Pathways to Detection of Strongly-Bound Inorganic Species: The Vibrational and Rotational Spectral Data of AlH2OH, HMgOH, AlH2NH2, and HMgNH2

Small, inorganic hydrides are likely hiding in plain sight, waiting to be detected toward various astronomical objects. AlH₂OH can form in the gas phase via a downhill pathway, and the present, high-level quantum chemical study shows that this molecule exhibits bright infrared features for anharmonic fundamentals in regions above and below that associated with polycyclic aromatic hydrocarbons. AlH₂OH along with HMgOH, HMgNH₂, and AlH₂NH₂ are also polar with AlH₂OH having a 1.22 D dipole moment. AlH₂OH and likely HMgOH have nearly unhindered motion of the hydroxyl group but are still strongly bonded. This could assist in gas phase synthesis, where aluminum oxide and magnesium oxide minerals likely begin their formation stages with AlH₂OH and HMgOH. This work provides the spectral data necessary to classify these molecules such that observations as to the buildup of nanoclusters from small molecules can possibly be confirmed.

1 Introduction

Currently, Al–O bonds are known in evolved stars and one exoplanet atmosphere in the form of AlOH and AlO (Tenenbaum and Ziurys, 2009; Tenenbaum and Ziurys, 2010; Takigawa et al., 2017; Chubb et al., 2020). Silicon monoxide has been observed toward Sgr B2 (Wilson et al., 1971), but no other small molecules containing Si–O or even Mg–O bonds have yet to be reported in the astrochemical literature (McGuire, 2018). Differently, crystalline forms of minerals containing Si, Mg, and O have been observed spectroscopically. One of the most notable cases is the mineral enstatite (MgSiO₃), whose infrared features have been noted toward NGC 6302 (Mölster et al., 2001, Mölster et al., 2002). Most of these enstatite features fall in the 17–50 μm region of the observered spectrum with those features from 2.4–12 μm attributed to carbon-rich materials like polycyclic aromatic hydrocarbons (PAHs). Hence, crystalline structures with Mg–O and Si–O bonds are perceived in at least one astronomical object. However, the region from 12–17 μm does not have a broad consensus as to the origins of these features, partially due to instrumental artifacts affecting the ISO spectrum. Additionally, O-rich evolved stars will not have PAH features in the 2–20 μm region, but only other silicate features. Therefore, any strong vibrational features in this region might aid in identification if they do not overlap with the strong Si–O–Si modes (Mölster et al., 2002).

Most of the anharmonic vibrational frequencies for the related and previously explored OAlOH molecule fall at 12.82 μm (the internal Al–O stretch) or longer directly in this “uncertain area of spectrum” (Mölster et al., 2001) from high-level quantum chemical computations (Fortenberry et al., 2020). This is also in line with (MO)₂ molecules where M = Mg, Al, Si, P, S, Ca, and Ti and also where all of the spectral features of these molecules lie below 12 μm with many of these also above 17 μm (Westbrook and Fortenberry, 2020). Similar spectra behavior has also been noted in the enstatite monomer (Valencia et al., 2020). These fundamental vibrational frequencies also possess notable intensities making them more observable than molecules containing the more abundant carbon atoms that are often the central atom of astrochemical analyses.

Recent work has shown that the strongest bonds between atoms on the first three rows of the periodic table (i.e. a majority of the most common elements in the Universe) are between one part oxygen and another part from one of aluminum, silicon, and magnesium, respectively (Doerksen and Fortenberry, 2020). Granted, this is after the astrophysically-depleted Be, B, and F atoms are discounted. The strongest of the remaining bonds is between the aluminum and oxygen atoms in AlH₂OH which is likely one of the first refractory chemical bonds. Further Al and O additions continue to build the material such that covalent network nanocrystals form followed by larger macromolecular solids in the form of common minerals. These mineral nanocrystals then form dust grains that eventually aggregate into rocky bodies like meteors or, ultimately, planets. Therefore, something more than a coincidence may be present between bond strength and elemental abundance in rocky bodies like the Earth, but determination of any such relationship is remains to be tested fully.

Previous, high-level quantum chemical computations show that water reacts with the simplest aluminum hydride, AlH₃, to form AlH₂OH and molecular hydrogen via an exothermic pathway producing a net of 30.5 kcal/mol with a submerged transition state lying 3.8 kcal/mol below the relative energy of the starting materials (Swinnen et al., 2009). Consequently, AlH₂OH could readily form in the atmospheres of massive stars, in protoplanetary disks, or even in molecular clouds. This gas phase pathway for the creation of AlH₂OH also produces omnipresent hydrogen molecules which would provide no further evidence for such a reaction potentially allowing such a pathway to remain hidden in plain sight. The work by Swinnen et al., (2009) is actually motivated by alternative energy applications in the production of H₂ from common materials like water. Even so, the known presence of water in stellar atmospheres (McGuire, 2018) and perceived presence of aluminium trihydride (which is likely unobserved due to its lack of a permanent dipole moment rendering it rotationally dark) imply that such a reaction could be common under interstellar conditions. The regions where AlH₂OH may be found will be dependent upon the abundance of the necessary starting materials, constraining the regions where it may be detected. Conversely, detection of this molecule would strongly imply the presence of AlH₃ and H₂O in the gas phase, and give an implication as to the presence of the rotationally-dark AlH₃ molecule.

Furthermore, this same work by Swinnen et al., (2009) shows that H₂O + 2AlH₃ → Al₂H₆O + H₂, where Al₂H₆O possesses a highly symmetric structure and an Al–O–Al motif, is also strongly exothermic producing 71 kcal/mol of energy. Curiously, the H₂O + BH₃ → BH₂OH + H₂ reaction has the transition state 11.8 kcal/mol above the starting materials (Swinnen et al., 2009). Such a barrier would stop any gas-phase astrochemical reactions before the reaction could progress, but this may be limited to second-row atoms due to the small charge density.

The present work utilizes similar quantum chemical computations as employed previously for OAlOH and AlOH (Fortenberry et al., 2020) to produce molecular structures, energies, and spectroscopic data for the four molecules at the nexus of strongly bound and containing highly abundant atoms as determined in earlier work (Doerksen and Fortenberry, 2020): AlH₂OH, HMgOH, AlH₂NH₂, and HMgNH₂. Additionally, these structures are known to challenge conventional thinking in that AlH₂OH is planar, HMgOH is linear, and the two N-containing species are $C_{2v}$ structures (Alabugin et al., 2014; Fugel et al., 2018; Sheridan and Ziurys, 2000; Xin et al., 2000; Grotjahn et al., 2001; Burton et al., 2019). This is most succinctly described as resulting from exceptionally strong yet floppy polarized covalent bonding between the two heavy atoms (Doerksen and Fortenberry, 2020; Fortenberry et al., 2020). In any case, their spectral features will be computed via quartic force fields (QFFs) which are fourth-order Taylor series expansions of the internuclear Hamiltonian. Their utilization defined with accurate electronic structure methods have previously produced anharmonic fundamental vibrational frequencies to within 0.70% error as well as B and C rotational constants to within 0.12% error of gas phase experiment (Huang et al., 2011; Fortenberry et al., 2012a, Fortenberry et al., 2012b; Zhao et al., 2014; Morgan and Fortenberry, 2015; Theis and Fortenberry, 2016; Bizzocchi et al., 2017; Kitchens and Fortenberry, 2016; Fortenberry and Francisco, 2017; Fuente et al., 2017; Wagner et al., 2018; Fortenberry and Lee, 2019; Gardner et al., 2021). The accuracy of such methods has led to the first interstellar observation of HOCO⁺ in the ${\nu }_5=1$ state (Bizzocchi et al., 2017) as well as the first laboratory observation of ArOH⁺ (Wagner et al., 2018), both based on previously existing quantum chemical data produced in our group (Fortenberry et al., 2012b; Theis and Fortenberry, 2016).

2 Computational Details

Two QFFs are utilized in this work. Both are based on coupled cluster theory at the singles, doubles, and perturbative triples [CCSD(T)] level of theory (Raghavachari et al., 1989; Shavitt and Bartlett, 2009; Crawford and Schaefer III, 2000), but one utilizes the explicitly correlated F12b formalism (CCSD(T)-F12b) (Adler et al., 2007). This level of theory solely employs the cc-pVTZ-F12 basis set (Peterson et al., 2008; Yousaf and Peterson, 2008; Knizia et al., 2009) and will be referred to from here on as the F12-TZ approach. The other method is a composite scheme based on canonical CCSD(T) but with considerations for complete basis set (CBS) limit extrapolations (“C”), core electron correlation (“cC”), and relativity (“R”) to give the so-called CcCR QFF (Fortenberry et al., 2011). The F12-TZ QFF has been shown to produce fundamental anharmonic vibrational frequencies nearly coincident with the much more costly CcCR method (Agbaglo et al., 2019; Agbaglo and Fortenberry, 2019a; Agbaglo and Fortenberry, 2019b), but the composite method is still required for accurate rotational constants (Gardner et al., 2021). The F12-TZ QFF will be utilized on all four molecules of the present study. The CcCR will only be employed for HMgOH and AlH₂OH due to the lower number of displacements required for HMgOH compared to the other molecules and also the prevalance of oxygen over nitrogen in most astrophysical media.

Both QFFs utilize the MOLPRO 2015.1 software package (Werner et al., 2015) for the electronic structure computations, and both begin with geometry optimizations. The F12-TZ approach simply but tightly optimizes the geometry at this level of theory, with gradients converged to less than 10^–8 Å or radians. The CcCR QFF reference geometry is based on CCSD(T)/aug-cc-pV5Z, or aug-cc-pV(5 + d)Z for Al and Mg (Dunning, 1989; Kendall et al., 1992; Peterson and Dunning, 1995), structures corrected for shifts in the structure brought about by inclusion of core electron correlation. The Martin-Taylor (MT) core correlating basis set (Martin and Taylor, 1994) is utilized for CCSD(T) computations with the core electrons included and excluded. The difference in the MT structures is then added to the CCSD(T)/aug-cc-pV5Z geometry. Relativity has no marked effect on the reference geometries (Huang and Lee, 2008; Huang and Lee, 2009).

From this reference geometry, displacements are made to produce the actual QFF. Bond lengths are displaced by 0.005 Å per each step and angles/torsions by 0.005 radians. The coordinate system employed for ${{}^1\text{Σ}}^{+}$ HMgOH is similar to that used in other tetraatomic $C_{\infty v}$ structures (Fortenberry and Lukemire, 2015; Novak and Fortenberry, 2017) with a QFF requiring 625 points and is defined from Figure 1A as:

$S_1\left(\sigma \right)={\text{H}}_1\text{–Mg}(1)$

$S_2\left(\sigma \right)=\text{Mg–O}(2)$

$S_3\left(\sigma \right)={\text{O–H}}_2(3)$

$S_4\left({\pi }_x\right)=\angle {\left({\text{H}}_1\text{–Mg–O}\right)}_x(4)$

$S_5\left({\pi }_x\right)=\angle {\left({\text{Mg–O–H}}_2\right)}_x(5)$

$S_6\left({\pi }_y\right)=\angle {\left({\text{H}}_1\text{–Mg–O}\right)}_y(6)$

$S_7\left({\pi }_y\right)=\angle {\left({\text{Mg–O–H}}_2\right)}_y.(7)$

FIGURE 1

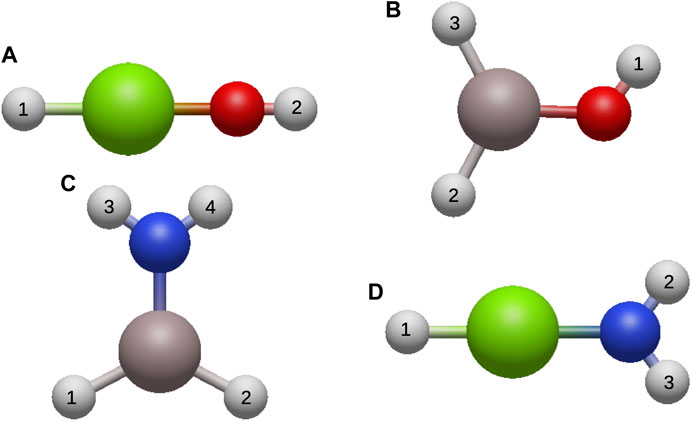
FIGURE 1. The Optimized Structures of (A) HMgOH, (B) AlH₂OH, (C) AlH₂NH₂, and (D) HMgNH₂ with H atoms in white, O in red, N in blue, Mg in green, and Al in gray.

${{}^{1}A}_1$ AlH₂OH has straightforward simple-internal coordinate system with 3,161 points as defined from the atoms in Figure 1B:

$S_1\left(a\text{'}\right)={\text{H}}_1\text{–O}(8)$

$S_2\left(a\text{'}\right)=\text{O–Al}(9)$

$S_3\left(a\text{'}\right)={\text{Al–H}}_2(10)$

$S_4\left(a\text{'}\right)={\text{Al–H}}_3(11)$

$S_5\left(a\text{'}\right)=\angle \left({\text{H}}_1\text{–O–Al}\right)(12)$

$S_6\left(a\text{'}\right)=\angle \left({\text{O–Al–H}}_2\right)(13)$

$S_7\left(a\text{'}\right)=\angle \left({\text{O–Al–H}}_3\right)(14)$

$S_8\left(a\text{''}\right)=\tau \left({\text{H}}_1{\text{–O–Al–H}}_2\right)(15)$

$S_9\left(a\text{''}\right)=\tau \left({\text{H}}_1{\text{–O–Al–H}}_3\right).(16)$

${{}^{1}A}_1$ HMgNH₂ has 1,613 points in its coordinate system, where “OPB” represents an out-of-plane bending motion:

$S_1\left(a_1\right)={\text{H}}_1\text{–Mg}(17)$

$S_2\left(a_1\right)={\text{H}}_1\text{–N}(18)$

$S_3\left(a_1\right)=\frac{1}{\sqrt{2}}\left[\left({\text{N–H}}_2\right)+\left({\text{N–H}}_3\right)\right](19)$

$S_4\left(a_1\right)=\frac{1}{\sqrt{2}}\left[\angle \left({\text{Mg–N–H}}_2\right)+\angle \left({\text{Mg–N–H}}_3\right)\right](20)$

$S_5\left(b_2\right)=\frac{1}{\sqrt{2}}\left[\left({\text{N–H}}_2\right)-\left({\text{N–H}}_3\right)\right](21)$

$S_6\left(b_2\right)=\frac{1}{\sqrt{2}}\left[\angle \left({\text{Mg–N–H}}_2\right)-\angle \left({\text{Mg–N–H}}_3\right)\right](22)$

$S_7\left(b_2\right)=\angle {\left({\text{H}}_1\text{–Mg–N}\right)}_x(23)$

$S_8\left(b_1\right)=\angle {\left({\text{H}}_1\text{–Mg–N}\right)}_y(24)$

$S_9\left(b_1\right)=OPB\left({\text{Mg–N–H}}_2{\text{–H}}_3\right).(25)$

The ${{}^{1}A}_1$ AlH₂NH₂ symmetry-internal coordinate system is of a similar construction as that for ${\text{CH}}_2{\text{NH}}_2^{+}$ (Thackston and Fortenberry, 2018) and its 4,493 points:

$S_1\left(a_1\right)=\text{Al}–\text{N}(26)$

$S_2\left(a_1\right)=\frac{1}{\sqrt{2}}\left[\left({\text{Al–H}}_1\right)+\left({\text{Al–H}}_2\right)\right](27)$

$S_3\left(a_1\right)=\frac{1}{\sqrt{2}}\left[\left({\text{N–H}}_3\right)+\left({\text{N–H}}_4\right)\right](28)$

$S_4\left(a_1\right)=\frac{1}{\sqrt{2}}\left[\angle \left({\text{N–Al–H}}_1\right)+\angle \left({\text{N–Al–H}}_2\right)\right](29)$

$S_5\left(a_1\right)=\frac{1}{\sqrt{2}}\left[\angle \left({\text{Al–N–H}}_3\right)+\angle \left({\text{Al–N–H}}_4\right)\right](30)$

$S_6\left(b_2\right)=\frac{1}{\sqrt{2}}\left[\left({\text{Al–H}}_1\right)-\left({\text{Al–H}}_2\right)\right](31)$

$S_7\left(b_2\right)=\frac{1}{\sqrt{2}}\left[\left({\text{N–H}}_3\right)-\left({\text{N–H}}_4\right)\right](32)$

${\text{S}}_8\left(b_2\right)=\frac{1}{\sqrt{2}}\left[\angle \left({\text{N–Al–H}}_1\right)-\angle \left({\text{N–Al–H}}_2\right)\right](33)$

$S_9\left(b_2\right)=\frac{1}{\sqrt{2}}\left[\angle \left({\text{Al–N–H}}_3\right)-\angle \left({\text{Al–N–H}}_4\right)\right](34)$

$S_{10}\left(b_1\right)=\frac{1}{\sqrt{2}}\left[\tau \left({\text{H}}_3{\text{–N–Al–H}}_1\right)-\tau \left({\text{H}}_4{\text{–N–Al–H}}_2\right)\right](35)$

$S_{11}\left(b_1\right)=\frac{1}{\sqrt{2}}\left[\tau \left({\text{H}}_4{\text{–N–Al–H}}_1\right)-\tau \left({\text{H}}_3{\text{–N–Al–H}}_2\right)\right](36)$

$S_{12}\left(a_2\right)=\frac{1}{\sqrt{2}}\left[\tau \left({\text{H}}_3{\text{–N–Al–H}}_1\right)+\tau \left({\text{H}}_4{\text{–N–Al–H}}_2\right)\right].(37)$

The F12-TZ QFF only requires energies at each point at this level of theory. The CcCR QFF requires CCSD(T)/aug-cc-pVTZ, aug-cc-pVQZ, and aug-cc-pV5Z (with the tight d functions assumed for Mg and Al) energies computed at each point and extrapolated via a three-point formula to the CBS limit (Martin and Lee, 1996). Each point has CCSD(T)/MT computations with and without the core electrons included as well as scalar relativity (Douglas and Kroll, 1974) from CCSD(T)/cc-pVTZ-DK energies with and without the relativity turned on. For either QFF, the fitting of the points is done by means of a least squared procedure where the sum of squared residuals are on the order of 10^–16 a.u.² or less for all system including the F12-TZ QFF for AlH₂NH₂. The resulting force constants are transformed from simple-internal or symmetry-internal coordinates into more generic Cartesian coordinates using the INTDER program (Allen et al., 2005). Then, the SPECTRO program (Gaw et al., 1991) utilizes rotational and vibrational perturbation theory at second-order (VPT2) to produce the rotational constants and the fundamental vibrational frequencies (Mills, 1972; Watson, 1977; Papousek and Aliev, 1982). SPECTRO can not only treat Fermi resonances, but polyads of these resonances for more accurate descriptions of the frequencies (Martin and Taylor, 1997). The resonances included are: a $2{\nu }_9={\nu }_9+{\nu }_7={\nu }_4={\nu }_5$ polyad for AlH₂OH; $2{\nu }_3={\nu }_2$ and $2{\nu }_4={\nu }_3$ type-1 Fermi resonances for HMgOH; a $2{\nu }_5={\nu }_4$ type-1 Fermi resonance and a $2{\nu }_7=2{\nu }_8=2{\nu }_9={\nu }_8+{\nu }_7={\nu }_9+{\nu }_6={\nu }_5$ Fermi resonance polyad for HMgNH₂; and two polyads for AlH₂NH₂, $2{\nu }_6=2{\nu }_7=2{\nu }_8={\nu }_7+{\nu }_6={\nu }_5$ and $2{\nu }_{11}=2{\nu }_{12}={\nu }_6={\nu }_7$.

MP2/aug-cc-pVTZ double-harmonic intensities are computed with the Gaussian09 program (Møller and Plesset, 1934; Frisch et al., 2009) and have previously been shown to be reliable for semi-quantitative descriptions of the fundamental intensities (Yu et al., 2015; Finney et al., 2016; Westbrook and Fortenberry, 2020). These are also reported for the molecules of interest. The equilibrium dipole moments have all been computed within Molpro at the F12-TZ level at the corresponding reference geometries for this level of theory.

3 Results and Discussion

3.1 –OH Species

Of the four molecules examined in this work, AlH₂OH is the most polar. Its rotational constants, given in Table 1, show a clear near-prolate character (κ = −0.97) and a dipole moment (Table 2) of 1.22 D. This is even higher than the 1.11 D dipole moment of AlOH (Fortenberry et al., 2020) and should help facilitate detection through rotational spectroscopy. There is little deviation of the dipole moment from the principle axis (${\mu }_x$ is 0.05 D) since only the hydrogen bonded to the oxygen perturbs the symmetry within the plane of the molecule. The nearly equivalent Al–H₁ and Al–H₂ bond lengths (∼1.58 Å) also contribute to this even though their bond angles to the oxygen atom vary by roughly 4°. The vibrationally-excited rotational constants are further reported in Table 1 as the A-Reduced Hamiltonian quartic and sextic distortion constants are in Table 2.

TABLE 1

TABLE 1. Geometry and rotational constants for AlH₂OH.

TABLE 2

TABLE 2. Quartic and sextic constants for AlH₂OH.

Most of the vibrational frequencies agree well between the CcCR and F12-TZ approaches. This is especially true of the harmonic frequencies, but, as has been observed previously (Fortenberry et al., 2020), the anharmonic frequencies diverge more. This is most pronounced in the ${\nu }_9$ frequency. Likely, the F12-TZ result is more correct since it relies upon a single level of theory. The composite CcCR has competing factors that can work against one another and provide spurious results for coordinates with flat potentials or where different levels of theory predict notably different minima (Morgan and Fortenberry, 2015; Bassett and Fortenberry, 2017; Trabelsi et al., 2019). The rotation of the O–H is small with a barrier of 3.3 kcal/mol for a relaxed F12-TZ scan of coordinate $S_8$ with step sizes of 2.0°. During the optimizations for the scan the ∠(H₁–O–Al) increases to nearly 150° when $S_8=90\text{°}$ creating an even more near-prolate structure. The constrained optimization has the maximum at 4.4 kcal/mol further implying the largely unhindered motion of the hydroxyl group even without the enlargement of ∠(H₁–O–Al). Even so, this Al–O bond is notably stronger than any C−C or C−O single bond (Doerksen and Fortenberry, 2020). In spite of this nearly free rotation, the motion does not plague as deeply the anharmonic vibrational frequencies for AlH₂OH as those reported for OAlOH (Fortenberry et al., 2020) likely due to the slightly deeper energy well and since the 424.1 cm⁻¹ anharmonic frequency for AlH₂OH ${\nu }_9$ would require at least three quanta to excite above the barrier.

The vibrational frequencies imply that this molecule should be detectable in the infrared. All of the double-harmonic intensities from Table 3 are at least on the order of that for the antisymmetric stretch in water (∼70 km/mol) if not two or even three or more times greater. The strongly polarized Al−O bond is borne out in the 203 km/mol intensity for ${\nu }_4$ which is dominated by this heavy atom stretching motion. This frequency at 864.7 cm⁻¹ for CcCR is equivalent to 11.56 μm, at the end of the infrared region typically associated with PAHs (Mölster et al., 2001). Hence, the lower-frequency vibrational frequencies will all fall in the infrared wavelength regions between 12 and 17 µm that do not have widespread consensus as to their origins. The hydride stretches associated with the aluminum atom have much brighter intensities than the O−H stretch. The O−H stretch for AlH₂OH, at 3,773.6 cm⁻¹ or 2.65 μm for CcCR, is actually more than 250 cm⁻¹ higher than 3,681 cm⁻¹ for methanol (Shimanouchi, 1972).

TABLE 3

TABLE 3. Vibrational Frequencies (in cm⁻¹) of AlH₂OH with MP2/aug-cc-pVTZ Intensities in Parentheses (in km/mol).

The HMgOH molecule is not nearly as polar as the AlH₂OH, but its 0.57 D dipole moment (Table 4) should still support a potential detection through rotational spectroscopy or radioastronomical observation. The CcCR Mg−O bond length of 1.782 Å is notably longer than the 1.695 Al−O bond in the equivalent aluminum structure owing to the slightly weaker (but still quite strong) bonding present for the magnesium-bearing molecule. This also produces a slightly smaller $B_0$ at 12,699.2 MHz compared to the 13,550 MHz $B_{eff}$, where $B_{eff}$ = (B + C)/2, for AlH₂OH even with less mass in HMgOH.

TABLE 4

TABLE 4. Geometry and spectroscopic constants of HMgOH.

Again, F12-TZ and CcCR are mostly in agreement with one another for HMgOH save for the ${\nu }_5$ bend once more involving bending of the hydroxyl moiety. Neither method can adequately treat this mode, similar to the bend in AlOH (Fortenberry et al., 2020). Even so, nearly unhindered rotation coupled to strong bonding is a hallmark of these polarized covalent bonds. The fundamental anharmonic vibrational frequencies, given in Table 5, also display large intensities with ${\nu }_4$ being one of the largest for those reported in this work. The three motions not classified as hydride stretches all fall below 13 μm. The 3,861.6 cm⁻¹ O−H stretch is once more higher in frequency than methanol, and the ${\nu }_2$ Mg−H stretch at 1,604.4 cm⁻¹ is much lower than either of the Al−H stretches in AlH₂OH. However, this value and that of ${\nu }_3$ have experimental references (Kauffman et al., 1984). The Ar matrix results are in line with the presently and previously (Sakai and Jordan, 1986; Yang et al., 2011) computed values implying that actual gas phase frequencies should be somewhere in the region we have computed for each fundamental.

TABLE 5

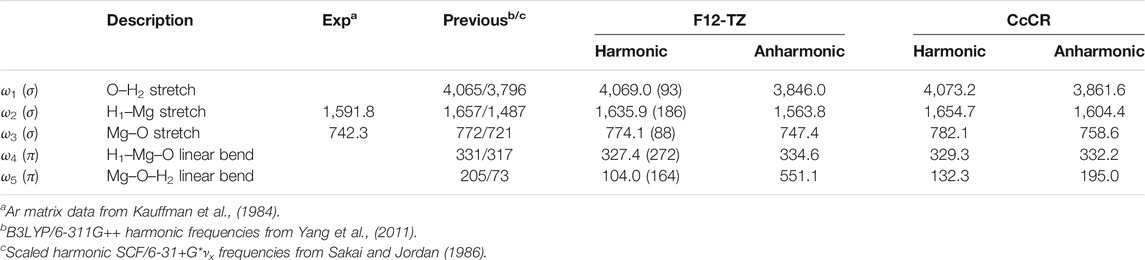
TABLE 5. Vibrational frequencies (in cm⁻¹) of HMgOH with MP2/aug-cc-pVTZ intensities in parentheses (in km/mol).

3.2 –NH₂ Species

HMgNH₂ is even more prolate than AlH₂OH with the A rotational constant a factor of more than 30 larger than B or C (Table 6) and κ = −0.998, but is less polar at 0.62 D (Table 7). The $B_{eff}$ for HMgNH₂ is 11,213.43 MHz putting it in between that of the known inorganic, interstellar MgCN and SiO molecules. The Mg−N bond is relatively long at more than 1.9 Å, which makes sense in light of the fact that Al and O create stronger bonds than either Mg or N, much less a Mg−N bond, in these types of polarized covalent interactions (Doerksen and Fortenberry, 2020).

TABLE 6

TABLE 6. Geometry and rotational constants for HMgNH₂.

TABLE 7

TABLE 7. Quartic and sextic constants for HMgNH₂.

The CcCR QFF is not utilized for this molecule due to time constraints in the publication process. However, the F12-TZ QFF vibrational frequencies have been shown above to be comparable to those from CcCR and potentially more reliable for the low-frequency modes. The ${\nu }_8$ out-of-plane bending fundamental reported in Table 8 has the highest intensity by far of those computed here at 342 km/mol. This mode actually exhibits a positive anharmonicity along with the other lower-frequency fundamental, ${\nu }_9$, with the anharmonic value of 307.8 cm⁻¹, 13.8 cm⁻¹ above the harmonic value. While this type of result raises questions about the fundamentals computed, such behavior is not uncommon for molecules with nearly linear geometries (Fortenberry et al., 2012a). The non-hydride stretching fundamentals all lie below 14.8 μm coinciding with the Mg−N stretch at 674.5 cm⁻¹.

TABLE 8

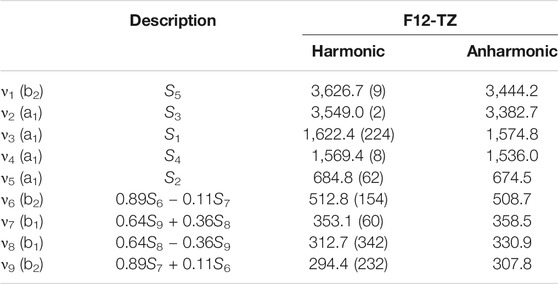
TABLE 8. Vibrational Frequencies (in cm⁻¹) of HMgNH₂ with MP2/aug-cc-pVTZ intensities in parentheses (in km/mol).

The number of points necessary to define the QFF increases dramatically for AlH₂NH₂ making F12-TZ the most practical choice of QFF for analysis of this molecule. AlH₂NH₂ has rotational constants (Table 9) similar to those present in the related AlH₂OH molecule but with a slightly lower $B_{eff}$ of 12,223.02 MHz. The dipole moment (1.08 D) is given in Table 10 along with the other spectroscopic constants. Again, the dipole moment is comparable to but less than the same observable in AlH₂OH. Hence, the rotational spectrum of AlH₂NH₂ will mirror that of the hydroxide.

TABLE 9

TABLE 9. Geometry and rotational constants of AlH₂NH₂.

TABLE 10

TABLE 10. Quartic and sextic constants of AlH₂NH₂.

Significantly more previous experimental and high-level theoretical data exist for the vibrational frequencies of AlH₂NH₂ than any of the other four molecules examined in this work. Both of the previous (Davy and Jaffrey, 1994; Grant and Dixon, 2005) coupled cluster harmonic frequency sets corroborate well the present F12-TZ results shown in Table 11 implying that the harmonic foundation for the subsequent QFF computations is grounded. The Ar matrix data (Himmel et al., 2000) perform a similar benchmark for the F12-TZ QFF anharmonic vibrational frequencies. Most frequencies agree between present theory and this previous experiment to within 10 cm⁻¹ or so. The notable exceptions are ${\nu }_2$, which is understandable as this is the antisymmetric N−H stretch, as well as the ${\nu }_{11}$$b_1$ NH₂ out-of-plane bend. However, some of these bands could be misassigned. Specifically, the ${\nu }_2$ antisymmetric stretch given experimentally at 3,499.7 cm⁻¹ matches the F12-TZ anharmonic frequencies better for the ${\nu }_1$ symmetric N−H stretch at 3,496.8 cm⁻¹, and both the symmetric and antisymmetric N−H stretches have similar intensities from the present MP2/aug-cc-pVTZ computations. Regardless, the F12-TZ anharmonic frequencies are performing as expected compared to these Ar matrix data once more showing that the present computations will guide future gas phase spectral analysis.

TABLE 11

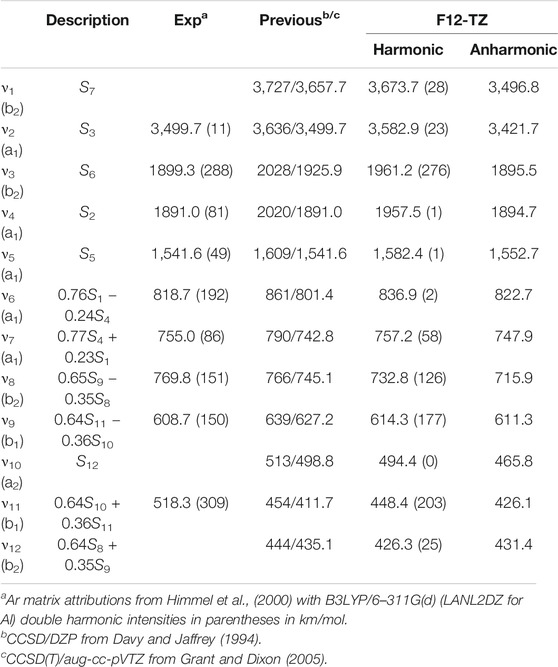
TABLE 11. Vibrational Frequencies (in cm⁻¹) of AlH₂NH₂ with MP2/aug-cc-pVTZ Intensities in Parentheses (in km/mol).

Beyond such benchmarks, the most notable item for the vibrational spectrum of AlH₂NH₂ is that the Al−H stretches, especially the ${\nu }_3$ antisymmetric stretch at 1895.5 cm⁻¹ or 5.2757 μm, will be the most visible for gas phase experimental detection or any astronomical observation. The ${\nu }_5$ symmetric Al−N−H bend sits at frequencies just below this value, but the other seven frequencies lie beyond 12.1 μm. The ${\nu }_6$ Al−N stretch is 822.7 cm⁻¹ or 12.15 μm and correlates well with previous Ar matrix experimental data (818.7 cm⁻¹). The ${\nu }_{10}$$a_2$ twisting mode is vibrationally dark by symmetry, but all of the other low frequency fundamentals (save for ${\nu }_{12}$) have bright fundamentals. This definitely populates the 12–17 μm region as well as beyond 20 μm for ${\nu }_{11}$ and ${\nu }_{12}$.

4 Conclusion

AlH₂OH is a detectable and likely interstellar molecule waiting for observation. Previous work has shown its kinetic and thermodynamic formation are favorable in the gas phase from AlH₃, which is likely to be present, and water, which is abundant. The notable dipole moment and infrared intensities for AlH₂OH should allow for detection in simulated astrophysical contexts utilizing the spectral data produced here. Furthermore, the largely unhindered rotation of the hydroxyl group is typical of what recent work has shown for similar molecules with Al−O−H motifs. This does not appear to be negatively affecting the predicted anharmonic frequencies here as much as has been reported previously.

AlH₂OH along with HMgOH, HMgNH₂, and AlH₂NH₂ share many similarities in that the O−H and N−H stretches have smaller intensities but have frequencies above those found in molecules not containing third-row atoms. Most frequencies for these molecules come in roughly three sets: 1) the second-row hydride stretches in the 2.5–3.0 μm range above that typically associated with PAHs; 2) the third-row hydride stretches and second-row hydride bends between 5.0–6.7 μm in regions typically associated with bending in PAHs; and 3) the >12 μm range for the heavy atom stretches and other bend/dihedral fundamental frequencies. The first and last of these three imply that such frequencies rest in infrared spectral windows less clouded with seemingly ubiquitous PAHs. Hence, these molecules may prove to be novel candidates for understanding the provenance for many currently unidentified interstellar infrared emission and absorption features, and may viable candidates for detection with the upcoming James Webb Space Telescope. Additionally, all four molecules are near-prolate (if not linear) and polar allowing for rotational and radioastronomical observation. The data provided herein should aid in growing the census of simple inorganic molecules observed in space.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

AW gathered the data. AW and MD analyzed and formatted the data. RF provided management and funding. All three wrote and edited the paper.

Funding

All funding sources have been declared.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work has been supported by NSF Grant OIA-1757220, NASA Grant NNX17AH15G, and the University of Mississippi. Additionally, computational resources have been provided in part by the Mississippi Center for Supercomputing Research funded through NSF Grant CHE-1338056.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2021.643348/full#supplementary-material.

References

Adler, T. B., Knizia, G., and Werner, H. J. (2007). A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys. 127, 221106. doi:10.1063/1.2817618

PubMed Abstract | CrossRef Full Text | Google Scholar

Agbaglo, D., and Fortenberry, R. C. (2019a). The performance of CCSD(T)-F12/aug-cc-pVTZ for the computation of anharmonic fundamental vibrational frequencies. Int. J. Quantum Chem. 119, e25899. doi:10.1002/qua.25899

CrossRef Full Text | Google Scholar

Agbaglo, D., and Fortenberry, R. C. (2019b). The performance of explicitly correlated wavefunctions [CCSD(T)-F12b] in the computation of anharmonic vibrational frequencies. Chem. Phys. Lett. 734, 136720. doi:10.1016/j.cplett.2019.136720

CrossRef Full Text | Google Scholar

Agbaglo, D., Lee, T. J., Thackston, R., and Fortenberry, R. C. (2019). A small molecule with pah vibrational properties and a detectable rotational spectrum: (C)C₃H₂, cyclopropenylidenyl carbene. Astrophys. J. 871, 236. doi:10.3847/1538-4357/aaf85a

CrossRef Full Text | Google Scholar

Alabugin, I. V., Bresch, S., and Manoharan, M. (2014). Hybridization trends for main group elements and expandingthe bentâs rule beyond carbon: more than electronegativity. J. Phys. Chem. A. 118, 3663–3677. doi:10.1021/jp502472u

PubMed Abstract | CrossRef Full Text | Google Scholar

Allen, W. D., et al. (2005). INTDER 2005 is a General Program Written by W. D. Allen and Coworkers, which performs vibrational analysis and higher-order non-linear transformations.

Bassett, M. K., and Fortenberry, R. C. (2017). Symmetry breaking and spectral considerations of the surprisingly floppy C₃H radical and the related dipole-bound excited state of C₃H⁻. J. Chem. Phys. 146, 224303. doi:10.1063/1.4985095

PubMed Abstract | CrossRef Full Text | Google Scholar

Bizzocchi, L., Lattanzi, V., Laas, J., Spezzano, S., Giuliano, B. M., Prudenzano, D., et al. (2017). Accurate sub-millimetre rest frequencies for HOCO⁺ and DOCO⁺ ions. Astronom. Astrophys. 602, A34. doi:10.1051/0004-6361/201730638

CrossRef Full Text | Google Scholar

Burton, M. A., Russ, B. T., Bucchino, M. P., Sheridan, P. M., and Ziurys, L. M. (2019). Quadrupole coupling in alkali metal amides MNH₂(${\tilde{X}}^2{A}_1$): an experimental and computational study. J. Mol. Spectrosc. 365, 111211. doi:10.1016/j.jms.2019.111211

CrossRef Full Text | Google Scholar

Chubb, K. L., Min, M., Kawashima, Y., Helling, C., and Waldmann, I. (2020). Aluminium oxide in the atmosphere of hot Jupiter WASP-43b. Astronom. Astrophys. 639, A3. doi:10.1051/0004-6361/201937267

CrossRef Full Text | Google Scholar

Crawford, T. D., and Schaefer, H. F. (2000). “An introduction to coupled cluster theory for computational chemists,” in Reviews in computational chemistry. Editors K. B. Lipkowitz, and D. B. Boyd (New York: Wiley), 14, 33–136.

Google Scholar

Davy, R. D., and Jaffrey, K. L. (1994). Aluminum-nitrogen multiple bonds in small a1nh molecules: structures and vibrational frequencies of AlNH₂, AlNH₃, and AlNH₄. J. Phys. Chem. 98, 8930–8936. doi:10.1021/j100087a019

CrossRef Full Text | Google Scholar

Doerksen, E. S., and Fortenberry, R. C. (2020). A coincidence between bond strength, atomic abundance, and the composition of rocky materials. ACS Earth Sp. Chem. 4, 812–817. doi:10.1021/acsearthspacechem.0c00029

CrossRef Full Text | Google Scholar

Douglas, M., and Kroll, N. M. (1974). Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. 82, 89–155. doi:10.1016/0003-4916(74)90333-9

CrossRef Full Text | Google Scholar

Dunning, T. H. (1989). Gaussian basis sets for use in correlated molecular calculations. i. the atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023. doi:10.1063/1.456153

CrossRef Full Text | Google Scholar

Finney, B., Fortenberry, R. C., Francisco, J. S., and Peterson, K. A. (2016). A spectroscopic case for SPSi detection: the third-row in a single molecule. J. Chem. Phys. 145, 124311. doi:10.1063/1.4963337

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Francisco, J. S., Crawford, T. D., and Lee, T. J. (2012a). Fundamental vibrational frequencies and spectroscopic constants of HOCS⁺, HSCO⁺, and isotopologues via quartic force fields. J. Phys. Chem. A. 116, 9582–9590. doi:10.1021/jp3073206

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Francisco, J. S., Crawford, T. D., and Lee, T. J. (2012b). Quartic force field predictions of the fundamental vibrational frequencies and spectroscopic constants of the cations HOCO⁺ and DOCO⁺. J. Chem. Phys. 136, 234309. doi:10.1063/1.4729309

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., Trabelsi, T., and Francisco, J. S. (2020). Anharmonic frequencies and spectroscopic constants of OAlOH and AlOH: strong bonding but unhindered motion. J. Phys. Chem. A. 124, 8834–8841. doi:10.1021/acs.jpca.0c07945

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., and Francisco, J. S. (2017). On the detectability of the ${\tilde{X}}^{2}A\text{''}$ HSS, HSO, and HOS radicals in the interstellar medium. Astrophys. J. 835, 243. doi:10.3847/1538-4357/aa582d

CrossRef Full Text | Google Scholar

Fortenberry, R. C., Huang, X., Francisco, J. S., Crawford, T. D., and Lee, T. J. (2011). The trans-HOCO radical: fundamental vibrational frequencies, quartic force fields, and spectroscopic constants. J. Chem. Phys. 135, 134301. doi:10.1063/1.3643336

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortenberry, R. C., and Lee, T. J. (2019). Computational vibrational spectroscopy for the detection of molecules in space. Annu. Rep. Comput. Chem. 15, 173–202. doi:10.1016/bs.arcc.2019.08.006

CrossRef Full Text | Google Scholar

Fortenberry, R. C., and Lukemire, J. A. (2015). Electronic and rovibrational quantum chemical analysis of C₃P⁻: the next interstellar anion? Mon. Not. R. Astron. Soc. 453, 2824–2829. doi:10.1093/mnras/stv1844

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2009). Gaussian 09 Revision D.01. Wallingford CT: Gaussian Inc.

Fuente, A., Goicoechea, J. R., Pety, J., Gal, R. L., Martín-Doménech, R., Gratier, P., et al. (2017). First detection of interstellar S₂H. Astrophys. J. Lett. 851, 49. doi:10.3847/2041-8213/aaa01b

CrossRef Full Text | Google Scholar

Fugel, M., Beckmann, J., Jayatilaka, D., Gibbs, G. V., and Grabowsky, S. (2018). A variety of bond analysis methods, one answer? an investigation of the element-oxygen bond of hydroxides H_nXOH. Chem. Eur. J. 24, 6248–6261. doi:10.1002/chem.201800453

PubMed Abstract | CrossRef Full Text | Google Scholar

Gardner, M. B., Westbrook, B. R., Fortenberry, R. C., and Lee, T. J. (2021). Highly-accurate quartic force fields for the prediction of anharmonic rotational constants and fundamental vibrational frequencies. Spectrochim. Acta A: Mol. Biomol. Spectrosc., 248, 119184. doi:10.1016/j.saa.2020.119184 (in press).

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaw, J. F., Willets, A., Green, W. H., and Handy, N. C. (1991). “SPECTRO: a program for the derivation of spectrscopic constants from provided quartic force fields and cubic dipole fields,” in Advances in molecular vibrations and collision dynamics. Editors J. M. Bowman, and M. A. Ratner (Greenwich, Connecticut: JAI Press, Inc.), 170–185.

Google Scholar

Grant, D. J., and Dixon, D. A. (2005). Thermodynamic properties of molecular borane phosphines, alane amines, and phosphine alanes and the [BH₄⁺][PH₄⁺], [AlH₄⁻][NH₄⁺], and [AlH₄⁻][PH₄⁺] salts for chemical hydrogen storage systems from ab initio electronic structure theory. J. Phys. Chem. A. 109, 10138–10147. doi:10.1021/jp054152y

PubMed Abstract | CrossRef Full Text | Google Scholar

Grotjahn, D. B., Sheridan, P. M., Al Jihad, I., and Ziurys, L. M. (2001). First synthesis and structural determination of a monomeric, unsolvated lithium amide. J. Am. Chem. Soc. 123, 5489–5494. doi:10.1021/ja003422h

PubMed Abstract | CrossRef Full Text | Google Scholar

Himmel, H.-J., Downs, A. J., and Greene, T. M. (2000). Thermal and photochemical reactions of aluminum, gallium, and indium atoms (M) in the presence of ammonia: generation and characterization of the species MNH₃, HMNH₂, MNH₂, and H₂MNH₂. J. Am. Chem. Soc. 122, 9793–9807. doi:10.1021/ja001313x

CrossRef Full Text | Google Scholar

Huang, X., and Lee, T. J. (2008). A procedure for computing accurate ab initio quartic force fields: application to HO₂⁺ and H₂O. J. Chem. Phys. 129, 044312. doi:10.1063/1.2957488

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, X., and Lee, T. J. (2009). Accurate ab initio quartic force fields for NH₂⁻ and CCH⁻ and rovibrational spectroscopic constants for their isotopologs. J. Chem. Phys. 131, 104301. doi:10.1063/1.3212560

CrossRef Full Text | Google Scholar

Huang, X., Taylor, P. R., and Lee, T. J. (2011). Highly accurate quartic force field, vibrational frequencies, and spectroscopic constants for cyclic and linear C₃H₃⁺. J. Phys. Chem. A. 115, 5005–5016. doi:10.1021/jp2019704

PubMed Abstract | CrossRef Full Text | Google Scholar

Kauffman, J. W., Hauge, R. H., and Margrave, J. L. (1984). Infrared matrix isolation studies of the interactions of magnesium, calcium, strontium, and barium atoms and small clusters with water. High Temp. Sci. 18, 97.

Google Scholar

Kendall, R. A., Dunning, T. H., and Harrison, R. J. (1992). Electron affinities of the first-row atoms revisited. systematic basis sets and wave functions. J. Chem. Phys. 96, 6796–6806. doi:10.1063/1.462569

CrossRef Full Text | Google Scholar

Kitchens, M. J. R., and Fortenberry, R. C. (2016). The rovibrational nature of closed-shell third-row triatomics: HOX and HXO, X = Si⁺, P, S⁺, and Cl. Chem. Phys. 472, 119–127. doi:10.1016/j.chemphys.2016.03.018

CrossRef Full Text | Google Scholar

Knizia, G., Adler, T. B., and Werner, H. J. (2009). Simplified CCSD(T)-F12 methods: theory and benchmarks. J. Chem. Phys. 130, 054104. doi:10.1063/1.3054300

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, J. M. L., and Lee, T. J. (1996). The atomization energy and proton affinity of nh₃. an ab initio calibration study. Chem. Phys. Lett. 258, 136–143. doi:10.1016/0009-2614(96)00658-6

CrossRef Full Text | Google Scholar

Martin, J. M. L., and Taylor, P. R. (1997). Accurate ab initio quartic force field for trans-HNNH and treatment of resonance polyads. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 53, 1039–1050. doi:10.1016/s1386-1425(96)01869-0

CrossRef Full Text | Google Scholar

Martin, J. M. L., and Taylor, P. R. (1994). Basis set convergence for geometry and harmonic frequencies. are ℎ functions enough?. Chem. Phys. Lett. 225, 473–479. doi:10.1016/0009-2614(94)87114-0

CrossRef Full Text | Google Scholar

McGuire, B. A. (2018). 2018 census of interstellar, circumstellar, extragalactic, protoplanetary disk, and exoplanetary molecules. Astrophys. J. Suppl. Ser. 239 (17), 48. doi:10.3847/1538-4365/aae5d2

CrossRef Full Text | Google Scholar

Mills, I. M. (1972). “Vibration-rotation structure in asymmetric- and symmetric-top molecules,” in Molecular spectroscopy - modern research. Editors K. N. Rao, and C. W. Mathews (New York: Academic Press), 115–140.

CrossRef Full Text | Google Scholar

Møller, C., and Plesset, M. S. (1934). Note on an approximation treatment for many-electron systems. Phys. Rev. 46, 618–622.

Google Scholar

Mölster, F. J., Lim, T. L., Sylvester, R. J., Waters, L. B. F. M., Barlow, M. J., Beintema, D. A., et al. (2001). The complete ISO spectrum of NGC 6302. Astronom. Astrophys. 372, 165–172. doi:10.1051/0004-6361:20010465

CrossRef Full Text | Google Scholar

Mölster, F. J., Waters, L. B. F. M., and Tielens, A. G. G. M. (2002). Crystalline silicate dust around evolved stars II. The crystalline silicate complexes. Astronom. Astrophys. 382, 222–240. doi:10.1051/0004-6361:20011551

CrossRef Full Text | Google Scholar

Morgan, W. J., and Fortenberry, R. C. (2015). Theoretical rovibronic treatment of the $\tilde{X}{ }^2{\text{Σ}}^{+}$ and $\tilde{A}{}^2\text{Π}$ states of C2H and the $\tilde{X}{}^1{\text{Σ}}^{+}$ state of C2H- from quartic force fields. J. Phys. Chem. A. 119, 7013–7025. doi:10.1021/acs.jpca.5b03489

PubMed Abstract | CrossRef Full Text | Google Scholar

Novak, C. M., and Fortenberry, R. C. (2017). Vibrational frequencies and spectroscopic constants of three, stable noble gas molecules: NeCCH+, ArCCH+, and ArCN+. Phys. Chem. Chem. Phys. 19, 5230–5238. doi:10.1039/c6cp08140a

PubMed Abstract | CrossRef Full Text | Google Scholar

Papousek, D., and Aliev, M. R. (1982). Molecular vibration-rotation spectra. Amsterdam: Elsevier.

Peterson, K. A., Adler, T. B., and Werner, H. J. (2008). Systematically convergent basis sets for explicitly correlated wavefunctions: the atoms H, He, B-Ne, and Al-Ar. J. Chem. Phys. 128, 084102, doi:10.1063/1.2831537

PubMed Abstract | CrossRef Full Text | Google Scholar

Peterson, K. A., and Dunning, T. H. (1995). Benchmark calculations with correlated molecular wave functions. vii. binding energy and structure of the hf dimer. J. Chem. Phys. 102, 2032–2041. doi:10.1063/1.468725

CrossRef Full Text | Google Scholar

Raghavachari, K., Trucks, G. W., Pople, J. A., and Head-Gordon, M. (1989). A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 157, 479–483. doi:10.1016/s0009-2614(89)87395-6

CrossRef Full Text | Google Scholar

Sakai, S., and Jordan, K. D. (1986). Squared and vibrational frequencies of HBeOH, HBOH, HCOH, HMgOH, HAlOH, and HSiOH. Chem. Phys. Lett. 130, 103–110. doi:10.1016/0009-2614(86)80434-1

CrossRef Full Text | Google Scholar

Shavitt, I., and Bartlett, R. J. (2009). Many-body methods in chemistry and physics: MBPT and coupled-cluster theory. Cambridge: Cambridge University Press.

CrossRef Full Text

Sheridan, P. M., and Ziurys, L. M. (2000). Laboratory detection of the MgNH2 radical ($\tilde{X}{ }^2{A}_1$). Astrophys. J. 540, L61–L64. doi:10.1086/312859

CrossRef Full Text | Google Scholar

Shimanouchi, T. (1972). Tables of molecular vibrational frequencies consolidated volume I. National Bureau of Standards, 1–160.

Swinnen, S., Nguyen, V. S., Sakai, S., and Nguyen, M. T. (2009). Calculations suggest facile hydrogen release from water using boranes and alanes as catalysts. Chem. Phys. Lett. 472, 175–180. doi:10.1016/j.cplett.2009.02.078

CrossRef Full Text | Google Scholar

Takigawa, A., Kamizuka, T., Tachibana, S., and Yamamura, I. (2017). Dust formation and wind acceleration around the aluminum oxide-rich AGB star W Hydrae. Sci. Adv. 3, eaao2149. doi:10.1126/sciadv.aao2149

PubMed Abstract | CrossRef Full Text | Google Scholar

Tenenbaum, E. D., and Ziurys, L. M. (2010). Exotic metal molecules in oxygen-rich envelopes: detection of AlOH ($\tilde{X}{}^1{\text{Σ}}^{+}$) in VY Canis Majoris. Astrophys. J. 712, L93–L97. doi:10.1088/2041-8205/712/1/l93

CrossRef Full Text | Google Scholar

Tenenbaum, E. D., and Ziurys, L. M. (2009). Millimeter detection of AlO ($\tilde{X}{}^2{\text{Σ}}^{+}$): metal oxide chemistry in the envelope of vy canis majoris. Astrophys. J. 694, L59–L63. doi:10.1088/0004-637x/694/1/l59

CrossRef Full Text | Google Scholar

Thackston, R., and Fortenberry, R. C. (2018). Quantum chemical spectral characterization of CH₂NH₂⁺ for remote sensing of titan’s atmosphere. Icarus 299, 187–193. doi:10.1016/j.icarus.2017.07.029

CrossRef Full Text | Google Scholar

Theis, R. A., and Fortenberry, R. C. (2016). Potential interstellar noble gas molecules: ArOH⁺ and NeOH⁺ rovibrational analysis from quantum chemical quartic force fields. Mol. Astrophys. 2, 18–24. doi:10.1021/acsomega.6b00249

CrossRef Full Text | Google Scholar

Trabelsi, T., Davis, M. C., Fortenberry, R. C., and Francisco, J. S. (2019). Spectroscopic investigation of [Al,N,C,O] refractory molecules. J. Chem. Phys. 151, 244303. doi:10.1063/1.5125268

PubMed Abstract | CrossRef Full Text | Google Scholar

Valencia, E. M., Worth, C. J., and Fortenberry, R. C. (2020). Enstatite (MgSiO₃) and forsterite (Mg₂SiO₄) monomers and dimers: highly-detectable infrared and radioastronomical molecular building blocks. Mon. Not. R. Astron. Soc. 492, 276–282. doi:10.1093/mnras/stz3209

CrossRef Full Text | Google Scholar

Wagner, J. P., McDonald, D. C., and Duncan, M. A. (2018). An argon oxygen covalent bond in the ArOH⁺ molecular ion. Angew. Chem. Int. Ed. Engl. 57, 5081–5085. doi:10.1002/anie.201802093

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, J. K. G. (1977). “Aspects of quartic and sextic centrifugal effects on rotational energy levels,” in Vibrational spectra and structure. Editor J. R. During (Amsterdam: Elsevier), 1–89.

Google Scholar

Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R., Schütz, M., Celani, P., et al. (2015). Molpro, version 2015.1, a package of ab initio programs. http://www.molpro.net.

Westbrook, B. R., and Fortenberry, R. C. (2020). Anharmonic frequencies of (MO)₂ & related hydrides for M = Mg, Al, Si, P, S, Ca, & Ti and heuristics for predicting anharmonic corrections of inorganic oxides. J. Phys. Chem. A. 124, 3191–3204. doi:10.1021/acs.jpca.0c01609

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, R. W., Penzias, A. A., Jefferts, K. B., Kutner, M., and Thaddeus, P. (1971). Discovery of interstellar silicon monoxide. Astrophys. J. 167, L97–L100. doi:10.1086/180769

CrossRef Full Text | Google Scholar

Xin, J., Brewster, M. A., and Ziurys, L. M. (2000). The pure rotational spectrum of gas-phase NaNH2 ($\tilde{X}{ }^1{A}_1$). Astrophys. J. 530, 323–328. doi:10.1086/308373

CrossRef Full Text | Google Scholar

Yang, W., Han, Z., Zhou, J., Liu, J., and Cen, K. (2011). Theoretical study on the reaction of magnesium with water in the gas-phase. Int. J. Hydrogen Energy 36, 10608–10613. doi:10.1016/j.ijhydene.2011.05.112

CrossRef Full Text | Google Scholar

Yousaf, K. E., and Peterson, K. A. (2008). Optimized auxiliary basis sets for explicitly correlated methods. J. Chem. Phys. 129, 184108. doi:10.1063/1.3009271

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, Q., Bowman, J. M., Fortenberry, R. C., Mancini, J. S., Lee, T. J., Crawford, T. D., et al. (2015). The structure, anharmonic vibrational frequencies, and intensities of NNHNN⁺. J. Phys. Chem. A. 119, 11623–11631. doi:10.1021/acs.jpca.5b09682

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, D., Doney, K. D., and Linnartz, H. (2014). Laboratory gas-phase detection of the cyclopropenyl cation (-C₃H₃⁺.). Astrophys. J. 791, L28. doi:10.1088/2041-8205/791/2/l28

CrossRef Full Text | Google Scholar