A. Bemporad- INAF, Turin Astrophysical Observatory, Pino Torinese, Italy
After the launch of STEREO twin spacecraft, and most recently of Solar Orbiter and Parker Solar Probe spacecraft, the next mission that will explore Sun-Earth interactions and how the Sun modulates the Heliosphere will be the “Lagrange” mission, which will consist of two satellites placed in orbit around L1 and L5 Sun-Earth Lagrangian points. Despite the significant novelties that will be provided by such a double vantage point, there will be also missing information, that are briefly discussed here. For future heliospheric missions, an alternative advantageous approach that has not been considered so far would be to place two twin spacecraft not in L1 and L5, but in L4 and L5 Lagrangian points. If these two spacecraft will be equipped with in situ instruments, and also remote sensing instruments measuring not only photospheric but also coronal magnetic fields, significant advancing will be possible. In particular, data provided by such a twin mission will allow to follow the evolution of magnetic fields from inside the Sun (with stereoscopic helioseismology), to its surface (with classical photospheric magnetometers), and its atmosphere (with spectro-polarimeters); this will provide a tremendous improvement in our physical understanding of solar activity. Moreover, the L4-L5 twin satellites will take different interesting configurations, such as relative quadrature, and quasi-quadrature with the Earth, providing a baseline for monitoring the Sun-to-Earth propagation of solar disturbances.
Introduction: State of the Art
One of the main target of Space Weather is to provide alerts to the human society before the occurrence of a geomagnetic storm, within the reasonable amount of time required to prevent possible consequences for human technologies and activities (see e.g., Schrijver et al., 2015; Eastwood et al., 2018). For these reasons, in 2009 ESA started the Space Situation Awareness (SSA) program (see e.g., Opgenoorth et al., 2019 and references therein), working on three main areas: Space Weather (SWE), Near-Earth Objects (NEO), and Space Surveillance and Tracking (SST), with SSA Program Office located at ESOC Darmstad (Germany). Focusing on main progresses for SW activities, over the last 12 years lot of developments have been implemented, such as (but not limited to) the SW data center (SWDC) located at ESA Redu Space Services Station in Belgium, and the ESA SSA SW coordination center (SSCC) in Bruxelles (established in 2013), with integrate information provided also by the Met Office Space Weather Operations Center in United Kingdom (established in 2014).
In particular, SSCC is coordinating a common effort at European level, the SW Service Network including 5 “Expert Service Centers” (ESCs) and consisting of ∼40 European teams collaborating to provide products and services for customers. These centers heavily rely on space-based data provided by remote sensing instruments. Hence, under the SSA program ESA is also expanding the use of data provided by existing missions (e.g., PROBA-2, SOHO, Gaia, SWARM), but also studying the deployment of new SW sensors to be hosted on future missions, and supporting the development of a new mission called “Lagrange” (Hapgood, 2017). This mission will be entirely dedicated to SW monitoring, and will consist of two satellites placed in orbit around the Sun-Earth Lagrangian points L1 and L5; the mission development is now in Phase B, and its launch is planned for 2025, when the development of SW services mentioned above will also be ready to integrate the data coming from “Lagrange” mission (Kraft, 2017).
Among the different Sun-Earth Lagrangian points, in the development of the “Lagrange” mission a preference was given to L1 and L5 points mostly because L1 offers a very good vantage point to measure local conditions of interplanetary plasma just before its interaction with the Earth’s magnetosphere, and a good point to monitor the solar hemisphere facing the Earth, while L5 offers a good vantage point to constrain the arrival time of CMEs (Vourlidas, 2015; Rodriguez et al., 2020) and detect with remote sensing instruments the arrival of Active Regions or equatorial coronal holes before their appearance behind the solar limb visible from the Sun-Earth line (Hapgood, 2017).
Given the inherent complexity of physical phenomena related with solar activity (including for instance the emergence of magnetic flux, the accumulation of magnetic energy in the solar atmosphere, the destabilization of magnetic configurations, the acceleration of plasma and particles, etc …), the research dealing with single specific case studies failed so far to identify clear and common universal phenomena occurring in every event (see e.g., Chen, 2011; Liu, 2020), although unified models have been recently proposed (Wyper et al., 2017). On the other hand, the huge number of studies performed over the last decades on eruptive events from the Sun demonstrates that a statistical knowledge of these phenomena (e.g., Wheatland, 2005; McKenna-Lawlor et al., 2006; Song et al., 2009; Ma et al., 2010; Morgan et al., 2012) based on large catalogs (e.g., Gopalswamy et al., 2009; Rotti et al., 2020) is not sufficient to provide reliable forecast of Space Weather conditions, also because of limited duration of solar-terrestrial datasets (see e.g., discussion by Hapgood, 2011). Over the last ∼10 years, a rising number of researchers moved their interest to the promising research fields of Artificial Intelligence and Machine Learning (see review by Camporeale, 2019) applied to solar and i.p. physics data for SW forecasting purposes, for instance to predict the occurrence of solar eruptions and flares (e.g., Ahmed et al., 2013; Benvenuto et al., 2018; Florios et al., 2018), predict geomagnetic storms (e.g., Sexton et al., 2019), and to detect and classify solar events (Martens et al., 2012; Armstrong and Fletcher 2019; Hughes et al., 2019). These methods are really promising, but it is maybe too early to know what will be the new results that these methods will provide in the end.
Motivations: The Need for Magnetic Field Measurements
In general, learning a phenomenon does not necessarily imply a real physical understanding of it, but the latter is needed to generalize new discoveries about Sun-Earth interactions (Hapgood, 2011), and also to apply the same concepts for instance to the interaction of other planets in the Solar System with the Sun, or to other planetary systems orbiting solar-type stars in our Galaxy. Without a real understanding of solar-terrestrial physics (e.g., Tsurutani et al., 2020), any significant change in the background, stationary, or “average” conditions that were used to “learn” anything about the complex behavior of the Sun-Earth system even over one full solar cycle, will make the system likely unpredictable when extreme Carrington-like events will happen (Riley et al., 2018). In this perspective, SW prediction capabilities we are developing could fail just when we will need them most. Hence, it is hard to believe that real SW prediction capabilities will ever be developed in the end without going through a real understanding of physical phenomena driving the solar variability and the corresponding planetary response. Moreover, significant advancing in our forecasting capabilities will necessary require a much deeper understanding of the origin on the Sun and propagation/evolution in the interplanetary medium of these disturbances.
Now, because the majority of phenomena occurring on the Sun are driven by magnetic fields and related plasma physical phenomena, this means in particular that we need a better understanding of how the magnetic fields are generated in the solar interior, how their emergence through the photosphere, their storage and release in the lower corona, and the final connection with our planet. Hence, a mission specifically dedicated to these objectives is needed. In fact, previous solar missions demonstrate the potential of remote sensing observations combined with in situ instrument data acquired from multiple points of view, but much more attention is required to the origin and evolution of solar magnetic fields.
Unfortunately, continuous monitoring of the magnetic fields on the Sun is currently possible only for one single layer of this star: the photosphere (see Kleint and Gandorfer 2017). Over this surface, magnetic field measurements are possible thanks to the Zeeman splitting of some spectroscopic lines, related with the strength of the magnetic field. These measurements are currently available 24 h per day only for the solar hemisphere visible along the Sun-Earth line. On the other hand, field measurements in the above layers of the Sun have been proven to be possible with spectro-polarimetry both in the chromosphere (e.g., Kano et al., 2012) and the corona (Tomczyk and McIntosh 2009) by using Zeeman and Hanle effects (see also Raouafi et al., 2016; Yang et al., 2020). Unfortunately, coronal field measurements are acquired so far only along the Sun-Earth line, hence on the plane of sky of the solar corona as seen from Earth. This means that at present (under favorable conditions) we can measure coronal magnetic fields related with sunspots and active regions located on the limb whose photospheric fields cannot be measured, while we can measure photospheric fields of these regions when they are located in the visible hemisphere when the corresponding coronal fields cannot be measured. So, at present magnetic fields cannot be measured at the same time from the photosphere to the corona. As a result, it is at present impossible to fully understand how the magnetic energy is transferred from the photosphere to the corona, how it is stored in the corona, and why the excess energy is finally released when the system is destabilized, leading to solar flares, CMEs, and SEP acceleration. Having information of photospheric-to-coronal magnetic fields is of paramount importance to forecast geomagnetic storms in advance, because the magnetic structure of the flux rope embedded in the eruption is the most crucial parameter to determine the strength of the space weather effects (see e.g., Kilpua et al., 2019), and our current capability to provide that information is very modest.
To solve this significant lack of information, many different extrapolation methods have been developed to reconstruct the coronal fields starting from the measured photospheric fields (see Wiegelmann, 2008; Régnier, 2013 and references therein), but the agreement between the location and orientation of the reconstructed fieldlines and the observed EUV coronal loops (usually assumed to match the fieldlines) is only marginal (Sandman et al., 2009), in particular above active regions where significant deviations from the lower energy potential field configuration are present (Aschwanden, 2013). A better correspondence with EUV features is provided for instance by non-linear Force-free field extrapolations (e.g., Guo et al., 2012; James et al., 2018) or time-dependent magneto-frictional methods (e.g., Pomoell et al., 2019), but these models provide a good reconstruction only for regions located near the solar disk center, and because measurements of the above coronal fields are missing, more quantitative comparisons are not possible. Moreover, these extrapolation methods start from photospheric field measurements acquired when the active regions are observed in the visible hemisphere, and these fields can be compared only with EUV features visible on-disk in the inner corona (h < 1.3 Rsun), while a comparison with coronal features extending at higher altitudes requires off-limb observations (as those recently provided by PAROBA2/SWAP; O’Hara et al., 2019), and again these observations are daily available only along the Sun-Earth line. Hence, a comparison between the extrapolated coronal fieldlines and the observed coronal features requires to assume that these fields are not changed significantly over the time required (3–7 days) for the active region observed on disk to move at the limb dragged by solar rotation.
The situation was marginally improved thanks to the STEREO mission (Kaiser et al., 2008), that provided for the first time observations of coronal structures on a plane of the sky aligned with the Sun-Earth line, but (because STEREO spacecraft are orbiting the Sun along the Earth orbit, but drifting away from Earth at an average rate of about 22.5° per year) this happened only for short periods during the mission. Moreover, unfortunately the STEREO spacecraft didn’t have on-board any photospheric field magnetometer, and not even any coronal field magnetometer. In the near future the situation will be slightly improved thanks to Solar Orbiter mission (Müller et al., 2013), which is carrying on-board a photospheric magnetometer (Solanki et al., 2020), a coronagraph (Antonucci et al., 2020) and a Heliospheric Imager (Howard et al., 2020), but remote sensing observations will be acquired only during specific time windows, and only a few of them will occur with the spacecraft in quadrature with respect to the Earth.
As anticipated, to overcome these limits ESA is now developing the “Lagrange” mission (Hapgood, 2017), with the aim to put in stable orbits two satellites around the L1 and L5 Sun-Earth Lagrangian points. In particular, the real novelty of the mission will be represented by the satellite put in orbit around the L5 point, something that has never been attempted before. From this vantage point, the remote sensing instruments on-board the spacecraft (including a photospheric field magnetometer) will continuously monitor coronal off-limb features located near the plane of the sky close to the Sun-Earth line, and the interplanetary propagation of solar disturbances expanding toward Earth. It will be possible for the first time to measure with remote sensing data photospheric fields of active regions crossing the solar limb as seen from Earth and before their arrival with solar rotation on the hemisphere pointing toward our planet. Moreover, in situ data acquired in L5 will detect possible high-speed streams and Stream Interaction Regions before their arrival on Earth ∼4.5 days later dragged by rotation of the Parker spiral. These are likely the main reasons why the L5 point was chosen instead of L4 for the “Lagrange” mission.
Nevertheless, there are few important considerations to be made. First of all, neither of the two “Lagrange” satellites will carry on-board an instrument to measure with spectro-polarimetry coronal magnetic fields. Hence, without a coronal magnetometer, it will be again necessary to extrapolate these fields in the corona, starting from photospheric field measurements: a mission carrying on board such an instrument will be still missing in the near future. For this reason, similar instruments have been proposed as a payload not only for past missions (e.g., Peter et al., 2012), but also more recently1 in response to the call for “white papers” for the long-term planning of ESA science program (MiMOSA mission).
Second, we have to consider that the L5 point is not located in quadrature with the Earth, but at an angle from the Sun-Earth line of 60°, which is not the ideal location to monitor solar eruptions propagating toward the Earth. This angular separation may not appear significant, considering also the angular expansion of solar eruptions, but the visible light emission observed by coronagraphs maximizes on the so-called “Thomson sphere,” and this limit their visibility in the inner corona to the instrument plane-of-sky (see review by Rouillard, 2011). The spacecraft in L5 will be likely placed in a stable “Trojan” orbit (Llanos et al., 2012), which is almost elliptical, with amplitude of the orbit depending mostly on the chosen transfer trajectory and transfer time from the low Earth parking orbit, and two extreme cases can be considered here. For instance, if the spacecraft will be inserted in a small amplitude Trojan orbit (even down to ∼100 km) around L5, the remote sensing instruments will never observe the corona in quadrature with the Earth. On the other hand, if the spacecraft will be inserted in a large amplitude Trojan orbit (up to ∼0.25–0.50 AU), the spacecraft will spend a half of its time very close to the quadrature configuration, and the second half very far from this configuration. The period of any of these orbits around L5 is about one year (Llanos et al., 2012). In summary: both in the first and in the second case a single spacecraft placed in L5 will never be able to monitor continuously the Sun in quasi-quadrature with respect to the Earth.
Third, we also have to remember that, considering the path followed by Solar Energetic Particles (SEPs) during their propagation in the interplanetary space, the most dangerous Active Regions (in terms of possible SW effects) are those located not at the center of the solar hemisphere as seen from the Sun-Earth line, but those located Westward, typically around 45–60° West (see review by Reames, 2013). This phenomenon is related with the Sun-Earth magnetic connectivity through the Parker spiral of interplanetary magnetic field, making an angle of about 45° with respect to the radial direction at the Earth’s orbit. As a consequence, photospheric magnetic fields for these dangerous Active Regions cannot be observed at all from a spacecraft located in L5 (because the region will appear behind the limb as seen from that vantage point), and can be only marginally observed from a spacecraft located in L1 or along the Sun-Earth line (because the best measurement of photospheric fields provides the line-of-sight component of these fields, unless vector magnetograms are employed, whose data have a well-known ±180° azimuthal ambiguity, Gary and Hagyard, 1990). Hence, the best location to measure magnetic fields of Active Regions magnetically connected with the Earth will be nor L5, neither L1, but the L4 Lagrangian point.
Looking Forward: The Advantages of a Twin L4-L5 Mission
A solution to all the above missing capabilities of the previous (e.g., STEREO), current (e.g., Solar Orbiter), and near future (e.g., “Lagrange”) missions will be covered instead by a new mission concept, consisting of twin spacecraft to L4 and L5, briefly described here. An example of a combined views of photosphere and corona that will be provided by L4 and L5 is shown in Figure 1: the unique combination of these data would allow to monitor the same Active Region and its impact on the overlying atmosphere from the limb to the disk center at the same time, allowing to follow the emergence of photospheric fields, the accumulation of coronal fields, and their release from a side and face perspectives. Considering the limited amount of space and the aims of this paper, I will not review here the need for a mission carrying remote sensing instruments capable to measure at the same time not only the photospheric, but also the coronal magnetic fields with spectro-polarimetry. The interested reader may refer for instance to the recent paper by Raouafi et al. (2016), or to the review by Kleint and Gandorfer (2017), and references therein.
FIGURE 1. Example of a possible combination of data acquired from L5 (top row), L1 (middle row), and L4 (bottom row) vantage point. The different columns show the visible photosphere (left column), the inner corona (middle left column), and the corresponding photospheric fields (middle right column) and coronal field azimuth (right column). The location of the same sunspot group is outlines with a circle.
What will be discussed here instead is the importance to consider a similar suite of instruments on-board a twin mission to the L4 and L5 vantage points; this idea was first proposed by Bemporad et al. (2014) in a mission concept named “HeMISE (Helio-Magnetism Investigation from the Sun to Earth).” Let us consider here two twin spacecraft, carrying in situ and remote sensing instruments measuring photospheric and coronal fields, and being located in stable orbits around L4 and L5 Lagrangian points. This configuration will have many advantages, briefly summarized here. The two spacecraft could be placed both in close orbit around L4 and L5, thus keeping almost all the time a relative separation angle of about ∼120° each other, and ∼60° with respect to the Sun-Earth line. During a solar eruption, the same event would be observed expanding above the limb from one view point (thus allowing an early determination of kinematical properties of CMEs and shocks), and face-on above the disk (the perfect location to study the flare and SEP acceleration), as it is shown in Figure 2 bottom left panel. Nevertheless, this configuration seems not the best option for scientific and monitoring purposes.
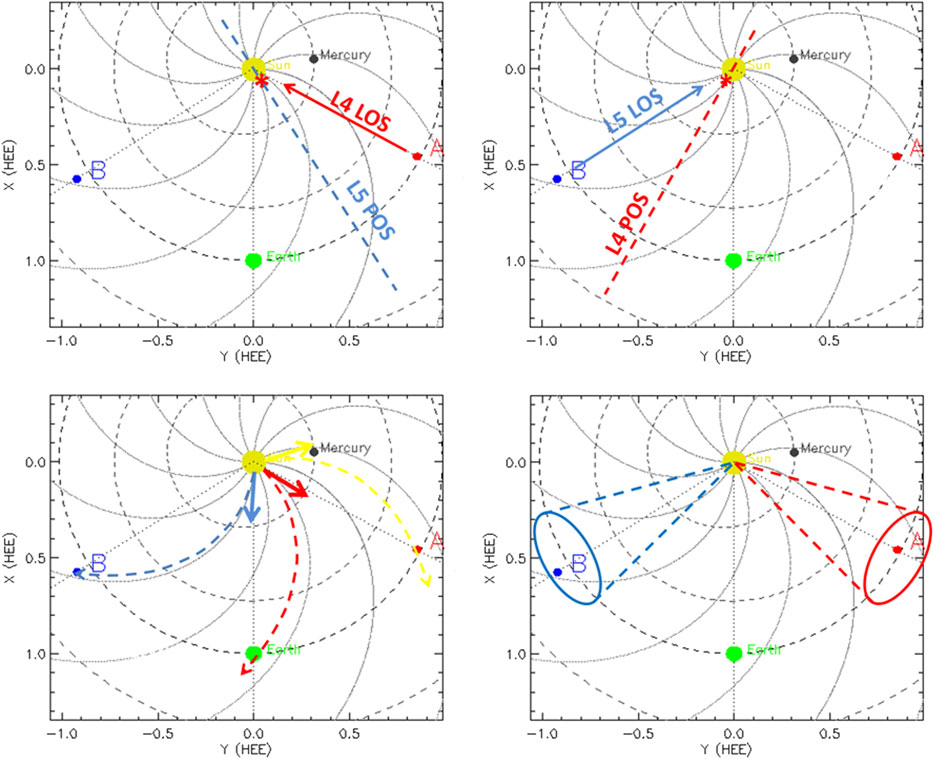
FIGURE 2. Example of possible advantages offered by the twin L4-L5 mission proposed here. Top panels: the plane-of-sky (POS) of remote sensing instruments will allow to observe limb events from one spacecraft that will be observed as events at the center of solar disk from the other spacecraft. Bottom left: combinations of remote sensing and in situ data will allow to study CMEs propagating at different direction (blue, red, and yellow arrows) and also to sample the associated SEP fluxes propagating along the Parker spiral arms (blue, red, and yellow dashed lines). Bottom right: during their Trojan stable orbits around L4 and L5 the twin spacecraft will go from relative quadrature to quasi-quadrature with the Earth (dashed lines). These drawings are based on the plot provided by the STEREO orbit tool2 and showing the location of STEREO spacecraft when the mission passed nearby L4 and L5 points (October 2009).
More interestingly, the two spacecraft could be placed in a much broader Trojan orbit around L4 and L5, having for instance an orbital amplitude (corresponding to two times the maximum radius measured from center of the libration orbit) of about 0.52 AU (Llanos et al., 2012). In this case, during the orbital period of about one year, each spacecraft will change its longitudinal angle with respect to the Sun-Earth line from a maximum amplitude of about 75°, down to a minimum amplitude around 45° (Figure 2, bottom right panel). Then, with two spacecraft in L4 and L5 two possible cases can be considered: 1) synchronous orbits, and 2) asynchronous orbits shifted by half a orbital period. If the two orbits around L4 and L5 (separated by an angular distance by 120°) are synchronized, then the separation angle between the two spacecraft will change from a maximum of 150° (quasi-opposition) to a minimum of 90° (quadrature), with both spacecraft closer/farther to the quasi-quadrature configuration with the Earth in the same period of time. On the other hand, in the case of asynchronous orbits shifted by half a orbital period, the separation angle between the two spacecraft will be almost constant during the mission, and the two spacecraft will move alternatively closer and farther from the quasi-quadrature with the Earth.
The first configuration 1) will provide very interesting cases from the scientific point of view. In particular, during quadratures between the two spacecraft photospheric fields sampled by one view point will be observed at the same time in the lower corona, off-limb with coronagraphic spectro-polarimetric data acquired from the second view-point. Photospheric fields measured by one spacecraft will be combined with coronal fields measured by the second spacecraft in quasi-quadrature, thus providing for the first time a continuous coverage of solar magnetic fields through the solar atmosphere. Hence, it will be possible for the first time to really understand how the emergence of magnetic fields in the photosphere directly affect the coronal structures, providing completely new information for the origin of solar eruptions, occurrence of impulsive events, acceleration of solar wind (stereoscopic coronal magnetometry). More than that, during the rest of the whole mission it will be possible in general to perform 3D reconstruction of solar stationary features in the inner corona, 3D reconstructions of CMEs and their kinematic, and stereoscopic helioseismology. In particular, it will be possible to study the 3D propagation of waves in the solar interior down to the tachocline from two points of view, opening the possibility for stereoscopic global helioseismology. The feasibility of research in this latter topic will be tested for the first time with the forthcoming Solar Orbiter data, but this mission will acquire only limited datasets during specific remote sensing periods, while satellites in stable orbits around L4 and L5 will cover potentially years of evolution of the Sun, and a long-term data coverage is of fundamental importance to understand the whole solar cycle evolution.
On the other hand, the second configuration 2) with the two orbits around L4 and L5 shifted by half a period will be the more suitable one for SW monitoring applications. The reason is that in this case one of the two spacecraft will be alternatively closer and farther from the quasi-quadrature configuration with the Earth. This means that among two spacecraft, one of them will be ever closer to the best configuration to monitor solar transients propagating toward the Earth. These resulting will be sampled by the heliospheric imagers on-board the spacecraft, covering almost the whole range of distances from the Sun to the Earth (like H1 and H2 imagers on-board STEREO). This will allow continuous 3D reconstructions of solar transients propagating to the Earth, hence providing a ideal mission for space weather studies. The same scientific cases mentioned above (3D reconstructions and stereoscopic helioseismology) will be also possible, with the advantage that the separation angle between the twin spacecraft will be almost constant with time, and this will reduce the long-term variability of data analysis for helioseismology. This configuration of L4-L5 satellites, complemented with measurements from L1 or from the Earth, would provide nearly continuous boundary conditions for coronal field models.
Moreover, considering again the geometry of interplanetary magnetic field spiral, very interesting science cases will be provided by the possible combinations of remote sensing and in situ data. The unique vantage point offered by the spacecraft in L5 will allow to detect in situ SEPs propagating along the Parker spiral and related with geo-effective ICMEs with the source region located near the center of the visible hemisphere as seen from the Sun-Earth line. On the other hand, the spacecraft in L4 will detect in situ the transit of ICMEs associated with SEP streams affecting the Earth. When the spacecraft will be in quasi-quadrature configuration, in the case of a CME directed toward one of them, the same eruption will be observed with remote sensing data as limb event from one spacecraft, and sampled later on with in situ data from the other spacecraft (Figure 2, bottom left panel). Last but not least, the L4 vantage point will allow to monitor Active Regions magnetically connected with the Earth with standard photopsheric magnetograms, thus helping the forecasting of flares accelerating SEP fluxes toward the Earth.
Summary and Conclusion
This paper briefly summarized the current state and future directions of solar and heliospheric physics human investigation. Among the current and proposed future missions exploring the Heliosphere, a possible combination of twin satellites orbiting around the L4 and L5 Sun-Earth Lagrangian point has never been proposed. The advantages and new knowledge of such a configuration were briefly described here: in particular, if the spacecraft will be equipped not only with “classical” remote sensing and in situ instruments, but also with coronal magnetometers, the combination of data acquired by the L4-L5 perspectives will provide a new knowledge of magnetic fields evolution across different layers of the Sun, and will also allow to monitor almost continuously in quasi-quadrature configuration the Sun-Earth interactions.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author acknowledges S. Fineschi and M. Romoli for useful discussions in the preparation of some of the ideas proposed here.
Footnotes
1https://www.cosmos.esa.int/web/voyage-2050/white-papers
2https://stereo-ssc.nascom.nasa.gov/where/
References
Ahmed, O. W., Qahwaji, R., Colak, T., Higgins, P. A., Gallagher, P. T., Bloomfield, D. S., et al. (2013). Solar flare prediction using advanced feature extraction, machine learning, and feature selection. Sol. Phys. 283 (1), 157–175. doi:10.1007/s11207-011-9896-1
Antonucci, E., Romoli, M., Andretta, V., Fineschi, S., Heinzel, P., Moses, J. D., et al. (2020). Metis: the solar orbiter visible light and ultraviolet coronal imager. Astron. Astrophys. 642, A10. doi:10.1051/0004-6361/201935338
Armstrong, J. A., and Fletcher, L. (2019). Fast solar image classification using deep learning and its importance for automation in solar physics. Sol. Phys. 294 (6), 80. doi:10.1007/s11207-019-1473-z
Aschwanden, M. J. (2013). A nonlinear force-free magnetic field approximation suitable for fast forward-fitting to coronal loops. III. the free energy. Sol. Phys. 287 (1-2), 369–389. doi:10.1007/s11207-012-0203-6
Bemporad, A., Fineschi, S., Focardi, M., Landini, F., Romoli, M., and Pancrazzi, M. (2014). “HeMISE (Helio-Magnetism Investigation from the Sun to Earth): a twin spacecraft mission at the Sun-Earth Lagrangian points L4 and L5” in 40th COSPAR scientific assembly, Moscow, Russia, 2-10 August 2014, 15–14.
Benvenuto, F., Piana, M., Campi, C., and Massone, A. M. (2018). A hybrid supervised/unsupervised machine learning approach to solar flare prediction. Astrophys. J. 853 (1), 90. doi:10.3847/1538-4357/aaa23c
Camporeale, E. (2019). The challenge of machine learning in space weather: nowcasting and forecasting. Space Weather 17 (8), 1166. doi:10.1029/2018sw002061
Chen, P. F. (2011). Coronal mass ejections: models and their observational basis. Living Rev. Solar Phys. 8, 1. doi:10.12942/lrsp-2011-1
Eastwood, J. P., Hapgood, M., Biffis, E., Benedetti, D., Bisi, M. M., Green, L., et al. (2018). Quantifying the economic value of space weather forecasting for power grids: an exploratory study. Space Weather 16, 2052–2067. doi:10.1029/2018sw002003
Florios, K., Kontogiannis, I., Park, S.-H., Guerra, J. A., Benvenuto, F., Bloomfield, D. S., et al. (2018). Forecasting solar flares using magnetogram-based predictors and machine learning. Sol. Phys. 293 (2), 28. doi:10.1007/s11207-018-1250-4
Gary, G. A., and Hagyard, M. J. (1990). Transformation of vector magnetograms and the problems associated with the effects of perspective and the azimuthal ambiguity. Sol. Phys. 126, 21.
Gopalswamy, N., Yashiro, S., Michalek, G., Stenborg, G., Vourlidas, A., Freeland, S., et al. (2009). The SOHO/LASCO CME catalog. Earth, Moon Planets 104 (1), 295. doi:10.1007/s11038-008-9282-7
Guo, Y., Ding, M. D., Liu, Y., Sun, X. D., DeRosa, M. L., Wiegelmann, T., et al. (2012). Modeling magnetic field structure of a solar active region corona using nonlinear force-free Fields in spherical geometry. Astrophys. J. 760, 47. doi:10.1088/0004-637x/760/1/47
Hapgood, M. (2017). L1L5Together: report of workshop on future missions to monitor space weather on the Sun and in the solar wind using both the L1 and L5 Lagrange points as valuable viewpoints. Space Weather 15, 654. doi:10.1002/2017sw001638
Hapgood, M. A. (2011). Towards a scientific understanding of the risk from extreme space weather. Adv. Space Res. 47, 2059. doi:10.1016/j.asr.2010.02.007
Howard, R. A., Vourlidas, A., Colaninno, R. C., Korendyke, C. M., Plunkett, S. P., Carter, M. T., et al. (2020). The solar orbiter heliospheric imager (SoloHI). Astron. Astrophys.. 642, A13. doi:10.1051/0004-6361/201935202
Hughes, J. M., Hsu, V. W., Seaton, D. B., Bain, H. M., Darnel, J. M., Krista, L., et al. (2019). Real-time solar image classification: assessing spectral, pixel-based approaches. J. Space Weather Space Clim. 9, A38. doi:10.1051/swsc/2019036
James, A. W., Valori, G., Green, L. M., Liu, Y., Cheung, M. C. M., Guo, Y., and Driel-Gesztelyi, L. v. (2018). An observationally constrained model of a flux rope that formed in the solar corona. Astrophys. J. Lett. 855, L16. doi:10.3847/2041-8213/aab15d
Kaiser, M. L., Kucera, T. A., Davila, J. M., Cyr, O. C. St., Guhathakurta, M., Christian, E., et al. (2008). The STEREO mission: an introduction. Space Sci. Rev. 136 (1), 5. doi:10.1007/s11214-007-9277-0
Kano, R., Bando, T., Narukage, N., Ishikawa, R., Tsuneta, S., Katsukawa, Y., et al. (2012). Chromospheric Lyman-alpha spectro-polarimeter (CLASP). Proc. SPIE 8443, 84434F. doi:10.1117/12.925991
Kilpua, E. K. J., Lugaz, N., Mays, M. L., and Temmer, M. (2019). Forecasting the structure and orientation of earthbound coronal mass ejections. Space Weather 17, 498–526. doi:10.1029/2018sw001944
Kraft, S. (2017). Remote sensing optical instrumentation for enhanced space weather monitoring from the L1 and L5 Lagrange points. Proc. SPIE 10562, 105620F–105622F. doi:10.1117/12.2296100
Kleint, L., and Gandorfer, A. (2017). Prospects of solar magnetometry-from ground and in space. Space Sci. Rev. 210, 397. doi:10.1007/s11214-015-0208-1
Liu, R. (2020). Magnetic flux ropes in the solar corona: structure and evolution toward eruption. Res. Astron. Astrophys. 20 (10), 165. doi:10.1088/1674-4527/20/10/165
Llanos, P. J., Miller, J. K., and Hintz, G. (2012). Navigation analysis for an L5 mission in the Sun-Earth system. Adv. Astronautical. Sci. 142, 11–503. doi:10.13140/2.1.2069.4402
Ma, S., Attrill, G. D. R., Golub, L., and Lin, J. (2010). Statistical study of coronal mass ejections with and without distinct low coronal signatures. Astrophys. J. 722 (1), 289. doi:10.1088/0004-637x/722/1/289
Martens, P. C. H., Attrill, G. D. R., Davey, A. R., Engell, A., Farid, S., Grigis, P. C., et al. (2012). Computer vision for the solar dynamics observatory (SDO). Sol. Phys. 275 (1-2), 79. doi:10.1007/s11207-010-9697-y
McKenna-Lawlor, S. M. P., Dryer, M., Kartalev, M. D., Smith, Z., Fry, C. D., Sun, W., et al. (2006). Near real-time predictions of the arrival at Earth of flare-related shocks during Solar Cycle 23. J. Geophys. Res. 111 (A11), A11103. doi:10.1029/2005ja011162
Morgan, H., Byrne, J. P., and Habbal, S. R. (2012). Automatically detecting and tracking coronal mass ejections. I. separation of dynamic and quiescent components in coronagraph images. Astrophys. J., 752 (2), 144. doi:10.1088/0004-637x/752/2/144
Müller, D., Marsden, R. G., Cyr, O. C. St., and Gilbert, H. (2013). Solar orbiter. exploring the Sun-Heliosphere connection. Sol. Phys. 285 (1-2), 25. doi:10.1007/s11207-012-0085-7
Opgenoorth, H. J., Wimmer-Schweingruber, R. F., Belehaki, A., Berghmans, D., Hapgood, M., Hesse, M., et al. (2019). Assessment and recommendations for a consolidated European approach to space weather - as part of a global space weather effort. J. Space Weather Space Clim. 9, A37. doi:10.1051/swsc/2019033
O’Hara, J. P., Mierla, M., Podladchikova, O., D’Huys, E., and West, M. J. (2019). Exceptional extended field-of-view observations by PROBA2/SWAP on 2017 April 1 and 3. Astrophys. J. 883, 59. doi:10.3847/1538-4357/ab3b08
Peter, H., Abbo, L., Andretta, V., Auchère, F., Bemporad, A., Berrilli, F., et al. (2012). Solar magnetism eXplorer (SolmeX). Exploring the magnetic field in the upper atmosphere of our closest star. Exp. Astron. 33 (2-3), 271. doi:10.1007/s10686-011-9271-0
Pomoell, J., Lumme, E., and Kilpua, E. (2019). Time-dependent data-driven modeling of active region evolution using energy-optimized photospheric electric fields. Sol. Phys. 294 (4), 41. doi:10.1007/s11207-019-1430-x
Raouafi, N. E., Riley, P., Gibson, S., Fineschi, S., and Solanki, S. K. (2016). Diagnostics of coronal magnetic fields through the Hanle Effect in UV and IR lines. Front. Astron. Space Sci. 3. doi:10.3389/fspas.2016.00020
Reames, D. V. (2013). The two sources of solar energetic particles. Space Sci. Rev. 175 (1-4), 53–92. doi:10.1007/s11214-013-9958-9
Régnier, S. (2013). Magnetic field extrapolations into the corona: success and future improvements. Sol. Phys. 288 (2), 481. doi:10.1007/s11207-013-0367-8
Riley, P., Baker, D., Liu, Y. D., Verronen, P., Singer, H. J., and Güdel, M. (2018). Extreme space weather events: from cradle to grave. Space Sci. Rev., 214 (1), 21. doi:10.1007/s11214-017-0456-3
Rodriguez, L., Scolini, C., Mierla, M., Zhukov, A. N., and West, M. J. (2020). Space weather monitor at the L5 point: a case study of a CME observed with STEREO B. Space Weather 18 (10), e02533. doi:10.1029/2020sw002533
Rotti, S. A., Martens, P. C. H., and Aydin, B. (2020). A catalog of solar flare events observed by the SOHO/EIT. ApJS 249 (2), 20. doi:10.3847/1538-4365/ab9a42
Rouillard, A. P. (2011). Relating white light and in situ observations of coronal mass ejections: a review. J. Atmos. Solar-Terrestrial Phys. 73 (10), 1201. doi:10.1016/j.jastp.2010.08.015
Sandman, A. W., Aschwanden, M. J., DeRosa, M. L., Wülser, J. P., and Alexander, D. (2009). Comparison of STEREO/EUVI loops with potential magnetic field models. Sol. Phys. 259 (1), 1–11. doi:10.1007/s11207-009-9383-0
Schrijver, C. J., Kauristie, K., Aylward, A. D., Denardini, D. M., Gibson, S. E., Glover, A., et al. (2015). Understanding space weather to shield society: A global road map for 2015–2025 commissioned by COSPAR and ILWS. Adv. Space Res. 55 (12), 2745–2807. doi:10.1016/j.asr.2015.03.023
Sexton, S., Nykyri, K., and Ma, X. (2019). Kp forecasting with a recurrent neural network. J. Space Weather Space Clim. 9, A19. doi:10.1051/swsc/2019020
Solanki, S. K., del Toro Iniesta, J. C., Woch, J., Gandorfer, A., Hirzberger, J., Alvarez-Herrero, A., et al. (2020). The polarimetric and helioseismic imager on solar orbiter. Astron. Astrophys. 642, A11. doi:10.1051/0004-6361/201935325
Song, H., Tan, C., Jing, J., Wang, H., Yurchyshyn, V., and Abramenko, V. (2009). Statistical assessment of photospheric magnetic features in imminent solar flare predictions. Sol. Phys. 254 (1), 101. doi:10.1007/s11207-008-9288-3
Tomczyk, S., and McIntosh, S. W. (2009). Time-distance seismology of the solar corona with CoMP. Astrophys. J. 697 (2), 1384. doi:10.1088/0004-637x/697/2/1384
Tsurutani, B. T., Lakhina, G. S., and Hajra, R. (2020). The physics of space weather/solar-terrestrial physics (STP): what we know now and what the current and future challenges are. Nonlin. Process. Geophys. 27, 7. doi:10.5194/npg-27-75-2020
Vourlidas, A. (2015). Mission to the sun-earth L5Lagrangian point: an optimal platform for space weather research. Space Weather 13, 197–201. doi:10.1002/2015sw001173
Wheatland, M. S. (2005). A statistical solar flare forecast method. Space Weather 3 (7), S07003. doi:10.1029/2004sw000131
Wiegelmann, T. (2008). Nonlinear force-free modeling of the solar coronal magnetic field. J. Geophys. Res. 113 (A3), A03S02. doi:10.1029/2007ja012432
Wyper, P. F., Antiochos, S. K., and DeVore, C. R. (2017). A universal model for solar eruptions. Nature 544 (7651), 452. doi:10.1038/nature22050
Keywords: space weather, future missions, open problems, solar physics, solar eruptions
Citation: Bemporad A (2021) Possible Advantages of a Twin Spacecraft Heliospheric Mission at the Sun-Earth Lagrangian Points L4 and L5. Front. Astron. Space Sci. 8:627576. doi: 10.3389/fspas.2021.627576
Received: 09 November 2020; Accepted: 20 January 2021;
Published: 31 March 2021.
Edited by:
Luca Sorriso-Valvo, Institute for Space Physics (Uppsala), SwedenReviewed by:
Scott William McIntosh, National Center for Atmospheric Research (UCAR), United StatesEmilia Kilpua, University of Helsinki, Finland
Copyright © 2021 Bemporad. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A. Bemporad, YWxlc3NhbmRyby5iZW1wb3JhZEBpbmFmLml0