- Institute of Geophysics and Meteorology, University of Cologne, Cologne, Germany
The magnetospheres of the outer planets exhibit turbulent phenomena in an environment which is qualitatively different compared to the solar wind or the interstellar medium. The key differences are the finite sizes of the magnetospheres limited by their physical boundaries, the presence of a strong planetary background magnetic field and spatially very inhomogeneous plasma properties within the magnetospheres. Typical turbulent fluctuations possess amplitudes much smaller than the background field and are characterized by Alfvén times, which can be smaller than the non-linear interaction time scales. The magnetospheres of the outer planets are thus interesting laboratories of plasma turbulence. In Jupiter's and Saturn's magnetospheres, turbulence is well-established thanks to the in-situ measurements by several spacecraft, in particular the Galileo and Cassini orbiter. In contrast, the fluctuations in Uranus' and Neptune's magnetospheres are poorly understood due to the lack of sufficient data. Turbulence in the outer planets' magnetospheres have important effects on the systems as a whole. The dissipation of the turbulent fluctuations through wave-particle interaction is a significant heat source, which can explain the large magnetospheric plasma temperatures. Similarly, turbulent wave fluctuations strongly contribute to the acceleration of particles responsible for the planet's auroras.
1. Introduction and Origin of Turbulence
All four outer planets of the solar system, Jupiter, Saturn, Uranus, and Neptune, possess strong internal dynamo magnetic fields with polar field strength of ~ 2,000,000, 40,000, 100,000, and 90,000 nT, respectively (Connerney, 2007; Ness, 2010). They are also fast rotators with periods of 9.9, 10.7, 17.2, and 16.1 h, respectively (Seidelmann et al., 2002). These two effects lead to large and rotationally dominated magnetospheres with average magnetopause standoff distances on the sub-solar side of 65, 20, 20, and 26 planetary radii, respectively (Bagenal, 2009, 2013; Vasyliūnas, 2009).
One of the most important difference between the magnetospheres of the outer planets and the magnetosphere of Earth is the presence of large mass sources well inside the outer planets' magnetospheres and the resultant effects generated by the associated radial mass transport. In case of Jupiter, its inner Galilean moon Io, located deeply within the magnetosphere at 6 RJ, produces about 103 kg s−1 of SO2, which eventually gets ionized (Thomas et al., 2004). An additional, but smaller source of mass is its moon Europa with about 50 kg s−1 of H2O (Bagenal and Dols, 2020). In case of Saturn, the mass source is the moon Enceladus, with a time-variable injection rate of 200–1,000 kg s−1 of H2O (Dougherty et al., 2009; Fleshman et al., 2010; Saur et al., 2011; Hedman et al., 2013). In case of Uranus and Neptune, also major moons orbit within their magnetosphere. However, their mass loss rates are not well-constrained. They are considered smaller compared to those in the magnetospheres of Jupiter and Saturn based on the significantly smaller mass densities in the magnetospheres of Uranus and Neptune (e.g., Bagenal, 2009, 2013).
The centrifugal force in the fast rotating magnetospheres causes the plasma to be concentrated near the equatorial regions (called plasma sheets, see Figure 1) and drives transport of plasma radially outward. Due to conservation of angular momentum the outward moving plasma does not to fully corotate with the planet. This generates two types of magnetospheric stresses: Stretched magnetic field lines in the radial direction from the radial transport (see Figure 1) and bend backed magnetic field lines in azimuthal direction due to the subcorotating plasma. These magnetic stresses couple to the planets' ionospheres and cause transport of angular momentum between the planets' ionospheres and magnetospheres (Hill, 2001; Goldreich and Farmer, 2007). The stress balance is however not in steady state, but constantly disturbed due to non-continuous radial transport of plasma, which is observed to occur through the interchange of mass loaded magnetic flux tubes with adjacent less loaded flux tubes further out (Kivelson et al., 1997). The imbalance of magnetic stresses cause Alfvén waves to propagate along the magnetic field to achieve stress balance. The Alfvén wave packages are partially reflected at the ionospheres or other boundaries, such as large density gradients of the plasma sheet. The resulting counter-propagating Alfvén wave packages interact non-linearly and thus generate a turbulent cascade (Saur et al., 2002; Saur et al., 2018). On the MHD scales the magnetospheric plasma sheet is thought to be a key region where the cascade is being driven (Saur et al., 2002).
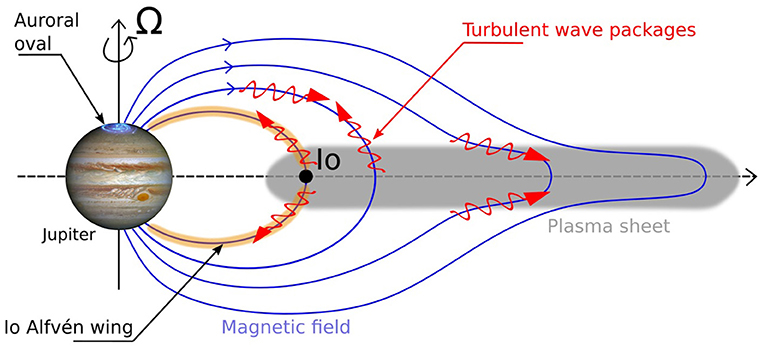
Figure 1. Sketch of turbulent wave packages in Jupiter's magnetosphere. The interaction of counter-propagating Alfvén wave packages generates a turbulent cascade. Waves packages are reflected at the ionosphere of Jupiter or other density gradients in the magnetosphere.
The non-linear interaction of counter-propagating wave packages is the fundamental building block of MHD and plasma turbulence. It is established observationally, theoretically and in numerical modeling (e.g., Goldreich and Sridhar, 1995; Howes and Nielson, 2013). There are several key differences between turbulence in the solar wind (e.g., Bruno and Carbone, 2013) and the turbulence in the magnetospheres of the outer planets. The magnetospheric fluctuations are small amplitude fluctuations δB≪B0 compared to the dominant magnetospheric background field B0. The magnetospheres are also finite in size. This implies that turbulent scales are bound and a maximum length scale for the inertial range of turbulence exists. It also causes reflection of the wave packages at the ionospheric boundaries. Additionally the magnetospheres are highly inhomogeneous with large densities and small magnetic field strength in the magnetospheric plasma sheets and vice versa at high latitudes (see Figure 1). Therefore, the generator region, i.e., where the turbulent cascade is driven, and the dissipation regions of the turbulent fluctuations do not need to be spatially collocated (Saur et al., 2018). Another interesting difference between the solar wind and the magnetospheres of the outer planets is that the composition of ions has a much larger spread in mass. The solar wind is mostly composed of H+ and He++ compared to H+, O+, S+, H2O+ … in Jupiter's or Saturn's magnetospheres. This causes a larger spread of gyro frequencies and inertial length scales and will influence the pathways of turbulent dissipations.
In the reminder of this review we will present observations of turbulent fluctuations in Jupiter's and Saturn's magnetospheres. Additionally, we discuss their impact on overall properties of these magnetospheres such as aurora or temperature structure.
2. Magnetospheric Turbulence
Turbulence and its implications for the magnetospheres of Jupiter and Saturn have been studied by a number of authors. There are no published studies about turbulence in the magnetospheres of Uranus and Neptune due to a lack of appropriate data.
2.1. Jupiter Magnetosphere
Turbulence in Jupiter's magnetosphere has been investigated on various levels of detail. Before the Galileo epoch, Nishida (1976) considered whistler mode turbulence for pitch angle diffusion of energetic electrons and ions. Barbosa (1981) and Barbosa et al. (1984) investigated ion heating due to high-frequency kilohertz plasma wave turbulence and low frequency Alfvénic turbulence, respectively. Glassmeier (1995) suggests a Kolmogorov-type of turbulence in the very low-frequency, milli-Hertz, range based on Voyager magnetic field measurements.
Magnetic field measurements by the Galileo orbiter led to a dedicated turbulence analysis by Saur et al. (2002). The analysis covered the magnetic field fluctuations in Jupiter's middle magnetosphere (9–24 RJ) within the magnetohydrodynamic (MHD) range between 2.8 × 10−4 and 3.6 × 10−2 Hz, i.e., below the ion cyclotron frequency. Even though the relative velocity between the magnetospheric plasma and the spacecraft is much smaller compared to spacecraft in the solar wind, the Taylor theorem can still be applied (Saur et al., 2013). The properties of the magnetic field fluctuations in Jupiter's middle magnetosphere differ from those in the solar wind. In the Jovian system, the ratio of the magnetic fluctuations δB compared to the background magnetic field B0 is less than 10−1, while it is of order unity in the solar wind. A weak turbulence cascade is expected in Jupiter's middle magnetosphere based on the ratio ϵ = τA/τnl between the Alfvén time τA and the non-linear interaction time τnl. This ratio ϵ lies in the range of 0.06 to 0.34 and is indicative of weak turbulence (Ng and Bhattacharjee, 1997; Galtier et al., 2000). Magnetic field fluctuations parallel to the background magnetic field exhibit a power law with spectral index of –2 (Saur et al., 2002) also indicative of weak turbulence (Ng and Bhattacharjee, 1997; Galtier et al., 2000). The other components often show deviations from clear power laws possibly due to other perturbations in the Jupiter's highly dynamic magnetosphere or locally non-fully developed turbulent cascades.
Turbulence in Jupiter's magnetosphere has subsequently been analyzed by Tao et al. (2015) who combined low and high-time resolution magnetic field data of the Galileo spacecraft within MHD and kinetic scales, i.e., within 1 × 10−4 Hz to 1 Hz. The resultant magnetic field spectra show spectral breaks well-organized by the ion scales (i.e., ion cyclotron frequency, the Doppler-shifted ion inertial length scales and the ion gyroradius, which assume similar values in Jupiter's middle magnetosphere). For frequencies smaller than those associated with the ion scales, the spectral indices lie in the range of –0.6 and –1.9 and for higher frequencies within the range of –1.7 and –2.5 (Tao et al., 2015). The authors also show that the turbulence is intermittent, in particular in the equatorial region of Jupiter's magnetospheric plasma.
2.2. Saturn Magnetosphere
Saturn's magnetosphere also hosts small scale turbulent magnetic field fluctuations as demonstrated by von Papen et al. (2014). The average amplitudes of the fluctuations compared to the magnetospheric background field assumes values of δB/B = 0.07. An exemplary spectrum is shown in Figure 2. On MHD scales the spectral slope of the fluctuations perpendicular and parallel to the background magnetic field varies between –0.8 and –1.7. At ion scales, i.e., near the ion inertial length scale or the Doppler-shifted ion gyroradius, a spectral break occurs, with a sub-ion, i.e., high-frequency, slope of –2.3 inside of a radial distances of 9 RS (see Figure 2). Further outside in the magnetosphere the sub-ion spectrum steepens to –2.6. These slopes could be consistent with turbulence of kinetic Alfvén waves. The probability density function of the fluctuations have non-Gaussian tails and a power law increase of the flatness indicates that the turbulence is intermittent (von Papen et al., 2014). The turbulence on the kinetic scales is estimated to be strong in Saturn's magnetosphere with ϵ > 1, i.e., the non-linear time is shorter than the wave propagation time, which could result from Saturn's weaker planetary magnetic field compared to Jupiter's field.
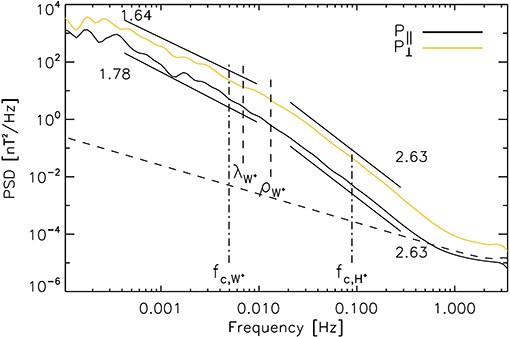
Figure 2. Power spectral density (PSD) of turbulent magnetic field fluctuations in Saturn's magnetosphere (from von Papen et al., 2014). P⊥ and P∥ refer to the power spectral densities of fluctuations perpendicular and parallel to the background magnetic field, respectively. and indicate the Doppler shifted ion inertial length scale and gyroradius of water ions, respectively, and and are the cyclotron frequencies of water ions and protons, respectively.
In a follow-up study, von Papen and Saur (2016) investigated the spatial and temporal structure of the magnetospheric turbulence. In local time coordinates, enhanced fluctuations are seen at noon, possibly resulting from flux tube interchanges (e.g., Kivelson et al., 1997), which are considered a prime source of the turbulence. In a frame rotating with Saturn, increased fluctuations are seen at 65° southern and 250° northern magnetic phase. The later correlation is enigmatic and is related to the still unresolved planetary period oscillations of Saturn (Espinosa and Dougherty, 2000; Gurnett et al., 2009; Provan et al., 2009; von Papen and Saur, 2016). The oscillations might result from a coupling between Saturn's atmosphere, ionosphere and magnetosphere. The variability in the turbulence can thus be considered as an effect of the Alfvénic energy fluxes underlying these coupling processes. The spatial variability of the turbulent fluctuations in Saturn's magnetosphere has been subsequently studied by Kaminker et al. (2017). The authors also found enhanced fluctuations between 10 hr and 20 hr local time and the turbulence to be more quiet between 3 hr and 9 hr local time.
2.3. Large Scale Implications of Turbulence
In addition to serving as a laboratory for turbulence studies, the fluctuations in the outer planets' magnetospheres have major implications on overall properties of their planetary systems.
2.3.1. Magnetospheric Heating
The magnetospheres of Jupiter and Saturn possess ion temperatures which strongly increase from the plasma source regions radially outwards by approximately two orders of magnitude to values up to nearly 108 K (Bagenal and Delamere, 2011). These observations are considered a long standing puzzle since major energy input rates are required to explain these temperature increases. Otherwise the radial transport of magnetospheric plasma would lead to adiabatic cooling with distance. Dissipation of turbulent magnetic field fluctuations is a very powerful energy source which can explain the temperature increase.
First suggestions of the importance of turbulent heating in Jupiter's magnetosphere in addition to pickup energization and subsequent radial transport date back to Barbosa et al. (1984). Based on the observed spatial distribution of the magnetic field fluctuations and a model for a weak turbulent cascade, Saur (2004) calculated the dissipation rate in Jupiter's middle magnetosphere to a total amount of 5 × 1012 W and demonstrated that this rate and its spatial distribution can explain the observed radial temperature profile (Frank and Paterson, 2002). To a similar conclusion came Ng et al. (2018) who used a radial transport model based on advection and not on flux tube diffusion as in Saur (2004). The turbulent dissipation rates are consistent with the required heating rate independently extracted from Galileo spacecraft observations by Bagenal and Delamere (2011). A possible dissipation mode could be ion cyclotron damping in particular of the heavy sulfur and oxygen ions of Jupiter's magnetosphere (Saur et al., 2018). In Saturn's magnetosphere the dissipation of the magnetic field fluctuations based on a strong turbulence model could provide power on the order of 1011 W (von Papen and Saur, 2016; Kaminker et al., 2017; Neupane et al., 2021), which is roughly consistent with the energy needed to heat the magnetosphere to its observed temperatures (Bagenal and Delamere, 2011).
2.3.2. Aurora
Jupiter's main auroral oval lies on magnetic field lines that map to an equatorial distance of about 20–30 RJ (e.g., Clarke et al., 1998, 2002; Hill, 2001) The turbulent power of the magnetic fluctuations in Jupiter's magnetosphere maximizes at the same radial distance (Saur et al., 2003). This distance is also the region where the corotation of Jupiter's magnetosphere breaks down and magnetospheric-ionospheric coupling currents maximize as derived by Hill (1979, 2001) and Cowley and Bunce (2001). The turbulent fluctuations result from the non-steady radial transport and the resultant imbalanced stresses between the magnetosphere and Jupiter's ionosphere. The stress balance is achieved by Alfvén waves propagating between both regions. When the Alfvén waves reach the polar regions of the magnetosphere, the perpendicular length scales of the Alfvén waves grow small due to Jupiter's increasing magnetic field. Just above the ionosphere, the electron inertial length scale assumes its large values of ~50 km due to the low electron density. When the turbulent cascade reaches this scale, the fluctuations are subject to electron Landau damping resulting in stochastically accelerated electrons (Saur et al., 2018). This process is consistent with the bi-directional and energetically broad band electron distributions recently measured by the Juno spacecraft (e.g., Mauk et al., 2017; Clark et al., 2018). These electrons are one of the key contributors to Jupiter's main auroral oval. Magnetic field fluctuations measured by the Juno spacecraft near the auroral particle acceleration region showed a spectrum with a slope of –2.29 ± 0.09 within 0.5–5 × 10−1 Hz (Gershman et al., 2019). They could be due to kinetic/inertial Alfvén waves, however, the underlying turbulent processes for this spectrum are not fully clear yet as, e.g., the Alfvén velocity is close to the speed of light in this region. The aurora of Saturn is less well-understood, but also within Saturn's magnetosphere bi-directional energetically broad band electron beams have been observed on field lines which are connected to the aurora (Saur et al., 2006; Mitchell et al., 2009) and which appear to be driven by stochastic, turbulent processes (von Papen and Saur, 2016).
2.4. Turbulence in Alfvén wings of the Moons
A new and evolving area of turbulence research in the outer planets' magnetosphere are the Alfvén wings generated by the moons. In Figure 1, we exemplarily show Jupiter's moon Io. The moon is an obstacle to the rotating magnetospheric plasma and generates Alfvén waves, which propagate along the rotating background magnetic field toward Jupiter. In the rest frame of each moon two standing waves develop (north and south, respectively). They are referred to as Alfvén wings (Goertz, 1980; Neubauer, 1980, 1998; Saur et al., 2013). The moons can thus be considered as gigantic Alfvén wave antenna. The Alfvén wings are reflected at gradients of the background density and generate filamented structures (Chust et al., 2005; Hess et al., 2011). The magnetic field fluctuations in Io's Alfvén wings at high latitudes have been recently measured by the Juno spacecraft. Their spectrum is consistent with a power law spectral index of –2.35 ± 0.07 within 0.1–800 Hz (Sulaiman et al., 2020). When the filamented waves approach kinetic scales, wave-particle interaction sets in and can energize electrons through electron Landau damping and ions through cyclotron damping (Hess et al., 2010; Saur et al., 2018; Szalay et al., 2018, 2020b). Similar particle acceleration processes have also been observed in the Alfvén wings of Europa (Allegrini et al., 2020) and Ganymede (Szalay et al., 2020a).
2.5. Magnetosheaths' of Jupiter and Saturn
Turbulence in the magnetosheaths of the outer planets has received very little attention to date. Turbulence in the magnetosheaths is distinct from turbulence within the outer planets' magnetospheres. The magnetosheaths are characterized by large amplitude magnetic fluctuations δB/B0 ~ 1 (Hadid et al., 2015). The ultimate source of free energy stems from the shocked solar wind plasma with Alfvén Mach numbers as high as ~100 (Masters et al., 2013), which causes enhanced plasma temperatures and large plasma beta turbulence.
Alexandrova and Saur (2008) analyzed turbulent magnetic field fluctuations in Saturn's magnetosheath obtained the Cassini spacecraft and identified Alfvén vortices similar to those found in Earth's magnetosheath. Alfvén vortices are non-linear magnetic structures associated with sheared velocity perturbations propagating obliquely to the external field. Hadid et al. (2015) also studied Saturn's magnetosheath and calculated power-spectral energy densities of the magnetic field fluctuations with a ~f−1 scaling at MHD scales and an ~f−2.6 scaling at sub-ion scales. The authors also found based on the compressibility of magnetic and density fluctuations that compressible magnetosonic slow modes at MHD scales dominate rather than the Alfvén mode. Magnetic field turbulence in Jupiter's magnetosheath was studied by Bolzan and Echer (2014) based on Ulysses measurements. Bolzan and Echer (2014) considered a similar frequency range as Hadid et al. (2015), but fitted the power spectral density to only one power law instead of two and thus found an average slope of around −2.
3. Discussion: Outstanding Issues and Outlook
For a more comprehensive understanding of turbulence in the outer planets' magnetospheres further measurements and studies are required. The Galileo spacecraft recorded only a small fraction of its mission in a high-frequency modus. The Juno spacecraft is currently exploring the high latitude regions of Jupiter's magnetosphere including the moons' Alfvén wings. With its instrumentation and its polar orbit detailed studies of turbulence and the associated wave-particle processes of turbulent dissipation are on their way.
New missions with appropriate instrumentation to Uranus and Neptune are being discussed (e.g., Arridge et al., 2014), but no mission has been decided upon. The orientations of the planetary magnetic moments at Uranus and Neptune are highly tilted compared to the planets' spin axis. Also the plasma densities and the magnetic field fluctuations in these magnetospheres are much smaller compared to those of Jupiter and Saturn. It will be interesting to see how these properties influences the possible turbulent nature of the field and plasma fluctuations.
Further studies are warranted on where and what types of turbulent cascades are driven in the magnetospheres of the outer planets. For example, are there cascades on kinetic scales outside the plasma sheets? Also a better understanding of the nature of the dissipation mechanisms of the turbulent fluctuations and the resultant ion or electron distribution functions is an important matter. Further observational studies might aim to better resolve the effects of the various dissipation and turbulent break scales expected to occur at the inertial lengths scales and the gyroradii of the electrons and the various ion species, respectively. Because the magnetospheres are highly inhomogeneous, the spatial variability of these parameters and their effects can be more easily studied compared to the solar wind. Suggestions for the roles of Landau and ion cyclotron damping of Alfvénic turbulence in the magnetosphere of Jupiter have been made (e.g., Saur et al., 2018). However, the role of other wave modes or non-resonant wave-particle interaction processes warrant further analysis.
Numerical simulations with hybrid or particle-in-cell models can be a useful tool to better understand the dissipation mechanisms and the associated transport of particles and energy (e.g., Delamere et al., 2021). Future models could focus on more realistic magnetic field geometries with current sheets and inhomogeneous plasma densities along field lines.
Turbulence in the magnetosheaths of the outer planets have not received much attention. Dedicated study might investigate the structure of turbulence downstream of the planets' bow shocks to test the universality of turbulent evolution in Earth's and other planets' magnetosheaths. In the much larger magnetosheath of the outer planets' turbulence might evolve toward a more fully developed turbulent states compared to Earth. While turbulence in the middle magnetospheres of Jupiter and Saturn is unique due to the plasma of the moons and the fast rotating planets, the existence of turbulence in the magnetospheric tails and the magnetosheaths could be universal across all magnetized planets.
Turbulent fluctuations might be used as a diagnostic tool to probe the interior of the icy moons in the outer solar system. Icy moons, such as Europa or Ganymede, possess subsurface water oceans (Kivelson et al., 2000, 2002; Saur et al., 2010, 2015). These saline and thus electrically conductive oceans have been detected through electromagnetic induction caused by time-variable magnetospheric fields. For existing observations only the ~10 h rotation period of Jupiter could be applied. Turbulent fluctuations provide a broad range of frequencies which can be used in future induction studies to additionally probe the interior of the moons (e.g., with JUICE or Europa Clipper data).
In summary, compared to the solar wind or the interstellar medium, the magnetospheres of the outer planets are complementary laboratories to study plasma turbulence. These magnetospheres are distinct due the planets' large background magnetic fields, the bound and inhomogeneous nature of the turbulent systems, where the location of the turbulent cascade and the turbulent dissipation are not necessarily collocated.
Author Contributions
JS selected the material for this review and wrote the manuscript.
Funding
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant Agreement No. 884711).
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
JS thanks Sascha Janser for helpful comments on the manuscript and Filip Elekes for the graphics support.
References
Alexandrova, O., and Saur, J. (2008). Alfvén vortices in Saturn's magnetosheath: cassini observations. Geophys. Res. Lett. 35:L15102. doi: 10.1029/2008GL034411
Allegrini, F., Gladstone, G. R., Hue, V., Clark, G., Szalay, J. R., Kurth, W. S., et al. (2020). First report of electron measurements during a Europa footprint tail crossing by juno. Geophys. Res. Lett. 47:e89732. doi: 10.1029/2020GL089732
Arridge, C. S., Achilleos, N., Agarwal, J., Agnor, C. B., Ambrosi, R., André, N., et al. (2014). The science case for an orbital mission to Uranus: exploring the origins and evolution of ice giant planets. Planet. Space Sci. 104, 122–140. doi: 10.1016/j.pss.2014.08.009
Bagenal, F. (2009). “Comparative planetary environmnents,” in Heliophysics: Plasma Physics of the Local Cosmos, eds G. Siscoe and C. J. Schrijver (Cambridge: Cambridge University Press), 360
Bagenal, F. (2013). “Planetary magnetospheres,” in Planets, Stars and Stellar Systems. Volume 3: Solar and Stellar Planetary Systems, eds T. D. Oswalt, L. M. French, and P. Kalas (Dordrecht: Springer, Media), 251. doi: 10.1007/978-94-007-5606-9_6
Bagenal, F., and Delamere, P. A. (2011). Flow of mass and energy in the magnetospheres of Jupiter and Saturn. J. Geophys. Res. Space Phys. 116:A05209. doi: 10.1029/2010JA016294
Bagenal, F., and Dols, V. (2020). The space environment of Io and Europa. J. Geophys. Res. Space Phys. 125:e27485. doi: 10.1029/2019JA027485
Barbosa, D. (1981). Dissipation and turbulent heating of plasma in Jupiter's magnetosphere. Geophys. Res. Lett. 8, 1111–1114.
Barbosa, D., Eviatar, A., and Siscoe, G. (1984). On the acceleration of energetic ions in Jupiter's magnetosphere. J. Geophys. Res. 89, 3789–3800.
Bolzan, M. J. A., and Echer, E. (2014). A multifractal approach applied to the magnetic field turbulence in Jupiter's magnetosheath. Planet. Space Sci. 91, 77–82. doi: 10.1016/j.pss.2013.12.004
Bruno, R., and Carbone, V. (2013). The solar wind as a turbulence laboratory. Liv. Rev. Solar Phys. 10:2. doi: 10.12942/lrsp-2013-2
Chust, T., Roux, A., Kurth, W. S., Gurnett, D. A., Kivelson, M. G., and Khurana, K. K. (2005). Are Io's Alfvén wings filamented? Galileo observations. Planet. Space Sci. 53, 395–412.
Clark, G., Tao, C., Mauk, B. H., Nichols, J., Saur, J., Bunce, E. J., et al. (2018). Precipitating electron energy flux and characteristic energies in jupiter's main auroral region as measured by Juno/JEDI. J. Geophys. Res. Space Phys. 123, 7554–7567. doi: 10.1029/2018JA025639
Clarke, J. T., Ajello, J., Ballester, G. E., Jaffel, L. B., Connerney, J. E. P., Gérard, J.-C., et al. (2002). Ultaviolet emissions from the magnetic footprints of Io, Ganymede and Europa on Jupiter. Nature 415, 997–1000. doi: 10.1038/415997a
Clarke, J. T., Ballester, G. E., Trauger, J., Ajello, J., Pryor, W., Tobiska, K., et al. (1998). Hubble Space Telescope imaging of Jupiter's UV aurora during the Galileo orbiter mission. J. Geophys. Res. 103, 20217–20236.
Connerney, J. E. P. (2007). “Planetary magnetism,” in Planets and Moons, Treatise on Geophysics, ed G. Schubert (Amsterdam: Elsevier), 281–298.
Cowley, S. W. H., and Bunce, E. J. (2001). Origin of the main auroral oval in Jupiter's coupled magnetosphere-ionosphere system. Planet. Space Sci. 49, 1067–1088. doi: 10.1016/S0032-0633(00)00167-7
Delamere, P. A., Ng, C. S., Damiano, P. A., Neupane, B. R., Johnson, J. R., Burkholder, B., et al. (2021). Kelvin-helmholtz related turbulent heating at Saturn's magnetopause boundary. J. Geophys. Res. Space Phys. 126:e28479. doi: 10.1029/2020JA028479
Dougherty, M. K., Esposito, L. W., and Krimigis, S. M. (2009). Saturn From Cassini-Huygens. Dordrecht: Springer.
Espinosa, S., and Dougherty, M. (2000). Periodic perturbations in saturn's magnetic field. Geophys. Res. Lett. 27, 2785–2788. doi: 10.1029/2000GL000048
Fleshman, B. L., Delamere, P. A., and Bagenal, F. (2010). A sensitivity study of the Enceladus torus. J. Geophys. Res. Planets 115:E04007. doi: 10.1029/2009JE003372
Frank, L. A., and Paterson, W. R. (2002). Galileo observations of electron beams and thermal ions in Jupiter's magnetosphere and their relationship to the auroras. J. Geophys. Res. 107:1478. doi: 10.1029/2001JA009150
Galtier, S., Nazarenko, S. V., Newell, A. C., and Pouquet, A. (2000). A weak turbulence theory for incompressible magnetohydrodynamics. J. Plasma Phys. 63, 447–488. doi: 10.1017/S0022377899008284
Gershman, D. J., Connerney, J. E. P., Kotsiaros, S., DiBraccio, G. A., Martos, Y. M., Viñas, A. F., et al. (2019). Alfvénic fluctuations associated with jupiter's auroral emissions. Geophys. Res. Lett. 46, 7157–7165. doi: 10.1029/2019GL082951
Glassmeier, K.-H. (1995). Ultralow-frequency pulsations: Earth and Jupiter compared. Adv. Space Res. 16, 209–218.
Goldreich, P., and Farmer, A. J. (2007). Spontaneous axisymmetry breaking of the external magnetic field at Saturn. J. Geophys. Res. Space Phys. 112:A05225. doi: 10.1029/2006JA012163
Goldreich, P., and Sridhar, S. (1995). Toward a theory of interstellar turbulence. II. Strong Alfvénic turbulence. Astrophys. J. 438, 763–775.
Gurnett, D. A., Lecacheux, A., Kurth, W. S., Persoon, A. M., Groene, J. B., Lamy, L., et al. (2009). Discovery of a north-south asymmetry in Saturn's radio rotation period. Geophys. Res. Lett. 36:L16102. doi: 10.1029/2009GL039621
Hadid, L. Z., Sahraoui, F., Kiyani, K. H., Retinò, A., Modolo, R., Canu, P., et al. (2015). Nature of the MHD and kinetic scale turbulence in the magnetosheath of Saturn: cassini observations. Astrophys. J. Lett. 813:L29. doi: 10.1088/2041-8205/813/2/L29
Hedman, M. M., Gosmeyer, C. M., Nicholson, P. D., Sotin, C., Brown, R. H., Clark, R. N., et al. (2013). An observed correlation between plume activity and tidal stresses on Enceladus. Nature 500, 182–184. doi: 10.1038/nature12371
Hess, S. L. G., Delamere, P., Dols, V., Bonfond, B., and Swift, D. (2010). Power transmission and particle acceleration along the Io flux tube. J. Geophys. Res. Space Phys. 115:A06205. doi: 10.1029/2009JA014928
Hess, S. L. G., Delamere, P. A., Dols, V., and Ray, L. C. (2011). Comparative study of the power transferred from satellite-magnetosphere interactions to auroral emissions. J. Geophys. Res. Space Phys. 116:A01202. doi: 10.1029/2010JA015807
Hill, T. W. (2001). The Jovian auroral oval. J. Geophys. Res. 106, 8101–8107. doi: 10.1029/2000JA000302
Howes, G. G., and Nielson, K. D. (2013). Alfvén wave collisions, the fundamental building block of plasma turbulence. I. Asymptotic solution. Phys. Plasmas 20:072302. doi: 10.1063/1.4812805
Kaminker, V., Delamere, P. A., Ng, C. S., Dennis, T., Otto, A., and Ma, X. (2017). Local time dependence of turbulent magnetic fields in Saturn's magnetodisc. J. Geophys. Res. Space Phys. 122, 3972–3984. doi: 10.1002/2016JA023834
Kivelson, M. G., Khurana, K. K., Russell, C. T., Volwerk, M., Walker, J., and Zimmer, C. (2000). Galileo magnetometer measurements: a stronger case for a subsurface ocean at Europa. Science 289, 1340–1343. doi: 10.1126/science.289.5483.1340
Kivelson, M. G., Khurana, K. K., Russell, C. T., and Walker, R. J. (1997). Intermittent short-duration magnetic field anomalies in the Io torus: evidence for plasma interchange? grl 24, 2127. doi: 10.1029/97GL02202
Kivelson, M. G., Khurana, K. K., and Volwerk, M. (2002). The permanent and inductive magnetic moments of Ganymede. Icarus 157, 507–522. doi: 10.1006/icar.2002.6834
Masters, A., Stawarz, L., Fujimoto, M., Schwartz, S. J., Sergis, N., Thomsen, M. F., et al. (2013). Electron acceleration to relativistic energies at a strong quasi-parallel shock wave. Nat. Phys. 9, 164–167. doi: 10.1038/nphys2541
Mauk, B. H., Haggerty, D. K., Paranicas, C., Clark, G., Kollmann, P., Rymer, A. M., et al. (2017). Juno observations of energetic charged particles over Jupiter's polar regions: analysis of monodirectional and bidirectional electron beams. Geophys. Res. Lett. 44, 4410–4418. doi: 10.1002/2016GL072286
Mitchell, D. G., Kurth, W. S., Hospodarsky, G. B., Krupp, N., Saur, J., Mauk, B. H., et al. (2009). Ion conics and electron beams associated with auroral processes on Saturn. J. Geophys. Res. Space Phys. 114:A02212. doi: 10.1029/2008JA013621
Ness, N. F. (2010). Space exploration of planetary magnetism. Space Sci. Rev. 152, 5–22. doi: 10.1007/s11214-009-9567-9
Neubauer, F. M. (1980). Nonlinear standing Alfvén wave current system at Io: theory. J. Geophys. Res. 85, 1171–1178.
Neubauer, F. M. (1998). The sub-Alfvénic interaction of the Galilean satellites with the Jovian magnetosphere. J. Geophys. Res. 103, 19843–19866.
Neupane, B. R., Delamere, P. A., Ma, X., Ng, C. S., Burkholder, B., and Damiano, P. (2021). On the nature of turbulent heating and radial transport in Saturn's magnetosphere. J. Geophys. Res. Space Phys. 126:e27986. doi: 10.1029/2020JA027986
Ng, C. S., and Bhattacharjee, A. (1997). Scaling of anisotropic spectra due to the weak interaction of shear-Alfvén wave packets. Phys. Plasma 4, 605–610.
Ng, C. S., Delamere, P. A., Kaminker, V., and Damiano, P. A. (2018). Radial transport and plasma heating in Jupiter's magnetodisc. J. Geophys. Res. Space Phys. 123, 6611–6620. doi: 10.1029/2018JA025345
Nishida, A. (1976). Outward diffusion of energetic particles from the Jovian radiation belt. J. Geophys. Res. 81, 1771–1773.
Provan, G., Andrews, D. J., Arridge, C. S., Coates, A. J., Cowley, S. W. H., Milan, S. E., et al. (2009). Polarization and phase of planetary-period magnetic field oscillations on high-latitude field lines in Saturn's magnetosphere. J. Geophys. Res. Space Phys. 114, A02225. doi: 10.1029/2008JA013782
Saur, J. (2004). Turbulent heating of Jupiter's magnetosphere. Astrophys. J. Lett. 602, L137–L140. doi: 10.1086/382588
Saur, J., Duling, S., Roth, L., Jia, X., Strobel, D. F., Feldman, P. S., et al. (2015). The search for a subsurface ocean in Ganymede with Hubble Space Telescope observations of its auroral ovals. J. Geophys. Res. Space Phys. 120, 1715–1737. doi: 10.1002/2014JA020778
Saur, J., Feldman, P. D., Roth, L., Nimmo, F., Strobel, D. F., Retherford, K. D., et al. (2011). Hubble space telescope/Advanced camera for surveys observations of Europa's atmospheric ultraviolet emission at Eastern elongation. Astrophys. J. 738:153. doi: 10.1088/0004-637X/738/2/153
Saur, J., Grambusch, T., Duling, S., Neubauer, F. M., and Simon, S. (2013). Magnetic energy fluxes in sub-Alfvénic planet star and moon planet interactions. Astron. Astrophys. 552:A119. doi: 10.1051/0004-6361/201118179
Saur, J., Janser, S., Schreiner, A., Clark, G., Mauk, B. H., Kollmann, P., et al. (2018). Wave-particle interaction of Alfvén waves in jupiter's magnetosphere: auroral and magnetospheric particle acceleration. J. Geophys. Res. Space Phys. 123, 9560–9573. doi: 10.1029/2018JA025948
Saur, J., Mauk, B. H., Mitchell, D. G., Krupp, N., Khurana, K. K., Livi, S., et al. (2006). Anti-planetward auroral electron beams at Saturn. Nature 439, 699–702. doi: 10.1038/nature04401
Saur, J., Neubauer, F. M., and Glassmeier, K.-H. (2010). Induced magnetic fields in solar system bodies. Space Sci. Rev. 152, 391–421. doi: 10.1007/s11214-009-9581-y
Saur, J., Politano, H., Pouquet, A., and Matthaeus, W. (2002). Evidence for weak MHD turbulence in the middle magnetosphere of Jupiter. Astron. Astrophys. 386:699. doi: 10.1051/0004-6361:20020305
Saur, J., Pouquet, A., and Matthaeus, W. (2003). An acceleration mechanism for the generation of the main auroral oval on Jupiter. Geophys. Res. Lett. 30:1260. doi: 10.1029/2002GL015761
Seidelmann, P. K., Abalakin, V. K., Bursa, M., Davies, M. E., de Bergh, C., Lieske, J. H., et al. (2002). Report of the IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites: 2000. Celest. Mech. Dynam. Astron. 82, 83–111. doi: 10.1023/A:1013939327465
Sulaiman, A. H., Hospodarsky, G. B., Elliott, S. S., Kurth, W. S., Gurnett, D. A., Imai, M., et al. (2020). Wave-particle interactions associated with io's auroral footprint: evidence of alfven, ion cyclotron, and whistler modes. Geophys. Res. Lett. 47:e2020GL088432. doi: 10.1029/2020GL088432
Szalay, J. R., Allegrini, F., Bagenal, F., Bolton, S. J., Bonfond, B., Clark, G., et al. (2020a). Alfvénic acceleration sustains Ganymede's footprint tail aurora. Geophys. Res. Lett. 47:e86527. doi: 10.1029/2019GL086527
Szalay, J. R., Bagenal, F., Allegrini, F., Bonfond, B., Clark, G., Connerney, J. E. P., et al. (2020b). Proton acceleration by Io's Alfvénic interaction. J. Geophys. Res. Space Phys. 125:e27314. doi: 10.1029/2019JA027314
Szalay, J. R., Bonfond, B., Allegrini, F., Bagenal, F., Bolton, S., Clark, G., et al. (2018). In situ observations connected to the Io footprint tail aurora. J. Geophys. Res. Planets 123, 3061–3077. doi: 10.1029/2018JE005752
Tao, C., Sahraoui, F., Fontaine, D., Patoul, J., Chust, T., Kasahara, S., et al. (2015). Properties of Jupiter's magnetospheric turbulence observed by the Galileo spacecraft. J. Geophys. Res. Space Phys. 120, 2477–2493. doi: 10.1002/2014JA020749
Thomas, N., Bagenal, F., Hill, T. W., and Wilson, J. K. (2004). “The Io neutral clouds and plasma torus,” in Jupiter: The Planet, Satellites and Magnetosphere, Vol. 1, eds F. Bagenal, T. E. Dowling, and W. B. McKinnon (Cambridge: Cambridge University Press), 561–591.
Vasyliūnas, V. M. (2009). “Fundamentals of planetary magnetospheres,” in Heliophysics: Plasma Physics of the Local Cosmos, eds G. Siscoe and C. J. Schrijver (Cambridge: Cambridge University Press), 256.
von Papen, M., and Saur, J. (2016). Longitudinal and local time asymmetries of magnetospheric turbulence in Saturn's plasma sheet. J. Geophys. Res. Space Phys. 121, 4119–4134. doi: 10.1002/2016JA022427
Keywords: turbulence, outer planets, magnetosphere, wave turbulence, wave-particle interaction, aurora
Citation: Saur J (2021) Turbulence in the Magnetospheres of the Outer Planets. Front. Astron. Space Sci. 8:624602. doi: 10.3389/fspas.2021.624602
Received: 31 October 2020; Accepted: 23 March 2021;
Published: 20 May 2021.
Edited by:
Joseph Eric Borovsky, Space Science Institute, United StatesReviewed by:
Fran Bagenal, University of Colorado Boulder, United StatesMostafa El-Alaoui, UCLA Department of Physics and Astronomy, United States
Copyright © 2021 Saur. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joachim Saur, c2F1ciYjeDAwMDQwO2dlby51bmkta29lbG4uZGU=
 Joachim Saur
Joachim Saur