
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Astron. Space Sci. , 23 March 2021
Sec. Space Physics
Volume 8 - 2021 | https://doi.org/10.3389/fspas.2021.622570
This article is part of the Research Topic The Role of Turbulence in the Solar Wind, Magnetosphere, Ionosphere Dynamics View all 22 articles
There is a vast amount of evidence that suggests that the geomagnetic tail is like a turbulent wake behind an obstacle. Large-scale vortices in the wake are able to generate turbulent transport that takes place both along the plasma sheet, in the X and Y directions, and across the plasma sheet, in the Z direction. Thus, turbulent fluctuations in all directions should be taken into consideration when analyzing plasma transport in the plasma sheet, and stability of the plasma sheet configurations. In this review, we summarize and discuss the main results of large and middle scale magnetospheric turbulence yielded by data analysis and modeling. We also identify changes in the description of the magnetospheric dynamics connected with the existence of turbulent fluctuations in the tail.
Formation of turbulent wake behind an obstacle is a well-known phenomenon observed in the gas and fluid flows with a high Reynolds number. An example of such a wake behind a flying bullet can be seen in Figure 1 adapted from (http://waterocket.explorer.free.fr/aerodynamics.htm). As it is well known, the sound and Alfvénic Reynolds numbers in the magnetosphere of the Earth are larger than ∼1011 (Borovsky and Funsten, 2003a). The magnetic field of the Earth represents an obstacle for the solar wind flow. That is why the formation of a turbulent wake behind such obstacle is very natural even in the case of a laminar flow in front of it. In fact, the solar wind flow is not laminar, and there are many works describing its turbulent properties. On the other hand, the existence of well-defined structures and the lack of evidence of mixing in the solar wind as it moves outward through the inner heliosphere is now intensively discussed (Borovsky, 2008; Borovsky, 2020a; Borovsky, 2020b). Regardless, the main solar wind macro parameters are highly fluctuating, and the properties of the turbulent flow behind the Earth’s magnetic dipole should depend on those random fluctuations. The effect of the solar wind turbulence on the magnetospheric activity was discussed by D’Amicis et al. (2020). They show “the major role of the solar wind turbulence as a driver of geomagnetic activity especially at high latitudes” and at the same time “the geomagnetic response strongly affected by the intrinsic dynamics of the magnetosphere”. They also stressed, that “strong variations in the geomagnetic field occur even in absence of large solar wind perturbations.”
The change of the solar wind flow at the bow shock leads to the formation of a turbulent magnetosheath behind it. The level of fluctuations in the magnetosheath is an order of magnitude larger than in the solar wind. Although the term “turbulent magnetosheath” does exist since the first space measurements (Antonova et al., 2012), the attention to the importance of the study of this phenomenon was captured mainly during the last years. Detailed reviews of such studies can be found in the current Topic Issue. The existence of turbulent magnetosheath should be taken into account during the analysis of the properties of magnetospheric turbulence and the magnetospheric dynamics.
Currently there are a lot of studies of turbulence in the Earth’s magnetosphere at the MHD scale [see, for example, references in (Borovsky et al., 2020)]. Despite this, until now the most popular analytical and computer models that describe the magnetospheric dynamics consider only the laminar flows in the geomagnetic tail. In this paper, we summarize the main results of the study of magnetospheric turbulence and try to understand the reasons of why the laminar flow models are so widely used. We also try to analyze the results of the models, which consider the turbulent transport as one of the main factors that determines the magnetospheric dynamics. A complete review of all results obtained is beyond the scope of this paper. We only try to identify the key unsolved topics in the study of the magnetospheric turbulence and to show why such studies are very important for the solution of a number of the key magnetospheric problems. Our current work is mainly concentrated on the analysis of the inertial or driving scales of tail turbulence, leaving the dissipative scale beyond the scope of this review.
The paper is organized as follows: The second section contains the historical review of the main stages of the study of the magnetospheric turbulence as well as the analysis of the properties of the turbulent transport in the geomagnetic tail. The third section contains the analysis of the main reasons, which make the studies of magnetospheric turbulent wake difficult. The fourth section is dedicated to the discussion of the results of the turbulent plasma sheet modeling. In this section, we also analyze the advantages of studies of the magnetostatic equilibrium that take into account the turbulence for the description of several magnetospheric processes. The fifth section contains the discussion of the connection between the plasma sheet turbulence and the large-scale magnetospheric convection. The six section contains the analyzes the role of the eddy diffusion in solving problems caused by the use of models based on laminar flow. The last section is dedicated to discussions and conclusions.
A clear manifestation of the existence of low frequency magnetospheric turbulence was obtained through spectral analysis of geomagnetic indexes [see (Consolini et al., 1996; Uritsky and Pudovkin, 1998; Stepanova et al., 2003; etc.)]. Consolini et al. (1996) examined the structure of fluctuations in the auroral electrojet index and found them to be multifractal. The noncoincidence of forms of Fourier-spectra of the solar wind parameters and the AE-fluctuation spectra shown by Uritsky and Pudovkin (1998) evidenced the existence of the inner magnetospheric sources of turbulent fluctuations of the auroral electrojets. Such finding was in close agreement with the numerous low altitude auroral observations of fluctuating electric fields, amplitudes of which are much larger than the large-scale dawn-dusk electric field. Numerous results of auroral plasma measurements also clearly demonstrated the existence of nonequipotential magnetic field lines. Turbulent fluctuations of the electric field in the plasma sheet were observed by Maynard et al. (1982), Petersen et al. (1984), Hoshino et al. (1994), etc. These fluctuations have mainly electrostatic nature.
Even the first observations in the geomagnetic tail (Sonett et al., 1960) showed the presence of strong fluctuations of the main magnetospheric parameters. It is necessary to mention that James Dungey, the author of the first theory, explaining the dependence of magnetospheric dynamics on the direction and value of the interplanetary magnetic field (IMF), considered the observed fluctuations as the main difficulty for the validity of his approach (Dungey, 1961; Dungey, 1962). He stressed the importance to study “the effect of turbulence.” However, at the beginning of the space age, the possibilities to analyze turbulent flows were limited and the systematic study of the characteristics of turbulent plasma flows have started only during the last decades.
Antonova (1985) summarized the results of magnetospheric observations leading to the suggestion about the dominant role of turbulence in the dynamics of the magnetospheric plasma sheet. It was suggested that the observed turbulence is mainly connected to the excitation of drift instabilities due to the nonhomogeneous distribution of magnetospheric plasma. It was also suggested that the magnetospheric turbulence includes embedded vortices connected to the large scale two vortex magnetospheric convection. Figure 2A shows a system of such vortices. Simultaneously Montgomery (1987) pointed out that the plasmas of the Earth's magnetotail should not behave in a laminar-flow fashion, owing to the high fluid and magnetic Reynolds numbers of the plasma sheet. He stressed that laminar-flow models of the magnetosphere and magnetotail “seem unlikely.” Unfortunately, despite of these works, most researches were convinced that it would be possible to describe the main processes in the magnetosphere in the frame of the laminar models of plasma flow.
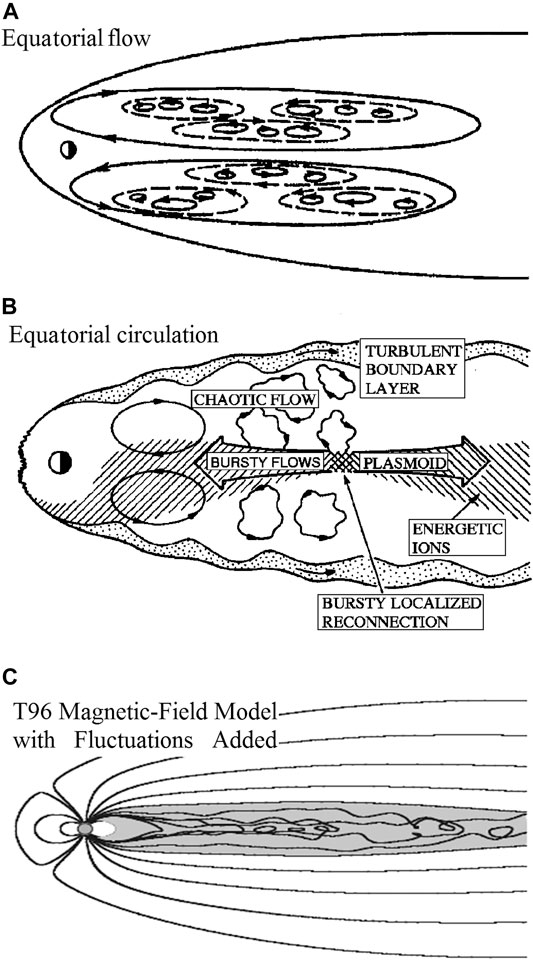
FIGURE 2. Early schemes of the plasma sheet turbulent flows at the equatorial plane of (A)Antonova (1985), (B)Kennel (1995) and in the meridian cross section (C)Borovsky and Funsten (2003a).
The study of plasma sheet turbulence was driven by the discovery of the bursty-bulk-flow (BBF) events by Baumjohann et al. (1989), Baumjohann et al. (1990a) and the analysis of plasma sheet bulk velocity and magnetic field fluctuations (Angelopoulos et al., 1992; Angelopoulos et al., 1996; Angelopoulos et al., 1999; Borovsky et al., 1997; Borovsky et al., 1998). It was clearly shown, that the observed picture of plasma flow at the equatorial plane strongly differs from the large scale magnetospheric convection. Figure 2B shows the adapted from Kennel (1995) and discussed by Angelopoulos et al. (1999) scheme of localized bursty-flows that drive the vortical turbulent flows. It was suggested that the BBF appears as a result of reconnection processes. Not only the bulk velocity, but also the magnetic field in the plasma sheet is highly fluctuating and can result in a snarling of the magnetic field lines. Figure 2C adapted from (Borovsky and Funsten, 2003a) shows a sketch of the turbulent magnetic field of the plasma sheet constructed by adding noise to the Tsyganenko-96 magnetic field model.
The quantitative study of the hydrodynamic properties of plasma sheet turbulence started with the papers of (Borovsky et al., 1997; Borovsky et al., 1998; Borovsky and Funsten, 2003a). It was shown using the ISEE-2 plasma and magnetic field measurements that the amplitudes of the bulk velocity fluctuations are much larger than the average velocities: δVx/Vx>>1, δVy/Vy>>1 and amplitudes of the magnetic field fluctuations are comparable with its mean value δB/B ∼ 0.5. Later, Yermolaev et al. (1995) obtained the same picture in the Z and Y directions using data of the Interball/Tail probe. According to Borovsky et al. (1997), Borovsky et al. (1998), the correlation time for velocity fluctuations at geocentric distance ∼20 RE is ∼2 min, and for the magnetic field is ∼8 min. The mixing length of the average plasma sheet is ∼10,000 km (Borovsky et al., 1998). It was shown that the distributions of the occurrence of the plasma-sheet bulk flows P (vx) and P (vy) has two components: i) an isotropic distribution of flows at low flow velocities and ii) an anisotropic distribution of fast flows. Such asymmetry appears due to the presence of BBF in the X and Y components of the inner plasma sheet flows. The distribution of slower flows was fitted by Borovsky et al. (1997) by the exponential functions:
Borovsky et al. (1997) and Borovsky and Funsten (2003a) showed that the plasma-sheet material appears to be well mixed in density and temperature. They stressed that the persistent (many-minute) laminar flow is not observed and the turbulence may be strongly driven rather than well developed. It is interesting to mention that the values of plasma flow are significantly larger during the intervals of steady magnetospheric convection than they are during active times. Neagu et al. (2002), Neagu et al. (2005) found no significant dependence of the amplitude of the ion velocity and magnetic field fluctuations on the distance from the Earth toward the geomagnetic tail, the dawn-tail distance and on the distance from the neutral sheet.
Subsequent results obtained by Antonova (2000), Ovchinnikov et al. (2000), Schödel et al. (2001), Ovchinnikov et al. (2002), Troshichev et al. (2002), Uritsky et al. (2002), Neagu et al. (2002), Uritsky et al. (2003), Neagu et al. (2005), Stepanova et al. (2005), Stepanova et al. (2006), Antonova (2008), Uritsky et al. (2008), Stepanova et al. (2009), Uritsky et al. (2009), Stepanova et al. (2011), etc. supported the validity of early findings and permitted to obtain a number of statistical dependencies. Ovchinnikov et al. (2002), Stepanova et al. (2005), Stepanova et al. (2009), Stepanova et al. (2011) showed that the level of velocity fluctuations strongly depends on the phase of magnetospheric substorm. It increases after a substorm onset and then slowly decreases during 1–2 h.
The BBFs are frequently considered as the main source of the observed plasma sheet fluctuations. They are composed by flow bursts lasting ∼1 min and are commonly observed at substorm growth, expansion and recovery phases. Nonetheless, many BBF occur without classical substorm signatures during pseudo-breakups and auroral brightening. The BBF occurrence rate peaks close to midnight, and the variance of the remnant flow during high AE is stronger at midnight than at nearby sectors. This result supports the conclusion of Kennel (1995) that the geomagnetic tail is in a state of bimodal convection, whereby the potential flow is stagnant unless it is driven by localized flow bursts. Nagai et al. (1998) showed using the Geotail observations that the fast flows tend to be observed around the near-Earth pre-midnight sector. Petrukovich et al. (2001) calculated the angles between the vectors of fast earthward plasma flow and the local magnetic field. In the low-β (where β is the plasma parameter) parts of the geomagnetic tail, the fast flows were found to be nearly field-aligned. In the high-β plasma sheet the average angle was larger than 45°. The width of the flow channel, which represents the typical large-scale characteristic scale of the flow used to calculate the Reynolds number, has been estimated from the statistical analysis of Cluster spacecraft multi-point measurements by Sergeev et al. (2000), Nakamura et al. (2004). It was shown that the full width of the flow channel is 2–3 RE in the “dawn-dusk” direction and 1.5–2 RE in the “north-south” direction. Recently Sitnov et al. (2019) summarized the main results of the BBF study.
Borovsky et al. (1997) found that within the plasma sheet the slope of the power spectral density vs. frequency for plasma flow velocity and magnetic field varied from −0.8 to −2.0 and from −1.6 to −3.0, respectively. Different types of Reynolds numbers can be derived for the flows in the plasma sheet reflecting different aspects of turbulent flows (Borovsky and Funsten 2003a; Weygand et al., 2005). In particular, Weygand et al., (2005) showed that the level of intermittency in the central plasma sheet differs from that observed for the outer plasma sheet. They examined the magnetic field spectral indices in the field-aligned coordinate system and found that their range was quite broad (average of −2.0 ± 0.4). The transverse magnetic field component inside the central plasma sheet in the Y direction had a spectra index of −1.56 ± 0.04, and the mean eddy scale size found in this study was 6,000 km.
The study of plasma velocity fluctuations has been limited by a low time resolution of particle spectra measurements in comparison to the magnetic measurements, and by contamination caused by many sources. That is why the main progress in the study of plasma sheet turbulence was done due to the analysis of spectra of magnetic fluctuations using Cluster magnetometer observations (Vörös et al., 2003; Vörös et al., 2004; Vörös et al., 2006; Vörös et al., 2019; Volwerk et al., 2004; Weygand et al., 2005). It was shown, that the turbulence in the plasma sheet is a mixture of Alfvénic wavy turbulence and of eddy 2-D turbulence. A strong correlation between the maximum perpendicular flow velocity and the turbulence power for maximum velocities 150 ≤ v⊥max≤ 400 km/s was found. It was also shown that the presence of BBFs significantly changes the spectral index or scaling index. Hoshino et al. (1994) showed that fluctuations of the magnetic field observed in the distant plasma sheet are characterized by a “kink” Fourier power law spectrum that can be approximated by two power law functions with two different spectral indices (Zelenyi et al., 2015).
The behavior of magnetospheric turbulence is hard to comprehend because it is almost impossible to discriminate between spatial and temporal variations even using data from multipoint satellite missions as THEMIS, CLUSTER and MMS. That is why the determination of properties of magnetospheric turbulence in most cases is still limited to the method proposed by Borovsky et al. (1997), Borovsky et al. (1998) for calculations of fluctuations of hydrodynamic velocities and their autocorrelation times [see also (Ovchinnikov et al. (2000), Antonova (2000), Ovchinnikov et al. (2002), Antonova (2008); Troshichev et al. (2002)] for the implementation of this method). It allows us to determine the turbulent flow velocities vrms and their components and the autocorrelation time τauto when the mean flow velocity is small compared with the turbulent flow velocities. Borovsky et al. (1997) considered the autocorrelation time as a measure of the persistence of a fluctuating velocity and calculated it by analyzing the autocorrelation function:
Four methods were proposed for the determination of τauto (Borovsky et al., 1997), the most popular of which is based on the determination of the time interval during which the curve A (τ) has fallen to the value A (τ) = 1/e. Finally, the method proposed by Borovsky et al. (1998) permits to estimate the coefficient of eddy diffusion as:
and analyze the transport of the plasma sheet material.
The first evaluation of the coefficient of eddy diffusion made by Borovsky et al. (1998) gave a very high value of D = 2.6∙105 km2 s−1. Nearly the same eddy diffusion coefficients were reported by (Ovchinnikov et al., 2000; Stepanova et al., 2005; 2009; Stepanova et al., 2011; Pinto et al., 2011). In particular, Stepanova et al. (2009), Stepanova et al. (2011) obtained the statistical distribution of the coefficients of eddy diffusion for quiet time and different phases of magnetospheric substorm. The use of the Interball/Tail probe satellite data allowed Stepanova et al. (2009) to determine Dzz and Dyy components of the eddy diffusion tensor, meanwhile the use of the THEMIS satellites permitted to obtain all three diagonal components of this tensor Dzz, Dyy and Dxx (Stepanova et al., 2011). However, it is necessary to mention that the presence of BBF might strongly affect the results of Dxx calculations and this value should be used with caution. Figure 3A shows the comparison of the dependence of Dzz on the radial distance for different phases of the magnetospheric substorm from (Stepanova et al., 2009) (red diamonds) and (Stepanova et al., 2011) (green diamonds). Figure 3B shows the same results for Dyy from (Stepanova et al., 2009) (blue squares) and (Stepanova et al., 2011) (dark blue squares). It is possible to note that the eddy diffusion coefficients obtained using the data from the THEMIS mission are smaller than the coefficients obtained from the Interball/Tail probe observations. It can be explained considering that during the first years of the THEMIS mission the geomagnetic activity was very low, and the eddy diffusion is expected to be lower for the time interval used for that studies (2008–2010). Pinto et al. (2011) obtained the instantaneous radial distribution of eddy diffusion coefficients using the data of the THEMIS satellites located along the midnight meridian. It was shown that the level of turbulence is greatly decreased at geocentric distances smaller than ∼10 RE. Slightly lower values of eddy diffusion coefficients were obtained in the distant tail by Troshichev et al. (2002). The same eddy diffusion coefficient values ∼105 km2/s were obtained by Nagata et al. (2008) for northward IMF orientation. Wang et al. (2010) analyzed plasma sheet transport and estimated the diffusion coefficients Dyy and Dxx associated with fluctuating drift to be ∼105–106 km2/s.
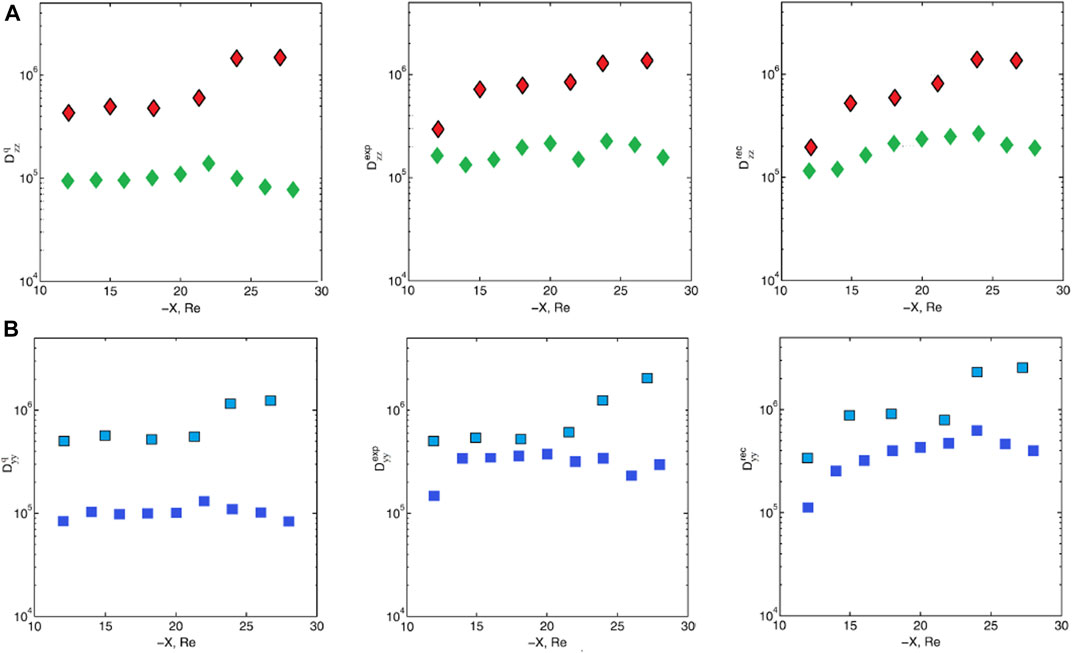
FIGURE 3. Comparison of the dependencies of Dzz(A) and Dyy(B) on the radial distance and on the phase of magnetospheric substorm (q, quiet; exp, expansion; rec, recovery) from (Stepanova et al., 2009) (red diamonds and blue squares) and (Stepanova et al., 2011) (green diamonds and dark blue squares).
As it will be shown in the next sections, the introduction of eddy diffusion transport makes it possible to overcome the limitations of the ordinary MHD approach for the description of large-scale magnetospheric processes. To date, the necessary formalism has been developed only for gases in the absence of a magnetic field (Klimontovich, 1990; Klimontovich, 1999). Nonetheless, even a simplified analysis could be very useful.
Our analysis of characteristics of turbulent plasma flows leads to a natural question: Why do the most popular models describe the magnetospheric plasma flows in a laminar fashion? They have been developed in parallel with the models of the radiation belts formation, where the radial diffusion is recognized as the most important mechanism. The simplest answer is because of the real simplicity of such models and the possibility in a number of cases to obtain more or less reasonable results. Nonetheless, the explanation of this popularity is not so simple and can be related to three main reasons.
The first reason is a comparatively small number of works dedicated to the magnetospheric turbulence in comparison with the solar wind turbulence. It is related to the viability of use of the Taylor’s hypothesis for the solar wind, which allows us to transform the length scale l into the time scale t via a simple relation: l = t × VSW, where VSW is the solar wind velocity. This relation permits in case of the solar wind to obtain spectra of turbulent fluctuations in a wide range of scales, meanwhile it is very difficult or even impossible to separate spatial and temporal variations inside the magnetosphere, especially for large vortices, even using multisatellite observation.
The second reason is that the plasma sheet configuration differs from the turbulent wake in hydrodynamic fluid. The scale of plasma sheet in Z direction is much smaller than the scale in Y direction. The formation of the plasma sheet is possible to model using global MHD codes and assuming the preexistence of particle sources in the magnetosphere [see (Watanabe and Sato, 1990) and results of later MHD simulations]. As a result of this modeling, the plasma sheet region extends widely in the equatorial plane and is considerably compressed perpendicular to it. However, taking into account the high values of the coefficient of eddy diffusion Dzz it is difficult to understand why such configuration could exist for a comparatively long time. In the next section we shall show that the observed structure of the quasistable magnetospheric turbulent wake as a sheet-like structure can be clearly explained taking into account the compression of this wake by the dawn-dusk electric field.
The third, and from our point of view the most important reason is related to the problem of the auroral oval mapping. Even the first results of auroral observations (Chamberlain, 1961) showed that the quiet time auroral arcs could exist for many hours, which is difficult to imagine if the roots of such arcs are embedded into the turbulent medium. For a long time, it has been widely assumed that the auroral oval maps to the plasma sheet. This assumption was based on the use of the magnetic field models with predefined configuration of current systems (Antonova et al., 2018). Nonetheless, the results of the topological mapping, based on the use of the plasma pressure as a “tracer” along a magnetic field line, indicated (Antonova et al., 2014; Antonova et al., 2015), that most of auroral oval is mapped to the surrounding the Earth plasma ring at geocentric distances from ∼7 to ∼10 RE (Kirpichev et al., 2016). As the level of velocity and magnetic field fluctuations decreases at the distances <10 RE (Stepanova et al., 2009; Stepanova et al., 2011; Pinto et al., 2011), the roots of quiet auroral arcs can be formed in a comparatively stable region. Therefore, the third obstacle to model the magnetosphere as a turbulent wake is caused by an erroneous auroral oval mapping.
The experimental evidences of high levels of fluctuations having a turbulent character encourage the development of models that would take into account both the turbulent transport and the modification of particle distribution functions due to interaction with turbulent electric and magnetic fields. It is an endeavor that could be reached in the future. For now, we can only present a few results, which can be useful for the future studies.
The most popular models of the large scale magnetospheric dynamics, known as the ideal MHD models, are developed using the MHD finite difference codes. That is why the results of such modeling should be used with caution taking into account the effect of numerical resistivity. Frequently such numerical codes break the frozen-in condition and are not able to produce high magnetic Reynolds numbers. These models reproduce the magnetic field line reconnection in the geomagnetic tail at different distances depending on the grid spacing scale. Nonetheless, even this kind of models reproduce the formation of medium scale vortexes in the plasma sheet after reconnection (Birn et al., 1999; Birn et al., 2011). It is necessary to mention also that MHD models describe the formation of vortices that appeared due to development of Kelvin-Helmholtz instability at the magnetospheric flanks stating from (Miura, 1984). Latest results employed the fully kinetic model were obtained by (Nakamura et al., 2020).
When the computer codes combine both the low resistivity and small grid spacing, it is possible to obtain comparatively large values of the magnetic Reynolds number and to model the formation of the turbulent plasma sheet under idealized southward (El-Alaoui et al., 2010) and northward (El-Alaoui et al., 2012) IMF. These models were able to reproduce some features of the plasma sheet turbulence, including the nested vortices at multiple scales. The largest scales were associated with the reconnection outflows and the diversion of high-speed flows. El-Alaoui et al. (2010), El-Alaoui et al. (2012) also found that the power spectral densities (PSDs) had the characteristics of a turbulent flow and showed the three scale ranges expected from theory: the energy-containing range, the inertial range, and the dissipative range. They selected the formation of localized reconnection regions as the main process driving turbulence in the plasma sheet.
However, the appearance of numerical resistivity is not the unique and even not the main problem of the ideal MHD models. It is necessary to take into account that the contribution of the pressure gradients in the generalized Ohm’s law can be significant. In collisionless plasma, this law has the form:
where me and ne are the mass and density of electrons, mi and ni are the mass and density of ions,
The first term in the right-hand side of Eq. 3 is named the Hall term. Priest and Forbes (2000) stressed that only in case of strong collisional plasma in weak magnetic field this term can be neglected. The scale of the Hall term if V ≠ VA is equal (Priest and Forbes, 2000):
where
This means that in collisionless MHD with Hall currents, the electrons are the unique plasma component, which is frozen to the magnetic field. The plasma flow in such a case deviates from the motion of the magnetic field lines. Hall currents are observed in the magnetotail [see Nagai et al. (2003) and later observations]. The validation of the frozen in condition for electrons and electron reconnection was one of the main goals of the MMS mission (Burch et al., 2016a). The electron reconnection was used to explain the observations of the super-Alfvénic electron jets, not accompanied by the ion outflows (Burch et al., 2016b; Phan et al., 2018). Although the MMS observations captivated the attention to the study and modeling of the turbulent processes at small and medium scales [see (Stawarz et al., 2015; Ergun et al., 2018; Califano et al., 2020) and references therein], it is not clear how these studies could help to clarify the main properties of the large-scale magnetospheric dynamics.
Therefore, in spite of significant advantages of different MHD models in the analysis of magnetospheric turbulence and dynamics, there are some important problems which solution requires a different approach. This includes the magnetospheric configurations with slow in comparison with the Alfvén velocity plasma motions like the central plasma sheet where the averaged flow velocities are ∼30 km/s (Angelopoulos et al., 1993), and hence V << VA. At the same time, for this and similar regions it is necessary to take into account the presence of the turbulent eddy diffusion and the role of the turbulent transport due to the large values of obtained eddy diffusion coefficients.
It is well known that when the flow velocity is much smaller than the Alfvén and sound velocities, the analyzed plasma configuration is in magnetostatic equilibrium [j × B] = ∇p. Here we discuss the simplest case of the isotropic plasma pressure. Plasma velocity across the plasma sheet is fast only in case of the tail flapping; meanwhile plasma velocity along the sheet is comparable with the Alfvén velocity only inside the BBF. Therefore, it is possible to analyze the properties of the plasma sheet using the condition of magnetostatic equilibrium as it was done in many papers. It is necessary to note that the existence of stress balance p + (B2/2μ0)≈const across the plasma sheet and the plasma pressure isotropy were experimentally verified by Baumjohann et al. (1990b), Kistler et al. (1993), Petrukovich et al. (1999), Wang et al. (2013), etc. The plasma sheet is a well-defined structure that exists in spite of the presence of turbulent fluctuations. Therefore, it is necessary to understand why such structure is formed and how it is supported in the collisionless plasma with turbulent fluctuations. It is necessary to mention that the existence of high level of turbulent fluctuations can lead to the appearance of eddy viscosity (Borovsky and Funsten, 2003b). Nonetheless, the eddy diffusion transport is more relevant for the Earth’s plasma sheet where plasma pressure is nearly isotropic.
In order to include the turbulent transport to the description of the large-scale processes in the geomagnetic tail it is necessary to use a special system of hydrodynamic transport equations. To our knowledge, such system of equations has not been developed for collisionless plasma yet. However, the turbulent diffusion was included to the system of hydrodynamic equations by Klimontovich (1990), starting from the equation of mass conservation, which can be written as:
where ρ is the mass density, V is the bulk velocity (averaged on turbulent fluctuations) and D is the space diffusion coefficient. In a presence of the magnetic field, the coefficients of space diffusion can have different values along and perpendicular to the magnetic field and are determined by the properties of the turbulence. Taking into account such feature, Eq. 7 can be used in the first approximation for the description of plasma transport. It shows that the distribution of plasma density does not change if the expression in round brackets is equal to zero, leading to the appearance of quasistatic distributions.
Observed conservation of pressure balance across the plasma sheet permits to use the condition of magnetostatic equilibrium as an empirical relation thereby connecting the magnetic field and the plasma pressure. A more careful analysis will require the inclusion of magnetic field fluctuations. However, at first approximation it is possible to suggest that they are not so large in comparison with the regular field [∼0.5 in accordance with (Borovsky et al., 1997)]. In this case, it is possible to solve the Grad-Shafranov equation and to determine the magnetic field distribution across the plasma sheet in the tail approximation of Birn and Schindler (1983).
Such approach was used in the Antonova and Ovchinnikov (1996a; Antonova and Ovchinnikov,1996b; Antonova and Ovchinnikov, 1999; Antonova and Ovchinnikov, 2001) model developed to explain the existence of the quasistable plasma sheet in the presence of turbulent transport. As it was mentioned in Reasons for the Popularity of Laminar Flow Models, the concept of the plasma sheet as a turbulent wake behind an obstacle has attracted little attention due to an unusual configuration of such turbulent wake, in comparison to the wake commonly observed in ordinary fluids. In the geomagnetic tail, it only takes up part of the volume behind the obstacle and is located between the tail lobes. However, it is well known that such configuration is observed only under southward IMF orientation (IMF Bz < 0). When the IMF turns northward for a comparatively long time, the tail lobes fill with plasma from the plasma sheet (Frank et al., 1986). Such filling leads to the appearance of polar cap arcs and the formation of theta-aurora. One of the main differences between the periods of IMF Bz < 0 and of IMF Bz > 0 is the value of the dawn-dusk electric field, which is much stronger for the southward IMF orientation. The particle drift along the Z axis in the SM coordinate system generates the lobe plasma flow directed from the tail lobes to the center of the plasma sheet, where the plasma density has a maximum. Eq. 5 shows that the turbulent transport, directed opposite to the plasma pressure gradient, can compensate the regular transport if the averaged bulk velocity
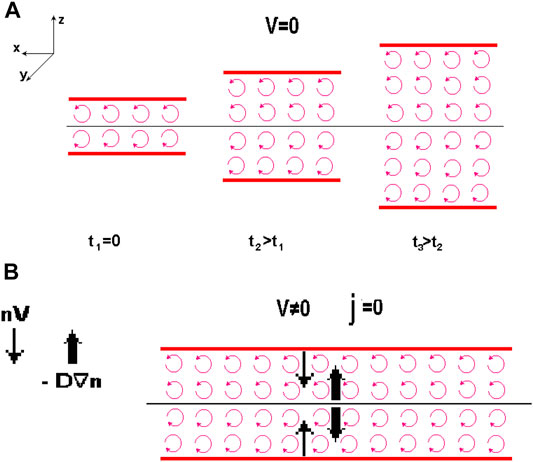
FIGURE 4. Scheme illustrating the formation of the turbulent plasma sheet. Case (A) corresponds to the expansion of the sheet due to eddy diffusion when the regular flow velocity V = 0, case (B) corresponds to the quasistable configuration, when the regular velocity to the tail center compensates the eddy diffusion.
Figure 5 shows an example of plasma pressure distribution obtained using (Antonova and Ovchinnikov, 1996a; Antonova and Ovchinnikov,1996b; Antonova and Ovchinnikov, 1999) model at geocentric distances X = −30 RE when
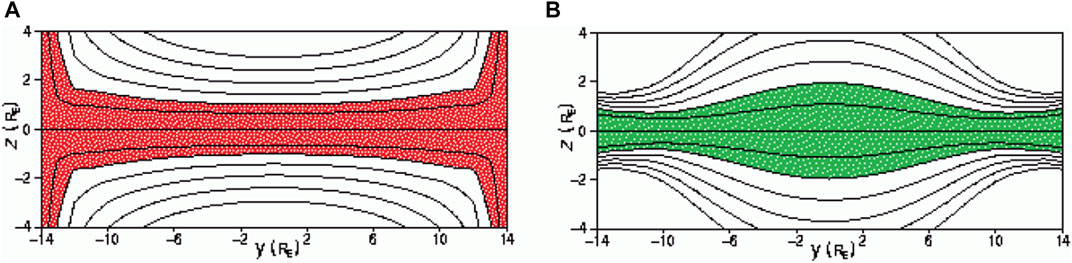
FIGURE 5. An example of plasma pressure distribution in the plasma sheet at geocentric distance X = −30 RE, (A) when
The main achievement of the discussed model is the prediction of the value of the eddy diffusion coefficient Dzz by Antonova and Ovchinnikov (1996a), Antonova and Ovchinnikov (1996b), before it was obtained experimentally in many works, starting from Borovsky et al. (1998) [see the discussion in (Antonova, 2000; Ovchinnikov et al., 2000; Ovchinnikov and Antonova, 2017)]. Later, Stepanova and Antonova (2011) made a direct verification of the main predictions of the model. Despite its simplicity, the discussed model shows how the existence of turbulent transport could explain the observed formation of quasistable structures, which are compressed by the regular plasma motions, compared with the classical schemes where such compression leads to the appearance of reconnection.
To date the mechanisms of the formation of the plasma sheet turbulence are not clear, and continue to be discussed. The formation of the large-scale vortices with scales ∼10,000 km is of particular interest, as they make the main contribution to the turbulent transport. The existence of magnetospheric vortices was first demonstrated using data of simultaneous ISSE-1 and ISEE-2 observations by Hones et al. (1979) and analyzed in detail by Birn et al. (1985). Study and modeling of such vortices were later connected to the development of Kelvin-Helmholtz instability at the magnetospheric flanks. Latest analysis of Nakamura et al. (2020) showed how the formation of vortices is related to the level of solar wind fluctuations.
Study of BBF formation leads to the description of vortex formation at the center of the plasma sheet. According to the model of Birn et al. (1999), Birn et al. (2011), the vortices could appear as a result of reconnection. The large-scale vortices of such type were successfully identified in many works using multisatellite observations (Keiling, et al., 2009; Keika et al., 2009; Panov et al., 2010; Tang, 2012; etc.). Unfortunately, these studies were done in (X, Y) plane only, and the structure of vortices in Z direction remains unclear.
El-Alaoui et al. (2010), El-Alaoui et al. (2012) considered the energy-containing scale of magnetospheric turbulence as the largest scale being associated with reconnection outflows and the diversion of high-speed flows. Therefore, the eddy vortices were considered as a driving or integral scale of the tail turbulence. Nonetheless, the appearance of such vortices is a consequence of the large-scale magnetospheric flows. These flows increase when IMF Bz < 0. That shows their deep connection with the large-scale magnetospheric convection. A strong connection between the eddy diffusion and the large-scale magnetospheric convection is also described in the model of the turbulent plasma sheet proposed by Antonova and Ovchinnikov (1996a), bAntonova and Ovchinnikov (1996b), Antonova and Ovchinnikov (1999).
Properties of the large-scale magnetospheric convection have been obtained by many tools and are well known [see (Weimer, 1996)]. The nature of the observed large-scale magnetospheric convection was widely discussed in multiple works since the beginning of Space Age. The viscous interaction and reconnection models were the most popular ones for a long time. However, both mechanisms were not considered a source of large-scale vortices at driving or integral scale of turbulence. Borovsky et al. (2020) stressed that the viscous interaction is neither quantified nor understood. The observed high level of magnetosheath and plasma sheet turbulence is the main obstacle to the applicability of the Dungey (1961) reconnection model.
The discovery of a system of large-scale field-aligned currents by Iijima and Potemra (1976) was crucial for the understanding of the large-scale magnetospheric convection. It became clear that the dawn-dusk electric field in the polar cap and, hence, the large-scale two vortex magnetospheric convection are supported by the Region I field-aligned currents of Iijima and Potemra. The source of the Region 1 currents in the equatorial plane is located inside the plasma sheet and the outer part of the ring current (Antonova et al., 2006; Xing et al., 2009; Antonova et al., 2018). The most probable mechanism of generation of both Region II and Region I currents is related to the existence of the plasma pressure gradients. Strong arguments in favor this mechanism were provided by Troshichev (1982). In particular, Antonova and Ganushkina (1997) showed that the Region I field-aligned currents can be supported by the azimuthal plasma pressure gradients, which appear due to azimuthal asymmetry of the magnetoshere modulated by the IMF. The detailed discussion about the action of this mechanism is beyond the scope of this paper. For the description of turbulent processes in the magnetosphere, it is only important to stress that such mechanism produces the large-scale two vortex convection flows.
The inverted V structures in the auroral oval containing the field-aligned potential drop are a clear result of a medium scale vortex formation in the region of the upward field-aligned current (see Figure 1 in (Antonova and Ovchinnikov, 1999) which schematically shows the structure of the electrostatic field and its equipotentials typically observed in the inverted-V quiet auroral band). It is necessary to remind that the electric field in the inverted V structure is much larger than the large-scale dawn-dusk electric field, and it increases with the distance from the ionosphere. We assume that the medium-scale vortices such as inverted-V structures should form part of the plasma sheet turbulence. However, their connection with smaller vortices that produce the eddy diffusion in the plasma sheet is not clear yet.
Our analysis shows that mechanisms of generation of the plasma sheet turbulence are deeply connected to the plasma pressure gradients in the magnetosphere, including the driving or integral scale vortices–the two-vortex convection and the eddy vortices, responsible for the eddy diffusion transport.
The convection crisis is one of the main problems of the slow motion of plasma from the tail to the Earth inside the plasma sheet. Ericson and Wolf (1980), Birn and Schindler (1983) showed that the adiabatic plasma transport in case of the laminar convection should lead to an increase of plasma pressure in the plasma sheet, which was never observed. The adiabatic laminar convection assumes the conservation of particles in a magnetic flux tube and an increase of their temperature in accordance with the adiabatic law, i.e. particle and heat fluxes between the flux tubes are not allowed. Analyzing this problem, Kivelson and Spence (1988) showed that under quiet geomagnetic conditions a quasi-static adiabatic convection is possible in a magnetotail of finite width. However, the problem continued to exist for more disturbed conditions. The existence of turbulent electric field fluctuations and eddy diffusion naturally removes this problem (Antonova, 1985; Antonova and Tverskoy, 1998), as the turbulent fluctuations of the magnetic field do not allow to use such concepts as the magnetic flux tube and the adiabatic transport. It is necessary to note also that particle trajectory in fluctuating magnetic and therefore fluctuating electric field becomes stochastic, when the Larmor radius of a particle is comparable with the field inhomogeneity. In contrast to the commonly used adiabatic model, the behavior of particle pressure in the plasma sheet was determined by Antonova and Ovchinnikov (1996a), Antonova and Ovchinnikov (1996b), Antonova and Ovchinnikov (1999) as the pressure balance in Z direction described by the flaring-tail model of Tverskoy (1968) and Kennel (1995).
Consideration of the high level of plasma sheet fluctuations is also fundamental for the understanding of the nature of magnetospheric substorms. According to (Akasofu, 1964), an isolated substorm onset starts with the brightening of the equatorward auroral arc. Such arc is mapped to the equatorial plane at geocentric distance ∼7 RE [see arguments summarized by Antonova et al. (2018)], i.e., near the inner boundary of the outer part of the ring current. Dispersionless injection boundary is also located at such distances (Lopez et al., 1990; Spanswick et al., 2010). Such features mean the development of an instability able to produce auroral brightening and local particle acceleration. It is difficult to imagine how this instability would develop in the presence of turbulent fluctuations in the plasma sheet, assuming that the auroral oval is mapped to that region, as suggested in many works. On the contrary, the mapping of the auroral oval to the outer part of the ring current does not lead to such consequences, considering that the level of turbulent fluctuations before substorm vanishes in this region, as mentioned in Study of Magnetospheric Turbulence and Its Main Characteristics.
It is necessary to mention, that the BBFs are frequently discussed as an onset trigger in the tail. They are observed during the substorm growth, expansion and recovery phases. Nonetheless, many BBFs occur without classical substorm signatures during pseudo-breakups and auroral brightening and produce the auroral streamers. Many substorm onsets are not preceded by the arrival of streamers [see references in (Antonova et al., 2009; Sitnov et al., 2019)]. Therefore, the existence of plasma sheet turbulence including BBFs is a strong argument in favor of the location of the instability responsible for a substorm onset at comparatively small geocentric distances, that agrees with the onset observations.
During a long history of study of substorms different mechanisms of substorm onset were discussed. Most models based on the reconnection in the tail suppose the existence of the laminar plasma flow and the regular character of the magnetic field before the reconnection onset including the models which take into account the Hall term and electron inertia [see, for example (Shay et al., 2003)]. Therefore, variations of plasma sheet velocity and magnetic field constantly observed in the plasma sheet create real difficulties for such models, giving preference for models of substorm onset located at geocentric distances <10 RE such as the current disruption models (Lui, 2001) and development of upward field-aligned current instability (Antonova, 2002; Stepanova et al., 2002).
One more problem, which naturally appears in connection with the plasma sheet turbulence, is the presence of beams and fast plasma motions, which are attributed to the magnetic reconnection leading to the change of a large-scale magnetic configuration. However, as was mentioned earlier, most of the BBFs do not produce any substantial changes like generation of geomagnetic substorms. To understand such contradiction, it is necessary to remind that the plasma sheet turbulence is a mixture of the Alfvénic wavy turbulence and eddy 2-D turbulence. Therefore, the Alfvénic disturbances constantly exist in the plasma sheet. Relations (3) and (4) show that the ideal MHD in such a case is applicable when the scale of perturbed region is larger than the ion inertial length. This means that the traditional reconnection models can describe the processes inside such regions, which can be only a small part of the entire turbulent region. In such a case, the local reconnection phenomena can be considered as an intrinsic property of the collisionless turbulence and local reconnection phenomena leading to the BBF formation as a part of the tail turbulence development. The reconnection-like phenomena observed inside the turbulent magnetosheath (Yordanova et al., 2016; Vörös et al., 2017) and the plasma sheet (El-Alaoui et al., 2013) are strong evidences in favor of such approach. The magnetostatically quasistable configuration with slow averaged flow velocity can be formed in such a case.
In this review, we have summarized published results in which the plasma sheet in Earth’s magnetosphere has been regarded as a turbulent wake behind an obstacle formed due to high Reynolds number values. Traditional hydrodynamics shows that a turbulent wake should be formed even in the case of a laminar flow before an obstacle. In the magnetosphere, we deal not only with high Reynolds numbers, but also with the interaction between the geomagnetic field and the turbulent solar wind. These solar wind turbulent fluctuations are strongly amplified after crossing the bow shock, forming the plasma flows in the magnetosheath. Here, we have briefly summarized the results of plasma velocity and magnetic field fluctuations in the geomagnetic tail, focusing on the MHD scales, as turbulent motion on such scales makes the main contribution to the plasma transport and mixing. Despite an evident analogy between the turbulent wake behind an obstacle observed in the ordinary flows and the turbulent geomagnetic tail, this approach for the magnetospheric dynamics is not popular. In the following, we analyzed the potential reasons leading to this situation. We consider that in addition to simplicity of laminar models it is possible to identify three reasons:
• The difficulties in studies of turbulent plasma flows and especially in the detection of large vortices, even using data of multisatellite observations.
• The sheet-like structure of the plasma sheet, which is located between the tail lobes with a very low plasma density, meanwhile the ordinary turbulent wake fills up all region behind an obstacle.
• >The erroneous assumption of the mapping of the auroral oval to the plasma sheet, which contradicts the observations of nearly stationary auroral arcs during quiet periods.
In this paper, we have shown that it is possible to overcome all the above mentioned difficulties by considering the latest observational and theoretical works about the morphological mapping of the auroral oval into the equatorial plane. It is important to stress that these works showed that the main part of the auroral oval maps to the outer part of the ring current.
We analyze results of theoretical studies of tail turbulence using the results of the ideal MHD models and the model of the plasma sheet, in which regular flow across the sheet is compensated by eddy diffusion. Here we have pointed out the real advantages of such approach. We have also analyzed the main difficulties of the ideal MHD models, which commonly have not been discussed, connected to the inapplicability of the frozen-in condition. It is well known that in the magnetosphere the averaged plasma velocity is much smaller than the Alfvén velocity. In this case we cannot use the aforementioned approach and the ideal MHD cannot describe plasma systems in magnetostatic equilibrium. Nevertheless, it was possible to obtain the results of near to ideal MHD modeling reproducing the main features of plasma sheet turbulence including comparatively large-scale vortices.
The model of the plasma sheet based on the validity of the plasma and magnetic field pressure balance across the sheet is able to explain the plasma sheet thinning during substorm growth phase due to increase of the dawn-dusk electric field. This model also explains its thickening during expansion phase due to an increase in turbulence and eddy diffusion. It can also help to understand the mechanism of tail lobe filling by the plasma sheet plasma during IMF Bz > 0. Development of such mechanism permitted to predict the values of the eddy diffusion coefficients, which were obtained later experimentally, using data of ISEE-2, Interball/Tail Probe, Geotail, CLUSTER and Themis satellites. It takes away the problem of a sheet like turbulent wake behind an obstacle. Nonetheless, this model requires further development and additional verification.
Direct observations of vortices on the scales of ∼1–2 RE showed the reliability to consider the plasma sheet as a turbulent wake behind an obstacle. We discuss a deep connection between the plasma sheet turbulence and the large-scale magnetospheric convection. This relation is analyzed with the aim to identify the vortices corresponding to the driving or integral scale of the tail turbulence. We consider that the large-scale two-vortex magnetospheric convection generated by the magnetospheric plasma pressure gradients is a real source of energy for the turbulence development and may be the driving or integral vortex of such turbulence. However, these suggestions require further investigation.
In this paper we have discussed a number of long standing magnetospheric problems, which are removed due to the existence of the turbulent plasma sheet, including the convection crisis problem. This problem ceases to exist because in case of the turbulent plasma sheet a number of particles in the magnetic flux tube is not conserved, and the approximation of adiabatic compression is not valid for the slow plasma motion. The problem of the location of the substorm expansion phase onset inside the magnetosphere at geocentric distances ∼7 RE also obtains a reasonable explanation as the instability leading to the first auroral arc brightening can be developed only in a region which is comparatively stable before an onset.
We suggest that the long-standing problem of the role of reconnection phenomena on the magnetospheric dynamics obtain new aspect that requires additional discussion. It became clear that the reconnection phenomena are observed inside the turbulent regions and can be considered as a part of the turbulent tail dynamics.
In summary, the plasma sheet turbulence corresponds to an important part of the magnetospheric dynamics and should be studied in detail for the adequate description of the magnetospheric processes.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The work of MS was supported by Universidad de Santiago de Chile through the grant: DICYT N° 042031S.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We are grateful for numerous and fruitful discussions on this topic with our colleagues from the Skobeltsyn Institute of Nuclear Physics Moscow State University, the Space Research Institute RAS in Russian Federation, and the Physics Departments at the Universidad de Santiago and Universidad de Chile.
Akasofu, S.-I. (1964). The development of the auroral substorm. Planet. Space Sci. 12, 273–282. doi:10.1016/0032-0633(64)90151-5
Angelopoulos, V., Baumjohann, W., Kennel, C. F., Coroniti, F. V., Kivelson, M. G., Pellat, R., et al. (1992). Bursty bulk flows in the inner central plasma sheet. J. Geophys. Res. 97 (A4), 4027–4039. doi:10.1029/91JA02701
Angelopoulos, V., Kennel, C. F., Coroniti, F. V., Pellat, R., Spence, H. E., Kivelson, M. G., et al. (1993). Characteristics of ion flow in the quiet state of the inner plasma sheet. Geophys. Res. Lett. 20, 1711–1714. doi:10.1029/93GL00847
Angelopoulos, V., Coroniti, F. V., Kennel, C. F., Kivelson, M. G., Walker, R. J., Russell, C. T., et al. (1996). Multipoint analysis of a bursty bulk flow event on April 11, 1985. J. Geophys. Res. 101 (A5), 4967–4989. doi:10.1029/95JA02722
Angelopoulos, V., Mukai, T., and Kokubun, S. (1999). Evidence for intermittency in Earth's plasma sheet and implications for self-organized criticality. Phys. Plasmas 6 (11), 4161–4168. doi:10.1063/1.873681
Antonova, E. E. (1985). On nonadiabatic diffusion and adjustment of concentration and temperature in the plasma sheet of the Earth’s magnetosphere. Geomagn. Aeron. 25, 623–627.
Antonova, E. E. (2000). Large scale magnetospheric turbulence and the topology of magnetospheric currents. Adv. Space Res. 25 (7/8), 1567–1570. doi:10.1016/S0273-1177(99)00669-9
Antonova, E. E. (2002). The results of Interball/Tail probe observations the inner magnetosphere substorm onset and particle acceleration. Adv. Space Res. 30 (7), 1671–1676. doi:10.1016/S0273-1177(02)00434-9
Antonova, E. E. (2008). Magnetospheric turbulence and properties of magnetospheric dynamics. Adv. Space Res. 41, 1677–1681. doi:10.1016/j.asr.2007.05.057
Antonova, E. E., and Ganushkina, N. Y. (1997). Azimuthal hot plasma pressure gradients and dawn-dusk electric field formation. J. Atmos. Solar-Terrestrial Phys. 59, 1343–1354. doi:10.1016/S1364-6826(96)00169-1
Antonova, E. E., and Ovchinnikov, I. L. (1996a). Equilibrium of a turbulent current sheet and the current sheet of geomagnetic tail. Geomagn. Aeron. (Engl. Transl.). 36, 597–601.
Antonova, E. E., and Ovchinnikov, I. L. (1996b). Current sheet with medium scale developed turbulence and the formation of the plasma sheet of Earth’s magnetosphere and solar prominences. Adv. Space Res. 19, 1919–1922. doi:10.1016/S0273-1177(97)00101-4
Antonova, E. E., and Ovchinnikov, I. L. (1999). Magnetostatically equilibrated plasma sheet with developed medium-scale turbulence: structure and implications for substorm dynamics. J. Geophys. Res. 104, 17289–17297. doi:10.1029/1999JA900141
Antonova, E. E., and Ovchinnikov, I. L. (2001). The model of turbulent plasma sheet during IMF Bz > 0. Adv. Space Res. 28 (12), 1747–1752. doi:10.1016/S0273-1177(01)00541-5
Antonova, E. E., and Tverskoy, B. A. (1998). On the nature of electric fields in the Earth’s inner magnetosphere (a review). Int. J. Geomagn. Aeron. 1 (1), 9–21.
Antonova, E. E., Kirpichev, I. P., and Stepanova, M. V. (2006). Field-aligned current mapping and the problem of the generation of magnetospheric convection. Adv. Space Res. 38, 1637–1641. doi:10.1016/j.asr.2005.09.042
Antonova, E. E., Kornilov, I. A., Kornilova, T. A., Kornilova, T. A., Kornilov, O. I., and Stepanova, M. V. (2009). Features of auroral breakup obtained using data of ground-based television observations: case study. Ann. Geophys. 27, 1413–1422. doi:10.5194/angeo-27-1413-2009
Antonova, E. E., Pulinets, M. S., Riazantseva, M. O., Znatkova, S. S., Kirpichev, I. P., and Stepanova, M. V. (2012). Turbulence in the magnetosheath and the problem of plasma penetration inside the magnetosphere. Exploring the solar wind, ed. M. Lazar (INTECHOPEN.COM). Chapter 18, pp. 417–438.
Antonova, E. E., Vorobjev, V. G., Kirpichev, I. P., and Yagodkina, O. I. (2014). Comparison of the plasma pressure distributions over the equatorial plane and at low altitudes under magnetically quiet conditions. Geomagn. Aeron. 54, 278–281. doi:10.1134/S0016793214030025
Antonova, E. E., Vorobjev, V. G., Kirpichev, I. P., Yagodkina, O. I., and Stepanova, M. V. (2015). Problems with mapping the auroral oval and magnetospheric substorms. Earth Planets Space 67, 166. doi:10.1186/s40623-015-0336-6
Antonova, E. E., Stepanova, M., Kirpichev, I. P., Ovchinnikov, I. L., Vorobjev, V. G., Yagodkina, O. I., et al. (2018). Structure of magnetospheric current systems and mapping of high latitude magnetospheric regions to the ionosphere. J. Atmos. Solar-Terrestrial Phys. 177, 103–114. doi:10.1016/j.jastp.2017.10.013
Baumjohan, W., and Treuman, R. (1996). Basic space plasma Physics. London, UK: Imperial College Press, 156–158.
Baumjohann, W., Paschmann, G., and Cattell, C. A. (1989). Average plasma properties in the central plasma sheet. J. Geophys. Res. 94, 6597–6606. doi:10.1029/JA094iA06p06597
Baumjohann, W., Paschmann, G., and Lühr, H. (1990a). Characteristics of high-speed ion flows in the plasma sheet. J. Geophys. Res. 95, 3801–3809. doi:10.1029/JA095iA04p03801
Baumjohann, W., Paschmann, G., and Lühr, H. (1990b). Pressure balance between lobe and plasma sheet. Geophys. Res. Lett. 17 (1), 45–48. doi:10.1029/GL017i001p00045
Birn, J., Hones, E. W., Bame, S. J., and Russell, C. T. (1985). Analysis of 16 plasma vortex events in the geomagnetic tail. J. Geophys. Res. 90, 7449–7456. doi:10.1029/JA090iA08p07449
Birn, J., Hesse, M., Haerendel, G., Baumjohann, W., and Shiokawa, K. (1999). Flow braking and the substorm current wedge. J. Geophys. Res. 104, 19895–19903. doi:10.1029/1999JA900173
Birn, J., Nakamura, R., Panov, E. V., and Hesse, M. (2011). Bursty bulk flows and dipolarization in MHD simulations of magnetotail reconnection. J. Geophys. Res. 116. doi:10.1029/2010JA016083
Birn, J., and Schindler, K. (1983). Self-consistent theory of three-dimensional convection in the geomagnetic tail. J. Geophys. Res. 88 (A9), 6969–6980. doi:10.1029/GL007i011p0089710.1029/ja088ia09p06969
Borovsky, J. E., Elphic, R. C., Funsten, H. O., and Thomsen, M. F. (1997). The Earth's plasma sheet as a laboratory for flow turbulence in high-β MHD. J. Plasma Phys. 57, 1–34. doi:10.1017/S0022377896005259
Borovsky, J. E., Thomsen, M. F., Elphic, R. C., and Elphic, R. C. (1998). The driving of the plasma sheet by the solar wind. J. Geophys. Res. 103 (A8), 17617–17639. doi:10.1029/97JA02986
Borovsky, J. E. (2008). Flux tube texture of the solar wind: strands of the magnetic carpet at 1 AU? J. Geophys. Res. 113. doi:10.1029/2007JA012684
Borovsky, J. E., and Funsten, H. O. (2003a). MHD turbulence in the Earth's plasma sheet: dynamics, dissipation, and driving. J. Geophys. Res. 108 (A7), 1284. doi:10.1029/2002JA009625
Borovsky, J. E., and Funsten, H. O. (2003b). Role of solar wind turbulence in the coupling of the solar wind to the Earth's magnetosphere. J. Geophys. Res. 108 (A6), 1246. doi:10.1029/2002JA009601
Borovsky, J. E. (2020a). Plasma and magnetic-field structure of the solar wind at inertial-range scale sizes discerned from statistical examinations of the time-series measurements. Front. Astron. Space Sci. 7, 20. doi:10.3389/fspas.2020.00020
Borovsky, J. E. (2020b). The compression of the heliospheric magnetic structure by interplanetary shocks: is the structure at 1AU a manifestation of solar-wind turbulence or is it fossil structure from the sun? Front. Astron. Space Sci. 7, 582564. doi:10.3389/fspas.2020.582564
Borovsky, J. E., Delzanno, G. L., Valdivia, J. A., Moya, P. S., Stepanova, M., Birn, J., et al. (2020). Outstanding questions in magnetospheric plasma physics: the pollenzo view. J. Atmos. Solar-Terrestrial Phys. 208, 105377. doi:10.1016/j.jastp.2020.105377
Burch, J. L., Torbert, R. B., Phan, T. D., Chen, L. J., Moore, T. E., Ergun, R. E., et al. (2016b). Electron-scale measurements of magnetic reconnection in space. Science 352, aaf2939. doi:10.1126/science.aaf2939
Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L. (2016a). Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9
Califano, F., Cerri, S. S., Faganello, M., Laveder, D., Sisti, M., and Kunz, M. W. (2020). Electron-only reconnection in plasma turbulence. Front. Phys. 8, 317. doi:10.3389/fphy.2020.00317
Consolini, G., Marcucci, M. F., and Candidi, M. (1996). Multifractal structure of auroral electrojet index data. Phys. Rev. Lett. 76, 4082–4085. doi:10.1103/PhysRevLett.76.4082
Consolini, G., Kretzschmar, M., Lui, A. T. Y., Zimbardo, G., and Macek, W. M. (2005). On the magnetic field fluctuations during magnetospheric tail current disruption: a statistical approach. J. Geophys. Res. 110, A07202. doi:10.1029/2004JA010947
Dungey, J. W. (1961). Interplanetary magnetic field and the auroral zones. Phys. Rev. Lett. 6 (1), 47–48. doi:10.1103/PhysRevLett.6.47
Dungey, J. W. (1962). The interplanetary magnetic field and the auroral zones. Tech. Rep. 157. Pennsylvania, USA: The Pennsylvania State University, Scientific Report, University Park.
D’Amicis, R., Telloni, D., and Bruno, R. (2020). The effect of solar-wind turbulence on magnetospheric activity. Front. Phys. 8, 604857. doi:10.3389/fphy.2020.604857
El-Alaoui, M., Ashour-Abdalla, M., Richard, R. L., Goldstein, M. L., Weygand, J. M., and Walker, R. J. (2010). Global magnetohydrodynamic simulation of reconnection and turbulence in the plasma sheet. J. Geophys. Res. 115. doi:10.1029/2010JA015653
El-Alaoui, M., Richard, R. L., Ashour-Abdalla, M., Walker, R. J., and Goldstein, M. L. (2012). Turbulence in a global magnetohydrodynamic simulation of the Earth's magnetosphere during northward and southward interplanetary magnetic field. Nonlin. Process. Geophys. 19, 165–175. doi:10.5194/npg-19-165-2012
El-Alaoui, M., Richard, R. L., Ashour-Abdalla, M., Goldstein, M. L., and Walker, R. J. (2013). Dipolarization and turbulence in the plasma sheet during a substorm: THEMIS observations and global MHD simulations. J. Geophys. Res. Space Phys. 118, 7752–7761. doi:10.1002/2013JA019322
Ergun, R. E., Goodrich, K. A., Wilder, F. D., Ahmadi, N., Holmes, J. C., Eriksson, S., et al. (2018). Magnetic reconnection, turbulence, and particle acceleration: observations in the Earth's magnetotail. Geophys. Res. Lett. 45, 3338–3347. doi:10.1002/2018GL076993
Ericson, G. M., and Wolf, R. A. (1980). Is the steady convection possible in the Earth’s magnetotail. Geophys. Res. Lett. 7 (11), 897–900. doi:10.1029/GL007i011p00897
Frank, L. A., Craven, J. D., Gurnett, D. A., Shawhan, S. D., Weimer, D. R., Burch, J. L., et al. (1986). The theta aurora. J. Geophys. Res. 91 (A3), 3177–3224. doi:10.1029/JA091iA03p03177
Hones, E. W., Paschmann, G., Bame, S. J., Asbridge, J. R., Sckopke, N., and Schindler, K. (1978). Vortices in magnetospheric plasma flow. Geophys. Res. Lett. 5, 1059–1062. doi:10.1029/GL005i012p01059
Hoshino, M., Nishida, A., Yamamoto, T., and Kokubun, S. (1994). Turbulent magnetic field in the distant magnetotail: bottom-up process of plasmoid formation? Geophys. Res. Lett. 21, 2935–2938. doi:10.1029/94GL02094
Iijima, T., and Potemra, T. A. (1976). The amplitude distribution of field-aligned currents at northern high latitudes observed by Triad. J. Geophys. Res. 81, 2165–2174. doi:10.1029/JA081i013p02165
Keika, K., Nakamura, R., Volwerk, M., Angelopoulos, V., Baumjohann, W., Retinò, A., et al. (2009). Observations of plasma vortices in the vicinity of flow-braking: a case study. Ann. Geophys. 27, 3009–3017. doi:10.5194/angeo-27-3009-2009
Keiling, A., Angelopoulos, V., Runov, A., Weygand, J., Apatenkov, S. V., Mende, S., et al. (2009). Substorm current wedge driven by plasma flow vortices: THEMIS observations. J. Geophys. Res. 114, a. doi:10.1029/2009JA014114
Kennel, C. F. (1995). Convection and substorms. Paradigm of magnetospheric phenomenology. Oxford University Press, 408.
Kirpichev, I. P., Yagodkina, O. I., Vorobjev, V. G., and Antonova, E. E. (2016). Position of projections of the nightside auroral oval equatorward and poleward edges in the magnetosphere equatorial plane. Geomagn. Aeron. 56, 407–414. doi:10.1134/S001679321604006X
Kistler, L. M., Baumjohann, W., Nagai, T., and Möbius, E. (1993). Superposed epoch analysis of pressure and magnetic field configuration changes in the plasma sheet. J. Geophys. Res. 98 (A6), 9249–9258. doi:10.1029/93JA00630
Kivelson, M. G., and Spence, H. E. (1988). On the possibility of quasi-static convection in the quiet magnetotail. Geophys. Res. Lett. 15 (13), 1541–1544. doi:10.1029/GL015i013p01541
Klimontovich, Y. L. (1990). Turbulent motion and the structure of chaos. The new approach to the statistical theory of open systems. Dordrecht: Kluwer Academic Publishers, 317.
Lopez, R. E., Sibeck, D. G., McEntire, R. W., and Krimigis, S. M. (1990). The energetic ion substorm injection boundary. J. Geophys. Res. 95, 109–117. doi:10.1029/JA095iA01p00109
Lui, A. T. Y. (2001). Multifractal and intermittent nature of substorm-associated magnetic turbulence in the magnetotail. J. Atmos. Solar-Terrestrial Phys. 63, 1379–1385. doi:10.1016/S1364-6826(00)00239-X
Maynard, N. C., Heppner, J. P., and Aggson, T. L. (1982). Turbulent electric fields in the nightside magnetosphere. J. Geophys. Res. 87 (A3), 1445–1454. doi:10.1029/JA087iA03p01445
Miura, A. (1984). Anomalous transport by magnetohydrodynamic Kelvin-Helmholtz instabilities in the solar wind-magnetosphere interaction. J. Geophys. Res. 89, 801–818. doi:10.1029/JA089iA02p00801
Montgomery, D. (1987). “Remarks on the mhd problem of generic magnetospheres and magnetotails,” in Magnetotail Physics. Editor A. T. Y. Lui (Baltimore: Johns Hopkins University Press), 203.
Nagai, T., Fujimoto, M., Saito, Y., Machida, S., Terasawa, T., Nakamura, R., et al. (1998). Structure and dynamics of magnetic reconnection for substorm onsets with Geotail observations. J. Geophys. Res. 103, 4419–4440. doi:10.1029/97JA02190
Nagai, T., Shinohara, I., Fujimoto, M., Machida, S., Nakamura, R., Saito, Y., et al. (2003). Structure of the Hall current system in the vicinity of the magnetic reconnection site. J. Geophys. Res. 108 (A10), 1357. doi:10.1029/2003JA009900
Nagata, D., Machida, S., Ohtani, S., Saito, Y., and Saito, T. (2008). Solar wind control of plasma number density in the near-Earth plasma sheet: three-dimensional structure. Ann. Geophys. 26, 4031–4049. doi:10.5194/angeo-26-4031-2008
Nakamura, R., Baumjohann, W., Mouikis, C., Kistler, L. M., Runov, A., Volwerk, M., et al. (2004). Spatial scale of high-speed flows in the plasma sheet observed by Cluster. Geophys. Res. Lett. 31, a. doi:10.1029/2004GL019558
Nakamura, T. K. M., Stawarz, J. E., Hasegawa, H., Narita, Y., Franci, L., Wilder, F. D., et al. (2020). Effects of fluctuating magnetic field on the growth of the kelvin‐helmholtz instability at the Earth's magnetopause. J. Geophys. Res. Space Phys. 125, e2019JA027515. doi:10.1029/2019JA027515
Neagu, E., Borovsky, J. E., Gary, S. P., Jorgensen, A. M., Baumjohann, W., and Treumann, R. A. (2005). Statistical survey of magnetic and velocity fluctuations in the near-Earth plasma sheet: international Sun Earth Explorer (ISEE-2) measurements. J. Geophys. Res. 110, A05203. doi:10.1029/2004JA010448
Neagu, E., Borovsky, J. E., Thomsen, M. F., Gary, S. P., Baumjohann, W., and Treumann, R. A. (2002). Statistical survey of magnetic field and ion velocity fluctuations in the near-Earth plasma sheet: active Magnetospheric Particle Trace Explorers/Ion Release Module (AMPTE/IRM) measurements. J. Geophys. Res. 107, 1098. doi:10.1029/2001JA000318
Ovchinnikov, I. L., and Antonova, E. E. (2017). Turbulent transport of the Earth magnitisphere: review of the results of observations and modeling. Geomagn. Aeron. 57 (6), 655–663. doi:10.1134/S0016793217060081
Ovchinnikov, I. L., Antonova, E. E., and Yermolaev, Y. I. (2000). Determination of the turbulent diffusion coefficient in the plasma sheet using the project INTERBALL data. Cosmic Res. 38, 557–561. doi:10.1023/a:1026686600686
Ovchinnikov, I. L., Antonova, E. E., and Yermolaev, Y. I. (2002). Plasma sheet heating during substorm and the values of the plasma sheet diffusion coefficient obtained on the base of interball/tail probe observations. Adv. Space Res. 30 (7), 1821–1824. doi:10.1016/S0273-1177(02)00456-8
Panov, E. V., Nakamura, R., Baumjohann, W., Angelopoulos, V., Petrukovich, A. A., Retinò, A., et al. (2010). Multiple overshoot and rebound of a bursty bulk flow. Geophys. Res. Lett. 37, L08103. doi:10.1029/2009GL041971
Paschmann, G., Haaland, S., and Treumann, R. (2002). Auroral plasma physics. Space Sci. Rev. 103 (1-4), 1–485. doi:10.1023/A:1023030716698
Petersen, A., Cattell, C. A., Falthammar, C. G., Formisano, V., Lindqvist, P. A., Mozer, F., et al. (1984). Quasistatic electric field measurements with spherical double probes on the GEOS and ISEE satellites. Space Sci. Rev. 37 (3/4), 269–312. doi:10.1007/BF00226365
Petrukovich, A. A., Baumjohann, W., Nakamura, R., Schödel, R., and Mukai, T. (2001). Are earthward bursty bulk flows convective or field-aligned? J. Geophys. Res. 106 (A10), 21211–21215. doi:10.1029/2001JA900019
Petrukovich, A. A., Mukai, T., Kokubun, S., Romanov, S. A., Saito, Y., Yamamoto, T., et al. (1999). Substorm-associated pressure variations in the magnetotail plasma sheet and lobe. J. Geophys. Res. 104 (A3), 4501–4513. doi:10.1029/98JA02418
Phan, T. D., Eastwood, J. P., Shay, M. A., Drake, J. F., Sonnerup, B. U. Ö., Fujimoto, M., et al. (2018). Electron magnetic reconnection without ion coupling in Earth's turbulent magnetosheath. Nature 557, 202–206. doi:10.1038/s41586-018-0091-5
Pinto, V., Stepanova, M., Antonova, E. E., and Valdivia, J. A. (2011). Estimation of the eddy-diffusion coefficients in the plasma sheet using THEMIS satellite data. J. Atmos. Solar-Terrestrial Phys. 73, 1472–1477. doi:10.1016/j.jastp.2011.05.007
Priest, E., and Forbes, T. (2000). “Introduction,” in Magnetic reconnection: MHD theory and applications (Cambridge: Cambridge University Press), 1–47. doi:10.1017/CBO9780511525087.002
Schödel, R., Baumjohann, W., Nakamura, R., Sergeev, V. A., and Mukai, T. (2001). Rapid flux transport in the central plasma sheet. J. Geophys. Res. 106 (A1), 301–313. doi:10.1029/2000JA90015910.1029/2000ja900139
Sergeev, V. A., Sauvaud, J.-A., Popescu, D., Kovrazhkin, R. A., Liou, K., Newell, P. T., et al. (2000). Multiple-spacecraft observation of a narrow transient plasma jet in the Earth's plasma sheet. Geophys. Res. Lett. 27 (6), 851–854. doi:10.1029/1999GL010729
Shay, M. A., Drake, J. F., Swisdak, M., Dorland, W., and Rogers, B. N. (2003). Inherently three dimensional magnetic reconnection: a mechanism for bursty bulk flows? Geophys. Res. Lett. 30, 1345. doi:10.1029/2002GL016267
Sitnov, M., Birn, J., Ferdousi, B., Gordeev, E., Khotyaintsev, Y., Merkin, V., et al. (2019). Explosive magnetotail activity. Space Sci. Rev. 215, 31. doi:10.1007/s11214-019-0599-5
Sonett, C. P., Judge, D. L., Sims, A. R., Sims, A. R., and Kelso, J. M. (1960). A radial rocket survey of the distant geomagnetic field. J. Geophys. Res. 65, 55–68. doi:10.1029/JZ065i001p000551960
Spanswick, E., Reeves, G. D., Donovan, E., and Friedel, R. H. W. (2010). Injection region propagation outside of geosynchronous orbit. J. Geophys. Res. 115. doi:10.1029/2009JA015066
Stawarz, J. E., Ergun, R. E., and Goodrich, K. A. (2015). Generation of high-frequency electric field activity by turbulence in the Earth's magnetotail. J. Geophys. Res. Space Phys. 120, 1845–1866. doi:10.1002/2014JA020166
Stepanova, M. V., Antonova, E. E., Bosqued, J. M., Kovrazhkin, R. A., and Aubel, K. R. (2002). Asymmetry of auroral electron precipitations and its relationship to the substorm expansion phase onset. J. Geophys. Res. 107 (A7), 1134. doi:10.1029/2001JA003503
Stepanova, M. V., Antonova, E. E., and Troshichev, O. A. (2003). Intermittency of magnetospheric dynamics through non-Gaussian distribution function of PC-index fluctuations. Geophys. Res. Lett. 30 (3), 1127. doi:10.1029/2002GL0107010.1029/2002gl016070
Stepanova, M., Vucina-Parga, T., Antonova, E., Ovchinnikov, I., and Yermolaev, Y. (2005). Variation of the plasma turbulence in the central plasma sheet during substorm phases observed by the Interball/tail satellite. J. Atmos. Solar-Terrestrial Phys. 67, 1815–1820. doi:10.1016/j.jastp.2005.01.013
Stepanova, M. V., Antonova, E. E., Foppiano, A. J., and Rosenberg, T. J. (2006). Intermittency in the auroral absorption fluctuations as manifestation of magnetospheric turbulence. Adv. Space Res. 37 (3), 559–565. doi:10.1016/j.asr.2005.04.112
Stepanova, M., Antonova, E. E., Paredes-Davis, D., Ovchinnikov, I. L., and Yermolaev, Y. I. (2009). Spatial variation of eddy-diffusion coefficients in the turbulent plasma sheet during substorms. Ann. Geophys. 27, 1407–1411. doi:10.5194/angeo-27-1407-200910.5194/angeo-27-1407-2009
Stepanova, M., and Antonova, E. E. (2011). Modeling of the turbulent plasma sheet during quiet geomagnetic conditions. J. Atmos. Solar-Terrestrial Phys. 73, 1636–1642. doi:10.1016/j.jastp.2011.02.009
Stepanova, M., Pinto, V., Valdivia, J. A., and Antonova, E. E. (2011). Spatial distribution of the eddy diffusion coefficients in the plasma sheet during quiet time and substorms from THEMIS satellite data. J. Geophys. Res. 116, A00I24. doi:10.1029/2010JA015887
Tang, C. L. (2012). A plasma flow vortex in the magnetotail and its related ionospheric signatures. Ann. Geophys. 30, 537–544. doi:10.5194/angeo-30-537-2012
Troshichev, O. A. (1982). Polar magnetic disturbances and field-aligned currents. Space Sci. Rev. 32, 275–360. doi:10.1007/BF00167945
Troshichev, O. A., Antonova, E. E., and Kamide, Y. (2002). Inconsistency of magnetic field and plasma velocity variations in the distant plasma sheet: violation of the "frozen-in" criterion? Adv. Space Res. 30 (12), 2683–2687. doi:10.1016/S0273-1177(02)80382-9
Uritsky, V. M., and Pudovkin, M. I. (1998). Low frequency 1/f-like fluctuations of the AE-index as a possible manifestation of self-organized criticality in the magnetosphere. Ann. Geophys. 16 (12), 1580–1588. doi:10.1007/s00585-998-1580-x
Uritsky, V. M., Klimas, A. J., Vassiliadis, D., Chua, D., and Parks, G. (2002). Scale-free statistics of spatiotemporal auroral emissions as depicted by POLAR UVI images: dynamic magnetosphere is an avalanching system. J. Geophys. Res. 107 (A12), 1426. doi:10.1029/200100028110.1029/2001ja000281
Uritsky, V. M., Klimas, A. J., and Vassiliadis, D. (2003). Evaluation of spreading critical exponents from the spatiotemporal evolution of emission regions in the nighttime aurora. Geophys. Res. Lett. 30 (15), 1813. doi:10.1029/2002GL016556
Uritsky, V. M., Donovan, E., Klimas, A. J., and Spanswick, E. (2008). Scale-free and scale-dependent modes of energy release dynamics in the nighttime magnetosphere. Geophys. Res. Lett. 35, L21101. doi:10.1029/2008GL035625
Uritsky, V. M., Donovan, E., Klimas, A. J., and Spanswick, E. (2009). Collective dynamics of bursty particle precipitation initiating in the inner and outer plasma sheet. Ann. Geophys. 27, 745–753. doi:10.5194/angeo-27-745-2009
Volwerk, M., Vörös, Z., Baumjohann, W., Nakamura, R., Runov, A., Zhang, T. L., et al. (2004). Multi-scale analysis of turbulence in the Earth's current sheet. Ann. Geophys. 22, 2525–2533. doi:10.5194/angeo-22-2525-2004
Vörös, Z., Baumjohann, W., Nakamura, R., Runov, A., Zhang, T. L., Volwerk, M., et al. (2003). Multi-scale magnetic field intermittence in the plasma sheet. Ann. Geophys. 21, 1955–1964. doi:10.5194/angeo-21-1955-2003
Vörös, Z., Baumjohann, W., Nakamura, R., Volwerk, M., Runov, A., Zhang, T. L., et al. (2004). Magnetic turbulence in the plasma sheet. J. Geophys. Res. 109, A11215. doi:10.1029/2004JA010404
Vörös, Z., Baumjohann, W., Nakamura, R., Volwerk, M., and Runov, A. (2006). Bursty bulk flow driven turbulence in the Earth's plasma sheet. Space Sci. Rev. 122, 301–311. doi:10.1007/s11214-006-6987-7
Vörös, Z., Yordanova, E., Varsani, A., Genestreti, K. J., Khotyaintsev, Y. V., Li, W., et al. (2017). MMS observation of magnetic reconnection in the turbulent magnetosheath. J. Geophys. Res. Space Phys. 122, 11,442–11,467. doi:10.1002/2017JA024535
Vörös, Z., Yordanova, E., Khotyaintsev, Y. V., Varsani, A., and Narita, Y. (2019). Energy conversion at kinetic scales in the turbulent magnetosheath. Front. Astron. Space Sci. 6, 60. doi:10.3389/fspas.2019.00060
Wang, C.-P., Lyons, L. R., Nagai, T., Weygand, J. M., and Lui, A. T. Y. (2010). Evolution of plasma sheet particle content under different interplanetary magnetic field conditions. J. Geophys. Res. 115. doi:10.1029/2009JA015028
Wang, C.-P., Yue, C., Zaharia, S., Xing, X., Lyons, L., Angelopoulos, V., et al. (2013). Empirical modeling of plasma sheet pressure and three-dimensional force-balanced magnetospheric magnetic field structure: 1. observation. J. Geophys. Res. Space Phys. 118, 6154–6165. doi:10.1002/jgra.50585
Watanabe, K., and Sato, T. (1990). Global simulation of the solar wind-magnetosphere interaction: the importance of its numerical validity. J. Geophys. Res. 95 (A1), 75–88. doi:10.1029/JA095iA01p00075
Weimer, D. R. (1996). A flexible, IMF dependent model of high-latitude electric potentials having "Space Weather" applications. Geophys. Res. Lett. 23 (18), 2549–2552. doi:10.1029/96GL02255
Weygand, J. M., Kivelson, M. G., Khurana, K. K., Schwarzl, H. K., Thompson, S. M., McPherron, R. L., et al. (2005). Plasma sheet turbulence observed by Cluster II. J. Geophys. Res. 110, A01205. doi:10.1029/2004JA010581
Xing, X., Lyons, L. R., Angelopoulos, V., Larson, D., McFadden, J., Carlson, C., et al. (2009). Azimuthal plasma pressure gradient in quiet time plasma sheet. Geophys. Res. Lett. 36, L14105. doi:10.1029/2009GL038881
Yermolaev, Y. I., Petrukovich, A. A., Zelenyj, L. M., Antonova, E. E., Ovchinnikov, I. L., and Sergeev, V. A. (1995). Investigation of the structure and dynamics of the plasma sheet: the CORALL experiment of the INTERBALL project. Kosmicheskie Issledovaniia 38 (1), 16–(22.) [In Russian].
Yordanova, E., Vörös, Z., Varsani, A., Graham, D. B., Norgren, C., Khotyaintsev, Y. V., et al. (2016). Electron scale structures and magnetic reconnection signatures in the turbulent magnetosheath. Geophys. Res. Lett. 43, 5969–5978. doi:10.1002/2016GL069191
Keywords: magnetosphere, plasma sheet, medium and large-scale turbulence, pressure balance, substorm
Citation: Antonova EE and Stepanova MV (2021) The Impact of Turbulence on Physics of the Geomagnetic Tail. Front. Astron. Space Sci. 8:622570. doi: 10.3389/fspas.2021.622570
Received: 28 October 2020; Accepted: 10 February 2021;
Published: 23 March 2021.
Edited by:
Luca Sorriso-Valvo, Institute for Space Physics (Uppsala), SwedenReviewed by:
Gaetano Zimbardo, University of Calabria, ItalyCopyright © 2021 Antonova and Stepanova. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Elizaveta E. Antonova, ZWxpemF2ZXRhLmFudG9ub3ZhQGdtYWlsLmNvbQ==; Marina V. Stepanova, bWFyaW5hLnN0ZXBhbm92YUB1c2FjaC5jbA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.