- 1Department of Physics and Astronomy, UCLA, Los Angeles, CA, United States
- 2Community Coordinated Modeling Center, NASA GSFC, Greenbelt, MD, United States
- 3Department of Physics, CUA, Washington, DC, United States
- 4Department of Earth, Planetary, and Space Sciences, University of California, Los Angeles, CA, United States
- 5Department of Mathematics, KU Leuven, Leuven, Belgium
- 6Space Science Institute, Boulder, CO, United States
- 7University of Maryland Baltimore County, Baltimore, MD, United States
Magnetohydrodynamic (MHD) turbulent flows are found in the solar wind, the magnetosheath and the magnetotail plasma sheet. In this paper, we review both observational and theoretical evidence for turbulent flow in the magnetotail. MHD simulations of the global magnetosphere for southward interplanetary magnetic field (IMF) exhibit nested vortices in the earthward outflow from magnetic reconnection that are consistent with turbulence. Similar simulations for northward IMF also exhibit enhanced vorticity consistent with turbulence. These result from Kelvin-Helmholtz (KH) instabilities. However, the turbulent flows association with reconnection fill much of the magnetotail while the turbulent flows associated with the KH instability are limited to a smaller region near the magnetopause. Analyzing turbulent flows in the magnetotail is difficult because of the limited extent of the tail and because the flows there are usually sub-magnetosonic. Observational analysis of turbulent flows in the magnetotail usually assume that the Taylor frozen-in-flow hypothesis is valid and compare power spectral density vs. frequency with spectral indices derived for fluid turbulence by Kolmogorov in 1941. Global simulations carried out for actual magnetospheric substorms in the tail enable the results of the simulations to be compared directly with observed power spectra. The agreement between the two techniques provides confidence that the plasma sheet plasma is actually turbulent. The MHD results also allow us to calculate the power vs. wave number; results that also support the idea that the tail is turbulent.
Introduction
One of the primary goals of current investigations in space physics is to understand how electromagnetic energy stored in the magnetotail is transferred to plasma energy. Turbulence is a multi-scale phenomenon that mediates the transport of energy, mass, and momentum. Unsteady, but nonrandom fluctuations in the magnetic and electric fields and flows characterize turbulence (e.g., Karimabadi et al., 2013). Turbulent spectra have been observed in many space plasmas. For example, turbulent fluctuation spectra have been found in the solar wind (Coleman, 1968; Matthaeus and Goldstein 1982; Roberts et al., 1987a; Roberts et al., 1987b; Tu et al., 1989; Marsch and Tu, 1990; Sahraoui et al., 2010), in the magnetosheath (Zimbardo et al., 2010; Li et al., 2020) and in the magnetosphere (Borovsky et al., 1997; Lui 2001; Weygand 2005; Weygand et al., 2006; Weygandf et al., 2007). In the magnetosphere, turbulence exists over a wide range of scales from large scale magnetohydrodynamic (MHD) flows to kinetic dissipation scales (see Zimbardo et al., (2010) for a review of turbulence studies in the geospace environment including both the magnetosheath and the magnetosphere). Emphasis in this paper is on our understanding of the MHD turbulence, its consequences for transport and dynamics, and, specifically, its relationship to magnetic reconnection, with a focus on the magnetotail. In particular, several studies have presented evidence that turbulence in the plasma sheet is an important mechanism for energizing plasma in the magnetotail (Borovsky et al., 1997; Angelopoulos et al., 1999; Chang, 1999; Klimas, 2000; Borovsky and Funsten 2003; Weygand et al., 2007).
In general, turbulence in plasmas can be thought of as resulting from oscillations in velocity or magnetic field driven by nonlinear processes at large scales (Kadomtsev, 1965) and as vorticity in fluid motion where the inertial forces in the vortices are larger than the forces that are damping the eddies (Leung and Gibson, 2004). The turbulence in any medium transfers energy from the largest scales to small dissipation scales, but, in some circumstances, can involve an inverse transfer from small scales to large scales (Frisch and Kolmogorov, 2001). Observations of turbulent fluctuations in the solar wind have been discussed for decades. For example, one of the primary goals of the Parker Solar Probe mission (Nature 2019) is to find the source of the Alfvénic turbulence in the solar corona. Compared to the solar wind, there are relatively few observational studies of turbulence in the magnetosphere. Such studies as there are include observations of the fluctuations in the magnetic field, plasma, and electric field measurements associated with power in both the inertial range and the dissipation range. A schematic of this process is shown in Figure 1. The large scales, or energy containing scales, will drive turbulence to an inertial range that, in fluid turbulence, was shown by Kolmogorov (1941) to have a power spectral index as a function of wave number that is –5/3. In this range of scales, turbulent eddies will break-down until dissipation causes the spectrum to steepen as viscosity damps the eddies. The beginning of the dissipative range is the Taylor scale (Kolmogorov 1941) scale and it is at this (kinetic scale) that heating occurs as the fluctuations are damped. In space, one generally measures time series, so that the power spectra are usually shown as a function of frequency but the validity of such a representation depends on the nature of the background flow and the properties of the fluctuations and often is determined by the validity of the Taylor frozen-in-flow hypothesis (Taylor, 1938), which is discussed in more detail below.

FIGURE 1. Schematic of a typical power spectral density plot for turbulent solar wind. The lowest frequencies are at the energy containing scales and the dissipation range is at the highest frequencies. The correlation scale (left most dashed gray line) separates energy containing scales and the inertial range while the Kolmogorov scale (right most dashed gray line) is between the inertial range and the dissipation range. The third scale on the schematic is the Taylor scale (middle dashed gray line), the scale at which eddies start to damp out, (Adapted from Goldstein et al. (1995)).
In this review, we first consider in Observations of Turbulence in the Magnetotail the observational evidence that turbulence exists in the tail. The approach used for studies of solar wind turbulence is not directly applicable to the magnetotail because contrary to the case in the solar wind, boundary effects are often important and the fluctuations may not satisfy conditions required of a random stationary process (Matthaeus and Goldstein, 1982; Perri and Balogh, 2010) which justifies construction of power spectra. In the super-Alfvénic solar wind flow, one can usually assume the validity of the Taylor frozen-in-flow hypothesis (Taylor, 1938) which justifies the transformation from frequency spectra to wave number. The Taylor hypothesis states that frequency ω relates linearly to the wave vector k (i.e., ω = k v, where v is the plasma velocity) when the magnetic field evolves on a timescale longer than the time it takes it to flow past the spacecraft. In the magnetotail, the flow rarely exceeds the Alfvén speed and thus time and spatial scales are difficult to separate and determining the power spectrum of fluctuations as a function of wavenumber is challenging. Therefore, it is difficult to determine unambiguously the spectra of observed fluctuations. The flow speeds in the magnetosheath are usually higher and use of the Taylor hypothesis is frequently valid.
Consequently, we include a discussion of a variety of analysis methods in our discussion of fluctuations in the tail. In addition, analysis techniques used for studies of magnetic reconnection in the magnetotail can be applied to analyze the nature of the observed flows.
A number of generation mechanisms including flow shear instabilities such as the Kelvin-Helmholtz instability and flows from reconnection have been proposed (Matthaeus et al., 1984; Montgomery 1987; Angelopoulos et al., 1993; Borovsky et al., 1997; Lui 2001; Antonova and Ovchinnikov, 2002; Vörös et al., 2003). In Magnetohydrodynamic Simulations of Turbulence in the Magnetotail, we review work on evaluating the mechanisms by using MHD simulations. Finally, in Some Unsolved Questions About Turbulence That can be Addressed Using Modeling, we consider several unsolved problems associated with turbulence in the tail and discuss future simulations to address them.
Observations of Turbulence in the Magnetotail
A simplistic method suggesting the presence of turbulent fluctuations in a time series is to examine the spectral index in the inertial range of the power spectra. Kolmogorov (1941) used dimensional analysis to argue that the spectral index for fully developed fluid turbulence should be -5/3 for spectra of power vs. wavenumber. Perhaps surprisingly, this value is frequently observed in the fluctuating magnetic fields of the solar wind and magnetosheath (also see, Podesta et al. (2007)). On the other hand, Kraichnan (1965) found a value of -3/2 for ideal isotropic incompressible MHD turbulence. The difference between the neutral fluid values and magnetized fluid value comes from the number of degrees of freedom in the fluid. In both derivations, the rate of energy transfer from the driving scale of the spectra to the dissipation range of the spectrum was held constant. Whether or not the energy transfer rate is constant is important for differentiating Kraichnan and Kolmogorov type turbulence from intermittent turbulence. In intermittent turbulence, the energy transfer rate may not be constant and the turbulence may not yet be fully developed.
Within the plasma sheet, Borovsky et al. (1997) used ISEE-2 data and found for the plasma flow velocities that the slope of the power spectral density vs. frequency was -0.8 to -2.0 while that for the magnetic fieldit was between −1.6 and −3.0. Borovsky et al. (1997) used a “random sweeping model to approximate the conversion from wavenumber to frequency. (Even though these values include the theoretical value they do not confirm the presence of turbulent flows in the plasma sheet). Several different phenomena can explain these values including waves and/or driving phenomena, or it could be that the time series is neither stationary nor fully developed. Borovsky and Funsten (2003) suggested that this range of spectral indices could result from boundary effects or a combination of driving mechanisms each with different spectral indices. Weygand et al. (2005) found spectral indices in Cluster plasma sheet magnetic field data that were closer to −2 for the inertial range but did not take into account the speed of the flows. Vӧrӧs et al. (2004), also using Cluster magnetic field data, obtained a value of −2.6, but it is not clear if this value applies to the inertial range, dissipation range, or somewhere in between. Ergun et al. (2014) used MMS data and found a clear spectral index of −5/3 within the magnetic field inertial range, but a spectral index closer −3/2 in the electric field inertial range data. Chaston et al. (2012) found a similar value within the inertial range for electric field power spectra using THEMIS plasma sheet electric field data. Overall, the studies show that for slow speed flow the Taylor hypothesis is not valid but may be valid for high speed flows like those associated with magnetic reconnection. More work on this is needed.
Kozak et al. (2018) used the magnetic field measurements from four spacecraft of the Cluster mission for the analysis of turbulent processes in Earth’s magnetotail. They obtained power-law scaling of the generalized diffusion coefficient indicating the presence of super-diffusion processes. Prior to the dipolarization, the spectral index was in the range between −1.68 and −2.08 while in the dipolarization on larger time scales the index was between −2.2 and −1.53. However, when they examined the data in the dipolarization on smaller time scales they found that the range was −2.89 to −2.35. They also report that the break in the spectra occurs at approximately the average proton gyrofrequency.
The wide range of spectral indices from the magnetic field and electric field data suggests the presence of intermittent turbulence within the plasma sheet. One method of determining the presence of intermittent turbulence is to look for non-self-similar scaling of the fluctuation probability distribution function. A number of studies have demonstrated that non-self-similar scaling of probability distribution functions exists within the plasma sheet (Weygand et al., 2005; Weygand et al., 2006; Stawarz et al., 2015]. To determine if there is non-self-similar scaling, one constructs probability distribution functions of the fluctuations across a range of times and calculates the kurtosis (i.e., fourth moment) for each distribution. If the kurtosis systematically decreases with increasingly temporal separation in the time series, then most likely the turbulence is intermittent (Weygand et al., 2006). All three of these studies found that magnetic field fluctuations observed with Cluster and THEMIS exhibited non-self-similar scaling of probability distributions during geomagnetic active periods within the plasma sheet. Both Stawarz et al. (2015) and Weygand et al. (2005) used single spacecraft observations to show non-self-similar scaling, which requires that the Taylor hypothesis applies, and suggests that the fluctuations are evolving slowly with respect to the time required for the plasma to flow past the spacecraft and are consequently frozen in the flow. Weygand et al. (2006) took this method one step further and avoided assuming the Taylor hypothesis by using pairs of Cluster spacecraft separated in space to show that non-self-similar scaling is present within the plasma sheet magnetic field. This non-self-similar scaling demonstrated the presence of intermittent turbulence in the plasma sheet. Thus much of the prior work suggests that turbulence is present in the plasma sheet, but that it may not be fully developed or may be intermittent.
Assuming that turbulence is present in the plasma sheet, we can determine the three fundamental associated scale lengths, viz., the correlation scale, the Taylor scale, and the Kolmogorov scale (Goldstein et al., 1995; Weygand et al., 2007). The correlation scale is the energy-containing scale and the scale at which the inertial range turbulent cascade begins to exhibit a power spectrum. The Taylor scale is the scale at which the turbulent eddies begin to damp out, and the Kolmogorov scale is the point at which dissipation begins (Figure 1). A series of studies by Weygand et al., 2007; Weygand et al., 2009; Weygand et al., 2010) used Cluster spacecraft pairs over many years combining many different intervals to produce two-dimensional cross correlation maps of the magnetic field fluctuations within the plasma sheet. An example of such a map is shown in Figure 2. From these maps, we can determine correlation scales and Taylor scales. The correlation scale is the 1/e folding distance on the correlation vs. spacecraft separation curve and the Taylor scale is the radius of curvature of the two point cross correlation function of the magnetic field fluctuations at the origin (Matthaeus et al., 2005; Weygand et al., 2007). Weygand et al., 2007; Weygand et al., 2009; Weygand et al., 2010) found that the correlation scale and Taylor scale varied with their angle with respect to the mean magnetic field direction for geomagnetically quiet and moderate conditions. The correlation scale and Taylor scale were longest along the mean magnetic field (about 16,400 km and 2900 km, respectively) and shortest perpendicular to the field (9200 km and 1100 km, respectively). In the plasma sheet, the resulting two-dimensional correlation maps were similar to the two-dimensional correlation maps of quasi two-dimensional turbulence observed in the slow solar wind (Dasso et al., 2005; Weygand et al., 2011), suggesting the presence of quasi two-dimensional turbulence within the plasma sheet. Physically, the correlation scale is associated with the approximate thickness of the plasma sheet and/or driving scales and the Taylor scale is expected to be about the same size or larger than an ion gyroradius in the plasma sheet (∼700 km). Weygand et al. (2009) suggested that the difference in the Taylor scale size with magnetic field direction (Figure 2) might be related to dispersive and dissipative effects. Similar differences were noted in the solar wind in the same paper.
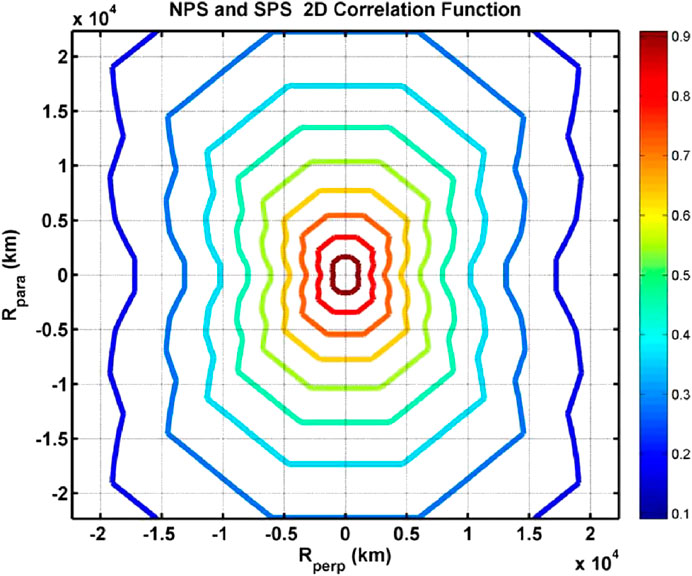
FIGURE 2. Correlation contour plot for the plasma sheet. Correlations calculated for one quadrant were mirrored into the other quadrants. Rperp is the separation perpendicular to the mean magnetic field direction and Rpara is the separation parallel to the magnetic field direction. The color bar gives the value of the cross correlation coefficient (Weygand et al., 2009).
The correlation scale (λCS) and the Taylor scale (λTS) derived from the two-dimensional correlation maps can be employed to determine an effective magnetic Reynolds number (Reff = (λCS/λTS)2) for the plasma sheet. The effective magnetic Reynolds number (i.e., Lundqvist number) is an important parameter to help validate numerical MHD models and it suggests where dissipation scale or, for Hall effects, dispersion become important. Weygand et al. (2009), Weygand et al., (2010) obtained effective magnetic Reynolds numbers between 10 and 110 for the plasma sheet. These values are similar to Lundqvist numbers for magnetospheric MHD models, but atre significantly smaller than 1600 reported in Vӧrӧs et al. (2006). El-Alaoui et al., (2010) estimated the magnetic Reynolds number from an MHD simulation to be between 100 and 1000 except near sites of reconnection where the Reynolds number is less than 10.
The statistical studies used to investigate observations of turbulence can also be applied to simulations, which enables us to compare more directly observations that indicate turbulence with the simulations. The focus of this review is on global MHD calculations of turbulence in the magnetotail but we should mention additional modeling studies using other techniques. Several calculations have modeled particle motion in turbulent fields (e.g. Taktakishvili et al. (2001), Greco et al., (2002), Zimbardo et al. (2003) We discuss the MHD simulation results in more detail in Magnetohydrodynamic Simulations of Turbulence in the Magnetotail.
Magnetohydrodynamic Simulations of Turbulence in the Magnetotail
The MHD equations written in primitive form illustrate the nonlinear terms responsible for MHD turbulence.
where ρ is the mass density, v is the plasma flow velocity, B is the magnetic field vector, P is the thermal pressure, µo is the permeability of free space, and
In the magnetotail at the largest scales, well described by MHD, flows driven on the scale of the entire system, break up into structures that cascade to smaller scales in an (energy cascade) (El-Alaoui et al., 2010). Borovsky and Funsten (2003) argue that plasma sheet turbulence is due to vortices, or eddies as shown in two dimensions in Matthaeus and Montgomery (1980). In the plasma sheet, turbulence produces intense mixing (Antonova and Ovchinnikov, 1999; Antonova and Ovchinnikov, 2002). A number of local (e.g. Nykyri and Otto, 2001; Nykyri et al., 2006b) and global MHD simulation studies have shown vortices forming at the magnetopause (e.g., Hwang et al., 2011; El-Alaoui et al., 2012; Hwang et al., 2012; Sorathia et al., 2019) and in the tail (e.g., Ashour-Abdalla et al., 1999; Fairfield et al., 2000; White et al., 2001; Ashour-Abdalla et al., 2002; Slinker et al., 2003; Hasegawa et al., 2004; Walker et al., 2006; Collado-Vega et al., 2007; Claudepierre et al., 2008; Hwang et al., 2011; Sorathia et al., 2019). However, the expected behavior in three dimensions has yet to be studied in any depth. Vortices observed at the magnetopause occur for both northward and southward interplanetary magnetic field (IMF) and have been interpreted as nonlinear Kelvin-Helmholtz waves (e.g. Hwang et al., 2011; El-Alaoui et al., 2012; Hwang et al., 2012; Sorathia et al., 2019). The vortices reported in the tail were, in general, not associated with boundary oscillations. For example, Ashour-Abdalla et al. (2002), Walker et al. (2006) found large-scale vortices in the central plasma sheet during simulations of prolonged intervals with southward IMF.
The results from idealized global MHD simulations of the solar wind-magnetosphere ionosphere system driven by simplified solar wind and IMF conditions (constant solar wind with either southward or northward IMF), exhibit field fluctuations with spectral properties similar to the observations (El-Alaoui et al., 2012). An interesting feature revealed by these simulations is that the fluctuation energy is transported to small regions of high dissipation as described by, for example Wan et al., (2012). However, MHD cannot reveal the processes causing the dissipation. The statistical properties of the observed fluctuations indicate that localized regions of high-dissipation are formed (see, for example, a study carried out in the solar wind by Greco et al., (2009)). The simulations show that these fluctuations are associated with reconnection (El-Alaoui et al., 2009; El-Alaoui et al., 2010). However, it is unknown whether large-scale turbulence enhances, diminishes, breaks up, or otherwise affects the micro-processes involved in magnetic reconnection. Investigating this theoretically requires particle-in-cell (PIC) simulations. However, local PIC simulations of the reconnection region do not include the substantial energy input from large-scale turbulence. It is thus important to include the large scale driving as well as the microscopic dissipation in the same calculation as was done, for example, in Wu et al., (2013).
We have recently introduced a method to couple the large scale drivers to the local kinetic scales. In this approach (Walker et al., 2019), the MHD results provide the initial state and the driving boundary conditions for a particle-in-cell simulation of a substantial portion of the magnetosphere. The use of the implicit moment method as implemented in the iPic3D code (Markidis et al., 2010) allows one to consider larger domain sizes within the kinetic approach. The approach has been shown to introduce correctly the physics of reconnection at electron scales, replicating the presence of electron crescent-shaped distributions (Lapenta et al., 2017) and of unsteady reconnection processes feeding further into the turbulence cascade (Ashour-Abdalla et al., 2016) and resulting in electron (Ashour-Abdalla et al., 2015) and ion (Lapenta et al., 2016) energization. The kinetic level of description also reveals instabilities both near the reconnection site (Lapenta, 2008; Walker et al., 2018) and in the outflow (Divin et al., 2015; Lapenta et al., 2015) that further drive (Pucci et al.,2017; Lapenta et al., 2018) and impact energy exchanges (Lapenta et al., 2016; Lapenta et al., 2020a). For instance, Lapenta et al. (2020b) argue that turbulent acceleration is responsible for the formation of power law tails in the distribution functions of energetic electrons.
Turbulence for idealized conditions
El-Alaoui et al., (2010) examined results from a 3D MHD simulation of the magnetosphere with nominal solar wind parameters and a southward IMF. They demonstrated that flows in the plasma sheet were consistent with turbulence. This global MHD simulation required very small grid spacing (<0.13 RE) to resolve flow vortices and turbulence in the plasma sheet. The simulation was run with southward IMF (5 nT) for 240 min followed by a northward IMF of the same magnitude. They found that fluctuations and eddies occurred under these steady driving conditions. In the tail, the regions of high grid resolution were large, including the near earth and mid-magnetotail regions. Snapshots taken during the southward IMF interval are in Figure 3. Three variables are superimposed in areas on the equatorial plane. The color contours display the BZ component of the magnetic field, the black arrows show flows in the plane and the white isocontours give the locations of the last closed field lines. Localized reconnection can be identified by flow reversals, from earthward to tailward, associated with reversals in the BZ component of the magnetic field. The BZ component was complex during this interval with filament like structure where it was large and positive at several locations. A spacecraft encountering this would see dipolarization front like signatures in the magnetic field. Vortices are apparent earthward of the reconnection (panel a). Nested within the larger vortices are smaller vortices (panel b) and within the smaller vortices we find even small vortices (panel c). This pattern of nested vortices exists throughout the magnetotail earthward of the reconnection sites throughout the simulation.
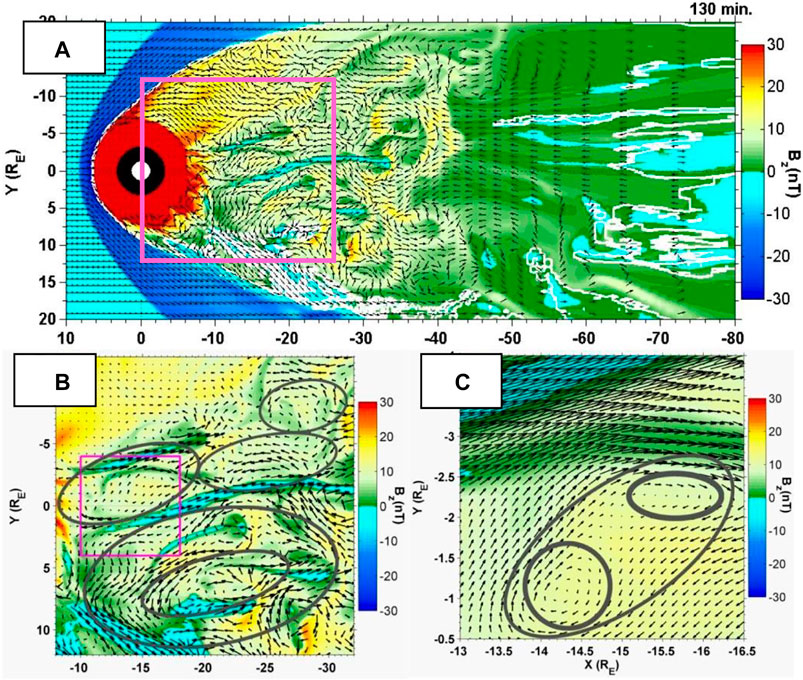
FIGURE 3. BZ color contours and flow vectors (arrows) at time 130 min in the equatorial plane. Panel (A) shows the global scale configuration; panel (B) shows the meso-scale vortices expanded; and panel (C) shows further expansion of a selected region. Note that Bz changes sign tailward of about 50 RE and is very patchy at this time. (After El-Alaoui et al. (2010)).
Figure 4 shows the power spectral density (PSD) in the tail (Figure 4A) with the Kolmogorov [1941] spectrum superimposed. The slope changes to –3 at ∼30 mHz, which we interpret as the dissipation regime. A qualitatively similar change in slope is also observed in the solar wind (e.g., Alexandrova, 2008; Chen et al., 2010; Sahraoui et al., 2010) and in the magnetosphere (e.g., Vörös et al., 2005; Nykyri et al., 2006a; Matthaeus et al., 2008).
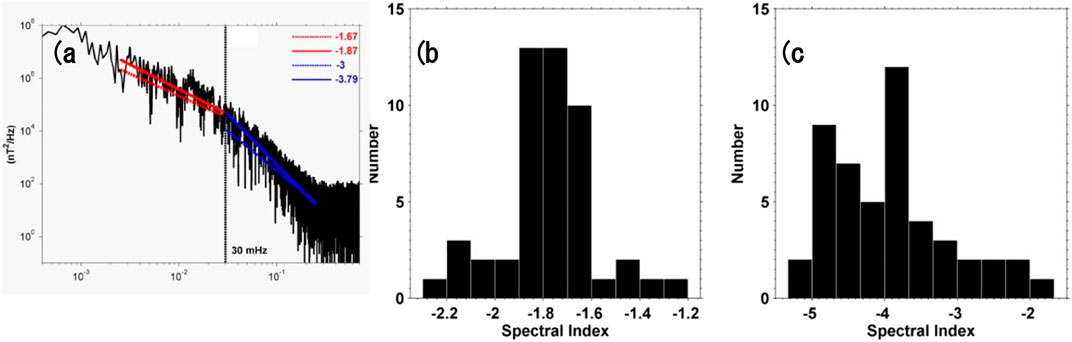
FIGURE 4. (A) Power spectra for BZ at x = −15 RE, y = −5 RE and z = 0 for southward IMF. Histograms of (B) inertial range PSD slopes (C) Dissipative range PSD slopes for southward IMF. (After El-Alaoui et al., 2010).
We computed inertial and dissipative range PSD slopes at forty-nine locations in the equatorial magnetotail. All of the PSDs at these locations exhibited the three frequency ranges defined above: the driving (energy containing) range, the inertial range, and the dissipative range. We constructed histograms of the spectral slopes for the inertial ranges (Figure 4B) and for dissipative ranges (Figure 4C) for southward IMF. We found that the PSDs have a median value of −1.77 while in the dissipative range the median value is −3.9 although the distribution is broad. In a statistical distribution of observed spectra Weygand et al. (2005) found a peak in the distribution of slopes at a spectral index of −2.0 and a weak secondary peak at a slope of −1.6. There is a trend toward more negative slopes for more tailward locations.
MHD simulations require a source of dissipation for reconnection to occur. One way to provide dissipation is to add an extra term of the form ηJ where η is a resistivity and J is the current density in Ohm’s law (El-Alaoui, 2001; El-Alaoui et al., 2009). Dissipation in the simulation contributes to plasma sheet turbulence in two ways. On a large scale, it leads to reconnection that drives the turbulent flows and on small scales it dissipates the energy. It is important to have this term in the MHD code. For instance, without this term reconnection does not occur in the tail (Raeder et al., 2001).
While the turbulent flows in these calculations are related to reconnection, turbulent flows in the magnetotail associated with the Kelvin-Helmholtz (KH) instability also have been reported. Observations of changes in the magnetopause position consistent with KH have been discussed by numerous authors (e.g., Sckopke et al., 1981; Song et al., 1988; Chen et al., 1993; Fairfield et al., 2000). Intervals with northward IMF provide an opportunity to investigate boundary oscillations in the absence of strong flows from plasma sheet reconnection. For instance, several studies have reported vortices forming along the flank boundaries from MHD simulations (Li et al., 2009; El-Alaoui et al., 2010; Sorathia et al., 2019). They indicated that the KH instability was likely the source but noted that reconnection also was occurring at high latitudes in the polar cusp region (Hwang et al., 2012). Li et al. (2009) argued that the combined processes form a cold dense boundary layer. All of the papers indicated that the process was turbulent. A typical example of the resulting flows based on the El-Alaoui et al. (2010) simulation is shown in Figure 5. Power spectral densities at different locations for the northward IMF interval are shown in Figure 6. The PSD power law indices in the inertial range had more variation than in the southward case but were still consistent with turbulence. The PSD power law indices in the dissipative range also varied widely but were generally more negative than in the inertial range.
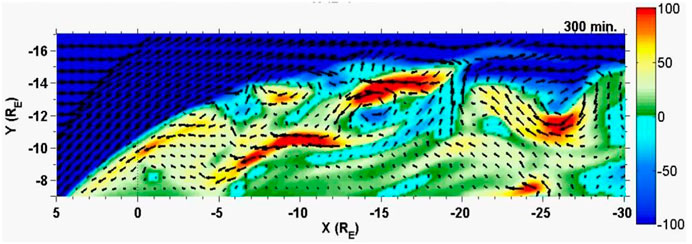
FIGURE 5. Northward IMF results at 300 min. Shown are color contours of Vx and flow vectors at the dawn flank to show the existence of waves consistent with the Kelvin-Helmholtz instability. (Adapted from El-Alaoui et al. (2010)).
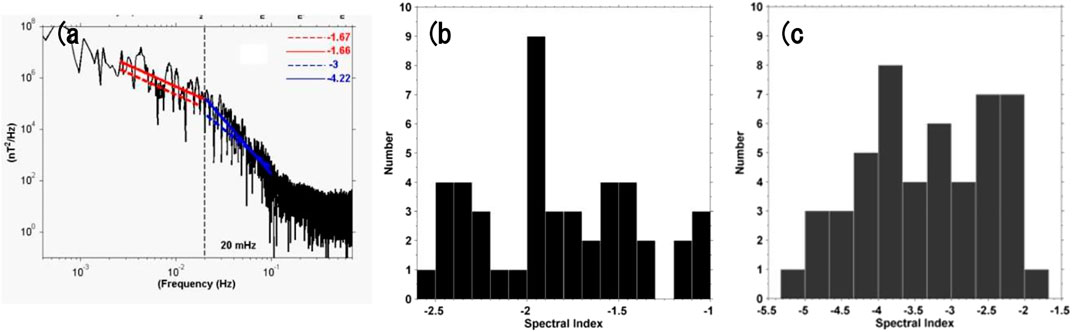
FIGURE 6. (A) Power spectra for BZ at x = −20 RE, y = −5 RE and z = 0 for northward IMF. Panel (B) contains a histogram of (B) inertial range PSD slopes and panel (C) has dissipative range PSD slopes for northward IMF (After El-Alaoui et al. (2010)).
The pattern of vorticity in the tail was much more extensive for the southward IMF. This suggests that reconnection driven flows are more important than the KH instability for driving the tail into a turbulent state. However, more work needs to be done to quantify the relative contributions of reconnection and KH.
Our ability to correctly resolve the turbulent cascade resulted in large part from recent improvements in the resolution of MHD simulations [e.g., Guild et al., 2008; El-Alaoui et al., 2009). The success in simulating the overall form of turbulent spectrum (Figure 4,6) gives us confidence That the details of dissipation may not significantly affect that overall turbulent spectrum.
MHD turbulence in simulated substorms
El-Alaoui et al., (2013) investigated the properties of fluctuations during a February 7, 2009 substorm in which the WIND spacecraft provided solar wind data. The simulation of this substorm suggests that the configuration of the tail and its evolution is very complex. The simulation results and THEMIS observations in the magnetotail were remarkably similar to dipolarizations and strong flows (see Figures 3,4 of El-Alaoui et al., (2013) for a detailed comparison between the observed magnetic field and flows and the simulation). As has been reported in previous substorm simulation studies (e.g. Ashour-Abdalla et al., (2015)) a large dipolarization grows by accreting smaller earthward-moving dipolarization fronts (DFs). In this case the dipolarizations were associated with a strong channel of earthward flow that formed a large vortex near earth. Figure 7 shows two snapshots of the flows, Bz and the thermal pressure in the plasma sheet (maximum pressure surface) at two times. The plots on the left are from 0359UT and those on the right are from 0405UT. Dipolarizations from reconnection at about X = −15RE have moved into the inner tail. The flows in these channels, combined with lower velocity return flows, form several large vortices in the plasma sheet.
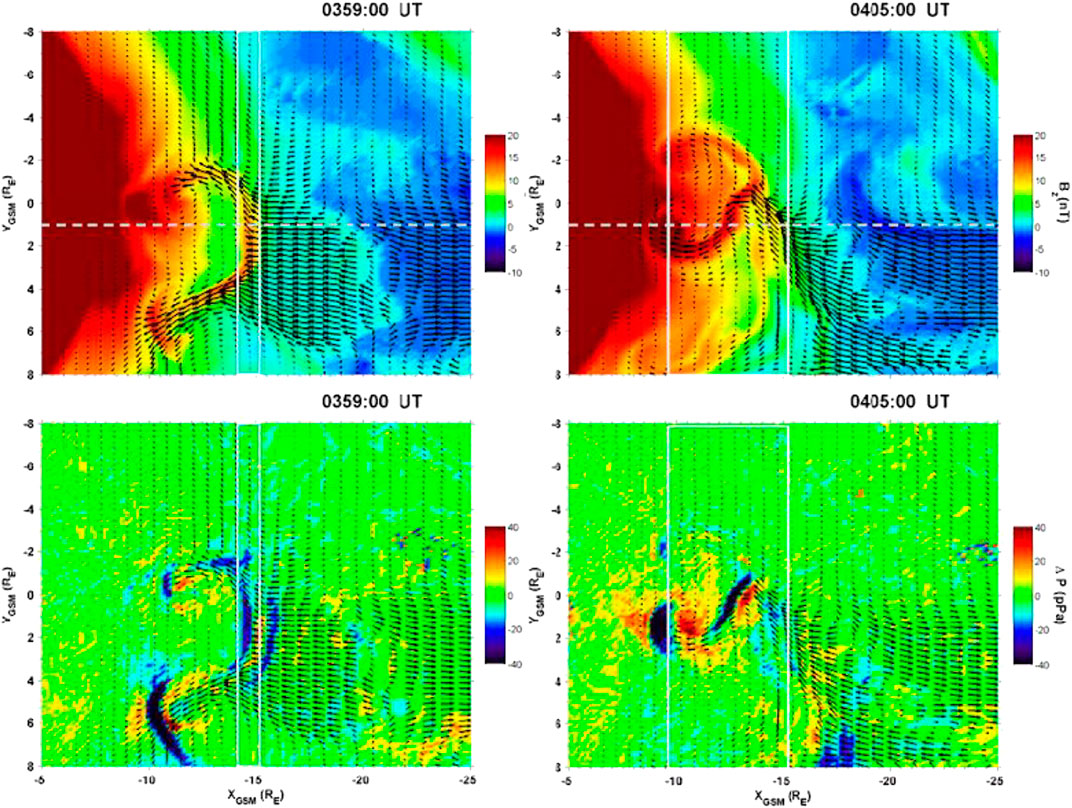
FIGURE 7. MHD results on the maximum pressure surface at two times (GSM coordinates). In the top panel, color contours show Bz and the black arrows give the flow velocity. Dipolarization fronts are located between the vertical white lines. Dipolarization fronts are clearly visible as areas of high magnetic fields which are moving earthward. The bottom panels show the change in thermal pressure from a baseline 10 s before. (After El-Alaoui et al., (2013)).
The panels in Figure 8 show successive blowups of Bz and the flows at 407UT. Within the larger vortices, we find smaller nested vortices like those found in the generic simulation described above, although the vortex structure is more complex in the event driven case (compare Figure 3 with Figures 7,8). These vortices form the low frequency end of the turbulent cascade.
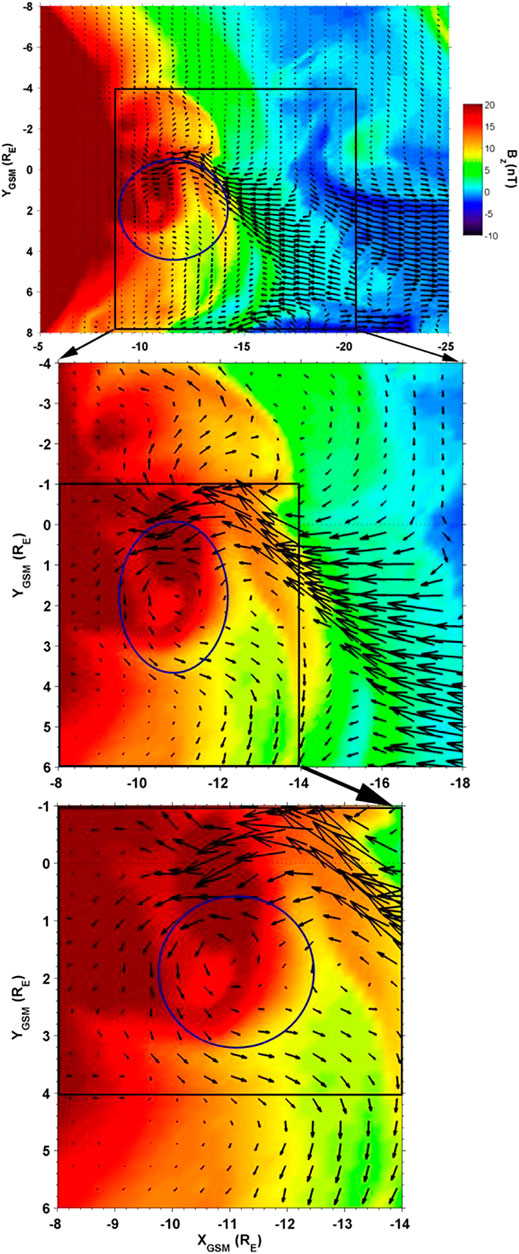
FIGURE 8. Details on the maximum pressure surface of Bz and the flow showing vortices at 0407 UT. Vortices occur on multiple time and spatial scales. (After El-Alaoui et al., 2013).
The MHD simulation and the observations show that the magnetotail mesoscale structures (e.g., dipolarizations, flow channels, localized reconnection sites, and flow vortices) during a substorms are in a state of rapid change. In Figure 9, we have compared the spectra of Bz from times between 0200 UT and 0500 UT, at z = −3 RE and y = −2 RE for three x values (−10 RE, −12 RE, and −14 RE) with observations at THEMIS P5. The driving, inertial and dissipative scales appear in both the observations and the simulation. The slope of the spectrum in the MHD results at high frequencies becomes nearly flat as the MHD time-step size (typically between 0.01 and 0.1 s) is approached. The slopes in the upper right corner of the figure come from least squares fits to the results. The simulation (black) power levels in the driving and inertial ranges frequently overlap those observed (red). The spectral indices in the inertial ranges are similar, with an observed index at P5 of −1.74 and values from −1.85 to −1.80 from the simulation. The frequency between the inertial range and the dissipative range appears to be about 30 mHz. This feature is similar to that found in the generic cases. The numerical experiments with generic simulations have shown that the overall level of dissipation in the simulation controls the location of this breakpoint (El-Alaoui et al., 2013) but does not affect the driving and inertial ranges. Although the resistivity in the MHD model gives the observed frequency where the slope changes, it does not tell us which physical mechanisms dissipate energy at the high-frequencies.
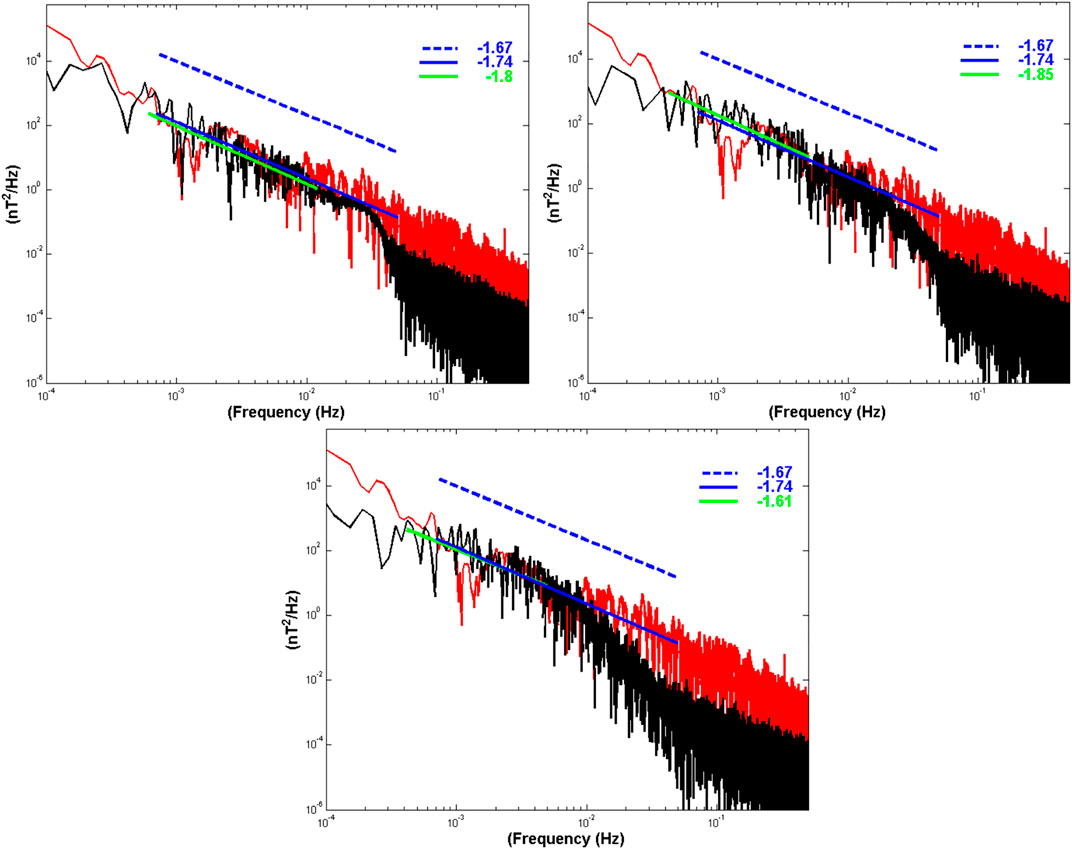
FIGURE 9. The panels show PSDs for BZ at the three locations in the MHD simulation. Values from the simulation are black and at THEMIS P5 observations are red. The solid blue (green) lines are least squares fits in the inertial range for the data (MHD results). The dashed blue lines have the slopes of -5//3.
Probability distribution functions (PDFs) enable us to characterize the turbulent flows. In particular, the fourth moment of the PDF (the kurtosis) provides a measure of non-Gaussian nature of the wings of the PDF. If the kurtosis of the PDF decreases with increasing lag (τ) the turbulence is said to be intermittent. In plasma flows, intermittent turbulence occurs if dissipation is localized to specific regions of space. Figure 10 shows the PDFs from this simulation as black curves and PDFs constructed from THEMES P5 observations in red using three lags (10, 200 and 900s). The black dotted line gives values from a Gaussian. The numbers at the top of the panels give the kurtosis. A Gaussian distribution has a kurtosis of three while the larger values reflect energy in the wings of the distributions. The kurtosis tends to decrease for increasing lags consistent with the expectations of intermittency. Similar results in the solar wind were found in Wu et al. (2013).
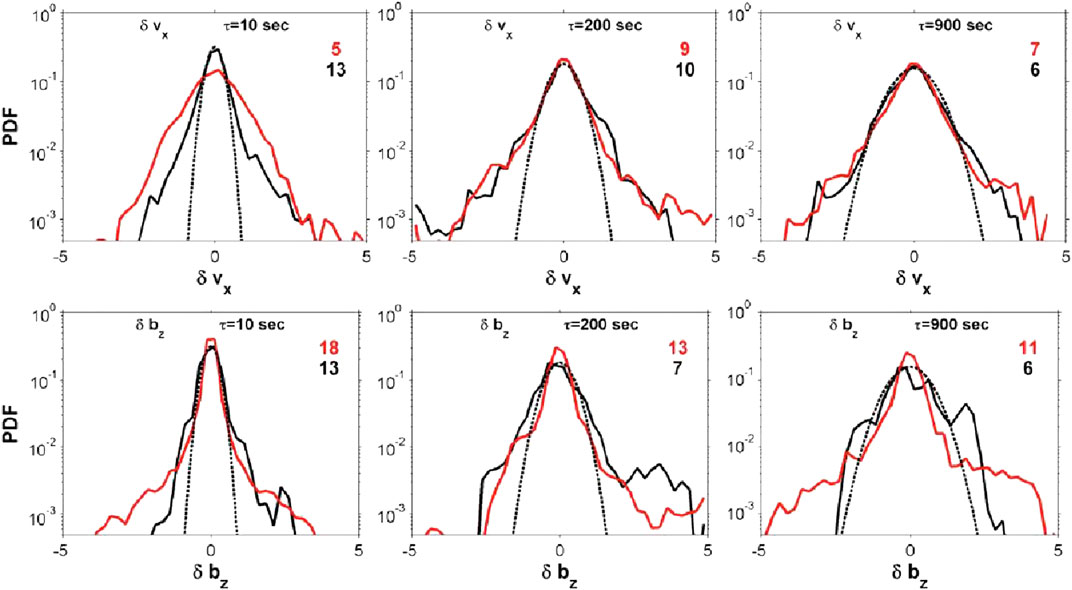
FIGURE 10. Probability Distribution Functions calculated from the simulation (black) and from THEMIS P5 observations (red). The top panels are based on the Vx component of velocity and bottom panels are based on Bz. The dashed line is a Gaussian fit. The numbers at the top give the kurtosis. (From El-Alaoui et al., 2013).
The vorticity in both the generic case (Figure 3) and the event simulation (Figure 7) suggest a strong interaction between the reconnection generated flows and the tail becoming turbulent. As discussed in Observations of Turbulence in the Magnetotail, the Taylor hypothesis may not be applicable to the tail under all flow conditions. One advantage of simulations is that we can calculate the power in k space. We computed spatial power spectra in the region between −10 and −22RE in x and −4 to 8RE in y at the maximum pressure surface (El-Alaoui et al., 2016). The fluctuations in this box were transformed to k space by using a Fourier transform. This yields the power at the allowed wavenumbers in the square domain. These are given by
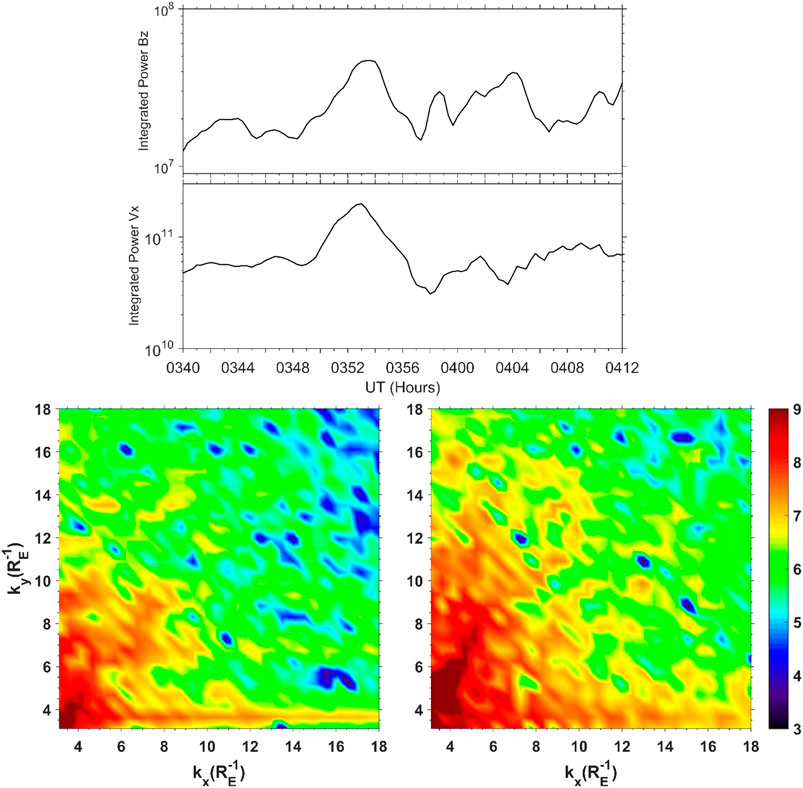
FIGURE 11. Time history of total small and mesoscale spectral power in the vicinity of flow channels and dipolarizations. For the region between −10 and −22RE in x and −4 to 8RE in y, the sum of the power in all x and y for mode numbers greater than two was computed (top two panels). The top panel shows the result for Bz, in units of nT2, and the panel below it shows the result for Vx, in units of (km/s)2. The lower two panels show the power, in units of (RE · km/s)2, vs. wavenumber at two times, 0344 UT on the left and 0353 UT on the right. (After El-Alaoui et al. (2016)).
The top panels of Figure 11 give the summed power vs. time. The maxima in the Bz and Vx power correspond with the evolution of the mesoscale structures in the magnetotail. The largest feature is a major increase in Vx power starting at 0349 UT and peaking at 0353 UT. An increase in Bz power starts at about the same time and peaks a few minutes later. The start of this increase corresponds to the formation of a narrow, intense flow channel and a large dipolarization noted above. At 0353, this large dipolarization has reached about x = −10.5 RE.
The February 7, 2009 substorm provides a rare example in the literature of a case where both observations and a simulations have been compared directly. There is considerable work from both the data analysis and the simulations that support the conclusion that localized reconnection-driven earthward flows can generate turbulent fluctuations in the tail. Observations of localized reconnection regions with strong high-speed outflow support the idea that reconnection is an important process driving turbulence in the plasma sheet (Vörös et al., 2006; Angelopoulos et al., 1999). Huang et al., (2012) and Osman et al., (2015) have analyzed the magnetic field fluctuations observed by Cluster during a period of strong earthward plasma sheet flow (∼1200 km/s). The magnetic field fluctuations are consistent with turbulence. Localized dissipation may drive these fast flows by enabling localized reconnection. The resulting outflow jets can initiate a turbulent cascade. For example, when a high-speed flow such as a bursty bulk flow (BBF) reaches the near-Earth region, that flow is diverted leading to large vortices that are several RE across [e.g., Vörös et al., 2006]. The February 7, 2009 MHD simulation of the magnetosphere shows this explicitly. In the MHD results strong narrow flow channels form (Wiltberger et al., 2000; Ashour-Abdalla et al., 2002; Walker et al., 2006; Ge et al., 2011; Birn and Hesse, 2013) at the driving scales for turbulent vortices (e.g., El-Alaoui et al., 2013). In turn, the turbulent eddies can feedback on the reconnection process as well, leading to a very complex interplay between turbulence and dissipation (Matthaeus and Lamkin, 1986; El-Alaoui et al., 2012; Donato et al., 2013). The existence of turbulent eddies may contribute to the patchiness of the reconnection occurring in MHD simulations (El-Alaoui et al., 2010). Borovsky and Funsten (2003) investigated dissipation of the turbulence and argued for small-scale eddy dissipation where the vortices dissipate energy due to reconnection. Overall the results from all of these studies strongly support the idea that fast earthward flows drive large scale vortices that initiate turbulence.
Some Unsolved Questions About Turbulence That can be Addressed Using Modeling
The simulation and data studies discussed make a strong case that flows associated with reconnection are turbulent. However, the dissipation in the MHD models used in this review depends on an additional term in Ohm’s law. The extra term has free parameters so the fluid models provide little information about the physics of the dissipation region. One challenge in modeling turbulent flows in the tail is to include the physics of dissipation on a global scale. We need a model that can extend our basic understanding of kinetic turbulence and the transition between fluid and kinetic effects. Such a model would be a combined simulation that would resolve macroscopic motions and at the same time resolve ion and electron scales. It would cover the MHD turbulent cascade at large scales (inertial range) as well as Hall (dispersive) and kinetic (dissipation) ranges. Such simulations need to capture energetic exchanges at all scales. Fluid turbulence transfers the energy of large-scale flows to small-scale fluctuations and heat. As turbulence develops, the large-scale flow breaks up into vortices that cascade down to smaller and smaller scales where energy dissipates as heat. This represents a cascade of energy from the large energy-containing scales, through intermediate scales to small scales where heating occurs. In the magnetotail, the energy at the largest scales comes from the interaction between the magnetosphere and the solar wind, while at the smallest scales the dissipation is due to wave particle interactions and reconnection occurring on length scales of the ion Larmor radius or smaller. In the magnetotail, turbulence is complicated by the coupling between velocity and magnetic field fluctuations. Furthermore, turbulence in the kinetic regime involves specific normal modes of the plasma with spatial scales associated with specific waves, e.g., lower hybrid, or ion cyclotron waves.
We have recently developed (Walker et al., 2019) a model that combines simulations that resolve the macroscopic evolution and simulations that resolve ion and electron scales. The new method covers the MHD turbulent cascade at large scales (inertial range) as well as Hall (dispersive) and kinetic (dissipation) ranges. In the application to the study of turbulence, these simulations capture energetic exchanges at all scales. Fluid turbulence transfers the energy of large-scale flows to small-scale fluctuations and heat. As turbulence develops, the large-scale flow breaks up into vortices that cascade down to smaller and smaller scales where energy dissipates as heat. This represents a cascade of energy from the large energy-containing scales, through intermediate scales to small scales where heating occurs. At the magnetopause, the energy at the largest scales comes from the interaction between the magnetosphere and the solar wind, while at the smallest scales the dissipation is due to wave particle interactions and reconnection occurring on length scales of the ion Larmor radius or smaller. In the magnetotail, turbulence is complicated by the coupling between velocity and magnetic field fluctuations. Furthermore, turbulence in the kinetic regime involves specific normal modes of the plasma with spatial scales associated with specific waves, e.g., lower hybrid, or ion cyclotron waves. It has long been recognized that the plasma distributions in the tail have non-thermal tails (a κ distribution). Recently, Lapenta et al. (2020b) have used this approach to model the acceleration of tail plasma to form this high-energy tail distribution. They argue that the main acceleration mechanism is turbulent acceleration. A similar conclusion was reached by Ergun et al. (2020) based on observations from the Magnetospheric Multi-Scale (MMS) mission.
The MMS observations come from four closely spaced satellites that provide the opportunity to investigate the turbulence in wave number space without the necessity of invoking the Taylor hypothesis. Combined with the latest kinetic simulation, these data (e.g., Ergun et al., 2018; Li et al., 2020; Ergun et al., 2020) offer great potential for understanding the importance of turbulence for acceleration in the tail and provide the community with a way to better understand the mechanisms of dissipation.
Specific issues that need to be examined include the scale of the dissipation region and its distribution in space. Fluid turbulence can develop into a state with dissipation localized in small regions of sharp gradients. How does this dissipation work in the plasma sheet when kinetic physics is included? How does dissipation occur in different regions? Is dissipation found near structures like thin current sheets (as in Wu et al., 2013), dipolarization fronts and the separatrices the result of distinct or the same processes? How do the flows become turbulent (e.g. velocity shears as in Ruffolo et al. (2020))? How important are turbulent flows for plasma heating by energy transfer from magnetic energy to particle and wave energy?
The magnetotail provides a unique laboratory for studying turbulence and reconnection. In the solar wind, turbulence has been investigated in depth for a long time (e.g. Coleman, 1968; Roberts et al., 1987a; Roberts et al., 1987b) but it is driven from the Sun over very large distances and long times but there is also evidence of reconnection driven turbulence in the solar wind (Gosling et al., 2010). In contrast in the magnetotail plasma sheet, the driving forces are well confined and comparatively short-term, developing in a few minutes over just tens of thousands of km.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by NASA NNX17AB83G and NSF-2040319. We also acknowledge NASA THEMIS contract NAS5-02099 and NASA HPDE contract 80GSFC17C0018 at UCL. The MHD computations were performed by using the Comet supercomputer at San Diego, part of the Extreme Science and Engineering Discovery Environment (XSEDE). This program is supported by grant number ACI-1548562 from the National Science Foundation. The data produced by the simulations are stored on local machines and are available upon request to the lead author.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Alexandrova, O. (2008). Solar wind vs magnetosheath turbulence and Alfvén vortices. Nonlin. Process. Geophys. 15, 95–108. doi:10.5194/npg-15-95-2008
Angelopoulos, V., Kennel, C. F., Coroniti, F. V., Pellat, R., Spence, H. E., Kivelson, M. G., et al. (1993). Characteristics of ion flow in the quiet state of the inner plasma sheet. Geophys. Res. Lett. 20 (16), 1711–1714. doi:10.1029/93GL00847
Angelopoulos, V., Mukai, T., and Kokubun, S. (1999). Evidence for intermittency in Earth's plasma sheet and implications for self-organized criticality. Phys. Plasmas 6 (11), 4161. doi:10.1063/1.873681
Antonova, E. E., and Ovchinnikov, I. L. (1999). Magnetostatically equilibrated plasma sheet with developed medium-scale turbulence: structure and implications for substorm dynamics. J. Geophys. Res. 104 (A8), 17289. doi:10.1029/1999JA900141
Antonova, E. E., and Ovchinnikov, I. L. (2002). Reconnection in the conditions of developed turbulence. Adv. Space Res. 29 (7), 1063–1068. doi:10.1016/S0273-1177(02)00022-4
Ashour-Abdalla, M., El-Alaoui, M., Coroniti, F. V., Walker, R. J., and Peroomian, V. (2002). A new convection state at substorm onset: results from an MHD study. Geophys. Res. Lett. 29 (20), 26. doi:10.1029/2002GL015787
Ashour-Abdalla, M., El-Alaoui, M., Peroomian, V., Walker, R. J., Zelenyi, L. M., Frank, L. A., et al. (1999). Localized reconnection and substorm onset on Dec. 22, 1996. Geophys. Res. Lett. 26, 3545. doi:10.1029/1999gl003630
Ashour-Abdalla, M., Lapenta, G., Walker, R., El‐Alaoui, M., Liang, H., Zhou, M., and Goldstein, M. L. (2016). Identifying the electron diffusion region in a realistic simulation of Earth's magnetotail. Geophys. Res. Lett. 43 (12), 6005–6011.
Ashour-Abdalla, M., Lapenta, G., Walker, R. J., El‐Alaoui, M., and Liang, H. (2015). Multiscale study of electron energization during unsteady reconnection events. J. Geophys. Res. Space Phys. 120 (6), 4784–4799.
Birn, J., and Hesse, M. (2013). The substorm current wedge in MHD simulations. J. Geophys. Res. Space Phys. 118 (6), 3364–3376. doi:10.1002/jgra.50187
Borovsky, J. E., Elphic, R. C., Funsten, H. O., and Thomsen, M. F. (1997). The Earth's plasma sheet as a laboratory for flow turbulence in high-β MHD. J. Plasma Phys. 57 (1), 1–34. doi:10.1017/S0022377896005259
Borovsky, J. E., and Funsten, H. O. (2003). MHD turbulence in the Earth’s plasma sheet: dynamics, dissipation, and driving. J. Geophys. Res. 108 (A7). doi:10.1029/2002JA009625
Chang, T. (1999). Self-organized criticality, multi-fractal spectra, sporadic localized reconnections and intermittent turbulence in the magnetotail. Phys. Plasmas 6 (1), 4137–4145. doi:10.1063/1.873678
Chaston, C. C., Bonnell, J. W., Clausen, L., and Angelopoulos, V. (2012). Energy transport by kinetic-scale electromagnetic waves in fast plasma sheet flows. J. Geophys. Res. 117, A09202. doi:10.1029/2012JA017863
Chen, C. H., Horbury, T. S., Schekochihin, A. A., Wicks, R. T., Alexandrova, O., and Mitchell, J. (2010). Anisotropy of solar wind turbulence between ion and electron scales. Phys. Rev. Lett. 104 (2), 255002. doi:10.1103/PhysRevLett.104.255002
Chen, S., Doolen, G., Herring, J., Kraichnan, R., Orszag, S., and She, Z. (1993). Far-dissipation range of turbulence. Phys. Rev. Lett. 70 (20), 3051–3054. doi:10.1103/PhysRevLett.70.3051
Claudepierre, S. G., Elkington, S. R., and Wiltberger, M. (2008). Solar wind driving of magnetospheric ULF waves: pulsations driven by velocity shear at the magnetopause. J. Geophys. Res. 113, A05218. doi:10.1029/2007JA012890
Coleman, P. J. J. (1968). Turbulence, viscosity, and dissipation in the solar-wind plasma. ApJ 153, 371. doi:10.1086/149674
Collado-Vega, Y. M., Kessel, R. L., Shao, X., and Boller, R. A. (2007). MHD flow visualization of magnetopause boundary region vortices observed during high-speed streams. J. Geophys. Res. 112, A06213. doi:10.1029/2006JA012104
Dasso, S., Milano, L. J., Matthaeus, W. H., and Smith, C. W. (2005). Anisotropy in fast and slow solar wind fluctuations. ApJ 635, L181–L184. doi:10.1086/499559
Divin, A., Khotyaintsev, Y. V., Vaivads, A., André, M., Markidis, S., and Lapenta, G. (2015). Evolution of the lower hybrid drift instability at reconnection jet front. J. Geophys. Res. Space Phys. 120 (4), 2675–2690. doi:10.1002/2014ja020503
Donato, S., Greco, A., Matthaeus, W. H., Servidio, S., and Dmitruk, P. (2013). How to identify reconnecting current sheets in incompressible Hall MHD turbulence. J. Geophys. Res. Space Phys. 118 (7), 4033–4038. doi:10.1002/jgra.50442
El-Alaoui, M. (2001). Current disruption during November 24, 1996, substorm. J. Geophys. Res. 106 (A4), 6229–6245.
El-Alaoui, M., Ashour-Abdalla, M., Richard, R. L., Goldstein, M. L., Weygand, J. M., and Walker, R. J. (2010). Global magnetohydrodynamic simulation of reconnection and turbulence in the plasma sheet. J. Geophys. Res. 115, A12236. doi:10.1029/2010JA015653
El-Alaoui, M., Ashour-Abdalla, M., Walker, R. J., Peroomian, V., Richard, R. L., Angelopoulos, V., et al. (2009). Substorm evolution as revealed by THEMIS satellites and a global MHD simulation. J. Geophys. Res. 114, A08221. doi:10.1029/2009JA014133
El-Alaoui, M., Richard, R. L., Ashour-Abdalla, M., Goldstein, M. L., and Walker, R. J. (2013). Dipolarization and turbulence in the plasma sheet during a substorm: THEMIS observations and global MHD simulations. J. Geophys. Res. Space Phys. 118 (12), 7752–7761. doi:10.1002/2013JA019322
El-Alaoui, M., Richard, R. L., Ashour-Abdalla, M., Walker, R. J., and Goldstein, M. L. (2012). Turbulence in a global magnetohydrodynamic simulation of the Earth's magnetosphere during northward and southward interplanetary magnetic field. Nonlin. Process. Geophys. 19 (2), 165–175. doi:10.5194/npg-19-165-2012
El-Alaoui, M., Richard, R. L., Nishimura, Y., and Walker, R. J. (2016). Forces driving fast flow channels, dipolarizations, and turbulence in the magnetotail. J. Geophys. Res. Space Phys. 121 (11), 63–111. doi:10.1002/2016JA023139
Ergun, R. E., Ahmadi, N., Kromyda, L., Schwartz, S. J., Chasapis, A., Hoilijoki, S., et al. (2020). Observations of particle acceleration in magnetic reconnection-driven turbulence. ApJ 898, 154. doi:10.3847/1538-4357/ab9ab6
Ergun, R. E., Goodrich, K. A., Stawarz, J. E., Andersson, L., and Angelopoulos, V. (2015). Large-amplitude electric fields associated with bursty bulk flow braking in the Earth's plasma sheet. J. Geophys. Res. Space Phys. 120, 1832–1844. doi:10.1002/2014JA020165
Ergun, R. E., Goodrich, K. A., Wilder, F. D., Ahmadi, N., Holmes, J. C., Eriksson, S., et al. (2018). Magnetic reconnection, turbulence, and particle acceleration: observations in the earth's magnetotail. Geophys. Res. Lett. 45, 3338–3347. doi:10.1002/2018gl076993
Fairfield, D. H., Otto, A., Mukai, T., Kokubun, S., Lepping, R. P., Steinberg, J. T., et al. (2000). Geotail observations of the Kelvin-Helmholtz instability at the equatorial magnetotail boundary for parallel northward fields. J. Geophys. Res. 105 (A9), 21159–21173. doi:10.1029/1999ja000316
Frisch, U., and Kolmogorov, A. N. (2001). Turbulence: the legacy of A.N. Kolmogorov. Cambridge, United Kingdom: Cambridge University Press
Ge, Y. S., Raeder, J., Angelopoulos, V., Gilson, M. L., and Runov, A. (2011). Interaction of dipolarization fronts within multiple bursty bulk flows in global MHD simulations of a substorm on 27 February 2009. J. Geophys. Res. 116 (A5), 57. doi:10.1029/2010JA015758
Goldstein, M. L., Roberts, D. A., and Matthaeus, W. H. (1995). Magnetohydrodynamic turbulence in the solar wind. Annu. Rev. Astron. Astrophys. 33, 283–325. doi:10.1146/annurev.aa.33.090195.001435
Gosling, J. T., Teh, W.-L., and Eriksson, S. (2010). A torsional Alfvén wave embedded within a small magnetic flux rope in the solar wind. ApJ 719, L36. doi:10.1088/2041-8205/719/1/L36
Greco, A., Matthaeus, W. H., Servidio, S., Chuychai, P., and Dmitruk, P. (2009). Statistical analysis of discontinuities in solar wind ACE data and comparison with intermittent MHD turbulence. ApJ 691 (2), L111–L114. doi:10.1088/0004-637X/691/2/L111
Greco, A., Taktakishvili, A. L., Zimbardo, G., Veltri, P., and Zelenyi, L. M. (2002). Ion dynamics in the near-Earth magnetotail: magnetic turbulence versus normal component of the average magnetic field. J. Geophys. Res. 107 (A10), 1267. doi:10.1029/2002JA009270
Guild, T. B., Spence, H. E., Kepko, E. L., Merkin, V., Lyon, J. G., Wiltberger, M., et al. (2008). Geotail and LFM comparisons of plasma sheet climatology: 2. Flow variability. J. Geophys. Res. Atmos. 113 (A4). doi:10.1029/2007JA012613
Hasegawa, H., Fujimoto, M., Phan, T. D., Rème, H., Balogh, A., Dunlop, M. W., et al. (2004). Transport of solar wind into Earth's magnetosphere through rolled-up Kelvin-Helmholtz vortices. Nature 430 (7001), 755–758. doi:10.1038/nature02799
Huang, S. Y., Zhou, M., Sahraoui, F., Vaivads, A., Deng, X. H., André, M., et al. (2012). Observations of turbulence within reconnection jet in the presence of guide field. Geophys. Res. Lett. 39 (11), L11104. doi:10.1029/2012GL052210
Hwang, K.-J., Goldstein, M. L., Kuznetsova, M. M., Wang, Y., Viñas, A. F., and Sibeck, D. G. (2012). The first in situ observation of Kelvin-Helmholtz waves at high-latitude magnetopause during strongly dawnward interplanetary magnetic field conditions. J. Geophys. Res. 117 (A8), a. doi:10.1029/2011JA017256
Hwang, K.-J., Kuznetsova, M. M., Sahraoui, F., Goldstein, M. L., Lee, E., and Parks, G. K. (2011). Kelvin-Helmholtz waves under southward interplanetary magnetic field. J. Geophys. Res. 116, A08210. doi:10.1029/2011JA016596
Karimabadi, H., Roytershteyn, V., Wan, M., Matthaeus, W. H., Daughton, W., Wu, P., et al. (2013). Coherent structures, intermittent turbulence, and dissipation in high-temperature plasmas. Phys. Plasmas 20 (1), 012303. doi:10.1063/1.4773205
Klimas, A. J., Valdivia, J. A., Vassiliadis, D., Baker, D. N., Hesse, M., and Takalo, J. (2000). Self-organized criticality in the storm phenomenon and its relation to localized reconnection in the magnetospheric plasma sheet. J. Geophys. Res. 105 (A8), 18765–18780. doi:10.1029/1999ja000319
Kolmogorov, A. N. (1941). The local structure of turbulence in incompressible viscous fluid for very large Reynolds’ numbers. Dokl. Akad. Nauk SSSR 30, 301–305.
Kozak, L. V., Petrenko, B. A., Lui, A. T. Y., Kronberg, E. A., Grigorenko, E. E., and Prokhorenkov, A. S. (2018). Turbulent processes in the Earth's magnetotail: spectral and statistical research. Ann. Geophys. 36, 1303–1318. doi:10.5194/angeo-36-1303-2018
Kraichnan, R. H. (1965). Inertial-range spectrum of hydromagnetic turbulence. Phys. Fluids 8, 1385. doi:10.1063/1.1761412
Lapenta, G., Ashour‐Abdalla, M., Walker, R. J., and El Alaoui, M. (2016). A multiscale study of ion heating in Earth's magnetotail. Geophys. Res. Lett. 43 (2), 515–524. doi:10.1002/2015gl066689
Lapenta, G., Berchem, J., El Alaoui, M., and Walker, R. (2020b). Turbulent energization of electron power law tails during magnetic reconnection. Phys. Rev. Lett. Appear. 125 (22), 225101. doi:10.1103/PhysRevLett.125.225101
Lapenta, G., Berchem, J., Zhou, M., Walker, R. J., El‐Alaoui, M., Goldstein, M. L., et al. (2017). On the origin of the crescent‐shaped distributions observed by MMS at the magnetopause. J. Geophys. Res. Space Phys. 122, 2024–2039. doi:10.1002/2016JA023290
Lapenta, G., El Alaoui, M., Berchem, J., and Walker, R. (2020a). Multiscale MHD‐kinetic PIC study of energy fluxes caused by reconnection. J. Geophys. Res. Space Phys. 125, e2019JA027276. doi:10.1029/2019ja027276
Lapenta, G., Goldman, M. V., Newman, D. L., and Markidis, S. (2016). Energy exchanges in reconnection outflows. Plasma Phys. Controlled Fusion 59 (1), 014019. doi:10.1088/0741-3335/59/1/014019
Lapenta, G., Markidis, S., Goldman, M. V., and Newman, D. L. (2015). Secondary reconnection sites in reconnection-generated flux ropes and reconnection fronts. Nat. Phys 11 (8), 690–695. doi:10.1038/nphys3406
Lapenta, G., Pucci, F., Olshevsky, V., Servidio, S., Sorriso-Valvo, L., Newman, D. L., et al. (2018). Nonlinear waves and instabilities leading to secondary reconnection in reconnection outflows. J. Plasma Phys. 84 (1). doi:10.1017/s002237781800003x
Lapenta, G. (2008). Self-feeding turbulent magnetic reconnection on macroscopic scales. Phys. Rev. Lett. 100 (23), 235001. doi:10.1103/PhysRevLett.100.235001
Leung, P.-T., and Gibson, C. H. (2004). Turbulence and fossil turbulence in oceans and lakes. Chin. J. Ocean. Limnol. 22, 1–23. doi:10.1007/bf02842796
Li, W., Raeder, J., Øieroset, M., and Phan, T. D. (2009). Cold dense magnetopause boundary layer under northward IMF: results from THEMIS and MHD simulations. J. Geophys. Res. 114, A00C15. doi:10.1029/2008JA013497
Lui, A. T. Y. (2001). Multifractal and intermittent nature of substorm-associated magnetic turbulence in the magnetotail. J. Atmos. Solar-Terrestrial Phys. 63 (13), 1379–1385. doi:10.1016/S1364-6826(00)00239-X
Markidis, S., Lapenta, G., and Rizwan-Uddin, G. (2010). Multi-scale simulations of plasma with iPIC3D. Mathematics Comput. Simulation 80, 1509–1519. doi:10.1016/j.matcom.2009.08.038
Marsch, E., and Tu, C.-Y. (1990). On the radial evolution of MHD turbulence in the inner heliosphere. J. Geophys. Res. 95 (A6), 8211. doi:10.1029/JA095iA06p08211
Matthaeus, W. H., Dasso, S., Weygand, J. M., Milano, L. J., Smith, C. W., and Kivelson, M. G. (2005). Spatial correlation of solar-wind turbulence from two-point measurements. Phys. Rev. Lett. 95 (2), 231101. doi:10.1103/PhysRevLett.95.231101
Matthaeus, W. H., Pouquet, A., Mininni, P. D., Dmitruk, P., and Breech, B. (2008). Rapid alignment of velocity and magnetic field in magnetohydrodynamic turbulence. Phys. Rev. Lett. 100 (8), 085003. doi:10.1103/PhysRevLett.100.085003
Matthaeus, W. H., Ambrosiano, J. J., and Goldstein, M. L. (1984). Particle acceleration by turbulent magnetohydrodynamic reconnection. Phys. Rev. Lett. 53 (15), 1449–1452. doi:10.1103/PhysRevLett.53.1449
Matthaeus, W. H., and Lamkin, S. L. (1986). Turbulent magnetic reconnection. Phys. Fluids 29 (8), 2513. doi:10.1063/1.866004
Matthaeus, W. H., and Goldstein, M. L. (1982). Stationarity of magnetohydrodynamic fluctuations. J. Geophys. Res. Atmos. 87 (A12), 10347–10354. doi:10.1029/JA087iA12p10347
Matthaeus, W. H., and Montgomery, D. C. (1980). “Selective decay hypothesis at high mechanical and magnetic Reynolds numbers,” in Nonlinear dynamics. Editors H. H. G. Hellman (New York, NY: New York Academy of Sciences), 203.
Montgomery, D. (1987). “Remarks on the MHD problem of generic magnetospheres and magnetotails,” in Magnetotail physics. Editor A. T. Y. Lui (Baltimore, MD: Johns Hopkins University Press), 203–204.
Nykyri, K., Grison, B., Cargill, P. J., Lavraud, B., Lucek, E., Dandouras, I., et al. (2006a). Origin of the turbulent spectra in the high-altitude cusp: Cluster spacecraft observations. Ann. Geophys. 24, 1057–1075. doi:10.5194/angeo-24-1057-2006
Nykyri, K., Otto, A., Lavraud, B., Mouikis, C., Kistler, L. M., Balogh, A., et al. (2006b). Cluster observations of reconnection due to the Kelvin-Helmholtz instability at the dawnside magnetospheric flank. Ann. Geophys. 24, 2619. doi:10.5194/angeo-24-2619-2006
Nykyri, K., and Otto, A. (2001). Plasma transport at the magnetospheric boundary due to reconnection in Kelvin-Helmholtz vortices. Geophys. Res. Lett. 28, 3565. doi:10.1029/2001gl013239
Osman, K. T., Kiyani, K. H., Matthaeus, W. H., Hnat, B., Chapman, S. C., and Khotyaintsev, Yu. V. (2015). Multi-spacecraft measurement of turbulence within a magnetic reconnection jet. Available at: http://arxiv.org/abs/1508.04179.
Perri, S., and Balogh, A. (2010). Stationarity in solar wind flows, ApJ, 714, 937. doi:10.1088/0004-637X/714/1/937
Podesta, J. J., Roberts, D. A., and Goldstein, M. L. (2007). Spectral exponents of kinetic and magnetic energy spectra in solar wind turbulence. ApJ 664, 543. doi:10.1086/519211
Pucci, F., Servidio, S., Sorriso-Valvo, L., Olshevsky, V., Matthaeus, W. H., Malara, F., et al. (2017). Properties of turbulence in the reconnection exhaust: numerical simulations compared with observations. ApJ 841 (1), 60. doi:10.3847/1538-4357/aa704f
Raeder, J., McPherron, R. L., Frank, L. A., Kokubun, S., Lu, G., Mukai, T., et al. (2001). Global simulation of the Geospace Environment Modeling substorm challenge event. J. Geophys. Res. 106 (A1), 323–337. doi:10.1029/2000JA000605
Roberts, D. A., Goldstein, M. L., Klein, L. W., and Matthaeus, W. H. (1987b). Origin and evolution of fluctuations in the solar wind: helios observations and Helios-Voyager comparisons. J. Geophys. Res. 92 (A11), 12023. doi:10.1029/JA092iA11p12023
Roberts, D. A., Klein, L. W., Goldstein, M. L., and Matthaeus, W. H. (1987a). The nature and evolution of magnetohydrodynamic fluctuations in the solar wind: Voyager observations. J. Geophys. Res. 92 (A10), 11021. doi:10.1029/JA092iA10p11021
Ruffolo, D., Matthaeus, W. H., Chhiber, R., Usmanov, A. V., Yang, Y. R., and Bandyopadhyay, R. (2020). Shear-driven transition to Isotropically turbulent solar wind outside the Alfvén critical zone. ApJ 902, 94. doi:10.3847/1538-4357/abb594
Sahraoui, F., Goldstein, M. L., Belmont, G., Canu, P., and Rezeau, L. (2010). Three dimensional anisotropic k spectra of turbulence at subproton scales in the solar wind. Phys. Rev. Lett. 105 (13), 13–24. doi:10.1103/PhysRevLett.105.131101
Sckopke, N., Paschmann, G., Haerendel, G., Sonnerup, B. U. Ö., Bame, S. J., Forbes, T. G., et al. (1981). Structure of the low-latitude boundary layer, J. Geophys. Res., 86, 2099.
Slinker, S. P., Fedder, J. A., Sibeck, D. G., Lyon, J. G., Frank, L. A., and Mukai, T. (2003). Simulation of magnetopause oscillations observed January 9, 1996. Geophys. Res. Lett. 30 (11), 1569. doi:10.1029/2003GL017063
Song, Y., and Lysak, R. L. (1988). Turbulent generation of auroral currents and fields-A spectral simulation of two-dimensional MHD turbulence. Geophys. Monogr. Ser. 44, 197–203. doi:10.1029/GM044p0197
Sorathia, K., Merkin, V. G., Ukhorskiy, A. Y., Allen, R. C., Nykyri, K., and Wing, S. (2019). Solar wind ion entry into the magnetosphere during northward IMF. J. Geophys. Res. Space Phys. 124, 5461–(5481.)
Stawarz, J. E., Ergun, R. E., and Goodrich, K. A. (2015). Generation of high-frequency electric field activity by turbulence in the Earth’s magnetotail. J. Geophys. Res. Space Phys. 120, 1845–1866. doi:10.1002/2014JA020166
Taktakishvilli, A. L., Greco, A., Veltri, P., Zimbardo, G., Zelenyi, L. M., and Milovanov, A. V. (2001). Magnetic turbulence and ion dynamics in the magnetotail. Astrophysics Space Sci. 277, 71–79.
Taylor, G. I. (1938). The spectrum of turbulence. Proc. R. Soc. London, Ser. A. 164, 476–490. doi:10.1098/rspa.1938.0032
Tu, C.-Y., Marsch, E., and Thieme, K. M. (1989). Basic properties of solar wind MHD turbulence near 0.3 AU analyzed by means of Elsässer variables. J. Geophys. Res. 94 (A9), 11739. doi:10.1029/JA094iA09p11739
Vörös, Z., Baumjohann, W., Nakamura, R., Volverk, M., Schwarzl, H., Balogh, A., et al. (2005). Dissipation scale in the Earth’s plasma sheet estimated from Cluster measurements, Nonlin. Processes Geophys. 12, 725–732. doi:10.5194/npg-12-725-2005
Vörös, Z., Baumjohann, W., Nakamura, R., Runov, A., Zhang, T. L., Volwerk, M., et al. (2003). Multi-scale magnetic field intermittence in the plasma sheet. Ann. Geophys. 21 (9), 1955–1964. doi:10.5194/angeo-21-1955-2003
Vörös, Z., Baumjohann, W., Nakamura, R., Volwerk, M., and Zhang, T. L. (2004). Wavelet analysis of magnetic turbulence in the Earth’s plasma sheet, Phys. Plasmas, 11. J. Geophys. Res. Space Phys. 109, 1333.
Vörös, Z., Leubner, M. P., and . Baumjohann, W. (2006). Cross-scale coupling-induced intermittency near interplanetary shocks. J. Geophys. Res. 111 (A2). doi:10.1029/2005JA011479
Walker, R. J. M., Ashour-Abdalla, M., El Alaoui, M., and Coroniti, F. V. (2006). Magnetospheric convection during prolonged intervals with southward interplanetary magnetic field. J. Geophys. Res. 111, A10219. doi:10.1029/2005JA011541
Walker, R. J., Lapenta, G., Berchem, J., El-Alaoui, M., and Schriver, D. (2019). Embedding particle-in-cell simulations in global magnetohydrodynamic simulations of the magnetosphere. J. Plasma Phys. 85 (1), 905850109. doi:10.1017/S0022377819000072
Walker, R. J., Lapenta, G., Liang, H., Berchem, J., El‐Alaoui, M., and Goldstein, M. L. (2018). Structure and dynamics of three‐dimensional magnetotail reconnection. J. Geophys. Res. Space Phys. 123 (10), 8241–8260. doi:10.1029/2018JA025509
Wan, M., Matthaeus, W. H., Karimabadi, H., Roytershteyn, V., Shay, M., Wu, P., et al. (2012). Intermittent dissipation at kinetic scales in collisionless plasma turbulence. Phys. Rev. Lett. 109 (19). doi:10.1103/PhysRevLett.109.195001
Weygand, J. M., Kivelson, M. G., Khurana, K. K., Schwarzl, H. K., Thompson, S. M., McPherron, R. L., et al. (2005). Plasma sheet turbulence observed by cluster II. J. Geophys. Res. 110, A01205. doi:10.1029/2004JA010581
Weygand, J. M., Kivelson, M. G., Khurana, K. K., Schwarzl, H. K., Walker, R. J., Balogh, A., et al. (2006). Non-self-similar scaling of plasma sheet and solar wind probability distribution functions of magnetic field fluctuations. J. Geophys. Res. 111 (A11), A08102. doi:10.1029/2006JA011820
Weygand, J. M., Matthaeus, W. H., Dasso, S., and Kivelson, M. G. (2011). Correlation and Taylor scale variability in the interplanetary magnetic field fluctuations as a function of solar wind speed. J. Geophys. Res. 116 (A8), A08102. doi:10.1029/2011JA016621
Weygand, J. M., Matthaeus, W. H., Dasso, S., Kivelson, M. G., Kistler, L. M., and Mouikis, C. (2009). Anisotropy of the Taylor scale and the correlation scale in plasma sheet and solar wind magnetic field fluctuations. J. Geophys. Res. 114 (A), 07213. doi:10.1029/2008JA013766
Weygand, J. M., Matthaeus, W. H., Dasso, S., Kivelson, M. G., and Walker, R. J. (2007). Taylor scale and effective magnetic Reynolds number determination from plasma sheet and solar wind magnetic field fluctuations. J. Geophys. Res. 112 (A10), A10201. doi:10.1029/2007JA012486
Weygand, J. M., Matthaeus, W. H., El-Alaoui, M., Dasso, S., and Kivelson, M. G. (2010). Anisotropy of the Taylor scale and the correlation scale in plasma sheet magnetic field fluctuations as a function of auroral electrojet activity. J. Geophys. Res. Space Phys. 115 (A), A12250. doi:10.1029/2010JA01599
White, W. W., Shoendorf, J. A., Siebert, K. D., Maynard, N. C., Weimer, D. R., Wilson, G. L., et al. (2001). MHD simulation of magnetospheric transport at the mesoscale. in Space weather. Editors P. Song, H. Singer, and G. Siscoe (Washington, DC: AGU).
Wiltberger, M., Pulkkinen, T. I., Lyon, J. G., and Goodrich, C. C. (2000). MHD simulation of the magnetotail during the December 10, 1996, substorm. J. Geophys. Res. 105 (A12), 27649. doi:10.1029/1999JA000251
Wu, P., Perri, S., Osman, K., Wan, M., Matthaeus, W. H., Shay, M. A., et al. (2013). Intermittent heating in solar wind and kinetic simulations. Astrophys. J. Lett. 763 (2), L30. doi:10.1088/2041-8205/763/2/L30
Zimbardo, G., Greco, A., Sorriso-Valvo, L., Perri, S., Vörös, Z., Aburjania, G., et al. (2010). Magnetic turbulence in the geospace environment. Space Sci. Rev. 156 (1–4), 89–134. doi:10.1007/s11214-010-9692-5
Keywords: turbulence, Magnetohydrodynamic, magnetotail, plasma sheet, reconnection
Citation: El-Alaoui M, Walker RJ, Weygand JM, Lapenta G and Goldstein ML (2021) Magnetohydrodynamic Turbulence in the Earth’s Magnetotail From Observations and Global MHD Simulations. Front. Astron. Space Sci. 8:620519. doi: 10.3389/fspas.2021.620519
Received: 23 October 2020; Accepted: 04 February 2021;
Published: 22 March 2021.
Edited by:
Gaetano Zimbardo, University of Calabria, ItalyReviewed by:
Antonella Greco, Università della Calabria, ItalyHui Li, National Space Science Center (CAS), China
Copyright © 2021 El-Alaoui, Walker, Weygand, Lapenta and Goldstein. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mostafa El-Alaoui, bW9zdGFmYUBwaHlzaWNzLnVjbGEuZWR1
 Mostafa El-Alaoui
Mostafa El-Alaoui Raymond J. Walker
Raymond J. Walker James M. Weygand4
James M. Weygand4 Giovanni Lapenta
Giovanni Lapenta Melvyn L. Goldstein
Melvyn L. Goldstein