Black Hole Science With the Laser Interferometer Space Antenna

Sesana, Alberto

doi:10.3389/fspas.2021.601646

MINI REVIEW article

Front. Astron. Space Sci., 18 February 2021

Sec. Cosmology

Volume 8 - 2021 | https://doi.org/10.3389/fspas.2021.601646

This article is part of the Research Topic Gravitational Waves: A New Window to the Universe View all 9 articles

Black Hole Science With the Laser Interferometer Space Antenna

Alberto Sesana*

Department of Physics G. Occhialini, University of Milano - Bicocca, Piazza della Scienza 3, Milano, Italy

The author reviews the scientific potential of the Laser Interferometer Space Antenna (LISA), a space-borne gravitational wave (GW) observatory to be launched in the early 30s. Thanks to its sensitivity in the milli-Hz frequency range, LISA will reveal a variety of GW sources across the Universe, from our Solar neighborhood potentially all the way back to the Big Bang, promising to be a game changer in our understanding of astrophysics, cosmology, and fundamental physics. This review dives in the LISA Universe, with a specific focus on black hole science, including the formation and evolution of massive black holes in galaxy centers, the dynamics of dense nuclei and formation of extreme mass ratio inspirals, and the astrophysics of stellar-origin black hole binaries.

1 Introduction

Despite the wealth of revolutionary results already delivered (Abbott et al., 2019), gravitational wave (GW) astronomy is still in its infancy. LIGO (Abbott et al., 2009) and Virgo (Acernese et al., 2015) are in fact only sensitive to binary systems of $≲ 100 M_{⊙}$ out to $z \approx 1$ , leaving us still blind to the vast majority of GW sources in the Universe. This will profoundly change within the next 2 decades, when GW revelation instruments and techniques will access sources covering a much larger spectrum of masses (upto $10^{10} M_{⊙}$ ) essentially anywhere in the Universe. The 3G detectors Einstein Telescope (Punturo et al., 2010) and Cosmic Explorer (Reitze et al., 2019) will cover the Hz to kilo-Hz frequency range, populated by binaries of compact objects (CO) of different nature, out to high redshift. Neutron star binaries (NSBs) will be observed out to $z > 2$ at a rate of tens of thousands per year, and similar rates are expected for black hole binaries (BHBs) which will be observable out to $z \approx 20$ (Van Den Broeck, 2014). Interestingly, the extension of the sensitivity window down to few Hz will open up the uncharted land of intermediate mass black holes (Jani et al., 2019). At the opposite end of the frequency and source mass spectrum, radio millisecond pulsar data, collected and analyzed by pulsar timing array (PTA, Foster and Backer, 1990) collaborations (Desvignes et al., 2016; Arzoumanian et al., 2018; Kerr et al., 2020), are the gateway to the $μ - Hz$ to nano-Hz frequency range. Here, the expectation is to detect a stochastic GW background (GWB) emerging from the incoherent superposition of signals from a cosmic population of massive black hole binaries (MBHBs), forming in the aftermath of galaxy mergers occurring along the assembly of cosmic structures (Sesana et al., 2008; Ravi et al., 2012). The international PTA (IPTA, Verbiest et al., 2016) is working in this direction and with the advent of the Square Kilometer Array (SKA, Dewdney et al., 2009), there is also the expectation to resolve the most massive inspiralling individual MBHBs in the Universe (Sesana et al., 2009; Kelley et al., 2018).

The bridging milli-Hz frequency window will be explored from space, thanks to the Laser Interferometer Space Antenna (LISA Amaro-Seoane et al., 2017), one of the next large missions of the European Space Agency with the participation of NASA, to be flown in the early 30s. Being sensitive to the milli-Hz frequency band, from $\approx 0.1$ milli-Hz to 0.1Hz, LISA is ideally suited to probe GW sources across the mass and distance scales, from the Solar neighborhood to the Big Bang. Starting from our backyard, contrary to ground-based detectors and PTAs, LISA is expected to observe a bonanza of sources within the Milky Way (MW). Those include millions of galactic compact objects (COs), mostly double white dwarfs (DWDs), building up an unresolved confusion noise around 0.5–2 milli-Hz (Nelemans et al., 2001). Up to 20 k such DWDs will be individually resolvable (Nissanke et al., 2012), along with several tens of NSBs (Lau et al., 2020) and few BHBs (Seto, 2016; Sesana et al., 2020). Moreover, LISA has the unique potential to detect the presence of planets around nearby DWDs (Tamanini and Danielski, 2019) and perhaps dozens of brown dwarfs and substellar objects orbiting SgrA^* (Freitag, 2003), known as X-MRI (Amaro-Seoane, 2019). LISA will detect many more BHBs outside the MW, being sensitive to the early inspiral of these systems centuries to weeks before they enter the ground-based detector sensitivity band, out to $z \approx 0.5$ Sesana (2016). COs inspiralling onto MBHs, known as extreme mass ratio inspirals (EMRIs), can be detected out to $z \approx 2$ Babak et al. (2017), whereas coalescing massive black hole binaries MBHBs in the mass range $10^{4} M_{⊙} < M < 10^{7} M_{⊙}$ can be seen anywhere in the Universe Klein et al. (2016). Last but not least, the frequency range covered by LISA makes it sensitive to TeV energy scales, where a stochastic GWB might be produced in the early Universe by, e.g., first-order phase transitions or cosmic defects like strings and loops. A visual summary of selected LISA sources is depicted in Figure 1, from Amaro-Seoane et al. (2017). The observation of each class of sources will provide invaluable insights in astrophysics, cosmology, and fundamental physics, which is beyond what can be reasonably tackled within the few pages of this review. We therefore focus on a subset of sources, specifically MBHBs, EMRIs, and BHBs, highlighting their astrophysical potential in particular. The payouts of studying fundamental physics with low frequency GWs are extensively described in a dedicated LRR article Gair et al. (2013), whereas a comprehensive review of cosmological GWBs with much focus on LISA can be found in Caprini and Figueroa (2018).

FIGURE 1

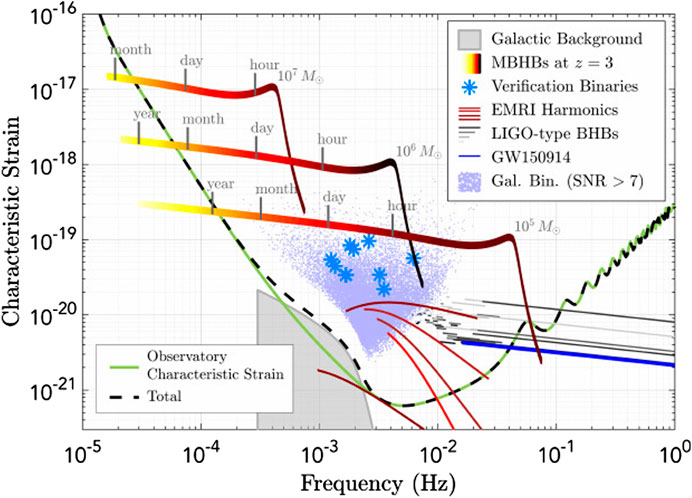
FIGURE 1. The dimensionless “characteristic strain” of GW sources in the LISA frequency band. The nominal detector sensitivity is shown by the green line. Displayed are tracks of three equal MBHBs at $z = 3$ with total masses of $10^{5}, 10^{6}, 10^{7} M_{⊙}$ , the first five harmonics of an EMRI at $z = 1.2$ (red solid lines), a sample of stellar-mass BHBs (black solid lines), and several thousands of resolvable galactic binaries (blue dots). The subset of known “verification binaries” is shown with blue asterisks. The “confusion noise” arising from the millions of galactic binaries that cannot be resolved individually is shown by the gray shaded area (Amaro-Seoane et al., 2017).

2 Massive Black Hole Binaries

MBHBs are expected to form in large number along the cosmic history (Volonteri et al., 2003). Pairing in the aftermath of galaxy mergers, they are tracers of structure formation in the Universe and can be seen by LISA out to $z > 20$ , beyond the foreseeable capabilities of any electromagnetic (EM) observation. The poor knowledge of protogalaxy and black hole seed formation at high redshift is mirrored in the large uncertainties in detection rate predictions (e.g., Sesana et al., 2011; Barausse et al., 2020). Nonetheless, LISA is expected to observe between a few and a hundred MBHB coalescences per year. The unique potential of this observatory is shown in Figure 2, where LISA signal-to-noise ratio (S/N) contours for equal-mass, nonspinning binaries are superimposed to the differential distribution of mergers occurring in 4 years (the nominal mission lifetime) in the chirp mass-redshift plane, as predicted by four selected MBH evolution models (Bonetti et al., 2019).

FIGURE 2

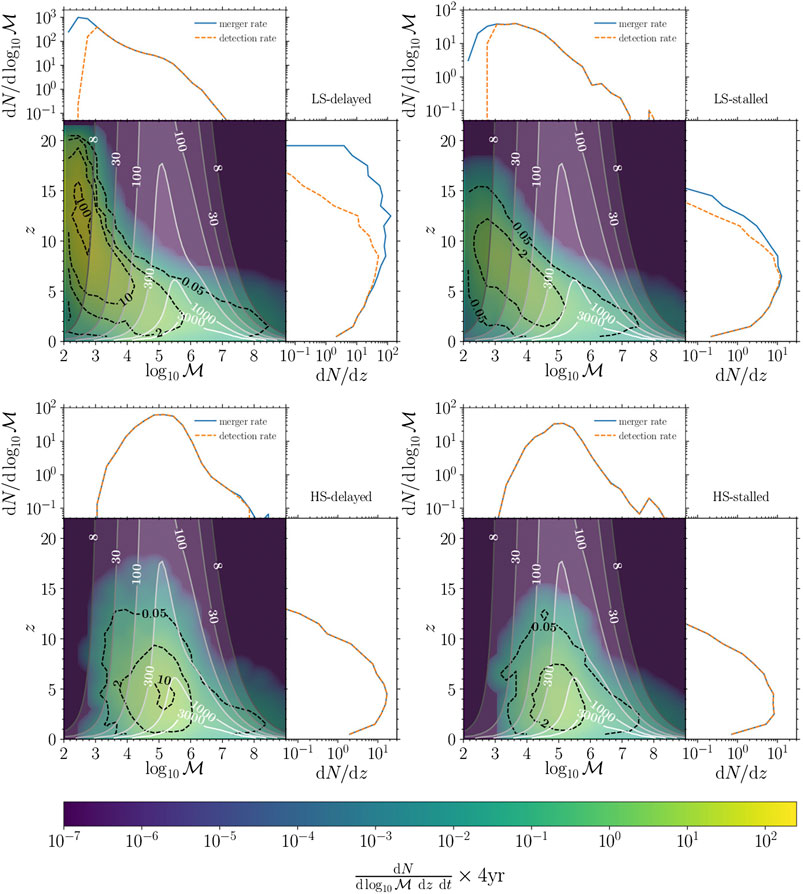
FIGURE 2. LISA observational capabilities vs. predicted MBHB merger rates in the chirp mass-redshift plane. In each panel, gray shaded contours show the S/N of LISA observations for equal-mass, nonspinning binaries. The superimposed yellow-green color gradient with black dashed contours represents the differential number of mergers during the planned 4-year mission lifetime. From the upper-left panel, clockwise, we show four different astrophysical models: LS-delayed, LS-stalled, HS-stalled, and HS-delayed (Bonetti et al., 2019, for details). For each model, the upper and right-side panels show the merger rate (blue line) and detection rate (orange line) distributions marginalized over redshift and chirp mass, respectively (Bonetti et al., 2019).

In the case of high-mass seeds from direct collapse shown in the bottom panels of the figure (see Woods et al., 2018, for a recent review), LISA can see essentially every single merger occurring within the observable Universe. If instead seeds are produced as remnants of popIII stars (Madau and Rees, 2001), as in the top panels of the figure, LISA will miss the first round of mergers, but it will still probe the subsequent growth history of MBHs out to $z \approx 20$ . In the latter case, an intriguing possibility is to complement LISA with ground-based 3G observations to fully reconstruct the cosmic history of those systems (see, e.g., Jani et al., 2019). In any case, LISA will provide a unique sample of up to several hundred MBHB coalescences: a potential revolution in physics and astronomy.

2.1 Extracting Information

MBHBs will generally enter the LISA band during their inspiral, completing thousands of cycles before merging within the detector’s band. This will allow the accumulation of such high S/N that the main source of error in the parameter recovery, at least for the loudest sources, might come from inaccuracies in the available waveforms rather than from the intrinsic detector noise. In fact, currently available inspiral-merger-ringdown (IMR) waveforms (Bohé et al., 2017; Khan et al., 2018) are not even close to the needed level of accuracy. This is particularly critical for tests of GR with, e.g., ringdown spectroscopy (Berti et al., 2006; Gair et al., 2013), which relies on measuring tiny deviations from the higher multipoles of the ringdown radiation compared to GR expectations (Baibhav et al., 2018), especially to extract information from the higher multipoles of the radiation (Baibhav and Berti, 2019).

Nonetheless, waveforms employed so far include most of the relevant physics and can therefore provide a reliable estimate of LISA’s capabilities. As an example, Klein et al. (2016) carried out a comprehensive study based on spinning precessing post-Newtonian waveforms, corrected for the enhancement in S/N provided by adding merger and ringdown. They found that LISA can recover individual redshifted masses, i.e., $(1 + z) M$ , to better than $1 %$ for loud sources at $z < 5$ . To get the intrinsic mass, however, one must know the redshift to the source, which is computed from the $D_{L}$ measurement, by assuming a fiducial cosmology. At $z > 1$ , LISA will measure $D_{L}$ to a few% accuracy, and weak lensing will affect the $D_{L} - z$ conversion adding another few% error (Shapiro et al., 2010). Considering both effects, LISA will provide an estimate of individual source frame masses within <10% relative accuracy for sources at $z < 5$ . Note that such precise measurements are today available only for MBHs in the local Universe, including SgrA^* [Ghez et al. (2008), Gillessen et al. (2009), M87 Event Horizon Telescope Collaboration et al. (2019a), Event Horizon Telescope Collaboration et al. (2019b)], and few systems powering megamaser Miyoshi et al. (1995). The other relevant property of astrophysical MBHs is their spin magnitude and orientation, which are notoriously difficult to measure and are as of today estimated (with large uncertainties) only for $\approx 20$ systems in the low-redshift Universe (see, e.g., Reynolds, 2014). Moving to the early epoch of structure formation, estimating parameters of systems at $z > 10$ will be more challenging. In particular, the error on $D_{L}$ tends to become much larger; nonetheless LISA can still place a 95% lower limit to the source redshift of $\approx 0.66 z$ (Sesana, 2013).

2.2 MBH Cosmic History Reconstruction

Because of its excellent parameter estimation capabilities, LISA will deliver an unprecedented catalog of MBHB coalescences that will provide precious information about their formation and evolution along the cosmic history (Sesana et al., 2011). This is because the mass, redshift, and spin distribution of LISA events carry the imprint of the underlying physics driving their formation and evolution, including the origin, abundance, mass function, and redshift distribution of the first seeds; the detailed properties of the subsequent accretion processes driving their mass growth; the dynamical details of the pairing and hardening process of MBHBs forming in the aftermath of galaxy mergers, for example, the seeding mechanism as a direct impact on the number of observable sources. Astrophysical low (popIII) and high (direct collapse) mass seed scenarios have been extensively explored and result in very different number of mergers in the LISA band. Furthermore, the MBH seeding process can be connected to the production of primordial BHs in the early Universe (Khlopov, 2010; Clesse and García-Bellido, 2015), a scenario that can be tested by LISA as more quantitative predictions of merger rates become available. On the other hand, measured MBH spins are mainly determined by the geometry of the accretion flow, with prolonged accretion in a defined plane resulting in efficient MBH spin-ups (Thorne, 1974), in contrast to the spin-down caused by interaction with cold gas clouds incoming from random directions (King et al., 2005). Mergers also play a role in determining the magnitude and relative orientation of the MBH spins: in gas rich environment, interaction with a putative massive circumbinary disk (Perego et al., 2009) tends to align individual spins with the binary angular momentum, whereas spins of MBHBs merging in gas poor environment are expected to be randomly oriented (Bogdanović et al., 2007). Moreover, the redshift distribution of detected systems is strongly affected by the time required for the binary to complete its journey from kpc scales down to final coalescence, following the host galaxy merger (Bonetti et al., 2019; Barausse et al., 2020). One of the main challenges of future astrophysical modeling will be to make the best out of the LISA dataset to address the “inverse problem” of reconstructing the MBHB cosmic history from observations. In a proof-of-concept study, Sesana et al. (2011) showed that LISA can separate different seed models (popIII vs. direct collapse) and accretion geometries (coherent vs. chaotic), with only a handful of events.

2.3 EM Counterparts and Multimessenger Astronomy

Occurring at the very center of galaxy merger remnants, MBHBs form and evolve within a dense environment that might favor the presence of EM signals matching the inspiral and coalescence of the pair. As mentioned above, in gas rich environments, binaries are expected to be surrounded by a massive circumbinary disk. Gas can leak from the inner edge of the disc, feeding minidiscs around individual MBHs (Farris et al., 2014), resulting in a number of distinctive EM signals. For example, feeding of the minidiscs might be modulated over the period of the binary, eventually resulting in a periodicity of their emission (Tang et al., 2018); the cavity evacuated by the binary torques, removing a significant portion of the inner disc, will produce a distinctive shape of the UV continuum (Tanaka et al., 2012); streams can produce periodic nonthermal X-ray bursts upon impact onto the outer edge of the minidiscs (Roedig et al., 2014); finally, the inverse Compton upscatter of photons in the corona might produce distinctive double Kα lines (Sesana et al., 2012).The main challenge will be the detection and identification of all those putative features. Being an omnidirectional detector, LISA sky localization capabilities are mostly determined by the evolution of the antenna response function as it moves along its orbit around the Sun. For MBHBs this will allow localization of $z < 2$ sources within $Δ Ω < 10 (0.5) \deg^{2}$ weeks (hours) before coalescence (McWilliams et al., 2010; Mangiagli et al., 2020). This is a remarkable feat foe GW astronomy, allowing for searches with optical, radio, and X-ray wide-field instruments, such as LSST (LSST Science Collaboration et al., 2009), SKA, and Athena (McGee et al., 2020). After merger, the high S/N added at coalescence, LISA sky localization will improve to several arcminutes; deeper EM observations might then reveal a number of features related to the postmerger dynamics of the surrounding medium. These include the birth of a quasar as the gas in the circumbinary disc refills the cavity and is efficiently accreted (Milosavljević and Phinney, 2005), the launch of a relativistic jet (Palenzuela et al., 2010), or nonthermal emission from shocks prompted within the disk by the sudden change of the potential due to gravitational recoil (Rossi et al., 2010). Convincing identification of any such counterpart would be an unprecedented milestone in accretion physics, opening up the study of interaction between gravity and matter in the time-dependent, strong field regime of a merging binary, as well as probing accretion onto MBHs of known masses and spins thus allowing, among other things, testing theoretical conjectures linking MBH spins to jet launching (Blandford and Znajek, 1977). Last but not least, joint EM and GW detections of MBHB will provide a unique class of standard sirens, extending up to $z > 5$ (Tamanini et al., 2016), thus probing the expansion history of the Universe in uncharted territory.

3 Extreme Mass Ratio Inspirals

EMRIs are distinct from MBHBs both in their properties and their origin. As the name indicates, they are binaries involving objects of very different masses, generally a MBH interacting with a CO that can be a WD, NS, or stellar-mass BH. Consequently, their origin is not related to galaxy mergers or, more broadly, to the hierarchical structure formation paradigm but is rooted in the relativistic dynamics of dense nuclei. Sitting at galactic centers, in fact, MBHs are surrounded by a dense distribution of stars and COs. In such a dense environment, the central MBH can “capture” a stellar BH as a result of several dynamical processes, including different flavor of relaxation mechanisms deflecting BHs onto low angular momentum orbits or the tidal breakup of a compact binary close to the MBH. The captured BH will then inspiral onto the central MBH completing millions of orbits before eventually plunging into it (Amaro-Seoane, 2018). The detection of the resulting GW signal poses a major challenge for GW modelers, since it requires matching hundreds of thousands of cycles with accurate enough waveform templates (Barack and Cutler, 2004; Barack, 2009; Chua and Gair, 2015; Chua et al., 2017). But payouts are well worth the investment of theoretical and computational resources. Upon detection EMRIs will deliver unprecedented measurements of the system parameters, including the central MBH mass and spin to a precision of $< 10^{- 4}$ , a luminosity distance accuracy of a few percent, and sky localization within ≈1deg² (Barack and Cutler, 2004; Babak et al., 2017), making them formidable probes of MBH astrophysics, fundamental physics, and cosmology.

Capable of detecting EMRIs out to $z \approx 2$ , LISA will detect from few to thousands of these systems per year (Babak et al., 2017). Very uncertain rates stem from poorly known underlying physics, meaning that EMRIs will provide a new wealth of information about the conditions of dense nuclei, in particular the mass function and occupation fractions of dormant MBHs in the mass range $10^{5} M_{⊙} - 10^{6} M_{⊙}$ , difficult to probe by other means (Gair et al., 2010). Source abundance and individual EMRI parameters, such as eccentricity and orbital inclination, will help constrain their formation channel, shedding new light on extreme dynamics in dense nuclei (Amaro-Seoane, 2018). A fraction of EMRIs might also form and evolve within AGN discs (Levin, 2007). If this is the case, drag from the disc will leave distinctive signatures in the waveform, giving us access to the conditions of the plasma in the midplane of optically thick accretion discs, something that is beyond the reach of photon-based astronomy (Kocsis et al., 2011; Barausse et al., 2014). Exquisite parameter estimation accuracy makes EMRIs unique tools for probing space-time. For example, the central MBH quadrupole moment can be measured to a fractional precision of $< 10^{- 4}$ , allowing the detection of tiny deviation from Kerr geometry. Finally, although generally lacking EM counterparts, the excellent measurement of EMRIs distance and sky location will allow for effectively determining their redshift via statistical methods. Estimates suggest that $H_{0}$ could be measured to an accuracy of ≈1% with an ensemble of 20 EMRIs detected out to $z \approx 0.5$ (MacLeod and Hogan, 2008).

4 STELLAR-MASS Black Hole Binaries and Multiband Detections

Last but not least, LISA will observe stellar-mass BHBs still far from coalescence, before they enter the ground-based detector band. This was soon realized after the detection of GW150914, a system so massive and nearby that would have been observed by LISA with S/N $\approx 5$ about five years before coalescence (Sesana, 2016). Subsequent studies have demonstrated that LISA can detect several tens of BHBs, up to hundreds of years before coalescence. A fraction of them will be caught in the last few years of inspiral and will cross all the way to the LIGO-Virgo band, paving the way to multiband GW astronomy (Kyutoku and Seto, 2016; Sesana, 2017; Gerosa et al., 2019). LISA will localize these multiband sources within ≈0.1deg², predicting their coalescence time with an error of <10s. We will therefore be in the unprecedented position of knowing exactly where and when a BHB is going to merge, a condition that will allow prepointing of EM facilities to search for possible counterparts coincident with the merger with a depth which is inconceivable with wide-field monitors (Sesana, 2016). Reconstructing the phase evolution of the system across 5 decades in frequency, and possibly fine-tuning the sensitivity of Earth-based detectors, will lead to improved tests of general relativity [Barausse et al. (2016), Carson and Yagi (2019), Berti et al. (2019), Chamberlain and Yunes (2017), Tso et al. (2018), Gnocchi et al. (2019)]. As an example, observations of the same source in the early and late inspiral will place unique constraints on additional emission multipoles (Barausse et al., 2016).

Even without multiband observations, detecting stellar-origin BHBs with LISA may have important astrophysical implications. Far from coalescence, LISA can measure the eccentricity (e) of these binaries as long as $e ≳ 10^{- 3}$ at GW frequencies $f \sim 10^{- 2}$ Hz (Nishizawa et al., 2016). Field binaries are expected to have small eccentricities at these frequencies (Kowalska et al., 2011); therefore these measurements can be used to discriminate between the dynamical and field formation channels (Breivik et al., 2016; Nishizawa et al., 2017; Samsing and D’Orazio, 2018). Combined with ground-based spin measurements, LISA eccentricity measurements can have an important role in our understanding of BHB formation. If the rate turns out to be large, specific stellar subpopulations could potentially be constrained (e.g., Gerosa et al., 2019). Cosmology will also benefit. Similar to EMRIs, the sky location and distance of at least a subset of these systems can be precise enough that we could use them as standard candles, allowing for an independent statistical measurement of $H_{0}$ within a few percent accuracy (Kyutoku and Seto, 2017; Del Pozzo et al., 2018).

5 Conclusion

The future of GW astronomy is going to be loud. Building on the successes of LIGO and Virgo, the GW community is investing in a number of projects that will tremendously expand our knowledge of the dark side of the Universe. 3G ground-based detectors will observe hundreds of thousands CO mergers across the Universe and PTAs will unveil the most massive black hole binaries in the Universe. In this context, LISA will be one of our finest ears on the Universe. By surveying the milli-Hz frequency band, LISA will detect a variety of GW sources, across several decades in the mass scale, from the Solar neighborhood back to the formation of the first cosmic structure, promising an unprecedented revolution in our understanding of the Universe.

Acknowledgments

The author is supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program ERC-2018-COG under grant agreement No. 818691 (B Massive). The author is also indebted to Emanuele Berti for early contributions to this review.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abbott, B. P., Abbott, R., Adhikari, R., Ajith, P., Allen, B., Allen, G., et al. (2009). LIGO: the laser interferometer gravitational-wave observatory. Rept. Prog. Phys. 72, 076901. doi:10.1088/0034-4885/72/7/076901