The Relevance of Nuclear Reactions for Standard Solar Models Construction

The fundamental processes by which nuclear energy is generated in the Sun have been known for many years. However, continuous progress in areas such as neutrino experiments, stellar spectroscopy and helioseismic data and techniques requires ever more accurate and precise determination of nuclear reaction cross sections, a fundamental physical input for solar models. In this work, we review the current status of (standard) solar models and present a complete discussion on the relevance of nuclear reactions for detailed predictions of solar properties. In addition, we also provide an analytical model that helps understanding the relation between nuclear cross sections, neutrino fluxes and the possibility they offer for determining physical characteristics of the solar interior. The latter is of particular relevance in the context of the conundrum posed by the solar composition, the solar abundance problem, and in the light of the first ever direct detection of solar CN neutrinos recently obtained by the Borexino collaboration. Finally, we present a short list of wishes about the precision with which nuclear reaction rates should be determined to allow for further progress in our understanding of the Sun.

1 Introduction

The history of solar models, or standard solar models (SSMs) to be more precise, is formed by three large chapters related to the type of observational and experimental data about the solar interior that existed at any given time. The first part of this history comprises the period over which only neutrino data were available, and it spans about 20 years, from the mid 60 s to the early 80 s of the past century. During that period, the solar neutrino problem was seen by many as having an origin in the complexities involved in building accurate and precise SSMs, a fundamental part of which is determined by the nuclear reaction rates involved in the generation of the solar nuclear energy. Around the end of that era, the precision of nuclear reaction rates involved in the chains of reactions leading to the production of the different solar neutrino fluxes were on the order to 20–30%. These uncertainties may seem large for present day standards. However, if some faith was put in their accuracy, these uncertainties were small enough that associating the solar neutrino problem to nuclear cross section measurements was highly unlikely (Bahcall et al., 1982).

In the mid 80s helioseismology, the study of solar oscillations, evolved into a precision branch of solar physics. The sensitivity of the frequency spectrum of these global pressure waves to the details of the interior solar structure allowed their reconstruction by means of inversion methods (see e.g., Deubner and Gough (1984); Christensen-Dalsgaard et al. (1985)), in particular of the solar interior sound speed. This (r)evolution peaked during the second half of the 1990s with the establishment of the Global Oscillation Network Group (GONG), a network of six instruments established around the world that carried out resolved radial velocity measurements of the solar surface (Harvey et al., 1996) and with the launch of the SoHO satellite, both of which provided rich helioseismic datasets. In turn, this led to determination of the solar interior properties with precision of better than 1% (and in some cases even an order of magnitude better) (Gough et al., 1996). These results led to the appearance of a new generation of SSMs (Bahcall et al., 1995; Christensen-Dalsgaard et al., 1996), which were successful in satisfying the tight observational constraints imposed by helioseismology, leaving little room for an astrophysical solution to the solar neutrino problem, as had originally been suggested a few years earlier (Elsworth et al., 1990). Simultaneously, Super-Kamiokande (Fukuda, 1998; Fukuda et al., 2001) led to the precise measurement of ⁸B neutrino flux which, in combination with the results of radiochemical experiments Homestake (Cleveland et al., 1998), Gallex (Hampel et al., 1999) and SAGE (Abdurashitov et al., 1999) strongly hinted at the existence of solar neutrino oscillations, result confirmed just a few years later by SNO results (Ahmad et al., 2001; Ahmad et al., 2002). The needs of refined nuclear reaction rates imposed by the type and quality of the new observational and experimental data led to famous revisions of nuclear reaction rates such as NACRE (Angulo et al., 1999) and in particular that of Solar Fusion I (Adelberger, 1998). In the latter, a critical analysis of the accumulated experimental and theoretical data was performed and consensus values were provided for all relevant nuclear reactions affecting energy generation and neutrino production in the Sun. The improvement in the uncertainties, in particular, was about a factor of to 2, leading to typical errors around 10%. Simultaneously, several authors used helioseismic inversion of the solar sound speed to determine, or at least set constraints, on the proton-proton reaction rate, showing that its value had to be within about 15% of its theoretically determined value (degl’Innocenti et al., 1998; Schlattl et al., 1999; Antia and Chitre, 1999; Turck-chièze et al., 2001; Antia and Chitre, 2002).

The combination of helioseismic constraints and the discovery of neutrino oscillations changed the focus of interest of SSMs. In particular, the accurate and precise determination of neutrino fluxes from individual reactions started playing a fundamental role in the determination of the neutrino oscillation parameters. SSMs became a fundamental source of information, a reference, not just for astrophysics, but for particle physics as well. In 2007, the final and present chapter in this history started when Borexino presented the first measurement of the ⁷Be neutrinos (Arpesella et al., 2008), originating from a subdominant branch of reactions, the so-called pp-II branch of the pp-chain that accounts for about 10% of the energy generation of the Sun. Further work by Borexino led to an almost complete characterization of the spectrum of neutrinos from the pp-chain (Agostini et al., 2018). Together with the very precise measurement of the ⁸B flux from SNO (Aharmim, 2013) and Super-Kamiokande (Abe, 2016), we have come full circle and results from solar neutrino experiments can now be used to learn about the properties of the Sun. This is timely. There is a lingering dispute about which is the detailed chemical composition of the Sun, the solar abundance problem (Section 2.1), that is intimately linked to the uncertainties in our knowledge of radiative opacities in the solar interior. Solar neutrino data can in principle be used to disentangle this problem (Haxton and Serenelli, 2008; Serenelli et al., 2013; Villante et al., 2014), in particular if the promising results by Borexino on solar CN neutrinos (Agostini et al., 2020a) can be further improved. But progress along this line depends crucially on the accuracy and precision with which nuclear reaction rates are known. The latest compilation, Solar Fusion II (Adelberger, 2011), and subsequent work on specific reactions (Section 2), show on average a factor of two improvement with respect to the status 10–15 years ago, and 5% uncertainties are nowadays typical. But further work is still needed; uncertainties from nuclear reactions still have a non negligible role in the overall SSMs error budget.

In Section 2 we summarize the current status of SSMs, review the solar abundance problem, the SSM predictions on the solar neutrino spectrum and the status of nuclear reaction rates affecting model predictions. Section 3 presents an analytical formation of the relation between nuclear reaction rates and solar model properties both for reactions from the pp-chains and CNO-cycles. Section 4 reviews results from numerical SSM calculations, including a detailed assessment of uncertainties and highlighting where progress is most needed, and revises the possibility of using future CN neutrino measurements to determine the solar core C + N abundance.

2 Standard Solar Models

SSMs are a snapshot in the evolution of a 1 ${\text{M}}_{\odot }$ star, calibrated to match present-day surface properties of the Sun. Two basic assumptions in SSM calculations are: 1) after the phase of star formation the Sun was chemically homogenized as a result of the fully convective phase during its contracting along the Hayashi track and before nuclear reactions start altering its initial composition and, 2) at all moments during its evolution up to the present solar age ${\tau }_{\odot }=4.57$ Gyr mass loss is negligible. The calibration is done by adjusting the mixing length parameter (${\alpha }_{\text{MLT}}$) and the initial helium and metal mass fractions ($Y_{\text{ini}}$ and $Z_{\text{ini}}$, respectively), in order to satisfy the constraints imposed by the present-day solar luminosity ${\text{L}}_{\odot }=3.8418\times {10}^{33}\text{erg}{\text{s}}^{-1}$, radius ${\text{R}}_{\odot }=6.9598\times {10}^{10}\text{cm}$ (Bahcall et al., 2006), and surface metal to hydrogen abundance ratio ${\left(\text{Z}/\text{X}\right)}_{\odot }$, see section 2.1. As a result of this procedure, SSM has no free parameters and completely determines the physical properties of the Sun. It can be then validated (or falsified) by other observational constraints, in particular by those provided by solar neutrino fluxes measurements and helioseismic frequencies determinations.

The physics input in the SSM is rather simple and it accounts for: convective and radiative transport of energy, chemical evolution driven by nuclear reactions, microscopic diffusion of elements which comprises different processes but among which gravitational settling dominates. Over more than 25 years, since the modern version of the SSM was established with the inclusion of microscopic diffusion (Bahcall and Pinsonneault, 1992; Christensen-Dalsgaard et al., 1993), the continuous improvement of the constitutive physics has brought about the changes and the evolution of SSMs. In particular, a lot of effort has gone into experimental and theoretical work on nuclear reaction rates. But changes in radiative opacities and the equation of state were also relevant. We take here as a reference the results of recent SSM calculations by Vinyoles et al. (2017), the so-called Barcelona 2016 (B16, for short) SSMs, which are based on the following state of the art ingredients. The equation of state is calculated consistently for each of the compositions used in the solar calibrations by using FreeEOS (Cassisi et al., 2003). Atomic radiative opacities are from the Opacity Project (OP) (Badnell et al., 2005), complemented at low temperatures with molecular opacities from Ferguson et al. (2005). Nuclear reaction rates for the pp-chain and CNO-bicycle, which are described in more details in the following section, are from the Solar Fusion II compilation (Adelberger, 2011) with important updates for the rates of $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$ (Marcucci et al., 2013; Tognelli et al., 2015; Acharya et al., 2016), ${}^7\text{B}\text{e}{\left(\text{p},\gamma \right)}^8\text{B}$ (Zhang et al., 2015) and ¹⁴$\text{N}{\left(\text{p},\gamma \right)}^{15}\text{O}$ (Marta, 2011) reactions. Microscopic diffusion coefficients are computed as described in Thoul et al. (1994). Convection is treated according to the mixing length theory (Kippenhahn and Weigert, 1990). The atmosphere is gray and modeled according to a Krishna-Swamy $T-\tau$ relationship (Krishna Swamy, 1966).

2.1 The Solar Composition Problem

The solar surface composition, determined with spectroscopic techniques, is a fundamental input in the construction of SSMs. The development of three dimensional hydrodynamic models of the solar atmosphere, of techniques to study line formation under non-local thermodynamic conditions and the improvement in atomic properties (e.g., transition strengths) have led since 2001 to a complete revision of solar abundances. Table 1 lists the abundances determined by different authors for the most relevant metals in solar modeling: GN93 (Grevesse and Noels, 1993), GS98 (Grevesse and Sauval, 1998), AGSS09 (Asplund et al., 2009), C11 (Caffau et al., 2011) and AGSS15 (Scott et al., 2015a; Scott et al., 2015b; Grevesse et al., 2015). Note that only abundances relative to hydrogen can be obtained from spectroscopy because the intensity of spectroscopic lines is measured relative to a continuum that is determined by the hydrogen abundance in the solar atmosphere. The last row in the table gives the total photospheric present-day metal-to-hydrogen ratio ${\left(\text{Z}/\text{X}\right)}_{\odot }$ and it is the quantity used as observational constraint to construct a solar model. In fact, the solar composition set used in solar models determines not only ${\left(\text{Z}/\text{X}\right)}_{\odot }$ but also the relative abundances of metals in the models. In this sense, $Z_{\text{ini}}$ acts as a normalization factor that, together with $Y_{\text{ini}}$ and the relation $X_{\text{ini}}+Y_{\text{ini}}+Z_{\text{ini}}=1$, determines completely the initial composition of the model.

TABLE 1

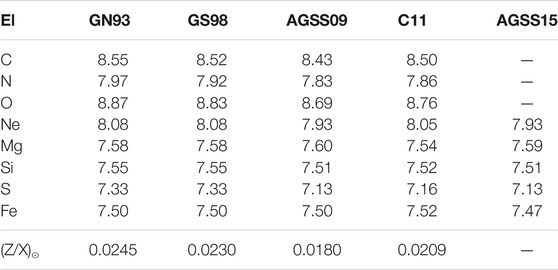
TABLE 1. Solar photospheric composition through time and authors for most relevant metals in solar modeling. Abundances are given in the standard astronomical scale ${\mathit{ϵ}}_i={\text{log}}_{10}\left(n_i/n_{\text{H}}\right)+12$, where $n_i$ is the number density of a given atomic species.

There is no complete agreement among authors, and some controversy still remains as to what the best values for the new spectroscopic abundances are. However, there is consensus in that all determinations of the solar metallicity based on the new generation of spectroscopic studies yield a solar metallicity lower than older spectroscopic results (Grevesse and Noels, 1993; Grevesse and Sauval, 1998), in particular for the volatile and most abundant C, N, and O. For refractories elements, like Fe, Si, Mg and S that have important role in solar modeling being important contributors to the radiative opacity, meteorites offer a very valuable alternative method (see e.g., Lodders et al. (2009)) and, in fact, elemental abundances determined from meteorites have been historically more robust than spectroscopic ones.

Considering that uncertainties in element abundances are difficult to quantify, it has become customary to consider two canonical sets of abundances to which we refer to as high metallicity (HZ) and low metallicity (LZ) solar admixtures, see e.g., Serenelli et al. (2011); Vinyoles et al. (2017) as reference assumptions for SSM calculations. These are obtained by using the photospheric (volatiles) + meteoritic (refractories) abundances from GS98 and AGSS09 respectively, and are reported in Table 2. In the last column, we give the fractional differences $\delta z_i\equiv z_i^{\text{HZ}}/z_i^{\text{LZ}}-1$ where $z_i\equiv Z_i/X$ is the ratio of the $i-$ element abundance with that of hydrogen, to facilitate comparison among the two admixtures. Even if GS98 abundances are presumably surpassed by the more recent determinations, they are still considered as a valid option to construct solar models because they lead to a temperature stratification that well reproduces the helioseismic constraints.

TABLE 2

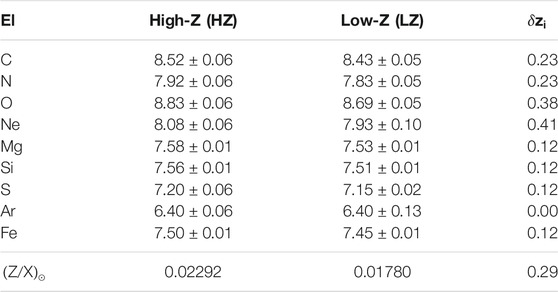
TABLE 2. The two canonical HZ and LZ solar mixtures given as ${\mathit{ϵ}}_i={\text{log}}_{10}\left(n_i/n_{\text{H}}\right)+12$. The two compilations are obtained by using the photospheric (volatiles) + meteoritic (refractories) abundances from GS98 and AGSS09 respectively, and correpond to the admixture labeled as GS98 and AGSS09met in Vinyoles et al. (2017).

This can be better appreciated by considering Table 3 and Figure 1 where we compare theoretical predictions of SSMs implementing HZ and LZ surface composition with helioseismic determinations of the surface helium abundance $Y_{\text{s}}$, of the convective envelope depth $R_{\text{CZ}}$ and the solar sound speed $c_{\odot }\left(r\right)$. We see that solar models implementing the LZ abundances fail to reproduce all helioseismic probes of solar properties. This disagreement constitutes the so-called solar abundance problem (Basu and Antia, 2004; Bahcall et al., 2005a; Delahaye and Pinsonneault, 2006) that has defied a complete solution. All proposed modifications to physical processes in SSMs offer, at best, only partial improvements in some helioseismic probes (e.g. Guzik et al. (2005); Castro et al. (2007); Basu and Antia (2008); Guzik and Mussack (2010); Serenelli et al. (2011)). An alternative possibility is to consider modifications to the physical inputs of SSMs at the level of the constitutive physics, radiative opacities in particular. The effective opacity profile in the solar interior results from the combination of the reigning thermodynamic conditions, including composition, and the atomic opacity calculations at hand. Early works (Montalban et al., 2004; Bahcall et al., 2005b) already suggested that a localized increase in opacities could solve or, at least, alleviate the disagreement of low-Z solar models with helioseismology. Refs. (Christensen-Dalsgaard et al., 2009; Villante, 2010) have concluded that a tilted increase in radiative opacities, with a few percent increase in the solar core and a larger (15–20%) increase at the base of the convective envelope could lead to low-Z SSMs that would satisfy helioseismic probes equally as well as SSMs based on the older, higher, metallicities.

TABLE 3

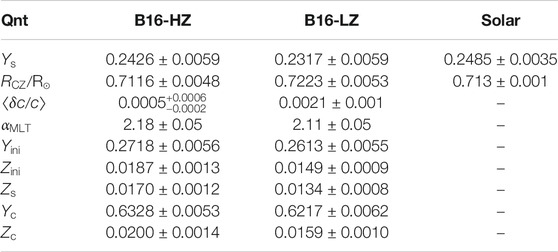
TABLE 3. Main characteristics of SSMs with different surface composition (Vinyoles et al., 2017). The observational values for $Y_{\text{s}}$ and $R_{\text{CZ}}$ are taken from Basu and Antia (2004) and Basu and Antia (1997), respectively. The quantity $\delta \text{c}/\text{c}=\left({\text{c}}_{\odot }-{\text{c}}_{\text{mod}}\right)/{\text{c}}_{\text{mod}}$ is the fractional difference between sound speed helioseismic determination and model prediction.

FIGURE 1

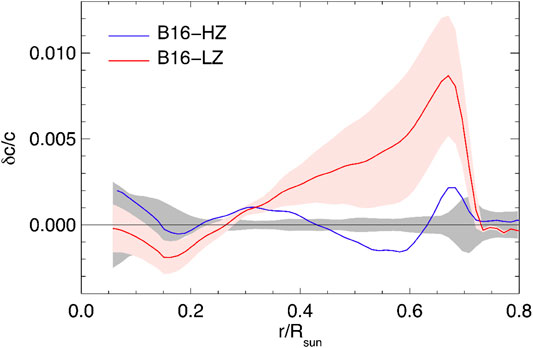
FIGURE 1. Fractional sound speed difference in the sense $\delta \text{c}/\text{c}=\left({\text{c}}_{\odot }-{\text{c}}_{\text{mod}}\right)/{\text{c}}_{\text{mod}}$. Gray shaded regions corresponds to errors from helioseismic inversion procedure. Red shaded region corresponds to uncertainties in SSM predictions which we chose to plot around the B16-LZ central value (solid red line). An equivalent relative error band holds around the central value of the B16-HZ central value (solid blue line) which we do not plot for the sake of clarity.

Recent years have seen a surge of activity in theoretical calculations of atomic radiative opacities. Updated calculations (Badnell et al., 2005) by the Opacity Project have led the way, followed by OPAS (Blancard et al., 2012; Mondet et al., 2015), STAR (Krief et al., 2016b) and a new version of OPLIB, the opacities from Los Alamos (Colgan et al., 2016). For conditions in solar interiors, all theoretical opacities agree with each other within few %. Interestingly Bailey et al. (2015), have presented the first ever measurement of opacity under conditions very close to those at the bottom of the solar convective envelope. While the experiment has been carried out only for iron, their conclusion is that all theoretical calculations predict a too low Rosseland mean opacity, at a level of $7\pm 4\text{\%}$, for the temperature and density combinations realized in the experiment. Further experimental work on chromium and nickel opacities was carried out (Nagayama et al., 2019) to help evaluate discrepancies between experimental and theoretical resuls on iron opacity. Results point toward a shortcomings that affect models, particularly in the case of open electronic L-shell configurations such as is present in iron at the base of the convective envelope. Also, the disagreement between theoretical and measured line shapes for the three elements indicates shortcomings in the theoretical understanding of atomic interaction with the plasma. On the other hand, the results also indicated that the quasicontinuum opacity determined experimentally agrees well with the chromium and nickel experiments, contrary to results from the iron experiment. However, the chromium and nickel experiments were carried out at lower temperatures than those used in the original iron experiment, which suggests that the problem of missing quasicontinuum opacity might have an unknown temperature dependence, or that a systematic error affected the high temperature iron measurements. Moreover, Ref. (Krief et al., 2016a) in a recent theoretical analysis of line broadening modeling in opacity calculations, have found that uncertainties linked to this are larger at the base of the convective envelope than in the core. These arguments suggest that opacity calculations are more accurate in the solar core than in the region around the base of the convective envelope. To take this into account, opacity uncertainty was modeled in B16-SSM calculations in terms of two parameters, ${\kappa }_a$ and ${\kappa }_b$, that can change both the scale and the temperature dependence of opacity according to $\delta k\left(T\right)={\kappa }_a+\left({\kappa }_b/\text{Δ}\right)\text{log}\left(T/T_{\text{c}}\right)$, where $\delta \kappa$ is the fractional opacity variation, $\text{Δ}=\text{log}\left(T_{\text{c}}/T_{\text{CZ}}\right)$, $T_{\text{c}}=15.6\times {10}^6\text{K}$ and $T_{\text{CZ}}=2.3\times {10}^6\text{K}$ are the temperatures at the solar center and at the bottom of the convective zone, respectively. The parameters ${\kappa }_a$ and ${\kappa }_b$ have been treated as independent random variables with mean equal to zero and dispersions ${\sigma }_a=2\text{\%}$ and ${\sigma }_b=6.7\text{\%}$, corresponding to opacity uncertainty ${\sigma }_{\text{in}}={\sigma }_a=2\text{\%}$ at the solar center and ${\sigma }_{\text{out}}={\left({\sigma }_a^2+{\sigma }_b^2\right)}^{1/2}=7\text{\%}$ at the base of the convective region.

2.2 Nuclear Reactions in the Sun

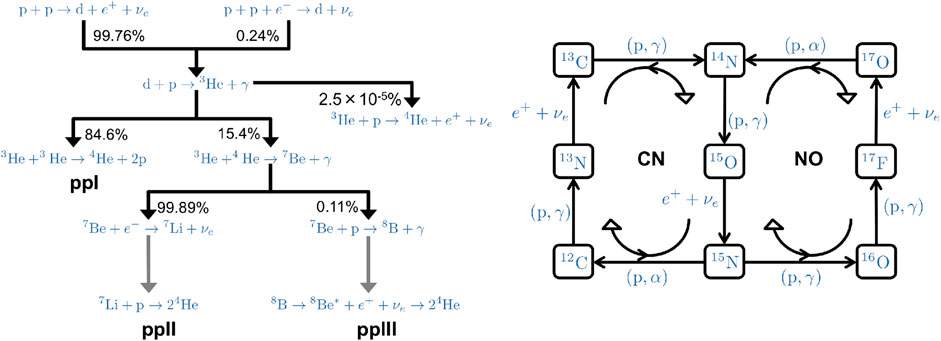
The overall effect of nuclear reactions in the Sun, as in any other star in hydrogen burning stage, is the conversion:

$4\text{p}+2e^{-}\to \left(4\text{H}\text{e}\right)+2{\nu }_{\text{e}}(1)$

with the production of a fixed amount of energy $Q=4m_{\text{p}}+2m_{\text{e}}-m_4{}_{\text{He}}=26.7\text{MeV}$ per synthesized ⁴He nucleus. Most of this energy is released in the solar plasma and slowly diffuses toward the solar surface supporting the radiative luminosity of the Sun. A small fraction of it, that depends on the specific channel by which hydrogen burning proceeds, is emitted in neutrinos. According to SSM calculations, the two neutrinos carry away about $0.6\text{MeV}$ on the average.

The SSM predicts that most of the solar energy ($>99\text{\%}$) is produced by the pp-chain, i.e. the hydrogen fusion reaction chain displayed in the left panel of Figure 2. The pp-chain is mostly initiated by $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$ reaction and, to a minor extent, by electron capture reaction $\text{p}\left(\text{p}{e}^{-},{\nu }_e\right)\text{d}$ and has several possible terminations that depend on the specific mechanism by which helium-3 nuclei, which are produced by $\text{d}\left(\text{p},\gamma \right){}^3\mathrm{H}\mathrm{e}$ reaction, are converted to heavier elements. In the Sun, the dominant mechanism is ${}^3\mathrm{H}\mathrm{e}{\left({}^3\mathrm{H}\mathrm{e},2p\right)}^4\text{H}\mathrm{e}$ that corresponds to the so-called pp-I termination of the pp-chain. Alternatively, helium-3 can undergo ${}^3\mathrm{H}\mathrm{e}{\left({}^4\mathrm{H}\mathrm{e},\gamma \right)}^7\mathrm{B}\mathrm{e}$ reaction with the effect of producing beryllium-7. Depending on the destiny of ${}^7\mathrm{B}\mathrm{e}$, that can be processed either by the electron capture ${}^7\text{B}\text{e}{\left(e^{-},{\nu }_e\right)}^7\text{L}\text{i}$ or by the (largely sub-dominant) proton capture reaction ${}^7\mathrm{B}\mathrm{e}{\left(\text{p},\gamma \right)}^8\text{B}$, one obtains the pp-II or the pp-III terminations of the chain. Finally, a very small amount of helium-4 nuclei is produced by ${}^3\text{H}\text{e}\left(\text{p},e^{+}{\nu }_e\right){}^4\mathrm{H}\mathrm{e}$ reaction. The relative importance of the different branches of the pp-chain depends primarily on the core temperature of the Sun and on the cross section of specific reactions, as will be discussed in next section. The numbers given in Figure 2 show the branching ratios in the present Sun. According to SSM calculations, the central temperature and density of the present Sun are $T_{\text{c}}\simeq 15.6\times {10}^6\text{K}$ and ${\rho }_{\text{c}}\simeq 150\text{g}{\text{cm}}^{-3}$ and they decrease as a function of the solar radius as it is shown in Figure 3. Most of the solar luminosity is produced in the region $r\underset{˜}{<}0.2R_{\odot }$ that contains about $30\text{\%}$ of the total mass of the Sun. In this region we observe a relevant increase (decrease) of the helium-4 (hydrogen) mass fraction Y (X), as a result of hydrogen burning during the Sun lifetime. The helium-3 mass fraction ($X_3$) has a non monotonic behavior, explained by the fact that ³$\mathrm{H}\mathrm{e}$ burning time is larger than the age of the Sun for $r\underset{˜}{>}0.3R_{\odot }$ and thus helium-3 accumulates proportionally to the efficiency of $\text{d}{\left(\text{p},\gamma \right)}^3\mathrm{H}\mathrm{e}$ reaction. In the energy-producing core, however, ${}^3\text{H}\text{e}$ nuclei are efficiently converted to heavier elements by nuclear processes (mainly by ${}^3\mathrm{H}\mathrm{e}\left({}^3\mathrm{H}\mathrm{e},2p\right){}^4\text{H}\mathrm{e}$), and the abundance $X_3$ is equal to the equilibrium value.

FIGURE 2

FIGURE 2. Left Panel: The pp-chain; Right Panel: The CNO-bicycle.

FIGURE 3

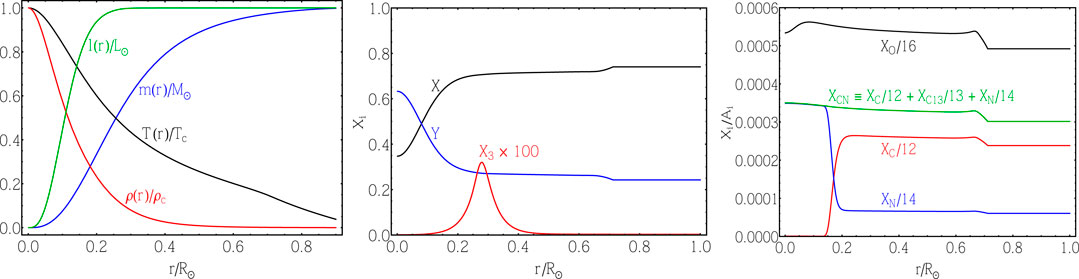
FIGURE 3. Left Panel: The behavior of temperature T and density ρ (scaled to central values $T_{\text{c}}$ and ${\rho }_{\text{c}}$) and of mass m and luminosity l (scaled to total mass $M_{\odot }$ and luminosity $L_{\odot }$) as a function of the solar radius. Middle Panel: The abundances of hydrogen (X), helium-4 (Y) and helium-3 ($X_3$) in the present Sun; Right Panel: The abundances of CNO elements in the present Sun.

An alternative hydrogen burning mechanism is provided by the CNO-bicycle that is displayed in the right panel of Figure 2. The CNO-bicycle uses carbon, nitrogen and oxygen nuclei that are present in the core of the Sun as catalysts for hydrogen fusion. It is composed by two different branches, i.e. the CN-cycle and the NO-cycle, whose relative importance depends on the outcome of proton capture reaction on nitrogen-15. In the Sun, the ¹⁵$\text{N}\left(\text{p},\alpha \right)$¹²C channel is largely dominant and so, in practice, the CNO-bicycle is reduced to the CN-cycle with a marginal contribution by the NO-cycle. Note that the CN-cycle conserves the total number of ¹²C and ¹⁴N nuclei in the core of the Sun, but alters their distribution as it burns into equilibrium, eventually achieving equilibrium abundances proportional to the inverse of the respective rates, see right panel of Figure 3. The reactions controlling conversion of ¹²C and ¹⁴N in the solar core and the approach to equilibrium are ¹²$\mathrm{C}\left(\text{p},\gamma \right)$¹³N and ¹⁴N${\left(\text{p},\gamma \right)}^{15}\text{O}$: these are the next-to-slowest and slowest rates in the CN-cycle, respectively. The temperature above which the ¹²C burning time through ¹²$\mathrm{C}\left(\text{p},\gamma \right)$¹³N is smaller than the Sun’s lifetime is $T\sim {10}^7\text{K}$. In the SSM, the entire energy-producing core, $r\lesssim 0.2R_{\odot }$ and $m\lesssim 0.3M_{\odot }$ is at temperature larger than this value, so that nearly all of the core’s carbon-12 is converted to nitrogen-14. The slower ¹⁴$\mathrm{N}{\left(\text{p},\gamma \right)}^{15}\text{O}$: reaction determines whether equilibrium is achieved. The ¹⁴N burning time is shorter than the age of the Sun for $T\gtrsim 1.3\times {10}^7\text{K}$. Therefore equilibrium for the CN cycle is reached only for $R\underset{˜}{<}0.1R_{\odot }$, corresponding to the central 7% of the Sun by mass. Consequently, over a significant portion of the outer core, ¹²C is converted to ¹⁴N, but further reactions are inhibited by the ¹⁴$\mathrm{N}{\left(\text{p},\gamma \right)}^{15}\text{O}$ bottleneck.

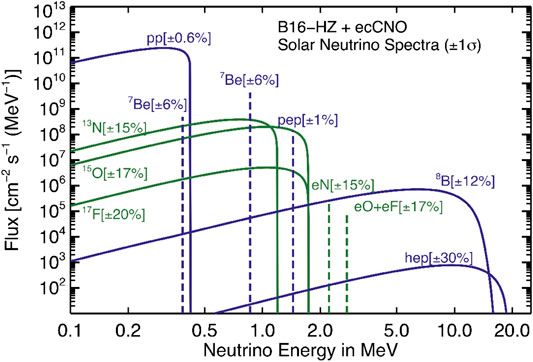
A very effective tool to investigate nuclear energy generation in the Sun is provided by neutrinos which are necessarily produced along with ${}^4\mathrm{H}\mathrm{e}$ nuclei during hydrogen burning, in order to satisfy lepton number conservation. Neutrinos free stream in the solar plasma and reach the Earth in about 8 min where they can be detected by solar neutrino experiments. While the total amount of neutrinos produced in the Sun can be easily estimated from the solar luminosity constraint, i.e., the assumption that the luminosity radiated from the surface of the Sun is exactly counterbalanced by the amount of energy produced by hydrogen fusion reactions in the solar core (see e.g., Bahcall (2002); Degl’Innocenti et al. (1997); Vissani (2019) for a detailed discussion), the evaluation of their spectrum requires the knowledge of the individual rates of neutrino producing reactions and thus the construction of a complete solar model. We report in Figure 4 and Table 4, the SSM predictions for the different components of the solar neutrino flux, named according to the specific reaction by which they are produced (Vinyoles et al., 2017). We also include, for completeness, ecCNO neutrinos, i.e. neutrinos produced by electron capture reaction in the CNO-bicycle (in addition to the “standard” CNO neutrinos produced by β decays of ¹³$\text{N}$, ¹⁵$\text{O}$ and ¹⁷$\text{F}$) that were originally calculated in Bahcall (1990); Stonehill et al. (2004) and recently reevaluated in Villante (2015)^a. The two columns “B16-HZ” and “B16-LZ” reported in Table 4 are obtained by considering two different options for the solar surface composition, as it discussed in Section 2.1. During the last few decades, solar neutrino experiments have allowed us to determine with great accuracy most of the components of the solar flux. As an example, ${}^7\mathrm{B}\mathrm{e}$ and $\text{B}8$ neutrino fluxes are measured with accuracy better than $\sim 3\text{\%}$ by Borexino (Agostini et al., 2018), Super-Kamiokande (Abe, 2016) and SNO (Aharmim, 2013). The pp and pep-neutrino flux can be determined with $\lesssim 1\text{\%}$ accuracy by assuming the solar luminosity constraint, see e.g., Bergstrom et al. (2016). These fluxes, however, have been also directly measured by Borexino (Bellini et al., 2012; Bellini, 2014; Agostini et al., 2018) with $\sim 10\text{\%}$ and $\sim 17\text{\%}$ accuracy, respectively. Finally, Borexino has recently obtained the experimental identification of CNO neutrinos (Agostini et al., 2020a), providing the first direct evidence that CNO-bicycle is active in the Sun.

FIGURE 4

FIGURE 4. The solar neutrino spectrum.

TABLE 4

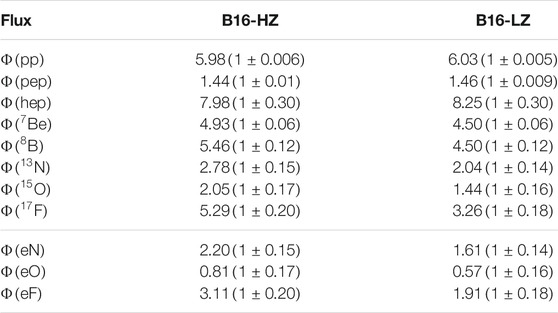
TABLE 4. Solar neutrino fluxes predicted by SSMs with different surface composition (Vinyoles et al., 2017). Units are: ${10}^{10}\left(\text{pp}\right)$, ${10}^9{(}^7\text{Be})$, ${10}^8\left(\text{pep},{}^{13}\text{N},{}^{15}\text{O}\right)$, ${10}^6{(}^8\text{B}{,}^{17}\text{F})$, ${10}^5\left(\text{eN},\text{eO}\right)$ and ${10}^3\left(\text{hep},\text{eF}\right){\text{cm}}^{-2}{\text{s}}^{-1}$.

2.3 Nuclear Reaction Rates

The cross sections of nuclear reaction in pp-chain and in CNO-bicycle are fundamental inputs for SSM calculations. Even if the focus of this work is on the role of nuclear rates for solar modeling (more than on reviewing the present situation for cross section measurements and calculations), we believe that it is useful to briefly discuss the adopted assumptions for the B16-SSM (Vinyoles et al., 2017). whose results have been previously discussed. The nuclear rates adopted for these models are from the Solar Fusion II compilation (Adelberger, 2011) with few relevant changes summarized in the following.

• $\mathbf{p}\left(\mathbf{p},{\mathbf{e}}^{+}{\mathit{\nu }}_{\mathbf{e}}\right)\mathbf{d}$: The astrophysical factor $S_{11}\left(E\right)$ has been recalculated in Marcucci et al. (2013) by using chiral effective field theory framework, including the P-wave contribution that had been previously neglected. For the leading order they obtain $S_{11}\left(0\right)=\left(4.03\pm 0.006\right)\cdot {10}^{-25}\text{MeV}\text{b}$. More recently, and also using chiral effective field theory, $S_{11}\left(E\right)$ was calculated by Acharya et al. (2016), resulting in $S_{11}\left(0\right)={4.047}_{-0.032}^{+0.024}\cdot {10}^{-25}\text{MeV}\text{b}$. This is in very good agreement with result from Marcucci et al. (2013). Ref. Acharya et al. (2016) have performed a more thorough assessment of uncertainty sources leading to an estimated error of 0.7%, much closer to the 1% uncertainty which was obtained by Adelberger (2011). In B16-SSM calculations, the astrophysical factor $S_{11}\left(E\right)$ is taken from Marcucci et al. (2013) with a conservative 1% error estimate Vinyoles et al. (2017).

• ${}^7\mathbf{B}\mathbf{e}{\left(\mathbf{p},\mathit{\gamma }\right)}^8\mathbf{B}$: Solar Fusion II recommended value is $S_{17}\left(0\right)=\left(2.08\pm 0.07\pm 0.14\right)\cdot {10}^{-5}\text{MeV}\text{b}$ (Adelberger, 2011), where the first error term comes from uncertainties in the different experimental results and the second one from considering different theoretical models employed for the low-energy extrapolation of the rate. Ref. (Zhang et al., 2015) presented a new low-energy extrapolation $S_{17}\left(0\right)=\left(2.13\pm 0.07\right)\cdot {10}^{-5}\text{MeV}\text{b}$, based on Halo Effective Field Theory, which allows for a continuous parametric evaluation of all low-energy models. Marginalization over the family of continuous parameters then amounts to marginalizing the results over the different low-energy models. In B16-SSM calculations, it was conservatively adopted an intermediate error between those from Zhang et al. (2015) and Adelberger (2011). The adopted value is $S_{17}\left(0\right)=\left(2.13\pm 0.1\right)\cdot {10}^{-5}\text{MeV}\text{b}$. The derivatives of the astrophysical factor were updated by using the recommended values in Zhang et al. (2015).

• ${}^{14}\mathbf{N}{\left(\mathbf{p},\mathit{\gamma }\right)}^{15}\mathbf{O}$: Ref. (Marta, 2011) presented cross-section data for this reaction obtained at the Laboratory for Underground Nuclear Astrophysics (LUNA) experiment. With the new data and using R-matrix analysis they recommend the value for the ground-state capture of $S_{GS}\left(0\right)=\left(0.20\pm 0.05\right)\cdot {10}^{-3}\text{MeV}\text{b}$. Combined with other transitions (see Table XI in that work) this leads to $S_{114}\left(0\right)=\left(1.59\cdot {10}^{-3}\right)\text{MeV}\text{b}$, about 4% lower than the previous recommended value in Ref. (Adelberger, 2011). The derivatives and the errors remain unchanged.

• ${}^3\mathbf{H}\mathbf{e}{{(}^4\mathbf{H}\mathbf{e},\mathit{\gamma })}^7\mathbf{B}\mathbf{e}$: Two recent analyses (deBoer et al., 2014; Iliadis et al., 2016) have provided determinations of the astrophysical factor that differs by about $6\text{\%}$ (to be compared with a claimed accuracy equal to $4\text{\%}$ and $2\text{\%}$ for deBoer et al. (2014) and Iliadis et al. (2016), respectively). Considering that the results from deBoer et al. (2014) and Iliadis et al. (2016) bracket the previously adopted value from Adelberger (2011), the latter was considered as preferred choice in Vinyoles et al. (2017).

Finally, Salpeter’s formulation of weak screening (Salpeter, 1954) is adopted. The validity of this formulation for solar conditions, where electrons are only weakly degenerate, has been discussed in detail in Gruzinov and Bahcall (1998), where a more sophisticated approach was shown to lead, to within differences of about 1%, to Salpeter’s result. Other proposed deviations from this formulation have been discussed at length in Bahcall et al. (2002), including different approaches to dynamic screening, and shown to be flawed or not well physically motivated. More recent calculations of dynamic screening (Mao et al., 2009; Mussack and Dappen, 2011) still leave, however, some room for discussion on this topic. In the weak screening limit, and in conditions under which screening is not numerically large, the dominant scaling is with the product of the charge of the two reacting nuclei. In the solar core, screening enhancement is about 5% for $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$, 20% for ${}^3\text{H}\text{e}\left({}^4\text{H}\text{e},\gamma \right){}^7\text{B}\text{e}$ and ${}^7\text{B}\text{e}\left(\text{p},\gamma \right){}^8\text{B}$, and 40% for ${}^{14}\text{N}{\left(\text{p},\gamma \right)}^{15}\text{O}$.

3 The Role of Nuclear Reactions

In the following, we discuss the role of nuclear reactions in SSM construction. Among nuclear processes, the $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$ reaction is the only one that can affect the temperature stratification of the Sun. Indeed, this process determines the global efficiency of hydrogen burning in the Sun. The other reactions in the pp-chain and in the CNO-cycle have a minor importance in this respect. However, they have a crucial role in determining the relative rates of the different pp-chain terminations and the efficiency of the CNO-cycle, thus affecting the predictions for the different components of the solar neutrino spectrum.

3.1 The pp-Reaction Rate and the Central Temperature of the Sun

In SSM calculations, where the Sun is assumed to be in thermal equilibrium, the rate of the pp-reaction is basically determined by the solar luminosity. Indeed, by considering that helium-4 is mainly produced by ${}^3\mathrm{H}\mathrm{e}\left({}^3\mathrm{H}\mathrm{e},2p\right){}^4\mathrm{H}\mathrm{e}$, we arrive at the conclusion that the integrated pp-rate in the Sun is ${\lambda }_{11}\sim 2L_{\odot }/Q_{\text{I}}$, where $Q_{\text{I}}=Q-2{\langle E_{\nu }\rangle }_{\text{pp}}\sim 26.2\text{MeV}$ is the energy released in the solar plasma when ${}^4\mathrm{H}\mathrm{e}$ is synthesized through pp-I termination. In the previous expression, we considered that the average energy of neutrinos produced by $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$ is ${\langle E_{\nu }\rangle }_{\text{pp}}=0.265\text{MeV}$ and we took into account that, at equilibrium, the pp-I termination involves twice the pp-reaction in order to feed the process ${}^3\mathrm{H}\mathrm{e}\left({}^3\mathrm{H}\mathrm{e},2p\right){}^4\mathrm{H}\mathrm{e}$.

Being the reaction rate fixed by the observed luminosity, the cross section of $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$ determines the central temperature of the Sun, as it is explained in the following. The rate ${\lambda }_{11}$ can be expressed as:

${\lambda }_{11}={{\displaystyle \int }}^{\text{}}{d}^{3}r\frac{{\rho }^2}{m_{\text{u}}^2}\frac{X^2}{2}{\langle \sigma v\rangle }_{11}(2)$

where ρ is the density, $m_{\text{u}}$ is the atomic mass unit, X is the hydrogen mass fraction and ${\langle \sigma v\rangle }_{11}$ is the reaction rate per particle pair of the $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$ reaction. The above integral involves, in principle, the entire solar structure but it gets a non-vanishing contribution only from the inner core of the Sun at $r\le 0.3R_{\odot }$. This can be appreciated by looking at Figure 5 where we show the differential rates $\left(1/{\lambda }_{\text{ij}}\right)\left(d{\lambda }_{\text{ij}}/dr\right)$ for the $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$ (black), $\text{p}\left(\text{p}{e}^{-},{\nu }_e\right)\text{d}$ (blue), ${}^3\mathrm{H}\mathrm{e}\left({}^4\mathrm{H}\mathrm{e},\gamma \right){}^7\mathrm{B}\mathrm{e}$ (red), ${}^7\mathrm{B}\mathrm{e}\left(\text{p},\gamma \right){}^8\text{B}$ (green) and ${}^3\mathrm{H}\mathrm{e}{\left(\text{p},e^{+}{\nu }_e\right)}^4\text{H}\text{e}$ (purple) reactions as a function of the solar radius. The different curves are all normalized to one in order to facilitate comparison among them. These curves also corresponds to the normalized production rates of pp, pep, ⁷Be, ⁸B and hep neutrinos, respectively^b.

FIGURE 5

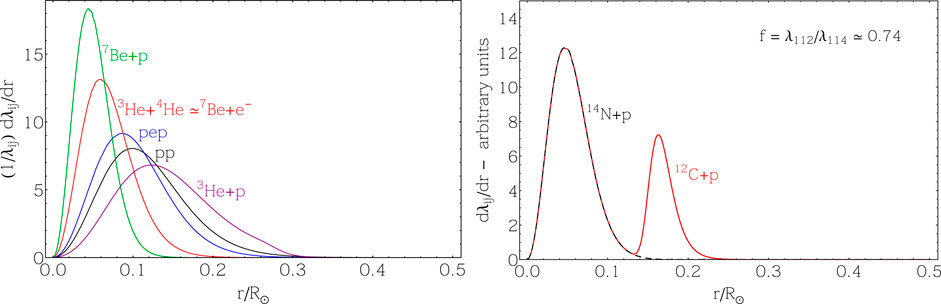
FIGURE 5. The differential rates for nuclear reactions in the pp-chain (Left Panel) and CN-cycle (Right Panel). The curves in the left panel have been normalized to one to facilitate comparison among them. The curves in the right panel are not normalized to emphasize that reactions ¹²$\text{C}{\left(\text{p},\gamma \right)}^{13}\text{N}$ and ¹⁴$\text{N}{\left(\text{p},\gamma \right)}^{15}\text{O}$ have the same rate in the equilibrium region.

Taking into account that $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$ reaction is active in a narrow region of the Sun at $r_0\simeq 0.1R_{\odot }$ whose physical conditions are similar to those at the solar center, we write the approximate scaling law:

${\lambda }_{11}\propto {\rho }_{\text{c}}^2{X}_{\text{c}}^2{S}_{11}{T}_{\text{c}}^{{\gamma }_{11}}(3)$

where the notation $Q_{\text{c}}$ indicates that the generic quantity Q is evaluated at the center of the Sun, $S_{11}$ is the astrophysical factor of the pp-reaction and we considered that ${\langle \sigma v\rangle }_{11}\propto S_{11}{T}_{\text{c}}^{{\gamma }_{11}}$ with ${\gamma }_{11}\simeq 4$. Eq. 3 implies the following linearized relationship:

$\delta {\lambda }_{11}\simeq 2\delta {\rho }_{\text{c}}+2\delta X_{\text{c}}+{\gamma }_{11}\delta T_{\text{c}}+\delta S_{11},$(3.1)

where $\delta Q$ indicates the fractional variation of the quantity Q with respect to the reference SSM value. The above expression contains input parameters for solar model construction, i.e. the astrophysical factor $S_{11}$, and structural parameters, like e.g., the temperature, density and hydrogen abundance in the core of the Sun which are the result of solar model self-calibrated calculations. In principle, a modification of $S_{11}$ induces a change of the solar structure and, thus, the different terms in the r.h.s of Eq. 3.1 are correlated. In order to keep $\delta {\lambda }_{11}\simeq 0$, an increase of the astrophysical factor $\delta S_{11}\ge 0$ has to be counterbalanced by an opposite contribution $2\delta {\rho }_{\text{c}}+2\delta X_{\text{c}}+{\gamma }_{11}\delta T_{\text{c}}\le 0$. This is achieved by varying the initial helium and metal abundance of the Sun according to $\delta Y_{\text{ini}}=0.6\delta S_{11}$ and $\delta Z_{\text{ini}}\simeq -0.10\delta S_{11}$ with the effect of obtaining a (slightly) colder solar core. We obtain numerically:

$\delta T_{\text{c}}\sim -0.13\delta S_{11}(4)$

that will be useful in the following to understand the effects of $S_{11}$ variations on the various components of the solar neutrino spectrum. In Figure 6, we show the effect of a 10% increase of $S_{11}$ on the temperature profile of SSMs and on the helioseismic observable quantities $\delta c\left(r\right)$ and $\delta \rho \left(r\right)$.

FIGURE 6

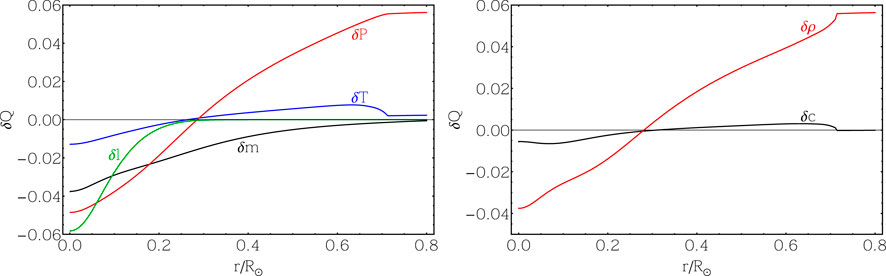
FIGURE 6. The effects of a $10\text{\%}$ increase of the astropysical factor of $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$ reaction on the physical properties of the Sun (left Panel) and on helioseismic observable quantities $\delta c\left(r\right)$ and $\delta \rho \left(r\right)$(right Panel). The fractional variations $\delta Q$ are calculated with respect to the reference SSM predictions.

3.2 The Dependence of Neutrino Fluxes on the Central Temperature of the Sun and on Nuclear Reaction Cross Sections

Even a small modification of the central temperature of the Sun reflects into large variations of solar neutrino fluxes. By considering the arguments discussed in Bahcall and Ulmer (1996); Degl’Innocenti et al. (1997), we discuss the dependence of solar neutrino fluxes on the core temperature of the Sun, highlighting the role of nuclear reactions for determining the branching ratios of the different pp-chain terminations and the efficiency of the CNO-bicycle.

3.2.1 PP-Chain Neutrino Fluxes

The pp-neutrino flux:

The vast majority of the solar neutrino emission is due to pp-neutrinos whose flux $\text{Φ}\left(\text{pp}\right)$ is directly linked to ${\lambda }_{11}$ being $\text{Φ}\left(\text{pp}\right)={\lambda }_{11}/\left(4\pi D^2\right)$ where $D=1\text{A}.\text{U}.$ is the Sun-Earth distance. According to discussion in the previous Section, the rate ${\lambda }_{11}$ is directly fixed by solar luminosity and thus $\text{Φ}\left(\text{pp}\right)$ is expected to be independent from the central temperature of the Sun and nuclear reaction cross sections. This result is obtained by assuming that pp-I is the only mechanism for helium-4 production by nuclear reaction in the Sun. A more accurate description can be obtained by taking into account the contribution the secondary branches of the pp-chain (namely, the pp-II termination) initiated by the ${}^3\mathrm{H}\mathrm{e}\left({}^3\mathrm{H}\mathrm{e},\gamma \right){}^7\mathrm{B}\mathrm{e}$ which provides an alternative ³$\text{H}\text{e}$ burning mechanism to the most common ${}^3\mathrm{H}\mathrm{e}\left({}^3\mathrm{H}\mathrm{e},2p\right){}^4\mathrm{H}\mathrm{e}$. In this assumption, we have:

$L_{\odot }=Q_{\text{I}}{\lambda }_{33}+Q_{\text{II}}{\lambda }_{34}(5)$

where ${\lambda }_{33}$ and ${\lambda }_{34}$ are the integrated rate of the ${}^3\mathrm{H}\mathrm{e}\left({}^3\mathrm{H}\mathrm{e},2p\right){}^4\mathrm{H}\mathrm{e}$ and ${}^3\mathrm{H}\mathrm{e}\left({}^4\mathrm{H}\mathrm{e},\gamma \right){}^7\mathrm{B}\mathrm{e}$ reactions, while $Q_{\text{I}}=26.20\text{MeV}$ and $Q_{\text{II}}=25.65\text{MeV}$ give the amount of energy, corrected for neutrino emission, delivered in the plasma when ${}^4\mathrm{H}\mathrm{e}$ is produced through pp-I and pp-II termination, respectively. By considering that ${\lambda }_{11}=2{\lambda }_{33}+{\lambda }_{34}$ at equilibrium, we arrive at the conclusion that (Bahcall and Ulmer, 1996):

$\text{Φ}\left(\text{pp}\right)=\frac{1}{4\pi D^2}\left(\frac{2{\text{L}}_{\odot }}{Q_{\text{I}}}-{\lambda }_{34}\right)(6)$

where we considered that $Q_{\text{I}}\simeq Q_{\text{II}}$. While the first term in the r.h.s of the above equation is constant, the rate ${\lambda }_{34}$ depends on the temperature of the plasma and on nuclear reaction cross sections. If we take into account that ${\lambda }_{34}\propto S_{34}\cdot {\left(S_{11}/S_{33}\right)}^{1/2}\cdot T_{\text{c}}^{{\beta }_{\text{Be}}}$ with ${\beta }_{\text{Be}}\sim 11$, as motivated later in this section, we obtain the following relationship

$\delta \text{Φ}\left(\text{pp}\right)=-\eta \delta S_{34}-\frac{\eta }{2}\left(\delta S_{11}-\delta S_{33}\right)+{\beta }_{\text{pp}}\delta T_{\text{c}}(7)$

that gives the fractional variation of the flux $\delta \text{Φ}\left(\text{pp}\right)$ as a function of fractional variation of the core temperature $\delta T_{\text{c}}$ and of the astrophysical factors $\delta S_{ij}$. The coefficients in the above equation correspond to the logarithmic derivatives of $\text{Φ}\left(\text{pp}\right)$ with respect to these quantities and are given by $\eta ={\lambda }_{34}/{\lambda }_{11}\simeq \text{Φ}{(}^7\text{B}\text{e})/\text{Φ}\left(\text{pp}\right)\simeq 0.08$ and ${\beta }_{\text{pp}}=-\eta {\beta }_{\text{Be}}\simeq -0.9$, showing that the pp-neutrino flux is a decreasing function of the central temperature of the Sun.

The pep-neutrino flux:

The pep-neutrinos are produced by electron capture reaction $\text{p}\left(\text{p}{e}^{-},{\nu }_e\right)\text{d}$ which is linked to the β-decay process $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$ by well-known nuclear physics. Since the two processes depend on the same allowed nuclear matrix element, the ratio between their rates is determined by the available reaction phase spaces and by the electron density $n_e$ of the solar plasma only. It can be determined with $\sim 1\text{\%}$ precision for the conditions of the solar interior and is mildly dependent on the properties of the solar plasma, being roughly proportional to $T_{\text{c}}^{-1/2}{n}_e$ (see e.g., Adelberger (2011) for a review). We can thus assume $\text{Φ}\left(\text{pep}\right)\propto T_{\text{c}}^{1/2}\text{Φ}\left(\text{pp}\right)$, allowing us to conclude:

$\delta \text{Φ}\left(\text{pep}\right)=-\eta \delta S_{34}-\frac{\eta }{2}\left(\delta S_{11}-\delta S_{33}\right)+{\beta }_{\text{pep}}\delta T_{\text{c}}(8)$

where ${\beta }_{\text{pep}}={\beta }_{\text{pp}}-1/2\simeq -1.4$, and we neglected effects related to possible density and chemical composition variations in the solar core.

The ⁷Be-neutrino flux:

The formation of beryllium-7 through ${}^3\text{H}\text{e}\left({}^4\text{H}\text{e},\gamma \right){}^7\text{B}\text{e}$ leads to neutrino production through the electron capture reaction ${}^7\text{B}\text{e}\left(e^{-},{\nu }_e\right){}^7\text{L}\text{i}$. This process largely dominates over the competing proton-capture reaction whose effects are discussed in the following paragraph. Taking this into account, the Be-neutrino flux can be directly estimated from the rate of the ${}^3\text{H}\text{e}\left({}^4\text{H}\text{e},\gamma \right){}^7\text{B}\text{e}$ reaction by using $\text{Φ}\left({}^7\text{B}\text{e}\right)={\lambda }_{34}/\left(4\pi D^2\right)$. The rate ${\lambda }_{34}$ is given by:

${\lambda }_{34}={{\displaystyle \int }}^{\text{}}{d}^{3}r\frac{{\rho }^2}{m_{\text{u}}^2}\frac{X_{3}Y}{12}{\langle \sigma v\rangle }_{34}(9)$

where Y ($X_3$) is the helium-4 (helium-3) mass fraction and ${\langle \sigma v\rangle }_{34}$ is the reaction rate per particle pair of ${}^3\mathrm{H}\mathrm{e}\left({}^3\mathrm{H}\mathrm{e},\gamma \right){}^7\mathrm{B}\mathrm{e}$. The amount of helium-4 nuclei in the present Sun is determined by the assumed initial abundance $Y_{\text{ini}}$ and by nuclear processes that have converted hydrogen into helium during the Sun evolution. We may thus expect that Y depends on nuclear cross sections, in particular on $S_{11}$ that determines the global efficiency of hydrogen burning. This dependence is however marginal because the product ${\text{L}}_{\odot }{\tau }_{\odot }$ essentially provides an observational determination of the integrated solar luminosity (and thus of the total amount of helium synthesized by nuclear reactions during the Sun lifetime). The helium-3 abundance in the solar core depends instead on the temperature $T_{\text{c}}$ and on the cross sections of the $\text{p}\left(\text{p},e^{+}{\nu }_e\right)\text{d}$ and ³$\text{H}\text{e}{(}^3\text{H}\text{e},2p)$⁴He reactions. It can be indeed calculated by using the equilibrium condition

$X_3\simeq X_{3,\text{eq}}=3X\sqrt{\frac{{\langle \sigma v\rangle }_{11}}{2{\langle \sigma v\rangle }_{33}}}(10)$

where X is the hydrogen mass fraction. Considering that ${\langle \sigma v\rangle }_{ij}\propto S_{ij}{T}_{\text{c}}^{{\gamma }_{ij}}$, this can be rewitten as $X_{3,\text{c}}\propto {\left(S_{11}/S_{33}\right)}^{1/2}\cdot T_{\text{c}}^{\left({\gamma }_{11}-{\gamma }_{33}\right)/2}$ where we neglected effects related to possible hydrogen abundance variations^c. This expression, combined with Eq. 9, allows us to conclude that:

$\text{Φ}\left(7\text{B}\text{e}\right)\propto S_{34}\cdot {\left(S_{11}/S_{33}\right)}^{1/2}\cdot T_{\text{c}}^{{\beta }_{\text{Be}}}(11)$

or, equivalently,

$\delta \text{Φ}\left(7\text{B}\text{e}\right)=\delta S_{34}+\frac{1}{2}\left(\delta S_{11}-\delta S_{33}\right)+{\beta }_{\text{Be}}\delta T_{\text{c}}(12)$

where ${\beta }_{\text{Be}}={\gamma }_{34}+\left({\gamma }_{11}-{\gamma }_{33}\right)/2\sim 11$. Note that the ⁷Be-neutrino flux does not depends on the cross section of ${}^7\mathrm{B}\mathrm{e}\left(e^{-},{\nu }_e\right){}^7\mathrm{L}\mathrm{i}$, due to the fact that (almost) the totality of beryllium-7 nuclei produced by ${}^3\mathrm{H}\mathrm{e}\left({}^4\mathrm{H}\mathrm{e},\gamma \right){}^7\mathrm{B}\mathrm{e}$ are expected to decay through this reaction.

The ⁸B-neutrino flux:

The ⁸B neutrinos constitute a largely subdominant component of the solar flux which is produced when ${}^7\mathrm{B}\mathrm{e}$ nuclei capture a proton (instead of an electron) producing ${}^8\text{B}$ (instead of ⁷$\text{L}\text{i}$). The ⁸B-neutrino flux is thus given by $\text{Φ}\left({}^8\text{B}\right)=r\text{Φ}\left({}^7\mathrm{B}\mathrm{e}\right)$ where $r\equiv {\lambda }_{17}/{\lambda }_{e7}$ is the ratio between proton and electron capture rates on beryllium-7. The parameter r scales as $r\propto \left(S_{17}/S_{e7}\right)\cdot T_{\text{c}}^{\alpha }$ where $\alpha ={\gamma }_{17}+\left(1/2\right)$ and we have considered that ${\langle \sigma v\rangle }_{\text{e}7}\propto S_{e7}{T}_{\text{c}}^{-1/2}$ for electron capture reaction. Taking this into account, we obtain the following scaling law:

$\text{Φ}\left(8\text{B}\right)\propto \left(S_{17}/S_{e7}\right)\cdot S_{34}\cdot {\left(S_{11}/S_{33}\right)}^{1/2}\cdot T_{\text{c}}^{{\beta }_{\text{B}}}(13)$

that also corresponds to:

$\delta \text{Φ}\left(8\text{B}\right)=\left(\delta S_{17}-\delta S_{e7}\right)+\delta S_{34}+\frac{1}{2}\left(\delta S_{11}-\delta S_{33}\right)+{\beta }_{\text{B}}\delta T_{\text{c}}(14)$

with ${\beta }_{\text{B}}={\beta }_{\text{Be}}+{\gamma }_{17}+1/2\simeq 24$. The large value of ${\beta }_{\text{B}}$ indicates that ⁸B neutrinos are a very sensitive probe of the core temperature of the Sun.

3.2.2 The CNO Neutrino Fluxes

The neutrino fluxes produced in the CN-cycle by β-decay (and electron capture reactions) of ¹³N and ¹⁵O nuclei, besides depending on the solar central temperature, are approximately proportional to the stellar-core number abundance of CN elements. This dependence is relevant to understand the role of cross section for CNO-neutrino production. Moreover, as it is discussed in Haxton and Serenelli (2008); Haxton et al. (2013), it permits us to use CNO neutrinos, in combination with other neutrino fluxes, to directly probe the chemical composition of the Sun.

The ¹⁵O-neutrino flux:

This component of the solar neutrino spectrum is determined by the production rate of oxygen-15 by ¹⁴$\text{N}{\left(\text{p},\gamma \right)}^{15}\text{O}$ reaction in the core of the Sun. It can be calculated as $\text{Φ}{(}^{15}\text{O})={\lambda }_{114}/\left(4\pi D^2\right)$ where the rate ${\lambda }_{114}$, given by:

${\lambda }_{114}={{\displaystyle \int }}^{\text{}}{d}^{3}r\frac{{\rho }^2}{m_{\text{u}}^2}\frac{X{X}_{14}}{14}{\langle \sigma v\rangle }_{114}(15)$

is proportional to the nitrogen-14 mass fraction $X_{14}$ in the solar core (see Figure 3) and to the reaction rate per particle pair ${\langle \sigma v\rangle }_{114}$ of the ¹⁴N (p,γ)¹⁵O reaction. The above integral get a non vanishing contribution from a narrow region at $r\lesssim 0.1R_{\odot }$ whose conditions are similar to that at the solar center, see Figure 5. We thus write the approximate scaling law:

$\text{Φ}\left(15\text{O}\right)\propto {\lambda }_{114}\propto X_{14,\text{c}}{S}_{114}{T}_{\text{c}}^{{\beta }_{\text{O}}}(16)$

where $S_{114}$ is the astrophysical factor of the ¹⁴N (p,γ)¹⁵O reaction, we considered that ${\langle \sigma v\rangle }_{114}\propto S_{114}{T}_{\text{c}}^{{\gamma }_{114}}$ and we defined ${\beta }_{\text{O}}={\gamma }_{114}\simeq 20$. Eq. 16 implies the following linearized relationship:

$\delta \text{Φ}\left(15\text{O}\right)=\delta X_{14,\text{c}}+\delta S_{114}+{\beta }_{\text{O}}\delta T_{\text{c}}(17)$

In the above expressions, we neglected effect related to possible variations of the density and of the hydrogen abundance in the solar core, since these are expected to be small. We instead explicitly considered the dependence of $\text{Φ}\left({\text{O}}^{15}\right)$ on the central abundance of nitrogen-14 which is essentially determined, as it is explained in the following, by the total abundances of CN elements in the solar core. It is useful to remark that, being the CNO cycle sub-dominant, a modification of its efficiency does not alter the solar luminosity and does not require a readjustement of the central temperature. Moreover, carbon and nitrogen give a marginal contribution to the opacity of the solar plasma and thus a variation of their abundances do not alter the temperature stratification. As a result of this, we can consider the different terms in Eq. 17 as independent.

The ¹³N-neutrino flux:

The flux of ¹³N-neutrinos can be calculated $\text{Φ}{(}^{13}\text{N})={\lambda }_{112}/\left(4\pi D^2\right)$ where ${\lambda }_{112}$ is the total rate of the ¹²$\text{C}{\left(\text{p},\gamma \right)}^{13}\text{N}$ reaction in the Sun. This is given by:

${\lambda }_{112}={{\displaystyle \int }}^{\text{}}{d}^{3}r\frac{{\rho }^2}{m_{\text{u}}^2}\frac{X{X}_{12}}{12}{\langle \sigma v\rangle }_{112}(18)$

where $X_{12}$ is the carbon-12 mass fraction and ${\langle \sigma v\rangle }_{112}$ is the reaction rate per particle pair of ¹²C (p,γ)¹³N. We can write:

${\lambda }_{112}={\lambda }_{114}+{\lambda }_{112}^{\left(\text{ne}\right)}(19)$

where the quantity:

${\lambda }_{112}^{\left(\text{ne}\right)}={{\displaystyle \int }}^{\text{}}{d}^{3}r\frac{{\rho }^2}{m_{\text{u}}^2}X[\frac{X_{12}}{12}{\langle \sigma v\rangle }_{112}-\frac{X_{14}}{14}{\langle \sigma v\rangle }_{114}](20)$

gives the contribution to the total rate produced in the region of the Sun where the CN-cycle is incomplete. The above integral vanishes indeed for $r\le 0.13R_{\odot }$ where the equilibrium condition for the CN-cycle ensures that $\left(X_{12}/12\right){\langle \sigma v\rangle }_{112}-\left(X_{14}/14\right){\langle \sigma v\rangle }_{114}=0$. This can be appreciated in the right panel of Figure 5 where we show the differential rate $d{\lambda }_{114}/dr$ and $d{\lambda }_{112}/dr$ of ¹⁴$\text{N}{\left(\text{p},\gamma \right)}^{15}\text{O}$ (black) and ¹²$\text{C}{\left(\text{p},\gamma \right)}^{13}\text{N}$ (red) reactions as a function of the solar radius r.

Eq. 19 implies that $\text{Φ}{(}^{13}\text{N})$ can be decomposed as the sum:

$\text{Φ}\left(13\text{N}\right)=\text{Φ}\left(15\text{O}\right)+\text{Φ}{\left(13\text{N}\right)}^{\left(\text{ne}\right)}(21)$

where the quantity $\text{Φ}{\left(13\text{N}\right)}^{\left(\text{ne}\right)}\equiv {\lambda }_{112}^{\left(\text{ne}\right)}/\left(4\pi D^2\right)$ represents the neutrino flux produced in the region $0.13\underset{˜}{<}r/R_{\odot }\underset{˜}{<}0.25$, where ¹⁴$\text{N}{\left(\text{p},\gamma \right)}^{15}\text{O}$ reaction is not effective. This component of the flux scales as:

$\text{Φ}{\left(13\text{N}\right)}^{\left(\text{ne}\right)}\propto X_{12}\left(r_{\text{ne}}\right)S_{112}{T}_{\text{c}}^{{\gamma }_{114}}(22)$

where we considered that ${\langle \sigma v\rangle }_{112}\propto S_{112}{T}_{\text{c}}^{{\gamma }_{112}}$ with ${\gamma }_{112}\simeq 18$ and we neglected effects related to possible variations of density and hydrogen abundance. Note that the carbon-12 mass fraction in Eq. 22 is evaluated at $r_{\text{ne}}\simeq 0.16R_{\odot }$ where the out-of-equilibrium ¹³N-neutrino production rate is maximal, see Figures 3, 5. In principle, the temperature should be also evaluated at this position. However, we can take the central value $T_{\text{c}}$ as representative for the entire energy producing region, motivated by the fact that $T\left(r\right)$ (differently from $X_{12}\left(r\right)$) is slowly varying in the solar core. Eq. 22 implies the following relationship:

$\delta \text{Φ}{\left(13\text{N}\right)}^{\left(\text{ne}\right)}=\delta X_{12}\left(r_{\text{ne}}\right)+\delta S_{112}+{\gamma }_{112}\delta T_{\text{c}}(23)$

that combined with Eq. 17 gives:

$\delta \text{Φ}\left(13\text{N}\right)=f[\delta X_{14,\text{c}}+\delta S_{114}+{\gamma }_{114}\delta T_{\text{c}}]+\left(1-f\right)[\delta X_{12}\left(r_{\text{ne}}\right)+\delta S_{112}+{\gamma }_{112}\delta T_{\text{c}}](24)$

where $f=\text{Φ}{(}^{15}\text{O})/\text{Φ}{(}^{13}\text{N})=0.74$ is the ratio between ¹⁵O and ¹³N neutrino fluxes in SSMs (Vinyoles et al., 2017).

The abundance of carbon and nitrogen in the core of the Sun.

Eqs. 17, 24 describe the dependence of the CN-neutrino fluxes from the abundances of nitrogen $X_{14,\text{c}}$ and carbon $X_{12}\left(r_{\text{ne}}\right)$ at the center of the Sun and close to $r_{\text{ne}}=0.16R_{\odot }$, respectively. These abundances are determined by the formation and chemical evolution history of the Sun, i.e. by the initial solar composition and by the subsequent action of nuclear reactions and elemental diffusion, as it is described in the following. Let us first consider that the CN-cycle conserves the total number of CN-nuclei in the core of the Sun. This is shown in Figure 3 by the behavior of the quantity:

$\mathcal{N}\equiv X_{12}/12+X_{13}/13+X_{14}/14(25)$

which is proportional to the total carbon + nitrogen number density ($X_{13}$ represents the carbon-13 mass abundance) and it is nearly constant in the solar core despite the action of nuclear reactions. In the SSM paradigm, the radial dependence of $\mathcal{N}$ is only due to elemental diffusion so that we can write:

$\mathcal{N}\left(r\right)={\mathcal{N}}_{\text{ini}}[1+\text{Δ}\left(r\right)](26)$

where ${\mathcal{N}}_{\text{ini}}$ is the initial carbon + nitrogen abundance that is assumed to be uniform in the solar structure while the function $\text{Δ}\left(r\right)$ describes the effects of gravitational settling. It takes the value ${\text{Δ}}_{\text{c}}=0.06$ at the center of the Sun that can be considered also representative for $r_{\text{ne}}=0.16R_{\odot }$, and ${\text{Δ}}_{\text{s}}=-0.09$ in external convective envelope according to SSM calculations (Vinyoles et al., 2017). It is useful to connect the core composition to photospheric abundances since these are observationally constrained by spectroscopic measurements. We thus write:

${\mathcal{N}}_{\text{c}}={\mathcal{N}}_{\text{s}}[1+{\text{Δ}}^{\left(\text{cs}\right)}](27)$

where ${\mathcal{N}}_{\text{s}}$ (${\mathcal{N}}_{\text{c}})$ is the carbon + nitrogen abundance in the external convective envelope (at the center) of the Sun while ${\text{Δ}}^{\left(\text{cs}\right)}=\left({\text{Δ}}_{\text{c}}-{\text{Δ}}_{\text{s}}\right)/\left(1+{\text{Δ}}_{\text{s}}\right)=0.16$ represents the fractional difference between core and surface abundances.

The abundance $X_{14,\text{c}}$ that controls the equilibrium production of CN-neutrinos is directly related to total abundance of carbon and nitrogen in the core of the Sun. Indeed, for $r\lesssim 0.1R_{\odot }$ the CN-cycle is complete and all available carbon is essentially transformed into nitrogen, giving $X_{14,\text{c}}\simeq 14{\mathcal{N}}_{\text{c}}$ (see Figure 3). We thus obtain the relation $\delta X_{14,\text{c}}=\delta {\mathcal{N}}_{\text{c}}$ that, by taking advantage of Eqs. 25, 27), can be rewritten as:

$\delta X_{14,\text{c}}=a\delta X_{14,\text{s}}+\left(1-a\right)\delta X_{12,\text{s}}+b\left({\text{Δ}}^{\left(\text{cs}\right)}-0.16\right)(28)$

where $b=1/\left(1+0.16\right)=0.86$, $a=6\xi /\left(6\xi +7\right)\simeq 0.20$ and $\xi =\left(X_{\text{N},\text{s}}/X_{\text{C},\text{s}}\right)\simeq 0.30$ is the surface nitrogen-to-carbon ratio in SSM. The first two terms of the r.h.s in the above equation describe the effects produced by a variation of the surface composition. A modification of the chemical composition profile that is instead produced either “primordially” (e.g., by assuming that the Sun was not born chemical homogenous) or during the evolution (e.g., by anomalous diffusion) on time scales longer than carbon and nitrogen burning time at the solar center, is instead described in terms of a variation of ${\text{Δ}}^{\left(\text{cs}\right)}$ from the SSM value, i.e., by assuming ${\text{Δ}}^{\left(\text{cs}\right)}-0.016\ne 0$.

A slightly more involved expression is obtained for the abundance $X_{12}\left(r_{\text{ne}}\right)$ that controls the non-equilibrium production of ¹³N-neutrinos. In the relevant region $0.13\lesssim r/R_{\odot }\lesssim 0.25$, the carbon-12 abundance differs from the surface value $X_{12,\text{s}}$ due to the action of elemental diffusion and ¹²$\text{C}{\left(\text{p},\gamma \right)}^{13}\text{N}$ reaction only, since further reactions are inhibited by the bottleneck. It can be approximately described as

$X_{12}\left(r_{\text{ne}}\right)\simeq X_{12,\text{s}}[1+{\text{Δ}}^{\left(\text{cs}\right)}]\text{exp}\left(-{\overline{\mathrm{}}}_{112}\left(r_{\text{ne}}\right)t_{\odot }\right)(29)$

where the quantity ${\overline{\mathrm{}}}_{112}$ represents the carbon-12 burning rate

${\mathrm{}}_{112}=\frac{\rho X}{m_u}{\langle \sigma v\rangle }_{112}(30)$

averaged over the Sun lifetime, see Appendix for details. The maximal neutrino production is achieved at $r_{\text{ne}}\simeq 0.16R_{\odot }$ where the integrated burning rate is ${\overline{\mathrm{}}}_{112}\left(r_{\text{ne}}\right)t_{\odot }\simeq 1$. Indeed, in the inner core where ${\overline{\mathrm{}}}_{112}{t}_{\odot }\gg 1$, carbon-12 abundance is too low to efficiently feed ¹²$\text{C}{\left(\text{p},\gamma \right)}^{13}\text{N}$ reaction. On the other hand, the carbon-12 burning time is much larger than solar age (and thus ¹²$\text{C}{\left(\text{p},\gamma \right)}^{13}\text{N}$ reaction is not effective) in more external regions where ${\overline{\mathrm{}}}_{112}\ll \left(1/t_{\odot }\right)$, as can be understood by considering that ${\mathrm{}}_{112}\simeq {\overline{\mathrm{}}}_{112}$. Taking this into account, we obtain the following relation:

$\delta X_{12}\left(r_{\text{ne}}\right)=\delta X_{12,\text{s}}+b\left({\text{Δ}}^{\left(\text{cs}\right)}-0.16\right)-\delta S_{112}-{\gamma }_{112}\delta T_{\text{c}}(31)$

where we considered that ${\overline{\mathrm{}}}_{112}\left(r_{\text{ne}}\right)\propto S_{112}{T}_{\text{c}}^{{\gamma }_{112}}$.

The final expressions the CN neutrino fluxes.

By using the above equations, we are able to calculate the dependence of neutrino fluxes produced in the CN-cycle on the properties of the Sun. By using Eqs. 28, 31 into Eqs. 17, 24, we obtain:

$\begin{array}{l}\delta \text{Φ}\left(15\text{O}\right)={\beta }_{\text{O}}\delta T_{\text{c}}+\left(1-a\right)\delta X_{12,\text{s}}+a\delta X_{14,\text{s}}+b\left({\text{Δ}}^{\left(\text{cs}\right)}-0.16\right)+\delta S_{114}\\ \delta \text{Φ}\left(13\text{N}\right)={\beta }_{\text{N}}\delta T_{\text{c}}+\left(1-a^{\text{′}}\right)\delta X_{12,\text{s}}+a^{\text{′}}\delta X_{14,\text{s}}+b\left({\text{Δ}}^{\left(\text{cs}\right)}-0.16\right)+f\delta S_{114}\end{array}(32)$

with ${\beta }_{\text{O}}=20$, $f=0.74$, $a=0.2$, $b=0.86$, ${\beta }_{\text{N}}\equiv f{\beta }_{\text{O}}=15$ and $a\text{'}\equiv fa=0.15$. Note that, in the derivation of the second equation, we took into account that the third and the fourth terms in the r.h.s of Eq. 31 cancels the dependence of $\text{Φ}{{(}^{13}\text{N})}^{\left(\text{ne}\right)}$ on $S_{112}$ and $T_{\text{c}}$ expressed in Eq. 23. This is due to the fact that, as far as the ¹³N-neutrino (non equilibrium) production rate is concerned, the effect of ¹²$\text{C}{\left(\text{p},\gamma \right)}^{13}\text{N}$ cross section enhancement is compensated by the reduction of residual carbon-12 abundance due the more efficient carbon burning.

4 Numerical Results and Nuclear Uncertainties

The expressions obtained for the neutrino fluxes can be compared with the results of SSMs calculations. In particular, the numerical coefficients in Eqs. 7, 8, 12, 14 , 32 should reproduce the logarithmic derivatives of the neutrino fluxes with respect to the astrophysical factors of the relevant nuclear cross sections reported in Table 5. We see that a good agreement exists, indicating that all the major physical effects are included in our discussion and correctly described. In the case of $S_{11}$, we have to take into account that the role of this parameter is twofold; indeed, besides altering the efficiency of pp-reaction (at fixed temperature), this parameter also induces a variation of the central temperature of the Sun as described by Eq. 4. This effect, combined with the strong temperature dependence of the fluxes, allow us to understand the large values for logarithmic derivatives reported in the first column of Table 5.

TABLE 5

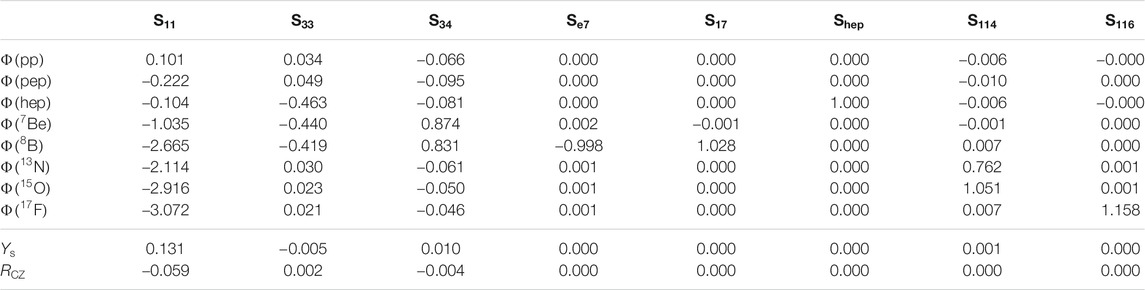
TABLE 5. The logarithmic derivatives $\alpha \left(Q,I\right)$ of the solar neutrino fluxes with respect to nuclear input parameters calculated in B16-HZ SSMs.

For completeness, we also discuss in the last two rows of Table 5 the dependence of the helioseismic observable quantities $Y_{\text{s}}$ (surface helium abundance) and $R_{\text{CZ}}$ (depth of the convective envelope) on nuclear reactions cross sections. We see that $S_{11}$ is the only nuclear parameter that affects the predictions for these quantities. The effects of $S_{11}$ modifications on sound speed and density profiles are shown in the right panel of Figure 6. Finally, Table 6 gives the logarithmic derivatives of neutrino fluxes and helioseismic quantities on other input parameters (beside nuclear cross sections) which are necessary to construct SSMs. These are: the solar age (age), luminosity (lumi) and the diffusion coefficients (diffu); the opacity of solar plasma whose uncertainty is described in terms of two parameters ${\kappa }_a$ and ${\kappa }_b$ defined in Section 2.1; the surface abundances of key elements (C, N, O, Ne, Mg, Si, S, Ar, Fe) which are determined through spectroscopic measurements as discussed in Section 2.1. We can see that the logarithmic derivatives of the CN-neutrino fluxes with respect to the surface carbon and nitrogen abundances are correctly predicted by Eq. 32.

TABLE 6

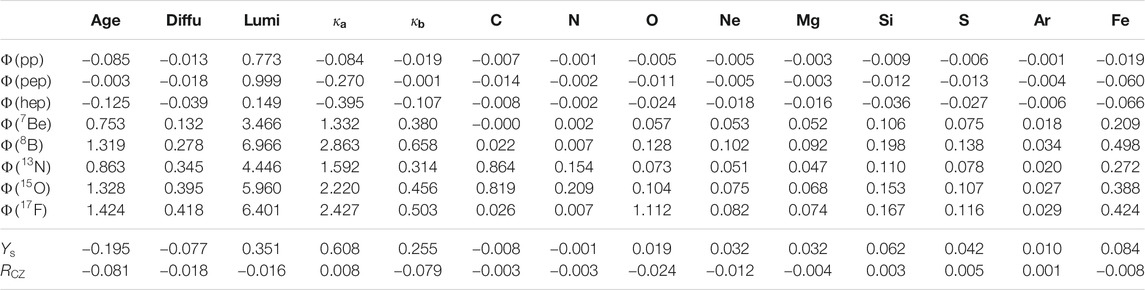
TABLE 6. The logarithmic derivatives $\alpha \left(Q,I\right)$ of the solar neutrino fluxes with respect to solar properties that produce environmental effects and chemical composition parameters calculated in B16-HZ SSMs.

The uncertainties in solar properties leading to environmental effects and chemical composition parameters, together with uncertainties in nuclear reaction cross sections propagate to SSM predictions which are affected by a theoretical (or model) error that can be estimated by Monte-Carlo techniques and/or linear propagation. By using this approach, the fractional error ${\sigma }_Q$ on a generic SSM prediction Q can be obtained as the sum (in quadrature) of different contributions, according to:

${\sigma }_Q^2={\displaystyle \sum }_I{\left[\alpha \left(Q,I\right)\right]}^2{\sigma }_I^2(33)$

where $I=age,lumi,\dots$ indicates a specific input, ${\sigma }_I$ represents its fractional uncertainty and $\alpha \left(Q,I\right)\equiv d\text{ln}Q/d\text{ln}I$ is the logarithmic derivative of Q with respect to I. Table 7 contains the uncertainties ${\sigma }_I$ that have been considered for the construction of B16-SSMs (the surface composition errors are reported in Table 2), see Vinyoles et al. (2017) for details. By using these values, one is able to estimate the contribution $\delta Q_I\equiv \alpha \left(Q,I\right){\sigma }_I$ of each input parameter to the total error budget of Q. The dominant error sources for solar neutrino fluxes and helioseismic quantities are given in Table 8.^d

TABLE 7

TABLE 7. The fractional uncertainties of enviromental and nuclear input parameters in SSM construction.

TABLE 8

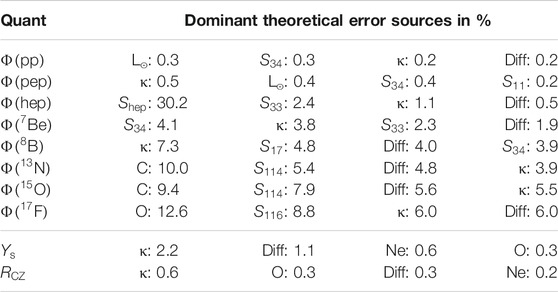
TABLE 8. Dominant theoretical error sources for neutrino fluxes and for the main characteristics of the SSM.

Focusing on nuclear reactions, we note that, despite the progress in the field, they are still an important uncertainty source for neutrino fluxes. In particular, the error contributions from $S_{34}$ and $S_{17}$ are comparable to or larger than the uncertainties in the experimental determinations of $\text{Φ}{(}^8\text{B})$ and $\text{Φ}\left({}^7\text{B}\text{e}\right)$. As discussed in Vinyoles et al. (2017), the ability of solar neutrinos produced in the pp-chain to play a significant role in constraining physical conditions in the solar interior depends, although it is not the only factor, on pinning down errors of nuclear reaction rates to just $\sim 2\text{\%}$. For CN fluxes, we see that $S_{114}$ is the dominant error source if composition is left aside. This is particularly relevant, especially in consideration of the fact that Borexino has just opened the era of CNO neutrino detection, obtaining for the first time $\sim 5\sigma$ direct experimental evidence for a non vanishing flux from the Sun (Agostini et al., 2020a).

For a correct evaluation of the importance of nuclear cross section, it should be remarked that, while neutrino fluxes generally change with variation in any of the input parameters, SSM predictions are strongly correlated with a single output parameter, the core temperature $T_{\text{c}}$ (Bahcall and Ulmer, 1996; Degl’Innocenti et al., 1997; Haxton and Serenelli, 2008; Serenelli et al., 2013). As a consequence, a multi-dimensional set of variations of enviromental and chemical composition parameters $\left\{\delta I\right\}$ often collapses to a one-dimensional dependence on $\delta T_{\text{c}}$, where $\delta T_{\text{c}}$ is an implicit function of the variations $\left\{\delta I\right\}$. The dominance of $T_{\text{c}}$ as the controlling parameter for neutrino fluxes can be exploited to cancel out uncertainties in the analysis of solar neutrino data. One can indeed form weighted ratios $\text{Φ}\left({\nu }_1\right)/\text{Φ}{\left({\nu }_2\right)}^{x_{12}}$, or equivalently weighted fractional differences $\delta \text{Φ}\left({\nu }_1\right)-x_{12}\delta \text{Φ}\left({\nu }_2\right)$ with respect to SSM predictions that are nearly independent of $T_{\text{c}}$ and thus marginally affected by environmental effects and chemical composition, using the residual dependence on selected parameters to learn something about them.

In Haxton and Serenelli (2008); Serenelli et al. (2013), it was suggested to combine the CN-neutrino fluxes with the boron neutrino flux that, due to the exquisite precision of current experimental results and the large temperature sensitivity can be efficiently used as solar thermometer. As can be understood by considering Eqs. 14, 32, the following combinations can be formed:

$\begin{array}{c}\delta \text{Φ}\left(15\text{O}\right)-x\delta \text{Φ}\left(8\text{B}\right)=\left(1-a\right)\delta X_{12,\text{s}}+a\delta X_{14,\text{s}}+b\left({\text{Δ}}^{\left(\text{cs}\right)}-0.16\right)\\ +\delta S_{114}-x\left(\frac{\delta S_{11}}{2}-\frac{\delta S_{33}}{2}+\delta S_{34}+\delta S_{17}-\delta S_{e7}\right)\end{array}(34)$

$\begin{array}{c}\delta \text{Φ}\left(13\text{N}\right)-x^{\prime }\delta \text{Φ}\left(8\text{B}\right)=\left(1-a^{\prime }\right)\delta X_{12,\text{s}}+a^{\prime }\delta X_{14,\text{s}}+b\left({\text{Δ}}^{\left(\text{cs}\right)}-0.16\right)\\ +\delta S_{114}-x^{\prime }\left(\frac{\delta S_{11}}{2}-\frac{\delta S_{33}}{2}+\delta S_{34}+\delta S_{17}-\delta S_{e7}\right)\end{array}(35)$

where $x={\beta }_{\text{O}}/{\beta }_{\text{B}}\simeq 0.8$ and $x\text{'}=fx\simeq 0.6$, that are independent from $\delta T_{\text{c}}$. This possibility is extremely important because it allows us to cancels out the dependence on the radiative opacity (implicit in $\delta T_{\text{c}}$). The uncertainty of available opacity calculations is indeed not easily quantified and may be potentially underestimated. Moreover, it breaks the degeneracy between composition and opacity effects on solar observable properties. Indeed, the considered flux combinations only depend on the carbon and nitrogen abundance in the solar core allowing us to test the chemical composition and evolution of the Sun. The first two terms in the r.h.s of Eqs. 34, 35 quantify the effects of a variation of the surface C and N abundances. A change of the diffusion efficiency is instead described in terms of a variation of ${\text{Δ}}^{\left(\text{cs}\right)}$ from the SSM value, i.e., by assuming ${\text{Δ}}^{\left(\text{cs}\right)}-0.016\ne 0$. It should be remarked that the ability to probe solar composition by using this approach is only limited by experimental accuracy of flux determinations and by nuclear cross section uncertainties.

While the above relationships are based on the simplified arguments discussed in the previous section, the optimal combinations $\delta \text{Φ}\left({\nu }_1\right)-x_{12}\delta \text{Φ}\left({\nu }_2\right)$, or equivalently weighted ratios $\text{Φ}\left({\nu }_1\right)/\text{Φ}{\left({\nu }_2\right)}^{x_{12}}$, can be determined by using the power-law coefficients from Vinyoles et al. (2017) given in Table 6. The parameter $x_{12}$ is obtained by minimizing the residual

$\rho ={\displaystyle \sum }_{I=1}^N{\left[\alpha \left({\nu }_1,I\right)-x_{12}\alpha \left({\nu }_2,I\right)\right]}^2{\sigma }_I^2(36)$

where the sum extends to the N input parameters whose dependence we want to cancel out and ${\sigma }_I$ are the corresponding uncertainties. The minimal value for ρ gives the intrinsic error in the considered approach. This method, originally proposed by Haxton and Serenelli (2008); Serenelli et al. (2013), has been recently adapted to Borexino (Agostini et al., 2020b). By taking into account that the measured CNO neutrino signal in Borexino is basically probing $\delta {\varphi }_{\text{CNO}}^{\text{BX}}\equiv \xi \delta \text{Φ}{(}^{15}\text{O})+\left(1-\xi \right)\delta \text{Φ}{(}^{13}\text{N})$ with $\xi =0.764$ , it was concluded that the surface composition of the Sun can be probed by the combination:

$\delta R_{\text{CNO}}^{\text{BX}}-0.716\delta \text{Φ}\left(8\text{B}\right)=0.814\delta X_{12,\text{s}}+0.191\delta X_{14,\text{s}}\pm 0.5\text{\%}\left(\text{env}\right)\pm 9.1\text{\%}\left(\text{nucl}\right)\pm 2.8\text{\%}\left(\text{diff}\right)(37)$

where $\delta R_{\text{CNO}}^{\text{BX}}$ is the fractional difference of the observed CNO signal with respect to SSM expectations and the quoted uncertainties are obtained by propagating errors of SSM input parameters. The error budget is presently dominated by the uncertainty of the CNO signal Borexino measurement. However, a relevant error ($\sim 10\text{\%}$) is also provided by nuclear reactions, with the largest contributions coming from $S_{114}$ (7.6%), $S_{34}$ (3.4%), and $S_{17}$ (3.5%). In the perspective of future improvements of the CNO signal determination, it is evidently important to have reliable and accurate determinations of these cross sections.

5 Concluding Remarks

A fundamental part in solar model calculations is the knowledge of the rates of nuclear reactions involved in the generation of solar nuclear energy. During the last decades, we experienced a substantial progress in the accuracy of SSM calculations that was made possible, among the other ingredients, by the continuous improvements of nuclear cross sections that are now typically determined with $\sim 5\text{\%}$ accuracy. However, SSMs have now to challenge new puzzles, like e.g., the solar composition problems. Moreover, SSM neutrino flux predictions, which are directly affected to nuclear cross sections uncertainties, have to be compared against very accurate observational determinations, having errors at few % level or better e.g., for $\text{Φ}\left({}^7\text{B}\text{e}\right)$ and $\text{Φ}\left({}^8\text{B}\right)$.

As a consequence, further work is needed on the side of nuclear reactions. Indeed, nuclear uncertainties have a non negligible role in SSMs error budget. As an example, the error contributions from $S_{34}$ and $S_{17}$ are about a factor 2 larger than the uncertainties in the experimental determinations of $\text{Φ}{(}^7\text{B}\text{e})$ and $\text{Φ}{(}^8\text{B})$. As it is discussed in Vinyoles et al. (2017), the few percent systematics in the determination of these reaction rates is still a relevant source of difficulty in using neutrino fluxes as constraints to solar model properties. The astrophysical factor $S_{114}$ is morevoer a relevant error source for CN neutrino fluxes. This last point is particularly important after Borexino opened the era of CNO neutrino detection, obtaining the first ever direct evidence of a non vanishing CN neutrino signal from the Sun. In the perspective of future and more accurate measurements, nuclear uncertainties can become a limiting factor in the possibility to use the CN-neutrinos, in combination with ⁸B neutrinos, to directly probe the solar composition, thus addressing the solar composition problem. At the moment, the nuclear error contribution to CN-core abundance uncertainty is $\sim 10\text{\%}$, see Eq. 37. This is comparable to the error in CN-surface abundance determinations (0.05 dex in LZ composition) and only a factor $\sim 2$ smaller than the difference between HZ and LZ results, which can be regarded as an estimate of the systematic shift in the surface abundances produced by advances in stellar spectroscopy during the last 20 years. We remark that a high accuracy determination of the solar core composition could be used not only to discriminate among different solar surface admixtures but also to test the chemical evolution scheme employed by SSMs, e.g., by verifying the effect of elemental diffusion according to which core abundances are expected to be $\sim 15\text{\%}$ larger than surface values.

In conclusion, it would be desirable to further improve our knowledge of nuclear cross sections, in particular for ³$\text{H}\text{e}{(}^4\text{H}\text{e},\gamma )$⁷Be, ⁷$\text{B}\text{e}\left(\text{p},\gamma \right)$⁸B and ¹⁴$\text{N}{\left(\text{p},\gamma \right)}^{15}\text{O}$ reactions. As we discussed in the introduction, the history of SSMs appears to be formed by three large chapters, during which the knowledge of nuclear rates improved at each stage by about a factor two with respect to the previous period, up to the present situation in which the leading cross section in pp-chain and CN-cycle are typically determined with $\sim 5\text{\%}$ accuracy. The ambitious goal for the next stage could be a further factor $\sim 2$ reduction, in such a way that nuclear reactions uncertainties will not represent a limiting factor in constraining the physical conditions of solar interior.

Author Contribitions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

FV acknowledges support by ‘Neutrino and Astroparticle Theory Network’ under the program PRIN 2017 funded by the Italian Ministry of Education, University and Research (MIUR) and INFN Iniziativa Specifica TAsP. AS acknowledges support by the Spanish Government through the MICINN grant PRPPID 2019–108709GB-I00.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix: the ¹²C abundance in non-equilibrium region

In the region $0.13\lesssim r/R_{\odot }\lesssim 0.25$, the CN-cycle is incomplete; carbon-12 is partially burned by ¹²$\text{C}{\left(\text{p},\gamma \right)}^{13}\text{N}$ while nitrogen-14 is not effectively processed by ¹⁴$\text{N}{\left(\text{p},\gamma \right)}^{15}\text{O}$ reaction. If we neglect elemental diffusion, the equation that describes the time evolution of carbon-12 is (in lagrangian coordinates):

$\frac{\partial X_{12}}{\partial t}=-X_{12}{\mathrm{}}_{112}(38)$

where the carbon-12 burning rate ${\mathrm{}}_{112}$ is given by:

${\mathrm{}}_{112}=\frac{\rho X}{m_u}{\langle \sigma v\rangle }_{112}(39)$

The solution of Eq. 38 is:

$X_{12}=X_{12,\text{ini}}\text{exp}\left(-{\overline{\mathrm{}}}_{112}{t}_{\odot }\right)(40)$

where $X_{12,\text{ini}}$ is the initial abundance and ${\overline{\mathrm{}}}_{112}$ is given by:

${\overline{\mathrm{}}}_{112}\equiv \frac{1}{t_{\odot }}{{{\displaystyle \int }}^{\text{}}}_0^{t_{\odot }}dt{\mathrm{}}_{112}.(41)$

We include a-posteriori the effecs of elemental diffusion by replacing $X_{12,\text{ini}}\to X_{12,\text{ini}}\left(1+\text{Δ}\left(r\right)\right)$ with the function $\text{Δ}\left(r\right)$ defined in Eq. 26. We can then recast in terms of the surface carbon abundance, obtaining:

$X_{12}=X_{12,\text{s}}\left[1+{\text{Δ}}^{\left(\text{cs}\right)}\right]\text{exp}\left(-{\overline{\mathrm{}}}_{112}{t}_{\odot }\right).(42)$

where ${\text{Δ}}^{\left(\text{cs}\right)}=0.16$ is the fractional difference between core and surface abundances induced by elemental diffusion.

^aIn order to take into account the new inputs in B16-SSM calculations, the ecCNO fluxes given in Table 4 have been scaled with respect to the values quoted in Villante (2015) proportionally to the corresponding β-decay fluxes. This follows from the assumption that the ratio of electron capture and beta decay processes in the Sun is equal to what evaluated in Villante (2015).

^bNote that the rate of ${}^3\text{H}\text{e}{(}^4\text{H}\text{e},\gamma ){}^7\text{B}\text{e}$ is basically equal to that of the neutrino producing reaction ${}^7\text{B}\text{e}\left(e^{-},{\nu }_e\right){}^7\text{L}\text{i}$

^cWe evaluate the exponents ${\gamma }_{ij}$ by using ${\gamma }_{ij}\simeq {\left(E_0\right)}_{ij}-2/3$ where ${\left(E_0\right)}_{ij}$ is the Gamov peak energy of the considered reaction, see e.g., Bahcall and Ulmer (1996).

^dThe total error due to opacity is obtained by combining in quadrature the contributions from ${\kappa }_a$ and ${\kappa }_b$.

References

Abdurashitov, J., Gavrin, V. N., Girin, S. V., Gorbachev, V. V., Ibragimova, T. V., Kalikhov, A. V., et al. (1999). Measurement of the solar neutrino capture rate with gallium metal. Phys. Rev. C 60, 055801. doi:10.1103/PhysRevC.60.055801

CrossRef Full Text | Google Scholar

Abe, K. (2016). Solar neutrino measurements in super-kamiokande-IV. Phys. Rev. D 94, 052010. doi:10.1103/PhysRevD.94.052010

CrossRef Full Text | Google Scholar

Acharya, B., Carlsson, B. D., Ekström, A., Forssén, C., and Platter, L. (2016). Uncertainty quantification for proton-proton fusion in chiral effective field theory. Phys. Lett. B7 60, 584–589. doi:10.1016/j.physletb.2016.07.032

CrossRef Full Text | Google Scholar

Adelberger, E. G. (2011). Solar fusion cross sections II: the pp chain and CNO cycles. Rev. Mod. Phys. 83, 195. doi:10.1103/RevModPhys.83.195

CrossRef Full Text | Google Scholar

Adelberger, E. G. (1998). Solar fusion cross-sections. Rev. Mod. Phys. 70, 1265–1292. doi:10.1103/RevModPhys.70.1265

CrossRef Full Text | Google Scholar

Agostini, M., Altenmüller, K., and The Borexino Collaboration., (2018). Comprehensive measurement of -chain solar neutrinos. Nature 562, 505–510. doi:10.1038/s41586-018-0624-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Agostini, M., Altenmüller, K., and The Borexino Collaboration., (2020a). First direct experimental evidence of CNO neutrinos. Nature 587, 577–582. doi:10.1038/s41586-020-2934-0

CrossRef Full Text | Google Scholar

Agostini, M., Altenmüller, K., and The Borexino Collaboration., (2020b). Sensitivity to neutrinos from the solar CNO cycle in Borexino. Eur. Phys. J. C 80. doi:10.1140/epjc/s10052-020-08534-2

CrossRef Full Text | Google Scholar

Aharmim, B. (2013). Combined analysis of all three phases of solar neutrino data from the sudbury neutrino observatory. Phys. Rev. C 88, 025501. doi:10.1103/PhysRevC.88.025501

CrossRef Full Text | Google Scholar

Ahmad, Q., Allen, R C., Andersen, T C., Anglin, J D., Barton, J C., Beier, E W., et al. (2002). Direct evidence for neutrino flavor transformation from neutral current interactions in the Sudbury Neutrino Observatory. Phys. Rev. Lett. 89, 011301. doi:10.1103/PhysRevLett.89.011301

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmad, Q., Allen, R C., Andersen, T C., Anglin, J D., Barton, J C., Beier, E W., et al. (2001). Measurement of the rate of interactions produced by solar neutrinos at the Sudbury Neutrino Observatory. Phys. Rev. Lett. 87, 071301. doi:10.1103/PhysRevLett.87.071301

PubMed Abstract | CrossRef Full Text | Google Scholar

Angulo, C., Arnould, M., Rayet, M., Descouvemont, P., Baye, D., Leclercq-Willain, C., et al. (1999). A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. 656, 3–183. doi:10.1016/S0375-9474(99)00030-5

CrossRef Full Text | Google Scholar

Antia, H. M., and Chitre, S. M. (2002). Helioseismic limit on heavy element abundance. Astron. Astrophys. 393, L95–L98. doi:10.1051/0004-6361:20021253

CrossRef Full Text | Google Scholar

Antia, H. M., and Chitre, S. M. (1999). Limits on the proton-proton reaction cross-section from helioseismology. Astron. Astrophys. 347, 1000–1004.

Google Scholar

Arpesella, C., Back, H. O., Bellini, G. B., Balata, M., Benzinger, J., Leclercq-Willain, C., et al. (2008). Direct measurement of the Be-7 solar neutrino flux with 192 Days of Borexino data. Phys. Rev. Lett. 101, 091302. doi:10.1103/PhysRevLett.101.091302

PubMed Abstract | CrossRef Full Text | Google Scholar

Asplund, M., Grevesse, N., Sauval, A. J., and Scott, P. (2009). The chemical composition of the Sun. Annu. Rev. Astron. Astrophys. 47, 481–522. doi:10.1146/annurev.astro.46.060407.145222

CrossRef Full Text | Google Scholar

Badnell, N. R., Bautista, M. A., Butler, K., Delahaye, F., Mendoza, C., Palmeri, P., et al. (2005). Up-dated opacities from the opacity Project. Mon. Not. Roy. Astron. Soc. 360, 458–464. doi:10.1111/j.1365-2966.2005.08991.x

CrossRef Full Text | Google Scholar

Bahcall, J. N., Basu, S., Pinsonneault, M., and Serenelli, A. M. (2005a). Helioseismological implications of recent solar abundance determinations. Astrophys. J. 618, 1049–1056. doi:10.1086/426070

CrossRef Full Text | Google Scholar

Bahcall, J. N., Brown, L. S., Gruzinov, A., and Sawyer, R. (2002). The Salpeter plasma correction for solar fusion reactions. Astron. Astrophys. 383, 291–295. doi:10.1051/0004-6361:20011715

CrossRef Full Text | Google Scholar

Bahcall, J. N., Huebner, W. F., Lubow, S. H., Parker, P. D., and Ulrich, R. K. (1982). Standard solar models and the uncertainties in predicted capture rates of solar neutrinos. Rev. Mod. Phys. 54, 767–799. doi:10.1103/RevModPhys.54.767

CrossRef Full Text | Google Scholar

Bahcall, J. N. (1990). Line versus continuum solar neutrinos. Phys. Rev. D41, 2964. doi:10.1103/PhysRevD.41.2964

CrossRef Full Text | Google Scholar

Bahcall, J. N., and Pinsonneault, M. H. (1992). Standard solar models, with and without helium diffusion, and the solar neutrino problem. Rev. Mod. Phys. 64, 885–926. doi:10.1103/RevModPhys.64.885

CrossRef Full Text | Google Scholar

Bahcall, J. N., Pinsonneault, M. H., and Wasserburg, G. J. (1995). Solar models with helium and heavy-element diffusion. Rev. Mod. Phys. 67, 781–808. doi:10.1103/RevModPhys.67.781

CrossRef Full Text | Google Scholar

Bahcall, J. N., Serenelli, A. M., and Basu, S. (2006). 10,000 standard solar models: a Monte Carlo simulation. Astrophys. J. Suppl. 165, 400–431. doi:10.1086/504043

CrossRef Full Text | Google Scholar

Bahcall, J. N., Serenelli, A. M., and Basu, S. (2005b). New solar opacities, abundances, helioseismology, and neutrino fluxes. Astrophys. J. Lett. 621, L85–L88. doi:10.1086/428929

CrossRef Full Text | Google Scholar

Bahcall, J. N. (2002). The Luminosity constraint on solar neutrino fluxes. Phys. Rev. C65, 025801. doi:10.1103/PhysRevC.65.025801

CrossRef Full Text | Google Scholar

Bahcall, J. N., and Ulmer, A. (1996). The Temperature dependence of solar neutrino fluxes. Phys. Rev. D53, 4202–4210. doi:10.1103/PhysRevD.53.4202

CrossRef Full Text | Google Scholar

Bailey, J. E., Nagayama, T., Loisel, G. P., Rochau, G. A., Blancard, C., Colgan, J., et al. (2015). A higher-than-predicted measurement of iron opacity at solar interior temperatures. Nature 517, 56–59. doi:10.1038/nature14048

PubMed Abstract | CrossRef Full Text | Google Scholar

Basu, S., and Antia, H. M. (2004). Constraining solar abundances using helioseismology. Astrophys. J. 606, L85. doi:10.1086/421110

CrossRef Full Text | Google Scholar

Basu, S., and Antia, H. M. (2008). Helioseismology and solar abundances. Phys. Rep. 457, 217–283. doi:10.1016/j.physrep.2007.12.002

CrossRef Full Text | Google Scholar

Basu, S., and Antia, H. M. (1997). Seismic measurement of the depth of the solar convection zone. Mon. Not. Roy. Astron. Soc. 287, 189–198. doi:10.1093/mnras/287.1.189

CrossRef Full Text | Google Scholar

Bellini, G., Benziger, J., Bick, D., Bonetti, S., Bonfini, G., Bravo, D., et al. (2012). First evidence of pep solar neutrinos by direct detection in Borexino. Phys. Rev. Lett. 108, 051302. doi:10.1103/PhysRevLett.108.051302

PubMed Abstract | CrossRef Full Text | Google Scholar

Bellini, G. (2014). Neutrinos from the primary proton-proton fusion process in the Sun. Nature 512, 383–386. doi:10.1038/nature13702

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergstrom, J., Gonzalez-Garcia, M. C., Maltoni, M., Pena-Garay, C., Serenelli, A. M., and Song, N. (2016). Updated determination of the solar neutrino fluxes from solar neutrino data. JHEP 03, 132. doi:10.1007/JHEP03(2016)132

CrossRef Full Text | Google Scholar

Blancard, C., Cossé, P., and Faussurier, G. (2012). Solar mixture opacity calculations using detailed configuration and level accounting treatments. Astrophys. J. 745, 10. doi:10.1088/0004-637X/745/1/10

CrossRef Full Text | Google Scholar

Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., and Bonifacio, P. (2011). Solar chemical abundances determined with a CO5BOLD 3D model atmosphere. Sol. Phys. 268, 255. doi:10.1007/s11207-010-9541-4

CrossRef Full Text | Google Scholar

Cassisi, S., Salaris, M., and Irwin, A. W. (2003). The initial helium content of galactic globular cluster stars from the r-parameter: comparison with the cmb constraint. Astrophys. J. 588, 862. doi:10.1086/374218

CrossRef Full Text | Google Scholar

Castro, M., Vauclair, S., and Richard, O. (2007). Low abundances of heavy elements in the solar outer layers: comparisons of solar models with helioseismic inversions. Astron. Astrophys. 463, 755–758. doi:10.1051/0004-6361:20066327

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Dappen, W., Ajukov, S. V., Anderson, E. R., Antia, H. M., Basu, S., et al. (1996). The current state of solar modeling. Science 272, 1286–1292. doi:10.1126/science.272.5266.1286

PubMed Abstract | CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Di Mauro, M. P., Houdek, G., and Pijpers, F. (2009). On the opacity change required to compensate for the revised solar composition. Astron. Astrophys. 494, 205. doi:10.1051/0004-6361:200810170

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Duvall, J., T. L., , Gough, D. O., Harvey, J. W., Rhodes, J., et al. (1985). Speed of sound in the solar interior. Nature 315, 378–382. doi:10.1038/315378a0

CrossRef Full Text | Google Scholar

Christensen-Dalsgaard, J., Proffitt, C. R., and Thompson, M. J. (1993). Effects of diffusion on solar models and their oscillation frequencies. Astrophys. J. Lett. 403, L75. doi:10.1086/186725

CrossRef Full Text | Google Scholar

Cleveland, B., Daily, T., Davis, J., Raymond, Distel, J. R., Lande, K., Lee, C., et al. (1998). Measurement of the solar electron neutrino flux with the Homestake chlorine detector. Astrophys. J. 496, 505–526. doi:10.1086/305343

CrossRef Full Text | Google Scholar

Colgan, J., Kilcrease, D. P., Magee, N. H., Sherrill, M. E., Abdallah, J., J., Hakel, P., et al. (2016). A new generation of Los Alamos opacity tables. Astrophys. J. 817, 116. doi:10.3847/0004-637X/817/2/116

CrossRef Full Text | Google Scholar

deBoer, R. J., Görres, J., Smith, K., Uberseder, E., Wiescher, M., Kontos, A., et al. (2014). Monte Carlo uncertainty of the He3(alpha,gamma)Be7 reaction rate. Phys. Rev. C90, 035804. doi:10.1103/PhysRevC.90.035804

CrossRef Full Text | Google Scholar

Degl’Innocenti, S., Dziembowski, W. A., Fiorentini, G., and Ricci, B. (1997). Helioseismology and standard solar models. Astropart. Phys. 7, 77–95. doi:10.1016/S0927-6505(97)00004-2

CrossRef Full Text | Google Scholar

degl’Innocenti, S., Fiorentini, G., and Ricci, B. (1998). Helioseismology and p+p → d + e ⁺ ν_e in the sun. Phys. Lett. B 416, 365–368. doi:10.1016/S0370-2693(97)01197-0

CrossRef Full Text | Google Scholar

Delahaye, F., and Pinsonneault, M. (2006). The solar heavy element abundances. 1. constraints from stellar interiors. Astrophys. J. 649, 529–540. doi:10.1086/505260

CrossRef Full Text | Google Scholar

Deubner, F.-L., and Gough, D. (1984). Helioseismology: oscillations as a diagnostic of the solar interior. Annu. Rev. Astron. Astrophys. 22, 593–619. doi:10.1146/annurev.aa.22.090184.003113

CrossRef Full Text | Google Scholar

Elsworth, Y., Howe, R., Isaak, G. R., McLeod, C. P., and New, R. (1990). Evidence from solar seismology against non-standard solar-core models. Nature 347, 536–539. doi:10.1038/347536a0

CrossRef Full Text | Google Scholar

Ferguson, J. W., Alexander, D. R., Allard, F., Barman, T., Bodnarik, J. G., Hauschildt, P. H., et al. (2005). Low temperature opacities. Astrophys. J. 623, 585–596. doi:10.1086/428642

CrossRef Full Text | Google Scholar

Fukuda, S., Fukuda, Y., Ishitsuka, M., Itow, Y., Kajita, T., Kameda, J., et al. (2001). Solar B-8 and hep neutrino measurements from 1258 days of Super-Kamiokande data. Phys. Rev. Lett. 86, 5651–5655. doi:10.1103/PhysRevLett.86.5651

PubMed Abstract | CrossRef Full Text | Google Scholar

Fukuda, Y. (1998). Measurements of the solar neutrino flux from Super-Kamiokande’s first 300 days. Phys. Rev. Lett. 81, 1158–1162. doi:10.1103/PhysRevLett.81.1158

CrossRef Full Text | Google Scholar

Gough, D. O., Kosovichev, A. G., Toomre, J., Anderson, E., Antia, H. M., Basu, S., et al. (1996). The seismic structure of the sun. Science 272, 1296–1300. doi:10.1126/science.272.5266.1296

PubMed Abstract | CrossRef Full Text | Google Scholar

Grevesse, N., and Noels, A. (1993). “Cosmic abundances of the elements,”. Origin and evolution of the elements. Editors N. Prantzos, E. Vangioni-Flam, and M. Casse (Tokyo, Japan: Cambridge University Press), 15–25.

Google Scholar

Grevesse, N., and Sauval, A. J. (1998). Standard solar composition. Space Sci. Rev. 85, 161–174. doi:10.1023/A:1005161325181

CrossRef Full Text | Google Scholar

Grevesse, N., Scott, P., Asplund, M., and Sauval, A. J. (2015). The elemental composition of the Sun III. The heavy elements Cu to Th. Astron. Astrophys. 573, A27. doi:10.1051/0004-6361/201424111

CrossRef Full Text | Google Scholar

Gruzinov, A. V., and Bahcall, J. N. (1998). Screening in thermonuclear reaction rates in the sun. Astrophys. J. 504, 996–1001. doi:10.1086/306116

CrossRef Full Text | Google Scholar

Guzik, J. A., and Mussack, K. (2010). Exploring mass loss, low-Z accretion, and convective overshoot in solar models to mitigate the solar abundance problem. Astrophys. J. 713, 1108–1119. doi:10.1088/0004-637X/713/2/1108

CrossRef Full Text | Google Scholar

Guzik, J. A., Watson, L., and Cox, A. N. (2005). Can enhanced diffusion improve helioseismic agreement for solar models with revised abundances?. Astrophys. J. 627, 1049–1056. doi:10.1086/430438

CrossRef Full Text | Google Scholar

Hampel, W., Handt, J., Heusser, G., Kiko, J., Kirsten, T., Laubenstein, M., et al. (1999). GALLEX solar neutrino observations: results for GALLEX IV. Phys. Lett. B 447, 127–133. doi:10.1016/S0370-2693(98)01579-2

CrossRef Full Text | Google Scholar

Harvey, J. W., Hill, F., Hubbard, R. P., Kennedy, J. R., Leibacher, J. W., Pintar, J. A., et al. (1996). The global oscillation network group (GONG) Project. Science 272, 1284–1286. doi:10.1126/science.272.5266.1284

PubMed Abstract | CrossRef Full Text | Google Scholar

Haxton, W. C., Hamish Robertson, R. G., and Serenelli, A. M. (2013). Solar neutrinos: status and prospects. Annu. Rev. Astron. Astrophys. 51, 21–61. doi:10.1146/annurev-astro-081811-125539

CrossRef Full Text | Google Scholar

Haxton, W. C., and Serenelli, A. M. (2008). CN-cycle solar neutrinos and Sun’s primordial core metalicity. Astrophys. J. 687, 678–691. doi:10.1086/591787

CrossRef Full Text | Google Scholar

Iliadis, C., Anderson, K., Coc, A., Timmes, F., and Starrfield, S. (2016). Bayesian estimation of thermonuclear reaction rates. Astrophys. J. 831, 107. doi:10.3847/0004-637X/831/1/107

CrossRef Full Text | Google Scholar

Kippenhahn, R., and Weigert, A. (1990). Stellar structure and evolution. Berlin Heidelberg, New York: Springer, 606.

Krief, M., Feigel, A., and Gazit, D. (2016a). Line broadening and the solar opacity problem. Astrophys. J. 824, 98. doi:10.3847/0004-637X/824/2/98

CrossRef Full Text | Google Scholar

Krief, M., Feigel, A., and Gazit, D. (2016b). Solar opacity calculations using the super-transition-array method. Astrophys. J. 821, 45. doi:10.3847/0004-637X/821/1/45

CrossRef Full Text | Google Scholar

Krishna Swamy, K. S. (1966). Profiles of strong lines in K-dwarfs. Astrophys. J. 145, 174. doi:10.1086/148752

CrossRef Full Text | Google Scholar

Lodders, K., Palme, H., and Gail, H.-P. (2009). Abundances of the elements in the solar system. Landolt Börnstein, 712. doi:10.1007/978-3-540-88055-4˙3410.1007/978-3-540-88055-4_34

CrossRef Full Text | Google Scholar

Mao, D., Mussack, K., and Dappen, W. (2009). Dynamic screening in solar plasma. Astrophys. J. 701, 1204–1208. doi:10.1088/0004-637X/701/2/1204

CrossRef Full Text | Google Scholar

Marcucci, L. E., Schiavilla, R., and Viviani, M. (2013). Proton-proton weak capture in chiral effective field theory. Phys. Rev. Lett. 110, 192503. doi:10.1103/PhysRevLett.110.192503

PubMed Abstract | CrossRef Full Text | Google Scholar

Marta, M. (2011). The 14N(p,gamma)15O reaction studied with a composite germanium detector. Phys. Rev. C83, 045804. doi:10.1103/PhysRevC.83.045804

CrossRef Full Text | Google Scholar

Mondet, G., Blancard, C., Cossé, P., and Faussurier, G. (2015). Opacity calculations for solar mixtures. Astrophys. J. Supp. 220, 2. doi:10.1088/0067-0049/220/1/2

CrossRef Full Text | Google Scholar

Montalban, J., Miglio, A., Noels, A., Grevesse, N., and Di Mauro, M. (2004). Solar model with CNO revised abundances. ESA Spec. Publ. 559, 574

Google Scholar

Mussack, K., and Dappen, W. (2011). Dynamic screening correction for solar p-p reaction rates. Astrophys. J. 729, 96. doi:10.1088/0004-637X/729/2/96

CrossRef Full Text | Google Scholar

Nagayama, T., Bailey, J. E., Loisel, G. P., Dunham, G. S., Rochau, G. A., Blancard, C., et al. (2019). Systematic study of L -shell opacity at stellar interior temperatures. Phys. Rev. Lett. 122, 235001. doi:10.1103/PhysRevLett.122.235001

PubMed Abstract | CrossRef Full Text | Google Scholar

Salpeter, E. (1954). Electron screening and thermonuclear reactions. Austral. J. Phys. 7, 373–388. doi:10.1071/PH540373

CrossRef Full Text | Google Scholar

Schlattl, H., Bonanno, A., and Paternò, L. (1999). Signatures of the efficiency of solar nuclear reactions in the neutrino experiments. Phys. Rev. D 60, 113002. doi:10.1103/PhysRevD.60.113002

CrossRef Full Text | Google Scholar

Scott, P., Asplund, M., Grevesse, N., Bergemann, M., and Sauval, A. J. (2015a). The elemental composition of the Sun II. The iron group elements Sc to Ni. Astron. Astrophys. 573, A26. doi:10.1051/0004-6361/201424110

CrossRef Full Text | Google Scholar

Scott, P., Grevesse, N., Asplund, M., Sauval, A. J., Lind, K., Takeda, Y., et al. (2015b). The elemental composition of the Sun I. The intermediate mass elements Na to Ca. Astron. Astrophys. 573, A25. doi:10.1051/0004-6361/201424109

CrossRef Full Text | Google Scholar

Serenelli, A. M., Haxton, W. C., and Pena-Garay, C. (2011). Solar models with accretion. I. Application to the solar abundance problem. Astrophys. J. 743, 24. doi:10.1088/0004-637X/743/1/24

CrossRef Full Text | Google Scholar

Serenelli, A., Peña-Garay, C., and Haxton, W. C. (2013). Using the standard solar model to constrain solar composition and nuclear reaction S factors. Phys. Rev. D 87, 043001. doi:10.1103/PhysRevD.87.043001

CrossRef Full Text | Google Scholar

Stonehill, L. C., Formaggio, J. A., and Robertson, R. G. H. (2004). Solar neutrinos from CNO electron capture. Phys. Rev. C 69, 015801. doi:10.1103/PhysRevC.69.015801

CrossRef Full Text | Google Scholar

Thoul, A. A., Bahcall, J. N., and Loeb, A. (1994). Element diffusion in the solar interior. Astrophys. J. 421, 828–842. doi:10.1086/173695

CrossRef Full Text | Google Scholar

Tognelli, E., Degl’Innocenti, S., Marcucci, L. E., and Prada Moroni, P. G. (2015). Astrophysical implications of the proton-proton cross section updates. Phys. Lett. B 742, 189–194. doi:10.1016/j.physletb.2015.01.033

CrossRef Full Text | Google Scholar

Turck-chièze, S., Nghiem, P., Couvidat, S., and Turcotte, S. (2001). Solar internal composition and nuclear reaction rates in the light of helioseismology. Sol. Phys. 200, 323–342. doi:10.1023/A:1010365125791

CrossRef Full Text | Google Scholar

Villante, F. L. (2010). Constraints on the opacity profile of the sun from helioseismic observables and solar neutrino flux measurements. Astrophys. J. 724, 98–110. doi:10.1088/0004-637X/724/1/98

CrossRef Full Text | Google Scholar

Villante, F. L. (2015). ecCNO solar neutrinos: a challenge for gigantic ultra-pure liquid scintillator detectors. Phys. Lett. B 742, 279–284. doi:10.1016/j.physletb.2015.01.043

CrossRef Full Text | Google Scholar

Villante, F. L., Serenelli, A. M., Delahaye, F., and Pinsonneault, M. H. (2014). The chemical composition of the Sun from helioseismic and solar neutrino data. Astrophys. J. 787, 13. doi:10.1088/0004-637X/787/1/13

CrossRef Full Text | Google Scholar

Vinyoles, N., Serenelli, A. M., Villante, F. L., Basu, S., Bergström, J., Gonzalez-Garcia, M. C., et al. (2017). A new generation of standard solar models. Astrophys. J. 835, 202. doi:10.3847/1538-4357/835/2/202

CrossRef Full Text | Google Scholar

Vissani, F. (2019). “Luminosity constraint and entangled solar neutrino signals,” in Solar Neutrinos. Editors M. Meyer and K. Zuber. 121–141.

CrossRef Full Text

Zhang, X., Nollett, K. M., and Phillips, D. R. (2015). Halo effective field theory constrains the solar ⁷Be + p →⁸B + gamma rate. Phys. Lett. B 751, 535–540. doi:10.1016/j.physletb.2015.11.005

CrossRef Full Text | Google Scholar