- 1Dipartimento di Scienze Fisiche e Chimiche, Università degli Studi dell’Aquila, L'Aquila, Italy
- 2Laboratori Nazionali del Gran Sasso (LNGS), Istituto Nazionale di Fisica Nucleare (INFN), Assergi, Italy
- 3Institute of Space Sciences (ICE, CSIC), Barcelona, Spain
- 4Institut D’Estudis Espacials de Catalunya (IEEC), Barcelona, Spain
The fundamental processes by which nuclear energy is generated in the Sun have been known for many years. However, continuous progress in areas such as neutrino experiments, stellar spectroscopy and helioseismic data and techniques requires ever more accurate and precise determination of nuclear reaction cross sections, a fundamental physical input for solar models. In this work, we review the current status of (standard) solar models and present a complete discussion on the relevance of nuclear reactions for detailed predictions of solar properties. In addition, we also provide an analytical model that helps understanding the relation between nuclear cross sections, neutrino fluxes and the possibility they offer for determining physical characteristics of the solar interior. The latter is of particular relevance in the context of the conundrum posed by the solar composition, the solar abundance problem, and in the light of the first ever direct detection of solar CN neutrinos recently obtained by the Borexino collaboration. Finally, we present a short list of wishes about the precision with which nuclear reaction rates should be determined to allow for further progress in our understanding of the Sun.
1 Introduction
The history of solar models, or standard solar models (SSMs) to be more precise, is formed by three large chapters related to the type of observational and experimental data about the solar interior that existed at any given time. The first part of this history comprises the period over which only neutrino data were available, and it spans about 20 years, from the mid 60 s to the early 80 s of the past century. During that period, the solar neutrino problem was seen by many as having an origin in the complexities involved in building accurate and precise SSMs, a fundamental part of which is determined by the nuclear reaction rates involved in the generation of the solar nuclear energy. Around the end of that era, the precision of nuclear reaction rates involved in the chains of reactions leading to the production of the different solar neutrino fluxes were on the order to 20–30%. These uncertainties may seem large for present day standards. However, if some faith was put in their accuracy, these uncertainties were small enough that associating the solar neutrino problem to nuclear cross section measurements was highly unlikely (Bahcall et al., 1982).
In the mid 80s helioseismology, the study of solar oscillations, evolved into a precision branch of solar physics. The sensitivity of the frequency spectrum of these global pressure waves to the details of the interior solar structure allowed their reconstruction by means of inversion methods (see e.g., Deubner and Gough (1984); Christensen-Dalsgaard et al. (1985)), in particular of the solar interior sound speed. This (r)evolution peaked during the second half of the 1990s with the establishment of the Global Oscillation Network Group (GONG), a network of six instruments established around the world that carried out resolved radial velocity measurements of the solar surface (Harvey et al., 1996) and with the launch of the SoHO satellite, both of which provided rich helioseismic datasets. In turn, this led to determination of the solar interior properties with precision of better than 1% (and in some cases even an order of magnitude better) (Gough et al., 1996). These results led to the appearance of a new generation of SSMs (Bahcall et al., 1995; Christensen-Dalsgaard et al., 1996), which were successful in satisfying the tight observational constraints imposed by helioseismology, leaving little room for an astrophysical solution to the solar neutrino problem, as had originally been suggested a few years earlier (Elsworth et al., 1990). Simultaneously, Super-Kamiokande (Fukuda, 1998; Fukuda et al., 2001) led to the precise measurement of 8B neutrino flux which, in combination with the results of radiochemical experiments Homestake (Cleveland et al., 1998), Gallex (Hampel et al., 1999) and SAGE (Abdurashitov et al., 1999) strongly hinted at the existence of solar neutrino oscillations, result confirmed just a few years later by SNO results (Ahmad et al., 2001; Ahmad et al., 2002). The needs of refined nuclear reaction rates imposed by the type and quality of the new observational and experimental data led to famous revisions of nuclear reaction rates such as NACRE (Angulo et al., 1999) and in particular that of Solar Fusion I (Adelberger, 1998). In the latter, a critical analysis of the accumulated experimental and theoretical data was performed and consensus values were provided for all relevant nuclear reactions affecting energy generation and neutrino production in the Sun. The improvement in the uncertainties, in particular, was about a factor of to 2, leading to typical errors around 10%. Simultaneously, several authors used helioseismic inversion of the solar sound speed to determine, or at least set constraints, on the proton-proton reaction rate, showing that its value had to be within about 15% of its theoretically determined value (degl’Innocenti et al., 1998; Schlattl et al., 1999; Antia and Chitre, 1999; Turck-chièze et al., 2001; Antia and Chitre, 2002).
The combination of helioseismic constraints and the discovery of neutrino oscillations changed the focus of interest of SSMs. In particular, the accurate and precise determination of neutrino fluxes from individual reactions started playing a fundamental role in the determination of the neutrino oscillation parameters. SSMs became a fundamental source of information, a reference, not just for astrophysics, but for particle physics as well. In 2007, the final and present chapter in this history started when Borexino presented the first measurement of the 7Be neutrinos (Arpesella et al., 2008), originating from a subdominant branch of reactions, the so-called pp-II branch of the pp-chain that accounts for about 10% of the energy generation of the Sun. Further work by Borexino led to an almost complete characterization of the spectrum of neutrinos from the pp-chain (Agostini et al., 2018). Together with the very precise measurement of the 8B flux from SNO (Aharmim, 2013) and Super-Kamiokande (Abe, 2016), we have come full circle and results from solar neutrino experiments can now be used to learn about the properties of the Sun. This is timely. There is a lingering dispute about which is the detailed chemical composition of the Sun, the solar abundance problem (Section 2.1), that is intimately linked to the uncertainties in our knowledge of radiative opacities in the solar interior. Solar neutrino data can in principle be used to disentangle this problem (Haxton and Serenelli, 2008; Serenelli et al., 2013; Villante et al., 2014), in particular if the promising results by Borexino on solar CN neutrinos (Agostini et al., 2020a) can be further improved. But progress along this line depends crucially on the accuracy and precision with which nuclear reaction rates are known. The latest compilation, Solar Fusion II (Adelberger, 2011), and subsequent work on specific reactions (Section 2), show on average a factor of two improvement with respect to the status 10–15 years ago, and 5% uncertainties are nowadays typical. But further work is still needed; uncertainties from nuclear reactions still have a non negligible role in the overall SSMs error budget.
In Section 2 we summarize the current status of SSMs, review the solar abundance problem, the SSM predictions on the solar neutrino spectrum and the status of nuclear reaction rates affecting model predictions. Section 3 presents an analytical formation of the relation between nuclear reaction rates and solar model properties both for reactions from the pp-chains and CNO-cycles. Section 4 reviews results from numerical SSM calculations, including a detailed assessment of uncertainties and highlighting where progress is most needed, and revises the possibility of using future CN neutrino measurements to determine the solar core C + N abundance.
2 Standard Solar Models
SSMs are a snapshot in the evolution of a 1
The physics input in the SSM is rather simple and it accounts for: convective and radiative transport of energy, chemical evolution driven by nuclear reactions, microscopic diffusion of elements which comprises different processes but among which gravitational settling dominates. Over more than 25 years, since the modern version of the SSM was established with the inclusion of microscopic diffusion (Bahcall and Pinsonneault, 1992; Christensen-Dalsgaard et al., 1993), the continuous improvement of the constitutive physics has brought about the changes and the evolution of SSMs. In particular, a lot of effort has gone into experimental and theoretical work on nuclear reaction rates. But changes in radiative opacities and the equation of state were also relevant. We take here as a reference the results of recent SSM calculations by Vinyoles et al. (2017), the so-called Barcelona 2016 (B16, for short) SSMs, which are based on the following state of the art ingredients. The equation of state is calculated consistently for each of the compositions used in the solar calibrations by using FreeEOS (Cassisi et al., 2003). Atomic radiative opacities are from the Opacity Project (OP) (Badnell et al., 2005), complemented at low temperatures with molecular opacities from Ferguson et al. (2005). Nuclear reaction rates for the pp-chain and CNO-bicycle, which are described in more details in the following section, are from the Solar Fusion II compilation (Adelberger, 2011) with important updates for the rates of
2.1 The Solar Composition Problem
The solar surface composition, determined with spectroscopic techniques, is a fundamental input in the construction of SSMs. The development of three dimensional hydrodynamic models of the solar atmosphere, of techniques to study line formation under non-local thermodynamic conditions and the improvement in atomic properties (e.g., transition strengths) have led since 2001 to a complete revision of solar abundances. Table 1 lists the abundances determined by different authors for the most relevant metals in solar modeling: GN93 (Grevesse and Noels, 1993), GS98 (Grevesse and Sauval, 1998), AGSS09 (Asplund et al., 2009), C11 (Caffau et al., 2011) and AGSS15 (Scott et al., 2015a; Scott et al., 2015b; Grevesse et al., 2015). Note that only abundances relative to hydrogen can be obtained from spectroscopy because the intensity of spectroscopic lines is measured relative to a continuum that is determined by the hydrogen abundance in the solar atmosphere. The last row in the table gives the total photospheric present-day metal-to-hydrogen ratio
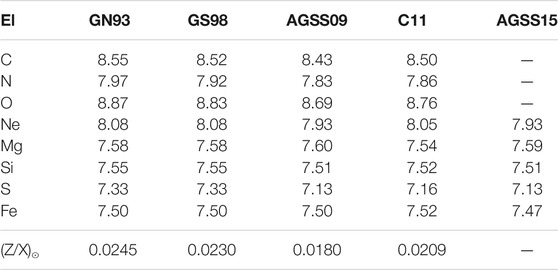
TABLE 1. Solar photospheric composition through time and authors for most relevant metals in solar modeling. Abundances are given in the standard astronomical scale
There is no complete agreement among authors, and some controversy still remains as to what the best values for the new spectroscopic abundances are. However, there is consensus in that all determinations of the solar metallicity based on the new generation of spectroscopic studies yield a solar metallicity lower than older spectroscopic results (Grevesse and Noels, 1993; Grevesse and Sauval, 1998), in particular for the volatile and most abundant C, N, and O. For refractories elements, like Fe, Si, Mg and S that have important role in solar modeling being important contributors to the radiative opacity, meteorites offer a very valuable alternative method (see e.g., Lodders et al. (2009)) and, in fact, elemental abundances determined from meteorites have been historically more robust than spectroscopic ones.
Considering that uncertainties in element abundances are difficult to quantify, it has become customary to consider two canonical sets of abundances to which we refer to as high metallicity (HZ) and low metallicity (LZ) solar admixtures, see e.g., Serenelli et al. (2011); Vinyoles et al. (2017) as reference assumptions for SSM calculations. These are obtained by using the photospheric (volatiles) + meteoritic (refractories) abundances from GS98 and AGSS09 respectively, and are reported in Table 2. In the last column, we give the fractional differences
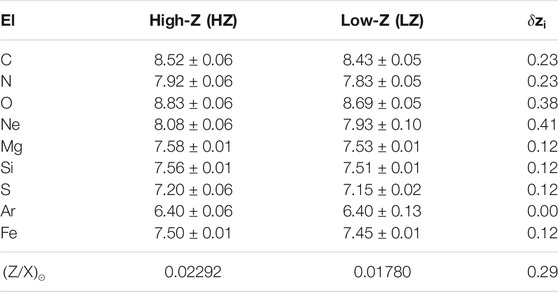
TABLE 2. The two canonical HZ and LZ solar mixtures given as
This can be better appreciated by considering Table 3 and Figure 1 where we compare theoretical predictions of SSMs implementing HZ and LZ surface composition with helioseismic determinations of the surface helium abundance
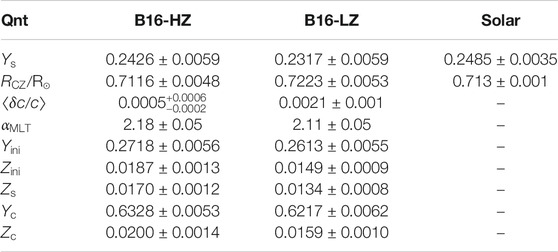
TABLE 3. Main characteristics of SSMs with different surface composition (Vinyoles et al., 2017). The observational values for
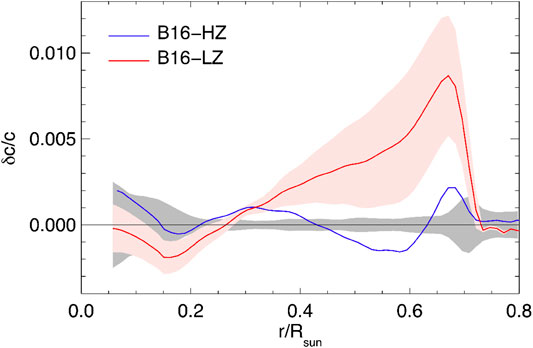
FIGURE 1. Fractional sound speed difference in the sense
Recent years have seen a surge of activity in theoretical calculations of atomic radiative opacities. Updated calculations (Badnell et al., 2005) by the Opacity Project have led the way, followed by OPAS (Blancard et al., 2012; Mondet et al., 2015), STAR (Krief et al., 2016b) and a new version of OPLIB, the opacities from Los Alamos (Colgan et al., 2016). For conditions in solar interiors, all theoretical opacities agree with each other within few %. Interestingly Bailey et al. (2015), have presented the first ever measurement of opacity under conditions very close to those at the bottom of the solar convective envelope. While the experiment has been carried out only for iron, their conclusion is that all theoretical calculations predict a too low Rosseland mean opacity, at a level of
2.2 Nuclear Reactions in the Sun
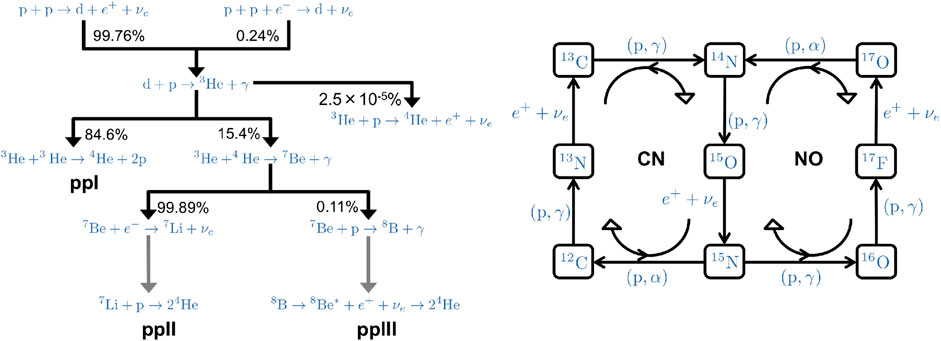
The overall effect of nuclear reactions in the Sun, as in any other star in hydrogen burning stage, is the conversion:
with the production of a fixed amount of energy
The SSM predicts that most of the solar energy (
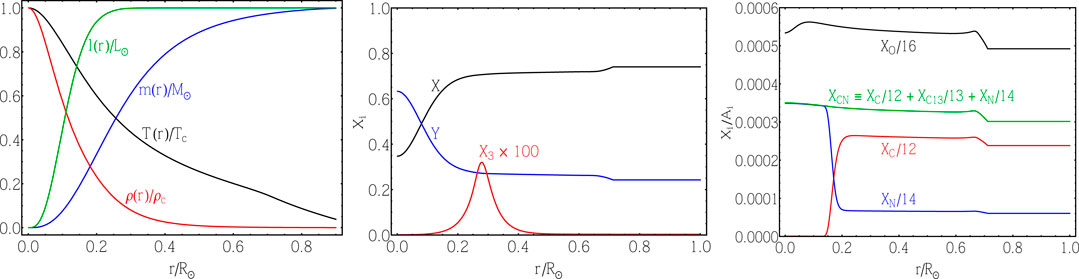
FIGURE 3. Left Panel: The behavior of temperature T and density ρ (scaled to central values
An alternative hydrogen burning mechanism is provided by the CNO-bicycle that is displayed in the right panel of Figure 2. The CNO-bicycle uses carbon, nitrogen and oxygen nuclei that are present in the core of the Sun as catalysts for hydrogen fusion. It is composed by two different branches, i.e. the CN-cycle and the NO-cycle, whose relative importance depends on the outcome of proton capture reaction on nitrogen-15. In the Sun, the 15
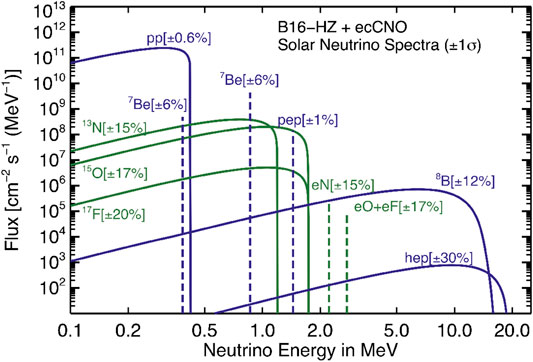
A very effective tool to investigate nuclear energy generation in the Sun is provided by neutrinos which are necessarily produced along with
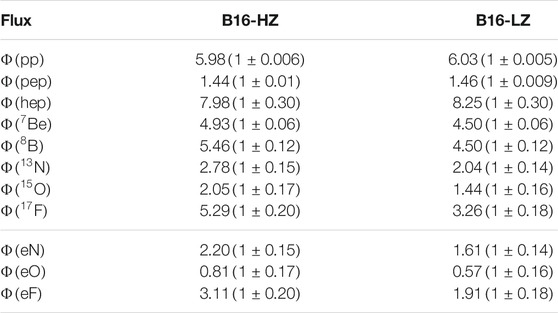
TABLE 4. Solar neutrino fluxes predicted by SSMs with different surface composition (Vinyoles et al., 2017). Units are:
2.3 Nuclear Reaction Rates
The cross sections of nuclear reaction in pp-chain and in CNO-bicycle are fundamental inputs for SSM calculations. Even if the focus of this work is on the role of nuclear rates for solar modeling (more than on reviewing the present situation for cross section measurements and calculations), we believe that it is useful to briefly discuss the adopted assumptions for the B16-SSM (Vinyoles et al., 2017). whose results have been previously discussed. The nuclear rates adopted for these models are from the Solar Fusion II compilation (Adelberger, 2011) with few relevant changes summarized in the following.
•
•
•
•
Finally, Salpeter’s formulation of weak screening (Salpeter, 1954) is adopted. The validity of this formulation for solar conditions, where electrons are only weakly degenerate, has been discussed in detail in Gruzinov and Bahcall (1998), where a more sophisticated approach was shown to lead, to within differences of about 1%, to Salpeter’s result. Other proposed deviations from this formulation have been discussed at length in Bahcall et al. (2002), including different approaches to dynamic screening, and shown to be flawed or not well physically motivated. More recent calculations of dynamic screening (Mao et al., 2009; Mussack and Dappen, 2011) still leave, however, some room for discussion on this topic. In the weak screening limit, and in conditions under which screening is not numerically large, the dominant scaling is with the product of the charge of the two reacting nuclei. In the solar core, screening enhancement is about 5% for
3 The Role of Nuclear Reactions
In the following, we discuss the role of nuclear reactions in SSM construction. Among nuclear processes, the
3.1 The pp-Reaction Rate and the Central Temperature of the Sun
In SSM calculations, where the Sun is assumed to be in thermal equilibrium, the rate of the pp-reaction is basically determined by the solar luminosity. Indeed, by considering that helium-4 is mainly produced by
Being the reaction rate fixed by the observed luminosity, the cross section of
where ρ is the density,
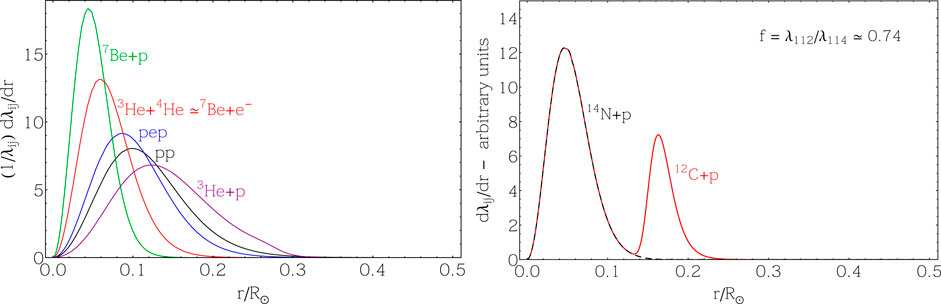
FIGURE 5. The differential rates for nuclear reactions in the pp-chain (Left Panel) and CN-cycle (Right Panel). The curves in the left panel have been normalized to one to facilitate comparison among them. The curves in the right panel are not normalized to emphasize that reactions 12
Taking into account that
where the notation
where
that will be useful in the following to understand the effects of
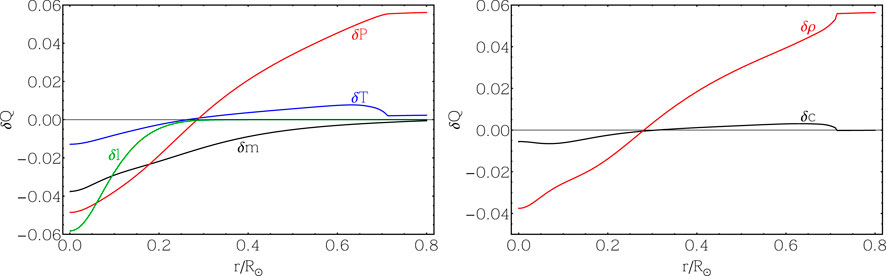
FIGURE 6. The effects of a
3.2 The Dependence of Neutrino Fluxes on the Central Temperature of the Sun and on Nuclear Reaction Cross Sections
Even a small modification of the central temperature of the Sun reflects into large variations of solar neutrino fluxes. By considering the arguments discussed in Bahcall and Ulmer (1996); Degl’Innocenti et al. (1997), we discuss the dependence of solar neutrino fluxes on the core temperature of the Sun, highlighting the role of nuclear reactions for determining the branching ratios of the different pp-chain terminations and the efficiency of the CNO-bicycle.
3.2.1 PP-Chain Neutrino Fluxes
The pp-neutrino flux:
The vast majority of the solar neutrino emission is due to pp-neutrinos whose flux
where
where we considered that
that gives the fractional variation of the flux
The pep-neutrino flux:
The pep-neutrinos are produced by electron capture reaction
where
The 7Be-neutrino flux:
The formation of beryllium-7 through
where Y (
where X is the hydrogen mass fraction. Considering that
or, equivalently,
where
The 8B-neutrino flux:
The 8B neutrinos constitute a largely subdominant component of the solar flux which is produced when
that also corresponds to:
with
3.2.2 The CNO Neutrino Fluxes
The neutrino fluxes produced in the CN-cycle by β-decay (and electron capture reactions) of 13N and 15O nuclei, besides depending on the solar central temperature, are approximately proportional to the stellar-core number abundance of CN elements. This dependence is relevant to understand the role of cross section for CNO-neutrino production. Moreover, as it is discussed in Haxton and Serenelli (2008); Haxton et al. (2013), it permits us to use CNO neutrinos, in combination with other neutrino fluxes, to directly probe the chemical composition of the Sun.
The 15O-neutrino flux:
This component of the solar neutrino spectrum is determined by the production rate of oxygen-15 by 14
is proportional to the nitrogen-14 mass fraction
where
In the above expressions, we neglected effect related to possible variations of the density and of the hydrogen abundance in the solar core, since these are expected to be small. We instead explicitly considered the dependence of
The 13N-neutrino flux:
The flux of 13N-neutrinos can be calculated
where
where the quantity:
gives the contribution to the total rate produced in the region of the Sun where the CN-cycle is incomplete. The above integral vanishes indeed for
Eq. 19 implies that
where the quantity
where we considered that
that combined with Eq. 17 gives:
where
The abundance of carbon and nitrogen in the core of the Sun.
Eqs. 17, 24 describe the dependence of the CN-neutrino fluxes from the abundances of nitrogen
which is proportional to the total carbon + nitrogen number density (
where
where
The abundance
where
A slightly more involved expression is obtained for the abundance
where the quantity
averaged over the Sun lifetime, see Appendix for details. The maximal neutrino production is achieved at
where we considered that
The final expressions the CN neutrino fluxes.
By using the above equations, we are able to calculate the dependence of neutrino fluxes produced in the CN-cycle on the properties of the Sun. By using Eqs. 28, 31 into Eqs. 17, 24, we obtain:
with
4 Numerical Results and Nuclear Uncertainties
The expressions obtained for the neutrino fluxes can be compared with the results of SSMs calculations. In particular, the numerical coefficients in Eqs. 7, 8, 12, 14 , 32 should reproduce the logarithmic derivatives of the neutrino fluxes with respect to the astrophysical factors of the relevant nuclear cross sections reported in Table 5. We see that a good agreement exists, indicating that all the major physical effects are included in our discussion and correctly described. In the case of
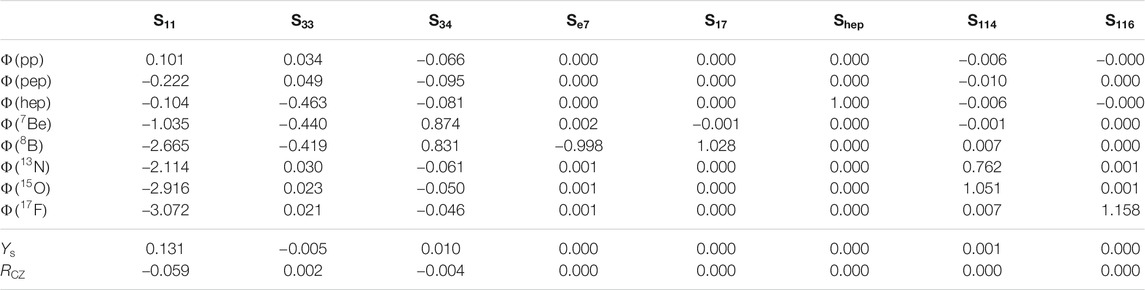
TABLE 5. The logarithmic derivatives
For completeness, we also discuss in the last two rows of Table 5 the dependence of the helioseismic observable quantities
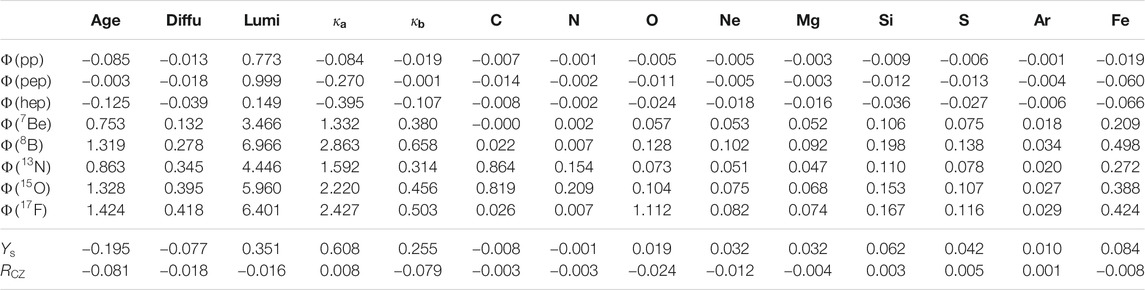
TABLE 6. The logarithmic derivatives
The uncertainties in solar properties leading to environmental effects and chemical composition parameters, together with uncertainties in nuclear reaction cross sections propagate to SSM predictions which are affected by a theoretical (or model) error that can be estimated by Monte-Carlo techniques and/or linear propagation. By using this approach, the fractional error
where

TABLE 7. The fractional uncertainties of enviromental and nuclear input parameters in SSM construction.
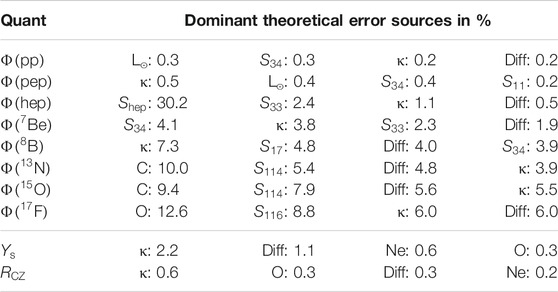
TABLE 8. Dominant theoretical error sources for neutrino fluxes and for the main characteristics of the SSM.
Focusing on nuclear reactions, we note that, despite the progress in the field, they are still an important uncertainty source for neutrino fluxes. In particular, the error contributions from
For a correct evaluation of the importance of nuclear cross section, it should be remarked that, while neutrino fluxes generally change with variation in any of the input parameters, SSM predictions are strongly correlated with a single output parameter, the core temperature
In Haxton and Serenelli (2008); Serenelli et al. (2013), it was suggested to combine the CN-neutrino fluxes with the boron neutrino flux that, due to the exquisite precision of current experimental results and the large temperature sensitivity can be efficiently used as solar thermometer. As can be understood by considering Eqs. 14, 32, the following combinations can be formed:
where
While the above relationships are based on the simplified arguments discussed in the previous section, the optimal combinations
where the sum extends to the N input parameters whose dependence we want to cancel out and
where
5 Concluding Remarks
A fundamental part in solar model calculations is the knowledge of the rates of nuclear reactions involved in the generation of solar nuclear energy. During the last decades, we experienced a substantial progress in the accuracy of SSM calculations that was made possible, among the other ingredients, by the continuous improvements of nuclear cross sections that are now typically determined with
As a consequence, further work is needed on the side of nuclear reactions. Indeed, nuclear uncertainties have a non negligible role in SSMs error budget. As an example, the error contributions from
In conclusion, it would be desirable to further improve our knowledge of nuclear cross sections, in particular for 3
Author Contribitions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
FV acknowledges support by ‘Neutrino and Astroparticle Theory Network’ under the program PRIN 2017 funded by the Italian Ministry of Education, University and Research (MIUR) and INFN Iniziativa Specifica TAsP. AS acknowledges support by the Spanish Government through the MICINN grant PRPPID 2019–108709GB-I00.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix: the 12C abundance in non-equilibrium region
In the region
where the carbon-12 burning rate
The solution of Eq. 38 is:
where
We include a-posteriori the effecs of elemental diffusion by replacing
where
aIn order to take into account the new inputs in B16-SSM calculations, the ecCNO fluxes given in Table 4 have been scaled with respect to the values quoted in Villante (2015) proportionally to the corresponding β-decay fluxes. This follows from the assumption that the ratio of electron capture and beta decay processes in the Sun is equal to what evaluated in Villante (2015).
bNote that the rate of
cWe evaluate the exponents
dThe total error due to opacity is obtained by combining in quadrature the contributions from
References
Abdurashitov, J., Gavrin, V. N., Girin, S. V., Gorbachev, V. V., Ibragimova, T. V., Kalikhov, A. V., et al. (1999). Measurement of the solar neutrino capture rate with gallium metal. Phys. Rev. C 60, 055801. doi:10.1103/PhysRevC.60.055801
Abe, K. (2016). Solar neutrino measurements in super-kamiokande-IV. Phys. Rev. D 94, 052010. doi:10.1103/PhysRevD.94.052010
Acharya, B., Carlsson, B. D., Ekström, A., Forssén, C., and Platter, L. (2016). Uncertainty quantification for proton-proton fusion in chiral effective field theory. Phys. Lett. B7 60, 584–589. doi:10.1016/j.physletb.2016.07.032
Adelberger, E. G. (2011). Solar fusion cross sections II: the pp chain and CNO cycles. Rev. Mod. Phys. 83, 195. doi:10.1103/RevModPhys.83.195
Adelberger, E. G. (1998). Solar fusion cross-sections. Rev. Mod. Phys. 70, 1265–1292. doi:10.1103/RevModPhys.70.1265
Agostini, M., Altenmüller, K., and The Borexino Collaboration., (2018). Comprehensive measurement of -chain solar neutrinos. Nature 562, 505–510. doi:10.1038/s41586-018-0624-y
Agostini, M., Altenmüller, K., and The Borexino Collaboration., (2020a). First direct experimental evidence of CNO neutrinos. Nature 587, 577–582. doi:10.1038/s41586-020-2934-0
Agostini, M., Altenmüller, K., and The Borexino Collaboration., (2020b). Sensitivity to neutrinos from the solar CNO cycle in Borexino. Eur. Phys. J. C 80. doi:10.1140/epjc/s10052-020-08534-2
Aharmim, B. (2013). Combined analysis of all three phases of solar neutrino data from the sudbury neutrino observatory. Phys. Rev. C 88, 025501. doi:10.1103/PhysRevC.88.025501
Ahmad, Q., Allen, R C., Andersen, T C., Anglin, J D., Barton, J C., Beier, E W., et al. (2002). Direct evidence for neutrino flavor transformation from neutral current interactions in the Sudbury Neutrino Observatory. Phys. Rev. Lett. 89, 011301. doi:10.1103/PhysRevLett.89.011301
Ahmad, Q., Allen, R C., Andersen, T C., Anglin, J D., Barton, J C., Beier, E W., et al. (2001). Measurement of the rate of interactions produced by solar neutrinos at the Sudbury Neutrino Observatory. Phys. Rev. Lett. 87, 071301. doi:10.1103/PhysRevLett.87.071301
Angulo, C., Arnould, M., Rayet, M., Descouvemont, P., Baye, D., Leclercq-Willain, C., et al. (1999). A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. 656, 3–183. doi:10.1016/S0375-9474(99)00030-5
Antia, H. M., and Chitre, S. M. (2002). Helioseismic limit on heavy element abundance. Astron. Astrophys. 393, L95–L98. doi:10.1051/0004-6361:20021253
Antia, H. M., and Chitre, S. M. (1999). Limits on the proton-proton reaction cross-section from helioseismology. Astron. Astrophys. 347, 1000–1004.
Arpesella, C., Back, H. O., Bellini, G. B., Balata, M., Benzinger, J., Leclercq-Willain, C., et al. (2008). Direct measurement of the Be-7 solar neutrino flux with 192 Days of Borexino data. Phys. Rev. Lett. 101, 091302. doi:10.1103/PhysRevLett.101.091302
Asplund, M., Grevesse, N., Sauval, A. J., and Scott, P. (2009). The chemical composition of the Sun. Annu. Rev. Astron. Astrophys. 47, 481–522. doi:10.1146/annurev.astro.46.060407.145222
Badnell, N. R., Bautista, M. A., Butler, K., Delahaye, F., Mendoza, C., Palmeri, P., et al. (2005). Up-dated opacities from the opacity Project. Mon. Not. Roy. Astron. Soc. 360, 458–464. doi:10.1111/j.1365-2966.2005.08991.x
Bahcall, J. N., Basu, S., Pinsonneault, M., and Serenelli, A. M. (2005a). Helioseismological implications of recent solar abundance determinations. Astrophys. J. 618, 1049–1056. doi:10.1086/426070
Bahcall, J. N., Brown, L. S., Gruzinov, A., and Sawyer, R. (2002). The Salpeter plasma correction for solar fusion reactions. Astron. Astrophys. 383, 291–295. doi:10.1051/0004-6361:20011715
Bahcall, J. N., Huebner, W. F., Lubow, S. H., Parker, P. D., and Ulrich, R. K. (1982). Standard solar models and the uncertainties in predicted capture rates of solar neutrinos. Rev. Mod. Phys. 54, 767–799. doi:10.1103/RevModPhys.54.767
Bahcall, J. N. (1990). Line versus continuum solar neutrinos. Phys. Rev. D41, 2964. doi:10.1103/PhysRevD.41.2964
Bahcall, J. N., and Pinsonneault, M. H. (1992). Standard solar models, with and without helium diffusion, and the solar neutrino problem. Rev. Mod. Phys. 64, 885–926. doi:10.1103/RevModPhys.64.885
Bahcall, J. N., Pinsonneault, M. H., and Wasserburg, G. J. (1995). Solar models with helium and heavy-element diffusion. Rev. Mod. Phys. 67, 781–808. doi:10.1103/RevModPhys.67.781
Bahcall, J. N., Serenelli, A. M., and Basu, S. (2006). 10,000 standard solar models: a Monte Carlo simulation. Astrophys. J. Suppl. 165, 400–431. doi:10.1086/504043
Bahcall, J. N., Serenelli, A. M., and Basu, S. (2005b). New solar opacities, abundances, helioseismology, and neutrino fluxes. Astrophys. J. Lett. 621, L85–L88. doi:10.1086/428929
Bahcall, J. N. (2002). The Luminosity constraint on solar neutrino fluxes. Phys. Rev. C65, 025801. doi:10.1103/PhysRevC.65.025801
Bahcall, J. N., and Ulmer, A. (1996). The Temperature dependence of solar neutrino fluxes. Phys. Rev. D53, 4202–4210. doi:10.1103/PhysRevD.53.4202
Bailey, J. E., Nagayama, T., Loisel, G. P., Rochau, G. A., Blancard, C., Colgan, J., et al. (2015). A higher-than-predicted measurement of iron opacity at solar interior temperatures. Nature 517, 56–59. doi:10.1038/nature14048
Basu, S., and Antia, H. M. (2004). Constraining solar abundances using helioseismology. Astrophys. J. 606, L85. doi:10.1086/421110
Basu, S., and Antia, H. M. (2008). Helioseismology and solar abundances. Phys. Rep. 457, 217–283. doi:10.1016/j.physrep.2007.12.002
Basu, S., and Antia, H. M. (1997). Seismic measurement of the depth of the solar convection zone. Mon. Not. Roy. Astron. Soc. 287, 189–198. doi:10.1093/mnras/287.1.189
Bellini, G., Benziger, J., Bick, D., Bonetti, S., Bonfini, G., Bravo, D., et al. (2012). First evidence of pep solar neutrinos by direct detection in Borexino. Phys. Rev. Lett. 108, 051302. doi:10.1103/PhysRevLett.108.051302
Bellini, G. (2014). Neutrinos from the primary proton-proton fusion process in the Sun. Nature 512, 383–386. doi:10.1038/nature13702
Bergstrom, J., Gonzalez-Garcia, M. C., Maltoni, M., Pena-Garay, C., Serenelli, A. M., and Song, N. (2016). Updated determination of the solar neutrino fluxes from solar neutrino data. JHEP 03, 132. doi:10.1007/JHEP03(2016)132
Blancard, C., Cossé, P., and Faussurier, G. (2012). Solar mixture opacity calculations using detailed configuration and level accounting treatments. Astrophys. J. 745, 10. doi:10.1088/0004-637X/745/1/10
Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., and Bonifacio, P. (2011). Solar chemical abundances determined with a CO5BOLD 3D model atmosphere. Sol. Phys. 268, 255. doi:10.1007/s11207-010-9541-4
Cassisi, S., Salaris, M., and Irwin, A. W. (2003). The initial helium content of galactic globular cluster stars from the r-parameter: comparison with the cmb constraint. Astrophys. J. 588, 862. doi:10.1086/374218
Castro, M., Vauclair, S., and Richard, O. (2007). Low abundances of heavy elements in the solar outer layers: comparisons of solar models with helioseismic inversions. Astron. Astrophys. 463, 755–758. doi:10.1051/0004-6361:20066327
Christensen-Dalsgaard, J., Dappen, W., Ajukov, S. V., Anderson, E. R., Antia, H. M., Basu, S., et al. (1996). The current state of solar modeling. Science 272, 1286–1292. doi:10.1126/science.272.5266.1286
Christensen-Dalsgaard, J., Di Mauro, M. P., Houdek, G., and Pijpers, F. (2009). On the opacity change required to compensate for the revised solar composition. Astron. Astrophys. 494, 205. doi:10.1051/0004-6361:200810170
Christensen-Dalsgaard, J., Duvall, J., T. L., , Gough, D. O., Harvey, J. W., Rhodes, J., et al. (1985). Speed of sound in the solar interior. Nature 315, 378–382. doi:10.1038/315378a0
Christensen-Dalsgaard, J., Proffitt, C. R., and Thompson, M. J. (1993). Effects of diffusion on solar models and their oscillation frequencies. Astrophys. J. Lett. 403, L75. doi:10.1086/186725
Cleveland, B., Daily, T., Davis, J., Raymond, Distel, J. R., Lande, K., Lee, C., et al. (1998). Measurement of the solar electron neutrino flux with the Homestake chlorine detector. Astrophys. J. 496, 505–526. doi:10.1086/305343
Colgan, J., Kilcrease, D. P., Magee, N. H., Sherrill, M. E., Abdallah, J., J., Hakel, P., et al. (2016). A new generation of Los Alamos opacity tables. Astrophys. J. 817, 116. doi:10.3847/0004-637X/817/2/116
deBoer, R. J., Görres, J., Smith, K., Uberseder, E., Wiescher, M., Kontos, A., et al. (2014). Monte Carlo uncertainty of the He3(alpha,gamma)Be7 reaction rate. Phys. Rev. C90, 035804. doi:10.1103/PhysRevC.90.035804
Degl’Innocenti, S., Dziembowski, W. A., Fiorentini, G., and Ricci, B. (1997). Helioseismology and standard solar models. Astropart. Phys. 7, 77–95. doi:10.1016/S0927-6505(97)00004-2
degl’Innocenti, S., Fiorentini, G., and Ricci, B. (1998). Helioseismology and p+p → d + e + νe in the sun. Phys. Lett. B 416, 365–368. doi:10.1016/S0370-2693(97)01197-0
Delahaye, F., and Pinsonneault, M. (2006). The solar heavy element abundances. 1. constraints from stellar interiors. Astrophys. J. 649, 529–540. doi:10.1086/505260
Deubner, F.-L., and Gough, D. (1984). Helioseismology: oscillations as a diagnostic of the solar interior. Annu. Rev. Astron. Astrophys. 22, 593–619. doi:10.1146/annurev.aa.22.090184.003113
Elsworth, Y., Howe, R., Isaak, G. R., McLeod, C. P., and New, R. (1990). Evidence from solar seismology against non-standard solar-core models. Nature 347, 536–539. doi:10.1038/347536a0
Ferguson, J. W., Alexander, D. R., Allard, F., Barman, T., Bodnarik, J. G., Hauschildt, P. H., et al. (2005). Low temperature opacities. Astrophys. J. 623, 585–596. doi:10.1086/428642
Fukuda, S., Fukuda, Y., Ishitsuka, M., Itow, Y., Kajita, T., Kameda, J., et al. (2001). Solar B-8 and hep neutrino measurements from 1258 days of Super-Kamiokande data. Phys. Rev. Lett. 86, 5651–5655. doi:10.1103/PhysRevLett.86.5651
Fukuda, Y. (1998). Measurements of the solar neutrino flux from Super-Kamiokande’s first 300 days. Phys. Rev. Lett. 81, 1158–1162. doi:10.1103/PhysRevLett.81.1158
Gough, D. O., Kosovichev, A. G., Toomre, J., Anderson, E., Antia, H. M., Basu, S., et al. (1996). The seismic structure of the sun. Science 272, 1296–1300. doi:10.1126/science.272.5266.1296
Grevesse, N., and Noels, A. (1993). “Cosmic abundances of the elements,”. Origin and evolution of the elements. Editors N. Prantzos, E. Vangioni-Flam, and M. Casse (Tokyo, Japan: Cambridge University Press), 15–25.
Grevesse, N., and Sauval, A. J. (1998). Standard solar composition. Space Sci. Rev. 85, 161–174. doi:10.1023/A:1005161325181
Grevesse, N., Scott, P., Asplund, M., and Sauval, A. J. (2015). The elemental composition of the Sun III. The heavy elements Cu to Th. Astron. Astrophys. 573, A27. doi:10.1051/0004-6361/201424111
Gruzinov, A. V., and Bahcall, J. N. (1998). Screening in thermonuclear reaction rates in the sun. Astrophys. J. 504, 996–1001. doi:10.1086/306116
Guzik, J. A., and Mussack, K. (2010). Exploring mass loss, low-Z accretion, and convective overshoot in solar models to mitigate the solar abundance problem. Astrophys. J. 713, 1108–1119. doi:10.1088/0004-637X/713/2/1108
Guzik, J. A., Watson, L., and Cox, A. N. (2005). Can enhanced diffusion improve helioseismic agreement for solar models with revised abundances?. Astrophys. J. 627, 1049–1056. doi:10.1086/430438
Hampel, W., Handt, J., Heusser, G., Kiko, J., Kirsten, T., Laubenstein, M., et al. (1999). GALLEX solar neutrino observations: results for GALLEX IV. Phys. Lett. B 447, 127–133. doi:10.1016/S0370-2693(98)01579-2
Harvey, J. W., Hill, F., Hubbard, R. P., Kennedy, J. R., Leibacher, J. W., Pintar, J. A., et al. (1996). The global oscillation network group (GONG) Project. Science 272, 1284–1286. doi:10.1126/science.272.5266.1284
Haxton, W. C., Hamish Robertson, R. G., and Serenelli, A. M. (2013). Solar neutrinos: status and prospects. Annu. Rev. Astron. Astrophys. 51, 21–61. doi:10.1146/annurev-astro-081811-125539
Haxton, W. C., and Serenelli, A. M. (2008). CN-cycle solar neutrinos and Sun’s primordial core metalicity. Astrophys. J. 687, 678–691. doi:10.1086/591787
Iliadis, C., Anderson, K., Coc, A., Timmes, F., and Starrfield, S. (2016). Bayesian estimation of thermonuclear reaction rates. Astrophys. J. 831, 107. doi:10.3847/0004-637X/831/1/107
Kippenhahn, R., and Weigert, A. (1990). Stellar structure and evolution. Berlin Heidelberg, New York: Springer, 606.
Krief, M., Feigel, A., and Gazit, D. (2016a). Line broadening and the solar opacity problem. Astrophys. J. 824, 98. doi:10.3847/0004-637X/824/2/98
Krief, M., Feigel, A., and Gazit, D. (2016b). Solar opacity calculations using the super-transition-array method. Astrophys. J. 821, 45. doi:10.3847/0004-637X/821/1/45
Krishna Swamy, K. S. (1966). Profiles of strong lines in K-dwarfs. Astrophys. J. 145, 174. doi:10.1086/148752
Lodders, K., Palme, H., and Gail, H.-P. (2009). Abundances of the elements in the solar system. Landolt Börnstein, 712. doi:10.1007/978-3-540-88055-4˙3410.1007/978-3-540-88055-4_34
Mao, D., Mussack, K., and Dappen, W. (2009). Dynamic screening in solar plasma. Astrophys. J. 701, 1204–1208. doi:10.1088/0004-637X/701/2/1204
Marcucci, L. E., Schiavilla, R., and Viviani, M. (2013). Proton-proton weak capture in chiral effective field theory. Phys. Rev. Lett. 110, 192503. doi:10.1103/PhysRevLett.110.192503
Marta, M. (2011). The 14N(p,gamma)15O reaction studied with a composite germanium detector. Phys. Rev. C83, 045804. doi:10.1103/PhysRevC.83.045804
Mondet, G., Blancard, C., Cossé, P., and Faussurier, G. (2015). Opacity calculations for solar mixtures. Astrophys. J. Supp. 220, 2. doi:10.1088/0067-0049/220/1/2
Montalban, J., Miglio, A., Noels, A., Grevesse, N., and Di Mauro, M. (2004). Solar model with CNO revised abundances. ESA Spec. Publ. 559, 574
Mussack, K., and Dappen, W. (2011). Dynamic screening correction for solar p-p reaction rates. Astrophys. J. 729, 96. doi:10.1088/0004-637X/729/2/96
Nagayama, T., Bailey, J. E., Loisel, G. P., Dunham, G. S., Rochau, G. A., Blancard, C., et al. (2019). Systematic study of L -shell opacity at stellar interior temperatures. Phys. Rev. Lett. 122, 235001. doi:10.1103/PhysRevLett.122.235001
Salpeter, E. (1954). Electron screening and thermonuclear reactions. Austral. J. Phys. 7, 373–388. doi:10.1071/PH540373
Schlattl, H., Bonanno, A., and Paternò, L. (1999). Signatures of the efficiency of solar nuclear reactions in the neutrino experiments. Phys. Rev. D 60, 113002. doi:10.1103/PhysRevD.60.113002
Scott, P., Asplund, M., Grevesse, N., Bergemann, M., and Sauval, A. J. (2015a). The elemental composition of the Sun II. The iron group elements Sc to Ni. Astron. Astrophys. 573, A26. doi:10.1051/0004-6361/201424110
Scott, P., Grevesse, N., Asplund, M., Sauval, A. J., Lind, K., Takeda, Y., et al. (2015b). The elemental composition of the Sun I. The intermediate mass elements Na to Ca. Astron. Astrophys. 573, A25. doi:10.1051/0004-6361/201424109
Serenelli, A. M., Haxton, W. C., and Pena-Garay, C. (2011). Solar models with accretion. I. Application to the solar abundance problem. Astrophys. J. 743, 24. doi:10.1088/0004-637X/743/1/24
Serenelli, A., Peña-Garay, C., and Haxton, W. C. (2013). Using the standard solar model to constrain solar composition and nuclear reaction S factors. Phys. Rev. D 87, 043001. doi:10.1103/PhysRevD.87.043001
Stonehill, L. C., Formaggio, J. A., and Robertson, R. G. H. (2004). Solar neutrinos from CNO electron capture. Phys. Rev. C 69, 015801. doi:10.1103/PhysRevC.69.015801
Thoul, A. A., Bahcall, J. N., and Loeb, A. (1994). Element diffusion in the solar interior. Astrophys. J. 421, 828–842. doi:10.1086/173695
Tognelli, E., Degl’Innocenti, S., Marcucci, L. E., and Prada Moroni, P. G. (2015). Astrophysical implications of the proton-proton cross section updates. Phys. Lett. B 742, 189–194. doi:10.1016/j.physletb.2015.01.033
Turck-chièze, S., Nghiem, P., Couvidat, S., and Turcotte, S. (2001). Solar internal composition and nuclear reaction rates in the light of helioseismology. Sol. Phys. 200, 323–342. doi:10.1023/A:1010365125791
Villante, F. L. (2010). Constraints on the opacity profile of the sun from helioseismic observables and solar neutrino flux measurements. Astrophys. J. 724, 98–110. doi:10.1088/0004-637X/724/1/98
Villante, F. L. (2015). ecCNO solar neutrinos: a challenge for gigantic ultra-pure liquid scintillator detectors. Phys. Lett. B 742, 279–284. doi:10.1016/j.physletb.2015.01.043
Villante, F. L., Serenelli, A. M., Delahaye, F., and Pinsonneault, M. H. (2014). The chemical composition of the Sun from helioseismic and solar neutrino data. Astrophys. J. 787, 13. doi:10.1088/0004-637X/787/1/13
Vinyoles, N., Serenelli, A. M., Villante, F. L., Basu, S., Bergström, J., Gonzalez-Garcia, M. C., et al. (2017). A new generation of standard solar models. Astrophys. J. 835, 202. doi:10.3847/1538-4357/835/2/202
Vissani, F. (2019). “Luminosity constraint and entangled solar neutrino signals,” in Solar Neutrinos. Editors M. Meyer and K. Zuber. 121–141.
Keywords: solar physics, solar models, nuclear reactions, nuclear astrophysics, solar neutrino fluxes
Citation: Villante FL and Serenelli A (2021) The Relevance of Nuclear Reactions for Standard Solar Models Construction. Front. Astron. Space Sci. 7:618356. doi: 10.3389/fspas.2020.618356
Received: 16 October 2020; Accepted: 11 December 2020;
Published: 02 March 2021.
Edited by:
Scilla Degl’Innocenti, University of Pisa, ItalyReviewed by:
Sarbani Basu, Yale University, United StatesWick Haxton, University of California, Berkeley, United States
Copyright © 2021 Villante and Serenelli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francesco L. Villante, dmlsbGFudGVAbG5ncy5pbmZuLml0
 Francesco L. Villante
Francesco L. Villante Aldo Serenelli
Aldo Serenelli