The Study of Key Reactions Shaping the Post-Main Sequence Evolution of Massive Stars in Underground Facilities

The chemical evolution of the Universe and several phases of stellar life are regulated by minute nuclear reactions. The key point for each of these reactions is the value of cross-sections at the energies at which they take place in stellar environments. Direct cross-section measurements are mainly hampered by the very low counting rate and by cosmic background; nevertheless, they have become possible by combining the best experimental techniques with the cosmic silence of an underground laboratory. In the nineties, the LUNA (Laboratory for Underground Nuclear Astrophysics) collaboration opened the era of underground nuclear astrophysics, installing first a homemade 50 kV and, later on, a second 400 kV accelerator under the Gran Sasso mountain in Italy: in 25 years of experimental activity, important reactions responsible for hydrogen burning could have been studied down to the relevant energies thanks to the high current proton and helium beams provided by the machines. The interest in the next and warmer stages of star evolution (i.e., post-main sequence and helium and carbon burning) drove a new project based on an ion accelerator in the MV range called LUNA-MV, able to deliver proton, helium, and carbon beams. The present contribution is aimed to discuss the state of the art for some selected key processes of post-main sequence stellar phases: ¹²C(α,γ)¹⁶O and ¹²C+¹²C are fundamental for helium and carbon burning phases, and ¹³C(α,n)¹⁶O and ²²Ne(α,n)²⁵Mg are relevant to the synthesis of heavy elements in AGB stars. The perspectives opened by an underground MV facility will be highlighted.

Introduction

The hypothesis that the energy which powers the Sun comes from thermonuclear reactions seems to be mainly due to Eddington (1920) and Aston. After the discovery of nuclear reactions by Rutherford in the twenties, it became clear that only the enormous amount of energy stored in the nuclei and released during fusion reactions was able to support the Sun luminosity for a time period compatible with the geological datings (von Weizsäcker, 1938; Bethe and Critchfield, 1938): by fact, in order to properly understand the chemical evolution and the stellar energy engine, it is fundamental to precisely know how light nuclei are converted to heavier ones.

According to current theories, the first nuclei were formed through a network of nuclear reactions in the Big Bang nucleosynthesis (BBN), a few minutes after the Big Bang. BBN left our Universe containing about 75% hydrogen and 24% helium by mass, with some traces of lithium and deuterium. The composition of the present Universe is not very different from the primordial one, with the total mass elements heavier than hydrogen and helium (“metals” according to the astronomers) at the level of a few percent. Stars fuse light elements to heavier ones in their cores, up to iron and nickel in the more massive stars.

The most important stellar properties that determine the evolutionary fate of a star are its mass and its composition (Rolfs and Rodney, 1988; Iliadis, 2015): the larger the mass, the larger the temperature in the core. The star composition influences which reactions dominate the burning processes.

When a low-mass star like the Sun runs out of hydrogen in the core, it becomes a red giant star, fusing H to He via the CNO cycle in a shell surrounding an inert He core. When the core temperature reaches 100 million K, the He nuclei in the core have sufficient kinetic energy to fuse to C (helium burning), forming ¹²C in a two-stage process. Subsequent fusion with another helium nucleus produces ¹⁶O nuclei. This process, in symbols ¹²C(α,γ)¹⁶O, is the main source of the carbon and oxygen found in the Universe, including that in our bodies, and represents by fact the “Holy Grail” of nuclear astrophysics since the C/O ratio at the end of helium burning greatly affects the subsequent evolution of the star. At some point, when He in the core is exhausted, the stars start to burn He in a shell surrounding the inert C/O core, in addition to burning H to He in a shell surrounding the He-burning region. This phase, referred to as the asymptotic giant branch (AGB), is characterized by thermal instabilities: at a given time, the burning shells extinguish and the low-mass star will end its existence as a white dwarf, consisting mainly of C and O and supported by electron degeneracy pressure.

Massive stars evolve very differently from low-mass stars. After the end of a burning phase, the core contracts gravitationally, and the temperature increase can be sufficient to ignite the next and heavier nuclear fuel. In the case of masses larger than 11M_ʘ, after undergoing He burning, the core experiences further burning episodes referred to as C, Ne, O, and Si burning. The duration of each subsequent nuclear burning phase decreases significantly. There are two main reasons: the first is that each burning phase releases by far less energy per unit mass with respect to the previous phase; the second that an increasing fraction of energy is radiated away by neutrinos. Therefore, while H burning may continue for many million years, C burning typically lasts hundreds of days and Si burning may run out in just one day. After the last advanced burning stage (Si burning), the core consists mainly of iron isotopes: no more energy can be generated through fusion reactions. The core contracts and when it exceeds the Chandrasekhar mass limit, it collapses until the density of nuclear matter is reached. As a consequence of the neutron degeneracy pressure, the core rebounds and produces an outgoing shock wave. The wave heats and compresses the overlying layers of the star, consisting of successive shells of Si, O, Ne, and C; thus, more episodes of nucleosynthesis, referred to as explosive Si, O, Ne, and C burning, take place.

The creation of elements heavier than iron occurs mainly through neutron-capture processes, eventually followed by beta-decays in the so-called slow process (s-process) (Käppeler et al., 2011) and rapid process (r-process). The r-process dominates in environments with higher free neutrons fluxes and it produces heavier elements and more neutron-rich isotopes than the s-process. Supernovae explosions and neutron star mergers are potential sites for the r-process. The s-process is slow in the sense that there is enough time for beta-decays to occur before another neutron is captured: a network of reactions produces stable isotopes by moving along the valley of beta-decay stable isobars. This process primarily occurs within ordinary stars, particularly AGB stars, where the neutron flux is sufficient to cause neutron captures to recur every 10–100 years, much slower than for the r-process, which requires 100 captures per second.

The key point for each of these reactions is the value of cross-sections at the energies at which they take place in stellar environments. For most stellar scenarios, the changes in the system are slower than the collision time between the ions or atoms inside the stars; thus, the temperature profile is well-defined: the thermonuclear reaction rate depends on the Maxwell–Boltzmann velocity distribution and on the cross-section σ(E) energy dependence (Rolfs and Rodney, 1988). Typical stellar temperatures for main sequence low-mass stars correspond to peak energies of the Maxwell–Boltzmann distribution of $k_{\text{B}}T\sim 0.9-90\text{keV}$. In the case of more massive stars during advanced burning stages, peak energies can be as high as a few MeV. For charged particles induced reactions, these energies are typically well below the Coulomb barrier due to the nuclei electrostatic repulsion and the nuclear reactions proceed via tunnel effect. As a consequence, the low values of the cross-sections, ranging from picobarn to femtobarn and even lower, prevent their measurements in a laboratory at the Earth’s surface where the signal-to-background ratio is too small mainly because of cosmic rays. The observed energy dependence of the cross-section at high energies is extrapolated to astrophysically relevant energies leading to substantial uncertainties. In particular, the reaction mechanism might change, or there might be the contribution of unknown resonances that could completely dominate the reaction rate at the stellar energies.

In the nineties, the LUNA collaboration proved that the installation of the experiments in a deep underground laboratory, the Gran Sasso National Laboratory, is a successful approach: for the first time, nuclear astrophysics measurements with very low counting rates down to few events per month became a reality.

The high current hydrogen and helium beams provided by the 50 kV (Greife et al., 1994) and, later on, by the LUNA-400 kV accelerators (Formicola et al., 2003) allowed for the investigation, for the first time at stellar energies, of the most important reactions responsible for the hydrogen burning in the Sun, such as ${}^3\text{He}\left({}^3\text{He},2p\right){}^4\text{H}\text{e}$ (Bonetti et al., 1999), and for the BBN such as ${}^2\text{H}\left(\text{p},\gamma \right){}^3\text{H}\text{e}$ (Casella et al., 2002; Mossa et al., 2020).

Full descriptions of LUNA and of several results obtained in 25 years of experimental activity can be found in recent review articles (Broggini et al., 2018; Cavanna and Prati, 2018; Broggini et al., 2019).

Such achievements have motivated two proposals for similar facilities in China (Liu et al., 2016) and in the United States (Robertson et al., 2016).

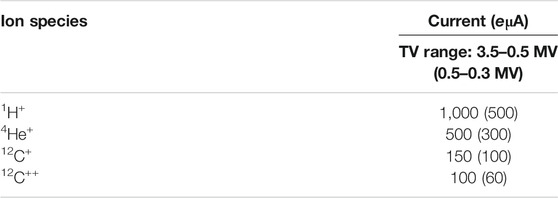
The importance of extending such precise studies to the processes relevant to the late and warmer stages of star evolution (post-main sequence phases and helium and carbon burning) has motivated the LUNA collaboration to acquire a new and more powerful 3.5 MV single-ended accelerator. The new machine will deliver ion beams of H⁺, ⁴He⁺, ¹²C⁺, and ¹²C⁺⁺ in the energy range from 0.350 to 7 MeV with 100 µA–1 mA intensity currents, depending on the ion species and on the energy value.

In the following sections, first, we will focus on the technical aspects, which are important for an underground nuclear astrophysics experiment. Then, the state of the art and the expected improvements from underground measurements are presented for some selected key processes of post-main sequence stellar phases: in detail, ¹³C(α,n)¹⁶O and ²²Ne(α,n)²⁵Mg are sources of neutrons for the s-process in AGB stars and during hydrostatic evolution of massive stars and the ¹²C(α,γ)¹⁶O and the ¹²C+¹²C reactions are key processes of helium and carbon burning, respectively.

In conclusion, the commissioning phase of the new accelerator will be detailed, together with highlights about the exciting perspectives opened by the new facility in a larger time window scenario.

The MV Facility at Gran Sasso

The MV facility will be hosted in the north side of Hall B in the Gran Sasso Laboratory and will consist of an accelerator room with concrete walls and a multistory building housing the control room and technical facilities. The concrete walls and ceiling (thickness of 80 cm) of the accelerator room will act as neutron shielding.

Nuclear astrophysics experiments require both high beam currents and a well-defined and stable beam energy: to perform reliable energy scans of the targets, the accelerator terminal voltage must be stable to <1 keV over many hours and to <0.1 keV over 1 h. A precise energy value is mandatory because of the almost exponential energy dependence of the cross-section induced by the tunnel effect probability: a small fluctuation of the beam energy would cause a large uncertainty in the measured cross-section value. Since, for some reactions, long data taking times are expected, the ion source must be able to run stably overnight without human intervention.

A 3.5 MV linear DC accelerator was specifically developed by High Voltage Engineering to meet the stringent requirements on beam intensity and stability (Sen et al., 2019). The machine will deliver ion beams into two different beamlines via a 35° switching analyzing magnet. Two independent target stations for solid and gas targets will be located at a 2 m distance from the analyzing magnet. The LUNA-MV accelerator is single-ended; i.e., it has an ion source and an injector block located inside the accelerator tank in the high-voltage terminal.

The need for high-intensity protons and carbon ions in the 2⁺ charge state were the reasons to prefer an electron cyclotron resonance (ECR) ion source for the accelerator.

The accelerator operates at a terminal voltage (TV) range of 300 kV–3.5 MV, while the ion source can operate at 30 kV–40 kV. In the present system, high-intensity beam currents should be maintained over a large dynamic range: by considering a 1 mA current capability in the case of a proton beam, the beam power can be as high as 3.5 kW. To guarantee voltage stability for longer time periods (>1 h), a high-precision, low-temperature coefficient (<5 ppm°C) resistor chain is used to measure the TV. Beam intensities on target for H, He, and C ions are reported in Table 1. Compared to previous Singletron accelerators, the LUNA-MV has improved specifications for TV stability and ripple (10⁻⁵). Beam energy reproducibility is in the order of 10⁻⁴. A detailed description can be found in Sen et al. (2019).

TABLE 1

TABLE 1. Beam intensity on target.

For practical considerations, targets for direct measurements of nuclear cross-sections on stable nuclides are typically in either solid or gaseous state. The basic aspects of such targets are similar for experiments underground and on the surface, but certain requirements are emphasized for experiments deep underground to fully embrace the advantages of the location. In the case of a solid target, the beam energy loss occurs in a relatively small volume. The resulting power density, up to the order of 10²–10³ W/cm² at LUNA 400 if the beam is stopped in the target, requires the target to be cooled to avoid an increase of temperature that would damage the target or accelerate beam-induced target degradation. For targets on inert backing material, such as those produced by evaporation, sputtering, or implantation, water cooling behind the target is often used to dissipate the heat. The maximal power densities attainable on target will increase with the next generation of underground accelerators, either because of higher beam energies at comparable intensities (such as the MV facility at Gran Sasso) or due to further increased beam intensities (cf. JUNA Liu et al. 2016) compared to LUNA 400. Efforts are underway to adopt and advance techniques from surface experiments, such as cooling for high-powered targets (Wolfgang Hammer et al., 1986) or large-area reaction targets (Chen et al., 2020), to overcome thermal limitations on the beam intensity in future underground experiments. Even with best efforts in cooling, the performance of solid targets degrades under the beam, which is seen, for example, in a reduction of target thickness or changes in the target stoichiometry. In the regime of low-energy nuclear astrophysics experiments, solid targets typically have to be replaced after an irradiation corresponding to accumulated 10⁰–10¹ (particle) Coulombs of the beam on target. This is an important practical aspect for the use of massive shielding against environmental radiation in low-background measurement. Compared to experiments on the surface, where secondary cosmic radiation on shielding materials results in diminishing returns beyond a certain thickness of shielding, much more massive shielding setups of lead and copper have been used at LUNA 400 (Caciolli et al., 2009), where for experiments with solid targets, easy access to the target had to be secured (Boeltzig et al., 2018). More sophisticated, i.e., larger and multilayered, shielding configurations are foreseen in the future as a consequence of an improved understanding of the relevant backgrounds and allowed by the more spacious target station layout at the new MV facility. Target access requirements will continue to be central in future experiments with these setups that employ solid targets.

The effects of target degradation may be avoided, wherever possible, by choosing targets in the gaseous form: a windowless gas target system offers stability over the long data taking periods, up to several weeks, if needed. Another advantage is chemical purity. Solid targets are rarely made by an element alone: possible changes in the stoichiometry should be continuously monitored during the running time.

The gas target system presently in use at the LUNA-400 accelerator is shown in Figure 1. It consists of three differential pumping stages, the target chamber, the gas pipeline, and a recycling system (see Figure 1). Three pumping stages produce a strong pressure gradient between the interaction chamber and the beamline. A water-cooled collimator is placed between adjacent pumping stages, provides the correct gas flow, and determines the pressure drop. The gas target system can either recycle the gas or let it flow away.

FIGURE 1

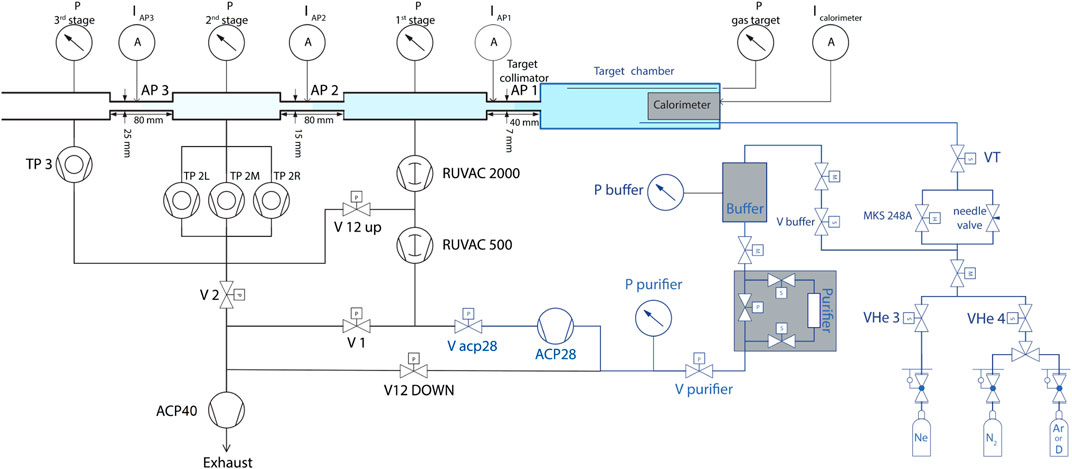
FIGURE 1. Differential pumping system schematic. The beam comes from the accelerator on the left, passes through the apertures AP3, AP2, and AP1, enters the target chamber, and stops on the calorimeter.

The gas enters the interaction chamber close to the beam stop and flows into the first pumping stage, where 99.5% of the gas is pumped away through a roots pump. Approximately 0.5% of the gas also goes in the second pumping stage, where it is pumped by three turbomolecular pumps. A small amount of gas flows in the third pumping stage through and is pumped away by a turbomolecular pump. A roots pump collects the gas from the previous pumps and is itself connected to the roughing pump or the recycling pump, depending on the running mode.

The target volume, typically 10–40 cm long, is surrounded by the detectors and is delimited by the chamber walls, the calorimeter, and the target chamber collimator. The latter does not only collimate the beam but also makes the pressure decrease steeply towards the first pumping stage.

The ionization of the target gas and the neutralization of the beam prevent the electrical reading of the beam current and a power compensation calorimeter with a constant temperature gradient is used to monitor the beam intensity (Ferraro et al., 2018a; Ferraro et al., 2018b). For the proper characterization of a windowless gas target, the density and the efficiency of the detectors profile along the beam path must be known. The density profile is usually measured using a mock-up scattering chamber equipped with measurement ports for capacitive pressure gauges and thermoresistors. The efficiency profile is, in turn, measured by moving radioactive sources along the beamline. Another method is the resonance scan technique: the target system is filled with selected gases such as ¹⁴N or ²¹Ne and their narrow, strong resonances are excited with a proton beam of proper energy. The resonance position is then moved along the target by changing the beam energy accordingly. Gas target setups usually ask for heavier detector shielding systems due to the larger dimensions.

The LUNA laboratory is protected by 1,400 m of dolomite rock from cosmic ray–induced effects. This rock overburden completely suppresses the hadronic and the soft electromagnetic component of cosmic rays. Muons are able to penetrate inside the mountain, but their flux is mitigated by about six orders of magnitude when compared with the Earth surface: this makes typically negligible also muon-induced radiations, such as spallation neutrons or cosmogenic-unstable nuclides. Long-lived radioisotopes such as the ones produced by the natural ²³⁸U and ²³²Th decay chains or ⁴⁰K are present in any laboratory and do not depend on depth but rather on the radiopurity of rocks, buildings, and detector materials. The induced gamma radiations can be mitigated by a suitable passive shielding surrounding the target and the detectors, usually consisting of selected low-background lead and freshly refined electrolytic copper. For the deep underground setting of LUNA, a shielding of 15–25 cm lead with low ²¹⁰Pb content lined at the inside with 5 cm electrolytic copper has been found to give excellent background capabilities, as shown in Figure 2. Impurities in the detector and target, on the other hand, must be minimized by proper material selection.

FIGURE 2

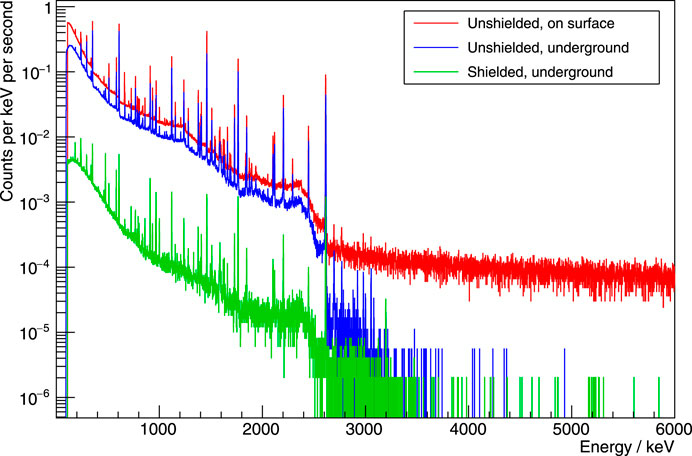
FIGURE 2. γ-ray background spectra taken with a HPGe detector in the surface laboratory (red line), at Gran Sasso (blue), and at Gran Sasso with 15 cm lead shield (green).

From the point of view of neutron background, the underground location allows for a reduction of 3 orders of magnitude with respect to above-ground measurements (Figure 3) even without any further shielding. To further increase the sensitivity in view of neutron emitting reactions that are going to be studied with the MV facility, a deep study devoted to selection material was performed to reduce intrinsic background of detectors such as ³He counters. We recall that a typical counter consists of a gas-filled tube with a high voltage applied across the anode and cathode: a neutron passing through the tube will interact with a ³He atom to produce tritium and a proton. These two particles ionize the surrounding gas atoms to create charges, which in turn ionize other gas atoms in an avalanche-like multiplication process.

FIGURE 3

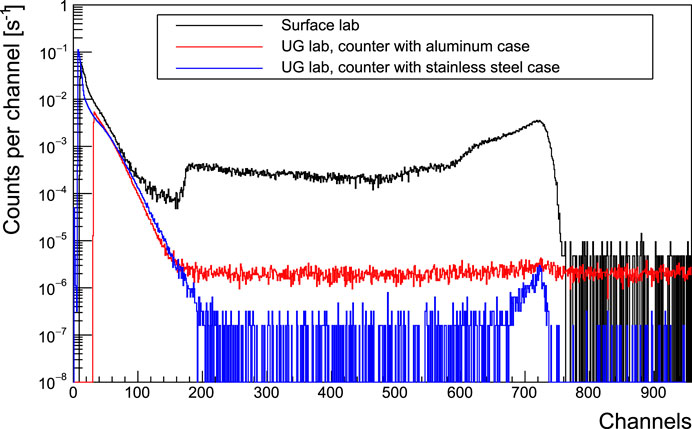
FIGURE 3. Comparison of neutron background measured by means of ³He counters: the black one is measured in a surface laboratory. Blue and red spectra are measured in the LNGS underground laboratory by means of counters with stainless steel and aluminum cases, respectively.

Indeed, alpha particle decays, coming from impurities of uranium and thorium in the counter cases, represent the main source of intrinsic background. By selecting stainless steel cases instead of standard aluminum ones, a reduction of one order of magnitude was achieved as shown in Figure 3: the blue and the red spectra were measured in the Gran Sasso with stainless steel and aluminum counters, respectively. The black spectrum is the background in a surface lab with a stainless steel counter. As a matter of fact, the new MV facility, together with the extremely low gamma and neutron background achieved by the LUNA collaboration, provides a unique sensitivity to assess the key processes of post-main sequence stellar burning.

Neutron Sources for the s-Process

The basic idea of the s-process was born in the 50's, with the famous article by Burbidge et al. (1957). It consists of a series of “slow” neutron captures and β-decays along the neutron-rich side of the valley of stability, close to the stability line. This process is responsible for the production of about half of the elemental abundances between iron and bismuth, as stated in Käppeler et al. (2011), the other part being produced by the rapid neutron-capture process (r-process) and, to a lesser extent, by the proton capture processes.

The s-process takes place in a low neutron flux, where the neutron-capture rate is lower than the β-decay rate of the resulting unstable nuclei. Such conditions are satisfied in the helium-burning shell of low-mass thermally pulsing stars in the AGB (main s-process) or in the helium-burning core of massive stars in the Red Giant Branch (weak s-process). The main s-process is mostly responsible for the production of elements with $90\le A\le 209$ (i.e., from zirconium to bismuth), while the weak s-process contributes to elements in the range $56\le A\le 90$ (i.e., from iron to zirconium).

It is well established that the ¹³C(α,n)¹⁶O reaction (Q_value = 2.216 MeV) is the principal neutron source for the main s-process, while the major neutron source of weak s-process is the ²²Ne(α,n)²⁵Mg reaction (Q_value = −0.478 keV). The cross-section of both these reactions greatly depends on temperature, the existence of excited states close to the reaction threshold, and the initial abundances of the interacting species.

The Main s-Process and the ¹³C(α,n)¹⁶O Reaction

Käppeler (1999) attributed the formation of the main s-process elements to thermally pulsing stars in the asymptotic giant branch (TP-AGB) with mass $1.5M_{\odot }<M\le 3M_{\odot }$. More recently, Cristallo et al. (2018) indicated a slightly broader mass interval, between 1.2 and 4M_ʘ.

The structure of TP-AGB stars is organized in the following layers: a carbon-oxygen core, a He-burning shell, a He-rich intershell, a H-burning shell, and a H-rich envelope. While the H-burning shell produces helium, the core contracts and heats up the basis of the He-burning shell, whose energy production increases. Eventually, the energy produced by the He-burning shell is not anymore radiated away efficiently and a thermonuclear runaway occurs, known as “helium shell flash” or “thermal pulse.” This translates into an expansion of the He-rich intershell and the cooldown of the H-burning shell, which extinguishes. Also, the He-burning shell is affected by the expansion and cools down until extinction. A new contraction takes over and causes the initial reignition of the H-burning shell and of the He-burning shell afterward, until another thermal pulse occurs. A reservoir of ¹³C, produced via the ${}^{12}\text{C}\left(\text{p},\gamma \right){}^{13}\text{N}\left({\beta }^{+}\nu \right){}^{13}\text{C}$ reaction chain, forms the so-called ¹³C pocket at the interface between the He-rich intershell and the H-rich envelope. As of today, the exact formation mechanism of such a pocket is still debated, as stated by Cristallo et al. (2018). During this phase, which lasts some 10⁴ years, the ¹³C(α,n)¹⁶O reaction takes place and provides neutrons for the main s-process.

In the article by Cristallo et al. (2018), the authors claim that, in the most metal-rich stellar models with an almost solar composition, a small amount of ¹³C might survive and be engulfed into the convective zone generated by the incoming thermal pulse. This scenario would affect several branching points along the s-process path, and excesses of ⁶⁰Fe, ⁸⁶Kr, ⁸⁷Rb, or ⁹⁶Zr are expected compared to the radiative (low neutron density) ¹³C burst. The unburned ¹³C left at the end of the interpulse and available to produce neutrons in the subsequent pulse depends on the rate of the ¹³C(α,n)¹⁶O reaction.

The relevant astrophysical temperature for this process is ∼0.1 GK, corresponding to a Gamow energy window between 140 and 250 keV. Indeed, the energy range of interest could be even larger, as discussed in the research by Kimura and Bonasera (2013), since the S(E) factor is energy-dependent. In Figure 4, the level scheme of ¹³C(α,n)¹⁶O nuclear reaction process is shown. The excited states of interest for AGB nucleosynthesis are highlighted in green and red. In particular, green levels are broad states which must be taken into account for any ¹³C(α,n)¹⁶O cross-section evaluation in the astrophysical region of interest. These are the (1/2)⁺ near-threshold state and the (3/2)⁺ at $E_x=7239\text{keV}$.

FIGURE 4

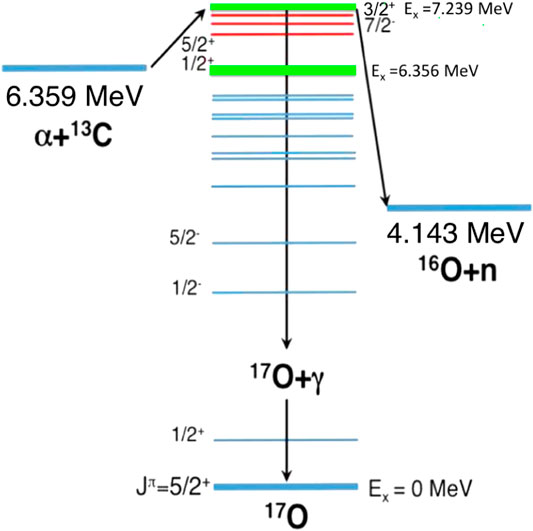
FIGURE 4. (Colour online) Schematic diagram adapted from Cristallo et al. (2018) of the ¹³C(α,n)¹⁶O nuclear reaction process, together with the competing exit channel ¹⁷O+γ. The excited states of interest for AGB nucleosynthesis are highlighted in green.

It is important to mention that the energy level of the near-threshold state is debated: Ajzenberg-Selove (1986) attributed to this state as subthreshold energy of $E_x=-\left(3\pm 8\right)\text{keV}$, while recently a study by Faestermann et al. (2015) deduced a positive energy value at $E_x=\left(4.7\pm 3.0\right)\text{keV}$.

State-of-the-Art

A conspicuous number of measurements of the ¹³C(α,n)¹⁶O cross-section have been carried out over the past 45 years.

We focus the attention on crucial direct and indirect measurements performed as follows.

The following are some of the direct measurements performed:

Drotleff et al. (1993) measured the cross-section of the ¹³C(α,n)¹⁶O reaction in the 370–1000 keV energy range with ³He proportional counters embedded in a moderating polyethylene matrix. This is still the dataset with the lowest point ever measured with direct measurement. The low-energy points reveal a S-factor enhancement, possibly due to a 1/2⁺ subthreshold resonance, mentioned by Ajzenberg-Selove (1986).

Brune et al. (1993) used ³He counters to measure the resonances of the ¹³C(α,n)¹⁶O reaction, at E_α = 656 and 802 keV: the authors concluded that the resonance strengths for these two states are too weak, compared to the nonresonant contribution, to affect the stellar reaction rates;

Harissopulos et al. (2005) measured the ¹³C(α,n)¹⁶O reaction absolute cross-section in an energy range E = 0.8–8 MeV in steps of 10 keV with a setup similar to Drotleff’s one. The main aim of the measurement was the geoneutrino background subtraction required by neutrino experiments such as Borexino and Kamland, as explained in the study by Araki et al. (2005). An overall uncertainty of 4% was achieved.

Heil et al. (2008) promoted a new study of the ¹³C(α,n)¹⁶O cross-section in the energy range E = 420–900 keV. Heil used a different approach, employing a n-γ converter consisting of a Cd-doped paraffin sphere surrounded with 42 BaF₂γ detectors. In the central hole, a neutron converter was installed. A detailed uncertainties analysis is described in the article. The authors recognized the main source of systematic error as the change of target stoichiometry caused by the buildup during the beam irradiation. At higher energies, overall uncertainties could be reduced to the level of 5%.

Recent measurements at high energy are due to Febbraro et al. (2020), covering the same energy range spanned by Harissopulos. They improved the precision and accuracy by means of a setup sensitive to the neutron energies, also measuring the excited state transitions via secondary γ-ray detection. With this setup, they discriminated against neutrons emitted from different energy groups and they could measure the individual partial cross-sections of the ¹³C(α,n)¹⁶O reaction to the ground state and second excited state of the ¹⁶O final nucleus.

At low energies, uncertainties of direct measurements are larger than 50%: they are dominated by the low counting statistics caused by unfavorable S/N ratio.

Moreover, going down in energy, direct measurements face limits of the fast dropping of the cross-section due to the Coulomb barrier and the increase of the screening effect.

For this reason, complementary indirect studies have been developed to better constrain the cross-section of this neutron source in the relevant energy region for astrophysics. These measurements were mostly aimed to determine the spectroscopic factor and/or the asymptotic normalization coefficient (ANC) of the 1/2+ level of ¹⁷O near threshold, which represents the largest source of uncertainty at low energies. Kubono et al. (2003) evaluated a spectroscopic factor S_α = 0.01, but data were reanalyzed by Keeley et al. (2003), indicating a factor of 40 larger contributions. The ANC method was approached for the first time in the work by Johnson et al. (2006) that used the ${}^6\text{L}\text{i}\left({}^{13}\text{C},\text{d}\right){}^{17}\text{O}$ sub-Coulomb transfer reaction. These results were recently revisited in the article by Avila et al. (2015).

Other indirect measurements were obtained with the Trojan Horse Method (THM): in this approach, projectiles (or targets) are selected and described as clusters of two particles in quasi-free kinematics. One is involved in reaction, while the other constituent cluster, called the spectator nucleus “s,” is emitted without interacting with the system. For further information on the method, one could refer to Tumino et al. (2018a) and Tumino et al. (2018b). Using this technique, the ${}^{13}\text{C}\left({}^6\text{L}\text{i},\text{n}{}^{16}\text{O}\right)\text{d}$ reaction was studied in quasi-free kinematic conditions (the deuteron inside the ⁶Li beam is considered as a spectator to the three-body reaction), as described in La Cognata et al. (2013). This work covered an energy range between −0.3 and 1.2 MeV and allowed studing the near-threshold resonance at $E_x=6356\text{keV}$. In general, THM results need to be normalized to selected direct data and their uncertainty strongly depends on the choice of the reference direct measurements: in the first THM analysis by La Cognata et al. (2013), data were scaled to the astrophysical S-factor recommended by Heil et al. in the energy region between ∼0.6 and 1.2 MeV. As a result, a THM S-factor was good in agreement with the direct ones, but with a squared Coulomb-modified ANC $\left(7.7\pm 0.3\right){\text{fm}}^{-1}$, it was not in agreement with independent assessments of the ANCs, whose weighted average is $\left(3.9\pm 0.5\right){\text{fm}}^{-1}$. After the new evaluation of the near-threshold resonance energy by Faestermann et al. (2015), setting its center at 4.7 keV above the ¹³C–α threshold, data by THM were reanalyzed by Trippella and La Cognata (2017), normalizing experimental data with respect to the ANC parameter of the threshold resonance obtained by Avila et al. (2015). Trippella obtained an ANC value of (3.6 ± 0.7) fm^{− 1}, in agreement with literature.

Data from the most recent works (direct and indirect methods) are shown in Figure 5.

FIGURE 5

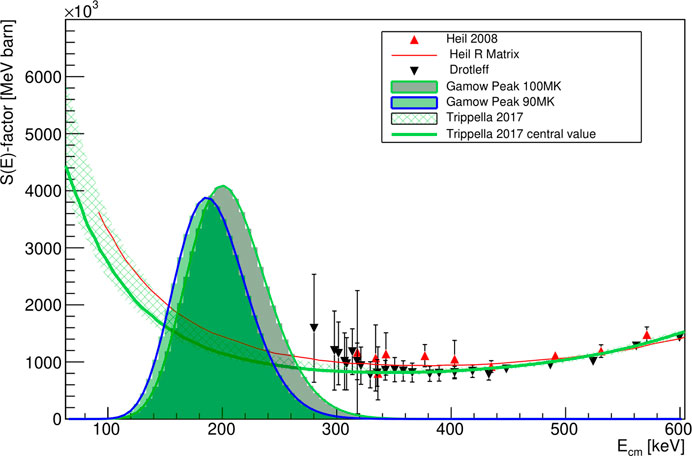
FIGURE 5. Selection of most recent ¹³C(α,n)¹⁶O measurements. Among the direct measurements, the Drotleff and the Heil data are represented, indicated by black triangles and red triangles, respectively. The solid red curve indicates the R matrix extrapolation by Heil. The most recent indirect measurement by THM by Trippella et al. is indicated by the green squared area and the central value is the green curve. In the plot, the Gamow window for two different stellar scenarios is drawn.

From direct measurements (high uncertainties at low energy and a large scatter in absolute values among datasets) and indirect measurements (e.g., discrepancy in the spectroscopic factor evaluation and uncertain normalization of THM), there is a clear indication that more direct data with about 10% overall uncertainty are mandatory at both low and high energy.

The LUNA Direct Measurement

Taking advantage of the low environmental background of LNGS and the highly intense and stable alpha beam provided by the LUNA 400 accelerator, recently the LUNA collaboration put huge efforts into the measurement of the ¹³C(α,n)¹⁶O cross-section at low energy with the goal to reach an overall uncertainty near 10%. A detector based on 18 ³He counters arranged in a polyethylene moderator has been developed in order to maximize its efficiency. ¹³C targets used during the measurement at LUNA have been produced evaporating 99% ¹³C isotopically enriched powder on tantalum backing using the evaporator installed at the nuclear institute of research Atomki (Debrecen, Hungary). Hereby, the key points of the LUNA experiment are summarized. As already said before, the installation of the accelerator in the LNGS underground laboratory allows a neutron background reduction of 3 orders of magnitude with respect to above-ground measurements. Moreover, special attention was paid to reduce the α particle intrinsic background from detectors.

A further step for the background reduction was performed, acquiring the raw preamplifiers signals coming from detectors with Caen V1724 digitizers and rejecting alpha signals with a pulse shape discrimination analysis described in the article by Balibrea-Correa et al. (2018). This allowed reaching an overall background in the whole detector of about 1 count/h, 2 orders of magnitude lower than previous experiments performed in surface laboratories as described in the article by Csedreki et al. (2019).

Possible beam-induced background sources were investigated shooting alpha beam on blank tantalum backings. The neutron detection rate was compatible with the background measurement, making negligible the in-beam background.

The degradation monitoring under an intense alpha beam is crucial during the cross-section measurement performed at LUNA. The well-known NRRA (Nuclear Resonant Reaction Analysis) technique is not applicable due to the lack of resonances in the dynamic energy range of the accelerator. For this reason, a new method of analysis was developed.

Data taking at LUNA consisted in long α-beam runs with accumulated charges of ≈1C per run, interspersed by short proton-beam runs with moderator opened and HPGe detector in close geometry, with typical accumulated charges of 0.2 C at most. During the last mentioned proton run, the target degradation can be checked by performing a gamma shape analysis on the direct capture deexcitation to the ground state peak of ¹³C(p,γ)¹⁴N reaction with the HPGe detector.

Further information and details can be found in the study by Ciani et al. (2020).

Thanks to the unprecedented background reduction for this kind of direct measurement and the novel approach to monitoring target degradation, it was possible to measure the experimental yield of the ¹³C(α,n)¹⁶O reaction in an energy range from 400 keV down to 305 keV in laboratory system energy, 40 keV lower than data in the literature: for the first time, LUNA collaboration measured with a direct technique cross-section inside the Gamow window reaching unprecedented overall uncertainty (<20%). Final results and astrophysical implications will be published within the end of 2020.

The LUNA collaboration is planning to extend the measurement of the ¹³C(α,n)¹⁶O at higher energies at the new MV facility in the LNGS laboratory. This will give the unique possibility of providing a complete dataset over a wide energy range and avoiding renormalization to other datasets with unknown systematic uncertainties.

The Weak s-Process and the ²²Ne(α,n)²⁵Mg Reaction

About half of the elements between iron and yttrium ($56\mathrm{\lesssim }A\mathrm{\lesssim }90$) are produced via the weak s-process in massive stars with initial mass M > 8M_ʘ (Käppeler et al., 2011). In such stars, ²²Ne is a byproduct of He-burning starting from preexisting CNO isotopes.

The reaction ²²Ne(α,n)²⁵Mg has a negative Q-value of −478 keV and requires relatively high temperatures to be ignited. At the base of the convective envelope around the He core of massive stars, the temperature is sufficiently high (>0.25 GK) to make this reaction a relevant source of neutrons for the weak s-process until core He-burning extinguishes (Peters, 1968; Couch et al., 1974; Lamb et al., 1977; Prantzos et al., 1990; Raiteri et al., 1991a). Its effectiveness as a neutron source, though, depends also on the cross-section of the competing reaction, ²²Ne(α,γ)²⁶Mg.

When core He-burning runs out, ²²Ne is still rather abundant [about 1% in mass as claimed in the article by Pignatari et al. (2010)] and the reaction ²²Ne(α,n)²⁵Mg is reactivated during shell C burning (Raiteri et al., 1991b) at a temperature of about 1 GK. At this stage, the ¹²C(¹²C,α)²⁰Ne process yields α particles (Arnett and Truran, 1969) and even larger neutron fluxes are provided as a consequence of the higher temperature.

Besides the broad interest in the main neutron source in the weak s-process, some contributions also to the main s-process are worth mentioning in low-mass (M < 3M_ʘ) AGB stars during thermal pulses (Gallino et al., 1988; Hollowell and Iben, 1988) and in intermediate-mass ($4M_{\odot }<M<8M_{\odot }$) AGB stars (Bisterzo et al., 2014; Bisterzo et al., 2015), whereas predicted abundances of ⁸⁶Kr, ⁸⁷Rb, and ⁹⁶Zr are at variance with observations (Lugaro et al., 2003; Garcia-Hernandez et al., 2006; Garcia-Hernandez et al., 2007; Garcia-Hernandez et al., 2009; van Raai et al., 2012).

State-of-the-Art

Considering the weak s-process during core He-burning, the low-energy part of the Gamow window of the ²²Ne(α,n)²⁵Mg reaction extends down to the boundary of the (α,n) threshold, located at $E_{\alpha ,\text{lab}}=575\text{keV}$. At such low energies, measurements have so far suffered from low signal and high background, especially because of the small cross-section. For this reason, different groups only succeeded to directly study the resonances down to $E_{\alpha ,\text{lab}}=830\text{keV}$ (see Figure 6). Other attempts to study the resonances at lower energies by means of indirect methods often obtained inconsistent results. In the following, we summarize the most relevant direct studies of this reaction.

FIGURE 6

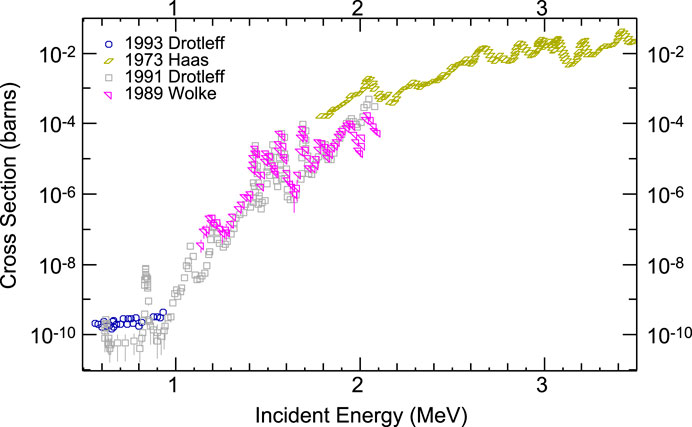
FIGURE 6. A subset of the previous measurements of the ²²Ne(α,n)²⁵Mg reaction cross-section. Data retrieved from the EXFOR database version of October 8, 2020. Blue circles are upper limits.

Back in the 60s, Ashery (1969) discovered that this reaction proceeds through many resonances in the compound nucleus. Other experimental studies conducted by Haas and Bair (1973), Mak et al. (1974), and Wolke et al. (1989) reported about 1 MeV and above.

Harms et al. (1991) investigated the energy range between $E_{\alpha ,\text{lab}}=0.73$ and 2.10 MeV with a windowless, recirculating gas target system and two ³He ionization chambers in close geometry. The resonance at $E_{\alpha ,\text{lab}}=830\text{keV}$ was clearly detected, but it was not possible to show the existence of resonances at lower energies. Soon after, Drotleff et al. (1991)Drotleff et al. (1993) explored a lower energy range using the same gas target and an improved 4π detector, including two concentric circles of eight ³He counters in a polyethylene moderator. Despite the improved sensitivity, no new low-energy resonances were observed in this experiment.

Giesen et al. (1993) performed a direct measurement with implanted ²²Ne targets to search for low-energy resonances. The background from ${}^{11}\text{B}\left(\alpha ,\text{n}\right){}^{14}\text{N}$, however, limited the sensitivity at lower energies. At the same time, they investigated the excited levels with natural parity in ²⁶Mg thanks to an indirect technique, the α-transfer.

Later, Jaeger et al. (2001) developed a new detector with twelve ³He counters arranged in an optimized geometry. This upgrade allowed achieving a sensitivity of ∼10 pb and constraining the strength of the $E_{\alpha ,\text{lab}}=830\text{keV}$ resonance to $\omega \gamma =\left(118\pm 11\right)\mathrm{\mu }\text{eV}$. The upper limit on the tentative resonance at $E_{\alpha ,\text{lab}}=633\text{keV}$ was significantly lowered. Based on these results, Jaeger et al. (2001) calculated the reaction rate under the assumption that the strength of the hypothetical resonance at $E_{\alpha ,\text{lab}}=633\text{keV}$ was at 10% of its observed upper limit. However, the occurrence of such a resonance was ruled out by Longland et al. (2009), who demonstrated that the corresponding excited state at $E_x=\mathrm{11,150}\text{keV}$ in ²⁶Mg has unnatural parity.

At that time, it was clear that only a very low-background setup in an underground laboratory could have made possible a direct investigation of the resonances at lower energies.

The focus then moved to the evaluation of the reaction rate and its implications, mostly using direct cross-section measurements at relatively high energy and indirect data.

Longland et al. (2012) used a sophisticated statistical approach to calculate the ²²Ne(α,n)²⁵Mg reaction rate, including a careful treatment of the uncertainties. This led to a reduction of the uncertainties on calculated rates and raised the need for new, more precise and more sensitive measurements.

Bisterzo et al. (2015) estimated the impact of the ²²Ne(α,n)²⁵Mg uncertainty on the isotopic abundances close to and within the branching of the s-path for the main s-process. They provided a new evaluation of the reaction rate that was a factor of 2 higher than Longland et al. (2012). Even if this new rate was still able to reproduce the contribution of s-only isotopes from the main s-process within the solar uncertainties, Bisterzo et al. (2015) underlined how a sizeable change could be caused by low-energy resonances.

In the following years, several indirect studies attempted to improve the knowledge of this reaction. A new experimental investigation by Talwar et al. (2016) used α inelastic scattering to identify the important resonances and the α transfer technique to indirectly measure their width. The resulting ²²Ne(α,n)²⁵Mg reaction rate was close to the rate in Longland et al. (2012). Soon after, Massimi et al. (2017) studied neutron-capture reactions on ²⁵Mg, observing several excited states of ²⁶Mg and in particular at $E_x=11.112\text{MeV}$. In the same article, an R-matrix analysis was developed to assign spin and parity values to the excited states in ²⁶Mg without ambiguity and to calculate the upper limits on the reaction rates of the ²²Ne(α,n)²⁵Mg and ²²Ne(α,γ)²⁶Mg reactions. In the same work, Massimi et al. (2017) studied the impact of these new rates on the evolution of stars with initial mass M between 2 and 25M_ʘ. It was observed that for a 25M_ʘ star, the uncertainty of the ²²Ne(α,n)²⁵Mg reaction rate was responsible for large differences in the weak s-process abundances, up to a factor of 50 in the Sr region. Noticeable changes were also found in intermediate-mass AGB models (IMS-AGBs, $3<M/M_{\odot }<7$) with an increase of ∼50% in the abundances of Y and La.

The continued interest in this reaction is demonstrated by two very recent experimental studies by Ota et al. (2020) and Jayatissa et al. (2020) with α transfer reactions: Ota et al. (2020) studied the ${}^{22}\text{N}\text{e}\left({}^6\text{L}\text{i},\text{d}\right){}^{26}\text{M}\text{g}$ in inverse kinematics, detecting outgoing deuterons and ^25,26Mg in coincidence. In addition, Jayatissa et al. (2020) studied the ${}^{22}\text{N}\left({}^7\text{L}\text{i},\text{t}\right){}^{26}\text{M}\text{g}$ reaction.

The new evaluation of the reaction rate, based on spin-parity assignments by Jayatissa et al. (2020) combined with data from Ota et al. (2020), resulted in lower rates than previous evaluations, especially at low temperatures (see Figure 7). The lower rate is also the result of excluding an excited state at $E_x=11.112\text{MeV}$, corresponding to $E_{\alpha ,\text{lab}}=598\text{keV}$, observed by Massimi et al. (2017) and not observed in these studies.

FIGURE 7

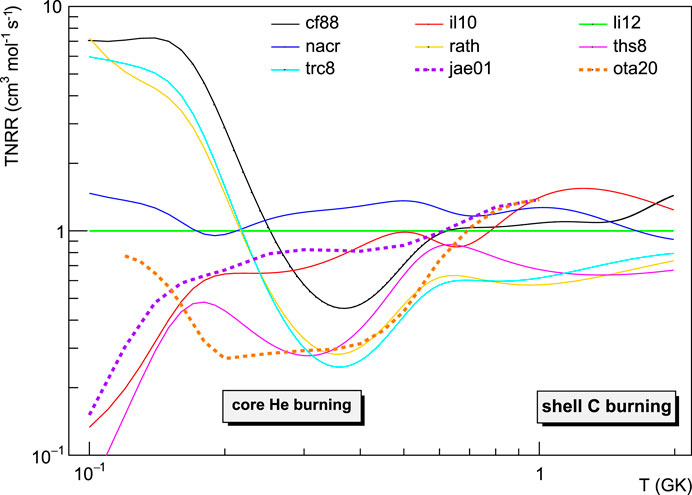
FIGURE 7. A subset of the ²²Ne(α,n)²⁵Mg reaction rate evaluations, relative to Longland et al. (2012). Solid lines refer to the evaluations reported in the JINA REACLIB database as in Cyburt et al. (2010). In particular, cf88 = Caughlan and Fowler (1988); nacr = Angulo et al. (1999); rath = Rauscher and Thielemann (2000); ths8 = Cyburt et al. (2010); il10 = Iliadis et al. (2010); trc8 = REFIT: Cyburt et al. (2010); li12 = Longland et al. (2012). Dashed lines: jae01 = Jaeger et al. (2001); ota20 = Ota et al. (2020).

In conclusion, the thermonuclear reaction rate of this reaction is still largely uncertain: several evaluations are present in the literature (see Figure 7), based on theoretical considerations, direct and indirect measurements, differing up to a factor of 5 in the temperature range relevant to the s-process in core He burning. The presence of low-energy resonances in the ²²Ne(α,n)²⁵Mg reaction below $E_{\alpha ,\text{lab}}=830\text{keV}$ is expected, based on known levels in ²⁶Mg, but no such resonances have been directly observed yet. Nevertheless, they might contribute significantly to the reaction rate around 0.2 GK and cause sizeable changes in the prediction of weak s-process abundances.

The direct measurement of the ²²Ne(α,n)²⁵Mg reaction cross-section will be carried out at the new MV facility at LNGS (Guglielmetti, 2014; Prati, 2019), using a windowless gas target (see Figure 1) of enriched ²²Ne. Such an experiment could provide precise and accurate cross-section measurements down to about $E_{\alpha ,\text{lab}}\sim 600\text{keV}$. Most of the background is expected to be due to the ¹¹$\text{B}{\left(\alpha ,\text{n}\right)}^{14}\text{N}$ reaction, as already reported by past experiments; therefore, a proper reduction of contaminants poses a crucial challenge, combined with the development of an optimized detector setup.

SHADES (Scintillator-He3 Array for Deep underground Experiments on the S-process) is an ERC starting grant (Grant agreement ID: 852016), recently awarded to realize a new setup for the measurement of the ²²Ne(α,n)²⁵Mg reaction at energies of astrophysical interest. SHADES includes the development of a novel neutron detector and a gas target to be used at LUNA. The detector combines an array of ³He counters with their high detection efficiency and liquid scintillators, which act as moderators for the reaction neutrons while at the same time providing information on the neutron energy. The combination of ³He tubes and scintillator, together with recently studied signal processing techniques, as shown in Balibrea-Correa et al. (2018), will be able to limit backgrounds from external and internal sources and a beam-induced background to acceptable levels. The new detector will allow an increase of at least two orders of magnitude in sensitivity, allowing for the first time a measurement of the reaction cross-section in the energy range relevant to the s-process in core He burning.

The ¹²C(α,γ)¹⁶O Reaction

The reaction ¹²C(α,γ)¹⁶O competes with the so-called triple-α process (${}^4\text{H}\text{e}+{}^4\text{H}\text{e}\to {}^8\text{B}\text{e}$ followed by ${}^4\text{H}\text{e}+{}^8\text{B}\text{e}\to {}^{12}\text{C}$) during stellar helium burning (Burbidge et al., 1957). The astrophysical rates of both reactions influence the ratio of ¹²C/¹⁶O produced during the helium-burning phase, which in turn determines the following steps of stellar evolution. Due to the central role of these nuclides, understanding their ratio in helium burning has been identified as a problem of “paramount importance” for nuclear astrophysics, as shown in Fowler (1984). Compared to the triple-α process, the cross-section of ¹²C(α,γ)¹⁶O is significantly less well-known and, in spite of extensive experimental efforts, a better understanding of this reaction remains desirable. A recent comprehensive review on the state of understanding ¹²C(α,γ)¹⁶O can be found in deBoer et al. (2017).

Owing to the sharp drop of the charged particle reaction cross-sections towards the energy regions relevant for astrophysics, direct measurements in the energy region of interest are not available, making extrapolations necessary. Such extrapolations are challenging due to the nuclear structure of the compound nucleus ¹⁶O: the cross-section in the energy range of interest is characterized by the presence of broad resonances (including subthreshold states). It is crucial to study the interference between states of the same J^π but also to account for angular effects from the interference of processes with different J^π (as outlined in deBoer et al., 2017). In particular, the E1 and E2 components of capture to the ground state are of comparable strength in the energy range of interest, and the extrapolated cross-section is very sensitive to the interference of these two components.

Different experimental approaches have been taken to directly study the ¹²C(α,γ)¹⁶O reaction: in normal kinematics, a fixed ¹²C target (solid or gaseous) is bombarded by α particles, detecting γ-rays from the reaction; inverse kinematics employs a ¹²C beam impinging on a helium target. Inverse kinematics experiments have been performed as measurements of the γ-rays from the reaction or detecting the ¹⁶O nuclei in a recoil separator (Kremer et al., 1988; Schürmann et al., 2005; Matei et al., 2006; Schürmann et al., 2011). Studies of the inverse reaction ${}^{16}\text{O}\left({\gamma }_0,\text{p}\right){}^{12}\text{C}$ at high-intensity γ-ray facilities allow us to infer information on the ground state transitions. Other reactions to study the nuclear structure of ¹⁶O are used to constrain extrapolations of the reaction ¹²C(α,γ)¹⁶O in frameworks such as R-matrix theory in deBoer et al. (2017).

When measuring the γ-rays from reaction, angular distribution measurements at multiple detector angles yield information to disentangle the E1 and E2 components, while a total absorption spectroscopy setup, detecting the total γ-ray energy, yields the total cross-section with a large detection efficiency. Figure 8 summarizes the current situation of direct measurements, showing recent direct measurements of this reaction at low energies for illustration. These measurements extend down to about 0.9 MeV center of mass energy but are characterized by increasing uncertainties when approaching these low energies. As the cross-section drops rapidly towards these energies, backgrounds—environmental and beam-induced—are increasingly relevant. For example, experiments in normal kinematics are affected by backgrounds from the reaction ¹³C(α,n)¹⁶O, which has a cross-section that is of the order of 10⁶ times that of ¹²C(α,γ)¹⁶O. Neutrons can produce background signals directly in the detector or through secondary radiation in the environment of the detector. This background can be reduced by using ¹²C targets depleted in ¹³C or with the help of bunched beams that allow disentangling the prompt γ-ray signal from neutron-induced backgrounds by time of flight.

FIGURE 8

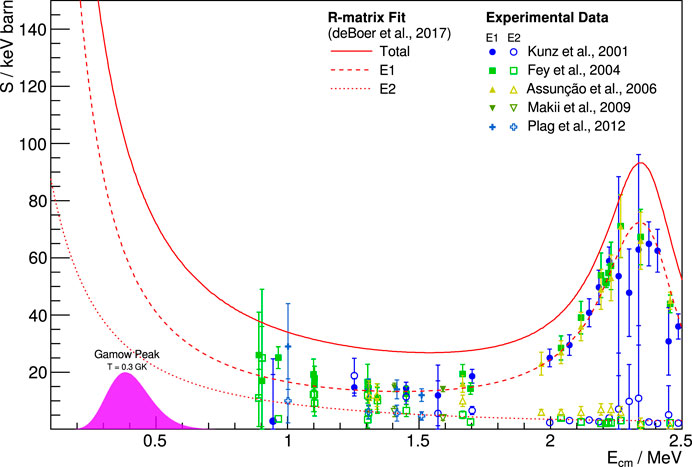
FIGURE 8. Overview of recent experimental data (Kunz et al., 2001; Fey, 2004; Assunção et al., 2006; Makii et al. 2009; Plag et al., 2012) for the ground state capture in ¹²C(α,γ)¹⁶O, with the results of R-matrix fits from deBoer et al. (2017) for comparison. All data are unscaled. The location of the Gamow window for a stellar temperature of 0.3 GK is shown for reference.

Additional data at lower energies are desirable to better constrain the energy dependence of the extrapolation, and further experiments will aim to shed light on it in the future. Direct measurements are expected to contribute to this effort by pushing the lower limit for the available cross-section data further below 1 MeV center of mass energy. This includes promising measurements with a recoil mass separator, as in Fujita et al. (2015). On the side of the new underground accelerator facilities, new exciting opportunities for the study of this reaction will become available shortly. Measurements of ¹²C(α,γ)¹⁶O are among the scientific goals of the new MV facility at LNGS and the Felsenkeller shallow-underground accelerator laboratory for nuclear astrophysics, as in Bemmerer et al. (2018). Both accelerators will provide beams not only of α particles but also of carbon ions, allowing for underground measurements of this reaction in inverse kinematics. The scientific program of JUNA at JPL, as outlined in Liu (2017), includes the study of ¹²C(α,γ)¹⁶O as well. To take full advantage of the high-intensity α beam and the deep underground location of JUNA, the minimization of beam-induced backgrounds, such as those created on ¹³C, has been identified as crucial.

The ¹²C+¹²C Reaction

At the end of the core helium burning, the central part of the star becomes more massive, contracts, and heats up. The contraction and the possible consequent collapse can be halted by the ignition of carbon burning or by the pressure of degenerate electrons. There are several factors preventing the ignition temperature before carbon burning is reached prior to electron degeneracy. For instance, plasma neutrinos are produced near the center of the star and they cause a decrease in the central temperature while leaving it. In addition, in the case of intermediate-mass stars, the second dredge-up further reduces the temperature of the star core, with the convective envelope penetrating into the H-exhausted shell. Depending on the star mass, it may attain the physical condition for C burning or become a carbon-oxygen white dwarf. The minimum initial mass of a star able to experience a C-burning phase is called $M_{\text{up}}$. The value of $M_{\text{up}}$ was proposed for the first time by Becker and Iben (1980), who found $M_{\text{up}}=9M_{\odot }$ for a star with nearly solar composition. However, there are many uncertainties: those affecting the ¹²C+¹²C and ¹²C+α rates are the most important nuclear ones. As a matter of fact, the value of $M_{\text{up}}$ separates the progenitors of C-O white dwarfs, novae, and type Ia supernovae from those of core-collapse supernovae, neutron stars, and stellar-mass black holes. Finally, if the star mass is slightly higher than $M_{\text{up}}$, an off-center carbon ignition takes place in degenerate conditions and the star may end its life as an O-Ne white dwarf.

Stellar models predict that carbon burning, triggered by the ¹²C+¹²C, occurs for center of mass energies between 0.9 and 3.4 MeV. The reaction can proceed through different channels corresponding to the emission of a photon, a neutron, a proton, one or two α particles, or a ⁸Be nucleus. Among these channels, the two most relevant are the ${}^{12}\text{C}\left({}^{12}\text{C},\text{p}\right){}^{23}\text{N}\text{a}$ and ${}^{12}\text{C}\left({}^{12}\text{C},\text{α}\right){}^{20}\text{N}\text{e}$; alpha particles can produce neutrons through ¹³C(α,n)¹⁶O and ²²Ne(α,n)²⁵Mg reactions. These neutrons are fundamental for the synthesis of elements heavier than Fe through the s-process.

The ¹²C+¹²C reaction rate at the center of mass energies $\approx 1.5\text{MeV}$ also affects the physical conditions in the SNIA explosion. In particular, carbon burning can be ignited in an explosive condition when the material is accreted on the surface of a white dwarf in a close binary system, as in Bravo et al. (2011). A variation in the rate would modify the extension of the convective core prior to the explosion, the degree of neutronization, and the temperature at the beginning of the thermonuclear runaway. The knowledge of SNIA is fundamental in cosmology since these systems allow the measurements of distances and of the expansion rate of high redshift galaxies Tutusaus et al. (2019).

Unfortunately, the Gamow window of the ¹²C+¹²C reaction, 0.7–3.4 MeV depending on the astrophysical scenario, is much lower than the height of the Coulomb barrier, 6.7 MeV approximately, making the direct measurement of the cross-section extremely difficult.

State-of-the-Art

The two most relevant channels in the ¹²C+¹²C reaction are the emission of protons and α particles, with a Q-value of 2.24 MeV and 4.62 MeV, respectively. The proton and alpha channels can be measured by detecting either the charged particles or the gamma decay. In particular, the largest branching is for the deexcitation of the first excited state to the ground state of the ²³Na or ²⁰Ne. Above 2 MeV, the first excited state transition to the ground state accounts for approximately 50% of the total cross-section and produces photons of 440 keV and 1634 keV in the case of proton or alpha emission, respectively.

The challenge in obtaining a reliable measurement of the ¹²C+¹²C cross-section at low energies is related to its exponentially falling behavior, which produces a very low counting rate; in this scenario, any natural or beam-induced background can seriously affect the measurement. The latter is due to impurities in the carbon target, mainly hydrogen and deuterium, because they can form bonds with carbon. The main background related to the gamma measurements comes from the ${}^2\text{H}\left({}^{12}\text{C},{\text{p}}_1\gamma \right){}^{13}\text{C}$ and ${}^1\text{H}\left({}^{12}\text{C},\gamma \right){}^{13}\text{N}$ reactions, as detailed in the experimental work by Spillane et al. The Compton background of the primary peaks could completely dominate the carbon fusion γ-ray peaks, as in Spillane et al. (2007). As far as the particle measurements are concerned, it is kinematically impossible to find protons in the carbon fusion region of interest if the particle detectors are placed at backward angles.

The most recent articles focusing on the ¹²C+¹²C cross-section measurement at low energies are summarized as follows.

Jiang et al. (2018) have recently measured the ¹²C+¹²C fusion cross-section in the energy range 2.5–5 MeV. The authors studied the two main channels: ${}^{12}\text{C}\left({}^{12}\text{C},\text{p}\right){}^{23}\text{N}\text{a}$ and ${}^{12}\text{C}\left({}^{12}\text{C},\alpha \right){}^{20}\text{N}\text{e}$ at Argonne National Laboratory using a Gammasphere array of 100 Compton-suppressed Ge spectrometers in coincidence with silicon detectors. The measurement was pushed down to 2.84 MeV and 2.96 MeV for the p and α channels, respectively; the results are in good agreement with other measurements using γSpillane et al. (2007) and charged particle detection Zickefoose et al. (2018), but with smaller uncertainties.

Tumino et al. (2018a) and Tumino et al. (2018b) measured the cross-section of the ${}^{12}\text{C}\left({}^{12}\text{C},\text{p}\right){}^{23}\text{N}\text{a}$ and ${}^{12}\text{C}\left({}^{12}\text{C},\alpha \right){}^{20}\text{N}\text{e}$ reactions through the indirect THM. A 30 MeV beam was delivered on a natural carbon target; charged particles were detected through ΔE-E position-sensitive silicon detectors. The THM results for α and p channels are in good agreement with direct data except for the 2.14 MeV region, where the claim of a strong resonance by previous works Spillane et al. (2007) is not confirmed. Instead, the indirect data show a resonance at 2.095 MeV, one order of magnitude less intense with respect to the 2.14 MeV resonance found by Spillane in the ${}^{20}\text{N}\text{e}+\alpha$ channel and of similar intensity in the ${}^{23}\text{N}\text{a}+\text{p}$ one. In addition, several low-energy resonances are evident below 1.5 MeV, never detected before in a direct measurement. The results of the THM raised some criticism, as in Mukhamedzhanov et al. (2019), mainly because of the neglected Coulomb interaction between ²H, the spectator nucleus in the THM, and ²⁴Mg.

${}^{12}\text{C}\left({}^{12}\text{C},\text{p}\right){}^{23}\text{N}\text{a}$ has also been measured by Zickefoose et al. (2018) in the 2–4 MeV energy range by particle spectroscopy. The beam, provided by the tandem accelerator of the Center for Isotopic Research on the Cultural and Environmental (CIRCE) heritage, was sent onto highly ordered pyrolytic graphite targets; protons were detected through ΔE-E silicon detectors. The total S-factor, including also the contribution of the α channel, has been obtained using the ratio between the p-channel and total S-factor provided by Becker et al. (1981). Due to the poor statistics and beam-induced background problems, this work needs a further experimental effort to improve the knowledge of the total S-factor in the relevant energy range. For this reason, the experimental campaign continued with a new study devoted to the reduction of light species contaminant, especially ¹H and ²H in the carbon targets, as in Morales-Gallegos et al. (2018). Measurements were done with natural graphite and highly ordered pyrolytic graphite targets. ¹H and ²H content were reduced up to 70–85% by means of diffusion at high temperatures (higher than 1,000°C). A further reduction of a factor of 2.5 was obtained, enclosing the scattering chamber in dry nitrogen to minimize leaks into the rest gas within the chamber. The bulk contamination finally achieved by the authors is 0.3 ppm. Further measurements are planned with the new experimental setup.

An upper limit on the ¹²C+¹²C S-factor has been recently suggested from the measurement of the ¹²C+¹³C reaction by Zhang et al. (2020); in fact, it has been observed that the ¹²C+¹³C and ¹³C+¹³C cross-sections at energies below and above the Coulomb barrier are upper bounds of the nonresonant contribution of the ¹²C+¹²C cross-section. The measurement of the ¹³C+¹³C reaction was performed by studying the ${}^{12}\text{C}\left({}^{13}\text{C},\text{p}\right){}^{24}\text{N}\text{a}$ channel; ²⁴Na has a half-life of 15.0 h, allowing an activation measurement. The resulting upper limit on the ¹²C+¹²C S-factor agrees nicely with available direct experimental data down to ≈2.5 MeV, while for lower energies, the THM results are significantly higher compared to the Zhang upper limit. However, this result should be taken with caution, considering that the obtained upper limit is only valid for the nonresonant component of the ¹²C+¹²C cross-section. Recent theoretical calculations of the ¹²C+¹²C subbarrier fusion cross-section highlighting the role of resonances can be found in Bonasera and Natowitz (2020).

Another step forward in the knowledge of the ¹²C+¹²C rate has been recently moved by Fruet et al. (2020). They performed a direct measurement down to ≈2.2 MeV using the particle-gamma coincidence technique. The experiment was performed at the Andromede accelerator facility at IPN Orsay, France, with a ¹²C beam, maximum beam current of 2 pμA for astrophysically relevant energies, impinging on a natural carbon target. Charged particles were detected through three annular silicon strip detectors covering 30% of the total solid angle. For gamma-ray detection, an array of LaBr₃(Ce) scintillator detectors has been employed. The results are in good agreement with the data reported by Jiang et al. (2018) and Tumino et al. (2018a), Tumino et al. (2018b). However, a more prominent resonance has been observed around 3.8 MeV compared to other measurements (Spillane et al., 2007; Zickefoose et al., 2018).

The most recent measurement of the ¹²C+¹²C cross-section has been performed by Tan et al. (2020) at the University of Notre Dame. The simultaneous detection of protons and alphas, through a silicon detector array, and γ-rays with a 109% HPGe detector, allowed for particle-γ coincidence technique. The S-factor upper limit at 2.2 MeV for proton (p₁) and alpha (α₁) channels is lower than THM data. We note that the upper limit for the proton channel disagrees significantly with the recent measurement of Fruet et al. (2020). The discrepancy is less evident, but still present, for the alpha channel. In the energy region between 2.5 and 3 MeV, there is some tension between the results of Tan et al. (2020) and previous measurements Jiang et al. (2018) for both proton and alpha channels. The S-factor results at the center of mass energies above 4 MeV agree nicely with other data.

A comparison between the total S-factor values obtained by Spillane et al. (2007), Jiang et al. (2018), Tumino et al. (2018a), Tumino et al. (2018b), Fruet et al. (2020), and Tan et al. (2020) is shown in Figure 9. It should be underlined that Tumino et al. (2018a), Tumino et al. (2018b) data are normalized to direct measurements, so a difference in the absolute value of the S-factor can also be attributed to systematic errors affecting direct data. Significant discrepancies between the results of the reported experiments are evident in the whole energy range and, for this reason, a further experimental effort is needed.

FIGURE 9

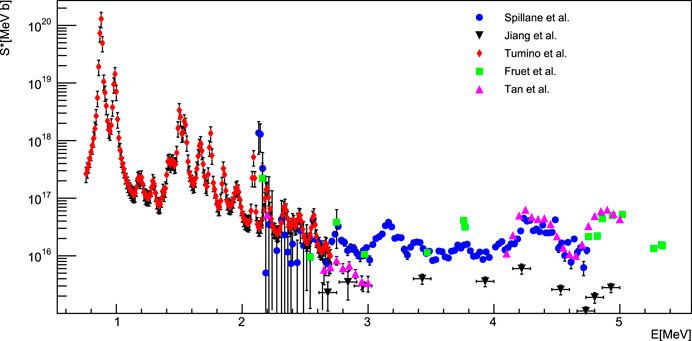
FIGURE 9. S-factor values obtained by Spillane et al. (2007), Jiang et al. (2018), Tumino et al. (2018a), Tumino et al. (2018b), Fruet et al. (2020), and Tan et al. (2020).

The Measurement in an Underground Laboratory

An underground location, such as the one of the LUNA experiment, is the perfect environment to perform the measurement of the ¹²C+¹²C cross-section detecting γ-rays emitted in the decay of the ²³Na and ²⁰Ne excited states. A high-efficiency and ultralow intrinsic background germanium detector (HPGe) is suitable for the measurement in combination with a massive lead shielding to avoid the contribution of the low-energy gamma-rays coming from the decay of the ²³⁸U and ²³²Th chains. In Figure 10, the counting rate, expressed in counts per day, is reported as a function of the interaction energy. To calculate the rate, the S-factor provided by Spillane et al. (2007) has been adopted, considering that the decay of the first excited state to the ground state accounts for ≈50% of the total cross-section and produces photons of 440 keV and 1634 keV in the case of proton or alpha emission, respectively. It is evident that if the trend of the S-factor observed by Tumino et al. (2018a), Tumino et al. (2018b) is confirmed, the reaction rates can be higher by 1–3 orders of magnitude. The two horizontal lines represent a typical rate of γ background measured at LNGS with a shielded setup, as in Caciolli et al. (2009) (blue and red line for 440 keV and 1636 keV γ energies, respectively). In particular, for the proton channel, crucial issues are the choice of the materials to limit the intrinsic contaminants and proper detectors shielding. In addition, constant nitrogen fluxing around the setup could help to further reduce the background, avoiding radon contaminants. The γ-detection efficiency adopted in the calculation is just a standard value; new high-efficiency setups will be developed for future measurements. From a rough estimation considering the data provided by Spillane et al. (2007) and the setup described in Figure 10, we can say that the dominant contribution to the background for the proton channel will come from the environmental radioactivity if a 0.3 ppm H contamination level is achieved in the targets (Morales-Gallegos et al., 2018) making the induced background not an issue at least down to ∼2 MeV. The limitation in the alpha channel is conversely related to the low rate. To provide the total cross-section, the measurement of the charged particle channels is also needed. In this case, the advantage of the underground location is less evident but still present; in fact, secondary particles produced by the passage of cosmic rays through the detectors could contribute to the background and they are effectively reduced at LNGS (Bruno et al., 2015).

FIGURE 10

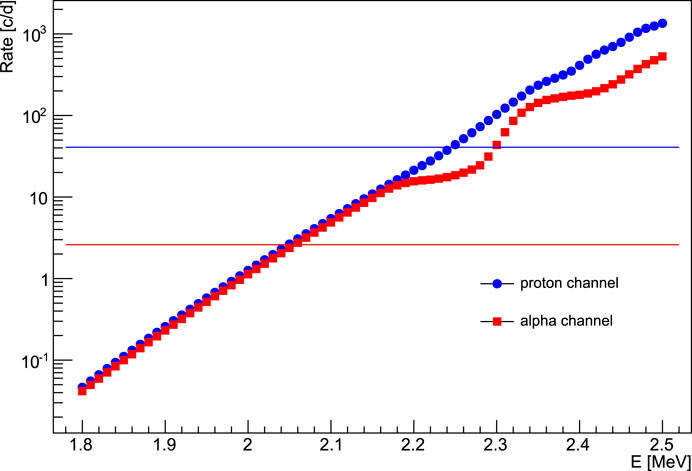
FIGURE 10. Counting rate, in counts per day, obtained considering data provided by Spillane et al. (2007), a γ detection efficiency of 6% and 2% for 440 keV and 1636 keV γ energies, respectively, and a beam current of 50–150 μA. The two horizontal lines represent a typical rate of γ background measured at LNGS with a shielded setup Caciolli et al. (2009) (blue and red lines for 440 keV and 1636 keV γ energies, respectively).

Conclusions

The enhancement in the sensitivity provided by the strong background reduction in an underground laboratory, together with the best experimental techniques, have made it possible, during twenty-five years of LUNA activity, to take clear steps forward in the knowledge of nuclear processes relevant to astrophysical scenarios. The installation of a new MV accelerator in the Gran Sasso laboratory will allow over a broad time window of at least twenty years extending these studies to key processes of helium, carbon, and neon burning phases. Even if more extensively studied, also other important processes of H burning will be better constrained, thanks to the new facility. An example is the ${}^{14}\text{N}\left(\text{p},\gamma \right){}^{15}\text{O}$ reaction, presently known only at energies well above the Gamow peak. By combining the existing LUNA 400 kV machine with new LUNA-MV facility, it will be possible to cover the necessary energy range with a sufficient overlap and without any hole between 200 keV and 1.5 MeV, allowing the reduction of the systematics in the extrapolations down to the 5% level. The ${}^{14}\text{N}\left(\text{p},\gamma \right){}^{15}\text{O}$ reaction will also be suitable to perform the commissioning and the tuning of the LUNA-MV accelerator.

As already said, the success of the LUNA approach has motivated similar facilities already in operation in the United States or under construction in the Republic of China. This worldwide effort will allow in the next decades taking important steps forward in the field of nuclear astrophysics.

Author Contributions

SZ wrote the introduction and the conclusion, GC the section on ¹³C(α,n) reaction, FF the section on ²²Ne(α,n) reaction, AB the section on ¹²C(α,γ), and FC the section on ¹²C+¹²C.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ajzenberg-Selove, F. (1986). Energy levels of light nuclei A = 16–17. Nucl. Phys. A 460, 1–110. doi:10.1016/0375-9474(86)90038-2

CrossRef Full Text | Google Scholar

Angulo, C., Arnould, M., Rayet, M., Descouvemont, P., Baye, D., Leclercq-Willain, C., et al. (1999). A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A 656, 3–183. doi:10.1016/S0375-9474(99)00030-5

CrossRef Full Text | Google Scholar

Araki, T., Enomoto, S., Furuno, K., Gando, Y., Ichimura, K., Ikeda, H., et al. (2005). Experimental investigation of geologically produced antineutrinos with KamLAND. Nature 436, 499–503. doi:10.1038/nature03980

PubMed Abstract | CrossRef Full Text | Google Scholar

Arnett, W. D., and Truran, J. W. (1969). Carbon-burning nucleosynthesis at constant temperature. Astrophys. J. 157, 339. doi:10.1086/150072

CrossRef Full Text | Google Scholar

Ashery, D. (1969). Study of the ²²Ne(α, n)²⁵Mg reaction: a possible source of stellar neutrons. Nucl. Phys. A 136, 481–495. doi:10.1016/0375-9474(69)90122-5

CrossRef Full Text | Google Scholar

Assunção, M., Fey, M., Lefebvre-Schuhl, A., Kiener, J., Tatischeff, V., Hammer, J. W., et al. (2006). E1 and E2 S factors of ¹²C(α, γ₀)¹⁶O from γ-ray angular distributions with a 4π-detector array. Phys. Rev. C 73, 055801. doi:10.1103/PhysRevC.73.055801

CrossRef Full Text | Google Scholar

Avila, M. L., Rogachev, G. V., Koshchiy, E., Baby, L. T., Belarge, J., Kemper, K. W., et al. (2015). New measurement of the α asymptotic normalization coefficient of the 1/2+ state in ¹⁷O at 6.356 MeV that dominates the ¹³C(α,n)¹⁶O reaction rate at temperatures relevant for the s process. Phys. Rev. C 91, 048801. doi:10.1103/PhysRevC.91.048801

CrossRef Full Text | Google Scholar

Balibrea-Correa, J., Ciani, G. F., Buompane, R., Cavanna, F., Csedreki, L., Depalo, R., et al. (2018). Improved pulse shape discrimination for high pressure ³He counters. Nucl. Instrum. Methods Phys. Res. Sect. A 906, 103–109. doi:10.1016/j.nima.2018.07.086

CrossRef Full Text | Google Scholar

Becker, H. W., Kettner, K. U., Rolfs, C., and Trautvetter, H. P. (1981). The ¹²C+¹²C reaction at subcoulomb energies (ii). Zeitschrift für Physik A Atoms Nucl. 303, 305–312. doi:10.1007/BF01421528

CrossRef Full Text | Google Scholar

Becker, S. A., and Iben, J. I. (1980). The asymptotic giant branch evolution of intermediate-mass stars as a function of mass and composition. II. Through the first major thermal pulse and the consequences of convective dredge-up. Astrophys. J. 237, 111–129. doi:10.1086/157850

CrossRef Full Text | Google Scholar

Bemmerer, D., Cowan, T. E., Grieger, M., Hammer, S., Hensel, T., Junghans, A. R., et al. (2018). Felsenkeller 5 MV underground accelerator: towards the holy Grail of nuclear astrophysics ¹²C(α, γ)¹⁶O. EPJ Web Conf. 178, 01008. doi:10.1051/epjconf/201817801008

CrossRef Full Text | Google Scholar

Bethe, A., and Critchfield, C. (1938). The Formation of deuterons by proton combination. Phys. Rev. 54, 248. doi:10.1103/PhysRev.54.248

CrossRef Full Text | Google Scholar

Bisterzo, S., Gallino, R., Käppeler, F., Wiescher, M., Imbriani, G., Straniero, O., et al. (2015). The branchings of the main s-process: their sensitivity to α-induced reactions on ¹³C and ²²Ne and to the uncertainties of the nuclear network. Mon. Not. R. Astron. Soc. 449, 506–527. doi:10.1093/mnras/stv271

CrossRef Full Text | Google Scholar

Bisterzo, S., Travaglio, C., Gallino, R., Wiescher, M., and Käppeler, F. (2014). Galactic chemical evolution and solar s-process abundances: dependence on the ¹³C-pocket structure. Astrophys. J. 787, 10. doi:10.1088/0004-637X/787/1/10

CrossRef Full Text | Google Scholar

Boeltzig, A., Best, A., Imbriani, G., Junker, M., Aliotta, M., Bemmerer, D., et al. (2018). Improved background suppression for radiative capture reactions at LUNA with HPGe and BGO detectors. J. Phys. G Nucl. Part. Phys. 45, 025203. doi:10.1088/1361-6471/aaa163

CrossRef Full Text | Google Scholar

Bonasera, A., and Natowitz, J. B. (2020). Calculation of the ¹²C+¹²C sub-barrier fusion cross section in an imaginary-time-dependent mean field theory. Phys. Rev. C 102, 061602. doi:10.1103/PhysRevC.102.061602

CrossRef Full Text | Google Scholar

Bonetti, R., Broggini, C., Campajola, L., Corvisiero, P., D’Alessandro, A., Dessalvi, M., et al. (1999). First measurement of the ³He(³He, 2p)⁴He cross-section down to the lower edge of the solar Gamow peak. Phys. Rev. Lett. 82, 5205–5208. doi:10.1103/PhysRevLett.82.5205

CrossRef Full Text | Google Scholar

Bravo, E., Piersanti, L., Domínguez, I., Straniero, O., Isern, J., and Escartin, J. A. (2011). Type Ia supernovae and the ¹²C+¹²C reaction rate. Astron. Astrophys. 535, A114. doi:10.1051/0004-6361/201117814

CrossRef Full Text | Google Scholar

Broggini, C., Bemmerer, D., Caciolli, A., and Trezzi, D. (2018). LUNA: Status and prospects. Prog. Part. Nucl. Phys. 98, 55–84. doi:10.1016/j.ppnp.2017.09.002

CrossRef Full Text | Google Scholar

Broggini, C., Straniero, O., Taiuti, M., De Angelis, G., Benzoni, G., Bruno, G., et al. (2019). Experimental nuclear astrophysics in Italy. Rivista del Nuovo Cimento. 42, 103–152. doi:10.1393/ncr/i2019-10157-1

CrossRef Full Text | Google Scholar

Brune, C. R., Licot, I., and Kavanagh, R. W. (1993). Low-energy resonances in ¹³C(α,n). Phys. Rev. C 48, 3119–3121. doi:10.1103/PhysRevC.48.3119

CrossRef Full Text | Google Scholar

Bruno, C. G., Scott, D. A., Formicola, A., Aliotta, M., Davinson, T., Anders, M., et al. (2015). Resonance strengths in the ^17,18O(p, α)^14,15N reactions and background suppression underground. Eur. Phys. J. A 51, 94. doi:10.1140/epja/i2015-15094-y

CrossRef Full Text | Google Scholar

Burbidge, E. M., Burbidge, G. R., Fowler, W. A., and Hoyle, F. (1957). Synthesis of the elements in stars. Rev. Mod. Phys. 29, 547–650. doi:10.1103/RevModPhys.29.547

CrossRef Full Text | Google Scholar

Caciolli, A., Agostino, L., Bemmerer, D., Bonetti, R., Broggini, C., Confortola, F., et al. (2009). Ultra-sensitive in-beam γ-ray spectroscopy for nuclear astrophysics at LUNA. Eur. Phys. J. A 39, 179–186. doi:10.1140/epja/i2008-10706-3

CrossRef Full Text | Google Scholar

Casella, C., Costantini, H., Lemut, A., Limata, B., Bonetti, R., Broggini, C., et al. (2002). First measurement of the d(p,γ)³He cross section down to the solar Gamow peak. Nucl. Phys. A 706, 203–216. doi:10.1016/S0375-9474(02)00749-2

CrossRef Full Text | Google Scholar

Caughlan, G. R., and Fowler, W. A. (1988). Thermonuclear reaction rates. Atomic Data Nucl. Data Tables 40, 283–334. doi:10.1016/0092-640X(88)90009-5

CrossRef Full Text | Google Scholar

Cavanna, F., and Prati, P. (2018). Direct measurement of nuclear cross-section of astrophysical interest: results and perspectives. Int. J. Mod. Phys. A 33, 1843010–1843346. doi:10.1142/S0217751X18430108

CrossRef Full Text | Google Scholar

Chen, C., Li, Y. J., Zhang, H., and Li, Z. H. (2020). Preparation of large-area isotopic magnesium targets for the ²⁵Mg(p, γ)²⁶Al experiment at JUNA. Nucl. Sci. Tech. 31, 91. doi:10.1007/s41365-020-00800-y

CrossRef Full Text | Google Scholar

Ciani, G. F., Csedreki, L., Balibrea-Correa, J., Best, A., Aliotta, M., Barile, F., et al. (2020). A new approach to monitor ¹³C-targets degradation in situ for ¹³C(α,n)¹⁶O cross-section measurements at LUNA. Eur. Phys. J. A 56, 75. doi:10.1140/epja/s10050-020-00077-0

CrossRef Full Text | Google Scholar

Couch, R. G., Schmiedekamp, A. B., and Arnett, W. D. (1974). S-PROCESS nucleosynthesis in massive stars: core helium burning. Astrophys. J. 190, 95–100. doi:10.1086/152851

CrossRef Full Text | Google Scholar

Cristallo, S., Cognata, M. L., Massimi, C., Best, A., Palmerini, S., Straniero, O., et al. (2018). The importance of the ¹³C(α, n)¹⁶O reaction in asymptotic giant branch stars. Astrophys. J 859, 105. doi:10.3847/1538-4357/aac177

CrossRef Full Text | Google Scholar

Csedreki, L., Ciani, G. F., Best, A., Balibrea-Correa, J., and Gyürky, G. (2019). “The LUNA neutron detector array for the direct measurement of the ¹³C(α, n)¹⁶O nuclear reaction,” in Nuclei in the Cosmos XV. Editors A. Formicola, M. Junker, L. Gialanella, and G. Imbriani (Cham: Springer International Publishing)), 331–334.

CrossRef Full Text | Google Scholar

Cyburt, R. H., Amthor, A. M., Ferguson, R., Meisel, Z., Smith, K., Warren, S., et al. (2010). The JINA Reaclib database: its recent updates and impact on type-I X-ray bursts. Astrophys. J. Suppl. 189, 240–252. doi:10.1088/0067-0049/189/1/240

CrossRef Full Text | Google Scholar

deBoer, R., Görres, J., Wiescher, M., Azuma, R., Best, A., Brune, C., et al. (2017). The ¹²C(α, γ)¹⁶O reaction and its implications for stellar helium burning. Rev. Mod. Phys. 89, 035007. doi:10.1103/RevModPhys.89.035007

CrossRef Full Text | Google Scholar

Drotleff, H. W., Denker, A., Hammer, J. W., Knee, H., Küchler, S., Streit, D., et al. (1991). New22Ne(α,n)25Mg-resonances at very low energies relevant for the astrophysical s-process. Z. Physik A - Hadrons and Nuclei, 338, 367–368. doi:10.1007/BF01288203

CrossRef Full Text | Google Scholar

Drotleff, H. W., Denker, A., Knee, H., Soine, M., Wolf, G., Hammer, J. W., et al. (1993). Reaction rates of the s-process neutron sources ²²Ne(α, n)²⁵Mg and ¹³C(α, n)¹⁶O. Astrophys. J. 414, 735. doi:10.1086/173119

CrossRef Full Text | Google Scholar

Eddington, A. S. (1920). The internal Constitution of the stars. Sci. Mon. 11, 297–303.

Google Scholar

Faestermann, T., Mohr, P., Hertenberger, R., and Wirth, H. F. (2015). Broad levels in ¹⁷O and their relevance for the astrophysical s process. Phys. Rev. C 92, 052802. doi:10.1103/PhysRevC.92.052802

CrossRef Full Text | Google Scholar

Febbraro, M., deBoer, R. J., Pain, S. D., Toomey, R., Becchetti, F. D., Boeltzig, A., et al. (2020). New ¹³C(α,n)¹⁶O cross section with implications for neutrino mixing and geoneutrino measurements. Phys. Rev. Lett. 125, 062501. doi:10.1103/PhysRevLett.125.062501

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferraro, F., Takács, M. P., Piatti, D., Mossa, V., Aliotta, M., Bemmerer, D., et al. (2018a). A high-efficiency gas target setup for underground experiments, and redetermination of the branching ratio of the 189.5 kev ²²Ne(p, γ)²³Na resonance. Eur. Phys. J. A 54, 44. doi:10.1140/epja/i2018-12476-7

CrossRef Full Text | Google Scholar

Ferraro, F., Takács, M. P., Piatti, D., Mossa, V., Cavanna, F., Aliotta, M., et al. (2018b). Direct capture cross section and the Ep= 71 and 105 keV Resonances in the 22Ne(p,γ)23Na reaction. Phys. Rev. Lett., 121, 172701. doi:10.1103/PhysRevLett.121.172701

CrossRef Full Text | Google Scholar

Fey, M. (2004). Im Brennpunkt der Nuklearen Astrophysik: Die Reaktion ¹²C(α, γ)¹⁶O. Stuttgart: Ph.D. Universität Stuttgart.

Google Scholar

Formicola, A., Imbriani, G., Junker, M., Bemmerer, D., Bonetti, R., Broggini, C., et al. (2003). The LUNA II 400 kV accelerator. Nucl. Instrum. Methods A 507, 609–616. doi:10.1016/S0168-9002(03)01435-9

CrossRef Full Text | Google Scholar

Fowler, W. A. (1984). The quest for the origin of the elements. Science 226, 922–935. doi:10.1126/science.226.4677.922

PubMed Abstract | CrossRef Full Text | Google Scholar

Fruet, G., Courtin, S., Heine, M., Jenkins, D. G., Adsley, P., Brown, A., et al. (2020). Advances in the direct study of carbon burning in massive stars. Phys. Rev. Lett. 124, 192701. doi:10.1103/PhysRevLett.124.192701

PubMed Abstract | CrossRef Full Text | Google Scholar

Fujita, K., Yamaguchi, H., Ban, T., Hamamoto, K., Narikiyo, Y., Tao, N., et al. (2015). Direct measurement of the ⁴He(¹²C, ¹⁶O)γ total cross section near stellar energies. EPJ Web Conf. 93, 03005. doi:10.1051/epjconf/20159303005

CrossRef Full Text | Google Scholar

Gallino, R., Busso, M., Picchio, G., Raiteri, C. M., and Renzini, A. (1988). On the role of low-mass asymptotic giant branch stars in producing a solar system distribution of s-process isotopes. Astrophys. J. Lett. 334, L45. doi:10.1086/185309

CrossRef Full Text | Google Scholar

Garcia-Hernandez, D. A., Garcia-Lario, P., Plez, B., Manchado, A., D’Antona, F., Lub, J., et al. (2007). Lithium and zirconium abundances in massive galactic O-rich AGB stars. Astron. Astrophys. 462, 711–730. doi:10.1051/0004-6361:20065785

CrossRef Full Text | Google Scholar

Garcia-Hernandez, D. A., Garcia-Lario, P., Plez, B., D’Antona, F., Manchado, A., and Trigo-Rodriguez, J. M. (2006). Rubidium-rich asymptotic giant branch stars. Science 314, 1751–1754. doi:10.1126/science.1133706

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia-Hernandez, D. A., Manchado, A., Lambert, D. L., Plez, B., Garcia-Lario, P., D’Antona, F., et al. (2009). Rb-rich asymptotic giant branch stars in the magellanic clouds. Astrophys. J 705, L31–L35. doi:10.1088/0004-637x/705/1/l31

CrossRef Full Text | Google Scholar

Giesen, U., Browne, C., Görres, J., Graff, S., Iliadis, C., Trautvetter, H. P., et al. (1993). The astrophysical implications of low-energy resonances in ²²Ne+α. Nucl. Phys. 561, 95–111. doi:10.1016/0375-9474(93)90167-V

CrossRef Full Text | Google Scholar

Greife, U., Arpesella, C., Barnes, C., Bartolucci, F., Bellotti, E., Broggini, C., et al. (1994). Laboratory for underground nuclear astrophysics (LUNA). Nucl. Instrum. Methods Phys. Res. Sect. A 350, 327–337. doi:10.1016/0168-9002(94)91182-7

CrossRef Full Text | Google Scholar

Guglielmetti, A. (2014). The LUNA experiment at gran Sasso laboratory. EPJ Web Conf. 78, 07001. doi:10.1051/epjconf/20147807001

CrossRef Full Text | Google Scholar

Haas, F. X., and Bair, J. K. (1973). Total neutron yield from the (α,n) reaction on ^21,22Ne. Phys. Rev. C 7, 2432–2436. doi:10.1103/PhysRevC.7.2432

CrossRef Full Text | Google Scholar

Harissopulos, S., Becker, H. W., Hammer, J. W., Lagoyannis, A., Rolfs, C., and Strieder, F. (2005). Cross section of the ¹³C(α,n)¹⁶O reaction: a background for the measurement of geo-neutrinos. Phys. Rev. C 72, 062801. doi:10.1103/PhysRevC.72.062801

CrossRef Full Text | Google Scholar

Harms, V., Kratz, K. L., and Wiescher, M. (1991). Properties of ²²Ne(α, n)Mg resonances. Phys. Rev. C 43, 2849–2861. doi:10.1103/PhysRevC.43.2849

CrossRef Full Text | Google Scholar

Heil, M., Detwiler, R., Azuma, R. E., Couture, A., Daly, J., Görres, J., et al. (2008). The ¹³C(α,n) reaction and its role as a neutron source for the s process. Phys. Rev. C 78, 025803. doi:10.1103/PhysRevC.78.025803

CrossRef Full Text | Google Scholar

Hollowell, D., and Iben, J. (1988). Nucleosynthesis of solar system material in a low-mass, low-metallicity asymptotic giant branch star. Astrophys. J. Lett. 333, L25. doi:10.1086/185279

CrossRef Full Text | Google Scholar

Iliadis, C., Longland, R., Champagne, A., Coc, A., and Fitzgerald, R. (2010). Charged-particle thermonuclear reaction rates: ii. tables and graphs of reaction rates and probability density functions. Nucl. Phys. 841, 31–250. doi:10.1016/j.nuclphysa.2010.04.009

CrossRef Full Text | Google Scholar

Iliadis, C. Nuclear physics of stars. Physics textbook. (Weinheim: Wiley-VCH), 2 edn. (2015). OCLC.

CrossRef Full Text | Google Scholar

Jaeger, M., Kunz, R., Mayer, A., Hammer, J. W., Staudt, G., Kratz, K. L., et al. (2001). ²²Ne(α, n)²⁵Mg: the key neutron source in massive stars. Phys. Rev. Lett. 87, 202501. doi:10.1103/PhysRevLett.87.202501

PubMed Abstract | CrossRef Full Text | Google Scholar

Jayatissa, H., Rogachev, G., Goldberg, V., Koshchiy, E., Christian, G., Hooker, J., et al. (2020). Constraining the ²²Ne(α, γ)²⁶Mg and ²²Ne(α, n)²⁵Mg reaction rates using sub-Coulomb α-transfer reactions. Phys. Lett. B 802, 135267. doi:10.1016/j.physletb.2020.135267

CrossRef Full Text | Google Scholar

Jiang, C. L., Santiago-Gonzalez, D., Almaraz-Calderon, S., Rehm, K. E., Back, B. B., Auranen, K., et al. (2018). Reaction rate for carbon burning in massive stars. Phys. Rev. C 97, 012801. doi:10.1103/PhysRevC.97.012801

CrossRef Full Text | Google Scholar

Johnson, E. D., Rogachev, G. V., Mukhamedzhanov, A. M., Baby, L. T., Brown, S., Cluff, W. T., et al. (2006). Astrophysical reaction rate for the neutron-generator reaction ¹³C(α,n)¹⁶O in asymptotic giant branch stars. Phys. Rev. Lett. 97, 192701. doi:10.1103/PhysRevLett.97.192701

PubMed Abstract | CrossRef Full Text | Google Scholar

Käppeler, F., Gallino, R., Bisterzo, S., and Aoki, W. (2011). The s process: nuclear physics, stellar models, and observations. Rev. Mod. Phys. 83, 157–193. doi:10.1103/RevModPhys.83.157

CrossRef Full Text | Google Scholar

Käppeler, F. (1999). The origin of the heavy elements: the s process. Prog. Part. Nucl. Phys. 43 (43), 419–483.

Google Scholar

Keeley, N., Kemper, K., and Khoa, D. T. (2003). DWBA analysis of the ¹³C(⁶Li,d)¹⁷O reaction at 10 MeV/nucleon and its astrophysical implications. Nucl. Phys. 726, 159–172. doi:10.1016/S0375-9474(03)01622-1

CrossRef Full Text | Google Scholar

Kimura, S., and Bonasera, A. (2013). Gamow peak approximation near strong resonances. Phys. Rev. C 87, 058801. doi:10.1103/PhysRevC.87.058801

CrossRef Full Text | Google Scholar

Kremer, R. M., Barnes, C. A., Chang, K. H., Evans, H. C., Filippone, B. W., Hahn, K. H., et al. (1988). Coincidence measurement of the ¹²C(α, γ)¹⁶O cross section at low energies. Phys. Rev. Lett. 60, 1475–1478. doi:10.1103/PhysRevLett.60.1475

PubMed Abstract | CrossRef Full Text | Google Scholar

Kubono, S., Abe, K., Kato, S., Teranishi, T., Kurokawa, M., Liu, X., et al. (2003). Determination of the Subthreshold state contribution in ¹³C(α,n)¹⁶O, the main neutron-source reaction for the s process. Phys. Rev. Lett. 90, 062501. doi:10.1103/PhysRevLett.90.062501

PubMed Abstract | CrossRef Full Text | Google Scholar

Kunz, R., Jaeger, M., Mayer, A., Hammer, J. W., Staudt, G., Harissopulos, S., et al. (2001). ¹²C(α, γ)¹⁶O: the key reaction in stellar nucleosynthesis. Phys. Rev. Lett. 86, 3244–3247. doi:10.1103/PhysRevLett.86.3244

PubMed Abstract | CrossRef Full Text | Google Scholar

La Cognata, M., Spitaleri, C., Trippella, O., Kiss, G. G., Rogachev, G. V., Mukhamedzhanov, A. M., et al. (2013). On the measurement of the ¹³C(α,n)¹⁶O S-factor at negative energies and its influence on the s-process. Astrophys. J 777, 143. doi:10.1088/0004-637X/777/2/143

CrossRef Full Text | Google Scholar

Lamb, S. A., Howard, W. M., Truran, J. W., and Iben, J. I. (1977). Neutron-capture nucleosynthesis in the helium-burning cores of massive stars. Astrophys. J. 217, 213–221. doi:10.1086/155571

CrossRef Full Text | Google Scholar

Liu, W., Li, Z., He, J., Tang, X., Lian, G., An, Z., et al. (2016). Progress of Jinping underground laboratory for nuclear astrophysics (JUNA). Science China physics. Mech. Astron. 59, 642001. doi:10.1007/s11433-016-5785-9

CrossRef Full Text | Google Scholar

Liu, W. P. (2017). Underground nuclear astrophysics experiment JUNA in China. J. Phys. Soc. Japan. 758, 335c. doi:10.7566/JPSCP.14.011101

CrossRef Full Text | Google Scholar

Longland, R., Iliadis, C., and Karakas, A. I. (2012). Reaction rates for the s-process neutron source ²²Ne+α. Phys. Rev. C 85, 065809. doi:10.1103/PhysRevC.85.065809

CrossRef Full Text | Google Scholar

Longland, R., Iliadis, C., Rusev, G., Tonchev, A. P., deBoer, R. J., Görres, J., et al. (2009). Photoexcitation of astrophysically important states in ²⁶Mg. Phys. Rev. C 80, 055803. doi:10.1103/PhysRevC.80.055803

CrossRef Full Text | Google Scholar

Lugaro, M., Herwig, F., Lattanzio, J. C., Gallino, R., and Straniero, O. (2003). s-process nucleosynthesis in asymptotic giant branch stars: a test for stellar evolution. Astrophys. J 586, 1305–1319. doi:10.1086/367887

CrossRef Full Text | Google Scholar

Mak, H. B., Ashery, D., and Barnes, C. (1974). Cross sections of the ²¹Ne(α, n)²⁴Mg and ²²Ne(α, n)²⁵Mg reactions at low energies of astrophysical interest. Nucl. Phys. 226, 493–505. doi:10.1016/0375-9474(74)90496-5

CrossRef Full Text | Google Scholar

Makii, H., Nagai, Y., Shima, T., Segawa, M., Mishima, K., Ueda, H., et al. (2009). E1 and E2 cross sections of the ¹²C(α, γ₀)¹⁶O reaction using pulsed α beams. Phys. Rev. C 80, 065802. doi:10.1103/PhysRevC.80.065802

CrossRef Full Text | Google Scholar

Massimi, C., Altstadt, S., Andrzejewski, J., Audouin, L., Barbagallo, M., Bécares, V., et al. (2017). Neutron spectroscopy of ²⁶Mg states: constraining the stellar neutron source ²²Ne(α, n)²⁵Mg. Phys. Lett. B 768, 1–6. doi:10.1016/j.physletb.2017.02.025

CrossRef Full Text | Google Scholar

Matei, C., Buchmann, L., Hannes, W. R., Hutcheon, D. A., Ruiz, C., Brune, C. R., et al. (2006). Measurement of the cascade transition via the first excited state of ¹⁶O in the ¹²C(α, γ)¹⁶O reaction, and its S factor in stellar helium burning. Phys. Rev. Lett. 97, 242503. doi:10.1103/PhysRevLett.97.242503

PubMed Abstract | CrossRef Full Text | Google Scholar

Morales-Gallegos, L., Aliotta, M., Bruno, C. G., Buompane, R., Davinson, T., De Cesare, M., et al. (2018). Reduction of deuterium content in carbon targets for ¹²C+¹²C reaction studies of astrophysical interest. Eur. Phys. J. A 54, 132. doi:10.1140/epja/i2018-12564-8

CrossRef Full Text | Google Scholar

Mossa, V., Stöckel, K., Cavanna, F., Ferraro, F., Aliotta, M., Barile, F., et al. (2020). Setup commissioning for an improved measurement of the D(p,γ)³He cross section at Big Bang Nucleosynthesis energies. Eur. Phys. J. A 56, 144. doi:10.1140/epja/s10050-020-00149-1

CrossRef Full Text | Google Scholar

Mukhamedzhanov, A. M., Pang, D. Y., and Kadyrov, A. S. (2019). Astrophysical factors of ¹²C+¹²C fusion extracted using the trojan horse method. Phys. Rev. C 99, 064618. doi:10.1103/PhysRevC.99.064618

CrossRef Full Text | Google Scholar

Ota, S., Christian, G., Lotay, G., Catford, W., Bennett, E., Dede, S., et al. (2020). Decay properties of ²²Ne+α resonances and their impact on s-process nucleosynthesis. Phys. Lett. B 802, 135256. doi:10.1016/j.physletb.2020.135256

CrossRef Full Text | Google Scholar

Peters, J. G. (1968). Nucleosynthesis by the s-PROCESS in stars of 9 and 15 solar masses. Astrophys. J. 154, 225. doi:10.1086/149753

CrossRef Full Text | Google Scholar

Pignatari, M., Gallino, R., Heil, M., Wiescher, M., Käppeler, F., Herwig, F., et al. (2010). The weak s-process in massive stars and its dependence on the neutron capture cross sections. Astrophys. J 710, 1557–1577. doi:10.1088/0004-637x/710/2/1557

CrossRef Full Text | Google Scholar

Plag, R., Reifarth, R., Heil, M., Käppeler, F., Rupp, G., Voss, F., et al. (2012). ¹²C(α, γ)¹⁶O studied with the Karlsruhe 4π BaF₂ detector. Phys. Rev. C 86, 015805. doi:10.1103/PhysRevC.86.015805

CrossRef Full Text | Google Scholar

Prantzos, N., Hashimoto, M., and Nomoto, K. (1990). The s-process in massive stars: yields as a function of stellar mass and metallicity. Astron. Astrophys. 234, 211.

Google Scholar

Prati, P. (2019). “Nuclei in the Cosmos XV”, in Nuclear reaction of astrophysical interest with LUNA projects. Editors A. Formicola, M. Junker, L. Gialanella, and G. Imbriani (Cham: Springer), 247–252.

CrossRef Full Text | Google Scholar

Raiteri, C. M., Busso, M., Gallino, R., Picchio, G., and Pulone, L. (1991a). S-process nucleosynthesis in massive stars and the weak component. I. Evolution and neutron captures in a 25 M_sun star. Astrophys. J. 367, 228. doi:10.1086/169622

CrossRef Full Text | Google Scholar

Raiteri, C. M., Busso, M., Gallino, R., and Picchio, G. (1991b). S-process nucleosynthesis in massive stars and the weak component. II. Carbon burning and galactic Enrichment. Astrophys. J. 371, 665. doi:10.1086/169932

CrossRef Full Text | Google Scholar

Rauscher, T., and Thielemann, F. K. (2000). Astrophysical reaction rates from statistical model calculations. Atom. Data Nucl. Data Tables 75, 1–351. doi:10.1006/adnd.2000.0834

CrossRef Full Text | Google Scholar

Robertson, D., Couder, M., Greife, U., Strieder, F., and Wiescher, M. (2016). Underground nuclear astrophysics studies with CASPAR. EPJ Web Conf. 109, 09002. doi:10.1051/epjconf/201610909002

CrossRef Full Text | Google Scholar

Rolfs, C., and Rodney, W. (1988). Cauldrons in the Cosmos. Chicago: The University of Chicago Press.

Google Scholar

Schürmann, D., Di Leva, A., Gialanella, L., Kunz, R., Strieder, F., De Cesare, N., et al. (2011). Study of the 6.05 MeV cascade transition in ¹²C(α, γ)¹⁶O. Phys. Lett. B 703, 557–561. doi:10.1016/j.physletb.2011.08.061

CrossRef Full Text | Google Scholar

Schürmann, D., Di Leva, A., Gialanella, L., Rogalla, D., Strieder, F., De Cesare, N., et al. (2005). First direct measurement of the total cross-section of ¹²C(α, γ)¹⁶O. Eur. Phys. J. A 26, 301–305. doi:10.1140/epja/i2005-10175-2

CrossRef Full Text | Google Scholar

Sen, A., Domínguez-Cañizares, G., Podaru, N., Mous, D., Junker, M., and Imbriani, G. (2019). A high intensity, high stability 3.5 MV Singletron^TM accelerator. Nucl. Instrum. Methods Phys. Res. B 460, 390–395. doi:10.1016/j.nimb.2018.09.016

CrossRef Full Text | Google Scholar

Spillane, T., Raiola, F., Rolfs, C., Schürmann, D., Strieder, F., Zeng, S., et al. (2007). ¹²C+¹²C fusion reactions near the Gamow energy. Phys. Rev. Lett. 98, 122501. doi:10.1103/PhysRevLett.98.122501

PubMed Abstract | CrossRef Full Text | Google Scholar

Talwar, R., Adachi, T., Berg, G. P. A., Bin, L., Bisterzo, S., Couder, M., et al. (2016). Probing astrophysically important states in the ²⁶Mg nucleus to study neutron sources for the s process. Phys. Rev. C 93, 055803. doi:10.1103/PhysRevC.93.055803

CrossRef Full Text | Google Scholar

Tan, W. P., Boeltzig, A., Dulal, C., deBoer, R. J., Frentz, B., Henderson, S., et al. (2020). New measurement of ¹²C+¹²C fusion reaction at astrophysical energies. Phys. Rev. Lett. 124, 192702. doi:10.1103/PhysRevLett.124.192702

PubMed Abstract | CrossRef Full Text | Google Scholar

Trippella, O., and Cognata, M. La. (2017). Concurrent application of ANC and THM to assess the ¹³C(α,n)¹⁶O absolute cross section at astrophysical energies and possible consequences for neutron production in low-mass AGB stars. Astrophys. J. 837, 41. doi:10.3847/1538-4357/aa5eb5

CrossRef Full Text | Google Scholar

Tumino, A., Spitaleri, C., La Cognata, M., Cherubini, S., Guardo, G. L., Gulino, M., et al. (2018a). An increase in the ¹²C+¹²C fusion rate from resonances at astrophysical energies. Nature 557, 687–690. doi:10.1038/s41586-018-0149-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Tumino, A., Spitaleri, C., Cherubini, S., D´Agata, G., Luca, G., Gulino, M., et al. (2018b). The trojan horse method in nuclear astrophysics. EPJ Web Conf. 184, 01016. doi:10.1051/epjconf/201818401016

CrossRef Full Text | Google Scholar

Tutusaus, I., Lamine, B., and Blanchard, A. (2019). Model-independent cosmic acceleration and redshift-dependent intrinsic luminosity in type-Ia supernovae. Astron. Astrophys. 625, A15. doi:10.1051/0004-6361/201833032

CrossRef Full Text | Google Scholar

van Raai, M. A., Lugaro, M., Karakas, A. I., García-Hernández, D. A., and Yong, D. (2012). Rubidium, zirconium, and lithium production in intermediate-mass asymptotic giant branch stars. Astron. Astrophys. 540, A44. doi:10.1051/0004-6361/201117896

CrossRef Full Text | Google Scholar

von Weizsäcker, C. F. (1938). Über Elementumwandlungen im Innern der Sterne, ii. Phys. Z. 39, 633–646.

Google Scholar

Wolfgang Hammer, J., Bulski, G., Grum, W., Kratschmer, W., Postner, H., and Schleussner, G. (1986). Scorpion, the Stuttgart scattering facility for fast polarized neutrons. Nucl. Instrum. Methods Phys. Res. Sect. A. 244, 455–476. doi:10.1016/0168-9002(86)91069-7

CrossRef Full Text | Google Scholar

Wolke, K., Becker, H. W., Rolfs, C., Schröder, U., Trautvetter, H. P., Harms, V., et al. (1989). Helium burning of ²²Ne. Zeitschrift für Physik A Hadrons Nucl. 334, 491–510. doi:10.1007/BF01294757

CrossRef Full Text | Google Scholar

Zhang, N., Wang, X., Tudor, D., Bucher, B., Burducea, I., Chen, H., et al. (2020). Constraining the ¹²C+¹²C astrophysical S-factors with the ¹²C+¹³C measurements at very low energies. Phys. Lett. B 801, 135170. doi:10.1016/j.physletb.2019.135170

CrossRef Full Text | Google Scholar

Zickefoose, J., Di Leva, A., Strieder, F., Gialanella, L., Imbriani, G., De Cesare, N., et al. (2018). Measurement of the ¹²C(¹²C, p)²³Na cross section near the Gamow energy. Phys. Rev. C 97, 065806. doi:10.1103/PhysRevC.97.065806

CrossRef Full Text | Google Scholar