Statistical Analysis of Magnetic Field Fluctuations in Coronal Mass Ejection-Driven Sheath Regions

We report a statistical analysis of magnetic field fluctuations in 79 coronal mass ejection- (CME-) driven sheath regions that were observed in the near-Earth solar wind. Wind high-resolution magnetic field data were used to investigate 2 h regions adjacent to the shock and ejecta leading edge (Near-Shock and Near-LE regions, respectively), and the results were compared with a 2 h region upstream of the shock. The inertial-range spectral indices in the sheaths are found to be mostly steeper than the Kolmogorov −5/3 index and steeper than in the solar wind ahead. We did not find indications of an $f^{-1}$ spectrum, implying that magnetic fluctuation properties in CME sheaths differ significantly from planetary magnetosheaths and that CME-driven shocks do not reset the solar wind turbulence, as appears to happen downstream of planetary bow shocks. However, our study suggests that new compressible fluctuations are generated in the sheath for a wide variety of shock/upstream conditions. Fluctuation properties particularly differed between the Near-Shock region and the solar wind ahead. A strong positive correlation in the mean magnetic compressibility was found between the upstream and downstream regions, but the compressibility values in the sheaths were similar to those in the slow solar wind (<0.2), regardless of the value in the preceding wind. However, we did not find clear correlations between the inertial-range spectral indices in the sheaths and shock/preceding solar wind properties, nor with the mean normalized fluctuation amplitudes. Correlations were also considerably lower in the Near-LE region than in the Near-Shock region. Intermittency was also considerably higher in the sheath than in the upstream wind according to several proxies, particularly so in the Near-Shock region. Fluctuations in the sheath exhibit larger rotations than upstream, implying the presence of strong current sheets in the sheath that can add to intermittency.

1 Introduction

Coronal mass ejections (CMEs; Webb and Howard, 2012) are huge expulsions of plasma and field from the Sun that propagate at supersonic speeds into the heliosphere. When a CME is sufficiently faster than the preceding solar wind, a fast-forward shock develops ahead of it. Plasma and field are compressed at the shock and accumulate ahead of the leading edge of the CME ejecta to form a sheath region (e.g., Kilpua et al., 2017a). CME sheaths are large-scale heliospheric structures that are of wide interest in both fundamental plasma physics and space weather contexts. Sheaths comprise layers of inhomogeneous plasma and field (Kaymaz and Siscoe, 2006; Siscoe et al., 2007) and thus exhibit highly variable structure with various embedded plasma waves, discontinuities, and reconnection exhausts (e.g., Kataoka et al., 2005; Ala-Lahti et al., 2018, 2019). On average, sheaths have considerably higher solar wind density, dynamic pressure, Alfvén Mach number, and power in magnetic field fluctuations than the CME ejecta (e.g., Guo et al., 2010; Kilpua et al., 2013; Myllys et al., 2016; Kilpua et al., 2019). This compressed and turbulent state has been invoked to explain why sheaths couple so efficiently with the Earth’s magnetosphere and drive intense space weather disturbances (e.g., Tsurutani et al., 1988; Huttunen and Koskinen, 2004; Myllys et al., 2016; Kilpua et al., 2017b). Enhanced turbulence in the solar wind can particularly intensify viscous interaction at the magnetopause and drive stronger geomagnetic activity (e.g., Borovsky and Funsten, 2003; Jankovičová et al., 2008; Osmane et al., 2015). CME sheaths differ from planetary magnetosheaths in various ways (e.g., Siscoe et al., 2007); unlike planetary magnetosheaths, they share properties of both “expansion” and “propagation” sheaths and are formed gradually over several days, as the CME propagates in interplanetary space. The lateral deflection of solar wind plasma around the CME is relatively reduced and, as a consequence, plasma and field pile up at the CME nose rather than flow around it. CME shocks are also generally weaker than planetary bow shocks. Despite their importance, CME-driven sheaths are still relatively little studied. In particular, their formation and small-scale structure are currently poorly understood, and there is no solid understanding of turbulence and intermittency in sheath regions.

We briefly summarize below recent works that have investigated magnetic field fluctuations in CME sheaths in more detail. Moissard et al. (2019) studied fluctuation power, anisotropy, and compressibility in 42 CME sheaths using ACE 1 s magnetic field data. The authors found that, at fluctuation timescales ranging between 20 s and 7.5 min, sheaths have on average higher fluctuation power, lower anisotropy, and higher compressibility than in the solar wind ahead or the CME flux rope behind. Good et al. (2020a) performed a case study of a CME-driven sheath detected by MESSENGER at ∼0.5 AU and then by STEREO-B at 1.08 AU while the spacecraft were almost radially aligned. The CME shock was quasi-parallel at MESSENGER and quasi-perpendicular at STEREO-B; the sheath behind the quasi-parallel shock closer to the Sun showed greater differences to the local upstream wind than the sheath at ∼ 1 AU behind the quasi-perpendicular shock. For instance, the sheath at MESSENGER exhibited relatively more large-angle fluctuations and higher compressibility than the upstream solar wind. The inertial-range spectral slope steepened in the sheath plasma between MESSENGER and STEREO-B. Kilpua et al. (2020) conducted a detailed analysis of three sheath regions observed by the Wind spacecraft at Lagrangian point L1. In contrast to the studies described above, which investigated sheath intervals globally, Kilpua et al. (2020) studied three separate regions within the sheath: a region close to the shock, in the middle of the sheath, and close to the ejecta leading edge, each 1 h in duration. All three sheaths had enhanced fluctuations, intermittency, and compressibility when compared to the solar wind ahead, with differences being most pronounced close to the shock. The approach of studying separate sheath subregions was motivated by the fact that plasma and field properties often vary considerably within a given sheath and that different physical mechanisms causing field fluctuations are in action close to the shock and near the ejecta leading edge. Close to the shock, field fluctuations are associated with shock compression and alignment of preceding fluctuations (e.g., Neugebauer et al., 1993; Kataoka et al., 2005). In addition, shock heating produces temperature anisotropy that provides free energy for generation of mirror mode and Alfvén ion cyclotron waves (e.g., Ala-Lahti et al., 2018, 2019). Near the ejecta leading edge, in turn, draping of the magnetic field about the ejecta can lead to large-amplitude out-of-ecliptic field variations (Gosling and McComas, 1987; McComas et al., 1988).

It is also an interesting question as to how fluctuation properties in CME sheaths relate to the driver properties and upstream conditions. For example, Moissard et al. (2019) found that the sheaths of fast CMEs encountering turbulent solar wind and with high Mach number shocks have on average the highest levels of turbulence and lowest anisotropy in their fluctuations. For quasi-parallel shocks and high upstream beta, turbulent energy and anisotropy were both lower. In Kilpua et al. (2020), the greatest differences between the sheath and solar wind ahead were found for the event associated with a strong and fast quasi-parallel shock, but we also note that a slow sheath behind a weak and quasi-perpendicular shock had enhanced level of fluctuations. This is in contrast with Good et al. (2020a), who found very little differences for a slow sheath behind quasi-perpendicular shock near 1 AU. This could be because Kilpua et al. (2020), as described above, investigated three separate regions. Another interesting finding in Kilpua et al. (2020) was that the region adjacent to the ejecta leading edge resembled relatively closely the solar wind ahead, in particular, the slower sheaths investigated.

The spectrum of solar wind turbulence has been extensively investigated. In the inertial range, slow solar wind shows larger variability and usually steeper slopes than fast solar wind. Spectral slopes are often generally close to the Kolmogorov index $\left(-5/3\right)$ near 1 AU (e.g., Smith et al., 2006; Borovsky, 2012; Bruno, 2019; Verscharen et al., 2019; Chen et al., 2020). The typical kinetic-range spectral index in the solar wind is −2.8 (e.g., Alexandrova et al., 2013; Bruno et al., 2017; Huang et al., 2017), but shallower values have also been reported (e.g., Sahraoui et al., 2009). Kilpua et al. (2020) found that, in most of the sheath subregions investigated, spectral slopes departed from Kolmogorov turbulence and also from Kraichnan turbulence (slope −3/2). Observations did not match well with the standard p-model of intermittency, but the extended p-model in its Kraichnan form yielded the most consistent agreement with the observations and spectral slopes determined from the spectra. This implies that turbulence in sheaths is generally not fully developed at the orbit of the Earth, and/or that current models are not well suited for describing turbulence in CME sheaths. Kinetic-range spectral indices were consistently shallower than −2.8, which could imply that the turbulent cascade is still ongoing (Sahraoui et al., 2010).

Within planetary magnetosheaths, MHD spectral indices close to −1 have been reported throughout the inertial range at locations close to the bow shock, with the index steepening toward the more commonly observed Kolmogorov index deeper in the magnetosheath (Hadid et al., 2015; Huang et al., 2017, 2020). The authors suggest that this may arise from the bow shock “resetting” the turbulence and generating randomly distributed fluctuations at the MHD scale. Spectral indices in the kinetic range were shallower than −2.8, close to the bow shock, but then steepened toward the magnetopause, approaching the −2.8 value more typically seen in the upstream solar wind.

Spectral slopes of magnetic field and density fluctuations upstream and downstream of interplanetary shocks have also been investigated in detail in some recent studies, with the emphasis of these studies placed on the role of the shock in modifying fluctuation properties. For example, Pitňa et al. (2016) and Riazantseva et al. (2017) analyzed high-resolution plasma data by the Spektr-R spacecraft and showed that the MHD-range slopes of density fluctuations were approximately conserved across the shock transition, while the study by Borovsky (2020) reported that the MHD-range slopes for magnetic field and velocity fluctuations are steeper in the downstream than upstream. Pitňa et al. (2017) also investigated the decay of MHD-scale turbulent energy behind interplanetary shocks, finding that this decay does not begin immediately after the shock but when the contribution of kinetic processes becomes negligible.

In this study, we perform a statistical analysis of fluctuation properties in CME-driven sheath regions. We use high time-resolution observations from the Wind spacecraft located in the near-Earth solar wind. The key science questions we pose are the following: What are distributions of spectral slopes (kinetic and MHD) in sheaths and how do they depend on the properties of the sheath, shock, and solar wind ahead? What are the distributions of compressibility, intermittency, and normalized magnetic field fluctuations in sheaths? How do these compare to the equivalent parameters and distributions in the solar wind and in planetary magnetosheaths? Similar to Kilpua et al. (2020), we investigate separate regions in the sheath. This present study focuses on the regions close to the shock and CME leading edge.

The paper is organized as follows: In Section 2, we describe the data and methods used, and in Section 3, the results are presented. Section 4 summarizes and discusses the results.

2 Spacecraft Data and Methods

High-resolution magnetic field data from the Magnetic Fields Investigation (MFI; Lepping et al., 1995) instrument of the Wind spacecraft (Ogilvie and Desch, 1997) have been used in this study. The data were obtained from the NASA Goddard Space Flight Center Coordinated Data Analysis Web¹ (CDAWeb). The time resolution of the data varies from 0.046 s to 1.84 s. For the majority of events, resolution was 0.092 s and all data were interpolated to this cadence.

The solar wind plasma measurements were obtained from the Solar Wind Experiment (SWE; Ogilvie et al., 1995) instrument on-board Wind. These data were available at 90 s resolution.

Shock parameters were taken from the Heliospheric Shock database, developed and maintained at the University of Helsinki (http://ipshocks.fi/; Kilpua et al., 2015).

2.1 Methods

Sheath events listed by Kilpua et al. (2019) for the years 1997–2018 with some additional events listed by Regnault et al. (2020) have been analyzed in this study. OMNI data were used to identify sheaths in the list given by Kilpua et al. (2019); a few sheaths with Wind data gaps were excluded, leaving a total of 79 sheaths analyzed in the present study (Supplementary Table S1). The duration of the sheaths in study varied from ∼5 to ∼20 h, with the mean duration of 10.1 h.

An example of a sheath region in the near-Earth solar wind is shown in Figure 1. Wind 1 min magnetic field data and 90 s plasma data are shown. The red vertical line indicates the shock, and the blue vertical line indicates the ejecta leading edge (LE). We study two subregions (orange-shaded) within the sheath separately: 1) the Near-Shock region, extending 2 h from the shock into the sheath but excluding the 5 min closest to the shock, and 2) the Near-LE region, covering 2 h closest to the ejecta but excluding the 5 min closest to the leading edge. The fixed 2 h intervals were selected for this study (instead of fractional time) to capture the regions with distinct physical processes likely occurring closest to the shock and the CME-leading edge and providing the same statistical conditions. The leading edge times were adjusted to exclude boundary layers (BLs) that are regularly observed between the sheath and ejecta (Wei et al., 2003a). These BLs form due to interaction between the CME ejecta and the preceding solar wind and exhibit magnetic structure distinct to that in the sheath or ejecta (e.g., Wei et al., 2003a, Wei et al., 2003b; Zhou et al., 2019). The properties in these subregions are compared to conditions in the solar wind ahead (SW-Ahead). This region was selected to extend 2 h into the upstream wind, ending 1 h before the shock. The 1 h before the shock was excluded to avoid foreshock regions that are typically observed for ∼30 min upstream for CME-driven shocks (Kajdič et al., 2012). At the shock, the field magnitude and plasma parameters jump simultaneously. Compared to the preceding solar wind and trailing ejecta, the sheath has compressed plasma (i.e., high temperature and density) and large-amplitude changes in the magnetic field direction and the plasma and field parameters have high variability. The ejecta leading edge is marked by clear decreases in plasma density and temperature and a clear drop in magnetic field variability.

We define magnetic field fluctuations as

$\delta \mathbf{B}=\mathbf{B}\left(t\right)-\mathbf{B}\left(t+\tau \right),$

where τ is the timescale of the fluctuation (or timelag between two sample points) and the amplitude of the fluctuation is $\delta B=\left|\delta \mathbf{B}\right|$. Fluctuations have been analyzed for successively doubled values of the base data time resolution of 0.092 s, such that t ranges from 0.092 to 754 s. We note that this approach is particularly suitable for analyzing CME-driven sheaths (e.g., compared to standard Fourier analysis, where a global average across the analyzed interval would be subtracted from all data points) since magnetic field variability is relatively high and the direction and magnitude of the field can change over relatively short time intervals.

FIGURE 1

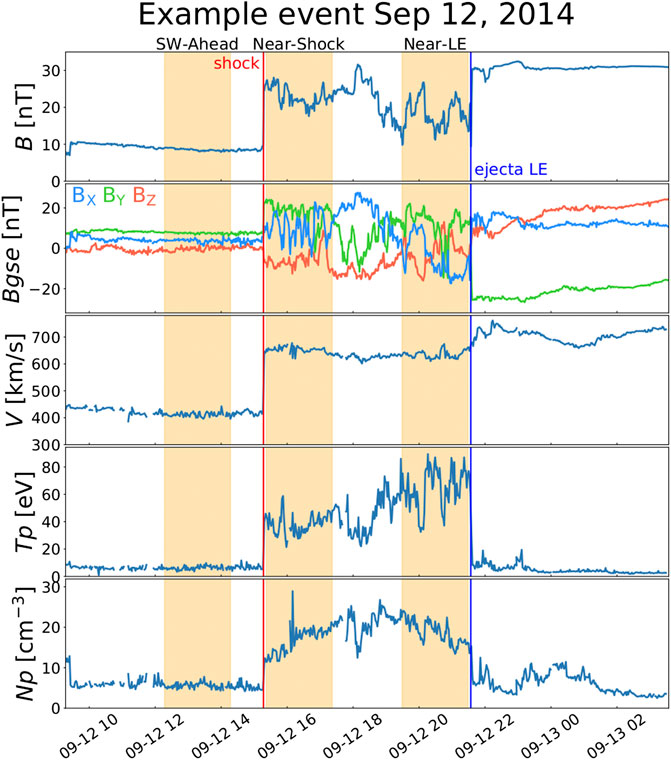
FIGURE 1. Example of a CME-driven sheath region in the near-Earth solar wind as observed by the Wind spacecraft on September 12, 2014. The panels show from top to bottom the following: (A) magnetic field magnitude; (B) magnetic field components in GSE coordinates; (C) solar wind speed; (D) solar wind temperature; and (E) solar wind density. The red vertical line indicates the shock time and the blue vertical line indicates the ejecta leading edge (LE) time. The orange-shaded regions show the solar wind ahead (SW-Ahead), Near-Shock region, and Near-LE region, each 2 h in duration.

The spectral break between the inertial and kinetic ranges is expected to occur close to the ion cyclotron frequency. In the top panels of Figure 2, distributions of ion cyclotron times ($t_{ci}$) for the solar wind (SW) ahead, Near-Shock region, and Near-LE region are shown. The ion cyclotron frequency in the spacecraft frame derived with Taylor’s hypothesis is given by

$f_{ci}=\frac{\langle v\rangle }{\langle v_{th}\rangle }\frac{e\langle B\rangle }{2\pi m_i}$

and $t_{ci}=1/f_{ci}$. Here, $\langle v\rangle$, $\langle v_{th}\rangle$, and $\langle B\rangle$ are the averages of the solar wind speed, thermal speed, and magnetic field magnitude, respectively. We calculate $t_{ci}$ values as averages over the investigated 2 h intervals. Figure 2 shows that $t_{ci}$ values are largely >0.2–0.3 s. The three smallest time lags (i.e., 0.092, 0.18, and 0.37 s) are thus taken to be representative of the kinetic range.

FIGURE 2

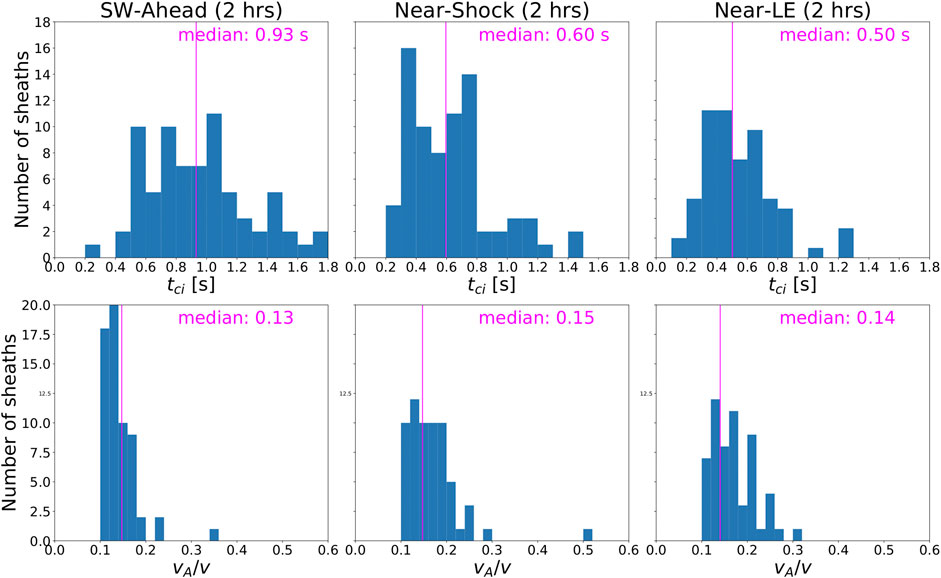
FIGURE 2. Distribution of ion cyclotron times ($t_{ci}$) in 0.1 s bins (top panels) and ratios of Alfvén speed to solar wind speed ($v_A/v$) in bins of width 0.02 in the solar wind ahead (SW-Ahead), Near-Shock region, and Near-LE region (bottom panels).

We investigate magnetic field fluctuations in the spacecraft frame rather than the solar wind (plasma) frame. The validity of the transformation from spacecraft frequency to wavenumber thus needs some justification. In this context, the Taylor hypothesis states that, when the timescales of magnetic field fluctuations are sufficiently less than the timescale of the rapidly flowing solar wind, the path taken by the observing spacecraft through the solar can be considered as an instantaneous spatial cut (Taylor, 1938; Matthaeus and Goldstein, 1982). The validity of this assumption can be assessed with the $v_A/v\mathrm{\hspace{1em}\lesssim \hspace{1em}}1$ ratio (Howes et al., 2014), where $v_A$ is the Alfvén speed and v is the solar wind speed. The bottom panels of Figure 2 show the distribution of $v_A/v$ values. It is clear that for all cases, the Taylor hypothesis is valid.

3 Results

3.1 Spectral Indices

The distributions of $\delta B$ in each subregion of each sheath were determined as functions of timelag τ. For each subregion, the mean values of the distributions, $\langle \delta B\rangle$, were plotted vs. the corresponding τ values with log-log scales. The slopes were calculated from linear regression fits to $lo{g}_{10}(\langle \delta B\rangle$) as a function of $lo{g}_{10}\left(\tau \right)$. The slopes of these curves are straightforwardly related to k-space spectral indices (e.g., Matteini et al., 2018).

Figure 3 shows the histograms of spectral indices in the Near-Shock and Near-LE regions for three different timelag ranges (6–47, 24–188, and 94–754 s) in the inertial range, each containing four values. The pink vertical lines indicate the median values of the distributions. The Kolmogorov (5/3) and Kraichnan (3/2) spectral slopes are indicated by cyan and green vertical lines, respectively.

FIGURE 3

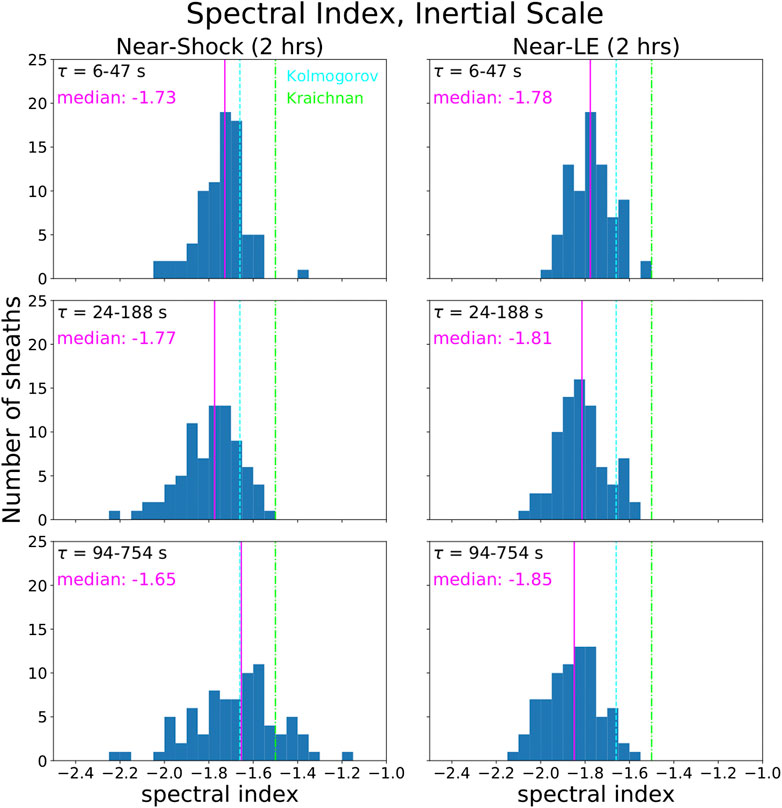
FIGURE 3. Histograms of inertial-range spectral slopes in the Near-Shock sheath subregions (left panels) and Near-LE subregions (right panels), with bin widths of 0.05. Spectral indices were calculated for three different timelag ranges, each containing four values. The dashed cyan vertical line indicates the Kolmogorov index, and the dash-dotted green vertical line indicates the Kraichnan index. The pink vertical lines indicate the distribution medians.

The histograms show that spectral indices mostly vary within the interval ∼ [−2.0, −1.6] for the inertial range. The spread in indices increases as the timelag range moves to larger timescales. At the largest timescales for the Near-Shock region, the distributions extend to shallower values, reaching ∼−1.3. Otherwise, practically all measured slopes are steeper than the Kraichnan index and the bulk of the distributions are also at values steeper than the Kolmogorov index. There is thus no evidence of −1 slopes in the investigated timelag ranges. The comparison of the left and right panels shows that there are no drastic differences between the slopes in the Near-Shock and Near-LE regions. However, the slopes are slightly shallower in the Near-Shock region than in the Near-LE region with the median values closer to the Kolmogorov index (and matching the Kolmogorov index for the largest timescale range).

It should be noted that the 2 h intervals used here to calculate the spectral indices include field fluctuations that may have evolved over considerably different times between different events and within the 2 h intervals themselves. This effect can be explored by estimating the time since the plasma was shocked, given by Borovsky (2020) as $\text{Δ}t=\left(\text{Δ}{t}_{ps}{V}_{sh,x}\right)/\left(V_{sh,x}-V_{p,x}\right)$. Here, $V_{sh,x}$ is the shock speed along the Sun-Earth line, $V_{p,x}$ is the plasma speed in the sheath, and $\text{Δ}{t}_{ps}$ is the time difference between shock observation and the point within the sheath investigated at L1. We define here $\text{Δ}{t}_{ps}$ using the center point of the Near-Shock and Near-LE regions and for $V_{p,x}$, we use 10 min averages around those points. For the Near-Shock region, $\text{Δ}{t}_{ps}$ is constant (3,900 s), while for the Near-LE region, it varies depending on the duration of the sheath. For example, if we take the shock speed of $V_{sh,x}=522\mathrm{km}/\mathrm{s}$ (the average for our data set) and assume $V_{p,x}=480\mathrm{km}/\mathrm{s}$ throughout the Near-Shock region (a reasonable approximation since the speed typically stays relatively constant in the sheath), $\text{Δ}t$ varies from ∼60 min to 25 h. There are some obvious sources of uncertainties in this approach, e.g., it assumes that both $V_{sh,x}$ and $V_{p,x}$ stay unchanged from the point where the plasma was shocked to L1 (which can be a considerable fraction of 1 AU) and radial propagation. In addition, the shock speed determination can have significant uncertainties (e.g., Schwartz, 2000). We note that the analysis is particularly problematic for the Near-LE region. The field and plasma in that region may not even have been always processed by the shock but piled up in the sheath during the earlier stages of the CME evolution when the shock was not there or was very weak.

The top panels of Figure 4 show the scatter plot of the inertial-range spectral slopes and $\text{Δ}t$ for the timescale 24–188 s. We note that for a significant fraction of events, $\text{Δ}t$ became negative or unrealistically large (>120 h, i.e., larger than the typical Sun-to-Earth transit time of a CME). Firstly, the figure shows that $\text{Δ}t$ values are larger in the Near-LE region than in the Near-Shock region. This reflects that the field and plasma in the Near-LE region are in a more evolved state (longer time since processing). Secondly, there is a large variability in the obtained $\text{Δ}t$ values for both regions. However, a weak trend exists for the Near-Shock region; indices are shallowest when $\text{Δ}t$ is small, i.e., when the plasma was most recently shocked and when the interval was still dominated by the influence of the shock (consistent e.g. with Pitňa et al., 2017). When the time since the processing increases, it is likely that various small-scale structures develop in the sheath (e.g., current sheets) that steepen the slopes. The bottom panels of Figure 4 show the scatter plot of the inertial-range spectral slopes and $V_{sh,x}$. Although the scatter is again large for the Near-Shock region, the figure shows that the steepest slopes are associated with the slowest shocks, and, conversely, that the fastest shocks are related to shallower spectral indices. This result is partly a reflection of the fact that faster shocks are associated with higher solar wind speeds, which in turn are associated with shallower spectral indices (e.g., Chen et al., 2013).

FIGURE 4

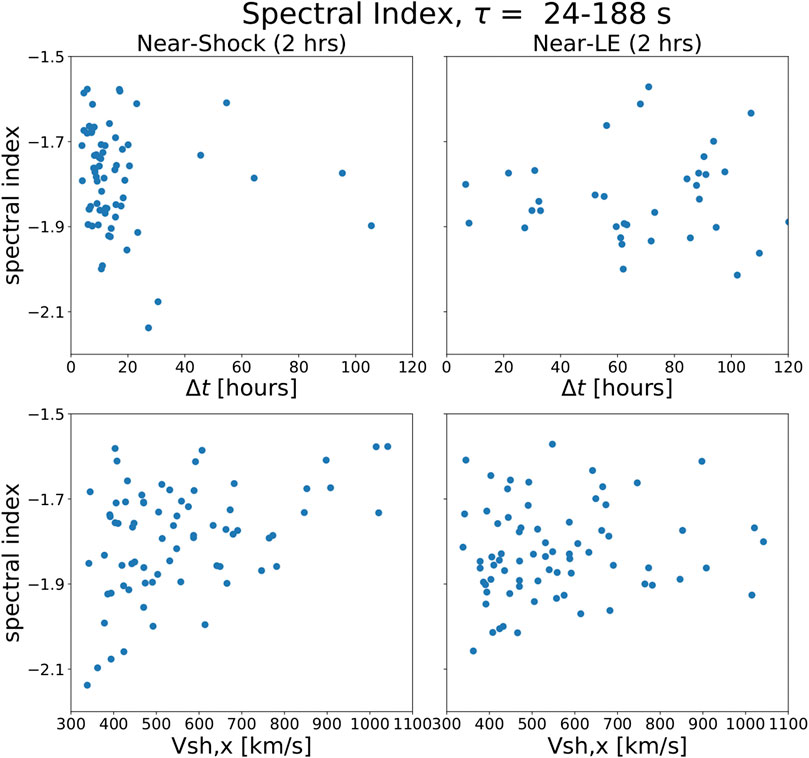
FIGURE 4. Scatter plot of inertial-range spectral slopes calculated for the timescale 24–188 s vs. (top panels) the time since the plasma was processed ($\text{Δ}t$) and (bottom panels) shock speed in the radial direction ($V_{sh,x}$).

The distribution of kinetic-range spectral indices is shown in Figure 5. Indices were calculated for the three smallest time lags and for one timelag range only. The blue lines in the figure indicate the −2.8 slope found in several previous solar wind studies (see Introduction), and the pink lines give the distribution medians. The kinetic-range indices vary within the interval ∼ [−2.6, −2.0] with median values at −2.40 and −2.32 for the Near-Shock and Near-LE regions, respectively. The figure shows that the measured spectral indices are all shallower than −2.8. We note that the values could have been affected by ion cyclotron timescales being close to or even smaller than the upper limit of the analyzed time range for some cases, the use of only three points in the calculation, and the potentially larger relative contribution of magnetometer noise to these smaller amplitude fluctuations.

FIGURE 5

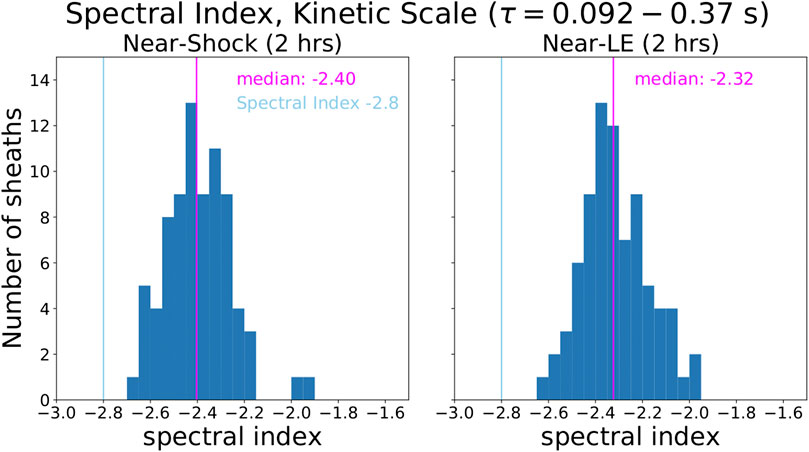
FIGURE 5. Histograms of kinetic-range spectral slopes in the Near-Shock subregions (left panel) and Near-LE sheath subregions (right panel). The blue line indicates the −2.8 slope identified in previous solar wind studies. The pink lines indicate the median values of the distributions.

Figure 6 shows scatter plots of the inertial-range spectral index in the sheath vs. various parameters that characterize the preceding solar wind, the sheath, and the CME driver. The top two rows show plots for the Near-Shock region and the bottom two rows show plots for the Near-LE region. Solar wind parameters include the mean upstream speed ($V_{\text{upstream}}$), inertial-range spectral index (${\alpha }_{\text{upstream}}$), and plasma beta (${\beta }_{\text{upstream}}$) calculated as the average over the 2 h SW-Ahead region (see Section 2.2). Also included are the shock magnetosonic Mach number ($M_{\text{ms}}$), shock angle (${\theta }_{Bn}$), i.e., the angle between the shock normal and upstream magnetic field direction, and the angle, ϕ, between the shock normal and radial direction. The last parameter can be used as a rough proxy of the spacecraft crossing distance from the apex of the CME (e.g., Janvier et al., 2015; Savani et al., 2015); small values of ϕ indicate that the CME is crossed close to the apex, while larger values indicate crossing through the flank or leg of the CME. Finally, $V_{\text{sheath}}$ gives the mean solar wind speed in the Near-Shock and Near-LE regions and $V_{\text{exp}}$ gives the expansion speed of the driving CME ejecta. The expansion speed is calculated as the difference between the ejecta leading edge and trailing edge speeds (note that in some cases, the speed profile in the ejecta increases toward the trailing edge, giving a positive expansion speed). Pearson correlation coefficients ($cc$) are also indicated in each panel.

FIGURE 6

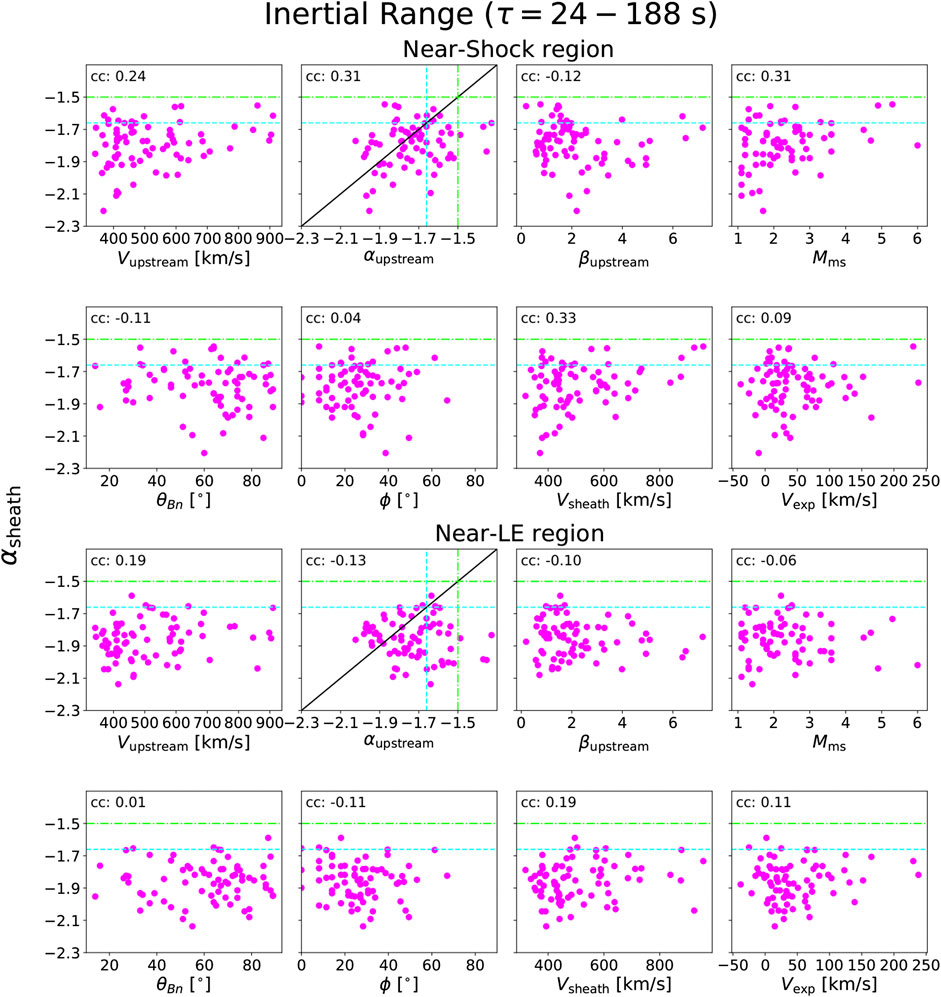
FIGURE 6. Scatter plots of sheath inertial-range spectral indices in the Near-Shock region (top two rows) and Near-LE region (bottom two rows) vs. a range of plasma parameters. The parameters include the upstream wind speed ($V_{\text{upstream}}$), upstream spectral index (${\alpha }_{\text{upstream}}$), upstream plasma beta (${\beta }_{\text{upstream}}$), shock magnetosonic Mach number ($M_{\text{ms}}$), shock angle (${\theta }_{Bn}$), angle between the shock normal and radial direction (ϕ), mean speed in the sheath ($V_{\text{sheath}}$), and expansion speed of the driving CME ejecta ($V_{\text{exp}}$). The Pearson correlation coefficients ($cc$) are included in each panel. The cyan dashed and green dash-dotted lines indicate the Kolmogorov (−1.67) and Kraichnan (−1.50) spectral indices, respectively.

First, it is clear from Figure 6 that there are no strong ($cc>0.60$) or moderate ($cc=0.40-0.59$) correlations. All coefficients show either weak ($cc=0.20-0.39$) or very weak to nonexistent ($cc=0-0.19$) correlation. Only vague trends can be discerned for some of the parameters, and this is the case only for the Near-Shock region: Those sheaths that are preceded by slow solar wind ($V_{\text{upstream}}\mathrm{\lesssim }$ 450 km/s) have a larger spread in their spectral indices than the sheaths preceded by a fast ($V_{\text{upstream}}\mathrm{\gtrsim }600\mathrm{km}/\mathrm{s}$) solar wind. The latter are associated with shallower slopes, which are confined within the range ∼ [−1.9, −1.5]. The scatter plot for $V_{\text{sheath}}$ is very similar to that of $V_{\text{upstream}}$. The panel ${\alpha }_{\text{upstream}}$ shows that, for the Near-Shock region, there is a weak tendency for the shallowest (steepest) spectral indices in the preceding solar wind to correspond to shallower (steeper) indices in the sheath, but the spread is significant. For the Near-LE region, in turn, there is only a very weak (negative) correlation. The dashed line ($y=x$) highlights that spectral indices steepen from the solar wind ahead to the sheath in most cases, both for the Near-Shock and Near-LE regions. However, there exist a considerable number of events for which indices become shallower, but these mostly cluster close to the dashed line.

The spectral indices in sheaths behind the strongest shocks tend to be shallower and have a smaller spread, particularly so for the Near-Shock region, while weaker shocks are associated with a wide range of spectral indices. The majority of interplanetary shocks at 1 AU are quasi-perpendicular (e.g., Kilpua et al., 2015), and this was also the case for the events analyzed here. Figure 6 shows that they are associated with a large range of spectral indices. For the Near-Shock region in particular, quasi-parallel shocks are in turn associated with a narrower range of spectral indices, ∼[−1.9, −1.5]. The angles between the radial direction and shock normal (ϕ) are generally small, indicating that the majority of the events included in this study were sheaths ahead of CMEs that were crossed relatively close to the apex. There is no notable correlation between ϕ and the spectral indices. The cyan dashed and green dash-dotted lines indicate the Kolmogorov (−1.67) and Kraichnan (−1.50) spectral indices, respectively.

3.2 Partial Variance of Increments

The partial variance of increments (PVI) method (e.g., Greco et al., 2008) allows intermittent structures in time series data to be identified. The time series of the PVI parameter is defined as

$PVI=\frac{\left|\delta \mathbf{B}\right|}{\sqrt{\langle |\delta \mathbf{B}{|}^2\rangle }},(1)$

where the field increment $\delta \mathbf{B}$ is as defined previously. In the denominator, the average is taken over the interval from 1 h before the start of the SW-Ahead region to 1 h after the end of the Near-LE region. The results can be affected by the selection of the interval where the average is calculated. However, a few intervals were checked (from a few minutes to 2 h), and the results were very similar. PVI values >3 are considered to be intermittent structures (e.g., Bruno, 2019; Zhou et al., 2019).

Figure 7 shows the probability distribution functions (PDFs) for all 79 sheaths at four τ values, one in the kinetic range (0.18 s) and three in the inertial range (12, 94, and 754 s). At each τ value, PDFs for the SW-Ahead, Near-Shock region, and Near-LE region are shown separately.

FIGURE 7

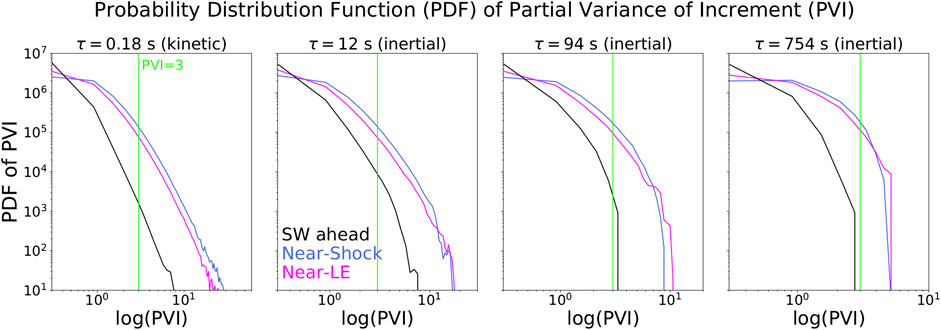
FIGURE 7. PDFs of PVI for four different time lags. PDFs for the SW-Ahead (black), Near-Shock (blue) region, and Near-LE (magenta) region are shown. The green vertical lines indicate the $PVI=3$ threshold for intermittent structures.

For all timelags considered, the sheath subregions clearly have higher probability for large PVI values than the solar wind ahead, suggesting that they contain more intermittent structures. The Near-Shock region has generally slightly higher probability for large PVI values than the Near-LE region, except at the very end of the high PVI tail.

We note that PDFs in Figure 7 include the values for all sheaths, meaning that the high PVI tails (particularly at the very largest values) could come from a few events only. To explore this possibility, we show in Table 1 the number of the three regions for which three strong PVI thresholds ($PVI=3$, $PVI=5$, and PVI $=7$) were exceeded, requiring that at least 100 samples of 0.092 s exceeded the threshold during the 2 h interval. The majority of Near-Shock regions have $PVI>3$ and $PVI>5$ values and the majority of Near-LE regions $PVI>3$ values. In contrast to the solar wind ahead, strong $PVI$ values occurred only in a few cases. The strongest PVI values > 7 occurred only in about 20% of the Near-Shock and Near-LE regions. SW-Ahead completely lacked these strongest PVI values.

TABLE 1

TABLE 1. The occurrence of high PVI values.

3.3 Fluctuation Amplitudes

Normalized fluctuation amplitudes are defined as $\delta B/B$, where B is the magnetic field amplitude calculated over the interval t (i.e., between times t and $t+\tau$). The maximum angular deviation of the magnetic field is 180°, and thus, $\delta B/B$ must be always $\mathrm{\lesssim }2$ for noncompressible (Alfvénic) fluctuations, while fluctuations in the field with values $>2$ must be at least partly compressive (see also discussion in Chen et al., 2015). Note that fluctuations with $\delta B/B$$<2$ can also be partly compressive.

The histograms of mean normalized fluctuation amplitudes, $\langle \delta B/B\rangle$, are shown in Figure 8 for SW-Ahead, Near-Shock region, and Near-LE region. No spectral slopes −1 were found in this study. The $\langle \delta B/B\rangle$ values are <1 for all timescales except for a few Near-Shock and Near-LE regions for the largest timescale shown (754 s). As shown by Matteini et al. (2018), the break between the inertial and $f^{-1}$ range occurs when the $\langle \delta B/B\rangle \sim 1$. Another feature clearly visible from the figure is that $\langle \delta B/B\rangle$ values spread considerably with increasing timelag. Figure 8 also shows that the median $\langle \delta B/B\rangle$ (magenta lines) are highest in the Near-Shock region and smallest in the SW-Ahead region (expect for $\tau =12\mathrm{s}$, for which the smallest values occurs in the Near-LE region).

FIGURE 8

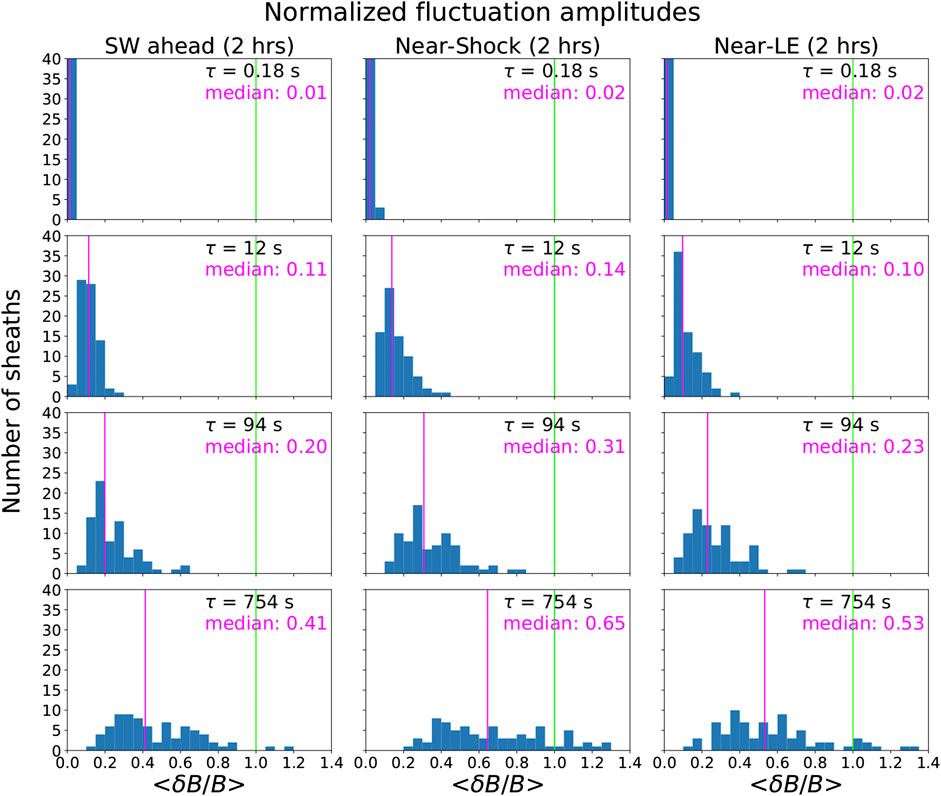
FIGURE 8. Histograms of mean normalized fluctuation amplitudes ($\langle \delta B/B\rangle$) in the (left) solar wind ahead, (middle) Near-Shock region, and (right) Near-LE region. The green vertical line shows $\langle \delta B/B\rangle =1$.

There are some large $\delta B/B$ values in the sheaths although the distributions are dominated by $\delta B/B<1$ for all timescales investigated. Table 1 also shows the number of cases with $\delta B/B$ exceeding three different thresholds for the timelag $\tau =94\mathrm{s}$. $\delta B/B>\sqrt{2}$ indicates significant rotation of the field direction, i.e., over 90° for purely rotational fluctuations, while the values $\delta B/B>2$ correspond to at least partly compressional fluctuations as explained above. The number of cases for which the thresholds are exceeded is largest for the Near-Shock region and smallest for the solar wind ahead. In particular, the differences are clear for $\delta B/B>2$. This threshold was exceeded only for 11 cases in the solar wind ahead, but in almost half of the cases in the Near-Shock regions.

The top panels of Figure 9 show $\langle \delta B/B\rangle$ in the solar wind ahead vs. in the sheath. The top left panel shows the results for the Near-Shock region and right panels for the Near-LE region. The color-coding of the points indicates the value of the shock magnetosonic Mach number ($M_{sh}$). Pearson correlation coefficients are shown in each panel. The figure shows that $\langle \delta B/B\rangle$ statistically tends to be larger in the Near-Shock region than in the SW-Ahead region. The small fraction of events at or below the $x=y$ dashed line may have been due to spatial inhomogeneities in the plasma (e.g., events where the upstream wind happened to contain fluctuations with larger than usual amplitudes). Although we infer the preshock to postshock evolution, it should be noted that the comparison is spatial in strict terms and that different field and plasma (with potentially different preshocked properties) are probed upstream and downstream.

FIGURE 9

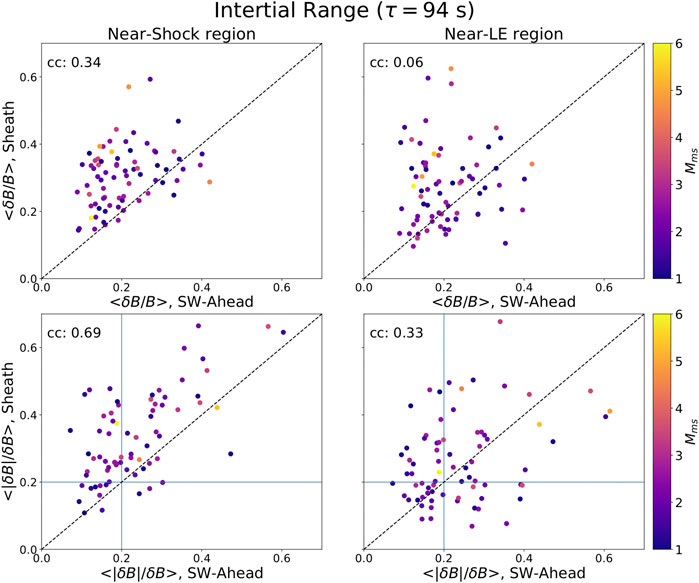
FIGURE 9. Scatter plots of (top) mean normalized fluctuation amplitudes ($\langle \delta B/B\rangle$) and (bottom) mean magnetic compressibility ($\langle \delta \left|B\right|/\delta B\rangle$) in the solar wind ahead (SW-Ahead) vs. in the sheath. The left panels show the results for the Near-Shock region and right panels for the Near-LE region. The symbols are color-coded with shock magnetosonic Mach number ($M_{sh}$). In the bottom panels, the vertical line shows $\langle \delta \left|B\right|/\delta B\rangle =0.2$, which is the upper threshold for values typically observed in the fast solar wind. The Pearson correlation coefficients are shown in each panel.

The majority of Near-LE regions also have higher $\langle \delta B/B\rangle$ than the SW-Ahead region, but there are more cases when the value is smaller. For the Near-LE region, the data are uncorrelated, while there is a weak positive correlation ($cc=0.34$) for the Near-Shock region. The events with the largest $\langle \delta B/B\rangle$ have some tendency to be associated with stronger shocks, but there is no strong ordering with the shock $M_{ms}$.

3.4 Compressibility

The previous section indicated that sheaths embed at least some compressible fluctuations. The level of magnetic compressibility can be approximated with $\delta \left|B\right|/\delta B$, i.e., the change in magnitude as a fraction of the total fluctuation amplitude. Figure 10 shows the mean value of magnetic compressibility ($\langle \delta \left|B\right|/\delta B\rangle$) in the same three regions and four timescales as in Figure 8. The lime vertical lines indicate $\delta \left|B\right|/\delta B=0.2$, corresponding to the cutoff value found for the fast solar wind by Matteini et al. (2018). The authors found considerably larger compressibility for the slow solar wind, consistent with the suggestion that low compressibility limits the value of $\delta B/B$ in the fast wind.

FIGURE 10

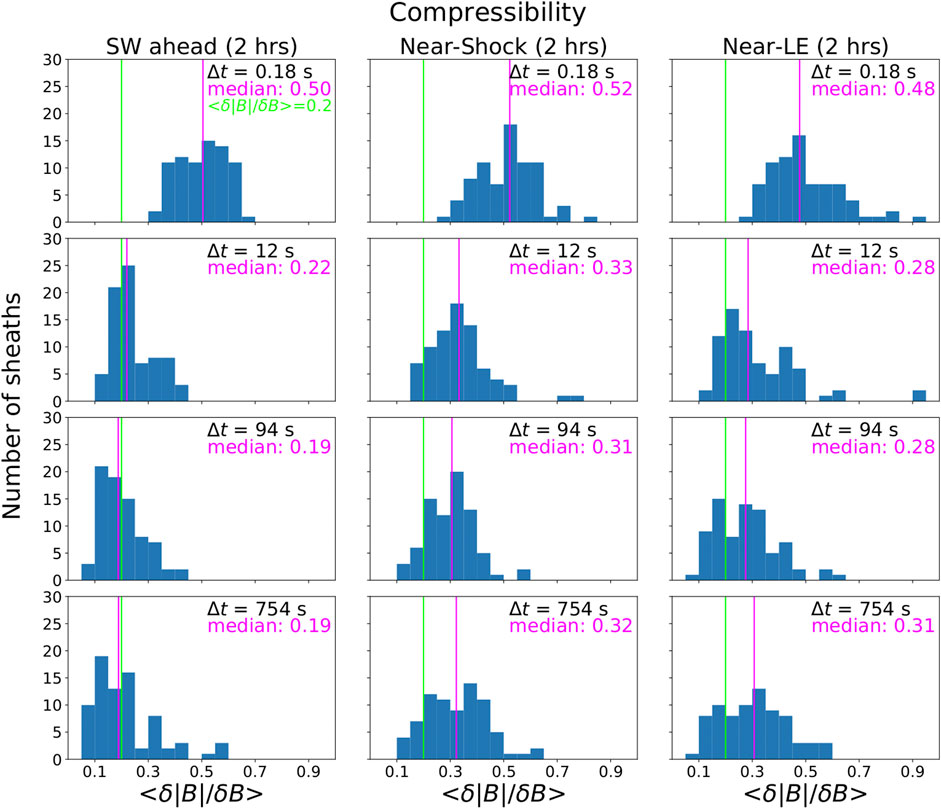
FIGURE 10. Histograms of mean magnetic compressibility ($\langle \delta \left|B\right|/\delta B\rangle$) in the solar wind ahead (left panels), Near-Shock region (middle panels), and Near-LE region (right panels). The green vertical line shows $\langle \delta \left|B\right|/\delta B\rangle =0.2$, which is the upper threshold for values typically observed in the fast solar wind.

Figure 10 shows that the level of magnetic compressibility is larger in the kinetic range than in the inertial range (all $\langle \delta \left|B\right|/\delta B\rangle$ values are $>0.2$ in the kinetic range), consistent with several previous studies in the solar wind (e.g., Chen et al., 2015; Matteini et al., 2018; Šafránková et al., 2019; Good et al., 2020a). While the median $\langle \delta \left|B\right|/\delta B\rangle$ is similar between all regions investigated, the values are more spread in the sheath than in the solar wind ahead. In the inertial range, the SW-Ahead shows a considerable amount of cases with $\langle \delta \left|B\right|/\delta B\rangle$ values < 0.2 and clearly lower medians than what are found in the sheath. For both sheaths regions, the majority of cases still have $\langle \delta \left|B\right|/\delta B\rangle >0.2$ at all inertial-scale timelag ranges investigated. In the Near-LE regions, $\langle \delta \left|B\right|/\delta B\rangle$ values are slightly smaller than in the Near-Shock region but still considerably larger than in the SW-Ahead. This implies that compressibility in the sheaths more closely resembles that observed in the slow solar wind, regardless of the compressibility in the solar wind ahead.

The bottom panels of Figure 9 show $\langle \delta \left|B\right|/\delta B\rangle$ in the solar wind ahead vs. the sheath. The vertical line shows the $\langle \delta \left|B\right|/\delta B\rangle =0.2$ threshold discussed above. Similar to the mean normalized fluctuation amplitudes, the compressibility is larger in the Near-Shock region than in the SW-Ahead region for the clear majority of the cases, while there is a considerable amount of cases with $\langle \delta \left|B\right|/\delta B\rangle$ value smaller in the Near-LE region. For the Near-Shock region, there is a strong positive correlation (0.69) in the data, while the correlation is weak for the Near-LE region. There is again no clear ordering with the shock $M_{ms}$.

Finally, in Figure 11, we explore the magnetic field rotation and compressibility in more detail (see, e.g., Chen et al. 2015). The top panels show the rotation angle α, defined over timescale t and at time t, as follows:

$\alpha \left(t,\tau \right)={\text{cos}}^{-1}\left[\frac{\mathbf{B}\left(t\right)\cdot \mathbf{B}\left(t+\tau \right)}{\left|\mathbf{B}\left(t\right)\right|\cdot \left|\mathbf{B}\left(t+\tau \right)\right|}\right].$

FIGURE 11

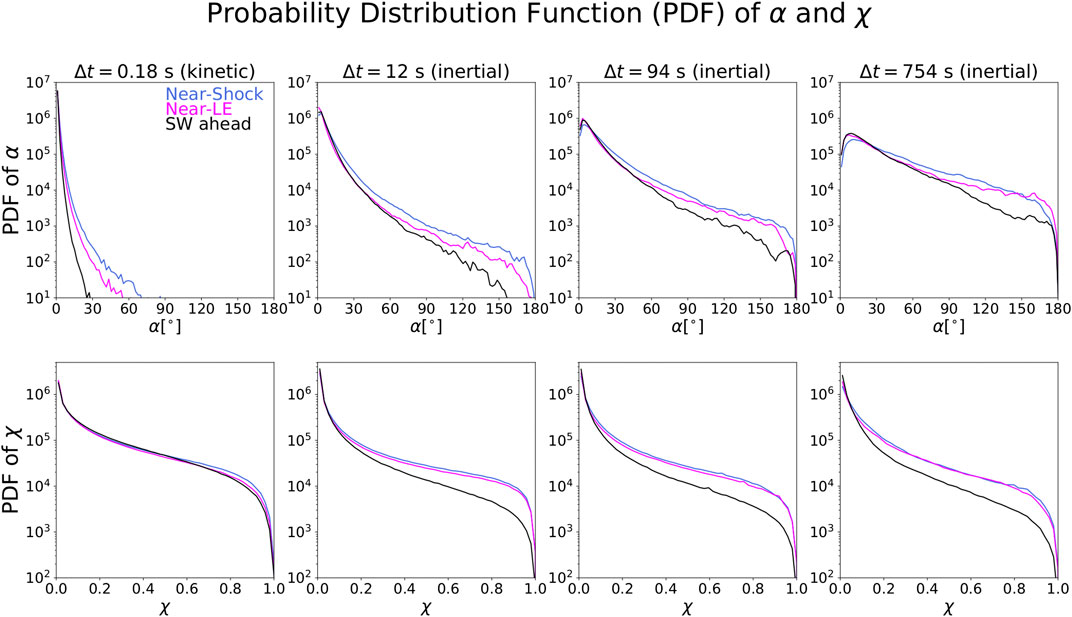
FIGURE 11. Probability distribution function (PDF) of (top) rotation angle α and (bottom) parameter χ for SW-Ahead, Near-Shock region, and Near-LE region. The results are shown for four timelags.

The maximum rotation possible is ${180}^{\circ }$, and $\alpha =0^{\circ }$ for purely compressive fluctuations. The bottom panels show the parameter χ, which gives a measure of the degree to which the magnetic field changes magnitude during a rotation:

$\chi \left(t,\tau \right)=\frac{|\delta B/B-2\text{sin}\left(\alpha /2\right)|}{\delta B/B}.$

Here, $\chi =0$ for a pure rotation without any change in the magnitude, while $\chi =1$ for a magnitude change without any rotation.

Figure 11 shows that both a and $\chi$ values are clearly larger in the sheath than in the solar wind ahead. This suggests the presence of coherent structures (current sheets with large rotations, plasma interfaces, magnetic holes, etc.) and more compressible fluctuations. There is not much difference in the values between the Near-LE and Near-Shock regions.

4 Summary and Discussion

We have performed a statistical investigation of the fluctuation properties in CME-driven sheath regions. In total, 79 sheaths observed in the near-Earth solar wind by the Wind spacecraft between 1997 and 2018 were included in this study. Three different regions were studied, each 2 h in duration: 1) solar wind ahead (SW-Ahead), 2) Near-Shock, and 3) Near-LE. Near-Shock and Near-LE regions are within the sheath, the former adjacent to the shock and the latter adjacent to the ejecta leading edge.

The key findings can be summarized as follows:

•Sheaths had on average steeper inertial-range spectral indices than the Kolmogorov and Kraichnan indices. However, the range of indices was relatively large (∼[−2.2, −1.3]) and was larger for slow sheaths and sheaths preceded by slow solar wind.

•Pearson correlations between the inertial-range spectral indices in the sheath and selected shock, sheath, ejecta, and upstream parameters were mostly very weak or negligible. Some weak correlations were found only for the Near-Shock region; fast sheaths behind strong shocks (high $M_{ms}$) preceded by faster wind tend to have the shallowest spectral indices. Weak correlation was also found with the speed and spectral index in the solar wind ahead.

•On average, sheaths had larger normalized magnetic field fluctuation amplitudes, $\langle \delta B/B\rangle$, than the solar wind ahead. This was particularly the case for the Near-Shock region. The range and median of $\langle \delta B/B\rangle$ values also increased with increasing timelag.

•A weak correlation in $\langle \delta B/B\rangle$ between the SW-Ahead and Near-Shock region was found, while the data were uncorrelated for the Near-LE region.

•Sheaths had higher magnetic compressibility, $\langle \delta \left|B\right|/\delta B\rangle$, than the solar wind ahead. For the majority of cases, $\langle \delta \left|B\right|/\delta B\rangle$ values were >0.2. The compressibility was somewhat higher in the Near-Shock region than in the Near-LE region.

•A strong positive correlation was found for the compressibility between the upstream wind and Near-Shock region, while for the Near-LE region, the correlation was weak.

•Sheaths have clearly larger intermittency than the solar wind ahead. This result is particularly clear in the PVI analysis showing that sheaths have regular strong PVI values (>3), consistent with findings of Zhou et al. (2019). Steeper spectral indices than Kolmogorov’s (and steeper than in the upstream wind) and the presence of fluctuations exhibiting large magnetic field rotation and compressibility (larger $\langle \delta \left|B\right|/\delta B\rangle$, α and χ parameters) support high intermittency. Intermittency was slightly higher in the Near-Shock region than in the Near-LE region.

The results of this study confirm many findings of the case studies by Kilpua et al. (2020) and Good et al. (2020a). Sheaths have on average enhanced normalized fluctuation amplitudes, compressibility, and intermittency, and their spectral slopes in the majority of cases are steeper than Kolmogorov’s. Borovsky (2020) performed an extensive statistical analysis of magnetic field and velocity fluctuations upstream and downstream of 109 interplanetary shocks and also found enhanced normalized fluctuation amplitudes downstream, as well as low correlation coefficients between the downstream and upstream values. Note that, however, their work uses partly different approaches as well as that SIR and CME-driven shocks are combined with categorization that is based on the type of the solar wind the shock propagates into. Increased compressibility in the sheaths when compared to ambient wind was also reported in a statistical study by Moissard et al. (2019) (performed over the whole sheath and fluctuations ranging between 20 s and 7.5 min). We note that the compressibility values we obtained here are generally higher than those found in the downstream of interplanetary shocks by Šafránková et al. (2019). The authors also showed that compressibility of fluctuations (defined as the ratio of PSDs of perpendicular to parallel magnetic field fluctuations) increased with increasing plasma beta. The relatively large compressibility values obtained in our study could also be explained by most sheaths, being high-beta structures. The increased intermittency in density fluctuations in terms of substantial deviations from the Gaussian distribution functions from upstream to downstream of interplanetary shocks was also reported by Riazantseva et al. (2017). In agreement, Kilpua et al. (2020) reported stronger deviations from Gaussian distributions for magnetic field fluctuations for three ICME sheaths.

The observed smaller spread in the inertial-range spectral indices and shallower slopes, closer to Kolmogorov’s, for fast sheaths ($\mathrm{\gtrsim }600\mathrm{km}/\mathrm{s}$) than for slow sheaths ($\mathrm{\lesssim }450\mathrm{km}/\mathrm{s}$) is in agreement with the previous studies in the solar wind in general (see the Introduction section). The statistical study by Borovsky (2020) found also steeper slopes downstream than upstream of interplanetary shocks.

As discussed in the Introduction section, in planetary magnetosheaths, $f^{-1}$ spectrum is commonly observed at the MHD scale, with an absence of the Kolmogorov inertial range close to the nose of the bow shock. This has been interpreted as a sign of bow shock resetting the turbulence (e.g., Huang et al., 2017). We did not find indication of the $f^{-1}$ spectrum in CME sheaths. The lack of $f^{-1}$ spectrum could be related to CME shocks being typically considerably weaker (∼2, e.g., Kilpua et al., 2015) than planetary bow shocks (∼5–10). Our study however included a few stronger shocks (Mach numbers between 4 and 6), and for those either, no $f^{-1}$ spectrum was found. We point out that the majority of the events included in this study were cases where the CME was crossed relatively close to the nose, implying that if the $f^{-1}$ spectrum would be a common feature of CME sheaths, we would have expected to detect it. As discussed already in Section 3.1, the results can be affected significantly by the investigated regions including fluctuations that have evolved over different times since processes by the shock. Our analysis following the approach in Borovsky (2020) and comparison of slopes with the shock speed suggest a tendency that regions most recently processed by the shock have the shallowest slopes, implying that structures such as current sheets increasingly develop in the sheath as the CME propagates forward.

In the kinetic range, spectral slopes varied in the range of [−2.7, −2.0] and were thus shallower than the nominal value reported in solar wind (∼−2.8). Shallower than nominal kinetic-range slopes could be attributed to continuing energy cascade (e.g., Sahraoui et al., 2009; see also discussion in the study by Kilpua et al., 2020). The spread in the kinetic-range spectral indices in turn was smaller than in the inertial-range indices, contrary to, e.g., a study by Smith et al. (2006) in solar wind in general. As mentioned in Section 3.1, the results could be affected by the Wind data capturing only the upper part of kinetic range, the use of only three points in the calculation of the kinetic-range slopes, and the magnetometer noise level. In addition, the shape of the spectrum can change as a function of the distance from the shock due to exponential decay of the spectrum, as shown for density fluctuations, e.g., in the study by Pitňa et al. (2017).

Although the lack of MHD-scale spectrum suggest that CME-driven shocks are not resetting the turbulence at a similar extent than planetary bow shocks, fluctuation properties in sheaths were observed to be distinctly different from the upstream. This was particularly the case for the Near-Shock region. The increased compressibility and normalized fluctuation amplitudes indicate that new (at least partly) compressible fluctuations are developed in the sheath. This is supported by the general lack of correlation between the spectral indices in the sheath and preceding solar wind found in this work and consistent with the results of case studies by Good et al. (2020a) and Kilpua et al. (2020). These results are also consistent with Borovsky (2020) who reported no correlation between the upstream and downstream values of spectral indices. The present statistical study also confirms the finding of Kilpua et al. (2020) that the Near-LE region is more similar to upstream conditions regarding its mean fluctuation properties. The particularly weak/negligible correlations between the sheath and shock/upstream conditions for the Near-LE region suggests that fluctuation properties have further evolved deeper in the sheath and/or are affected by processes at the ejecta leading edge. The field line draping generates field fluctuations and could provide some free energy for the generation of plasma waves (e.g., Ala-Lahti et al., 2019), and its importance should increase with the speed and expansion speed of the ejecta (e.g., Gosling and McComas, 1987; McComas et al., 1988). No clear trend was found with either of these with the spectral slopes in the Near-LE region, but a more detailed comparison of turbulent properties close to the ejecta leading edge and driver characteristics would be needed. The correlation between the shock/upstream parameters and spectral slopes in the Near-Shock region was also weak at best. We note that for some parameters investigated, low correlations can be affected by their values clustering to a relatively limited range. For example, the strong $M_{ms}>3$ and fast ($V_{sh}>600$) shocks were related to the shallowest slopes in the Near-Shock region, but their numbers were small when compared to weaker and slower shocks. We also found that in contrast with the planetary magnetosheaths (e.g., Hadid et al., 2015), spectral slopes in CME sheaths do not vary significantly from the nose toward the flanks of the CME ejecta. However, as mentioned above, most events in our study were sheaths behind centrally crossed CMEs, and therefore, no strong conclusions can be drawn.

As summarized above, sheaths were found to have a higher intermittency than solar wind ahead according to several used proxies. It is an interesting question as to what extent the increased intermittency in CME sheath is related to intermittency of turbulent cascade, or is it rather the consequence of the frequent presence of coherent small-scale magnetic structures in the sheath, such as currents sheets, reconnection exhausts, and flux tube boundaries. These coherent magnetic structures could be “relics from the Sun” (e.g., Owens et al., 2011) or formed actively by the processes at the CME shock and leading edge as the CME propagates through the solar wind. Their presence would be detected as high PVI structures and steepen the spectral slopes. This could also shed light on another interesting question why CME sheaths as high magnetic field structures do not exhibit shallower Kraichnan–Iroshinikov spectral slopes (−1.5). Li et al. (2012) suggested that the initially Kraichnan–Iroshinikov-type spectra in the solar wind could steepen due to the presence of current sheets (see also Borovsky, 2010). Another possibility is that turbulent cascade is anisotropic giving the ∼ −5/3 slope in perpendicular direction as suggested by Goldreich and Sridhar (1995). In sheath regions perpendicular to turbulence dominates (e.g., Moissard et al., 2019; Good et al., 2020b) as is typical in general in the solar wind.

It is also an interesting question as to how much fluctuation properties in CME-driven sheaths differ from downstream regions behind SIR-driven shocks. Both are compressive large-scale structures in the solar wind but have different generation mechanisms and differences in their shock properties. Only a relatively small fraction (∼26%) of SIRs has fully developed leading shocks at the Earth’s orbit (e.g., Jian et al., 2006). SIR-driven shocks are also typically weaker and slower than the shocks associated with CMEs and have on average higher upstream plasma beta (e.g., Kilpua et al., 2015). The higher plasma beta can affect generation of plasma waves and, therefore, fluctuation properties.

This statistical study shows that CME-driven sheath regions have their own distinct magnetic field fluctuation properties that are partly distinct from planetary magnetosheaths. Except for compressibility, correlation between downstream values is only weak or negligible. In addition, spectral indices in sheaths did not show clear trends with the shock properties. For example, this is quite different for the case of the terrestrial magnetosheath downstream with a quasi-parallel and a quasi-perpendicular bow shock geometry, where there is clear difference between the turbulence spectral indices, fluctuation levels, compressibility, and occurrence of current sheets (Yordanova et al., 2020). This emphasizes the need for more detailed investigation on how solar wind turbulent properties evolve in the transition through the shock into the sheath, e.g., by finding cases where the spacecraft are probing simultaneously the solar wind upstream, the shock, and the sheath. In addition, multispacecraft encounters within the single sheath would allow better probing on how spectral indices and fluctuation properties change with the distance from the apex of the CME and better comparison with planetary magnetosheath. Higher-resolution magnetic field data would also allow probing more extensively the kinetic range in CME-driven sheath regions. Now, we covered only the upper end of the kinetic range that likely affects the results. Solar Orbiter (Müller et al., 2013) and Parker Solar Probe (Fox et al., 2016) can also shed new insight into CME sheaths (e.g., Good et al., 2020b) and allow investigation on how fluctuation properties in CME sheaths evolve in the inner heliosphere.

Data Availability Statement

Wind data are publicly available at NASA’s Coordinated Data Analysis Web (CDAWeb) database (https://cdaweb.sci.gsfc.nasa.gov/index.html/).

Author Contributions

EK did the main data analysis and compiled the figures. EK and SG planned majority of the research and approaches to be used in the study. All authors (EK, SG, MA-L, AO, DF, MJ, LH, and EY) contributed to the methods and physical interpretations and to the writing of the paper.

Funding

This manuscript has received funding from the SolMAG project (ERC-COG 724391) funded by the European Research Council (ERC) in the framework of the Horizon 2020 Research and Innovation Programme, and the Academy of Finland project SMASH 1310445. The results presented in here have been achieved under the framework of the Finnish Centre of Excellence in Research of Sustainable Space (Academy of Finland grant number 1312390), which we gratefully acknowledge. EY's research is supported by the Swedish Contingencies Agency, gran 2016-2102.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge A. Szabo for the Wind/MFI data and K. Ogilvie for the Wind/SWE data.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2020.610278/full#supplementary-material.

Footnotes

¹http://cdaweb.gsfc.nasa.gov/

References

Ala-Lahti, M., Kilpua, E. K. J., Souček, J., Pulkkinen, T. I., and Dimmock, A. P. (2019). Alfvén ion cyclotron waves in sheath regions driven by interplanetary coronal mass ejections. J. Geophys. Res. Space. 124, 3893–3909. doi:10.1029/2019JA026579

CrossRef Full Text | Google Scholar

Ala-Lahti, M. M., Kilpua, E. K. J., Dimmock, A. P., Osmane, A., Pulkkinen, T., and Souček, J. (2018). Statistical analysis of mirror mode waves in sheath regions driven by interplanetary coronal mass ejection. Ann. Geophys. 36, 793–808. doi:10.5194/angeo-36-793-2018

CrossRef Full Text | Google Scholar

Alexandrova, O., Chen, C. H. K., Sorriso-Valvo, L., Horbury, T. S., and Bale, S. D. (2013). Solar wind turbulence and the role of ion instabilities. Space Sci. Rev. 178, 101–139. doi:10.1007/s11214-013-0004-8

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2020). A statistical analysis of the fluctuations in the upstream and downstream plasmas of 109 strong-compression interplanetary shocks at 1 AU. J. Geophys. Res. C Oceans Atmos. 125, e27518. doi:10.1029/2019JA027518

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2010). Contribution of strong discontinuities to the power spectrum of the solar wind. Phys. Rev. Lett. 105, 111102. doi:10.1103/PhysRevLett.105.111102 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Borovsky, J. E., and Funsten, H. O. (2003). Role of solar wind turbulence in the coupling of the solar wind to the Earth’s magnetosphere. J. Geophys. Res. C Oceans Atmos. 108, 1246. doi:10.1029/2002JA009601

CrossRef Full Text | Google Scholar

Borovsky, J. E. (2012). The velocity and magnetic field fluctuations of the solar wind at 1 AU: statistical analysis of Fourier spectra and correlations with plasma properties. J. Geophys. Res. Space. 117, A05104. doi:10.1029/2011JA017499

CrossRef Full Text | Google Scholar

Bruno, R. (2019). Intermittency in solar wind turbulence from fluid to kinetic scales. Earth Space Sci. 6, 656–672. doi:10.1029/2018EA000535

CrossRef Full Text | Google Scholar

Bruno, R., Telloni, D., DeIure, D., and Pietropaolo, E. (2017). Solar wind magnetic field background spectrum from fluid to kinetic scales. Mon. Not. Roy. Astron. Soc. 472, 1052–1059. doi:10.1093/mnras/stx2008

CrossRef Full Text | Google Scholar

Chen, C. H. K., Bale, S. D., Bonnell, J. W., Borovikov, D., Bowen, T. A., Burgess, D., et al. (2020). The evolution and role of solar wind turbulence in the inner heliosphere. LABEL:@jnlApJS. 246, 53. doi:10.3847/1538-4365/ab60a3

CrossRef Full Text | Google Scholar

Chen, C. H. K., Bale, S. D., Salem, C. S., and Maruca, B. A. (2013). Residual energy spectrum of solar wind turbulence. LABEL:@jnlApJ. 770, 125. doi:10.1088/0004-637X/770/2/125

CrossRef Full Text | Google Scholar

Chen, C. H. K., Matteini, L., Burgess, D., and Horbury, T. S. (2015). Magnetic field rotations in the solar wind at kinetic scales. Mon. Not. Roy. Astron. Soc. 453, L64–L68. doi:10.1093/mnrasl/slv107

CrossRef Full Text | Google Scholar

Fox, N. J., Velli, M. C., Bale, S. D., Decker, R., Driesman, A., Howard, R. A., et al. (2016). The solar Probe plus mission: humanity’s first visit to our star. Space Sci. Rev. 204, 7–48. doi:10.1007/s11214-015-0211-6

CrossRef Full Text | Google Scholar

Goldreich, P., and Sridhar, S. (1995). Toward a theory of interstellar turbulence. II. Strong alfvenic turbulence. LABEL. 438, 763. doi:10.1086/175121

CrossRef Full Text | Google Scholar

Good, S. W., Ala-Lahti, M., Palmerio, E., Kilpua, E. K. J., and Osmane, A. (2020a). Radial evolution of magnetic field fluctuations in an interplanetary coronal mass ejection sheath. Astrophys. J. 893, 110. doi:10.3847/1538-4357/ab7fa2

CrossRef Full Text | Google Scholar

Good, S. W., Kilpua, E. K. J., Ala-Lahti, M., Osmane, A., Bale, S. D., and Zhao, L. L. (2020b). Cross helicity of the 2018 november magnetic cloud observed by the parker solar Probe. LABEL. 900, L32. doi:10.3847/2041-8213/abb021

CrossRef Full Text | Google Scholar

Gosling, J. T., and McComas, D. J. (1987). Field line draping about fast coronal mass ejecta - a source of strong out-of-the-ecliptic interplanetary magnetic fields. Geophys. Res. Lett. 14, 355–358. doi:10.1029/GL014i004p00355

CrossRef Full Text | Google Scholar

Greco, A., Chuychai, P., Matthaeus, W. H., Servidio, S., and Dmitruk, P. (2008). Intermittent MHD structures and classical discontinuities. Geophys. Res. Lett. 35, L19111. doi:10.1029/2008GL035454

CrossRef Full Text | Google Scholar

Guo, J., Feng, X., Zhang, J., Zuo, P., and Xiang, C. (2010). Statistical properties and geoefficiency of interplanetary coronal mass ejections and their sheaths during intense geomagnetic storms. J. Geophys. Res. C Oceans Atmos. 115, A09107. doi:10.1029/2009JA015140

CrossRef Full Text | Google Scholar

Hadid, L. Z., Sahraoui, F., Kiyani, K. H., Retinò, A., Modolo, R., Canu, P., et al. (2015). Nature of the MHD and kinetic scale turbulence in the magnetosheath of saturn: cassini observations. LABEL. 813, L29. doi:10.1088/2041-8205/813/2/L29

CrossRef Full Text | Google Scholar

Howes, G. G., Klein, K. G., and TenBarge, J. M. (2014). Validity of the taylor hypothesis for linear kinetic waves in the weakly collisional solar wind. Astrophys. J. 789, 106. doi:10.1088/0004-637X/789/2/106

CrossRef Full Text | Google Scholar

Huang, S. Y., Hadid, L. Z., Sahraoui, F., Yuan, Z. G., and Deng, X. H. (2017). On the existence of the Kolmogorov inertial range in the terrestrial magnetosheath turbulence. Astrophys. J. Lett. 836, L10. doi:10.3847/2041-8213/836/1/L10

CrossRef Full Text | Google Scholar

Huang, S. Y., Wang, Q. Y., Sahraoui, F., Yuan, Z. G., Liu, Y. J., Deng, X. H., et al. (2020). Analysis of turbulence properties in the mercury plasma environment using MESSENGER observations. LABEL. 891, 159. doi:10.3847/1538-4357/ab7349

CrossRef Full Text | Google Scholar

Huttunen, K., and Koskinen, H. (2004). Importance of post-shock streams and sheath region as drivers of intense magnetospheric storms and high-latitude activity. Ann. Geophys. 22, 1729–1738. doi:10.5194/angeo-22-1729-2004

CrossRef Full Text | Google Scholar

Jankovičová, D., Vörös, Z., and Imkanin, J. Å. (2008). The effect of upstream turbulence and its anisotropy on the efficiency of solar wind magnetosphere coupling. Nonlinear Process Geophys. 15, 523–529. doi:10.5194/npg-15-523-2008

CrossRef Full Text | Google Scholar

Janvier, M., Dasso, S., Démoulin, P., Masías-Meza, J. J., and Lugaz, N. (2015). Comparing generic models for interplanetary shocks and magnetic clouds axis configurations at 1 AU. J. Geophys. Res. C Oceans Atmos. 120, 3328–3349. doi:10.1002/2014JA020836

CrossRef Full Text | Google Scholar

Jian, L., Russell, C. T., Luhmann, J. G., and Skoug, R. M. (2006). Properties of stream interactions at one AU during 1995 2004. LABEL:@jnlSol. Phys. 239, 337–392. doi:10.1007/s11207-006-0132-3

CrossRef Full Text | Google Scholar

Kajdič, P., Blanco-Cano, X., Aguilar-Rodriguez, E., Russell, C. T., Jian, L. K., and Luhmann, J. G. (2012). Waves upstream and downstream of interplanetary shocks driven by coronal mass ejections. J. Geophys. Res. C Oceans Atmos. 117, A06103. doi:10.1029/2011JA017381

CrossRef Full Text | Google Scholar

Kataoka, R., Watari, S., Shimada, N., Shimazu, H., and Marubashi, K. (2005). Downstream structures of interplanetary fast shocks associated with coronal mass ejections. Geophys. Res. Lett. 32, L12103. doi:10.1029/2005GL022777

CrossRef Full Text | Google Scholar

Kaymaz, Z., and Siscoe, G. (2006). Field-line draping around ICMES. Sol. Phys. 239, 437–448. doi:10.1007/s11207-006-0308-x

CrossRef Full Text | Google Scholar

Kilpua, E., Koskinen, H. E. J., and Pulkkinen, T. I. (2017a). Coronal mass ejections and their sheath regions in interplanetary space. Living Rev. Sol. Phys. 14, 5. doi:10.1007/s41116-017-0009-6 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Kilpua, E. K. J., Balogh, A., von Steiger, R., and Liu, Y. D. (2017b). Geoeffective properties of solar transients and stream interaction regions. Space Sci. Rev. 212, 1271–1314. doi:10.1007/s11214-017-0411-3

CrossRef Full Text | Google Scholar

Kilpua, E. K. J., Fontaine, D., Good, S. W., Ala-Lahti, M., A., O., , Palmerio, E., et al. (2020). Magnetic field fluctuation properties of coronal mass ejection-driven sheath regions in the near-Earth solar wind. Ann. Geophys. 28, 999–1017. doi:10.5194/angeo-38-999-2020

CrossRef Full Text | Google Scholar

Kilpua, E. K. J., Fontaine, D., Moissard, C., Ala-Lahti, M., Palmerio, E., Yordanova, E., et al. (2019). Solar wind properties and geospace impact of coronal mass ejection-driven sheath regions: variation and driver dependence. Space Weather. 17, 1257–1280. doi:10.1029/2019SW002217

CrossRef Full Text | Google Scholar

Kilpua, E. K. J., Hietala, H., Koskinen, H. E. J., Fontaine, D., and Turc, L. (2013). Magnetic field and dynamic pressure ULF fluctuations in coronal-mass-ejection-driven sheath regions. Ann. Geophys. 31, 1559–1567. doi:10.5194/angeo-31-1559-2013

CrossRef Full Text | Google Scholar

Kilpua, E. K. J., Lumme, E., Andreeova, K., Isavnin, A., and Koskinen, H. E. J. (2015). Properties and drivers of fast interplanetary shocks near the orbit of the Earth (1995-2013). J. Geophys. Res. C Oceans Atmos. 120, 4112–4125. doi:10.1002/2015JA021138

CrossRef Full Text | Google Scholar

Lepping, R. P., Acũna, M. H., Burlaga, L. F., Farrell, W. M., Slavin, J. A., Schatten, K. H., et al. (1995). The wind magnetic field investigation. Space Sci. Rev. 71, 207–229. doi:10.1007/BF00751330

CrossRef Full Text | Google Scholar

Li, G., Qin, G., Hu, Q., and Miao, B. (2012). Effect of current sheets on the power spectrum of the solar wind magnetic field using a cell model. Adv. Space Res. 49, 1327–1332. doi:10.1016/j.asr.2012.02.008

CrossRef Full Text | Google Scholar

Müller, D., Marsden, R. G., StCyr, O. C., and Gilbert, H. R. (2013). Solar orbiter. Exploring the sun-heliosphere connection. Sol. Phys. 285, 25–70. doi:10.1007/s11207-012-0085-7

CrossRef Full Text | Google Scholar

Matteini, L., Stansby, D., Horbury, T. S., and Chen, C. H. K. (2018). On the 1/f spectrum in the solar wind and its connection with magnetic compressibility. Astrophys. J. Lett. 869, L32. doi:10.3847/2041-8213/aaf573

CrossRef Full Text | Google Scholar

Matthaeus, W. H., and Goldstein, M. L. (1982). Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res.-Space. 87, 6011–6028. doi:10.1029/JA087iA08p06011

CrossRef Full Text | Google Scholar

McComas, D. J., Gosling, J. T., Winterhalter, D., and Smith, E. J. (1988). Interplanetary magnetic field draping about fast coronal mass ejecta in the outer heliosphere. J. Geophys. Res. Space. 93, 2519–2526. doi:10.1029/JA093iA04p02519

CrossRef Full Text | Google Scholar

Moissard, C., Fontaine, D., and Savoini, P. (2019). A study of fluctuations in magnetic cloud-driven sheaths. J. Geophys. Res. Space. 124, 8208–8226. doi:10.1029/2019JA026952

CrossRef Full Text | Google Scholar

Myllys, M., Kilpua, E. K. J., Lavraud, B., and Pulkkinen, T. I. (2016). Solar wind-magnetosphere coupling efficiency during ejecta and sheath-driven geomagnetic storms. J. Geophys. Res. C Oceans Atmos. 121, 4378–4396. doi:10.1002/2016JA022407

CrossRef Full Text | Google Scholar

Neugebauer, M., Clay, D. R., and Gosling, J. T. (1993). The origins of planar magnetic structures in the solar wind. J. Geophys. Res. Space. 98, 9383–9390. doi:10.1029/93JA00216

CrossRef Full Text | Google Scholar

Ogilvie, K. W., Chornay, D. J., Fritzenreiter, R. J., Hunsaker, F., Keller, J., Lobell, J., et al. (1995). SWE, A comprehensive plasma instrument for the wind spacecraft. Space Sci. Rev. 71, 55–77. doi:10.1007/BF00751326

CrossRef Full Text | Google Scholar

Ogilvie, K. W., and Desch, M. D. (1997). The wind spacecraft and its early scientific results. Adv. Space Res. 20, 559–568. doi:10.1016/S0273-1177(97)00439-0

CrossRef Full Text | Google Scholar

Osmane, A., Dimmock, A. P., and Pulkkinen, T. I. (2015). Universal properties of mirror mode turbulence in the Earth’s magnetosheath. Geophys. Res. Lett. 42, 3085–3092. doi:10.1002/2015GL063771

CrossRef Full Text | Google Scholar

Owens, M. J., Wicks, R. T., and Horbury, T. S. (2011). Magnetic discontinuities in the near-earth solar wind: evidence of in-transit turbulence or remnants of coronal structure? LABEL:@jnlSol. Phys. 269, 411–420. doi:10.1007/s11207-010-9695-0

CrossRef Full Text | Google Scholar

Pitňa, A., Šafránková, J., Němeček, Z., and Franci, L. (2017). Decay of solar wind turbulence behind interplanetary shocks. Astrophys. J. 844, 51. doi:10.3847/1538-4357/aa7bef

CrossRef Full Text | Google Scholar

Pitňa, A., Šafránková, J., Němeček, Z., Goncharov, O., Němec, F., Přech, L., et al. (2016). Density fluctuations upstream and downstream of interplanetary shocks. LABEL:@jnlApJ. 819, 41. doi:10.3847/0004-637X/819/1/41

CrossRef Full Text | Google Scholar

Regnault, F., Janvier, M., Démoulin, P., Auchère, F., Strugarek, A., Dasso, S., et al. (2020). 20 years of ACE data: how superposed epoch analyses eeveal generic features in interplanetary CME profiles. J. Geophys. Res. 125, e28150. doi:10.1029/2020JA028150

CrossRef Full Text | Google Scholar

Riazantseva, M. O., Budaev, V. P., Rakhmanova, L. S., Borodkova, N. L., Zastenker, G. N., Yermolaev, Y. I., et al. (2017). Intermittency of the solar wind density near the interplanetary shock. Geomagn. Aeron. 57, 645–654. doi:10.1134/S001679321706010X

CrossRef Full Text | Google Scholar

Šafránková, J., Němeček, Z., Němec, F., Verscharen, D., Chen, C. H. K., Ďurovcová, T., et al. (2019). Scale-dependent polarization of solar wind velocity fluctuations at the inertial and kinetic scales. LABEL:@jnlApJ. 870, 40. doi:10.3847/1538-4357/aaf239

CrossRef Full Text | Google Scholar

Sahraoui, F., Goldstein, M. L., Belmont, G., Canu, P., and Rezeau, L. (2010). Three dimensional anisotropic κ spectra of turbulence at subproton scales in the solar wind. Phys. Rev. Lett. 105, 131101. doi:10.1103/PhysRevLett.105.131101 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Sahraoui, F., Goldstein, M. L., Robert, P., and Khotyaintsev, Y. V. (2009). Evidence of a cascade and dissipation of solar-wind turbulence at the electron gyroscale. Phys. Rev. Lett. 102, 231102. doi:10.1103/PhysRevLett.102.231102 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Savani, N. P., Vourlidas, A., Szabo, A., Mays, M. L., Richardson, I. G., Thompson, B. J., et al. (2015). Predicting the magnetic vectors within coronal mass ejections arriving at Earth: 1. Initial architecture. Space Weather. 13, 374–385. doi:10.1002/2015SW001171

CrossRef Full Text | Google Scholar

Schwartz, S. J. (2000). SSI Scientific Report SR-001. “Shock and discontinuity normals, Mach numbers, and related parameters,” in Analysis Methods for Multispacecraft Data. Editors G. Paschmann, and P.W. Daly (London, United Kingdom: Internation Space Science Institute), 472.

Google Scholar

Siscoe, G., MacNeice, P. J., and Odstrcil, D. (2007). East-west asymmetry in coronal mass ejection geoeffectiveness. Space Wea. 5, S04002. doi:10.1029/2006SW000286

CrossRef Full Text | Google Scholar

Smith, C. W., Hamilton, K., Vasquez, B. J., and Leamon, R. J. (2006). Dependence of the dissipation range spectrum of interplanetary magnetic fluctuationson the rate of energy cascade. Astrophys. J. Lett. 645, L85–L88. doi:10.1086/506151

CrossRef Full Text | Google Scholar

Taylor, G. I. (1938). Production and dissipation of vorticity in a turbulent fluid. Proc. Roy. Soc. Lond. A. 164, 15–23. doi:10.1098/rspa.1938.0002

CrossRef Full Text | Google Scholar

Tsurutani, B. T., Gonzalez, W. D., Tang, F., Akasofu, S. I., and Smith, E. J. (1988). Origin of interplanetary southward magnetic fields responsible for major magnetic storms near solar maximum (1978-1979). J. Geophys. Res. Space. 93, 8519–8531. doi:10.1029/JA093iA08p08519

CrossRef Full Text | Google Scholar

Verscharen, D., Klein, K. G., and Maruca, B. A. (2019). The multi-scale nature of the solar wind. Living Rev. Sol. Phys. 16, 5. doi:10.1007/s41116-019-0021-0 |

PubMed Abstract | CrossRef Full Text | Google Scholar

Webb, D. F., and Howard, T. A. (2012). Coronal mass ejections: observations. Living Rev. Sol. Phys. 9, 3. doi:10.12942/lrsp-2012-3

CrossRef Full Text | Google Scholar

Wei, F., Liu, R., Fan, Q., and Feng, X. (2003a). Identification of the magnetic cloud boundary layers. J. Geophys. Res. C Oceans Atmos. 108, 1263. doi:10.1029/2002JA009511

CrossRef Full Text | Google Scholar

Wei, F., Liu, R., Feng, X., Zhong, D., and Yang, F. (2003b). Magnetic structures inside boundary layers of magnetic clouds. Geophys. Res. Lett. 30, 2283. doi:10.1029/2003GL018116

CrossRef Full Text | Google Scholar

Yordanova, E., Vörös, Z., Raptis, S., and Karlsson, T. (2020). Current sheet statistics in the magnetosheath. Front. Astron. Space Sci. 7, 2. doi:10.3389/fspas.2020.00002

CrossRef Full Text | Google Scholar

Zhou, Z., Zuo, P., Feng, X., Wang, Y., Jiang, C., and Song, X. (2019). Intermittencies and local heating in magnetic cloud boundary layers. Sol. Phys. 294, 149. doi:10.1007/s11207-019-1537-0

CrossRef Full Text | Google Scholar