
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
METHODS article
Front. Astron. Space Sci., 19 November 2020
Sec. Space Physics
Volume 7 - 2020 | https://doi.org/10.3389/fspas.2020.595929
This article is part of the Research TopicNew Challenges in Space Plasma Physics: Open Questions and Future Mission ConceptsView all 13 articles
Insufficiently accurate magnetic-field-line mapping between the aurora and the equatorial magnetosphere prevents us from determining the cause of many types of aurora. An important example is the longstanding question of how the magnetosphere drives low-latitude (growth-phase) auroral arcs: a large number of diverse generator mechanisms have been hypothesized but equatorial magnetospheric measurements cannot be unambiguously connected to arcs in the ionosphere, preventing the community from identifying the correct generator mechanisms. Here a mission concept is described to solve the magnetic-connection problem. From an equatorial instrumented spacecraft, a powerful energetic-electron beam is fired into the atmospheric loss cone resulting in an optical beam spot in the upper atmosphere that can be optically imaged from the ground, putting the magnetic connection of the equatorial spacecraft’s measurements into the context of the aurora. Multiple technical challenges that must be overcome for this mission concept are discussed: these include spacecraft charging, beam dynamics, beam stability, detection of the beam spot in the presence of aurora, and the safety of nearby spacecraft.
One of the unsolved problems of magnetospheric physics is the cause of the various types of auroral forms (Lanchester, 2017; Denton, 2019). This is particularly the case for auroral arcs (Denton et al., 2016; Borovsky et al., 2020a), where an unknown generator mechanism in the equatorial and near-equatorial magnetosphere extracts power and current from the magnetosphere to drive an auroral arc that dissipates energy in the ionosphere and atmosphere. This is sketched in Figure 1. A large number of diverse generator mechanisms have been hypothesized (e.g., Borovsky, 1993; Haerendel, 2011; Haerendel, 2012; Borovsky et al., 2020b) but equatorial magnetospheric measurements have not been unambiguously connected to arecs in the ionosphere, preventing scientists from identifying the correct generator mechanisms. For quiescent auroral arcs, even the form of energy that is extracted from the magnetosphere (magnetic energy, ion thermal energy, electron thermal energy, flow kinetic energy, …) is not known. The auroral community understands the near-Earth acceleration processes quite well (e.g., field-aligned potentials and Alfven-wave electron acceleration) but does not understand the equatorial energy-conversion processes driving these near-Earth processes; nor does the community understand the origin of the Alfvenic energy. The aurora is a manifestation of complex processes operating in the distant magnetosphere; the desire to use optical images of the aurora as television-screen view of magnetospheric processes (e.g., Akasofu, 1965; Mende, 2016a;
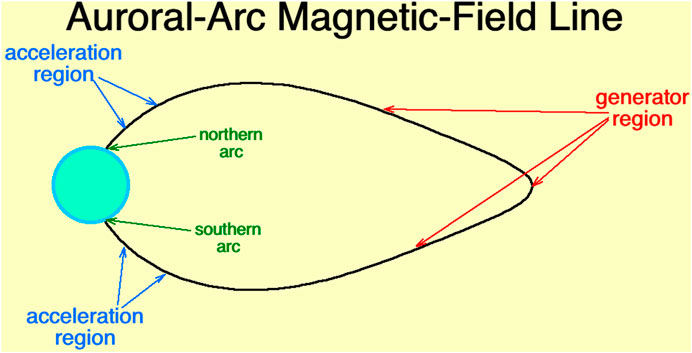
FIGURE 1. A sketch of the equatorial magnetospheric spacecraft firing an electron beam into the northern loss cone where the beam spot can be located by a ground-based camera. Conjugate northern and southern auroral arcs are noted in the upper atmosphere, the near-Earth acceleration regions for auroral-arc electrons are indicated, and the equatorial and near-equatorial regions where the auroral-arc generator mechanisms operate are noted.
Mende, 2016b) is impeded by not knowing what processes act to create the various auroral forms.
The foundation of the auroral-cause problem is an inability to unambiguously connect equatorial magnetospheric measurements to the various auroral forms. Static magnetic models of the magnetosphere (e.g., Tsyganenko, 1989; Tsyganenko and Sitnov, 2007; Sitnov et al., 2008) are not sufficiently accurate to magnetically map ionospheric features into the equatorial electron plasma sheet, particularly into the high-Reynolds-number magnetotail (Borovsky et al., 1997; Voros et al., 2004; El-Alaoui et al., 2010; Stepanova et al., 2011; El-Alaoui et al., 2012). Tests of the accuracy of magnetic-field-line mapping with the standard magnetic-field models have found very large errors for the nightside magnetosphere (Thomsen et al., 1996; Weiss et al., 1997; Ober et al., 2000; Shevchenko et al., 2010; Nishimura et al., 2011), even in the quasi-dipolar regions. For quiescent, low-latitude (growth-phase) auroral arcs there are two schools of thought about the equatorial location of the source of the arc: one school assume that the arc is in the dipolar portion of the nightside magnetosphere (e.g., McIlwain, 1975; Meng et al., 1979; Kremser et al., 1988; Mauk and Meng, 1991; Pulkkinen et al., 1991; Lu et al., 2000; Motoba et al., 2015) and a second school has the source of the arc in the stretched magnetotail (e.g., Yahnin et al., 1997; Yahnin et al., 1999; Birn et al., 2004a; Birn et al., 2004b; Birn et al., 2012; Sergeev et al., 2012; Hsieh and Otto, 2014): our ability to map magnetic-field lines in the nightside magnetosphere is insufficient to determine which is the correct location.
Developing the technology to attain accurate “Magnetosphere-to-Ionosphere Field-Line-Tracing Technology” has been cited as an “instrument development need and emerging technology” necessary for the future of space science (National Research Council, 2012). For several decades a team of researchers centered around Los Alamos National Laboratory has worked to develop a viable spacecraft mission to unambiguously determine the magnetic connection between equatorial-magnetospheric measurements and optical auroral observations (Borovsky et al., 1998; Borovsky, 2002; NASA, 2003; NASA, 2006; Delzanno et al., 2016; Borovsky and Delzanno, 2019; Borovsky et al., 2020c). That research team has consisted of auroral observers, magnetospheric instrument designers, optical physicists, ionospheric physicists, plasma physicists, spacecraft systems scientists, and two compact-accelerator design groups. That mission concept (and the technical challenges that it must overcome) is the focus of this brief report.
As sketched in Figure 1, the mission concept is for a magnetospheric spacecraft to carry an electron accelerator, to fire an electron beam along the magnetospheric magnetic field into the atmospheric loss cone, and with a ground-based camera to optically image the beam spot in the upper atmosphere. If that is accomplished then it is unambiguously known that a measurement taken by the magnetospheric spacecraft magnetically connects to the location in the ionosphere where the beam spot is imaged (Note that one can also approximately account for the eastward curvature-drift shift of the electron beam to more-accurately identify the magnetic location of the spacecraft.)
There are a number of challenges with this simple concept, and a good deal of research has been performed to overcome those difficulties: the technical challenges include spacecraft charging, beam aiming, beam dynamics and stability, and the detection of the beam spot in the presence of aurora. The major challenges and the associated mission-design tradeoffs are discussed in Sections 3 and 4.
Mission concepts have been examined that involve either (A) a single magnetospheric spacecraft making measurements and carrying an electron accelerator or (B) a swarm of measuring spacecraft with one member of the swarm carrying the electron accelerator. The spacecraft carrying the accelerator will also carry a power-storage system and a plasma contactor (for spacecraft-charging mitigation). The purpose of a swarm is to measure perpendicular-to-B gradients in the magnetosphere, which are important for diverting perpendicular magnetospheric currents into field-aligned currents, a critical part of the processes of driving of auroral arcs; the perpendicular gradients of interest are ion-pressure gradients, electron-pressure gradients, mass-density gradients, temperature gradients, flow shear, and gradients in the field strength, and the cross products of the various gradients are of interest (cf. eq. 12 of Strangeway 2012 or eq. 1 of Borovsky et al. 2020b). As analyzed in Borovsky et al. 2020c, the measurement requirements for quiescent auroral arcs in the equatorial magnetosphere appear in Table 1. For some theories of auroral arcs (e.g., Schindler and Birn, 2002; Birn et al., 2004a; Birn et al., 2012; Yang et al., 2013; Hsieh and Otto, 2014; Coroniti and Pritchett, 2014), Hall effects are important and so measuring both the perpendicular ion flow and the perpendicular electron flow is desirable; this can be accomplished by measuring both the ion flow and the electric field.
Two mission concepts have been considered. The first, Magnetosphere-Ionosphere Observatory (MIO) (Borovsky et al., 1998; Borovsky, 2002) consists of a tight (100’s of km) swarm of spacecraft in the equator at geosynchronous orbit (6.6 RE where RE is the radius of the Earth), with a single ground-based observatory in the vicinity of the swarm’s magnetic footpoints. In Figure 2 the location at 100 km altitude of the magnetic footpoint of a spacecraft in the geographic equator at geosynchronous orbit is estimated using the T89 (Tsyganenko, 1989) and the IGRF (Maus et al., 2005) magnetic-field models. The spacecraft is located in the “Alaska sector” of geosynchronous orbit where the geographic and geomagnetic equators are close to each other. The “observatory” in the figure is located at Eagle, Alaska (64o47´N,121o12´W). The red circles in Figure 2 are the angle from zenith where the 100 km altitude is seen by the observatory. In Figure 3 a similar plot is made for a spacecraft in the geographic equator at geosynchronous orbit in the “Scandinavian sector”. The ground-based observatory would have at least one camera dedicated to beam spot imaging, although, owing to uncertainty in the estimation of the magnetic-footpoint location using magnetic-field models, a network of beamspotting cameras around the observatory location will probably be needed. The observatory would have cameras for auroral imaging and other instrumentation for ionospheric physics. In the MIO mission concept a ground-based radar could be used to help locate the beam spot (e.g., Izhovkina et al., 1980; Uspensky et al., 1980; Zhulin et al., 1980; Marshall et al., 2014); additionally the radar could be used for physics studies with the electron beam as an element of upper-atmosphere experiments. Other instrumentation at the observatory could be ionosondes, an ionospheric heater, a wave transmitter, and a magnetometer network. An important aspect of the MIO mission concept is the ability to concentrate ground-based infrastructure at a single location.
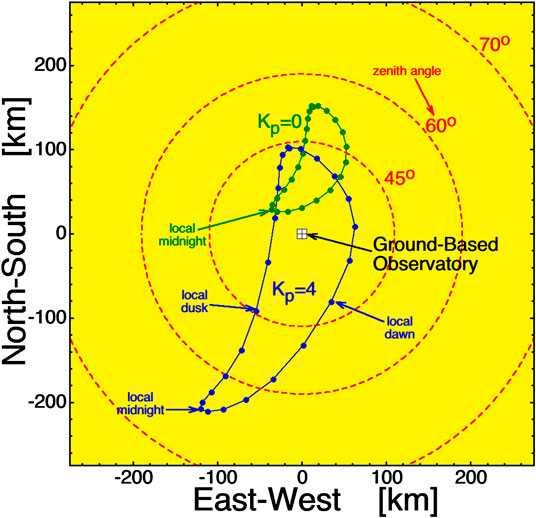
FIGURE 2. Looking down onto Alaska, the approximate location each hour of the day in Winter of the magnetic footpoint at 100 km altitude of a spacecraft in the geosynchronous orbit geographic equator is plotted. The green points are for Kp = 0 and the blue points are for Kp = 4. The observatory is located at Eagle, Alaska. The red circles are the zenith angle of the 100 km altitude as seen from the ground-based observatory.
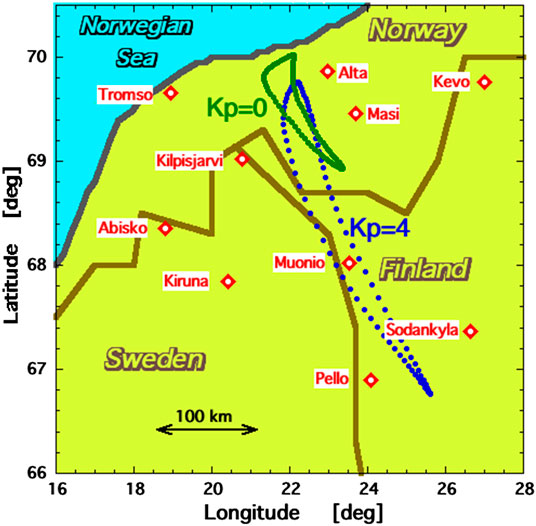
FIGURE 3. Looking down onto Scandinavia, the approximate location each hour of the day in Winter of the magnetic footpoint at 100 km altitude of a spacecraft in the geosynchronous orbit geographic equator is plotted. The green points are for Kp = 0 and the blue points are for Kp = 4.
The second mission concept, called connections (Borovsky et al., 2020c), has a swarm of spacecraft in an eccentric orbit and takes advantage of the Canadian TREx (Transition Region Explorer) (Spanswick et al., 2018) network of auroral cameras. Orbits are chosen with periods of 24 h so that the magnetic footpoint of the swarm wanders over Western Canada with a 24-h period. A 5 RE by 8 RE orbit was studied for its desirable footpoint locations (Borovsky et al., 2020c); note with an 8-RE apogee, the spacecraft swarm can magnetically map further downtail than 8 RE owing to orbital inclination and dipole tilt. The approximate magnetic-footpoint locations for the 5 RE by 8 RE 24-h orbit are shown as the blue curve in Figure 4 and the approximate footpoint locations of a 4 RE by 8 RE 24-h orbit are also shown as the yellow curve in Figure 4. In Figure 4 the field-of-views of the individual (Transition Region Explorer) TREx cameras are indicated as the red circles. An eccentric 24 h orbit can better sample the stretched-magnetotail portion of the nightside magnetosphere than can a circular geosynchronous orbit.
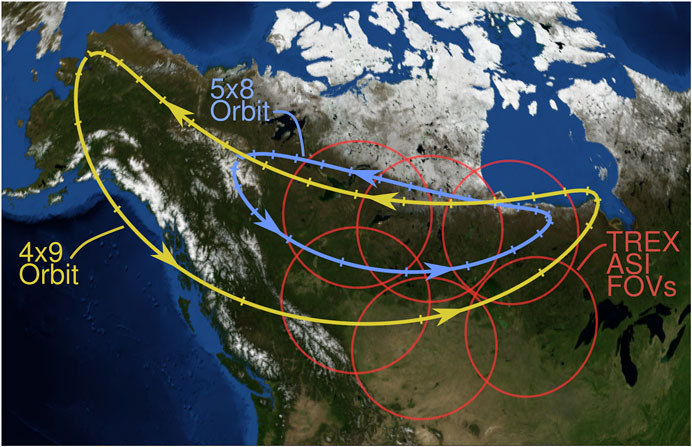
FIGURE 4. The estimated magnetic footpoints over Canada and the (Transition Region Explorer) TREx fields of view of two elliptical orbits: a 5 RE × 8 RE 24 hr-period orbit (blue) and a 4 RE × 9 RE 24 h orbit (yellow). The arrows on the footpoint curves are the temporal direction of the movement of the footpoint relative to the ground. The red circles are the fields-of-view at 100 km altitude of the present (Transition Region Explorer) TREx cameras. The low-latitude portions of the footpoint curves correspond to spacecraft perigee’s and the hash marks on the footpoint curves are at 1 h intervals in the 24 h orbits.
Four challenges that must be overcome for this magnetospheric-electron-beam mission concept are discussed in this section.
The most critical issue for operating a high-power electron beam from an ungrounded spacecraft in the tenuous magnetospheric plasma is spacecraft charging. The beam must deposit sufficient power (∼5 kW) in the upper atmosphere to be seen in the presence of ongoing aurora: if the beam energy is 50 keV then a beam current of 100 mA is required and if the beam energy is 1 MeV then a beam current of 5 mA is required. Firing the beam will result in a fraction of a Coulomb of negative being removed from the spacecraft in a time on the order of 1 s. A substantial computer-simulation-based research effort (Delzanno et al., 2015a; Delzanno et al., 2015b; Delzanno et al., 2016; Lucco Castello et al., 2018), supported by laboratory experiments (Miars et al., 2020), has demonstrated that the operation of a plasma contactor releasing a high-density charge-neutral plasma plume before and during a beam firing can greatly mitigate the charging of the spacecraft during the beam operation. Contrary to prior discussion of an emitted plasma plume acting to collect charge from the ambient plasma (e.g., Hastings and Blandino, 1989; Gerver et al., 1990; Williams and Wilbur, 1990; Davis et al., 1991), the research effort demonstrated that the surface of the plasma plume acts as an ion emitter, producing an ion current equal to the current of the electron beam.
Getting the electron beam from the spacecraft in the magnetospheric equator to the atmosphere involves aiming the beam into the atmospheric loss cone, fitting the beam within the loss cone, ensuring that the propagating beam is stable, and ensuring that the propagating beam electrons are not scattered by magnetospheric plasma waves.
Assuming that the magnetic-field strength in the auroral upper atmosphere is ∼0.5 Gauss, the radius of the atmospheric loss cone is 2.5o if the spacecraft is in a 100 nT field (e.g., in geosynchronous orbit) and the radius is 1.1o if the spacecraft is in a 20 nT field (e.g., in the stretched magnetotail). Knowledge of the direction of the ambient magnetic field to an accuracy of about 0.5o is needed, and an ability to aim the beam with an accuracy of about 0.5o is also needed. A complication to the aiming into the loss cone occurs if the electron beam is very energetic: finite-gyroradii effects shift the direction of the loss cone eastward (for electrons) from the local magnetic-field direction (Il’ina et al., 1993; Mozer, 1966; Porazik et al., 2014; Powis et al., 2019; Willard et al., 2019; Borovsky et al., 2020c). For a dipole magnetic field the magnitude of this eastward angular shift is easily predictable (Mozer, 1966; Borovsky et al., 2020c), but for non-dipolar magnetic fields this shift is not predictable and a space experiment would need to determine the loss-cone shift by repeatedly test firing the electron beam with differing amounts of eastward shift while ground cameras work to detect the beam spot. If onboard energy-storage resources are limited, this would not be desirable, and if the optical beam-spot-location image analysis is not instantaneous, this trial-and-error methodology cannot be implemented.
After the electron beam is emitted from the accelerator and as it travels along the Earth’s magnetic field, the nonzero net negative space charge of the beam acts to repulsively accelerate beam electrons transverse to the magnetic field; this transverse acceleration results in a spread of pitch angles of the beam electrons, turning a narrowly focused beam into a “shotgun” (cf. Appendix B of Borovsky, 2002). The space charge per unit length of the beam Q/L is given by Q/L = Ibeam/vbeam, where Ibeam is the current of the beam and vbeam is the speed of the beam. The beam power Pbeam is Pbeam = IbeamVbeam, where Vbeam is the beam voltage (accelerator energy). The speed of the beam increases with the beam voltage. For the same amount of beam power, a high-voltage beam has less current and higher speed, hence it has much less charge per unit length Q/L, and the space-charge transverse spreading of the beam is much less. Figure 2 of Borovsky et al., (2020c) looks at the maximum power of a beam that will stay within the loss cone as a function of the beam voltage. Greater beam voltage is very advantageous from the beam-spreading point of view.
Calculating the stability of the electron beam propagating through the ambient magnetospheric plasma is an ongoing area of research. Fortunately, the powerful electrostatic two-stream instabilities are greatly weakened by the fact that the beam has a small cylindrical cross section (Galvez and Borovsky, 1988). Relativistic electron beams have been calculated to be stable to electromagnetic hose and filamentation instabilities (Gilchrist et al., 2001; Neubert and Gilchrist, 2002; Neubert and Gilchrist, 2004). Experimentally, similar beams have been detected after long-distance propagation through the magnetosphere. Beams with energies of up to 40 keV were propagated long distances through the magnetosphere in the Echo series of experiments (Hallinan et al., 1990; Winckler, 1992) and electron beams of 27 keV, 0.5 Amp and 15 keV, 0.5 Amp on the two ARAKS experiments were propagated 8.2 RE through the magnetosphere without disruption (Pellat and Sagdeev, 1980; Lavergnat, 1982).
Finally, an issue of ongoing research is estimating the amount of pitch-angle scattering that beam electrons will undergo from the action of ambient magnetospheric plasma waves when the spacecraft is in various locations of the magnetosphere during different levels of geomagnetic activity. The degree of pitch-angle scattering will vary significantly with the beam voltage. At higher (relativistic) beam voltages electromagnetic ion-cyclotron (EMIC) waves and whistler-mode chorus are of concern, as is field-line curvature acting to scatter the beam. At lower beam voltages whistler-mode chorus and electromagnetic electron-cyclotron waves are of concern. Section 6.3 of Borovsky et al. (2020c) provides some preliminary estimates of the amount of pitch-angle scattering of beam electrons in the nightside magnetosphere: those estimates are favorable for the beam surviving from the equator to the atmosphere. Note also that (electromagnetic ion-cyclotron) EMIC waves are prevalent in the noon and afternoon sectors and not prevalent in the nightside auroral zone (Clausen et al., 2011; Usanova et al., 2012).
To produce a beam spot that is optically detectable from the ground in the presence of active aurora, a beam power of 5 kW or more needs to be deposited in the atmosphere. Each 1 kW of beam power results in about 1.1 W of 4278 Å emission [Bryant et al., 1970) and about 3 W of 3914 Å emission. The spectral lines emitted by the beam spot will be the same spectral lines as emitted by the electron aurora. The beam spot will be cylindrical, 10’s of m in diameter across the magnetic field and ∼10 km long along the magnetic field; this will produce a multi-pixel streak in the camera images. The technology of optically detecting the illuminated footpoint from the ground has been verified: electron beams with less than 5 kW of power have been optically detected from the ground after they have propagated through the magnetosphere into the upper atmosphere. Two examples are the detection of a 3.4 kW beam by Davis et al. (1980) during the NASA 12.18 NE beam experiment and the detection of a 2.4 kW beam in the Echo-4 experiment by Hallinan et al. (1990) using a ground-based image-orthicon television. In the Echo-4 experiment, the beamspot was imaged after the beam had propagated twice through the magnetosphere at L = 6.5. To identify the beam spot in the presence of aurora, an on-off temporal blink pattern of beam firings must be used along with temporal processing of the camera images to locate the blinking streak. If the mission has a “scientist in the loop” commanding the firing of the beam as the beam spot crosses critical auroral features, the image processing must be automatic and prompt.
For beams of 10’s of keV the beam spot altitude is around 90–100 km; for beams of 1 MeV the beam spot altitude is around 60 km. If the beam has a narrow spread of pitch angles, the beam spot altitude can be raised by aiming the beam away from the center of the loss cone. At 60 km there is some collisional quenching of the 3914 and 4278 Å prompt emission bands (Marshall et al., 2014; Borovsky et al., 2020c), so more beam power is required to image the beam spot. Unless it is overhead of the camera, a beam spot at 60 km altitude will also suffer more extinction from Rayleigh scattering (Penndorf, 1957; International Telephone and Telegraph Corporation, 1977), again requiring more beam power.
Since there are other spacecraft in orbit around the Earth, an important aspect to consider is whether the electron beam emitted could intercept another spacecraft and induce catastrophic charging on it. After the beam is emitted, it expands and contracts periodically with time due to space-charge and Lorentz forces as well as due to spreading in pitch angle and energy due to the electron accelerator design (Borovsky, 2002; Powis et al., 2019). As a result the beam current density will change significantly along the beam path. Any mission design will need a beam-safety plan. To estimate the beam flux to another spacecraft, the beam dynamics must be modeled and beam-connection dwell times with other spacecraft must be calculated using orbital considerations.
From preliminary calculations of the dynamics of a 1 MeV 10 mA beam in the dipolar magnetosphere with a criterion that the current flux to a second spacecraft must be less than 10−6 A/m2 yields a “current safety distance” of 0.5 RE along the Earth’s magnetic field from the accelerator to another spacecraft. In the tenuous plasma of the magnetosphere an electron beam flux of 10−6 A/m2 would only induce ∼1 kV of spacecraft charging to the second spacecraft.
There are many tradeoffs that must be made in designing a mission. A major tradeoff is whether to have a single-observatory geosynchronous mission or an elliptic orbit distributed-camera-network mission (cf. Sect. 2). Two other major tradeoffs are discussed below.
The accelerator technology for relativistic (∼MeV) vs. nonrelativistic (10’s-of-keV) beams differs:10’s-of-keV beams can be produced with direct-current electron guns that accelerate the electrons through a static potential drop whereas MeV beams must be produced with a radio-frequency electron accelerator that accelerates the electrons with a propagating wavefront. Direct-current electron guns with 10’s of keV energies and 10’s of kW powers have been flown in space numerous times (Winckler et al., 1975; O’Neil et al., 1978; Rappaport et al., 1993; Prech et al., 1995; McNutt et al., 1995; Prech et al., 2018), while a radio-frequency accelerator has only been flown once (a 1-MeV H− beam) (Pongratz, 2018). Designs for compact space-based relativistic-electron accelerators are underway (Lewellen et al., 2019) and spaceflight tests of the accelerator concepts are planned (Reeves et al., 2020).
The advantages of a relativistic electron accelerator over a 10’s-of-keV electron gun are 1) lower beam space charge for the same beam power, resulting in a beam with less angular spread to more-easily fit into the loss cone, and 2) lower total charge removed from the spacecraft in a beam pulse, requiring less-stringent spacecraft-charging mitigation. For beam energies below a few 10’s of keV, the space charge of the beam drastically limits the amount of beam power that can be delivered into the loss cone.
The disadvantages of a relativistic accelerator compared with a 10’s-of-keV electron gun are 1) a lower-altitude beam spot subject to quenching, 2) for a non-dipole magnetic field the location of the loss cone is not known, 3) more difficulty in steering the beam mechanically or electrostatically, 4) there can be accelerator-thermal issues that de-tune the radio-frequency cavities after several beam firings, and 5) there are more-critical safety considerations for other spacecraft. For beams with energies above about 1 MeV, the loss-cone shift becomes severe.
The relativistic vs. nonrelativistic beams will also have tradeoffs concerning beam stability and scattering and the accelerator and gun will have tradeoffs concerning the power-conversion efficiency and mass of the required energy-storage system. For any mission with a powerful electron beam, energy storage will require substantial spacecraft mass.
A spinning spacecraft is better, in general, for measuring plasma properties and fields. Spinning has the distinct advantage that offsets in the magnetometer can be corrected, resulting in a more-accurate determination of the magnetic field direction for beam aiming. If a relativistic accelerator is used, which will have a length of 1 m or so, mechanically steering the accelerator into the moving loss cone seen by a spinning spacecraft will be challenging. At relativistic energies, electrostatic steering of the electron beam after it exits the accelerator is very limited in angle.
A 3-axis stabilized spacecraft makes it easier to direct the beam into the loss cone, particularly if a long (0.5-s or 1-s) beam pulse is used. A de-spun platform on a spinning spacecraft is another option.
Note that if an electron drift instrument (Torbert et al., 2016) is used to measure the electric field, that instrument works in concert with a magnetometer and magnetometer offsets can be detected and corrected, even on a non-spinning spacecraft.
Most of the work on the development of this magnetospheric-electron-beam mission concept has been motivated by the desire to understand the generator mechanisms of low-latitude quiescent auroral arcs (Borovsky, 2002; Delzanno et al., 2016; Borovsky et al., 2020c). However, such a beam experiment could be used to explore a wide variety of scientific problems.
The magnetospheric causes of various other types of aurora could be investigated if there is appropriate instrumentation on the magnetospheric accelerator spacecraft or the swarm spacecraft. Discerning the causes of other aurora may require wave measurements, cold-ion and cold-electron measurements, and particle-anisotropy measurements: examples of this would be the diffuse and pulsating aurora. Other auroral forms include undulations of the equatorward auroral boundary, omega bands, torches, black aurora, and patches. Investigating high-latitude auroral forms such as streamers or high-latitude Alfvenic arcs will require a spacecraft orbit that is eccentric.
The mapping of boundaries and regions between the magnetosphere and the ionosphere could be unambiguously performed with a magnetospheric-electron-beam spacecraft, provided it is instrumented to identify those boundaries and regions. Of interest are the mapping to the ionosphere of a) the inner edge of the electron plasma sheet, b) the remnant layer, c) the plasmapause, d) detached plasmasphere regions, e) ion-isotropy boundaries, f) substorm-injection boundaries, and g) the Earthward edge of the cross-tail current sheet. The magnetospheric boundaries (a)–(f) are clearly seen at the geosynchronous-orbit equator: the magnetic field at geosynchronous orbit often exhibits a stretched-tail morphology at local midningt (cf. Figure 11 of Borovsky and Denton (2010)) but boundary (g) is ambiguous to detect in the magnetosphere. Conversely, the mapping of ionospheric troughs out into the magnetosphere is of interest.
The magnetic connections between magnetospheric and ionospheric processes such as SAPS, SAID, STEVE, convection reversals, and bursty bulk flows could be determined with certainty. An eccentric orbit provides more-regular access to these various phenomena, in particular to bursty bulk flows.
Magnetosphere-ionosphere coupling can be studied by comparing temporal onsets of convection in the magnetosphere (via spacecraft flow measurements) with temporal onsets of ionospheric convection (measured, for example, by the SuperDARN radar network (Greenwald et al., 1995; Baker et al., 2011; Bristow et al., 2016)) and could answer questions about when and where the magnetosphere drives ionospheric convection and when and where the ionosphere drives magnetospheric convection.
Finally, there is an extensive literature describing how energetic electron beams could be used to study mesospheric chemistry (Neubert et al., 1990; Marshall et al., 2019), atmospheric electricity (Banks et al., 1990; Neubert et al., 1990; Neubert and Gilchrist, 2004; Marshall et al., 2019; Sanchez et al., 2019; Borovsky et al., 2020c), atmospheric electron-attachment physics and electrical conductivity (Banks et al., 1990; Neubert et al., 1996; Neubert and Gilchrist, 2004; Borovsky, 2017), and plasma-wave generation (Carlsten et al., 2018; Delzanno and Roytershteyn, 2019; Reeves et al., 2020).
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.
All authors performed research on this mission concept and contributed information for the manuscript.
Work at the Space Science Institute was supported by the NASA Heliophysics LWS program via award NNX16AB75G, and by the NSF GEM Program via grant AGS-2027569, by the NASA Heliophysics Guest Investigator Program via award NNX17AB71G, by the NSF SHINE program via grant AGS-1723416.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors thank Phil Barker. Joachim Birn, Bruce Carlsten, Mike Collier, Eric Donovan, Eric Dors, Phil Fernandes, Reiner Friedel, Brian Gilchrist, Ray Greenwald, Herb Funsten, Gerhard Haerendel, Mike Holloway, Larry Kepko, Dave Klumpar, Dave Knudsen, Brian Larsen, Omar Leon, John Lewellen, Grant Mairs, Bob Marshall, Barry Mauk, Dave McComas, Liz McDonald, Steve Mende, Tom Moore, Dinh Nguryen, Jeff Nielsen, Craig Pollock, Tuija Pulkkinen, John Raitt, Geoff Reeves, Vadim Roytershteyn, Mike Ruohoniemi, Ennio Sanchez, Howard Singer, Jan Sojka, Emma Spanswick, Steve Storms, Bob Strangeway, Don Thompson, Michelle Thomsen. Roy Torbert, Maria Usanova, Hans Vaith, and Brent White for their assistance in developing this mission concept and in overcoming its challenges. JEB was supported by the NASA Heliophysics LWS program via award NNX16AB75G, by the NSF GEM Program via grant AGS-2027569, by the NASA Heliophysics Guest Investigator Program via award NNX17AB71G, and by the NSF SHINE program via grant AGS-1723416. GLD was supported by the Los Alamos National Laboratory (LANL) Directed Research and Development (LDRD) Program under Project 20170423ER. LANL is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (DOE) under Contract 89233218CNA000001.
Baker, J. B. H., Ruohoniemi, J. M., Ribiro, A. J., Clausen, L. B. N., Greenwald, R. A., Frissell, N. A., et al. (2011). SuperDARN ionospheric space weather. IEEE A&E Systems Mag. 26:30–34.
Banks, P. M., Fraser-Smith, A. C., and Gilchrist, B. E. (1990). Ionospheric modification using relativistic electron beams. AGARD Conference Proceedings 485, (Loughton, United Kingdom: Specialised Printing Services Limited), 22-1–22-18.
Birn, J., Dorelli, J. C., Hesse, M., and Schindler, K. (2004a). Thin current sheets and loss of equilibrium: Three-dimensional theory and simulations. J. Geophys. Res. 109, A02217. doi:10.1029/2003ja010303
Birn, J., Schindler, K., and Hesse, M. (2012). Magnetotail Aurora Connection: The Role of Thin Current Sheets. Geophys. Monogr. Ser. 197, 337. doi:10.1029/2011gm001182
Birn, J., Schindler, K., and Hesse, M. (2004b). Magnetotail aurora connections: The role of thin current sheets. Geophys. Monogr. Ser. 197, 337. doi:10.1029%2F2011GM001182
Borovsky, J. E. (1993). Auroral arc thicknesses as predicted by various theories. J. Geophys. Res. 98, 6101. doi:10.1029/92ja02242
Borovsky, J. E., Birn, J., Echim, M. M., Fujita, S., Lysak, R. L., Knudsen, D. J., et al. (2020b). Quiescent discrete auroral arcs: A review of magnetospheric generator mechanisms, Space Sci. Rev. 216, 1. doi:10.1007/s11214-019-0619-5
Borovsky, J. E., Delzanno, G. L., Dors, E. E., Thomsen, M. F., Sanchez, E. R., Henderson, M. G., et al. (2020c). Solving the auroral-arc-generator question by using an electron beam to unambiguously connect critical magnetospheric measurements to auroral images. J. Atmos. Sol. Terr. Phys. 206, 105310. doi:10.1016/j.jastp.2020.105310
Borovsky, J. E., Delzanno, G. L., Valdivia, J. A., Moya, P. S., Stepanova, M., Birn, J., et al. (2020a). Outstanding questions in magnetospheric plasma physics: The Pollenzo view. J. Atmos. Sol. Terr. Phys. 208, 105377. doi:10.1016/j.jastp.2020.105377
Borovsky, J. E., and Delzanno, J. L. (2019). Space active experiments: The future. Front. Astron. Space Sci. 6, 31. doi:10.3389/fspas.2019.00031
Borovsky, J. E., and Denton, M. H. (2010). On the heating of the outer radiation belt to produce high fluxes of relativistic electrons: Measured heating rates at geosynchronous orbit for high-speed stream-driven storms. J. Geophys. Res. 115, A12206. doi:10.1029/2010ja015342
Borovsky, J. E. (2017). Electrical conductivity channels in the atmosphere produced by relativistic-electron microbursts from the magnetosphere. J. Atmos. Sol. Terr. Phys. 155, 22. doi:10.1016/j.jastp.2017.01.004
Borovsky, J. E., Elphic, R. C., Funsten, H. O., and Thomsen, M. F. (1997). The Earth's plasma sheet as a laboratory for flow turbulence in high-β MHD. J. Plasma Phys. 57, 1. doi:10.1017/s0022377896005259
Borovsky, J. E., Greenwald, R. A., Hallinan, T. J., Horwitz, J. L., Kelley, M. C., Klumpar, D. M., et al. (1998). The magnetosphere-ionosphere facility: a satellite cluster in geosynchronous orbit connected to ground-based observatories. Eos Trans. Amer. Geophys Union. 79 (45), F744.
Borovsky, J. E., (2002). The Magnetosphere-Ionosphere Observatory (MIO). Los Alamos National Laboratory https://www.lanl.gov/csse/MIOwriteup.pdf.
Bristow, W. A., Hampton, D. L., and Otto, A. (2016). High‐spatial‐resolution velocity measurements derived using Local Divergence‐Free Fitting of SuperDARN observations J. Geophys. Res. Space Phys. 121, 1349. doi:10.1002/2015ja021862
Bryant, D. A., Courtier, G. M., Skovli, G., Lindalen, H. R., Aarsnes, K., and Måseide, K. (1970). Electron density and electron flux in a glow aurora. J. Atmos. Terr. Phys. 32, 1695. doi:10.1016/0021-9169(70)90175-3
Carlsten, B. E., Colestock, P. L., Cunningham, G. S., Delzanno, G. L., Dors, E. E., Holloway, M. A., et al. (2018). Radiation-belt remediation using space-based antennas and electron beams. IEEE Trans. Plasma Sci. 47, 2045. doi:10.1109%2FTPS.2019.2910829
Clausen, L. B. N., Baker, J. B. H., Ruohoniemi, J. M., and Singer, H. J. (2011). ULF wave characteristics at geosynchronous orbit during the recovery phase of geomagnetic storms associated with strong electron acceleration. J. Geophys. Res. Space Phys. 116, A09203. doi:10.1029/2011ja016823
Coroniti, F. V., and Pritchett, P. L. (2014). The quiet evening auroral arc and the structure of the growth phase near-Earth plasma sheet. J. Geophys. Res. Space Phys. 119, 1827. doi:10.1002/2013ja019435
Davis, T. N., Hess, W. N., Trichel, M. C., Wescott, E. M., Hallinan, T. J., Stenbaek-Nielsen, H. C., et al. (1980). Artificial aurora conjugate to a rocket-borne electron accelerator. J. Geophys. Res. 85, 1722. doi:10.1029/ja085ia04p01722
Davis, V. A., Katz, I., Mandell, M. J., and Parks, D. E. (1991). Model of electron collecting plasma contactors. J. Spacecr. Rockets. 28, 292–298. doi:10.2514/3.26243
Delzanno, G. L., Borovsky, J. E., Thomsen, M. F., Gilchrist, B. E., and Sanchez, E. (2016). Can an electron gun solve the outstanding problem of magnetosphere-ionosphere connectivity?. J. Geophys. Res. Space Phys. 121, 6769. doi:10.1002/2016ja022728
Delzanno, G. L., Borovsky, J. E., Thomsen, M. F., and Moulton, J. D. (2015a). Future beam experiments in the magnetosphere with plasma contactors: The electron collection and ion emission routes. J. Geophys. Res. Space Phys. 120, 3588. doi:10.1002/2014ja020683
Delzanno, G. L., Borovsky, J. E., Thomsen, M. F., Moulton, J. D., and MacDonald, E. A. (2015b). Future beam experiments in the magnetosphere with plasma contactors: How do we get the charge off the spacecraft?. J. Geophys. Res. Space Phys. 120, 3647. doi:10.1002/2014ja020608
Delzanno, G. L., and Roytershteyn, V. (2019). High‐Frequency Plasma Waves and Pitch Angle Scattering Induced by Pulsed electron Beams. J. Geophys. Res. Space Phys. 124, 7543. doi:10.1029/2019ja027046
Denton, M. H., Borovsky, J. E., Stepanova, M., and Valdivia, J. A. (2016). Unsolved Problems of Magnetospheric Physics. J. Geophys. Res. 121, 10783. doi:10.1002/2016ja023362
Denton, M. H. (2019). Some unsolved problems of magnetospheric physics, in Magnetospheres in the Solar System. Washington, DC: AGU Books, in press.
El-Alaoui, M., Ashour-Abdalla, M., Richard, R. L., Goldstein, M. L., Weygand, J. M., and Walker, R. J. (2010). Global magnetohydrodynamic simulation of reconnection and turbulence in the plasma sheet. J. Geophys. Res. 115, A12236. doi:10.1029/2010ja015653
El-Alaoui, M., Richard, R. L., Walker, R. J., Goldstein, M. L., R. J., , et al. (2012). Turbulence in a global magnetohydrodynamic simulation of the Earth's magnetosphere during northward and southward interplanetary magnetic field. Nonlinear Process Geophys. 19, 165. doi:10.5194/npg-19-165-2012
Galvez, M., and Borovsky, J. E. (1988). The electrostatic two-stream instability driven by slab-shaped and cylindrical beams injected into plasmas. Phys. Fluids. 31, 857. doi:10.1063/1.866767
Gerver, M. J., Hastings, D. E., and Oberhardt, M. R. (1990). Theory of plasma contactors in ground-based experiments and low earth orbit. J. Spacecr. Rockets., 27 (4), 391. doi:10.2514/3.26156
Gilchrist, B. E., Khazanov, G., Krause, L., and Neubert, T. (2001). Study of Relativistic electron Beam Propagation in the Atmosphere-Ionosphere-Magnetosphere. Tech. Rep. AFRL-VS-TR-2001-1505, Air Force Research Lab, Hanscom AFB, MA.
Greenwald, R. A., Baker, K. B., Dudeney, J. R., Pinnock, M., Jones, T. B., Thomas, E. C., et al. (1995). DARN/SuperDARN. Space Sci. Rev. 71, 761. doi:10.1007/bf00751350
Haerendel, G. (2012). Auroral Generators: A Survey. Geophys. Monogr. Ser. 197, 347. doi:10.1029/2011gm001162
Haerendel, G. (2011). Six auroral generators: A review. J. Geophys. Res. Atmos. 116, 347–354. doi:10.1029/2010ja016425
Hallinan, T. J., Winckler, J., Malcolm, P., Stenbaek-Nielsen, H. C., and Baldridge, J. (1990). Conjugate echoes of artificially injected electron beams detected optically by means of new image processing. J. Geophys. Res. Space Phys. 95, 6519. doi:10.1029/ja095ia05p06519
Hastings, D. E., and Blandino, J. (1989). Bounds on Current Collection From the Far Field by Plasma Clouds in the Ionosphere. J. Geophys. Res. 94, 2737. doi:10.1029/ja094ia03p02737
Hsieh, M.-S., and Otto, A. (2014). The influence of magnetic flux depletion on the magnetotail and auroral morphology during the substorm growth phase. J. Geophys. Res. Space Physics. 119, 3430. doi:10.1002/2013ja019459
Il’ina, A. N., Il’in, V. D., Kuznetsov, S. N., Yushkov, B. Y., Amirkhanov, I. V., and Il’in, I. V. (1993). Model of nonadiabatic charged-particle motion in the field of a magnetic dipole. J. Exp. Theor. Phys. Lett. 77, 246.
International Telephone and Telegraph Corporation (1977). Reference Data for Radio Engineers. Sect. 28, Fig. 32, Howard Sams and Co., Indianapolis, For. Ind.
Izhovkina, N. I., JKosik, J. C., Pyatsi, A. K., Reme, H., Saint-Marc, A., Sverdlov, J. L., et al. (1980). Comparison between experimental and theoretical conjugate points locations in the Araks experiments. Ann. Geophys. 36, 319.
Kremser, G., Korth, A., Ullaland, S. L., Perraut, S., Roux, A., Pedersen, A., et al. (1988). Field-aligned beams of energetic electrons (16 keV ≤E≤ 80 keV) observed at geosynchronous orbit at substorm onsets. J. Geophys. Res. 93, 14453. doi:10.1029/ja093ia12p14453
Lanchester, B. (2017). Some remaining mysteries in the aurora. Astron. Geophys. 58, 3–17. doi:10.1093/astrogeo/atx098
Lavergnat, J. (1982). The French-Soviet experiment ARAKS: Main results. in Artificial Particle Beams in Space Plasma Studies, Grandal, B. (ed.), pg. 87, Plenum , New York.
Lewellen, J. W., Buechler, C. B., Carlsten, B. F., Dale, G. E., Holloway, M. A., Patrick, D., et al. (2019). Space borne electron accelerator design. Front. Astron. Space Sci. 6, 35. doi:10.3389/fspas.2019.00035
Lu, G., Brittnacher, M., Parks, G., and Lummerzheim, D. (2000). On the magnetospheric source regions of substorm-related field-aligned currents and auroral precipitation. J. Geophys. Res. Atmos. 105, 18483. doi:10.1029/1999ja000365
Lucco Castello, F., Delzanno, G. L., Borovsky, J. E., Miars, G., Leon, O., and Gilchrist, B. E. (2018). Spacecraft-charging mitigation of a high-power electron beam emitted by a magnetospheric spacecraft: simple theoretical model for the transient of the spacecraft potential. J. Geophys. Res. Space Phys. 123. 6424. doi:10.1029%2F1999JA000365
Marshall, R. A., Xu, W., Kero, A., Kabirzadeh, R., and Sanchez, E. (2019). Atmospheric effects of a relativistic electron beam injected from above: chemistry, electrodynamics, and radio scattering. Front. Astron. Space Sci. 6, 6. doi:10.3389/fspas.2019.00006
Marshall, R. A., Nicolls, M., Sanchez, E., Lehtinen, N. G., and Neilson, J. (2014). Diagnostics of an artificial relativistic electron beam interacting with the atmosphere. J. Geophys. Res. Space Phys. 119, 8560. doi:10.1002/2014ja020427
Mauk, B. H., and Meng, C.-I. (1991). The aurora and middle magnetospheric processes, in Auroral Physics, edited by C.-I. Meng, M. J. Rycroft, and L. A. Frank (Cambridge: Cambridge Press), 223.
Maus, S., Macmillan, S., Chrnova, T., Choi, S., Dater, D., Golovkov, V., et al. (2005). The 10th-generation International Geomagnetic Reference Field. Geophys. J. Int. 161, 561.
McIlwain, C. E. (1975). “Auroral electron beams near the magnetic equator,” in Physics of the Hot Plasma in the Magnetosphere, Editor B. Hultqvist and L. Stenflo (New York, NY: Plenum), 91.
McNutt, R. L., Rieder, R. J., Keneshea, T. J., LePage, A. J., Rappaport, S. A., and Paulsen, D. E. (1995). Energy deposition in the upper atmosphere in the EXCEDE III experiment. Adv. Space Res. 15 (12), 13. doi:10.1016/0273-1177(95)00002-v
Mende, S. B. (2016a). Observing the magnetosphere through global auroral imaging: 1. Observables. J. Geophys. Res. Space Phys. 121, 10623. doi:10.1002/2016ja022558
Mende, S. B. (2016b). Observing the magnetosphere through global auroral imaging: 2. Observing techniques. J. Geophys. Res. Space Phys. 121, 10638. doi:10.1002/2016ja022607
Meng, C.-I., Mauk, B., and McIlwain, C. E. (1979). Electron precipitation of evening diffuse aurora and its conjugate electron fluxes near the magnetospheric equator. J. Geophys. Res. 84, 2545. doi:10.1029/ja084ia06p02545
Miars, G. C., Delzanno, G. L., Gilchrist, B. E., Leon, O., and Lucco Castello, F. (2020). Ion Emission from a Positively Biased Hollow Cathode Plasma, IEEE Trans. Plasma Sci. 48, 2693. doi:10.1109/tps.2020.3004553
Motoba, T., Ohtani, S., Anderson, B. J., Korth, H., Mitchell, D., Lanzerotti, L. J., et al. (2015). On the formation and origin of substorm growth phase/onset auroral arcs inferred from conjugate space-ground observations. J. Geophys. Res. Space Phys. 120, 8707. doi:10.1002/2015ja021676
Mozer, F. S. (1966). Proton trajectories in the radiation belts. J. Geophys. Res. 71, 2701. doi:10.1029/jz071i011p02701
NASA (2006). Heliophysics: The New Science of the Sun-Solar System Connection: Recommended Roadmap for Science and Technology 2005-2035. Washington, DC: National Aereonautics and Space Administration.
NASA, (2003). Sun-Earth Connection Roadmap 2003-2028, http://www.dept.aoe.vt.edu/∼cdhall/courses/aoe4065/NASADesignSPs/SEC_2003_roadmap_full.pdf.
National Research Council (2012). Magnetosphere-to-ionosphere field-line tracing technology, in Solar and Space Physics: A Science for a Technological Society, (Washington, D. C: National Academies Press), 333–334.
Neubert, T., Banks, P. M., Gilchrist, B. E., Fraser-Smith, A. C., Williamson, P. R., Raitt, W. J., et al. (1990). The interaction of an artificial electron beam with the Earth's upper atmosphere: Effects on spacecraft charging and the near-plasma environment. J. Geophys. Res. 95, 12209. doi:10.1029/ja095ia08p12209
Neubert, T., and Gilchrist, B. E. (2002). Particle simulations of relativistic electron beam injection from spacecraft. J. Geophys. Res. 107, 1167. doi:10.1029/2001ja900102
Neubert, T., and Gilchrist, B. E. (2004). Relativistic electron beam injection from spacecraft: performance and applications. Adv. Space Res. 34, 2409. doi:10.1016/j.asr.2003.08.081
Neubert, T., Gilchrist, B., Wilderman, S., Habash, L., and Wang, H. J. (1996). Relativistic electron beam propagation in the Earth's atmosphere: Modeling results. Geophys. Res. Lett. 23, 1009. doi:10.1029/96gl00247
Nishimura, Y., Bortnik, J., Li, W., Thorne, R. M., Lyons, L. R., Angelopoulos, V., et al. (2011). Estimation of magnetic field mapping accuracy using the pulsating aurora-chorus connection. Geophys. Res. Lett. 38, L14110. doi:10.1029/2011gl048281
O’Neil, R. R., Shepherd, O., Reidy, W. P., Carpenter, J. W., Davis, T. N., Newell, D., et al. (1978). Excede 2 test, an artificial auroral experiment: ground-based optical measurements. J. Geophys. Res. 83, 3281. doi:10.1029/JA083iA07p03281
Ober, D. M., Maynard, N. C., Burke, W. J., Moen, J., Egeland, A., Sandholt, P. E., et al. (2000). Mapping prenoon auroral structures to the magnetosphere. J. Geophys. Res. 105, 27519. doi:10.1029/2000ja000009
Pellat, R., and Sagdeev, R. Z. (1980). Concluding remarks on the ARAKS experiments. Ann. Geophys. 36, 443.
Penndorf, R. (1957). Tables of the Refractive Index for Standard Air and the Rayleigh Scattering Coefficient for the Spectral Region between 02 and 200 μ and Their Application to Atmospheric Optics. J. Opt. Soc. Am. 47, 176. doi:10.1364/josa.47.000176
Pongratz, M. B. (2018). History of Los Alamos participation in active experiments in space. Front. Phys. 6, 144. doi:10.3389/fphy.2018.00144
Porazik, P., Johnson, J. R., Kaganovich, I., and Sanchez, E. (2014). Modification of the loss cone for energetic particles. Geophys. Res. Lett. 41, 8107. doi:10.1002/2014gl061869
Powis, A. T., Porazik, P., Greklek-Mckeon, M., Amin, K., Shaw, D., Kaganovich, I. D., et al. (2019). Evolution of a relativistic electron beam for tracing magnetospheric field lines. Front. Astron. Space Phys. 6, 69. doi:10.3389/fspas.2019.00069
Prech, L., Nemecek, Z., Šafránková, J., Šimunek, J., Truhlík, V., and Shutte, N. M. (1995). Response of the electron energy distribution to an artificially emitted electron beam: APEX experiment. Adv. Space Res. 15 (12), 33. doi:10.1016/0273-1177(95)00007-2
Prech, L., Ruzhin, Y. Y., Dokukin, V. S., Nemecek, Z., and Safrankova, J. (2018). Overview of APEX Project results. Front. Astron. Space Sci. 5, 46. doi:10.3389/fspas.2018.00046
Pulkkinen, T. I., Koskinen, H. E. J., and Pellinen, R. J. (1991). Mapping of auroral arcs during substorm growth phase. J. Geophys. Res. 96, 21087. doi:10.1029/91ja01960
Rappaport, S. A., Rieder, R. J., Reidy, W. P., McNutt, R. L., Atkinson, J. J., and Paulsen, D. E. (1993). Remote X ray measurements of the electron beam from the EXCEDE III Experiment. J. Geophys. Res. 98, 19093. doi:10.1029/93ja01154
Reeves, G., Delzanno, G. L., Fernandez, P., Yakymenko, K., Carlsten, B., Lewellen, J., et al. (2020). The Beam Plasma Interactions Experiment: An active experiment using pulsed electron beams. Front. Astron. Space Sci. 7, 23. doi:10.3389/fspas.2020.00023
Sanchez, E. R., Powis, A. T., Kagonovich, I. D., Marshall, R., Porazik, P., Johnson, J., et al. (2019). Relativistic particle beams as a resournce to solve outstanding problems in space physics. Front. Astron. Space Sci. 6, 71. doi:10.3389/fspas.2019.00071
Schindler, K., and Birn, J. (2002). Models of two-dimensional embedded thin current sheets from Vlasov theory. J. Geophys. Res. 107, SMP20. doi:10.1029/2001ja000304
Sergeev, V. A., Chernyaev, I. A., Dubyagin, S. V., Miyashita, Y., Angelopoulos, V., Boakes, P. D., et al. (2012). Energetic particle injections to geostationary orbit: Relationship to flow bursts and magnetospheric state. J. Geophys. Res. 117, A10207. doi:10.1029/2011ja017154
Shevchenko, I. G., Sergeev, V., Kubyshkina, M., Angelopoulos, V., Glassmeier, K. H., and Singer, H. J. (2010). Estimation of magnetosphere-ionosphere mapping accuracy using isotropy boundary and THEMIS observations. J. Geophys. Res. 115, A11206. doi:10.1029/2010ja015354
Sitnov, M. I., Tsyganenko, N. A., Ukhorskiy, A. Y., and Brandt, P. C. (2008). Dynamical data-based modeling of the storm-time geomagnetic field with enhanced spatial resolution. J. Geophys. Res. 113, A07218. doi:10.1029/2007ja013003
Spanswick, E., Donovan, E., Liang, J., Weatherwax, A. T., Skone, S., Hampton, D. L., et al. (2018). First-Light Observations from the Transition Region explorer (TREx) Ground-Based Network. American Geophysical Union, Fall Meeting, abstract SM23B-04,2018AGUFMSM23B.04S
Stepanova, M., Pinto, V., Valdivia, J. A., and Antonova, E. E. (2011). Spatial distribution of the eddy diffusion coefficients in the plasma sheet during quiet time and substorms from THEMIS satellite data. J. Geophys. Res. Atmos. 116, A00I24. doi:10.1029/2010ja015887
Strangeway, R. J. (2012). The relationship between magnetospheric processes and auroral field-aligned current morphology. Geophys. Monogr. Ser. 197, 355. doi:10.1029/2012gm001211
Thomsen, M. F., McComas, D. J., Reeves, G. D., and Weiss, L. A. (1996). An observational test of the Tsyganenko (T89a) model of the magnetospheric field. J. Geophys. Res. 101, 24827. doi:10.1029/96ja02318
Torbert, R. B., Vaith, H., Granoff, M., Widholm, M., Gaidos, J. A., Briggs, B. H., et al. (2016). The electron drift instrument for MMS. Space Sci. Rev. 199, 283. doi:10.1007/s11214-015-0182-7
Tsyganenko, N. A. (1989). A magnetospheric magnetic field model with a warped tail current sheet. Planet. Space Sci. 37, 5. doi:10.1016/0032-0633(89)90066-4
Tsyganenko, N. A., and Sitnov, M. I. (2007). Magnetospheric configurations from a high-resolution data-based magnetic field model. J. Geophys. Res. Atmos. 112, A06225. doi:10.1029/2007ja012260
Usanova, M. E., Mann, I. R., Bortnik, J., Shao, L., and Angelopoulos, V. (2012). THEMIS observations of electromagnetic ion cyclotron wave occurrence: dependence on AE, SYMH, and solar wind dynamic pressure. J. Geophys. Res., 117, 172. doi:10.1029/2012ja018049
Uspensky, M. V., Timopheev, E. E., and Sverdlov, Y. L. (1980). “Araks” Doppler radar measurements of the ionospheric effects of artificial electron beam in the North hemisphere. Ann. Geophys. 36, 303.
Voros, Z., Baumjohann, W., Nakamura, R., Volwerk, M., Runov, A., Zhang, T. L., et al. (2004). Magnetic turbulence in the plasma sheet. J. Geophys. Res. Atmos. 109, A11215. doi:10.1029%2F2004JA010404
Weiss, L. A., Thomsen, M. F., Reeves, G. D., and McComas, D. J. (1997). An Examination of the Tsyganenko (T89A) Field Model Using a Database of Two-Satellite Magnetic Conjunctions. J. Geophys. Res. 102, 4911. doi:10.1029/96ja02876
Willard, J. M., Johnson, J. R., Snelling, J. M., Powis, A. T., Kaganovich, I. D., and Sanchez, E. R. (2019). Effect of field-line curvature on the ionospheric accessibility of relativistic electron beam experiments. Front. Astron. Space Sci. 6, 56. doi:10.3389/fspas.2019.00056
Williams, J. D., and Wilbur, P. J. (1990). Experimental study of plasma contactor phenomena, J. Spacecr. Rockets., 27 (6), 634–641. doi:10.2514/3.26192
Winckler, J. R., Arnoldy, R. L., and Hendrickson, R. A. (1975). Echo 2: A study of electron beams injected into the high-latitude ionosphere from a large sounding rocket. J. Geophys. Res. 80, 2083. doi:10.1029/ja080i016p02083
Winckler, J. R. (1992). Controlled experiments in the earth's magnetosphere with artifical electron beams. Rev. Mod. Phys. 64, 859. doi:10.1103/revmodphys.64.859
Yahnin, A. G., Sergeev, V. A., Gvozdevsky, B. B., and Vennerstrøm, S. (1997). Magnetospheric source region of discrete auroras inferred from their relationship with isotropy boundaries of energetic particles. Ann. Geophys. 15, 943. doi:10.1007/s00585-997-0943-z
Yahnin, A. G., Sergeev, V. A., Gvozdevsky, B. B., and Vennerstrom, S. (1999). Reply. Ann. Geophys. 17, 42. doi:10.1007/s005850050734
Yang, J., Wolf, R. A., Toffoletto, F. R., and Sazykin, S. (2013). RCM-E simulation of substorm growth phase arc associated with large-scale adiabatic convection. Geophys. Res. Lett. 40, 6017. doi:10.1002/2013gl058253
Keywords: aurora, space experiments, magnetosphere, ionosphere, electron beams
Citation: Borovsky JE, Delzanno GL and Henderson MG (2020) A Mission Concept to Determine the Magnetospheric Causes of Aurora. Front. Astron. Space Sci. 7:595929. doi: 10.3389/fspas.2020.595929
Received: 18 August 2020; Accepted: 28 September 2020;
Published: 19 November 2020.
Edited by:
Luca Sorriso-Valvo, National Research Council, ItalyReviewed by:
Octav Marghitu, Space Science Institute, RomaniaCopyright © 2020 Borovsky, Delzanno and Henderson. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joseph E. Borovsky, amJvcm92c2t5QHNwYWNlc2NpZW5jZS5vcmc=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.