The Discrepancy Between Simulation and Observation of Electric Fields in Collisionless Shocks

Recent time series observations of electric fields within collisionless shocks have shown that the fluctuating, electrostatic fields can be in excess of one hundred times that of the quasi-static electric fields. That is, the largest amplitude electric fields occur at high frequencies, not low. In contrast, many if not most kinetic simulations show the opposite, where the quasi-static electric fields dominate, unless they are specifically tailored to examine small-scale instabilities. Further, the shock ramp thickness is often observed to fall between the electron and ion scales while many simulations tend to produce ramp thicknesses at least at or above ion scales. This raises numerous questions about the role of small-scale instabilities and about the ability to directly compare simulations with observations.

1 Introduction

Collisionless shock waves are an ubiquitous phenomenon in heliospheric and astrophysical plasmas. They most often manifest as a nonlinearly steepened fast magnetosonic-whistler wave that has reached a stable balance between steepening and some form of irreversible energy dissipation. If a balance is reached, a stationary shock ramp is formed. The shock ramp is the part of shock transition region between upstream and downstream with an abrupt, discontinuity-like change in number density (n_S where s is the particle species), pressure¹, quasi-static² magnetic field magnitude vector (B_o), and bulk flow velocity (V_bulk). The thickness of this ramp is thought to depend upon macroscopic shock parameters like the fast mode Mach number (M_f), shock normal angle, ${\theta }_{Bn}$ (e.g., quasi-perpendicular shocks satisfy ${\theta }_{Bn}$$\ge$ 45^°), and upstream averaged plasma beta (Sagdeev, 1966; Coroniti, 1970; Tidman & Krall, 1971; Galeev, 1976; Kennel et al., 1985).

The term collisionless derives from the fact that the shock ramp thickness ranges from several electron inertial lengths³ to an ion inertial length with the majority below ∼35 ${\lambda }_e$ (Hobara et al., 2010; Mazelle et al., 2010). In contrast, the collisional mean free path of a thermal proton can be on the order of 1 AU or $\mathrm{\gtrsim }$10⁷${\lambda }_e$ (Wilson et al., 2018; Wilson et al., 2019a). Thus, fast mode shocks in astrophysical plasmas cannot be regulated by Coulomb collisions (with the exception of, perhaps, stellar photospheres and/or chromospheres or interstellar medium) like shock waves in dense neutral fluids similar to Earth’s atmosphere. The proposed phenomenon thought to act as dissipation mechanisms are dispersive radiation (Galeev and Karpman, 1963; Stringer, 1963; Morton, 1964; Sagdeev, 1966; Tidman and Northrop, 1968; Tidman and Northrop, 1968; Decker and Robson, 1972; Krasnoselskikh et al., 2002), macroscopic quasi-static field effects (Scudder et al., 1986a; Scudder et al., 1986b; Scudder et al., 1986c; Schwartz et al., 1988; Hull and Scudder, 2000; Mitchell and Schwartz, 2013; Mitchell and Schwartz, 2014), particle reflection (Edmiston and Kennel, 1984; Kennel et al., 1985; Kennel, 1987), and wave-particle interactions (Sagdeev, 1966; Coroniti, 1970; Gary, 1981; Papadopoulos, 1985).

The topic of interest for this study is electric fields in observations and simulations, so we will limit the discussion to wave-particle interactions and macroscopic quasi-static field effects. Further, given that the primary discrepancy between simulations and observations lies in the lack of large amplitude, high frequency electrostatic waves in the former, we will limit the discussion to high frequency electrostatic waves. Note that some PIC simulations do generate the electrostatic waves of interest but the simulations are often tailored to generate the modes (e.g., isolated simulation mimicking shock foot region) by artificially injecting known free energy sources (e.g., initialize with two counter-streaming beams). Therefore, all of the modes listed in the following discussion have been generated in PIC simulations (Dyrud and Oppenheim, 2006; Matsukiyo and Scholer, 2006; Matsukiyo and Scholer, 2012; Muschietti and Lembège, 2017; Saito et al., 2017). However, as will be shown, parameters like the wavelengths and amplitudes tend to differ from those in observations, sometimes significantly.

Recent work using time series electric field data has shown that the common electrostatic wave modes near collisionless shocks include lower hybrid waves (LHWs), ion acoustic waves (IAWs), electrostatic solitary waves (ESWs), waves radiated by the electron cyclotron drift instability (ECDI), and Langmuir waves (Filbert and Kellogg, 1979; Mellott and Greenstadt, 1988; Kellogg, 2003; Wilson et al., 2007; Pulupa and Bale, 2008; Walker et al., 2008; Wilson et al., 2010; Breneman et al., 2013; Wilson et al., 2014a; Wilson et al., 2014b; Chen et al., 2018; Goodrich et al., 2018; Goodrich et al., 2019). The properties of these modes are summarized in Table 1 and discussed in detail below.

TABLE 1

TABLE 1. Common Electrostatic Waves at/near Collisionless Shocks.

Electrostatic LHWs have been theorized to play a critical role in collisionless shock dynamics for decades (Papadopoulos, 1985; Tidman and Krall, 1971; Wu et al., 1984) but observations of their electrostatic form have been limited (Mellott and Greenstadt, 1988; Walker et al., 2008; Wygant et al., 1987). They are present in spacecraft observations at frequencies, in the spacecraft frame, near the local lower hybrid resonance frequency⁴. They are linearly polarized nearly perpendicular to B_o with $k{\lambda }_e$$\mathrm{\lesssim }$ 1. They are thought to be driven unstable by the free energy in currents (Lemons and Gary, 1978), ion velocity rings (Akimoto et al., 1985a), modified two stream instability (MTSI)⁵ (Gladd, 1976; Lemons and Gary, 1977; Wu et al., 1983; Wu et al., 1984), electron beams (Papadopoulos and Palmadesso, 1976), and/or heat flux carrying electrons (Marsch and Chang, 1983). These modes are important for collisionless shock dynamics because they can stochastically accelerate both thermal electrons (parallel to B_o) and ions (perpendicular to B_o) to suprathermal energies (Wu et al., 1984; Cairns and McMillan, 2005).

Electrostatic IAWs have been observed in the solar wind and near collisionless shocks for over 40 years (Fredricks et al., 1968; Fredricks et al., 1970a; Gurnett and Anderson, 1977; Gurnett et al., 1979; Kurth et al., 1979). They present in spacecraft observations at frequencies, in the spacecraft frame, above the proton plasma frequency⁶ (due to the Doppler effect), typically in the ∼1–10 kHz range in the solar wind near 1 AU. They are observed as linearly polarized (mostly parallel to B_o but sometimes at small oblique angles), modulated sine waves with bursty wave envelopes lasting 10 s of ms (Wilson et al., 2007; Wilson et al., 2010; Wilson et al., 2014a; Wilson et al., 2014b). They have been shown to have wavelengths on the order of a few to several Debye lengths⁷, or 10–100 s of meters near 1 AU (Fuselier and Gurnett, 1984; Breneman et al., 2013; Goodrich et al., 2018; Goodrich et al., 2019). They are thought to be driven unstable by the free energy in currents (Biskamp et al., 1972; Lemons and Gary, 1978), temperature gradients (Allan and Sanderson, 1974), electron heat flux (Dum et al., 1980; Henchen et al., 2019), or ion/ion streaming instabilities (Auer et al., 1971; Akimoto and Winske, 1985; Akimoto et al., 1985b; Goodrich et al., 2019) or they can result from a nonlinear wave-wave process (Cairns and Robinson, 1992; Dyrud and Oppenheim, 2006; Kellogg et al., 2013; Saito et al., 2017). These modes are important for collisionless shock dynamics because they can stochastically accelerate thermal electrons (parallel to B_o) generating self-similar velocity distribution functions (VDFs) or the so called “flattop” distributions (Vedenov, 1963; Sagdeev, 1966; Dum et al., 1974; Dum, 1975; Dyrud and Oppenheim, 2006). They are also capable of stochastically accelerating the high energy tail of the ion VDF (parallel to B_o) (Dum et al., 1974). Note that the generation of the flattop has recently been interpreted as evidence of inelastic collisions (Wilson et al., 2019a; Wilson et al., 2019b; Wilson et al., 2020).

ESWs present in spacecraft observations as short duration (few ms), bipolar electric field pulses parallel to B_o and monopolar perpendicular (Behlke et al., 2004; Wilson et al., 2007; Wilson et al., 2010; Wilson et al., 2014b). They tend to be on Debye scales and are thought to be BGK phase space holes (Ergun et al., 1998; Cattell et al., 2005; Franz et al., 2005; Vasko et al., 2018). ESWs can be driven unstable by electron beams (Ergun et al., 1998; Cattell et al., 2005; Franz et al., 2005), ion beams (Vasko et al., 2018), modified two-stream instability (MTSI) (Matsukiyo and Scholer, 2006), or the produce of high frequency wave decay (Singh et al., 2000). Until recently, it was thought all ESWs outside the auroral acceleration region were electron holes. However, work by (Vasko et al., 2018) and (Wang et al., 2020) suggest that many of the ESWs in the terrestrial bow shock are not only ion holes, they do not propagate exactly along B_o as was previously thought. ESWs are important in collisionless shock dynamics because they can trap incident electrons (Dyrud and Oppenheim, 2006; Lu et al., 2008) or ions (Vasko et al., 2018; Wang et al., 2020), depending on the type of hole. They have also been shown to dramatically heat ions (Ergun et al., 1998), and/or couple to (or directly cause) the growth of IAWs (Dyrud and Oppenheim, 2006), whistler mode waves (Singh et al., 2001; Lu et al., 2008; Goldman et al., 2014), LHWs (Singh et al., 2000).

The ECDI is driven by the free energy in the relative drift between the incident electrons and shock-reflected ions (Forslund et al., 1970; Forslund et al., 1971; Lampe et al., 1972; Matsukiyo and Scholer, 2006; Muschietti and Lembège, 2013). They also range from Debye to electron thermal gyroradius scales (Breneman et al., 2013) and present in spacecraft observations as mixtures of Doppler-shifted IAWs and electron Bernstein modes. The polarization of these modes can be confusing, presenting as shaped like a tadpole or tear drop, with one part of the “tadpole” nearly parallel to B_o (i.e., IAW part) and the other nearly orthogonal (i.e., the Bernstein mode part) (Wilson et al., 2010; Breneman et al., 2013; Wilson et al., 2014b; Goodrich et al., 2018). This results from the coupling between two modes that are normally orthogonal to each other in their electric field oscillations. ECDI-driven modes are important for collisionless shocks because they can resonantly interact with the bulk of the ion VDF, generate a suprathermal tail on the ion VDF, and strongly heat the electrons perpendicular to B_o (Forslund et al., 1970; Forslund et al., 1972; Lampe et al., 1972; Muschietti and Lembège, 2013).

Langmuir waves have been observed upstream of collisionless shocks for decades (Gurnett and Anderson, 1977; Filbert and Kellogg, 1979; Kellogg et al., 1992; Cairns, 1994; Bale et al., 1998; Bale et al., 1999; Malaspina et al., 2009; Soucek et al., 2009; Krasnoselskikh et al., 2011). These waves have $k{\lambda }_e$$\mathrm{\lesssim }$ 1 (Soucek et al., 2009; Krasnoselskikh et al., 2011) and rest frame frequencies satisfying $f_{rest}$$\mathrm{\lesssim }$$f_{pe}$. Langmuir waves are driven unstable by electron beams and/or nonlinear wave decay (Pulupa et al., 2010; Kellogg et al., 2013). They tend to be linearly polarized nearly parallel to B_o when electrostatic but some do exhibit circular polarization when electromagnetic (Bale et al., 1998; Malaspina and Ergun, 2008). Langmuir waves are relevant to collisionless shock dynamics in that they dissipate the free energy in reflected electron beams and can mode convert to generate free mode emissions that can serve as remote detection signatures (Cairns, 1994; Bale et al., 1999; Pulupa et al., 2010).

In summary, the most commonly observed electrostatic wave modes near collisionless shocks are IAWs, ESWs, ECDI-driven modes, and Langmuir waves. Electrostatic LHWs are less commonly observed, which may be due to instrumental effects as many electric field instruments (Bonnell et al., 2008; Bougeret et al., 2008; Cully et al., 2008) have been designed with gain roll-offs at ∼1–10 Hz (low- or high-pass filters), which happens to be the typical value of f_lh in the solar wind near 1 AU. It may also be that electrostatic LHWs are just less commonly generated or damp very quickly in collisionless shocks. Langmuir waves tend to occur upstream of the shock in regions filled with shock reflected electron beams (Cairns, 1994; Bale et al., 1999; Wilson et al., 2007; Pulupa et al., 2010). Although they can be common in the upstream, they tend to be much less so in the ramp and immediate downstream region. Therefore, the remaining discussion will focus on the most commonly observed Debye-scale, electrostatic modes: IAWs, ESWs, and ECDI-driven modes. These three modes are observed in and around both quasi-parallel and quasi-perpendicular shocks. The only macroscopic shock parameters on which they appear to depend are the shock density compression ratio and M_f [e.g., Wilson et al., 2007; Wilson et al., 2014a; Wilson et al., 2014b]. The ECDI-driven modes tend not to be observed for M_f$\mathrm{\lesssim }$ 3, since they require sufficient reflected ions to initiate the instability. Part of the reason for the lack of dependence on shock geometry is that the fluctuations in the foreshock upstream of a quasi-parallel shock, for instance, locally rotate the magnetic field to quasi-perpendicular geometries and some can even locally reflect/energize particles [e.g., Wilson et al., 2013; Wilson et al., 2016].

2 Historical Context

2.1 Spacecraft Observations

Early spacecraft electric field observers had very limited resources, compared to modern day, in memory, computational power, and spacecraft telemetry. As such, the common practice was to perform onboard computations to generate Fourier spectra for predefined frequency ranges (Fredricks et al., 1968; Fredricks et al., 1970a; Fredricks et al., 1970b; Rodriguez and Gurnett, 1975). These Fourier spectra are spectral intensity data averaged over fixed time and frequency intervals, which has been more recently shown to significantly underestimate the instantaneous wave amplitude (Tsurutani et al., 2009). The underestimation led to some confusion in multiple areas of research because the estimated wave amplitudes from the spectra were too small to noticeably impact the dynamics of the system in question.

For instance, for decades the radiation belt community had relied upon such dynamic spectra and came to conclusion that the whistler mode waves (e.g., chorus and hiss) were typically in the $\mathrm{\lesssim }$1 mV/m amplitude range. The advent of time series electric field data led to the discovery that some of these modes could have amplitudes in excess of ∼30 mV/m (Santolík et al., 2003). Later the STEREO spacecraft were launched and the electric field instruments were one of the first to be turned on. This led to the discovery of extremely large amplitude whistler mode waves with $\mathrm{\gtrsim }$200 mV/m (Cattell et al., 2008). The discovery provoked an investigation of Wind observations as it passed through the radiation belt some 60$+$ times early in its lifetime. The result was a series of papers using Wind and STEREO that all showed consistent observations of large amplitude whistler mode waves with $\mathrm{\gtrsim }$100 mV/m (Kellogg et al., 2010; Breneman et al., 2011; Kellogg et al., 2011; Kersten et al., 2011; Wilson et al., 2011; Breneman et al., 2012). These results altered the design and scientific direction of NASA’s Van Allen Probes mission.

Similar issues arose in observations of collisionless shock waves. The early work using dynamic spectra data found electrostatic waves with spacecraft frame frequencies, f_sc, greater than a few hundred hertz to have amplitudes of, at most, a few 10s of mV/m but typically smaller in the few mV/m range (Fredricks et al., 1970b; Rodriguez and Gurnett, 1975). Numerous theoretical studies had suggested that small-scale, high frequency waves were an important dissipation mechanism to regulate the nonlinear steepening of collisionless shock waves (Sagdeev, 1966; Tidman and Krall, 1971; Papadopoulos, 1985). However, such small amplitude electric field observations raised doubts about the ability of the high frequency modes to supply sufficient dissipation to maintain a stable shock.

The first published example (of which the authors are aware) of a time series electric field component observed by a spacecraft within a collisionless shock was presented in Wygant et al. (1987) observed by the ISEE-1 probe. The observation was one of the first pieces of evidence that the dynamic spectra plots were not fully capturing the electric field dynamics because the data showed electric fields up to nearly ∼100 mV/m. Later work using the Wind spacecraft found ESWs in the terrestrial bow shock with amplitudes in excess of ∼100 mV/m (Bale et al., 1998; Bale et al., 2002). A few bow shock crossings were observed with the Polar spacecraft, which found nonlinear, electrostatic IAWs within the shock with amplitudes up to ∼80 mV/m (Hull et al., 2006). The picture starting to emerge was that high frequency, electrostatic waves were common and large amplitude in collisionless shocks. Note that the occurrence rate of electrostatic waves was already implied by studies using dynamic spectra data, but not such large amplitude.

Wilson et al. (2007) examined waveform capture data of electrostatic waves above the proton cyclotron frequency, f_pp, from the Wind spacecraft finding a positive correlation between peak wave amplitude and shock strength, i.e., stronger shocks had larger amplitude waves. They also observed that ion acoustic waves were the dominant electrostatic mode within the shock ramp. Shortly after, a study (Wilson et al., 2010) of a supercritical shock showed evidence of waves radiated by the ECDI. Since then, a series of papers using MMS (Chen et al., 2018; Goodrich et al., 2018; Goodrich et al., 2019), STEREO (Breneman et al., 2013), THEMIS (Wilson et al., 2014a; Wilson et al., 2014b), and Wind (Breneman et al., 2013) have examined these electrostatic waves in collisionless shocks.

While the discussion has almost exclusively focused on fluctuating electric fields, $\delta E$, it is critical to discuss quasi-static electric fields, E_o, as well. The primary obstacle to accurate E_o measurements results from the lack of a stable ground in spacecraft observations (Scime et al., 1994a; Scime et al., 1994b; Scudder et al., 2000; Pulupa et al., 2014; Lavraud and Larson, 2016) and the sheath that forms around the conducting surfaces (Ergun et al., 2010), which alters how the instrument couples to the plasma. It is beyond the scope of this study to discuss, in detail, the difficulties associated with such measurements, but some context can be gained by reviewing some recent electric field instrument papers (Wygant et al., 2013; Bale et al., 2016; Ergun et al., 2016; Lindqvist et al., 2016). In lieu of a proper E_o measurement in the plasma rest frame, we can estimate the convective electric field, E_c = -V_sw × B_o (where V_sw is the bulk flow solar wind velocity in the spacecraft frame)⁸. Since the parameters in most simulations are scaled or normalized, we will use the dimensionless ratio $\delta E/E_o$ when comparing spacecraft and simulation results. Unless otherwise specified, E_o$=$E_c in these contexts.

Prior to the launch of MMS, there were several studies that attempted to measure the cross shock electric field but each suffered from inaccuracies or under resolved electric field measurements which kept the issue of its magnitude in doubt (Dimmock et al., 2011; Dimmock et al., 2012; Wilson et al., 2014a; Wilson et al., 2014b). The launch of MMS allowed researchers, for the first time, to probe E_o with sufficient cadence and accuracy to properly measure the cross shock electric field in an interplanetary shock (Cohen et al., 2019). Note that the E_o measured in this study peaked at $\mathrm{\lesssim }$1.5 mV/m, i.e., comparable to or smaller than the magnitude of E_c (which was $\mathrm{\lesssim }$4 mV/m in this study). Therefore, we will assume E_o as being comparable to E_c in magnitude throughout and will just refer to E_o instead of both. Even so, there is some discrepancy because such a measurement is extremely difficult at the terrestrial bow shock and detailed MMS observations showed that the electron dynamics seemed to be dominated by a combination of magnetosonic-whistler modes and electrostatic IAWs and ECDI waves (Chen et al., 2018).

The current picture from observations is summarized in the following. In the studies where the quasi-static electric field could be reliably measured (Cohen et al., 2019) or approximated from measurements (Wilson et al., 2014a; Wilson et al., 2014b; Goodrich et al., 2018; Goodrich et al., 2019), the findings were that $\delta E$ is consistently much larger than E_o, i.e., $\delta E$$\gg$E_o. Some of these works attempted to quantify the impact on the dynamics of the system due to $\delta E$ vs. E_o, finding $\delta E$ dominated (Wilson et al., 2014a; Wilson et al., 2014b; Chen et al., 2018; Goodrich et al., 2018). Chen et al. (Chen et al., 2018) examined in great detail the evolution of the electron distribution through the shock finding that a magnetosonic-whistler wave accelerated the bulk of the incident distribution which rapidly became unstable to high frequency, electrostatic IAWs that scattered the electrons into the often observed flattop distribution [Wilson et al., 2019b; Wilson et al., 2019a; Wilson et al., 2020, and references therein]. This seems to somewhat contradict the results of Cohen et al. (2019) and others who argued that a quasi-static cross shock potential is dominating the shock and particle dynamics. What all of these studies do agree upon is that $\delta E$$\gg$E_o. Note that the purpose of comparing the fluctuating to the quasi-static field here is to help compare with simulations, which normalize the electric fields by the upstream E_c value or something similar.

Figure 1 shows seven waveform captures observed by the Wind spacecraft’s WAVES instrument (Bougeret et al., 1995) while passing through the quasi-perpendicular terrestrial bow shock. The first column shows the x-antenna electric field ($\delta E_x$), the second the y-antenna electric field ($\delta E_y$), and the third hodograms of $\delta E_y$ vs. $\delta E_x$. The local B_o is projected onto each hodogram shown as a magenta line⁹. Each row shows a different waveform capture/snapshot that is ∼17 ms in duration. The first column contains a double-ended arrow in each panel illustrating the scale associated with 200 mV/m. The first two rows show examples of ESWs mixed with ECDI-driven waves, the third and fourth rows show ECDI-driven waves, and the fifth through seventh rows show IAWs. The distinguishing features are as follows: the ESWs have an isolated, bipolar pulse with either a linear or figure eight-like polarization and a nearly flat frequency (spacecraft frame) spectrum response in the ∼0.2–10 kHz range (not shown); the IAWs exhibit symmetric $\delta E_x$ and $\delta E_y$ about zero, are linearly polarized along B_o, and have a broad frequency peak (spacecraft frame) in the ∼2–10 kHz range (not shown); and the ECDI exhibit asymmetric $\delta E_x$ and $\delta E_y$ fluctuations about zero, their polarization is not always linear along B_o, and the frequency peak (spacecraft frame) is in the ∼0.5–10 kHz range with superposed cyclotron harmonics (not shown). For reference, the upstream average convective for this bow shock crossing is E_c ∼ 3.5 mV/m.

FIGURE 1

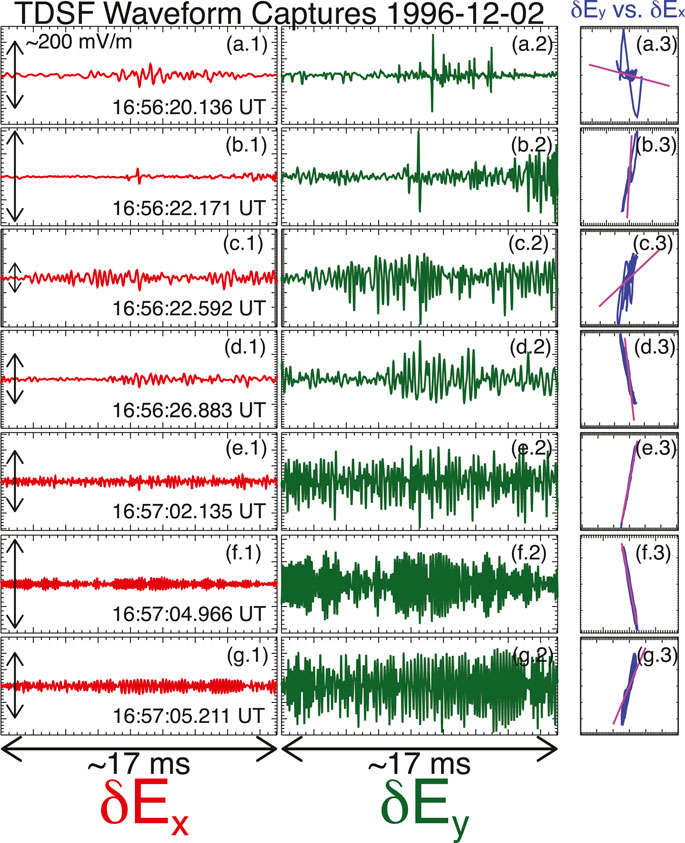
FIGURE 1. Example of six waveform captures observed by Wind while crossing the Earth’s quasi-perpendicular bow shock on 1996-12-02. Each row corresponds to, by column, the X vs time, Y vs time, and Y vs X hodogram (in instrument coordinates) from the Wind/WAVES time domain sampler (TDS) instrument (Bougeret et al., 1995). Each waveform capture/snapshot is ∼17 ms in duration. The quasi-static magnetic field projection is shown as the magenta line in hodograms (Adapted from Figure 3.6 in Wilson (2010).

2.2 Kinetic Simulations

Kinetic simulations of shocks are challenging due to the need to resolve global structure of the shock (generally associated with ${\lambda }_i$¹⁰) and the relatively long time scales associated with it simultaneously with short spatial (${\lambda }_{De}$) and fast temporal scales (f_pe) associated with instabilities.

Early kinetic particle-in-cell (PIC) simulations were much more limited by computational constraints than those performed today. A common approach to scaling the problem in order reduce the computational load is to consider one- or two-dimensional problems and to reduce ratios of the ion-to-electron mass, $\frac{M_i}{m_e}$, and electron plasma-to-cyclotron frequency, $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$, while keeping the plasma β and the size of the problem in units of ${\lambda }_i$ comparable to the physical system of interest. Further computational trade-offs include altering the simulation resolution (i.e., number of grid cells), the number of particles per cell for particle codes or velocity-space resolution for continuum Vlasov codes (Yang et al., 2013). Since the frequencies and the growth rates of the instabilities of interest are associated with certain characteristic time scales, such a re-scaling may significantly alter the development and the role of instabilities in the simulations. For example, reducing $\frac{M_i}{m_e}$ lowers the threshold for Buneman instability (Hoshino and Shimada, 2002) by reducing the difference between electron and ion thermal speeds. Values of $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$ were also expected and found to inhibit the growth of certain wave modes like Bernstein modes (Matsukiyo and Scholer, 2006; Muschietti and Lembège, 2013; Muschietti and Lembège, 2017). What’s more, the $\frac{M_i}{m_e}$ ratio was shown to dramatically affect the macroscopic profile of the shock magnetic field (Scholer and Matsukiyo, 2004) and affect the growth of what are now viewed as critical instabilities like the MTSI (Umeda et al., 2012a; Umeda et al., 2012b; Umeda et al., 2014). Thus the re-scaling approach must be carefully chosen based upon its expected impact on the phenomena of interest.

Some of the first two-dimensional PIC simulations using realistic $\frac{M_i}{m_e}$ was presented by (Matsukiyo and Scholer, 2006). Since then, the community has made efforts to compromise somewhat on $\frac{M_i}{m_e}$ in order to increase $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$, to more realistic values (i.e., 50–100 in solar wind near 1 AU) (Muschietti and Lembège, 2013) used ratios of $\frac{M_i}{m_e}$$=$ 400 and $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$$=$ 10 to examine the higher harmonics of Bernstein modes associated with the ECDI. More typical values for the latter fall in the ∼2–4 range for recent simulations (Umeda et al., 2014; Matsukiyo and Matsumoto, 2015; Zeković, 2019). However, much larger values have been used in cases where one can reduce the simulation to one spatial dimension (Umeda et al., 2019).

Despite all of the progress made since the early full PIC simulations, there still remains two striking discrepancies between observations and many simulations: the amplitude and wavelength at which the strongest electric fields are observed and inconsistencies in the thickness of the shock ramp. The second issue is more obvious from cursory examinations of simulation results, so we will discuss it first. As previously discussed, observations consistently show that the shock ramp thickness, L_sh, tends to satisfy 5 < $L_{sh}/{\lambda }_e$$<$ 40 (Hobara et al., 2010; Mazelle et al., 2010). However, PIC simulations, even with realistic mass ratio, often generate shock ramps with thicknesses satisfying $L_{sh}/{\lambda }_e$$>$ 43, i.e., exceeding proton inertial length (Scholer and Burgess, 2006), while some generate more realistically thin ramps (Matsukiyo and Scholer, 2012; Yang et al., 2013). Yang et al. (Yang et al., 2013) concluded that the shock ramp thickness decreased with increasing $\frac{M_i}{m_e}$ but increased with increasing ion plasma beta. Note however that (Matsukiyo & Scholer, 2012) used ∼20% finer grid resolution, twice as many particles per cell, and smaller plasma betas than (Scholer & Burgess, 2006). However, (Yang et al., 2013) used fewer particles per cell and smaller $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$ than both (Matsukiyo and Scholer, 2012) and (Scholer and Burgess, 2006). It is important to note that it’s still not clear what physical or numerical parameters controls the ramp thickness in simulations or observations or even what the relevant physical scale is (e.g. ${\lambda }_e$ or ${\lambda }_{De}$).

Note that the thickness of the magnetic ramp of a collisionless shock is not significantly affected by the presence of corrugation/ripples (Johlander et al., 2016) other than the temporal dependence that can occur during reformation (Mazelle et al., 2010). The spatial extent of the entire transition region can indeed be increased by such oscillations but the magnetic gradient scale length does not appear to be significantly affected. The biggest limiation to determining the shock ramp thickness in data is time resolution. More recent spacecraft like THEMIS (Angelopoulos, 2008) and MMS (Burch et al., 2016) have, for instance, fluxgate magnetometers that return 3-vector components 128 times every second, which is more than sufficient to resolve the bow shock ramp. The bow shock moves slower in the spacecraft frame than interplanetary shocks, so time resolution is more of a constraint for examining the shock ramp thickness of interplanetary shocks. Even so, the 128 sps of the THEMIS and MMS fluxgate magnetometers is still sufficient for most interplanetary shocks.

As previously discussed, observations consistently show $\delta E/E_o$$>$ 50 for fluctuations with wavelengths at or below a few 10s of Debye lengths (Wilson et al., 2014a; Wilson et al., 2014b; Chen et al., 2018; Goodrich et al., 2018), i.e., λ $\mathrm{\lesssim }$ few 10s of ${\lambda }_{De}$. Most shock simulations find values satisfying $\delta E/E_o$$<$ 10 and the scales at which the largest electric field fluctuations occur tend to satisfy $k{\lambda }_e$$<$ 1 (Scholer and Matsukiyo, 2004; Matsukiyo and Scholer, 2006; Scholer and Burgess, 2007; Lembège et al., 2009; Umeda et al., 2012a; Umeda et al., 2014; Matsukiyo and Matsumoto, 2015). We note that explicit fully kinetic PIC simulations tend to have spatial grid resolution of a few ${\lambda }_{De}$, since such scales must be resolved for numerical stability. It has long been known that unrealistically small values of $\frac{M_i}{m_e}$ and $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$ can lead to unrealistically large electric field amplitudes for modes with $k{\lambda }_e$$<$ 1 (Hoshino and Shimada, 2002; Comişel et al., 2011; Zeković, 2019). Although the three main modes discussed herein have been successfully identified in PIC simulations, they were either unrealistically small in amplitude or at different spatial scales or not excited unless the simulation was specifically tailored for that instability.

It is worth noting the severe computational costs of using fully realistic plasma parameters. The separation of spatial scales satisfies ${\lambda }_i/{\lambda }_{De}$$=$$\sqrt{\frac{M_i}{m_e}}{\beta }_e^{-1/2}\left(\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}\right)$ or ${\lambda }_e/{\lambda }_{De}$$=$$\left(\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}\right)\left(\frac{\sqrt{2}{V}_{Ae}}{V_{Te}}\right)$$=$$\sqrt{\frac{2}{{\beta }_e}}\left(\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}\right)$ or ${\lambda }_e/{\lambda }_{De}$$=$$\frac{V_{Te}}{\sqrt{2}c}$, where $V_{Ae}$$=$$\frac{B_o}{\sqrt{{\mu }_o{n}_e{m}_e}}$$=$${\lambda }_e{\text{Ω}}_{ce}$ and ${\beta }_e$$=$$\frac{2{\mu }_o{n}_e{k}_B{T}_e}{B_o^2}$$=$${\left(\frac{V_{Te}}{\text{Ω}ce{\lambda }_e}\right)}^2$. If we use typical examples from 1 AU solar wind observations (see Section 3 for values) and let ${\beta }_e$ ∼ 1, then ${\lambda }_i/{\lambda }_{De}$ ∼ 4,000–20,000. The separation of temporal scales goes as $\left(\frac{{\omega }_{pi}}{{\text{Ω}}_{ci}}\right)$$=$$\sqrt{\frac{M_i}{m_e}}\left(\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}\right)$, which is again $\sim$4,000–20,000¹¹. The computational cost of any given simulation scales as ${\left(\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}\right)}^{d+1}{\left(\frac{M_i}{m_e}\right)}^{\left(d+1\right)/2}$, where d is the number of spatial dimensions used in the simulation. Thus, one can see that increasing $\left(\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}\right)$ from ∼10 to 100, even in a one-dimensional simulation, is at least 100 times more computationally expensive. It is also the case that simulations often use shock speeds satisfying V_Tp < V_Te < U_shn while shocks in the solar wind tend to satisfy $V_{Tp}$$<$$U_{shn}$$\ll$$V_{Te}$$\ll$c (see Section 3 for values and definitions). For explicit PIC codes, there are additional computational expenses since the time steps are tied to the grid cell size, which raises the order of both $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$ and $\frac{M_i}{m_e}$ by one. Therefore, it can be seen that we are approaching a computational wall and it may require new classes of simulation codes to overcome these limitations if we hope to use fully realistic plasma parameters.

3 Example Observations Versus Simulations

In this section we will present two example observations made by the THEMIS (Angelopoulos, 2008) and MMS (Burch et al., 2016) missions to further illustrate the difference in magnitude between $\delta E$ and E_o. We will also present PIC simulation results with parameters representative of a wide class of simulations discussed in the literature. The purpose is to illustrate some limitations of simulations to provoke advancement in closing the gap between observations and simulations of collisionless shocks.

Figure 2 shows a direct comparison between $\delta E$ and E_o observed by THEMIS-C during a terrestrial bow shock crossing adapted from Wilson III et al. (2014a) and Wilson III et al. (2014b). The study examined the energy dissipation rates estimated from (J ⋅ E) (i.e., from Poynting’s theorem) due to the observed electric fields, E, and estimated current densities¹², J. They expanded $({\mathbf{j}}_{\mathrm{o}}+\delta \mathbf{j})\cdot ({\mathbf{E}}_o+\delta \mathbf{E})$ and found that $({\mathbf{J}}_{\mathrm{o}}\cdot \delta \mathbf{E})$ was the dominant term¹³, i.e., the fluctuating fields acted to limit the low frequency currents in/around the shock. Two important things were found: the magnitude of $({\mathbf{j}}_{\mathrm{o}}\cdot \delta \mathbf{E})$ and changes in this term were much larger than (j_o ⋅ E_o); the signs of the changes in $({\mathbf{j}}_{\mathrm{o}}\cdot \delta \mathbf{E})$ and (j_o ⋅ E_o) are opposite. The second point was interpreted to imply that the fluctuating fields were giving energy to the particles and the quasi-static fields were gaining energy from the particles. In short, the main conclusion from (Wilson III et al., 2014a; Wilson III et al., 2014b) was to illustrate that not only are the fluctuating electric fields large, they could potentially contribute enough energy transfer to compete with quasi-static fields. Prior to this study, the view by many in the community was that these fluctuating fields were completely negligible or just a minor, secondary effect. More recent, independent studies have performed similar analyses using different spacecraft and came to similar conclusions (Chen et al., 2018; Goodrich et al., 2018; Hull et al., 2020).

FIGURE 2

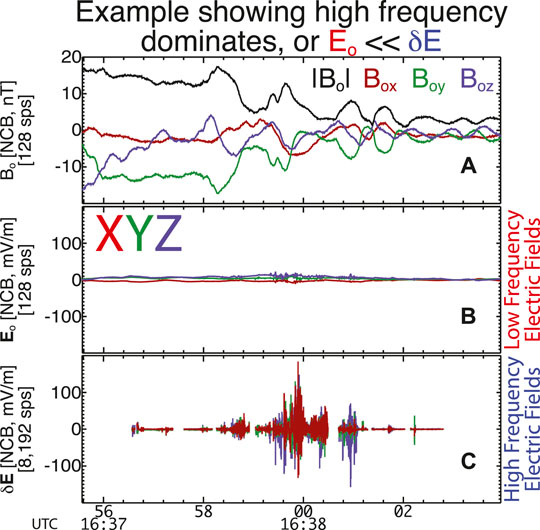
FIGURE 2. An example terrestrial bow shock crossing observed by THEMIS-C on 2009-09-05. Panel (A) shows the magnetic field magnitude (black) and three normal incidence frame coordinate basis (NCB) (Scudder et al., 1986a) components vs time at 128 samples/second (sps) observed by the fluxgate magnetometer (Auster et al., 2008). Panel (B) shows the DC-coupled electric field at 128 sps observed by EFI (Bonnell et al., 2008; Cully et al., 2008). Panel (C) shows the AC-coupled electric field at 8,192 sps observed by EFI. Note that Panels (B,C) share the same vertical axis range for direct comparison (Adapted from Figure I:2 in Wilson et al. (2014a)).

Figure 3 provides another example directly comparing $\delta E$ and E_o observed by two MMS spacecraft during a terrestrial bow shock crossing. The electric fields are shown in the De-spun, Sun-pointing, L-vector system or DSL (Angelopoulos, 2008). For each spacecraft, E_o,j$\mathrm{\lesssim }$ 10 mV/m was satisfied for the entire interval with most time steps satisfying E_o,j$\mathrm{\lesssim }$ 5 mV/m. In contrast, the peak-to-peak $\delta E_j$ values commonly exceed 100 mV/m in bursty, short duration, wave packet intervals. Note that even the electric field instrument on MMS has limitations in its accuracy for frequencies below ∼1 Hz (Ergun et al., 2016; Lindqvist et al., 2016). Thus, even with the significantly improved instrument technology and design of MMS, the observations consistently show $\delta E$$\gg$E_o.

FIGURE 3

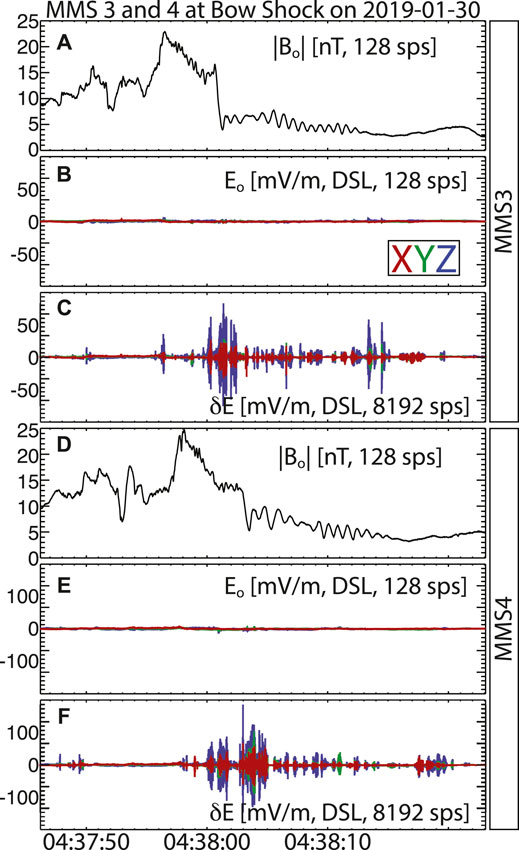
FIGURE 3. An example terrestrial bow shock crossing observed by MMS3 and MMS4 on 2019-01-30. Panels (A,D) show the magnetic field magnitude (black) vs time at 128 sps observed by the fluxgate magnetometer (Russell et al., 2016). Panels (B,E) show the DC-coupled electric field components at 128 sps observed by the electric field instrument (Ergun et al., 2016; Lindqvist et al., 2016). Panels (C,F) show the AC-coupled electric field at 8,192 sps. Note that Panels (B,C,E) share the same vertical axis range for direct comparison.

As a practical list of reference values, we present one-variable statistics of solar wind parameters from the same data set as in Wilson et al. (2018) and all interplanetary (IP) shocks in the Harvard Smithsonian’s Center for Astrophysics Wind shock database¹⁴. The following will show parameters as $X_{5\text{\%}}$$\mathrm{\lesssim }$X$\mathrm{\lesssim }$$X_{95\text{\%}}$, $\tilde{X}$ [units], for the entire data set, where $X_{y\text{\%}}$ is the y^th percentile and $\tilde{X}$ is the median. First, the typical parameters for over 400 IP shocks are as follows:

1.10 $\mathrm{\lesssim }$M_f$\mathrm{\lesssim }$ 4.60, ∼1.91 [N/A];

1.15 $\mathrm{\lesssim }$M_A$\mathrm{\lesssim }$ 6.24, ∼2.41 [N/A];

36.6 $\mathrm{\lesssim }$U_shn$\mathrm{\lesssim }$ 329.9, ∼98.2 [km/s];

79.6 $\mathrm{\lesssim }$V_shn$\mathrm{\lesssim }$ 762.3, ∼418.5 [km/s];

22.2 $\mathrm{\lesssim }$${\theta }_{Bn}$$\mathrm{\lesssim }$ 87.7, ∼63.8 [deg];

where U_shn is the upstream average flow speed in the shock rest frame and V_shn is the upstream average shock speed in the spacecraft frame. Note that the values of M_f, M_A, and U_shn will all be, on average, larger for most bow shocks in the interplanetary medium. These values are only meant to serve as a statistical baseline for reference. For example, the 11 bow shock crossings in Wilson et al. (2014a); Wilson et al. (2014b) satisfied 3.1 $\mathrm{\lesssim }$M_A$\mathrm{\lesssim }$ 21.9. Next, we present some typical plasma parameters¹⁵ near 1 AU in the solar wind:

80.2 $\mathrm{\lesssim }$f_ce$\mathrm{\lesssim }$ 409, ∼162 [Hz];

0.04 $\mathrm{\lesssim }$f_cp$\mathrm{\lesssim }$ 0.22, ∼0.09 [Hz];

17.2 $\mathrm{\lesssim }$f_pe$\mathrm{\lesssim }$ 42.5, ∼26.3 [kHz];

371 $\mathrm{\lesssim }$f_pp$\mathrm{\lesssim }$ 944, ∼578 [Hz];

1,579 $\mathrm{\lesssim }$V_Te$\mathrm{\lesssim }$ 2,411, ∼1975 [km/s];

21.9 $\mathrm{\lesssim }$V_Tp$\mathrm{\lesssim }$ 76.9, ∼40.2 [km/s];

1.03 $\mathrm{\lesssim }$${\rho }_{ce}$$\mathrm{\lesssim }$ 4.62, ∼2.28 [km];

32.5 $\mathrm{\lesssim }$${\rho }_{cp}$$\mathrm{\lesssim }$ 186, ∼88.8 [km];

1.12 $\mathrm{\lesssim }$${\lambda }_e$$\mathrm{\lesssim }$ 2.77, ∼1.82 [km];

50.5 $\mathrm{\lesssim }$${\lambda }_p$$\mathrm{\lesssim }$ 129, ∼82.5 [km];

4.74 $\mathrm{\lesssim }$${\lambda }_{De}$$\mathrm{\lesssim }$ 13.8, ∼8.58 [m];

where f_cs is the cyclotron frequency of species s, f_ps is the plasma frequency of species s, $V_{Ts}$ is the most probable thermal speed of species s¹⁶, ${\rho }_{cs}$ is the thermal gyroradius of species s¹⁷, ${\lambda }_e$ is the inertial length of species s, and ${\lambda }_{De}$ is the electron Debye length. Next, we present ratios of some typical plasma parameters near 1 AU in the solar wind:

176 $\mathrm{\lesssim }$${\lambda }_e/{\lambda }_{De}$$\mathrm{\lesssim }$ 269, ∼215 [N/A];

131 ≲${\rho }_{ce}/{\lambda }_{De}$$\mathrm{\lesssim }$ 670, ∼255 [N/A];

8,000 $\mathrm{\lesssim }$${\lambda }_p/{\lambda }_{De}$$\mathrm{\lesssim }$ 12,160, ∼9,757 [N/A];

0.34 $\mathrm{\lesssim }$${\lambda }_e/{\rho }_{ce}$$\mathrm{\lesssim }$ 1.63, ∼0.83 [N/A];

92.4 $\mathrm{\lesssim }$$f_{pe}/f_{ce}$$\mathrm{\lesssim }$ 474, ∼180 [N/A];

4.79 $\mathrm{\lesssim }$$V_{Te}/{\langle U_{shn}\rangle }_{95\text{\%}}$$\mathrm{\lesssim }$ 7.31, ∼5.99 [N/A];

43.1 $\mathrm{\lesssim }$$V_{Te}/{\langle U_{shn}\rangle }_{5\text{\%}}$$\mathrm{\lesssim }$ 65.9, ∼54.0 [N/A];

0.53 $\mathrm{\lesssim }$$V_{Te}/c$$\mathrm{\lesssim }$ 0.80, ∼0.66 [%];

where ${\langle U_{shn}\rangle }_{y\text{\%}}$ is the y^th percentile of U_shn presented earlier in this section and c is the speed of light in vacuum.

Figure 4 shows example one-dimensional cuts at three different time steps taken from a PIC simulation. The simulation parameters are as follows: ${\theta }_{Bn}$ ∼ 60 deg, $M_A$ ∼ 6.5, $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$ ∼ 4, $\frac{M_i}{m_e}$ ∼ 900, $\text{Δ}$ ∼ 1 ${\lambda }_{De}$ (where $\text{Δ}$ is the grid cell size), initially 1,000 particles per cell, and ${\lambda }_e/{\lambda }_{De}$ ∼ 8 (i.e., ∼27 times smaller than median solar wind values near 1 AU). All of the panels show data in normalized units. The electric field is normalized to the initial upstream averaged convective electric field, -V×B, i.e., the same E_o referenced for spacecraft observations. Thus, in the upstream the E_z component has an offset of unity. The normalization for n_e and B are just the initial upstream average values of the magnitude of each. All fields are measured in the simulation frame, where the shock moves in the positive x direction with the speed of approximately 2 V_A.

FIGURE 4

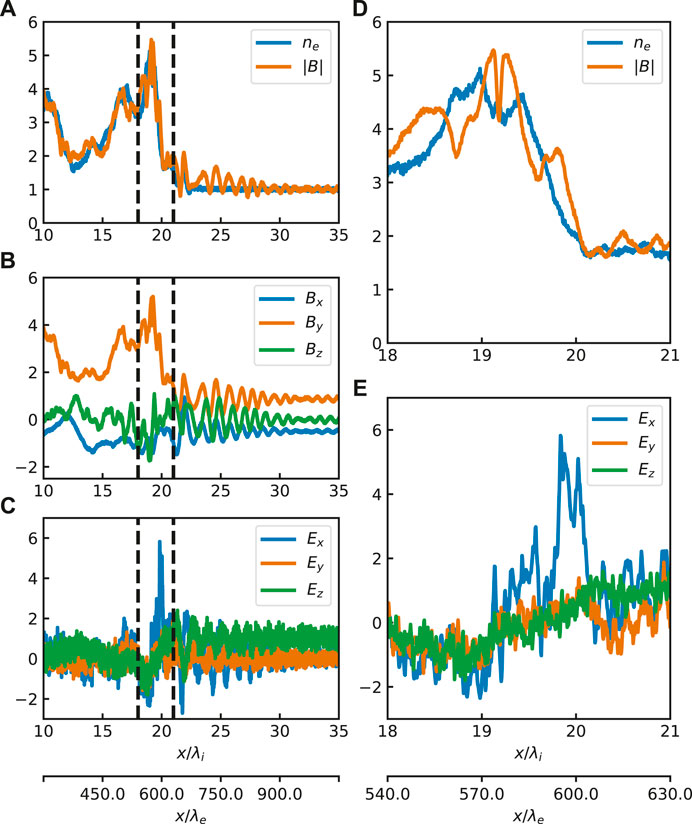
FIGURE 4. An example taken from a PIC simulation with the shock normal along the x-direction. Each plot shows a 1D cut through the middle of 2D simulation domain. Panel (A) shows the magnetic field magnitude, B (orange), and the electron number density, n_e (blue), vs. spatial position x. Panels (B,C) show the components of magnetic field (B) and the electric field (E). Panels (D,E) show a zoomed region of panels (A,C) respectively. The boundaries of the zoomed region are indicated by vertical dashed lines in panels (A–C). All fields are measured in the simulation frame, where the shock moves in the positive x direction with the speed of ∼2 V_A.

One can see that the largest values of $\left|\mathbf{E}\right|$ rarely exceed 2 (i.e., only short intervals >2 but peak only at ∼6), similar to the simulations discussed previously. Further, the spatial scales at which these fields are maximized is on ${\lambda }_e$ scales whereas observations show maximum electric fields at ${\lambda }_{De}$ scales. One can also see that the ramp, e.g., B in panel (D), is about L_sh ∼ 28 ${\lambda }_e$ (or ∼0.9 ${\lambda }_i$) thick, similar to observations that typically show ramps satisfying L_sh < 35 ${\lambda }_e$ (or <0.8 ${\lambda }_i$) (Hobara et al., 2010; Mazelle et al., 2010). The simulation does, however, generate the ubiquitous whistler precursor train upstream of the shock ramp (Wilson et al., 2012; Wilson et al., 2017). Yet it is still not clear what parameter or parameters are controlling the shock ramp thickness and electric field amplitudes at very small spatial scales in simulations.

4 Discussion

We have presented examples illustrating that spacecraft observations of collisionless shocks consistently show $\delta E$$\gg$E_o where $\delta E$ is due to electrostatic fluctuations satisfying $k{\lambda }_{De}$$\mathrm{\lesssim }$ 1 with frequencies well above f_lh. In contrast, most PIC simulations of collisionless shocks show considerably smaller amplitude of electrostatic fluctuations. This is true even when the simulation uses realistic $\frac{M_i}{m_e}$ and plasma betas.

Further, many simulations still generate shock ramps satisfying $L_{sh}/{\lambda }_e$ > 43, i.e., thicker than most observations. However, much more progress has been made on this front where Yang et al. (2013) concluded that the shock ramp thickness decreased with increasing $\frac{M_i}{m_e}$ but increased with increasing ion plasma beta. There is still the question of whether $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$ plays a role in the simulated values of L_sh, though Yang et al. (2013) was able to produce realistic thicknesses despite only having $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$$=$ 2.

Another potential issue that was not explicitly discussed in detail is that of the separation between ${\lambda }_e$ and ${\lambda }_{De}$, but these are controlled by $\frac{M_i}{m_e}$ and $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$. As previously shown, statistical solar wind parameters satisfy ${\lambda }_e/{\lambda }_{De}$ ∼ 215 (or ${\lambda }_p/{\lambda }_{De}$ ∼ 9,757) while simulations often have much smaller vales of ${\lambda }_p/{\lambda }_{De}$ ∼ 70–500 (or ${\lambda }_e/{\lambda }_{De}$ ∼ 7–40) (Umeda et al., 2011; Umeda et al., 2012a; Umeda et al., 2014; Savoini and Lembège, 2015). It is also the case that simulations often use shock speeds satisfying V_Tp < V_Te < U_shn < c while shocks in the solar wind tend to satisfy $V_{Tp}$$<$$U_{shn}$$\ll$$V_{Te}$$\ll$c.

The origins of the discrepancy between the observation that $\delta E$$\gg$$E_o$ for electrostatic fluctuations satisfying $k{\lambda }_{De}$$\mathrm{\lesssim }$ 1 remain unclear. The ratios $\frac{M_i}{m_e}$ and $\frac{{\omega }_{pe}}{{\text{Ω}}_{ce}}$ are the most likely parameters since they control the separation of spatial and temporal scales between the instabilities of interest and the global shock scales in an obvious manner. A lack of spatial resolution in most simulations may also be a factor. The purpose of this work is to motivate both observational and simulation communities to bridge the gap find closure with this issue. Without an accurate reproduction of the high frequency, large amplitude waves it is not possible to determine at what scales the electric fields dominate the energy dissipation through collisionless shocks.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://cdaweb.gsfc.nasa.gov.

Author Contributions

LW wrote most of the content and generated all the observational data figures presented herein. L-JC provided critical contributions to the bridge between observations and simulations. VR provided critical contributions to simulation techniques and limitations induced by the variation of different normalized parameters.

Funding

The work was supported by the International Space Science Institute’s (ISSI) International Teams program. LW was partially supported by Wind MO&DA grants and a Heliophysics Innovation Fund (HIF) grant. Contributions of VR were supported by NASA grant 80NSSC18K1649. Computational resources supporting this work were provided by the NASA High-End Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank B. Lembège, R. A. Treumann, M. Hesse, J. TenBarge, and J. Juno for useful discussions of kinetic simulations.

Footnotes

¹P_s = n_sk_BT_s, where T_s is the temperature of species s.

²Note we use the term quasi-static instead of background here since electromagnetic fluctuations near shocks in the solar wind can have amplitudes larger than the surrounding mean. That is, quasi-static refers to the lowest frequency response of an instrument, for practical purposes, but one can think of it as the effective background field.

³${\lambda }_s=\frac{c}{{\omega }_{ps}}$ where s is the particle species.

⁴$f_{lh}=\sqrt{f_{ce}{f}_{cp}}$, where f_cs is the cyclotron frequency of species s ($=$$\frac{q_s{B}_o}{m_s}$ where q_s is the total charge, and m_s is the mass of species s).

⁵There are two modes radiated by the MTSI at collisionless shocks, both of which are very obliquely propagating and have real frequencies near or below f_lh. The two free energy sources for the MTSIs are between incident electrons and reflected ions and incident electrons and incident ions.

⁶$2\pi f_{ps}=\sqrt{\frac{n_{s}q{s}^2}{{\epsilon }_o{m}_s}}$ where s is the particle species.

⁷${\lambda }_{De}=\sqrt{\frac{{\epsilon }_{o}k{}_B{T}_e}{n_e{e}^2}}$ where n_e is the electron number density.

⁸E_c has typical values satisfying ∼0.1–3 mV/m in the solar wind near Earth. In contrast, the waves shown in Figure 1 have $\delta E$$\mathrm{\gtrsim }$ 100–300 mV/m, thus $\delta E/E_o$$>$ 50.

⁹Note that the data is taken in the ecliptic plane to within ∼1^° and the fraction of the local B_o in this plane exceeds 89% for all events except the first two rows.

¹⁰The size of the problem may significantly exceed ${\lambda }_i$, for example when upstream turbulence in quasi-parallel shocks must be included.

¹¹Note that ${\omega }_{pe}/{\text{Ω}}_{ci}$ is larger by an additional factor of $\sqrt{M_i/m_e}$.

¹²Note that similar current densities have been found using multi-spacecraft techniques (Hull et al., 2020) supporting the results in Wilson III et al. (2014a) and Wilson III et al. (2014b).

¹³Note that Q^o in this context is not the quasi-static terms in quasi-linear or linear theory but that from the DC-coupled measurements. Further, $\delta Q$ is the fluctuating terms from these theories but the AC-coupled measurements, thus there is no a priori requirement that $\langle \delta Q\rangle$$=$ 0.

¹⁴https://www.cfa.harvard.edu/shocks/wi_data/.

¹⁵Note that none of these are Doppler-shifted.

¹⁶$V_{Ts}=\sqrt{\frac{{2k}_B{T}_s}{m_s}}.$

¹⁷${\rho }_{cs}=\frac{V_{Ts}}{{\text{Ω}}_{cs}}.$

References

Akimoto, K., and Winske, D. (1985). Ion-acoustic-like waves excited by the reflected ions at the earth’s bow shock. J. Geophys. Res. 90, 12095. doi:10.1029/JA090iA12p12095

CrossRef Full Text | Google Scholar

Akimoto, K., Papadopoulos, K., and Winske, D. (1985b). Ion-acoustic instabilities driven by an ion velocity ring. J. Plasma Phys. 34, 467–479. doi:10.1017/S0022377800003019

CrossRef Full Text | Google Scholar

Akimoto, K., Papadopoulos, K., and Winske, D. (1985a). Lower-hybrid instabilities driven by an ion velocity ring. J. Plasma Phys. 34, 445–465. doi:10.1017/S0022377800003007

CrossRef Full Text | Google Scholar

Allan, W., and Sanderson, J. J. (1974). Temperature gradient drive ion acoustic instability. Plasma Phys. 16, 753–767. doi:10.1088/0032-1028/16/8/005

CrossRef Full Text | Google Scholar

Angelopoulos, V. (2008). The THEMIS mission. Space Sci. Rev. 141, 5–34. doi:10.1007/s11214-008-9336-1

CrossRef Full Text | Google Scholar

Auer, P. L., Kilb, R. W., and Crevier, W. F. (1971). Thermalization in the earth’s bow shock. J. Geophys. Res. 76, 2927–2939. doi:10.1029/JA076i013p02927

CrossRef Full Text | Google Scholar

Auster, H. U., Glassmeier, K. H., Magnes, W., Aydogar, O., Baumjohann, W., Constantinescu, D., et al. (2008). The THEMIS fluxgate magnetometer. Space Sci. Rev. 141, 235–264. doi:10.1007/s11214-008-9365-9

CrossRef Full Text | Google Scholar

Bale, S. D., Goetz, K., Harvey, P. R., Turin, P., Bonnell, J. W., Dudok de Wit, T., et al. (2016). The FIELDS instrument suite for solar probe plus. Measuring the coronal plasma and magnetic field, plasma waves and turbulence, and radio signatures of solar transients. Space Sci. Rev. 204, 49–82. doi:10.1007/s11214-016-0244-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Bale, S. D., Hull, A., Larson, D. E., Lin, R. P., Muschietti, L., Kellogg, P. J., et al. (2002). Electrostatic turbulence and debye-scale structures associated with electron thermalization at collisionless shocks. Astrophys. J. 575, L25–L28. doi:10.1086/342609

CrossRef Full Text | Google Scholar

Bale, S. D., Kellogg, P. J., Goetz, K., and Monson, S. J. (1998). Transverse z-mode waves in the terrestrial electron foreshock. Geophys. Res. Lett. 25, 9–12. doi:10.1029/97GL03493

CrossRef Full Text | Google Scholar

Bale, S. D., Reiner, M. J., Bougeret, J. L., Kaiser, M. L., Krucker, S., Larson, D. E., et al. (1999). The source region of an interplanetary type II radio burst. Geophys. Res. Lett. 26, 1573–1576. doi:10.1029/1999GL900293

CrossRef Full Text | Google Scholar

Behlke, R., André, M., Bale, S. D., Pickett, J. S., Cattell, C. A., Lucek, E. A., et al. (2004). Solitary structures associated with short large-amplitude magnetic structures (SLAMS) upstream of the Earth’s quasi-parallel bow shock. Geophys. Res. Lett. 31, 16805. doi:10.1029/2004GL019524

CrossRef Full Text | Google Scholar

Biskamp, D., von Hagenow, K. U., and Welter, H. (1972). Computer studies of current-driven ion-sound turbulence in three dimensions. Phys. Lett. 39, 351–352. doi:10.1016/0375-9601(72)90090-4

CrossRef Full Text | Google Scholar

Bonnell, J. W., Mozer, F. S., Delory, G. T., Hull, A. J., Ergun, R. E., Cully, C. M., et al. (2008). The electric field instrument (EFI) for THEMIS. Space Sci. Rev. 141, 303–341. doi:10.1007/s11214-008-9469-2

CrossRef Full Text | Google Scholar

Bougeret, J. L., Goetz, K., Kaiser, M. L., Bale, S. D., Kellogg, P. J., Maksimovic, M., et al. (2008). S/WAVES: the radio and plasma wave investigation on the STEREO mission. Space Sci. Rev. 136, 487–528. doi:10.1007/s11214-007-9298-8

CrossRef Full Text | Google Scholar

Bougeret, J. L., Kaiser, M. L., Kellogg, P. J., Manning, R., Goetz, K., Monson, S. J., et al. (1995). Waves: the radio and plasma wave investigation on the wind spacecraft. Space Sci. Rev. 71, 231–263. doi:10.1007/BF00751331

CrossRef Full Text | Google Scholar

Breneman, A., Cattell, C., Kersten, K., Paradise, A., Schreiner, S., Kellogg, P. J., et al. (2013). STEREO and Wind observations of intense cyclotron harmonic waves at the Earth’s bow shock and inside the magnetosheath. J. Geophys. Res. 118, 7654–7664. doi:10.1002/2013JA019372

CrossRef Full Text | Google Scholar

Breneman, A., Cattell, C., Wygant, J., Kersten, K., Wilson, L. B., Dai, L., et al. (2012). Explaining polarization reversals in STEREO wave data. J. Geophys. Res. 117, A04317. doi:10.1029/2011JA017425

CrossRef Full Text | Google Scholar

Breneman, A., Cattell, C., Wygant, J., Kersten, K., Wilson, L. B., Schreiner, S., et al. (2011). Large-amplitude transmitter-associated and lightning-associated whistler waves in the Earth’s inner plasmasphere at L $<$2. J. Geophys. Res. 116, A06310. doi:10.1029/2010JA016288

CrossRef Full Text | Google Scholar

Burch, J. L., Moor, T. E., Torbert, R. B., and Giles, B. L. (2016). Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 199, 5–21. doi:10.1007/s11214-015-0164-9

CrossRef Full Text | Google Scholar

Cairns, I. H. (1994). Fine structure in plasma waves and radiation near the plasma frequency in Earth’s foreshock. J. Geophys. Res. 99, 23505. doi:10.1029/94JA01997

CrossRef Full Text | Google Scholar

Cairns, I. H., and McMillan, B. F. (2005). Electron acceleration by lower hybrid waves in magnetic reconnection regions. Phys. Plasmas. 12, 102110. doi:10.1063/1.2080567

CrossRef Full Text | Google Scholar

Cairns, I. H., and Robinson, P. A. (1992). Theory for low-frequency modulated Langmuir wave packets. Geophys. Res. Lett. 19, 2187–2190. doi:10.1029/92GL02632

CrossRef Full Text | Google Scholar

Cattell, C., Dombeck, J., Wygant, J., Drake, J. F., Swisdak, M., Goldstein, M. L., et al. (2005). Cluster observations of electron holes in association with magnetotail reconnection and comparison to simulations. J. Geophys. Res. 110, A01211. doi:10.1029/2004JA010519

CrossRef Full Text | Google Scholar

Cattell, C., Wygant, J. R., Goetz, K., Kersten, K., Kellogg, P. J., von Rosenvinge, T., et al. (2008). Discovery of very large amplitude whistler-mode waves in Earth’s radiation belts. Geophys. Res. Lett. 35, L01105. doi:10.1029/2007GL032009

CrossRef Full Text | Google Scholar

Chen, L. J., Wang, S., Wilson, L. B., Schwartz, S. J., Gershman, D. J., Bessho, N., et al. (2018). Electron bulk acceleration and thermalization at Earth’s quasi-perpendicular bow shock. Phys. Rev. Lett. 120, 225101. doi:10.1103/PhysRevLett.120.225101

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, I. J., Schwartz, S. J., Goodrich, K. A., Ahmadi, N., Ergun, R. E., Fuselier, S. A., et al. (2019). High-resolution measurements of the cross-shock potential, ion reflection, and electron heating at an interplanetary shock by MMS. J. Geophys. Res. 124, 3961–3978. doi:10.1029/2018JA026197

CrossRef Full Text | Google Scholar

Comişel, H., Scholer, M., Soucek, J., and Matsukiyo, S. (2011). Non-stationarity of the quasi-perpendicular bow shock: comparison between cluster observations and simulations. Ann. Geophys. 29, 263–274. doi:10.5194/angeo-29-263-2011

CrossRef Full Text | Google Scholar

Coroniti, F. V. (1970). Dissipation discontinuities in hydromagnetic shock waves. J. Plasma Phys. 4, 265–282. doi:10.1017/S0022377800004992

CrossRef Full Text | Google Scholar

Cully, C. M., Ergun, R. E., Stevens, K., Nammari, A., and Westfall, J. (2008). The THEMIS digital fields board. Space Sci. Rev. 141, 343–355. doi:10.1007/s11214-008-9417-1

CrossRef Full Text | Google Scholar

Decker, G., and Robson, A. E. (1972). Instability of the whistler structure of oblique hydromagnetic shocks. Phys. Rev. Lett. 29, 1071–1073. doi:10.1103/PhysRevLett.29.1071

CrossRef Full Text | Google Scholar

Dimmock, A. P., Balikhin, M. A., and Hobara, Y. (2011). Comparison of three methods for the estimation of cross-shock electric potential using Cluster data. Ann. Geophys. 29, 815–822. doi:10.5194/angeo-29-815-2011

CrossRef Full Text | Google Scholar

Dimmock, A. P., Balikhin, M. A., Krasnoselskikh, V. V., Walker, S. N., Bale, S. D., and Hobara, Y. (2012). A statistical study of the cross-shock electric potential at low Mach number, quasi-perpendicular bow shock crossings using cluster data. J. Geophys. Res. 117, A02210. doi:10.1029/2011JA017089

CrossRef Full Text | Google Scholar

Dum, C. T. (1975). Strong-turbulence theory and the transition from Landau to collisional damping. Phys. Rev. Lett. 35, 947–950. doi:10.1103/PhysRevLett.35.947

CrossRef Full Text | Google Scholar

Dum, C. T., Chodura, R., and Biskamp, D. (1974). Turbulent heating and quenching of the ion sound instability. Phys. Rev. Lett. 32, 1231–1234. doi:10.1103/PhysRevLett.32.1231

CrossRef Full Text | Google Scholar

Dum, C. T., Marsch, E., and Pilipp, W. (1980). Determination of wave growth from measured distribution functions and transport theory. J. Plasma Phys. 23, 91–113. doi:10.1017/S0022377800022170

CrossRef Full Text | Google Scholar

Dyrud, L. P., and Oppenheim, M. M. (2006). Electron holes, ion waves, and anomalous resistivity in space plasmas. J. Geophys. Res. 111, A01302. doi:10.1029/2004JA010482

CrossRef Full Text | Google Scholar

Edmiston, J. P., and Kennel, C. F. (1984). A parametric survey of the first critical Mach number for a fast MHD shock. J. Plasma Phys. 32, 429–441. doi:10.1017/S002237780000218X

CrossRef Full Text | Google Scholar

Ergun, R. E., Carlson, C. W., McFadden, J. P., Mozer, F. S., Muschietti, L., Roth, I., et al. (1998). Debye-scale plasma structures associated with magnetic-field-aligned electric fields. Phys. Rev. Lett. 81, 826–829. doi:10.1103/PhysRevLett.81.826

CrossRef Full Text | Google Scholar

Ergun, R. E., Malaspina, D. M., Bale, S. D., McFadden, J. P., Larson, D. E., Mozer, F. S., et al. (2010). Spacecraft charging and ion wake formation in the near-Sun environment. Phys. Plasmas. 17, 072903. doi:10.1063/1.3457484

CrossRef Full Text | Google Scholar

Ergun, R. E., Tucker, S., Westfall, J., Goodrich, K. A., Malaspina, D. M., Summers, D., et al. The axial double probe and fields signal processing for the MMS mission. Space Sci. Rev. 199, (2016). 167–188. doi:10.1007/s11214-014-0115-x

CrossRef Full Text | Google Scholar

Filbert, P. C., and Kellogg, P. J. (1979). Electrostatic noise at the plasma frequency beyond the earth’s bow shock. J. Geophys. Res. 84, 1369–1381. doi:10.1029/JA084iA04p01369

CrossRef Full Text | Google Scholar

Forslund, D., Morse, R., Nielson, C., and Fu, J. (1972). Electron cyclotron drift instability and turbulence. Phys. Fluids. 15, 1303–1318. doi:10.1063/1.1694082

CrossRef Full Text | Google Scholar

Forslund, D. W., Morse, R. L., and Nielson, C. W. Electron cyclotron drift instability. Phys. Rev. Lett. 25, (1970). 1266–1270. doi:10.1103/PhysRevLett.25.1266

CrossRef Full Text | Google Scholar

Forslund, D. W., Morse, R. L., and Nielson, C. W. (1971). Nonlinear electron-cyclotron drift instability and turbulence. Phys. Rev. Lett. 27, 1424–1428. doi:10.1103/PhysRevLett.27.1424

CrossRef Full Text | Google Scholar

Franz, J. R., Kintner, P. M., Pickett, J. S., and Chen, L. J. (2005). Properties of small-amplitude electron phase-space holes observed by Polar. J. Geophys. Res. 110, A09212. doi:10.1029/2005JA011095

CrossRef Full Text | Google Scholar

Fredricks, R. W., Coroniti, F. V., Kennel, C. F., and Scarf, F. L. (1970a). Fast time-resolved spectra of electrostatic turbulence in the earth’s bow shock. Phys. Rev. Lett. 24, 994–998. doi:10.1103/PhysRevLett.24.994

CrossRef Full Text | Google Scholar

Fredricks, R. W., Crook, G. M., Kennel, C. F., Green, I. M., Scarf, F. L., Coleman, P. J., et al. (1970b). OGO 5 observations of electrostatic turbulence in bow shock magnetic structures. J. Geophys. Res. 75, 3751–3768. doi:10.1029/JA075i019p03751

CrossRef Full Text | Google Scholar

Fredricks, R. W., Kennel, C. F., Scarf, F. L., Crook, G. M., and Green, I. M. (1968). Detection of electric-field turbulence in the earth’s bow shock. Phys. Rev. Lett. 21, 1761–1764. doi:10.1103/PhysRevLett.21.1761

CrossRef Full Text | Google Scholar

Fuselier, S. A., and Gurnett, D. A. (1984). Short wavelength ion waves upstream of the earth’s bow shock. J. Geophys. Res. 89, 91–103. doi:10.1029/JA089iA01p00091

CrossRef Full Text | Google Scholar

Galeev, A. A. (1976). “Collisionless shocks,” in Physics of solar planetary environments; Proceedings of the International Symposium on Solar-Terrestrial Physics, Boulder, CO, June 7–18, 1976. Vol. 1. (A77-44201 20-88). Editor D. J. Williams (Washington, D.C.: American Geophysical Union). 464–490.

Google Scholar

Galeev, A. A., and Karpman, V. I. (1963). Turbulence theory of a weakly nonequilibrium low-density plasma and structure of shock waves. Sov. Phys.–JETP. 17, 403–409.

Google Scholar

Gary, S. P. (1981). Microinstabilities upstream of the earth’s bow shock – a brief review. J. Geophys. Res. 86, 4331–4336. doi:10.1029/JA086iA06p04331

CrossRef Full Text | Google Scholar

Gladd, N. T. (1976). The lower hybrid drift instability and the modified two stream instability in high density theta pinch environments. Plasma Phys. 18, 27–40. doi:10.1088/0032-1028/18/1/002

CrossRef Full Text | Google Scholar

Goldman, M. V., Newman, D. L., Lapenta, G., Andersson, L., Gosling, J. T., Eriksson, S., et al. (2014). Čerenkov emission of quasiparallel whistlers by fast electron phase-space holes during magnetic reconnection. Phys. Rev. Lett. 112, 145002. doi:10.1103/PhysRevLett.112.145002

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodrich, K. A., Ergun, R. E., Schwartz, S. J., Wilson, L. B., Johlander, A., Newman, D., et al. (2019). Impulsively reflected ions: a plausibile mechanism for ion acoustic wave growth in collisionless shocks. J. Geophys. Res. 124, 1855–1865. doi:10.1029/2018JA026436

CrossRef Full Text | Google Scholar

Goodrich, K. A., Ergun, R. E., Schwartz, S. J., Wilson, L. B., Newman, D., Wilder, F. D., et al. (2018). MMS observations of electrostatic waves in an oblique shock crossing. J. Geophys. Res. 123, 9430–9442. doi:10.1029/2018JA025830

CrossRef Full Text | Google Scholar

Gurnett, D. A., and Anderson, R. R. (1977). Plasma wave electric fields in the solar wind - initial results from HELIOS 1. J. Geophys. Res. 82, 632–650. doi:10.1029/JA082i004p00632

CrossRef Full Text | Google Scholar

Gurnett, D. A., Neubauer, F. M., and Schwenn, R. (1979). Plasma wave turbulence associated with an interplanetary shock. J. Geophys. Res. 84, 541–552. doi:10.1029/JA084iA02p00541

CrossRef Full Text | Google Scholar

Henchen, R. J., Sherlock, M., Rozmus, W., Katz, J., Masson-Laborde, P. E., Cao, D., et al. (2019). Measuring heat flux from collective Thomson scattering with non-Maxwellian distribution functions. Phys. Plasmas. 26, 032104. doi:10.1063/1.5086753

CrossRef Full Text | Google Scholar

Hobara, Y., Balikhin, M., Krasnoselskikh, V., Gedalin, M., and Yamagishi, H. (2010). Statistical study of the quasi-perpendicular shock ramp widths. J. Geophys. Res. 115, 11106. doi:10.1029/2010JA015659

CrossRef Full Text | Google Scholar

Hoshino, M., and Shimada, N. (2002). Nonthermal electrons at high Mach number shocks: electron shock surfing acceleration. Astrophys. J. 572, 880–887. doi:10.1086/340454

CrossRef Full Text | Google Scholar

Hull, A. J., and Scudder, J. D. (2000). Model for the partition of temperature between electrons and ions across collisionless, fast mode shocks. J. Geophys. Res. 105, 27323–27342. doi:10.1029/2000JA900105

CrossRef Full Text | Google Scholar

Hull, A. J., Larson, D. E., Wilber, M., Scudder, J. D., Mozer, F. S., Russell, C. T., et al. (2006). Large-amplitude electrostatic waves associated with magnetic ramp substructure at Earth’s bow shock. Geophys. Res. Lett. 33, 15104. doi:10.1029/2005GL025564

CrossRef Full Text | Google Scholar

Hull, A. J., Muschietti, L., Le Contel, O., Dorelli, J. C., and Lind, P. A. (2020). MMS observations of intense whistler waves within earth’s supercritical bow shock: source mechanism and impact on shock structure and plasma transport. J. Geophys. Res. 125, e27290. doi:10.1029/2019JA027290

CrossRef Full Text | Google Scholar

Johlander, A., Schwartz, S. J., Vaivads, A., Khotyaintsev, Y. V., Gingell, I., Peng, I. B., et al. (2016). Rippled quasiperpendicular shock observed by the magnetospheric multiscale spacecraft. Phys. Rev. Lett. 117, 165101. doi:10.1103/PhysRevLett.117.165101

PubMed Abstract | CrossRef Full Text | Google Scholar

Kellogg, P. J. (2003). Langmuir waves associated with collisionless shocks; a review. Planet. Space Sci. 51, 681–691. doi:10.1016/j.pss.2003.05.001

CrossRef Full Text | Google Scholar

Kellogg, P. J., Cattell, C. A., Goetz, K., Monson, S. J., and Wilson, L. B. (2010). Electron trapping and charge transport by large amplitude whistlers. Geophys. Res. Lett. 37, L20106. doi:10.1029/2010GL044845

CrossRef Full Text | Google Scholar

Kellogg, P. J., Cattell, C. A., Goetz, K., Monson, S. J., and Wilson, L. B. (2011). Large amplitude whistlers in the magnetosphere observed with wind-waves. J. Geophys. Res. 116, A09224. doi:10.1029/2010JA015919

CrossRef Full Text | Google Scholar

Kellogg, P. J., Goetz, K., Howard, R. L., and Monson, S. J. (1992). Evidence for Langmuir wave collapse in the interplanetary plasma. Geophys. Res. Lett. 19, 1303–1306. doi:10.1029/92GL01016

CrossRef Full Text | Google Scholar

Kellogg, P. J., Goetz, K., Monson, S. J., and Opitz, A. (2013). Observations of transverse Z mode and parametric decay in the solar wind. J. Geophys. Res. 118, 4766–4775. doi:10.1002/jgra.50443

CrossRef Full Text | Google Scholar

Kennel, C. F. (1987). Critical Mach numbers in classical magnetohydrodynamics. J. Geophys. Res. 92, 13427–13437. doi:10.1029/JA092iA12p13427

CrossRef Full Text | Google Scholar

Kennel, C. F., Edmiston, J. P., and Hada, T. (1985). “A quarter century of collisionless shock research,” in Collisionless shocks in the heliosphere: a tutorial review. Geophysics monograph series. Editors R. G. Stone, and B. T. Tsurutani (Washington, D.C.: AGU), Vol. 34, 1–36. doi:10.1029/GM034p0001

CrossRef Full Text | Google Scholar

Kersten, K., Cattell, C. A., Breneman, A., Goetz, K., Kellogg, P. J., Wygant, J. R., et al. (2011). Observation of relativistic electron microbursts in conjunction with intense radiation belt whistler-mode waves. Geophys. Res. Lett. 38, L08107. doi:10.1029/2011GL046810

CrossRef Full Text | Google Scholar

Krasnoselskikh, V. V., Dudok de Wit, T., and Bale, S. D. (2011). Determining the wavelength of Langmuir wave packets at the Earth’s bow shock. Ann. Geophys. 29, (2011). 613–617. doi:10.5194/angeo-29-613-2011

CrossRef Full Text | Google Scholar

Krasnoselskikh, V. V., Lembège, B., Savoini, P., and Lobzin, V. V. (2002). Nonstationarity of strong collisionless quasiperpendicular shocks: theory and full particle numerical simulations. Phys. Plasmas. 9, 1192–1209. doi:10.1063/1.1457465

CrossRef Full Text | Google Scholar

Kurth, W. S., Gurnett, D. A., and Scarf, F. L. (1979). High-resolution spectrograms of ion acoustic waves in the solar wind. J. Geophys. Res. 84, 3413–3419. doi:10.1029/JA084iA07p03413

CrossRef Full Text | Google Scholar

Lampe, M., Manheimer, W. M., McBride, J. B., Orens, J. H., Papadopoulos, K., Shanny, R., et al. (1972). Theory and simulation of the beam cyclotron instability. Phys. Fluids. 15, 662–675. doi:10.1063/1.1693961

CrossRef Full Text | Google Scholar

Lavraud, B., and Larson, D. E. (2016). Correcting moments of in situ particle distribution functions for spacecraft electrostatic charging. J. Geophys. Res. 121, 8462–8474. doi:10.1002/2016JA022591

CrossRef Full Text | Google Scholar

Lembège, B., Savoini, P., Hellinger, P., and Trávníček, P. M. (2009). Nonstationarity of a two-dimensional perpendicular shock: competing mechanisms. J. Geophys. Res. 114, A03217. doi:10.1029/2008JA013618

CrossRef Full Text | Google Scholar

Lemons, D. S., and Gary, S. P. Current-driven instabilities in a laminar perpendicular shock. J. Geophys. Res. 83, (1978). 1625–1632. doi:10.1029/JA083iA04p01625

CrossRef Full Text | Google Scholar

Lemons, D. S., and Gary, S. P. (1977). Electromagnetic effects on the modified two-stream instability. J. Geophys. Res. 82, 2337–2342. doi:10.1029/JA082i016p02337

CrossRef Full Text | Google Scholar

Lindqvist, P. A., Olsson, G., Torbert, R. B., King, B., Granoff, M., Rau, D., et al. (2016). The spin-plane double probe electric field instrument for MMS. Space Sci. Rev. 199, 137–165. doi:10.1007/s11214-014-0116-9

CrossRef Full Text | Google Scholar

Lu, Q. M., Lembège, B., Tao, J. B., and Wang, S. (2008). Perpendicular electric field in two-dimensional electron phase-holes: a parameter study. J. Geophys. Res. 113, A11219. doi:10.1029/2008JA013693

CrossRef Full Text | Google Scholar

Malaspina, D. M., and Ergun, R. E. (2008). Observations of three-dimensional Langmuir wave structure. J. Geophys. Res. 113, A12108. doi:10.1029/2008JA013656

CrossRef Full Text | Google Scholar

Malaspina, D. M., Li, B., Cairns, I. H., Robinson, P. A., Kuncic, Z., and Ergun, R. E. Terrestrial foreshock Langmuir waves: STEREO observations, theoretical modeling, and quasi-linear simulations. J. Geophys. Res. 114, (2009). A12101. doi:10.1029/2009JA014493

CrossRef Full Text | Google Scholar

Marsch, E., and Chang, T. Electromagnetic lower hybrid waves in the solar wind. J. Geophys. Res. 88, (1983). 6869–6880. doi:10.1029/JA088iA09p06869

CrossRef Full Text | Google Scholar

Matsukiyo, S., and Matsumoto, Y. (2015). Electron acceleration at a high beta and low Mach number rippled shock. J. Phys. Conf. 642, 012017. doi:10.1088/1742-6596/642/1/012017

CrossRef Full Text | Google Scholar

Matsukiyo, S., and Scholer, M. (2012). Dynamics of energetic electrons in nonstationary quasi-perpendicular shocks. J. Geophys. Res. 117, A11105. doi:10.1029/2012JA017986

CrossRef Full Text | Google Scholar

Matsukiyo, S., and Scholer, M. (2006). On microinstabilities in the foot of high Mach number perpendicular shocks. J. Geophys. Res. 111, A06104. doi:10.1029/2005JA011409

CrossRef Full Text | Google Scholar

Mazelle, C., Lembège, B., Morgenthaler, A., Meziane, K., Horbury, T. S., Génot, V., et al. (2010). Self-reformation of the quasi-perpendicular shock: CLUSTER observations. Proc. 12th Intl. Solar Wind Conf. 1216, 471–474. doi:10.1063/1.3395905

CrossRef Full Text | Google Scholar

Mellott, M. M., and Greenstadt, E. W. (1988). Plasma waves in the range of the lower hybrid frequency – ISEE 1 and 2 observations at the earth’s bow shock. J. Geophys. Res. 93, 9695–9708. doi:10.1029/JA093iA09p09695

CrossRef Full Text | Google Scholar

Mitchell, J. J., and Schwartz, S. J. (2014). Isothermal magnetosheath electrons due to nonlocal electron cross talk. J. Geophys. Res. 119, 1080–1093. doi:10.1002/2013JA019211

CrossRef Full Text | Google Scholar

Mitchell, J. J., and Schwartz, S. J. Nonlocal electron heating at the Earth’s bow shock and the role of the magnetically tangent point. J. Geophys. Res. 118, (2013). 7566–7575. doi:10.1002/2013JA019226

CrossRef Full Text | Google Scholar

Morton, K. W. (1964). Finite amplitude compression waves in a collision-free plasma. Phys. Fluids. 7, 1800–1815. doi:10.1063/1.2746780

CrossRef Full Text | Google Scholar

Muschietti, L., and Lembège, B. (2013). Microturbulence in the electron cyclotron frequency range at perpendicular supercritical shocks. J. Geophys. Res. 118, 2267–2285. doi:10.1002/jgra.50224

CrossRef Full Text | Google Scholar

Muschietti, L., and Lembège, B. (2017). Two-stream instabilities from the lower-hybrid frequency to the electron cyclotron frequency: application to the front of quasi-perpendicular shocks. Ann. Geophys. 35, 1093–1112. doi:10.5194/angeo-35-1093-2017

CrossRef Full Text | Google Scholar

Papadopoulos, K. (1985). “Microinstabilities and anomalous transport,” in Collisionless shocks in the heliosphere: a tutorial review. Geophysics Monograph Series. Editors R. G. Stone, and B. T. Tsurutani (Washington, DC: AGU), Vol. 34, 59–90. doi:10.1029/GM034p0059

CrossRef Full Text | Google Scholar

Papadopoulos, K., and Palmadesso, P. (1976). Excitation of lower hybrid waves in a plasma by electron beams. Phys. Fluids. 19, 605. doi:10.1063/1.861501

CrossRef Full Text | Google Scholar

Pulupa, M., and Bale, S. D. (2008). Structure on interplanetary shock fronts: type II radio burst source regions. Astrophys. J. 676, 1330–1337. doi:10.1086/526405

CrossRef Full Text | Google Scholar

Pulupa, M. P., Bale, S. D., and Kasper, J. C. (2010). Langmuir waves upstream of interplanetary shocks: dependence on shock and plasma parameters. J. Geophys. Res. 115, A04106. doi:10.1029/2009JA014680

CrossRef Full Text | Google Scholar

Pulupa, M. P., Bale, S. D., Salem, C., and Horaites, K. (2014). Spin-modulated spacecraft floating potential: observations and effects on electron moments. J. Geophys. Res. 119, 647–657. doi:10.1002/2013JA019359

CrossRef Full Text | Google Scholar

Rodriguez, P., and Gurnett, D. A. (1975). Electrostatic and electromagnetic turbulence associated with the earth’s bow shock. J. Geophys. Res. 80, 19–31. doi:10.1029/JA080i001p00019

CrossRef Full Text | Google Scholar

Russell, C. T., Anderson, B. J., Baumjohann, W., Bromund, K. R., Dearborn, D., Fischer, D., et al. (2016). The magnetospheric multiscale magnetometers. Space Sci. Rev. 199, 189–256. doi:10.1007/s11214-014-0057-3

CrossRef Full Text | Google Scholar

Sagdeev, R. Z. (1966). Cooperative phenomena and shock waves in collisionless plasmas. Rev. Plasma Phys. 4, 23.

Google Scholar

Saito, S., Nariyuki, Y., and Umeda, T. (2017). Generation of intermittent ion acoustic waves in whistler-mode turbulence. Phys. Plasmas. 24, 072304. doi:10.1063/1.4990443

CrossRef Full Text | Google Scholar

Santolík, O., Gurnett, D. A., Pickett, J. S., Parrot, M., and Cornilleau-Wehrlin, N. (2003). Spatio-temporal structure of storm-time chorus. J. Geophys. Res. 108, 1278. doi:10.1029/2002JA009791

CrossRef Full Text | Google Scholar

Savoini, P., and Lembège, B. (2015). Production of nongyrotropic and gyrotropic backstreaming ion distributions in the quasi-perpendicular ion foreshock region. J. Geophys. Res. 120, 7154–7171. doi:10.1002/2015JA021018

CrossRef Full Text | Google Scholar

Scholer, M., and Burgess, D. (2006). Transition scale at quasiperpendicular collisionless shocks: full particle electromagnetic simulations. Phys. Plasmas. 13, 062101. doi:10.1063/1.2207126

CrossRef Full Text | Google Scholar

Scholer, M., and Burgess, D. (2007). Whistler waves, core ion heating, and nonstationarity in oblique collisionless shocks. Phys. Plasmas. 14, 072103. doi:10.1063/1.2748391

CrossRef Full Text | Google Scholar

Scholer, M., and Matsukiyo, S. (2004). Nonstationarity of quasi-perpendicular shocks: a comparison of full particle simulations with different ion to electron mass ratio. Ann. Geophys. 22, 2345–2353. doi:10.5194/angeo-22-2345-2004

CrossRef Full Text | Google Scholar

Schwartz, S. J., Thomsen, M. F., Bame, S. J., and Stansberry, J. (1988). Electron heating and the potential jump across fast mode shocks. J. Geophys. Res. 93, 12923–12931. doi:10.1029/JA093iA11p12923

CrossRef Full Text | Google Scholar

Scime, E. E., Bame, S. J., Feldman, W. C., Gary, S. P., Phillips, J. L., and Balogh, A. (1994b). Regulation of the solar wind electron heat flux from 1 to 5 AU: ULYSSES observations. J. Geophys. Res. 99, 23401–23410. doi:10.1029/94JA02068

CrossRef Full Text | Google Scholar

Scime, E. E., Phillips, J. L., and Bame, S. J. (1994a). Effects of spacecraft potential on three-dimensional electron measurements in the solar wind. J. Geophys. Res. 99, 14769–14776. doi:10.1029/94JA00489

CrossRef Full Text | Google Scholar

Scudder, J. D., Aggson, T. L., Mangeney, A., Lacombe, C., and Harvey, C. C. (1986a). The resolved layer of a collisionless, high beta, supercritical, quasi-perpendicular shock wave. I–rankine-Hugoniot geometry, currents, and stationarity. J. Geophys. Res. 91, 11019–11052. doi:10.1029/JA091iA10p11019

CrossRef Full Text | Google Scholar

Scudder, J. D., Aggson, T. L., Mangeney, A., Lacombe, C., and Harvey, C. C. (1986b). The resolved layer of a collisionless, high beta, supercritical, quasi-perpendicular shock wave. II - dissipative fluid electrodynamics. J. Geophys. Res. 91, 11053–11073. doi:10.1029/JA091iA10p11053

CrossRef Full Text | Google Scholar

Scudder, J. D., Cao, X., and Mozer, F. S. (2000). Photoemission current-spacecraft voltage relation: key to routine, quantitative low-energy plasma measurements. J. Geophys. Res. 105, 21281–21294. doi:10.1029/1999JA900423

CrossRef Full Text | Google Scholar

Scudder, J. D., Mangeney, A., Lacombe, C., Harvey, C. C., and Wu, C. S. (1986c). The resolved layer of a collisionless, high beta, supercritical, quasi-perpendicular shock wave. III – Vlasov electrodynamics. J. Geophys. Res. 91, 11075–11097. doi:10.1029/JA091iA10p11075

CrossRef Full Text | Google Scholar

Singh, N., Loo, S. M., Wells, B. E., and Deverapalli, C. (2000). Three-dimensional structure of electron holes driven by an electron beam. Geophys. Res. Lett. 27, 2469–2472. doi:10.1029/2000GL003766

CrossRef Full Text | Google Scholar

Singh, N., Loo, S. M., and Wells, B. E. (2001). Electron hole as an antenna radiating plasma waves. Geophys. Res. Lett. 28, 1371–1374. doi:10.1029/2000GL012652

CrossRef Full Text | Google Scholar

Soucek, J., Santolík, O., Dudok de Wit, T., and Pickett, J. S. (2009). Cluster multispacecraft measurement of spatial scales of foreshock Langmuir waves. J. Geophys. Res. 114, A02213. doi:10.1029/2008JA013770

CrossRef Full Text | Google Scholar

Stringer, T. E. (1963). Low-frequency waves in an unbounded plasma. J. Nuclear Energy. 5, 89–107. doi:10.1088/0368-3281/5/2/304

CrossRef Full Text | Google Scholar

Tidman, D. A., and Krall, N. A. (1971). Shock waves in collisionless plasmas. New York, NY: John Wiley & Sons.

Google Scholar

Tidman, D. A., and Northrop, T. G. (1968). Emission of plasma waves by the Earth’s bow shock. J. Geophys. Res. 73, 1543–1553. doi:10.1029/JA073i005p01543

CrossRef Full Text | Google Scholar

Tsurutani, B. T., Verkhoglyadova, O. P., Lakhina, G. S., and Yagitani, S. (2009). Properties of dayside outer zone chorus during HILDCAA events: loss of energetic electrons. J. Geophys. Res. 114, A03207. doi:10.1029/2008JA013353

CrossRef Full Text | Google Scholar

Umeda, T., Kidani, Y., Matsukiyo, S., and Yamazaki, R. (2014). Dynamics and microinstabilities at perpendicular collisionless shock: a comparison of large-scale two-dimensional full particle simulations with different ion to electron mass ratio. Phys. Plasmas. 21, 022102. doi:10.1063/1.4863836

CrossRef Full Text | Google Scholar

Umeda, T., Kidani, Y., Matsukiyo, S., and Yamazaki, R. (2012b). Microinstabilities at perpendicular collisionless shocks: a comparison of full particle simulations with different ion to electron mass ratio. Phys. Plasmas. 19, 042109. doi:10.1063/1.3703319

CrossRef Full Text | Google Scholar

Umeda, T., Kidani, Y., Matsukiyo, S., and Yamazaki, R. (2012a). Modified two-stream instability at perpendicular collisionless shocks: full particle simulations. J. Geophys. Res. 117, A03206. doi:10.1029/2011JA017182

CrossRef Full Text | Google Scholar

Umeda, T., Yamao, M., and Yamazaki, R. (2011). Cross-scale coupling at a perpendicular collisionless shock. Planet. Space Sci. 59, 449–455. doi:10.1016/j.pss.2010.01.007

CrossRef Full Text | Google Scholar

Umeda, T., Yamazaki, R., Ohira, Y., Ishizaka, N., Kakuchi, S., Kuramitsu, Y., et al. (2019). Full particle-in-cell simulation of the interaction between two plasmas for laboratory experiments on the generation of magnetized collisionless shocks with high-power lasers. Phys. Plasmas. 26, 032303. doi:10.1063/1.5079906

CrossRef Full Text | Google Scholar

Vasko, I. Y., Mozer, F. S., Krasnoselskikh, V. V., Artemyev, A. V., Agapitov, O. V., Bale, S. D., et al. (2018). Solitary waves across supercritical quasi-perpendicular shocks. Geophys. Res. Lett. 45, 5809–5817. doi:10.1029/2018GL077835

CrossRef Full Text | Google Scholar

Vedenov, A. A. (1963). Quasi-linear plasma theory (theory of a weakly turbulent plasma). J. Nucl. Energy. 5, 169–186. doi:10.1088/0368-3281/5/3/305

CrossRef Full Text | Google Scholar

Walker, S. N., Balikhin, M. A., Alleyne, H. S. C. K., Hobara, Y., André, M., and Dunlop, M. W. (2008). Lower hybrid waves at the shock front: a reassessment. Ann. Geophys. 26, 699–707. doi:10.5194/angeo-26-699-2008

CrossRef Full Text | Google Scholar

Wang, R., Vasko, I. Y., Mozer, F. S., Bale, S. D., Artemyev, A. V., Bonnell, J. W., et al. (2020). Electrostatic turbulence and debye-scale structures in collisionless shocks. Astrophys. J. Lett. 889, L9. doi:10.3847/2041-8213/ab6582

CrossRef Full Text | Google Scholar

Wilson, L. B. (2010). The microphysics of collisionless shocks. PhD thesis, University of Minnesota. Publication Number: AAT 3426498; ISBN: 9781124274577; Minneapolis, MN: Advisor: Cynthia Cattell.

Google Scholar

Wilson, L. B., Cattell, C., Kellogg, P. J., Goetz, K., Kersten, K., Hanson, L., et al. (2007). Waves in interplanetary shocks: a wind/WAVES study. Phys. Rev. Lett. 99, 041101. doi:10.1103/PhysRevLett.99.041101

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, L. B., Cattell, C. A., Kellogg, P. J., Goetz, K., Kersten, K., Kasper, J. C., et al. (2010). Large-amplitude electrostatic waves observed at a supercritical interplanetary shock. J. Geophys. Res. 115, A12104. doi:10.1029/2010JA015332

CrossRef Full Text | Google Scholar

Wilson, L. B., Cattell, C. A., Kellogg, P. J., Wygant, J. R., Goetz, K., Breneman, A., et al. (2011). The properties of large amplitude whistler mode waves in the magnetosphere: propagation and relationship with geomagnetic activity. Geophys. Res. Lett. 38, L17107. doi:10.1029/2011GL048671

CrossRef Full Text | Google Scholar

Wilson, L. B., Chen, L. J., Wang, S., Schwartz, S. J., Turner, D. L., Stevens, M. L., et al. (2019a). Electron energy partition across interplanetary shocks: II. Statistics. Astrophys. J. 245. doi:10.3847/1538-4365/ab5445

CrossRef Full Text | Google Scholar

Wilson, L. B., Chen, L. J., Wang, S., Schwartz, S. J., Turner, D. L., Stevens, M. L., et al. (2020). Electron energy partition across interplanetary shocks: III. Analysis. Astrophys. J. 893. doi:10.3847/1538-4357/ab7d39

CrossRef Full Text | Google Scholar

Wilson, L. B., Chen, L. J., Wang, S., Schwartz, S. J., Turner, D. L., Stevens, M. L., et al. (2019b). Electron energy partition across interplanetary shocks: I. Methodology and data product. Astrophys. J. 243. doi:10.3847/1538-4365/ab22bd

CrossRef Full Text | Google Scholar

Wilson, L. B., Koval, A., Sibeck, D. G., Szabo, A., Cattell, C. A., Kasper, J. C., et al. (2013). Shocklets, SLAMS, and field-aligned ion beams in the terrestrial foreshock. J. Geophys. Res. 118, 957–966. doi:10.1029/2012JA018186

CrossRef Full Text | Google Scholar

Wilson, L. B., Koval, A., Szabo, A., Breneman, A., Cattell, C. A., Goetz, K., et al. (2012). Observations of electromagnetic whistler precursors at supercritical interplanetary shocks. Geophys. Res. Lett. 39, L08109. doi:10.1029/2012GL051581

CrossRef Full Text | Google Scholar

Wilson, L. B., Koval, A., Szabo, A., Stevens, M. L., Kasper, J. C., Cattell, C. A., et al. (2017). Revisiting the structure of low Mach number, low beta, quasi-perpendicular shocks. J. Geophys. Res. 122, 9115–9133. doi:10.1002/2017JA024352

CrossRef Full Text | Google Scholar

Wilson, L. B., Sibeck, D. G., Breneman, A. W., Le Contel, O., Cully, C., Turner, D. L., et al. (2014a). Quantified energy dissipation rates in the terrestrial bow shock: 1. Analysis techniques and methodology. J. Geophys. Res. 119, 6455–6474. doi:10.1002/2014JA019929

CrossRef Full Text | Google Scholar

Wilson, L. B., Sibeck, D. G., Breneman, A. W., Le Contel, O., Cully, C., Turner, D. L., et al. (2014b). Quantified energy dissipation rates in the terrestrial bow shock: 2. Waves and dissipation. J. Geophys. Res. 119, 6475–6495. doi:10.1002/2014JA019930

CrossRef Full Text | Google Scholar

Wilson, L. B., Sibeck, D. G., Turner, D. L., Osmane, A., Caprioli, D., and Angelopoulos, V. (2016). Relativistic electrons produced by foreshock disturbances observed upstream of the Earth’s bow shock. Phys. Rev. Lett. 117, 215101. doi:10.1103/PhysRevLett.117.215101

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, L. B., Stevens, M. L., Kasper, J. C., Klein, K. G., Maruca, B., Bale, S. D., et al. (2018). The Statistical Properties of Solar Wind Temperature Parameters Near 1 au. Astrophys. J. Suppl. 236, 41. doi:10.3847/1538-4365/aab71c

CrossRef Full Text | Google Scholar

Wu, C. S., Winske, D., Papadopoulos, K., Zhou, Y. M., Tsai, S. T., and Guo, S. C. (1983). A kinetic cross-field streaming instability. Phys. Fluids. 26, 1259–1267. doi:10.1063/1.864285

CrossRef Full Text | Google Scholar

Wu, C. S., Winske, D., Tanaka, M., Papadopoulos, K., Akimoto, K., Goodrich, C. C., et al. (1984). Microinstabilities associated with a high Mach number, perpendicular bow shock. Space Sci. Rev. 37, 63–109. doi:10.1007/BF00213958

CrossRef Full Text | Google Scholar

Wygant, J. R., Bensadoun, M., and Mozer, F. S. (1987). Electric field measurements at subcritical, oblique bow shock crossings. J. Geophys. Res. 92, 11109–11121. doi:10.1029/JA092iA10p11109

CrossRef Full Text | Google Scholar

Wygant, J. R., Bonnell, J. W., Goetz, K., Ergun, R. E., Mozer, F. S., Bale, S. D., et al. (2013). The electric field and waves instruments on the radiation belt storm probes mission. Space Sci. Rev. 179, 183–220. doi:10.1007/s11214-013-0013-7

CrossRef Full Text | Google Scholar

Yang, Z., Lu, Q., Gao, X., H, C., Yang, H., Liu, Y., et al. (2013). Magnetic ramp scale at supercritical perpendicular collisionless shocks: full particle electromagnetic simulations. Phys. Plasmas. 20, 092116. doi:10.1063/1.4821825

CrossRef Full Text | Google Scholar

Zeković, V. (2019). Resonant micro-instabilities at quasi-parallel collisionless shocks: cause or consequence of shock (re)formation. Phys. Plasmas. 26, 032106. doi:10.1063/1.5050909

CrossRef Full Text | Google Scholar