Experimental Nuclear Astrophysics With the Light Elements Li, Be and B: A Review

Light elements offer a unique opportunity for studying several astrophysical scenarios from Big Bang Nucleosynthesis to stellar physics. Understanding the stellar abundances of light elements is key to obtaining information on internal stellar structures and mixing phenomena in different evolutionary phases, such as the pre-main-sequence, main-sequence or red-giant branch. In such a case, light elements, i.e., lithium, beryllium and boron, are usually burnt at temperatures of the order of 2–5 × 10⁶ K. Consequently, the astrophysical S(E)-factor and the reaction rate of the nuclear reactions responsible for the burning of such elements must be measured and evaluated at ultra-low energies (between 0 and 10 keV). The Trojan Horse Method (THM) is an experimental technique that allows us to perform this kind of measurements avoiding uncertainties due to the extrapolation and electron screening effects on direct data. A long Trojan Horse Method research program has been devoted to the measurement of light element burning cross sections at astrophysical energies. In addition, dedicated direct measurements have been performed using both in-beam spectroscopy and the activation technique. In this review we will report the details of these experimental measurements and the results in terms of S(E)-factor, reaction rate and electron screening potential. A comparison between astrophysical reaction rates evaluated here and the literature will also be given.

1 Introduction

Lithium, beryllium and boron (hereafter LiBeB, for simplicity) are carriers of important information in several domain of astrophysics, from primordial Big Bang Nucleosynthesis (BBN) to cosmic ray nucleosyntheis (GCR nucleosynthesis) and stellar nucleosynthesis (both for quiescent and explosive scenarios).

Primordial nucleosynthesis is one of the three pillars of the Big Bang theory together with Hubble expansion and the relic Cosmic Microwave Background (CMB) radiation. Although a strong agreement exists between BBN theoretical predictions for ²H and ^3,4He abundances, the long-standing debate about the cosmological Li-problem is far from solved (Pitrou et al., 2018). The primordial lithium abundances (Li)¹ are derived from metal-poor main sequence halo star observations. These stars show a remarkably constant value of Li/H since the metallicity [Fe/H] varies (for [Fe/H] < −1.5 and $T_{\text{eff}}$ above ∼5,900 K), leading to the so called Spite plateau [see, e.g., (Spite and Spite, 1982; Meléndez et al., 2010; Sbordone et al., 2010), and references therein]. An averaged value of (Li/H)_obs = $\left({1.58}_{-0.28}^{+0.35}\right)$ × 10⁻¹⁰ is currently accepted, as reported in (Sbordone et al., 2010). By comparing (Li/H)_obs with the most recent inferred lithium abundances (Li/H)_BBN ∼ (5.623) × 10⁻¹⁰ (Pitrou et al., 2018), we can find a discrepancy of a factor of ∼3.6. Several efforts have been made within pure nuclear physics in the recent years to alleviate this deviation, as in the case of the recent cross section measurements of the ⁷Be(n,p) ⁷Li and ⁷Be(n,α) ⁴He neutron-induced reactions (Barbagallo et al., 2016; Lamia et al., 2017; Damone et al., 2018; Lamia et al., 2019), which affect the total ⁷Li primordial abundance. Despite these efforts or new physics in BBN models [see e.g. (Fields, 2011; Goudelis et al., 2016; Coc and Vangioni, 2017)] or possible stellar depletion mechanisms [diffusion, mass-loss, accretion (Vauclair and Charbonnel, 1995; Richard et al., 2005; Fu et al., 2015; Tognelli et al., 2020)], the Li-problem seems to be far from the solution. For completeness, the BBN calculations of (Coc et al., 2012) allow us to get the primordial abundances of boron (¹¹B), N(¹¹B)/N(H) ≈ 3 × 10⁻¹⁶ and beryllium N(⁹Be)/N(H) ≈ 3 × 10⁻¹⁸ at very low values with respect the ones observed up to now in halo-stars (Tan et al., 2009; Primas, 2010; Boesgaard et al., 2011).

Galactic cosmic ray (GCR) nucleosynthesis is responsible for the production of most cosmic ⁹Be through spallation reactions induced by the interaction of high-energy particles with CNO nuclei in the interstellar medium (Lemoine et al., 1998; Fields and Olive, 1999). Additionally, GCR nucleosynthesis allows one to explain LiBeB abundances and isotopic ratios, although only in the late 90s was it made clear that additional sources for the production of ⁷Li and ¹¹B were needed. An indisputable “signature” of the GCR action is the increase of Be and B abundances with the metallicity (Fields and Olive, 1999; Prantzos, 2012; Prantzos et al., 2017). For Milky Way disc stars with [Fe/H] larger than about −1.5, [Li/H] increases with [Fe/H] from the Spite plateau value up to its solar value (Lambert and Reddy, 2004). Nevertheless, it is widely recognized that GCR nucleosyntesis cannot account for the total lithium abundance observed in the galactic disc, and stellar nucleosynthesis contributes significantly (Prantzos et al., 2017).

Stellar burning effectively depletes LiBeB at stellar depths where temperatures of few 10⁶ K are reached, ranging from T ≈ 2 × 10⁶ K for ⁶Li to T ≈ 4–5 × 10⁶ K for boron isotopes. Their surface abundances are strongly influenced by the nuclear burnings as well as by the extension of the convective envelope (see e.g., Deliyannis et al., 2000; Jeffries, 2006). The prediction of light element abundances in stars still represents an unsolved and challenging task for astrophysics since it strongly depends on the adopted input physics in theoretical models e.g., nuclear reaction rates, opacity of the stellar matter, equation of state, efficiency of microscopic diffusion, etc. (see e.g., Piau and Turck-Chièze, 2002; D’Antona and Montalbán, 2003; Montalbán and D’Antona, 2006; Tognelli et al., 2012) as well as on the assumed external convection efficiency. In addition, since the first observational evidences from Li abundances in Hyades (∼600 My) and Pleiades (∼70 My) open clusters (Spite and Spite, 1986), the light elements LiBeB problem has also been confirmed by the existence of a less-pronounced Be-dip connected with Li-dip, by the Li–Be and Be–B correlation and by the (nearly) constant B abundances in the open clusters (Boesgaard et al., 2004; Boesgaard et al., 2005; Boesgaard et al., 2019). Astronomical observations suggest that lithium and beryllium are depleted in F-type MS stars in middle-aged clusters (such as those detected in the Hyades or Praesepe, ∼600 My). On the other hand, there is no evidence of this depletion in F-type PMS stars, as revealed by observations of young open clusters [for ages ≤150–200 My (Boesgaard et al., 2004; Sestito and Randich, 2005)]. The discrepancies between astronomical observations and stellar models could be overcome if non-standard stellar mixing, mainly induced by stellar rotation, is taken into account (Stephens et al., 1997; Boesgaard et al., 2016). In addition, explosive scenario could significantly contribute to the light element abundances, particularly ⁷Li ones. Carbon-oxygen (CO) novae have been recently studied as possible contributors for galactic lithium-7 production in the work of Starrfield et al. (2019) thanks to the large contribution of ⁷Be present in the ejected material of a Nova explosion, which later decays into ⁷Li. Lithium and boron abundances could also be used to constrain neutrino driven nucleosynthesis, as recently suggested by Kusakabe et al. (2019).

2 The Role of the Trojan Horse Method in Nuclear Astrophysics

LiBeB are easily burnt by proton capture reactions at temperatures of few million Kelvin. At such temperatures, the (p,α) channel dominates the total proton-capture cross section. In order to evaluate the energy range at which such processes occur, the general formula of the Gamow window could be applied (Rolfs and Rodney, 1988):

$E_0=1.22{\left(Z_x^2{Z}_X^2\mu T_6^2\right)}^{\frac{1}{3}}\text{keV}$

$\text{Δ}{E}_0=0.749{\left(Z_x^2{Z}_X^2\mu T_6^5\right)}^{\frac{1}{6}}\text{keV},$

where E₀ is the central energy and $\text{Δ}{E}_0$ the Gamow window’s width, Z_x and Z_X are the atomic numbers of the two interacting particles, µ their reduced mass and T₆ the temperature of the stellar plasma in million degrees Kelvin. Table 1 summarizes the value of E₀ and $\text{Δ}{E}_0$ for the proton induced reactions on LiBeB of interest for the stellar burning conditions as given in Section 1.

TABLE 1

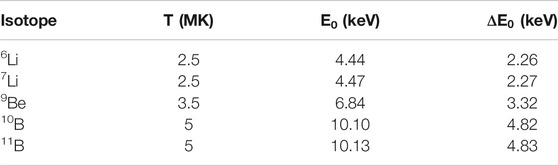
TABLE 1. Central energy and width of the Gamow windows for the proton-induced reactions on LiBeB at temperatures, typical of their stellar burning as discussed in Section 1, expressed in millions of Kelvin.

At such energies, the direct measurement of a charged-particle-induced reaction cross section is hindered by the Coulomb barrier penetration probability, which suppresses nuclear cross sections to the nano or picobarn scale. Moreover, a further difficulty in performing ultra-low energy cross section measurements is related to the presence of the electron screening effect due to the electronic cloud surrounding the interacting particles in a terrestrial laboratory measurement (Rolfs and Rodney, 1988). Indeed, nuclear reaction cross sections measured in the laboratory exhibit an enhancement, with respect to the bare-nucleus ones, given by (Rolfs and Rodney, 1988)

$f_{enh}=\frac{{\sigma }_{sh}}{{\sigma }_b}\approx \text{exp}\left(\pi \eta \frac{U_e}{E}\right),(1)$

σ_sh being the shielded nuclear cross section measured in the laboratory, σ_b the bare-nucleus cross section, η the Sommerfeld parameter (Rolfs and Rodney, 1988) and U_e the electron screening potential in the laboratory. The combined effects of Coulomb barrier penetration and electron screening make it difficult to access the Gamow energy window, leaving extrapolation as the most common way to extract the S(E)-factor

$S\left(E\right)=E\sigma \left(E\right)exp\left(2\pi \eta \right)(2)$

down to the relevant energies.

The knowledge of the S(E)-factor allows us to evaluate the reaction rate through the following formula:

$N_A\langle \sigma v\rangle ={\left(\frac{8}{\pi \mu }\right)}^{\frac{1}{2}}\frac{N_A}{{\left(kT\right)}^{\frac{3}{2}}}{{{\displaystyle \int }}^{\text{}}}_0^{\infty }S\left(E\right)e^{-2\pi \eta -\frac{E}{kT}}dE(3)$

where E is the center-of-mass energy.

Extrapolation procedures are difficult to perform, as the electron screening phenomenon is far from completely understood. Indeed, large deviations are present when comparing the electron screening potential U_e values intervening in Eq. 1, as deduced in the laboratory alongside the ones predicted by theoretical models. Such a deviation inevitably makes extrapolation procedures difficult, as the enhanced cross section values measured in a laboratory cannot properly be revealed from any electron screening potential value known a priori (Adelberger et al., 2011).

Thanks to the development of experimental techniques and the improvement of devoted theoretical formalism, several indirect methods have been proposed in the last years to access the astrophysically relevant energy region without the use of any extrapolation procedure (Tribble et al., 2014). Among them, the Trojan Horse Method is a powerful tool for measuring the bare-nucleus cross section of a binary reaction of interest for astrophysics at Gamow energies without the influence of Coulomb suppression or electron screening phenomena.

THM allows us to extract the cross section of an astrophysically relevant A(x, c)C reaction by selecting the quasi-free (QF) component of a suitable 2 → 3 body reaction a(A, cC)s (Baur, 1986; Spitaleri, 1991; Spitaleri et al., 2003; Spitaleri et al., 2004; Tribble et al., 2014; Spitaleri et al., 2016; Spitaleri et al., 2019). Nucleus a, called the “Trojan-horse (TH) nucleus”, exhibits a dominant $a=x\oplus s$ cluster configuration probability with a low x − s binding energy. In addition, the radial wave function for the x − s configuration is known from independent studies. The 2 → 3 body reaction occurs at energies higher than the A + a Coulomb barrier, thus causing the breakup of a into its components x and s directly in the nuclear field. In the quasi-free conditions, the “spectator” s maintains in the exit channel the same momentum distribution it had in a before the occurrence of the break-up, i.e., only x takes part to the binary reaction as “participant”. The role of the x − s binding energy is of primary importance since it allows for compensating the energy of the incoming projectile down to astrophysical energies (Tribble et al., 2014; Spitaleri et al., 2016; Spitaleri et al., 2019). Thus, THM data will be not affected by Coulomb barrier penetration effects or screening phenomena (Assenbaum et al., 1987) since the interaction A − x switches on in the nuclear field.

Taking advantage of the Plane Wave Impulse Approximation (PWIA), it is possible to relate the a(A,cC)s reaction cross section to the A(x,c)C one through the relation (Tribble et al., 2014; Spitaleri et al., 2016; Spitaleri et al., 2019):

$\frac{d^3\sigma }{d{E}_{c}d{\text{Ω}}_{c}d{\text{Ω}}_C}\propto \text{KF}\cdot {\left|\text{Φ}\left(\overrightarrow{{\text{p}}_{\text{xs}}}\right)\right|}^2\cdot {\frac{d\sigma }{d\text{Ω}}|}_{cm}^{HOES}(4)$

where:

• the kinematical factor KF is function of masses, momenta and angles of the outgoing particles;

• ${\left|\text{Φ}\left(\overrightarrow{{\text{p}}_{\text{xs}}}\right)\right|}^2$ is the squared modulus of the Fourier transform of the radial wave function for the x − s motion. Depending on the selected TH-nucleus, it can be described through the Hulthén, Hänkel or Eckart functions;

• $d\sigma /d\text{Ω}{|}_{cm}^{HOES}$ is the half-off-energy-shell (HOES) A(x,c)C differential cross section at the center of mass energy E_cm = E_cC − Q. Q is the A(x,c)C Q-value while E_cC is the relative c–C energy measured in laboratory. This quantity is the HOES since the transferred particle x, with mass m_x, is virtual; the corresponding energy and momentum do not obey the mass-shell equation ${\text{E}}_x={\text{k}}_x^2{\text{/}(2\text{m}}_x)\text{.}$ In QF conditions, the relative A – x energy is given by $E_{Ax}=p_{Ax}^2/\left(2{\mu }_{Ax}\right)-{\mathit{ϵ}}_{sx},$ being ${\mathit{ϵ}}_{sx}$ the binding energy of the TH-nucleus. Since the outgoing c–C particles are “real”, the energy-momentum relation is restored in the exit channel (Tribble et al., 2014).

More advanced techniques have also been developed for resonant reactions (see for instance Sergi et al., 2015) together with the modified R-matrix approach of Mukhamedzhanov et al. (2008), La Cognata et al. (2011) for multiresonant reactions (Guardo et al., 2017; Indelicato et al., 2017; Tumino et al., 2018). Recently, an extension to RIB's induced reactions has been also provided, as discussed in Cherubini et al. (2015), Pizzone et al. (2016), Lamia et al. (2019).

3 Study Cases: LiBeB Burning Reactions

The THM has largely been applied to shed light on cross section measurements for the light element burning processes. In the following, some of the most important results concerning the study of the ^6,7Li(p,α)^3,4He, ⁹Be(p,α)⁶Li and ^10,11B(p,α)^7,8Be reactions will be reported.

3.1 The ⁶Li(p,α)³He Burning Reaction

3.1.1 Direct Measurement

The ⁶Li(p,α)³He reaction has been studied at low energies (<1 MeV) by several groups. Among them, the direct measurement of Engstler et al. (1992) covers the energy range between 10 and 500 keV and provides an extrapolated S(E)-factor to zero energy S(0) = 3.09 ± 1.23 MeV barns, where the 40% error accounts for the uncertainty on the absolute cross section. Concerning the electron screening potential, the authors derived a value of U_e = 470 ± 150 eV (by considering cross section measurements on atomic lithium targets) and U_e = 440 ± 150 eV (by considering cross section measurements on molecular lithium targets). The direct measurements by Cruz et al. (2005), Cruz et al. (2008) provide the most recent direct study of the ⁶Li(p,α)³He reaction. The energy ranges spanned 30–100 keV and 90–1740 keV, respectively, using different lithium-implanted targets. The extrapolated zero-energy S(E)-factor was S(0) = 3.52 ± 0.08 MeV barns, while the extracted electron screening potential was U_e = 237 ± 111 eV (Li₂ WO₄ target) (Cruz et al., 2008).

The theoretical value provided by the adiabatic limit is $U_e^{ad}=175\text{eV}\text{.}$

3.1.2 Trojan Horse Method Measurement

The THM low-energy investigation of the ⁶Li(p,α)³He reaction was performed in two different measurements. In Tumino et al. (2003), the ⁶Li(p,α)³He reaction was studied by means of THM applied to the ²H(⁶Li,α³He)n QF reaction. The experiment was performed at Laboratori Nazionali del Sud in Catania by means of a 25 MeV ⁶Li beam provided by the SMP Tandem van de Graaff accelerator, which was delivered on a 250 µg/cm²-thick deuterated polyethylene CD₂ target. Beam energy and angular displacement of the detection setup were selected following the standard procedure for THM experiments, as discussed in Spitaleri et al. (2016).

Silicon position-sensitive detectors (PSD) were placed inside the CAMERA2000 scattering chamber to cover the phase space region where the quasi-free reaction mechanism is expected to be dominant. Kinematical conditions allowed us to measure the excitation function in a center-of-mass energy range from 2 MeV down to 40 keV. In order to get the ⁶Li(p,α)³He reaction cross section in absolute units, TH data have been normalized to direct data from Engstler et al. (1992). The zero-energy S(E)-factor obtained was S(0) = 3.00 ± 0.19 MeV barns. The error is only statistical, while an additional ∼11% error was due to the normalization procedure.

The second THM study (Tumino et al., 2004) was performed at the 4 MV Tandem accelerator of the Dynamitron Tandem Laboratorium in Bochum with the aim of exploring lower energies with respect the measurement of Tumino et al. (2003). For such a purpose, a 14 MeV ⁶Li beam was used, allowing us to investigate down to about 10 keV in the center-of-mass energy. The simultaneous fit of the two THM data sets confirmed a zero energy S(E)-factor S(0) = 3.00 ± 0.19 MeV barns (Tumino et al., 2003; Tumino et al., 2004). Moreover, an estimation of electron screening potential was provided: U_e = 450 ± 100 eV. More details regarding the TH measurements can be found in Tumino et al. (2003) and Tumino et al. (2004). Pizzone et al. (2005) evaluated the reaction rate, taking into account TH bare-nucleus cross section and evaluating its impact on the lithium abundance during the PMS phase.

In Lamia et al. (2013) a new evaluation of the ⁶Li(p,α)³He S(E)-factor was performed due to the recent availability of direct data. In detail, the direct measurements of Cruz et al. (2008) were included in the data set necessary for THM normalization together with the ones available in the NACRE compilation (Angulo et al., 1999). A new normalization procedure was consequently made for the THM data (Tumino et al., 2004) with the advantage of the small uncertainties on the new set of direct data (Cruz et al., 2008). The final result of the investigation made in Lamia et al. (2013) is reported in Figure 1 as red squares, while black dots represent TH data from Tumino et al. (2003). The two TH data set have been fitted with a third-order polynomial function (black line in Figure 1) with the aim of extracting the zero-energy S(E)-factor:

$S\left(E\right)=3.44-3.50E+1.74E^2+0.23E^3\text{MeV}\text{barns}(5)$

FIGURE 1

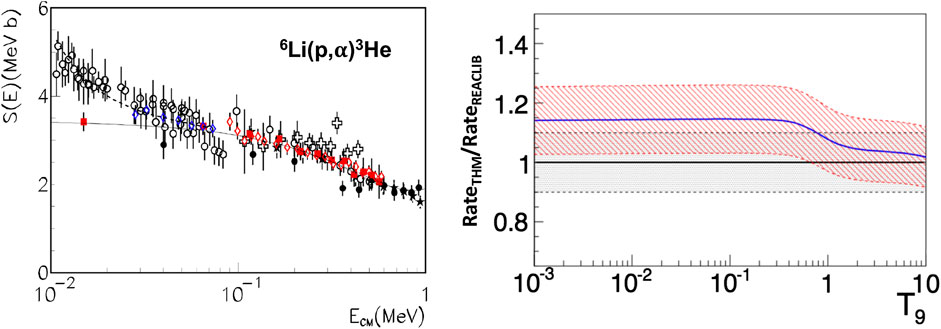
FIGURE 1. Left panel S(E)-factor for the ⁶Li(p,α)³He reaction. TH data from Lamia et al. (2013) (red squares) normalized to the available direct measurements of Elwyn et al. (1979), Kwon et al. (1989), Cruz et al. (2008). Black dots represent TH data from Tumino et al. (2003). The full line is the result of the polynomial fit of TH data. Dashed line is the result of the fit of Engstler et al. (1992) and Cruz et al. (2005) data to extract the electron screening potential. Right panel The ratio between the THM reaction rate of Lamia et al. (2013) compared with the one reported in Cyburt et al. (2010) [Figures adapted from Lamia et al. (2013)].

The obtained value was S(0) = 3.44 ± 0.35 MeV barns, where the quoted error accounts for the statistical error on the TH experimental points (∼7% an average) and on the direct data as well (∼7% an average), while a ∼3% uncertainty was due to the normalization procedure.

The electron screening potential was then extracted following the standard procedure adopted for these kinds of measurements so far, i.e., by fitting the low-energy (<70 keV) data of Engstler et al. (1992) and Cruz et al. (2005) via Eq. 1, considering the bare-nucleus cross section given by Eq. 5 and leaving U_e as the only free parameter. This led to the value of U_e = 355 ± 100 eV, where the error takes into account a ∼12% related to the uncertainties in the low-energy direct data of Engstler et al. (1992) (more details in Lamia et al., 2013). The result of the fit is shown in Figure 1 (left side) as dashed line.

Lamia et al. (2013) provide also a new evaluation of the ⁶Li(p,α)³He reaction rate at astrophysical energies, deduced via Eq. (3). The reaction rate given in Lamia et al. (2013) was then compared with the one reported in the JINA-REACLIB compilation (Cyburt et al., 2010), as reported in the left panel of Figure 1. The TH result deviates at low temperatures from the one of Cyburt et al. (2010), showing an increase of about ∼5–15% as the temperature decreases from 1 down to 10⁻³ T₉.

The astrophysical impact of the TH reaction rate (with respect to the one from the widely used NACRE compilation) was evaluated by Lamia et al. (2013) in which the focus was on PMS stellar models by use of the FRANEC stellar evolution code (Degl’Innocenti et al., 2008; Dell’Omodarme et al., 2012; Tognelli et al., 2012). The greatest differences are present for those stars that efficiently burn ⁶Li, which correspond to stars in the mass interval 0.6–1.2M_ʘ; in this case, the adoption of the recent TH reaction rate reduces the lithium abundance by ∼15%. However, the current ⁶Li reaction rate and its estimated uncertainty introduce variations on the surface lithium abundance in stellar models that are less important than those caused by the uncertainties on other physics input and parameters used in stellar evolutionary codes, such as the uncertainty on the radiative opacity, equation of state, outer boundary conditions, convection efficiency and initial chemical composition (see, e.g., Tognelli et al., 2012).

3.2 The ⁷Li(p,α)⁴He Burning Reaction

3.2.1 Direct Measurements

Several direct cross section measurements were dedicated to the study of the ⁷Li(p,α)⁴He reaction. A thorough list is reported in Lamia et al. (2012a) together with the results in terms of S(E)-factor and electron screening potential. In particular, Engstler et al. (1992) measured the ⁷Li(p,α)⁴He reaction over the c.m. energy range from ∼1 MeV down to ∼30 keV. The extrapolated zero-energy S(E)-factor was S(0) = 59 ± 23 keV barns, where the error is derived from the absolute cross-section determination, while the obtained electron screening potential values were U_e = 300 ± 280 eV for atomic lithium target and U_e = 300 ± 160 eV for molecular lithium target. The experimental results in Engstler et al. (1992) are included in the NACRE compilation (Angulo et al., 1999). The latest direct measurements are discussed in Cruz et al. (2005) and Cruz et al. (2008). The two measurements covered the following c. m. energy range 30–100 keV and 90–1740 keV respectively, providing a data set with lower uncertainties with respect previous measurements. To extract the zero-energy S(E)-factor, data have been fitted by an R-matrix calculation, obtaining $S\left(0\right)={55.6}_{-1.7}^{+0.8}\text{keV}\text{barns}\text{.}$ The measured electron screening potential was $U_e={237}_{-77}^{+133}\text{eV}\text{.}$ For completeness, we report the theoretical value $U_e^{ad}$ = 175 eV provided by the adiabatic limit.

3.2.2 Trojan Horse Method Measurements

A number of THM experiments have been dedicated to the study of the ⁷Li(p,α)⁴He reaction. In particular, the TH measurement of the low-energy ⁷Li(p,α)⁴He bare-nucleus S(E)-factor was reported in Aliotta et al. (2000), Lattuada et al. (2001) while an extended measurement also at higher energies (i.e., up to ∼3 MeV in center of mass) was reported in Tumino et al. (2006). In both the experimental works Aliotta et al. (2000) and Lattuada et al. (2001), the deuteron was used as the TH nucleus because of its $\text{p}\oplus \text{n}$ structure. In Tumino et al. (2006), ³He was instead used because of its $\text{p}\oplus \text{d}$ structure. The agreement between the two different THM measurements, where different TH-nuclei were adopted, was the experimental confirmation of the so-called “polar-invariance” of THM measurements, as extensively discussed in Pizzone et al. (2011), Pizzone et al. (2013).

Focusing on the work by Lattuada et al. (2001), the ⁷Li(p,α)⁴He cross section measurement was performed by applying the THM to the QF ²H(⁷Li,αα)n reaction. The experiment was performed at Laboratori Nazionali del Sud (Catania, Italy) using a ⁷Li beam at three different energies: 19.0, 19.5 and 20.0 MeV delivered onto a 250 µg/cm²-thick CD₂ target. The outgoing α particles were detected by means of PSD displaced in order to cover the kinematic region at which a strong contribution from the QF reaction mechanism is expected. The excitation function for the ⁷Li(p,α)⁴He reaction was measured in the energy range 10–400 keV. More details about the experimental setup and data analysis can be found in Lattuada et al. (2001).

To obtain the zero-energy S(E)-factor, TH data were normalized to the direct ones of Engstler et al. (1992) and then fitted via a second-order polynomial. This procedure leads to a value of S(0) = 55 ± 3 keV barns, where the error is only statistical. The data also suffer from a systematic error of ∼10% caused by the normalization procedure to the direct data (Engstler et al., 1992).

The THM results were included in a review paper regarding solar fusion cross sections (Adelberger et al., 2011), where the recommended value is S(0) = 55 ± 6 keV barns.

TH data were then used to evaluate the astrophysical impact in the framework of the solar lithium problem and primordial nucleosynthesis (Pizzone et al., 2003). The obtained solar lithium abundance agree, within 5%, with the ones based on NACRE compilation (Angulo et al., 1993).

Lamia et al. (2012a) provided a new THM investigation by adopting the more recent direct measurements (Cruz et al., 2008) for re-normalizing the TH data of Lattuada et al. (2001). The improved TH S(E)-factor was fitted via a second order polynomial obtaining to the following function:

$S\left(E\right)=53+213E-336E^2\text{keV}\text{barns}(6)$

being E the energy in the c.m. system. The TH S(E)-factor is reported on the left-hand side of Figure 2 as black dots, and the figure also shows direct data from Cruz et al. (2005) and Cruz et al. (2008) (red and blue circles, respectively) and the result of the fit (Eq. 6, black line).

FIGURE 2

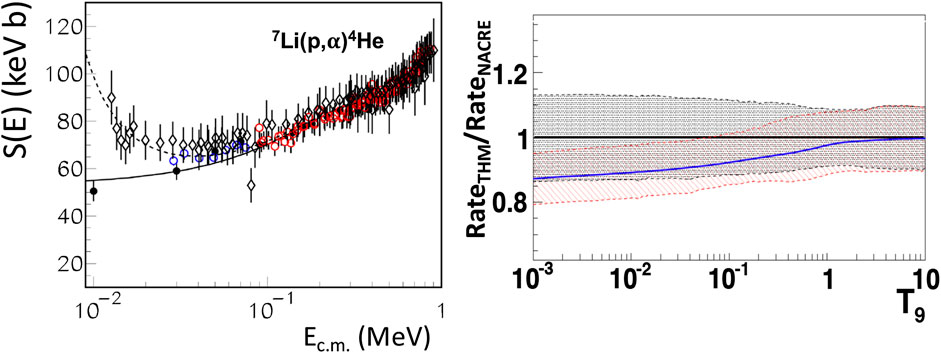
FIGURE 2. Left panel S(E)-factor for the ⁷Li(p,α)⁴He reaction. Black dots are TH data after the new normalization to Cruz et al. (2008). Red and blue circles represent data from Cruz et al. (2005) and Cruz et al. (2008), respectively. Open diamonds represent Engstler et al. (1992) data. The full line is the result of the polynomial fit of TH data, while the dashed line is the fit to the low-energy (<60 keV) direct data of Engstler et al. (1992) and Cruz et al. (2005). Right panel The ratio between the THM reaction rate of Lamia et al. (2012a) and the one of NACRE (Angulo et al., 1993) [This figure has been adapted from the ones of Lamia et al. (2012a)].

The obtained value for the bare-nucleus zero-energy S(E)-factor was S(0) = 53 ± 5 keV barns, where the error takes into account a ∼4% related to the normalization procedure, a ∼6% due to the statistics of the TH data and to an error of ∼6% related to the uncertainty of the direct data average (Cruz et al., 2008), as discussed in details in Lamia et al. (2012a).

Thanks to the low-energy behavior of the ⁷Li(p,α)⁴He bare-nucleus cross section given by Eq. 6, the electron screening potential was determined by fitting the low-energy (<60 keV) direct data of Engstler et al. (1992) and Cruz et al. (2005) with Eq. (1). The obtained value for the electron screening potential was U_e = 425 ± 60 eV, where the error is mainly due to the ∼14% uncertainty on data from Engstler et al. (1992). The resulting fitting curve is shown in Figure 2 (left side) as a dashed line, while open diamonds represent (Engstler et al., 1992) data.

In order to evaluate the astrophysical impact of the new ⁷Li(p,α)⁴He S(E)-factor, the reaction rate was then calculated in the temperature range ∼0.01 < T₉ < ∼2. The reaction rate deviates from ∼5 to ∼13% as the temperature decreases from T₉ = 1 down to T₉ = 10⁻³ with respect the NACRE one (see right panel of Figure 2). This called for further evaluations on astrophysical sites. In particular, the impact of the TH reaction rate was evaluated on a solar-metallicity RGB star. The authors found no significant variations of lithium abundance (Lamia et al., 2012a). In the case of primordial BBN, ⁷Li is mainly burnt through its (p,α) destruction channel while ⁷Be come into play for its production. The role of ⁷Li(p,α)⁴He has been thus also taken into account in the work of Pizzone et al. (2014), and, more recently, the neutron-induced reactions on ⁷Be have also been evaluated (Barbagallo et al., 2016; Damone et al., 2018; Lamia et al., 2019). Such studies conclude that it is unlikely that the solution of ⁷Li cosmological problem could be related to these nuclear physics processes.

3.3 The ⁹Be(p,α)⁶Li Burning Reaction

3.3.1 Direct Measurements

In astrophysical environments, ⁹Be is mainly depleted by proton capture via the ⁹Be(p,α)⁶Li and ⁹Be(p,d)⁸Be reactions within a Gamow energy (E_G) ranging from about 3 keV (for stellar nucleosynthesis) to 100 keV (for primordial nucleosynthesis), which makes it an exquisite probe of depletion mechanisms in stellar evolution and inhomogeneous BBN.

In order to accurately calculate the depletion of ⁹Be, the cross sections for these reactions must be known at Gamow energies. Several direct measurements of the ⁹Be(p,α)⁶Li and ⁹Be(p,d)⁸Be reactions at low energies have been reported (Sierk and Tombrello, 1973; Zahnow et al., 1997; Brune et al., 1998; Kaihong et al., 2018; Zhang et al., 2020), as listed in Table 2. However, reaction rates for the ⁹Be destruction channels still come with large uncertainties owing to large errors induced by extrapolation to the low energy of astrophysical interest.

TABLE 2

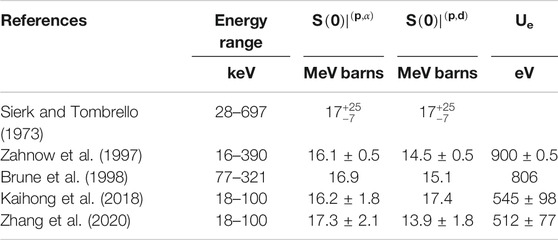
TABLE 2. List of the extracted S(0) factor and the electron screening potential U_e value of different direct measurements of ⁹Be destroyed reactions.

3.3.2 Trojan Horse Method Measurements

The THM has been used in order to extract the bare-nucleus S(E)-factor of the ⁹Be(p,α)⁶Li reaction at astrophysical energies avoiding extrapolations free of Coulomb suppression and electron screening effect.

The first indirect measurement of the ⁹Be(p,α)⁶Li S(E)-factor was carried out at INFN-LNS in Catania (Romano et al., 2006), using THM by properly selecting the QF-contribution of the three-body reaction ²H(⁹Be,α⁶Li)n. Deuterons were used as TH nuclei because of the obvious $d=\left(p\oplus n\right)$ structure with a weak binding energy of 2.225 MeV and the p − n relative motion mainly occurring in s-wave. The experiment was performed by using a 22 MeV, 2–5 pnA ⁹Be beam impinging onto a 190 µg/cm²-thick deuterated polyethylene target CD₂. Particle detection was performed by using two silicon $\text{ΔE}-\text{E}$ telescopes in coincidence, with a PSD as the E stage. Angular distributions were investigated, thus allowing us to study the resonant contribution at ∼250 keV (⁹Be-p c.m. energy) due to the population of the 6.87 MeV ¹⁰B (J^π = 1⁻) excited level. The preliminary astrophysical S(E)-factor was then extracted and compared to direct data, although the poor energy resolution (∼90 keV) prevented us from accessing the S(0)-factor and determining the electron screening potential. More details about the adopted experimental setup and data analysis can be found in Romano et al. (2006).

To completely study the reaction, and thanks to both experimental and theoretical improvements to the method, a further THM experiment has been performed at the CIAE (China Institute of Atomic Energy, Beijing, China) (Wen et al., 2008; Wen et al., 2011; Wen et al., 2016). The ⁹Be beam energy was 22.35 MeV. A strip CD₂ target of about 155 µg/cm² in thickness and 1.5 mm in width was used in order to limit the beam spot size and decrease the angle uncertainty.

Here, experimental results reported in Wen et al. (2008) are discussed. For the first time, an intermediate process, ⁹Be + ²H → ⁹Be + p + n, was considered as one criterion of the QF condition. As a result, most of the sequential decay processes were eliminated by using the new QF-selection, as seen in Figure 3. In order to obtain the astrophysical S(E)-factor, the experimental TH data have then been normalized to the direct ones (Zahnow et al., 1997), thus allowing us to get a zero-energy S(E)-factor S(0) = 21.0 ± 0.8 MeV barns. The THM S(E)-factor is reported in Figure 4 as red points. From the comparison with low-energy data of Zahnow et al. (1997), the electron screening potential energy U_e = 676 ± 86 eV was extracted. This value is significantly higher than that predicted by current theoretical models $(U_e^{ad}=240\text{eV})\text{,}$ whereas it is lower than U_e = 900 eV or U_e = 830 eV (Zahnow et al., 1997), being the second value extracted from direct measurements with inclusion of the −26 keV subthreshold resonance due to the 6.56 MeV ¹⁰B level (Zahnow et al., 1997). The U_e value is sensitive to low energy points; if compared with another set of direct data from Kaihong et al. (2018), the extracted U_e will be about 500 eV.

FIGURE 3

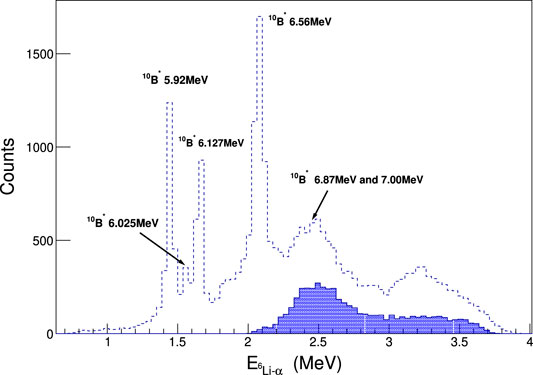
FIGURE 3. The spectrum of ${\mathrm{E}}_{{\mathrm{6}}_{\mathit{Li}-\alpha }}$ with QF-cut. The filled solid histogram is restricted by the condition that the assumed intermediate breakup process ⁹Be + ²H → ⁹Be + p + n is one criterion of the QF process. Without this restriction, the energy region of the QF process overlaps with that of the sequential decay via the 5.92, 6.025, 6.127, 6.56, 6.87 and 7.00 MeV ¹⁰B levels (dashed histogram). The picture is adapted from ref. Wen et al. (2008).

FIGURE 4

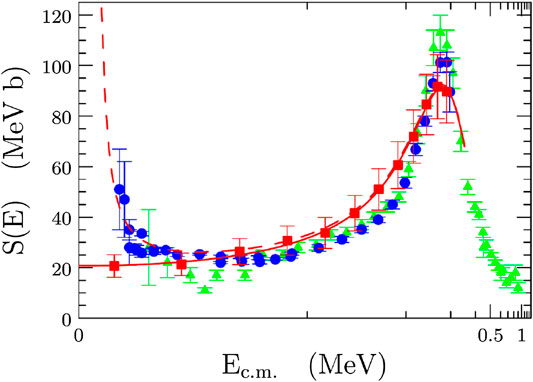
FIGURE 4. The S(E)-factor of ⁹Be(p,α)⁶Li via THM (red points) compared to the direct data (green and blue points). The solid red curve describes the fit of the bare-nucleus THM data, leading to S(0) = 21.0 ± 0.8 MeV barns. The red dashed line describes the enhancing caused by electron screening effects with a fitted value of U_e = 676 ± 86 eV, as given in Wen et al. (2008).

The measured THM zero-energy S(E)-factor deviates by a factor 1.23 from the one of the NACRE compilation, which adopts a low-energy extrapolation, leading to $S\left(0\right)={17}_{-7}^{+25}\text{MeV}\text{barns}$. In Lamia et al. (2015) the astrophysical impact of THM S(E)-factor is evaluated. The reaction rate at astrophysical energies has been deduced via Eq. 3 by using the p + ⁹Be bare-nucleus S(E)-factor of Wen et al. (2008) integrated from 200 keV down to about 10 keV. An analytical form of the thermonuclear reaction rate was derived as the following:

$N_A\langle \sigma v\rangle =\text{exp}\left[a_1+\frac{a_2}{T_9}+\frac{a_3}{T_9^{1/3}}+a_4\times T_9^{1/3}+a_5\times T_9+a_6\times T_9^{5/3}+a_7\times \text{ln}{T}_9\right](7)$

where the a_i coefficients have been left as free parameters for the ⁹Be(p,α)⁶Li reaction. The temperature T₉ is expressed in units of 10⁹ K and the final reaction rate given in (cm³mol⁻¹s⁻¹). The resulting a_i coefficients are listed in Lamia et al. (2015). As discussed in Lamia et al. (2015), at temperatures lower than 10⁸ K, the THM S(E)-factor reduces the reaction rate uncertainties from 70–90% (Angulo et al., 1999) to about 20%.

The impact of such a variation on the surface beryllium abundance of PMS stars was investigated in Lamia et al. (2015). In stars, beryllium is destroyed by two reactions, 1) ⁹Be(p,α)⁶Li (R₁) and 2) ⁹Be(p,2α)²H (R₂). At temperatures typical of ⁹Be burning, the reaction rates have a ratio R₁/R₂ ≈ 1.2, and the two channels are thus both important to correctly follow the temporal evolution of ⁹Be abundance. The impact of upgrading only the first channel is thus partially masked by the fact that the second is unmodified. The total expected variation of the resulting ⁹Be destruction rate due to only the upgrade of R₁ is thus smaller than the actual relative change of R₁. With respect to NACRE, the TH reaction rate is about 25% larger but, for what we just discussed, the net effect on beryllium destruction rate is expected to be of the order of 14%. As expected, the adoption of TH reaction rate reduces the level of Be destruction in stars at a given age. The effect depends on the stellar mass, and only in the case of stars that show a large Be depletion (0.10 ≤ M/M_ʘ ≤ 0.45), the reaction rate upgrade significantly affects surface ⁹Be abundance up to a difference of 0.3–0.4 dex in the surface logarithmic abundances.

3.4 The ¹⁰B(p,α)⁷Be Burning Reaction

3.4.1 Direct Measurements

Because of the presence of a l = 0 resonance at 10 keV (¹⁰B–p c.m. system energy), the experimental measurement of the ¹⁰B(p,α)⁷Be reaction S(E)-factor at energies of astrophysical interest is very important to the avoidance of possible uncertainties caused by the extrapolation procedure. This resonance, due to the 8.699 MeV J^π = 5⁺/2 of ¹¹C, rises exactly at the Gamow energy for typical boron quiescent burning (see Table 1). The ¹⁰B(p,α)⁷Be reaction has been studied by many groups in the past, but only two direct measurements (Youn et al., 1991; Angulo et al., 1993) have provided an estimation of the S(E)-factor at the Gamow energy by means of an extrapolation procedure from data at higher energy. In particular, Angulo et al. (1993) declared for the S(E)-factor at the resonance energy the value of S(10) = 2,870 ± 500 MeV barns. Regarding the electron screening potential, the adopted value is U_e = 430 ± 80 eV, deduced from the direct measurement of the ¹¹B(p,α)⁸Be S(E)-factor under the hypothesis of no isotopic dependence of U_e (Assenbaum et al., 1987). The theoretical value provided by the adiabatic limit is $U_e^{ad}$ = 340 eV.

The ¹⁰B(p,α)⁷ Be astrophysical S(E)-factor is enhanced both by the presence of the 10 keV resonance and by the effect of electron screening. In this framework, indirect low-energy measurements of the ¹⁰B(p,α)⁷Be cross section performed with the THM are pivotal to disentangling the two components and avoiding possible uncertainty due to the extrapolation procedure. Unfortunately, high-energy data available in literature until recently did not provide a reliable reference for normalization. Indeed, the energy range between 200 keV and 2 MeV was poorly explored, and there was some tension between the two existing data sets (see Figure 6). Moreover, direct data from Youn et al. (1991), between 200 and 500 keV, were scaled by a factor of 1.83 to obtain a better agreement with lower-energy data.

3.4.2 ¹⁰B(p,α)⁷Be Cross Section Measurements via Activation Method at Legnaro National Laboratories

To solve the discrepancies existing in the intermediate energy range, a number of new measurements have been performed recently at different facilities, including one experiment at the Legnaro National Laboratories (Italy).

At stellar energies, the ¹⁰B(p,α)⁷Be reaction proceeds through two different transitions: it can either populate the ground state of ⁷Be (hereafter called the α₀ channel) or leave ⁷Be in its first excited state (hereafter called α₁ channel), which then de-excites emitting a γ ray of E_γ = 429 keV. Subsequently, ⁷Be decays to ⁷Li via electron capture with a half life of 53.22 days. Then, 10.44% of these decays in turn populate the first excited state of ⁷Li, which then goes to the ground state by the emission of a E_γ = 477.6 keV γ ray.

Because of the properties outlined above, the ¹⁰B(p,α)⁷Be reaction can be investigated with different, complementary approaches, involving the detection of α particles, gamma rays or with the activation technique (Iliadis, 2007). The latter allows us to derive the number of ⁷Be nuclei produced by the reaction through off-beam gamma spectroscopy, detecting the 477.6 keV γ rays emitted in ⁷Be decay. The activation technique offers the advantage of being free of beam-induced background. Moreover, counting facilities are often equipped with passive shields around the gamma detectors in order to suppress environmental radioactivity and increase the sensitivity to small cross sections. On the other hand, when counting ⁷Be nuclei with the activation method it is not possible to disentangle the α₀ and α₁ channels. Though the α₀ channel dominates the total cross section at low energies, its contribution to the total cross section is of the order of 10% at 1 MeV.

The ¹⁰B(p,α₁)⁷Be cross section is also not well constrained at energies between 500 keV and 2 MeV. In this energy range, the dominant contribution to the cross section comes from a resonance at 1,500 keV. Two pioneering experiments performed in the 1950s (Brown et al., 1951; Day and Huus, 1954) provided contradictory results on the value of the cross section on top of the resonance. As a consequence (Day and Huus, 1954), adopted the average cross section at the peak to normalize its data. Following experiments made the picture even more complicated, finding cross sections up to a factor of two lower (Hunt et al., 1957).

Given the discrepancies existing in the literature, both in the α₀ and α₁ channel, two separate experiments were performed at the AN2000 accelerator of the INFN National Laboratories of Legnaro: the first exploited the activation method (using the formalism discussed in Scott et al. (2012), Di Leva et al. (2014) for the total cross section (Caciolli et al., 2016) and the second was devoted to detecting only the prompt γ rays produced by the α₁ channel (Caciolli et al., 2019).

The AN2000 accelerator was installed at the INFN-LNL in 1971 and can provide proton and α beams in an energy range from 250 keV up to 2.2 MeV. A sketch of the experimental setups is shown in Figure 5, while a detailed description of the chamber and the beam current measurement can be found in Caciolli et al. (2016), Caciolli et al. (2019).

FIGURE 5

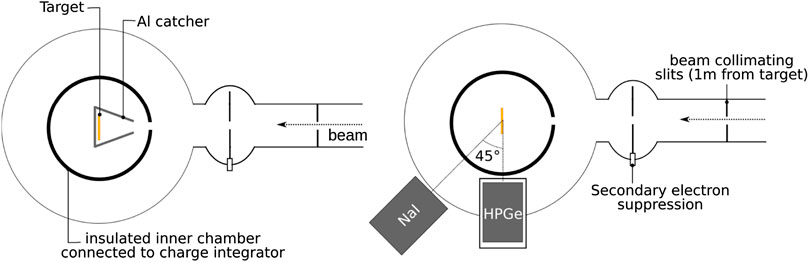
FIGURE 5. Sketch of the experimental setup used for the study of the ¹⁰B(p,α)⁷Be reaction at LNL with the activation technique (left) and with prompt-gamma spectroscopy (right).

For the measurement with the activation technique, no detectors were needed during the irradiation, and the ⁷Be decays were counted in a dedicated low counting level facility (Caciolli et al., 2012; Xhixha et al., 2013) after removing the sample from the beamline. For the measurement of the α₁ cross section, two gamma-ray detectors were placed around the scattering chamber: a high-purity germanium detector at 90° and a sodium iodide detector at 45°.

Results from the two experiments are summarized in Figure 6, together with literature cross sections. ¹⁰B(p,α)⁷Be total cross section data cover the energy range E_c.m. = 249–1,182 keV, providing a link between literature data sets in an energy region that was poorly explored. ¹⁰B(p,α₁)⁷Be data span the range E_c.m. = 348–1795 keV and cover the resonance at 1,400 keV.

FIGURE 6

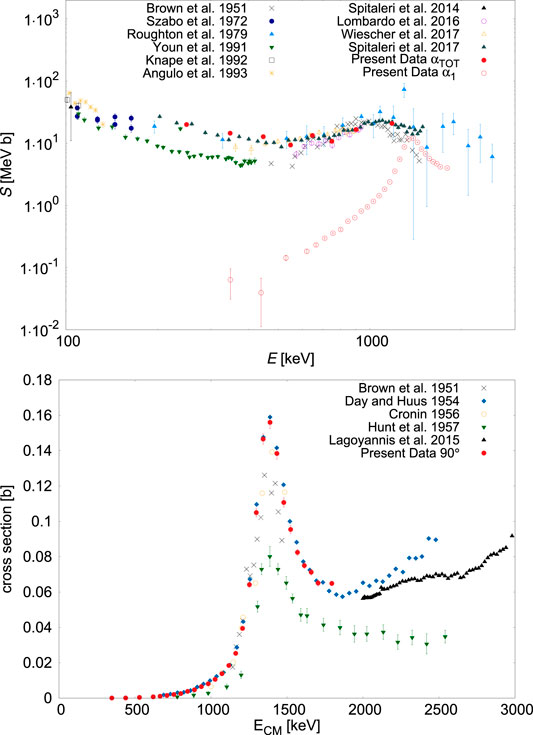
FIGURE 6. Upper panel: Total astrophysical S(E)-factor for the ¹⁰B(p,α)⁷Be reaction. Lower panel: Cross section for the ¹⁰B(p,α1)⁷Be reaction channel.

The new total cross section data are in good agreement with old data from Roughton et al. (1979), but error bars are greatly reduced. There is also a fair agreement with data from Lombardo et al. (2016), published concurrently. Present data confirm the destructive interference pattern between the 10 keV and the 500 keV resonances. This results in a decrease in the astrophysical factor above 500 keV. Below 500 keV, some tension still exists between present data and more recent results published in Wiescher et al. (2017). Further investigations will be needed to address this issue. Moreover, in order to obtain a reliable and consistent R-matrix fit of all data sets, new data extending up to 3 MeV are needed to better constraint the four resonances dominating the cross section.

3.4.3 Trojan Horse Method Measurements

A first attempt of studying the ¹⁰B(p,α₀)⁷Be reaction at stellar energies through THM was discussed in Lamia et al. (2007). Starting from that, an improved THM measurement was performed by Spitaleri et al. (2014), applying THM to the ²H(¹⁰B,α₀⁷Be)n three-body reaction. The experiment was carried out at LNS by means of a 24.5 MeV ¹⁰B beam delivered on a 200 µg/cm² thick CD₂ target. The deuteron was thus used as the TH nucleus. Thanks to the devoted experimental setup, an energy resolution of ∼30 keV in the ¹⁰B + p c.m. system was reached, thus allowing the proper separation of the 8.699 MeV resonance of interest from the sub-threshold peak due to the population of the 8.654 MeV J^π = 7⁺/2 level of ¹¹C (Spitaleri et al., 2014). By means of the standard procedure and by following the factorization reported in Eq. 4, the spectator momentum distribution and half-off energy shell cross section were deduced via the PWIA formalism. In order to extract the S(E)-factor in absolute units, TH data have been normalized to direct ones available in literature at that time (Youn et al., 1991; Angulo et al., 1993) in an energy range of 50–100 keV, where the electron screening effect is negligible. Due to the experimental resolution affecting TH data, the normalization procedure is not straightforward. The detailed procedure is described in Spitaleri et al. (2014). Authors highlighted a possible presence of systematic effects in the energy region where the two direct data sets overlap, underlining the need of a new direct measurement in this energy range (Spitaleri et al., 2014) (see also Section 3.4). The measured TH bare-nucleus S(E)-factor at the Gamow energy peak was S(10 keV) = 3,127 ± 583 Mev barns. As extensively described in Spitaleri et al. (2014), the effect of experimental resolution has been removed from the obtained results and the quoted error accounts for statistical, sub-threshold subtraction, normalization and channel radius uncertainties.

The THM study provided the first independent measurement of the electron screening U_e for the ¹⁰B(p,α₀)⁷Be reaction since the adopted value derived from applying the so-called isotopic independence hypothesis for electron screening. The obtained result was U_e = 240 ± 200 eV where the error derives from the uncertainties affecting TH S(E)-factor.

Thanks to the broad-energy range direct measurements of Lombardo et al. (2016), Caciolli et al. (2016) (see Section 3.4.2) and Wiescher et al. (2017), a further THM S(E)-factor determination was performed by Spitaleri et al. (2017). The ²H(¹⁰B,α₀⁷Be)n reaction measurement was performed at the Pelletron–Linac laboratory - Departamento de Fisica Nuclear (DFN) in São Paolo, Brazil. The Tandem accelerator provided a 27 MeV ¹⁰B beam sent on a 200 µg/cm²-thick CD₂ target. For the first time the astrophysical factor of the ¹⁰B(p,α₀)⁷Be reaction has been measured over a wide energy range, from 5 keV to 1.5 MeV, in a single experiment and with a reduction of the normalization error from ∼18–20% to ∼4%. In Figure 7 TH data has been reported (black diamonds) together with TH data from Spitaleri et al. (2014) (black stars) and direct data from Caciolli et al. (2016) (green triangles) Lombardo et al. (2016), (grey triangles) Roughton et al. (1979), (purple circles) (Angulo et al. (1999), (blue circles) and Youn et al. (1991) (red squares). A very good agreement was found between the direct data and the TH ones. The investigation of the ¹⁰B(p,α₀)⁷Be reaction in a wide energy range suggested the performance of a devoted R-matrix fit of the deduced S(E) TH data (dashed line in Figure 7). The details of this calculation, together with the interesting spectroscopic implication on ¹¹C levels, are described in Spitaleri et al. (2017). Consequently, a more accurate evaluation of the S(E)-factor was provided S(10 keV) = 2,942 ± 398 MeV barns [relative error 13.5% with respect to 18.6% in Spitaleri et al. (2014)] as well as of the electron screening potential, U_e = 240 ± 50 eV [relative error 20.8% with respect to 83.3% in Spitaleri et al. (2014)].

FIGURE 7

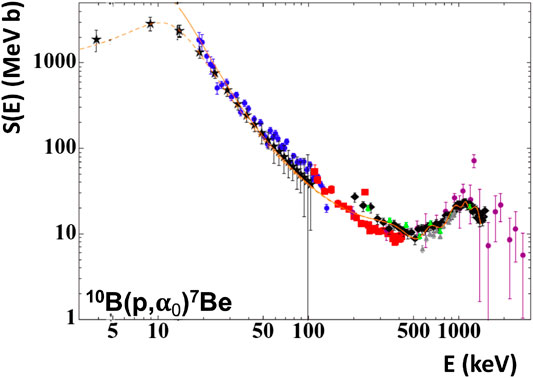
FIGURE 7. S(E)-factor for the ¹⁰B(p,α₀)⁷Be reaction. The following data set are reported: TH data from Spitaleri et al. (2017) (black diamonds) and from Spitaleri et al. (2014) (black stars) and direct data from Caciolli et al. (2016) (green triangles), Lombardo et al. (2016) (grey triangles), Roughton et al. (1979) (purple circles), Angulo et al. (1999) (blue circles) and Youn et al. (1991) (red squares). The dashed line represent the R-matrix fit performed on TH data (Spitaleri et al., 2017). [Figure adapted from Spitaleri et al. (2017)].

The latest THM study is discussed in Cvetinović et al., 2018. The experiment was performed at LNS applying THM to the ²H(¹⁰B,α₀⁷Be)n three-body reaction. Particular attention has been paid to the improvement of the experimental resolution. In particular, thanks to the reduction of the CD₂ target thickness, set at 56 µg/cm² (Rapisarda et al., 2018), an energy resolution of 17 keV in the ¹⁰B + p c.m. system has been obtained, allowing for a better separation between the 10 keV resonance and the subthreshold level. Moreover, the experimental resolution allowed for the first time in a THM study the separation and the independent study of the α₀ (Cvetinović et al., 2018) and α₁ channel (Rapisarda et al., 2018). As a further improvement, the experimental setup allowed for a measurement of the S(E)-factor in a wide energy range from 3 keV up to 2.2 MeV expanding the explored energy range with respect to the previous THM measurement (Spitaleri et al., 2017). In this way, TH data have been normalized to the R-matrix calculation provided in Spitaleri et al. (2017) in a wide energy range, reducing the normalization error to about 2.8%. The obtained value for S(E)-factor is S(10 keV) = 2,950 ± 291 MeV barns, which is in agreement with the previous results but with a reduced relative error of 9.9%. The declared electron screening potential value is U_e = 391 ± 74 eV relative error 18.9%.

Lamia et al. (2015) provided an evaluation of the reaction rate for the ¹⁰B(p,α)⁷Be reaction based on the TH S(E)-factor from Spitaleri et al. (2014), resulting in the analytical form already given by Eq. 3 with the corresponding coefficients listed in Lamia et al. (2015). The TH reaction rate has been compared with the NACRE compilation (Angulo et al., 1999) and with the more recent NACREII (Xu et al., 2013). A first result concerned the reduction of reaction rate uncertainties at lower temperatures, that is, close to the Gamow peak typical of quiescent boron burning. Moreover, at temperatures of 2–5 × 10⁶ K, the TH reaction rate deviated with respect to the NACRE one, being ∼25–30% lower.

Astrophysical implications of the evaluated ¹⁰B(p,α)⁷Be burning rate on surface abundances of pre-MS stars are exhaustively discussed in Lamia et al. (2015). The reduction of the reaction rate by about 25–30% in the temperature range characteristic of the ¹⁰B stellar destruction is especially relevant for stars with masses between about 0.1–0.3M_ʘ. The TH reaction rate significantly reduces the level of ¹⁰B depletion, with a logarithmic abundance variation up to 0.9–1 dex for those stars that undergo a strong surface ¹⁰B depletion, as discussed in detail in Lamia et al. (2015). Unfortunately, at the moment, it is difficult to observe ¹⁰B in cool stars where the largest impact of the reaction rate is expected but only few data are available to test the models predictions.

3.5 The ¹¹B(p,α)⁸Be Burning Reaction

3.5.1 Direct Measurements

At low energies the ¹¹B(p,α)⁸Be astrophysical S(E)-factor is characterized by the presence of two resonances that rise at about ∼150 keV and ∼600 keV (¹¹B – p center of mass energy) due to the formation of the 16.106 MeV (J^π = 2⁺) and 16.570 MeV (J^π = 2⁻) ¹²C excited levels. In particular, the α₀ channel S(E)-factor is characterized by the presence of the l = 1 ∼150 keV level superimposed on a non-resonant contribution, while the ∼600 keV resonance is excluded because of spin-parity selection rules. On the other hand, both levels contribute to the reaction yield of the α₁ channel.

The direct measurements of the ¹¹B(p,α)⁸Be reaction cross section at energy of astrophysical interest are reported in Segel et al. (1965), Davidson et al. (1979), Becker et al. (1987), Angulo et al. (1993). In particular, the extrapolated astrophysical S(E)-factor was provided in Becker et al. (1987) for α₀ and α₁ channels. The obtained values are S(0) = 2.1 MeV barns (α₀) and S(0) = 195 MeV barns (α₁). No evaluation of the electron screening potential was provided in Becker et al. (1987). A further measurement of the astrophysical S(E)-factor (α₀ + α₁ channels) in the energy range from E_cm = 132 keV down to E_cm = 18.73 keV was given in Angulo et al. (1993). In this paper, the authors declared an electron screening potential of U_e = 430 ± 80 eV. This value turns out to be higher than the upper limit provided by the adiabatic model $U_e^{ad}=340\text{eV,}$ confirming the systematic discrepancy between experimental and theoretical values of the electron screening potential. All the direct measurements are above the Gamow energy and both S(0) and U_e are obtained with extrapolation procedures.

3.5.2 Trojan Horse Method Measurements

The first measurement of the ¹¹B(p,α₀)⁸Be reaction cross section covering the whole energy region of astrophysical interest was reported in Spitaleri et al. (2004). THM was applied to the three-body reaction ²H(¹¹B,α₀⁸Be)n using a 27 MeV ¹¹B beam impinging on a CD₂ target where the deuteron provide the virtual proton. This study represented an important validity test for THM since it showed the possibility to measure resonances at low energy, below the Coulomb barrier of the interacting nuclei. The poor experimental resolution suffered by the discussed THM measurement pushed to proceed further in the experimental work, as shown in Lamia et al. (2008), Lamia et al. (2012b). THM was again applied to the ²H(¹¹B,α₀⁸Be)n three-body reaction, and a 27 MeV ¹¹B beam was delivered on a CD₂ target about 170 µg/cm² thick. The detection setup allowed the detection of α particles in coincidence with ⁸Be. α particles coming from the three-body reaction were detected by PSDs. ⁸Be events were reconstructed following the procedure described in Spitaleri et al. (2004) and in Lamia et al. (2008) using a Dual Position Sensitive Detector made up of two PSDs mounted one above the other, and this guaranteed the coincident detection of the two α particles coming from the ⁸Be decay. More details on the experimental setup are provided in Lamia et al. (2012b). In order to improve the experimental resolution, significant efforts were made on the selection of the quasi-free events, disentangling the events of interest from those produced by sequential mechanism (Lamia et al., 2012b). Additionally, a devoted study was performed on the neutron momentum distribution. In more detail, the experimental momentum distribution (black points of Figure 8) was compared with both PWIA (black line) and DWBA calculations (dashed line). For DWBA calculations, the FRESCO code was adopted by using optical potential parameters adjusted from those of Perey and Perey (1976), as performed in several THM papers such as La Cognata et al. (2010a), La Cognata et al. (2010b), Sergi et al. (2010). In the FRESCO calculation, optical potentials are used for the following systems: ²H-¹¹B and n-¹²C (for distorted waves evaluation in both entrance and exit channel, respectively), n-p and p-¹¹B (to calculate the bound state wave functions) and the core–core potential n-¹¹B. In total, the calculation involves several parameters besides a normalization factor, fixed by scaling the theoretical distribution to the experimental one (black dots of Figure 8). Both calculations agree nicely at low-neutron momenta (below 30 MeV/c for the present case), i.e., at those values of interest for THM application. This shows once more the goodness of the approach via the most simple PWIA factorization of Eq. 4 (see Lamia et al., 2012b for details).

FIGURE 8

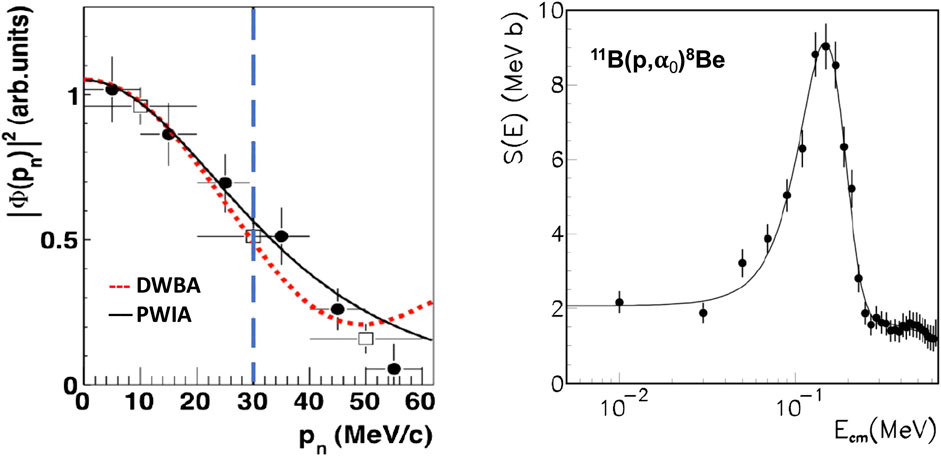
FIGURE 8. Left panel Experimental momentum distribution of the neutron spectator (black and open points) compared with the Hulthén wave function in momentum space (black curve) and the DWBA calculation (red dashed). Only the data with momenta lower than 30 MeV/c were considered for the analysis. Right panel S(E)-factor for the ¹¹B(p,α₀)⁸Be reaction. Black points represent the THM data while the solid line represents the fit given in terms of Eq. 8 [Figures adapted from Lamia et al. (2012b)].

The extracted excitation function can be described by the resonance contribution due to the resonance at E_cm = 150 keV (l = 1), superimposed onto a non-resonant contribution (l = 0). TH data have been normalized to direct data provided by Becker et al. (1987) after a spread-out procedure to take into account the THM experimental resolution (∼40 keV). In particular the non-resonant contribution has been normalized in an energy range between 400 and 600 keV, while for the resonant part areas under the peak have been equalized. TH data have been fitted with a function given by the incoherent sum of a second order polynomial and a Gauss function in order to take in to account the non-resonant and resonant contributions to the reaction cross section, obtaining the following function:

$S{\left(E\right)}_{{\alpha }_0}^{THM}=2.04-1.37E+0.12E^2+7.28\times \text{exp}\left[-0.5{\left(\frac{E-0.148}{0.044}\right)}^2\right]\text{MeV}\text{barns}(8)$

The obtained bare-nucleus TH zero-energy S(E)-factor for ¹¹B(p,α₀)⁸Be reaction is S(0) = 2.07 ± 0.41 MeV barns, where the total error takes into account the following: the statistical error on the experimental points (∼10%), the uncertainties on the normalization procedure (∼10%) and the systematic uncertainties due to the choice of the cut-off radius in the Coulomb penetrability function (∼14%). The TH S(0) value and the one extrapolated from direct measurement are in agreement within the experimental errors. In the right panel of Figure 8, the TH S(E)-factor evaluated in Lamia et al. (2012b) is shown (black points) together with the fit obtained from Eq. 8. Taking advantage of direct data reported in Angulo et al. (1993) and of the bare-nucleus TH S(E)-factor the electron screening potential U_e has been evaluated. The extracted value U_e = 472 ± 160 eV is in agreement with the value provided in Angulo et al. (1993)U_e = 430 ± 80 eV and higher than the upper limit predicted by the adiabatic limit U_e = 340 eV (Lamia et al., 2012b).

4 Conclusions

This paper has provided a review on the experimental studies performed through the application of the Trojan Horse Method and devoted to the measurement of the light elements LiBeB burning cross section at the low energies of interest for astrophysics. Moreover, experimental results obtained by means of the activation technique have been discussed as well. For each (p,α) channel of interest in the LiBeB problem, we discussed the S(E)-factor evaluation, the determination of the electron screening potential and the reaction rate evaluation together with the comparison with the most recent direct data available in literature. Table 3 provides an overview of the zero-energy S(E)-factor and electron screening potential values of the discussed reactions, as obtained via THM.

TABLE 3

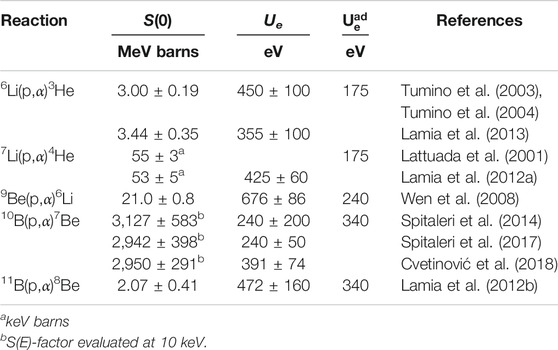
TABLE 3. Overview of THM astrophysical S(E)-factor and electron screening potential for the discussed reactions. Theoretical values for electron screening potential according to the adiabatic approximation $U_e^{ad}$ are reported for completeness.

Despite the efforts made, open issues are still present. In addition to the nuclear astrophysics field, the study of the ¹¹B(p,α)⁸Be is of interest also for the plasma fusion community since the ¹¹B+p process is considered one of the best candidates for the aneutronic fusion. In this framework, detailed information is needed also on the ¹¹B(p,α₁)⁸Be reaction, whose cross section is about two orders of magnitude higher than the α₀ channel. A dedicated THM study will provide more information on the contribution of the α₁ channel (Lamia et al., 2012b).

Moreover, natural boron fuel used for aneutronic fusion is composed by ∼19% of ¹⁰B, whose interaction with protons produces ⁷Be a radioactive isotope (T_1/2 = 53.22 ± 0.06 days). In order to evaluate a safe ¹¹B enrichment level to avoid radioprotection issues, an accurate measurement of the ¹⁰B(p,α)⁷Be cross-section is necessary for both α₀ and α₁ channels. In this framework, starting from the results obtained by Rapisarda et al. (2018), a new THM study will be dedicated to the ¹⁰B(p,α₁)⁷Be in a wide energy range, including the low energy of astrophysical interest.

Author Contributions

Nuclear data were analyzed by G.G.R., L.L., R.D., A.C., C.L., R.G.P., S.R., C.S. and Q.W. S.D.I., E.T. and S.P. took care of the astrophysical impact of these data. All the listed authors contributed to the writing of the paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge “Programma ricerca di ateneo UNICT 2020-22 linea2” and “Starting grant 2020” of University of Catania. CL and QW acknowledge the partial support of National Natural Science Foundation of China (10575132, 11075218, 12075031). RD acknowledges funding from Italian Ministry of Education, University and Research (MIUR) through the “Dipartimenti di eccellenza” project Science of the Universe.

Footnotes

¹Here, Li is the sum of lithium-6 and lithium-7 abundances. BBN predicts ⁶Li abundances lower that the ⁷Li ones. Metal-poor main sequence stars exhibit a negligible amount of ⁶Li compared to the ⁷Li ones (Lind et al., 2013).

References

Adelberger, E. G., García, A., Robertson, R. G. H., Snover, K. A., Balantekin, A. B., Heeger, K., et al. (2011). Solar fusion cross sections. II. The pp chain and CNO cycles. Rev. Mod. Phys. 83, 195–246. doi:10.1103/RevModPhys.83.195

CrossRef Full Text | Google Scholar

Aliotta, M., Spitaleri, C., Lattuada, M., Musumarra, A., Pizzone, R. G., Tumino, A., et al. (2000). Improved information on electron screening in ⁷Li(p,α)α using the Trojan-horse method. Eur. Phys. J. A. 9, 435–437. doi:10.1007/s100500070001

CrossRef Full Text | Google Scholar

Angulo, C., Arnould, M., Rayet, M., Descouvemont, P., Baye, D., Leclercq-Willain, C., et al. (1999). A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. 656, 3–183. doi:10.1016/S0375-9474(99)00030-5

CrossRef Full Text | Google Scholar

Angulo, C., Engstler, S., Raimann, G., Rolfs, C., Schulte, W. H., and Somorjai, E. (1993). The effects of electron screening and resonances in (p,α) reactions on ¹⁰B and ¹¹B at thermal energies. Zeitschrift fur Physik A Hadrons and Nuclei. 345, 231–242. doi:10.1007/BF01293350

CrossRef Full Text | Google Scholar

Assenbaum, H. J., Langanke, K., and Rolfs, C. (1987). Effects of electron screening on low-energy fusion cross sections. Zeitschrift fur Physik A Hadrons and Nuclei. 327, 461–468.

CrossRef Full Text | Google Scholar

Barbagallo, M., Musumarra, A., Cosentino, L., Maugeri, E., Heinitz, S., Mengoni, A., et al. (2016). ⁷Be(n,α)⁴He reaction and the cosmological lithium problem: measurement of the cross section in a wide energy range at n_TOF at CERN. Phys. Rev. Lett. 117, 152701. doi:10.1103/PhysRevLett.117.152701

PubMed Abstract | CrossRef Full Text | Google Scholar

Baur, G. (1986). Breakup reactions as an indirect method to investigate low-energy charged-particle reactions relevant for nuclear astrophysics. Phys. Lett. B. 178, 135–138. doi:10.1016/0370-2693(86)91483-8

CrossRef Full Text | Google Scholar

Becker, H. W., Rolfs, C., and Trautvetter, H. P. (1987). Low-energy cross sections for ¹¹B(p, 3α). Zeitschrift fur Physik A Hadrons and Nuclei. 327, 341–355.

CrossRef Full Text | Google Scholar

Boesgaard, A. M., Armengaud, E., and King, J. R. (2004). Beryllium abundances in F and G Dwarfs in Praesepe and other young clusters from Keck HIRES observations. Astrophys. J. 605, 864–873. doi:10.1086/382943

CrossRef Full Text | Google Scholar

Boesgaard, A. M., Deliyannis, C. P., and Steinhauer, A. (2005). Boron depletion in F and G Dwarf stars and the beryllium-boron correlation. Astrophys. J. 621, 991–998. doi:10.1086/427687

CrossRef Full Text | Google Scholar

Boesgaard, A. M., Lum, M. G., and Deliyannis, C. P. (2019). Correlated depletion and dilution of lithium and beryllium revealed by subgiants in M 67. arXiv e-printsarXiv:1910.07656

CrossRef Full Text | Google Scholar

Boesgaard, A. M., Lum, M. G., Deliyannis, C. P., King, J. R., Pinsonneault, M. H., and Somers, G. (2016). Boron abundances across the “Li-Be dip” in the Hyades cluster. Astrophys. J. 830, 49. doi:10.3847/0004-637X/830/1/49

CrossRef Full Text | Google Scholar

Boesgaard, A. M., Rich, J. A., Levesque, E. M., and Bowler, B. P. (2011). Beryllium and Alpha-element abundances in a large sample of metal-poor stars. Astrophys. J. 743, 140. doi:10.1088/0004-637X/743/2/140

CrossRef Full Text | Google Scholar

Brown, A., Snyder, C., Fowler, W., and Lauritsen, C. (1951). Phys. Rev. 82, 159.

CrossRef Full Text | Google Scholar

Brune, C., Geist, W., Karwowski, H., Ludwig, E., and Veal, K. (1998). ¹¹B(p,α)⁸Be and ⁹Be(p,α)⁶Li and reactions at low energies. Phys. Rev. C. 57, 3437–3446.

CrossRef Full Text | Google Scholar

Caciolli, A., Baldoncini, M., Bezzon, G., Broggini, C., Buso, G., Callegari, I., et al. (2012). A new fsa approach for in situ γ ray spectroscopy. Sci. Total Environ. 414, 639–645. doi:10.1016/j.scitotenv.2011.10.071

PubMed Abstract | CrossRef Full Text | Google Scholar

Caciolli, A., Depalo, R., Broggini, C., La Cognata, M., Lamia, L., Menegazzo, R., et al. (2016). A new study of ¹⁰B(p,α)⁷Be reaction at low energies. Eur. Phys. J. A. 52, 136. doi:10.1140/epja/i2016-16136-8

CrossRef Full Text | Google Scholar

Caciolli, A., Depalo, R., and Rigato, V. (2019). A new study of the ¹⁰B(p,α₁)⁷Be reaction from 0.35 to 1.8 MeV. Eur. Phys. J. A. 55, 171. doi:10.1140/epja/i2019-12859-2

CrossRef Full Text | Google Scholar

Cherubini, S., Gulino, M., Spitaleri, C., Rapisarda, G. G., La Cognata, M., Lamia, L., et al. (2015). First application of the Trojan horse method with a radioactive ion beam: study of the ¹⁹F (p,α)¹⁴O reaction at astrophysical energies. Phys. Rev. C. 92, 015805. doi:10.1103/PhysRevC.92.015805

CrossRef Full Text | Google Scholar

Coc, A., Goriely, S., Xu, Y., Saimpert, M., and Vangioni, E. (2012). Standard big bang nucleosynthesis up to CNO with an improved extended nuclear network. Astrophys. J. 744, 158. doi:10.1088/0004-637X/744/2/158

CrossRef Full Text | Google Scholar

Coc, A., and Vangioni, E. (2017). Primordial nucleosynthesis. Int. J. Mod. Phys. E. 26, 1741002. doi:10.1142/S0218301317410026

CrossRef Full Text | Google Scholar

Cruz, J., Fülöp, Z., Gyürky, G., Raiola, F., di Leva, A., Limata, B., et al. (2005). Electron screening in ⁷Li(p,α)α and ⁶Li(p, α)³He for different environments. Phys. Lett. B. 624, 181–185. doi:10.1016/j.physletb.2005.08.036

CrossRef Full Text | Google Scholar

Cruz, J., Luis, H., Fonseca, M., Fülöp, Z., Gyürky, G., Raiola, F., et al. (2008). Experimental study of proton-induced nuclear reactions in Li. J. Phys. G Nucl. Phys. 35, 014004. doi:10.1088/0954-3899/35/1/014004

CrossRef Full Text | Google Scholar

Cvetinović, A., Spitaleri, C., Spartá, R., Rapisarda, G. G., Puglia, S. M. R., La Cognata, M., et al. (2018). Trojan horse measurement of the 10B(p,α⁰)⁷Be cross section in the energy range from 3 keV to 2.2 MeV. Phys. Rev. C. 97, 065801. doi:10.1103/PhysRevC.97.065801

CrossRef Full Text | Google Scholar

Cyburt, R. H., Amthor, A. M., Ferguson, R., Meisel, Z., Smith, K., Warren, S., et al. (2010). The JINA REACLIB Database: its recent updates and impact on type-I X-ray bursts. Astrophys. J. Suppl. 189, 240–252. doi:10.1088/0067-0049/189/1/240

CrossRef Full Text | Google Scholar

Damone, L., Barbagallo, M., Mastromarco, M., Mengoni, A., Cosentino, L., Maugeri, E., et al. (2018). ⁷Be(n,p)⁷Li reaction and the cosmological lithium problem: measurement of the cross section in a wide energy range at n_TOF at CERN. Phys. Rev. Lett. 121, 042701. doi:10.1103/PhysRevLett.121.042701

PubMed Abstract | CrossRef Full Text | Google Scholar

Davidson, J. M., Berg, H. L., Lowry, M. M., Dwarakanath, M. R., Sierk, A. J., and Batay-Csorba, P. (1979). Low energy cross sections for ¹⁰B(p, 3α). Nucl. Phys. 315, 253–268. doi:10.1016/0375-9474(79)90647-X

CrossRef Full Text | Google Scholar

Day, R. B., and Huus, T. (1954). Gamma radiation from bombarded by protons. Phys. Rev. 95, 1003–1006. doi:10.1103/PhysRev.95.1003

CrossRef Full Text | Google Scholar

Degl’Innocenti, S., Prada Moroni, P. G., Marconi, M., and Ruoppo, A. (2008). The FRANEC stellar evolutionary code. Astrophys. Space Sci. 316, 25–30. doi:10.1007/s10509-007-9560-2

CrossRef Full Text | Google Scholar

Deliyannis, C. P., Pinsonneault, M. H., and Charbonnel, C. (2000). “Sinks of light elements in stars - Part I (invited paper),” in The light elements and their evolution. Editors L da Silva, R de Medeiros, and M Spite (IAU Symposium), 198, 61.

CrossRef Full Text | Google Scholar

Dell’Omodarme, M., Valle, G., Degl’Innocenti, S., and Prada Moroni, P. G. (2012). The Pisa stellar evolution data base for low-mass stars. Astron. Astrophys. 540, A26. doi:10.1051/0004-6361/201118632

CrossRef Full Text | Google Scholar

Di Leva, A., Scott, D. A., Caciolli, A., Formicola, A., Strieder, F., Aliotta, M., et al. (2014). Underground study of the ¹⁷O(p,γ)¹⁹F reaction relevant for explosive hydrogen burning. Phys. Rev. C. 89, 015803. doi:10.1103/PhysRevC.89.015803

CrossRef Full Text | Google Scholar

D’Antona, F., and Montalbán, J. (2003). Efficiency of convection and Pre-Main Sequence lithium depletion. Astron. Astrophys. 412, 213–218. doi:10.1051/0004-6361:20031410

CrossRef Full Text | Google Scholar

Elwyn, A. J., Holland, R. E., Davids, C. N., Meyer-Schützmeister, L., Mooring, F. P., and Ray, J. W. (1979). Cross sections for the ⁷Li(p,He)³He reaction at energies between 0.1 and 3.0 MeV. Phys. Rev. C. 20, 1984. doi:10.1103/PhysRevC.20.1984

CrossRef Full Text | Google Scholar

Engstler, S., Raimann, G., Angulo, C., Greife, U., Rolfs, C., Schröder, U., et al. (1992). Isotopic dependence of electron screening in fusion reactions. Zeitschrift fur Physik A Hadrons and Nuclei. 342, 471–482. doi:10.1007/BF01294958

CrossRef Full Text | Google Scholar

Fields, B. D., and Olive, K. A. (1999). The revival of galactic cosmic-ray nucleosynthesis?. Astrophys. J. 516, 797–810. doi:10.1086/307145

CrossRef Full Text | Google Scholar

Fields, B. D. (2011). The primordial lithium problem. Annu. Rev. Nucl. Part Sci. 61, 47–68. doi:10.1146/annurev-nucl-102010-130445

CrossRef Full Text | Google Scholar

Fu, X., Bressan, A., Molaro, P., and Marigo, P. (2015). Lithium evolution in metal-poor stars: from pre-main sequence to the Spite plateau. Monthly Notices of the RAS. 452, 3256–3265. doi:10.1093/mnras/stv1384

CrossRef Full Text | Google Scholar

Goudelis, A., Pospelov, M., and Pradler, J. (2016). Light particle solution to the cosmic lithium problem. Phys. Rev. Lett. 116, 211303. doi:10.1103/PhysRevLett.116.211303

PubMed Abstract | CrossRef Full Text | Google Scholar

Guardo, G. L., Spitaleri, C., Lamia, L., Gulino, M., La Cognata, M., Tang, X., et al. (2017). Assessing the near threshold cross section of the ¹⁷O(n,α)¹⁴C reaction by means of the Trojan horse method. Phys. Rev. C. 95, 025807. doi:10.1103/PhysRevC.95.025807

CrossRef Full Text | Google Scholar

Hunt, S. E., Pope, R. A., and Evans, W. W. (1957). Investigation of the gamma radiation produced by irradiating with protons in the energy range 0.7 to 3.0 mev. Phys. Rev. 106, 1012–1015. doi:10.1103/PhysRev.106.1012

CrossRef Full Text | Google Scholar

Iliadis, C. (2007). Nuclear physics of stars. New York: Wiley

CrossRef Full Text | Google Scholar

Indelicato, I., La Cognata, M., Spitaleri, C., Burjan, V., Cherubini, S., Gulino, M., et al. (2017). New improved indirect measurement of the ¹⁸F(p,α)¹⁵O reaction at energies of astrophysical relevance. Astrophys. J. 845, 19. doi:10.3847/1538-4357/aa7de7

CrossRef Full Text | Google Scholar

Jeffries, R. D. (2006). Pre-main-sequence lithium depletion (Chemical abundances and mixing in stars in the Milky Way and its satellites., 163. New York, NY: Springer, 163. 978-3-540-34135-2

CrossRef Full Text | Google Scholar

Kaihong, F., Qian, Z., Bingjun, C., Zhengwei, Z., Qiang, W., Tieshan, W., et al. (2018). Direct measurement of astrophysical factor S(E) and screening potential for reaction at low energy. Phys. Lett. B. 785, 262–267

CrossRef Full Text | Google Scholar

Kusakabe, M., Cheoun, M. K., Kim, K. S., Hashimoto, Ma., Ono, M., Nomoto, K., et al. (2019). Supernova neutrino process of ¹⁰Li and ¹¹B revisited. Astrophys. J. 872, 164. doi:10.3847/1538-4357/aafc35

CrossRef Full Text | Google Scholar

Kwon, J. U., Kim, J. C., and Sung, B. N. (1989). Low-energy cross sections for the ¹⁰Li(p, He)³He reaction. Nucl. Phys. 493, 112–123. doi:10.1016/0375-9474(89)90535-6

CrossRef Full Text | Google Scholar

La Cognata, M., Mukhamedzhanov, A. M., Spitaleri, C., Indelicato, I., Aliotta, M., Burjan, V., et al. (2011). The fluorine destruction in stars: first experimental study of the ¹⁹F(p, α⁰)¹⁶O reaction at astrophysical energies. Astrophys. J. Lett. 739, L54. doi:10.1088/2041-8205/739/2/L54

CrossRef Full Text | Google Scholar

La Cognata, M., Spitaleri, C., Mukhamedzhanov, A., Banu, A., Cherubini, S., Coc, A., et al. (2010a). A novel approach to measure the cross section of the ¹⁷O(p, α)¹⁴N resonant reaction in the 0-200 keV energy range. Astrophys. J. 708, 796–811. doi:10.1088/0004-637X/708/1/796

CrossRef Full Text | Google Scholar

La Cognata, M., Spitaleri, C., Mukhamedzhanov, A., Goldberg, V., Irgaziev, B., Lamia, L., et al. (2010b). DWBA momentum distribution and its effect on. THM. Nucl. Phys. A. 834, 658–660. doi:10.1016/j.nuclphysa.2010.01.116

CrossRef Full Text | Google Scholar

Lambert, D. L., and Reddy, B. E. (2004). Lithium abundances of the local thin disc stars. Month. Notices RAS. 349, 757–767. doi:10.1111/j.1365-2966.2004.07557.x

CrossRef Full Text | Google Scholar

Lamia, L., Mazzocco, M., Pizzone, R. G., Hayakawa, S., La Cognata, M., Spitaleri, C., et al. (2019). Cross-section measurement of the cosmologically relevant ⁷Be(n,α)⁴He reaction over a broad energy range in a single experiment. Astrophys. J. 879, 23. doi:10.3847/1538-4357/ab2234

CrossRef Full Text | Google Scholar

Lamia, L., Romano, S., Carlin, N., Cherubini, S., Crucillà, V., de Moura, M. M., et al. (2007). Boron depletion: indirect measurement of the ¹¹B(p,α)⁴Be S(E)-factor. Nucl. Phys. 787, 309–314. doi:10.1016/j.nuclphysa.2006.12.049

CrossRef Full Text | Google Scholar

Lamia, L., Spitaleri, C., Bertulani, C. A., Hou, S. Q., La Cognata, M., Pizzone, R. G., et al. (2017). On the determination of the ⁷Be(n,α)⁴He reaction cross section at BBN energies. Astrophys. J. 850, 175. doi:10.3847/1538-4357/aa965c

CrossRef Full Text | Google Scholar

Lamia, L., Spitaleri, C., Burjan, V., Carlin, N., Cherubini, S., Crucillà, V., et al. (2012b). New measurement of the ¹¹B(p,α)⁴Be bare-nucleus S(E) factor via the Trojan horse method. J. Phys. G Nucl. Phys. 39, 015106. doi:10.1088/0954-3899/39/1/015106

CrossRef Full Text | Google Scholar

Lamia, L., Spitaleri, C., Carlin, N., Cherubini, S., Del Szanto, M. G., Gulino, M., et al. (2008). Indirect study of (p,ant) and (n,ant) reactions induced on boron isotopes. Nuovo Cimento C Geophys. Space Phys. C. 31, 423–431. doi:10.1393/ncc/i2009-10303-2

CrossRef Full Text | Google Scholar

Lamia, L., Spitaleri, C., La Cognata, M., Palmerini, S., and Pizzone, R. G. (2012a). Recent evaluation of the ¹⁰Li(p, α)⁴He reaction rate at astrophysical energies via the Trojan Horse method. Astron. Astrophys. 541, A158. doi:10.1051/0004-6361/201219014

CrossRef Full Text | Google Scholar

Lamia, L., Spitaleri, C., Pizzone, R. G., Tognelli, E., Tumino, A., Degl’Innocenti, S., et al. (2013). An updated ¹⁰Li(p, α)⁴He reaction rate at astrophysical energies with the Trojan Horse method. Astrophys. J. 768, 65. doi:10.1088/0004-637X/768/1/65

CrossRef Full Text | Google Scholar

Lamia, L., Spitaleri, C., Tognelli, E., Degl’Innocenti, S., Pizzone, R. G., and Prada Moroni, P. G. (2015). Astrophysical impact of the updated ⁴Be(p,α)¹¹Li and ¹⁰B(p,α)³Be reaction rates as deduced by THM. Astrophys. J. 811, 99. doi:10.1088/0004-637X/811/2/99

CrossRef Full Text | Google Scholar

Lattuada, M., Pizzone, R. G., Typel, S., Figuera, P., Miljanić, D., Musumarra, A., et al. (2001). The bare astrophysical S(E) factor of the ¹¹Li(p, α)α reaction. Astrophys. J. 562, 1076–1080. doi:10.1086/323868

CrossRef Full Text | Google Scholar

Lemoine, M., Vangioni-Flam, E., and Cassé, M. (1998). Galactic cosmic rays and the evolution of light elements. Astrophys. J. 499, 735–745. doi:10.1086/305650

CrossRef Full Text | Google Scholar

Lind, K., Melendez, J., Asplund, M., Collet, R., and Magic, Z. (2013). The lithium isotopic ratio in very metal-poor stars. Astron. Astrophys. 554, A96. doi:10.1051/0004-6361/201321406

CrossRef Full Text | Google Scholar

Lombardo, I., Dell’Aquila, D., Conte, F., Francalanza, L., La Cognata, M., Lamia, L., et al. (2016). New investigations of the ¹¹B(p,α)⁴Be reaction at bombarding energies between 0.6 and 1 MeV. J. Phys. G Nucl. Phys. 43, 045109. doi:10.1088/0954-3899/43/4/045109

CrossRef Full Text | Google Scholar

Meléndez, J., Casagrande, L., Ramírez, I., Asplund, M., and Schuster, W. J. (2010). Observational evidence for a broken Li Spite plateau and mass-dependent Li depletion. Astron. Astrophys. 515, L3. doi:10.1051/0004-6361/200913047

CrossRef Full Text | Google Scholar

Montalbán, J., and D’Antona, F. (2006). New light on the old problem of lithium pre-main sequence depletion: models with 2D radiative-hydrodynamical convection. Monthly Notices of the RAS. 370, 1823–1828. doi:10.1111/j.1365-2966.2006.10600.x

CrossRef Full Text | Google Scholar

Mukhamedzhanov, A. M., Blokhintsev, L. D., Irgaziev, B. F., Kadyrov, A. S., La Cognata, M., Spitaleri, C., et al. (2008). Trojan Horse as an indirect technique in nuclear astrophysics. J. Phys. G Nucl. Phys. 35, 014016. doi:10.1088/0954-3899/35/1/014016

CrossRef Full Text | Google Scholar

Perey, C. M., and Perey, F. G. (1976). Compilation of Phenomenological optical-model parameters 1954-1975. Atomic Data Nucl. Data Tables. 17, 1. doi:10.1016/0092-640X(76)90007-3

CrossRef Full Text | Google Scholar

Piau, L., and Turck-Chièze, S. (2002). Lithium depletion in pre-main-sequence solar-like stars. Astrophys. J. 566, 419–434. doi:10.1086/324277

CrossRef Full Text | Google Scholar

Pitrou, C., Coc, A., Uzan, J. P., and Vangioni, E. (2018). Precision big bang nucleosynthesis with improved Helium-4 predictions. Phys. Rep. 754, 1–66. doi:10.1016/j.physrep.2018.04.005

CrossRef Full Text | Google Scholar

Pizzone, R. G., Roeder, B. T., McCleskey, M., Trache, L., Tribble, R. E., Spitaleri, C., et al. (2016). Trojan Horse measurement of the ¹⁸F(p,α)¹⁵O astrophysical S(E)-factor. Eur. Phys. J. A. 52, 24. doi:10.1140/epja/i2016-16024-3

CrossRef Full Text | Google Scholar

Pizzone, R. G., Spartá, R., Bertulani, C. A., Spitaleri, C., La Cognata, M., Lalmansingh, J., et al. (2014). Big bang nucleosynthesis revisited via Trojan Horse method measurements. Astrophys. J. 786, 112. doi:10.1088/0004-637X/786/2/112

CrossRef Full Text | Google Scholar

Pizzone, R. G., Spitaleri, C., Bertulani, C. A., Mukhamedzhanov, A. M., Blokhintsev, L., La Cognata, M., et al. (2013). Updated evidence of the Trojan horse particle invariance for the ²H(d, p)³H reaction. Phys. Rev. C. 87, 025805. doi:10.1103/PhysRevC.87.025805

CrossRef Full Text | Google Scholar

Pizzone, R. G., Spitaleri, C., Lamia, L., Bertulani, C., Mukhamedzhanov, A., Blokhintsev, L., et al. (2011). Trojan horse particle invariance studied with the Li6(d,α)He4 and Li7(p,α)He4 reactions. Phys. Rev. C. 83, 045801. doi:10.1103/PhysRevC.83.045801

CrossRef Full Text | Google Scholar

Pizzone, R. G., Spitaleri, C., Lattuada, M., Cherubini, S., Musumarra, A., Pellegriti, M. G., et al. (2003). Proton-induced lithium destruction cross-section and its astrophysical implications. Astron. Astrophys. 398, 423–427. doi:10.1051/0004-6361:20021700

CrossRef Full Text | Google Scholar

Pizzone, R. G., Tumino, A., degl’Innocenti, S., Spitaleri, C., Cherubini, S., Musumarra, A., et al. (2005). Trojan Horse estimate of bare nucleus astrophysical S(E)-factor for the ⁶Li(p,α)³He reaction and its astrophysical implications. Astron. Astrophys. 438, 779–784. doi:10.1051/0004-6361:20052863

CrossRef Full Text | Google Scholar

Prantzos, N., de Laverny, P., Guiglion, G., Recio-Blanco, A., and Worley, C. C. (2017). The AMBRE project: a study of Li evolution in the Galactic thin and thick discs. Astron. Astrophys. 606, A132. doi:10.1051/0004-6361/201731188

CrossRef Full Text | Google Scholar

Prantzos, N. (2012). Production and evolution of Li, Be, and B isotopes in the Galaxy. Astron. Astrophys. 542, A67. doi:10.1051/0004-6361/201219043

CrossRef Full Text | Google Scholar

Primas, F. (2010). “Beryllium and boron in metal-poor stars,” in Light elements in the Universe. Editors C Charbonnel, M Tosi, F Primas, and C Chiappini (IAU Symposium), 268, 221–230. doi:10.1017/S1743921310004163

CrossRef Full Text | Google Scholar

Rapisarda, G. G., Spitaleri, C., Cvetinović, A., Spartà, R., Cherubini, S., Guardo, G. L., et al. (2018). Study of the ¹¹B(p,α)⁴Be reaction by means of the Trojan Horse method. Eur. Phys. J. A. 54, 189. doi:10.1140/epja/i2018-12622-3

CrossRef Full Text | Google Scholar

Richard, O., Michaud, G., and Richer, J. (2005). Implications of WMAP observations on Li abundance and stellar evolution models. Astrophys. J. 619, 538–548. doi:10.1086/426470

CrossRef Full Text | Google Scholar

Rolfs, C., and Rodney, W. (1988). Book Review: Cauldrons in the cosmos: nuclear astrophysics., 42. Chicago: U Chicago Press, 71. doi:10.1063/1.2811016

CrossRef Full Text | Google Scholar

Romano, S., Lamia, L., Spitaleri, C., Li, C., Cherubini, S., Gulino, M., et al. (2006). Study of the ⁹Be(p,α)⁶Li reaction via the Trojan Horse method. Eur. Phys. J. A Hadrons Nucl. 27, 221–225

CrossRef Full Text | Google Scholar

Roughton, N. A., Fritts, M. R., Peterson, R. J., Zaidins, C. S., and Hansen, C. J. (1979). Thick-target measurements and astrophysical thermonuclear reaction rates: proton-induced reactions. Atom. Data Nucl. Data Tables. 23, 177. doi:10.1016/0092-640X(79)90004-4

CrossRef Full Text | Google Scholar

Sbordone, L., Bonifacio, P., Caffau, E., Ludwig, H. G., Behara, N. T., González Hernández, J. I., et al. (2010). The metal-poor end of the Spite plateau. I. Stellar parameters, metallicities, and lithium abundances. Astron. Astrophys. 522, A26. doi:10.1051/0004-6361/200913282

CrossRef Full Text | Google Scholar

Scott, D. A., Caciolli, A., Di Leva, A., Formicola, A., Aliotta, M., Anders, M., et al. (2012). First direct measurement of the O(p,γ)F reaction cross section at Gamow energies for classical novae. Phys. Rev. Lett. 109, 202501. doi:10.1103/PhysRevLett.109.202501

PubMed Abstract | CrossRef Full Text | Google Scholar

Segel, R. E., Hanna, S. S., and Allas, R. G. (1965). States in C Between 16.4 and 19.6 MeV. Phys. Rev. 139, 818–830. doi:10.1103/PhysRev.139.B818

CrossRef Full Text | Google Scholar

Sergi, M. L., Spitaleri, C., La Cognata, M., Coc, A., Mukhamedzhanov, A., Burjan, S. V., et al. (2010). New high accuracy measurement of the O¹⁷(p,α)N¹⁴ reaction rate at astrophysical temperatures. Phys. Rev. C. 82, 032801. doi:10.1103/PhysRevC.82.032801

CrossRef Full Text | Google Scholar

Sergi, M. L., Spitaleri, C., La Cognata, M., Lamia, L., Pizzone, R. G., Rapisarda, G. G., et al. (2015). Improvement of the high-accuracy ¹⁷O(p,α)¹⁴N reaction-rate measurement via the Trojan Horse method for application to ¹⁷O nucleosynthesis. Phys. Rev. C. 91, 065803. doi:10.1103/PhysRevC.91.065803

CrossRef Full Text | Google Scholar

Sestito, P., and Randich, S. (2005). Time scales of Li evolution: a homogeneous analysis of open clusters from ZAMS to late-MS. Astron. Astrophys. 442, 615–627. doi:10.1051/0004-6361:20053482

CrossRef Full Text | Google Scholar

Sierk, A. J., and Tombrello, T. A. (1973). The ⁹Be(p,α) and (p, d) cross sections at low energies. Nucl. Phys. 210, 341–354

CrossRef Full Text | Google Scholar

Spitaleri, C., Cherubini, S., del Zoppo, A., di Pietro, A., Figuera, P., Gulino, M., et al. (2003). The Trojan Horse method in nuclear astrophysics. Nucl. Phys. 719, C99. doi:10.1016/S0375-9474(03)00975-8

CrossRef Full Text | Google Scholar

Spitaleri, C., La Cognata, M., Lamia, L., Mukhamedzhanov, A. M., and Pizzone, R. G. (2016). Nuclear astrophysics and the Trojan Horse method. European Physical Journal A. 52, 77. doi:10.1140/epja/i2016-16077-2

CrossRef Full Text | Google Scholar

Spitaleri, C., La Cognata, M., Lamia, L., Pizzone, R. G., and Tumino, A. (2019). Astrophysics studies with the Trojan Horse method. Eur. Phys. J. A. 55, 161. doi:10.1140/epja/i2019-12833-0

CrossRef Full Text | Google Scholar

Spitaleri, C., Lamia, L., Puglia, S. M. R., Romano, S., La Cognata, M., Crucillà, V., et al. (2014). Measurement of the 10 keV resonance in the B¹⁰⁽p,α)Be⁷ reaction via the Trojan Horse method. Phys. Rev. C. 90, 035801. doi:10.1103/PhysRevC.90.035801

CrossRef Full Text | Google Scholar

Spitaleri, C., Lamia, L., Tumino, A., Pizzone, R. G., Cherubini, S., del Zoppo, A., et al. (2004). The ¹¹B(p,α)⁸Be reaction at sub-Coulomb energies via the Trojan-horse method. Phys. Rev. C. 69, 055806. doi:10.1103/PhysRevC.69.055806

CrossRef Full Text | Google Scholar

Spitaleri, C. (1991). Problems of fundamental modern Physics, II. Proceedings. 28, 21–36

CrossRef Full Text | Google Scholar

Spitaleri, C., Puglia, S. M. R., La Cognata, M., Lamia, L., Cherubini, S., Cvetinović, A., et al. (2017). Measurement of the ¹¹B(p,α)⁸Be cross section from 5 keV to 1.5 MeV in a single experiment using the Trojan horse method. Phys. Rev. C. 95, 035801. doi:10.1103/PhysRevC.95.035801

CrossRef Full Text | Google Scholar

Spite, F., and Spite, M. (1982). Abundance of lithium in unevolved halo stars and old disk stars - interpretation and consequences. Astron. Astrophys. 115, 357–366

CrossRef Full Text | Google Scholar

Spite, M., and Spite, M. (1986). Astron. Astrophys. 115, 357

CrossRef Full Text | Google Scholar

Starrfield, S., Bose, M., Iliadis, C., Hix, W. R., Woodward, C. E., and Wagner, R. M. (2019). Carbon-oxygen classical novae are galactic li producers as well as potential supernova ia progenitors. .arXiv e-printsarXiv:1910.00575

CrossRef Full Text | Google Scholar

Stephens, A., Boesgaard, A. M., King, J. R., and Deliyannis, C. P. (1997). Beryllium in lithium-deficient F and G stars. Astrophys. J. 491, 339–358. doi:10.1086/304933

CrossRef Full Text | Google Scholar

Tan, K. F., Shi, J. R., and Zhao, G. (2009). Beryllium abundances in metal-poor stars. Monthly Notices of the RAS. 392, 205–215. doi:10.1111/j.1365-2966.2008.14027.x

CrossRef Full Text | Google Scholar

Tognelli, E., Degl’Innocenti, S., and Prada Moroni, P. G. (2012). ⁷Li surface abundance in pre-main sequence stars. Testing theory against clusters and binary systems. Astron. Astrophys. 548, A41. doi:10.1051/0004-6361/201219111

CrossRef Full Text | Google Scholar

Tognelli, E., Prada Moroni, P. G., Degl’Innocenti, S., Salaris, M., and Cassisi, S. (2020). Protostellar accretion in low mass metal poor stars and the cosmological lithium problem. arXiv e-printsarXiv:2004.14857

CrossRef Full Text | Google Scholar

Tribble, R. E., Bertulani, C. A., La Cognata, M., Mukhamedzhanov, A. M., and Spitaleri, C. (2014). Indirect techniques in nuclear astrophysics: a review. Rep. Prog. Phys. 77, 106901. doi:10.1088/0034-4885/77/10/106901

PubMed Abstract | CrossRef Full Text | Google Scholar

Tumino, A., Spitaleri, C., di Pietro, A., Figuera, P., Lattuada, M., Musumarra, A., et al. (2003). Validity test of the “Trojan horse” method applied to the ⁷Li(p,α)⁴He reaction. Phys. Rev. C. 67, 065803. doi:10.1103/PhysRevC.67.065803

CrossRef Full Text | Google Scholar

Tumino, A., Spitaleri, C., La Cognata, M., Cherubini, S., Guardo, G. L., Gulino, M., et al. (2018). An increase in the ¹²C + ¹²C fusion rate from resonances at astrophysical energies. Nature. 557, 687–690. doi:10.1038/s41586-018-0149-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Tumino, A., Spitaleri, C., Pappalardo, L., Cherubini, S., Zoppo, A. D., La Cognata, M., et al. (2004). Indirect study of the astrophysically relevant ⁷Li(p, α)³He reaction by means of the Trojan Horse method. Prog. Theor. Phys. Suppl. 154, 341–348. doi:10.1143/PTPS.154.341

CrossRef Full Text | Google Scholar

Tumino, A., Spitaleri, C., Sergi, M. L., Kroha, V., Burjan, V., Cherubini, S., et al. (2006). Validity test of the Trojan Horse Method applied to the ⁷Li + p → α + α reaction via the ³He break-up. Eur. Phys. J. A. 27, 243–248. doi:10.1140/epja/i2006-08-038-1

CrossRef Full Text | Google Scholar

Vauclair, S., and Charbonnel, C. (1995). Influence of a stellar wind on the lithium depletion in halo stars: a new step towards the lithium primordial abundance. Astron. Astrophys. 295, 715

CrossRef Full Text | Google Scholar

Wen, Q. G., Li, C. B., Zhou, S. H., Irgaziev, B., Fu, Y. Y., Spitaleri, C., et al. (2016). Experimental study to explore the ⁹Be-induced nuclear reaction via the Trojan horse method. Phys. Rev. C. 93, 035803

CrossRef Full Text | Google Scholar

Wen, Q. G., Li, C. B., Zhou, S. H., Meng, Q. Y., Spitaleri, C., Tumino, A., et al. (2011). A new approach to select the quasifree mechanism in the Trojan horse method. J. Phys. G Nucl. Part. Phys. 38, 085103

CrossRef Full Text | Google Scholar

Wen, Q. G., Li, C. B., Zhou, S. H., Meng, Q. Y., Zhou, J., Li, X. M., et al. (2008). Trojan horse method applied to ⁹Be(p,α)⁶Li at astrophysical energies. Phys. Rev. C. 78, 035805

CrossRef Full Text | Google Scholar

Wiescher, M., deBoer, R. J., Görres, J., and Azuma, R. E. (2017). Low energy measurements of the ¹⁰B(p,α)⁷Be reaction. Phys. Rev. C. 95, 044617. doi:10.1103/PhysRevC.95.044617

CrossRef Full Text | Google Scholar

Xhixha, G., Bezzon, G. P., Broggini, C., Buso, G. P., Caciolli, A., Callegari, I., et al. (2013). The worldwide norm production and a fully automated gamma-ray spectrometer for their characterization. J. Radioanal. Nucl. Chem. 295, 445–457. doi:10.1007/s10967-012-1791-1

CrossRef Full Text | Google Scholar

Xu, Y., Takahashi, K., Goriely, S., Arnould, M., Ohta, M., and Utsunomiya, H. (2013). NACRE II: an update of the NACRE compilation of charged-particle-induced thermonuclear reaction rates for nuclei with mass number A<16. Nucl. Phys. 918, 61–169. doi:10.1016/j.nuclphysa.2013.09.007

CrossRef Full Text | Google Scholar

Youn, M., Chung, H. T., Kim, J. C., Bhang, H. C., and Chung, K. H. (1991). The ¹⁰B(p, α)⁴Be reaction in the thermonuclear energy region. Nucl. Phys. 533, 321–332. doi:10.1016/0375-9474(91)90493-P

CrossRef Full Text | Google Scholar

Zahnow, D., Rolfs, C., Schmidt, S., and Trautvetter, H. P. (1997). Low-energy S(E) factor of ⁹Be(p,α)⁶Li and .¹¹B(p,α)⁸Be. Zeitschrift fur Physik A Hadrons Nucl. 359, 211–218. doi:10.1007/s002180050389

CrossRef Full Text | Google Scholar

Zhang, Q., Huang, Z., Hu, J., Chen, B., and Fang, K. (2020). Astrophysical S(E) for the ¹¹B(p,d)⁶Li and ¹¹B(p,α)⁸Be reactions by direct measurement. Astrophys. J. 893, 126

CrossRef Full Text | Google Scholar