- 1Discipline of Astronomy Astrophysics and Space Engineering, Indian Institute of Technology Indore, Indore, India
- 2Center of Excellence in Space Sciences India, Indian Institute of Science Education and Research Kolkata, Mohanpur, India
Coronal mass ejections and high speed solar streams serve as perturbations to the background solar wind that have major implications in space weather dynamics. Therefore, a robust framework for accurate predictions of the background wind properties is a fundamental step toward the development of any space weather prediction toolbox. In this pilot study, we focus on the implementation and comparison of various models that are critical for a steady state, solar wind forecasting framework. Specifically, we perform case studies on Carrington rotations 2,053, 2,082, and 2,104, and compare the performance of magnetic field extrapolation models in conjunction with velocity empirical formulations to predict solar wind properties at Lagrangian point L1. Two different models to extrapolate the solar wind from the coronal domain to the inner-heliospheric domain are presented, namely, a) Kinematics based [Heliospheric Upwind eXtrapolation (HUX)] model, and b) Physics based model. The physics based model solves a set of conservative equations of hydrodynamics using the PLUTO code and can additionally predict the thermal properties of solar wind. The assessment in predicting solar wind parameters of the different models is quantified through statistical measures. We further extend this developed framework to also assess the polarity of inter-planetary magnetic field at L1. Our best models for the case of CR2053 gives a very high correlation coefficient (∼0.73–0.81) and has an root mean square error of (∼75–90 km s−1). Additionally, the physics based model has a standard deviation comparable with that obtained from the hourly OMNI solar wind data and also produces a considerable match with observed solar wind proton temperatures measured at L1 from the same database.
Introduction
Space weather refers to the dynamic conditions on the Sun and in the intervening Sun–Earth medium that can severely influence the functioning of space-borne and ground based technical instruments thereby affecting human life. Predicting the impact of space weather thereby becomes an essential task. In particular, explosive events on the Sun that include solar flares, coronal mass ejections (CMEs) and solar energetic particles play a crucial role in influencing space weather (Schwenn, 2006). The ambient solar wind being the medium in which the CMEs propagate also plays a significant role in influencing space weather, particularly, high speed solar wind streams which contribute to about 70% of geomagnetic activity outside of the solar maximum phase (Richardson et al., 2000). Therefore, understanding and predicting the key properties of the ambient solar wind is a crucial component of space weather modeling (Owens and Forsyth, 2013).
Magnetic field is a key ingredient that threads the solar plasma and governs the dynamical properties of solar wind. Observational measurements of field strengths in tenuous coronal environments is a challenging task even today. Thus, modeling coronal plasma requires extrapolating magnetic fields at the photosphere in the coronal region. Typically, a potential field source surface solution [PFSS (Altschuler and Newkirk, 1969), is adopted to extend photospheric magnetic fields up-to the source surface, usually set at
The various forecasting models over time have shown considerable progress in our understanding of modeling the macro-physical solar wind properties. One of the key ingredients that is critical for space weather modeling is the interplay of micro-physical turbulent and particle acceleration processes with macro-physical dynamics. Several attempts have been made to include effects of energy contained in sub-grid turbulence and multi-fluid aspects in modeling of solar wind [CORHEL (Downs et al., 2016), AWSoM (Sokolov et al., 2016), CRONOS (Usmanov et al., 2014; Wiengarten et al., 2016; Usmanov et al., 2018)]. In general, handling of large separation of scales required to consistently model such an interplay of length scales is a challenging task. Such a multi-scale nature of problem is also experienced in astrophysical plasma modeling and several astrophysical codes are working in direction of developing a hybrid framework that bridges this wide gap. In particular, recent development of hybrid particle module for PLUTO code (Mignone et al., 2018; Vaidya et al., 2018) to model particle acceleration at shocks and its subsequent non-thermal emission. Further, PLUTO code supports adaptive mesh refinement and various non-ideal MHD processes including magnetic resistivity (Mignone et al., 2012) and Hall-MHD. The code also has support for anisotropic thermal conduction (Vaidya et al., 2017) and optical thin cooling. In last 5 years, problems pertaining to solar and magnetospheric physics have also been tackled with PLUTO code (Reale et al., 2016; Sarkar et al., 2017; Bharati Das et al., 2019; Réville et al., 2020). The goal of this work is to develop a space weather modeling framework in conjunction with PLUTO code aiming to utilize the additional functionalities of the code for modeling the micro-physical aspects of Sun–Earth environment.
In this first study, our focus is to compare the various coronal and inner heliospheric models for solar wind forecasting and the assessment of their predictive performance. The paper is arranged in the following manner—the details of the methods implemented for the forecasting framework are described in Section 2. The results from various models adopted for forecasting of solar wind velocity for a couple of case studies along with statistical assessment of their accuracy are elaborated in Section 3. Finally, Section 4 discusses the various features of the forecasting framework along with limitations and future outlook.
Methodology
The region between the solar photosphere and the Lagrangian point L1 is divided into two zones. The inner coronal zone extends from the photosphere up-to 5
• To calculate the magnetic fields in the coronal region through various extrapolation methods of the input observed photospheric magnetic field.
• Applying the velocity empirical relations based on the field line properties obtained from extrapolation at the outer boundary of the coronal region.
• Extending the velocity estimates from the outer boundary of the coronal region up-to Lagrangian point L1 for comparison with observations.
Detailed procedure followed for each of the above steps is described in this section.
Magnetic Field Extrapolation
Forecasting of solar wind across the domain requires accurate magnetic field solutions extrapolated from the solar surface to the outer boundaries of the coronal domain. The magnetic field extrapolations are carried out up to a distance of 5
Just above the photospheric region, the magnetic energy density is greater than the plasma energy density and magnetic effects dominate. One can assume this region to be current free and thus, use the potential formulation for the magnetic fields (Schatten et al., 1968). This current free assumption is valid inside a sphere of radius of about 2.5
In the region outside the source surface, the magnetic fields are extrapolated using the Schatten Current Sheet (SCS) model (Schatten, 1972). The SCS model extends the magnetic fields from the source surface to a distance of 5
Velocity Empirical Relations
Based on the magnetic field structure (Reiss et al., 2019) obtained by from the field extrapolation methods, we generate a velocity map for the solar wind using some empirical velocity mapping models. We employ two different empirical models for the velocity calculations described in the sections below.
Wang–Sheeley Model
The Wang–Sheeley (WS) model depends on a parameter, called the expansion factor of the coronal flux tubes to calculate Solar Wind velocities. The expansion factor (
where
where,
Wang–Sheeley–Arge Model
The Wang–Sheeley–Arge (WSA) (Arge et al., 2003) is a model that also incorporates the effect of minimum angular distance of foot point of the field line from coronal hole, along with the expansion factor. It is believed that coronal holes produce fast streams of solar wind. So the position of the field line’s foot point in coronal hole plays a very important role. The empirical relation from the WSA model (Riley et al., 2015) used in the present work is
The parameters
Extrapolation Into the Heliospheric Domain
The WS and WSA model gives us the solar wind maps at the outer boundary of the coronal domain i.e., at 2.5
Heliospheric Upwind eXtrapolation
The Heliospheric Upwind eXtrapolation (HUX) model assumes the solar-wind flow at the outer boundary of the coronal domain to be time-ϕstationary. The extrapolation of the solar wind velocities in an r-grid can be then be kinetically approximated using
where
Physics Based Modeling Using PLUTO Code
With an aim to incorporate the effects of some of the physical aspects in solar wind extrapolation, we describe a physics based modeling approach that involves solving a set of conservative equations using the Godunov scheme based Eulerian grid code, PLUTO (Mignone et al., 2007).
For this pilot study, we assume the solar wind to be hydrodynamic and solve the following set of compressible equations in 2D polar co-ordinates (r, ϕ):
where, ρ is the density of the fluid, P being the isotropic thermal pressure,
The above equations are solved in a non-inertial frame where the inner radial boundary rotates with the rate equal to the solar rotation rate. Further to simplify we neglect the Coriolis and centrifugal terms as their contribution is rather small in determining the steady flow structure of the solar wind (Pomoell and Poedts, 2018). The computational grid in polar co-ordinates ranges in the radial direction from 5
Initially, the computational domain is filled with a static gas with number density of 1 cm−3 and thermal sound speed of 180 km s−1. The choice of initial conditions does not affect final steady state wind solution as the material injected from the inner boundary wash away these initial values to obtain a new steady state. Radial velocity is prescribed at the inner boundary from the WSA mapping. The inner boundary is also made to rotate with respect to the computational domain with a rate equal to the solar rotational time period which is 27.3 days. As a general rule, boundary conditions can be specified for only those characteristics that are outgoing (away from the boundary). Since we have a supersonic inflow boundary condition, all the characteristics are pointing away from the boundary and therefore, along with the prescription of solar wind velocity, one would need to prescribe the density and pressure at the inner radial boundary as well. Following (Pomoell and Poedts, 2018), we prescribe the number density (n) and pressure at the inner radial boundary in following manner:
where
Model Definitions
Using the combination of various magnetic field extrapolation, velocity empirical relations and method of extrapolating velocity field within the inner heliosphere, we have defined 6 different models. The combinations used for each of these models are shown in Figure 1. Models 1 and 2 involves magnetic field extrapolation using PFSS (without SCS) and velocity extrapolation in inner heliosphere using the HUX model. The difference between them is the choice of velocity empirical relation. In the other set of models 3 and 4a, the magnetic fields are extrapolated using PFSS+SCS. The empirical velocity relation employed for Model 3 is WS and that for Model 4a is WSA. Velocity field in both these models are extrapolated from 5
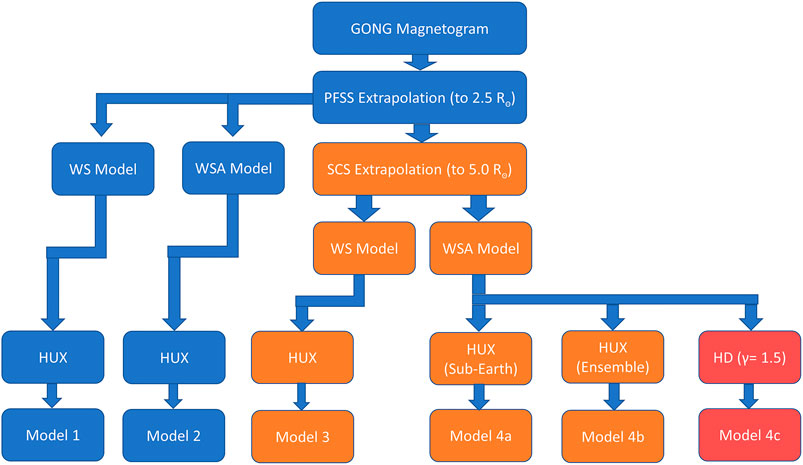
FIGURE 1. A flowchart of the models that have been utilized in the present work. The various combinations of coronal and inner heliospheric models have been categorized into six different models: 1, 2, 3, 4a, 4b, and 4c.
Statistical Measures of Forecast Performance
The performance of a forecast can be determined by comparing the forecast outcome of continuous variables (e.g., velocity) to the observed values. We calculated several scalar measures of forecast accuracy which has previously been used to determine forecast performances by (Reiss et al., 2016; Wu et al., 2020). Given a set of modeled values
The Mean absolute error can be considered as a measure of the overall error in forecast of a model. Another such measure is the Mean Absolute Percentage error (MAPE) which is given by
The Root Mean Square Error or RMSE is also used sometimes as a performance statistic for a model and is given by
Another important measure in determining the forecast performance is the Pearson Correlation Coefficient (CC) which is a parameter used to estimate the correlation between the observed values and the model values. In addition to this, another measure is the standard deviation of the time series of each of the individual model outputs and its comparison with the estimate from observed data. These measures are estimated for all the models considered and discussed in Section 3.5 for the three Carrington rotations CR2053, CR2082 and CR2104 considered in our study.
Results
In this section, we present our results using the methodology described above for the three case studies spanning the declining phase of cycle 23, near the solar minimum and the rising phase of solar cycle 24. In particular, we consider CR 2053 (from 2007/02/04 to 2007/03/04), CR 2082 (from 2009/04/05 to 2009/05/03) and CR 2104 (from 2010/11/26 to 2010/12/24).We also demonstrate the assessment of performance of the different forecasting models considered for these cases.
Case Studies
CR2053 represents a relatively quiet phase of the Sun during the decline of the solar cycle number 23. Six active regions were identified regions during the period of CR2053 (Fazakerley et al., 2016) that can also be seen in our input synoptic magnetogram (Figure 2A). All the active region lie close to the L1 footprint and thus are expected to have pertinent effects on the solar wind velocities.
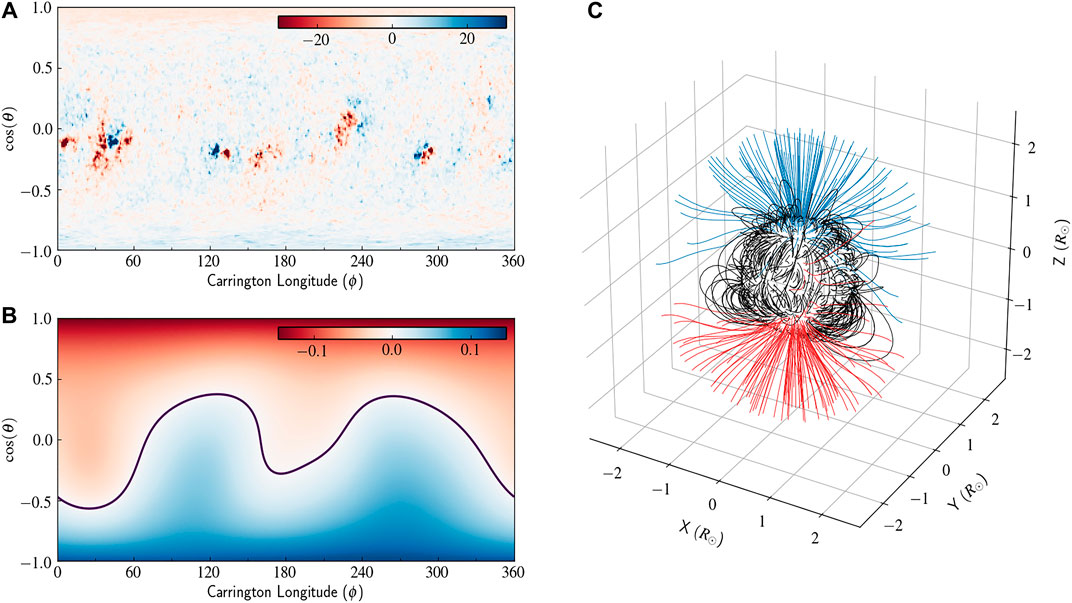
FIGURE 2. Panel (A) shows the photspheric magnetic flux density (in Gauss) from a standard synoptic magnetogram obtained from GONG for CR 2053, panel (B) shows the magnetic flux density measured in Gauss obtained from PFSS extrapolation at the source surface (2.5
As a first step, we calculated the PFSS solution for this Carrington rotation. The GONG magnetogram data which is given as input to PFSS and the output solution obtained using pfsspy are shown in Figure 2. A 3D map of field lines joining the photosphere to the PFSS source surface at 2.5
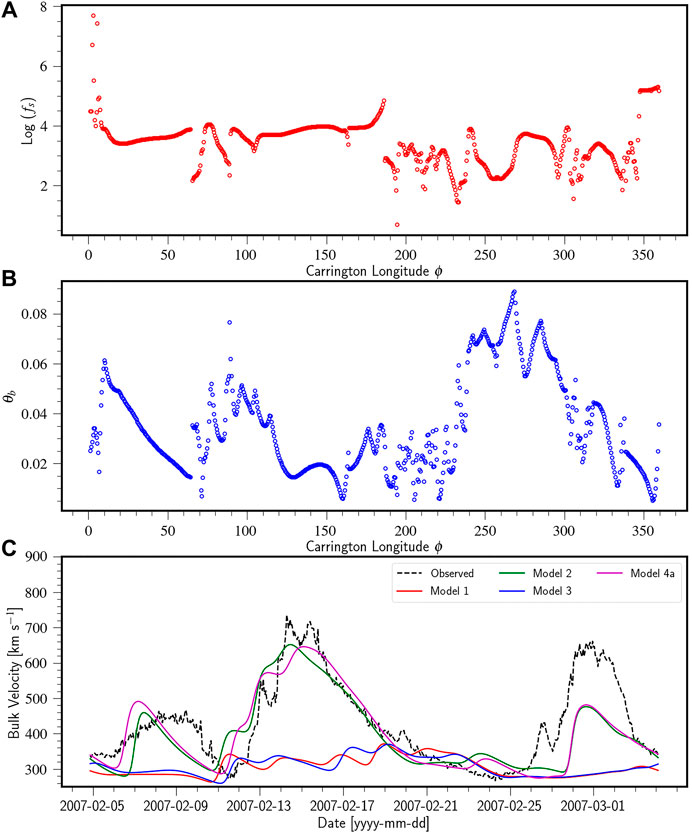
FIGURE 3. Panel (A) and panel (B) show plots of
We observe that the WS model gives an inaccurate representation of the solar wind velocities and the contrast between the slow wind and the fast streams are not satisfactorily reproduced. For example, during the first phase of high speed stream peaking on 2007-02-15, variations are observed in values of
The case of CR2082 also illustrates the quiet phase of the Sun, in-fact it lies at the solar minimum at the end of cycle 23. The input GONG magnetogram is shown in Figure 4A. The solution obtained from PFSS at the source surface shows a rather bipolar structure, where the polarity inversion line is relativity straight lying around the co-latitude
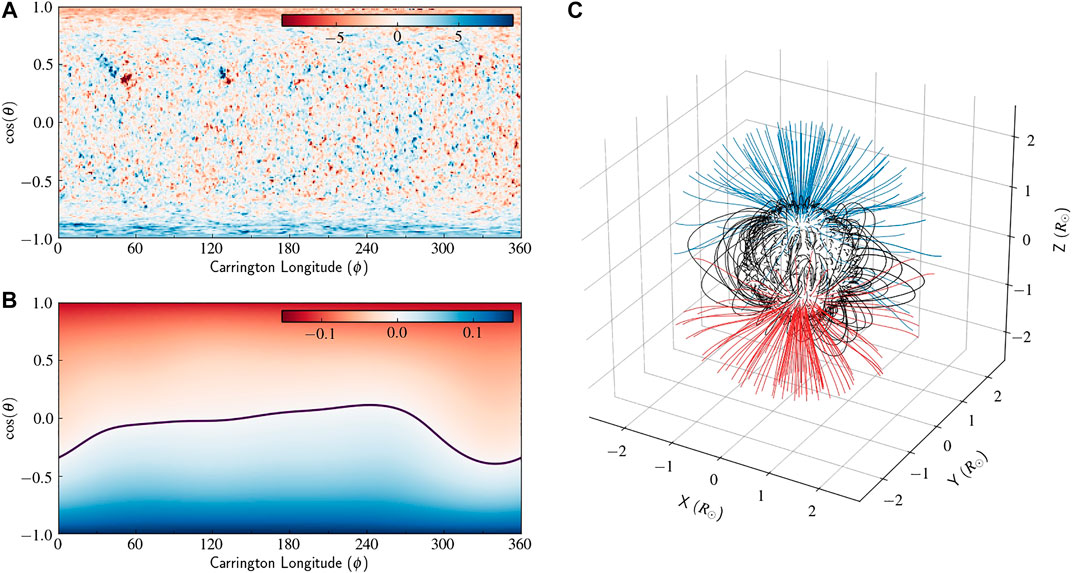
FIGURE 4. The PFSS input and output in a similar layout as Figure 2 for CR 2082.
Extrapolated field lines from PFSS solution and ones that are augmented with SCS model are used to obtain the values of the expansion factor
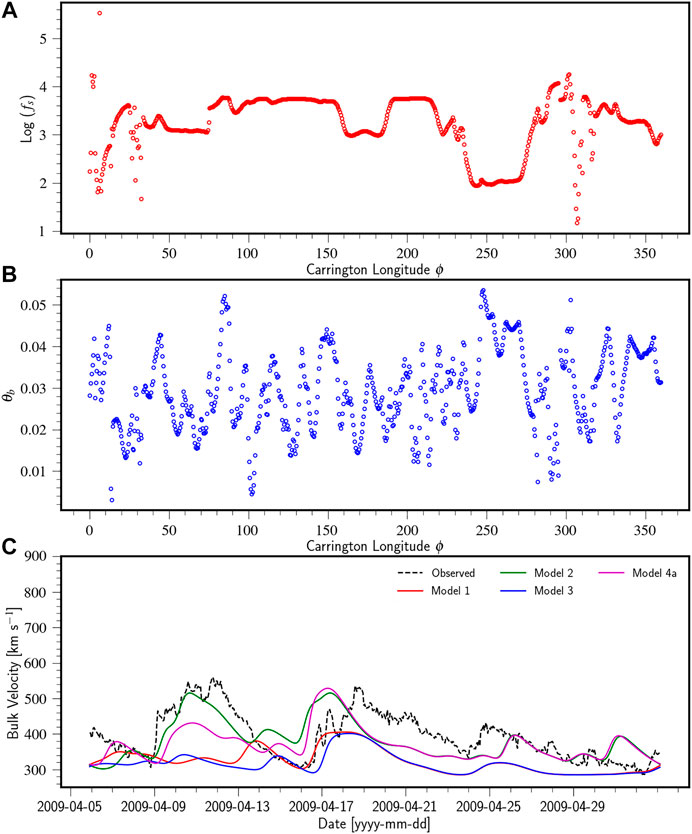
FIGURE 5. Panel (A) and panel (B) show plots of
We have also carried out the same analysis using the same set of model parameters (see Eq. 3) for the case of CR 2104 that represents the rising phase of the solar cycle 24. We find similar trend even for this case as solar wind velocity estimates from Model 2 and Model 4a that involves WSA empirical relation presents a better match with observations as compared those obtained from Model 1 and Model 3.
Ensemble Forecasting
Numerical extrapolation models like HUX are computationally less demanding than HD or 3D MHD models. Such numerical models are thus used to study a large set of initial conditions by a method known as ensemble forecasting. Ensemble forecasting has been widely used to constrain terrestrial weather and is an important tool to determine model performance and also helps to set uncertainty bounds to the model output. A solar wind forecast model is considered to be a very uncertain one if the ensemble members produce drastically different results (Reiss et al., 2019).
To study the variations introduced in our model output due to an uncertainty in determining source that contribute to solar wind measured at L1, we created an ensemble of latitudes centered around our expected sub-earth latitude at a distance of ±1°, ±2.5°, ±5°, ±10°, and ±15°. The change in sub-earth latitude changes the field lines under consideration which in turn effects the parameters associated with the field lines (e.g.,
Figure 6 shows the forecast obtained from the ensemble of sub-earth latitudes by using Model 4a for all three cases CR 2053, CR 2082, and CR 2104 The dashed line in the figures represent the ensemble median for the respective cases. We have also plotted the velocity obtained by considering zero uncertainties in the the sub-earth latitudes and the same is plotted as a black solid line. The dark and light shades around the median represent the
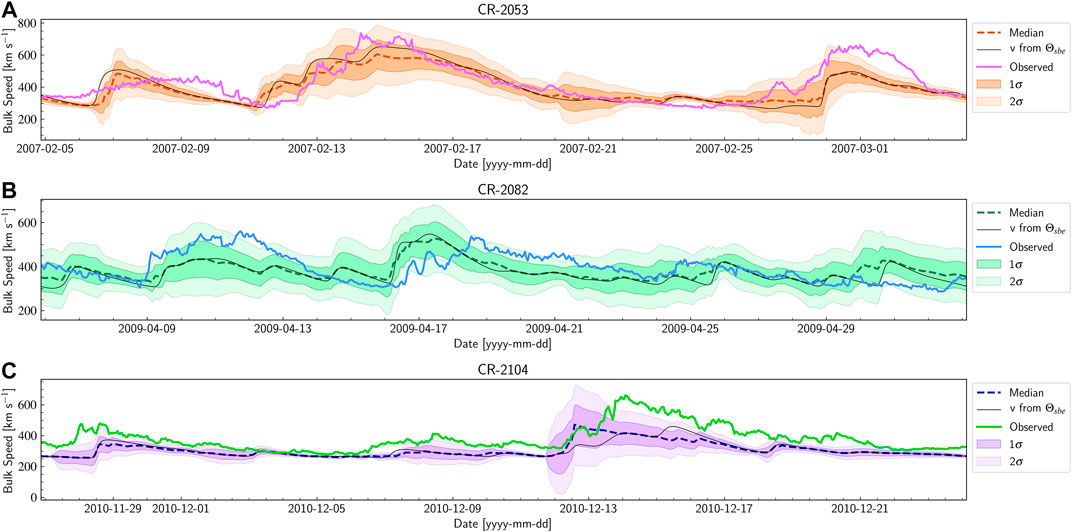
FIGURE 6. A plot of the ensemble forecast for CR 2053 (panel (A)), CR 2082 (panel (B)) and CR 2104 (panel (C)) along with the observed velocities. The black solid line in each plot represents the velocities obtained without incorporating the uncertainty. The dashed line in each of the plots represent the respective ensemble median values and the darker and lighter shades around the median values represent the 1σ and 2σ error expected during the forecast, respectively.
Assessing Interplanetary Magnetic Field Polarity
In addition to predicting the solar wind velocity, we also assess the polarity of the magnetic field lines at L1 assuming a Parker spiral magnetic field configuration between Sun and Earth [see (Jian et al., 2015)] We evaluate the corresponding longitude at L1 for each CR longitude at 5
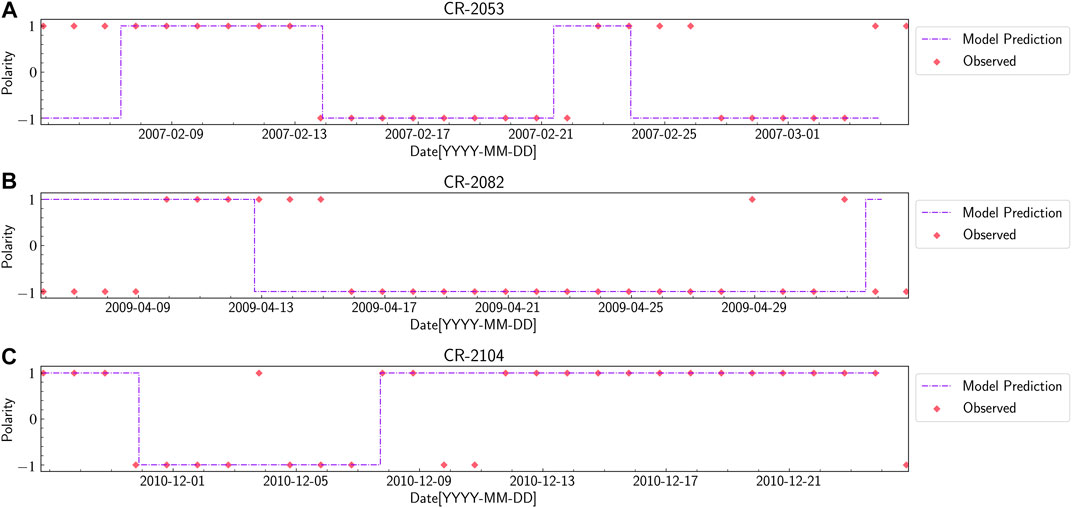
FIGURE 7. A plot showing the magnetic field polarity forecast at L1 for CR 2053 (A), CR 2082 (B) and CR 2104 (C) along with the observed values from OMNI database. The red diamonds represent the daily average value of polarity of radial component of the interplanetary magnetic field at L1. The purple dashed line are the polarity of the transformed radial component of field lines at L1 in the GSE/GSM co-ordinate frame.
Forecasting From Physics Based Modeling
Two dimensional hydrodynamic simulation runs with initial conditions described in Section 2.3.2 provide a time dependent solar wind forecasting framework. Plasma is injected in the computational domain from the inner rotating radial boundary at each time step. Empirical values of velocities obtained from the WSA model using the sub-earth point field lines are used as input conditions for the hydrodynamic simulations in the inner boundary placed at 5
In the initial transient phase, the plasma propagates outwards toward the outer boundary from where it leaves the domain. Subsequent to this transient phase, a steady state solar wind is established in the domain. The steady state radial velocity [X-Y plane] in units of km s−1 from the simulation after a one solar rotation time period of 27.3 days is shown in the Figure 8A for CR2053. The black dashed circle represents the radial distance corresponding to L1 point (
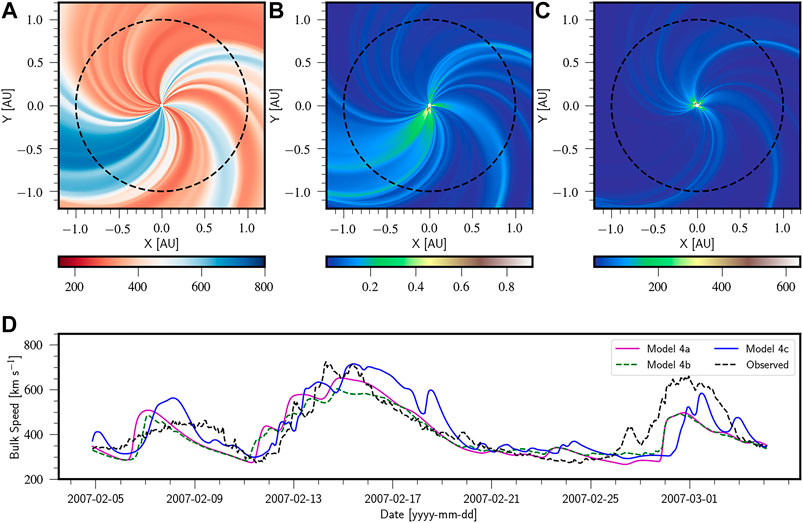
FIGURE 8. Quantities of the solar wind obtained from the physics based model (A) radial velocity, (B) proton temperature in MK, and (C) number density in cm−3, the black dashed line in each of these panels represents the L1 position at 1 AU. Panel (D) shows comparison of variation in bulk speed in km s−1 at L1 point for CR 2053 for Models 4a, 4b and 4c with hourly averaged observed values. The X-axis in panel (D) represents the time in yyyy-mm-dd format.
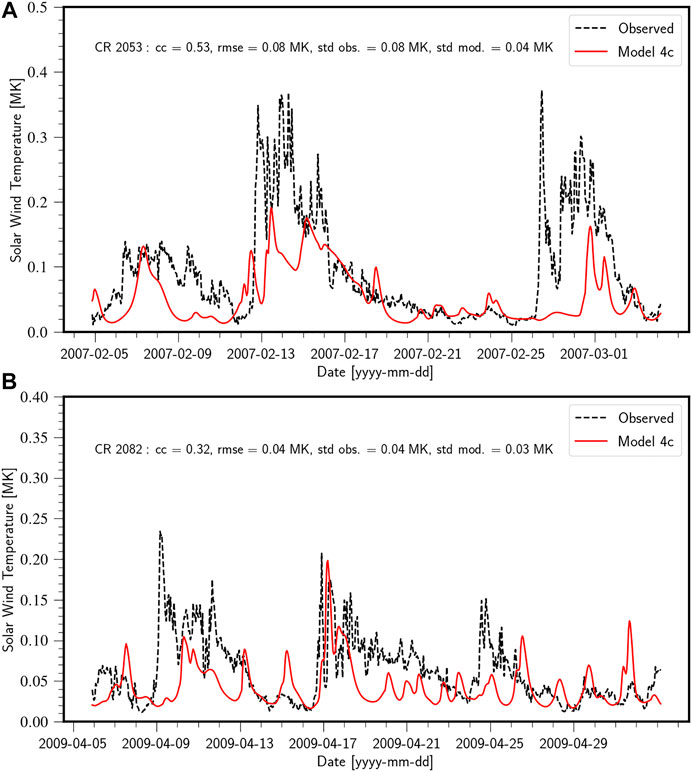
FIGURE 9. (A) Comparison of the proton temperature estimated from the model 4c (red solid line) at Lagrangian point L1 with hourly averaged observed values (black dashed line) obtained from OMNI database for CR2053. The statistical analysis of the forecast performance are mentioned in the panel. (B) Comparison of proton temperature estimates from model 4c and observations for the case of CR 2082. The color scheme is same as the panel above.
Quantifying Predictive Performance Using Statistical Analysis
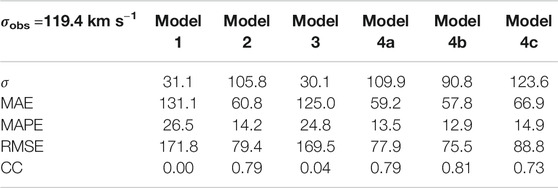
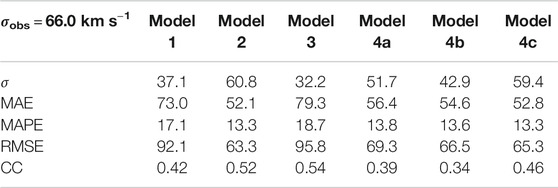
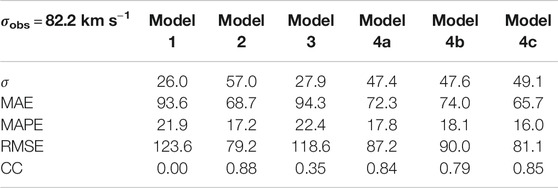
Statistical measures (see Section 2.5) quantifying forecast performance for CR 2053, CR 2082, and CR 2104 are presented in Table 1, 2, and 3, respectively. The standard deviation of the observed time series for CR2053 is 119.4 km s−1. Model 4c was able to reproduce this standard deviation quite satisfactorily (123.6 km s−1). All models for CR 2053 involving the WS model failed to produce reasonable agreement with the observations, which can be inferred from the extremely low value of the correlation coefficient (∼0). We believe that this is due to the proximity of the coronal holes to the equator, whereby open field lines emerging from these holes drive high speed streams. The WS empirical model disregards the size of coronal holes in its empirical relation and fails to capture this effect. The presence of a significant number of coronal holes on the magnetogram that are close to the sub-earth latitudes thus necessitates the use of the WSA model for velocity mapping on the inner boundary. CR2082 on the other hand has a significantly lesser number of coronal holes (Petrie and Haislmaier, 2013). And thus even the models involving the WS velocity mapping show acceptable CC values (0.42–0.54). The highest CC for CR 2053 is produced by model 4b (CC = 0.81) which represents the ensemble median of the sub-earth latitude variations, however the same cannot be said for CR 2082 as all the other models produce a greater CC and lower error values than that of the ensemble median. This reinforces the statement that the ensemble average does not always produce a more accurate representation of the velocity profile.
A graphical representation and analysis of various forecasting models implemented in this work are represented in a Taylor diagram (Taylor, 2001). The Taylor plots for CR 2053, CR 2082, and CR 2104 are given in Figure 10 The radial distance from the origin represents the standard deviation, the azimuthal coordinate represent the correlation coefficient (CC). In addition to this, one more set of arcs are drawn, centered at the reference (observed) standard deviation on the X axis that represent the RMS error for the models. In general a solar wind model is considered to be a good model if it has a high correlation coefficient (CC), low RMS error, and having a similar standard deviation to the observed time series of velocities (Reiss et al., 2016) and in a Taylor plot it would lie close to the smallest circle on the X axis. For the case of CR 2053, Model 1 and Model 3 lie very close to the vertical axis indicating very low CC value and thus are considered to have poor forecast performance. Model 4b has the highest CC value and comparatively low errors, but it lies relatively far from the observed standard deviation curve. The physics based models, Model 4c is seen to have standard deviation profiles well in agreement with the observed values along with a good CC. We thus assert that Model 4b and 4c are the best representations of the velocity profiles for CR 2053. For the case of CR 2082, Model 4c and Model 2 has a standard deviation closest to that of the observed value of ∼60 km s−1 and Model 2 has the lowest error values (in terms of RMSE, MAE and MAPE). The CC of model 3 is one of the highest in the models considered followed closely by Model 2. Model 3 however has larger values of all the errors considered showing that even though its correlated well with the observed values, the model is prone to errors which would result in inaccurate output solar wind velocity profiles. Model 4a, 4b, and 4c have similar but low values of MAE, MAPE and RMSE, and CC lying in the range of (∼0.34–0.46). Based on the above analysis for the assumed set of WSA parameters, Model 2 performs better for CR2082 closely followed by models 4c and 4a. For the case of CR 2104, the predicted standard deviation is less as compared to the observed values for all the models. The predictions from model 1 and 3 have low CC value and RMSE around 120 km/s and indicating a poor forecast performance. The CC of models 2, 4a, 4b, and 4c is as high as 0.8 and the RMSE for these models ranges between 80 and 90 km s. This suggests these models have a better forecast performance as was the case in CR 2053.
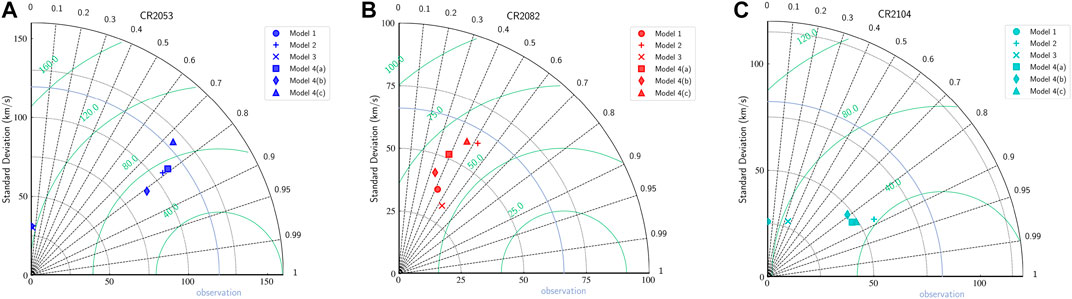
FIGURE 10. Taylor Plots for CR 2053 (A), CR 2082 (B) and CR 2104 (C) summarizing the performance of various models in each case. The blue curve concentric to the standard deviation curves represents the standard deviation of the observed time series. The green curves with centers on the X axis serve as ticks for the RMSE.
Discussions and Summary
In this pilot study, we have developed a python module toward constructing a robust framework for accurate predictions of a steady state background solar wind model using various empirical and extrapolation formulations. This framework is also integrated with physics based modeling using PLUTO code. The entire workflow is a combination of a) extrapolating the magnetic fields to the outer coronal domain using magnetic models such as PFSS and SCS, b) mapping the velocities in the outer coronal domain using models such as WS and WSA, and c) extrapolating the velocities to L1 using extrapolation techniques such as HUX as well as hydrodynamic propagation of the velocities using PLUTO. We have studied various combinations of the coronal magnetic models as well as velocity extrapolation models in view of three different Carrington rotations, CR 2053, CR 2082, and CR 2104. We were successfully able to generate velocity profiles well in agreement with the observed values.
Even though the the models involving the WS velocity mapping performed relatively well for the case of CR 2082 when compared to the equivalent models of the other CRs in this study, it performed very poorly when applied to CR 2053 and CR 2104. The WSA model on the other hand has shown consistently superior performance for all the CRs with lesser error measures in these cases than the WS model. The WS model also failed to capture the contrast between the slow and fast solar wind streams and thus produced velocity profiles with significantly lesser standard deviation than the observed profile. We infer from this that the WSA model is superior to the WS model for the cases and parameters considered in this work.
In general, the models with a combination of PFSS + SCS for magnetic field extrapolation paired with the WSA model for velocity mapping (models 4a, 4b, and 4c) had the best performance in all the cases, CR 2053, CR 2082 as well as CR 2104. This can be seen as near identical standard deviations of the output velocity pattern in Model 4a and Model 4c paired with a very high correlation coefficient (∼0.73–0.81) and relatively low errors for the case of CR 2053 (Table 1) and CR 2104 (Table 3). For CR 2082, Model 4a and Model 4c had standard deviations which are close to that of the observed profile. We note that Model 3 performed quite well in case of CR 2082 with a high CC (∼0.53) but with higher errors than the other models. However, it showed a lack of consistency in performance with very poor results in case of CR 2053. We observe that Model 2 also performed well for all three CRs which can be seen in its high CC values and low errors.
Model 4c that employs PFSS+SCS and WSA velocity empirical relation with physics based extrapolation, gives us an additional advantage of being able to determine the thermal properties of the solar wind which also showed good correlation with the observed values (see Figure 9). This model also naturally takes into account the acceleration of the solar wind during its propagation. The standard deviation of the Model 4c velocity profile also had good agreement with the observations with high CC values (0.73 for CR 2053, 0.46 for CR 2082 and 0.85 for CR 2104). The Model 4c thus has its own pros and cons. The pros being the ability to determine additional solar wind properties than what HUX or HUXt can offer, and the cons being that it takes significantly more computational resources.
Ensemble forecasting helps provide a rather clear quantification of the uncertainty associated with the predictions. We have chosen a total of 11 realisations covering a latitude range of
Even though ensemble forecasting can provide a rather clear statistical uncertainty prediction of the model, it has been seen that various other uncertainties can creep in that are solely dependent on the choice of the input magnetograms. Riley et al. (2014) highlighted that magnetograms from various observatories show significant differences in magnetic field measurements. In-spite of the fact that one can quantify the conversion factors between various independent datasets, there is no particular observatory that can produce a ground truth dataset for the input magnetograms. Additionally, one can improve the WSA model performance using time-dependent flux transport model based magnetograms (e.g., Schrijver and De Rosa, 2003; Arge et al., 2010; Arge et al., 2013). Quantifying the effects of input magnetograms on model performance is beyond the scope of this paper and shall be addressed in a future study.
The statistical parameters represented in the Taylor diagrams indicate the accuracy of our current forecasting framework. Typically, for an accurate forecasting model, low RMSE, high CC and similar standard deviation with observed values are expected. The forecasting presented in this paper uses the same set of parameters (except
We would like to point out that the free parameters used for the WS and WSA empirical relations cannot be universally applied for all CRs and must be individually tuned for a particular case scenario. This is evident from our use of the same set of free parameters for all the CRs which results in significantly different performances. Additionally, the statistical estimates have indicated that in case of CR 2082, the model with PFSS+WSA have performed slightly better than its counterpart including SCS. In this particular case, this could perhaps be related to over-estimation of magnetic field lines contributing to solar wind speeds at L1 by SCS. However, through the ensemble modeling we have demonstrated the estimation from Model 4a is within the 2σ bounds. Improving the accuracy and performance of SCS extrapolation will be considered in our further studies.
The caveat of hydrodynamic models (Model 4c) is that it solves the equations on a plane and does not contain the magnetic information of the Sun–Earth system on which state-of-the-art 3D MHD model are based. However, even without the magnetic field information and having a 2D geometry, the HD models capture many important aspects of the solar wind. Model 4c facilitate better physical insight in the behavior of solar wind than the HUX models (4a and 4b). Model 4c (HD) can thus be seen as a halfway point between HUX and full MHD models.
In summary, we have successfully produced velocity maps for the cases considered and also matched our results with additional observable eg, proton temperature. This pilot study is the first step in developing an indigenous space weather framework which is an absolute need of hour as Indian Space Research Organization (ISRO) is coming up with Aditya-L1 to study the properties of Sun at L1 (https://www.isro.gov.in/aditya-l1-first-indian-mission-to-study-sun). A full-fledged 3D-MHD run of solar wind using PLUTO code will be carried out in our subsequent paper for predicting other observable quantities like the number density and IMF magnetic field. Further, including the propagation of CMEs in such a realistic solar wind background would be carried out with an aim to study its impact on space weather.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author.
Author Contributions
SK developed the python pipeline that was able to obtain the velocity of solar wind at L1 for various models following the flowchart described in the paper. AP utilised the data and formulated the statistical framework for quantifying the performance of forecasting. He also contributed significantly in writing the text. BV did the overall supervision of the work and contributed in integrating the data from python pipeline into PLUTO code for physics based simulations runs.
Acknowledgments
The authors acknowledge the comments from the referees that have helped in significantly improving the manuscript. We also thank the support from Indian Institute of Technology Indore. The calculations are done using the computational resources available in the institute. BV is heading the Max Planck Partner Group at IIT Indore and would like to thank the same for financial support.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Altschuler, M. D., and Newkirk, G. (1969). Magnetic fields and the structure of the solar corona. I: Methods of calculating coronal fields. Sol. Phys. 9, 131–149. doi:10.1007/BF00145734
Arge, C. N., and Pizzo, V. J. (2000). Improvement in the prediction of solar wind conditions using near-real time solar magnetic field updates. J. Geophys. Res. Space Phys. 105, 10465–10480. doi:10.1029/1999JA000262
Arge, C. N., Odstrcil, D., Pizzo, V. J., and Mayer, L. R. (2003). “Improved method for specifying solar wind speed near the sun,” in Solar wind ten of American Institute of Physics conference series. Editors M. Velli, R. Bruno, F. Malara, and B. Bucci, Vol. 679, 190–193. doi:10.1063/1.1618574
Arge, C. N., Henney, C. J., Koller, J., Compeau, C. R., Young, S., MacKenzie, D., et al. (2010). “Air force data assimilative photospheric Flux transport (ADAPT) model,” in Twelfth international solar wind conference of American Institute of Physics conference series. Editors M. Maksimovic, K. Issautier, N. Meyer-Vernet, M. Moncuquet, and F. Pantellini, Vol. 1216, 343–346. doi:10.1063/1.3395870
Arge, C. N., Henney, C. J., Hernandez, I. G., Toussaint, W. A., Koller, J., and Godinez, H. C. (2013). “Modeling the corona and solar wind using ADAPT maps that include far-side observations,” in Solar wind 13 of American Institute of Physics conference series. Editors G. P. Zank, J. Borovsky, R. Bruno, J. Cirtain, S.Cranmer, H. Elliott, et al. , Vol. 1539, 11–14. doi:10.1063/1.4810977
Bharati Das, S., Basak, A., Nandy, D., and Vaidya, B. (2019). Modeling star-planet interactions in far-out planetary and exoplanetary systems. Astrophys. J. 877, 80. doi:10.3847/1538-4357/ab18ad
Downs, C., Lionello, R., Mikić, Z., Linker, J. A., and Velli, M. (2016). Closed-field coronal heating driven by wave turbulence. Astrophys. J. 832, 180. doi:10.3847/0004-637X/832/2/180
Fazakerley, A. N., Harra, L. K., and van Driel-Gesztelyi, L. (2016). An investigation of the sources of earth-directed solar wind during Carrington rotation 2053. Astrophys. J. 823, 145. doi:10.3847/0004-637X/823/2/145
Henley, E. M., and Pope, E. C. D. (2017). Cost-loss analysis of ensemble solar wind forecasting: space weather use of terrestrial weather tools. Space Weather 15, 1562–1566. doi:10.1002/2017SW001758
Jian, L. K., MacNeice, P. J., Taktakishvili, A., Odstrcil, D., Jackson, B., Yu, H.-S., et al. (2015). Validation for solar wind prediction at earth: comparison of coronal and heliospheric models installed at the ccmc. Space Weather 13, 316–338. doi:10.1002/2015SW001174
Lionello, R., Linker, J. A., and Mikić, Z. (2009). Multispectral emission of the sun during the first whole sun month: magnetohydrodynamic simulations. Astrophys. J. 690, 902–912. doi:10.1088/0004-637X/690/1/902
MacNeice, P., Jian, L. K., Antiochos, S. K., Arge, C. N., Bussy-Virat, C. D., DeRosa, M. L., et al. (2018). Assessing the quality of models of the ambient solar wind. Space Weather 16, 1644–1667. doi:10.1029/2018SW002040
McGregor, S. L., Hughes, W. J., Arge, C. N., and Owens, M. J. (2008). Analysis of the magnetic field discontinuity at the potential fieldsource surface and schatten current sheet interface in the Wang–Sheeley–Arge model. J. Geophys. Res. 113, 23–27. doi:10.1029/2007ja012330
Mignone, A., Bodo, G., Massaglia, S., Matsakos, T., Tesileanu, O., Zanni, C., et al. (2007). PLUTO: a numerical code for computational astrophysics. Astrophys. J. Suppl. Ser. 170, 228–242. doi:10.1086/513316
Mignone, A., Bodo, G., Vaidya, B., and Mattia, G. (2018). A particle module for the PLUTO code. I. an implementation of the MHDPIC equations. Astrophys. J. 859, 13. doi:10.3847/1538-4357/aabccd
Mignone, A., Zanni, C., Tzeferacos, P., van Straalen, B., Colella, P., and Bodo, G. (2012). The PLUTO code for adaptive mesh computations in astrophysical fluid dynamics. Astrophys. J. Suppl. Ser. 198, 7. doi:10.1088/0067-0049/198/1/7
Odstrcil, D., Riley, P., and Zhao, X. P. (2004). Numerical simulation of the 12 May 1997 interplanetary CME event. J. Geophys. Res. Space Phys. 109, A02116. doi:10.1029/2003JA010135
Owens, M. J., and Forsyth, R. J. (2013). The heliospheric magnetic field. Living Rev. Sol. Phys. 10, 5. doi:10.12942/lrsp-2013-5
Owens, M. J., and Riley, P. (2017). Probabilistic solar wind Forecasting using large ensembles of near-sun conditions with a simple one-dimensional “upwind” scheme. Space Weather 15, 1461–1474. doi:10.1002/2017SW001679
Owens, M., Lang, M., Barnard, L., Riley, P., Ben-Nun, M., Scott, C. J., et al. (2020). A computationally efficient, time-dependent model of the solar wind for use as a surrogate to three-dimensional numerical magnetohydrodynamic simulations. Sol. Phys. 295, 43. doi:10.1007/s11207-020-01605-3
Petrie, G. J. D., and Haislmaier, K. J. (2013). Low-latitude coronal holes, decaying active regions, and global coronal magnetic structure. Astrophys. J. 775, 100. doi:10.1088/0004-637X/775/2/100
Pomoell, J., and Poedts, S. (2018). EUHFORIA: European heliospheric forecasting information asset. J. Space Weather Space Clim. 8, A35. doi:10.1051/swsc/2018020
Reale, F., Orlando, S., Guarrasi, M., Mignone, A., Peres, G., Hood, A. W., et al. (2016). 3D MHD modeling of twisted coronal loops. Astrophys. J. 830, 21. doi:10.3847/0004-637X/830/1/21
Reiss, M. A., Temmer, M., Veronig, A. M., Nikolic, L., Vennerstrom, S., Schöngassner, F., et al. (2016). Verification of high-speed solar wind stream forecasts using operational solar wind models. Space Weather 14, 495–510. doi:10.1002/2016SW001390
Reiss, M. A., MacNeice, P. J., Mays, L. M., Arge, C. N., Möstl, C., Nikolic, L., et al. (2019). Forecasting the ambient solar wind with numerical models. I. on the implementation of an operational framework. Astrophys. J. Suppl. 240, 35. doi:10.3847/1538-4365/aaf8b3
Réville, V., Velli, M., Rouillard, A. P., Lavraud, B., Tenerani, A., Shi, C., et al. (2020). Tearing instability and periodic density perturbations in the slow solar wind. Astrophys. J. 895, L20. doi:10.3847/2041-8213/ab911d
Richardson, I. G., Cliver, E. W., and Cane, H. V. (2000). Sources of geomagnetic activity over the solar cycle: relative importance of coronal mass ejections, high-speed streams, and slow solar wind. J. Geophys. Res.: Space Phys. 105, 18203–18213. doi:10.1029/1999JA000400
Riley, P., and Lionello, R. (2011). Mapping solar wind streams from the sun to 1 au: a comparison of techniques. Sol. Phys. 270 (2), 575–592. doi:10.1007/s11207-011-9766-x
Riley, P., Ben-Nun, M., Linker, J. A., Mikic, Z., Svalgaard, L., Harvey, J., et al. (2014). A multi-observatory inter-comparison of line-of-sight synoptic solar magnetograms. Astrophys. J. 289, 769–792. doi:10.1007/s11207-013-0353-1
Riley, P., Linker, J. A., and Arge, C. N. (2015). On the role played by magnetic expansion factor in the prediction of solar wind speed. Space Weather 13, 154–169. doi:10.1002/2014SW001144
Sarkar, A., Vaidya, B., Hazra, S., and Bhattacharyya, J. (2017). Simulating coronal loop implosion and compressible wave modes in a flare hit active region. ArXiv e-prints.
Schatten, K. H. (1972). Current sheet magnetic model for the solar corona. NASA Special Publ. 308, 44.
Schatten, K. H., Wilcox, J. M., and Ness, N. F. (1968). A model of interplanetary and coronal magnetic fields. Sol. Phys. 6, 442–455. doi:10.1007/BF00146478
Schrijver, C. J., and De Rosa, M. L. (2003). Photospheric and heliospheric magnetic fields. Astrophys. J. 212, 165–200. doi:10.1023/A:1022908504100
Schwenn, R. (2006). Space weather: the solar perspective. Living Rev. Sol. Phys. 3, 2. doi:10.12942/lrsp-2006-2
Sokolov, I. V., van der Holst, B., Manchester, W. B., Ozturk, D. C. S., Szente, J., Taktakishvili, A. R., et al. (2016). Threaded-field-lines model for the low solar corona powered by the Alfven wave turbulence. arXiv:1609.04379.
Taylor, K. E. (2001). Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res.: Atmosphere 106, 7183–7192. doi:10.1029/2000JD900719
Tóth, G., van der Holst, B., Sokolov, I. V., De Zeeuw, D. L., Gombosi, T. I., Fang, F., et al. (2012). Adaptive numerical algorithms in space weather modeling. J. Comput. Phys. 231, 870–903. doi:10.1016/j.jcp.2011.02.006
Usmanov, A. V., Goldstein, M. L., and Matthaeus, W. H. (2014). Three-fluid, three-dimensional magnetohydrodynamic solar wind model with eddy viscosity and turbulent resistivity. Astrophys. J. 788, 43. doi:10.1088/0004-637X/788/1/43
Usmanov, A. V., Matthaeus, W. H., Goldstein, M. L., and Chhiber, R. (2018). The steady global corona and solar wind: a three-dimensional MHD simulation with turbulence. Transp. Heat. 865, 25. doi:10.3847/1538-4357/aad687
Vaidya, B., Prasad, D., Mignone, A., Sharma, P., and Rickler, L. (2017). Scalable explicit implementation of anisotropic diffusion with Runge-Kutta-Legendre super-time stepping. Astrophys. J. 472, 3147–3160. doi:10.1093/mnras/stx2176
Vaidya, B., Mignone, A., Bodo, G., Rossi, P., and Massaglia, S. (2018). A particle module for the PLUTO code: II-hybrid framework for modeling non-thermal emission from relativistic magnetized flows. ArXiv e-prints
Wang, Y. M., and Sheeley, N. R. (1989). Solar wind speed and coronal flux-tube expansion. Astrophys. J. 355, 726–732. doi:10.1086/168805 | .
Wang, Y. M., and Sheeley, N. R. (1995). Solar implications of ULYSSES interplanetary field measurements. 447, L143. doi:10.1086/309578
Wiengarten, T., Oughton, S., Engelbrecht, N. E., Fichtner, H., Kleimann, J., and Scherer, K. (2016). A generalized two-component model of solar wind turbulence and ab initio diffusion mean-Free paths and drift lengthscales of cosmic rays. Astrophys. J. 833, 17. doi:10.3847/0004-637X/833/1/17
Wu, C.-C., Liou, K., Wood, B. E., Plunkett, S., Socker, D., Wang, Y. M., et al. (2020). Modeling inner boundary values at 18 solar radii during solar quiet time for global three-dimensional time-dependent magnetohydrodynamic numerical simulation. J. Atmos. Sol. Terr. Phys. 201, 105211. doi:10.1016/j.jastp.2020.105211
Keywords: solar wind, sun–earth connection, sun: magnetic fields, sun: heliosphere, method: numerical, space weather modeling
Citation: Kumar S, Paul A and Vaidya B (2020) A Comparison Study of Extrapolation Models and Empirical Relations in Forecasting Solar Wind. Front. Astron. Space Sci. 7:572084. doi: 10.3389/fspas.2020.572084
Received: 12 June 2020; Accepted: 16 October 2020;
Published: 23 November 2020.
Edited by:
Stefaan Poedts, KU Leuven, BelgiumReviewed by:
Meng Jin, Lockheed Martin Solar and Astrophysics Laboratory (LMSAL), United StatesJiansen He, Peking University, China
Copyright © 2020 Kumar, Paul and Vaidya. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sandeep Kumar, c3NhbmRlZXBzaGFybWEyMDFAZ21haWwuY29t
 Sandeep Kumar
Sandeep Kumar Arghyadeep Paul
Arghyadeep Paul