Investigating Dark Energy Equation of State With High Redshift Hubble Diagram

Several independent cosmological data, collected within the last 20 years, revealed the accelerated expansion rate of the Universe, usually assumed to be driven by the so called dark energy, which, according to recent estimates, provides now about 70% of the total amount of matter-energy in the Universe. The nature of dark energy is yet unknown. Several models of dark energy have been proposed: a non-zero cosmological constant, a potential energy of some self interacting scalar field, effects related to the non-homogeneous distribution of matter, or effects due to alternative theories of gravity. Recently, it turned out that the standard flat ΛCDM is disfavored (at 4σ) when confronted with a high redshift Hubble diagram, consisting of supernovae of type Ia (SNIa), quasars (QSOs), and gamma ray-bursts (GRBs) (Lusso and Risaliti, 2016; Lusso et al., 2019; Risaliti and Lusso, 2019). Here we use the same data to investigate if this tension is confirmed, using a different approach: actually in Lusso and Risaliti (2016), Lusso et al. (2019), and Risaliti and Lusso (2019), the deviation between the best fit model and the ΛCDM model was noticed by comparing cosmological parameters derived from cosmographic expansions of their theoretical predictions and observed high redshift Hubble diagram. In this paper we use a substantially different approach, based on a specific parametrization of the redshift dependent equation of state (EOS) of dark energy component w(z). Our statistical analysis is aimed to estimate the parameters characterizing the dark energy EOS: our results indicate (at > 3σ level) an evolving dark energy EOS, while the cosmological constant Λ has a constant EOS, w_Λ = −1. This result not only confirms the tension previously detected but shows that it is not an artifact of cosmographic expansions.

1. Introduction

Recent observations of supernovae of type Ia (SNIa) indicate that the expansion rate of the Universe is accelerating (Perlmutter et al., 1998, 1999; Riess et al., 1998, 2007; Astier et al., 2006; Amanullah et al., 2010). This unexpected result was confirmed by analysis of small-scale anisotropies in temperature of the cosmic microwave background radiation (CMBR) (Planck Collaboration, 2016), and other cosmological data. The observed acceleration is due to so called dark energy, that, in a fluid dynamics approach can be represented by a medium with a negative EOS, $w<-\frac{1}{3}$. According to observational estimates, dark energy provides now about 70% of matter energy in the Universe.

However the nature of dark energy, is unknown. A large variety of models of dark energy have been introduced, including a cosmological constant (Carroll, 2001), or scalar field (see for instance, Alam et al., 2003; Peebles and Ratra, 2003; Sahni et al., 2003).

The accelerated expansion of the Universe could be also expression of the inhomogeneous distribution of matter (see for instance, Clarkson and Maartens, 2010), or effects due to alternative theories of gravity.

Therefore the cause of the accelerated expansion of the Universe remains one of the most important open question in Cosmology and Physics: any new, independent measurement related to the expansion rate of the cosmological background, specially in different ranges of redshift, may shed new light on this topic and provide non-trivial test of the standard cosmological model (see Riess et al., 2018a,b).

Indeed, recently, other cosmological probes have entered the game: the first ones are Ghirlanda et al. (2004) and Firmani et al. (2005) using long GRBs; Eisenstein et al. (2005) using the imprints of the BAOs in the large-scale structure; Chávez et al. (2016) using HII galaxies; Negrete et al. (2017) using extreme quasars.

Recently, Lusso and Risaliti (2016) and Risaliti and Lusso (2019) have shown that the combination of supernovae and quasars can extend and further constrain cosmological models. In Lusso et al. (2019), some of us found a tension between theoretical predictions of the ΛCDM model and a high-redshift Hubble diagram, on the basis of cosmographic expansions of the observable quantities.

Actually, cosmography allows to investigate the kinematic features of the evolution of the universe, assuming only that the space time geometry is described by the Friedman-Lemaitre-Robertson-Walker metric, and adopting Taylor expansions, in the traditional approach, or logarithmic polynomial expansions, in a generalized approach (Lusso and Risaliti, 2016; Risaliti and Lusso, 2019), of basic cosmological observables.

From observational data it is possible to constrain the cosmographic parameters, and their probability distributions. These constraints can provide information about the nature of dark energy (Demianski et al., 2017a), and are model independent, but depend on the properties of convergence of the cosmographic series.

Here we approach this tension from a different point of view, and try to figure out from the observations whether the dark energy equation of state (EOS) evolve or not. Actually it turns out that the cosmological constant Λ has a constant EOS, w_Λ = −1, whereas in most cosmological models, following a fluid dynamics approach, we can introduce at least an effective EOS of dark energy, depending on the redshift z. This happens, for instance, in extended theories of gravity (Demianski et al., 2006, 2008; Piedipalumbo et al., 2012, 2015), or in an interacting quintessence cosmology (Piedipalumbo et al., 2020): actually in the generalized Friedman equations, that drive the dynamics of these models, we can identify effective density and pressure terms, and define effective EOS. Understanding from the data whether or not the dark energy EOS is constant, independently of any assumptions on its nature, is, therefore, a daunting yet rewarding task of probing the evolution of dark energy (Piedipalumbo et al., 2014).

Here we parameterize w(z) using the Chevallier-Polarski-Linder (CPL) model (Chevallier and Polarski, 2001; Linder, 2003). Noteworthy in this regard is that we do not intend to use the CPL model to test its robustness in providing reliable reconstruction of dark energy models, as for instance in Linden and Virey (2008) and Scherrer (2015), but, rather, infer from high redshift data if the dark energy EOS is constant or not, and, therefore, if the expansion rate is compatible with the flat ΛCDM model.

Actually, despite the ΛCDM enormous success, some tensions and problem have been detected: a combined analysis of the Planck angular power spectra with different luminosity distance measurements are in strong disagreement with the flat ΛCDM (Di Valentino et al., 2020). Moreover, it turns out that there are some tensions among the values of cosmological parameters inferred from independent datasets. The most famous and persisting one is related to the value of the Hubble constant H₀ as measured by Planck and recently by Choi et al. (2020) with respect the value extracted from Cepheid-calibrated local distance ladder measurements (see for instance, Riess et al., 2019) (the so called H₀ tension).

Several papers present interesting attempt to solve this tension. For instance, Poulin et al. (2019) propose an early dark energy model to resolve the Hubble tension. They assume existence of a scalar field that adds dark energy equal to about 10% of the energy density at the end of the radiation-dominated era at z ≃ 3, 500, and then it dilutes; after that the energy density components are the same as in the ΛCDM model. Another example is the consequence of string theory that predicts existence of an axiverse, i.e., a huge number of extremely light particles with very peculiar physical properties. It seems that a simple modification of the physical properties of these particles is enough to accommodate the Hubble tension (Kamionkowski et al., 2014).

In our analysis we use the (SNIa) Hubble diagram (Union2.1 compilation), the gamma-ray burst (GRBs) and QSOs Hubble diagram. We also use Gaussian priors on the distance from the Baryon Acoustic Oscillations (BAO), and the Hubble constant h, these priors have been included in order to help break the degeneracies among model parameters. To constrain cosmological parameters we perform Monte Carlo Markov Chain (MCMC) simulations. The structure of the paper is as follows. In section 2 we describe the CPL parametrization used in our analysis. In section 3 we describe the data sets, and in section 4 we describe the statistical analysis and present our results. General discussion of our results and conclusions are presented in section 5.

2. Parametrization of the Dark Energy EOS

Available now observational data imply that the expansion rate of the Universe is accelerating. This accelerated expansion is conveniently described by the standard ΛCDM cosmological model. However, to test if the accelerated expansion is due to the non-zero cosmological constant it is necessary to consider a more general model of evolving dark energy that can be described by a simple equation of state (EOS)

$\begin{array}{ll}{p}_{de}(z)=w(z){\rho }_{de}(z),& (1)\end{array}$

where ρ_de is the effective energy density of dark energy and p_de(z) is its pressure. The proportionality coefficient w(z) determines the dark energy EOS. When w(z) = −1 the cosmological constant plays the role of dark energy.

In the standard spatially flat Friedman-Lemaitre-Robertson-Walker model the scale factor a(t) is determined by the Friedman equations:

$\begin{array}{ll}{H}^2={(\frac{\stackrel{.}{a}}{a})}^2=\frac{8\pi G}{3}({\rho }_m+{\rho }_{de}),& (2)\end{array}$

$\begin{array}{ll}\frac{\ddot{a}}{a}=-\frac{4\pi G}{3}({\rho }_m+{\rho }_{de}+3p_{de}),& (3)\end{array}$

where H is the Hubble parameter, the dot denotes the derivative with respect to the cosmic time t, and ρ_m is the density of non-relativistic matter. When the Universe is filled in with other non-interacting matter components their energy density ρ_i and pressure p_i are related by EOS for each component of the cosmological fluid p_i = w_iρ_i and i = 1, …, n. Non-relativistic matter is usually considered to be pressure less so it is characterized by w = 0. The cosmological constant can be treated as a medium with w = −1. The non-interacting matter components satisfy the continuity equation

$\begin{array}{ll}\frac{\dot{{\rho }_i}}{{\rho }_i}=-3H\left(1+\frac{p_i}{{\rho }_i}\right)=-3H\left[1+w_i(t)\right].& (4)\end{array}$

In the later stages of evolution of the Universe its dynamics is determined only by two components: the non-relativistic matter and dark energy. In this case the Friedman equation (2) can be rewritten as

$\begin{array}{ll}H(z,\theta )=H_0\sqrt{{\Omega }_m{(z+1)}^3+(1-{\Omega }_m)g(z,\theta )},& (5)\end{array}$

where ${\Omega }_m=\frac{8\pi G{\rho }_m}{3H_0^2}$ is the matter density parameter, and $g(z,\theta )=\frac{{\rho }_{de}(z)}{{\rho }_{de}(0)}=\text{exp}(3{\int }_0^z\frac{w(x,\theta )+1}{x+1}dx)$. Here w(z, θ) characterizes the dark energy EOS and θ = (θ₁, …, θ_n) are additional parameters that describe different models of dark energy. Using the Hubble parameter (5) we define the luminosity distance in the standard way as

$\begin{array}{ll}{d}_L(z,\theta )=\frac{c}{H_0}(1+z){\displaystyle {\int }_0^z}\frac{d\zeta }{H(\zeta ,\theta )}.& (6)\end{array}$

Moreover we can define the angular diameter distance and the volume distance as:

$\begin{array}{ll}{d}_A(z,\theta )=\frac{c}{H_0}\frac{1}{1+z}{\displaystyle {\int }_0^z}\frac{d\zeta }{H(\zeta ,\theta )},& (7)\end{array}$

$\begin{array}{ll}{d}_V(z,\theta )={\left[(1+z)d_A{(z,\theta )}^2\frac{cz}{H(z,\theta )}\right]}^{\frac{1}{3}}.& (8)\end{array}$

To compare predictions of different models of dark energy with high redshift Hubble diagram we use the standard definition of the distance modulus:

$\begin{array}{ll}\mu (z,\theta )=25+5\text{ log }{d}_L(z,\theta ).& (9)\end{array}$

Several different models of dark energy were proposed so far. Here to simplify our analysis we use a two parametric EOS proposed by Chevalier, Polarski and Linder (CPL)

$\begin{array}{ll}w(z)=w_0+w_1\frac{z}{1+z},& (10)\end{array}$

where w₀ and w₁ are constants to be determined by the fitting procedure. From the assumed form of w(z) it is clear that

$\begin{array}{ll}{\displaystyle \underset{z\to 0}{\text{lim }}}w(z)=w_0,& (11)\end{array}$

$\begin{array}{ll}{\displaystyle \underset{z\to \infty }{\text{lim }}}w(z)=w_0+w_1.& (12)\end{array}$

To check if properties of dark energy change in time it is necessary to use high redshift data to find out if w₁ is zero or not.

3. The Data Sets

To perform our analysis and determine the basic cosmological parameters, we construct a Hubble diagram by combining four data samples. In our analysis we build up a Hubble diagram spanning a wide redshift range as shown in Figure 1. To this aim we combine different data sets.

FIGURE 1

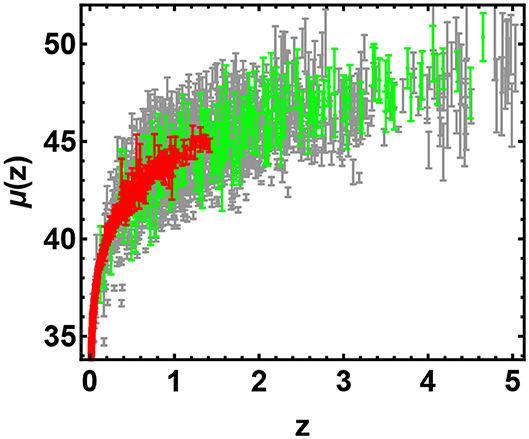
Figure 1. Hubble diagram of SNIa (red points), quasars (gray points), and GRBs (green points), with their respective 1σ uncertainties.

3.1. Supernovae Ia

SNIa observations gave the first strong indication of the recent accelerating expansion of the Universe (Riess et al., 1998; Perlmutter et al., 1999). In our analysis we use the recently updated Supernovae Cosmology Project Union 2.1 compilation (Suzuki et al., 2012), containing 580 SNIa, spanning the redshift range (0.015 ≤ z ≤ 1.4). We compare the theoretical distance modulus μ(z), based on the definition of the distance modulus in different cosmological models:

$\begin{array}{ll}\mu (z_j)=5{\text{ log}}_{10}(D_L(z_j,\{{\theta }_i\}))+{\mu }_0,& (13)\end{array}$

where D_L(z_j, {θ_i}) is the Hubble free luminosity distance, and θ_i indicates the set of parameters that appear in different dark energy equations of state considered in our analysis. The parameter μ₀ encodes the Hubble constant and the absolute magnitude M. We used an alternative version of the χ²:

$\begin{array}{ll}{\tilde{\chi }}_{\text{SN}}^2(\{{\theta }_i\})=c_1-\frac{c_2^2}{c_3},& (14)\end{array}$

where

$\begin{array}{ll}{c}_1={\displaystyle \sum _{j=1}^{N_{SNIa}}}\frac{{\left(\mu (z_j;{\mu }_0=0,\{{\theta }_i\})-{\mu }_{obs}(z_j)\right)}^2}{{\sigma }_{\mu ,j}^2},& (15)\end{array}$

$\begin{array}{l}{c}_2={\displaystyle \sum _{j=1}^{N_{SNIa}}\frac{{\left(\mu (z_j;{\mu }_0=0,\{{\theta }_i\}-{\mu }_{obs}(z_j)\right)}^2}{{\sigma }_{\mu ,j}^2}},\\ c_3={\displaystyle \sum _{j=1}^{N_{SNIa}}\frac{1}{{\sigma }_{\mu ,j}^2}}.& (16)\end{array}$

It is worth noting that

$\begin{array}{ll}{\chi }_{\text{SN}}^2({\mu }_0,\{{\theta }_i\})=c_1-2c_2{\mu }_0+c_3{\mu }_0^2,& (17)\end{array}$

which clearly has a minimum for ${\mu }_0=\frac{c_2}{c_3}$, so that.

$\begin{array}{l}{\tilde{\chi }}_{\text{SN}}^2\equiv {\chi }_{\text{SN}}^2({\mu }_0=\frac{c_2}{c_3},\{{\theta }_i\}).\end{array}$

3.2. Gamma-Ray Burst Hubble Diagram

Gamma-ray bursts are visible up to high redshifts thanks to the enormous released energy, and therefore are good candidates for our high-redshift cosmological investigations. They show non-thermal spectra which can be empirically modeled with the Band function, i.e., a smoothly broken power law with parameters: the low–energy spectral index α, the high energy spectral index β and the roll–over energy E₀. Their spectra show a peak corresponding to a specific (and observable) value of the photon energy E_p = E₀(2 + α); indeed it turns out that for GRBs with measured spectrum and redshift it is possible to evaluate the intrinsic peak energy, E_p,i = E_p(1 + z) and the isotropic equivalent radiated energy

$\begin{array}{ll}{E}_{\text{iso}}=4\pi d_L(z,\theta ){(1+z)}^{-1}{\displaystyle {\int }_{1/(1+z)}^{10^4/(1+z)}}EN(E)dE,& (18)\end{array}$

where N(E) is the Band function:

$\begin{array}{l}N(E)=\{\begin{array}{cc}A{\left(\frac{E}{100keV}\right)}^{\alpha }\text{exp}\left(\frac{-E}{E_0}\right),\hfill & (\alpha -\beta )\ge 0,\hfill \\ A{\left(\frac{(\alpha -\beta )E}{100keV}\right)}^{\alpha -\beta }\text{exp}(\alpha -\beta ){\left(\frac{E}{100keV}\right)}^{\beta },\hfill & (\alpha -\beta )E_0\le E,\hfill \end{array}\hfill \end{array}$

E_p,i and E_iso span several orders of magnitude (GRBs cannot be considered standard candles), and show distributions approximated by Gaussians plus a tail at low energies. However in 2002, based on a small sample of BeppoSAX, it turned out that E_p,i is strongly correlated with E_iso (Amati et al., 2002). This correlation, commonly called Amati relation within the GRB community, has been confirmed in subsequent observations and provide a reliable instrument to standardize GRBs as a distance indicator, in a way similar to t the Phillips relation to standardize SNIa (see, for instance, Amati et al., 2008; Demianski et al., 2017a,b, and reference therein). It is clear from Equation (18) that, in order to get the isotropic equivalent radiated energy, E_iso it is necessary to specify the fiducial cosmological model and its basic parameters. But we want to use the observed properties of GRBs to derive the cosmological parameters. Several procedures to overcome this circular situation have been proposed (see for instance, Schaefer, 2007; Basilakos and Perivolaropoulos, 2008; Demianski et al., 2011; Amati et al., 2019).

Here we performed our analysis using a GRB Hubble diagram data set obtained by calibrating the E_p,i– E_iso correlation on a SNIa data (Demianski et al., 2017a,b). Actually we applied a local regression technique to estimate the distance modulus μ(z) from the SCP Union2 compilation. To obtain an estimation of μ(z_i) we order the SNIa dataset according to increasing values of |z − z_i|. Therefore, we select the first n = αN_SNIa, where α is a user selected value and N_SNIa the total number of SNIa. Then we fit a first order polynomial to these data, weighting each SNIa with the corresponding value of an appropriate weight function, like, for instance

$\begin{array}{ll}W(u)=\{\begin{array}{cc}{(1-|u{|}^2)}^2\hfill & \left|u\right|\le 1\hfill \\ 0\hfill & \left|u\right|\ge 1.\hfill \end{array}\hfill & (19)\end{array}$

The zeroth order term is the best estimate of μ(z). The error on μ(z) is provided by the root mean square of the weighted residuals with respect to the best fit value. In Equation (19) u = |z − z_i|/Δ and Δ indicates the maximum value of the |z − z_i| over the chosen subset. Having estimated the distance modulus at redshift z in a model independent way, we can fit the E_p,i – E_iso correlation using the local regression reconstructed μ(z) in Equation (18). It is worth noting that we already discussed some aspects of this topic in our previous papers (Demianski et al., 2011, 2017b), where, apart from other issues, we described how it is possible to simultaneously constrain the calibration parameters and the set of cosmological parameters: we found that the calibration parameters are fully consistent with the results obtained from the SNIa calibrated data.

In order to investigate a possible z dependence of the correlation coefficients, in the calibration procedure we added terms representing the z-evolution, which are assumed to be power-law functions: $g_{iso}(z)={(1+z)}^{k_{iso}}$ and $g_p(z)={(1+z)}^{k_p}$ (Demianski et al., 2017b). Therefore, $E_{\text{iso}}^{\prime }=\frac{E_{\text{iso}}}{g_{iso}(z)}$ and $E_{\text{p},\text{i}}^{\prime }=\frac{E_{\text{p},\text{i}}}{g_p(z)}$ are the de-evolved quantities included in a 3D correlation:

$\begin{array}{l}\text{log}\left[\frac{E_{\text{iso}}}{1\text{ erg}}\right]=b+a\text{ log}\left[\frac{E_{\text{p},\text{i}}}{300\text{ keV}}\right]+\\ \begin{array}{l}+\left(k_{iso}-a{k}_p\right)\text{log }(1+z).\end{array}& (20)\end{array}$

This de-evolved correlation was calibrated applying the same local regression technique previously adopted (Demianski et al., 2017a,b), but considering a 3D Reichart likelihood:

$\begin{array}{l}{L}_{Reichart}^{3D}(a,k_{iso},k_p,b,{\sigma }_{int})=\\ \frac{1}{2}\frac{\sum \text{log}({\displaystyle {\sigma }_{int}^2}+{\sigma }_{y_i}^2+a^2{\sigma }_{x_i}^2)}{\text{log}(1+a^2)}\\ \begin{array}{l}+\frac{1}{2}{\displaystyle \sum }\frac{{(y_i-a{x}_i-(k_{iso}-\beta )z_i-b)}^2}{{\displaystyle {\sigma }_{int}^2}+{\sigma }_{x_i}^2+a^2{\sigma }_{x_i}^2},\end{array}& (21)\end{array}$

where β = a k_p. We also used the MCMC method to maximize the likelihood and ran five parallel chains and the Gelman-Rubin convergence test. We found that $a=1.87_{-0.09}^{+0.08}$, k_iso = −0.04 ± 0.1; β = 0.02 ± 0.2 ; ${\sigma }_{int}=0.35_{-0.03}^{+0.02}$, so that $b=52.8_{-0.06}^{+0.03}$. After fitting the correlation and estimating its parameters, we used them to construct the GRB Hubble diagram. Detailed discussion of the GRBs sample and possible selection effects is presented also in Amati et al. (2008), Ghirlanda et al. (2008), Nava et al. (2011), Amati and Della Valle (2013), Demianski et al. (2017b), and Dainotti and Amati (2018).

3.3. Quasars

A physical relation has been observed between the optical-UV disk and the X-ray corona consisting in a log-log relation between their respective fluxes. From previous studies, Lusso and Risaliti (2016) found out a dispersion varying between 0.35 and 0.4 dex in this correlation. Their first sample was further reduced by eliminating quasars with host galaxy contamination, reddening, X-ray obscured objects and radio loudness (Lusso and Risaliti, 2016) to reach a dispersion of 0.21-0.24 dex. The quasar sample used here is presented in Lusso et al. (2019) and Risaliti and Lusso (2019) and consists of 1,598 sources in the redshift range 0.04 < z < 5.1. Distance moduli have been estimated by calibrating the power-law correlation between the ultraviolet and the X-ray emission observed in quasars (Lusso and Risaliti, 2016; Lusso et al., 2019; Risaliti and Lusso, 2019). More details on the sample are provided in Lusso et al. (2019).

3.4. H(z) Data

The Hubble parameter depends on the differential age of the Universe and can be measured using the cosmic chronometers: usually, dz is obtained from spectroscopic surveys, and, if cosmic chronometers are identified, we can measure dt, in the redshift interval dz. We used a list of 28 H(z) measurements, compiled in Farroq and Ratra (2013). The Hubble parameter H(z) can be measured through the differential age technique, based on passively evolving red galaxies as cosmic chronometers. Actually it turns out that H(z) depends on the differential variation of the cosmic time with redshift according to the following relation:

$\begin{array}{ll}H(z)=-\frac{1}{1+z}{\left(\frac{dt}{dz}\right)}^{-1}.& (22)\end{array}$

The term $\left(\frac{dt}{dz}\right)$, is estimated from the age of old stellar populations in red galaxies from their high resolution spectra.

3.5. BAOs

In order to reduce the degeneracy among cosmological parameters we also use some constraints from standard rulers. Actually the BAOs, which are related to imprints of the primordial acoustic waves on the galaxy power spectrum, are widely used as such rulers. In order to use BAOs as constraints, we follow Percival et al. (2010) by first defining :

$\begin{array}{ll}{d}_z=\frac{r_s(z_d)}{d_V(z)},& (23)\end{array}$

with z_d being the drag redshift, d_V(z) the volume distance, and r_s(z) the comoving sound horizon given by :

$\begin{array}{ll}{r}_s(z)=\frac{c}{\sqrt{3}}{\displaystyle {\int }_0^{{(1+z)}^{-1}}}\frac{da}{a^{2}H(a)\sqrt{1+(3/4){\Omega }_b/{\Omega }_{\gamma }}},& (24)\end{array}$

here Ω_γ is the radiation density parameter. We fix r_s(z_d) = 152.6 Mpc and the volume distance is defined in Equation (8). The values of d_z at z = 0.20 and z = 0.35 have been estimated by Percival et al. (2010) using the SDSS DR7 galaxy sample (Percival et al., 2010) so that we define ${\chi }_{BAO}^2={\text{D}}^T{\text{C}}_{BAO}^{-1}\text{C}$ with ${\text{D}}^T=(d_{0.2}^{obs}-d_{0.2}^{th},d_{0.35}^{obs}-d_{0.35}^{th})$ and C_BAO is the BAO covariance matrix.

4. Statistical Analysis

To compare the high-redshift data described above with the CPL parametrization, we use a Bayesian approach, and we apply the MCMC method to maximize the likelihood function ${L}(\text{p})$:

$\begin{array}{l}{L}(\text{p})\propto \frac{\text{exp}(-{\chi }_{GRB}^2/2)}{{(2\pi )}^{\frac{{{N}}_{GRB}}{2}}|{\text{C}}_{GRB}{|}^{1/2}}\frac{\text{exp}(-({\chi }_{QSO}^2/2)}{{(2\pi )}^{\frac{{{N}}_{QSO}}{2}}|{\text{C}}_{QSO}{|}^{1/2}}\\ \times \frac{\text{exp}(-{\chi }_{SNIa}^2/2)}{{(2\pi )}^{\frac{{{N}}_{SNIa}}{2}}|{\text{C}}_{SNIa}{|}^{1/2}}\frac{\text{exp}(-{\chi }_{BAO}^2/2)}{{(2\pi )}^{{{N}}_{BAO}/2}|{\text{C}}_{BAO}{|}^{1/2}}\\ \times \frac{\text{exp}(-{\chi }_H^2/2)}{{(2\pi )}^{{{N}}_H/2}|{\text{C}}_H{|}^{1/2}}.& (25)\end{array}$

In the Equation (25)

$\begin{array}{ll}{\chi }^2(\text{p})={\displaystyle \sum _{i,j=1}^N}\left(x_i-x_i^{th}(\text{p})\right)C_{ij}^{-1}\left(x_j-x_j^{th}(\text{p})\right),& (26)\end{array}$

where p denotes the parameters that determine the cosmological model, N is the number of data point. C_ij is the covariance matrix (C_{SNIa/GRB/QSO/H} indicates the SNIa/GRBs/QSO/H covariance matrix). The term $\frac{\text{exp}(-{\chi }_H^2/2)}{{(2\pi )}^{{{N}}_H/2}|{\text{C}}_H{|}^{1/2}}$ in Equation (25) is the likelihood relative to H(z). It is worth noting that by joining the GRB and QSO Hubble diagrams we can probe the background cosmological expansion over a redshift range more appropriate for studying dark energy than the one covered by SNIa only. We used a Metropolis-Hastings algorithm: we start from an initial parameter vector θ^start, and we generate a new trial vector θ^next from a tested density f(θ^next, θ^start), which represents the conditional probability of θ^next, given θ^start. The probability of accepting the new vector θ^next is described by

$\begin{array}{ll}F({\theta }^{\text{next}},{\theta }^{\text{start}})=min\left\{1,\frac{{L}(\text{d}|{\theta }^{\text{next}})Pr({\theta }^{\text{next}})f({\theta }^{\text{next}}{\theta }^{\text{start}})}{{L}(\text{d}|{\theta }^{\text{next}})Pr({\theta }^{\text{start}})f({\theta }^{\text{next}},{\theta }^{\text{start}})}\right\}& (27)\end{array}$

where d are the data, ${L}(\text{d}|{\text{p}}^{\prime })\propto \text{exp}(-{\chi }^2/2)$ is the likelihood function, Pr(θ) is the prior on the parameters. Moreover, we assume that f(θ^start, θ^next) ∝ exp(−Δθ²/2δ²), with Δθ = (θ^start − θ^next), and the dispersion δ = 15% for any step.

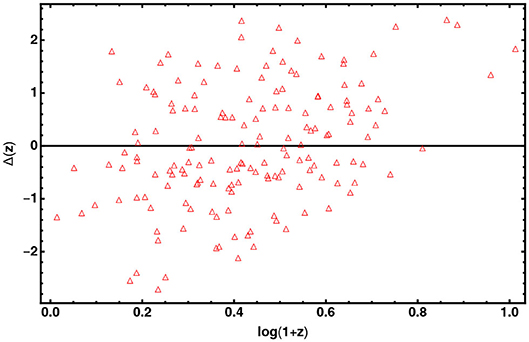
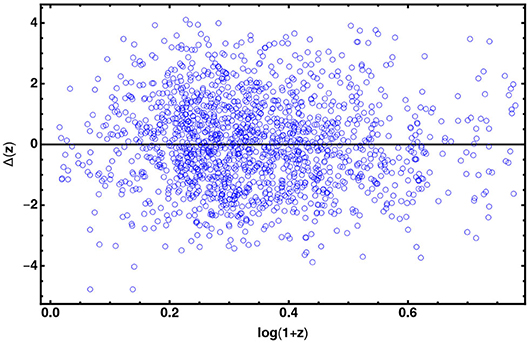
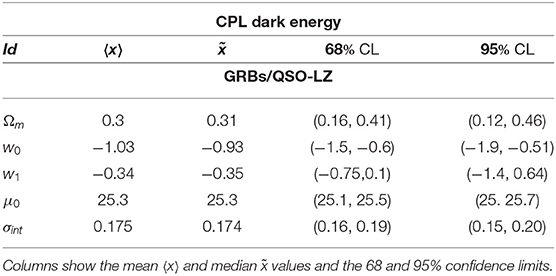
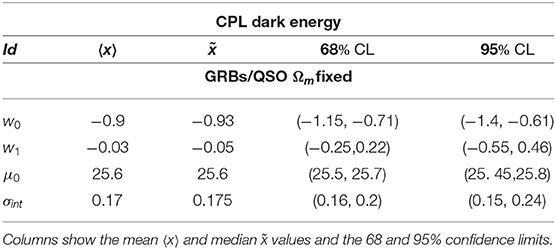
In order to sample the space of parameters, we run three parallel chains and use the Gelman-Rubin test to control the convergence of the chains. We use uniform priors for the parameters. After that we conservatively discard the first 30% of the point iterations at the beginning of any MCMC run, and thin the chains, we finally extract the constraints on cosmological parameters by co-adding the thinned chains. Histograms of the parameters from the merged chains were used to estimate the median values and confidence ranges. In Tables 1, 2 we report results of our analysis. It is worth noting that σ_int is the observed dispersion of the QSO Hubble diagram, and it is of order of 0.2 dex. If we compare this value with dispersion in the Hubble diagram of SNIa, which is σ_SN ~ 0.07 at z ~ 1, it turns out that QSOs provide the same cosmological information as SNIa. For the GRBs Hubble diagram we do not provide the observed dispersion here, because it has been evaluated during the calibration of the E_p,i – E_iso correlation and used to estimates the error bars in the GRB Hubble diagram. In Figures 2–4 we show 2D confidence regions: it turns out that the dark energy EOS does evolve with redshift, and the ΛCDM model, i.e., w₀ = −1 and w₁ = 0 is disfavored (at more than 3σ) with all the data, thus showing the importance of independent and complementary data sets, specially in different ranges of redshift. Actually our results, not based on cosmographic expansions, confirm the tension between predictions of the ΛCDM model and observations found previously in Lusso and Risaliti (2016), Lusso et al. (2019), and Risaliti and Lusso (2019). In order to highlight that this result is due to the contribution of the high redshift QSO and GRB Hubble diagram we first used these sample only: the results are shown in Table 2 (right panel). In Figures 5, 6 we plot the distribution of the residuals as a function of redshift for the GRB and QSO samples. It turns out that the amplitude of the scatter of the residuals show no significant trend with redshift. Moreover, the deviation from the ΛCDM model emerges at high redshifts: it turns out that if we select GRBs and QSOs at z ≤ 1, the corresponding Hubble diagram is well-reproduced by the standard flat ΛCDM, as shown in Table 3¹. Similarly when we fit the GRB and QSO Hubble diagram fixing Ω_m = 0.31, as we show in Table 4, we found that the ΛCDM with Ω_m = 0.31 reproduces the data at 1σ. Finally it is worth noting that future missions, like, the THESEUS observatory (Amati et al., 2018) for GRBs, and eRosita all sky survey for QSOs (Lusso, 2020) will substantially increase the number of data usable to construct the Hubble diagram at high redshift and so help to probe the nature of dark energy. Actually the main power of the GRB and QSO Hubble diagram for cosmological investigations lies in the high-redshift regime, where it is possible to discriminate among different cosmological models and also different theories of gravity.

TABLE 1

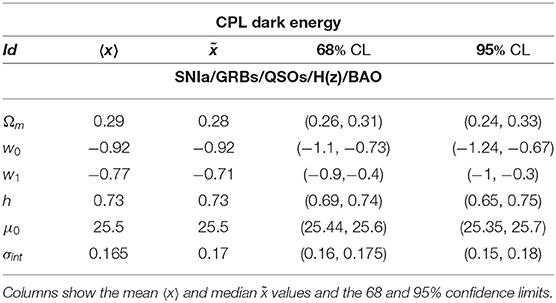
Table 1. Constraints on the CPL parameters from different data: combined SNIa, GRBs, and QSOs Hubble diagrams, H(z) data sets, and BAO data.

TABLE 2

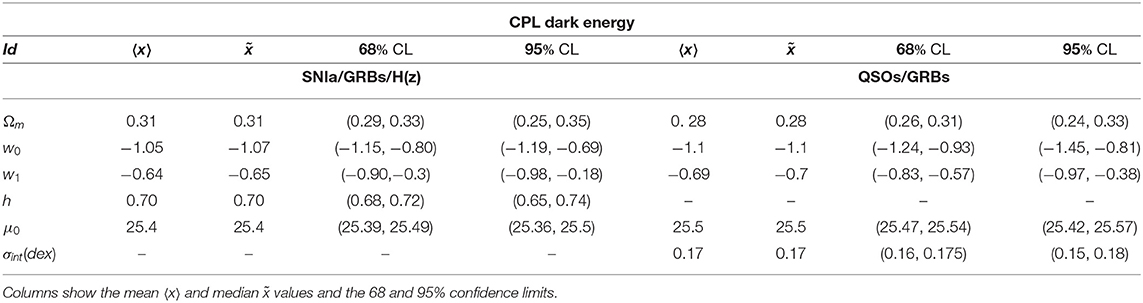
Table 2. Constraints on the CPL parameters from different data: combined SNIa and GRB Hubble diagrams, and H(z) data sets (Left Panel); QSO and GRB Hubble diagram (Right Panel).

FIGURE 2

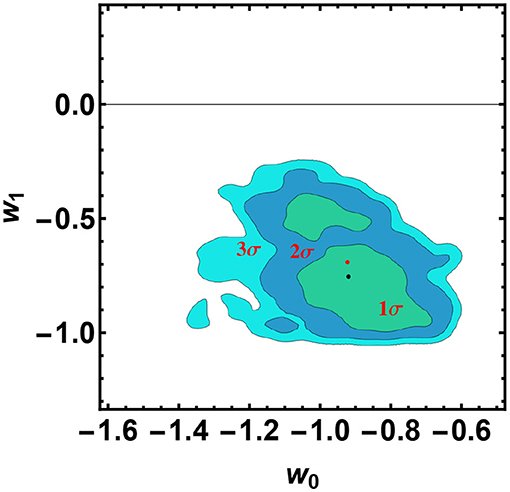
Figure 2. 2D confidence regions in the w₀ − w₁ plane for the CPL model, obtained from all the data sets. It turns out that the case w₀ = −1, w₁ = 0, corresponding to the standard ΛCDM model, is disfavored at 3σ, in full agreement with the results of Lusso et al. (2019) that use a different approach. The red and black points correspond to the best fit value and the mean, respectively.

FIGURE 3

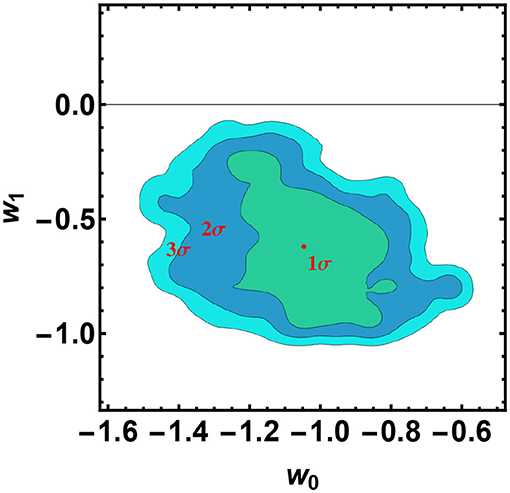
Figure 3. 2D confidence regions in the w₀ − w₁ plane for the CPL model, obtained from SNIa, GRB Hubble diagram and the H(z) measurements. It turns out that the case w₀ = −1, w₁ = 0, corresponding to the ΛCDM model, is disfavored at more than 3σ. The red point corresponds to the best fit value and the mean, respectively, that in this case are indistinguishable.

FIGURE 4

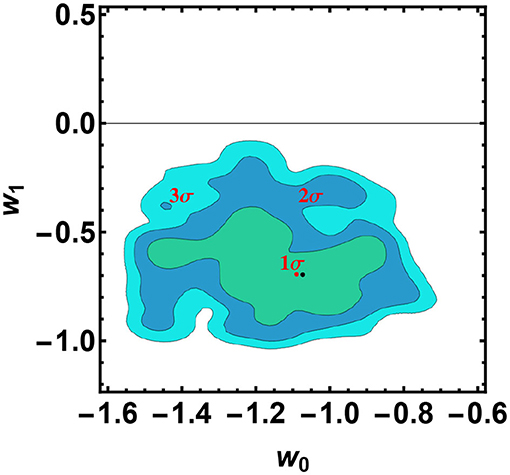
Figure 4. 2D confidence regions in the w₀ − w₁ plane for the CPL model, obtained from the QSO and GBR Hubble diagram: it turns out that the case w₀ = −1, w₁ = 0, corresponding to the standard ΛCDM model, is disfavored at 3σ. The red and black points correspond to the best fit value and the mean, respectively.

FIGURE 5

Figure 5. Distribution of the Hubble diagram residuals as a function of z for the GRBs sample.

FIGURE 6

Figure 6. Distribution of the Hubble diagram residuals as a function of z for the QSOs sample.

TABLE 3

Table 3. Constraints on the CPL parameters from GRB and QSO Hubble diagram at z ≤ 1.

TABLE 4

Table 4. Constraints from GRB and QSO Hubble diagram, setting Ω_m = 0.31.

5. Conclusions

The nature of the dark energy and the origin of the accelerated expansion of the Universe remain one of the most challenging open questions in Physics and Cosmology. The flat ΛCDM model is the most popular cosmological model used by the scientific community. However, despite its enormous successes, some problems have been detected: quite recently it turned out that there is a tension (at more than 3σ) between cosmological and local measurements of the Hubble constant (Riess et al., 2019). Moreover, recently in Lusso and Risaliti (2016), Demianski et al. (2019), Lusso et al. (2019), and Risaliti and Lusso (2019), another tension has been also reported between predictions of the ΛCDM model and the Hubble Diagram of SNIa and quasars. With the aim of clarifying this result, we concentrated on the possibility to detect, from different and independent data, evidence of a redshift evolution of the dark energy equation of state: we performed statistical analysis to constrain the dark energy EOS, using the simple CPL parametrization. Our high redshift Hubble diagram provides a clear indication (at 3σ level) of an evolving dark energy EOS, thus confirming the previous results (Demianski et al., 2019), and highlight the importance, to explore the cosmological expansion, of using independent probes and exploring large ranges of redshift. It turns out that the deviation from the standard ΛCDM is due just to the QSO and GRBs Hubble diagrams. Moreover, it is important for z > 1: if, indeed we limit our analysis to z ≤ 1 the ΛCDM reproduces the data at 1σ. The residuals do not present any significant trend systematic with redshift: this evidence further proves that our results are not affected by systematics. With future missions, like, the THESEUS observatory, and the eRosita all-sky survey, that will substantially increase the number of GRBs and QSOs usable to construct the Hubble diagram it will be possible to better test the nature of dark energy.

Data Availability Statement

Most of the data underlying this article are available in literature and are appropriately cited in the bibliography. The GRBs data are provided by the corresponding author.

Author Contributions

EP has written most of the text. All the authors contributed to the analysis and critically reviewed the entire paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge financial contribution from the agreement ASI-INAF n.2017-14-H.O. MD was grateful to the INFN for financial support through the Fondi FAI GrIV. EP acknowledges the support of INFN Sez. di Napoli (Iniziativa Specifica QGSKY).

Footnotes

1. ^It is worth noting that the values of the QSOs and GRBs distance module are not absolute, thus cross calibration parameters are needed (for both GRBs and QSOs data). Therefore, the Hubble constant H₀ is degenerate with these calibration parameters, and it cannot be constrained.

References

Alam, U., Sahni, V., Saini, T. D., and Starobinsky, A. A. (2003). Exploring the expanding universe and dark energy using the statefinder diagnostic. Mon. Not. R. Astron. Soc. 344:1057. doi: 10.1046/j.1365-8711.2003.06871.x

CrossRef Full Text | Google Scholar

Amanullah, R., Lidman, C., Rubin, D., Aldering, G., Astier, P., Barbary, K., et al. (2010). Spectra and hubble space telescope light curves of six type Ia supernovae at 0.511 < z < 1.12 and the Union2 compilation. Astrophys. J. 716, 712–738. doi: 10.1088/0004-637X/716/1/712

CrossRef Full Text | Google Scholar

Amati, L., D'Agostino, R., Luongo, O., Muccino, M., and Tantalo, M. (2019). Addressing the circularity problem in the E_p,i-E_iso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. 486, L46–L51. doi: 10.1093/mnrasl/slz056

CrossRef Full Text | Google Scholar

Amati, L., and Della Valle, M. (2013). Measuring cosmological parameters with gamma ray bursts. Int. J. Mod. Phys. D 22:1330028. doi: 10.1142/S0218271813300280

CrossRef Full Text | Google Scholar

Amati, L., Frontera, F., Tavani, M., in't Zand, J. J. J., Antonelli, A., Costa, E., et al. (2002). Intrinsic spectra and energetics of BeppoSAX gamma-ray bursts with known redshifts. Astron. Astrophys. 390, 81–89. doi: 10.1051/0004-6361:20020722

CrossRef Full Text | Google Scholar

Amati, L., Guidorzi, C., Frontera, F., Della Valle, M., Finelli, F., Landi, R., et al. (2008). Measuring the cosmological parameters with the E_p,i-E_iso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. 391, 577–584. doi: 10.1111/j.1365-2966.2008.13943.x

CrossRef Full Text | Google Scholar

Amati, L., O'Brien, P., Goetz, P., Bozzo, E., Tenzer, C., Frontera, F., et al. (2018). The THESEUS space mission concept: science case, design and expected performances. Adv. Space Res. 62, 191–244. doi: 10.1016/j.asr.2018.03.010

CrossRef Full Text | Google Scholar

Astier, P., Guy, J., Regnault, N., Pain, R., Aubourg, E., Balam, D., et al. (2006). The supernova legacy survey: measurement of Ω_M, Ω_Λ and w from the first year data set. Astron. Astrophys. 447, 31–48. doi: 10.1051/0004-6361:20054185

CrossRef Full Text | Google Scholar

Basilakos, S., and Perivolaropoulos, L. (2008). Testing gamma-ray bursts as standard candles. Mon. Not. R. Astron. Soc. 391, 411–419. doi: 10.1111/j.1365-2966.2008.13894.x

CrossRef Full Text | Google Scholar

Carroll, S. M. (2001). The cosmological c. Liv. Rev. Relat. 4:1. doi: 10.12942/lrr-2001-1

CrossRef Full Text | Google Scholar

Chávez, R., Plionis, M., Basilakos, S., Terlevich, R., Terlevich, E., Melnick, J., et al. (2016). Constraining the dark energy equation of state with H II galaxies. Mon. Not. R. Astron. Soc. 462, 2431–2439. doi: 10.1093/mnras/stw1813

CrossRef Full Text | Google Scholar

Chevallier, M., and Polarski, D. (2001). Accelerating universes with scaling dark matter. Int. J. Mod. Phys. D 10, 213–223. doi: 10.1142/S0218271801000822

CrossRef Full Text | Google Scholar

Choi, S., Hasselfield, M., Ho, S. P. P., Koopman, B., Lungu, M., Abitbol, M. H., et al. (2020). The Atacama cosmology telescope: a measurement of the cosmic microwave background power spectra at 98 and 150 GHz. arXiv 2007.07289.

Google Scholar

Clarkson, C., and Maartens, R. (2010). Inhomogeneity and the foundations of concordance cosmology. Classic. Quant. Grav. 27:124008. doi: 10.1088/0264-9381/27/12/124008

CrossRef Full Text | Google Scholar

Dainotti, M. G., and Amati, L. (2018). Gamma-ray burst prompt correlations: selection and instrumental effects. Publ. Astron. Soc. Pac. 987:051001. doi: 10.1088/1538-3873/aaa8d7

CrossRef Full Text | Google Scholar

Demianski, M., Piedipalumbo, E., and Rubano, C. (2011). The gamma-ray bursts Hubble diagram in quintessential cosmological models. Mon. Not. R. Astron. Soc. 411, 1213–1222. doi: 10.1111/j.1365-2966.2010.17751.x

CrossRef Full Text | Google Scholar

Demianski, M., Piedipalumbo, E., Rubano, C., and Scudellaro, P. (2008). Cosmological models in scalar tensor theories of gravity and observations: a class of general solutions. Astron. Astrophys. 481, 279–294. doi: 10.1051/0004-6361:20067045

CrossRef Full Text | Google Scholar

Demianski, M., Piedipalumbo, E., Rubano, C., and Tortora, C. (2006). Accelerating universe in scalar tensor models–comparison of theoretical predictions with observations. Astron. Astrophys. 454, 55–66. doi: 10.1051/0004-6361:20054601

CrossRef Full Text | Google Scholar

Demianski, M., Piedipalumbo, E., Sawant, D., and Amati, L. (2017a). Cosmology with gamma-ray bursts. II. Cosmography challenges and cosmological scenarios for the accelerated universe. Astron. Astrophys. 598:A113. doi: 10.1051/0004-6361/201628911

CrossRef Full Text | Google Scholar

Demianski, M., Piedipalumbo, E., Sawant, D., and Amati, L. (2017b). Cosmology with gamma-ray bursts. I. The hubble diagram through the calibrated E_p,i-E_iso correlation. Astron. Astrophys. 598:A112. doi: 10.1051/0004-6361/201628909

CrossRef Full Text | Google Scholar

Demianski, M., Piedipalumbo, E., Sawant, D., and Amati, L. (2019). High redshift constraints on dark energy models and tension with the flat. LCDM model. arXiv 1911.08228.

Google Scholar

Di Valentino, E., Melchiorri, A., and Silk, J. (2020). Mapping the Chevallier-Polarski-Linder parametrization onto physical dark energy Models. arXiv 2003.04935.

Google Scholar

Eisenstein, D. J., Zehavi, I., Hogg, D. W., Scoccimarro, R., Blanton, M. R., Nichol, R. C., et al. (2005). Detection of the Baryon acoustic peak in the large-scale correlation function of SDSS luminous red galaxies. Astrophys. J. 633, 560–574. doi: 10.1086/466512

CrossRef Full Text | Google Scholar

Farroq, O., and Ratra, B. (2013). Hubble parameter measurement constraints on the cosmological deceleration-acceleration transition redshift. Astrophys. J. 766:L7. doi: 10.1088/2041-8205/766/1/L7

CrossRef Full Text | Google Scholar

Firmani, C., Ghisellini, G., Ghirlanda, G., and Avila-Reese, V. (2005). The peak luminosity-peak energy correlation in gamma-ray bursts. Mon. Not. R. Astron. Soc. 360, L45–L49. doi: 10.1111/j.1745-3933.2005.00043.x

CrossRef Full Text | Google Scholar

Ghirlanda, G., Ghisellini, G., Lazzati, D., and Firmani, C. (2004). Gamma-ray bursts: new rulers to measure the universe. Astrophys. J. 613, L13–L16. doi: 10.1086/424915

CrossRef Full Text | Google Scholar

Ghirlanda, G., Nava, L., Ghisellini, G., Firmani, C., and Cabrera, J. I. (2008). The E_peak-E_iso plane of long gamma-ray bursts and selection effects. Mon. Not. R. Astron. Soc. 387:319. doi: 10.1111/j.1365-2966.2008.13232.x

CrossRef Full Text | Google Scholar

Kamionkowski, M., Pradler, J., and Walker, D. G. E. (2014). Dark energy from the string axiverse. Phys. Rev. Lett. 113:251302. doi: 10.1103/PhysRevLett.113.251302

PubMed Abstract | CrossRef Full Text | Google Scholar

Linden, S., and Virey, J. M. (2008). Test of the Chevallier-Polarski-Linder parametrization for rapid dark energy equation of state transitions. Phys. Rev D 78:023526. doi: 10.1103/PhysRevD.78.023526

CrossRef Full Text | Google Scholar

Linder, E. V. (2003). Exploring the expansion history of the universe. Phys. Rev. Lett. 90:091301. doi: 10.1103/PhysRevLett.90.091301

PubMed Abstract | CrossRef Full Text | Google Scholar

Lusso, E. (2020). Cosmology with quasars: predictions for eROSITA from a quasar hubble diagram. Front. Astron. Space Sci. 7:8. doi: 10.3389/fspas.2020.00008

CrossRef Full Text | Google Scholar

Lusso, E., Piedipalumbo, E., Risaliti, G., Paolillo, M., Bisogni, S., Nardini, E., et al. (2019). Tension with the flat ΛCDM model from a high-redshift hubble diagram of supernovae, quasars, and gamma-ray bursts. Astron. Astrophys. 628:L4. doi: 10.1051/0004-6361/201936223

CrossRef Full Text | Google Scholar

Lusso, E., and Risaliti, G. (2016). The tight relation between X-ray and ultraviolet luminosity of quasars. Astrophys. J. 819:154. doi: 10.3847/0004-637X/819/2/154

CrossRef Full Text | Google Scholar

Nava, L., Ghirlanda, G., Ghisellini, G., and Celotti, A. (2011). Spectral properties of 438 GRBs detected by Fermi/GBM. Astron. Astrophys. 530:21. doi: 10.1051/0004-6361/201016270

CrossRef Full Text | Google Scholar

Negrete, C. A., Dultzin, D., Marziani, P., Sulentic, J. W., Esparza-Arredondo, D., Martínez-Aldama, M. L., et al. (2017). Quasars as cosmological standard candles. Front. Astron. Space Sci. 4:59. doi: 10.3389/fspas.2017.00059

CrossRef Full Text | Google Scholar

Peebles, P. J. E., and Ratra, B. (2003). The cosmological constant and dark energy. Rev. Mod. Phys. 75, 559–606. doi: 10.1103/RevModPhys.75.559

CrossRef Full Text | Google Scholar

Percival, W. J., Reid, B. A., Eisenstein, D. J., Bahcall, N. A., Budavari, T., Frieman, J. A., et al. (2010). Baryon acoustic oscillations in the sloan digital sky survey data release 7 galaxy sample. Mon. Not. R. Astron. Soc. 401, 2148–2168. doi: 10.1111/j.1365-2966.2009.15812.x

CrossRef Full Text | Google Scholar

Perlmutter, S., Aldering, G., Della Valle, M., Deustua, S., Ellis, R. S., Fabbro, S., et al. (1998). Discovery of a supernova explosion at half the age of the Universe. Nature 391, 51–54. doi: 10.1038/34124

CrossRef Full Text | Google Scholar

Perlmutter, S., Aldering, G., Goldhaber, G., Knop, R., Nugent, P., Castro, P. G., et al. (1999). Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 517, 565–586. doi: 10.1086/307221

CrossRef Full Text | Google Scholar

Piedipalumbo, E., De Laurentis, M., and Capozziello, S. (2020). Noether symmetries in interacting quintessence cosmology. Phys. Dark Univ. 27:100444. doi: 10.1016/j.dark.2019.100444

CrossRef Full Text | Google Scholar

Piedipalumbo, E., della Moglie, E., and Cianci, R. (2015). Updated f(T) gravity constraints from high-redshift cosmography. Int. J. Mod. Phys. D 24:1550100. doi: 10.1142/S021827181550100X

CrossRef Full Text | Google Scholar

Piedipalumbo, E., Della Moglie, E., De Laurentis, M., and Scudellaro, P. (2014). High-redshift investigation on the dark energy equation of state. Mon. Not. R. Astron. Soc. 441, 3643–3655. doi: 10.1093/mnras/stu790

CrossRef Full Text | Google Scholar

Piedipalumbo, E., Scudellaro, P., Esposito, G., and Rubano, C. (2012). On quintessential cosmological models and exponential potentials. Gen. Rel. Grav. 44, 2611–2643. doi: 10.1007/s10714-012-1421-9

CrossRef Full Text | Google Scholar

Planck Collaboration (2016). Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 594:A13. doi: 10.1051/0004-6361/201525830

CrossRef Full Text | Google Scholar

Poulin, V., Smith, T. L., Karwal, T., and Kamionkowski, M. (2019). Early dark energy can resolve the hubble tension. Phys. Rev. Lett. 122:221301. doi: 10.1103/PhysRevLett.122.221301

PubMed Abstract | CrossRef Full Text | Google Scholar

Riess, A. G., Casertano, S., Yuan, W., Macri, L., Bucciarelli, B., Lattanzi, M. G., et al. (2018b). Milky way cepheid standards for measuring cosmic distances and application to Gaia DR2: implications for the hubble constant. Astrophys. J. 861:126. doi: 10.3847/1538-4357/aac82e

CrossRef Full Text | Google Scholar

Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., and Scolnic, D. (2019). Large magellanic cloud cepheid standards provide a 1% foundation for the determination of the hubble constant and stronger evidence for physics beyond ΛCDM. Astrophys. J. 876:85. doi: 10.3847/1538-4357/ab1422

CrossRef Full Text | Google Scholar

Riess, A. G., Filippenko, A. V., Challis, P., Clocchiatti, A., Diercks, A., Garnavich, P. M., et al. (1998). Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 116, 1009–1038. doi: 10.1086/300499

CrossRef Full Text | Google Scholar

Riess, A. G., Rodney, S. A., Scolnic, D. M., Shafer, D. L., Strolger, L. G., Ferguson, H. C., et al. (2018a). Type Ia supernova distances at redshift >1.5 from the hubble space telescope multi-cycle treasury programs: the early expansion rate. Astrophys. J. 853:126. doi: 10.3847/1538-4357/aaa5a9

CrossRef Full Text | Google Scholar

Riess, A. G., Strolger, L. G., Casertano, S., Ferguson, H. C., Mobasher, B., Gold, B., et al. (2007). New hubble space telescope discoveries of type Ia supernovae at z ≥ 1: narrowing constraints on the early behavior of dark energy. Astrophys. J. 659, 98–121. doi: 10.1086/510378

CrossRef Full Text | Google Scholar

Risaliti, G., and Lusso, E. (2019). Cosmological constraints from the hubble diagram of quasars at high redshifts. Nat. Astron. 3, 272–277. doi: 10.1038/s41550-018-0657-z

CrossRef Full Text | Google Scholar

Sahni, V., Saini, T. D., Starobinsky, A. A., and Alam, U. (2003). Statefinder–a new geometrical diagnostic of dark energy. JETP Lett. 77:201. doi: 10.1134/1.1574831

CrossRef Full Text | Google Scholar

Schaefer, B. E. (2007). The hubble diagram to redshift >6 from 69 gamma-ray bursts. Astrophys. J. 660, 16–46. doi: 10.1086/511742

CrossRef Full Text | Google Scholar

Scherrer, R. J. (2015). Mapping the Chevallier-Polarski-Linder parametrization onto physical dark energy models. Phys. Rev. D 92:043001. doi: 10.1103/PhysRevD.92.043001

CrossRef Full Text | Google Scholar

Suzuki, N., Rubin, D., Lidman, C., Aldering, G., Amanullah, R., Barbary, K., et al. (2012). The hubble space telescope cluster supernova survey: V. Improving the dark energy constraints above z > 1 and building an early-type-hosted supernova sample. Astrophys. J. 746:85. doi: 10.1088/0004-637X/746/1/85

CrossRef Full Text | Google Scholar