
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
METHODS article
Front. Astron. Space Sci., 19 March 2021
Sec. Stellar and Solar Physics
Volume 7 - 2020 | https://doi.org/10.3389/fspas.2020.438870
This article is part of the Research TopicThe Future of AsteroseismologyView all 19 articles
Using our non-local and time-dependent theory of convection and a fixed set of convective parameters
Convection occurs within most stars. Convection brings about the transport and exchange of energy and momentum, and the mixing of matter in the stellar interior. Therefore, it strongly influences the structure, evolution, and pulsational stability of stars. Unfortunately, up to now no perfect convection theory has been accepted by the community. The most popularly applied convection theory is still the mixing-length theory (MLT, Bohm-Vitense, 1958). The most obvious advantage of MLT is its straightforwardness in physical picture and simplicity of use. However, the MLT is not a dynamic theory following the hydrodynamic equations and turbulence theory, but is a phenomenological theory based on a simple analogy of turbulence with the kinetic theory of gas molecules. As such, it cannot give an exact description for turbulent convection, particularly for non-local and time-dependent convection. We developed a non-local and time-dependent theory of convection (Xiong et al., 1980; Xiong, 1981; Xiong, 1989; Xiong et al., 1997; Deng et al., 2006) based on hydrodynamic equations and turbulence theory in order to improve the treatment of overshooting in the calculation of stellar structure and evolution, and the treatment of coupling between convection and oscillations in the calculations of stellar oscillations. In Part Ⅰ of this article, a non-local and time-dependent theory of convection developed by us was briefly described, and its applications in theoretical calculations of the structure of the solar convection zone, of massive star evolution, and of the lithium depletion in the atmospheres of late-type dwarfs were presented. Here in Part Ⅱ, we illustrate its applications in the calculations of stellar oscillations. These applications are not only the primary motivation of our research on convective theory, but also the means for testing convection theory.
Stellar pulsation theory is being perfected thanks to the continuous work of generations of researchers for over 7 decades. Among others, we name four classical books by Ledoux and Walreven (1958), Cox (1980), Unno et al. (1989), and Aerts et al. (2011). They review the major research completed during that period of time. The remaining problems in stellar pulsation theory are almost all related to convection or non-linear theory. This paper is limited to the subjects of turbulent convection and the pulsational stability of stars.
Convection theory is still the most uncertain factor which prevents a clear understanding of oscillations in low-temperature stars. For low-temperature stars, dynamic coupling between convection and oscillations (through the exchange of momentum, i.e., turbulent pressure and turbulent viscosity) has at least as much, or possibly a larger effect than thermodynamic coupling (through the exchange of energy, i.e., convective enthalpy flux) on pulsational stability. The local description of convection has to be abandoned when turbulent pressure is taken into account in the equations of stellar structure, otherwise numerical calculations become unstable (Xiong, 1980). Our non-local and time-dependent theory of convection (Xiong, 1980; Xiong, 1981; Xiong, 1989; Xiong et al., 1997; Deng et al., 2006) is based on hydrodynamic equations and turbulence theory (Hinze, 1975); therefore, it has a more solid foundation in hydrodynamics, and provides a more precise description for the dynamic behavior of turbulent convection. Our formulation has the following advantages in the calculations of stellar oscillations:
(1) Our theory can be used for the treatment of both the thermodynamic (through the turbulent enthalpy flux) and dynamic coupling (through turbulent Reynolds stress, i.e., turbulent pressure and turbulent viscosity) between convection and oscillations in a self-consistent way.
(2) Our theory applies not only to radial oscillations but also to non-radial oscillations of stars in a self-consistent way, because our radiation-hydrodynamic equations are written in a general tensor format, which can deal not only with the exchange of energy and momentum in the radial direction, but also in the horizontal direction.
(3) In most calculations of non-adiabatic oscillations, the problematic rapidly oscillatory solutions are due to the local treatment method (Keeley, 1977; Baker and Gough, 1979; Gonczi and Osaki, 1980). Our time-dependent convection theory is non-local, so they have been effectively suppressed, and even completely removed (Xiong et al., 1998b; see also Figures 1–3 in the present paper).
(4) The pulsation stability is insensitive to convective parameters used. It is almost independent of the choice of convective parameters within a rather wide range (Xiong et al., 2015).
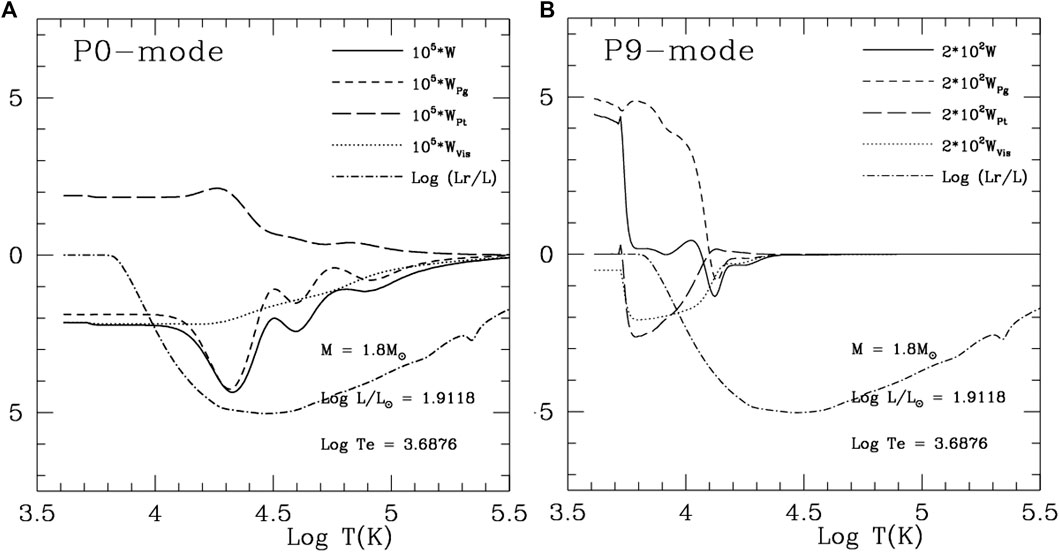
FIGURE 1. Cumulative work
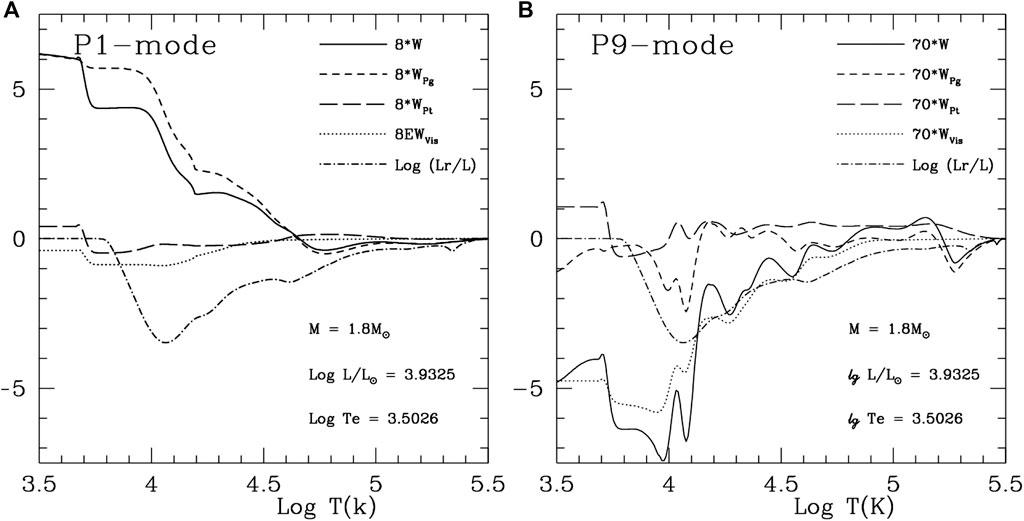
FIGURE 2. The same as Figure 1, but for a high-luminosity red giant.
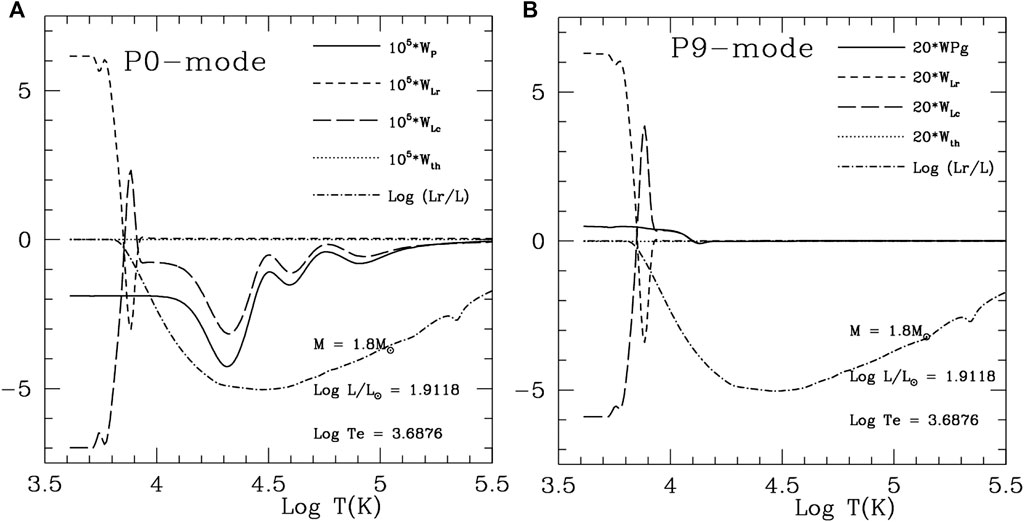
FIGURE 3. Gas pressure
Linearizing our system of radiation-hydrodynamic equations for the calculation of stellar structure and oscillations in Eqs. (2), (3′), (4′), (5) and Eqs. 18‐21 in Part I, we produce the non-adiabatic radial and non-radial pulsation equations. They are more complex than other theories, they are a system of differential equations of orders 10 and 16, respectively. For the adiabatic oscillation, the equations of energy conservation in Eq. (4′), and auto-correlation and cross-correlation for turbulent velocity and temperature in Eqs. 18‐21 can be removed, the adiabatic radial and non-radial pulsation equations will be simplified to orders 2 and 6. Therefore, the complexity and all the advantages mentioned above are due to our more accurate treatment of the convection problem. This should be the price for a more accurate convection theory, and it is worth it. The wave-scattering by inhomogeneous turbulent medium was neglected in the pulsation equations. Further investigation is needed.
In Theoretical Instability Strips, we present our theoretical instability strips in the H-R diagram. Recent progress in research of
By using our non-local and time-dependent theory of convection and a fixed set of convective parameters
Figure 4 shows the pulsationally unstable low-order non-radial
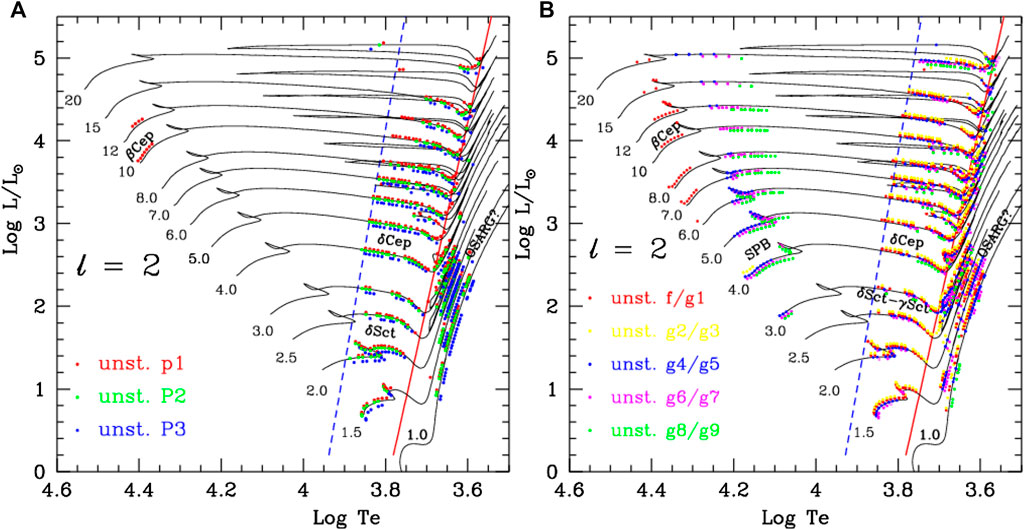
FIGURE 4. Pulsationally unstable (colored, filled circles) low-degree
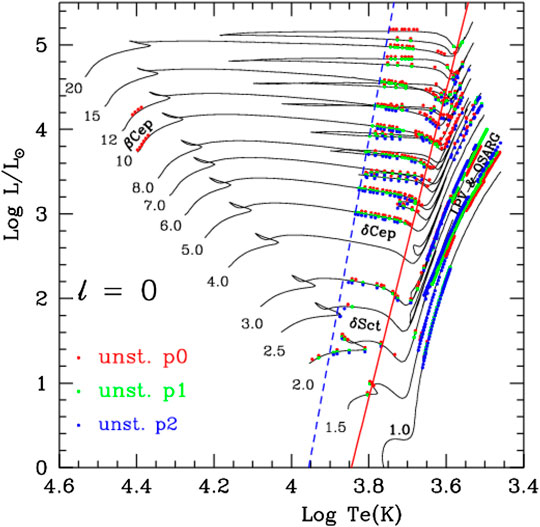
FIGURE 5. Pulsationally unstable radial low-order modes (colored, filled circles as labeled in the figure) in the H-R diagram for evolutionary models of 1–20
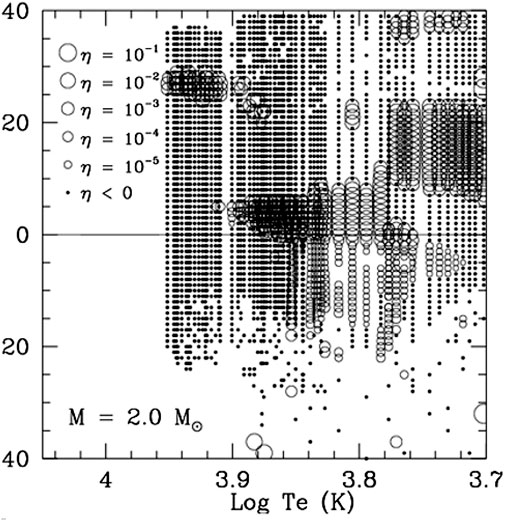
FIGURE 6. Stable (small filled circles) and unstable (open circles) low-degree
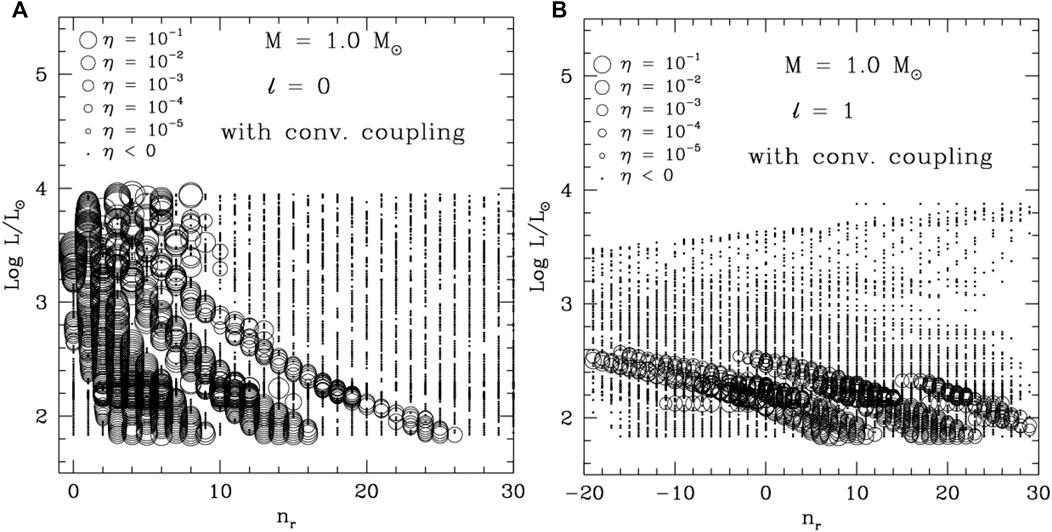
FIGURE 7. (A) Pulsationally stable (small filled circles) and unstable (open circles) radial modes on the
Studies of
Studies of luminous variable red giants have progressed significantly in the past 2 decades thanks to OGLE (Soszynski et al., 2004; Soszynski et al., 2005; Soszynski et al., 2007; Soszynski et al., 2009), MACHO (Wood, 2000), and similar projects. The existence of the red edge of the Cepheid instability strip is due to damping from thermodynamic coupling between convection and oscillations (through thermal energy exchange, namely convective enthalpy flux). Therefore, fora long time, convection was understood as a pure damping mechanism for the oscillations of stars. Why are there various red variables in the low-temperature area beyond the Cepheid instability strip? This is still an outstanding and disputed subject. Xiong et al. (1998a); Xiong and Deng, (2007) studied in detail the coupling between convection and oscillations, and showed that there is a Mira instability strip in the low-temperature and high-luminosity area of the H-R diagram. Turbulent pressure plays an important role in the excitation of luminous red variables. OGLE and MACHO observations not only greatly enhanced the database, but also offered the best opportunity for studies of the luminous variable stars. By using our non-local and time-dependent theory of convection and the same set of convection parameters
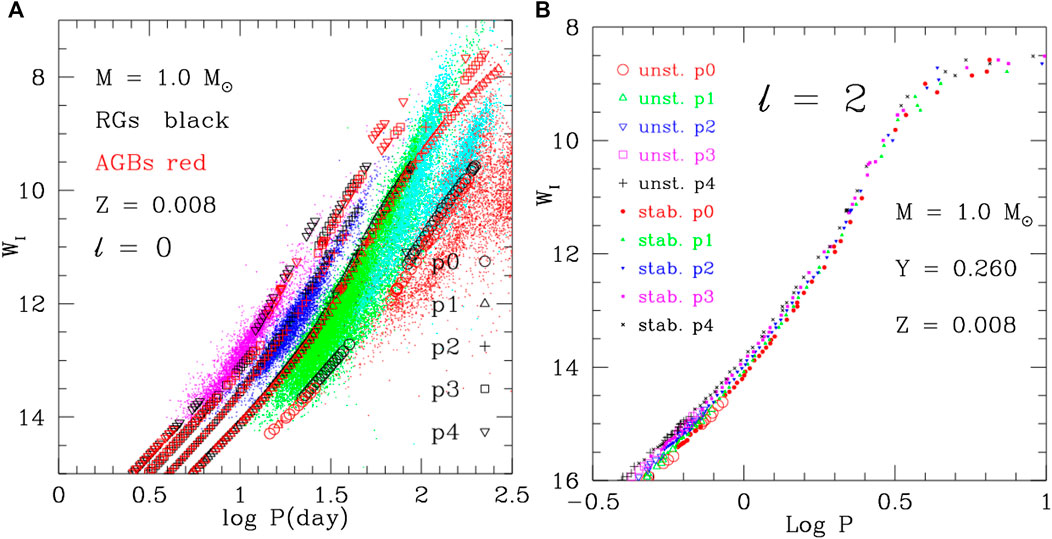
FIGURE 8. Period-luminosity diagram of low-order radial (panel a) and non-radial (panel b) modes for evolutionary models of RGs (black) and AGBs (red) with mass
The observed sequences A′, A, B, C′, and C of luminous red variables in the LMC are shown by magenta, blue, green, cyan, and red points in Figure 8A using data from the OGLE-Ⅲ catalog of LPVs in the LMC (Soszynski et al., 2004; Soszynski et al., 2005; Soszynski et al., 2009).
The sequences C-A′ are commonly interpreted as different pulsation modes. But there is disagreement on the modal assignment. Based on the period ratios, Takayama et al. (2013) suggested that they can be explained by radial and low-degree non-radial (
Studies for luminous red variables have greatly advanced our understanding, but there are still many outstanding problems:
(1) What kinds of variables are the OGLE small amplitude variable red giants (OSARGs)? Why are they so different from Miras and semi-regular variables located in the sequences of C and C’ (Soszynski et al., 2004)?
(2) Are there true oscillation modes with period ratios ∼1 and ∼0 in the observed Petersen diagram, or are these spurious modes due to insufficient observations (Soszynski et al., 2004)?
(3) It can be seen from Figures 4A,B, 8A,B, 7A,B,, that all the non-radial modes are stable for low-mass
Cumulative work is a convenient and efficient way to investigate the excitation and damping mechanism. Not only can the magnitude be estimated quantitatively for each component of excitation and damping, but also the location of these components can be identified. We give a simple derivation of cumulative work. Linearizing the average equation of momentum conservation in Eq. 3 in part I and neglecting the molecular viscous term (it is far smaller than any other terms in the equation), we have,
where
where
The value of
where
where
where
The first term in the brackets of Eq. 13 is the buoyancy work, that is, the conversion rate from thermal energy into turbulent kinetic energy, so its contribution for
Linearizing Eqs. (18) and (19) in Part Ⅰ and neglecting the third-order correlation terms, we have
Eqs. 4–16 are our expressions for cumulative work in the general case of non-radial oscillations. They will reduce to the radial expression for
Figure 9 shows the frequency dependences of the excitation and damping effects of turbulent pressure, viscosity, and convective enthalpy flux.
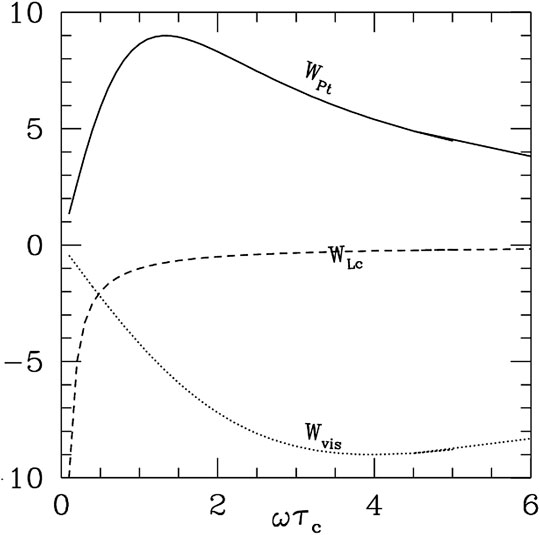
FIGURE 9. Frequency dependence of the excitation and damping effects of turbulent pressure (solid line), turbulent viscosity (dotted line), and convective enthalpy flux (dashed line) on stellar oscillations. The ordinate is used in any unit.
There is a red edge for the Cepheid (and Cepheid-like) instability strip in the H-R diagram due to convective damping, as mentioned in the previous section. Therefore, convection for a long time was thought of as a purely damping mechanism for stellar oscillations. Convection is not, in fact, a pure damping effect for stellar oscillations, as described in Cumulative Work Analysis for the Excitation and Damping Mechanism. The relative contributions of turbulent pressure, turbulent viscosity, and convective enthalpy flux for excitation and damping of modes change with stellar parameters (mass, luminosity, and effective temperature) and the pulsation frequency (or, alternatively, the radial order and spherical harmonic degree) of the mode. Therefore, the net effect of convection is sometimes to dampen, and sometimes to excite an oscillation mode. Figure 7 shows the pulsationally stable and unstable modes in the
where
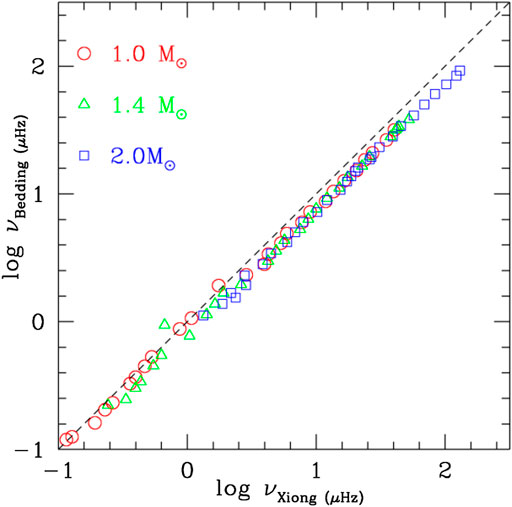
FIGURE 10. Comparison of our theoretical prediction of the maximally unstable mode based on pulsation calculations (abscissa) with the semi-empirical scaling relation (ordinate) for the p-mode peak of stochastically excited modes (Kjeldsen and Bedding, 1995).
In the cumulative work analysis (Cumulative Work Analysis for the Excitation and Damping Mechanism) and in our theoretical calculations of non-adiabatic oscillations (Theoretical Instability Strips,
Figure 1 shows the cumulative work
Therefore, it can be found from the above analysis that the variable red giants of high luminosity are self-exciting. The excitation and stabilization of the oscillations result from the combined effects of the radiative κ-mechanism and the coupling between convection and oscillations. Turbulent pressure plays a significant role in the excitation of variable red giants. This may also be true for the intermediate-luminosity red giants.
Convection is an important and outstanding problem in astrophysics. Collectively, we have studied this subject for over fifty years. Our goal is to develop a stellar convection theory that is exact enough and simple enough in order to improve the treatment of overshooting in the calculations of stellar structure and evolution as well as the treatment of coupling between convection and oscillations in the theoretical calculations of stellar oscillations. In the present papers (including Parts Ⅰ and Ⅱ), a brief description of a time-dependent theory of convection developed by us (in Part Ⅰ) was presented, and the progress of its application in the theoretical calculations of stellar structure and evolution (in Part Ⅰ) and of stellar oscillations (in Part Ⅱ) was reviewed. Our theoretical results achieve obvious improvements over the MLT formulation, which can be summarized as follows:
(1) Structure of the solar convection zone: Using our non-local convection theory, we calculated a model of the entire convective envelope of the Sun and studied the structure of both the upper and lower overshooting zones in detail (in Part Ⅰ; Unno et al., 1985;Xiong and Cheng, 1992;Xiong and Deng, 2001;Deng et al., 2006). The results show that turbulent velocity and temperature fluctuations penetrate deeply into the convectively stable zone and decrease exponentially with
(2) Overshooting mixing and the evolution of massive stars: By using our non-local convection theory in chemically inhomogeneous stars (Xiong, 1981), we calculated the evolution of massive stars through the hydrogen burning stage (Xiong, 1986). The so-called semi-convection contradiction (Schwarzchild and Harm, 1958) is removed automatically, as predicted by us. The convectively neutral stability follows neither the Schwarzschild criterion nor that of Ledoux.
(3) Lithium depletion in stellar atmospheres: By using our non-local convection theory in chemically inhomogeneous stars (Xiong, 1981), we calculated the lithium depletion in the atmosphere of the Sun and late-type dwarfs (in Part Ⅰ). The theoretical predictions agree well with observations of lithium abundances in the atmosphere of the Sun (Figures 9, 11 in Part Ⅰ; Xiong and Deng, 2002) and of member stars of Galactic open clusters of different ages (Figure 11 in Part Ⅰ; Xiong and Deng, 2009).
(4) Pulsational stability of stars: Linearizing the radiation-hydrodynamic equations for the calculation of stellar structure and oscillations in Eqs. (2), (3′), (4′), (5), and (18–21) in Part Ⅰ, we can obtain a set of linear equations for radial and non-radial non-adiabatic oscillations. The radiative κ-mechanism and the thermodynamic- (through the convective enthalpy flux) and dynamic- (through the turbulent Reynolds Stress, i.e., turbulent pressure and turbulent viscosity) coupling between convection and oscillations have been taken into account in a self-consistent way. With a slight modification, the ε-mechanism can be also included, if it is needed. Apart from damping due to the scattering and refraction of sound waves by inhomogeneous turbulent elements and stochastic excitation, they cover almost all the excitation and damping mechanisms for classical variables and variable red giants. By using our non-adiabatic oscillation equations and a fixed set of convective parameters
(5) Excitation and damping mechanisms of red giants were studied in detail: They are excited by the combined effects of the κ-mechanism and coupling between convection and oscillations. Convective flux and turbulent viscosity are found to always have a damping effect. The damping effect of the convective flux is inversely proportional to the mode frequency, so it plays an important role in stabilizing the low-order modes and in defining the red edge of the instability strip. The damping effect of turbulent viscosity reaches its maximum at the point in the star where
(6) The pulsation amplitude growth rates of high-frequency p-modes, which are high-order radial/non-radial modes trapped in the surface region of a star, are overestimated by our theory for low-luminosity low-temperature stars, because up to now we have had no reliable theory to treat and estimate the damping effect due to the scattering and refraction of sound waves by inhomogeneous turbulent elements and neglected it in our theoretical calculations of non-adiabatic oscillations. Our theoretical results for non-adiabatic oscillations are not as reliable for high-frequency p-modes of low-luminosity low-temperature stars, so we should be very cautious about interpreting them. However, our theoretical results for non-adiabatic oscillations are reliable for the classical variables and high-luminosity red giants, because these have low-order modes trapped in the deep interior of the stars that are only lightly influenced by this damping. This inference has been supported by the fact that our theoretical results of non-adiabatic oscillations are in good agreement with observed mode instability from classic variables to high-luminosity red giants (Figures 4–6, 8). This may be also true for intermediate-luminosity red giants. Our prediction that low-luminosity red giants might exhibit unstable intermediate-order modes still needs confirmation. It is also an uncertain prediction since we have not yet determined the range of stellar parameters for which our approach (neglecting the damping effects due to wave scattering and refraction by inhomogeneous turbulent elements) is valid. The ultimate solution to this problem depends on developing a theory for treating the damping effects due to the scattering and refraction of sound waves by inhomogeneous turbulent elements. This problem can be resolved in the not-too-distant future.
It is necessary to emphasize the following two points:
(1) The successes mentioned above do not only apply to an individual problem, but our theory is successful for many important problems in a wide field of stellar structure, evolution, and oscillations.
(2) Our non-local and time-dependent theory of convection includes three adjustable parameters of convection
All the successes mentioned above show that our dynamic theory of convection is roughly correct. It describes the dynamic behavior of turbulent convection more accurately than the MLT calculations. However, there are some difficulties in the calculations of the structure of the convective envelope for yellow giants and supergiants with Te∼6000–7000 K and for high-luminosity red giants. The evolutionary calculations with our non-local convection theory have been successful only for the hydrogen-burning stage of massive stars with initial mass M >
(1) An inadequate numerical method for converging the calculations
(2) Inadequacies of the convection theory
In the derivation of our convection theory, it was assumed that the turbulence is quasi-isotropic and the relative fluctuations of temperature and density are much less than 1. So, our convection theory is applicable only for extensive (the scale of the convection zone is much larger than one pressure scale height) and subsonic convection. The convection zone becomes somewhat narrow in the surface convection zone of yellow giants and in the convective cores of intermediate-mass stars as well as at late evolutionary stages. In surface convection zones, the convective velocity increases with increasing stellar luminosity. Convection becomes nearly sonic or even locally supersonic for luminous red giants and supergiants. So, it is not difficult to understand why the convergence of numerical calculations would become difficult in the cases mentioned above, in which convection conditions deviate from quasi-isotropic or become locally supersonic.
In comparison with MLT, our theory has obvious advantages for the treatment of the dynamic problems of non-local and time-dependent convection. Its weaknesses are a lack of straightforwardness in the physical picture and the fact that the application becomes more complex in comparison with MLT. So, it is difficult to popularize. Up to now, it was only used by a small number of members within our own group and collaborators. There are many remaining problems to be addressed in the theory itself and its practicality. It is impossible to have a perfect convection theory until a better understanding of turbulence has been achieved. Our non-local and time-dependent theory is only one among numerous theoretical approaches for turbulent convection. The existence of different viewpoints and contention are very normal and helpful for the development of science. The applications of our theory in calculations of stellar convective envelope structure and oscillations have achieved some progress. However, more advances are necessary for the treatment of overshooting mixing in the late stages of stellar evolution using a completely non-local convection theory. We expect that more astronomers, hydrodynamicists, and applied mathematicians will join the collaborations for the research of convection theory and relevant problems.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
The author confirms being the sole contributor of this work and has approved it for publication.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was supported by the National Nature Science Foundation of China (NSFC) through Grant No. 1137069. We would like to thank L. Deng and Dr C. Zhang for their valuable discussion. We thank Guzik and reviewer 3 for their kind help in revising the paper. I dedicate this article to my mentor, Prof. Wasaburo Unno. I thank him very much for his attention and support for our work over the years.
Aerts, C., Christensen-Dalsgaard, J., and Kurtz, D. W. (2010). Astroseismology. Berlin, Germany: Springer.
Alexander, D. R., and Ferguson, J. W., (1994). Low-temperature rosseland opacities. Astrophys. J. 437, 879. doi:10.1086/175039
Baker, N. H., and Gough, D. O. (1979). Pulsations of model RR Lyrae stars. Astrophys. J. 234, 232. doi:10.1086/157492
Balona, A., and Dziembowski, W. A. (2011). Kepler observations of δ Scuti stars. Mon. Not. Roy. Astron. Soc. 417, 591–601. doi:10.1111/j.1365-2966.2011.19301.x
Balona, L. A., Guzik, J. A., Uytterhoeven, K., Smith, J. C., Tenenbaum, P., and Twicken, J. D. (2011). The Kepler view of γ Doradus stars. Mon. Not. Roy. Astron. Soc. 415, 3531–3538. doi:10.1111/j.1365-2966.2011.18973.x
Bertelli, G., Girardi, L., Marigo, P., and Nasi, E. (2008). Scaled solar tracks and isochrones in a large region of the Z–Y plane. Astron. Astrophys. 484, 815–830. doi:10.1051/0004-6361:20079165
Bertelli, G., Nasi, E., Girardi, L., and Marigo, P. (2009). Scaled solar tracks and isochrones in a large region of the Z–Y plane. Astron. Astrophys. 508, 355–369. doi:10.1051/0004-6361/200912093
Brun, A. S., Turck-Chieze, S., and Zahn, J. P. (1999). Standard solar models in the light of new helioseismic constraints. ii. mixing below the convective zone. Astrophys. J. 525, 1032–1041. doi:10.1086/307932
Buchler, J. R., and Szabo, R. (2007). Beat cepheids as probes of stellar and galactic metallicity. Astrophys. J. 660, 723–731. doi:10.1086/513071
Bohm-Vitense, T. R., and Stothers, R. B. (1958). Über die Wasserstoffkonvektionszone in Sternen Verschiedener Effektivtemperaturen und Leuchtkräfte. Mit 5 Textabbildungen, Z. Astrophys. 46, 108.
Chandrasekhar, S. (1939). An introduction to the study of stellar structure. Chicago, IL: University of Chicago Press.
Chiosi, C., Wood, P. R., Bertelli, G., Bressan, A., and Mateo, M. (1992). On the mass discrepancy of the Cepheid stars. Astrophys. J. 385, 205–216.
Christensen-Dalsgaard, J., Däppen, W., Ajukov, S. V., Anderson, E. R., Antia, H. M., Basu, S., et al. (1996). The current state of solar modeling. Science 272, 1286–1292. doi:10.1126/science.272.5266.1286
Christensen-Dalsgaard, J., and Di Mauro, M. P. (2007). Stellar evolution and seismic tools for asteroseismology—diffusive processes in stars and seismic analysis. Editors C. W. Straka, Y. Lebreton, and M. J. P. G. Monteiro (Les Ulis, France: EDP Sciences), 26.
Cox, J. P., and Tabor, J. E. (1976). Radiative opacity tables for 40 stellar mixtures. ApJS 31, 271.
Däppen, W., Mihalas, D., Hummer, D. G., and Mihalas, B. W. (1988). The equation of state for stellar envelopes. III—thermodynamic quantities. Astrophys. J. 332, 261–270. doi:10.1086/166650
Deng, L., and Xiong, D. R. (2001). The β Cephei instability strip. Mon. Not. R. Astron. Soc. 327, 881.
Deng, L., Xiong, D. R., and Chan, K. L. (2006). An anisotropic nonlocal convection theory. Astrophys. J. 643, 426–437. doi:10.1086/502707
Dupret, M-A., Grigahcene, A., Garrido, R., Gabriel, M., and Scuflaire, R. (2005). Convection-pulsation coupling-II. Excitation and stabilization mechanisms in δ Sct and γ Dor stars. Astron. Astrophys. 435, 927. doi:10.1051/0004-6361:20041817
Eggen, O. J. (1977). The classification of instrinsic variables VII. The medium -amplitude red variables. ApJ 213, 767.
Eggen, O. J. (1972a). The classification of intrinsic variable stars. 1. The Red variables of type N. Astrophys. J. 174, 45–55. doi:10.1086/151467
Eggen, O. J. (1972b). The classification of intrinsic variable stars. II. The red variables of S and related types. Astrophys. J. 177, 489–507.
Eggen, O. J. (1973a). The classification of intrinsic variable. III. Calibration of the luminosities of small amplitude red variables in the old disk population. Astrophys. J. 180, 857–870. doi:10.1086/152012
Eggen, O. J. (1973b). The classification of intrinsic variables. IV. Very-small-amplitude, very-short-period red variables. Astrophys. J. 184, 793–799.
Eggen, O. J. (1975). The classification of intrinsic variables. V. The large-amplitude variables. Astrophys. J. 195, 661–678.
Gieren, W. P. (1988). The Galactic Cepheid period-luminosity relation from the visual surface brightness method. Astrophys. J. 329, 790–796.
Gingerich, O., Noyes, R. W., Kalkofen, W., and Cuny, Y. (1971). The Harvard-Smithsonian reference atmosphere. Sol. Phys. 18, 347–365. doi:10.1007/BF00149057
Gonczi, G., and Osaki, Y. (1980). On local theory of time-dependent convection in the stellar pulsation problem. A&A. 84, 304.
Gough, D. O. (1979). Some theoretical remarks on solar oscillations, in Nonradial and Nonlinear Stellar Pulsation. Berlin, Germany: Springer-Verlog, p. 273.
Grigahcene, A., Antoci, V., Balona, L., Catanzaro, G., Daszyńska-Daszkiewicz, J., Guzik, J. A., et al. (2010). Hybrid γ doradus-δ Scuti pulsators: new insights into the Physics of the oscillations from kepler observations. Astrophys. J. 713, 192–197. doi:10.1088/2041-8205/713/2/L192
Guzik, J. A., Farag, E., and Ostrowski, J. (2020). Investigating opacity modifications and reaction rate uncertainties to resolve the cepheid mass discrepancy. arxiv. doi:10.204073G2020/62
Guzik, J. A., Kaye, A. B., Bradley, P. A., Cox, A. N., and Neuforge, C. (2000). Driving the gravity-mode pulsations in γ Doradus variables. Astrophys. J. 542, 57.
Hareter, M. (2012). Preliminary results on γ Dor and δ Sct γ Dor hybrids in the CoRoT exo field of LRa01. Astron. Nachr. 333, 1048–1050. doi:10.1002/asna.201211790
Higgins, E. R., and Vink, J. S. (2020). Theoretical investigation of the Humphreys–Davidson limit at high and low metallicity. Astron. Astrophys. 635, 175–186. doi:10.1051/0004-6361/201937374
Houdek, G. (2000). Delta Scuti and related stars. Editors M. Breger, and M. H. Montgomery (San Francisco: Astronomical Society Pacific), 210, 454.
Hummer, D. G., and Mihalas, D. (1988). The equation of state for stellar envelopes. I. An occupation probability formalism for the truncation of internal partition functions. Astrophys. J. 331, 794. doi:10.1086/166600
Humphreys, R. (1978). Studies of luminous stars in nearby galaxies. I. Supergiants and O stars in the Milky Way, 38, 309.
Humphreys, R., and Davidson, K. (1979). Studies of luminous stars in nearby galaxies. III-Comments on the evolution of the most massive stars in the Milky Way and the Large Magellanic Cloud. Astrophys. J. 232, 409–420.
Keel, S. L., and Canfield, R. C. (1978). The height variation of velocity and temperature fluctuations in the solar photosphere. Astron. Astrophys. 70, 169–179.
Keeley, D. A. (1977). Linear stability analysis of stellar models by the inverse iteration method. ApJ. 211, 926.
Keller, S. C., and Wood, P. C. (2002). Large magellanic cloud bump cepheids: probing the stellar mass-luminosity relation. Astrophys. J. 578, 144–150.
Kjeldsen, H., and Bedding, T. R. (1995). Amplitudes, of stellar oscillations: the implications for asteroseismology. A&A. 293, 87.
Komm, R., Mattig, R. W., and Nesis, A. (1991). The small-scale velocity field in the solar photosphere. Astron. Astrophys. 243, 251–262.
Ledoux, P., and Walraven, T. (1958). Handbuch der physic. Editor S. Flugg (Berlin: Springer-Verlag), Vol. 51, 353.
Leighton, R. B., Noyes, R. W., and Simon, G. W. (1962). Velocity fields in the solar atmosphere. I. Preliminary report. Astrophys. J. 135, 474.
Madore, B. F. (1982). The period-luminosity relation. IV-Intrinsic relations and reddenings for the Large Magellanic Cloud Cepheids. Astrophys. J. 253, 575–579.
Maeder, B. F. (1981). Grids of evolutionary models for the upper part of HR diagram. Mass loss and turning of some red supergiants into WR Stars. A&A. 102, 401.
Mihalas, D., Däppen, W., and Hunmer, D. G. (1988). The equation of state for stellar envelopes. II-Algorithm and selected results. Astrophys. J. 331, 815–825.
Moskalik, P., Buchler, J. R., and Marom, M. N. (1992). Toward a resolution of the bump and beat Cepheid mass discrepancies. Astrophys. J. 385, 685–693.
Moskalik, P., and Dziembowski, W. A. (1992). New opacities and the origin of the Beta Cephei pulsation. Astron. Astrophys. 256, L5–L8.
Nasis, A., and Mattig, W. (1989). The height dependence of vertical and horizontal velocities attributed to the convective overshoot in the solar atmosphere. Astron. Astrophys. 221, 130–136.
Pamyatnykh, A. A. (2000). Delta Scuti and related stars. Editor M. Breger, and M. H. Montgomery (San Francisco: Astronomical Society Pacific), 210, 215.
Petersen, J. O. (1992). Studies of Cepheid-type variability. X-Kappa-effect-functions for period ratios. Astron. Astrophys. 265, 555–562.
Richard, O., Vauclair, S., Charbonnel, C., et al. (1996). New solar models including helioseismological constraints and light-element depletion. A&A. 312, 1000.
Rodgers, A. W. (1970). The masses of pulsating stars. Mon. Not. Roy. Astron. Soc. 151, 133–140. doi:10.1093/mnras/151.1.133
Rogers, F. J., and Iglesias, C. A. (1992). Radiative atomic Rosseland mean opacity tables. Astrophys. J. Suppl. Ser. 79, 507–568.
Sarro, L. M., Debosscher, J., Neiner, C., Bello-Garcia, A., González-Marcos, A., Prendes-Gero, B., et al. (2013). Improved variability classification of CoRoT targets with Giraffe spectra. Astron. Astrophys. 550, 120. doi:10.1051/0004-6361/201220184
Schootemeijer, A., Nanger, N., and Grin, N. J. (2019). Constraining mixing in massive stars in the small magellanic cloud. A&A 625A, 132.
Schwarzscild, M., and Harm, R. (1958). Evolution of very massive stars. Astrophys. J. 128, 348. doi:10.1086/146548
Simon, N. R. (1995). ASPC series. Editors S. J. Adelman, and W. L. Weise (San Francisco: Astronomical Society Pacific), Vol. 78, 211.
Soszynski, I., Dziembowski, W. A., Udalski, A., Kubaik, M. K., Szymanski, G., Pietrzynski, L., et al. (2007). The optical gravitational lensing experiment. Period-luminosity relations of variable red giant stars. Acta Astronom. 57, 201–225.
Soszynski, I., Udalski, A., Szymansi, M. K., Kubiak, M., et al. (2009). The optical gravitational lensing experiment. The OGLE-III catalog of variable stars. IV. Long-period variables in the large magellanic cloud. Acta Astronom. 59, 239–253.
Soszynski, I., Udalski, A., Kubiak, M., Szymanski, M. K., Pietrzynski, G., Zebrun, K., et al. (2005). The optical gravitational lensing experiment. Miras and semiregular variables in the Large Magellanic Cloud. Acta Astronom. 55, 331–348.
Soszynski, I., Udalski, A., Kubiak, M., Szymanski, M., Peitrzynski, G., Zebrun, K., et al. (2004). The Optical Gravitational Lensing Experiment. Small Amplitude Variable Red Giants in the Magellanic Clouds. Acta Astronom. 54, 129.
Spiegel, E. A. (1963). A generalization of the mixing-length theory of turbulent convection. Astrophys. J. 138, 216.
Stellingwerf, R. F. (1982). Convection in pulsating stars. I—nonlinear hydrodynamics. II—RR Lyrae convection and stability. Astrophys. J. 262, 330–343.
Stello, D., Bruntt, H., Kjeldsen, H., Bedding, T. R., Arentoft, T., Gilliland, R. L., et al. (2007). Multisite campaign on the open cluster M67—II. Evidence for solar-like oscillations in red giant stars. Mon. Not. Roy. Astron. Soc. 377, 584–594. doi:10.1111/j.1365-2966.2007.11585.x
Stobie, R. S. (1969). Cepheid pulsation—I: numerical technique and test calculations. Mon. Not. Roy. Astron. Soc. 144, 461–484. doi:10.1093/mnras/144.4.461
Stothers, R. B. (1991). Observational tests of convective core overshooting in stars of intermediate to high mass in the Galaxy. Astrophys. J. 383, 820–836. doi:10.1086/170840
Takayama, I., Saio, H., and Ita, Y. (2013). On the pulsation modes of OGLE small amplitude red giant variables in the LMC. Mon. Not. Roy. Astron. Soc. 431, 3189–3195. doi:10.1093/mnras/stt398
Tian, B., Men, H., Deng, L., Xiong, D.-R., and Cao, H.-L. (2003). Statistics of the instability strip of Cephei stars. Chin. J. Astron. Astrophys. 2, 125–132. doi:10.1088/1009-9271/3/2/125
Trabucchi, M., Wood, P. R., Montalbán, J., Marigo, P., Pastorelli, G., and Giradi, L. (2017). A new interpretation of the period–luminosity sequences of long-period variables. Astrophys. J. 847, 139. doi:10.3847/1538-4357/aa8998
Travis, L. D., and Matsushima, S. (1973). The role of CONVECT10N in stellar atmospheres. Observable effects of convection in the solar atmosphere. Astrophys. J. 180, 975–986. doi:10.1086/152020
Ulrich, R. K. (1970). The five-minute oscillations on the solar surface. Astrophys. J. 162, 993. doi:10.1086/150731
Unno, W., Kondo, M.-A., and Xiong, D. R. (1985). Solar convection zone given by nonlocal mixing-length theory. Publ. Astron. Soc. Jpn. 37, 235–244.
Unno, W., Osaki, Y., and Ando, H., (1989). Nonradial oscillations of stars. 2nd Edn. Tokyo: University of Tokyo Press.
Unno, W. (1969). Theoretical studies on stellar stability, II. Undisturbed convective nongrey atmospheres. Publ. Astron. Soc. Jpn. 21, 240.
Uytterhoeven, K., Moya, A., Grigahcene, A., Guzik, J. A., Gutiérrez-Soto, J., Smalley, B., et al. (2011). The Kepler characterization of the variability among A- and F-type stars. Astron. Astrophys. 534, 125. doi:10.1051/0004-6361/201117368
Wood, P. R. (2019). Modelling long-period variables—I. A new grid of O-rich and C-rich pulsation models. Mon. Not. Roy. Astron. Soc., 482, 929–949. doi:10.1093/mnras/sty2745
Wood, P. R. (2015). Oscillatory convective modes in red giants: a possible explanation of the long secondary periods. Mon. Not. Roy. Astron. Soc., 448, 3829. doi:10.1093/mnras/stv1587
Xiong, D. R., and Deng, L. (2009). Lithium depletion in late-type dwarfs. Mon. Not. Roy. Astron. Soc., 395, 2013–2028. doi:10.1111/j.1365-2966.2009.14581.x
Xiong, D. R. (1981). Statistical theory of non-local convection in chemically inhomogeneous stars. SciSn 24, 1406.
Xiong, D. R., Cheng, Q. L., and Deng, L. (1997). Nonlocal time-dependent convection theory. ApJS 108, 529.
Xiong, D. R., Cheng, Q. L., and Deng, L. (1998b). Turbulent convection and pulsational stability of variable stars. II. Oscillations of RR lyrae and horizontal branch red variable stars. Astrophys. J. 500, 465.
Xiong, D. R., and Deng, L. (2001). The structure of the solar convective overshooting zone. MNRAS 327, 1137.
Xiong, D. R., and Deng, L. (2002). The extent of the solar overshooting zone deduced from Li abundance. MNRAS 336, 511.
Xiong, D. R., Deng, L., and Cheng, Q. L. (1998a). Turbulent convection and pulsational stability of variable stars. I. Oscillations of long-period variables. Astrophys. J. 499, 355.
Xiong, D. R., Deng, L., Zhang, C., and Wang, K. (2016). Turbulent convection and pulsation stability of stars—II. Theoretical instability strip for δ Scuti and γ Doradus stars. Mon. Not. Roy. Astron. Soc. 457, 3163–3177. doi:10.1093/mnras/stw047
Xiong, D. R. (1986). The evolution of massive stars using a non-local theory of convection. Astron. Astrophys. 167, 239–246.
Xiong, D. R., and Cheng, Q. L. (1992). A note on the mixing length theory and massive star evolution. Chin. J. Astron. Astrophys. 254, 362.
Xiong, D. R., and Deng, L. (2011). Pulsationally unstable nonradial modes in upper main sequence. ACASn, 52, 115.
Xiong, D. R., and Deng, L. (2010). Non-adiabatic oscillations of the low- and intermediate-degree modes of the Sun. Mon. Not. Roy. Astron. Soc. 405, 2759–2767. doi:10.1111/j.1365-2966.2010.16662.x
Xiong, D. R., and Deng, L. (2013). Solar-like and Mira-like oscillations of stars—a uniform excitation mechanism. RAA 13, 1269.
Xiong, D. R. (1989). Radiation-hydrodynamic equations for stellar oscillations. Astron. Astrophys. 209, 126–134.
Zhang, C., Deng, L., Xiong, D., and Christensen-Dalsgaard, J. (2012). Sound-speed inversion of the Sun using a nonlocal statistical convection theory. Astrophys. J. Lett 759, L14. doi:10.1088/2041-8205/759/1/L14
Keywords: variables, interior-stars, convection-stars, oscillations-stars, evolution-stars
Citation: Xiong D-r (2021) Convection Theory and Related Problems in Stellar Structure, Evolution, and Pulsational Stability II. Turbulent Convection and Pulsational Stability of Stars. Front. Astron. Space Sci. 7:438870. doi: 10.3389/fspas.2020.438870
Received: 26 November 2018; Accepted: 28 October 2020;
Published: 19 March 2021.
Edited by:
Joyce Ann Guzik, Los Alamos National Laboratory (DOE), United StatesReviewed by:
Marc-Antoine Dupret, University of Liège, BelgiumCopyright © 2021 Xiong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Da-run Xiong, eGlvbmdkckBwbW8uYWMuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.