Current Sheet Statistics in the Magnetosheath

Yordanova, Emiliya; Vörös, Zoltán; Raptis, Savvas; Karlsson, Tomas

doi:10.3389/fspas.2020.00002

ORIGINAL RESEARCH article

Front. Astron. Space Sci., 07 February 2020

Sec. Space Physics

Volume 7 - 2020 | https://doi.org/10.3389/fspas.2020.00002

This article is part of the Research Topic Improving the Understanding of Kinetic Processes in Solar Wind and Magnetosphere: From CLUSTER to MMS View all 10 articles

Current Sheet Statistics in the Magnetosheath

$\nEmiliya Yordanova$ Emiliya Yordanova¹^*

Zoltán Vörös^2,3

Savvas Raptis⁴

Tomas Karlsson⁴

¹Swedish Institute of Space Physics, Uppsala, Sweden
²Space Research Institute, Austrian Academy of Sciences, Graz, Austria
³Geodetic and Geophysical Institute, Research Centre for Astronomy and Earth Sciences (RCAES), Sopron, Hungary
⁴Space and Plasma Physics, Royal Institute of Technology, Stockholm, Sweden

The magnetosheath (MSH) plasma turbulence depends on the structure and properties of the bow shock (BS). Under quasi-parallel (Q_||) and quasi-perpendicular (Q_⊥) BS configurations the electromagnetic field and plasma quantities possess quite distinct behavior, e.g., being highly variable and structured in the Q_|| case. Previous studies have reported abundance of thin current sheets (with typical scales of the order of the plasma kinetic scales) in the Q_|| MSH, associated with magnetic reconnection, plasma heating, and acceleration. Here we use multipoint observations from Magnetospheric MultiScale (MMS) mission, where for the first time a comparative study of discontinuities and current sheets in both MSH geometries at very small spacecraft separation (of the order of the ion inertial length) is performed. In Q_|| MSH the current density distribution is characterized by a heavy tail, populated by strong currents. There is high correlation between these currents and the discontinuities associated with large magnetic shears. Whilst, this seems not to be the case in Q_⊥ MSH, where current sheets are virtually absent. We also investigate the effect of the discontinuities on the scaling of electromagnetic fluctuations in the MHD range and in the beginning of the kinetic range. There are two (one) orders of magnitude higher power in the magnetic (electric) field fluctuations in the Q_|| MSH, as well as different spectral scaling, in comparison to the Q_⊥ MSH configuration. This is an indication that the incoming solar wind turbulence is completely locally reorganized behind Q_⊥ BS while even though modified by Q_|| BS geometry, the downstream turbulence properties are still reminiscent to the ones upstream, the latter confirming previous observations. We show also that the two geometries are associated with different temperature anisotropies, plasma beta, and compressibility, where the Q_⊥ MSH is unstable to mostly mirror mode plasma instability, while the Q_|| MSH is unstable also to oblique and parallel fire-hose, and ion-cyclotron instabilities.

1. Introduction

The interaction between the supersonic and superalfvénic solar wind with the Earth's magnetic field results in the formation of the terrestrial bow shock (BS). The BS geometry depends on the local orientation of the interplanetary magnetic field (IMF) and the shock normal, i.e., on the angle θ_BN. When θ_BN is smaller than 45°, the configuration of the BS and the adjacent downstream magnetosheath (MSH) is called—quasi-parallel (Q_||); when the angle is larger than 45°, it is called quasi-perpendicular (Q_⊥). The plasma dynamics of the two geometries is quite different. The Q_|| MSH being magnetically connected to the solar wind strongly interacts with the upstream transients and discontinuities hitting the bow shock (BS). The MSH turbulence is also influenced by the various instabilities generated by the reflected at the BS ions in the upstream foreshock region. An example is high-speed magnetosheath jets (e.g., Archer and Horbury, 2013; Hietala and Plaschke, 2013; Plaschke et al., 2013) that are believed to be connected to ripples on the BS, created by downstream-convected foreshock fluctuations, triggered by the counterstreaming ions (Hao et al., 2016). Such ripples can allow the solar wind plasma to cross the BS with only weak deceleration, resulting in the high-speed flows in the magnetosheath (Franci et al., 2016). It should be noted, however, that the bow shock ripples are intrinsic and may possibly be created by other mechanisms as well (Sundberg et al., 2016), even in the case of Q_⊥ BS (Fuselier, 2013). Another product of upstream-downstream interaction is the Hot Flow Anomaly (HFA) (Zhang et al., 2013)—when a solar wind tangential discontinuity with appropriate orientation intersects the BS, a hot core of the back-streaming ions with lower ram pressure, and compressed plasma edges associated with weak shock waves develop, which eventually deform the magnetopause.

In difference, to the Q_|| MSH geometry, there is a sharp increase of the magnetic field magnitude and abrupt deceleration of the plasma in Q_⊥ MSH. Also, the fluctuations of the plasma parameters characterizing the MSH region with Q_⊥ geometry have lower amplitude. Particle energization is mainly caused by the adiabatic and non-adiabatic compressions across the shock. Typical for the Q_⊥ MSH is the ion temperature anisotropy (with respect to the magnetic field), arising from ion reflection and adiabatic compression of ions transmitted at the shock (Johlander et al., 2018). In turn, the temperature anisotropy give rise to the Alfvén ion cyclotron (AIC) instability, for the case of proton plasma β_p < 1, and mirror mode (MM) instability, for β_p > 1. Various simulations have shown the importance of AIC waves at and near the BS (Burgess et al., 2016 and references therein). On the other hand, MM are often observed closer to the magnetopause where the temperature anisotropy is higher (Dimmock et al., 2015). The resulted waves from AIC and MM instabilities, together with the magnetic compressibility, affect the fluctuation anisotropy and their spectral properties (Breuillard et al., 2018).

Most of our observational knowledge about incompressible collisionless magnetohydrodynamic (MHD) turbulence comes from the solar wind (Bruno and Carbone, 2013). It agrees with the classical view of turbulent cascade developing due to non-linear interactions from the large scales where the energy is injected, then being transferred without any loses in the inertial range, and finally being dissipated at the smaller than the ion and electron scales via wave-particle interactions and magnetic reconnection. The inertial range appears as a power law in the power spectral density (PSD) of the fluctuations with Kolmogorov slope −5/3. However, an intrinsic feature of solar wind turbulence is the coexistence of intermittent spatio-temporal structures (e.g., discontinuities and current sheets) along with the turbulent fluctuations. The intermittency is identified as the departure of the probability distribution functions (PDFs) of magnetic field increments from Gaussian statistics (Marsch and Tu, 1994) and it is associated with the formation of sharp gradients. The gradients are important at the small scale end of the MHD range and they reflect the available energy in the turbulent energy cascade which can potentially generate various structures such as current sheets (CSs), (Karimabadi et al., 2014; Matthaeus et al., 2015 and references there in) and magnetic reconnection, (Karimabadi et al., 2014; Matthaeus et al., 2015; Treumann and Baumjohann, 2015). On the other hand again, such coherent structures are of fundamental importance because they become the focal place where energy is dissipated.

Solar wind discontinuities are broadly studied in the past years (Matthaeus et al., 2015 and reference there in). However, their origin is still debated: they are seen either as the boundaries of small scale flux ropes produced in the solar corona (Borovsky, 2008), or alternatively as being locally generated by the turbulent cascade (Carbone et al., 1990). It is worth noting, that both views do not exclude each other. Similarly to the solar wind, the magnetosheath turbulence is also intermittent (Yordanova et al., 2008). The discontinuities can be locally generated or convected from the solar wind to the MSH. Cluster observations showed that turbulence generated thin proton-scale CSs are ubiquitous in the magnetosheath downstream of a Q_|| bow shock (Vörös et al., 2016). In recent numerical (Wan et al., 2015) and other observational studies in the Q_|| MSH, it was evidenced that dissipation, plasma acceleration, plasma heating, and magnetic reconnection occurs at such narrow CSs (Sundqvist et al., 2007; Chasapis et al., 2015, 2018; Eriksson et al., 2016; Yordanova et al., 2016; Phan et al., 2018; Vörös et al., 2019).

As a whole, independently on its geometry, the MSH is a unique plasma laboratory because the turbulence there is high plasma beta (β) and it is compressional, i.e., a type of turbulence which does not occur often in the solar wind, except during short time transient CME sheaths, and we know very little about. In addition, the occurrence and origin of discontinuities in Q_⊥ MSH is largely unknown. Therefore, we aim here to assess the differences in the magnetosheath turbulence properties and structure in an event where MMS measurements are available from the two configurations. This paper is organized as follows: in section 2 we present the determination of the magnetosheath configuration and the discontinuity detection tool; in section 3 the investigated data set is described; in section 4 the results from the comparison are shown, which are finally discussed in the last section 5.

2. Methods

In order to verify and distinguish between the Q_⊥ and Q_|| MSH, we apply a set of criteria based on the magnetic field variance, the temperature anisotropy, and the high energy ion flux. The classification algorithm is based on the local magnetosheath MMS data rather than the associated solar wind upstream measurements. This was done for several reasons. Available solar wind data is usually artificially propagated to the BS from L1, producing an uncertainty regarding the exact time. This is due to the fact that the propagating models are not fully accurate and the BS shape and position are dynamically changing. Additionally, the MMS orbit does not have a constant distance from the BS, which makes the associated upstream values require further propagation inside the MSH depending on the MMS position, providing further uncertainty to the associated solar wind values. Finally, there are several cases where there is no solar wind data available that can be associated to MMS measurements.

Initially, the Partial Variance of Increments (PVI) method was proposed for detection of coherent structures in the solar wind turbulence from single point observations and MHD numerical simulations (Greco et al., 2008, 2009). Later, it was also adapted to multipoint measurements for the magnetosheath region (Chasapis et al., 2015; Vörös et al., 2016). PVI is by definition the partial variance of magnetic field increments (ΔB_ij(t) = B_i(t) − B_j(t)), estimated between two points of measurements, in our case—by pairs of spacecraft:

\begin{array}{l} P V I_{i j} (t) = \sqrt{\frac{∣ Δ B_{i j} (t) ∣^{2}}{〈 ∣ Δ B_{i j} ∣^{2} 〉}}, & (1) \end{array}

where the average 〈·〉 is taken over the whole interval, and i, j = 1,2,3,4 is the MMS spacecraft number. It is worth noting that the PVI method from multipoint measurement will be sensitive to structures with size comparable to the distance between spacecraft.

In addition, the rotation of the magnetic field between two spacecraft, i.e., magnetic field shear angle, can be estimated as:

\begin{array}{l} α_{i j} (t) = \cos^{- 1} \frac{B_{i} (t) \cdot B_{j} (t)}{∣ B_{i} (t) ∣ \cdot ∣ B_{j} (t) ∣} . & (2) \end{array}

Previously was reported that a correlation between PVI and α exists—high PVI and high magnetic shears are indication that the detected discontinuity is a current sheet (Chasapis et al., 2015). It was also shown that such current sheets are associated with local increase of electron temperature and energy dissipation at electron scales (Chasapis et al., 2018). On the contrary, when the PVIs and the magnetic shear angles are small, these parameters measure a stochastic noise.

We note that simulations (Zhang et al., 2015) and observations (Wang et al., 2013) of the discontinuities in the solar wind has revealed that plasma heating is more significant around tangential discontinuities than rotational discontinuities. However, in our case, the PVI (Equation 1) as an identifier of current sheets, together with the magnetic shear angle (Equation 2), were calculated between the spacecraft pairs with separation distances between the electron and ion gyroradius scales. In such a case, the small-scale sub-gyro-scale current sheets found for the given spacecraft separations do not necessarily correspond to discontinuities existing in magnetohydrodynamics (Balikhin et al., 2014).

3. Data

In this work, we use measurements from the four identical spacecraft of the MMS mission, whose objective is to investigate the plasma processes at kinetic scales in the Earth's magnetosphere. The magnetic field data, sampled at 16 Hz were obtained by the Flux Gate Magnetometer (FGM) instrument (Russell et al., 2014). The Electric field Double Probe (EDP) instrument provides the electric field data with sampling of 32 Hz (Lindqvist et al., 2016). Finally, the electron and ion moments were available from the Fast Plasma Investigation (FPI) instrument (Pollock et al., 2016), sampled with spacecraft spin frequency of 4.5 s. During 2016-01-03/05:00-06:00 UTC, the spacecraft were in the magnetosheath region close to the subsolar region at (9,−7,−1) R_E in GSE coordinates. The fleet was in tetrahedron formation with separation between spacecraft of ~36 km. For the sake of comparison, the interval under investigation was selected such that MMS consequently passed through Q_⊥ and then through Q_|| BS geometry, so that both cases are subjected to similar upstream plasma conditions. Four minutes (05:28-05:32 UTC) in the transition from one region to the other are excluded from the analysis to ensure that the parameters we compare are typical for the respective MSH configuration. The average plasma parameters are shown in Table 1. The difference between the four spacecraft are insignificant therefore, we choose the values corresponding to MMS4.

TABLE 1

Table 1. Averaged parameters and the respective variance (gray) for quasi-perpendicular (Q_⊥) and (Q_||) MSH.

4. Results

Figure 1 (top to bottom) shows the spectrogram of the ion differential energy flux, the ion temperature anisotropy with respect to the magnetic field, and the ion plasma beta during the selected event. It is clearly seen that in the interval 05:30-06:00 UTC, there are much larger fluctuations than the ones observed in the period 05:00-05:30 UTC, indicating that the magnetosheath is subjected to a different bow shock geometry: first MMS was sampling a Q_⊥ MSH and then got immersed in a Q_|| MSH (the border between the two configurations is marked with the black dash line in Figure 1). We distinguish between the two cases, according to the criteria described in the section 2, based on the magnetic field variance, temperature anisotropy, and high ion differential energy flux (DEF). It is known, that the temperature anisotropy is typically higher in Q_⊥ MSH compared to Q_|| one (Fuselier et al., 1994), which is supported by our estimation in Figure 1 (middle panel), where the ion temperature (T_⊥) perpendicular to the magnetic field is higher than the one in the parallel direction (T_||) for all spacecraft. In the Q_|| MSH (to the right of the black vertical line) the temperature anisotropy is small, and fluctuates around 1. Further, the variance of the magnetic field components is also higher in the Q_|| configuration. This is true for the other plasma parameters (see Table 1), e.g., plasma density, resulting in the ion plasma beta (β) shown in Figure 1 (bottom panel). Note that despite the different variability (with β occasionally reaching values from tens to hundreds in Q_|| MSH), β > 1 in both geometries, which is characteristic for the magnetosheath, and shows that in general, the plasma pressure dominates the magnetic one. This is opposite to the case of the low plasma β of the upstream solar wind. The most striking difference between the two configurations, however, is the ion differential energy flux that is observed in Q_|| MSH, while being completely absent in Q_⊥ MSH (Fuselier, 2013) (Figure 1, top panel). One can see also much more discrete structure in the energy band in the Q_|| MSH vs. the smooth featureless energy spectrum in the Q_⊥ case.

FIGURE 1

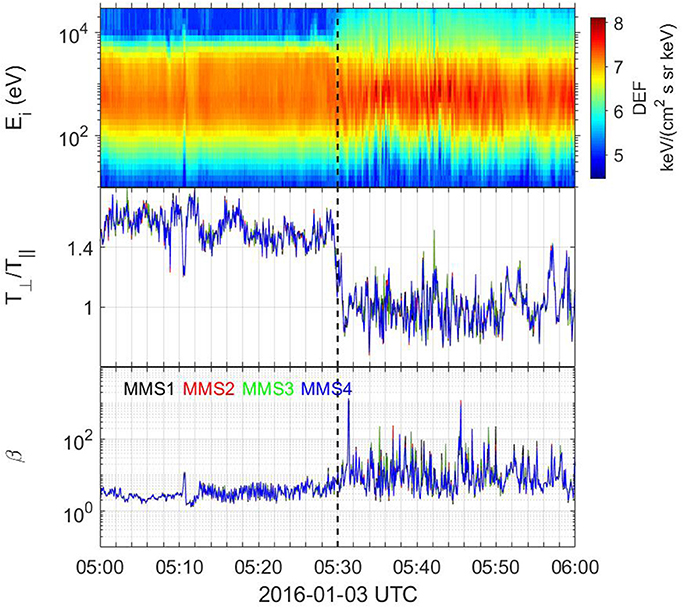
Figure 1. Top to bottom: Differential energy flux for ions for MMS4, temperature anisotropy in perpendicular and parallel directions to the background magnetic field, and plasma beta for MMS1-4. The vertical black dashed line marks the transition between the Q_⊥ MSH (left) to the Q_|| MSH (right) intervals.

The visual inspection of the wave forms of the magnetic field (Figure 2, top panels) shows that in the Q_⊥ MSH (left) the fluctuations of the components are small, the field intensity is strong, the components are well-separated and there are no directional changes. On the other hand, in the Q_|| MSH (right), the variability of the magnetic field is very high (see also Table 1), the components nearly overlap with sudden changes of sign, and the field magnitude is lower. The “turbulence” level δB/B₀ ≈ 0.9 (for δB > 0.001 Hz), i.e., the fluctuations are of the order of the background magnetic field. This is opposite to δB/B₀ ≈ 0.2 for Q_⊥ MSH, meaning that we can assume the validity of mean-field approximation since the fluctuations are quite small. The described behavior is typical for the respective geometries (Lucek et al., 2005).

FIGURE 2

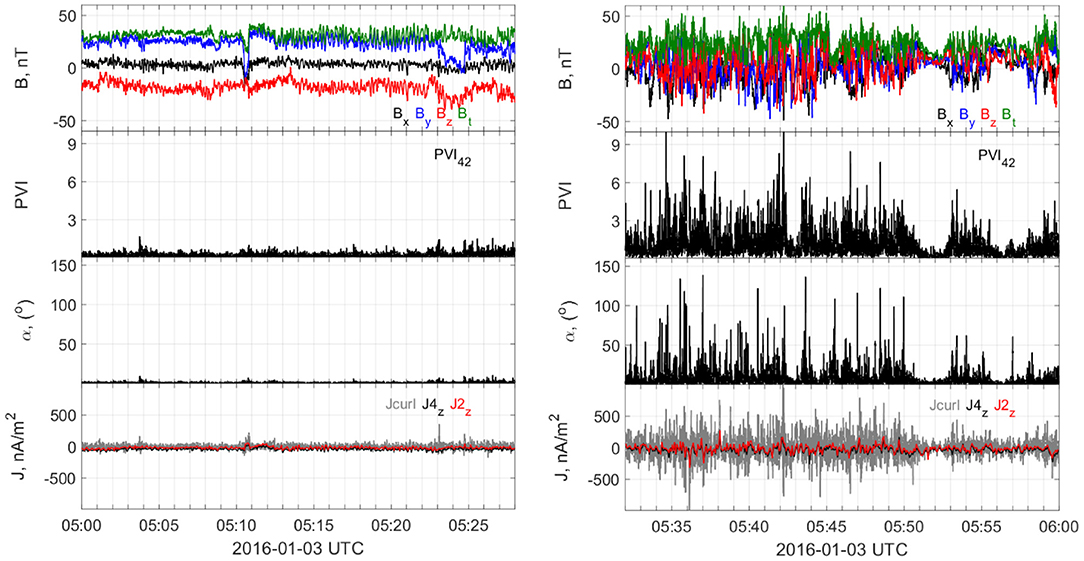
Figure 2. (Left) from top to bottom: Magnetic field magnitude and components, PVI for MMS4 and MMS2 pair of spacecraft, magnetic shear angle, and current density from curlometer (J_curl, gray) and plasma currents for MMS4 (J4_z, black) and MMS2 (J2_z, black) in the Q_⊥ MSH; (Right) Same as on the left in the Q_|| MSH.

Next, we search for coherent structures by calculating PVI from the magnetic field increments for all pairs of spacecraft. Figure 2 presents the PVI (annotated as PVI₄₂) in the plot and the magnetic vector rotations for the example of MMS 4 and 2 pair (Figure 2, middle panels). The results from the other pairs of spacecraft are very similar. Over the time scale of 0.25 s (defined by the spacecraft separation and the plasma bulk speed), the PVI in the Q_|| MSH is characterized by abundance of strong peaks (PVI > 3). Some of the strongest PVI values are also associated with large magnetic field shear angles (α > 100), implying that the detected structures are current sheets. On the contrary, in the Q_⊥ MSH, however, there is a complete absence of any such activity—PVI hardly reaches 1.5 and the magnetic shear is less than 10°. Thanks to the multipoint MMS measurements and the availability of both plasma components (electrons and ions), we can estimate the current density in two ways: from the curlometer technique (J_curl = (∇×B)/μ₀, μ₀—the magnetic constant, Dunlop et al., 2002), and from the plasma measurements, and then relate it to the PVI and magnetic shear. Figure 2 (bottom panels), shows the J_z component of the plasma current and the same component of the current from the curlometer. It is worth noting that in this comparison, we cannot benefit from the highest particle resolution because it is not available for such long intervals as the one in hand. However, the spacecraft are so close to each other that the curlometer current is better resolved, and we can see the presence of strong small-scale currents throughout the Q_|| MSH, where they are also well-correlated with the PVI peaks and large magnetic rotations. Despite the low (spin) resolution, the plasma current follows closely the curlometer current. Previously, such very good correlation between the PVI and the high intensity curlometer current has also been demonstrated on the basis of Cluster multipoint measurements (Chasapis et al., 2017).

Further, we compare the distribution of PVI > 3 as a function of the magnetic shear α for the two MSH geometries (Figure 3, left panel). The distribution is obtained by combining the PVIs from all pairs of spacecraft. The threshold is chosen such that the statistics represents the stronger discontinuities that may be related to current sheets. Note again that, PVI detection here is limited to the time scale of the spacecraft separation (~0.25 s). In the Q_⊥ MSH, the PVI is concentrated mostly at magnetic rotation under 10°, and there is no PVI values above 20°. At the same time, the PVI histogram for Q_|| case has counts in the entire range of angles. The distribution maximum is ~30° and has heavy tail for α > 90°. It is known from MHD simulations (Greco et al., 2009) and observations (Vörös et al., 2016) that the heavy tail belongs to the presence of current currents. This is also confirmed here by the histogram of the current density shown in Figure 3 (right panel). Similar to the PVI histogram, the current distribution has heavy tail due to strong currents in Q_|| MSH extending up to 1000 nA/m², while J has mostly values <200 nA/m² in the Q_⊥. In fact, we performed a single test (not shown) and deduced that the few counts of the maximum current in Q_⊥ MSH belong to the two structures at 05:11 and 05:22-05:25 UTC (Figure 2, top and bottom panels and the isolated light blue bar at ~370 nA/m² in Figure 3, right panel). Alternative possibility for the current sheets origin, is that they have very likely been convected from the solar wind into the magnetosheath since WIND observations (not shown) reveal non-stationary solar wind at the times corresponding to our event. It is difficult to attribute in the plasma moments an indication that these discontinuities are locally generated, due to the low sampling resolution at the spacecraft spin.

FIGURE 3

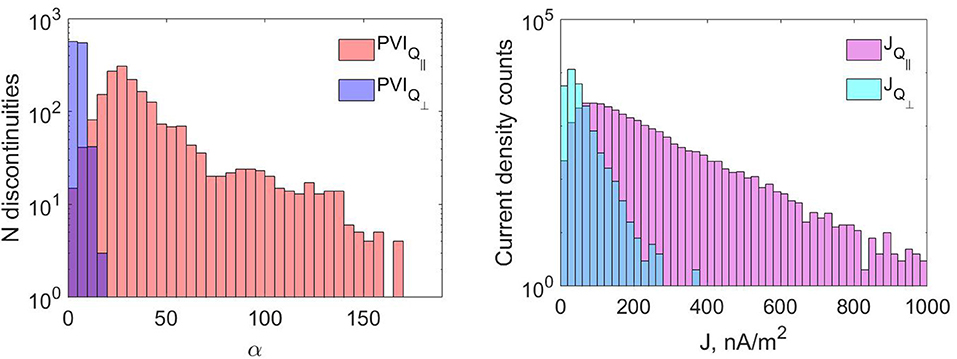
Figure 3. (Left) PVI calculated from magnetic field increments, in bins of 5 degrees shear angle for all pairs of MMS for threshold PVI > 3; (Right) Current density from curlometer method in bins of 20 nA/m². Note, the shorter Y range in the left panel.

Further, we investigate the correlation between the current intensity from the curlometer and the PVI (Figure 4). We consider here only the Q_|| MSH interval, given the very small PVI activity and current intensity in the Q_⊥ MSH. In gray are plotted all PVI values, showing wide spread. Since, as described earlier, PVI is proportional to the current, we look at the correlation between the current and only those PVI values that are associated with magnetic rotation angles larger than 100° (black dots). The obtained correlation with this conditioning is quite good with coefficient of 0.7. The large current densities or PVI's (Servidio et al., 2011), associated with large magnetic shear angles (Vörös et al., 2016; Yordanova et al., 2016) can correspond to potentially reconnecting current sheets.

FIGURE 4

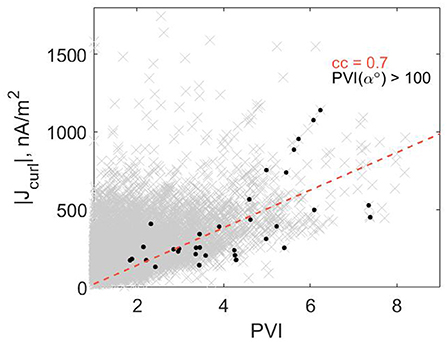
Figure 4. Current magnitude from curlometer vs all PVI values (gray) in the case of Q_|| MSH. The black dots correspond to PVI conditioned for magnetic shear larger than 100°. The red dashed line represents the correlation with coefficient 0.7, between the current and the conditioned PVI.

To characterize further the magnetosheath fluctuations and make a comparison between the two MSH geometries, we compute the PSD of the magnetic and electric field fluctuations for Q_⊥ in Figure 5 (left panel) and Q_|| MSH (right panel). The PSD is calculated from FFT using Welch method with Hanning window and 75% overlap between the data segments. The annotated spectral indices are obtained by linear fitting over certain frequency ranges of the averaged from all spacecraft PSD. Since, the observed PSD is obtained in frequency domain, to interpret the spectral scaling in terms of turbulence regimes we need to transform the temporal scales into spacial scales. This is done by assuming the Taylor hypothesis, where the intrinsic plasma fluctuations evolve much slower than the bulk plasma speed, therefore they are considered frozen-in in the flow (Taylor, 1938). Taylor hypothesis is usually well-satisfied in the solar wind (Perri et al., 2017). In our event, the bulk flow and the Alfvén velocity have close magnitude (see Table 1), which potentially could invalidate this assumption. Recent numerical simulation however, demonstrated that even for high beta cases the spectral slopes are preserved but shifted in fluctuation level (Perri et al., 2017). Also, the presence of zero-frequency structures, such as current sheets, do not violate the Taylor hypothesis. This has been confirmed by MMS observations, where the assumption was successfully applied in a case of electron reconnection in the MSH (Stawarz et al., 2019). Considering our results, we are mindful that the validity of the Taylor hypothesis may be uncertain for our event.

FIGURE 5

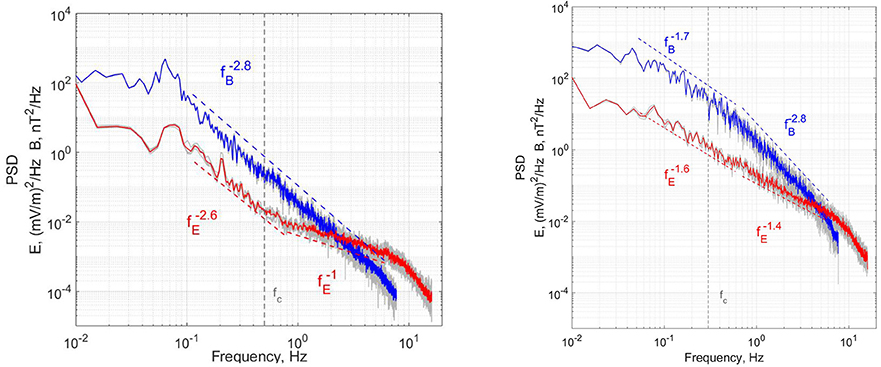
Figure 5. (Left) PSD of the average over the four MMS spacecraft magnitudes of the electric (red) and magnetic (blue) fields over-plotted on the spectrum from each spacecraft (gray) for the Q_⊥ MSH; (Right) Same as on the left in the Q_|| MSH. The vertical gray dashed line marks the respective gyrofrequency f_c for each MSH geometry. The error in the spectral slopes are very small and are reported in the text.

In both MSH configurations the PSD shows power law behavior. However, the spectral shape and the power content are distinctly different between the two geometries. In the Q_⊥ MSH, the PSD has single power law for the magnetic field (–2.8), extending over one decade (0.1–6 Hz) with the ion gyrofrequency f_c ~0.5 Hz. The electric field power law at the low frequency is rather short (0.1–0.8 Hz), with close spectral slope –2.6 close to the magnetic field one. A second shallower regime can be recognized starting at 0.8 Hz in the electric fluctuations above 0.8 Hz with spectral index –1 in the range 0.8–6 Hz. There is a bump at 0.05–0.1 Hz in the spectra, probably due to the presence of mirror modes (MM) commonly occurring in the Q_⊥ MSH at such frequencies. Their typical appearance as wave-train of dips in the magnetic field observations can be distinguished in the period 05:12-05:28 UTC (Figure 2, top left panel). MM are characterized by anticorrelation between the magnetic field and plasma density and can also appear as trains of peaks in the magnetic field magnitude. From a large statistical study (Dimmock et al., 2015), it has been shown that the upstream Alfvén Mach number M_A controls the MM formation as dips, when M_A is small, or peaks when M_A is large. A possible scenario has been proposed recently in a numerical study for the development of turbulent cascade in the absence of inertial range, i.e., without Kolmogorov scaling (Franci et al., 2017). It was attributed to the interplay between magnetic reconnection and plasma turbulence. However, this scenario cannot explain the same power law in the MHD and sub-ion regimes in the reported here Q_⊥ MSH, because there are no strong current sheets and large magnetic field rotations observed that could serves as possible reconnection sites, thus this issue still remains an open question.

In the Q_|| MSH, on the other hand, there are nearly two orders of magnitude higher spectral content in the magnetic field and one order higher power in the electric field. At the lower frequencies (0.05–0.6 Hz), the spectral index of the magnetic fluctuations is –1.7, which is close to theoretical Kolmogorov one of fully developed turbulence in the inertial range. A spectral break is observed at 0.6 Hz (near f_c ~0.3 Hz), followed by a second steeper power law (–2.8) in the higher frequency domain up to 6 Hz. The electric field scaling in the inertial range is –1.6, which is slightly shallower than the magnetic field spectral slope, but also close to the Kolmogorov one. Above the break at 0.6 Hz at higher frequency, the power law becomes somewhat shallower (–1.4). All of these differences imply that the plasma turbulence in the Q_|| MSH must be substantially different from the one in the Q_⊥ MSH. This will be discussed in more details in the next section. For the sake of completeness, we have estimated the uncertainty in the estimation of the spectral slope by considering each individual MMS spacecraft and by varying the frequency ranges over which the spectral fit is performed. We found that the slopes are rather stable with very small errors—for Q_⊥ MSH, the electric field spectral slope in the MHD domain is –2.61 ± 0.03, in the kinetic range it is –0.97 ± 0.08; and the magnetic field one is –2.79 ± 0.01. In the case of Q_|| MSH the electric field scales as –1.59 ± 0.03 in the MHD domain, and –1.38 ± 0.03 in the kinetic range; respectively, the magnetic field index in the MHD range is –1.79 ± 0.02, and in the kinetic one it is –2.77 ± 0.04.

The Q_|| and Q_⊥ MSH configurations are clearly associated with different ion temperature anisotropies, plasma β and compressibility distributions. Figure 6 shows the scatterplots for β_|| vs. ion temperature anisotropy ratio T_⊥/T_||, with color coded parallel compressibility $C_{| |} = δ B_{| |}^{2} / (δ B_{| |}^{2} + δ B_{⊥}^{2})$ . The colored dashed lines correspond to the thresholds of ion cyclotron (black), mirror mode (red), oblique (magenta) and parallel fire-hose (green) plasma instabilities (Hellinger et al., 2006), respectively. In the Q_⊥ MSH (Figure 6, left), C_|| falls in the range of T_⊥/T_|| values between 1.2 and 2, and for β_|| roughly between 1 and 10, being at and over the ion cyclotron threshold and mostly concentrated around mirror mode threshold. C_|| is also larger in the Q_⊥ MSH than in the Q_|| one (Figure 6, right). In the latter case β_|| is roughly between 2 and 100 and T_⊥/T_|| is between 0.7 and 1.5, being over the instability thresholds for larger values of β_||.

FIGURE 6

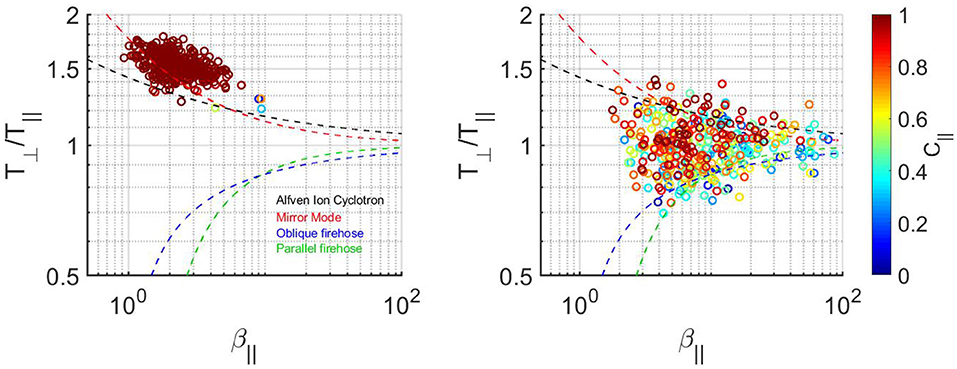
Figure 6. (Left) Parallel compresibility C_|| (color code) as a function of proton temperature anisotropy and parallel plasma beta β_|| for the Q_⊥ MSH; (Right) Same as on the left for the Q_|| MSH. The thresholds for the different plasma instabilites are shown with dashed lines in color.

5. Discussion

The PVI method provides a relatively simple tool to find in the data small volumes of concentrated field gradients that are linked to coherent structures, i.e., to intermittency. This was demonstrated for the first time by Greco et al. (2008) on the basis of 3D Hall MHD numerical simulation. In a more recent simulation, it was predicted that the large current density corresponds to strong PVI peaks in reconnecting current sheets (Donato et al., 2013). This correspondence was confirmed experimentally in the Q_|| MSH with the high resolution Cluster (Vörös et al., 2016; Chasapis et al., 2017) and MMS (Yordanova et al., 2016) data.

In the Q_|| MSH presented here, the intermittency and the related current sheets appear in the burstiness of the PVI (Figure 2, middle panel), and the non-Gaussian PVI and current distributions (Figure 3). Although there is a clear statistical difference in the current distribution between the two geometries, there can exist a few current sheets reaching 200 nA/m² also in the Q_⊥ case. Our results demonstrate that perhaps it is not the mean values or medians of distributions which are important, but the large current values in the tail, which correspond to the strongest current sheets and probably have the largest influence on dissipation during a time interval. In a recent study, based on MMS magnetosheath data (Stawarz et al., 2019), it has also been shown that the distributions of magnetic field increments and currents are highly non-Gaussian with heavy tails due to reconnecting electron-scale current sheets. The authors have demonstrated that a link exist between the power law spectrum and magnetic reconnection, where below the ion gyroradius, the magnetic field PSD exhibits higher steepening the more current sheets are evidenced to reconnect. In Q_|| MSH this may be one mechanism for dissipating energy. It is worth noting that it is hard to speculate whether the current sheets are generated by turbulence in the MSH. For example, some current sheets can be generated in the solar wind or by the upstream BS, then convected downstream. When current sheets are generated by turbulence, they are obviously part of the turbulence, perhaps being associated with some additional self-organizing processes in the turbulent cascade, and this is not fully understood yet. Nevertheless, in both cases (current sheets as part of turbulence or generated by some other mechanisms), the study of these structures can be helpful in understanding the different nature of fluctuations in Q_⊥ and Q_|| MSH.

While, as discussed already, there is abundance of small-scale current sheets in Q_|| MSH (Retinò et al., 2007; Vörös et al., 2016), associated with magnetic reconnection (Vörös et al., 2016; Yordanova et al., 2016; Phan et al., 2018) and energy dissipation (Sundqvist et al., 2007; Chasapis et al., 2018), in the Q_⊥ MSH the fluctuations do not contain strong currents and the magnetic field is not changing directions (Figure 2). Given that current sheets are not present in Q_⊥, another dissipation mechanism might be at play. It was suggested that the kinetic processes are driven by electrostatic solitary waves at frequency > 100 Hz (Breuillard et al., 2018), which is unfortunately way outside the range available in our data set. Recently the damping of waves due to wave-particle interactions and the dissipation of ion-cyclotron waves in the Q_⊥ MSH has been studied by He et al. (2019). They have found that the dissipation of ion-cyclotron wave energy occurs preferentially in the direction perpendicular to the mean magnetic field. This could partially explain the observed perpendicular temperature anisotropy seen in the Q_⊥ MSH (Figure 1, bottom panel and Figure 6, left plot).

The power of the electromagnetic fluctuations in the Q_⊥ MSH is much lower seemingly mostly concentrated near a low frequency bump, followed by steep (–2.8) slope at higher frequency (Figure 5, left panel). Similar bump was reported in Breuillard et al. (2018) and it was attributed to mirror modes, below which they also observe the same scaling. Such steep power law extended over the two frequency decades was reported in another Q_⊥ MSH case study from INTERBALL-1 measurements (Shevyrev and Zastenker, 2005), where the authors attributed the steeper PSD at low frequency to the mixture of MHD waves, including MM.

A statistical study of magnetosheath data from Cluster spacecraft revealed that the spectral slope in the MHD domain changes from –1 to –1.6 from the BS toward the flanks close to the magnetopause (Huang et al., 2017). Thus, the upstream solar wind turbulence is modified by the BS serving as a generator of additional fluctuations downstream in the magnetosheath. However, no significant dependence on θ_BN of the spectra have been found. On the contrary, they have found that the scaling in sub-ion range is independent on the distance from the BS. The MMS data studied here show similar trend—the spectral index in the frequency range around and above the ion gyro frequency have similar to –2.8 spectral slope for both BS geometries. The same scaling in the kinetic range was observed in another MMS magnetosheath comparison between Q_⊥ MSH and Q_|| MSH (Breuillard et al., 2018). However, they also detected an additional range with Kolmogorov—like scaling (–1.6) in the Q_|| case at 0.02–0.2 Hz, similarly to our results of slope close to Kolmogorov –1.7 at 0.05–0.6 Hz.

The spectra of the electric field show that in the MHD frequency range the power law follows closely the one of the magnetic field (Figure 5), in the respective MSH geometry. Previous comparison of magnetic and electric field fluctuations from Cluster measurements in the case of high plasma β ≥ 1 solar wind (Bale et al., 2005) and in the magnetosheath (Matteini et al., 2017) have also reported similar scaling in the MHD range. It was also found that, below the ion scales and before the electron scales are reached, the magnetic field PSD steepens while the electric field one becomes shallower. Another feature is that the electric field power dominates the magnetic field one in the kinetic range. The theoretical prediction is that at sub-ion scales the magnetic and electric field decouple and the relation between their spectral slopes is: α_E = α_B − 2 (Sahraoui et al., 2009; Franci et al., 2018). We see similar trend in our results even though not exact - the shallower electric spectral slope leads to –1.8 difference in the fields scaling in the Q_⊥ MSH, while in the Q_|| the relation is –1.4. The reason for the non-exact relation in our case is probably due to the rather short frequency range of the power laws estimation. Another possibility is that, the relation between the slope is specifically valid for perpendicular component of the electric field and the parallel component of the magnetic field and not for the field magnitudes as in our case (Franci et al., 2018). The flattening of the electric field spectrum at high frequency could also explained by the high level noise at the small scales.

Further, as in the previously discussed high β cases the electric field power is higher than the magnetic field at higher frequency. This has been attributed to the contribution of the non-ideal terms in the Ohm's law (Franci et al., 2018). From a numerical prediction it is expected that in the MHD range the magnetic field power law is the same regardless plasma β (Franci et al., 2016). In the high frequency range, however, the spectral index is expected to become shallower the higher the plasma β: from –3.5 (β ~ 0.01) to –2.9 (β > 1), the latter being close to the β conditions in our case. Finally, statistical study based on Cluster (Dwivedi et al., 2019) and case study based on MMS (Breuillard et al., 2018) magnetosheath observations support the idea that the magnetic field turbulence cascade with –2.8 scaling at the high frequency range in the magnetosheath results from the non-linear evolution of KAW.

In summary, in this work we have investigated the magnetosheath turbulence downstream Q_⊥ and Q_|| BS geometry by means of multipoint MMS measurements at very small spacecraft separations of the order of ion scales. In particular, we have focused on the differences in the fluctuations and occurrences of structures downstream of the different BS geometries. We have shown that while in the Q_|| MSH there is abundance of discontinuities and very strong currents associated with large rotations in the magnetic field (known from previous studies), in the Q_⊥ MSH these are absent, which has not been reported before. Both regions exhibit high plasma β because of the compression and higher plasma density, however the fluctuations in all plasma variables in Q_|| are significantly more intense than in Q_⊥ MSH. The power of the magnetic field is about two orders higher in the Q_|| than in the Q_⊥ MSH. The electric field intensity in the Q_⊥ case is one order weaker. Further, in the Q_⊥ geometry the Kolmogorov scaling is missing, which still remains an open question. One possibility suggested in the literature before, is that the turbulence did not have enough time to develop fully due the close proximity of the bow shock and the transit time through the magnetosheath being too short in comparison with the non-linear time of the intrinsic Alfvénic fluctuations in the inertial range. On the contrary, in the Q_|| MSH we still observed the inertial range, supporting previously suggested interpretation that the solar wind turbulence survives to some extend the transition through the BS. Finally, we have found that for large plasma β the plasma is unstable to AIC and predominantly MM instability in the Q_⊥ MSH, while in the Q_|| MSH it is unstable to AIC, MM, and oblique and parallel fire-hose instabilities.

We conclude here that the different scaling and intrinsic turbulence structure would suggest that the plasma heating and dissipation occur by means of different mechanisms in the two magnetosheath configurations. Obviously, in the absence of simultaneous multi-point observations at the locations both of the bow shock and magnetosheath, we were not able to connect the magnetosheath observations directly with the details of shock physics upstream. However, we believe that the statistical investigations in Q_⊥ and Q_|| MSH can help us to improve our understanding about dayside solar wind-magnetosphere interactions.

Data Availability Statement

MMS data are available at the MMS Science Data Center (https://lasp.colorado.edu/mms/sdc).

Author Contributions

EY and ZV designed the study. EY prepared the data and performed the analysis. SR and TK selected the time interval. All authors have contributed to the discussion and writing of the manuscript.

Funding

EY was funded by the Swedish Contingency Agency, grant 2016-2102. ZV was supported by the Austrian FWF under contract P28764-N27. SR and TK acknowledge support from SNSA grant 90/17.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors acknowledge the MMS team. EY acknowledge A.P. Dimmock for the fruitful discussions.

References

Archer, M. O., and Horbury, T. S. (2013). Magnetosheath dynamic pressure enhancements: occurrence and typical properties. Ann. Geophys. 31, 319–331. doi: 10.5194/angeo-31-319-2013