- 1Department of Astrophysical Sciences, Princeton University, Princeton, NJ, United States
- 2Max-Planck-Institut für Plasmaphysik, Garching, Germany
- 3School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
Turbulence and kinetic processes in magnetized space plasmas have been extensively investigated over the past decades via in-situ spacecraft measurements, theoretical models and numerical simulations. In particular, multi-point high-resolution measurements from the Cluster and MMS space missions brought to light an entire new world of processes, taking place at the plasma kinetic scales, and exposed new challenges for their theoretical interpretation. A long-lasting debate concerns the nature of ion and electron scale fluctuations in solar-wind turbulence and their dissipation via collisionless plasma mechanisms. Alongside observations, numerical simulations have always played a central role in providing a test ground for existing theories and models. In this Perspective, we discuss the advances achieved with our 3D3V (reduced and fully) kinetic simulations, as well as the main questions left open (or raised) by these studies. To this end, we combine data from our recent kinetic simulations of both freely decaying and continuously driven fluctuations to assess the similarities and/or differences in the properties of plasma turbulence in the sub-ion range. Finally, we discuss possible future directions in the field and highlight the need to combine different types of numerical and observational approaches to improve the understanding of turbulent space plasmas.
1. Introduction
With the establishment of satellite space missions, the near-Earth environment and the solar wind have provided unique opportunities to explore the physics of weakly collisional, magnetized plasmas (e.g., Bruno and Carbone, 2013; Chen, 2016; Verscharen et al., 2019). In particular, increasingly accurate in-situ measurements of plasma fluctuations and particle distribution functions from Cluster and MMS have uncovered an entire new world of kinetic processes occurring in plasma turbulence (e.g., Alexandrova et al., 2009, 2012, 2013; Sahraoui et al., 2009, 2010; Chen et al., 2010, 2019; Greco et al., 2016; Narita et al., 2016; Chasapis et al., 2017; Chen and Boldyrev, 2017; Huang et al., 2017; Roberts et al., 2017; Servidio et al., 2017). These observations highlight a change in the turbulent cascade at plasma microscales, challenging the community for a consistent theory of kinetic-range turbulence. In fact, several collisionless plasma processes may be simultaneously at play and compete with each other in determining the nature of ion-scale and electron-scale fluctuations (e.g., Stawicki et al., 2001; Galtier and Bhattacharjee, 2003; Howes et al., 2008a; Gary and Smith, 2009; Schekochihin et al., 2009; Boldyrev and Perez, 2012; He et al., 2012; Podesta, 2012; Boldyrev et al., 2013; Matthaeus et al., 2014; Passot and Sulem, 2015, 2019; Kunz et al., 2018; Passot et al., 2018) and, consequently, how free energy cascades in phase space (e.g., Schekochihin et al., 2008; Servidio et al., 2017; Adkins and Schekochihin, 2018; Cerri et al., 2018; Eyink, 2018; Pezzi et al., 2018; Kawazura et al., 2019). Many observations at ion and sub-ion scales, specifically, suggest that turbulent fluctuations exhibit properties mainly typical of kinetic Alfvén waves (KAWs) (Leamon et al., 1998; Sahraoui et al., 2009; Podesta and TenBarge, 2012; Salem et al., 2012; Chen et al., 2013; Kiyani et al., 2013; Chen, 2016; Lacombe et al., 2017). The emergence of KAW-like fluctuations in kinetic turbulence has been also supported by means of a large number of theoretical and numerical works (e.g., Hollweg, 1999; Stawicki et al., 2001; Gary and Nishimura, 2004; Howes et al., 2008a; Gary and Smith, 2009; Sahraoui et al., 2012; TenBarge et al., 2012; Vásconez et al., 2014, 2015; Franci et al., 2015; Cerri et al., 2016; Pucci et al., 2016; Zhao et al., 2016; Valentini et al., 2017; Grošelj et al., 2019). Some of these studies rely on the so-called spectral field ratios, which provide a measure of the wave-like polarization properties of the turbulent fluctuations, as compared to what linear theory predicts (see, e.g., Boldyrev et al., 2013) and section 3.
In the above context, direct numerical simulations play a key role by providing a controlled test ground for different theories, providing information not accessible to observations. Enormous efforts have been recently made to understand 3D kinetic turbulence via numerical experiments (e.g., Howes et al., 2008b; Gary et al., 2012; TenBarge and Howes, 2013; Vasquez et al., 2014; Servidio et al., 2015; Told et al., 2015; Wan et al., 2015, 2016; Bañón Navarro et al., 2016; Comişel et al., 2016; Cerri et al., 2017b, 2018; Hughes et al., 2017a,b; Kobayashi et al., 2017; Franci et al., 2018a,b; Grošelj et al., 2018, 2019; Arzamasskiy et al., 2019; Roytershteyn et al., 2019; Zhdankin et al., 2019). In this Perspective, we combine data from our recent 3D3V studies (Cerri et al., 2017b; Franci et al., 2018b; Grošelj et al., 2019) to investigate whether common turbulence features exist in all three independently performed simulations (section 2), thus indicating a certain “universality” of kinetic-scale turbulence. Moreover, we also highlight possible model-dependent differences between the 3D hybrid-kinetic and fully kinetic simulations. We mention that this approach follows the general idea of adopting different models (and/or implementations) to study turbulent heating and dissipation in collisionless plasmas that was initiated within the “Turbulent Dissipation Challenge” framework (Parashar et al., 2015). Here we extend similar comparative analysis of the spectral properties that have been previously performed in a reduced two-dimensional setup (see Cerri et al., 2017a; Franci et al., 2017; Grošelj et al., 2017) to the more realistic three-dimensional geometry (section 3), and we present a new analysis of our data based on local structure functions (section 4). Finally, we discuss possible implications for sub-ion-scale turbulence and future directions emerging from this study (section 5).
2. Data Sets
In the following, we consider three recent kinetic simulations in a six-dimensional phase space (“3D3V”) using: (i) CAMELIA, a hybrid particle-in-cell (PIC) code with massless electrons (Franci et al., 2018a), (ii) HVM, an Eulerian hybrid-Vlasov code with finite electron-inertia effects (Valentini et al., 2007), and (iii) OSIRIS, a fully kinetic PIC code (Fonseca et al., 2002, 2013). Unless otherwise specified, parallel (||) and perpendicular (⊥) directions are defined with respect to the global mean magnetic field B0 = B0ez. Franci et al. (2018b) employed the CAMELIA code to investigate freely decaying, Alfvénic fluctuations in a cubic box (L|| = L⊥ = 128di with 5123 grid points and 2048 particles per cell (ppc)) for βi = βe = 0.5, where is the species beta. Cerri et al. (2017b) instead adopted the HVM code to study freely decaying compressive fluctuations in an elongated box (L|| = 2L⊥ ≃ 63di with 3842 × 64 grid points in real space, and 513 points in a velocity space bounded by |v/vth, i| ≤ 5) for βi = βe = 1 and with a reduced ion-electron mass ratio of mi/me = 100 (viz. including de-effects in a generalized Ohm's law). Spectral filters were applied at runtime, determining a cutoff in the turbulent spectrum at k⊥di > 20 and at kzdi > 2. Finally, Grošelj et al. (2019) use the OSIRIS code to investigate continuously driven Alfvénic fluctuations in a βi ≈ βe ≈ 0.5 plasma with mi/me = 100. An elongated box was used (L|| = 2.56L⊥ ≃ 48.3di with 9282 × 1920 grid points and 150 ppc per species). An example of in a two-dimensional cut perpendicular to B0 is given in Figure 1A, along with a schematic representation of these simulations in the (k⊥, k||) plane (Figure 1B).
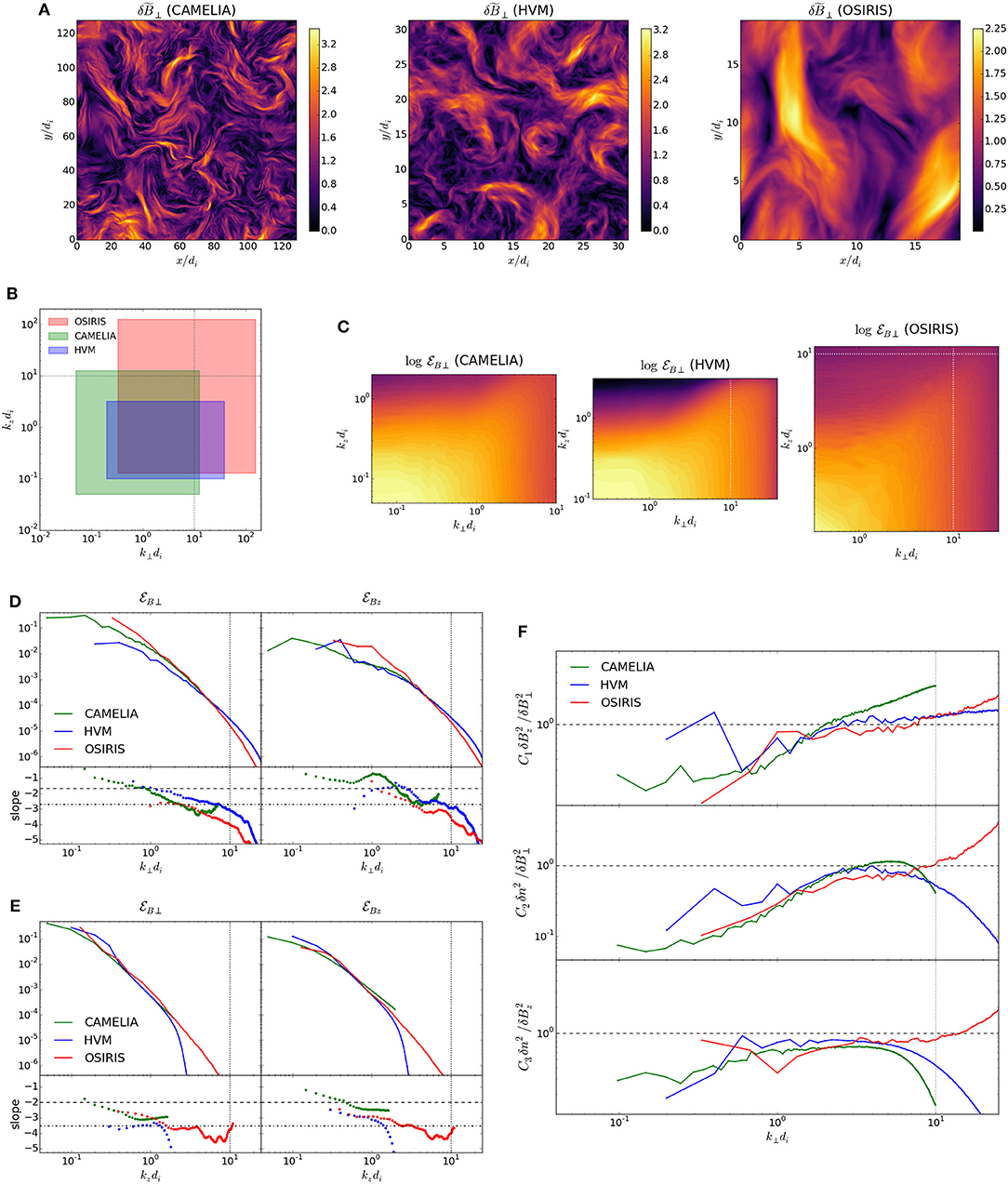
Figure 1. (A) in a plane perpendicular to B0. (B) Nominal wavenumber-space representation of simulations. (C) δB⊥ spectrum in (k⊥, kz) space. White dotted lines mark kde = 1. (D) Top panels: reduced spectra vs. k⊥di. Spectra have been shifted (see text). Bottom panels: local spectral exponents. Horizontal lines denote −5/3 (dashed) and −8/3 (dash-dotted) slopes. Vertical dotted line marks k⊥de = 1. (D) Same as (E), but vs. kzdi. Here −2 (dashed) and −7/2 (dash-dotted) slopes are marked for reference. (F) Spectral ratios vs. k⊥, normalized to the asymptotic KAW prediction (dashed horizontal lines; see text for details).
In the following, the analysis of freely decaying simulations (viz., CAMELIA and HVM) is performed at the peak of the turbulent activity (cf., e.g., Servidio et al., 2015), while for the continuously driven OSIRIS run we consider the turbulence at the end of the simulation when the kinetic range spectra appear converged. Following Franci et al. (2018b) and Grošelj et al. (2019), PIC data have been filtered before performing the analysis to remove spectral regions dominated by particle noise. The OSIRIS data have been filtered for k⊥di > 30 or kzdi > 12 and downsampled to a grid 4642 × 640. Note that OSIRIS simulations require to resolve the Debye scale, while the physical scales of interest are well represented at a lower resolution. A short-time average over ΔtΩce = 2 (Ωce being the electron cyclotron frequency) was also performed to further reduce electron-scale noise (Grošelj et al., 2019). The CAMELIA data have been filtered for k⊥di > 10 or kzdi > 2. We also considered alternative filtering approaches confirming that our results are not very sensitive to such particular choice.
3. Spectral Slopes and Normalized Field Ratios
Here we review and compare the standard set of spectral properties in our independently performed 3D kinetic simulations, namely the slopes of the turbulence power spectra and the spectral field ratios. Early theoretical predictions for sub-ion-range turbulence (e.g., Cho and Lazarian, 2004; Schekochihin et al., 2009) proposed a spectral scaling for the magnetic energy spectrum. However, solar wind observations typically exhibit much steeper magnetic spectra, namely (e.g., Alexandrova et al., 2009, 2013; Sahraoui et al., 2010; Chen, 2016; Kobayashi et al., 2017; Sorriso-Valvo et al., 2018). Similar spectral exponents were also reported in recent 3D kinetic simulations (Told et al., 2015; Cerri et al., 2017b, 2018; Franci et al., 2018a,b; Grošelj et al., 2018, 2019; Arzamasskiy et al., 2019). Recently, refined predictions were proposed to explain steeper spectra. Those include intermittency corrections (Boldyrev and Perez, 2012), dissipative effects (Howes et al., 2011; Passot and Sulem, 2015), and reconnection-mediated turbulence (Loureiro and Boldyrev, 2017; Mallet et al., 2017a). Further insight into the nature of kinetic-scale turbulence can be obtained from the spectral field ratios, which have been used to detect wave-like polarization properties in solar-wind turbulence and in kinetic simulations (e.g., Sahraoui et al., 2009; Salem et al., 2012; TenBarge et al., 2012; Chen et al., 2013; Kiyani et al., 2013; Cerri et al., 2017b; Franci et al., 2018b; Grošelj et al., 2018).
In Figure 1C the two-dimensional Fourier spectra, , are shown. The wavenumber region (k⊥, kz) occupied by the turbulent fluctuations already highlights the anisotropic nature of the cascade, with energy preferentially flowing to high k⊥. However, note that the 2D Fourier spectrum may exhibit a weaker anisotropy than the one typical of turbulent eddies, which are elongated along the local field direction (see, e.g., Cho and Vishniac, 2000). We perform a local analysis of anisotropy in section 4.1.
In Figures 1D,E, the reduced 1D spectra, (upper panels), and their local slope (lower panels) are reported. To remove the effects of different energy injection conditions, the k⊥-spectra have been normalized so that they overlap in the sub-ion range, at k⊥di ≃ 5. According to the spectral anisotropy in Figure 1C, the kz-spectra have been consequently matched at kzdi ≃ 0.5. For our choice of low-pass filter (see section 2), CAMELIA spectra artificially flatten beyond k⊥di ≳ 7 due to PIC noise, and therefore we do not show CAMELIA data in this range in Figure 1D. Overall, the spectral slopes are consistent with each other, although the spectra obtained from the three simulations do not quite assume a universal shape. Close to the box scale, the spectral exponents are likely affected by the turbulence injection details. It is also possible that some of the sub-ion scale spectral exponents are not fully converged in terms of the box size (which was different for each simulation) and of the limited extent of sub-ion range itself. 3D3V simulations with a significantly larger sub-ion range are required to clarify this point. To some degree, differences at sub-ion scales could also be physical. In particular, the HVM simulation includes electron inertia effects in Ohm's law, while the OSIRIS results include the full electron kinetics, such as electron Landau damping and finite electron Larmor radius corrections. It is interesting to notice that OSIRIS spectra become steeper than the hybrid counterparts beyond k⊥di ≳ 3, for our particular choice of the mass ratio (mi/me = 100). This feature has been usually explained in terms of electron Landau damping (Grošelj et al., 2017; Chen et al., 2019), which is not included in the hybrid-kinetic model.
In Figure 1F, we report the comparison of spectral ratios, (top), (middle), and (bottom). The ratios are normalized to the β-dependent kinetic Alfvén wave (KAW) eigenvalue from asymptotic linear theory ( and k|| ≪ k⊥), namely C1 = (2 + β)/β, C2 = (2 + β)β/4, and , where β = βi + βe (see, e.g., Boldyrev et al., 2013, for details). In the normalized units, asymptotic KAW theory predicts a value of unity for all three ratios. This is essentially the result of KAWs developing a certain degree of magnetic compressibility at sub-ion scales, which sets the relation between δB⊥ and δB||, and requiring that compressive magnetic fluctuations are pressure balanced, which in turn provides a relation between δB|| and δn (see, e.g., Schekochihin et al., 2009; Boldyrev et al., 2013). As found in previous studies (e.g., Salem et al., 2012; TenBarge et al., 2012; Chen et al., 2013; Cerri et al., 2017b; Franci et al., 2018b; Grošelj et al., 2018), the spectral field ratios are overall consistent with KAW-like turbulence at sub-ion scales. This is not completely surprising, as both in CAMELIA and OSIRIS simulations, Alfvénic fluctuations are injected. On the other hand, compressible magnetic fluctuations (i.e., including δB||) are injected in HVM run, and yet KAW-like fluctuations still develop. It was also proposed that KAWs may, quite generally, emerge as a result of Alfvén waves interacting with large-scale inhomogeneities (Pucci et al., 2016). Thus, the KAW-like spectral properties at sub-ion scales appear to be a relatively robust feature, independent of the details of the turbulent fluctuations injected at the MHD scales (cf. Cerri et al., 2017a). While the results are overall consistent, some differences are also seen, most notably in the high-k⊥ range (k⊥di ≳ 10), which could be presumably attributed to various numerical artifacts. However, some deviations could also relate to differences between the hybrid-kinetic and fully kinetic model [for instance, some dispersion relation properties not being exactly the same (e.g., Told et al., 2016)].
So are the sub-ion-scale field polarizations indeed KAW-like? As discussed above, recent observations and kinetic simulations are consistent with such idea, although linear wave predictions are not necessarily satisfied precisely (e.g., Chen et al., 2013; Kiyani et al., 2013; Cerri et al., 2017b; Franci et al., 2018b). Chen et al. (2013) report an average value of 0.75 for the normalized ratio , whereas (asymptotic) KAW theory predicts a value of unity. That latter may be due to different reasons, among which we remark the following two: (i) sub-ion-range turbulence is not made of purely KAW-like fluctuations, and/or (ii) the asymptotic conditions that are used in the derivation of linear theory predictions are not met exactly because of the limited sub-ion range of scales and/or because of the inherently non-linear dynamics of turbulence. These two explanations are not mutually exclusive, of course. Indeed, sub-ion-scale turbulence can in principle include contributions from wave-like fluctuations of other nature. This may include fluctuations consistent with whistler (e.g., Gary and Smith, 2009), ion-cyclotron (e.g., Omidi et al., 2014; Zhao et al., 2018), or ion Bernstein waves (e.g., Podesta, 2012; Del Sarto et al., 2017; Grošelj et al., 2017), to name a few. On the other hand, the spectral ratios could also deviate from linear KAW predictions as a result of non-linear dynamics. For example, Boldyrev et al. (2013) propose that, specifically the (normalized) ratio may fall somewhat below the KAW prediction due to a (yet to be investigated) non-linear effect, analogous to the residual-energy phenomenon in MHD turbulence.
4. Multi-Point Structure Functions
Beyond energy spectra, fluctuations across different scales may be investigated in more detail via structure functions, i.e., the moments of local field increments (e.g., Frisch, 1995; Biskamp, 2008). Two-point structure functions, (m being the order), are most common. However, these cannot quantitatively produce the correct scaling for fluctuations with power spectra steeper than ~ k−3, assuming a clean power-law spectrum (Falcon et al., 2007; Cho and Lazarian, 2009). Therefore, structure functions using more than two points are generally required at kinetic scales. Essentially, higher-order increments yield a scale decomposition that is more effective in filtering out the large-scale fluctuations below k ≈ π/ℓ in spectral space, where ℓ is the increment scale. We also mention that if the signal is a polynomial of degree , its corresponding 2nd-order, -point structure function vanishes (Cho, 2019). This makes multi-point structure functions more suitable for the analysis of relatively smooth signals with steep spectra (Schneider et al., 2004). A detailed review of -point increments, as well as their physical interpretation can be found in Cho (2019). Here, we consider for some field f(x) the conditional, five-point structure functions:
where is the (normalized) field increment, 〈… 〉x is a space average, and ϑBloc is the angle between the increment vector ℓ and the local mean magnetic field Bloc. The term “conditional” implies that Sm are defined as conditional averages of |Δf(x, ℓ)|m, using only those points in the statistical sample that fall within a given (narrow) range for ℓ and ϑBloc. We also considered three-point structure functions (see Figure 2A) and, for a limited number of cases, seven-point structure functions (not shown). Comparison between the three-point, five-point and seven-point structure functions shows not only qualitative similarities among the three cases, but an apparent quantitative convergence with increasing number of points. We chose to illustrate the results in Figure 2 in terms of five-point structure functions in order to provide better constraints for the theoretical predictions. Similar to two-point increments, where the local mean field is often defined as Bloc(x, ℓ) = [B(x) + B(x + ℓ)]/2 (e.g., Cho and Vishniac, 2000; Mallet et al., 2016), we obtain Bloc by averaging over the points used for the increment. For five-point increments, a reasonable definition is Bloc(x, ℓ) = [B(x + 2ℓ) + 4B(x + ℓ) + 6B(x) + 4B(x−ℓ) + B(x−2ℓ)]/16. It is straightforward to check that such mean field definition filters out fluctuations around the scale of the increment ~ ℓ, while preserving the contribution from scales larger than ℓ.
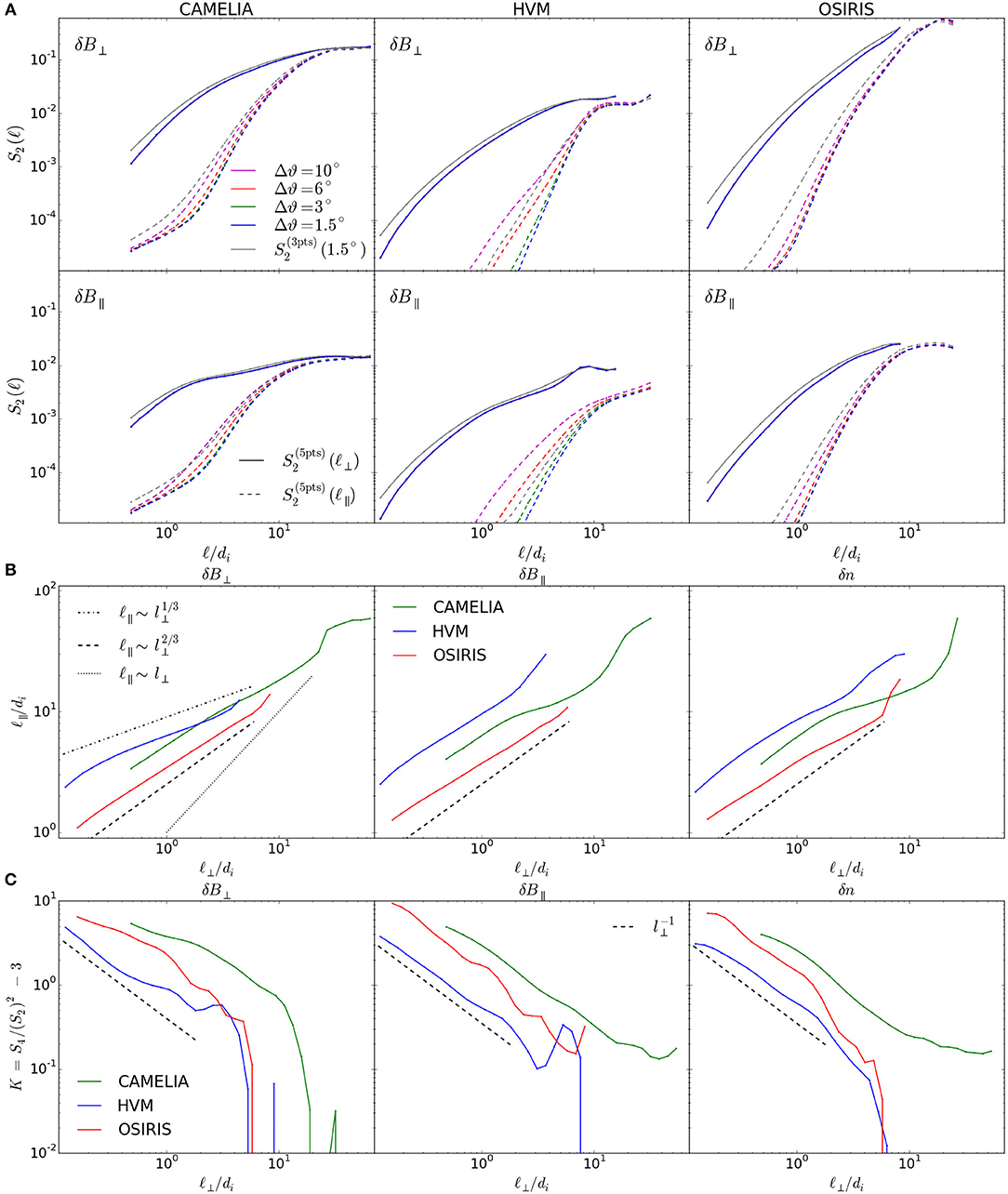
Figure 2. (A) Five-points, 2nd-order structure functions, , of δB⊥ (top row) and δB|| (bottom row) vs. ℓ⊥ (continuous lines) and ℓ|| (dashed lines). Here, || and ⊥ are defined with respect to the local field direction (i.e., δB|| ≠ δBz) with different angular tolerance, Δϑ (colored lines; see text for definition). with Δϑ = 1.5° are also shown for reference (gray lines). (B) Anisotropy scaling, ℓ||(ℓ⊥), of δB⊥ (left panel), δB|| (central panel), and δn (right panel), derived from with nominal resolution. Three reference scalings are also shown. (C) Excess kurtosis, vs. ℓ⊥ for δB⊥ (left panel), δB|| (central panel), and δn (right panel). A 1/ℓ⊥ scaling is given for reference.
In what follows, we consider field-perpendicular, , and field-parallel, , five-point structure functions of the magnetic field and density fluctuations, where Δϑ represents a finite angular tolerance used in practice to determine the local perpendicular and parallel directions. We reduce Δϑ until the scalings appear converged. The field increments, from which we obtain the conditional structure functions, are evaluated at every grid point. In each grid point and at every scale, increments are sampled along random directions. The numbers of these random directions per grid point have been tested to provide a statistically significant (i.e., converged) sample. The sample that is used in the following is such that any structure function Sm(ℓ, ϑBloc) counts at least 1.5 × 105 points per scale ℓ, in any given band for ϑBloc.
4.1. Spectral Anisotropy
A delicate point concerns the sub-ion-range spectral anisotropy, (cf., e.g., Schekochihin et al., 2009; Boldyrev and Perez, 2012; Cerri et al., 2018; Landi et al., 2019). As is known from MHD, electron-MHD (EMHD), and kinetic-reduced-MHD (KRMHD) turbulence (Cho and Vishniac, 2000; Cho and Lazarian, 2009; Meyrand et al., 2019), the true anisotropy is often revealed only when measured with respect to the local, scale-dependent mean magnetic-field direction. Somewhat contradicting estimates, obtained with different methods, for the sub-ion-scale anisotropy have been presented in recent works. Here, we revisit this issue using the above-mentioned implementation of five-point structure functions, consistently applied to all data.
In Figure 2A we show the perpendicular and parallel second-order structure function scalings, and in Figure 2B we show the inferred anisotropy, ℓ||(ℓ⊥). The characteristic parallel length ℓ||(ℓ⊥) at a given perpendicular scale ℓ⊥ is obtained by finding the value of ℓ||, at which the amplitudes of S2(ℓ||) and S2(ℓ⊥) match. To illustrate the sensitivity to the local mean field direction, we show in Figure 2A the convergence with respect to the angular tolerance Δϑ. The parallel scalings appear converged at Δϑ ≃ 3° for CAMELIA data and at around Δϑ ≃ 1.5° for HVM, whereas the OSIRIS results are somewhat less sensitive to Δϑ (converging already for Δϑ ≃ 6°). This difference may occur because OSIRIS simulation exhibits the weakest anisotropy (in absolute values). Physically, Δϑ should be approximately no larger than ~ ℓ⊥/ℓ|| of the small-scale turbulent eddies. Thus, smaller Δϑ are needed if a stronger anisotropy develops at the energy-containing scales.
All quantities seem to converge to a scaling close to (although δB⊥ fluctuations in HVM exhibit a scaling closer to 1/3 over the range of scales across ℓ ⊥ ~ di(= ρi)). It is worth noticing, however, that this is not the end of the story, as the scaling is not quite 2/3 and additional effects such as B-field curvature may slightly change the anisotropy. Indeed, the field increments are taken along a straight line. If the local magnetic field lines are significantly curved over the extent of the increment stencil (= 4ℓ for five-point increments), the field increments will mix contributions from different field lines, in which case the anisotropy may be somewhat underestimated. It is worth mentioning that a scaling was proposed in Boldyrev and Perez (2012), based on a filling-factor correction for the fluctuation energy. Assuming the energy is concentrated in intermittent, two-dimensional structures as in Boldyrev and Perez (2012), the filling factor should scale as . The filling factor may be approximately estimated from the inverse scaling of the excess kurtosis (Matthaeus et al., 2015; see section 4.2). Our results shown in Figure 2C are indeed roughly consistent with an excess kurtosis scaling , although this approximate scaling is overall better satisfied for δB∥ and δn than for δB⊥. Finally, we mention that an alternative anisotropy estimate, based on a spectral band-pass filter (Cho and Lazarian, 2009), gives a somewhat stronger anisotropy than the five-point structure functions (not shown). On the other hand, qualitatively similar results are still obtained for all data. Thus, all simulations analyzed exhibit a similar sub-ion-scale anisotropy according to the particular diagnostics employed. Therefore, the differences that were previously reported in the literature could be mainly related to the different methods employed.
4.2. Intermittency: The “Saturation Problem”
Another relevant feature of kinetic plasma turbulence is the excess kurtosis of the fluctuations, . The increase of K(ℓ⊥) above zero is a measure of non-Gaussian statistics of the turbulent fluctuations (Frisch, 1995; Matthaeus et al., 2015). As seen in Figure 2C, the excess kurtosis gradually increases above the Gaussian value throughout the sub-ion scale range. Moreover, similar statistical trends are seen for δB⊥, δB∥, and δn [note that we take here the component of δB⊥ parallel to ℓ × Bloc to estimate the flatness of δB⊥ (see also Kiyani et al., 2013)]. In apparent contrast with our results, a number of observational studies of solar wind turbulence find non-Gaussian, yet nearly scale-independent turbulence statistics at sub-ion scales (Kiyani et al., 2009, 2013; Wu et al., 2013; Chen et al., 2014). Thus, it appears a process operates in the solar wind that saturates the turbulence statistics already near the transition to sub-ion scales (ℓ⊥ ≲ di). What could be the reason for this apparent contradiction? One clear difference is that the solar-wind fluctuations are already heavily non-Gaussian at MHD scales (Salem et al., 2009), whereas our 3D kinetic simulations do not quite share the same feature due to the limited simulation domain. We mention that even large-size 2D kinetic simulations (e.g., Wan et al., 2012; Franci et al., 2015; Leonardis et al., 2016) did not yet achieve K(ℓ⊥) ≫ 1 in the MHD range (ℓ⊥ ≫ di). In this context, it may be worth pointing out that intermittency in MHD turbulence is commonly associated with the emergence of sheetlike structures (e.g., Chandran et al., 2015; Matthaeus et al., 2015; Mallet and Schekochihin, 2017), which may break apart via the tearing instability (causing the field lines to reconnect), once their perpendicular aspect ratio exceeds a critical threshold (Matthaeus and Lamkin, 1986; Boldyrev and Loureiro, 2017; Mallet et al., 2017b). For sub-ion-scale turbulence, the possible role of magnetic reconnection has been as well highlighted in a number of recent works (e.g., Franci et al., 2016, 2017; Cerri and Califano, 2017; Loureiro and Boldyrev, 2017; Mallet et al., 2017a; Papini et al., 2019). Moreover, a recent observational study (Vech et al., 2018) argued that the spectral break at the tail of the MHD cascade may be controlled by reconnection. Therefore, the phenomenology of the cascade may critically depend on the morphology of the intermittent structures at the transition into the kinetic range (Mallet et al., 2017a). If the structures are indeed sufficiently sheetlike to be tearing unstable, collisionless reconnection might be one possible process that limits the growth of the sub-ion scale kurtosis (see also Biskamp et al., 1990; Chen et al., 2014). However, alternative possibilities such as collisionless damping of the fluctuations cannot be ruled out at this stage.
5. Concluding Remarks
So, what is the nature of sub-ion-scale fluctuations? From our independently performed 3D3V (hybrid and fully) kinetic simulations, a picture consistent with KAW turbulence phenomenology emerges. Moreover, our results imply a scale-dependent anisotropy, together with intermittent statistics of magnetic and density fluctuations at sub-ion scales. Thus, we conclude that within the range of parameters explored here, the statistical properties of ion-scale plasma turbulence (at β ~ 1) definitely show a certain degree of similarity, regardless of the precise details of the large-scale energy injection. On the other hand, slight differences can also be identified, some of which may be also model-dependent.
A number of key aspects will have to await the next-generation of 3D3V kinetic simulations. Ideally, future numerical experiments should aim to resolve both larger (MHD) scales, as well as a broader range between the ion and the electron scales by adopting significantly higher (if not realistic) mass ratios. These two aspects indeed appear to be both required in order to achieve (i) a possible saturation of the kurtosis at ion scales and (ii) a relevant sub-ion range of scales before electron-scale effects significantly come into play. Moreover, different aspects other than the spectral and statistical properties of the turbulent fluctuations will need to be considered in characterizing kinetic-range turbulence, as for instance, the dissipation mechanisms of turbulent fluctuations under different plasma conditions and the consequent energy partition among different species (e.g., Matthaeus et al., 2016; Parashar et al., 2018; Arzamasskiy et al., 2019; Kawazura et al., 2019; Zhdankin et al., 2019).
While certain progress was definitely achieved in recent years, many other plasma regimes and setups may need to be explored, and the process(es) underlying a possible universality of kinetic-range plasma turbulence (e.g., magnetic reconnection) need to be fully worked out. Moreover, a few relevant discrepancies between numerical simulations, theories and in-situ observations appear. These “anomalies” definitely call for an explanation by the space physics community. In this context, advances cannot be achieved without investing in next-generation multi-spacecraft missions. Multi-point in situ measurements of turbulent fluctuations from a large number of spacecrafts are indeed fundamental in order to disentangle the non-linear spatio-temporal character of plasma turbulence (see, e.g., Klein et al., 2019; Matthaeus et al., 2019; TenBarge et al., 2019). This includes answering fundamental questions about, for instance, (i) the distribution of turbulent energy in space and time, (ii) the three-dimensional anisotropic structure of energy transfer across scales, (iii) the high-order statistics of the fluctuations, and (iv) the validity of Taylor's hypothesis over a broad range of time and spatial scales. Alongside observations, advances in computational capabilities are required to perform more realistic numerical simulations as discussed above, and compare these with spacecraft measurements. Finally, following the same spirit promoted by the “Turbulent Dissipation Challenge” (Parashar et al., 2015), we would like to end this Perspective by stressing that our community could benefit from comparisons such as the one performed here, involving various codes, models and diagnostics.
Note added: Arzamasskiy et al. (2019) recently reported a scale-independent anisotropy at ion scales (i.e., ℓ∥ ~ ℓ⊥) based on a set of 3D driven hybrid-kinetic turbulence simulations. Using our structure function diagnostic applied to their data, we were able to qualitatively (and quantitatively) reproduce their result. A more detailed investigation along these lines is currently ongoing, but beyond the scope of this Perspective and will be presented elsewhere.
Data Availability Statement
The data used in this study are available from the authors upon reasonable request.
Author Contributions
SC, DG, and LF provided their HVM, OSIRIS, and CAMELIA simulation data, respectively. SC performed the spectral analysis, produced the figures, and wrote the paper, taking into account suggestions from DG and LF. DG implemented and performed the structure function analysis. All authors discussed the results.
Funding
SC was supported by the National Aeronautics and Space Administration under Grant No. NNX16AK09G issued through the Heliophysics Supporting Research Program. LF was supported by the UK Science and Technology Facilities Council (STFC) grant ST/P000622/1.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
SC and DG acknowledge the generous hospitality of the Wolfgang Pauli Institute in Vienna, where the first discussions leading to this work took place. We acknowledge PRACE for awarding us access to Marconi at CINECA, Italy, where the calculations with the HVM code were performed under the grant No. 2017174107. The Cray XC40, Shaheen, at the King Abdullah University of Science and Technology (KAUST) in Thuwal, Saudi Arabia was utilized for the simulation performed with the OSIRIS code. LF acknowledges PRACE for awarding him access to Cartesius at SURFsara, the Netherlands, through the DECI-13 (Distributed European Computing Initiative) call (project HybTurb3D) where the HPIC simulation was performed, and INAF and CINECA for awarding him access to Marconi within the framework of the MoU New Frontiers in Astrophysics: HPC and New Generation Data Exploration (project INA17_C4A26), where new further analysis of the HPIC data has been performed. The authors would like to acknowledge the OSIRIS Consortium, consisting of UCLA and IST (Lisbon, Portugal) for the use of OSIRIS 3.0 and for providing access to the OSIRIS 3.0 framework. SC acknowledges Dr. C. Cavazzoni and Dr. M. Guarrasi (CINECA, Italy) for their contributions to HVM code parallelization, performance and implementation on Marconi-KNL. The authors also acknowledge useful discussions with Alfred Mallet, Lev Arzamasskiy, Bill Dorland, Matt Kunz, Simone Landi, Emanuele Papini, Frank Jenko, and David Burgess.
References
Adkins, T., and Schekochihin, A. A. (2018). A solvable model of Vlasov-kinetic plasma turbulence in FourierHermite phase space. J. Plasma Phys. 84:905840107. doi: 10.1017/S0022377818000089
Alexandrova, O., Chen, C. H. K., Sorriso-Valvo, L., Horbury, T. S., and Bale, S. D. (2013). Solar wind turbulence and the role of ion instabilities. Space Sci. Rev. 178, 101–139. doi: 10.1007/s11214-013-0004-8
Alexandrova, O., Lacombe, C., Mangeney, A., Grappin, R., and Maksimovic, M. (2012). Solar wind turbulent spectrum at plasma kinetic scales. Astrophys. J. 760:121. doi: 10.1088/0004-637X/760/2/121
Alexandrova, O., Saur, J., Lacombe, C., Mangeney, A., Mitchell, J., Schwartz, S. J., et al. (2009). Universality of solar-wind turbulent spectrum from MHD to electron scales. Phys. Rev. Lett. 103:165003. doi: 10.1103/PhysRevLett.103.165003
Arzamasskiy, L., Kunz, M. W., Chandran, B. D. G., and Quataert, E. (2019). Hybrid-kinetic simulations of ion heating in alfvénic turbulence. Astrophys. J. 879:53. doi: 10.3847/1538-4357/ab20cc
Bañón Navarro, A., Teaca, B., Told, D., Groselj, D., Crandall, P., and Jenko, F. (2016). Structure of plasma heating in gyrokinetic alfvénic turbulence. Phys. Rev. Lett. 117:245101. doi: 10.1103/PhysRevLett.117.245101
Biskamp, D., Welter, H., and Walter, M. (1990). Statistical properties of two-dimensional magnetohydrodynamic turbulence. Phys. Fluids B 2:3024.
Boldyrev, S., Horaites, K., Xia, Q., and Perez, J. C. (2013). Toward a theory of astrophysical plasma turbulence at subproton scales. Astrophys. J. 777:41. doi: 10.1088/0004-637X/777/1/41
Boldyrev, S., and Loureiro, N. F. (2017). Magnetohydrodynamic turbulence mediated by reconnection. Astrophys. J. 844:125. doi: 10.3847/1538-4357/aa7d02
Boldyrev, S., and Perez, J. C. (2012). Spectrum of kinetic-alfvén turbulence. Astrophys. J. Lett. 758:L44. doi: 10.1088/2041-8205/758/2/L44
Bruno, R., and Carbone, V. (2013). The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10:2. doi: 10.12942/lrsp-2013-2
Cerri, S. S., and Califano, F. (2017). Reconnection and small-scale fields in 2D-3V hybrid-kinetic driven turbulence simulations. New J. Phys. 19:025007. doi: 10.1088/1367-2630/aa5c4a
Cerri, S. S., Califano, F., Jenko, F., Told, D., and Rincon, F. (2016). Subproton-scale cascades in solar wind turbulence: driven hybrid-kinetic simulations. Astrophys. J. Lett. 822:L12. doi: 10.3847/2041-8205/822/1/L12
Cerri, S. S., Franci, L., Califano, F., Landi, S., and Hellinger, P. (2017a). Plasma turbulence at ion scales: a comparison between particle in cell and Eulerian hybrid-kinetic approaches. J. Plasma Phys. 83:705830202. doi: 10.1017/S0022377817000265
Cerri, S. S., Kunz, M. W., and Califano, F. (2018). Dual phase-space cascades in 3D hybrid-vlasov-maxwell turbulence. Astrophys. J. Lett. 856:L13. doi: 10.3847/2041-8213/aab557
Cerri, S. S., Servidio, S., and Califano, F. (2017b). Kinetic cascade in solar-wind turbulence: 3D3V hybrid-kinetic simulations with electron inertia. Astrophys. J. Lett. 846:L18. doi: 10.3847/2041-8213/aa87b0
Chandran, B. D. G., Schekochihin, A. A., and Mallet, A. (2015). Intermittency and alignment in strong RMHD turbulence. Astrophys. J. 807:39. doi: 10.1088/0004-637X/807/1/39
Chasapis, A., Matthaeus, W. H., Parashar, T. N., Fuselier, S. A., Maruca, B. A., Phan, T. D., et al. (2017). High-resolution statistics of solar wind turbulence at kinetic scales using the magnetospheric multiscale mission. Astrophys. J. Lett. 844:L9. doi: 10.3847/2041-8213/aa7ddd
Chen, C. H. K. (2016). Recent progress in astrophysical plasma turbulence from solar wind observations. J. Plasma Phys. 82:535820602. doi: 10.1017/S0022377816001124
Chen, C. H. K., and Boldyrev, S. (2017). Nature of kinetic scale turbulence in the Earth's magnetosheath. Astrophys. J. 842:122. doi: 10.3847/1538-4357/aa74e0
Chen, C. H. K., Boldyrev, S., Xia, Q., and Perez, J. C. (2013). Nature of subproton scale turbulence in the solar wind. Phys. Rev. Lett. 110:225002. doi: 10.1103/PhysRevLett.110.225002
Chen, C. H. K., Horbury, T. S., Schekochihin, A. A., Wicks, R. T., Alexandrova, O., and Mitchell, J. (2010). Anisotropy of solar wind turbulence between ion and electron scales. Phys. Rev. Lett. 104:255002. doi: 10.1103/PhysRevLett.104.255002
Chen, C. H. K., Klein, K. G., and Howes, G. G. (2019). Evidence for electron Landau damping in space plasma turbulence. Nat Commun. 10:740. doi: 10.1038/s41467-019-08435-3
Chen, C. H. K., Sorriso-Valvo, L., Šafránková, J., and Němeček, Z. (2014). Intermittency of solar wind density fluctuations from ion to electron scales. Astrophys. J. Lett. 789:L8. doi: 10.1088/2041-8205/789/1/L8
Cho, J. (2019). A technique for removing large-scale variations in regularly and irregularly spaced data. Astrophys. J. 874:75. doi: 10.3847/1538-4357/ab06f3
Cho, J., and Lazarian, A. (2004). The anisotropy of electron magnetohydrodynamic turbulence. Astrophys. J. Lett. 615, L41–L44. doi: 10.1086/425215
Cho, J., and Lazarian, A. (2009). Simulations of electron magnetohydrodynamic turbulence. Astrophys. J. 701, 236–252. doi: 10.1088/0004-637X/701/1/236
Cho, J., and Vishniac, E. T. (2000). The anisotropy of magnetohydrodynamic Alfvénic turbulence. Astrophys. J. 539, 273–282. doi: 10.1086/309213
Comişel, H., Nariyuki, Y., Narita, Y., and Motschmann, U. (2016). On the role of ion-scale whistler waves in space and astrophysical plasma turbulence. Ann. Geophys. 34, 975–984. doi: 10.5194/angeo-34-975-2016
Del Sarto, D., Pegoraro, F., and Tenerani, A. (2017). ‘Magneto-elastic' waves in an anisotropic magnetised plasma. Plasma Phys. Control. Fusion 59:045002. doi: 10.1088/1361-6587/aa56bd
Eyink, G. L. (2018). Cascades and dissipative anomalies in nearly collisionless plasma turbulence. Phys. Rev. X 8:041020. doi: 10.1103/PhysRevX.8.041020
Falcon, E., Fauve, S., and Laroche, C. (2007). Observation of intermittency in wave turbulence. Phys. Rev. Lett. 98:154501. doi: 10.1103/PhysRevLett.98.154501
Fonseca, R. A., Silva, L. O., Tsung, F. S., Decyk, V. K., Lu, W., Ren, C., et al. (2002). OSIRIS: a three-dimensional, fully relativistic particle in cell Code for modeling plasma based accelerators. Lecture Notes Comput. Sci. 2331:342–351. doi: 10.1007/3-540-47789-636
Fonseca, R. A., Vieira, J., Fiuza, F., Davidson, A., Tsung, F. S., Mori, W. B., et al. (2013). Exploiting multi-scale parallelism for large scale numerical modelling of laser wakefield accelerators. Plasma Phys. Control. Fusion 55:124011. doi: 10.1088/0741-3335/55/12/124011
Franci, L., Cerri, S. S., Califano, F., Landi, S., Papini, E., Verdini, A., et al. (2017). Magnetic reconnection as a driver for a sub-ion-scale cascade in plasma turbulence. Astrophys. J. Lett. 850:L16. doi: 10.3847/2041-8213/aa93fb
Franci, L., Hellinger, P., Guarrasi, M., Chen, C. H. K., Papini, E., Verdini, A., et al. (2018a). Three-dimensional simulations of solar wind turbulencewith the hybrid code camelia. J. Phys. Conf. Ser. 1031:012002. doi: 10.1088/1742-6596/1031/1/012002
Franci, L., Landi, S., Matteini, L., Verdini, A., and Hellinger, P. (2015). High-resolution hybrid simulations of kinetic plasma turbulence at proton scales. Astrophys. J. 812:21. doi: 10.1088/0004-637X/812/1/21
Franci, L., Landi, S., Matteini, L., Verdini, A., and Hellinger, P. (2016). Plasma beta dependence of the ion-scale spectral break of solar Wind turbulence: high-resolution 2D hybrid simulations. Astrophys. J. 833:91. doi: 10.3847/1538-4357/833/1/9
Franci, L., Landi, S., Verdini, A., Matteini, L., and Hellinger, P. (2018b). Solar wind turbulent cascade from MHD to sub-ion scales: large-size 3D hybrid particle-in-cell simulations. Astrophys. J. 853:26. doi: 10.3847/1538-4357/aaa3e8
Frisch, U. (1995). Turbulence. The Legacy of A. N. Kolmogorov. Cambridge: Cambridge University Press.
Galtier, S., and Bhattacharjee, A. (2003). Anisotropic weak whistler wave turbulence in electron magnetohydrodynamics. Phys. Plasmas 10, 3065–3076. doi: 10.1063/1.1584433
Gary, S. P., Chang, O., and Wang, J. (2012). Forward cascade of whistler turbulence: three-dimensional particle-in-cell simulations. Astrophys. J. 755:142. doi: 10.1088/0004-637X/755/2/142
Gary, S. P., and Nishimura, K. (2004). Kinetic Alfvén waves: linear theory and a particle-in-cell simulation. J. Geophys. Res. 109:A02109. doi: 10.1029/2003JA010239
Gary, S. P., and Smith, C. W. (2009). Short-wavelength turbulence in the solar wind: linear theory of whistler and kinetic Alfvén fluctuations. J. Geophys. Res. 114:A12105. doi: 10.1029/2009JA014525
Greco, A., Perri, S., Servidio, S., Yordanova, E., and Veltri, P. (2016). The complex structure of magnetic field discontinuities in the turbulent solar wind. Astrophys. J. 823:L39. doi: 10.3847/2041-8205/823/2/L39
Grošelj, D., Cerri, S. S., Bañón Navarro, A., Willmott, C., Told, D., Loureiro, N. F., et al. (2017). Fully kinetic versus reduced-kinetic modeling of collisionless plasma turbulence. Astrophys. J. 847:28. doi: 10.3847/1538-4357/aa894d
Grošelj, D., Chen, C. H. K., Mallet, A., Samtaney, R., Schneider, K., and Jenko, F. (2019). Kinetic turbulence in astrophysical plasmas: waves and/or structures? Phys. Rev. X 9:031037. doi: 10.1103/PhysRevX.9.031037
Grošelj, D., Mallet, A., Loureiro, N. F., and Jenko, F. (2018). Fully kinetic simulation of 3D kinetic Alfvén Turbulence. Phys. Rev. Lett. 120:105101. doi: 10.1103/PhysRevLett.120.105101
He, J., Tu, C., Marsch, E., and Yao, S. (2012). Do oblique Alfvén/Ion-cyclotron or fast-mode/whistler waves dominate the dissipation of solar wind turbulence near the proton inertial length? Astrophys. J. Lett. 745:L8. doi: 10.1088/2041-8205/745/1/L8
Howes, G. G., Cowley, S. C., Dorland, W., Hammett, G. W., Quataert, E., and Schekochihin, A. A. (2008a). A model of turbulence in magnetized plasmas: implications for the dissipation range in the solar wind. J. Geophys. Res. 113:A05103. doi: 10.1029/2007JA012665
Howes, G. G., Dorland, W., Cowley, S. C., Hammett, G. W., Quataert, E., Schekochihin, A. A., et al. (2008b). Kinetic simulations of magnetized turbulence in astrophysical plasmas. Phys. Rev. Lett. 100:065004. doi: 10.1103/PhysRevLett.100.065004
Howes, G. G., Tenbarge, J. M., and Dorland, W. (2011). A weakened cascade model for turbulence in astrophysical plasmas. Phys. Plasmas 18, 102305–102305. doi: 10.1063/1.3646400
Huang, S. Y., Hadid, L. Z., Sahraoui, F., Yuan, Z. G., and Deng, X. H. (2017). On the existence of the kolmogorov inertial range in the terrestrial magnetosheath turbulence. Astrophys. J. Lett. 836:L10. doi: 10.3847/2041-8213/836/1/L10
Hughes, R. S., Gary, S. P., and Wang, J. (2017a). Particle-in-cell simulations of electron and ion dissipation by whistler turbulence: variations with electron β. Astrophys. J. 835:L15. doi: 10.3847/2041-8213/835/1/L15
Hughes, R. S., Gary, S. P., Wang, J., and Parashar, T. N. (2017b). Kinetic Alfvén turbulence: electron and ion heating by particle-in-cell simulations. Astrophys. J. Lett. 847:L14. doi: 10.3847/2041-8213/aa8b13
Kawazura, Y., Barnes, M., and Schekochihin, A. A. (2019). Thermal disequilibration of ions and electrons by collisionless plasma turbulence. Proc. Natl. Acad. Sci. U.S.A 116, 771–776. doi: 10.1073/pnas.1812491116
Kiyani, K. H., Chapman, S. C., Khotyaintsev, Y. V., Dunlop, M. W., and Sahraoui, F. (2009). Global scale-invariant dissipation in collisionless plasma turbulence. Phys. Rev. Lett. 103:075006. doi: 10.1103/PhysRevLett.103.075006
Kiyani, K. H., Chapman, S. C., Sahraoui, F., Hnat, B., Fauvarque, O., and Khotyaintsev, Y. V. (2013). Enhanced magnetic compressibility and isotropic scale invariance at sub-ion larmor scales in solar wind turbulence. Astrophys. J. 763:10. doi: 10.1088/0004-637X/763/1/10
Klein, K. G., Alexandrova, O., Bookbinder, J., Caprioli, D., Case, A. W., Chandran, B. D. G., et al. (2019). [Plasma 2020 Decadal] multipoint measurements of the solar wind: a proposed advance for studying magnetized turbulence. arXiv [Pre-print]. arXiv:1903.05740.
Kobayashi, S., Sahraoui, F., Passot, T., Laveder, D., Sulem, P. L., Huang, S. Y., et al. (2017). Three-dimensional simulations and spacecraft observations of sub-ion scale turbulence in the solar wind: influence of landau damping. Astrophy. J. 839:122. doi: 10.3847/1538-4357/aa67f2
Kunz, M. W., Abel, I. G., Klein, K. G., and Schekochihin, A. A. (2018). Astrophysical gyrokinetics: turbulence in pressure-anisotropic plasmas at ion scales and beyond. J. Plasma Phys. 84:715840201. doi: 10.1017/S0022377818000296
Lacombe, C., Alexandrova, O., and Matteini, L. (2017). Anisotropies of the magnetic field fluctuations at kinetic scales in the solar wind: cluster observations. Astrophys. J. 848:45. doi: 10.3847/1538-4357/aa8c06
Landi, S., Franci, L., Papini, E., Verdini, A., Matteini, L., and Hellinger, P. (2019). Spectral anisotropies and intermittency of plasma turbulence at ion kinetic scales. arXiv [Pree-print]. arXiv:1904.03903.
Leamon, R. J., Smith, C. W., Ness, N. F., Matthaeus, W. H., and Wong, H. K. (1998). Observational constraints on the dynamics of the interplanetary magnetic field dissipation range. J. Geophys. Res. 103, 4775–4788. doi: 10.1029/97JA03394
Leonardis, E., Sorriso-Valvo, L., Valentini, F., Servidio, S., Carbone, F., and Veltri, P. (2016). Multifractal scaling and intermittency in hybrid Vlasov-Maxwell simulations of plasma turbulence. Phys. Plasmas 23:022307. doi: 10.1063/1.4942417
Loureiro, N. L., and Boldyrev, S. (2017). Collisionless reconnection in magnetohydrodynamic and kinetic turbulence. Astrophys. J. 850:182.
Mallet, A., and Schekochihin, A. A. (2017). A statistical model of three-dimensional anisotropy and intermittency in strong alfvénic turbulence. Mon. Not. R. Astron. Soc. 466:3918. doi: 10.1093/mnras/stw3251
Mallet, A., Schekochihin, A. A., and Chandran, B. D. G. (2017a). Disruption of Alfvénic turbulence by magnetic reconnection in a collisionless plasma. J. Plasma Phys. 83:905830609. doi: 10.1017/S0022377817000812
Mallet, A., Schekochihin, A. A., and Chandran, B. D. G. (2017b). Disruption of sheet-like structures in Alfvénic turbulence by magnetic reconnection. Mon. Not. R. Astron. Soc. 468, 4862–4871. doi: 10.1093/mnras/stx670
Mallet, A., Schekochihin, A. A., Chandran, B. D. G., Chen, C. H. K., Horbury, T. S., Wicks, R. T., et al. (2016). Measures of three-dimensional anisotropy and intermittency in strong alfvénic turbulence. Mon. Not. R. Astron. Soc. 459:2130. doi: 10.1093/mnras/stw802
Matthaeus, W. H., Bandyopadhyay, R., Brown, M. R., Borovsky, J., Carbone, V., Caprioli, D., et al. (2019). [Plasma 2020 Decadal] the essential role of multi-point measurements in turbulence investigations: the solar wind beyond single scale and beyond the Taylor Hypothesis. arXiv [Pre-print]. arXiv:1903.06890.
Matthaeus, W. H., and Lamkin, S. L. (1986). Turbulent magnetic reconnection. Phys. Fluids 29, 2513–2534.
Matthaeus, W. H., Oughton, S., Osman, K. T., Servidio, S., Wan, M., Gary, S. P., et al. (2014). Nonlinear and linear timescales near kinetic scales in solar wind turbulence. Astrophys. J. 790:155. doi: 10.1088/0004-637X/790/2/155
Matthaeus, W. H., Parashar, T. N., Wan, M., and Wu, P. (2016). Turbulence and proton-electron heating in kinetic plasma. Astrophys. J. Lett. 827:L7. doi: 10.3847/2041-8205/827/1/L7
Matthaeus, W. H., Wan, M., Servidio, S., Greco, A., Osman, K. T., Oughton, S., et al. (2015). Intermittency, nonlinear dynamics and dissipation in the solar wind and astrophysical plasmas. Philos. Trans. Roy. Soc. Lond. Ser. A 373:20140154. doi: 10.1098/rsta.2014.0154
Meyrand, R., Kanekar, A., Dorland, W., and Schekochihin, A. A. (2019). Fluidization of collisionless plasma turbulence. Proc. Natl. Acad. Sci. U.S.A. 116, 1185–1194. doi: 10.1073/pnas.1813913116
Narita, Y., Nakamura, R., Baumjohann, W., Glassmeier, K.-H., Motschmann, U., Giles, B., et al. (2016). On electron-scale whistler turbulence in the solar wind. Astrophys. J. Lett. 827:L8. doi: 10.3847/2041-8205/827/1/L8
Omidi, N., Isenberg, P., Russell, C. T., Jian, L. K., and Wei, H. Y. (2014). Generation of ion cyclotron waves in the corona and solar wind. J. Geophys. Res. 119, 1442–1454. doi: 10.1002/2013JA019474
Papini, E., Franci, L., Landi, S., Verdini, A., Matteini, L., and Hellinger, P. (2019). Can hall magnetohydrodynamics explain plasma turbulence at sub-ion scales? Astrophys. J. 870:52. doi: 10.3847/1538-4357/aaf003
Parashar, T. N., Matthaeus, W. H., and Shay, M. A. (2018). Dependence of kinetic plasma turbulence on plasma β. Astrophys. J. Lett. 864:L21. doi: 10.3847/2041-8213/aadb8b
Parashar, T. N., Salem, C., Wicks, R. T., Karimabadi, H., Gary, S. P., and Matthaeus, W. H. (2015). Turbulent dissipation challenge: a community-driven effort. J. Plasma Phys. 81:905810513. doi: 10.1017/S0022377815000860
Passot, T., and Sulem, P. L. (2015). A model for the non-universal power law of the solar wind sub-ion-scale magnetic spectrum. Astrophys. J. Lett. 812:L37. doi: 10.1088/2041-8205/812/2/L37
Passot, T., and Sulem, P. L. (2019). Imbalanced kinetic Alfv\'en wave turbulence: from weak turbulence theory to nonlinear diffusion models for the strong regime. arXiv [Pre-print]. arXiv:1902.04295.
Passot, T., Sulem, P. L., and Tassi, E. (2018). Gyrofluid modeling and phenomenology of low-βe Alfvén wave turbulence. Phys. Plasmas 25:042107. doi: 10.1063/1.5022528
Pezzi, O., Servidio, S., Perrone, D., Valentini, F., Sorriso-Valvo, L., Greco, A., et al. (2018). Velocity-space cascade in magnetized plasmas: numerical simulations. Phys. Plasmas. 25:060704. doi: 10.1063/1.5027685
Podesta, J. J. (2012). The need to consider ion Bernstein waves as a dissipation channel of solar wind turbulence. J. Geophys. Res. 117:A07101. doi: 10.1029/2012JA017770
Podesta, J. J., and TenBarge, J. M. (2012). Scale dependence of the variance anisotropy near the proton gyroradius scale: additional evidence for kinetic Alfvén waves in the solar wind at 1 AU. J. Geophys. Res. 117:A10106. doi: 10.1029/2012JA017724
Pucci, F., Vásconez, C. L., Pezzi, O., Servidio, S., Valentini, F., Matthaeus, W. H., et al. (2016). From Alfvén waves to kinetic Alfvén waves in an inhomogeneous equilibrium structure. J. Geophys. Res. 121, 1024–1045. doi: 10.1002/2015JA022216
Roberts, O. W., Narita, Y., and Escoubet, C. P. (2017). Direct measurement of anisotropic and asymmetric wave vector spectrum in ion-scale solar wind turbulence. Astrophys. J. 851:L11. doi: 10.3847/2041-8213/aa9bf3
Roytershteyn, V., Boldyrev, S., Delzanno, G. L., Chen, C. H. K., Grošelj, D., and Loureiro, N. F. (2019). Numerical study of inertial kinetic-alfvén turbulence. Astrophys. J. 870:103. doi: 10.3847/1538-4357/aaf288
Sahraoui, F., Belmont, G., and Goldstein, M. L. (2012). New insight into short-wavelength solar wind fluctuations from vlasov theory. Astrophys. J. 748:100. doi: 10.1088/0004-637X/748/2/100
Sahraoui, F., Goldstein, M. L., Belmont, G., Canu, P., and Rezeau, L. (2010). Three dimensional anisotropic k spectra of turbulence at subproton scales in the solar wind. Phys. Rev. Lett. 105:131101. doi: 10.1103/PhysRevLett.105.131101
Sahraoui, F., Goldstein, M. L., Robert, P., and Khotyaintsev, Y. V. (2009). Evidence of a cascade and dissipation of solar-wind turbulence at the electron gyroscale. Phys. Rev. Lett. 102:231102. doi: 10.1103/PhysRevLett.102.231102
Salem, C., Mangeney, A., Bale, S. D., and Veltri, P. (2009). Solar wind magnetohydrodynamics turbulence: anomalous scaling and role of intermittency. Astrophys. J. 702:537. doi: 10.1088/0004-637X/702/1/537
Salem, C. S., Howes, G. G., Sundkvist, D., Bale, S. D., Chaston, C. C., Chen, C. H. K., et al. (2012). Identification of kinetic Alfvén wave turbulence in the solar wind. Astrophys. J. Lett. 745:L9. doi: 10.1088/2041-8205/745/1/L9
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Plunk, G. G., et al. (2008). Gyrokinetic turbulence: a nonlinear route to dissipation through phase space. Plasma Phys. Control. Fusion 50:124024. doi: 10.1088/0741-3335/50/12/124024
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E., et al. (2009). Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. 182, 310–377. doi: 10.1088/0067-0049/182/1/310
Schneider, K., Farge, M., and Kevlahan, N. (2004). “Spatial intermittency in two-dimensional turbulence: a wavelet approach,” in Woods Hole Mathematics, Perspectives in Mathematics and Physics, Vol 34, eds N. Tongring and R. C. Penner (Singapore: World Scientific), 302–328. doi: 10.1142/97898127013980007
Servidio, S., Chasapis, A., Matthaeus, W. H., Perrone, D., Valentini, F., Parashar, T. N., et al. (2017). Magnetospheric multiscale observation of plasma velocity-space cascade: hermite representation and theory. Phys. Rev. Lett. 119:205101. doi: 10.1103/PhysRevLett.119.205101
Servidio, S., Valentini, F., Perrone, D., Greco, A., Califano, F., Matthaeus, W. H., et al. (2015). A kinetic model of plasma turbulence. J. Plasma Phys. 81:325810107. doi: 10.1017/S0022377814000841
Sorriso-Valvo, L., Carbone, F., Perri, S., Greco, A., Marino, R., and Bruno, R. (2018). On the statistical properties of turbulent energy transfer rate in the inner heliosphere. Sol. Phys. 293:10. doi: 10.1007/s11207-017-1229-6
Stawicki, O., Gary, S. P., and Li, H. (2001). Solar wind magnetic fluctuation spectra: dispersion versus damping. J. Geophys. Res. 106, 8273–8282. doi: 10.1029/2000JA000446
TenBarge, J. M., Alexandrova, O., Boldyrev, S., Califano, F., Cerri, S. S., Chen, C. H. K., et al. (2019). [Plasma 2020 Decadal] Disentangling the spatiotemporal structure of turbulence using multi-spacecraft data. arXiv [Preprint]. arXiv:1903.05710.
TenBarge, J. M., and Howes, G. G. (2013). Current sheets and collisionless damping in kinetic plasma turbulence. Astrophys. J. Lett. 771:L27. doi: 10.1088/2041-8205/771/2/L27
TenBarge, J. M., Podesta, J. J., Klein, K. G., and Howes, G. G. (2012). Interpreting magnetic variance anisotropy measurements in the solar wind. Astrophys. J. 753:107. doi: 10.1088/0004-637X/753/2/107
Told, D., Cookmeyer, J., Muller, F., Astfalk, P., and Jenko, F. (2016). Comparative study of gyrokinetic, hybrid-kinetic and fully kinetic wave physics for space plasmas. New J. Phys. 18:065011. doi: 10.1088/1367-2630/18/6/065011
Told, D., Jenko, F., TenBarge, J. M., Howes, G. G., and Hammett, G. W. (2015). Multiscale nature of the dissipation range in gyrokinetic simulations of alfvénic turbulence. Phys. Rev. Lett. 115:025003. doi: 10.1103/PhysRevLett.115.025003
Valentini, F., Trávníček, P., Califano, F., Hellinger, P., and Mangeney, A. (2007). A hybrid-Vlasov model based on the current advance method for the simulation of collisionless magnetized plasma. JCoPh 225, 753–770. doi: 10.1016/j.jcp.2007.01.001
Valentini, F., Vásconez, C. L., Pezzi, O., Servidio, S., Malara, F., and Pucci, F. (2017). Transition to kinetic turbulence at proton scales driven by large-amplitude kinetic Alfvén fluctuations. Astron. Astrophys. 599:A8. doi: 10.1051/0004-6361/201629240
Vásconez, C. L., Pucci, F., Valentini, F., Servidio, S., Matthaeus, W. H., and Malara, F. (2015). Kinetic alfvén wave generation by large-scale phase mixing. Astrophys. J. 815:7. doi: 10.1088/0004-637X/815/1/7
Vásconez, C. L., Valentini, F., Camporeale, E., and Veltri, P. (2014). Vlasov simulations of kinetic Alfvén waves at proton kinetic scales. Phys. Plasmas 21:112107. doi: 10.1063/1.4901583
Vasquez, B. J., Markovskii, S. A., and Chandran, B. D. G. (2014). Three-dimensional hybrid simulation study of anisotropic turbulence in the proton kinetic regime. Astrophys. J. 788:178. doi: 10.1088/0004-637X/788/2/178
Vech, D., Mallet, A., Klein, K. G., and Kasper, J. C. (2018). Magnetic reconnection may control the ion-scale spectral break of solar wind turbulence. Astrophys. J. Lett. 855:L27. doi: 10.3847/2041-8213/aab351
Verscharen, D., Klein, K. G., and Maruca, B. A. (2019). The multi-scale nature of the solar wind. arXiv [Pre-print]. arXiv:1902.03448.
Wan, M., Matthaeus, W. H., Karimabadi, H., Roytershteyn, V., Shay, M., Wu, P., et al. (2012). Intermittent dissipation at kinetic scales in collisionless plasma turbulence. Phys. Rev. Lett. 109:195001. doi: 10.1103/PhysRevLett.109.195001
Wan, M., Matthaeus, W. H., Roytershteyn, V., Karimabadi, H., Parashar, T., Wu, P., et al. (2015). Intermittent dissipation and heating in 3D kinetic plasma turbulence. Phys. Rev. Lett. 114:175002. doi: 10.1103/PhysRevLett.114.175002
Wan, M., Matthaeus, W. H., Roytershteyn, V., Parashar, T. N., Wu, P., and Karimabadi, H. (2016). Intermittency, coherent structures and dissipation in plasma turbulence. Phys. Plasmas 23:042307. doi: 10.1063/1.4945631
Wu, P., Perri, S., Osman, K., Wan, M., Matthaeus, W. H., Shay, M. A., et al. (2013). Intermittent heating in solar wind and kinetic simulations. Astrophys. J. Lett. 763:L30. doi: 10.1088/2041-8205/763/2/L30
Zhao, G. Q., Feng, H. Q., Wu, D. J., Liu, Q., Zhao, Y., Zhao, A., et al. (2018). Statistical study of low-frequency electromagnetic cyclotron waves in the solar wind at 1 AU. J. Geophys. Res. 123, 1715–1730. doi: 10.1002/2017JA024979
Zhao, J. S., Voitenko, Y. M., Wu, D. J., and Yu, M. Y. (2016). Kinetic Alfvén turbulence below and above ion cyclotron frequency. J. Geophys. Res. 121, 5–18. doi: 10.1002/2015JA021959
Keywords: magnetic fields, plasma turbulence, solar wind, kinetic plasma simulations, turbulence intermittency, plasma waves
Citation: Cerri SS, Grošelj D and Franci L (2019) Kinetic Plasma Turbulence: Recent Insights and Open Questions From 3D3V Simulations. Front. Astron. Space Sci. 6:64. doi: 10.3389/fspas.2019.00064
Received: 26 June 2019; Accepted: 20 September 2019;
Published: 11 October 2019.
Edited by:
Denise Perrone, Agenzia Spaziale Italiana, ItalyReviewed by:
Christian L. Vásconez, National Polytechnic School, EcuadorStephen Peter Gary, Space Science Institute, United States
Copyright © 2019 Cerri, Grošelj and Franci. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Silvio Sergio Cerri, c2NlcnJpJiN4MDAwNDA7YXN0cm8ucHJpbmNldG9uLmVkdQ==
 Silvio Sergio Cerri
Silvio Sergio Cerri Daniel Grošelj
Daniel Grošelj Luca Franci
Luca Franci