Reconstruction of a Highly Twisted Magnetic Flux Rope for an Inter-active-region X-Class Solar Flare

Solar eruptions are manifestation of explosive release of magnetic energy in the Sun's corona. Large solar eruptions originate mostly within active regions, where strong magnetic fields concentrate on the solar surface. Here we studied the magnetic field structure for an exception, which is a peculiar GOES X1.2 flare accompanied with a very fast coronal mass ejection taking place between two active regions, where the magnetic field is relatively weak. The pre-flare magnetic field is reconstructed from the SDO/HMI vector magnetogram, using a non-linear force-free field extrapolation method. It is found that prior to the flare, there is a highly twisted magnetic flux rope with magnetic field lines winding over 6 turns, which connects the border of a leading sunspot of one active region and the following polarity of the neighboring active region. The basic configuration of the flux rope is consistent with the observed sigmoidal coronal loops and filament channels by SDO/AIA. It resides rather low-lying between the active regions such that the torus instability is not able to be triggered. Thus, it is likely that, due to the strong magnetic twist, the kink instability of the flux rope triggers the eruption.

1. Introduction

The catastrophic energy-conversion phenomena, such as solar flares and coronal mass ejections (CMEs) from the sun can heavily influence the space weather and human activities in modern society. Now it is well-recognized that the Sun's magnetic field plays a key role in such solar explosive transients (Forbes et al., 2006; Chen, 2011; Shibata and Magara, 2011; Cheng et al., 2017; Guo et al., 2017), thus it is paramount to understand the underlying magnetic field structure for a reliable forecast of solar eruptions. Strong flares and CMEs originated mostly from solar active regions (ARs), where high concentrations of magnetic field clusters (Toriumi and Wang, 2019). In particular, major flares (e.g., those above GOES X-class) occurred predominantly from the site of magnetic polarity inversion lines (PILs) at the photosphere which possess strong magnetic shear as well as high magnetic gradient. Such PILs are often found in δ-sunspot groups (that is, two sunspots with inverse signs of magnetic polarity share the same penumbra), possibly as a result of colliding of magnetic flux tubes during their emergence from right below the photosphere (Fang and Fan, 2015).

However, there are exceptions, although rather few. By surveying the flare events above GOES M5 with 45° from the disk center between 2010 and 2016 (Toriumi et al., 2017), it is found that, out of a total number of 51 flares, there are 2 events that took place between ARs where the PIL is in a relatively weak field without significant magnetic shear and gradient. Among them is an X1.2 flare, and this inter-AR flare produced an extremely fast CME (above 1,800 km/s). From a space weather perspective, this is an important event as forecasters expected a significant impact (a G3 class geomagnetic storm or higher) on the Earth, yet it did not occur. Thus, attentions have been attracted in many papers to study the CME propagation, attempting to reveal why it is significantly deflected from the solar disk center to the Mars by a longitude of over 40° (Mays et al., 2015; Möstl et al., 2015; Wang et al., 2015; Zheng et al., 2016; Zagainova and Fainshtein, 2018). Nevertheless, it is still not clear what is the source magnetic field structure that triggers the eruption. Why such a weak field region can produce such strong flare and fast CME?

In this paper, using a coronal magnetic field reconstruction method, we reveal that prior to the flare, there is a highly twisted magnetic flux rope (MFR) with magnetic twist number reaching over 6 turns. Overall, the configuration of MFR is consistent with the observed sigmoidal coronal loops and filament channels, and it is likely the source structure leading to the eruption of the flare and CME through kink instability. The rest of the paper is organized as follows: section 2 present the observations; section 3 gives a brief description of the coronal magnetic reconstruction method; section 4 shows the reconstructed MFR, and finally conclusions are made in section 5.

2. Observations

The X1.2 flare occurred between two neighboring ARs, numbered as NOAA 11944 and 11943, on 2014 January 7, associated with a very fast halo CME with linear speed of ~1,830 km/s. Figure 1 shows the source region and the flare loops observed by the Solar Dynamics Observatory (SDO), as well as the CME observed by STEREO. The flare started at 18:04 UT, peaked at 18:32 UT and ended at 18:58 UT. As shown in Figure 1, the flare site (or the CME source region) is located at S12W08, which is close to the disk center, between the ARs 11944 (S09W01) and 11943 (S11W19).

FIGURE 1

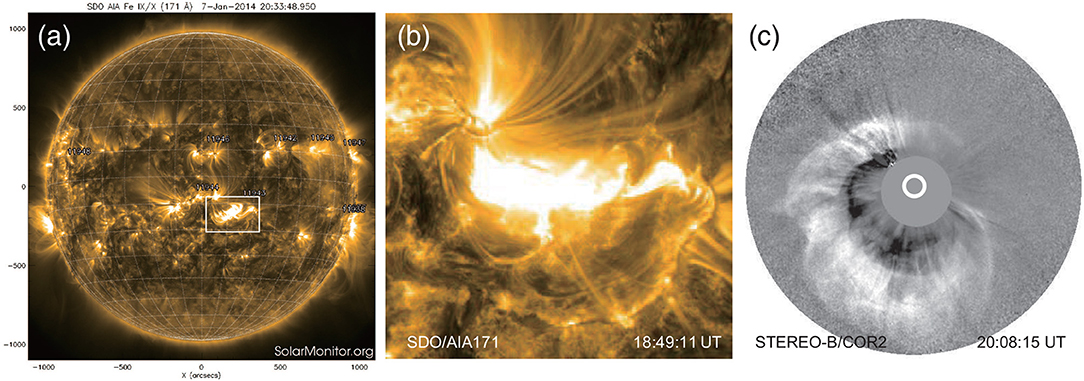
Figure 1. (a) Location of the flare site in a full-disk SDO/AIA 171 Å image. The number of the ARs are labeled, and the boxed region denotes the flare site. (b) Enlarged view of the flaring loops during the X1.2 flare. (c) A running difference image of the CME from the flare region observed by STEREO-B/COR2.

In Figure 2, we further show the source region with SDO/HMI magnetogram. Three ARs cluster forming a complicate system, which is usually very active for eruptions because of the underlying complex magnetic topology. There are mainly four polarities of two pairs forming the ARs 11944 and 11943, respectively. The leading sunspot of AR 11944 has a positive polarity (P1, which has a field strength up to ~3,000 G), and a high-gradient PIL divides it with its following sunspot of polarity N1. However, the X1.2 flare did not take place along this strong-gradient PIL. Rather, it occurred mainly along the relatively weak-gradient PIL dividing P1 and the negative polarity (N2) of the neighboring AR, 11943, thus the negative polarity (N1) of AR 11944 barely contributed to the flare. Furthermore, there are secondary flare ribbons extending along the PIL of AR 11943 (N2-P2), as it seems that N2 is surrounded by P1 and P2.

FIGURE 2

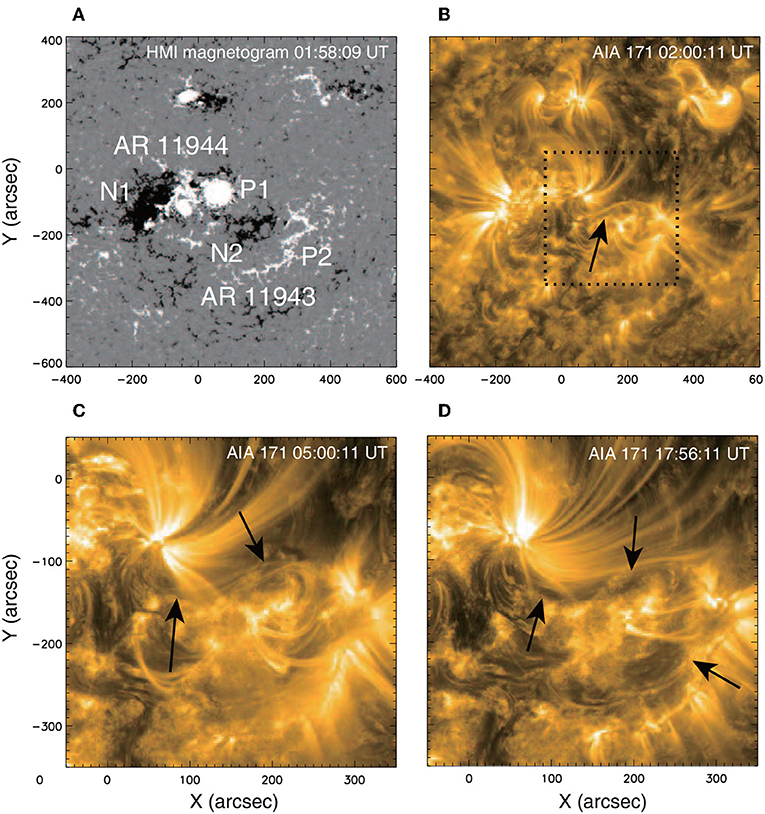
Figure 2. (A) SDO/HMI magnetogram showing the distribution of magnetic polarities around the flare site. The main polarities are labeled as N1 and P1, which constitute AR 11944, and N2 and P2, which constitute AR 11943. The flare occurred mainly in association with P1 and N2. (B) SDO/AIA 171 Å image of the same field view of (A). The arrow remarks a sigmoidal coronal loop in the flare site. (C) Enlarged view of the sigmoid as well as a filament as denoted by the arrows. (D) The filament channels as denoted by the arrows.

There are several pieces of evidences indicating the existence of a long MFR between the two ARs prior to the flare. Firstly, there is a sigmoidal coronal loop connecting P1 and N2 (Figures 2B,C), which has a length of at least 300 arcsec. The west elbow is more prominent, roughly following the PIL between polarities N2 and P2. Secondly, almost co-aligned with the sigmoidal loop, there is a filament observed in AIA images (see Figure 2C). Last, a filament channel, which is relatively dark, can be clearly seen in the AIA 171 Å image a few hours before the flare (Figure 2D). Overall its structure is complex and rather segmented, but the major part of the filament channel has a very similar S shape as the sigmoidal loops. Wang et al. (2015) has performed a NLFFF reconstruction for this region using the Wiegelmann (2004)'s NLFFF code. Although they also conjectured that an MFR exists in the flare site, but the NLFFF code failed to reproduce such an MFR.

3. Coronal Magnetic Field Reconstruction

We carried out 3D magnetic field reconstruction for the pre-flare corona from the SDO/HMI vector magnetograms using the CESE–MHD–NLFFF code (Jiang and Feng, 2013). In particular, we used the data product of the Space-weather HMI Active Region Patch (SHARP, Bobra et al., 2014), in which the 180° ambiguity has been resolved by using the minimum energy method, the coordinate system has been modified via the Lambert method, and the projection effect has been corrected. Here the magnetogram is taken at the time of 17:48 UT, about 20 min before the flare. The CESE–MHD–NLFFF code is based on an MHD-relaxation method which seeks approximately force-free equilibrium. It solves a set of modified zero-β MHD equations with a friction force using an advanced conservation-element/solution-element (CESE) space-time scheme on a non-uniform grid with parallel computing (Jiang et al., 2010; Duan et al., 2018). The code also utilizes adaptive mesh refinement and a multi-grid algorithm to optimize the relaxation process. This model has been tested by different benchmarks including a series of analytic force-free solutions (Low and Lou, 1990) and numerical MFR models (Titov and Démoulin, 1999). The results of extrapolation reproduced from SDO/HMI are in good agreement with corresponding observable features like filaments, coronal loops, and sigmoids (Jiang and Feng, 2013; Jiang et al., 2014). Especially, among the NLFFF methods that use solely vector magnetograms as input, it seems that only the CESE–MHD–NLFFF code can reconstruct MFR in a weak field region, for example, Jiang et al. (2014) successfully reconstructed a large-scale MFR corresponding to an intermediate filament in the boundary of the AR 11283. In this paper, we applied the same code to the inter-AR region producing the X1.2 flare. It should be noted that there are other ways for modeling MFR in such weak-field region, for instance, the flux-rope insertion method (Su and van Ballegooijen, 2012) can also reconstruct MFR matching observations by inserting an MFR following observed filament channel into a background potential field. In particular, an MFR was also reconstructed in a weak field region between two ARs (Zhou et al., 2019) using the flux-rope insertion method.

4. The MFR

From the reconstructed field, MFR can be precisely located by calculating the magnetic twist number T_w in the whole computation volume, which is defined by

$\begin{array}{ll}{T}_w={\displaystyle {\int }_L}\frac{(\nabla \times B)·B}{4\pi B^2}dl& (1)\end{array}$

where the integral is taken along the length L of the magnetic field line from one footpoint on the photosphere to the other (Liu et al., 2016). We find a right-handed, significantly twisted MFR, indicating a positive helicity. In Figure 3, we show the iso-surfaces with T_w = 3 and T_w = 6, which are the surfaces of a flux volume with field-line winding number above 3 and 6 turns, respectively. Although interrupted by many small-scale structures, the volume of the strong twisted flux is coherent, forming a forward S shape, in agreement with the sigmoidal loops seen in AIA 171 Å image as well as the filament channel seen in the AIA 304 Å image. The maximum value of T_w in the MFR reaches ~6.5, and the corresponding field line can be a proxy of the axis of the rope, as suggested by Liu et al. (2016). In the bottom panels, we show sampled magnetic field lines of the rope with different colors, and the rope axis is colored in white. As can be seen, the field lines start from the penumbra of the big sunspot of AR 11944, wind tightly around the axis, run very lowly above the bottom surface in the central part, and finally end in the negative polarity (N2) of AR 11943.

FIGURE 3

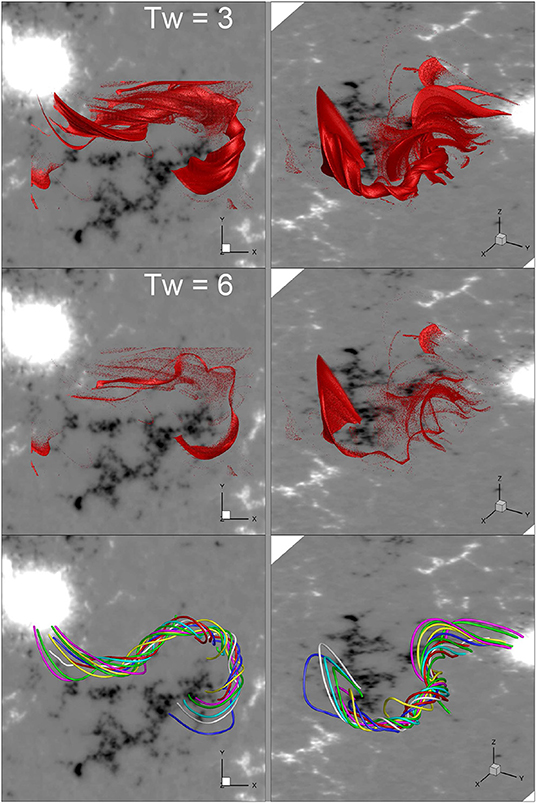
Figure 3. Top: iso-surface of magnetic twist number T_w = 3 in two different angles of view. Middle: iso-surface of magnetic twist number T_w = 6. Bottom: sampled magnetic field lines of the MFR in different views. Note that the lines colored in white represent the axis of the rope, i.e., the one that possesses the maximum value of T_w = 6.5.

With the data of magnetic field, we can search the location where the filament material can likely be sustained. Such place are magnetic dips where the magnetic field lines concave upward such that the magnetic tension points upward to support the heavy cold filament mass. The magnetic dips are defined as locations where $\overrightarrow{B}\cdot \nabla B_z>0$ and B_z = 0. In Figure 4, we show the magnetic dips. There is clearly a spine of magnetic dips, which extend to a height of ~7 Mm above the photosphere, and overall the shape looks co-spatial with the filament observed in AIA 171 Å image in Figure 2C.

FIGURE 4

Figure 4. Two different views of distribution of magnetic dips, which is shown by the colored structures, and the colors represent the heights of the dips.

We further study the ideal MHD instabilities of the MFR. There are two kinds of ideal instabilities that prevail in the study of eruption of coronal MFRs. One is the torus instability (TI) which occurs if the strapping field that stabilizing the MFR decreases with height too fast, and the control parameter is its decay index (Kliem and Török, 2006). The decay index n is defined as

$\begin{array}{ll}n=\frac{dlog(B)}{dlog(h)}& (2)\end{array}$

where B denotes the strapping field stabilizing the MFR and h is the height. Theoretically derived threshold for the decay index is found in the range of 1–2 (Kliem and Török, 2006; Fan and Gibson, 2007; Török and Kliem, 2007; Aulanier et al., 2010; Démoulin and Aulanier, 2010). In Figure 5, we show the MFR and its strapping flux, which is approximated by the potential field model based on the vertical component of the magnetogram. As can be seen the magnetic flux connecting the big sunspot of P1 and the negative polarity N2 plays the main role in confining the MFR. In the right panel of Figure 5, we show an iso-surface of decay index n = 0.5, above which the decay index is larger than 0.5. As can be clearly seen, the main body of the MFR situated below the iso-surface. Regarding that the TI threshold is mostly above 1, we concluded that this MFR is far below such threshold and the TI cannot be the trigger of the eruption.

FIGURE 5

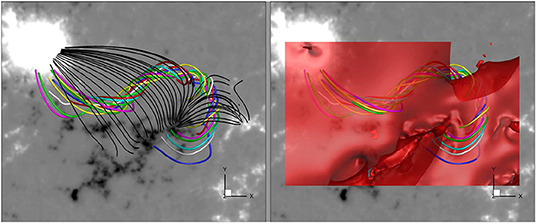
Figure 5. Left: the color lines represent the MFR, while the black lines show sampled field lines of the strapping field overlying the MFR. These field lines are plotted using the potential field model extrapolated from the vertical component of the magnetogram. Right: the red, transparent surface is the iso-surface with magnetic decay index n = 0.5, and as can be seen, the significant part of the MFR is below the surface.

Then we consider the other instability, the kink instability (KI, Török and Kliem, 2005). If the MFR is twisted too much, KI occurs with the rope axis experiences an eruptive deformation. Unfortunately, there seems to be no unique value for the threshold of KI, since it depends on many details of the MFR, for example, the overall shape, the distribution of magnetic twist, the aspect ratio, etc. Theoretical and numerical investigations have shown the KI threshold, which is a critical value of the magnetic twist number, seems to reside in the range of 1.25–2.5 turns (Fan and Gibson, 2003; Török et al., 2004; Török and Kliem, 2005). However, since these results are derived using a simple and idealized MFR models, for example, a half-circle current torus (Titov and Démoulin, 1999), while the MFRs reconstructed from the real data often show very different configurations with strong asymmetry and non-uniform magnetic twist, thus it is not easy to apply directly the theoretical values to the reconstructed solution. Here the reconstructed MFR has a very large magnetic twist as well as a rather complex configuration. Considering the strong twist, the KI is most likely the candidate of the eruption trigger. We should also remind the readers that cautions are needed here because different coronal field reconstruction methods might give very different results with the same magnetogram. Further analysis of the formation and growth of the MFR is necessary to see how the magnetic twist evolves before the eruption. Also the magnetic-reconnection trigger cannot be excluded here because of the complex magnetic topology of the flare site. It has been found that the MFR's overlying magnetic field has a null-point-like magnetic topology (Wang et al., 2015), and the flare has a large, almost circular-shaped weak ribbon. Thus, the breakout reconnection model might also play a role in triggering the flare. A further investigation is deserved for studying the background magnetic topology as well as its evolution associated with the development of the MFR.

5. Conclusions

In this paper, we studied the coronal magnetic field for a peculiar inter-AR, X-class eruptive flare which occurred in a relatively weak-field region between two ARs. Using the CESE–MHD–NLFFF code and the SDO/HMI vector magnetogram, we reconstructed a highly twisted MFR before the flare, which is not found in previous NLFFF extrapolations (e.g., Wang et al., 2015). The existence of such pre-flare MFR is indicated by several pieces of evidences, such as the sigmoidal coronal loops, the filament and filament channel, and the overall configuration of the reconstructed MFR resembles well with all these observed features. The MFR has a maximum magnetic twist number of 6.5, but resides rather low-lying between the ARs such the TI is not able to be triggered. It is likely that, due to the strong magnetic twist, the KI of the MFR triggers the eruption.

Thus we can provide an answer to the question as arised in section 1: why such a weak field region can produce such strong flare and fast CME? Although the flare occurred in the weak-field region as indicated by the magnetogram, overlying the weak-field region is a highly twisted MFR which connects the penumbra of a leading sunspot of one active region and the following polarity of the neighboring active region. Thus, the magnetic field of the MFR is actually not weak, and more importantly, its high twist and large size indicate that lots of non-potential energy is accumulated in the large volume. It can provide free magnetic energy to power the flare and meanwhile it offers a mechanism for trigger the eruption by, possibly, KI of the MFR. Last, it should be noted that the existence of a highly twisted MFR in such a weak-field region seems unusual since the magnetogram shows no significant magnetic shear. Further investigation on the existence of the MFR in different time and particularly on how it was formed will be carried out in the near future.

Data Availability Statement

All datasets generated for this study are included in the manuscript/supplementary files.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was jointly supported by National Natural Science Foundation of China (NSFC 41822404, 41731067, 41574170, 41531073), the Fundamental Research Funds for the Central Universities (Grant No. HIT.BRETIV.201901), the China Postdoctoral Science Foundation (2018M641812), and Shenzhen Technology Project JCYJ20180306171748011. Data from observations are courtesy of NASA SDO/AIA and the HMI science teams.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with the authors CJ and AD.

References

Aulanier, G., Török, T., Démoulin, P., and DeLuca, E. E. (2010). Formation of torus-unstable flux ropes and electric currents in erupting sigmoids. Astrophys. J. 708, 314–333. doi: 10.1088/0004-637X/708/1/314

CrossRef Full Text | Google Scholar

Bobra, M. G., Sun, X., Hoeksema, J. T., Turmon, M., Liu, Y., Hayashi, K., et al. (2014). The helioseismic and magnetic imager (HMI) vector magnetic field pipeline: SHARPs–space-weather HMI active region patches. Sol. Phys. 289, 3549–3578. doi: 10.1007/s11207-014-0529-3

CrossRef Full Text | Google Scholar

Chen, P. F. (2011). Coronal mass ejections: Models and their observational basis. Liv. Rev. Sol. Phys. 8:1. doi: 10.12942/lrsp-2011-1

CrossRef Full Text | Google Scholar

Cheng, X., Guo, Y., and Ding, M. (2017). Origin and structures of solar eruptions I: magnetic flux rope. Sci. China Earth Sci. 60, 1383–1407. doi: 10.1007/s11430-017-9074-6

CrossRef Full Text | Google Scholar

Démoulin, P., and Aulanier, G. (2010). Criteria for flux rope eruption: non-equilibrium versus torus instability. Astrophys. J. 718, 1388–1399. doi: 10.1088/0004-637X/718/2/1388

CrossRef Full Text | Google Scholar

Duan, A. Y., Zhang, H., and Lu, H. Y. (2018). 3D MHD simulation of the double-gradient instability of the magnetotail current sheet. Sci. China Technol. Sci. 61, 104–111. doi: 10.1007/s11431-017-9158-7

CrossRef Full Text | Google Scholar

Fan, Y., and Gibson, S. E. (2003). The emergence of a twisted magnetic flux tube into a preexisting coronal arcade. Astrophys. J. 589, L105–L108. doi: 10.1086/375834

CrossRef Full Text | Google Scholar

Fan, Y., and Gibson, S. E. (2007). Onset of coronal mass ejections due to loss of confinement of coronal flux ropes. Astrophys. J. 668, 1232–1245. doi: 10.1086/521335

CrossRef Full Text | Google Scholar

Fang, F., and Fan, Y. (2015). δ-sunspot formation in simulation of active-region-scale flux emergence. Astrophys. J. 806:79. doi: 10.1088/0004-637X/806/1/79

CrossRef Full Text | Google Scholar

Forbes, T. G., Linker, J. A., Chen, J., Cid, C., Kóta, J., Lee, M. A., et al. (2006). CME theory and models. Space Sci. Rev. 123, 251–302. doi: 10.1007/s11214-006-9019-8

CrossRef Full Text | Google Scholar

Guo, Y., Cheng, X., and Ding, M. (2017). Origin and structures of solar eruptions II: magnetic modeling. Sci. China Earth Sci. 60, 1408–1439. doi: 10.1007/s11430-017-9081-x

CrossRef Full Text | Google Scholar

Jiang, C., and Feng, X. (2013). Extrapolation of the solar coronal magnetic field from SDO/HMI magnetogram by a CESE-MHD-NLFFF code. Astrophys. J. 769:144. doi: 10.1088/0004-637X/769/2/144

CrossRef Full Text | Google Scholar

Jiang, C., Wu, S. T., Feng, X., and Hu, Q. (2014). Nonlinear force-free field extrapolation of a coronal magnetic flux rope supporting a large-scale solar filament from a photospheric vector magnetogram. Astrophys. J. Lett. 786:L16. doi: 10.1088/2041-8205/786/2/L16

CrossRef Full Text | Google Scholar

Jiang, C. W., Feng, X. S., Zhang, J., and Zhong, D. K. (2010). AMR simulations of magnetohydrodynamic problems by the CESE method in curvilinear coordinates. Sol. Phys. 267, 463–491. doi: 10.1007/s11207-010-9649-6

CrossRef Full Text | Google Scholar

Kliem, B., and Török, T. (2006). Torus instability. Phys. Rev. Lett. 96:255002. doi: 10.1103/PhysRevLett.96.255002

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, R., Kliem, B., Titov, V. S., Chen, J., Wang, Y., Wang, H., et al. (2016). Structure, stability, and evolution of magnetic flux ropes from the perspective of magnetic twist. Astrophys. J. 818:148. doi: 10.3847/0004-637X/818/2/148

CrossRef Full Text | Google Scholar

Low, B. C., and Lou, Y. Q. (1990). Modeling solar force-free magnetic fields. Astrophys. J. 352, 343–352. doi: 10.12942/lrsp-2012-5

CrossRef Full Text | Google Scholar

Mays, M. L., Thompson, B. J., Jian, L. K., Colaninno, R. C., Odstrcil, D., Möstl, C., et al. (2015). Propagation of the 7 January 2014 CME and resulting geomagnetic non-event. Astrophys. J. 812:145. doi: 10.1088/0004-637X/812/2/145

CrossRef Full Text | Google Scholar

Möstl, C., Rollett, T., Frahm, R. A., Liu, Y. D., Long, D. M., Colaninno, R. C., et al. (2015). Strong coronal channelling and interplanetary evolution of a solar storm up to Earth and Mars. Nat. Commun. 6:7135. doi: 10.1038/ncomms8135

PubMed Abstract | CrossRef Full Text | Google Scholar

Shibata, K., and Magara, T. (2011). Solar flares: magnetohydrodynamic processes. Liv. Rev. Sol. Phys. 8:6. doi: 10.12942/lrsp-2011-6

CrossRef Full Text | Google Scholar

Su, Y., and van Ballegooijen, A. (2012). Observations and magnetic field modeling of a solar polar crown prominence. Astrophys. J. 757:168. doi: 10.1088/0004-637X/757/2/168

CrossRef Full Text | Google Scholar

Titov, V. S., and Démoulin, P. (1999). Basic topology of twisted magnetic configurations in solar flares. Astron. Astrophys. 351, 707–720.

Google Scholar

Toriumi, S., Schrijver, C. J., Harra, L. K., Hudson, H., and Nagashima, K. (2017). Magnetic properties of solar active regions that govern large solar flares and eruptions. Astrophys. J. 834:56. doi: 10.3847/1538-4357/834/1/56

CrossRef Full Text | Google Scholar

Toriumi, S., and Wang, H. (2019). Flare-productive active regions. Liv. Rev. Sol. Phys. 16:3. doi: 10.1007/s41116-019-0019-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Török, T., and Kliem, B. (2005). Confined and ejective eruptions of kink-unstable flux ropes. Astrophys. J. Lett. 630, L97–L100. doi: 10.1086/462412

CrossRef Full Text | Google Scholar

Török, T., and Kliem, B. (2007). Numerical simulations of fast and slow coronal mass ejections. Astron. Nachr. 328, 743–746. doi: 10.1002/asna.200710795

CrossRef Full Text | Google Scholar

Török, T., Kliem, B., and Titov, V. S. (2004). Ideal kink instability of a magnetic loop equilibrium. Astron. Astrophys. 413, L27–L30. doi: 10.1051/0004-6361:20031691

CrossRef Full Text | Google Scholar

Wang, R., Liu, Y. D., Dai, X., Yang, Z., Huang, C., and Hu, H. (2015). The role of active region coronal magnetic field in determining coronal mass ejection propagation direction. Astrophys. J. 814:80. doi: 10.1088/0004-637X/814/1/80

CrossRef Full Text | Google Scholar

Wiegelmann, T. (2004). Optimization code with weighting function for the reconstruction of coronal magnetic fields. Sol. Phys. 219, 87–108. doi: 10.1023/B:SOLA.0000021799.39465.36

CrossRef Full Text | Google Scholar

Zagainova, Y. S., and Fainshtein, V. G. (2018). Comparison of features of the generation of coronal mass ejections with variable velocity in the field of view of LASCO coronagraphs. Geomag. Aeron. 58, 966–972. doi: 10.1134/S0016793218070253

CrossRef Full Text | Google Scholar

Zheng, R., Chen, Y., and Wang, B. (2016). Slipping magnetic reconnections with multiple flare ribbons during an X-class solar flare. Astrophys. J. 823:136. doi: 10.3847/0004-637X/823/2/136

CrossRef Full Text | Google Scholar

Zhou, G. P., Tan, C. M., Su, Y. N., Shen, C. L., Tan, B. L., Jin, C. L., et al. (2019). Multiple magnetic reconnections driven by a large-scale magnetic flux rope. Astrophys. J. 873:23. doi: 10.3847/1538-4357/ab01cf

CrossRef Full Text | Google Scholar