Impact of Cosmological and Astrophysical Constraints on Dark Matter Simplified Models

Studies of dark matter models lie at the interface of astrophysics, cosmology, nuclear physics, and collider physics. Constraining such models entails the capability to compare their predictions to a wide range of observations. In this review, we present the impact of global constraints to a specific class of models, called dark matter simplified models. These models have been adopted in the context of collider studies to classify the possible signatures due to dark matter production, with a reduced number of free parameters. We classify the models that have been analyzed so far and for each of them we review in detail the complementarity of relic density, direct, and indirect searches with respect to the LHC searches. We also discuss the capabilities of each type of search to identify regions where individual approaches to dark matter detection are the most relevant to constrain the model parameter space. Finally we provide a critical overview on the validity of the dark matter simplified models and discuss the caveats for the interpretation of the experimental results extracted for these models.

1. Introduction

The presence of dark matter, postulated at the beginning of last century (Jeans, 1922; Kapteyn, 1922; Oort, 1932; Zwicky, 1933; see Bertone and Hooper, 2016; de Swart et al., 2017 for a review), has been nowadays confirmed by several observations in cosmology and astrophysics. Besides precision measurements on its abundance from the cosmic microwave background and large scale structures, which state ${\Omega }_{\text{DM}}{h}^2=0.1198\pm 0.00015$ (Planck Collaboration et al., 2016), there is only gravitational evidence for this dark component while its nature and properties are completely unknown. Baryons can constitute only the 4% of the total energy content of the universe, not enough to explain the entire matter content of the universe (~30%). This fact supports a non-baryonic origin for the dark matter particles, most likely arising in models beyond the Standard Model (SM) of particle physics, as SM neutrinos were relativistic in the early universe. Several theoretically motivated extensions of the SM, such as supersymmetry or universal extra-dimensions, provide dark matter candidates which fall into the category of WIMPs (Weakly Interacting Massive Particles). These particles are usually neutral, stable at least on cosmological scale, and with a mass in the GeV-TeV energy range. In this review we will comply with the WIMP paradigm and use WIMPs and dark matter interchangeably, even though other possibilities exist (see e.g., Marsh, 2016; Drewes et al., 2017) and the references therein.

With the generic hypothesis that WIMPs interact with the SM particles, a multitude of experimental approaches have been undertaken to detect it. These methods range from dark matter searches in underground detectors (Akerib et al., 2017; Amole et al., 2017; Aprile et al., 2017a) via the scattering of WIMPs off nuclei (direct detection), to observations of gamma rays, cosmic rays, and neutrinos, produced by dark matter annihilation in astrophysical environments (indirect detection) (see e.g., Aartsen et al., 2016; Aguilar et al., 2016; Albert et al., 2017; Ambrosi et al., 2017), and dedicated searches for missing energy signals at colliders (see e.g., Abercrombie et al., 2015; Boveia et al., 2016) (production). Yet, despite the enormous experimental effort, the dark matter detection remains a challenge and our understanding of dark matter properties limited, hence WIMP models can span many orders of magnitude in dark matter masses and interaction strengths. This makes it difficult to efficiently study all possible scenarios and models. It is necessary to find a strategy to combine the maximum amount of available experimental information in the most efficient way to: (i) carve out the dark matter models which are inconsistent with experimental observations; (ii) to highlight the most promising regions for discovery in the model parameter space, in the light of the near future dark matter search program; (iii) to highlight the complementarity among the diverse dark matter search methods. Dark matter simplified models (DMsimps from hereafter) represent a convenient framework where to achieve these objectives, and will be the main focus of the review.

In these past few years, the dark matter program at the LHC has set the trend to follow the avenue of DMsimps (Abdallah et al., 2015; Abercrombie et al., 2015; Boveia et al., 2016; Albert et al., 2017a), as compared to the Effectivfe Field Theory (EFT) approach or as compared to the study of complete dark matter models. EFT states that the dark matter is the only accessible particle at our experiment, while all the other states that might characterize the dark sector are kinematically unaccessible. This is a valid framework when the masses of all particles mediating the interaction between the dark matter and the SM particles are assumed to be larger than the energy scale of the process. The limitations of this approach, at least as far as the LHC searches are concerned (Goodman and Shepherd, 2011; March-Russell et al., 2012; Shoemaker and Vecchi, 2012; Buchmueller et al., 2014; Busoni et al., 2014a,b,c; Bell et al., 2015; De Simone and Jacques, 2016), have now been recognized by the theoretical and experimental communities. Basically as soon as the momentum transfer of the process is near or larger than the mass of the mediator, EFT breaks down and the micro-physics describing the process needs to be taken into account. As far as it concerns dark matter direct detection, the momentum transfer is about a few MeV, hence EFT is a well-defined framework that can be used unless the mediator mass is of the order the MeV. Dark matter indirect detection lies in between the two cases described above and will be discussed in details in the paper. Notice that nowadays EFT at the LHC is a useful tool to grasp complementary information for instance for high scale (Belyaev et al., 2017) or for strongly interacting (Bruggisser et al., 2016) dark matter models.

The opposite approach with respect to EFT stands in considering UV (ultraviolet) complete theoretical models, motivated for instance by solving the hierarchy or the little hierarchy problems, such as supersymmetric models. These models have been and still are being extensively investigated in dedicated study programs, by both the theoretical and experimental communities. The complication arising from such models is the large number of free parameters: at present the dark matter data have not enough constraining power (the only measurement so far being the dark matter relic density) to select specific values of these free parameters of the theory space, hence it is common to end up with degeneracies among the parameters. Conversely, complete models usually feature complex dark sectors with interesting correlations among observables that cannot be reproduced by the EFT or simple models.

These simple models, called DMsimps, are constituted by the addition to the SM particle content of a dark matter candidate which communicates with at least the SM quarks via one mediator. This minimalistic construction consists in expanding the EFT interaction by introducing a new state that mediates the interactions of the dark matter (and of the dark sector¹) with the SM. Simplified models are typically characterized by three or four free parameters: the dark matter mass m_DM, the WIMP-SM g_DM, and mediator-SM g_SM couplings (or equivalently the coupling WIMP-SM-mediator y) and the mediator mass m_med. So far, they have proven useful to categorize the dark matter searches at the LHC and to set up an easy framework for comparison with direct and indirect searches of dark matter. There are however several caveats emerging from the use of DMsimps in relation with LHC searches and direct/indirect dark matter searches, which are currently driving these models, which might seem purely phenomenological constructions, into more natural bottom-up theoretical models (Albert et al., 2017b).

The rest of this review is organized as follows. Section 2 provides a general overview on the dark matter searches, ranging from cosmology to collider. Section 3 presents the state of art of current DMsimps, with respect to all the dark matter searches presented in the previous section. A special focus is given to the cosmological and astrophysical constraints, as collider constraints are described in depth in many reviews and recommendation papers (see e.g., Abdallah et al., 2015; Abercrombie et al., 2015; Boveia et al., 2016; De Simone and Jacques, 2016; Arcadi et al., 2017; Kahlhoefer, 2017; Morgante, 2018) and the references therein. In particular section 3.1 considers s-channel mediator models and distinguishes the case of spin-0, spin-1, and spin-2 bosons, whereas section 3.2 reviews the status of t-channel models. Section 4 discusses the theoretical caveats of DMsimps, while section 5 presents potential avenues for the future. We have tried to present the material in a self-contained form as much as possible, so that the review might serve as an introduction for the beginner and as a reference guide for the practitioner.

2. Overview on Dark Matter Searches

2.1. Cosmological Constraints, Astrophysical, and Direct Searches

In this section we provide the theoretical basic ingredients to compute cosmological, astrophysical, or scattering signals from the DMsimps. For each type of search we discuss whether it is pertinent to use the EFT approximation or if the micro-physics processes should be fully taken into account. A summary plot is provided in Figure 1. We also discuss the theoretical assumptions and uncertainties related to each type of search, and how these are interpreted in terms of DMsimps. Finally we briefly review the cosmological constraints on dark matter as well as the several astroparticle searches that are currently running. These constraints will be used to assess the complementarity of searches on the DMsimp parameter space in section 3.

FIGURE 1

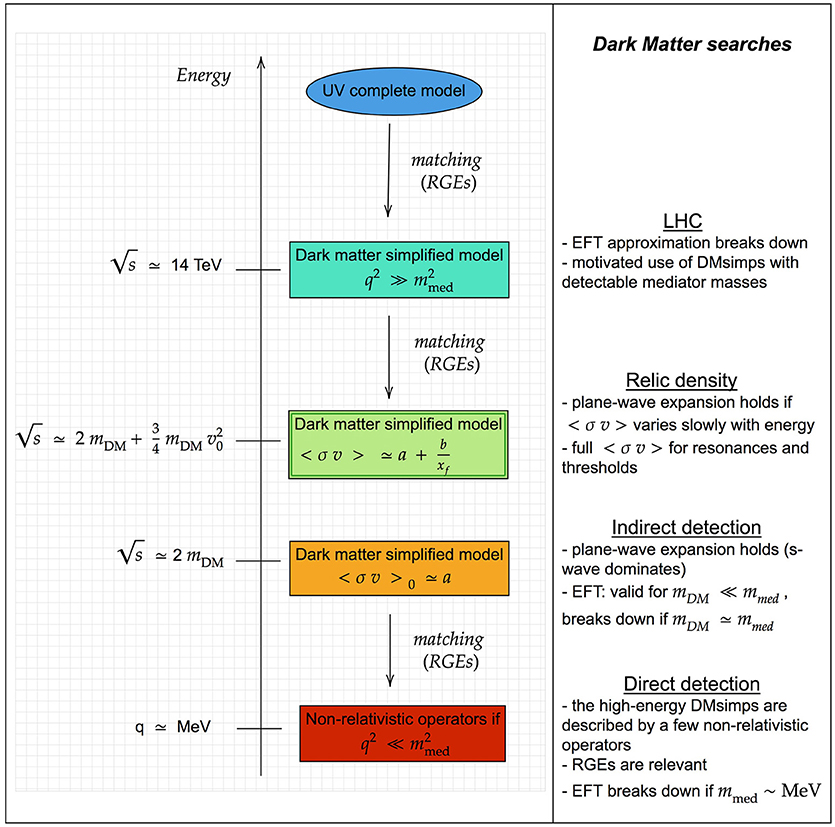
Figure 1. Schematic overview of the dark matter searches together with the energy scale typically involved in each of them.

2.1.1. Dark Matter Relic Density

In the standard scenario, dark matter is considered a non-relativistic thermal relic in the early universe, which freezes out at x_f = T/m_DM (with T being the temperature of the thermal bath). Its relic abundance is given roughly by the following approximate solution of the evolution equation (see e.g., Srednicki et al., 1988; Kolb and Turner, 1990):

$\begin{array}{ll}{\Omega }_{\text{DM}}{h}^2\propto \frac{0.2\times 10^{-9}\text{GeV}}{\langle \sigma v\rangle },& (1)\end{array}$

where Ω_DM is as usual the ratio between the dark matter energy density and the critical density of the universe, h is the reduced Hubble parameter (h = H₀/100 km s⁻¹ Mpc⁻¹, with H₀ being the Hubble constant today), and σv is the thermally averaged annihilation cross section. The interaction of the particles needs to be extremely weak in order to achieve ${\Omega }_{\text{DM}}{h}^2~0.1$. To have an idea of the size of the coupling leading to the correct relic density, it is instructive to see what happens by considering a coupling with the strength of the weak interaction, $\sigma v~G_F^2{m}_{\text{DM}}^2~10^{-9}\text{Ge}{\text{V}}^{-2}~3\times 10^{-26}\text{c}{\text{m}}^3/s$ (G_F is the Fermi constant): this is just right in the ballpark to achieve the measured ${\Omega }_{\text{DM}}{h}^2$ for particles with masses around 100 GeV. Hence WIMPs have extremely small but non-vanishing interaction couplings with the SM; the size of the couplings depend on the mass of the WIMP and is typically of the order or smaller than the weak interaction for dark matter particles in the GeV-TeV range² to account for all the relic density. This is what is intended with the WIMP paradigm.

The inverse proportionality between Ω_DM and the thermal averaged cross section dictates that: (i) the stronger the interaction rate is, the more depleted is the dark matter number density and as a consequence its relic abundance is too low (“under-abundant” dark matter, namely it contributes to ${\Omega }_{\text{DM}}{h}^2$ by some %); (ii) annihilation processes for WIMPs are less efficient, the dark matter particles freeze out at early time and at present time have a significant abundance that matches ${\Omega }_{\text{DM}}{h}^2$; (iii) the dark matter particles are too feebly interacting, hence they decouple too early and over-close the universe (“over-abundant” dark matter).

If 〈σv〉 varies slowly with energy, it can be expanded in plane waves Srednicki et al. (1988):

$\begin{array}{ll}\langle \sigma v\rangle =\langle a+b{v}^2+c{v}^4+\dots \rangle =a+\frac{3}{2}\frac{b^{\prime }}{x}+\frac{15}{8}\frac{c}{x^2}+\dots ,& (2)\end{array}$

where b = 3/2b′. Typically freeze out occurs at x_f ~ 20 − 30 leading to a most probable velocity v₀ of the order of 0.25c: corrections proportional to x⁻¹ are indeed relevant with respect to the a term and need to be taken into account (notice that the back of the envelop estimate in Equation (1) is valid only for a pure s-wave 〈σv〉). Additionally, there might be selection rules at play that make the s-wave term vanishing. This occurs for several DMsimps, as we will discuss in the next section, which end up having p-wave dominated annihilation cross sections.

There are circumstances in which the non-relativistic expansion of 〈σv〉 in Equation (2) breaks down (Gondolo and Gelmini, 1991; Griest and Seckel, 1991; Edsjo and Gondolo, 1997):

• Resonant annihilation: The annihilation cross section is not a smooth function of the centre-of-mass-energy s in the vicinity of an s-channel resonance. For m_DM ≤ 2m_med the additional kinetic energy provided by the thermal bath brings s on top of the resonance and the annihilation cross section increases drastically. Conversely, for m_DM > 2m_med the additional kinetic energy brings s even further away from the resonance, hence the annihilation cross section decreases quickly.

• Opening of new annihilation channels: a fraction of dark matter particles might have a kinetic energy, given by their thermal distribution in the early universe, sufficient to annihilate into heavier particles, which are above the threshold. This again leads to a rapid enhancement of 〈σv〉.

• Co-annihilation: if there are one or more particles heavier than the dark matter but close in mass (roughly speaking the difference in mass should be at most 10% of the dark matter mass), these are present as well in the thermal bath in the early universe and contribute to the relic abundance of the dark matter with annihilation processes among themselves and with the dark matter. These processes should be taken into account in the Boltzmann equation that leads to ${\Omega }_{\text{DM}}{h}^2$ with an effective 〈σv〉, the weighted sum over all annihilation processes (see for details Edsjo and Gondolo, 1997).

In these cases it is necessary to rely on the full computation of the thermally averaged cross section without approximations as well as to solve the complete Boltzmann equation to evaluate precisely ${\Omega }_{\text{DM}}{h}^2$. This is the standard procedure encoded in the public tools for dark matter [see e.g., micrOMEGAs (Belanger et al., 2018), DarkSUSY (Bringmann et al., 2018), and MadDM (Ambrogi et al., 2018), etc.]. As we will see in section 3, the model parameter space of DMsimps often features the correct relic density in a tuned-region m_DM ~ 2m_med, relying on resonant annihilation, and several threshold openings are at play in setting ${\Omega }_{\text{DM}}{h}^2$. This is schematically resumed in Figure 1.

The dark matter relic density is the only precision measurement we have so far. As already anticipated in the introduction, it has been measured with great accuracy by the Planck satellite (Planck Collaboration et al., 2016). This measurement, combined with large scale structure data, gives: ${\Omega }_{\text{DM}}{h}^2=0.1198\pm 0.00015$. The experimental error is at the level of ‰, two orders of magnitude smaller than the associated theoretical error, typically quoted around ${O}(10\%)$.

There are a certain number of caveats when considering the relic density as a constraint for DMsimps, which have to be taken into account in the interpretation of the complementarity of searches:

• DMsimps provide an extension of the SM particle content into the most minimalistic dark sector possible, constituted solely by the dark matter and an extra mediator. If the dark/new physics sector contains more particles, two types of processes can alter the relic density value: (i) there are additional mediators, opening up new annihilation channels including resonance effects; (ii) co-annihilation (Edsjo and Gondolo, 1997), if there are particles heavier but close in mass with the dark matter mass $(\Delta m\underset{\sim }{<}(O)(10\%))$. The region allowed by relic density in the DMsimp set up should be considered then as a subset of the whole allowed model parameter space.

• DMsimps focus particularly on studying and constraining the dark matter-quark couplings, which are accessible at the LHC. However if the dark matter couples to other SM species, additional annihilation diagrams can have a significant impact on the model parameter space allowed by the relic density constraint by opening up new annihilation thresholds. Other couplings, such as dark matter—lepton couplings, start to be considered as well (Albert et al., 2017a) in the context of di-lepton searches. In these cases the interpretation of the allowed relic density regions becomes more robust (cfr. the other caveats).

• The constraint on ${\Omega }_{\text{DM}}{h}^2$ relies on the assumption that the dark matter is a thermal relic. Other viable assumptions to bring ${\Omega }_{\text{DM}}{h}^2$ to the observed value, are for instance: (i) the dark matter is non-thermally produced; (ii) the cosmological evolution of our universe is rather different than the one described by the Standard Cosmological model. For example, late-time entropy injection (Bramante and Unwin, 2017) can decrease the dark matter relic density, while late gravitino decays in supersymmetric theories can increase the neutralino relic abundance (Allahverdi et al., 2012).

In section 3, we will discuss the combination of dark matter searches in full generality, with and without considering the relic density as relevant constraint. Notice that all caveats described above spoil the model-independent approach of DMsimps, as they rely on the specificity of the dark matter model.

2.1.2. Dark Matter Direct Detection

As the dark matter particles move in the Milky Way halo, it is worthwhile to explore the possibility to detect them. This can be done directly in underground terrestrial detectors, sensitive to the nuclear recoil caused by the passing wind of dark matter particles. From a theoretical point of view, in direct detection, the crucial quantity is the scattering cross section of dark matter particles off a nucleon, in a deeply non-relativistic regime. Indeed the momentum transfer in the collision is of the order of a few to tens of MeV, as the speed of the incoming WIMP is of the order of v ~ 10⁻³c. As a consequence, direct detection can be safely treated in term of EFT³, except when the mediator mass connecting the dark matter and the SM quarks becomes of the order of the momentum transfer $(m_{\text{med}}^2\sim q^2\sim (O)(10\text{MeV}))$, as resumed in Figure 1.

It has been shown that the scattering process between the dark and ordinary matter can be expressed in terms of a limited number of relativistic degrees of freedom, which give rise to a basis of non-relativistic operators. As a matter of fact, any process of elastic scattering between the dark matter and the nucleon can be expressed as a combination of this basis in a unique way, irrespective of the details of the high-energy dark matter model. This basis is constituted by 12 operators, here we report the most relevant for the discussion of section 3 using the notation of (Cirelli et al., 2013):

$\begin{array}{lll}{{O}}_1^{\text{NR}}& =& 1,{{O}}_4^{\text{NR}}={\text{s}}_{\text{DM}}·{\text{s}}_{\text{N}},\\ {{O}}_6^{\text{NR}}& =& ({\text{s}}_{\text{DM}}·\text{q})({\text{s}}_{\text{N}}·\text{q}),{{O}}_8^{\text{NR}}={\text{s}}_{\text{DM}}·{\text{v}}^{\perp },\\ {{O}}_9^{\text{NR}}& =& i{\text{s}}_{\text{DM}}·({\text{s}}_{\text{N}}\times \text{q}),& (3)\end{array}$

Starting from the DMsimp Lagrangian, which describes the interaction of the dark matter with the quarks, it is necessary first to determine the dark matter-nucleon effective Lagrangian. Secondly, the elastic scattering occurs with the whole nucleus, due to the small WIMP speed in the galactic halo. Therefore, one needs to properly take into account the composite structure of the nucleus which results in the appearance of nuclear form factors in the cross section. Nuclear form factors parametrize the loss of coherence in the scattering with increasing exchanged momentum. In Table 1, we provide the list of non-relativistic operators relevant for the DMsimps presented in section 3 and their matching with the matrix element involving the whole nucleus. We refer to Cirigliano et al. (2012), Cirelli et al. (2013), Fitzpatrick et al. (2013), and De Simone and Jacques (2016) for the rigorous definition of the non-relativistic operator basis and for the detailed direct detection analyses⁴.

TABLE 1

Table 1. List of direct detection EFT operators WIMP-nuclei for fermionic and scalar dark matter arising from the DMsimp high-energy interaction Lagrangians discussed in the paper.

Concerning the experimental state of art for direct detection, a huge experimental effort has been deployed in the past years, that features nowadays more than 10 different experiments currently running toward unprecedented sensitivities. Several orders of magnitude in the WIMP-nucleus elastic interaction have been constrained by past and current experiments. As far as it concerns spin-independent elastic scattering, which occurs when the dark matter interacts with all the nucleons (it is proportional to the atomic number of the nucleus, A²), the most notable experiments are XENON1T (Aprile et al., 2017a), LUX (Akerib et al., 2017), and PANDAX-II (Fu et al., 2017) for intermediate WIMP masses, CDMSLite (SuperCDMS Collaboration et al., 2018) and CRESST-II (Angloher et al., 2016) at low WIMP masses. XENON1T excludes at 90% confidence level (CL) WIMP-nucleon cross sections of about 8 × 10⁻⁴⁷cm² for dark matter masses of 30 GeV. The usual spin-independent scattering cross section corresponds to the operator ${{O}}_1^{\text{NR}}$ of Table 1. If present in the underlying particle physics model, this operator dominates over all other non-relativistic operators. Spin-dependent scattering occurs when the dark matter interacts with the spin of the unpaired proton or neutron of the nucleus. PICO 60 Amole et al. (2017) detains the most constraining bound for spin-dependent scattering on proton so far. Only a few experiments are sensitive to the spin-dependent interaction on neutron (mostly dual phase xenon or nobel liquid/gas detectors) and the strongest exclusion bound is held by the LUX LUX Collaboration et al. (2017) experiment. The spin-dependent operator currently considered by the experimental collaborations is ${{O}}_4^{\text{NR}}$. Exclusion limits for the other operators are provided in Cirelli et al. (2013), even thought at present these exclusion bounds are a bit outdated. On the experimental side, the XENON collaboration has started to use the non-relativistic operator description and has released exclusion limits based on the XENON100 data (Aprile et al., 2017b).

Direct detection is affected by several astrophysical uncertainties related for instance to the description of the dark matter velocity distribution at the Sun position and to the local dark matter density. There are two different approaches to deal with these uncertainties: either perform a likelihood analysis and marginalize or profile over them (see e.g., Strigari and Trotta, 2009; Arina et al., 2011; Bertone et al., 2012; Arina, 2014), either use the so-called halo-independent method (see e.g., Fox et al., 2011; Gondolo and Gelmini, 2012; Del Nobile et al., 2013). In most of the analyses described in section 3, astrophysical uncertainties are not taken into account, hence we will not consider this matter any further.

2.1.3. Dark Matter Indirect Detection

Dark matter indirect detection relies on the principle that dark matter particles in galactic halos annihilate into SM particles. These SM particles subsequently undergo decays, showering and hadronization and lead to a continuum flux of cosmic rays, gamma rays, and neutrinos. In the case where the dark matter annihilates via loop-induced processes into a pair of photons or a photon and a boson, the signal is characterized by a sharp spectral feature such as a gamma-ray line. Dark matter annihilation takes place in several astrophysical environments and at different epochs in the evolution of the universe, from cosmological down to solar system scales. As dark matter indirect detection encompasses a large variety of searches, in this review we describe only the searches that have been directly used as complementary probes together with LHC dark matter searches and/or direct detection to constrain DMsimps. Those involve mainly gamma rays, neutrinos and anti-protons at galactic scales. For a detailed review on dark matter indirect detection we refer the reader to (e.g., Cirelli, 2015; Gaskins, 2016; Slatyer, 2017).

Before going into the details of the specific searches and theoretical predictions, let us mention two generic features concerning the flux of particles produced by dark matter annihilation. This quantity is proportional to

1. 〈σv〉₀. This is defined as the velocity averaged annihilation cross section computed at present time. Annihilation in galactic halos occurs in a highly non-relativistic regime with an centre-of-mass-energy provided by $\sqrt{s}=2m_{\text{DM}}$ as the typical mean velocities characterizing the dark matter halo are negligible. For instance in the Milky Way the most probable velocity of dark matter particles is $v_0~10^{-3}c~230\text{km}/\text{s}$ (Schoenrich et al., 2010), while it is even lower in dwarf Spheroidal galaxies (dSphs), $v_0~10^{-5}c~8\text{km}/\text{s}$ (Bonnivard et al., 2015), hence in indirect searches the non-relativistic expansion of 〈σv〉₀ in plane waves is a fairly good approximation. The dominant term that is in the reach of current astrophysical probe is the s-wave: 〈σv〉₀ ≃ a. If this term is absent due to some selection rule, the model is most likely unconstrained from indirect detection. Notice that the EFT approach remains valid and can be used for m_DM ≪ m_med. This is summarized in Figure 1.

2. $\text{d}{N}_f/\text{d}{E}_f\equiv \sum _i{B}_i\text{d}{N}_f^i/\text{d}{E}_f$. This is defined as the energy spectrum of the particle species f (with $f=\gamma ,{\nu }_l,e^{+},\bar{p}$, and l is the neutrino flavor, l = e, μ, τ) at production where annihilation occurred. The index i runs over all possible annihilation final states of the dark matter model, each of them with a branching ratio B_i. The final states are typically SM pairs of particles, however new particles beyond the SM can appear as well, which will subsequently decay into SM particles. We will see in section 3 that this option is realized in several DMsimps.

3. Typically the experimental searches present the limits in a model-independent way, supposing a branching ratio of 100% into one species of SM particles and assuming that ${\Omega }_{\text{DM}}{h}^2$ matches the observed value. To compare a specific dark matter model with the experimental exclusion limits, the most rigorous procedure is to recompute the upper bound for that particular model by means of the experimental likelihoods. If this is not possible, one can combine the experimental exclusion bounds after having rescaled them by the appropriate branching ratio. This procedure should be a good approximation provided the energy spectrum of the specific model does not differ too much from the energy spectrum for which each respective upper bound has been computed. The micrOMEGAs and DarkSUSY numerical tools rely on tabulated energy spectra for all possible SM final states and for dark matter masses ranging from 5 to 100 TeV. The MadDM tool (Ambrogi et al., 2018) allows to generate the energy spectrum in both model-independent and model-dependent ways for any possible dark matter mass.

Similarly to direct detection, indirect detection is affected by astrophysical uncertainties related to the dark matter density distribution in galactic halos, by the propagation parameters for cosmic rays, etc. Whenever relevant, we will discuss the comparison between different dark matter searches and the indirect detection limits based on different assumptions on the astrophysics.

Gamma-ray searches

The gamma-ray flux from dark matter annihilation from a direction ψ in the sky, averaged over an opening angle Δψ, is given by:

$\begin{array}{ll}\frac{\text{d}\Phi }{\text{d}{E}_{\gamma }}(E_{\gamma },\psi )=\frac{{\langle \sigma v\rangle }_0}{2m_{\chi }^2}{\displaystyle \sum _i}{B}_i\frac{\text{d}{N}_{\gamma }^i}{\text{d}{E}_{\gamma }}\frac{1}{4\pi }{\displaystyle {\int }_{\psi }}\frac{\text{d}\Omega }{\Delta \psi }{\displaystyle {\int }_{\mathrm{\text{los}}}}{\rho }^2(\psi ,l)\text{d}l.& (4)\end{array}$

For dark matter particles with distinct particle and antiparticle Equation (4) is multiplied by an additional factor of 1/2. The two integrals, over the angle and the line of sight (los), define the astrophysical J factor $(J\equiv {\int }_{\psi }\text{d}\Omega /\Delta \psi {\int }_{\mathrm{\text{los}}}{\rho }^2(\psi ,l)\text{d}l)$. The J factor encodes the information about the astrophysical environment (experimental window) where annihilation occurs (is sought) and the dark matter density profile.

We start by illustrating the gamma-ray constraints from dSphs, which are dark matter dominated objects (Mateo, 1998; Weisz et al., 2011; Brown et al., 2012; Coureau et al., 2014). The Fermi-LAT satellite looks for a gamma-ray emission from these Milky Way satellite galaxies, and so far, no excess in gamma rays has been observed.⁵ Hence the Fermi-LAT collaboration has set upper bounds at 95% CL on the continuum prompt photon flux produced by dark matter annihilation (Ackermann et al., 2015a; Albert et al., 2017). From these bounds, it has publicly released upper limits for the annihilation rate into $b\bar{b}$ and τ⁺ τ ⁻ final states as a function of the dark matter mass. The $b\bar{b}$ channel is an example of “soft” channel that produces photons mostly from the decay of neutral pions produced in hadronisation, while the τ⁺ τ ⁻ is a “hard” channel that generates photons from final state radiation, scaling as E⁻¹, on top of the photons coming from π⁰ decays. The Fermi-LAT team has performed a stacked likelihood analysis for 45 dSphs. The resulting profile function for each dSph has been released publicly and can be used to compare for instance DMsimps with dSphs data from the 6 years Fermi-LAT data (Pass 8 event reconstruction algorithm)⁶. These likelihood functions have been implemented in the last MadDM version (see Ambrogi et al., 2018) for details, and can be used for any generic dark matter model. Gamma-ray constraints from dSPhs are subject to astrophysical uncertainties mostly related to the determination of the J factor. These uncertainties are particularly large in the case of the latest dSPhs discovered, which are ultra-faint dwarf galaxies, for details (see Bonnivard et al., 2015). In addition to the prompt photon flux, there are also contribution from inverse Compton scattering generated by charged propagating particles. These are often neglected while computing the exclusion limits on the dark matter annihilation rate, however could have an impact for m_DM ≥ 100 GeV. Hence the exclusion bounds for large dark matter masses should be regarded as conservative.

Another search, used in the complementarity framework of DMsimps, looks for gamma-ray spectral features toward the Galactic Centre. These spectral features encompass gamma-ray lines, narrow boxes (see e.g., Ibarra et al., 2015a) and sharp edges in the prompt photon energy spectrum coming for instance from internal bremsstrahlung processes (see e.g., Giacchino et al., 2013; Toma, 2013). The most constraining exclusion limits on the dark matter annihilation rate into gamma-ray lines are provided by the Fermi-LAT satellite (Ackermann et al., 2015b) for m_DM < 500 GeV and the HESS telescope for dark matter masses up to 25 TeV (Abramowski et al., 2013; Abdalla et al., 2016). These searches suffer of large astrophysical uncertainties related to the dark matter density profile, included in the J factor, and to the background modeling of the Galactic Centre ⁷.

Neutrino searches

If dark matter particles scatter in heavy astrophysical bodies such as the Sun, they can lose enough energy to become gravitationally trapped inside it. Dark matter particles start to accumulate in the center of these celestial bodies, where subsequently dark matter annihilation sets in (see e.g., Steigman et al., 1978; Press and Spergel, 1985; Silk et al., 1985; Gould, 1987; Ritz and Seckel, 1988; Kamionkowski, 1991; Jungman et al., 1996; Bergstrom et al., 1997; Gondolo et al., 2004; Blennow et al., 2008; Peter, 2009; Sivertsson and Edsjo, 2012). In the Sun, constituted primarily by hydrogen, the dark matter capture occurs mainly by spin-dependent elastic scattering [even thought the spin-independent scattering on nucleons, ${\sigma }_n^{\text{SI}}$, can also play a role, as it is enhanced by the A² term for heavy nuclei (Gondolo et al., 2004)]. The Sun is opaque to all dark matter annihilation products but neutrinos, which can escape the Sun surface and be detected by Earth based telescopes such as IceCube and Super-Kamiokande (Choi et al., 2015). The annihilation rate can become large enough to lead to an equilibrium between dark matter capture and annihilation. In this case 〈σv〉₀ and the elastic cross section on proton, ${\sigma }_p^{\text{SD}}$, become two related quantities that can be trade one for the other. This assumption is used for computing experimentally the exclusion bounds on the WIMP-nucleon elastic cross section. The IceCube collaboration has set stringent upper limits, competitive with those of direct detection searches for spin-dependent scattering (Aartsen et al., 2013, 2016), by the non observation of GeV-TeV scale neutrinos coming from the Sun direction. The exclusion bounds publicly released, at 90% CL, are based on IceCube data with 79 strings including DeepCore and are given for the following final states, “hard”channels (W⁺W⁻, τ⁺ τ ⁻, ZZ, $\nu \bar{\nu }$) and “soft” channels ($b\bar{b}$, $t\bar{t}$, gg and hh).

The equilibrium assumption helps in the interpretation and comparison of dark matter exclusion limits coming from direct and indirect detection in terms of WIMP-quark coupling; this is particularly appreciable for DMsimp models, which often do include only these couplings. There is however an emergent caveat: direct detection experiments have pushed the upper bound on the spin-independent and spin-dependent cross-section to lower and lower values for which the equilibrium assumption starts to break down (Arina et al., 2017). Depending then on the size of 〈σv〉₀ and ${\sigma }_n^{\text{SI},\text{SD}}$, the useful representation of exclusion bounds in terms of elastic scattering might not provide anymore a correct physical interpretation.

Anti-proton searches

Searches for dark matter annihilation products in local charged cosmic-ray fluxes can be highly sensitive, especially due to the low backgrounds for antimatter produced by astrophysical processes. A major challenge for these searches is the identification of the locations of the sources of cosmic rays due to their propagation throughout the Milky Way, conversely to the case of gamma rays and neutrinos, which do not diffuse and trace their source. Anti-protons have been recognized as important messengers not only for cosmic ray physics but constitute one of the primary channels in the dark matter searches (Silk and Srednicki, 1984; Silk et al., 2010). This idea has been further reinforced by the data released recently by the AMS 02 satellite (Aguilar et al., 2016), which have an amazing statistical precision and extend up to 450 GeV. The authors of (Giesen et al., 2015) and (Cuoco et al., 2018) have provided an analysis of these data in terms of exclusion limits for the dark matter velocity averaged annihilation cross section as a function of m_DM at 95% CL for the $b\bar{b}$, gg, $q\bar{q}$, $t\bar{t}$, μ⁺ μ ⁻, W⁺W⁻, hh, and γγ final states. These bounds (especially $b\bar{b}$) are used to assess the constraining power of anti-proton searches for DMsimps in some of the analyses presented in section 3.

The exclusion limits on the dark matter annihilation rate from anti-protons suffer of very large astrophysical uncertainties. The exclusion limits can fluctuate upwards or downwards by one order of magnitude at low dark matter masses, mainly because of uncertainties in the propagation parameters in our galaxy and of solar modulation. The choice of the dark matter density profile is not the main cause of the lack of precision. For details we refer to Cirelli (2015), Giesen et al. (2015), Cuoco et al. (2018) and the references therein.

2.2. LHC Dark Matter Searches

In this section we summarize very briefly the main dark matter searches pursued by the LHC experimental collaborations. For a detailed information, we refer the reader to (e.g., Abercrombie et al., 2015; De Simone and Jacques, 2016; Albert et al., 2017a; Kahlhoefer, 2017; Morgante, 2018) and the references therein.

During the LHC Run 2, ATLAS and CMS have gone the avenue of dark matter simplified models to classify and categorize all possible final states arising in the dark matter search program. This method has been validated by the Dark Matter forum (Abercrombie et al., 2015) and further supported by the LHC Dark Matter Working Group, established as the successor of the Dark Matter Forum⁸.

The main bulk of dark matter searches at colliders is constituted by signatures with missing transverse energy ($\cancel{E}$_T) in the final state, due to the pair-produced dark matter particles which elusively leave the detector with no trace. The mediator, produced by Drell-Yan or gluon fusion and decaying invisibly into a pair of dark matter particles, can be looked for by tagging an energetic jet, coming typically from initial state radiation, which balances the missing energy from the final state. These are the most relevant searches for DMsimps undertook so far by the ATLAS and CMS collaborations and are called mono-X + $\cancel{E}$_T searches, where X stems for a jet, a photon, a vector boson, a Higgs, and multi-jets (from 2 to 6 jets) + $\cancel{E}$_T. All these searches require 2m_DM < < m_med and possible that the mediator has a large branching ratio into dark matter and SM particles (large g_DM and especially large g_SM). Once these conditions are met, the searches are not very sensitive to the actual mass of the dark matter particle. This is the reason why LHC searches are more sensitive to very light dark matter masses, close the ${O}(1)$ GeV with respect to direct detection searches (Boveia et al., 2016). Additionally to mono-X + $\cancel{E}$_T searches, a certain number of DMsimps can be constrained by recasting searches in supersymmetric simplified models or by $t\bar{t}+{\cancel{E}}_T$ searches.

Both the experimental and theoretical communities have recognized that resonance searches for the mediator can be as powerful as the $\cancel{E}$_T signals in DMsimps, or in some case be even more constraining (see e.g., Arina et al., 2016; Albert et al., 2017a). These searches are based on the principle that, after its production by proton collisions, the mediator does not necessarily decay into dark matter particles but can decay back into SM final states. This is always the case for m_med < 2m_DM, as the invisible decay channel is closed; it is also satisfied for g_SM > g_DM, condition that leads to a small branching ratio into dark matter particles and a large branching ratio into visible SM species. Besides the two requirements above these searches as well are not very sensitive to the dark matter exact mass value. In general the most relevant resonance searches, depending on the specific of the DMsimp, are $t\bar{t}$, 4 tops, di-photons, di-leptons, and di-jets. The sensitivity of each search depends on the specificity of the DMsimp under investigation. For instance, di-jet signals are irrelevant for scalar mediators, while $t\bar{t}$ pair production and di-photons reveal very useful (Arina et al., 2016). Conversely spin-1 mediators are easily probed via di-jets and mono-X signatures (Chala et al., 2015; du Pree et al., 2016).

Notice that the discovery of an anomalous signals in a mono-X + $\cancel{E}$_T search at the LHC would not imply the discovery of dark matter, contrary to the case of direct and indirect detection searches. Hence a potential discovery at colliders needs to be supported by further evidence in direct or indirect searches, in order to fully identify the dark matter candidate. On the other hand, in case of new findings, LHC is able to provide an accurate characterization of the new mediator particle, while direct and indirect detection are more loosely sensitive to it.

3. Current Status of Dark Matter Simplified Models

Since the start of the LHC Run 2 and the publication of the DM forum recommendations (Abercrombie et al., 2015), the number of works studying DMsimps has increased exponentially. DMsimps have been adopted for their minimalistic structure to provide the SM with a dark matter particle, in the sense that they represent the minimal extension of the EFT approach used in the LHC Run 1 dark matter searches. The EFT operators are opened up by introducing a particle mediating the interaction between the dark matter and the SM particles (the so-called mediator). They are simple enough to allow the LHC experimental collaborations to categorize all possible dark matter signals they can give rise to. A general classification stems from the class of vertices that characterize the model: Lagrangians featuring WIMP-WIMP-mediator and SM-SM-mediator type interactions identify models with an s-channel mediator, while Lagrangians characterized by WIMP-SM-mediator interactions define a t-channel mediator. In s-channel models, the mediator is always a color singlet, while in t-channel models it can be either a colored particle or a color singlet (even though this second possibility, is less appealing for the collider phenomenology). Nonetheless, the definition of DMsimp is not unique, especially as far as it concerns the mediator nature. Some works consider Higgs portal models as part of the DMsimp category (see e.g., Abdallah et al., 2015; De Simone and Jacques, 2016), while others do not include the SM Higgs boson in this context (Abercrombie et al., 2015; Boveia et al., 2016). For the rest of the section we will use the definition of DMsimp as provided in Abercrombie et al. (2015) and Boveia et al. (2016):

• There can be only one new mediator at a time that defines the interaction between the dark matter and the SM quarks. Namely the dark matter and the mediator are the only particle accessible by current experiments. The presence of additional new particles in the dark sector is assumed not to modify sensibly the physics described by DMsimps. This assumption allows to introduce a very limited set of new free parameters (typically four). The mediator can have spin-0, spin-1/2, spin-1, and spin-2. The category of scalar mediators, however, does not include the Higgs boson (and no mixing with it is considered). We will comment on Higgs portal models in section 4.

• The new interaction should not violate the exact and approximate accidental global symmetries of the SM. For instance this means that baryon and lepton number conservation of the SM should be preserved by this interaction. Additionally, the new mediating particle can produce large flavor violating effects. By enforcing that the flavor structure of the couplings between the dark matter and the ordinary particles follows the same structure as in the SM, it is ensured that DMsimps do not violate flavor constraints. This assumption is called Minimal Flavor Violation (MFV) (D'Ambrosio et al., 2002), for a detailed discussion (see e.g., Abdallah et al., 2015).

• Another recommendation concerns the nature of the dark matter particle. It is suggested to consider Dirac fermionic candidates only, because LHC searches are rather insensitive to the spin of the dark matter particles. As the $\cancel{E}$_T searches are based on cut-and-count analyses, minor changes in the kinematic distributions of the visible particle are expected to have little effect on these analyses, besides the fact the Majorana particles forbid some processes allowed for Dirac particles. However, whenever possible, we will review cases that go beyond the Dirac fermionic dark matter assumption, as the dark matter annihilation and elastic scattering cross sections do depend on the dark matter spin. Different selection rules are at play depending whether the dark matter is a real scalar, a complex scalar, a Dirac or Majorana fermion, leading to suppressions or enhancements of direct or indirect detection signals. These selection rules change drastically the complementarity picture of dark matter searches and need to be considered and investigated further. Table 2 provides a summary of the sensitivity of each dark matter search as a function of the DMsimp and of the spin of the dark matter particle, considered in this review.

TABLE 2

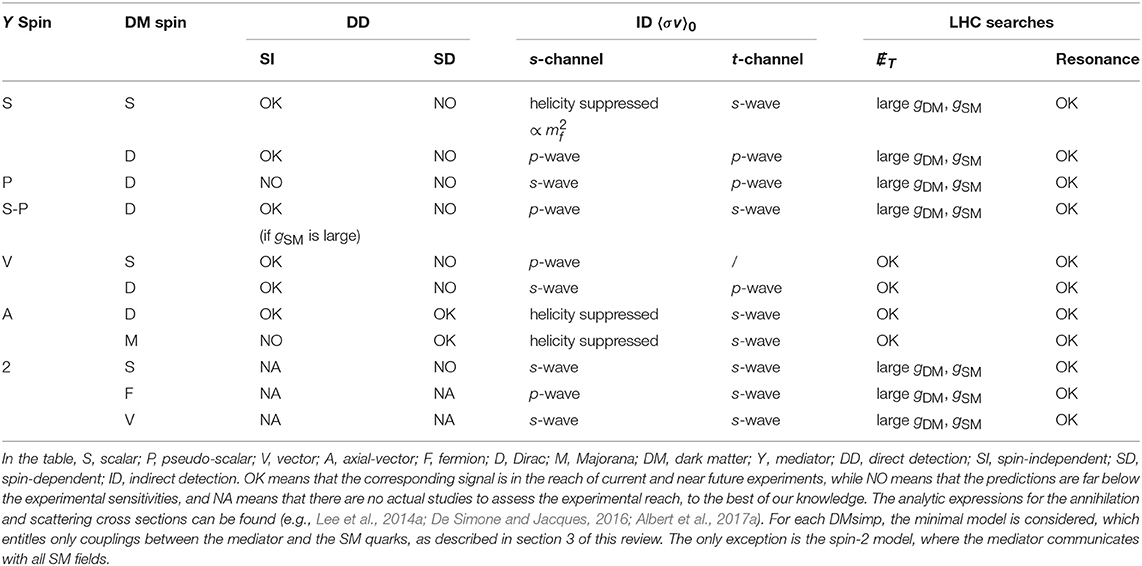
Table 2. Schematic summary of the complementarity of dark matter searches for the DMsimps, taking into account the spins and nature of both mediator and dark matter particles.

Most of DMsimps considered in this review have been implemented in FeynRules (Alloul et al., 2014) and are publicly available for download in the repository of the DMsimp framework⁹. DMsimps for s-channel mediators include three different choices for the spin of the WIMP (Dirac fermion, real scalar and complex scalar for spin-0 and spin-1 mediators, and real scalar, Dirac fermion and vector dark matter for spin-2 mediators). Typically, the numerical tools used to compute the dark matter relic density and astrophysical constraints are micrOMEGAs (Belanger et al., 2018) and MadDM (Ambrogi et al., 2018). In the MadGraph_aMC@NLO platform (Alwall et al., 2011, 2014), one-loop and NLO (next-to-leading order) computations in QCD and EW interactions can be automatically performed in models beyond the SM. This framework allows to compute accurate and precise predictions for production cross sections and distributions of dark matter particles produced at the LHC in association for instance with a mono-jet, mono-photon, mono-Z or mono-Higgs (see e.g., Backović et al., 2015; Mattelaer and Vryonidou, 2015; Arina et al., 2016; Das et al., 2017). It is known that higher order QCD corrections impact not only the production rate but also the shape of the distributions. Most of s-channel DMsimps do include NLO corrections to the matrix elements and parton shower matching and merging. Indeed these higher order terms pertain only to the initial state and originate only from SM processes, hence they can be factorized with respect to the leading order (LO) process accounting for the production of the uncolored mediator and dark matter particles. Conversely the implementation of NLO corrections into t-channel DMsimp is much more involved, due to the colored nature of the mediator, which do not allow anymore to factorize initial and final state corrections. Typically t-channel DMsimps are LO models, unless stated otherwise. The NLO DMsimps [implemented with NloCT (Degrande, 2015)] are also available at the DMsimp framework webpage⁹. As far as it concerns the DMsimp predictions for relic density, direct and indirect detection, NLO corrections are typically not considered. The automatization of loop-induced, one-loop and NLO processes is currently under development in a future release of MadDM, which is now a MadGraph_aMC@NLO plugin and hence inherits all its features, including the capabilities of automatically generate the above-mentioned processes for dark matter observables.

As the literature about DMsimps is vast, we consider and discuss only a few selected representative papers, whereas we try to be as exhaustive as possible with the references. In the following sections we provide the interaction Lagrangian for DMsimps we consider and the relevant details for the analyses we review. We take into consideration in general only mediator-quark couplings; couplings to leptons or other SM particles are switched on whenever relevant.

3.1. s-Channel Mediator Models

3.1.1. Spin-0 Mediator

The material presented in this section is based on these selected reference papers (Haisch and Re, 2015; Arina et al., 2016; Banerjee et al., 2017), as they nicely exemplify the main features of scalar and pseudo-scalar mediators in the s-channel by performing comprehensive studies of the model, including astrophysical and cosmological dark matter searches.

We focus on the case of Dirac dark matter (X), with spin-0 mediator (Y₀) coupling to the matter fields of the SM (the dependence on the dark matter spin is briefly summarized in Table 2). The interaction Lagrangians is defined as:

$\begin{array}{ll}{{L}}_X^{Y_0}=\bar{X}(g_{\text{DM}}^S+i{g}_{\text{DM}}^P{\gamma }_5)X{Y}_0,& (5)\end{array}$

and

$\begin{array}{cc}{{L}}_{\text{SM}}^{Y_0}={\displaystyle \sum _{i,j}\left[\overline{d_i}\frac{y_{ij}^d}{\sqrt{2}}(g_{d_{ij}}^S+i{g}_{d_{ij}}^P{\gamma }_5)d_j+\overline{u_i}\frac{y_{ij}^u}{\sqrt{2}}(g_{u_{ij}}^S+i{g}_{u_{ij}}^P{\gamma }_5)u_j\right]}{Y}_0,& (6)\end{array}$

where d and u denote down- and up-type quarks, respectively, (i, j=1,2,3) are flavor indices, $g_{\text{DM}}^{S/P}$ are the scalar/pseudo-scalar WIMP-Y₀ couplings. Following the prescriptions of MFV, the couplings of the mediator to the SM particles are proportional to the particle masses and normalized to the SM Yukawa couplings, $y_{ii}^f=\sqrt{2}{m}_f/v$ and v being the Higgs vacuum expectation value, and all flavor off-diagonal couplings are set to zero. This choice of couplings ensures that: (i) the structure of flavor changing neutral current processes of the SM is preserved by the introduction of new physics; (ii) that all flavor violating transitions are governed by the Cabibbo-Kobayashi-Maskawa matrix.

The pure scalar and pure pseudo-scalar mediator scenarios, which we will review in the rest of the section, are given by setting the parameters in the Lagrangians (5) and (6) to:

$\begin{array}{ll}{g}_{\text{DM}}^S\equiv g_{\text{DM}}\text{ and }{g}_{\text{DM}}^P=0,& (7)\end{array}$

$\begin{array}{ll}{g}_{u_{ii}}^S=g_{d_{ii}}^S\equiv g_{\text{SM}}\text{ and }{g}_{u_{ii}}^P=g_{d_{ii}}^P=0,& (8)\end{array}$

and

$\begin{array}{ll}{g}_{\text{DM}}^S=0\text{ and }{g}_{\text{DM}}^P\equiv g_{\text{DM}},& (9)\end{array}$

$\begin{array}{ll}{g}_{u_{ii}}^S=g_{d_{ii}}^S=0\text{ and }{g}_{u_{ii}}^P=g_{d_{ii}}^P\equiv g_{\text{SM}},& (10)\end{array}$

respectively. With the simplification of a single universal coupling for the SM-Y₀ interactions, the model has only four independent parameters, i.e., two couplings and two masses:

$\begin{array}{ll}\left\{g_{\text{SM}},g_{\text{DM}},m_{\text{DM}},m_{\text{med}}\right\}.& (11)\end{array}$

The MFV assumption implies that we can even further neglect the contributions of all quarks but the top-quark in the model, as it has the largest Yukawa coupling. This is certainly an optimal approximation for LHC studies, while dark matter searches are sensitive to all quark flavors. The assumption however that $g_{\text{SM}}\equiv g_{u_{33}}^{S/A}$ provides a good description of the phenomenology of the model, as the inclusion of all other quark flavors has the effect of globally decreasing the value of g_SM needed to achieve the same cross section.

The Lagrangians of Equations (5) and (6) induce dimension-five couplings of the mediator to gluons and photons via top-quark loop diagrams. These loop-induced operators are relevant for both astrophysical and collider searches for dark matter. For a scalar Y₀, the couplings of the mediator to gluons and photons are given, at the leading order, by the effective operators:

$\begin{array}{ll}{{L}}_g^{Y_0}=-\frac{1}{4}\frac{g_g(Q^2)}{v}{G}_{\mu \nu }^a{G}^{a,\mu \nu }{Y}_0\mathrm{\text{and }}{{L}}_{\gamma }^{Y_0}=-\frac{1}{4}\frac{g_{\gamma }(Q^2)}{v}{F}_{\mu \nu }{F}^{\mu \nu }{Y}_0,& (12)\end{array}$

with the effective couplings being

$\begin{array}{cc}{g}_g(Q^2)=g_{\text{SM}}\frac{{\alpha }_s}{3\pi }\frac{3}{2}{F}_S\left(\frac{4m_t^2}{Q^2}\right)\text{and}{g}_{\gamma }(Q^2)=g_{\text{SM}}\frac{8{\alpha }_e}{9\pi }\frac{3}{2}{F}_S\left(\frac{4m_t^2}{Q^2}\right),& (13)\end{array}$

where Q² denotes the virtuality of the s-channel resonance, while F_S is the one-loop form factor

$\begin{array}{ll}{F}_S(x)=x{\displaystyle [}1+(1-x){arctan}^2(\frac{1}{\sqrt{x-1}}){\displaystyle ]}.& (14)\end{array}$

Similar expressions can be retrieved for the pseudo-scalar case (see e.g., Haisch and Re, 2015; Arina et al., 2017). Because of the hierarchy between the strong and the electromagnetic couplings (${\alpha }_s^2/{\alpha }_e^2~100$), the Y₀ partial width into a pair of gluons is always larger than the one into a pair of photons. The expressions for tree level and loop-induced partial widths are provided in Arina et al. (2016).

Let us first discuss the case of pure scalar Y₀ and summarize briefly all the relevant LHC and dark matter searches to constrain its parameter space:

• LHC $\cancel{\mathbf{E}}$_T searches. As this DMsimp features Yukawa-type couplings, the most relevant tree-level process at the LHC is dark matter pair production associated with a top-quark pair (CMS Collaboration, 2014). Similarly to Higgs production, at one loop, gluon fusion gives rise to $\cancel{E}$_T + jet signatures (Khachatryan et al., 2015a), mono-Z (Khachatryan et al., 2016) and mono-h (Aad et al., 2016), which are phenomenologically relevant.

• LHC mediator searches. The mediator is produced in association with top-quark pairs (Aad et al., 2015a), or via the loop-induced gluon fusion process. These searches are relevant for mediators produced on-shell, or close to on-shell, which decay back into top pairs if kinematically allowed, or a pair of jets (CMS, 2015) or photons (Khachatryan et al., 2015b). For the heavy mediator case, the four-top final state (Khachatryan et al., 2014) can be also relevant.

• Relic density. The dark matter achieves the correct relic density in three separated regions. If m_DM > m_med the relic density is set by the t-channel annihilation into a pair of mediators. Above the top threshold, resonant annihilation into top-quark pairs is efficient enough to lead to the correct value for ${\Omega }_{\text{DM}}{h}^2$. For m_DM < m_t the resonant annihilation into a pairs of gluon leads to the correct relic density for a very fine tuned part of the parameter space. This is due to the very small decay width into gluons.

• Indirect detection. All annihilation processes are p-wave suppressed, hence all fluxes of gamma rays, cosmic rays and neutrinos produced by this model are well below the present and future reach of indirect detection probes.

• Direct detection. The interaction Lagrangians in Equations (5) and (6), after some manipulations to express it in terms of nucleus instead of nucleons, reduces to the operator $\bar{X}X\bar{N}N$. This is equivalent to the ${{O}}_1^{\text{NR}}$ operator (see Table 1), which corresponds to the usual spin-independent interaction. The scalar DMsimp is hence highly constrained by the XENON1T and LUX experimental upper bounds.

All the leading order relevant diagrams for Y₀ and dark matter production at the LHC and dark matter annihilation/scattering in astroparticle experiments are summarized in Figures 2, 3.

FIGURE 2

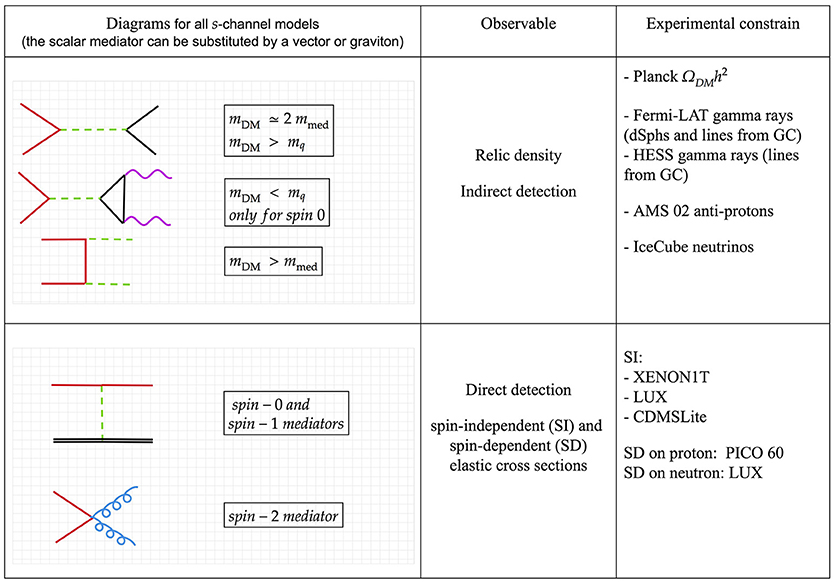
Figure 2. Summary of the leading diagrams contributing to dark matter astrophysical and cosmological searches in the s-channel DMsimps. Color code: red lines denote the dark matter particles, black lines are for SM fermions, purple lines for SM vector bosons, blue lines for gluons and green lines (dashed for the scalar mediator) for the mediator. The spin-1 and spin-2 cases are obtained simply by replacing Y₀ with the spin-1 and spin-2 mediators, except for the case of direct detection, where the first diagram contributes to SI and SD for spin-0 and spin-1, while the second diagram is for the spin-2 case in the minimalistic model. GC stands for Galactic Centre.

FIGURE 3

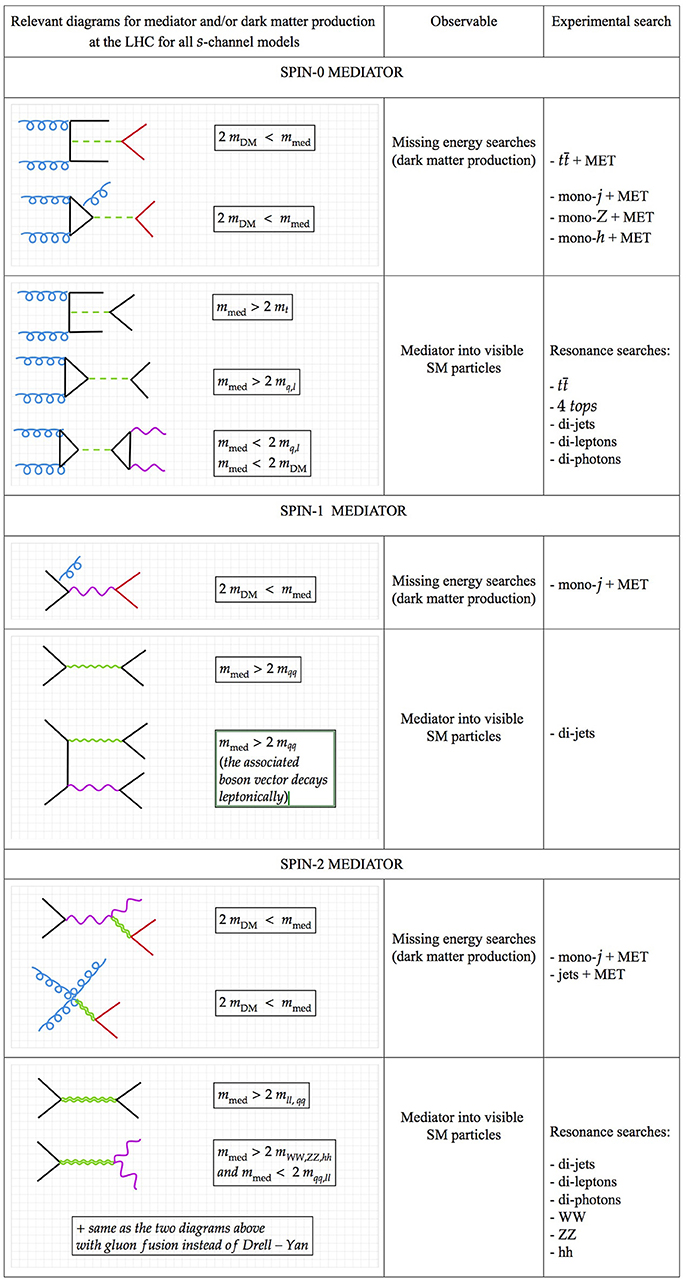
Figure 3. Schematic of leading order diagrams contributing to dark matter and mediator searches at the LHC in the s-channel DMsimps. MET stands for missing transverse energy. The color code is as in Figure 2.

The result of the comprehensive studies are presented in Figures 4–6, from Haisch and Re (2015), Arina et al. (2016), and Ambrogi et al. (2018), assuming a narrow width approximation. Figure 4 illustrates the mono-jet + $\cancel{E}$_T constraints on fixed slices of the model parameter space (red regions). It is clear that mono-jets + $\cancel{E}$_T searches constrain the model parameter space for large values of the Y₀-SM coupling, g_SM ≥ 3.5. The same couplings contribute to the direct detection signal, ${\sigma }_n^{\text{SI}}\propto g_{\text{SM}}^2{g}_{\text{DM}}^2/m_{\text{med}}^4$, and lead to large elastic scattering cross sections, already excluded by LUX (blue solid line). Also shown is the EFT limit, which sets in for heavy mediators. Notice that mono-jets (and mono-X) + $\cancel{E}$_T searches are sensitive to the region m_med > 2m_DM, where typically the dark matter over-closes the universe, if considered as a pure thermal relic. Figure 5A, illustrates the reach of the $t\bar{t}+{\cancel{E}}_T$ search at 8 TeV, where NLO simulations, that reduce the theoretical errors, are used. Similarly to the case of mono-jets + $\cancel{E}$_T, the mediator should be heavier than twice the dark matter mass, in order to be able to decay into invisible states; and the constraints are sensitive to large g_SM couplings. In Figure 5B we show the behavior of the relic density calculation for a 2D scan over the mass parameters and couplings fixed at 1 [this is one of the benchmark point recommended by the LHC DM working group (Boveia et al., 2016)]. The black line represents the values of masses that achieve the correct ${\Omega }_{\text{DM}}{h}^2$, the blue region denotes under-abundant dark matter (mostly leaving in the region m_DM > m_med and dominated by the t-channel annihilation into mediator pairs), while the gray region stands for over-abundant dark matter (mostly covering the region m_med > 2m_DM, where $\cancel{E}$_T searches are relevant). Figure 6 illustrates a comprehensive parameter space sampling of the model, with the assumption that the dark matter is a thermal relic and constitutes 100% of the matter content of the universe. Couplings are freely varied in between 10⁻⁴ and π. The relic density measurement rules out completely the region sensitive to $\cancel{E}$_T searches, while direct detection disfavors at 90% CL regions with a light mediator for a wide range of m_DM. Resonance searches are relevant and constrain the region m_DM > m_t. Di-photons are sensitive to the parameter space m_med < 2m_t, while the $t\bar{t}$ and 4 top searches are sensitive to m_med > 2m_t. A summary of the search sensitivities is provided in Table 2.

FIGURE 4

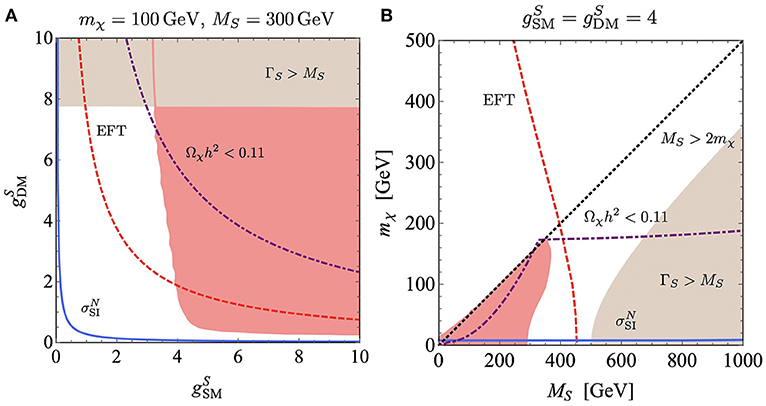
Figure 4. DMsimp: s-channel spin-0 scalar mediator and Dirac dark matter. (A) Present mono-jet exclusion region at 95% CL (red contour and region within) for scalar mediators in a 2D scan of the parameter space in the $\left\{g_{\text{DM}}^S,g_{\text{SM}}^S\right\}$-plane. The fixed values of the two parameters over which the scan is not performed are indicated in each panel. For comparison, we show the region Γ_S > M_S (brown, with Γ_S being the mediator width), the LUX 90% CL exclusion limits on ${\sigma }_n^{\text{SI}}$ (solid blue curve, excludes above and on the right of the curve), the parameter space for under-abundant dark matter (${\Omega }_{\text{DM}}{h}^2<0.11$, dot-dashed purple line), the EFT limit (red dashed line) and the region for which M_S > 2m_χ (black dotted line). (B) Same as (A) in the {m_χ, M_S}-plane. Figures taken from Haisch and Re (2015). The reader can identify $g_{\text{DM}}^S=g_{\text{DM}}$, $g_{\text{SM}}^S=g_{\text{SM}}$, m_χ = m_DM and M_S = m_med with respect to the convention used in the review. Haisch and Re (2015) is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.

FIGURE 5

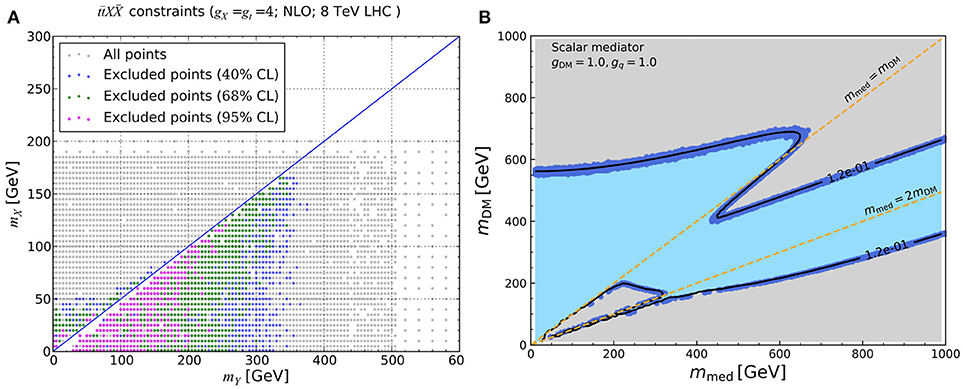
Figure 5. DMsimp: s-channel spin-0 scalar mediator and Dirac dark matter. (A) Constraints from the CMS 8TeV $t\bar{t}+{\cancel{E}}_T$ analysis in the {m_X, m_Y}-plane. The top and dark matter couplings to the mediator are set to 4, as labeled. The next to leading order (NLO) exclusions are shown. Figure taken from Arina et al. (2016). The reader can identify m_X = m_DM and m_Y = m_med with respect to the convention used in the review. (B) Dark matter relic density in the {m_DM, m_med}-plane. The gray region denotes over-abundant dark matter, while the light blue region is for under-abundant dark matter. The black solid line/dark blue points denote the parameter space for which the dark matter has the correct relic density. The orange dashed lines stand for m_med = m_DM and m_med = 2m_DM, as labeled. The couplings are fixed at the values labeled in the plot. Figure taken from Ambrogi et al. (2018). The reader can identify g_q = g_SM with respect to the convention used in the review. Arina et al. (2016) is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited, while (Ambrogi et al., 2018) is distributed with a non-exclusive arXiv license.

FIGURE 6

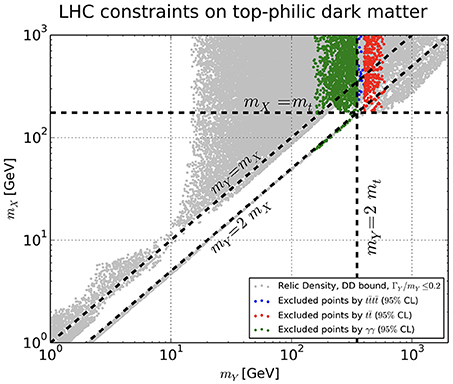
Figure 6. DMsimp: s-channel spin-0 scalar mediator and Dirac dark matter. Results of a 4D parameter sampling projected onto the {m_X, m_Y}-plane, assuming a scenario of thermal dark matter. All gray points satisfy the relic density, narrow width assumption and direct detection constraints. The white region with m_X < m_Y is excluded by relic density constraints (over-closure of the universe), while in the left upper corner the white region is excluded by the LUX and CDMSLite upper limits at 90% CL. LHC constraints are imposed by the colored points, as labeled. The green points are excluded by the di-photon searches, the red points are excluded by $t\bar{t}$ searches and the blue points by the four-top search. Figure taken from Arina et al. (2016). The reader can identify m_X = m_DM and m_Y = m_med with respect to the convention used in the review. Arina et al. (2016) is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.

Moving on to the pure pseudo-scalar case (Banerjee et al., 2017), the relevant LHC and dark matter searches are:

• LHC $\cancel{\mathbf{E}}$_T searches. These are the same as for the scalar case.

• LHC mediator searches. These are the same as for the scalar case. By switching on the couplings to leptons, an additional relevant search is the production via gluon fusion or in association with a pair of bottom-quarks, of the mediator decaying into a pair of τ leptons (A → τ⁺ τ ⁻) (CMS Collaboration, 2016d). This holds for a scalar Y₀ as well.

• Indirect detection. The annihilation channels with Y₀ exchanged in the s-channel are s-wave dominated (i.e., $X\bar{X}\to gg,t\bar{t}$), hence the pseudo-scalar mediator model can be constrained by gamma-ray and cosmic-ray searches.

• Direct detection. Direct detection is not sensitive to pseudo-scalar mediators. This can be understood by looking at Table 1: the high-energy Lagrangians of the pure pseudo-scalar case are mapped into ${{O}}_6^{NR}$. This non-relativistic operator is suppressed by the momentum transfer to the fourth power, hence the current direct detection experiments are insensitive to it, unless the mediator is of the order of the MeV Arina et al. (2015).

The result of the analysis are illustrated in Figure 7 from Banerjee et al. (2017). Figure 7A shows all astrophysical and cosmological constraints for the dark matter: Fermi-LAT exclusion limits from dSphs are more stringent than both anti-proton bounds (as well as more robust in terms of astrophysical uncertainties) and gamma-ray line searches. Figure 7B shows the most stringent dark matter constraints combined with the LHC searches. A thermal relic scenario lives in the narrow band in between the black and the red solid lines. It is a narrow region because it is dominated by resonant s-channel annihilation, which is fine tuned however occurs in all dark matter models featuring an s-channel mediator. $\cancel{E}$_T searches probe a region which is already challenged by the Fermi-LAT dSph constraints. On the other hand, di-photons, $t\bar{t}$ and τ leptons can probe the mediator mass as low as 100 GeV and challenge the left-hand side region where dark matter is a viable thermal relic. The projection for the exclusion bounds coming from the Fermi-LAT satellite after 15 years of operation (red dashed line) shows that these data can basically probe the whole parameter space of the model (everything on the left hand side of the curve is excluded). Notice that additional dark states and mediators can affect the relic density and indirect detection regions. However the changes are supposed to go both in the same directions, hence the region allowed by Planck and Fermi-LAT will remain narrow. LHC bounds for m_med < 2m_t can change sensibly if additional scalars are introduced, as new decay channels will become available; conversely the constraints for m_med > 2m_t are robust and will be qualitatively unaltered.

FIGURE 7

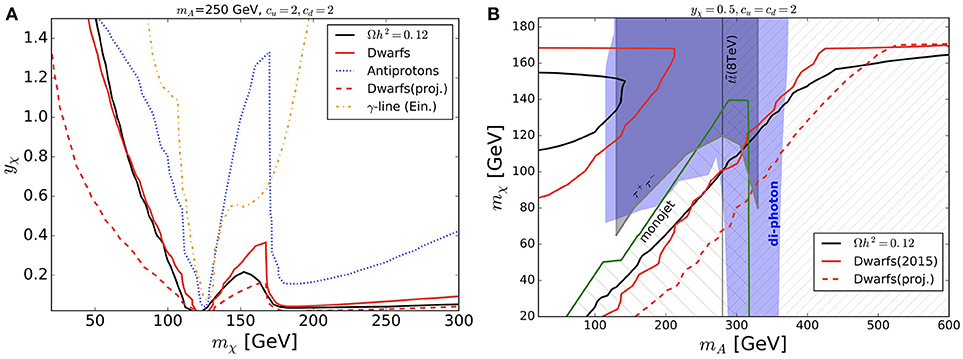
Figure 7. DMsimp: s-channel spin-0 pseudo-scalar mediator and Dirac dark matter. (A) Dark matter constraints on the model parameter space in the {y_χ, m_χ}-plane. The other parameters are fixed as labeled. Below the black line the universe is over-closed, while the region above the red solid line is excluded by the Fermi-LAT dSph gamma-ray searches. The region above the dotted blue line is disfavored by AMS 02 anti-proton measurements, whereas the region above the yellow dot-dashed line is excluded at 95% CL by gamma-ray line searches from the Galactic Center. The red dashed curve denotes the expected sensitivity of the Fermi-LAT searches in dSPhs after 15 years of data. (B) Dark matter and collider searches presented in the {m_χ, m_A}-plane. The other parameters are fixed as labeled. If considered as thermal relic the dark matter allowed region is contained in between the red and black solid lines. The shaded regions are excluded by LHC searches at 95% CL: mono-jet (hatched green), A → τ⁺ τ ⁻ (gray), di-photons (blue), and $t\bar{t}$ (hatched gray). Figures taken from Banerjee et al. (2017). The reader can identify m_χ = m_DM and m_A = m_med, c_u = c_d = g_SM and y_χ = g_DM with respect to the convention used in the review. Banerjee et al. (2017) is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.

Other studies of the spin-0 case are for instance (Buckley et al., 2015; Harris et al., 2015; Dolan et al., 2016; du Pree et al., 2016), while details on loop-induced process for mono-jet + MET can be found in Haisch et al. (2013), Buckley et al. (2015), Harris et al. (2015), Haisch and Re (2015), and Backović et al. (2015). Leptonic couplings have been introduced in e.g., Albert et al. (2017a). Similarly, Y₀ couplings to the SM gauge bosons are discussed in Neubert et al. (2015).

3.1.2. Spin-1 Mediator

The material discussed in this section is based on these selected (Chala et al., 2015; Carpenter et al., 2016; Heisig et al., 2016; Albert et al., 2017a), that exhaustively exemplify the main features of vector and axial-vector mediators in the s-channel and perform comprehensive studies of the model, including astrophysical and cosmological dark matter searches.

The interaction Lagrangian of a spin-1 mediator (Y₁) with a Dirac fermion dark matter particle (X) is given by:

$\begin{array}{ll}{{L}}_X^{Y_1}=\bar{X}{\gamma }_{\mu }(g_{\text{DM}}^V+g_{\text{DM}}^A{\gamma }_5)X{Y}_1^{\mu },& (15)\end{array}$

and with quarks by:

$\begin{array}{ll}{{L}}_{\text{SM}}^{Y_1}={\displaystyle \sum _{i,j}}[\overline{d_i}{\gamma }_{\mu }(g_{d_{ij}}^V+g_{d_{ij}}^A{\gamma }_5)d_j+\overline{u_i}{\gamma }_{\mu }(g_{u_{ij}}^V+g_{u_{ij}}^A{\gamma }_5)u_j]Y_1^{\mu },& (16)\end{array}$

where $g_{\text{DM}}^{V/A}$ and $g_{u/d_{ij}}^{V/A}$ are the vector/axial-vector couplings of the dark matter and quarks with Y₁. For a Majorana dark matter candidate the vector coupling is not allowed.

The pure vector and pure axial-vector mediator scenarios are obtained by setting the parameters in the Lagrangians (15) and (16) to

$\begin{array}{ll}{g}_X^V\equiv g_{\text{DM}}\text{ and }{g}_X^A=0,& (17)\end{array}$

$\begin{array}{ll}{g}_{u_{ii}}^V=g_{d_{ii}}^V\equiv g_{\text{SM}}\text{ and }{g}_{u_{ii}}^A=g_{d_{ii}}^A=0& (18)\end{array}$

and

$\begin{array}{ll}{g}_X^V=0\text{ and }{g}_{X_D}^A\equiv g_{\text{DM}},& (19)\end{array}$

$\begin{array}{ll}{g}_{u_{ii}}^V=g_{d_{ii}}^V=0\text{ and }{g}_{u_{ii}}^A=g_{d_{ii}}^A\equiv g_{\text{SM}},& (20)\end{array}$

respectively, where we assume quark couplings to the mediator to be flavor universal and set all flavor off-diagonal couplings to zero. Similarly to the case of spin-0 mediator, this model has only four free parameters, defined as in Equation (28). The universality assumption of the couplings is also justified by gauge invariance, which sets very tight constraints on the relation among couplings (see e.g., Bell et al., 2015). Even though the Lagrangians presented above do not preserve gauge invariance, the assumption of having different couplings to up- and down-type quarks, as e.g., in Chala et al. (2015), can lead to artificial enhanced cross sections which are not representative of gauge invariant theories.

In this model the couplings to leptons are not considered, hence it can be seen as a lepto-phobic Z′ model (see e.g., Duerr and Fileviez Perez, 2015). Leptonic couplings are indeed very tightly constrained by di-lepton resonant searches (Dudas et al., 2009; Arcadi et al., 2014; Lebedev and Mambrini, 2014) and can be switched off to allow to have large quark couplings.

Let us first discuss the complementarity of searches for the case of a pure vectorial Z′ model, hence the dark matter candidate can only be a Dirac fermion (Chala et al., 2015; Carpenter et al., 2016; du Pree et al., 2016).

• LHC $\cancel{\mathbf{E}}$_T searches. ATLAS and CMS searches for jets in association with $\cancel{E}$_T (due to initial state radiation of a gluon) place strong constraints on this model (Aad et al., 2015b; Khachatryan et al., 2015a).

• LHC mediator searches. The di-jet final state is a very important complementary channel, as it has been pointed out in Chala et al. (2015). Di-jets can be produced via Y₁ Drell-Yan process or via associated production. Stringent bounds for di-jet invariant mass above 1 TeV are provided by ATLAS (ATLAS Collaboration, 2013; Aad et al., 2015c) and CMS (Khachatryan et al., 2015c), while complementary and equally tight bounds for smaller masses are provided by the UA2 (Alitti et al., 1993) experiment and the Tevatron CDF experiment (Aaltonen et al., 2009).

• Relic density. The dark matter achieves the correct relic density in a small narrow band for fixed couplings. If m_DM > m_med the relic density is set by the t-channel annihilation into a pair of mediators, which is an s-wave process proportional to $g_{\text{DM}}^4$. For g_DM ~ 1 this cross section is small and the dark matter is under-abundant. For the benchmark points chosen by the LHC Dark matter working group (Albert et al., 2017a), the correct relic density is achieved by the exchange in the s-channel of a Y₁, leading to resonant annihilation into quark pairs, which is also s-wave. Of course, the introduction of leptonic couplings can change this classification.

• Indirect detection. 〈σv〉₀ receives contributions from the same channels that fix the relic density. For the details on the annihilation cross section we refer to Albert et al. (2017a). However in the literature, at the best of our knowledge, there are no results on constraints from Fermi-LAT dSph gamma-ray searches that include the t-channel term.

• Direct detection. The interaction Lagrangians in Equations (15) and (16) are equivalent to ${{O}}_1^{\text{NR}}$, see Table 1. This non-relativistic operator describes the usual spin-independent elastic scattering off nuclei. The vector model is hence highly constrained by the XENON1T and LUX experimental upper bounds.

The leading order relevant diagrams for Y₁ and dark matter production at the LHC and dark matter annihilation/scattering in astroparticle experiments are summarized in Figures 2, 3 (the same holds for the pure axial-vector mediator).

Figure 8A, from Chala et al. (2015), shows the complementarity of collider, cosmological and direct detection searches, with fixed couplings g_SM = g_DM = 1. Basically the whole parameter space of the model is strongly disfavored by the current limits of direct detection experiments. Di-jets and mono-jets have a rather smaller impact on the model parameter space. Notice however that, contrary to the case of spin-0 mediator, collider searches are sensitive to smaller values of g_SM, even of the order of ${O}(0.1)$. Mono-X searches are more sensitive to the region for which m_med > 2m_DM, in which the DMsimp features over-abundant dark matter. This assumption can be circumvented by invoking for instance dark matter non thermal production or entropy injection. Conversely, di-jet constraints are rather independent of the dark matter mass and cover all dark matter regions. Constraints from Fermi-LAT dSphs have been discussed in Carpenter et al. (2016): the parameter space of the model is most restricted for m_med ~ 2m_DM, because of the enhancement in 〈σv〉₀ due to the resonance. If the vector mediator is much heavier than the dark matter, the total annihilation cross section drops and the parameter space becomes suddenly less constrained. This can be understood by the fact that annihilation occurs far away from the resonance, hence 〈σv〉₀ decreases quickly.

FIGURE 8

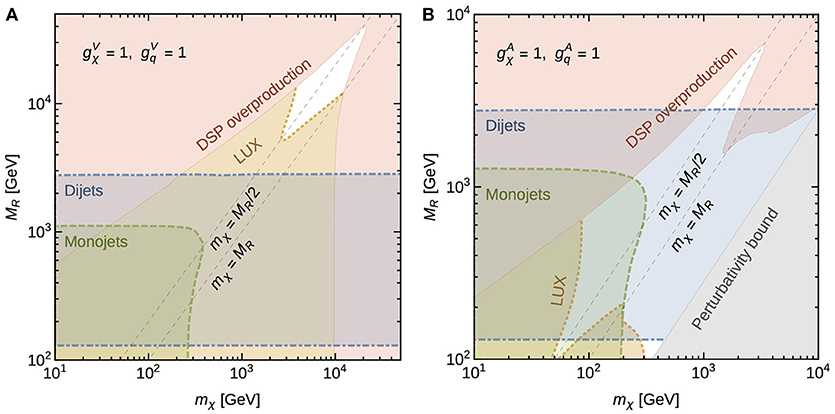
Figure 8. DMsimp: s-channel spin-1 vector (A) and axial-vector (B) mediator and Dirac dark matter. (A) Combined constraints at 95% CL from the LUX experiment (orange dotted line and orange shaded region), from mono-jet searches (green dashed line and green shaded region) and di-jets (blue dot-dashed line and region in between) in the {M_R, m_χ}-plane for fixed couplings, as labeled. We also show the region that over-closes the universe (red) and the region excluded by perturbativity (gray). (B) Same as (A). The reader can identify m_χ = m_DM and M_R = m_med, $g_{\chi }^{V/A}=g_{\text{DM}}$, and $g_q^{V/A}=g_{\text{SM}}$ with respect to the convention used in the review. Figures taken from Chala et al. (2015), distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.

Moving to the axial-vector case, the dark matter can be either Dirac or Majorana. The most relevant dark matter searches are (Chala et al., 2015; du Pree et al., 2016; Heisig et al., 2016):

• LHC $\cancel{\mathbf{E}}$_T searches and mediator searches. These are exactly the same as in the pure vector case described above.

• Relic density. The s-channel process is helicity suppressed if $g_{\text{DM}}^V=0$, namely it is proportional to $m_q^2$, while the t-channel is s-wave, taken properly into account in the analysis in Albert et al. (2017a).

• Indirect detection. In the analyses performed so far there are no bounds from gamma-ray or cosmic-ray searches because the t-channel process has not been properly taken into account. However, relevant constraints for the model parameter space arise from the IceCube upper limits on ${\sigma }_p^{\text{SD}}$, where all annihilation processes contributing to 〈σv〉₀ have been properly taken into account.

• Direct detection. Spin-independent elastic scattering is superseded by the ordinary spin-dependent elastic scattering (corresponding to ${{O}}_4^{\text{NR}}$ in Table 1). This operator is less constrained by direct detection experiments with respect to ${{O}}_1^{\text{NR}}$. The most constraining experiment is LUX for ${\sigma }_n^{\text{SD}}$.

The right panel of Figure 8 from Chala et al. (2015), describes the complementarity of collider, cosmological and direct detection searches, with fixed couplings g_SM = g_DM = 1, for the axial-vector model. The impact of the LUX exclusion limit is rather reduced with respect to the pure vector case. Hence collider bounds have a nice degree of complementarity for this model, disfavoring the majority of the viable parameter space. The gray region is excluded by the perturbativity bound, obtained by imposing $m_{\text{med}}>g_{\text{DM}}^4{m}_{\text{DM}}\sqrt{4\pi }$, which comes from the requirement that the annihilation cross section remains well-behaved at large dark matter masses. Figure 9, from Heisig et al. (2016), shows the impact of the IceCube bounds on the model parameter space for fixed product of the couplings and for a narrow Y₁ width (Figure 9A) and for a large mediator width (Figure 9B), as Γ_Y1 ≡ Γ_V is taken as a free parameter. In the very narrow width approximation, di-jet constraints are irrelevant, while mono-jet + $\cancel{E}$_T searches are much less affected by changes in the mediator width. The exclusion bound stemming from LUX does not depend on the mediator width, and remains unchanged in the two cases and constrain the DMsimp parameter space where dark matter is either a thermal relic or under-abundant. The IceCube exclusion limit has a subtle dependence on the mediator width, as the annihilation rate is sensitive to both the s-channel process, which depends on g_SM × g_DM, and on the t-channel process, which depends only on g_DM, for m_DM ≥ m_med¹⁰. In Figure 9A, IceCube and LUX probe a complementary region, in which m_DM > m_med, with respect to LHC searches. LUX constraints are relevant at intermediate dark matter masses, while IceCube lower limits overtake all other constraints at large dark matter masses. In case of a large mediator width, the IceCube bound overlaps with the di-jet constraints. From a refined analysis on di-jets in Fairbairn et al. (2016), it has been shown that for m_med < 3 TeV and Γ_Y1 > 0.25m_med, the collider constraints disfavor the possibility that the WIMP-quark interactions are responsible for setting the dark matter relic density. A summary of the search sensitivities and their dependency on the dark matter nature is provided in Table 2.

FIGURE 9

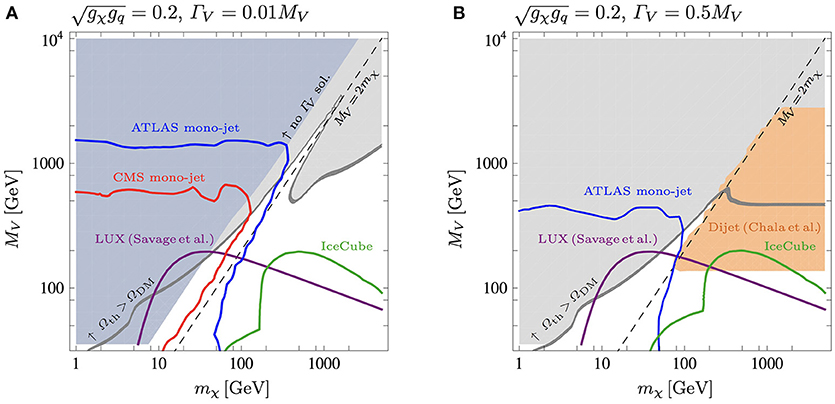
Figure 9. DMsimp: s-channel spin-1 axial-vector mediator and Majorana dark matter. (A) Combined constraints in the {M_V, m_χ}-plane for fixed couplings and for a narrow mediator width Γ_V = 0.01M_V, as labeled. We show the region disfavored by mono-jet searches from ATLAS (blue solid line including the region below and on the left) and CMS (red solid line including the region below and on the left), both at 95% CL, the LUX exclusion bound (purple solid line and region below) and by IceCube searches (green solid line and region below it), both at 90% CL.The light gray region stands for over-abundant dark matter, while the gray band denotes the region where the dark matter relic density matches the observed one. The blue region does not allow for a consistent solution of Γ_V in terms of M_v, m_χ and $\sqrt{g_{\chi }{g}_q}$ within this DMsimp. (B): Same as (A) for a large mediator width Γ_V = 0.5M_V. The orange region denotes the constraint from di-jets searches. Figures taken from Heisig et al. (2016). The reader can identify m_χ = m_DM and M_V = m_med, g_q = g_SM and g_χ = g_DM with respect to the convention used in the review. Permission to reuse the figures from Heisig et al. (2016) have been granted under the license RNP/18/004002.

The LHC Dark Matter working group has suggested to consider leptonic couplings as well (Albert et al., 2017a). These should be however at least one order of magnitude smaller than the mediator-quark couplings, to not completely exclude the model. Interestingly couplings to neutrinos would also be present because of gauge invariance requirements; these couplings will supply an additional $\cancel{E}$_T channel with the consequences of enhancing certain mono-X + $\cancel{E}$_T signals.

Other studies of the spin-1 DMsimps are for instance (Buchmueller et al., 2015; Harris et al., 2015; Jacques and Nordstrom, 2015; Bell et al., 2016a; Brennan et al., 2016; du Pree et al., 2016; Fairbairn et al., 2016; Jacques et al., 2016). The latter papers in the list already consider a gauge invariant completion of the Z′ model, instead of the DMsimp Lagangrians in Equations (15) and (16). This issue will be discussed in section 4.

3.1.3. Spin-2 Mediator

The material presented in this section is based on these selected (Lee et al., 2014a; Kraml et al., 2017; Zhang et al., 2017), as they exemplify the main features of a spin-2 mediator in the s-channel as compared with LHC searches and indirect detection searches. The literature on spin-2 mediator is rather reduced with respect to the spin-0 and spin-1 cases. Relevant works are provided by these (Garcia-Cely and Heeck, 2016; Dillon and Sanz, 2017; Dillon et al., 2017; Rueter et al., 2017; Zhu and Zhang, 2017; Yang and Li, 2018).

Even though the exchange of a graviton in the s-channel is not considered in the recommendations of the LHC Dark Matter working group (Boveia et al., 2016), it entails several features in common with the DMsimp philosophy. It is possible to build a dark matter simplified model out of a gravity-mediated dark matter model proposed in Lee et al. (2014b), even though it requires a dedicated validation work, as such model is, in general, not renormalizable. This type of models have as well driven a lot of attention at the time of the 750 GeV excess in the di-photon channel (see e.g., Han et al., 2016; Martini et al., 2016; Arun and Saha, 2017) and the references therein.

The definition of the model follows the approach of DMsimps. We consider dark matter particles which interact with the SM particles via an s-channel spin-2 mediator. The interaction Lagrangian of a spin-2 mediator (Y₂) with the dark matter (X) is given by Lee et al. (2014b):

$\begin{array}{ll}{{L}}_X^{Y_2}=-\frac{1}{\Lambda }{g}_X^T{T}_{\mu \nu }^X{Y}_2^{\mu \nu },& (21)\end{array}$

where Λ is the scale parameter of the theory, $g_X^T$ is the coupling between Y₂ and the dark matter, and $T_{\mu \nu }^X$ is the energy–momentum tensor of the dark matter field. The energy–momentum tensors of the dark matter are:

$\begin{array}{lll}{T}_{\mu \nu }^{X_R}& =-\frac{1}{2}{g}_{\mu \nu }({\partial }_{\rho }{X}_R{\partial }^{\rho }{X}_R-m_X^2{X}_R^2)+{\partial }_{\mu }{X}_R{\partial }_{\nu }{X}_R,& (22)\end{array}$

$\begin{array}{l}{T}_{\mu \nu }^{X_D}=-g_{\mu \nu }({\overline{X}}_{D}i{\gamma }_{\rho }{\partial }^{\rho }{X}_D-m_X{\overline{X}}_D{X}_D)+\frac{1}{2}{g}_{\mu \nu }{\partial }_{\rho }({\overline{X}}_{D}i{\gamma }^{\rho }{X}_D)+\frac{1}{2}\\ {\overline{X}}_{D}i({\gamma }_{\mu }{\partial }_{\nu }+{\gamma }_{\nu }{\partial }_{\mu })X_D-\frac{1}{4}{\partial }_{\mu }({\overline{X}}_{D}i{\gamma }_{\nu }{X}_D)-\frac{1}{4}{\partial }_{\nu }({\overline{X}}_{D}i{\gamma }_{\mu }{X}_D),& (23)\end{array}$

$\begin{array}{lll}{T}_{\mu \nu }^{X_V}& =-g_{\mu \nu }(-\frac{1}{4}{F}_{\rho \sigma }{F}^{\rho \sigma }+\frac{m_X^2}{2}{X}_{V\rho }{X}_V^{\rho })+F_{\mu \rho }{F}_{\nu }^{\rho }+m_X^2{X}_{V\mu }{X}_{V\nu },& (24)\end{array}$

where F_μν is the field strength tensor. We consider three dark matter spins: a real scalar (X_R), a Dirac fermion (X_D), and a vector (X_V). The interaction Lagrangian with the SM particles is:

$\begin{array}{ll}{{L}}_{\text{SM}}^{Y_2}=-\frac{1}{\Lambda }{\displaystyle \sum _i}{g}_i^T{T}_{\mu \nu }^i{Y}_2^{\mu \nu },& (25)\end{array}$

where i denotes the SM fields: the Higgs doublet (H), quarks (q), leptons (ℓ), and SU(3)_C, SU(2)_L and U(1)_Y gauge bosons (g, W, B). Following (Ellis et al., 2013; Englert et al., 2013), the phenomenological coupling parameters are defined as:

$\begin{array}{ll}{g}_i^T=\left\{g_H^T,g_q^T,g_{\ell }^T,g_g^T,g_W^T,g_B^T\right\}& (26)\end{array}$

without assuming any UV complete model. Notice that the interaction Lagrangian in Equation (25) defines couplings of the graviton with all SM fields. This hypothesis is more generic with respect to the standard assumptions of the DMsimps, where the mediator interacts only with the quark sector. The energy-momentum tensors of the SM fields are similar to Equation (22) and their explicit expression is provided in e.g., Das et al. (2017).

Complying with the DMsimp idea, it is instructive to consider universal couplings between the spin-2 mediator and the SM particles:

$\begin{array}{ll}{g}_H^T=g_q^T=g_{\ell }^T=g_g^T=g_W^T=g_B^T\equiv g_{\text{SM}}.& (27)\end{array}$

With this simplification, the model has only four independent parameters¹¹, two masses and two couplings, as for the other DMsimps considered so far:

$\begin{array}{ll}\left\{m_X,m_Y,g_{\text{DM}}/\Lambda ,g_{\text{SM}}/\Lambda \right\}.& (28)\end{array}$

This scenario with a universal coupling to SM particles is realized, e.g., in the original Randall–Sundrum model of localized gravity (Randall and Sundrum, 1999). With this choice of couplings the mediator decays mainly into gluons and light quarks, while the di-photon branching ratio is only ~5%. The decay into top-quarks or vector bosons is relevant when kinematically allowed. As already discussed in the case of spin-1 mediator, the Y₂-neutrino coupling leads to $\cancel{E}$_T signals that are independent of the decays into dark matter particles and provide additional $\cancel{E}$_T channels for the mono-X signals.

In the following, to exemplify the complementarity of dark matter searches, we will focus on vectorial dark matter.

• LHC $\cancel{\mathbf{E}}$_T searches. The Y₂ production is mostly initiated by gluon fusion at low masses, which suppresses mono-photon, mono-Z and mono-W signals, as they can occur only in quark initiated processes. Hence the most constraining missing energy searches for the spin-2 model are a single mono-jet + $\cancel{E}$_T (ATLAS Aaboud et al., 2016a) and 2–6 jets + $\cancel{E}$_T (ATLAS Aaboud et al., 2016b).

• LHC mediator searches. Resonance searches from LHC Run 2 data [ATLAS (ATLAS Collaboration, 2016a,b,c,d,e,f; CMS Collaboration, 2016a) and CMS (CMS Collaboration, 2015, 2016b,c; Khachatryan et al., 2017a,b; Sirunyan et al., 2017a)] give strong constraints on the graviton mass in between few hundreds of GeV and several TeV. The considered final states are $jj,ll,\gamma \gamma ,W^{+}{W}^{-},ZZ,hh,b\bar{b},t\bar{t}$.

• Relic density. The dark matter can achieve the correct relic density via the s-channel exchange of a graviton, especially in the region m_med ~ 2m_med, and via t-channel annihilation into a pairs of Y₂, which subsequently decay into SM particles, in the region m_DM < m_med. Both annihilation channels are s-wave in the case of vectorial dark matter. The analytic expression for these channels are provided in Lee et al. (2014a).

• Indirect detection. Annihilation via s-channel into SM particles with Y₂ exchange can produce both a continuum photon spectrum and gamma-ray lines. Both signals can be constrained by Fermi-LAT and HESS spectral feature searches at the Galactic Centre and by Fermi-LAT dSph exclusion limits. Additionally the t-channel annihilation process can give rise to box-shaped gamma-ray signatures (see e.g., Ibarra et al., 2015a), which are however only poorly constrained by Fermi-LAT searches for spectral features toward the Galactic Centre (Lee et al., 2014a).

• Direct detection. The WIMP-gluon interaction is relevant for direct searches: this coupling generates a twist-2 operator which induces a spin-independent cross-section dark matter-nucleon. This cross section can be in tension with the XENON1T for dark matter masses below roughly 400 GeV (see Chu et al., 2012; Lee et al., 2014b) for the case of scalar dark matter. However, we couldn't find a dedicated analysis illustrating how direct detection impacts the whole DMsimp spin-2 parameter space. The elastic cross section WIMP-nuclei can receive additional contributions in non minimalistic models (Lee et al., 2014a).

The diagrams for dark matter annihilation are illustrated in Figure 1, while the mediator production at the LHC is shown in Figure 3.

At present, to the best of our knowledge, there are actually no comprehensive studies of spin-2 models, which encompass both LHC and dark matter searches, except for Zhang et al. (2017). We however refrain from using their results to illustrate the main features of this model, as they perform a random scan of the full parameter space. While this is certainly instructive, it is not necessarily the most optimal pedagogical approach to begin with. For the sake of the discussion, we choose to show 2D parameter scans, even though they do not show the complementarity of searches.

Figure 10, from Lee et al. (2014a); Kraml et al. (2017), resumes the constraints on slices of the DMsimp parameter space stemming from LHC searches for a massive graviton, Figure 10A, and the dark matter gamma-ray searches, Figure 10B. From Figure 10A, we clearly see that the di-photon and the di-lepton resonance searches provide the most stringent limit in the whole mediator mass range, constraining Λ/g_SM > 100 TeV for graviton masses below 1 TeV. These searches are rather independent on the exact dark matter mass value. Mono-jets + $\cancel{E}$_T searches become competitive for large values of g_SM and, if the Y₂ decays into γγ and ll, are heavily suppressed. In Figure 10B, we show the impact of gamma-ray searches. For m_DM < m_med, the exclusion limits from gamma-ray lines provided by Fermi-LAT disfavor at 95% CL the model parameter space compatible with the thermal relic assumptions, as the dark matter annihilates mainly into gg and γγ. For m_DM > m_med the thermal relic scenario is compatible with Fermi-LAT dSph upper limits and with the HESS gamma-ray line searches, which are the most sensitive constraints for large dark matter masses.

FIGURE 10

Figure 10. DMsimp: s-channel spin-2 mediator. (A): Summary of the 13 TeV LHC constraints in the {Λ/g_SM, m_Y}-plane. The other parameters are fixed as labeled. The differences among the different dark matter spins is not visible in the limits from the resonance searches (as labeled in the plots), conversely to the case of jets + $\cancel{E}$_T searches (red lines as labeled). Regions below each lines are disfavored at 95% CL. Information on the mediator width-to-mass ratio is provided by the gray dotted lines. Figure taken from Kraml et al. (2017). The reader can identify m_Y = m_med, g_X = g_DM and m_X = m_DM with respect to the convention used in the review. (B): Gamma-ray bounds from Fermi-LAT (d.G., line, G.C.) and HESS telescope (lines) are shown in case of vector dark matter in the {m_G/Λ, M_X}-plane, for a fixed graviton mass as labeled. Couplings are not universal, but fixed at g_X = 1, g_V = g_g = g_γ = 0.3 and g_h = 0, and m_G/Λ corresponds to the Y₂-WIMP coupling g_DM. The green line corresponds to the region of parameter space achieving the correct ${\Omega }_{\text{DM}}{h}^2$. Figure taken from Lee et al. (2014a). The reader can identify M_X = m_DM and m_G = m_med with respect to the convention used in the review, while d.G. and G.C. stand for dSphs and Galactic Center respectively. Both Kraml et al. (2017) and Lee et al. (2014a) are distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.

Fermionic and scalar dark matter particles are more loosely constrained by current gamma-ray searches with respect to vectorial dark matter particles, as 〈σv〉₀ is suppressed by p-wave or d-wave respectively. LHC constraints are less sensitive to the dark matter spin. The sensitivity to the dark matter particle nature depends on the hierarchy between g_DM and g_SM: for g_DMSM only jets + $\cancel{E}$_T searches can differentiate among the spin of the dark matter candidate; for g_SM >> g_DM all searches become sensitive to the dark matter nature. It turns out that the vectorial case is the most constrained model, while the scalar DMsimp is the less constrained and the fermionic case lies in between.

3.2. t-Channel Mediator Models

In this section we discuss the phenomenology of t-channel DMsimps and their current state of art with respect to the experimental situation. t-channel models couple directly the dark matter sector with the SM fermions (primarily quarks), leading to a different phenomenology with respect to s-channel models. The fields in the dark sector are both odd under a Z₂ symmetry to ensure the stability of the dark matter candidate, while in s-channel models the mediator is usually assumed to be even under the Z₂ symmetry¹². As a consequence, LHC searches are always characterized by $\cancel{E}$_T signals, as the mediator is produced each time in combination with a dark matter particle. In order to connect the dark matter via t-channel with SM quarks there are two main possibilities: scalar dark matter and fermionic mediator, or fermionic dark matter and scalar mediator. The dark matter cannot have color charge, hence the mediator has to be colored. Additionally, to comply to MFV, either the mediator or the dark matter should have a flavor index. Here we assume to be the former case. For uncolored mediator models see (Garny et al., 2015), while for flavored dark matter we refer to Agrawal et al. (2012, 2014); Kile (2013). From the point of view of QCD corrections, the t-channel and s-channel models are very different, as in the former the mediator can be either neutral or colored, rendering more involved the treatment of NLO corrections. This has not been yet fully investigated in the literature, due to its complexity.

Among the vast literature on t-channel models (see e.g., Blumlein et al., 1997; Cao et al., 2009; Bell et al., 2011, 2012, 2016b; Barger et al., 2012; Bai and Berger, 2013, 2014; Garny et al., 2013, 2014, 2018; Giacchino et al., 2013, 2014, 2016; Toma, 2013; An et al., 2014; Chang et al., 2014a,b; Ibarra et al., 2014, 2015b; Papucci et al., 2014; Yu, 2014; Abdallah et al., 2015; Abercrombie et al., 2015; Brennan et al., 2016; Bringmann et al., 2016; Carpenter et al., 2016; De Simone and Jacques, 2016; Goyal and Kumar, 2016; El Hedri et al., 2017), we choose to present the results obtained in Colucci et al. (2018) for the case of scalar dark matter and fermionic mediator, which is the most updated analysis at the time of writing. For the case of fermionic dark matter and scalar mediator we discuss the results presented in Garny et al. (2015), which is a comprehensive review paper focusing on t-channel simplified models alike the supersymmetric one.

Let us first discuss the case of scalar dark matter candidate S and a vector-like fermionic mediator T. We assume that the dark matter is a SU(2)_L singlet, hence it cannot couple at tree level with the weak gauge bosons. Consequently the dark matter hyper-charge is zero, in order to obtain an electrically neutral particle. The dark matter can couple to either right-handed or left-handed SM fermions. Here we assume a couplings with right-handed quarks, in particular only with the third generation. The main reason is dictated by the fact that right-handed couplings to quarks play a major role for the LHC and direct detection phenomenology and the Yukawa of the top is the largest coupling. The mediator T should be a color triplet, have opposite hyper-charge with respect to the right-handed quarks and be a singlet under SU(2)_L. The interaction Lagrangian between WIMPs and the SM quarks is then given by Colucci et al. (2018):

$\begin{array}{ll}{{L}}_S^T=yS\bar{T}{P}_{R}t+\text{h}.\text{c}.,& (29)\end{array}$

where P_R is the right-handed chirality projector, and we have neglected the quartic term connecting the dark matter particle with the SM Higgs doublet, in the spirit of DMsimp construction. With these assumptions the model has only three free parameters:

$\begin{array}{ll}\left\{m_{\text{DM}},m_{\text{med}},y\right\}.& (30)\end{array}$

This model considers top-philic dark matter, which might seem more ad- hoc than a generic framework where the dark matter couples to all generations. However, this is enough to comprehend all the relevant phenomenology, as in the limit m_DM > m_t, the results are strictly equivalent as for the case in which the dark matter couples to the light quark (or lepton) generations only. Moreover, at energies comparable with the top mass, the computation of QCD and bremsstrahlung corrections are much more involved than in the chiral limit, hence it is relevant to have the most general framework where to treat them. We are not providing any detail on this part and refer to (Bringmann et al., 2017; Colucci et al., 2018) the interested reader. Notice that if the dark matter was coupled to all three quark generations with three different vector-like fermionic mediators, MFV requirements would enforce the three mediator masses to be equal, as well as their couplings with WIMPs and quarks.

The dark matter constraints for this model are:

• LHC searches with $\cancel{\mathbf{E}}$_T. There are two types of searches particularly relevant for this model: (i) supersymmetric searches of scalar top partners [LEP (Abbiendi et al., 2002) and LHC (CMS Collaboration, 2017; Sirunyan et al., 2018)], recasted to constrain the vector-like fermionic mediator of the model, which is strongly interacting and leads to mainly $t\bar{t}+{/\cancel{\mathbf{E}}}_T$ signals; (ii) the usual dark matter searches characterized by a mono-jet + $\cancel{E}$_T (Aaboud et al., 2016a, 2018; Sirunyan et al., 2017b,c) (actually the most updated mono-j searches do include more than one hard jet). NLO QCD corrections and matching with the parton showers have been taken into account, in order to comply with the state-of-art modeling of the LHC signals for the s-channel case.

• Relic density. There are several annihilation processes contributing to ${\Omega }_{\text{DM}}{h}^2$, depending on the model parameter space region. For m_DM >> m_t the chiral limit is valid and virtual internal bremsstrahlung (VIB) adds a significative contribution to the tree level leading order t-channel diagram, which is helicity suppressed and the first non-zero term depends on v⁴ (d-wave). Decreasing m_DM just above the top threshold, the tree level t-channel diagram, which is s-wave, is the leading contribution to 〈σv〉₀. Below the top mass, loop-induced processes into γγ and gg can play a role (similarly to the spin-0 top-philic dark matter presented in section 3.1.1), while, for m_DM ≲ m_t the off-shell decay t* → Wb is relevant. Additionally, if the dark matter and the mediator masses are close in mass (within 10%) co-annihilation between S and T is also relevant, as well as T annihilations.

• Indirect detection. For m_DM < m_t, annihilation via the loop induced process into pairs of gluons dominates. This leads to a prompt photon spectrum. The γγ final state is subdominant with respect to the gg final state as already discussed in section 3.1.1, however it gives rise to box-shaped gamma-ray signals (the width of the box depends on the mass hierarchy between S and T: if they are quasi degenerate the box is very narrow, otherwise it is a wide box). For m_DM ~ m_t, the dominant annihilation channel is the tree level t-channel, $SS\to t\bar{t}$, which leads to a continuum spectrum of prompt photons, detectable by the Fermi-LAT dSph searches. The same process can be constrained with the anti-proton data released by AMS 02. VIB with the emission of a photon, a gluon or a weak boson, has been demonstrated to be the dominant contribution in the chiral limit (m_DM >> m_t) (see e.g., Bell et al., 2011; Giacchino et al., 2013, 2014, 2016; Bringmann et al., 2016, 2017). The emission of an additional vector boson lifts the helicity suppression and gives rise to sizeable 〈σv〉₀. If S and T are nearly degenerate in mass, the $SS\to t\bar{t}\gamma$ process dominates the VIB contribution. This photon emission gives rise to a sharp spectral feature, that can be constrained with current gamma-ray line searches. Indeed, the present telescope resolution does not allow to discriminate among the sharp edge due to VIB or a true gamma-ray line (Garny et al., 2015). Direct annihilation of the dark matter into photon pairs via box diagram is on the same foot as VIB. On the other hand the annihilation process $SS\to t\bar{t}g$ contributes to the continuum photon spectrum.

• Direct detection. An effective coupling WIMP-gluons generates a spin-independent contribution to the elastic scattering cross section, which is, for m_DM < m_t, in tension with the XENON1T bound. Conversely for m_DM > m_t, ${\sigma }_n^{\text{SI}}$ is negligible and below the neutrino background (Billard et al., 2014).

The relevant diagrams contributing to all dark matter searches in this DMsimp are shown in Figure 11, while the dependency on the dark matter spin is summarized in Table 2.

FIGURE 11

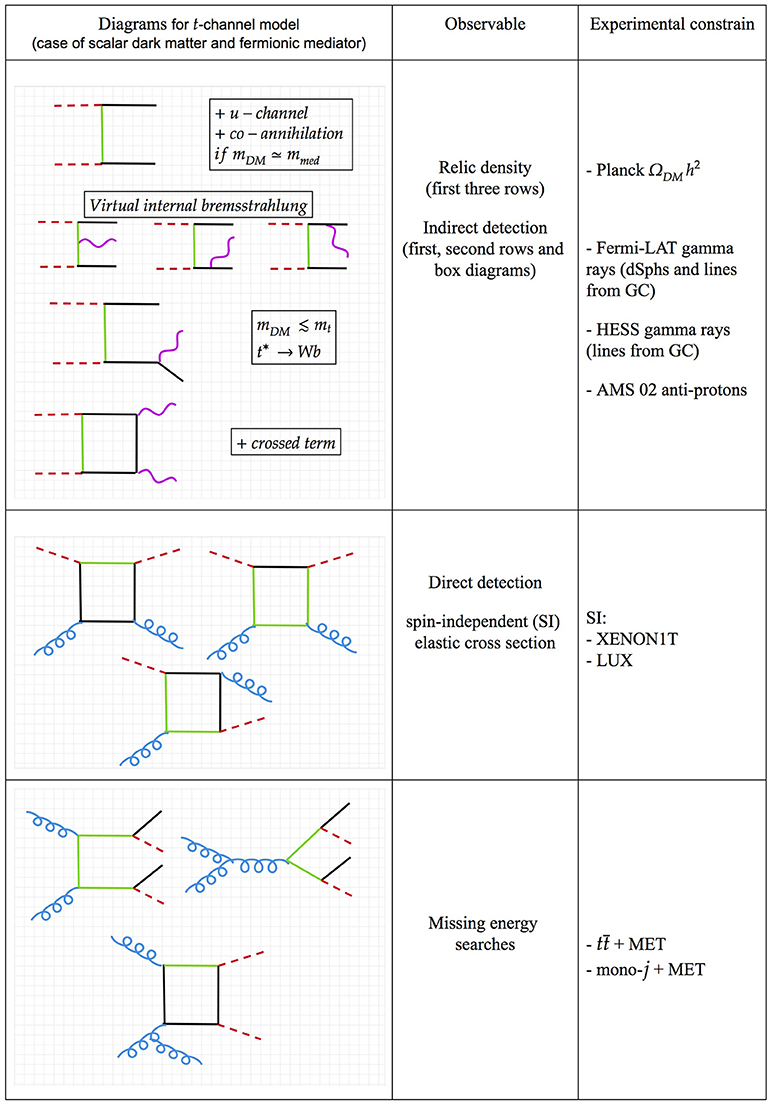
Figure 11. Schematic of leading order diagrams contributing to all dark matter searches in the t-channel DMsimps with scalar dark matter and fermionic mediator. The diagrams contributing to LHC searches are specifically drawn for the case of the top-philic model discussed in section 3.2 [for generic fermionic mediator the reader is referred to De Simone and Jacques (2016) and the references therein]. The case of Majorana dark matter and scalar mediator is easily obtained from the above diagrams. For fermionic dark matter there is an additional spin-dependent contribution to the direct detection elastic scattering cross section. MET stands for missing transverse energy. The color code is as in Figure 2.

The results of the comprehensive dark matter study are illustrated in Figure 12A. Under the assumption that the dark matter is a thermal relic, the complementarity of dark matter searches is clearly shown in the plot. Direct detection experiments probe the region for m_DM < m_t, while Fermi-LAT, HESS and AMS 02 are sensitive to a mass range from roughly m_t up to 500 GeV. This shows that anti-matter constraints can be competitive with gamma-ray searches, modulo the larger astrophysical uncertainties. LEP searches constrain the most lightest values of m_DM, while CMS searches cover a parameter space orthogonal to indirect detection. In particular multi-jets + $\cancel{E}$_T searches loose quickly sensitivity with the increase of the dark matter mass, however the $t\bar{t}+{/\cancel{E}}_T$ searches are effective in the regime where the decay T → St happens far from threshold. Notice that if the decay channel T → St is closed, the mediator becomes long-lived. This case requires further dedicated studies.

FIGURE 12

Figure 12. DMsimp: t-channel. (A) Combined constraints from direct and indirect detection and collider searches in the {(m_T/m_S − 1), m_S}-plane. The gray regions stand for either under-abundant or for over-abundant dark matter for fermionic mediator and scalar WIMPs. The red region is excluded at 90% CL by XENON1T, while the red dashed line indicates the region of parameter above the neutrino floor hence detectable by direct detection. The green regions are excluded by Fermi-LAT dSph constraints on gamma rays and by anti-protons (Cuoco et al., 2018). The orange region denotes the expected sensitivity of 15 years of data taking by Fermi-LAT. The magenta and blue regions show constraints on scalar top production at LEP and at the LHC, while mono-X + $\cancel{E}$_T searches disfavor the dark blue region at 95% CL. Figure taken from Colucci et al. (2018). The reader can identify m_T = m_med and m_S = m_DM with respect to the convention used in the review. (B) Same as (A) for Majorana dark matter and scalar mediator. The color code is: gray regions denote under- and over-abundant dark matter, while the green regions are disfavored at 95% CL by jet(s) searches + $\cancel{E}$_T. The red regions are excluded by XENON100 and LUX at 90% CL. The blue contour levels show the ratio between the excluded annihilation cross section and the thermal cross section. The regions inside these contour lines are disfavored if the gamma-ray flux from dark matter annihilation is enhanced relative to the Einasto profile (Einasto and Haud, 1989) by the corresponding factor (more cuspy profiles or presence of substructures). Figure taken from Garny et al. (2015). The reader can identify m_χ = m_DM and m_η = m_med with respect to the convention used in the review. Both Colucci et al. (2018) and Garny et al. (2015) are distributed under the non-exclusive arXiv license.

The Majorana dark matter DMsimp exhibits only few differences with respect to the scalar dark matter model presented above. We summarize here the most important. Under the same assumptions made for the fermionic mediator, the interaction Lagrangian with only a single generation of light quark (considering the model in Garny et al., 2015) is given by:

$\begin{array}{ll}{{L}}_S^T=y{\tilde{T}}^{*}\bar{X}{P}_{R}q+\text{h}.\text{c}.,& (31)\end{array}$

where now the dark matter field is denoted by X and the mediator by $\tilde{T}$ and q is the light quark, which we assume to be the u flavor for concreteness for the rest of the section. This Majorana model is very close to the simplified model considered in supersymmetric searches at the LHC, as it is implemented in the Minimal Supersymmetric Model with only light quarks and the neutralino, except that the coupling y is not fixed at the weak scale but can be varied freely.

• LHC searches with $\cancel{\mathbf{E}}$_T. As for the fermionic dark matter case, the most stringent searches are given by jets + $\cancel{E}$_T and mono-jet + $\cancel{E}$_T. The first arises from the direct production of the colored mediator that further decays into the dark matter and light quarks. The latter stems from the loop-induced production of a dark matter pair that recoils against a jet.

• Relic density. The annihilation processes contributing to the dark matter relic density are analogous to the case of scalar dark matter in the chiral limit. In this limit, the XX → u_Ru_R process is p-wave suppressed.

• Indirect detection. This is completely analogous to the scalar dark matter case in the chiral limit, except that the t-channel tree level annihilation diagram is still helicity suppressed and the first non zero term in the chiral limit is p-wave. The authors in Garny et al. (2015) consider as well the exclusion limits on ${\sigma }_p^{\text{SD}}$ stemming from IceCube. The vector boson generating the neutrino flux from the Sun arises from VIB: XX → u_Ru_RV and subsequently V = W, Z, h shower and hadronise and produce a continuum spectrum for the neutrinos. The IceCube bounds are less performant that direct detection searches to constrain the model parameter space, hence are not shown in the following.

• Direct detection. With respect to the diagrams shown in Figure 11, the elastic cross section off nucleus receives an additional contribution from the s-channel exchange of $\tilde{T}$, which is not present in the scalar dark matter case. There is a small contribution from the spin-independent operator, while the leading contributions to the elastic cross section are proportional to a combination of ${{O}}_4^{\text{NR}}$, ${{O}}_8^{\text{NR}}$, and ${{O}}_9^{\text{NR}}$, which are spin-dependent operators. Still the most constraining bounds on the model come from spin-independent limits from the LUX experiment, as these are orders of magnitude more sensitive than the spin-dependent upper bounds.

The results of the comprehensive dark matter study are illustrated in Figure 12B. The picture is rather similar to the case of scalar dark matter, assuming a thermal dark matter scenario. Constraints from jets + $\cancel{E}$_T are relevant for large mass splitting between X and $\tilde{T}$, because after its production the mediator has a larger phase space for its decay into the dark matter and the light quark, leading to harder jets. Direct detection is sensitive to smaller mass splitting, while mono-jet +$\cancel{E}$_T searches are sensitive to the quasi degenerate region. Gamma rays probe the model parameter space in the intermediate m_DM mass range.

The Dirac dark matter DMsimp is different from the Majorana case reported above, as far as it concerns the dark matter studies. The elastic scattering cross section is dominated by spin-independent because of the contribution from vectorial currents, which are null in case of Majorana fermions. Hence, thermal Dirac dark matter models get strongly constrained by current direct detection experiments, which combined with LHC searches, completely disfavor the thermal hypothesis for such model (see De Simone and Jacques, 2016) for details.

As a concluding remark, in general a colored t-channel mediator scenario will be probed to a large extent by next generation experiments, assuming thermal dark matter production and perturbativity of the coupling.

4. Caveats of Dark Matter Simplified Models

DMsimps represent an improvement with respect to the use of EFT for collider dark matter searches during LHC Run 1. However, most of them are still considered not the ideal benchmark models over which categorize the dark matter searches and their complementarity. The main reason of concern is related to the fact that most of the DMsimps are not gauge invariant, thus not renormalisable (see e.g., Bell et al., 2015, 2016a,b, 2017a; Englert et al., 2016; Haisch et al., 2016; Kahlhoefer et al., 2016). The most striking example is provided by the spin-1 mediator with axial-vector couplings to fermions. The interaction Lagrangians provided in section 3.1.2 are not gauge invariant unless a dark Higgs is introduced to give mass to the Z′ mediator, and hence to unitarise its longitudinal component. As a consequence, the most minimalistic self consistent model would feature two mediators, an additional scalar along with the Z′. The presence of a second mediator would change the phenomenology of the model, which is not anymore well described by the single mediator assumption.

The s-channel scalar mediator case is not gauge invariant unless Y₀ mixes with the Higgs boson, because the dark matter is a singlet under the SM gauge symmetries (see e.g., Lopez-Val and Robens, 2014; Khoze et al., 2015; Baek et al., 2016; Costa et al., 2016; Dupuis, 2016; Robens and Stefaniak, 2016; Wang et al., 2016; Balazs et al., 2017). The mixing with the Higgs boson introduces a major modification in the building of the next generation of DMsimps, as the model parameter space then becomes constrained by measurements of the Higgs properties. This has motivated two types of scenarios: (i) models that communicate with the SM via the Higgs portal through the mixing parameters, or even models for which the scalar mediator is the Higgs itself; (ii) to avoid the tight constraints stemming from Higgs physics, Y₀ mixes with an additional doublet similarly to a two Higgs doublet model. Likewise, pseudo-scalar DMsimps (Goncalves et al., 2017) can be made theoretically consistent by promoting them to double mediator models. Two Higgs doublet models are well motivated theoretically, arising in several UV complete models such as supersymmetry, or other extensions of the SM (see e.g., Fayet, 1976; Gunion and Haber, 1986; Amaldi et al., 1991; Carena et al., 1996; Branco et al., 2012; Bhattacharyya and Das, 2016) and the references therein.

We will not discuss more in details here these issues and the proposed solutions. There is already a quite vast literature along the lines of the two Higgs doublet models and Higgs portals. The interested reader is referred to e.g., (Boveia et al., 2016; De Simone and Jacques, 2016; Duerr et al., 2016; Albert et al., 2017b; Baek et al., 2017; Bauer et al., 2017; Bell et al., 2017b; Ellis et al., 2017; Ko et al., 2017).

5. Future Prospects

The focus of this review has been to describe the state-of-art of dark matter simplified models, as defined by the LHC Dark Matter Working group, with respect to the current dark matter searches. In particular we have discussed the degree of complementarity of LHC searches (mono-jet + $\cancel{E}$_T, jets + $\cancel{E}$_T, resonance searches), dark matter direct and indirect detection searches (gamma-ray, anti-matter, and neutrino searches) in several scenarios: s-channel mediator with spin-0 and spin-1 and Dirac dark matter, s-channel mediator with spin-2 and vectorial dark matter, t-channel mediator with either scalar dark matter and fermionic mediator or vice-versa. DMsimps provide a simple framework where to define, categorize, and compare the current reach of dark matter searches, as well as the expected sensitivity of forthcoming experiments. These comprehensive analyses are a powerful tool to understand the dynamics underlying the various dark matter searches, modulo their interpretation being subject to the caveats described in the previous section. Keeping in mind the main assumption that the dark matter and the mediator are the only particles of the dark sector accessible at current and future experiments, we can formulate few general statements from the global analyses presented in this review, after having presented the forthcoming particles and astroparticle probes.

Experimentally, the close future is quite promising as there is a rich program expected to start soon and produce results in the next decade or so. Concerning the future of direct detection, starting from 2019, there are several experiments planned able to probe WIMP-nucleon cross section of the order of the neutrino floor (${\sigma }_n^{\text{SI}}~10^{-48}\text{c}{\text{m}}^2$ for m_DM ~ 30 GeV), see XENONnT (Aprile et al., 2016), LZ (Mount et al., 2017), and DARWIN (Aalbers et al., 2016). At low WIMP mass, around 3-4 GeV, exciting progresses are expected by SuperCDMS SNOLAB (Agnese et al., 2017), by CRESST III (Strauss et al., 2016), and by EDELWEISS-III (Arnaud et al., 2018), which can probe elastic spin-independent cross sections as low as 10⁻⁴⁴cm². Concerning indirect detection, the Cherenkov Telescope Array (Acharya et al., 2013) (CTA) is one of the major advancements in the gamma-ray searches as it will be sensitive to the energy range in between 20 and 300 TeV. Starting from 2022, while operating, it will provide unprecedented complementary results to direct detection and LHC searches, as it will be sensitive to dark matter masses up to 100 TeV. These future probes, together with the LHC Run 3 foreseen for 2021, can vastly extend the coverage of the dark matter parameter space of simplified models (see e.g., Balazs et al., 2017; Baum et al., 2017; Bertone et al., 2017). More precisely:

• s-channel scalar mediator: The spin-0 odd mediator can be probed either by direct detection, which is actually the most promising dark matter search for this model, either by LHC. Indirect detection searches are insensitive to this model, as 〈σv〉 is p-wave suppressed. XENONnT, with one year of exposure, can probe most of the dark matter region from 10 GeV up to roughly 200 GeV, with couplings $g_{\text{DM}}\times g_{\text{SM}}>10^{-3}$ (see Arina et al., 2016). Mono-X + missing energy searches can probe the region where the dark matter achieves the relic density by resonant annihilation up to mediator masses of 1 TeV and dark matter masses up to 500 GeV, for couplings of order 1. More promising are LHC resonant searches, that can probe much higher mediator masses (see e.g., Balazs et al., 2017; Banerjee et al., 2017; Baum et al., 2017; Bertone et al., 2017.

This case is an example of how LHC searches for dark matter with mono-X and missing energy, direct dark matter searches and indirect dark matter searches in general probe regions of the model parameter space which are complementary to each other. Direct detection has better sensitivity than LHC searches in the intermediate dark matter mass range, while LHC performs better in the small dark matter range, where however the dark matter is often not viable as thermal relic (it is either over-abundant or under-abundant, depending on the model). The relic density constraint can be avoided by assuming for instance a non thermal dark matter scenario. Because of the complementarity of searches, for instance a non-detection in direct detection does not preclude a positive detection at the LHC or at gamma-ray telescopes.

• s-channel pseudoscalar mediator: This case has the same phenomenology as the scalar mediator, as far as it concerns the LHC searches. On the contrary of the scalar mediator case, it is completely elusive for direct detection searches but con be probed by indirect detection (Banerjee et al., 2017). Indirect dark matter searches extend to heavier dark matter masses with respect to LHC and direct detection exploring TeV candidates. The searches for gamma-rays from dSph galaxies after 15 years will cover basically all the parameter space where the dark matter has the correct relic density, except for the region where ${\Omega }_{\text{DM}}{h}^2$ is obtained via resonant annihilation.

• s-channel vector mediator: This model, with Majorana dark matter, is an example of models that are already disfavoured as thermal relic by the combination of LHC and direct detection searches (Fairbairn et al., 2016). By reversing the argument, we can assert that if a signal is seen in the mono-X + $\cancel{E}$_T searches, the thermal dark matter hypothesis is under test. This can be solved: (i) by invoking a more complex dark sector, where co-annihilation and new annihilation channels can open up the thermal relic parameter space; (ii) dark matter is produced via additional non-thermal mechanisms to dilute/increase its relic abundance down/up to the observed value. If we do not consider the thermal relic hypothesis, the most LHC promising searches are dijets, that can probe vector mediator masses up to few TeV (Fairbairn et al., 2016) and dark matter direct detection. Conversely gamma-ray searches are poorly sensitive to the mode, the CTA telescope can probe regions of the model that are already excluded by the combination of di-jets searches and XENON1T (Balázs et al., 2017).

• s-channel spin-2 mediator: The spin-2 mediator model has been poorly investigated so far and deserves future careful comprehensive analyses. The literature available so far suggests that vectorial dark matter candidates in the TeV range can give rise to gamma-ray line signals partly in the reach of CTA (Zhang et al., 2017), if ${\langle \sigma v\rangle }_{\gamma \gamma }>5\times 10^{-28}c{m}^3/s$. Current constraints seem to suggest that diphoton and dilepton searches are potentially the best way to hunt for gravitons in DMsimps at the LHC (Kraml et al., 2017).

• t-channel mediator: The t-channel model parameter space, under the hypothesis of thermal dark matter, will be almost entirely probed by future generation experiments. XENONnT can almost entirely probe the dark matter region for mediator masses below the top-quark mass, while the gamma-ray searches in dSphs performed by Fermi-LAT in 15 years can probe the model for mediator masses in between the top-quark mass and roughly 500 GeV. Larger mediator masses can be probed by mono-X searches of LHC Run 3 (Colucci et al., 2018).

It is crucial to keep looking for dark matter with a comprehensive approach relying in simplified bottom-up scenarios. Some theoretical shrewdnesses are in place. The use of gauge invariant models certainly constitutes a must, however theoretical predictions can be improved along other directions, which are often neglected. For instance, the wide separation of scales involved in constraining WIMP models, from the LHC to indirect detection and to direct detection, is often neglected. The authors in (D'Eramo and Procura, 2015) have shown that the running of EFT operators from the mediator mass scale to the nuclear scales probed by direct searches via one-loop Renormalisation Group Equations (RGEs) has an impact for models that would in generally not be constrained by direct detection searches because suppressed by the momentum transfer or by the WIMP velocity. These models can be excluded as a consequence of spin-independent couplings induced by SM loops.

In case of a positive signal at the LHC in a SM + $\cancel{E}$_T channel, the identification of the dark matter is non-trivial, as opposed to the characterization of the mediator. Luckily all dark matter searches, even though they feature a certain degree of complementarity, also probe common regions of the parameter space. In an optimistic scenario, a signal can be detected in multiple experiments allowing to pin point both the nature of the dark matter and the characteristics of the model.

Lastly, the Sun has been recently proposed as target to constrain a specific class of DMsimps, in which the mediator is light (MeV range) and long-lived (Arina et al., 2017; Leane et al., 2017). LHC searches are insensitive to this type of mediators, which can however be observed in gamma rays. The Sun is opaque to all dark matter annihilation products but neutrinos and the neutral and weakly interacting mediators (the mechanism that produces the mediators inside the Sun is the same as for the neutrino signal). If these mediators are long-lived enough to decay outside the Sun, they could lead to characteristic gamma-ray signatures detectable within 10 years of Fermi-LAT mission, and in 1 year of full exposure of ground water Cherenkov telescopes (HAWC Abeysekara et al., 2013 and LHAASO Zhen, 2014; He, 2016). Models with long-lived MeV mediators are actually very constrained by beam dump experiments and cosmology (Arina et al., 2017). Their entire parameter space can be probed by next generation of intensity experiments, such as NA62 (Doebrich, 2017) and SHiP (Alekhin et al., 2016). Hence dark matter simplified models not only serve as benchmark for high-energy studies but they can be exploited as a bridge relying the high-energy frontiers with the intensity frontiers.

Author Contributions

The author confirms being the sole contributor of this work and approved it for publication.

Funding

This review article has been supported by the Innoviris grant ATTRACT Brains for Brussels 2015 (BECAP 2015-BB2B-4).

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author would like to acknowledge Fabio Maltoni, Luca Mantani, and Kentarou Mawatari for useful discussions about various aspects of the dark matter simplified models. She is also grateful to Jan Heisig for a careful reading of the manuscript and for providing useful comments.

Footnotes

1. ^If the dark sector consists of more than one new mediating particle, DMsimps take into account the effect only of the lightest state that can be produced at the LHC.

2. ^An upper bound on the WIMP mass of ${O}(100)TeV$ stems from the requirement of perturbative unitarity (Griest and Kamionkowski, 1990), while a lower bound is much more debated and model dependent. In certain models m_DM > 10 GeV not to spoil recombination (Planck Collaboration et al., 2016), for other models m_DM > 4 GeV (Lee and Weinberg, 1977), etc.

3. ^This approximation is satisfied by the DMsimp framework, which typically features mediators heavier than GeV.

4. ^On a side note, except for (Cirelli et al., 2013), the publicly available dark matter numerical tools do not use the general description of direct detection in terms of non-relativistic operators, at the best of our knowledge at the time of writing.

5. ^There are four dSphs recently discovered by DES (Abbott et al., 2005), which, taken individually, show a slight excess over the background, of the order of 2σ. Other analyses (see e.g., Geringer-Sameth et al., 2015; Hooper and Linden, 2015) have pointed out similarly a possible excess over the background. The excess disappears once the data are stacked with the other dSph data.

6. ^Dataset (2015). Available online at: https://www-glast.stanford.edu/pub_data/1203/.

7. ^In this review we do not consider the Galactic Center excess at low dark matter masses. For details, we refer the reader to (e.g., Gaskins, 2016) and the references therein.

8. ^We chose not to provide any reference here for the specific searches conducted by ATLAS and CMS, and to provide the references in the next section, referring to the data sets actually used in the analyses discussed in this review.

9. ^Dataset (2015). Available online at: http://feynrules.irmp.ucl.ac.be/wiki/DMsimp.

10. ^The exclusion bounds are not rescaled, as the authors assume that the dark matter makes up 100% of the matter content of the universe in the white region. Thermal production is then supplemented by some other mechanism to achieve the observed value of ${\Omega }_{\text{DM}}{h}^2$.

11. ^We have dropped the superscript T for simplicity.

12. ^In DMsimp s-channel models, the mediator cannot be odd under the Z₂ otherwise for m_med < m_DM it would be playing the role of dark matter candidate.

References

Aaboud, M., Aad, G., Abbott, B., Abdallah, J., Abdinov, O., Abeloos, B., et al. (2016a). Search for new phenomena in final states with an energetic jet and large missing transverse momentum in pp collisions at $\sqrt{s}=13$TeV using the ATLAS detector. Phys. Rev. D94:032005. doi: 10.1103/PhysRevD.94.032005

CrossRef Full Text | Google Scholar

Aaboud, M., Aad, G., Abbott, B., Abdallah, J., Abdinov, O., Abeloos, B., et al. (2016b). Search for squarks and gluinos in final states with jets and missing transverse momentum at $\sqrt{s}=13$ TeV with the ATLAS detector. Eur. Phys. J. C76:392. doi: 10.1140/epjc/s10052-016-4184-8

CrossRef Full Text | Google Scholar

Aaboud, M., Aad, G., Abbott, B., Abdallah, J., Abdinov, O., Abeloos, B., et al. (2018). Search for dark matter and other new phenomena in events with an energetic jet and large missing transverse momentum using the ATLAS detector. J. High Energy Phys. 1:126. doi: 10.1007/JHEP01(2018)126

CrossRef Full Text | Google Scholar

Aad, G., Abbott, B., Abdallah, J., Abdel Khalek, S., Abdinov, O., Aben, R., et al. (2015b). Search for new phenomena in final states with an energetic jet and large missing transverse momentum in pp collisions at $\sqrt{s}=8$ TeV with the ATLAS detector. Eur. Phys. J. C75:299. doi: 10.1140/epjc/s10052-015-3639-7

CrossRef Full Text | Google Scholar

Aad, G., Abbott, B., Abdallah, J., Abdel Khalek, S., Abdinov, O., Aben, R., et al. (2015c). Search for new phenomena in the dijet mass distribution using p−p collision data at $\sqrt{s}=8$ TeV with the ATLAS detector. Phys. Rev. D91:052007. doi: 10.1103/PhysRevD.91.052007

CrossRef Full Text | Google Scholar

Aad, G., Abbott, B., Abdallah, J., Abdinov, O., Aben, R., Abolins, M., et al. (2015a). A search for $t\overline{t}$ resonances using lepton-plus-jets events in proton-proton collisions at $\sqrt{s}=8$ TeV with the ATLAS detector. J. High Energy Phys. 8:148. doi: 10.1007/JHEP08(2015)148

CrossRef Full Text | Google Scholar

Aad, G., Abbott, B., Abdallah, J., Abdinov, O., Aben, R., Abolins, M., et al. (2016). Search for dark matter produced in association with a Higgs boson decaying to two bottom quarks in pp collisions at $\sqrt{s}=8$ TeV with the ATLAS detector. Phys. Rev. D93:072007. doi: 10.1103/PhysRevD.93.072007

CrossRef Full Text | Google Scholar

Aalbers, J., Agostini, F., Alfonsi, M., Amaro, F. D., Amsler, C., Aprile, E., et al. (2016). DARWIN: towards the ultimate dark matter detector. J. Cosmol. Astropart. Phys. 1611:017. doi: 10.1088/1475-7516/2016/11/017

CrossRef Full Text | Google Scholar

Aaltonen, T., Adelman, J., Akimoto, T., Álvarez González, B., Amerio, S., Amidei, D., et al. (2009). Search for new particles decaying into dijets in proton-antiproton collisions at s**(1/2) = 1.96-TeV. Phys. Rev. D79:112002. doi: 10.1103/PhysRevD.79.112002

CrossRef Full Text | Google Scholar

Aartsen, M. G., Abbasi, R., Abdou, Y., Ackermann, M., Adams, J., Aguilar, J. A., et al. (2013). Search for dark matter annihilations in the Sun with the 79-string IceCube detector. Phys. Rev. Lett. 110:131302. doi: 10.1103/PhysRevLett.110.131302

PubMed Abstract | CrossRef Full Text | Google Scholar

Aartsen, M. G., Abraham, K., Ackermann, M., Adams, J., Aguilar, J. A., Ahlers, M., et al. (2016). Improved limits on dark matter annihilation in the Sun with the 79-string IceCube detector and implications for supersymmetry. JCAP 1604:022. doi: 10.1088/1475-7516/2016/04/022

CrossRef Full Text | Google Scholar

Abbiendi, G., Ainsley, C., Akesson, P., Alexander, G., Allison, J., Amaral, P., et al. (2002). Search for scalar top and scalar bottom quarks at LEP. Phys. Lett. B545, 272–284. doi: 10.1016/S0370-2693(02)02808-3

CrossRef Full Text | Google Scholar

Abbott, T, Abdalla, F. B., Aleksic, J., Allam, S., Amara, A., Bacon, D., et al. (2005). The dark energy survey. arXiv: astro-ph/0510346.

PubMed Abstract

Abdalla, H., Abramowski, A., Aharonian, F., Ait Benkhali, F., Akhperjanian, A. G., Andersson, T., et al. (2016). H.E.S.S. limits on linelike dark matter signatures in the 100 GeV to 2 TeV energy range close to the Galactic Center. Phys. Rev. Lett. 117:151302. doi: 10.1103/PhysRevLett.117.151302

PubMed Abstract | CrossRef Full Text | Google Scholar

Abdallah, J., Araujo, H., Arbey, A., Ashkenazi, A., Belyaev, A., Berger, J., et al. (2015). Simplified models for dark matter searches at the LHC. Phys. Dark Univ. 9–10, 8–23. doi: 10.1016/j.dark.2015.08.001

CrossRef Full Text

Abercrombie, D., Akchurin, N., Akilli, E., Alcaraz Maestre, J., Allen, B., Alvarez Gonzalez, B., et al. (2015). Dark Matter Benchmark Models for Early LHC Run-2 Searches: Report of the ATLAS/CMS Dark Matter Forum.

Abeysekara, A. U., Alfaro, R., Alvarez, C., Álvarez, J. D., Arceo, R., Arteaga-Velázquez, J. C., et al. (2013). Sensitivity of the high altitude water cherenkov detector to sources of multi-TeV gamma rays. Astropart. Phys. 50–52, 26–32. doi: 10.1016/j.astropartphys.2013.08.002

CrossRef Full Text | Google Scholar

Abramowski, A., Acero, F., Aharonian, F., Akhperjanian, A. G., Anton, G., Balenderan, S., et al. (2013). Search for photon-linelike signatures from dark matter annihilations with H.E.S.S. Phys. Rev. Lett. 110:041301. doi: 10.1103/PhysRevLett.110.041301

PubMed Abstract | CrossRef Full Text | Google Scholar

Acharya, B. S. A. M., Croston, J. H., Granot, J., and Hardcastle, M.J. (2013). Introducing the CTA concept. Astropart. Phys. 43, 3–18. doi: 10.1016/j.astropartphys.2013.01.007

CrossRef Full Text | Google Scholar

Ackermann, M., Ajello, M., Albert, A., Anderson, B., Atwood, W. B., Baldini, L., et al. (2015b). Updated search for spectral lines from Galactic dark matter interactions with pass 8 data from the Fermi Large Area Telescope. Phys. Rev. D91:122002. doi: 10.1103/PhysRevD.91.122002

CrossRef Full Text | Google Scholar

Ackermann, M., Albert, A., Anderson, B., Atwood, W. B., Baldini, L., Barbiellini, G., et al. (2015a). Searching for dark matter annihilation from milky way dwarf spheroidal galaxies with six years of Fermi Large Area Telescope Data. Phys. Rev. Lett. 115:231301. doi: 10.1103/PhysRevLett.115.231301

PubMed Abstract | CrossRef Full Text | Google Scholar

Agnese, R., Anderson, A. J., Aramaki, T., Arnquist, I., Baker, W., Barker, D., et al. (2017). Projected Sensitivity of the SuperCDMS SNOLAB experiment. Phys. Rev. D95:082002. doi: 10.1103/PhysRevD.95.082002

CrossRef Full Text | Google Scholar

Agrawal, P., Batell, B., Hooper, D., and Lin, T. (2014). Flavored dark matter and the galactic center gamma-ray excess. Phys. Rev. D90:063512. doi: 10.1103/PhysRevD.90.063512

CrossRef Full Text | Google Scholar

Agrawal, P., Blanchet, S., Chacko, Z., and Kilic, C. (2012). Flavored Dark Matter, and its implications for direct detection and colliders. Phys. Rev. D86:055002. doi: 10.1103/PhysRevD.86.055002

CrossRef Full Text | Google Scholar

Aguilar, M., Ali Cavasonza, L., Alpat, B., Ambrosi, G., Arruda, L., Attig, N., et al. (2016). Antiproton flux, antiproton-to-proton flux ratio, and properties of elementary particle fluxes in primary cosmic rays measured with the alpha magnetic spectrometer on the international space station. Phys. Rev. Lett. 117:091103. doi: 10.1103/PhysRevLett.117.091103

PubMed Abstract | CrossRef Full Text | Google Scholar

Akerib, D. S., Alsum, S., Araújo, H. M., Bai, X., Bailey, A. J., Balajthy, J., et al. (2017). Results from a search for dark matter in the complete LUX exposure. Phys. Rev. Lett. 118:021303. doi: 10.1103/PhysRevLett.118.021303

PubMed Abstract | CrossRef Full Text | Google Scholar

Albert, A., Anderson, B., Bechtol, K., Drlica-Wagner, A., Meyer, M., Sánchez-Conde, M., et al. (2017). Searching for dark matter annihilation in recently discovered milky way satellites with Fermi-LAT. Astrophys. J. 834:110. doi: 10.3847/1538-4357/834/2/110

CrossRef Full Text | Google Scholar

Albert, A., Backovié, M., Boveia, A., Buchmueller, O., Busoni, G., De Roeck, A., et al. (2017a). Recommendations of the LHC Dark Matter Working Group: comparing LHC searches for heavy mediators of dark matter production in visible and invisible decay channels. arXiv:1703.05703.

Google Scholar

Albert, A., Bauer, M., Brooke, J., Buchmueller, O., Cerdeno, D. G., Citron, M., et al. (2017b). Towards the next generation of simplified Dark Matter models. Phys. Dark Univ. 16, 49–70. doi: 10.1016/j.dark.2017.02.002

CrossRef Full Text | Google Scholar

Alekhin, S., Altmannshofer, W., Asaka, T., Batell, B., Bezrukov, F., Bondarenko, K., et al. (2016). A facility to Search for Hidden Particles at the CERN SPS: the SHiP physics case. Rept. Prog. Phys. 79:124201. doi: 10.1088/0034-4885/79/12/124201

PubMed Abstract | CrossRef Full Text | Google Scholar

Alitti, J., Ambrosini, G., Ansari, R., Autiero, D., Bareyre, P., Bertram, I. A., et al. (1993). A Search for new intermediate vector mesons and excited quarks decaying to two jets at the CERN $\bar{p}p$ collider. Nucl. Phys. B400, 3–24. doi: 10.1016/0550-3213(93)90395-6

CrossRef Full Text | Google Scholar

Allahverdi, R., Dutta, B., and Sinha, K. (2012). Non-thermal higgsino dark matter: cosmological motivations and implications for a 125 GeV Higgs. Phys. Rev. D86:095016. doi: 10.1103/PhysRevD.86.095016

CrossRef Full Text | Google Scholar

Alloul, A., Christensen, N. D., Degrande, C., Duhr, C., and Fuks, B. (2014). FeynRules 2.0 - A complete toolbox for tree-level phenomenology. Comput. Phys. Commun. 185, 2250–2300. doi: 10.1016/j.cpc.2014.04.012

CrossRef Full Text | Google Scholar

Alwall, J., Frederix, R., Frixione, S., Hirschi, V., Maltoni, F., Mattelaer, O., et al. (2014). The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. J. High Energy Phys. 7:079. doi: 10.1007/JHEP07(2014)079

CrossRef Full Text | Google Scholar

Alwall, J., Herquet, M., Maltoni, F., Mattelaer, O., and Stelzer, T. (2011). MadGraph 5 : going beyond. J. High Energy Phys. 6:128. doi: 10.1007/JHEP06(2011)128

CrossRef Full Text | Google Scholar

Amaldi, U., de Boer, W., and Furstenau, H. (1991). Comparison of grand unified theories with electroweak and strong coupling constants measured at LEP. Phys. Lett. B260, 447–455. doi: 10.1016/0370-2693(91)91641-8

CrossRef Full Text | Google Scholar

Ambrogi, F., Arina, C., Backovic, M., Heisig, J., Maltoni, F., Mantani, L., et al. (2018). MadDM v.3.0: A Comprehensive Tool for Dark Matter Studies.

Ambrosi, G., An, Q., Asfandiyarov, R., Azzarello, P., Bernardini, P., Bertucci, B., et al. (2017). Direct detection of a break in the teraelectronvolt cosmic-ray spectrum of electrons and positrons. Nature 552, 63–66. doi: 10.1038/nature24475

CrossRef Full Text | Google Scholar

Amole, C., Ardid, M., Arnquist, I. J., Asner, D. M., Baxter, D., Behnke, E., et al. (2017). Dark Matter search results from the PICO-60 C₃F₈ bubble chamber. Phys. Rev. Lett. 118:251301. doi: 10.1103/PhysRevLett.118.251301

CrossRef Full Text | Google Scholar

An, H., Wang, L. T., and Zhang, H. (2014). Dark matter with t-channel mediator: a simple step beyond contact interaction. Phys. Rev. D89:115014. doi: 10.1103/PhysRevD.89.115014

CrossRef Full Text | Google Scholar

Angloher, G., Bento, A., Bucci, C., Canonica, L., Defay, X., Erb, A., et al. (2016). Results on light dark matter particles with a low-threshold CRESST-II detector. Eur. Phys. J. C76:25. doi: 10.1140/epjc/s10052-016-3877-3

CrossRef Full Text | Google Scholar

Aprile, E., Aalbers, J., Agostini, F., Alfonsi, M., Amaro, F. D., Anthony, M., et al. (2016). Physics reach of the XENON1T dark matter experiment. J. Cosmol. Astropart. Phys. 1604:027. doi: 10.1088/1475-7516/2016/04/027

CrossRef Full Text | Google Scholar

Aprile, E., Aalbers, J., Agostini, F., Alfonsi, M., Amaro, F. D., Anthony, M., et al. (2017a). First Dark Matter Search Results from the XENON1T Experiment. Phys. Rev. Lett. 119:181301. doi: 10.1103/PhysRevLett.119.181301

PubMed Abstract | CrossRef Full Text | Google Scholar

Aprile, E., Aalbers, J., Agostini, F., Alfonsi, M., Amaro, F. D., Anthony, M., et al. (2017b). Effective field theory search for high-energy nuclear recoils using the XENON100 dark matter detector. Phys. Rev. D96:042004. doi: 10.1103/PhysRevD.96.042004

CrossRef Full Text | Google Scholar

Arcadi, G., Dutra, M., Ghosh, P., Lindner, M., Mambrini, Y., Pierre, M., et al. (2017). The waning of the WIMP? A review of models, searches, and constraints. arXiv: 1703.07364.

Google Scholar

Arcadi, G., Mambrini, Y., Tytgat, M. H. G., and Zaldivar, B. (2014). Invisible Z′ and dark matter: LHC vs LUX constraints. J. High Energy Phys. 3:134. doi: 10.1007/JHEP03(2014)134

CrossRef Full Text | Google Scholar

Arina, C. (2014). Bayesian analysis of multiple direct detection experiments. Phys. Dark Univ. 5–6, 1–17. doi: 10.1016/j.dark.2014.03.003

CrossRef Full Text

Arina, C., Backović, M., Conte, E., Fuks, B., Guo, J., Heisig, J., et al. (2016). A comprehensive approach to dark matter studies: exploration of simplified top-philic models. J. High Energy Phys. 11:111. doi: 10.1007/JHEP11(2016)111

CrossRef Full Text | Google Scholar

Arina, C., Backović, M., Heisig, J., and Lucente, M. (2017). Solar γ rays as a complementary probe of dark matter. Phys. Rev. D96:063010. doi: 10.1103/PhysRevD.96.063010

CrossRef Full Text | Google Scholar

Arina, C., Del Nobile, E., and Panci, P. (2015). Dark matter with pseudoscalar-mediated interactions explains the DAMA signal and the Galactic Center Excess. Phys. Rev. Lett. 114:011301. doi: 10.1103/PhysRevLett.114.011301

PubMed Abstract | CrossRef Full Text | Google Scholar

Arina, C., Hamann, J., and Wong, Y. Y. Y. (2011). A Bayesian view of the current status of dark matter direct searches. J. Cosmol. Astropart. Phys. 1109:022. doi: 10.1088/1475-7516/2011/09/022

CrossRef Full Text | Google Scholar

Arnaud, Q., Armengaud, E., Augier, C., Benoît, A., Bergé, L., Billard, J., et al. (2018). Optimizing EDELWEISS detectors for low-mass WIMP searches. Phys. Rev. D97:022003. doi: 10.1103/PhysRevD.97.022003

CrossRef Full Text | Google Scholar

Arun, M. T., and Saha, P. (2017). Gravitons in multiply warped scenarios: At 750 GeV and beyond. Pramana 88:93. doi: 10.1007/s12043-017-1387-y

CrossRef Full Text | Google Scholar

ATLAS Collaboration (2013). Search for a Dijet Resonance Produced in Association with a Leptonically decayingw or Z Boson with the ATLAS Detector at √s = 8TeV. ATLAS-CONF-2013-074. Geneva: CERN.

ATLAS Collaboration (2016a). Search for Pair Production of Higgs Bosons in the 4bs with bar symbol Final State Using Proton—Proton Collisions at √s = 13 TeV with the ATLAS Detector. ATLAS-CONF-2016-049. Geneva: CERN.

ATLAS Collaboration (2016b). Search for Diboson Resonance Production in the l νqq Final State Using pp Collisions at √s = 13 TeV With the ATLAS Detector at the LHC. ATLAS-CONF-2016-062. Geneva: CERN.

ATLAS Collaboration (2016c). Search for New Phenomena in Dijet Events with the ATLAS Detector at √s = 13 TeV with 2015 and 2016 Data. ATLAS-CONF-2016-069. Geneva: CERN.

ATLAS Collaboration (2016d). Search for New Light Resonances Decaying to Jet Pairs and Produced in Association with a Photon or a Jet in Proton-Proton Collisions at √s = 13 TeV with the ATLAS Detector. ATLAS-CONF-2016-070. Geneva: CERN.

ATLAS Collaboration (2016e). Searches for Heavy ZZ and ZW Resonances in the llqq and vvqq Final States in pp Collisions at √s = 13 TeV with the ATLAS Detector. ATLAS-CONF-2016-082. Geneva: CERN.

ATLAS Collaboration (2016f). Search for Resonances in the Mass Distribution of Jet Pairs with One or Two Jets Identified as b-jets with the ATLAS Detector with 2015 and 2016 Data. ATLAS-CONF-2016-060.

Backović, M., Kraemer, M., Maltoni, F., Martini, A., Mawatari, K., and Pellen, M. (2015). Higher-order QCD predictions for dark matter production at the LHC in simplified models with s-channel mediators. Eur. Phys. J. C75:482. doi: 10.1140/epjc/s10052-015-3700-6

CrossRef Full Text | Google Scholar

Baek, S., Ko, P., and Li, J. (2017). Minimal renormalizable simplified dark matter model with a pseudoscalar mediator. Phys. Rev. D95:075011. doi: 10.1103/PhysRevD.95.075011

CrossRef Full Text | Google Scholar

Baek, S., Ko, P., Park, M., Park, W. I., and Yu, C. (2016). Beyond the Dark matter effective field theory and a simplified model approach at colliders. Phys. Lett. B756, 289–294. doi: 10.1016/j.physletb.2016.03.026

CrossRef Full Text | Google Scholar

Bai, Y., and Berger, J. (2013). Fermion portal Dark Matter. J. High Energy Phys. 11:171. doi: 10.1007/JHEP11(2013)171

CrossRef Full Text | Google Scholar

Bai, Y., and Berger, J. (2014). Lepton portal Dark Matter. J. High Energy Phys. 8:153. doi: 10.1007/JHEP08(2014)153

CrossRef Full Text | Google Scholar

Balázs, C., Conrad, J., Farmer, B., Jacques, T., Li, T., Meyer, M., et al. (2017). Sensitivity of the Cherenkov Telescope Array to the detection of a dark matter signal in comparison to direct detection and collider experiments. Phys. Rev. D96:083002. doi: 10.1103/PhysRevD.96.083002

CrossRef Full Text | Google Scholar

Balazs, C., Fowlie, A., Mazumdar, A., and White, G. (2017). Gravitational waves at aLIGO and vacuum stability with a scalar singlet extension of the Standard Model. Phys. Rev. D95:043505. doi: 10.1103/PhysRevD.95.043505

CrossRef Full Text | Google Scholar

Banerjee, S., Barducci, D., Bélanger, G., Fuks, B., Goudelis, A., and Zaldivar, B. (2017). Cornering pseudoscalar-mediated dark matter with the LHC and cosmology. J. High Energy Phys. 7:080. doi: 10.1007/JHEP07(2017)080

CrossRef Full Text | Google Scholar

Barger, V., Keung, W. Y., and Marfatia, D. (2012). Bremsstrahlung in dark matter annihilation. Phys. Lett. B707, 385–388. doi: 10.1016/j.physletb.2012.01.001

CrossRef Full Text | Google Scholar

Bauer, M., Haisch, U., and Kahlhoefer, F. (2017). Simplified dark matter models with two Higgs doublets: I. Pseudoscalar mediators. J. High Energy Phys. 5:138. doi: 10.1007/JHEP05(2017)138

CrossRef Full Text | Google Scholar

Baum, S., Catena, R., Conrad, J., Freese, K., and Krauss, M. B (2017). Determining Dark Matter properties with a XENONnT/LZ signal and LHC-Run3 mono-jet searches. arXiv: 1709.06051.

Google Scholar

Belanger, G., Boudjema, F., Goudelis, A., Pukhov, A., and Zaldivar, B. (2018). micrOMEGAs5.0: freeze-in.

Bell, N. F., Busoni, G., and Sanderson, I. W. (2017b). Two higgs doublet dark matter portal. arXiv: 1710.10764.

Google Scholar

Bell, N. F., Cai, Y., Dent, J. B., Leane, R. K., and Weiler, T. J. (2015). Dark matter at the LHC: effective field theories and gauge invariance. Phys. Rev. D92:053008. doi: 10.1103/PhysRevD.92.053008

CrossRef Full Text | Google Scholar

Bell, N. F., Cai, Y., and Leane, R. K. (2016a). Dark Forces in the Sky: Signals from Z' and the Dark Higgs. J. Cosmol. Astropart. Phys. 1608:001. doi: 10.1088/1475-7516/2016/08/001

CrossRef Full Text | Google Scholar

Bell, N. F., Cai, Y., and Leane, R. K. (2016b). Mono-W dark matter signals at the LHC: simplified model analysis. J. Cosmol. Astropart. Phys. 1601:051. doi: 10.1088/1475-7516/2016/01/051

CrossRef Full Text | Google Scholar

Bell, N. F., Cai, Y., and Leane, R. K. (2017a). Impact of mass generation for spin-1 mediator simplified models. J. Cosmol. Astropart. Phys. 1701:039. doi: 10.1088/1475-7516/2017/01/039

CrossRef Full Text | Google Scholar

Bell, N. F., Dent, J. B., Galea, A. J., Jacques, T. D., Krauss, L. M., and Weiler, T. J. (2011). W/Z Bremsstrahlung as the dominant annihilation channel for dark Matter, revisited. Phys. Lett. B706, 6–12. doi: 10.1016/j.physletb.2011.10.057

CrossRef Full Text | Google Scholar

Bell, N. F., Dent, J. B., Galea, A. J., Jacques, T. D., Krauss, L. M., and Weiler, T. J. (2012). Searching for Dark Matter at the LHC with a Mono-Z. Phys. Rev. D86:096011. doi: 10.1103/PhysRevD.86.096011

CrossRef Full Text | Google Scholar

Belyaev, A., Panizzi, L., Pukhov, A., and Thomas, M. (2017). Dark Matter characterization at the LHC in the Effective Field Theory approach. J. High Energy Phys. 4:110. doi: 10.1007/JHEP04(2017)110

CrossRef Full Text | Google Scholar

Bergstrom, L., Edsjo, J., and Gondolo, P. (1997). Indirect neutralino detection rates in neutrino telescopes. Phys. Rev. D55, 1765–1770. doi: 10.1103/PhysRevD.55.1765

CrossRef Full Text

Bertone, G., Bozorgnia, N., Kim, J. S., Liem, S., McCabe, C., Otten, S., et al. (2017). IdentifyingWIMP dark matter from particle and astroparticle data. arXiv: 1712.04793.

Google Scholar

Bertone, G., Cerdeno, D. G., Fornasa, M., Ruiz de Austri, R., Strege, C., and Trotta, R. (2012). Global fits of the cMSSM including the first LHC and XENON100 data. J. Cosmol. Astropart. Phys. 1201:015. doi: 10.1088/1475-7516/2012/01/015

CrossRef Full Text | Google Scholar

Bertone, G., and Hooper, D. (2016). A history of dark matter. Rev. Mod. Phys. arXiv:1605.04909.

Google Scholar

Bhattacharyya, G., and Das, D. (2016). Scalar sector of two-Higgs-doublet models: a minireview. Pramana 87:40. doi: 10.1007/s12043-016-1252-4

CrossRef Full Text | Google Scholar

Billard, J., Strigari, L., and Figueroa-Feliciano, E. (2014). Implication of neutrino backgrounds on the reach of next generation dark matter direct detection experiments. Phys. Rev. D89:023524. doi: 10.1103/PhysRevD.89.023524

CrossRef Full Text | Google Scholar

Blennow, M., Edsjo, J., and Ohlsson, T. (2008). Neutrinos from WIMP annihilations using a full three-flavor Monte Carlo. J. Cosmol. Astropart. Phys. 0801:021. doi: 10.1088/1475-7516/2008/01/021

CrossRef Full Text | Google Scholar

Blumlein, J., Boos, E., and Kryukov, A. (1997). Leptoquark pair production in hadronic interactions. Z. Phys. C76, 137–153. doi: 10.1007/s002880050538

CrossRef Full Text | Google Scholar

Bonnivard, V., Combet, C., Daniel, M., Funk, S., Geringer-Sameth, A., Hinton, J. A., et al. (2015). Dark matter annihilation and decay in dwarf spheroidal galaxies: the classical and ultrafaint dSphs. Mon. Not. Roy. Astron. Soc. 453, 849–867. doi: 10.1093/mnras/stv1601

CrossRef Full Text | Google Scholar

Boveia, A., Buchmueller, O., Busoni, G., D'Eramo, F., De Roeck, A., De Simone, A., et al. (2016). Recommendations on presenting LHC searches for missing transverse energy signals using simplified s-channel models of dark matter. arXiv:1603.04156.

Google Scholar

Bramante, J., and Unwin, J. (2017). Superheavy Thermal Dark Matter and Primordial Asymmetries. J. High Energy Phys. 2:119. doi: 10.1007/JHEP02(2017)119

CrossRef Full Text | Google Scholar

Branco, G., Ferreira, P. M., Lavoura, L., Rebelo, M. N., Sher, M., and Silva, J. P. (2012). Theory and phenomenology of two-Higgs-doublet models. Phys. Rept. 516, 1–102. doi: 10.1016/j.physrep.2012.02.002

CrossRef Full Text | Google Scholar

Brennan, A. J., McDonald, M. F., Gramling, J., and Jacques, T. D. (2016). Collide and conquer: constraints on simplified Dark Matter models using Mono-X Collider Searches. J. High Energy Phys. 5:112. doi: 10.1007/JHEP05(2016)112

CrossRef Full Text | Google Scholar

Bringmann, T., Calore, F., Galea, A., and Garny, M. (2017). Electroweak and Higgs Boson Internal Bremsstrahlung: General considerations for Majorana dark matter annihilation and application to MSSM neutralinos. J. High Energy Phys. 9:041. doi: 10.1007/JHEP09(2017)041

CrossRef Full Text | Google Scholar

Bringmann, T., Edsjo, J., Gondolo, P., Ullio, P., and Bergstrom, L. (2018). DarkSUSY 6 : an advanced tool to compute dark matter properties numerically. arXiv: 1802.03399.

Google Scholar

Bringmann, T., Galea, A. J., and Walia, P. (2016). Leading QCD corrections for indirect dark matter searches: a fresh look. Phys. Rev. D93:043529. doi: 10.1103/PhysRevD.93.043529

CrossRef Full Text | Google Scholar

Brown, T. M., Tumlinson, J., Geha, M., Kirby, E. N., VandenBerg, D. A., Muñoz, R. R., et al. (2012). The primeval populations of the Ultra-Faint dwarf galaxies. Astrophys. J. 753:L21. doi: 10.1088/2041-8205/753/1/L21

CrossRef Full Text | Google Scholar

Bruggisser, S., Riva, F., and Urbano, A. (2016). The last gasp of dark matter effective theory. J. High Energy Phys. 11:069. doi: 10.1007/JHEP11(2016)069

CrossRef Full Text | Google Scholar

Buchmueller, O., Dolan, M. J., Malik, S. A., and McCabe, C. (2015). Characterising dark matter searches at colliders and direct detection experiments: Vector mediators. J. High Energy Phys. 1:037. doi: 10.1007/JHEP01(2015)037

CrossRef Full Text | Google Scholar

Buchmueller, O., Dolan, M. J., and McCabe, C. (2014). Beyond effective field theory for dark matter searches at the LHC. J. High Energy Phys. 1:025. doi: 10.1007/JHEP01(2014)025

CrossRef Full Text | Google Scholar

Buckley, M. R., Feld, D., and Goncalves, D. (2015). Scalar simplified models for Dark Matter. Phys. Rev. D91:015017. doi: 10.1103/PhysRevD.91.015017

CrossRef Full Text | Google Scholar

Busoni, G., De Simone, A., Gramling, J., Morgante, E., and Riotto, A. (2014b). On the validity of the effective field theory for dark matter searches at the LHC, part II: complete analysis for the s-channel. J. Cosmol. Astropart. Phys. 1406:060. doi: 10.1088/1475-7516/2014/06/060

CrossRef Full Text | Google Scholar

Busoni, G., De Simone, A., Jacques, T., Morgante, E., and Riotto, A. (2014c). On the validity of the effective field theory for dark matter searches at the LHC part III: analysis for the t-channel. J. Cosmol. Astropart. Phys. 1409:022. doi: 10.1088/1475-7516/2014/09/022

CrossRef Full Text | Google Scholar

Busoni, G., De Simone, A., Morgante, E., and Riotto, A. (2014a). On the validity of the effective field theory for dark matter searches at the LHC. Phys. Lett. B728, 412–421. doi: 10.1016/j.physletb.2013.11.069

CrossRef Full Text | Google Scholar

Cao, Q. H., Ma, E., and Shaughnessy, G. (2009). Dark Matter: the leptonic connection. Phys. Lett. B673, 152–155. doi: 10.1016/j.physletb.2009.02.015

CrossRef Full Text | Google Scholar

Carena, M., Quiros, M., and Wagner, C. E. M. (1996). Effective potential methods and the Higgs mass spectrum in the MSSM. Nucl. Phys. B461, 407–436. doi: 10.1016/0550-3213(95)00665-6

CrossRef Full Text | Google Scholar

Carpenter, L. M., Colburn, R., Goodman, J., and Linden, T. (2016). Indirect detection constraints on s and t channel simplified models of Dark Matter. Phys. Rev. D94:055027. doi: 10.1103/PhysRevD.94.055027

CrossRef Full Text | Google Scholar

Chala, M., Kahlhoefer, F., McCullough, M., Nardini, G., and Schmidt-Hoberg, K. (2015). Constraining dark sectors with Monojets and Dijets. J. High Energy Phys. 7:089. doi: 10.1007/JHEP07(2015)089

CrossRef Full Text | Google Scholar

Chang, S., Edezhath, R., Hutchinson, J., and Luty, M. (2014a). Effective WIMPs. Phys. Rev. D89:015011. doi: 10.1103/PhysRevD.89.015011

CrossRef Full Text | Google Scholar

Chang, S., Edezhath, R., Hutchinson, J., and Luty, M. (2014b). Leptophilic Effective WIMPs. Phys. Rev. D90:015011. doi: 10.1103/PhysRevD.90.015011

CrossRef Full Text | Google Scholar

Choi, K., Abe, K., Haga, Y., Hayato, Y., Iyogi, K., Kameda, J., et al. (2015). Search for neutrinos from annihilation of captured low-mass dark matter particles in the Sun by Super-Kamiokande. Phys. Rev. Lett. 114:141301. doi: 10.1103/PhysRevLett.114.141301

PubMed Abstract | CrossRef Full Text | Google Scholar

Chu, X., Hambye, T., Scarna, T., and Tytgat, M. H. G. (2012). What if Dark Matter gamma-ray lines come with Gluon Lines? Phys. Rev. D86:083521. doi: 10.1103/PhysRevD.86.083521

CrossRef Full Text | Google Scholar

Cirelli, M. (2015). Status of indirect (and direct) dark matter searches. arXiv: 1511.02031.

Google Scholar

Cirelli, M., Del Nobile, E., and Panci, P. (2013). Tools for model-independent bounds in direct dark matter searches. J. Cosmol. Astropart. Phys. 1310:019. doi: 10.1088/1475-7516/2013/10/019

CrossRef Full Text

Cirigliano, V., Graesser, M. L., and Ovanesyan, G. (2012). WIMP-nucleus scattering in chiral effective theory. J. High Energy Phys. 10:025. doi: 10.1007/JHEP10(2012)025

CrossRef Full Text | Google Scholar

CMS (2015). Search for Resonances Decaying to Dijet Final States at √s = 8 TeV with Scouting Data. CMS-PAS-EXO-14-005. Geneva: CERN.

CMS Collaboration (2014). Search for the Production of Dark Matter in Association with Top Quark Pairs in the Single-lepton Final State in pp Collisions at √s = 8 TeV. CMS-PAS-B2G-14-004.

CMS Collaboration (2015). Search for Massive Resonances Decaying into Pairs of boosted Wand Z Bosons at √s = 13 TeV. CMS-PAS-EXO-15-002.

CMS Collaboration (2016a). Search for new high-mass resonances in the dilepton final state using proton-proton collisions at $\sqrt{s}=13$ TeV with the ATLAS detector.

CMS Collaboration (2016b). Search for a High-Mass Resonance Decaying into a Dilepton Final State in 13 fb−1 of pp Collisions at √s = 13 TeV. CMS-PAS-EXO-16-031.

CMS Collaboration (2016c). Search for t.t Resonances in Boosted Semileptonic Final States in pp Collisions at √s = 13 TeV. CMS-PAS-B2G-15-002.

CMS Collaboration (2016d). Search for a Neutral MSSMHiggs Boson Decaying into τ τ with 12.9 fb−1 of Data at √s = 13 TeV. CMS-PAS-HIG-16-037.

CMS Collaboration (2017). Search for supersymmetry in events with at least one soft lepton, low jet multiplicity, and missing transverse momentum in proton-proton collisions at $\sqrt{s}=13\text{T}\text{e}\text{V}$.

Colucci, S., Fuks, B., Giacchino, F., Lopez Honorez, L., Tytgat, M. H. G., and Vandecasteele, J. (2018). Top-philic vector-like portal to scalar Dark Matter. Phys. Rev. D98:035002. doi: 10.1103/PhysRevD.98.035002

CrossRef Full Text | Google Scholar

Costa, R., Muehlleitner, M., Sampaio, M. O. P., and Santos, R. (2016). Singlet extensions of the standard model at LHC Run 2: benchmarks and comparison with the NMSSM. J. High Energy Phys. 6:034. doi: 10.1007/JHEP06(2016)034

CrossRef Full Text | Google Scholar

Courteau, S., Cappellari, M., de Jong, R. S., Dutton, A. A., Emsellem, E., Hoekstra, H., et al. (2014). Galaxy masses. Rev. Mod. Phys. 86, 47–119. doi: 10.1103/RevModPhys.86.47

CrossRef Full Text | Google Scholar

Cuoco, A., Heisig, J., Korsmeier, M., and Kraemer, M. (2018). Constraining heavy dark matter with cosmic-ray antiprotons. J. Cosmol. Astropart. Phys. 1804:004. doi: 10.1088/1475-7516/2018/04/004

CrossRef Full Text | Google Scholar

D'Ambrosio, G., Giudice, G. F., Isidori, G., and Strumia, A. (2002). Minimal flavor violation: an Effective field theory approach. Nucl. Phys. B645, 155–187. doi: 10.1016/S0550-3213(02)00836-2

CrossRef Full Text | Google Scholar

Das, G., Degrande, C., Hirschi, V., Maltoni, F., and Shao, H. S. (2017). NLO predictions for the production of a spin-two particle at the LHC. Phys. Lett. B770, 507–513. doi: 10.1016/j.physletb.2017.05.007

CrossRef Full Text | Google Scholar

De Simone, A., and Jacques, T. (2016). Simplified models vs. effective field theory approaches in dark matter searches. Eur. Phys. J. C76, 367. doi: 10.1140/epjc/s10052-016-4208-4

CrossRef Full Text | Google Scholar

de Swart, J., Bertone, G., and van Dongen, J. (2017). How dark matter came to matter Nat. Astron. 1:0059. doi: 10.1038/s41550017-0059

CrossRef Full Text | Google Scholar

Degrande, C. (2015). Automatic evaluation of UV and R2 terms for beyond the Standard Model Lagrangians: a proof-of-principle. Comput. Phys. Commun. 197, 239–262. doi: 10.1016/j.cpc.2015.08.015

CrossRef Full Text | Google Scholar

Del Nobile, E., Gelmini, G., Gondolo, P., and Huh, J. H. (2013). Generalized halo independent comparison of direct dark matter detection data. J. Cosmol. Astropart. Phys. 1310:048. doi: 10.1088/1475-7516/2013/10/048

CrossRef Full Text | Google Scholar

D'Eramo, F., and Procura, M. (2015). Connecting Dark Matter UV complete models to direct detection rates via effective field theory. J. High Energy Phys. 4:054. doi: 10.1007/JHEP04(2015)054

CrossRef Full Text | Google Scholar

Dillon, B. M., Han, C., Lee, H. M., and Park, M. (2017). KK graviton resonance and cascade decays in warped gravity. Int. J. Mod. Phys. A32:1745006. doi: 10.1142/S0217751X17450063

CrossRef Full Text | Google Scholar

Dillon, B. M., and Sanz, V. (2017). Kaluza-Klein gravitons at LHC2. Phys. Rev. D96:035008. doi: 10.1103/PhysRevD.96.035008

CrossRef Full Text | Google Scholar

Doebrich, B. (2017). “Searches for very weakly-coupled particles beyond the Standard Model with NA62,” in Proceedings of the 13th “Patras” Workshop on Axions, WIMPs and WISPs, PATRAS 2017.

Google Scholar

Dolan, M. J., Spannowsky, M., Wang, Q., and Yu, Z. H. (2016). Determining the quantum numbers of simplified models in $t\bar{t}X$ production at the LHC. Phys. Rev. D94:015025. doi: 10.1103/PhysRevD.94.015025

CrossRef Full Text | Google Scholar

Drewes, M., Lasserre, T., Merle, A., Mertens, S., Adhikari, R., Agostini, M., et al. (2017). A white paper on keV sterile neutrino dark matter. JCAP 1701:025. doi: 10.1088/1475-7516/2017/01/025

CrossRef Full Text | Google Scholar

du Pree, T., Hahn, K., Harris, P., and Roskas, C. (2016). Cosmological constraints on dark matter models for collider searches. arXiv: 1603.08525.

Google Scholar

Dudas, E., Mambrini, Y., Pokorski, S., and Romagnoni, A. (2009). (In)visible Z-prime and dark matter. J. High Energy Phys. 8:014. doi: 10.1088/1126-6708/2009/08/014

CrossRef Full Text | Google Scholar

Duerr, M., and Fileviez Perez, P. (2015). Theory for baryon number and Dark Matter at the LHC. Phys. Rev. D91:095001. doi: 10.1103/PhysRevD.91.095001

CrossRef Full Text | Google Scholar

Duerr, M., Kahlhoefer, F., Schmidt-Hoberg, K., Schwetz, T., and Vogl, S. (2016). How to save the WIMP: global analysis of a dark matter model with two s-channel mediators. J. High Energy Phys. 9:042. doi: 10.1007/JHEP09(2016)042

CrossRef Full Text | Google Scholar

Dupuis, G. (2016). Collider constraints and prospects of a scalar singlet extension to Higgs portal Dark Matter. J. High Energy Phys. 7:008. doi: 10.1007/JHEP07(2016)008

CrossRef Full Text | Google Scholar

Edsjo, J., and Gondolo, P (1997). Neutralino relic density including coannihilations. Phys. Rev. D56, 1879–1894.

Google Scholar

Einasto, J, and Haud, U. (1989). Galactic models with massive corona. I - Method. II - Galaxy. Astron. Astrophys. 223, 89–106.

Google Scholar

El Hedri, S., Kaminska, A., de Vries, M., and Zurita, J. (2017). Simplified phenomenology for colored dark sectors. J. High Energy Phys. 4:118. doi: 10.1007/JHEP04(2017)118

CrossRef Full Text | Google Scholar

Ellis, J., Fairbairn, M., and Tunney, P. (2017). Anomaly-Free Dark Matter Models are not so Simple. J. High Energy Phys. 8:053. doi: 10.1007/JHEP08(2017)053

CrossRef Full Text | Google Scholar

Ellis, J., Fok, R., Hwang, D. S., Sanz, V., and You, T. (2013). Distinguishing ‘Higgs’ spin hypotheses using γγ and WW* decays. Eur. Phys. J. C73:2488. doi: 10.1140/epjc/s10052-013-2488-5

CrossRef Full Text | Google Scholar

Englert, C., Goncalves-Netto, D., Mawatari, K., and Plehn, T. (2013). Higgs quantum numbers in Weak Boson Fusion. J. High Energy Phys. 1:148. doi: 10.1007/JHEP01(2013)148

CrossRef Full Text | Google Scholar

Englert, C., McCullough, M., and Spannowsky, M. (2016). S-Channel Dark Matter simplified models and unitarity. Phys. Dark Univ. 14, 48–56. doi: 10.1016/j.dark.2016.09.002

CrossRef Full Text | Google Scholar

Fairbairn, M., Heal, J., Kahlhoefer, F., and Tunney, P. (2016). Constraints on Z? models from LHC dijet searches and implications for dark matter. J. High Energy Phys. 9:018. doi: 10.1007/JHEP09(2016)018

CrossRef Full Text | Google Scholar

Fayet, P. (1976). Supersymmetry and weak, electromagnetic and strong interactions. Phys. Lett. 64B:159. doi: 10.1016/0370-2693(76)90319-1

CrossRef Full Text | Google Scholar

Fitzpatrick, A. L., Haxton, W., Katz, E., Lubbers, N., and Xu, Y. (2013). The effective field theory of dark matter direct detection. J. Cosmol. Astropart. Phys. 1302:004. doi: 10.1088/1475-7516/2013/02/004

CrossRef Full Text | Google Scholar

Fox, P. J., Kribs, G. D., and Tait, T. M. P. (2011). Interpreting dark matter direct detection independently of the local velocity and density distribution. Phys. Rev. D83:034007. doi: 10.1103/PhysRevD.83.034007

CrossRef Full Text | Google Scholar

Fu, C., Cui, X., Zhou, X., Chen, X., Chen, Y., Fang, D., et al. (2017). Spin-dependent weakly-interacting-massive-particle?Nucleon cross section limits from first data of PandaX-II experiment. Phys. Rev. Lett. 118:071301. doi: 10.1103/PhysRevLett.118.071301

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia-Cely, C., and Heeck, J. (2016). Indirect searches of dark matter via polynomial spectral features. J. Cosmol. Astropart. Phys. 1608:023. doi: 10.1088/1475-7516/2016/08/023

CrossRef Full Text | Google Scholar

Garny, M., Heisig, J., Hufnagel, M., and Luelf, B. (2018). Top-philic dark matter within and beyond the WIMP paradigm. Phys. Rev. D97:075002. doi: 10.1103/PhysRevD.97.075002

CrossRef Full Text | Google Scholar

Garny, M., Ibarra, A., Pato, M., and Vogl, S. (2013). Internal bremsstrahlung signatures in light of direct dark matter searches. J. Cosmol. Astropart. Phys. 1312:046. doi: 10.1088/1475-7516/2013/12/046

CrossRef Full Text | Google Scholar

Garny, M., Ibarra, A., Rydbeck, S., and Vogl, S. (2014). Majorana Dark Matter with a coloured mediator: collider vs direct and indirect searches. J. High Energy Phys. 6:169. doi: 10.1007/JHEP06(2014)169

CrossRef Full Text | Google Scholar

Garny, M., Ibarra, A., and Vogl, S. (2015). Signatures of Majorana dark matter with t-channel mediators. Int. J. Mod. Phys. D24:1530019. doi: 10.1142/S0218271815300190

CrossRef Full Text | Google Scholar

Gaskins, J. M. (2016). A review of indirect searches for particle dark matter. Contemp. Phys. 57, 496–525. doi: 10.1080/00107514.2016.1175160

CrossRef Full Text | Google Scholar

Geringer-Sameth, A., Walker, M. G., Koushiappas, S. M., Koposov, S. E., Belokurov, V., Torrealba, G., et al. (2015). Indication of gamma-ray emission from the newly discovered dwarf galaxy reticulum II. Phys. Rev. Lett. 115:081101. doi: 10.1103/PhysRevLett.115.081101

PubMed Abstract | CrossRef Full Text | Google Scholar

Giacchino, F., Ibarra, A., Lopez Honorez, L., Tytgat, M. H. G., and Wild, S. (2016). Signatures from scalar Dark Matter with a vector-like quark mediator. J. Cosmol. Astropart. Phys. 1602:002. doi: 10.1088/1475-7516/2016/02/002

CrossRef Full Text | Google Scholar

Giacchino, F., Lopez-Honorez, L., and Tytgat, M. H. G. (2013). Scalar dark matter models with significant internal bremsstrahlung. J. Cosmol. Astropart. Phys. 1310:025. doi: 10.1088/1475-7516/2013/10/025

CrossRef Full Text | Google Scholar

Giacchino, F., Lopez-Honorez, L., and Tytgat, M. H. G. (2014). Bremsstrahlung and gamma ray lines in 3 scenarios of Dark Matter annihilation. J. Cosmol. Astropart. Phys. 1408:046. doi: 10.1088/1475-7516/2014/08/046

CrossRef Full Text | Google Scholar

Giesen, G., Boudaud, M., Genolini, Y., Poulin, V., Cirelli, M., Salati, P., et al. (2015). AMS-02 antiprotons, at last! Secondary astrophysical component and immediate implications for Dark Matter. J. Cosmol. Astropart. Phys. 1509:023. doi: 10.1088/1475-7516/2015/9/023

CrossRef Full Text | Google Scholar

Goncalves, D., Machado, P. A. N., and No, J. M. (2017). Simplified models for Dark Matter face their consistent completions. Phys. Rev. D95:055027. doi: 10.1103/PhysRevD.95.055027

CrossRef Full Text | Google Scholar

Gondolo, P., Edsjo, J., Ullio, P., Bergstrom, L., Schelke, M., and Baltz, E. A. (2004). DarkSUSY: Computing supersymmetric dark matter properties numerically. J. Cosmol. Astropart. Phys. 0407:008. doi: 10.1088/1475-7516/2004/07/008

CrossRef Full Text | Google Scholar

Gondolo, P., and Gelmini, G. (1991). Cosmic abundances of stable particles: Improved analysis. Nucl. Phys. B360, 145–179. doi: 10.1016/0550-3213(91)90438-4

CrossRef Full Text | Google Scholar

Gondolo, P., and Gelmini, G. B. (2012). Halo independent comparison of direct dark matter detection data. J. Cosmol. Astropart. Phys. 1212:015. doi: 10.1088/1475-7516/2012/12/015

CrossRef Full Text | Google Scholar

Goodman, J., and Shepherd, W. (2011). LHC bounds on UV-complete models of dark matter. arXiv:1111.2359.

Google Scholar

Gould, A. (1987). Resonant enhancements in WIMP capture by the Earth. Astrophys. J. 321:571. doi: 10.1086/165653

CrossRef Full Text

Goyal, A., and Kumar, M. (2016). Fermionic Dark Matter in a simple t-channel model. J. Cosmol. Astropart. Phys. 1611:001. doi: 10.1088/1475-7516/2016/11/001

CrossRef Full Text | Google Scholar

Griest, K., and Kamionkowski, M. (1990). Unitarity limits on the mass and radius of dark matter particles. Phys. Rev. Lett. 64:615.

PubMed Abstract | Google Scholar

Griest, K., and Seckel, D. (1991). Three exceptions in the calculation of relic abundances. Phys. Rev. D43, 3191–3203. doi: 10.1103/PhysRevD.43.3191

CrossRef Full Text | Google Scholar

Gunion, J. F., and Haber, H. E. (1986). Higgs Bosons in supersymmetric models. 1. Nucl. Phys. B272:1. doi: 10.1016/0550-3213(93)90653-7

CrossRef Full Text | Google Scholar

Haisch, U., Kahlhoefer, F., and Tait, T. M. P. (2016). On Mono-W signatures in Spin-1 simplified models. Phys. Lett. B760, 207–213. doi: 10.1016/j.physletb.2016.06.063

CrossRef Full Text | Google Scholar

Haisch, U., Kahlhoefer, F., and Unwin, J. (2013). The impact of heavy-quark loops on LHC dark matter searches. J. High Energy Phys. 7:125. doi: 10.1007/JHEP07(2013)125

CrossRef Full Text | Google Scholar

Haisch, U., and Re, E. (2015). Simplified dark matter top-quark interactions at the LHC. J. High Energy Phys. 6:078. doi: 10.1007/JHEP06(2015)078

CrossRef Full Text | Google Scholar

Han, C., Lee, H. M., Park, M., and Sanz, V. (2016). The diphoton resonance as a gravity mediator of dark matter. Phys. Lett. B755, 371–379. doi: 10.1016/j.physletb.2016.02.040

CrossRef Full Text | Google Scholar

Harris, P., Khoze, V. V., Spannowsky, M., and Williams, C. (2015). Constraining dark sectors at colliders: beyond the effective theory approach. Phys. Rev. D91:055009. doi: 10.1103/PhysRevD.91.055009

CrossRef Full Text | Google Scholar

He, H. (2016). Design Highlights and Status of the LHAASO Project. PoS ICRC2015.

Heisig, J., Kraemer, M., Pellen, M., and Wiebusch, C. (2016). Constraints on Majorana Dark Matter from the LHC and IceCube. Phys. Rev. D93:055029. doi: 10.1103/PhysRevD.93.055029

CrossRef Full Text | Google Scholar

Hooper, D., and Linden, T (2015). On the gamma-ray emission from reticulum II other dwarf galaxies. J. Cosmol. Astropart. Phys. 1509:016. doi: 10.1088/1475-7516/2015/09/016

CrossRef Full Text | Google Scholar

Ibarra, A., Lamperstorfer, A. S., López-Gehler, S., Pato, M., and Bertone, G. (2015a). On the sensitivity of CTA to gamma-ray boxes from multi-TeV dark matter. J. Cosmol. Astropart. Phys. 1509:048. doi: 10.1088/1475-7516/2015/09/048

CrossRef Full Text | Google Scholar

Ibarra, A., Pierce, A., Shah, N. R., and Vogl, S. (2015b). Anatomy of coannihilation with a scalar top partner. Phys. Rev. D91:095018. doi: 10.1103/PhysRevD.91.095018

CrossRef Full Text | Google Scholar

Ibarra, A., Toma, T., Totzauer, M., and Wild, S. (2014). Sharp gamma-ray spectral features from scalar dark matter annihilations. Phys. Rev. D90:043526. doi: 10.1103/PhysRevD.90.043526

CrossRef Full Text | Google Scholar

Jacques, T., Katz, A., Morgante, E., Racco, D., Rameez, M., and Riotto, A. (2016). Complementarity of DM searches in a consistent simplified model: the case of Z? J. High Energy Phys. 10:071. doi: 10.1007/JHEP10(2016)071

CrossRef Full Text | Google Scholar

Jacques, T., and Nordstrom, K. (2015). Mapping monojet constraints onto Simplified Dark Matter Models. J. High Energy Phys. 6:142. doi: 10.1007/JHEP06(2015)142

CrossRef Full Text | Google Scholar

Jeans, J. H. (1922). The motions of stars in a Kapteyn Universe. MNRAS 82, 122–132. doi: 10.1093/mnras/82.3.122

CrossRef Full Text | Google Scholar

Jungman, G., Kamionkowski, M., and Griest, K. (1996). Supersymmetric dark matter. Phys. Rept. 267, 195–373. doi: 10.1016/0370-1573(95)00058-5

CrossRef Full Text | Google Scholar

Kahlhoefer, F. (2017). Review of LHC dark matter searches. Int. J. Mod. Phys. A32:1730006. doi: 10.1142/S0217751X1730006X

CrossRef Full Text | Google Scholar

Kahlhoefer, F., Schmidt-Hoberg, K., Schwetz, T., and Vogl, S. (2016). Implications of unitarity and gauge invariance for simplified dark matter models. J. High Energy Phys. 2:016. doi: 10.1007/JHEP02(2016)016

CrossRef Full Text | Google Scholar

Kamionkowski, M. (1991). Energetic neutrinos from heavy neutralino annihilation in the sun. Phys. Rev. D44, 3021–3042. doi: 10.1103/PhysRevD.44.3021

CrossRef Full Text | Google Scholar

Kapteyn, J. C. (1922). First attempt at a theory of the arrangement and motion of the sidereal system. ApJS 55:302. doi: 10.1086/142670

CrossRef Full Text | Google Scholar

Khachatryan, V., Sirunyan, A. M., Tumasyan, A., Adam, W., AÇilar, E., Bergauer, T., et al. (2015b). Search for diphoton resonances in the mass range from 150 to 850 GeV in pp collisions at $\sqrt{s}=8$ TeV. Phys. Lett. B750, 494–519. doi: 10.1016/j.physletb.2015.09.062

CrossRef Full Text | Google Scholar

Khachatryan, V., Sirunyan, A. M., Tumasyan, A., Adam, W., Açilar, E., Bergauer, T., et al. (2016). Search for dark matter and unparticles produced in association with a Z boson in proton-proton collisions at $\sqrt{s}=8$ TeV. Phys. Rev. D93:052011. doi: 10.1103/PhysRevD.93.052011

CrossRef Full Text | Google Scholar

Khachatryan, V., Sirunyan, A. M., Tumasyan, A., Adam, W., AÇilar, E., Bergauer, T., et al. (2017a). Search for high-mass diphoton resonances in proton-proton collisions at 13 TeV and combination with 8 TeV search. Phys. Lett. B767, 147–170. doi: 10.1016/j.physletb.2017.01.027

CrossRef Full Text | Google Scholar

Khachatryan, V., Sirunyan, A. M., Tumasyan, A., Adam, W., AÇilar, E., Bergauer, T., et al. (2017b). Search for heavy resonances decaying to tau lepton pairs in proton-proton collisions at $\sqrt{s}=13$ TeV. J. High Energy Phys. 2:048. doi: 10.1007/JHEP02(2017)048

CrossRef Full Text | Google Scholar

Khachatryan, V., Sirunyan, A. M., Tumasyan, A., Adam, W., Bergauer, T., Dragicevic, M., et al. (2014). Search for Standard Model Production of Four Top Quarks in the Lepton + Jets Channel in pp Collisions at $\sqrt{s}=8$ TeV. J. High Energy Phys. 11:154. doi: 10.1007/JHEP11(2014)154

CrossRef Full Text | Google Scholar

Khachatryan, V., Sirunyan, A. M., Tumasyan, A., Adam, W., Bergauer, T., Dragicevic, M., et al. (2015a). Search for dark matter, extra dimensions, and unparticles in monojet events in proton-proton collisions at $\sqrt{s}=8$ TeV. Eur. Phys. J. C75:235. doi: 10.1140/epjc/s10052-015-3451-4

CrossRef Full Text | Google Scholar

Khachatryan, V., Sirunyan, A. M., Tumasyan, A., Adam, W., Bergauer, T., Dragicevic, M., et al. (2015c). Search for resonances and quantum black holes using dijet mass spectra in proton-proton collisions at $\sqrt{s}=8$ TeV. Phys. Rev. D91:052009. doi: 10.1103/PhysRevD.91.052009

CrossRef Full Text | Google Scholar

Khoze, V. V., Ro, G., and Spannowsky, M. (2015). Spectroscopy of scalar mediators to dark matter at the LHC and at 100 TeV. Phys. Rev. D92:075006. doi: 10.1103/PhysRevD.92.075006

CrossRef Full Text | Google Scholar

Kile, J. (2013). Flavored Dark Matter: a review. Mod. Phys. Lett. A28:1330031. doi: 10.1142/S0217732313300310

CrossRef Full Text | Google Scholar

Ko, P., Natale, A., Park, M., and Yokoya, H. (2017). Simplified DM models with the full SM gauge symmetry : the case of t-channel colored scalar mediators. J. High Energy Phys. 1:086. doi: 10.1007/JHEP01(2017)086

CrossRef Full Text | Google Scholar

Kolb, E. W., and Turner, M. S. (1990). The Early Universe. Front. Phys. 69, 1–547.

Google Scholar

Kraml, S., Laa, U., Mawatari, K., and Yamashita, K. (2017). Simplified dark matter models with a spin-2 mediator at the LHC. Eur. Phys. J. C77:326. doi: 10.1140/epjc/s10052-017-4871-0

CrossRef Full Text | Google Scholar

Leane, R. K., Ng, K. C. Y., and Beacom, J. F. (2017). Powerful solar signatures of long-lived dark mediators. Phys. Rev. D95:123016. doi: 10.1103/PhysRevD.95.123016

CrossRef Full Text | Google Scholar

Lebedev, O., and Mambrini, Y. (2014). Axial dark matter: the case for an invisible Z? Phys. Lett. B734,350–353. doi: 10.1016/j.physletb.2014.05.025

CrossRef Full Text | Google Scholar

Lee, B. W., and Weinberg, S. (1977). Cosmological lower bound on heavy-neutrino masses. Phys. Rev. Lett. 39, 165–168.

Google Scholar

Lee, H.M., Park, M., and Sanz, V. (2014a). Gravity-mediated (or Composite) Dark Matter confronts astrophysical data. J. High Energy Phys. 5:063. doi: 10.1007/JHEP05(2014)063

CrossRef Full Text | Google Scholar

Lee, H. M., Park, M., and Sanz, V. (2014b). Gravity-mediated (or Composite) Dark Matter. Eur. Phys. J. C74:2715. doi: 10.1140/epjc/s10052-014-2715-8

CrossRef Full Text | Google Scholar

Lopez-Val, D., and Robens, T. (2014). Δr and the W-boson mass in the singlet extension of the standard model. Phys. Rev. D90:114018. doi: 10.1103/PhysRevD.90.114018

CrossRef Full Text | Google Scholar

Akerib, D. S., Alsum, S., Araújo, H. M., Bai, X., Bailey, A. J., et al. (2017). Limits on spin-dependent WIMP-nucleon cross section obtained from the complete LUX exposure. Phys. Rev. Lett. 118:251302. doi: 10.1103/PhysRevLett.118.251302

PubMed Abstract | CrossRef Full Text | Google Scholar

March-Russell, J., Unwin, J., and West, S. M. (2012). Closing in on asymmetric dark matter I: model independent limits for interactions with quarks. J. High Energy Phys. 8:029. doi: 10.1007/JHEP08(2012)029

CrossRef Full Text | Google Scholar

Marsh, D. J. E. (2016). Axion cosmology. Phys. Rept. 643, 1–79. doi: 10.1016/j.physrep.2016.06.005

CrossRef Full Text | Google Scholar

Martini, A., Mawatari, K., and Sengupta, D. (2016). Diphoton excess in phenomenological spin-2 resonance scenarios. Phys. Rev. D93:075011. doi: 10.1103/PhysRevD.93.075011

CrossRef Full Text | Google Scholar

Mateo, M. (1998). Dwarf galaxies of the Local Group. Ann. Rev. Astron. Astrophys. 36, 435–506. doi: 10.1146/annurev.astro.36.1.435

CrossRef Full Text | Google Scholar

Mattelaer, O., and Vryonidou, E. (2015). Dark matter production through loop-induced processes at the LHC: the s-channel mediator case. Eur. Phys. J. C75:436. doi: 10.1140/epjc/s10052-015-3665-5

CrossRef Full Text | Google Scholar

Morgante, E. (2018). Simplified dark matter models. arXiv: 1804.01245.

Google Scholar

Mount, B. J., Hans, S., Rosero, R., Yeh, M., Chan, C., Gaitskell, R. J., et al. (2017). LUX-ZEPLIN (LZ) Technical Design Report.

Neubert, M., Wang, J., and Zhang, C. (2015). Higher-order QCD predictions for dark matter production in mono-Z searches at the LHC. J. High Energy Phys. 2:082. doi: 10.1007/JHEP02(2016)082

CrossRef Full Text | Google Scholar

Oort, J. H. (1932). The force exerted by the stellar system in the direction perpendicular to the galactic plane and some related problems. Bull. Astron. Inst. Netherlands 6, 249.

Google Scholar

Papucci, M., Vichi, A., and Zurek, K. M. (2014). Monojet versus the rest of the world I: t-channel models. J. High Energy Phys. 11:024. doi: 10.1007/JHEP11(2014)024

CrossRef Full Text | Google Scholar

Peter, A. H. G. (2009). Dark matter in the solar system II: WIMP annihilation rates in the Sun. Phys. Rev. D79:103532. doi: 10.1103/PhysRevD.79.103532

CrossRef Full Text | Google Scholar

Ade, P. A. R., Aghanim, N., Arnaud, M., Ashdown, M., Aumont, J., et al. (2016). Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 594:A13. doi: 10.1051/0004-6361/201525830

CrossRef Full Text | Google Scholar

Press, W. H., and Spergel, D. N. (1985). Capture by the sun of a galactic population of weakly interacting massive particles. Astrophys. J. 296, 679–684. doi: 10.1086/163485

CrossRef Full Text | Google Scholar

Randall, L., and Sundrum, R. (1999). A Large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 83, 3370–3373. doi: 10.1103/PhysRevLett.83.3370

CrossRef Full Text | Google Scholar

Ritz, S., and Seckel, D. (1988). Detailed neutrino spectra from cold dark matter annihilations in the Sun. Nucl. Phys. B304, 877–908. doi: 10.1016/0550-3213(88)90660-8

CrossRef Full Text | Google Scholar

Robens, T., and Stefaniak, T. (2016). LHC benchmark scenarios for the real higgs singlet extension of the standard model. Eur. Phys. J. C76:268. doi: 10.1140/epjc/s10052-016-4115-8

CrossRef Full Text | Google Scholar

Rueter, T. D., Rizzo, T. G., and Hewett, J. L. (2017). Gravity-mediated Dark Matter annihilation in the Randall-Sundrum Model. J. High Energy Phys. 10:094. doi: 10.1007/JHEP10(2017)094

CrossRef Full Text | Google Scholar

Schoenrich, R., Binney, J., and Dehnen, W. (2010). Local kinematics and the local standard of rest. Mon. Not. Roy. Astron. Soc. 403:1829. doi: 10.1111/j.1365-2966.2010.16253.x

CrossRef Full Text | Google Scholar

Shoemaker, I. M., and Vecchi, L. Unitarity Monojet bounds on models for DAMA, CoGeNT, CRESST-II. (2012). Phys. Rev. D86:015023. doi: 10.1103/PhysRevD.86.015023

CrossRef Full Text

Silk, J., Moore, B., Diemand, J., Bullock, J., Kaplinghat, M., Strigari, L., et al. (2010). Particle Dark Matter: Observations, Models and Searches Cambridge: Cambridge Univ. Press.

Silk, J., Olive, K. A., and Srednicki, M. (1985). The Photino, the Sun and high-energy neutrinos. Phys. Rev. Lett. 55, 257–259. doi: 10.1103/PhysRevLett.55.257

PubMed Abstract | CrossRef Full Text | Google Scholar

Silk, J., and Srednicki, M. (1984). Cosmic ray anti-protons as a probe of a photino dominated Universe. Phys. Rev. Lett. 53:624. doi: 10.1103/PhysRevLett.53.624

CrossRef Full Text | Google Scholar

Sirunyan, A.M., Tumasyan, A., Adam, W, Asilar, E., Bergauer, T., Brandstetter, J., et al. (2017c). Search for new physics in final states with an energetic jet or a hadronically decaying W or Z boson and transverse momentum imbalance at √s = 13 TeV. arXiv: 1712.02345.

Google Scholar

Sirunyan, A. M., Tumasyan, A., Adam, W., AÇilar, E, Bergauer, T, Brandstetter, J, et al. (2017a). Search for dijet resonances in proton-proton collisions at $\sqrt{s}=13$ TeV and constraints on dark matter and other models. Phys. Lett. B769, 520–542. doi: 10.1016/j.physletb.2017.02.012

CrossRef Full Text | Google Scholar

Sirunyan, A. M., Tumasyan, A., Adam, W., Ambrogi, F., Asilar, E., Bergauer, T., et al. (2018). Search for top squarks and dark matter particles in opposite-charge dilepton final states at $\sqrt{s}=13$ TeV. Phys. Rev. D97:032009. doi: 10.1103/PhysRevD.97.032009

CrossRef Full Text | Google Scholar

Sirunyan, A. M., Tumasyan, A., Adam, W., Asilar, E., Bergauer, T., Brandstetter, J., et al. (2017b). Search for dark matter produced with an energetic jet or a hadronically decaying W or Z boson at $\sqrt{s}=13$ TeV. J. High Energy Phys. 7:014. doi: 10.1007/JHEP07(2017)014

CrossRef Full Text | Google Scholar

Sivertsson, S., and Edsjo, J. (2012). WIMP diffusion in the solar system including solar WIMP-nucleon scattering. Phys. Rev. D85:123514. doi: 10.1103/PhysRevD.85.123514

CrossRef Full Text | Google Scholar

Slatyer, T. R. (2017). “TASI lectures on indirect detection of dark matter,” in Theoretical Advanced Study Institute in Elementary Particle Physics: Anticipating the Next Discoveries in Particle Physics (TASI 2016) (Boulder, CO).

Srednicki, M., Watkins, R., and Olive, K. A. (1988). Calculations of relic densities in the early universe. Nucl. Phys. B310:693.

Google Scholar

Steigman, G., Sarazin, C. L., Quintana, H., and Faulkner, J. (1978). Dynamical interactions and astrophysical effects of stable heavy neutrinos. Astron. J. 83, 1050–1061. doi: 10.1086/112290

CrossRef Full Text | Google Scholar

Strauss, R., Angloher, G., Bento, A., Bucci, C., Canonica, L., Defay, X., et al. (2016). The cresst-III low-mass wimp detector. J. Phys. 718:042048. doi: 10.1088/1742-6596/718/4/042048

CrossRef Full Text | Google Scholar

Strigari, L. E., and Trotta, R. (2009). Reconstructing WIMP properties in direct detection experiments including galactic dark matter distribution uncertainties. J. Cosmol. Astropart. Phys. 0911:019. doi: 10.1088/1475-7516/2009/11/019

CrossRef Full Text | Google Scholar

Agnese, R., Anderson, A. J., Aralis, T, Aramaki, T., Arnquist, I. J., et al. (2018). Low-mass dark matter search with CDMSlite. Phys. Rev. D97:022002. doi: 10.1103/PhysRevD.97.022002

CrossRef Full Text | Google Scholar

Toma, T. (2013). Internal bremsstrahlung signature of real scalar dark matter and consistency with thermal relic density. Phys. Rev. Lett. 111:091301. doi: 10.1103/PhysRevLett.111.091301

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z. W., Steele, T. G., Hanif, T., and Mann, R. B. (2016). Conformal complex singlet extension of the standard model: scenario for Dark Matter and a Second Higgs Boson. J. High Energy Phys. 8:065. doi: 10.1007/JHEP08(2016)065

CrossRef Full Text | Google Scholar

Weisz, D. R., Dalcanton, J. J., Williams, B. F., Gilbert, K. M., Skillman, E. D., Seth, A. C., et al. (2011). The ACS Nearby Galaxy Survey Treasury VIII. The Global Star Formation Histories of 60 Dwarf Galaxies in the Local Volume. Astrophys. J. 739:5. doi: 10.1088/0004-637X/739/1/5

CrossRef Full Text | Google Scholar

Yang, D., and Li, Q. (2018). Probing the Dark Sector through Mono-Z Boson Leptonic Decays. J. High Energy Phys. 2:090. doi: 10.1007/JHEP02(2018)090

CrossRef Full Text | Google Scholar

Yu, J. H. (2014). Vector fermion-portal dark Matter: direct detection and galactic center gamma-ray excess. Phys. Rev. D90:095010. doi: 10.1103/PhysRevD.90.095010

CrossRef Full Text | Google Scholar

Zhang, C., Cui, M. Y., Feng, L., Fan, Y. Z., and Ren, Z. Z. (2017). γ-ray emission signals in the massive graviton mediated dark matter model. Nucl. Phys. B916, 208–218. doi: 10.1016/j.nuclphysb.2017.01.003

CrossRef Full Text | Google Scholar

Zhen, C. (2014). LHAASO: Science and Status. Frascati Phys. Ser. 58:331.

Google Scholar

Zhu, R., and Zhang, Y. (2017). Graviton-mediated dark matter model explanation the DAMPE electron excess and search at e⁺e⁻ colliders. arXiv: 1712.01143.

Google Scholar

Zwicky, F. (1933). Spectral displacement of extra galactic nebulae. Helv. Phys. Acta 6, 110–127.