Black Hole Mass Estimation in Type 1 AGN: Hβ vs. Mg II Lines and the Role of Balmer Continuum

Here we investigate the Hβ and Mg II spectral line parameters used for the black hole mass (M_BH) estimation for a sample of Type 1 Active Galactic Nuclei (AGN) spectra selected from the Sloan Digital Sky Survey (SDSS) database. We have analyzed and compared the virialization of the Hβ and Mg II emission lines, and found that the Hβ line is more confident virial estimator than Mg II. We have investigated the influence of the Balmer continuum emission to the M_BH estimation from the UV parameters, and found that the Balmer continuum emission can contribute to the overestimation of the M_BH on average for ~5% (up to 10%).

1. Introduction

Several methods are used to estimate central black hole (BH) mass M_BH in galaxies (for review see e.g., Marziani and Sulentic, 2012; Shen, 2013; Ilić and Popović, 2014; Peterson, 2014). For Type 1 AGN, the most appropriate methods for the M_BH estimation are those using the strong broad emission lines (BELs), as the most prominent features in their spectra. The virial methods (see Peterson et al., 2004; Vestergaard and Peterson, 2006) are based on the assumption that the Broad Line Region (BLR) gas is bounded to the central BH (see Gaskell, 2009) and the main broadening mechanism of the BELs is the Keplerian motion around the supermassive BH, so the full width at half maximum (FWHM) of BELs indicates the velocity of the emitting gas. We should note that in principle the line dispersion much better represents this motion (Peterson et al., 2004; Collin et al., 2006), however in order to find the line dispersion one should assume some type of line profile (that may be very complex), therefore the FWHM is often used instead of the line dispersion.

One of these methods is based on the R–L relationship (see e.g., Bentz et al., 2006), the outcome of the reverberation mapping (see Blandford and McKee, 1982; Peterson et al., 2004, etc.), which enables the estimation of the photometric radius from only one epoch spectrum (see e.g., Vestergaard and Peterson, 2006). An alternative method for M_BH estimation using the BEL parameters is based on the gravitational redshift in the broad line profiles (see Zheng and Sulentic, 1990; Popović et al., 1995; Bon et al., 2015; Jonić et al., 2016; Liu et al., 2017). The advantage of this method is that it does not depend on the BLR inclination, unlike the virial methods.

There are many unresolved questions relevant for the application of these methods. For example, since the BLR geometry could be complex (see e.g., Sulentic et al., 2000; Popović et al., 2004; Gaskell, 2009, etc.), it is essential to confirm if the virial assumption is correct for all BELs which are used in the methods for the M_BH estimation and if the gravitational redshift could be measured from the BELs complex shapes, or if it may be suppressed by some other effects.

The most frequently used BELs as the virial estimators are the broad Hβ (in the optical) and Mg II (in the UV) lines (see Marziani and Sulentic, 2012). Both, Hβ and Mg II lines have complex profiles, which should be considered if these lines are used for the M_BH estimation. Extracting refined Hβ and Mg II profiles is a difficult task and it is essential for an accurate M_BH estimation. Especially since the broad Hβ overlaps with a numerous optical Fe II lines, the [O III] doublet and the Hβ narrow line component, while the Mg II line overlaps with a numerous UV Fe II lines. Finally, the presence of the Balmer continuum for λ < 3,646Å, is contributing to the uncertainty of the M_BH estimation from the UV parameters and it has to be subtracted for obtaining the pure power law luminosity in the UV band.

In this paper we first present the models of the optical Fe II, UV Fe II emission and Balmer continuum, that could give more precise measurements of the optical and UV parameters [Hβ and Mg II broad line profiles, power law luminosity at λ = 3,000Å, as L_λ(3,000Å)] used for the M_BH estimation. Then, we analyze the virialization assumption for the Hβ and Mg II broad lines, and the influence of the Balmer continuum to the M_BH estimation from the UV parameters.

2. The Sample and Analysis

The used sample consists of the 287 spectra of Type 1 AGN, obtained from the SDSS Data Release 7 (DR7). The sample is the same as in Kovačević-Dojčinović and Popović (2015) where the detailed description of the sample selection criteria is given. For the investigation of the virialization of the emission regions, we exclude all spectra with the blue asymmetry, which resulted with the sample of 123 objects used in this research of the Hβ and Mg II profiles (see Jonić et al., 2016). In the future work we plan to investigate in more details radio properties for this sample, and to search for the connection between the radio-loudness and M_BH.

2.1. Model of the Optical Emission Lines in 4,000–5,500Å: Extracting the Pure Broad Hβ Profile

To obtain a pure broad Hβ component, the narrow Hβ and [O III] lines have to be carefully subtracted, as well as the optical Fe II lines. After correcting the spectra for the Galactic reddening and the cosmological redshift, and subtracting the underlying continuum, we applied the multi-Gaussian fitting procedure in 4,000–5,500Å range, described in details in Kovačević et al. (2010) and Kovačević-Dojčinović and Popović (2015). In the fitting procedure, the number of free parameters was reduced assuming that the lines or the line components which originate from the same emission region, have the same widths and shifts. Therefore all narrow Balmer lines (Hδ, Hγ, and Hβ) have the same widths and shifts as [O III] lines, since we assume that they all originate from the Narrow Line Region (NLR). The broad part of the Balmer lines was modeled with two Gaussian functions representing the emission from the Intermediate Line Region (ILR) and from the Very Broad Line Region (VBLR) (see Popović et al., 2004; Bon et al., 2006, 2009; Hu et al., 2008).

We have made a Fe II template as a sum of the most prominent Fe II lines, described with Gaussian functions, with the same widths and shifts, since we assumed that all optical Fe II lines were originating from the same emission region. The number of free parameters was reduced by calculating the relative intensities for the Fe II lines with the same lower term of transition (see Kovačević et al., 2010). Finally, the Fe II template was described with five parameters of intensity, width, shift, and temperature, which was included in the calculation of the relative intensities. For more details about the optical Fe II template see Kovačević et al. (2010) and Shapovalova et al. (2012), and this Fe II template is also available on line (http://servo.aob.rs/FeII_AGN). The example of the spectral decomposition in 4,000–5,500Å range is shown in the optical part in Figure 1.

FIGURE 1

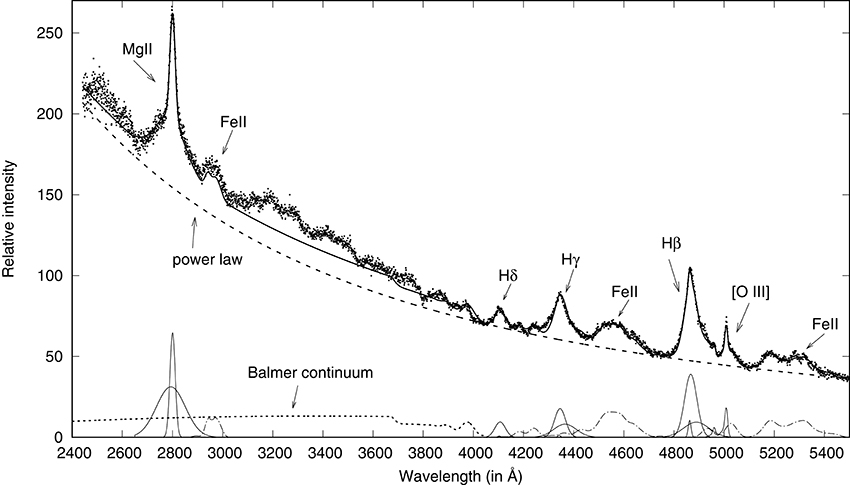
Figure 1. The example of the decomposition of the UV-optical pseudo-continuum (power law + Balmer continuum) and emission lines in ranges 2,650–3,050Å and 4,000–5,500Å for object SDSS J014942.50+001501.7. The observations are denoted with dots, the sum of pseudo-continuum and emission line model with solid line, and the power law continuum with dashed line. Bellow, the Balmer continuum is given with dotted line, and UV/optical Fe II templates with dotted-dashed line and all emission lines with solid line.

2.2. The Balmer Continuum Model

The UV pseudo-continuum consists of the power law, which represents the emission from the accretion disc and the bump at 3,000Å, which represents the sum of the blended, high-order broad Balmer lines, and the Balmer continuum (λ < 3,646Å). In order to measure the flux or luminosity of the power law at UV spectral range (e.g., 3,000Å), one needs to subtract the Balmer continuum emission first (see Figure 1). The model of the Balmer continuum first given in Kovačević et al. (2014), is based on the function for the Balmer continuum given in Grandi (1982) for the case of a partially optically thick cloud, with one degree of freedom decreased, as the intensity of the Balmer continuum was calculated, obtaining in that way lower uncertainty. The intensity of the Balmer continuum was estimated at the Balmer edge (λ = 3,646Å), as a sum of the intensities of all high-order Balmer lines at the same wavelength. All broad Balmer lines were represented with one Gaussian function only, with the same width and shift of a prominent Balmer line, and their relative intensities were taken from the literature or were calculated (see Kovačević et al., 2014). Therefore, if only one prominent Balmer line was fitted (e.g., Hβ), and the shift, width, and intensity were obtained from that fit, than the fluxes of all other Balmer lines would be known, and the Balmer continuum at the Balmer edge could be calculated. Finally, with this model, the UV pseudo-continuum was fitted with four free parameters: the width, shift, and intensity of the one prominent Balmer line, and the exponent of the power law. An example of the Balmer continuum fit is shown below in Figure 1.

2.3. Model of the UV Emission Lines in 2,650–3,050Å: Extracting the Pure Mg II Profile

We performed the spectral decomposition in 2,650–3,050Å range in order to estimate the pure Mg II profile, which overlaps with the UV Fe II lines (Figure 1). The Mg II line was fitted with two Gaussian functions, the one that represents the line core and the other that fits the line wings (see Kovačević-Dojčinović and Popović, 2015), and a sum of those two components represents the broad Mg II line. The narrow Mg II line was not detected in analyzed spectra. The numerous Fe II lines in the range 2,650–3,050Å were all fitted with the Fe II template presented in Popović et al. (2003) and Kovačević-Dojčinović and Popović (2015). The Fe II lines in the 2,650–3,050Å range were divided into four multiplets, and relative intensities of the lines within each multiplet were taken from literature. Finally, the Fe II template was described with six parameters: four parameters for the intensity, line width, and shift. The example of the spectral decomposition in the 2,650–3,050Å range with UV pseudo-continuum fit is shown in the UV part in Figure 1.

2.4. Measuring the Spectral Parameters

From the pure broad profiles of the Hβ and Mg II lines, we measured the FWHM of these lines, as well as Full Width at 10% of the Maximum (FW10%M). The asymmetries of these lines (intrinsic shifts) were measured at different levels of the line maximal intensity (at 50%, z₅₀ and at 10%, z₁₀), as the centroid shift with respect to the broad line peak (see Jonić et al., 2016, their Figure 2). The luminosity of the continuum was calculated using the formula given in Peebles (1993) with adopted cosmological parameters of Ω_M = 0.3, Ω_Λ = 0.7, Ω_k = 0, and Hubble constant H_o = 70 km s⁻¹ Mpc⁻¹. The virial M_BH for the UV parameters [FWHM Mg II, L_λ(3, 000)] was calculated using the formula given in Wang et al. (2009) [their Equation (9), for γ = 2].

3. Results

3.1. Testing the Virialization of the Broad Hβ and Mg II Lines

If the emission gas in the BLR is virialized, one can expect to observe correlations between the widths and the gravitational redshifts of the BELs, which comes from the equations for the M_BH estimation by the virial method using the line width (see Zheng and Sulentic, 1990; Peterson et al., 2004). The expected relation is: z_G ~ FWHM², i.e., log(z_G) ~ log(FWHM) (see Jonić et al., 2016). This correlation is expected since at the same distance from a BH the line is broadened by the gravitational rotational effect which depends from the distance as ~ $\sqrt{\frac{M}{r}}$, and by the gravitational shift (red-shifting of photons) that also depends from the distance as ~ $\frac{M}{r}$ (see Popović et al., 1995).

We investigated correlation between the intrinsic shifts, as indicators of the gravitational redshifts, and the widths of the Hβ or the Mg II lines, at different levels (50 and 10%) of their maximal intensity, for the sample of 123 Type 1 AGNs with the red asymmetry in BELs. We have found that the width of the Hβ line is well correlated with the line's intrinsic shift measured at the 50% and at the 10% of the maximal intensity. However, in the case of the Mg II line, the correlation between the Mg II width and intrinsic shift is detected only at the 50% of the line maximal intensity, whereas at the 10% of the line maximal intensity an anti-correlation is seen (for more detail see Jonić et al., 2016).

Note here that the literature in the field presents comparisons on the use of the optical and the UV lines, like Hβ and Mg II, as virial estimators of the M_BH in AGN, pointing out that in some cases Mg II is more reliable as M_BH estimator then Hβ (e.g., Marziani et al., 2013, and references therein). However, it has been shown that the Mg II wings are emitted from the weakly gravitationally bounded gas (see Kovačević-Dojčinović and Popović, 2015; Jonić et al., 2016), i.e., the assumption of virialization may be problem in using Mg II line as the BH mass estimator.

3.2. Influence of the Blamer Continuum to the M_BH Estimation Using the UV Spectral Parameters

We calculated the luminosity at 3,000Å before [L_λ(3,000Å)_tot] and after the Balmer continuum [L_λ(3,000Å)_pow] contribution was subtracted. In the sample of 287 Type 1 AGN spectra, the Balmer continuum contributes to the continuum L_λ(3,000Å) on average for ~10%, with the maximal value of 18%. The ratios of the L_λ(3,000Å), with and without the Balmer continuum contribution, are shown on the histogram (Figure 2A). The majority of the equations for the M_BH estimation using the UV parameters neglect the contribution of the Balmer continuum (see e.g., McLure and Jarvis, 2002; Vestergaard and Osmer, 2009). Wang et al. (2009) give the relation for the assessment of M_BH using the FWHM Mg II and L_λ(3,000Å), assuming that after subtraction of the Balmer continuum, the L_λ(3,000Å) is the pure power law continuum, therefore we then compared M_BH calculated with and without consideration of the Balmer continuum contribution. We got that the Balmer continuum increased M_BH on average for ~5% (0.02 dex), with the maximal value of the M_BH overestimation up to 10% (0.04 dex). The ratio of the M_BH estimates before and after the Balmer continuum subtraction is shown in Figure 2B. The comparison of M_BH values before (index “tot”) and after the Balmer continuum subtractions (index “pow”) are also given in Figure 3, where the correlation coefficients ρ (ρ_tot = 0.783 and ρ_pow = 0.786), P-values (P_tot = 0 and P_pow = 0) and linear best-fit (y = a*x+b) coefficients are given: slope a, (a_tot = 0.85 and a_pow = 0.84) and y-intercept b, (b_tot = 1.36 and b_pow = 1.43). It can be seen that the influence of the Balmer continuum to the M_BH estimation is so small that it barely changes the correlation coefficient (ρ) or the coefficients of the linear best-fit (a, b) between the M_BH estimated with the optical and the one estimated with the UV parameters. Also, it seams that removing the Balmer continuum does not affect the outliers in this relationship.

FIGURE 2

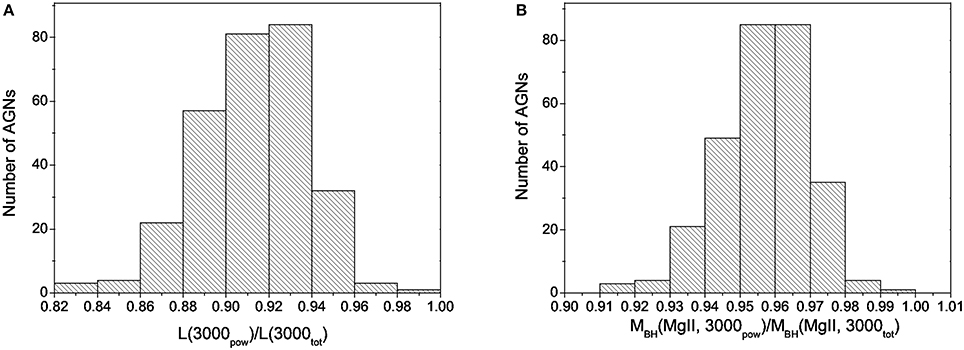
Figure 2. (A) The ratio of the continuum L_λ(3,000Å) before [L(3,000_tot)] and after [L(3,000_pow)] the Balmer continuum subtraction. (B) The ratio of the M_BH estimate before [M_BH (L_tot)] and after [M_BH (L_pow)] the Balmer continuum subtraction.

FIGURE 3

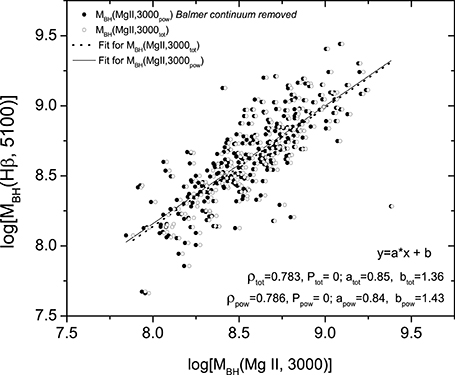
Figure 3. The relation of the M_BH[Hβ, L_λ(5,100Å)] vs. M_BH[MgII, L_λ(3,000Å)] before (index “tot,” open circles) and after the Balmer continuum subtraction (index “pow,” full circles). The corresponding correlation coefficients, P-values, and coefficients of the liner best-fit are also given.

4. Conclusions

Here we have used the sample of the SDSS Type 1 AGN spectra to compare the most frequently used emission lines for the M_BH estimation, Hβ (in the optical band) and Mg II (in the UV band), in order to assess which line is better virial estimator and thus more convenient for that purpose. We investigated how the Balmer continuum affect the BH mass estimation using the UV parameters.

From our investigation we can outline the following conclusions:

I) The Hβ line is a more reliable virial estimator than the Mg II line, since the expected linear relationship between logarithms of the widths (influenced by the Keplerian motion) and red asymmetries (caused by the gravitational redshift) was evidenced for both lines when measured at the 50% of the line maximal intensities, but when measured in the line wings (at the 10% of the line maximal intensities) the expected relationship was present only for Hβ (see Jonić et al., 2016).

II) The disregard of the Balmer continuum emission, in the case of the M_BH estimation using the UV parameters [Mg II, L_λ(3,000Å)], causes the overestimation of the M_BH on average for ~5% (0.02 dex) and up to 10% (0.04 dex).

At the end, let us note that similar investigation should be performed on the sample where more reliable methods for mass measurements (as e.g., reverberation) should be applied to explore the influence of the Balmer continuum and this we postpone for our future work. Moreover, some additional effects (as e.g., relativistic jets) can significantly affect line profiles, i.e., the radio loudness which can indicate the presence of relativistic jets, therefore in the future work radio properties of the sample should also be explored.

Author Contributions

JK, SM, and LP: Developing concept of the work; the acquisition, analysis and interpretation of data for the work; drafting the work and revising it critically for important intellectual content; final approval of the version to be published; being accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The work is a part of the project 176001 financed by the Ministry of Education, Science, Technology and Development, Republic of Serbia.

References

Bentz, M. C., Peterson, B. M., Pogge, R. W., Vestergaard, M., and Onken, C. A. (2006). The radius-luminosity relationship for active galactic nuclei: the effect of host-galaxy starlight on luminosity measurements. Astrophys. J. 644, 133–142. doi: 10.1086/503537

CrossRef Full Text | Google Scholar

Blandford, R. D., and McKee, C. F. (1982). Reverberation mapping of the emission line regions of seyfert galaxies and quasars. Astrophys. J. 255, 419–439.

Google Scholar

Bon, E., Popović, L. Č., Gavrilović, N., La Mura, G., and Mediavilla, E. (2009). Contribution of a disc component to single-peaked broad lines of active galactic nuclei. Mon. Not. R. Astron. Soc. 400, 924–936. doi: 10.1111/j.1365-2966.2009.15511.x

CrossRef Full Text | Google Scholar

Bon, E., Popović, L. Č., Ilić, D., and Mediavilla, E. (2006). Stratification in the broad line region of AGN: the two-component model. New Astron. Rev. 50, 716–719. doi: 10.1016/j.newar.2006.06.015

CrossRef Full Text | Google Scholar

Bon, N., Bon, E., Marziani, P., and Jovanović, P. (2015). Gravitational redshift of emission lines in the AGN spectra. Astrophys. Space Sci. 360:7. doi: 10.1007/s10509-015-2555-5

CrossRef Full Text | Google Scholar

Collin, S., Kawaguchi, T., Peterson, B. M., and Vestergaard, M. (2006). Systematic effects in measurement of black hole masses by emission-line reverberation of active galactic nuclei: eddington ratio and inclination. Astron. Astrophys. 456, 75–90. doi: 10.1051/0004-6361:20064878

CrossRef Full Text | Google Scholar

Gaskell, C. M. (2009). What broad emission lines tell us about how active galactic nuclei work. New Astron. Rev. 53, 140–148. doi: 10.1016/j.newar.2009.09.006

CrossRef Full Text | Google Scholar

Grandi, S. A. (1982). The 3000 bump in quasars. Astrophys. J. 255, 25–38.

Google Scholar

Hu, C., Wang, J. M., Ho, L. C., Chen, Y.-M., Bian, W.-H., and Xue, S.-J. (2008). Hβ profiles in quasars: evidence for an intermediate-line region. Astrophys. J. 683:L115. doi: 10.1086/591848

CrossRef Full Text | Google Scholar

Ilić, D., and Popović, L. Č. (2014). Supermassive black holes and spectral emission lines. J. Phys. Conf. Ser. 548:012002. doi: 10.1088/1742-6596/548/1/012002

CrossRef Full Text | Google Scholar

Jonić, S., Kovačević-Dojčinović, J., Ilić, D., and Popović, L. Č. (2016). irilization of the broad line region in active galactic nuclei: connection between sshifts and widths of broad emission lines. Astrophys. Space Sci. 361:101. doi: 10.1007/s10509-016-2680-9

CrossRef Full Text | Google Scholar

Kovačević, J., Popović, L. Č., and Dimitrijević, M. S. (2010). Analysis of optical Fe II emission in a sample of active galactic nucleus spectra. Astrophys. J. Suppl. 189, 15–36. doi: 10.1088/0067-0049/189/1/15

CrossRef Full Text | Google Scholar

Kovačević, J., Popović, L. Č., and Kollatschny, W. (2014). A model for the balmer pseudocontinuum in spectra of type 1 AGNs. Adv. Space Res. 54, 1347–1354. doi: 10.1016/j.asr.2013.11.035

CrossRef Full Text | Google Scholar

Kovačević-Dojčinović, J., and Popović, L. Č. (2015). The connections between the UV and optical Fe ii emission lines in type 1 AGNs. Astrophys. J. Suppl. 221:35. doi: 10.1088/0067-0049/221/2/35

CrossRef Full Text | Google Scholar

Liu, H. T., Feng, H. C., and Bai, J. M. (2017). A new method to measure the virial factors in the reverberation mapping of active galactic nuclei. Mon. Not. R. Astron. Soc. 466, 3323–3330. doi: 10.1093/mnras/stw3261

CrossRef Full Text | Google Scholar

Marziani, P., Sulenti, J. W., Plauchu-Frayn, I., and del Olmo, A. (2013). Is MgIIλ2800 a reliable virial broadening estimator for quasars? Astron. Astrophys. 555:16. doi: 10.1051/0004-6361/201321374

CrossRef Full Text | Google Scholar

Marziani, P., and Sulentic, J. W. (2012). Estimating black hole masses in quasars using broad optical and UV emission lines. New Astron. Rev. 56, 49–63. doi: 10.1016/j.newar.2011.09.001

CrossRef Full Text | Google Scholar

McLure, R. J., and Jarvis, M. J. (2002). Measuring the black hole masses of high-redshift quasars. Mon. Not. R. Astron. Soc. 337, 109–116. doi: 10.1046/j.1365-8711.2002.05871.x

CrossRef Full Text | Google Scholar

Peebles, P. J. E. (1993). Principles of Physical Cosmology. Princeton, NJ: Princeton University Press.

Google Scholar

Peterson, B. M. (2014). Measuring the masses of supermassive black holes. Space Sci. Rev. 183, 253–275. doi: 10.1007/s11214-013-9987-4

CrossRef Full Text | Google Scholar

Peterson, B. M., Ferrarese, L., Gilbert, K. M., Kaspi, S., Malkan, M. A., Maoz, D., et al. (2004). Central masses and broad-line region sizes of active galactic nuclei. II. A homogeneous analysis of a large reverberation-mapping database. Astrophys. J. 613, 682–699. doi: 10.1086/423269

CrossRef Full Text | Google Scholar

Popović, L. Č., Mediavilla, E., Bon, E., and Ilić, D. (2004). Contribution of the disk emission to the broad emission lines in AGNs: two-component model. Astron. Astrophys. 423, 909–918. doi: 10.1051/0004-6361:20034431

CrossRef Full Text | Google Scholar

Popović, L. Č., Mediavilla, E. G., Bon, E., Stanić, N., and Kubičela, A. (2003). The line emission region in III Zw 2: kinematics and variability. Astrophys. J. 599, 185–192. doi: 10.1086/379277

CrossRef Full Text | Google Scholar

Popović, L. Č., Vince, I., Atanacković-Vukmanović, O., and Kubičela, A. (1995). Contribution of gravitational redshift to spectral line profiles of seyfert galaxies and quasars. Astron. Astrophys. 293, 309–314.

Google Scholar

Shapovalova, A. I., Popović, L. Č., Burenkov, A. N., Chavushyan, V. H., Ilić, D., Kovačević, A., et al. (2012). Spectral optical monitoring of the narrow-line seyfert 1 Galaxy Ark 564. Astrophys. J. Suppl. 202:10. doi: 10.1088/0067-0049/202/1/10

CrossRef Full Text | Google Scholar

Shen, Y. (2013). The mass of quasars. Bull. Astron. Soc. India 41, 61–115.

Google Scholar

Sulentic, J. W., Marziani, P., and Dultzin-Hacyan, D. (2000). Phenomenology of broad emission lines in active galactic nuclei. Annu. Rev. Astron. Astrophys. 38, 521–571. doi: 10.1146/annurev.astro.38.1.521

CrossRef Full Text | Google Scholar

Vestergaard, M., and Osmer, P. S. (2009). Mass functions of the active black holes in distant quasars from the large bright quasar survey, the bright quasar survey, and the color-selected Sample of the SDSS fall equatorial stripe. Astrophys. J. 699, 800–816. doi: 10.1088/0004-637X/699/1/800

CrossRef Full Text | Google Scholar

Vestergaard, M., and Peterson, B. M. (2006). Determining central black hole masses in distant active galaxies and quasars. II. Improved optical and UV scaling relationships. Astrophys. J. 641, 689–709. doi: 10.1086/500572

CrossRef Full Text | Google Scholar

Wang, J.-G., Dong, X.-B., Wang, T.-G., Ho, L. C., Yuan, W., Wang, H., et al. (2009). Estimating black hole masses in active galactic nuclei using the Mg II λ2800 emission line. Astrophys. J. 707, 1334–1346. doi: 10.1088/0004-637X/707/2/1334

CrossRef Full Text | Google Scholar

Zheng, W., and Sulentic, J. W. (1990). Internal redshift difference and central mass in QSOs. Astrophys. J. 350, 512–517.

Google Scholar