- 1Department of Oral and Maxillofacial Surgery / Oral Pathology, Dutch Experiment Support Center, VU University Medical Center and Academic Centre for Dentistry Amsterdam, Amsterdam, Netherlands
- 2TEC-MMG LIS Lab, European Space Agency Technology Center, Noordwijk, Netherlands
Due to the cumbersome nature of performing real microgravity—spaceflight research scientists have been searching for alternatives to perform simulated microgravity or partial gravity experiments on Earth. For more than a century one uses the slow rotating clinostat as developed by von Sachs at the end of the nineteenth century. Since then, the fast rotating clinostat, the 3D clinostat or the random positioning machine, the rotating wall vessels, tail suspension and bed rest head down tilt and lately the levitating magnets have been introduced. Several of these simulation systems provide some similarities of the responses and phenotypes as seen in real microgravity experiments. However, one should always realize that we cannot reduce gravity on Earth, other than the relative short duration free fall studies in e.g., drop towers or parabolic aircraft. In this paper we want to explore the possibility to apply centrifuges to simulate microgravity or maybe better to simulate hypo-gravity. This Reduced Gravity Paradigm, RGP is based on the premise that adaptations seen going from a hypergravity level to a lower gravity are similar as changes seen going from unit gravity to microgravity.
Introduction
When we want to explore the impact of a certain parameter it is quite useful when we are able to vary such a parameter either in time and / or magnitude. This is what we do with exploring gravity. We can bring its magnitude to a minimum by going into free fall or increase its magnitude using centrifuges. The latter is relatively simple, however, to go into extended duration free fall one needs to make use of orbital spacecraft like the International or Chinese Space Stations or un-manned platforms. Such in-flight experiments and studies are still rare, expensive and logistically unreliable. Scientists have been exploring alternatives for long duration free fall, microgravity or better near weightlessness studies. One of the earlier known publication on the subject of microgravity simulation was from Julius von Sachs (1879) who slowly rotated flax (Linum usitatissimum) and cress (Lepidium sativum) around their horizontal axes. Von Sachs coined the term “klinostat” for such a device. Later other models such as regular (Newcombe, 1904; Dedolph et al., 1967) and fast rotating clinostats (Briegleb, 1967), 3D clinostats (Hoson et al., 1997), the Random Positioning Machine (van Loon, 2007; Borst and van Loon, 2009) or the Rotating Wall Vessel (Schwarz et al., 1992) were developed in order to improve on the initial design. Another microgravity simulation is by making use of the magnetic properties of atoms via magnetic levitation (Beaugnon and Tournier, 1991; Berry and Geim, 1997). For rodent studies the tail suspension model is often used while the space analog for humans would be the 6 degree head down tilt bed rest (See also Beysens and van Loon, 2015a).
Although the devices were and still are widely used one should also understand the limitations and artifacts associated with their applications (e.g., Brown et al., 1976; Laurinavicius et al., 1998; Leguy et al., 2011; Moes et al., 2011).
Gravity is generated by mass as defined by Sir Newton's 2nd law. However, gravity can also be generated by an accelerating object such as a rocket. It was Einstein who showed, for the first time, that there is no physical demonstrable difference between acceleration generated by mass or generated by linear accelerations, the equivalence principle. The fact that for a sample in a centrifuge we speak of acceleration while we deal with a centrifuge running at a constant speed has to do with the fact that the sample is constantly changing direction, forced to do so being attached or fixed somehow to a center of rotation. If the sample would detach from the centrifuge it will, because of its inertia, fly off in a straight line. It would not be accelerated anymore and “loses” its weight. The latter applies when such a centrifuge would be running in space in a place where there is hardly any gravity field from a nearby moon, planet or any other celestial body. One should note, however, that absolute zero gravity does not exist (Beysens and van Loon, 2015b). So it is because of the samples' inertia and the rotation of the centrifuge that one generates gravity. The magnitude of this gravity depends on the radius of the centrifuge and the angular velocity or speed of rotation. The sample experiences a centripetal acceleration ac = ω2r, where ω is angular velocity (rad s−1) and r the centrifuge arm radius (in m).
In life sciences plant research, it was Sir Knight who exposed garden beans (Phaseolus vulgaris) to centrifugal forces and showed the direction of growth of both shoots and roots was the resultant of both Earth 1 g and the artificial gravitation as generated by his water wheel centrifuge (Knight, 1806).
Centrifuges are applied in various disciplines mainly in material and particle technology like for separation (Sahuquillo et al., 1999; Kuang et al., 2015), for nanomaterials classification (Wohlleben, 2012), casting (Huisman et al., 1994; Liu and Barnett, 2002; Dikel et al., 2005; Velhinho and Rocha, 2011), combustion (Merzhanov, 1995), but also in areas like geology (Gopal Madabhushi, 2004; Costa et al., 2016), life sciences in plants (Musgrave et al., 2009; Herranz et al., 2013; Hoson and Wakabayashi, 2015), single cells (Loesberg et al., 2006; Tavakolinejad et al., 2015), animals (van Loon, 2001; van Loon et al., 2005; Tateishi et al., 2015) and humans (Akima et al., 2005; van Loon et al., 2012; Goswami et al., 2015).
Examples of the RGP Hypothesis
But how can we use centrifuges for microgravity simulation? This hypothesis is based on the principle of the “Reduced Gravity Paradigm,” RGP (Figure 1). With this paradigm we are not focusing on the absolute acceleration values but on the responses generated because of the delta between two accelerations levels.
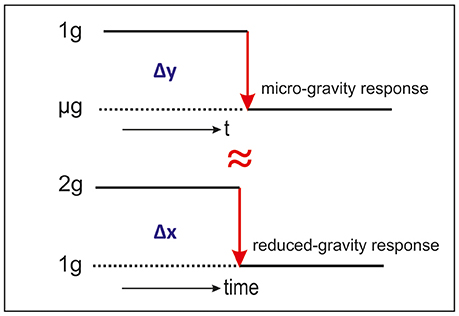
Figure 1. Graphic representation of the Reduced Gravity Paradigm, RGP. Delta between μg and 1 g is (nearly) the same as between 2 and 1 g.
In space and gravity related research the focus has been to study near weightlessness (microgravity). Samples are brought into near weightlessness or free fall either in drop towers, parabolic and suborbital flights, sounding rockets or with Earth orbiting missions (see Figure 1 Δy). The delta acceleration in such cases is unit gravity, 1 g, 9.81 ms−2 (excluding the launch acceleration). But what would the response of these same samples be if we go from a steady 2 g to a 1 g level (see Figure 1 Δx)? Could we expect the same or a similar response?
It is not improbable to presume that such a reduction in gravitational load from 2 to 1 g would display comparable responses as going into free fall coming from a 1 g state. However, since free fall is such an exceptional environment, where phenomena as convection, buoyancy, sedimentation or hydrostatic pressure are no longer present, we could expect a different response in long duration experiments.
The RGP is best applied for a stable and steady system at a certain higher g level combined with measuring a, relatively, fast responding phenomenon when reducing the acceleration load. In the next part we will attend to some experimental configurations addressing the boundary conditions for a RGP set-up across various disciplines ranging from plant cell biology to human physiology. These past studies will provide insight how to best configure a RGP experiment.
Figure 2A is an example of hyper-g adaptation of mice from a study by Oshima et al. (2007). Mice were subjected to 2 g in a 7.25 m radius centrifuge. Apparently 4 h exposure to 2 g is not yet sufficient to reach a steady state for COX-1, COX-2, and VEGF expression in these animals. The mice need to adapt 24 h in order to stabilize these protein levels. Figure 2B shows that steady states might be different for different organs within an animal as is shown by the level of the stress protein HSP70 in rats exposed to 2.5 × g for either 24 h (acute) or 7 months (chronic) acceleration (van Loon et al., 2005).
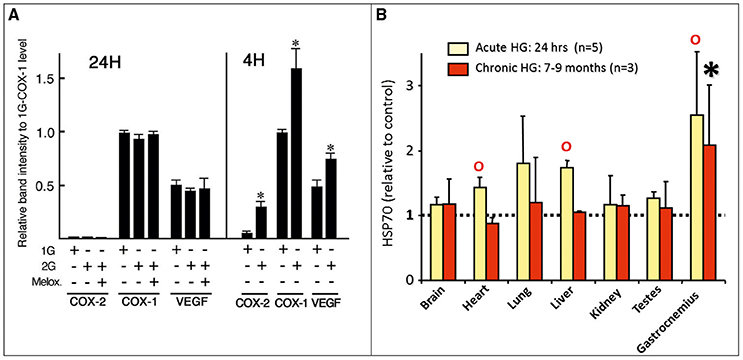
Figure 2. Examples of reaching steady states. (A) Mice exposed to 2 g for 4 or 24 h. Stable levels of COX-1, COX-2, and VEGF in heart tissue seems to be reached at 24 h (from Oshima et al., 2007, with permission). (B) Rats exposed for either 24 h or 7 months to 2.5 g (van Loon et al., 2005). In both figures data are means ± S.D., *and oidentifies significance of <0.05 with respect to 1 g controls.
Figure 3A is an example of how a RGP experiment set-up could look like. In this study by Kozeko and Kordyum (2009) pea seedling (Pisum sativum) are exposed to various levels of hypergravity (HG) for 1 h each. After the HG exposure the samples are brought back to 1 g for either one or 24 h and the content of Hsp70 was measured. However, it appears that a 1 h exposure to hyper-g is not sufficient to reach a steady state regarding Hsp70 in these seedlings as can be seen especially in the 10 and 14 g groups (Figure 3A).
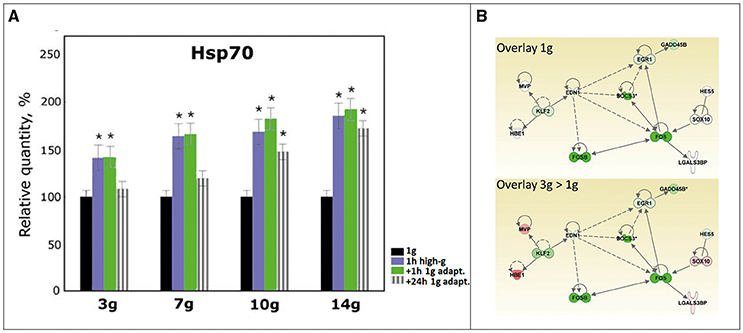
Figure 3. (A) Example Hsp70 content of pea seedlings exposed to 1 h hyper-gravity levels ranging from 3 to 14 g. After HG exposure the seedlings were left for either 1 or 24 h to re-adapt to 1 g. Data are means ±SD. * indicate values that are statistically different from control (p ≤ 0.05). (Reproduced from Kozeko and Kordyum, 2009, with permission). (B) Example of a Reduced Gravity Paradigm experiment execution. A specific gene network was identified that specifically responds to a 1 day reduced gravity, i.e., going from 5 days at 3 g to 1 day at 1 g (from Aceto et al., 2015).
Figure 3B shows part of the results of a study where zebra fish (Danio rerio) were exposed for 6 days at control conditions at 1 g (Figure 3B, top panel) or one group exposed to 3 g for 5 days and then exposed to a relative reduced gravity of 1 g for 1 day (Figure 3B, lower panel). From this study a network composed of 7 genes (FOS, FOSB, EGR1, EDN1, SOCS3, GADD45B, KLF2) was identified which is affected by the altered gravity conditions, indicating that they represent a central network that is affected by gravitational conditions and are rapidly (within 24 h) adapted to the reduced gravity conditions. Five additional genes (MVP, HBE1, HES5, SOX10, LGALS3BP) were only affected after 1 day at lower gravity (3 > 1 g), indicating that they may be actually involved in the mechanism for rapid adaptation to lower gravity and might be expected to change when exposed to real free fall conditions.
There are also very clear indications of the RGP emerging from studies on the vestibular system. European scientist astronauts of the D1 Spacelab mission identified that an exposure for 60–90 min at 3 gx and then reduce it to 1 g elicited the same effects as a transition from 1 g to real free fall μg (Nooij et al., 2007). It is remarkable to note that the post-centrifuge phenomenon remains for several hours after high g exposure, especially since the vestibular system is one of the fastest responding sensor systems with respect to gravity. A similar phenomenon was described for fish. The vestibular related looping behavior often seen in fish when entering free fall was also reported for animals that were shifted from a high to a lower g-level (Von Baumgarten et al., 1972; Rahmann et al., 1996).
The application of the RGP has its restrictions and limitations. An important prerequisite for a successful RGP experiment is that the system needs to be in a stable / steady state condition at the high g level before lowering the acceleration. Also, the best results are to be expected from fast responding systems. Such systems will react due to the reduced gravity load while not yet responding, too much, to the actual g level the sample is exposed to and, in due time, completely adapted to.
Figure 4 displays some scenarios in gravity related research. A regular scenario in, for example, a sounding rocket experiment would be going from A1 to A2 for fast responding system. When using on on-board 1 g centrifuge it would follow the red lines A1–A3. At T0 the experiment is launched. At T1 and T2 the rocket motor is stopped and the samples are in 1 g for the on-board 1 g centrifuge (T1) or in free fall (T2), respectively.
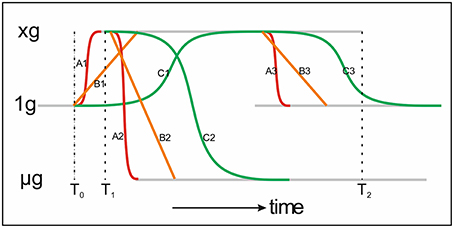
Figure 4. This is a cartoon illustrating gravity levels (gray lines) and (biological) systems response times. Fast responding systems (red line, A1–A3), linearly somewhat intermediate responding systems (orange line, B1–B3) and slow responding systems (green line, C1–C3). When a sample is launched is goes from 1 g to × g, delta y, for a fast responding systems going through A1. When going into free fall after launch the fast system would follow A2, delta y + delta x. In this representation the times for both fast and slow responding systems regarding a Reduced Gravity Paradigm are set properly.
Figure 5A displays the possible responses in a RGP protocol. At T0 we intend to bring the system in a steady state condition in order to later perform the microgravity simulation. We would have a successful measurement when we would stop the centrifuge at T1 and measure the fast responding system (red line, A1–A3) measured at T2. However, when the system has not reached a steady state yet (orange B1 and green C1 lines) a measurement at T2 does not reflect a full reduced gravity response. (In order not to make the graph too complex, I left out the impact of 1 g. In such a case we need to adapt the system longer at the higher g level). A comparable limitation might arise in parabolic flight experiments (Figure 5B). The rapid cycling between 1 g, 1.8 g, and μg might for especially slow responding systems (orange and green lines) “contaminate” the actual microgravity measurements. A parabola length from T1 to T2 is sufficient for fast changes (red line, A3) but for an intermediated responding system one would need a parabola length of T1–T3. Even more time is required for slow responding systems (green line) although part of the slow responding system might have contributed to the fast and intermediate signals.
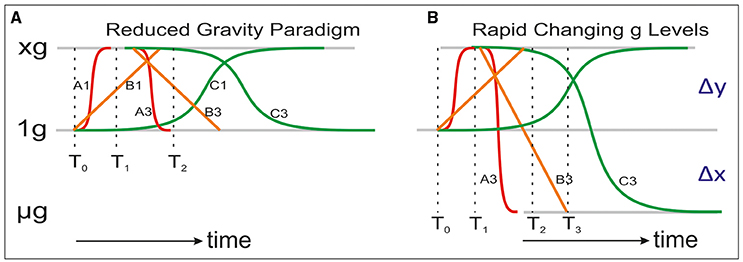
Figure 5. This is a cartoon illustrating in more detail the (A) Reduced Gravity Paradigm (RGP) or (B) a real free fall experiment with rapidly changing g levels (e.g., a parabolic flight experiment). Fast responding systems (red line, A1–A3), linearly somewhat intermediate responding systems (orange line, B1–B3) and slow responding systems (green line, C1–C3).
The Gravity Continuum
Finally it is interesting and necessary to note the phenomenon of the “Gravity Continuum” where we also make use of centrifuges in order to predict the value or behavior of a system at a partial- or micro-gravity condition (Figure 6). The basis for this paradigm is the extrapolation of the data of a series of hypergravity experiments as represented as red dots in Figure 6. The theory is that a system would continue to behave similarly as it does coming from higher g levels going toward 1 g. The results could have a linear (orange line Figure 6) or some exponential relationship (green and black lines). Examples of the gravity continuum can be found in humans (Bergstedt, 1961), animal research (Ronca, 2003; Wade, 2005) but also in combustion sciences (Lewis, 1973; Merzhanov, 1995) or geological studies (de Vet, 2010). Comparable results from applying both the gravity continuum and RGP in the same study strengthen the final results.
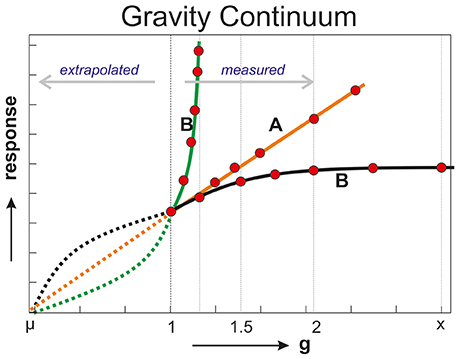
Figure 6. Cartoon of the Gravity Continuum. The red dots represent measurements at various hyper-g values. Connecting lines based on the measurements (solid) can be extrapolated (dotted lines) to lower g conditions.
Conclusion
Application of the Reduced Gravity Paradigm, RGP, within a study provides, in the first place, a basic knowledge and understanding of how a system responds to altered gravity conditions. In hypergravity studies often the more classical end point measurements at a certain g-level are applied. However, preferably on-line measurements of dynamic changes going from a lower to a hyper-gravity level provides a wealth of knowledge on gravity adaptations. On the other hand, with the RGP one focuses more on the changes going into lower g levels. The RGP should be further explored on cell, tissue and system level both in plants, animal and humans.
Although the concept of RGP has to some extend been used in previous studies a systematic approach would provide insight on whether the RGP is a valid concept or if other responses are more pertinent. Such an approach requires the execution of protocols in real free fall conditions to verify their validity. When the RGP hypothesis is proven to be valid it will provide a cheap and reliable way to generate simulated microgravity and thus provide insight in the effect of real microgravity onto a system. It provides an additional simulated microgravity paradigm complementing systems like clinostats, RPMs, tail suspension, tilt tables etcetera.
As with other ground-based simulation paradigms the real response to reduced gravity always need to be verified in actual spaceflight free fall conditions.
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I would like to thank the support of the European Space Agency via the ESA contract 4000107455/12/NL/PA for the TEC-MMG LIS Lab. Also thanks for Mrs. Astrid Fredriksz for critically reading the manuscript.
References
Aceto, J., Nourizadeh-Lillabadi, R., Marée, R., Dardenne, N., Jeanray, N., Wehenkel, L., et al. (2015). Zebrafish bone and general physiology are differently affected by hormones or changes in gravity. PLoS One 10:e0126928. doi: 10.1371/journal.pone.0126928
Akima, H., Katayama, K., Sato, K., Ishida, K., Masuda, K., Takada, H., et al. (2005). Intensive cycle training with artificial gravity maintains muscle size during bed rest. Aviat. Space Environ. Med. 76, 923–929.
Beaugnon, E., and Tournier, R. (1991). Levitation of organic materials. Nature 349, 470. doi: 10.1038/349470a0
Bergstedt, M. (1961). The effect of gravitational force on the vestibular caloric test. Acta Otolaryngol. 53, 551–562. doi: 10.3109/00016486109126523
Berry, M. V., and Geim, A. K. (1997). Of flying frogs and levitrons. Eur. J. Phys. 18, 307–313. doi: 10.1088/0143-0807/18/4/012
Beysens, D. A., and van Loon, J. J. W. A. (2015a). Generation and Applications of Extra-Terrestrial Environments on Earth. Aalborg: Rivers Publishers.
Beysens, D. A., and van Loon, J. J. W. A. (2015b). “The space gravity environment,” in Generation and Applications of Extra-Terrestrial Environments on Earth, eds D. A. Beysens and J. J. W. A. van Loon (Aalborg: Rivers Publishers), 5–9.
Borst, G., and van Loon, J. J. W. A. (2009). Technology and developments for the Random Positioning Machine, RPM. Microgravity Sci. Technol. 21, 287–292. doi: 10.1007/s12217-008-9043-2
Briegleb, W. (1967). In: modell fuer schwerlosichkeits-simulation an mikroorganismen. Naturwissenschaften 54, 67. doi: 10.1007/BF00590841
Brown, A., Dahl, A. O., and Chapman, D. K. (1976). Limitation on the use of the horizontal clinostat as a gravity compensator. Plant Physiol. 58, 127–130. doi: 10.1104/pp.58.2.127
Costa, C. M. L., Zornberg, J. G., Bueno, B. D., and Costa, Y. D. J. (2016). Centrifuge evaluation of the time-dependent behavior of geotextile-reinforced soil walls. Geotext. Geomembr. 44, 188–200. doi: 10.1016/j.geotexmem.2015.09.001
Dedolph, R. R., Oemick, D. A., Wilson, B. R., and Smith, G. R. (1967). Causal basis of gravity stimulus nullification by clinostat rotation. Plant Physiol. 42, 1373–1383. doi: 10.1104/pp.42.10.1373
de Vet, S. (2010). Down Wind & Down Slope. Chap. 3. Gravitational influences. Master thesis. University of Amsterdam.
Dikel, M., Uster, A., and Kuskonmaz, N. (2005). Centrifuged casting of ductile iron using composite mold. Materialwissenschaft und Werkstofftechnik 36, 32–35. doi: 10.1002/mawe.200400844
Gopal Madabhushi, S. P. (2004). Modelling of earthquake damage using geotechnical centrifuges. Curr. Sci. 87, 1405–1416.
Goswami, N., Bruner, M., Xu, D., Bareille, M. P., Beck, A., Hinghofer-Szalkay, H., et al. (2015). Short-arm human centrifugation with 0.4g at eye and 0.75g at heart level provides similar cerebrovascular and cardiovascular responses to standing. Eur. J. Appl. Physiol. 115, 1569–1575. doi: 10.1007/s00421-015-3142-8
Herranz, R., Manzano, A. I., van Loon, J. J. W. A., Christianen, P. C., and Medina, F. J. (2013). Proteomic signature of Arabidopsis cell cultures exposed to magnetically induced hyper- and microgravity environments. Astrobiology 13, 217–224. doi: 10.1089/ast.2012.0883
Hoson, T., Kamisaka, S., Masuda, Y., Yamashita, M., and Buchen, B. (1997). Evaluation of the three dimensional clinostat as a simulator of weightlessness. Planta 203, 187–197. doi: 10.1007/PL00008108
Hoson, T., and Wakabayashi, K. (2015). Role of the plant cell wall in gravity resistance. Phytochemistry 112, 84–90. doi: 10.1016/j.phytochem.2014.08.022
Huisman, W., Graule, T., and Gauckler, L. J. (1994). Centrifugal slip casting of zirconia (TZP) J. Eur. Ceram. Soc. 13, 33–39. doi: 10.1016/0955-2219(94)90055-8
Knight, T. A. (1806). On the direction of the radicle and germen during the vegetation of seeds. Philos. Trans. R. Soc. Lond. Biol. Sci. 99, 108–120.
Kozeko, L., and Kordyum, E. (2009). Effect of hypergravity on the level of heat shock proteins 70 and 90 in pea seedlings. Microgravity Sci. Technol. 21, 175–178. doi: 10.1007/s12217-008-9044-1
Kuang, X. X., Jiao, J. J., and Liu, K. (2015). Numerical studies of vertical Cl, δ2H and δ18O profiles in the aquifer–aquitard system in the Pearl River Delta, China. Hydrol. Process 29, 4199–4209. doi: 10.1002/hyp.10483
Laurinavicius, R., Svegzdiene, D., Buchen, B., and Sievers, A. (1998). Determination of the threshold acceleration for the gravitropic stimulation of cress roots and hypocotyls. Adv. Space Res. 21, 1203–1207. doi: 10.1016/S0273-1177(97)00636-4
Leguy, C. A. D., Delfos, R., Pourquie, M. J. B. M., Poelma, C., Krooneman, J., Westerweel, J., et al. (2011). Fluid motion for microgravity simulations in a random positioning machine. Gravit. Space Biol. 25, 36–39.
Lewis, G. D. (1973). Centrifugal-force effects on combustion. Symp. Combustion 14, 413–419. doi: 10.1016/S0082-0784(73)80040-2
Liu, J., and Barnett, S. A. (2002). Thin Yttrium-stabilized Zirconia electrolyte solid oxide fuel cells by centrifugal casting. J. Am. Ceram. Soc. 85, 3096–3098. doi: 10.1111/j.1151-2916.2002.tb00588.x
Loesberg, W. A., Walboomers, X. F., van Loon, J. J, and Jansen, J. A. (2006). The effect of combined hypergravity and micro-grooved surface topography on the behaviour of fibroblasts. Cell Motil. Cytoskeleton 63, 384–394. doi: 10.1002/cm.20132
Merzhanov, A. G. (1995). “Combustion and structure formation in SHS processes under microgravity conditions: SHS plans for microgravity experiments,” in NASA Lewis Research Center, The 3rd International Microgravity Combustion Workshop (Cleveland: NASA Lewis Research Center), 159–164.
Moes, M. J. A., Gielen, J. C., Bleichrodt, R.-J., van Loon, J. J. W. A., Christianen, P. C. M., and Boonstra, J. (2011). Simulation of microgravity by magnetic levitation and random positioning: effect on human A431 cell morphology. Microgravity Sci. Technol. 23, 249–261. doi: 10.1007/s12217-010-9185-x
Musgrave, M. E., Kuang, A., Allen, J., Blasiak, J., and van Loon, J. J. W. A. (2009). Brassica rapa L. seed development in hypergravity. Seed Sci. Res. 19, 63–72. doi: 10.1017/S0960258509303360
Newcombe, F. C. (1904). Limitations of the klinostat as an instrument for scientific research. Science 20, 376–379. doi: 10.1126/science.20.507.376-b
Nooij, S. A. E., Bos, J. E., Groen, E. L., Bles, W., and Ockels, W. J. (2007). Space sickness on Earth. Microgravity Sci. Technol. 19, 113–117. doi: 10.1007/BF02919464
Oshima, M., Suzaki, H., Guo, X., and Oshima, H. (2007). Increased level of serum vascular endothelial growth factor by long term exposure to hypergravity. Exp. Anim. 56, 309–313. doi: 10.1538/expanim.56.309
Rahmann, H., Hilbig, R., Flemming, J., and Slenzka, K. (1996). Influence of long-term altered gravity on the swimming performance of developing cichlid fish: including results from the 2nd German Spacelab Mission D-2. Adv. Space Res. 17, 121–124. doi: 10.1016/0273-1177(95)00623-M
Ronca, A. E. (2003). Studies toward birth and early mammalian development in space. Adv. Space Res. 32, 1483–1490. doi: 10.1016/S0273-1177(03)90385-1
Sahuquillo, A., López-Sánchez, J. F., Rubio, R., Rauret, G., Thomas, R. P., Davidson, C. M., et al. (1999). Use of a certified reference material for extractable trace metals to assess sources of uncertainty in the BCR three-stage sequential extraction procedure Anal. Chim. Acta 382, 317–327. doi: 10.1016/S0003-2670(98)00754-5
Schwarz, R. P., Goodwin, T. J., and Wolf, D. A. (1992). Cell culture for three-dimensional modeling in rotating-wall vessels: an application of simulated microgravity. J. Tissue Cult. Methods 14, 51–57. doi: 10.1007/BF01404744
Tateishi, R., Akiyama, N., Miyauchi, M., Yoshinaga, R., Sasanuma, H., Kudo, T., et al. (2015). Hypergravity provokes a temporary reduction in CD4+CD8+ thymocyte number and a persistent decrease in medullary thymic epithelial cell frequency in mice. PLoS ONE 10:e0141650. doi: 10.1371/journal.pone.0141650
Tavakolinejad, A., Rabbani, M., and Janmaleki, M. (2015). Effects of hypergravity on adipose-derived stem cell morphology, mechanical property and proliferation. Biochem. Biophys. Res. Commun. 464, 473–479. doi: 10.1016/j.bbrc.2015.06.160
van Loon, J. J. W. A. (2001). Hypergravity studies in the Netherlands. J. Gravit. Physiol. 8, 139–142.
van Loon, J. J. W. A. (2007). Some history and use of the Random Positioning Machine, RPM, in gravity related research. Adv. Space Res. 39, 1161–1165. doi: 10.1016/j.asr.2007.02.016
van Loon, J. J. W. A., Baeyens, J. P., Berte, J., Blanc, S., ter Braak, L., Bok, K., et al. (2012). A large human centrifuge for exploration and exploitation research. Annales Kinesiologiae 3, 107–121.
van Loon, J. J. W. A., Tanck, E., van Nieuwenhoven, F., Snoeckx, L. H. E. H., de Jong, H. A. A., and Wubbels, R. J. (2005). A brief overview of animal hypergravity studies. J. Grav. Physiol. 12, 5–10.
Velhinho, A., and Rocha, L. A. (2011). Longitudinal centrifugal casting of metal-matrix functionally graded composites: an assessment of modelling issues. J. Mater. Sci. 46, 3753–3765. doi: 10.1007/s10853-011-5289-y
Von Baumgarten, R. G, Baldrighi, and, G., and Shillinger, G. L. (1972). Vestibular behavior of fish during diminished g-force and weightlessness. Aerosp. Med. 43, 626–632.
von Sachs, F. G. J. R. (1879). Über Ausschliessung der geotropischen und heliotropischen Krümmungen wärend des Wachsthums. Würzburger Arbeiten 2, 209–225.
Wade, C. E. (2005). “Responses across the gravity continuum: hypergravity to microgravity,” in Experimentation with Animal Models in Space, ed G. Sonnenfeld (Amsterdam: Elsevier B.V.).
Keywords: microgravity simulation, centrifuges, hypergravity, partial-gravity, reduced gravity paradigm, space flight, ground based research
Citation: van Loon JJWA (2016) Centrifuges for Microgravity Simulation. The Reduced Gravity Paradigm. Front. Astron. Space Sci. 3:21. doi: 10.3389/fspas.2016.00021
Received: 30 March 2016; Accepted: 10 June 2016;
Published: 19 July 2016.
Edited by:
Martin Bojowald, The Pennsylvania State University, USAReviewed by:
Kazuharu Bamba, Fukushima University, JapanRaul Herranz, Centro de Investigaciones Biológicas-CSIC, Spain
Copyright © 2016 van Loon. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jack J. W. A. van Loon, ai52YW5sb29uQHZ1bWMubmw=
 Jack J. W. A. van Loon
Jack J. W. A. van Loon