Cluster Physics with Merging Galaxy Clusters

Collisions between galaxy clusters provide a unique opportunity to study matter in a parameter space which cannot be explored in our laboratories on Earth. In the standard ΛCDM model, where the total density is dominated by the cosmological constant (Λ) and the matter density by cold dark matter (CDM), structure formation is hierarchical, and clusters grow mostly by merging. Mergers of two massive clusters are the most energetic events in the universe after the Big Bang, hence they provide a unique laboratory to study cluster physics. The two main mass components in clusters behave differently during collisions: the dark matter is nearly collisionless, responding only to gravity, while the gas is subject to pressure forces and dissipation, and shocks and turbulence are developed during collisions. In the present contribution we review the different methods used to derive the physical properties of merging clusters. Different physical processes leave their signatures on different wavelengths, thus our review is based on a multifrequency analysis. In principle, the best way to analyze multifrequency observations of merging clusters is to model them using N-body/hydrodynamical numerical simulations. We discuss the results of such detailed analyses. New high spatial and spectral resolution ground and space based telescopes will come online in the near future. Motivated by these new opportunities, we briefly discuss methods which will be feasible in the near future in studying merging clusters.

1. Introduction

According to our most successful structure formation models, the cosmological constant (Λ) dominated cold dark matter (ΛCDM) models, structures form in a hierarchical process due to gravitational instabilities. Small positive density fluctuations collapse first, then massive structures form by merging and smooth accretion. This model predicts that numerous galaxy clusters are in some stage of merging at any epoch. During this merging process the gravitational potential energy of the infalling groups and subclusters is dissipated, and heats up the gas. Large clusters gain most of their mass by merging with less massive halos, as opposed to secondary infall of unprocessed gas (e.g., Muldrew et al., 2015).

Galaxy clusters are usually classified into two broad categories: relaxed and non-relaxed clusters. Many different quantitative methods have been proposed to classify galaxy clusters and identify dynamically active clusters. Based on X-ray observations, the most common parameters used to classify clusters have been power ratios, the ratios of the squares of the multiple moments of the 2D gravitational potential of the cluster to that of the monopole term (Buote and Tsai, 1995), and centroid shifts in the X-ray flux (Mohr et al., 1993).

Recently, Parekh et al. (2015) carried out an extensive study of galaxy clusters classification based on X-ray observations. They found that the most useful parameters are: the Gini, M20, and Concentration. The Gini parameter describes the non-uniformity of X-ray flux distribution in the image pixels, for uniform distribution, G = 0 (Lotz et al., 2004). M20 is based on the second moment of the flux distribution in pixels; it is a measure of the relative contribution of the brightest 20% pixels (Lotz et al., 2004). The Concentration depends on the ratio between radii enclosing 80 and 20% of the total X-ray flux from a cluster (Bershady et al., 2000). Parekh et al. found that non-relaxed clusters exhibit low Gini and Concentration (< 0.4 and < 1), numbers and high M20 (> −1.4) values.

Radio observations have also been used to identify dynamically active clusters. Radio halos and relics have been associated with merging clusters, while mini-halos were found in relaxed clusters (for a review see Feretti et al., 2012).

Optical spectroscopic surveys have been used to study the line of sight (LOS) velocity distribution of cluster galaxies, and infer the dynamical state of clusters. One of the most popular indicators of dynamical activity is the offset between the brightest cluster galaxy (BCG) and the X-ray surface brightness peak. Large offset signals a merging cluster or a recent merger (Poole et al., 2007). Recently, Wen and Han (2013) used different statistical parameters to describe the dynamical states of 2092 clusters using the Sloan Digital Sky Survey (SDSS). They classified only 28% of clusters as relaxed. Wen and Han found that the dominance (the difference between the brightest and second brightest cluster galaxies), the absolute magnitude of the brightest cluster galaxies, and the amplitude of the flux from radio halos correlate well with the dynamical state of clusters.

Merging of galaxy clusters and groups generate turbulence and bulk flows in the intracluster gas (ICG). Infalling massive halos loose gas due to ram pressure stripping. Assuming a spherical geometry, a simple approximation suggests that gas is removed at large where the ram pressure is greater than the pressure in the ICG of the infalling cluster/group, $P_{ram}\propto {\rho }_{gas}{\text{v}}_{rel}^2\ge P_{gas}(r)$, where ρ_gas and v_rel are the gas density of the infalling halo and its relative velocity to the ICG of the main cluster (e.g., Gunn and Gott, 1972).

If the mass ratio is large (~ 10), cold fronts may be generated in cool core clusters due to sloshing induced by the passage of the infalling halo (Ascasibar and Markevitch, 2006; for a review see Markevitch and Vikhlinin, 2007). Massive cluster mergers with small mass ratios may produce a bow shock in front of the infalling cluster followed by a contact discontinuity (“cold front”), which separates the gas of the two colliding components. In the opposite direction a shock is propagating outward in the ICG of the subcluster. These two shocks are thought to be responsible for the double radio relics found in some merging galaxy clusters (e.g., van Weeren et al., 2011a,b; Bonafede et al., 2012).

In the cases of large velocity, the dark matter surface density peaks, the X-ray, and the centroids of the Sunyaev-Zel'dovich (SZ) signal (Section 2.3) do not coincide. Offsets between them are generated by the different behavior of the collisionless component, the dark matter, and the collisional gas during the merging process: the dark matter responds only to gravity, and therefore the core of the infalling cluster passes through that of the main cluster relatively unchanged, but the gas is subject to hydrodynamical effects, which cause large disturbances, shocks and contact discontinuities.

Major mergers are the most energetic events since the Big Bang, (~10⁶³ ergs). The ΛCDM models predict that the infall velocities of massive merging systems are typically 500–700 km s⁻¹, with a tail extending to higher velocities (Thompson and Nagamine, 2012). Recent observations of several massive merging clusters suggest a high-velocity tail in the velocity distribution extending out to ≳ 3000 km s⁻¹. The most famous example of these high-velocity mergers is the so called “Bullet cluster” (1E0657-56). We discuss this merging cluster in more detail in Section 6. The Bullet cluster was the first merging system which provided direct evidence for the existence of dark matter (Markevitch et al., 2002; Markevitch, 2005). In the left panel in Figure 1 we show a multi-frequency image of the Bullet cluster with the mass surface density reconstructed from weak lensing superimposed (Clowe et al., 2006). The mass surface densify is dominated by the most massive component, the dark matter, which is about 82% of the total mass. The X-ray emission is due to the ICG the most massive component of the ordinary matter (~16%), conventionally called baryonic matter in astrophysics, because the mass of ordinary matter is dominated by baryons (protons and neutrons), and not electrons, which are actually leptons. The optical emission is dominated by the least massive component, the cluster galaxies (~2%). The displacement of the gas from the dark matter is clearly visible.

FIGURE 1

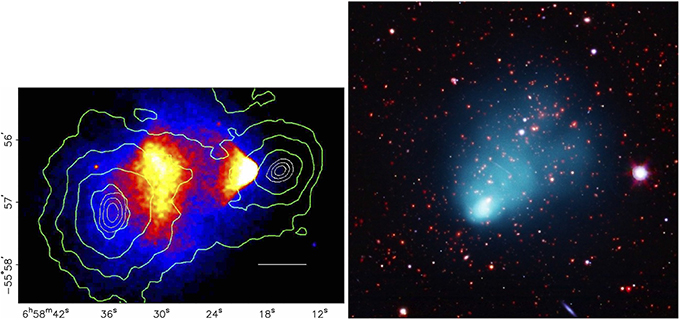
Figure 1. Multi-frequency/component images of merging clusters of galaxies. Left panel: Chandra image of the “Bullet cluster” with green contours showing the projected total mass distribution from gravitational lensing observations (from Clowe et al., 2006). The white contours show the errors in the mass peaks (68.3%, 95.5%, and 99.7% CL). Right panel: A multi-frequency image of “El Gordo”. X-ray emission from NASA's Chandra X-ray Observatory shown in blue, optical image from the European Southern Observatory's Very Large Telescope (VLT) and infrared emission from the NASA's Spitzer Space Telescope in red and orange (from Menanteau et al., 2012).

Since the discovery of the Bullet cluster, several other merging clusters have been found with a bullet-cluster-like morphology. As an example, we show a multifrequency (X-ray and optical) image of “El Gordo” (ACT-CT J0102-4915) in the right panel of Figure 1. El Gordo is a recently discovered very massive high redshift merging cluster (Marriage et al., 2011; Menanteau et al., 2012) showing a unique, bullet-like X-ray morphology, followed by a “twin tailed” structure. Also, several other merging clusters have been found with significant offsets between the mass surface density and peaks of the X-ray emission and SZ signal (e.g., MACS J0025.4-1222: Bradač et al., 2008; CL J0152-1347: Massardi et al., 2010; A2163: Bourdin et al., 2011; MACS J0744.8+3927 and CL J1226.9+3332: Korngut et al., 2011; MACS J0717.5+3745: Mroczkowski et al., 2012; DLSCL J0916.2+2951: Dawson et al., 2012; ZwCl 1234.0+02916: Dahle et al., 2013; SL2S J08544-0121: Gastaldello et al., 2014).

2. Multifrequency Observations of Galaxy Clusters

2.1. Optical/Near-Infrared Observations

Galaxy clusters were discovered as galaxy overdensities in the sky. The first statistically complete sample of galaxy clusters based on image plates obtained by the Palomar Observatory Sky Survey was published by Abell (1958). For many years catalogs of clusters were assembled using only optical observations.

The most straightforward quantities we can measure based on O/NIR observations of a cluster are the luminosities, angular positions, shapes, and redshifts of galaxies located in the cluster region. From these quantities it is straightforward to derive the number and luminosity distribution of the cluster galaxies, and their radial velocities relative to the cluster center assuming that they are all at the distance of the cluster. Note that the distance to the cluster is much larger than the distance between cluster galaxies, thus the errors in radial velocities are negligible due to this assumption.

From the distortion of the shapes of background galaxies due to gravitational lensing, the surface mass distribution can be derived, which is a LOS integral of the total density:

$\begin{array}{ll}\Sigma (x,y)={{\displaystyle \int }}_{z_1}^{z_2}{\rho }_t(r)dz\prime ,& (1)\end{array}$

where ρ_t(r) is the total mass density, the sum of the dark matter, the ICG and stars, ρ_t(r) = ρ_d(r) + ρ_g(r) + ρ_s(r), and the physical position within the cluster, r = (x, y, z′) is expressed as angular coordinates here. A derivation of the mass surface density based on gravitational lensing needs more assumptions due to the low signal-to-noise (S/N) ratio of lensing observations, thus we will discuss it in more details in Section 3.1.

2.2. X-Ray Observations

The most massive baryonic component of galaxy clusters is the ICG. The low density, high temperature gas trapped in the gravitational potential of the cluster is heated up to ~10⁸ K during cluster formation as a result of conversion of gravitational potential to heat. At these temperatures the most efficient radiation mechanism is thermal bremsstrahlung in the X-ray band. X-ray emission from clusters also contain emission lines from partially ionized atoms, which can be used to study the chemical composition, and certain physical properties of the ICG. Galaxy clusters can be identified as large scale extended sources in the X-ray band.

X-ray observations measure the flux density, F_X(x, y) (in, e.g., ergs s⁻¹ cm⁻² Hz⁻¹), in the direction, x, y, in the sky, which is related to the integrated X-ray emissivity, ϵ, (in, e.g., ergs s⁻¹ cm⁻³ Hz⁻¹), over the LOS:

$\begin{array}{ll}{F}_X(x,y)=\frac{1}{4\pi D_L^2}{{\displaystyle \int }}_{{\nu }_1∕(1+z)}^{{\nu }_2∕(1+z)}{{\displaystyle \int }}_{z_1}^{z_2}ϵ(\rho ,T_g,Z_{ab};\nu )dz\prime d\nu ,& (2)\end{array}$

where the inner integral is along the LOS (z′ axis), the outer integral is over the observed frequency band, (ν₁, ν₂) the (1 + z) factors convert observed frequencies to emitted ones at the source at redshift z, the inner integral is over the LOS through the cluster, from z₁ to z₂, D_L is the luminosity distance to the cluster, ρ(r) and T_g(r) are the gas density and temperature, Z_ab(r) is the abundance of heavy elements, and the emissivity at frequency ν can be expressed as

$\begin{array}{ll}ϵ(\rho ,T_g,Z_{ab};\nu )=n_e{\displaystyle \sum _{i,Z}}{n}_{i,Z}\Lambda (T_e,Z_i;\nu ),& (3)\end{array}$

where electron and ion number densities, n_e(r) and n_i,Z(r) are known functions of ρ, T_e (usually assuming T_e = T_g), and the cooling function, Λ(T_e, Z_i; ν), depends only the frequency, the electron temperature and physical constants (we ignore the telescope response function here). The angular coordinates can be expressed as a function of the distance to the cluster. In a narrow spectral band, from Equation (2), we obtain an approximation for the X-ray intensity,

$\begin{array}{ll}{I}_X(x,y;\nu )=\frac{F_X(x,y)}{\Delta \nu },& (4)\end{array}$

where Δν is the size of the frequency bin. The frequency bin has to be fine enough to resolve the narrowest spectral lines expected. If the geometry (the shape) of the cluster is known, I_X(x, y; ν) can be inverted and we can derive ρ(r), T_g(r), and Z_ab(r). In practice, we usually assume a simple geometry for the cluster, spherical or ellipsoidal, however, this approximation breaks down for dynamically active clusters.

2.3. Radio Observations

The distribution of the ICG can also be studied using radio observations. The change in the cosmic microwave background (CMB) due to inverse-Compton scatterings (IC) of cold photons of the CMB off electrons in the hot ICG is called the SZ effect (Sunyaev and Zel'dovich, 1980; for recent reviews see Rephaeli, 1995; Birkinshaw, 1999; Carlstrom et al., 2002). If the cluster is not moving relative to the Hubble flow and the ICG is in thermal equilibrium (or in local thermodynamic equilibrium, LTE), this is called the thermal SZ (TSZ) effect. Additional changes in the CMB may be caused by radial motion of the cluster or bulk velocity in the ICG, which is called the kinematic SZ (KSZ) effect. We measure the sum of these two effects,

$\begin{array}{ll}{T}_{SZ}(x,y;\nu )=T_{TSZ}(x,y;\nu )+T_{KSZ}(x,y;\nu ),& (5)\end{array}$

where, using the single scattering approximation, the TSZ effect can be expressed as

$\begin{array}{ll}\Delta T_{TSZ}(x,y,\nu )=T_{CMB}\frac{{\sigma }_T{k}_B}{m_e{c}^2}{{\displaystyle \int }}_{z_1}^{z_2}{g}_{TSZ}(x_{\nu },T_e)n_e(r)T_e(r)dz\prime ,& (6)\end{array}$

and the KSZ effect as

$\begin{array}{ll}\Delta T_{KSZ}(x,y,\nu )=T_{CMB}\frac{{\sigma }_T}{c}{{\displaystyle \int }}_{z_1}^{z_2}{g}_{KSZ}(x_{\nu },T_e)n_e(r)v_r(r)dz\prime ,& (7)\end{array}$

where T_CMB = 2.72548 ± 0.00057 K is the temperature of the CMB (Fixsen, 2009), v_r(r) is the radial (LOS) velocity of the ICG, σ_T is the Thomson cross section, k_B is the Boltzmann constant, m_e and c is the mass of the electron and the speed of light, and the frequency dependences are:

$\begin{array}{ll}{g}_{TSZ}(x_{\nu },T_e)=g_T(x_{\nu })+{\delta }_{RT}(T_e,x_{\nu }),& (8)\end{array}$

and

$\begin{array}{ll}{g}_{KSZ}(x_{\nu },T_e)=g_K(x_{\nu })+{\delta }_{RK}(T_e,x_{\nu }),& (9)\end{array}$

where

$\begin{array}{ll}g(x_{\nu })=x_{\nu }\frac{e^{x_{\nu }}+1}{e^{x_{\nu }}-1}-4,& (10)\end{array}$

and

$\begin{array}{ll}{g}_K(x_{\nu })=-\frac{x_{\nu }^2{e}^x}{{(e^{x_{\nu }}-1)}^2},& (11)\end{array}$

where the dimensionless frequency is x_ν = hpν/(k_B T_CMB), where h_p is the Planck constant.

The relativistic corrections, δ_RT and δ_RK, can be found in, e.g., Nozawa et al. (1998a) and Nozawa et al. (1998b). The effect of multiple scatterings due to the relativistic SZ effect was studied using analytic approximations by Itoh et al. (2001), and performing Monte Carlo simulations by Molnar and Birkinshaw (1999). These corrections were found to be negligible.

In most applications the relativistic corrections can be ignored, and, assuming an isothermal static cluster, in the Rayleigh-Jeans (RJ) limit we obtain:

$\begin{array}{ll}\frac{\Delta T_{RJ}}{T_{CMB}}(x,y)=-2y_C(x,y)-\tau (x,y)\frac{v_r}{c},& (12)\end{array}$

where v_r is the radial peculiar velocity of the cluster, and y_C is the Compton y parameter, $y_C(x,y)=\tau (x,y)k_B{T}_e(x,y)∕(m_e{c}^2)$, where τ(x, y) is the LOS optical depth.

Similarly to X-ray observations, we need to know the geometry of the cluster to derive the three-dimensional (3D) distribution of n_e(r), T_e(r), and v_r(r). From Equation (12) it is clear that in the RJ limit we measure the sum of both TSZ and KSZ effects, and, in some cases of merging clusters some care is needed in analyzing the SZ data (e.g., Mroczkowski et al., 2012). For example, for a 10 keV subcluster moving with v_r = 3000 km s⁻¹, $[\Delta T_{KSZ}/\Delta T_{TSZ}){]}_{RJ}\propto (v_r/c)/(2k_B{T}_e(x,y)/(m_e{c}^2)~0.25$, i.e., the KSZ effect is 25% of the TSZ effect.

3. Physics of Dark Matter from Merging Galaxy Clusters

3.1. Total Mass Distribution from Gravitational Lensing

In principle, the best way to derive the total mass distribution of a galaxy cluster is to use gravitational lensing, the bending of light rays due to mass concentrations (Schneider et al., 1992, for a more recent review see e.g., Bartelmann, 2010). In the case of gravitational lensing by a galaxy cluster, the distances between the source, the lens, and the observer are large, thus we can assume that all the mass of the deflector is in a plane perpendicular to the LOS, the lens plane. This is called the thin lens approximation. In this case, choosing our z′ axis parallel to the LOS, the bending angle becomes:

$\begin{array}{cc}\alpha (r_{2D})=-\frac{4G}{c^2}\int \frac{\Sigma (r_{2D}^{\prime })}{b^2}bdx\prime dy\prime ,& (13)\end{array}$

where $\text{b}={\text{r}}_{2D}-{\text{r}}_{2D}^{\prime }$, where r_2D and ${\text{r}}_{2D}^{\prime }$ are 2D vectors, $r_{2D}^{\prime }=(x\prime ,y\prime )$, Σ is the surface mass density (Equation 1). The bending angle can be expressed using the 2-dimensional gravitational deflection potential, ϕ_2D(x, y), as

$\begin{array}{ll}\alpha (x,y)=\frac{2}{c^2}\nabla {\varphi }_{2D}(x,y),& (14)\end{array}$

where ∇ is the 2D gradient operator in the lens plane, and the 2D gravitational deflection potential is defined as the LOS integral of the 3D Newtonian potential,

$\begin{array}{ll}{\varphi }_{2D}(x,y)={\displaystyle \int }\varphi (x,y,z\prime )dz\prime .& (15)\end{array}$

Using the thin lens approximation, we can project the distances between the source and its image onto the source plane, and obtain the lens equation, which, in angular coordinates, becomes:

$\begin{array}{ll}{\theta }^I={\theta }^S+\frac{D_{LS}}{D_{OS}}\alpha ={\theta }^S+\widehat{\alpha },& (16)\end{array}$

where θ^S and θ^I are the source and image coordinates, and we defined the reduced bend-angle, $\widehat{\alpha }$. Defining the 2D scaled deflection potential, ψ_2D, as

$\begin{array}{ll}{\psi }_{2D}(\theta )=\frac{2D_{LS}}{D_{OL}{D}_{OS}} {{\displaystyle \int }}^{\text{}}\varphi (x,y,z\prime )dz\prime ,& (17)\end{array}$

where x = D_OLθ₁ and y = D_OLθ₂, the lens equation becomes

$\begin{array}{ll}{\theta }^S={\theta }^I-\widehat{\alpha }={\theta }^I-{\nabla }_{\theta }{\psi }_{2D}({\theta }^I),& (18)\end{array}$

where ∇_θ is to be taken with respect to the angular coordinates, θ₁ and θ₂, thus ∇_θ = D_OL∇, where ∇ acts on the Cartesian coordinates x and y in the lens plane.

It is convenient to define the convergence field, κ(θ), the dimensionless measure of the surface mass density, as

$\begin{array}{ll}\kappa (\theta )=\frac{1}{{\Sigma }_{crit}}\Sigma (\theta ),& (19)\end{array}$

where we defined the critical surface mass density, Σ_crit,

$\begin{array}{ll}{\Sigma }_{crit}=\frac{c^2}{4\pi G}\frac{D_{OS}}{D_{LS}{D}_{OL}},& (20)\end{array}$

where D_OS and D_OL are the angular diameter distances from the observer to the source and the lens (defecting cluster), and D_LS is the distance from the lens to the source. For a lens at a redshift of 0.3, a source at z = 1, and H₀ = 70 km s⁻¹ Mpc⁻¹, the critical surface mass density is Σ_crit = 1.18 g cm⁻². The scaled deflection angle can be expressed with these new variables as

$\begin{array}{cc}\widehat{\alpha }(\theta )=\frac{1}{\pi }\int \frac{\kappa (\theta \prime )}{|\theta \prime {|}^2}\theta \prime d\theta \prime ,& (21)\end{array}$

and the scaled 2D deflection potential becomes

$\begin{array}{ll}{\psi }_{2D}(\theta )=\frac{1}{\pi }{\displaystyle \int }\kappa (\theta \prime )\ln |\theta \prime |d\theta \prime .& (22)\end{array}$

The gravitational bending of the light depends only on the mass distribution of the lensing object, therefore these measurements are not sensitive to the dynamical state of galaxy clusters. As a consequence, for a merging clusters of galaxy, the total mass can be derived from lensing independently from the viewing angle of the system. The mass is dominated by dark matter, thus the gravitational lensing derived dark matter can be used as an approximation for the dark matter distribution. In some cases of merging clusters the gas is removed from their dark matter potential wells, and thus lensing measurements give directly the dark matter distribution (e.g., Bullet cluster; see left panel in Figure 1). In general, lensing observations of merging clusters allow us to derive the total masses and locations of the projected centers of subclusters, which can be used to constrain the phase of the collision (e.g., the time after the first core passage), subject to projection effects.

Gravitational lensing has two main regimes: (1) strong lensing, which is based on strong, non-linear image distortions of background galaxies, is sensitive to the mass distribution only in the core of clusters; (2) weak lensing, which is the linear regime of image distortion, it is a result of small distortions of background galaxies caused by slowly varying weak gravitational field outside of the core out to the virial radius of clusters.

Using strong lensing to reconstruct the mass distribution in a galaxy cluster, the deflection field is calculated using Equation (13) assuming models of the mass distributions for the background galaxies and the cluster, and the positions of the observed and calculated images of background galaxies are compared. The process is iterated until convergence (e.g., Broadhurst et al., 2005; for non-parametric methods see, e.g., Diego et al., 2005).

In the case of weak lensing, we can rewrite the lens equation using physical coordinates in the 2D lens plane, where it is straightforward to represent the observations. In component notation, the lens equation becomes:

$\begin{array}{ll}{y}_i=x_i-{\widehat{\alpha }}_i(x_1,x_2),& (23)\end{array}$

where y_i and x_i (i = 1, 2) are the 2D coordinates in the source and lens planes. This equation clearly describes a coordinate transformation between the lens plane to the source plane. This is a non-linear transformation due to the deflection angle field, ${\widehat{\alpha }}_i(x_1,x_2)$. However, in the case of weak lensing, the distortions are small and we can do a Taylor expansion to first order of this transformation, which can be expressed as:

$\begin{array}{ll}{y}_i(x_1,x_2)\approx \frac{\partial y_i}{\partial x_j}{|}_0{x}_j=A_{ij}{x}_j,& (24)\end{array}$

where the Jacobian of the transformation, A_ij, using Equation (23), is

$\begin{array}{ll}{A}_{ij}={\delta }_{ij}-\frac{\partial {\widehat{\alpha }}_i}{\partial x_j}={\delta }_{ij}-\frac{{\partial }^2\psi }{\partial x_i\partial x_j}.& (25)\end{array}$

Using the convergence field, κ(x₁, x₂), and introducing the shear tensor field, Γ(x₁, x₂), with components γ₁ and γ₂, also referred to as a two component pseudo-vector field, γ, the isotropic and traceless part of the lensing Jacobian can be separated, and we obtain,

$\begin{array}{ll}\kappa =\frac{1}{2}({\psi }_{11}+{\psi }_{22}),\hfill & (26)\hfill \end{array}$

$\begin{array}{ll}{\gamma }_1=\frac{1}{2}(-{\psi }_{11}+{\psi }_{22}),\hfill & (27)\hfill \end{array}$

$\begin{array}{ll}{\gamma }_2=\frac{1}{2}({\psi }_{12}+{\psi }_{21}),\hfill & (28)\hfill \end{array}$

and

$\begin{array}{ll}\Gamma =\left(\begin{array}{ll}{\gamma }_1\hfill & {\gamma }_2\hfill \\ {\gamma }_2\hfill & -{\gamma }_1\hfill \end{array}\right).& (29)\end{array}$

With these variables, the Jacobian of the transformation becomes

$\begin{array}{ll}A=(1-\kappa )\left(\begin{array}{ll}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right)-\left(\begin{array}{ll}{\gamma }_1\hfill & {\gamma }_2\hfill \\ {\gamma }_2\hfill & -{\gamma }_1\hfill \end{array}\right)=(1-\kappa )I_{2D}-\Gamma ,& (30)\end{array}$

where I_2D is the 2D identity matrix. Since A is a real and symmetric matrix, it can be diagonalized and written as

$\begin{array}{cc}A=(1-\kappa \prime )\left(\begin{array}{ll}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right)-\gamma \prime \left(\begin{array}{ll}1\hfill & 0\hfill \\ 0\hfill & -1\hfill \end{array}\right),& (31)\end{array}$

where (${\gamma \prime )}^2={({\gamma }_1\prime )}^2+{({\gamma }_2\prime )}^2$. This form clearly shows that the convergence is responsible for isotropic distortion of a background galaxy, (magnifying or de-magnifying it, i.e., changes the surface area of the galaxy) and γ′ describes a shear distortion.

The shear coefficients, γ_{1, 2}, can be derived from observations defining complex ellipticities using

$\begin{array}{ll}ϵ={ϵ}_1+i{ϵ}_2=\frac{1-b/a}{1+b/a}{e}^{2i\varphi },& (32)\end{array}$

where a and b are the major and minor axis of the ellipse and ϕ is the position angle. The average ellipticities measured from observations are related to the shear and convergence in that region as

$\begin{array}{cc}\langle ϵ\rangle =\frac{\gamma }{1-\kappa },& (33)\end{array}$

where the angle brackets refer to averages over an area of the sky. In the limits of small distortions, i.e., the weak lensing approximation, γ ≪ 1 and κ ≪ 1, thus the averaged ellipticities directly give the shear fields γ₁(θ) ≈ 〈ϵ₁(θ)〉 and γ₂(θ) ≈ 〈ϵ₂(θ)〉. The convergence can be derived from

$\begin{array}{cc}\kappa (\theta )=\frac{1}{\pi }{\displaystyle \int }{d}^2\theta \prime D^{*}(\theta -\theta \prime )\gamma (\theta \prime ),& (34)\end{array}$

where D* is the complex conjugate of the convolution kernel, γ = γ₁ + iγ₂,

$\begin{array}{ll}D(\theta )=\frac{({\theta }_2^2-{\theta }_1^2)-2i{\theta }_1{\theta }_2}{{\theta }^4},& (35)\end{array}$

and the mass surface density as Σ(θ) = Σ_crκ(θ) (this is called the Kaiser-Squires algorithm; Kaiser and Squires, 1993).

The angular resolution of strong lensing is much higher than that of the weak lensing, because in order to measure the weak lensing signal, it is necessary to average out the intrinsic ellipticities of background galaxies. The best way to derive the mass distribution in clusters using gravitational lensing is to combine these two methods.

Gravitational lensing measurements are very difficult. Massive components can be mapped accurately, but the S/N ratio is much smaller for less massive components, and, as a consequence, the errors in their amplitudes and locations are higher. The 3D distribution of the total mass can be derived either by assuming a geometry for the mass distribution applicable to relaxed clusters, or using N-body/hydrodynamical simulations to model the system, which is the best method for merging clusters (see Section 6).

Large observing programs using the Hubble Space Telescope (HST) provide deep galaxy cluster observations for gravitational lensing analysis: the Cluster Lensing And Supernova survey with Hubble (CLASH, Postman et al., 2012) and the Frontiers Fields (http://www.stsci.edu/hst/discretionary-campaigns/discretionary-frontier-fields/). These new data make a more accurate derivation of the mass distribution in the core of clusters possible by increasing the number of multiple lensed background galaxies (CLASH: Umetsu et al., 2014, 2015b; Merten et al., 2015; Frontier Fields: Lam et al., 2014; Diego et al., 2015a,b; Jauzac et al., 2015).

3.2. Physical Properties of Dark Matter: Cross Section

Overwhelming evidence shows that the mass of galaxy clusters is dominated by dark matter (DM). However, as of today, no DM particles have been detected. The most popular candidates for DM are weakly interacting massive particles (WIMPs) and axions. WIMPs are predicted by R-parity-conserving supersymmetry (SUSY) theory, a very popular extension to the standard model of particle physics predicting a number of hypothetical particles (e.g., Kolb and Turner, 1990). WIMPs are assumed to be interacting via gravity and the weak interaction only, and have a large mass (> 1 GeV). Axions are hypothetical particles introduced to explain the strong charge–parity problem associated with the non-trivial nature of the vacuum in quantum chromodynamics (QCD), which is part of our standard model of particle physics. Sterile (right handed) neutrinos, hypothetical particles which do not take part in the weak interaction, suggested by some extensions of the standard model, were also proposed as candidates for dark matter (e.g., Dodelson and Widrow, 1994). One of the main arguments against these heavy particles is that they should decay and produce line emission in the X-ray band at a frequency depending on their mass, which has not been found yet.

Recently, analyzing XMM observations of a sample of galaxy clusters and M31, some evidence has been found for the existence of an unidentified X-ray line at 3.5 keV, which is suggested to be a decay line of a sterile neutrino with a mass of 7 keV in energy units (Boyarsky et al., 2014; Bulbul et al., 2014). This line was identified in the Chandra data as well, but it has not been found in the ACIS-I spectrum of the Virgo cluster. At this point it cannot be ruled out that this line is due to instrumental effects or to an unidentified atomic line. The suggested decay line is very weak (with an equivalent width of only about 1 eV) in the vicinity of known atomic lines.

Merging galaxy clusters provided the first direct evidence for the existence of dark matter. Large offsets between the X-ray emission due to the collisional baryonic matter in the ICG, and the mass concentrations derived from gravitational lensing marking the centers of the two colliding clusters in the Bullet cluster clearly showed that most of the mass in clusters consists of collisionless particles, as we would expect based on our ΛCDM models. It was soon realized that, in principle, the offsets between the dark matter centers and those of the baryonic component (ICG and galaxies) provide a possibility to measure the self-interacting cross section of dark matter. The offsets in the Bullet cluster were the first to derive upper limits on the self-interacting cross section (Markevitch et al., 2004; Randall et al., 2008).

Since the first constraint, several merging clusters have been used to put upper limits on the cross section of the dark matter (e.g., MACSJ0025.4-1222: Bradač et al., 2008; A520: Clowe et al., 2012; Jee et al., 2012, A2744: Merten et al., 2011; DLSCL J0916.2+2951: Dawson et al., 2012). The best constraints on the interaction cross section of DM particles using these merging clusters were σ_D ∕m_D ≲ 1cm²g⁻¹. It is also possible to use a sample of minor mergers and derive constraints on the dark matter cross section. Recently Harvey et al. (2015), applying statistical methods to analyze the offset between the gas, the dark matter, and the galaxy component of merging clusters observed with the HST and Chandra X-ray observatory, derived the tightest limit for the dark matter cross section: σ_D ∕ m_D ≤ 0.47 cm²g⁻¹.

Using offsets between bright central galaxies and the centroids of the DM mass surface density in dense cores of galaxy clusters can also be used to study dark matter cross section. Using HST imaging of four BCGs in the core region of A3827 and VLT/MUSE integral field spectroscopy data, Massey et al. (2015) claimed to find the most accurate offset between stellar and dark matter centroids of $1.62_{-0.49}^{+0.47}$ kpc. Assuming that this is due to DM scatterings exclusively, they derived ${\sigma }_D∕m_D~1.07\pm 0.7\times 10^{-4}{(t_{in}∕10^9\text{yrs})}^{-2}$ cm²g⁻¹, where t_in is the time interval of the infall. However, they acknowledged that at these length scales the gravitational forces do not dominate and other interactions may also cause these offsets. Using the same data, Kahlhoefer et al. (2015) derived a much larger cross section, σ_D ∕ m_D ~ 1.5 or 3cm²gr⁻¹ (depending on whether assuming contact interaction or an effective force for the interaction). As opposed to Massey et al. (2015), Kahlhoefer et al. (2015) assumed that the effective drag force on the DM subhalo is not constant during the evolution of the system. Note, however, that this DM cross section is larger than some of the upper limits derived earlier based on cluster mergers.

The explanation of offsets between peaks of mass surface density and the gas distribution based on the merging scenario assuming ΛCDM cosmological models is questionable in some merging clusters. Since the DM and the galaxies are nearly collisionless, we expect that they move together during merging. For example. it was found that, in spite of the violent collision taking place in the Bullet cluster, the galaxies associated with the infalling subcluster still track its DM center well. However, in A520, a DM peak was found without an overdensity of galaxies in the middle of the cluster near the X-ray peak associated with the ICG, surrounded by three DM peaks which coincide with galaxy density peaks (Mahdavi et al., 2007). The physical reason for the existence of this DM peak without a galaxy density enhancement in A520 is still a subject of debate. One possible explanation would be that it is due to collisions between DM particles (Jee et al., 2012, 2014; however see Clowe et al., 2012). In A2744, an extended X-ray emission was found at large physical distances from the DM mass peaks (Merten et al., 2011). As of today, no merging scenario can explain all observed features of this object (Merten et al., 2011; Medezinski et al., 2016). Clearly, detailed numerical simulations are necessary to find out whether an explanation based on ΛCDM is possible.

4. Physics of the Intracluster Gas

The ICG is the most massive baryonic component of galaxy clusters. As we mentioned, we observe integrated physical quantities of the ICG, thus, in general we need to apply deprojection techniques to derive their 3D distribution. However, some physical quantities can be derived from observations of merging clusters independently of the viewing angle. We discuss these first.

4.1. Total Thermal Energy of Electrons

The total thermal energy of electrons can be derived from observations without any further assumptions. The TSZ effect (Equation 6) may be expressed, ignoring relativistic corrections, as a line of sight integral of the electron pressure:

$\begin{array}{ll}\frac{\Delta T_{TSZ}}{T_{CMB}}(\nu )=\frac{{\sigma }_T{g}_T(\nu )}{m_e{c}^2}{\displaystyle {{\displaystyle \int }}_{-R_{vir}}^{R_{vir}}{n}_e(r)k_B{T}_e(r)dz\prime =\frac{2{\sigma }_T{g}_T(\nu )}{3m_e{c}^2}{U}_e,}& (36)\end{array}$

where U_e = ∫(3∕2)n_e(r)k_BT_e(r)dV, is the total thermal energy of the electrons, and we assumed that the cluster gas is bounded by the virial radius, R_vir. This non-relativistic approximation is valid for most part of the cluster at low radio frequencies. The total pressure of the ICG can be derived from the electron pressure if the gas composition and temperature are known.

4.2. Thermodynamical Properties of the ICG from X-Ray and SZ Observations

The derivation of the 3D intrinsic physical properties of the ICG, the density, and temperature, ρ_g(r), T_g(r), is not trivial for merging clusters. The reason for this is that we observe integrated quantities along the LOS, and in order to derive the 3D physical quantities we need to deproject the observed quantities, which can be done exactly only if we know the geometry of the cluster. This deprojection is usually done assuming a distribution with a simple symmetry, such as spherical or ellipsoidal, which works well only for relaxed clusters (e.g., Sarazin, 1988; Reiprich et al., 2013; Molnar, 2015).

In the case of merging clusters, the 3D geometry is usually guessed from the observed 2D image. Menanteau et al. (2012) developed a method to deproject X-ray images assuming cylindrical symmetry with the axis lying in the plane of the sky, and applied their method to analyze Chandra observations of El Gordo. They used the geometry derived from X-ray observations to model the SZ signal in this system. This is a better approximation than a spherical model for the geometry of the gas in merging clusters, but it is only realistic if the impact parameter of the collision is negligible. Korngut et al. (2011) analyzed Mustang (SZ) and Chandra (X-ray) observations of MACS J0744.8+3927, and modeled the shock assuming elliptical geometry. SZ observations of merging clusters have also been analyzed using “pseudo-pressure” maps derived from X-ray observations (e.g., Mroczkowski et al., 2012).

Relativistic corrections to the SZ effect measured at different frequencies depend on the temperature of the ICG. In principle, this can also be used to derive the temperature distribution in the ICG (e.g., Prokhorov et al., 2011; Chluba et al., 2013). Prokhorov et al. (2011) discussed how merging clusters can be studied using the relativistic SZ effect. Chluba et al. (2013) showed that variations in the temperature along the LOS can introduce bias in the derived temperature and peculiar velocity.

If it is possible, the best way to carry out the deprojection is to perform full N-body/hydrodynamical simulations tailored to the observations of the merging cluster. We discuss these methods in detail in Section 6.

4.3. Constraining Transport Processes of the ICG using Merging Clusters

High angular resolution X-ray observations provided evidence that the transport processes (heat conduction and viscosity) in the ICG have been suppressed relative to those expected based on the mean fee path due to the Coulomb interaction for particles crossing the cold front from the inner to the outer part of the cold front. The mean fee path of these particles can be expressed as

$\begin{array}{ll}{\lambda }_C=15\text{\hspace{0.17em}kpc}\left(\frac{T_{e,1}}{T_{e,2}}\right)\left(\frac{G(1)}{G(\sqrt{T_{e,1}/T_{e,2}}]}\right){\left[\frac{T_{e,2}}{7\text{keV}}\right]}^2\left[\frac{n_{e,2}}{{10}^{-3}{\text{cm}}^{-\text{3}}}\right],& (37)\end{array}$

where n_e and T_e are the electron densities and temperatures in the regions 1 or 2, and G(x) = (${E}$(x) − x${E}$(x))∕(2x²), where ${E}$(x) is the error function (Markevitch and Vikhlinin, 2007), sometimes also been referred to as the “Spitzer value” (Spitzer, 1962).

High-resolution X-ray observations carried out by the Chandra mission found shocks in the ICG, as well as unexpected sharp density and temperature discontinuities, called “cold fronts” (for reviews see Markevitch and Vikhlinin, 2007 and Ghizzardi et al., 2010). Cold fronts were found to be contact discontinuities: two regions of gas with different temperatures and densities but with no pressure jump between them separated by a boundary surface. Two types of cold fronts have been identified. One is interpreted as a result of sloshing of the ICG in the main cluster with a cool core due to its displacement from equilibrium in its DM potential well due to minor mergers. In this case the gas on the two sides of the cold font belong to the same cluster, and their motion is tangential (Keshet et al., 2010). The other type of cold front separates the two regions of ICG of the main and infalling subcluster following the bow shock in the main cluster due to major mergers. In the rest of this review we refer to cold fronts following bow shocks in major mergers as “contact discontinuities” for easy reference.

X-ray observations suggest that the width of cold fronts may be significantly smaller than the Coulomb free mean path. The cold front found in A3667 has a width of ≲3 kpc, while the local Coulomb mean free path is estimated to be λ_C ≈ 12 kpc (Vikhlinin et al., 2001). Similar results were obtained analyzing contact discontinuities in other clusters (e.g., Ettori and Fabian, 2000). In the merging cluster A2146, the width of the bow shock and the reverse shock were found to be ≲12 kpc and ≲6 kpc, but the they found that λ_C ≈ 21 kpc and λ_C ≈ 23 kpc (Russell et al., 2012). In galaxy group merger RXJ0751.3+5012, the width of the CD was found to be 2.4±0.7 kpc (leading edge in the NE core component; Russell et al., 2014). The width of contact discontinuities suggest a large gradient of the temperature across them within less than the Coulomb mean free path.

The heat conductivity has also ben found to be suppressed relative to an estimate based on the Coulomb interaction, usually refereed to as the “Spitzer conduction,”

$\begin{array}{ll}{\kappa }_S=4.6\times {10}^{13}\text{ergs\hspace{0.17em}}{\text{s}}^{-1}{\text{cm}}^{-\text{1}}{\text{K}}^{-\text{1}}{\left[\frac{T_e}{{10}^8\text{K}}\right]}^{5/2}{\left[\frac{\ln {\Lambda }_C}{40}\right]}^{-1},& (38)\end{array}$

where T_e is the electron temperature (conductivity is mainly due to electrons), and ln Λ_C is the Coulomb logarithm (Spitzer, 1962; Sarazin, 1988). The effective conductivity is often expressed as a fraction of the Spitzer conductivity, κ = f_Sκ_S. Eckert et al. (2014), using XMM-Newton observations of a galaxy group falling into the massive cluster A2142, found that f_C ≲ 0.0025. Eckert et al. used the time scale of diffusion due to conductivity, which smoothes sharp temperature edges, to the time scale the ram pressure stripped tail of the infalling group survived (≳600 Myr).

The first explanation for the narrow width of cold fronts and shocks was that the flow of the ambient ICM around the dense subcluster core will stretch the initially tangled magnetic field lines to form a draping layer with a magnetic field parallel to the front. Transport processes are significantly suppressed perpendicular to magnetic field lines in a plasma because charged particles get trapped and circle around the field liens with a very small gyroradius, much smaller than the Coulomb mean free path. This assumption was used to explain the narrow width of contact discontinuities and shocks in merging clusters and groups: in A3667 (Vikhlinin et al., 2001), A2146 (Russell et al., 2012), and RXJ0751.3+5012 (Russell et al., 2014). This explanation was supported by MHD numerical simulations including anisotropic heat conduction and assuming a uniform magnetic field perpendicular to the path of the infalling cluster carried out by Asai et al. (2005). They suggested that the magnetic field lines wrapping around the infalling subcluster suppress the heat conduction across them. Asai et al. argue that without magnetic field in the ICG a cold front cannot be maintained because isotropic heat conduction from the hot ambient plasma would rapidly heats the cold subcluster plasma.

The latest detailed study using long exposure (500 k) Chandra observations of the cold fronts in the core of the Virgo cluster found that the northern part of the front is < 2.5 kpc (99% confidence level, CL). Comparing the observations with MHD numerical simulations, the presence of Kelvin-Helmholtz instability would imply that the effective viscosity of the ICG is suppressed by more than an order of magnitude with respect to the isotropic Spitzer viscosity (Werner et al., 2015).

Detailed numerical simulations question the magnetic draping scenario for suppression of transport processes at cold fronts and shocks in the ICG. MHD simulations suggest that magnetic draping suppresses the conduction only by a factor of a few (ZuHone et al., 2013). Simulations also suggest, that magnetic draping is broken near the cold front due to tangled magnetic fields and the increased magnetic pressure (Ruszkowski et al., 2014).

A more straightforward explanation for the significantly suppressed transport processes is that a thin shock surface is developed where the kinetic energy of the colliding plasma is dissipated due to collective plasma instabilities. Fluctuations in the electron and ion distributions lead to electric currents which generate magnetic fields even in an unmagnetized plasma. As a consequence of these processes we expect the width of a shock in the ICG to be in the order of the ion inertial length,

$\begin{array}{ll}{\lambda }_{pi}=c/{\omega }_{pi}=2.33\times {10}^{-10}\text{pc\hspace{0.17em}}{\left[\frac{n_i}{{10}^{-3}{\text{cm}}^{-\text{3}}}\right]}^{-1/2},& (39)\end{array}$

where ω_pi and n_i are the plasma frequency and number density of ion i (e.g., Treumann, 2009; Bykov et al., 2015). We expect the width of cold fronts and shocks to be a few times this inertial length, which is many orders of magnitude less than the Coulomb mean free path (Equation 37). In addition, if external magnetic fields exist, the width of the shocks will be limited perpendicular to the magnetic field, by the gyroradius, for an ion is

$\begin{array}{ll}{r}_{gyro}\approx 2\times {10}^{-9}\text{pc}{\left[\frac{T_e}{{10}^8\text{K}}\right]}^{1/2}{\left[\frac{B}{1\mu \text{G}}\right]}^{-1},& (40)\end{array}$

which is of similar order as the inertial length (Equation 39).

4.4. Constraining Turbulence in the ICG from X-Ray Observations

As a consequence of the hierarchical structure formation, merging of massive objects generate large scale turbulence and bulk motion. Largest eddies in the order of 100s of kpc with velocities ~400 km s⁻¹ were found in cosmological simulations (e.g., Norman and Bryan, 1999). Similar results were found in numerical simulations of binary cluster mergers (e.g., Ricker and Sarazin, 2001). Turbulence plays an important role in determining the structure of clusters by transporting heat, and providing non-thermal pressure to the ICG.

Numerical simulations suggest that turbulent motions of the ICG caused by mergers and shocks provide a significant non-thermal pressure support which varies as a function of radius (e.g., Norman and Bryan, 1999; Dolag et al., 2005; Rasia et al., 2006; Vazza et al., 2006, 2009; Iapichino and Niemeyer, 2008; Lau et al., 2009; Molnar et al., 2010). Observations confirm that non-thermal pressure support is important in clusters at the core and the outer regions (e.g., Chiu and Molnar, 2012; Morandi and Limousin, 2012; Morandi et al., 2012; Umetsu et al., 2015a).

The contributions to non-thermal pressure support from turbulence and residual bulk motion generated by hierarchical structure formation, if not accounted for, introduce bias in cluster mass determinations, and therefore in cosmological parameters derived using clusters. Turbulence may also accelerate relativistic electrons, which are responsible for the emission in diffuse radio sources in clusters and amplify magnetic fields (Dolag et al., 2008; Ferrari et al., 2008). Turbulence generated by cluster mergers and AGN feedback is thought to be able to heat the cluster cores of cool core clusters and prevent them from overcooling and forming too many stars. Numerical simulations demonstrated that a large amount of energy is deposited in the central region of clusters due to a major merger providing a significant turbulent pressure support (about 10% of the total pressure; Paul et al., 2011).

Hydrodynamical flows become turbulent, when their Reynolds number is high. The Reynolds number is defined as the ratio of inertial forces to viscous forces. It can be approximated as Re ≈ ML∕λ, where M is the Mach number, L is the characteristic size of the cluster and λ is the relevant free mean path. We expect the ICG, where M is a few, L ≈ 1 Mpc and λ ≈ 1 kpc, Re is the order of 1000 assuming the Coulomb free mean path, or even larger if we take the reduction of the mean free path by magnetic field, is highly turbulent (e.g., Sarazin, 1988; Molnar, 2015).

With the new generation of high angular resolution X-ray telescopes on board Chandra and XMM-Newton it has become possible to study turbulence in the ICG for the first time. In the case of isotropic and homogeneous turbulence, a statistical model is possible, and it can be shown that the velocity energy spectrum, E_v, the kinetic energy per unit mass at wave number k, is $E_v(k)~{ϵ}^{2∕3}{k}^{-5∕3}$, where ϵ is the kinetic energy per unit mass (Kolmogorov, 1941). Schuecker et al. (2004) used the result for the gas pressure fluctuation spectrum, $E_p(k)~{ϵ}^{4∕3}{k}^{-7∕3}$, to derive constraints on turbulence based on X-ray observations of the Coma cluster of galaxies, and found that it is compatible with a Kolmogorov type turbulence spectrum ($E_v(k)~k^{-5∕3}$).

Recently Gaspari and Churazov (2013) used the power spectrum of the gas density fluctuations (δ = δρ∕ρ) derived from X-ray observations of the Coma cluster to constrain turbulence. They used N-body/hydrodynamical simulations (FLASH) including conduction with no viscosity to derive an empirical relation between the amplitude of the gas density fluctuation (δ = δρ∕ρ) spectrum, A_δ(k), defined as $A_{\delta }(k)=\sqrt{P_{\delta }(k)4\pi k^3}$, where P_δ(k) is the power spectrum, as a function of wavelength, k, and the characteristic Mach number of the turbulence, M_ch. They found that the normalization of the characteristic amplitude of the density fluctuation spectrum, is linearly proportional to the Mach number: A_δ(k)|_max ∝ M_ch. The characteristic Mach number was found to be M_ch ~ 0.45.

4.5. Constraining Turbulence and Resonant Line Scatterings from X-Ray Lines

It is very difficult to characterize turbulence in the ICG based on observations of X-ray emission lines. Since thermal broadening is proportional to $T_i^{-1∕2}$, and the amplitude of turbulence is independent of temperature, the best way to measure turbulence is to use emission lines of heavy elements with high abundance (to get as much photons in the line as possible). The different ionization stages (depending on the temperature of the ICG) of Iron seems to be the best choice to study turbulence.

Turbulence causes line broadening and a unique line profile, as well as shifts in the line centroid (Inogamov and Sunyaev, 2003). Turbulence suppresses the optical depth of resonant lines due to a shift in frequency caused by the Doppler effect, thus observations of resonant lines can also be used to study turbulence (Churazov et al., 2004; Gastaldello and Molendi, 2004). We illustrate the effect of turbulence on emission lines in the left panel in Figure 2 (from Zhuravleva et al., 2013). In this panel we show simulated spectra of the emerging line from the Perseus cluster with and without resonant scattering turbulence.

FIGURE 2

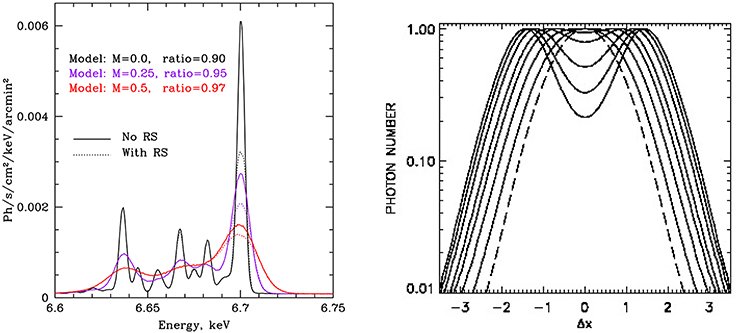
Figure 2. Comparison between different line shapes from clusters due to turbulence and resonant line scatterings. Left panel: Simulated spectra of the emerging line from the Perseus cluster with and without resonant scattering (solid and dotted lines), and with and without turbulence (M = 0.5, 0.25 and 0, in units of the Mach number of the turbulent velocity; Figure 6 from Zhuravleva et al., 2013). Right panel: Shapes of emerging lines due to resonant scatterings with different optical depths from Monte Carlo simulations. Solid lines represent emergent lines with central optical depths of τ₀ = 0.5, 1, 1.5, 2, 3, 4, and 5 (5 is the broadest). The un-scattered, thermally broadened emission line is shown with a dashed line (from Molnar et al., 2006). The frequency shift is expressed in units of the thermal Doppler shift (Δx = Δν∕Δν_D).

The maximum optical depth of the continuum radiation and most emission lines are very low (τ₀≲0.01), thus the emergent radiation is thin. However, as it has been pointed out by Gil'fanov et al. (1987), resonant lines of ions of heavy elements may have optical depths larger than unity in clusters. Strong resonance lines have large transition probabilities, and thus high probabilities of scattering in the high density core of clusters, and subsequently being reemited in a different direction, depending on their scattering distribution function. Photons in these lines suffer multiple scatterings, and as a result, the line shapes and intensities change (Gil'fanov et al., 1987; Shigeyama, 1998); moreover, the line amplitudes are reduced along the line of sight through the core of the cluster and enhanced through the outer regions.

Resonant line scatterings change the observed X-ray surface brightness distribution in a cluster as a function of the LOS optical depth. The X-ray surface density along a LOS close to the center of the cluster, for example, is reduced. Resonant scatterings also change the shape of the emergent line from clusters. We illustrate the effect of resonant line scattering on the line shape in the right panel in Figure 2 (for a detailed description see Molnar et al., 2006). As it can be seen from this figure, the line flattens at the line center, and at high central optical depths, τ₀, a unique double peaked line profile develops toward the cluster center.

Ignoring scatterings can cause an underestimate in the abundances based on resonance lines (see for example, Shigeyama, 1998; Akimoto et al., 2000). Scatterings can also polarize the emission lines (Sazonov et al., 2002). The line shape is also affected by gas motion in clusters. This can reduce the optical depth of all lines by Doppler broadening (Churazov et al., 2004). Therefore, resonance scattering on emission lines can be used to probe velocity fields and turbulence in clusters (for a review of the effects of resonant line scatterings on X-ray spectra see Churazov et al., 2010).

Using XMM-Newton observations, Sakelliou et al. (2002) found no sign for resonant scatterings in M87. On the other hand, Xu et al. (2002) found evidence for resonant line scatterings in NGC 4636 in the outskirts of the Virgo cluster. In the Perseus cluster resonant scatterings were ruled out based on an analysis of the Fe XXVI K lines (Churazov et al., 2004; Gastaldello and Molendi, 2004). However, Sanders et al. (2005) argue that the existence of Hα filaments in the core of Perseus suggests no turbulence. Based on resonance lines of Fe XXIV and Fe XXIII, Sanders et al. (2005) conclude that, in Perseus, resonance scattering may be the cause of the apparent central drop in metal abundances.

Constraints on turbulent velocities were derived by measuring the suppression of resonant line amplitudes due to scatterings (e.g., Werner et al., 2009). It is difficult to measure turbulence with the spectral resolution of today's X-ray detectors. Turbulence broadens the line profile due to the Doppler effect. Currently only the Reflection Grating Spectrometers (RGS1 and RGS2) on board of XMM-Newton provide the necessary effective area and spectral resolution to possibly measure line broadening due to turbulence. Spectroscopic observations of clusters with bright central emission (cool core clusters) were used to put upper limits on turbulence using RGS1 and RGS2 (Sanders et al., 2010, 2011). Recently Pinto et al. (2015) derived upper limits on turbulence in 44 groups and clusters of galaxies using XMM-Newton data. They found an upper limit of 500 km s⁻¹ for half of their sources, while a few objects were consistent with large turbulence with upper limits of about 500 km s⁻¹. Pinto et al. found a velocity broadening of ≳1000 km s⁻¹ (±1000 km s⁻¹) in one group of galaxies, NGC507, which is most likely due to previous merging activity. Turbulence < 500 km s⁻¹ may be caused by bubbles inflated by previous AGN activity (e.g., Brüggen et al., 2005). Larger turbulence is probably generated by merging due to hierarchical structure formation. Note that these results are subject to systematic errors due to the fact that the XMM-Newton RGS instruments are slitless spectrographs, and thus line broadening can also be caused by finite extension of the source. Observations carried out by the future mission Astro-H will not have this systematic effect.

Separation of the effect of line broadening due to turbulence and resonant line scattering can be performed based on line ratios of resonant and thin lines (e.g., Shang and Oh, 2013; Zhuravleva et al., 2013), as well as using their different line shapes (as demonstrated by Molnar et al., 2006). Mild turbulence may leave some lines with optical depth larger than unity, so that it remains possible to determine the optical depth from the line shapes. In such cases we could use the shapes of optically-thin lines as a template and calculate the broadening due to resonance line scattering. Resonant line scatterings can also be identified using line ratios between resonant lines and other lines, for example using intensity ratios between triplet lines of helium-like ions. The He like FeXXV K line triplet at 6.7 keV is especially useful due to the high relative abundance of Fe. In the left panel in Figure 3 we show the complex line structure of the FeXXV K line complex with and without resonant scattering (from Zhuravleva et al., 2013). The strongest line is the resonance line at 6.7 keV. Since the amplitude of the resonant line is reduced as a function of its optical depth, the ratio between these lines is proportional to the optical depth to resonant line scatterings. In the right panel in Figure 3 we illustrate the effects of resonant line scatterings and turbulence on the FeXXV K line complex. Here we show theoretical model spectra with and without resonant line scattering, as well as with and without turbulence (Zhuravleva et al., 2013). Points with error bars represent simulated data based on a 100 ks Astro-H observation of the core region (0.5′ ≤ r ≤ 1′) of the Perseus Cluster.

FIGURE 3

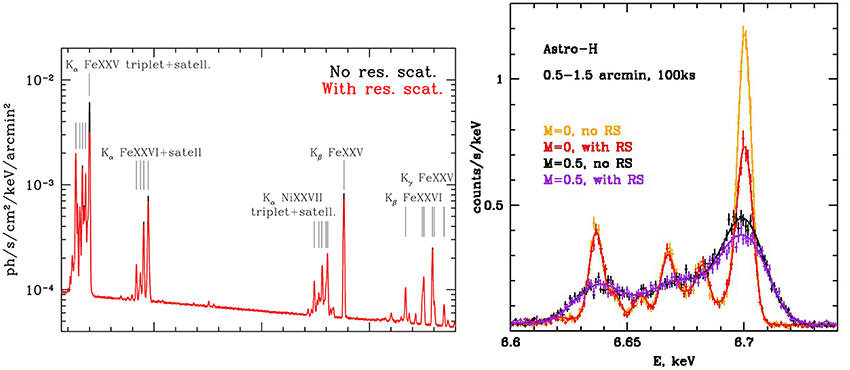
Figure 3. Left panel: Simulated spectrum around the Fe xxv line complex for the Perseus cluster with and without resonant scattering (black and red lines; the red lines cover most of the emission lines; Figure 4a from Zhuravleva et al., 2013). Right panel: Simulated spectra of an Astro-H observation of 100 ks of the core region of the Perseus Cluster (data points; from Zhuravleva et al., 2013). The solid lines represent theoretical model spectra with (red and magenta lines) and without (yellow and black lines) resonant line scattering and with (black and magenta lines) and without (yellow and red lines) turbulence.

Gaspari et al. (2014) using high-resolution hydrodynamical simulations concluded that Astro-H should be able to detect turbulence in the ICG, and suggested that, in massive clusters a 200 km s⁻¹ broadening of the Fe XXV emission line would be detectable. Ota et al. (2015) studied how well the Astro-H mission is going to be able to constrain bulk motion and turbulence in clusters. The did not take into account resonant line scatterings, which are not important outside of the core of clusters. They demonstrated that the spherically averaged velocity profiles can be derived within 20% error from Astro-H observations of the 6.7 keV Fe XXV line complex in clusters, however, they pointed out that even relaxed clusters, the significant azimuthal variations in the ICM velocities should be taken into account. Ota et al. also show that Astro-H should be able to directly measure the hydrostatic mass bias with an accuracy of ≲5%.

4.6. Large Scale Diffuse Radio Emission from Galaxy Clusters

The large scale diffuse radio emission due to synchrotron radiation has been observed in many galaxy clusters. This diffuse synchrotron emission indicates the existence of non-thermal electrons accelerated to relativistic energies by magnetic fields in the ICG. Diffuse radio emission in clusters can be divided into three main categories: halos, mini halos, and relics (for a recent review see Feretti et al., 2012). Radio halos and relics seem to be associated with merging clusters, mini-halos are concentrated at the center of some cool-core clusters usually containing a powerful radio galaxy. Non-thermal relativistic particles can be generated in cluster mergers by direct particle acceleration at the merger shocks or by indirect processes as a result of turbulence.

Radio halos are found at the center of merging clusters extending out to large radii, ≳1 Mpc. Their smooth radio emission is unpolarized with a steep power law spectrum, ∝ ν^−α (α = 1.2 − 2). Radio halo emission is probably due to turbulent acceleration of electrons, which is a random process similar to the second-order Fermi acceleration. This enhanced turbulence is thought to be generated by ongoing or a recent merger event (e.g. Fujita et al., 2003; Cassano and Brunetti, 2005). Brunetti and Lazarian (2011) carried out a detailed study of particle acceleration due to compressible hydrodynamical turbulence in magnetized ICG.

Radio relics extend to Mpc scales showing an elongated shape. Relics are located in the outer regions of merging clusters (e.g., the “Sausage”: CIZAJ2242.8+ 5301; van Weeren et al., 2010, and the “Toothbrush”: 1RXS 0603.3+4214; van Weeren et al., 2012). Radio emission from relics is highly polarized and have a steep spectrum. Relics indicate the existence of non-thermal electrons in the outskirts of clusters with field strength in the order of ~1μG. The radio emission from relics is likely due to a diffusive shock acceleration, a first order Fermi acceleration (e.g., Drury, 1983), generated by merger shocks. This mechanism assumes that the particles scatter back and forth crossing the shock surface and gain energy at each crossing, which is comparable to the energy of the particle (ΔE ~ E). The acceleration efficiency is mainly determined by the Mach number of the shock. The spectral index of the synchrotron emission, α, which can be derived from radio observations, is related to the index of the energy distribution as α = (p − 1) ∕ 2. From the index of the energy distribution, p, the compression ratio, r = ρ₂ ∕ ρ₁, can be derived, because it is related to the index of the electron energy distribution, p, N = E^−p, as p = (r + 2)∕(r − 1). Finally, the Mach number of the merging shock can be derived using the Rankine-Hugoniot jump conditions (for details see Section 5.1.1). Cosmological simulations suggest that emission from relics may be powered by reaccelerated fossil electrons (Pinzke et al., 2013).

Recently, the diffusive shock acceleration explanation for the origin of emission from radio relics has been challenged. The Mach numbers derived from spectral indexes of the radio emission from the relics in two clusters, 1RXS J0603.3+4214 (“Toothbrush cluster”) and CIZA J2242.8+5301, were found to be about 4, twice as large as those derived from XMM-Newton and Chandra observations (1RXS J0603.3+4214, the “Toothbrush cluster”: Ogrean et al., 2013 and CIZA J2242.8+5301: Ogrean et al., 2014). Also, Vazza et al. (2015) found that diffusive shock acceleration cannot explain the synchrotron radio emission from relics and the observed upper limits for the expected γ-ray emission from them simultaneously, unless unrealistically large magnetic fields are assumed (much larger than 10μG). However, note that, the Mach number derived from the gas temperature jumps at the shock based on X-ray observations may be significantly biased (Molnar et al., 2013b). The results of Vazza et al. (2015) depend on a lot of assumptions, and they used a simplified spherically symmetric semi-analytical model of expanding merger shocks in clusters to reconstruct the propagation history of shocks. Clearly, more work is necessary to clarify the particle acceleration mechanisms and their role in the generation of radio relics.

In principle, combining the synchrotron radio emission form relics and their γ, -ray emission, the ratio of kinetic energies between electrons and protons due to the acceleration, K_e/K_p, can be derived. We expect that relativistic protons accelerated by shocks will collide with thermal protons in the ICG, and generate pions and other mesons, p + p → p + p + nπ, and the charged pions will decay to produce electrons and positrons, ${\pi }^{\pm }\to e^{\pm }+{\nu }_{\left[e,\mu \right]}+{\bar{\nu }}_{\left[\mu ,e\right]}$, where e and μ is square brackets refer to electron and muon neutrinos, and the line over ν refer to their antiparticles. As of today, γ-ray emission has not been observed from galaxy clusters (e.g., Ackermann et al., 2014; Griffin et al., 2014; Zandanel and Ando, 2014).

4.7. Cluster Magnetic Fields from Radio Observations

The existence of magnetic fields in galaxy clusters has been established based on synchrotron emission from diffuse radio sources and Faraday rotation observations of polarized radio galaxies within or in background of clusters (e.g., Carilli and Taylor, 2002). A magnetized plasma is birefringent, i.e., the photon propagation speed depends on the orientation of its circular polarization (e.g., Spitzer, 1978). Synchrotron emission in a background radio galaxy produces linearly polarized photons, which can be represented as a sum of circularly polarized photons. Since circularly polarized photons propagate with different velocities in magnetized plasma, a rotation of the polarization plane will result. This is called Faraday rotation. The angle of the Faraday rotation is proportional to the rotation measure, R_B, and the wavelength of the photon,

$\begin{array}{ll}\Delta \phi =R_B{\lambda }^2,& (41)\end{array}$

where the rotation measure is defined, and expressed in radians m⁻², as

$\begin{array}{cc}\begin{array}{l}{R}_B=\frac{e^3}{2\pi m_e^2{c}^4}\int dz{n}_e{B}_{\parallel }=8.12\times {10}^{-6}\\ \int \left[\frac{dz}{1\text{kpc}}\right]\left[\frac{n_e}{{10}^{-2}{\text{cm}}^{-3}}\right][\frac{B_{\parallel }}{1\mu \text{G}}],\end{array}& (42)\end{array}$

where n_e is the electron number density, B_∥ is the magnitude of the magnetic field parallel to the LOS integral over z. The original polarization angle of the background radio emission is unknown, but since the amount of Faraday rotation depends on the photon wavelength, the difference in the polarization can be measured, and thus the cluster magnetic field estimated.

The first Faraday rotation measurements established that clusters of galaxies have a rotation measure of R_B ≈ 100 m⁻², which, assuming a characteristic electron density of $n_e=10^{-3}$ cm⁻³ and length of 500 kpc, gives B_∥ ≈ 0.1μG (Jaffe, 1980). In general, observations of the Faraday rotation indicate that the intra-cluster magnetic fields are of the order of 1–10 μG decreasing as a function of the distance from the center with high filling factors up to Mpc scale (e.g., Andernach et al., 1988; Giovannini et al., 1993; Bonafede et al., 2010, 2013; for a review see Feretti et al., 2012).

The luminosity of the synchrotron radiation can also be used to derive a lower bound on the magnetic field assuming the minimum energy of the emitting electrons required to produce the measured luminosity (Burbidge, 1959; for a detailed discussion see Miley, 1980). This minimum energy requirement is close to equipartition between the kinetic energy of electrons and the energy of the magnetic field, U_kin = (3/4)U_B, thus equipartition is often used as an approximation to the magnetic field. It is possible to estimate the magnetic field without the minimum energy requirement. Using radio and X-ray spectra of the Coma cluster and assuming particle acceleration models, the magnetic field was found to be smoothly declining from 2±1μG in the cluster center, to 0.3 ± 0.1μG at 1 Mpc, confirming the results based on the minimum energy requirement (Brunetti et al., 2001).

In principle, the magnetic field in clusters can be derived directly from observations of the radio synchrotron emission and the inverse Compton emission from the same non-thermal electron population, because the inverse Compton flux depends on the electron density, while synchrotron flux depends on the electron density and the magnetic field (Rephaeli, 1977; for a recent review see Rephaeli et al., 2008). The inverse Compton emission in the hard X-ray/γ-ray band has to be measured as an excess emission relative to the thermal emission from the cluster. This is a very difficult measurement, even with the new generation of satellites. Observations carried out using Swift and NuSTAR have not confirmed the detection of non-thermal emission from clusters (Wik et al., 2009, 2012, 2014; Gastaldello et al., 2015).

Magnetic fields play an important role in the ICG. They suppress transport processes (heat conduction, viscosity) and instabilities (Kelvin-Helmholtz) by reducing the mean free path from that derived from Coulomb collisions. Magnetic pressure, $P_M=B^2/4\pi$, where B is the magnetic field strength, may also contribute to the pressure equilibrium at the core and the outer regions of clusters (e.g., Laganá et al., 2010).

4.8. Non-Thermal Pressure from Multi-Wavelength Observations

As a consequence of ongoing hierarchical structure formation and various feedback mechanisms (AGN, star formation), we expect that the ICG is not in perfect hydrostatic equilibrium. Cosmological simulations demonstrated that the ICG may not be in strict hydrostatic equilibrium even in relaxed clusters (Evrard, 1990; Norman and Bryan, 1999). Simulations suggest that the non-thermal pressure support depends on the radial distance from the cluster center (Norman and Bryan, 1999; Rasia et al., 2004; Dolag et al., 2005; Rasia et al., 2006; Vazza et al., 2006, 2009; Iapichino and Niemeyer, 2008; Lau et al., 2009; Burns et al., 2010; Molnar et al., 2010; Suto et al., 2013; Nelson et al., 2014). Based on simulations, Kravtsov, et al. (2002) found that in relaxed clusters the non-thermal pressure support increases with distance from the cluster center reaching about 20–30% at the outer regions. Analyzing high-resolution cosmological simulations, Molnar et al. (2012) found a significant non-thermal pressure contribution to the equilibrium pressure, ~30%, at the center of relaxed clusters, decreasing to a minimum in the core region (0.1R_vir), and an increasing up to ~30–45% at the virial radius.

High resolution cosmological simulations were used to parameterize the contribution to the equilibrium pressure from gas turbulence as a function of radius (Shaw et al., 2010; Battaglia et al., 2012). It has been shown recently, that if the radial coordinate is scaled by the mass over density relative to the mean mass density and not the critical density, the contribution to the non-thermal pressure from turbulence can be derived with no direct dependence of the redshift, however, a small correction is necessary due to the mass accretion history of clusters (Nelson et al., 2014).

Random turbulent flows remaining from previous merger events were suggested to be the main contributions to the non-thermal pressure (Rasia et al., 2004; Lau et al. 2009). Acceleration of the gas was also suggested as the origin of the lack of hydrostatic equilibrium in clusters based on the Euler equation instead of the Jeans equation (Suto et al., 2013).

Multiwavelength observations confirm the lack of strict hydrostatic equilibrium in relaxed galaxy clusters. The most straightforward way to test the assumption of hydrostatic equilibrium and quantify the non-thermal pressure contribution is to derive the pressure necessary for hydrostatic equilibrium from the total mass determined from gravitational lensing observations using the equation of hydrostatic equilibrium,

$\begin{array}{ll}\nabla P_{HE}(r)=-{\rho }_g\nabla \Phi (r),& (43)\end{array}$

where Φ(r) is the potential generated by all matter. The gas thermal pressure, P_th is derived from gas density and temperature distribution using X-ray and/or SZ observations, in practice (in principle high resolution multi-wavelength SZ observations could also be applied), assuming the ideal gas law P ∝ ρ_gT_g. The difference defines the non-thermal pressure contribution: P_nth = P_HE − P_th. This method was used to test the strict hydrostatic equilibrium in galaxy clusters A1689 (Molnar et al., 2010; Morandi et al., 2011; Limousin et al., 2013; Umetsu et al., 2015a), A383 (Morandi and Limousin, 2012), A1835 (Morandi et al., 2012), and MS 2137 (Chiu and Molnar, 2012).

The exact physical origin of the lack of hydrostatic equilibrium in clusters is currently a subject of active research. The most important mechanisms proposed to provide non-thermal pressure support in galaxy clusters are turbulence, magnetic and cosmic ray pressure. These contributions may be separated, for example, assuming a functional form for them and fitting the profiles to observations. Assuming spherical geometry, Laganá et al. (2010) adopted this method to separate the different contributions to non-thermal pressure using X-ray and lensing observations of clusters. Their results suggest that all three components contribute significantly to the non-thermal pressure, contributions from magnetic and cosmic ray pressure dominating in the center of cool core clusters. However, as they note, their results may be subject to systematic effects due to the parameterization used for these contributions. Non-thermal pressure support from different physical mechanisms may be related to each other. Magneto-hydrodynamical simulations assuming anisotropic conduction suggest that magneto-thermal instability can drive turbulence which can provide 5–30% of the hydrostatic equilibrium pressure to balance gravity in the outer parts of clusters (Parrish et al., 2012).

The physical understanding of non-thermal pressure support is essential in using clusters of galaxies as cosmological probes. Ignoring non-thermal pressure support when constructing scaling relations which link the cluster observables (X-ray luminosity, temperature, etc). to the mass distribution predicted by cosmological models leads to biases in the derived cosmological parameters (e.g., Rasia et al., 2006; Battaglia et al., 2012; Nelson et al., 2014). Understanding non-thermal pressure support is also important when using the angular power spectrum of the thermal SZ effect for cosmology (e.g., Bhattacharya et al., 2012; Hill and Sherwin, 2013; Crawford et al., 2014; George et al., 2015). The contribution originating from non-thermal pressure to the amplitude of the thermal SZ power spectrum may reach 60% (Battaglia et al., 2010; Shaw et al., 2010; Trac et al., 2011).

We discuss how the non-thermal pressure support can be constrained using detailed numerical simulations and multi-frequency observations of merging galaxy clusters in Section 6.1.

5. Kinematics of Merging Galaxy Clusters

In this section we discuss how the velocity of the different mass components in merging clusters can be derived. We start with an approximation which can be used to derive the 3D velocity of the infalling cluster, then we describe different methods to derive the tangential and radial velocity components, and shock velocities of the gas.

5.1. Relative 3D Velocity Based on O/NIR Spectroscopy: an Approximation

The 3D relative velocity at the phase of observation of a merging cluster can be approximated using a simplified model of gravitational collapse introduced by Beers et al. (1982). This approximation is very useful when no additional information is available for the merging cluster, and it can also be used as a check for other methods (e.g., Molnar et al., 2013b).

This dynamical model assumes that a spherical perturbation with the total mass of the merging cluster is expanding with the universe and then collapses. This model has a physical meaning until the first core passage, however, assuming time symmetry, it may be used after that as a rough approximation. If no bound model can be found, there is still an unbound solution, also considered sometimes when applying this model. However, this out-going solution describes an overdensity perturbation expanding with the universe and never collapsing, which, in a case of a merging cluster, has no physical meaning. The lack of a bound solution means that the observed merging system may be in contradiction with the ΛCDM models of structure formation.

This dynamical model treats the infalling cluster as a test particle moving in the gravitational field of a main cluster with a total mass of the system in an expanding background. It assumes that the test particle start out at zero spatial separation on a radial orbit ignoring a likely finite angular momentum of the system and any tidal forces due to the large scale structure. In this case the system can be described by the well-known parametric solution of the spherical collapse model based on the general relativistic Einstein's field equations,

$\begin{array}{ll}R=\frac{R_{max}}{2}(1-\cos \chi )\hfill & (44)\hfill \end{array}$

$\begin{array}{ll}V={\left[\frac{2GM}{R_{max}}\right]}^{1/2}\frac{\sin \chi }{1-\cos \chi }\hfill & (45)\hfill \end{array}$

$\begin{array}{ll}t={\left[\frac{R_{max}^3}{8GM}\right]}^{1∕2}\left(\chi -sin\chi \right),\hfill & (46)\hfill \end{array}$

where M is the total mass of the system, R and V are the 3D distance and the relative velocity between the two components, t is the time elapsed since zero separation, R(t = 0) = 0, which is assumed to be equal to the age of the universe at the redshift of the merging system, R_max is the distance at maximum separation, G is the gravitational constant, and χ is the development angle (e.g., Peebles, 1993).

The rotation angle between the line of collision and the plane of the sky, θ, connects the observables: R_p, the distance between the two components projected to the plane of the sky and relative radial velocity, V_r, to the equations of the spherical collapse model: R_p = Rcosθ and V_r = Vcosθ. Substituting the observables into the equations above, we can derive a relation between the rotation angle, θ and the development angle (Gregory and Thompson, 1984), we find

$\begin{array}{ll}tan\theta =\frac{t{V}_r}{R_p}\frac{{(cos\chi -1)}^2}{sin\chi (\chi -sin\chi )}.& (47)\end{array}$

Using Equations (44–47), the development angle, χ and the 3D velocity, V, can be derived.

This model has been used to estimate the relative velocities of merging clusters recently (e.g., Bourdin et al., 2011; Girardi et al., 2011; Maurogordato et al., 2011; Molnar et al., 2013b). Molnar et al. (2013b) compared 3D relative velocities derived from this simplified dynamical model and from full N-body/hydrodynamical simulations for A1750, a merging cluster before the first core passage (see Discussion in Section 6.2), and found that the simplified model provided a good approximation.

5.1.1. Shock Velocities of the Gas Component from Observations of Radio Relics

The 3D shock velocity of the gas in merging clusters can be derived using spectroscopic observations of synchrotron radiation from radio relics (for a recent review see, e.g., Feretti et al., 2012). Radio relics, located in the outer regions of merging clusters extend to Mpc scales showing an elongated shape (e.g., the “Sausage”: CIZAJ2242.8+ 5301 van Weeren et al., 2010, and the “Toothbrush”: 1RXS 0603.3+4214 van Weeren et al., 2012). Radio emission from relics is highly polarized and has a steep spectrum. Relics indicate the existence of non-thermal electrons accelerated to relativistic energies by magnetic fields located in the outskirts of clusters with field strength in the order of ~1μG. The radio emission from relics is likely due to first order Fermi acceleration generated by merging shocks. Cosmological simulators suggest that emission from relics may be powered by reaccelerated fossil electrons (Pinzke et al., 2013).

Assuming that the electrons are accelerated via the first–order Fermi acceleration mechanism (e.g., Drury, 1983), the compression ratio, r = ρ₂/ρ₁, is related to the index of the electron energy distribution, p, N = E^−p, as p = (r + 2)/(r − 1). This is a diffusive mechanism, the particles scatter back and forth crossing the shock surface and gain energy at each crossing, which is comparable to the energy of the particle (ΔE ~ E). The acceleration efficiency is mostly determined by the Mach number of the shock. The spectral index of the synchrotron emission, which can be derived from radio observations, is related to the index of the energy distribution as α = (p − 1)/2. Thus, the compression ratio can be derived from radio observations.

Using the Rankine-Hugoniot jump conditions for the shock, the compression ratio can be expressed as a function of the Mach number of the shock as

$\begin{array}{ll}\frac{1}{r}=\frac{2}{\gamma +1}\frac{1}{M^2}+\frac{\gamma -1}{\gamma +1},& (48)\end{array}$

where the Mach number, M = M₁ = v₁/c_s1, where v₁ and c_s1 are the gas velocity relative to the shock and the sound speed in the pre-shocked gas. The ICG is assumed to be monatomic in most applications, thus γ = 5/3. The speed of the pre-shocked gas v₁ (and thus the shock speed in the frame of the pre-shocked gas, v_sh = |v₁|) and the speed of the shocked gas, v₂, can be derived from the compression ratio, r = v₁/v₂. This method was used by Lindner et al. (2014) to estimate the relative velocity of the infalling subcluster in El Gordo assuming that the NW relic is associated with the merger shock. Note, however, that our simulations based on the observed X-ray morphology (Molnar and Broadhurst, 2015) show that the NW relic is on the opposite side of the merging system, thus it is not related to the merging shock directly. Also, the shock velocity may not be a good approximation for the relative velocity of the dark matter components of a merging system. It has been demonstrated, that the velocity of the shock front relative to the gas of the main cluster may be very different from the velocity of the infalling cluster relative to the main cluster (e.g., Springel and Farrar, 2007).

5.2. Tangential Velocities

5.2.1. Tangential Velocities of the Dark Matter from Radio Observations

Tangential velocities of the components of merging clusters, in principle, can be derived based on the Birkinshaw-Gull (BG) effect (first derived by Birkinshaw and Gull, 1983). The BG effect, the changes in the CMB caused by frequency shifts due to moving gravitational lenses, can be expressed as

$\begin{array}{ll}\frac{\Delta \nu }{{\nu }_0}={\gamma }_v{\beta }_T^L·\delta ,& (49)\end{array}$

where ${\gamma }_T^L=v_T^L/c$, and δ is the bend angle due to gravitational lensing. In the case of a spherical cluster, this reduces to

$\begin{array}{ll}\frac{\Delta \nu }{{\nu }_0}={\gamma }_v{\beta }_T^L\delta cos\phi ,& (50)\end{array}$

where φ is the angle in the sky measured from the direction of the tangential velocity of the moving lens.

The frequency change due to the BG effect, taking the motion of the source and the observer into account, in first order in velocity (FOV), was derived by Wucknitz and Sperhake (2004). They obtained:

$\begin{array}{ll}\frac{\Delta \nu }{{\nu }_0}=\left[{\beta }_T^L-\frac{D_{LS}}{D_{OS}}{\beta }_T^O-\frac{D_{OL}}{D_{OS}}\frac{1+z_L}{1+z_S}{\beta }_T^S\right]·\delta ,& (51)\end{array}$

where β_T = v_T/c and D denote tangential velocity and angular diameter distance, and the indices, O, L, and S refer to the observer, the lens, and the source. Equation (51) clearly shows that the frequency shift depends on the relative velocities between the source, the lens, and the observer, and it is zero when the quantity in the bracket vanishes. We expect that the peculiar velocities of the field galaxies, especially at large redshifts, are quite small. The peculiar velocity of the observer (our Heliocentric velocity relative to the CMB) is only $c{\beta }^O=v^O=369.0\pm 0.99$ km s⁻¹ (Hinshaw et al., 2009), and we can measure only tangential velocities on the order of a few 1000 km s⁻¹, thus we can ignore the last two terms in most applications, and use Equation (49) (e.g., Molnar et al., 2013a). In principle, the BG effect can be used to derive our peculiar velocity relative to CMB using a sample of massive galaxy clusters.

However, it is very difficult to measure the BG effect using individual clusters because the bending angle generated by a massive galaxy cluster is ≲1′, thus the frequency shift is very small: $\Delta \nu /{\nu }_0\lesssim {10}^{-6}{v}_T/(1000{\text{km s}}^{\text{-1}})$, or ΔT_BG ≲ ±3μK in temperature units (e.g., Molnar and Birkinshaw, 2000). The sensitivity of the SZ instruments on Planck is in the order of 1μK, but have low angular resolution. A statistical measurement of clusters in a bulk flow may still be possible by stacking clusters. The BG effect in individual clusters can be measured only with high-angular resolution radio telescopes sensitive to μK signals on large angular scales, which may be possible based on imaging observations by the next generation ground based radio interferometers, such as, for example, the Atacama Large Millimeter/Submillimeter Array (ALMA).

Although the frequency change due to the BG effect is small, it still would be important to measure it because no other methods exist to constrain tangential motion of the main mass component, the dark matter, of clusters. Velocity fields of massive objects derived from observations can be compared to those predicted by different cosmological models, and thus they provide an important test for cosmological models.

5.2.2. Tangential Velocities of the Dark Matter from O/NIR Observations

Optical/Near infrared (O/NIR) observations can be used to derive tangential velocities of the main mass components (essentially the dark matter components), in principle, based on frequency changes due to the BG effect. The frequency shifts of emission lines from individual background galaxies caused by the BG effect cannot be measured, because frequency shifts due to other effects are not known (e.g., cosmological redshift, peculiar velocity). However, Molar and Birkinshaw (2003) suggested that the BG effect may be used to derive tangential velocities of clusters by measuring frequency shifts between multiple images of the same background galaxy using high-resolution spectroscopic observations.

Following up this idea, Molnar et al. (2013a) demonstrated that the tangential velocity of the “bullet” in the Bullet cluster may be measurable using spectra observed by the new generation high-spectral resolution ground based interferometer, ALMA. In merging galaxy clusters, the frequency shifts due to the different moving components can be added together, as a good approximation, because the shifts are small. In a binary merging cluster, such as the Bullet cluster, Equation (49), becomes, in velocity units,

$\begin{array}{ll}V(x,y)={\nu }_{T1}·{\delta }_1+{\nu }_{T2}·{\delta }_2,& (52)\end{array}$

where the 2D vector fields v_{T1, 2} and δ_{1, 2} represent the tangential velocities and the deflection angles of the main cluster (1) and the bullet (2). The difference between the maximum and minimum frequency shifts due to the tangential motion of the bullet is 1.2 km s⁻¹.

5.3. Radial Velocities

5.3.1. Radial Velocities of the Galaxy Components from Optical Spectroscopy

Spectroscopic observations with the new generation of ground based observatories make it possible to study substructure and galaxy kinematics in galaxy clusters based their phase-space distribution. Due to observational constraints, the phase space coordinates for each galaxy is reduced to two coordinates in the configuration space (the angular coordinates in the sky) and the LOS velocity derived from the redshift of the galaxy (e.g., Owers et al., 2011; Boschin et al., 2013; Girardi et al., 2015).

The most straightforward way to derive relative radial velocities of the galaxy components in merging clusters is to measure the Doppler shift using O/NIR spectroscopy. The Doppler shift between two emission lines is proportional to the LOS relative velocity, v_r:

$\begin{array}{ll}\frac{{\nu }_2-{\nu }_1}{{\nu }_1}=\frac{\Delta {\nu }_{1,2}}{{\nu }_1}=\frac{{\nu }_r}{c},& (53)\end{array}$

where ν₁ and ν₂ are the frequencies of the line centers. If we assume that the subclusters are at the same distance from us, the observed redshift of a galaxy can be decomposed to a cosmological term due to the expansion of the universe and to a Doppler shift due to the LOS velocity of the galaxy. This is a good approximation, because, if two clusters seem to interact, the cluster centers should be only a few Mpc away form each other, and ignoring this distance introduces only ~100 km s⁻¹. error in the measured radial velocities. Note, that in principle, it is possible to correct for this effect if we model the merging system using full N-body/hydrodynamical simulations. Combining these spectroscopic measurements with a dynamical analysis, we can determine which component is closer to us and which is farther.

As an example, we show the radial velocity distribution in two merging clusters: A2744 and A1750 in Figure 4 (left and right panels; from Owers et al., 2011 and Molnar et al., 2013b). Gaussian fits were used to determine the relative radial velocities of the subclusters in both clusters. A Gaussian distribution is often assumed for galaxy velocities in clusters because they are expected to relax to an equilibrium configuration. This may be a good assumption around the core region even in merging clusters. Owers et al. (2011) used the Kayes Mixture Model algorithm to fit Gaussians to the galaxy velocity distributions near the center of the two components of A2744. We show their results on the left panel in Figure 4 for the main cluster and the northern component. The northern component is closer to us moving away from us with a radial velocity of ~2900 km s⁻¹ relative to the main component. In the right panel, we show the velocity distribution of all galaxies in the field of A1750, as well as Gaussian fits to the galaxy velocities extracted near the core of the two subclusters. A dynamical analysis of A1750 based on N-body/hydrodynamical simulations shows that the southern subcluster is closer to us moving away form us toward the northern component with a radial velocity of ~960 km s⁻¹ (Molnar et al., 2013b).

FIGURE 4

Figure 4. The distribution of number of galaxies as a function of LOS velocity in two merging clusters of galaxies. Left panel: Distribution of galaxies for two partitions in A2744 are shown in green and red lines; dashed line represents the sum of the two Gaussians (from Owers et al., 2011). Right panel: Dash-dotted line shows all galaxies in the area of A1750. Number distribution of galaxies around the two centers of the merging cluster are shown with solid and dashed lines (from Molnar et al., 2013b).

5.3.2. Radial Velocities of the ICG from X-Ray Spectroscopy

The relative radial velocity of the gas components in merging clusters can be derived from high resolution X-ray spectroscopy based on the Doppler shift between emission lines using Equation (53), where the frequencies of the line centers, ν₁ and ν₂, are usually expressed in keV in X-ray astronomy (e.g., as in the left panel in Figure 5). However, with the present spectral resolution of X-ray instruments, this is a difficult measurement with substantial systematic errors.

FIGURE 5

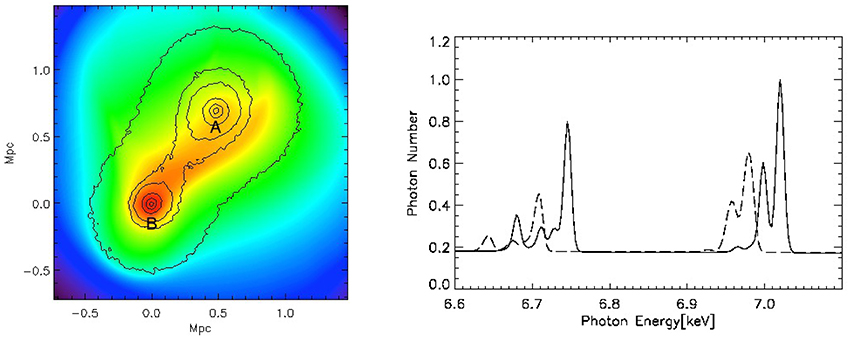
Figure 5. Left panel: X-ray surface brightness image based on an N-body/hydrodynamical simulation (FLASH) for the merging cluster El Gordo (from Molnar and Broadhurst, 2015). Black contours represent the dark matter distribution. The dark matter centers of the main and the infalling cluster are marked with A and B. Right panel: Simulated spectra around the Fe K line complex extracted from our FLASH simulation (shown in the left panel) around A and B; dashed and solid lines). The frequency shift due to the relative LOS velocity (1900 kms⁻¹) between A and B can be seen clearly.

The frequency change due to Doppler shift was used to derive the relative velocity between the main and infalling cluster in A2256 by Tamura et al. (2011) using the XIS instrument on Suzaku, which is appropriate for extended sources. They found a relative velocity of v_r = 1500±300(stat)±300(sys) km s⁻¹ (with statistical and systematic errors) between these components. The future X-ray mission Astro-H will have a high spectral resolution of ~7 eV (compare the spectral resolution of 120 eV of the XIS on Suzaku at 6 keV photon energy), and reduced systematics, which will make it an ideal tool to measure radial velocity differences between the gas components of merging clusters, and study radial gas motion in clusters in general.

As an illustration of the capabilities of the Astro-H X-ray mission, we show a simulated X-ray surface brightness image of El Gordo based on FLASH simulations and simulated spectra associated with the two components of this massive merging cluster in Figure 5 (Molnar and Broadhurst, 2015). In the left panel, the false color image is the X-ray emission, the black contours represent the dark matter distribution. The projection angle for the simulation was chosen to reproduce the observed features this system the best. The infalling cluster is moving from north-west toward south-east, just passed the core of the main cluster. The dark matter centers of the main and the infalling clusters are marked with A and B. The LOS gas radial velocity difference between A and B derived from the best fit simulation was found to be Δv_r = 1900km s⁻¹. This causes a large shift due to Doppler effect in the spectrum, as it is illustrated in the right panel in Figure 5. In this panel we show spectra extracted from simulation generated by APEC X-ray emission models including thermal broadening and the Doppler shift due to the line of sight motion of the ICG. The areas of the extraction regions were chosen to give about the same counts. The spectral resolution of ~7 eV of Astro-H should be sufficient to measure a relative velocity of few hundred km s⁻¹ in merging clusters.

5.3.3. Radial Velocities of the ICG from the KSZ Effect

The change on the CMB due to the LOS motion of the galaxy cluster, the kinematic SZ (KSZ) effect (Sunyaev and Zel'dovich, 1980) can be expressed as a fractional radiation temperature change at frequency ν,

$\begin{array}{ll}\frac{\Delta T_{KSZ}(\nu )}{T_{CMB}}=-\frac{x_{\nu }^2{e}^x}{{(e^{x_{\nu }}-1)}^2}\frac{v_r}{c}\tau ,& (54)\end{array}$

where the dimensionless frequency is x_ν = h_P ν ∕ (k_B T_CMB), T_CMB is the temperature of the CMB, and τ is the LOS optical depth. In the Rayleigh-Jeans frequency regime, it becomes simply

$\begin{array}{ll}\frac{\Delta T_{KSZ}^{RJ}(\nu )}{T_{CMB}}=-\frac{{\nu }_r}{c}\tau .& (55)\end{array}$

Relativistic corrections for the KSZ effect were also calculated and found to be small (Nozawa et al., 1998b).

It is very difficult to measure of the KSZ effect due to its small amplitude. The KSZ signal was not detected statistically using WMAP and Planck observations, only upper limits were placed on the rms in the peculiar velocities of galaxy clusters (Osborne et al., 2011; Planck Collaboration et al., 2014). Hand et al. (2012) found evidence for the KSZ effect using statistical methods. They used maps derived from Atacama Cosmology Telescope (ALMA) observations and identified galaxy clusters based on a luminous galaxy catalog derived from the Baryon Oscillation Spectroscopic Survey, (part of the Sloan Digital Sky Survey III).

Measurements of the KSZ effect in individual massive clusters have been proven even more difficult. In general, the upper limits on radial peculiar velocities derived based on the KSZ effect were large, and no significant detections were reported (e.g., Mauskopf et al., 2012; Mroczkowski et al., 2012; Zemcov et al., 2012).

The first significant detection of the KSZ effect was performed by Sayers et al. (2013) using Caltech Submilimeter Observatory/Bolocam observations of MACS J0717.5+3745 in two frequency bands: 140 and 268 GHz (see also Mroczkowski et al., 2012). Sayers et al. derived a radial peculiar velocity of v_r = +3450 ± 900 km s⁻¹. This result is in a good agreement with that based on optical spectroscopy: ${\nu }_r=+{3238}_{-242}^{+252}$ (Ma et al., 2009).

5.4. Relative Velocity of the Gas Component in Merging Clusters

When the main plane of the collision (the plane containing the two mass centers and the relative velocity vector) is close to the plane of the sky, shocks and contact discontinuities generated by the collision can be clearly identified and analyzed, and the shock velocity of the gas can be derived. Cold fronts have been found in many galaxy clusters (for review see Markevitch and Vikhlinin, 2007; Owers et al., 2009; Ghizzardi et al., 2010). Shock fronts have been detected only in a few merging clusters besides the Bullet cluster (e.g., A520: Markevitch et al., 2005; A754: Macario et al., 2011; A2744: Owers et al., 2011; A2146: Russell et al., 2012; 1RXS J0603.3+4214, the “Toothbrush”: Ogrean et al., 2013; RXJ0751.3+5012: Russell et al., 2014; CIZA J2242.8+5301: Ogrean et al., 2014).

5.4.1. Velocity of the Gas from Merging Shocks

Shocks in the intracluster plasma are expected to be collisionless because the mean free path of particles is large. A thin shock surface is developed where the kinetic energy of the colliding plasma is dissipated due to collective plasma instabilities. Fluctuations in the electron and ion distributions lead to electric currents which generate magnetic fields even in an unmagnetized plasma. As a consequence of these processes we expect the width of a shock in the ICG to be in the order of the ion inertial length, λ_i = c∕ω_pi, where ω_pi is the plasma frequency for ion i (e.g., Treumann, 2009). In addition, if external magnetic fields exist, the width of the shocks will be limited by the gyroradius perpendicular to the magnetic field. Cosmological simulations suggest that the shocked gas in clusters is heated up only to mildly relativistic temperatures with T_shock ≲ 100 keV even for high infall velocity shocks, as merger simulations indicate (e.g., Molnar et al., 2012).

When two clusters collide, first a contact discontinuity forms where the edges of the ICG (at the accretion shock of each cluster) of the two components touch. This contact surface is generated because the two distinct gas components cannot penetrate each other. As the two clusters approach each other, the gas on the two sides get compressed and reach near pressure equilibrium (there are some contributions from ram pressure), The compressed gas pushes against the undisturbed ICG, and when the velocities on both sides exceed the sound speed in the gas, two shocks are formed. As the collision proceeds, the infalling cluster passes through the core of the more massive main component, and a bow shock forms as it reaches the outer regions of the gas of the main cluster, where the temperature drops and thus the sound speed is lower, The most famous example of a merging cluster at this stage is the Bullet cluster (see left panel in Figure 1).

An upper limit for the Mach numbers we expect in merging clusters can be derived by assuming that the infall velocity of the smaller subcluster would be about the escape velocity, v_esc. Based on this argument, we obtain M ≲ v_esc ∕ c_s, where c_s is the sound speed in the gas of the main cluster, thus we expect the Mach number to be M ≲ 4. However, this is an overestimate for two reasons: (1) massive clusters collect matter from a region of about 10 Mpc in radius, not from infinity; (2) the expansion of the Universe reduces the infall velocity derived applying Newtonian mechanics.

Assuming that no energy is lost at the shock due to radiation, particle acceleration, etc., the well-known Rankine–Hugoniot jump conditions across a shock front would determine the physical properties of the gas after the shock passed (Rankine, 1870; Hugoniot, 1889). Since the characteristic lengths of the physical processes that determine the properties of the shock are usually much smaller than the curvature of the shock, we can assume that the shock surface is flat. It is convenient to choose a coordinate system which is moving with the shock velocity (so v_sh = 0). In this coordinate system, the speed of the pre-shocked gas, v₁ = −v_sh, where v_sh is the speed of the shock as it is moving in the frame of the pre-shock gas. We use indices 1 and 2 for the gas properties in the pre- and post-shock gas hereafter. Integrating the mass, momentum and energy conservation equations, the jump conditions can be derived:

$\begin{array}{l}{\rho }_1{\nu }_1={\rho }_2{\nu }_2\hfill \\ P_1+{\rho }_1{\nu }_1^2=P_2+{\rho }_2{\nu }_2\hfill \\ h_1+\frac{1}{2}{\nu }_1^2=h_2+{\rho }_2{\nu }_2,\hfill & (56)\hfill \end{array}$

where h_i = ϵ_i + P_i ∕ ρ_i is the enthalpy, and ϵ_i is the internal energy per unit mass of the pre- and post-shock gas (i = 1 or 2). Assuming that the gas is a perfect fluid, ϵ = [1∕(γ − 1)]P∕ρ, where γ is the adiabatic index (the ratio of the specific heats). In the case of the almost fully ionized ICG, which can be regarded as a monatomic ideal gas, γ = 5∕3. From Equation (56), we obtain the jump conditions:

$\begin{array}{l}\frac{P_2}{P_1}=\frac{2\gamma }{\gamma +1}{M}^2-\frac{\gamma -1}{\gamma +1}\\ \frac{{\rho }_1}{{\rho }_2}=\frac{1}{r}=\frac{2}{\gamma +1}\frac{1}{M^2}-\frac{\gamma -1}{\gamma +1},& (57)\end{array}$

where r is the compression, r = ρ₂ ∕ ρ₁ = v₁ ∕ v₂, with a maximum value of 4, and M is the Mach number in the pre-shocked gas, M = M₁.

The temperatures and densities can be determined from X-ray spectroscopy. The compression can be derived from the measured X-ray temperature,

$\begin{array}{ll}\frac{1}{r}={\left[\frac{1}{4}{\left(\frac{\gamma +1}{\gamma -1}\right)}^2{\left(\frac{T_2}{T_1}-1\right)}^2+\frac{T_2}{T_1}\right]}^{1∕2}-\frac{1}{2}\left(\frac{T_2}{T_1}-1\right),& (58)\end{array}$

as suggested by Markevitch et al. (1999). The compression can be used to derive the Mach number from the temperature jump using

$\begin{array}{ll}{\nu }_{sh}=\frac{r}{{(r-1)}^{1/2}}{\left[\frac{k_B{T}_1}{\mu m_p}\left(\frac{T_2}{T_1}-\frac{1}{r}\right)\right]}^{1/2},& (59)\end{array}$

where μ is the mean molecular weight. This method was used to determine shock velocities in several clusters (e.g., Markevitch et al., 1999; Markevitch and Vikhlinin, 2001).

The Mach number can be derived from the shock compression, r = ρ₂∕ρ₁, determined from X-ray observations using the Rankine–Hugoniot jump conditions as

$\begin{array}{ll}M(r)={\left[\frac{2r}{\gamma +1-r(\gamma -1)}\right]}^{1∕2},& (60)\end{array}$

and, using the Mach number, the shock velocity can be derived from the pre-shock sound speed obtained from X-ray observations as v_sh = Mc_s1. The relative velocity of the infalling cluster can be derived assuming that it is the same as the shock velocity, v₂ = v_sh, although this has been shown to be an overestimate (e.g., Springel and Farrar, 2007). The Mach number can also be derived from the pressure jump based on the Rankine-Hugoniot jump conditions, as

$\begin{array}{ll}M={\left[\frac{(\gamma +1)P_2∕P_1+\gamma -1}{2\gamma }\right]}^{1∕2}.& (61)\end{array}$

In the case of strong shocks, the Mach number and the shock velocity are well constrained by the pressure jump, Equation (61), since these quantities grow without limit with increasing Mach number. The Mach number in weak shocks is more sensitive to small changes in the compression, thus, in this case, Equation (60) can be used. Using these techniques, the shock velocities have been found in the range of 2000–5000 km s⁻¹ (e.g., Markevitch et al., 2002, 2005; Russell et al., 2012).

In principle, the opening angle, θ_M, of the Mach cone can also be used to derive the Mach number, if the shock is well visible: M = 1∕ sinθ_M. This method is not too reliable, however, since pressure gradients and substructure affect this simple scaling with angle. The distance to the stagnation point on the contact discontinuity (separating the two gas components of the colliding clusters) from the mid point of the bow shock, d_st (connecting the line of the stagnation point and the center of a spherical infalling cluster) and the radius of the curvature of the contact discontinuity, R_cd, can also be used to derive the Mach number, since the ratio d_st∕R_cd is a function of M² − 1 for a spherical discontinuity (Schreier, 1982). Due to the fact that the subcluster is not a hard sphere, the existence of pressure gradients, substructure, ram pressure stripping, and substructure makes it difficult to use this method with accuracy.

5.4.2. Velocity of the Gas from Contact Discontinuities

Contact discontinuities (cold fronts) following the bow shock in merging clusters can also be used to derive the physical parameters of the gas (for a review see Markevitch and Vikhlinin, 2007). As the infalling subcluster gas is pushing the gas of the main cluster ahead, a shock forms if the Mach number, M = M₁ = v₁∕c_s1 > 1, where v₁ and c_s1 are the speed and sound speed in the pre-shock gas. At the center of the contact discontinuity, where the flow of the gas of the main cluster is separated and starts flowing around the gas of the infalling cluster, there is a zero velocity point (relative to the moving cluster), which is called the stagnation point. The pressure ratio of at the stagnation point, P_st, and the pre-shock gas, P₁, can be expressed as

$\begin{array}{ll}\frac{P_{st}}{P_1}=\{\begin{array}{ll}{[1+0.5(\gamma -1)M^2]}^{\gamma /(\gamma -1)}\hfill & M\le 1\hfill \\ M^2{[0.5(\gamma +1)]}^{(\gamma +1)/(\gamma -1)}[\gamma -(\gamma -1)/\hfill & \hfill \\ (2M^2){]}^{1/(1-\gamma )}\hfill & M>1.\hfill \end{array}& (62)\end{array}$

where M is the Mach number in the pre-shocked gas.

In principle, determining the Mach number of strong shocks from the pressure ratio is better then using the compression, since it is increasing with Mach number without limit, so a small error in the ratio will not lead to a large error in the Mach number. Unfortunately the pressure ratio might not be determined if the gas on one side is too hot and low density, as it can be seen in cold fronts, where a colder gas is plunging through the hot gas of the main cluster (as in the Bullet cluster, because of the low photon counts ahead of the discontinuity; Markevitch et al., 2002). This problem can be solved by recognizing that at a contact discontinuity the pressure is continuous, so we can determine the pressure on the other side of the discontinuity, where the density is much higher, and thus more photons are available for spectroscopy. Using this approach, the Mach number for the upstream gas can be obtained, and from that, the velocity of the shock, v_sh = v₁ = M₁c_s1. Merger velocities have been derived using this technique for several systems (e.g., Mazzotta et al., 2001; Vikhlinin et al., 2001; Kempner et al., 2002).

Systematic errors in the determination of the Mach number from these methods are due to non-uniform distribution of gas temperature and density, substructures, and projection effects. Particularly, the determination of the temperature is difficult, since we observe the integrated spectrum along the LOS. Attempts to deproject the temperature distribution in the LOS have been made using different weightings: spectroscopic, mass weighed, emission weighted (Mazzotta et al., 2004).

In the case of relaxed clusters, a simple geometry can be assumed (e.g., spherical or ellipsoidal), and a reliable deprojection can be performed. For example, a simultaneous spectral model can be fitted using LOS volume weighting assuming that the cluster is spherically symmetric and piecewise constant density and temperature distribution (“onion shell model”) using an X-ray spectral fitting package (as it was done for ellipsoidal geometry in Chiu and Molnar, 2012). Merging clusters, however, are far from equilibrium, thus no simple geometry can be assumed to describe them.

It has been shown that, due to the unknown projection angle (the angle between the LOS and the main plane of collision), systematic errors in the temperature deprojection can be substantial (Molnar et al., 2013b). Errors in the temperature lead to bias in the derived Mach number. As it was demonstrated by Molnar et al. (2012) and Molnar et al. (2013b), systematic errors from deprojection can be minimized by using self-consistent N-body/hydrodynamical numerical simulations of merging galaxy clusters. The advantage of these numerical simulations is that, as long as substructures in the clusters before collision are not substantial, they will be washed out by the energetic merging event, and the features of the shock, which are used to determine the shock velocity and the Mach number of the collision, are not affected by them.

6. Physical Properties of Merging Clusters from Numerical Simulations

In principle, the best way to analyze merging clusters is to model the system using self-consistent N-body/hydrodynamical simulations constrained by multifrequency observations. Merging clusters are not in dynamical equilibrium. Their structure and evolution are determined by complex non-linear physical processes. The dark matter components react only to gravity, the ICG responsive to pressure forces and various feedback mechanisms (heating, cooling, etc.). As a consequence, it is not possible to use conventional methods, which assume spherical or ellipsoidal geometry, to analyze observations of merging galaxy clusters.

Merging galaxy cluster simulations can be cast into two main categories: (i) simulations starting from cosmological initial conditions, and (ii) idealized cluster simulations, which assume simplified cluster models and follow their collisions. Both techniques have advantages and disadvantages (e.g., Molnar, 2015). Based on cosmological simulations, the general properties of merging clusters can be studied using the resimulation technique (e.g., Paul et al., 2011). Simulations based on initial conditions generated by controlled Gaussian statistic for the density field to simulate individual clusters is also possible (e.g., Mathis et al., 2005). Alternatively, multi-scale initial conditions can be used, in which case there is no need for resimulation (Hahn and Abel, 2011). These simulations are more realistic, but it is not possible to have full control over the initial conditions of the collision (infalling velocity, impact parameter, dark matter and gas distribution, etc…) to fit the resulting merging system to observations.

Idealized merging cluster simulations set up the initial conditions just before the collision and run the simulations in a Newtonian reference frame. The disadvantages of idealized merging simulations are that they adopt a symmetric cluster shape (mostly spherical), they lack of substructure and the large scale structure (filaments, infalling galaxies, etc…), and assume hydrostatic equilibrium (e.g., Ricker and Sarazin, 2001; Ritchie and Thomas, 2002; McCarthy et al., 2007; Poole et al., 2008; ZuHone, 2011; Molnar et al., 2012).

Self-consistent 3D merging cluster simulations, which took into account the mass of the gas and coupled gravity, adopting different implementation of N-body techniques, were first carried out using the method of smoothed particle hydrodynamics (SPH; Pearce, Thomas and Couchman, 1994; Roettiger et al., 1999a,b; Roettiger and Flores, 2000). The first N-body/magneto-hydrodynamical (MHD) simulations of merging clusters were carried out by Roettiger et al. (1999a). Roettiger et al. demonstrated that the magnetic field can be amplified as a consequence of merging. These simulations were used to analyze the merging cluster A3367, which contains double radio relics in the outskirts of the cluster, and concluded that the relics are a consequence of a 5:1 mass slightly off-axis merging nearly in the plane of the sky. The same method was used to model A3266 as a 2.5:1 off axis merger, and predicted that the rotation of the gas of the main component due to the angular momentum generated by merging might be observable in the future with a new generation of high-spectral resolution X-ray instruments (Roettiger and Flores, 2000).

Off-center collisions of equal mass clusters using different impact parameters were carried out by Ricker (1998), who studied the dependence of the virialization time, X-ray luminosity, and structure of the merger on the impact parameter. It was found that the X-ray luminosity increases due to merging as a function of the impact parameter. Ritchie and Thomas (2002) confirmed that merging can increase the X-ray luminosity and temperature substantially. They also showed that cool cores in clusters might be disrupted if the impact parameter is small enough and the mass ratio is not too large (e.g., less than 8:1). Merging cluster simulations with different mass ratios and impact parameters found that large scale turbulent motions are generated by merging with up to a few hundred kpc in sizes of eddies (Ricker and Sarazin, 2001).

SPH simulations were used to study electron-ion equilibration and non-thermal emission from off axis mergers (Takizawa, 2000). SPH merging cluster simulations assuming cool core clusters carried out by Poole et al. (2006) suggest that the offset between X-ray and mass surface density centroids is the best measure of how much the cluster deviates from dynamical equilibrium. These simulations demonstrate that a merging cluster at a redshift of 0.1 would exhibit no signs of dynamical activity after the second core passage on a 50 ks Chandra observation, although it takes another ~2 Gyr for the system to virialize.

N-body/MHD simulations of binary merging clusters found that merging amplifies the magnetic field perpendicular to the axis of collision (Takizawa, 2008). N-body/hydrodynamical simulations carried out to study electron-ion equilibration state in shocks due to cluster merging showed that there is a significant departure from equilibrium (Akahori and Yoshikawa, 2010). Detailed high resolution Eulerian AMR simulations (using FLASH) of binary cluster mergers were performed to study gas sloshing and entropy generation and the effect of different initial conditions by ZuHone et al. (2010) and ZuHone (2011). Binary merger simulations using SPH and Eulerian (FLASH) codes were carried out by Mitchell et al. (2009) to compare the results for mixing and turbulence for these two different methods. Mitchell et al. showed that SPH codes artificially suppress turbulence, while AMR codes treat them more realistically (see also Agertz et al., 2007).

Most merging cluster simulations have been carried out to study the astrophysics of merging systems and to understand how the dark matter and gas components interact. A large offset was found in the Bullet cluster, between the gravitational center of the bullet (derived from lensing observations) and the gas component derived from X-ray imaging (Clowe et al., 2006). In the Bullet cluster (left panel in Figure 1) the infalling subcluster seems to be plunging through the central region of the main cluster like a bullet showing an X-ray bright wedge shape morphology at the interface of the two ICG components. This merging cluster provided the first direct evidence for the existence of dark matter in large scales (Clowe et al., 2006). Detailed N-body/hydrodynamical simulations of binary mergers have been carried out to explain the morphology of the X-ray and mass surface density and the offset between the X-ray and mass peaks in the Bullet cluster (Springel and Farrar, 2007; Mastropietro and Burkert, 2008; Lage and Farrar, 2014).

The offsets between the dark matter peaks, the X-ray, and SZ centroids are generated by the different behavior of the collisionless component, the dark matter, and the collisional gas during the merging process: the dark matter responds only to gravity, and therefore the core of the infalling cluster passes through that of the main cluster relatively unchanged, but the gas is subject to hydrodynamical effects, which cause large disturbances, shocks and contact discontinuities. The amplitude of the offsets between the dark matter and the gas peaks is determined by the relative strength of the gravitational force, which is trying to keep the gas locked into the potential well of the dark matter, and the ram pressure, which is acting to remove it.

A quantitative study of the offsets between the peaks of the mass surface density (dominated by dark matter, thus often just refer to as dark matter mass peak), X-ray emission, and SZ effect amplitude as a function of the masses of the components, the impact parameter, and the infall velocity using self-consistent N-body/hydrodynamical simulations of merging galaxy clusters we carried out by Molnar et al. (2012). They demonstrated that, in general, large infall velocities are necessary to produce offsets in the order of ≳100 kpc as long as the impact parameter is not close to zero. Mergers with small impact parameters may produce large offsets just because the gas of the infalling cluster cannot penetrate through that of the main cluster.

When interpreting multifrequency observations of merging clusters, it is possible to use results from simulations already performed, but the best way to analyze these systems is to carry out a series of simulations to reproduce the observations. This makes it possible to constrain quantitatively some important input parameters. As of today only a few detailed studies of merging clusters have been carried out to interpret multifrequency observations: Cl 0024+17 (ZuHone et al., 2009); CIZA J2242.8+5301 (van Weeren et al., 2011a); CL J0152-1347 (Molnar et al., 2012); 1RXS J0603.3+4214 (Brüggen, et al., 2012); using the AMR code FLASH; A3376 (Machado and Lima Neto, 2013) using the SPH code GADGET-2; El Gordo using GADGET-3 (Donnert, 2014), and the FLASH (Molnar and Broadhurst, 2015). All these merging clusters are in the phase soon after the first core passage, when the progenitors can be clearly identified and the morphology of the system is relatively simple. Detailed simulations were carried out to analyze the pre-merger cluster A1750, and it was demonstrated that they can also be used to constrain the initial parameters of the collision (Molnar et al., 2013b).

These numerical simulations assume the initial kinematics of the collision (velocities, impact parameters) and parameterized models for initial distribution of the DM and the gas. Since the parameter space is quite large, the question of uniqueness naturally arises. Assuming that the adopted model is correct, Molnar et al. (2012) demonstrated that observations in O/NIR (mass surface density), X-ray and radio (SZ effect) bands strongly constrain the initial parameters of the collision, and thus merging simulations can be used to uniquely determine them. It is possible, however, that we can obtain a viable solution assuming a different model. A detailed study of model parameterization has not been done yet.

6.1. Analyzing Merging Clusters after the First Core Passage

The best constraints on all initial parameters for a binary merger can be derived for a cluster observed just after the first core passage. The morphology of the X-ray emission and the offsets between the mass peaks, the X-ray and SZ centroids are sensitive to most initial parameters.

As an example of an analysis of a merging cluster after the first core passage using full N-body/hydrodynamical simulations we show the results for the massive merging cluster, El Gordo (Molnar and Broadhurst, 2015). The simulations were constrained by the X-ray morphology, the mass distribution (from gravitational lensing; Jee et al., 2014), and the relative LOS velocity of the two components (derived from optical spectroscopy; Menanteau et al., 2012). The detailed numerical modeling made it possible to constrain the infall velocity, the impact parameter, and the initial masses of the two merging clusters (≃2250 km s⁻¹, ≃300 kpc, 1.4 × 10¹⁵ M_⊙ and 7.5 × 10¹⁴ M_⊙). The numerical simulations also suggested a physical explanation for the cometary structure with a “twin tail” feature in the X-ray morphology observed by Chandra (right panel in Figure 1): tidally stretched gas is responsible for the northern X-ray tail along the collision axis between the mass peaks, the southern tail, which lies off axis, marks compressed and shock heated gas due to the less massive infalling component (left panel in Figure 5).

Constraining physical parameters of the ICG using detailed numerical models for individual merging galaxy clusters has just started. We illustrate the power of this method on the extreme merging cluster, the Bullet cluster. The most recent N-body/MHD binary merger simulations to explain O/NIR and X-ray observations of the Bullet cluster were performed by Lage and Farrar (2014). The initial models for the clusters assumed triaxial geometry with a Navarro–Frenk–White (NFW; Navarro et al., 1997) distribution for the dark matter density and a triaxial β-model (Cavaliere and Fusco-Femiano, 1978) with three different exponents and core radii (three simple β model multiplied) in hydrostatic equilibrium with the dark matter. Parametric models were assumed for viscosity and the cluster magnetic field. Non-thermal pressure support was taken into account when calculating gas cooling assuming that it is a constant fraction of the thermal pressure. Images of X-ray emission and SZ effect were generated using the reduced temperature.

We show the results of Lage and Farrar in Figures 6, 7. In the left panel in Figure 6 we show the mass surface density derived from observations and simulations based on the best fit model. The X-ray surface brightness in the 0.5–2 keV band is shown in the right panel. The effect of the magnetic field is illustrated in Figure 7. As a result of magnetic pressure, Lage and Farrar found that the amplitude and the position of the X-ray peak is shifted. As we can see from these figures, the simulations reproduced the observed mass surface density, and X-ray surface brightness well, but the resulting average metallicity, Z_ab = 0.78 Z_⊙, non-thermal pressure fraction, 0.52, and peak magnetic field, B₀ = 63μG, seem to be too high for clusters. Note that the parametric forms of the distribution of viscosity and magnetic field are not well constrained by observations. As a consequence, a simultaneous fitting for all parameters may adjust the fitted parameters to compensate for modeling errors, and as a result, the derived parameters would be biased. This might be the cause of the large values of some fitted parameters. A study of the correlation between parameters would help to clarify the situation.

FIGURE 6

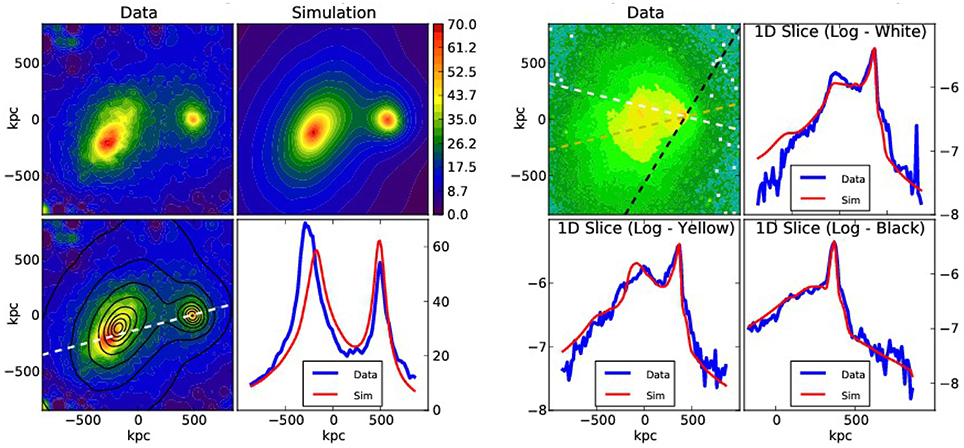
Figure 6. Data and the results based on the best fit simulations for the Bullet cluster. Left Panel: The mass distribution reconstructed from weak lensing data and from simulations are shown in the first row, the data with contours from the best fit simulation shown in left panel in the second row. The right panel in the second row displays the mass distribution from the data and from simulations along the cut shown as dashed line in the left panel. Right Panel: The X-ray surface brightness distribution in the range of 0.5–2 keV is shown in the left panel in the first row. The other three panels show the data and the simulations along three cuts marked as white, yellow, and black dashed lines (from Lage and Farrar, 2014).

FIGURE 7

Figure 7. The effect of the ICG magnetic field on the X-ray flux in the range of 0.5–2 keV. The peak of the X-ray emission is shifted as a result of magnetic pressure. Left Panel: First row (left and right panels): X-ray surface brightness from data and simulations assuming B₀ = 61μG for the amplitude of the magnetic field (note that $B\propto {\rho }_g^{2∕3}$ was assumed). Second row: left panel: data with contours from simulations over-plot; right panel: X-ray surface brightness along a cut marked as a dashed line on the left panel. Right Panel: Same as left panel but assuming B₀ = 0.01μG (from Lage and Farrar, 2014).

Numerical models of merging clusters can also be used to locate areas in the cluster where the LOS gas velocity can be measured with maximal S/N ratio for future high-spectral resolution missions such as Astro-H (see Section 5.3.3). For example, even without a map of the mass surface density, we can identify the dark matter centers of the main and the infalling clusters from where we expect the largest signal, the LOS relative velocity difference in the LOS between the two gas components (as marked with A and B in Figure 5).

6.2. Analyzing Pre-Merger Clusters

Perhaps it is the most straightforward to analyze merging clusters before the first core passage, because they are less disturbed due to the collision. Only a small volume of their gas component is affected by adiabatic gas compression and shocks, and the tidal distortions in their dark matter distributions are small, thus the initial conditions of the gas and dark matter distributions in the two merging clusters, in principle, can be straightforwardly derived. In this case, the numerical simulations are needed only to constrain the geometry of the collision, and the relative infall velocity.

We illustrate techniques applicable to analyze pre-merger clusters based on an analysis of A1750. Molnar et al. (2013b) carried out detailed N-body/hydrodynamical simulations using FLASH to model this system. A1750 contains two massive cluster components located at a mean redshift of z = 0.086. Optical and X-ray observations of this merging system were used to constrain the initial parameters of this system. The two components can be seen elongated in the northwest–southeast direction in the X-ray image of the cluster (left panel in Figure 8). The simulations were constrained by the projected mass centers of the two subclusters marked by their X-ray peaks (since we do not expect a large offset between mass centers and X-ray peaks before the first core passage), the projected X-ray temperature across the interaction region (with a maximum of ~6 keV; 3rd panel from the left in Figure 8), and the relative radial velocities derived from optical spectroscopic observations (left panel in Figure 4). The simulated X-ray surface brightness and temperature distributions based on the best fit model with M₁ = 2.0 × 10¹⁴ M_⊙ and M₂ = 1.8 × 10¹⁴ M_⊙, an impact parameter of P = 150 kpc, and an infall velocity of 1400 km s⁻¹ are shown in the 2nd and 4th panel from the left in Figure 4; from Molnar et al., 2013b). The surface brightness is low in the interaction region. As a consequence, the temperature shows large variations in the map (3rd panel from the left in Figure 8), thus we used an average temperature in the interaction region as a function of the distance between the two X-ray peaks (a one dimensional distribution).

FIGURE 8

Figure 8. Images of X–ray surface brightness and projected temperature (in units of keV) of A1750 from Chandra observations and from the FLASH simulation with an impact velocity of 1400 km s⁻¹, which is the best match to observations (Molnar et al., 2013b). From left to right: exposure corrected X–ray surface brightness maps from observations and simulation, projected temperature maps from observations and simulation.

Molnar et al. (2013b) demonstrated that, in the case of mergers before the first core passage, the temperature of the compressed/shocked region can be used to put strong constraints on the infall velocity, and that the shape of the temperature distribution is sensitive to the impact parameter. They found that the temperature distribution derived from X-ray observations depends on the viewing angle of the system, and quantified the effect. Thus, due to projection effects, the Mach number derived directly from X-ray observations may also be biased since it depends on the temperature jump at the shock (as we described it in Section 5.4.1).

7. Summary and Future Prospects

In this contribution, we presented a new, interesting interdisciplinary field, merging clusters of galaxies. In summary: merging clusters are important for astrophysics and provide a unique tool for cosmology. The extreme physical environment in massive merging clusters amplifies the otherwise small effects due to, for example, viscosity, conduction, and magnetic field in the ICG. Merging clusters trace the velocity distribution of massive halos, which can be used to test cosmological models.

We demonstrated that in order to interpret multifrequency observations of merging clusters, detailed N-body/hydrodynamical simulations are necessary. The mass surface density derived from O/NIR observations can be used to constrain the masses for the simulations and the phase of the collision. Optical spectroscopy is necessary to derive the LOS velocity of the components, and make it possible to use the phase space distribution of cluster galaxies to identify substructures. X-ray and SZ observations of the ICG can be used to derive the thermodynamical state of the ICG, analyze shocks and contact discontinuities, and constrain the geometry of the collision. High resolution X-ray spectroscopy will provide information on turbulence and the LOS motion of the gas. Observations of radio halos and relics along with X-ray observations can be used to study non-thermal particle population in clusters and constrain magnetic fields in the ICG. A detailed modeling of an extreme merging system, such as, for example, the Bullet cluster, using N-body/magneto-hydrodynamical simualations make it possible to constrain the initial parameters and the geometry of the merging clusters and derive constraints on viscosity, conduction, and magnetic fields in the ICG simultaneously.

In the next decade, we expect that a number of large observational projects will provide us a plethora of new data making it possible to improve our understanding of the physics of clusters of galaxies, and use them as a precision cosmological tool, complementary to other methods. Merging galaxy clusters will play an important role in this process. New powerful computational technology and code development will make it possible to model these new multifrequency data on merging clusters using more sophisticated N-body/magneto-hydrodynamical simulations including more realistic heating and cooling effects, transport processes, and, when necessary, radiative transfer tailored for each observed system.

In the O/NIR band, ground-based broad-band imaging surveys are already under way (e.g., Pan-STARRS, KIDS, VIKING, DES, and UKIDSS). In the near future (~2020), a large survey program, the Large Synoptic Survey Telescope (LSST)¹ is planned using an 8-m-class telescope dedicated to a 10-year survey of the southern sky (Abell et al., 2009).

A 4-year all-sky survey will be carried out in the X-ray band by the extended ROentgen Survey with an Imaging Telescope Array (eROSITA²) scheduled for launch in 2016 (Merloni et al., 2012). Astro-H³, the X-ray/soft Gamma-ray space-based pointing observatory developed by the Japan Aerospace Exploration Agency (JAXA) with participation from NASA and ESA, is planned for launch in 2016. The primary goal of this mission is to study clusters of galaxies and cluster physics using the high spectral-resolution X-ray detectors on board. The high spectral-resolution is achieved by using a micro calorimeter detector array, which provides a constant spectral resolution over the entire detected frequency range.

In the near future (~2021), a large FOV, and high angular (~5″), and spectral resolution (~2.5 eV) a large satellite mission, the International X-ray Observatory (IXO), is planned in an international collaboration including NASA, ESA, and JAXA. This mission will be capable of preforming, for the first time, X-ray polarimetry. IXO will carry four different instruments: (1) An X-ray Micro-calorimeter Spectrometer (XMS) with 2.5 eV spectral resolution; (2) A combined Wide Field Imager (WFI) and Hard X-ray Imager (HXI) with a FOV of 18′ sensitive in the photon energy range of 0.3–40 keV; (3) An X-ray grating spectrometer with a resolving power of ~3000 in the soft X-ray band, and (4) An X-ray polarimeter. One of the major goals of IXO is to map bulk motions and turbulence in galaxy clusters. The imaging instrument planned to operate in the hard X-ray energy band (10–40 keV) on board of IXO, with its high sensitivity and angular resolution, will make it possible to study non-thermal emission from clusters by detecting the expected inverse Compton emission due to high-energy electrons, and map its angular distribution. Combining IXO and future sensitive high-resolution radio interferometric observations, the properties and evolution of magnetic fields in the ICG can be studied.

Several large projects are planned to observe clusters of galaxies based on their SZ signal and the large scale structure in different wavebands. In the radio/submm band, the wide field bolometer array with broad frequency coverage and high sensitivity, Cerro Chajnantor Atacama Telescope (CCAT)⁴, is planned to come online in 2017. CCAT is a large collaborative project involving universities from Canada, Germany, and the US. It will be the highest elevation large permanent ground-based telescope in the world. It has a large, 25 m aperture telescope with frequency coverage of 200–2200 μm (1499–1362.5 GHz) and a FOV of 1° with an angular resolution of 3.5″. High spatial resolution millimeter-wave observations of the SZ effect in galaxy clusters coupled with submillimeter observations to remove contamination from cluster members and lensed galaxies will provide a unique opportunity to study the ICG.

The largest ground-based radio interferometer, the Atacama Large Millimeter Array (ALMA)⁵, is already operational in its first phase since 2013. ALMA is a very expensive international project, a result of merging three large projects: the Millimeter Array of the USA, the Large Southern Array of the European Union, and the Large Millimeter Array of Japan. This interferometer will operate in the 30–1000 GHz band using 50 antennas with 12 m in diameter, with an extension of 4 12-m antennas and 12 smaller, 7-m, antennas, in a compact configuration to improve the capability to observe more extended sources, the Atacama Compact Array (ACA). Since June 2014, 34 out of the planned 50 12-m antennas of the full ALMA configuration, and two 12-m antennas and 9 smaller, 7-m antennas of ACA are operational. ALMA observations will provide maps of clusters at an angular resolution of ~5″ (Yamada et al., 2012). Although ALMA observations of accretion shocks in galaxy clusters and tangential motion of clusters will be a very difficult (Molnar et al., 2009, 2013a), shocks in merging clusters should be observable (Yamada et al., 2012). Thus, we expect that ALMA will provide us a unique opportunity to study shock fronts and relativistic electrons produced during cluster mergers even at high redshifts, which is not possible with X-ray observations due to the 1 ∕ (1 + z)⁴ dependence of the X-ray flux. The frequency dependence of the high-angular resolution maps generated by ALMA will allow us to study gas motion based on the kinematic Sunyaev-Zel'dovich (KSZ) effect, the electron temperature distribution based on the relativistic corrections to the thermal Sunyaev-Zel'dovich (TSZ) effect, and the effect of non-thermal electrons (e.g., Colafrancesco et al., 2011; Prokhorov et al., 2011). Mapping high-redshift galaxy clusters with ALMA's high spatial resolution and sensitivity is essential to asses the dynamical state of these clusters, which is necessary when using individual clusters for cosmology. However, these cluster observations at frequency bands higher than 100 GHz will become too time consuming due to the small effective beam size and higher system temperature (Yamada et al., 2012).

Our main goal to go beyond a simple review of past research on cluster physics with merging clusters of galaxies and discuss the opportunities the new data from instruments available currently and the near future was to show how important and interesting this field is, and inspire young scientists to consider working on this exciting new field.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^http://www.lsst.org/lsst

2. ^http://www.mpe.mpg.de/eROSITA

3. ^http://heasarc.gsfc.nasa.gov/docs/astroh

4. ^http://www.ccatobservatory.org/index.cfm/page/index.htm.

5. ^http://www.almascience.org.

References

Abell, G. O. (1958). The distribution of rich clusters of galaxies. Astrophys. J. Suppl. 3, 211–288. doi: 10.1086/190036

CrossRef Full Text | Google Scholar

Abell, P. A., Allison, J., Anderson, S. F., Scott F., Andrew, J. R., Angel, J. R. P., et al., (2009). The LSST Science Collaboration. LSST Science Book, Version 2.0. arXiv:0912.0201, 1–596.

Ackermann, M., Ajello, M., Albert, A., Allafort, A., Atwood, W. B., Baldini, L., et al. (2014). Search for cosmic-ray-induced gamma-ray emission in galaxy clusters. Astrophys. J. 787, 1–26. doi: 10.1088/0004-637x/787/1/18

CrossRef Full Text | Google Scholar

Agertz, O., Moore, B., Stadel, J., Potter, D., Miniati, F., Read, J., et al. (2007). Fundamental differences between SPH and grid methods. Mon. Not. Roy. Astron. Soc. 380, 963–978. doi: 10.1111/j.1365-2966.2007.12183.x

CrossRef Full Text | Google Scholar

Akahori, T., and Yoshikawa, K. (2010). Non-equilibrium ionization state and two-temperature structure in the Bullet Cluster 1E 0657-56. Publ. Astron. Soc. Jpn. 62, 335–345. doi: 10.1093/pasj/62.2.335

CrossRef Full Text | Google Scholar

Akimoto, F., Furuzawa, A., Tawara, Y., and Yamashita, K. (2000). Iron k-line analysis of clusters of galaxies with the resonance scattering effect. Adv. Space Res. 25, 603–606. doi: 10.1016/S0273-1177(99)00809-1

CrossRef Full Text | Google Scholar

Andernach, H., Han, T., Sievers, A., Reuter, H.-P., Junkes, N., and Wielebinski, R. (1988). A radio survey of clusters of galaxies. VI - more observations of 34 Abell cluster areas at 11.1, 6.3 and 2.8 CM and a preliminary statistical review of data in papers I–VI. Astron. Astrophys. Suppl. 73, 265–324.

Google Scholar

Asai, N., Fukuda, N., and Matsumoto, R. (2005). Three-dimensional MHD simulations of X-ray emitting subcluster plasmas in cluster of galaxies. Adv. Space Res. 36, 636–642. doi: 10.1016/j.asr.2005.04.041

CrossRef Full Text | Google Scholar

Ascasibar, Y., and Markevitch, M. (2006). The origin of cold fronts in the cores of relaxed galaxy clusters. Astrophys. J. 650, 102–127. doi: 10.1086/506508

CrossRef Full Text | Google Scholar

Bartelmann, M. (2010). TOPICAL REVIEW gravitational lensing. Classical Quantum Grav. 27, 1–72. doi: 10.1088/0264-9381/27/23/233001

CrossRef Full Text | Google Scholar

Battaglia, N., Bond, J. R., Pfrommer, C., and Sievers, J. L. (2012). On the cluster physics of Sunyaev-Zel'dovich and X-ray surveys. I. The influence of feedback, non-thermal pressure, and cluster shapes on YM scaling relations. Astrophys. J. 758, 74–96. doi: 10.1088/0004-637X/758/2/74

CrossRef Full Text | Google Scholar

Battaglia, N., Bond, J. R., Pfrommer, C., Sievers, J. L., and Sijacki, D. (2010). Simulations of the Sunyaev-Zel'dovich power spectrum with active galactic nucleus feedback. Astrophys. J. 725, 91–99. doi: 10.1088/0004-637X/725/1/91

CrossRef Full Text | Google Scholar

Beers, T. C., Geller, M. J., and Huchra, J. P. (1982). Galaxy clusters with multiple components. I - the dynamics of Abell 98. Astrophys. J. 257, 23–32. doi: 10.1086/159958

CrossRef Full Text | Google Scholar

Bershady, M. A., Jangren, A., and Conselice, C. J. (2000). Structural and photometric classification of galaxies. I. Calibration based on a nearby galaxy sample. Astron. J. 119, 2645. doi: 10.1086/301386

CrossRef Full Text | Google Scholar

Bhattacharya, S., Nagai, D., Shaw, L., Crawford, T., and Holder, G. P. (2012). Bispectrum of the Sunyaev-Zel'dovich effect. Astrophys. J. 760, 5–15. doi: 10.1088/0004-637X/760/1/5

CrossRef Full Text | Google Scholar

Birkinshaw, M. (1999). The Sunyaev-Zel'dovich effect. Phys. Rep. 310, 97–195. doi: 10.1016/S0370-1573(98)00080-5

CrossRef Full Text | Google Scholar

Birkinshaw, M., and Gull, S. F. (1983). A test for transverse motions of clusters of galaxies. Nature 302, 315–317. doi: 10.1038/302315a0

CrossRef Full Text | Google Scholar

Bonafede, A., Brüeggen, M., van Weeren, R., Vazza, F., Giovannini, G., Ebeling, H., et al. (2012). Discovery of radio haloes and double relics in distant MACS galaxy clusters: clues to the efficiency of particle acceleration. Mon. Not. Roy. Astron. Soc. 426, 40–56. doi: 10.1111/j.1365-2966.2012.21570.x

CrossRef Full Text | Google Scholar

Bonafede, A., Feretti, L., Murgia, M., Govoni, F., Giovannini, G., Dallacasa, D., et al. (2010). The Coma cluster magnetic field from Faraday rotation measures. Astron. Astrophys. 513, 1–21. doi: 10.1051/0004-6361/200913696

CrossRef Full Text | Google Scholar

Bonafede, A., Vazza, F., Brüggen, M., Murgia, M., Govoni, F., Feretti, L., et al. (2013). Measurements and simulation of Faraday rotation across the Coma radio relic. Mon. Not. Roy. Astron. Soc. 433, 3208–3226. doi: 10.1093/mnras/stt960

CrossRef Full Text | Google Scholar

Boschin, W., Girardi, M., and Barrena, R. (2013). The dynamical status of ZwCl 2341.1+0000: a very elongated galaxy structure with a complex radio emission. Mon. Not. Roy. Astron. Soc. 434, 772–783. doi: 10.1093/mnras/stt1070

CrossRef Full Text | Google Scholar

Buote, D. A., and Tsai, J. C. (1995). The reliability of X-ray constraints of intrinsic cluster shapes. Astrophys. J. 439, 29–41. doi: 10.1086/175148

CrossRef Full Text | Google Scholar

Bourdin, H., Arnaud, M., Mazzotta, P., Pratt, G. W., Sauvageot, J.-L., Martino, R. (2011). A2163: Merger events in the hottest Abell galaxy cluster. II. Subcluster accretion with galaxy-gas separation. Astron. Astrophys. 527, 1–13. doi: 10.1051/0004-6361/201014907

CrossRef Full Text | Google Scholar

Boyarsky, A., Ruchayskiy, O., Iakubovskyi, D., and Franse, J. (2014). Unidentified line in X-ray spectra of the andromeda galaxy and Perseus galaxy cluster. 113, 1–11. doi: 10.1103/physrevlett.113.251301

PubMed Abstract | CrossRef Full Text | Google Scholar

Bradač, M., Allen, S. W., Treu, T., Ebeling, H., Massey, R., Glenn Morris, R., et al. (2008). Revealing the properties of dark matter in the merging cluster MACS J0025.4-1222. Astrophys. J. 687, 959–967. doi: 10.1086/591246

CrossRef Full Text | Google Scholar

Broadhurst, T., Benítez, N., Coe, D., Sharon, K., Zekser, K., White, R., et al. (2005). Strong-lensing analysis of A1689 from deep advanced camera images. Astrophys. J. 621, 53–88. doi: 10.1086/426494

CrossRef Full Text | Google Scholar

Brunetti, G., and Lazarian, A. (2011). Acceleration of primary and secondary particles in galaxy clusters by compressible MHD turbulence: from radio haloes to gamma-rays. Mon. Not. Roy. Astron. Soc. 410, 127–142. doi: 10.1111/j.1365-2966.2010.17457.x

CrossRef Full Text | Google Scholar

Brunetti, G., Setti, G., Feretti, L., and Giovannini, G. (2001). Particle reacceleration in the Coma cluster: radio properties and hard X-ray emission. Mon. Not. Roy. Astron. Soc. 320, 365–378. doi: 10.1046/j.1365-8711.2001.03978.x

CrossRef Full Text | Google Scholar

Brüggen, M., Hoeft, M., and Ruszkowski, M. (2005). X-Ray line tomography of AGN-induced motion in clusters of galaxies. Astrophys. J. 628, 153–159. doi: 10.1086/430732

CrossRef Full Text | Google Scholar

Brüggen, M., van Weeren, R. J., and Röttgering, H. J. A. (2012). Simulating the toothbrush: evidence for a triple merger of galaxy clusters. Mon. Not. Roy. Astron. Soc. 425, L76–L80. doi: 10.1111/j.1745-3933.2012.01304.x

CrossRef Full Text

Bulbul, E., Markevitch, M., Foster, A., Smith, R. K., Loewenstein, M., and Randall, S. W. (2014). Detection of an unidentified emission line in the stacked X-ray spectrum of galaxy clusters. Astrophys. J. 789, 1–23. doi: 10.1088/0004-637x/789/1/13

CrossRef Full Text | Google Scholar

Burbidge, G. R. (1959). Estimates of the total energy in particles and magnetic field in the non-thermal radio sources. Astrophys. J. 129, 849–852. doi: 10.1086/146680

CrossRef Full Text | Google Scholar

Burns, J. O., Skillman, S. W., and O'Shea, B. W. (2010). Galaxy clusters at the edge: temperature, entropy, and gas dynamics near the virial radius. Astrophys. J. 721, 1105–1112. doi: 10.1088/0004-637X/721/2/1105

CrossRef Full Text | Google Scholar

Bykov, A. M., Churazov, E. M., Ferrari, C., Forman, W. R., Kaastra, J. S., Klein, U., et al. (2015). Structures and components in galaxy clusters: observations and models. Space Sci. Rev. 188, 141–185. doi: 10.1007/s11214-014-0129-4

CrossRef Full Text | Google Scholar

Carilli, C. L., and Taylor, G. B. (2002). Cluster magnetic fields. Annu. Rev. Astron. Astrophys. 40, 319–348. doi: 10.1146/annurev.astro.40.060401.093852

CrossRef Full Text

Carlstrom, J. E., Holder, G. P., and Reese, E. D. (2002). Cosmology with the Sunyaev-Zel'dovich effect. Annu. Rev. Astron. Astrophys. 40, 643–680. doi: 10.1146/annurev.astro.40.060401.093803

CrossRef Full Text | Google Scholar

Cassano, R., and Brunetti, G. (2005). Cluster mergers and non-thermal phenomena: a statistical magneto-turbulent model. Mon. Not. Roy. Astron. Soc. 357, 1313–1329. doi: 10.1111/j.1365-2966.2005.08747.x

CrossRef Full Text | Google Scholar

Cavaliere, A., and Fusco-Femiano, R. (1978). The distribution of hot gas in clusters of galaxies. Astrophys. J. 70, 677–684.

Google Scholar

Chiu, I.-N. T., and Molnar, S. M. (2012). Testing hydrostatic equilibrium in galaxy cluster MS 2137. Astrophys. J. 756, 1–10. doi: 10.1088/0004-637X/756/1/1

CrossRef Full Text | Google Scholar

Chluba, J., Switzer, E., Nelson, K., and Nagai, D. (2013). Sunyaev-Zeldovich signal processing and temperature-velocity moment method for individual clusters. Mon. Not. Roy. Astron. Soc. 430, 3054–3069. doi: 10.1093/mnras/stt110

CrossRef Full Text | Google Scholar

Churazov, E., Forman, W., Jones, C., Sunyaev, R., and Böhringer, H. (2004). XMM-Newton observations of the Perseus cluster - II. Evidence for gas motions in the core. Mon. Not. Roy. Astron. Soc. 347, 29–35. doi: 10.1111/j.1365-2966.2004.07201.x

CrossRef Full Text | Google Scholar

Churazov, E., Zhuravleva, I., Sazonov, S., and Sunyaev, R. (2010). Resonant scattering of X-ray emission lines in the hot intergalactic medium. Space Sci. Rev. 157, 193–209. doi: 10.1007/s11214-010-9685-4

CrossRef Full Text | Google Scholar

Clowe, D., Bradač, M., Gonzalez, A. H., Markevitch, M., Randall, S. W., Jones, C., et al. (2006). A direct empirical proof of the existence of dark matter. Astrophys. J. Lett. 648, L109–L113. doi: 10.1086/508162

CrossRef Full Text | Google Scholar

Clowe, D., Markevitch, M., Bradač, M., Gonzalez, A. H., Mi Chung, S., Massey, R., et al. (2012). On dark peaks and missing mass: a weak-lensing mass reconstruction of the merging cluster system A520. Astrophys. J. 758, 128–143. doi: 10.1088/0004-637X/758/2/128

CrossRef Full Text | Google Scholar

Colafrancesco, S., Marchegiani, P., and Buonanno, R. (2011). Untangling the atmosphere of the Bullet cluster with Sunyaev-Zel'dovich effect observations. Astron. Astrophys. 527, L1–L5. doi: 10.1051/0004-6361/201016037

CrossRef Full Text | Google Scholar

Crawford, T. M., Schaffer, K. K., Bhattacharya, S., Aird, K. A., Benson, B. A., Bleem, L. E., et al. (2014). A measurement of the secondary-CMB and millimeter-wave-foreground bispectrum using 800 deg2 of South Pole Telescope data. Astrophys. J. 784, 143–163. doi: 10.1088/0004-637X/784/2/143

CrossRef Full Text | Google Scholar

Dahle, H., Sarazin, C. L., Lopez, L. A., Kouveliotou, C., Patel, S. K., Rol, E., et al. (2013). The Burst cluster: dark matter in a cluster merger associated with the short gamma-ray burst, GRB 050509B. Astrophys. J. 772, 23–37. doi: 10.1088/0004-637X/772/1/23

CrossRef Full Text | Google Scholar

Dawson, W. A., Wittman, D., Jee, M., Gee, P., Hughes, J. P., Tyson, J. A., et al. (2012). Discovery of a dissociative galaxy cluster merger with large physical separation. Astrophys. J. Lett. 747, L42–L47. doi: 10.1088/2041-8205/747/2/L42

CrossRef Full Text | Google Scholar

Diego, J. M., Broadhurst, T., Molnar, S. M., Lam, D., and Lim, J. (2015a). Free-form lensing implications for the collision of dark matter and gas in the Frontier Fields cluster MACS J0416.1-2403. Mon. Not. Roy. Astron. Soc. 447, 3130–3149. doi: 10.1093/mnras/stu2660

CrossRef Full Text | Google Scholar

Diego, J. M., Broadhurst, T., Zitrin, A., Lam, D., Lim, J., Ford, H. C., et al. (2015b). Hubble Frontier Field free-form mass mapping of the massive multiple-merging cluster MACSJ0717.5+3745. Mon. Not. Roy. Astron. Soc. 451, 3920–3932. doi: 10.1093/mnras/stv1168

CrossRef Full Text | Google Scholar

Diego, J. M., Protopapas, P., Sandvik, H. B., and Tegmark, M. (2005). Non-parametric inversion of strong lensing systems. Mon. Not. Roy. Astron. Soc. 360, 477–491. doi: 10.1111/j.1365-2966.2005.09021.x

CrossRef Full Text | Google Scholar

Dodelson, S., and Widrow, L. M. (1994). Sterile neutrinos as dark matter. Phys. Rev. Lett. 72, 17–20. doi: 10.1103/PhysRevLett.72.17

PubMed Abstract | CrossRef Full Text | Google Scholar

Dolag, K., Bykov, A. M., and Diaferio, A. (2008). Non-thermal processes in cosmological simulations. Space Sci. Rev. 134, 311–335. doi: 10.1007/s11214-008-9319-2

CrossRef Full Text | Google Scholar

Dolag, K., Vazza, F., Brunnetti, G., and Tormen, G. (2005). Turbulent gas motions in galaxy cluster simulations: the role of smoothed particle hydrodynamics viscosity. Mon. Not. Roy. Astron. Soc. 364, 753–772. doi: 10.1111/j.1365-2966.2005.09630.x

CrossRef Full Text | Google Scholar

Donnert, J. M. F. (2014). Initial conditions for idealized clusters mergers, simulating ‘El Gordo’. Mon. Not. Roy. Astron. Soc. 438, 1971–1984. doi: 10.1093/mnras/stt2291

CrossRef Full Text | Google Scholar

Drury, L. O. (1983). An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rep. Prog. Phys. 46, 973–1027. doi: 10.1088/0034-4885/46/8/002

CrossRef Full Text | Google Scholar

Eckert, D., Molendi, S., Owers, M., Gaspari, M., Venturi, T., Rudnick, L., et al. (2014). The stripping of a galaxy group diving into the massive cluster A2142. Astron. Astrophys. 570, 1–10. doi: 10.1051/0004-6361/201424259

CrossRef Full Text | Google Scholar

Ettori, S., and Fabian, A. C. (2000). Chandra constraints on the thermal conduction in the intracluster plasma of A2142. Mon. Not. Roy. Astron. Soc. 317, L57–L59. doi: 10.1046/j.1365-8711.2000.03899.x

CrossRef Full Text | Google Scholar

Evrard, A. E. (1990). Formation and evolution of X-ray clusters - a hydrodynamic simulation of the intracluster medium. Astrophys. J. 363, 349–366. doi: 10.1086/169350

CrossRef Full Text | Google Scholar

Ferrari, C., Govoni, F., Schindler, S., Bykov, A. M., and Rephaeli, Y. (2008). Observations of extended radio emission in clusters. Space Sci. Rev. 134, 93–118. doi: 10.1007/s11214-008-9311-x

CrossRef Full Text | Google Scholar

Feretti, L., Giovannini, G., Govoni, F., and Murgia, M. (2012). Clusters of galaxies: observational properties of the diffuse radio emission. Astron. Astrophys. Rev. 20, 1–60. doi: 10.1007/s00159-012-0054-z

CrossRef Full Text | Google Scholar

Fixsen, D. J. (2009). The temperature of the cosmic microwave background. Astrophys. J. 707, 916–920. doi: 10.1088/0004-637X/707/2/916

CrossRef Full Text | Google Scholar

Fujita, Y., Takizawa, M., and Sarazin, C. L. (2003). Nonthermal emissions from particles accelerated by turbulence in clusters of galaxies. Astrophys. J. 584, 190–202. doi: 10.1086/345599

CrossRef Full Text | Google Scholar

Gaspari, M., and Churazov, E. (2013). Constraining turbulence and conduction in the hot ICM through density perturbations. Astron. Astrophys. 559, 1–18. doi: 10.1051/0004-6361/201322295

CrossRef Full Text | Google Scholar

Gaspari, M., Churazov, E., Nagai, D., Lau, E. T., and Zhuravleva, I. (2014). The relation between gas density and velocity power spectra in galaxy clusters: high-resolution hydrodynamic simulations and the role of conduction. Astron. Astrophys. 569, 1–15. doi: 10.1051/0004-6361/201424043

CrossRef Full Text | Google Scholar

Gastaldello, F., Limousin, M., Foëx, G., Muñoz, R. P., Verdugo, T., Motta, V., et al. (2014). Dark matter-baryons separation at the lowest mass scale: the Bullet Group. Mon. Not. Roy. Astron. Soc. 442, L76–L80. doi: 10.1093/mnrasl/slu058

CrossRef Full Text | Google Scholar

Gastaldello, F., and Molendi, S. (2004). Ni Abundance in the core of the Perseus cluster: an answer to the significance of resonant scattering. Astrophys. J. 600, 670–680. doi: 10.1086/379970

CrossRef Full Text | Google Scholar

Gastaldello, F., Wik, D. R., Molendi, S., Westergaard, N. J., Hornstrup, A., Madejski, G., et al. (2015). A NuSTAR observation of the center of the Coma cluster. Astrophys. J. 800, 139–146. doi: 10.1088/0004-637X/800/2/139

CrossRef Full Text | Google Scholar

George, E. M., Reichardt, C. L., Aird, K. A., Benson, B. A., Bleem, L. E., Carlstrom, J. E., et al. (2015). A measurement of secondary cosmic microwave background anisotropies from the 2500 square-degree SPT-SZ survey. Astrophys. J. 799, 1–22. doi: 10.1088/0004-637X/799/2/177

CrossRef Full Text | Google Scholar

Ghizzardi, S., Rossetti, M., and Molendi, S. (2010). Cold fronts in galaxy clusters. Astron. Astrophys. 516, 1–20. doi: 10.1051/0004-6361/200912496

CrossRef Full Text | Google Scholar

Gil'fanov, M. R., Sunyaev, R. A., and Churazov, E. M. (1987). Radial brightness profiles of resonance X-ray lines in galaxy clusters. Sov. Astron. Lett. 13, 7–18.

Giovannini, G., Feretti, L., Venturi, T., Kim, K.-T., and Kronberg, P. P. (1993). The halo radio source Coma C and the origin of halo sources. Astrophys. J. 406, 399–406. doi: 10.1086/172451

CrossRef Full Text | Google Scholar

Girardi, M., Bardelli, S., Barrena, R., Boschin, W., Gastaldello, F., and Nonino, M. (2011). Internal dynamics of Abell 2254: a merging galaxy cluster with a clumpy, diffuse radio emission. Astron. Astrophys. J. 536, 1–20. doi: 10.1051/0004-6361/201117332

CrossRef Full Text | Google Scholar

Girardi, M., Mercurio, A., Balestra, I., Nonino, M., Biviano, A., Grillo, C., et al. (2015). CLASH-VLT: Substructure in the galaxy cluster MACS J1206.2-0847 from kinematics of galaxy populations. Astron. Astrophys. J. 579, 1–19. doi: 10.1051/0004-6361/201425599

CrossRef Full Text | Google Scholar

Gregory, S. A., and Thompson, L. A. (1984). The A2197 and A2199 galaxy clusters. Astron. Astrophys. J. 286, 422–436. doi: 10.1086/162617

CrossRef Full Text | Google Scholar

Griffin, R. D., Dai, X., and Kochanek, C. S. (2014). New limits on gamma-ray emission from galaxy clusters. Astrophys. J. Lett. 795, L21–L25. doi: 10.1088/2041-8205/795/1/L21

CrossRef Full Text | Google Scholar

Gunn, J. E., and Gott, J. R. III. (1972). On the infall of matter into clusters of galaxies and some effects on their evolution. Astrophys. J. 176, 1–19. doi: 10.1086/151605

CrossRef Full Text | Google Scholar

Hahn, O., and Abel, T. (2011). Multi-scale initial conditions for cosmological simulations. Mon. Not. Roy. Astron. Soc. 415, 2101–2121. doi: 10.1111/j.1365-2966.2011.18820.x

CrossRef Full Text | Google Scholar

Hand, N., Addison, G. E., Aubourg, E., Battaglia, N., Battistelli, E. S., Bizyaev, D., et al. (2012). Evidence of galaxy cluster motions with the kinematic Sunyaev-Zel'dovich effect. Phys. Rev. Lett. 109, 1–6. doi: 10.1103/PhysRevLett.109.041101

PubMed Abstract | CrossRef Full Text | Google Scholar

Harvey, D., Massey, R., Kitching, T., Taylor, A., and Tittley, E. (2015). The nongravitational interactions of dark matter in colliding galaxy clusters. Science 347, 1462–1465. doi: 10.1126/science.1261381

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill, J. C., and Sherwin, B. D. (2013). Cosmological constraints from moments of the thermal Sunyaev-Zel'dovich effect. Phys. Rev. D 87, 1–14. doi: 10.1103/PhysRevD.87.023527

CrossRef Full Text | Google Scholar

Hinshaw, G., Weiland, J. L., Hill, R. S., Odegard, N., Larson, D., Bennett, C. L., et al. (2009). Five-year Wilkinson Microwave Anisotropy Probe observations: data processing, sky maps, and basic results. Astrophys. J. Suppl. 180, 225–245. doi: 10.1088/0067-0049/180/2/225

CrossRef Full Text | Google Scholar

Hugoniot, A. (1889). Sur la propagation du mouvement dans les corps et spcialement dans les gaz parfaits (deuxi8Fme partie). J. Ecol. Polytech. 58, 1–125.

Iapichino, L., and Niemeyer, J. C. (2008). Hydrodynamical adaptive mesh refinement simulations of turbulent flows - II. Cosmological simulations of galaxy clusters. Mon. Not. Roy. Astron. Soc. 388, 1089–1100. doi: 10.1111/j.1365-2966.2008.13518.x

CrossRef Full Text | Google Scholar

Inogamov, N. A., and Sunyaev, R. A. (2003). Turbulence in clusters of galaxies and X-ray line profiles. Astron. Lett. 29, 791–824. doi: 10.1134/1.1631412

CrossRef Full Text | Google Scholar

Itoh, N., Kawana, Y., Nozawa, S., and Kohyama, Y. (2001). Relativistic corrections to the multiple scattering effect on the Sunyaev-Zel'dovich effect in the isotropic approximation. Mon. Not. Roy. Astron. Soc. 327, 567–576. doi: 10.1046/j.1365-8711.2001.04740.x

CrossRef Full Text | Google Scholar

Jaffe, W. J. (1980). On the morphology of the magnetic field in galaxy clusters. Astrophys. J. 241, 925–927. doi: 10.1086/158407

CrossRef Full Text | Google Scholar

Jauzac, M., Richard, J., Jullo, E., Clement, B., Limousin, M., Kneib, J.-P., et al. (2015). Hubble Frontier fields: a high-precision strong-lensing analysis of the massive galaxy cluster Abell 2744 using ~180 multiple images. Mon. Not. Roy. Astron. Soc. 452, 1437–1446. doi: 10.1093/mnras/stv1402

CrossRef Full Text | Google Scholar

Jee, M. J., Hoekstra, H., Mahdavi, A., and Babul, A. (2014). Hubble Space Telescope/Advanced Camera for Surveys confirmation of the dark substructure in A520. Astrophys. J. 783, 1–18. doi: 10.1088/0004-637x/783/2/78

CrossRef Full Text | Google Scholar

Jee, M. J., Mahdavi, A., Hoekstra, H., Babul, A., Dalcanton, J. J., Carroll, P., et al. (2012). A Study of the dark core in A520 with the Hubble Space Telescope: the mystery deepens. Astrophys. J. 747, 1–8. doi: 10.1088/0004-637X/747/2/96

CrossRef Full Text | Google Scholar

Kaiser, N., and Squires, G. (1993). Mapping the dark matter with weak gravitational lensing. Astrophys. J. 404, 441–450. doi: 10.1086/172297

CrossRef Full Text | Google Scholar

Kahlhoefer, F., Schmidt-Hoberg, K., Kummer, J., and Sarkar, S. (2015). On the interpretation of dark matter self-interactions in Abell 3827. Mon. Not. Roy. Astron. Soc. 452, L54–L58. doi: 10.1093/mnrasl/slv088

CrossRef Full Text | Google Scholar

Kempner, J. C., Sarazin, C. L., and Ricker, P. M. (2002). Chandra observations of A85: merger of the south subcluster. Astrophys. J. 579, 236–246. doi: 10.1086/342748

CrossRef Full Text | Google Scholar

Keshet, U., Markevitch, M., Birnboim, Y., and Loeb, A. (2010). Dynamics and magnetization in galaxy cluster cores traced by X-ray cold fronts. Astrophys. J. Lett. 719, L74–L78. doi: 10.1088/2041-8205/719/1/L74

CrossRef Full Text | Google Scholar

Kolb, E. W., and Turner, M. T. (1990). The Early Universe. Vol. 69. Boston, MA: Addison–Wesley.

Google Scholar

Kolmogorov, A. (1941). The local structure of turbulence in incompressible viscous fluid for very large Reynolds' numbers. Akad. Nauk. SSSR Dok. 30, 301–305.

Korngut, P. M., Dicker, S. R., Reese, E. D., Mason, B. S., Devlin, M. J., Mroczkowski, T., et al. (2011). MUSTANG high angular resolution Sunyaev-Zel'dovich effect imaging of substructure in four galaxy clusters. Astrophys. J. 734, 10–17. doi: 10.1088/0004-637X/734/1/10

CrossRef Full Text | Google Scholar

Kravtsov, A. V., Klypin, A., and Hoffman, Y. (2002). Constrained simulations of the real universe. II. Observational signatures of intergalactic gas in the local supercluster region. Astrophys. J. 571, 563–575. doi: 10.1086/340046

CrossRef Full Text | Google Scholar

Laganá, T. F., de Souza, R. S., and Keller, G. R. (2010). On the influence of non-thermal pressure on the mass determination of galaxy clusters. Astron. Astrophys. J. 510, 1–10. doi: 10.1051/0004-6361/200911855

CrossRef Full Text

Lage, C., and Farrar, G. (2014). Constrained simulation of the Bullet cluster. Astrophys. J. 787, 144–162. doi: 10.1088/0004-637X/787/2/144

CrossRef Full Text | Google Scholar

Lam, D., Broadhurst, T., Diego, J. M., Lim, J., Coe, D., Ford, H. C., et al. (2014). A rigorous free-form lens model of A2744 to meet the Hubble Frontier Fields challenge. Astrophys. J. 797, 98–125. doi: 10.1088/0004-637X/797/2/98

CrossRef Full Text | Google Scholar

Lau, E. T., Kravtsov, A. V., and Nagai, D. (2009). Residual gas motions in the intracluster medium and bias in hydrostatic measurements of mass profiles of clusters. Astrophys. J. 705, 1129–1138. doi: 10.1088/0004-637X/705/2/1129

CrossRef Full Text | Google Scholar

Limousin, M., Morandi, A., Sereno, M., Meneghetti, M., Ettori, S., Bartelmann, M., et al. (2013). The three-dimensional shapes of galaxy clusters. Space Sci. Res. 177, 155–194. doi: 10.1007/s11214-013-9980-y

CrossRef Full Text | Google Scholar

Lindner, R. R., Baker, A. J., Hughes, J. P., Battaglia, N., Gupta, N., Knowles, K., et al. (2014). The radio relics and halo of El Gordo, a massive z = 0.870 cluster merger. Astrophys. J. 786, 1–12. doi: 10.1088/0004-637X/786/1/49

CrossRef Full Text | Google Scholar

Lotz, J. M., Primack, J., and Madau, P. (2004). A new nonparametric approach to galaxy morphological classification. Astron. J. 128, 163-182. doi: 10.1086/421849

CrossRef Full Text | Google Scholar

Ma, C.-J., Ebeling, H., and Barrett, E. (2009). An X-ray/optical study of the complex dynamics of the core of the massive intermediate-redshift cluster MACS J0717.5+3745. Astrophys. J. Lett. 693, L56–L60. doi: 10.1088/0004-637X/693/2/L56

CrossRef Full Text | Google Scholar

Macario, G., Markevitch, M., Giacintucci, S., Brunetti, G., Venturi, T., and Murray, S. (2011). A shock front in the merging galaxy cluster a754: X-ray and radio observations. Astrophys. J. 728, 82–90. doi: 10.1088/0004-637X/728/2/82

CrossRef Full Text | Google Scholar

Machado, R. E. G., and Lima Neto, G. B. (2013). Simulations of the merging galaxy cluster Abell 3376. Mon. Not. Roy. Astron. Soc. 430, 3249–3260. doi: 10.1093/mnras/stt127

CrossRef Full Text | Google Scholar

Mahdavi, A., Hoekstra, H., Babul, A., Balam, D. D., and Capak, P. L. (2007). A dark core in Abell 520. Astrophys. J. 668, 806–814. doi: 10.1086/521383

CrossRef Full Text | Google Scholar

Markevitch, M. (2005). Chandra observation of the most interesting cluster in the universe. arXiv:astro-ph/0511345, 1–4.

Markevitch, M., Gonzalez, A. H., Clowe, D., Vikhlinin, A., Forman, W., Jones, C., et al. (2004). Direct constraints on the dark matter self-interaction cross section from the merging galaxy cluster 1E 0657-56. Astrophys. J. 606, 819–824. doi: 10.1086/383178

CrossRef Full Text | Google Scholar

Markevitch, M., Gonzalez, A. H., David, L., Vikhlinin, A. Murray, S. Forman, W., et al. (2002). A textbook example of a bow shock in the merging galaxy cluster 1E 0657-56. Astrophys. J. Lett. 567, L27–L31. doi: 10.1086/339619

CrossRef Full Text | Google Scholar

Markevitch, M., Govoni, F., Brunetti, G., and Jerius, D. (2005). Bow shock and radio halo in the merging cluster A520. Astrophys. J. 627, 733–738. doi: 10.1086/430695

CrossRef Full Text | Google Scholar

Markevitch, M., Sarazin, C.L., and Vikhlinin, A. (1999). Physics of the merging clusters Cygnus A, A3667, and A2065. Astrophys. J. 521, 526–530. doi: 10.1086/307598

CrossRef Full Text | Google Scholar

Markevitch, M., and Vikhlinin, A. (2001). Merger shocks in galaxy clusters A665 and A2163 and their relation to radio halos. Astrophys. J. 563, 95–102. doi: 10.1086/323831

CrossRef Full Text | Google Scholar

Markevitch, M., and Vikhlinin, A. (2007). Shocks and cold fronts in galaxy clusters. Phys. Rep. 443, 1–57. doi: 10.1016/j.physrep.2007.01.001

CrossRef Full Text | Google Scholar

Marriage, T. A., Acquaviva, V., Ade, P. A. R., Aguirre, P., Amiri, M., Appel, J. W., et al. (2011). The Atacama Cosmology Telescope: Sunyaev-Zel'dovich-selected galaxy clusters at 148 GHz in the 2008 survey. Astrophys. J. 737, 1–10. doi: 10.1088/0004-637x/737/2/61

CrossRef Full Text | Google Scholar

Massardi, M., Ekers, R. D., Ellis, S. C., and Maughan, B. (2010). High angular resolution observation of the Sunyaev-Zel'dovich effect in the massive z 0.83 cluster CL J0152-1357. Astrophys. J. Lett. 718, L23–L26. doi: 10.1088/2041-8205/718/1/L23

CrossRef Full Text | Google Scholar

Massey, R., Williams, L., Smit, R., Swinbank, M., Kitching, T. D., Harvey, D., et al. (2015). The behaviour of dark matter associated with four bright cluster galaxies in the 10 kpc core of Abell 3827. Mon. Not. Roy. Astron. Soc. 449, 3393–3406. doi: 10.1093/mnras/stv467

CrossRef Full Text | Google Scholar

Mastropietro, C., and Burkert, A. (2008). Simulating the Bullet cluster. Mon. Not. Roy. Astron. Soc. 389, 967–688. doi: 10.1111/j.1365-2966.2008.13626.x

CrossRef Full Text | Google Scholar

Mathis, H., Lavaux, G., Diego, J. M., and Silk, J. (2005). On the formation of cold fronts in massive mergers. Mon. Not. Roy. Astron. Soc. 357, 801–818. doi: 10.1111/j.1365-2966.2004.08589.x

CrossRef Full Text | Google Scholar

Maurogordato, S., Sauvageot, J. L., Bourdin, H., Cappi, A., Benoist, C., Ferrari, C., et al. (2011). Merging history of three bimodal clusters. Astron. Astrophys. J. 525, 1–19. doi: 10.1051/0004-6361/201014415

CrossRef Full Text | Google Scholar

Mauskopf, P. D., Horner, P. F., Aguirre, J., Bock, J. J., Egami, E., Glenn, J., et al. (2012). A high signal-to-noise ratio map of the Sunyaev-Zel'dovich increment at 1.1-mm wavelength in Abell 1835. Mon. Not. Roy. Astron. Soc. 421, 224–234. doi: 10.1111/j.1365-2966.2011.20295.x

CrossRef Full Text | Google Scholar

Mazzotta, P., Markevitch, M., Vikhlinin, A., Forman, W. R., David, L. P., and van Speybroeck, L. (2001). Chandra observation of RX J1720.1+2638: a nearly relaxed cluster with a fast-moving core? Astrophys. J. 555, 205–214. doi: 10.1086/321484

CrossRef Full Text | Google Scholar

Mazzotta, P., Rasia, E., Moscardini, L., and Tormen, G. (2004). Comparing the temperatures of galaxy clusters from hydrodynamical N-body simulations to Chandra and XMM-Newton observations. Mon. Not. Roy. Astron. Soc. 354, 10–24. doi: 10.1111/j.1365-2966.2004.08167.x

CrossRef Full Text | Google Scholar

McCarthy, I. G., Bower, R. G., Balogh, M. L., Voit, G. M., Pearce, F. R., Theuns, T., et al. (2007). Modelling shock heating in cluster mergers - I. Moving beyond the spherical accretion model. Mon. Not. Roy. Astron. Soc. 376, 497–522. doi: 10.1111/j.1365-2966.2007.11465.x

CrossRef Full Text | Google Scholar

Medezinski, E., Umetsu, K., Okabe, N., Nonino, M., Molnar, S., Massey, R., et al. (2016). Frontier fields: Subaru weak-lensing analysis of the merging galaxy cluster A2744. Astrophys. J. 748, 1–16. doi: 10.3847/0004-637X/817/1/24

CrossRef Full Text

Menanteau, F., Hughes, J. P., Sifón, C., Hilton, M., González, J. Infante, L., et al. (2012). The Atacama Cosmology Telescope: ACT-CL J0102-4915 el gordo, a massive merging cluster at redshift 0.87. Astrophys. J. 748, 7–24. doi: 10.1088/0004-637X/748/1/7

CrossRef Full Text | Google Scholar

Merloni, A., Predehl, P., Becker, W., Böhringer, H., Boller, T., Brunner, H., et al. (2012). eROSITA science book: mapping the structure of the energetic universe. arXiv:1209.3114.

Google Scholar

Merten, J., Coe, D., Dupke, R., Massey, R., Zitrin, A., Cypriano, E. S., et al. (2011). Creation of cosmic structure in the complex galaxy cluster merger Abell 2744. Mon. Not. Roy. Astron. Soc. 417, 333–347. doi: 10.1111/j.1365-2966.2011.19266.x

CrossRef Full Text | Google Scholar

Merten, J., Meneghetti, M., Postman, M., Umetsu, K., Zitrin, A., Medezinski, E., et al. (2015). CLASH: The concentration-mass relation of galaxy clusters. Astrophys. J. 806, 1–26. doi: 10.1088/0004-637x/806/1/4

CrossRef Full Text | Google Scholar

Miley, G. (1980). The structure of extended extragalactic radio sources. Annu. Rev. Astron. Astrophys. 18, 165–218. doi: 10.1146/annurev.aa.18.090180.001121

CrossRef Full Text | Google Scholar

Mitchell, N. L., McCarthy, I. G., Bower, R. G., Theuns, T., and Crain, R. A. (2009). On the origin of cores in simulated galaxy clusters. Mon. Not. Roy. Astron. Soc. 395, 180–196. doi: 10.1111/j.1365-2966.2009.14550.x

CrossRef Full Text | Google Scholar

Mohr, J. J., Fabricant, D. G., and Geller, M. J. (1993). An X-ray method for detecting substructure in galaxy clusters - application to Perseus, A2256, Centaurus, Coma, and Sersic 40/6. Astrophys. J. 413, 492–505. doi: 10.1086/173019

CrossRef Full Text | Google Scholar

Molnar, S. M. (2015). Cosmology with Clusters of Galaxies. New York, NY: Nova Science Publishers.

Google Scholar

Molnar, S. M., and Birkinshaw, M. (1999). Inverse Compton scattering in mildly relativistic plasma. Astrophys. J. 523, 78–86. doi: 10.1086/307718

CrossRef Full Text | Google Scholar

Molnar, S. M., and Birkinshaw, M. (2000). Contributions to the power spectrum of cosmic microwave background from fluctuations caused by clusters of galaxies. Astrophys. J. 537, 542–554. doi: 10.1086/309042

CrossRef Full Text | Google Scholar

Molnar, S. M., and Birkinshaw, M. (2003). Determining tangential peculiar velocities of clusters of galaxies using gravitational lensing. Astrophys. J. 586, 731–734. doi: 10.1086/346071

CrossRef Full Text | Google Scholar

Molnar, S. M., Birkinshaw, M., and Mushotzky, R. F. (2006). Determining distances to clusters of galaxies using resonant X-ray emission lines. Astrophys. J. Lett. 643, L73–L76. doi: 10.1086/505301

CrossRef Full Text | Google Scholar

Molnar, S. M., and Broadhurst, T. (2015). A hydrodynamical solution for the ‘twin-tailed’ colliding galaxy cluster ‘El Gordo’. Astrophys. J. 800, 37–45. doi: 10.1088/0004-637X/800/1/37

CrossRef Full Text | Google Scholar

Molnar, S. M., Broadhurst, T., Umetsu, K., Zitrin, A., Rephaeli, R., and Shimon, M. (2013a). Tangential velocity of the dark matter in the Bullet cluster from precise lensed image redshifts. Astrophys. J. 774, 70–80. doi: 10.1088/0004-637X/774/1/70

CrossRef Full Text | Google Scholar

Molnar, S. M., Chiu, I.-N. T., Broadhurst, T., and Stadel, J. G. (2013b). The pre-merger impact velocity of the binary cluster A1750 from X-ray, lensing, and hydrodynamical simulations. Astrophys. J. 779, 63–73. doi: 10.1088/0004-637X/779/1/63

CrossRef Full Text | Google Scholar

Molnar, S. M., Chiu, I.-N., Umetsu, K., Chen, P., Hearn, N., Broadhurst, T., et al. (2010). Testing strict hydrostatic equilibrium in simulated clusters of galaxies: implications for A1689. Astrophys. J. Lett. 724, L1–L4. doi: 10.1088/2041-8205/724/1/L1

CrossRef Full Text | Google Scholar

Molnar, S. M., Hearn, N., Haiman, Z., Bryan, G., Evrard, A. E., and George, L. (2009). Accretion shocks in clusters of galaxies and their SZ signature from cosmological simulations. Astrophys. J. 696, 1640–1656. doi: 10.1088/0004-637X/696/2/1640

CrossRef Full Text | Google Scholar

Molnar, S. M., Hearn, N. C., and Stadel, J. G. (2012). Merging galaxy clusters: offset between the Sunyaev-Zel'dovich effect and X-ray peaks. Astrophys. J. 748, 45–54. doi: 10.1088/0004-637X/748/1/45

CrossRef Full Text | Google Scholar

Morandi, A., and Limousin, M. (2012). Triaxiality, principal axis orientation and non-thermal pressure in Abell 383. Mon. Not. Roy. Astron. Soc. 421, 3147–3158. doi: 10.1111/j.1365-2966.2012.20537.x

CrossRef Full Text | Google Scholar

Morandi, A., Limousin, M., Rephaeli, Y., Umetsu, K., Barkana, R., Broadhurst, T., et al. (2011). Triaxiality and non-thermal gas pressure in Abell 1689. Mon. Not. Roy. Astron. Soc. 416, 2567–2573. doi: 10.1111/j.1365-2966.2011.19175.x

CrossRef Full Text | Google Scholar

Morandi, A., Limousin, M., Sayers, J., Golwala, S. R., Czakon, N. G., Pierpaoli, E., et al. (2012). X-ray, lensing and Sunyaev-Zel'dovich triaxial analysis of Abell 1835 out to R₂₀₀. Mon. Not. Roy. Astron. Soc. 425, 2069–2082. doi: 10.1111/j.1365-2966.2012.21196.x

CrossRef Full Text | Google Scholar

Mroczkowski, T., Dicker, S., Sayers, J., Reese, E. D., Mason, B., Czakon, N., et al. (2012). A multi-wavelength study of the Sunyaev-Zel'dovich effect in the triple-merger cluster MACS J0717.5+3745 with Mustang and Bolocam. Astrophys. J. 761, 47–61. doi: 10.1088/0004-637X/761/1/47

CrossRef Full Text | Google Scholar

Muldrew, S. I., Hatch, N. A., and Cooke, E. A. (2015). What are protoclusters? - Defining high-redshift galaxy clusters and protoclusters. Mon. Not. Roy. Astron. Soc. 452, 2528–2539. doi: 10.1093/mnras/stv1449

CrossRef Full Text | Google Scholar

Navarro, J. F., Frenk, C. S., and White, S. D. M. (1997). A universal density profile from hierarchical clustering. Astrophys. J. 490, 493–508. doi: 10.1086/304888

CrossRef Full Text | Google Scholar

Nelson, K., Lau, E. T., and Nagai, D. (2014). Hydrodynamic simulation of non-thermal pressure profiles of galaxy clusters. Astrophys. J. 792, 25–32. doi: 10.1088/0004-637X/792/1/25

CrossRef Full Text | Google Scholar

Nelson, K., Lau, E. T., Nagai, D., Rudd, D. H., and Yu, L. (2014). Weighing Galaxy clusters with gas. II. On the origin of hydrostatic mass bias in ΛCDM galaxy clusters. Astrophys. J. 782, 1–9. doi: 10.1088/0004-637X/782/2/107

CrossRef Full Text | Google Scholar

Norman, M. L. and Bryan, G. L. (1999). “Cluster turbulence,” in The Radio Galaxy Messier 87, Proceedings of a Workshop Held at Ringberg Castle, Tegernsee, Germany. (Lecture Notes in Physics), Vol. 530, eds H.-J. Röser and K. Meisenheimer (Berlin: Springer), 106–115. doi: 10.1007/BFb0106425

CrossRef Full Text

Nozawa, S., Itoh, N., and Kohyama, Y. (1998a). Relativistic thermal bremsstrahlung Gaunt factor for the intracluster plasma. Astrophys. J. 507, 530–557. doi: 10.1086/306352

CrossRef Full Text | Google Scholar

Nozawa, S., Itoh, N., and Kohyama, Y. (1998b). Relativistic corrections to the Sunyaev-Zeldovich effect for clusters of galaxies. II. Inclusion of peculiar velocities. Astrophys. J. 508, 17–24. doi: 10.1086/306401

CrossRef Full Text | Google Scholar

Ogrean, G. A., Brüggen, M., van Weeren, R. J., Röttgering, H., Croston, J. H., and Hoeft, M. (2013). Challenges to our understanding of radio relics: X-ray observations of the Toothbrush cluster. Mon. Not. Roy. Astron. Soc. 433, 812–824. doi: 10.1093/mnras/stt776

CrossRef Full Text | Google Scholar

Ogrean, G. A., Brüggen, M., van Weeren, R., Röttgering, H. J. A., Simionescu, A., Hoeft, M., et al. (2014). Multiple density discontinuities in the merging galaxy cluster CIZA J2242.8+5301. Mon. Not. Roy. Astron. Soc. 440, 3416–3425. doi: 10.1093/mnras/stu537

CrossRef Full Text | Google Scholar

Osborne, S. J., Mak, D. S. Y., Church, S. E., and Pierpaoli, E. (2011). Measuring the galaxy cluster bulk flow from WMAP data. Astrophys. J. 737, 1–20. doi: 10.1088/0004-637X/737/2/98

CrossRef Full Text | Google Scholar

Ota, N., Nagai, D., and Lau, E. T. (2015). Testing Astro-H measurements of bulk and turbulent gas motions in galaxy clusters. arXiv:1507.02730, 1–11.

Owers, M. S., Nulsen, P. E. J., Couch, W. J., and Markevitch, M. (2009). A high fidelity sample of cold front clusters from the Chandra archive. Astrophys. J. 704, 1349–1370. doi: 10.1088/0004-637X/704/2/1349

CrossRef Full Text | Google Scholar

Owers, M. S., Randall, S. W., Nulsen, P. E. J., Couch, W. J., David, L. P., and Kempner, J. C. (2011). The dissection of Abell 2744: a rich cluster growing through major and minor mergers. Astrophys. J. 728, 27–53. doi: 10.1088/0004-637X/728/1/27

CrossRef Full Text | Google Scholar

Parekh, V., van der Heyden, K., Ferrari, C., Angus, G., and Holwerda, B. (2015). Morphology parameters: substructure identification in X-ray galaxy clusters. Astron. Astrophys. J. 575, 1–28. doi: 10.1051/0004-6361/201424123

CrossRef Full Text | Google Scholar

Parrish, I. J., McCourt, M., Quataert, E., and Sharma, P. (2012). Turbulent pressure support in the outer parts of galaxy clusters. Mon. Not. Roy. Astron. Soc. 419, L29–L33. doi: 10.1111/j.1745-3933.2011.01171.x

CrossRef Full Text | Google Scholar

Paul, S., Iapichino, L., Miniati, F., Bagchi, J., and Mannheim, K. (2011). Evolution of shocks and turbulence in major cluster mergers. Astrophys. J. 726, 17–31. doi: 10.1088/0004-637X/726/1/17

CrossRef Full Text | Google Scholar

Peebles, P. J. E. (1993). Principles of Physical Cosmology. Princeton, NJ: Princeton University Press.

Google Scholar

Pearce, F. R., Thomas, P. A., and Couchman, H. M. P. (1994). Head-on mergers of systems containing gas. Mon. Not. Roy. Astron. Soc. 268, 953–965. doi: 10.1093/mnras/268.4.953

CrossRef Full Text | Google Scholar

Pinto, C., Sanders, J. S., Werner, N., de Plaa, J., Fabian, A. C., Zhang, Y.-Y., et al. (2015). Chemical Enrichment RGS cluster Sample (CHEERS): constraints on turbulence. Astron. Astrophys. J. 575, 1–16. doi: 10.1051/0004-6361/201425278

CrossRef Full Text | Google Scholar

Pinzke, A., Oh, S. P., and Pfrommer, C. (2013). Giant radio relics in galaxy clusters: reacceleration of fossil relativistic electrons? Mon. Not. Roy. Astron. Soc. 435, 1061–1082. doi: 10.1093/mnras/stt1308

CrossRef Full Text | Google Scholar

Planck Collaboration, Ade, P. A. R., Aghanim, N., Arnaud, M., Ashdown, M., Aumont, J., et al. (2014). Planck intermediate results. XIII. Constraints on peculiar velocities. Astron. Astrophys. 561, 1–21. doi: 10.1051/0004-6361/201321299

CrossRef Full Text

Poole, G. B., Babul, A., McCarthy, I. G., Fardal, M. A., Bildfell, C. J., Quinn, T., et al. (2007). The impact of mergers on relaxed X-ray clusters II. Effects on global X-ray and SunyaevZel'dovich properties and their scaling relations. Mon. Not. Roy. Astron. Soc. 380, 437–454. doi: 10.1111/j.1365-2966.2007.12107.x

CrossRef Full Text | Google Scholar

Poole, G. B., Babul, A., McCarthy, I. G., Sanderson, A. J. R., and Fardal, M. A. (2008). The impact of mergers on relaxed X-ray clusters - III. Effects on compact cool cores. Mon. Not. Roy. Astron. Soc. 391, 1163–1175. doi: 10.1111/j.1365-2966.2008.14003.x

CrossRef Full Text | Google Scholar

Poole, G. B., Fardal, M. A., Babul, A., McCarthy, I. G., Quinn, T., and Wadsley, J. (2006). The impact of mergers on relaxed X-ray clusters - I. Dynamical evolution and emergent transient structures. Mon. Not. Roy. Astron. Soc. 373, 881–905. doi: 10.1111/j.1365-2966.2006.10916.x

CrossRef Full Text | Google Scholar

Postman, M., Coe, D., Benítez, N., Bradley, L., Broadhurst, T., Donahue, M., et al. (2012). The cluster lensing and supernova survey with Hubble: an overview. Astrophys. J. Suppl. 199, 1–23. doi: 10.1088/0067-0049/199/2/25

CrossRef Full Text | Google Scholar

Prokhorov, D. A., Colafrancesco, S., Akahori, T., Million, E. T., Nagataki, S., and Yoshikawa, K. (2011). A high-frequency study of the Sunyaev-Zel'dovich effect morphology in galaxy clusters. Mon. Not. Roy. Astron. Soc. 416, 302–310. doi: 10.1111/j.1365-2966.2011.19037.x

CrossRef Full Text | Google Scholar

Randall, S. W., Markevitch, M., Clowe, D., Gonzalez, A. H., and Bradač, M. (2008). Constraints on the self-interaction cross section of dark matter from numerical simulations of the merging galaxy cluster 1E 0657-56. Astrophys. J. 679, 1173-1180. doi: 10.1086/587859

CrossRef Full Text | Google Scholar

Rankine, W. J. M. (1870). On the thermodynamic theory of waves of finite longitudinal disturbance. Philos. Trans. R. Soc. 160, 277–288. doi: 10.1098/rstl.1870.0015

CrossRef Full Text | Google Scholar

Rasia, E., Ettori, S., Moscardini, L., Mazzotta, P., Borgani, S., Dolag, K., et al. (2006). Systematics in the X-ray cluster mass estimators. Mon. Not. Roy. Astron. Soc. 369, 2013–2024. doi: 10.1111/j.1365-2966.2006.10466.x

CrossRef Full Text | Google Scholar

Rasia, E., Tormen, G., and Moscardini, L. (2004). A dynamical model for the distribution of dark matter and gas in galaxy clusters. Mon. Not. Roy. Astron. Soc. 351, 237–252. doi: 10.1111/j.1365-2966.2004.07775.x

CrossRef Full Text | Google Scholar

Reiprich, T. H., Basu, K., Ettori, S., Israel, H., Lovisari, L., Molendi, S., et al. (2013). Outskirts of galaxy clusterss. Space Sci. Rep. 177, 195–245. doi: 10.1007/s11214-013-9983-8

CrossRef Full Text | Google Scholar

Rephaeli, Y. (1977). Spatial distribution of Compton-produced X-ray flux from rich and regular clusters of galaxies. Astrophys. J. 212, 608–615. doi: 10.1086/155083

CrossRef Full Text | Google Scholar

Rephaeli, Y. (1995). Comptonization of the cosmic microwave background. Annu. Rev. Astron. Astrophys. 33, 541–579. doi: 10.1146/annurev.aa.33.090195.002545

PubMed Abstract | CrossRef Full Text | Google Scholar

Rephaeli, Y., Nevalainen, J., Ohashi, T., and Bykov, A. M. (2008). Nonthermal phenomena in clusters of galaxies. Space Sci. Rep. 134, 71–92. doi: 10.1007/s11214-008-9314-7

CrossRef Full Text | Google Scholar

Ricker, P. M. (1998). Off-center collisions between clusters of galaxies. Astrophys. J. 496, 670–692. doi: 10.1086/305393

CrossRef Full Text | Google Scholar

Ricker, P. M., and Sarazin, C. L. (2001). Off-axis cluster mergers: effects of a strongly peaked dark matter profile. Astrophys. J. 561, 621–644. doi: 10.1086/323365

CrossRef Full Text | Google Scholar

Ritchie, B. W., and Thomas, P. A. (2002). Hydrodynamic simulations of merging clusters of galaxies. Mon. Not. Roy. Astron. Soc. 329, 675–688. doi: 10.1046/j.1365-8711.2002.05027.x

CrossRef Full Text | Google Scholar

Roettiger, K., Burns, J., and Stone, J. M. (1999b). A cluster merger and the origin of the extended radio emission in Abell 3667. Astrophys. J. 518, 603–612. doi: 10.1086/307327

CrossRef Full Text | Google Scholar

Roettiger, K., and Flores, R. (2000). A prediction of observable rotation in the intracluster medium of Abell 3266. Astrophys. J. 538, 92–97. doi: 10.1086/309132

CrossRef Full Text | Google Scholar

Roettiger, K., Stone, J. M., and Burns, J. (1999a). Magnetic field evolution in merging clusters of galaxies. Astrophys. J. 518, 594–602. doi: 10.1086/307298

CrossRef Full Text | Google Scholar

Russell, H. R., Fabian, A. C., McNamara, B. R., Edge, A. C., Sanders, J. S., Nulsen, P. E. J., et al. (2014). The bow shock, cold fronts and disintegrating cool core in the merging galaxy group RX J0751.3+5012. Mon. Not. Roy. Astron. Soc. 444, 629–641. doi: 10.1093/mnras/stu1469

CrossRef Full Text | Google Scholar

Russell, H. R., McNamara, B. R., Sanders, J. S., Fabian, A. C., Nulsen, P. E. J., Canning, R. E. A., et al. (2012). Shock fronts, electron-ion equilibration and ICM transport processes in the merging cluster Abell 2146. Mon. Not. Roy. Astron. Soc. 423, 236–255. doi: 10.1111/j.1365-2966.2012.20808.x

CrossRef Full Text | Google Scholar

Ruszkowski, M., Brüggen, M., Lee, D., and Shin, M.-S. (2014). Impact of magnetic fields on ram pressure stripping in disk galaxies. Astrophys. J. 784, 1–13. doi: 10.1088/0004-637x/784/1/75

CrossRef Full Text | Google Scholar

Sakelliou, I., Peterson, J. R., Tamura, T., Paerels, F. B. S., Kaastra, J. S., Belsole, E., et al. (2002). High resolution soft X-ray spectroscopy of M 87 with the reflection grating spectrometers on XMM-Newton. Astron. Astrophys. 391, 903–909. doi: 10.1051/0004-6361:20020900

CrossRef Full Text | Google Scholar

Sanders, J. S., Fabian, A. C., and Dunn, R. J. H., (2005). Non-thermal X-rays, a high-abundance ridge and fossil bubbles in the core of the Perseus cluster of galaxies. Mon. Not. Roy. Astron. Soc. 360, 133–140. doi: 10.1111/j.1365-2966.2005.09016.x

CrossRef Full Text | Google Scholar

Sanders, J. S., Fabian, A. C., and Smith, R. K. (2011). Constraints on turbulent velocity broadening for a sample of clusters, groups and elliptical galaxies using XMM-Newton. Mon. Not. Roy. Astron. Soc. 410, 1797–1812. doi: 10.1111/j.1365-2966.2010.17561.x

CrossRef Full Text | Google Scholar

Sanders, J. S., Fabian, A. C., Smith, R. K., and Peterson, J. R. (2010). A direct limit on the turbulent velocity of the intracluster medium in the core of Abell 1835 from XMM-Newton. Mon. Not. Roy. Astron. Soc. 402, L11–L15. doi: 10.1111/j.1745-3933.2009.00789.x

CrossRef Full Text | Google Scholar

Sarazin, C. L. (1988). X-Ray Emission from Clusters of Galaxies. Cambridge: Cambridge University Press.

Google Scholar

Sayers, J., Mroczkowski, T., Zemcov, M., Korngut, P. M., Bock, J., Bulbul, E., et al. (2013). A measurement of the kinetic Sunyaev-Zeldovich signal toward MACS J0717.5+3745. Astrophys. J. 778, 52–71. doi: 10.1088/0004-637X/778/1/52

CrossRef Full Text | Google Scholar

Sazonov, S. Y., Churazov, E. M., and Sunyaev, R. A. (2002). Polarization of resonance X-ray lines from clusters of galaxies. Mon. Not. Roy. Astron. Soc. 333, 191–201. doi: 10.1046/j.1365-8711.2002.05390.x

CrossRef Full Text | Google Scholar

Schneider, P., Ehlers, J., and Falco, E. E. (1992). Gravitational Lenses, Vol. XIV. Berlin; Heidelberg; New York, NY: Springer-Verlag.

Google Scholar

Schreier, S. (1982). Compressible Flow. New York, NY: Wiley.

Google Scholar

Schuecker, P., Finoguenov, A., Miniati, F., Böhringer, H., and Briel, U. G. (2004). Probing turbulence in the Coma galaxy cluster. Astron. Astrophys. J. 426, 387–397. doi: 10.1051/0004-6361:20041039

CrossRef Full Text | Google Scholar

Shang, C., and Oh, S. P. (2013). Disentangling resonant scattering and gas motions in galaxy cluster emission line profiles. Mon. Not. Roy. Astron. Soc. 433, 1172–1184. doi: 10.1093/mnras/stt790

CrossRef Full Text | Google Scholar

Shaw, L. D., Nagai, D., Bhattacharya, S., and Lau, E. T. (2010). Impact of cluster physics on the Sunyaev-Zel'dovich power spectrum. Astrophys. J. 725, 1452–1465. doi: 10.1088/0004-637X/725/2/1452

CrossRef Full Text | Google Scholar

Shigeyama, T., (1998). Resonance line scattering modifies X-ray surface brightness of elliptical galaxies. Astrophys. J. 497, 587–593. doi: 10.1086/305498

CrossRef Full Text | Google Scholar

Spitzer, L. (1962). Physics of Fully Ionized Gases, 2nd Edn. New York, NY: Wiley-Interscience.

Google Scholar

Spitzer, L. (1978). Physical Processes in the Interstellar Medium. New York, NY: Wiley-Interscience.

Google Scholar

Springel, V., and Farrar, G. R. (2007). The speed of the ‘bullet’ in the merging galaxy cluster 1E0657-56. Mon. Not. Roy. Astron. Soc. 380, 911–925. doi: 10.1111/j.1365-2966.2007.12159.x

CrossRef Full Text | Google Scholar

Sunyaev, R. A. and Zel'dovich, Y. B. (1980). Microwave background radiation as a probe of the contemporary structure and history of the universe. Annu. Rev. Astron. Astrophys. 18, 537–560. doi: 10.1146/annurev.aa.18.090180.002541

CrossRef Full Text | Google Scholar

Suto, D., Kawahara, H., Kitayama, T., Sasaki, S., Suto, Y., and Cen, R. (2013). Validity of hydrostatic equilibrium in galaxy clusters from cosmological hydrodynamical simulations. Astrophys. J. 767, 79–89. doi: 10.1088/0004-637X/767/1/79

CrossRef Full Text | Google Scholar

Takizawa, M. (2000). Off-center mergers of clusters of galaxies and nonequipartition of electrons and ions in the intracluster medium. Astrophys. J. 532, 183–192. doi: 10.1086/308550

CrossRef Full Text | Google Scholar

Takizawa, M. (2008). N-body + magnetohydrodynamical simulations of merging clusters of galaxies: characteristic magnetic field structures generated by bulk flow motion. Astrophys. J. 687, 951–958. doi: 10.1086/592059

CrossRef Full Text | Google Scholar

Tamura, T., Hayashida, K., Ueda, S., and Nagai, M. (2011). Discovery of gas bulk motion in the galaxy cluster Abell 2256 with Suzaku. Publ. Astron. Soc. Jpn. 63, S1009–S1017. doi: 10.1093/pasj/63.sp3.s1009

CrossRef Full Text | Google Scholar

Thompson, R., and Nagamine, K. (2012). Pairwise velocities of dark matter haloes: a test for the Λ Cold Dark Matter model using the Bullet cluster. Mon. Not. Roy. Astron. Soc. 419, 3560–3570. doi: 10.1111/j.1365-2966.2011.20000.x

CrossRef Full Text | Google Scholar

Trac, H., Bode, P., and Ostriker, J. P. (2011). Templates for the Sunyaev-Zel'dovich angular power spectrum. Astrophys. J. 727, 1–14. doi: 10.1088/0004-637x/727/2/94

CrossRef Full Text | Google Scholar

Treumann, R. A. (2009). Fundamentals of collisionless shocks for astrophysical application, 1. Non-relativistic shocks. Astron. Astrophys. Rev. 17, 409–535. doi: 10.1007/s00159-009-0024-2

CrossRef Full Text | Google Scholar

Umetsu, K., Medezinski, E., Nonino, M., Merten, J., Postman, M., Meneghetti, M., et al. (2014). CLASH: Weak-lensing shear and magnification analysis of 20 galaxy clusters. Astrophys. J. 795, 1–25. doi: 10.1088/0004-637x/795/2/163

CrossRef Full Text | Google Scholar

Umetsu, K., Sereno, M., Medezinski, E., Nonino, M., Mroczkowski, T., Diego, J. M., et al. (2015a). Three-dimensional multi-probe analysis of the galaxy cluster A1689. Astrophys. J. 806, 207. doi: 10.1088/0004-637X/806/2/207

CrossRef Full Text | Google Scholar

Umetsu, K., Zitrin, A., Gruen, D., Merten, J., Donahue, M., and Postman, M. (2015b). CLASH: Joint analysis of strong-lensing, weak-lensing shear and magnification data for 20 galaxy clusters. arXiv:1507.04385, 1–26.

van Weeren, R. J., Brüggen, M., Röttgering, H. J. A., and Hoeft, M. (2011a). Using double radio relics to constrain galaxy cluster mergers: a model of double radio relics in CIZA J2242.8+5301. Mon. Not. Roy. Astron. Soc. 418, 230–243. doi: 10.1111/j.1365-2966.2011.19478.x

CrossRef Full Text | Google Scholar

van Weeren, R. J., Hoeft, M., Röttgering, H. J. A., Brüggen, M., Intema, H. T., and van Velzen, S. (2011b). A double radio relic in the merging galaxy group RX J0751.3+5012. Astron. Astrophys. J. 528, 1–13. doi: 10.1051/0004-6361/201016185

CrossRef Full Text | Google Scholar

van Weeren, R. J., Röttgering, H. J. A., Brüggen, M., and Hoeft, M. (2010). Particle acceleration on megaparsec scales in a merging galaxy cluster. Science 330, 347–357. doi: 10.1126/science.1194293

PubMed Abstract | CrossRef Full Text | Google Scholar

van Weeren, R. J., Röttgering, H. J. A., Intema, H. T., Rudnick, L., Brggen, M., Hoeft, M., et al. (2012). The “toothbrush-relic': evidence for a coherent linear 2-Mpc scale shock wave in a massive merging galaxy cluster? Astron. Astrophys. J. 546, 1–21. doi: 10.1051/0004-6361/201219000

CrossRef Full Text | Google Scholar

Vazza, F., Brunetti, G., Kritsuk, A., Wagner, R., Gheller, C., and Norman, M. (2009). Turbulent motions and shocks waves in galaxy clusters simulated with adaptive mesh refinement. Astron. Astrophys. J. 504, 33–43. doi: 10.1051/0004-6361/200912535

CrossRef Full Text | Google Scholar

Vazza, F., Eckert, D., Brüggen, M., and Huber, B. (2015). Electron and proton acceleration efficiency by merger shocks in galaxy clusters. Mon. Not. Roy. Astron. Soc. 451, 2198–2211. doi: 10.1093/mnras/stv1072

CrossRef Full Text | Google Scholar

Vazza, F., Tormen, G., Cassano, R., Brunetti, G., and Dolag, K. (2006). Turbulent velocity fields in smoothed particle hydrodymanics simulated galaxy clusters: scaling laws for the turbulent energy. Mon. Not. Roy. Astron. Soc. 369, L14–L18. doi: 10.1111/j.1745-3933.2006.00164.x

CrossRef Full Text | Google Scholar

Vikhlinin, A., Markevitch, M., and Murray, S. M. (2001). A moving cold front in the intergalactic medium of A3667. Astrophys. J. 551, 160–171. doi: 10.1086/320078

CrossRef Full Text | Google Scholar

Wen, Z. L., and Han, J. L. (2013). Substructure and dynamical state of 2092 rich clusters of galaxies derived from photometric data. Mon. Not. Roy. Astron. Soc. 436, 275-293. doi: 10.1093/mnras/stt1581

CrossRef Full Text | Google Scholar

Werner, N., Zhuravleva, I., Churazov, E., Simionescu, A., Allen, S. W., Forman, W., et al. (2009). Constraints on turbulent pressure in the X-ray haloes of giant elliptical galaxies from resonant scattering. Mon. Not. Roy. Astron. Soc. 398, 23–32. doi: 10.1111/j.1365-2966.2009.14860.x

CrossRef Full Text | Google Scholar

Werner, N., ZuHone, J. A., Zhuravleva, I., Ichinohe, Y., Simionescu, A., Allen, S. W., et al. (2015). Deep Chandra observation and numerical studies of the nearest cluster cold front in the sky. Mon. Not. Roy. Astron. Soc. 455, 846-858. doi: 10.1093/mnras/stv2358

CrossRef Full Text | Google Scholar

Wik, D. R., Hornstrup, A., Molendi, S., Madejski, G., Harrison, F. A., Zoglauer, A., et al. (2014). NuSTAR observations of the Bullet cluster: constraints on inverse compton emission. Astrophys. J. 792, 1–24. doi: 10.1088/0004-637X/792/1/48

CrossRef Full Text | Google Scholar

Wik, D. R., Sarazin, C. L., Finoguenov, A., Finoguenov, A., Matsushita, K., Nakazawa, K., et al. (2009). A Suzaku search for nonthermal emission at hard X-ray energies in the Coma cluster. Astrophys. J. 696, 1700–1711. doi: 10.1088/0004-637X/696/2/1700

CrossRef Full Text | Google Scholar

Wik, D. R., Sarazin, C. L., Zhang, Y.-Y., Baumgartner, W. H., Mushotzky, R. F., Tueller, J., et al. (2012). The Swift Burst Alert Telescope perspective on non-thermal emission in HIFLUGCS galaxy clusters. Astrophys. J. 748, 1–26. doi: 10.1088/0004-637X/748/1/67

CrossRef Full Text | Google Scholar

Wucknitz, O., and Sperhake, U. (2004). Deflection of light and particles by moving gravitational lenses. Phys. Rev. D 69, 1–13. doi: 10.1103/physrevd.69.063001

CrossRef Full Text | Google Scholar

Xu, H., Kahn, S. M., Peterson, J. R., Behar, E., Paerels, F. B. S., Mushotzky, R. F., et al. (2002). High-resolution observations of the elliptical galaxy NGC 4636 with the reflection grating spectrometer on board XMM-Newton. Astrophys. J. 579, 600–606. doi: 10.1086/342828

CrossRef Full Text | Google Scholar

Yamada, K., Kitayama, T., Takakuwa, S., Iono, D., Tsutsumi, T., Kohno, K., et al. (2012). Imaging simulations of the Sunyaev-Zel'dovich effect for ALMA. Publ. Astron. Soc. Jpn. 64, 1–26. doi: 10.1093/pasj/64.5.102

CrossRef Full Text | Google Scholar

Zandanel, F., and Ando, S. (2014). Constraints on diffuse gamma-ray emission from structure formation processes in the Coma cluster. Mon. Not. Roy. Astron. Soc. 440, 663–671. doi: 10.1093/mnras/stu324

CrossRef Full Text | Google Scholar

Zemcov, M., Aguirre, J., Bock, J., Bradford, C. M., Czakon, N., Glenn, J., et al. (2012). High spectral resolution measurement of the Sunyaev-Zel'dovich effect null with Z-Spec. Astrophys. J. 749, 114–126. doi: 10.1088/0004-637X/749/2/114

CrossRef Full Text | Google Scholar

Zhuravleva, I., Churazov, E., Sunyaev, R., Sazonov, S., Allen, S. W., Werner, N., et al. (2013). Resonant scattering in the Perseus cluster: spectral model for constraining gas motions with Astro-H. Mon. Not. Roy. Astron. Soc. 435, 3111–3121. doi: 10.1093/mnras/stt1506

CrossRef Full Text | Google Scholar

ZuHone, J. A. (2011). A parameter space exploration of galaxy cluster mergers. I. Gas mixing and the generation of cluster entropy. Astrophys. J. 728, 54–77. doi: 10.1088/0004-637X/728/1/54

CrossRef Full Text | Google Scholar

ZuHone, J. A., Markevitch, M., and Johnson, R. E. (2010). Stirring up the pot: can cooling flows in galaxy clusters be quenched by gas sloshing? Astrophys. J. 717, 908–928. doi: 10.1088/0004-637X/717/2/908

CrossRef Full Text | Google Scholar

ZuHone, J. A., Ricker, P. M., Lamb, D. Q., and Karen Yang, H.-Y. (2009). Rings of dark matter in collisions between clusters of galaxies. Astrophys. J. 696, 694–700. doi: 10.1088/0004-637X/696/1/694

CrossRef Full Text | Google Scholar

ZuHone, J. A., Markevitch, M., Ruszkowski, M., and Lee, D. (2013). Cold fronts and gas sloshing in galaxy clusters with anisotropic thermal conduction. Astrophys. J. 762, 69–85. doi: 10.1088/0004-637X/762/2/69

CrossRef Full Text | Google Scholar