- 1Department of Chemistry, Norwegian University of Science and Technology (NTNU), Trondheim, Norway
- 2School of Chemical and Process Engineering, University of Leeds, Leeds, United Kingdom
The Open Lock-In Amplifier (OLIA) is a microcontroller-based digital lock-in amplifier built from a small number of inexpensive and easily sourced electronic components. Despite its small credit card-sized form-factor and low build-cost of around US$35, OLIA is a capable instrument that offers many features associated with far costlier commercial devices. Key features include dual-phase lock-in detection at multiple harmonic frequencies up to 50 kHz, internal and external reference modes, adjustable levels of input gain, a choice between low-pass filtering and synchronous filtering, noise estimation, and a comprehensive programming interface for remote software control. OLIA comes with an optional optical breakout board that allows noise-tolerant optical detection down to the 40-pW level. OLIA and its breakout board are released here as open hardware, with technical diagrams, full parts-lists, and source-code for the firmware.
1 Introduction
The measurement of weak signals in the presence of strong background noise is a ubiquitous problem in analytical science. In circumstances where the target signal varies only slowly with time, lock-in detection is an effective and easily implemented solution (Meade, 1982; Stimpson et al., 2019; Kishore and Akbar, 2020; Wang et al., 2023). In the lock-in method, a known modulation frequency is imposed on the target signal (e.g., by modulating the stimulus at the same frequency), and noise and interfering signals at other frequencies are eliminated by means of analogue or digital signal processing.
At its simplest, the lock-in approach requires just three elements: a waveform generator, a mixer, and a low-pass filter: the waveform generator produces a periodic signal of frequency
In this paper we report a simple, yet versatile, digital lock-in amplifier (LIA) based on a microcontroller development board and a small number of inexpensive, analogue components. While there have been a few previous reports of microcontroller-based LIAs (Bengtsson, 2012; Hofmann et al., 2012; Kim, 2014; Wang et al., 2017; Harvie et al., 2021; Pollastrone et al., 2023), only a small number have been released on a fully open basis (with complete design files, build instructions and source-code), and few have sought to replicate the full range of functionality offered by high-end commercial instruments. Our goal in releasing OLIA is to provide an inexpensive, easily upgraded, intermediate performance digital lock-in amplifier that is suitable for a wide range of physical measurements. We have prioritised simplicity of design and affordability over performance, but OLIA is nonetheless a capable instrument, and we believe it will find many uses in teaching and research. Key applications include optical detection, harmonic analysis, and impedance analysis.
Core functionality offered by OLIA includes: 1) dual-phase detection at multiple harmonic frequencies up to 50 kHz; 2) the choice between internal or external referencing; 3) the ability to select different time constants and varying levels of gain/reserve; 4) noise estimation; and 5) the option to select synchronous filtering at low modulation frequencies for faster settling times.
2 Overview of lock-in detection
We begin with a brief description of the lock-in procedure as implemented in OLIA. Figure 1 shows a block diagram, summarising the analysis procedure. The digitised input signal
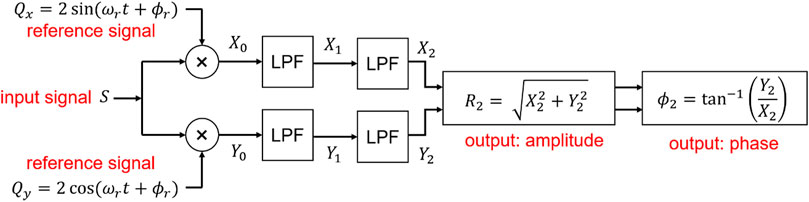
FIGURE 1. Block diagram summarising analysis procedure. An input signal
The lock-in amplifier generates two internal reference signals
and
where
In the first stage of lock-in amplification, the input signal
and
Hence, for the typical case
In the second stage of lock-in amplification we sequentially pass the intermediate output signals
Only when the frequency of the incoming signal is closely matched to the frequency of the reference signal (
and
where the first term in each expression is a constant that depends only on the amplitude of the incoming signal and the phase difference between the incoming signal and the reference signal. After two-stage DC filtering, we therefore obtain
and
where
From Eqs 5a, 5b, we obtain expressions for the amplitude and relative phase of the input signal
and
It follows from the above analysis, that a lock-in amplifier set to a reference frequency
The effective bandwidth is equal to twice the cut-off frequency of the low-pass filter (since signal frequencies just above and just below
Note, in the above analysis we assumed that the reference signals
3 Implementation
OLIA is housed on a credit card-sized, two-sided printed circuit board (PCB) that accommodates hardware for analogue signal conditioning and a Teensy 4.0 microcontroller development board for signal sampling, digital signal processing, and external communication (Figure 2A). A separate break-out board is provided for optical detection (Figure 2B).

FIGURE 2. (A) Photograph of OLIA’s fully assembled printed circuit board (PCB). Inputs and outputs are made via two 4-pin terminal blocks (blue and white boxes, respectively). A 2-pin terminal block (green box) provides power pass-through from the USB port of the Teensy 4.0 (red box), which is used to both power the device and provide a connection to an external computer for data handling. We recommend using a quick-connect magnetic USB cable and connector as shown in the photo to prevent damage to the fragile micro-USB connector from repeated connection and disconnection. A potentiometer (yellow box) is used to bring OLIA into a lock condition with an external reference signal when it is operating in external referencing mode. (B) Photograph of break-out board for optical detection. Terminal blocks are used to supply power (green box) to the integrated DC servo circuit and the OPT101 amplified photodiode, and for electrical access (white box) to the output signal that feeds into OLIA. The amplified photodiode is soldered on the opposite side of the board in the position indicated by the red box. Complete schematics for the two PCBs are provided in the Supplementary Material.
4 Analogue signal conditioning
The first stage of the analogue conditioning circuit on OLIA’s PCB is a bipolar programmable gain amplifier (PGA) that offers amplification levels of 0 (“off”), 1, 2, 4, 8, 16, 32 and 64, while the second stage is a summing amplifier (S1 in Supplementary Figure S4) that converts a bipolar input signal in the range −1.65 V to +1.65 V into a unipolar output signal in the range 0–3.3 V, allowing it to be sampled by a built-in (unipolar) analogue-to-digital converter (ADC0) on the microcontroller. The third stage is a unity-gain low-pass filter with a cut-off frequency of 94 kHz, slightly less than half the default 200-kHz digitisation rate used by ADC0. The purpose of the low-pass filter is to attenuate noise and interferences above the 100-kHz Nyquist frequency of ADC0, and so reduce sampling artefacts due to aliasing. Full details of the signal conditioning circuitry are provided in Supplementary Figure S4.
A separate signal processing board containing an OPT101 amplified silicon photodiode and a DC servo circuit is also provided for optical detection (see Figure 2B; Supplementary Figure S5), with the servo circuit dynamically compensating any DC output from the photodiode due to (slowly varying) ambient light that would otherwise saturate ADC0. The DC servo circuit allows weak optical signals at the lock-in frequency to be measured even in the presence of strong ambient light.
5 Digital signal processing
5.1 Internal referencing
OLIA can operate with either an internal or an external reference signal. In the internal referencing mode, the lock-in procedure is carried out as follows. A 3.3 V square-wave equal in frequency and phase to
and
The sample values
5.2 External referencing
In the external referencing mode, the digitisation rate is determined by an incoming 3.3 V TTL reference signal of frequency
The approximate frequency of the TTL signal is measured via a digital input pin of the microcontroller, which connects internally to a hardware counter on the microcontroller. For
and
where
5.3 Lock-in detection
The lock-in procedure is implemented entirely in the digital domain at 64-bit double precision using the microcontroller’s built-in FPU. Multiplying
and
The low-pass filtering step is carried out by exponentially averaging
and
where
The exponential filtering stage is repeated using the same
and
Finally, we determine the amplitude
and
Note, the above procedure may be repeated using higher harmonics of the reference signals to obtain the amplitude and phase of higher harmonics of the incoming signal. Since all calculations are done entirely in the digital domain using the same input signal
5.4 Synchronous filtering
From Eqs 4a, 4b, it is evident that the outputs of the two multipliers contain significant components at the sum frequency
As an alternative to exponential low-pass filtering, the outputs
5.5 Noise estimation
A live estimation of the noise level is obtained by determining the exponentially weighted standard deviation
where
where
6 Graphical user interface (GUI)
The lock-in calculations described above are carried out internally on the FPU of the Teensy 4.0 microcontroller. The microcontroller sends out new values for
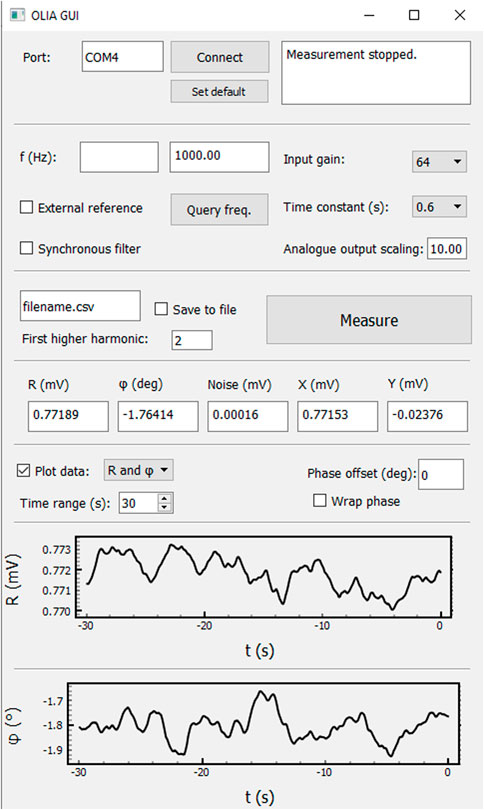
FIGURE 3. Screenshot of Python-based graphical user interface used for controlling OLIA and visualising and saving data. The application window includes controls for connecting to OLIA’s serial interface (top), and a text window (top right) for displaying messages relating to the measurement status, e.g., out-of-range signals and connection status. Controls for setting measurement parameters such as the modulation frequency, input gain, time constant, and the lowest requested higher harmonic are also present. Two checkboxes are provided for switching between internal or external referencing and low-pass or synchronous filtering. A file-name may be specified for live data logging. The numerical values of
The Python application allows the user to select between internal and external referencing. In internal referencing mode, it is possible to modify the modulation frequency from 1 Hz to 50 kHz, the analogue input gain from zero to 64, and the time constant from 0.01 to 10 s. To obtain the optimum signal-to-noise ratio (SNR), the input gain should be set as high as possible without saturating the ADC. If the input to the ADC is too high, an overload message is displayed in the text box located at the top-right corner of the GUI interface. (Note, low input gain is equivalent to high dynamic reserve so, if the signal is masked by a high level of noise, it may be necessary to use a low input gain to avoid noise-induced saturation of the ADC). For a reliable measurement, it is advisable to wait approximately ten time-constants after any change (e.g., after switching on a sensor, loading a new sample in an experimental set-up, or changing a measurement parameter) to provide sufficient time for the lock-in output to stabilise. Hence, for a typical time constant of 0.6 s, a wait time of at least 6 s is recommended. For modulation frequencies below 100 Hz that would require high exponential filter time constants and long associated wait times, it is possible to select synchronous filtering and obtain a new output every time period (at the expense of increased measurement noise).
In internal referencing mode, the digitisation rate
A real-time plot of lock-in output at the fundamental frequency is displayed on the GUI front panel, with the option to select between (
The external referencing mode is selected by ticking the appropriate checkbox on the GUI front panel, and offers equivalent functionality to the internal referencing mode. The button “Query freq.” should be pressed immediately after switching to external referencing mode to determine the frequency of the external reference signal and hence allow OLIA to determine the appropriate digitisation rate. The potentiometer P1 must then be manually adjusted (by rotating the tuning knob on the PCB) until the PLL circuit achieves phase locking; an error message “lock failure” is displayed on the front panel until P1 has been set to a suitable value. “Query freq.” should also be pressed whenever the frequency of the reference signal changes appreciably, so that the digitisation rate is kept at an appropriate value.
7 Selected results
In this section, we present illustrative results obtained using OLIA. For convenience, we refer to the doubly filtered lock-in outputs
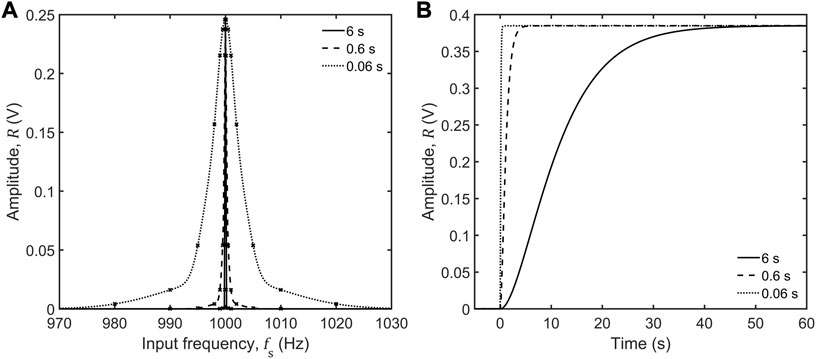
FIGURE 4. (A) Measured amplitude
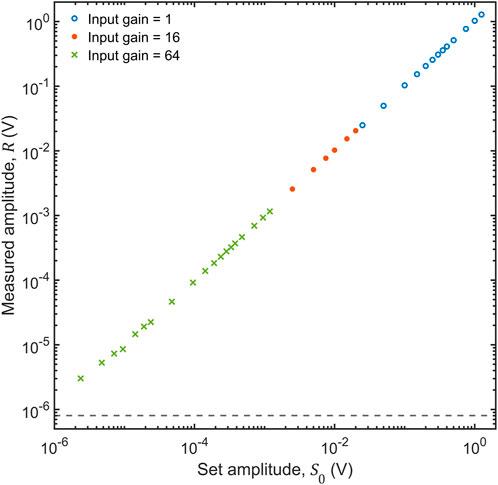
FIGURE 5. Measured amplitude
The most common use of a lock-in amplifier is to measure a target signal of known fixed frequency in the presence of interfering signals at other frequencies. Figure 4A shows—for a fixed internal reference frequency
The drawback of using higher
where
Figure 5 shows—for a sinusoidal input of frequency 1 kHz—the effect on the measured amplitude
Figure 6A shows—for a sinusoidal input of magnitude ∼240 mV and frequency 1 kHz—the effect on the measured phase of varying the relative phase
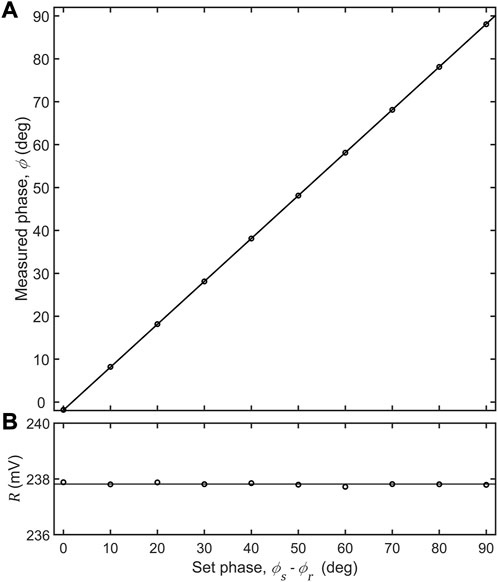
FIGURE 6. (A) Measured phase
Figure 7A shows—for a filter time constant of 6 s and sinusoidal input signals of amplitude ∼1 mV and frequency 1 kHz—the influence of varying levels of white noise on the measured
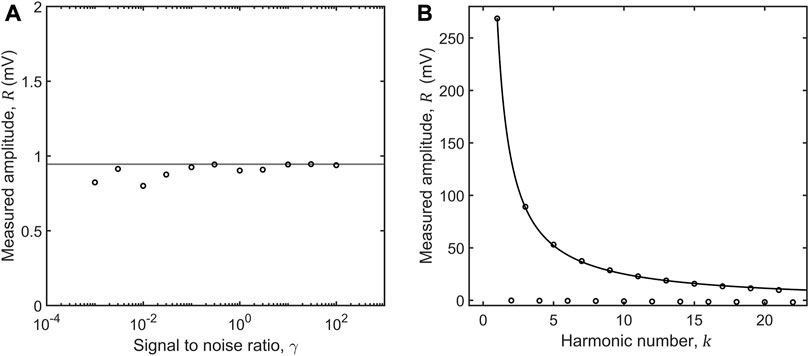
FIGURE 7. (A) Measured amplitude
A common application of a lock-in amplifier is to carry out a Fourier decomposition of an incoming signal by carrying out lock-in detection at harmonics of the fundamental signal frequency. Figure 7B shows the measured amplitude
Figure 8 shows the normalised signal amplitude versus signal frequency
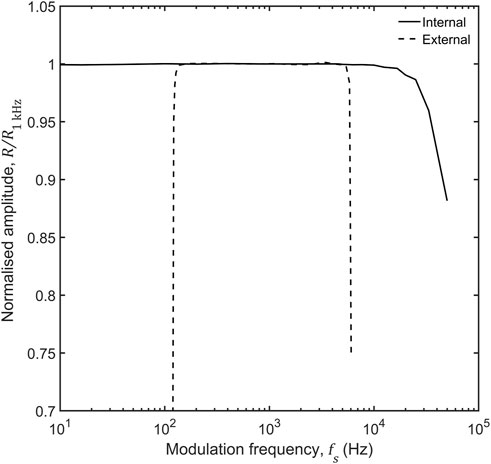
FIGURE 8. Normalised measured amplitude vs. modulation frequency for input signals of fixed amplitude ∼200 mV and zero phase; data were obtained using a time constant of 0.6 s, an input gain of 1, and reference frequencies matched to the frequency of the incoming signal. The measured amplitude has been normalised to the value recorded at 1 kHz. The solid and dotted lines denote data acquired using internal and external referencing, respectively.
Using an external square-wave reference derived from an external waveform generator, reliable measurements were obtained over a narrower frequency range from 130 Hz to 6 kHz, with the frequency multiplier circuit exhibiting unreliable locking outside of this range. Within the working range, the results obtained by external referencing closely matched those obtained by internal referencing. If required the working range of the PLL could be modified by changing the value of capacitor C1 in the PLL, with higher capacitances pushing the working range to lower frequencies and vice versa.
Figure 9 shows optical measurements obtained using OLIA and its companion optical breakout board, which houses an OPT101 amplified photodiode and a DC servo circuit to zero-out DC offsets caused by ambient light or non-ideality of the photodiode’s built-in amplifier (see Supplementary Figure S5). To carry out the measurements, a 635-nm LED driven at 1 kHz by OLIA’s square wave reference voltage was focused directly onto the OPT101 photodiode, while a beam-splitter directed a fixed fraction of the light onto a (non-amplified) silicon photodiode connected to an electrometer (6517A, Keithley) operating as a sensitive current meter. The electrometer’s integration time was set to the longest possible value of 200 ms (equal to 200 periods of the modulating signal), and the entire optical setup was sealed in a light-proof enclosure, so that the average current recorded by the electrometer was directly proportional to the average photon flux falling on the OPT101 photodetector. Plotting the amplitude recorded by OLIA versus the average photon flux falling on the OPT101 photodetector (in arbitrary units) revealed a linear response, spanning more than five orders of magnitude. The measured amplitude at the lower end of the linearity range was 0.016 mV, which for an amplified photodiode sensitivity of approximately 0.43 V/μW, implies a detection limit of around 40 pW (0.016 mV
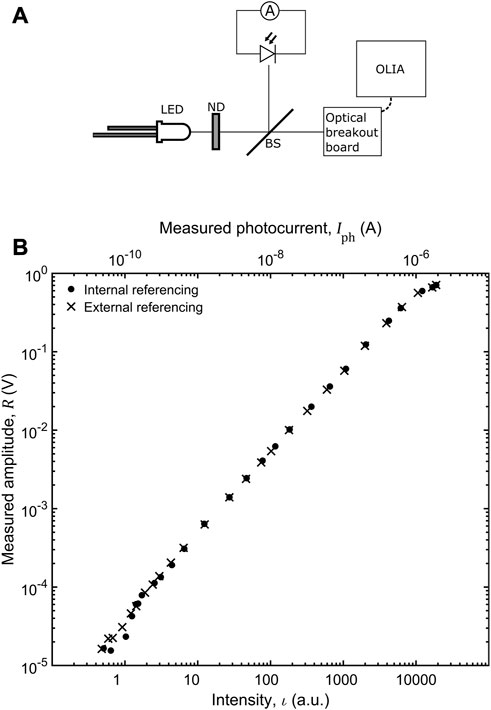
FIGURE 9. (A) Optical setup used to test the performance of OLIA and its optical breakout board. Modulated light from an LED is attenuated using a series of neutral density filters (ND) before striking a glass microscope slide that serves as a beam-splitter. The transmitted light strikes the amplified silicon photodiode on the optical breakout board, and the output signal from the breakout board is connected to the input terminals of OLIA. The reflected light strikes a separate photodiode, and the resulting photocurrent is measured using an electrometer. The photocurrent measured by the electrometer is proportional to the intensity of light incident on OLIA’s photodiode. (B) Plot of amplitude
8 Potential modifications
There are many ways in which OLIA could be further improved, without substantially increasing the cost or complexity of design, and we mention the most obvious enhancements here. Firstly, digitisation of the input signal is currently carried out using the built-in ADC on the Teensy 4.0 microcontroller, which has a low effective bit-depth of 12 and high input noise; switching to a high performance 16- or 18-bit bipolar ADC would improve dynamic range and lower measurement noise (while also removing the need for the summing amplifier S1), bringing the performance closer to high-end instruments.
The antialiasing filter has a slow second-order roll-off at 94 kHz, providing only weak attenuation of signals above the 100 kHz Nyquist frequency; a better choice would be a separate, specialised low-pass anti-aliasing filter such as the eighth-order LTC1564 (Analog devices), which could be doubly cascaded if necessary. We further note that the antialiasing filter in the current design has a fixed cut-off frequency. Using a dynamically tuneable anti-aliasing filter (such as the LTC1564) would allow run-time adjustment of the digitisation rate, which in turn would allow more harmonics to be simultaneously measured (at lower digitisation rates).
The frequency multiplier used in the external reference mode requires manual tuning (via a mechanical potentiometer) and is restricted to a frequency range of 130 Hz to 5 kHz. Modifications to the design of the frequency multiplier would eliminate the need for manual tuning and widen the operating range.
The Teensy 4.0 microcontroller development board has no internal DAC; switching to a different DAC-equipped microcontroller or adding an external DAC chip would allow for the generation of sinusoidal analogue reference signals and/or a faster analogue output of the
Finally, it would be useful to develop a range of breakout boards offering, e.g., overload protection or tuneable current or voltage pre-amplification. There is also much scope for providing additional functionality at a software level, e.g., by using chirped reference signals to investigate frequency effects (Sonnaillon and Bonetto, 2007).
Most of these changes would be simple to incorporate into the current design, providing better performance and/or enhanced functionality without adding substantially to OLIA’s current US$35 build cost. Hence the current implementation of OLIA, as described here, offers a promising springboard for developing enhanced future versions that can further narrow the performance and functionality gap with (far costlier) high-end commercial systems.
9 Conclusion
In conclusion OLIA is an inexpensive microcontroller-based digital lock-in amplifier that offers much of the functionality associated with high-end instruments. Key features include dual-phase detection at multiple harmonic frequencies up to 50 kHz, internal and external reference modes, adjustable levels of input gain from 1 to 64, a choice between low-pass filtering and synchronous filtering, noise estimation, and a comprehensive programming interface for remote control. With a build cost of just US$35, OLIA’s design prioritises affordability over performance. Nonetheless, it is a capable instrument that permits the measurement of signals over six orders of magnitude, with excellent linearity and good noise rejection. OLIA also comes with an optional optical breakout board that integrates an amplified silicon photodiode with a DC servo circuit, permitting sensitive measurements down to the 40-pW level even in the presence of strong ambient illumination. We are hopeful OLIA will find uses in a wide variety of cost-sensitive applications that require noise-tolerant signal recovery over a wide dynamic range. Finally we note that, although OLIA is intended to be a research-grade instrument, its low cost and fully open design should also make it an attractive option for laboratory-based teaching.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: Zenodo, at DOI: https://doi.org/10.5281/zenodo.7334355.
Author contributions
AH designed and built hardware, wrote software and performed experiments. Both AH and JdM contributed to conceptualisation, algorithm design, data analysis and preparing the manuscript.
Funding
This work was supported through a grant from the Research Council of Norway (Grant No. 262152) and the NTNU Nano Impact Fund.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsens.2023.1102176/full#supplementary-material
References
Barragán, L. A., Artigas, J. I., Alonso, R., and Villuendas, F. (2001). A modular, low-cost, digital signal processor-based lock-in card for measuring optical attenuation. Rev. Sci. Instrum. 72, 247–251. doi:10.1063/1.1333046
Bengtsson, L. E. (2012). A microcontroller-based lock-in amplifier for sub-milliohm resistance measurements. Rev. Sci. Instrum. 83, 075103. doi:10.1063/1.4731683
Finch, T. (2009). Incremental calculation of weighted mean and variance. Cambridge, United Kingdom: University of Cambridge
Harvie, A. J., Yadav, S. K., and de Mello, J. C. (2021). A sensitive and compact optical detector based on digital lock-in amplification. HardwareX 10, e00228. doi:10.1016/j.ohx.2021.e00228
Hofmann, M., Bierl, R., and Rueck, T. (2012). “Implementation of a dual-phase lock-in amplifier on a TMS320C5515 digital signal processor,” in 2012 5th European DSP Education and Research Conference (EDERC) (IEEE), 20–24. doi:10.1109/EDERC.2012.6532217
Kim, C.-W. (2014). A microcontroller-based lock-in amplifier for capacitive sensors. J. Sens. Sci. Technol. 23, 24–28. doi:10.5369/JSST.2014.23.1.24
Kishore, K., and Akbar, S. A. (2020). Evolution of lock-in amplifier as portable sensor interface platform: A review. IEEE Sens. J. 20, 10345–10354. doi:10.1109/JSEN.2020.2993309
Meade, M. L. (1982). Advances in lock-in amplifiers. J. Phys. E 15, 395–403. doi:10.1088/0022-3735/15/4/001
Pollastrone, F., Piccinini, M., Pizzoferrato, R., Palucci, A., and Montereali, R. M. (2023). Fully-digital low-frequency lock-in amplifier for photoluminescence measurements. Analog. Integr. Circuits Signal Process. doi:10.1007/s10470-022-02125-9
Probst, P. A., and Collet, B. (1985). Low-frequency digital lock-in amplifier. Rev. Sci. Instrum. 56, 466–470. doi:10.1063/1.1138324
Sonnaillon, M. O., and Bonetto, F. J. (2007). Lock-in amplifier error prediction and correction in frequency sweep measurements. Rev. Sci. Instrum. 78, 014701. doi:10.1063/1.2428269
Stimpson, G. A., Skilbeck, M. S., Patel, R. L., Green, B. L., and Morley, G. W. (2019). An open-source high-frequency lock-in amplifier. Rev. Sci. Instrum. 90, 094701. doi:10.1063/1.5083797
Wang, J., Wang, Z., Ji, X., Liu, J., and Liu, G. (2017). A simplified digital lock-in amplifier for the scanning grating spectrometer. Rev. Sci. Instrum. 88, 023101. doi:10.1063/1.4974755
Keywords: open hardware, lock-in amplification, signal detection, optical sensing, digital signal processing (DSP), electronics
Citation: Harvie AJ and de Mello JC (2023) OLIA: An open-source digital lock-in amplifier. Front. Sens. 4:1102176. doi: 10.3389/fsens.2023.1102176
Received: 18 November 2022; Accepted: 16 March 2023;
Published: 30 March 2023.
Edited by:
Massood Atashbar, Western Michigan University, United StatesReviewed by:
Damon Miller, Western Michigan University, United StatesYang Deng, University of Pennsylvania, United States
Copyright © 2023 Harvie and de Mello. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrew J. Harvie, YS5qLmhhcnZpZUBsZWVkcy5hYy51aw==; John C. de Mello, am9obi5kZW1lbGxvQG50bnUubm8=
 Andrew J. Harvie
Andrew J. Harvie John C. de Mello
John C. de Mello