- 1Department of Earth and Environmental Sciences, University of Waterloo, Waterloo, ON, Canada
- 2Kansas Geological Survey, University of Kansas, Lawrence, KS, United States
Both natural processes and human activities alter streamflow conditions, which can significantly affect streambank erosion and stability, leading to consequences such as sedimentation of reservoirs, contamination of streams, loss of productive land, and damage to infrastructure. Hydrological conditions, which are often controlled by water management decisions and infrastructure (e.g., reservoirs and dams), are a major factor affecting streambank erosion and stability. Extensive research has explored the relationships between hydrology, water management, and streambank stability. However, limited studies directly address the impacts of water management decisions, particularly reservoir operations, on the driving mechanisms of streambank stability such as changes in pore water pressure, pressure differentials between the surface and subsurface, and gravitational forces versus shear stress. This study builds upon these existing concepts by integrating them into a model that accounts for both the effects of water management and inherent hydrologic conditions on streambank stability.
The module estimates streambank stability using a factor of safety approach, with hydrologic conditions derived from an established integrated hydrologic model, HydroGeoSphere, coupled with the surface water operations model, OASIS. This module is validated and then demonstrated using simulations from the Lower Republican River Basin in Kansas, United States. Results indicate that several water management decisions, such as groundwater pumping and timing of reservoir releases, may negatively affect streambank stability by changing pore water pressure, the weight of the bank material, and the pressure differential between the surface and the subsurface. Given that most of the rivers and streams of the world are regulated by reservoir operations, this work demonstrates that water management practices need to be considered in simulations of streambank stability.
1 Introduction
Land use changes, combined with shifting hydrologic conditions, have a significant impact on sediment transport in river systems. Factors such as urbanization, construction of water conservancy projects, groundwater withdrawals, and climate change all contribute to these changing dynamics. For example, the construction of dams and reservoirs was found to decrease downstream sediment loads significantly due to reservoir trapping efficiency (Yang et al., 2007), and groundwater pumping and the subsequent decline in groundwater levels can destabilize streambank materials through pore pressure changes (Casagli et al., 1999). Increased stream discharge due to precipitation events or reservoir releases can also increase streambank erosion through increased shear stress (Springston, 2007). Bank erosion has been shown to be a major contributor to overall watershed sediment yields and is essentially controlled by two dominant processes: hydraulic forces acting on the channel boundary (e.g., shear stresses) and gravitational forces acting on the channel banks (e.g., hydrostatic stresses) (Simon et al., 2000). When they occur concurrently, streamflow can erode the bank toe, which increases the bank angle and, subsequently, the gravitational forces acting upon the bank, resulting in instability and bank failure when those forces exceed the shear strength of the bank material (e.g., Osman and Thorne, 1988). Therefore, it is critical to understand how water management affects hydrologic conditions, streambank stability, and, ultimately, sediment loading within managed watersheds.
In this study, the focus is on hydrostatic pressure and its role in streambank stability. Hydrostatic pressure results from the weight of water acting directly on the bank, leading to elevated pore water pressure within the soil. This pressure weakens the soil’s internal cohesion, making the bank more prone to failure. Unlike velocity-induced shear stress, which results from the dynamic forces of flowing water, hydrostatic pressure is a static force that plays a critical role in destabilizing the streambank by altering pore water conditions (Rinaldi et al., 2004; Fox et al., 2007; Shields et al., 2009). Building on previous work, such as that of Brookfield and Layzell (2019) which focused on shear stresses, this paper emphasizes hydrostatic pressure as the primary factor contributing to streambank failure and explores its implications for future erosion modeling and stability assessments.
Some recent studies, such as those by Bigham et al. (2024) and Kadhim et al. (2024) have investigated sediment dynamics and streambank stability, focusing on factors like flow velocity, slope angle, soil type and flow regulations. However, they do not directly address the impacts of water management decisions, particularly reservoir operations, on the driving mechanisms of streambank stability. This study builds upon these existing concepts by further developing a model that accounts for both the effects of water management and inherent hydrologic conditions, including hydrostatic pressure, on streambank stability.
Streambank failures occur in various forms, with planar failures being particularly common in steep, cohesive banks, and are the focus of this work. These failures involve sections of the bank sliding along a nearly flat plane, forming a wedge shape slide or slab failure, due to a combination of increased pore water pressure and weakened internal cohesion (Osman and Thorne, 1988; Langendoen, 2000; Simon et al., 2000; Chu-Agor et al., 2008; Midgley et al., 2012). In addition to planar failures, other types of failures, such as rotational failure, cantilever failure and piping or sapping failure, can also significantly impact streambank stability (e.g., Langendoen, 2000; Rinaldi and Darby, 2007; Patsinghasanee et al., 2018). A thorough understanding of these failure mechanisms is essential for accurately assessing the stability of streambanks in different hydrological conditions.
Hydrologic models are commonly used to simulate hydrological processes and support water management decisions (Midgley et al., 2012). Many models are available for simulating integrated (surface and subsurface) hydrologic conditions (e.g., Brunner and Simmons, 2012; Maxwell et al., 2015; Taie Semiromi and Koch, 2019) and water management strategies (e.g., Hydrologics, 2009; Valerio et al., 2010; Qiu et al., 2019); however, they do not capture streambank erosion processes. Several models that simulate or quantify streambank stability exist (e.g., Midgley et al., 2012; Chu-Agor et al., 2008; Simon et al., 2000; Langendoen, 2000; Osman and Thorne, 1988); however, these models do not directly link to the influence of water management decisions on the hydrologic conditions driving erosion. Recent studies have explored related topics, such as modeling rainfall-induced landslides using the concept of local factor of safety (Abbasov et al., 2024) and investigating slope stability influenced by reservoir water level fluctuations and precipitation (Kafle et al., 2022), which highlight the effect reservoir operations can have on local slope stability. However, these studies do not provide a modeling framework to simulate both the temporal and spatial changes in groundwater and surface water conditions and their effects on streambank stability.
Some research has examined the links between hydrology, water management, and streambank stability, addressing the importance of factors such as pore water pressure, shear stress, and pressure differentials. The mechanisms driving changes in pore water pressure are often tied to variations in groundwater levels and reservoir releases, which can alter the balance of forces within streambank material, affecting stability (e.g., Casagli et al., 1999). Additionally, the pressure differential between the surface and subsurface influences the rate of bank erosion, as sudden changes in water levels can destabilize streambanks by creating imbalanced forces (e.g., Simon et al., 2000). For example, while surface water levels may fall quickly from a precipitation event, the streambanks may take longer to drain. This causes a difference between the subsurface pore pressure in the streambanks and the adjoining surface water. Without the hydrostatic pressure provided by surface water, the streambanks are more susceptible to failure.
This work builds on an existing modeling framework that captures the integrated surface/subsurface flow system, including water management (e.g., reservoir operations, surface diversions, groundwater pumping). This framework couples the control volume, finite element integrated hydrologic model, HydroGeoSphere (HGS) (Aquanty, 2023), with the optimized linear programming-based surface water operations model, OASIS (Hydrologics, 2009), which was also linked to a module that estimates fluvial erosion in previous research (Brookfield and Layzell, 2019). Here, a streambank stability module is developed to run independently or coupled to the HGS modeling framework to investigate how streambank stability may change due to changes in surface and subsurface hydrologic conditions caused by water management decisions.
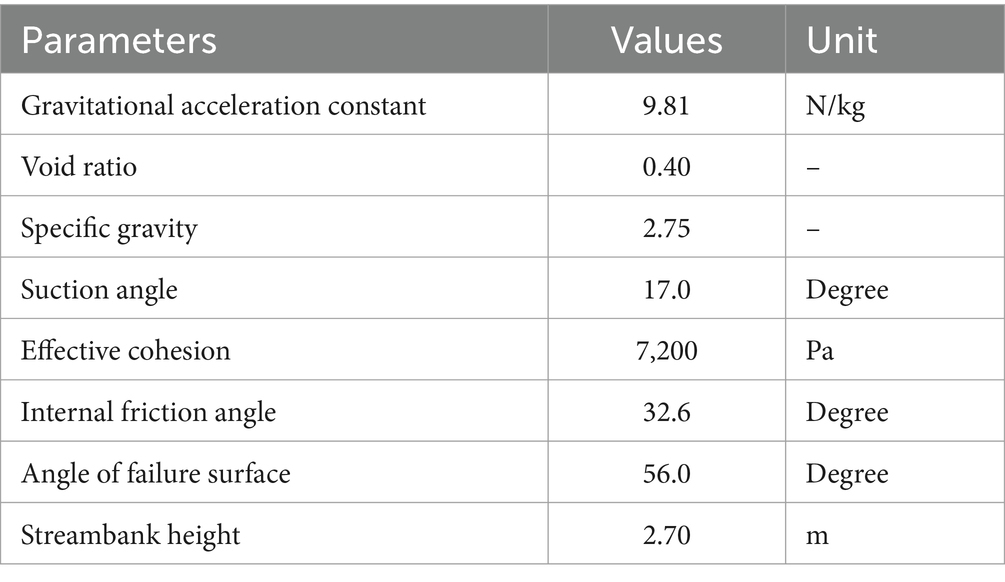
All models used in this study require parameterization to represent real-world conditions accurately. Some key parameters such as effective cohesion, internal friction angle, suction angle, and bank geometry are measured through field methods including soil sampling, groundwater monitoring, and Borehole Shear Testing, which are discussed in detail in the following sections.
The primary objective of this study is to investigate how water management decisions, including reservoir operations and groundwater pumping, affect streambank stability. We hypothesize that changes in pore water pressure, surface-subsurface pressure differentials, and hydrologic conditions are critical drivers of streambank instability. Additionally, this work aims to develop a computationally efficient module that simulates these effects using the simplified factor of safety approach. The combination of both scientific inquiry and module development allows for a more comprehensive understanding of streambank erosion processes. Addressing issues such as water availability, sediment loading, and streambank stability is crucial for many regions globally (e.g., Yang et al., 2007), including the demonstration site of the Republican River Basin.
2 Module development and validation
A streambank stability module was developed in Python to work with output from the integrated hydrologic model, HydroGeoSphere (HGS), which was previously coupled with the surface water operations model, OASIS. The module takes the data output from the coupled HGS/OASIS model, such as surface and subsurface hydrologic conditions (e.g., pore water pressure, groundwater levels), and estimates streambank stability using the simplified factor of safety (Fs) approach, through one-way feedback from HGS/OASIS to the module. The HGS and OASIS models are iteratively coupled, providing two-way feedback at each OASIS timestep, ensuring the surface water operations modelled by OASIS are reflected in the hydrologic conditions simulated by HGS (Brookfield et al., 2017).This is consistent with the approach used to simulated fluvial erosion with HGS/OASIS presented by Brookfield and Layzell (2019). In this work, we focus on simulating planar failure, a common type of streambank failure where a section of the bank slides along a nearly flat plane. This occurs when changes in pore water pressure reduce the shear strength of the bank material, leading to instability (Langendoen, 2000).
2.1 Module development
To minimize data and computational requirements, streambank stability is estimated using the Fs approach with the Vertical Slides Method (Langendoen, 2000). In this approach, streambanks are separated into several vertical slices (Figure 1). Fs is estimated using a physically-based approach, based on (1) the forces acting on a streambank, with normal forces, shear forces, and gravity acting in the vertical direction, and (2) hydrostatic forces, with components perpendicular to gravity (Figure 2). An Fs value of less than 1 indicates an unstable streambank, values significantly greater than one are considered stable, and values at or just above 1 indicate streambanks that are at high risk of becoming unstable (Langendoen, 2000).
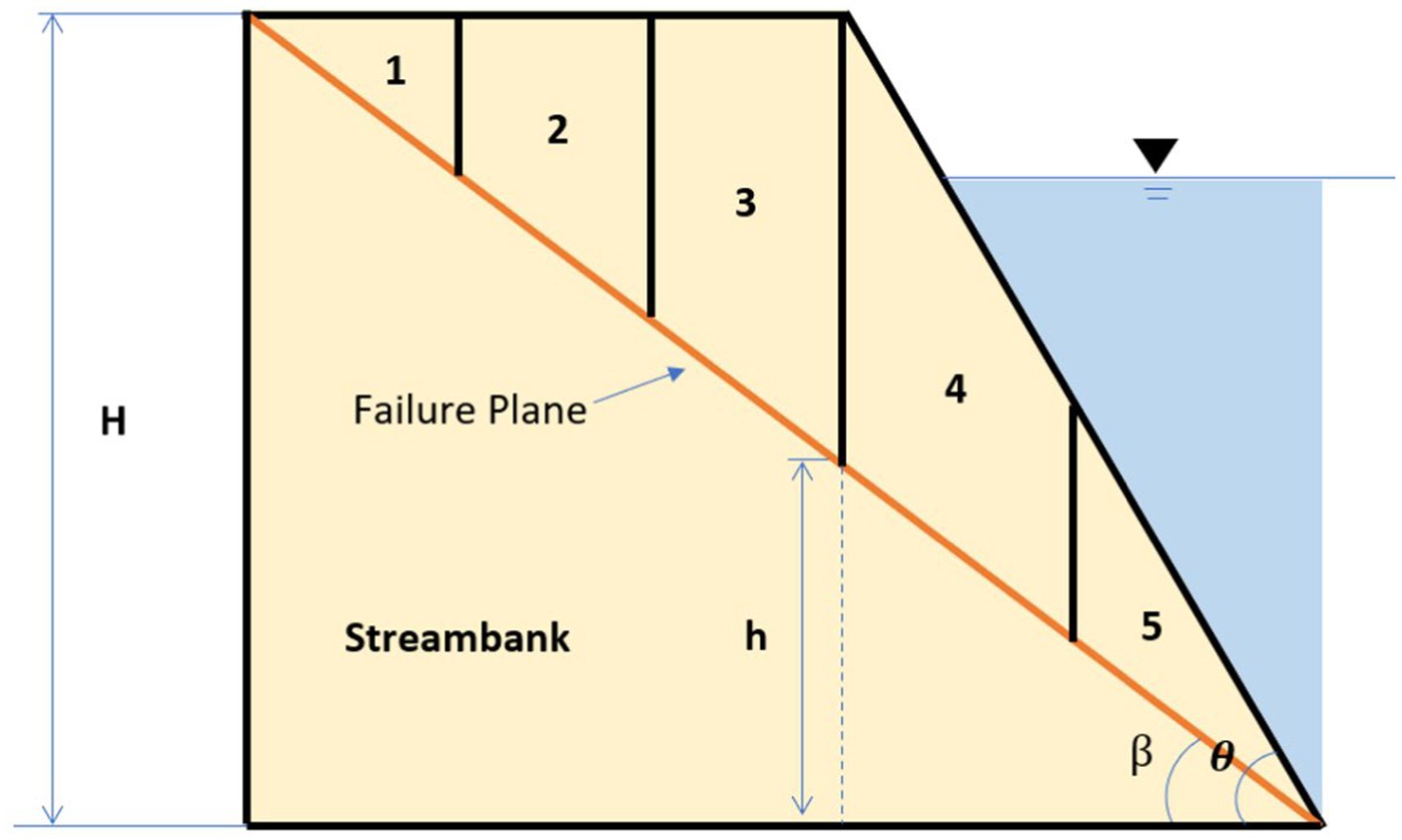
Figure 1. A simplified streambank cross-section split into five slices, where H is the height of the streambank, β is the angle of the failure plane, θ is the angle of the streambank, and h is the height of the failure plane at any point along the cross-section.
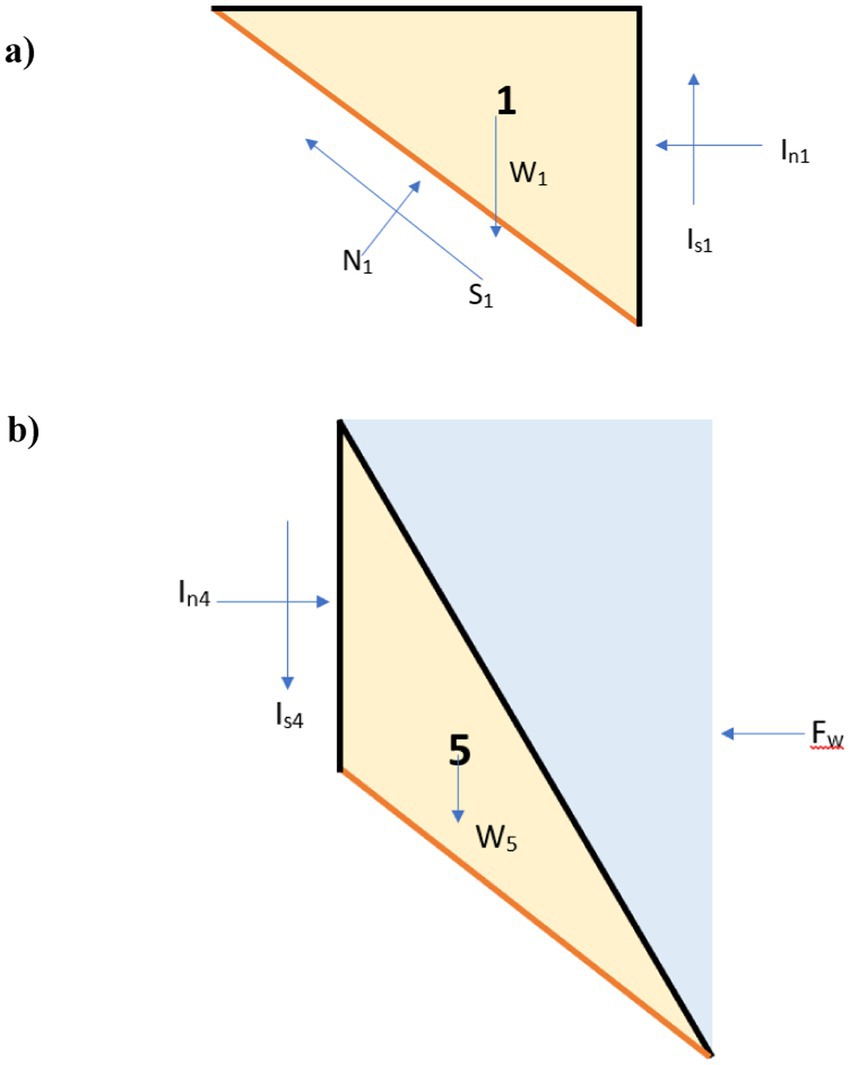
Figure 2. Forces acting on streambank cross-section (A) slice one and (B) slice 5 (cf. Figure 1), where N is the normal force, S is the shear force on the slide’s base, W is the weight, Is is the vertical interslice shear force, In is the horizontal interslice shear force and Fw is the hydrostatic force.
Forces acting on each slice are calculated separately and combined using the approach outlined in Langendoen (2000), with the Fs value determined by Equation 1 (Simon, 2006).
Where cj’ is the effective cohesion (Pa), Lj is the length of the slice base (m), Sj is the shear force mobilized at the base of the slice (N), ϕbj is an angle indicating the increase in shear strength for an increase in matric suction (degree), Uj is the porewater force on the base of the slice (N), ϕ’j is the effective angle of internal friction (degree), β is the angle of the failure plane (degree), Nj is the normal force (N), and Fw is the hydrostatic force along the whole streambank (N). Full details of the approach, including the development of a user interface, are provided in the Supplementary material.
Due to the limitations of this simplified, computationally-frugal method and the governing equation, this module is suited for scenarios where changes in hydrostatic pressure drive instability, rather than velocity-induced shear stress. Future work aims to include velocity-induced shear stress in the estimation of streambank stability. Full details of the approach, including the development of a user interface, are provided in the Supplementary material.
2.2 Module verification
As no analytical solutions or exact replicates of our approach are available to verify the developed streambank stability module, we utilize results from a similar and commonly used model, the Bank Stability and Toe Erosion Model (BSTEM) (US Army Corps of Engineers, 2015) for verification and a layer-refining approach to ensure convergence with increased spatial resolution. BSTEM is an Excel-based numerical tool used to assess streambank stability and predict toe erosion by analyzing soil mechanics, hydraulic effects, and vegetation impact, which is widely used by engineers, hydrologists, and environmental scientists. The default parameters used in the verification scenarios are provided in Table 1. The Fs values simulated by BSTEM and the module developed here are compared using different bank angles, bank heights, suction angles, friction angles, and effective cohesion values. The governing equations used by the two models are slightly different, as the streambank stability module uses the slices method (Vertical Slices Method), which is considered a “more classical geotechnical approach to planar failure” (US Army Corps of Engineers, 2015); however, BSTEM uses the layer method. The calculated normal force will be slightly different when using those two methods, and the slices method results are expected to be higher than layer methods without considering tension (US Army Corps of Engineers, 2015). Consistent with this, the module developed in this work has higher Fs values compared to BSTEM under the conditions assessed here (Figure 3). This suggests that our model estimates higher stability under similar conditions. However, the trends in Fs values under changing conditions are similar, and both models show similar increases/decreases in the factor of safety as the tested parameters change (Figure 3 for bank angle; Supplementary Figures S1–S4 for other parameters).
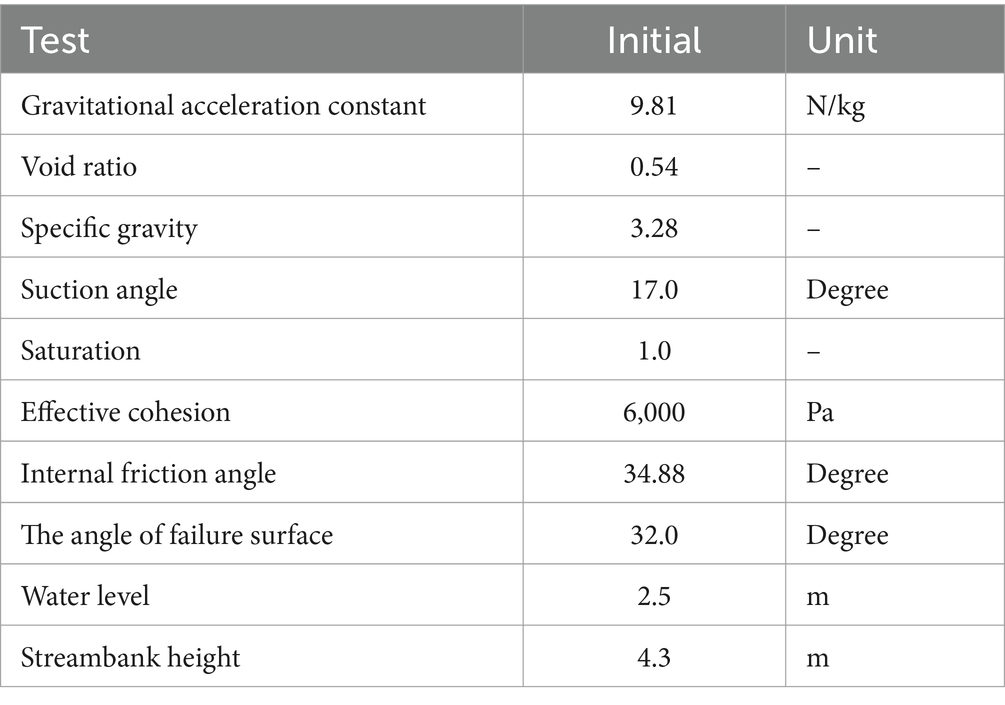
Table 1. Module Verification Data from Sutarto et al. (2014).
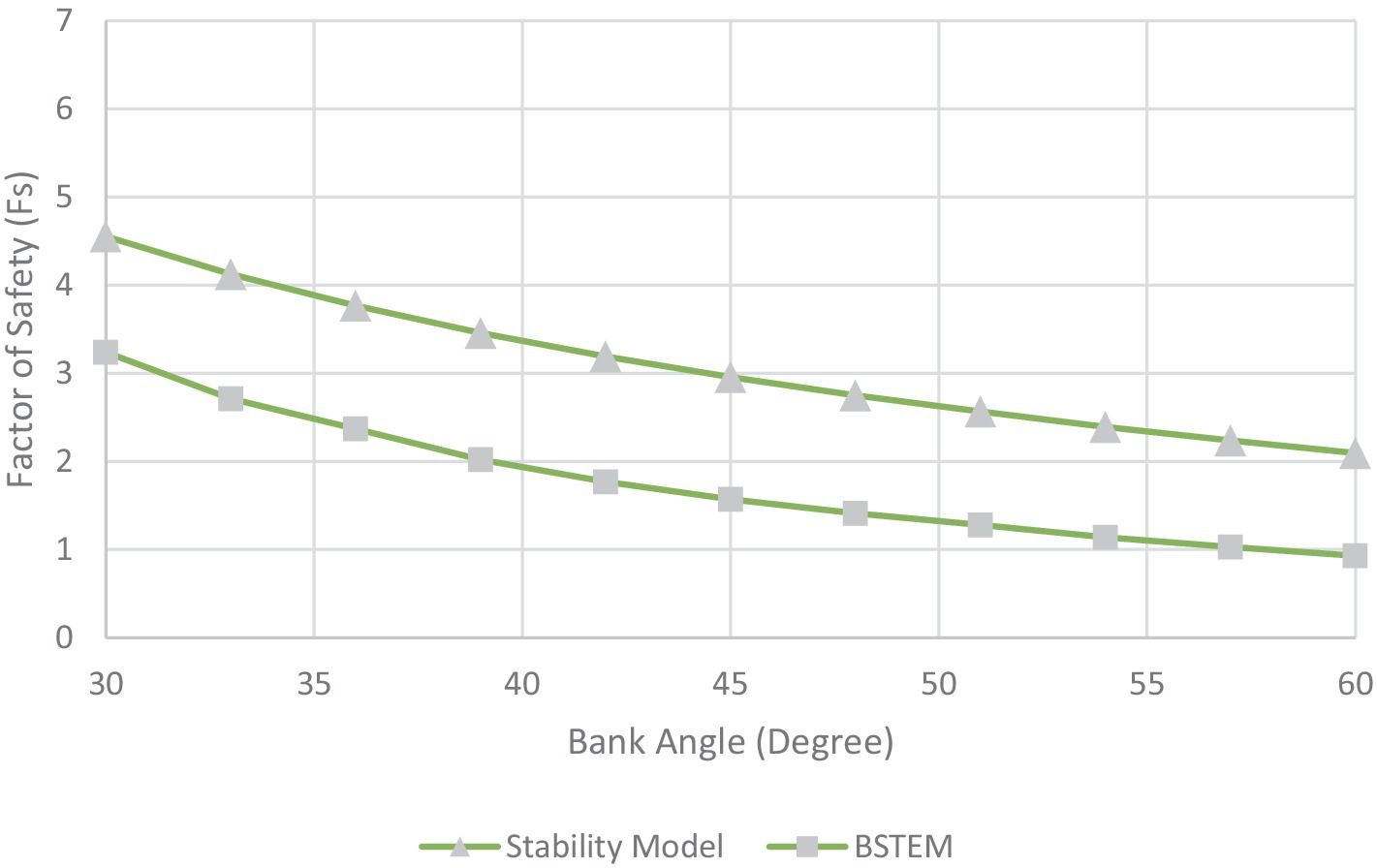
Figure 3. Factor of safety results from BSTEM and the streambank stability module across different bank angles.
The differences in Fs values between the streambank stability module and BSTEM could be attributed to several factors, including differences in the governing equations, simulation methods, approximate calculation methods, assumptions made, and streambank characterization. Each model is underpinned by its unique set of fundamental equations; as mentioned before, the BSTEM uses the layer method, which is different from the stability model, and the choice of numerical simulation methods can notably influence a model’s precision and responsiveness to parameter changes. The equations used in these test cases, though not identical, model equivalent physical processes. It is argued that comparing different approaches to the same physical processes can still provide valuable insights. Furthermore, each model employs its own strategies to simplify these complex systems, which can result in discrepancies between their outputs. However, given the consistency between trends in BSTEM and the module developed here, and the limited availability of other verification examples, the new module is considered representative of changing streambank stability conditions.
In the case of the streambank stability module developed in this work, it operates under the premise that the streambank is homogeneous and isotropic for ease of calculation. This simplification process encompasses factors such as soil cohesion, internal friction angles, the weight of the soil, moisture levels, and vegetative impact. However, in reality, streambanks are relatively heterogeneous in all these factors. Such variability can lead to noteworthy differences in model accuracy.
The newly developed module was also tested for spatial convergence. Using consistent input parameters, the number of slices varied from 2 to 100. Results indicate for the test case that the module converges to about 3.69 with 20 slices but approaches a reasonable estimate of 3.70 with about five slices (Figure 4). As a greater number of slices increases the computational burden of the module, it is ideal to balance accuracy with computational demand and therefore, we recommend using at least five slices in future simulations.
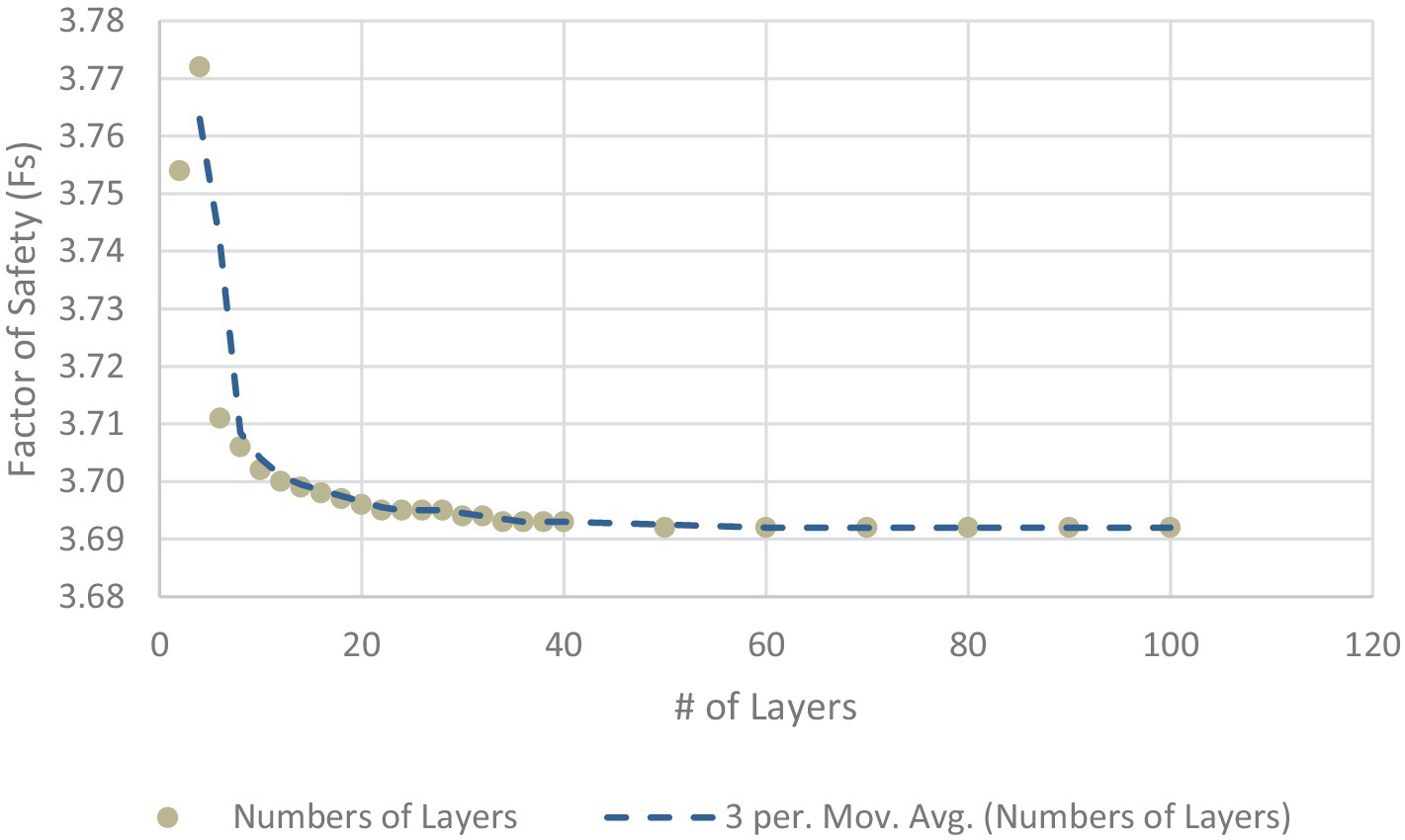
Figure 4. The factor of safety results from the streambank stability module vary with the number of vertical layers.
3 Module demonstration
The new streambank stability module is applied to a drainage basin with existing coupled HGS/OASIS simulation results (Brookfield and Gnau, 2016). The goal is to demonstrate the module’s ability to discern temporal and spatial differences in streambank stability due to changing hydrologic conditions, including those induced by water management practices.
3.1 Site description
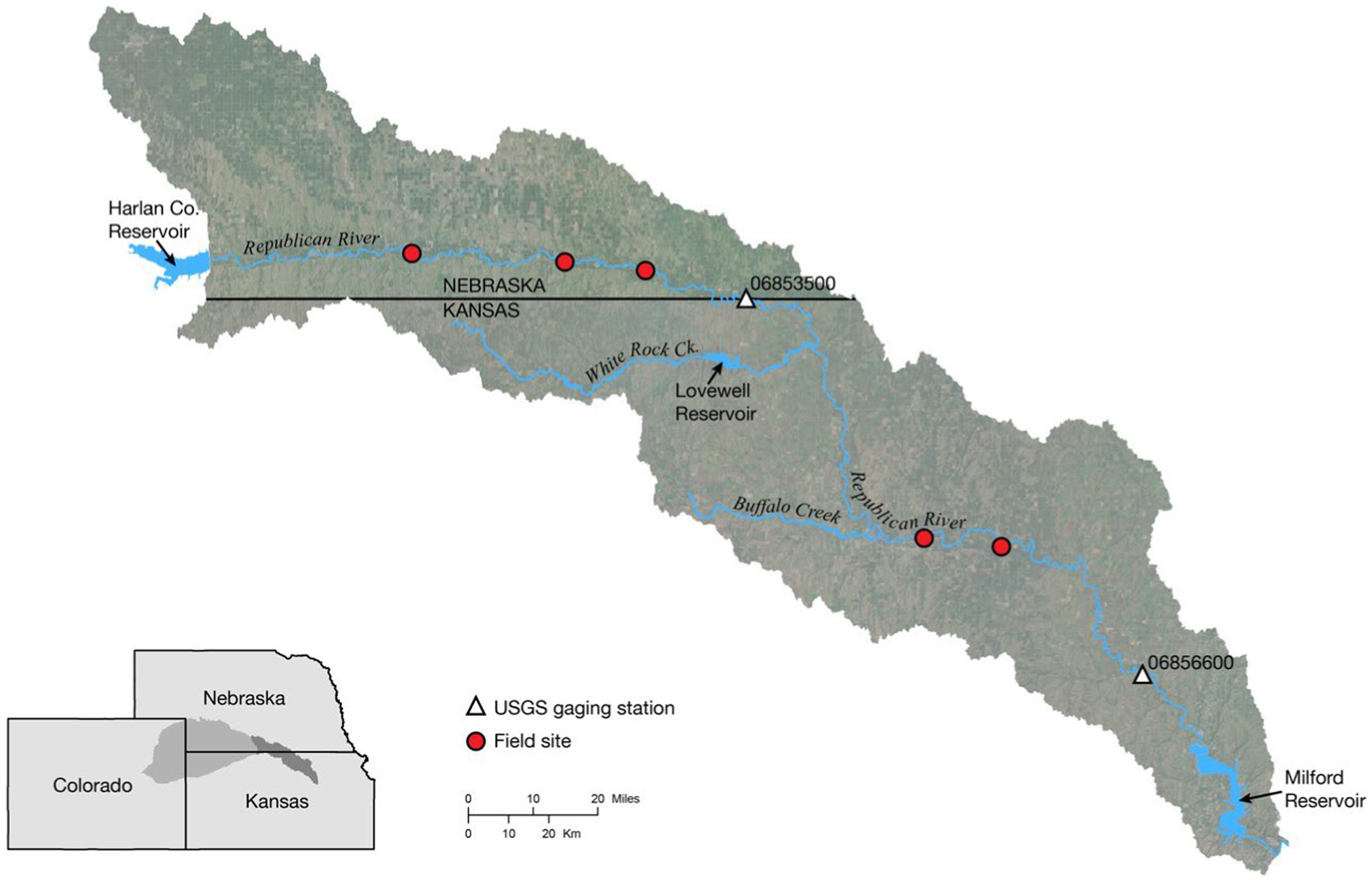
The Lower Republican River Basin (LRRB) is located in southern Nebraska and northern Kansas (Figure 5). The entire Republican River basin covers approximately 65,000 km2, with the rivers originating in northeastern Colorado (U.S. Department of the Interior, 2016). Approximately 31% of the basin is in Colorado, 30% is in Kansas, and 39% is in Nebraska. The dominant use of water in the basin is for agriculture, although water is also used for domestic, industrial, recreational, and wildlife purposes (U.S. Department of the Interior, 2016). Although aquifers underlie most of the basin, the basin is overallocated, and water resources are limited. As such, water management planning in the basin is directly linked to the economic health of the region. Brookfield and Gnau (2016) coupled HGS and OASIS to simulate future water resources in the LRRB (Brookfield and Gnau, 2016), and Brookfield and Layzell (2019) expanded this model to include fluvial erosion to consider some components of sediment transport in the basin.
3.2 Module parameterization
For the streambank stability module, several parameters were estimated from previous literature (e.g., void ratio and specific gravity), and others were measured in the field (e.g., bank height). In order to provide field constraints for the streambank stability module, cohesion (c’) and internal friction angle (Φ’) were measured at five locations in the LRRB (Figure 5) using a Borehole Shear Test (BST) device (Lutenegger and Hallberg, 1981). For each test, an expandable shear head was lowered into a 3-inch diameter borehole augured to a given depth in the streambank. An initial normal stress was applied to the material by expanding the shear head for 15 min. A vertical force was then applied to the shear head by a hand crank, and the peak shear stress was recorded. The test was repeated with progressively higher normal stresses applied to the material in order to construct a failure envelope and determine the variables c’ and Φ.’ At each field site, BST tests were performed at different depths, depending on the alluvial stratigraphy and sedimentology. Three tests were repeated to test for variability. Values representative of average site conditions and measurements are used for this module demonstration (Table 2). Results from the coupled HGS/OASIS model for the LRRB are used to characterize hydrologic conditions for this demonstration (Brookfield et al., 2017) specifically surface water depth, groundwater levels, and pore pressure. These hydrologic conditions varied spatially throughout the basin.
To demonstrate how hydrologic conditions resulting from precipitation events and water management decisions (e.g., reservoir releases) affect streambank stability, results from the coupled HGS/OASIS model were selected for two different periods, reflecting “wet” and “dry” conditions. The two periods selected were July 2005 (severe drought) and July 2010 (wet conditions) based on regional climate data from the National Integrated Drought Information System (Drought.Gov, 2022). It should be noted that due to pervasive dry conditions in the basin over the past several decades, the “wet” scenario is characterized by a return to more normal hydrologic conditions (i.e., lack of severe drought) rather than abnormally wet conditions (i.e., extreme flooding). Streamflow was significantly lower in 2005 compared to 2010 at both the USGS gaging station near Hardy, NE (Station 06853500), just downstream of Harlan County Reservoir, and the gaging station at Clay Center, KS (Station 06856600), which is downstream of the inflow from Lovewell Reservoir via White Rock Creek (Figures 5, 6). Average groundwater levels across the basin also were much lower in 2005 compared to 2010, at 415.2 masl and 439.1 masl, respectively. Stream discharge at Hardy averaged 3.98 m3/s in July 2005 compared to 72.72 m3/s in July 2010, and downstream at Clay Center averaged 0.94 m3/s in July 2005 compared to 7.73 m3/s in July 2010. Water management in the LRRB, both between the wet and dry scenarios and between the two reservoirs, was also notably different. For example, in 2005 (dry scenario), Harlan Reservoir released no water and releases from Lovewell Reservoir were limited (Figure 7), likely due to lack of water availability as well as the administration of the Republican River Compact that allocates the waters of the river among the states of Colorado, Nebraska, and Kansas. In 2010 (wet scenario), both reservoirs released significantly more water as water storage demands had likely been met (Figure 7). The pattern of reservoir releases contributed to observed differences in streamflow. For example, in 2005 consistently low flows at the Hardy gage were a product of both drought conditions as well as lack of releases from Harlan Reservoir (Figures 6A, 7A). In contrast, releases from Lovewell Reservoir in the summer of 2005 were able to maintain streamflow at the Clay Center gage (Figures 6B, 7B). These differences allow us to simulate three different hydrologic conditions as a result of reservoir management: (1) wetter conditions when water is released from both reservoirs (2010); (2) dry conditions when water is unavailable for release (2005, upstream of White Rock Creek); and (3) dry conditions where water is available for release (2005, downstream of White Rock Creek).
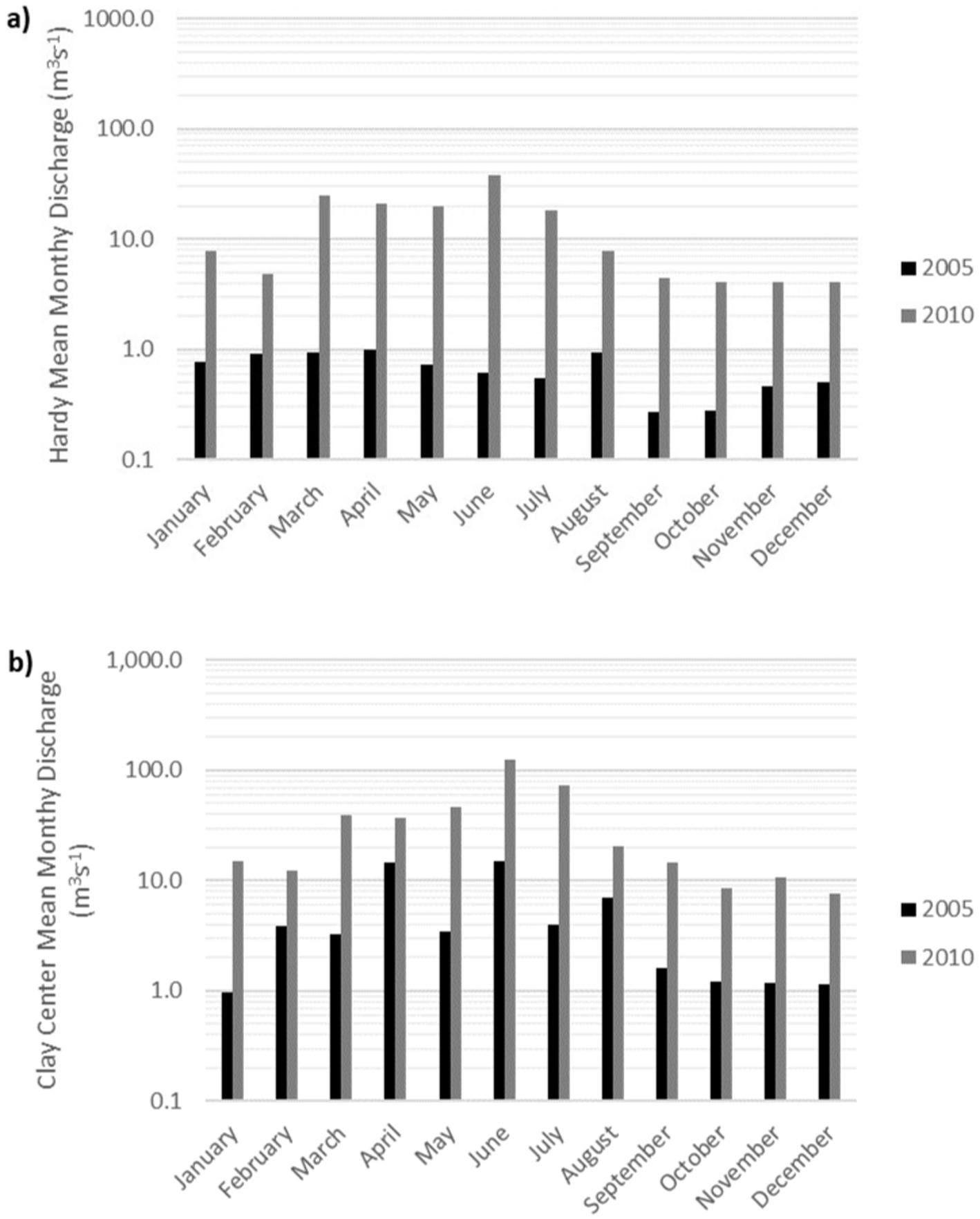
Figure 6. Log-scale of average monthly streamflow for the Republican River in 2005 and 2010 (A) near Hardy, NE (USGS gage 06853500) and (B) at Clay Center, KS (USGS gage 06856600).

Figure 7. Average monthly discharge for 2005 and 2010 from (A) Harlan County Reservoir and (B) Lovewell Reservoir.
4 Results
The Fs results are displayed spatially, using ArcGIS, at points that align with nodal coordinates from the HGS/OASIS simulations. A total of 737 HGS nodes along streams are simulated for each scenario. The wet and dry scenario results are presented independently. To facilitate a comparison between results from the two scenarios, a 1:1 plot comparing Fs values under wet and dry conditions is included (Figure 8) for each node along the main stem of the Republican River with an unstable streambank in at least one of the scenarios. As shown in the plot, most values fall below the 1:1 line, indicating that the factor of safety is consistently, and sometimes substantially, lower under wet conditions than under dry conditions for the same locations.
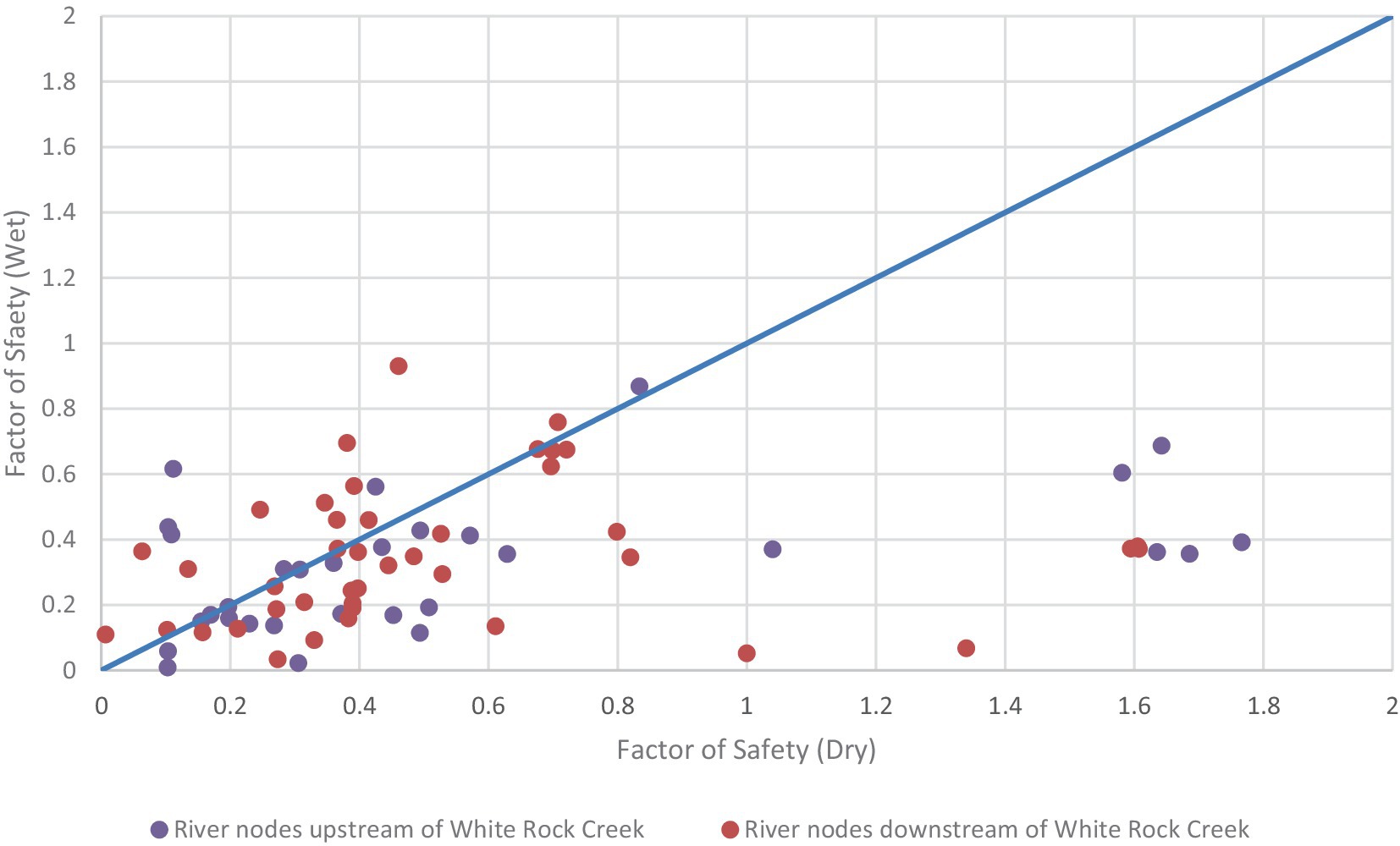
Figure 8. Relationship between the factor of safety values under wet (high precipitation and elevated groundwater levels) and dry (low precipitation and reduced groundwater levels) conditions.
When comparing the regions upstream of White Rock Creek (purple) and downstream of White Rock Creek (red) segments, it becomes apparent that upstream nodes show a broader range of factor of safety values between the model scenarios, with several points displaying higher stability under dry conditions (points located in bottom-right portion of Figure 8). This may be due the differences in reservoir releases in the regions upstream and downstream of White Rock Creek. The upstream region is affected by releases from Harlan Reservoir, which had no releases in the dry scenario (2005) but did have releases in the wet scenario (2010, Figure 7). In contrast, downstream segments are influenced by releases from both Harlan and Lovewell Reservoirs, and Lovewell released water more consistently in both scenarios (Figure 7). This would contribute to the factor of safety values clustering more closely together and shows generally lower stability in wet conditions.
4.1 Wet scenario
Simulation results for the wet scenario indicate a total of 92 unstable nodal locations, with 83 unstable locations along the main rivers of the basin (Figure 9). For the 737 HGS nodes along the main stem of the Republican River and major tributaries (White Rock Creek and Buffalo Creek), the average Fs was 2.03, ranging from 0.01 to 2.34. The locations of potential failure are distributed relatively evenly throughout the LRRB, although the number of unstable locations declines slightly in the upper reaches of the basin (Figure 9).
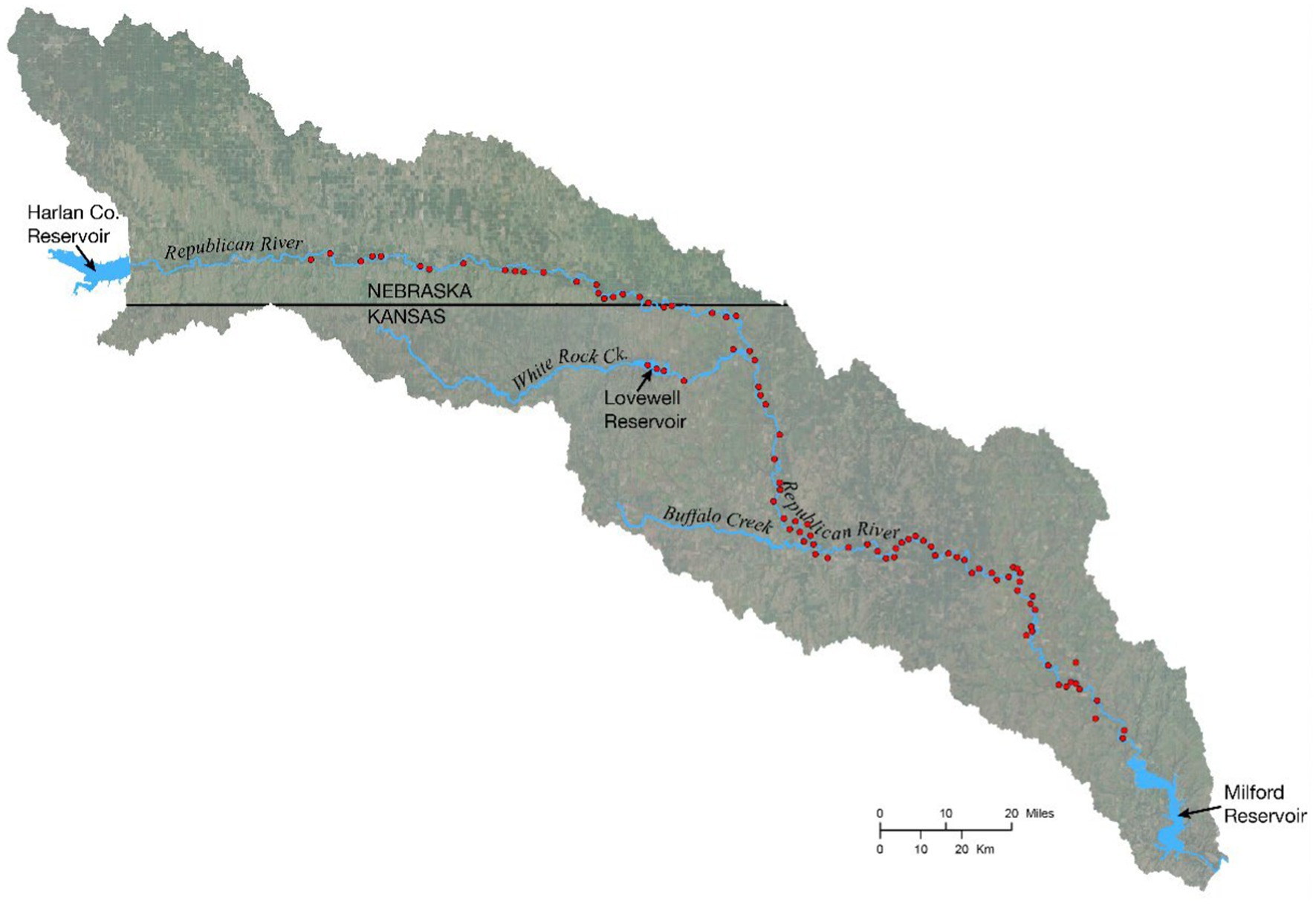
Figure 9. Map of streambank instability for the wet scenario. Red circles indicate nodes where streambank failure is predicted to occur (Fs ≤ 1).
4.2 Dry scenario
Results for the dry scenario indicate a total of 84 unstable nodal locations, with 70 along the main stem of the Republican River and major tributaries (Figure 10). For the 737 HGS nodes along these sections, the average Fs was 2.07, with a range from 0.01 to 2.34. In this scenario, the spatial distribution of unstable nodes is similar to the wet scenario for the lower half of the LRRB (i.e., downstream of White Rock Creek). However, there are notably fewer unstable locations located in the upper half of the basin, particularly closer to Harlan County Reservoir, which released no water during this period.
Figure 10. Map of streambank instability for the dry scenario. Red circles indicate nodes where streambank failure is predicted to occur (Fs ≤ 1).
5 Discussion
As shown in Figures 8–10, the stability of streambanks in the LRRB is not the same under wet and dry conditions. There are parts of the basin where streambank stability is similar between scenarios, particularly in the lower half of the basin, which received water from reservoir releases under both wet and dry conditions (Figures 6, 7). However, streambanks in the upstream portion of the basin are more stable under dry conditions with no reservoir releases. This observation is likely due to the equilibrium, or lack thereof, between the surface and groundwater levels. Consistently low streamflow and groundwater levels result in low streambank saturation levels, thereby reducing the effect of gravitational forces (W1 and W5 in Figure 2) and inhibiting bank failure. If reservoir releases occur during dry periods, then we would expect downstream surface water levels to be higher relative to natural conditions, which could increase the hydrostatic force (Fw in Figure 2B) on the streambank and further support bank stability. However, prolonged increases in streamflow from reservoir releases can also increase the streambank pore pressure from bank infiltration, Saturation of the bank also increases the weight (i.e., gravitational forces), so that when releases cease and stream stage falls, the bank becomes more unstable (higher W and lower Fs). Moreover, the situation is further complicated under wet conditions by increased soil loading from precipitation events and pore pressures due to high saturation levels. This is likely the reason for increased instability in the wet scenario (precipitation + reservoir releases) and the downstream portion of LRRB during the dry scenario (reservoir releases).
Following this reasoning, we note that in July 2005, streamflow did not respond to precipitation events until the last event of the month (Figure 11A), as opposed to July 2010, where the stream responded to both precipitation events and reservoir releases (Figure 11B). Based on these patterns, we infer that under dry conditions, the soil moisture was so low in July 2005 that infiltrating water from precipitation was retained in the soil rather than transferred through the streambanks to the river by throughflow. However, in July 2010 (wet scenario), we infer that soil moisture levels were high enough to promote the throughflow of infiltrating water to the river, thereby increasing pore pressures in streambanks. While the modelled and observed stream stage at the Hardy gaging station was much lower than at the Clay Center gaging station for both the wet and dry scenario, likely due to differences in reservoir releases between the Harlan and Lovewell reservoirs, it is reasonable to propose that the stream levels were lower than they would have been under natural flow conditions (no reservoirs). This would cause a disequilibrium between the pore pressure of the streambanks (high) and the confining pressure from streamflow (low), contributing to streambank instability under wet conditions. These inferences are supported by simulated and observed groundwater levels, which were much higher in 2010 than in 2005. This higher ambient soil moisture increased the weight of the streambank material, thereby promoting streambank instability and bank failure. While not definitive from the available information, these inferences provide a conceptual idea of how water management could impact streambank stability in the LRRB, and are consistent with other studies (e.g., Kafle et al., 2022).
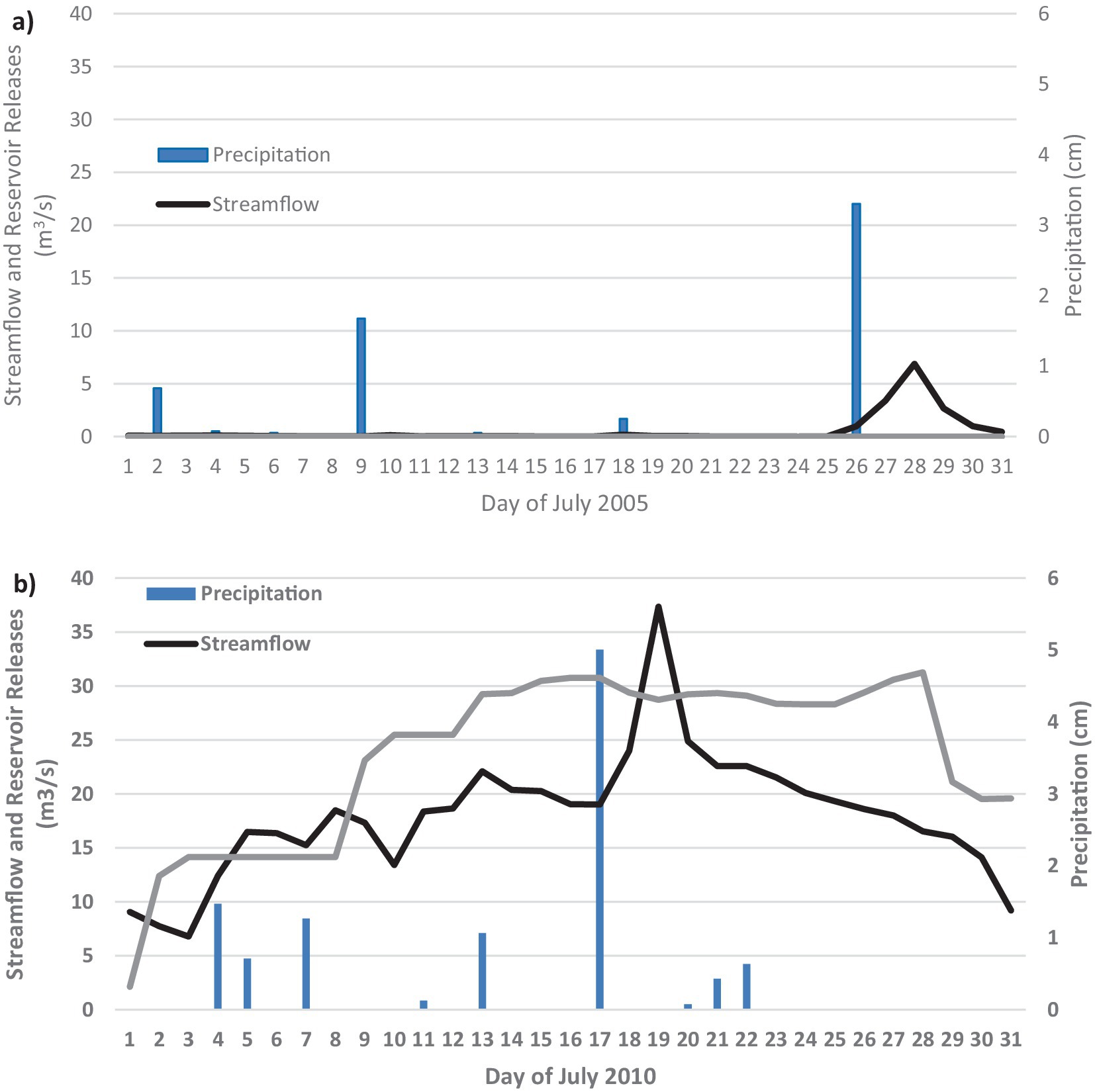
Figure 11. Response of streamflow at the USGS gage station near Hardy, NE, to Harlan Reservoir releases and precipitation in (A) July 2005 and (B) July 2010.
In this study, we recognize several factors that may contribute to errors and uncertainties in the modeling approach and application. First, the simplified methods used may not fully capture real-world complexities including all of the different streambank failure methods, as discussed in the model development, limiting the model’s ability to accurately represent site conditions. Additionally, the HEC-RAS method (For further details, please refer to the supplementary material, Page 5) applied in our analysis may not always yield the minimum factor of safety value under certain conditions, such as when there are monotonic relationships between failure angle and factor of safety (US Army Corps of Engineers, 2015), which could affect the reliability of stability predictions. Another source of uncertainty is the assumption of homogeneous soil properties in the vertical profile. In reality, soil types and properties can vary significantly with depth, impacting both pore pressure distribution and overall stability. Future work could include sensitivity analyses and refinements in parameter selection to address these limitations, enhancing the model’s accuracy and applicability.
6 Conclusions
Here, the impact of changing hydrologic conditions, driven in part by water management decisions, on streambank stability is studied by developing a new module that estimates FS using results from coupled HGS/OASIS simulations. This module was verified using a previously published, commonly used model (BSTEM) and was tested for spatial convergence. The module was then applied to wet and dry scenarios in the LRRB for demonstration. In applying the verified module to the LRRB, it is evident that water management decisions can have an impact on the stability of streambanks. Results indicated that streambanks were less stable under the wet conditions than dry conditions, likely due to a combination of increased pore water pressures and soil loading. These conditions resulted from increased soil saturation levels and reservoir controlled streamflows that were likely lower than what would have naturally occurred. This was most evident in the upstream portion of the basin studied in this work, where noticeable differences in streambank stability between the wet and dry scenarios were evident. The upstream reservoir (Harlan County Reservoir) released no water during the dry scenario, resulting in very low streamflows in the upper part of the basin. In the lower half of the basin, releases from Lovewell Reservoir augmented downstream streamflow, and, as a result, streambank stability was found to be similar to that of the wet scenario in downstream reaches.
This research intends to provide a tool for the preliminary assessment of streambank stability under hydrologic conditions driven by water management decisions and operations. In future work, we will further explore more spatially variable streambank conditions and simulate longer continuous periods to capture the dynamic interactions and temporal variations in streambank stability. The work presented in this manuscript introduces a modeling framework that is suited for this future work. Additionally, we will investigate how changes in water management practices induced by climate change can affect streambank stability. We believe this future work can provide an even more comprehensive understanding of the factors influencing streambank erosion and stability within the context of water management decisions.
Data availability statement
The original contributions presented in the study are publicly available. This data can be found here: Federated Research Data Repository (FRDR); Wei, Q., Brookfield, A., Layzell, A. (2024). Quantifying the Effects of Water Management Decisions on Streambank Stability, https://doi.org/10.20383/103.01126.
Author contributions
QW: Validation, Writing – original draft, Writing – review & editing, Software, Visualization. AB: Supervision, Writing – original draft, Writing – review & editing, Formal analysis, Funding acquisition, Validation. AL: Data curation, Investigation, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by a US Geological Survey Section 104(b) grant via the Kansas Water Resource Institute (PI Layzell) and the Natural Science and Engineering Research Council of Canada Discovery Grant Program (PI Brookfield).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2024.1430374/full#supplementary-material
References
Abbasov, R., Fahs, M., Younes, A., Nowamooz, H., Jørgen Måløy, K., and Toussaint, R. (2024). Modeling rainfall-induced landslide using the concept of local factor of safety: uncertainty propagation and sensitivity analysis. Comput. Geotech. 167:106102. doi: 10.1016/j.compgeo.2024.106102
Aquanty (2023) Aquanty. Available at: https://www.aquanty.com (Accessed February 22, 2023).
Bigham, K. A., Keane, T. D., and Moore, T. L. (2024). Effect of flow regulation on streambank erosion: a perspective downstream of a flood control dam, Kansas, USA. River Res. Appl. 40, 14–28. doi: 10.1002/rra.4212
Brookfield, A. E., and Gnau, C. (2016). Optimizing water Management for Irrigation under Climate Uncertainty: evaluating operational and structural alternatives in the lower Republican River basin, Kansas, USA. Water Resour. Manag. 30, 607–622. doi: 10.1007/s11269-015-1180-y
Brookfield, A., Gnau, C., and Wilson, B. (2017). Incorporating surface water operations in an integrated hydrologic model: model development and application to the lower Republican River basin, United States. J. Hydrol. Eng. 22:04016065. doi: 10.1061/(ASCE)HE.1943-5584.0001486
Brookfield, A. E., and Layzell, A. L. (2019). Simulating the effects of reservoir management strategies on fluvial Erosion. Water Resour. Manag. 33, 4983–4995. doi: 10.1007/s11269-019-02380-y
Brunner, P., and Simmons, C. T. (2012). HydroGeoSphere: a fully integrated, physically based hydrological model. Groundwater 50, 170–176. doi: 10.1111/j.1745-6584.2011.00882.x
Casagli, N., Rinaldi, M., Gargini, A., and Curini, A. (1999). Pore water pressure and streambank stability: results from a monitoring site on the Sieve River, Italy. Earth Surf. Process. Landf. 24, 1095–1114. doi: 10.1002/(SICI)1096-9837(199911)24:12<1095::AID-ESP37>3.0.CO;2-F
Chu-Agor, M. L., Wilson, G. V., and Fox, G. A. (2008). Numerical modeling of Bank instability by seepage Erosion undercutting of layered streambanks. J. Hydrol. Eng. 13, 1133–1145. doi: 10.1061/(ASCE)1084-0699(2008)13:12(1133)
Drought.Gov (2022) National Integrated Drought Information System. Available at: https://www.drought.gov/ (Accessed September 30, 2022).
Fox, G. A., Wilson, G. V., Simon, A., Langendoen, E. J., Akay, O., and Fuchs, J. W. (2007). Measuring streambank erosion due to ground water seepage: correlation to bank pore water pressure, precipitation and stream stage. Earth Surf. Process. Landf. 32, 1558–1573. doi: 10.1002/esp.1490
Hydrologics (2009). OASIS with OCL, model version 3.10.8, GUI version 4.6.16. New York, NY, USA: Hydrologics.
Kadhim, J., Waheed, M. Q., Hussein, H. A., and al-Wakel, S. F. A. (2024). Experimental study on the effect of flow velocity and slope on stream Bank stability (part I). Civil Eng. J. 10, 2631–2644. doi: 10.28991/CEJ-2024-010-08-013
Kafle, L., Xu, W. J., Zeng, S. Y., and Nagel, T. (2022). A numerical investigation of slope stability influenced by the combined effects of reservoir water level fluctuations and precipitation: a case study of the Bianjiazhai landslide in China. Eng. Geol. 297:106508. doi: 10.1016/j.enggeo.2021.106508
Langendoen, E. J. (2000) CONCEPTS - CONservational Channel evolution and pollutant transport system: stream corridor version 1.1. U.S. Department of Agriculture (USDA). Available at: https://www.ars.usda.gov (Accessed November 2022).
Lutenegger, A. J., and Hallberg, G. R. (1981). Borehole shear test in geotechnical investigations. In: Laboratory Shear Strength of Soil, STP740-EB:0. Eds. R. N. Yong and F. C. Townsend, ASTM International.
Maxwell, R. M., Condon, L. E., and Kollet, S. J. (2015). A high-resolution simulation of groundwater and surface water over most of the continental US with the integrated hydrologic model ParFlow v3. Geosci. Model Dev. 8, 923–937. doi: 10.5194/gmd-8-923-2015
Midgley, T. L., Fox, G. A., and Heeren, D. M. (2012). Evaluation of the Bank stability and toe Erosion model (BSTEM) for predicting lateral streambank retreat on Ozark streams. Geomorphology, 145–146, 107–114. doi: 10.1016/j.geomorph.2011.12.044
Osman, A. M., and Thorne, C. R. (1988). Riverbank stability analysis. I: theory. J. Hydraul. Eng. 114, 134–150. doi: 10.1061/(ASCE)0733-9429(1988)114:2(134)
Patsinghasanee, S., Kimura, I., Shimizu, Y., and Nabi, M. (2018). Experiments and modelling of cantilever failures for cohesive riverbanks. J. Hydraul. Res. 56, 76–95. doi: 10.1080/00221686.2017.1300194
Qiu, J., Yang, Q., Zhang, X., Huang, M., Adam, J. C., and Malek, K. (2019). Implications of water management representations for watershed hydrologic modeling in the Yakima River basin. Hydrol. Earth Syst. Sci. 23, 35–49. doi: 10.5194/hess-23-35-2019
Rinaldi, M., Casagli, N., Dapporto, S., and Gargini, A. (2004). Monitoring and modelling of pore water pressure changes and riverbank stability during flow events. Earth Surf. Process. Landf. 29, 237–254. doi: 10.1002/esp.1042
Rinaldi, M., and Darby, S. E. (2007). Modelling river-bank-erosion processes and mass failure mechanisms: progress towards fully coupled simulations. Dev. Earth Surf. Process. 11, 213–239. doi: 10.1016/S0928-2025(07)11126-3
Shields, F. D., Simon, A., and Dabney, S. M. (2009). Streambank dewatering for increased stability. Hydrol. Process. 23, 1537–1547. doi: 10.1002/hyp.7286
Simon, A. (2006) ‘A model of streambank stability incorporating hydraulic erosion and the effects of riparian vegetation’, Proceedings of the Eighth Federal Interagency Sedimentation Conference (8thFISC).
Simon, A., Curini, A., Darby, S. E., and Langendoen, E. J. (2000). Bank and near-bank processes in an incised channel. Geomorphology 35, 193–217. doi: 10.1016/S0169-555X(00)00036-2
Springston, G. (2007). Report on streambank stability assessment techniques Vermont geological survey technical Report. VGTR2007-1. Vermont Geological Survey.
Sutarto, T., Papanicolaou, T., Wilson, C., and Langendoen, E. (2014). Stability analysis of semicohesive streambanks with CONCEPTS: Coupling field and laboratory investigations to quantify the onset of fluvial erosion and mass failure. J. Hydraul. Eng. 140:04014041. doi: 10.1061/(ASCE)HY.1943-7900.0000899
Taie Semiromi, M., and Koch, M. (2019). Analysis of spatio-temporal variability of surface–groundwater interactions in the Gharehsoo river basin, Iran, using a coupled SWAT-MODFLOW model. Environ. Earth Sci. 78:201. doi: 10.1007/s12665-019-8206-3
U.S. Department of the Interior. (2016). Republican River Basin Study: Final Executive Summary Report. Bureau of Reclamation Technical Service Center, Denver, Colorado. Available at: https://www.usbr.gov
US Army Corps of Engineers (2015) HEC-RAS USDA-ARS Bank Stability & toe Erosion Model (BSTEM), Technical Reference and User’s manual. Available at: https://www.hec.usace.army.mil/confluence/rasdocs/rassed1d/1d-sediment-transport-technical-reference-manual/bstem-technical-reference-manual/steps-in-a-bank-failure-analysis (Accessed May 30, 2023).
Valerio, A., Rajaram, H., and Zagona, E. (2010). Incorporating groundwater-surface water interaction into river management models. Groundwater 48, 661–673. doi: 10.1111/j.1745-6584.2010.00702.x
Keywords: streambank stability, integrated water resources management, porewater pressure, reservoir operations, water management decisions
Citation: Wei Q, Brookfield A and Layzell A (2024) Quantifying the effects of water management decisions on streambank stability. Front. Water. 6:1430374. doi: 10.3389/frwa.2024.1430374
Edited by:
Matteo Camporese, University of Padua, ItalyReviewed by:
Marwan Fahs, National School for Water and Environmental Engineering, FranceBenjamin Mary, Instituto de Ciencias Agrarias, Spain
Copyright © 2024 Wei, Brookfield and Layzell. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Q. Wei, cXVhbi53ZWlAdXdhdGVybG9vLmNh
 Q. Wei
Q. Wei A. Brookfield
A. Brookfield A. Layzell2
A. Layzell2