Performance comparison of physics-based and machine learning assisted multi-fidelity methods for the management of coastal aquifer systems

Kopsiaftis, George; Kaselimi, Maria; Protopapadakis, Eftychios; Voulodimos, Athanasios; Doulamis, Anastasios; Doulamis, Nikolaos; Mantoglou, Aristotelis

doi:10.3389/frwa.2023.1195029

ORIGINAL RESEARCH article

Front. Water, 30 June 2023

Sec. Water and Hydrocomplexity

Volume 5 - 2023 | https://doi.org/10.3389/frwa.2023.1195029

This article is part of the Research Topic Multifidelity Modelling for Optimization and Analysis of Subsurface and Surface Water Systems View all 4 articles

Performance comparison of physics-based and machine learning assisted multi-fidelity methods for the management of coastal aquifer systems

$\r\nGeorge Kopsiaftis$ George Kopsiaftis¹^*

Maria Kaselimi²

Eftychios Protopapadakis³

Athanasios Voulodimos⁴

Anastasios Doulamis²

Nikolaos Doulamis²

Aristotelis Mantoglou¹

¹Laboratory of Reclamation Works and Water Resources Management, School of Rural, Surveying and Geoinformatics Engineering, National Technical University of Athens, Athens, Greece
²Laboratory of Photogrammetry, School of Rural, Surveying and Geoinformatics Engineering, National Technical University of Athens, Athens, Greece
³School of Information Sciences, Department of Applied Informatics, University of Macedonia, Thessaloniki, Greece
⁴Artificial Intelligence and Learning Systems Laboratory, School of Electrical and Computer Engineering, National Technical University of Athens, Athens, Greece

In this work we investigate the performance of various lower-fidelity models of seawater intrusion in coastal aquifer management problems. The variable density model is considered as the high-fidelity model and a pumping optimization framework is applied on a hypothetical coastal aquifer system in order to calculate the optimal pumping rates which are used as a benchmark for the lower-fidelity approaches. The examined lower-fidelity models could be classified in two categories: (1) physics-based models, which include several widely used variations of the sharp-interface approximation and (2) machine learning assisted models, which aim to improve the efficiency of the SI approach. The Random Forest method was utilized to create a spatially adaptive correction factor for the original sharp-interface model, which improves its accuracy without compromising its efficiency as a lower-fidelity model. Both the original sharp-interface and Machine Learning assisted model are then tested in a single-fidelity optimization method. The optimal pumping rated which were calculated using the Machine Learning based SI model sufficiently approximate the solution from the variable density model. The Machine Learning assisted approximation seems to be a promising surrogate for the high-fidelity, variable density model and could be utilized in multi-fidelity groundwater management frameworks.

1. Introduction

Seawater intrusion (SWI) models based on density-dependent approach constitute an accurate and realistic emulation of the saltwater/freshwater interaction and movement in coastal aquifers, since they incorporate several components of the physical processes, such as the dispersion mechanism (Simmons, 2005; Younes et al., 2009, 2022; Dokou and Karatzas, 2012; Werner et al., 2013; Karatzas and Dokou, 2015; Kourgialas et al., 2015; Fahs et al., 2022). However, variable density (VD) models are computationally demanding and entail considerably long runtimes, as the mathematical description of the model consists of a coupled partial differential equation system, which require the implementation of complex and time-consuming numerical methods (e.g., finite differences or finite element methods). The long simulation runtimes, usually lead to an unmanageable overall computational burden for several real-life applications that require a considerable number of iterations, such as simulation-optimization problems and inverse modeling in coastal aquifers, sensitivity and uncertainty analysis or the development of decision support systems in coastal water resources systems (Asher et al., 2015). A common approach to mitigate the excessive computational cost is the use of approximation models, which aim to simulate the same physical process considering only few components of the real physical system (Simpson et al., 2001; Forrester et al., 2008; Razavi et al., 2012). These low-complexity models—which are often called surrogate models, metamodels, lower-fidelity (LF) models, response surfaces etc.—are much quicker compared to the high-fidelity (HF) models, but they have lower fidelity, i.e., the degree of the realism of a simulation model (Razavi et al., 2012).

Approximation models are gradually gaining ground in many aspects of water resources, such as groundwater modeling. A thorough survey of the surrogate models in water resources is presented in the work of Razavi et al. (2012) and Asher et al. (2015). According to Razavi et al. (2012) there are two main categories of the surrogate models: (i) the statistical or empirical data-driven models, which emulate the HF model responses, and (ii) the physically-based surrogates, which are usually a simplified version of the original HF model.

On the broad category of the data-driven surrogate models, Machine Learning (ML) algorithms demonstrated good performance in reproducing the outcomes of HF models. One of the first to use an ML assisted metamodeling strategy for SWI was Bhattacharjya et al. (2007), who employed an Artificial Neural Network (ANN) to predict the concentration at specified observation locations at different times in a coastal aquifer. Trichakis et al. (2011) also used ANNs to model the groundwater levels in a karstified groundwater system. Roy and Datta (2017a) utilized the fuzzy C-means clustering algorithm to predict the extent of SWI, while Lal and Datta (2018) employed Support Vector Machines (SVM) as a ML regressor to predict the salinity concentration at specified monitoring wells and compared the results with a genetic programming (GP) based surrogate model. Kopsiaftis et al. (2019b) investigated several ML algorithms, such as Gaussian Process Regression (GPR), SVMs, RFs, and ANNs, regarding their ability to estimate the location of a critical isohaline.

In a number of studies, the data-driven surrogate models were exploited in groundwater management strategies. For example, Kourakos and Mantoglou (2009) coupled a simulation-optimization framework with an ANN model to reduce the computational burden arising from the VD simulations. In the same context, Kourakos and Mantoglou (2013) integrated modular neural networks into a multi-objective management scheme, whereas Ataie-Ashtiani et al. (2014) developed an efficient, ANN-based multi-objective system for groundwater management in freshwater lenses of small islands. Christelis and Mantoglou (2016b) used cubic radial basis functions (RBFs) in an adaptive-recursive metamodeling framework which provided optimal pumping rates which approximated the global optimum. Christelis et al. (2018) emphasized on the joint use of HF and LF models to improve the efficiency of a surrogate-based optimization framework under limited computational budgets and for problems of different dimensionality.

In some recent studies, researchers investigate the efficiency of the weighted combination of several surrogate models in the form of ensemble models. Sreekanth and Datta (2011) proposed an ensemble model based on the genetic programming algorithm. Roy and Datta (2017b,c) examined ensemble versions of multivariate adaptive regression spline and adaptive neuro-fuzzy inference systems respectively, in coastal aquifer pumping optimization problems to control the encroachment of SWI. Kopsiaftis et al. (2019a) utilized three well established physically-based surrogate models in groundwater management problems following a tow-step approach—first they solved a pumping optimization problem with each model separately, and then with all the possible combinations. The results indicated that in most cases the ensemble model predictions outperformed the individual surrogate models. Christelis and Mantoglou (2016a, 2019) introduced a variable-fidelity approach in pumping optimization of coastal aquifers to leverage the LF model features and specifically the reduced simulation runtimes.

In this paper we propose a method that combines a physical-based surrogate model and a data driven model, which—to the best of our knowledge—has not been used in coastal aquifer management problems. The core idea of the method lies on the correction of existing approaches, which, as mentioned before, are widely-used and of significant usefulness in seawater intrusion problems. In the following section of the paper, we initially investigate well-established, physical-based surrogate models of SWI, regarding their efficiency in coastal aquifer management problems. The preliminary results indicate that the use of single-fidelity models may have several limitations in capturing the extent of SWI for a wide range of coastal aquifer parameter values (e.g., pumping rates and recharge). To address this problem, the combined use of models of various fidelities is investigated in this paper, which could enhance their adaptability in different aquifer geometries and flow conditions. To this end, a data-driven model—specifically the Random Forest (RF) method—is utilized to increase the fidelity of a widely used physically-based SWI model. It is worth mentioning that the RF algorithms, as implemented in this study, is univariate and that Bayesian optimization is employed in the surrogate model, to improve its efficiency. The proposed correction method is applied on a hypothetical unconfined coastal aquifer and the calculated SWI extent is compared to the results of three additional physically-based surrogate models, that is the original model before the correction and its two main modifications under moderate and intensive pumping.The examined aquifer is a typical coastal aquifer in arid and semi-arid Mediterranean islands, which spans an approximate area of 20km². The ML assisted LF model outperformed the examined surrogate models in capturing the VD SWI extent. To test its usefulness in applications of practical interest, the proposed LF model is subsequently incorporated in a pumping optimization framework demonstrating a good performance, comparable to VD model.

The remainder of this work is structured as follows: Section 2 analyzes the mathematical formulation of all the examined SWI models, including the HF model, the previous well-established LF approximations, and finally the proposed RF assisted model, whereas Section 3 presents the optimization framework for a coastal aquifer management problem. Section 4 provides the experimental results, including the comparison of the proposed method with previous approached, and the implementation of the pumping optimization framework. Finally, Section 5 concludes the paper.

2. Seawater intrusion models and application aquifer

Several mathematical models of different complexity have been proposed to describe SWI in coastal aquifers. As already mentioned in Section 1, in the present study we employ models of two fidelity options to simulate SWI: (i) a 3D VD model representing the HF case, and (ii) a 2D SI model as the LF case. The LF model does not consider the dispersion mechanism—is the driving force of seawater/freshwater mixing—leading to a model of reduced complexity. In the following sections we briefly present the mathematical formulation of all the SWI models.

2.1. Variable density model

VD models are based on the spatial variability of groundwater density, which ranges from saline water density to freshwater density. The density changes because of the mixing of freshwater and seawater, which results in the existence of a transition zone across the entire coastline. The width and exact position of the zone depends on the aquifer parameters and the pumping regime. In the current paper, thermal and viscosity effects are neglected and the density changes are attributed only to concentration effect. The mathematical formulation of the VD model has been thoroughly analyzed in several works (e.g., Frind, 1982; Kolditz et al., 1998; Younes et al., 2009; Pool and Carrera, 2011; Kourgialas et al., 2015; Fahs et al., 2022). In this study thesis the notation proposed by (Guo and Langevin, 2002; Langevin et al., 2008) is followed in order to be consistent with the SEAWAT numerical code, which is utilized for the VD simulations.

In general, the flow and solute-transport equations are used to describe mathematically the VD model. The two equations form a coupled differential equation system, which could be expressed as follows

\begin{array}{l} - ▽ \cdot (ρ q) + ρ_{s} q_{s} = ρ S_{f} \frac{\partial h_{f}}{\partial t} + n \frac{\partial ρ}{\partial C} \frac{\partial C}{\partial t} & (1) \end{array}

\begin{array}{l} - ▽ \cdot (D \cdot ▽ C) - ▽ \cdot (v C) - \frac{q_{s}}{n} C_{s} = \frac{\partial C}{\partial t} & (2) \end{array}

where ρ is fluid density, q is the Darcy velocity vector, ρ_s is the density of water entering from a source of leaving through a sink, q_s is the volumetric flow rate per unit volume of porous medium representing sources and sinks, S_f is the specific storage, h_f is the freshwater head, n is the porosity, C is the solute concentration, D is the hydrodynamic dispersion tensor, v is the fluid velocity vector, and C_s is the solute concentration of water entering or leaving through sources and sinks respectively. Since solute reaction is not considered, fluid density is only a function of the solute concentration C, according to the following equation

\begin{array}{l} ρ = ρ_{o} (1 + \frac{ϵ}{C_{s} - C_{o}} (C - C_{o})) & (3) \end{array}

in which ρ_o is the freshwater density, ϵ is the density difference ratio (Equation 3), C_o is reference concentration, and C_s is the maximum concentration. In this paper, the following values are used for the parameters of Equation (3): ρ_o = 1.000kg/m³, C_o = 0kg/m³, and C_s = 35kg/m³.

The density difference ratio is expressed as

\begin{array}{l} ϵ = \frac{ρ_{s} - ρ_{f}}{ρ_{f}} & (4) \end{array}

where ρ_s stands for the maximum seawater density. In this study, we consider ρ_s = 1025kg/m³.

The Darcy flux term q of Equation (1) for constant viscosity and freshwater properties could be expressed as

\begin{array}{l} q_{x} = - K_{f x} (\frac{\partial h_{f}}{\partial x}) \\ q_{y} = - K_{f y} (\frac{\partial h_{f}}{\partial y}) \\ q_{z} = - K_{f z} (\frac{\partial h_{f}}{\partial z} + \frac{ρ - ρ_{f}}{ρ}) & (5) \end{array}

where q_x, q_y, and q_z are the components of the specific discharge in the principal directions, K_fx, K_fy, and K_fz are the components of the freshwater hydraulic conductivity in the same directions and ρ_f is the freshwater density.

Equations (1)–(5) are the mathematical representation of VD approach of seawater intrusion. The well-established SEAWAT code is used to solve numerically the above equation set. SEAWAT is a modular finite-difference computer code created by USGS, which couples MODFLOW and MT3DMS, in order to solve iteratively the fluid flow and solute transport equations (Guo and Langevin, 2002).

2.2. Sharp interface model

The SI model employed in the present work is based on the single flow potential formulation proposed by Strack (1976). The Strack's approach considers three basic assumptions: (1) the Dupuit-Forchheimer approximation, (2) Ghyben-Herzberg approximation, and (3) Hydrostatic conditions in the saltwater zone. For steady state conditions, the incorporation of the three assumptions result in a simplified one-fluid, 2D SWI model, which, for the general case of irregular-shaped aquifers with spatially variable parameters (e.g., hydraulic conductivity and recharge), could be solved numerically using a groundwater flow code (Mantoglou et al., 2004). The differential equations used to calculate the flow potential in an unconfined coastal aquifer has the following form

\begin{array}{l} \frac{\partial}{\partial x} (K \frac{\partial ϕ}{\partial x}) + \frac{\partial}{\partial y} (K \frac{\partial ϕ}{\partial y}) + N - Q (x, y) = 0 & (6) \end{array}

where K = K(x, y) is the hydraulic conductivity of the aquifer, which is usually considered as a function of the spatial coordinates (x, y), N is the aquifer recharge, and Q(x, y) represents the distributed well pumping rates. The flow potential ϕ_τ at the location of the toe in an unconfined aquifer is calculated from the following equations (Mantoglou, 2003).

\begin{array}{l} ϕ_{τ} = \frac{(1 + ϵ) ϵ}{2} d^{2} & (7) \end{array}

where d denotes the thickness of the aquifer from the horizontal bottom to the sea level. From the flow potential value field we are able to calculate the exact location of the sharp interface toe, which is of considerable interest in coastal aquifer management problems.

2.3. Sharp interface model modifications

The SI model proposed by Strack (1976) and adopted in several studies (e.g., Werner et al., 2012; Ketabchi and Ataie-Ashtiani, 2015) have been widely used to simulate SWI in coastal aquifers or pumping optimization problems in coastal aquifers (e.g., Mantoglou, 2003; Mantoglou et al., 2004). However, it has been observed in several previous studies (e.g., Dausman et al., 2010; Koussis et al., 2015; Kopsiaftis et al., 2019a) that for a specific set of pumping rates the SI model tends to overestimate the extent of the seawater wedge compared to the variable density approach, which is considered as a reference result for the estimation of seawater intrusion. Llopis-Albert and Pulido-Velazquez (2014) further examined the efficiency of the Ghyben-Herzberg based SI model in producing comparable results with the VD model, within a range in the values of critical hydrogeological parameters and defined several limitations in the validity of the SI model.

In order to eliminate the discrepancy between the two models, several correction methods have been recently proposed (e.g., Pool and Carrera, 2011; Koussis et al., 2012, 2015; Lu et al., 2016; Werner, 2017; Koussis and Mazi, 2018; Christelis et al., 2019), which aim to incorporate the effect of the dispersion mechanism and improve the accuracy of the SI approach. Pool and Carrera (2011) were the first to suggest a novel formula to extend Strack's equations to the case of the mixing zone. In particular, they proposed an multiplication factor for the saltwater-freshwater density ratio, which is expressed as an empirical equation of specific physical parameters of the aquifer. The multiplication factor has the following form

\begin{array}{l} ϵ^{*} = ϵ [1 - {(\frac{a_{T}}{d})}^{1 / 6}] & (8) \end{array}

where ϵ^* is the modified buoyancy factor or saltwater-freshwater density ratio and a_T is transverse dispersivity. This specific correction factor has been widely used in a number of studies (e.g., Lu et al., 2012; Christelis and Mantoglou, 2013; Lu and Werner, 2013; Lu and Luo, 2014; Koussis et al., 2015). Lu and Werner (2013) proposed a modification of the (Pool and Carrera, 2011) correction factor. Specifically, they performed a significant number of variable density simulations and suggested that the 1/6 exponent of Equation (8) should be replaced with 1/4. In a more recent study, Christelis and Mantoglou (2016a) observed that in highly pumped aquifers, the value of the density ratio that allows the SI to resemble the salinity spatial distribution depends not only on the aquifer physical parameters included in Equation (8), but also on the well pumping rates. In order to incorporate this effect, they suggested a dynamic adjustment of the density ratio during the pumping optimization process. In this case, the correction is based on the modification of the density ratio in an intermediate optimization step, which minimizes the discrepancy between the VD and SI models. Kopsiaftis et al. (2019a) compared the SWI extent based on five models: (i) the VD model, (ii) the Strack SI model, (iii) the Pool and Carrera (2011) correction, (iv) the Lu and Werner (2013), and (v) several combinations of the above SI models, in the form of ensemble SI model prediction. In the same study, the authors used all the examined models in a pumping optimization model and concluded that the ensemble solutions provide promising results. The ensemble SI prediction could be expressed as follows

\begin{array}{l} Ŷ_{e n s} = \sum_{i = 1}^{P} w_{i} Y_{i} & (9) \end{array}

where Ŷ_ens is the ensemble prediction of the toe, P is the number of the individual SI models, w_i is the weight corresponding to Y_i toe prediction of the i-th SI model. In the present work, three SI models are examined for the ensemble prediction of the toe: (1) the original Strack SI model Strack (1976), (2) the modified Strack model proposed by Pool and Carrera (2011), and (3) the modified Strack model proposed by Lu and Werner (2013). The contribution of the three SI models is considered equal, thus the weights are w₁ = w₂ = w₃ = 1/3 and the Ŷ_ens is calculated as the average value of the individual SI model predictions.

2.4. Multi-fidelity approach of seawater intrusion

In this work an implicit correction of the Strack (1976) SI model is investigated using the position of a specific isohaline, which represents the extent of SWI based on the variable density approach. In the multi-fidelity (MF) related literature, the proposed correction is denoted as additive correction (e.g., Alexandrov and Lewis, 2001; Zhou et al., 2016; Giselle Fernandez-Godino et al., 2019) and, in general, it could be described as an additive shift of the low-fidelity response y_LF(x) to yield the high-fidelity response y_HF(x). The correction has the following general mathematical form Giselle Fernandez-Godino et al. (2019).

\begin{array}{l} ŷ_{M F} (x) = ŷ_{L F} (x) + \hat{δ} (x) & (10) \end{array}

where ŷ_MF(x) is the MF surrogate model, $\hat{δ} (x)$ is the surrogate constructed to model the discrepancy between the y_HF(x) and y_LF(x) at data point where we have model computations for both the HF and LF models. For the groundwater application examined in the present work, the input vector x corresponds to the vector Q of the pumping rates.

In this study, RF method was utilized as the discrepancy function $\hat{δ} (x)$ . RF algorithm is an ensemble learning technique for solving both classification and regression problems. RFs can be used to predict continuous target variable based on a set of input features. Each decision tree in the forest is built using a random subset of the available features, and the final output is obtained by averaging the predictions of all the trees. This results in a more stable and accurate model than using a single decision tree, as it reduces the risk of overfitting and the impact of noisy or irrelevant features. Ho (1998) was the first to embed a random subspace method in decision forest. Breiman (2001) further extended the algorithm and introduced the term “Random Forests”. RFs have been widely used in several components of the water resources field under different context. For example, Papacharalampous et al. (2018, 2019) aimed at forecasting several hydrological processes and parameters (e.g., temperature and precipitation time-sires) and they compared the outcomes with stochastic methods. A popular implementation of RF refers to the predictive modeling of several groundwater pollution sources, which is crucial in areas with significant agricultural or urban growth, especially in arid and semi-arid climates (e.g., Wheeler et al., 2015; Canion et al., 2019; Knoll et al., 2019; Messier et al., 2019; Ouedraogo et al., 2019; Lahjouj et al., 2020; Pham et al., 2021; He et al., 2022). Other noteworthy applications of RF are the prediction of groundwater levels (e.g., Wang et al., 2018; Saha et al., 2022), assessment of drought impact on groundwater potential (Masroor et al., 2021), classification of surface-groundwater interaction (Yang et al., 2019), identification of potential sites for groundwater artificial recharge (Norouzi and Shahmohammadi-Kalalagh, 2019; Naghibi et al., 2020), investigation of the spatial and temporal variations of soil salinity (Fathizad et al., 2020) and modeling of the shallow water table at high spatial resolution to calculate the risk for groundwater-induced flood events (Koch et al., 2019).

It should be noted that in the present work, in order to capture the complex relation between the well pumping rates and the proposed additive correction factor, the 0.1 kg /m³ isohaline and the corresponding SI toe are divided in several segments and a RF model is trained for the edge points of each segment. Thus, the proposed correction demonstrated good adaptive capabilities, which are further analyzed in Section 4.3.

3. Pumping optimization framework

In general, the objective of the groundwater management problem in the areas adjacent to the sea is the maximization of freshwater extraction while meeting several environmental criteria, which usually include the control of hydraulic head or the extent of SWI. In the present paper, we adopt a simulation-optimization approach to solve the groundwater management problem in coastal aquifers. The decision variables are the well pumping rates Q_i, i = 1, 2, …, n, where n is the total number of wells. This approach is applied on both the VD and the SI models. However, the formulation slightly differs in the two SWI models, since each one of them has different output.

In the case of the VD model, the optimization problem has the following mathematical form (Kourakos and Mantoglou, 2013; Christelis and Mantoglou, 2016a; Christelis et al., 2019).

\begin{array}{l} {\begin{cases} min - \sum_{i = 1}^{n} Q_{i} \\ s.t. x_{i}^{C_{i}} (Q_{1}, \dots, Q_{n}) \leq x w_{i}, \forall i = 1, \dots, n \\ h_{i} (Q_{1}, \dots, Q_{n}) \geq 0, \forall i = 1, \dots, n \\ Q_{min} \leq Q_{i} \leq Q_{max}, i = 1, \dots, n \end{cases} & (11) \end{array}

where $x_{i}^{C_{i}} (Q_{1}, \dots, Q_{n})$ represents the distance of a critical isohaline—which is a function of the pumping rates and corresponds to a concentration value equal to C_i—from the coastline at the bottom of the aquifer. Here, the 0.1 kg/m³ isohaline was selected as representative for SWI extent. According to the first constraint, SWI should not exceed the location of the i-th well denoted by xw_i. Likewise, the hydraulic head in the i-th well should not drop below the sea level. Finally, Q_min and Q_max defines the minimum and maximum allowed pumping rates for each well, respectively.

In the case of SI model, the extent of SWI is defined by the location of the equipotential line ϕ_τ which corresponds to the intersection of the SI with the bottom of the aquifer (toe of the SWI wedge). The value ϕ_τ of the toe is calculated by Equation (7) and its location is specified as a contour line of the potential flow field, which results from the solution of Equation (6). The mathematical expression of the optimization framework is similar to the one in Equation (11), with their main difference being that $x_{i}^{C_{i}} (Q_{1}, \dots, Q_{n})$ is substituted with $x_{i}^{ϕ_{τ}} (Q_{1}, \dots, Q_{n})$ , which represents the distance of the toe from the coastline and it is a function of the well pumping rates and the hydraulic head h_i(Q₁, …, Q_n) with ϕ_i(Q₁, …, Q_n), which denotes potential flow at the well locations. Similarly to the VD case, the constraints in the SI optimization framework prevent the toe from reaching the well locations and ensure that the potential flow remains above the sea level.

To solve the above optimization problems, we employed the evolutionary annealing-simplex (EAS) algorithm Efstratiadis and Koutsoyiannis (2002), a heuristic optimization algorithm that proved to be quite efficient in coastal aquifer management (Kourakos and Mantoglou, 2009; Christelis and Mantoglou, 2016b; Christelis and Hughes, 2018; Kopsiaftis et al., 2019a). To apply the EAS algorithm, the constraints in Equation (11) were incorporated in the objective function in the form of penalty terms (Christelis et al., 2018).

\begin{array}{l} min f (Q) = {\begin{cases} - \sum_{i = 1}^{n} Q_{i}, if \forall j; (g^{j} (Q) \leq 0), j = 1, \dots, 2 n \\ M_{g} \sum_{i = 1}^{2 n} {[max (g^{j}, 0)]}^{2}, if \exists j; g^{j} (Q) > 0, j = 1, \dots, 2 n \end{cases} & (12) \end{array}

where M_g is the number of constraint function violations, Q is the vector of the decision variables and g^j(Q) is a term that contains all the constraints of Equation (11). It should be noted that Equation (12) applies for both the VD and the SI model.

4. Experimental results

4.1. Experiment setup

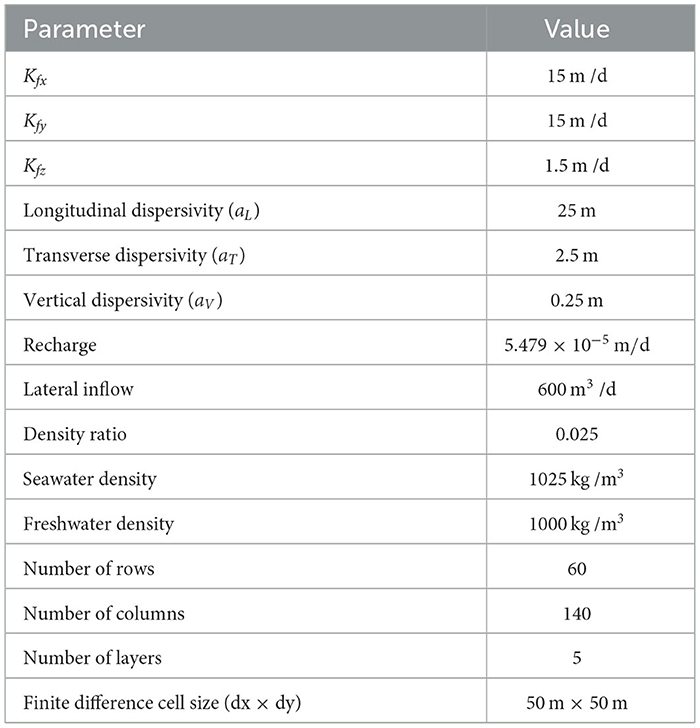
The SWI models described in Sections 2.1–2.3, as well as the optimization frameworks of Section 2.1 are applied on a hypothetical unconfined aquifer of a simplified rectangular shape. The horizontal dimensions of the examined aquifer are L × W = 7.000m × 3.000m and the base of the aquifer is considered horizontal and is located at a depth of -25 m below sea level. Along the coastline, a hydrostatic boundary condition is set with a constant salinity concentration of 35 kg /m³. Also, a specified flux is applied along the entire inland boundary, while the remaining boundaries—lateral and aquifer bottom—are considered impermeable. The aquifer is considered to be homogeneous and anisotropic with regard to the hydraulic conductivity and is pumped through ten fully penetrating wells. Finally, a uniform recharge replenishes the aquifer along its upper boundary. It should be noted that for both the recharge and the well pumping rates we used constant average values throughout the entire 50-year simulation period. Figure 1 is a conceptual representation of the coastal aquifer model, while Table 1 includes all the model's parameters. Each VD simulation requires approximately 75 s in a i7-4770 CPU of 3.7 GHz, 16 GB RAM to complete. The duration of the corresponding SI simulation is in the order of 0.3 s. The significant difference in computational time between the two SWI models highlights the benefit of the SI approach and its usefulness in applications which require a large number of simulations, such as a simulation-optimization method in groundwater management problems.

FIGURE 1

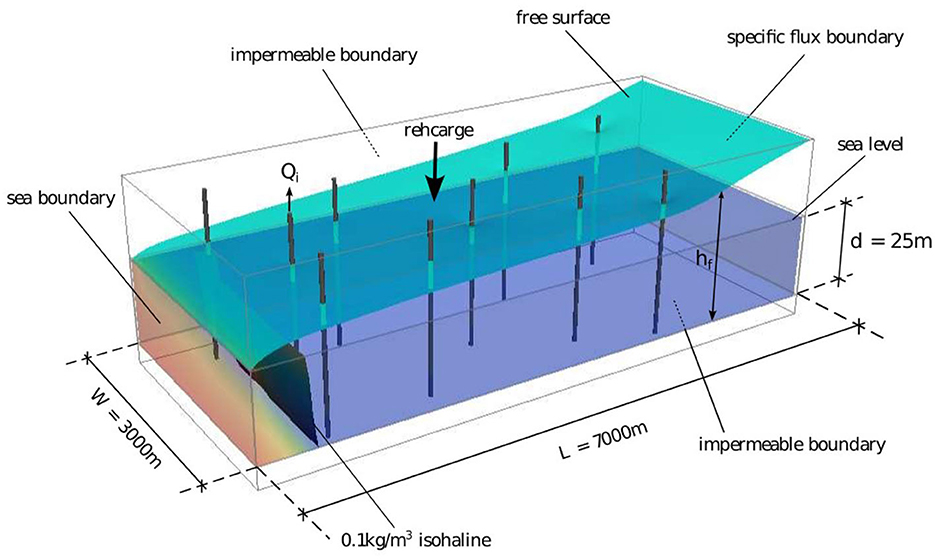
Figure 1. Conceptual model of the examined unconfined coastal aquifer, presenting the size of the aquifer, the boundary conditions, the location of the wells and an indicative location of the critical 0.1 kg/m³ isohaline.

TABLE 1

Table 1. Parameter values of the variable density model.

4.2. Comparison of seawater intrusion models

As already mentioned in Section 4.1, there is a clear advantage to utilizing the SI model rather than the VD model for groundwater management applications, due to its computational efficiency. In the present study, we further examine the correction of the SI model discussed in Section 2.3 by searching for any potential spatial dependencies of the density ratio, which would lead not to a unique correction factor for the entire flow field—as in previous studies—but to a locally adapted modification of the SI toe. To this end, we create a large dataset of 5, 000 pumping scenarios using the Latin Hypercube Sampling (LHS) statistical method. The pumping scenarios are applied on both the VD and SI models and subsequently the locations of the 0.1 kg /m³ isohaline and the SI toe are extracted from the concentration results and the flow potential field, respectively. Figures 2A, B depict the advancement of SWI for the VD model and the four variations of the SI model which include: (i) the original Strack model, (ii) the Pool and Carrera (2011) correction, (iii) the Lu and Werner (2013) correction, and (iv) the ensemble SI model described in Section 2.3. The results indicates that for low pumping rates the model proposed by Strack (Strack, 1976) outperforms the other SI models. However, in high pumping rate scenarios—which is of practical interest for groundwater management problems—the Strack model overestimates the extend of SWI, while the Lu and Luo (2014) models seems to capture more accurately the benchmark VD solution. The ensemble model toe closer resembles the shape of the 0.1 kg /m³ isohaline, though shifted several hundred meters inland. Overall, the results demonstrate a considerable dependency of the SI models' efficiency on the total pumping rates, confirming the findings of previous studies (e.g., Christelis and Mantoglou, 2016a).

FIGURE 2

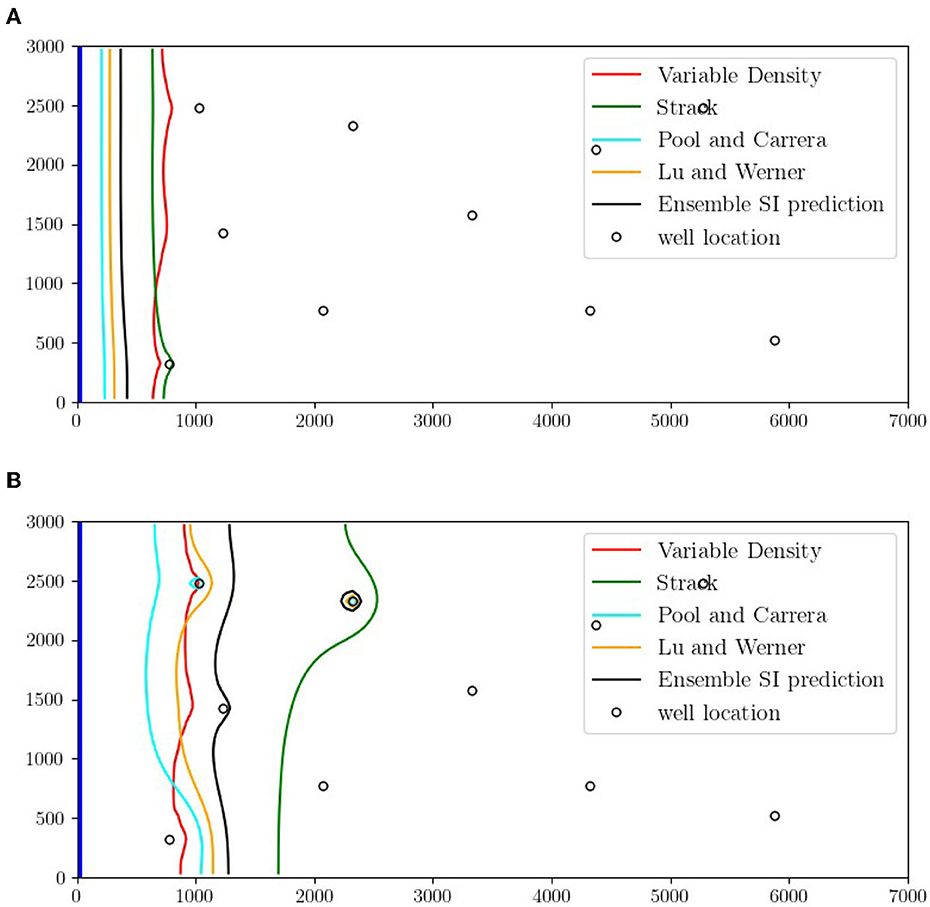
Figure 2. Top view of the bottom layer of the aquifer depicting the advancement of SWI for the VD model and the four variations of the SI model based on the same sets of pumping rates. (A) Results comparison based on a low total pumping scenario. (B) Results comparison based on a high total pumping scenario.

In order to define possible spatial dependencies of the correction factor both the 0.1 kg /m³ isohaline and the SI toe based on Strack's model were divided in an equal number of segments and the correction of the latter was examined at the endpoints of each segment. In the hypothetical aquifer of the present study we selected a dense segmentation of the lines to achieve a relatively comprehensive and complete analysis. In particular, following the finite different discretization of the numerical models, we divided both lines into 59 segments. For each one of the segments' endpoints and for each pumping scenario we calculated an optimal density ratio that minimizes the distance between the two points. This problem is equivalent to calculating the potential flow value at each point of the 0.1 kg /m³ isohaline through an interpolation method, and then solve Equation (7) for ϵ. Figure 3 presents the optimal values for the 5, 000 pumping scenarios, for three segments of the a the critical isohaline, representing both the northern and the southern part of the aquifer, as well as the middle area. The figure leads to the following two key conclusions

• The optimal values of the correction factor has a strong dependence on the pumping rates. In particular, the optimal values tend to reduce as the total pumping rates increase.

• The optimal correction factor follows the same pattern in all the segments of the compared lines. However, its mean value and range differs indicating a spatial variability, which should be further investigated.

FIGURE 3

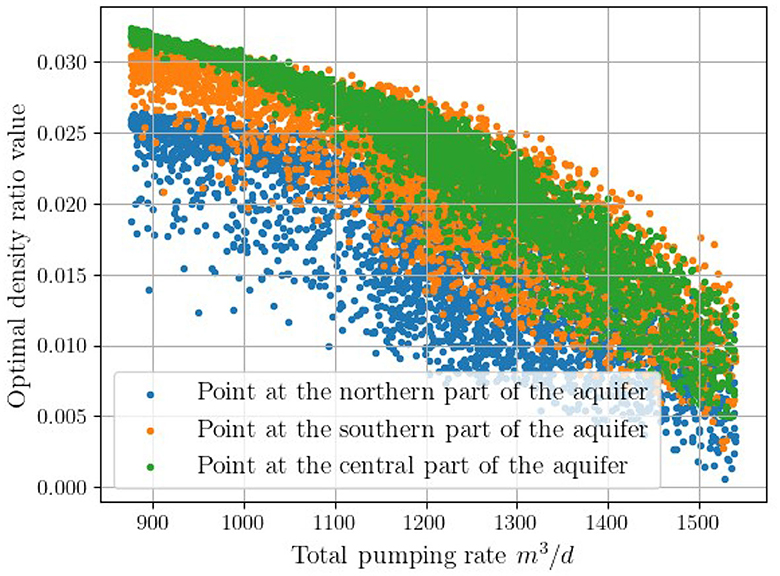
Figure 3. Optimal density ratio in relation to the total pumping rates for the 5,000 pumping rate scenarios. Each color corresponds to a point located at different part of the aquifer.

4.3. Sharp interface correction based on random forests

The findings and observations of Section 4.2 suggest that the correction factor proposed in earlier studies for the Strack SI model (e.g., Pool and Carrera, 2011; Lu and Werner, 2013), enhance the determination of the toe position considerably, aligning with the benchmark VD approach. However, it has certain limitations and its overall precision is contingent on the pumping regime. Furthermore, applying a uniform correction factor across the entire flow field does not have the capability to adapt to the specific conditions of distinct areas within the aquifer, which—for the case of homogeneous aquifer, like the hypothetical aquifer examined in the present study—are mostly related to the relative position of the wells and the applied pumping rates.

Following the line segmentation approach of Section 4.2, a total number of 60 points is selected from both the 0.1 kg /m³ and the SI toe based on Strack model, as depicted in Figure 4. The arrows in the figure denote the intended correction for indicative points of the line. In order to investigate a spatially variable correction factor, we utilize a ML method, and particularly the RF algorithm described in Section 2.3. The training sample consists of 4, 000 variable sets, representing the 80% of the total sample. Each variable set has 11 parameters, namely the pumping rates of the 10 extraction wells and the initial position of the examined point relative to the coastline. The output set consists of a single variable, that is the distance of the examined SI toe point from its relative point lying on the 0.1 kg /m³ isohaline. Figure 5 schematically presents the overall concept of the proposed method in contrast to a typical approach in coastal aquifer managements problems. Regarding the RF based correction of the SI, the following points should be mentioned

• A multiple input/single output version of the RF algorithm was implemented in the present study. Thus, one RF model was developed and trained for each one of the points of the SI toe.

• Contrary to previous studies, we adopted a direct correction of the location of the SI toe and not an indirect correction through the modification of the density ratio. Modeling the distance of the examined line points seems to provide a relatively smooth corrected line, while the density ratio solution tends to overestimate or underestimate the displacement of the toe points, as small changes in the parameter value lead to a non-proportional correction.

FIGURE 4

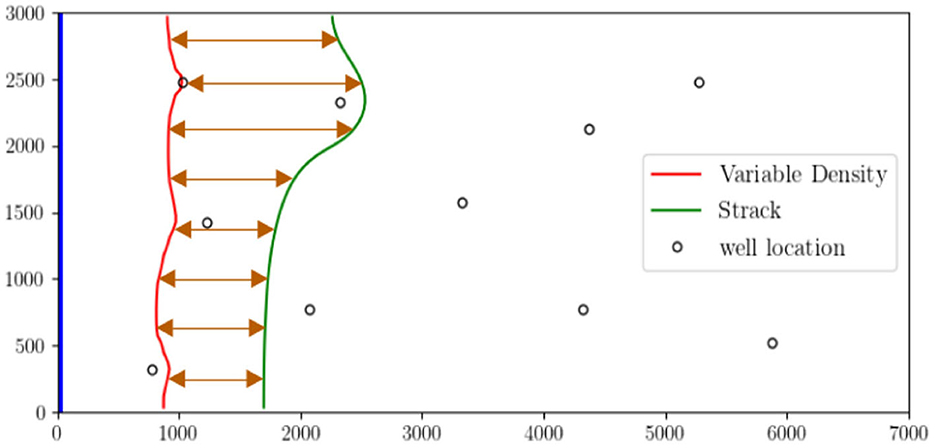
Figure 4. Relative position of the 0.1 kg/m³ isohaline and the SI toe based on the Strack model. The arrows indicate the correction for each one of the points of the SI toe. A RF model is developed and trained for each one of the SI toe points.

FIGURE 5

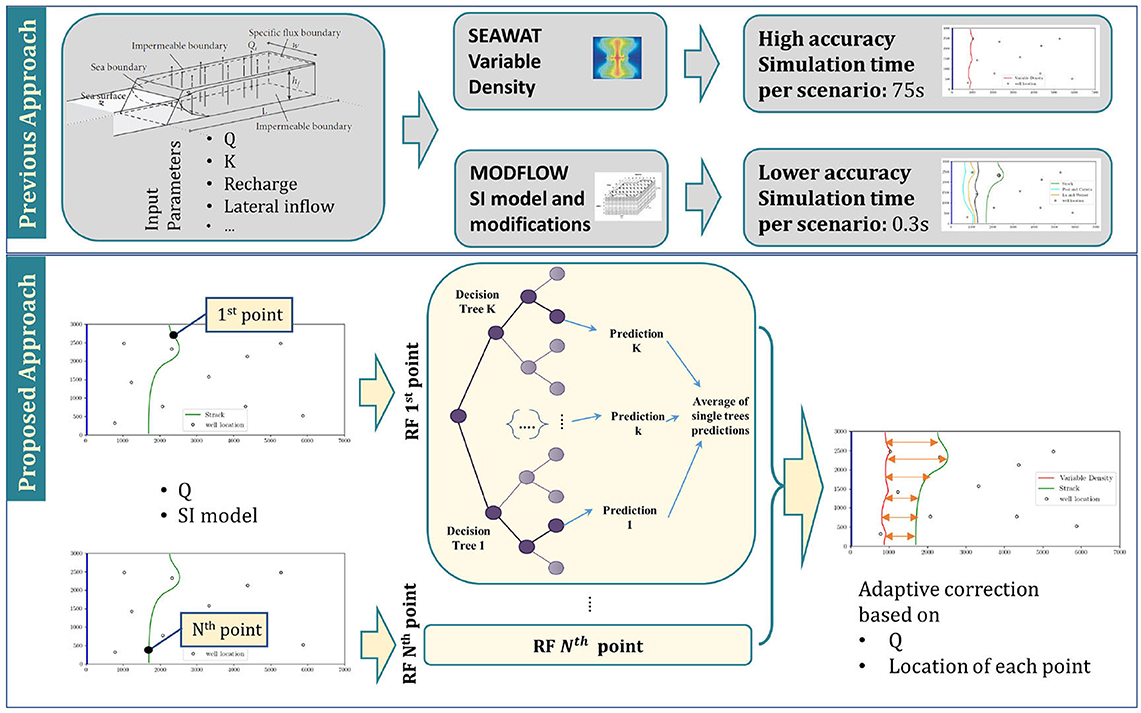
Figure 5. Overall concept of the proposed RF method for the correction of the Strack's based SI toe.

In our experiments, we used a k-fold cross-validation technique to mitigate possible overfitting and achieve a more robust evaluation of the RF models' generalization ability. The train dataset is divided into k = 5 subsets (folds) of equal size. The RF hyperparameters were optimized using Bayesian optimization over these 5k-fold cross-validation sets. Table 2 summarizes the optimizable variables and the corresponding value ranges. The number of splits falls within the range of 1 to 3995.

TABLE 2

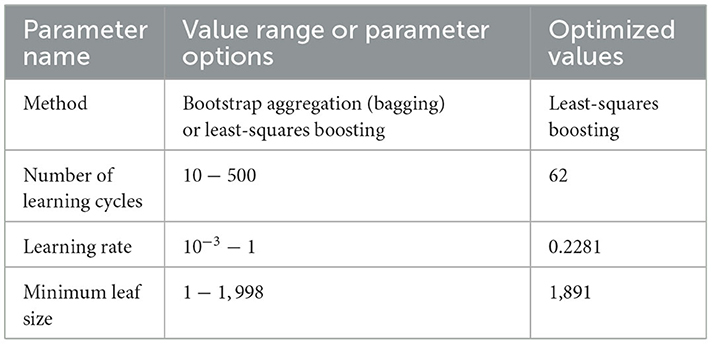
Table 2. Value ranges of optimized hyperparameters of RF and indicative optimized values for one of the 60 points of the SI toe.

For the evaluation of the RF models performance we use as metrics the mean absolute error (MAE), the root mean squared error (RMSE), and the R-squared (R²), which are defined as follows:

\begin{array}{l} MAE = \frac{\sum_{i = 1}^{N} | y_{i} - ŷ_{i} |}{N} & (13a) \end{array}

\begin{array}{l} RMSE = \sqrt{\frac{\sum_{i = 1}^{N} {(y_{i} - ŷ_{i})}^{2}}{N}} & (13b) \end{array}

\begin{array}{l} R^{2} = 1 - \frac{\sum_{i = 1}^{N} {(y_{i} - ŷ_{i})}^{2}}{\sum_{i = 1}^{N} {(y_{i} - ȳ_{i})}^{2}} & (13c) \end{array}

where N is the number of variable sets in the train or test dataset, y_i represents the true values of the modeled parameter, ŷ_i stands for the estimated values and ȳ_i is the mean value of the parameter. These metrics are applied in both training and test sets.

In order to ensure the accuracy and robustness of the final RF models, the entire training and validation process was repeated five times for all the examined points of the SI toe. The performance metrics were computed for each one of the five output values datasets. The repetition of the process allowed the approximate quantification of the uncertainty of the proposed method. The uncertainty is provided as the standard deviation of the metrics (e.g., MAE) over the five repetitions. In particular, the calculations for the MAE are based on the following formula:

\begin{array}{l} SD = \sqrt{\frac{\sum_{i = 1}^{r} {({MAE}_{i} - \bar{MAE})}^{2}}{r}} & (14) \end{array}

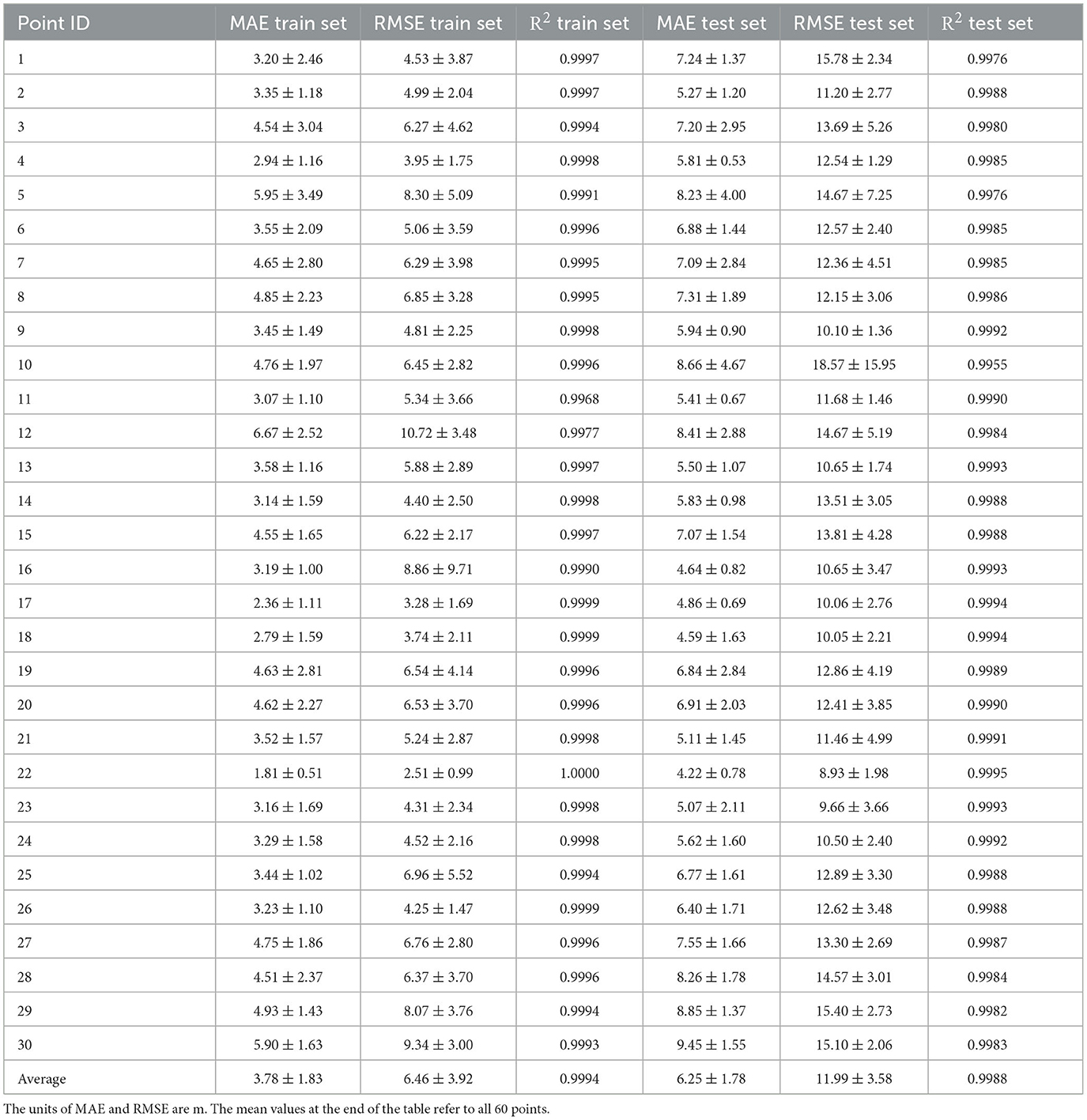
Table 3 contains the values of the statistical measurements used to evaluate the performance of the proposed method, namely the mean absolute error (MAE), the root mean square error (RMSE) and the R². For the MAE we also provide the corresponding standard deviation. It should be noted that the values listed in the table are the averages over the five repetitions of the calculation process for half of the 60 points selected from the SI toe. Given the magnitude of the examined parameter and the size of the finite difference cell, the MAE and RMSE values are considered satisfactory. At the bottom of the table, we also provide the average values of all the metrics over the entire set of points. Regarding the high values of the R², the use of the cross-validation approach and the repetition of the process minimize the possibility of overfitting and ensure the model's generalization ability. The proposed methodology significantly improves the location of the SI toe, with respect to the 0.1 kg /m³ isohaline.

TABLE 3

Table 3. Performance evaluation of the proposed method for half of the examined points.

4.4. Pumping optimization results

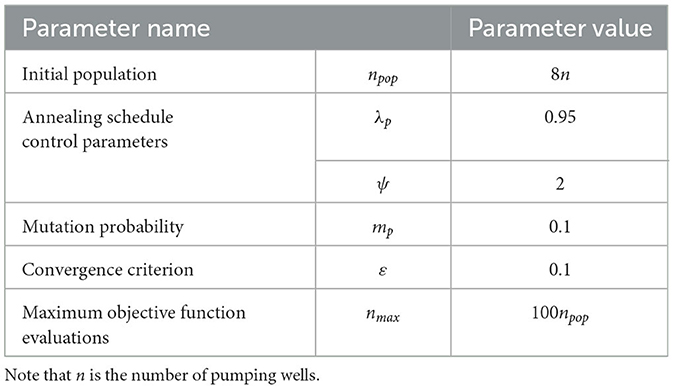
In order to test the usefulness of the proposed LF model in pumping optimization problems, we apply the optimization framework described in Section 3 on the unconfined hypothetical aquifer. For consistency, we solved the optimization problem not only for the HF model, but also for the original Strack model. The parameters of the EAS optimization algorithm are listed in Table 4 and their values are set based on the work of Efstratiadis and Koutsoyiannis (2002), Tsoukalas et al. (2016) and Christelis and Mantoglou (2019). The optimization is terminated if at least one of the following criteria is met: (i) the convergence criterion ε reaches its preset value, and (ii) the number of objective function evaluations exceeds the maximum number n_max.

TABLE 4

Table 4. Parameter values of the EAS optimization algorithm.

Table 5 contains the optimal pumping rates for the examined HF and LF models. As expected, the Strack's SI model provides a relatively low estimation of the total pumping rates, which does not exceed 75% of the VD optimal results. Using the proposed correction of the SI significantly improved the results, allowing the extraction of a freshwater amount that corresponds to 95% of the VD estimation. Furthermore, it is worth mentioning that the evaluation of the optimal pumping rates with the VD optimization framework confirms that it is a feasible solution, since none of the constraint functions was violated. Figure 6 shows the 0.1 kg /m³ isohaline corresponding to the optimal pumping rates for the two examined SI models. The RF-based correction of the Strack SI model provides a solution which approaches the benchmark VD solution, without violating the constraint set.

TABLE 5

Table 5. Optimal pumping rates for the HF (VD) model and the two LF models: (i) the original Strack SI model, and (ii) the corrected SI model using the RF (RF-SI).

FIGURE 6

Figure 6. Projection of the 0.1 kg/m³ isohaline at the bottom of the aquifer, which correspond to the VD evaluation of the optimal pumping rates for two SI models: (i) the original Strack model and (ii) the corrected SI model based on RF. The VD optimal solution is also included for comparison purposes.

5. Conclusions

Due to the low computational budget and the relatively easy implementation the SI models are considered a promising surrogate model for the more accurate, but computationally expensive VD model. For this reason, the SI model have been extensively investigated in a number of previous studies. Most of them focus on improving the Strack SI models by modifying the density ratio. The present work aims to provide a ML based correction of the original Strack SI model. In a first step, the Strack model and three modifications were examined in several pumping levels. From the corresponding SWI extent it was evident that the behavior is significantly influenced by the total amount of the freshwater extraction, thus imposing limitations in their ability to function as effective substitutes for the VD model. This observation required further investigation, and to this end we calculated an optimal density ratio that minimizes the discrepancy between the SI toe and the 0.1 kg /m³ isohaline. Despite the fact that the optimized density ratio corrected the location of the SI toe, it failed to encapsulate possible local conditions in the flow field (e.g., interaction between neighboring pumping wells).

The above findings highlighted the need to search for a regionally adapted correction factor, and to achieve this goal, the SI toe was divided in several segments, which were examined individually with respect to the density ratio. A considerable number of simulations were performed using both the VD and the SI approach and based on the results a secondary inverse problem setup was implemented to calculate the optimal values of the correction factor. The outcome confirmed the spatial variability of the examined parameter, in terms of the magnitude and value range. In order to model the regional dependency of the correction factor, the RF algorithm was utilized for each one of the individual points of the Strack SI toe. In particular, instead of using the density ratio as a correction factor, the point to point distance between the SI toe and the 0.1 kg /m³ isohaline was selected as the output of the ML method. Based on the RF evaluation metrics—specifically, the MAE and RMSE results for both the train and test data sets—, the proposed correction demonstrates a good performance, with a mean accuracy in the order of 5 − 10 m.

Subsequently, the proposed correction factor was incorporated in a coastal aquifer optimization framework. The estimated optimal pumping rates provided feasible solutions, which approximated the benchmark VD optimal results within a 5% margin. To the best of our knowledge, this is the first study that examines in detail the spatial variability of the SI correction and implements the correction in a coastal aquifer pumping optimization problem. Overall, the proposed method is yielding promising results and could be used as an accurate and robust LF model in coastal aquifer management problems. Future research will focus on further scrutinizing the effectiveness of the proposed method in different aquifer setups and real applications.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

GK and MK: conceptualization and visualization. GK, MK, EP, and AV: methodology and formal analysis. GK, MK, EP, AV, AD, ND, and AM: validation and writing—review and editing. GK: investigation and data curation. GK, MK, and EP: resources and writing—original draft preparation. MK, EP, AV, AD, ND, and AM: supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This paper was supported by the European Union Funded project euPOLIS Integrated NBS-based Urban Planning Methodology for Enhancing the Health and Well-being of Citizens: the euPOLIS Approach under the Horizon 2020 program H2020-EU.3.5.2., grant agreement no 869448.

Acknowledgments

This work was supported by computational time granted from the National Infrastructures for Research and Technology S.A. (GRNET) in the National HPC facility ARIS-under project ID pa211104 (MLGM).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alexandrov, N. M., and Lewis, R. M. (2001). An overview of first-order model management for engineering optimization. Opt. Eng. 2, 413–430. doi: 10.1023/A:1016042505922