- 1Department of Biological Systems Engineering, University of Nebraska–Lincoln, Lincoln, NE, United States
- 2Department of Environmental Resources Engineering, SUNY College of Environmental Science and Forestry, Syracuse, NY, United States
- 3Departments of Ecology and Evolutionary Biology, Kansas Biological Survey-Center for Ecological Research, University of Kansas, Lawrence, KS, United States
- 4Pacific Northwest National Laboratory, Richland, WA, United States
- 5School of the Environment, Washington State University, Pullman, WA, United States
- 6Department of Food Science and Technology, Nebraska Food for Health Center, University of Nebraska–Lincoln, Lincoln, NE, United States
Microbial decomposition of organic matter (OM) in river corridors is a major driver of nutrient and energy cycles in natural ecosystems. Recent advances in omics technologies enabled high-throughput generation of molecular data that could be used to inform biogeochemical models. With ultrahigh-resolution OM data becoming more readily available, in particular, the substrate-explicit thermodynamic modeling (SXTM) has emerged as a promising approach due to its ability to predict OM degradation and respiration rates from chemical formulae of compounds. This model implicitly assumes that all detected organic compounds are bioavailable, and that aerobic respiration is driven solely by thermodynamics. Despite promising demonstrations in previous studies, these assumptions may not be universally valid because OM degradation is a complex process governed by multiple factors. To identify key drivers of OM respiration, we performed a comprehensive analysis of diverse river systems using Fourier-transform ion cyclotron resonance mass spectrometry OM data and associated respiration measurements collected by the Worldwide Hydrobiogeochemistry Observation Network for Dynamic River Systems (WHONDRS) consortium. In support of our argument, we found that the incorporation of all compounds detected in the samples into the SXTM resulted in a poor correlation between the predicted and measured respiration rates. The data-model consistency was significantly improved by the selective use of a small subset (i.e., only about 5%) of organic compounds identified using an optimization method. Through a subsequent comparative analysis of the subset of compounds (which we presume as bioavailable) against the full set of compounds, we identified three major traits that potentially determine OM bioavailability, including: (1) thermodynamic favorability of aerobic respiration, (2) the number of C atoms contained in compounds, and (2) carbon/nitrogen (C/N) ratio. We found that all three factors serve as “filters” in that the compounds with undesirable properties in any of these traits are strictly excluded from the bioavailable fraction. This work highlights the importance of accounting for the complex interplay among multiple key traits to increase the predictive power of biogeochemical and ecosystem models.
1. Introduction
Microorganisms play a significant role in maintaining the elemental balance in natural ecosystems. By degrading complex organic matter (OM), microbes recycle essential nutrients (e.g., carbon, nitrogen, and phosphorus) back into the ecosystem and release carbon dioxide into the atmosphere (Pomeroy, 1974; Sun et al., 1997; Findlay and Sinsabaugh, 1999; Benner, 2003; Kellerman et al., 2015; Hu et al., 2022). Therefore, biogeochemical models must consider the significant role of microbes in OM degradation, which is influenced by multiple biotic and abiotic factors, including chemical traits of substrates, biological traits of microbes, and extracellular enzymes, as well as their dynamic interactions. All of these factors play a role in governing OM degradation and must be accounted for in models to achieve accurate predictions of microbial respiration rates (Moorhead et al., 2013; Song et al., 2020). The development of microbial-explicit (Todd-Brown et al., 2012; Wieder et al., 2015; Allison, 2017; Sulman et al., 2018), enzyme-explicit (Moorhead et al., 2013; Song et al., 2014, 2017; Song and Liu, 2015), and substrate-explicit models (Garayburu-Caruso et al., 2020a,b; Song et al., 2020) demonstrates ongoing efforts to improve our understanding of complex OM degradation process in this regard.
With the increasing availability of ultrahigh-resolution OM data, the substrate-explicit thermodynamic modeling (SXTM) developed by Song et al. (2020) is particularly valuable due to its capability of using the chemical formulae of organic compounds to predict aerobic respiration rates. Notably, the SXTM can handle complex formulae, including compounds with a high number of carbon (C) atoms, which constitute the majority of measured compounds in the ecosystem. In a previous study, the SXTM predicted the variation in respiration rates between two sites with distinct vegetation densities by incorporating ultrahigh-resolution Fourier-transform ion cyclotron resonance mass spectrometry (FTICR-MS) OM data (Song et al., 2020). Primary assumptions made in these predictions were that: (1) all detected organic compounds are bioavailable for aerobic respiration, and (2) the aerobic respiration of OM is driven by their thermodynamic favorability. Despite successful demonstrations in previous studies, these assumptions are not universally valid, and therefore, need further evaluation.
Clearly, not all organic compounds are readily decomposable by microbes (or bioavailable)—rather, only a small fraction of compounds in the OM pool may be effectively utilized over a given time for microbial metabolism (Sun et al., 1997). The bioavailability of OM is dependent on various factors, including chemical heterogeneity (Thurman, 1985; Kellerman et al., 2015) that affects the recalcitrance and thermodynamics, steric hindrances of OM localized in small pores or protected within soil/mineral aggregates (Marschner and Kalbitz, 2003; Schmidt et al., 2011; Lavallee et al., 2020), non-uniform spatiotemporal distributions of temperature, vegetation, moisture and nutrients (Marschner and Kalbitz, 2003), fluctuating occurrence and concentration of organic compounds (Schmidt et al., 2011; Merder et al., 2021), diversity and dynamics of microbial communities (Giovannoni et al., 1990), and multiple biotransformation pathways (Findlay and Sinsabaugh, 1999). The complexity of the controls of OM bioavailability hinders the mechanistic understanding of how the dynamic interplay between the governing factors drives OM degradation. Even in well-controlled lab incubation experiments, the bioavailable fractions of organic compounds detected in ultrahigh-resolution molecular datasets are not easily distinguished, which poses a serious challenge in incorporating the OM data into quantitative biogeochemical modeling for robust predictions of carbon and nutrient cycles (D'Andrilli et al., 2015; Hu et al., 2022).
Earlier studies that condense rich and distributed properties of OM into collective bulk parameters lose critical information needed to understand the relations between substrate chemistry and microbial activity (Findlay and Sinsabaugh, 1999; Merder et al., 2021). Some studies partially accounted for the distinction between bioavailable and non-bioavailable fractions by identifying labile and recalcitrant compounds (D'Andrilli et al., 2015; Hu et al., 2022), respectively. However, the bioavailability of OM is often dictated by several interdependent factors (Marschner and Kalbitz, 2003), therefore, OM degradation is best described by concurrently accounting for various dimensions of OM characteristics (Hu et al., 2022). Moreover, to our knowledge, no studies have attempted to predict the microbial aerobic respiration rates by distinctly accounting for just the bioavailable fraction of the detected compounds.
In this work, we propose a computational method combining the SXTM with an optimization approach that enables identifying a subset of organic compounds that are potentially bioavailable under aerobic conditions from a set of measured compounds. As a case study, we analyzed the high-throughput ultrahigh-resolution FTICR-MS OM data from diverse river systems collected by the Worldwide Hydrobiogeochemistry Observation Network for Dynamic River Systems [WHONDRS; Stegen and Goldman (2018), Goldman et al. (2020), Toyoda et al. (2020), https://whondrs.pnnl.gov] consortium. While our initial estimation of aerobic respiration rates using the SXTM (Song et al., 2020) that ignores OM bioavailability resulted in a poor correlation with measured values, the model prediction was significantly improved by incorporating a small subset of bioavailable portion identified using an optimization algorithm. Through a subsequent analysis of the subset of compounds selected by the model, three primary chemical traits emerged as potential drivers of OM bioavailability: thermodynamic favorability of aerobic respiration, the number of C atoms present in compounds, and the C/N ratio. These findings suggest that to develop predictive models of biogeochemical and ecosystem processes, we must shift our focus from searching for individual key parameters to integrative analysis of multiple factors and their interactions.
2. Methods
2.1. Thermodynamic estimation of microbial oxidative degradation of organic matter
We use the SXTM developed by Song et al. (2020) that enables converting chemical formulae of detected organic compounds into stoichiometric and kinetic equations to infer microbial aerobic respiration kinetics of individual compounds. The model derives a stoichiometric equation for metabolic reaction by considering the energetic coupling between catabolic (energy production through substrate degradation) and anabolic (energy consumption for cell synthesis) reactions.
First, catabolic reaction is formulated by balancing a pair of redox half reactions for an electron donor (i.e., organic compound) and an electron acceptor (i.e., oxygen) (Rittmann and McCarty, 2001; Kleerebezem and Van Loosdrecht, 2010). Anabolic reaction is also derived based on the mass and electron balances for the carbon and nitrogen sources, where the carbon source is the electron donor for heterotrophic organisms and ammonium is chosen as the nitrogen source.
The final metabolic reaction is obtained by combining catabolic and anabolic reactions using the parameter λi [defined in Eq. (1)] such that the energy is balanced. We evaluate thermodynamic favorability of aerobic respiration of organic compounds based on λi, which denotes the number of times the catabolic reaction of ith compound needs to proceed to provide the energy required for the synthesis of a unit C-mole of biomass (CMB) (Hoijnen et al., 1992; Song et al., 2020):
Given the definition, smaller λ denotes greater thermodynamic favorability, and as a result, λ is inversely associated with the microbial aerobic respiration rates in theory. In Eq. (1), Gi, cat and Gi, ana are the Gibbs free energies of catabolic and anabolic reactions, respectively, which are computed using the stoichiometric coefficients of the respective reactions:
Here, is the stoichiometric coefficient of k-th component in the reaction, is the Gibbs energy of formation of the respective component, and the subscript and superscript r denotes the reaction, i.e., r = [cat, ana]. Following this, the remaining unknowns in Eq (1), i.e., the dissipation energy, ΔGi, dis, and λi, are estimated using the thermodynamic electron equivalents model (TEEM) (Mccarty, 2007). Lastly, the stoichiometric coefficient for the overall metabolic reaction is given as follows:
where , , and yi are the vectors containing stoichiometric coefficients for various chemical species involved in the catabolic, anabolic, and the overall metabolic reactions, respectively.
Then, the model formulates the microbial growth kinetics for oxidative degradation of OM based on thermodynamic theory by linking the stoichiometry coefficients of organic carbon and O2 in the metabolic reaction (Quéméner and Bouchez, 2014):
Here, rO2,i (mol-O2/CMB.h) is the specific respiration rate of ith compound defined per CMB, yO2, i and yOC,i are the stoichiometric coefficients of O2 and organic carbon (normalized per CMB), μi and μmax (1/h) are the actual and maximum specific growth rate of microbiome, Vh is the harvest volume (volume of the environment surrounding microbes in which they can access substrates for harvesting energy), whereas [OCi] and [O2] are the respective substrate volumetric molar concentrations. As the Vh and the concentrations of individual organic compounds are unknown from qualitative OM data, we can take them collectively as tuning parameters to represent different levels of substrate limitations. If the supply of organic carbon is limited with excessive O2 supply, the concentration of organic carbon becomes the rate-limiting factor, indicating a C-limited microbial reaction, while the opposite is also true. Likewise, when the supply of C and O2 are both restricted, the microbial reaction is both C- and O2-limited. We can enforce various levels of C and O2 limitation in estimating aerobic respiration rates by tuning the parameters [i.e., Vh[OCi] and Vh[O2]] in Eq. (4). For example, microbial growth and respiration rates will not be limited by substrate concentrations when Vh[OCi] and Vh[O2] tend to large values, where , and vice versa. Therefore, we tested a range of values for the parameters and systematically chose a set of values to estimate the respiration rates under C-limited, O2-limited and both C- and O2-limited conditions (see Supplementary Figure S1). Additionally, we assume a unity value for μmax which is also unknown, resulting in defined as the respiration rate normalized per unit maximum specific growth rate of microbiome (mol-O2/CMB):
The use of the same value of μmax implicitly assumes that the microbial growth kinetics does not vary significantly across samples. The formulation in Eq. (5) is used to represent the model respiration rates throughout the rest of this work, but we drop the prime notation from for brevity. A more detailed derivation of the aerobic respiration kinetics and thermodynamic favorability is given in Song et al. (2020).
2.2. Estimation of overall aerobic respiration and thermodynamic favorability in samples containing organic matter
We can represent the overall oxidative respiration rate in a given sample by taking an average of the model-estimated rates of all detected organic compounds in the sample. However, not all detected compounds may be actively involved in biogeochemical transformations given the variable bioavailability of compounds. To better represent microbial processes, we only consider a subset of compounds that are presumably bioavailable:
Here, rO2, ij is the normalized respiration rate of ith compound detected in jth sample, is the overall respiration rate in jth sample, and nj is the total number of compounds detected in jth sample. In the summation, we only account for the set of bioavailable compounds (), which means that non-bioavailable compounds are presumed not respired (assigned zero rates) in the sample. Similarly, we can compute the overall thermodynamic favorability of aerobic respiration in jth sample as:
Here, as we cannot assign zero values to λ by definition, we exclude non-bioavailable compounds from the average calculation by using which is the total number of bioavailable compounds in jth sample. To this end, we employ a model optimization pipeline to identify a subset of bioavailable compounds (detailed in the following section) that can adequately represent the overall microbial activity in samples.
2.3. Model optimization pipeline for identification of bioavailable organic matter
In this work, we examine FTICR-MS and measured aerobic respiration data collected from various river corridors as part of the WHONDRS Summer 2019 Sampling Campaign (Figure 1A). The FTICR-MS assigns chemical formula to detected organic compounds, and the respiration rates are measured by determining the rate of oxygen depletion (i.e., mg-O2/L.h) in batch experiments conducted under aerobic conditions over the span of about 2 h (Goldman et al., 2020).
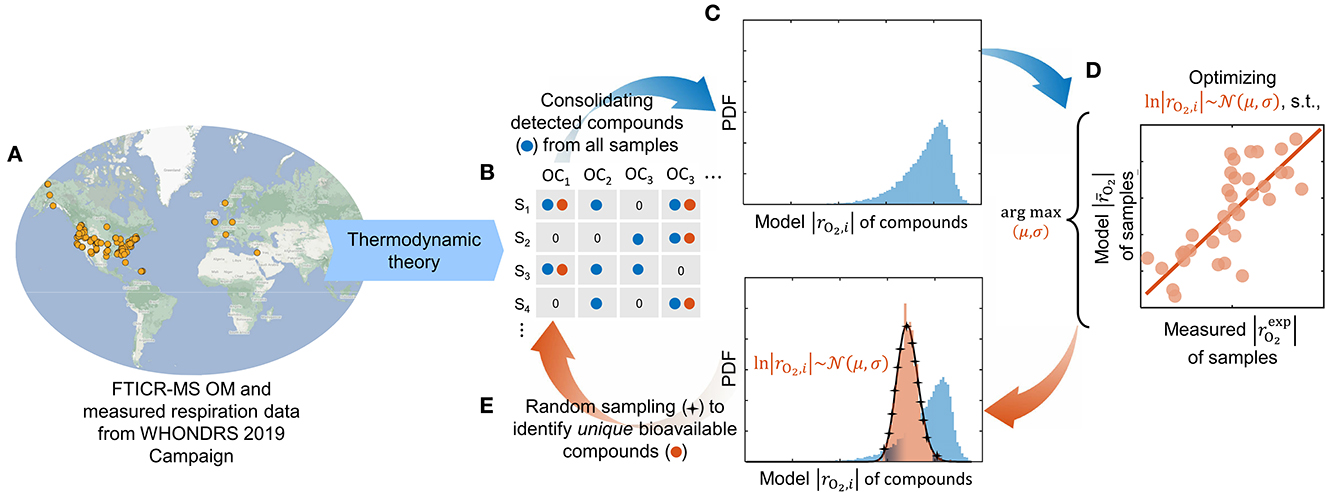
Figure 1. Modeling workflow depicting our optimization pipeline to identify bioavailable OM. Ultrahigh-resolution OM data is used to estimate the oxidative respiration kinetics of individual organic compounds based on thermodynamic theory (A). The model-estimated respiration rates of detected compounds (blue) from all samples (B) are consolidated into a composite distribution (C). A lognormal distribution function is optimized (within the domain of the composite distribution) such that it maximizes the correlation of model respiration rates with experimentally measured rates of each sample (D). A set of unique compounds that are potentially bioavailable (orange) is identified by randomly sampling the optimized distribution function (E). The overall respiration in each sample is computed by taking an average of model respiration rates of only bioavailable compounds detected in the respective sample. Compounds that are not detected in the sample are omitted from the calculation, whereas detected compounds that are not chosen as bioavailable are assigned zero respiration rates.
The experimental setting and measurement led to the thermodynamic model formulation as described in Section 2.1 that quantifies the aerobic respiration rate by taking oxygen as the terminal electron acceptor. Using the model, we estimate the aerobic respiration rates (i.e., O2 consumption rate) for detected compounds from all samples (Figure 1B) and consolidate the rates to form a composite distribution (Figure 1C). Note that distinct composite distributions can be collated for different cases of assumed substrate limitations (see Supplementary Figure S2). As the sample-specific maximum microbial growth rate is unknown, we present the model respiration rate per unit maximum specific growth rate of the microbiome with the unit mol-O2/CMB (Section 2.1). Although the predicted rates are in different units than measured data (and therefore no direct comparison of their absolute values would be possible), it is still an adequate proxy of microbial activity that can be directly correlated with the measured absolute volumetric respiration rates.
Subsequently, we optimize a lognormal distribution function by calibrating the mean (μ) and standard deviation (σ) within the domain of the respective composite distribution to maximize the correlation between the model respiration rates and measured (experimental) rates of each sample (Figure 1D), by minimizing the sum of squares of residuals:
Here, is the measured respiration rates in samples, and the overall model respiration rate () only accounts for the bioavailable compounds detected in respective samples following Eq. (6). We used “fmincon” on MATLAB® R2022a to perform the optimization. Throughout this work, it shall be understood that we presume the compounds chosen by our model optimization as bioavailable. To identify unique bioavailable compounds, we randomly sample the lognormal distribution function in each iteration of the optimizer and locate the closest resembling compound (in terms of model respiration rates of individual compounds) from the composite distribution (Figure 1E). We enforce sampling without replacement, i.e., if a compound is selected more than once, we pick the next closely resembling compound from the composite distribution. The number of compounds picked from the distribution would affect the performance of the optimizer and the correlation between model outcome and measured data. In this work, the sampling size is fixed at 5% of the size of the composite distribution (the rationale for this choice is discussed in Section 3.2).
3. Results
3.1. Model-data correlation is significantly improved by selectively incorporating a subset of bioavailable organic matter
As alluded to in Section 2.1, we used the parameters Vh[OCi] and Vh[O2] of the SXTM to estimate the aerobic respiration kinetics under varying substrate limitations—C-limited, O2-limited, and both C- and O2-limited conditions. As expected, the correlations between the model and measured respiration rates are negative and poor when we assumed that all detected compounds in respective samples were being respired during laboratory experiments (Figure 2, top in blue), regardless of substrate limitations. To ensure that our selection of parameter values had no bearing on causing the observed negative correlations, we thoroughly examined various values for the parameters that correspond to low, moderate, and severe limitations of C and O2 in Supplementary Figure S3, confirming that the negative correlations persist in all the examined cases. Conversely, when we only account for the chosen bioavailable compounds, the correlations are vastly improved and positive (Figure 2, bottom in orange). Moreover, the positive correlation considering only the bioavailable compounds is the highest when C is limited and lowest when O2 is limited, consistent with the common understanding that natural ecosystems are more limited by C than O2. Therefore, for the remainder of this work, we have specifically focused on analyzing the results under C-limited condition due to its relevance to the natural ecosystems. The results support our initial argument that OM in the ecosystem has variable bioavailability, where only a subset of compounds is being respired and contributes to the measured respiration rates. We explain the choice of bioavailable compounds in the following section.
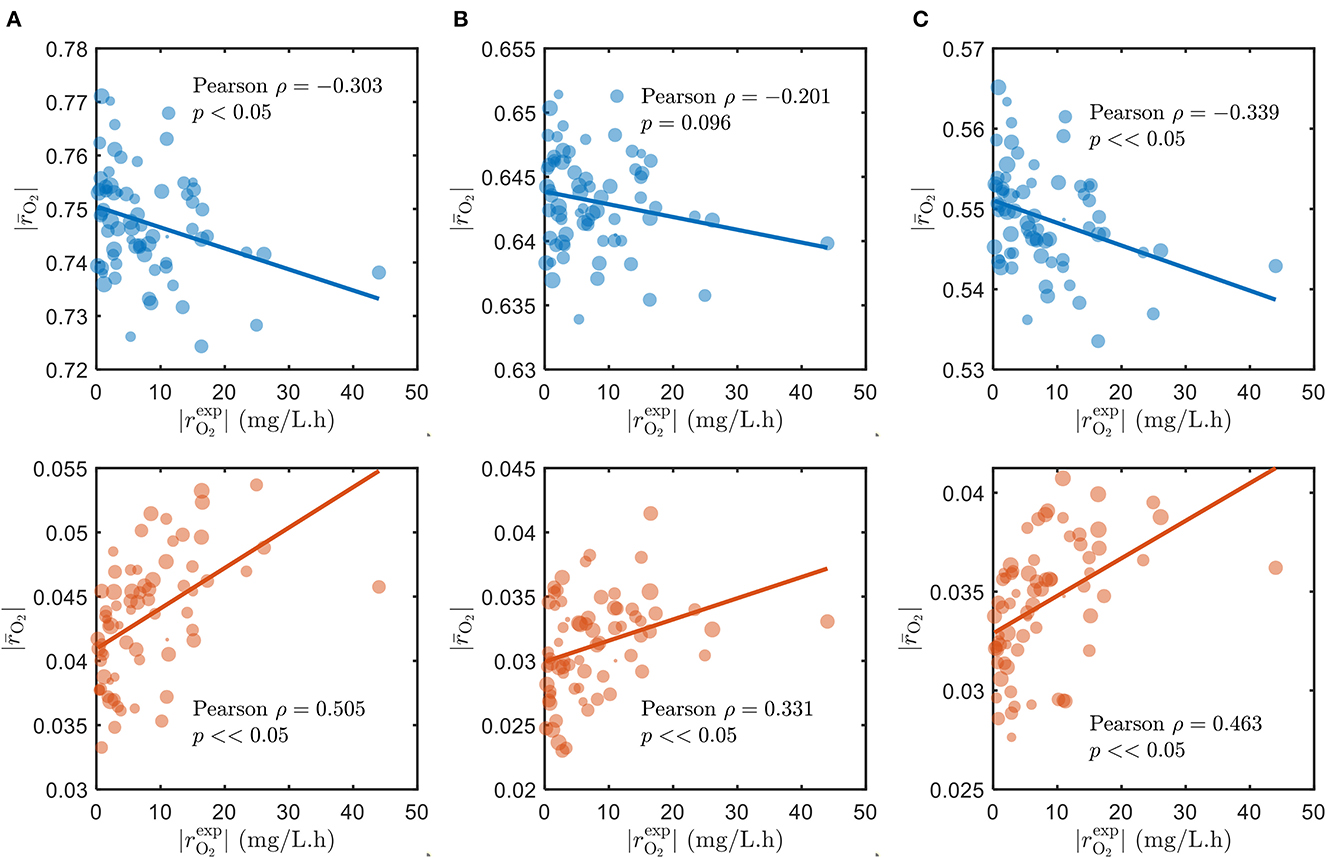
Figure 2. Correlations of model oxidative respiration rates against experimental respiration rates under (A) C-limited, (B) O2-limited, and (C) both C- and O2-limited conditions. The top panels (blue) show the correlations when assuming that all detected compounds in respective samples are respired, and the bottom panels (orange) show the results when only the chosen bioavailable compounds detected in respective samples are respired. The size of markers denotes the number of compounds detected (blue) and the number of chosen bioavailable compounds detected (orange) in respective samples.
3.2. Sampling optimized lognormal distribution to identify bioavailable organic matter
While the optimized lognormal distribution (see Section 2.3) gives an overview of the individual aerobic respiration rates of bioavailable compounds, we still must identify actual compounds that make up the distribution through random sampling to compute the overall respiration rates in samples. While the number of compounds that make up the optimized distribution (i.e., bioavailable fraction) depends on various environmental factors, the OM data from FTICR-MS does not allow to directly account for those sample-specific factors in determining the fraction. Therefore, we employed a statistical approach to estimate the value, that is, the sampling population size should be aptly chosen to ensure the sampled population fits the distribution adequately, whilst also maximizing the correlation between the model and measured respiration rates. A disproportionately large or small sampling population size may cause the sampled population to extend beyond (due to excessive sampling without replacement to identify unique compounds) or inadequately fill the optimized distribution, respectively. To gauge the fitness of sampling population sizes, we use a scaled metric, , where ρ is the Pearson coefficient for correlation between model and measured respiration rates, and ΔO,S is the deviation (sum of squares of residuals) between the optimized distribution and sampled population. The scaled metric is penalized when the correlation between the model and measured respiration rates is poor and/or when the sampled population does not sufficiently match the optimized distribution. Based on this metric, we observe a steady improvement in correlation and the distribution fit up to a population size of 5% (see Supplementary Figure S4A). However, beyond this point up until 25% population size, the metric exhibits inconsistent measures due to random sampling (although a linear fit would display a nearly flat plateau at this region), and a steady decline is observed at larger population sizes. Consequently, we conclude that a 5% sampling population size is optimal for selecting bioavailable compounds from the composite distribution. This conclusion is supported by the consistent value of the metric and the absence of any significant additional advantage in sampling more compounds.
Without any ad hoc constraints to the optimization routine, the model respiration rates of the chosen bioavailable compounds are narrowly distributed (i.e., a proper subset) and with a lower mean than the composite distribution (see Supplementary Figure S4B). Therefore, the outcome again supports our conjecture that only a portion of the detected compounds is bioavailable, and any further inclusion of compounds will hurt the correlation with measured respiration rates. However, it should be clarified that the lower mean of respiration rates of bioavailable compounds should not be construed as an unfavorable choice for the microbiome, as the estimated thermodynamic-based kinetics are only realized when the compounds are ideally consumed, while there are many factors that affect the consumption (recalcitrance, steric hindrance, metabolic constraints, etc.). Thus, the bioavailability of OM cannot be fully described by respiration kinetics alone and requires the consideration of interdependencies with other factors as well (see Sections 3.3 and 3.4). Lastly, the chosen bioavailable compounds make up between 5 and 6% of detected compounds in individual samples (see Supplementary Figure S4C), which means that there are no samples with none or purely bioavailable compounds (under- or over-represented, respectively) that can introduce computational artifacts to the analysis. Previous studies have similarly reported a slight variability in bioavailable fractions between diverse environments/samples (Sondergaard and Middelboe, 1995).
3.3. Thermodynamic favorability of aerobic respiration is not the sole driver of the bioavailability of organic matter
A systematic evaluation of factors governing the bioavailability of OM has been lacking, but we can now assess potential factors with the identification of a subset of bioavailable compounds in this work. The higher mean of λ (thermodynamically less favorable), and lower mean of carbon use efficiency (CUE, see Supplementary material for derivation) of chosen bioavailable compounds (Figure 3) are opposite to our expectation from a purely thermodynamic perspective. Moreover, compounds with a lower number of C (and concomitantly, lower C/N and molecular weights) are seemingly more bioavailable than others. Conversely, the bioavailability is not distinguished based on the spatial distribution or occupancy (ranging between 0 and 1 for when the compound is not detected in any sample or detected in all samples, respectively) of compounds across the samples. Hence, it is apparent that oxidative respiration of OM may not be solely driven by thermodynamics, but rather possibly influenced by multiple interdependent factors (Marschner and Kalbitz, 2003). As alluded to in the preceding section, the estimated thermodynamic properties of organic compounds are expected outcomes if the compounds are ideally consumed. However, there are many other factors that can equally dictate the consumption of the compounds. The trends in Figure 3 motivate interpretations considering the interdependencies between various key properties of OM, which we explore in the following section.
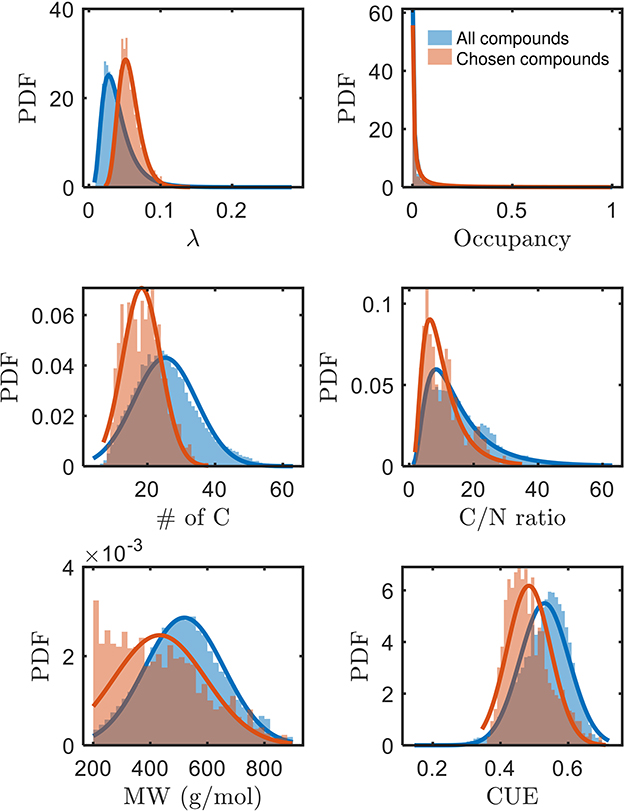
Figure 3. Comparison of various properties of chosen bioavailable compounds (orange) against detected compounds from all samples (blue) under C-limited condition. The differences in the PDFs between the two sets of compounds across all properties are statistically significant (p≪0.05). MW, molecular weight; CUE, carbon use efficiency.
3.4. C/N ratio, number of C atoms, and thermodynamic favorability of aerobic respiration jointly determine the bioavailability of organic matter
We established in the preceding section that the bioavailability of OM is presumably driven by multiple interdependent factors. All pairwise associations between relevant properties of OM are displayed in Supplementary Figure S5. Here, we highlight the correlations of the threshold element ratio (TER) vs. the C/N ratio and the number of C vs. λ that showed meaningful interrelations as possible factors governing the bioavailability of OM. TER is the balanced requirement of C/N ratio for the growth and maintenance of microbiome (Sterner and Elser, 2003; Soong et al., 2020), evaluated based on the carbon and nitrogen use efficiencies as well as assumed biomass composition (see Supplementary material for mathematical derivations). Microbiomes are limited by both C and N when the growth substrate C/N ratio matches the TER, whereas a mismatch results in disproportionate utilization of C and N in the environment (C/N > TER → C surplus, N deficit; C/N < TER → C deficit, N surplus).
The chosen bioavailable compounds are mainly composed of compounds in the vicinity of C/N ≈ TER (Figure 4A), that is, the bioavailability of OM is driven by the need to satisfy the balanced C and N requirements of the microbiome to fuel growth and maintenance through efficient utilization of energy sources. However, there are some chosen bioavailable compounds with relatively higher C/N than the TER. When examined in detail, compound of a relatively low to moderate number of C and molecular weight (MW) were also included in the bioavailable OM pool (Figures 5B, C, respectively), but the effect of λ is not substantial in this context (Figure 5A). Nevertheless, the significance of λ should not be discounted, as we observe a clear-cut exclusion of thermodynamically unfavorable compounds (high λ) from the bioavailable OM pool (Figure 4B). Likewise, compounds with a large number of C (potentially recalcitrant compounds) are also strictly excluded from the bioavailable OM pool despite high thermodynamic favorability. This suggests that thermodynamics and the number of C atoms have clear quantitative cutoffs, where the compounds beyond the cutoffs appear to be unavailable for microbial aerobic respiration. Conversely, bioavailability is mainly determined by the TER requirement among compounds that have few C atoms and low λ. The effect of the TER requirement on the bioavailability of OM is more apparent in Figure 6, where we further examine the compounds not chosen as bioavailable despite falling within the cutoff limits for high λ and number of C (compounds in the regions marked as I and II in Figure 4B). The compounds from group I are not chosen as bioavailable as their C/N ratios largely deviate from TER distribution, whereas the chosen bioavailable compounds show more comparable distributions, especially the median values (Figure 6). Although compounds from group II also have relatively comparable C/N and TER distributions, they are compounds with a higher number of C for about the same level of λ as chosen compounds, which is less desirable than compounds with an equally minimal number of C and λ (cf. Figures 4B, 6).
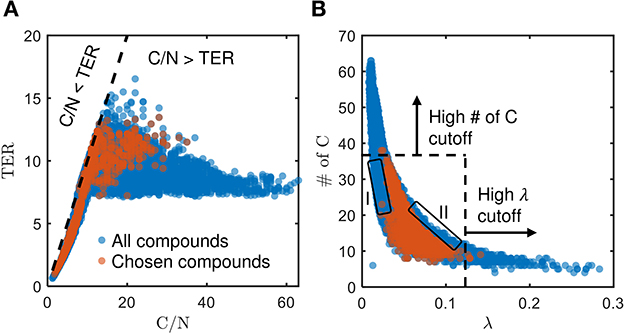
Figure 4. Distribution of (A) threshold element ratio (TER) against C/N ratio, and (B) number of C against λ, of chosen bioavailable compounds (orange) compared against compounds collectively detected in all samples (blue) under C-limited condition. The diagonal dashed line in (A) represents the region that corresponds to C/N = TER, whereas the dashed lines in (B) represent the cutoff thresholds of properties for bioavailable OM. Compounds that stray away from the diagonal line, and the compounds in the regions marked as I and II that are not chosen as bioavailable despite falling within the cutoff limits for high λ and number of C, are examined further in Figures 5, 6, respectively.
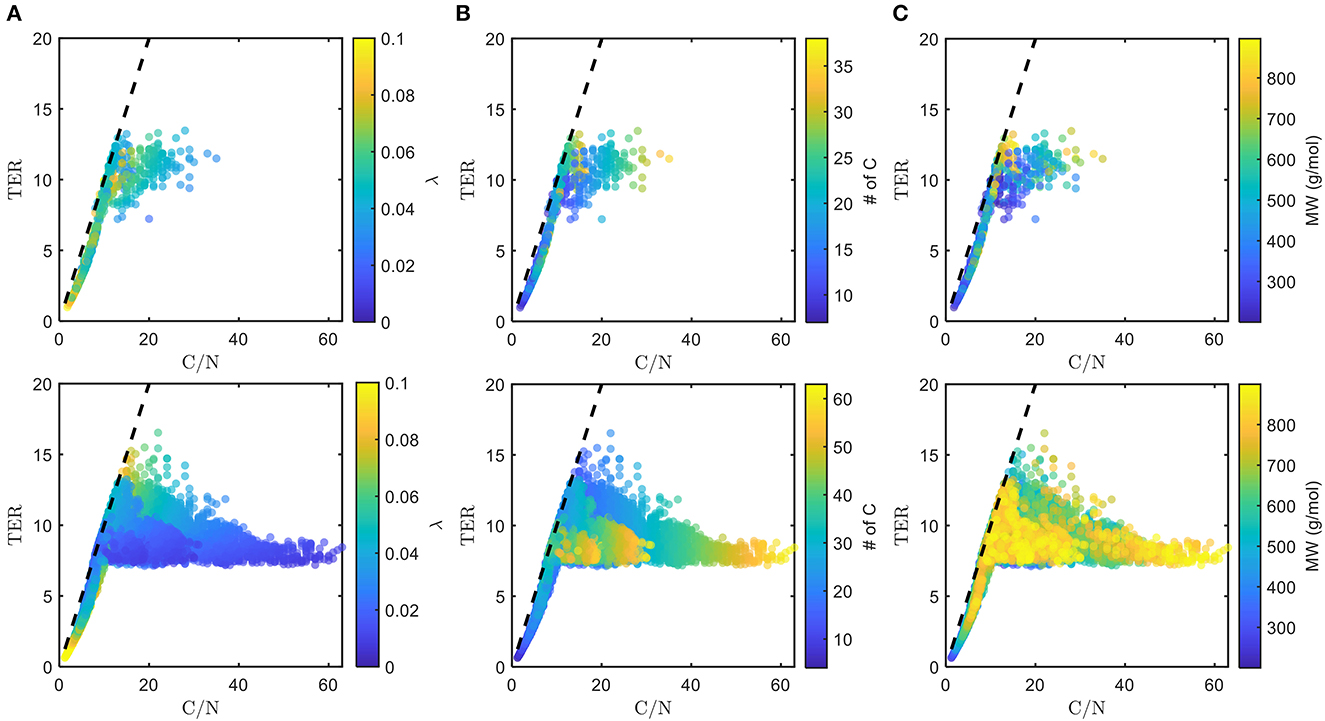
Figure 5. Distributions of threshold element ratio (TER) against C/N ratio with heatmaps of (A) λ, (B) number of C, and (C) molecular weight (MW), of chosen bioavailable compounds (top) compared with detected compounds from all samples (bottom) under C-limited condition. The diagonal dashed lines represent the region that corresponds to C/N = TER. Here, we show how thermodynamic and molecular properties (in addition to the TER requirement, cf. Figure 4A) dictate the choice of bioavailable compounds.
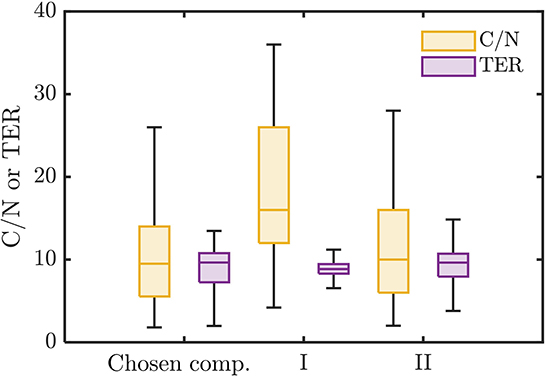
Figure 6. Distributions of C/N ratio and threshold element ratio (TER) of the chosen bioavailable compounds compared against compounds from groups I and II of non-bioavailable compounds in the marked regions in Figure 4B.
4. Discussion
Identifying bioavailable fractions is challenging given the heterogeneous and highly complex mixture of organic compounds in aquatic systems. Applying thermodynamic theory alone through SXTM (Song et al., 2020) to the detected metabolite data failed to adequately represent the aerobic respiration rates measured by laboratory experiments. This is because the thermodynamic model estimates the potential aerobic reactivity of organic compounds while the actual utilization of compounds in the environment is also dependent on many other factors.
In this study, we investigate the impact of incorporating the variable bioavailability of OM, among other potential factors, on enhancing the model prediction and representation of OM degradation. Using an optimization approach, we identified a subset of compounds that vastly improved the prediction of aerobic respiration rates. By analyzing the chosen subset of compounds that is presumably bioavailable during the respiration rate measurements under aerobic conditions, we showed that enhanced thermodynamics and respiration kinetics alone does not necessarily guarantee the respiration of OM. Hence, interdependencies with additional chemical traits and metabolic elements should also be considered. Particularly, we showed that the C/N ratio, number of C, and thermodynamic favorability all jointly influence OM bioavailability, but we may see one or more of these predicting factors dictate OM decomposition depending on the details of a given OM assemblage. Compounds with an exceedingly high number of C atoms or a very low thermodynamic favorability are omitted from the bioavailable fraction altogether. From the pool of compounds that satisfy the criteria imposed by the number of C atom and thermodynamic favorability, those with a C/N ratio that matches the TER are preferentially bioavailable.
While many studies have previously explored the controls of microbial utilization of OM (Sun et al., 1997; Benner, 2003; Schmidt et al., 2011; D'Andrilli et al., 2015; Hu et al., 2022), we have identified the potential controlling factors of OM bioavailability through an unbiased approach without assuming any bioavailability-promoting OM properties a priori. Consistent with our findings, previous studies have clearly shown that only fractions of the OM present in natural aquatic systems support microbial metabolism and suggest the significance of chemical traits such as C and N contents on OM bioavailability (Sun et al., 1997; Benner, 2003; D'Andrilli et al., 2015). Findlay and Sinsabaugh (1999) and Benner (2003) agree that C/N ratio is a good indicator of bioavailability given that microbes are generally more nitrogen-rich relative to OM. For example, compounds with high C/N is not easily respired without external sources of inorganic nutrient N to compensate for the N deficit (Cotner and Heath, 1990; Kroer, 1993), which makes N-rich compounds more bioavailable (Benner, 2003). Agreeably, high C/N compounds are not chosen as bioavailable in our work, but rather compounds that are balanced with respect to their C/N ratio (i.e., C/N ≈ TER), which are also co-incidentally N-rich, make up the bioavailable fraction. Further, high MW (i.e., associated with a high number of C) is linked to recalcitrant compounds (D'Andrilli et al., 2015) that especially make up the less or non-bioavailable fractions of OM pools (Hu et al., 2022), which is also coherent with our results where compounds with a high number of C are excluded from the bioavailable fraction.
The compounds that are not chosen by our model as bioavailable OM should not be necessarily interpreted as not involved in the biochemical transformations. The dynamics of non-bioavailable OM may be considerably low where their decomposition will be heavily influenced by stochastic elements (e.g., spatial and seasonal fluctuations) such that the deterministic effects of bioavailability become diluted and insignificant (Hu et al., 2022). It is also worth noting that the experimental respiration rates of samples that were used to characterize the OM bioavailability in this study were measured during the initial stages of incubations over the span of about 2 h, during which O2 may serve as the main terminal electron acceptor as reflected in the model formulation. The time scale of the incubation experiment is also deemed acceptable given that the reactivity of OM is most apparent in the early stages of decomposition, where the compounds are most susceptible to degradation (Benner, 2003).
Besides aerobic respiration kinetics, the overall thermodynamic favorability of a sample is also often used as an indicator of biogeochemical transformations. Typically, we would expect a negative correlation between λ and respiration rates solely based on thermodynamic theory, but we find that the correlations with the measured respiration rates are positive regardless of accounting for all detected compounds or only the chosen bioavailable compounds in respective samples, across various levels of substrate limitations (see Supplementary Figure S6). This finding is expected as we have previously established that OM aerobic respiration is not solely driven by thermodynamics, but rather influenced by multiple interdependent factors (see Sections 3.3 and 3.4). An equally reasonable explanation for this observation is that the metabolic diversity (i.e., compositional differences in microbial communities and the amount of microbial biomass) across different samples would impose variable kinetics of degradation of OM as steered by the dominant biological functionalities. Microbes are known to possess high substrate specificity (Hu et al., 2022) as the ability to degrade various organic compounds is not equally distributed among microbial taxa (Martinez et al., 1996). Therefore, microbial and OM compositions will both affect and be affected by each other (Findlay and Sinsabaugh, 1999; Marschner and Kalbitz, 2003). Spatially diverse datasets, such as the one used in this work, have a higher likelihood of containing biologically diverse samples collected from various locations and environments. As a result, we may not observe adequate correlations with measured respiration when we pool all the samples together. Conversely, we may see improved correlations if we classify the samples based on biological similarities. For instance, a previous study (Song et al., 2020) showed better correlations between λ and measured microbial activity as the work involved data from localized regions, which presumably encompass microbiomes that are biologically more similar.
Related to the issues above, we have assumed that the microbiomes in all samples share biological similarities [i.e., microbiome growth kinetics defined by μmax in Eq. (5) are consistent across all samples] due to data limitations in this work, which may not be true in general contexts. Therefore, how and to what degree the correlations between model and measured respiration rates could be improved by accounting for the variation of microbial community composition and growth kinetics would be an important issue to investigate in the future, which requires additional data analysis and significant model extension. While we attributed molecular reactivity driven by chemical traits as the major factors governing the decomposition of OM, the results also hinted at the influence of metabolic factors (i.e., microbial requirements for C and N). Therefore, future studies should also focus on the inclusion of microbiome-explicit biochemical transformation pathways (Hu et al., 2022) in analyzing OM degradation. This can be accomplished by tracing organic carbon transformations in FTICR-MS data (Stegen et al., 2018) or through the incorporation of additional biological data (metagenome, metatranscriptome). Further, some compounds (which may be part of bioavailable OM) may have inadvertently gone undetected in OM data due to the variations in production and transformation rates (Hu et al., 2022), but they too can be recovered by identifying active biochemical transformation pathways from additional biological data. To this end, our approach here can be easily extended to account for sample-specific microbiome characteristics to assess the effect on OM bioavailability, as well as to identify contextual microbiome-metabolite interactions when analyzed jointly with auxiliary multi-omics data.
Data availability statement
The codes and data used in this study are provided in the GitHub repository at https://github.com/WHONDRS-Crowdsourced-Manuscript-Effort/Topic6. This study uses the data from the larger Worldwide Hydrobiogeochemistry Observation Network for Dynamic River Systems (WHONDRS; https://whondrs.pnnl.gov) Summer 2019 Sampling Campaign containing surface water and sediment data from 97 river corridors which are openly accessible through Environmental Systems Science Data Infrastructure for a Virtual Ecosystem (ESS-DIVE—https://data.ess-dive.lbl.gov), under doi: 10.15485/1603775 and doi: 10.15485/1729719 Supplementary material that support this study are given in the online version of this article. Further inquiries can be directed to the corresponding author.
Author contributions
FA and H-SS developed optimization methods used for identifying bioavailable OM. FA performed computational analyses and drafted out the article, which were reviewed, edited, and approved by all authors. All authors contributed to the design of the research.
Funding
JS and TS were supported by the River Corridor Science Focus Area (SFA) project at Pacific Northwest National Laboratory (PNNL) funded by the U.S. Department of Energy, Office of Biological and Environmental Research, Environmental System Science program. FA and H-SS were supported by the same through a subcontract with PNNL's River Corridor SFA. YY was supported by the New York State Center of Excellence in Healthy Water Solutions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2023.1169701/full#supplementary-material
References
Allison, S. D. (2017). Building predictive models for diverse microbial communities in soil. Microb. Biomass. 141−166. doi: 10.1142/9781786341310_0006
Benner, R. (2003). Molecular indicators of the bioavailability of dissolved organic matter. Aquat. Ecosyst. 121−137. doi: 10.1016/B978-012256371-3/50006-8
Cotner, J. B., and Heath, R. T. (1990). Iron redox effects on photosensitive phosphorus release from dissolved humic materials. Limnol. Oceanogr. 35, 1175–1181. doi: 10.4319/lo.1990.35.5.1175
D'Andrilli, J., Cooper, W. T., Foreman, C. M., and Marshall, A. G. (2015). An ultrahigh-resolution mass spectrometry index to estimate natural organic matter lability. Rapid Commun. Mass Spectrom. 29, 2385–2401. doi: 10.1002/rcm.7400
Findlay, S., and Sinsabaugh, R. L. (1999). Unravelling the sources and bioavailability of dissolved organic matter in lotic aquatic ecosystems. Mar. Freshw. Res. 50, 781–790. doi: 10.1071/MF99069
Garayburu-Caruso, V. A., Danczak, R. E., Stegen, J. C., Renteria, L., McCall, M., Goldman, A. E., et al. (2020a). Using community science to reveal the global chemogeography of river metabolomes. Metabolites. 10, 1–20. doi: 10.3390/metabo10120518
Garayburu-Caruso, V. A., Stegen, J. C., Song, H. S., Renteria, L., Wells, J., Garcia, W., et al. (2020b). Carbon Limitation Leads to Thermodynamic Regulation of Aerobic Metabolism. Environ. Sci. Technol. Lett. 7, 517–524. doi: 10.1021/acs.estlett.0c00258
Giovannoni, S. J., Britschgi, T. B., Moyer, C. L., and Field, K. G. (1990). Genetic diversity in Sargasso Sea bacterioplankton. Nature. 345, 60–63. doi: 10.1038/345060a0
Goldman, A. E., Arnon, S., Bar-Zeev, E., Chu, R. K., Danczak, R. E., Daly, R. A., et al. (2020). “WHONDRS summer 2019 sampling campaign: global river corridor sediment fticr-ms, dissolved organic carbon, aerobic respiration, elemental composition, grain size, and total nitrogen and organic carbon content,” in River Corridor Watershed Biogeochem. SFA Worldw. Hydrobiogeochemistry Obs. Netw. Dyn. River Syst. (WHONDRS), ESS-DIVE Repos.
Hoijnen, J. J., van Loosdrecht, M. C. M., and Tijhuis, L. (1992). A black box mathematical model to calculate auto- and heterotrophic biomass yields based on Gibbs energy dissipation. Biotechnol. Bioeng. 40, 1139–1154. doi: 10.1002/bit.260401003
Hu, A., Jang, K. S., Meng, F., Stegen, J., Tanentzap, A. J., Choi, M., et al. (2022). Microbial and environmental processes shape the link between organic matter functional traits and composition. Environ. Sci. Technol. 56, 10504–10516. doi: 10.1021/acs.est.2c01432
Kellerman, A. M., Kothawala, D. N., Dittmar, T., and Tranvik, L. J. (2015). Persistence of dissolved organic matter in lakes related to its molecular characteristics. Nat. Geosci. 8, 454–457. doi: 10.1038/ngeo2440
Kleerebezem, R., and Van Loosdrecht, M. C. M. (2010). A generalized method for thermodynamic state analysis of environmental systems. Crit. Rev. Environ. Sci. Technol. 40, 1–54. doi: 10.1080/10643380802000974
Kroer, N. (1993). Bacterial growth efficiency on natural dissolved organic matter. Limnol. Oceanogr. 38, 1282–1290. doi: 10.4319/lo.1993.38.6.1282
Lavallee, J. M., Soong, J. L., and Cotrufo, M. F. (2020). Conceptualizing soil organic matter into particulate and mineral-associated forms to address global change in the 21st century. Glob. Chang. Biol. 26, 261–273. doi: 10.1111/gcb.14859
Marschner, B., and Kalbitz, K. (2003). Controls of bioavailability and biodegradability of dissolved organic matter in soils. Geoderma. 113, 211–235. doi: 10.1016/S0016-7061(02)00362-2
Martinez, J., Smith, D. C., Steward, G. F., and Azam, F. (1996). Variability in ectohydrolytic enzyme activities of pelagic marine bacteria and its significance for substrate processing in the sea. Aquat. Microb. Ecol. 10, 223–230. doi: 10.3354/ame010223
Mccarty, P. L. (2007). Thermodynamic electron equivalents model for bacterial yield prediction : modifications and comparative Evaluations. 97, 377–388. doi: 10.1002/bit.21250
Merder, J., Röder, H., Dittmar, T., Feudel, U., Freund, J. A., Gerdts, G., et al. (2021). Dissolved organic compounds with synchronous dynamics share chemical properties and origin. Limnol. Oceanogr. 66, 4001–4016. doi: 10.1002/lno.11938
Moorhead, D. L., Rinkes, Z. L., Sinsabaugh, R. L., and Weintraub, M. N. (2013). Dynamic relationships between microbial biomass, respiration, inorganic nutrients and enzyme activities: informing enzyme-based decomposition models. Front. Microbiol. 4, 1–12. doi: 10.3389/fmicb.2013.00223
Pomeroy, L. R. (1974). The ocean's food web, a changing paradigm. Bioscience. 24, 499–504. doi: 10.2307/1296885
Quéméner, E. D., and Bouchez, T. (2014). A thermodynamic theory of microbial growth. ISME J. 8, 1747–1751. doi: 10.1038/ismej.2014.7
Rittmann, B. E., and McCarty, P. L. (2001). Environmental Biotechnology: Principles and Applications, 1st ed. New York, NY: McGraw-Hill Education.
Schmidt, M. W. I., Torn, M. S., Abiven, S., Dittmar, T., Guggenberger, G., Janssens, I. A., et al. (2011). Persistence of soil organic matter as an ecosystem property. Nature. 478, 49–56. doi: 10.1038/nature10386
Sondergaard, M., and Middelboe, M. (1995). A cross-system analysis of labile dissolved organic carbon. Mar. Ecol. Prog. Ser. 118, 283–294. doi: 10.3354/meps118283
Song, H.-S., Cannon, W., Beliaev, A., and Konopka, A. (2014). Mathematical modeling of microbial community dynamics: a methodological review. Processes. 2, 711–752. doi: 10.3390/pr2040711
Song, H.-S., Thomas, D. G., Stegen, J. C., Li, M., Liu, C., Song, X., et al. (2017). Regulation-structured dynamic metabolic model provides a potential mechanism for delayed enzyme response in denitrification process. Front. Microbiol. 8, 1–12. doi: 10.3389/fmicb.2017.01866
Song, H. S., and Liu, C. (2015). Dynamic metabolic modeling of denitrifying bacterial growth: the cybernetic approach. Ind. Eng. Chem. Res. 54, 10221–20227. doi: 10.1021/acs.iecr.5b01615
Song, H. S., Stegen, J. C., Graham, E. B., Lee, J. Y., Garayburu-Caruso, V. A., Nelson, W. C., et al. (2020). Representing organic matter thermodynamics in biogeochemical reactions via substrate-explicit modeling. Front. Microbiol. 11, 1–16. doi: 10.3389/fmicb.2020.531756
Soong, J. L., Fuchslueger, L., Marañon-Jimenez, S., Torn, M. S., Janssens, I. A., Penuelas, J., et al. (2020). Microbial carbon limitation: the need for integrating microorganisms into our understanding of ecosystem carbon cycling. Glob. Chang. Biol. 26, 1953–1961. doi: 10.1111/gcb.14962
Stegen, J. C., and Goldman, A. E. (2018). WHONDRS: a community resource for studying dynamic river corridors. mSystems. 3, 1–4. doi: 10.1128/mSystems.00151-18
Stegen, J. C., Johnson, T., Fredrickson, J. K., Wilkins, M. J., Konopka, A. E., Nelson, W. C., et al. (2018). Influences of organic carbon speciation on hyporheic corridor biogeochemistry and microbial ecology. Nat. Commun. 9, 1–11. doi: 10.1038/s41467-018-02922-9
Sterner, R. W., and Elser, J. J. (2003). 7. Stoichiometry in Communities: Dynamics and Interactions. Ecol. Stoichiom. 262–312. doi: 10.1515/9781400885695-011
Sulman, B. N., Moore, J. A. M., Abramoff, R., Averill, C., Kivlin, S., Georgiou, K., et al. (2018). Multiple models and experiments underscore large uncertainty in soil carbon dynamics. Biogeochemistry. 141, 109–123. doi: 10.1007/s10533-018-0509-z
Sun, L., Perdue, E. M., Meyer, J. L., and Weis, J. (1997). Use of elemental composition to predict bioavailability of dissolved organic matter in a Georgia river. Limnol. Oceanogr. 42, 714–721. doi: 10.4319/lo.1997.42.4.0714
Todd-Brown, K. E. O., Hopkins, F. M., Kivlin, S. N., Talbot, J. M., and Allison, S. D. (2012). A framework for representing microbial decomposition in coupled climate models. Biogeochemistry. 109, 19–33. doi: 10.1007/s10533-011-9635-6
Toyoda, J. G., Goldman, A. E., Arnon, S., Bar-Zeev, E., Chu, R. K., Danczak, R. E., et al. (2020). “WHONDRS Summer 2019 Sampling Campaign: Global River Corridor Surface Water FTICR-MS, NPOC, TN, Anions, and Stable Isotopes,” in River Corridor Watershed Biogeochem. SFA Worldw. Hydrobiogeochemistry Obs. Netw. Dyn. River Syst. (WHONDRS), ESS-DIVE Repos.
Keywords: river biogeochemistry, organic matter bioavailability, chemical traits, thermodynamic favorability, model optimization
Citation: Ahamed F, You Y, Burgin A, Stegen JC, Scheibe TD and Song H-S (2023) Exploring the determinants of organic matter bioavailability through substrate-explicit thermodynamic modeling. Front. Water 5:1169701. doi: 10.3389/frwa.2023.1169701
Received: 20 February 2023; Accepted: 15 June 2023;
Published: 04 July 2023.
Edited by:
Martin Thullner, Federal Institute for Geosciences and Natural Resources, GermanyReviewed by:
Adrian Mellage, University of Kassel, GermanyArjun Chakrawal, Stockholm University, Sweden
Copyright © 2023 Ahamed, You, Burgin, Stegen, Scheibe and Song. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hyun-Seob Song, hsong5@unl.edu
 Firnaaz Ahamed
Firnaaz Ahamed Yaqi You
Yaqi You Amy Burgin3
Amy Burgin3 James C. Stegen
James C. Stegen Timothy D. Scheibe
Timothy D. Scheibe Hyun-Seob Song
Hyun-Seob Song