A critical mini-review on the low-field nuclear magnetic resonance investigation of pore coupling effects in near-surface environments

Soto Bravo, Francisca; Zhang, Chi

doi:10.3389/frwa.2023.1059128

MINI REVIEW article

Front. Water, 05 May 2023

Sec. Water and Critical Zone

Volume 5 - 2023 | https://doi.org/10.3389/frwa.2023.1059128

This article is part of the Research Topic Women in Critical Zone Science View all 7 articles

A critical mini-review on the low-field nuclear magnetic resonance investigation of pore coupling effects in near-surface environments

$\r\nFrancisca Soto Bravo&#x;$ Francisca Soto Bravo¹^†

Chi Zhang^1,2^*^†

¹Environmental Geophysics, Institute of Meteorology and Geophysics, Faculty of Earth Sciences, Geography and Astronomy, University of Vienna, Vienna, Austria
²State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan, China

The assessment and monitoring of groundwater resources is of increasing importance to ensure the continuous supply of fresh water for human activity and endangered ecosystems. These groundwater resources include fully saturated aquifers, water in unsaturated soil, and water trapped as rock moisture in weathered bedrocks. Low-field nuclear magnetic resonance (NMR) is a method with unique sensitivity to pore water, as it is based on the magnetization and relaxation behavior of the spin magnetic moment of hydrogen atoms forming water molecules. It is a cost-effective and minimally-invasive technology that can help characterize the pore structures and the groundwater distribution and transport in different types of subsurface materials. However, the interpretation of NMR data from samples with complex bimodal or multimodal porous geometries requires the consideration of pore coupling effects. A pore-coupled system presents significant magnetization exchange between macro- and micropores within the measurement time, making the independent characterization of each pore environment difficult. Developing a better understanding of pore coupling is of great importance for the accurate estimation of hydrogeological parameters from NMR data. This mini-review presents the state-of-art in research exploring the two factors controlling pore coupling: surface geochemistry and network connectivity, summarizes existing experimental and numerical modeling approaches that have been used to study pore coupling and discusses the pore coupling effects in fully and partially saturated conditions. At the end of this review, we outline major knowledge gaps and highlight the research needs in the vadose zone.

1. Introduction

The exploration and management of groundwater resources is of increasing importance in the context of climate change. Monitoring aquifers and understanding the transport of water and contaminants through soil is vital to elucidate critical zone functions, forecast ecosystem processes, and ensure the sustainable exploitation of groundwater resources.

The low-field nuclear magnetic resonance (NMR) method, based on the relaxation behavior of protons within external magnetic fields, is a non-invasive geophysical method gaining popularity for near-surface research, especially for hydrogeologic investigations. Due to its unique direct sensitivity to pore water, NMR is used to characterize the structure of porous media and to quantitatively estimate water contents and distributions. The deployment of low-field NMR measurements can be done in the laboratory (labNMR) with benchtop instrument for core samples, as a logging tool in boreholes (bNMR), or at Earth's surface using Earth's magnetic field (sNMR) (Behroozmand et al., 2015; Binley et al., 2015). Numerous laboratory studies and field applications encouraged the development of low-field NMR techniques including theory, modeling, inversion, and field instrumentation (Behroozmand et al., 2015). Besides groundwater exploration and aquifer characterization, other NMR applications include the monitoring of infiltration processes in controlled flood events (e.g., Walsh et al., 2014), the delineation of weathering profiles in fractured rocks (e.g., Flinchum et al., 2019), the study of frost damage (e.g., Ding et al., 2020) and freeze-thaw processes in general (e.g., An et al., 2022), as well as the monitoring of melting soil (e.g., Watanabe and Wake, 2009) and permafrost (e.g., Parsekian et al., 2013; Kass et al., 2017; Sullivan, 2022). Further applications for near surface characterization, as well as detailed explanations on the working principles of NMR, are reviewed in Behroozmand et al. (2015).

The key assumption that each pore environment relaxes independently fails when interpreting NMR signals in scenarios presenting pore coupling effects. Pore coupling distorts the NMR-gained relaxation time distributions, characterizing an averaged version of the pore network instead of identifying individual pore environments (e.g., Grunewald and Knight, 2009). This represents a non-negligible effect in accurately applying NMR tools in heterogeneous subsurface materials with dual or multimode pore systems, where magnetisation can be exchanged between pore environments during the NMR measurement. Pore coupling effects were first described by Brownstein and Tarr (1979) and have been observed in fully-saturated rocks and unconsolidated material through laboratory measurements (e.g., Toumelin et al., 2003; Anand and Hirasaki, 2007; Grunewald and Knight, 2009) and numerical simulation studies (e.g., Mohnke and Klitzsch, 2010; Chi and Heidari, 2015; Mitchell et al., 2019). It is important to understand and quantify pore coupling effects and the factors that drive their occurrence and severity.

Although magnetisation exchange can take place in multiple settings beyond the critical zone, e.g., in organic rich shale (Washburn and Cheng, 2017), and research on the application of NMR in unconventional reservoirs under multi-phase and pore coupling conditions (e.g., Singer et al., 2020; Elsayed et al., 2022) has greatly contributed to the understanding and interpretation of NMR data and fluid relaxation, this mini-review focuses on water interactions between the pore environments in near-surface conditions. We summarize the approaches used to investigate pore coupling effects using NMR, discuss the connectivity between pore environments and the pore wall's surface geochemistry as two factors controlling the degree of coupling, and highlight the most pressing open questions for further research opportunities, particularly for application in the vadose zone.

2. Basic concepts of NMR

NNR measurements are based on the behavior of the magnetic spin of protons inside changing magnetic fields. In the presence of an applied constant magnetic field, the spins of hydrogen atoms inside geologic material containing pore water align along the field direction at their characteristic Larmor frequency. A secondary radio frequency pulse perturbs this alignment by exciting the spins, causing increased magnetization in the system. After removing this secondary pulse, the hydrogen atoms precess and decay back to equilibrium in a process called relaxation. The initial magnitude of the relaxation decay is proportional to water content. Relaxation is enhanced when the protons, diffusing inside the pore space, encounter the pore's wall. This process is called surface relaxation (T_{1S, 2S}). Besides surface relaxation, Equation (1) outlines other relaxation mechanisms for both longitudinal (T₁) and transverse (T₂) relaxation times—bulk relaxation (T_{1B, 2B}) takes place spontaneously in the fluid, depending on its physical properties and without the influence of the pore wall, while diffusion relaxation (T_2D) occurs in inhomogeneous magnetic fields and only affects transverse relaxation (T₂).

\begin{array}{l} \frac{1}{T_{relax}} = \frac{1}{T_{1, 2}} = \frac{1}{T_{1 B, 2 B}} + \frac{1}{T_{1 S, 2 S}} + \frac{1}{T_{2 D}} & (1) \end{array}

Both bulk and diffusion relaxation are considerably slower compared to surface relaxation and can often be neglected. Though they do not provide information about the pore's structure, in certain scenarios (e.g., in systems with large pore spaces or inside strong magnetic gradients) they must be considered for a correct interpretation (e.g., Dlugosch et al., 2013; Costabel et al., 2018, 2022).

Brownstein's parameter μ differentiates between fast, intermediate and slow diffusion regimes and is defined by Equation (2), where L₂ is the average distance traveled by a proton during the NMR measurement and D is the self-diffusion coefficient of water. Fast diffusion, with a μ value below 0.1 (Ryu, 2009), is a precondition for the tradition interpretation of NMR signals (Brownstein and Tarr, 1979). Further considerations regarding to diffusion regimes can be found e.g., in Müller-Petke et al. (2015).

\begin{array}{l} μ = \frac{relaxation rate}{diffusion rate} = \frac{ρ / L_{2}}{D / L_{2}^{2}} = \frac{ρ L_{2}}{D} & (2) \end{array}

Other scenarios that requires extra careful interpretation of the NMR signal are pore-coupled systems. Here, the diffusing protons are able to move between pore environments during the NMR measurement time, leading to distorted relaxation time distributions where the peaks are no longer representing the distinct pore environments but an average of the whole sample (e.g., Grunewald and Knight, 2009). In pore-coupled systems, the average pore size is smaller than the diffusion length scale, l, defined by the Einstein equation for self-diffusion (see Equation 3) where D is the self-diffusion coefficient of water (a temperature dependant constant) and T is the time scale of the NMR measurement.

\begin{array}{l} l = \sqrt{6 D T} & (3) \end{array}

For a system in the fast diffusion regime and without pore coupling effects, Equation (1) can be written as Equation (4), where S_por stands for the pore's surface area-to-volume ratio. Thus, the relaxation time (T₁ or T₂) can be used to estimate pore size distribution, irreducible and movable liquid saturation, surface area-to-volume ratios, and hydraulic conductivity under saturated condition (e.g., Coates et al., 1999).

\begin{array}{l} \frac{1}{T_{1, 2}} = \frac{1}{T_{1 S, 2 S}} = ρ S_{p o r} & (4) \end{array}

While the violation of the fast diffusion regime and the pore coupling effects are only of relevance in specific scenarios and for certain type of materials, they can lead to serious misinterpretations of the NMR data if they are ignored or overlooked.

3. Pore coupling effects

As NMR gains popularity in new fields of research and starts to be deployed in new conditions or to study more complex materials (Behroozmand et al., 2015; Schmidt and Rempe, 2020), it is of great importance to identify the scenarios in which pore coupling must be considered and to describe how it will affect the NMR signals (Grunewald and Knight, 2009). Pore coupling effects arise due to the magnetization exchange between pore environments of different characteristic pore sizes during the NMR measurement time (Ramakrishnan et al., 1998) and can be observed both in T₁ and T₂ distributions as the merging of two peaks (Grunewald and Knight, 2009), as well as in 2D T₂−T₂- or T₁−T₂-maps as off-diagonal peaks (Song, 2012). Figure 1 shows a comparison between uncoupled (Figure 1A) and coupled scenarios (Figure 1B) in relation to the simple modeled behavior of diffusing hydrogen atoms inside pore spaces. In Figure 1B, the diffusing spins of protons (indicated with blue and red) move through both pore environments, resulting in merged relaxation peaks and a reduced amplitude of the fast peak as some protons diffuse out of the micropores without relaxing (Figure 1D). Figures 1C, D show the exemplary relaxation time distributions for uncoupled and coupled scenarios. 2D T₂−T₂-maps (Figures 1E, F) are measurements to detect the chemical shift of protons and monitor the exchange of water among different pore environments during designed experimental mixing periods (Song, 2012). In pore coupled environment (Figure 1F), the magnetization can be exchanged between environments multiple times during the NMR measurement, leading to shifts in the peaks away from the diagonal and asymmetry in cross-peaks (Song, 2012; Zhang and Zhang, 2021).

FIGURE 1

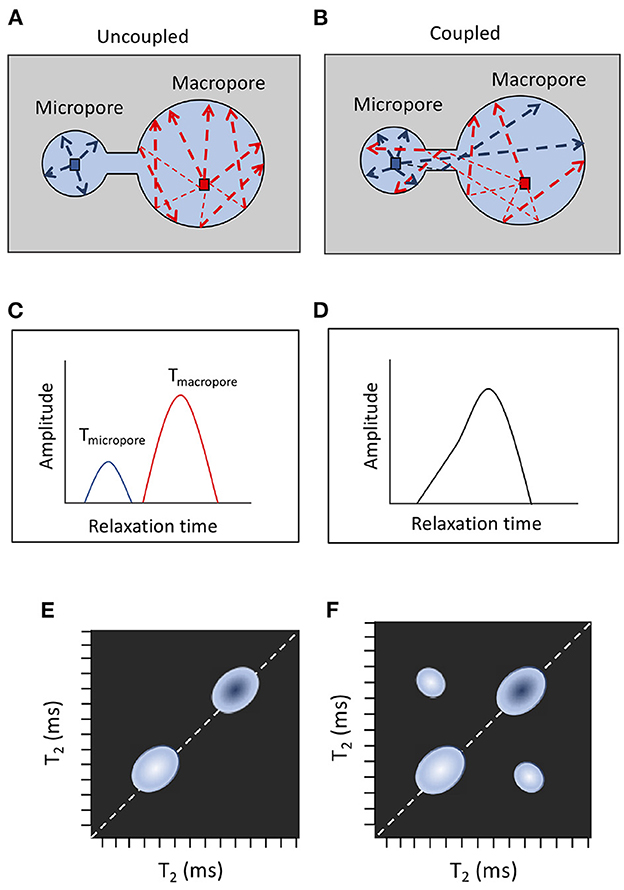
Figure 1. Comparison of an uncoupled and a coupled scenario. Panels (A, B) illustrate the movement of one exemplary hydrogen atom as it diffuses through the pore spaces. Panels (C, D) represent the corresponding relaxation time distribution curves, while panels (E, F) represent the corresponding 2D T₂-T₂-maps.

Pore coupling affects the interpretation of NMR data in respect to the water distribution within the sample and the characterization of the pore network's structure, e.g., leading to an underestimation of total micropore volume and/or the underestimation of the macropore's characteristic sizes (Grunewald and Knight, 2009). The identification of pore coupling-prone materials and the scenarios leading to stronger coupling, as well as the quantification of the pore coupled effects in NMR signals, is of great importance to utilize NMR to its full potential and avoid mistakes in the interpretation of the results.

3.1. Approaches to study pore coupling

Pore coupling effects have been studied experimentally and through numerical simulations in fully saturated environments.

A common method used in the laboratory to identify pore coupling effects involves comparing the NMR signals from fully saturated samples with those from centrifuged samples (with drained macropores and saturated micropores) (e.g., Toumelin et al., 2003; Anand and Hirasaki, 2007; Grunewald and Knight, 2009). The measurement obtained from the centrifuged samples provides a baseline for the fast relaxation peak in an uncoupled scenario, which can be used to isolate pore-coupled signals from the fully saturated measurement.

Numerical simulations on digitized or synthetic samples are great tools to study pore coupling as they allow for the targeted exploration of its controlling parameters. The typical numerical modeling workflow is depicted in Figure 2. A popular approach to simulate NMR relaxation using real geological geometries involves the creation of digital porous media from micro-CT images (e.g., Chi and Heidari, 2015). Two main simulation methods are predominant in literature: Random Walk (e.g., Talabi, 2008) and Finite Elements (e.g., Mohnke and Klitzsch, 2010; Mitchell et al., 2019). Furthermore, Mohnke et al. (2014) developed a Boltzmann Lattice framework, allowing for the joint simulation of NMR relaxation and transport properties in unsaturated environments. Several versions of the Random Walk method have been developed deviating from the traditional fix-step-size technique: in the First Arrival or First Passage approach (e.g., Toumelin et al., 2003; Mitchell et al., 2019) the step-size of the walkers depends on its proximity to the pore wall, while, in the Variable-Step-Size approach (e.g., Zhang et al., 2011; Carneiro et al., 2013), each walker moves at changing step-sizes with its own internal clock. Furthermore, Toumelin et al. (2007) developed a Random Walk capable of modeling a CPMG pulse sequence. Mitchell et al. (2019) compares the First Arrival Random Walk to the Finite Elements Method (FEM) and argues that FEM provides greater versatility by allowing for more arbitrary pore geometries, while reducing computational costs and uncertainties by solving the diffusion equations in the eigenvalue domain (thus skipping the inversion step). Simulating NMR relaxation using Finite Elements approaches can be straightforward employing licensed-software such as COMSOL Multiphysics (COMSOL Multiphysics, 1998) or open-software such as OpenFoam (Weller et al., 1998) (e.g., Tandon and Heidari, 2018). The development and publication of open-access simulation codes for open-software would reduce the barriers for using FEM to simulate NMR signals of complicated scenarios.

FIGURE 2

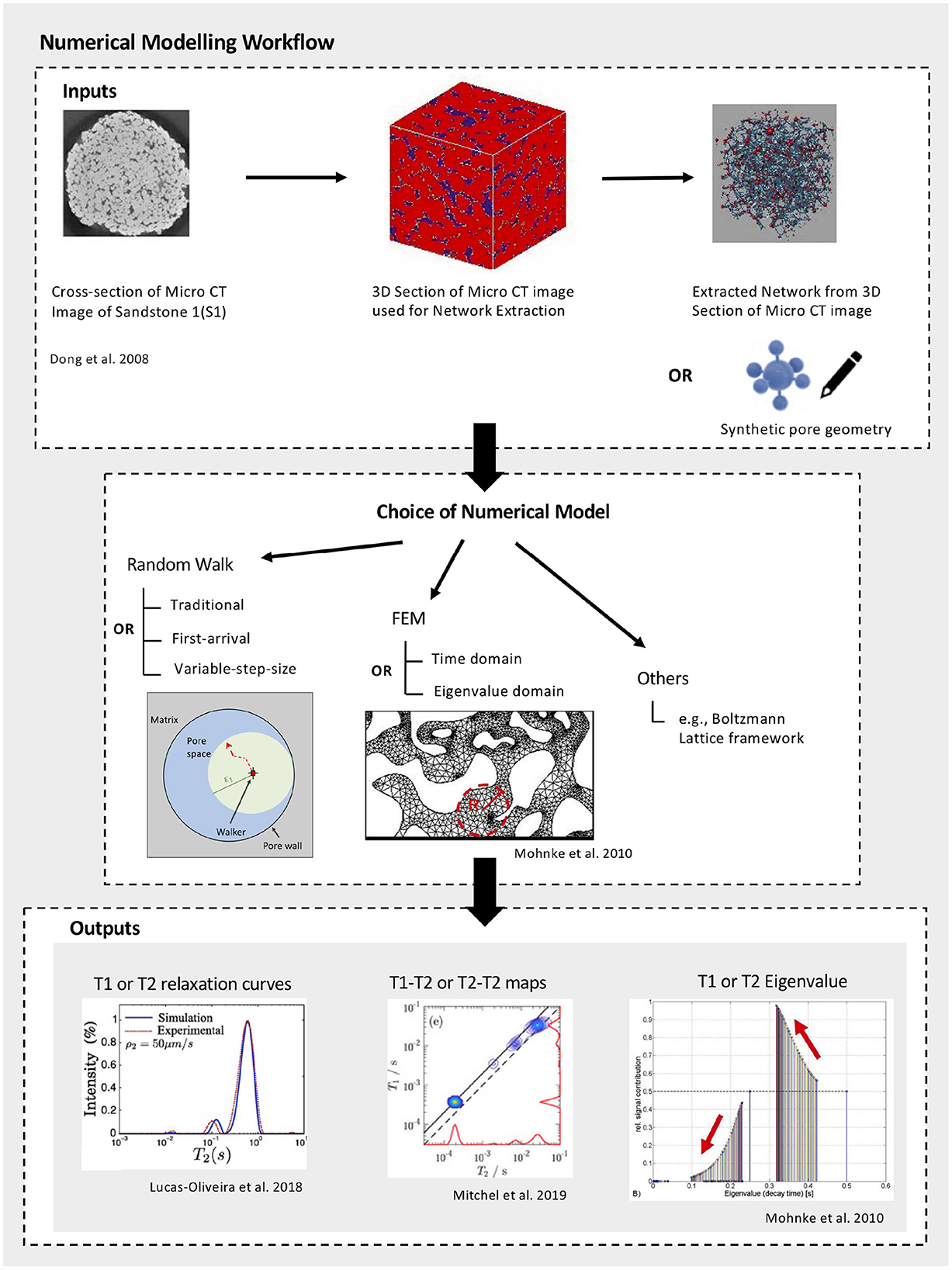
Figure 2. Typical workflow for the numerical modeling of pore coupling effects on NMR data. With images from Dong and Blunt (2008); Mohnke and Klitzsch (2010); Lucas-Oliveira et al. (2018), and Mitchell et al. (2019).

Moreover, multiple studies have used 2D approaches, such as T₂−T₂-maps (see Figures 1E, F), to detect and quantify pore coupling (e.g., Washburn and Callaghan, 2006; Mitchell et al., 2019; Zhang and Zhang, 2021). Although T₂−T₂-maps are great tools to identify a pore-coupled sample, they require more demanding experimental techniques than 1D approaches (Fleury and Soualem, 2009), with evidence suggesting that no additional pore couple strength information can be obtained from T₂−T₂-maps, in comparison to T₁- or T₂-distributions (Johnson and Schwartz, 2014).

3.2. Factors controlling pore coupling

From literature, two main factors controlling pore coupling are identified in existing studies: surface geochemistry and network connectivity.

The surface geochemistry of the pore's wall, in particular related to the rock's mineralogy, can be quantified through the surface relaxivity value (ρ). Surface relaxivity ρ is an empirical factor describing the wall's ability to enhance relaxation (Bergman et al., 1995). It will increase in the presence of paramagnetic material in the grain such as manganese(II) or iron(III) (Bryar et al., 2000), and is also affected by pore fluid properties (e.g., Anand and Hirasaki, 2007) and temperature (e.g., Godefroy et al., 2002). Higher surface relaxivity values will lead to faster relaxation processes, thus weakening pore coupling effects. The role of surface geochemistry in pore coupling effects has been probed experimentally using iron-coated silica gels by Daughney et al. (2000) and Grunewald and Knight (2009), with changing saturation fluids by Anand and Hirasaki (2007) and Fleury and Soualem (2009), and via numerical simulations (e.g., Mitchell et al., 2019). Furthermore, since both surface relaxivity and the fluid's diffusion coefficient are temperature dependent, a rise in temperature has been found to enhance pore coupling (Toumelin et al., 2003; Anand et al., 2008).

The parameters affecting the pore's network connectivity will change depending on the network's model representing the sample. Three well-studied, pore coupling-prone network geometries can be identified in literature: shales, modeled as systems with macro- and micropores connected through pore throats (e.g., Washburn, 2014), clay-lined sandstones, modeled as systems where NMR relaxation predominantly takes place in the micropores surrounding round-shaped macropores (e.g., Anand and Hirasaki, 2007), and carbonate rocks, often understood through the micrograin consolidation model, with a cubic packing of spherical porous grains, each comprised by non-porous micrograins (e.g., Schwartz et al., 2013). For the simpler geometry of pores connected by throats, the influence of the throat sizes on pore-coupling strength has been studied numerically by Mohnke and Klitzsch (2010) (throat length) and Ghomeshi et al. (2018) (throat diameter). Their results show that better connected geometries with shorter and wider throats have stronger pore coupling.

For clay-lined geometries, Anand and Hirasaki (2007) introduces a parameter, α, to quantify the degree of pore coupling (see Equation 5), with higher α values signaling weaker pore coupling. This parameter recognizes the key fact that the total volume available for a spin to diffuse in (i.e., the macropore and the micropore volume) is decoupled from the available active surface for spin relaxation (i.e., the micropore surface area). Relaxation is assumed to only take place in the micropores because of the much larger surface available in comparison to macropores.

\begin{array}{l} α = β η μ = β \frac{L_{2}}{L_{1}} \frac{L_{2} ρ}{D} = \frac{β ρ}{D} \frac{L_{2}^{2}}{L_{1}} & (5) \end{array}

Where μ is the Brownstein's parameter, η is the aspect ratio (L₂/L₁), L₂ is defined as the half length to the middle of the macropore, and L₁ as the half-distance between clay flakes. β is a parameter controlled by geometry-factors described in Equation (6), where ϕ is the total porosity of the sample, ϕ_μ the microporosity and ϕ_m the macroporosity.

\begin{array}{l} β = \frac{ϕ_{μ} (1 - ϕ_{m})}{ϕ} & (6) \end{array}

By adjusting the definition of L₂ and L₁, α can also be applied to the micrograin consolidation model (e.g., Souza et al., 2016; Mitchell et al., 2019), as in Equation (7), where R_g is the microporous grain's radius and R_μ the micropore radius, ρ is the surface relaxivity, D is the diffusivity of water, and β is the geometrical parameter described by Equation (6).

\begin{array}{l} α_{grain} = \frac{ρ β R_{g}^{2}}{D R_{μ}} & (7) \end{array}

These established equations suggest that increased grain radius leads to the weakening of the pore coupling. This relationship was also tested and verified experimentally and numerically by Anand and Hirasaki (2007) and Mitchell et al. (2019).

4. Discussion—Knowledge gaps

4.1. The vadose zone

The study of pore coupling effects has so far been limited to fully-saturated conditions. The NMR method, nevertheless, has great potential for studying unsaturated conditions and fluid-flow processes in the vadose zone (Costabel and Yaramanci, 2011; Walsh et al., 2014; Flinchum et al., 2019; Tian, 2021); it can provide information regarding water availability, distribution and movement, and has already been used to study infiltration mechanisms (e.g., Walsh et al., 2014), draining processes (e.g., Mohnke et al., 2014), water availability for plants in form of rock moisture (e.g., Rempe and Dietrich, 2018; Schmidt and Rempe, 2020; Zhang and Zhang, 2021), among others.

However, to address some of these research questions, e.g., for the study of physico-chemical processes in the soil (e.g., wetting or swelling), an accurate measurement of water distribution within different pore environments is crucial and only possible if eventual distortions of the NMR signals, related to pore coupling effects, are accounted for. This is also relevant, and must still be examined, e.g., for the estimation of water retention curves from NMR measurements in the saturated material (e.g., Jaeger et al., 2009; Costabel and Hiller, 2021). Furthermore, the complexity and heterogeneity of top-soils may lead to large differences in surface relaxivity values for neighboring pore environments (e.g., Jaeger et al., 2009; Benavides et al., 2017); the effect such heterogeneous ρ distribution will have on pore coupling remains to be investigated. Likewise unexplored, remains whether a potential transition from the slow into the fast diffusion regime, observed in analytical models with a decrease in saturation level (Costabel, 2011), would translate to a reduction on pore coupling effects. Whether pore coupling strength can be used as an estimator of the degree of connectivity between the pores (Carneiro et al., 2014; Tian, 2021) to evaluate hydraulic conductivity and estimate permeability, is, similarly, an interesting open question, with potential applications to determine, e.g., soil contaminants' flow speed and extent.

Due to the inherent characteristics of the vadose zone, the complexity of interpretation and modeling of NMR signals increases. Three further factors controlling NMR relaxation must be considered in relation to pore coupling: level of saturation, water retention function, and pore shape. The pore-filling and draining mechanism, such as the specific order in which pore environments fill or drain, and possible hysteresis are of great interest and can be explored using NMR (e.g., Mohnke and Klitzsch, 2010; Falzone and Keating, 2016; Zhang and Zhang, 2021). Additionally, studies such as Costabel and Yaramanci (2011) and Mohnke et al. (2015) investigated the influence of the pore shape on the hydraulic properties and found that sharp angles are capable of withholding small water quantities as they drain. Understanding how these three factors impact pore coupling effects in unsaturated conditions is essential to expand the use of NMR for practical environmental applications in the vadose zone, which plays important retention and buffering roles and supports crucial ecosystem functions.

4.2. Karst aquifers

Karst aquifers are the source of about a quarter of the world's potable water (Clifford and Williams, 2007) and feature highly heterogeneous networks formed through the chemical weathering of soluble rocks. These creates conduits with free surface flow and high flow rate, as well as confined flow with various porosity and permeability values. Due to these unique features, karst aquifers are sensitive to hydro-meteorological changes and are highly vulnerable to external forcings, such as contamination (Hartmann et al., 2014; Goldscheider et al., 2020). Due to their inter- and intragranular porosity and their low- to mid- surface relaxivity, carbonate systems are highly prone to pore coupling (Ramakrishnan et al., 1998). However, the coupling effects in carbonate system and their effects on the relaxation behavior of mesopores, or of pores in a wider range of sizes, is understudied.

Detailed experimental investigation into pore coupling effects in carbonate rocks is required for full utilization of NMR in karst aquifers. Moreover, the improvement of image processing steps are required to better extract pore networks from carbonate samples via improved segmentation (Lucas-Oliveira et al., 2018), which will allow for advanced simulations of the NMR responses in pore coupled carbonate systems.

5. Closing remarks

Low-field NMR is an emerging technology within the hydrogeophysics community with significant potential for practical applications in near-surface environments and for critical zone research due to its non-invasive, cost-efficient, direct sensitivity to pore water. Much information can be gained from improving and extending the applications of NMR in different environments. In order to achieve its full potential, a better understanding of NMR signals in complex scenarios is required. This includes, though it is not limited to, the understanding of pore coupling effects in fully and partially saturated environments.

In the past years, with improvements in the understanding of NMR signals in partially saturated environments, the application of NMR in the vadose zone has expanded, yet pore coupling effects remain understudied in unsaturated conditions. Technological advances have allowed for more sophisticated numerical simulation methods to study pore coupling in more complex geometries, and the original definition of pore coupling has been expanded to include different pore networks or even diffusion between pores and microfractures (Chi and Heidari, 2015). The development and identification of better techniques to study pore coupling (e.g., FEM over Random Walk or T₂-distributions over T₂ − T₂-maps) has brought this emerging field forward.

Developing our understanding of NMR relaxation in pore-coupled unsaturated environments, as well as in complex geometries with a wider range of pore sizes or lower surface relaxivities, would improve the interpretation of NMR data and lead to its broader applications in near-surface environments. Furthermore, studying the relation between coupling degree and network connectivity opens the possibility of using pore coupling as a connectivity estimator in unknown samples or for larger scale field application (Carneiro et al., 2014) and should be seen as more than a disturbance in the NMR signal.

Author contributions

FS: figures and writing. CZ: concept and writing. All authors contributed to the article and approved the submitted version.

Funding

This work was funded by State Key Laboratory of Geomechanics and Geotechnical Engineering (SKlGGE), Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, provided the funding Z019003.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, R., Zhang, X., Wang, Y., Liu, X., Chen, C., and Gong, J. (2022). Freeze–thaw impact on sandy clay in artificial frozen walls: an investigation of shear strength and pore-size distribution. Int. J. Geomech. 22, 04022230. doi: 10.1061/(ASCE)GM.1943-5622.0002489

PubMed Abstract | CrossRef Full Text | Google Scholar

Anand, V., and Hirasaki, G. (2007). Diffusional coupling between micro and macroporosity for NMR relaxation in sandstones and grainstones. Petrophysics 48, 289–307.

Google Scholar

Anand, V., Hirasaki, G., and Fleury, M. (2008). NMR diffusional coupling: effects of temperature and clay distribution. Petrophysics 49, 362–372.

Google Scholar

Behroozmand, A. A., Keating, K., and Auken, E. (2015). A review of the principles and applications of the NMR technique for near-surface characterization. Surv. Geophys. 36, 27–85. doi: 10.1007/s10712-014-9304-0