Explicit simulation of environmental gas tracers with integrated surface and subsurface hydrological models

Delottier, Hugo; Peel, Morgan; Musy, Stéphanie; Schilling, Oliver S.; Purtschert, Roland; Brunner, Philip

doi:10.3389/frwa.2022.980030

ORIGINAL RESEARCH article

Front. Water, 28 September 2022

Sec. Water and Hydrocomplexity

Volume 4 - 2022 | https://doi.org/10.3389/frwa.2022.980030

This article is part of the Research Topic Advances and Emerging Methods in Tracer Hydrogeology View all 5 articles

Explicit simulation of environmental gas tracers with integrated surface and subsurface hydrological models

$\nHugo Delottier$ Hugo Delottier¹^*

Morgan Peel¹

Stéphanie Musy²

Oliver S. Schilling^3,4

Roland Purtschert²

Philip Brunner¹

¹Centre for Hydrogeology and Geothermics (CHYN), Faculty of Science, University of Neuchâtel, Neuchâtel, Switzerland
²Climate and Environmental Physics and Oeschger Center for Climate Change Research, Faculty of Science, University of Bern, Bern, Switzerland
³Hydrogeology, Department of Environmental Sciences, University of Basel, Basel, Switzerland
⁴Eawag, Swiss Federal Institute of Aquatic Science and Technology, Dübendorf, Switzerland

Environmental gas tracers allow inferring groundwater travel times and mixing ratios. Their concentrations are commonly interpreted with simplified and indirect approaches that are conceptually at odds with the high degree of complexity found in natural systems. However, the information content of the tracers can potentially be fully explored through the explicit simulation of an advection-dispersion transport equation, for example using integrated surface-subsurface hydrological models (ISSHMs). These integrated models can be used to explicitly simulate environmental tracers in complex environments. ISSHMs are usually variably saturated flow models. However, these models do not explicitly simulate gas partitioning with the aqueous phase, restricting explicit simulation of gas tracers to fully saturated conditions or to tracers with very low solubilities. We propose a mathematical formulation for the production of environmental gas tracers that are emanated in the subsurface. The production is scaled according to gas/water partitioning and water saturation, which is already computed by the model. Therefore, ISSHMs can now be used to their full potential to explicitly simulate tracer concentrations under variably saturated and dynamic conditions. The new formulation has been successfully verified against reference simulations provided with a multi-phase flow and transport model. In addition, explicit simulation of ²²²Rn and ³⁷Ar groundwater concentrations in a synthetic alluvial river-groundwater system was demonstrated, for the first time, with an ISSHM.

Introduction

Hydrologic environmental tracers are widely distributed in the near-surface environment of the Earth, such that their abundance facilitates their consideration for studying a range of subsurface flow processes (Cook and Herczeg, 2012; Partington et al., 2020; Dwivedi et al., 2022). Many environmental tracers (e.g., CFCs, N₂, O₂, Ar, Ne, Kr, He, Xe, CH₄, CO₂, ²²²Rn, and SF₆) are gases that dissolve into water. These environmental gas tracers can be either natural (e.g., ³⁹Ar, ⁸⁵Kr) or anthropogenic (e.g., CFCs, SF₆) and their concentrations can either remain stable, increase (production) and/or decrease (decay) in the subsurface as a function of time.

The residence time of water in the subsurface is the sum of the transit times through the unsaturated and saturated zones. Residence times can be obtained from the decay of radioactive tracers and from tracers that are produced (accumulating tracers) in the subsurface. Therefore, their measured concentrations can be used to determine pathways and timescales (i.e., ages) of groundwater (Kazemi et al., 2006).

Tracer concentrations are usually considered for estimating apparent ages that are then used in the calibration of hydrological models (Van Huijgevoort et al., 2016; Schilling et al., 2017a, 2019, 2022). However, these simplified and indirect approaches are conceptually at odds with the high degree of complexity found in natural systems (McCallum et al., 2015, 2017; Peel et al., 2022). The explicit simulation of tracer mass-transport through the solution of an advection-dispersion equation is a promising pathway that can potentially increase the information contained in the tracers (Goode, 1996; Turnadge and Smerdon, 2014). A zero-order source term (or boundary condition) can be used to consider environmental tracers that are produced in the subsurface.

Gases that are emanated in the unsaturated media will partition between the aqueous and gaseous phases as a function of their solubility in water and water saturation. Therefore, a rigorous way to model accumulating tracers in a numerical flow model requires the consideration of both gas and liquid phases to allow exchanges between the two. For gases with high solubilities (e.g., ²²²Rn), deep unsaturated zones, and for tracers where the concentration is a function of depth (e.g., Ar isotopes), the consideration of a gas phase in the model is a prerequisite for robust tracer simulation.

The consideration of both gas and liquid phases requires the use of multiphase fluid flow and transport models that solve the advection-dispersion equation. HYDRUS, NUFT, and Getflows (Nitao, 1998; Tosaka et al., 2000; Simunek et al., 2016) are examples of multiphase flow and transport models. However, these mechanistic models are computationally demanding and are therefore usually preferred for controlled experiments and to model mass-transport in unsaturated soils (Guillon et al., 2016).

In groundwater hydrology, the simulation of the unsaturated zone along with the groundwater flow domain and the surface water flow domain can be done using integrated surface and subsurface hydrologic models (ISSHM) (Sebben et al., 2013; Paniconi and Putti, 2015). These integrated models are particularly well-suited to study complex hydrodynamic behaviors such as river-groundwater interactions that characterize shallow subsurface environments (Brunner et al., 2017). HydroGeoSphere (Brunner and Simmons, 2012; Aquanty Inc., 2022), ParFlow (Kollet and Maxwell, 2008), or OpenGeoSys (Kolditz et al., 2012) are examples of such integrated models. Some of these models allow the explicit simulation of tracers in the saturated zone of the aquifer. For instance, explicit modeling or a radiogenic tracer such as ²²²Rn has been recently proposed with HydroGeoSphere (Gilfedder et al., 2019). However, most of the integrated models are single-phase flow, preventing the consideration of a gas phase in the unsaturated zone. Thus, the zero-order source, which allows a tracer to be produced in the subsurface, does not consider gas/water partitioning, potentially leading to an overly large concentration in the unsaturated zone, as the produced tracer accumulates in a smaller volume of water compared to what would be the case under full saturation.

To overcome this issue we propose a simplified mathematical formulation for the production of environmental gas tracers that are emanated in the subsurface, which allows the solute mass production rate for variably saturated conditions to be scaled according to the degree of saturation and the gas/water partitioning coefficient. The proposed formulation is designed for single-phase surface and subsurface flow and transport in integrated hydrological models that are capable of simulating variably saturated subsurface flow. In the present study this formulation was implemented in the ISSHM HydroGeoSphere (HGS) and is called via the “Zero-order source with partitioning” command (Aquanty Inc., 2022). The new formulation in HGS was validated against an explicit multiphase flow and transport reference case implemented in the software HYDRUS-1D (Simunek et al., 2016). The capability of the new formulation is illustrated for a river-groundwater flow system where ²²²Rn and ³⁷Ar are explicitly simulated.

Mathematical formulation

An instant-equilibration mass balance

The present section introduces the derivation of the proposed instant-equilibration mass-balance to scale the production of dissolved gas tracers according to the degree of water saturation of the subsurface. An underlying assumption is that any produced amount of tracer will partition immediately into both the gas and aqueous phases. In a small test volume V_test, we can write:

\begin{array}{l} \frac{δ Q_{t r a c e r, t o t}^{p r o d}}{δ t} = P_{s a t} V_{p o r e} & (1) \end{array}

where, $δ Q_{t r a c e r, t o t}^{p r o d}$ [M] is the amount of tracer produced in a small time increment δt [T], P_sat [M·L⁻³·T⁻¹] is the total tracer production rate (assumed independent of the degree of water saturation), and V_pore [L³] is the pore volume of the matrix (porosity × V_test).

If we assume that the amount of tracer δ $Q_{t r a c e r}^{p r o d}$ is partitioned into both gas and aqueous phases, we can write the following mass balance relationship:

\begin{array}{l} δ Q_{t r a c e r}^{p r o d} = δ Q_{t r a c e r, w a t e r}^{p r o d} + δ Q_{t r a c e r, a i r}^{p r o d} = δ C_{t r a c e r, w a t e r}^{p r o d} V_{w a t e r} \\ + δ C_{t r a c e r, a i r}^{p r o d} V_{a i r} & (2) \end{array}

where, $δ Q_{t r a c e r, w a t e r}^{p r o d}$ and $δ Q_{t r a c e r, a i r}^{p r o d}$ are the amounts of produced tracer [M] which go into the liquid and gas phases, respectively. Similarly, $δ C_{t r a c e r, w a t e r}^{p r o d}$ and $δ C_{t r a c e r, a i r}^{p r o d}$ are changes in tracer concentrations from the zero-order source [M·L⁻³] in the given volumes of water V_water [L³] and air V_air [L³].

Assuming a solubility law of the form $H^{c c} = \frac{C_{w a t e r}}{C_{a i r}}$ with instant equilibration, we can write:

\begin{array}{l} δ Q_{t r a c e r}^{p r o d} = H^{c c} δ C_{t r a c e r, a i r}^{p r o d} V_{w a t e r} + δ C_{t r a c e r, a i r}^{p r o d} V_{a i r} \\ = δ C_{t r a c e r, a i r}^{p r o d} (H^{c c} V_{w a t e r} + V_{a i r}) & (3) \end{array}

If we divide both sides by V_pore, we get:

\begin{array}{l} \frac{1}{V_{p o r e}} δ Q_{t r a c e r}^{p r o d} = δ C_{t r a c e r, a i r}^{p r o d} \frac{H^{c c} V_{w a t e r} + V_{a i r}}{V_{p o r e}} \\ = δ C_{t r a c e r, a i r}^{p r o d} (H^{c c} S_{w} + S_{a}) & (4) \end{array}

where, S_w and S_a = 1−S_w are respectively, the degree of water and air saturations [–]. Therefore, by combining Equation (4) with Equation (1) we can write:

\begin{array}{l} P_{s a t} = \frac{1}{V_{p o r e}} \frac{δ Q_{t r a c e r}^{p r o d}}{δ t} = \frac{δ C_{t r a c e r, a i r}^{p r o d}}{δ t} (H^{c c} S_{w} + [1 - S_{w}]) & (5) \end{array}

Which can also be written as follows:

\begin{array}{l} \frac{δ C_{t r a c e r, a i r}^{p r o d}}{δ t} = \frac{P_{s a t}}{H^{c c} S_{w} + [1 - S_{w}]} & (6) \end{array}

If we define the effective production rate in water P_eff [M·L⁻³·T⁻¹] as the amount of tracer input only into the water phase per unit time, we can write:

\begin{array}{l} P_{e f f} = \frac{δ C_{t r a c e r, w a t e r}^{p r o d}}{δ t} = H^{c c} \frac{δ C_{t r a c e r, a i r}^{p r o d}}{δ t} = \frac{H^{c c} P_{s a t}}{H^{c c} S_{w} + [1 - S_{w}]} & (7) \end{array}

This formulation (Equation 7) is equivalent to the original zero-order source as implemented in HGS (production per unit aquifer volume) in the limit H^cc → ∞ (i.e., no partitioning) and for S_w = 1 regardless of H^cc. This means that all produced species remain in the aqueous phase. In the case H^cc → 0, the tracer is immediately volatilized. Mean groundwater age, defined with the age-mass concept (Goode, 1996), can be estimated directly by setting H^cc = 1 with a solute mass production rate equal to the aquifer porosity and with a decay constant of zero (no decay of mean age).

Equation 7 assumes that every produced atom in the unsaturated zone partitions immediately into both gas and aqueous phases according to a fixed partitioning coefficient. Thus, the proposed formulation is equivalent to an equilibrium solute transport model where the mass of volatilized tracer, which in theory would interact with groundwater in case of variations in water saturation, is not considered. The phase-equilibrium partitioning coefficient H^cc, is considered constant, synonymous with isothermal conditions. Moreover, H^cc is a well-constrained parameter as it strictly depends on water temperature and the considered species. Interested readers should refer to Cook and Herczeg (2012) and Schubert et al. (2012) for default values of H^cc for ²²²Rn and ³⁷Ar, respectively.

The hypothesis of saturation-independent emanation is supported by the fact that ²²²Rn (and likely ³⁷Ar) emanation has been shown to reach its maximum value at moderate degrees of water saturation, typically between 0.2 and 0.3 (e.g., Sun and Furbish, 1995; Zhuo et al., 2006). Indeed, the presence of a thin moisture film on the surface of mineral grains will prevent produced atoms recoiled into the pore space from embedding into adjacent grains, as recoil ranges of atoms in water are orders of magnitude lower than those in air. Only in very dry conditions and low residual water contents in the porous medium can this hypothesis no longer be justified.

Verification

To verify the proposed instant-equilibration mass balance as newly implemented in HGS, simulations of ²²²Rn in an unsaturated medium using HGS are compared with explicit multi-phase simulations using HYDRUS-1D. HYDRUS-1D is based on a finite element model that solves Richard's equation for variably-saturated subsurface flow and Fickian-based advection-dispersion equations for heat and mass transport.

In the proposed experiment, HYDRUS-1D was used to solve the advection-dispersion solute transport equations with a linear equilibrium between the aqueous and the gaseous phases. Diffusion in both aqueous and gas phases were considered to be instantaneous (i.e., equilibrium transport). Moreover, we did not consider the effects of adsorption-desorption and we have assumed no immobile fraction of water. Thus, the advection-dispersion equation can be written in the following form:

\begin{array}{l} \frac{\partial θ c}{\partial t} + \frac{\partial a g}{\partial t} = \frac{\partial}{\partial x} (θ D^{w} \times \frac{\partial c}{\partial x}) + \frac{\partial}{\partial x} (a D^{g} \times \frac{\partial g}{\partial x}) \\ - \frac{\partial q c}{\partial x} - (μ_{w} θ c + μ_{g} a g) + (γ_{w} θ + γ_{g} a) & (8) \end{array}

where, c and g are solute concentrations in the aqueous [M·L⁻³] and gaseous [M·L⁻³] phases, respectively; θ [L³·L⁻³] is the water content, ρ [M·L⁻³] is the soil bulk density, a [L³·L⁻³] is the air content, D^w [L²·T⁻¹] is the dispersion coefficient for the aqueous phase, D^g [L²·T⁻¹] is the diffusion coefficient for the gas phase, q [L·T⁻¹] is the volumetric fluid flux density, μ_w and μ_g [T⁻¹] are first-order rate (decay) constants for solutes in the aqueous and gas phases, respectively; γ_w and γ_g [M·L⁻³·T⁻¹] are zero-order rate constants (or source) for the aqueous and gas phases, respectively.

Furthermore, equilibrium exchange between water and gas concentrations of the solute in the soil system was assumed. The adsorption isotherm was considered linear. The concentrations in the aqueous and in the gas phases (c and g) are related by a linear expression of the form:

\begin{array}{l} g = k_{g} \times c (9) & (9) \end{array}

where, k_g [-] is an empirical constant equal to (K_H·R_u·T_A)⁻¹, in which K_H [M·T²·M⁻¹·L⁻²] is Henry's law coefficient, R_u [M·L²·T⁻²·K⁻¹·M⁻¹] is the universal gas constant and T_A [K] is the absolute temperature. The advection-dispersion equations were solved in the gas and in the aqueous phases, thus permitting the simulation of solute transport simultaneously in both the aqueous and gas phases.

²²²Rn production

²²²Rn is produced as an intermediary product in the ²³⁸U decay chain, and is released into groundwater as a result of the alpha decay of matrix-bound ²²⁶Ra (Cecil and Green, 2000). This radioactive noble gas with a half-life of 3.82 days is commonly used in groundwater hydrology as a tracer of surface water—groundwater interactions, as ²²²Rn activities in groundwater are often orders of magnitude higher than those in surface water (Cecil and Green, 2000). Upon infiltration of surface water with low ²²²Rn activities into the subsurface, ²²²Rn concentrations will gradually increase until they reach secular equilibrium after ~15–20 days (Hoehn and Von Gunten, 1989). Therefore, it has been extensively used to study very young groundwater dynamics and mixing [i.e., timescales of several hours to a few weeks (Cook et al., 2008; Bourke et al., 2014; Cartwright and Gilfedder, 2015; Peel et al., 2022)]. Assuming spatially homogenous ²²²Rn production, the relationship between production rate per unit pore volume γ_Rn [M·L⁻³·T⁻¹] and equilibrium ²²²Rn activity concentration in groundwater $C_{R n, e q}^{S a t}$ [M·L⁻³] is given by the following equation:

\begin{array}{l} C_{R n, e q}^{S a t} = \frac{γ_{R n}}{λ_{R n}} (10) & (10) \end{array}

where, λ_Rn [T⁻¹] is the ²²²Rn decay constant. The value for $C_{R n, e q}^{S a t}$ , which is site specific since it is closely related to aquifer geochemistry and mineral texture, has been considered homogenous for the present study, and set to 15 Bq·l⁻¹ (e.g., Popp et al., 2021).

Model set-up

As a verification experiment, a one-dimensional soil column 5-m thick uniformly discretized with 0.05 m vertical intervals is considered for both HYDRUS-1D and HGS.

In both models, the soil column was assumed homogeneous and variably saturated flow was solved using the van Genuchten—Mualem model with the fitting parameters α [L⁻¹] and β [–] set to 3.48 and 1.75, respectively, simulating a typical alluvial gravel (Dann et al., 2009; Schilling et al., 2020). The residual soil water content was set to 0.095 and the porosity to 0.41. A value of 1 m·d⁻¹ was used for the saturated hydraulic conductivity. The tortuosity parameter in the conductivity function was set to 0.5. The longitudinal horizontal dispersivity was set to 0.1 m, while the transverse dispersivities were set to 0.01 m. A pore pressure of 0 was applied to nodes at the bottom (z = −5m) of the column, making the bottom of the soil model a constant water table elevation.

For HYDRUS-1D, the bulk density was set to 1.593 g·cm⁻³. In Equation 9, which controls the interaction between the liquid and the gas concentrations, the empirical constant k_g was set to 2.155 (-), which is the inverse of the partitioning coefficient H^cc as defined in Equation 3. The first-order rate (decay) constant for ²²²Rn was set to 0.1814 d⁻¹ for all phases. The γ_w, and γ_g zero-order rate constants were set to 2721 Bq·m⁻³·d⁻¹, which has been derived from Equation 10, assuming a saturated ²²²Rn activity $C_{R n, e q}^{S a t}$ of 15 Bq·l⁻¹.

Flow and transport through the soil column were simulated according to two scenarios: (i) drainage conditions and (ii) recharge conditions. The soil column was initially considered fully saturated with water. For scenario (i), the model was run without any infiltration fluxes at the top so that the soil column is progressively drained until a pseudo steady-state condition was reached after 365 days (Figure 1B). We refer to pseudo steady-state as transient simulations that reaches a dynamic equilibrium state, that is, a point at which there is minimal drift in the model states (similar to actual steady-state conditions). Starting from this new pseudo steady-state condition, for scenario (ii), a constant input flux of 0.1 m·d⁻¹ was then considered at the top of the column, simulating an extremely high infiltration flux. The model was then run for another 365 days until a new pseudo steady-state condition was reached (Figure 1D). To evaluate the performance of the HGS simulations in transient conditions, snapshots of dissolved ²²²Rn activities were also taken five days after the beginning of each simulation scenario (Figures 1A,C). For a majority of locations, the simulated saturation profiles of HGS and HYDRUS-1D were nearly identical (Supplementary Figure A1), therefore allowing direct comparisons of the tracer concentrations simulated with the two different software.

FIGURE 1

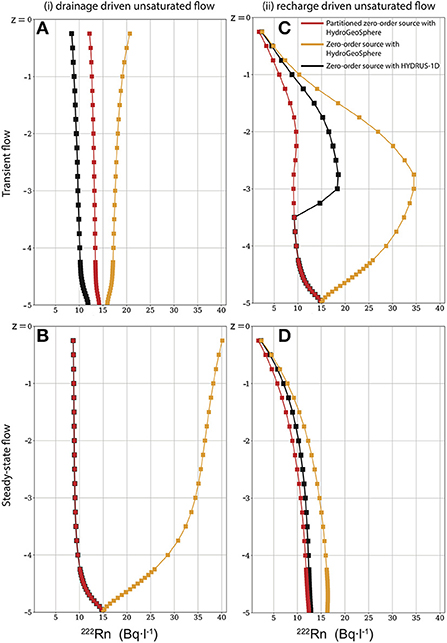
Figure 1. Concentrations of ²²²Rn in water for a synthetic one-dimensional soil column model under (A) drainage driven transient (t = 5 days) flow, (B) drainage driven steady-state flow, (C) recharge driven transient (t = 5 days) flow, and (D) recharge driven steady-state flow.

Results

Under drainage driven flow and transport (scenario (i); Figures 1A,B), a perfect match of the simulation of ²²²Rn after 365 days was reached with HYDRUS-1D (under consideration of explicit multi-phase flow) and HGS (under consideration of the new partitioned zero-order source production), demonstrating the consistency of the simplified approach under pseudo steady-state conditions. After five days of drainage (i.e., highly transient conditions), the HGS-based simulations with partitioned zero-order source production slightly overestimated the ²²²Rn concentrations compared to the multi-phase flow simulations with HYDRUS-1D. This reflects the ability of HYDRUS-1D to explicitly account for ²²²Rn in both the gas and liquid phases. When the saturation drops, dissolved ²²²Rn concentrations re-equilibrate with those in the gas phase; in other words, a drop in saturation will lead to the volatilization of some of the dissolved ²²²Rn to the gas phase and therefore a reduction of the concentration in the aqueous phase. In HGS, the gas phase is not simulated explicitly and the ²²²Rn concentration in water is therefore not directly affected by changes in saturation; only production is scaled, which leads to an overestimation of ²²²Rn activities in water after five days of transient simulation of drainage.

Under recharge driven flow (scenario (ii); Figures 1C,D), the opposite mechanism occurs, and ²²²Rn concentrations in water are slightly underestimated with HGS compared to HYDRUS-1D in highly transient conditions. As in the drainage scenario, the difference is more pronounced under transient conditions compared to the pseudo steady-state, when the simulated concentration profiles of both codes almost match. The reason for the mismatch lies in the fact that once the saturation increases within the soil column because of the constant input flux from the top, dissolved ²²²Rn concentrations start to increase as a result of soil matrix production, but also because of the dissolution of ²²²Rn from the gas phase into the water. Again, as in HGS, the gas phase is not explicitly simulated, dissolved ²²²Rn concentrations in the soil column tend to be underestimated compared to the explicit multi-phase simulations with HYDRUS-1D.

Under both drainage and recharge conditions, more realistic simulations were obtained with HGS when the zero-order source was partitioned with the water saturation (red lines in Figure 1). When the production of ²²²Rn was not scaled according to water saturation (i.e., unpartitioned zero-order source), the ²²²Rn concentrations in the unsaturated soil column were significantly overestimated by HGS because the same amount of total produced tracer mass accumulated in a comparatively smaller volume of water (orange lines in Figure 1). Although some discrepancies between HYDRUS-1D and HGS with the proposed partitioned zero-order source along a one-dimensional unsaturated soil column could be identified, the improvement achieved with the partitioned zero-order source implementation is significant, resulting in nearly matching pseudo steady-state conditions under both drainage and recharge conditions. The proposed partitioned zero-order source approach is thus a highly efficient and simplified, yet realistic, way to include simulations of environmental gas tracers in the unsaturated zone for applications involving both surface and the subsurface flow processes, especially where the application of computationally demanding and complex two-phase flow models is not desirable or practical.

Illustrative example

The simulation of environmental gas tracer concentrations with a single-phase ISSHM is illustrated below using a more realistic and complex model configuration. For this purpose, a synthetic alluvial plain model was used for the simulation of ²²²Rn and ³⁷Ar mass-transport. The consideration of both ²²²Rn and ³⁷Ar was motivated by their short half-lives, making these tracers particularly well-suited to track recently infiltrated surface water in shallow alluvial aquifers (Brunner et al., 2017; Schilling et al., 2017a).

³⁷Ar production

³⁷Ar is a rare radioactive isotope of argon with a half-life of 34.95 ± 0.08 days (Renne and Norman, 2001). A originally ³⁷Ar free water parcel that enters the subsurface reaches 88% of the secular production-decay equilibrium after three half-lives of ³⁷Ar, i.e., after approximately 110 days. In the shallow underground, ³⁷Ar atoms are primarily produced by cosmogenic neutron activation of calcium (⁴⁰Ca(n,α)³⁷Ar), and to some extent spallation of potassium (³⁹K(n,p2n)³⁷Ar) (Fabryka-Martin, 1988; Loosli and Purtschert, 2005; Riedmann and Purtschert, 2011). The flux of fast cosmogenic neutrons is exponentially attenuated with depth on a length scale, which is proportional to the density of the medium without of its elemental composition (Gosse and Phillips, 2001). Other production reactions, e.g., induced by muons or by neutrons from (α, n) reactions can be neglected in the depth range considered here (Spannagel and Fireman, 1972; Heisinger et al., 2002; Sramek et al., 2017). The depth dependent production rate $^{37} P_{(z) r}$ in (atoms·yr⁻¹·cm⁻³) has been parameterized through a production function equation (Guillon et al., 2016) and can be described as follows:

\begin{array}{l} _{}^{37} P_{(z) r} = ([C a] + 0.38 [K]) \times X_{s c} \times P_{0} \\ \times e^{- \frac{z}{Λ} [(1 - n) ρ_{g} + n ρ_{w} S_{w}]} & (11) \end{array}

where, Ca and K are calcite and potassium contents in (mg·kg⁻¹), X_SC (-) is a scaling factor for latitude and altitude, P_o (atoms·cm⁻³·yr⁻¹·mgCa⁻¹·kg_rock) is the surface production normalized for sea level and high latitude (SLHL) (Fabryka-Martin, 1988) and for Ca and K content. Λ (g.cm⁻²) is the attenuation length for fast neutron in soils/rocks. z (g·cm⁻²) is the product of depth below ground surface (cm) and water density (g.cm⁻³), n (-) is the porosity. ρ_g (g·cm⁻³) is the grain density and S_w (-) is the water saturation.

From the above production function, the daily production of ³⁷Ar in water $^{37} P_{(z) w}$ (atoms·m⁻³·d⁻¹) can be computed as follows:

\begin{array}{l} _{}^{37} P_{(z) w} = \frac{_{}^{37} P_{(z) r} \times [\frac{ϵ}{n}] \times 10^{6}}{365} & (12) \end{array}

where, ϵ (-) is the emanation factor, which was determined by irradiation experiments (Johnson et al., 2021; Musy et al., 2022). The attenuation length of cosmogenic fast neutrons depends on the density of the material crossed. Along a given column of water, the saturation and porosity is 1 in Equation 11, resulting in a lower density and higher attenuation length compared to a same column of rocks. Thus, ³⁷Ar production below a stream (³⁷P_stream) is reduced compared to the production in the aquifer at the same depth. The reduction factor depends on the height of the water column h (cm) and the water density ρ_w (g·cm⁻³) such that:

\begin{array}{l} _{}^{37} P_{s t r e a m} =_{}^{37} P_{(z) w} \frac{- h \times ρ_{w}}{Λ} & (13) \end{array}

Most of the parameters related to the production of ³⁷Ar should be measured in the field so that realistic concentrations of ³⁷Ar can be generated. Therefore, measurements from a pre-alpine alluvial aquifer were here considered to define the values for the parameters introduced in this section (Table 1). As the attenuation length parameter itself cannot be measured directly in the field, for the illustrative model it has been manually estimated such that the secular equilibrium profile in a virtual background piezometer (Figure 2) reproduces a ³⁷Ar secular equilibrium profile determined from measurements of ³⁷Ar activity concentrations in a sandy-gravel aquifer in the Swiss pre-Alps (Schilling et al., 2017a).

TABLE 1

Table 1. Parameter values involved in the production of ³⁷Ar from fast cosmic ray neutrons.

FIGURE 2

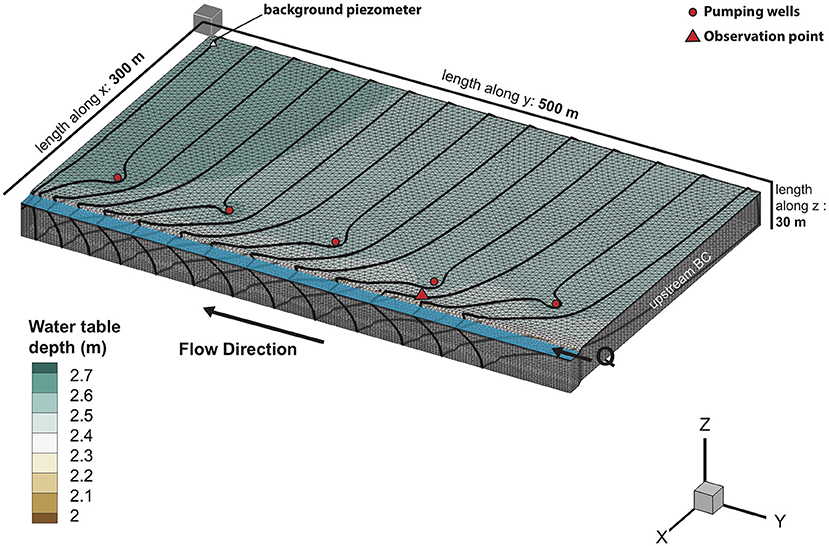
Figure 2. Conceptual model for the synthetic alluvial plain model. The bright blue area represents the stream, which is in losing condition. Five wells separated by a distance of 100 m are located at 50 m from the stream. The virtual background piezometer has been used to estimate the attenuation length for ³⁷Ar production function. The observation point has been used to generate one-dimensional concentration profiles as illustrated in Figure 4. Solid black lines are groundwater head equipotential, illustrating losing river conditions and the influence of pumping wells.

Model set-up

The HGS model for the synthetic alluvial river-groundwater system has a spatial extent of 300 × 500 × 30 m along the x-, y-, and z-directions, respectively (Figure 2). The alluvial plain was gently inclined toward the stream outlet with a slope of 0.003 m/m in the y-direction and discretized with a 2D unstructured triangular mesh with lateral internodal spacing ranging from 4 m along the stream to 7 m on the alluvial plain. The 2D mesh was generated with AlgoMesh (HydroAlgorithmics Pty Ltd, 2016). The model consists of 41 layers of elements used to discretize the alluvial plain in the z-direction, with an exponential range of layer thicknesses varying from 0.05 m at the surface without exceeding more than 1 m at depth (Figure 2). This relatively fine vertical discretization has been chosen to appropriately simulate the vertical and exponential decrease of ³⁷Ar emanation rates. The resulting 3D mesh has a total of 2,87,615 nodes for 5,44,000 elements.

The stream was conceptualized as a 20 m wide and 2 m deep channel (Figure 2). As in all ISSHM, streamflow was simulated explicitly, allowing infiltration of stream water and exfiltration of groundwater to arise naturally, that is, without the need to specify additional internal boundary conditions. Stream water inflow at the upstream end of the model was conceptualized as a second-type (specified flux) boundary condition (BC) with a value of 2 m³·s⁻¹. Surface water outflow was implemented as a critical depth BC to nodes in the stream. Due to very rough surface usually found in alluvial streams, a high value for Manning's n (1.7 × 10⁻⁶ d·m^−1/3) was used. To ensure pressure continuity between the surface and the subsurface, the coupling length (i.e., the first-order exchange coefficient), was set to a low value of 0.001 m (Liggett et al., 2012).

The aquifer was conceptualized as a homogeneous sandy gravel porous medium with a van Genuchten α of 3.40 m⁻¹, a van Genuchten β of 1.71 (-), and a residual water saturation of 0.05 (-). The hydraulic conductivity (K) and porosity (n) of the homogeneous aquifer were set to 500 m·d⁻¹ and 0.15, respectively, mimicking typical values for sandy-gravel aquifers (Schilling et al., 2017a, 2020). A head-dependent flux (Cauchy-type) BC was used for both the upstream and the downstream groundwater BC. Constant hydraulic heads equal to 99.5 and 93.20 m were considered at the upstream (y = 0 m) and downstream boundary (y = 500 m) of the model, respectively, with a conductance of 5.8 m²·s⁻¹. These boundary conditions were manually adjusted to favor natural losing river conditions. Additionally, five pumping wells were implemented as one-dimensional vertical line elements (along the x-axis = 235 m) screened between 80 and 90 m. From each well, 45 l·s⁻¹ where abstracted via a nodal flux BC set at an elevation of 82 m (Figure 2). Focusing on losing stream conditions was also preferred to better illustrate the use of these natural gas tracers to track the recent infiltration of surface water into a groundwater body. Note that pumping in the wells was not considered when the attenuation length for the ³⁷Ar production function was manually adjusted to reproduce the secular equilibrium profile of ³⁷Ar. This choice was made to ensure that the ³⁷Ar background piezometer (Figure 2) was in secular equilibrium. The lateral model boundaries (x = 0 m and x = 300 m), and the bottom boundary, were assumed to be impermeable. No riverbed was considered, and it was assumed that the stream is fully connected to the aquifer [see Brunner et al. (2009) and Schilling et al. (2017b) for implications]. A meteoric groundwater recharge BC was applied (300 mm·y⁻¹) at the top nodes of the subsurface flow domain to favor vertical flow in the unsaturated zone. The result of this flow model configuration is a shallow water table aquifer (≃ 2.5 m thick unsaturated and 27.5 m thick saturated zone) with a losing river all along the model and localized drawdown at the pumping wells (Figure 2). The proposed model design was inspired by the common configuration of bank filtration wells in mountainous river corridors.

The lateral transport BC, at x = 0 m and x = 300 m, and bottom boundaries, were set as zero mass gradients. The upstream boundary of the model, at y = 500 m, was set as a third-type BC with fixed concentrations at secular equilibrium. Surface nodes act as discharge and/or recharge points regarding the mass gradient between the surface and the subsurface. Due to the negligible atmospheric concentrations as well as the volatility of both ²²²Rn and ³⁷Ar, a zero concentration BC was specified for the surface nodes. Based on the scaling relationships of Schulze-Makuch (2005), the longitudinal dispersivity of the current transport model was set to 5 m, while the transverse dispersivities were set to 0.5 m. Within the matrix, radiogenic production of ²²²Rn and ³⁷Ar was set according to the new partitioning zero-order source, while the disintegration was simulated with a first-order decay. The ²²²Rn aquifer production rate per unit pore volume was computed from Equation 10. The production of ³⁷Ar was computed from Equations 11, 12. For the elements below the stream, the production of ³⁷Ar is slightly attenuated according to Equation 13, assuming a constant water column with a thickness of 1 m. The phase-equilibrium partitioning coefficient H^cc was assigned a value of 0.35 for ²²²Rn and 0.04182 for ³⁷Ar in mole fraction ratio as defined in Equation 3 for 10°C water temperature.

Results

The model was forced with constant boundary conditions and run long enough to reach secular equilibrium for both ²²²Rn and ³⁷Ar. A comparison of the simulated concentrations of ³⁷Ar at the virtual background piezometer shows that the simulations of ³⁷Ar are in agreement with the secular equilibrium profile estimated from the real-world sandy gravel alluvial aquifer that was used for calibration of the attenuation length parameter (Supplementary Figure A2). The fast neutron attenuation length was estimated at 98 g·cm⁻², which is of the same order as empirically established values (Phillips et al., 2001). Note that the apparent attenuation length observed at the background piezometer is the combined result of depth-dependent production and dispersive smoothing.

The simulated concentrations of ²²²Rn and ³⁷Ar with the synthetic alluvial plain model under pumping conditions are illustrated in Figure 3. For both gas tracers, for a given depth, groundwater concentrations increase with distance from the stream. This is an expected pattern as the freshly infiltrated water from the stream lowers the groundwater concentrations of ²²²Rn and ³⁷Ar. Minimum concentrations are located directly underneath the losing stream, corresponding to the location where surface water infiltrates into subsurface. The effect of depth-dependent ³⁷Ar production is clearly visible in the groundwater concentrations.

FIGURE 3

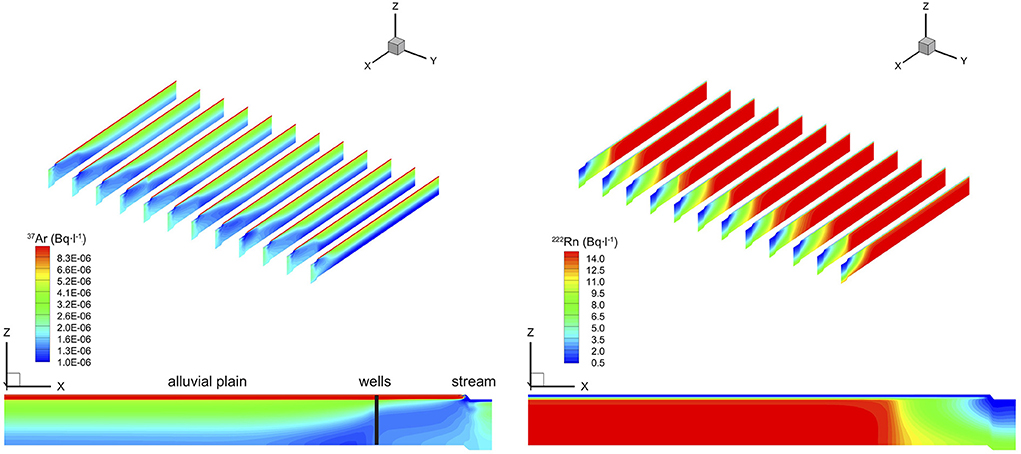
Figure 3. Simulated steady-state ³⁷Ar and ²²²Rn concentrations (Bq·l⁻¹) for the synthetic alluvial plain model with the proposed zero-order source feature. Cross sections below are taken at y = 20 m.

The pumping at the wells induces faster flow paths from the edge of the riverbank toward the wells (Figure 3). Thus, high groundwater flow velocities are located between the riverbank and the well corridor, where drawdown is induced by the pumping wells. Within these high flow paths or capture zones, recently infiltrated water spends less time in upper layers and is thus less concentrated in ³⁷Ar compared to other stretches along the stream. The low production rates located in the deeper layers are not sufficient to increase the concentrations of ³⁷Ar and the low concentration signals allow tracking the recently infiltrated surface water (Figure 3). In contrast, the production of ²²²Rn was assumed independent of depth and therefore, concentrations are only related to by residence times in the alluvial aquifer (Figure 3).

Additionally, at the location of the observation point inside the model domain (see Figure 2), vertical one-dimensional profiles of ³⁷Ar and ²²²Rn tracer concentrations can be drawn across the 27.5 m saturated portion of the aquifer, thus focusing on groundwater tracer concentrations (Figure 4). The main interest is to evaluate the impact of simulating tracer concentrations in the unsaturated zone on tracer concentrations in groundwater, which correspond to measurements usually gathered in the field. In this section, in addition to the standard (non-partitioning) zero-order source and the proposed new zero-order source with partitioning, a (non-partitioning) zero-order source with saturation threshold (which neglects the production of tracers below a given saturation threshold, assumed here at 99%) is also considered. A saturation threshold fixed at 99% restricts the production of tracers to the saturated zone, essentially neglecting the production of tracers in the unsaturated zone. Groundwater concentration profiles are thus computed for ³⁷Ar and ²²²Rn with these three approaches.

FIGURE 4

Figure 4. Simulated pseudo steady-state ³⁷Ar and ²²²Rn groundwater concentrations (Bq·l⁻¹) profiles for the synthetic alluvial plain model with the (non-partitioning) zero-order source (orange), the zero-order source with partitioning (red) and the (non-partitioning) zero-order source with saturation threshold (green). The left side plots illustrate the concentration difference (in %) between the zero-order source with partitioning (red) and the (non-partitioning) zero-order source with saturation threshold (green). The solid horizontal blue line indicates the location of the water table.

For both tracers, the one-dimensional profiles show that the standard zero-order source implementation, which doesn't scale the production of tracers in the unsaturated zone, leads to a systematic overestimation of the tracer concentrations in groundwater (Figure 4). This large overestimation (up to one order of magnitude for ³⁷Ar) illustrates the limited capacity of the standard zero-order source implementation to model gas-tracer production in variably saturated conditions, which must usually be considered when studying river-groundwater environments (Brunner et al., 2017).

Alternatively, when the tracer production is completely neglected in the unsaturated zone using the zero-order source with saturation threshold implementation, the concentrations in the groundwater are likely to be underestimated for both ²²²Rn and ³⁷Ar (Figure 4). These are consistent simulation results since the infiltrated water that reached the water table is less concentrated when the unsaturated zone production of these tracers is ignored, potentially reducing the groundwater concentrations close to the water table. This illustrates the major interest of the proposed zero-order source with partitioning for tracers with high solubility but also for tracers that are heterogeneously emanated in the subsurface and where tracer production in the unsaturated zone cannot be ignored.

Despite a lower solubility of ³⁷Ar compared to ²²²Rn, production of ³⁷Ar is exponentially decreasing with depth and a high proportion of the concentration (50% at the observation point location) is neglected when the tracer is not simulated in the unsaturated zone (Figure 4). This is less significant for ²²²Rn (difference at about 15% at the observation point location) because production is considered homogeneous and so the impact of not including the larger production in the unsaturated zone is minimized. However, recent studies have shown that ²²²Rn emanations rates can be highest within the first few meters below the surface (Mullinger et al., 2009; Peel et al., 2022). High ²²²Rn production rates in the shallow part of the aquifer might have significant effects on measured ²²²Rn concentrations in groundwater and the proposed zero-order source with partitioning implementation would significantly improve the simulation of ²²²Rn in such systems. For both tracers, neglecting the production in the unsaturated zone can significantly influence the groundwater concentrations up to 10 m below the ground surface for our river-groundwater alluvial model. Yet more pronounced differences are expected for thick unsaturated zones and highly dynamic transient conditions.

Discussion

Limitation of the partitioning zero-order source production

In the preceding sections, it has been shown that a more consistent simulation of environmental gas tracer concentrations can be achieved with single-phase ISSHMs if the production in the unsaturated zone is considered with the proposed instant-equilibration mass-balance formulation (i.e., the zero-order source with partitioning). However, it should be noted that the verification section has underlined some limitations under strongly transient conditions since the gas phase is not explicitly simulated. Thus, while the proposed methodology represents a clear and computationally highly efficient improvement of the current capacity of single-phase ISSHMs to explicitly simulate environmental gas tracers, consistent simulation of environmental gas tracer concentrations in the unsaturated zone, should be done with a multi-phase flow and transport model.

Conclusions

A zero-order source implementation that scales the production of environmental gas tracers according to the water saturation and gas/water partitioning has been proposed. The new implementation, labeled as a zero-order source with partitioning, is based on an instant-equilibration mass-balance and allows realistic simulations of environmental gas tracers in the unsaturated zone with single-phase, variably saturated hydrologic models. The new feature, which has been implemented in HydroGeoSphere, has been verified against a multi-phase fluid flow and transport model (HYDRUS-1D). As illustrated in the verification and illustration examples, the application of the proposed partitioning of tracer production rates can significantly improve the consistency of simulations of environmental gas tracer concentrations under variably saturated conditions. The method is particularly well-suited to enhance the capacity of integrated surface and subsurface hydrologic models (ISSHMs) to explicitly simulate environmental gas tracers in steady-state and dynamic conditions, although some limitations has been shown for extremely dynamic contexts. In addition to the presentation of the new zero-order source with partitioning, we demonstrate for the first time the explicit and simultaneous simulation of ²²²Rn alongside ³⁷Ar under variably-saturated conditions with an ISSHM. These tracers have so far not been jointly simulated.

Data availability statement

Data used for this study are supplied as SI Dataset P2 available for download from HydroShare (https://www.hydroshare.org/resource/9cee88f43ce6401c92f05c12706308e7/).

Author contributions

HD: writing—original draft preparation, investigation, software, conceptualization, methodology. MP: writing—review and editing, conceptualization, and methodology. SM: writing—review and editing, and conceptualization. OS: writing—review and editing. RP: writing—review and editing. PB: writing—review and editing, conceptualization, supervision, and funding acquisition. All authors contributed to the article and approved the submitted version.

Funding

HD and MP acknowledge the funding provided by the Swiss National Science Foundation (SNSF; grant number 200021_179017).

Acknowledgments

The authors acknowledge the Aquanty Inc. scientific team for their support and assistance during the implementation of the zero-order source with partitioning feature into the numerical model code HydroGeoSphere.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2022.980030/full#supplementary-material

References

Aquanty Inc. (2022). HydroGeoSphere Theory Manual. Waterloo, ON. p. 101.

Bourke, S. A., Cook, P. G., Shanafield, M., Dogramaci, S., and Clark, J. F. (2014). Characterisation of hyporheic exchange in a losing stream using radon-222. J. Hydrol. 519, 94–105. doi: 10.1016/j.jhydrol.2014.06.057

ORIGINAL RESEARCH article

Explicit simulation of environmental gas tracers with integrated surface and subsurface hydrological models

Introduction

Mathematical formulation

An instant-equilibration mass balance

Verification

222Rn production

Model set-up

Results

Illustrative example

37Ar production

Model set-up

Results

Discussion

Limitation of the partitioning zero-order source production

Conclusions

Data availability statement

Author contributions

Funding

Acknowledgments

Conflict of interest

Publisher's note

Supplementary material

References

²²²Rn production

³⁷Ar production