A review of machine learning concepts and methods for addressing challenges in probabilistic hydrological post-processing and forecasting

Probabilistic forecasting is receiving growing attention nowadays in a variety of applied fields, including hydrology. Several machine learning concepts and methods are notably relevant toward addressing the major challenges of formalizing and optimizing probabilistic forecasting implementations, as well as the equally important challenge of identifying the most useful ones among these implementations. Nonetheless, practically-oriented reviews focusing on such concepts and methods, and on how these can be effectively exploited in the above-outlined essential endeavor, are currently missing from the probabilistic hydrological forecasting literature. This absence holds despite the pronounced intensification in the research efforts for benefitting from machine learning in this same literature. It also holds despite the substantial relevant progress that has recently emerged, especially in the field of probabilistic hydrological post-processing, which traditionally provides the hydrologists with probabilistic hydrological forecasting implementations. Herein, we aim to fill this specific gap. In our review, we emphasize key ideas and information that can lead to effective popularizations, as such an emphasis can support successful future implementations and further scientific developments. In the same forward-looking direction, we identify open research questions and propose ideas to be explored in the future.

Background information, basic terminology and review overview

“Prediction” is a broad and generic term that describes any process for obtaining guesses of unseen variables based on any available information, as well as each of these guesses. On the other hand, “forecasting” is a more specific term that describes any process for issuing predictions for future variables based on information (which most commonly takes the form of time series) about the present and the past, with these particular predictions being broadly called “forecasts”. Forecasting is a key theme and topic for this study. Therefore, in what follows, the general focus will be on it and not on prediction in general, although many of the statements and methods that will be referring to it are equally relevant and applicable to other prediction types.

The origins of forecasting trace back to the early humans and their pronounced need for certainty in the practical endeavor of supporting their various everyday life decisions (Petropoulos et al., 2022). Thus, forecasting has met until today and still meets numerous implementations, formal and informal. Independently of their exact categorization and features, the formal implementations of forecasting rely, in principal, on concepts, theory and practice that originate from or can be attributed to the predictive branch of statistical modeling, although forecasting is also considered as an entire field on its own because of the major role that the temporal dependence plays in the formulation of its methods. The predictive branch of statistical modeling exhibits profound and fundamental differences with respect to the descriptive and explanatory ones, as it is thoroughly explained in Shmueli (2010). All these three statistical modeling branches and their various tasks are known to have utility and value themselves with no exceptions; still, the ultimate goal behind all of them, even behind (the majority of) the other prediction tasks, should be forecasting (Billheimer, 2019).

Overall, the various forecasts can be categorized in many ways. Regular groupings of forecasts are those based on the forecast horizon or lead time. The most common relevant categories are the ones known under the terms “one-step ahead” and “multi-step ahead” forecasts (which appear extensively, for instance, in the general forecasting and the energy forecasting literatures; see, e.g., Bontempi and Taieb, 2011; Taieb et al., 2012), as well as those known under the terms “real-time,” “short-range,” “medium-range” and “long-range” forecasts (which appear extensively, for instance, in the meteorological and hydrological forecasting literatures; see, e.g., Gneiting and Raftery, 2005; Yuan et al., 2015). In the context of the same categorization rule, the terms “short-term,” “medium-term” and “long-term” forecasts also appear broadly (see, e.g., Regonda et al., 2013; Yuan et al., 2015). Other meaningful groupings are based on the temporal scale at which the forecasting takes place. In this context, the various categories and terms range from the “sub-seasonal” to the “seasonal” or even the “annual” and “inter-annual” forecasts (see, e.g., Gneiting and Raftery, 2005; Yuan et al., 2015). Obviously, the lead time and the temporal scale of the forecasts are related to each other. Another distinction between forecasts can be made based on whether they refer to continuous or categorical variables, with the former case consisting the most common one in the literature and, thus, also the general focus of this study.

In the context of another regular categorization rule, one category includes the best-guess forecasts, which are best guesses for future variables, each taking the form of a single value. These forecasts have been traditionally and predominantly supporting decision making in almost every applied field (Gneiting and Katzfuss, 2014), including hydrology (Krzysztofowicz, 2001). Their most common formal implementations for the case of continuous variables are the mean- (also known as “expected-”) and the median-value forecasts, which are simply the mean and median values, respectively, of their corresponding predictive probability distributions (i.e., the probability distributions of the targeted future variables conditioned upon the data and models utilized for the forecasting; see, e.g., Gelman et al., 2013, for the mathematical formulation of this definition). Best-guess forecasts are else referred to in the forecasting literature as “best-estimate,” “single-value,” “single-valued,” “single-point” or even more broadly as “point” forecasts, while sometimes they are additionally said to correspond to the “conditional expectation,” the “conditional mean” or the “conditional median” of the future variable of interest [see, e.g., the terminology adopted for such forecasts in Holt (2004), Giacomini and Komunjer (2005), Gneiting (2011), Torossian et al. (2020), Hyndman and Athanasopoulos (2021), Chapter 1.7].

A best-guess forecast can be obtained by utilizing traditional and more modern time series (also referred to as “stochastic”) models [e.g., those by Brown (1959), Winters (1960), Box and Jenkins (1970), Holt (2004), Hyndman and Khandakar (2008)] or supervised machine and statistical learning algorithms for regression or classification [e.g., those listed and documented in Hastie et al. (2009), James et al. (2013)] under proper formulations, which largely depend on the exact forecasting problem under consideration. Another well-established way for issuing best-guess forecasts in hydrological settings is based on the hydrological modeling literature and consists in running process-based rainfall-runoff models (i.e., models that are built based on process understanding for taking information on rainfall and other meteorological variables as their inputs to give runoff or streamflow in their output) in forecast mode (i.e., by using meteorological forecasts as inputs; Klemeš, 1986). These models are also extensively exploited in simulation mode (i.e., by using meteorological observations as inputs; Klemeš, 1986) and can be classified into conceptual and physically-based models [see, e.g., the relevant examples provided in Todini (2007), as well as the 36 conceptual rainfall-runoff models in Knoben et al. (2020)]. Note here that the terms “simulation” and “prediction” are used as synonymous in the hydrological modeling literature (Beven and Young, 2013). In what follows, we will be using the term “hydrological forecasting” to exclusively refer to the forecasting of runoff or streamflow variables (which, in its best-guess form, could be made, for instance, by following one of the above-outlined approaches) and their extreme behaviors, although the same term is also used relatively frequently in the literature for the forecasting of other hydrometeorological and hydroclimatic variables, such as the rainfall, water quality, soil moisture and water supply ones. The term “hydrological forecast” will be used accordingly.

The alternative to issuing best-guess forecasts is issuing probabilistic forecasts, which include almost always best-guess forecasts and, at the same time, provide additional information about the predictive probability distributions. More precisely, a probabilistic forecast can take either (i) the form of an entire predictive probability distribution (Krzysztofowicz, 2001; Gneiting and Katzfuss, 2014), with Bayesian statistical models consisting the earliest formal procedures for obtaining this particular form [see, e.g., the work by Roberts (1965)], or (ii) comprehensively reduced forms that might include single quantile or interval forecasts [see, e.g., the remarks on the usefulness and importance of such forecasts in Chatfield (1993), Giacomini and Komunjer (2005)] or, more commonly, sets of such forecasts that might additionally comprise a mean-value forecast [see, e.g., the forecast examples in Hyndman and Athanasopoulos (2021), Chapter 1.7]. Indeed, such reduced forms can effectively summarize the corresponding entire predictive probability distributions for technical applications. Simulations of the predictive probability distribution, which are usually obtained in Bayesian settings using Monte Carlo Markov Chain (MCMC)-based techniques, or characterizations of the predictive probability distribution using ensemble members can be said to belong to both the above categories (Bröcker, 2012).

A quantile forecast is simply a quantile of the corresponding predictive probability distribution and might also be referred to in the literature under the alternative terms “conditional quantile,” “predictive quantile” or “forecast quantile” or even as a “point” forecast corresponding to a specific “quantile level” [see, e.g., the terminology adopted in Giacomini and Komunjer (2005), Gneiting (2011)]. The latter level indicates the probability with which the quantile forecasts should exceed their corresponding actual future values. Moreover, an interval forecast is simply defined by two quantile forecasts, provided that these quantile forecasts correspond to different quantile levels, and is alternatively referred to under the terms “predictive interval” or “prediction interval” [see, e.g., the terminology adopted in Chatfield (1993), Lichtendahl et al. (2013), Abdar et al. (2021), Hyndman and Athanasopoulos (2021), Chapter 1.7], with the most common prediction intervals being by far the central ones (i.e., intervals bounded by symmetric level quantiles). The p% (central) prediction intervals, with p taking values larger than 0 and smaller than 100, are considered to have an optimal coverage (i.e., maximum reliability) if they include the actual future values with frequency p%. Examples of probabilistic hydrological forecasts are presented in Figure 1.

FIGURE 1

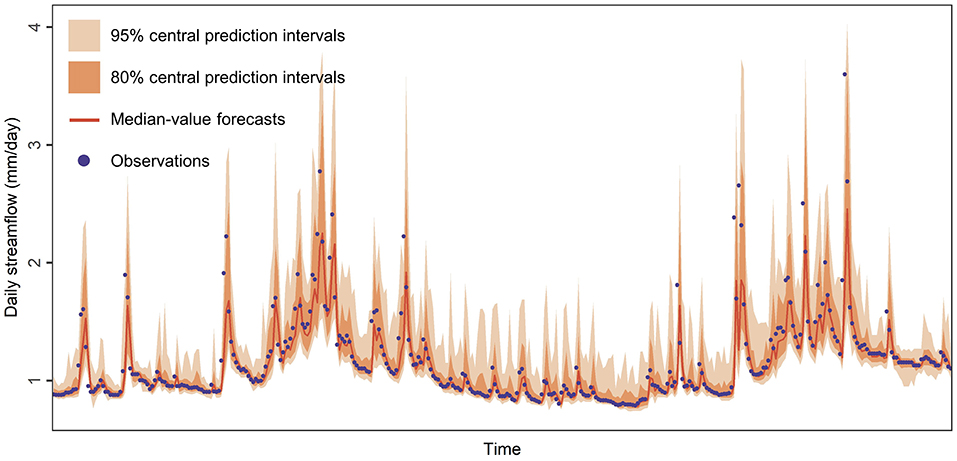
Figure 1. Probabilistic one-day ahead forecasts that are consisted of (i) median-value forecasts (depicted with a red line), (ii) 80% central prediction intervals (depicted with a dark orange ribbon) and (iii) 95% central prediction intervals (depicted with a light orange ribbon) for a daily streamflow time series (depicted with purple points).

Probabilistic forecasting in general, and probabilistic hydrological forecasting in particular, is receiving growing attention nowadays for multiple reasons that include: (a) the increasing embracement of the concept of predictive uncertainty [i.e., a fundamental mathematical concept that underlies probabilistic forecasting and has been thoroughly placed in a hydrological context by Todini (2007)]; and (b) the larger degree of information that the probabilistic forecasts can offer to the practitioners compared to the best-guess forecasts. Extensive discussions on this latter point can be found in Krzysztofowicz (2001). These discussions rotate around the rapidly expanding belief that probabilistic forecasts are an “essential ingredient of optimal decision making” (Gneiting and Katzfuss, 2014), which also consists the key premise that underlies a variety of important research efforts and advancements, both in hydrology and beyond. In spite of these efforts and advancements, probabilistic forecasting is still a relatively new endeavor and, therefore, it carries with it numerous fresh challenges that need to be formally recognized and addressed in an optimal way (Gneiting and Katzfuss, 2014). Perhaps the most fundamental, and at the same time universal across disciplines, umbrella methodological challenges from the entire pool are those of formalizing and optimizing probabilistic forecasting implementations, as well as that of identifying the most useful ones among the various implementations.

Machine learning concepts and methods can provide effective and straightforward solutions to these specific challenges. Indeed, we have recently witnessed the transfer of some notably useful machine learning concepts and methods in the field of probabilistic hydrological forecasting and, even more frequently, in its sister field of “probabilistic hydrological post-processing”. This latter field can be defined as the one that comprises a wide range of statistical methods (which include but are not limited to machine learning ones) for issuing probabilistic hydrological forecasts and, more generally, probabilistic hydrological predictions by using the best-guess outputs of process-based rainfall-runoff models as predictors in regression settings [see, e.g., a review of such methods in Li et al. (2017)]. Although the term “post-processing” is sometimes also used to refer to best-guess procedures that are limited to improving the accuracy of best-guess outputs of process-based rainfall-runoff models, only its probabilistic version is relevant herein. This specific version relies on models that can offer accuracy improvements as well, but their utility in the overall framework is not limited to such improvements.

A considerable part of the “probabilistic hydrological post-processors” are being (i) broadly referred to as methods for estimating (and advancing our perception of) the “uncertainty” of the various hydrological predictions or simulations [see, e.g., related definitions in Montanari (2011)], and (ii) tested with the process-based rainfall-runoff model being run in simulation mode [see, e.g., the modeling works by Montanari and Brath (2004), Montanari and Grossi (2008), Solomatine and Shrestha (2009), Montanari and Koutsoyiannis (2012), Bourgin et al. (2015), Dogulu et al. (2015), Sikorska et al. (2015), Farmer and Vogel (2016), Bock et al. (2018), Papacharalampous et al. (2019, 2020b), Tyralis et al. (2019a), Li D. et al. (2021), Sikorska-Senoner and Quilty (2021), Koutsoyiannis and Montanari (2022), Quilty et al. (2022), Romero-Cuellar et al. (2022)]. Notably, reviews, overviews and popularizations that focus on the above-referred to as existing and useful machine learning concepts and methods are currently missing from the probabilistic hydrological post-processing and forecasting literatures.

This scientific gap exists despite the large efforts being made toward summarizing and fostering the use of machine learning in hydrology [see, e.g., the reviews by Solomatine and Ostfeld (2008), Raghavendra and Deka (2014), Mehr et al. (2018), Shen (2018), Tyralis et al. (2019b)] and in best-guess hydrological forecasting [see, e.g., the reviews by Maier et al. (2010), Sivakumar and Berndtsson (2010), Abrahart et al. (2012), Yaseen et al. (2015), Zhang et al. (2018)]. It also exists despite the comparably large efforts made for strengthening progress in the field of ensemble hydrological forecasting [see, e.g., the review by Yuan et al. (2015)]. This latter field [see, e.g., the methods in Regonda et al. (2013), Pechlivanidis et al. (2020), Girons Lopez et al. (2021), Liu et al. (2022)] offers a well-established way of issuing operational probabilistic hydrological forecasts. In the related typical implementations, process-based rainfall-runoff models are utilized in forecast mode with ensembles of meteorological forecasts (which are created on a regular basis by atmospheric scientists to meet a wide range of applications; Gneiting and Raftery, 2005) in their input to deliver an ensemble of point hydrological forecasts that collectively constitute the output probabilistic forecast.

In this work, we aim to fill the above-identified gap toward formalizing the exploitation of machine and statistical learning methods (and their various extensions) for probabilistic hydrological forecasting given hydrological and meteorological inputs that can be but are not necessarily the same to those required for ensemble hydrological forecasting. Indeed, only such a formalization can allow making the most of the multiple possibilities offered by the algorithmic modeling culture (see Breiman, 2001b, for extensive and enlightening discussions on this culture and its implications) in practical probabilistic hydrological forecasting settings. For achieving our aim, we first summarize the qualities of a good probabilistic hydrological forecasting method in Section What is a good method for probabilistic hydrological forecasting. We then select the most relevant machine learning concepts and methods toward ensuring these qualities, and briefly review their related literature in Section Machine learning for probabilistic hydrological forecasting. In our review, we emphasize key ideas and information that can lead to effective popularizations and syntheses of the concepts and methods under investigation, as such an emphasis could support successful future implementations and further scientific developments in the field. In the same forward-looking direction, we identify open research questions and propose ideas to be explored in the future. Lastly, we summarize and conclude the work by further discussing its most important aspects in terms of practical implications in Section Summary, discussion and conclusions.

What is a good method for probabilistic hydrological forecasting

The title of this section emulates the successfully “eye-catching” title “What is the ‘best' method of forecasting?” that was given to the seminal review paper by Chatfield (1988) from the forecasting field. This same paper begins by stating that the reader who expects a simple answer to the question consisting the paper's title might eventually get disappointed by the contents of the paper, although some general guidelines are still provided in it. Indeed, a universally best forecasting method does not exist and, therefore, instead of pursuing its proper definition and its finding, one should pursue making the most of multiple good forecasting methods by using, each time, the most relevant one (or ones) depending on exact formulation of the forecasting task to be undertaken [see, e.g., discussions by Jenkins (1982), Chatfield (1988)]. However, even the definition of a good forecasting method in terms of specific qualities can get quite challenging and is mostly equivalent to the definition of a useful forecasting method [see, e.g., discussions by Jenkins (1982), Chatfield (1988), Hyndman and Khandakar (2008), Taylor and Letham (2018)], thereby rotating around a wide variety of considerations to be optimally weighed against each other in the important direction of effectively making the targeted future quantities and events more manageable on a regular basis for the practitioners.

Among these considerations, obtaining skillful probabilistic forecasts (with the term “skillful” and its relatives being used herein to imply high predictive performance from perspectives that do not necessarily involve skill scores; for the definition and examples of the latter, see Gneiting and Raftery, 2007) is perhaps by far the easiest to perceive and recognize. In fact, probabilistic forecasting aims at reducing the uncertainty around predicted future quantities and events (with the importance of this target having been recognized in hydrology with the 20^th of the 23 major unsolved problems; Blöschl et al., 2019), similarly to what applies to best-guess forecasting, but from a conditional probabilistic standpoint. Thus, the more skillful the probabilistic forecasts, the less uncertain and the more manageable can become for the practitioner the predicted future quantities and events. Probabilistic predictions and forecasts are, in principle, considered to be skillful (again in a more general sense than the one relying on skill scores) when the sharpness of the predictive probability distributions is maximized, subject to reliability, on the basis of the available information set (Gneiting and Katzfuss, 2014). This constitutes indeed the formal criterion for assessing probabilistic predictions and forecasts. In this criterion, the term “reliability” refers to the degree of coverage of the actual future values by the various prediction intervals (or the probability with which the quantile forecasts exceed their corresponding actual future values; see again related remarks in Section Background information, basic terminology and review overview). Moreover, the term “sharpness” refers to how wide or narrow the predictive probability distributions and, thus, the various prediction intervals are. Scoring rules that are proper for the general task of probabilistic forecasting, with this propriety being evaluated strictly in terms of meeting the above criterion, include the quantile, interval and continuous ranked probability scoring rules, among others, with the latter of them being broadly referred to in the literature under its abbreviation “CRPS”. These scoring rules and their documentations can be found, for instance, in Dunsmore (1968), Gneiting and Raftery (2007) and Gneiting (2011). Notably, scoring rules that evaluate either reliability or sharpness alone are not proper for the task; yet, they could have some usefulness in terms of interpreting proper comparative evaluations. Also notably, the same criterion is not appropriate for assessing the skill of the probabilistic forecasts of extreme events (Brehmer and Strokorb, 2019), in a similar way that the root mean square error (RMSE) is not appropriate for assessing best-guess forecasts of extreme events [see also discussions in Tyralis and Papacharalampous (2022)], and consequently the forecast evaluation in this special case necessarily reduces into the computation of scores that are not designed particularly for probabilistic forecasts (e.g., point summaries of the tails of the predictive probability distributions; Lerch et al., 2017) or it relies on the most recent developments for adjusting scoring rules to meet such special requirements [see, e.g., the developments by Taggart (2022)].

Aside from skill, there are several additional, but still crucial, considerations driving the formulation and selection of forecasting methods that are mostly overlooked in the vast majority of research papers, both those appearing in hydrology and beyond. Indeed, not all the methodological developments can be exploited in technical and operational contexts, and even some of the most skillful probabilistic forecasting methods might not be useful in practice, at least considering the current limitations. Among the most characteristic considerations are, therefore, those for meeting the various requirements accompanying the ambitious, yet necessary and fully achievable, endeavor of forecasting “at scale” (Taylor and Letham, 2018). These requirements have been enumerated and extensively discussed in the context of probabilistic hydrological post-processing and forecasting by Papacharalampous et al. (2019), and include those for (a) a massive number of forecasts and (b) a massive variety of “situations” and quantities to be forecasted, thereby imposing the development of fully automatic, widely applicable and computationally fast (or at least affordable) forecasting methods. Importantly, a large degree of automation should not be interpreted to imply a small degree of flexibility in the forecasting method's formulation, as the opposite should actually hold [see, e.g., the examples by Hyndman and Khandakar (2008), Taylor and Letham (2018)]. This form of flexibility is indeed required, for instance, in terms of dealing with diverse conditions of data availability (either for accelerating forecasting solutions by making the most of the available data, or even for assuring the delivery of forecasts in conditions of poor data availability). It should further ensure any proper adjustment and special treatment that might be required for achieving optimality in terms of skill and for dealing with special categories of future events and quantities (e.g., extremes).

Moreover, simplicity, straightforwardness, interpretability and explainability could also be recognized as qualities of a good forecasting method, although their definition is more subjective than the definition of other qualities (such as those of skill, applicability and automation) and their consideration (or not) largely depends on the forecaster and the user of the forecasts. In fact, these rather secondary and optional qualities could make the forecasts easier to trust and handle in practice, thereby making a forecasting method more useful [see, e.g., discussions by Chatfield (1988), Januschowski et al. (2020)]. Even further from such benefits, simplicity and straightforwardness could be additionally important in terms of minimizing the computational cost, while interpretability and explainability can also offer scientific insights, along with a solid ground for future methodological developments, and are considered particularly important in hydrology. Lastly, a probabilistic forecasting method is sometimes judged on the basis of the exact form of its outputs, specifically from whether these outputs take the form of entire predictive probability distributions or reduced forms (which, however, can resemble quite satisfactorily entire predictive probability distributions, provided that they comprise forecasts for multiple statistics of theirs), with the former form being somewhat easier to interpret and follow, especially for unexperienced users of the forecasts.

Machine learning for probabilistic hydrological forecasting

Quantile, expectile, distributional and other regression algorithms

There is a widespread misconception in hydrology that machine and statistical learning algorithms cannot provide probabilistic predictions and forecasts unless they get merged with other models within wider properly designed frameworks and, thus, a large amount of research efforts are devoted toward addressing this particular challenge. However, this challenge could be safely skipped (thereby saving research efforts for devoting them to other challenges) by adopting suitable developments that are originally made beyond hydrology, specifically those that are founded on the top of the pioneering concept of going “beyond mean regression” (Kneib, 2013). Indeed, there are already whole families of machine and statistical learning regression algorithms that are explicitly designed to provide, in a straightforward and direct way, probabilistic predictions and forecasts. Also notably, a considerable portion of the implementations of these algorithms are made available in open source software after being optimally programmed by computer scientists and are equally user-friendly as the typical, broadly known regression algorithms (for mean regression). These families are outlined in the present section, with emphasis on the most well-received by the hydrological community and, at the same time, most practically appealing ones, while additional details on their similarities and differences with respect to their fundamentals and underlying assumptions can be found, for instance, in review paper by Kneib et al. (2021).

The quantile regression algorithms consist one of the most characteristic families for moving “beyond mean regression”. These algorithms provide quantile predictions and forecasts (according to the definitions and illustrative examples provided in Section Background information, basic terminology and review overview) in their output, and include, among others, the linear-in-parameters quantile regression algorithm (that is most commonly referred to simply as “quantile regression” in the literature; Koenker and Bassett, 1978), as well as its autoregressive variant (Koenker and Xiao, 2006) and additional extensions [see, e.g., their summary by Koenker (2017)]. Other typical examples of quantile regression algorithms (or, more generally, algorithms that can support quantile estimation, among other learning tasks) include the k-nearest neighbors for quantile estimation (Bhattacharya and Gangopadhyay, 1990), quantile regression forests (Meinshausen, 2006), generalized random forests for quantile estimation (Athey et al., 2019), gradient boosting machines (Friedman, 2001), model-based boosting based on linear or non-linear models (Bühlmann and Hothorn, 2007; Hofner et al., 2014) and quantile regression neural networks [originally introduced by Taylor (2000) and later improved by Cannon (2011)], while there are also quantile autoregression neural networks (Xu et al., 2016), composite quantile regression neural networks (Xu et al., 2017), quantile deep neural networks (Tagasovska and Lopez-Paz, 2019), composite quantile regression long short-term memory networks (Xie and Wen, 2019), quantile regression long short-term memory networks with exponential smoothing components (Smyl, 2020) and quantile regression neural networks for mixed sampling frequency data (Xu et al., 2021). Additional examples from this same algorithmic family include the XGBoost (eXtreme Gradient Boosting machine; Chen and Guestrin, 2016) and LightGBM (Light Gradient Boosting Machine; Ke et al., 2017) algorithms for estimating predictive quantiles, the random gradient boosting algorithm (which combines random forests and boosting; Yuan, 2015) and optimized versions from a practical point of view (Friedberg et al., 2020; Gasthaus et al., 2020; Moon et al., 2021).

As the above-reported names largely indicate, all these algorithms are close relatives (variants) of broadly known mean regression algorithms, such as the linear regression [see, e.g., documentations in James et al. (2013), Chapter 3], k-nearest neighbors [see e.g., documentations in Hastie et al. (2009), Chapter 2.3.2], random forests (Breiman, 2001a), boosting algorithms [see e.g., documentations in Hastie et al. (2009), Chapter 10], neural networks [see e.g., documentations in Hastie et al. (2009), Chapter 11] and deep neural networks (Hochreiter and Schmidhuber, 1997; Lecun et al., 2015). Therefore, similarly to them, their relative performance depends largely on the real-world problem that needs to be solved, and they can also differ notably with each other in terms of interpretability and flexibility (with these two algorithmic features being broadly recognized as incompatible to each other; see, e.g., James et al., 2013, Chapter 2.1.3, for characteristic examples on their trade-off). Indeed, they span from the most interpretable (least flexible) statistical learning ones (e.g., quantile regression) to less interpretable (more flexible) machine and deep learning ones (e.g., quantile regression forests and quantile deep neural networks). Theoretical details supporting their exact formulations can be found, for instance, in the references that are provided in the above paragraph or in the longer list of references in Torossian et al. (2020) and are out of the scope of this work, which is practically oriented.

Given this specific orientation, it is important to explain in simple terms the key idea behind the majority of the quantile regression algorithms. This specific idea was first conceived and successfully implemented by Koenker and Bassett (1978) for formulating the simplest quantile regression algorithm (Waldmann, 2018) and is very simple itself. For its herein provided popularization, let us begin by supposing one of our most familiar problems, the typical (i.e., the mean) regression problem. For solving this specific problem, an algorithm needs to “learn” how the mean of the response variable changes with the changes of the predictor variables. For achieving this, the least-square error objective function or some other similarly conceptualized error function is routinely incorporated into the algorithm and guides its training by consisting the loss function that is minimized. Let us now suppose that we are not interested in the future mean of the response variable, but instead that we are interested in that future value of streamflow at time t that will be exceeded with probability 10%. In this case, the algorithm needs to “learn” how the streamflow quantile of level 0.90 changes with the changes of the predictor variables. For achieving this, the quantile scoring function (else referred to as “pinball loss” function in the literature; see, e.g., Gneiting and Raftery, 2007; Gneiting, 2011, for the its definition) can be incorporated (instead of the least-square loss function) into the algorithm for placing the focus on the targeted streamflow quantile, thereby effectively allowing the algorithm's straightforward training for probabilistic prediction and forecasting. This training is then made by exploiting the formal criterion for achieving skillful probabilistic predictions and forecasts (see Section What is a good method for probabilistic hydrological forecasting).

In a nutshell, most of the quantile regression algorithms (e.g., the quantile regression, linear boosting, gradient boosting machine and quantile regression neural network ones) are trained by minimizing the quantile scoring function separately for each quantile level, while among the most characteristic examples of quantile regression algorithms that do not rely on this particular minimization, but on other optimization procedures, are the quantile regression forests and the generalized random forests for quantile regression. Independently of the exact optimization procedure applied, there exist clear guidance in the literature and, more precisely, in Waldmann (2018) on when quantile regression algorithms consist a befitting choice. In brief, this is the case when: (a) there is interest in events at the “limit of probability” (i.e., further than the most central parts of the predictive probability distributions); (b) there is no information at hand on which probability distribution models represent sufficiently the predictive probability distributions (or such information is hard to deduce); (c) there are numerous outliers among the available observations of the dependent variable; and (d) heteroscedasticity needs to be modeled. Based on the above-summarized guidance, we understand that probabilistic hydrological forecasting can indeed benefit from the family of quantile regression algorithms in the direction of issuing skillful probabilistic forecasts. In fact, several algorithms from this specific family have already been found relevant to this task and have been tested in the field of probabilistic hydrological post-processing, including the simplest linear-in-parameters [e.g., in Weerts et al. (2011), López López et al. (2014), Dogulu et al. (2015), Bogner et al. (2017), Wani et al. (2017), Papacharalampous et al. (2019, 2020a,b), Tyralis et al. (2019a)] and several machine learning [e.g., in Bogner et al. (2016, 2017), Papacharalampous et al. (2019), Tyralis et al. (2019a)] ones.

Probabilistic hydrological post-processing through quantile regression algorithms has been extensively discussed as a culture-integrating approach to probabilistic hydrological prediction and forecasting by Papacharalampous et al. (2019). The relevant discussions are primarily based on the overview by Todini (2007), in which the process-based rainfall-runoff models and the data-driven algorithms (with the latter including, among others, all the machine and statistical learning ones) are summarized as two different “streams of thought” (or cultures) that need to be harmonized “for the sake of hydrology”. A basic probabilistic hydrological post-processing methodology comprising a process-based rainfall-runoff model and a quantile regression algorithm, is summarized in Figure 2. Notably, this methodology could be further enriched in multiple ways. For instance, information from multiple process-based rainfall-runoff models could be exploited [see, e.g., related discussions by Montanari and Koutsoyiannis (2012)], while the same applies for other additional predictors. Such predictors could include various types of meteorological forecasts (and possibly entire ensembles of such forecasts), and past or present hydrological and meteorological observations. Of course, the utilization of best-guess hydrological forecasts as predictors (see again Figure 2) is not absolutely necessary, which practically means that probabilistic hydrological forecasting can be made without applying post-processing. Although both the absolute and relevant performance of probabilistic hydrological post-processors might (and is rather expected to) depend on whether the process-based rainfall-runoff model is applied in simulation or in forecast mode, the possible solutions and the various pathways toward addressing the challenges of formalizing, optimizing and selecting probabilistic hydrological post-processors using machine learning do not. Still, a clear distinction between these two modeling contexts is necessary when trying to benefit from past post-processing works for achieving optimal machine learning solutions. Similarly, the absolute and relevant performance of machine learning methods might depend on whether they are applied in post-processing or more direct probabilistic hydrological forecasting contexts.

FIGURE 2

Figure 2. Basic formulation of probabilistic hydrological post-processing for providing probabilistic hydrological forecasts in the period T₃ using a process-based rainfall-runoff model in forecast mode (i.e., with meteorological forecasts as its inputs; Klemeš, 1986) and a machine or statistical learning algorithm, along with best-guess meteorological forecasts and hydrological observations. The machine or statistical learning algorithm could originate from any of the families summarized in Section Quantile, expectile, distributional and other regression algorithms. For most of the quantile regression algorithms, steps 3 and 4 comprise in practice multiple trainings and runs, respectively, with each of them referring to a different quantile level, until all the quantile hydrological forecasts consisting the probabilistic hydrological forecast are issued. For example, for obtaining the probabilistic hydrological forecasts of Figure 1 through probabilistic hydrological post-processing using quantile regression neural networks (with the latter being the selected machine learning algorithm), steps 3 and 4 would comprise 5 trainings and 5 runs, respectively.

Overall, there are two ways for improving predictive performance: (i) improving the prediction algorithm; and (ii) discovering new informative predictors. For dealing with the latter of these challenges, the computation of variable importance scores [see, e.g., the reviews on the topic by Grömping (2015), Wei et al. (2015)] is often suggested in the machine learning literature. Indeed, variable importance information helps us understand which predictors are the most relevant to improving predictive performance in each task [see, e.g., relevant investigations in a probabilistic hydrological post-processing context by Sikorska-Senoner and Quilty (2021)], with this relevance being larger for the predictors with the larger scores. The variable importance scores can be classified into two main categories, which are known under the terms (Linardatos et al., 2020; Kuhn, 2021): (a) “model-specific” (indicating that the application is restricted only to a specific family of algorithms); and (b) “model-agnostic” or “model-independent” (indicating that the application can be made in every possible algorithm). Their open source implementations are coupled with several machine and statistical learning algorithms (e.g., in linear models, random forests, partial least squares, recursive partitioning, bagged trees, boosted trees, multivariate adaptive regression splines—MARS, nearest shrunken centroids and cubist; Kuhn, 2021). As perhaps proven by their popularity beyond hydrology, the most easy- and straightforward-to-compute for the task of probabilistic hydrological forecasting are those incorporated into the generalized random forest algorithm and into several boosting variants for quantile regression. Related summaries and literature information can be found in Tyralis et al. (2019b) and Tyralis and Papacharalampous (2021a). The various variable importance scores are implementations of the concept of explainable machine learning [see, e.g., the reviews on the topic by Linardatos et al. (2020), Roscher et al. (2020), Belle and Papantonis (2021)], which is known for its utility for gaining scientific insights from machine learning algorithms, thereby achieving a deviation from “black box” solutions. Notably, this specific concept can take various additional forms of articulation and expression, which can also facilitate successful future implementations and an improved understanding of the forecasts by the practitioners.

In particular as regards the remarkably wide applicability characterizing the various quantile regression algorithms (most probably because of their non-parametric nature), with this particular applicability being sufficient even for meeting the strict operational requirements accompanying the endeavor of probabilistic hydrological forecasting, the reader is referred to the works by Papacharalampous et al. (2019) and Tyralis et al. (2019a). Indeed, these specific works present large-scale multi-site evaluations across the contiguous United States that could be possible only for widely applicable algorithms. The former of these works additionally presents the computational times spent for running the following six quantile regression algorithms in probabilistic hydrological post-processing: (i) quantile regression, (ii) generalized random forests for quantile regression, (iii) generalized random forests for quantile regression emulating quantile regression forests, (iv) gradient boosting machine based on trees, (v) boosting based on linear models and (vi) quantile regression neural networks. It further provides detailed information on how to implement these algorithms using open source software.

Aside from the above-discussed advantages, quantile regression algorithms also share a few characteristic drawbacks (Waldmann, 2018). Indeed, the vast majority of these algorithms estimate separately predictive quantiles at different quantile levels. This implies some inconvenience in their utilization (in the sense that additional automation is required with respect to that already incorporated in the various open software implementations). Most importantly, it can cause quantile crossing, which however can be treated ad hoc by the forecaster (with this treatment requiring additional automated procedures). Also notably, parameter estimation is harder in quantile regression than in standard regression, while another drawback of quantile regression algorithms that is worthy to discuss is their inappropriateness for dealing with the important challenge of predicting extreme quantiles. Indeed, this inappropriateness could be a crucial limitation for the case of flood forecasting. Still, in such cases, proper extensions and close relatives of quantile regression algorithms could be applied. Indeed, Tyralis and Papacharalampous (2022) have recently proposed a new probabilistic hydrological post-processing method based on extremal quantile regression (Wang et al., 2012; Wang and Li, 2013). This method extrapolates predictions issued by the quantile regression algorithm to high quantiles by exploiting properties of the Hill's estimator from the extreme value theory, while similar extensions for other quantile regression algorithms could also be possible. Another worth-mentioned modification that can be applied to any of these algorithms, inspired by the already existing quantile regression long short-term memory networks with exponential smoothing components by Smyl (2020), is the addition of a trend component for dealing with changing weather conditions beyond variability. In fact, the latter can be modeled directly by the quantile regression algorithms.

Other close relatives of the quantile regression algorithms are the expectile regression ones, which focus on conditional expectiles instead of conditional quantiles. Expectiles are the least squares analogs of the quantiles. Indeed, they are generalizations of the mean, in the same way that the quantiles are generalizations of the median. Among the existing expectile regression algorithms are the expectile regression (Newey and Powell, 1987) and the expectile regression neural networks (Jiang et al., 2017). Notably, expectile regression algorithms (in their original forms) are a completely unexplored topic for probabilistic hydrological post-processing and forecasting contexts. Therefore, future research could investigate their place and usefulness in such contexts. Overall, it might be important to note that, similar to what applies for the quantile regression algorithms, the expectile regression algorithms should be expected to be more useful in the cases where there is no sufficient information at hand about the predictive probability distributions.

On the contrary, however, in the cases where such information exists, the distributional (else known as “parametric”) algorithms should be expected to excel. These algorithms include several machine and statistical learning ones, which are usually referred to under the term “distributional regression” algorithms. Among them are the GAMLSS (Generalized Additive Models for Location, Scale and Shape; Rigby and Stasinopoulos, 2005) and its extension in Bayesian settings, i.e., the BAMLSS (Bayesian Additive Models for Location, Scale, and Shape; Umlauf et al., 2018), as well as the distributional regression forests (Schlosser et al., 2019), a boosting GAMLSS model (Mayr et al., 2012), the NGBoost (Natural Gradient Boosting) model for probabilistic prediction (Duan et al., 2020) and the Gaussian processes for distributional regression (Song et al., 2019). Other distributional regression algorithms are the deep distribution regression algorithm (Li R. et al., 2021), the marginally calibrated deep distributional regression algorithm (Klein et al., 2021) and the DeepAR model for probabilistic forecasting with autoregressive recurrent networks (Salinas et al., 2020). Notably, distributional regression algorithms could be also modified similarly to the quantile regression ones for dealing in an improved way with the special case of changing conditions beyond variability. Moreover, they could be applied with heavy-tailed distributions for approaching the other special case of predicting the extreme quantiles of the real-world distributions (that appear due to weather and climate extremes), thereby consisting alternatives to the previously discussed extensions of quantile regression based on the extreme value theory (see again Tyralis and Papacharalampous, 2022).

Aside from the machine and statistical learning algorithms belonging to the above-outlined families, there are numerous others that can also provide probabilistic predictions and forecasts in a straightforward way (at least for dealing with the casual forecasting cases, while their modification or extension based on traditional statistics may be possible for special cases, such as changes beyond variability and extremes). Such algorithms are the BART (Bayesian Additive Regression Trees; Chipman et al., 2012) and their heteroscedastic variant (Pratola et al., 2020), which are regarded as boosting variants. Another machine learning algorithm that is notably relevant to the task of probabilistic hydrological forecasting is the dropout ensemble (Srivastava et al., 2014). This deep learning algorithm has been proved to be equivalent to Bayesian approximation (Gal and Ghahramani, 2016) and has already been proposed for estimating predictive hydrological uncertainty by Althoff et al. (2021). Its automated variant for probabilistic forecasting can be found in Serpell et al. (2019), while open software implementations of many other models, mostly deep learning ones, can be found in Alexandrov, et al. (2020). Also notably, comprehensive reviews on deep learning and neural networks for probabilistic modeling can be found in Lampinen and Vehtari (2001), Khosravi et al. (2011), Abdar et al. (2021) and Hewamalage et al. (2021), where the interested reader can find numerous new candidates for performing probabilistic hydrological forecasting, thereby enriching the deep learning toolbox whose compilation has just started in the field [see, e.g., relevant works by Althoff et al. (2021), Li D. et al. (2021)].

Lastly, it is important to highlight that benefitting from the field of machine learning does not only include the identification and transfer (and perhaps even the modification) of various relevant machine and statistical learning algorithms. Indeed, more abstract inspirations sourced from this field can also lead to useful practical solutions. Characteristic examples of such inspirations are the concepts of “quantile-based hydrological modeling” (Tyralis and Papacharalampous, 2021b) and “expectile-based hydrological modeling” (Tyralis et al., 2022). These concepts offer the most direct and straightforward probabilistic hydrological forecasting solutions using process-based rainfall-runoff models. In fact, the latter can be simply calibrated using the quantile or the expectile loss function for delivering quantile or expectile hydrological predictions and forecasts.

The “no free lunch” theorem on the a priori distinction between algorithms

In practice, several themes are routinely integrated for the formulation and selection of skillful forecasting methods. Among them are those for exploiting sufficient information that we might already have at hand about the exact forecasting problem to be undertaken and the various methods composing our toolbox. Characteristic examples of such themes appear extensively in previous sections and in the literature, and include the a priori distinction and selection of models based on their known properties, as well as the inclusion of useful data for the present and the past (and perhaps also the inclusion of useful forecasts) in the input of the various models. Indeed, in the above section we referred to the guidance by Waldmann (2018) for summarizing when the various quantile regression algorithms should be viewed as befitting modeling choices and when they should be expected to be more skillful than distributional regression or other distributional methods for probabilistic prediction and forecasting [e.g., the Bayesian ones in Geweke and Whiteman (2006)], and vice-versa. We also referred to the concept of explainable machine learning and its pronounced relevance to the well-recognized endeavor of discovering new informative predictor variables for our algorithms. Even further, we highlighted the fact that quantile regression algorithms do not consist optimal choices (in their original forms) when extreme events need to be predicted and forecasted, and discussed how the capabilities of these same algorithms can be extended into the desired direction.

Themes such as the above are undoubtedly important in the endeavor of formulating and selecting skillful forecasting methods. Yet, it is equally important for the forecaster to recognize the following fact: such themes and tools can only guide us through parts of the entire way and this is probably why a different family of themes is also routinely exploited toward an optimal selection between forecasting models. This latter family is founded on the top of scoring rules, and includes themes such as those of “forecast evaluation,” “empirical evaluation,” “empirical comparison” and “benchmarking”. Indeed, the a priori distinction between models based on theoretical properties is not possible most of the times and, even when it is, it cannot always optimally support the selection between models. In fact, our knowledge on which properties matter the most in achieving optimal practical solutions might be limited or might be based on hardly relevant assumptions that should be avoided [e.g., assumptions stemming from descriptive or explanatory investigations, while the focus should be in the actual forecasting performance; see relevant discussions in Shmueli (2010)]. On the top of everything else, the various model properties are analytically derived and hold for infinite samples, while the samples used as inputs for forecasting are finite. Based on the above considerations, empirical evaluations, comparisons and benchmarking of forecasting models cannot be skipped when we are interested at maximizing the skill.

Importantly, there is a theorem underlying the discussions of this section, which is known as the “no free lunch” theorem (Wolpert, 1996). This theorem is of fundamental importance for conducting proper benchmark evaluations and comparisons of methods for forecasting (and not only), and it was originally formulated for machine and statistical learning algorithms, as there are indeed whole groups of such algorithms that cannot be distinguished with each other to any extent, regarding their skill, based on their theoretical properties. In simple terms, the “no free lunch” theorem implies that, among the entire pool of relevant algorithms for dealing with a specific problem type (which, for the case of probabilistic hydrological forecasting, might include the various quantile regression algorithms that are enumerated in Section Quantile, expectile, distributional and other regression algorithms), there is no way for someone to tell in advance with certainty which of them will perform the best for one particular problem case (e.g., within a specific probabilistic hydrological forecasting case study). Indeed, there is “no free lunch” in the utilization of any machine or statistical learning algorithm, as there is “no free lunch” in the utilization of any model. Notably, the “no free lunch” theorem also implies that any empirical evidence that we might have for a specific case study cannot be interpreted as general empirical evidence and, therefore, forecast comparisons within case studies cannot support optimal selections between models, as it is also thoroughly explained in Boulesteix et al. (2018); nonetheless, there are still ways for the forecasters to deal with the “no free lunch” theorem in a meaningful sense. The most characteristic of these ways are discussed in detail in Sections Massive multi-site datasets and large-scale benchmarking and Forecast combinations, ensemble learning and meta-learning.

Massive multi-site datasets and large-scale benchmarking

An effective way for dealing with the “no free lunch” theorem toward maximizing the benefits and reducing the risks, in terms of predictive skill, of machine and statistical learning algorithms (and not only) is through the concept of “large-scale benchmarking”. This concept relies on the use of massive datasets (i.e., datasets that comprise multiple and diverse real-world cases, and sometimes also simulated toy cases) and multiple models, with the latter necessarily including benchmarks (e.g., simple or traditional models). Large-scale benchmarking consists the main concept underlying all the “large-scale comparison” studies, which are incomparably fewer than the “model development” studies in all the disciplines, while the opposite should actually hold to ensure that the strengths and limitations of the various models are well-understood and well-handled in practice (Boulesteix et al., 2018). It is also the core concept of the “M,” “Kaggle” and other well-established series of competitions that appear in the forecasting and machine learning fields. Such competitions have a vital utility toward providing the community with properly formulated, independent and, therefore, also highly trustable evaluations of widely applicable and fully automated forecasting and/or machine learning methods. They are extensively discussed (by, e.g., Fildes and Lusk, 1984; Chatfield, 1988; Clements and Hendry, 1999; Armstrong, 2001; Fildes and Ord, 2002; Athanasopoulos and Hyndman, 2011; Fildes, 2020; Castle et al., 2021; Januschowski et al., 2021; Lim and Zohren, 2021; Makridakis et al., 2021) and reviewed (by, e.g., Hyndman, 2020; Bojer and Meldgaard, 2021) beyond hydrology, where the interested reader can find details about their history and characteristics. In particular as regards the fundamental necessity of utilizing benchmarks in forecast evaluation works, the reason behind it can be found in the outcomes of the already completed competitions. Indeed, simple (or less sophisticated) methods might perform surprisingly well in comparison to more sophisticated methods in some types of forecasting (and other) problems (Hyndman and Athanasopoulos, 2021, Chapter 5.2).

In what follows, discussions on the practical meaning of large-scale benchmarking are provided. For these discussions, let us suppose a pool of probabilistic prediction methods from which we wish to select one (or more) for performing probabilistic hydrological forecasting (e.g., through post-processing). Among others, these candidate methods could include multiple machine and statistical learning ones, with each being defined not only by a specific algorithm (e.g., one of those enumerated in Section Quantile, expectile, distributional and other regression algorithms) but also by a specific set of predictor variables and by specific parameters (which are also commonly referred to as “hyperparameters”), or alternatively by the algorithm and automated procedures for predictor variable and parameter selection. For achieving optimal practical solutions in this particular context, we specifically wish to know the probabilistic hydrological forecasting “situations” in which it is more likely for each candidate to work better than the remaining ones. Note here that the various probabilistic hydrological forecasting “situations” of our interest could be defined by all the time scales and forecast horizons of our interest, by all the situations of data availability with which we might have to deal in practice, by all the quantile and prediction interval levels of our interest, by all the streamflow magnitudes of our interest or by other hydroclimatic conditions (e.g., those defined as “climate zones” by the various climate classification systems), or even by all these factors and several others. Since there is no theoretical solution to the above-outlined problem (see again discussions in Section The “no free lunch” theorem on the a priori distinction between algorithms), we can only provide empirical solutions to it. These latter solutions can, then, be derived through extensively comparing the performance of all the candidates in a large number and wide range of problem cases, which should collectively well-represent the various types of probabilistic hydrological forecasting “situations” being of interest to us. That is what large-scale benchmarking is, in its full potential, and that is why its value should be apprised in the direction of making the most of multiple good methods (e.g., for probabilistic hydrological forecasting) and not in the direction of selecting a single “best” method (see again Section What is a good method for probabilistic hydrological forecasting).

In brief, if we empirically prove through large-scale benchmarking that a probabilistic hydrological forecasting method performs on average better in terms of skill than the remaining ones (see again Section What is a good method for probabilistic hydrological forecasting, for a summary of the criteria and scoring rules that should guide such comparisons) for a sufficiently large number of cases representing a specific type of probabilistic hydrological forecasting “situations,” then we have found that it is “safer” to use this specific method than using any of the remaining ones for this same type of probabilistic hydrological forecasting “situations” in the future. By repeating this procedure for all the possible categories of probabilistic hydrological forecasting “situations” (after properly defining them based on the various practical needs), the forecaster can increase the benefits and reduce the risks stemming from the use of multiple probabilistic hydrological forecasting methods. Given this pronounced relevance of large-scale benchmarking toward maximizing predictive skill, ensuring compliance with the various practical considerations accompanying the endeavor of formulating and selecting probabilistic hydrological forecasting methods (see again Section What is a good method for probabilistic hydrological forecasting) gains some additional importance. Indeed, only the widely applicable, fully automated and computationally fast methods can be extensively investigated and further improved, if necessary, before applied in practice (or perhaps even discarded, but still having served a purpose as benchmarks for others). These same methods are also the only whose long-run future performance can be known in advance to a large extent, and include many machine and statistical learning ones, a considerable portion of which are enumerated in Section Quantile, expectile, distributional and other regression algorithms.

At this point, it is also important to highlight that there are multiple open multi-site datasets comprising both hydrological and meteorological information, thereby being appropriate for performing large-scale benchmarking (at least for the daily and coarser temporal scales) in probabilistic hydrological post-processing and forecasting [e.g., those by Newman et al. (2015), Addor et al. (2017), Alvarez-Garreton et al. (2018), Chagas et al. (2020), Coxon et al. (2020), Fowler et al. (2021), Klingler et al. (2021)]. Examples of studies utilizing such datasets to support a successful formulation and selection of skillful probabilistic hydrological forecasting or, more generally, probabilistic hydrological prediction methods also exist. Nonetheless, such examples mostly refer to single-method evaluations (or benchmarking) either in post-processing contexts [e.g., those in Farmer and Vogel (2016), Bock et al. (2018), Papacharalampous et al. (2020b)] or in ensemble hydrological forecasting contexts [e.g., those in Pechlivanidis et al. (2020), Girons Lopez et al. (2021)].

Ensemble hydrological forecasting can be (mostly) regarded as the well-established alternative in operational hydrology to the machine learning methods outlined in Section Quantile, expectile, distributional and other regression algorithms, independently of whether or not some type of post-processing is involved in the overall framework for probabilistic forecasting (or prediction). Still, some common data-related challenges are shared between these alternatives, as machine learning, too, should ideally be informed by “state-of-the-art” datasets comprising weather and/or climate forecasts to be then applied in operational mode. Although there are massive datasets comprising meteorological and hydrological forecasts and observations [see, e.g., those investigated in Pechlivanidis et al. (2020), Girons Lopez et al. (2021)], the methods for ensemble weather forecasting keep updating. In such cases, the data that are actually available for (i) the training of the machine learning algorithms and (ii) the calibration of the hydrological models might be changing over time. Dealing with this particularity is somewhat more critical for forecasting with machine learning algorithms, because of the well-known importance of large data samples for their training. Approaches referred to under the term “online learning” (see, e.g., Martindale et al., 2020) could partly serve toward this important direction and could, thus, be investigated in this endeavor. Such approaches do not require a static dataset.

As regards the examples of large-scale comparisons and benchmarking of multiple machine and statistical learning methods, these are even rarer in the field, with the ones conducted in probabilistic hydrological post-processing contexts being available in Papacharalampous et al. (2019) and Tyralis et al. (2019a). These two works can effectively guide the application of quantile regression algorithms in probabilistic hydrological forecasting. Indeed, although their large-scale results refer exclusively to the modeling “situations” determined by their experimental settings (i.e., the daily temporal scale, a specific process-based rainfall-runoff model, specific conditions of data availability and predictors, etc.), the re-formulation and extension of their methodological contribution to other hydrological forecasting settings would be a straightforward process, from an algorithmic point of view, and could be made in the future to answer those research questions that are still open on the relative performance of the various quantile regression algorithms in the field.

Of course, many more open research questions exist and concern the various families of machine learning algorithms that are discussed in Section Quantile, expectile, distributional and other regression algorithms, with some of them being completely unexplored. In particular, it would be useful for the hydrological forecaster to know how these families and their algorithms compare with each other, as well as to other families and their methods, with the latter possibly including several well-established alternatives that do not originate from the machine learning literature (e.g., the traditional Hydrologic Model Output Statistics—HMOS method; Regonda et al., 2013). Indeed, such information is currently missing from the literature. The various comparisons could be conducted, both in terms of skill and in more practical terms, in probabilistic hydrological forecasting for the various modeling “situations” exhibiting practical relevance, as this would allow making the most of the entire available toolbox in technical and operational settings. For achieving this, it would also be useful to deliver large-scale findings on predictor variable importance through explainable machine learning (see again the related remarks in Section Quantile, expectile, distributional and other regression algorithms), as such results could replace automated procedures for predictor variable selection with (mostly) satisfactorily results, thereby saving considerable time in operational settings. Massive multi-site datasets could also support hyperparameter selection investigations. Although these latter investigations could, indeed, be beneficial, it might be preferable to skip them (in favor of addressing other research questions) by simply selecting the predefined hyperparameter values that have been made available in the various open source implementations of the algorithms. According to Arcuri and Fraser (2013), these specific values are expected to lead to satisfactory performance in most cases (probably because they are selected based on extensive experimentation).

Forecast combinations, ensemble learning and meta-learning

Another way for dealing with the “no free lunch” theorem in a meaningful sense is based on the concept of “ensemble learning,” a pioneering concept appearing in the community of machine learning that is equivalent to the concept of “forecast combinations” from the forecasting field. In forecasting through ensemble learning, instead of using one individual algorithm, an ensemble of algorithms is used [see, e.g., the seminal paper by Bates and Granger (1969) and the review papers by Clemen (1989), Granger (1989), Timmermann (2006), Wallis (2011), Sagi and Rokach (2018), Wang et al. (2022)]. The latter algorithms are known as “base learners” in the machine learning field, and are trained and then applied in forecast mode independently of each other. Their independent forecasts are finally combined with another learner, which is known as the “combiner” and is “stacked” on top of the base learners, with the final output being a single forecast (and the independent forecasts provided by the base learners being discarded after their combination). Notably, the term “ensemble learning” should not be confused with the terms “ensemble simulation” and “ensemble forecast” (or the term “ensemble forecasting”), which refer to formulations in which the entire ensemble of independent simulations or forecasts constitutes the probabilistic prediction or forecast [see, e.g., the model output forms in Montanari and Koutsoyiannis (2012), Hemri et al. (2013), Sikorska et al. (2015), Quilty et al. (2019), Pechlivanidis et al. (2020), Girons Lopez et al. (2021)].

The simplest form of ensemble learning and “stacking” of algorithms is simple averaging, in which the combiner does not have to be trained, as it simply computes the average of the forecasts of the various base learners. For instance, the forecasts of quantile regression, quantile regression forests and quantile regression neural networks for the streamflow quantile of level 0.90 (i.e., three forecasts) can be averaged to produce a new forecast (i.e., one forecast), while the averaging of distributions is also possible. Some quite appealing properties and concepts are known to be related to simple averaging. Among them are the “wisdom of the crowd” and the “forecast combination puzzle”. The “wisdom of the crowd” can be harnessed through simple averaging (Lichtendahl et al., 2013; Winkler et al., 2019) to increase robustness in probabilistic hydrological post-processing and forecasting using quantile regression algorithms [see related empirical proofs in Papacharalampous et al. (2020b)] or potentially machine and statistical learning algorithms from the remaining families that are summarized in Section Quantile, expectile, distributional and other regression algorithms. By increasing robustness, one reduces the risk of delivering poor quality forecasts at every single forecast attempt. Overall, simple averaging is known to be hard to beat in practice, in the long run, for many types of predictive modeling “situations” [see relevant discussions by De Gooijer and Hyndman (2006), Smith and Wallis (2009), Lichtendahl et al. (2013), Graefe et al. (2014), Hsiao and Wan (2014), Winkler (2015), Claeskens et al. (2016)], thereby leading to the challenging puzzle of beating this simple form of stacking with more sophisticated stacking (Wolpert, 1992) and meta-learning forecast combination methods. Alternative possibilities for combining forecasts include Bayesian model averaging (see, e.g., Hoeting et al., 1999, for a related historical and tutorial review); yet, stacking has been theoretically proved to have some optimal properties in comparison to this alternative when the focus is on predictive performance (Yao et al., 2018).

In hydrology, the concept of ensemble learning has been extensively implemented for combining both best-guess forecasts (by, e.g., Diks and Vrugt, 2010; Xu et al., 2018; Huang et al., 2019; Papacharalampous and Tyralis, 2020; Tyralis et al., 2021) and probabilistic predictions (by, e.g., Vrugt and Robinson, 2007; Hemri et al., 2013; Bogner et al., 2017; Papacharalampous et al., 2019, 2020a,b; Tyralis et al., 2019a; Li et al., 2022), with the Bayesian model averaging implementation being by far the most popular one. Probabilistic hydrological predictions of different machine learning quantile regression algorithms have been combined through simple averaging [by Papacharalampous et al. (2019), Tyralis et al. (2019a)] and through stacking [by Tyralis et al. (2019a)] in the context of probabilistic hydrological post-processing, and related large-scale benchmark tests have also been performed (by the same works). These benchmark tests stand as empirical proofs that simple averaging and stacking can offer considerable improvements in terms of skill in probabilistic hydrological prediction at the daily time scale, while similar large-scale investigations for the most specific case of probabilistic hydrological forecasting at the same and at other time scales with large practical relevance (and for various conditions of data availabilities) could be the subject of future research. Such investigations could also focus on the combination of probabilistic hydrological forecasts that have been previously issued based on different members of ensemble meteorological forecasts. Of course, the overall benefit from the use of ensemble learning methods should be also apprised again according to Section What is a good method for probabilistic hydrological forecasting. Aside from the secondary considerations enumerated in this latter section, which are indeed met to a considerably lesser degree when forecast combinations are performed, the remaining considerations can be met quite satisfactorily, yet to a degree that largely depends on the choice of the base learners. That additionally implies that, ideally, the various combiners should be tested with as many different sets of base learners as possible in the context of large-scale benchmarking for optimizing long-run forecasting skill [see, e.g., the experimental setting in Papacharalampous and Tyralis (2020)]. Also notably, large-scale benchmark tests that examine the combination of entire predictive probability distributions are still missing from the hydrological literature and are, thus, recommended as future research.

Lastly, discussions should focus on the meta-learning approach to forecasting [see, e.g., some of the first relevant formulations for performing best-guess forecasting by Wang et al. (2009), Lemke and Gabrys (2010), Matijaš et al. (2013), Montero-Manso et al. (2020), Talagala et al. (2021)]. This approach is built on the reasonable premise that improvements in terms of skill can be obtained by conditioning upon time series features the weights with which the forecast combination is performed. This relatively recent idea can be interpreted in the sense that one method might be more skilful than others in forecasting time series with specific ranges of characteristics (with these characteristics standing as a new additional way for defining various modeling “situations” of interest for the forecasters) and implies the automation of practical forecasting systems that are necessarily trained through large-scale benchmarking in the direction of making the most of multiple forecasting methods (see again Section Massive multi-site datasets and large-scale benchmarking). Among the most typical time series features are the various autocorrelation, partial autocorrelation, long-range dependence, entropy, temporal variation, seasonality, trend, lumpiness, stability, non-linearity, linearity, spikiness and curvature features [see the numerous examples in Wang et al. (2006), Fulcher et al. (2013), Fulcher and Jones (2014), Hyndman et al. (2015), Kang et al. (2017, 2020), Fulcher (2018)], while the length and time scale of a time series could also be viewed as its features. Such general-purpose time series features for data science have been found relevant in interpreting the skill of best-guess hydrological forecasts at the monthly temporal scale in Papacharalampous et al. (2022), and are of fundamental and practical interest in hydrology [see, e.g., the central themes, concepts and directions provided by Montanari et al. (2013)], especially in its stochastic branch.

Still, meta-learning consists a completely unexplored endeavor for the sister fields of probabilistic hydrological post-processing and forecasting. Given that the benefits from it could be considerably large [see again previous successful formulations for best-guess forecasting in Wang et al. (2009), Lemke and Gabrys (2010), Matijaš et al. (2013), Montero-Manso et al. (2020), Talagala et al. (2021)], future research could be devoted to its exploration at the various temporal scales exhibiting practical relevance and for various data availability conditions. For this particular exploration, a variety of probabilistic forecasting methods (including, among others, those relying on the algorithms mentioned in Section Quantile, expectile, distributional and other regression algorithms) and a variety of time series features could be considered. It is, lastly, highly relevant to note that meta-learning methods for probabilistic hydrological forecasting could also be formulated around hydrological signatures, which have already been used for interpreting, from a process-oriented perspective, the performance of probabilistic hydrological forecasting methods by Pechlivanidis et al. (2020) and Girons Lopez et al. (2021). Hydrological signatures are, indeed, the analogous of time series features in the catchment hydrology field, where the interested reader can find details about them [see, e.g., their taxonomies in McMillan et al. (2017) and McMillan (2020)].

Summary, discussion and conclusions

Machine learning can provide straightforward and effective methodological solutions to many practical problems, including various probabilistic prediction and forecasting ones. With this practically-oriented review, we believe to have enriched the hydrological forecaster's toolbox with the most relevant machine learning concepts and methods for addressing the following major challenges in probabilistic hydrological forecasting: (a) how to formalize and optimize probabilistic forecasting implementations; and (b) how to identify the most useful among these implementations. The machine learning concepts and methods are summarized in Figure 3. We have thoroughly reviewed their literature by emphasizing key information that can lead to effective popularizations. We have also assessed the degree to which the field has already benefitted from them, and proposed ideas and pathways that could bring further scientific developments by also building upon existing knowledge, traditions and practices. The proposed pathways include both formal (and, thus, quite strict) ones and more abstract inspirations sourced from the machine learning field. Most importantly, we have proposed a united view that aims at making the most of multiple (typically as many as possible) methods, including but not limited to machine learning ones, by maximizing the benefits and reducing the risks from their use.

FIGURE 3

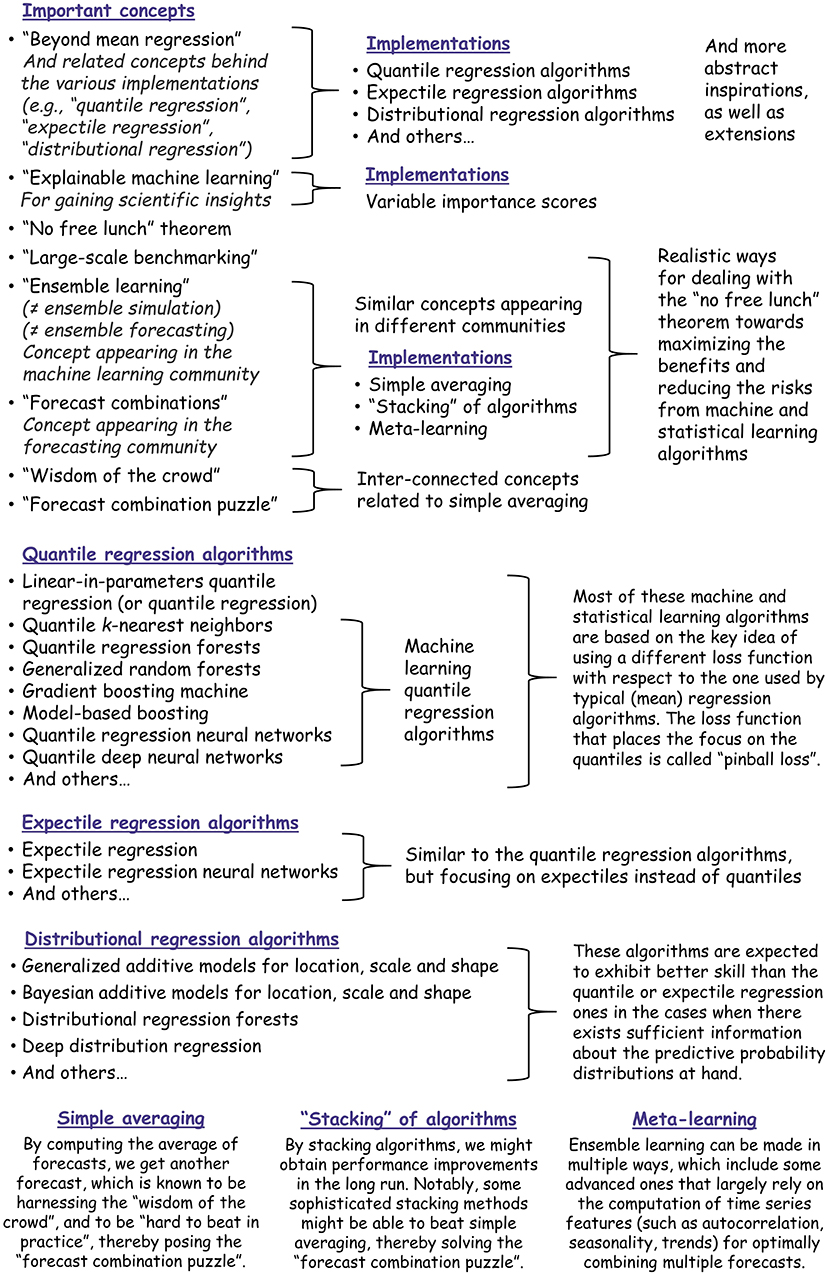
Figure 3. A practically-oriented synthesis of the most relevant machine learning concepts and methods for performing probabilistic hydrological post-processing and forecasting. The various procedures consisting probabilistic hydrological post-processing, in its basic formulation, are summarized in Figure 2.

Fostering research efforts under this united view is indeed particularly important, especially when the aim is at maximizing predictive skill. Natural companions in such a demanding endeavor are open science and open research [see, e.g., the related guidance in Hall et al. (2022)], which are often overlooked in practice despite their vital significance. This review extensively discussed, among others, the fundamental relevance of massive open datasets to identifying the strengths and limitations of the various methods (both of the already available and the newly proposed ones) toward accelerating probabilistic hydrological forecasting solutions based on key discussions by Boulesteix et al. (2018), and based on the concept behind the forecasting and machine learning competitions. It also highlighted the importance of open software [see, e.g., packages in the R and Python programming languages, which are documented in R Core Team (2022) and Python Software Foundation (2022), respectively] for enriching the toolbox of the hydrological forecaster with algorithms that are optimally programmed (in many cases by computer scientists) and widely tested in various modeling “situations” before released. Overall, we believe that the summaries of the guidelines and considerations provided by this review are equally (and perhaps even more) important than the summaries of the various algorithms that are also provided. We would, therefore, like to conclude by emphasizing the need for formalizing research efforts as these guidelines and considerations imply.

Author contributions

Both authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

The authors are sincerely grateful to the Research Topic Editors for inviting the submission of this paper, to the Handling Editor for his additional work on it, and to the Reviewers for their constructive suggestions and remarks. Portions of this paper have been discussed by the authors in a popular science fashion in the HEPEX (Hydrologic Ensemble Prediction EXperiment) blog post entitled Machine learning for probabilistic hydrological forecasting. This blog post is available online at the following link: https://hepex.inrae.fr/machine-learning-for-probabilistic-hydrological-forecasting.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdar, M., Pourpanah, F., Hussain, S., Rezazadegan, D., Liu, L., Ghavamzadeh, M., et al. (2021). A review of uncertainty quantification in deep learning: techniques, applications and challenges. Information Fusion 76, 243–297. doi: 10.1016/j.inffus.2021.05.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Abrahart, R. J., Anctil, F., Coulibaly, P., Dawson, C. W., Mount, N. J., See, L. M., et al. (2012). Two decades of anarchy? Emerging themes and outstanding challenges for neural network river forecasting. Prog. Phys. Geogr. 36, 480–513. doi: 10.1177/0309133312444943

CrossRef Full Text | Google Scholar

Addor, N., Newman, A. J., Mizukami, N., and Clark, M. P. (2017). The CAMELS data set: catchment attributes and meteorology for large-sample studies. Hydrol. Earth Sys. Sci. 21, 5293–5313. doi: 10.5194/hess-21-5293-2017

CrossRef Full Text | Google Scholar

Alexandrov, A., Benidis, K., Bohlke-Schneider, M., Flunkert, V., Gasthaus, J., Januschowski, T., et al. (2020). Gluonts: probabilistic and neural time series modeling in Python. J. Machine Learn. Res. 21, 1–6.

Google Scholar

Althoff, D., Rodrigues, L. N., and Bazame, H. C. (2021). Uncertainty quantification for hydrological models based on neural networks: the dropout ensemble. Stoch. Environ. Res. Risk Assess. 35, 1051–1067. doi: 10.1007/s00477-021-01980-8

CrossRef Full Text | Google Scholar

Alvarez-Garreton, C., Mendoza, P. A., Boisier, J. P., Addor, N., Galleguillos, M., Zambrano-Bigiarini, M., et al. (2018). The CAMELS-CL dataset: catchment attributes and meteorology for large sample studies – Chile dataset. Hydrol. Earth Sys. Sci. 22, 5817–5846. doi: 10.5194/hess-22-5817-2018

CrossRef Full Text | Google Scholar

Arcuri, A., and Fraser, G. (2013). Parameter tuning or default values? An empirical investigation in search-based software engineering. Empir. Softw. Eng. 18, 594–623. doi: 10.1007/s10664-013-9249-9

CrossRef Full Text | Google Scholar

Armstrong, J. S. (2001). Should we redesign forecasting competitions? Int. J. Forecast. 17, 542–545

Google Scholar

Athanasopoulos, G., and Hyndman, R. J. (2011). The value of feedback in forecasting competitions. Int. J. Forecast. 27, 845–849. doi: 10.1016/j.ijforecast.2011.03.002

CrossRef Full Text | Google Scholar

Athey, S., Tibshirani, J., and Wager, S. (2019). Generalized random forests. Ann. Stat. 47, 1148–1178. doi: 10.1214/18-AOS1709

CrossRef Full Text | Google Scholar

Bates, J. M., and Granger, C. W. J. (1969). The combination of forecasts. J. Oper. Res. Soc. 20, 451–468. doi: 10.1057/jors.1969.103

CrossRef Full Text | Google Scholar

Belle, V., and Papantonis, I. (2021). Principles and practice of explainable machine learning. Front. Big Data 4, 688969. doi: 10.3389/fdata.2021.688969

PubMed Abstract | CrossRef Full Text | Google Scholar

Beven, K., and Young, P. (2013). A guide to good practice in modeling semantics for authors and referees. Water Resour. Res. 49, 5092–5098. doi: 10.1002/wrcr.20393

CrossRef Full Text | Google Scholar

Bhattacharya, P. K., and Gangopadhyay, A. K. (1990). Kernel and nearest-neighbor estimation of a conditional quantile. Ann. Stat. 18, 1400–1415. doi: 10.1214/aos/1176347757

PubMed Abstract | CrossRef Full Text | Google Scholar

Billheimer, D. (2019). Predictive inference and scientific reproducibility. Am. Stat. 73, 291–295. doi: 10.1080/00031305.2018.1518270

CrossRef Full Text | Google Scholar

Blöschl, G., Bierkens, M. F. P., Chambel, A., Cudennec, C., Destouni, G., Fiori, A., et al. (2019). Twenty-three Unsolved Problems in Hydrology (UPH) – a community perspective. Hydrol. Sci. J. 64, 1141–1158. doi: 10.1080/02626667.2019.1620507

CrossRef Full Text | Google Scholar

Bock, A. R., Farmer, W. H., and Hay, L. E. (2018). Quantifying uncertainty in simulated streamflow and runoff from a continental-scale monthly water balance model. Adv. Water Resour. 122, 166–175. doi: 10.1016/j.advwatres.2018.10.005

CrossRef Full Text | Google Scholar

Bogner, K., Liechti, K., and Zappa, M. (2016). Post-processing of stream flows in Switzerland with an emphasis on low flows and floods. Water 8, 115. doi: 10.3390/w8040115

CrossRef Full Text | Google Scholar

Bogner, K., Liechti, K., and Zappa, M. (2017). Technical note: combining quantile forecasts and predictive distributions of streamflows. Hydrol. Earth Sys. Sci. 21, 5493–5502. doi: 10.5194/hess-21-5493-2017

CrossRef Full Text | Google Scholar

Bojer, C. S., and Meldgaard, J. P. (2021). Kaggle forecasting competitions: an overlooked learning opportunity. International J. Forecast. 37, 587–603. doi: 10.1016/j.ijforecast.2020.07.007

CrossRef Full Text | Google Scholar

Bontempi, G., and Taieb, S. B. (2011). Conditionally dependent strategies for multiple-step-ahead prediction in local learning. Int. J. Forecast. 27, 689–699. doi: 10.1016/j.ijforecast.2010.09.004

CrossRef Full Text | Google Scholar

Boulesteix, A. L., Binder, H., Abrahamowicz, M., and Sauerbrei, W. (2018). Simulation Panel of the STRATOS Initiative. On the necessity and design of studies comparing statistical methods. Biometrical J. 60, 216–218. doi: 10.1002/bimj.201700129

PubMed Abstract | CrossRef Full Text | Google Scholar

Bourgin, F., Andréassian, V., Perrin, C., and Oudin, L. (2015). Transferring global uncertainty estimates from gauged to ungauged catchments. Hydrol. Earth Sys. Sci. 19, 2535–2546. doi: 10.5194/hess-19-2535-2015

CrossRef Full Text | Google Scholar

Box, G. E. P., and Jenkins, G. M. (1970). Time Series Analysis: Forecasting and Control. San Francisco, United States: Holden-Day Inc.

Google Scholar

Brehmer, J. R., and Strokorb, K. (2019). Why scoring functions cannot assess tail properties. Electron. J. Stat. 13, 4015–4034. doi: 10.1214/19-EJS1622

CrossRef Full Text | Google Scholar

Breiman, L. (2001a). Random forests. Mach. Learn. 45, 5–32. doi: 10.1023/A:1010933404324

CrossRef Full Text | Google Scholar

Breiman, L. (2001b). Statistical modeling: the two cultures (with comments and a rejoinder by the author). Stat. Sci. 16, 199–231. doi: 10.1214/ss/1009213726

CrossRef Full Text | Google Scholar

Bröcker, J. (2012). Evaluating raw ensembles with the continuous ranked probability score. Q. J. R. Meteorol. Soc. 138, 1611–1617. doi: 10.1002/qj.1891

CrossRef Full Text | Google Scholar

Brown, R. G. (1959). Statistical Forecasting for Inventory Control. New York, United States: McGraw-Hill Book Co.

Google Scholar

Bühlmann, P., and Hothorn, T. (2007). Boosting algorithms: regularization, prediction and model fitting. Stat. Sci. 22, 477–505. doi: 10.1214/07-STS242

CrossRef Full Text | Google Scholar

Cannon, A. J. (2011). Quantile regression neural networks: implementation in R and application to precipitation downscaling. Comput. Geosci. 37, 1277–1284. doi: 10.1016/j.cageo.2010.07.005

CrossRef Full Text | Google Scholar

Castle, J. L., Doornik, J. A., and Hendry, D. F. (2021). Forecasting principles from experience with forecasting competitions. Forecasting 3, 138–165. doi: 10.3390/forecast3010010

CrossRef Full Text | Google Scholar

Chagas, V. B. P., Chaffe, P. L. B., Addor, N., Fan, F. M., Fleischmann, A. S., Paiva, R. C. D., et al. (2020). CAMELS-BR: hydrometeorological time series and landscape attributes for 897 catchments in Brazil. Earth Sys. Sci. Data 12, 2075–2096. doi: 10.5194/essd-12-2075-2020

CrossRef Full Text | Google Scholar

Chatfield, C. (1988). What is the ‘best' method of forecasting? J. Appl. Stat. 15, 19–38. doi: 10.1080/02664768800000003

CrossRef Full Text | Google Scholar

Chatfield, C. (1993). Calculating interval forecasts. J. Bus. Econ. Stat. 11, 121–135. doi: 10.1080/07350015.1993.10509938

CrossRef Full Text | Google Scholar

Chen, T., and Guestrin, C. (2016). XGBoost: a scalable tree boosting system. KDD '16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 785–794. doi: 10.1145/2939672.2939785

CrossRef Full Text | Google Scholar

Chipman, H. A., George, E. I., and McCulloch, R. E. (2012). BART: Bayesian additive regression trees. Ann. Appl. Stat. 6, 266–298. doi: 10.1214/09-AOAS285

PubMed Abstract | CrossRef Full Text | Google Scholar

Claeskens, G., Magnus, J. R., Vasnev, A. L., and Wang, W. (2016). The forecast combination puzzle: a simple theoretical explanation. Int. J. Forecast. 32, 754–762. doi: 10.1016/j.ijforecast.2015.12.005

CrossRef Full Text | Google Scholar

Clemen, R. T. (1989). Combining forecasts: a review and annotated bibliography. Int. J. Forecast. 5, 559–583. doi: 10.1016/0169-2070(89)90012-5

CrossRef Full Text | Google Scholar

Clements, M. P., and Hendry, D. F. (1999). On winning forecasting competitions in economics. Spanish Econ. Rev. 1, 123–160. doi: 10.1007/s101080050006

CrossRef Full Text | Google Scholar

Coxon, G., Addor, N., Bloomfield, J. P., Freer, J., Fry, M., Hannaford, J., et al. (2020). CAMELS-GB: hydrometeorological time series and landscape attributes for 671 catchments in Great Britain. Earth Sys. Sci. Data 12, 2459–2483. doi: 10.5194/essd-12-2459-2020

CrossRef Full Text | Google Scholar

De Gooijer, J. G., and Hyndman, R. J. (2006). 25 years of time series forecasting. Int. J. Forecast. 22, 443–473. doi: 10.1016/j.ijforecast.2006.01.001

CrossRef Full Text | Google Scholar

Diks, C. G., and Vrugt, J. A. (2010). Comparison of point forecast accuracy of model averaging methods in hydrologic applications. Stoch. Environ. Res. Risk Assess. 24, 809–820. doi: 10.1007/s00477-010-0378-z

CrossRef Full Text | Google Scholar

Dogulu, N., López López, P., Solomatine, D. P., Weerts, A. H., and Shrestha, D. L. (2015). Estimation of predictive hydrologic uncertainty using the quantile regression and UNEEC methods and their comparison on contrasting catchments. Hydrol. Earth Sys. Sci. 19, 3181–3201. doi: 10.5194/hess-19-3181-2015

CrossRef Full Text | Google Scholar

Duan, T., Avati, A., Ding, D. Y., Thai, K. K., Basu, S., Ng, A., et al. (2020). NGBoost: natural gradient boosting for probabilistic prediction. Proceedings of Machine Learning Research 119, 2690–2700.

PubMed Abstract | Google Scholar

Dunsmore, I. R. (1968). A Bayesian approach to calibration. J. Royal Stat. Soc.: B. (Methodol.) 30, 396–405. doi: 10.1111/j.2517-6161.1968.tb00740.x

CrossRef Full Text | Google Scholar

Farmer, W. H., and Vogel, R. M. (2016). On the deterministic and stochastic use of hydrologic models. Water Resour. Res. 52, 5619–5633. doi: 10.1002/2016WR019129

CrossRef Full Text | Google Scholar

Fildes, R. (2020). Learning from forecasting competitions. Int. J. Forecast. 36, 186–188. doi: 10.1016/j.ijforecast.2019.04.012

CrossRef Full Text | Google Scholar

Fildes, R., and Lusk, E. J. (1984). The choice of a forecasting model. Omega 12, 427–435. doi: 10.1016/0305-0483(84)90042-2

CrossRef Full Text | Google Scholar

Fildes, R., and Ord, K. (2002). “Forecasting competitions: their role in improving forecasting practice and research,” in A Companion to Economic Forecasting, eds M. P. Clements and D. F. Hendry (Oxford: Blackwell Publishing), 322–353. doi: 10.1002/9780470996430.ch15

CrossRef Full Text | Google Scholar

Fowler, K. J. A., Acharya, S. C., Addor, N., Chou, C., and Peel, M. C. (2021). CAMELS-AUS: hydrometeorological time series and landscape attributes for 222 catchments in Australia. Earth Sys. Sci. Data 13, 3847–3867. doi: 10.5194/essd-13-3847-2021

CrossRef Full Text | Google Scholar

Friedberg, R., Tibshirani, J., Athey, S., and Wager, S. (2020). Local linear forests. J. Comput. Graph. Stat. 30, 503–517. doi: 10.1080/10618600.2020.1831930

CrossRef Full Text | Google Scholar

Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Ann. Stat. 29, 1189–1232. doi: 10.1214/aos/1013203451

CrossRef Full Text | Google Scholar

Fulcher, B. D. (2018). “Feature-based time-series analysis,” in Feature Engineering for Machine Learning and Data Analytics, eds G. Dong and H. Liu (CRC Press), 87–116. doi: 10.1201/9781315181080-4

CrossRef Full Text | Google Scholar

Fulcher, B. D., and Jones, N. S. (2014). Highly comparative feature-based time-series classification. IEEE Trans. Knowl. Data Eng. 26, 3026–3037. doi: 10.1109/TKDE.2014.2316504

CrossRef Full Text | Google Scholar

Fulcher, B. D., Little, M. A., and Jones, N. S. (2013). Highly comparative time-series analysis: the empirical structure of time series and their methods. J. Royal Soc. Interface 10, 20130048. doi: 10.1098/rsif.2013.0048

PubMed Abstract | CrossRef Full Text | Google Scholar

Gal, Y., and Ghahramani, Z. (2016). Dropout as a Bayesian approximation: representing model uncertainty in deep learning. Proceedings of Machine Learning Research 48, 1050–1059

Google Scholar

Gasthaus, J., Benidis, K., Wang, Y., Rangapuram, S. S., Salinas, D., Flunkert, V., et al. (2020). Probabilistic forecasting with spline quantile function RNNs. Proceedings of Machine Learning Research 89, 1901–1910

Google Scholar

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., Rubin, D. B., et al. (2013). Bayesian Data Analysis, Third Edition. Chapman and Hall/CRC. doi: 10.1201/b16018

CrossRef Full Text | Google Scholar

Geweke, J., and Whiteman, C. (2006). “Chapter 1 Bayesian forecasting,” in Handbook of Economic Forecasting, eds G. Elliott, C.W. J. Granger, and A. Timmermann 1, 3–80. doi: 10.1016/S1574-0706(05)01001-3

CrossRef Full Text | Google Scholar

Giacomini, R., and Komunjer, I. (2005). Evaluation and combination of conditional quantile forecasts. J. Bus. Econ. Stat. 23, 416–431. doi: 10.1198/073500105000000018

CrossRef Full Text | Google Scholar

Girons Lopez, M., Crochemore, L., and Pechlivanidis, I. G. (2021). Benchmarking an operational hydrological model for providing seasonal forecasts in Sweden. Hydrol. Earth Sys. Sci. 25, 1189–1209. doi: 10.5194/hess-25-1189-2021

CrossRef Full Text | Google Scholar

Gneiting, T. (2011). Making and evaluating point forecasts. J. Am. Stat. Assoc. 106, 746–762. doi: 10.1198/jasa.2011.r10138

CrossRef Full Text | Google Scholar

Gneiting, T., and Katzfuss, M. (2014). Probabilistic forecasting. Ann. Rev. Stat. Appl. 1, 125–151. doi: 10.1146/annurev-statistics-062713-085831

CrossRef Full Text | Google Scholar

Gneiting, T., and Raftery, A. E. (2005). Weather forecasting with ensemble methods. Science 310, 248–249. doi: 10.1126/science.1115255

PubMed Abstract | CrossRef Full Text | Google Scholar

Gneiting, T., and Raftery, A. E. (2007). Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 102, 359–378. doi: 10.1198/016214506000001437

CrossRef Full Text | Google Scholar

Graefe, A., Armstrong, J. S., Jones, R. J. Jr., and Cuzán, A. G. (2014). Combining forecasts: an application to elections. Int. J. Forecast. 30, 43–54. doi: 10.1016/j.ijforecast.2013.02.005

CrossRef Full Text | Google Scholar

Granger, C. W. J. (1989). Invited review combining forecasts—twenty years later. J. Forecast. 8, 167–173. doi: 10.1002/for.3980080303

CrossRef Full Text | Google Scholar

Grömping, U. (2015). Variable importance in regression models. Wiley Interdisciplinary Reviews: computational Statistics 7, 137–152. doi: 10.1002/wics.1346

CrossRef Full Text | Google Scholar

Hall, C. A., Saia, S. M., Popp, A. L., Dogulu, N., Schymanski, S. J., Drost, N., et al. (2022). A hydrologist's guide to open science. Hydrol. Earth Sys. Sci. 26, 647–664. doi: 10.5194/hess-26-647-2022

CrossRef Full Text | Google Scholar

Hastie, T., Tibshirani, R., and Friedman, J. H. (2009). The Elements of Statistical Learning: Data Mining, Inference and Prediction, second edition. New York, NY: Springer. doi: 10.1007/978-0-387-84858-7

CrossRef Full Text | Google Scholar

Hemri, S., Fundel, F., and Zappa, M. (2013). Simultaneous calibration of ensemble river flow predictions over an entire range of lead times. Water Resour. Res. 49, 6744–6755. doi: 10.1002/wrcr.20542

CrossRef Full Text | Google Scholar

Hewamalage, H., Bergmeir, C., and Bandara, K. (2021). Recurrent neural networks for time series forecasting: current status and future directions. Int. J. Forecast. 37, 388–427. doi: 10.1016/j.ijforecast.2020.06.008

CrossRef Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780. doi: 10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoeting, J. A., Madigan, D., Raftery, A. E., and Volinsky, C. T. (1999). Bayesian model averaging: a tutorial. Stat. Sci. 14, 382–401. doi: 10.1214/ss/1009212519

CrossRef Full Text | Google Scholar

Hofner, B., Mayr, A., Robinzonov, N., and Schmid, M. (2014). Model-based boosting in R: a hands-on tutorial using the R package mboost. Comput. Stat. 29, 3–35. doi: 10.1007/s00180-012-0382-5

CrossRef Full Text | Google Scholar

Holt, C. C. (2004). Forecasting seasonals and trends by exponentially weighted moving averages. Int. J. Forecast. 20, 5–10. doi: 10.1016/j.ijforecast.2003.09.015

CrossRef Full Text | Google Scholar

Hsiao, C., and Wan, S. K. (2014). Is there an optimal forecast combination? J. Econom. 178, 294–309. doi: 10.1016/j.jeconom.2013.11.003

CrossRef Full Text | Google Scholar

Huang, H., Liang, Z., Li, B., Wang, D., Hu, Y., Li, Y., et al. (2019). Combination of multiple data-driven models for long-term monthly runoff predictions based on Bayesian model averaging. Water Resour. Manage. 33, 3321–3338. doi: 10.1007/s11269-019-02305-9

CrossRef Full Text | Google Scholar

Hyndman, R. J. (2020). A brief history of forecasting competitions. Int. J. Forecast. 36, 7–14. doi: 10.1016/j.ijforecast.2019.03.015

CrossRef Full Text | Google Scholar

Hyndman, R. J., and Athanasopoulos, G. (2021). Forecasting: Principles and Practice. Melbourne, Australia: OTexts. Available online at: https://otexts.com/fpp3 (accessed June 5, 2022).

Google Scholar

Hyndman, R. J., and Khandakar, Y. (2008). Automatic time series forecasting: the forecast package for R. J. Stat. Softw. 27, 1–22. doi: 10.18637/jss.v027.i03

CrossRef Full Text | Google Scholar

Hyndman, R. J., Wang, E., and Laptev, N. (2015). Large-scale unusual time series detection. 2015 IEEE International Conference on Data Mining Workshop (ICDMW), Atlantic City, NJ, 1616–1619. doi: 10.1109/ICDMW.2015.104

PubMed Abstract | CrossRef Full Text | Google Scholar

James, G., Witten, D., Hastie, T., and Tibshirani, R. (2013). An Introduction to Statistical Learning. New York: Springer. doi: 10.1007/978-1-4614-7138-7

CrossRef Full Text | Google Scholar

Januschowski, T., Gasthaus, J., Wang, Y., Salinas, D., Flunkert, V., Bohlke-Schneider, M., et al. (2020). Criteria for classifying forecasting methods. Int. J. Forecast. 36, 167–177. doi: 10.1016/j.ijforecast.2019.05.008

CrossRef Full Text | Google Scholar

Januschowski, T., Wang, Y., Torkkola, K., Erkkilä, T., Hasson, H., and Gasthaus, J. (2021). Forecasting with trees. Int. J. Forecast. doi: 10.1016/j.ijforecast.2021.10.004

CrossRef Full Text | Google Scholar

Jenkins, G. M. (1982). Some practical aspects of forecasting in organizations. J. Forecast. 1, 3–21. doi: 10.1002/for.3980010103

CrossRef Full Text | Google Scholar

Jiang, C., Jiang, M., Xu, Q., and Huang, X. (2017). Expectile regression neural network model with applications. Neurocomputing 247, 73–86. doi: 10.1016/j.neucom.2017.03.040

CrossRef Full Text | Google Scholar

Kang, Y., Hyndman, R. J., and Li, F. (2020). GRATIS: GeneRAting TIme Series with diverse and controllable characteristics. Stat. Anal. Data Min.: ASA Data Sci. J. 13, 354–376. doi: 10.1002/sam.11461

CrossRef Full Text | Google Scholar

Kang, Y., Hyndman, R. J., and Smith-Miles, K. (2017). Visualising forecasting algorithm performance using time series instance spaces. Int. J. Forecast. 33, 345–358. doi: 10.1016/j.ijforecast.2016.09.004

CrossRef Full Text | Google Scholar

Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., et al. (2017). LightGBM: a highly efficient gradient boosting decision tree. Adv. Neural Inform. Process. Sys. 30, 3146–3154.

Google Scholar

Khosravi, A., Nahavandi, S., Creighton, D., and Atiya, A. F. (2011). Comprehensive review of neural network-based prediction intervals and new advances. IEEE Trans. Neural Networks 22, 1341–1356. doi: 10.1109/TNN.2011.2162110

PubMed Abstract | CrossRef Full Text | Google Scholar

Klein, N., Nott, D. J., and Smith, M. S. (2021). Marginally calibrated deep distributional regression. J. Comput. Graph. Stat. 30, 467–483. doi: 10.1080/10618600.2020.1807996

CrossRef Full Text | Google Scholar

Klemeš, V. (1986). Operational testing of hydrological simulation models. Hydrol. Sci. J. 31, 13–24. doi: 10.1080/02626668609491024

CrossRef Full Text | Google Scholar

Klingler, C., Schulz, K., and Herrnegger, M. (2021). LamaH-CE: LArge-SaMple DAta for hydrology and environmental sciences for Central Europe. Earth Sys. Sci. Data 13, 4529–4565. doi: 10.5194/essd-13-4529-2021

CrossRef Full Text | Google Scholar

Kneib, T. (2013). Beyond mean regression. Stat. Model. 13, 275–303. doi: 10.1177/1471082X13494159

CrossRef Full Text | Google Scholar

Kneib, T., Silbersdorff, A., and Säfken, B. (2021). Rage against the mean – a review of distributional regression approaches. Econ. Stat. doi: 10.1016/j.ecosta.2021.07.006

CrossRef Full Text | Google Scholar

Knoben, W. J. M., Freer, J. E., Peel, M. C., Fowler, K. J. A., and Woods, R. A. (2020). A brief analysis of conceptual model structure uncertainty using 36 models and 559 catchments. Water Resour. Res. 56, e2019WR025975. doi: 10.1029/2019WR025975

CrossRef Full Text | Google Scholar

Koenker, R. W. (2017). Quantile regression: 40 years on. Annu. Rev. Econom. 9, 155–176. doi: 10.1146/annurev-economics-063016-103651

CrossRef Full Text | Google Scholar

Koenker, R. W., and Bassett, G. Jr. (1978). Regression quantiles. Econometrica 46, 33–50. doi: 10.2307/1913643

CrossRef Full Text | Google Scholar

Koenker, R. W., and Xiao, Z. (2006). Quantile autoregression. J. Am. Stat. Assoc. 101, 980–990. doi: 10.1198/016214506000000672

CrossRef Full Text | Google Scholar

Koutsoyiannis, D., and Montanari, A. (2022). Bluecat: a local uncertainty estimator for deterministic simulations and predictions. Water Resour. Res. 58, e2021WR031215. doi: 10.1029/2021WR031215

CrossRef Full Text | Google Scholar

Krzysztofowicz, R. (2001). The case for probabilistic forecasting in hydrology. J. Hydrol. 249, 2–9. doi: 10.1016/S0022-1694(01)00420-6

CrossRef Full Text | Google Scholar

Kuhn, M. (2021). caret: classification and regression training. R Package Version 6.0–88. Available online at: https://CRAN.R-project.org/package=caret (accessed June 5, 2022).

Google Scholar

Lampinen, J., and Vehtari, A. (2001). Bayesian approach for neural networks—review and case studies. Neural Networks 14, 257–274. doi: 10.1016/S0893-6080(00)00098-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Lecun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature 521, 436–444. doi: 10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemke, C., and Gabrys, B. (2010). Meta-learning for time series forecasting and forecast combination. Neurocomputing 73, 10–12. doi: 10.1016/j.neucom.2009.09.020

CrossRef Full Text | Google Scholar

Lerch, S., Thorarinsdottir, T. L., Ravazzolo, F., and Gneiting, T. (2017). Forecaster's dilemma: extreme events and forecast evaluation. Stat. Sci. 32, 106–127. doi: 10.1214/16-STS588

CrossRef Full Text | Google Scholar

Li, D., Marshall, L., Liang, Z., and Sharma, A. (2022). Hydrologic multi-model ensemble predictions using variational Bayesian deep learning. J. Hydrol. 604, 127221. doi: 10.1016/j.jhydrol.2021.127221

CrossRef Full Text | Google Scholar

Li, D., Marshall, L., Liang, Z., Sharma, A., and Zhou, Y. (2021). Characterizing distributed hydrological model residual errors using a probabilistic long short-term memory network. J. Hydrol. 603, 126888. doi: 10.1016/j.jhydrol.2021.126888

CrossRef Full Text | Google Scholar

Li, R., Reich, B. J., and Bondell, H. D. (2021). Deep distribution regression. Comput. Stat. Data Anal. 159, 107203. doi: 10.1016/j.csda.2021.107203

CrossRef Full Text | Google Scholar

Li, W., Duan, Q., Miao, C., Ye, A., Gong, W., Di, Z., et al. (2017). A review on statistical postprocessing methods for hydrometeorological ensemble forecasting. Wiley Interdisciplinary Reviews: Water 4, e1246. doi: 10.1002/wat2.1246

CrossRef Full Text | Google Scholar

Lichtendahl, K. C. Jr., Grushka-Cockayne, Y., and Winkler, R. L. (2013). Is it better to average probabilities or quantiles? Manage. Sci. 59, 1594–1611. doi: 10.1287/mnsc.1120.1667

CrossRef Full Text | Google Scholar

Lim, B., and Zohren, S. (2021). Time-series forecasting with deep learning: a survey. Philosophical Transactions of the Royal Society A 379, 20200209. doi: 10.1098/rsta.2020.0209

PubMed Abstract | CrossRef Full Text | Google Scholar

Linardatos, P., Papastefanopoulos, V., and Kotsiantis, S. (2020). Explainable AI: a review of machine learning interpretability methods. Entropy 23, 18. doi: 10.3390/e23010018

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, J., Yuan, X., Zeng, J., Jiao, Y., Li, Y., Zhong, L., et al. (2022). Ensemble streamflow forecasting over a cascade reservoir catchment with integrated hydrometeorological modeling and machine learning. Hydrol. Earth Sys. Sci. 26, 265–278. doi: 10.5194/hess-26-265-2022

CrossRef Full Text | Google Scholar

López López, P., Verkade, J. S., Weerts, A. H., and Solomatine, D. P. (2014). Alternative configurations of quantile regression for estimating predictive uncertainty in water level forecasts for the upper Severn River: a comparison. Hydrol. Earth Sys. Sci. 18, 3411–3428. doi: 10.5194/hess-18-3411-2014

CrossRef Full Text | Google Scholar

Maier, H. R., Jain, A., Dandy, G. C., and Sudheer, K. P. (2010). Methods used for the development of neural networks for the prediction of water resource variables in river systems: current status and future directions. Environ. Model. Software 25, 891–909. doi: 10.1016/j.envsoft.2010.02.003

CrossRef Full Text | Google Scholar

Makridakis, S., Fry, C., Petropoulos, F., and Spiliotis, E. (2021). The future of forecasting competitions: design attributes and principles. INFORMS J. Data Sci. doi: 10.1287/ijds.2021.0003

CrossRef Full Text | Google Scholar

Martindale, N., Ismail, M., and Talbert, D. A. (2020). Ensemble-based online machine learning algorithms for network intrusion detection systems using streaming data. Information 11, 315. doi: 10.3390/info11060315

CrossRef Full Text | Google Scholar

Matijaš, M., Suykens, J. A., and Krajcar, S. (2013). Load forecasting using a multivariate meta-learning system. Expert Sys. Appl. 40, 4427–4437. doi: 10.1016/j.eswa.2013.01.047

CrossRef Full Text | Google Scholar

Mayr, A., Fenske, N., Hofner, B., Kneib, T., and Schmid, M. (2012). Generalized additive models for location, scale and shape for high dimensional data: a flexible approach based on boosting. J. Royal Stat. Soc. C. (Appl. Stat.) 61, 403–427. doi: 10.1111/j.1467-9876.2011.01033.x

PubMed Abstract | CrossRef Full Text | Google Scholar

McMillan, H. (2020). Linking hydrologic signatures to hydrologic processes: a review. Hydrol. Process. 34, 1393–1409. doi: 10.1002/hyp.13632

CrossRef Full Text | Google Scholar

McMillan, H., Westerberg, I., and Branger, F. (2017). Five guidelines for selecting hydrological signatures. Hydrol. Process. 31, 4757–4761. doi: 10.1002/hyp.11300

CrossRef Full Text | Google Scholar

Mehr, A. D., Nourani, V., Kahya, E., Hrnjica, B., Sattar, A. M. A., Yaseen, Z. M., et al. (2018). Genetic programming in water resources engineering: a state-of-the-art review. J. Hydrol. 566, 643–667. doi: 10.1016/j.jhydrol.2018.09.043

CrossRef Full Text | Google Scholar

Meinshausen, N. (2006). Quantile regression forests. J. Machine Learn. Res. 7, 983–999

Google Scholar

Montanari, A. (2011). “Uncertainty of hydrological predictions,” in Treatise on Water Science 2, ed P. A. Wilderer (Elsevier), 459–478. doi: 10.1016/B978-0-444-53199-5.00045-2

CrossRef Full Text | Google Scholar

Montanari, A., and Brath, A. (2004). A stochastic approach for assessing the uncertainty of rainfall-runoff simulations. Water Resour. Res. 40, W01106. doi: 10.1029/2003WR002540

CrossRef Full Text | Google Scholar

Montanari, A., and Grossi, G. (2008). Estimating the uncertainty of hydrological forecasts: a statistical approach. Water Resour. Res. 44, W00B08. doi: 10.1029/2008WR006897

CrossRef Full Text | Google Scholar

Montanari, A., and Koutsoyiannis, D. (2012). A blueprint for process-based modeling of uncertain hydrological systems. Water Resour. Res. 48, W09555. doi: 10.1029/2011WR011412

CrossRef Full Text | Google Scholar

Montanari, A., Young, G., Savenije, H. H. G., Hughes, D., Wagener, T., Ren, L. L., et al. (2013). “Panta Rhei—Everything Flows”: change in hydrology and society—The IAHS Scientific Decade 2013–2022. Hydrol. Sci. J. 58, 1256–1275. doi: 10.1080/02626667.2013.809088

CrossRef Full Text | Google Scholar

Montero-Manso, P., Athanasopoulos, G., Hyndman, R. J., and Talagala, T. S. (2020). FFORMA: feature-based forecast model averaging. Int. J. Forecast. 36, 86–92. doi: 10.1016/j.ijforecast.2019.02.011

CrossRef Full Text | Google Scholar

Moon, S. J., Jeon, J.-J., Lee, J. S. H., and Kim, Y. (2021). Learning multiple quantiles with neural networks. J. Comput. Graph. Stat. 30, 1238–1248. doi: 10.1080/10618600.2021.1909601

CrossRef Full Text | Google Scholar

Newey, W. K., and Powell, J. L. (1987). Asymmetric least squares estimation and testing. Econometrica 55, 819–847. doi: 10.2307/1911031

CrossRef Full Text | Google Scholar

Newman, A. J., Clark, M. P., Sampson, K., Wood, A., Hay, L. E., Bock, A., et al. (2015). Development of a large-sample watershed-scale hydrometeorological data set for the contiguous USA: data set characteristics and assessment of regional variability in hydrologic model performance. Hydrol. Earth Sys. Sci. 19, 209–223. doi: 10.5194/hess-19-209-2015

CrossRef Full Text | Google Scholar

Papacharalampous, G. A., Koutsoyiannis, D., and Montanari, A. (2020a). Quantification of predictive uncertainty in hydrological modelling by harnessing the wisdom of the crowd: methodology development and investigation using toy models. Adv. Water Resour. 136, 103471. doi: 10.1016/j.advwatres.2019.103471

CrossRef Full Text | Google Scholar

Papacharalampous, G. A., and Tyralis, H. (2020). Hydrological time series forecasting using simple combinations: big data testing and investigations on one-year ahead river flow predictability. J. Hydrol. 590, 125205. doi: 10.1016/j.jhydrol.2020.125205

CrossRef Full Text | Google Scholar

Papacharalampous, G. A., Tyralis, H., Koutsoyiannis, D., and Montanari, A. (2020b). Quantification of predictive uncertainty in hydrological modelling by harnessing the wisdom of the crowd: a large-sample experiment at monthly timescale. Adv. Water Resour. 136, 103470. doi: 10.1016/j.advwatres.2019.103470

CrossRef Full Text | Google Scholar

Papacharalampous, G. A., Tyralis, H., Langousis, A., Jayawardena, A. W., Sivakumar, B., Mamassis, N., et al. (2019). Probabilistic hydrological post-processing at scale: why and how to apply machine-learning quantile regression algorithms. Water 11, 2126. doi: 10.3390/w11102126

CrossRef Full Text | Google Scholar

Papacharalampous, G. A., Tyralis, H., Pechlivanidis, I., Grimaldi, S., and Volpi, E. (2022). Massive feature extraction for explaining and foretelling hydroclimatic time series forecastability at the global scale. Geosci. Front. 13, 101349. doi: 10.1016/j.gsf.2022.101349

CrossRef Full Text | Google Scholar

Pechlivanidis, I. G., Crochemore, L., Rosberg, J., and Bosshard, T. (2020). What are the key drivers controlling the quality of seasonal streamflow forecasts? Water Resour. Res. 56, e2019WR026987. doi: 10.1029/2019WR026987

CrossRef Full Text | Google Scholar

Petropoulos, F., Apiletti, D., Assimakopoulos, V., Babai, M. Z., Barrow, D. K., Taieb, S. B., et al. (2022). Forecasting: theory and practice. Int. J. Forecast. 38, 705–871. doi: 10.1016/j.ijforecast.2021.11.001

CrossRef Full Text | Google Scholar

Pratola, M. T., Chipman, H. A., George, E. I., and McCulloch, R. E. (2020). Heteroscedastic BART via multiplicative regression trees. J. Comput. Graph. Stat. 29, 405–417. doi: 10.1080/10618600.2019.1677243

CrossRef Full Text | Google Scholar

Python Software Foundation (2022). Python Language Reference. Available online at: http://www.python.org (accessed June 5, 2022).

Google Scholar

Quilty, J., Adamowski, J., and Boucher, M. A. (2019). A stochastic data-driven ensemble forecasting framework for water resources: a case study using ensemble members derived from a database of deterministic wavelet-based models. Water Resour. Res. 55, 175–202. doi: 10.1029/2018WR023205

CrossRef Full Text | Google Scholar

Quilty, J. M., Sikorska-Senoner, A. E., and Hah, D. (2022). A stochastic conceptual-data-driven approach for improved hydrological simulations. Environ. Model. Software 149, 105326. doi: 10.1016/j.envsoft.2022.105326

CrossRef Full Text | Google Scholar

R Core Team (2022). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. Available online at: https://www.R-project.org (accessed June 5, 2022).

Google Scholar

Raghavendra, S., and Deka, P. C. (2014). Support vector machine applications in the field of hydrology: a review. Appl. Soft Comput. 19, 372–386. doi: 10.1016/j.asoc.2014.02.002

CrossRef Full Text | Google Scholar

Regonda, S. K., Seo, D. J., Lawrence, B., Brown, J. D., and Demargne, J. (2013). Short-term ensemble streamflow forecasting using operationally-produced single-valued streamflow forecasts – a Hydrologic Model Output Statistics (HMOS) approach. J. Hydrol. 497, 80–96. doi: 10.1016/j.jhydrol.2013.05.028

CrossRef Full Text | Google Scholar

Rigby, R. A., and Stasinopoulos, D. M. (2005). Generalized additive models for location, scale and shape. J. Royal Stat. Soc.: C. (Appl. Stat.) 54, 507–554. doi: 10.1111/j.1467-9876.2005.00510.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberts, H. V. (1965). Probabilistic prediction. J. Am. Stat. Assoc. 60, 50–62. doi: 10.1080/01621459.1965.10480774

CrossRef Full Text | Google Scholar

Romero-Cuellar, J., Gastulo-Tapia, C. J., Hernández-López, M. R., Prieto Sierra, C., and Francés, F. (2022). Towards an extension of the model conditional processor: predictive uncertainty quantification of monthly streamflow via Gaussian mixture models and clusters. Water 14, 1261. doi: 10.3390/w14081261

CrossRef Full Text | Google Scholar

Roscher, R., Bohn, B., Duarte, M. F., and Garcke, J. (2020). Explainable machine learning for scientific insights and discoveries. IEEE Access 8, 42200–42216. doi: 10.1109/ACCESS.2020.2976199

PubMed Abstract | CrossRef Full Text | Google Scholar

Sagi, O., and Rokach, L. (2018). Ensemble learning: a survey. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 8, e1249. doi: 10.1002/widm.1249

CrossRef Full Text | Google Scholar

Salinas, D., Flunkert, V., Gasthaus, J., and Januschowski, T. (2020). DeepAR: probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 36, 1181–1191. doi: 10.1016/j.ijforecast.2019.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlosser, L., Hothorn, T., Stauffer, R., and Zeileis, A. (2019). Distributional regression forests for probabilistic precipitation forecasting in complex terrain. Ann. Appl. Stat. 13, 1564–1589. doi: 10.1214/19-AOAS1247

CrossRef Full Text | Google Scholar

Serpell, C., Araya, I., Valle, C., and Allende, H. (2019). Probabilistic forecasting using Monte Carlo dropout neural networks. Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications, 387–397. doi: 10.1007/978-3-030-33904-3_36

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, C. (2018). A trans-disciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 54, 8558–8593. doi: 10.1029/2018WR022643

CrossRef Full Text | Google Scholar

Shmueli, G. (2010). To explain or to predict? Stat. Sci. 25, 289–310. doi: 10.1214/10-STS330

CrossRef Full Text | Google Scholar

Sikorska, A. E., Montanari, A., and Koutsoyiannis, D. (2015). Estimating the uncertainty of hydrological predictions through data-driven resampling techniques. J. Hydrol. Eng. 20, A4014009. doi: 10.1061/(ASCE)HE.1943-5584.0000926

CrossRef Full Text | Google Scholar

Sikorska-Senoner, A. E., and Quilty, J. M. (2021). A novel ensemble-based conceptual-data-driven approach for improved streamflow simulations. Environ. Model. Software 143, 105094. doi: 10.1016/j.envsoft.2021.105094

CrossRef Full Text | Google Scholar

Sivakumar, B., and Berndtsson, R. (2010). Advances in Data-Based Approaches for Hydrologic Modeling and Forecasting. Singapore: World Scientific Publishing Company. doi: 10.1142/7783

CrossRef Full Text | Google Scholar

Smith, J., and Wallis, K. F. (2009). A simple explanation of the forecast combination puzzle. Oxf. Bull. Econ. Stat. 71, 331–355. doi: 10.1111/j.1468-0084.2008.00541.x

CrossRef Full Text | Google Scholar

Smyl, S. (2020). A hybrid method of exponential smoothing and recurrent neural networks for time series forecasting. Int. J. Forecast. 36, 75–85. doi: 10.1016/j.ijforecast.2019.03.017

CrossRef Full Text | Google Scholar

Solomatine, D. P., and Ostfeld, A. (2008). Data-driven modelling: some past experiences and new approaches. J. Hydroinform. 10, 3–22. doi: 10.2166/hydro.2008.015

CrossRef Full Text | Google Scholar

Solomatine, D. P., and Shrestha, D. L. (2009). A novel method to estimate model uncertainty using machine learning techniques. Water Resour. Res. 45. doi: 10.1029/2008WR006839

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, H., Diethe, T., Kull, M., and Flach, P. (2019). Distribution calibration for regression. Proceedings of Machine Learning Research 97, 5897–5906

Google Scholar

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: a simple way to prevent neural networks from overfitting. J. Machine Learn. Res. 15, 1929–1958

PubMed Abstract | Google Scholar

Tagasovska, N., and Lopez-Paz, D. (2019). Single-model uncertainties for deep learning. Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, Canada

Google Scholar

Taggart, R. (2022). Evaluation of point forecasts for extreme events using consistent scoring functions. Q. J. Royal Meteorol. Soc. 148, 306–320. doi: 10.1002/qj.4206

CrossRef Full Text | Google Scholar

Taieb, S. B., Bontempi, G., Atiya, A. F., and Sorjamaa, A. (2012). A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. Expert Sys. Appl. 39, 7067–7083. doi: 10.1016/j.eswa.2012.01.039

CrossRef Full Text | Google Scholar

Talagala, T. S., Li, F., and Kang, Y. (2021). FFORMPP: feature-based forecast model performance prediction. Int. J. Forecast. 38, 920–943. doi: 10.1016/j.ijforecast.2021.07.002

CrossRef Full Text | Google Scholar

Taylor, J. W. (2000). A quantile regression neural network approach to estimating the conditional density of multiperiod returns. J. Forecast. 19, 299–311. doi: 10.1002/1099-131x(200007)19:4<299::aid-for775>3.3.co;2-m

CrossRef Full Text | Google Scholar

Taylor, S. J., and Letham, B. (2018). Forecasting at scale. Am. Stat. 72, 37–45. doi: 10.1080/00031305.2017.1380080

CrossRef Full Text | Google Scholar

Timmermann, A. (2006). “Chapter 4 forecast combinations,” in Handbook of Economic Forecasting, eds G. Elliott, C.W. J. Granger, and A. Timmermann 1, 135–196. doi: 10.1016/S1574-0706(05)01004-9

CrossRef Full Text | Google Scholar

Todini, E. (2007). Hydrological catchment modelling: past, present and future. Hydrol. Earth Sys. Sci. 11, 468–482. doi: 10.5194/hess-11-468-2007

CrossRef Full Text | Google Scholar

Torossian, L., Picheny, V., Faivre, R., and Garivier, A. (2020). A review on quantile regression for stochastic computer experiments. Reliab. Eng. Sys. Saf. 201, 106858. doi: 10.1016/j.ress.2020.106858

CrossRef Full Text | Google Scholar

Tyralis, H., and Papacharalampous, G. A. (2021a). Boosting algorithms in energy research: a systematic review. Neural Comput. Appl. 33, 14101–14117. doi: 10.1007/s00521-021-05995-8

CrossRef Full Text | Google Scholar

Tyralis, H., and Papacharalampous, G. A. (2021b). Quantile-based hydrological modelling. Water 13, 3420. doi: 10.3390/w13233420

CrossRef Full Text | Google Scholar

Tyralis, H., and Papacharalampous, G. A. (2022). Hydrological Post-Processing for Predicting Extreme Quantiles. Available online at: https://arxiv.org/abs/2202.13166 (accessed June 5, 2022).

Google Scholar

Tyralis, H., Papacharalampous, G. A., Burnetas, A., and Langousis, A. (2019a). Hydrological post-processing using stacked generalization of quantile regression algorithms: large-scale application over CONUS. J. Hydrol. 577, 123957. doi: 10.1016/j.jhydrol.2019.123957

CrossRef Full Text | Google Scholar

Tyralis, H., Papacharalampous, G. A., and Khatami, S. (2022). Expectile-Based Hydrological Modelling for Uncertainty Estimation: Life After Mean. Available online at: https://arxiv.org/abs/2201.05712 (accessed June 5, 2022).

Google Scholar

Tyralis, H., Papacharalampous, G. A., and Langousis, A. (2019b). A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 11, 910. doi: 10.3390/w11050910

CrossRef Full Text | Google Scholar

Tyralis, H., Papacharalampous, G. A., and Langousis, A. (2021). Super ensemble learning for daily streamflow forecasting: large-scale demonstration and comparison with multiple machine learning algorithms. Neural Comput. Appl. 33, 3053–3068. doi: 10.1007/s00521-020-05172-3

CrossRef Full Text | Google Scholar

Umlauf, N., Klein, N., and Zeileis, A. (2018). BAMLSS: Bayesian additive models for location, scale, and shape (and beyond). J. Comput. Graph. Stat. 27, 612–627. doi: 10.1080/10618600.2017.1407325

CrossRef Full Text | Google Scholar

Vrugt, J. A., and Robinson, B. A. (2007). Treatment of uncertainty using ensemble methods: comparison of sequential data assimilation and Bayesian model averaging. Water Resour. Res. 43, W01411. doi: 10.1029/2005WR004838

CrossRef Full Text | Google Scholar

Waldmann, E. (2018). Quantile regression: a short story on how and why. Stat. Model. 18, 203–218. doi: 10.1177/1471082X18759142

CrossRef Full Text | Google Scholar

Wallis, K. F. (2011). Combining forecasts–forty years later. Appl. Financ. Econ. 21, 33–41. doi: 10.1080/09603107.2011.523179

CrossRef Full Text | Google Scholar

Wang, H. J., and Li, D. (2013). Estimation of extreme conditional quantiles through power transformation. J. Am. Stat. Assoc. 108, 1062–1074. doi: 10.1080/01621459.2013.820134

CrossRef Full Text | Google Scholar

Wang, H. J., Li, D., and He, X. (2012). Estimation of high conditional quantiles for heavy-tailed distributions. J. Am. Stat. Assoc. 107, 1453–1464. doi: 10.1080/01621459.2012.716382

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Hyndman, R. J., Li, F., and Kang, Y. (2022). Forecast Combinations: An Over 50-Year Review. Available online at: https://arxiv.org/abs/2205.04216 (accessed June 5, 2022).

Google Scholar

Wang, X., Smith, K., and Hyndman, R. J. (2006). Characteristic-based clustering for time series data. Data Min. Knowl. Discov. 13, 335–364. doi: 10.1007/s10618-005-0039-x

CrossRef Full Text | Google Scholar

Wang, X., Smith-Miles, K., and Hyndman, R. (2009). Rule induction for forecasting method selection: meta-learning the characteristics of univariate time series. Neurocomputing 72, 2581–2594. doi: 10.1016/j.neucom.2008.10.017

CrossRef Full Text | Google Scholar

Wani, O., Beckers, J. V. L., Weerts, A. H., and Solomatine, D. P. (2017). Residual uncertainty estimation using instance-based learning with applications to hydrologic forecasting. Hydrol. Earth Sys. Sci. 21, 4021–4036. doi: 10.5194/hess-21-4021-2017

CrossRef Full Text | Google Scholar

Weerts, A. H., Winsemius, H. C., and Verkade, J. S. (2011). Estimation of predictive hydrological uncertainty using quantile regression: examples from the National Flood Forecasting System (England and Wales). Hydrol. Earth Sys. Sci. 15, 255–265. doi: 10.5194/hess-15-255-2011

CrossRef Full Text | Google Scholar

Wei, P., Lu, Z., and Song, J. (2015). Variable importance analysis: a comprehensive review. Reliab. Eng. Sys. Saf. 142, 399–432. doi: 10.1016/j.ress.2015.05.018

CrossRef Full Text | Google Scholar

Winkler, R. L. (2015). Equal versus differential weighting in combining forecasts. Risk Anal. 35, 16–18. doi: 10.1111/risa.12302

PubMed Abstract | CrossRef Full Text | Google Scholar

Winkler, R. L., Grushka-Cockayne, Y., Lichtendahl, K. C., and Jose, V. R. R. (2019). Probability forecasts and their combination: a research perspective. Decision Anal. 16, 239–260. doi: 10.1287/deca.2019.0391

CrossRef Full Text | Google Scholar

Winters, P. R. (1960). Forecasting sales by exponentially weighted moving averages. Manage. Forecast. 6, 324–342. doi: 10.1287/mnsc.6.3.324

CrossRef Full Text | Google Scholar

Wolpert, D. H. (1992). Stacked generalization. Neural Networks 5, 241–259. doi: 10.1016/S0893-6080(05)80023-1

CrossRef Full Text | Google Scholar

Wolpert, D. H. (1996). The lack of a priori distinctions between learning algorithms. Neural Comput. 8, 1341–1390. doi: 10.1162/neco.1996.8.7.1341

CrossRef Full Text | Google Scholar

Xie, Z., and Wen, H. (2019). Composite Quantile Regression Long Short-Term Memory Network. Artificial Neural Networks and Machine Learning – ICANN 2019: Text and Time Series 513–524. doi: 10.1007/978-3-030-30490-4_41

CrossRef Full Text | Google Scholar

Xu, L., Chen, N., Zhang, X., and Chen, Z. (2018). An evaluation of statistical, NMME and hybrid models for drought prediction in China. J. Hydrol. 566, 235–249. doi: 10.1016/j.jhydrol.2018.09.020

CrossRef Full Text | Google Scholar

Xu, Q., Deng, K., Jiang, C., Sun, F., and Huang, X. (2017). Composite quantile regression neural network with applications. Expert Sys. Appl. 76, 129–139. doi: 10.1016/j.eswa.2017.01.054

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Q., Liu, S., Jiang, C., and Zhuo, X. (2021). QRNN-MIDAS: a novel quantile regression neural network for mixed sampling frequency data. Neurocomputing 457, 84–105. doi: 10.1016/j.neucom.2021.06.006

CrossRef Full Text | Google Scholar

Xu, Q., Liu, X., Jiang, C., and Yu, K. (2016). Quantile autoregression neural network model with applications to evaluating value at risk. Appl. Soft Comput. 49, 1–12. doi: 10.1016/j.asoc.2016.08.003

CrossRef Full Text | Google Scholar

Yao, Y., Vehtari, A., Simpson, D., and Gelman, A. (2018). Using stacking to average Bayesian predictive distributions. Bayesian Anal. 13, 917–1003. doi: 10.1214/17-BA1091

CrossRef Full Text | Google Scholar

Yaseen, Z. M., El-Shafie, A., Jaafar, O., Afan, H. A., and Sayl, K. N. (2015). Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 530, 829–844. doi: 10.1016/j.jhydrol.2015.10.038

CrossRef Full Text | Google Scholar

Yuan, S. (2015). Random gradient boosting for predicting conditional quantiles. J. Stat. Comput. Simulat. 85, 3716–3726. doi: 10.1080/00949655.2014.1002099

CrossRef Full Text | Google Scholar

Yuan, X., Wood, E. F., and Ma, Z. (2015). A review on climate-model-based seasonal hydrologic forecasting: physical understanding and system development. Wiley Interdisciplinary Reviews: Water 2, 523–536. doi: 10.1002/wat2.1088

CrossRef Full Text | Google Scholar

Zhang, Z., Zhang, Q., and Singh, V. P. (2018). Univariate streamflow forecasting using commonly used data-driven models: literature review and case study. Hydrol. Sci. J. 63, 1091–1111. doi: 10.1080/02626667.2018.1469756

CrossRef Full Text | Google Scholar