Efficacy of Riparian Buffers in Phosphorus Removal: A Meta-Analysis

Efficacious use of riparian buffers (RBs) is a mitigation strategy that can protect water quality in the face of climate change and agricultural intensification. We investigated the efficacy of RBs in reducing phosphorus (P) and identified effective RB designs using two quantitative meta-analytic approaches, i.e., traditional random-effects meta-analysis and Bayesian mixed-effects regression, to synthesize the results from 36 peer-reviewed articles. We found that the overall P removal efficacy of RBs is 54.5% with a 95% confidence interval (46.1, 61.6), as indicated by our traditional meta-analysis, and 51.3% on average with a 95% confidence level (19.6, 71.2), as estimated by our Bayesian meta-analysis. The effectiveness of RBs was reduced by soil that was either bare, water-saturated, or covered by snowmelt. The interactive effect of width and slope on P removal in RBs varied considerably across different soils, leading to a larger variation in P removal efficacy, as compared to other studies. Our results show that width is the predominant determinant for P retention efficiency in clay soil RBs, whereas in sandy soil RBs, slope is the leading factor. Our findings can provide policymakers and managers with RB design criteria to maximize P retention.

Introduction

Growing human population together with climate change is likely to lead to the degradation of water quality in lakes, rivers, and oceans. Meeting the caloric needs of expanding human populations will necessitate agricultural intensification as well as the expansion of the land area in agricultural production (Keating et al., 2014; Kummu et al., 2017). Agricultural expansion and intensification are likely to result in increasing flows of nutrients to adjacent water bodies. Phosphorus (P) is a primary component of agricultural fertilizer, and the leakage of P from agriculture to adjacent waterways leads to decrease in water quality through eutrophication and harmful algae blooms (HABs) (Bennett et al., 2001; Scheffer et al., 2001). In addition, climate change is expected to increase the sensitivity of water bodies to the influx of P; increasing water temperature over longer periods of time contributes to eutrophication and more frequent and intensive HABs (Zia et al., 2016; Nazari-Sharabian et al., 2018). The expected effect of climate change and agricultural intensification and expansion reduce water quality with negative impacts on ecosystem function as well as human health.

Riparian buffers (RBs) are a potential mitigation strategy that can reduce the transport of P to adjacent waterways, thus, protecting water quality in the face of climate change and agricultural intensification. In agricultural watersheds, excess P produced by farms is transported via overland runoff. RBs are often considered one of the most effective best management practices (BMPs) to improve water quality in lake systems, as they can intercept P-reducing transport to adjacent waterways. As a result, substantial governmental funds are appropriated annually to establish RBs. For example, as of the fiscal year 2012, the Conservation Reserve Program (CRP) reported that ~0.35 million hectares of RBs were installed on a continuous basis either through the Conservation Reserve Enhancement Program (CREP) or non-CREP in the U.S. (USDA, 2012). On average, US$326 and US$230 were paid for each hectare of CREP and non-CREP enrollment, respectively, on a continuous basis in 2012 across the U.S. This leads to our inquiry into RBs' effectiveness in intercepting P through a quantitative literature review.

The efficacy of RBs for nutrient mitigation is driven by multiple factors (Dorioz et al., 2006). Most previous reviews of RBs are either qualitative (e.g., McDowell et al., 2004; Dorioz et al., 2006; Hoffmann et al., 2009; Cole et al., 2020) or, if quantitative, mainly assess the effects of at most four aspects of RB design and implementation (e.g., Mayer et al., 2007; Zhang et al., 2010; Sweeney and Newbold, 2014; Land et al., 2016). We evaluated the effects of a wider spectrum of RB parameters on P removal efficacy by employing two quantitative meta-analytic approaches, namely, traditional and regression meta-analyses. Using two meta-analytic approaches is helpful in drawing inferences given that a wider spectrum of RB parameters is assessed in this study than in other studies in the literature. We considered the effect of seven RB specifications, including two continuous variables (i.e., width and slope) and five categorical variables (i.e., soil, vegetation, P application practices in adjacent fields, on-site infiltration capacity, and P transport pathway). Traditional meta-analysis was used to infer P reduction levels by considering a categorical parameter one at a time. We used a regression meta-analysis to infer P reduction levels given a consideration of all RB parameters simultaneously with synergistic effects.

In summary, this study expands the existing quantitative RB reviews by using a larger sample size, accounting for more factors and their interactions, and using two meta-analytic approaches for improving statistical inferences. The results of this study can help guide the design of RBs and maximize the effectiveness of governmental RB funds to reduce P transport from farms.

Materials and Methods

Data Collection

We used three databases, i.e., Web of Science, Science Direct, and Google Scholar, to locate peer-reviewed studies reporting the P removal efficacy of RBs. In the scope of this article, we considered RBs, riparian zones, buffer strips, vegetated filter strips, and grass strips to be synonymous. We selected studies (1) that were published within a 25-year time period between January 1990 and June 2015, (2) in which study sites were located in the USA or Canada, (3) that had provided P reduction in the forms of total phosphorus (TP), particulate phosphorus (PP), dissolved phosphorus (DP), or P in agricultural settings, (4) in which control experiments were performed, and (5) that are not review studies. We included studies reporting any of the four P forms (i.e., TP, PP, DP, and P) to increase the number of potential studies; TP is assumed to measure both dissolved and particulate P in a sample in routine P analyses (Sheppard et al., 2006). Our search strategy for Google Scholar, which was conducted in June 2015, included setting the publication date of studies to <25 years and using the phrase “riparian buffer effectiveness in reducing Total phosphorus or Particulate Phosphorous” in which “riparian buffer” was also replaced with “riparian buffer zone,” “vegetated buffer,” “vegetated buffer strip,” “vegetated filter strip,” and “grass strip” for further search. Our literature search procedure is summarized in a flowchart (Figure 1) conforming to the statement of Preferred Reporting Items for Systematic reviews and Meta-Analyses (PRISMA) suggested by Moher et al. (2009). A total of 36 peer-reviewed articles were selected for further review. We assessed the methodological quality of these 36 studies using “hierarchy of evidence quality (Table 1),” modified by Pullin and Knight (2003) and commonly used by system review studies in environmental science. We also assessed the publication bias of these 36 studies using a funnel plot and Egger's test.

FIGURE 1

Figure 1. PRISMA flow diagram of our literature search.

TABLE 1

Table 1. Hierarchy of evidence quality.

We summarized the study design features of these 36 studies in Table A1. Soil descriptions from these studies were clustered into four classes using the USDA soil textural triangle (USDA, 1987). These four classes, ordered by ascending grain size, are clay, silt, loam, or sand. Each class indicates the predominant soil in an RB, though it is not necessarily the only class present. This soil clustering introduces uncertainties; however, a collapsed stratification was necessary for evaluating the effects of RB soil on P removal.

We used discrete categories to represent on-site infiltration capacity, because quantitative measurements (e.g., infiltration rate, rainfall intensity, and runoff velocity) commonly used for determining this parameter were not often provided by the 36 studies. As shown in Table A1, on-site infiltration capacity was determined based on runoff source and its relative effects on soil. This parameter was denoted as low, medium, or indeterminate. The sites monitored under naturally occurred or simulated rainfall were denoted as medium-level infiltration capacity. The sites observed under hydraulically overloaded conditions, flooded irrigation, or wet rainfall season were coded with low infiltration capacity. The RBs monitored during snowmelt were coded as indeterminate infiltration capacity, because additional measurements for determining meltwater infiltration, such as thickness of snow cover and timing of snowmelt, were not available (Iwata et al., 2010).

Discrete levels, i.e., low, medium, or high, were also used to describe P inputs in the fields adjacent to RBs, because most studies did not measure P in these fields. Category assignments were based on nutrient types applied in these fields. Applications of manure, fertilizer, wastewater, crop residuals, and chemicals in adjacent fields were considered high P inputs. On-site sediment and biosolids were regarded as medium P inputs. If nutrients were not applied in adjacent fields, this was coded as low.

Two classes representing P removal pathways were assigned based on sample locations, namely, surface and subsurface. The surface pathway indicates P transport via surface runoff. The subsurface pathway encompasses P transport either through subsurface flow or soil.

P measurements were not consistent across the reviewed studies. P entering (M₀) or leaving (M_e) RBs were measured as mass, flux, or flow-weighted concentration. Some of the 36 studies also provided P removal efficacy, $R_d=100\left(1-\frac{M_e}{M_0}\right)$. Due to this heterogeneity, we chose to use P removal efficacy, which is based on the ratio of M_e to M₀, rather than the difference between M₀ and M_e. P removal efficacy of RBs in the scope of this study, denoted as R_d, is expressed as

$\begin{array}{ll}{R}_d=100\left(1-\frac{M_e}{M_0}\right)=100(1-R_r)& (1)\end{array}$

where R_r is termed the P response ratio of RBs.

While the majority of the published studies report that RBs are generally effective in reducing P, there exists a wide variation in P removal efficacy estimates in the literature. For example, of the 36 published studies reviewed here (Table A1), Pratt and Fox (2009) reported P removal efficacy estimates ranging between −2,400 and 72.2%, while Lim et al. (1998) reported a range between 75.5 and 94.1%. This wide range of estimates could be attributed to the variations in the RB specifications, such as design parameters (e.g., width and vegetation) and site characteristics (e.g., slope, soil, on-site infiltration capacity, weather condition during experiments, and nutrient application practices in agricultural fields). In addition, differences in study designs (e.g., experimental design, methods, and choice of observation parameters) may also contribute to the uncertainty of P removal efficacy of RBs.

Meta-Analysis Frameworks

Meta-analysis is a useful technique for synthesizing information from various data sources. In traditional meta-analysis, commonly used by medical, health, and ecological sciences (Mrozek and Taylor, 2002), statistical details are pooled across studies by assigning weights to each based on their data sizes (Hedges et al., 1999; Kulinskaya et al., 2008; Borenstein et al., 2009, 2010). The overall outcome of an intervention is then estimated by summing the weighted means of all studies. However, regression meta-analysis can also be used to conduct a meta-analysis, e.g., in studies of nutrient removal efficacy of RBs (e.g., Mayer et al., 2007; Zhang et al., 2010; Sweeney and Newbold, 2014). In these examples, pooled evidence came from the original raw data, rather than from each study's weighted estimate of interest (e.g., P removal efficacy).

We used two meta-analysis frameworks to assess the effects of RB design specifications on P removal efficacy, namely, traditional random-effects meta-analysis and mixed-effects regression meta-analysis using Bayesian methods. The latter accounts for both fixed and random effects. We encompassed random-effects because the idiosyncrasies of the studies reviewed lead to significant variations from both within- and between-groups. We evaluated the effects of predictors (shown in Table 2) on R_r in natural logarithm space and then transformed the results back to real space, because ln(R_r) can be well-approximated by normal distribution. This ensures that the confidence intervals of R_r and R_d resulting from our meta-analyses are reliable (Hedges et al., 1999).

TABLE 2

Table 2. Descriptions of the variables used in our meta-analysis.

Traditional Random-Effects Meta-Analysis

We followed the traditional meta-analysis procedures suggested by Hedges et al. (1999) to evaluate the effects of RB characteristics on ln(R_r). First, we estimated the mean (${\overline{L}}_j$) and within-study variance (${\widehat{V}}_j$) of ln(R_r) for each study (j) using Equations (3) and (4). Given that the mean of R_r for each study (j) is:

$\begin{array}{ll}{{\overline{R}}_r}_j=\frac{{{\overline{M}}_e}_j}{{{\overline{M}}_0}_j},& (2)\end{array}$

where ${{\overline{M}}_0}_j$ and ${{\overline{M}}_e}_j$ represent the means of M₀ and M_e (i.e., P entering and leaving an RB) within a study; assuming ${{\overline{M}}_0}_j$ is non-negative,

$\begin{array}{ll}{\overline{L}}_j=ln({{\overline{R}}_r}_j)=ln({{\overline{M}}_e}_j)-ln({{\overline{M}}_0}_j)& (3)\end{array}$

and

$\begin{array}{ll}{\widehat{V}}_j=\frac{{{S{D}_e}_j}^2}{{n_e}_j{{{\overline{M}}_e}_j}^2}+\frac{{{S{D}_0}_j}^2}{{n_0}_j{{{\overline{M}}_0}_j}^2}& (4)\end{array}$

where S_D0j and S_Dej denote the standard deviations of M₀ and M_e, and n_0j and n_ej denote the corresponding sample sizes. The 100(1 − α/2)% confidence interval of ln(R_r) for each study, accounting only for the within-study variance, was estimated by

$\begin{array}{ll}{\overline{L}}_j\pm z_{\alpha /2}\sqrt{{\widehat{V}}_j}& (5)\end{array}$

where z_α/2 denotes the Z statistic at two-sided type I error α. The corresponding confidence interval of R_r was estimated by the exponential of Equation (5).

Next, we estimated the between-study variance ($\widehat{T}$) based on the assigned weight of each study (w_j) and the heterogeneity statistic (Q):

$\begin{array}{ll}\widehat{T}=\frac{Q-(k-1)}{{\displaystyle {\sum }_{j=1}^k}{w}_j-\frac{{\displaystyle {\sum }_{j=1}^k}{w_j}^2}{{\displaystyle {\sum }_{j=1}^k}{w}_j}}& (6)\end{array}$

where k is the number of total studies, $w_j=\frac{1}{{\widehat{V}}_j}$, and

$\begin{array}{ll}Q={\displaystyle \sum _{j=1}^k{w}_j}{({\overline{L}}_j)}^2-\frac{{({\displaystyle {\sum }_{j=1}^k{w}_j}{\overline{L}}_j)}^2}{{\displaystyle {\sum }_{j=1}^k{w}_j}}.& (7)\end{array}$

We then estimated the combined weight for each study ($w_j^{*}$) by accounting for both within-study variance (${\widehat{V}}_j$) and between-study variance ($\widehat{T}$): $w_j^{*}=\frac{1}{{\widehat{V}}_j+\widehat{T}}$. The confidence interval of ln(R_r) for each study, accounting for both variances, was estimated by the following equation:

$\begin{array}{ll}{\overline{L}}_j\pm z_{\alpha /2}\sqrt{{\widehat{V}}_j+\widehat{T}}.& (8)\end{array}$

The mean of ln(R_r) pooled across studies, factoring in both variances, was then estimated by the following equation:

$\begin{array}{ll}\overline{L^{*}}=\overline{{ln(R_r)}^{*}}=\frac{{\displaystyle {\sum }_{j=1}^k}{w}_j^{*}{\overline{L}}_j}{{\displaystyle {\sum }_{j=1}^k}{w}_j^{*}}.& (9)\end{array}$

We used a more accurate estimate of standard error of $\overline{L^{*}}$, because the number of studies included in our review and the within-study sample sizes were small (Hedges et al., 1999):

$\begin{array}{l}SE\left(\overline{L^{*}}\right)\\ =\sqrt{\frac{1}{{\displaystyle {\sum }_{j=1}^k}{w}_j^{*}}\left\{1+4{\displaystyle \sum _{j=1}^k}\frac{1}{d{f}_j}{\left(\frac{w_j^{*}}{w_j}\right)}^2\frac{w_j^{*}\left[\left({\displaystyle {\sum }_{j=1}^k}{w}_j^{*}\right)-w_j^{*}\right]}{{\left({\displaystyle {\sum }_{j=1}^k}{w}_j^{*}\right)}^2}\right\}}& (10)\end{array}$

where the degrees of freedom are given as d_fj = n_0j + n_ej − 2. The confidence interval for $\overline{L^{*}}$ was then estimated by

$\begin{array}{ll}\overline{L^{*}}\pm z_{\alpha /2}SE(\overline{L^{*}}).& (11)\end{array}$

The confidence interval of R_r pooled across all studies was computed by the exponential of Equation (11).

The heterogeneity statistic, Q, in Equation (7) was used to test the null hypothesis. The null hypothesis was rejected when Q exceeded 100(1 − α)% of the chi-squared distribution with a degree of freedom of k-1 and one-sided type I error α. Rejection, meaning the between-study variance is not zero, suggests that random-effects must be considered.

Next, to assess the effects of the selected RB characteristics on P removal efficacy and their variations, we conducted categorical traditional random-effects meta-analyses with respect to different categorizations of RB observations. As shown in Table 2, these categorizations were P inputs in adjacent fields (PF), P removal pathway (PW), on-site infiltration capacity (IC), vegetation (V1), and soil (SO). Random-effects assumption was also tested using Q here.

Mixed-Effects Regression Meta-Analysis Using Bayesian Modeling

Similar to previous review studies (Mayer et al., 2007; Zhang et al., 2010; Sweeney and Newbold, 2014), our mixed-effects regression meta-analysis was developed based on the exponential decay function

$\begin{array}{ll}{R}_r=\frac{M_e}{M_0}=e^{X{\beta }_f+Z{\beta }_r+\epsilon }& (12)\end{array}$

where β_f represents a fixed-effects vector associated with a known design matrix X, β_r is a random-effects vector with a known design matrix Z, and a random normal variate $\epsilon ~(0,{{\sigma }_{\epsilon }}^2)$ models the effects of unobservable influences. β_r was assumed to arise from a distribution with mean μ_βr and variance-covariance matrix Σ_βr. We assumed that a linear combination of RB characteristics correlates with ln(R_r). The fixed-effects vector X consisted of both numerical and categorical variables (Table 2). The numerical variables were width (W) and slope (SL), and the categorical variables were vegetation (V2), soil (SO), P inputs in adjacent fields (PF2), on-site infiltration capacity (IC), and P removal pathway (PW). The mixed-effects regression meta-analysis simultaneously fitted a curve to each subset of data grouped by the categorical variables. Observations in these data subsets were mutually exclusive. Using Equation (1), multiple non-linear curves were derived to explain the effects of continuous predictors (e.g., width) on P removal efficacy (R_d) given different subsets of data. We used Bayesian model averaging (Raftery et al., 2015) to select several fixed-effects models with high posterior probability; then, we used stepwise regression based on Akaike information criterion (AIC) to identify the most parsimonious and plausible mixed-effects model. The use of Bayesian model averaging and AIC for model selection are well-illustrated by Hoeting et al. (1999) and Bolker et al. (2009), respectively. We estimated the confidence intervals of both random- and fixed-effects using Stan, a probabilistic programming language for Bayesian inference and optimization (Gelman et al., 2015). Berger and Berry (1988) provided detailed explanations concerning the advantages of using Bayesian analysis over traditional hypothesis test when pooling multiple data sources.

Results

The methodological quality of the 36 studies included is fair (Table 3) according to the assessment of hierarchy of evidence quality (Pullin and Knight, 2003). The relatively symmetrical funnel plot (Figure 2) indicates that publication bias is absent, which was also confirmed by Egger's test (Egger et al., 1997) with a p-value of 0.45.

TABLE 3

Table 3. Methodological quality assessment of all studies included in this article.

FIGURE 2

Figure 2. Funnel plot with the 95% confidence interval region.

Overall P Removal Efficacy Estimated by the Traditional Meta-Analysis

Generally, RBs are effective P removal interventions (Figure 3). The overall mean of P removal efficacy (R_d) pooled across 35 studies was 54.5% with a 95% confidence level (46.1, 61.6), while the means of R_d for each study ranged from −128.2 to 94.7%. Of the 36 studies reviewed, 35 were included in the traditional random-effects meta-analysis. Wagner et al.'s (2008) study was excluded because it only provided one observation, making the estimation of within-study variance impossible.

FIGURE 3

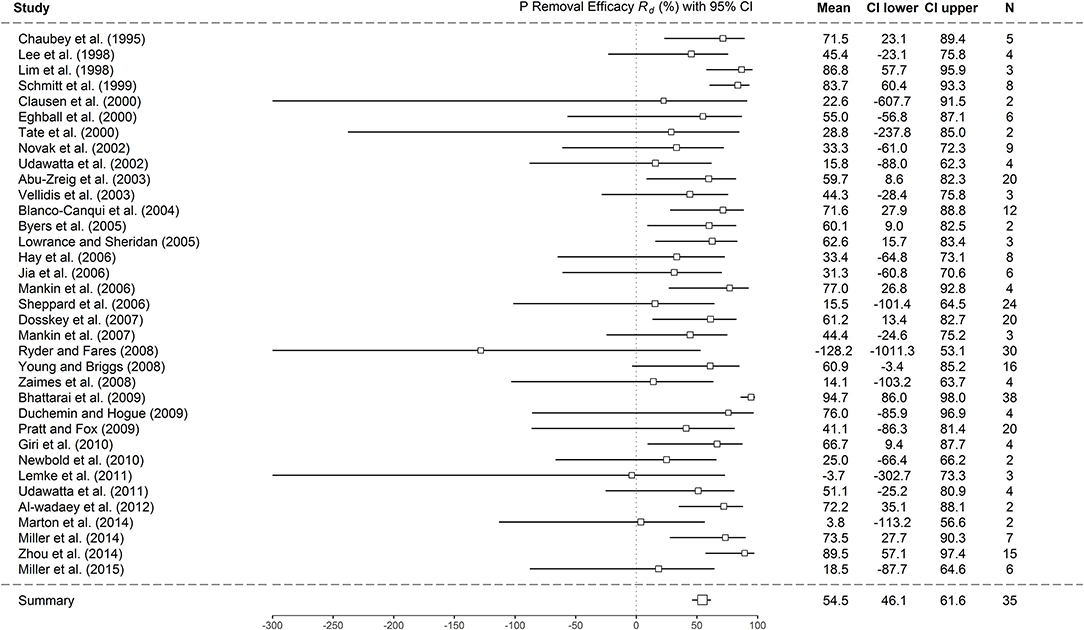
Figure 3. Plot showing the mean and 95% confidence interval of P removal efficacy (R_d) for each of the 35 studies. The P removal efficacy pooled from these 35 studies is shown in the “Summary” row. N represents the number of RB observations of a study or, for the case of “Summary,” the number of studies pooled.

P removal efficacy varied not only across studies but also within a study (Figure 3). The hypothesis test on Q (Equation 8) further confirmed that the between-study variation of P removal efficacy was too large to be overlooked. The within-study variations of some of these 35 studies (e.g., Clausen et al., 2000; Tate et al., 2000; Sheppard et al., 2006; Ryder and Fares, 2008; Duchemin and Hogue, 2009; Lemke et al., 2011) were so large that P removal efficacy of RBs was statistically not different than zero.

Riparian buffers were most likely to be ineffective in P removal under four conditions, namely, (1) RBs were installed next to fields with low P input, (2) RBs were installed to mitigate P transport through subsurface pathways, (3) the infiltration capacity of RB soil was low or intermediate, and (4) RBs were not vegetated (Figure 4). The RBs planted with grass plus trees were generally less effective than the grass or tree-only RBs. The P removal efficacy of RBs varied given soil compositions; generally, the clay RBs were the most effective, followed by silt, sand, and loam RBs.

FIGURE 4

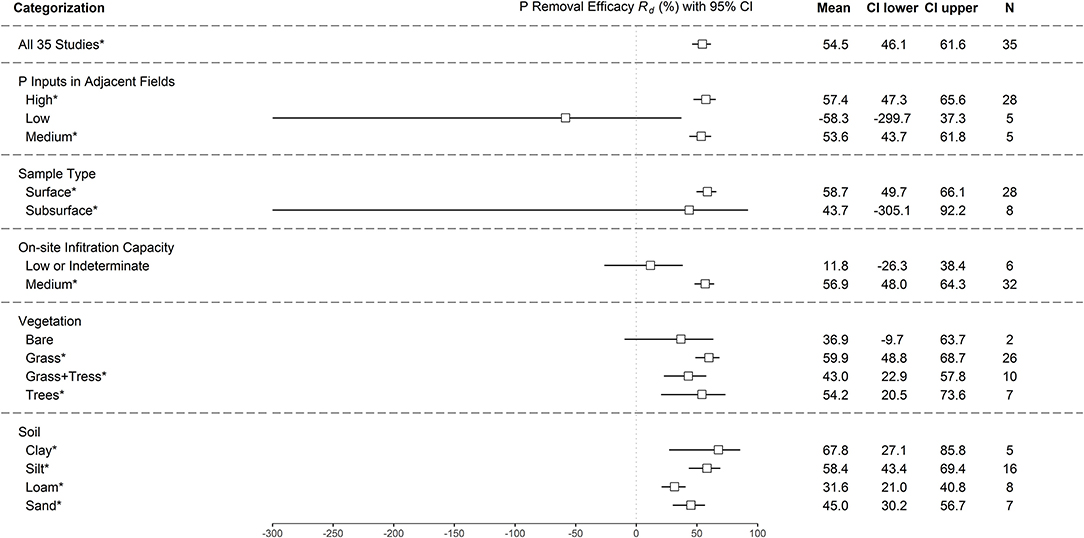
Figure 4. Plot showing the mean and 95% confidence interval of P removal efficacy (R_d) given multiple categorization schemes. Here, N represents the number of studies included in each category. ^* indicates between-study variance is significant.

P Removal Efficacy Given Predominant RB Features: The Results of Mixed-Effects Regression Meta-Analysis

A total of 283 RB observations collected from 30 studies were included in the mixed-effects regression meta-analysis after we excluded the incomplete records. We applied Bayesian model averaging and a stepwise procedure to select the best-fit regression model that can be explained by physical P removal mechanisms (Table 4). The fit of the best model had an R² = 0.66, meaning that the predictors explained 66% of the variation of the P response ratio to RBs (R_r). The intercept, of this mixed-effects model, represents that the average P removal efficacy of an RB can achieve under the condition that the RB is adjacent to a field where “above medium level of P” is applied. The variables modeled as having random effect include study (j), vegetation (V2), P inputs in adjacent fields (PF2), and flow pathway (PW), as described in Table 2.

TABLE 4

Table 4. The best regression model.

In this mixed-effect model, the intercept represents the average P removal efficacy an RB can achieve under the condition where an RB is adjacent to a field where “above medium level of P” was applied. The variables modeled as having random effect include study (j), vegetation (V2), P inputs in adjacent fields (PF2), and flow pathway (PW).

The coefficients of these variables add to the intercept term, namely, P inputs in adjacent fields (at low), width interacting with soil (clay, silt, loam, and sand), and slope interacting with soil. A negative coefficient indicates that an increase in a predictor improved the P removal efficacy of RBs, while a positive value means that an increase in the predictor reduced P removal efficiency. Multiple non-linear curves (Table 5) were derived from the regression results (Table 4) to explain the interactive effects of width and slope on P removal efficacy given different subsets of data. The RBs that were installed adjacent to the fields applied with an above medium level of P injections regardless of soil, vegetation, and flow pathway were generally effective in removing P (Figure 5). The P removal efficacy of these RBs was averaged at 51.3% with a 95% confidence level (19.6, 71.2), when both width and slope were approaching zero (Table 5). Here, 51.3% was derived from 100(1 − e^−0.72), where the intercept was estimated at −0.72 (Table 4). Conversely, the low P-input RBs that were the neighboring fields applied with a very minimal level of P regardless of soil, vegetation, and pathway were generally not effective in reducing P from already low levels. The P removal efficacy of those low P-input RBs was averaged at −51.6%, equal to 100(1 − e^0.42), when both width and slope were zero (refer to Tables 4, 5 for detail). The value of 0.42 is the sum of intercept (−0.72) and P inputs as low (1.14). At low levels of P input, RBs can sometimes act as sources of P. However, P flux leaching from such RBs, when in weight or concentration, was very small because the denominator of the percentage was infinitesimal (i.e., P transporting from the adjacent fields where P level is low). Moreover, a 1 m increase in buffer width of a clay RB significantly improved P removal to 52.4 from 51.3% (p < 0.01). A 1% increase in the slope of a sandy RB significantly improved P removal to 65.4 from 51.3%. However, width increase in silt, loam, or sand RBs did not significantly increase P removal efficacy from its base level of 51.3%. Similarly, slope variation in clay, silt, or loam RBs had minimal impact on adjusting P removal efficacy. Vegetation (V2), pathway (PW), and on-site infiltration capacity (IC) were dropped from the best model because their effect on P removal was insignificant. However, some models that were not selected using our model selection criteria indicated that bare RBs hinder P removal efficacy, while vegetated RBs reinforce P removal efficacy. The power of vegetation in removing P, i.e., ranking from high to low, is grass, trees, and grass + trees, although the within-group difference was not statistically significant.

TABLE 5

Table 5. Functional forms of the best regression model that explain the relationship of P retention effectiveness (R_d), slope, and width of riparian buffers.

FIGURE 5

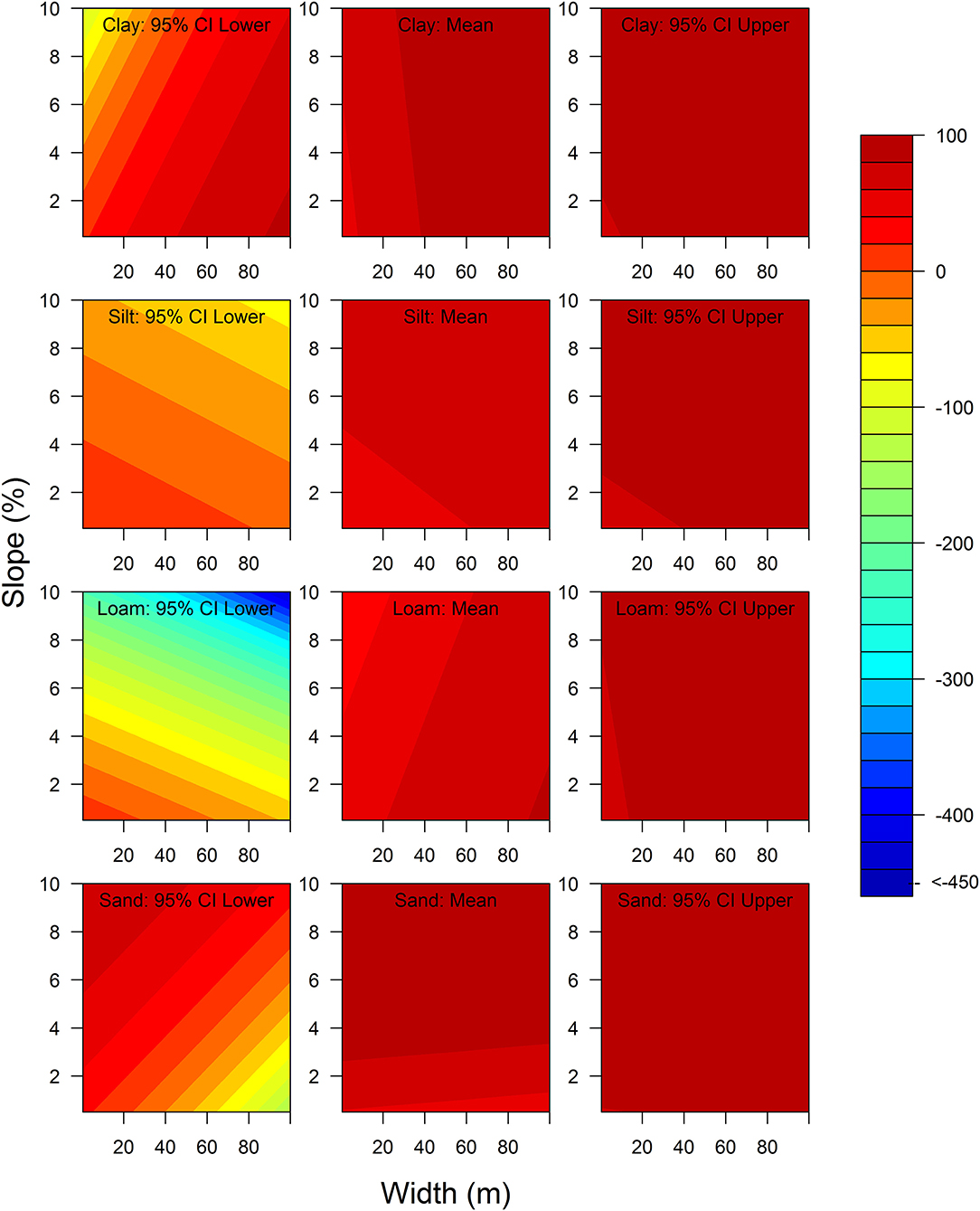
Figure 5. The contours of P removal efficacy (mean and the 95% confidence interval) given RB width, slope, and soil type for the RBs installed adjacent to the fields with at least medium level of P application.

Discussion

Riparian buffers are generally effective in retaining P. As shown in Figure 3, the mean P removal efficacy of RBs is 54.5% with a 95% confidence interval (46.1, 61.6). However, Figure 3 also suggests that the variations of within- and between-studies are large. While the large within-study variation of P removal efficacy rises from a wide spectrum of RB characteristics within a study, the large between-study variation is contributed by the idiosyncrasies of individual studies. For example, the studies investigating the P removal of RBs from both surface and subsurface pathways often reported a large difference in P removal between surface and subsurface pathways (Clausen et al., 2000; Duchemin and Hogue, 2009). Moreover, some studies reported large variations given that a small number of RB observations were collected (e.g., Marton et al., 2014).

The RBs with certain characteristics are more effective in removing P (Figure 4 and Table 5). P is removed through RBs via different mechanisms depending on the design and specifications of RBs. The soil of the RBs that were adjacent to the fields without nutrient applications and ineffective in further reducing low levels of P from surface runoff was predominantly clay or loam (Table 5). Dissolved P eroding from clays in such RBs may have eclipsed P removal (Sheppard et al., 2006). Moreover, such RBs were planted with trees of ~25 years old. These mature forested RBs may have become sources of dissolved P leaching from vegetation and soil, because plant and microbial uptakes are generally considered transient P pools (Hoffmann et al., 2009). Our inference that RBs are effective in removing P in the overland runoff but have a very less quantitative impact on P retention through subsurface pathways (Figure 4) is supported by Hoffmann et al. (2009). Figure 4 also suggests that the RBs covered by snowmelt or with saturated soil are ineffective in Uusi-Kämppä (2005) also found that the RBs during snowmelt were ineffective in P removal. Frozen and dormant vegetation during snowmelt may have accelerated the release of dissolved P (Sheppard et al., 2006) or are biologically inactive, causing RBs to be ineffective in P removal. Saturated soil may impede runoff infiltration and sedimentation and accelerate erosion within RBs, reducing the amounts of dissolved P infiltrated and particulate P trapped and remobilizing particulate P from soil. Lastly, the inefficacy of bare RBs in P removal (Figure 4) may be due to the increasing risk of erosion during rainfall events, making such RBs act as P sources. Some alternative regression models (with poorer goodness-of-fit) also support these findings regarding the effect of the pathway, on-site infiltration capacity, and vegetation.

The soil of RBs greatly affects their P removal efficacy (Figure 4). In an RB, P is removed through different combinations of P removal mechanisms depending on the RB soil properties, such as particle size and chemical composition. While both runoff infiltration and P sorption may be active simultaneously in an RB, infiltration that reduces sediment mobilization may be the dominant mechanism in larger particle size soil (Hay et al., 2006; Sheppard et al., 2006; Al-wadaey et al., 2012), whereas P sorption may be the major P removal mechanism in smaller particle size soil, such as clay (Abu-Zreig et al., 2003). In addition to soil clay content, many studies also suggested that P sorption and desorption also depend on pH, other chemical compounds (e.g., Fe, Ca, or Al), and organic matter (e.g., Khalid et al., 1977; Vadas et al., 2005; Leader et al., 2008; Idris and Ahmed, 2012).

The interactive effect of width and slope on P removal in RBs varies across soil types (Figures 5, 6). Figures 5 and 6 show that the complexity of P retention in RBs can be captured by a non-linear functional form (Table 5). The motivation of fitting a non-linear functional form to complex data is driven by the concept that P retention in RBs is dictated by a specific physical process, which can be rendered in nuanced expressions given varied combinations of parameters. Table 5 shows that the use of discrete variables dissects the complex system into multiple subsystems with respect to environmental conditions (e.g., soil, P inputs in adjacent fields). The interactive effect of width, slope, and soil indicates that the balance between P sorption, desorption, sedimentation, and remobilization may vary depending on the combination of width, slope, and soil, respectively. If sorption is the primarily P removal mechanism in the clay RBs, then our finding that increasing width significantly improved P removal in clay RBs suggests that sorption by clay may be improved by increasing residence time in such RBs. It is worth noting that our results suggest that sandy RBs with steeper slope are more effective in reducing P (Table 4). This inference is heavily weighted by the three RBs with the steepest slope (i.e., 5%), which are also the most effective in reducing P in shallow groundwater. The other 10 RBs in this group only reduce P minimally to moderately in surface flow. While this conclusion is counterintuitive for surface flow transport, a steeper slope with sandy soil can increase retention time for infiltrated water before the soil is saturated, thus increasing P absorption through roots. This also shows that three outliers of a small sample size (N = 13 for sandy RBs in Table 5) can greatly influence the outcomes.

FIGURE 6

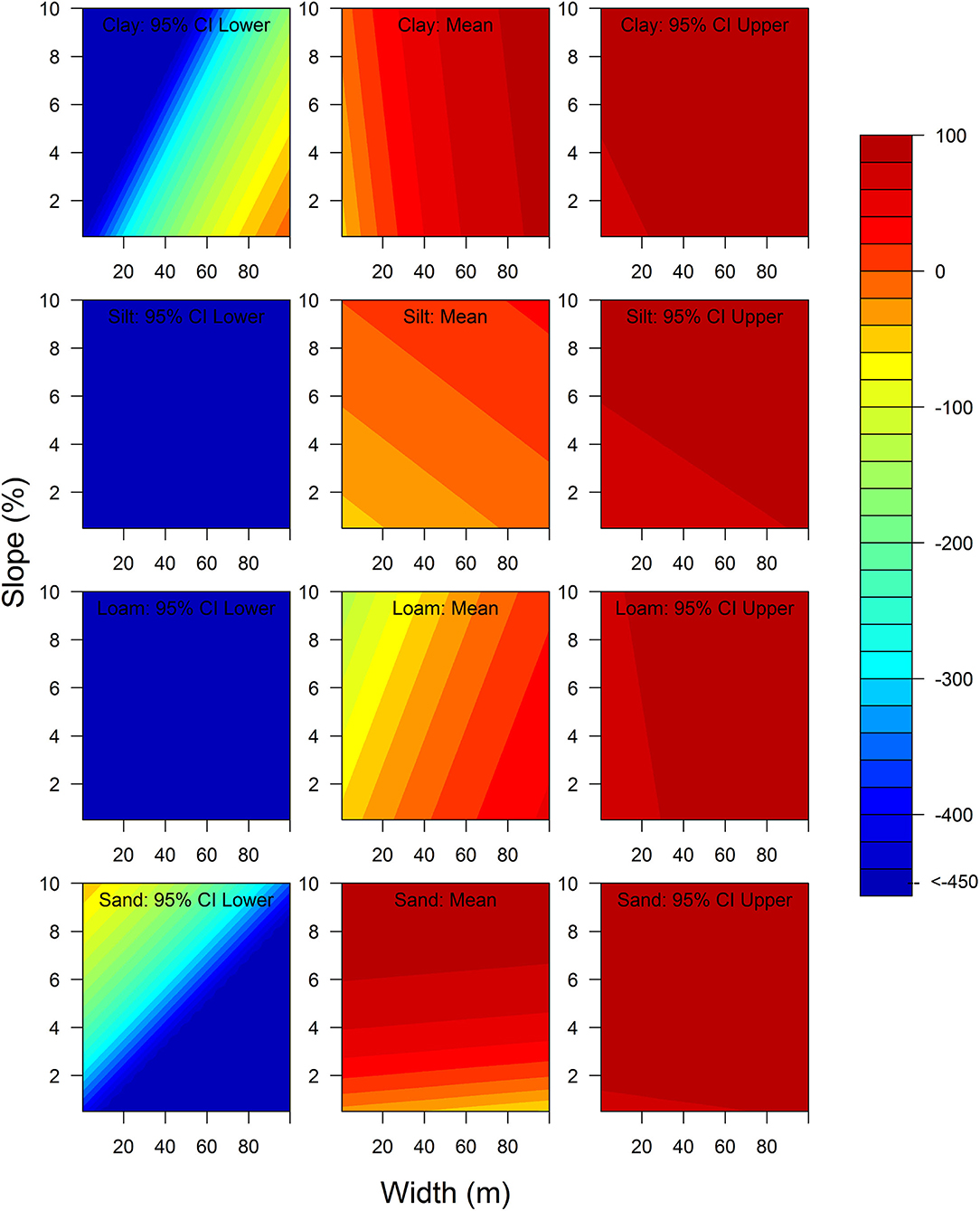
Figure 6. The contours of P removal efficacy (mean and the 95% confidence interval) given RB width, slope, and soil type for the RBs installed adjacent to the fields without P application.

Grass, grass mixed with tree, and tree RBs are equally effective in removing P (Figure 4). Moreover, our regression analyses show that bare RBs remove less P, while vegetated RBs remove more P. Although grass has the largest increase in P removal capacity, followed by trees and then by grass + trees, the within-group differences are very small. These findings contradict those reported by Zhang et al. (2010) but agree with those reported by Hoffmann et al. (2009). Zhang et al. (2010) suggested that the RBs planted with trees are more effective in retaining P than those with grass or grass plus trees. Overall, our traditional meta-analysis showed that the mean of P removal efficacy pooled from all RB observations was 54.4%. Our regression results suggest that P removal efficacy was 51.3% for the RBs adjacent to the fields applied with medium to high P when width and slope were approaching zero. These estimates (54.4 and 51.3%) are higher than the value of 30.5% estimated by Zhang et al. (2010) for grass RBs and mixed grass and tree RBs. However, our estimate is similar to their estimate of 59.8% for tree RBs. We found that all vegetated RBs, i.e., grass, grass mixed with trees, and trees, are equally effective. Our results suggest that the effect of RB width on P removal efficacy for baseline clay RBs is −0.023, which is similar to −0.03 reported by Zhang et al. (2010), in which the effect of RB soil type was not investigated. However, our estimates of the effect of width in the loam, silt, and sand RBs (ranging from −0.010 to 0.0025) are smaller than −0.03. In summary, our results suggest that P removal efficacy (R_d) of RBs is dictated by a complex process that involves the interaction of width, slope, soil, and P level in the adjacent fields. The determinants of RB efficacy involve more factors than that suggested by Zhang et al. (2010). The number of RB observations included in our regression meta-analysis is larger (N = 283) than that of Zhang et al. (2010) (N = 52) and Mayer et al. (2007) (N = 88). Our model also gives better goodness-of-fit (R² = 0.66) than that of Zhang et al. (2010) (R² = 0.48). Our results suggest that the effects of width and slope on P removal in RBs vary with soil type, rather than a simple positive correlation between width and P removal efficacy. These large variations in the effects of width and slope for the silt, loam, and sand RBs give rise to large uncertainty in the P removal efficacy of specific RB designs. In addition, soil type may be the key to better control the uncertainty.

Conclusion

This study provides not only the effect size of P removal efficacy of RBs but also its uncertainty using two approaches to meta-analysis, namely, traditional random-effects meta-analysis and mixed-effects regression meta-analysis with Bayesian modeling. Our traditional random-effects meta-analysis indicates that generally, P removal efficacy of RBs is 54.5% with a 95% confidence interval (46.1, 61.6). Our mixed-effects regression meta-analysis suggests that the RBs that were installed adjacent to the fields applied with at least a medium level of nutrients can achieve an average of 51.3% of P removal with a 95% confidence level (19.6, 71.2), while width and slope are approaching zero. By accounting for the effects of soil, we are able to provide P removal estimates given specific soil and evaluate the effects of soil combined with RB width and slope on P removal. Our results suggest that the effects of RB width and slope on P removal vary substantially given RB soil type. This indicates that dominant P removal mechanisms in RBs vary given the interactions of the influential RB specifications, such as width, slope, soil, and P application practice in adjacent fields. Moreover, compared to other qualitative P efficacy reviews, this study suggests a larger variation in P removal efficacy of RBs and of the effects of RB width and slope on P removal. This finding cautions both policymakers and practitioners that optimal RB width and slope for P removal depend on on-site soil and the level of nutrient additions in adjacent fields. Moreover, policymakers should consider the large variations in both P removal efficacy and the effect of width and slope, when designing government programs for encouraging the implementation of RBs. Our analyses were limited by the low number of RB with trees present, hindering our assessment of vegetation effect. We hope this study will lead to future studies that further investigate the complex set of characteristics that determine P removal by RBs.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding authors.

Author Contributions

YT, AZ, and BB conceived of the presented idea. HZ collected the data. HZ and YT processed the data and performed the analysis. YT and BB developed the theoretical framework for analysis. YT, HZ, and BB contributed to the interpretation of the results. YT took the lead in writing the manuscript. All authors provided critical feedback and helped shape the research, analysis and manuscript. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by Vermont EPSCoR with funds from the National Science Foundation Grant EPS-1101317 and EPS-1556770.

Author Disclaimer

The views expressed in this document are solely those of the authors, not those of the National Science Foundation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2022.882560/full#supplementary-material

References

Abu-Zreig, M., Rudra, R. P., Whiteley, H. R., Lalonde, M. N., and Kaushik, N. K. (2003). Phosphorus removal in vegetated filter strips. J. Environ. Qual. 32, 613–619. doi: 10.2134/jeq2003.6130

PubMed Abstract | CrossRef Full Text | Google Scholar

Al-wadaey, A., Wortmann, C. S., Franti, T. G., Shapiro, C. A., and Eisenhauer, D. E. (2012). Effectiveness of grass filters in reducing phosphorus and sediment runoff. Water Air Soil Pollut. 223, 5865–5875. doi: 10.1007/s11270-012-1322-2

CrossRef Full Text | Google Scholar

Bennett, E. M., Carpenter, S. R., and Caraco, N. F. (2001). Human impact on erodable phosphorus and eutrophication: a global perspective increasing accumulation of phosphorus in soil threatens rivers, lakes, and coastal oceans with eutrophication. Bioscience 51, 227–234. doi: 10.1641/0006-3568(2001)051[0227:HIOEPA]2.0.CO;2

CrossRef Full Text | Google Scholar

Berger, J. O., and Berry, D. A. (1988). Statistical analysis and the illusion of objectivity. Am. Sci. 76, 159–165.

Bolker, B. M., Brooks, M. E., Clark, C. J., Geange, S. W., Poulsen, J. R., Stevens, M. H. H., et al. (2009). Generalized linear mixed models: a practical guide for ecology and evolution. Trends Ecol. Evol. 24, 127–135. doi: 10.1016/j.tree.2008.10.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Borenstein, M., Hedges, L. V., Higgins, J. P., and Rothstein, H. R. (2009). Introduction to Meta-Analysis. Wiley Online Library.

Borenstein, M., Hedges, L. V., Higgins, J. P. T., and Rothstein, H. R. (2010). A basic introduction to fixed-effect and random-effects models for meta-analysis. Res. Synth. Methods 1, 97–111. doi: 10.1002/jrsm.12

PubMed Abstract | CrossRef Full Text | Google Scholar

Clausen, J., Guillard, K., Sigmund, C., and Dors, K. M. (2000). Water quality changes from riparian buffer restoration in Connecticut. J. Environ. Qual. 29, 1751–1761. doi: 10.2134/jeq2000.00472425002900060004x

CrossRef Full Text | Google Scholar

Cole, L. J., Stockan, J., and Helliwell, R. (2020). Managing riparian buffer strips to optimise ecosystem services: a review. Agric. Ecosyst. Environ. 296, 106891. doi: 10.1016/j.agee.2020.106891

CrossRef Full Text | Google Scholar

Dorioz, J. M., Wang, D., Poulenard, J., and Trévisan, D. (2006). The effect of grass buffer strips on phosphorus dynamics-a critical review and synthesis as a basis for application in agricultural landscapes in France. Agric. Ecosyst. Environ. 117, 4–21. doi: 10.1016/j.agee.2006.03.029

CrossRef Full Text | Google Scholar

Duchemin, M., and Hogue, R. (2009). Reduction in agricultural non-point source pollution in the first year following establishment of an integrated grass/tree filter strip system in southern Quebec(Canada). Agric. Ecosyst. Environ. 131, 85–97. doi: 10.1016/j.agee.2008.10.005

CrossRef Full Text | Google Scholar

Egger, M., Smith, G. D., Schneider, M., and Minder, C. (1997). Bias in meta-analysis detected by a simple, graphical test. BMJ 315, 629–634. doi: 10.1136/bmj.315.7109.629

PubMed Abstract | CrossRef Full Text | Google Scholar

Gelman, A., Lee, D., and Guo, J. (2015). Stan a probabilistic programming language for Bayesian inference and optimization. J. Educ. Behav. Statistics. 40, 147–158. doi: 10.3102/1076998615606113

CrossRef Full Text | Google Scholar

Hay, V., Pittroff, W., Tooman, E. E., and Meyer, D. (2006). Effectiveness of vegetative filter strips in attenuating nutrient and sediment runoff from irrigated pastures. J. Agric. Sci. 144, 349–360. doi: 10.1017/S0021859606006216

CrossRef Full Text | Google Scholar

Hedges, L. V., Gurevitch, J., and Curtis, P. S. (1999). The meta-analysis of response ratios in experimental ecology. Ecology 80, 1150–1156. doi: 10.1890/0012-9658(1999)080[1150:TMAORR]2.0.CO;2

CrossRef Full Text | Google Scholar

Hoeting, J. A., Madigan, D., Raftery, A. E., and Volinsky, C. T. (1999). Bayesian model averaging: a tutorial. Statistical Sci. 14, 382–401.

Hoffmann, C. C., Kjaergaard, C., Uusi-Kämppä, J., Hansen, H. C. B., and Kronvang, B. (2009). Phosphorus retention in riparian buffers: review of their efficiency. J. Environ. Qual. 38, 1942–1955. doi: 10.2134/jeq2008.0087

PubMed Abstract | CrossRef Full Text | Google Scholar

Idris, O. A., and Ahmed, H. S. (2012). Phosphorus sorption capacity as a guide for phosphorus availability of selected Sudanese soil series. Afr. Crop Sci. J. 20, 59–65.

Iwata, Y., Hayashi, M., Suzuki, S., Hirota, T., and Hasegawa, S. (2010). Effects of snow cover on soil freezing, water movement, and snowmelt infiltration: a paired plot experiment. Water Resources Res. 46:W09504. doi: 10.1029/2009WR008070

CrossRef Full Text | Google Scholar

Keating, B. A., Herrero, M., Carberry, P. S., Gardner, J., and Cole, M. B. (2014). Food wedges: Framing the global food demand and supply challenge towards 2050. Glob. Food Secur. 3, 125–132. doi: 10.1016/j.gfs.2014.08.004

CrossRef Full Text | Google Scholar

Khalid, R. A., Patrick, W. H., and DeLaune, R. D. (1977). Phosphorus sorption characteristics of flooded soils 1. Soil Sci. Soc. Am. J. 41, 305–310. doi: 10.2136/sssaj1977.03615995004100020026x

CrossRef Full Text | Google Scholar

Kulinskaya, E., Morgenthaler, S., and Staudte, R. G. (2008). Meta Analysis: A Guide to Calibrating and Combining Statistical Evidence. John Wiley & Sons.

Kummu, M., Fader, M., Gerten, D., Guillaume, J. H. A., Jalava, M., Jägermeyr, J., et al. (2017). Bringing it all together: linking measures to secure nations' food supply. Curr. Opin. Environ. Sustain. 29, 98–117. doi: 10.1016/j.cosust.2018.01.006

CrossRef Full Text | Google Scholar

Land, M., Granéli, W., Grimvall, A., Hoffmann, C. C., Mitsch, W. J., Tonderski, K. S., et al. (2016). How effective are created or restored freshwater wetlands for nitrogen and phosphorus removal? A systematic review. Environ. Evid. 5, 9. doi: 10.1186/s13750-016-0060-0

CrossRef Full Text | Google Scholar

Leader, J., Dunne, E., and Reddy, K. (2008). Phosphorus sorbing materials: sorption dynamics and physicochemical characteristics. J. Environ. Qual. 37, 174–181. doi: 10.2134/jeq2007.0148

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemke, A., Kirkham, K., Lindenbaum, T., Herbert, M., Tear, T., Perry, W., et al. (2011). Evaluating agricultural best management practices in tile-drained subwatersheds of the Mackinaw River, Illinois. J. Environ. Qual. 40, 1215–1228. doi: 10.2134/jeq2010.0119

PubMed Abstract | CrossRef Full Text | Google Scholar

Lim, T., Edwards, D. R., Workman, S., Larson, B., and Dunn, L. (1998). Vegetated filter strip removal of cattle manure constituents in runoff. Trans. ASAE 41, 1375–1381. doi: 10.13031/2013.17311

CrossRef Full Text | Google Scholar

Marton, J. M., Fennessy, M. S., and Craft, C. B. (2014). Functional differences between natural and restored wetlands in the Glaciated Interior Plains. J. Environ. Qual. 43, 409–417. doi: 10.2134/jeq2013.04.0118

PubMed Abstract | CrossRef Full Text | Google Scholar

Mayer, P. M., Reynolds, S. K., McCutchen, M. D., and Canfield, T. J. (2007). Meta-analysis of nitrogen removal in riparian buffers. J. Environ. Qual. 36, 1172–1180. doi: 10.2134/jeq2006.0462

PubMed Abstract | CrossRef Full Text | Google Scholar

McDowell, R., Biggs, B., Sharpley, A., and Nguyen, L. (2004). Connecting phosphorus loss from agricultural landscapes to surface water quality. Chem. Ecol. 20, 1–40. doi: 10.1080/02757540310001626092

CrossRef Full Text | Google Scholar

Moher, D., Liberati, A., Tetzlaff, J., Altman, D. G., and Group, P. (2009). Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. PLoS Med. 6:e1000097. doi: 10.1371/journal.pmed.1000097

PubMed Abstract | CrossRef Full Text | Google Scholar

Mrozek, J. R., and Taylor, L. O. (2002). What determines the value of life? A meta-analysis. J. Policy Anal. Manage. 21, 253–270. doi: 10.1002/pam.10026

PubMed Abstract | CrossRef Full Text | Google Scholar

Nazari-Sharabian, M., Ahmad, S., and Karakouzian, M. (2018). Climate change and eutrophication: a short review. Eng. Technol. Appl. Sci. Res. 8, 3668–3672. doi: 10.48084/etasr.2392

CrossRef Full Text | Google Scholar

Pratt, W., and Fox, T. (2009). Streamside management zones effectiveness for protecting water quality after forestland application of biosolids. J. Environ. Qual. 38, 2106–2120. doi: 10.2134/jeq2008.0350

PubMed Abstract | CrossRef Full Text | Google Scholar

Pullin, A. S., and Knight, T. M. (2003). Support for decision making in conservation practice: an evidence-based approach. J. Nat. Conserv. 11, 83–90. doi: 10.1078/1617-1381-00040

CrossRef Full Text | Google Scholar

Raftery, A., Hoeting, J., Volinsky, C., Painter, I., Yeung, K. Y., Sevcikova, M. H., et al. (2015). Bayesian Model Averaging.

Ryder, M., and Fares, A. (2008). Evaluating cover crops (sudex, sunn hemp, oats) for use as vegetative filters to control sediment and nutrient loading from agricultural runoff in a hawaiian watershed 1. J. Am. Water Resources Assoc. 44, 640–653. doi: 10.1111/j.1752-1688.2008.00189.x

CrossRef Full Text | Google Scholar

Scheffer, M., Carpenter, S., Foley, J. A., Folke, C., and Walker, B. (2001). Catastrophic shifts in ecosystems. Nature 413, 591–596. doi: 10.1038/35098000

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheppard, S. C., Sheppard, M. I., Long, J., Sanipelli, B., and Tait, J. (2006). Runoff phosphorus retention in vegetated field margins on flat landscapes. Can. J. Soil Sci. 86, 871–884. doi: 10.4141/S05-072

CrossRef Full Text | Google Scholar

Sweeney, B. W., and Newbold, J. D. (2014). Streamside forest buffer width needed to protect stream water quality, habitat, and organisms: a literature review. J. Am. Water Resources Assoc. 50, 560–584. doi: 10.1111/jawr.12203

CrossRef Full Text | Google Scholar

Tate, K. W., Nader, G. A., Lewis, D. J., Atwill, E. R., and Connor, J. M. (2000). Evaluation of buffers to improve the quality of runoff from irrigated pastures. J Soil Water Conserv. 55, 473–478.

USDA (1987). Soil Mechanics: Level I, Module 3, USDA Textural Soil Classification Study Guide.

USDA (2012). Conservation Reserve Program Annual Summary and Enrollment Statistics.

Uusi-Kämppä, J. (2005). Phosphorus purification in buffer zones in cold climates. Ecol. Eng. 24, 491–502. doi: 10.1016/j.ecoleng.2005.01.013

CrossRef Full Text | Google Scholar

Vadas, P. A., Kleinman, P. J. A., Sharpley, A. N., and Turner, B. L. (2005). Relating soil phosphorus to dissolved phosphorus in runoff. J. Environ. Qual. 34, 572–580. doi: 10.2134/jeq2005.0572

PubMed Abstract | CrossRef Full Text | Google Scholar

Wagner, D., Elliott, H., Brandt, R., and Jaiswal, D. (2008). Managing biosolids runoff phosphorus using buffer strips enhanced with drinking water treatment residuals. J. Environ. Qual. 37, 1567–1574. doi: 10.2134/jeq2007.0338

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X. Y., Liu, X. M., Zhang, M. H., Dahlgren, R. A., and Eitzel, M. (2010). A review of vegetated buffers and a meta-analysis of their mitigation efficacy in reducing nonpoint source pollution. J. Environ. Qual. 39, 76–84. doi: 10.2134/jeq2008.0496

PubMed Abstract | CrossRef Full Text | Google Scholar

Zia, A., Bomblies, A., Schroth, A. W., Koliba, C., Isles, P. D. F., Tsai, Y., et al. (2016). Coupled impacts of climate and land use change across a river-lake continuum: Insights from an integrated assessment model of Lake Champlain's Missisquoi Basin, 2000–2040. Environ. Res. Lett. 11:114026. doi: 10.1088/1748-9326/11/11/114026

CrossRef Full Text | Google Scholar