Capturing Regional Differences in Flood Vulnerability Improves Flood Loss Estimation

Flood vulnerability is quantified by loss models which are developed using either empirical or synthetic approaches. In reality, processes influencing flood risk are stochastic and loss predictions bear significant uncertainty, especially due to differences in vulnerability across exposed objects and regions. However, many state-of-the-art flood loss models are deterministic, i.e., they do not account for data and model uncertainty. The Bayesian Data-Driven Synthetic (BDDS) model was one of the first approaches that used empirical data to reduce the prediction errors at object-level and enhance the reliability of synthetic flood loss models. However, the BDDS model does not account for regional differences in vulnerability which may result in over-/under-estimation of losses in some regions. In order to overcome this limitation, this study introduces a hierarchical parameterization of the BDDS model which enhances synthetic flood loss model predictions by quantifying regional differences in vulnerability. The hierarchical parameterization makes optimal use of the process information contained in the overall data set for the various regional applications, so that it is particularly suitable for cases in which only a small amount of empirical data is available. The implementation and performance of the hierarchical parametrization is demonstrated with the Multi-Colored Manual (MCM) loss functions and empirical damage dataset from the UK consisting of residential buildings from the regions Appleby, Carlisle, Kendal and Cockermouth that suffered losses during the 2015 flood event. The developed model improves prediction accuracy of flood loss compared to MCM by reducing the absolute error and bias by at least 23 and 90%, respectively. The model reliability in terms of hit rate (i.e., the probability that the observed value lies in the 90% high density interval of predictions) is 88% for residential buildings from the same regions used for calibration and 73% for residential buildings from new regions. The approach is of high practical relevance for all regions where only limited amounts of empirical flood loss data is available.

Introduction

Flood loss models are an essential component of risk analyses. Loss models quantify the vulnerability of exposed assets to different hazard characteristics. Flood loss models are developed based on the synthetic approach (e.g., Penning-Rowsell and Chatterton, 1977; Smith, 1994), the empirical approach (e.g., Elmer et al., 2010; Merz et al., 2013) or a combination of both (Wagenaar et al., 2018). The empirical approach includes statistical models developed using empirical data e.g., survey data concerning flood loss and influencing factors of flood loss (Elmer et al., 2010; Rözer et al., 2019). Synthetic loss models are based on what-if scenarios and expert and engineering methods (Smith, 1994; Merz et al., 2010). They are not based on statistical analysis of observed data (Penning-Rowsell and Chatterton, 1977). Due to scarcity of empirical data, the synthetic models are rarely validated against observed loss (Gerl et al., 2016). Thus, despite the high standardization of the synthetic models, they may result in biased and uncertain loss predictions (Merz et al., 2010). However, in regions where only small amounts of empirical flood loss data is available they seem to be the only possible approach for loss estimation. Flood vulnerability often varies across regions (Vogel et al., 2018). Regional characteristics such as predominant building types, past flood experience, and socio-economic aspects drive flood vulnerability (Jongman et al., 2012). Owing to these constraints, flood loss models, both empirical and synthetic, trained on particular regions do not perform well when transferred as such to other regions (Cammerer et al., 2013; Figueiredo et al., 2018; Wagenaar et al., 2018).

Hierarchical Bayesian approaches can be theoretically conceptualized and implemented to capture causal effects (Kruschke and Vanpaemel, 2015). A Hierarchical Bayesian Model for flood loss prediction using empirical data has been developed to capture spatiotemporal variability in damage processes (Sairam et al., 2019b) and variability across flood types (Mohor et al., 2021). Calibrating a synthetic model with available empirical loss data within a probabilistic framework resulted in a Bayesian Data-driven Synthetic (BDDS) model that captures the flood vulnerability of households and enhances the reliability of loss predictions, especially for data-scarce regions (Sairam et al., 2020). The BDDS model is formulated based on the premise that the observed loss values and predictions from synthetic loss models may be seen as components of a statistical model in which the predictions from the synthetic loss model are considered as an exogenous variable (one that is determined outside the model and imposed on the model). In the model formulation, the synthetic loss predictions explain the observed loss values. The BDDS is a fully probabilistic model which enhances the synthetic flood loss functions by associating probability distributions to their deterministic loss predictions. Depending on the available empirical data and level-of-detail in the synthetic model, the vulnerability differences at the object (household) -level can be captured by the BDDS model. Building characteristics, past flood experiences, risk management, warning lead time, warning quality, and private precaution are some of the aspects that strongly influence households' flood vulnerability and consequently flood loss (Bubeck et al., 2012; Hudson et al., 2014; Sairam et al., 2019a; Kreibich et al., 2021). Since it is time consuming and expensive to collect data concerning these aspects at the object (household)-level, and only possible after a flood event, such detailed data is scarce in many regions. However, ignoring these aspects may lead to biased estimates of flood loss in an entire region.

The objective of this study is to develop a fully probabilistic model that provides uncertainty quantification and explicitly accounts for regional differences in flood vulnerability. We propose a hierarchical parameterization of the BDDS model at region-level. The implementation and performance of the model is demonstrated using the Multi-Colored Manual (MCM) loss functions and empirical loss data of residential buildings from the regions Appleby, Carlisle, Kendal and Cockermouth that were affected by the 2015 flood event in the UK. The model is tested to enhance the predictive capability of MCM for residential buildings from the regions used for training and from new regions. Furthermore, vulnerability differences across these regions are inferred from the model parameters.

Data and Model

Cumbria Floods, 2015

In December 2015, storm Desmond affected the North Western part of the UK causing an extreme flood event in Cumbria with a return period of 800–1,000 years. The event was characterized by heavy rainfall, high temperature and soil moisture. The event resulted in losses between £520 and £662 Million (Szonyi et al., 2016). In many parts of Cumbria, the inundation was a result of overtopped flood walls. The flood affected regions were characterized by different levels of preparedness. Properties behind the flood walls experienced inundation depth of almost 3 meters and inundation duration of up to 48 h. Many of these properties, especially in big cities like Carlisle had low awareness regarding the residual risk—in this context, residual risk refers to the chance of failure of structural adaptation such as dikes and flood walls leading to increased flood risk. Due to the lack of awareness, they had not prepared for a flooding. In contrast, residential properties in rural regions such as the Appleby region which were not protected by structural measures, showed high awareness and had implemented many property-level precautionary measures. The Cocker region had been already severely affected during the 2009 flood. After 2009, the flood walls along Cocker river were raised and at-risk properties undertook private precaution. These measures resulted in lower water depths as well as reduced loss in this region during the 2015 flood.

After the 2015 event, computer-aided telephone surveys were undertaken targeting the households that had suffered flood loss. The households were from the towns of Appleby, Kendal, Carlisle and Cockermouth located in the region of Cumbria. The survey consisted of questions concerning the flood characteristics (water depth, duration), building characteristics (type, construction year), preparedness (private precautionary measures, emergency measures, warning information etc.) and incurred loss to building structure and contents. The reconstruction costs for the houses were obtained from the Association of British Insurers (https://www.abi.org.uk/). The datasets that contained water depth and building loss information were selected for this analysis. This resulted in a dataset with 33 flood damaged residential buildings. All these datasets provide information pertaining to the initial appraisal of the MCM. The responses from the households are summarized per region in Table 1.

TABLE 1

Table 1. Summary of empirical data: sample size of complete records; medians of water depth in meters, duration in hours, warning lead time in hours, absolute building loss in £, and reconstruction value in £.

Multi-Colored Manual

The Multi-Colored Manual (MCM) (Penning-Rowsell et al., 2013) presents a deterministic flood loss model that estimates flood losses in Sterling. The MCM provides a range of synthetically-generated absolute losses corresponding to water depths for residential and non-residential properties to provide national consistent values for appraisals. The loss functions are based on the best ownership and economic values available from market-based surveys and synthetically generated loss functions.

For residential properties, unique loss functions are provided for different types of flooding, duration of inundation, warning lead time, building type, year of construction and social class; and estimates of loss are provided for the building fabric and contents along with the costs for cleaning and drying. In this study, we utilize MCM loss functions relevant to residential building fabric and divide the absolute loss estimates by the reconstruction cost to obtain an estimate of relative loss (rloss). Since empirical data concerning social class was not available, an initial MCM assessment for building fabric loss was performed utilizing different loss functions based on type of flooding, water depth, duration of inundation, warning lead time, building type and year of building construction.

Results

Exploratory Data Analysis

MCM provides a multi-variable synthetic model that captures damage processes affecting residential buildings based on building and hazard characteristics explained in Section Multi-Colored Manual. Flood damage processes are stochastic and there is variability in damage processes across buildings, events and regions. It is unlikely to sufficiently capture all loss influencing factors and processes using a deterministic model. During the 2015 flood there was heterogeneity across the affected regions in terms of flood awareness, flood experience and implementation of private precautionary measures.

In order to understand the potential regional variability, the agreement between observed loss and MCM predictions are analyzed in Figure 1. The empirical loss obtained from post-event surveys (observed relative loss) is represented as $\widetilde{rloss}$ and the MCM predictions are represented as rloss_MCM. Since MCM is a deterministic model, a single value of rloss_MCM is obtained for each building.

FIGURE 1

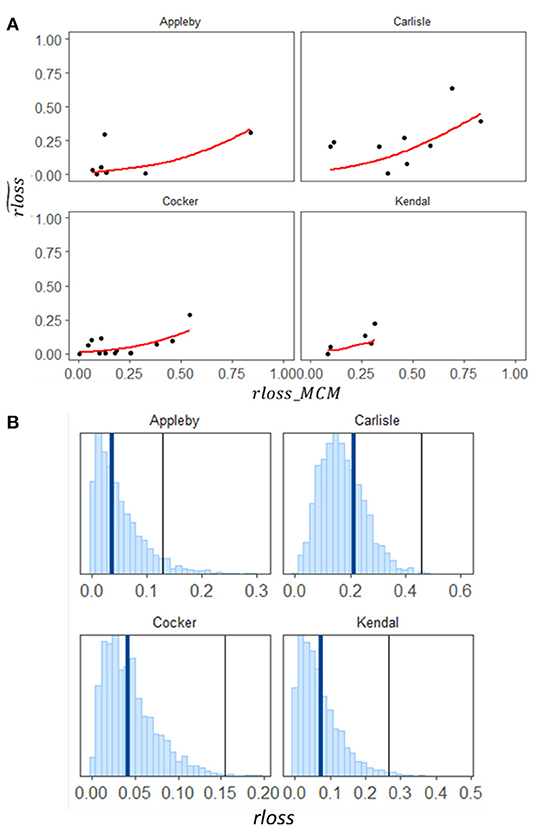
Figure 1. (A) Region-wise scatter plot of MCM predictions against observed loss (black points) with reference 1:1-line (gray line) and predictions using hierarchical parameterization of the BDDS model (red line); (B) Region-wise posterior predictions using hierarchical parameterization of the BDDS model (histogram) along with median observed loss (blue line) and median of MCM estimate (black line).

From Figure 1A, we see that most of the MCM predictions fall below the reference line, thus, we can infer that MCM consistently overestimates flood loss. A negative intercept in the fit of residuals may potentially compensate for this over-estimation.

Hierarchical Parameterization and Bayesian Inference

The hierarchical parameterization of the BDDS model is aimed at minimizing the deviation of MCM predictions from the observed data, resulting in better prediction capabilities for regions within and outside the training area. The model is fully probabilistic which provides estimates of model reliability based on the predictive distributions.

The region-level parameterization considers differences in vulnerability across regions. Based on the exploratory data analysis performed in Section Exploratory Data Analysis, the empirical loss as the dependent variable is regressed against the MCM estimation. Thus, the vulnerability of a household is modeled using a logit transformed linear relationship between the MCM loss prediction and the observed loss conditioned on the region in which the household is located (Equations 2, 3). Figure 1A shows the model fit plotted over observed losses against MCM estimation. The significance of the model structure (linear relationship) is measured using the threshold based on the Region Of Practical Equivalence (ROPE) for Bayesian models (Kruschke, 2018). The ROPE is a region around 0 corresponding to practically no effect or negligible magnitude (i.e., the model parameter is not significant). The proportion of posterior distribution of parameter outside the ROPE is used to either accept or reject the Bayesian parameters. The significance test for the developed model shows that both parameters λ_r and ε_r has 100% of the posterior distribution outside the ROPE.

$\begin{array}{ll}{\widetilde{rloss}}_i|{rloss\text{\_}MCM}_i~Beta({\alpha }_i,{\beta }_i)& (1)\end{array}$

$\begin{array}{ll}{\alpha }_i={\mu }_i\times {\phi }_r;{\beta }_i=(1-{\mu }_i)\times {\phi }_r& (2)\end{array}$

$\begin{array}{ll}{\mu }_i=invlogit({\lambda }_r\times {rloss\text{\_}MCM}_i+{\epsilon }_r)& (3)\end{array}$

In equations 2 and 3, subscripts i and r refer to individual buildings and the region in which they are located. $\widetilde{rloss}$ is modeled as a beta distribution with logit transformation, since, unbounded distributions might result in implausible values for $\widetilde{rloss}$ (Rözer et al., 2019). The beta distribution holds two parameters α and β which are algebraically determined using location parameter μ and variance parameter φ (Equation 3). μ is a logit transformed function of the MCM predictions (rloss_MCM) with parameters slope (λ), intercept (ε). The parameters φ, λ and ε vary across the four regions. They are made up of two components, the fixed component which is common to all regions and the varying component which determined the variability in damage processes across the regions conditioned on the MCM predictions. Equations 2 and 3 are comprised of three fixed parameters, one for each of the φ, λ and ε; twelve region-level parameters, four (number of regions) for each of the φ, λ and ε; three standard deviations governing the variability across regions for each of the φ, λ, and ε; one correlation coefficient between varying λ and ε. The parameters of this multi-level model structure are estimated using Bayesian inferences.

Bayesian inference allows us to include our assumptions regarding damage processes as priors and available empirical data as evidence for updating. Bayes' Theorem (Equation 4) tells us that the posterior distribution of our parameters depends on the likelihood of the data and our prior estimation of the parameter distributions.

$\begin{array}{ll}p(\theta |y)=\frac{\tilde{p}(y|\theta )p(\theta )}{p(y|\theta )p(\theta )d\theta }& (4)\end{array}$

The posterior distribution of our parameter estimates is represented by p(θ|y). Our prior belief about the distribution of the parameters is represented by p(θ). We initially provide priors that describe our general belief about the distribution of the parameters. For example, in Equation 3, φ is required to be positive and hence given an un-informative generic prior, gamma(0.01, 0.01). Similarly, the standard deviation terms that govern variability at each level in the hierarchy are given weakly informative priors which are constrained to be positive. e.g., half-student t priors (Gelman, 2006). We also provide un-informative generic priors to λ and ε to estimate the model parameters based on the availability of evidence from empirical loss data using the likelihood estimate p(y|θ). The model parameters are approximated using MCMC (Markov Chain Monte Carlo) sampling implemented using the software Stan (Carpenter et al., 2017). Stan uses Hamiltonian Monte Carlo sampling, which uses the gradient of the log probability to speed up convergence and parameter exploration.

Model Performances and Inferences

The validation of the models is performed based on assessment metrics: Mean Absolute Error—MAE (Equation 5) and Mean Bias Error—MBE (Equation 6). These metrics measure the model's predictive capability using a point estimate as the predicted rloss (e.g., deterministic estimate or median of the predictive distribution). MAE represents the magnitude of the error (precision) and MBE represents the direction of the error bias (over-/under-estimation- accuracy). With respect to MAE and MBE, the Hierarchical parametrization of the BDDS model can be directly compared with the MCM predictions.

In contrast to the deterministic MCM, the BDDS is a probabilistic model which provides a predictive distribution from which Hit Rate (HR, Equation 7) and Interval Score (Equation 8, Gneiting and Raftery, 2007) can be determined. The HR represents the percentage of predictions where the observed data falls into the 90% High Density Interval (HDI) of the prediction (HDI₉₀; values between the 5th and 95th percentiles of the distribution); the interval score (IS) is the width of the 90% HDI (HDI₉₀). The IS is penalized, if the prediction lies outside the 90% HDI. The HR and IS are measures of model reliability.

$\begin{array}{ll}MAE=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|r\widetilde{los}{s}_i-rlos{s}_i\right|}& (5)\end{array}$

$\begin{array}{ll}MBE=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}r\widetilde{los}{s}_i-rlos{s}_i}& (6)\end{array}$

$\begin{array}{ll}HR=\frac{1}{n}{\displaystyle \sum _{i=1}^n{h}_i;h_i=}1ifrlos{s}_i\in HD{I}_{90i};0,otherwise& (7)\end{array}$

$\begin{array}{l}IS=HD{I}_{90i}+\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{2}{\beta }}\left(\min \left(HD{I}_{90i}\right)-r\widetilde{los}{s}_i\right)|r\widetilde{los}{s}_i\\ <\min \left(HD{I}_{90}\right)+\frac{2}{\beta }(r\widetilde{los}{s}_i-\max \left(HD{I}_{90i}\right)|\{r\widetilde{los}{s}_i\\ >\max \left(HD{I}_{90i}\right)& (8)\end{array}$

Where $\widetilde{rloss}$ is the observed rloss from empirical dataset, rloss is the 50th percentile of the predictive distribution and β = 1−(0.95−0.05), for 90% HDI.

In reality, we are interested in predicting losses of houses that are not in our training dataset. These include houses from the same regions used for training as well as houses from other regions. In order to test the models under a regional transfer scenario, we perform Leave-One-Out (LOO) and Out-Of-Region (OOR) cross validations (CV).

LOO-CV requires the model to be trained on n-1 buildings, where n is the total number of buildings. The loss of the left-out building is predicted. This is iteratively performed until the loss prediction is performed for all the buildings in the dataset. OOR-CV requires the model to be trained on all buildings from m-1 regions, where m is the total number of regions. The losses of the buildings in the left-out region is predicted. This is iteratively repeated until loss prediction is performed for buildings in all regions. The assessment of the model performances for LOO and OOR CV are given in Table 2.

TABLE 2

Table 2. Performance of MCM and hierarchical BDDS models.

The Hierarchical BDDS outperforms the deterministic MCM with least MAE and least absolute MBE (Table 2). The MAE and MBE are reduced by 52 and 93%, respectively, in the case of LOO-CV and by 23 and 90%, respectively, in the case of OOR-CV. The developed model, being probabilistic, also quantifies prediction reliability using IS and HR. The posterior predictive distribution corresponding to each region is shown in Figure 1B. These results show that calibrating the synthetic MCM function with available empirical data within a hierarchical probabilistic framework results in precise predictions with high reliability. That is, predictions from the developed model are consistently closer to the observed loss values than the MCM estimates.

Based on these validation tests, the Hierarchical BDDS model has higher prediction capability than the MCM for both scenarios (LOO-CV and OOR-CV). Nevertheless, the errors from LOO-CV are lower than the errors from OOR-CV. Similarly, the reliability measured using IS(HR) from LOO-CV is lower(higher) than the IS(HR) for OOR-CV. Based on these results, we infer that the model performance is also dependent on the quality and availability of empirical data from the regions to which the model is applied. Thus, using local empirical data for parametrization enhances the model's predictive capabilities.

The parameters from the model defined in Equations 2, 3 are provided in Table 3. The estimates are provided along with their standard deviations. The fixed intercept (ε) is negative, as presumed in Section Exploratory Data Analysis. The positive slope is also evident since we expect the MCM predictions to follow a similar trend as the observations. The model fit between MCM estimate and empirical loss is also validated by the 5th and 95th quantiles of the model coefficients being >0. The slope parameter shows the highest regional variability. Small values of φ represent high deviation (large credible interval of the beta distribution). Loss predictions from Carlisle and Appleby, the two highly impacted regions with varying levels of preparedness resulted in large predictive intervals, compared to the other regions. Additionally, Carlisle and Kendal with the highest intercept and slope, respectively have buildings that are more vulnerable than the other regions. This finding aligns with the fact that households in Carlisle and Kendal were unprepared for such an extreme event—the peak discharge of the 2015 event was almost 60% larger than the 2009 event which led to overtopping of the flood walls designed based on past flood levels. In particular, the households behind the flood walls suffered high losses as they felt safe and did not implement Property Level Resilience measures (MSCA ETN Early Stage Researchers, 2019). On the other hand, despite having had the least warning lead time and high flooding duration, the residential buildings in Appleby have the least slope, representing low increase in vulnerability with higher water depths. The environmental agency's (DEFRA) pilot implementation of Property Level Resilience measures in 199 properties in Appleby in 2007 is a potential reason for low vulnerability.

TABLE 3

Table 3. Model parameters estimate and standard deviation.

Conclusions

In this study, synthetic model calibration using a hierarchical Bayesian approach is demonstrated using a small sample of empirical flood loss data from the UK and the MCM. The resulting flood loss model is fully probabilistic and provides loss distributions which are precise and reliable. Using exploratory analysis of the MCM predictions and empirical loss data, the hierarchical parameterization included varying slope, intercept and deviation across regions.

The validation results proof that, the hierarchical parameterization of the BDDS model enhances the synthetic loss model by reducing the absolute error and bias by 23 and 90%, respectively, for residential buildings from new regions and by 52 and 93%, respectively, for residential buildings from the same regions used for training. The model reliability in terms of hit rate (i.e., the probability that the observed value lies in the 90% high density interval of predictions) is 88% for residential buildings from the same regions used for calibration and 73% for residential buildings from new regions and also captures flood vulnerability differences across regions. This is a promising step forward in calibrating synthetic models and determining reliability of flood loss predictions and can be further improved by including expert knowledge in the form of informative priors and region-level variables.

Since the empirical dataset used in this study is small and not representative of different flood damage processes in the UK, robust inferences concerning drivers of flood vulnerability cannot be made from this analysis. On the other hand, the results show the high value of good quality empirical flood loss data for developing reliable flood loss models, stressing the importance of post-event data collection campaigns.

The example of a successful enhancement of a synthetic model with very little empirical data stresses the practical relevance of the approach for the many regions worldwide where only limited amounts of flood loss data is available (or can be collected) but where reliable loss estimates are urgently needed. The explicit quantification of uncertainty in damage predictions driven by the quality of available data and expert knowledge contribute to making reliable risk management decisions at the household- and region-levels such as determining insurance premiums and implementation of flood protection.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

NS and HK: conceptualization. NS and KS: data and methodology. NS and MS: inferences. NS, HK, and MS: manuscript writing. All authors contributed to the article and approved the submitted version.

Funding

The research conducted within ETN System-Risk has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 676027 as well as from the project DECIDER (BMBF, 01LZ1703G).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bubeck, P., Botzen, W. J. W., Kreibich, H., and Aerts, J. C. J. H. (2012). Long-term development and effectiveness of private flood mitigation measures. Nat. Hazards Earth Syst. Sci. 12, 3507–3518. doi: 10.5194/nhess-12-3507-2012

CrossRef Full Text | Google Scholar

Cammerer, H., Thieken, A. H., and Lammel, J. (2013). Adaptability and transferability of flood loss functions in residential areas. Nat. Hazards Earth Syst. Sci. 13, 3063–3081. doi: 10.5194/nhess-13-3063-2013

CrossRef Full Text | Google Scholar

Carpenter, B., Gelman, A., Hoffman, M. D., Lee, D., Goodrich, B., Betancourt, M., et al. (2017). Stan: a probabilistic programming language. J. Stat. Softw. 76:1–32. doi: 10.18637/jss.v076.i01

CrossRef Full Text | Google Scholar

Elmer, F., Thieken, A. H., Pech, I., and Kreibich, H. (2010). Influence of flood frequency on residential building losses. Nat. Hazards Earth Syst. Sci. 10, 2145–2159. doi: 10.5194/nhess-10-2145-2010

CrossRef Full Text | Google Scholar

Figueiredo, R., Schröter, K., Weiss-Motz, A., Martina, M. L. V., and Kreibich, H. (2018). Multi-model ensembles for assessment of flood losses and associated uncertainty. Nat. Hazards Earth Syst. Sci. 18, 1297–1314. doi: 10.5194/nhess-18-1297-2018

CrossRef Full Text | Google Scholar

Gelman, A.. (2006). Multilevel (hierarchical) modeling: what it can and cannot do. Technometrics 48, 432–435. doi: 10.1198/004017005000000661

CrossRef Full Text | Google Scholar

Gerl, T., Kreibich, H., Franco, G., Marechal, D., and Schröter, K. (2016). A review of flood loss models as basis for harmonization and benchmarking. PLoS ONE 11, e0159791. doi: 10.1371/journal.pone.0159791

PubMed Abstract | CrossRef Full Text | Google Scholar

Gneiting, T., and Raftery, A. E. (2007). Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 102, 359–378. doi: 10.1198/016214506000001437

CrossRef Full Text | Google Scholar

Hudson, P., Botzen, W. J. W., Kreibich, H., Bubeck, P., and Aerts, J. C. J. H. (2014). Evaluating the effectiveness of flood damage mitigation measures by the application of propensity score matching. Nat. Hazards Earth Syst. Sci. 14, 1731–1747. doi: 10.5194/nhess-14-1731-2014

CrossRef Full Text | Google Scholar

Jongman, B., Kreibich, H., Apel, H., Barredo, J. I., Bates, P. D., Feyen, L., et al. (2012). Comparative flood damage model assessment: towards a European approach. Nat. Hazards Earth Syst. Sci. 2, 3733–3752. doi: 10.5194/nhess-12-3733-2012

CrossRef Full Text | Google Scholar

Kreibich, H., Müller, M., Schröter, K., and Thieken, A. H. (2021). New insights into flood warning reception and emergency response by affected parties. Nat. Hazards Earth Syst. Sci. 17, 2075–2092. doi: 10.5194/nhess-17-2075-2017

CrossRef Full Text | Google Scholar

Kruschke, J. K.. (2018). Rejecting or accepting parameter values in bayesian estimation. Adv. Methods Pract. Psychol. Sci. 1, 270–280. doi: 10.1177/2515245918771304

CrossRef Full Text | Google Scholar

Kruschke, J. K., and Vanpaemel, W. (2015). “Bayesian estimation in hierarchical models,” in The Oxford Handbook of Computational and Mathematical Psychology, eds J. R. Busemeyer, Z. Wang, J. T. Townsend, and A. Eidels (Oxford University Press), 279–299.

Google Scholar

Merz, B., Kreibich, H., and Lall, U. (2013). Multi-variate flood damage assessment: a tree-based data-mining approach. Nat. Hazards Earth Syst. Sci. 13, 53–64. doi: 10.5194/nhess-13-53-2013

CrossRef Full Text | Google Scholar

Merz, B., Kreibich, H., Schwarze, R., and Thieken, A. (2010). Review article Assessment of economic flood damage. Nat. Hazards Earth Syst. Sci. 10, 1697. doi: 10.5194/nhess-10-1697-2010

CrossRef Full Text | Google Scholar

Mohor, G. S., Thieken, A. H., and Korup, O. (2021). Residential flood loss estimated from Bayesian multilevel models. Nat. Hazards Earth Syst. Sci. 21, 1599–1614. doi: 10.5194/nhess-21-1599-2021

CrossRef Full Text | Google Scholar

MSCA ETN Early Stage Researchers. (2019). Flood Task Force Report: Retrospective Assessment and Comparison of the 2009 and 2015 Floods in Cumbria, UK. European Unions Horizon 2020 research and innovation program, System Risk ETN under grant agreement No 676027. Available online at: https://ec.europa.eu/research/participants/documents/downloadPublic?documentIds=080166e5c542ca1candappId=PPGMS (accessed on July 29, 2021).

Google Scholar

Penning-Rowsell, E., Priest, S., Parker, D., Morris, J., Tunstall, S., Viavattene, C., et al. (2013). Flood and Coastal Erosion Risk Management A Manual for Economic Appraisal. London: Routledge. doi: 10.4324/9780203066393

CrossRef Full Text | Google Scholar

Penning-Rowsell, E. C., and Chatterton, J. B. (1977). The Benefits of Flood Alleviation: A Manual of Assessment Techniques. Aldershot: Gower Technical Press.

Google Scholar

Rözer, V., Kreibich, H., Schröter, K., Müller, M., Sairam, N., Doss-Gollin, J., et al. (2019). Probabilistic models significantly reduce uncertainty in hurricane harvey pluvial flood loss estimates. Earths Fut. 7, 384–394. doi: 10.1029/2018EF001074

CrossRef Full Text | Google Scholar

Sairam, N., Schröter, K., Carisi, F., Wagenaar, D., Domeneghetti, A., Molinari, D., et al (2020): Bayesian Data-Driven approach enhances synthetic flood loss models. Environ. Model. Softw. 132, 104798. doi: 10.1016/j.envsoft.2020.104798.

CrossRef Full Text | Google Scholar

Sairam, N., Schröter, K., Lüdtke, S., Merz, B., and Kreibich, H. (2019a). Quantifying Flood vulnerability reduction via private precaution. Earths Fut. 7, 235–249. doi: 10.1029/2018EF000994

CrossRef Full Text | Google Scholar

Sairam, N., Schröter, K., Rözer, V., Merz, B., and Kreibich, H. (2019b). Hierarchical Bayesian approach for modeling spatiotemporal variability in flood damage processes. Wat. Resourc. Res. 55, 8223–8237. doi: 10.1029/2019WR025068

CrossRef Full Text | Google Scholar

Smith, D. I.. (1994). Flood damage estimation – A Review of urban stagedamage curves and loss functions. Water 20, 231–238.

Google Scholar

Szonyi, M., May, P., and Lamb, R. (2016). Flooding after Storm Desmond. Zurich Insurance Group. Available online at: https://www.jbatrust.org/wp-content/uploads/2016/08/flooding-after-storm-desmond-PUBLISHED-24-August-2016.pdf (accessed May 9, 2019).

Google Scholar

Vogel, K., Weise, L., Schröter, K., and Thieken, A. H. (2018). Identifying driving factors in flood-damaging processes using graphical models. Wat. Resourc. Res. 54, 8864–8889. doi: 10.1029/2018WR022858

CrossRef Full Text | Google Scholar

Wagenaar, D., Lüdtke, S., Schröter, K., Bouwer, L. M., and Kreibich, H. (2018). Regional and temporal transferability of multivariable flood damage models. Wat. Resourc. Res. 54, 3688–3703. doi: 10.1029/2017WR022233

CrossRef Full Text | Google Scholar