Temporal and Spatial Patterns of Groundwater Recharge Across a Small Watershed in the California Sierra Nevada Mountains

Mountain-block groundwater recharge is a crucial freshwater source in arid to semiarid watersheds worldwide; yet its quantification is difficult due to (1) hydrogeological heterogeneities especially in bedrock-dominated regimes, (2) drastic altitudinal ranges in climate, land use and land cover, and (3) mixing with deep groundwater derived from adjacent basins (i.e., interbasin groundwater flow). In this study, we test the utility of soil water-balance (SWB) modeling to quantify mountain-block groundwater recharge in the South Fork Tule River watershed in the California Sierra Nevada Mountains. This 1,018 km² watershed is instrumented with 3 USGS stream gages that allow for the development of a refined recharge (i.e., baseflow) calibration dataset via multi-objective optimization-based hydrograph separation. The SWB model was used to compute groundwater recharge and other water balance components at a daily time step using a 30-m grid cell size for a 40-year (1980–2019) study period. Mean annual recharge and runoff were estimated at 3.7 in/yr (3.0 m³/s) and 1.4 in/yr (1.2 m³/s), respectively, with modified Nash Sutcliffe Efficiency indices of 0.61 between baseflow and SWB-derived recharge, and 0.90 between hydrograph separation- and SWB-derived runoff. There is a strong correlation between annual recharge and rainfall (Pearson R = 0.95, p < 0.001) which attests to short residence times in the unsaturated zone and the immediate impact of droughts in 1990, 1999, and 2013. However, results of a modified Mann-Kendall trend analysis indicate no directional trends in recharge or runoff throughout the study period. Parameter sensitivity analyses reveal a persistent overprediction of recharge over baseflow that is particularly pronounced in the upper reaches of the watershed. This is likely related to the SWB model only considering soil characteristics at the surface and not simulating the fate of potential recharge below the root zone where it may be impeded from reaching the aquifer by shallow, impermeable bedrock. This limitation should be considered carefully for future water supply projections in this and comparable bedrock-dominated settings.

Introduction

Background

Mountain-block groundwater recharge (MBGR) represents the inflow of groundwater to lowland aquifers from adjacent mountains (Carling et al., 2012; Markovich et al., 2019). MBGR is a significant component of the hydrologic cycle, but it is notoriously difficult to quantify due to a lack of observational data (Kao et al., 2012; Yao et al., 2017; Markovich et al., 2019). The resulting uncertainty represents a key challenge in water sustainability assessments, particularly in arid to semiarid settings, such as the U.S. Southwest, where prolonged droughts coupled with drastically increasing water demands for agricultural and municipal supply resulted in widespread groundwater overdraft (Scanlon, 2004; Carling et al., 2012).

Early attempts to quantify MBGR at the watershed scale were based on empirically derived recharge to rainfall relationships (Maxey and Eakin, 1949), but more refined water balance models have shown to be the more reliable tools for this task (Healy and Scanlon, 2010). The main appeal of the water balance method is its universality and adaptability (Healy et al., 2007) because governing equations for the individual components (precipitation, evapotranspiration, etc.) do not specifically reflect mechanisms of subsurface flow and can thus be applied to diverse hydrologic settings (Healy and Scanlon, 2010). Governing equations can also be derived to reflect a variety of control volumes, from a column of soil (i.e., soil-water-balance) to an entire watershed (Healy et al., 2007). Additionally, as long-term climatic and hydrologic input data have become more readily available, recent water budget applications have facilitated new time series analyses of recharge (Dubois et al., 2021; Li et al., 2021).

A major limitation of the water balance method is its inability to capture compartmentalized water that transits in and out of the system on scales longer than the typical year-long scale watersheds are evaluated at (McDonnell, 2017). As an illustration, Martinec (1975) analyzed radioactive isotope tracers (i.e., tritium) in streams in the Swiss Alps, and found that snowpack runoff originated from precipitation that occurred several years prior to the actual measurement. Other issues arise from uncertain assumptions about hydrologic parameters such as changes in water storage, which is infrequently monitored so it is often wrongly approximated to be negligible (Flerchinger and Cooley, 2000; Scott and Biederman, 2019). Yet, in a study on groundwater recharge in the California Sierra Nevadas, Safeeq et al. (2021) found the water balance model to underestimate recharge when compared to estimates from groundwater well data, implying the importance of considering storage change in water balance approaches.

Several point-scale recharge estimation methods that rely on direct measurements at a specific location (i.e., a groundwater well) over time have been used to document MBGR. These include, e.g., assessments of groundwater table fluctuations (Healy and Cook, 2002); ionic mass balances for approximating gross inputs and outputs of water (Wilson and Guan, 2004; Aishlin and McNamara, 2011); and using isotope and noble gas geochemistry to estimate groundwater ages and recharge sources (Manning and Solomon, 2003, 2005; Anderson et al., 2005; Ma et al., 2009; Bowen et al., 2014; Markovich et al., 2021). While these approaches have shown to be useful in documenting MBGR, they have been of limited use for the quantification of MBGR rates due to the difficulty of obtaining sufficient data for a watershed-wide analysis. This is particularly a problem in mountainous settings where rainfall and recharge rates are typically highest in the undeveloped uplands, for which there are usually only limited groundwater well or aquifer parameter (e.g., specific yield) data available (Hagedorn et al., 2011). Groundwater well testing-based methods have, however, been widely used to derive calibration targets for water balance models despite uncertainty associated with scale (Singh et al., 2019; Walker et al., 2019). For instance, water table fluctuations represent current recharge events at the well screen, while an ionic mass balance represents mean recharge between where rainfall occurred and where water first entered the aquifer. Age dating tracers, in turn, represent mean recharge between where water first entered the aquifer and the groundwater discharge point, i.e., the well screen. Given these observations, it is not clear which of the groundwater well testing-based methods best resembles the potential recharge outputs of the water balance approach. Methods that rely on groundwater testing are further limited by groundwater mixing as in the U.S. Southwest, groundwater is often derived from long-screen wells intercepting multiple transmissive units. In those instances, groundwater often represents a complex mixture of modern, MBGR-derived proportions and premodern groundwater proportions, potentially derived externally via interbasin groundwater flow (IGF) (e.g., Bexfield et al., 2012; Hagedorn, 2015; Gardner et al., 2020).

Hydrograph separation and the quantification of baseflow has proven to be a valuable alternative to groundwater well testing for calibrating soil water balances and estimating MBGR rates. Baseflow includes only the groundwater input to streams, i.e., groundwater discharge, which by conservation of mass should equal groundwater recharge to the streams' drainage basin (Nielsen and Westenbroek, 2019). Several studies have demonstrated the utility of this approach (Lee et al., 2006; Zomlot et al., 2015; Trost et al., 2018; Day, 2019; Nielsen and Westenbroek, 2019). However, one problem of hydrograph separation is that available methods rely on subjective input parameters such as the choice of algorithm to connect lowest values in the stream hydrograph or the distinction of recession periods, etc. (Sloto and Crouse, 1996; Tan et al., 2009; Cheng et al., 2016). As a result, uncertainty in the baseflow output (and associated recharge calibration) is generally not addressed based on specific input parameter applicable to a specific setting, but rather through the use of an average value obtained from multiple methods run on default parameters (Day, 2019; Nielsen and Westenbroek, 2019). Recent studies have presented a new and more objective hydrograph separation approach that combines flow estimates from recursive digital filtering (RDF) with chemical mass balance through multi-objective optimization (Hagedorn, 2020; Hagedorn and Meadows, 2021). The utility of this method to provide calibration targets for water balance models in mountainous watersheds with pronounced spatiotemporal variability in the stream hydrograph and recharge has not yet been tested.

The purpose of this study is to apply the USGS Soil-Water-Balance (SWB) model (Westenbroek et al., 2018) in combination with optimized hydrograph separation to estimate MBGR in the South Fork Tule River watershed in the Sierra Nevada Mountains (California, USA). This watershed is largely undisturbed and has been instrumented with three USGS streamgages for multi-year stream hydrograph records (Hagedorn, 2020). SWB is based on a modified Thornthwaite-Mather soil-moisture accounting method (Thorthwaite and Mather, 1955, 1957) which estimates net infiltration of water out of the root zone by calculating excess soil moisture (i.e., potential recharge), where changes in the soil moisture reservoir is updated on a daily basis. The distinction of SWB calculating net infiltration rather than actual recharge lies in its lack of consideration of travel time of water to reach the groundwater system once infiltrating past the root-zone depth.

SWB has been applied in numerous studies, but few of which have encompassed mountain-front regions. Trost et al. (2018) used SWB to model groundwater recharge to the glacial aquifer system east of the Rocky Mountains, but did not adjust calibration parameters to specifically represent MBGR within the domain. As a result, calibration adjustments were made to best reflect average conditions across the watersheds which largely encompassed non-mountainous regions. Nielsen and Westenbroek (2019) developed a model for the state of Maine using a similar calibration approach and attempt to quantify parameter uncertainty through inverse (i.e., PEST; Doherty and Hunt, 2010) modeling. Importantly, this approach allows assessing the uncertainty resultant of user-defined input parameters such as runoff curve numbers, maximum net infiltration rates, and root-zone depths. However, the approach does not consider uncertainty associated in climate datasets, soil data mapped by the Natural Resources Conservation Service (NRCS), or land-use input grids, which tend to exert they highest influence on recharge magnitude based on previous SWB studies (Mair et al., 2013; Harlow and Hagedorn, 2018; Trost et al., 2018).

In this study, SWB was run over a 40-year dataset (1980–2019) placing special emphasis on the use of optimized baseflow calibration targets developed from 3 evenly distributed stream gages (Figure 1) to derive refined recharge estimates. The effects of user-defined input parameters on recharge magnitude were assessed in a sensitivity analysis. Furthermore, recharge and runoff outputs were analyzed through a series of Mann–Kendall (MK) trend tests, corrected for short-term autocorrelation effects to identify upward or downward trends over the course of the modeling period. This study provides valuable benchmark values of recharge and illuminates methodological limitations that require further study for improved recharge analysis in mountainous settings.

FIGURE 1

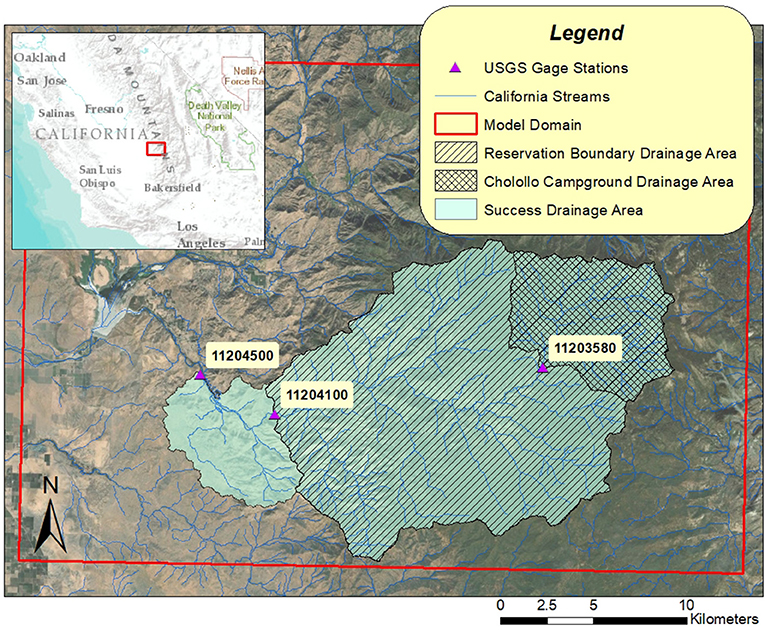
Figure 1. Location and extent of model domain with calibration subwatersheds and corresponding USGS gage stations.

Local Setting

The Tule River Basin is located in the southern-central section of Tulare County in south-central California (Figure 1). The headwaters of the South Fork Tule River lie in the southern Sierra Nevada Mountains, and it discharges into Lake Success to the west. The topography is characterized by steep western-facing slopes connecting the highlands with elevations around 2,000 m above sea level (asl) to the basin with elevations around 200 m asl.

This study area includes the 224 km² Tule River Indian Reservation on the south-central portion of the domain. One thousand one hundred and sixty-eight people reside on the reservation (U.S. Census Bureau, 2019) relying on both surface and groundwater resources from the South Fork Tule River Basin to meet water demands. Water deficits have become increasingly evident in late summer through early fall due to freshwater scarcity and lack of infrastructure (Natural Resources Consulting Engineers, GEI Consultants, Native American Rights Fund, and Kenney & Associates, 2013).

The region has a Mediterranean to semi-arid climate with warm, dry summers and cool, wet winters (State of California Department of Water Resources, 2014). Precipitation ranges from 67–79 inches in the alpine highlands to 31 inches in the western lowlands (State of California Department of Water Resources, 2014). Highest and lowest annual precipitation during the study period occurred in 1983 (50 in) (Figure 2a) and 2013 (8 in) (Figure 2b), respectively. The warmest year recorded during the study period was 2014, with an average maximum temperature of 23°C and minimum of 8°C (Figure 2c). The coolest year recorded was 1982 with average maximum and minimum temperatures of 19°C and 5°C, respectively (Figure 2d).

FIGURE 2

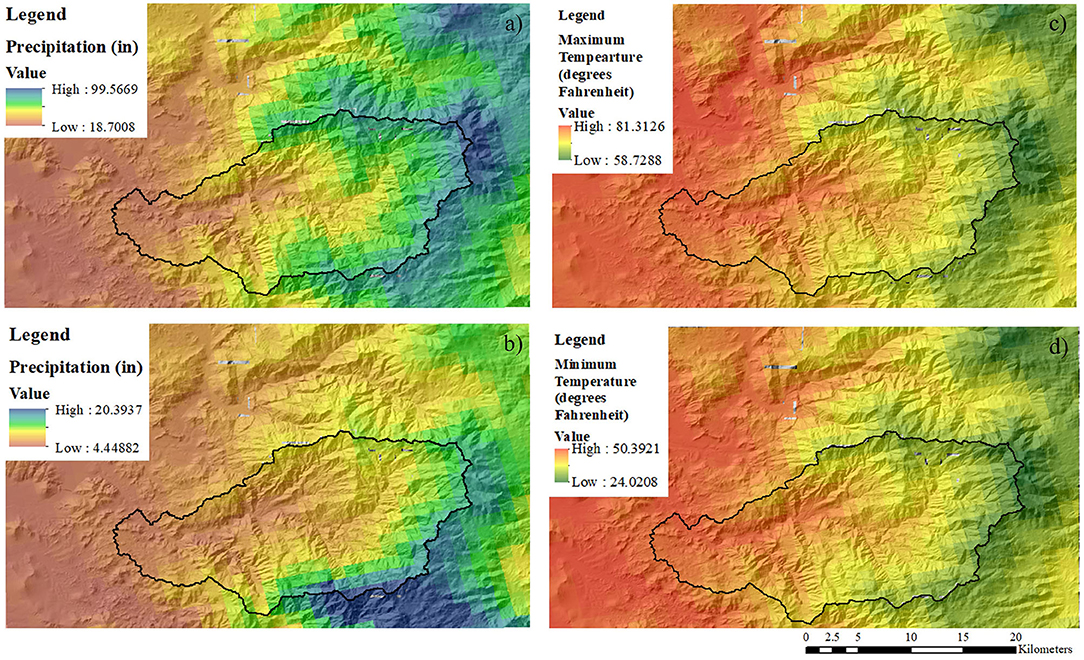
Figure 2. (a) Average annual precipitation high in 1983; (b) average annual precipitation low in 2013; (c) average annual maximum temperature high in 2014; (d) average annual minimal temperature low in 1982. Calibration watershed outlined in black.

Water demands are expected to be challenged by projected effects of climate change. According to the Joyce et al. (2009), the San Joaquin Valley, under low to medium-high intensity IPCC emission scenarios, should experience an increase in average annual temperature and the occurrence of droughts. Because of the resulting increase in evapotranspiration rates, crop water requirements are expected to rise in the San Joaquin Valley by about 5% (Joyce et al., 2009). Another climate model by VanRheenen et al. (2004) found that this projection could result in a reduced late spring snowpack by up to 50%. The Sierra snowpack alone accounts for nearly half of the surface water storage in California (Joyce et al., 2009), and mitigation techniques will need to accommodate for this temporal, spatial, and volumetric shift of water across the state. Furthermore, due to the combination of reduced snowpack, earlier melt, and increased evapotranspiration rates, high-elevation catchments with shallow soil, such as those throughout the Sierras, may lose their ability to carryover storage and buffer subsequent year streamflow (Safeeq and Hunsaker, 2016).

Land use across the model domain is largely distributed across four categories (96.8%): evergreen forest (40.2%), herbaceous land (34.3%), shrub/scrub (17.1%), and deciduous forest (5.2%) (Multi-Resolution Land Characteristics Consortium (MRLC), 2018) (Figure 3a). Based on the United States Department of Agriculture (USDA) NRCS classification of soils, ~70% of the model domain is made up of rock outcrop with slopes up to 75%. The majority of land in this category is overlain by thin soils. This has important implications for the analysis of this study, as input parameters of available water capacity and hydrologic soil group classifications may not be accurate for rock outcrops.

FIGURE 3

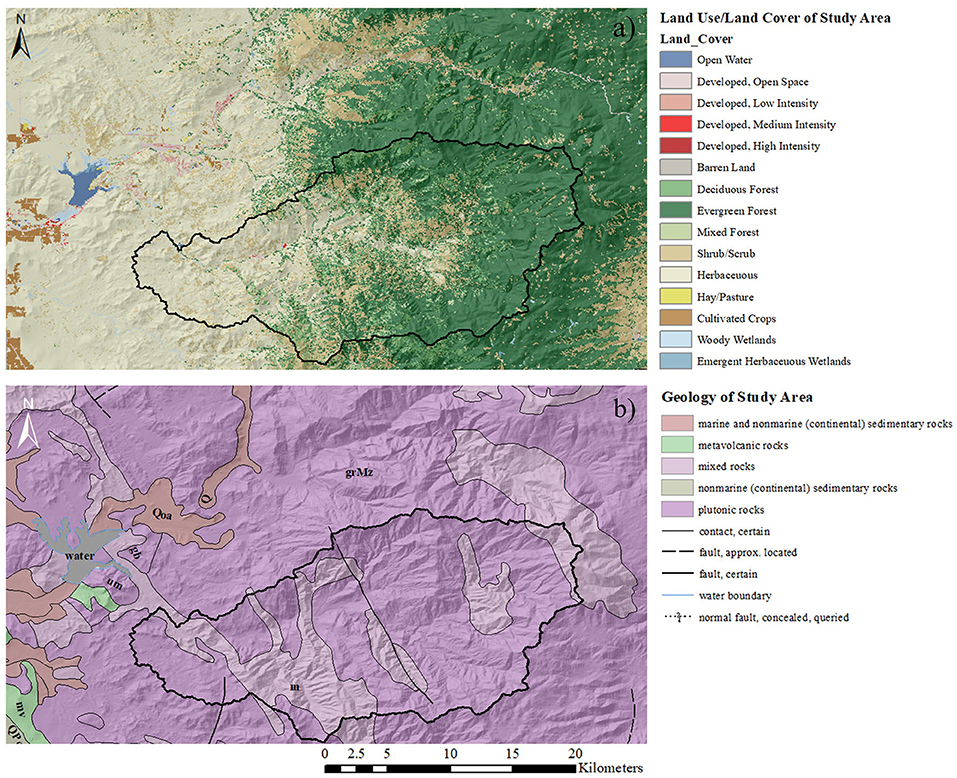
Figure 3. (a) Multi-Resolution Land Characteristics Consortium (MRLC) (2018) land use/land cover classification input raster of model domain. (b) Surficial geology units and faults across model domain (USGS). Calibration watershed outlined in black.

The geology of the model domain is dominated shallow crystalline bedrock of the Sierra Nevadan batholith which consists of Mesozoic plutonic rocks including granite, quartz monzonite, granodiorite, gabbro, and quartz diorite. Pockets of mixed pre-Cenozoic metasedimentary and metavolcanic rocks and Mesozoic ultramafic rocks are found in the southern portions of the model domain. Paleogene to Quaternary alluvial deposits dominate the western lowlands (Jennings et al., 2010) (Figure 3b).

The South Fork Tule River basin is characterized largely as an unconfined aquifer made up of Pliocene to Holocene-aged alluvial fan deposits. The unsaturated zone in this region is broken into a 5–7 ft thick soil root zone underlain by a vadose zone ranging from 49 to 164 ft thick (Ruud and Harter, 2002). The majority of the study area, however, is comprised of steeply-sloping plutonic rocks where soil layers are thin and the water table depth exceeds 6.6 ft (NRCS USDA, 2014), suggesting water storage in fractured-rock aquifers.

Five major fault systems have been mapped within the model domain (Figure 3b). Depending on fracture geometry, such features may act as either a conduit of flow (Barton et al., 1995; Thyne et al., 1999), creating an anomalously high hydraulic-conductivity region, or as an impediment to flow which may force water that would otherwise find its way to an adjacent aquifer to collect and remain within the bedrock (Mayer et al., 2007). Faults and fractures may also contribute to routing of water between basins, i.e., interbasin flow (Markovich et al., 2019). SWB is not equipped to simulate the effects of such geological heterogeneities on groundwater recharge.

Materials and Methods

Overview of SWB Model

SWB computes net infiltration out of the root zone (hereafter referred to as recharge) for each model cell as the difference between soil moisture for the current simulation day (θ_t) and the soil's field capacity (θ_FC):

$\begin{array}{ll}recharge={\theta }_t-{\theta }_{FC}& (1)\end{array}$

With:

$\begin{array}{ll}{\theta }_{FC}=TAW=AWC\times rootingdepth& (2)\end{array}$

Where TAW is the total available water and AWC is available water capacity, the latter representing the difference between a soil's field capacity and its permanent wilting point (θ_WP) (Barker et al., 2005). Soil moisture is estimated using a water-balance of the soil column:

$\begin{array}{l}{\theta }_t={\theta }_{t-1}+rainfall+runon+snowmelt\\ -interception-runoff-ET& (3)\end{array}$

Where θ_{(t −1)}is the soil moisture on the previous simulation day and ET is actual evapotranspiration.

In addition to soil moisture, SWB takes into consideration interception and snow as storage reservoirs. SWB calculates each component of the water balance equation using empirical methods in the following sequential order. First, precipitation is partitioned into rainfall or snowfall; the latter accounted for via a temperature-based snow index method (Westenbroek et al., 2010). On any given day, snow may accumulate, melt, or both. Next, rain or snow interception is simulated via the bucket method (Westenbroek et al., 2010), where a constant interception value specific to each land use type must be exceeded by rain or snowfall for infiltration to occur. Potential evapotranspiration (PET) is then calculated with the Jensen and Haise (1963) method, which was chosen because it was developed using evaporation data from a variety of vegetation grown in the western United States. This method is generally accepted as one of the more favorable for PET estimation where detailed meteorological data are unavailable, and its effective use particularly in semi-arid regions has been documented (Saeed, 1986; Al-Sha'lan and Salih, 1987; Shirmohammadi-Aliakbarkhani and Saberali, 2020).

Interim soil moisture is calculated to account for water that is potentially available for actual evapotranspiration (AET):

$\begin{array}{ll}{\theta }_{interim}={\theta }_{t-1}+rainfall+snowmelt+runon-runoff& (4)\end{array}$

Where θ_t−1 is the soil moisture on the previous day, runon includes water input to a cell from upslope cells and is determined according to downhill routing simulated by the input flow direction grid, and runoff was calculated using the curve number method (Cronshey et al., 1986). The curve number method defines runoff in relation to the difference between precipitation and an initial abstraction term, the latter representing all processes that might act to reduce runoff, including interception by plants and fallen leaves, depression storage, and infiltration (Woodward et al., 2003). Under wetter conditions a larger fraction of θ_interim is more readily available for AET than on drier days when soil moisture is more strongly held within the soil matrix (Dunne and Leopold, 1978). To simulate this, SWB calculates the fraction of interim soil moisture readily available for AET (f ) as:

$\begin{array}{ll}f=\frac{({\theta }_{interim}-{\theta }_{WP})}{({\theta }_{FC}-{\theta }_{WP})}& (5)\end{array}$

Where θ_WP is the wilting point of soil and θ_FC is the field capacity.

Lastly, AET from the soil storage reservoir is calculated using the Thornthwaite (1948) method as a function of f and PET:

$\begin{array}{ll}AET=PET\times f\left(\frac{{\theta }_{interim}}{{\theta }_{FC}}\right)& (6)\end{array}$

The year 1980 was ran as a “spin up” year to set initial conditions of percent soil moisture and snow cover storage. As such, 1980 SWB outputs were excluded from recharge analysis.

Model Inputs

The SWB model requires datasets of land use/land cover, flow direction, hydrologic soil group (HSG), and available water capacity. These include climate data and a land use lookup table with user-defined parameters for each land use and hydrologic soil group. The files, as well as their sources and roles in the model are described as follows:

Daily gridded climate data were obtained at a 1-km resolution from the National Oceanic and Atmospheric Administration (NOAA) Daymet database (Thornton et al., 2020). The data includes precipitation and maximum and minimum temperatures derived from the Daymet algorithm which interpolates and extrapolates ground-based observations across North America. Climate parameters in regions lacking instrumentation are derived from distance-weighted observational data from the nearest stations.

The land use grid was obtained through the USGS National Land Cover database (Multi-Resolution Land Characteristics Consortium (MRLC), 2018) at a resolution of 30 m. Land use types are categorized based on the Anderson Level II classification. Due to the minimal development in the area (total of 0.2% developed land), changes in land use over the course of the model run are considered negligible thus only one land use grid was considered over the 1980–2019 study period.

SWB assumes that surface and groundwater systems are coincident within the model domain, so a flow direction grid is used to route water to adjacent downslope cells. This grid was developed from a digital elevation model (DEM) (Gesch et al., 2002) following methods described by Harlow and Hagedorn (2018).

Available water capacity (AWC) AWC is used in combination with input parameter root-zone depth to calculate TAW (Equation 2), or the maximum amount of water able to be held in the soil reservoir. Gridded inputs of available water capacity were obtained from Soil Survey Geographic (SSURGO) (NRCS USDA, 2014) at a 100-m resolution (Figure 4a).

FIGURE 4

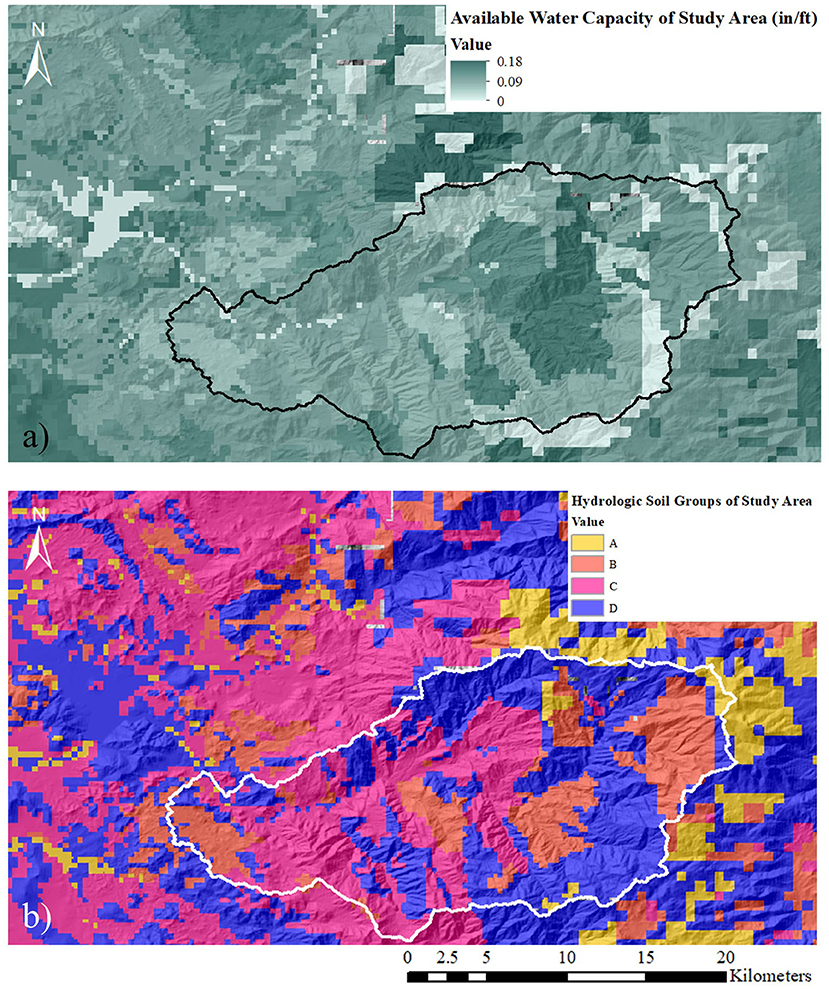
Figure 4. Soil characteristics input grids; (a) available water capacity of soil in inches of water per foot of soil; (b) distribution of hydrologic soil groups. Calibration watershed outlined in black.

Hydrologic soil groups (Figure 4b) are defined by USDA NRCS based on infiltration capacity of soils. A rating is determined for a specified volume of soil down to the depth of either the water table or an impermeable layer (whichever is shallower), based on the lowest hydraulic conductivity measured in the profile (Mockus et al., 1972). Four characteristic groups are recognized from A to D (represented in SWB as 1–4), where an A soil is described as having low runoff potential and high infiltration rates, and a D soil has low infiltration rates and high runoff potential when wetted (Cronshey et al., 1986). For the <1% of cells where no HSG was defined, an assignment to group D was given to produce the most conservative estimates of potential recharge and to prevent cells from being omitted from the model. Characteristic soil textures and corresponding infiltration rate ranges are summarized by Hawkins et al. (2009) based on categorization by the NRCS after studying qualities and properties of more than 14,000 soil series (Westenbroek et al., 2010).

The land use lookup table contains parameters for each land use and hydrologic soil group combination, including runoff curve numbers, maximum net infiltration rates, root zone depth, interception values for growing and non-growing seasons, and growing season start and end dates (Figure A1). Each parameter in this table is discussed in greater detail below.

A range of curve numbers typical for each HSG was derived by Hawkins et al. (2009), which was used along with previously published values specific to land use-HSG combinations in the land use lookup table of this study. SWB modifies these curve numbers according to the precipitation amounts from the previous 5-day period. Precipitation amounts are used to characterize soil-moisture conditions, which are differentiated into antecedent runoff conditions I, II, and III, or dry, average, and near saturation, respectively. Initially, curve numbers assigned in the land use lookup table are specified for antecedent runoff condition II (“normal” conditions). Higher soil moisture (i.e., antecedent runoff condition III) will force an increase in curve number from normal conditions because more runoff is likely to occur, while lower soil moisture yields a decrease in curve number (Mishra and Singh, 2003; Westenbroek et al., 2010).

Maximum net infiltration rates are used by the model as thresholds to prevent net infiltration estimates that are not typical given the soils and underlying geology in a given cell. Influxes of water occurring at a greater rate than the soil can accommodate is routed to runoff as rejected net infiltration. In this study, maximum rates were assigned as area-weighted averages for each land use-hydrologic soil group combination using saturated hydraulic conductivity data for each soil group (Web Soil Survey, 2014). Some calculated maximum infiltration rates were inconsistent with the expected trend of decreasing hydraulic conductivities from soil groups A-D, which has been ascribed in previous SWB model sensitivity studies to shallower root-zone depths and associated water competition between plant transpiration and infiltration in higher-rated soil types (Metropolitan Council, 2013; Smith and Westenbroek, 2015). The sensitivity of the model to these inconsistencies was explored in the calibration of the model.

Root-zone depths (the effective rooting depth of vegetation) is considered as the depth beyond which water becomes potential recharge. Measured data on root-zone depths are not available for this region, so this parameter was assumed equal to a “Restrictive Layer Depth” provided by SSURGO. A restrictive layer is defined as having properties that cause impedance of fluid movement or inhibit root growth. Determination of this parameter was accomplished in a similar procedure as the assignment of maximum infiltration rates: restrictive layer depths were entered into the soil polygon raster containing HSG assignments, and the resulting table was unionized with the land use raster. An area-weighted average root-zone depth was then calculated and entered into the land use lookup table.

Interception values for deciduous, evergreen, and mixed forest land use categories were derived from the literature for deciduous and evergreen species (Xiao et al., 2000), herbaceous grasses (Corbett and Crouse, 1968) and shrub/scrub vegetation (Hamilton and Rowe, 1949). Interception for open water; developed, open space; developed, high intensity; and barren land was set to 0 based on both observation via Google Earth imagery and subsequent determination of the lack of vegetation across these land use categories. Values for developed land of low and medium intensity were taken from Westenbroek et al. (2010). Due to lack of more relevant literature-published values and observation of similarities between land category characteristics, values for woody wetlands and emergent herbaceous wetlands were taken from Harlow and Hagedorn (2018). Interception by cultivated crop land typical of the San Joaquin Valley has to the authors' knowledge not been reliably studied, thus values were taken from suggested default values in the SWB v1.0 manual (Westenbroek et al., 2010). Hay/pastureland within the domain are similar in density and leaf size to vegetation categorized as herbaceous land, so the interception values were considered equal.

The growing season start and end dates were obtained through the NRCS Agricultural Applied Climate Information System (AgACIS) for Tulare County by taking the average of several station data (Fountain Springs, Lindsay, Milo, and Oak Opening) within the model domain which record the annual last spring and first fall freeze (Hedt, 2016). These dates are used in the land use lookup table to differentiate interception values for each land use type between their growing and non-growing seasons.

Model Calibration and Evaluation

A manual calibration was performed by adjusting parameters of the model with the objective of reaching an optimal correlation between SWB estimates of potential recharge and runoff to optimized baseflow and runoff derived from streamgage data. Direct runoff is calculated through hydrograph-separation as streamflow minus baseflow, which can be equated to the sum of SWB outputs “runoff outside” and “rejected net infiltration” (Nielsen and Westenbroek, 2019). “Runoff outside” includes direct runoff during a precipitation event or Hortonian overland flow (Chow et al., 1988), and “rejected net infiltration” includes any water in excess of the maximum infiltration capacity of the soil, or saturation overland flow (Chow et al., 1988).

The three streamgages—Cholollo Campground (CC) (station ID 11203580), Reservation Boundary (RB) (station ID 11204100), and Success (station ID 11204500)—are located along the South Fork Tule River and collectively capture the varying topographic and climatic regimes of the study area, with Cholollo Campground lying near the headwaters of the river, Reservation Boundary in the mid-slope region, and Success encompassing more of the lowland regions. Data from the CC and RB subwatersheds allowed for a calibration period between 2002–2019 and 2001–2019, respectively, and the Success subwatershed provided data for the calibration period 1981–1989. To perform calibration, gridded daily outputs of potential recharge and runoff were first processed to produce annual sums. The resultant grids were then clipped to the extent of the drainage area correspondent to each gage station, and spatially averaged for comparison to hydrograph-separation outputs.

Optimized baseflow and surface runoff constraints from multi-objective optimization from Hagedorn (2020) were used as calibration targets for Cholollo Campground and Reservation Boundary. The lack of time series specific conductivity data prevented optimized baseflow and runoff constraints for Success. Given this, the HYSEP sliding-interval method, implemented in the USGS Groundwater Toolbox program (v1.7; Zhai et al., 2015), was used to derive calibration targets for that gage.

To evaluate model performance the modified NSE (mNSE) index (Ritter and Muñoz-Carpena, 2013) was calculated for recharge and runoff estimates produced by SWB against streamflow-derived baseflow and runoff:

$\begin{array}{ll}mNSE=1-\frac{1}{{(n_i+1)}^2}with{n}_i=\frac{SD}{RMSE}-1& (7)\end{array}$

This statistic was chosen in favor over the NSE (Nash and Sutcliffe, 1970) to reduce the influence of outliers on model evaluation (McCuen et al., 2006). mNSE values range from –∞ to 1, where 1 indicates a perfect fit.

A modified Mann-Kendall (MK) trend test was used to identify trends in recharge and runoff time series produced by SWB. Trends were assessed using the R modifiedmk package (Patakamuri and O'Brien, 2021) following the methodology outlined by Hagedorn and Meadows (2021). We applied variance correction, pre-whitening and block bootstrapping techniques to account for autocorrelation effects typically present in daily hydrologic time series. Details on these procedures can be found in the reviews by Hamed and Ramachandra Rao (1998), Yue et al. (2002), Yue and Wang (2004), Hamed (2008), Khaliq et al. (2009), Önöz and Bayazit (2012), and Dinpashoh et al. (2014).

Modeled Recharge

Model Calibration

The baseline model run showed that SWB overpredicted recharge relative to hydrograph-separation derived recharge (i.e., baseflow), especially for the upper reach RB and CC drainages where steep topographic gradients and extensive bedrock outcrops prevail. This is consistent with findings from Nielsen and Westenbroek (2019), where SWB produced estimates of potential recharge significantly higher than baseflow values in mountainous regions of the U.S. State of Maine where abundant shallow bedrock outcrop exists. Additionally, because the root zone depth parameter was assumed as equal to the “Restrictive Layer Depth” value assigned by the USDA NRCS, it is possible that this depth is equal to the depth to bedrock in many regions of the domain, rather than a lower-permeability soil layer which would still allow water to infiltrate. However, SWB is able to accommodate lower potential recharge rates where impermeable surfaces are identified in the input (as defined in the land use lookup table). Taking this into consideration, the calibration process was performed in two phases:

Phase I followed standard adjustments to high uncertainty land use lookup table parameters with the overall goal of matching SWB estimates to hydrograph-separated baseflow and runoff. Adjustments made relative to the baseline model include: (1) increasing interception values by 10% (intercept10plus), (2) increasing root zone depths by 10% (rz10plus), (3) increasing curve numbers by 10% (cn10plus), and (4) adjusting maximum net infiltration rates to fit within typical ranges for HSG groups (from Hawkins et al., 2009) (maxinfilavg). Phase II involved adjusting model input parameters with the objective of simulating more impervious material where shallow bedrock exists within the model domain. The first adjustment was made by assigning HSG groups based on the distribution of bedrock in the domain (bedrock). By overlaying a surficial bedrock shapefile on the map of hydrologic soil groups, cells were reassigned to a value of D if bedrock exists in the majority of the cell. The description of an HSG of D is consistent with this assignment, as it includes “shallow soils over nearly impervious material” (Hawkins et al., 2009). The second adjustment made in Phase II was adding a value for “assumed imperviousness” in the land use lookup table (imperv). This parameter adds a percentage to the land-use type to which it is assigned that is treated as impervious. Land use types which were majorly underlain by shallow bedrock were given an assumed imperviousness value consistent with low density developed land (18%) (Westenbroek et al., 2018).

Despite efforts to simulate the effect of impervious bedrock present throughout the domain, mNSE values reveal no improvement relative to the baseline model by Phase II calibration. The RB subwatershed is entirely underlain by bedrock and encompasses the steepest-sloping regions of the domain (and associated thin soils). Estimates across RB produced the lowest mNSE values across all model runs. As an illustration, mNSE of predicted recharge for the RB subwatershed by the best-fit run is 0.34, while CC and Success subwatersheds produced mNSE values of 0.71 and 0.79, respectively. We attribute this low mNSE to the model's inability to address the fate of water below the root zone depth in bedrock-dominated units and units characterized by thin soils. If a bedrock layer exists above the water table depth, but below the root zone depth, all excess soil moisture is treated to reach the aquifer, even though the bedrock layer will impede vertical water movement if no fractures or dissolution features for water transport exist. In result, SWB consistently overpredicted recharge relative to baseflow (Figure 5). Additionally, SWB calculates the amount of water that is available for recharge (i.e., infiltrates past the rooting depth), however timing of recharge is not refined through this method. For instance, Smith and Westenbroek (2015) through calibration analysis of an SWB model developed for the state of Minnesota found that modeled, spatially-averaged potential recharge across the 35 watersheds in their domain was significantly more comparable to baseflow values derived from corresponding streamgages when compared as 15-year averages rather than annual-based averages.

FIGURE 5

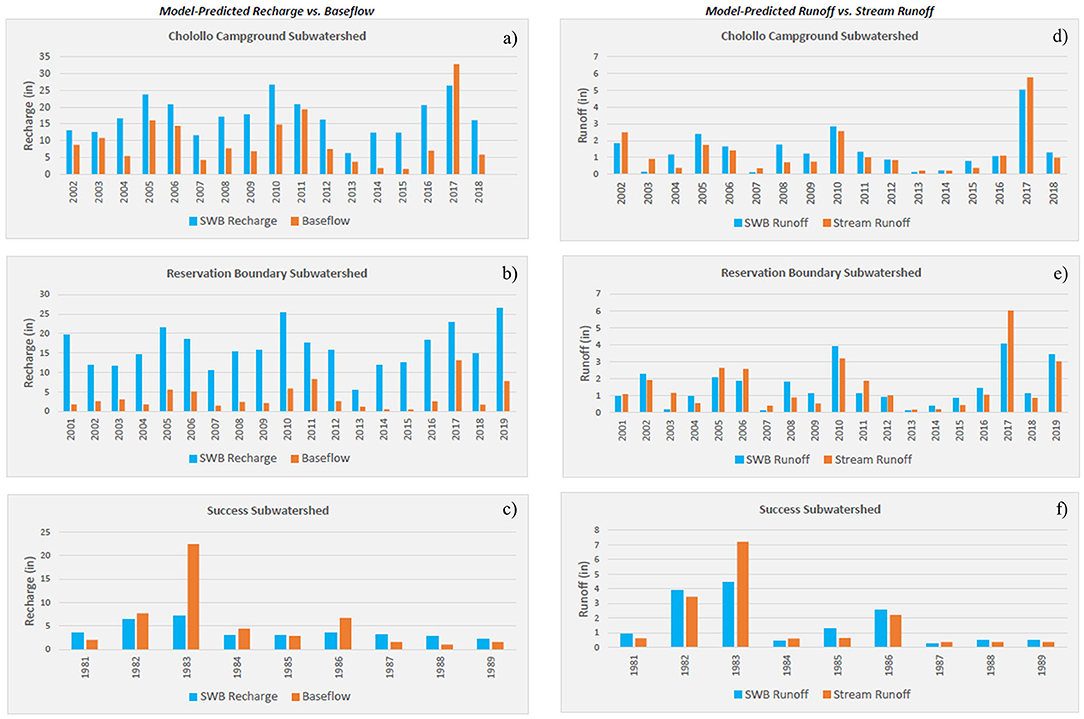
Figure 5. Bar charts of SWB-predicted recharge vs. baseflow (a,b Hagedorn, 2020; c HYSEP sliding-interval); bar charts of SWB-predicted runoff vs. stream runoff (d,e Hagedorn, 2020; f HYSEP sliding-interval).

The optimized model was determined as rz10plus, where root-zone depths were increased by 10%. Implications of increasing the root-zone depth include a larger soil-moisture reservoir and subsequently an increase in available moisture for ET, suggesting that ET amounts calculated in the baseline run may be underestimated. However, it is important to note that adjustments made in the calibration process often produced an improved model fit in one or more subwatersheds and a worsened fit in the others. For example, increasing root-zone depths by 10% improved modeled recharge estimates in the Success subwatershed relative to baseline, but resulted in a worsened fit in the CC subwatershed. This suggests model parameters may not reflect conditions specific to each subwatershed. There are also several parameter adjustments which produced an improved fit to one calibration target and a worsened fit to the other. Notably, maxinfilavg produced a better fit to baseflow relative to baseline, but a significantly worse fit to runoff indicating that those adjustments were not reflective of the true system. These analyses suggest that there is a lack of complexity in the SWB modeling structure to accommodate the various regimes present in a mountain-front region.

Spatial and Temporal Trends

Mean modeled annual recharge and runoff across the calibrated watershed are 3.7 in/yr (3.0 m³/s) at an mNSE of 0.61 and 1.4 in/yr (1.2 m³/s) at an mNSE 0.90, respectively. Estimates within the calibrated portion of the model (i.e., within the watershed boundary) were comparable to those produced in past studies conducted in similar regions. McCoy and Ladd (2019) developed an SWB model for fractured-rock aquifers in Virginia between 1996 and 2015 and estimated an average recharge of 5.3–8.1 in/yr (135–206 mm/yr). The average annual precipitation across the model domain was more than double that of the region studied herein, likely contributing to discrepancies between recharge estimates. Safeeq et al. (2021) applied a water balance method to watersheds in the Southern Sierra Critical Zone Observatory (SSCZO) and the Kings River Experimental Watersheds (KREW), which includes the Tule River watershed. They reported annual average estimates of recharge for a headwater catchment within KREW, just north of the Tule River watershed, at 8.22 in/yr (209 mm/yr) for the period 2009–2016. This headwater catchment is most similar in elevation and climatic conditions to the CC subwatershed, where SWB estimated average annual recharge at 16.7 in (478 mm) for the same time period.

The spatial distribution of recharge across the model grid (Figure 6) is similar to that of gross precipitation, suggesting a strong correlation between rainfall and recharge. This correlation is further supported with a linear regression analysis displayed in Figure 7. Recharge rates are highest near the headwaters of the river and lowest in mid-slope and lowlands in the study area, a pattern that is parallel to that of precipitation. Conversely, spatial distribution of recharge within the mid-slope region of the domain slightly differs from patterns of precipitation, likely a result of the downhill routing function implemented by SWB.

FIGURE 6

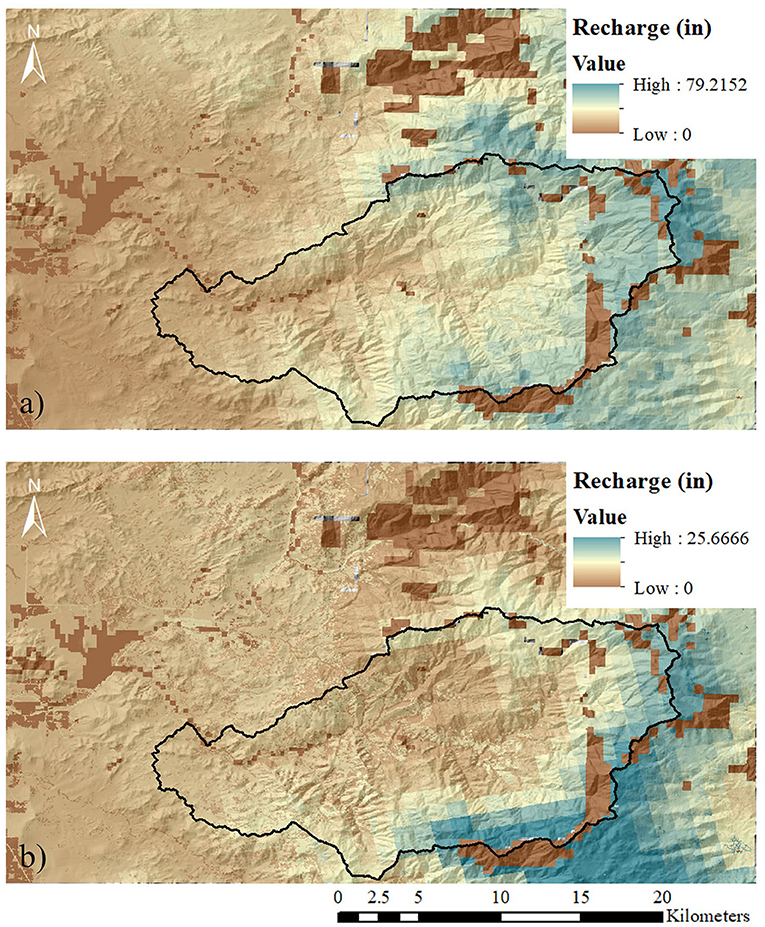
Figure 6. (a) Potential recharge distribution across model domain in highest recharge year 1983. (b) potential recharge distribution across model domain in lowest recharge year 2013. Calibration watershed outlined in black.

FIGURE 7

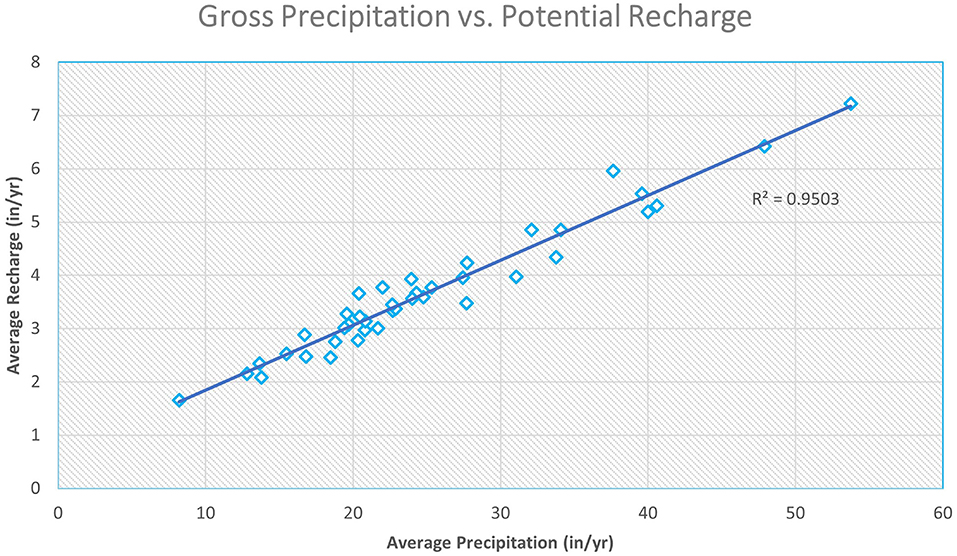
Figure 7. Linear regression plot of spatially-averaged gross precipitation vs. SWB recharge across calibrated watershed during study period.

On average, recharge in the calibrated portion of the domain accounted for 15% of gross precipitation during the study period. By comparison, Manna et al. (2016) found an average recharge-to-rainfall ratio in an upland sandstone aquifer in southern California of 4.2%, nearly four times lower than the ratio estimated herein. Conversely, Mair et al. (2013) computed SWB recharge to rainfall ratios across the island of Jeju in Korea of 42%. Schreiner-McGraw and Ajami (2021) applied an integrated surface water-groundwater model to simulate MBGR in the Kaweah River watershed in the Sierras of central California and found MBGR to account for 25-45% of annual precipitation. However, numerous dams and hydroelectric plants along the Kaweah strongly affect streamflow and it is not clear how this development was taken into account in the model calibration. Regardless, we attribute the discrepancy between our and previously published recharge to rainfall ratios for similar settings to the location of our calibration subwatersheds in relatively high-elevations and steeper terrains. More distributed calibration data for mid-stream and lowland streamgages are needed for a more reliable watershed-wide assessment of potential recharge and recharge to rainfall ratios.

Potential recharge estimates vary amongst land use types. Across the four most common land use types in the calibrated area (evergreen forest, herbaceous land, shrub/scrub, and deciduous forest) annual average recharge rates were 19.2 in (489 mm), 23.8 in (604 mm), 22.9 in (582 mm), and 23.1 in (586 mm), respectively. Rates within herbaceous land were highest among land use types, where average daily recharge range from 0 to 0.08 in (2 mm), attributed to low interception rates and high infiltration capacities. High intensity developed land makes up 0.01% of the calibrated area and yielded the lowest recharge rates amongst land use types with an average annual recharge of 1.1 in (26 mm). Low rates are likely a result of the high runoff potential of impervious surfaces common in this category.

Results of the optimized model showed that recharge estimates do not significantly vary between hydrologic soil group classifications. Across soil group A, recharge estimates averaged 21.2 in/yr (538 mm/yr). Soil group B yielded averaged recharge of 22.8 in/yr (580 mm/yr). Soil groups C and D produced average recharge of 22.2 in/yr (564 mm/yr) and 20.3 in/yr (516 mm/yr), respectively. Considering soil group alone, recharge estimates are expected to decrease from soil group A–D; however, since HSG classifications are only used by SWB as spatial reference for the distribution of parameters defined in the land use lookup table, these results suggest that those parameters may not be consistent with qualities characteristic of each HSG group. These inconsistencies likely arise from the uncertainty associated with the assignment of HSG assignments of the 70% rock outcrop makeup of the domain, as HSG classifications are designed for specific soil textures that do not consider hard rock.

Surficial geology in the calibrated area is made up of plutonic and metamorphic type rocks. Plutonic rocks underlie 72% of the calibrated model region, where recharge estimates averaged 22.3 in/yr (566 mm/yr). Metamorphic rocks underlie the remaining 28% of this area, where recharge estimates averaged 21.1 in/yr (537 mm/yr). Conversely, sedimentary rocks which are present outside the calibrated portion of the domain, yielded average recharge rates of 6.7 in/yr (170 mm/yr). The discrepancy between average annual recharge between hard-rock and soft-rock types is likely more an attribute of precipitation distribution across the domain, as SWB does not consider the effects of surficial geology on recharge potential; sedimentary rocks occupy the most western portions of the domain, where precipitation rates are the lowest. Recharge rates estimated by SWB for plutonic vs. sedimentary rock-dominated regions are uncharacteristic based upon typical porosity and permeability characteristics of these materials. Therefore, refined recharge estimation methods should be considered in this area through groundwater testing.

There is a strong temporal correlation between recharge and rainfall with a highest annual mean (7.2 in/yr or 5.9 m³/s) in the highest annual rainfall year of 1983 (Figure 6a) and the lowest recharge mean (1.7 in/yr or 1.4 m³/s) coinciding with the lowest rainfall year of 2013 (Figure 6b). However, modified MK tests corrected for autocorrelation reveal no significant upward or downward recharge trends over the 40-year modeling period (Figure 8a; Figure A2) suggesting that observed large-scale phenomena, i.e., a reduced Sierra snowpack due to recent warming and precipitation decreases, had no significant effects on recharge in the South Fork Tule watershed. Trend tests also show a slight decreasing trend in runoff over the model period, which would suggest that components of surface runoff are more influenced by climatic effects than recharge, however, assessed at p > 0.05 this trend is insignificant (Figure 8b; Figure A2). A key aspect of concern, however, is the declining recharge trend for the drought years 1990, 1999, and 2013 that suggests that effects of drought on low recharge outliers may become more exacerbated in the future. Extending the modeling time frame to longer; i.e., >50 yr periods would certainly increase the confidence in the trend analysis and should be considered in future follow up investigations.

FIGURE 8

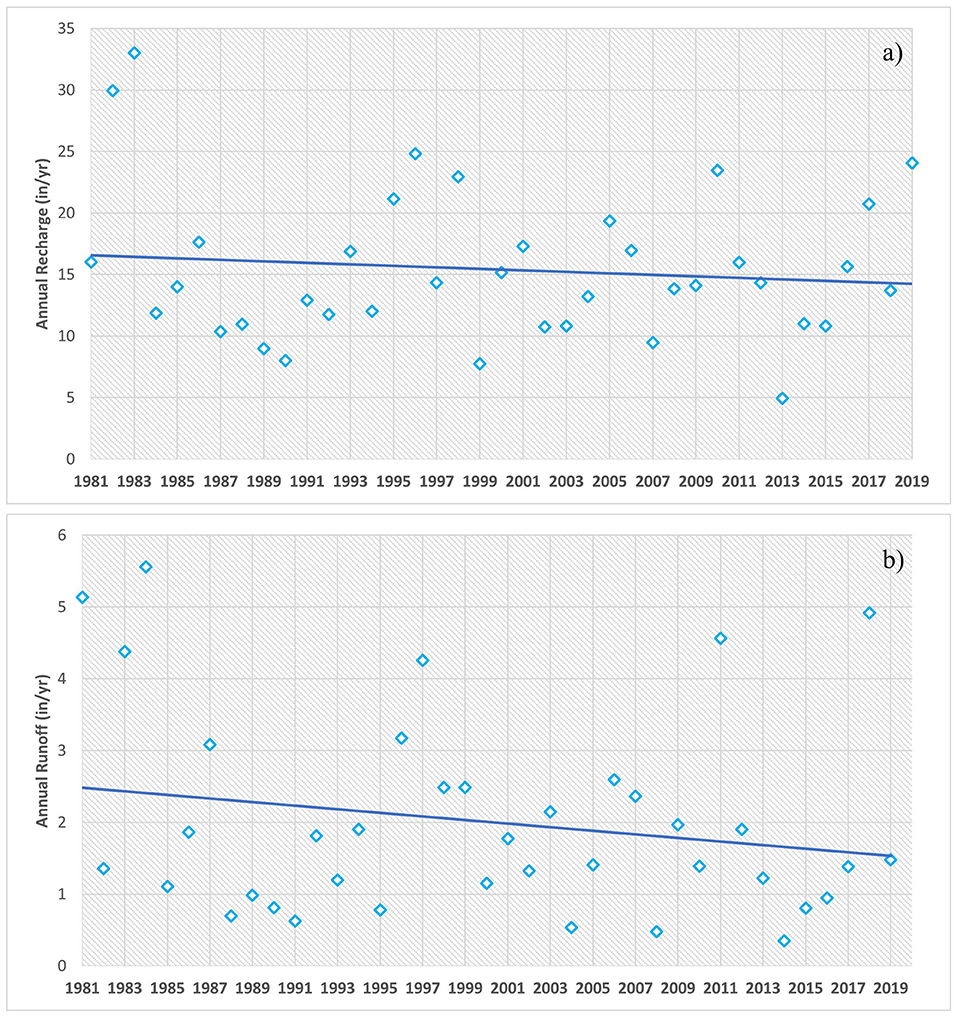
Figure 8. Linear regression plots of (a) SWB recharge and (b) runoff time series during study period.

Sensitivity Analysis

Results of the sensitivity analysis showed the difficult-to-measure maximum net infiltration rate (saturated hydraulic conductivity) and root zone depth parameters had the highest influence on recharge (Figure 9). Interception values displayed the lowest influence on predicted recharge, followed closely by hydrologic soil groups (bedrock). This is consistent with findings from Trost et al. (2018) who found that their model was most sensitive to the size of the soil-water reservoir, a function of root-zone depth and the maximum net infiltration rate. Our sensitivity analysis also revealed that maximum net infiltration rates had the largest influence on modeled runoff and were significantly more influential than any other parameter adjusted in calibration. Given these findings, it becomes clear that higher resolution soil conductivity and vegetation root zone depth is needed for improved and more reliable SWB applications.

FIGURE 9

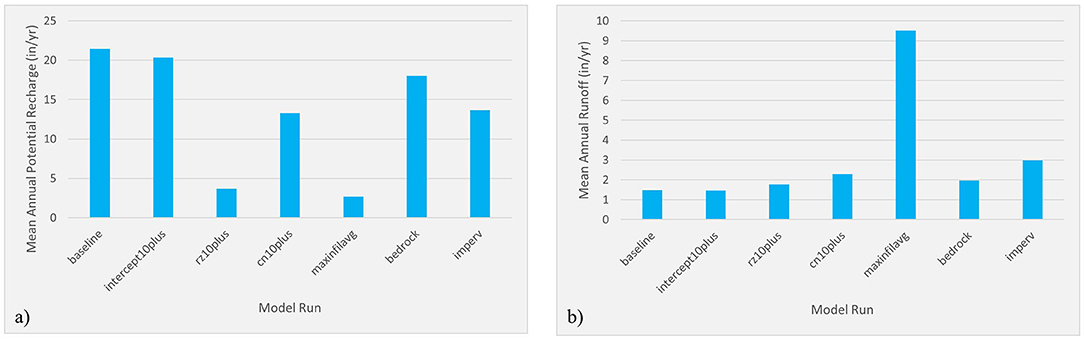
Figure 9. Sensitivity of model parameters to modeled (a) recharge (b) runoff. See text for description of model runs.

Limiting Assumptions

Limitations arise from assumptions made in the SWB model structure. SWB assumes that surface and groundwater flow paths are coincident, i.e., flow is routed strictly downhill according to the DEM-derived flow direction grid. However, it has been well-documented that interbasin flow occurs in mountain-block regimes and can constitute a significant portion of total recharge, especially in semi-arid to arid climates (Thyne et al., 1999; Belcher et al., 2009; Anderson et al., 2015). Specifically in plutonic rock mountain ranges, conduit flow via faults and fractures have shown to contribute a substantial amount of groundwater between basins with evidence from geochemical and isotopic signatures that differ from local recharge (Thyne et al., 1999).

While the SWB manual differentiates net infiltration estimates computed by the model from recharge in specifying that the code only simulates water that may move past the root zone depth, the potential recharge estimates for this particular region likely display larger discrepancies than in a non-mountain-front regime due to the influence of underlying impermeable bedrock. Fractures in bedrock are not simulated by the model, but likely contribute to channelized or “focused” infiltration across the model domain. Since the model only considers the subsurface above the root zone depth, it fails to accurately simulate recharge in regions where mapped soils overlie bedrock that is below the root zone (Nielsen and Westenbroek, 2019). Furthermore, this model code is not equipped to account for travel time of water to reach the groundwater aquifer, thus refined estimates of recharge timing are limited by this method.

For some soil groups, assigned AWC values do not reflect the ability of soils to drain, potentially leading to overestimates of recharge. For example, soils coded by SSURGO as A/D represent soils that are poorly drained which can significantly increase the capacity of soil to hold water, thus reducing the amount infiltrating out of the root zone (Nielsen and Westenbroek, 2019). Cells coded as A/D soils were considered as D soils to ensure the most conservative estimates. Sampling such soils was not possible within the scope of this project, which contributes to uncertainty.

Discussion and Conclusion

Watersheds in the U.S. Southwest are currently facing severe water supply challenges so reliable estimates of sustainable groundwater yields are critical for reservoir operation. This study aims at a quantification of locally derived MBGR for the period 1980–2019 through using of the SWB program in combination with optimized hydrograph separation. The calibrated model yielded mean estimates of annual potential recharge of 3.7 in/yr (3.0 m³/s; mNSE = 0.61) and runoff of 1.4 in/yr (1.2 m³/s; mNSE = 0.90). A complete set of groundwater and surface water extraction rates for municipal or agricultural supply is lacking for the study area, but a comparison of these rates to our estimates in follow up investigations could inform on overdraft risks in the area. Likewise, longer-term trend analyses are warranted in future investigations to better account for climate change induced impacts on recharge and surface runoff.

While SWB generated reasonable estimates of spatially-averaged recharge across the domain, inspection of results across individual calibration subwatersheds reveal that the model's ability to accurately calculate recharge is subject to significant spatial constraints. Recharge in the upper-reach regions, which are majorly underlain by impervious bedrock, are significantly overestimated by SWB which we attribute to the design of SWB to count any excess water simulated to move past the root-zone depth as potential recharge. In settings where an impermeable layer exists above the water table, but below the root-zone depth, this model structure fails to accurately consider the likely impedance the water encounters before, if ever, reaching the aquifer.

The recharge estimates presented in this study are within the range of previous values, which suggests that the model can produce reliable estimates of spatially-varying MBGR in complex mountainous settings. This can potentially facilitate a quantification of IGF to the watershed via comparison with estimates from other, groundwater testing-based methods that typically represent mixed systems affected by both MBGR and IGF components. Further modeling and field investigative study is needed to validate the model estimates and water balance parameters to completely assess the model's applicability to the California Sierra Nevadas and other mountainous settings.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

CM conducted modeling analysis. BH conducted MK trend analysis. Research was conceptualized and performed by CM and BH. All authors contributed to the article and approved the submitted version.

Funding

This study was supported by NSF grant HS-1936671 and CSU COAST SLR grant 210611. OA publication fees supplied by CSULB.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2022.815228/full#supplementary-material

Figure A1. Land use lookup table with parameters defined for each land use-HSG combination (HSG A–D as 1–4) for the baseline run. Highlighted cells display values inconsistent with expected pattern of consecutively decreasing infiltration rates from soil groups A–D.

Figure A2. MK Trend test results for annual recharge (R) and surface runoff (SR) in the South Fork Tule River watershed over time period 1981–2019. Trends are assessed at the 5% significance level.

References

Aishlin, P., and McNamara, J. P. (2011). Bedrock infiltration and mountain block recharge accounting using chloride mass balance. Hydrol. Processes. 25, 1934–1948. doi: 10.1002/hyp.7950

CrossRef Full Text | Google Scholar

Al-Sha'lan, S. A., and Salih, A. M. A. (1987). Evapotranspiration estimates in extremely arid areas. J. Irrigat. Drainage Eng. 113, 565–574. doi: 10.1061/(ASCE)0733-9437(1987)113:4(565)

CrossRef Full Text | Google Scholar

Anderson, K., Nelson, S., Mayo, A., and Tingey, D. (2005). Interbasin flow revisited: the contribution of local recharge to high-discharge springs, Death Valley, CA. J. Hydrol. 323, 276–302. doi: 10.1016/j.jhydrol.2005.09.004

CrossRef Full Text | Google Scholar

Anderson, M. P., Woessner, W. W., and Hunt, R. J. (2015). Applied Groundwater Modeling: Simulation of Flow and Advective Transport. London; San Diego, CA, Academic Press, 564.

Google Scholar

Barker, D., Beuerlein, J., Dorrance, A., Eckert, D., Eisley, B., Hammond, R., et al. (2005). Ohio Agronomy Guide, 14th Edn, Ohio State University Extension Bulletin, Vol. 472, 158. Available online at: https://agcrops.osu.edu/sites/agcrops/files/imce/fertility/Ohio_Agronomy_Guide_b472.pdf (accessed July 17, 2020).

Google Scholar

Barton, C. A., Zoback, M. D., and Moos, D. (1995). Fluid flow along potentially active faults in crystalline rock. Geology 23, 683–686. doi: 10.1130/0091-7613(1995)023<0683:FFAPAF>2.3.CO;2

CrossRef Full Text | Google Scholar

Belcher, W. R., Bedinger, M. S., Back, J. T., and Sweetkind, D. S. (2009). Interbasin flow in the Great Basin with special reference to the southern Funeral mountains and the source of Furnace Creek springs, Death Valley, California. U. S. J. Hydrol. 369, 30–43. doi: 10.1016/j.jhydrol.2009.02.048

CrossRef Full Text | Google Scholar

Bexfield, L. M., Jurgens, B. C., Crilley, D. M., and Christenson, S. C. (2012). Hydrogeology, Water Chemistry, and Transport Processes in the Zone of Contribution of a Public-Supply Well in Albuquerque, New Mexico, 2007–9. Reston, VA: U. S. Geological Survey Scientific Investigations Report 2011-5182, 114.

Google Scholar

Bowen, E. E., Hamada, Y., and O'Connor, B. L. (2014). Mapping mountain front recharge areas in arid watersheds based on a digital elevation model and land cover types. J. Water Resource Protect. 6, 756–771. doi: 10.4236/jwarp.2014.68072

CrossRef Full Text | Google Scholar

Carling, G. T., Mayo, A. L., Tingey, D., and Bruthans, J. (2012). Mechanisms, timing, and rates of arid region mountain front recharge. J. Hydrol. 428–429, 15–31. doi: 10.1016/j.jhydrol.2011.12.043

CrossRef Full Text | Google Scholar

Cheng, L., Zhang, L., and Brutsaert, W. (2016). Automated selection of pure base flows from regular daily streamflow data: objective algorithm. J. Hydrol. Eng. 21, 06016008. doi: 10.1061/(ASCE)HE.1943-5584.0001427

CrossRef Full Text | Google Scholar

Chow, V. T., Maidment, D. R., and Mays, L. W. (1988). Applied Hydrology. McGraw-Hill Series in Water Resources and Environmental Engineering. New York, NY: McGraw-Hill, 572.

Google Scholar

Corbett, E. S., and Crouse, R. B. (1968). Rainfall Interception by Annual Grass and Chaparral…Losses Compared. Berkeley, CA: Forest Service, U. S. Department of Agriculture Research Paper PSW-RP-48, 12.

Google Scholar

Cronshey, R., McCuen, N., Miller, N., Rawls, W., Robbins, S., and Woodward, D. (1986). Urban Hydrology for Small Watersheds. Washington, DC: U. S. Department of Agriculture, Soil Conservation Service, Engineering Division. Technical Release 55 (2nd ed.), 164.

Google Scholar

Day, E. S. (2019). Application of the USGS soil-water-balance (SWB) model to estimate spatial and temporal aspects of groundwater recharge in north-central Iowa (Thesis). Ames, IA: Iowa State University, 155.

Google Scholar

Dinpashoh, Y., Mirabbasi, R., Jhajharia, D., Abianeh, H. Z., and Mostafaeipour, A. (2014). Effect of short-term and long-term persistence on identification of temporal trends. J. Hydrol. Eng. 19, 617–625. doi: 10.1061/(ASCE)HE.1943-5584.0000819

CrossRef Full Text | Google Scholar

Doherty, J. E., and Hunt, R. J. (2010). Approaches to Highly Parameterized Inversion: A Guide to Using PEST for Groundwater-Model Calibration. Reston, VA: U. S. Geological Survey Scientific Investigations Report 2010-5169, 59. doi: 10.3133/sir20105169

CrossRef Full Text | Google Scholar

Dubois, E., Larocque, M., Gagné, S., and Meyzonnat, G. (2021). Simulation of long-term spatiotemporal variations in regional-scale groundwater recharge: contributions of a water budget approach in cold and humid climates. Hydrol. Earth Syst. Sci. 25, 6567–6589. doi: 10.5194/hess-25-6567-2021

CrossRef Full Text | Google Scholar

Dunne, T., and Leopold, L. (1978). Water in Environmental Planning. San Francisco, CA: Macmillan, 818.

Google Scholar

Flerchinger, G. N., and Cooley, K. R. (2000). A ten-year water balance of a mountainous semi-arid watershed. J. Hydrol. 237, 86–99. doi: 10.1016/S0022-1694(00)00299-7

CrossRef Full Text | Google Scholar

Gardner, P. M., Nelson, N. C., Heilweil, V. M., Solder, J. E., and Solomon, D. K. (2020). Rethinking a groundwater flow system using a multiple-tracer geochemical approach: a case study in Moab-Spanish Valley, Utah. J. Hydrol. 590, 125512. doi: 10.1016/j.jhydrol.2020.125512

CrossRef Full Text | Google Scholar

Gesch, D. B., Oimoen, M. J., Greenlee, S. K., Nelson, C. A., Steuck, M. J., and Tyler, D. J. (2002). “The national elevation data set,” in Photogrammetric Engineering and Remote Sensing, Vol. 68, 5–11.

Google Scholar

Hagedorn, B. (2015). Hydrochemical and 14C constraints on groundwater recharge and interbasin flow in an arid watershed: Tule Desert, Nevada. J. Hydrol. 523, 297–308. doi: 10.1016/j.jhydrol.2015.01.037

CrossRef Full Text | Google Scholar

Hagedorn, B. (2020). Hydrograph separation through multi objective optimization: revealing the importance of a temporally and spatially constrained baseflow solute source. J. Hydrol. 590, 125349. doi: 10.1016/j.jhydrol.2020.125349

CrossRef Full Text | Google Scholar

Hagedorn, B., El-Kadi, A. I., Mair, A., Whittier, R. B., and Ha, K. (2011). Estimating recharge in fractured aquifers of a temperate humid to semiarid volcanic island (Jeju, Korea) from water table fluctuations, and Cl, CFC-12 and 3H chemistry. J. Hydrol. 409, 650–662. doi: 10.1016/j.jhydrol.2011.08.060

CrossRef Full Text | Google Scholar

Hagedorn, B., and Meadows, C. (2021). Trend analyses of baseflow and BFI for undisturbed watersheds in Michigan—constraints from multi-objective optimization. Water 13, 564. doi: 10.3390/w13040564

CrossRef Full Text | Google Scholar

Hamed, K. H. (2008). Trend detection in hydrologic data: the Mann–Kendall trend test under the scaling hypothesis. J. Hydrol. 349, 350–363. doi: 10.1016/j.jhydrol.2007.11.009

CrossRef Full Text | Google Scholar

Hamed, K. H., and Ramachandra Rao, A. (1998). A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 204, 182–196. doi: 10.1016/S0022-1694(97)00125-X

CrossRef Full Text | Google Scholar

Hamilton, E. L., and Rowe, P. B. (1949). Rainfall Interception by Chaparral in California. Berkeley, CA: California Department of Natural Resources, Division of Forestry. Pacific Southwest Forest and Range Experiment Station.

Google Scholar

Harlow, J., and Hagedorn, B. (2018). SWB modeling of groundwater recharge on Catalina Island, California, during a period of severe drought. Water 11, 58. doi: 10.3390/w11010058

CrossRef Full Text | Google Scholar

Hawkins, R. H., Ward, T. J., Woodward, D. E., and Van Mullem, J. A. (2009). Curve Number Hydrology: State of the Practice. Reston, VA: American Society of Civil Engineers, 106.

PubMed Abstract | Google Scholar

Healy, R. W., and Cook, P. G. (2002). Using groundwater levels to estimate recharge. Hydrogeol. J. 10, 91–109. doi: 10.1007/s10040-001-0178-0

CrossRef Full Text | Google Scholar

Healy, R. W., and Scanlon, B. R. (2010). Estimating Groundwater Recharge. Cambridge: Cambridge University Press.

Google Scholar

Healy, R. W., Winter, T. C., LaBaugh, J. W., and Franke, O. L. (2007). Water budgets: foundations for effective water-resources and environmental management. U. S. Geol. Survey Circular 1308, 90. doi: 10.3133/cir1308

CrossRef Full Text | Google Scholar

Hedt, T. (2016). Agricultural Applied Climate Information System (AgACIS). Available online at: http://agacis.rcc-acis.org/.

Google Scholar

Jennings, C. W., Gutierrez, C., Bryant, W., Saucedo, G., and Wills, C. (2010). Geologic map of California: California Geological Survey California Geologic Data Map Series.

Google Scholar

Jensen, M. E., and Haise, H. R. (1963). Estimating evapotranspiration from solar radiation: American society of civil engineers. J. Irrig. Drain. Div. Proc. 89, 15–41.

Google Scholar

Joyce, B. A., Mehta, V. K., Purkey, D. R., Dale, L. L., and Hanemann, M. (2009). Climate Change Impacts on Water Supply and Agricultural Water Management in California's Western San Joaquin Valley, and Potential Adaptation Strategies. Berkeley, CA: California Climate Change Center, 69.

Google Scholar

Kao, Y.-H., Liu, C.-W., Wang, S.-W., and Lee, C.-H. (2012). Estimating mountain block recharge to downstream alluvial aquifers from standard methods. J. Hydrol. 426–427, 93–102. doi: 10.1016/j.jhydrol.2012.01.016

CrossRef Full Text | Google Scholar

Khaliq, M. N., Ouarda, T. B. M. J., Gachon, P., Sushama, L., and St-Hilaire, A. (2009). Identification of hydrological trends in the presence of serial and cross correlations. A review of selected methods and their application to annual flow regimes of Canadian rivers. J. Hydrol. 368, 117–130. doi: 10.1016/j.jhydrol.2009.01.035

CrossRef Full Text | Google Scholar

Lee, C.-H., Chen, W.-P., and Lee, R.-H. (2006). Estimation of groundwater recharge using water balance coupled with base-flow-record estimation and stable-base-flow analysis. Environ. Geol. 51, 73–82. doi: 10.1007/s00254-006-0305-2

CrossRef Full Text | Google Scholar

Li, X., Fernald, A. G., and Kang, S. (2021). Assessing long-term changes in regional groundwater recharge using a water balance model for New Mexico. JAWRA J. Am. Water Resources Assoc. 57, 807–827. doi: 10.1111/1752-1688.12933

CrossRef Full Text | Google Scholar

Ma, J., Ding, Z., Edmunds, W. M., Gates, J. B., and Huang, T. (2009). Limits to recharge of groundwater from Tibetan plateau to the Gobi desert, implications for water management in the mountain front. J. Hydrol. 364, 128–141. doi: 10.1016/j.jhydrol.2008.10.010

CrossRef Full Text | Google Scholar

Mair, A., Hagedorn, B., Tillery, S., El-Kadi, A. I., Westenbroek, S., Ha, K., and Koh, G.-W. (2013). Temporal and spatial variability of groundwater recharge on Jeju Island, Korea. J. Hydrol. 501, 213–226. doi: 10.1016/j.jhydrol.2013.08.015

CrossRef Full Text | Google Scholar

Manna, F., Cherry, J. A., McWhorter, D. B., and Parker, B. L. (2016). Groundwater recharge assessment in an upland sandstone aquifer of southern California. J. Hydrol. 541, 787–799, doi: 10.1016/j.jhydrol.2016.07.039

CrossRef Full Text | Google Scholar

Manning, A. H., and Solomon, D. K. (2003). Using noble gases to investigate mountain-front recharge. J. Hydrol. 275, 194–207. doi: 10.1016/S0022-1694(03)00043-X

CrossRef Full Text | Google Scholar

Manning, A. H., and Solomon, D. K. (2005). An integrated environmental tracer approach to characterizing groundwater circulation in a mountain block. Water Resources Res. 41. doi: 10.1029/2005WR004178. Available online at: https://agupubs-onlinelibrary-wiley-com.csulb.idm.oclc.org/doi/abs/10.1029/2005WR004178

CrossRef Full Text | Google Scholar

Markovich, K. H., Condon, L. E., Carroll, K. C., Purtschert, R., and McIntosh, J. C. (2021). A mountain-front recharge component characterization approach combining groundwater age distributions, noble gas thermometry, and fluid and energy transport modeling. Water Resources Res. 57. doi: 10.1029/2020WR027743. Available online at: https://agupubs-onlinelibrary-wiley-com.csulb.idm.oclc.org/action/showCitFormats?doi=10.1029%2F2020WR027743

CrossRef Full Text | Google Scholar

Markovich, K. H., Manning, A. H., Condon, L. E., and McIntosh, J. C. (2019). Mountain-block recharge: a review of current understanding. Water Resources Res. 55, 8278–8304. doi: 10.1029/2019WR025676

CrossRef Full Text | Google Scholar

Martinec, J. (1975). Subsurface flow from snowmelt traced by tritium. Water Resources Res. 11, 496–498. doi: 10.1029/WR011i003p00496

CrossRef Full Text | Google Scholar

Maxey, G. B., and Eakin, T. E. (1949). Ground Water in White River Valley, White Pine, Nye, and Lincoln Counties, Nevada: Nevada State Engineer, Water Resources Bulletin 8, 59.

Google Scholar

Mayer, A., May, W., Lukkarila, C., and Diehl, J. (2007). Estimation of fault-zone conductance by calibration of a regional groundwater flow model: Desert Hot Springs, California. Hydrogeol. J. 15, 1093–1106. doi: 10.1007/s10040-007-0158-0

CrossRef Full Text | Google Scholar

McCoy, K. J., and Ladd, D. E. (2019). Documentation of a Soil-Water-Balance Model to Estimate Recharge to Blue Ridge, Piedmont, and Mesozoic Basin Fractured-Rock Aquifers. Fauquier County, VA: U.S. Geological Survey Scientific Investigations Report 2019-5056. p. 22. doi: 10.3133/sir20195056

CrossRef Full Text | Google Scholar

McCuen, R. H., Knight, Z., and Cutter, A. G. (2006). Evaluation of the nash–sutcliffe efficiency index. J. Hydrol. Eng. 11, 597–602. doi: 10.1061/(ASCE)1084-0699(2006)11:6(597)

CrossRef Full Text | Google Scholar

McDonnell, J. J. (2017). Beyond the water balance. Nat. Geosci. 10, 396–396. doi: 10.1038/ngeo2964

CrossRef Full Text | Google Scholar

Metropolitan Council (2013). Wastewater and Water - Metro Model 3: Appendix A, Updated Daily Soil Water Balance (SWB) Model. Available online at: https://metrocouncil.org/Wastewater-Water/Planning~/Water-Supply-Planning/Metro-Model-3/MM3/MM3-Report-Appendix-A.aspx

Google Scholar

Mishra, S. K., and Singh, V. P. (2003). Soil Conservation Service Curve Number (SCS-CN) Methodology. Dordrecht: Springer Netherlands, Water Science and Technology Library, 42. doi: 10.1007/978-94-017-0147-1

CrossRef Full Text | Google Scholar

Mockus, V., Werner, J., Woodward, D. E., Nielsen, R., Dobos, R., Hjelmfelt, A., et al. (1972). “Hydrologic soil groups,” in National Engineering Handbook, Part 630 Hydrology (U.S. Department of Agriculture, Natural Resources Conservation Service), 13.

Google Scholar

Multi-Resolution Land Characteristics Consortium (MRLC) (2018). Multi-Resolution Land Characteristics Consortium (MRLC)National Land Cover Database 2011 (NLCD 2011). Available online at: https://data.nal.usda.gov/dataset/national-land-cover-database-2011-nlcd-2011

Google Scholar

Nash, J. E., and Sutcliffe, J. V. (1970). River flow forecasting through conceptual models part I — a discussion of principles. J. Hydrol. 10, 282–290. doi: 10.1016/0022-1694(70)90255-6

CrossRef Full Text | Google Scholar

Natural Resources Consulting Engineers GEI Consultants Native American Rights Fund, Kenney & Associates.. (2013). Water Settlement Technical Report: Tule River Indian Tribe. p. 108. Available online at: https://www.narf.org/nill/documents/NARF_water_settlements/Tule/20130600technical_report.pdf

Google Scholar

Nielsen, M. G., and Westenbroek, S. M. (2019). Groundwater Recharge Estimates for Maine Using a Soil-Water-Balance Model-25-Year Average, Range, and Uncertainty, 1991 to 2015. Reston, VA: U. S. Geological Survey Scientific Investigations Report 2019-5125, 56. doi: 10.3133/sir20195125

CrossRef Full Text | Google Scholar

Önöz, B., and Bayazit, M. (2012). Block bootstrap for Mann-Kendall trend test of serially dependent data: block bootstrap for mann-kendall trend test of serially dependent data. Hydrol. Processes 26, 3552–3560. doi: 10.1002/hyp.8438

CrossRef Full Text | Google Scholar

Patakamuri, S. K., and O'Brien, N. (2021). Modifiedmk: Modified Versions of Mann Kendall and Spearman's Rho Trend Tests. Available online at: https://cran.r-project.org/package=modifiedmk

Google Scholar

Ritter, A., and Muñoz-Carpena, R. (2013). Performance evaluation of hydrological models: statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 480, 33–45. doi: 10.1016/j.jhydrol.2012.12.004

CrossRef Full Text | Google Scholar

Ruud, N., and Harter, T. (2002). “A conjuctive use model for the Tule River groundwater basin in the San Joaquin Valley, California,” in Integrated Water Resources Management: A Selection of Papers Presented at the International Symposium on Integrated Water Resources Management held in April 2000 at the University of California, Davis, California, USA, Vol. 272, eds M. A. Mariño and International Association of Hydrological Sciences (Wallingford: IAHS Press; IAHS Publication), 167–173.

Google Scholar

Saeed, M. (1986). The estimation of evapotranspiration by some equations under hot and arid conditions. Trans. ASAE 29, 0434–0438. doi: 10.13031/2013.30168

CrossRef Full Text | Google Scholar

Safeeq, M., Bart, R. R., Pelak, N. F., Singh, C. K., Dralle, D. N., Hartsough, P, et al. (2021). How realistic are water-balance closure assumptions? A demonstration from the southern sierra critical zone observatory and kings river experimental watersheds. Hydrol. Processes 35. doi: 10.1002/hyp.14199. Available online at: https://www.fs.fed.us/psw/publications/wagenbrenner/psw_2021_wagenbrenner007_safeeq.pdf

CrossRef Full Text | Google Scholar

Safeeq, M., and Hunsaker, C. T. (2016). Characterizing runoff and water yield for headwater catchments in the Southern Sierra Nevada. J. Am. Water Resources Ass. 52, 1327–1346. doi: 10.1111/1752-1688.12457

CrossRef Full Text | Google Scholar

Scanlon, B. R. (2004). Evaluation of methods of estimating recharge in semiarid and arid regions in the Southwestern. U. S. Groundwater Recharge Desert Environ. Am. Geophys. Union 9, 235–254. doi: 10.1029/009WSA13

CrossRef Full Text | Google Scholar

Schreiner-McGraw, A. P., and Ajami, H. (2021). Combined impacts of uncertainty in precipitation and air temperature on simulated mountain system recharge from an integrated hydrologic model. Catchment Hydrol. Model. Approaches Preprint. 26, 1145–1164. doi: 10.5194/hess-2020-558

CrossRef Full Text | Google Scholar

Scott, R. L., and Biederman, J. A. (2019). Critical zone water balance over 13 years in a semiarid savanna. Water Resources Res. 55, 574–588. doi: 10.1029/2018WR023477

CrossRef Full Text | Google Scholar

Shirmohammadi-Aliakbarkhani, Z., and Saberali, S. F. (2020). Evaluating of eight evapotranspiration estimation methods in arid regions of Iran. Agric. Water Manage. 239, 106243. doi: 10.1016/j.agwat.2020.106243

CrossRef Full Text | Google Scholar

Singh, A., Panda, S. N., Uzokwe, V. N. E., and Krause, P. (2019). An assessment of groundwater recharge estimation techniques for sustainable resource management. Groundw. Sustain. Dev. 9, 100218. doi: 10.1016/j.gsd.2019.100218

CrossRef Full Text | Google Scholar

Sloto, R. A., and Crouse, M. Y. (1996). HYSEP: A Computer Program for Streamflow Hydrograph Separation and Analysis. Reston, VA: U. S. Geological Survey Water-Resources Investigations Report 96–4040, 51.

Google Scholar

Smith, E. A., and Westenbroek, S. M. (2015). Potential Groundwater Recharge for the State of Minnesota Using the Soil-Water-Balance Model, 1996-2010. Reston, VA: U. S. Geological Survey Scientific Investigations Report 2015-5038, 85. doi: 10.3133/sir20155038

CrossRef Full Text | Google Scholar

State of California Department of Water Resources (2014). Geology, Hydrology, Quality of Water, and Water Supply of the Three Rivers Area, California. Three Rivers Community Plan Community Plans. Fresno, CA: Division of Integrated Regional Water Management, South Central Region Office, Special Investigations and Regional Planning Branch.

Google Scholar

Tan, S. B., Lo, E. Y.-M., Shuy, E. B., Chua, L. H., and Lim, W. H. (2009). Hydrograph separation and development of empirical relationships using single-parameter digital filters. J. Hydrol. Eng. 14, 271–279. doi: 10.1061/(ASCE)1084-0699(2009)14:3(271)

CrossRef Full Text | Google Scholar

Thornthwaite, C. W. (1948). An approach toward a rational classification of climate. Geograph. Rev. 38, 55–94. doi: 10.2307/210739

CrossRef Full Text | Google Scholar

Thornton, M. M., Shrestha, R., Wei, Y., Thornton, P. E., Kao, S., and Wilson, B. E. (2020). DaymetDaymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 4: 0 MB. Oak Ridge, TN.

Google Scholar

Thorthwaite, C. W., and Mather, J. R. (1955). The water balanc. Lab. Climatol. Publ. Climatol. 8, 104.

Google Scholar

Thorthwaite, C. W., and Mather, J. R. (1957). Instructions and tables for computing potential evapotranspiration and the water balance. Lab. Climatol. Publ. Climatol. 10, 185–311.

Google Scholar

Thyne, G. D., Gillespie, J. M., and Ostdick, J. R. (1999). Evidence for interbasin flow through bedrock in the southeastern Sierra Nevada. GSA Bull. 111, 1600–1616. doi: 10.1130/0016-7606(1999)111<1600:EFIFTB>2.3.CO;2

CrossRef Full Text | Google Scholar

Trost, J. J., Roth, J. L., Westenbroek, S. M., and Reeves, H. W. (2018). Simulation of Potential Groundwater Recharge for the Glacial Aquifer System East of the Rocky Mountains, 1980–2011, Using the Soil-Water-Balance Model. Scientific Investigations Report Report 2018–5080, 64.

Google Scholar

U.S. Census Bureau (2019). American Community Servey 5-Year Estimates. Available online at: http://censusreporter.org/profiles/25200US4300R-tule-river-reservation/

Google Scholar

VanRheenen, N. T., Wood, A. W., Palmer, R. N., and Lettenmaier, D. P. (2004). Potential implications of PCM climate change scenarios for sacramento–San Joaquin River Basin Hydrology and Water Resources. Clim. Change 62, 257–281. doi: 10.1023/B:CLIM.0000013686.97342.55

CrossRef Full Text | Google Scholar

Walker, D., Parkin, G., Schmitter, P., Gowing, J., Tilahun, S. A., Haile, A. T., and Yimam, A. Y. (2019). Insights from a multi-method recharge estimation comparison study. Groundwater 57, 245–258. doi: 10.1111/gwat.12801

PubMed Abstract | CrossRef Full Text | Google Scholar

Web Soil Survey (2014). Soil Survey Staff, Natural Resources Conservation Service, United States Department of Agriculture. Available online at: http://websoilsurvey.sc.egov.usda.gov/

Google Scholar

Westenbroek, S. M., Engott, J. A., Kelson, V. A., and Hunt, R. J. (2018). SWB Version 2.0–A Soil-Water-Balance Code for Estimating Net Infiltration and Other Water-Budget Components. Reston, VA: U. S. Geological Survey Techniques and Methods Techniques and Methods, 130. doi: 10.3133/tm6A59

CrossRef Full Text | Google Scholar

Westenbroek, S. M., Kelson, V. A., Dripps, W. R., Hunt, R. J., and Bradbury, K. R. (2010). SWB—A Modified Thornthwaite-Mather Soil-Water-Balance Code for Estimating Groundwater Recharge. U. S. Geological Survey Techniques and Methods 6-A31, 60. doi: 10.3133/tm6A31

CrossRef Full Text | Google Scholar

Wilson, J. L., and Guan, H. (2004). Mountain-block hydrology and mountain-front recharge. Groundw. Recharge Desert Environ. Southwestern United States 9, 113–137. doi: 10.1029/009WSA08

CrossRef Full Text | Google Scholar

Woodward, D. E., Hawkins, R. H., Jiang, R., Hjelmfelt, A. T. Jr., Van Mullem, J. A., and Quan, Q. D. (2003). “Runoff curve number method: examination of the initial abstraction ratio,” in World Water & Environmental Resources Congress 2003 (Philadelphia, PA: American Society of Civil Engineers), 1–10. doi: 10.1061/40685(2003)308

CrossRef Full Text | Google Scholar

Xiao, Q. E., McPherson, S. L., Ustin, M. E., Grismer, M. E., and Simpson, J. R. (2000). Winter rainfall interception by two mature open-grown trees in Davis, California. Hydrol. Processes 14, 763–784. doi: 10.1002/(SICI)1099-1085(200003)14:4<763::AID-HYP971>3.0.CO;2-7

CrossRef Full Text | Google Scholar

Yao, Y., Zheng, C., Andrews, C., Zheng, Y., Zhang, A., and Liu, J. (2017). What controls the partitioning between baseflow and mountain block recharge in the Qinghai-Tibet Plateau?: mountainous groundwater flow system. Geophys. Res. Lett. 44, 8352–8358. doi: 10.1002/2017GL074344

CrossRef Full Text | Google Scholar

Yue, S., Pilon, P., Phinney, B., and Cavadias, G. (2002). The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Processes 16, 1807–1829. doi: 10.1002/hyp.1095

CrossRef Full Text | Google Scholar

Yue, S., and Wang, C. (2004). The Mann-Kendall Test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resources Manage. 18, 201–218. doi: 10.1023/B:WARM.0000043140.61082.60

CrossRef Full Text | Google Scholar

Zhai, T., Barlow, P. M., Cunningham, W. L., and Gray, M. (2015). Groundwater Toolbox: A Graphical and Mapping Interface for Analysis of Hydrologic Data. Reston, VA: U. S. Geological Survey.

Google Scholar

Zomlot, Z., Verbeiren, B., Huysmans, M., and Batelaan, O. (2015). Spatial distribution of groundwater recharge and base flow: assessment of controlling factors. J. Hydrol Regional Stud. 4, 349–368. doi: 10.1016/j.ejrh.2015.07.005

CrossRef Full Text | Google Scholar