Past and future evolution of the onshore-offshore groundwater system of a carbonate archipelago: The case of the Maltese Islands, central Mediterranean Sea

Offshore freshened groundwater (OFG) is groundwater with a salinity below that of seawater that is stored in sub-seafloor sediments and rocks. OFG has been proposed as an alternative solution to relieve water scarcity in coastal regions and to enhance oil recovery. Although OFG has been documented in most continental margins, we still have a poor understanding of the extent and flow characteristics of OFG systems, and their evolution through time. In view of the general absence of appropriate field data, paleohydrogeological models have been used. The majority of these models are based on 2D approaches, and they rarely consider the future evolution of OFG systems, especially in response to predicted climate change. Here we utilize recently acquired geological, geophysical and hydrogeological data from onshore and offshore the Maltese Islands, and employ 2D and 3D numerical models, to: (i) reconstruct the evolution of the onshore-offshore groundwater system during the last 188 ka, (ii) predict the evolution of the OFG system in response to climate-related changes. We show that the mechanisms emplacing OFG include a combination of active meteoric recharge at present as well as at sea-level lowstands. The Maltese onshore-offshore groundwater system is relatively dynamic, with 23% of groundwater being preserved in the last 18 ka. The control of geology is expressed by the more prevalent distribution of OFG north of the Great Fault, which is associated to the occurrence of low permeability units, and the asymmetry of the groundwater lens during the 18 ka lowstand. A 30% decrease in recharge predicted in the coming 100 years will diminish OFG extent by 38%, whereas sea-level rise will play a negligible role. At present the estimated volume of OFG is 1 km³, which could potentially provide an alternative supply of potable water to the Maltese Islands for 75 years. Exploitation of OFG with minimal salinization of onshore groundwater bodies would require locating pumping wells close to the coast.

1. Introduction

Offshore freshened groundwater [OFG; also termed offshore groundwater (Evans and Lizarralde, 2003), offshore fresh groundwater (Post et al., 2013), or subterranean estuary (Moore, 1999; Willard, 1999)] is groundwater stored in the pores of sediments or fractures of rocks in the sub-seafloor, and having a total dissolved solid concentration below that of seawater (Micallef et al., 2021). OFG has been documented in most continental margins (Post et al., 2013), although it predominantly occurs in siliciclastic passive margins, in water depths of 100 m and sub-seafloor depths of 200 m (Micallef et al., 2021). OFG can be emplaced by meteoric recharge (Kooi and Groen, 2001; Cohen et al., 2010; Thomas et al., 2019; Micallef et al., 2020, 2021), diagenesis (Kastner et al., 1991) or gas hydrate dissociation (Hesse and Harrison, 1981). Permeability contrasts (Zamrsky et al., 2020), connectivity of permeable and confining strata (Michael et al., 2016), buried paleochannels (Krantz et al., 2004), and faults (Varma and Michael, 2012) are the main geological elements controlling OFG distribution. There has been a growing interest in the study of OFG systems, especially in the last decade. This has largely been driven by their potential use as unconventional sources of water in coastal areas, where groundwater resources are being rapidly depleted or contaminated (Bakken et al., 2012; UN-Water, 2020), or to improve oil recovery (Person et al., 2017). OFG is also thought to play a key role in biogeochemical fluxes to the ocean (Michael et al., 2016), benthic and sub-seafloor biological systems (Moore, 1999), continental margin geomorphology (Johnson, 1939), and human migration patterns (Bailey and King, 2011), among others.

Our understanding of OFG is primarily based on borehole data (primarily chlorinity and total dissolved solids of extracted pore fluids) from legacy drilling campaigns and incidental discoveries (Micallef et al., 2021). Appropriate field data are limited, particularly in continental shelf environments. Direct observations of aquifer structure and properties, and geochemical characteristics, of OFG remain rare (Lofi et al., 2013; van Geldern et al., 2013). The mechanism and timing of OFG emplacement are often unknown, and the former has been confirmed by geochemical data for <10 records (Micallef et al., 2021). Downhole measurements of the physical characteristics of the OFG (e.g., flow velocity, direction, pressure) and residence times have never been performed. Detailed geophysical assessments of OFG systems, on the other hand, have only become available recently and for few locations (e.g., Gustafson et al., 2019; Attias et al., 2020; Micallef et al., 2020; Haroon et al., 2021).

As a result, important knowledge gaps still remain concerning the extent and flow characteristics of OFG systems, and evolution of these through time. To address these knowledge gaps at large spatial scales (e.g., margin) and temporal scales (e.g., glacial cycles), paleohydrogeological models have been used (e.g., Meisler et al., 1984; Kooi et al., 2000; Person et al., 2003; Marksammer et al., 2007; Cohen et al., 2010; DeFoor et al., 2011; Amir et al., 2013; Siegel et al., 2014; Morgan et al., 2018; Thomas et al., 2019; Micallef et al., 2020). The majority of these models are based on 2D approaches that take into consideration shore-normal topography-driven flow and varying sea-level conditions. They generally tend to reproduce the lateral extent of OFG, where this is documented in borehole data, and suggest that meteoric recharge during sea-level lowstands is the most common emplacement mechanism. 3D numerical modeling approaches, in comparison, remain rare and have primarily been applied to glaciated margins. For this reason, onshore-offshore and alongshore stratigraphic connectivity are poorly represented, which is problematic considering that shore-parallel flow regimes may be important in OFG systems (Micallef et al., 2020; Knight et al., 2021). A small number of studies have focused on the present and future evolution of OFG systems (e.g., Knight et al., 2018; Morgan et al., 2018; Yu and Michael, 2019). These are primarily 2D assessments, based on either analytical modeling or variable-density groundwater flow and transport modeling, which explore the link between onshore and offshore groundwater extraction. How OFG systems will respond to climate change—e.g., in terms of changes in groundwater recharge, water demand and sea-level—has still not been assessed.

The Maltese Islands, located in the central Mediterranean Sea, are a carbonate archipelago that has the highest population density in Europe and is one of the poorest countries globally in terms of water resources per inhabitant (FAO, 2003). Groundwater supplies ~50% of the potable water, and >16% of its volume is predicted to be lost due to climate change by 2100 (De Biase et al., 2021). Controlled-source electromagnetic and seismic reflection data from the seafloor offshore the SE of Malta were used to identify resistivity anomalies that were interpreted as indicative of OFG (Haroon et al., 2021). Numerical simulations suggest that an OFG body close the coast (~1 km) is actively recharging, whereas an isolated body at a distance of >3 km from the coast is likely a relict feature emplaced during the Last Glacial Maximum. The extent and characteristics of the freshened groundwater system offshore the Maltese Islands, how it has evolved in the past and how it will respond to climate change, remain poorly constrained.

In this study, we utilize recently acquired geological, geophysical and hydrogeological data from onshore and offshore the Maltese Islands, and employ 2D and 3D numerical models, to: (i) reconstruct the evolution of the Maltese onshore-offshore groundwater system during the last 188 ka in terms of extent, volume, salinity and velocity, (ii) predict the evolution of the OFG system in response to climate-related changes up to 2100.

2. Regional setting

The Maltese archipelago comprises the islands of Malta, Gozo and Comino, and three small islets. Outcropping across the archipelago are four main Oligo-Miocene sedimentary formations (Pedley et al., 1976). From bottom to top, these formations include: (i) Lower Coralline Limestone (1,000 m thick succession of shallow-water algal foraminiferal limestone); (ii) Globigerina Limestone (~200 m thick fine-grained biomicrite, made up of the Upper, Middle and Lower Globigerina Limestone members); (iii) Blue Clay (75 m of banded kaolinitic marls and clays); and (iv) Upper Coralline Limestone (~100 m thick shallow reef complex). This sedimentary sequence is disrupted by two normal fault systems (Illies, 1981; Gardiner et al., 1995). The most widespread system, which includes the Great Fault, trends ENE-WSW and was active intermittently between the Early Miocene and the mid-Pliocene. The second system trends NW-SE and was active during the late Pliocene to the Quaternary.

The archipelago generally tilts toward the NE, with cliffs reaching altitudes of 250 m along the western coast. Geomorphology is primarily controlled by tectonic activity, with mass movements, karstification, surface water and coastal erosion playing a secondary role (Alexander, 1988). The seafloor area considered for this study (i.e., from the coast down to a depth of 120 m; Figure 1) represents a submerged paleolandscape that is up to 10 km wide, gently sloping and hosting valleys, karstic landforms, paleoshorelines and deposits along the east (Micallef et al., 2013, 2019). Along the west, the shelf is comparably narrower. The predominant sediment type is muddy sand (Micallef et al., 2013).

FIGURE 1

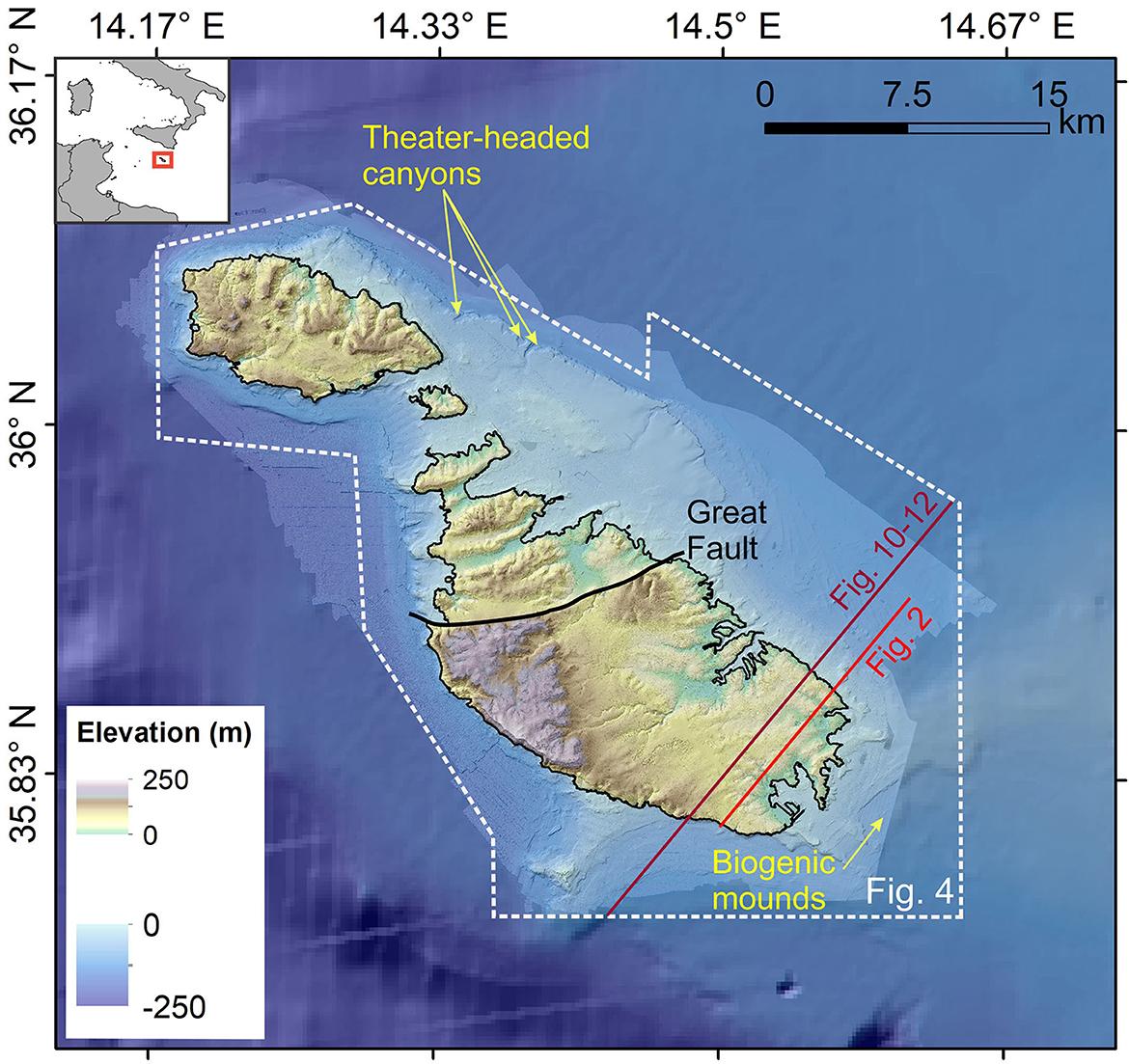
Figure 1. Topographic map of the Maltese Islands and the surrounding seafloor. Features of geological interest are denoted.

The Maltese Islands host three types of groundwater bodies (Bakalowicz and Mangion, 2003; Environment and Resources Authority, 2015; Pondthai et al., 2020; Lotti et al., 2021). The largest is the mean sea-level groundwater body, which is primarily hosted in the Lower Coralline Limestone formation. This comprises a freshwater Ghyben-Herzberg lens floating on seawater and is a key source of potable water. The other bodies have smaller areal extents and are hosted in the Upper Coralline Limestone formation, either as perched groundwater bodies above sea-level or in valleys below sea-level. Groundwater is primarily recharged by precipitation, which has a mean annual value of 550 mm (Galdies, 2011). The Maltese climate consists of hot, dry summers, and mild, wet winters, with most of the rain falling between October and February.

3. Materials and methods

3.1. Geological data

Onshore geological data for the Maltese Islands comprised: (i) a digital elevation model of the entire Maltese archipelago (1 m cell size; acquired during a 5.5 h flight in February 2012 using an IGI LiteMapper 6800 LiDAR system as part of the project “Development of Environmental Monitoring Strategy and Environmental Monitoring Baseline Surveys” funded by ERDF-156), (ii) a surface geological map (Pedley et al., 1976), and (iii) legacy and recent borehole logs (Costain and Messers, 1957; De Biase et al., 2021). Offshore geological data included: (i) multibeam echosounder data acquired offshore the eastern coast of the Maltese Islands during a number of expeditions (Micallef et al., 2013, 2019), (ii) >400 km² of bathymetric data acquired with a Hawkeye IIb bathymetric LiDAR sensor and an interferometric swath system (Kongsberg GeoSwath), collected as part of the project “Development of Environmental Monitoring Strategy and Environmental Monitoring Baseline Surveys” funded by ERDF-156, (iii) bathymetry from the remaining seafloor derived from EMODnet Bathymetry (https://www.emodnet-bathymetry.eu/), (iv) multichannel seismic reflection profiles, and (v) offshore boreholes and seafloor samples (as described in Micallef et al., 2019; Haroon et al., 2021).

3.2. 2D groundwater modeling

3.2.1. Modeling framework

The 2D approach is the most suitable to assess future scenarios of groundwater evolution at high spatial and temporal scales, and to determine the values of anisotropy factors to use in both 2D and 3D modeling approaches. The 2D model was designed to reconstruct the seafloor offshore the SE of Malta and assess the evolution of the groundwater system there in the future. We focus on this zone because it hosts the best indications, from a geophysical and numerical modeling point of view, for the occurrence of an OFG (Haroon et al., 2021). The variable density groundwater model SEAWAT (Langevin et al., 2008) was used to run 2D simulations of the mean sea-level groundwater body in SE Malta under transient conditions. The model domain includes a two-dimensional transect across SE Malta (Figure 2), developed by interpolating the interfaces between different formations from the geological map, boreholes and offshore seismic reflection data. The cross-section is oriented along the main groundwater flow direction, which is perpendicular to both the intersected coastlines. It has a total length of 19 km, including a 12 km onshore section and a 7 km offshore section, and a maximum height of 560 m. The NW edge of the section stops abruptly at the coastline due to the occurrence of a vertical cliff descending below sea-level. We have extended the section to the west coast to set the sea boundary condition for the model. The base of the model is set at a depth of 500 m below sea-level, which is significantly deeper than the freshwater–saltwater interface. The simulation domain is vertically discretized for the first 200 m, with thirty horizontal layers that have a constant thickness of ~10 m. The layers progressively increase in thickness, reaching 100 m at the bottom layer, in the remaining 300 m. This layout has been designed to facilitate the convergence of the solute transport equation in the zone where freshwater and saltwater interaction occurs (Zheng, 1990), and to reduce the computational burden where a high calculation precision was not required. The domain has been horizontally discretized by dividing each layer with 380 elements having a size of 50 × 50 m. Figure 2 shows the described model settings and the formations derived from the geological model.

FIGURE 2

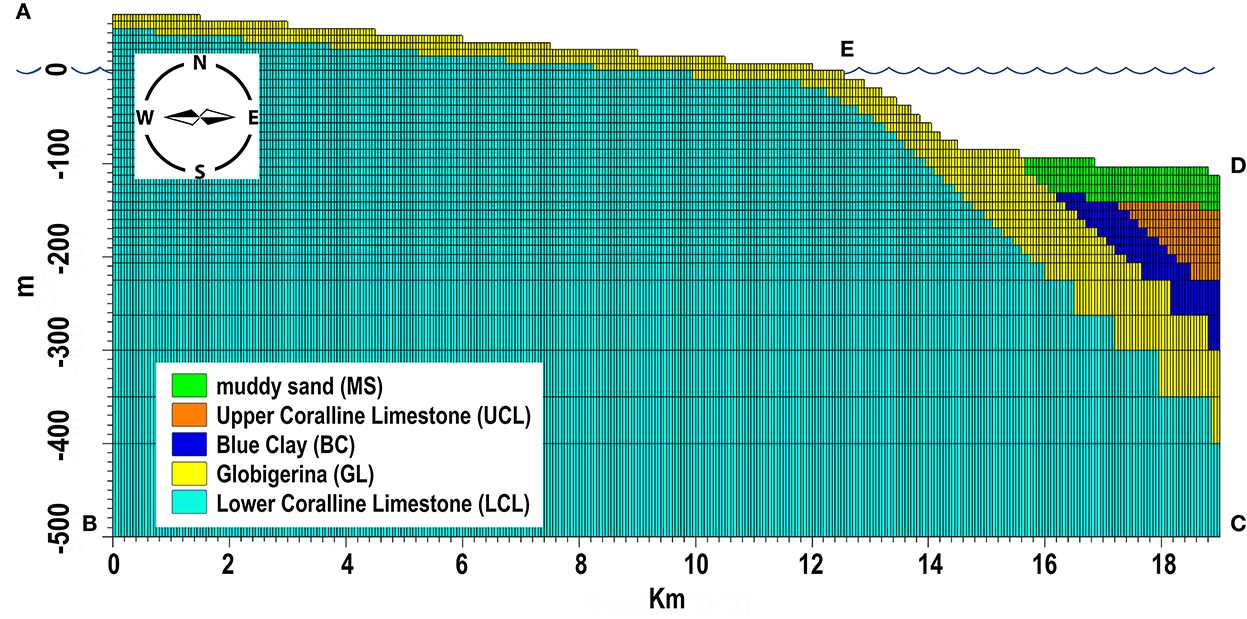
Figure 2. 2D model domain showing discretization settings and associated formations derived from the geological model. Location of profile in Figure 1.

The aquifer hosting the groundwater is considered as unconfined and each geological formation is modeled as homogeneous. There are no layers of impermeable material located both above and below the aquifer that cause it to be under pressure. The water table is at atmospheric pressure, and can thus rise and fall as a result of external forcings. The model layers are set to be “convertible”, which means that the model checks the hydraulic head value of each cell to determine if it is confined or not. Cells in convertible layers are either confined or unconfined depending on whether the head is above or below the top of the cell.

The aquifer bottom (boundary B-C in Figure 2) has been set as an impervious boundary for flow and transport. The seaward boundaries (left vertical edge A-B representing the steep cliff characterizing the coastline on that side; right vertical edge C-D and part of the top of the uppermost layer D-E representing the seafloor) are assumed to be at seawater hydrostatic pressure. On these boundaries, saltwater heads of 0 m have been assigned, a prescribed concentration of 35 g/L was set for entering fluxes and model calculated concentrations are applied for outcoming water flows.

3.2.2. Modeling parameters

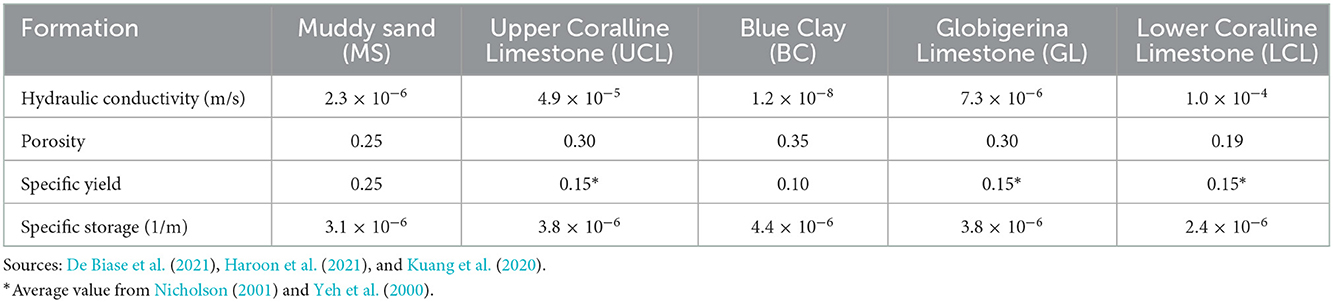
Hydraulic properties of the formations in the model are assigned according to the values shown in Table 1. The specific yield was derived from the studies of Nicholson (2001) and Yeh et al. (2000), whereas the specific storage was derived from the study by Kuang et al. (2020), who reviewed this parameter from 182 field sites that covered a wide range of aquifer materials.

TABLE 1

Table 1. Hydraulic parameters of the geological formations of the Maltese Islands.

The longitudinal dispersivity, which is used to represent the local variations in the velocity field of a groundwater solute in the direction of fluid flow, has been estimated using the empirical power law developed by Schulze-Makuch (2005):

$\begin{array}{ll}\alpha =c{(L)}^m& (1)\end{array}$

where α is longitudinal dispersivity [L], c is a parameter characteristic for a geological medium [L^1−m], L the flow distance [L], and m is the scaling exponent. These parameters have been quantified for unconsolidated sediments and consolidated rocks via the analysis of hundreds of data pairs. In the present study, the aforementioned parameters have been derived for carbonate rocks and a modeling scale of 20 km. The resulting longitudinal dispersivity is equal to 40 m and the transversal one is set to be a tenth of this value. The density of seawater is set to 1.025 g/cm³ (salt concentration of 35 g/L) while the density of freshwater is set to 1 g/cm³ (salt concentration of 0 g/L).

Onshore recharge equivalent to ~25% of the annual precipitation of 550 mm (FAO, 2003; Galdies, 2011) has been attributed to the top boundary A-E not covered by the sea, and was kept constant during the simulations. Simulations of ~5,000 year duration were run, with a starting salt concentration of 35 g/L in the aquifer, to reach the equilibrium conditions of the groundwater body generated and fed by the superficial freshwater recharge.

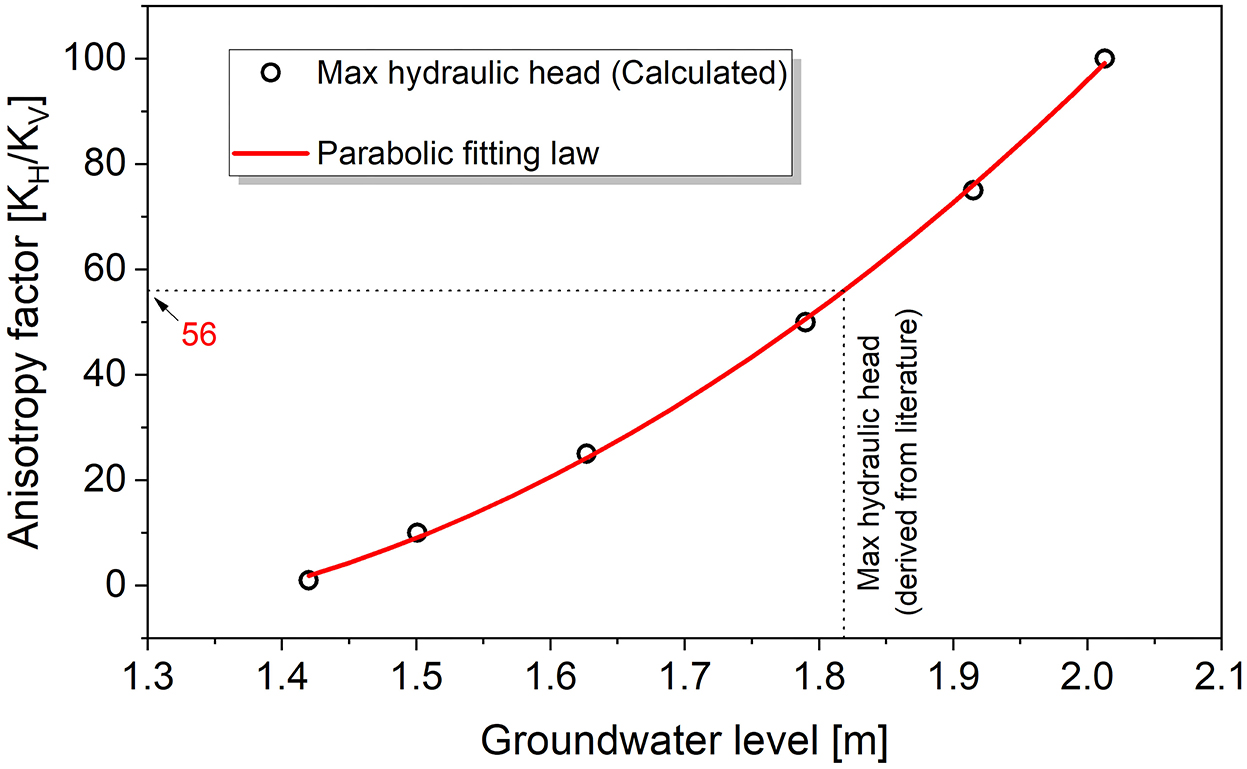
The anisotropy ratio between horizontal and vertical hydraulic conductivity (K_H/K_V), which plays a fundamental role in the formation and extension of OFG (e.g., Haroon et al., 2021), is not known. Six different values of anisotropy (1, 10, 25, 50, 75, and 100) were used to estimate groundwater hydraulic heads from the 2D model and compare them with the maximum reconstructed groundwater hydraulic head value in proximity of the transect area. No monitoring wells are located in that zone, but some information about the water table layout are available from the analyses realized in Environment and Resources Authority (2015), Monteiro et al. (2016), and De Biase et al. (2021) (e.g., the maximum hydraulic head achievable in the investigated section). Figure 3 shows the parabolic trend interpolating the simulated maximum hydraulic heads obtained for the different anisotropy factors. An anisotropy factor of 56 provided the match between the calculated maximum hydraulic head value and the one derived from the aforementioned studies. This value of anisotropy was thus used in all 2D and 3D numerical simulations.

FIGURE 3

Figure 3. Variation of maximum groundwater hydraulic head with respect to the anisotropy factor.

3.2.3. Simulation scenarios

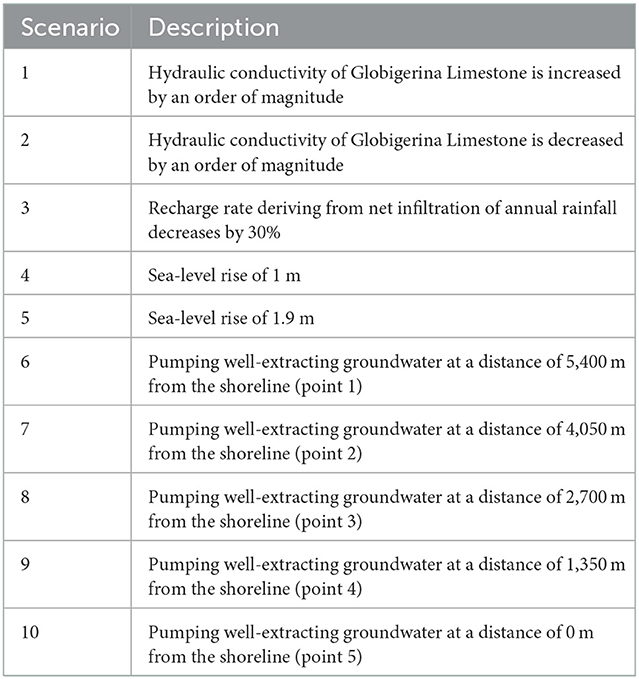
The model was first used to simulate the groundwater distribution along the SE Malta transect at present. Such present-day conditions were then used as initial conditions to investigate how groundwater distribution changes with respect to changes in:

i. Hydraulic conductivity of the Globigerina Limestone formation: The hydraulic conductivity of Globigerina Limestone is an order of magnitude lower than Lower Coralline Limestone. Such contrast is thought to play an important role in extending freshened groundwater offshore Malta. The Globigerina Limestone formation is actually made up of three members separated by conglomerate beds, so the hydraulic conductivity across the formation can vary by two orders of magnitude (De Biase et al., 2021). The impact of this variation on the extent of OFG is explored with our model.

ii. Decrease in recharge rate: Temperature increases of 2°C with respect to present conditions are expected in southern Europe in the next 100 years, in association with severe decreases in precipitation of up to 30% (Vautard et al., 2014). A 30% decrease in recharge rate has thus been considered.

iii. Increase in sea-level: Models for the Mediterranean region indicate that mean sea-level rise in 2100 will range from 52 to 190 cm (Adloff et al., 2015; Ciro Aucelli et al., 2017). Malta is characterized by gently to steeply sloping coasts and this limits the extent by which sea-level rise reduces the extent of the subaerial terrain. The hinterland portion, gained by the sea with the highest considered level rise, is well-below the cell extension of the model mesh. This aspect was therefore neglected and thus the extension of the modeling domain was kept constant. The simulation was therefore performed by gradually raising the saltwater boundary conditions first by 1 m, and then by 1.9 m in a second scenario over a period of 100 years.

iv. Position and extraction rates of onshore pumping wells: Simulations were also carried out to assess the effect of a pumping well-withdrawing at a sustainable flow rate at different distances from the shoreline, starting from the location of the highest hydraulic head. The well has a depth of −30 m with a 10 m filtering screen operating with a flow rate of 40 m³/d in view of a 50 m model width, which results in a value of 0.8 m³/(m·d). This extraction rate was determined in order to maximize its value whilst maintaining a salt concentration lower than 1 g/L for a simulation period of 100 years.

The simulation scenarios are summarized in Table 2.

TABLE 2

Table 2. 2D simulation scenarios (100 years duration).

3.3. 3D groundwater modeling

The 3D model focuses on a larger scale, coarser resolution representation of the archipelago in comparison to the 2D model, in order to reconstruct the past evolution of the onshore-offshore groundwater system over large time scales. 3D numerical simulations were implemented using the open-source, parallel, finite element code Elmer (2022). Darcy flow and the advection-diffusion equation for solute transport were solved using the formulation of Hartikainen (2018). Our transient 3D model includes the islands of Malta, Comino, and Gozo, and the adjacent seafloor down to a depth of 217 m below sea-level at present (Figure 4a). The finite element mesh was constructed using the LaGriT mesh generator (LaGriT, 2022) and consists of 2.5 million tetrahedra with 0.5 million nodes. 3D surfaces of the boundaries between adjacent geological formations were used to interpolate material properties of the formations onto the elements of the grid. The mesh extends down to a depth of 2 km, with vertical resolution that varies from ~3 m near the surface to ~50 m at the bottom of the domain. Horizontal mesh resolution is 1,000 m, except where the elevation is between 0 and −120 m, where the resolution is 250 m. This higher resolution was used to better resolve flow conditions at the freshwater-saltwater transition during sea-level fluctuations. The water table below the land surface for the islands of Malta, Gozo, and Comino was fixed and estimated based on the following analytical solution for steady-state groundwater flow equation:

$\begin{array}{ll}\frac{{\partial }^{2}h}{\partial x^2}=\frac{R}{T}& (2)\end{array}$

where R is recharge (0.003 m/d), T is transmissivity (1,000 m²/d), and x is the distance from the shoreline, which yields the value of the water table elevation, h, as a function of:

$\begin{array}{ll}h=\frac{R}{T}\left[Lx-\frac{x^2}{2}\right]& (3)\end{array}$

where L is the maximum radial distance from the shoreline to the center of the island.

FIGURE 4

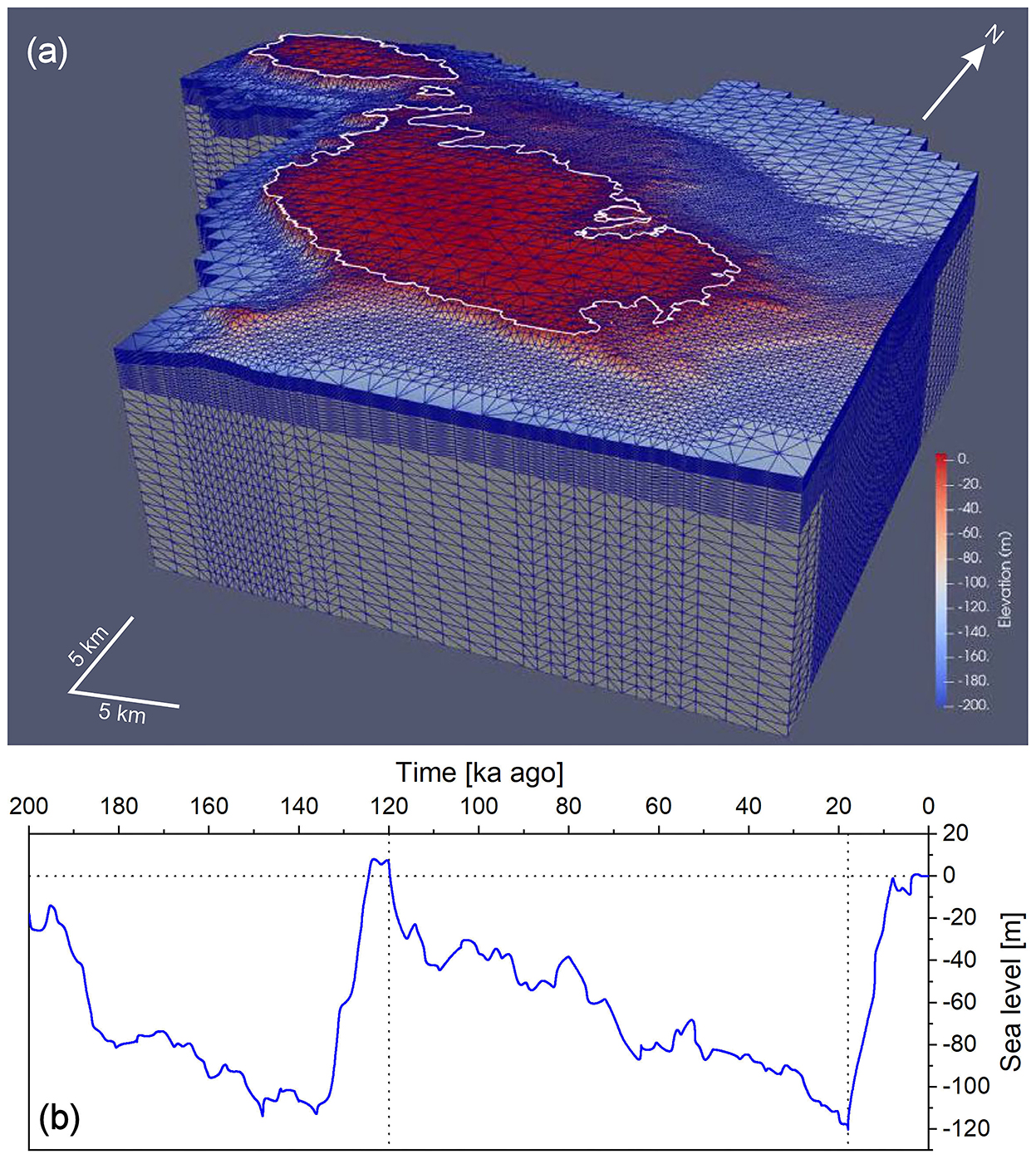
Figure 4. (a) The finite element mesh used for the 3D numerical groundwater simulations. Location of model in Figure 1. (b) Sea-level fluctuations from present day to 200 ka years ago derived from Hansen et al. (2013).

Elmer solves the groundwater pressure in Darcy's equation and the salinity in the advection diffusion equation sequentially using the Newton-Raphson iteration scheme. The finite element method uses the standard Galerkin method with residual-free bubbles for stabilization. An incomplete Lower-Upper factorization preconditioner was used on all equations, and a first-order backward differentiation formula was used for the time discretization (Elmer, 2022).

The model is isothermal, with groundwater properties calculated at 20°C. At the water table, a recharge boundary condition of 138 mm/a was prescribed based on rainfall and evapotranspiration data (FAO, 2003; Galdies, 2011), and kept constant during the simulations. Because the model does not solve for the water table elevation (it is fixed for all times), the groundwater pressure (or hydraulic head) is calculated and can vary during the simulation depending on the balance between groundwater flow and recharge. At the seafloor, a head boundary condition based on the water depth was imposed. Zero salinity was imposed at the land surface and sea water concentration was applied at the seafloor. On all vertical sides of the domain, a hydrostatic boundary condition was used and a no-flow condition was imposed at the bottom boundary.

Model runs simulated 188 ka (from Marine Isotope Stage 6) of groundwater flow and solute transport up to present day at time-steps of 1 a. Sea-level fluctuations for this period of time were derived from Hansen et al. (2013) (Figure 4b). The results presented in section 4.2 are for 120 ka BP (Marine Isotope Stage 5e), 18 ka BP (Marine Isotope Stage 2) and present conditions.

4. Results

4.1. 2D modeling results

4.1.1. Present-day scenario

Figure 5A shows the modeled groundwater salinity distribution at present conditions in SE Malta. This consists of a >13 km wide and ~120 m thick freshwater lens, which matches salinity data from deep boreholes in the region (Energy and Water Agency, unpublished data). The OFG body extends ~1 km from the coast, in agreement with the estimation of Haroon et al. (2021), which was based on a 20 ka numerical simulation that took into account sea-level fluctuations.

FIGURE 5

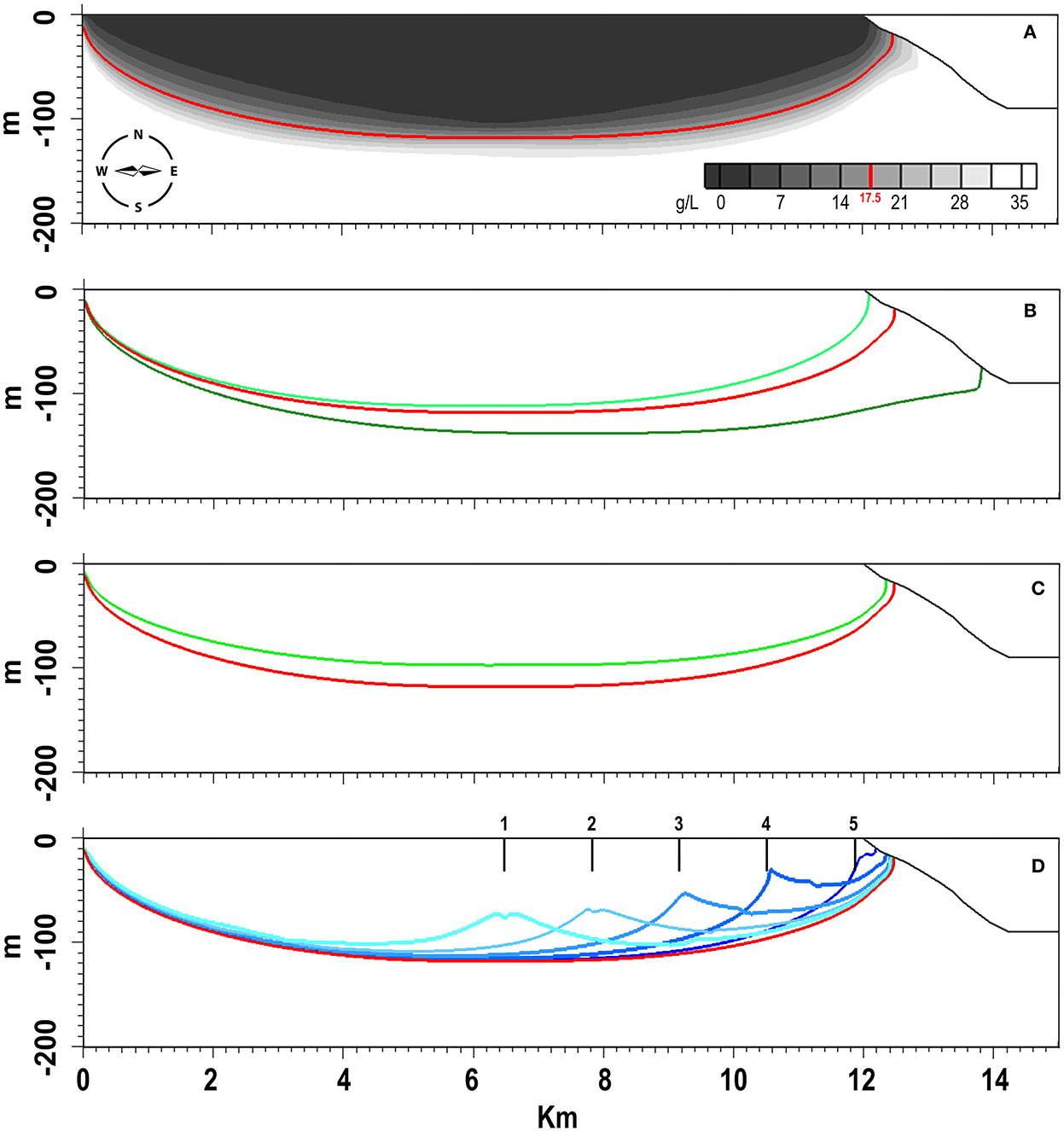
Figure 5. 2D numerical simulation results. For all figures, the contour lines represent the 17.5 g/L concentration, which stands at the transition between fresh and saltwater (0 and 35 g/L, respectively). Reference result from the calibrated model for present-day conditions is shown in red. (A) Simulated concentrations for an anisotropy factor of 56 and a time period of 5,000 years (until pseudo-stationarity conditions were achieved). (B) The impact of increased (light green) and decreased (dark green) hydraulic conductivity of the Globigerina Limestone formation on the dimensions of the groundwater body. (C) The impact of decreased surface recharge rate by 30% (green contour line). (D) Contour lines in shades of blue showing the extent of the groundwater body for five different scenarios (point 1: 5,400 m from shoreline; point 2: 4,050 m from shoreline; point 3: 2,700 m from shoreline; point 4: 1,350 m from shoreline; point 5: at shoreline) after a simulation time of 100 years).

This calibrated model allows us to assess the role of the Globigerina Limestone in the formation and extension of OFG. If the value of the hydraulic conductivity is increased by an order of magnitude (which is representative of the Lower Globigerina Limestone member and closer to the LCL formation), the contour for the 17.5 g/L concentration is just a few meters from shore (light green contour line in Figure 5B). This change in hydraulic conductivity also leads to a decrease of ~9 and 92% in the areas of the groundwater lens and OFG region, respectively. If the value of the hydraulic conductivity is decreased by an order of magnitude (which is representative of the Middle Globigerina Limestone member), the contour for the 17.5 g/L concentration is >2 km from shore (dark green contour line in Figure 5B). In the latter case, we observe an increase of 29% of the entire lens area, with the OFG area eight times larger than the reference result.

4.1.2. Influence of predicted climate change and pumping on OFG distribution

4.1.2.1. Decrease in recharge

The green contour line in Figure 5C represents the groundwater body extension obtained for a decrease of 30% in the recharge rate with respect to the one used in the calibrated model. The vertical extension of the groundwater body decreases by ~20 m at the point undergoing the greatest variation, while the OFG moves backward by ~200 m, resulting in an overall decrease of ~15% of the entire lens area and a decrease of 36% of the OFG area.

4.1.2.2. Increase in sea-level

Increases in sea-level of 1 and 1.9 m were simulated, starting from the calibrated model. Such changes in sea-level lift the interface between fresh and saltwater by a few centimeters, and this has no appreciable effect (in terms of the graphical result generated by our model) on both the mean sea-level groundwater body and the OFG configuration after 100 years.

4.1.2.3. Groundwater pumping

The last parameter that was explored with our 2D model was groundwater pumping and its impact on OFG. The contour lines in different shades of blue represent the estimated extent of the 17.5 g/L concentrations after a simulation time of 100 years for pumping wells operating at the same flow rate but different distances from the shoreline (Figure 5D). For locations 1 and 2 (5,400 and 4,050 m from shoreline, respectively), the extent of OFG is minimally affected by the pumping. The extent starts to decrease where the well is located at distances of <2,700 m from the shoreline (point 3). The decrease of the OFG area in this case is estimated to be 27%, while a loss of 55% is expected for pumping from point 4 (1,350 m from shoreline). The dark blue contour line, obtained after 100 years of constant water extraction for point 5 (at the shoreline), shows the almost complete disappearance of the OFG (95% reduction), although the onshore groundwater lens remains largely unchanged. In some scenarios (pumping from point 3, 4, and 5), a salt concentration < 1 g/L, with the extraction rate calibrated for point 1, cannot be maintained (Figure 6). In particular, the change of salt concentration with time at point 5, as calculated by our model, reaches a value of 2 g/L after just 1 year, and >13 g/L after 100 years of extraction (Figure 6).

FIGURE 6

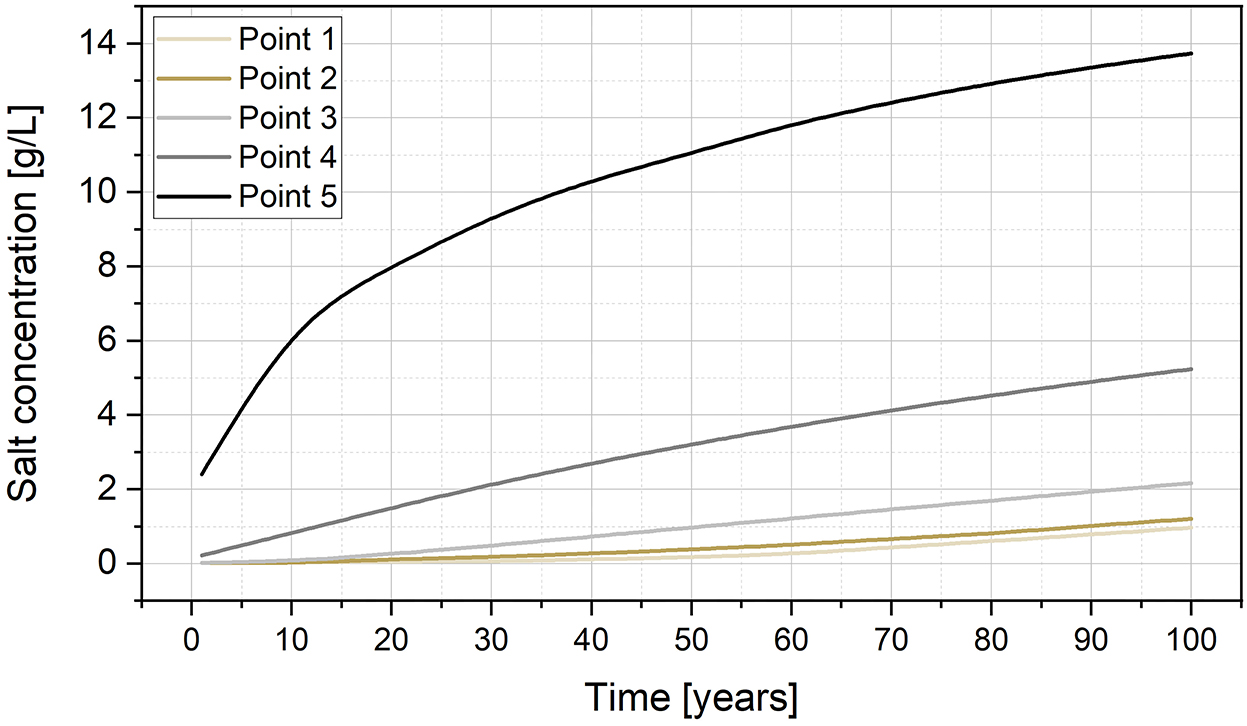
Figure 6. Variation of salt concentration with time calculated for pumping wells at the five points shown in Figure 5D.

4.2. 3D modeling results

The estimated volumes of groundwater, using the porosity values in Table 1, for the three time intervals are as follows:

i. 120 ka BP - total of 16 km³: 15 km³ onshore, 1 km³ offshore

ii. 18 ka BP - total of 97 km³: 85 km³ onshore, 12 km³ offshore

iii. Present - total of 22 km³: 21 km³ onshore, 1 km³ offshore.

These values are with respect to the coastline at the time. On average, ~25% of this groundwater volume has a PSU of <10.

The lateral extent of groundwater estimated by our 3D model at 120 ka, 18 ka and present is shown in Figures 7, 8. At 120 ka BP, when sea-level was 4–6 m higher than at present, OFG occurred along the coast between Mellieha and Valletta, with the largest extensions offshore Salini, Pembroke and Valletta (up to 2.8 km from the coast and a maximum thickness of 90 m). In the ensuing ~100 ka, the continental shelf was progressively exposed as sea-level dropped, promoting the expansion of the OFG across the shelf and beyond. The maximum extent of OFG was reached at the Last Glacial Maximum sea-level lowstand (18 ka), when OFG was primarily located offshore eastern Malta (up to 15 km from present coastline and a maximum thickness of 700 m) and, to a lesser extent, south and west of Malta, and east of Gozo. After the Last Glacial Maximum, the sea-level rose rapidly to reach present levels at 8 ka, driving the overall contraction of the OFG. At present, OFG is expected to predominantly occur between Malta and Gozo, and along the coast between Cirkewwa and Valletta, with the largest extensions offshore of St Paul's Bay, Salini and St Julian's (up to ~3 km from the coast and a maximum thickness of 100 m). This is in spatial agreement with the observed higher resistivity of the Blue Clay formation in CSEM line 2 offshore Cirkewwa and in CSEM line 6 offshore Salini (Haroon et al., 2021), in comparison to lower resistivities for Blue Clay elsewhere, which can be explained by fresher pore water. A resistivity anomaly (R1) was observed in Upper Coralline Limestone along CSEM line 6, although this was attributed to a decrease in porosity rather than a change in pore water salinity. A smaller extent of OFG is predicted offshore Birzebbuga, Lapsi, Golden Bay, and Gozo (Marsalforn to Ramla Bay, Dwejra). There are generally no indications of OFG in CSEM lines 5 and 8, which are located offshore north Malta and east Gozo, respectively, which is in agreement with our model results. There are two localized resistivity anomalies in these CSEM lines (R2 and R3), but these have also been attributed to reductions in porosity (Haroon et al., 2021). Offshore SE Malta, freshened groundwater is only predicted along the shoreline, rather than further offshore [as denoted by the localized resistivity anomaly R4 in CSEM line 9 (Haroon et al., 2021)]. We attribute to this to the coarse resolution of the 3D numerical model, which prevented the reconstruction of a small-scale OFG. A 2D profile extracted from the 3D model across the SE of Malta is shown in Figure 8. Whereas, the lens is largely symmetrical during sea-level highstands, it is thicker to the NE of Malta in comparison to the SW during the Last Glacial Maximum sea-level lowstand. Figure 9 shows the predicted groundwater velocity, which varies between 0.032 and 3.2 m/a at present, and which was at least an order of magnitude higher during the Last Glacial Maximum.

FIGURE 7

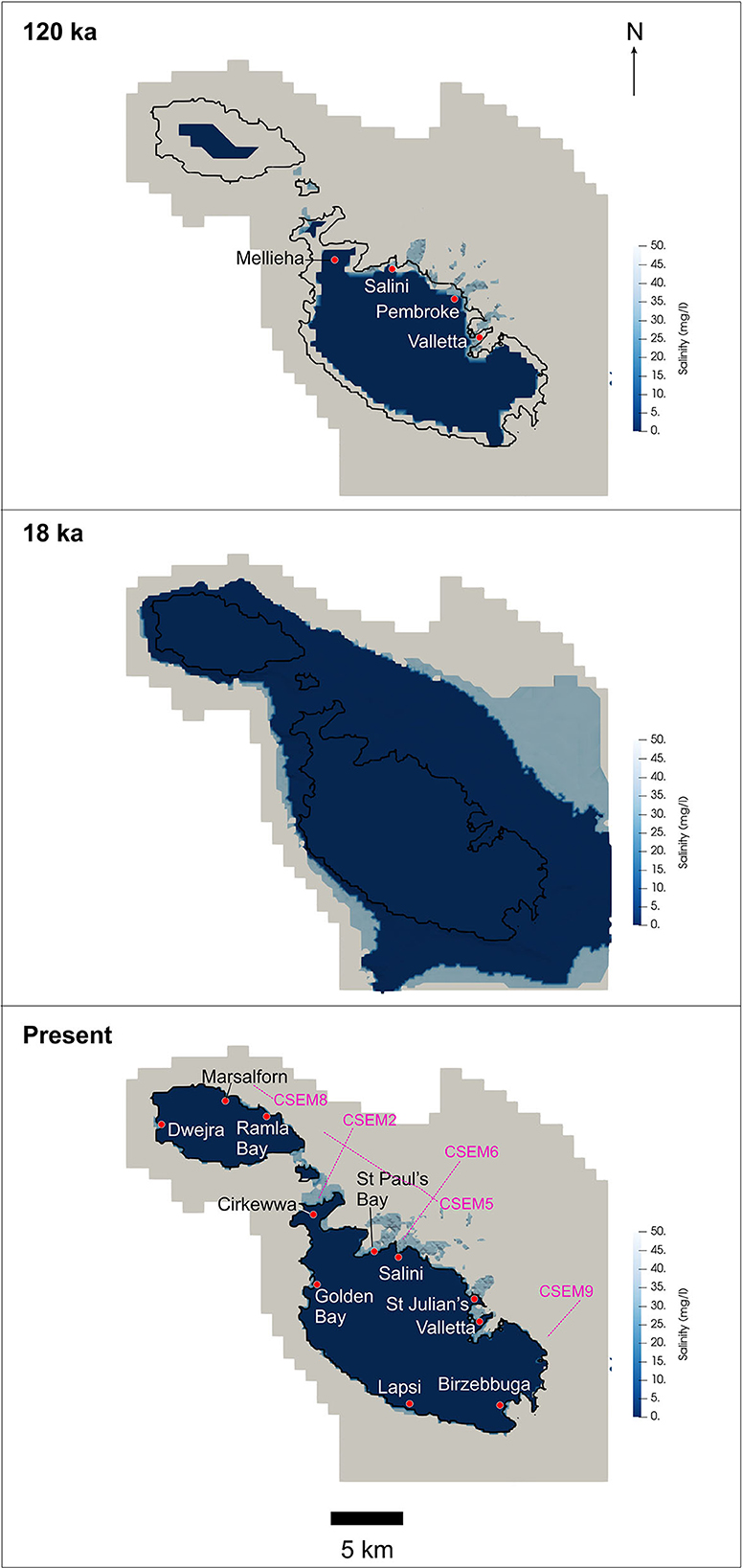
Figure 7. Estimated groundwater extent from the 3D model at three different time intervals. Only the salinity at the top of the groundwater body is shown.

FIGURE 8

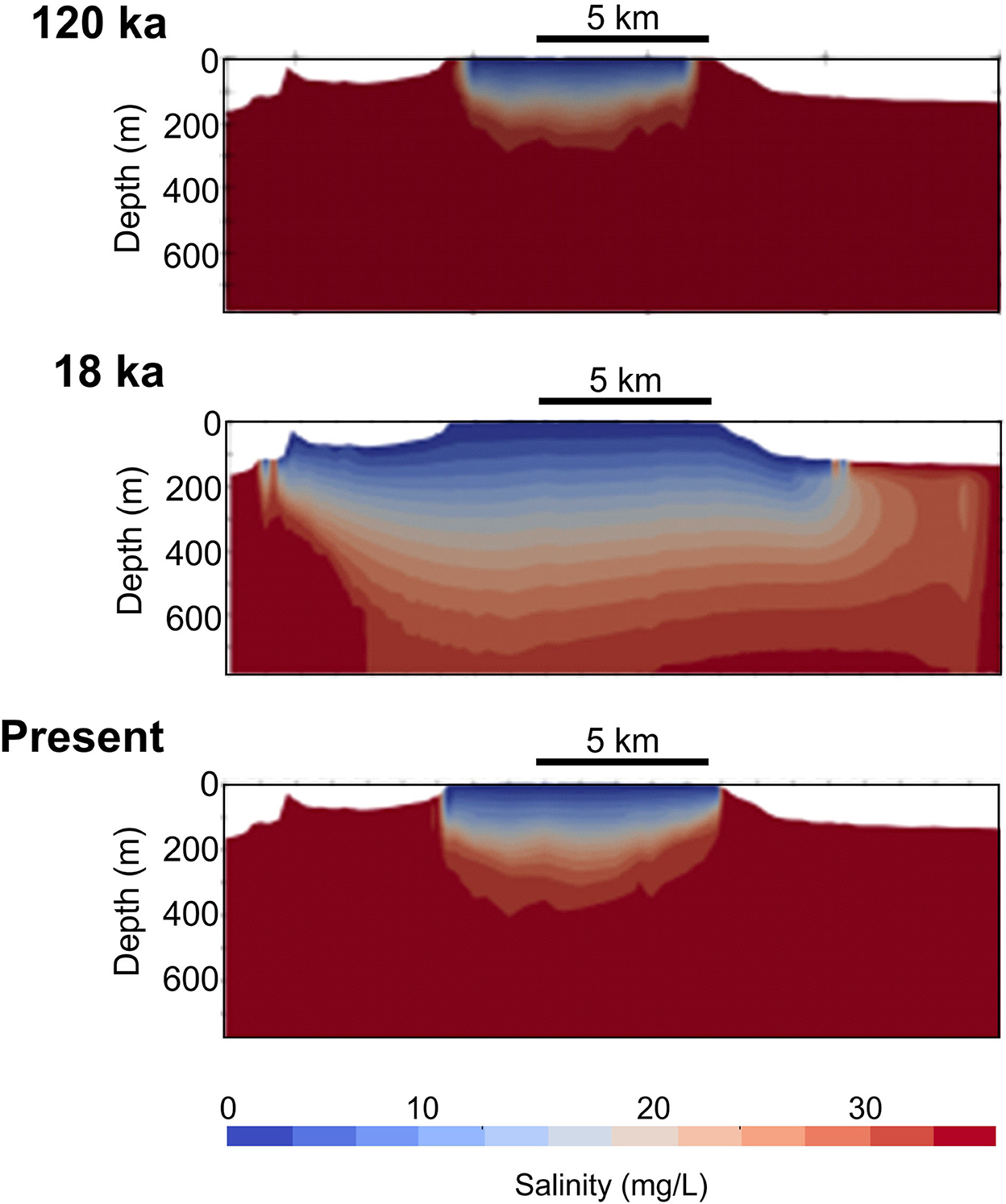
Figure 8. Salinity profile along SW-NE cross-section (location in Figure 1) at three different time intervals.

FIGURE 9

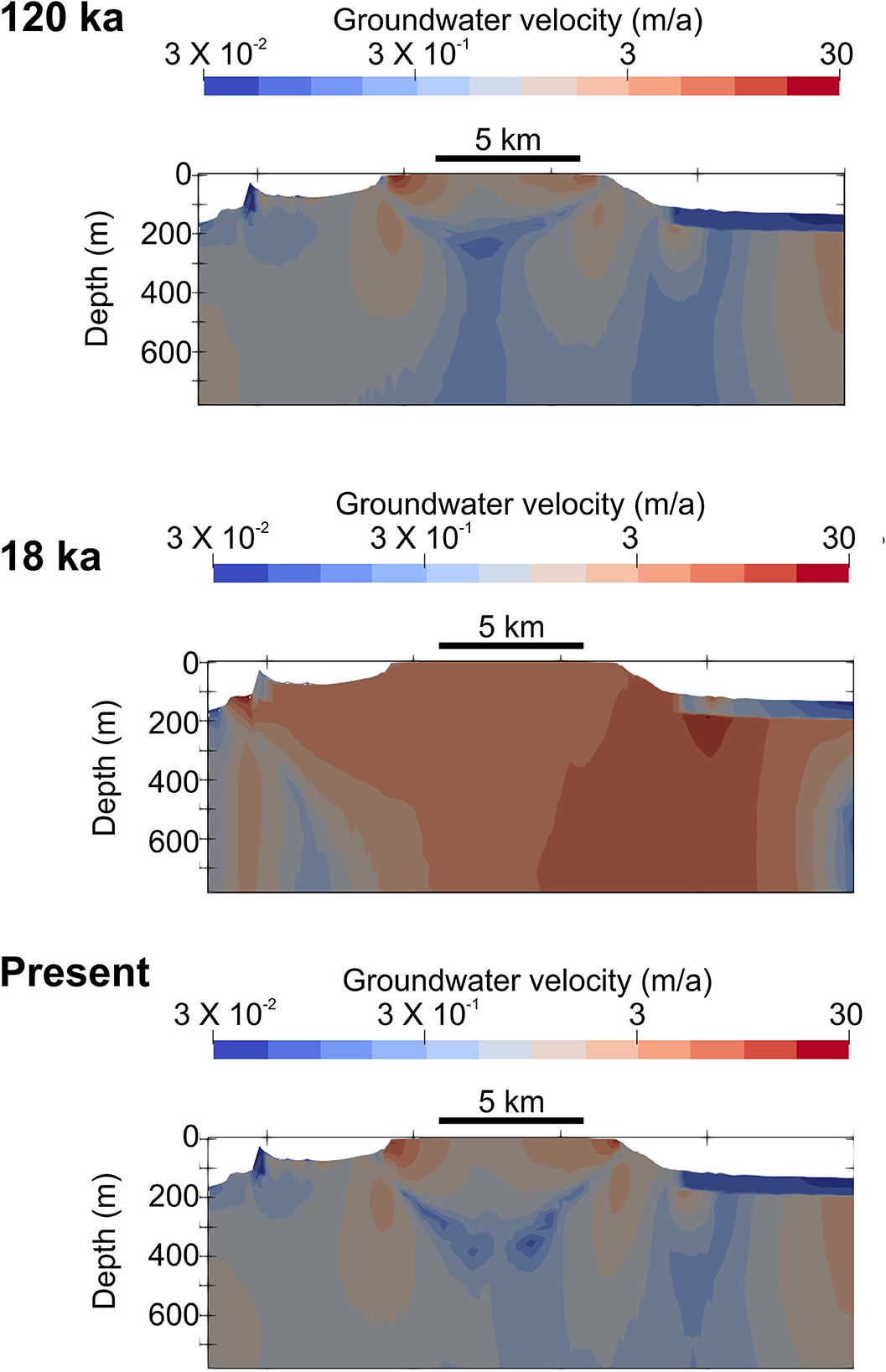
Figure 9. Estimated groundwater velocity along SW-NE cross-section (location in Figure 1) at three different time intervals.

5. Discussion and conclusions

5.1. OFG characteristics at present and their evolution in the past

Based on our modeling simulations, we can infer that:

i. The observed OFG distribution is strongly influenced by permeability and porosity distribution across the shelf. The occurrence of OFG at present is primarily located north of the Great Fault (Figure 7), which is where most of the Blue Clay is located (Haroon et al., 2021). South of the Great Fault, OFG is spatially more restricted and hosted by Globigerina Limestone. This, and the plot in Figure 5B, show the importance of lower permeability units in preserving OFG, either by improving its preservation or because of their role in providing a barrier to salt diffusion. Geological control is also reflected in the asymmetry of groundwater lens during Last Glacial Maximum (Figure 8), as this seems to follow the tilting of geological layers, and preferred recharge, toward the NE.

ii. Emplacement of OFG at distances of >1 km south of the Great Fault (e.g., offshore St Julian's), which is dominated by Globigerina and Lower Coralline Limestone formations with low coastal relief, can only be explained by recharge when sea-level was lower, followed by groundwater preservation in low permeability units when the sea-level rose again (e.g., Haroon et al., 2021). This emplacement mechanism is partly corroborated by the estimated faster groundwater velocities during the Last Glacial Maximum in comparison to present (Figure 9). North of the Great Fault, where Blue Clay is more prevalent, OFG extents of up to 3 km from the shoreline may be explained by active meteoric recharge in view of the low hydraulic conductivity of this formation (two orders of magnitude lower than Globigerina Limestone) and the higher coastal relief (Figure 5B).

iii. The onshore-offshore groundwater system of the Maltese Islands is relatively dynamic. Only 23% of the groundwater is preserved in the 18 ka between the Last Glacial Maximum and present, with the rest being replaced by seawater via density driven flows. The OFG interface moved landward at a rate of ~70 cm per year in the last 18 ka (Figure 7). This suggests that the freshwater emplaced across the Maltese shelf has a good chance of surviving an interglacial cycle, which would mean that the OFG we observe at present is likely a mixture of paleowaters emplaced during different sea-level lowstands. The preservation potential of the OFG offshore the Maltese Islands is comparable to that of the siliciclastic setting of the New Jersey margin, where 30–45% of initial OFG volume was preserved after 12 ka (Thomas et al., 2019).

iv. The extent of groundwater simulated for the Last Glacial Maximum spatially correlates with seafloor morphologies that have previously been attributed to groundwater seepage during sea-level lowstands (Figure 1). These morphologies include: (i) theater-headed canyons, which are inferred to form subaerially by seepage-driven slope failure associated with widening of joints and fractures in Upper Coralline Limestone, and creep of the underlying Blue Clay (Micallef et al., 2022), and (ii) biogenic mounds between 80 and 120 m below sea-level, which have been interpreted as authigenic carbonate edifices related to seepage at the coast or shallow seafloor (Bialik et al., 2022).

v. The estimated volume of freshened groundwater offshore the Maltese Islands at present is ~1 km³. This compares with ~0.013 km³ produced from various groundwater sources annually in the last 10 years (Hartfiel et al., 2020). If these water requirements were to be maintained constant and the OFG could be exploited, the latter would provide an alternative supply to onshore groundwater for ~75 years (if part of the OFG is desalinized).

5.2. Response of OFG system to climate-related changes and exploitation

i. Decrease in recharge is a key factor that will diminish the extent of the OFG emplaced by active meteoric recharge in the coming 100 years. Sea-level rise, in comparison, plays a negligible role. Older OFG emplaced during sea-level lowstands are not influenced by changes in recharge or sea-level for the timeframe considered, but only by salinization.

ii. Groundwater pumping at a rate of 40 m³/d can be sustainable at distance of >4 km from the coast. Considering that there are numerous wells located within 4 km of the coast [a few public pumping stations and many private wells; (Food and Agriculture Organisation (FAO) of the United Nations, 2006; Sapiano, 2015)], we infer that OFG may have already been inadvertently extracted from onshore wells in the past (e.g., Knight et al., 2018).

iii. If the pumping rate needs to be increased to cater for higher water demand in the near future, pumping at a distance of >4 km from the coast will also start impacting groundwater lens geometry and result in seawater intrusion, as suggested by Morgan et al. (2018). However, in case of extreme need, it might be possible to exploit significant volumes of OFG by locating wells close to the coast. The possibility of exploiting the brackish water in the OFG (which requires desalinization) represents a solution to be considered only in the case where the onshore groundwater body cannot be used or needs to be preserved.

5.3. Limitations

i. We have used static models where stratigraphy does not evolve with time. This is not problematic in the Maltese Islands because the bedrock geology has remained unchanged for the last 5 Ma. What changed was the deposition and removal of a thin layer of unconsolidated sediment above the bedrock during glacial cycles (Micallef et al., 2013).

ii. We did not account for surface water drainage and groundwater recharge fluctuations, because these are not well-constrained for the Maltese Islands in the past (e.g., Gambin et al., 2016).

iii. Faults have been shown to play an important role in controlling the groundwater flow regime of the Maltese Islands, primarily by enhancing or slowing down groundwater flow, depending on the flow direction (De Biase et al., 2021). Faults, and their influence on groundwater flow, have not been considered in either of our models.

iv. Karstic features are also not taken into consideration. These are known to occur onshore and offshore (Micallef et al., 2013; Calleja and Tonelli, 2019) and are expected to provide faster recharge and salinization of groundwater bodies.

v. We had to use 2D simulations to assess future scenarios because of the high spatial and temporal resolution required, which could not be achieved using a 3D approach.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MD, FC, and AM developed the main concept of this study. MD and FC were in charge of the 2D numerical modeling, whereas DC, CG, and TZ implemented the 3D numerical modeling. MD, FC, and AM interpreted the modeling results and wrote the manuscript, which was reviewed by DC, CG, and TZ. All authors contributed to the article and approved the submitted version.

Funding

This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 Research and Innovation program [grant agreement No. 677898 (MARCAN)]. MD acknowledges the European Commission for the financial support under the PON Research and Innovation 2014–2020, Action I.2 Researchers' Mobility Notice D.D. 407 of 02.27.2018—AIM Attraction and International Mobility—Line 1 Researchers' Mobility.

Acknowledgments

We thank the Energy and Water Agency, Mattia Martinelli, and Daniele Spatola for assistance with compiling the onshore geological database and Mark Person for assistance with modeling. We are grateful to the three reviewers for their insightful comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adloff, F., Somot, S., Sevault, F., Jordà, G., Aznar, R., Déqué, M., et al. (2015). Mediterranean Sea response to climate change in an ensemble of twenty first century scenarios. Clim. Dyn. 45, 2775–2802. doi: 10.1007/s00382-015-2507-3

CrossRef Full Text | Google Scholar

Alexander, D. (1988). A review of the physical geography of Malta and its significance for tectonic geomorphology. Quat. Sci. Rev. 7, 41–43. doi: 10.1016/0277-3791(88)90092-3

CrossRef Full Text | Google Scholar

Amir, N., Kafri, U., Herut, B., and Shalev, E. (2013). Numerical simulation of submarine groundwater flow in the coastal aquifer at the Palmahim Area, the Mediterranean Coast of Israel. Water Resour. Manag. 27, 4005–4020. doi: 10.1007/s11269-013-0392-2

CrossRef Full Text | Google Scholar

Attias, E., Thomas, D., Sherman, D., Ismail, K., and Constable, S. (2020). Marine electrical imaging reveals novel freshwater transport mechanism in Hawai‘i. Sci. Adv. 6, eabd4866. doi: 10.1126/sciadv.abd4866

PubMed Abstract | CrossRef Full Text | Google Scholar

Bailey, G. N., and King, G. C. (2011). Dynamic landscapes and human dispersal patterns: tectonics, coastlines, and the reconstruction of human habitats. Quat. Sci. Rev. 30, 1533–1553. doi: 10.1016/j.quascirev.2010.06.019

CrossRef Full Text | Google Scholar

Bakalowicz, M., and Mangion, J. (2003). The limestone aquifers of Malta: their recharge conditions from isotope and chemical surveys. Int. Assoc. Hydrol. Sci. 278, 49–54.

Google Scholar

Bakken, T. H., Ruden, F., and Mangset, L. E. (2012). Submarine groundwater: a new concept for the supply of drinking water. Water Resour. Manag. 26, 1015–1026. doi: 10.1007/s11269-011-9806-1

CrossRef Full Text | Google Scholar

Bialik, O. M., Varzi, A. G., Durán, R., Le Bas, T., Gauci, A., Savini, A., et al. (2022). Mesophotic depth biogenic accumulations (“biogenic mounds”) offshore the Maltese Islands, Central Mediterranean Sea. Front. Mar. Sci. 9, 803687. doi: 10.3389/fmars.2022.803687

CrossRef Full Text | Google Scholar

Calleja, I., and Tonelli, C. (2019). “Dwejra and Maqluba: Emblematic Sinkholes in the Maltese Islands,” in Landscapes and Landforms of the Maltese Islands, eds R. Gauci, and J. A. Schembri (Cham: Springer International Publishing), 129–139.

Google Scholar

Ciro Aucelli, P. P., Di Paola, G., Incontri, P., Rizzo, A., Vilardo, G., Benassai, G., et al. (2017). Coastal inundation risk assessment due to subsidence and sea level rise in a Mediterranean alluvial plain (Volturno coastal plain – southern Italy). Estuar. Coast. Shelf Sci. 198, 597–609. doi: 10.1016/j.ecss.2016.06.017

CrossRef Full Text | Google Scholar

Cohen, D., Person, M., Wang, P., Gable, C. W., Hutchinson, D., Marksamer, A., et al. (2010). Origin and extent of freshwater paleowaters on the Atlantic continental shelf, USA. Groundwater 48, 143–158. doi: 10.1111/j.1745-6584.2009.00627.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Costain, L., and Messers, R. (1957). Reports on Geological Investigations. Valletta: Government of Malta Water Supply.

De Biase, M., Chidichimo, F., Maiolo, M., and Micallef, A. (2021). The impact of predicted climate change on groundwater resources in a mediterranean archipelago: a modelling study of the Maltese Islands. Water 13, 3046. doi: 10.3390/w13213046

CrossRef Full Text | Google Scholar

DeFoor, W., Person, M., Larsen, H. C., Lizarralde, D., Cohen, D., and Dugan, B. (2011). Ice sheet–derived submarine groundwater discharge on Greenland's continental shelf. Water Resour. Res. 47. doi: 10.1029/2011WR010536

CrossRef Full Text | Google Scholar

Elmer (2022). Elmer. W07549. Available online at: https://www.csc.fi/web/elmer (accessed October 5, 2022).

Environment and Resources Authority (2015). The 2nd Water Catchment Management Plan for the Malta Water Catchment District (Marsa). 2015–2021.

Google Scholar

Evans, R. L., and Lizarralde, D. (2003), Geophysical evidence for karst formation associated with offshore groundwater transport: An example from North Carolina. Geochem. Geophys. Geosyst. 4, 1069. doi: 10.1029/2003GC0005108

CrossRef Full Text | Google Scholar

FAO (2003). “Review of world water resources by country,” in Water Reports (Rome: Food and Agriculture Organization of the United Nations).

Google Scholar

Food and Agriculture Organisation (FAO) of the United Nations (2006). Malta Water Resources Review (Rome).

Google Scholar

Galdies, C. (2011). The Climate of Malta: Statistics, Trends and Analysis. Valletta: National Statistics Office.

Google Scholar

Gambin, B., Andrieu-Ponel, V., Médail, F., Marriner, N., Peyron, O., Montade, V., et al. (2016). 7300 years of vegetation history and climate for NW Malta: a Holocene perspective. Clim. Past 12, 273–297. doi: 10.5194/cp-12-273-2016

CrossRef Full Text | Google Scholar

Gardiner, W., Grasso, M., and Sedgeley, D. (1995). Plio-Pleistocene fault movement as evidence for mega-block kinematics within the Hyblean-Malta Plateau, Central Mediterranean. J. Geodyn. 19, 35–51. doi: 10.1016/0264-3707(94)00006-9

CrossRef Full Text | Google Scholar

Gustafson, C., Key, K., and Evans, R. L. (2019). Aquifer systems extending far offshore on the U.S. Atlantic margin. Sci. Rep. 9, 8709. doi: 10.1038/s41598-019-44611-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, J. H., Sato, M., Russell, G., and Kharecha, P. (2013). Climate sensitivity, sea level and atmospheric carbon dioxide. Philos. Transact. R. Soc. A Math. Phys. Eng. Sci. 371, 20120294. doi: 10.1098/rsta.2012.0294

PubMed Abstract | CrossRef Full Text | Google Scholar

Haroon, A., Micallef, A., Jegen, M., Schwalenberg, K., Karstens, J., Berndt, C., et al. (2021). Electrical resistivity anomalies offshore a carbonate coastline: evidence for freshened groundwater? Geophys. Res. Lett. 48:e2020GL091909. doi: 10.1029/2020GL091909

CrossRef Full Text | Google Scholar

Hartfiel, L., Soupir, M., and Kanwar, R. S. (2020). Malta's water scarcity challenges: past, present, and future mitigation strategies for sustainable water supplies. Sustainability 12, 9835. doi: 10.3390/su12239835

CrossRef Full Text | Google Scholar

Hartikainen, J. (2018). Continuum Thermodynamic Modelling of Porous Medium With Application to Ground Freezing (Doctoral). Espoo: Aalto University.

Google Scholar

Hesse, R., and Harrison, W. E. (1981). Gas hydrates (clathrates) causing pore-water freshening and oxygen isotope fractination in deep-water sedimentary sections of terrigenous continental margins. Earth Planet. Sci. Lett. 55, 453–462. doi: 10.1016/0012-821X(81)90172-2

CrossRef Full Text | Google Scholar

Illies, J. H. (1981). Graben formation - The Maltese Islands, a case study. Tectonophysics 73, 151–168. doi: 10.1016/0040-1951(81)90182-7

CrossRef Full Text

Johnson, D. W. (1939). The Origin of Submarine Canyons: A Critical Review of Hypotheses. New York, NY: Columbia University Press.

Google Scholar

Kastner, M., Elderfield, H., and Martin, J. B. (1991). Fluids in convergent margins: what do we know about their composition, origin, role in diagenesis and importance for oceanic chemical fluxes? Philos. Transact. R. Soc. London 335, 243–259. doi: 10.1098/rsta.1991.0045

CrossRef Full Text | Google Scholar

Knight, A. C., Irvine, D. J., and Werner, A. D. (2021). Alongshore freshwater circulation in offshore aquifers. J. Hydrol. 593, 125915. doi: 10.1016/j.jhydrol.2020.125915

CrossRef Full Text | Google Scholar

Knight, A. C., Werner, A. D., and Morgan, L. K. (2018). The onshore influence of offshore fresh groundwater. J. Hydrol. 561, 724–736. doi: 10.1016/j.jhydrol.2018.03.028

CrossRef Full Text | Google Scholar

Kooi, H., Groen, J., and Leijnse, A. (2000). Modes of seawater intrusion during transgressions. Water Resour. Res. 36, 3581–3589. doi: 10.1029/2000WR900243

CrossRef Full Text | Google Scholar

Kooi, H., and Groen, K. (2001). Offshore continuation of coastal groundwater systems; predictions using sharp-interface approximations and variable-density flow modelling. J. Hydrol. 246, 19–35. doi: 10.1016/S0022-1694(01)00354-7

CrossRef Full Text | Google Scholar

Krantz, D. E., Manheim, F. T., Bratton, J. F., and Phelan, D. J. (2004). Hydrogeologic setting and ground water flow beneath a section of Indian River Bay, Delaware. Groundwater 42, 1035–1051. doi: 10.1111/j.1745-6584.2004.tb02642.x

CrossRef Full Text | Google Scholar

Kuang, X., Jiao, J. J., Zheng, C., Cherry, J. A., and Li, H. (2020). A review of specific storage in aquifers. J. Hydrol. 581, 124383. doi: 10.1016/j.jhydrol.2019.124383

CrossRef Full Text | Google Scholar

LaGriT (2022). LaGriT: Los Alamos Grid Toolbox. Available online at: https://lagrit.lanl.gov/ (accessed October 5, 2022).

Langevin, C. D., Thorne, D. T. Jr., Dausman, A. M., Sukop, M. C., and Guo, W. (2008). “SEAWAT Version 4: a computer program for simulation of multi-species solute and heat transport,” in U. S. Geological Survey Techniques and Methods (Reston, VA: USGS), 39.

Google Scholar

Lofi, J., Inwood, J., Proust, J. N., Monteverde, D. H., Loggia, D., Basile, C., et al. (2013). Fresh-water and salt-water distribution in passive margin sediments: insights from integrated ocean drilling program expedition 313 on the New Jersey Margin. Geosphere 9, 1–16. doi: 10.1130/GES00855.1

CrossRef Full Text | Google Scholar

Lotti, F., Borsi, I., Guastaldi, E., Barbagli, A., Basile, P., Favaro, L., et al. (2021). Numerically enhanced conceptual modelling (NECoM) applied to the Malta Mean Sea Level Aquifer. Hydrogeol. J. 29, 1517–1537. doi: 10.1007/s10040-021-02330-2

CrossRef Full Text | Google Scholar

Marksammer, A. J., Person, M., Day-Lewis, F. D., Lane, J. W., Cohen, D., Dugan, B., et al. (2007). “Integrating geophysical, hydrochemical, and hydrologic data to understand the freshwater resources on Nantucket Island, Massachusetts,” in Subsurface Hydrology: Data Integration for Properties and Processes, eds D. W. Hyndman, F. D. Day-Lewis, and K. Singha (AGU Water Resources Monograph).

Google Scholar

Meisler, H., Leahy, P. P., and Knobel, L. L. (1984). Effect of Eustatic Sea-Level Changes on Saltwater-Freshwater Relations in the Northern Atlantic Coastal Plain. U.S.G. Survey. U.S. Geological Survey.

Google Scholar

Micallef, A., Foglini, F., Le Bas, T., Angeletti, L., Maselli, V., Pasuto, A., et al. (2013). The submerged paleolandscape of the Maltese Islands: morphology, evolution and relation to quaternary environmental change. Mar. Geol. 335, 129–147. doi: 10.1016/j.margeo.2012.10.017

CrossRef Full Text | Google Scholar

Micallef, A., Person, M., Berndt, C., Bertoni, C., Cohen, D., Dugan, B., et al. (2021). Offshore freshened groundwater in continental margins. Rev. Geophys. 59, e2020RG000706. doi: 10.1029/2020RG000706

PubMed Abstract | CrossRef Full Text | Google Scholar

Micallef, A., Person, M., Haroon, A., Weymer, B. A., Jegen, M., Schwalenberg, K., et al. (2020). 3D characterisation and quantification of an offshore freshened groundwater system in the Canterbury Bight. Nat. Commun. 11, 1372. doi: 10.1038/s41467-020-14770-7

PubMed Abstract | CrossRef Full Text

Micallef, A., Saadatkhah, N., Spiteri, J., Rizzo, E., Capozzoli, L., Pace, L., et al. (2022). Groundwater seepage is a key driver in the formation of theatre-headed valleys in limestone. Geology 50, 686–690. doi: 10.1130/G49938.1

CrossRef Full Text

Micallef, A., Spatola, D., Caracausi, A., Italiano, F., Barreca, G., D'Amico, S., et al. (2019). Active degassing across the Maltese Islands (Mediterranean Sea) and implications for its neotectonics. Mar. Petrol. Geol. 104, 361–374. doi: 10.1016/j.marpetgeo.2019.03.033

CrossRef Full Text | Google Scholar

Michael, H. A., Scott, K. C., Koneshloo, M., Yu, X., Khan, M. R., and Li, K. (2016). Geologic influence on groundwater salinity drives large seawater circulation through the continental shelf. Geophys. Res. Lett. 43, 10782–10791. doi: 10.1002/2016GL070863

CrossRef Full Text | Google Scholar

Monteiro, J. P., Costa, L. R. D., Hugman, R., Sapiano, M., and Schembri, M. (2016). “Regional groundwater model of the Malta South Region,” in: MARSOL Project Deliverable N. D10.4.

Moore, W. S. (1999). The subterranean estuary: a reaction zone of ground water and sea water. Marine Chem. 65, 111–125. Available online at: https://www.sciencedirect.com/science/article/pii/S0304420399000146

PubMed Abstract | Google Scholar

Morgan, L. K., Werner, A. D., and Patterson, A. E. (2018). A conceptual study of offshore fresh groundwater behaviour in the Perth Basin (Australia): modern salinity trends in a prehistoric context. J. Hydrol. Reg. Stud. 19, 318–334. doi: 10.1016/j.ejrh.2018.10.002

CrossRef Full Text | Google Scholar

Nicholson, D. T. (2001). Pore properties as indicators of breakdown mechanisms in experimentally weathered limestones. Earth Surf. Process. Landforms 26, 819–838. doi: 10.1002/esp.228

CrossRef Full Text | Google Scholar

Pedley, H. M., House, M. R., and Waugh, B. (1976). The geology of Malta and Gozo. Proc. Geol. Assoc. 87, 325–341. doi: 10.1016/S0016-7878(76)80005-3

CrossRef Full Text | Google Scholar

Person, M., Dugan, B., Swenson, J., Urbano, L., Stott, C., Taylor, J., et al. (2003). Pleistocene hydrogeology of the Atlantic continental shelf, New England. Geol. Soc. Am. Bull. 115, 1324–1343. doi: 10.1130/B25285.1

CrossRef Full Text | Google Scholar

Person, M., Wilson, J. L., Morrow, N., and Post, V. E. A. (2017). Continental-shelf freshwater water resources and improved oil recovery by low-salinity waterflooding. Am. Assoc. Pet. Geol. Bull. 101, 1–18. doi: 10.1306/05241615143

CrossRef Full Text | Google Scholar

Pondthai, P., Everett, M. E., Micallef, A., Weymer, B. A., Faghih, Z., Haroon, A., et al. (2020). 3D characterization of a coastal freshwater aquifer in SE Malta (Mediterranean Sea) by time-domain electromagnetics. Water 12, 1566. doi: 10.3390/w12061566

CrossRef Full Text | Google Scholar

Post, V. E. A., Groen, J., Kooi, H., Person, M., Ge, S., and Edmunds, W. M. (2013). Offshore fresh groundwater reserves as a global phenomenon. Nature 504, 71–78. doi: 10.1038/nature12858

PubMed Abstract | CrossRef Full Text | Google Scholar

Sapiano, M. (2015). “Characterisation of the sea-level aquifer system in the Malta South region,” in MARSOL: Demonstrating Managed Aquifer Recharge as a Solution to Water Scarcity and Drought.

Schulze-Makuch, D. (2005). Longitudinal dispersivity data and implications for scaling behaviour. Groundwater 43, 443–456. doi: 10.1111/j.1745-6584.2005.0051.x

PubMed Abstract | CrossRef Full Text

Siegel, J., Person, M., Dugan, B., Cohen, D., Lizarralde, D., and Gable, C. (2014). Influence of late Pleistocene glaciations on the hydrogeology of the continental shelf offshore Massachusetts, USA, Geochem. Geophys. Geosyst. 15, 4651–4670. doi: 10.1002/2014GC005569

CrossRef Full Text | Google Scholar

Thomas, A. T., Reiche, S., Riedel, M., and Clauser, C. (2019). The fate of submarine fresh groundwater reservoirs at the New Jersey shelf, USA. Hydrogeol. J. 27, 2673–2694. doi: 10.1007/s10040-019-01997-y

CrossRef Full Text | Google Scholar

UN-Water (2020). UN-Water Analytical Brief on Unconventional Water Resources. Geneva: United Nations.

van Geldern, R., Hayashi, T., Bottcher, M. E., Mottl, M., Barth, J. A. C., and Stadler, S. (2013). Stable isotope geochemistry of pore waters and marine sediments from the New Jersey shelf: methane formation and fluid origin. Geosphere 9, 96–112. doi: 10.1130/GES00859.1

CrossRef Full Text | Google Scholar

Varma, S., and Michael, K. (2012). Impact of multi-purpose aquifer utilisation on a variable-density groundwater flow system in the Gippsland Basin, Australia. Hydrogeol. J. 20, 119–134. doi: 10.1007/s10040-011-0800-8

CrossRef Full Text | Google Scholar

Vautard, R., Gobiet, A., Sobolowski, S., Kjellström, E., Stegehuis, A., Watkiss, P., et al. (2014). The European climate under a 2°C global warming. Environ. Res. Lett. 9, 034006. doi: 10.1088/1748-9326/9/3/034006

CrossRef Full Text | Google Scholar

Willard, S. M. (1999). The subterranean estuary: a reaction zone of ground water and sea water. Mar. Chem. 65, 111–125. doi: 10.1016/S0304-4203(99)00014-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeh, Y. J., Lee, C. H., and Chen, S. T. (2000). A tracer method to determine hydraulic conductivity and effective porosity of saturated clays under low gradients. Groundwater 38, 522–529. doi: 10.1111/j.1745-6584.2000.tb00244.x

CrossRef Full Text | Google Scholar

Yu, X., and Michael, H. A. (2019). Offshore pumping impacts onshore groundwater resources and land subsidence. Geophys. Res. Lett. 46, 2553–2562. doi: 10.1029/2019GL081910

CrossRef Full Text | Google Scholar

Zamrsky, D., Karssenberg, M. E., Cohen, K. M., Bierkens, M. F. P., and Oude Essink, G. H. P. (2020). Geological heterogeneity of coastal unconsolidated groundwater systems worldwide and its influence on offshore fresh groundwater occurrence. Front. Earth Sci. 7, 339. doi: 10.3389/feart.2019.00339

CrossRef Full Text | Google Scholar

Zheng, C. (1990). MT3D: A Modular Three-Dimensional Transport Model for Simulation of Advection, Dispersion and Chemical Reactions of Contaminants in Groundwater Systems. Rockville, MD: S.S. Papadopulos & Associates.

Google Scholar