Hydroeconomic Analysis to Guide Climate Adaptation Plans

Successful climate adaptation needs to sustain food, water, and energy security in the face of elevated carbon emissions. Hydroeconomic analysis (HEA) offers considerable potential to inform climate adaptation plans where water is an important element of economic activity. This paper's contribution is to identify how HEA can inform climate adaptation plans by minimizing economic costs of responding to climate induced changes in water supplies. It describes what HEA is, why it is important, how researchers implement it, who has made significant contributions, and places where it has informed policy debates. It also describes future directions for the use of HEA to guide climate adaptation.

What Is Hydroeconomic Analysis

Structure and Function

Hydroeconomic analysis (HEA) typically consists of a spatially and temporally distributed computer aided mathematical model. HEA informs plans to improve the economic performance of water systems. Managers, water users, and stakeholders at various geographical levels face these challenges. They need answers to guide debates over the performance of alternative plans for managing river systems. When supported by a computer model, HEA described regional, basin scale, or multi-national hydrologic, engineering, institutional, economic, and environmental dimensions of river systems within a systematic integrated framework. An important motivation for the conduct of HEA is to improve the economic performance of water systems that need to adapt to climate change.

In an HEA, both demands for water use and supplies of water available are characterized hydrologically and economically. The integration of the physical hydrology and economic elements to support policy design is what makes the HEA so valuable. It uses science to guide improved economic conditions where money, capital, ecosystem services, and water at the right quantity, quality, timing, location, price, and cost are scarce.

An important characteristic of HEA is that neither demand nor supply are constant elements, but are flexible and change depending on demographic, institutional, income, and technical conditions in a river system. The flexibility of an HEA will become more apparent and valued in future years as their delivery lives up to their promise. These demands are for the development and use of water systems for meeting the needs for food, water, and energy security in the face of anticipated population growth, urbanization, and climate stressed water supplies. In conditions where the incremental cost of new water developments, especially environmental costs, are high, there is growing interest in finding optimized elements of demand reduction and supply expansion to guard against looming shortages. HEAs enable an informed alternative to the classical engineering approach of seeking out least cost developments to meet a fixed set of requirements. Attaching monetary values to system outputs elevates the capacity of planners to develop and manage a system using a single economic objective, total economic welfare, sometimes constrained by required non-economic outcomes.

HEA properly conducted, will help discover more economically efficient water allocations over uses, locations, and periods. Economic efficiency occurs when the discounted net present value of marginal benefits is equal in all uses, periods, and locations. Since water supplies rarely occur in one place, HEA offers a reliable method to describe movement of water or water improvements around a river system for those uses, periods, and locations so that that this equi-marginal principle is satisfied under the base level of information, as well as maintaining equality in the face of a steady stream of new information.

Simulation vs. Optimization

Two kinds of approaches have supported the conduct of HEA, simulation and optimization. Simulation models typically simulate water resource and water user behavior following a well-defined set of rules influencing water allocation, and system operations. The alternative approach is to build a model that optimizes water development, water system upgrades, and water allocated within a given system for a set period using a mathematically specified objective function while respecting various cultural, hydrological, food security, or cultural constraints. These are optimization models.

Simulation models are a good approach for experimenting with system operations when there is interest in detailed alternative strategies that are too complex for an optimized plan to found with gradient-based mathematical optimization solvers. Various complex rules can be set up for moving water through a river/aquifer/reservoir system. These rules can be specified mathematically, even with simple spreadsheet models, so they can answer a wide variety of questions for even a complex river system. They are attractive in part because they are unconstrained by convexity assumptions typically required for globally optimized solutions produced by mathematical programming models. Particle swarm (Poli et al., 2007) and ant colony (Dorigo and Blum, 2005) approaches have seen growing attention for handling non-convex systems when an optimization model is desired.

The greatest limitation of a simulation models comes from its greatest asset: there is no known systematic search algorithm developed to date for converging to an optimized solution. For this reason, they typically require an “absurd” number of trial-and-error iterations, with little guarantee of finding or even converging to the economically best system operation, system development plan, or system upgrade for adapting to climate change.

Modern computer algorithms allow investigation of Pareto frontiers by running a large set of model iterations, such as the work by Fu et al. (2013). While this approach is computationally demanding, some improvements have occurred since 2010. This author eagerly anticipates the day when the continuum between simulation and optimization becomes smaller and smoother. He anticipates the day when model solvers are readily available with simulation search algorithms, such as described by Salomon (1998), that effectively optimize water system choices where gradient search methods are not possible. One detailed comparison of simulation vs. optimization for water systems is found at (Draper et al., 2003).

Integration of Non-economic Goals

Numerous non-economic goals such as serving a minimum acceptable percentage of the population with safe drinking water, protecting habitat of a threatened or endangered species, or irrigating a certain amount of land with food staples where food security is weak, are common requirements for managers who develop and operate water systems. While a large number of non-market valuation techniques have been developed since the 1980s (Carson et al., 2001), attaching an economic value to a non-economic requirement may amount to barking up the wrong tree (Andersen, 2015), i.e., performing the wrong task well.

One of the more widely used methods for addressing goals that are difficult or unacceptable to value economically in an HEA is to use mathematical constraints requiring a set outcome at a set point in time. Alternatively, a benefit transfer exercise (Johnston and Rosenberger, 2010) can be taken from a historically studied site and transferred to the study site. Where a benefit transfer is undesirable or unworkable, the simple addition of a constraint to accompany measured economic values can be a more reliable method to squeeze the greatest amount of beneficial use from the water system for informing climate adaptation while protecting required uses. With addition of that constraint, a shadow price (marginal cost of respecting the constraint) typically results with most commercially available mathematical programing packages such as GAMS^®. By comparing alternative methods to supply the unpriced service, a simple comparison of the shadow price can give important insights into which method, for which sector, or at which location or time period the service should take place. For example if there is a large range of choices on timings and locations of pulse flows required to protect an important species, the plan with the lowest shadow price of protection is the most economically efficient protection measure.

Despite the attractiveness of assigning sufficient water to meet specified ecosystem services, this approach risks missing important ecosystem elements. Assigning various real ecosystem functions in the objective function complemented by their economic values (prices) to allow expressing ecological services on common denominator terms with economic values. The problem with this method is the lack of ecosystem function or economic price information that nearly always faces the model builder. Still, to the extent this information can be developed or transferred from another context, it is a fruitful approach to secure a biologically and economically consistent system of accounts.

Model Solvers

HEA is typically complex and needs to account for many moving parts happening at the same time to be useful for policy insights. The status of each moving part determines outcomes of other moving parts. Therefore, whatever solver is used will likely need to solve large systems of non-linear equations simultaneously. A good example is the need to move water over time and space to optimize a system of interrelated demands and supplies capacity to contribute to producer and consumer welfare. Even with no water elements at all, simply optimizing producer and consumer welfare from a series of goods for an interval of several periods presents a daunting task. Any single policy instrument has the potential to affect several demand and supply functions even at a single point in the system. When those points connect to several hydrologic elements, complexity expands quickly. The solver need to solve a large non-linear simultaneous equation system, and needs to find the highest economic point in the feasible space, another daunting task.

This author has found that GAMS^® can be an efficient framework for implementing linear, non-linear, and integer optimization. That system is flexible, open, self-documenting, and provides easy to follow links between the formulation of a model and the solution. Python^®, MATLAB^®, and R^® have also seen use for HEA.

Why: Climate Water, and Hydroeconomic Analysis

Climate

The ongoing search for technologies, policies, treaties, and other measures to sustainably limit worldwide carbon emission flows, reduce atmospheric carbon stocks, and reduce temperature elevation remains an important issue of our time. Climate mitigation has proven an elusive goal to date and will likely remain so unless something like climate clubs with sanctions for non-members are implemented internationally (Nordhaus, 2015, 2017). Technical and policy scholars have developed an extensive understanding of the science, technologies, institutions, and policies to control flows of carbon emissions and stocks of atmospheric carbon. Several analyses of national and international policy proposals like carbon taxes, cap-and-trade, various regulatory measures, climate clubs (Nordhaus, 2015), and integrated roadmaps (Rockstrom et al., 2017) have been undertaken. Yet neither of the most important international climate treaties to date, the Kyoto Protocol of 2005 or the Paris Accords of 2016 has reduced carbon emissions significantly.

Climate mitigation still has a long way to go, so this paper's objective is to addresses the more modest aim of HEA to address climate adaptation. Water is a big part of the climate story, so this work turns to water systems analysis in the search for better methods to support integrated assessments. Water has many complexities. Growing demands for water combined with increased variability of climate-induced water supplies in many parts the world is leading to in increasing array of challenges faced to supply adequate levels of water's six important dimensions: quantity, quality, timing, location, price, and cost. These challenges need to address water's four important characteristics, namely that it leaks, seeps, evaporates, and transpires, all of which experience impacts from climate change and policies to deal with it (Ward et al., 2019).

Since the early Twentieth century, there has been growing interest in the development of integrated assessment approaches of the sort described recently (Nordhaus, 2017) bring together under one roof the complex connections between hydrologic and economic systems. This integrated approach presents an efficient analytical framework to analyze water and climate connections for providing lasting solutions across a range of temporal, spatial, climate, and policy elements. HEA offers the potential to develop sturdy and reliable tools for discovering future affordable adjustments in water resources systems, including challenges of limiting carbon emissions. To address these challenges this review paper describes motivations for HEA, the nature of HEA, how HEA is conducted, who has done this work, where their applications have seen use, a time line over which they were built, as well as future challenges and opportunities.

History of Water Development and Use

Human history has evolved side by side with methods to treat and manage freshwater for drinking, irrigation, flood control, and sewage transport. Sustaining the earliest settlements depended on the finding ways to put to beneficial use water that could be found from rainfall, wells snowmelt, wells, and runoff. A 9000 year old well in Central China was discovered in 2018 (Toureille, 2018). The earliest human-built dams were of the gravity type, made of stone, brick, or concrete. Around 2950–2750 B.C, the Egyptians built the first known dam to reduce floods. They built the dam over a period of about 10 years but they never completed it, as a flood destroyed it. Despite failures, it was recognized early on that even small scale dams permitted greater crop production, longer growing seasons, and in some cases, reduced flood damages. Aqueducts have been used since ancient times (Temin, 2006) to move water over long distances for drinking and bathing.

Even in ancient times, planners who committed resources to this infrastructure and were responsible for overseeing their use believed that the economic benefits exceeded their large costs. Communities built these magnificent feats of engineering with little to no rigorous economic framework (Persky, 2001) for guidance. For quite some time, builders have received more rewards than counters. No civilization had developed or seen a consistent framework for measuring either benefits or the costs of expensive water development or delivery plans. Still, the need was there: a consistent and systematic method of assessing benefits and costs, supported by something like a modern HEA, would have contributed greatly to guiding scientifically and economically grounded choices of reducing the costs or dangers of a water problem.

Early human settlements needed to be economically or hydrologically near water, as water has always had a high ratio of weight to value, coming from a high transportation cost as a percentage of total value. Of course, for drinking, water has a high economic value, so its weight to value ratio was lower, giving rise to greater distances for which it was economically attractive to move water. Still, with few exceptions, engineers could not move water vast distances without better engineering methods than existed in ancient times (Harou et al., 2009). The growth of cities ultimately demanded development of sophisticated water transport systems, such as pipes, canals, and aqueducts, to bring water to people, with many unsuccessful attempts at devising workable methods to remove sewage at a large scale until late in the Nineteenth century.

By the early Twentieth century, engineering and technical advances enabled building large numbers of engineering projects such as water treatment facilities, reliable dams, extensive canal networks, and economical desalination facilities. Water infrastructure has successfully reduced flood damages, secured safe drinking water, developed pumping systems, provided electric power, and supplied water for crop irrigation, providing great economic benefits to billions. With improved scientific advances and sewer systems, water-related diseases such as typhoid and cholera, once pervasive, have been mostly eradicated in most industrialized regions. Today (2021), some large cities use water imported from hundreds of miles away (Hasnain and Alajlan, 1998).

Food production for more than half the world still depends to a large part on crop irrigation, for which water is sometimes moved great distances. For example, crop irrigation in southern New Mexico today comes from snowmelt from spring runoff 500 river miles away in the southern Colorado Rockies transported through the geographically and institutionally complex Rio Grande corridor (Ward and Pulido-Velazquez, 2008a; Ward et al., 2019). Nearly twenty percent of the world's electric power comes from hydroelectric sources.

Advances in economic principles and improvement in engineering methods continue to raise interest in and capacity to answer big questions about the economic performance of many emerging water choices, including construction of new water infrastructure, rehabilitation of old, drafting of legislation, water rights design, and much more. There is growing importance for a better understanding of the real economic costs of the full range of choices facing water planners today (2021). For centuries, there has been a need for a consistent framework for assessing the performance of water investments and plans. In Europe, the Water Framework Directive (Hering et al., 2010; Riegels et al., 2013) and its various daughter directive has been the guiding force. In the US, the need for this framework was established by the Flood Control Act of 1936 (Black, 2012), stating that federal support for flood control projects could not occur unless “the benefits to whomsoever they accrue, exceed the costs.”

The need for integrated assessments based on solid economic and hydrologic principles with widespread applicability is there. This assessment requirement is more important because many places still need new water delivery and treatment facilities. Moreover, existing facilities need maintenance and restoration to secure the continued flow of economic benefits. HEA offers a framework for guiding these hard choices.

Nature of Water Problems

River systems experiencing climate stress face threats to energy, food, water, and environmental security in much of the world, especially in more arid regions such as the Middle East, North Africa, Central Asia, Southern Europe, the Indian Subcontinent, dry parts of China, and much of western North America. Climate stress has elevated water scarcity internationally, with shortages or more poorly-timed water supplies expected to occur more often and with greater impact. More severe and costly droughts and floods in recent years elevate challenges of developing science-based approaches to guide planning for economically informed adaptation to climate water stress. So physical and economic characteristics unique to water make it more difficult to formulate affordable climate adaptation plans for water infrastructure and policy. Water has four special characteristics that cause special problems. Water transpires, evaporates, leaks, and seeps (Ward et al., 2019) all four of which make it difficult to establish private property rights, build infrastructure, enact comprehensive legislation governing its development and use, or get to people at the time, place, and form in which they need it. Even today, water has a low ratio of value to weight as it moves through the hydrologic cycle (Tui et al., 2013; Kovacs and Durand-Morat, 2020; Slater et al., 2020).

An extensive literature search on water policy concludes that despite thousands of contributions by hundreds of writers, six kinds of water problems stand out as needing attention. The six occur whenever water available for use is of the wrong quantity (Breshears et al., 2005), quality (Sweeney et al., 2004), location (Bird et al., 2016), timing (Ostrom, 2007), cost (Jacobson et al., 2015), or price (Coppola et al., 2003). Water also suffers from the classical market failures pathology, for which three of the best known are externalities (Huffaker and Whittlesey, 2000; Goor et al., 2010; Nagase and Uehara, 2011; Kuhn and Britz, 2012; Elbakidze et al., 2018; Gunawardena et al., 2018), common property (Black, 2012; Descheemaeker et al., 2016; Muneepeerakul and Anderies, 2017; Jeuland, 2020), and public goods (Simonovic, 2000; Booker et al., 2012; Boucher et al., 2012; Hudson and Botzen, 2019). Public goods present a special problem because they lead to the important free rider phenomenon, an important culprit in the international failure to reduce carbon emissions (Nordhaus, 2015, 2017).

Current Challenges

Many challenges face scientists, policy analysis, water system managers, and the public regarding sustaining water supply systems. The list below presents a sample of these challenges, and describes why HEA can contribute to their resolution.

Optimization Over Space, Time, Quality, Climate, and Policy

Optimization of water resources system design, management, and restoration has long been a desired goal by managers, researchers, and even some stakeholders. This author has traveled internationally to the developing world and seen the potential of optimizing water systems to support future water, food, and energy security. Especially in places where those securities are weak, the typically enthusiastic response is both surprising and satisfying.

Planners have understood the significance of optimization for many decades as an approach for water resource system design planning and management. One of the earliest written reports describing the need for system optimization coming from the experience of Miami Ohio Conservancy District Catastrophic Flood of 1918 (Bock, 1918). One of the early works taking a more systematic mathematical approach toward system optimization came from a 1996 work (Tufegdzic et al., 1996). Many works have shown awareness of the need for the application optimization techniques to support water system analysis (Brown et al., 2015), despite the fact that the earliest principles for rigorously applying linear programming with empirical data were not published in the west until 1948 (Dantzig, 1948).

Still, the interest in optimization for water systems has been around for a long time, at least as far back as the early days of the US Tennessee Value Authority (TVA) river basin planning efforts. For that organization, some of the principles guiding optimization thinking may have come from the Miami Ohio experience described above. A few of the better known applications in water system optimization have been applied to ground water management, control of sea water intrusion, irrigation reservoir management, improved cropping pattern, water quality improvements, reservoir system optimization, and many others.

Optimal Economic Growth

Several regions suffer water shortages or other water problems due to climate stress, previous poor water management, or population and economic expansion. Especially where several water problems face a region, economic optimization thinking can inform important choices for the future. Quantitative modeling through formal mathematical models to investigate effects of infrastructure or other water policy choices are needed to find a more optimized sustainable growth path. This optimized growth occurs on a path that maximizes discounted net present value of economic benefits. However, the path always changes in the face of new information, and needs optimized adjustments and updates.

While rigorous investigations of optimal economic growth have been around since early in the Twentieth century (Ramsey, 1928), few if any of those have been applied to address the complex and interdependent water problems today for which an economic optimization approach could produce important insights to guide policy. Still, summary works on HEA (Harou et al., 2009) offer hope for the future, which could see improved optimization software, more and better data, growing interest, and more widespread applications. The next sections describe a few of the many challenges facing water science, water policy, and water stakeholders that motivates improvement in HEA.

Reservoir Expansion and Operation

Water storage reservoirs, especially large ones that receive high inflow levels with high variability in those flows, are expensive to build and hard to operate efficiently (Goor et al., 2010; Gonzalez et al., 2020). While it is well-known that water project building programs need to optimize over the complex and interdependent elements of project timing, sizing, and sequencing (Becker and Yeh, 1974), there is no known systematic and agreed method to achieve this outcome to date (2021).

Even after reservoirs are built, their economically optimized operation poses additional complexities. Many come from the challenge of optimizing releases for various downstream users in various periods, when future inflows and their capacity to add to current storage volumes are uncertain. This point has been affirmed by the World Commission on Dams that concluded many large reservoir projects internationally are not living up to the level of economic benefits that could be supported by their storage capacity (Labadie, 2004).

The difficulty of economically optimizing a reservoir's performance is complicated when new uses emerge that were not originally part of the reservoir's authorization or building. That is, even when an economically optimized operation occurs, it is not always feasible to continually re-optimize in the face of changing demands, technology, and population. New uses or values can include urban uses from growing cities, minimum flow releases for ecosystem restoration, and the need to address shoreline development. One widely cited 2004 review article concluded that many reservoir operation plans and policies are not able to manage the system in a fully integrated way, falling back instead to piecemeal policy for addressing individual water use elements. Part of the difficulty of achieving this ambitious goal comes from the lack of fully integrated modeling approaches of the sort that can be made more rigorous by the development and use of HEA (Labadie, 2004).

Urban Water Supply

In many urban areas, especially in arid regions, large existing infrastructure systems transport water across hundreds of miles to support cities with economic solutions where water supplies are strained. Growing cities continue to seek out the least cost combination of demand reduction (conservation) and supply expansion from various new sources or measures, sometimes labeled integrated management. Despite the ease of describing the problem, integrated planning remains a considerable challenge in implementation. One series of works initiated in the 1980s with the Metropolitan Water District of southern California implemented this integrated management.

More recent works (Porse and Lund, 2016; Porse et al., 2017, 2018) have improved an integrated model of urban water management in southern California. They examined annualized costs with annualized benefits from a range of local and imported sources for additional supply compared to measures to promote demand reduction (conservation). Those works developed innovative approaches to urban water supply chains, including a series of sequential steps like finding, treating, distributing a networked water supply system, as well as recycling or reusing it. Their work relied heavily on integrated HEA, and serves as a model for water planners in growing cities worldwide facing actual or potential water stress and compounded with complex interacting measures to assure adequate and affordable supplies to end users.

Aquifer Management

Protecting aquifer sustainability can occur where discharge over the long term is no larger than recharge. While this is a desirable hydrologic outcome, aquifer protection can come at a high economic cost since water uses that currently put pumping to beneficial use may give rise to high economic values that would be lost if protection measures are implemented. That is, use patterns for which pumping exceeds recharge may be economically desirable under some conditions, especially where future benefits see heavy discounting compared the present. Ongoing evidence from climate stressed water supplies has brought about investigations using HEA (MacEwan et al., 2017) on the economic benefits and costs of various plans to protect aquifers.

Several works have been published since 2000 using HEA to assess management options for sustaining aquifers (Harou and Lund, 2008; Pulido-Velazquez et al., 2008; Pena-Haro et al., 2009, 2010, 2011; Varela-Ortega et al., 2011; Ward and Pulido-Velazquez, 2012; Molina et al., 2013; Foster et al., 2014, 2015; Kahil et al., 2016; Gohar et al., 2019; Ward et al., 2019). Despite these achievements, comparatively few academic works have investigated water use patterns that minimize or even simply control economic costs of protecting aquifers. One recent work (Ward et al., 2019) formulated an original approach to fill that need by building and demonstrating a basin scale optimization of North America's Middle Rio Grande Basin. That work permitted economic investigation of policies under debate to support aquifer protection, as well as posting results on a website available for regional stakeholders (SWIM, 2021). The posted model accounts for storage of groundwater and surface water at regional reservoirs, water use by irrigation, as well as environmental, domestic, recreational, and environmental uses. It also accounts for system inflows into two large reservoirs from surface supplies under several climate scenarios, for which the optimization model responds with groundwater pumping and recharge as well a surface water use. It also tracks evaporation and seepage, while responding to existing or potential institutional constraints influencing water use. The model works through use of an HEA that seeks and finds the maximum discounted net present value of economic benefits. These benefits are calculated by summing water use over uses, regions, and sectors from both surface water use and connected aquifers (Ward et al., 2019). Table 1 summarizes a few of these works.

TABLE 1

Table 1. Selected hydroeconomic analyses of groundwater pumping adaptations to climate change.

A difficult analytical challenge to addressing groundwater overdraft is the need to track hydrologic and economic processes over the complete water system since adjustments to pumping limits must somehow adapt to pumping use reductions. This makes for a considerable challenge with few simple and well-recognized approaches for handling this task. Still, if successful, integrated HEA has a potential to inform policy debates, since their goal is track hydrological, economic, and institutional elements of the system.

Drought Adaptation and Mitigation

Severe and sustained drought has been a problem for millennia. Drought has many dimensions (Wilhite et al., 2007): prolonged shortages in water supply, atmospheric drought consisting of below average precipitation, reduced surface supply runoff, increased pumping depth in aquifers. A drought onset can last for several months or even years. Yet it can be officially declared in a period as short as 2 weeks. Drought can produce damages to irrigated agriculture as well as drinking water supplies, a special problem with smaller utilities with weak backup water supply capacity. Even in tropical regions, extended dry seasons can elevate the likelihood of drought leading to fires (Wilson and Bowman, 1987; Enright and Goldblum, 1999; Finkele et al., 2006). Extended periods of heat or weak economic conditions can worsen drought conditions by increasing water evaporation or reducing the economic value of water (Harou et al., 2010). Investigations based on tree ring analysis (Cook and Jacoby, 1977; Ogle et al., 2000; Bragg, 2001) have uncovered remarkable insights into the history of drought. Because of the complexity of interacting elements, integrated HEA presents a prospective approach for informing comprehensive river basin management plans to inform sustainable water management policies (Kahil et al., 2015) including the special supporting role for water markets (Hanak et al., 2019).

Flood Damage Control

Gilbert White stated in his 1942 Ph.D. dissertation from the University of Chicago that “floods are an act of God but flood damage is an act of Man” (Macdonald et al., 2012). Floods occur when water overflows submerge land that is normally dry. Flood management falls under the discipline of hydrology. Floods continue to be a challenge for public health, urban planning, agriculture, civil engineering. Human alternations of the natural environment, such as forestry and road building, can increase the frequency, duration, intensity, and cost of flooding.

Historically, design standards and structural measures were the major approaches to flood management. Structural measures likes retention basins, dikes, and reservoirs, and levees, were planned and built to control up to a specified flood, such as a 100-year flood. Recently, this “flood control approach” has increasingly come under question. Recent works have seen alternative approaches to flood management, especially “flood risk management” (Merz et al., 2010). Economically efficient choices to address flood mitigation choices, especially human safety for protection against floods, requires good planning, and well-resourced plans. In light of these large resource requirements, it is important that analytical methods be developed to guide choices on the wise use of these resources.

Changes in thinking in recent years shifting away from flood hazard management to flood risk management has elevated emphasis on non-structural measures for controlling flood damages. Examples of such measures include spatial planning, elevating flood awareness, flood proofing, and increased and improved use of flood response systems, warning, and forecasting (Verkade and Werner, 2011). Flood risk is an important concept. It is defined as the expected monetary value of flood related damage and costs. Floods are stochastic events and therefore flood damage is a random event, so stochastic hydrology plays an important element in the search for economically efficient flood control measures. While the correct amount of damage at any place and time cannot be predicted with current statistical methods, the statistically expected annual value of flood damage can be determined if the probability distribution of flood damage, or damage frequency curve is known or can be found. This expected annual damage is a measure of flood risk. HEA has an important role to play. Important analytical elements of expected annual damages (EAD) include the flood frequency curve, the rating curve and the stage-damage curve, with and without a flood control structure or plan (Young and Loomis, 2005; Verkade and Werner, 2011).

An anonymous reviewer reminds that the Dutch are kings of HEA for systematically improving flood adaptation capacity. In the Netherlands, the whole country's flood plans since 1957 have been based on rigorous economic and statistical analysis of the sort done with principles guiding the development of HEA (Van Dantzig, 1956), recently updated in 2014 (Eijgenraam et al., 2014). Dutch scholars have produced a huge literature on risk-based flood management. They remain some of the world's leaders in this arena. In that country one-third of the land area lies below mean sea level. Without heavy flood control infrastructure invested over many years, 65% would be under water at high tide (Hoeksema, 2007).

Promoting Water Conservation

Facing climate water stress, increased fluctuations in water supply, growing populations, and increased water demands, and greater awareness of the need for future food, water, energy, and environmental security, many are searching for methods to promote water conservation, especially in irrigated agriculture, which is the world's largest user of water. Investments made in irrigation modernization, such converting from classical field flooding to modern drip irrigation, are believe to conserve water. However a number of studies using HEA have found that these kinds of conversions have led to increased water use, partly because of greater crop water use drip irrigation encourages associated with higher crop yields. While heavy public subsidies of drip irrigation can be good for raising farm incomes and increasing crop yields, the use of integrated HEA is consistently showing that they do not conserve water at a basin scale, as downstream and future users have often discovered reduced water availability.

One work from 2008 using a HEA for the Rio Grande Basin of North America showed that subsidies of water conservation technologies will not likely conserve water use under hydrologic and economic conditions that are seen in many of the world's river basins. Converting to more efficient irrigation technologies often limits flows and reduces aquifer recharge, so these policies enacted with high ambition to reduce water applications can increase net consumption of water. Finding programs that secure real and measurable water savings requires technologies and accounting procedures that carefully track and economically return water depletion reductions (Ward and Pulido-Velazquez, 2008b). Other works in recent years have come to the same conclusion (Rosenberg et al., 2007, 2008; Escriva-Bou et al., 2015, 2017, 2018; Grafton et al., 2018). One 2017 work done for the Food and Agricultural Organization reviewed the evidence from more than 200 studies on the water conserving effect of increasing irrigation efficiency and found that few to none saved water when carefully measured (Perry et al., 2017). Still, because of income gains and increased crop yields, we will likely continue to see incentives for modernization, but it needs to complemented by economic instruments to guard against the rebound effect of irrigation modernization (Berbel et al., 2015) for which that principle was first described by Jevons in 1865 (Dumont et al., 2013).

Enhancing Irrigation and Food Security

Recent forecasts of food supplies suggest that food prices for the near future will likely be stable over the longer term, but finding a way to allocate the food will be sometimes difficult, suggesting that making a serious dent in the malnutrition of many poor countries will present challenges. Because of low price elasticities of demand for food staples, modest reductions in crop production and yields can elevate food prices and increase malnutrition.

Irrigation will play a dominant role in protecting future food insecurity, since irrigated crop yields can be considerably higher than those from rainfed agriculture. For this potential to be realized, increased food production will need growing intensification of irrigated agriculture, as well as growing productivity of existing water supplies, made more difficult in light of ongoing climate water stress. Achieving these growth ambitions will need carefully planned and executed institutional analysis as well as better targeted policy design. Feeding 9 billion by 2050 (Godfray et al., 2010) through an expanded scale of irrigated agriculture raises pressures to bring marginal land into food production, with negative implications for environmental protection. Efficient irrigation and water development strategies need a better understanding of connections among water scarcity, effective water supply, food production, food distribution, and environmental protection.

Recent changes in water management models have elevated interest in the development of integrated multi-disciplinary methods for supporting water decision-making, for which one of the big ones could be improved HEA to support better tested water management strategies. HEA offers a blending of economic insights with hydrology and engineering processes. This combination brings about a more consistent and integrated framework to assess potential implications of a range of water management plans (Blanco-Gutierrez et al., 2013). Research on the role of HEA development and use enhance this understanding would produce high returns (Carruthers et al., 1997).

Poverty Reduction

Many of the world's poorest face considerable water insecurity and confront significant water-related risks partly as a consequence of living in places with unusually complex hydrology (Ray et al., 2015). These risks are made worse by typically weak and inaccessible water resources data in large parts of the world combined with ongoing increasing demands for scarce water heightened by economic development, climate change, and population growth. Much effort has been underway in recent years to develop a consistently measurable water poverty index (WPI) (Sullivan, 2002). This index is a composite connecting indicators of access to water and effective human welfare to assess the extent to which water scarcity affects numbers of people at scale.

Despite some limitations of the WPI (Garriga and Foguet, 2010) it does focus appropriately on the poor, who often face the highest burdens from weak access to water. Its strengths are that the WPI brings together economic, social, physical, and environmental faces connected to water scarcity as well as effective and affordable water access as well as capacity to use that water for economically productive ends. Five components of physical resources, access, capacity, use, and environmental evaluation have used to assemble this index. With access to this index, there appears to be considerable potential contributions by HEAs to inform least cost measures to elevate that index. For example a minimum acceptable level of each of a region's WPI elements or possibly a sufficiently high level of the overall WPI index could be established as a mathematical constraint in an HEA.

Rainwater Harvesting

Rainwater harvesting (RWH) pre-dates written records as a system for handling water supply needs where there is adequate reliable rainwater and large enough storage for its capture (Campisano et al., 2017). For urban use, RWH is typically consists of resources to collect, store, concentrate, treat rainwater from places of capture. These places include rooftops or other non-leaking surfaces to collect rainwater.

There are many urban uses of rainwater for domestic uses, but all such RWH activities seek to limit the demand placed on aquifers or other centrally supplied utility sources. Some scholars have suggested rainwater harvesting can make up a large percentage of use in some places, and have emphasized the considerable water conservation benefits associated with RWH implementation, most notably including reduced pressure on aquifers, and reduced pressures on river diversions as well as reduced costs of central utility delivery. Where economically attractive, RWH systems increase the self-sufficiency of certain water users who make the investment. Usually these investments, even when practiced require some kind of backup supply to handle demands when the rains fail to materialize.

Despite the well-recognized benefits of RWH, in certain dry regions where water rights to divert surface waters or pump aquifers are well-established, such as Colorado or New Mexico USA, RWH at scale could potentially impair existing water rights and thus present a legal and/or economic problem (Bretsen, 2017). Because of the important connection between rainwater harvesting and aquifer recharge and streamflows, HEAs offer considerable potential for cost benefit evaluations of RWH program designs.

Water Pricing

Water pricing can play a big role in signaling water's opportunity cost. Its opportunity water is an important piece of information used to guide a number of choices in water development, conservation, planning, and use. That opportunity cost of water is always in the foreground or background whenever there is scarcity in quality or quantity, because that cost involves a sacrifice to alternative uses. In an efficiently run water system, water users will always receive a signal of water's opportunity costs, enabling them to behave to use the water if their marginal value is higher than the opportunity cost, but not otherwise.

When water prices are established that ignore water's opportunity cost, the incremental cost from using an incremental unit of water are ignored as described well in Young and Loomis (2005). This lack of information can lead to important economic errors in water developments, purification decisions, and water allocations among competing demands, places, and periods. An HEA, carefully developed to jointly account for hydrology, economics, institutions, and finance, can provide an important tool to help guide better water planning and use decisions (Pulido-Velazquez et al., 2013). One of the more creative water pricing HEAs was done by Burn and McBean who build a dynamic programming model for capacity expansion with economies of scale, and used prices to dampen demand growth to develop plant expansion plans (Dandy et al., 1984; Burn and McBean, 1985).

Water Markets

Establishing water markets to facilitate water trading is one method of moving water from lower- to higher valued uses. The market system implements water trading by buying, selling, renting, leasing, or lending water rights or other entitlements to use water. The trade can either involve a permanent transfer of a water right can involve a contract for a change in water use for a short period. Trades that are successful at moving water to higher valued uses depend on differences in the marginal values across users to create incentives to move the water (Schwabe et al., 2020).

Water trading can encourage more economically efficient water use patterns because the market-determined price provides a motivation for users to trade water for cash, reallocating water from lower valued uses, such as fodder to higher valued uses such as urban water. This author has experienced some skepticism with stakeholders and policymakers in non-western cultures about the extent to which water markets can produce overall economic gains in practice as well as doubts about the ethical outcomes of water trading. These doubts are elevated when the higher valued urban uses has a large percentage of customers who cannot afford to pay the market-determined price of traded water. However, trading offers economic advantages over alternative water shortage sharing methods in terms of moving water to higher valued uses in drought periods compared to alternative methods for handling shortage. One of the more common alternatives is the legal Doctrine of Prior Appropriation (Tarlock, 2001) practiced in many parts of the American west.

Water Recycling and Reuse

Water recycling and reuse are growing in many places, even in wet locations that are not typically seen as facing water scarcity issues. Regions seeing growing applications of both include Israel, Australia, Western Europe, and the USA (Miller, 2006), though in most cases the percentage of re-used water is very small compared to total use. Of course, given our current understanding of the hydrologic cycle, an argument can be made that most water has always been recycled or reused at some level. While few doubt the desirability of reuse when it reduces the need for new supply development, and the technology has been shown to work, the big question centers around discovering those conditions in which it pays in the sense of producing benefits or revenues greater costs incurred (Rogers et al., 2002).

Moreover, certain kinds of reuse, such as direct or indirect potable use (toilet to tap), carry a considerable psychological stigma (Rozin et al., 2015) despite the confidence that some water engineers express in making public statements that it can be safe to drink. Several challenges face planners who are debating bringing in recycled or reused water as part of the delivery system (Miller, 2006). Two of the big ones include:

Incentivized pricing: Recycled water can be cheaper than the alternative where the latter is scarce. But where recycled water is priced higher than the alternative, few will use it (Rogers et al., 2002), a special problem that occurs when there is a weak customer base.

Safety: A big challenge is to find treatment technologies that safely and affordably remove dangerous chemicals like endocrine disruptors or other pathogens. Not only does it need to be safe, but the supplier needs to convince the water buying public it is so.

In any case, HEA can help discover where recycling and reuse is hydrologically and economically desirable. When water planners and engineers formulate a water reuse plan, they will need to account for the factors described above, and fold them together into an integrated package, for which HEA can be a contributing factor.

Benefit Sharing

Questions of economic efficiency, equity, and sustainability surrounding allocation of a water have been around for years. One idea with legs is the concept of benefit sharing. While there many versions of benefit sharing, one stands out, namely a policy or reallocation for which at least one party gains economically and none loses, also described as Pareto Improvement (Pareto, 1971; Baah-Kumi and Ward, 2020). Relative to an existing allocation of water system resources, an alternative allocation would be Pareto Efficient if at least one country gained and none lost. The search for Pareto Improving water policies, especially as they support investigations of climate planning is a classic use of an HEA. While there are many examples from the literature that can be discussed in detail, one with which this author is familiar was an investigation of opportunities for Pareto Improvement under the construction of the Grand Ethiopian Renaissance Dam (GERD) (Habteyes et al., 2015), that began filling in July 2020. This investigation has some generalizability, as new reservoir storage is seeing widespread attention as a climate adaptation plan (Rodell et al., 2009).

Tables 2–5 show an updated example of the results of that work, originally published in 2015, with a five percent increase in crops prices compared to the earlier work. In that earlier work, an HEA was conducted, for which the model is currently accessible at https://water-research.nmsu.edu/. The model seeks out and finds if any water sharing arrangement could maximize the discounted net present value of benefits after construction of the GERD, while constraining the model to supply as much water to the three downstream countries (Sudan, South Sudan, and Egypt) as would have occurred absent the dam. This may seem like a perpetual motion machine (impossible). In fact, the authors found that a very slow filling of GERD sourced by reduced irrigation diversions within Ethiopia upstream of the GERD could meet all historical downstream delivery requirements for which the filling would produce large hydroelectric economic values. These power values gained would be larger than the farm income losses from reduced Ethiopian water use in domestic irrigated agriculture. Results are presented for four conditions, with and without building and operation of the GERD (two policies) as well as historical vs. climate stressed water supplies from the Nile Basin's headwater supplies (multiplied by two states of nature) for a factorial design of four. These tables are, of course, unique to the hydrology and economics of the Nile Basin, but are generalizable to any basin where this kind of competition will become elevated in the face of future climate change.

TABLE 2

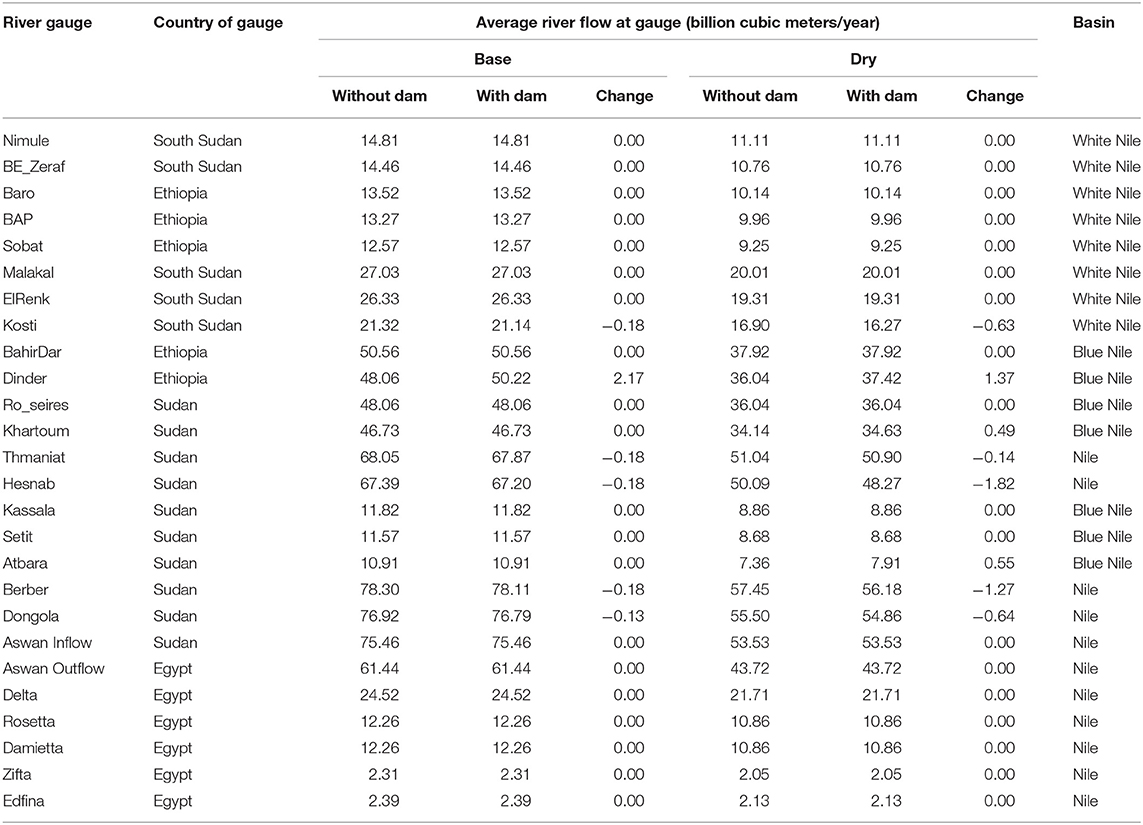
Table 2. Hydroeconomic model results illustration—predicted streamflow by gauge, policy, and scenario, averaged over 20 years, Nile Basin.

TABLE 3

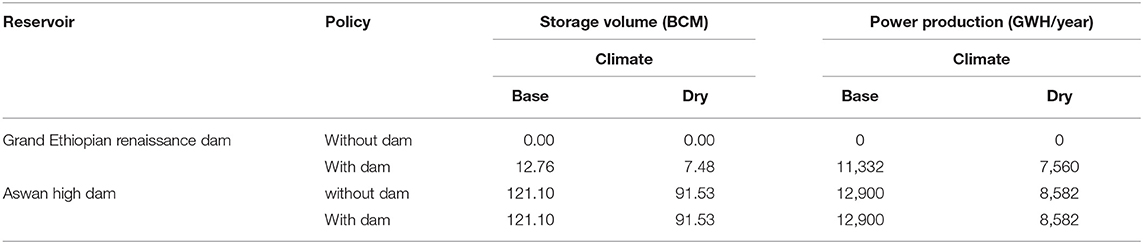
Table 3. Hydroeconomic model results illustration—storage volume and power produced by reservoir, policy and supply scenario, averaged over 20 years, Nile Basin.

TABLE 4

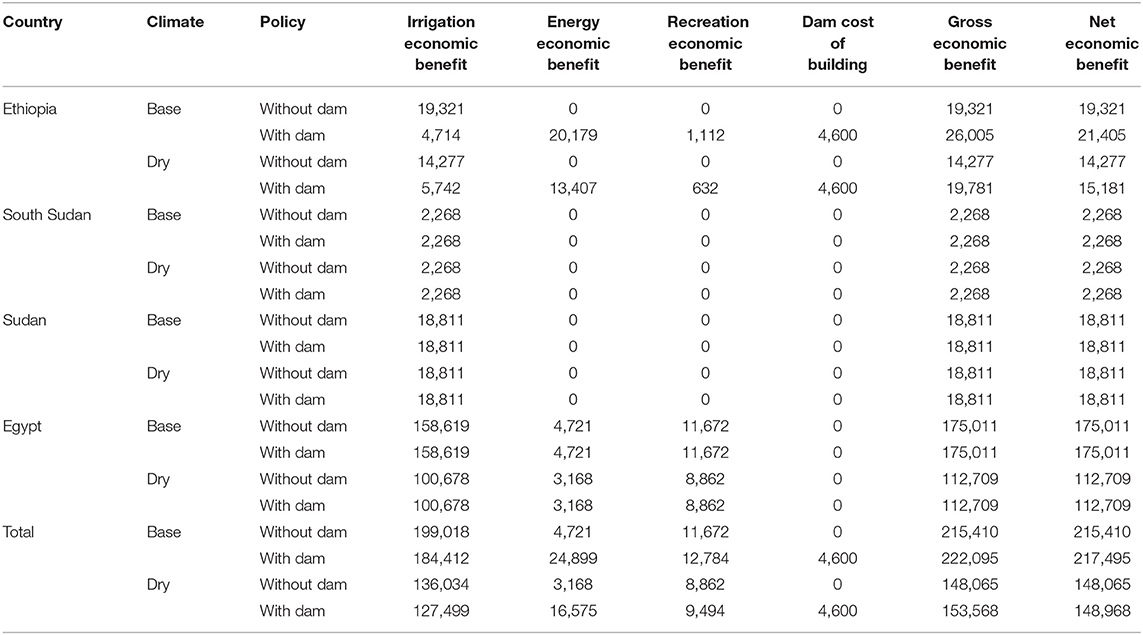
Table 4. Hydroeconomic model results illustration—total economic benefits by country, policy, water supply scenario, and water use, Nile Basin (discounted net present value, $US Million, summed over 20 years).

TABLE 5

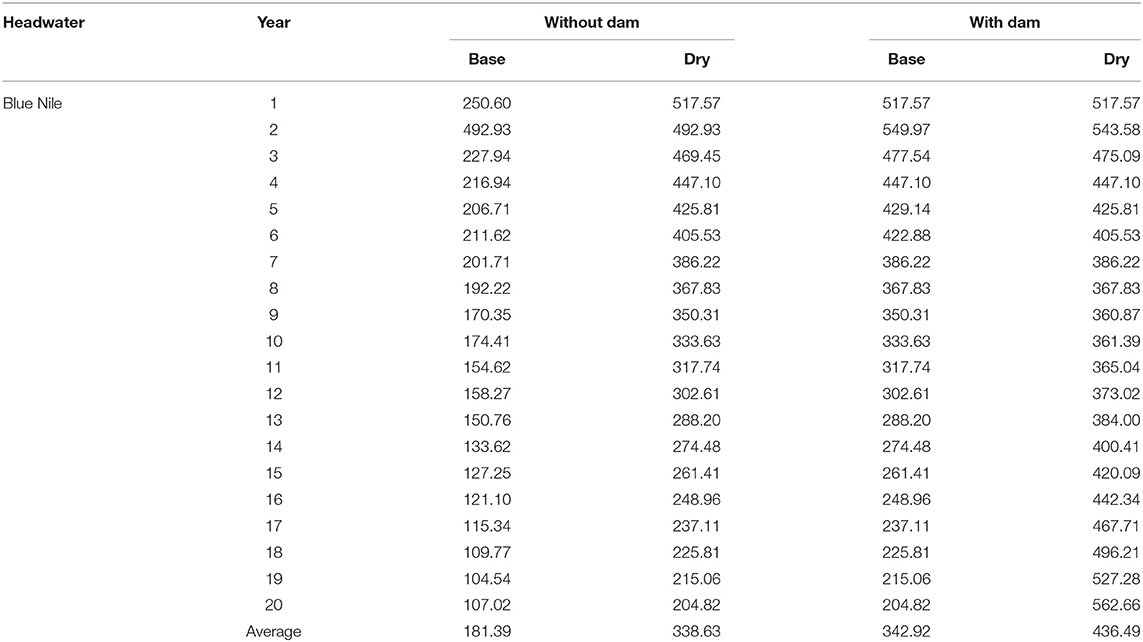
Table 5. Hydroeconomic model results illustration—economic value of one additional unit of water (shadow price) at Blue Nile headwater region above grand renaissance ethiopian dam, by year, policy, and climate scenario ($US Per 1,000 cubic meters).

Table 2 shows streamflows at the system important stream gauges in the four affected countries, while Table 3 shows storage volume and power production for each of the four conditions. This table shows unchanged conditions from power supplied by the Aswan Dam, with increases from the GERD, based on reductions in water use from irrigated agriculture. Table 4 shows that Ethiopia gains a small amount of economic welfare under these conditions even if they pay the full approximated cost of the dam, set for this model at $4.6 billion, while the other three countries show no welfare change. Table 5 shows the shadow price of water (Kuhn and Britz, 2012; Molinos-Senante et al., 2015; Gunawardena et al., 2018; Bierkens et al., 2019; Martinsen et al., 2019). The shadow price is the economic value of one additional unit of water if available at the headwaters or any other place that could be made available above the dam. The shadow price presents important information guiding the economic attractiveness of climate adaptation or mitigation plans. It measures the benefits of additional water, which can be compared side by side with incremental costs of making the water available. Notice that the shadow prices increase slightly with the dam compared to without, indicating a higher overall system economic performance made possible with the dam's construction and operation. It also shows a nearly twice is high level under climate stressed flows comparted to historical ones. These results are shown to illustrate the climate plan informing utility of a basin scale HEA where there are complex hydrological, economic, and political interactions that need to be sorted out.

How: Building an HEA

Economic and Physical Elements

As an optimization model, a reliable HEA rests on sound economics, solid hydrologic elements, reliable mathematical programming software, and data. An HEA is typically a special case of a general equilibrium (GE) model, of the sort taught in most university economics graduate programs. A general equilibrium model of an economy where water is a limiting resource attempts to understand that economy's structure building from the primary resources to factors affecting their supply and demand. Supply and demand for goods comes from market activity for those goods and from bounds set by availability of primary resources, such as land and water. GE modeling falls under the discipline of microeconomics, although some of GE models have attempted to explain macroeconomic fluctuations in things like aggregate employment, interest, and income (Keynes, 1936).

Beginning from an early work by Maass et al. (1962) water systems analysis, which later grew into formal HEA, started being modeled as system of sources, storage, use, and river point nodes joined by links reflecting river reaches, pipelines, canals, diversion points, and aquifer recharge locations. Water demands and use saw tracking and evaluation by their contribution to costs or benefits. The authors found in that early work that the network approach is understandable and can see use for economic optimization. In those networks, water needs to move throughout a system to produce the greatest possible net economic benefits while respecting important institutional, technical, and political constraints. A versatile method to express economic demands comes from representing demand with mathematical functions. These functions reflect total benefits and costs and their changes from changes in supply, reservoir release, pumping, or river diversion.

A typical microeconomic approach to GE models typically specifies two or more goods and two or more primary resource endowments. These models are often complex, attempt to simultaneously find equilibrium quantities and prices of all goods and all primary resources, and typically require mathematical programming software to produce numerical solutions. Most of the better mathematical programing solvers such as GAMS^® allow use of large sets of simultaneous equations that if specified as a convex model, such as quadratic programming (Nakashima, 2011; Zhang et al., 2019), can solve reliably. The objective function used for such models is typically producer plus consumer surplus summed over the goods, and for the case of dynamic models, summed over periods.

Production Functions

A classic way to explain the output of each (water-using) good is to build a mathematical production function, in which each sector's output is a mathematical function of water and other primary inputs, like land, labor, and infrastructure. Constant returns to scale can be imposed, for which a doubling of all primary inputs doubles output. This can be a straightforward exercise for water-using goods like domestic water supply, crop irrigation, livestock production (for which water is an indirect input by affecting forage supply), hydroelectric power, and key ecological assets.

It is theoretically best to permit substitution of other inputs for water, whether by specifying a finite number of fixed coefficients (limited substitution), or with a production function with the classical infinite number of input proportion choices. In either case, it is desirable to maintain output.

In the face of drought or other stresses to water supply that can be signaled to the water user through increased water prices, motivating substitution of other inputs for water.

Without substitution, economic theory has no systematic mechanism for handling things like water shortage or changes in water prices, as noted years ago by Solow (Solow, 1956) and by many others since. Input- output models with fixed input proportions makes it hard to discover the economic value of water supply or other primary resource increments (Young and Gray, 1985) that is consistent with the microeconomic theory of resource-user behavior.

Primary Resource Inputs

Total quantities of primary resource inputs like water and land, and their use by sector and time period are not too hard to find, and can be included in each commodity's production function. There are many kinds of production functions available, but the Cobb-Douglas and Constant Elasticity of Substitution (Uzawa, 1962) are two of the more commonly used. Both permit variable proportions in production, and use of standard econometric methods can estimate both.

Demand Functions/Demand Systems With Substitution

HEAs often see application to a small enough scale region for which commodity prices are not significantly affected by local water supplies or water policy choices like reservoir releases or new project developments. In those conditions, prices are constant. However, for larger regions like California where a large scale of produce is supplied, or New Mexico that contributes much of the US supply of pecans, each commodity's price will depend on its own supply as well as the price of substitutes since increased outputs traded nationally or internationally will affect prices. There are few HEAs published for which systems of demand function built into the model to be consistent with an utility theory (Vansoest et al., 1993). Consistency with consumer choice theory is desirable, because total spending on the goods produced by water and other resources is consistent with total incomes in the region in question.

One recent work (Esteve et al., 2015) from Spain analyzed a series of interrelated complex choices. It may have included partial demand systems. Price elasticities of demand are not that difficult to estimate or find from the literature, so even if the demand functions are not consistent with utility theory, having price depend on output, as affected by a water policy, is a plus. Two recent example of this came from a work that options investigated for alternative reservoir releases from various upstream storage locations in the Amu Darya Basin (Jalilov et al., 2015, 2016) of Central Asia.

With downward sloping demand functions, a mathematical programming package like GAMS^® should be able to find an optimized set of resource allocations that provide a tangency between aggregated welfare (consumer surplus) and a production possibilities frontier of the standard sort presented in international trade theory (Krugman et al., 2011). What is important to recognize in a HEA is that as water supplies continue to change, especially in basins with limited reservoir storage, the production possibilities shifts around from one period to the next, which means that the optimized tangency points linking production to consumption will also shift.

Institutional, Cultural, and Environmental Constraints

Water is one of the more important commodities whose production and use are governed by a wide array of institutional constraints (Jenkins and Lund, 2000). Many water uses carry considerable institutional importance that produce low or hard-to-measure economic values. There are many examples of this. A few include water uses to support food security (Habteyes and Ward, 2020), protection against demand hardening (Schwabe et al., 2020); ceremonial purposes (Cozzetto et al., 2013), access to affordable safe drinking water (Flanagan et al., 2012); recreation (Eiswerth et al., 2000); wetlands (Creel and Loomis, 1992); water quality protection (Randhir et al., 2001); pulse flows for endangered species (Loomis, 2000), restoration of ecosystem and watershed services, conservation, and a range of preservation uses (Stenger and Willinger, 1998). Many of these uses of water are difficult to measure economic values, for which their provision can sometimes by assured in a HEA by simple mathematical constraint equations or bounds.

Model Calibration

HEAs when built as optimization models without special calibration can make predictions of optimized behavior based on production and cost functions that do not reflect actual observed behavior of water users. One way to deal with this uncertainty originally proposed in 1995 by Howitt (1995), using the term “positive mathematical programming” (PMP) is to build an optimization model for which observed (privately-optimized) behavior is used to infer the underlying parameters of cost or production functions. If used in an optimization model, PMP can replicate the observed resource use behavior actually seen. This behavior comes from the “first order necessary conditions” (Intriligator, 2002) for optimal resource use.

Examples include the requirement that for any scarce resource like water, it will be used to the point where the value of its marginal product equals its input price. A follow up example of that original proposal came from a well-known 2012 paper that used a self-calibrating income-maximizing model of farm production using the California Statewide Agricultural Production Model. The coefficients of the model calibration were calculated to match observed cultivated areas and water application for selected crops in California's Central Valley (Medellin-Azuara et al., 2012). A similar approach was used for a HEA built for the Rio Grande Basin in New Mexico (Dagnino and Ward, 2012), described in more detail below.

Capacity Building

HEA, properly developed and understood, has considerable potential to inform important policy debates worldwide. Still, there seem to be few mechanisms to date for getting these models into the hands of the right people to permit systematic experimentation with policy proposals to inform current and emerging debates. This is a major limitation of HEA today (2021).

Universities offer degree programs, short courses, and overseas capacity building programs, all of which can pass along knowledge. For example, this author has worked with overseas partners in Israel, Spain, Australia, Saudi Arabia, Costa Rica, Afghanistan, Iraq, Uzbekistan, and Costa Rica, with future work possible in Kuwait, India, Mexico, and Panama, to name a few. Recent interactions since 2015 typically set up 1–2 week workshops on the development, application, interpretation, and adaptation of HEAs to actual local policy debates, such as how to most affordably and reliably protect food security under irrigation where water supplies or food import capacity is under stress or uncertain. Ministry or other staff assigned to enroll in these workshops are highly motivated, but have limited backgrounds in economics, engineering, institutional analysis, mathematical programming theory and practice, or all of these.

One reliable way to translate current knowledge of HEA into the toolkit of enthusiastic students is to enroll in a PhD program. Every university has its own way to make this happen, but one degree established at New Mexico State University in 2011 that is well-suited for this goal is its Water Science and Management. This interdisciplinary program, as currently organized, can give graduate students sufficient time, sometimes funding, and flexibility to gain confidence to develop these models. Successful PhD students take a range of classes in mathematical programming, microeconomic theory, and water engineering to get enough of the basics to build their own models. The author and his team normally use GAMS^®, but are told by many reliable sources of a number of competing optimization packages like Maple^®, MATLAB^®, and Python^® can do many of the same things.

A local team of water faculty and students invested a fair amount of time since 2016 posting and making accessible a medium scale HEA of the Middle Rio Grande Basin for New Mexico and West Texas (English), and Northern Mexico (Spanish) onto a regional web server. That model can currently (2021) be accessed at https://swim.cybershare.utep.edu/en/home. It allows the general public to run public scenarios, canned scenarios, or build their own scenarios. They can take away results sorted in a way targeted to their motivations, without absorbing large reams of undigested detail extraneous to their immediate interests.

Who and Where: Model Developers and Locations of Use

HEAs have seen contributions in parts of the world, with works from 45 previous years over 23 countries cited in the 2009 classic work (Harou et al., 2009). Among the 255 cited articles on hydroeconomic analysis found in a recent Web of Science search, more than half came from water issues addressed in a few parts of the world, mostly in arid regions, for which a few are summarized in Table 6.

TABLE 6

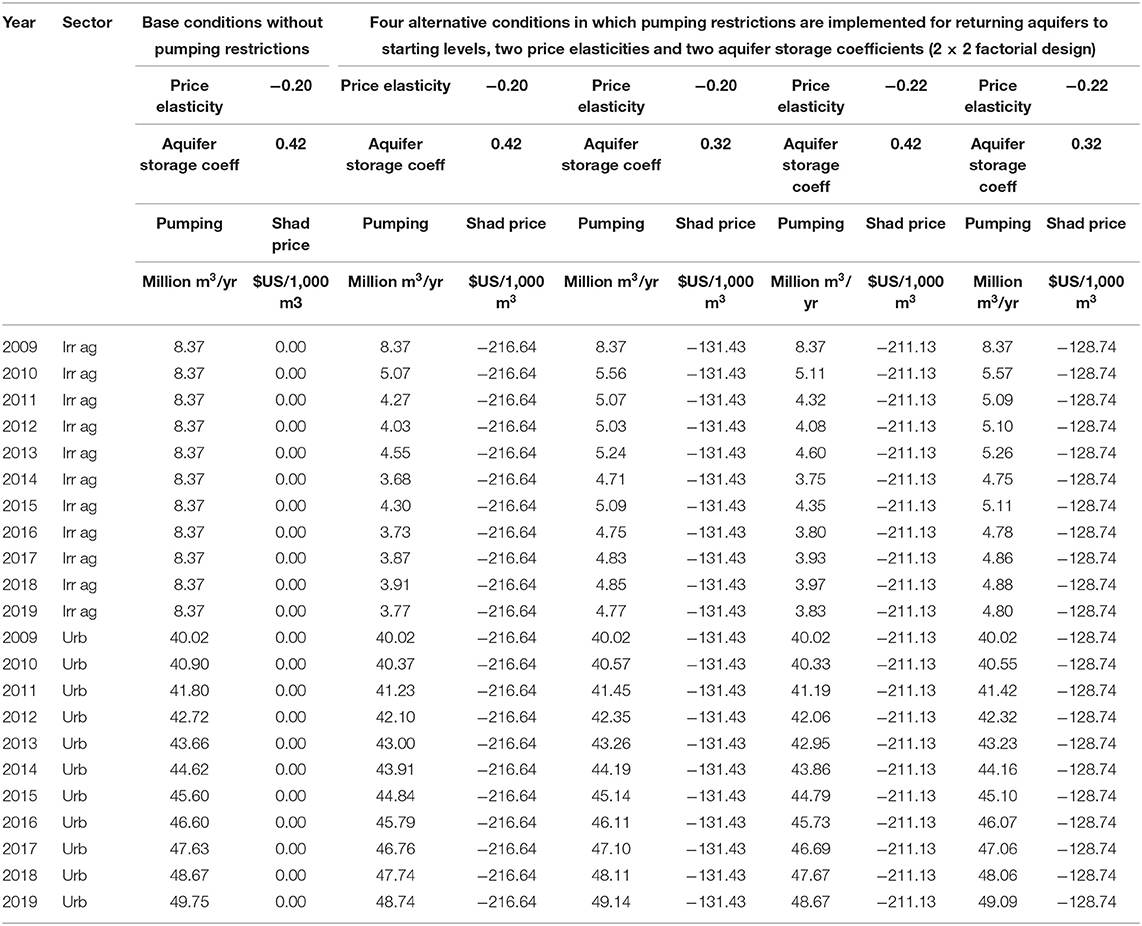
Table 6. Hydroeconomic model results illustration—water use and marginal value of additional water (shadow price) pumped by sector, urban price elasticity of demand, and aquifer storage coefficient, Nairobi Aquifer, Kenya, 2009–2019.

Arid regions are not the only communities needing guidance from HEAs developed and used. In some cases, the more humid regions face a number of water technology and policy issues, especially where water quality or water environments are important. Some of the better-known advances supported by the use of HEAs have come from application to flood control issues faced by the Netherlands and/or authored by Dutch researchers (Ngigi et al., 2005; Brouwer and Hofkes, 2008; Goor et al., 2010, 2011; George et al., 2011a,b; Verkade and Werner, 2011; Graveline et al., 2014; Satoh et al., 2017; Amjath-Babu et al., 2019).

One big contributing region for which water is a big policy challenge is southern Europe, notably Spain, Italy (D'Agostino et al., 2014), and Greece (Kourgialas and Karatzas, 2013; Riegels et al., 2013; Alamanos et al., 2019). Some of Europe's most and most notable have come from Spain, a county with a long history of drought and intense competition for water (Harou et al., 2009; Canals et al., 2010; Pena-Haro et al., 2010; Amores et al., 2013; Graveline et al., 2014; Foudi et al., 2015; Irabien and Darton, 2016; Kahil et al., 2016; Varela-Ortega et al., 2016; Escriva-Bou et al., 2017; Haro-Monteagudo et al., 2017; Ruperez-Moreno et al., 2017; Lopez-Nicolas et al., 2018; Crespo et al., 2019; Hervas-Gamez and Delgado-Ramos, 2020). A small number of researchers from Spain, as seen from this citation list, continues to produce a large number of influential works.

As the part of the world with the highest ratio of people to water, much work on HEAs have focused on the water problems of the Middle East. Examples include the works of Goor et al. (2010), Jeuland (2010), Satti et al. (2015), Siderius et al. (2016), Wu et al. (2016), Jeuland et al. (2017), Digna et al. (2018), Kahsay et al. (2019).

Central Asia has also received much attention, in part because of the considerable completion among higher elevation regions for hydroelectric power, irrigated agriculture at the lower regions, and environmental protection at other locations such as the Aral Sea. Examples include the papers of Jalilov et al. (2015, 2016), Bekchanov et al. (2015b, 2016, 2018), Bekchanov and Lamers (2016), Gunawardena et al. (2018).

The Indian Subcontinent has seen much attention in HEA application to local problems. These include work on water issues in India (Pande et al., 2011; Satoh et al., 2017; Zekri et al., 2017; Nechifor and Winning, 2018; Amjath-Babu et al., 2019; Pakhtigian et al., 2020), Bangladesh (Flanagan et al., 2012; Mullick et al., 2013; Ray et al., 2015; Amjath-Babu et al., 2019), and Pakistan (Yang et al., 2013, 2016a; Satoh et al., 2017; Amjath-Babu et al., 2019; Ali et al., 2020).

China has also had a long history of water issues, from which much recent attention has come from HEA work. Important works include those of Fischer and Sun (2001), Guan and Hubacek (2007, 2008), Cao et al. (2010), Han et al. (2014), Jiang et al. (2014), Zhao et al. (2014), Cheng and Li (2015), White et al. (2015), Yao et al. (2015), Davidsen et al. (2016), Wan et al. (2016), Yang et al. (2016b), Wu et al. (2017), Zhang et al. (2019), Meng et al. (2020).

Australia is a large country, with few people, little rainfall, several non-adjudicated river systems, and a considerable number of water challenges for which HEAs have been developed and used successfully (Enright and Goldblum, 1999; Finkele et al., 2006; Grafton and Jiang, 2011; Lester et al., 2011; Jiang and Grafton, 2012; Skurray et al., 2012; Davidson et al., 2013a,b; Qureshi et al., 2013).

Much of western North America is dry, and is a region that has produced many works with HEA foundations. A very short list includes (Ward and Pulido-Velazquez, 2008a, 2012; Harou et al., 2009; Medellin-Azuara et al., 2009; Booker et al., 2012; Hurd and Coonrod, 2012; Ruddell et al., 2014; Hrozencik et al., 2017; Porse et al., 2017, 2018; Wheeler et al., 2018; Levers et al., 2019; Ward et al., 2019). Many of the policy debates in that part of the world center on optimizing or even managing the competition for water for irrigation, flood control, urban water supply, and protecting key ecological assets.

Several very recent works in 2020 alone from many places internationally have looked at climate adaptation challenges (Alamanos et al., 2020; Baah-Kumi and Ward, 2020; Burek et al., 2020; Carolus et al., 2020; Dawoud, 2020; Do et al., 2020; Exposito et al., 2020; Goncalves et al., 2020; Graveline, 2020; Konapala and Mishra, 2020; Maneta et al., 2020; Meng et al., 2020; Pakhtigian et al., 2020; Sabbaghi et al., 2020; Slater et al., 2020; Tran et al., 2020; Turner et al., 2020).

When: Past Achievements and Future Needs

Past Achievements

There have been many achievements made possible by advances in HEA. One of the early first rate reviews of HEA was published in of 2009 by Harou et al. growing from several years' work spearheaded at the University of California, Davis (Harou et al., 2009). That work provided an excellent summary of the history of development of HEA going back to the mid Nineteenth century (Jules Dupuit), guidelines for an HEA construction, how those principles can be applied, and the kinds of advances then anticipated. Readers can find an excellent summary in that article, so there is little need to repeat its achievements here. Still, a brief update of other achievements in the world of HEA since that year is in order. More than 200 peer-reviewed articles dealing with HEA have been published since that time, so this brief review is necessarily limited to discussing some of the better known or most innovative efforts.

Soon after the above work appeared, one innovative work published in 2010 used HEA to assess implications of a low stabilization target of 400 ppm of CO₂ equivalent by 2100, concluding that this climate mitigation policy can be compatible with increased investment and technological advance. This was one of the early works noticing that HEA can be used to implement optimal growth models (Barker and Scrieciu, 2010).

Two 2010 works used HEA to gain insights into development of storage infrastructure and other policy options on the upper Blue Nile River Region of Ethiopia, a largely untapped source of water for hydropower and other uses. The authors pointed out that the use of HEA could elevate the insights by cost-benefit impacts of alternative methods for developing and managing a large scale storage reservoir in Ethiopia, a project that was initiated later in 2011. An important innovation of that work was its stochastic programming formulation to assess hydrologic uncertainty, determine water allocation policies that guard against hydrologic risk (Goor et al., 2010; Jeuland, 2010).

Another heavily cited work from 2010 from the UC Davis group boldly documented another new use of an HEA approach for drought adaptation and mitigation. The work was insightful and sometimes provocative. The authors synthesized a 72-year drought with 50% of mean historical inflows using stochastic sampling of historical dry years. HEA was used to assess how California could address an extreme drought using water trading, and found that water trading was a low cost way to make it through a severe and sustained drought, by moving low valued uses of water into higher valued uses through the mechanism of market incentives (Harou et al., 2010).

Yet another 2010 work summarized an effort to develop and use HEA for addressing water quality problems, with the goal of finding economically beneficial measures to control nitrate pollutions, for which the goal was to discover which programs produced benefits of the controls exceeding costs. A significant innovation achieved by that work was its capacity to characterize an economically efficient spatial and temporal allocation of variable fertilizer standards in agricultural basins that connected fertilizer applications with their fate and transport to various groundwater nitrate concentrations at several places in Spain (Pena-Haro et al., 2010). That work opened the door for several water quality policy assessments.

A pair of 2011 works presented an innovative approach for handling the competition for water for a basin in India. In it, the authors developed an integrated modeling framework with HEA elements for water resources planning and management for which the intent was to inform policy debates in India that influence water allocation and use. The application was implemented for India's Krishna Basin. The authors found that the competition for water is high there, for which transfers of water or water rights from irrigated agriculture from farms to cities is likely to grow in future years, since the economic value of water, where food is plentiful, is lower in agriculture than for cities and many other uses, such as hydropower. Of course, institutional mechanisms, such as market trading are needed to make this happen, sometimes difficult in cultures for which commercial motivations are weak (George et al., 2011a,b).

Another 2011 work advanced the cause of HEA taking a new look at multi-reservoir operation in a stochastic environment through the use of dual dynamic programming. Its innovation came by developing a method to handle the case that is common in hydropower management where the optimized head (difference between elevation of release point and generators) depends on the reservoir release trajectory over time. When the head is endogenous, there are many possibilities for local optima release paths failing the test of being globally optimal. Implementing their methodology was done by extending the scope of an earlier HEA developed by the authors in 2007 and 2008 for a multi-reservoir system where hydropower played an important role (Goor et al., 2011).

Another important work from 2011 presented innovations for handling flood risk using an interesting case study application in Scotland (Verkade and Werner, 2011). The authors used an analytical approach to assess economic benefits and costs of alternative of flood forecasting, warning and response (FFWR) systems in order to discover ones with a better economic performance. The innovation came through an HEA that permitted investigations of expected annual damage due to flooding, linked with the principle of relative economic value. Using an interesting case study of the White Cart Water River located in greater Glasgow, the authors focused on the Overlee gauging station as the river enters the city, an important place for better flood warning systems to be developed because of historically high damages to nearby residential areas. The authors found that an FFWR system that used a probabilistic forecast had the possibility of realizing higher benefits at all lead times considered, motivating a search for the concept of an (economically) optimal lead time.

An important 2012 review work by Booker et al. (2012) allowed HEA to take center stage, for which the authors applied several then-recent HEA innovations. Important advances in HEA policy models were described for integrating several sectors' demand and supply elements, as well as accounting for environmental benefits and costs with additional treatment of institutional constraints, like laws, regulations, and policies. More widespread expansions to river basins were seen as an important advance, such as developed in an earlier work by Booker (1995).

Another important 2012 contribution was an early work that addressed issues and opportunities for HEA focusing on the Mekong River Basin's development plans in south Asia. In that region, there remains considerable debate both inside and outside the basin over various water development and allocation policies. The authors concluded that future HEA could inform policy debates, especially if that work focused on integrating hydrologic and economic data. A comprehensive research effort can be complemented by the use of HEA to integrate conjunctive use of groundwater and surface water into decision support for regional planning (Johnston and Kummu, 2012).

A widely-cited work from 2013 addressed important water issues in the Murray-Darling Basin, Australia (Qureshi et al., 2013), and produced one of the first analyses on the water sector with the rest of the economy, focusing on Australia's food exports. Their findings showed climate water stressed, when modeled under its most severe conditions, along with other factors, will influence Australia's food exports. Despite its modest contribution to international food supplies, Australia contributes to international trade in several staples like wheat, meat, and some dairy products, for which shortages could elevate food prices. Furthermore, Australia's agricultural exports are of disproportionate importance within the South- and South-East Asian and Oceania region, both in terms of volume and for strategic reasons. The authors found that the use of HEA could help guide Australian planners in adapting to drought water stresses, as these models offer a comprehensive method for assessing policy options.

HEA saw an innovative advance in 2014 from a work shedding new light on optimization approaches to flood risk management (Zhao et al., 2014) when capacities to convey flood flows are scarce. The work formulated an economically optimized hedging set of rules for flood control operation of storage reservoirs for the case where there is important hydrological uncertainty, using mathematical programming and HEAs. The authors investigated three kinds of flood operations: (1) large anticipated floods requiring large volumes of reservoir storage, (2) medium anticipated floods requiring allocating most storage for the current period and less for future years, and (3) for small anticipated floods, for which reservoir space would be kept at or near empty in the current period. The HEA addressed the economic importance for trading off the incremental value of limited resources to manage floods in the case of uncertainty.

The year 2015 saw a significant contribution with the applications of HEA to energy policy using multi-criteria analysis. Making sustainable energy policy choices requires assessing energy supply options over a number of technical, social, environmental, and economic dimensions. Successfully making these comparisons using rigorous quantitative data is often lacking at the US national level. The authors developed a HEA to help guide these complex choices. Their findings taken over a number of scenarios showed that geothermal at that time scored best in sustainability for US energy suppliers. The HEA showed that several other energy supply measures provided considerable improvements for sustainability compared to fossil fuels or nuclear technologies. While natural gas combined cycle ranks high under economic and technical choices, renewables scored higher in both scenarios. This was one of the early works to bring energy and power into the same HEA (Klein and Whalley, 2015).

Soon after, 2016 saw an innovative new kind of HEA application for the case of a river basin in Central Asia. The need for this work came in part from increased debates among several the Central Asian countries, in particular Tajikistan, Afghanistan, Uzbekistan, and Turkmenistan, regarding the use of water for upstream hydroelectric power vs. downstream cotton production and environmental restoration at the Aral Sea. These debates continue to increase over the Rogun Dam on the Vakhsh River, an important tributary of the Amu Darya. What the authors described as an irrigation priority allocation system among the competing upstream-downstream demands could secure irrigation benefits to Uzbekistan with increased energy benefits to Tajikistan if managed well.

Even with these changes, energy output in the crop irrigation priority system would be inefficiently allocated throughout the year, resulting in large quantities of hydropower supplied during the crop growing season. Results showed that despite modeling results indicating a potential for a benefit sharing program to bring benefits to all, diplomatic success is required to achieve results theoretically indicated by models, especially important in transboundary basins (Jalilov et al., 2016).

One very recent contribution from 2019 (Amjath-Babu et al., 2019) used HEA to assess hydropower capacity development in the Koshi River Basin in the Himalayan region, near the rooftop of the world, making for an excellent opportunity to assess an intervention to support a regional commitments to the 2015 Paris Climate agreement. An HEA was conducted by linking a crop growth simulation model, a hydrological model, and an economic optimization model, something of a classic exercise in full integration. The goal of the authors was the use of sophisticated modeling to gain insights into measures to dissolve the vicious cycle of mass poverty brought on by the interrelated insecurities of energy, food, climate, and environment. An important contribution of their work was to address the potential of relying on the nexus by which hydropower, if developed, could pump groundwater for irrigation and food security, as well as enhance capacity to contribute to flood damage reduction goals. Another important innovation was that unlike a typical view that benefits of this kind of project is mostly limited to hydropower, the irrigation and flood damage reduction benefits can contribute to 40 percent of total benefits, if the reservoir system is managed efficiently. These findings have considerable implications for climate adaptation internationally.

Improvement Needs

Integrated Economic Frameworks

Economists developed principles with considerable rigor and elegance in the mid-1950s for recognizing and finding an optimal growth path that could see application to HEA. Yet, surprisingly few of those bright light insights have seen application to the choices of water managers and economic planners to inform policy ongoing policy debates over the role of water in sustainable development.

The problem occurs in which many economic development challenges related to water are typically addressed piecemeal, one period, one resource, one sector, one policy at a time. Such sequential piecemeal analysis risks successfully addressing one problem at a time, while worsening others (Liu et al., 2018). An integrated water nexus approach will simultaneously investigate then optimize the connecting elements among several sectors, resources, policies, and periods.

Because of the huge variability in ambition, spatial, sectorial, and temporal scope, integrated HEAs are hard to describe simply and harder to build, especially for beginners. With an attempt show a few of the policy informing features of an HEA, Table 7 shows results of a little toy-sized small scale HEA illustrating the integrated approach. It shows results of a little HEA that accounts simultaneously for a number of interacting elements for which the goal is insight to minimize the cost of sustaining an aquifer in the Nairobi region of Kenya. Any aquifer could have been chosen for which there are debates on pumping and protection. But the author is currently (2021) working on a Kenya aquifer sustainability project, so it seemed like a good place to turn for illustration.

TABLE 7

Table 7. Selected notable works since 2009 supported by hydroeconomic analysis.

Results show water use by pumping and shadow price pumped by sector, urban price elasticity of demand, and aquifer storage coefficient for the Nairobi Aquifer, Kenya, 2009–2019, for which the aquifer is described in more detail elsewhere (Oiro et al., 2018). Several elements are worth noticing. The first column shows results of an optimization mode that reproduce historical pumping levels by year along with (zero) shadow prices for two sectors. The shadow price under base conditions is zero, because there are no restrictions on the aquifer storage in any period that must occur. The positive mathematical programming (PMP) method, described elsewhere (Howitt, 1995; Dagnino and Ward, 2012) was used to assure that the model-optimized unrestricted observed pumping would match observed levels. The remaining four sets of columns show results of a tradeable permit system used to cut pumping back so that last period aquifer storage was at least as high as first period levels.

Results show a 2 × 2 factorial design (Wishart, 1938) of four re-optimized pumping plans according to four combinations of price elasticities (2) and aquifer storage coefficients (2) that did occur or could have occurred counterfactually (Parry, 1957). The mathematical optimization uses quadratic programming for which effects of the four alternative possible conditions spread require adjustments over sector and time period of the optimized water use plan in the face of new information. It shows several results:

• Optimized economic efficiency: The model was built by investigating water pumping patterns over the 11 year period 2009–2019 for the Nairobi Kenya aquifer (Kiptala et al., 2018). The historical pumping data for that aquifer showed an increased pump depth of about 2 meters each year over the 11 year period, indicating a clear stress to hydrologic and economic sustainability. The HEA was built to find adjustments to actual historical pumping needed to restore the aquifer to its starting (2009) depth and storage by the last year (2019). Economic theory makes us expect that pumping reduction would raise the scarcity of historical use, for which the optimized revised level of pumping makes the discounted marginal net present value of use equal in both sectors (agriculture and urban) and in all time periods. For base values of the two parameters, that shadow price is seen to be $216.64 per 1000 cubic meters from one unit increase in pumping in either sector or in any time period. The optimized physical pumping plan is different for each of the two sectors and is slightly different in each period. The quadratic program gives rise to well-known smooth pasting properties (Browne, 1995). That is one small change in data assumptions propagates smooth adjustments over time, use, and sector.

• Interdependence propagated throughout: All sectors compete for the same aquifer water pumped. So with a small change even in one parameter, such as price elasticity of demand, the model minimizes the cost adapting to the new information by reallocating water over sectors and time periods to minimize adjustment impacts. Results allow comparison of economically optimized pumping for each of the two sectors in all periods when new information shows the aquifer storage coefficient found to fall from 0.42 to 0.32, while the price elasticity is unchanged. Notice that pumping changes slightly in all periods for each sector. The shadow price of water, the marginal value of discounted net present value (DNPV), is also reduced by nearly half in moving from the initial optimal growth path ($216 per 1,000 cubic meters) to the new one ($131 per 1,000 cubic meter). However that shadow price is still constant across all periods and for both sectors, as required by theory.

• Intersectoral unity: When only the price elasticity of demand in the urban sector increases from a base level (−0.20) to a new level (−0.22), holding the storage coefficient at its initial level (0.42) pumping in both sectors and all years is affected. While total water use is not affected because of the terminal storage requirement, sharing of pumping adjustments takes place in both sectors, the one for which elasticity changed (urban) and the one for which it did not change (agriculture). So all water users in all periods adjust to new information, as any water utility manager knows. The scarcity value of water goes down as the price elasticity increases, indicating that water becomes less scarce when urban water users more easily shift out of water in the face of increased price. Such an increased price elasticity could occur if a new bottled water retailer came to town, bringing a greater ease of substitution of alternative water for utility supplied water.

• Conservation ambitions affect use. If a more ambitious levels of conservation (reduced water use) would have been required, say after detailed studies discovering lower levels of natural recharge, reduced pumping would have been required for all sectors and all time periods (not shown).

• Water sharing methods matter: Table 7 shows only one water institution, the equivalent of a pumping permit trading arrangement, by which market forces efficiently allocate shortage-sharing responsibilities, for which marginal discounted net present value is equal in all uses and time periods. Other water sharing methods work better in cultures where water trading is unacceptable. Alternative pumping shortage sharing methods can include arrangements like a proportional sharing of shortages or various priority allocation systems, such as a top priority going to urban uses. All these affect the (constrained) optimized pumping path as well as shadow prices. The spreadsheet that reproduces results in Table 7 are posted on the New Mexico State University web server at https://water-research.nmsu.edu/

Advancing beyond this little toy-sized example, HEA needs a more comprehensive underlying framework to distinguish their essential features from background details containing data from a particular time, sector, culture, or place. For the ambitious model builder, the ideal HEA would not be targeted to any single place, sector, or time, but would have complete upscalability and generalizability (Kahil et al., 2018). It would have a fixed set of mathematical equations that produced results for whatever context is needed, along the lines of the well-known and highly respected MODFLOW groundwater flow model built by the US Geological Survey (McDonald and Harbaugh, 2003; Barlow and Harbaugh, 2006).

One essential feature for recognizing the most desired economic efficiency of a plan comes when it can be shown the marginal discounted net present value (MDNPV) of changes that could be made in development or policy are equal in all directions in which change could occur. Moreover, a well-developed and useable HEA will show plans for which the MDNPV stays equal in the face of all new conditions that emerge, as shown in in Table 7.

Other Needs

A short list of advances called for in future HEAs appears below. It does not pretend to be comprehensive:

• Development of genetic algorithms (GA) for handling complex stochastic problems (Booker et al., 2012). GAs are motivated by the idea of Darwinian natural selection. They typically rely on biologically inspired concepts like selection, crossover, and mutation. They are one strategy for handling non-convexities commonly seen in water resources for which Newtonian gradient search methods cannot reliably find global optimum. Reservoir operators face pressures on timing releases of water. Releasing too much water immediately can threaten future supplies and costs, but not releasing enough creates immediate economic hardship downstream. A 2018 work examined the use of GAs showing how economic valuing of end-of-year carryover storage can achieve economically optimized levels of carryover storage in complex water resource systems (Khadem et al., 2018).

• Using remotely sensed data to connect observed hydrological and economic relations. One 2015 work showed hos this could be achieved (Medellin-Azuara et al., 2015).

• Greater application of HEA to politically difficult transboundary water issues, to address ongoing international debates over important systems like the Rhine, Meuse, Amu Darya, Tigris-Euphrates, Nile, Rio Grande, Colorado, Mekong, Indus, Brahmaputra, Ganges, Volga, and Amazon. Water negotiators who live in these basins need the help.

• More efforts and documented success in getting HEA models into the hands of water managers, stakeholders, technical advisers, and lawmakers. Most HEAs are ignored by most people most of the time. A water attorney in southern New Mexico told this author recently there are enough hydrological and economic models to build a road to Mars. How will yours be special, honest, unique, and used? One such HEA has been posted at the University of Texas El-Paso, and has opened up much discussion in the region, but it is only a start (SWIM, 2021).

• Better capacity for responding to unexpected conditions when they occur. This could occur by having an HEA in the tool kit to help expect the unexpected. Managers need a capacity for quickly developing a plan B when the plan A falls apart in the face of unanticipated conditions staring them in the face, for which fast and reliable action must occur. For example a good plan B model may assess the worthiness of importing large quantities of expensive water when local surface supplies fail to materialize or when local water supply system faces an unplanned health crisis (Hanna-Attisha et al., 2016) or when river supplies are hit with a toxic spill or terrorist attack (Ostfeld et al., 2008).

• Capacity to integrate climate, water, food, energy, and environment with the rest of the economy. Economic models typically have a limited physical basis, so HEAs developed since the early 2000s have already taken a big step ahead compared to other decision support models.

• Inclusion of water quality. A topic that of growing relevance is the case of new emerging contaminants or contaminants of emerging concern or CEC (Benson et al., 2017). In general, water quality has been seen as a problem coming from agricultural activities. However, CEC are mainly from urban and industrial sources. Addressing this in a coherent and consistent system is an important challenge for HEA.

• Model Calibration: Distinguishing Social and Private Optimization. The remarkable insights provided by Richard Howitt's 1995 work on positive mathematical programming (PMP) (Howitt, 1995) opened up new frontiers. Its foundation permitted calibration of models based on observed behavior that optimizes a private welfare function. A good example is discovering underlying parameters for crop irrigation behavior by simply watching the behavior of farmers optimize their incomes. Results of that behavior influenced with an optimization assumption is used to back-calculate parameters of a demand function or production function, since optimized behavior produces water use outcomes seen.

This remarkable insight permits solving an unconstrained optimization model that replicates historical behavior, the first step to predict future behavior under either status quo policies or new kinds of policies not implemented in the past. Replicating actual history is the first step toward more reliable predictions to the extent that underlying behavior does not change. Direct evidence is always desired for predicting the future, a fact that has been noted by many historians (Bunzl, 2004).

Socially Optimal Optimization: Even if PMP can support reconstructing drivers and outcomes of past behavior to forecast future behavior, it says nothing of social value of that behavior. So, for HEA to rise to its full potential, private behavioral predictions reconstructed by using PMP need guidance by social cost benefit to move observed private water outcomes onto a socially optimal growth path.

Conclusions

Water is a big part of the climate adaption story. This paper has searched that space for methods to promote integrated assessments. Growing demands for water combined with increased variability of climate induced water supplies in many parts the world is leading to in increasing array of challenges faced in the search for adequate levels of water's six important dimensions: quantity, quality, timing, location, price, and cost. The management of both climate and water suffer from the well-understood market failures of externalities, common property, public goods, and free riders, for which the development and use of HEAs offer hope for sustainable management.

The works and models summarized in this review describe modeling efforts illustrating the benefits to climate and water managers that can come from the use of HEAs to inform the choice of options for well-informed water management that deal with problems of water of the wrong quantity, quality, timing, location, price, and costs. A HEA includes but is not limited to economic optimization of water quantities for several uses for many sectors in several periods. A HEA can also give insights into improvements of infrastructure such as treatment plants and reservoir development and operation as well as new rules and laws that influence water use and its benefits.

Stakeholders will only believe and use a HEA if it produces predictions that square with historical behavior. Characterizing economic demands for water as opposed to engineering water requirements is especially difficult. Planners often forecast future use by using a straight edge ruler, but this method commonly fails. Demand forecasts expresses water use as a function of its price as well as other use predictors. An observed level of water use at a particular place at a point in the past provides no guarantee this use will continue into the future, especially in the face of changes in price, population, technology, or substitutes. Yet, solid economic principles alone are not enough to inform a trusted HEA. A good HEA needs to be based on solid modeling of the system hydrology, including things like crop ET, ecosystem water use, urban system use, and stream aquifer interaction that occurred in the past as well as those interaction that could occur in the future where different from the past.

Institutions like legislative enactments and new water right system will also affect water use outcomes. A common way to treat these in a HEA is to inserted mathematical constraints (Ward and Becker, 2015) to handle things like a proposed change in a water sharing system not yet been experienced (Ward et al., 2013; Bekchanov et al., 2015a; Gohar et al., 2015). Still the challenge comes from the fact that laws do not have quite the predictability as scientific principles. In summary, HEA will need more development if it is to see use for joint management of water along with other scarce resources like food, environment, and energy. Moreover, all this work needs to be conducted at the right temporal, sectoral, and spatial scale to address emerging challenges of population growth and climate change. In summary, this author sees a bright future for the use of HEA to guide climate adaptation policy.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Thanks are owed to the New Mexico State University Agricultural Experiment Station and US Geological Survey International Division for support of this paper.

References

Alamanos, A., Latinopoulos, D., Loukas, A., and Mylopoulos, N. (2020). Comparing two hydro-economic approaches for multi-objective agricultural water resources planning. Water Resour. Manag. 34, 4511–4526. doi: 10.1007/s11269-020-02690-6

CrossRef Full Text | Google Scholar

Alamanos, A., Latinopoulos, D., Papaioannou, G., and Mylopoulos, N. (2019). Integrated hydro-economic modeling for sustainable water resources management in data-scarce areas: the case of lake karla watershed in Greece. Water Resour. Manag. 33, 2775–2790. doi: 10.1007/s11269-019-02241-8

CrossRef Full Text | Google Scholar

Ali, S., Zhang, S. H., and Yue, T. J. (2020). Environmental and economic assessment of rainwater harvesting systems under five climatic conditions of Pakistan. J. Clean. Product. 259:120829. doi: 10.1016/j.jclepro.2020.120829

CrossRef Full Text | Google Scholar

Amjath-Babu, T. S., Sharma, B., Brouwer, R., Rasul, G., Wahid, S. M., Neupane, N., et al. (2019). Integrated modelling of the impacts of hydropower projects on the water-food-energy nexus in a transboundary Himalayan river basin. Appl. Energy 239, 494–503. doi: 10.1016/j.apenergy.2019.01.147

CrossRef Full Text | Google Scholar

Amores, M. J., Meneses, M., Pasqualino, J., Anton, A., and Castells, F. (2013). Environmental assessment of urban water cycle on Mediterranean conditions by LCA approach. J. Clean. Prod. 43, 84–92. doi: 10.1016/j.jclepro.2012.12.033

CrossRef Full Text | Google Scholar

Andersen, J. A. (2015). Barking up the wrong tree. On the fallacies of the transformational leadership theory. Leaders. Organ. Dev. J. 36, 765–777. doi: 10.1108/LODJ-12-2013-0168

CrossRef Full Text | Google Scholar

Baah-Kumi, B., and Ward, F. A. (2020). Poverty mitigation through optimized water development and use: Insights from the Volta Basin. J. Hydrol. 582:124548. doi: 10.1016/j.jhydrol.2020.124548

CrossRef Full Text | Google Scholar

Barker, T., and Scrieciu, S. S. (2010). Modeling low climate stabilization with E3MG: towards a 'new economics' approach to simulating energy-environment-economy system dynamics. Energy J. 31, 137–164. doi: 10.5547/ISSN0195-6574-EJ-Vol31-NoSI-6

CrossRef Full Text | Google Scholar

Barlow, P. M., and Harbaugh, A. W. (2006). USGS directions in MODFLOW development. Ground Water 44, 771–774. doi: 10.1111/j.1745-6584.2006.00260.x

CrossRef Full Text | Google Scholar

Becker, L., and Yeh, W. W. G. (1974). Optimal timing, sequencing, and sizing of multiple reservoir surface water supply facilities. Water Resour. Res. 10, 57–62. doi: 10.1029/WR010i001p00057

CrossRef Full Text | Google Scholar

Bekchanov, M., Bhaduri, A., and Ringler, C. (2015a). Potential gains from water rights trading in the Aral Sea Basin. Agric. Water Manag. 152, 41–56. doi: 10.1016/j.agwat.2014.12.011

CrossRef Full Text | Google Scholar

Bekchanov, M., and Lamers, J. P. A. (2016). The effect of energy constraints on water allocation decisions: the elaboration and application of a system-wide economic-water-energy model (SEWEM). Water 8:253. doi: 10.3390/w8060253

CrossRef Full Text | Google Scholar

Bekchanov, M., Ringler, C., and Bhaduri, A. (2018). A water rights trading approach to increasing inflows to the aral sea. Land Degrad. Dev. 29, 952–961. doi: 10.1002/ldr.2394

CrossRef Full Text | Google Scholar

Bekchanov, M., Ringler, C., Bhaduri, A., and Jeuland, M. (2015b). How would the Rogun Dam affect water and energy scarcity in Central Asia? Water Int. 40, 856–876. doi: 10.1080/02508060.2015.1051788

CrossRef Full Text | Google Scholar

Bekchanov, M., Ringler, C., Bhaduri, A., and Jeuland, M. (2016). Optimizing irrigation efficiency improvements in the Aral Sea Basin. Water Resour. Econ. 13, 30–45. doi: 10.1016/j.wre.2015.08.003

CrossRef Full Text | Google Scholar

Benson, R., Conerly, O. D., Sander, W., Batt, A. L., Boone, J. S., Furlong, E. T., et al. (2017). Human health screening and public health significance of contaminants of emerging concern detected in public water supplies. Sci. Total Environ. 579, 1643–1648. doi: 10.1016/j.scitotenv.2016.03.146

PubMed Abstract | CrossRef Full Text | Google Scholar

Berbel, J., Gutiérrez-Martín, C., Rodríguez-Díaz, J. A., Camacho, E., and Montesinos, P. (2015). Literature review on rebound effect of water saving measures and analysis of a Spanish case study. Water Resour. Manag. 29, 663–678. doi: 10.1007/s11269-014-0839-0

CrossRef Full Text | Google Scholar

Bierkens, M. F. P., Reinhard, S., de Bruijn, J. A., Veninga, W., and Wada, Y. (2019). The shadow price of irrigation water in major groundwater-depleting countries. Water Resour. Res. 55, 4266–4287. doi: 10.1029/2018WR023086

CrossRef Full Text | Google Scholar

Bird, M. I., O'Grady, D., and Ulm, S. (2016). Humans, water, and the colonization of Australia. Proc. Natl. Acad. Sci. U.S.A. 113, 11477–11482. doi: 10.1073/pnas.1608470113

CrossRef Full Text | Google Scholar

Black, P. E. (2012). The U.S. flood control program at 75: environmental issues. J. Am. Water Resour. Assoc. 48, 244–255. doi: 10.1111/j.1752-1688.2011.00609.x

CrossRef Full Text | Google Scholar

Blanco-Gutierrez, I., Varela-Ortega, C., and Purkey, D. R. (2013). Integrated assessment of policy interventions for promoting sustainable irrigation in semi-arid environments: A hydro-economic modeling approach. J. Environ. Manag. 128, 144–160. doi: 10.1016/j.jenvman.2013.04.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Bock, C. A. (1918). History of the Miami Flood Control Project. Davis, CA: University of California. Available online at: https://watershed.ucdavis.edu/shed/lund/Classes/MiamiConservancy.pdf

Google Scholar

Booker, J. F. (1995). Hydrologic and economic impacts of drought under alternatwe policy responses 1. JAWRA J. Am. Water Resour. Assoc. 31, 889–906. doi: 10.1111/j.1752-1688.1995.tb03409.x

CrossRef Full Text | Google Scholar

Booker, J. F., Howitt, R. E., Michelsen, A. M., and Young, R. A. (2012). Economics and the modeling of water resources and policies. Nat. Res. Model. 25, 168–218. doi: 10.1111/j.1939-7445.2011.00105.x

CrossRef Full Text | Google Scholar

Boucher, M. A., Tremblay, D., Delorme, L., Perreault, L., and Anctil, F. (2012). Hydro-economic assessment of hydrological forecasting systems. J. Hydrol. 416, 133–144. doi: 10.1016/j.jhydrol.2011.11.042

CrossRef Full Text | Google Scholar

Bragg, D. C. (2001). Potential relative increment (PRI): a new method to empirically derive optimal tree diameter growth. Ecol. Model. 137, 77–92. doi: 10.1016/S0304-3800(00)00433-6

CrossRef Full Text | Google Scholar

Breshears, D. D., Cobb, N. S., Rich, P. M., Price, K. P., Allen, C. D., Balice, R. G., et al. (2005). Regional vegetation die-off in response to global-change-type drought. Proc. Natl. Acad. Sci. U.S.A. 102, 15144–15148. doi: 10.1073/pnas.0505734102

PubMed Abstract | CrossRef Full Text | Google Scholar

Bretsen, S. N. (2017). Rainwater harvesting in colorado and the quandary of a taking. Tex. A&M J. Prop. L. 4:165. doi: 10.37419/JPL.V4.I3.1

CrossRef Full Text | Google Scholar

Brouwer, R., and Hofkes, M. (2008). Integrated hydro-economic modelling: Approaches, key issues and future research directions. Ecol. Econ. 66, 16–22. doi: 10.1016/j.ecolecon.2008.02.009

CrossRef Full Text | Google Scholar

Brown, C. M., Lund, J. R., Cai, X. M., Reed, P. M., Zagona, E. A., Ostfeld, A., et al. (2015). The future of water resources systems analysis: Toward a scientific framework for sustainable water management. Water Resour. Res. 51, 6110–6124. doi: 10.1002/2015WR017114

CrossRef Full Text | Google Scholar

Browne, S. (1995). Optimal investment policies for a firm with a random risk process: Exponential utility and minimizing the probability of ruin. Math. Operat. Res. 20, 937–958. doi: 10.1287/moor.20.4.937

CrossRef Full Text | Google Scholar

Bunzl, M. (2004). Counterfactual history: a user's guide. Am. Hist. Rev. 109, 845–858. doi: 10.1086/530560

CrossRef Full Text | Google Scholar

Burek, P., Satoh, Y., Kahil, T., Tang, T., Greve, P., Smilovic, M., et al. (2020). Development of the Community Water Model (CWatM v1.04) - a high-resolution hydrological model for global and regional assessment of integrated water resources management. Geosci. Model Dev. 13, 3267–3298. doi: 10.5194/gmd-13-3267-2020

CrossRef Full Text | Google Scholar

Burn, D. H., and McBean, E. A. (1985). Optimization modeling of water-quality in an uncertain environment. Water Resour. Res. 21, 934–940. doi: 10.1029/WR021i007p00934

CrossRef Full Text | Google Scholar

Campisano, A., Butler, D., Ward, S., Burns, M. J., Friedler, E., DeBusk, K., et al. (2017). Urban rainwater harvesting systems: research, implementation and future perspectives. Water Res. 115, 195–209. doi: 10.1016/j.watres.2017.02.056

PubMed Abstract | CrossRef Full Text | Google Scholar

Canals, L. M. I., Chapagain, A., Orr, S., Chenoweth, J., Anton, A., and Clift, R. (2010). Assessing freshwater use impacts in LCA, part 2: case study of broccoli production in the UK and Spain. Int. J. Life Cycle Assess. 15, 598–607. doi: 10.1007/s11367-010-0187-0

CrossRef Full Text | Google Scholar

Cao, S. Y., Lee, K. T., Ho, J. Y., Liu, X. N. A., Huang, E., and Yang, K. J. (2010). Analysis of runoff in ungauged mountain watersheds in sichuan, china using kinematic-wave-based GIUH model. J. Mountain Sci. 7, 157–166. doi: 10.1007/s11629-010-0256-7

CrossRef Full Text | Google Scholar

Carolus, J. F., Bartosova, A., Olsen, S. B., Jomaa, S., Veinbergs, A., Zilans, A., et al. (2020). Nutrient mitigation under the impact of climate and land-use changes: A hydro-economic approach to participatory catchment management. J. Environ. Manag 271:110976. doi: 10.1016/j.jenvman.2020.110976

PubMed Abstract | CrossRef Full Text | Google Scholar

Carruthers, I., Rosegrant, M. W., and Seckler, D. (1997). Irrigation and food security in the 21st century. Irrig. Drain. Syst 11, 83–101. doi: 10.1023/A:1005751232728

CrossRef Full Text | Google Scholar

Carson, R. T., Flores, N. E., and Meade, N. F. (2001). Contingent valuation: controversies and evidence. Environ. Resour. Econ. 19, 173–210. doi: 10.1023/A:1011128332243

CrossRef Full Text | Google Scholar

Cheng, G. D., and Li, X. (2015). Integrated research methods in watershed science. Sci. China Earth Sci. 58, 1159–1168. doi: 10.1007/s11430-015-5074-x

CrossRef Full Text | Google Scholar

Cook, E. R., and Jacoby, G. C. (1977). Tree-ring drought relationships in hudson valley, New-York. Science 198, 399–401. doi: 10.1126/science.198.4315.399

PubMed Abstract | CrossRef Full Text | Google Scholar

Coppola, E., Szidarovszky, F., Poulton, M., and Charles, E. (2003). Artificial neural network approach for predicting transient water levels in a multilayered groundwater system under variable state, pumping, climate conditions. J. Hydrol. Eng. 8, 348–360. doi: 10.1061/(ASCE)1084-0699(2003)8:6(348)

CrossRef Full Text | Google Scholar

Cozzetto, K., Chief, K., Dittmer, K., Brubaker, M., Gough, R., Souza, K., et al. (2013). Climate change impacts on the water resources of American Indians and Alaska natives in the US. Climatic Change 120, 569–584. doi: 10.1007/s10584-013-0852-y

CrossRef Full Text | Google Scholar

Creel, M., and Loomis, J. (1992). Recreational value of water to wetlands in the san joaquin valley - linked multinomial logit and count data trip frequency models. Water Resour. Res. 28, 2597–2606. doi: 10.1029/92WR01514

CrossRef Full Text | Google Scholar

Crespo, D., Albiac, J., Kahil, T., Esteban, E., and Baccour, S. (2019). Tradeoffs between water uses and environmental flows: a hydroeconomic analysis in the Ebro Basin. Water Res. Manag. 33, 2301–2317. doi: 10.1007/s11269-019-02254-3

CrossRef Full Text | Google Scholar

Dagnino, M., and Ward, F. A. (2012). Economics of agricultural water conservation: empirical analysis and policy implications. Int. J. Water Resour. Dev. 28, 577–600. doi: 10.1080/07900627.2012.665801

CrossRef Full Text | Google Scholar

D'Agostino, D. R., Scardigno, A., Lamaddalena, N., and El Chami, D. (2014). Sensitivity analysis of coupled hydro-economic models: quantifying climate change uncertainty for decision-making. Water Res. Manag. 28, 4303–4318. doi: 10.1007/s11269-014-0748-2

CrossRef Full Text | Google Scholar

Dandy, G. C., McBean, E. A., and Hutchinson, B. G. (1984). A model for constrained optimum water pricing and capacity expansion. Water Resour. Res. 20, 511–520. doi: 10.1029/WR020i005p00511

CrossRef Full Text | Google Scholar

Dantzig, G. B. (1948). Programming in a linear structure. Bull. Am. Math. Soc. 54, 1074–1074.

Google Scholar

Davidsen, C., Liu, S. X., Mo, X. G., Rosbjerg, D., and Bauer-Gottwein, P. (2016). The cost of ending groundwater overdraft on the North China Plain. Hydrol. Earth Syst. Sci. 20, 771–785. doi: 10.5194/hess-20-771-2016

CrossRef Full Text | Google Scholar

Davidson, B., Malano, H., Nawarathna, B., and Maheshwari, B. (2013a). The hydrological and economic impacts of changing water allocation in political regions within the peri-urban South Creek catchment in Western Sydney I: model development. J. Hydrol. 499, 339–348. doi: 10.1016/j.jhydrol.2013.06.052

CrossRef Full Text | Google Scholar

Davidson, B., Malano, H., Nawarathna, B., and Maheshwari, B. (2013b). The hydrological and economic impacts of changing water allocations in political regions within the peri-urban South Creek catchment in Western Sydney II: scenarios. J. Hydrol. 499, 349–359. doi: 10.1016/j.jhydrol.2013.06.030

CrossRef Full Text | Google Scholar

Dawoud, M. A. (2020). Groundwater economics in arid regions: Abu Dhabi Emirate case study. Desalin. Water Treat. 176, 84–93. doi: 10.5004/dwt.2020.25501

CrossRef Full Text | Google Scholar

Descheemaeker, K., Oosting, S. J., Tui, S. H. K., Masikati, P., Falconnier, G. N., and Giller, K. E. (2016). Climate change adaptation and mitigation in smallholder crop-livestock systems in sub-Saharan Africa: a call for integrated impact assessments. Reg. Environ. Change 16, 2331–2343. doi: 10.1007/s10113-016-0957-8

CrossRef Full Text | Google Scholar

Digna, R. F., Castro-Gama, M. E., van der Zaag, P., Mohamed, Y. A., Corzo, G., and Uhlenbrook, S. (2018). Optimal operation of the eastern nile system using genetic algorithm, and benefits distribution of water resources development. Water 10:921. doi: 10.3390/w10070921

CrossRef Full Text | Google Scholar

Do, P. R., Tian, F. Q., Zhu, T. J., Zohidov, B., Ni, G. H., Lu, H., et al. (2020). Exploring synergies in the water -food -energy nexus by using an integrated hydro -economic optimization model for the Lancang-Mekong River basin. Sci. Total Environ. 728:137996. doi: 10.1016/j.scitotenv.2020.137996

PubMed Abstract | CrossRef Full Text | Google Scholar

Dorigo, M., and Blum, C. (2005). Ant colony optimization theory: a survey. Theoret. Com. Sci. 344, 243–278. doi: 10.1016/j.tcs.2005.05.020

CrossRef Full Text | Google Scholar

Draper, A. J., Jenkins, M. W., Kirby, K. W., Lund, J. R., and Howitt, R. E. (2003). Economic-engineering optimization for California water management. J. Water Res. Plan. Manage. 129, 155–164. doi: 10.1061/(ASCE)0733-9496(2003)129:3(155)

CrossRef Full Text | Google Scholar

Dumont, A., Mayor, B., and López-Gunn, E. (2013). Is the rebound effect or Jevons paradox a useful concept for better management of water resources? Insights from the irrigation modernisation process in Spain. Aquat. Procedia. 1, 64–76. doi: 10.1016/j.aqpro.2013.07.006

CrossRef Full Text | Google Scholar

Eijgenraam, C., Kind, J., Bak, C., Brekelmans, R., den Hertog, D., Duits, M., et al. (2014). Economically efficient standards to protect the Netherlands against flooding. Interfaces 44, 7–21. doi: 10.1287/inte.2013.0721

CrossRef Full Text | Google Scholar

Eiswerth, M. E., Englin, J., Fadali, E., and Shaw, W. D. (2000). The value of water levels in water-based recreation: a pooled revealed preference/contingent behavior model. Water Resourc. Res. 36, 1079–1086. doi: 10.1029/1999WR900332

CrossRef Full Text | Google Scholar

Elbakidze, L., Vinson, H., Cobourn, K., and Taylor, R. G. (2018). Efficient groundwater allocation and binding hydrologic externalities. Res. Energy Econ. 53, 147–161. doi: 10.1016/j.reseneeco.2018.05.002

CrossRef Full Text | Google Scholar

Enright, N. J., and Goldblum, D. (1999). Demography of a non-sprouting and resprouting hakea species (Proteaceae) in fire-prone eucalyptus woodlands of southeastern Australia in relation to stand age, drought and disease. Plant Ecol. 144, 71–82. doi: 10.1023/A:1009839800864

CrossRef Full Text | Google Scholar

Escriva-Bou, A., Lund, J. R., and Pulido-Velazquez, M. (2015). Modeling residential water and related energy, carbon footprint and costs in California. Environ. Sci. Policy 50, 270–281. doi: 10.1016/j.envsci.2015.03.005

CrossRef Full Text | Google Scholar

Escriva-Bou, A., Lund, J. R., Pulido-Velazquez, M., Hui, R., and Medellin-Azuara, J. (2018). Developing a water-energy-GHG emissions modeling framework: insights from an application to California's water system. Environ. Model. Softw. 109, 54–65. doi: 10.1016/j.envsoft.2018.07.011

CrossRef Full Text | Google Scholar

Escriva-Bou, A., Pulido-Velazquez, M., and Pulido-Velazquez, D. (2017). Economic value of climate change adaptation strategies for water management in Spain's Jucar Basin. J. Water Res. Plan. Manag. 143:04017005. doi: 10.1061/(ASCE)WR.1943-5452.0000735

CrossRef Full Text | Google Scholar

Esteve, P., Varela-Ortega, C., Blanco-Gutierrez, I., and Downing, T. E. (2015). A hydro-economic model for the assessment of climate change impacts and adaptation in irrigated agriculture. Ecol. Econ. 120, 49–58. doi: 10.1016/j.ecolecon.2015.09.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Exposito, A., Beier, F., and Berbel, J. (2020). Hydro-Economic modelling for water-policy assessment under climate change at a river basin scale: a review. Water 12:1559. doi: 10.3390/w12061559

CrossRef Full Text | Google Scholar

Finkele, K., Mills, G. A., Beard, G., and Jones, D. A. (2006). National gridded drought factors and comparison of two soil moisture deficit formulations used in prediction of forest fire danger index in Australia. Austr. Meteorol. Magaz. 55, 183–197.

Google Scholar

Fischer, G., and Sun, L. X. (2001). Model based analysis of future land-use development in China. Agric. Ecosyst. Environ. 85, 163–176. doi: 10.1016/S0167-8809(01)00182-7

CrossRef Full Text | Google Scholar

Flanagan, S. V., Johnston, R. B., and Zheng, Y. (2012). Arsenic in tube well water in Bangladesh: health and economic impacts and implications for arsenic mitigation. Bull. World Health Organ. 90, 839–846. doi: 10.2471/BLT.11.101253

PubMed Abstract | CrossRef Full Text | Google Scholar

Foster, T., Brozovic, N., and Butler, A. P. (2014). Modeling irrigation behavior in groundwater systems. Water Resour. Res. 50, 6370–6389. doi: 10.1002/2014WR015620

CrossRef Full Text | Google Scholar

Foster, T., Brozovic, N., and Butler, A. P. (2015). Analysis of the impacts of well yield and groundwater depth on irrigated agriculture. J. Hydrol. 523, 86–96. doi: 10.1016/j.jhydrol.2015.01.032

CrossRef Full Text | Google Scholar

Foudi, S., Oses-Eraso, N., and Tamayo, I. (2015). Integrated spatial flood risk assessment: the case of Zaragoza. Land Use Policy 42, 278–292. doi: 10.1016/j.landusepol.2014.08.002

CrossRef Full Text | Google Scholar

Fu, G., Kapelan, Z., Kasprzyk, J. R., and Reed, P. (2013). Optimal design of water distribution systems using many-objective visual analytics. J. Water Resour. Plan. Manag. 139, 624–633. doi: 10.1061/(ASCE)WR.1943-5452.0000311

CrossRef Full Text | Google Scholar

Garriga, R. G., and Foguet, A. P. (2010). Improved method to calculate a water poverty index at local scale. J. Environ. Eng. 136, 1287–1298. doi: 10.1061/(ASCE)EE.1943-7870.0000255

CrossRef Full Text | Google Scholar

George, B., Malano, H., Davidson, B., Hellegers, P., Bharati, L., and Massuel, S. (2011a). An integrated hydro-economic modelling framework to evaluate water allocation strategies I: model development. Agric. Water Manag. 98, 733–746. doi: 10.1016/j.agwat.2010.12.004

CrossRef Full Text | Google Scholar

George, B., Malano, H., Davidson, B., Hellegers, P., Bharati, L., and Massuel, S. (2011b). An integrated hydro-economic modelling framework to evaluate water allocation strategies II: scenario assessment. Agric. Water Manag. 98, 747–758. doi: 10.1016/j.agwat.2010.12.005

CrossRef Full Text | Google Scholar

Godfray, H. C. J., Beddington, J. R., Crute, I. R., Haddad, L., Lawrence, D., Muir, J. F., et al. (2010). Food security: the challenge of feeding 9 billion people. Science. 327, 812–818. doi: 10.1126/science.1185383

PubMed Abstract | CrossRef Full Text | Google Scholar

Gohar, A. A., Amer, S. A., and Ward, F. A. (2015). Irrigation infrastructure and water appropriation rules for food security. J. Hydrol. 520, 85–100. doi: 10.1016/j.jhydrol.2014.11.036

CrossRef Full Text | Google Scholar

Gohar, A. A., Cashman, A., and Ward, F. A. (2019). Managing food and water security in Small Island states: new evidence from economic modelling of climate stressed groundwater resources. J. Hydrol. 569, 239–251. doi: 10.1016/j.jhydrol.2018.12.008

CrossRef Full Text | Google Scholar

Goncalves, J., Deschamps, P., Hamelin, B., Vallet-Coulomb, C., Petersen, J., and Chekireb, A. (2020). Revisiting recharge and sustainability of the North-Western Sahara aquifers. Reg. Environ. Change 20:47. doi: 10.1007/s10113-020-01627-4

CrossRef Full Text | Google Scholar

Gonzalez, J. M., Olivares, M. A., Medellin-Azuara, J., and Moreno, R. (2020). Multipurpose reservoir operation: a multi-scale tradeoff analysis between hydropower generation and irrigated agriculture. Water Resour. Manag. 34, 2837–2849. doi: 10.1007/s11269-020-02586-5

CrossRef Full Text | Google Scholar

Goor, Q., Halleux, C., Mohamed, Y., and Tilmant, A. (2010). Optimal operation of a multipurpose multireservoir system in the Eastern Nile River Basin. Hydrol. Earth Syst. Sci. 14, 1895–1908. doi: 10.5194/hess-14-1895-2010

CrossRef Full Text | Google Scholar

Goor, Q., Kelman, R., and Tilmant, A. (2011). Optimal multipurpose-multireservoir operation model with variable productivity of hydropower plants. J. Water Resour. Plan. Manag. 137, 258–267. doi: 10.1061/(ASCE)WR.1943-5452.0000117

CrossRef Full Text | Google Scholar

Grafton, R. Q., and Jiang, Q. (2011). Economic effects of water recovery on irrigated agriculture in the murray-darling basin. Austr. J. Agric. Resour. Econ. 55, 487–499. doi: 10.1111/j.1467-8489.2011.00545.x

CrossRef Full Text | Google Scholar

Grafton, R. Q., Williams, J., Perry, C. J., Molle, F., Ringler, C., Steduto, P., et al. (2018). The paradox of irrigation efficiency. Science 361, 748–750. doi: 10.1126/science.aat9314

CrossRef Full Text | Google Scholar

Graveline, N. (2020). Combining flexible regulatory and economic instruments for agriculture water demand control under climate change in Beauce. Water Resour. Econ. 29:100143. doi: 10.1016/j.wre.2019.100143

CrossRef Full Text | Google Scholar

Graveline, N., Majone, B., Van Duinen, R., and Ansink, E. (2014). Hydro-economic modeling of water scarcity under global change: an application to the Gallego river basin (Spain). Reg. Environ. Change 14, 119–132. doi: 10.1007/s10113-013-0472-0

CrossRef Full Text | Google Scholar

Guan, D., and Hubacek, K. (2007). Assessment of regional trade and virtual water flows in China. Ecol. Econ. 61, 159–170. doi: 10.1016/j.ecolecon.2006.02.022

CrossRef Full Text | Google Scholar

Guan, D., and Hubacek, K. (2008). A new and integrated hydro-economic accounting and analytical framework for water resources: a case study for North China. J. Environ. Manag. 88, 1300–1313. doi: 10.1016/j.jenvman.2007.07.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Gunawardena, A., White, B., Hailu, A., Wijeratne, E. M. S., and Pandit, R. (2018). Policy choice and riverine water quality in developing countries: an integrated hydro-economic modelling approach. J. Environ. Manag. 227, 44–54. doi: 10.1016/j.jenvman.2018.08.065

PubMed Abstract | CrossRef Full Text | Google Scholar

Habteyes, B. G., El-Bardisy, H., Amer, S. A., Schneider, V. R., and Ward, F. A. (2015). Mutually beneficial and sustainable management of Ethiopian and Egyptian dams in the Nile Basin. J. Hydrol. 529, 1235–1246. doi: 10.1016/j.jhydrol.2015.09.017

CrossRef Full Text | Google Scholar

Habteyes, B. G., and Ward, F. A. (2020). Economics of irrigation water conservation: dynamic optimization for consumption and investment. J. Environ. Manag. 258:110040. doi: 10.1016/j.jenvman.2019.110040

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, M. Y., Guo, S., Chen, H., Ji, X., and Li, J. S. (2014). Local-scale systems input-output analysis of embodied water for the Beijing economy in 2007. Front. Earth Sci. 8, 414–426. doi: 10.1007/s11707-014-0430-2

CrossRef Full Text | Google Scholar

Hanak, E., Escriva-Bou, A., Gray, B., Green, S., Harter, T., Jezdimirovic, J., et al. (2019). Water and the Future of the San Joaquin Valley. San Francisco, CA: Public Policy Institute of California.

Google Scholar

Hanna-Attisha, M., LaChance, J., Sadler, R. C., and Schnepp, A. C. (2016). Elevated blood lead levels in children associated with the flint drinking water crisis: a spatial analysis of risk and public health response. Am. J. Public Health 106, 283–290. doi: 10.2105/AJPH.2015.303003

PubMed Abstract | CrossRef Full Text | Google Scholar

Haro-Monteagudo, D., Solera, A., and Andreu, J. (2017). Drought early warning based on optimal risk forecasts in regulated river systems: application to the Jucar River Basin (Spain). J. Hydrol. 544, 36–45. doi: 10.1016/j.jhydrol.2016.11.022

CrossRef Full Text | Google Scholar

Harou, J. J., and Lund, J. R. (2008). Ending groundwater overdraft in hydrologic-economic systems. Hydrogeol. J. 16, 1039–1055. doi: 10.1007/s10040-008-0300-7

CrossRef Full Text | Google Scholar

Harou, J. J., Medellin-Azuara, J., Zhu, T. J., Tanaka, S. K., Lund, J. R., Stine, S., et al. (2010). Economic consequences of optimized water management for a prolonged, severe drought in California. Water Resour. Res. 46:W05522. doi: 10.1029/2008WR007681

CrossRef Full Text | Google Scholar

Harou, J. J., Pulido-Velazquez, M., Rosenberg, D. E., Medellin-Azuara, J., Lund, J. R., and Howitt, R. E. (2009). Hydro-economic models: concepts, design, applications, future prospects. J. Hydrol. 375, 627–643. doi: 10.1016/j.jhydrol.2009.06.037

CrossRef Full Text | Google Scholar

Hasnain, S. M., and Alajlan, S. A. (1998). Coupling of PV-powered RO brackish water desalination plant with solar stills. Desalination 116, 57–64. doi: 10.1016/S0011-9164(98)00057-5

CrossRef Full Text | Google Scholar

Hering, D., Borja, A., Carstensen, J., Carvalho, L., Elliott, M., Feld, C. K., et al. (2010). The European water framework directive at the age of 10: a critical review of the achievements with recommendations for the future. Sci. Total Environ. 408, 4007–4019. doi: 10.1016/j.scitotenv.2010.05.031

PubMed Abstract | CrossRef Full Text | Google Scholar

Hervas-Gamez, C., and Delgado-Ramos, F. (2020). Cross-Subsidies between water users in spain: the guadalquivir river basin case. Water Resour. Manag. 34, 4577–4591. doi: 10.1007/s11269-020-02675-5

CrossRef Full Text | Google Scholar

Hoeksema, R. J. (2007). Three stages in the history of land reclamation in the Netherlands. Irrig. Drain. 56, S113–S126. doi: 10.1002/ird.340

CrossRef Full Text | Google Scholar

Howitt, R. E. (1995). Positive mathematical-programming. Am. J. Agric. Econ. 77, 329–342. doi: 10.2307/1243543

CrossRef Full Text | Google Scholar

Hrozencik, R. A., Manning, D. T., Suter, J. F., Goemans, C., and Bailey, R. T. (2017). The heterogeneous impacts of groundwater management policies in the republican river Basin of Colorado. Water Resourc. Res. 53, 10757–10778. doi: 10.1002/2017WR020927

CrossRef Full Text | Google Scholar

Hudson, P., and Botzen, W. J. W. (2019). Cost-benefit analysis of flood-zoning policies: a review of current practice. Wiley Interdiscip. Rev. Water 6:e1387. doi: 10.1002/wat2.1387

CrossRef Full Text | Google Scholar

Huffaker, R., and Whittlesey, N. (2000). The allocative efficiency and conservation potential of water laws encouraging investments in on-farm irrigation technology. Agric. Econ. 24, 47–60. doi: 10.1111/j.1574-0862.2000.tb00092.x

CrossRef Full Text | Google Scholar

Hurd, B. H., and Coonrod, J. (2012). Hydro-economic consequences of climate change in the upper Rio Grande. Clim. Res. 53, 103–118. doi: 10.3354/cr01092

CrossRef Full Text | Google Scholar

Intriligator, M. D. (2002). Mathematical Optimization and Economic Theory. Englewood Cliffs, NJ: SIAM. doi: 10.1137/1.9780898719215

CrossRef Full Text | Google Scholar

Irabien, A., and Darton, R. C. (2016). Energy-water-food nexus in the Spanish greenhouse tomato production. Clean Technol. Environ. Policy 18, 1307–1316. doi: 10.1007/s10098-015-1076-9

CrossRef Full Text | Google Scholar

Jacobson, M. Z., Delucchi, M. A., Cameron, M. A., and Frew, B. A. (2015). Low-cost solution to the grid reliability problem with 100% penetration of intermittent wind, water, and solar for all purposes. Proc. Natl. Acad. Sci. U.S.A. 112, 15060–15065. doi: 10.1073/pnas.1510028112

PubMed Abstract | CrossRef Full Text | Google Scholar

Jalilov, S. M., Keskinen, M., Varis, O., Amer, S., and Ward, F. A. (2016). Managing the water-energy-food nexus: Gains and losses from new water development in Amu Darya River Basin. J. Hydrol. 539, 648–661. doi: 10.1016/j.jhydrol.2016.05.071

CrossRef Full Text | Google Scholar

Jalilov, S. M., Varis, O., and Keskinen, M. (2015). Sharing benefits in transboundary rivers: an experimental case study of central asian water-energy-agriculture nexus. Water 7, 4778–4805. doi: 10.3390/w7094778

CrossRef Full Text | Google Scholar

Jenkins, M. W., and Lund, J. R. (2000). Integrating yield and shortage management under multiple uncertainties. J. Water Resourc. Plan. Manage. 126, 288–297. doi: 10.1061/(ASCE)0733-9496(2000)126:5(288)

CrossRef Full Text | Google Scholar

Jeuland, M. (2010). Economic implications of climate change for infrastructure planning in transboundary water systems: an example from the Blue Nile. Water Resour. Res 46:W11556. doi: 10.1029/2010WR009428

CrossRef Full Text | Google Scholar

Jeuland, M. (2020). The economics of dams. Oxford Rev. Econ. Policy 36, 45–68. doi: 10.1093/oxrep/grz028

CrossRef Full Text | Google Scholar

Jeuland, M., Wu, X., and Whittington, D. (2017). Infrastructure development and the economics of cooperation in the Eastern Nile. Water Int. 42, 121–141. doi: 10.1080/02508060.2017.1278577

CrossRef Full Text | Google Scholar

Jiang, L., Wu, F., Liu, Y., and Deng, X. Z. (2014). Modeling the impacts of urbanization and industrial transformation on water resources in china: an integrated hydro-economic CGE analysis. Sustainability 6, 7586–7600. doi: 10.3390/su6117586

CrossRef Full Text | Google Scholar

Jiang, Q., and Grafton, R. Q. (2012). Economic effects of climate change in the Murray-Darling Basin, Australia. Agric. Syst. 110, 10–16. doi: 10.1016/j.agsy.2012.03.009

CrossRef Full Text | Google Scholar

Johnston, R., and Kummu, M. (2012). Water resource models in the mekong basin: a review. Water Resour. Manag. 26, 429–455. doi: 10.1007/s11269-011-9925-8

CrossRef Full Text | Google Scholar

Johnston, R. J., and Rosenberger, R. S. (2010). Methods, trends and controversies in contemporary benefit transfer. Econ. Surveys 24, 479–510. doi: 10.1111/j.1467-6419.2009.00592.x

CrossRef Full Text | Google Scholar

Kahil, M. T., Dinar, A., and Albiac, J. (2015). Modeling water scarcity and droughts for policy adaptation to climate change in arid and semiarid regions. J. Hydrol. 522, 95–109. doi: 10.1016/j.jhydrol.2014.12.042

CrossRef Full Text | Google Scholar

Kahil, M. T., Ward, F. A., Albiac, J., Eggleston, J., and Sanz, D. (2016). Hydro-economic modeling with aquifer-river interactions to guide sustainable basin management. J. Hydrol. 539, 510–524. doi: 10.1016/j.jhydrol.2016.05.057

CrossRef Full Text | Google Scholar

Kahil, T., Parkinson, S., Satoh, Y., Greve, P., Burek, P., Veldkamp, T. I. E., et al. (2018). A continental-scale hydroeconomic model for integrating water-energy-land nexus solutions. Water Resour. Res. 54, 7511–7533. doi: 10.1029/2017WR022478

CrossRef Full Text | Google Scholar

Kahsay, T. N., Arjoon, D., Kuik, O., Brouwer, R., Tilmant, A., and van der Zaag, P. (2019). A hybrid partial and general equilibrium modeling approach to assess the hydro-economic impacts of large dams - the case of the grand ethiopian renaissance dam in the Eastern Nile River basin. Environ. Model. Softw. 117, 76–88. doi: 10.1016/j.envsoft.2019.03.007

CrossRef Full Text | Google Scholar

Keynes, J. (1936). The General Theory of Employment, Interest and Money. London: Macmillan.

Google Scholar

Khadem, M., Rouge, C., Harou, J. J., Hansen, K. M., Medellin-Azuara, J., and Lund, J. R. (2018). Estimating the economic value of interannual reservoir storage in water resource systems. Water Resour. Res. 54, 8890–8908. doi: 10.1029/2017WR022336

CrossRef Full Text | Google Scholar

Kiptala, J. K., Mul, M. L., Mohamed, Y. A., and van der Zaag, P. (2018). Multiobjective Analysis of green-blue water uses in a highly utilized basin: case study of pangani basin, Africa. J. Water Resour. Plan. Manage. 144:12. doi: 10.1061/(ASCE)WR.1943-5452.0000960

CrossRef Full Text | Google Scholar

Klein, S. J. W., and Whalley, S. (2015). Comparing the sustainability of US electricity options through multi-criteria decision analysis. Energy Policy 79, 127–149. doi: 10.1016/j.enpol.2015.01.007

CrossRef Full Text | Google Scholar

Konapala, G., and Mishra, A. (2020). Dynamics of virtual water networks: role of national socio-economic indicators across the world. J. Hydrol 589:125171. doi: 10.1016/j.jhydrol.2020.125171

CrossRef Full Text | Google Scholar

Kourgialas, N. N., and Karatzas, G. P. (2013). A hydro-economic modelling framework for flood damage estimation and the role of riparian vegetation. Hydrol. Process. 27, 515–531. doi: 10.1002/hyp.9256

CrossRef Full Text | Google Scholar

Kovacs, K. F., and Durand-Morat, A. (2020). The influence of lateral flows in an aquifer on the agricultural value of groundwater. Nat. Resourc. Model. 33:e12266. doi: 10.1111/nrm.12266

CrossRef Full Text | Google Scholar

Krugman, P. R., Obstfeld, M., and Melitz, M. (2011). Resources and trade: the heckscher-ohlin model. Int. Econ. Theory Policy 13.

Kuhn, A., and Britz, W. (2012). Can hydro-economic river basin models simulate water shadow prices under asymmetric access? Water Sci. Technol. 66, 879–886. doi: 10.2166/wst.2012.251

PubMed Abstract | CrossRef Full Text | Google Scholar

Labadie, J. W. (2004). Optimal operation of multireservoir systems: state-of-the-art review. J. Water Res. Plan. Manag. 130, 93–111. doi: 10.1061/(ASCE)0733-9496(2004)130:2(93)

CrossRef Full Text | Google Scholar

Lester, R. E., Webster, I. T., Fairweather, P. G., and Young, W. J. (2011). Linking water-resource models to ecosystem-response models to guide water-resource planning - an example from the Murray - Darling Basin, Australia. Marine Freshw. Res. 62, 279–289. doi: 10.1071/MF09298

CrossRef Full Text | Google Scholar

Levers, L. R., Skaggs, T. H., and Schwabe, K. A. (2019). Buying water for the environment: a hydro-economic analysis of Salton Sea inflows. Agric. Water Manage. 213, 554–567. doi: 10.1016/j.agwat.2018.10.041

CrossRef Full Text | Google Scholar

Liu, J. G., Hull, V., Godfray, H. C. J., Tilman, D., Gleick, P., Hoff, H., et al. (2018). Nexus approaches to global sustainable development. Nat. Sust. 1, 466–476. doi: 10.1038/s41893-018-0135-8

CrossRef Full Text | Google Scholar

Loomis, J. B. (2000). Environmental valuation techniques in water resource decision making. J. Water Resourc. Plan. Manag. 126, 339–344. doi: 10.1061/(ASCE)0733-9496(2000)126:6(339)

CrossRef Full Text | Google Scholar

Lopez-Nicolas, A., Pulido-Velazquez, M., Rouge, C., Harou, J. J., and Escriva-Bou, A. (2018). Design and assessment of an efficient and equitable dynamic urban water tariff. Application to the city of Valencia, Spain. Environ. Model. Softw. 101, 137–145. doi: 10.1016/j.envsoft.2017.12.018

CrossRef Full Text | Google Scholar

Maass, A., Hufschmidt, M. M., Dorfman, R., Thomas. Jr, H. A., Marglin, S. A., and Fair, G. M. (1962). Design of Water-Resource Systems: New Techniques for Relating Economic Objectives, Engineering Analysis, Governmental Planning. Cambridge, MA: Harvard University Press. doi: 10.4159/harvard.9780674421042

CrossRef Full Text | Google Scholar

Macdonald, N., Chester, D., Sangster, H., Todd, B., and Hooke, J. (2012). The significance of Gilbert F. White's 1945 paper ‘human adjustment to floods' in the development of risk and hazard management. Progr. Phys. Geogr. 36, 125–133. doi: 10.1177/0309133311414607

CrossRef Full Text | Google Scholar

MacEwan, D., Cayar, M., Taghavi, A., Mitchell, D., Hatchett, S., and Howitt, R. (2017). Hydroeconomic modeling of sustainable groundwater management. Water Resour. Res. 53, 2384–2403. doi: 10.1002/2016WR019639

CrossRef Full Text | Google Scholar

Maneta, M. P., Cobourn, K., Kimball, J. S., He, M., Silverman, N. L., Chaffin, B. C., et al. (2020). A satellite-driven hydro-economic model to support agricultural water resources management. Environ. Model. Softw. 134:104836. doi: 10.1016/j.envsoft.2020.104836

CrossRef Full Text | Google Scholar

Martinsen, G., Liu, S. X., Mo, X. G., and Bauer-Gottwein, P. (2019). Optimizing water resources allocation in the Haihe River basin under groundwater sustainability constraints. J. Geogra. Sci. 29, 935–958. doi: 10.1007/s11442-019-1638-6

CrossRef Full Text | Google Scholar

McDonald, M. G., and Harbaugh, A. W. (2003). The history of MODFLOW. Ground Water 41, 280–283. doi: 10.1111/j.1745-6584.2003.tb02591.x

CrossRef Full Text | Google Scholar

Medellin-Azuara, J., Howitt, R. E., and Harou, J. J. (2012). Predicting farmer responses to water pricing, rationing and subsidies assuming profit maximizing investment in irrigation technology. Agric. Water Manag. 108, 73–82. doi: 10.1016/j.agwat.2011.12.017

CrossRef Full Text | Google Scholar

Medellin-Azuara, J., MacEwan, D., Howitt, R. E., Koruakos, G., Dogrul, E. C., Brush, C. F., et al. (2015). Hydro-economic analysis of groundwater pumping for irrigated agriculture in California's Central Valley, USA. Hydrogeol. J. 23, 1205–1216. doi: 10.1007/s10040-015-1283-9

CrossRef Full Text | Google Scholar

Medellin-Azuara, J., Mendoza-Espinosa, L. G., Lund, J. R., Harou, J. J., and Howitt, R. E. (2009). Virtues of simple hydro-economic optimization: Baja California, Mexico. J. Environ. Manag. 90, 3470–3478. doi: 10.1016/j.jenvman.2009.05.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, Y., Liu, J. G., Leduc, S., Mesfun, S., Kraxner, F., Mao, G. Q., et al. (2020). Hydropower production benefits more from 1.5 degrees c than 2 degrees C climate scenario. Water Res. Res 56. doi: 10.1029/2019WR025519

CrossRef Full Text | Google Scholar

Merz, B., Kreibich, H., Schwarze, R., and Thieken, A. (2010). Review article 'Assessment of economic flood damage'. Nat. Haz. Earth Syst. Sci. 10, 1697–1724. doi: 10.5194/nhess-10-1697-2010

CrossRef Full Text | Google Scholar

Miller, G. W. (2006). Integrated concepts in water reuse: managing global water needs. Desalination 187, 65–75. doi: 10.1016/j.desal.2005.04.068

CrossRef Full Text | Google Scholar

Molina, J. L., Pulido-Velazquez, M., Llopis-Albert, C., and Pena-Haro, S. (2013). Stochastic hydro-economic model for groundwater quality management using Bayesian networks. Water Sci. Technol. 67, 579–586. doi: 10.2166/wst.2012.598

PubMed Abstract | CrossRef Full Text | Google Scholar

Molinos-Senante, M., Hanley, N., and Sala-Garrido, R. (2015). Measuring the CO₂ shadow price for wastewater treatment: a directional distance function approach. Appl. Energy 144, 241–249. doi: 10.1016/j.apenergy.2015.02.034

CrossRef Full Text | Google Scholar

Mullick, M. R. A., Babel, M. S., and Perret, S. R. (2013). Marginal benefit based optimal water allocation: case of Teesta River, Bangladesh. Water Policy 15, 126–146. doi: 10.2166/wp.2013.004

CrossRef Full Text | Google Scholar

Muneepeerakul, R., and Anderies, J. M. (2017). Strategic behaviors and governance challenges in social-ecological systems. Earths Fut. 5, 865–876. doi: 10.1002/2017EF000562

CrossRef Full Text | Google Scholar

Nagase, Y., and Uehara, T. (2011). Evolution of population-resource dynamics models. Ecol. Econ. 72, 9–17. doi: 10.1016/j.ecolecon.2011.09.003

CrossRef Full Text | Google Scholar

Nakashima, T. (2011). Positive mathematical programming for farm planning: review. Jarq Japan Agric. Res. Q. 45, 251–258. doi: 10.6090/jarq.45.251

CrossRef Full Text | Google Scholar

Nechifor, V., and Winning, M. (2018). Global economic and food security impacts of demand-driven water scarcity-alternative water management options for a thirsty world. Water 10:1442. doi: 10.3390/w10101442

CrossRef Full Text | Google Scholar

Ngigi, S. N., Savenije, H. H. G., Rockstrom, J., and Gachene, C. K. (2005). Hydro-economic evaluation of rainwater harvesting and management technologies: farmers' investment options and risks in semi-arid Laikipia district of Kenya. Phys. Chem. Earth 30, 772–782. doi: 10.1016/j.pce.2005.08.020

CrossRef Full Text | Google Scholar

Nordhaus, W. (2015). Climate Clubs: overcoming free-riding in international climate policy. Am. Econ. Rev. 105, 1339–1370. doi: 10.1257/aer.15000001

CrossRef Full Text | Google Scholar

Nordhaus, W. D. (2017). Revisiting the social cost of carbon. Proc. Natl. Acad. Sci. U.S.A. 114, 1518–1523. doi: 10.1073/pnas.1609244114

CrossRef Full Text | Google Scholar

Ogle, K., Whitham, T. G., and Cobb, N. S. (2000). Tree-ring variation in pinyon predicts likelihood of death following severe drought. Ecology 81, 3237–3243. doi: 10.1890/0012-9658(2000)081[3237:TRVIPP]2.0.CO;2

CrossRef Full Text | Google Scholar

Oiro, S., Comte, J. C., Soulsby, C., and Walraevens, K. (2018). Using stable water isotopes to identify spatio-temporal controls on groundwater recharge in two contrasting East African aquifer systems. Hydrol. Sci. J. 63, 862–877. doi: 10.1080/02626667.2018.1459625

CrossRef Full Text | Google Scholar

Ostfeld, A., Uber, J. G., Salomons, E., Berry, J. W., Hart, W. E., Phillips, C. A., et al. (2008). The battle of the water sensor networks (BWSN): a design challenge for engineers and algorithms. J. Water Resourc. Plan. Manage. 134, 556–568. doi: 10.1061/(ASCE)0733-9496(2008)134:6(556)

CrossRef Full Text | Google Scholar

Ostrom, E. (2007). A diagnostic approach for going beyond panaceas. Proc. Natl. Acad. Sci. U.S.A. 104, 15181–15187. doi: 10.1073/pnas.0702288104

PubMed Abstract | CrossRef Full Text | Google Scholar

Pakhtigian, E. L., Jeuland, M., Dhaubanjar, S., and Pandey, V. P. (2020). Balancing intersectoral demands in basin-scale planning: the case of Nepal's western river basins. Water Resourc. Econ. 30:100152. doi: 10.1016/j.wre.2019.100152

CrossRef Full Text | Google Scholar

Pande, S., van den Boom, B., Savenije, H. H. G., and Gosain, A. K. (2011). Water valuation at basin scale with application to western India. Ecol. Econ. 70, 2416–2428. doi: 10.1016/j.ecolecon.2011.07.025

CrossRef Full Text | Google Scholar

Pareto, V. (1971). Manual of Political Economy. New York, NY: A. M. Kelley.

Google Scholar

Parry, W. T. (1957). Reexamination of the problem of counterfactual conditionals. J. Philos. 54, 85–94. doi: 10.2307/2022496

CrossRef Full Text | Google Scholar

Pena-Haro, S., Llopis-Albert, C., Pulido-Velazquez, M., and Pulido-Velazquez, D. (2010). Fertilizer standards for controlling groundwater nitrate pollution from agriculture: El Salobral-Los Llanos case study, Spain. J. Hydrol. 392, 174–187. doi: 10.1016/j.jhydrol.2010.08.006

CrossRef Full Text | Google Scholar

Pena-Haro, S., Pulido-Velazquez, M., and Llopis-Albert, C. (2011). Stochastic hydro-economic modeling for optimal management of agricultural groundwater nitrate pollution under hydraulic conductivity uncertainty. Environ. Model. Softw. 26, 999–1008. doi: 10.1016/j.envsoft.2011.02.010

CrossRef Full Text | Google Scholar

Pena-Haro, S., Pulido-Velazquez, M., and Sahuquillo, A. (2009). A hydro-economic modelling framework for optimal management of groundwater nitrate pollution from agriculture. J. Hydrol. 373, 193–203. doi: 10.1016/j.jhydrol.2009.04.024

CrossRef Full Text | Google Scholar

Perry, C., Steduto, P., and Karajeh, F. (2017). Does improved irrigation technology save water? A review of the evidence. Food Agric. Organ. United Nat. 42.

Google Scholar

Persky, J. (2001). Cost-benefit analysis and the classical creed. J. Econ. Perspect. 15, 199–208. doi: 10.1257/jep.15.4.199

CrossRef Full Text | Google Scholar

Poli, R., Kennedy, J., and Blackwell, T. (2007). Particle swarm optimization. Swarm Intell. 1, 33–57. doi: 10.1007/s11721-007-0002-0

CrossRef Full Text | Google Scholar

Porse, E., and Lund, J. (2016). Network analysis and visualizations of water resources infrastructure in california: linking connectivity and resilience. J. Water Resourc. Plan. Manag. 142. doi: 10.1061/(ASCE)WR.1943-5452.0000556

CrossRef Full Text | Google Scholar

Porse, E., Mika, K. B., Litvak, E., Manago, K. F., Hogue, T. S., Gold, M., et al. (2018). The economic value of local water supplies in Los Angeles. Nat. Sust. 1, 289–297. doi: 10.1038/s41893-018-0068-2

CrossRef Full Text | Google Scholar

Porse, E., Mika, K. B., Litvak, E., Manago, K. F., Naik, K., Glickfeld, M., et al. (2017). Systems analysis and optimization of local water supplies in Los Angeles. J. Water Resourc. Plan. Manage. 143:14. doi: 10.1061/(ASCE)WR.1943-5452.0000803

CrossRef Full Text | Google Scholar

Pulido-Velazquez, M., Alvarez-Mendiola, E., and Andreu, J. (2013). Design of efficient water pricing policies integrating basinwide resource opportunity costs. J. Water Res. Plan. Manag. 139, 583–592. doi: 10.1061/(ASCE)WR.1943-5452.0000262

CrossRef Full Text | Google Scholar

Pulido-Velazquez, M., Andreu, J., Sahuquillo, A., and Pulido-Velazquez, D. (2008). Hydro-economic river basin modelling: the application of a holistic surface-groundwater model to assess opportunity costs of water use in Spain. Ecol. Econ. 66, 51–65. doi: 10.1016/j.ecolecon.2007.12.016

CrossRef Full Text | Google Scholar

Qureshi, M. E., Hanjra, M. A., and Ward, J. (2013). Impact of water scarcity in Australia on global food security in an era of climate change. Food Policy 38, 136–145. doi: 10.1016/j.foodpol.2012.11.003

CrossRef Full Text | Google Scholar

Ramsey, F. P. (1928). A mathematical theory of saving. The Econ. J. 38, 543–559. doi: 10.2307/2224098

CrossRef Full Text | Google Scholar

Randhir, T. O., O'Connor, R., Penner, P. R., and Goodwin, D. W. (2001). A watershed-based land prioritization model for water supply protection. Forest Ecology and Management. 143, 47–56. doi: 10.1016/S0378-1127(00)00504-1

CrossRef Full Text | Google Scholar

Ray, P. A., Yang, Y. C. E., Wi, S., Khalil, A., Chatikavanij, V., and Brown, C. (2015). Room for improvement: hydroclimatic challenges to poverty-reducing development of the Brahmaputra River basin. Environ. Sci. Policy 54, 64–80. doi: 10.1016/j.envsci.2015.06.015

CrossRef Full Text | Google Scholar

Riegels, N., Pulido-Velazquez, M., Doulgeris, C., Sturm, V., Jensen, R., Moller, F., et al. (2013). Systems analysis approach to the design of efficient water pricing policies under the EU water framework directive. J. Water Resourc. Plan. Manage. 139, 574–582. doi: 10.1061/(ASCE)WR.1943-5452.0000284

CrossRef Full Text | Google Scholar

Rockstrom, J., Gaffney, O., Rogelj, J., Meinshausen, M., Nakicenovic, N., and Schellnhuber, H. J. (2017). Climate policy a roadmap for rapid decarbonization. Science 355, 1269–1271. doi: 10.1126/science.aah3443

CrossRef Full Text | Google Scholar

Rodell, M., Velicogna, I., and Famiglietti, J. S. (2009). Satellite-based estimates of groundwater depletion in India. Nature 460, 999–U80. doi: 10.1038/nature08238

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogers, P., De Silva, R., and Bhatia, R. (2002). Water is an economic good: How to use prices to promote equity, efficiency, and sustainability. Water Policy 4, 1–17. doi: 10.1016/S1366-7017(02)00004-1

CrossRef Full Text | Google Scholar

Rosenberg, D. E., Howitt, R. E., and Lund, J. R. (2008). Water management with water conservation, infrastructure expansions, and source variability in Jordan. Water Resour. Res 44. doi: 10.1029/2007WR006519

CrossRef Full Text | Google Scholar

Rosenberg, D. E., Tarawneh, T., Abdel-Khaleq, R., and Lund, J. R. (2007). Modeling integrated water user decisions in intermittent supply systems. Water Resour. Res 43. doi: 10.1029/2006WR005340

CrossRef Full Text | Google Scholar

Rozin, P., Haddad, B., Nemeroff, C., and Slovic, P. (2015). Psychological aspects of the rejection of recycled water: contamination, purification and disgust. Judge. Dec. Mak. 10, 50–63.

Google Scholar

Ruddell, B. L., Adams, E. A., Rushforth, R., and Tidwell, V. C. (2014). Embedded resource accounting for coupled natural-human systems: an application to water resource impacts of the western US electrical energy trade. Water Resourc. Res. 50, 7957–7972. doi: 10.1002/2013WR014531

CrossRef Full Text | Google Scholar

Ruperez-Moreno, C., Senent-Aparicio, J., Martinez-Vicente, D., Garcia-Arostegui, J. L., Calvo-Rubio, F. C., and Perez-Sanchez, J. (2017). Sustainability of irrigated agriculture with overexploited aquifers: the case of Segura basin (SE, Spain). Agric. Water Manag. 182, 67–76. doi: 10.1016/j.agwat.2016.12.008

CrossRef Full Text | Google Scholar

Sabbaghi, M. A., Nazari, M., Araghinejad, S., and Soufizadeh, S. (2020). Economic impacts of climate change on water resources and agriculture in Zayandehroud river basin in Iran. Agric. Water Manag. 241:106323. doi: 10.1016/j.agwat.2020.106323

CrossRef Full Text | Google Scholar

Salomon, R. (1998). Evolutionary algorithms and gradient search: similarities and differences. IEEE Trans. Evolut. Comput. 2, 45–55. doi: 10.1109/4235.728207

CrossRef Full Text | Google Scholar

Satoh, Y., Kahil, T., Byers, E., Burek, P., Fischer, G., Tramberend, S., et al. (2017). Multi-model and multi-scenario assessments of Asian water futures: the water futures and solutions (WFaS) initiative. Earths Fut. 5, 823–852. doi: 10.1002/2016EF000503

CrossRef Full Text | Google Scholar

Satti, S., Zaitchik, B., and Siddiqui, S. (2015). The question of Sudan: a hydro-economic optimization model for the Sudanese Blue Nile. Hydrol. Earth Syst. Sci. 19, 2275–2293. doi: 10.5194/hess-19-2275-2015

CrossRef Full Text | Google Scholar

Schwabe, K., Nemati, M., Landry, C., and Zimmerman, G. (2020). Water markets in the western united states: trends and opportunities. Water 12:233. doi: 10.3390/w12010233

CrossRef Full Text | Google Scholar

Siderius, C., Van Walsum, P. E. V., Roest, C. W. J., Smit, A., Hellegers, P., Kabat, P., et al. (2016). The role of rainfed agriculture in securing food production in the Nile Basin. Environ. Sci. Policy 61, 14–23. doi: 10.1016/j.envsci.2016.03.007

CrossRef Full Text | Google Scholar

Simonovic, S. P. (2000). Tools for water management - one view of the future. Water Int. 25, 76–88. doi: 10.1080/02508060008686799

CrossRef Full Text | Google Scholar

Skurray, J. H., Roberts, E. J., and Pannell, D. J. (2012). Hydrological challenges to groundwater trading: lessons from south-west Western Australia. J. Hydrol. 412, 256–268. doi: 10.1016/j.jhydrol.2011.05.034

CrossRef Full Text | Google Scholar

Slater, Y., Finkelshtain, I., Reznik, A., and Kan, I. (2020). Large-Scale desalination and the external impact on irrigation-water salinity: economic analysis for the case of Israel. Water Resourc. Res 56:e2019WR025657. doi: 10.1029/2019WR025657

CrossRef Full Text | Google Scholar

Solow, R. M. (1956). A contribution to the theory of economic-growth. Q. J. Econ. 70, 65–94. doi: 10.2307/1884513

CrossRef Full Text | Google Scholar

Stenger, A., and Willinger, M. (1998). Preservation value for groundwater quality in a large aquifer: a contingent-valuation study of the Alsatian aquifer. J. Environ. Manag. 53, 177–193. doi: 10.1006/jema.1998.0197

CrossRef Full Text | Google Scholar

Sullivan, C. (2002). Calculating a water poverty index. World Dev. 30, 1195–1210. doi: 10.1016/S0305-750X(02)00035-9

CrossRef Full Text | Google Scholar

Sweeney, B. W., Bott, T. L., Jackson, J. K., Kaplan, L. A., Newbold, J. D., Standley, L. J., et al. (2004). Riparian deforestation, stream narrowing, and loss of stream ecosystem services. Proc. Natl. Acad. Sci. U.S.A. 101, 14132–14137. doi: 10.1073/pnas.0405895101

PubMed Abstract | CrossRef Full Text | Google Scholar

SWIM. (2021). University of Texas at El Paso, Sustainable Water Through Integrated Management (SWIM). Available online at: https://swim.cybershare.utep.edu/en/home

Tarlock, A. D. (2001). The future of prior appropriation in the new west. Nat. Resourc. J. 41, 769–793. Available online at: https://www.jstor.org/stable/24888845

Google Scholar

Temin, P. (2006). The economy of the early Roman Empire. J. Econ. Perspect. 20, 133–151. doi: 10.1257/089533006776526148

CrossRef Full Text | Google Scholar

Toureille, C. (2018). Mysterious 9,000 years old wells discovered in Central China. New York, NY: International Business Times, Science. Available online at: https://www.ibtimes.co.uk/mysterious-9000-years-old-wells-discovered-central-china-1659531

Tran, D. Q., Kovacs, K. F., and West, G. H. (2020). Spatial economic predictions of managed aquifer recharge for an agricultural landscape. Agric. Water Manage. 241:106337. doi: 10.1016/j.agwat.2020.106337

CrossRef Full Text | Google Scholar

Tufegdzic, N., Frowd, R. J., and Stadlin, W. O. (1996). A coordinated approach for real-time short term hydro scheduling. IEEE Trans. Power Syst. 11, 1698–1704. doi: 10.1109/59.544630

CrossRef Full Text | Google Scholar

Tui, S. H. K., Blummel, M., Valbuena, D., Chirima, A., Masikati, P., van Rooyen, A. F., et al. (2013). Assessing the potential of dual-purpose maize in southern Africa: a multi-level approach. Field Crops Res. 153, 37–51. doi: 10.1016/j.fcr.2013.07.002

CrossRef Full Text | Google Scholar

Turner, S. W. D., Doering, K., and Voisin, N. (2020). Data-Driven reservoir simulation in a large-scale hydrological and water resource model. Water Resour. Res 56. doi: 10.1029/2020WR027902

CrossRef Full Text | Google Scholar

Uzawa, H. (1962). Production-functions with constant elasticities of substitution. Rev. Econ. Stud. 29, 291–299. doi: 10.2307/2296305

CrossRef Full Text | Google Scholar

Van Dantzig, D. (1956). Economic decision problems for flood prevention. Econ. J. Econ. Soc. 276–287. doi: 10.2307/1911632

CrossRef Full Text | Google Scholar

Vansoest, A., Kapteyn, A., and Kooreman, P. (1993). Coherency and regularity of demand systems with equality and inequality constraints. J. Econ. 57, 161–188. doi: 10.1016/0304-4076(93)90063-B

CrossRef Full Text | Google Scholar

Varela-Ortega, C., Blanco-Gutierrez, I., Esteve, P., Bharwani, S., Fronzek, S., and Downing, T. E. (2016). How can irrigated agriculture adapt to climate change? Insights from the Guadiana Basin in Spain. Reg. Environ. Change 16, 59–70. doi: 10.1007/s10113-014-0720-y

CrossRef Full Text | Google Scholar

Varela-Ortega, C., Blanco-Gutierrez, I., Swartz, C. H., and Downing, T. E. (2011). Balancing groundwater conservation and rural livelihoods under water and climate uncertainties: an integrated hydro-economic modeling framework. Glob. Environ. Change Hum. Policy Dimen. 21, 604–619. doi: 10.1016/j.gloenvcha.2010.12.001

CrossRef Full Text | Google Scholar

Verkade, J. S., and Werner, M. G. F. (2011). Estimating the benefits of single value and probability forecasting for flood warning. Hydrol. Earth Syst. Sci. 15, 3751–3765. doi: 10.5194/hess-15-3751-2011

CrossRef Full Text | Google Scholar

Wan, W. H., Zhao, J. S., Lund, J. R., Zhao, T. T. G., Lei, X. H., and Wang, H. (2016). Optimal hedging rule for reservoir refill. J. Water Res. Plan. Manag. 142. doi: 10.1061/(ASCE)WR.1943-5452.0000692

CrossRef Full Text | Google Scholar

Ward, F. A., Amer, S. A., and Ziaee, F. (2013). Water allocation rules in Afghanistan for improved food security. Food Sec. 5, 35–53. doi: 10.1007/s12571-012-0224-x

CrossRef Full Text | Google Scholar

Ward, F. A., and Becker, N. (2015). Cost of water for peace and the environment in Israel: an integrated approach. Water Resour. Res. 51, 5806–5826. doi: 10.1002/2014WR016783

CrossRef Full Text | Google Scholar

Ward, F. A., Mayer, A. S., Garnica, L. A., Townsend, N. T., and Gutzler, D. S. (2019). The economics of aquifer protection plans under climate water stress: new insights from hydroeconomic modeling. J. Hydrol. 576, 667–684. doi: 10.1016/j.jhydrol.2019.06.081

CrossRef Full Text | Google Scholar

Ward, F. A., and Pulido-Velazquez, M. (2008a). Efficiency, equity, and sustainability in a water quantity-quality optimization model in the Rio Grande basin. Ecol. Econ. 66, 23–37. doi: 10.1016/j.ecolecon.2007.08.018

CrossRef Full Text | Google Scholar

Ward, F. A., and Pulido-Velazquez, M. (2008b). Water conservation in irrigation can increase water use. Proc. Natl. Acad. Sci. U.S.A. 105, 18215–18220. doi: 10.1073/pnas.0805554105

PubMed Abstract | CrossRef Full Text | Google Scholar

Ward, F. A., and Pulido-Velazquez, M. (2012). Economic costs of sustaining water supplies: findings from the Rio Grande. Water Res. Manag. 26, 2883–2909. doi: 10.1007/s11269-012-0055-8

CrossRef Full Text | Google Scholar

Wheeler, K. G., Robinson, C. J., and Bark, R. H. (2018). Modelling to bridge many boundaries: the Colorado and Murray-Darling River basins. Reg. Environ. Change 18, 1607–1619. doi: 10.1007/s10113-018-1304-z

CrossRef Full Text | Google Scholar

White, D. J., Feng, K. S., Sun, L. X., and Hubacek, K. (2015). A hydro-economic MRIO analysis of the Haihe River Basin's water footprint and water stress. Ecol. Model. 318, 157–167. doi: 10.1016/j.ecolmodel.2015.01.017

CrossRef Full Text | Google Scholar

Wilhite, D. A., Svoboda, M. D., and Hayes, M. J. (2007). Understanding the complex impacts of drought: a key to enhancing drought mitigation and preparedness. Water Resour. Manag. 21, 763–774. doi: 10.1007/s11269-006-9076-5

CrossRef Full Text | Google Scholar

Wilson, B. A., and Bowman, D. (1987). Fire, storm, flood and drought - the vegetation ecology of howards peninsula, Northern territory, Australia. Austr. J. Ecol. 12, 165–174. doi: 10.1111/j.1442-9993.1987.tb00937.x

CrossRef Full Text | Google Scholar

Wishart, J. (1938). Field experiments of factorial design. J. Agric. Sci. 28, 299–306. doi: 10.1017/S002185960005067X

CrossRef Full Text | Google Scholar

Wu, F., Bai, Y. P., Zhang, Y. L., and Li, Z. H. (2017). Balancing water demand for the Heihe River Basin in Northwest China. Phys. Chem. Earth 101, 178–184. doi: 10.1016/j.pce.2017.07.002

CrossRef Full Text | Google Scholar

Wu, X., Jeuland, M., and Whittington, D. (2016). Does political uncertainty affect water resources development? The case of the Eastern Nile. Policy Soc. 35, 151–163. doi: 10.1016/j.polsoc.2016.07.001

CrossRef Full Text | Google Scholar

Yang, Y. C. E., Brown, C. M., Yu, W. H., and Savitsky, A. (2013). An introduction to the IBMR, a hydro-economic model for climate change impact assessment in Pakistan's Indus River basin. Water Int. 38, 632–650. doi: 10.1080/02508060.2013.830691

CrossRef Full Text | Google Scholar

Yang, Y. C. E., Ringler, C., Brown, C., and Mondal, M. A. H. (2016a). Modeling the agricultural water-energy-food nexus in the indus River Basin, Pakistan. J. Water Res. Plan. Manag. 142, 13. doi: 10.1061/(ASCE)WR.1943-5452.0000710

CrossRef Full Text | Google Scholar

Yang, Y. C. E., Wi, S., Ray, P. A., Brown, C. M., and Khalil, A. F. (2016b). The future nexus of the Brahmaputra River Basin: Climate, water, energy and food trajectories. Glob. Environ. Change Hum. Policy Dimen. 37, 16–30. doi: 10.1016/j.gloenvcha.2016.01.002

CrossRef Full Text | Google Scholar

Yao, M. T., Werners, S. E., Hutjes, R. W. A., Kabat, P., and Huang, H. Q. (2015). Sectorial Water Use Trends in the Urbanizing Pearl River Delta, China. PLoS ONE 10:e0115039. doi: 10.1371/journal.pone.0115039

PubMed Abstract | CrossRef Full Text | Google Scholar

Young, R. A., and Gray, S. L. (1985). Input-output models, economic surplus, and the evaluation of state or regional water plans. Water Resour. Res. 21, 1819–1823. doi: 10.1029/WR021i012p01819

CrossRef Full Text | Google Scholar

Young, R. A., and Loomis, J. B. (2005). Determining the Economic Value of Water. Washington, DC: Resources for the Future.

Google Scholar

Zekri, S., Madani, K., Bazargan-Lari, M. R., Kotagama, H., and Kalbus, E. (2017). Feasibility of adopting smart water meters in aquifer management: an integrated hydro-economic analysis. Agric. Water Manag. 181, 85–93. doi: 10.1016/j.agwat.2016.11.022

CrossRef Full Text | Google Scholar

Zhang, C. L., Yue, Q., and Guo, P. (2019). A nonlinear inexact two-stage management model for agricultural water allocation under uncertainty based on the heihe river water diversion plan. Int. J. Environ. Res. Public Health 16:1884. doi: 10.3390/ijerph16111884

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, T. T. G., Zhao, J. S., Lund, J. R., and Yang, D. W. (2014). Optimal hedging rules for reservoir flood operation from forecast uncertainties. J. Water Res. Plan. Manag. 140:432. doi: 10.1061/(ASCE)WR.1943-5452.0000432

CrossRef Full Text | Google Scholar