Triple Collocation Based Multi-Source Precipitation Merging

Multi-source precipitation merging has been used for improving global precipitation estimation accuracy. However, current merging techniques heavily rely on gauge-based precipitation and/or streamflow observations, which may contain substantial uncertainties over data-poor regions. This study provides a triple collocation (TC) based framework for merging multi-source precipitation products without the access of high-quality ground observations. In this framework, the error variances of the precipitation products are statistically estimated using TC, which are further employed in parameterizing a least-square-based precipitation merging framework. As validated against high-quality gauge observations collected over Europe, we demonstrate that TC can accurately estimate the relative errors of different precipitation products, which leads to robust multi-source precipitation merging. Results also demonstrate that the TC merged product significantly outperforms the parent products, which is noteworthy—given the strong skills of the reanalyzed (ERA-Interim) precipitation product over Europe. Since TC analysis does not rely on high-quality gauge observations, the proposed TC-based merging framework can be applied globally, and is expected to significantly contribute precipitation data merging over data-poor regions, e.g., Africa and South America.

1. Introduction

Precipitation is the key driving force of global hydrological cycle (Eltahir and Bras, 1996). Remotely sensed (RS) and reanalyzed global precipitation products are increasing available (e.g., Huffman et al., 1997; Dee et al., 2011; Ashouri et al., 2015; Funk et al., 2015), which may improve hydrological modeling accuracy over data-poor regions. However, inter-comparison studies suggest substantial inconsistency between different precipitation products, which is related to their input and model structural errors (Sun et al., 2018). Consequently, an optimal precipitation product may be achieved by merging all available precipitation products.

Statistically, the optimal merge of different precipitation products requires their error information, e.g., highly accurate products should receive larger weights during merging, and vice versa. The relative weights of different precipitation products are typically calculated using rain gauges and spatially interpolated to unobserved locations (e.g., Shrestha et al., 2011; Funk et al., 2015; Golian et al., 2015; Beck et al., 2019). The gauge-based approach ignores the uncertainty of rain gauges or precipitation networks (Villarini et al., 2008). As demonstrated in Dong and Crow (2018), observation errors can strongly bias the in-situ-based error metrics. As a result, spatially interpolating precipitation error statistics may contain substantial uncertainties over data-poor regions, e.g., Africa and South America (Chen et al., 2008).

Alternatively, precipitation products can be merged using a rainfall-runoff modeling framework (e.g., Chiang et al., 2007; Gebregiorgis and Hossain, 2011; Jiang et al., 2014; Hazra et al., 2019). In these studies, multi-source precipitation data are merged using randomly generated weights. The merged precipitation that leads to the most accurate streamflow estimates are considered as the optimally merged precipitation product. Although this hydrological modeling based approach does not rely on high-quality precipitation references, it is affected by hydrological model parameter and structural uncertainties (Beven and Binley, 1992; Renard et al., 2010; Crow et al., 2018). Additionally, this approach is limited to regions with high-quality streamflow observations.

Recently, triple collocation (TC) analysis (Stoffelen, 1998) has been proposed to estimate precipitation error without the reliance of gauge observations (Alemohammad et al., 2015; Massari et al., 2017; Li et al., 2018). Based on three noisy but independent measurements of a variable, TC analysis can solve for their error statistics using a set of linear equations. The robustness and the accuracy of TC in precipitation error analysis has been verified using high-density precipitation networks (e.g., Massari et al., 2017; Li et al., 2018; Dong et al., 2019b). These findings suggest that TC is ideal for precipitation merging—given accurate precipitation errors can be estimated globally without any access of high-quality in-situ observations. However, TC-based statistical tools have not been considered for current precipitation merging analyses.

This study aims to provide a framework that can optimally and objectively merge multi-source precipitation products using TC-based precipitation error information. The merged product is evaluated using spatially intensive gauge networks collected over Europe. The relative accuracy gain of the proposed merging framework is also demonstrated using independent gauge observations.

2. Materials and Methods

2.1. Precipitation Data

As mentioned above, TC analysis requires three independent precipitation products. Most of precipitation products use ground-based observations for correcting systematic errors. Therefore, it is challenging to obtain three strictly independent precipitation products. Nonetheless, previous studies demonstrate that soil moisture inverted, remotely sensed and model estimated precipitation products contain relatively independent precipitation errors, and can be used for TC analysis (Massari et al., 2017; Dong et al., 2019b). Therefore, precipitation products collected from these three categories were used for this study. The independency assumption was also revisited in the results section.

Based on land surface water balance, the SM2Rain precipitation product (Brocca et al., 2014, 2015) inverses the daily precipitation information from the Advanced Scatterometer (ASCAT) soil moisture retrievals (Wagner et al., 1999). In this study, we used the 0.25-degree daily SM2Rain product acquired from http://hydrology.irpi.cnr.it/download-area/sm2rain-data-sets/, which is available from 2007 to 2015 (denoted as “SM2Rain”). A detailed description of the SM2Rain algorithm can be found in Brocca et al. (2017).

The Remotely Sensed Information using Artificial Neural Networks for Climate Data Record (PERSIANN-CDR, denoted as “PER,” Ashouri et al., 2015) product was used as the second independent precipitation in the TC analysis. In PER, daily precipitation information is estimated using RS infrared data and artificial neural networks (ANN), with a spatial resolution of 0.25 degree. The climatology of the PER estimates are adjusted by the 2.5 degree monthly precipitation product from Global Precipitation Climatology Project (GPCP) product.

The daily reanalyzed ERA-Interim product (denoted as “ERA”; Dee et al., 2011) acquired from European Center for Medium-Range Weather Forecasts (ECMWF) was used as the third independent product for TC analysis. This 0.5 degree precipitation product is produced based on numerical weather modeling, and hence, relatively independent with both ground- and RS-based precipitation. The ERA product was resampled onto 0.25 degree spatial grids using nearest neighbor method (Beck et al., 2019).

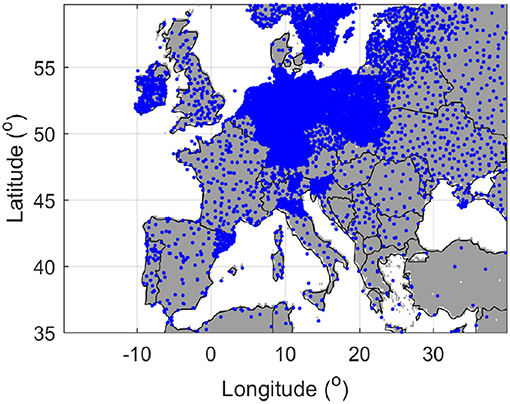
The latest (version 19.0e), ground-based, daily, EOBS precipitation (Cornes et al., 2018) was used for evaluating the skills of the original and the merged product (https://www.ecad.eu/download/ensembles/download.php). This EOBS dataset was developed by statistically interpolating ~15,000 ground rain gauges over the Europe (Figure 1).

FIGURE 1

Figure 1. Spatial distribution of rain gauges used in EOBS.

As mentioned above, the key goal of this study is to provide a statistical framework that can optimally merge multi-source precipitation products. Hence, our conclusions are qualitatively insensitive to the choice of the precipitation products—provided the TC assumptions are satisfied. However, for cases that are interested in generating the state-of-the-art precipitation estimates, parent products with latest versions should be considered.

2.2. Triple Collocation Analysis

In TC analysis, the error variance of a geophysical variable can be estimated using three noisy but independent measurements. It should be noted that TC is most robust for anomaly error characterization. This is because the climatology (mean seasonal cycle) of a geophysical product contains limited degree of freedom, and hence, climatology errors of different products can be cross-correlated and violate the TC assumption (Draper et al., 2013). Therefore, the goal of TC-based merging is to suppress the precipitation anomaly, instead of climatology, errors.

For a given grid cell, TC relates the zero-mean precipitation anomaly of a product (x) and the true signal (p) using a linear additive error model:

$\begin{array}{ll}\text{x}={\alpha }_x\text{p}+{ϵ}_x& (1)\end{array}$

where ϵ_x is the random precipitation anomaly error (Dong and Crow, 2018), with analogous equations for product y and z.

In the difference notation of TC analysis, one product is taken as a reference, and the other two products are scaled to this reference product to remove the dynamic range differences of different products (Draper et al., 2013). For example, taking x as a reference, the original products are scaled as:

$\begin{array}{ll}{\text{x}}^{*}=\text{x}& (2)\end{array}$

$\begin{array}{ll}{\text{y}}^{*}=\frac{a_x}{a_y}\text{y}& (3)\end{array}$

$\begin{array}{ll}{\text{z}}^{*}=\frac{a_x}{a_z}\text{z}& (4)\end{array}$

where x^*, y^*, and z^* are the scaled precipitation anomalies. Assuming the errors of the three products are mutually independent and orthogonal to the truth, the ratios of the scaling parameters can be estimated as (Draper et al., 2013):

$\begin{array}{ll}\frac{a_x}{a_y}=\frac{{\text{x}}^T\text{z}}{{\text{y}}^T\text{z}}& (5)\end{array}$

$\begin{array}{ll}\frac{a_x}{a_z}=\frac{{\text{x}}^T\text{y}}{{\text{z}}^T\text{y}}& (6)\end{array}$

After scaling, the error variances of the scaled products can be estimated as:

$\begin{array}{ll}{e}_x^{*}=\langle {({\text{x}}^{*}-{\text{y}}^{*})}^T({\text{x}}^{*}-{\text{z}}^{*})\rangle & (7)\end{array}$

$\begin{array}{ll}{e}_y^{*}=\langle {({\text{y}}^{*}-{\text{x}}^{*})}^T({\text{y}}^{*}-{\text{z}}^{*})\rangle & (8)\end{array}$

$\begin{array}{ll}{e}_z^{*}=\langle {({\text{z}}^{*}-{\text{x}}^{*})}^T({\text{z}}^{*}-{\text{y}}^{*})\rangle & (9)\end{array}$

where 〈.〉 represents the temporal average.

In addition to the error variances, TC can also estimate the product-truth correlation (i.e., the Pearson correlation coefficient between x and p), which is a widely used metric for precipitation accuracy evaluation:

$\begin{array}{ll}{R}_x=\sqrt{\frac{C_{x^{*}{y}^{*}}}{C_{x^{*}{x}^{*}}}}& (10)\end{array}$

where R_x is TC-estimated Pearson correlation coefficient between x^* and the true precipitation anomalies. The product-truth correlations of y and z can be estimated using analogous equations.

2.3. Precipitation Merging

As mentioned above, the proposed merging procedure is to suppress the precipitation anomaly errors, which is done by weighted averaging the scaled precipitation anomalies (i.e., x^*, y^*, and z^*). Based on the TC estimates, a least-square-based optimal merging can be formulated as:

$\begin{array}{ll}{\text{m}}^{*}={\text{x}}^{*}{w}_x+{\text{y}}^{*}{w}_y+{\text{z}}^{*}{w}_z& (11)\end{array}$

where m^* is the merged precipitation anomaly, and w_x, w_y, and w_z are the weights of the three products in precipitation merging. Following Yilmaz et al. (2012), the least-square solutions of the merging weights are calculated as:

$\begin{array}{ll}{w}_x=\frac{e_y^{*}{e}_z^{*}}{e_x^{*}{e}_y^{*}+e_y^{*}{e}_z^{*}+e_x^{*}{e}_z^{*}}& (12)\end{array}$

$\begin{array}{ll}{w}_y=\frac{e_x^{*}{e}_z^{*}}{e_x^{*}{e}_y^{*}+e_y^{*}{e}_z^{*}+e_x^{*}{e}_z^{*}}& (13)\end{array}$

$\begin{array}{ll}{w}_z=\frac{e_x^{*}{e}_y^{*}}{e_x^{*}{e}_y^{*}+e_y^{*}{e}_z^{*}+e_x^{*}{e}_z^{*}}& (14)\end{array}$

After adding a reference climatology to m^*, the multi-source merged precipitation time series was achieved (denoted as M1). The GPCP climatology was typically used as the reference climatology. However, to ensure our results are independent with gauge observations during the product validation step, we used ERA climatology as the reference climatology for simplicity.

Note that such merging procedure may falsely increase the precipitation occurrence. Hence, a second merged product (denoted as M2) was generated by removing precipitation events on days that reference precipitation is below the rain/no-rain threshold (taken as 1 mm/day in this study) from M1. Likewise, gauge-based rain/no-rain estimates were commonly used as the reference (Beck et al., 2019). However, to avoid any potential dependency of the merged and EOBS precipitation during validation, we used ERA dataset as the rain/no-rain reference in this study.

2.4. Gauge-Based Precipitation Evaluation

We first evaluated the accuracy of different products using their Pearson correlation coefficient with gauge-based EOBS data. The correlation metric directly reflects the overall accuracy of the precipitation products, which decreases with increased (total) error of a product.

The skill of a precipitation dataset in capturing the extreme events is crucial for hydrological applications. Hence, the biases of different products at the 85th and 95th EOBS observed precipitation percentiles were also considered.

Finally, widely used rain/no-rain detection metrics were used to evaluate the rain/no-rain detection skills of the merged product. The rain/no-rain consistency of a product and gauge-based precipitation time series are defined in Table 1. Based on these consistency estimates, the fraction of actual rainfall events captured by a product can be estimated using the probability of detection (POD):

$\begin{array}{ll}POD=\frac{A}{A+C}.& (15)\end{array}$

TABLE 1

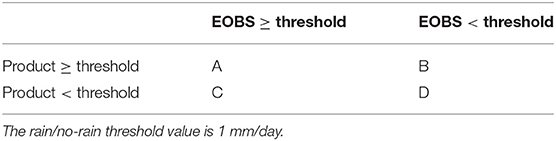
Table 1. Contingency table for comparing the rain/no-rain detected by precipitation gauge and products.

The tendency of a product for falsely reporting the precipitation events is captured by false-alarm-ratio (FAR):

$\begin{array}{ll}FAR=\frac{B}{A+B}.& (16)\end{array}$

Finally, the overall detection skill relative random binary sequences was measured using Heidke skill score (HSS):

$\begin{array}{ll}HSS=\frac{2(AD-BC)}{(A+C)(C+D)+(A+B)(B+D)}.& (17)\end{array}$

3. Results

3.1. Evaluation of TC Analysis

As shown above, different precipitation anomalies are merged according to their error statistics. Therefore, this section evaluates the accuracy and the robustness of the TC-based error estimates. According to the TC results, ERA has the highest product-truth correlation, relative to SM2Rain and PER (Figures 2a–c). Compared with ERA, SM2Rain and PER show stronger spatial variability in the precipitation accuracy. For instance, both SM2Rain and PER show the tendency of decreased precipitation estimation accuracy with increased latitude. In contrast, the accuracy of ERA is relatively spatially homogeneous. As expected, the precipitation anomaly error variance is reversely correlated with product-truth correlation. Hence, the precipitation anomaly errors (Figures 2d–f) provide same relative performance estimates of these three products. The relative accuracy of the three products is generally consistent with the amount of information being ingested in their precipitation estimation. For instance, SM2Rain mainly relies on ASCAT soil moisture retrievals. In contrast, ERA and PER use multi-source remote sensing and ground observations to constrain their precipitation estimates.

FIGURE 2

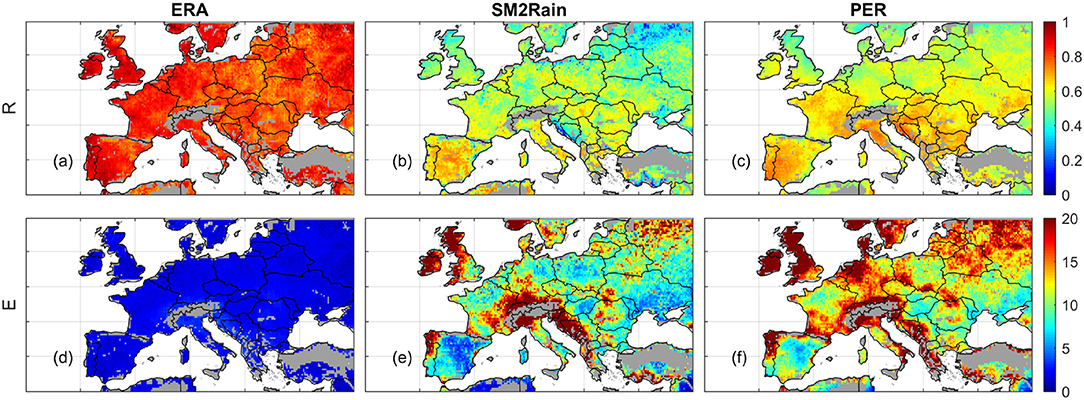
Figure 2. TC estimated product-truth correlation (R, first row) and standard deviation of precipitation error (E, mm/day, second row) of ERA (a,d), SM2Rain (b,e), and PER (c,f) precipitation anomalies.

Figure 3 provides gauge-based (EOBS estimated) ERA, SM2Rain and PER product-truth correlation, which is used for evaluating the TC results shown in Figure 2. As shown in section 1, the variance of the precipitation error is complicated by its dynamic range differences (i.e., the α values), which cannot be independently estimated using only gauge data. Hence, only product-truth correlation results are considered in Figure 3.

FIGURE 3

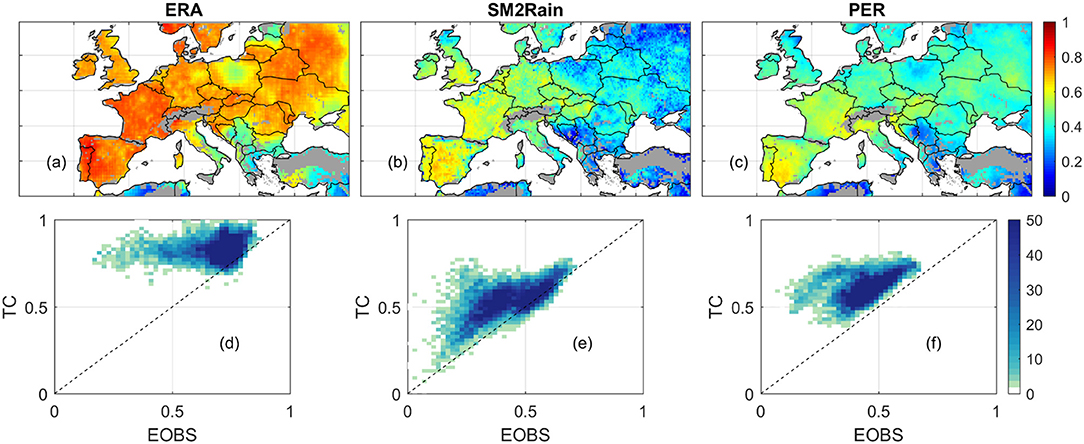
Figure 3. EOBS-based product-truth correlation of ERA, SM2Rain, and PER (a–c). The comparison of EOBS- and TC-based product-truth correlation estimates are shown in (d–f). Colors in (d–f) denotes the number of data points within a 0.05 [-] ×0.05 [-] grid.

Relative to TC estimates, EOBS-based ERA skills contain significantly higher spatial variability—comparing Figures 2a, 3a. Additionally, EOBS-based product-truth correlation is generally lower than TC estimates, particularly over regions that rain gauge density is relatively sparse (see Figure 1). Similar spatial differences of TC and EOBS estimates are also shown in the SM2Rain and PER results (Figures 3b,c).

These findings are entirely consistent with the analytical error propagation analysis shown in Dong and Crow (2018). They demonstrate that random errors typically bias product-truth correlation estimates low. Such random error impacts are implicitly handled in TC, but not considered in EOBS results. Hence, the inconsistency of TC and EOBS results are likely attributable to the spatial variability of EOBS accuracy due to its rain gauge density distribution (Figure 1). Additionally, the mutual consistency of TC and EOBS results is also partly determined by the spatial variability of the product-truth correlations. For instance, the product-truth correlation of ERA contains limited spatial variability (Figure 2a). As a result, any EOBS observation error will strongly affect the spatial distribution of product-truth correlation estimates, and by extension, the consistency between TC and EOBS results. In contrast, SM2Rain has strong spatial variability in product-truth correlation. Consequently, its spatial distribution is relatively less sensitive to the EOBS observation error impacts. Despite the unavoidable EOBS error impacts, the general consistency between TC- and EOBS-based product-truth correlation estimates is demonstrated (Figures 3d–f).

3.2. The Added Value of TC-Based Precipitation Merging

Based on the precipitation error estimated using TC (Figures 2d–f), we merged all the original precipitation anomalies using Equation (11). The reference precipitation climatology (ERA climatology in this case) was then added to the merged anomalies to achieve the merged precipitation product (M1). We also set M1 precipitation to the rain/no-rain threshold (1 mm/day) on days that ERA is below this threshold, which leads to the M2 product. Generally, M1 and M2 have very similar correlations with EOBS (Table 2). This suggests that the removal of false precipitation events in M2 has negligible impacts on the overall correlation metric (Table 2).

TABLE 2

Table 2. The EOBS evaluated product-truth correlations of TC-merged and ERA precipitation products.

Relative to the best parent product (i.e., ERA in this case), both M1 and M2 demonstrate significantly (paired t-test, at p = 0.05 confidence level, Table 2) improved correlations with EOBS. Given the strong skills of ERA in precipitation estimation over Europe, such accuracy gain is noteworthy.

It is known that capturing the extreme precipitation events is a challenge for remote-sensing and reanalyzed products. Figure 4 compares the biases of different products at the 85th and 95th percentiles of EOBS observations. SM2Rain demonstrates largest dry biases for the extreme precipitations (Figures 4c,d). SM2Rain estimates precipitation by inverting soil moisture retrievals. Consequently, it is insensitive to precipitation when surface soil is saturated. Therefore, SM2Rain has largest dry bias for extreme events, compared to other products. On average, the dry bias of M2 for extreme events has similar spatial patterns with ERA and PER. This is expected, since all the original products are biased low for extreme events, and least-squared based merging is not designed for adjusting such conditional biases.

FIGURE 4

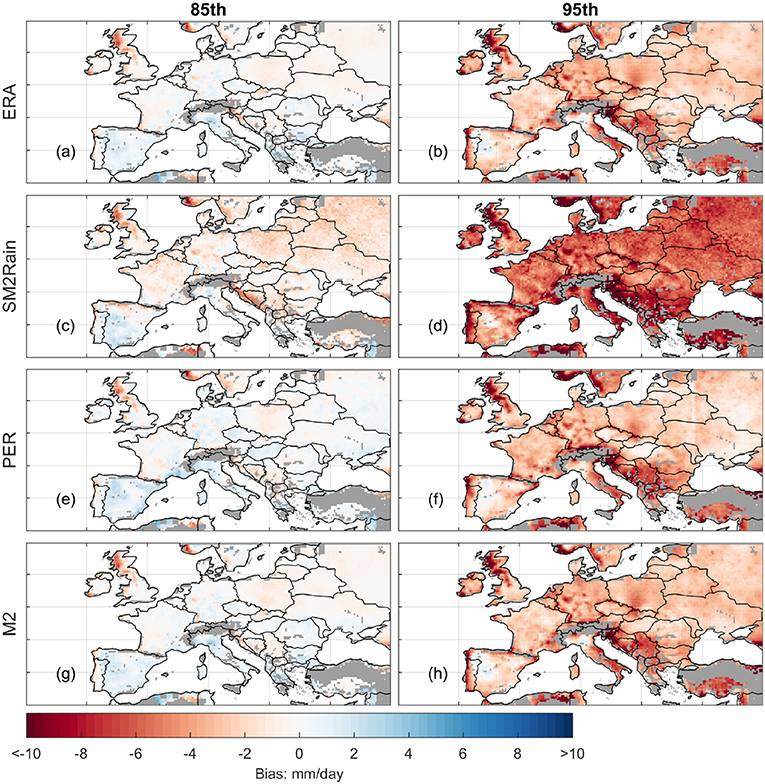
Figure 4. The biases of ERA (a,b), SM2Rain (c,d), PER (e,f), and M2 (g,h) at 85 and 95th percentile of EOBS precipitation observation.

3.3. Detection Errors of TC-Based Merging

Relative to M2, the POD of M1 is averagely 10% higher—suggesting M1 is more accurate in detecting the occurrence of precipitation events (Figures 5a,b). However, the FAR of M1 is approximately twice as high as M1 (Figures 5c,d). As a result, the overall detection score (HSS) of M1 is 0.2 to 0.3 [-] lower than M2.

FIGURE 5

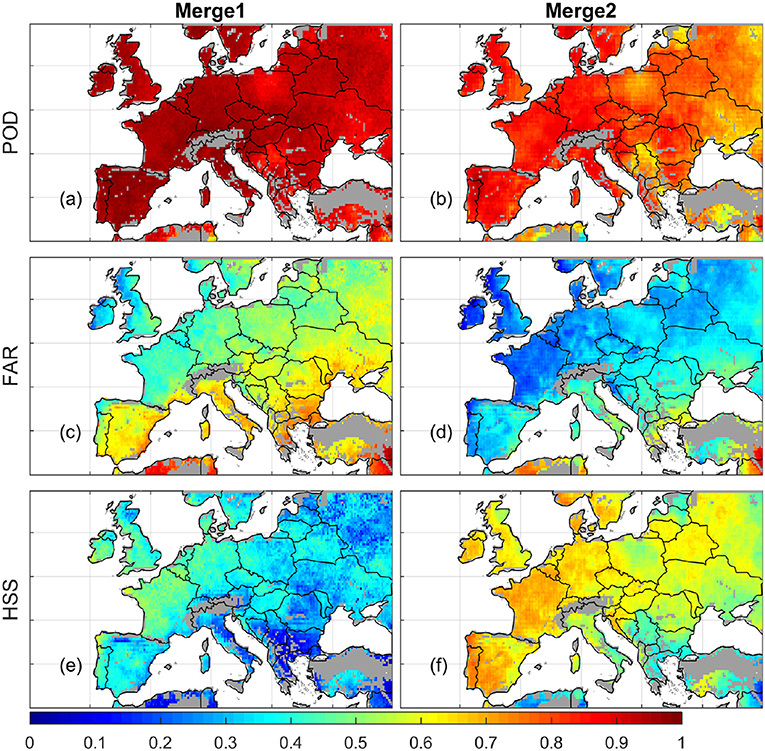
Figure 5. The detection skills of the merged products (a,b: POD; c,d: FAR; e,f: HSS). The left and right column represent merged precipitation without and with ERA-based false precipitation removal, respectively.

Figure 6 further investigates the differences of M1 and M2 detection skills. As shown in Figure 6, the percentage of rain days observed by EOBS is generally below 40%. However, the rain-day percentage of M1 is 30–40% higher than EOBS. Therefore, M1 has a higher POD due to the strong positive bias in precipitation occurrence detection. After removing the false precipitation events from M1 using ERA, M2 shows more realistic rain-day percentages (Figure 6c), which leads to improved precipitation detection skills (Figure 5f).

FIGURE 6

Figure 6. Percentage of rain days estimated using EOBS (a), M1 (b), and M2 (c) dataset.

4. Discussions and Conclusion

Optimal multi-source precipitation merging requires their error statistics, which are typically calculated using gauge data (e.g., Beck et al., 2019). However, gauge observation errors tend to bias the error statistics of different products (Dong and Crow, 2018; Dong et al., 2019b) and lead to sub-optimally merged precipitation datasets. The impacts of gauge observation error increase with decreased gauge density, and hence, the traditional merging techniques are expected to contain substantial uncertainties over data-poor regions, e.g., Africa and South America (Dong et al., 2019a).

To address this issue, this study proposed to use TC analysis for precipitation error estimation and data merging. In TC analysis, precipitation error statistics were estimated using three noisy but independent products, without any reliance on high-quality reference precipitation datasets. These TC-based error estimates were then used for parameterizing a least-square framework, which can statistically minimize the precipitation anomaly errors.

Based on the high-density gauge-based precipitation observations (EOBS), we first evaluated the TC-based precipitation error estimates. It is known that the observation errors of EOBS will unavoidably degrade the mutual consistency of TC- and EOBS-based precipitation error statistics. Nonetheless, a general consistency between TC- and EOBS-based evaluation results was still demonstrated. The TC-based precipitation merging also constantly outperformed the best parent product, i.e., ERA in this case. Note that ERA is known to have strong skills in precipitation estimation over Europe (Massari et al., 2017), and strongly outperforms other RS precipitation products (Figures 2, 3). Hence, any improvement relative to ERA is noteworthy.

However, a caveat of TC-based merging should be acknowledged. This type of merging is sensitive to false precipitation events of the original products. Consequently, the merged product is likely to contain relative high false alarm ratio (FAR)—see the M1 detection skills in Figure 5. However, we demonstrated that this issue can be easily addressed by removing false precipitation events using a reference product. As mentioned above, to ensure the independency of merged and gauge-based precipitation during validation, ERA was used for removing false rainfall events. At the global scale, gauge observations can be used for more accurate rain/no-rain determination (Beck et al., 2019).

It should be noted that the proposed TC-based merging framework is statistically optimal for independent products. However, it can be easily extended to optimally merge cross-correlated precipitation products. As demonstrated in Gruber et al. (2016), quadruple collocation (QC) can simultaneously estimate the error variance and inter-product error covariance of the input products. Based on these error statistics, the optimal weights of each product can be solved in analogous to Equations (12) to (14). Such QC-based merging may further benefit current multi-source precipitation framework for optimally combining independent and cross-correlated precipitation products (e.g., Beck et al., 2017, 2019).

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: EOBS: https://www.ecad.eu/download/ensembles/download.php; SM2Rain: http://hydrology.irpi.cnr.it/download-area/sm2rain-data-sets/; PERSIANN: https://climatedataguide.ucar.edu/climate-data/persiann-cdr-precipitation-estimation-remotely-sensed-information-using-artificial; ERA-Interim: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alemohammad, S., McColl, K., Konings, A., Entekhabi, D., and Stoffelen, A. (2015). Characterization of precipitation product errors across the US using multiplicative triple collocation. Hydrol. Earth Syst. Sci. 12, 2527–2559. doi: 10.5194/hessd-12-2527-2015

CrossRef Full Text | Google Scholar

Ashouri, H., Hsu, K.-L., Sorooshian, S., Braithwaite, D. K., Knapp, K. R., Cecil, L. D., et al. (2015). PERSIANN-CDR: daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 96, 69–83. doi: 10.1175/BAMS-D-13-00068.1

CrossRef Full Text | Google Scholar

Beck, H. E., van Dijk, A. I., Levizzani, V., Schellekens, J., Miralles, D. G., Martens, B., et al. (2017). MSWEP: 3-hourly 0.25 global gridded precipitation (1979-2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 21, 589–615. doi: 10.5194/hess-21-589-2017

CrossRef Full Text | Google Scholar

Beck, H. E., Wood, E. F., Pan, M., Fisher, C. K., Miralles, D. G., Van Dijk, A. I., et al. (2019). MSWEP V2 global 3-hourly 0.1 precipitation: methodology and quantitative assessment. Bull. Am. Meteorol. Soc. 100, 473–500. doi: 10.1175/BAMS-D-17-0138.1

CrossRef Full Text | Google Scholar

Beven, K., and Binley, A. (1992). The future of distributed models: model calibration and uncertainty prediction. Hydrol. Process. 6, 279–298. doi: 10.1002/hyp.3360060305

CrossRef Full Text | Google Scholar

Brocca, L., Ciabatta, L., Massari, C., Moramarco, T., Hahn, S., Hasenauer, S., et al. (2014). Soil as a natural rain gauge: estimating global rainfall from satellite soil moisture data. J. Geophys. Res. 119, 5128–5141. doi: 10.1002/2014JD021489

CrossRef Full Text | Google Scholar

Brocca, L., Crow, W. T., Ciabatta, L., Massari, C., De Rosnay, P., Enenkel, M., et al. (2017). A review of the applications of ascat soil moisture products. IEEE J. Select. Top. Appl. Earth Observ. Remote Sens. 10, 2285–2306. doi: 10.1109/JSTARS.2017.2651140

CrossRef Full Text | Google Scholar

Brocca, L., Massari, C., Ciabatta, L., Moramarco, T., Penna, D., Zuecco, G., et al. (2015). Rainfall estimation from in situ soil moisture observations at several sites in Europe: an evaluation of the SM2RAIN algorithm. J. Hydrol. Hydromech. 63, 201–209. doi: 10.1515/johh-2015-0016

CrossRef Full Text | Google Scholar

Chen, M., Shi, W., Xie, P., Silva, V., Kousky, V. E., Wayne Higgins, R., et al. (2008). Assessing objective techniques for gauge-based analyses of global daily precipitation. J. Geophys. Res. 113:D04110. doi: 10.1029/2007JD009132

CrossRef Full Text | Google Scholar

Chiang, Y.-M., Hsu, K.-L., Chang, F.-J., Hong, Y., and Sorooshian, S. (2007). Merging multiple precipitation sources for flash flood forecasting. J. Hydrol. 340, 183–196. doi: 10.1016/j.jhydrol.2007.04.007

CrossRef Full Text | Google Scholar

Cornes, R. C., van der Schrier, G., van den Besselaar, E. J., and Jones, P. D. (2018). An ensemble version of the e-obs temperature and precipitation data sets. J. Geophys. Res. 123, 9391–9409. doi: 10.1029/2017JD028200

CrossRef Full Text | Google Scholar

Crow, W., Chen, F., Reichle, R., Xia, Y., and Liu, Q. (2018). Exploiting soil moisture, precipitation, and streamflow observations to evaluate soil moisture/runoff coupling in land surface models. Geophys. Res. Lett. 45, 4869–4878. doi: 10.1029/2018GL077193

PubMed Abstract | CrossRef Full Text | Google Scholar

Dee, D. P., Uppala, S., Simmons, A., Berrisford, P., Poli, P., Kobayashi, S., et al. (2011). The ERA-interim reanalysis: configuration and performance of the data assimilation system. Quart. J. R. Meteorol. Soc. 137, 553–597. doi: 10.1002/qj.828

CrossRef Full Text | Google Scholar

Dong, J., Crow, W., Reichle, R., Liu, Q., Lei, F., and Cosh, M. H. (2019a). A global assessment of added value in the smap level 4 soil moisture product relative to its baseline land surface model. Geophys. Res. Lett. 46, 6604–6613. doi: 10.1029/2019GL083398

CrossRef Full Text | Google Scholar

Dong, J., and Crow, W. T. (2018). The added value of assimilating remotely sensed soil moisture for estimating summertime soil moisture-air temperature coupling strength. Water Resour. Res. 54, 6072–6084. doi: 10.1029/2018WR022619

CrossRef Full Text | Google Scholar

Dong, J., Crow, W. T., Duan, Z., Wei, L., and Lu, Y. (2019b). A double instrumental variable method for geophysical product error estimation. Remote Sens. Environ. 225, 217–228. doi: 10.1016/j.rse.2019.03.003

CrossRef Full Text | Google Scholar

Draper, C., Reichle, R., de Jeu, R., Naeimi, V., Parinussa, R., and Wagner, W. (2013). Estimating root mean square errors in remotely sensed soil moisture over continental scale domains. Remote Sens. Environ. 137, 288–298. doi: 10.1016/j.rse.2013.06.013

CrossRef Full Text | Google Scholar

Eltahir, E. A., and Bras, R. L. (1996). Precipitation recycling. Rev. Geophys. 34, 367–378. doi: 10.1029/96RG01927

CrossRef Full Text | Google Scholar

Funk, C., Peterson, P., Landsfeld, M., Pedreros, D., Verdin, J., Shukla, S., et al. (2015). The climate hazards infrared precipitation with stationsa new environmental record for monitoring extremes. Sci. Data 2:150066. doi: 10.1038/sdata.2015.66

PubMed Abstract | CrossRef Full Text

Gebregiorgis, A., and Hossain, F. (2011). How much can a priori hydrologic model predictability help in optimal merging of satellite precipitation products? J. Hydrometeorol. 12, 1287–1298. doi: 10.1175/JHM-D-10-05023.1

CrossRef Full Text | Google Scholar

Golian, S., Moazami, S., Kirstetter, P.-E., and Hong, Y. (2015). Evaluating the performance of merged multi-satellite precipitation products over a complex terrain. Water Resour. Manage. 29, 4885–4901. doi: 10.1007/s11269-015-1096-6

CrossRef Full Text | Google Scholar

Gruber, A., Su, C.-H., Crow, W. T., Zwieback, S., Dorigo, W., and Wagner, W. (2016). Estimating error cross-correlations in soil moisture data sets using extended collocation analysis. J. Geophys. Res. 121, 1208–1219. doi: 10.1002/2015JD024027

CrossRef Full Text | Google Scholar

Hazra, A., Maggioni, V., Houser, P., Antil, H., and Noonan, M. (2019). A Monte Carlo-based multi-objective optimization approach to merge different precipitation estimates for land surface modeling. J. Hydrol. 570, 454–462. doi: 10.1016/j.jhydrol.2018.12.039

CrossRef Full Text | Google Scholar

Huffman, G. J., Adler, R. F., Arkin, P., Chang, A., Ferraro, R., Gruber, A., et al. (1997). The global precipitation climatology project (GPCP) combined precipitation dataset. Bull. Am. Meteorol. Soc. 78, 5–20. doi: 10.1175/1520-0477(1997)078 <0005:TGPCPG>2.0.CO;2

CrossRef Full Text | Google Scholar

Jiang, S., Ren, L., Hong, Y., Yang, X., Ma, M., Zhang, Y., and Yuan, F. (2014). Improvement of multi-satellite real-time precipitation products for ensemble streamflow simulation in a middle latitude basin in South China. Water Resour. Manage. 28, 2259–2278. doi: 10.1007/s11269-014-0612-4

CrossRef Full Text | Google Scholar

Li, C., Tang, G., and Hong, Y. (2018). Cross-evaluation of ground-based, multi-satellite and reanalysis precipitation products: applicability of the triple collocation method across Mainland China. J. Hydrol. 562, 71–83. doi: 10.1016/j.jhydrol.2018.04.039

CrossRef Full Text | Google Scholar

Massari, C., Crow, W., and Brocca, L. (2017). An assessment of the performance of global rainfall estimates without ground-based observations. Hydrol. Earth Syst. Sci. 21, 4347–4361. doi: 10.5194/hess-21-4347-2017

CrossRef Full Text | Google Scholar

Renard, B., Kavetski, D., Kuczera, G., Thyer, M., and Franks, S. W. (2010). Understanding predictive uncertainty in hydrologic modeling: the challenge of identifying input and structural errors. Water Resour. Res. 46:W05521. doi: 10.1029/2009WR008328

CrossRef Full Text | Google Scholar

Shrestha, R., Houser, P. R., and Anantharaj, V. G. (2011). An optimal merging technique for high-resolution precipitation products. J. Adv. Model. Earth Syst. 3:M12003. doi: 10.1029/2011MS000062

CrossRef Full Text | Google Scholar

Stoffelen, A. (1998). Toward the true near-surface wind speed: error modeling and calibration using triple collocation. J. Geophys. Res. 103, 7755–7766. doi: 10.1029/97JC03180

CrossRef Full Text | Google Scholar

Sun, Q., Miao, C., Duan, Q., Ashouri, H., Sorooshian, S., and Hsu, K.-L. (2018). A review of global precipitation data sets: data sources, estimation, and intercomparisons. Rev. Geophys. 56, 79–107. doi: 10.1002/2017RG000574

CrossRef Full Text | Google Scholar

Villarini, G., Mandapaka, P. V., Krajewski, W. F., and Moore, R. J. (2008). Rainfall and sampling uncertainties: a rain gauge perspective. J. Geophys. Res. 113:D11102. doi: 10.1029/2007JD009214

CrossRef Full Text | Google Scholar

Wagner, W., Lemoine, G., and Rott, H. (1999). A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sens. Environ. 70, 191–207. doi: 10.1016/S0034-4257(99)00036-X

CrossRef Full Text | Google Scholar

Yilmaz, M., Crow, W., Anderson, M., and Hain, C. (2012). An objective methodology for merging satellite-and model-based soil moisture products. Water Resour. Res. 48:11502. doi: 10.1029/2011WR011682

CrossRef Full Text | Google Scholar