- RDI Unit on Environmental Sustainability Assessment and Circularity, Environmental Research and Innovation (ERIN) Department, Luxembourg Institute of Science and Technology (LIST), Belvaux, Luxembourg
Introduction
The sustainability evaluation of human/industrial systems related to products is commonly performed using life cycle methods:
• Life Cycle Assessment (LCA) is apprehended to estimate the environmental impact (ISO, 2006a,b; Schaubroeck et al., 2022).
• Social life cycle assessment is used to evaluate social impact (UNEP, 2020).
• Life cycle costing and related methods are used to estimate the financial/economic impact (Rödger et al., 2018).
• Life cycle sustainability assessment (LCSA) covers the overall sustainability impact, entailing all three pillars (environmental, social and economic) (Valdivia et al., 2021).
In these life cycle methods, a product system is evaluated that exists out of a series of processes interrelated with an object of study. For example, in consequential LCA, the product system would consist of all the processes that are induced by a product-related decision, e.g., extra demand of a product (Schaubroeck et al., 2021c). Modeling is needed to quantify process and flow amounts of all these processes (the life cycle inventory), and their subsequent related impacts. In practice, such modeling has commonly been done using Linear Inverse Modeling (LIM) based on matrix calculations for LCA (Heijungs and Suh, 2002). This has then also been apprehended for other life cycle methods such as LCSA (Heijungs, 2010, 2022). The equation that expresses this type of modeling is as follows:
In this equation, h is a vector (n × 1) of which the elements represent n multiple types of estimated impacts, Q is the characterization matrix (n × m) where the elements cover the impact amount of n types for the m elementary flows (emission or resources), B is the intervention matrix (m × o) where elements represent the elementary flow amount of m types for the amounts of the o processes/products, A is the technology matrix (o × o) that covers the amount of products/processes linked with other processes/products, and f as the vector (o × 1) that covers the product/process amounts related with the object of study. Quintessential is the use of matrix inversion (denoted with “A−1” in above equation). This represents the propagation of processes and associated flows of the studied product system, i.e., quantifying all the amounts of indirect processes that are associated with the initial object of study, e.g., a product, starting from the directly associated process, e.g., the one that provides the product (in the vector f ), using the prefixed direct relationships among processes specified in the original matrix, e.g., the technology matrix A. This inverse matrix calculation can be seen as in fact a closed expression of the iterative propagation at system level with linear relationships, under certain conditions, as expressed in the power series expansion version (where each term represents a further step of propagation at a system level) (Suh and Heijungs, 2007):
In this equation, I is the unit matrix.
However, there are two major issues with a fixed consideration of LIM for life cycle methods: (1) life cycle methods are not originally restricted to this type of modeling and (2) the limitations of LIM impede more accurate quantifications. Concerning the first issue, even in the ISO 14040-14044 (ISO, 2006a,b) standards on LCA, no specification on the type of mathematical relationship is presented. It is not restricted to linear and not to LIM. In other words, LCA is a method that covers a certain broad concept for which various mathematical and modeling frameworks can be developed, not just one, and this is moreover dependent on the selected goal, which is part of the LCA method. Historically speaking, LIM should never have been introduced as thé mathematical framework, as is presented in the title of the book on the fundamentals of Heijungs and Suh (2002) “The computational structure of life cycle assessment.” LIM is just a mathematical framework. On the second issue, for the sake of permitting more accurate modeling of environmental impact, the specific choice must be kept open for further advancements, which will be elaborated in this article. Any general mathematical framework for life cycle methods should thus ben an open framework where the type of mathematical relationship (linear, non-linear…) is not prefixed. Note that, even though accuracy cannot be completely evaluated in sustainability assessment methods such as LCA, especially concerning global level effects, accuracy could be verified and evaluated at intermediate flow level, process or subsystem level using empirical evidence (Schaubroeck et al., 2020), e.g., measured amount of CO2 emissions per transportation distance (which is not necessarily linear). This permits to check the accuracy of the modeling framework and mathematical relationships at such lower levels.
In literature, a more basic framework for life cycle methods in terms of a general iterative framework has been formulated (Schaubroeck et al., 2021a) and presented in a more correctly formulated way in the corrections published afterwards (Schaubroeck et al., 2021b). Although latter publications focused more on circular economy, the general implications and added value of its presented modeling framework for life cycle methods are there but may have gotten overlooked. I first recapitulate this more basic modeling framework, then newly present its openness to three major advancements and end with a discussion, elaborating on practical realization and a way forward.
The basic iterative modeling framework in short
The fundamentals of the iterative modeling framework exist in considering a network of processes that can be modeled in any way. The basic general equation of a process, equation 5b of the work of Schaubroeck et al. (2021b), is as follows:
In this equation, Fi is a flow amount (subscript may further contain a set of parameter values that specify flow i); t represents time; pp is a function that represents a certain process p (which may also be abstract); OC represents other condition parameters that in this case might influence the process. This equation also covers impact processes (social, economic, environmental). A distinction of processes belonging to the human/industrial system and those belonging to the environment in a broad way (i.e., covering anything but the human/industrial system), is optional and dependent on the goal. Moreover, flows could also imply stock additions or reductions (certain Fi), with associated storage processes (with particular pp). There can also be non-transformative processes such as market processes that specify new destinations as parameter values. This basic equation is not specific and not directly operational, but it is also not restricted to any type of mathematical relationships, and it is open to the practitioner to specify this.1 The goal of the study may implicate further mathematical restrictions on this equation. This mathematics would fit in an overall modeling framework. More precisely, after having specified the goal and scope of the study, which is a general aspect of any method, the stepwise procedures for the modeling framework are straightforward, following in particular an open conceptual framework for life cycle methods as recently argued in literature (Schaubroeck et al., 2022):
1. Start from the object of study as defined in the goal
2. Propagate and model the process chain, using equation 3, based on the relationships as defined in the goal and scope, possibly in a dynamic manner, i.e., which processes to consider is part of the modeling.
3. Aggregate results for final process flows of concern, optionally based on ethical considerations. There is no fixed mathematical procedure necessary for this, since for example prioritization instead of weighing may also occur (Schaubroeck and Rugani, 2017).
Step 1 and 2 are shortly exemplified for attributional and consequential submethods (Schaubroeck et al., 2021c). In case of the attributional submethod, the aim is to evaluate the product life cycle, starting from the process that provides the product of study and the processes that cover the human/industrial processes or abstract parts of it interlinked through physical and service flows in an additive manner, with subsequent impact processes that are consequentially caused by it. In case of the consequential submethod, the object of study is a decision and the further process chain covers the consequential processes that are induced by it. In practice, the framework can be presented in different forms and, the process modeling and interactions can be addressed using a variety of modeling techniques such as system dynamics (Onat et al., 2017) or agent based modeling (Wu et al., 2017) etc. LIM could be seen as just a certain version of this more broad modeling framework, which is more specific but also more limited. Particularly, in LIM, propagation is done stepwise at a system level, using linear relationships, with prefixed variables/relationships, as presented through power series expansion in equation 2. Keep in mind that practitioners should be diligent in providing metadata for the inventory and for the model, and they should make the customized model available as open-source code. This would be to ensure the transparency and reproducibility of the results.
Three main advancements of our framework
A first major advancement, compared to LIM, is the fact that our framework is not limited to linearity in amounts, technically speaking multilinearity (Heijungs, 2020), and direct linear relationships between amount variables. Note that we present linear formulations as an example in our work (Schaubroeck et al., 2021b), but the general equation in our work (equation 3 in this manuscript) is not delimited to linearity. Non-linearity is particularly relevant for consequential life cycle submethods, but can also be for other ones (Schaubroeck et al., 2021c; Li et al., 2022). Mathematical frameworks have been brought forward that update the factors in the matrices prior to LIM in a non-linear manner (Yang, 2016; Pizzol et al., 2021), boiling down to parametrization. These articles showcase as well the importance of considering non-linear effects. Yet, in the strict sense, those are not mathematical frameworks that solely resort to LIM, but they still use LIM to a certain degree and thus have also certain of its limitations.
A second major advancement is that our framework allows for the system to cover dynamics, i.e. continuously changing or developing (Cambridge English Dictionary, 2022) in the propagation of the system. Note that dynamic LCA encompasses both dynamics of systems and/or temporal differentiation, according to a latest review (Beloin-Saint-Pierre et al., 2020), and here we primarily focus on the dynamics of systems. Our framework permits dynamic effects as it does not prefix relationships as LIM does. In LIM, all the links and relative amounts between processes are prefixed in the to-be-inverted matrix on beforehand, of which then LIM follows these prefixed relationships. For example, product A is coming from process X or a collection of processes with fixed shares. However, in reality, the selected process will also depend on other drivers such as the demand for co-products, new product or material prices, new climate conditions, new policies, etc. that are occurring over the course of the propagation. Such aspects and limitations of LIM were already highlighted to a certain degree by Kätelhön et al. (2016). This openness to a dynamic nature in our framework implies that during propagation of the process chain, new relationships can be developed between processes, new processes considered, existing processes altered, i.e., amounts are changed. The world is after all dynamic and not static. Qin et al. (2021) exemplify this dynamic nature in a non-linear manner in the context of LCA for the dynamic selection of potato suppliers based on external conditions (change in demand, costs, maximum capacity etc.) influencing water consumption. The latter is based on optimisation. Another alternative is the use of technology choice models (Kätelhön et al., 2016). Note that it is strange that such modeling would be linked with only consequential LCA, since in attributional LCA the interlinked processes should as well be specified, among multiple alternatives. Covering dynamics could also be done by coupling with advanced agent-based or integrated assessment models (Baustert et al., 2019, in press; Beltran et al., 2020). Yet, again, this does not cover a full dynamic system propagation if the values are used to parametrize matrices with LIM or linear multiplications, whereas it should replace LIM eventually altogether. A more specific additional aspect that is also delimiting, as mentioned in our work (Schaubroeck et al., 2021a), is that “this linear inverse modeling approach, with or without power series expansion, [..] can only work if equal amounts of processes and flows are considered, or otherwise the matrix would not be square and calculations would not be possible. The latter implies that multiple drivers or influence for a process cannot be considered. For example, the fact that a process X will only occur if both its input flows are supplied is not considered.” To give an example, consider a multifunctional process 1 that provides products A and B, e.g., cogeneration providing heat and electricity through gas burning. Consider as well a process 2 that provides product A, e.g., heat produced through a conventional gas boiler, and a process 3 that provides product B, e.g., providing electricity from the grid. Consider hypothetically that, if products A and B are required up until their fixed product ratio, process 1 instead of processes 2 and 3 will cover this, and vice versa if these products are separately required or beyond their fixed product ratio. Now if products A and B are together required up until their fixed product ratio, the mathematical model should ideally run process 1 and not processes 2 and 3 separately. Consider the example of a factory that will operate a cogeneration unit if both heat and electricity are demanded, or otherwise a gas boiler if only heat is demanded, and taking electricity from the grid if only electricity is demanded, (see Figure 1). Such conditional dynamics cannot be considered in LIM at a systematic level during propagation. It is not that LIM cannot consider multifunctional processes in conjunction with separate processes (as mixes), but rather that their usage will be prefixed on beforehand by a certain amount or share, and will not dynamically be specified. Keep in mind that other types of dynamic effects exist. To conclude, the fact that our framework allows dynamic propagation is a step forward.
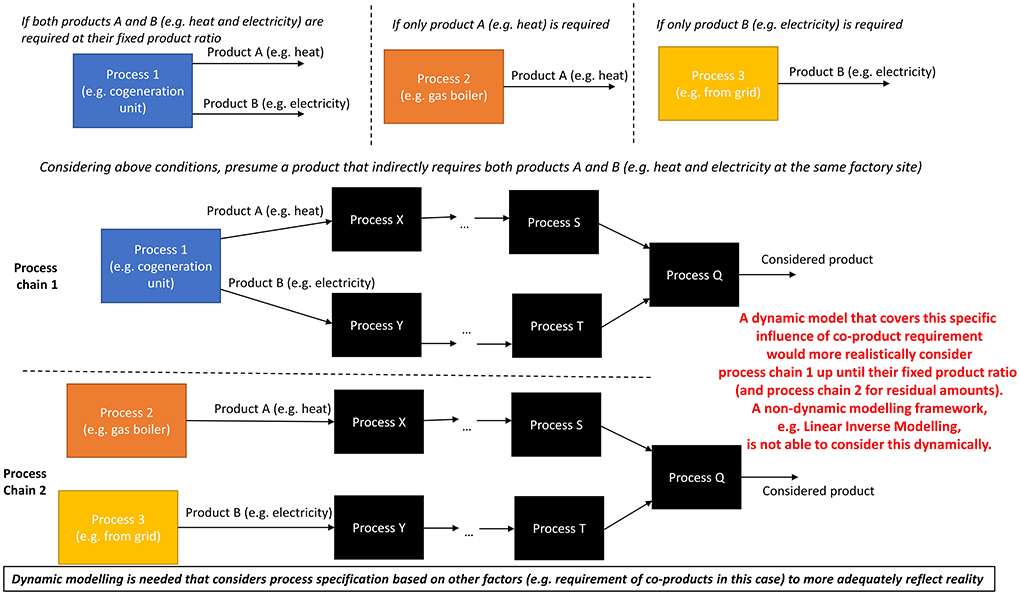
Figure 1. Example on dynamic modeling in the case of selection of a certain process, which provides two co-products, instead of alternative processes, when both co-products are required in a certain fixed product ratio. Note that other types of dynamic effects exist.
A third possible major advancement is that our framework does not necessarily exclude integrated, possibly synergetic and antagonistic non-linear effects between the cause-effect chains of sustainability pillars, which is relevant to cover (Guinée et al., 2011; Schaubroeck and Rugani, 2017), especially when going beyond the consideration of LCSA as a combination of Life Cycle Assessment, Social Life Cycle Assessment and Life Cycle Costing. In our framework we speak of impact in general, permitting integrated effects, whereas in the framework of Heijungs (Heijungs, 2010, 2022), environmental, social and economic impact characterization are computed separately: environmental flows (Benv) are only multiplied by environmental characterization factors (Qenv), similarly for economic and social impact. Other frameworks and cases out there have already considered integrated cause-effect chains in an LCSA context (Onat et al., 2016; Francis and Thomas, 2022). Moreover, the framework of Heijungs (2022) does also not consider feedback effects between inventory and impact modeling, whereas ours would. Yet, linear inverse modeling using matrix calculations could overcome the issue of integration and feedback loops, by considering complete matrices where also environmental, social and economic processes are integrated in networks with industrial processes, as presented in literature for the environmental processes (Heijungs, 1997; Schaubroeck et al., 2013; Weidema et al., 2018). Hence, it is not a general shortcoming.
A solely linear inverse modeling framework still cannot achieve the first and second advancements. The power series expansion variant of the inverse modeling (equation 2) has been used to add additional information, e.g., temporal differentiation to the calculated amounts (Beloin-Saint-Pierre et al., 2014), but it does not allow to overcome any of the essential first and second limitations.
Discussion: Practical realization and way forward
Concerning practical realization, the linear inverse modeling (LIM) framework is more readily operational and has been numerously applied to a database-level, which is its major advantage. Yet, limited operational iterative modeling frameworks and tools have been developed that explicitly ambition such a database-wide application, e.g., Temporalis (Cardellini et al., 2018) and DyPLCA (Tiruta-Barna et al., 2016; Pigné et al., 2020). Considering just these two frameworks, they are based on graph-based search algorithms that trace back processes along a prefixed process network graph, e.g., based on current process networks in databases. Please see the respective works for a more thorough explanation. For the DyPLCA framework (Pigné et al., 2020), there has been a full application at database level. There are issues with computational power at database level, limiting completeness in flow coverage in practice, but these can be overcome in due time. In the work of Pigné et al. (2020) is mentioned concerning the coverage of their framework of the flows considered in the analytical LIM approach that: “Carbon dioxide flows are considered, with a threshold of 10−4 leading to a coverage of 79%. It is estimated that 90% coverage would require more than 5 h of computation and 95% almost nine full days. Further optimization is needed to improve the coverage of emissions and to close the gap between numerical and analytical results.” Both frameworks are currently linear, pre-fixed, but could readily be converted to more open, integrated and non-linear versions. For non-linear modeling, process equations could be readily changed, possibly grouped by types of processes to facilitate execution. In the case of dynamics, specifically for graph-based search tools, dynamic graphs could be considered that can alter over time (Holme, 2015; Vernet et al., 2022).
Finally, the linear inverse modeling framework and computations based on matrices in the field of life cycle methods have been of major relevance and they still are in practice, but it is time to start moving more beyond them given their shortcomings by considering a more basic framework, as we present here, and the further development of derived specific, advanced and operational modeling frameworks. For the latter, taking over and combining modeling frameworks of other fields seems an efficient way forward, as presented in articles that are cited in this work and further literature (Yang and Heijungs, 2018; Huppes and Schaubroeck, 2022).
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Acknowledgments
I thank the reviewer for providing insightful comments that have helped to improve this manuscript.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^Using identical mathematical relationships facilitates application and grasping outcomes and differences, giving possibly the impression of guaranteed better comparability. Yet, since application and its accuracy depend considerably also on the specificity of the case, covered processes & flows and the used input data, in particular for life cycle methods, comparability is not solely affected by choosing certain mathematical relationships. It might be better to use similar accuracy, or quality as a partially subjective predictor, as a notion for comparability, which will depend on a combination of latter various aspects.
References
Baustert, P., Gutiérrez, T. N., Gibon, T., Chion, L., Ma, T.-Y., Mariante, G. L., et al. (2019). Coupling activity-based modeling and life cycle assessment—a proof-of-concept study on cross-border commuting in Luxembourg. Sustainability. 11, 4067. doi: 10.3390/su11154067
Baustert P. Igos E. Schaubroeck T. Chion L. Mendoza Beltran A. Stehfest E. (in Press). Integration of future water scarcity electricity supply into prospective LCA: application to the assessment of water desalination for the steel industry. J. Ind. Ecol. .
Beloin-Saint-Pierre, D., Albers, A., Hélias, A., Tiruta-Barna, L., Fantke, P., Levasseur, A., et al. (2020). Addressing temporal considerations in life cycle assessment. Sci. Total Environ. 743, 140700. doi: 10.1016/j.scitotenv.2020.140700
Beloin-Saint-Pierre, D., Heijungs, R., and Blanc, I. (2014). The ESPA (Enhanced Structural Path Analysis) method: a solution to an implementation challenge for dynamic life cycle assessment studies. Int. J. Life. Cycle Assess. 19, 861–871. doi: 10.1007/s11367-014-0710-9
Beltran, A. M., Cox, B., Mutel, C., Vuuren, D. P., van, Vivanco, D. F., Deetman, S., et al. (2020). When the background matters: using scenarios from integrated assessment models in prospective life cycle assessment. J. Ind. Ecol. 24, 64–79. doi: 10.1111/jiec.12825
Cambridge English Dictionary. (2022). dynamic [WWW Document]. Available online at: https://dictionary.cambridge.org/dictionary/english/dynamic (accessed April 21, 2022).
Cardellini, G., Mutel, C. L., Vial, E., and Muys, B. (2018). Temporalis, a generic method and tool for dynamic Life Cycle Assessment. Sci. Total Environ. 645, 585–595. doi: 10.1016/j.scitotenv.2018.07.044
Francis, A., and Thomas, A. (2022). A framework for dynamic life cycle sustainability assessment and policy analysis of built environment through a system dynamics approach. Sustain. Cities Soc. 76, 103521. doi: 10.1016/j.scs.2021.103521
Guinée, J. B., Heijungs, R., Huppes, G., Zamagni, A., Masoni, P., Buonamici, R., et al. (2011). Life cycle assessment: past, present, and future. Environ. Sci. Technol. 45, 90–96. doi: 10.1021/es101316v
Heijungs, R.. (1997). Economic drama and the environmental stage: formal derivation of algorithmic tools for environmental analysis and decision-support from a unified epistemological principle. [s.n.], S.l. doi: 10.1007/BF02978414
Heijungs, R.. (2010). Ecodesign—carbon footprint—life cycle assessment—life cycle sustainability analysis. A flexible framework for a continuum of tools. Environ. Clim. Technol. 4, 42–46. doi: 10.2478/v10145-010-0016-5
Heijungs, R.. (2020). Is mainstream LCA linear? Int. J. Life Cycle Assess. 25, 1872–1882. doi: 10.1007/s11367-020-01810-z
Heijungs, R.. (2022). The revised mathematics of life cycle sustainability assessment. J. Clean. Prod. 350:131380. doi: 10.1016/j.jclepro.2022.131380
Heijungs, R., and Suh, S. (2002). The computational structure of life cycle assessment, Eco-efficiency in industry and science v. 11. Dordrecht, Boston: Kluwer Academic Publishers. doi: 10.1007/978-94-015-9900-9_2
Holme, P.. (2015). Modern temporal network theory: a colloquium. Eur. Phys. J. B. 88, 234. doi: 10.1140/epjb/e2015-60657-4
Huppes, G., and Schaubroeck, T. (2022). Forecasting the future sustainability of technology choices: qualitative predictive validity of models as a complement to quantitative uncertainty. Front. Sustain. 3, 1–14. doi: 10.3389/frsus.2022.629653
Kätelhön, A., Bardow, A., and Suh, S. (2016). Stochastic technology choice model for consequential life cycle assessment. Environ. Sci. Technol. 50, 12575–12583. doi: 10.1021/acs.est.6b04270
Li, D., Tsang, M. P., and Kua, H. W. (2022). Editorial: non-linearity in life cycle assessment. Front. Sustain. 3, 1–2. doi: 10.3389/frsus.2022.883330
Onat, N. C., Kucukvar, M., Halog, A., and Cloutier, S. (2017). Systems thinking for life cycle sustainability assessment: a review of recent developments, applications, and future perspectives. Sustainability. 9, 706. doi: 10.3390/su9050706
Onat, N. C., Kucukvar, M., Tatari, O., and Egilmez, G. (2016). Integration of system dynamics approach toward deeping and broadening the life cycle sustainability assessment framework: a case for electric vehicles. Int. J. Life Cycle Assess. 21, 1009–1034. doi: 10.1007/s11367-016-1070-4
Pigné, Y., Gutiérrez, T. N., Gibon, T., Schaubroeck, T., Popovici, E., Shimako, A. H., et al. (2020). A tool to operationalize dynamic LCA, including time differentiation on the complete background database. Int. J. Life Cycle Assess. 25, 267–279. doi: 10.1007/s11367-019-01696-6
Pizzol, M., Sacchi, R., Köhler, S., and Anderson Erjavec, A. (2021). Non-linearity in the life cycle assessment of scalable and emerging technologies. Front. Sustain. 1, 1–16. doi: 10.3389/frsus.2020.611593
Qin, Y., Yang, Y., Cucurachi, S., and Suh, S. (2021). Non-linearity in marginal LCA: application of a spatial optimization model. Front. Sustain. 2, 1–8. doi: 10.3389/frsus.2021.631080
Rödger, J.-M., Kjær, L. L., and Pagoropoulos, A. (2018). "Life cycle costing: an introduction,” in: Life Cycle Assessment: Theory and Practice, eds M. Z. Hauschild, R. K. Rosenbaum, S. I. Olsen (Springer International Publishing, Cham), 373–399. doi: 10.1007/978-3-319-56475-3_15
Schaubroeck, T., Alvarenga, R. A. F., Verheyen, K., Muys, B., and Dewulf, J. (2013). Quantifying the environmental impact of an integrated human/industrial-natural system using life cycle assessment; a case study on a forest and wood processing chain. Environ. Sci. Technol. 47, 13578–13586. doi: 10.1021/es4046633
Schaubroeck, T., Baustert, P., Igos, E., and Benetto, E. (2020). Is a sustainability assessment a shot in the dark? How to deal with its nonquantified uncertainty? Environ. Sci. Technol. 54, 2051–2053. doi: 10.1021/acs.est.0c00450
Schaubroeck, T., Gibon, T., Igos, E., and Benetto, E. (2021a). Sustainability assessment of circular economy over time: Modelling of finite and variable loops and impact distribution among related products. Resour. Conserv. Recycl. 168, 105319. doi: 10.1016/j.resconrec.2020.105319
Schaubroeck, T., Gibon, T., Igos, E., and Benetto, E. (2021b). CORRECTION–sustainability assessment of circular economy over time: modeling of finite and variable loops and impact distribution among related products. Resour. Conserv. Recycl. 172, 105675. doi: 10.1016/j.resconrec.2021.105675
Schaubroeck, T., and Rugani, B. (2017). A revision of what life cycle sustainability assessment should entail: towards modeling the net impact on human well-being. J. Ind. Ecol. 21, 1464–1477. doi: 10.1111/jiec.12653
Schaubroeck, T., Schaubroeck, S., Heijungs, R., Zamagni, A., Brandão, M., and Benetto, E. (2021c). Attributional and consequential life cycle assessment: definitions, conceptual characteristics and modelling restrictions. Sustainability. 13, 7386. doi: 10.3390/su13137386
Schaubroeck, T., Schrijvers, D., Schaubroeck, S., Moretti, C., Zamagni, A., Pelletier, N., et al. (2022). Definition of product system and solving multifunctionality in ISO 14040–14044: inconsistencies and proposed amendments—toward a more open and general LCA framework. Front. Sustain. 3, 1–6. doi: 10.3389/frsus.2022.778100
Suh, S., and Heijungs, R. (2007). Power series expansion and structural analysis for life cycle assessment. Int. J. Life. Cycle. Assess. 12, 381–390. doi: 10.1065/lca2007.08.360
Tiruta-Barna, L., Pigné, Y., Navarrete Gutiérrez, T., and Benetto, E. (2016). Framework and computational tool for the consideration of time dependency in Life Cycle Inventory: proof of concept. J. Clean. Prod. 116, 198–206. doi: 10.1016/j.jclepro.2015.12.049
UNEP (2020). Guidelines for Social Life Cycle Assessment of Products and Organizations (2020). Benoît Norris, C., Traverso, M., Neugebauer, S., Ekener, E., Schaubroeck, T., Russo Garrido, S., et al. (eds.). United Nations Environment Programme (UNEP).
Valdivia, S., Backes, J. G., Traverso, M., Sonnemann, G., Cucurachi, S., Guinée, J. B., et al. (2021). Principles for the application of life cycle sustainability assessment. Int. J. Life Cycle Assess. 26, 1900–1905. doi: 10.1007/s11367-021-01958-2
Vernet, M., Pigné, Y., and Sanlaville, É. (2022). A study of connectivity on dynamic graphs: computing persistent connected components. 4OR-Q. J. Oper. Res. doi: 10.1007/s10288-022-00507-3
Weidema, B. P., Schmidt, J., Fantke, P., and Pauliuk, S. (2018). On the boundary between economy and environment in life cycle assessment. Int. J. Life Cycle Assess. 1839–1846. doi: 10.1007/s11367-017-1398-4
Wu, S. R., Li, X., Apul, D., Breeze, V., Tang, Y., Fan, Y., et al. (2017). Agent-based modeling of temporal and spatial dynamics in life cycle sustainability assessment: agent-based modeling of temporal and spatial dynamics in LCSA. J. Ind. Ecol. 21, 1507–1521. doi: 10.1111/jiec.12666
Yang, Y.. (2016). Two sides of the same coin: consequential life cycle assessment based on the attributional framework. J. Clean. Prod. 127, 274–281. doi: 10.1016/j.jclepro.2016.03.089
Keywords: life cycle assessment, sustainability assessment (SA), life cycle modeling, life cycle sustainability assessment, life cycle inventory (LCI)
Citation: Schaubroeck T (2022) A more basic modeling framework for life cycle methods to cover non-linear, dynamic, and integrated effects–looking beyond linear inverse modeling. Front. Sustain. 3:957017. doi: 10.3389/frsus.2022.957017
Received: 30 May 2022; Accepted: 14 July 2022;
Published: 01 August 2022.
Edited by:
Dingsheng Li, University of Nevada, Reno, United StatesReviewed by:
Simone Cornago, Singapore Institute of Manufacturing Technology (SIMTech), SingaporeCopyright © 2022 Schaubroeck. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thomas Schaubroeck, dGhvbWFzLnNjaGF1YnJvZWNrQGxpc3QubHU=
 Thomas Schaubroeck
Thomas Schaubroeck