Is the Evolution of Energy System Productive Structures Driven by a Physical Principle?

Introduction

The Constructal Principle has been proposed by Adrian Bejan in 1997 (Bejan, 1997) and then it has been used in literature to predict the shape and structure for a lot of physical flow systems (Bejan and Lorente, 2013; Bejan, 2017; Bejan and Errera, 2017; Bejan et al., 2017). It is often regarded as a possible 4th Law of Thermodynamics, stating the direction toward which a system evolves if it has access to some external resources to feed its internal fluxes, i.e., if it can stay far from equilibrium with its surrounding. In this case the well-known 2nd Law of Thermodynamics is not enough to predict system evolution, because this Law tells us that high entropy configurations are very likely to appear, when a system is approaching the thermodynamic equilibrium, for instance because it is isolated from its surrounding, or because no external resources are available. More recently (Reis, 2014), the Constructal Principle has been regarded to be an extension of the more famous Maximum Entropy Production Principle (MEP) (Martyusheva and Seleznev, 2006), previously formulated.

A generic production system may be described as a flow system if the production relation among components and processes are highlighted inside its model. This is the approach of the Thermoeconomic Analysis and Optimization, where the flows of Fuels (the external/internal resources consumed by a component or process) and Products (the useful flows produced for external/internal consumption) are used for describing the so-called Internal Economy of the system, instead of the actual material and energy flows that cross the control volumes of components and processes (see, for instance, Valero et al., 2006). The set of all Fuels and Products, connecting components and processes each other and with the outside, is named the Productive Structure of the system. It is worth noting that this kind of description may be suitable for all production systems, both natural and artificial, even if the great majority of applications in Literature deals with energy production systems. In any case, if the physical behavior of a generic productive structure has to be highlighted, the external resources that fed the productive structure itself have to be taken directly from the natural environment, rather than from some intermediate structure, governed by laws that are not completely known, such as society or the market.

In this paper, the Thermoeconomic Analysis and Optimization approach is briefly summarized, in particular for what concern the evaluation of all Fuels and Products by means of their exergy contents, then, the concept of Thermoeconomic Environment is defined and discussed with the aim of reconciling the Reference Environment, for exergy evaluation, and the consumption of environmental resources and residual emissions which inherently characterize every kind of production system. On these bases, the aim of the paper is to show that the Constructal Principle can provide information on the evolution of complex energy systems and that some noticeable aspects of the evolution of an energy system productive structure can be regarded as consequence of the Constructal Law. In particular, the widely accepted assumption that energy systems have to be optimized by minimizing the specific exergy cost of products, is shown to be a consequence of the Constructal Law. Additional consequences are the appearance of recycling flows inside the productive structure, supplying an explanation of the reason why the presence of recirculation flows is so widespread in production systems, both natural and technological, and a theoretical option for evaluating the exergy cost of residues and sub-products without the need of introducing any remediation technology in the evaluation. Therefore, the result that residues and sub-products cannot be indefinitely discharged in the Thermoeconomic Environment but they have to be generally converted into some kind of product by different (new) production processes, can be inferred on physical bases. This result supports the paradigm of the Circular Economy, as outlined by the Ellen MacArthur Foundation: “Looking beyond the current take-make-waste extractive industrial model, a circular economy aims to redefine growth, focusing on positive society-wide benefits. It entails gradually decoupling economic activity from the consumption of finite resources, and designing waste out of the system.”

The paper has to be regarded as a preliminary analysis with simple models: a three-step model for the production of electricity from solar sources, a Hubbert –like behavior for the availability of all resources, without explicitly introducing any type of differentiation, and a typical thermoeconomic model for defining the capital cost required by the production process. Nonetheless, even using a very simplified model of the system, it has been possible to define a new conceptual framework for Thermoeconomic analysis and to infer some interesting conclusions about both, the real meaning of the circular economy paradigm and the arising of recycling flows in natural and technological systems.

Thermoeconomic Optimization

The Thermoeconomic Optimization (TOP) can be generally defined as the effort of achieving a minimum consumption of total resources for obtaining a set of required products (named P). The key points are:

i. the total resources include both energy and material streams (the Fuels F) consumed at local level as inputs of the production process and all resources indirectly consumed for making all the plant components involved in the production system and for maintaining and operating the plant as a whole (the so called flows of fixed capital Z);

ii. all resources are regarded as energy resources; therefore, Fuels F and fixed capital Z have to be consistently measured.

In this perspective, the flows of fixed capital Z may be regarded as the indirect energy expense in order to arrange a proper set of constraints, for the energy conversion processes, which allow the formation of the required products P. Nevertheless, a problem arises from these general definitions: How different energy and material fuel streams and different kind of fixed capital can be consistently evaluated?

Different answers have been suggested in Literature by different kinds of analysis which, implicitly or explicitly, are supported as possible back ground for the TOP of goods and services production. Each analysis has positive aspects, but some draw back too, in view of TOP. For instance, Embodied Energy Analysis (EE) (Bullard and Herendeen, 1975) uses energy to measure all flows consumed and produced by both natural and technological systems. In this way the qualitative difference between heat and work is neglected. In addition, EE do not define in advance the control volume boundary for the whole system, so that the results obtained by different studies often cannot be compared.

The EMergy Analysis (EMA) (Brown and Herendeen, 1996; Odum, 2000) may be regarded as a similar approach, based on the energy evaluation of flows. Differently from EE, EMA introduces a standard for the origin of all production chains and for the limits of indirect energy supply: it prescribes that all energy inputs to the analyzed process have to be evaluated in terms of the solar energy that has been historically necessary for making available each of them. This can be a very difficult task indeed, and in most real-world cases, a substantial number of (rather arbitrary) assumptions have to be introduced in order of performing the analysis, which implies that the numerical results ought to be regarded as affected by a potentially relevant—and often irresolvable—degree of uncertainty. An additional difference consists in the fact that in the EE, the embodied energy allocation in case of bifurcations is supposed to be proportional to the energy or material content of each bifurcating flow, while the EMA introduces a peculiar set of rules, named Emergy Algebra, that prevents the Emergy budgets from being conservative. Although the Emergy Algebra is not devoid of a rational basis, its dogmatic application may result in some inconsistency, where technological and biological systems interact with each other (see, for instance, Reini and Valero, 2002; Sciubba, 2009; Gaggioli et al., 2014).

A wide group of methodologies aims to overcome the issue of the qualitative difference between the various forms of energy by using exergy for evaluating all energy and material flows. An almost complete review of those methodologies is beyond the scope of this paper and can be found in Rocco et al. (2014). In that paper, exergy based accounting methods are divided into two groups:

i  Monetary cost approach, using the monetary costs of Fuels F and fixed capital Z in order of consistently evaluate the different production factors,

ii Resource cost approach, using some assumptions in order of converting all fixed capital flows into exergy cost flows.

It is also highlighted that the first group (Rodríguez and Gaggioli, 1980; Valero et al., 1986; Tsatsaronis et al., 1993) assigns a unit cost equal to zero to natural resources as they are directly taken from the environment (crude) as well as to other externalities, like environmental pollution without remediation, therefore such a possible consequence of production may be regarded as a natural way for reducing the unit exergy cost of the products. On the other hand, the second group (Szargut, 1995; Sciubba, 2004) has to introduce some assumptions in order of converting all externalities into exergy cost flows; for instance, Szargut (1995) assumed the unit exergy cost of human labor were zero, or Sciubba (2004) supposed that a fixed ratio between monetary and exergy flows, in a defined economic context. The issue of incorporating human labor into exergy analysis has been recently addressed by Rocco and Colombo (2016), in the framework of the input-output economic analysis.

The control volume boundary for the whole system is not defined in advance not only in the ambit of EE, but also adopting various exergy based costing approaches. In these cases, the analyst is let free of fixing the limits of the considered production process, without the mandatory prescription of putting the external resources, that feed the productive structure, directly in relation with the consumption of natural resources, on conditions that a monetary cost were defined for each flow crossing the limits of the adopted control volume.

Thermoeconomic Environment

In this paper, the idea of a Thermoeconomic Environment (TE) is introduced with the aim of reconciling the Reference Environment, for exergy evaluation, and the consumption of environmental resources and residual emissions which inherently characterize every kind of production system. This approach allows to overcome the indetermination related to the control volume boundaries and it also allows the option of incorporating human labor and capital services into the exergy based TOP.

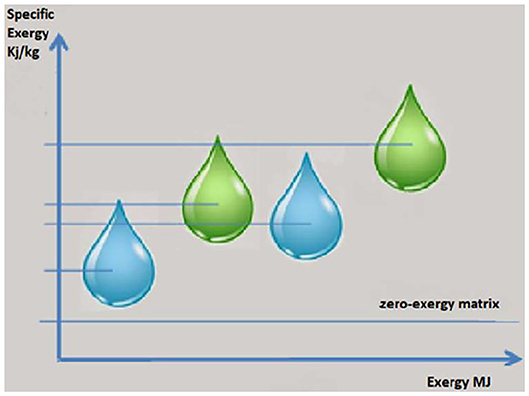
Consistently with the physical nature of real-world energy systems, which do not operate in a homogeneous environment, but they are fully immersed in the biosphere, the TE is a model of environment which may be defined as a set of reservoirs, where different kind of natural resources are confined; all reservoirs are surrounded by the zero-exergy matrix, which plays the role of the dead state for calculating the exergy of all flows inside the energy systems, as well as of all reservoirs (Figure 1), so that each available resource has a specific exergy content greater than zero and a specific exergy costs equal to 1, by hypothesis (see, for instance, Valero, Serra, and Uche Reis, 2014). The zero-exergy matrix can be defined as the dead state model proposed by Gaggioli and Petit (1977) or by Rodríguez and Gaggioli (1980).

FIGURE 1

Figure 1. A qualitative description of some reservoirs in the thermoeconomic environment.

The considered production system, jointly with all direct and indirect resources consumption chain, tracked back to the reservoirs inside the TE can be regarded as the system in its thermoeconomic environment.

It is worth noting that the confined condition of natural resource reservoirs is crucial: if the constraints that allow the confined condition of a particular resource are destroyed, the chemical compound that constitutes the resource is mixed with the zero-exergy matrix and some irreversible processes consume the exergy previously contained in the reservoir, reaching the thermodynamic equilibrium. In addition, each reservoir may be affected by some additional time and space constraints about its availability.

Notice that the idea of the TE, made by a zero-exergy matrix that embeds a set of reservoirs can be also useful for other purposes than the representation of natural non-renewable energy and material resources. For instance, the model could be enriched by defining an internal dynamics of the environment, or for representing the sequestration of a specific type of waste released by the production process. At present, this is one of the most popular options for mitigating the CO₂ accumulation in the atmosphere.

Notice finally that the TE is not too big to be modified by the considered production process, because the amount of exergy in each reservoir is limited and, in principle, it can be sensibly reduced by the exergy consumption of the production processes; moreover, also the zero-exergy matrix may change its temperature T° and its composition in consequence of its internal dynamics (for instance, the periodic oscillations of the availability of solar energy Reini and Casisi, 2016, 2020) or in consequence of the interaction with the global energy system. This could be regarded as a drawback, in view of a straightforward and unquestionable calculation of the exergy of all flows, but is crucial in the exergy cost evaluation of the residue flows released by the production process, as will be discussed in the following. In addition, looking for an exergetic evaluation of the environmental impact of pollutant emissions, should be regarded as physically inconsistent with the definition of an environment that is “too big to be modified” by whatever energy or material input flow affecting it.

An Energy System in the Thermoeconomic Environment

Let's consider an extended energy system, made up by a generic production system, plus the TE, plus all exergy streams and energy conversion processes connecting the considered production system to the TE, so that all Fuels F and fixed capital Z required, directly or indirectly, by the production system itself can be made available.

Notice that, in such an extended energy system there are no flows externally constrained (as may be, if the production system alone were considered). Therefore, it may be regarded, agreeing with Reis (2014), as a system with fixed forces and variable flows, for which the Constructal Principle can be shown to be equivalent to the MEP, so that all conclusions inferred in this work could be also inferred from the MEP, even if in a less straightforward way.

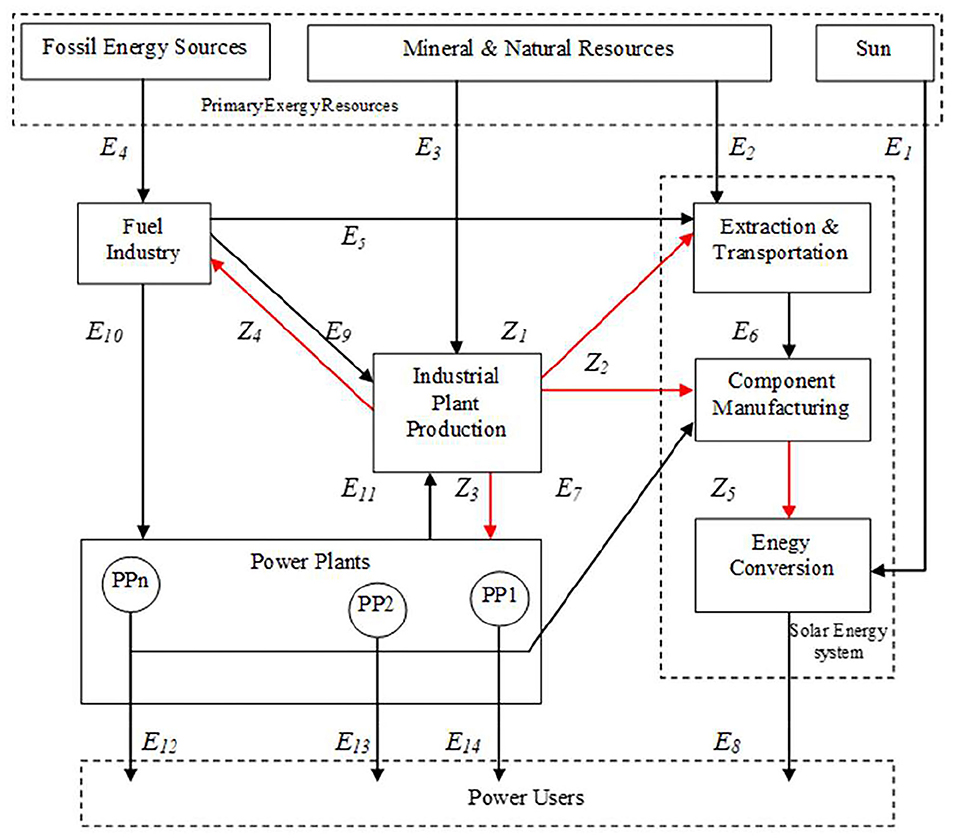
In Figure 2 a solar energy system is considered as an elementary example. It is made up of the three sub-systems highlighted inside the bold rectangle:

1. extraction and transportation of natural resources directly required;

2. manufacturing of the solar energy conversion plant;

3. conversion of solar radiation into electrical power.

FIGURE 2

Figure 2. The extended energy system for a solar energy production system.

Notice that, tracking back the indirect resource consumptions, some processes have to be taken into account (like manufacturing, or raw mineral extraction) which are not usually regarded as simultaneous with the main energy conversion phase; therefore, the extended energy system may be regarded as a life-cycle extended picture, rather than an instantaneous picture.

Alternatively, one might think that, during the normal operation of the energy conversion system, another similar system must be produced to replace the first at the end of its life cycle and, simultaneously, additional raw mineral resources have to be extracted for the production of the further energy conversion system and so on. In this way, the picture of the extended energy system may still be regarded as an instantaneous one.

The extended energy system in Figure 2 is very simple and is described by means of only three macro components, besides the solar energy system:

(a) the fuel industry sector, which supplies the proper fossil fuels required for the extraction and transportation of raw mineral resources, as well as for the industrial plant production sector and for the operation of power plants;

(b) the industrial plant production sector, supplying all fixed capital required by the other productive phases, except the fixed capital of the solar energy conversion plant, which is produced by sub-system 2 inside the control volume of the solar system itself.

(c) a set of power plants, which supplies the electric energy to all power users, including the Industrial plant production sector and the manufacturing of the solar energy conversion plant.

The flows connecting this extended production system to the TE can be easily inferred from Figure 2 and are summarized in Table 1.

TABLE 1

Table 1. Description of the flows in the extended energy production system in Figure 2.

Notice that the exergy cost and the exergy equivalents of money can be both inferred from the equation set containing the cost balance of each component inside the extended production system, provided that all flows produced by the same component had the same unit exergy cost (or the same exergy equivalent of money unit). This hypothesis is widely accepted in the ambit of Thermoeconomics and is known as the “P postulate” (Valero et al., 1986, 2006).

Constructal Law

In the previous paragraphs, the extended energy system has been defined as a network of flows, where different irreversible processes interact in order to extract exergy from the TE, obtaining one concentrated product flow in a defined site of the network. Therefore, the CL may be applied to the extended energy system as well as it has been applied in literature to a lot of physical flow systems, like river basins, sap ducts inside trees, pulmonary ducts, heat exchangers and so on (see, for instance, Ref. Bejan and Lorente, 2013; Bejan, 2017; Bejan and Errera, 2017; Bejan et al., 2017).

The CL states:

“For a finite-size flow system to persist in time (to survive) its configuration must evolve in such a way that it provides an easier access to the currents that flow through it” (Bejan, 1997).

Notice that this exergy based approach to the evolution of the productive structures of energy systems is consistent with the idea that exergy flows entail any process where the system evolves from one state to another, expressed by Lucia in (Lucia, 2013).

For the extended energy system in hands, the currents that flow through the system has to be identified with the electric power produced by the solar energy system in Figure 2, because it is the concentrated flow, required in a defined site of the network, which corresponds to the water mass flow rate at the mouth for a river basin, the total air flow in a lung, the total heat transmitted through a heat exchanger, and so on. In case of a different production system, the product could be identified with some kind of food, or simply the living biomass of a certain species, from a defined ecosystem.

In any case, the CL states that the evolution of the energy system will be in the direction of a production increase. It is worth noting that the new idea that allows to connect Thermoeconomics to the CL is simply to apply the latter, not only to physical flow systems (ducts, rivers, trees.) but also to flow systems made up of productive (or functional) relation, where the flowing magnitude may be not conserved, along the production process.

The expectation is that the CL could show us which productive structures are going to arise, or will persist, during the evolution of the energy system, and which other will be selected for the extinction, as well as the Second Law tells us that high entropy configurations are very likely to appear, when a system is approaching the thermodynamic equilibrium.

Unit Exergy Cost Reduction Principle

In the ECT, the direct and indirect consumption of exergy resources for obtaining a required product P is named the exergy cost of P and consequently the ratio between the exergy cost and P itself is named its unit exergy cost ($k_P^{*}$). In that approach the limits of the control volume are not prescribed by the theory but they are chosen by the analyst. This source of uncertainty can be overcome if we prescribe that all direct and indirect consumptions have to be tracked back to the TE, previously introduced. Let's name F_TE the sum of all direct and indirect Fuels received from the TE. The previous definitions can be summarized in Equation (1):

$\begin{array}{ll}{F}_{TE}=P{k}_P^{*}& (1)\end{array}$

Therefore, the production increase prescribed by the CL can be expressed as Equation (2):

$\begin{array}{ll}\delta P=(\delta F_{TE}{k}_P^{*}-F_{TE}\delta k_P^{*})/{(k_P^{*})}^2>0& (2)\end{array}$

In the framework of the CL, P represents the current that flows through the system (the water flow rate at the mouth for a river basin, or the power produced by the solar system in the extended energy system in Figure 2). F_TE represents the total exergy flow, available in the TE, to drive the process and $k_P^{*}$ represents the unit exergy cost to make the current flowing under the existing constraints, i.e., the “resistance to flow” (see, for instance Reis, 2008).

Whilst F_TE and $k_P^{*}$ are necessarily positive quantities, the sign of δF_TE depends on the behavior in time of the exploitation of resources from the TE. We can easily identify two main kinds of behaviors:

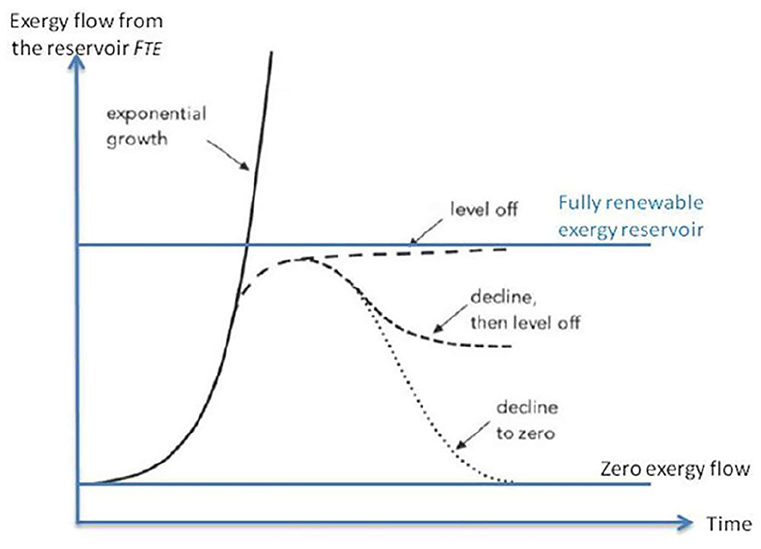
(a) Hubbert like, where a starting phase, characterized by an exponential (Malthusian) growth (Figure 3), is followed by a maximum (the Hubbert peak) and then by a declining phase, where δF_TE is negative (Bejan and Lorente, 2011);

(b) Sigma like, where the exponential starting phase is followed by a flex and then by an approximately constant value (asymptotically approached), where δF_TE is equal, or very close to zero.

FIGURE 3

Figure 3. Different kind of behavior for the exploitation of resources from the TE.

The first kind is characteristic of non-renewable resources, like fossil fuels, whilst the second one is characteristic of renewable resources, like solar energy. It is worth noting that both the Hubbert peak and the asymptotic value, in the first and second case, respectively, may depend on the technological development of the production system, or on the evolution stage of the ecosystem. An example of the last case, dealing with bacteria population evolution, can be found in Falkowski (1997); it can be regarded also as a demonstration that biological energy systems do modify the zero-exergy matrix of the TE.

In both cases (a) and (b), if the unrestricted availability of resources is over (i.e., when the finite size of the flow system plays a crucial role), the extraction of exergy resources from the TE is declining, or about constant. In the new situation of fuel shortage, the following Equation (3) may be assumed:

$\begin{array}{ll}\delta F_{TE}\le 0& (3)\end{array}$

By combining Equations (2) and (3) it can be easily inferred that the derivative of the unit exergy cost $k_P^{*}$ has to be strictly negative:

$\begin{array}{ll}\delta k_P^{*}<(\delta F_{TE}{k}_P^{*}/F_{TE})\to \delta k_P^{*}<0& (4)\end{array}$

In other words, the CL allows to infer a first conclusion about the evolution of (biological and artificial) energy systems: to persist in time, the unit exergy cost of their products have to reduce.

This is analogous to the general conclusion of the CL, that flow structures evolve in the direction of reducing the resistance to flow. Therefore, the unit exergy cost reduction has no more to be regarded as an axiom of TOP, but rather as a consequence of a physical principle that tells us which energy systems can persist in time (to survive) and which others would be selected for extinction. Bejan and Lorente (2008) have clearly highlighted, for an internal organ of an animal, how resistance to flow may be split in two contribution: “An organ destroys useful energy (i) by friction and heat and mass transfer irreversibilities because of the finite size of its flow passages and transfer surfaces and (ii) by having to be carried, constructed, and maintained (kept flowing) on the larger system (animal).” It can be easily inferred that, for a production process directly and indirectly fed by the exergy resources coming from the TE, the unit exergy cost of the product (resistance to flow) may be reduced in two ways: (i) reducing the specific consumption of each internal fuel, made available at the boundaries of the process (i.e., making the process more efficient), or (ii) adopting more efficient (more sustainable) supply chains, with lower unit exergy cost of the internal fuels they made available. It is worth noting that, in both ways, a reduction of the exergy destruction is obtained in the extended process, from the TE to the product P.

Moreover, by combining Equations (1) and (4) the following Equation (5) can be easily inferred:

$\begin{array}{ll}\delta k_P^{*}<\delta F_{TE}/P& (5)\end{array}$

Equation (5) means that there is a minimum reduction speed for the unit exergy cost of the of the product, above which the process may be more efficient, but it is not enough to persist in time (to survive). In this case, or when the exergy resources extracted from the TE decline to zero, the process has to switch to different resources, or it would approach its extinction.

The Creation of Recycling

During the evolution of the productive structure, two main strategies can be adopted for reducing the unit exergy cost of the products: (i) improving the exergy efficiency inside the considered process (i.e., reducing its specific exergy consumptions); (ii) identifying, inside the extended energy system, an available flow of the same nature of one of the fuels of the considered process, but at a lower unit exergy cost, with respect of the fuel actually consumed, and then modifying the productive structure of the extended energy system, in order of replacing the more resources-expensive fuel with the less one.

To exemplify these possible evolutions, let's consider that the fixed capital (Z₂) and the electric power (E₇) required by the manufacturing phase of the solar energy system in Figure 2, are not univocally fixed by the amount of input raw material (E₆), but they can be modified, in the sense that additional investment in fixed capital allows a saving in the need for electricity, and vice versa, without modify the efficiency (E₈/E₁) of the solar energy conversion phase. This approach is very common in the ambit of TOP (Tsatsaronis, 2011).

In the following, a trade-off is introduced between the capital intensity (Z₂/E₆) and the energy intensity (E₇/E₆) per unit of raw material processed, assuming that all the other components in the extended energy system do not vary their efficiency (or their technical production coefficients of Leontief, 1951).

To take also into account possible improved energy conversion strategies (for instance, as an effect of a technological development) an additional hypothesis is introduced, that a higher solar energy conversion efficiency may be achieved, but in that case the consumption of local resources of capital, or of exergy, would be higher.

Notice that the opposite case (lower consumption of capital and/or of exergy) does not require any optimal compromise to be identified, and has to be simply recognized as consistent with the unit exergy cost reduction principle and the Constructal Law. Then, the fixed capital Z₂ may be evaluated through Equation 6 (Tsatsaronis, 2011).

$\begin{array}{ll}\frac{Z_2}{E_6}=\frac{1}{{\left(\frac{E_7}{E_6}\right)}^n}\frac{m}{\left(\frac{E_1}{E_8}\right)-\frac{1}{{\eta }_M}}& (6)\end{array}$

where n and m are proper constants and η_M is the maximum realistic value for the efficiency of the energy conversion phase. In Figure 4, Equation 6 is plotted as a set parametric curves Z₂ = f (E₇/E₆, E₈/E₁), where the parameter is the efficiency of the energy conversion phase: η₈ = E₈/E₁. For each set of values (Z₂, E₇/E₆, E₈/E₁) the equation system containing the cost balance of each component inside the extended production system can be solved, and the exergy cost and the exergy equivalents of money can be calculated, for all flows Ei and Zj, respectively. The obtained unit exergy cost $k_8^{*}$ (of the electric power produced by the solar energy system) and $k_7^{*}$ (of the electric power consumed during the manufacturing phase—constant, in the considered example) are also plotted in Figure 4. Taking these reasonable hypotheses on the fixed capital (Z₂) into account, a possible evolution A-B-C-D can be highlighted, allowing a progressive reduction of the unit exergy cost of the Product E₈, consistently with the Constructal Law and the TOP.

FIGURE 4

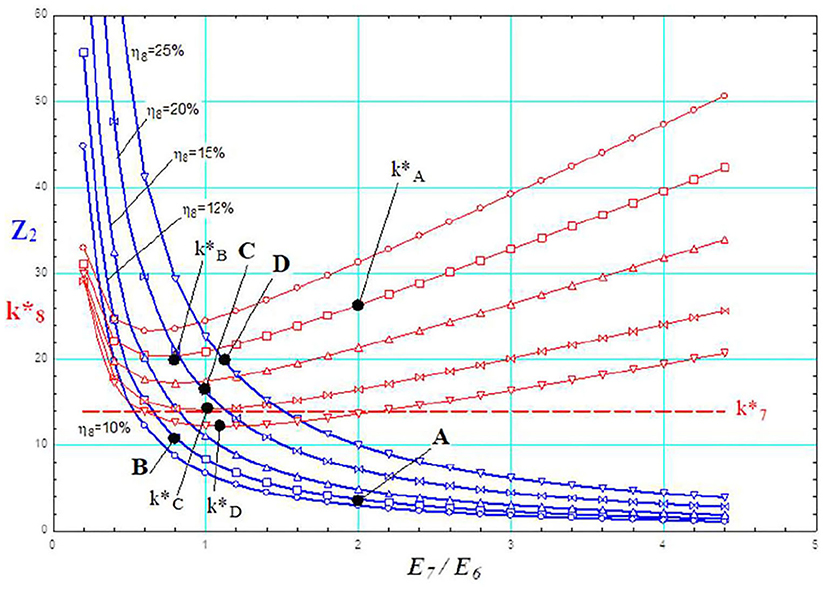
Figure 4. Parametric plot of the relation Z2 = f (E7/E6, E8/E1) evaluating the fixed capital cost for the manufacturing phase and the corresponding unit exergy cost k*8 for the solar system in Figure 2.

If the unit exergy cost reduction may go on enough, a condition is reached (point C in Figure 4) where $k_7^{*}$ = $k_8^{*}$. At that point, a further reduction can be achieved, not only by improving the exergy efficiency inside the process, but also by modifying the productive structure of the extended energy system; in fact, an alternative electric power flow is now available at the same unit exergy cost of flow E₇. This means that a part of the product E₈ can be split and recycled back in order of totally (or partially) replacing the flow E₇ as an input of the manufacturing phase.

It is worth noting that, in this case, the creation of a recycling inside the productive structure can be explained as a consequence of the CL, like the shape of a river basin.

Besides point C, a further unit exergy cost reduction of the product E₈ is still possible and it can be shown that the reduction is stronger for the productive structure containing the recycling of the power produced by the solar energy system (Reini, 2016). In other words, consistently with the CL, this recycling flows is expected to be reinforced during the evolution of the productive structure and the creation of internal recycling flows may be recognized as an important strategy of both natural and technological energy systems toward lower unit exergy cost of the products and more sustainable Supply Chains.

Strategies for the Disposal of Residues in the Thermoeconomic Environment

Leaving apart the elementary example, let's conclude discussing the relation between the unit exergy cost reduction principle and the different strategies for the disposal of residues in the TE. All energy systems generally include some flows, which are obtained during the production process, that are not products. Then, the system has to dispose them off (see, for instance, Liao et al., 2012). They are named residues and sub-products and the problem of their thermoeconomic evaluation is discussed, for instance, in Reini and Valero (2002) and in Torres et al. (2008). A different approach is suggested here, consistently with the CL and taking advantage by the definition of the TE. Three main options can be identified for the disposal of residues:

1. Disposing them off directly in the TE, without any kind of additional operation.

2. Neutralizing them; this option necessarily requires additional fuels and/or additional fixed capital (natural or artificial), in order of reducing the residues flows to an exergy level close to the zero-exergy matrix of the TE, or in order of creating a new confined reservoir inside the TE.

3. Converting them as input of some new process, which is able of obtaining some useful product.

The first option might be regarded as the most favorable, in view of the previous considerations about the unit exergy cost reduction principle. In fact, both second and third options imply an additional consumption of resource, with respect to the original system obtaining the product P. But this is true only if the disposal of residues does not affect the exergy stock in the TE. Keeping in mind that the TE is not unmodifiable in the present approach, its exergy stock can be reduced in two ways:

a) Modifying the zero-exergy matrix temperature (T°) or composition, so that a part of the reservoirs suffers a reduction of its exergy content;

b) Damaging the constraints that allow one or more reservoirs (including fresh water, fertile soil, etc.) to persist in their confined condition.

If the disposal of residues does affect the exergy stock in some way, it has an exergy cost which, in principle, may be very high, even if not easy to be evaluated. This cost has to be charged on the original system, so that the consequence of disposing directly the residues in the TE implies an increase in the unit exergy cost of the product, that is the opposite of what prescribed by the TOP and the CL to guarantee the persisting in time of the energy system.

On the contrary, the third disposal option is possibly the most favorable, because in this case the product P is discharged of some resource consumption, i.e., the part of the original resource consumption that is charge on the new Product (jointly with all the additional resources required for converting the old residue into the input of the new process). In this way the unit exergy cost of the main product P may decrease, consistently with the cost formation chain of the sub-products (Reini and Valero, 2002; Torres et al., 2008). In other words, this approach allow us to infer that no residues and sub-products may be indefinitely accumulated in the environment, but they have to be generally converted into some kind of product by different production processes, not because it is convenient, or because it is a moral duty, but because this allows the system to evolve avoiding extinction. It can be easily noted how this conclusion strongly supports the paradigm of the Circular Economy. In fact, the recycling flows here considered, for improving the efficiency of the supply chain, or for reducing the emission of residues affecting the exergy stock of the TE, may be more generally regarded as any product (or by-product) flow that is recirculated back ward in the production chain. In this sense, they may include some of the “R points” usually presented to describe the circular economy paradigm, in particular (Potting et al., 2017):

• R4 Repair: Repair and maintenance of defective product so it can be re-used with its original function.

• R6 Remanufacture: Use parts of discarded product in a new product with the same function.

• R8 Recycle: Process waste materials to re-obtain crude materials the same (high grade) or lower (low grade) quality.

• R9 Recover: Incineration of fuel waste material with energy recovery.

Conclusions

In the paper the concept of Thermoeconomic Environment (TE) has been introduced, and the possible application of the Constructal Theory to the evolution of the productive structure of any energy system (natural or artificial) has been discussed.

This approach allows to infer that the evolution of any energy system is strictly related to the exploitation of exergy resources from the TE; when the limited nature of the exploited exergy resources does not affect the system (typically, because it is too small) the latter evolves toward a continuous increment of the product, consistently with the Malthusian growth. But when the exergy extraction is declining, or constant, the evolution is driven by the effort of reducing the unit exergy cost of the product, either by increasing the efficiency of the internal components, or by modifying the productive structure of the extended energy system. Therefore, the unit exergy cost reduction principle has no more to be regarded as an axiom of TOP, but as a consequence of a physical principle that tells us which energy systems can persist in time (to survive) and which others would be selected for extinction.

When the productive structure of the extended energy system is modified to reduce the unit exergy cost of the product, recycling flows may be created inside the productive structure itself. It can be demonstrated that the presence of the recycle allows a further reduction of the unit exergy cost of the product, with respect to the reduction allowed by the components' efficiency improvement alone. Therefore, a wide variety of recycling flows is expected to appear and to be reinforced in both natural and artificial energy systems, consistently with the physical principle expressed by the CL. Then, the creation of internal recycling flows may be recognized as an important strategy of both natural and technological energy systems toward lower unit exergy cost of the products and more sustainable Supply Chains.

Finally, the definition of the TE allows (at least in principle) to properly identify the exergy cost of disposing off residues and sub-products directly in the environment, without any kind of additional operation. Their continuous accumulation in the environment directly implies an increment of the unit exergy cost of the product, exactly because the exergy stock of the TE is affected. Therefore, residues and sub-products cannot be indefinitely accumulated in the environment, but they have to be generally converted into some kind of product by different (new) production processes, supporting the paradigm of the Circular Economy and highlighting the importance of recycling not only for system efficiency, but for system surviving, as prescribed by the CL.

More generally, the results obtained may be regarded as the physical justifications, in the light of the Constructal Principle, of the evolutionary tendency toward the more and more complex and highly circular pathways that can be observed in both natural and artificial (energy) production systems.

The perspective of this research activity is to overcome the limitation of the simplified models here considered: a three-step model for the production of electricity from solar sources, a Hubbert –like behavior for the availability of all resources and a typical thermoeconomic model for defining the capital cost required by the production process. The expectation is to confirm the results here inferred also by using more complex and realistic models, and dealing with different kinds of renewable and non-renewable exergy resources, also quantitatively assessing the exergy cost linked to the impaired of the exergy stock of the geo-biosphere.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

MR and MC: conceptualization, methodology, validation, and writing—original draft preparation. MR: software, investigation, and data curation. MC: formal analysis, resources, writing—review and editing, and supervision. All authors: have read and agreed to the published version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Bejan, A. (1997). Advanced Engineering Thermodynamics. 2nd Edn. New York, NY: Wiley.

Google Scholar

Bejan, A. (2017). Evolution in thermodynamics. Appl. Phys. Rev. 4:011305. doi: 10.1063/1.4978611

CrossRef Full Text | Google Scholar

Bejan, A., Almerbati, A., and Lorente, S. (2017). Economies of scale: the physics basis. J. Appl. Phys. 121:044907. doi: 10.1063/1.4974962

CrossRef Full Text | Google Scholar

Bejan, A., and Errera, M. R. (2017). Wealth inequality: the physics basis. J. Appl. Phys. 121:124903. doi: 10.1063/1.4977962

CrossRef Full Text | Google Scholar

Bejan, A., and Lorente, S. (2008). Design With Constructal Theory. Hoboken, NJ: Wiley. doi: 10.1002/9780470432709

CrossRef Full Text | Google Scholar

Bejan, A., and Lorente, S. (2011). The constructal law origin of the logistics S curve. J. Appl. Phys. 110:024901. doi: 10.1063/1.3606555

CrossRef Full Text | Google Scholar

Bejan, A., and Lorente, S. (2013). Constructal law of design and evolution: physics, biology, technology, and society. J. Appl. Phys. 113:151301. doi: 10.1063/1.4798429

CrossRef Full Text | Google Scholar

Brown, M. T., and Herendeen, R. A. (1996). Embodied energy analysis and EMERGY analysis: a comparative view. Ecol. Econ. 19, 219–235. doi: 10.1016/S0921-8009(96)00046-8

CrossRef Full Text | Google Scholar

Bullard, C. W., and Herendeen, R. A. (1975). The energy cost of goods and services. Energy Policy 3, 268–278. doi: 10.1016/0301-4215(75)90035-X

CrossRef Full Text | Google Scholar

Falkowski, P. G. (1997). Evolution of the nitrogen cycle and its influence on the biological sequestration of CO2 in the ocean. Nature 387, 272–275. doi: 10.1038/387272a0

CrossRef Full Text | Google Scholar

Gaggioli, R., Reini, M., and Panel, I. (2014). Connecting 2nd law analysis with economics. Ecol. Energy Policy Entropy 16, 3903–3938. doi: 10.3390/e16073903

CrossRef Full Text | Google Scholar

Gaggioli, R. A., and Petit, P. J. (1977). Use the second law first. Chemtech 7, 496–506.

Google Scholar

Leontief, W. (1951). The Structure of American Economy, 1919–1939, an Empirical Application of Equilibrium Analysis. 2nd Edn. New York, NY: Oxford University Press.

Google Scholar

Liao, W., Heijungs, R., and Huppes, G. (2012). Thermodynamic analysis of human–environment systems: a review focused on industrial ecology. Ecol. Modell. 228, 76–88. doi: 10.1016/j.ecolmodel.2012.01.004

CrossRef Full Text | Google Scholar

Lucia, U. (2013). Exergy flows as bases of constructal law. Physica A 392, 6284–6287. doi: 10.1016/j.physa.2013.08.042

CrossRef Full Text | Google Scholar

Martyusheva, L. M., and Seleznev, V. D. (2006). Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 426, 1–45. doi: 10.1016/j.physrep.2005.12.001

CrossRef Full Text | Google Scholar

Odum, T. H. (2000). Emergy Accounting. Centre for Environmental Policy Environmental Engineering Science. Gainesville, FL: University of Florida.

Google Scholar

Potting, J., Hekkert, M., Worrell, E., and Hanemaaijer, A. (2017). Circular Economy: Measuring Innovation in the Product Chain. The Hague: PBL Netherlands Environmental Assessment Agency publication number: 2544.

Google Scholar

Reini, M. (2016). Constructal law & thermoeconomics. Int. J. Heat Technol. 34, S141–S146. doi: 10.18280/ijht.34S118

CrossRef Full Text | Google Scholar

Reini, M., and Casisi, M. (2016). “Exergy analysis with variable ambient conditions-ECOS 2016,” in Proceedings of the 29th International Conference on Efficiency, Cost, Optimisation, Simulation and Environmental Impact of Energy Systems.

Google Scholar

Reini, M., and Casisi, M. (2020). The Gouy-Stodola Theorem and the derivation of exergy revised. Energy 210:118486. doi: 10.1016/j.energy.2020.118486

CrossRef Full Text | Google Scholar

Reini, M., and Valero, A. (2002). “Towards a unified formulation of exergy cost theory and emergy algebra for ecological and technological energy system evaluation,” in Proceedings of the 2nd International Workshop on Advances in Energy Studies (Porto Venere), 591–603.

Google Scholar

Reis, A. H. (2008). “Emergence of shape and flow structure in Nature in the light of Constructal Theory,” in: Shape and Thermodynamics. International Workshop Florence (Florence).

Google Scholar

Reis, A. H. (2014). Use and validity of principles of extremum of entropy production in the study of complex systems. Ann. Phys. 346, 22–27. doi: 10.1016/j.aop.2014.03.013

CrossRef Full Text | Google Scholar

Rocco, M. V., and Colombo, E. (2016). Internalization of human labor in embodied energy analysis: definition and application of a novel approach based on environmentally extended input-output analysis. Appl. Energy 182, 590–601. doi: 10.1016/j.apenergy.2016.08.148

CrossRef Full Text | Google Scholar

Rocco, M. V., Colombo, E., and Sciubba, E. (2014). Advances in exergy analysis: a novel assessment of the extended exergy accounting method. Appl. Energy 113, 1405–1420. doi: 10.1016/j.apenergy.2013.08.080

CrossRef Full Text | Google Scholar

Rodríguez, L. S. J., and Gaggioli, R. A. (1980). Second law of a coal gasification process. Can. J. Chem. Eng. 58, 376–381. doi: 10.1002/cjce.5450580314

CrossRef Full Text | Google Scholar

Sciubba, E. (2004). From engineering economics to extended exergy accounting: a possible path from monetary to resource-based costing. J. Ind. Ecol. 8, 19–40. doi: 10.1162/1088198043630397

CrossRef Full Text | Google Scholar

Sciubba, E. (2009). Why emergy- and exergy analyses are not commensurable methods of system analysis, IJEx 6, 523–549. doi: 10.1504/IJEX.2009.026676

CrossRef Full Text | Google Scholar

Szargut, J. (1995). “Exergy and ecology,” in Proceedings of the Workshop: Second Law Analysis of Energy Systems, eds E. Sciubba, and M. J. Moran (Roma), 11–19.

Google Scholar

Torres, C., Valero, A., Rangel, V., and Zaleta, A. (2008). On the cost formation process of the residues. Energy 33, 144–152. doi: 10.1016/j.energy.2007.06.007

CrossRef Full Text | Google Scholar

Tsatsaronis, G. (2011). “Exergoeconomics and exergo-environmental analysis,” Thermodynamics and the Destruction of Resources, eds B. R. Bakshi, T. G. Gutowski, and D. P. Sekulic (New York, NY: Cambridge University Press), 377–401. doi: 10.1017/CBO9780511976049.019

CrossRef Full Text | Google Scholar

Tsatsaronis, G., Lin, L., and Pisa, J. (1993). Exergy costing in exergoeconomics. ASME J. Energy Resour. Technol. 115, 9–16. doi: 10.1115/1.2905974

CrossRef Full Text | Google Scholar

Valero, A., Lozano, M., and Muñoz, M. (1986). “A general theory of exergy saving”, in Computer-Aided Engineering and Energy Systems. Second Law Analysis and Modelling, Vol. 3. ed. by R. Gaggioli (New York, NY: ASME Book No. H0341C).

Google Scholar

Valero, A., Serra, L., and Uche, J. (2006). Fundamentals of exergy cost accounting and thermoeconomics. part i: theory. J. Energy Resour. Technol. 128, 1–8. doi: 10.1115/1.2134732

CrossRef Full Text | Google Scholar