- 1Positron Dynamics Inc, San Francisco, CA, United States
- 2Department of Physics and Astronomy, Texas Tech University, Lubbock, TX, United States
- 3Lawrence Livermore National Laboratory, Physical and Life Sciences Directorate, Livermore, CA, United States
The ionizing radiation properties of a fission fragment rocket engine concept are described in the context of a crewed Mars mission. This propulsion system could achieve very high specific impulses (>106 s) at a high power density (>kW/kg), utilizing micron-sized fissile fuel particles suspended in an aerogel matrix. The fission core is located within the bore of an electromagnet and external neutron moderator material. The low-density aerogel allows for radiative cooling of fuel particles while minimizing collisional losses with the fission fragments, leading to a more efficient use of fissile fuel in producing thrust compared to previous concepts. This paper presents the estimates of the steady-state ionizing radiation equivalent dose to the astronaut crew from both external (e.g., galactic cosmic rays) and internal (reactor) sources. The spacecraft design includes a centrifugation concept where the transit habitation module rotates around the spacecraft’s center of mass, providing artificial gravity to the crew and the separation distance to the nuclear core. We find that the fission fragment propulsion system combined with centrifugation could lead to reduced transit time, reduced equivalent radiation doses, and a reduced risk of long-term exposure to micro-g environments. Such a high-specific impulse propulsion system would enable other crewed fast transit, high delta-V interplanetary missions with payload mass fractions much greater than those of alternative propulsion architecture (chemical and solar electric).
1 Introduction
To address the urgent need for advanced propulsion solutions, we propose the development of an advanced nuclear rocket engine that is two orders of magnitude more propellent-efficient than all rocket engines currently being used to power today’s space vehicles. This rocket could achieve very high specific impulses at a high power density by utilizing fission fragments as the propellent. The critical technology development necessary to achieve this fission fragment rocket engine (FFRE) is a low-density nuclear core that provides a fission fragment with a high probability of escaping the core. All other nuclear rocket designs to date deposit the kinetic energy of their fission fragments in the nuclear fuel as heat, requiring a thermal conversion process to accelerate the rocket’s propellent, usually hydrogen (Gabrielli and Herdrich, 2015). The current proposed designs for a FFRE are massive, have significant thermal constraints, and/or require the implementation of complex designs, such as dusty plasma levitation, which limits the near-term viability (Clark and Sheldon, 2005).
Advanced propulsion systems with a higher specific impulse than chemical propellants are being investigated for crewed interplanetary missions (Kokan, 2021; Mason et al., 2022). For the baseline crewed Mars mission, the majority of ionizing radiation doses to the crew are caused by galactic cosmic rays (GCRs) during the transit to/from Earth and Mars. The current estimates for the equivalent radiation dose to the Mars crew are at or above the lifetime dose limits. To mitigate this risk, two strategies can be employed to reduce the absorbed dose given to the crew during transit: 1) increasing shielding or the distance from ionizing radiation sources and 2) reducing the transit time. However, various shielding strategies can be used to reduce the expected dose by adding shielding results to the added mass, most likely at the expense of a support system mass allocation (propellant, life support, etc.). Inadequate shielding presents an increased health risk over no shielding at all since high-energy GCRs cascade into many lower-energy charged particles that create even greater ionizing radiation risks for the crew. Hence, for a realistic spacecraft, shielding cannot completely solve the GCR problem. Here, we will investigate the benefits of using an FFRE to reduce transit time. In this case, both the GCR and the nuclear propulsion system will act as a source of ionizing radiation. Since increasing the distance between the crew and the FFRE core may also decrease the radiation dose, we include a baseline centrifugation concept to produce artificial gravity inside the transit habitation module (Clément and Bukley, 2007). The centrifugation concept also requires a long tethered or rigid structure between the spacecraft axis of rotation and the transit habitation module.
2 Aerogel FFRE design considerations
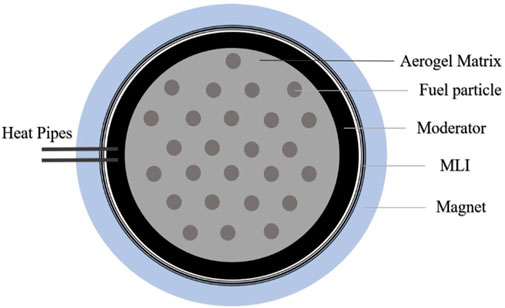
Fission fragments are heavy fragments of a nuclear core that have undergone a fission reaction. The two fission fragments typically carry more than 80% of the total energy released from the fission reaction. Having a high atomic mass, high charge state, and a very high velocity, they are an ideal propellant for a magnetic thrust nozzle. Unfortunately, fission fragments slow down rapidly inside solid matter (see Figure 1), so they must be generated in a fuel particle that is much smaller than the attenuation length scale (<10 um). These micron-sized fuel particle elements must also be accumulated such that a critical mass of fissile fuels is achieved, permitting a nuclear chain reaction to be initiated and sustained.
Satisfying both criticality and fission fragment escape is the largest challenge to developing a feasible FFRE concept. Chapline (1988) invented the FFRE and proposed to solve this problem by rotating micron-thick enriched fuel plates using a moderator structure and by extracting the fission fragment using a magnetic yoke. Clark and Sheldon (2005) suggested levitating a cloud of fissile dust particles inside a moderator and a magnet structure. As with the previous FFRE concepts, the aerogel matrix core relies on the high surface area (
Here, we will assume the unity emissivity (
Here,
Figure 2 shows that increasing the fission fragment escape fraction is the most important for enriched fuels with a lower critical mass (Am-242 m) and that a moderated core using Pu-239 or U-235 micron-sized particles could operate at temperatures well below the melting point of the fuel, even at lower fission fragment escape fractions. Thermal constraints on fuel particles are driven by the average fuel density and individual fuel particle size, FF range in oxide fuels, emissivity of the fuel, and the convective and radiative thermal transport properties of the aerogel matrix core.
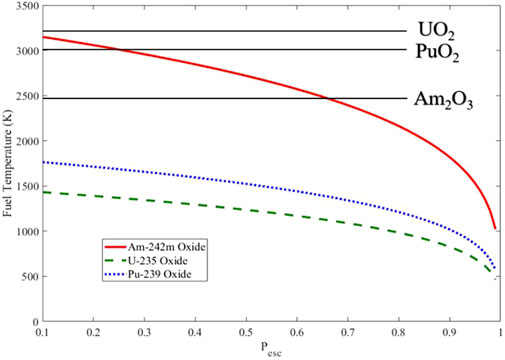
FIGURE 2. Oxide fuel temperatures as a function of the fission fragment escape fraction for the FFRE core operating at 1 GW power and a fuel particle radius of 1 micron. Solid horizontal lines indicate the approximate melting temperature of the fuel.
Practical limits on fuel particle fabrication lead to lower limits for the fuel size of about a micron, where the effective FF escape probability Pesc is 1. Combining this with the criticality requirements and the maximum fuel temperature operating point, we find that gigawatt (GW)-level powers are feasible with this approach. Fuels with a lower critical mass and a high thermal neutron fission cross section lead to lower volume reactors and higher power densities.
The energy loss process for heavy energetic particles in matter involves several regimes where different physical mechanisms dominate interactions between the particle and the attenuating medium. At very high velocities, when the particles are moving much faster than
A simple homogenous model of the aerogel core can be prepared with the fission fragment escape fraction from the fuel particle and an aerogel of the following thickness:
where
It is unlikely that this magnet can be built in space. Accounting for a finite width of the superconducting magnet, moderator, reflector, insulation, and cryostat, practical considerations limit the core width to approximately 6 m. The fairing width of the largest launch vehicle available in the near future is approximately 9 m (Elvis et al., 2023). We have not included the losses due to the finite Larmor radius of fission fragments and the possibility of impacts to the external walls or moderator structure. This is valid as long as the FF Larmor radius
Figure 4 shows that when the average fuel density is much greater than the supporting aerogel (
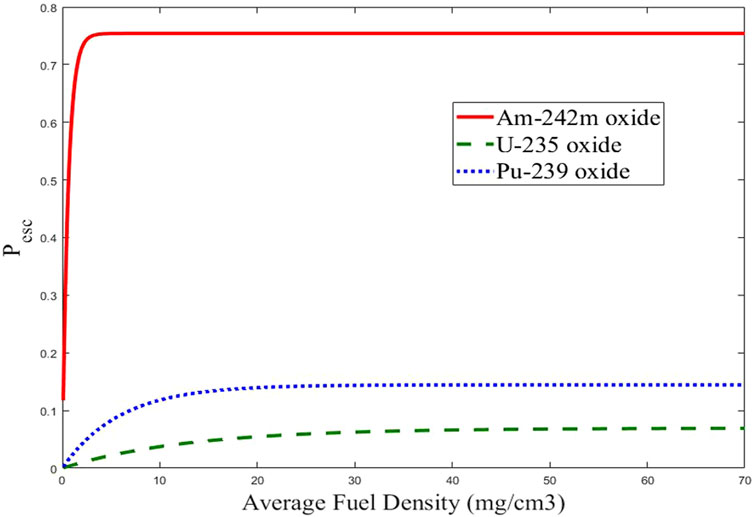
FIGURE 4. Fission fragment escape probability from a 6-m diameter FFRE core for three different oxide fuels as a function of the average fuel density, assuming an aerogel matrix density of 1 mg/cm3.
3 Propulsion performance
The FFRE thrust
where
For the Am-fueled FFRE core, this irradiance thermal load drops to approximately 20 MW/m2, which is near the expected first wall heat loads in compact fusion reactors (Dobran, 2012). High reflectance and emissivity coatings will be required to achieve steady-state thermal conditions that are within material limits.
4 FFRE spacecraft design and performance estimates
4.1 Baseline spacecraft in comparison to the NASA reference Mars mission
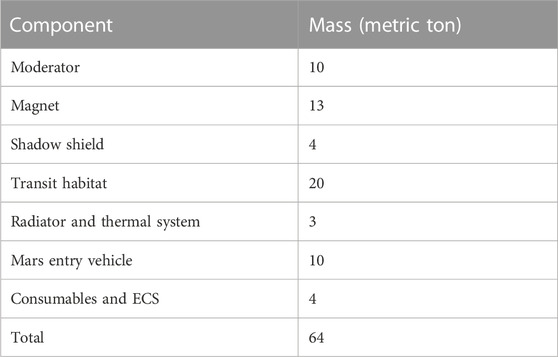
A notional spacecraft design for interplanetary missions is shown in Figure 5, including the FFRE propulsion element, radiator, transit habitation module, and shielding. To estimate the sizing of the transit hab, we will use the design from NASA’s Evolvable Mars Campaign (EMC), Mars transit habitat refinement activity (Simon, 2017), which was sized to support a crew of four for 1,100 days. The 22-metric ton (mt) transit hab design did not include artificial gravity, so we include a 20% margin on the structural mass and scale the consumable mass budget to the transit time using FFRE propulsion. Other differences include replacing 24-kW solar panels with a closed cycle Brayton (or other) power generation system, heat pipes, and radiators. Similar to the NASA EMC baseline, we do not include the Mars lander or Mars habitat components.
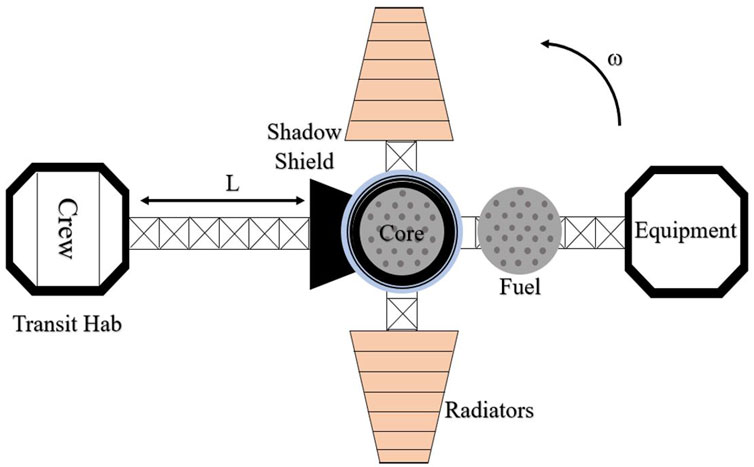
FIGURE 5. FFRE-based interplanetary crewed mission spacecraft layout. The spacecraft rotates to provide artificial gravity. Absorbed radiation doses to the crew come from external GCRs and the FFRE core.
Figure 5 shows an “equipment” module, which includes components less susceptible to radiation from the FFRE core and/or not required for crew transit. This may include the power processing unit, sensors, communication, navigation, or a crew reentry vehicle (e.g., Orion and Dragon) for aerocapture at interplanetary destinations with an atmosphere. The Mars Design Reference Mission (DRM) includes a provision for a 10-mt crew aerocapture reentry vehicle (Orion) capable of the maximum entry speed of 13 km/s (Drake et al., 2010).
4.2 Artificial gravity (centrifugation)
The FFRE-based design is well-suited to centrifugal rotation for producing artificial gravity with a CG at the FFRE core location as increasing the distance between the core and the transit hab will both reduce the rotation frequency required to achieve artificial gravity and improve the ionizing radiation environment due to the increased distance from the source. Centrifugation (rotation to provide artificial gravity-like acceleration) may provide a countermeasure to address the problems of bone loss, cardiovascular deconditioning, muscle weakening, sensorimotor and neuro-vestibular disturbances, and regulatory disorders (Clément et al., 2015). The low thrust (<100 N) properties of the FFRE also result in the reduced structural mass required in the high aspect ratio “arms” of the spacecraft.
4.3 Radiator sizing
The heat load on the moderator section
4.4 Magnet sizing
The high-temperature superconducting (HTS) magnet that provides the central solenoid field to direct fission fragments away from the core is the most massive component of the FFRE. The 6-m bore would approximately be the same size as the modern magnetic confinement fusion reactor designs (Mitchell et al., 2011). Here, we assume a magnet mass scaling of between 5 and 100 kg/Tm3. With an estimate of the FFRE mass, we can now calculate an approximate delta-V capability, as shown in Figure 6.
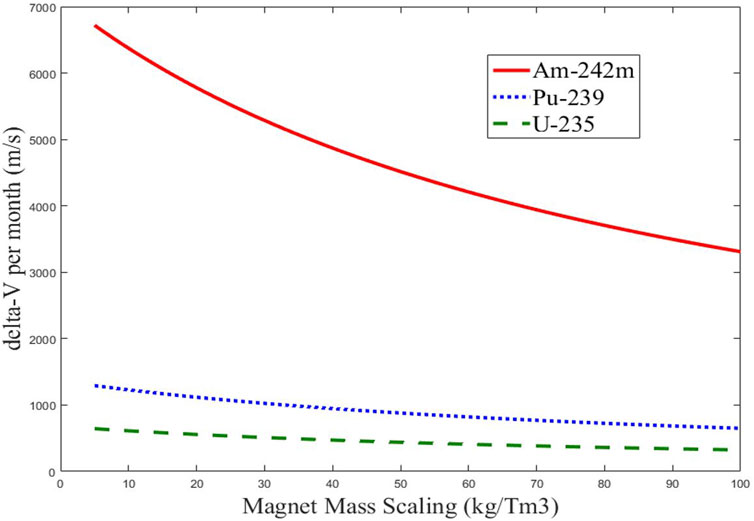
FIGURE 6. FFRE-based Mars crewed mission spacecraft delta-V capability per month of the operation at 1 GW power.
Figure 7 shows that for shorter mission durations like an Earth–Mars conjunction class, Pu-239 and U-235 FFRE may not be beneficial in reducing trip times and absorbed radiation doses. This is due to the lower thrust-to-weight ratio and a reduced fission fragment escape probability, described previously. The Am-242 m-fueled FFRE, however, shows a clear promise of achieving transit trajectories over shorter mission durations, such as the Earth–Mars transfer, with a delta-V per month capability in the 4–6 km/s range. An approximate mass budget is included in Table 1.
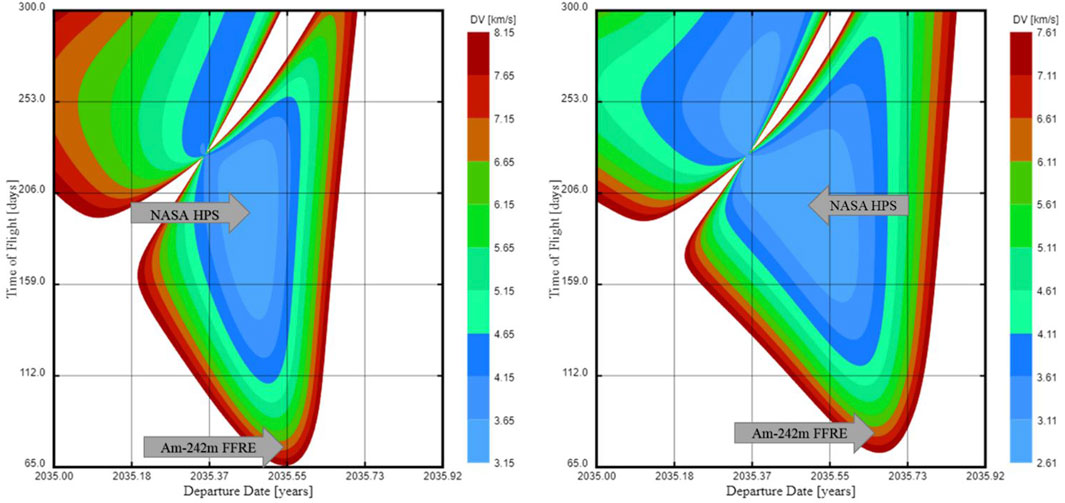
FIGURE 7. Porkchop plots (departure on the left and return on the right) for the Earth–Mars transfer using an approximate solution to Lambert’s problem described in Bombardelli et al. (2018). Gray arrows are the approximate location for NASA’s minimum delta-V approach with a hybrid propulsion system (HPS) and rapid transfer carried out using an Am-242 m-based FFRE. Figure is a modified image generated by EasyPorkchop software under public license GPLv3, copyright Juan Luis Gonzalo, Universidad Politécnica de Madrid (Technical University of Madrid).
5 Transit time estimates for the Earth–Mars transfer with FFRE propulsion
To estimate the transit times achievable with the propulsion system, we utilize an approximate solution to Lambert’s problem with the initial conditions in the circular Earth orbit at 800 km. It is likely that an FFRE propulsion system may be required to operate only outside the GEO to minimize fission fragment contamination, while starting in a lower energy orbit results in a more conservative delta-V and transit time estimate. The initial launch through the Earth’s atmosphere will require conventional chemical-rocket stages, and the transition to FF rocket propulsion may be determined through a future mission performance optimization calculation once the chemical rocket’s first stage’s performance characteristics are known.
Figure 7 shows that an Am-242 m FFRE operating at 1 GW could achieve an Earth–Mars transit time of 75 days at a delta-V of 7 km/s and a Mars–Earth transit time of 82 days at a delta-V of 6.5 km/s. This represents a 60% reduction in the total transit time vs. the NASA HPS baseline. Such a reduction is likely to result in further mass savings through a reduction in the food, consumable, environmental control system, and crew habitation support. In addition to the consumable/expendable mass reduction, the shorter transit time is likely to have a positive impact on the behavioral health and performance of the four-person crew (Whitmore et al., 2012). The transit time and delta-V calculations assume an impulsive input to delta-V, whereas the thrust-to-mass ratio of Am-242 m is quite low compared to that of chemical propulsion systems. If we assume a magnet mass scaling of less than 30 kg/Tm3, then the Earth–Mars transit delta-V can be achieved in less than half of the expected transit time. Future works will focus on more robust FFRE trajectory analyses using non-impulsive propulsion models.
6 Ionizing radiation dose estimates
The majority of health risks to the Mars crew will come from GCRs. These high-energy particles (∼GeV per nucleon) will strike the spacecraft, beginning a cascade of harmful radiation. To completely protect astronauts from GCR source radiation, we would require shielding equivalent to several meters of water. The development of DNA damage and cancer due to radiation is the primary concern for long-term astronaut health. NASA has determined a set of career radiation exposure limits for astronauts called the NASA Space Cancer Risk Model, which combines various components of the assessment of radiation-induced cancer risks for humans in space. The absorbed dose limits vary between 700 mSv and 1,150 mSv (Cucinotta, 2014). Current estimates for the absorbed dose during NASA DRM transit to/from Mars are approximately 1,200 mSv +/− 300 mSv, which corresponds to a risk of fatal cancer of nearly 4% for the Mars mission duration and a lifetime risk of 10%. This transit dose is calculated based on GCRs, and solar particle radiation, while less energetic, is much more variable and peaks during major solar storms, compounding the cancer risk of the crew. The large uncertainty in the estimated absorbed dose for the NASA DRM is mainly due to variability in solar particle radiation.
To estimate the absorbed dose for a rapid FFRE-based Hohmann transfer, we will assume the same transit habitat shielding (20 mg/cm2) and a core-to-habitat distance
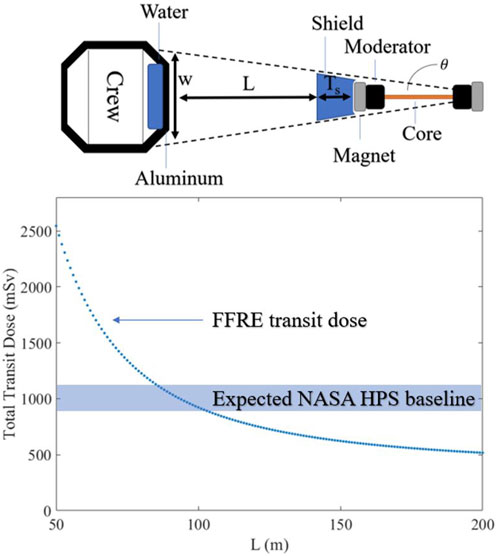
FIGURE 8. Total equivalent dose (blue dots) for an FFRE-based crewed Mars mission, including GCRs and reactor sources. The solid blue is the expected equivalent dose for the NASA HPS baseline. Furthermore, the geometry of the FFRE core, shielding, and transit hab is also shown (above).
where
The equivalent total dose given to the crew for the FFRE Mars mission (based on a magnet mass scaling of 50 kg/Tm3) is shown in Figure 8. The FFRE reactor operates at full power for approximately 40 days during the Earth–Mars and Mars–Earth transits.
For an FFRE-to-habitat distance greater than 100 m, the expected dose is less than the NASA HPS baseline. At L = 200, the transit dose drops to nearly half of the NASA HPS baseline. Given that the International Space Station (ISS) was constructed with a high aspect ratio for large (>100 m) structures in space, it is feasible that such a structure could be built. From a human physiological standpoint, it appears that the adaptation gravity gradient, Coriolis force, and cross-coupled accelerations limit the rotation rate of space habitats to less than approximately 4 RPM (Clément and Bukley, 2007). The low rotation rate lends itself to larger rotation radii (L >56 m) to produce 1 g of centrifugal acceleration. Therefore, a crewed FFRE-based interplanetary mission would likely take advantage of centrifugation with an arm radius in the 100–200 m range, with a rotation frequency in ∼RPM.
7 Discussion and future work
Clearly, the incredibly high specific impulse of the FFRE is not well-matched to the short-duration Mars transfer mission. At 1 GW operating power, the Mars transfer burns only 20 kg of the fissile fuel (Am-242 m), which represents less than 0.1% of the total spacecraft mass. Even with this low amount of fissile fuel, the core will need to be refueled “in situ” because of the low critical mass and low volumetric density of the core. For the Am-242 m FFRE Mars transfer mission described previously, it means replacing 20–40 cores (once every day) in a single transit. The engineering challenges associated with replacing an entire fission core may limit the feasibility of the concept; however, future works will look into the more continuous fueling of the aerogel matrix core with fission particles, alternative fuel-moderator geometries, and options for robotic core replacement. Since the FFRE will be emitting a large flux of relativistic and radioactive materials, the deposition of the exhausted fission fragments on other nearby spacecraft is observed in formation flights or in similar orbits. Although this is mitigated by the shorter half-life decay chains of most fission fragments, more work needs to be carried out to determine the impact of operating an FFRE in the Earth–Mars system.
The other method of increasing thrust for a given amount of power is to increase the mass flow rate of the propellant (see Eq. 3), at the expense of a specific impulse. For example, an FFRE “afterburner” configuration could inject a gas near the FFRE core or in between aerogel matrix fuel elements, transferring the kinetic energy (KE) from fission fragments to the gas via collision events. Since fission fragments are massive (80–160 u), the KE transfer process efficiency may be improved by using heavy noble gases (e.g., Kr, Xe, and Ar), where the noble gas density could be equal or greater than the surrounding aerogel matrix density, and the atomic mass of the noble gas is on the scale as the fission fragment mass. In this case, the low thermal conductivity of the aerogel would serve to insulate the fuel particles from the warm dense plasma of the noble gas generated during the thermalization of fission fragment particles. Since this process occurs in a strong magnetic field, a mirror configuration could serve to efficiently exhaust this plasma, generating thrust. Such an FFRE afterburner could also consist of a Penning trap of ions in order to increase the Coulomb interactions and momentum transfer between fission fragments and the afterburner fuel. Future works will also investigate how various afterburner FFRE configurations could result in higher thrust-to-weight ratios, shorter reactor “on” times, lower fission fuel burnup fractions, and lower absorbed equivalent doses given to the crew.
Another possible benefit of an FFRE vs. nuclear thermal propulsion (NTP) or nuclear electric propulsion (NEP) concepts in crewed spaceflight applications is the reduction in spent fuel radioactivity. By exhausting the fission fragment instead of capturing them in reactor fuel elements, an FFRE core may offer a lower total radiation dose to crew members over mission lifetimes. In future works, we will compare the total spent fuel radiation properties of a representative interplanetary crewed mission.
Astronauts embarking on a Mars mission using the current NASA approach have an approximate of 1 in 20 chances of dying of cancer during the mission due to radiation exposure. This may be acceptable for an initial high-risk exploration mission, but a different approach is needed to open up Mars for an extended and broader human presence. We have shown that a GW-scale FFRE could be used for rapid crewed Mars transits with a reduction in the total absorbed equivalent dose to the crew. Significant engineering challenges must be solved to make this system a reality. Although the production and enrichment of Am-242 m fuel is technically feasible, such a highly fissile enriched fuel remains a proliferation and safety concern. The supply chain for large scale productions is currently non-existent, and the lack of a commercial market for enriched Am-242 m will likely result in very high costs.
8 Conclusion
We have identified an important synergy between artificial gravity “centrifugation” and ionizing radiation shielding that point toward a 100-m scale rotating spacecraft as a feasible solution for reducing the negative health impacts on the crew during the Mars transit. If a large rotating spacecraft were to be built, it would likely leverage the recent advances of in-space manufacturing to assemble these large structures. Although a low-thrust, high-ISP propulsion option may not seem like the ideal solution for a Mars transit, the low thrust-to-weight ratio is well-matched to the “centrifugation” approach in the way that it reduces structural loads to the spacecraft that may not be capable of supporting large forces over long moment arms.
This research report introduces an alternative FFRE concept with a total mass of less than 70 metric tons using the Am-242 m fuel applied to the rapid Earth–Mars transfer mission. The shorter transit times, artificial gravity environment, and decreased total equivalent radiation dose may provide significant health benefits to crew members on other long-duration missions (e.g., Mars, Jupiter, and asteroid belts).
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
All authors contributed to the research reported here. RW conducted the FFRE design study, performance simulations, and prepared the first manuscript drafts. RD and GC contributed to the FFRE core design and criticality considerations. MH provided details on spacecraft considerations. All authors contributed to the article and approved the submitted version.
Funding
This work was partially supported by the NASA grant 80NSSC23K0592.
Acknowledgments
The authors would like to thank Shai Cohen for discussions on the FFRE core geometry.
Conflict of interest
Author RW was employed by Positron Dynamics Inc.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors RD and MH declared that they were editorial board members of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bombardelli, C., Juan, L. G., and Roa, J. (2018). Approximate analytical solution of the multiple revolution Lambert’s targeting problem. J. Guid. Control, Dyn. 41(3), 792–801. doi:10.2514/1.g002887
Cai, H., Jiang, Y., Feng, J., Zhang, S., Peng, F., Xiao, Y., et al. (2020). Preparation of silica aerogels with high temperature resistance and low thermal conductivity by monodispersed silica sol. Mater. Des. 191, 108640. doi:10.1016/j.matdes.2020.108640
Chapline, G. (1988). Fission fragment rocket concept. Nucl. Instrum. Methods Phys. Res. Sect. A 271 (1), 207–208. doi:10.1016/0168-9002(88)91148-5
Clark, R. L., and Sheldon, R. B. (2005). Dusty plasma based fission fragment nuclear reactor. Tucson, AZ: American Institute of Aeronautics and Astronautics, Inc.
G. Clément, and A. Bukley (Editors) (2007). Artificial gravity (Springer Science and Business Media), 20.
Clément, G. R., Bukley, A. P., and Paloski, W. H. (2015). Artificial gravity as a countermeasure for mitigating physiological deconditioning during long-duration space missions. Front. Syst. Neurosci. 9, 92. doi:10.3389/fnsys.2015.00092
Craven, P. (2014). “Lightweight damage tolerant radiators for in-space nuclear electric power and propulsion,” in 2014 national space and missile materials symposium (NSMMS), M14–M3712.
Cucinotta, F. A. (2014). Space radiation risks for astronauts on multiple international space station missions. PLoS One 9 (4), e96099. doi:10.1371/journal.pone.0096099
Dobran, F. (2012). Fusion energy conversion in magnetically confined plasma reactors. Prog. Nucl. Energy 60, 89–116. doi:10.1016/j.pnucene.2012.05.008
Drake, B. G., Hoffman, S. J., and Beaty, D. W. (2010). “Human exploration of Mars, design reference architecture 5.0,” in 2010 IEEE aerospace conference (IEEE).
Elvis, M., Lawrence, C., and Seager, S. (2023). Accelerating astrophysics with the SpaceX starship. Phys. Today 76(2), 40–45. doi:10.1063/pt.3.5176
Gabrielli, R. A., and Herdrich, G. (2015). Review of nuclear thermal propulsion systems. Prog. Aerosp. Sci. 79, 92–113. doi:10.1016/j.paerosci.2015.09.001
Hakim, M., and Shafrir, N. H. (1971). 252Cf fission fragment energy loss measurements in elementary gases and solids as compared with theory. Can. J. Phys. 49(23), 3024–3035. doi:10.1139/p71-358
Kokan, T. S. (2021). “Nuclear electric propulsion/chemical propulsion hybrid human mars exploration Campaign: first mars surface mission,” in AIAA propulsion and energy 2021 forum.
Mason, L. (2021). “Nuclear power concepts for high-power electric propulsion missions to mars,” in Nuclear and emerging Technologies for space (NETS).
Mason, Lee, Oleson, S., Jacobson, D., Schmitz, P., Qualls, L., Smith, M., et al. (2022). Nuclear power concepts and development strategies for high-power electric propulsion missions to mars. Nucl. Technol. 208, S52–S66. sup1. doi:10.1080/00295450.2022.2045180
Mitchell, N., Devred, A., Libeyre, P., Lim, B., and Savary, F. (2011). The ITER magnets: design and construction status. IEEE Trans. Appl. Supercond. 22(3), 4200809–4200809. doi:10.1109/tasc.2011.2174560
National Aeronautics and Space Administration (2015). Office of technology, policy, and strategy. Available at: https://www.nasa.gov/offices/oct/home/roadmaps/index.html.
Patil, S. P., Shendye, P., and Markert, B. (2020). Molecular investigation of mechanical properties and fracture behavior of graphene aerogel. J. Phys. Chem. B 124(28), 6132–6139. doi:10.1021/acs.jpcb.0c03977
Ronen, Y., and Leibson, M. J. (1987). An example for the potential applications of americium-242m as a nuclear fuel. Trans. Isr. Nucl. Soc. 14, V–42.
Simon, M. (2017). “NASA's advanced exploration systems Mars transit habitat refinement point of departure design,” in 2017 IEEE aerospace conference (IEEE).
Sun, H., Xu, Z., and Gao, C. (2013). Multifunctional, ultra-flyweight, synergistically assembled carbon aerogels. Adv. Mater. 25(18), 2554–2560. doi:10.1002/adma.201204576
Whitmore, M., Boyer, J., and Keith, H. (2012). “NASA-STD-3001, space flight human-system standard and the human integration design handbook,” in Industrial and systems engineering research conference. No. JSC-CN-25695.
Keywords: aerogel, fission fragment, propulsion, ionizing radiation, interplanetary
Citation: Weed R, Duncan RV, Horsley M and Chapline G (2023) Radiation characteristics of an aerogel-supported fission fragment rocket engine for crewed interplanetary missions. Front. Space Technol. 4:1197347. doi: 10.3389/frspt.2023.1197347
Received: 08 April 2023; Accepted: 17 August 2023;
Published: 08 September 2023.
Edited by:
Antonio Mattia Grande, Polytechnic University of Milan, ItalyReviewed by:
Andrew Higgins, McGill University, CanadaMichele Pasquali, Sapienza University of Rome, Italy
Copyright © 2023 Weed, Duncan, Horsley and Chapline. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ryan Weed, cnlhbi53ZWVkQHBvc2l0cm9uZHluYW1pY3MuY29t
 Ryan Weed
Ryan Weed R. V. Duncan
R. V. Duncan Matthew Horsley
Matthew Horsley George Chapline3
George Chapline3