- Center of Applied Space Technology and Microgravity, University of Bremen, Bremen, Germany
Introduction: A Direct Simulation Monte Carlo (DSMC) solver with a modified collisional routine is used to investigate an argon gas flow through a millimeter-scaled thruster nozzle with high-density ratios.
Method: The limiter scheme, denoted as the constant selection limiter (CSL), limits the possible number of selected collisional pairs to a constant value in accordance with the present simulation particles in the cell.
Results: Results of the CSL scheme are compared with the experimental and numerical results of a compressible Navier–Stokes solver and discussed in comparison with baseline DSMC simulations. The influence of collision limitation by the CSL is discussed on the stagnation pressure of the thruster and on thrust and specific impulse prediction. The application of the limiter scheme makes the prediction of stagnation pressure challenging in some cases.
Discussion: In contrast, thrust and specific impulse are predicted well, and their study remains valid. Investigated mass flow rates are 0.178 mg/s
1 Introduction
The direct simulation Monte Carlo (DSMC) method has been used to simulate rarefied flow fields in all kinds of geometries, for example, re-entering space capsules (Shang and Chen, 2013) or nozzle geometries (Zelesnik et al., 1994) and micro-electro-mechanical systems (MEMS) (Alexeenko et al., 2002; Titov et al., 2005a; Titov et al., 2005b; Roohi et al., 2009). The method, invented and described in its original form by Bird (1994), has proven to solve flow problems correctly, where the continuum approaches break down due to the strong effects of flow rarefaction. The DSMC approach has become a standard tool in solving micro-nozzle flow problems with high Knudsen numbers because it can handle the effects of viscous boundary layers, strongly affecting the flow itself due to the large ratio of nozzle wall area to the core volume of the flow (Gomez and Groll, 2016). The method is also used to correctly analyze thruster plume behavior beyond the nozzle’s exit (Ketsdever et al., 2005) and evaluate thrust at the nozzle exit plane.
In recent years, attempts have been made to extend simulation techniques to the whole range of flow regimes and Knudsen numbers. A way to extend the numerical capabilities is to use a hybrid approach by coupling two or more numerical methods best suited for each flow regime. For example, in nozzle flows, the high-density portion of the flow may be solved using a continuum-based method, defining a zone where the first method breaks down and transferring flow quantities to a kinetic approach to solve the rarefied part of the flow. Several different hybrid approaches are described in the literature, whereat in many approaches, the DSMC method is used to solve the rarefied portion of the flow. A coupling of Navier–Stokes and DSMC solvers has successfully been applied in the past (Ivanov et al., 1997; Wang et al., 2003). Despite the high efficiency of the continuum model at low Knudsen numbers, the transfer and interpolation of flow quantities to the kinetic method are challenging using this approach. Coupling can also be achieved by combining the DSMC method with another kinetic-based method, such as a BGK (Bhatnagar-Gross-Krook model) particle model (Macrossan, 2001; Kolobov et al., 2007). Here, the coupling is more straightforward but with the cost of computational speed because BGK particle models may have requirements for the cell size and time step similar to the DSMC method. A recent development that overcomes these strict requirements is the hybrid Fokker–Planck-DSMC algorithm, which was also successfully applied to nozzle flow test cases (Gorji and Jenny, 2015). A further example of a hybrid approach is the low diffusion particle method (Burt and Boyd, 2008; Burt and Boyd, 2009), which mainly replaces the collisional routines of the DSMC and can be seen as a quasi-hybrid.
The modification of the DSMC algorithm in a more direct way to raise the computational performance is an attractive idea. As only one single approach is used to solve the whole flow field, no transfer and interpolation of flow properties has to be done, and potential sources of error can be prevented. The DSMC method naturally yields the potential to solve a flow spanning over the whole range of flow regimes because the collisional term of the Boltzmann equation is solved directly, and sampling of macroscopic quantities is done in a statistical manner. Unfortunately, the DSMC method becomes numerically very expensive near or in the continuum regime when Knudsen numbers are low due to the huge number of collisions that have to be calculated (Busse et al., 2021; Kühn and Groll, 2021; Yu et al., 2023). According to Titov and Levin (2007) and Sharma and Long (2004), collisional computing time can take up to 60% of the overall computing time, depending on the method used (Muraviev et al., 2021). In order to reduce these costs, a common approach is to limit the number of possible collisions nc in a cell to a constant value per time step by nc = χ N, where χ is referred to as a limiter value and N is the number of test particles in the cell. The approach is valid as in the continuum regime, velocity relaxation to the equilibrium distribution is reached after a certain number of collisions, and further collisions would not change the distribution anymore.
The literature proposes several values for the limiter χ. For example, Sharma and Long (2004) used a value of χ = 0.75 to obtain results of blast impacts on building structures. However, this value was too low for certain problems, as Titov et al. (2005a)pointed out. With an applied value of χ = 0.75, large deviations occurred in the Maxwellian distribution of test particle velocities up to approximately 50%, especially in the throat region, where density, flow velocity, and temperature rapidly changed (Titov et al., 2005a). Titov and Levin (2007) used values of χ = 0.75 and χ = 2 for the limiter to extend the DSMC method to high-pressure MEMS nozzle flows. The combination of their proposed eDSMC method and the standard DSMC yielded good results for the investigated nozzle geometry for a value of χ = 2. Bartel et al. (1994)conducted another study with a limiter value of χ = 5.
A different technique to raise the computational performance of collision calculation, which has been denoted as a selection limiter, was reported by Zhang et al. (2008). The selection limiting procedure intervenes in the selection number calculation of the applied no-time-counter (NTC) scheme by multiplying the number of selected pairs nSP with a function S dependent on gradient length local Knudsen numbers KnGLL developed by Boyd et al. (1995) and Boyd et al. (2003). Here, the selection limiter function S becomes a unity in areas of large non-equilibrium, leaving nSP unaltered but decreasing nSP as the flow approximating the equilibrium state with a function of KnGLL. Results for a nozzle plume flow compared to the standard DSMC were in good agreement, whereas the evaluated collision limiter showed some deviations.
In the present study, a similar technique is described and used in the numerical study of a cold argon gas flow through an arcjet-like thruster geometry without an electric arc to reduce numerical costs on the collision calculation, denoting it as a constant selection limiter (CSL). In the proposed approach, we are limiting the number of selected pairs to a constant value per cell and time step, which is equal to two times that of the present test particles in the cell. If the number of selected pairs is lower than the limiter value, the collision calculation is unaltered.
In the following section, the solvers used and their modifications are described, followed by the experimental setup, which the numerical study was based on and which was used to obtain additional experimental results. The used numerical mesh and the applied boundary conditions are described thereafter. Numerical and experimental results for an argon gas flow are presented and discussed. The influence of flow rarefaction and proposed collision limiting (CSL) on the stagnation pressure and the prediction of thrust and specific impulse for the micro-nozzle flow are discussed. Hereby the referenced stagnation pressure is equivalent to the total pressure inside the thruster at the nozzle inlet. The computational performance of the scheme is also discussed in terms of speed-up factors.
2 Materials and methods
2.1 Numerical methods
2.1.1 Kinetic approach: DSMC solver
To model nozzle flows on a molecular basis, a modified version of the original implementation dsmcFoam by Scanlon et al. (2010) in the free software package of OpenFOAM, release 2.4, is used. The solver uses Bird’s original formulation for the NTC scheme (Bird, 2007) and sub-cell generation to reduce collision separation, to achieve nearest-neighbor collisions (Bird, 2007). The variable hard sphere collisional model with the addition of Larsen–Borgnakke energy exchange is implemented and used here, as well as diffusive and specular wall reflection models to simulate flows in arbitrary geometries (Scanlon et al., 2010).
In the original formulation, the inflow and outflow of the computational domain are achieved based on Bird’s equilibrium state formulation, which describes molecular flux quantities of a gas across a surface between the computational domain and an associated virtual volume (Bird, 1994). This treatment of mass flow on the boundary yields some challenges when simulating nozzle flows because velocity, temperature, and number density must be known. Conversely, the mass flow rate is usually a known quantity in experimental nozzle flow setups. Hence a modified inflow model is used here, modeling flow into the domain on the basis of the nozzle’s inlet cross-section Ain, molecular gas properties, and the mass flow rate min known from the experiment. A previous version of the inflow model was used by Groll et al. (2012), where some results were presented. The inflow particle flux
The number density nin is derived from
where M is the molecular mass and NA is the Avogadro constant. All molecules hitting an open domain border named in this manner are no longer deleted but reflected to create a steady inflow of molecules across the inlet boundary. The outflow of the numerical domain is modeled on the basis of Bird’s equilibrium state formulation (Bird, 1994), like in the original implementation.
The DSMC method becomes numerically very expensive when simulating continuum and near continuum flows, where the mean free path λ gets small, and the collision frequency ν rises, because the required computing time is mostly dependent on the movement and collision calculation of simulated particles. For the NTC scheme used in the present study, the number of collisions is evaluated as the number of selected pairs nSP, which describes the absolute number of colliding partners per cell in a time step:
where N is the number of present simulation particles in the chosen volume V during a time step Δt. The number of real molecules represented by a simulated particle is defined by nequi, and
The proposed CSL interferes directly by cutting of collisions at an average value of 2 N collisions for N present particles per cell and per time step.
Eq. 4 shows that the calculation is performed as in the original approach in Eq. 3 if the average number of 2 N collisions per particle is not reached in a cell.
2.1.2 Continuum approach: Navier–Stokes solver
Simulations are also performed using the Navier–Stokes solver, rhoCentralFoam. The solver developed and implemented in the OpenFOAM framework by Greenshields et al. (2010) uses semi-discrete, non-staggered upwind schemes of Kurganov and Tadmor (2000) (KT) and Kurganov et al. (2001) (KNT) to model compressible, transient, super- and hypersonic flows in arbitrary geometries. The fluid properties of the compressible flow are hereby transported through the cell faces via the interpolation of cell face fluxes for density, velocity, and temperature, which is stabilized by the so-called “dimension-by-dimension” reconstruction of the KT and KNT methods (Greenshields et al., 2010). The time discretization is performed by an Euler implicit scheme. The density-based approach is particularly suitable for problems with high gradients of density, which, for example, occur in shock waves, as shown by Greenshields et al. (2010). In addition, good numerical stability is achieved through the interpolation schemes. Hence, the solver is used as a second approach for result comparison.
2.2 Experimental setup
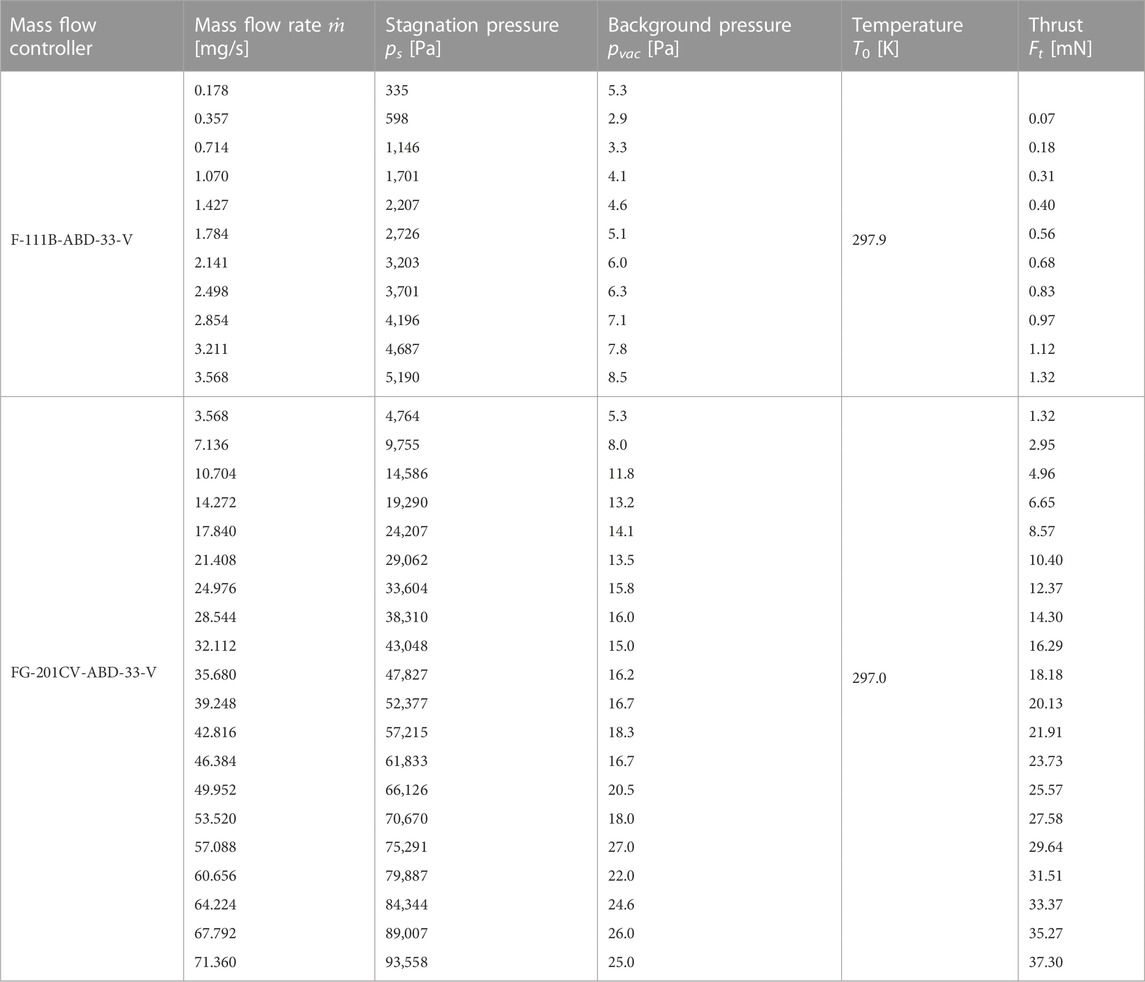
The experimental cold gas study is conducted on an arcjet thruster, whose sectional view is given in Figure 1A. The basic components are a tungsten de Laval nozzle acting as an anode, a tungsten cathode, body parts made of stainless steel, and sintered boron nitride insulators (Frieler and Groll, 2018). To specify the mass flow rate entering the thruster, thermal mass flow meters FG-201CV-ABD-33-V-DA-A1V and F-111B-ABD-33-V (in case two: separate valve, type F-004AC-LUU-33-V) from Bronkhorst1 are used to obtain argon mass flow rates of 0.178 mg/s
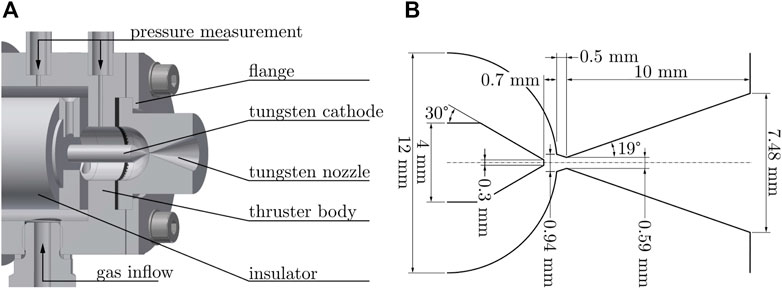
FIGURE 1. (A) Sectional view of the present nozzle geometry. (B) Schematic sectional view of the nozzle geometry.
2.3 Numerical mesh and case setup
2.3.1 Numerical meshes
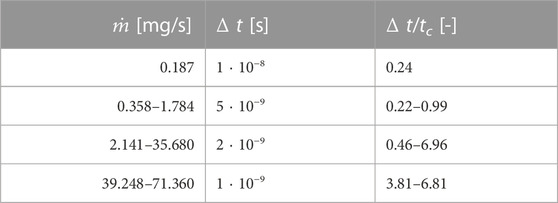
For the numerical study, three meshes are used: two for the CSL DSMC simulations and one additional for the Navier–Stokes simulation. The numerical meshes for the CSL DSMC simulations are generated based on the geometrical data presented in Figure 1B. An outlet domain of 15 mm by 7.5 mm is added to the nozzle to consider the downstream effects of boundary conditions on the nozzle flow plume and backflow effects. The application of an inlet domain was considered but rejected because no changes in flow properties could be observed after a certain distance upstream of the nozzle’s throat. The nozzle flow is considered axial symmetric. Hence, wedge meshes with an opening angle of 2.5° are used. The lower resolution mesh for the CSL DSMC simulations is shown in Figure 2, whereas only every 4th mesh line (not refined parts) is shown for accurate presentation. For the CSL DSMC simulations, mesh refinement is carefully applied to the stagnation part and the second half of the diffuser to achieve optimized parallel performance and higher numerical resolution on the nozzle’s exit plane (see red marked areas in Figure 2). According to Bird, the cell size Δ x for a baseline DSMC simulation should be chosen smaller than the local mean free path λ (Bird, 1994). As a selection limiter technique is used in the study, this strict limitation is softened and replaced by more classical restrictions of continuum-based theory as proposed by Titov and Levin (2007). For mass flow rates of 0.178 mg/s
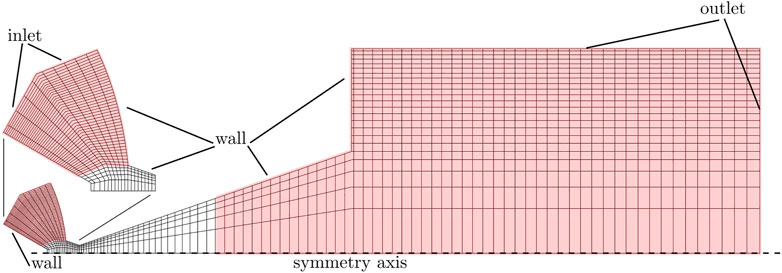
FIGURE 2. Numerical mesh of the thruster nozzle with an applied downstream domain. Only every 4th meshline is displayed. Inlet, outlet, and wall surfaces are marked. Red background coloring indicates areas where the mesh is refined.
To improve numerical stability for the Navier–Stokes simulations, the outlet domain of the third mesh is scaled up to 60 mm by 40 mm. Mesh convergence was previously tested with six different grid resolutions (Table 1). The coarsest had 15 by 10 cells in the nozzle’s throat area, whereas the finest had 360 by 40 cells in the same area. In all cases, the cell size for the rest of the mesh was scaled according to the throat area. The referenced cell height is scaled by the throat radius r* = 0.295 mm (Figure 1B). Tested mass flow rates were
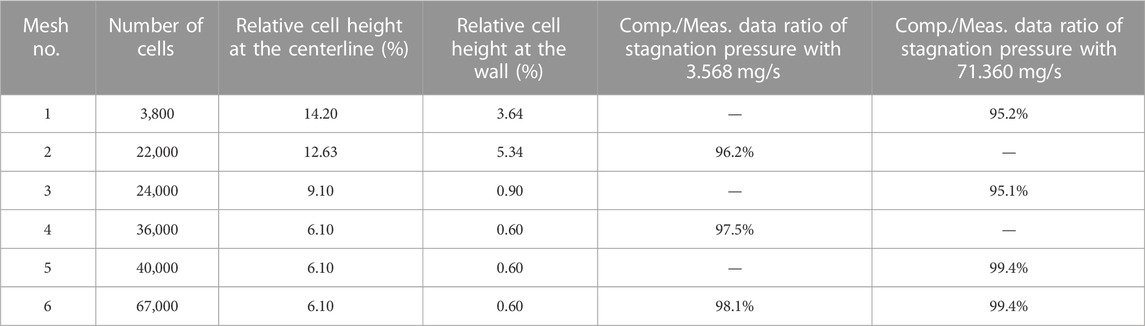
TABLE 1. Grid resolution and stagnation pressure convergence study. Tested meshes and data of the convergence study for Navier–Stokes simulations. The dimensionless cell height at the throat is given for the centerline and for the cell closest to the nozzle wall, whereat the cell height is scaled by the throat radius r*. Data for numerical stagnation pressures are scaled by the experimental values for the two investigated mass flow rates to give a dimensionless pressure relation.
2.3.2 Case setup and boundary conditions
Two sets of boundary conditions are used for the numerical simulations. As given in Eq. 1, the number of per-time-step initialized particles at the inlet surface for the DSMC simulations are calculated from experimental mass flow rates
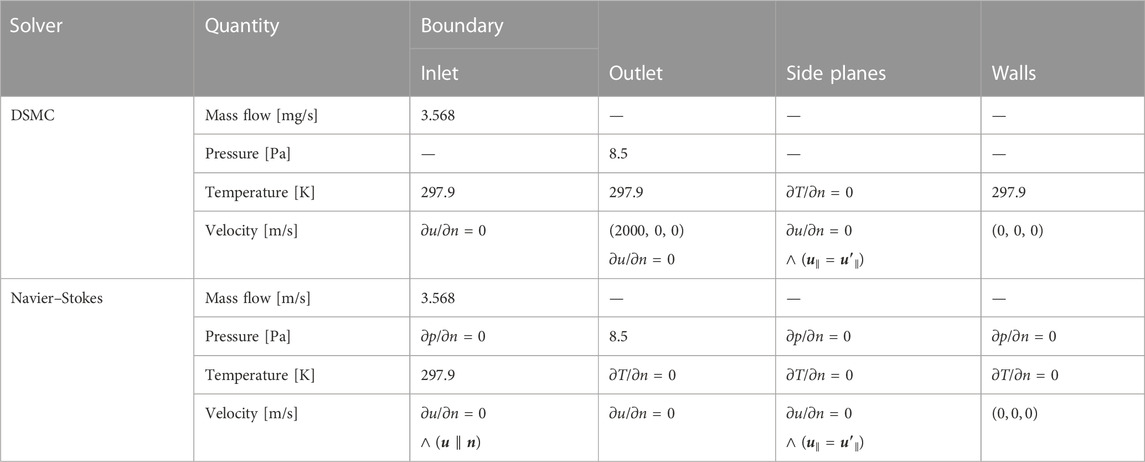
TABLE 3. Overview of the two sets of boundary conditions for the DSMC and the compressible Navier–Stokes simulations.
For the Navier–Stokes simulations, the specific heat capacity of argon is specified to cp = 520 J/kg K (VDI, 2013) and the molar mass to 39.95 kg/kmol (VDI, 2013). The temperature-dependent dynamic viscosity μ is calculated using Sutherland’s law (Sutherland, 1893) as follows:
where T is the temperature, Ts is the Sutherland temperature, and As is the Sutherland coefficient. For the results presented here, the Sutherland coefficient and temperature are calculated using experimental data from Clarke and Smith (1968). The obtained values are As = 1.9487 ⋅ 10−6 Pa s/
3 Results
3.1 Physical description of the nozzle flow
The numerical study presented in this work is based on an experimental series of argon mass flow rates performed on the presented thruster. Mass flow rates range from
For each of the experimentally investigated mass flow rates, numerical results are obtained using both methods. Altogether, 86 simulations were performed, giving a good data basis for the numerical investigation. Both solvers reached a steady state after a simulated time of approximately 3.5 m and were continued until a simulated time of approximately 6 m.
For the investigated range of mass flow rates, flow conditions from a continuum with Knudsen numbers below Kn = 0.01 to free flow conditions with Knudsen numbers over Kn = 10 are observed. For the highest mass flow rates, close to atmospheric conditions are reached inside the thruster, whereas plume flow conditions are in the free molecular range. Figure 3A shows the average Knudsen numbers obtained from baseline DSMC and CSL DSMC simulations at the nozzle’s throat and the exit plane over the range of investigated mass flow rates.
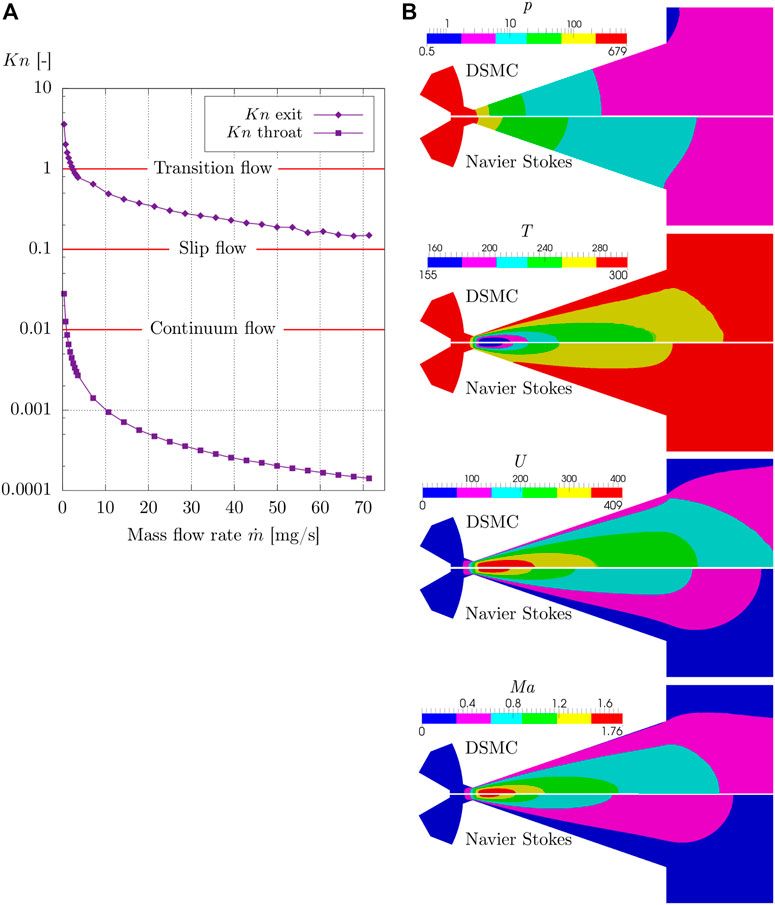
FIGURE 3. (A) Average throat and exit plane Knudsen numbers as a function of mass flow rates. (B) Pressure, temperature, velocity, and Mach number fields for a mass flow rate of
A clear dependency of the Knudsen number on the mass flow rate is seen. In the throat region of the thruster, Knudsen numbers stay in the continuum flow range for almost all investigated mass flow rates—the only exceptions are seen for the two smallest mass flow rates. In contrast, average exit plane values of the Knudsen number do not reach continuum flow or slip flow conditions, indicating that continuum-based assumptions may not be valid anymore.
As a result of the strong rarefaction of the flow, large deviations in numerical flow field distributions between the two solvers for pressure, velocity, temperature, and Mach number are present in Figure 3B for a mass flow rate of
The top picture presents the pressure drop along the nozzle. As a result of the large ratio of inlet area Ain to throat cross-section A*, the pressure keeps almost constant until the beginning of the converging nozzle throat, and most of the pressure drop occurs at the end of the throat and the beginning of the diffuser. The generated stagnation pressures close to the inlet differ by approximately 11% from each other, whereas the DSMC simulation indicates a faster pressure drop in the diffuser compared to the Navier–Stokes solver.
Results for the velocity distribution show a gentle acceleration of the fluid close to the nozzle throat with further acceleration throughout the diffuser in agreement with de Laval Nozzle theory. For the selected mass flow rate, the highest velocities are already reached in the first 20% of the diffuser, which indicates a non-ideal ratio of mass flow rate to diffuser length. Radial velocity distribution and the velocities at the diffuser walls differ significantly, with slip flow present in the DSMC solution caused by strong rarefaction effects of the expanding flow.
By accelerating the fluid, internal thermal energy is converted to kinetic energy, leading to a drop in temperatures in the diffuser. The lowest temperatures are reached where the highest velocities are present. Toward the end of the diffuser, the temperature distribution of the Navier–Stokes solution recovers faster toward ambient temperature.
The distribution of the Mach number separates the nozzle in a sub- and supersonic part. In accordance with the de Laval nozzle theory, Ma = 1 is reached at the end of the nozzle’s throat in both solutions. Then, the Mach number increases as the flow expands into the diffuser, reaching maximum values where velocity approaches maximum values and temperature is minimal.
3.2 Overprediction of stagnation pressure
To analyze the applicability of the proposed CSL DSMC, numerical and experimental stagnation pressures are compared for the full range of studied mass flow rates. Discussion of results is split to mass flow ranges of 0.178 mg/s
3.2.1 Lower mass flow rates
The left part of Figure 4 shows the results for stagnation pressures of the CSL DSMC and the Navier–Stokes solver in comparison to experimental values for mass flow rates of 0.178 mg/s
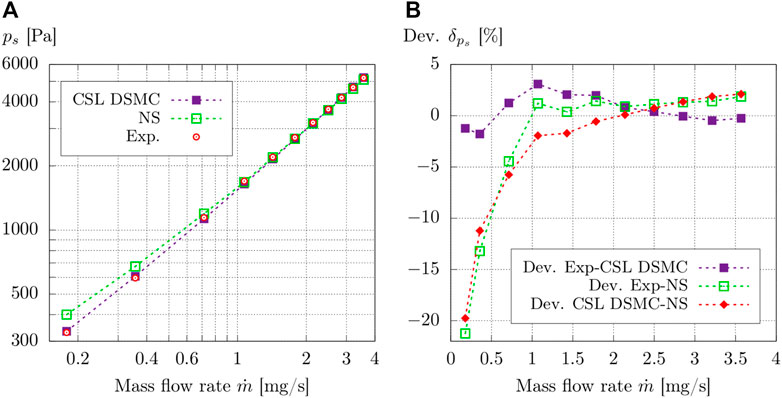
FIGURE 4. (A) Numerical and experimental stagnation pressures ps for mass flow rates of 0.178 mg/s
As the CSL DSMC solver can predict viscous losses more precisely for the strongly rarefied flow of the lower mass flow rates, deviations to experimental results are much smaller. For the two lowest measured mass flow rates, a slight overprediction of approximately 1.5% of the stagnation pressure is present for the CSL DSMC results. For mass flow rates of 0.714 mg/s
A reasonable relation is observed between the numerical results of the CSL DSMC and Navier–Stokes simulations, showing that with decreasing mass flow rates, the rarefaction effects of the flow exhibit a level the Navier–Stokes solver can handle, leading to apparent higher stagnation pressures in comparison to the CSL DSMC results. For mass flow rates over
3.2.2 Higher mass flow rates
In the left part of Figure 5, stagnation pressures of the CSL DSMC and the Navier–Stokes solutions are shown for mass flow rates of 3.568 mg/s
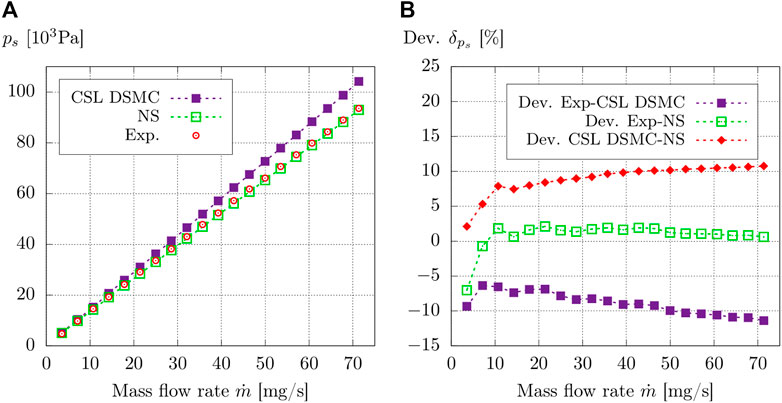
FIGURE 5. (A) Numerical and experimental stagnation pressures ps for mass flow rates of 3.568 mg/s
In contrast, the CSL DSMC results for the stagnation pressure do not reproduce the experimental values or the Navier–Stokes results. Although a decreasing overprediction from 9.3% to 6.4% of the experimental value is seen for the two lowest mass flow rates of
CSL DSMC and Navier–Stokes results are compared in Figure 5 to better understand the influence of the selection limiter scheme on the stagnation pressure and exclude possible errors from the experiment. By starting with a deviation of 2.1% at the handover mass flow rate of
3.2.3 Slowed down velocity relaxation
The deviations of the CSL DSMC results for the stagnation pressure from both experimental and numerical Navier–Stokes results are best explained regarding the centerline profiles of scaled density ρ/ρ0, temperature T/T0, and velocity U/Umax in Figure 6, where density ρ and temperature T are scaled by the stagnation values ρ0 and T0 of the CSL DSMC simulation, whereas the velocity profiles are scaled by the maximum velocity Umax reached by the particular CSL DSMC simulation. The axial position is scaled by the throat radius r* = 0.295 mm (Figure 1B), where zero indicates the throat position and a value of x/r* = 30 the nozzle’s exit plane.
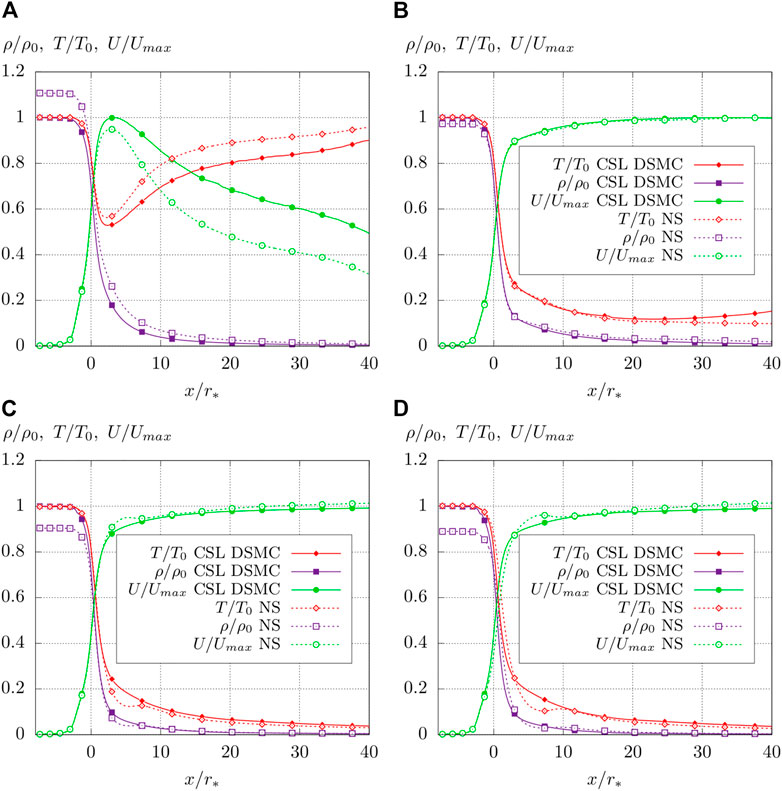
FIGURE 6. Centerline profiles of scaled density ρ/ρ0, temperature T/T0, and velocity U/Umax obtained by the CSL DSMC solver (continuous lines) and the Navier–Stokes solver (dashed lines) for four different mass flow rates. (A)
Due to the rarefaction of the flow for
With rising mass flow rates, Knudsen numbers in Figure 3A decrease to a level where no major effects on flow properties due to flow rarefaction can be seen on the centerline profiles for
Regarding higher mass flow rates of
3.2.4 Impact of the wall accommodation coefficient on predicted stagnation pressure
The impact of different wall accommodation coefficients σv on the stagnation pressure ps is investigated, as a variation of the coefficient may enhance the flow rate by raising the flow velocity close to the nozzle wall. Wall accommodation coefficients σv of 1.0, 0.9, 0.8, and 0.5 are investigated. A value of σv = 1.0 represents a fully diffusive reflection of particles from the wall, with an average tangential velocity of zero. For an assumed value of σv = 0.0, particles would be reflected in a specular manner, resulting in an inviscid flow with zero friction at the wall. As it can be assumed that the value of σv = 0.0 does not represent the physical flow, the lowest investigated value is σv = 0.5, where approximately half of the particles are scattered diffusively and specularly.
Table 5 presents obtained stagnation pressures from CSL DSMC simulations and relative deviations to experimental values for different accommodation coefficients for four mass flow rates. As can be seen, a steady decline of numerically obtained pressure for all mass flow rates is present when the coefficient is lowered. The lowest pressures are reached for σv = 0.5. In comparison to experimentally obtained stagnation pressures, two major effects can be seen. For the lower mass flow rates up to
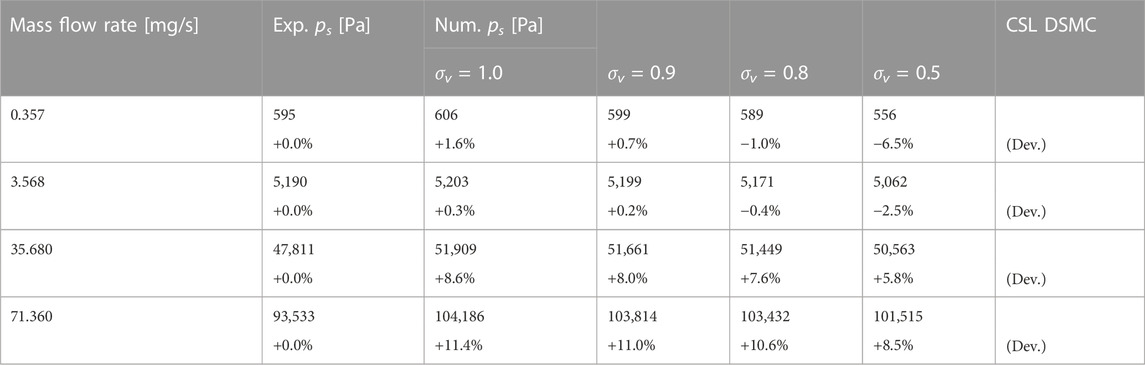
TABLE 5. Stagnation pressures of CSL DSMC simulations for different wall accommodation coefficients and mass flow rates.
4 Discussion
4.1 Comparison to baseline DSMC simulations
The overprediction of the stagnation pressure for the higher mass flow rates present in the CSL DSMC simulations should vanish if a DSMC simulation in accordance with the baseline criteria is applied. Hence, results for the CSL DSMC and Navier–Stokes simulations are compared to baseline DSMC simulations. Four mass flow rates of 0.357, 1.780, 3.568, and 7.136 mg/s are studied.
Table 6 presents results for the experimentally obtained stagnation pressure and for the three solvers. For the lowest mass flow rate of 0.357 mg/s, by applying the selection limiter scheme, no change in results for the pressure is present between baseline and CSL DSMC simulations. Deviations may only be within numerical uncertainty because baseline criteria for the time step and cell size are met in both simulations. The Navier–Stokes simulation clearly overpredicts the stagnation pressure.
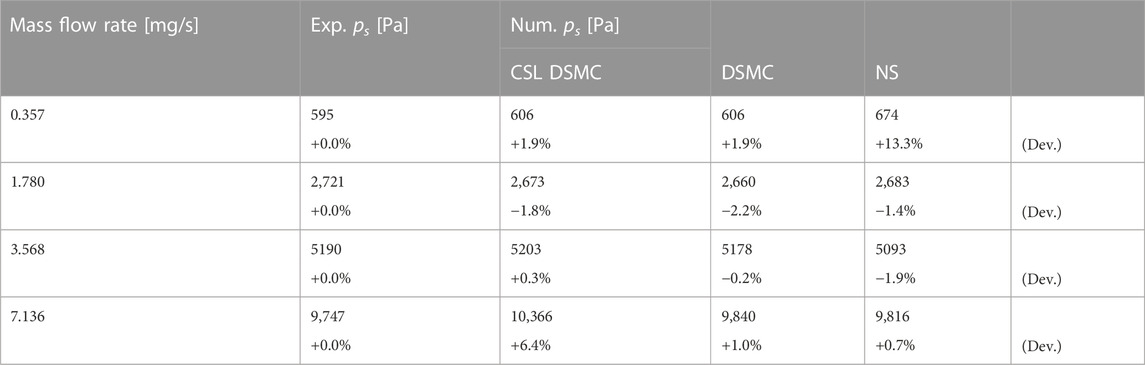
TABLE 6. Comparison of stagnation pressures of CSL DSMC, baseline DSMC, and NS simulations for mass flow rates between 0.357 and 7.136 mg/s.
For mass flow rates of 1.780 and 3.568 mg/s, only a little change in the stagnation pressure can be observed once again, comparing both CSL and baseline DSMC simulations. For 1.780 mg/s, both the DSMC and the Navier–Stokes simulations slightly underpredict the experimental value but within experimental error. However, a slight decrease of 0.4% can be seen regarding stagnation pressures for the CSL and baseline DSMC simulations. Regarding the results for a mass flow rate of 3.568 mg/s, a slight decrease of 0.5% in the stagnation pressure is obtained. Here, the effects of the selection limiter, enlarged time steps, and cell sizes may begin to show.
For the highest mass flow rate of 7.136 mg/s, shown in Table 6, the CSL DSMC simulation clearly overpredicts the experimental stagnation pressure of approximately 6.4% due to the applied selection limiter scheme. In contrast to that, the baseline DSMC simulation can predict the stagnation well, with a minor overprediction of approximately 1.0%, reaching almost the value of the Navier–Stokes simulation. Deviations between baseline DSMC and Navier–Stokes results may be within numerical uncertainty.
Table 6 shows that the effect of stagnation pressure overprediction vanishes if a baseline DSMC simulation is applied. The effects of the proposed selection limiter scheme and comparison to baseline DSMC simulations are also analyzed regarding centerline profiles of scaled flow properties, presented in Figure 7. For the lowest mass flow rate of 0.357 mg/s, no visible deviation between CSL and baseline DSMC is present over the whole nozzle. Even for mass flow rates of 1.780 and 3.568 mg/s, CSL and baseline DSMC basically predict the same profiles for scaled density ρ/ρ0, temperature T/T0, and velocity U/Umax. The small deviations in stagnation pressures shown in Table 6 may be present for the two mass flow rates.
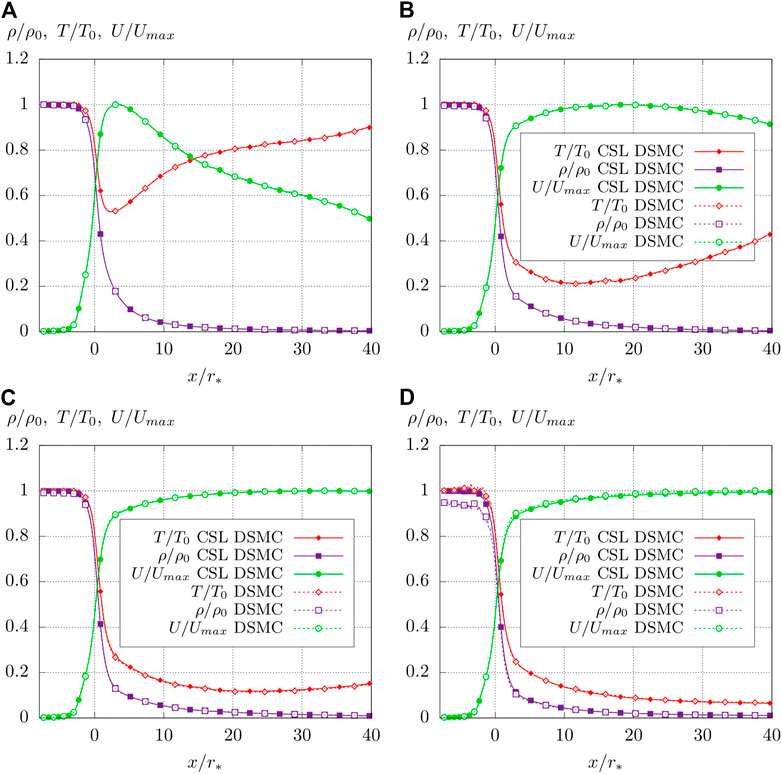
FIGURE 7. Centerline profiles of scaled density ρ/ρ0, temperature T/T0, and velocity U/Umax obtained by CSL DSMC simulations (continuous lines) and the baseline DSMC simulations (dashed lines) for four different mass flow rates. (A)
In contrast, deviations between CSL and baseline DSMC are present for a mass flow rate of 7.136 mg/s in Figure 7. As a result of the full velocity relaxation, the baseline DSMC simulation reaches slightly lower centerline densities ρ/ρ0 and higher velocities U/Umax directly after the nozzle throat at 0 ≤ x/r* ≤ 10. This, in return, leads to lower stagnation densities ρ/ρ0 and lower stagnation pressure obtained for the baseline DSMC simulation in Table 6 for 7.136 mg/s.
4.2 Thrust and specific impulse prediction
The second analysis of interest for the applicability is conducted on the dependency of predicted thrust and specific impulse using the CSL scheme. As differences between pressure values at the nozzle’s exit plane and measured background pressures of the far field are small for all examined mass flow rates, the effects of additional pressure drop on the generated thrust are neglected, and the numerical thrust for both used solvers is calculated by
where ρ is the density,
Numerically and experimentally obtained thrust forces for the investigated range of mass flow rates are shown on the left side of Figure 8. The lowest thrust forces are obtained for a mass flow rate of
With 0.357 mg/s
With a rising mass flow rate, the deviation between numerical results decreases rapidly, reaching a value of under 2.5% for
In summary, the CSL DSMC solver reproduces the experimental thrust better over the whole range of mass flow rates, which is remarkable as the results in Section 3.2 show an overprediction of the stagnation pressure caused by the applied selection limiter scheme for the higher mass flow rates. However, the pressure overprediction does not seem to have a huge effect on predicted thrust values, meaning that the study of exit plane and plume data is valid. An explanation for that behavior is given in Figure 9, showing the evolution of numerical thrust throughout the normalized diffuser length Dn.
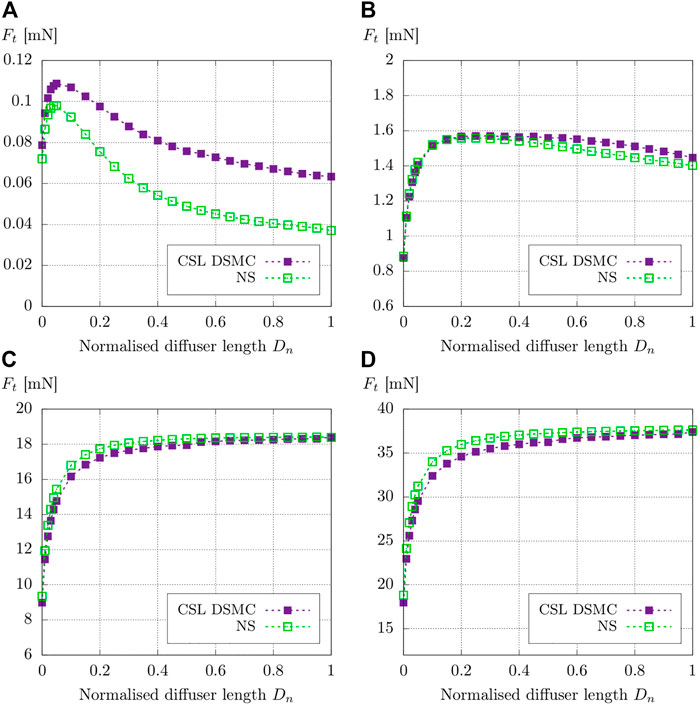
FIGURE 9. Evolution of thrust over the normalized length of the diffuser Dn for mass flow rates of (A)
Two major effects can be seen in Figure 9. For the smallest displayed mass flow rate of
In contrast, deviations based on the application of the selection limiter are present for
Figure 10A shows the results for the specific impulse Isp as a function of mass flow rate. As previously pointed out for the thrust forces in Figure 8, the apparent deviation between the two numerical results is present for mass flow rates below
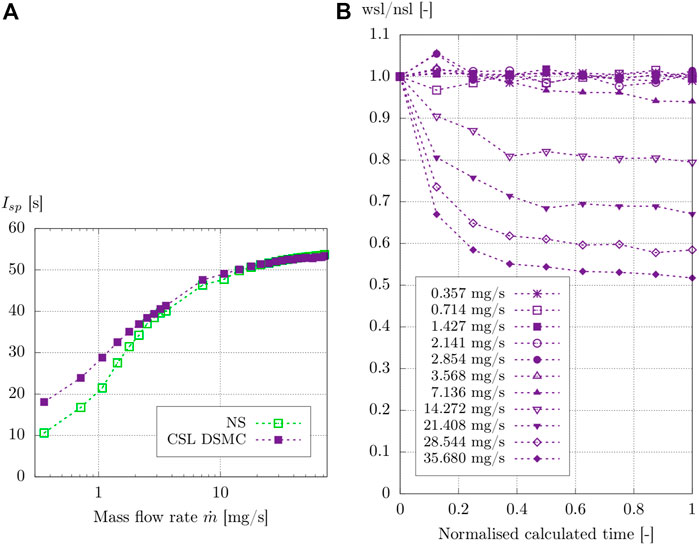
FIGURE 10. (A) Calculated exit plane specific impulses Isp for the CSL DSMC and the Navier–Stokes solver. (B) Relative computational speed-up.
4.3 Computational performance characterization of the scheme
The computational speed-up as a function of normalized calculated time for different mass flow rates is displayed in Figure 10B to characterize the performance. The dimensionless speed-up wsl/nsl is calculated as a fraction of two simulations, one with activated CSL (wsl) and one without (nsl). However, mesh size and time step are unaltered.
For displayed mass flow rates of 0.357 mg/s
5 Conclusion
An argon cold gas flow through a millimeter-scaled thruster nozzle geometry with high-density ratios was experimentally and numerically investigated using a compressible Navier–Stokes solver and a DSMC solver with a modified collisional routine, here denoted as CSL. To evaluate the applicability of the CSL DSMC for nozzle flow investigations, mass flow rates of 0.178 mg/s
The comparison of the numerical results with experimentally obtained stagnation pressures shows a clear overprediction by the Navier–Stokes solver for cases with rarefied gas flow and mass flow rates of 0.178 mg/s
In contrast, the DSMC method with applied CSL can reproduce the stagnation pressure well for the lower mass flow rates due to the kinetic nature of the method. By applying the CSL, the DSMC method overpredicts the stagnation pressure with rising mass flow rates up to a deviation of 11.4% from the experimental value for the largest mass flow rate studied. The impact of the wall accommodation coefficient is studied. A value of 0.9 to 0.8 for the coefficient could slightly improve results for the stagnation pressure for the lower mass flow rates. By applying a baseline DSMC simulation, the effects of the selection limiter scheme vanish, and the stagnation pressure is predicted correctly.
However, the results of the thrust and specific impulse prediction show that the applied CSL scheme does not alter the results, and the CSL DSMC can reproduce the experimental thrust and specific impulse for the higher mass flow rates. Results are in excellent agreement with the Navier–Stokes and experimental results. In addition, studied cases with lower mass flow rates, which are shown to be clearly in the rarefied flow regime, are naturally and correctly predicted by the CSL DSMC method.
Despite an overprediction of stagnation pressures, the CSL DSMC method is a suitable tool for predicting thrust and a specific impulse of cold gas micro-nozzle flows through the whole range of flow regimes.
By applying the CSL scheme, computational speed-up factors up to 0.51, dependent on the mass flow rate, could be achieved in the CSL DSMC simulations.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
TF and RG contributed to the conception and design of the study. TF performed the numerical computation. TF wrote the first draft of the manuscript. TF and RG wrote sections of the manuscript. All authors contributed to the manuscript revision and read and approved the submitted version.
Funding
The “North-German Supercomputing Alliance” (HLRN) provided computational time for the numerical study in this work (Funding ID: hbi00027).
Acknowledgments
The authors would like to thank Fionn Zeidler for his support in performing the numerical parameter studies and processing the simulation results.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1BRONKHORST HIGH-TECH B.V., Nijverheidsstraat 1A, NL-7261 AK Ruurlo (NL).
2First Sensor AG, Peter-Behrens-Straße 15, 12459 Berlin, Germany.
3Vision Engineering Ltd., Anton-Pendele-Str. 3, 82275 Emmering, Deutschland.
References
Alexeenko, A., Levin, D., Gimelshein, S., Collins, R., and Reed, B. (2002). Numerical modeling of axisymmetric and three-dimensional flows in microelectromechanical systems nozzles. AIAA J. 40, 897–904. doi:10.2514/3.15139
Bartel, T., Sterk, T., Payne, J., and Preppernau, B. (1994). “Dsmc simulation of nozzle expansion flow fields,” in 6th Joint Thermophysics and Heat Transfer Conference, Colorado Springs, CO. doi:10.2514/6.1994-2047
Bird, G. (1994). Molecular gas dynamics and the direct simulation of gas flows, vol. 42. Oxford, UK: Oxford Engineering Science Series, Clarendon Press.
Bird, G. (2007). “Sophisticated dsmc,” in Notes prepared for a short course at the DSMC07 meeting, Santa Fe, USA.
Boyd, I., Chen, G., and Candler, G. (1995). Predicting failure of the continuum fluid equations in transitional hypersonic flows. Phys. Fluids 7, 210–219. doi:10.1063/1.868720
Boyd, I., Ketsdever, A., and Muntz, E. (2003). Predicting breakdown of the continuum equations under rarefied flow conditions. AIP Conf. Proc. 663, 899–906. doi:10.1063/1.1581636
Burt, J., and Boyd, I. (2009). A hybrid particle approach for continuum and rarefied flow simulation. J. Comput. Phys. 228, 460–475. doi:10.1016/j.jcp.2008.09.022
Burt, J., and Boyd, I. (2008). A low diffusion particle method for simulating compressible inviscid flows. J. Comput. Phys. 227, 4653–4670. doi:10.1016/j.jcp.2008.01.020
Busse, C., Tsivilskiy, I., Hildebrand, J., and Bergmann, J. P. (2021). Numerical modeling of an inductively coupled plasma torch using openfoam. Comput. Fluids 216, 104807. doi:10.1016/j.compfluid.2020.104807
Clarke, A., and Smith, E. (1968). Low-temperature viscosities of argon, krypton, and xenon. J. Chem. Phys. 48, 3988–3991. doi:10.1063/1.1669725
Frieler, T., and Groll, R. (2018). A torsional sub-milli-Newton thrust balance based on a spring leaf strain gauge sensor. Rev. Sci. Instrum. 89, 075101. doi:10.1063/1.4996419
Gomez, J., and Groll, R. (2016). Pressure drop and thrust predictions for transonic micronozzle flows. Phys. Fluids 28, 022008. doi:10.1063/1.4942238
Gorji, M., and Jenny, P. (2015). Fokker–planck–dsmc algorithm for simulations of rarefied gas flows. J. Comput. Phys. 287, 110–129. doi:10.1016/j.jcp.2015.01.041
Greenshields, C. J., Weller, H. G., Gasparini, L., and Reese, J. (2010). Implementation of semi-discrete, non-staggered central schemes in a colocated, polyhedral, finite volume framework, for high-speed viscous flows. Int. J. Numer. Methods Fluids 63, 1–21.
Groll, R., Fastabend, F., and Rath, H. (2012). “Modelling transsonic flows through ring-shape thruster geometries with dsmc,” in ASME 2012 10th International Conference on Nanochannels, Microchannels, and Minichannels (New York City, USA: American Society of Mechanical Engineers (ASME)), 195–204.
Groll, R., and Gomez, J. (2016). Identifying microproduction inaccuracies with knudsen number depending correction functions. AIP Conf. Proc. 1786, 080012. doi:10.1063/1.4967605
Ivanov, S., Markelov, N., Kashkovsky, V., and Giordano, D. (1997). Numerical analysis of thruster plume interaction problems. Eur. Spacecr. Propuls. Conf. 398, 603.
Ketsdever, A., Lilly, T., Gimelshein, S., and Alexeenko, A. (2005). Experimental and numerical study of nozzle plume impingement on spacecraft surfaces. Tech. rep. DTIC Document.
Kolobov, V., Arslanbekov, R., Aristov, V., Frolova, A., and Zabelok, S. A. (2007). Unified solver for rarefied and continuum flows with adaptive mesh and algorithm refinement. J. Comput. Phys. 223, 589–608. doi:10.1016/j.jcp.2006.09.021
Kühn, C., and Groll, R. (2021). picfoam: An openfoam based electrostatic particle-in-cell solver. Comput. Phys. Commun. 262, 107853. doi:10.1016/j.cpc.2021.107853
Kurganov, A., Noelle, S., and Petrova, G. (2001). Semidiscrete central-upwind schemes for hyperbolic conservation laws and Hamilton–Jacobi equations. SIAM J. Sci. Comput. 23, 707–740. doi:10.1137/s1064827500373413
Kurganov, A., and Tadmor, E. (2000). New high-resolution central schemes for nonlinear conservation laws and convection–diffusion equations. J. Comput. Phys. 160, 241–282. doi:10.1006/jcph.2000.6459
Macrossan, M. (2001). A particle simulation method for the bgk equation. AIP Conf. Proc. 585, 426–433. doi:10.1063/1.1407592
Muraviev, A., Bashinov, A., Efimenko, E., Volokitin, V., Meyerov, I., and Gonoskov, A. (2021). Strategies for particle resampling in pic simulations. Comput. Phys. Commun. 262, 107826. doi:10.1016/j.cpc.2021.107826
Roohi, E., Darbandi, M., and Mirjalili, V. (2009). Direct simulation Monte Carlo solution of subsonic flow through micro/nanoscale channels. J. heat Transf. 131, 092402. doi:10.1115/1.3139105
Scanlon, T., Roohi, E., White, C., Darbandi, M., and Reese, J. (2010). An open source, parallel dsmc code for rarefied gas flows in arbitrary geometries. Comput. Fluids 39, 2078–2089. doi:10.1016/j.compfluid.2010.07.014
Shang, Z., and Chen, S. (2013). 3d dsmc simulation of rarefied gas flows around a space crew capsule using openfoam. Open J. Appl. Sci. 3, 35–38. doi:10.4236/ojapps.2013.31005
Sharma, A., and Long, L. N. (2004). Numerical simulation of the blast impact problem using the direct simulation Monte Carlo (dsmc) method. J. Comput. Phys. 200, 211–237. doi:10.1016/j.jcp.2004.03.015
Sutherland, W. (1893). Lii. the viscosity of gases and molecular force. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 36, 507–531. doi:10.1080/14786449308620508
Titov, E., Kumar, R., Levin, D., Gimelshein, N., Gimelshein, S., and Abe, T. (2008). Analysis of different approaches to modeling of nozzle flows in the near continuum regime. AIP Conf. Proc. 1084, 978. doi:10.1063/1.3076619
Titov, E., and Levin, D. (2007). Extension of the dsmc method to high pressure flows. Int. J. Comput. Fluid Dyn. 21, 351–368. doi:10.1080/10618560701736221
Titov, E., Zeifman, M., and Levin, D. (2005a). “Application of the kinetic and continuum techniques to the multi-scale flows in mems devices,” in 43rd AIAA Aerospace Sciences Meeting and Exhibit, 1399. doi:10.2514/6.2005-1399
Titov, E., Zeifman, M., and Levin, D. (2005b). “Examination of new dsmc methods for efficient modeling of mems device flows,” in 4th AIAA Theoretical Fluid Mechanics Meeting, Toronto, Ontario, 6–9. AIAA Paper. vol. 5058. doi:10.2514/6.2005-5058
Wang, W., Sun, Q., Boyd, I., Ketsdever, A., and Muntz, E. (2003). Assessment of a hybrid method for hypersonic flows. AIP Conf. Proc. 663, 923–930. doi:10.1063/1.1581639
Yu, S., Wu, H., Xu, J., Wang, Y., Gao, J., Wang, Z., et al. (2023). A generalized external circuit model for electrostatic particle-in-cell simulations. Comput. Phys. Commun. 282, 108468. doi:10.1016/j.cpc.2022.108468
Zelesnik, D., Micci, M., and Long, L. (1994). Direct simulation Monte Carlo model of low Reynolds number nozzle flows. J. Propuls. Power 10, 546–553. doi:10.2514/3.23807
Keywords: micro-nozzle, direct simulation Monte Carlo, cold gas thruster, rarefied gas flow, collision selector, collision limiter
Citation: Frieler T and Groll R (2023) Micro-nozzle flow and thrust prediction with high-density ratio using DSMC selection limiter. Front. Space Technol. 4:1114188. doi: 10.3389/frspt.2023.1114188
Received: 02 December 2022; Accepted: 06 February 2023;
Published: 13 March 2023.
Edited by:
Konstantinos Katsonis, DEDALOS Ltd., GreeceReviewed by:
Philippe Reynier, Ingénierie et Systèmes Avances, FranceAndrew Higgins, McGill University, Canada
Copyright © 2023 Frieler and Groll. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: R. Groll, Z3JvbGxAemFybS51bmktYnJlbWVuLmRl
 T. Frieler
T. Frieler R. Groll
R. Groll