- Emeritus Research Director, UMR 7190—Sorbonne-University, National Center for Scientific Research, Paris, France
We examine cases of stationary vortices that can appear inside spherical liquid drops in microgravity conditions. The first case is that of an incompressible external flow of uniform speed at infinity, leading the liquid in the drop by friction to form a Hill vortex. In the second case, the external fluid does not interact by friction with the liquid, but the drop is subjected to an axial temperature gradient causing a variation in surface tension. This time it is the induced movement which entrains the internal liquid. Note that the two situations can lead to the same Hill vortex. Combined effects are envisioned. We are also interested in the time factor in these phenomena.
1 Introduction
The drops of the sprays undergo various actions depending on their origin and the resulting physical situation in which they are found, such as watering spray, medical spray, automotive engine injector, rocket engine injector, etc. Their modeling includes on the one hand the examination on the scale of each individual drop, and on the other hand the study of the spray itself on a larger scale, as a constituent of a multiphase flow which is most often liquid-gas. Individual drop is often considered to be spherical. This is the case with small drops where capillary efforts are decisive for the establishment of sphericity. This simplicity of geometric shape is called into question in the case of large drops and as soon as they are subjected to significant forces of aerodynamic origin for example.1
For the sake of simplicity, we try during theoretical research to keep the spherical shape as long if possible.
The microgravity can be considered as a factor favorable to the spherical shape of the drops of average size which can allow experimental observation.
Finally, the study is also interested in applications to launchers. This dual fundamental/applied aspect makes the study of sprays a reason of choice recommended by CNES within the framework of Material Sciences.2
The exchanges between the individual drop and its gaseous environment are obviously different depending on whether there is evaporation-condensation or not. They concern the masses of the constituents, the momentum, and the energy. Each phase involved also undergoes motions and transfer phenomena.
For the flow of the spray itself, it is often necessary to model what happens inside the individual drops. The most classic is to characterize the latter by their radius, their mass, their temperature and their speed. The distribution in diameter and speed of the drops will always remain the essential element.
Nevertheless, it may be interesting to take care of the internal motions of medium-sized drops because these act on the exchanges at their surface. This is the problem that is proposed in this article, where we will therefore have to simultaneously study the external and internal flows of individual drops.
We have retained here the case of spherical liquid drops subjected either to a uniform external gas flow, or to a thermal gradient in an axial direction. We will see that Hill’s vortex modeling is an interesting solution for interior flows.
One of the major problems is that of the connection between the flow inside the drop-limiting sphere and the flow of the outside fluid.
Indeed, if we assume a perfect fluid on the outside, we can logically be led to admit perfect sliding conditions for this fluid at the level of the surface of the drop. But then how to admit that there is entrainment of the internal liquid in the drop by the external fluid?
The problem of the forces exerted on the drop by the external fluid is also posed regarding their resultant which is found to be zero! This constitutes the famous Dalembert paradox. We are then invited to consider the viscosity of the external fluid, at least in the close vicinity of the sphere, which leads to Stokes’ theory in the case of the rigid sphere. The results must also be modified to consider a liquid sphere. And in the presence of evaporation-condensation of the liquid it is even more complicated!
Finally, we know that for many linear problems one can superimpose elementary solutions. We will do this whenever possible, considering the nature of the fluids and the areas of validity that are the interior and exterior of the drop.
The origin of our study is related to the problem of combustion instabilities in rocket engines: It is established that the evaporation of droplets during combustion is the cause of amplification of HF vibrations generated by the engine (This model is mentioned in the appendix.). A feeded drop model was developed to represent the evaporating spray being. This model results from an improvement of that of Heidmann which did not consider the internal irreversibilities of the drop in evaporation. But if this model, with spherical symmetry, is well adapted to the velocity nodes (pressure anti-nodes) of standing sound waves, it is not suitable for the other zones of these waves presenting simultaneous pressure and velocity oscillations. These speed oscillations actually generate a break in the spherical symmetry, the consequences of which need to be analyzed.
2 Spherical Liquid Drop Subjected to a Uniform External Flow far away
Hill’s vortex is used to model the flow within a spherical liquid drop in the presence of relative external flow (Abramzon and Sirignano, 1989).
This vortex is a special case of a stationary motion of revolution of an incompressible inviscid fluid (Lamb, 1945). It is a rotational motion inside a sphere behaving with an irrotational external flow, so that by choosing suitably the multiplicative constant α of the stream function, the speeds of the two flows are identical to the surface of the sphere (Germain, 1986).
We first recall the equations of the fluid flow outside the sphere of radius R, and we will then determine the velocity field of the compatible steady liquid flow3 inside this same sphere (Prud’homme, 2012).
The stationary flow of a perfect fluid inside a sphere of radius R and the flow around this sphere are characteristic examples, shown in Figure 1.
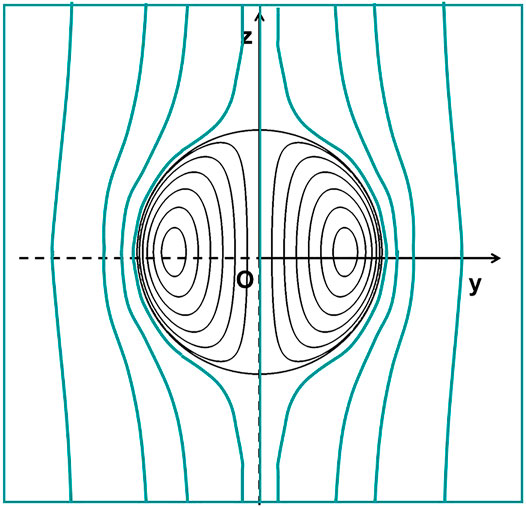
FIGURE 1. Liquid drop in the presence of an infinitely uniform flow: shape of the streamlines of the external and internal flows in a plane passing through the axis of symmetry.
2.1 Incompressible Fluids in Spherical Coordinates
2.1.1 Understanding the Coordinate System
The quantities
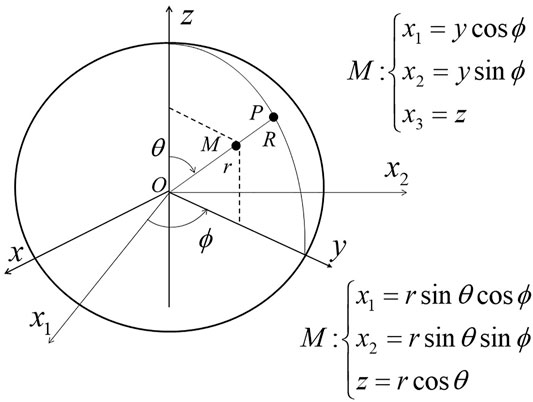
FIGURE 2. Definition of the spherical coordinates and representation of a sphere of radius R. The current point M can be inside or outside the considered sphere. p is the point of the half-line OM located at the surface of the sphere.
In the case of a symmetry around the axis Oz, one works in the plane
2.1.2 Continuity Equation
The continuity equation of an incompressible fluid is written in vectorial notations:
In the case of a symmetry of axis Oz, the motion is identical in each plane containing this axis.
The values of the various quantities of the fluid no longer depend on the angle
2.1.3 Expressions of the Stream Function in the Presence of a Sphere
We consider two kinds of flows: a flow irrotational (e) outside the sphere of radius R, and a rotational flow 1) with vorticity
Regarding the vorticity, zero on the outside, it is shown that we have
In the spherical coordinate system described above, we gets:
The stream functions
therefore:
In the problem of motion around a stationary sphere of radius R, the velocity
The calculations carried out with the stream function are summarized in Table 1. Theys are explicited hereafter.

TABLE 1. Correspondence between the coefficients for an external flow coming from the negative x with the velocity modulus
2.2 Flow Outside the Sphere
The steady flow of inviscid fluid outside the sphere is an irrotational flow. Its stream function (Figure 3) is (index e for exterior):
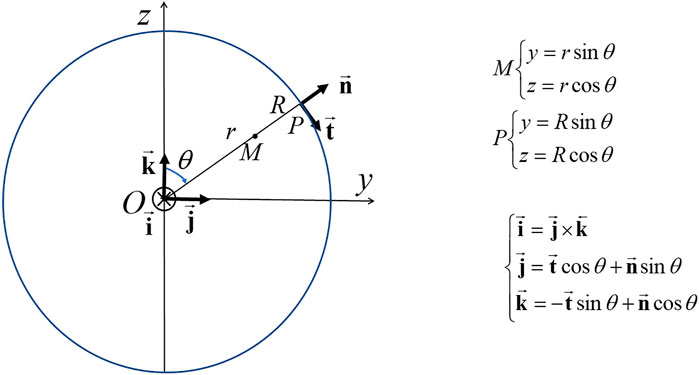
FIGURE 3. Definition of the coordinates in the y0z plane containing the axis of symmetry Oz. At the point p of the surface of the sphere of radius R, we define the unit vectors
The components of the velocity vector are:
Its streamlines are represented in Figure 4 with:
FIGURE 4. (A) Inner and outer streamlines, speed vectors
Maximum velocity:
Let us call
The velocity vectors of this flow and of the internal flow will be identical at any point on the surface of the sphere if the speed at infinity is suitably chosen:
2.3 Flow Inside the Sphere
2.3.1 Hill Vortex
The stream function of the form:
Corresponds to an internal rotational flow (ref. 4).
Knowing the stream function of the internal flow, we find the following radial and angular components of the velocity vector:
The results are shown in Figure 5.
FIGURE 5. (A) Streamlines calculated in the upper quarter plane passing through the axis.
Each value of the stream function corresponds to a toric surface. The limit value
The velocity vectors of the external flow are identical to those of the Hill vortex at any point on the surface of the sphere if the constants
One finds in this case:
Let us call
We therefore know how to determine the velocity field and the stream surfaces of the flows internal and external to the sphere (ref. iii). It has been shown that then the flows are compatible if
2.3.2 Remark About Viscous Fluid Vortex
The balance equation of the vortex vector in incompressible viscous fluid is written:
with, in spherical coordinates:
In the case of the flow inside the sphere, we find without difficulty for the Hill vortex:
The intensity
We set:
We then find:
The consequence is that Hill’s vortex, a solution of perfect fluid, is also a solution of the equations of viscous fluids.
In the case of external flow, we obviously have
3 Flows of a Spherical Liquid Drop Subjected to an Axial Thermal Gradient
3.1 Presentation of the Problem
The effect of an axial temperature field imposed on the internal motions of a liquid spherical drop has been studied by various authors. These movements are caused by the variations in surface tension induced and by the resulting Marangoni effect in viscous fluid.
We can cite in particular Bauer (Bauer, 1982), (Bauer, 1985), (Bauer and Eidel, 1987). For mathematical analysis, spherical harmonics are generally used.
In the article by Bauer (1982), a free-floating liquid drop is subjected on its surface to an axial temperature field inducing a thermal convection of Marangoni due to the variation of the surface tension. The stream function and the velocity distribution are determined analytically for the stationary and unsteady temperature fields, by solving the equation verified by the stream function using the associated Legendre functions of the first type. The particular case of a stable linear axial temperature field is evaluated numerically.
We consider the case of axial symmetry Oz, the liquid drop being centered in O. The equation of continuity of the flow of the supposedly incompressible liquid is written:
where u is the radial velocity and v the angular velocity5. We can therefore introduce the stream function ψ such that:
By removing the pressure from the unsteady momentum equations, and defining the operator:
It comes:
H.F. Bauer first deals with the stationary case by assuming constant the derivative of the surface tension
This temperature develops in a series of Legendre polynomials as follows:
With
The temperature distribution inside the spherical drop is given by:
with coefficients αn checking:
In the case of a temperature at the surface of the form
The temperature distribution inside the drop is then of the form
One thus solves the equation
and the fluxes cancellation conditions:
In the case of the linear axial temperature:
which corresponds to the case of the Hill vortex in Section 2.2.
Bauer also solves the problem in the case of an axial field of any stationary temperature, or with a periodic dependence in time.
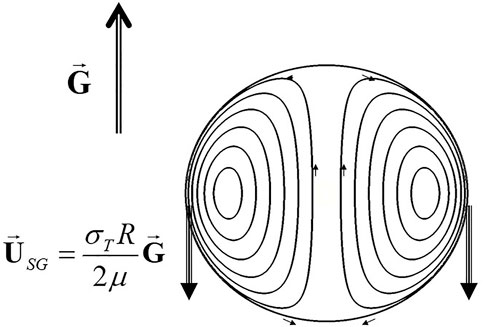
3.2 Thermo-Capillary Hill vortex
In the study by Bauer (1982), we notice that the solution obtained in the case of a constant axial thermal gradient was a Hill vortex with the same axis.6
The result can be obtained directly as follows. Consider a spherical drop of liquid whose surface is a phase separation of capillary tension
The motion of the liquid is organized in a Hill vortex, but if we assume that the outer fluid is inviscid and incompressible, it is at rest.
We can ask ourselves the following question: Which temperature field is capable of generating a Hill vortex as a result of the surface motion of the drop by thermo-capillary effect?
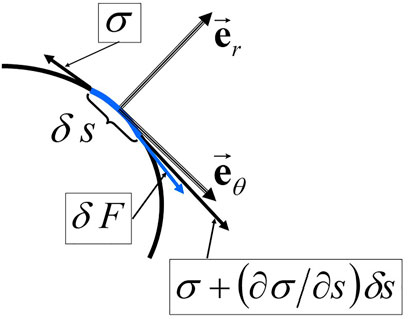
To answer this question, we establish the conditions of equilibrium to be verified between the capillary forces and the viscous forces at the surface of the sphere.
At point M, the velocity vector is (Figures 2,3, with
In p, that is to say for r = R, we have:
The balance of forces at a point on the capillary surface of the spherical drop involves the calculation of the tangential strain rate:
which makes it possible7 to express the tangential stress
One has:
This tangential stress is equal to:
It follows that
There is a constant gradient temperature field.
We can therefore give the following result:
A spherical liquid drop of constant density, subjected to a uniform and constant temperature gradient
3.3 Other Thermo-Capillary Flows
As indicated at the beginning of Section 3.1, Bauer also deals with instabilities in cases other than that of the constant axial thermal gradient.
In his 1985 paper, Bauer (ref.vi) studies the combined effects of Marangoni convection induced by a temperature gradient imposed on the free surface of a liquid sphere and natural convection from the residual microgravity field existing in an orbiting space laboratory. The case of a constant and linearly dependent axial residual gravity field was considered, for which the Stokes equation in the Boussinesq approximation was solved.
A dynamic Bond number derived from the ratio of the Grashof number, and the Reynolds number based on the Marangoni flow is introduced. It makes it possible to determine the predominance of the Marangoni effect if
The combined effects of Marangoni and natural convection are then studied. Streamlines, radial and angular velocity distributions have been obtained analytically. On the other hand, the isotherms are presented for different temperature distributions imposed on the free surface of the liquid sphere.
The dynamic Bond number introduced is by definition:
It compares the buoyancy force to the surface tension.
The main gravitational influence is due to the residual acceleration normal to the orbital path, in the plane of the orbit. It is created by the centrifugal acceleration of the space station in circular orbit and the acceleration of Newton.
When g is constant, we write
where β is the coefficient of thermal expansion of the liquid.
We then use the recurrence formulas of Legendre functions. The calculations lead to expressions of the stream function
The constants involved in these expressions are to be determined according to the boundary conditions at the surface of the liquid sphere.
In the absence of capillary effects, natural convection is obtained due to the residual gravity present at the location of the space station where the drop is located. We must then distinguish the case where liquid is in a rigid container from the case of the free surface
One also solves the situations where the internal motions of the drop of thermo-capillary origin are important, and we can thus predict the effects of residual gravity on these movements.
With regard to the field of gravity two situations are examined numerically: constant micro-gravity and linearly varying micro-gravity.
As for the field of temperature the field is linear axisymmetric
Results of the calculations carried out show in Figure 8 the possibility of notable differences with Hill’s vortices. Two-ring configurations of stream surfaces are observed (figures redrawn from the 1985 Bauer article) with a variable residual gravity field and quadratic temperature fields for
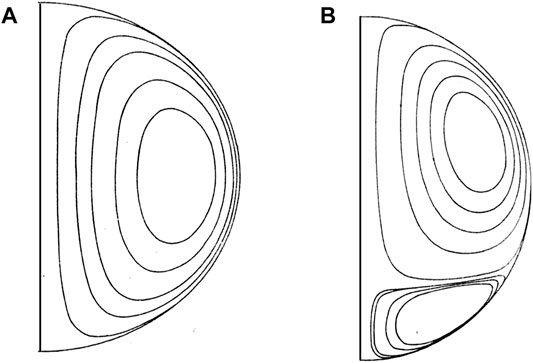
FIGURE 8. Streamlines of vortex rings in the presence of a variable gravity field (redrawn from Bauer 1985): (A) for a linear temperature field and (B) quadratic.
Another figure of the cited article also shows a case with two tore surfaces with a constant residual gravity field, the same quadratic temperature field and
4 Conclusion
We have presented Hill’s vortex as a structure that can appear inside liquid drops under two circumstances: infinitely uniform external fluid flow, thermal gradient along an axial direction. In both cases the speed of the fluid at the level of the surface of the drop is found to be proportional to the distance from the axis of symmetry.
The physical assumptions were:
1) The sphericity of the drop of constant radius.
2) The liquid: incompressible, expandable, or not, viscous but animated by a rotational motion of inviscid fluid in stationary regime.
3) The external fluid: at rest or animated by a uniform motion far away, inviscid irrotational or locally viscous.
4) Concerning the external liquid fluid interface:
o Simple contact surface or sliding surface,
o Identity of speeds: fluids-surface or only liquid-surface,
o With or without surface tension depending on the temperature. We took care to situate the case of the Hill vortex as a particular case of analysis by series of Legendre functions.
Outlook:
On the Hill vortex, it will be necessary to conclude on the birth and dissipation of this vortex by providing characteristic times (Gharib et al., 1998), (Chung, 1982).
On the Marangoni instability in a drop subjected to a radial thermal field with spherical symmetry, we will have to refine our formulation of the problem in spherical coordinates using the articles of Hoefsloot et al. (Hoefsloot et al., 1990), (Hoefsloot et al., 1992).
It would be interesting to study the effect of the thermo-capillary vortex on the evaporation of the drop (Shih and Megaridis, 1995), (Shih and Megaridis, 1996), in particular in the presence of thermal radiation (Niazmand and Ambarsooz, 2009) or acoustic excitation as we have done with other phenomena (Mauriot and Prud’homme, 2014).
Researchers are already interested in pursuing investigations on the subject8.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frspt.2022.835464/full#supplementary-material
Footnotes
1Paper proposed to Frontiers for “Transport Phenomena in Microgravity”, 13 October 2021.
2Indeed, linking work on microgravity research and space technologies is one of the objectives of the recommendations made during the CNES scientific prospective seminar in July 2004.
3That is to say with no velocity discontinuity at the interface.
4Ref. (Germain, 1986), p. 312.
5u and v were noted vr and vθ in Section 2.1.2.
6Unlike Section 2, the spherical drop is not in the presence of a well-defined external flow. This does not have a great importance if one neglects the interaction between the drop and the possible motions in its exterior.
7The surface forces are calculated from the speed field of the Hill vortex by introducing a viscosity, whereas this vortex is an inviscid fluid flow. This is not contradictory if we admit that it is a local influence and that the bulk of the flow is changed very little.
8In particular at the University of Lomé (Togo), and at the University of Abomey-Calavi (Benin).
References
Abramzon, B., and Sirignano, W. A. (1989). Droplet Vaporization Model for Spray Combustion Calculations. Int. J. Heat. Mass Transf. 32 (N° 9), 1605–1618. doi:10.1016/0017-9310(89)90043-4
Bauer, H. F. (1985). Combined Residual Natural and Marangoni Convection in a Liquid Sphere Subjected to a Constant and Variable Micro-gravity Field. Z. Angew. Math. Mech. 65, 461–470. doi:10.1002/zamm.19850651002
Bauer, H. F., and Eidel, W. (1987). Marangoni-convection in a Spherical Liquid System. Acta Astronaut. 15, 275–290. doi:10.1016/0094-5765(87)90073-7
Bauer, H. F. (1982). Marangoni-convection in a Freely Floating Liquid Sphere Due to Axial Temperature Field. Ing. Arch. 52, 263–273. doi:10.1007/bf00535319
Chung, J. N. (1982). The Motion of Particles inside a Droplet. Trans. ASME 104, 438–445. doi:10.1115/1.3245112
Gharib, M., Rambod, E., and Shariff, K. (1998). A Universal Time Scale for Vortex Ring Formation. J. Fluid Mech. 360, 121–140. doi:10.1017/s0022112097008410
Hoefsloot, H. C. J., Hoogstraten, H. W., Janssen, L. P. B. M., and Knobbe, J. W. (1992). Growth Factors for Marangoni Instability in a Spherical Liquid Layer under Zero-Gravity Conditions. Appl. Sci. Res. 49, 161–173. doi:10.1007/bf02984176
Hoefsloot, H. C. J., Hoogstraten, H. W., and Janssen, L. P. B. M. (1990). Marangoni Instability in a Liquid Layer Confined between Two Concentric Spherical Surfaces under Zero-Gravity Conditions. Appl. Sci. Res. 47, 357–377. doi:10.1007/bf00386244
Mauriot, Y., and Prud’homme, R. (2014). Assessment of Evaporation Equilibrium and Stability Concerning an Acoustically Excited Drop in Combustion Products. Comptes Rendus Mécanique 342, 240–253. doi:10.1016/j.crme.2014.02.004
Niazmand, H., and Ambarsooz, M. (2009). Effect of Slip and Marangoni Convection on Single Fuel Droplet Heat-Up in the Presence of Thermal Radiation. Kish Island: ICHEC.
Prud’homme, R. (2012). Flows and Chemical Reactions. WILEY/ISTE. Available at: http://www.iste.co.uk/index.php?f=a&ACTION=View&id=506.
Shih, A. T., and Megaridis, C. M. (1995). Suspended Droplet Evaporation Modeling in a Laminar Convective Environment. Combust. Flame 102, 256–270. doi:10.1016/0010-2180(94)00279-2
Shih, A. T., and Megaridis, C. M. (1996). Thermocapillary Flow Effects on Convective Droplet Evaporation. Int. J. Heat. Mass Transf. 39 (N°2), 247–257. doi:10.1016/0017-9310(95)00137-x
Glossary
D flow rate of a source
K intensity of a doublet
R gas constant, radius of a sphere
s curvilinear abscissa
S surface
T absolute temperature
Ω rotation speed
i, e flow resp.internal external
t, n resp.tangent, normal to the sphere of radius r
Keywords: Liquid drops, instabilities, velocity field, thermal field, Hill vortex
Citation: Prud'homme R (2022) Instabilities in a Spherical Liquid Drop. Front. Space Technol. 3:835464. doi: 10.3389/frspt.2022.835464
Received: 14 December 2021; Accepted: 28 March 2022;
Published: 24 May 2022.
Edited by:
Pradyumna Ghosh, Indian Institute of Technology (BHU), IndiaReviewed by:
Tatyana Lyubimova, Institute of Continuous Media Mechanics (RAS), RussiaOlga Lavrenteva, Technion Israel Institute of Technology, Israel
Copyright © 2022 Prud'homme. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Roger Prud'homme, cm9nZXIucHJ1ZGhvbW1lQHNvcmJvbm5lLXVuaXZlcnNpdGUuZnI=
 Roger Prud'homme
Roger Prud'homme