Spread spectrum modulation recognition based on phase diagram entropy

Wireless communication technologies are undergoing intensive study and are experiencing accelerated progress which leads to a large increase in the number of end-users. Because of this, the radio spectrum has become more crowded than ever. These previously mentioned aspects lead to the urgent need for more reliable and intelligent communication systems that can improve the spectrum efficiency. Specifically, modulation scheme recognition occupies a crucial position in the civil and military application, especially with the emergence of Software Defined Radio (SDR). The modulation recognition is an indispensable task while performing spectrum sensing in Cognitive Radio (CR). Spread spectrum (SS) techniques represent the foundation for the design of Cognitive Radio systems. In this work, we propose a new method of characterization of Spread spectrum modulations capable of providing relevant information for the process of recognition of this type of modulations. Using the proposed approach, results higher than 90% are obtained in the modulation classification process, thus bringing an advantage over the classical methods, whose performance is below 75%.

1 Introduction

Modulation recognition is increasingly important in civilian, commercial and military applications. It is used for cognitive radio, spectrum surveillance and management, software defined radio, source identification, and for many other applications (Iglesias et al., 2015; Ravi Kishore and Rao, 2017; Gacanin, 2019; Gui et al., 2019). The recognition accuracy has been a challenging issue because of the noise effect and multipath fading, as well as the increasing number of advanced modulation types. Considering these aspects, the automatic modulation recognition (AMR) would seem the most appropriate approach to extract representative features for the modulation in order to characterize them (Wu et al., 2008).

AMR methods can be classified into two categories: The likelihood-based (LB) methods and feature-based (FB) methods. The LB methods are based on decision theory, where the AMR is made by comparing the likelihood ratio with an appropriate theoretical threshold (Yang et al., 2004; Dobre et al., 2007). FB methods are based on the identification of defining features capable of discriminating between the analyzed signals. The most used features in FB scenarios are given by instantaneous features (Yu et al., 2019), high-order statistical features (Xiao-Ming and Zhong-Zhao, 2006), wavelet features (Huang et al., 2010) and time-frequency representations (Lee et al., 2020; Khan et al., 2022). But the performance of these FB methods largely depends on empirical feature extraction.

For the multipath interference and the low SNR ratio in CR communications, a commonly used technique is the spread spectrum communication (Reynders and Pollin, 2016; Qian et al., 2018). The spread spectrum method is a type of transmission in which the bandwidth occupied by the signal exceeds the minimum bandwidth required to transmit information. Spread spectrum transmissions are now widely used for secure communications, as well as for multiple access. Due to their low probability of interception, these signals increase the difficulty of spectrum surveillance. The most used modulations in spread spectrum communications include Chirp Spread Spectrum (CSS), Direct Sequence Spread Spectrum (DSSS) and Frequency Hopping Spread Spectrum (FHSS).

For AMR to be usable in most information interception scenarios, modulation recognition has to be completed in a blind manner, that is, the algorithm should be applied directly to the modulated signal with no prior knowledge (such as its phase, frequency, amplitude, etc.).

In (Yu et al., 2019) the authors used the instantaneous features, such as instantaneous amplitude, phase and frequency parameters on a Long Short-Term Memory (LSTM) network in order to differentiate between real DSSS and OFDM signals. For DSSS and OFDM signals, LSTM classifier has a good classification and recognition effect, but DSSS signals may be misclassified in OFDM signals. In general, the recognition accuracy using this approach can exceed 80%. In (Xiao-Ming and Zhong-Zhao, 2006) the authors used high order statistics to identify the DSSS modulations for low SNR values, obtaining good accuracy. They propose a new adaptive algorithm for the estimation of the fourth-order cumulant of stationary and non-stationary stochastic process based on an adaptive gain coefficient which offers very good results.

The second-generation wavelet kernel is applied from a Support Vector Machine (SVM) perspective in (Huang et al., 2010) to classify the individual transmitters from FHSS modulation, obtaining an average classification rate of 83.36%. The feasibility of this approach has been demonstrated for high values of SNR; the recognition rate is increased with increasing SNR. For values below $SNR=10dB$ this approach does not offer favorable results. To improve the discrimination of traditional ML algorithms for modeling visual-based time-frequency representations, the authors of (Khan et al., 2022) proposed linear discriminant analysis based on distance classifiers for classification of five types of FHSS modulation signals. This approach resulted in obtaining an accuracy of 90% for $SNR=3.5dB$. The thresholds used in this approach can be an impediment, because the choice of values is not automatic. The CSS signal recognition was improved in (Lee et al., 2020) by using the matched filter method on the spectrogram approach. The authors showed that the size of the matched filter can be doubled by applying a differential coding method and the performance is improved even if the SNR value is $SNR=0dB$.

In general, as we have seen previously, the large and similar number of modulations and the low level of SNR lead to a decrease in the accuracy of the classification due to the impossibility of identifying unique characteristics for each type of modulation. For example, in (Yu et al., 2019), under the condition of high SNR, the characteristics of the DSSS signal are more learnable and categorizable for the LSTM network. However, at low SNR, the characteristics of the DSSS signal are affected by noise, which directly affects the learning and classification of the LSTM network. In (Xiao-Ming and Zhong-Zhao, 2006) the adaptive algorithm is more useful to enhance the SNR of non-stationary stochastic process than the classical one, which contributes to an increase in the accuracy of the recognition process. As SNR decreases from zero, the adaptive algorithm changes less than the classical algorithm as well. It is shown in (Huang et al., 2010) that at high SNR values ($SNR=10dB$), the classification rate of the FHSS signals can be satisfactory. The results demonstrate that SNR has little influence on second-generation wavelet kernel function in classifying. In other words, this method has certain stability. But this is no longer valid for SNR below this value, the identification and recognition capacity falling to an unsatisfactory value. Also, the performance of the linear discriminant analysis method in (Khan et al., 2022) degraded for the FHSS signals at low SNR value because the frequencies of the signals are overlapping with the background noise. The visual method analyzed in (Lee et al., 2020) is the most susceptible to noise. At low SNR values, the spectrograms of CSS signals lose their interpretability and advanced processing techniques are needed to be able to eliminate the effects of noise. Although spectrograms are useful for highlighting frequency variations, depending on the type of analyzed signal and the amount of noise, they cannot always provide a satisfactory result of the signal recognition process.

That is why, in this paper, we propose a way to recognize the types of modulations specific to the spread spectrum using a data driven approach, independent of any model, namely, the phase diagram-based entropy (PDE). Considering the complexity of the used modulations, the phase diagram-based entropy brings out some hidden characteristics, this leading to the increase of the accuracy of the recognition process of the modulations.

The rest of this paper is organized as follows. In Section 2, we provide the basic information related to spread spectrum modulations. Section 3 details two theoretical approaches for modulation recognition that provide the comparative support in this paper. We present the approach of the phase diagram based entropy in Section 4. In Section 5 we detail the results of the signal characterization using our approach and the results of the modulation recognition process. We conclude our paper in Section 6.

2 Spread spectrum modulations

In this section, some theoretical notions about the three types of modulations analyzed in this paper will be presented.

2.1 Chirp Spread Spectrum (CSS)

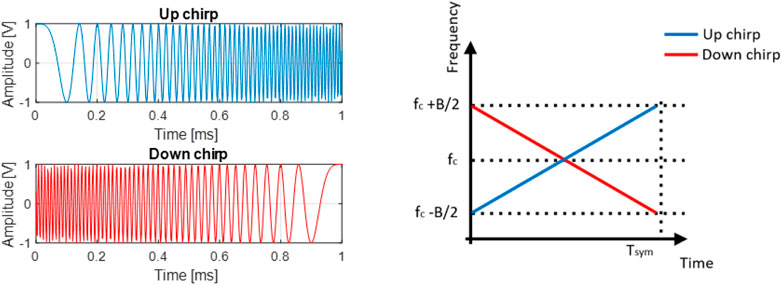
CSS communication system uses linear frequency-modulated chirps to represent the message symbols. It is known for its flexibility in providing tradeoffs between throughput and reception sensitivity. Due to its robustness against narrow-band interference and resistance against multi-path fading, CSS modulation has been adopted in various long-range wireless applications (Karapistoli et al., 2010; Raza et al., 2017). The chirp waveform can be described by:

$s\left(t\right)=\exp \left[j2\pi \left(f_{c}t+r{t}^2\right)\right],0\le t\le T_{sym}(1)$

where $f_c$ is center frequency, $r$ is the chirp rate and $T_{sym}$ is the symbol duration. If $r>0$ the chirp waveform is an up chirp called $s_u\left(t\right)$ and if $r<0$ the chirp waveform is a down chirp called $s_d\left(t\right)$.We can express Eq. 1 using the maximum and the minimum frequency as:

$s_u\left(t\right)=\exp \left[j2\pi t\left(f_{\min }+\frac{f_{\max }-f_{\min }}{T}t\right)\right](2)$

$s_d\left(t\right)=\exp \left[j2\pi t\left(f_{\max }+\frac{f_{\min }-f_{\max }}{T}t\right)\right](3)$

where $f_{\max }$ is maximum frequency and $f_{\min }$ is minimum frequency. The simplest form for a CSS signal is obtained according to the bit information and it is expressed as:

$s_{CSS}\left(t\right)=\left\{\begin{array}{cc}{s}_u\left(t\right),& if{b}_n=1\\ s_d\left(t\right),& if{b}_n=0\end{array}\right.(4)$

where $b_n$ is the bit sequence and $n$ is the bit index. In Figure 1 it is shown a representation for the up chirp $s_u\left(t\right)$ and the down chirp $s_d\left(t\right)$ in time and frequency domain.

FIGURE 1

FIGURE 1. The up chirp and the down chirp in time domain (left) and frequency domain (right).

The CSS modulation order is defined as $M=2^{SF}$, which means that each CSS symbol carries $SF$ (spreading factor) bits per encoded symbol. At baseband, each CSS symbol contains M complex samples, which are sent at a rate equal to the $B$ of the signal (Wang et al., 2008). Thus, the CSS symbol duration is given as $T_{sym}=M/B$. The chirp rate is the rate at which the frequency of a CSS signal changes over time and can be defined as:

$r=\frac{B}{T_{sym}}=\frac{B^2}{M}(5)$

The bandwidth $B$ is an important parameter in CSS modulation. Using a larger $B$ enhances the data rate and, at the same time, provides better immunity to narrow-band perturbations. The spreading factor, $SF$ is another important parameter. The range of communication may be greatly increased by increasing SF, but this comes at the expense of a lower transmission rate.

The CSS technique allows the symbol generation based on the $SF$ parameter, for a specific bandwidth, $B$. For example, if only chirp slope variation is used to encode digital data, only two different symbols are generated ($SF=1$). This would be the case described by Figure 1. If $SF$ increases, in order to distinguish between each symbol, a cyclic shift ($cs$) is used according to Eq. 6.

$cs=\frac{sv}{2^{SF}}{T}_{sym}(6)$

where $sv$ corresponds to the symbol value (0 to $2^{SF}-1$). The reference symbol is $sv=0$. Hence, the $cs$ parameter correspond to a time delay referenced to $T_{sym}$.

2.2 Direct Sequence Spread Spectrum (DSSS)

DSSS technology is a wideband modulation in which the original bit sequence is converted into a pseudo-random spreading sequence (Yue et al., 2003; Tsai, 2009). The direct-sequence modulation makes the transmitted signal wider in bandwidth than the information bandwidth. The pseudo-random code is modulated onto the information signal using several modulation techniques such as binary phase-shift keying (BPSK), quadrature phase-shift keying (QPSK) and so on. A transmission DSSS signal using BPSK modulation can be written as:

$s\left(t\right)=Ad\left(t\right)c\left(t\right)\cos \left(2\pi f_{0}t+{\theta }_0\right)(7)$

where $A$ denotes the amplitude of the signal, $d\left(t\right)$ is the data signal which will be transmitted, $c\left(t\right)$ is the spreading sequence, $f_0$ is the carrier frequency, and ${\theta }_0$ is the carrier phase. In Figure 2 we can see a representation of the DSSS signal generation.

FIGURE 2

FIGURE 2. DSSS transmitter block diagram.

DSSS significantly improves protection against interfering and jamming signals, especially narrowband and makes the signal less noticeable. In the DSSS systems, each user is assigned a unique code sequence that allows the user to spread the information signal across the assigned frequency band (Javed et al., 2020).

2.3 Frequency Hopping Spread Spectrum (FHSS)

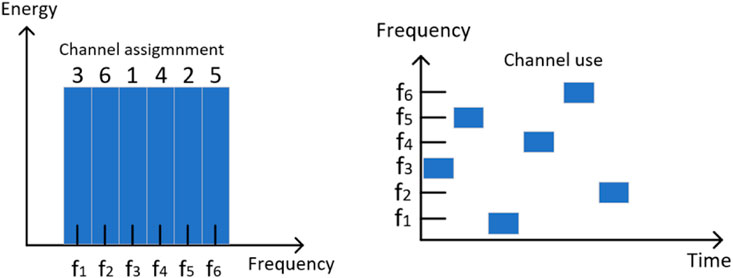
FHSS is a transmission technology used in wireless networks to generate spread spectrum by hopping the carrier frequency in a pseudo-random manner (Liu et al., 2017; Lei et al., 2018). For example, in a FHSS system, the transmitted signal is spread across multiple channels, as shown in Figure 3. The full bandwidth is divided into 6 channels, centred at $f_1$ through $f_6$. The signal hops between them in the following sequence: $f_3$, $f_5$, $f_1$, $f_4$, $f_6$ and $f_2$.

FIGURE 3

FIGURE 3. Channel assignment and channel use in FHSS.

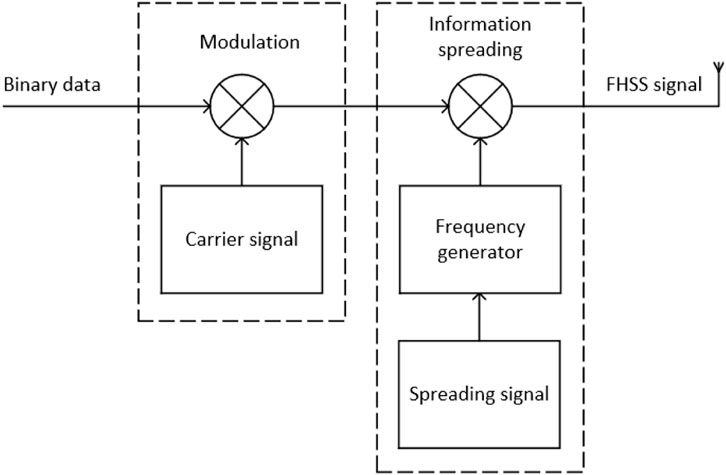
Figure 4 shows the block diagram of a typical FHSS transmitter. First, digital data is modulated usually using some digital-to-analogue scheme. This baseband signal is then modulated onto a carrier $c\left(t\right)$. The frequency of the carrier $c\left(t\right)$ that is the sequence of channels, depends on the spreading code, which is generated by a pseudo-random source.

FIGURE 4

FIGURE 4. FHSS transmitter block diagram.

The transmitted FHSS signal can be expressed as:

$s\left(t\right)=Ad\left(t\right)\cos \left(2\pi f_{i}t+{\theta }_i\right),i{T}_h\le t<\left(i+1\right)T_h(8)$

where $A$ denotes the amplitude of the signal, $d\left(t\right)$ is the data signal, $f_i$ is the carrier frequency, ${\theta }_i$ is the carrier phase and $T_h$ is frequency hopping rate.

Some of the advantages of using FHSS modulation are given by: improved privacy, avoiding interference and multi path fading, decreasing narrowband interference, increasing signal capacity, increasing the efficiency of bandwidth and the difficulty of interception. The transmission of a FHSS signal can share a frequency band with many types of conventional transmissions with minimal interference (Hong et al., 2013).

3 Classical approaches

In this section we detail two classic approaches used for modulation recognition that also provide the comparative support for the new proposed method based on the phase diagram analysis.

3.1 Wavelet transform approach

The wavelet transform is used to decompose a signal $s\left(t\right)$ into an orthonormal basis consisting of a family of functions $\psi \left(t\right)$ called wavelets, which is generated by time and scale modification of ${\psi }_0\left(t\right)$:

${\psi }_{m,n}\left(t\right)=\frac{1}{\sqrt{m}}{\psi }_0\left(\frac{t-n}{m}\right)(9)$

where ${\psi }_0\left(t\right)$ represents the generator wavelet, $m$ is the dilation factor and $n$ is the translation factor. A wavelet function is very concentrated in time or frequency. The central idea is based on the proposal of an orthonormal base elaborated from a mother wavelet, of average zero and its dilated and delayed variants (Eckmann et al., 1987). The signal is then projected into this base as:

$W_{\psi }\left(m,n\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}s\left(t\right){{\psi }_{m,n}}^{*}\left(t\right)dt(10)$

As a result of this projection, we obtain a two-dimensional function called continuous wavelet transform. From here the scalogram, which renders the signal energy distribution for the scale $m$ and the position in time $n$, can be derived as:

$S_W\left(m,n\right)={\left|W_{\psi }\left(m,n\right)\right|}^2(11)$

As a general remark on the use of this technique, one can say that the wavelet transform is able to quantify the time-frequency variations, but depends on the scale provided by the wavelet basis. That’s why in order to have a good wavelet representation, it is essential to determine the best suitable mother function which resembles as much as possible the analyzed transient signal.

3.2 Statistical approach

In the statistical approach are many sets of features that can be used in the signal recognition discrimination process. In this paper we use an approach based on the normalized central moments of the modulated signals. A central moment is a statistical moment that characterizes the probability distribution of a random variable with respect to its mean. The central moments are useful because they allow us to quantify properties of distributions in ways that are location-invariant, as in Eq. 12:

$c{m}_k=\frac{E{\left(s-\mu \right)}^k}{{\sigma }^k},k\ge 3(12)$

where $\mu$ is the mean of the signal $s$, $E\left(t\right)$ represents the expected value of the quantity $t$ and $\sigma$ is the standard deviation of the signal $s$ (Mallat, 2009).

It is important to note that the central moments are valid only for distributions that have well-defined first and second moments, with the second moment being non-zero. Fortunately, this criterion applies to the majority of distributions. By standardizing the moments, they become invariant to both location and scale.

4 Phase diagram-based entropy approach

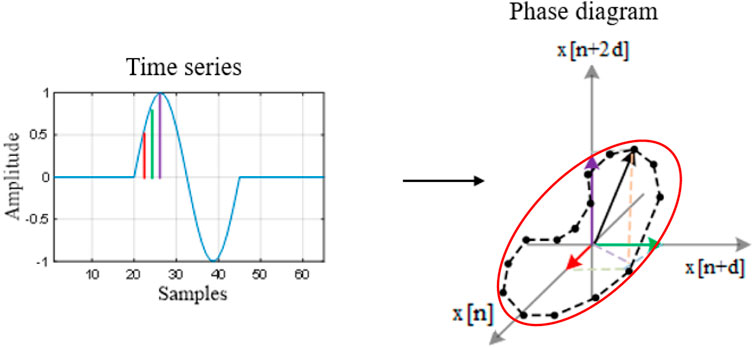
The phase diagram representation method is derived from the theory of nonlinear dynamical systems and it is a data–driven technique that makes no a priori assumption about the system (Zbilut and Webber, 1992; Davidson and Loughlin, 2000). Starting from a signal expressed as a time series, as in (13), the strategy for the phase diagram design is given by moving from the values of the signal to a new vector that defines the representation space as shown in Eq. 14:

$\mathbf{x}=\left\{x\left[1\right],x\left[2\right],...,x\left[N\right]\right\}(13)$

$\overrightarrow{v_{\left[\mathrm{i}\right]}}={\displaystyle \sum _{k=1}^m}x\left[\mathrm{i}+\left(k-1\right)d\right]\cdot \overrightarrow{e_k},i=1,...,M(14)$

where $\overrightarrow{v_{\left[i\right]}}$ are the vectors of the new representation space, $m$ is the embedding dimension, $d$ is the delay between the samples, $\overrightarrow{e_k}$ are the axis unit vectors and $M=N-\left(m-1\right)d$ . As can be seen, two new parameters appear in the new representation vectors: the delay, which is usually determined with the mutual information method (Marwan et al., 2007) and the embedding dimension, which is usually determined with false nearest neighbor method (Webber and Zbilut, 1994). In Figure 5, you can see a graphic example that shows the transition from the time series to the phase diagram.

FIGURE 5

FIGURE 5. Example of a time series and its phase diagram representation.

This new resulting representation space can provide several ways of quantifying the information of the analyzed signal. One of the things of interest that can be quantified from the phase diagram is the distances between the phase diagram vectors because this establishes the shape of the trajectory. Based on this, we have the possibility to quantify the distribution of the phase diagram vectors (Stanescu et al., 2021). In the quantification process we use a probabilistic approach and we are interested in determining the probability of the signal to pass through a specific region of the phase diagram. Mathematically, we determine the number of points, which are close within a distance $\mathrm{\sigma }$ for each vector and then we compute the ratio of number of close points to the total number of vectors as in Eq. 15:

$T_j\left(d,m,\sigma \right)=\frac{1}{N-\left(m-1\right)d}{\displaystyle \sum _{j=1,j\ne i}^{N-\left(m-1\right)d}}\mathrm{\Theta }\left(‖\overrightarrow{v_{\left[i\right]}}-\overrightarrow{v_{\left[j\right]}}‖-\sigma \right)(15)$

where $\mathrm{\Theta }$ is the Heaviside function, $\mathrm{\sigma }$ is the threshold distance used to determine the range between vectors and $‖\cdot ‖$ is the operator of the Euclidean distance. In this quantification, the choice of the distance threshold must be considered. We define it as the ratio between the product and the sum of the two semi-axes of the ellipse in which the phase diagram representation can be included, as shown in Figure 5, using Eq. 16:

$\sigma =\frac{ab}{\left(a+b\right)}(16)$

where $a$ is the major semi-axis of the ellipse and $b$ is the minor semi-axis of the ellipse.

Next, we determine the entropy information in the representation dimension of the phase diagram based on the number of total points, which satisfy the mentioned criterion, as described in Eq. 17.

$P\left(d,m,\sigma \right)=\frac{1}{N-\left(m-1\right)d}{\displaystyle \sum _{i=1}^{N-\left(m-1\right)d}}\log \left(T_i\left(d,m,\sigma \right)\right)(17)$

It is interesting to see how the entropy information change form one dimension to another, that’s why we define the phase diagram-based entropy as a gradient of entropy from one dimension to another as in Eq. 18. This approach is used to study the behavior of the signal by measuring the changes that occur as an increase of the embedding dimension (Stanescu et al., 2021).

$PDE\left(d,m,\sigma \right)=P\left(d,m,\sigma \right)-P\left(d,m+1,\sigma \right)(18)$

Thus, using this approach, we can successfully characterize the modulation signals in order to realize their recognition process. The advantages of the characterization of single carrier modulations based on the phase diagram approach were already shown in (Scripcaru et al., 2020; Stanescu et al., 2022; Stanescu et al., 2023). In order to address the characterization of different modulation, the sliding windows are used and the PDE is computed on each window.

5 Results

In this section we detail the results obtained in the characterization process of each type of modulation, then we discuss the accuracy of the recognition process by comparing our approach with other approaches used at the moment. The characterization of the signals will be done first in the noise-free scenario, after which the use of the approach in the presence of noise is studied.

5.1 CSS characterization

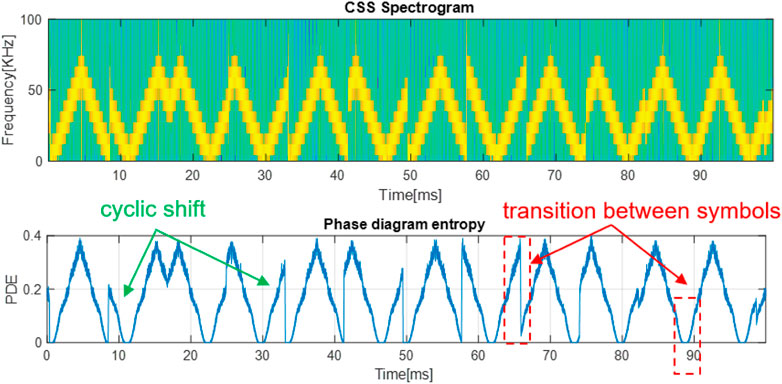
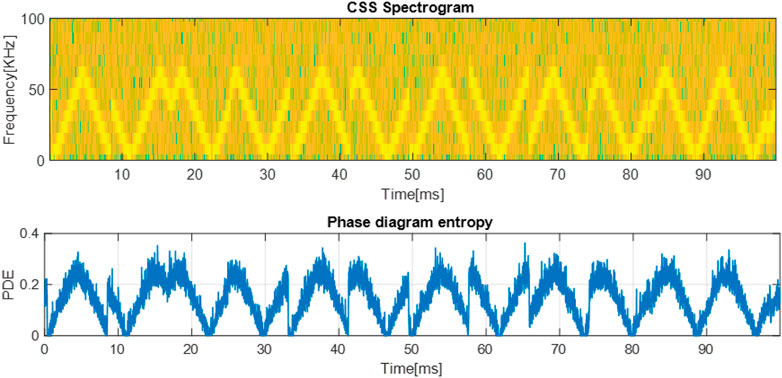
First, we analyze the CSS modulation. For this, we generate a CSS waveform, with the following parameters: the center frequency $f_c=35kHz$, the sweep bandwidth $B=70kHz$, the spreading factor $SF=10$, the symbol duration $T_{sym}=4ms$ and the sample frequency $f_s=1MHz$. In Figure 6 we can see the spectrogram of the generated CSS signal and the phase diagram entropy variation. In determining the spectrogram, the following parameters were used: a Hamming window of 128 samples size, the number of overlapped samples 120 and the number of Fast Fourier Transform points 128. To determine the phase diagram entropy variation, the following values were used for the necessary parameters: a sliding window of 50 samples, $m=3$, $d=2$ and $\mathrm{\sigma }=0.66$.

FIGURE 6

FIGURE 6. The CSS spectrogram and the PDE variation for $SNR\to \infty$.

As shown, the PDE variation highlights the cyclic shift of each symbol. Moreover, the symbols are delimited by global minima and maxima values of the PDE and sudden entropy drops as it can be seen marked with the red dashed line. These proprieties are also present in the case of the signal with $SNR=5dB$, where the PDE variation is a little more disturbed, as displayed in Figure 7.

FIGURE 7

FIGURE 7. The CSS spectrogram and the PDE variation for $SNR=5dB$.

After showing the potential of the PDE for the characterization of the CSS signal, we want to see what the PDE variation distribution looks like. The phase diagram entropy distribution is shown in their corresponding histograms. In Figure 8, are displayed the histograms of the PDE of the CSS signal in the two cases.

FIGURE 8

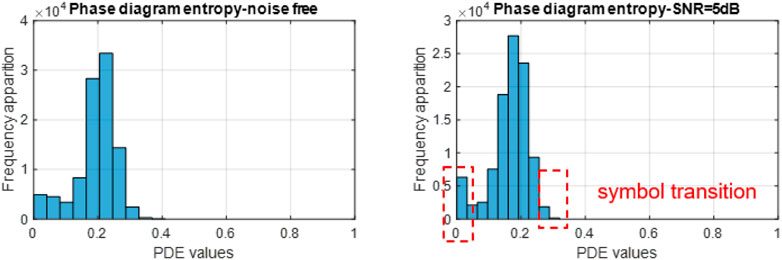
FIGURE 8. CSS signal phase diagram entropy histogram in the noise free case (left) and in the noisy case (right).

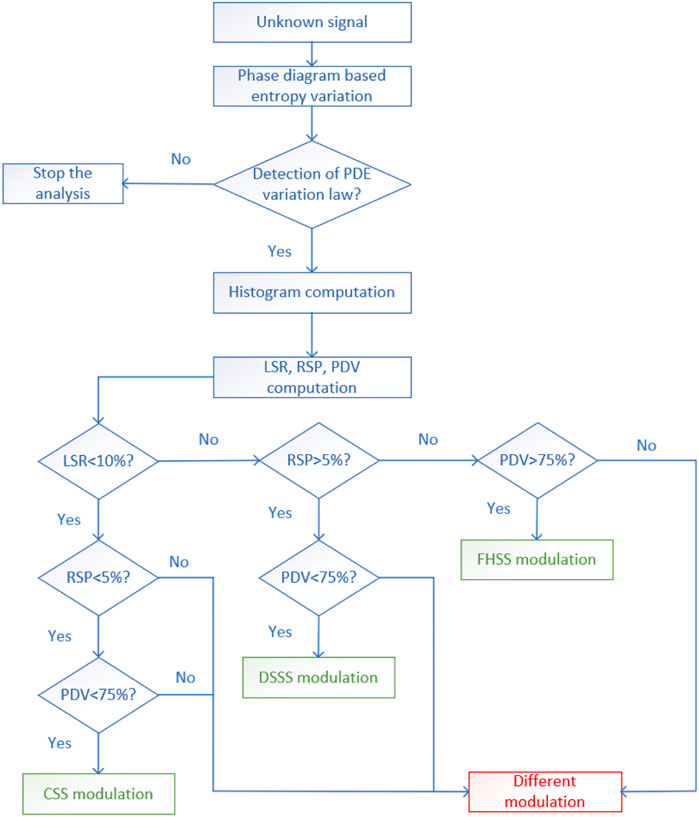
As we can see, the linear sweep of the signal quantified through the PDE values is grouped on the left side of the representation. We propose to quantify the transitions between CSS symbols based on the extremity bins of the histograms. Thus, we define the parameter Left Side Ratio (LSR) as the ratio between frequency of occurrence of the entropy values in extremity bins and frequency of occurrence of the remaining bins, as in Eq. 19:

$LSR=\frac{size\left(bi{n}_1\right)+size\left(bi{n}_{N_{bins}}\right)}{{\displaystyle \sum _{i=2}^{N_{bins}-1}}size\left(bi{n}_i\right)}(19)$

where $N_{bins}$ is the number of bins which contain at least one phase diagram entropy value. After the tests carried out, we conclude that this parameter is less than 10% regardless of the analyzed case (i.e., $SF$ values) and we decide to use it as an identifier for the analyzed phase diagram entropy variation which corresponds to a CSS signal.

5.2 DSSS characterization

In the analysis of the DSSS signal, we start from generating the 20 bits pattern with each bit, having a duration of $T_b=2ms$. Then we generate the pseudo-random bit pattern for spreading, which is the same for each transmitted bit. In our case the pseudorandom sequence for each bit is “01”. After that, we modulated the signal using a BPSK carrier with the following parameters: $A=1$, $f=100KHz$ and ${\theta }_{\mathrm{1,2}}=\left\{0,\pi \right\}$. In Figure 9 we can see the data encoding signal, the pseudorandom sequence and the DSSS signal.

FIGURE 9

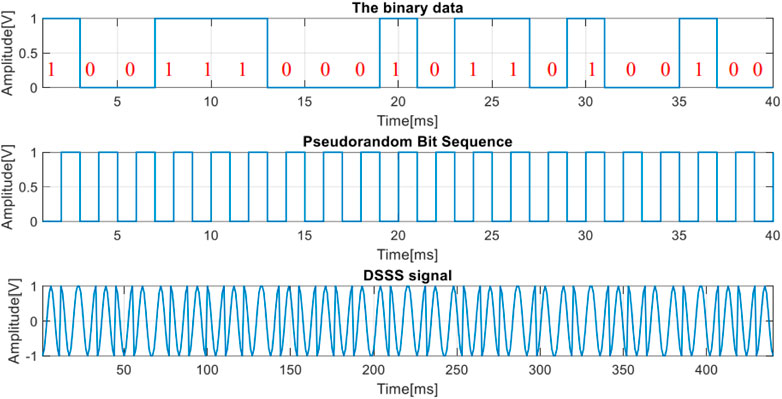
FIGURE 9. The data encoding signal (up), the pseudo-random sequence (middle) and the resulted DSSS signal.

In Figure 10 are displayed the DSSS signals and their PDE variation for the two cases. Each phase change of the DSSS signal leads to the appearance of a spike in the PDE variation. This is valid both in the noise free case and in the case of $SNR=5dB$, as can be seen on the right side of the figure. The phase diagram entropy follows the same principle, except that it is slightly disturbed.

FIGURE 10

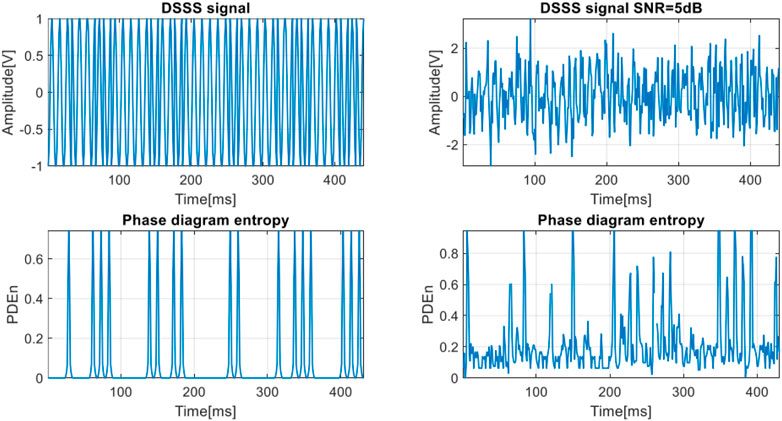
FIGURE 10. The DSSS signal and the phase diagram entropy variation for $SNR\to \infty$ (left) and the DSSS signal and the phase diagram entropy variation for $SNR=5dB$.

In order to increase the characterization capacity of the DSSS modulation, we analyze the PDE variation distribution. The histograms of the DSSS signal are displayed in Figure 11.

FIGURE 11

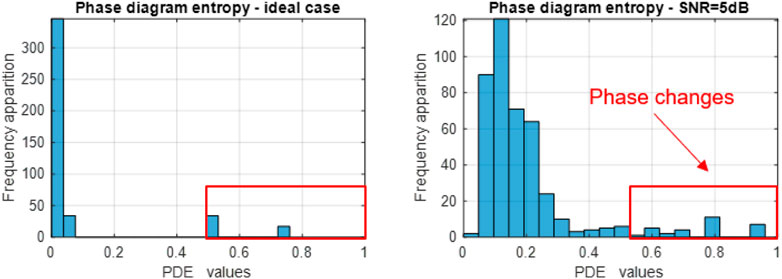
FIGURE 11. DSSS signal phase diagram entropy histogram in the noise free case (left) and in the noisy case (right).

We see that the transition between DSSS symbols, related to an increased value of PDE, is highlighted by the bins on the right side of the representation. In order to quantify this aspect, we define the Right-Side Proportion (RSP) as the ratio between the frequency of occurrence of the entropy values in the right half of the histogram representation and the total number of occurrences, as in Eq. 20:

$RSP=\frac{1}{N}{\displaystyle \sum _{i=N_{bins}/2}^{N_{bins}}}size\left(bi{n}_i\right)(20)$

where $N$ is the total number of samples and $N_{bins}$ is the number of bins which contain at least one phase diagram entropy value. After tests are performed, we found that the DSSS signal has an RSP >5%. Thus, the combination of the phase diagram-based entropy and the RSP parameter can be used to characterize the DSSS signal.

5.3 FHSS characterization

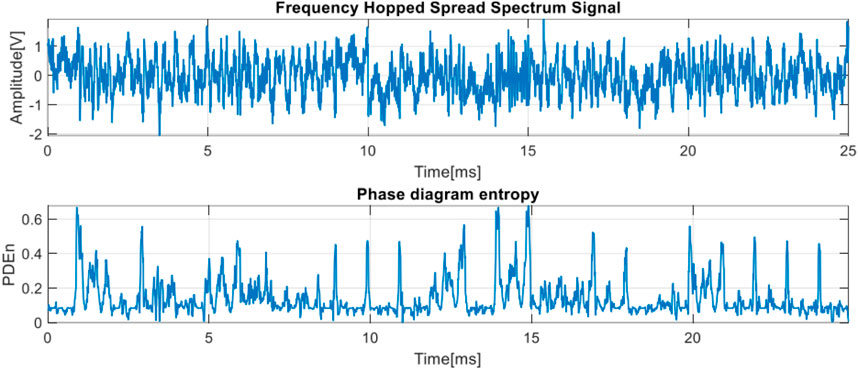
In the analysis of the FHSS signal, we start from generating the 25 bits pattern with each bit, having a duration of $T_b=1ms$. Then, we modulate the signal using a BPSK carrier with the following parameters: $A=1$, $f=100KHz$ and ${\theta }_{\mathrm{1,2}}=\left\{0,\pi \right\}$. After that, we generate the six random frequency hops to form the spread signal. This is how the FHSS signal is formed. In Figure 12 we can see the data encoded signal, the BPSK modulated signal, the spread signal with 6 frequencies and the FHSS signal.

FIGURE 12

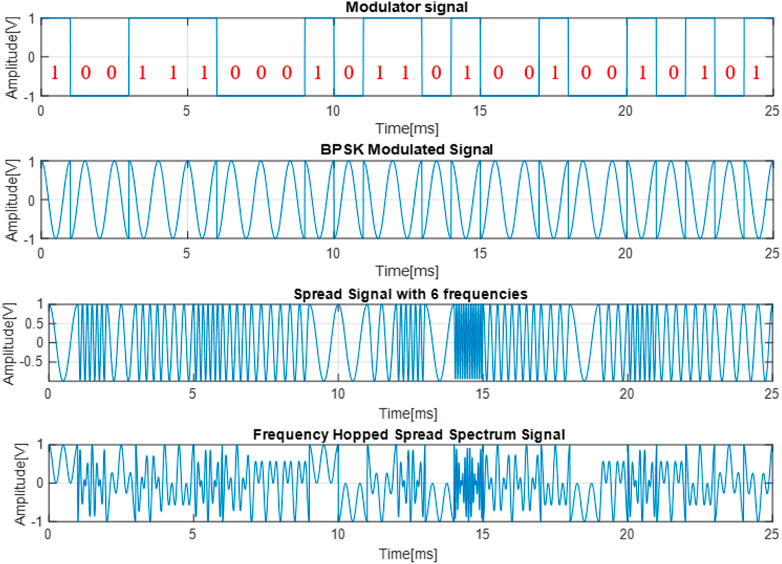
FIGURE 12. The data encoded signal, the BPSK modulated signal, the spread signal with 6 frequencies and the FHSS signal.

As can be seen in Figure 13, depending on the frequency of the signal we have a certain law of variation for the phase diagram entropy, each law being different from the other. Also, through the existence of more or less pronounced spikes, the transition from one frequency to another is captured. These observations are valid both in the noise free case and in the case of $SNR=5dB$, as shown in Figure 14.

FIGURE 13

FIGURE 13. The FHSS signal and the phase diagram entropy variation for $SNR\to \infty$.

FIGURE 14

FIGURE 14. The FHSS signal and the phase diagram entropy variation for $SNR=5dB$.

In order to strengthen the recognition of the modulation with the help of the phase diagram entropy, we also use the histogram to be able to help us in the noisier cases. Analyzing the histograms in Figure 15, we can see the tendency of the frequency of occurrence to decrease, starting with the maximum bin based on an exponential law with a subunit basis.

FIGURE 15

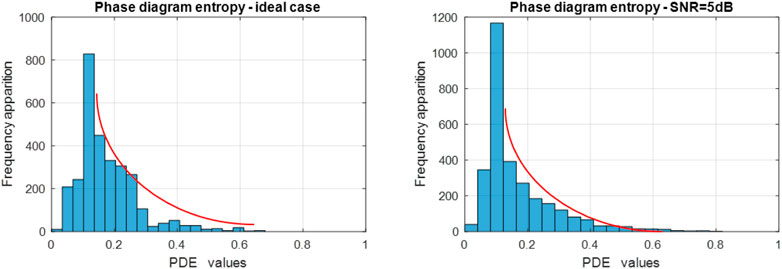
FIGURE 15. FHSS signal phase diagram entropy histogram in the noise free case (left) and in the noisy case (right).

Thus, we define the percentage of decreasing values (PDV) as the ratio between the frequency of occurrence of bins smaller than the bin with the most entropy values and the total number of values as in Eq. 21:

$PDV=\frac{1}{N}{\displaystyle \sum _{i=bi{n}_{\max }}^{N_{bins}}}size\left(bi{n}_i\right)(21)$

where $N$ is the total number of samples, $bi{n}_{\max }$ is the bin with the most frequency of occurrence and $N_{bins}$ is the number of bins which contain at least one phase diagram entropy value. After the tests carrier out, we found out that in order for the analyzed signal to be classified as FHSS, this parameter must be >75%. Thus, the combination of the phase diagram-based entropy and the PDV parameter can be used to characterize the FHSS signal.

5.4 Modulation recognition accuracy

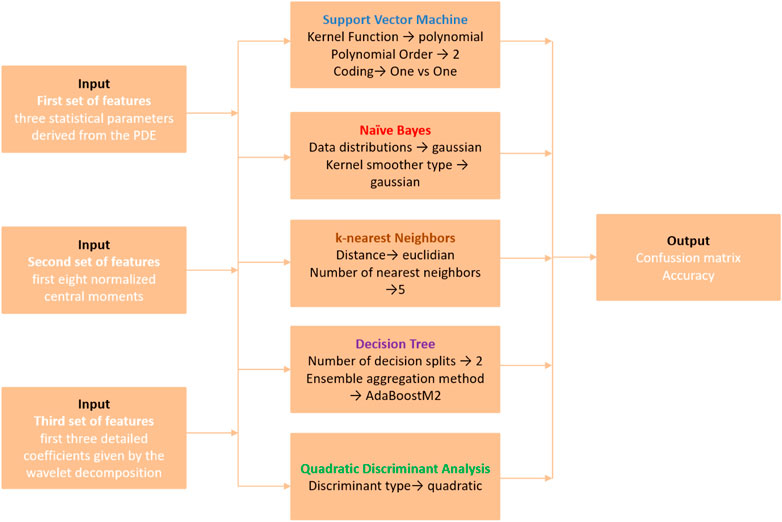
Based on the previous section, the approach that exploits the phase diagram-based entropy highlights unique characteristics for each type of spread spectrum modulation. Moreover, based on three statistical parameters derived from the PDE variation histograms, each modulation can be highlighted. Thus, Figure 16 presents the block diagram that we use to classify the spread spectrum modulations in totally blind conditions.

FIGURE 16

FIGURE 16. The block diagram for the classification of spread spectrum modulations.

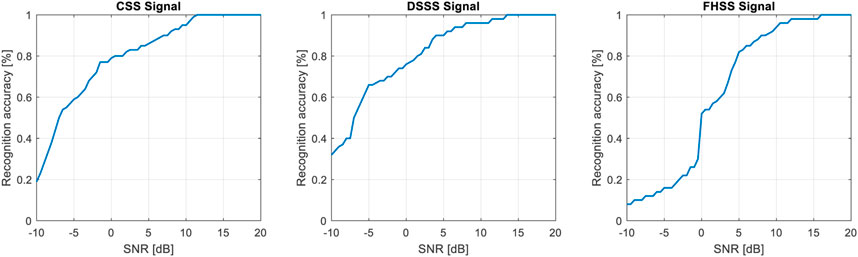
In order to see the accuracy of the proposed approach, we will further see how the recognition algorithm behaves in the presence of noise. Thus, in Figure 17 we see the recognition accuracy for the three types of signals. The accuracy was calculated for a set of 100 synthetic signals from each type of modulation. In the process of determining the accuracy, we used the algorithm described in the block diagram, for each modulated signal, analyzing the variation of the three statistical parameters extracted from the PDE. This procedure was repeated for a wide range of SNRs to be able to see the behavior of the algorithms in low SNR cases.

FIGURE 17

FIGURE 17. The recognition accuracy for the proposed approach for the spread spectrum signals.

The three graphs highlight a high accuracy for positive SNR values. For example, at $SNR=5dB$ the phase diagram entropy distribution for CSS signal recognition has an accuracy of 86%, for DSSS it has an accuracy of 90% and for FHSS signal 82%. To these accuracy values we add the advantages of the data-driven processing method which can highlight the particularities of each signal.

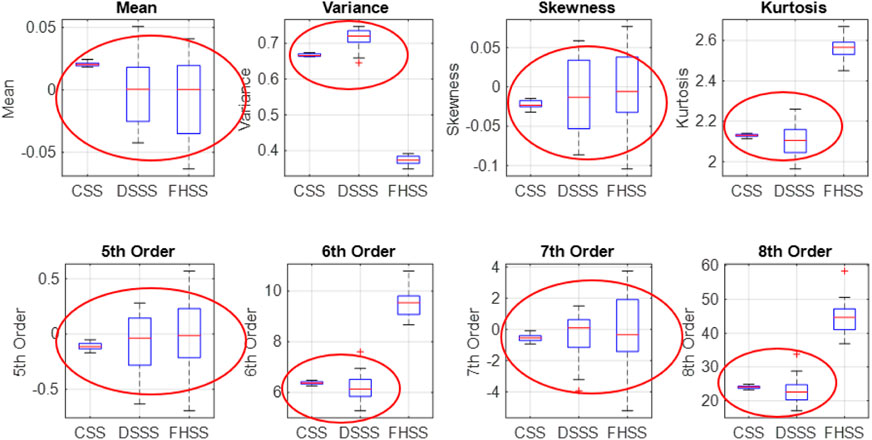
We turn our attention to some feature-based classic approaches for signal recognition in order to be able to compare the classical approaches with our proposal. We have as reference the spread spectrum signals for $SNR=5dB$. We start with a statistical approach based on the normalized central moments (Madhavan et al., 2013; Abu-Romoh et al., 2018) of the spread spectrum signals, shown in Figure 18:

FIGURE 18

FIGURE 18. The first eight normalized central moments of the spread spectrum signals.

As can be seen, this approach does not present a desirable procedure to be used because the information provided is not sufficient to recognize the modulation. Most of the moments have identical values for the three types of signals and cannot offer even a possibility to recognize them. Also, the values of these parameters do not highlight anything specific for each signal.

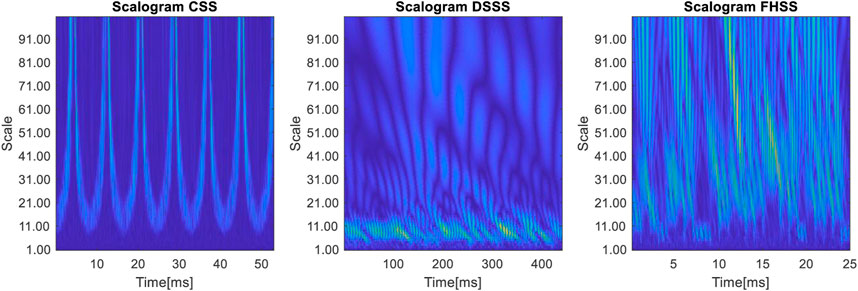
Another approach used in modulation recognition is that given by the use of the wavelet transform (Li et al., 2019; Al-Makhlasawy et al., 2021). Figure 19 shows the scalograms of the three signals, in the determination of which a 10th order Daubechies wavelet generator is used.

FIGURE 19

FIGURE 19. The scalograms of the three spread spectrum signals.

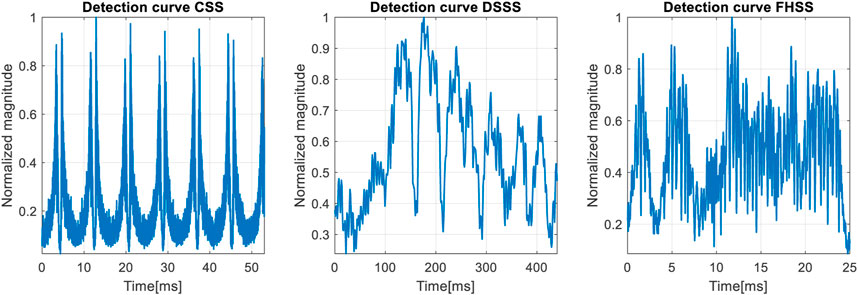
Analyzing the figure above, we notice that the analysis based on the wavelet transform has as a disadvantage the existence of a large number of representation scales and it is difficult to differentiate between scalograms based on these representations. One piece of information that we can quantify from these representations are the detection curves, shown in Figure 20.

FIGURE 20

FIGURE 20. The detection curves using the scalograms of the three spread spectrum signals.

The detection curve of the CSS signal highlights the five pulses, but for the other two signals, the information provided is not relevant and does not highlight anything specific.

From the scalograms we can also extracts the detail coefficients at the coarsest scale from the wavelet decomposition (Park et al., 2008; Kumar et al., 2017) of the three signals. Figure 21 shows these coefficients for three levels of the signals.

FIGURE 21

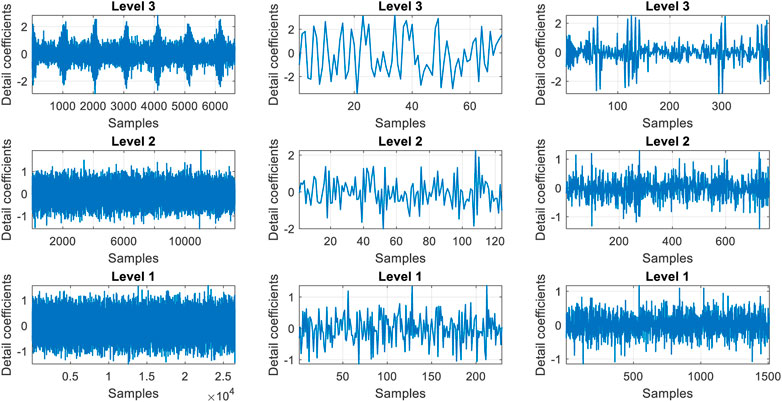
FIGURE 21. The detail coefficients for CSS signal (left), DSSS signal (middle) and FHSS signal (right).

The type of signal analyzed is too complicated to be characterized with these coefficients. Only the CSS signal shows some specific features in the detail coefficients of level 2 and 3, but the detail coefficients of the DSSS and FHSS signals cannot help in the recognition process of these modulations.

To highlight the capabilities of our approach, we use these two classic approaches as comparisons. The statistical approach uses the eight normalized central moments of the spread spectrum signals as features and the wavelet-based approach uses the three detail coefficients from the wavelet decomposition as features. Our approach consists in using the set consisting of the three statistical parameters derived from the PDE, namely, LSR, RSP and PDV as input for the ML classifiers. We use five Machine Learning classifiers: Support Vector Machine (SVM), Naïve Bayes (NB), k-Nearest Neighbors (kNN), Decision Tree (DT) and Quadratic Discriminant Analysis (QDA) in order to see which one is more appropriate for our classification process. The accuracy of the classification process is given by the confusion matrices obtained for the three sets of features. A visual representation of the input sets, the ML classifiers and the output is shown in Figure 22.

FIGURE 22

FIGURE 22. The illustration of the set of input features, the ML algorithms used and the output.

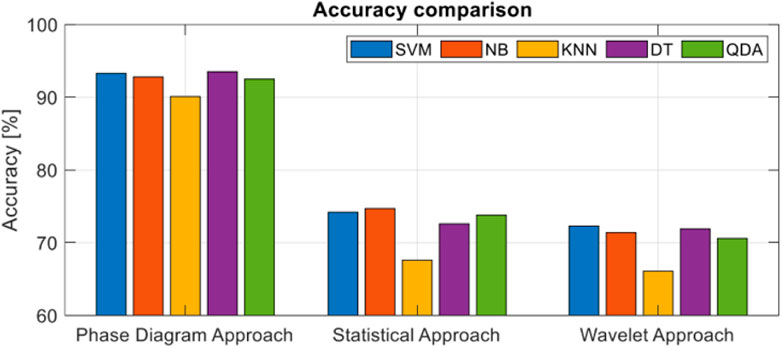
The classification result using the five ML classifiers is shown in Figure 23.

FIGURE 23

FIGURE 23. The classification accuracy using different approach and different classifiers.

The phase diagram-based approach offers the best results, with results over 90% depending on the classifier. The statistical approach provides poor results in terms of accuracy. Due to the fact that many of these moments are identical for the three classes of signals, the maximum accuracy we obtain is 74.7% using Naïve Bayes algorithm. The wavelet-based approach offers the worst results in the classification process of spread spectrum modulation. The maximum obtained for this approach is 72.3% using Support Vector Machine algorithm. The classical analysis methods, although they offer weaker results than the proposed method, have some advantages that can be used in certain contexts. For example, the statistical approach is simple to implement, it does not require the knowledge of additional information about the analyzed signal and the computational time related to this method is low. Also, the scalograms generated by the wavelet transform can be used with Deep Learning elements to increase the classification accuracy based on image classification algorithms.

From the perspective of ML algorithms, their functionality depends on the features used in the training process. Due to the particularities highlighted by the phase diagram entropy, DT offer a result of 93.5%, which is the highest, and kNN 90.2%, which is the lowest. The best results are obtained with DT because it is a non-parametric algorithm and it does not depend on probability distribution assumptions, working well on high-dimensional data. In addition, it uses a boosting algorithm to increase the performance. The worst results are obtained with kNN because kNN is a distance-based algorithm, this meaning that the cost of calculating the distance between a new point and each existing point is very high if we have a large dataset. That is why it does not work well with a high number of dimensions. In addition, kNN is a lazy algorithm and it does not have a training process in which the accuracy can be optimized.

6 Conclusion

Using the phase diagram entropy as a new alternative for the analysis of communication signals, we show the potential to extract important information about the analyzed signals and identify the type of modulations used, without prior knowledge. In this paper, we study the behavior in noisy backgrounds, of the parameters extracted from the spread spectrum signals using the phase diagram-based entropy and we propose some statistical parameters derived from the entropy distribution to recognize the signals. This approach proved to be very useful for the characterization and recognition of spread spectrum modulations being able to highlight defining characteristics for each type of modulation, which led to an accuracy higher than 90% in the classification process.

Three classes of spread spectrum modulations found in many commercial and military systems have been analyzed and characterized. The modulation recognition capability of the implemented algorithm is very high. Using this approach, we were able to highlight hidden features, invisible to other classical methods. We compared the proposed method with two feature-based classical methods based on high order statistical moments and wavelet transform. The results obtain using our approach exceed by more than 15% the results obtained using these classical approaches.

In our future work, we are planning to analyze a larger class of communication signals and study the capability of presented approach for higher orders of modulation. The robustness to the noise will be also addressed and we plan to refine our method to work at much lower SNR.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Conceptualization, DS, AD, and CI; methodology, DS; software, DS; validation, AD, CI, and AS; formal analysis, DS; investigation, DS, AD; resources, DS; data curation, CI; writing—original draft preparation, DS; writing—review and editing, AD and CI; visualization, DS; supervision, AS; project administration, AD; funding acquisition, CI; All authors contributed to the article and approved the submitted version.

Funding

This work has been supported by ALTUS project funded by SATT Linksium. The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study is funded by SATT Linksium.

Conflict of interest

The author AS declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abu-Romoh, M., Aboutaleb, A., and Rezki, Z. (2018). Automatic modulation classification using moments and likelihood maximization. IEEE Commun. Lett. 22 (5), 938–941. doi:10.1109/LCOMM.2018.2806489

CrossRef Full Text | Google Scholar

Al-Makhlasawy, R. M., Ghanem, H. S., Kassem, H. M., Elsabrouty, M., Hamed, H. F. A., Abd El-Samie, F. E., et al. (2021). Deep learning for wireless modulation classification based on discrete wavelet transform. Int. J. Commun. Syst. 34 (18). doi:10.1002/dac.4980

CrossRef Full Text | Google Scholar

Davidson, K. L., and Loughlin, P. J. (2000). Instantaneous spectral moments. J. Frankl. Inst. 337 (4), 421–436. doi:10.1016/S0016-0032(00)00034-X

CrossRef Full Text | Google Scholar

Dobre, O. A., Abdi, A., Bar-Ness, Y., and Su, W. (2007). Survey of automatic modulation classification techniques: Classical approaches and new trends. IET Commun. 1, 137. doi:10.1049/iet-com:20050176

CrossRef Full Text | Google Scholar

Eckmann, J.-P., Kamphorst, S. O., and Ruelle, D. (1987). Recurrence plots of dynamical systems. Europhys. Lett. 4, 973–977. doi:10.1209/0295-5075/4/9/004

CrossRef Full Text | Google Scholar

Gacanin, H. (2019). Autonomous wireless systems with artificial intelligence: A knowledge management perspective. IEEE Veh. Technol. Mag. 14, 51–59. doi:10.1109/MVT.2019.2920162

CrossRef Full Text | Google Scholar

Gui, G., Sari, H., and Biglieri, E. (2019). A new definition of fairness for non-orthogonal multiple access. IEEE Commun. Lett. 23, 1267–1271. doi:10.1109/LCOMM.2019.2916398

CrossRef Full Text | Google Scholar

Hong, S., Cheun, K., Lim, H., and Cho, S. (2013). Performance of M-ary turbo coded synchronous FHSS multiple access networks with noncoherent MFSK under Rayleigh fading channels. J. Commun. Netw. 15, 601–605. doi:10.1109/JCN.2013.000109

CrossRef Full Text | Google Scholar

Huang, J., Zhou, Y., Sun, N., Hu, Z., and Kang, Y. f. (2010). “Cruciate ligament reconstruction using LARS artificial ligament under arthroscopy: 81 cases report,” in Proceedings of the 2010 International Conference on Communications and Intelligence Information Security, Xi'an, China, October 2010, 160–164. doi:10.1109/ICCIIS.2010.39123

PubMed Abstract | CrossRef Full Text | Google Scholar

Iglesias, V., Grajal, J., Royer, P., Sanchez, M. A., Lopez-Vallejo, M., and Yeste-ojeda, O. A. (2015). Real-time low-complexity automatic modulation classifier for pulsed radar signals. IEEE Trans. Aerosp. Electron. Syst. 51, 108–126. doi:10.1109/TAES.2014.130183

CrossRef Full Text | Google Scholar

Javed, H., Khalid, M. R., and Soomro, H. (2020). “A novel practical method for blind detection of DSSS signal in multiple signals environment,” in Proceedings of the 2020 17th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, January 2020, 664–668. doi:10.1109/IBCAST47879.2020.9044593

CrossRef Full Text | Google Scholar

Karapistoli, E., Pavlidou, F.-N., Gragopoulos, I., and Tsetsinas, I. (2010). An overview of the IEEE 802.15.4a Standard. IEEE Commun. Mag. 48, 47–53. doi:10.1109/MCOM.2010.5394030

CrossRef Full Text | Google Scholar

Khan, M. T., Sha’ameri, A. Z., Zabidi, M. M. A., and Chia, C. C. (2022). “FHSS signals classification by linear discriminant in a multi-signal environment,” in Proceedings of the International e-Conference on Intelligent Systems and Signal Processing, Singapore, June 2022. Editors F. Thakkar, G. Saha, C. Shahnaz, and Y.-C. Hu, 143–155. doi:10.1007/978-981-16-2123-9_111370

CrossRef Full Text | Google Scholar

Kumar, S., Bohara, V. A., and Darak, S. J. (2017). “Automatic modulation classification by exploiting cyclostationary features in wavelet domain,” in Proceedings of the 2017 Twenty-Third National Conference on Communications (NCC), Chennai, India, March 2017, 1–6. doi:10.1109/NCC.2017.8077145

CrossRef Full Text | Google Scholar

Lee, J., An, J., Ra, H., and Kim, K. (2020). Long-range acoustic communication using differential chirp spread spectrum. Appl. Sci. 10 (24), 8835. doi:10.3390/app10248835

CrossRef Full Text | Google Scholar

Lei, Z., Yang, P., and Zheng, L. (2018). Detection and frequency estimation of frequency hopping spread spectrum signals based on channelized modulated wideband converters. Electronics 7, 170. doi:10.3390/electronics7090170

CrossRef Full Text | Google Scholar

Li, W., Dou, Z., Qi, L., and Shi, C. (2019). Wavelet transform based modulation classification for 5G and UAV communication in multipath fading channel. Phys. Commun. 34, 272–282. doi:10.1016/j.phycom.2018.12.019

CrossRef Full Text | Google Scholar

Liu, W., Huang, K., Zhou, X., and Durrani, S. (2017). Full-duplex backscatter interference networks based on time-hopping spread spectrum. IEEE Trans. Wirel. Commun. 16, 4361–4377. doi:10.1109/TWC.2017.2697864

CrossRef Full Text | Google Scholar

Madhavan, N., Vinod, A. P., Madhukumar, A. S., and Krishna, A. K. (2013). Spectrum sensing and modulation classification for cognitive radios using cumulants based on fractional lower order statistics. AEU - Int. J. Electron. Commun. 67 (6), 479–490. doi:10.1016/j.aeue.2012.11.004

CrossRef Full Text | Google Scholar

Mallat, S. G. (2009). A wavelet tour of signal processing: The sparse way. 3rd. Amsterdam; Boston: Elsevier/Academic Press.

Google Scholar

Marwan, N., Carmenromano, M., Thiel, M., and Kurths, J. (2007). Recurrence plots for the analysis of complex systems. Phys. Rep. 438, 237–329. doi:10.1016/j.physrep.2006.11.001

CrossRef Full Text | Google Scholar

Park, C.-S., Choi, J.-H., Nah, S.-P., Jang, W., and Kim, D. Y. (2008). “Automatic modulation recognition of digital signals using wavelet features and SVM,” in Proceedings of the 2008 10th International Conference on Advanced Communication Technology, Gangwon, Korea (South), February 2008, 387–390. doi:10.1109/ICACT.2008.4493784

CrossRef Full Text | Google Scholar

Qian, Y., Ma, L., and Liang, X. (2018). Symmetry chirp spread spectrum modulation used in LEO satellite internet of things. IEEE Commun. Lett. 22, 2230–2233. doi:10.1109/LCOMM.2018.2866820

CrossRef Full Text | Google Scholar

Ravi Kishore, T., and Rao, K. D. (2017). Automatic intrapulse modulation classification of advanced LPI radar waveforms. IEEE Trans. Aerosp. Electron. Syst. 53, 901–914. doi:10.1109/TAES.2017.2667142

CrossRef Full Text | Google Scholar

Raza, U., Kulkarni, P., and Sooriyabandara, M. (2017). Low power wide area networks: An overview. IEEE Commun. Surv. Tutorials 19, 855–873. doi:10.1109/COMST.2017.2652320

CrossRef Full Text | Google Scholar

Reynders, B., and Pollin, S. (2016). “Chirp spread spectrum as a modulation technique for long range communication,” in Proceedings of the 2016 Symposium on Communications and Vehicular Technologies (SCVT), Mons, Belgium, November 2016, 1–5. doi:10.1109/SCVT.2016.7797659

CrossRef Full Text | Google Scholar

Scripcaru, R., Nastasiu, D., Digulescu, A., Stanescu, D., Ioana, C., and Serbanescu, A. (2020). “On the potential of phase diagram analysis to identify the wide band modulations,” in Proceedings of the 2020 13th International Conference on Communications (COMM), Bucharest, Romania, June 2020, 55–58. doi:10.1109/COMM48946.2020.9141963

CrossRef Full Text | Google Scholar

Stanescu, D., Digulescu, A., Ioana, C., and Serbanescu, A. (2021). “A novel approach for characterization of transient signals using the phase diagram features,” in Proceedings of the 2021 IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS), Tel Aviv, Israel, November 2021, 299–304. doi:10.1109/COMCAS52219.2021.9629068

CrossRef Full Text | Google Scholar

Stanescu, D., Digulescu, A., Ioana, C., and Serbanescu, A. (2022). Modulation recognition of underwater acoustic communication signals based on phase diagram entropy. OCEANS 2022, 1–7. doi:10.1109/OCEANS47191.2022.9977145

CrossRef Full Text | Google Scholar

Stanescu, D., Nastasiu, D., Ioana, C., and Digulescu, A. (2023). Characterization of digital modulations using the phase diagram analysis. Eur. Phys. J. Special Top. 232 (1), 187–199. doi:10.1140/epjs/s11734-022-00744-x

CrossRef Full Text | Google Scholar

Tsai, Y.-R. (2009). M-ary spreading-code-phase-shift-keying modulation for DSSS multiple access systems. IEEE Trans. Commun. 57, 3220–3224. doi:10.1109/TCOMM.2009.11.050526

CrossRef Full Text | Google Scholar

Wang, Xiaowei, Fei, Minrui, and Li, Xin (2008). “Performance of chirp spread spectrum in wireless communication systems,” in Proceedings of the 2008 11th IEEE Singapore International Conference on Communication Systems, Guangzhou, China, November 2008, 466–469. doi:10.1109/ICCS.2008.4737227

CrossRef Full Text | Google Scholar

Webber, C. L., and Zbilut, J. P. (1994). Dynamical assessment of physiological systems and states using recurrence plot strategies. J. Appl. Physiology 76, 965–973. doi:10.1152/jappl.1994.76.2.965

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Hsiao-Chun, Saquib, M., and Yun, Zhifeng (2008). Novel automatic modulation classification using cumulant features for communications via multipath channels. IEEE Trans. Wirel. Commun. 7, 3098–3105. doi:10.1109/TWC.2008.070015

CrossRef Full Text | Google Scholar

Xiao-Ming, Z., and Zhong-Zhao, Z. (2006). “Parameter estimation of DSSS signals with modified fourth-order cumulants,” in Proceedings of the First International Conference on Innovative Computing, Information and Control - Volume I (ICICIC’06), Beijing, China, August 2006, 126–129. doi:10.1109/ICICIC.2006.1331

CrossRef Full Text | Google Scholar

Yang, Y., Chang, J.-N., Liu, J.-C., and Liu, C.-H. (2004). Maximum log-likelihood function-based QAM signal classification over fading channels. Wirel. Personal. Commun. 28, 77–94. doi:10.1023/B:WIRE.0000015422.23663.98

CrossRef Full Text | Google Scholar

Yu, X., Li, L., Yin, J., Shao, M., and Han, X. (2019). “Modulation pattern recognition of non-cooperative underwater acoustic communication signals based on LSTM network,” in Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, December 2019, 1–5. doi:10.1109/ICSIDP47821.2019.9173133

CrossRef Full Text | Google Scholar

Yue, Guangrong, Ge, Lijia, and Li, Shaoqian (2003). “Analysis of ultra wideband signal interference to DSSS receiver,” in Proceedings of the 2003 4th IEEE Workshop on Signal Processing Advances in Wireless Communications - SPAWC 2003, Rome, Italy, June 2003, 229–233. doi:10.1109/SPAWC.2003.1318956

CrossRef Full Text | Google Scholar

Zbilut, J. P., and Webber, C. L. (1992). Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett. A 171, 199–203. doi:10.1016/0375-9601(92)90426-M

CrossRef Full Text | Google Scholar