- 1Swartz Center for Computational Neuroscience, Institute for Neural Computation, University of California San Diego, La Jolla, CA, United States
- 2Canyon Crest Academy, San Diego, CA, United States
- 3Centre de Recherche Cerveau et Cognition (CerCo), CNRS, Université Paul Sabatier, Toulouse, France
- 4Institute of Noetic Sciences, Petaluma, CA, United States
- 5Psychological Methods and Evaluation, Institute of Psychology, University of Hagen, Hagen, Germany
- 6Division of Child and Adolescent Psychiatry, Cincinnati Children’s Hospital Medical Center, Cincinnati, OH, United States
- 7Department of Psychiatry, University of Cincinnati College of Medicine, Cincinnati, OH, United States
Independent component analysis (ICA) has been widely used for electroencephalography (EEG) analyses. However, ICA performance relies on several crucial assumptions about the data. Here, we focus on the granularity of data rank, i.e., the number of linearly independent EEG channels. When the data are rank-full (i.e., all channels are independent), ICA produces as many independent components (ICs) as the number of input channels (rank-full decomposition). However, when the input data are rank-deficient, as is the case with bridged or interpolated electrodes, ICA produces the same number of ICs as the data rank (forced rank deficiency decomposition), introducing undesired ghost ICs and indicating a bug in ICA. We demonstrated that the ghost ICs have white noise properties, in both time and frequency domains, while maintaining surprisingly typical scalp topographies, and can therefore be easily missed by EEG researchers and affect findings in unknown ways. This problem occurs when the minimum eigenvalue
Introduction
Independent component analysis (ICA) has been widely used in EEG studies for the purposes of both artifact rejection and signal extraction (Bell and Sejnowski, 1995; Makeig et al., 1996). The ICA model can be described as indicated in the following expression.
where
ICA relies on several assumptions and requirements to be reliable and accurate. Violating them may lead to inaccurate findings or even processing failure, depending on which assumption is violated. In this technical study, we focused on one of these cases in which ICA produces erroneous results without being detected by the algorithm. We also caution against the widely adopted, incorrect practice of re-referencing EEG data to average, which is a human error that also causes this issue.
Defining the problem: The effective rank deficiency
When we see multi-channel EEG recording as a matrix, the rank of the data refers to the number of linearly independent channels. For example, standard unipolarly referenced 64-ch EEG data have a data rank of 64. When the multi-channel data consist of linearly independent channels, the data are considered rank-full. On the other hand, if a pair of scalp electrodes adjacent to each other are bridged due to an injection of an excessive amount of saline water, for example, these pairs of electrodes are electrically connected and record identical signals redundantly. In this case, two channels have identical data and the data rank is no longer 64; it is reduced to 64–1 = 63. When the number of channels is larger than the number of linearly independent sources, the data are called rank-deficient. Data rank is important in ICA because ICA produces the same number of ICs as the data rank number, not the apparent number of scalp electrodes. When ICA is forced to produce more ICs than the data rank, the process fails and yields ghost ICs, at least in the case of implementation in EEGLAB (Delorme and Makeig, 2004). The ghost IC is akin to ICA’s “bug,” which we have examined to determine its properties in the time, frequency, and spatial domains.
Whether a pair of channels are linearly dependent or not is a qualitative question that can be answered with yes or no. However, the mathematical meaning of the rank has more granularity, as shown as follows. First, we applied the eigenvalue decomposition to the channel-by-channel covariance matrix of the input EEG data matrix. Next, we obtained the condition number
A very large condition number
Case 1: Incorrect re-referencing practice causes effective rank deficiency
In performing standard scalp-EEG preprocessing, there are two stages during which effective rank deficiency can occur. The first stage is re-referencing, which is often performed to the average potential because it is easy to calculate and it minimizes local bias if uniform electrode spacing is applied (Bertrand et al., 1985; Nunez and Srinivasan, 2006). However, the ‘problem’ arises from an incorrect implementation of average re-referencing, at least as observed in EEGLAB. First, we review the basic facts of EEG re-referencing in the following paragraphs.
It has been common practice to use a unipolar reference (i.e., potentials at multiple scalp locations are measured against a potential at one, often non-scalp, location) when recording scalp EEG data. The unipolarly referenced data have three key properties (Hu et al., 2019): 1) rank-deficient by 1; 2) no memory effect; and 3) orthogonal projector centering. The first property is the most important and naturally leads to the second property. We focus on the first two properties in the following paragraph.
The first property can be rephrased as follows: the unipolarly referenced scalp EEG data are always rank-deficient by 1 if the initial reference is taken into account. For those who have not yet considered this, the statement may sound counterintuitive and could even be a stumbling stone. Imagine the case of a simple bipolar recording: two electrodes record a one-channel signal as a difference (voltage is by definition a difference between potentials at two locations). This relation of two-electrodes-to-one-signal is the origin of rank deficiency by 1. Because unipolarly referenced recording can be understood as the parallel repetition of bipolar recordings for multiple electrodes while keeping the same reference location, the same rank deficiency by 1 is inherited. This is the EEG-context explanation to support the need for rank deficiency by 1 to be corrected before re-referencing. If we follow the convention that
The second property, the “no memory effect,” indicates that, as long as we follow the correct re-referencing, we can re-reference to any other location without changing the linear property of the data if the data are unipolarly referenced. In other words, one can re-reference unipolarly referenced EEG data offline from the original reference location A to the new reference location B, then from B to C, and from C to A, which brings back the original data without any change, regardless of the history of prior re-referencing processes. However, once we re-referenced to the average potential, for example, we would need to re-reference back to a unipolar reference with any chosen electrode for the next re-referencing. Repeating average-referencing after rejecting the initial reference electrode invalidates the data and should be avoided.
Based on these facts, there is no ambiguity about how to re-reference the data properly. Unfortunately, the current implementation of the re-referencing process in the past and current versions of EEGLAB (ver. 2022.0 or prior) does not follow this correct practice. Additionally, there are several implementation issues in the related solutions, which further complicate the problem:
1. EEGLAB does not account for the initial reference electrode. Therefore, EEGLAB reduces data rank by re-referencing. This violates the first and second properties described previously (Hu et al., 2019).
2. Although EEGLAB’s implementation of the ICA (pop_runica) includes an effective rank deficiency checker, the hard-coded detection of
3. Even if the data rank is ensured to be cleanly deficient by one [which can be detected by using the rank () function] through EEGLAB’s re-referencing process, EEGLAB calculates
In this study, we focused on these processes to quantify the margin of the effective rank deficiency. We report the influence of using the initial reference on
Case 2: Electrode interpolation can cause effective rank deficiency
The second common practice that can produce effective rank deficiency in EEG data is the spatial interpolation of rejected electrodes (considered artifactual) using non-linear methods such as spherical spline (Perrin et al., 1989), which is the default interpolation method implemented by EEGLAB. Although linear interpolation leads to a clean rank deficiency, non-linear methods result in interpolated electrode signals that are not exactly the weighted linear sum of other electrodes, leading to effective rank deficiency. Similar to Case 1, we quantified the effect of the non-linear electrode interpolation on
The goal of the current study
The study goals included the following: 1) to determine the effective
The second part was an investigation of how effective rank deficiency arises from the two EEG preprocessing stages, namely, incorrect re-referencing and electrode interpolation, using empirical EEG data and EEGLAB. Based on the critical threshold of
Materials and methods
Audio signal mixing simulation
As an homage to the original ICA demonstration performed in the late 1990s by four researchers from the Salk Institute (Terry Sejnowski, Te-Won Lee, Scott Makeig, and Tzyy-Ping Jung), we recorded the following four sentences as independent sound recordings:
“Independent component analysis is a new data tool that is sensitive to higher-order structure in multidimensional data” (JL).
“ICA is also a potentially important tool for data mining, factor analysis, clustering, and data compression” (SC).
“Neural networks that perform information maximization may emulate processes that drive evolution and brain organization” (MM).
“Infomax ICA is proving successful at modeling complex biological time series and imaging data” (TPJ).
These sound demonstrations are available at https://github.com/MakotoMiyakoshi/Effective-Rank-Deficiency.
In the current study, the audio files were recorded using a condenser microphone Perception 200 (AKG), a USB audio interface E-MU 0404 (Creative), and Thinkpad T42 (IBM) with a sampling rate of 44,100 Hz. Offline, the signals that were shorter than 9.288 s were zero-padded at the end, so they all were of equal length. The signals were z-scored.
The four-channel audio signals were mixed differently to generate four mixed signals. The mixing matrix
where
In addition to the required conditions relating to the goal of the study, we took advantage of this simulation to perform several confirmatory demonstrations in hope of helping novice ICA users directly experience important properties of ICA by listening to the decomposed signals, including 1) the time-invariant property by shuffling the 1-s time blocks before ICA; 2) undercomplete data decomposition by using four three-source mixings with four channels—see Chapter 13 of the book Independent Component Analysis (Hyvärinen et al., 2001); and 3) overcomplete data decomposition by using three four-source mixings with three channels. In addition, the difference between correct and incorrect re-referencing to average is demonstrated to provide an additional example that can be tested by ears. For these demonstrations, the following mixing matrix
Empirical EEG data demonstrations
We designed a demonstration of the two cases of effective rank deficiency caused by 1) incorrect re-referencing and 2) non-linear electrode interpolation using EEGLAB’s tutorial dataset (128 Hz sampling, 32 channels, 238.3 s), which was obtained from a previously published study (Makeig et al., 1999). To briefly describe the data, a visual attention experiment was performed, where stimuli appeared in any of five squares arrayed horizontally above a central fixation cross. In each experimental block, one (target) box was a color that was different from the rest. Whenever a square appeared in the target box, the subject was asked to respond quickly with a right thumb button press. If the stimulus was a circular disk, the subject was asked to ignore it. These data were constructed by concatenating 3-s epochs from one subject, each containing a target square in the attended location (“square” events, left-hemifield locations 1 or 2 only), followed by a button response (“rt” events). The data were stored in continuous data format to illustrate the process of epoch extraction from continuous data. There were 80 trials included in the analysis, regardless of the conditions.
For the case of incorrect average referencing, we compared two re-referencing approaches: one with the addition of the initial reference channel (i.e., a channel with zero-filled data) and the other approach without (current default method). We calculated
For the case of spherical spline channel interpolation (Perrin et al., 1989) implemented in the default EEGLAB option, we performed leave-one-out cross-validation (LOOCV) to balance the possible effect of spatial selection on the minimum eigenvalue obtained. The final number of channels used was 30, after rejecting two non-EEG channels. Mean values were reported.
The properties of the ghost ICs were evaluated for the case of spherical spline interpolation, in both the frequency (power spectral density, PSD) and time domains (event-related potential, ERP).
Results
Audio signal mixing simulation
Logarithmic variation of
The results from the ICA demonstration are summarized in Table 2. Note that the condition of random shuffling of the 1-s blocks should not impact ICA performance because all the time frames are shuffled differently to minimize learning bias at the beginning of each iteration of the gradient descent process. Also, note that, due to the lack of an effective countermeasure for the rank-deficient input data, the decomposition under the undercomplete condition failed. It was necessary to manually specify the correct rank number by using the “pca” option, which performs dimension reduction by rejecting principal components, as many as required, by counting the ones with the smallest eigenvalues. These results from the case of undercomplete ICA replicated the predictions made by the classic study on the nature of ICA (Hyvärinen et al., 2001). We will discuss the recommended solution for the case of EEG preprocessing in which data are known to be rank-deficient. The source audio signals, their linear mixings, and the decomposed signals obtained are available at https://github.com/MakotoMiyakoshi/Effective-Rank-Deficiency/.
Empirical EEG data demonstrations: Ghost ICs are ICA’s bug
For the case of re-referencing, the correct method, i.e., including the initial reference when re-referencing and then discarding the initial reference channel, resulted in a successful rank-full decomposition. Meanwhile, the incorrect method, i.e., without including the initial reference ICA, failed to decompose the signals. ICA failed for the case of non-linear electrode interpolation using spherical spline interpolation. These results are summarized in Table 3.
The spatial, temporal, and frequency properties of the ghost IC obtained are illustrated in Figure 1. The frequency domain analyses confirmed that the ghost IC did not follow the patterns of other ICs and showed unreasonable independence. The ghost IC’s flat PSD resembled white noise. In the time domain analysis, the ghost IC did not show visible ERP modulation. The ghost IC was ranked as the last IC among others, indicating it had the smallest variance. Visual inspection of the scalp topography of the ghost IC indicated surprisingly normal spatial distribution. The subsequent equivalent current dipole fitting produced a very good result, and the residual error was as small as the most dominant IC (i.e., the first-ranked IC after variance sorting; 3.5% vs. 3.6%, respectively). The scalp topography of the ghost IC showed overlap with the most dominant IC. This suggests the ghost IC’s dependence on the most dominant IC and the formation of a subspace.
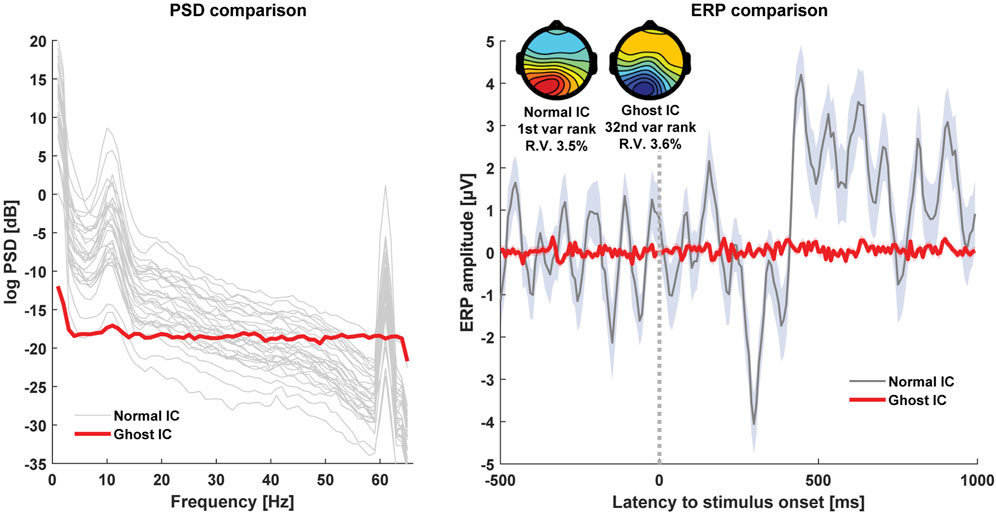
FIGURE 1. Left, power spectral density (PSD) of all the independent components (ICs) after applying spherical spline electrode interpolation. The PSD plot for the ghost IC is highlighted in red, and those for other ICs are represented in gray. Note that the ghost IC’s PSD does not follow the 1/f exponent or the large line noise at 60 Hz that is commonly present in other ICs. Right, ERP, the time-domain representation, of the ghost IC compared with the first-ranked (i.e., it had the largest variance) “Normal” IC. The shaded area indicates one standard error of the mean. The ghost IC was ranked as the last IC (i.e., it had the smallest variance), and the averaged potential did not show any ERP modulation. The ghost IC showed surprisingly normal spatial distribution with below-average (3.6% vs. mean 20.2%, SD 12.0) residual variance from the equivalent dipole fitting, and it largely overlapped with the “Normal” IC.
Discussion
What is the bug, after all?
The main problem we were motivated to address in this study is that even if the input data are confirmed to be rank-full (e.g., using MATLAB’s rank () function), under the condition where the minimum eigenvalue
The first goal of the study: To determine the practical threshold of
Although the effective threshold is expected to be dependent on each application, with the given conditions and tools that are described in this study, we determined that the critical threshold of
The second goal of the study: To confirm the signature of forced decomposition of rank-deficient data
In this study, we established a reproducible procedure to generate ghost ICs. We confirmed the properties of the ghost ICs as follows: 1) power spectral density (PSD) does not follow the pattern that all other ICs follow, such as the 1/f exponent, the alpha peak, or even the large 60-Hz line noise peak. The PSD of the ghost IC was rather flat, which indicates a resemblance to white noise; 2) the ghost IC did not show the temporal structure of the event-related potential, which is shown, as expected, by other ICs. This observation is in line with the PSD finding that the data appear similar to white noise; 3) counterintuitively, the scalp topography of the ghost IC had a normal appearance. The subsequent equivalent dipole fitting showed a good result, and the residual variance was below average. We speculated that the ghost IC may appear as an imperfect or broken subspace of the most dominant IC. If this is the case, it suggests that a ghost IC should be paired with a dominant IC with a largely overlapping scalp topography. Overall, the ghost IC showed clearly distinguishable properties in the time-frequency domain, which is a useful clue for suspect detection. Meanwhile, the presence of ghost ICs can be easily missed upon visual inspection of the IC scalp topographies.
The third goal of the study: To confirm the solution
The effective rank deficiency caused by EEGLAB’s re-referencing is a human error as there is no theoretical reason for data rank to become deficient during this operation. Although we wait for EEGLAB’s update and correction, we provide a modified function “reref.m” that can be used to overwrite the relevant code as a temporary patch to address the issue; the patch code can be downloaded at https://github.com/MakotoMiyakoshi/Effective-Rank-Deficiency. On the other hand, to address the effective rank deficiency introduced by non-linear electrode interpolation, the best solution is to explicitly input the effective rank for ICA, i.e., the number of eigenvalues larger than
Then, enter the obtained number as input for the “pca” option for runica.m or “pcakeep” for runamica.m. Meanwhile, we suggest changing the default behavior of the rank checker implemented in pop_runica () so that when it detects
Is using PCA before ICA always bad?
One study made a claim that applying the principal component analysis (PCA) before applying ICA for the sake of dimension reduction requires caution because abusing PCA for excessive dimension reduction deteriorates the quality of ICA (Artoni et al., 2018). This conclusion itself is not surprising based on the definition of lossy compression, i.e., greater dimension reduction at the cost of greater information loss. However, our confirmatory demonstrations using sound files showed that undercomplete ICA (i.e., number of sources < number of mixings) failed, and specifying the correct data rank by using PCA dimension reduction to manually set the rank-full decomposition helped ICA yield the sources correctly. The failure in the undercomplete decomposition and the use of PCA dimension reduction to make it effectively rank-full or reduce non-signal-subspace redundancy are predicted by the classical study on ICA, per Chapter 13 of the book by Hyvärinen et al. (2001). Thus, the study by Artoni and colleagues should not be taken as a message that using PCA before ICA is unconditionally bad. Rather, our view is that their study focused on the upper bound (i.e., abuse) of the use of PCA in preprocessing, while the study by Hyvärinen and colleagues focused on the lower bound (i.e., shortage) of the use of PCA. We recommend that PCA dimension reduction should be used whenever effective rank deficiency is detected. One important point Artoni and colleagues clarified, in our opinion, is that obtaining 95% of the variance after PCA reduction could be still considered aggressive, whereas Hyvärinen and colleagues casually hinted at 90% as a general idea. Because the scalp-recorded EEG data are heavily correlated due to volume conduction, the variance distribution across PCs is severely skewed. For the case of applying ICA to realistic scalp EEG recordings, it is an overcomplete decomposition (i.e., more sources than electrodes) as long as the data signal-to-noise ratio is reasonably high. Thus, for the standard EEG data decomposition, the recommended practice is to use PCA only for rank adjustment and to avoid possible overfitting (i.e., data length is too short for the number of electrodes). The EEGLAB developers have been suggesting a heuristic criterion, indicating that the input data length should be greater than (number of electrodes)2 x 20 (Makeig and Onton, 2011), given a 256 Hz sampling rate or lower. If the input data length is shorter than this criterion, the use of PCA is recommended to avoid overlearning. Unfortunately, the current implementation of the data rank checker in EEGLAB is suboptimal because it is unable to reduce the data rank using PCA to allow effective rank-full decomposition. We propose that the number of
Ambiguous status of the initial reference in the literature when re-referencing
The difference between “correct” and “incorrect” re-referencing could be trivial if the matrix inversion is not calculated; hence, the rank of data does not matter. Otherwise, the widely used spherical spline channel interpolation (Perrin et al., 1989; Kang et al., 2015) would have been considered an issue. However, as the use of a linear spatial filter including ICA became popular, the impact of the problem caused by effective rank deficiency also became non-negligible.
The literature on EEG research shows that one of the earliest studies on the use of average reference is a one-page article with a large schematic illustration that clearly shows the “rank-deficient by 1” property (Offner, 1950). Another early study clearly indicated that the initial reference is included when re-referencing the unipolarly referenced EEG to the average potential (Osselton, 1965). Thereafter, however, the status of the initial reference electrode when re-referencing became ambiguous. Whether the initial reference should be included or not is not discussed in a later theoretical study (Bertrand et al., 1985). Similarly, whether

FIGURE 2. Summary description of the problem, which relates to confusion about average referencing. There are 2 x 2 ways to calculate the average reference. Note that rank deficiency occurs only when using method A. For the case of method B, one may discard any one channel, except the initial reference, to retain the data rank
Future study
A potential future study on the issue of effective rank-deficient ICA includes an investigation of the validity of other ICs when a ghost IC appears. Because of the multivariate nature of ICA, obtaining one invalid IC could undermine the quality of all other ICs. However, as demonstrated in this study, a ghost IC may be paired with a certain normal IC as a pseudo-subspace, and the impact on other ICs may be limited. We attempted to address this in our study but encountered an issue with the reproducibility of the ICA. Using the same tutorial data, we confirmed that using the options “extended,” 1, “lrate,” 1e-5, and “maxsteps,” 2000 allowed reproducible results in IC scalp topographies and their variance-sorted orders across 10 runs. However, we decided not to include this test in the current report for practical purposes; when we find a ghost IC in our results, the whole batch of datasets processed using the same code should be re-processed anyway, for the sake of perfection. In that sense, investigating the validity of other ICs in the presence of a ghost IC is not very meaningful.
Conclusion
To conclude, effective rank deficiency occurs in electrode interpolation because the spherical spline interpolation is a non-linear method; however, it should not be a concern in re-referencing if re-referencing is applied correctly by including the initial reference. We propose a simple effective rank deficiency checker, which should be used to perform the effective rank-full decomposition as it reduces the data dimension using PCA dimension reduction whenever it detects effective rank deficiency. For future steps, it is advised that, when preprocessing EEG data, the proposed effective rank is explicitly calculated before using any solution involving matrix inversions.
Data availability statement
Publicly available datasets were analyzed in this study. The data can be found at https://github.com/MakotoMiyakoshi/Effective-Rank-Deficiency.
Author contributions
SH contributed to the original concept and the final solution indicated in the conclusion. HK and MM contributed to the conception and design of the study. JL, SC, and MM collected data and performed initial analysis. HK and MM analyzed the final data and generated figures and tables. MM contributed to contacting authors of previous studies. All authors contributed to the manuscript revision, and read and approved the submitted version.
Funding
MM and HK were supported by NSF 2011716 CRCNS US-Japan Research Proposal: A computational neuroscience approach to skill acquisition and transfer from visuo-haptic VR to the real-world. MM was supported by NINDS 5R01NS047293-16 ‘EEGLAB: Software for Analysis of Human Brain Dynamics’. HK and MM were supported by The Swartz Foundation (Old Field, New York). SH was supported by a grant of the German Research Foundation (DFG HO 5054/8-1). JL joined this project as a high school student via UC San Diego’s REHS and Pioneer Research programs.
Acknowledgments
The authors express gratitude to Tzyy-Ping Jung for helping them make the cocktail party problem by recording his voice and to Dezhong Yao, Joseph Dien, Ramesh Srinivasan, and Paul Nunez for insightful discussion and permission to cite personal communications with MM. They also thank Jason Palmer and Scott Makeig for helpful discussion, and Andreas Widmann for raising the issue of including vs. excluding the implicit reference in average re-referencing and its effect on data rank via discussion with MM in 2016.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Artoni, F., Delorme, A., and Makeig, S. (2018). Applying dimension reduction to EEG data by Principal Component Analysis reduces the quality of its subsequent Independent Component decomposition. Neuroimage 175, 176–187. doi:10.1016/j.neuroimage.2018.03.016
Bell, A. J., and Sejnowski, T. J. (1995). An information-maximization approach to blind separation and blind deconvolution. Neural comput. 7, 1129–1159. doi:10.1162/neco.1995.7.6.1129
Bertrand, O., Perrin, F., and Pernier, J. (1985). A theoretical justification of the average reference in topographic evoked potential studies. Electroencephalogr. Clin. Neurophysiology/Evoked Potentials Sect. 62, 462–464. doi:10.1016/0168-5597(85)90058-9
Collins, D. L., Neelin, P., Peters, T. M., and Evans, A. C. (1994). Automatic 3D intersubject registration of MR volumetric data in standardized Talairach space. J. Comput. Assist. Tomogr. 18, 192–205. doi:10.1097/00004728-199403000-00005
Delorme, A., and Makeig, S. (2004). Eeglab: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 134, 9–21. doi:10.1016/j.jneumeth.2003.10.009
Dien, J. (1998). Issues in the application of the average reference: Review, critiques, and recommendations. Behav. Res. Methods, Instrum. Comput. 30, 34–43. doi:10.3758/BF03209414
Dien, J. (2010). The ERP PCA Toolkit: An open source program for advanced statistical analysis of event-related potential data. J. Neurosci. Methods 187, 138–145. doi:10.1016/j.jneumeth.2009.12.009
Dong, L., Li, F., Liu, Q., Wen, X., Lai, Y., Xu, P., et al. (2017). MATLAB toolboxes for reference electrode standardization technique (REST) of scalp EEG. Front. Neurosci. 11, 601. doi:10.3389/fnins.2017.00601
Evans, A. C., Collins, D. L., Mills, S. R., Brown, E. D., Kelly, R. L., and Peters, T. M. (1993). “3D statistical neuroanatomical models from 305 MRI volumes,” in 1993 IEEE Conference Record Nuclear Science Symposium and Medical Imaging Conference, San Francisco, CA, USA, 31 October 1993 - 06 November 1993 (IEEE). doi:10.1109/NSSMIC.1993.373602
Hu, S., Yao, D., Bringas-Vega, M. L., Qin, Y., and Valdes-Sosa, P. A. (2019). The statistics of eeg unipolar references: Derivations and properties. Brain Topogr. 32, 696–703. doi:10.1007/s10548-019-00706-y
Hyvärinen, A., Karhunen, J., and Oja, E. (2001). Independent component analysis. 1st ed. New York: Wiley-Interscience.
Kang, S. S., Lano, T. J., and Sponheim, S. R. (2015). Distortions in EEG interregional phase synchrony by spherical spline interpolation: Causes and remedies. Neuropsychiatr. Electrophysiol. 1, 9. doi:10.1186/s40810-015-0009-5
Makeig, S., Bell, A., Jung, T.-P., and Sejnowski, T. (1996). Independent component analysis of electroencephalographic data. Adv. Neural Inf. Process. Syst. 8, 145–151.
Makeig, S., and Onton, J. (2011). ERP features and EEG dynamics. Oxford, United Kingdom: Oxford University Press. doi:10.1093/oxfordhb/9780195374148.013.0035
Makeig, S., Westerfield, M., Jung, T. P., Covington, J., Townsend, J., Sejnowski, T. J., et al. (1999). Functionally independent components of the late positive event-related potential during visual spatial attention. J. Neurosci. 19, 2665–2680. doi:10.1523/jneurosci.19-07-02665.1999
Nunez, P. L., and Srinivasan, R. (2006). Electric fields of the brain. 198. Madison Avenue, New York, New York: Oxford University Press, 10016. doi:10.1093/acprof:oso/9780195050387.001.0001
Offner, F. F. (1950). The EEG as potential mapping: The value of the average monopolar reference. Electroencephalogr. Clin. Neurophysiol. 2, 213–214. doi:10.1016/0013-4694(50)90040-x
Oostenveld, R., Fries, P., Maris, E., and Schoffelen, J.-M. (2011). FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011, 1–9. doi:10.1155/2011/156869
Osselton, J. W. (1965). Acquisition of EEG data by bipolar unipolar and average reference methods: A theoretical comparison. Electroencephalogr. Clin. Neurophysiol. 19, 527–528. doi:10.1016/0013-4694(65)90195-1
Perrin, F., Pernier, J., Bertrand, O., and Echallier, J. F. (1989). Spherical splines for scalp potential and current density mapping. Electroencephalogr. Clin. Neurophysiol. 72, 184–187. doi:10.1016/0013-4694(89)90180-6
Keywords: rank deficiency, principle component analysis, independent component analysis, dimension reduction, spherical spline interpolation, re-reference, average reference
Citation: Kim H, Luo J, Chu S, Cannard C, Hoffmann S and Miyakoshi M (2023) ICA’s bug: How ghost ICs emerge from effective rank deficiency caused by EEG electrode interpolation and incorrect re-referencing. Front. Sig. Proc. 3:1064138. doi: 10.3389/frsip.2023.1064138
Received: 07 October 2022; Accepted: 13 March 2023;
Published: 03 April 2023.
Edited by:
Rishi Raj Sharma, Defence Institute of Advanced Technology (DIAT), IndiaReviewed by:
Alina Santillan Guzman, Universidad Popular Autónoma del Estado de Puebla, MexicoAnurag Nishad, Birla Institute of Technology and Science, India
Copyright © 2023 Kim, Luo, Chu, Cannard, Hoffmann and Miyakoshi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Makoto Miyakoshi, TWFrb3RvLk1peWFrb3NoaUBjY2htYy5vcmc=
 Hyeonseok Kim
Hyeonseok Kim Justin Luo2
Justin Luo2 Shannon Chu
Shannon Chu Cedric Cannard
Cedric Cannard Sven Hoffmann
Sven Hoffmann Makoto Miyakoshi
Makoto Miyakoshi

