Robust Identification of the QRS-Complexes in Electrocardiogram Signals Using Ramanujan Filter Bank-Based Periodicity Estimation Technique

Plausibly, the first computerized and automated electrocardiogram (ECG) signal processing algorithm was published in the literature in 1961, and since then, the number of algorithms that have been developed to-date for the detection of the QRS-complexes in ECG signals is countless. Both the digital signal processing and artificial intelligence-based techniques have been tested rigorously in many applications to achieve a high accuracy of the detection of the QRS-complexes in ECG signals. However, since the ECG signals are quasi-periodic in nature, a periodicity analysis-based technique would be an apt approach for the detection its QRS-complexes. Ramanujan filter bank (RFB)-based periodicity estimation technique is used in this research for the identification of the QRS-complexes in ECG signals. An added advantage of the proposed algorithm is that, at the instant of detection of a QRS-complex the algorithm can efficiently indicate whether it is a normal or a premature ventricular contraction or an atrial premature contraction QRS-complex. First, the ECG signal is preprocessed using Butterworth low and highpass filters followed by amplitude normalization. The normalized signal is then passed through a set of Ramanujan filters. Filtered signals from all the filters in the bank are then summed up to obtain a holistic time-domain representation of the ECG signal. Next, a Gaussian-weighted moving average filter is used to smooth the time-period-estimation data. Finally, the QRS-complexes are detected from the smoothed data using a peak-detection-based technique, and the abnormal ones are identified using a period thresholding-based technique. Performance of the proposed algorithm is tested on nine ECG databases (totaling a duration of 48.91 days) and is found to be highly competent compared to that of the state-of-the-art algorithms. To the best of our knowledge, such an RFB-based QRS-complex detection algorithm is reported here for the first time. The proposed algorithm can be adapted for the detection of other ECG waves, and also for the processing of other biomedical signals which exhibit periodic or quasi-periodic nature.

1 Introduction

S. K. Yuen discoursed in his Ph.D. thesis (Yuen, 1976) that the cardiovascular diseases were the leading causes of death in the U.S. in 1972, and even in 2021 (Centers for Disease Control and Prevention, 2022) the statistic has not been altered. Perhaps the scenarios are even more alarming in the other parts of the globe. Therefore, it could be said undoubtedly that the research and development in the area of the computerized processing of the ECG signal and automated detection of cardiovascular diseases are to be carried out in higher pace, if the situation is to alter. An electrocardiogram (ECG) signal characterizes the electrical activity of the heart that arises from the depolarization and repolarization activities of the cardiac cells. ECG signals are recorded by means of electrodes that are placed on various standard locations on the body surface. An ECG signal is composed of waves such as P, QRS-complex and T waves, segments such as PR and ST segments and intervals such as R-to-R and P-to-R intervals, and the presence of any cardiac disorder is generally reflected in the shapes, patterns and durations of these waves, segments and intervals, respectively. Among all other waves and segments of an ECG signal, the QRS-complexes are the most salient regions as it contains the highest frequency spectrum and amplitude. Since the publication of the plausibly-first computerized ECG processing algorithm in 1961 (Pipberger et al., 1961), a multitude of algorithms are proposed in the literature to-date on the detection of the QRS-complexes in ECG signals. A methodological review (Berkayaa et al., 2018) suggests that these QRS-complex detection algorithms could be broadly categorized into two groups: 1) digital signal processing (Burguera, 2019; Hossain et al., 2019; Sharma et al., 2019; Zhang et al., 2020; Jorge et al., 2021; Modak et al., 2021; Morshedlou et al., 2021; Rahul et al., 2021; Tueche et al., 2021), and 2) artificial intelligence-based (Mehta and Lingayat, 2008; Merino et al., 2015; Chandra et al., 2019; Goovaerts et al., 2019; Chen and Maharatna, 2020; Jia et al., 2020; He et al., 2021).

Rahul et al. have proposed an amplitude and interval threshold-based QRS-complex detection algorithm in (Rahul et al., 2021). In (Rahul et al., 2021), first, the ECG signal is denoised using bandpass and moving average filters. Next, a series of static and dynamic amplitude-threshold values (7 threshold values in total) are applied on the denoised ECG signal to identify the plausible QRS-complexes. Though the run-time of the algorithm [run-time indicates the amount of time taken by an algorithm to process a certain amount of data (Cormen et al., 2009)] is low, the QRS-complex detection performance of the algorithm is poor compared to that of the state-of-the-art algorithms (Please see Table 6). A similar type of algorithm is proposed in (Tueche et al., 2021) by Tueche et al. In (Tueche et al., 2021), the ECG signal is first denoised, and then the denoised signal is squared to enhance the QRS-complex regions. Next, all the peaks of the enhanced signal are detected, and three different threshold values are applied on those detected peaks to separate out the real QRS-complexes. The algorithm is primarily implemented on software platform, and then it is also implemented on a microcontroller-based system to examine the likelihood of its success in real-time applications. The authors have claimed that they have not found any difference in the results that they obtained on both the software and hardware platforms. However, here also, as in the case of (Rahul et al., 2021), the QRS-complex detection performance of the algorithm (Tueche et al., 2021) is poor. A tunable-Q wavelet transform (TQWT)-based QRS-complex detection algorithm is proposed by Sharma et al. in (Sharma et al., 2019). A QRS-enhanced ECG signal is obtained from a number of suitably chosen wavelet sub-bands. Then, the correntropy of the QRS-enhanced signal is calculated. Finally, a threshold-based peak detection technique is used to identify the QRS complexes. However, neither the QRS-complex detection performance nor the runtime of the algorithm could compete with that of the state-of-the-art algorithms.

Processing of the ECG signals using deep learning models has become one of the most promising areas of research in the last few years. In their review (Hong et al., 2020), Hong et al. have found 109 published articles, which were focused only on the deep learning-based ECG processing algorithms, and all those articles were published after the year 2019. A U-Net and bidirectional long-short term memory-based QRS-complex detection algorithm is proposed in (He et al., 2021) by He et al. In (He et al., 2021), first, an ECG signal is denoised using a median filter and a wavelet transformation-based technique. The denoised signal is then segmented into blocks of length 10 s each. Those blocks are then fed to the deep learning model to train the classifier. However, even after rigorous training and testing, the algorithm is unable to detect the paced QRS-complexes. Moreover, the model demands high computational-memory, and it require a graphics processing unit to get implemented. Chen et al. have proposed a hierarchical clustering-based R-peak detection and discrete wavelet transform-based T-peak detection algorithm in (Chen and Maharatna, 2020). In (Chen and Maharatna, 2020), the ECG signal is first denoised using Butterworth lowpass and highpass filters to expel the high frequency noises and baseline wonder noise out, respectively, and the amplitude of the denoised signal is normalized within [0, 1]. Then the denoised ECG signal is broken into segments of length 1.2 s each and are processed sequentially. The amplitudes and slopes of all the ECG samples in each of the segment are calculated and then they are clustered into two, namely R-cluster and non-R-cluster. The cluster with a smaller number of samples is considered as the R-cluster, and those samples which belong to R-cluster are considered as the R-peaks. However, a window of length 1.2 s restricts the applicability of the algorithm on ECG signals where the heart rate varies between 50 and 100 beats/minute.

The objective and aim of this proposed research work are to design a high-efficient yet fast QRS-complex detection algorithm overriding the shortcomings of other state-of-the-art algorithms as mentioned above. The main contribution of this research work is that the proposed QRS-complex detection algorithm is 1) highly accurate compared to that of the state-of-the art algorithms, 2) less complex, 3) noise tolerant 4) fast and 5) able to identify the premature ventricular contraction and atrial premature contraction QRS-complexes. The novelty of the proposed algorithm lies both in its working principle and performance. It is worth mentioning that a Ramanujan filter bank-based QRS-complex detection algorithm exploiting the time-period estimation of the ECG signal is being proposed here for the first time, to the best of our knowledge.

The paper is organized as follows. The theoretical background of Ramanujan filter bank is presented in Section 2. Section 3 describes the proposed QRS-complex detection algorithm. The performance of the proposed algorithm is investigated in Section 4. Section 5 compares the performance of the proposed algorithm with that of other state-of-the-art algorithms. Limitation and the future direction of the proposed research work are outlined in Section 6. Finally, discussions and conclusions are drawn in Section 7.

2 Ramanujan Filter Bank

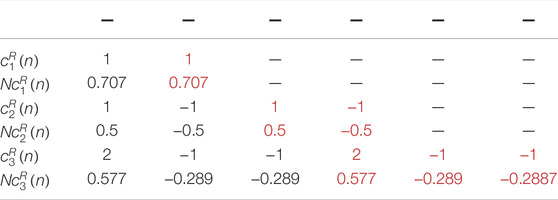
In 1918, the Indian mathematician Srinivasa Ramanujan introduced a new set of sequences, which is known as Ramanujan Sums (Ramanujan, 1918). Ramanujan sums (RS) are real sums defined as the $n^{th}$ powers of the $q^{th}$ primitive roots of unity. RS is defined as follows.

$c_q\left(n\right)={\displaystyle \sum _{\begin{array}{c}p=1\\ \left(p,q\right)=1\end{array}}^q\text{exp}\left(2\pi j\frac{p}{q}n\right)}(1)$

Where, $\left(p,q\right)=1$ indicates that $p$ and $q$ are co-prime, i.e., the greatest common divisor (GCD) is unity, and $-\infty \le n\le \infty$. The summation is obtained for only those values of $p$ that are coprime to $q$, and hence, $c_q\left(n\right)$ is periodic, i.e., $c_q\left(n+q\right)=c_q\left(n\right)$, and the period is equal to $q$. The RS can also be alternatively calculated as given below.

$c_q\left(n\right)=\mu \left(\frac{q}{GCD\left(q,n\right)}\right)\frac{\varnothing \left(q\right)}{\varnothing \left(\frac{q}{GCD\left(q,n\right)}\right)}(2)$

where, $\varnothing \left(q\right)$ is the Euler totient function which is a multiplicative arithmetic function defined for the positive integers and is given by the number of positive co-prime integers less than or equal to $q$. $\mu$ (n), which is known as the Mobius function, is also a multiplicative function and is zero for the positive integers which are not square-free (Sugavaneswaran et al., 2012). From Eq. 2 it can be noted that, $c_q\left(n\right)= \mu \left(q\right)$; if $\left(q,n\right)=1$, and $c_q\left(n\right)=\varnothing \left(q\right)$; if $\left(q,n\right)=q$. Another way of deriving the values of $c_q\left(n\right)$ is using the Euler’s formula; $e^{ix}=\cos x+i\sin x$. A few Ramanujan-sequences for one period is shown below, where $q \mathrm{ϵ}\left[\mathrm{1,6}\right]$.

$c_1\left(n\right)=1$

$c_2\left(n\right)=1,-1$

$c_3\left(n\right)=2,-1,-1$

$c_4\left(n\right)=2, 0,-2, 0$

$c_5\left(n\right)=4,-1,-1,-1,-1$

$c_6\left(n\right)=2, 1,-1,-2,-1, 1(3)$

It can be seen from Eq. 3 that the values of $c_q\left(n\right)$ are integer numbers despite the presence of the trigonometric function as shown in Eq. 1. The identification of the periodicity of a signal using RS has been well studied in (Sugavaneswaran et al., 2012; Chen et al., 2013; Tenneti and Vaidyanathan, 2015a; Tenneti and Vaidyanathan, 2015b; Vaidyanathan and Tenneti, 2015; Pei and Chang, 2017; Tenneti, 2018; Yadav et al., 2018; Saatci and Saatci, 2020). It has also been shown in (Mainardi et al., 2007) that a RS-based technique could better capture the periodicity of a signal better than that of a conventional discrete Fourier transform (DFT)-based method even in the presence of a Gaussian types of noise. The likelihood of application of RS in the context of biomedical signal processing is also reported by Mainardi et al. in (Mainardi et al., 2008).

If the RS is regarded as a digital filter having an impulse response $c_q\left(n\right)$, then its frequency response in $0\le \omega <2\pi$ is as given below.

$c=2\pi {\displaystyle \sum _{\begin{array}{c}1\le p\le q\\ \left(p,q\right)=1\end{array}}\sigma \left(\omega -\frac{2\pi p}{q}\right)}(4)$

From Eq. 4 it can be seen that the value of $C_q\left(e^{j\omega }\right)$ is non-zero only at the co-prime frequencies $2\pi p_i/q$ where $p_i$ is coprime to $q$; and zero elsewhere. Let us consider a periodic signal $x\left(n\right)$ with period $P_e$. Its Fourier transform can be written as below.

$X\left(e^{j\omega }\right)=\frac{2\pi }{P_e}{\displaystyle \sum _{l=0}^{P_e-1}X\left[l\right]\partial \left(\omega -\frac{2\pi l}{P_e}\right)}(5)$

If the signal $x\left(n\right)$ is passed through Ramanujan filter, by comparing Eqs 4, 5, it can be said that the output of the filter will be zero if neither of the Dirac functions in these two expressions coincide. However, for each value of $p$, such that $\frac{p}{q}=\frac{l}{P_e}$ for $0\le l\le P_e$, the output of Ramanujan filter could be non-zero. As $\left(p,q\right)=1$, Ramanujan filter $C_q\left(e^{j\omega }\right)$ outputs a non-zero value when $P_e$ is a multiple of $q$. The passband of Ramanujan filter is centered around its co-prime frequency. A collection of such filters for periods ranging from 1 to $P_e$ having impulse response $\left\{c_q\left(n\right)\right\}$; $1\le q\le N$ ($N$ is the length of the signal $x\left(n\right)$), is called the Ramanujan filter bank (RFB) (Tenneti and Vaidyanathan, 2015a), (Vaidyanathan and Tenneti, 2015), and a plot of the outputs of each of the filters for different values of $n$ is referred as the time-period plane plot of the signal.

3 The QRS-Complex Detection Algorithm

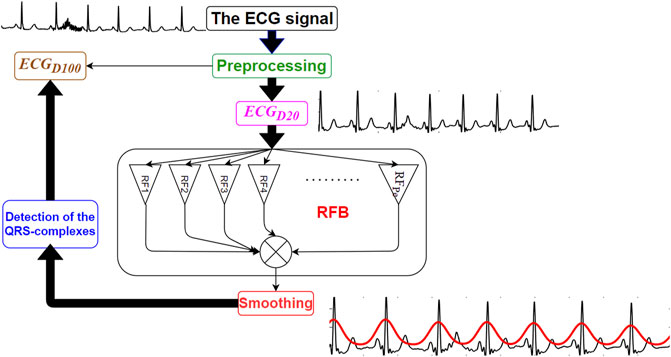
The proposed RFB-based QRS-complex detection algorithm can be divided into three major parts: 1) Preprocessing, 2) time-period analysis using RFB and the 3) identification of the QRS-complexes. Schematic diagram of the proposed algorithm is shown in Figure 1.

FIGURE 1

FIGURE 1. Schematic diagram of the proposed RFB-based QRS-complex detection algorithm.

3.1 Preprocessing

The clinical bandwidth of an ECG signal ranges between 0.5 and 100 Hz (Tompkins, 1993). In this research work the original ECG signal is denoised using two sets of filters. In the first set, a 4^th order zero-phase Butterworth bandpass filter having lower and upper cut-off frequencies 0.5 and 100 Hz, respectively, and a 4^th order zero-phase Butterworth notch filter is used to denoise the original ECG signal. The bandpass filter suppresses the out-of-band noises, and the notch filter suppresses the 50/60 Hz powerline interference noise. This version of the denoised signal is referred as $EC{G}_{D100}$ in this paper. In the second set, a 4^th order zero-phase Butterworth lowpass filter having a cutoff frequency of 20 Hz is used to denoised the original ECG signal, and this version of the denoised signal is referred as $EC{G}_{D20}$ in this paper. The roll-off rate of a Butterworth filter (-20dB/decade) is low compared to that of others such as a Chebyshev filter, but the frequency response of a Butterworth is flat within the passband. This is the main reason for what the Butterworth filters have been used in this research work. A Fourier decomposition-based efficient technique for the removal of baseline wander, powerline interference and other high frequency noises from the ECG signals is proposed in (Singhal et al., 2020) and (Singh et al., 2017). Such a technique could also be used for the removal of high and low frequency noises from the ECG signal.

Next, the amplitudes of both the $EC{G}_{D100}$ and $EC{G}_{D20}$ signals are normalized in between ±1. Undoubtedly, the $EC{G}_{D20}$ signal contains less clinical information as compared to that of its $EC{G}_{D100}$ counterpart, but it helps better identifying the QRS-complex regions. Figure 2 shows the example of an original ECG signal, its $EC{G}_{D100}$ and $EC{G}_{D20}$ versions.

FIGURE 2

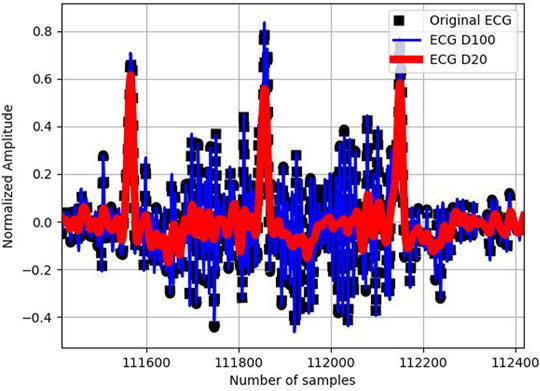
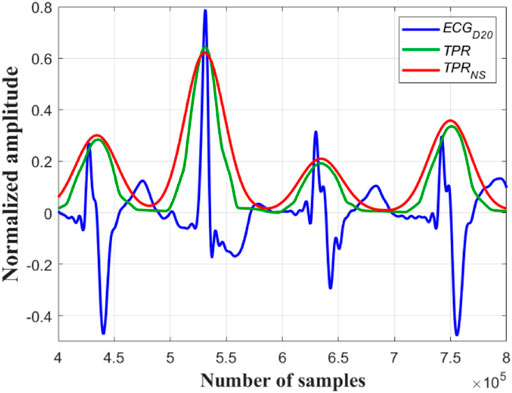
FIGURE 2. Original ECG signal (in black), its $EC{G}_{D100}$ (in blue) and $EC{G}_{D20}$ (in red) versions. The ECG signal is taken from MITDB: record #104 m.

3.2 Time-Period Analysis Using RFB

In this step, the $EC{G}_{D20}$ is fed to the input of the RFB. There are three parameters that are to be optimized in RFB: 1) the number of filters $\left(P_e\right)$, 2) the number of times the filter coefficients are to be repeated $\left(R_{cq}\right)$ and 3) the length of the average-filter $\left(R_{av}\right)$ (Tenneti, 2018), (Tenneti and Vaidyanathan, 2015b). Since, each of the filter in the bank captures different periodic components that are present in the input signal, the number of filters that are to be used are event-dependent. As the goal of this research work is to detect the QRS-complexes of the ECG signals, the number of filters that are to be used in the bank depend on the periodic property of the QRS-complexes. As per the cardio-physiologic definition (Goldberger, 2006), the width of a QRS-complex could stretch 120 milliseconds at most, and therefore, the number of the filters that are to be used has to be calculated based on this clinical information. However, as shown in Figure 3, a QRS-complex is not symmetric itself, i.e., the rise and fall times of a QRS-complex are not identical. Therefore, only the rise-time of a QRS-complex (∼60 milliseconds), i.e., the half of the maximum QRS-duration, is used in this research work to optimize the number of number filters that are required to track the periodicity of a QRS-complex in ECG signal and is calculated as given in Eq. 6.

$P_e=int\left(sampling frequency in Hz\times 0.06 seconds\right)(6)$

FIGURE 3

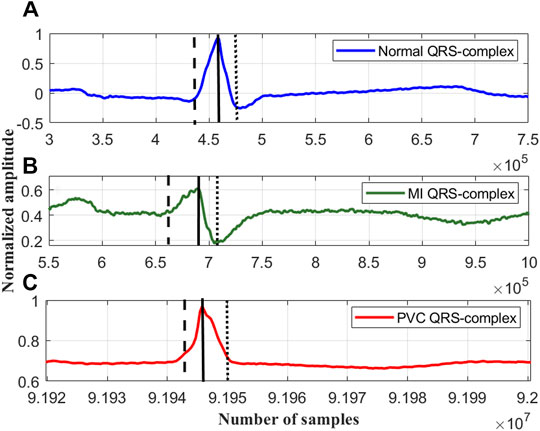
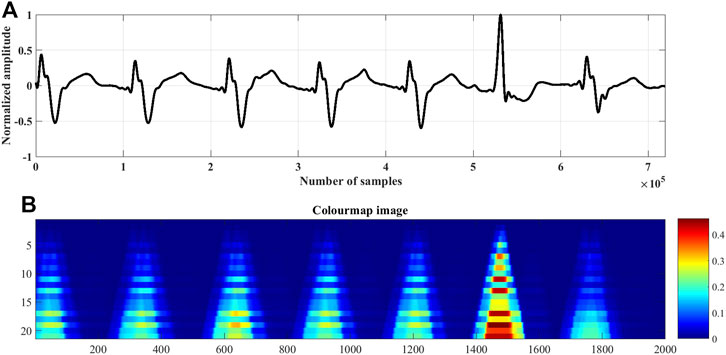
FIGURE 3. The rise and fall times of the QRS-complexes of a (A) normal ECG beat, lead I; record #s0273lrem, PTBDB, (B) myocardial infraction (MI) ECG beat, lead I; record #s0015lrem, PTBDB and (C) premature ventricular contraction (PVC) beat, lead V5; record # 104m, MITDB.

In the proposed research work it has been found experimentally, that repeating the coefficients of each of the Ramanujan filter twice $\left(R_{cq}=2\right)$, and a length of the average filter equals to six units $\left(R_{av}=6\right)$ provides an optimum QRS-complex detection performance. Next, after repetition, each set of the coefficients are normalized with their corresponding Euclidean norm. Eqs 7, 8 summarize the normalization operation, and Table 1 shows the coefficients of the RFB $\left(q \mathrm{ϵ}\left[\mathrm{1,3}\right]\right)$ and their corresponding normalized values after repetition. Two different colours; black and red are used in Table 1 for better showing the repetition.

$N{c}_q^R\left(n\right)=\frac{c_q^R\left(n\right)}{\Vert v\Vert }(7)$

$\Vert v\Vert =\sqrt{{\displaystyle \sum {\left|c_q^R\left(n\right)\right|}^2}}(8)$

where, $N{c}_q^R\left(n\right)$ is the set of a normalized Ramanujan filter coefficients, $c_q^R\left(n\right)$ is the set of a Ramanujan filter coefficients after repetition and $v$ is the Euclidean norm of $c_q^R\left(n\right)$.

TABLE 1

TABLE 1. The coefficients of the RFB $\left(q \mathrm{ϵ}\left[\mathrm{1,3}\right]\right)$ after repetition $\left(R_{cq}=2\right)$.

Now, the $EC{G}_{D20}$ signal is separately convoluted with each set of $N{c}_q^R\left(n\right)$. The convoluted data is denoted as $ConEC{G}_{D20}^q$. This step filters the $EC{G}_{D20}$ signal using the Ramanujan filter coefficients and tries to capture the periodicity of the QRS-complexes. Then, each of the $ConEC{G}_{D20}^q$ is again convoluted with the output of the average-filter. The average filter provides a smoothed version of the filtered data ($ConEC{G}_{D20}^q$). The steps, which are followed in performing the convolution operations are shown below.

for q =1 to $P_e$

 $Y\left(i\right) \leftarrow$ $EC{G}_{D20}$ $\ast N{c}_q^R\left(n\right)$

 $F_{av}\leftarrow$ ones((i× $R_{av}$), 1)

 $\Vert F_{av}\Vert =\sqrt{{\displaystyle \sum _{j=1}^{R_{av}}{\left|F_{av}\left(j\right)\right|}^2}}$

 $N{F}_{av}$ $\leftarrow$ $F_{av}/\Vert F_{av}\Vert$

 $FN{c}_q^R\left(n\right)\leftarrow$ $Y\left(i\right) \ast$ $N{F}_{av}$

 $Y\left(i\right)\leftarrow FN{c}_q^R\left(n\right)$

end

where, the command ‘ones((i× $R_{av}$), 1)’ creates a vector of length i × $R_{av}$, and it contains 1. $F_{av}$ is the Euclidean norm of $F_{av}$. $FN{c}_q^R\left(n\right)$ denotes the convoluted $EC{G}_{D20}$ signal using the coefficients of the $q^{th}$ Ramanujan filter. $Y\left(i\right)$ is a matrix of dimension $P_e\times N$, where $N$ is the length of $EC{G}_{D20}$. $Y$ is called the periodicity-matrix (Tenneti and Vaidyanathan, 2015b). For an example, if the sampling rate of the ECG signal is 360 Hz, then, the matrix $Y$ would have 21 rows. Therefore, following Eq. 6, 1) the 21st row of the matrix $Y$ would represents the periodicity of that ECG event which completes a period in 0.06 s, 2) the 20th row of the matrix $Y$ would represents the periodicity of that ECG event which completes a period in ∼0.055 s, and likewise 3) the 1st row of the matrix $Y$ would represents the periodicity of that ECG event which completes a period in ∼0.003 s. Figure 4 shows an $EC{G}_{D20}$ signal and the colour map of its corresponding periodicity-matrix. From this figure it can be seen that the RFB is not only able to capture the periodicity of the QRS-complexes, but it also shows a distinct periodic property for an abnormal QRS-complex. Figure 5 shows an $EC{G}_{D20}$ signal and its corresponding filtered outputs from the different filters in the bank.

FIGURE 4

FIGURE 4. (A) $EC{G}_{D20}$; record # 104m, MITDB, (B) colour map of its corresponding periodicity-matrix $Y$.

FIGURE 5

FIGURE 5. $EC{G}_{D20}$; record # 104m, MITDB, and $FN{c}_q^R\left(n\right)$ $\left(q \mathrm{ϵ}\left[\mathrm{1,21}\right]\right)$.

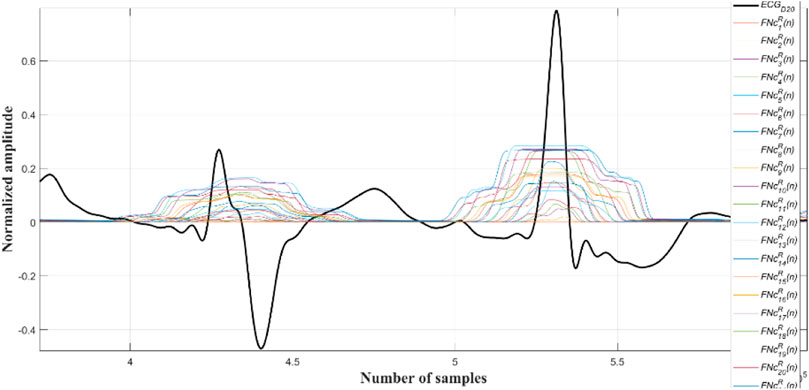
Next the outputs of all the Ramanujan filters are summed up so as to obtain a holistic time-period representation ($TPR$) of the $EC{G}_{D20}$ signal. Next, the $TPR$ data is smoothed using a Gaussian-weighted moving average filer, and then the amplitude of the smoothed data is normalized to $\pm 1$. The normalized smoothed data is denoted as $TP{R}_{NS}$. Figure 6 shows the example of an $EC{G}_{D20}$ signal, its corresponding $TPR$ and $TP{R}_{NS}$.

FIGURE 6

FIGURE 6. $EC{G}_{D20}$ in blue; record # 104m, MITDB, its $TPR$ in green, and $TP{R}_{NS}$ in red.

3.3 Identification of the QRS-Complexes

Now, all the peaks of the $TP{R}_{NS}$ data are detected and are mapped on to the $EC{G}_{D100}$ signal. The peaks on the $TP{R}_{NS}$ data indicate the probable R-peaks. As per the cardio-physiologic definition (Goldberger, 2006), the width of a QRS-complex could stretch 120 milliseconds at most. Then, the absolute-maximum amplitude is searched around each of the probable-peaks within a window of length $\pm 60$ milliseconds to locate the true R-peaks. Since, the $EC{G}_{D100}$ signal contains the necessary clinical information, the true R-peaks are detected on the $EC{G}_{D100}$ signal. Next, the Q and S peaks are detected using the algorithm, which is used in (Mukhopadhyay and Krishnan, 2020). If it is found that the polarity of the detected R-peak is positive, then the index of the minimum amplitude within a fixed time-window $t_1$ to $t_2$ is considered as the Q-peak, and the index of the minimum amplitude within a fixed time-window $t_2$ and $t_3$ is considered as the S-peak. Instead of a minimum amplitude, the index of the maximum amplitude is searched for detecting both the Q and S-peaks, if the polarity of the detected R-peak is found negative. Here, $t_1$ = index of the R-peak—60 milliseconds, $t_2$ = index of the R-peak, and $t_3$ = index of the R-peak + 60 milliseconds. As mentioned above, the duration of a QRS-complex could be 120 milliseconds at most (Goldberger, 2006), and this is the reason for which a half of the maximum QRS-duration (∼60 milliseconds) is used as the length of the window to look for the Q and S-peaks.

A close observation and analysis, which are listed below, reveal that the $TP{R}_{NS}$ data exhibits distinctly disparate patterns for a normal, premature ventricular contraction (PVC) and premature atrial contraction (APC) types of QRS-complexes. Figure 7 exemplifies these observations.

Observation #1: From Figure 7A, it can be seen that the amplitudes of the peaks and the valleys of the $TP{R}_{NS}$ do not differ much for a normal sinus rhythm.

Observation #2: Figure 7B shows that the amplitudes of the peaks of the $TP{R}_{NS}$ of the APC beats (the 4^th QRS-complex) do not differ much compared to that of the normal QRS-complexes. However, amplitudes of the valleys of the $TP{R}_{NS}$ of the APC beats significantly differ from that of the normal QRS-complexes.

Observation #3: Figure 7C shows that the amplitudes of both the peaks and the valleys of the $TP{R}_{NS}$ of the PVC beats (the 5^th QRS-complex) differs significantly compared to that of the normal QRS-complexes.

FIGURE 7

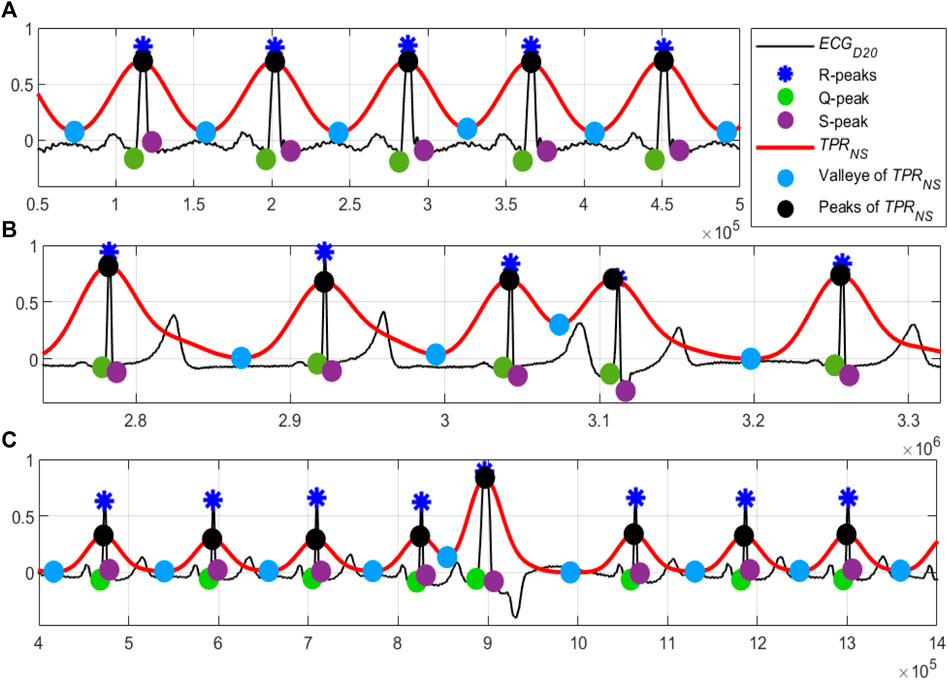
FIGURE 7. (A) Normal sinus rhythm; record #122m, MITDB, (B) the 4^th QRS-complex is an APC beat; record #113m, MITDB and (C) the 5^th QRS-complex is a PVC beats; record #119m, MITDB. The $EC{G}_{D100}$ signals, their corresponding $TP{R}_{NS}$, and the R-peaks in each of the three sub-figures are shown in black, red, and blue colours, respectively. The X and Y axes of all the three sub-figures are the number of samples and normalized amplitude, respectively.

Following these observations, the APC and PVC beats are segregated using the following steps.

$Step \#1:$ Detect the valleys of the $TP{R}_{NS}$ (peaks of the $TP{R}_{NS}$ are already detected during the detection of the QRS-complexes)

$Step \#2:$ $x\leftarrow$ amplitude of the $i^{th}$ peak of $TP{R}_{NS}$, $y\leftarrow$ amplitude of the $i-1^{th}$ peak of $TP{R}_{NS}$, $z\leftarrow$ amplitude of the $i^{th}$ valley of $TP{R}_{NS}$, $w\leftarrow$ amplitude of the $i-1^{th}$ valley of $TP{R}_{NS}$

$Step \#3:$ if (($x-y$)≥ $th$ and ($z-w$)≥ $th$

  the $i^{th}$ QRS-complex $\leftarrow$ PVC-beat

 elseif (($x-y)\le th$ and ($z-w$)≥ $th$

  the $i^{th}$ QRS-complex $\leftarrow$ APC-beat

 else

  the $i^{th}$ QRS-complex $\leftarrow$ normal QRS-complex

 end

After testing the proposed algorithm on a large number of ECG data of various pathological and arrhythmic classes, the value of $th$ is set to 0.2.

4 Performance Evaluation

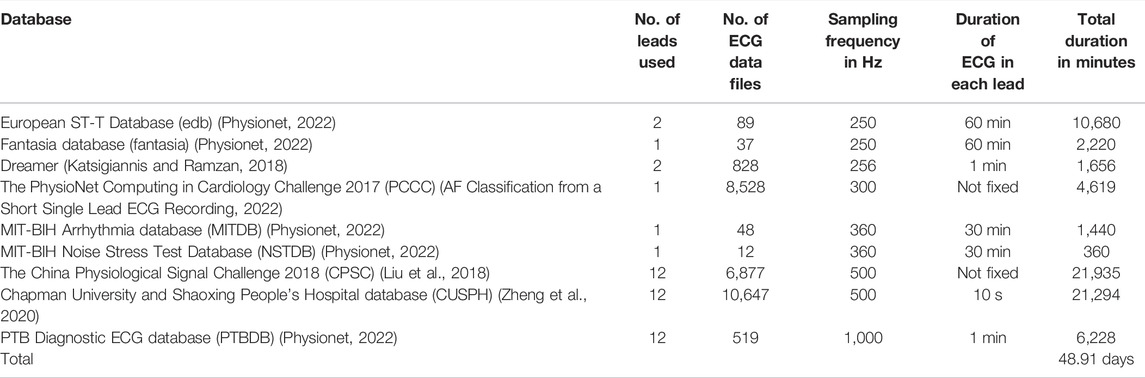
The ECG signals are collected from nine publicly available datasets, totaling a duration of 48.91 days, and are used as the performance evaluation testbed of the proposed algorithm. The details of these collected ECG signals are given in Table 2. The algorithm is implemented and tested on MATLAB platform with a computer having 64-bit Windows 10 operating system, 12 GB RAM and Intel Core i7 10510U central processing unit (CPU) 2.30 GHz. Five statistical metrices: sensitivity ($Se$), positive predictivity $\left(+P\right)$, detection accuracy $\left(Ac{c}_D\right)$, processing time $\left(T_{pro}\right)$ and $F1$ score $\left(F1\right)$ are used to assess the performance of the algorithm. These metrices are numerically expressed in Eqs 9–13.

$Se (\%)=\frac{TP}{TP+FN}\times 100(9)$

$+P (\%)=\frac{TP}{TP+FP}\times 100(10)$

$Ac{c}_D (\%)=\frac{TP}{Total no. of QRS complexes}\times 100(11)$

$T_{Pro}=Time taken to process the ECG signal in seconds(12)$

$F1(\%)=\frac{2\times TP}{\left(2\times TP\right)+FP+FN} \times 100(13)$

where, $TP$ is the total number of QRS-complexes, which the proposed algorithm has detected correctly. $FN$ is the total number of QRS-complexes, which the algorithm has failed to detect, and $FP$ is the total number of detections, which are not the real QRS-complexes, nevertheless, the proposed algorithm has detected those as the real QRS-complexes. In the context of the present research work, i.e., the QRS-complex detection, the sensitivity $\left(Se\right)$ is a measure of probability that an algorithm efficiently detects the true QRS-complexes among a given set of true QRS-complexes, and the positive predictivity $\left(+P\right)$ is a measure of probability that an algorithm efficiently detects only the true QRS-complexes among a given set of true and false QRS-complexes (Trevethan, 2017). The close the values of $Se$ and $+P$, $Ac{c}_D$ and $F1$ to 100%, and the lower the values of $FN$, $FP$ and $T_{Pro}$, the better the performance of the algorithm. Now, the performance of proposed RFB-based QRS-complex detection algorithm on MITDB is shown in Table 3, and the performance of the proposed algorithm in segregating the normal, APC and PVC beats on MITDB is shown in Table 4 in the form of a confusion matrix. The performance of the proposed algorithm is also tested on eight other datasets, and the results are shown in Table 5.

TABLE 2

TABLE 2. Details of the collected ECG signals.

TABLE 3

TABLE 3. Performance of proposed RFB-based QRS-complex detection algorithm on MITDB.

TABLE 4

TABLE 4. Performance of the proposed algorithm in segregating the normal, APC and PVC beats on MITDB.

TABLE 5

TABLE 5. Performance of the proposed algorithm on other ECG datasets.

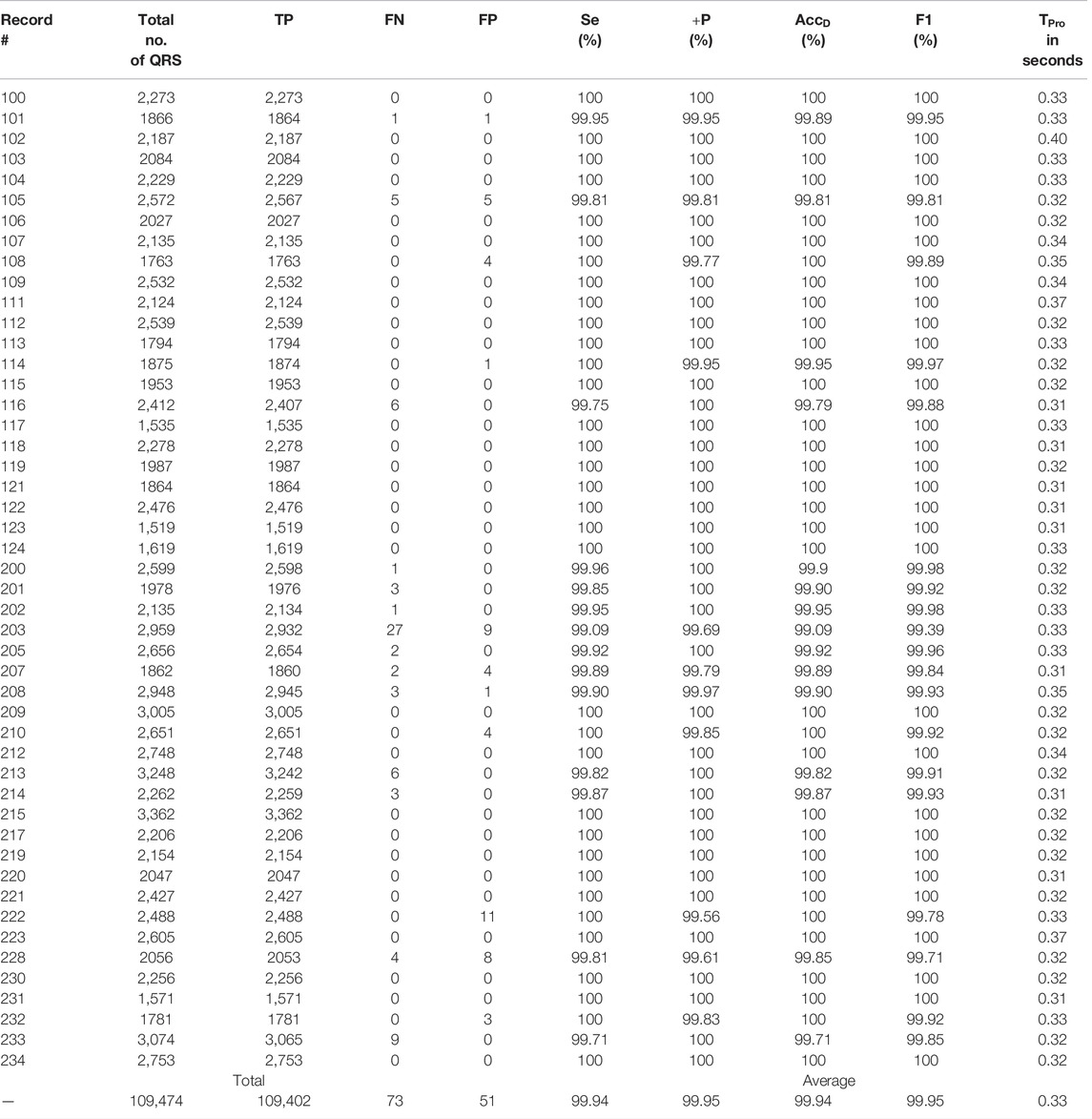
The proposed algorithm fails to detect a QRS-complex when its amplitude is too small compared to other such as a few of the QRS-complexes following a large motion artefact noise. On the other hand, the algorithm detects a non-QRS-complex as a QRS-complex when its amplitude is high, and the periodicity matches with that of a QRS-complex. From Table 3 it can be seen that the algorithm is unable to detect 27 QRS-complexes of the file number #203 m of MITDB. The reasons behind this are the presence of: 1) QRS-complexes of different morphologies, and 2) intense motion artifact noise. The ECG record #203 m of MITDB contains QRS-complexes of five different morphologies (normal, aberrated APC, PVC, fusion PVC) and of five different rhythms (normal sinus rhythm, atrial flutter, atrial fibrillation, ventricular trigeminy and ventricular tachycardia) (MIT-BIH Arrhythmia Database Directory, 2022). Such a combination intricates the task of interpretation of an ECG signal even for the cardiologists. On the other hand, the proposed algorithm detects 11 non-QRS-complexes in the ECG record #222. In this ECG record the QRS-complexes are annotated as atrial flutter. A few of those atrial flutters are detected as QRS-complexes. Figures 8–10 show the detected QRS-complexes, APC and PVC beats of the ECG signals of different databases. These figures portray the efficiency of the proposed algorithm in detection the QRS-complexes of different morphologies even in the presence of motion artifact noise.

FIGURE 8

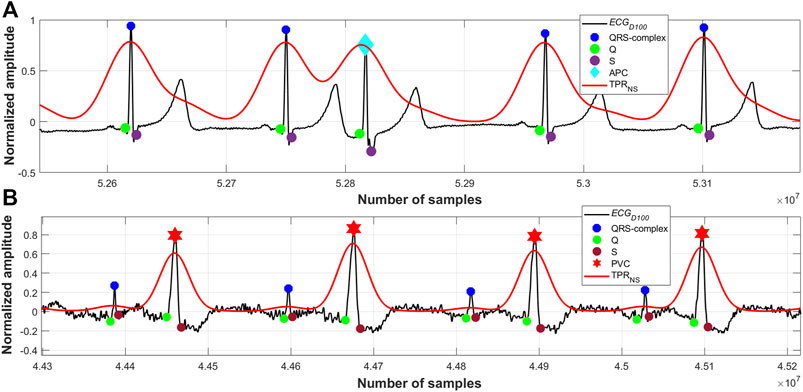
FIGURE 8. (A) Detected QRS-complexes and APC beats; record #113m, MITDB, (B) detected QRS-complexes and PVC beats; record #228m, MITDB.

Run-time of an algorithm is a function of the size of the input data file, and it is an important figure of merit. Run-time is used to measure the time complexity of an algorithm. Run-time of the proposed algorithm as a function of the length of the signal at different sampling rates are evaluated and shown in Figure 11. From this figure it is to be noted that the time complexity of the proposed algorithm varies almost linearly with the length of the signal and sampling rate. The proposed algorithm is primarily implemented on software platform, and hence, the space complexity and the power requirement are not considered in this research. However, the run-time of proposed algorithm can further be reduced by efficient code-optimization and implementation.

5 Performance Comparison

The performance of the proposed RFB-based QRS-complex detection algorithm on MITDB is compared with that of state-of-the-algorithms in Table 6. The numerical results of the other algorithms are collected from the respective articles.

TABLE 6

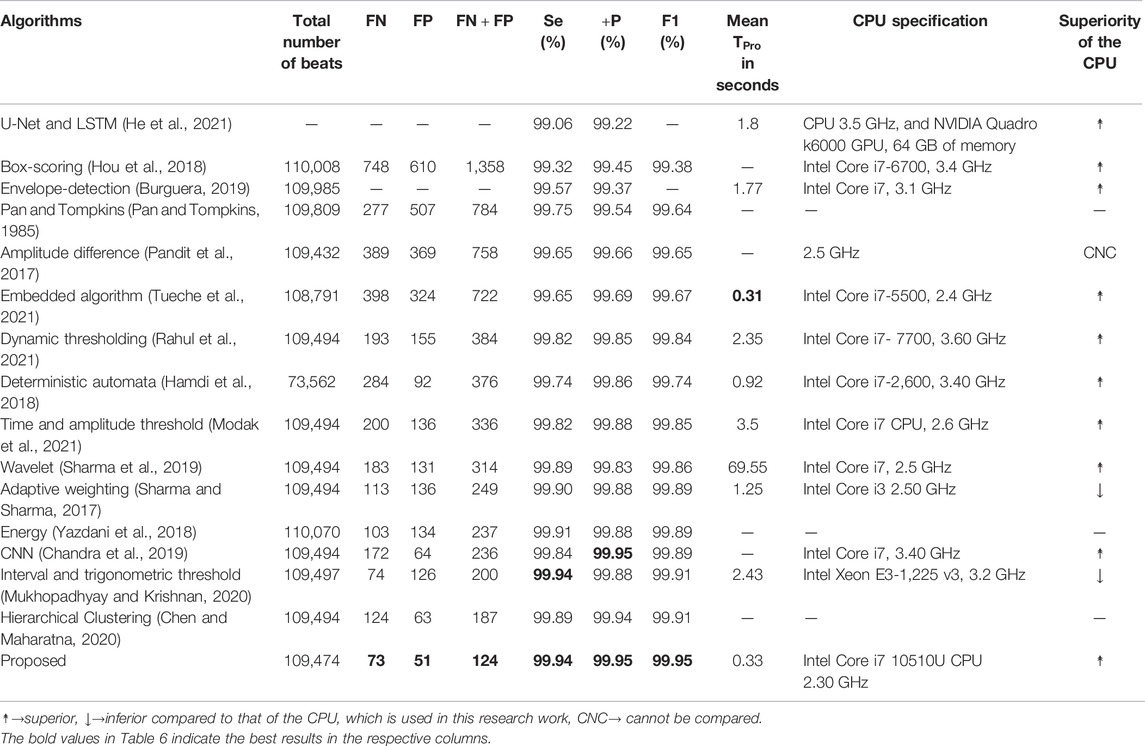
TABLE 6. Performance comparison of the proposed algorithm with a few other recently developed algorithms on MITDB.

Before going into a detail comparison, it is good to mention that the performance of all the algorithms, which are included in Table 6, are remarkably high. The $Se(\%)$, $+P(\%)$ and $F1$ score (except in (He et al., 2021) and (Burguera, 2019)) of all the algorithms are above 99%. However, there are a few more statistical parameters or figures-of-merit, which are also to be taken into consideration such as $FN$, $FP$ and the run-time $T_{Pro}$. Undoubtedly, the value of $T_{Pro}$ depends on the configuration of the system the algorithm is being tested on, and therefore, two additional columns, namely, the CPU specification and the superiority of the CPU, have been included in Table 6 so as to justify the comparison.

The $Se$ values of (Mukhopadhyay and Krishnan, 2020) and the proposed algorithm are identical, but the $+P$ and $F1$ score values of the proposed algorithm are better than that of (Mukhopadhyay and Krishnan, 2020). A direct comparison of $T_{Pro}$ between the proposed one and (Mukhopadhyay and Krishnan, 2020) is not possible as the system-configurations are different. In order to make a fair comparison, the algorithm which is proposed in (Mukhopadhyay and Krishnan, 2020) is run on the same CPU, which is used in this research. It has been found that the mean $T_{Pro}$ of (Mukhopadhyay and Krishnan, 2020) on MITDB is 0.72 s, when run on the same CPU which is used in this research. It suggests that the proposed algorithm is about 2.18 times faster than (Mukhopadhyay and Krishnan, 2020).

As the number of $FP$ detection of the proposed algorithm and (Chandra et al., 2019) are low; 51 and 64, respectively, the $+P$ values of both the algorithms are identical (99.95%). However, the number of $FN$ detection of (Chandra et al., 2019) is about 2.36 times high than that of the proposed one. The run-time of the algorithm is not mentioned.

The number of $FN$ and $FP$ detections of the tunable-Q wavelet transform-based technique (Sharma et al., 2019) are about 2.51 and 2.57 times, respectively, higher than that of the proposed algorithm. Even though, both the proposed algorithm and (Sharma et al., 2019) are implemented on Intel Core i7 processors, the proposed algorithm is about 210.76 times faster than that of (Sharma et al., 2019).

The number of $FN$ and $FP$ detections of the U-Net and LSTM-based QRS-complex detection algorithm are not mentioned in (He et al., 2021). The algorithm (He et al., 2021) is implemented on GPU-based system as it requires an intense training operation. Nonetheless, the proposed algorithm is about 5.45 times faster than that of (He et al., 2021).

In Table 6, seven metrics ($FN, FP$, $FN+FP$, $Se$, $+P$, $F1$ and $T_{Pro}$) are considered to compare the performance of the proposed RFB-based QRS-complex detection technique with that of the others on MITDB. It can be seen from Table 6 that the proposed algorithm: 1) solely holds the best results for four metrics ($FN, FP$, $FN+FP$ and $F1$), and 2) jointly holds the best results for two metrics ($Se$ and $+P$).

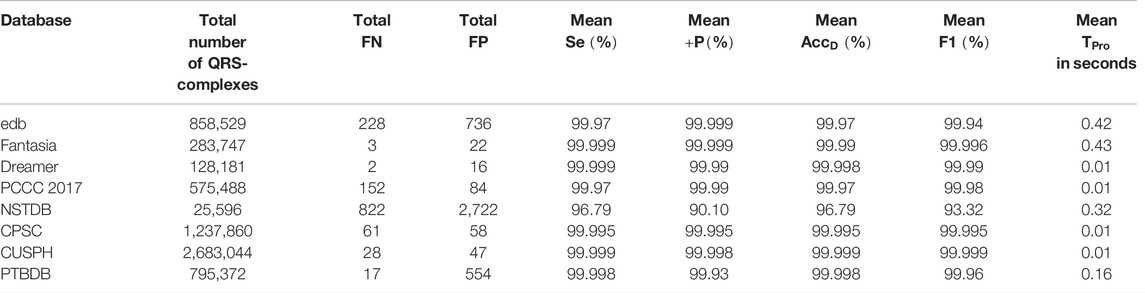
Now, the QRS-complex detection performance of the proposed RFB-based algorithm on other ECG databases is summarized and compared with a few recently developed algorithms in Table 7. It can be seen that the proposed algorithm performs equally well on other ECG datasets.

TABLE 7

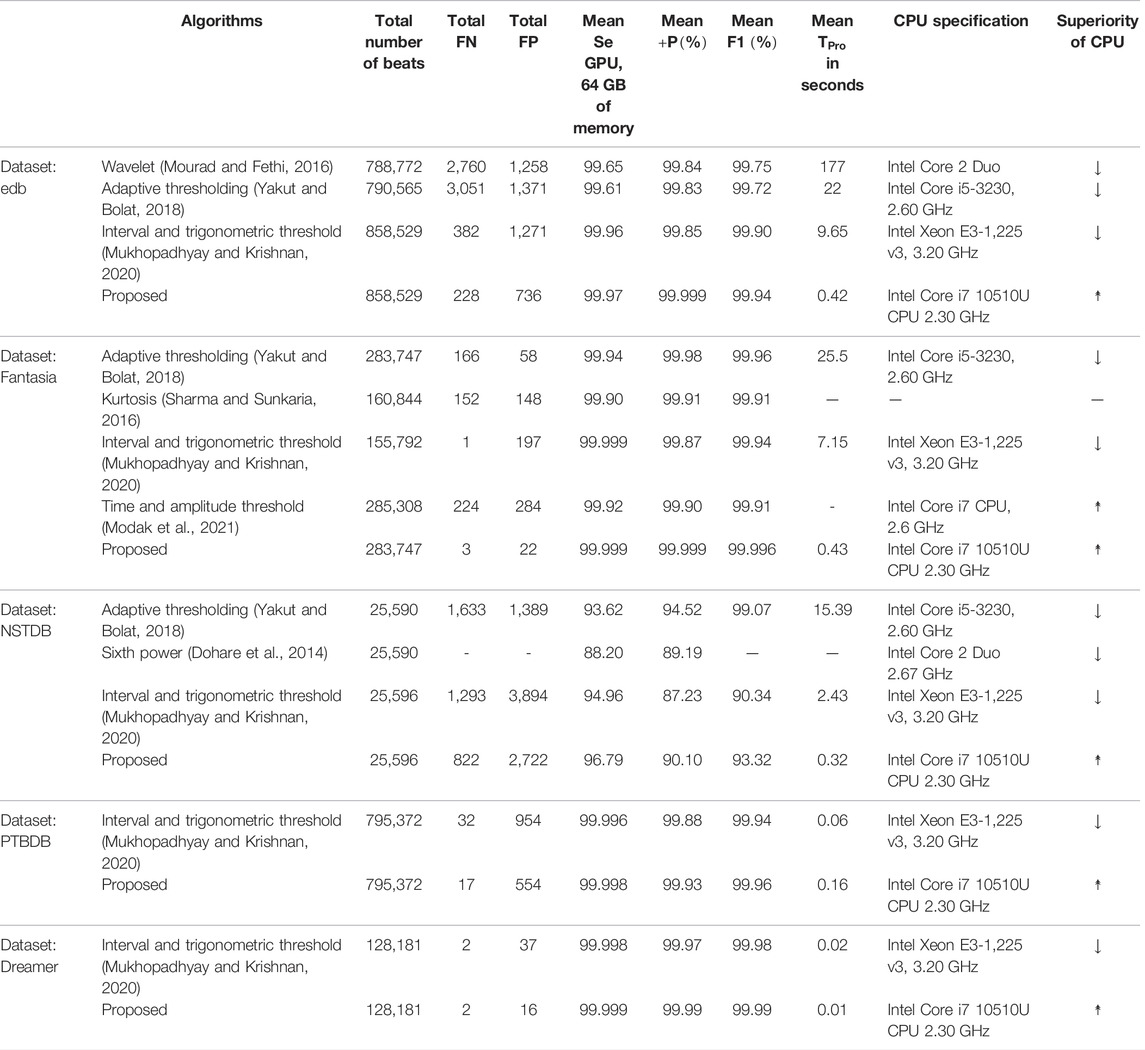
TABLE 7. Performance comparison of the proposed algorithm with a few other recently developed algorithms on non-MITDB ECG databases.

6 Limitation and Future Direction

It has been observed that sometimes the proposed algorithm fails to detect a few of the QRS-complexes following a large motion artefact noise when the amplitude of the noise is found to be around 10 times or more than that of the QRS amplitude. However, this limitation could be overcome by clipping the amplitude of such noises to a suitable level at the preprocessing stage. From Figure 9B it can also be seen that some of the noise-peaks of very low amplitude values have been wrongly detected by the algorithm as R-peaks. A suitably chosen threshold value could be applied on the $TP{R}_{NS}$ data at the time of detection of the QRS-complexes in order to eliminate these noise-peaks. In our future research we will explore the likelihood of detection of other arrhythmic QRS-complexes using their periodic and aperiodic traits. We will also extend the research work in 1) detecting the p and T waves using their corresponding time-period representations, and 2) processing other periodic/quasi-periodic biomedical signals such as photoplethysmogram, in our future research.

FIGURE 9

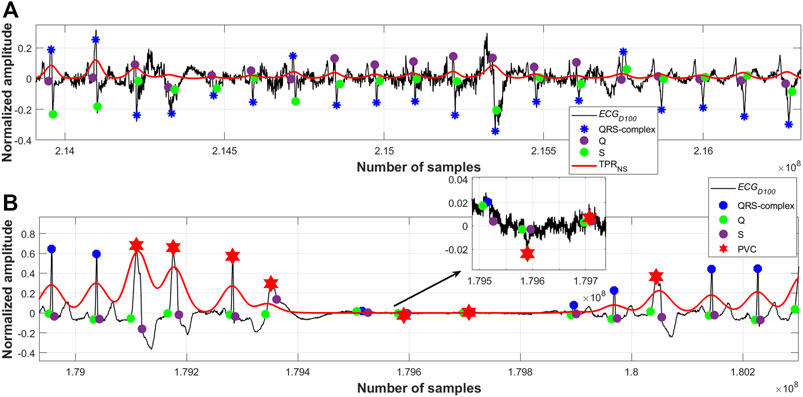
FIGURE 9. (A) Detected QRS-complexes; record #108m, MITDB, (B) detected QRS-complexes and PVC beats; record #208m, MITDB.

7 Conclusion and Discussion

A robust, reliable, fast and high-performance QRS-complex detection algorithm is proposed in this paper. It is worth mentioning that Ramanujan filter bank (RFB) is used in this research work for the detection of the QRS-complexes in ECG signals for the first time, to the best of our knowledge. The advantages of using RFB in detecting the QRS-complexes are multifold. First, the number of required filters in the bank and hence the filter-coefficients depends on the periodic property of the QRS-complexes. Since the periodic property of the QRS-complexes are well defined in the domain of cardio physiology, the required number of filters can easily be derived from the domain knowledge. In this research work it has been found that 1) the number of filters, which is equal to the sampling frequency times the half of the QRS duration; as defined in Eq. 6, and 2) the length of the average filter of unit 6; as described in Section 3.2, best suit in detecting the QRS-complexes in ECG signals. Therefore, the task of normalization of the sampling frequency, which is a prime prerequisite in many of the QRS-complex detection algorithms, could be avoided. Second, as described in Section 3.2, the main mathematical computation that is required to perform is the linear convolution operation only, and therefore the use of a mathematically as well as computationally intricated transformation technique could be avoided. Third, the runtime of the proposed algorithm is incredibly low. Fourth, the effect of the motion artifact types of noises on RFB is extremely low. Many of the QRS-complex detection algorithms detects the high amplitude motion artifact types of noises as the plausible QRS-complexes. This is because of the fact that both the frequency spectra and amplitude of the motion artifact noise and QRS-complex overlap. However, a motion artifact noise is not periodic in nature, and its periodic property does not match with that of the QRS-complexes. This is the main reason for what the false positive detection rate of the proposed algorithm low.

As per the cardio physiologic definition, the heights, frequencies, widths and also the periodicities of different arrhythmic QRS-complexes are different. Figures 7–10 manifest and corroborate this notion. A time-period representation clearly portrays and segregates a normal, premature ventricular contraction and atrial premature contraction QRS-complexes with their corresponding unique periodic patterns. In this research work, alongside detecting the normal QRS-complexes, two types of arrhythmic QRS-complexes (premature ventricular contraction and atrial premature contraction) are identified using a period-thresholding-based technique, and this has been done without the intervention of any ad hoc arrhythmic QRS-complex detection technique.

FIGURE 10

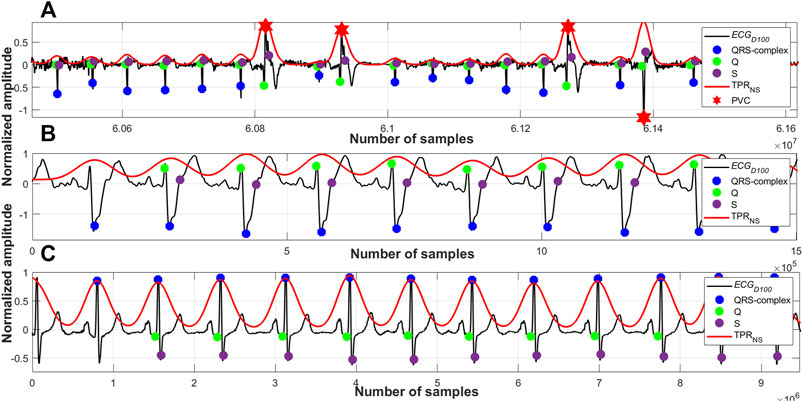
FIGURE 10. (A) Detected QRS-complexes and PVC beats; record #e0107m, edb, (B) detected QRS-complexes; record #A0001m, CPSC, (C) detected QRS-complexes; record #s0301lrem, PTBDB.

FIGURE 11

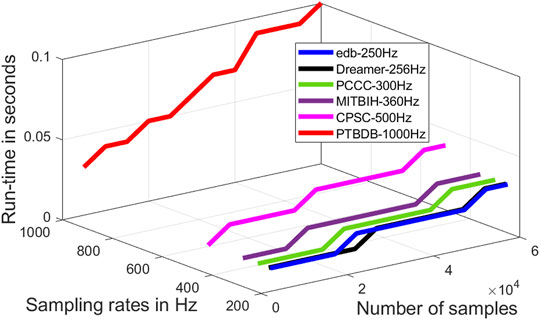
FIGURE 11. Run-time of the proposed algorithm as a function of the number of samples and sampling rates.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://physionet.org/about/database/.

Author Contributions

Both the authors; SM and SK, have equal contribution in this proposed research work and also in writing the paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank the funding provided by the Natural Sciences and Engineering Research Council (NSERC) Discovery Grant program of Canada.

References

AF Classification from a Short Single Lead Ecg Recording (2022). AF Classification from a Short Single Lead ECG Recording - the PhysioNet Computing in Cardiology Challenge 2017 v1.0.0. [Online]. Available at: https://physionet.org/content/challenge-2017/1.0.0/(Accessed April, 2022).

Google Scholar

Berkayaa, S. K., Uysal, A. K., Gunal, E. S., Erginc, S., Gunal, S., and Gulmezoglu, M. B. (2018). A Survey on ECG Analysis. Biomed. Signal Process. Control 43 (5), 216–235.

Google Scholar

Burguera, A. (2019). Fast QRS Detection and ECG Compression Based on Signal Structural Analysis. IEEE J. Biomed. Health Inf. 23 (1), 123–131. doi:10.1109/jbhi.2018.2792404

PubMed Abstract | CrossRef Full Text | Google Scholar

Centers for Disease Control and Prevention (2022). Centers for Disease Control and Prevention. [Online]. Available at: https://www.cdc.gov/nchs/fastats/leading-causes-of-death.htm (Accessed April, 2022).

Google Scholar

Chandra, B. S., Sastry, C. S., and Jana, S. (2019). Robust Heartbeat Detection from Multimodal Data via CNN-Based Generalizable Information Fusion. IEEE Trans. Biomed. Eng. 66 (3), 710–717. doi:10.1109/tbme.2018.2854899

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, G., Krishnan, S., and Bui, T. D. (2013). Matrix-Based Ramanujan-Sums Transforms. IEEE Signal Process. Lett. 20 (10), 941–944. doi:10.1109/lsp.2013.2273973

CrossRef Full Text | Google Scholar

Chen, H., and Maharatna, K. (2020). An Automatic R and T Peak Detection Method Based on the Combination of Hierarchical Clustering and Discrete Wavelet Transform. IEEE J. Biomed. Health Inf. 24 (10), 2825–2832. doi:10.1109/jbhi.2020.2973982

PubMed Abstract | CrossRef Full Text | Google Scholar

Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C. (2009). Introduction to Algorithms. Third edition July. Cambridge, MA, USA: The MIT Press.

Google Scholar

Dohare, A. K., Kumar, V., and Kumar, R. (2014). An Efficient New Method for the Detection of QRS in Electrocardiogram. Comput. Electr. Eng. 40 (5), 1717–1730. doi:10.1016/j.compeleceng.2013.11.004

CrossRef Full Text | Google Scholar

Goldberger, A. L. (2006). Clinical Electrocardiography, a Simplified Approach. 7th ed. Amsterdam, Netherlands: Elsevier.

Google Scholar

Goovaerts, G., Padhy, S., Vandenberk, B., Varon, C., Willems, R., and Van Huffel, S. (2019). A Machine-Learning Approach for Detection and Quantification of QRS Fragmentation. IEEE J. Biomed. Health Inf. 23 (5), 1980–1989. doi:10.1109/JBHI.2018.2878492

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamdi, S., Abdallah, A. B., and Bedoui, M. H. (2018). A Robust QRS Complex Detection Using Regular Grammar and Deterministic Automata. Biomed. Signal Process. Control 40 (2), 263–274. doi:10.1016/j.bspc.2017.09.032

CrossRef Full Text | Google Scholar

He, R., Liu, Y., Wang, K., Zhao, N., Yuan, Y., Li, Q., et al. (2021). Automatic Detection of QRS Complexes Using Dual Channels Based on U-Net and Bidirectional Long Short-Term Memory. IEEE J. Biomed. Health Inf. 25 (4), 1052–1061. doi:10.1109/jbhi.2020.3018563

CrossRef Full Text | Google Scholar

Hong, S., Zhou, Y., Shang, J., Xiao, C., and Sun, J. (2020). Opportunities and Challenges of Deep Learning Methods for Electrocardiogram Data: A Systematic Review. Comput. Biol. Med. 122 (7), 103801–103814. doi:10.1016/j.compbiomed.2020.103801

PubMed Abstract | CrossRef Full Text | Google Scholar

Hossain, M. B., Bashar, S. K., Walkey, A. J., McManus, D. D., and Chon, K. H. (2019). An Accurate QRS Complex and P Wave Detection in ECG Signals Using Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Approach. IEEE Access 7, 128869–128880. doi:10.1109/access.2019.2939943

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, Z., Dong, Y., Xiang, J., Li, X., and Yang, B. (2018). A Real-Time QRS Detection Method Based on Phase Portraits and Box-Scoring Calculation. IEEE Sensors J. 18 (9), 3694–3702. doi:10.1109/jsen.2018.2812792

CrossRef Full Text | Google Scholar

Jia, M., Li, F., Wu, J., Chen, Z., and Pu, Y. (2020). Robust QRS Detection Using High-Resolution Wavelet Packet Decomposition and Time-Attention Convolutional Neural Network. IEEE Access 8, 16979–16988.

CrossRef Full Text | Google Scholar

Jorge, R. R., Damas, I. D. L., Bila, J., and Škvor, J. (2021). Internet of Things-Assisted Architecture for QRS Complex Detection in Real Time. Internet Things 14 (2), 1–15. doi:10.1016/j.iot.2021.100395

CrossRef Full Text | Google Scholar

Katsigiannis, S., and Ramzan, N. (2018). DREAMER: A Database for Emotion Recognition through EEG and ECG Signals from Wireless Low-Cost Off-The-Shelf Devices. IEEE J. Biomed. Health Inf. 22 (1), 98–107. doi:10.1109/jbhi.2017.2688239

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, F., Liu, C., Zhao, L., Zhang, X., Wu, X., Xu, X., et al. (2018). An Open Access Database for Evaluating the Algorithms of Electrocardiogram Rhythm and Morphology Abnormality Detection. J. Med. imaging hlth Inf. 8 (7), 1368–1373. doi:10.1166/jmihi.2018.2442

CrossRef Full Text | Google Scholar

Mainardi, L., Bertinelli, M., and Sassi, R. (2008). Analysis of T-Wave Alternans Using the Ramanujan Transform. Comput. Cardiol. 14-17, 605–608. doi:10.1109/cic.2008.4749114

CrossRef Full Text | Google Scholar

Mainardi, L. T., Pattini, L., and Cerutti, S. (2007). Application of the Ramanujan Fourier Transform for the Analysis of Secondary Structure Content in Amino Acid Sequences. Methods Inf. Med. 46 (2), 126–129.

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehta, S. S., and Lingayat, N. S. (2008). SVM-based Algorithm for Recognition of QRS Complexes in Electrocardiogram. IRBM 29 (5), 310–317. doi:10.1016/j.rbmret.2008.03.006

CrossRef Full Text | Google Scholar

Merino, M., Gómez, I. M., and Molina, A. J. (2015). Envelopment Filter and K-Means for the Detection of QRS Waveforms in Electrocardiogram. Med. Eng. Phys. 37 (6), 605–609. doi:10.1016/j.medengphy.2015.03.019

PubMed Abstract | CrossRef Full Text | Google Scholar

MIT-BIH Arrhythmia Database Directory (2022). MIT-BIH Arrhythmia Database Directory. [Online]. Available at: https://archive.physionet.org/physiobank/database/html/mitdbdir/records.htm#203 (Accessed April, 2022).

Google Scholar

Modak, S., Taha, L. Y., and Abdel-Raheem, E. (2021). A Novel Method of QRS Detection Using Time and Amplitude Thresholds with Statistical False Peak Elimination. IEEE Access 9, 46079–46092. doi:10.1109/access.2021.3067179

CrossRef Full Text | Google Scholar

Morshedlou, F., Ravanshad, N., and Dehsorkh, H. R. (2021). An Ultra-low Power Analog QRS-Detection Circuit for Ambulatory ECG Monitoring. Int. J. Electron. Commun. 129 (2), 1–11. doi:10.1016/j.aeue.2020.153551

CrossRef Full Text | Google Scholar

Mourad, K., and Fethi, B. R. (2016). Efficient Automatic Detection of QRS Complexes in ECG Signal Based on Reverse Biorthogonal Wavelet Decomposition and Nonlinear Filtering. Measurement 94 (18), 663–670. doi:10.1016/j.measurement.2016.09.014

CrossRef Full Text | Google Scholar

Mukhopadhyay, S. K., and Krishnan, S. (2020). Robust Identification of QRS-Complexes in Electrocardiogram Signals Using a Combination of Interval and Trigonometric Threshold Values. Biomed. Signal Process. Control 61 (7), 1–12. doi:10.1016/j.bspc.2020.102007

CrossRef Full Text | Google Scholar

Pan, J., and Tompkins, W. J. (1985). A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. BME-32 (3), 230–236. doi:10.1109/tbme.1985.325532

PubMed Abstract | CrossRef Full Text | Google Scholar

Pandit, D., Zhang, L., Liu, C., Chattopadhyay, S., Aslam, N., and Lim, C. P. (2017). A Lightweight QRS Detector for Single Lead ECG Signals Using a Max-Min Difference Algorithm. Comput. Methods Programs Biomed. 144 (7), 61–75. doi:10.1016/j.cmpb.2017.02.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Pei, S.-C., and Chang, K.-W. (2017). Two-Dimensional Period Estimation by Ramanujan's Sum. IEEE Trans. Signal Process. 65 (19), 5108–5120. doi:10.1109/tsp.2017.2726986

CrossRef Full Text | Google Scholar

Physionet (2022). Physionet. [Online]. Available at: https://physionet.org/about/database/(Accessed April, 2022).

Google Scholar

Pipberger, H. V., Arms, R. J., and Stallmann, F. W. (1961). Automatic Screening of Normal and Abnormal Electrocardiograms by Means of a Digital Electronic Computer. Exp. Biol. Med. 106 (1), 130–132. doi:10.3181/00379727-106-26260

CrossRef Full Text | Google Scholar

Rahul, J., Sora, M., and Sharma, L. D. (2021). Dynamic Thresholding Based Efficient QRS Complex Detection with Low Computational Overhead. Biomed. Signal Process. Control 67 (5), 1–16. doi:10.1016/j.bspc.2021.102519

CrossRef Full Text | Google Scholar

Ramanujan, S. (1918). On Certain Trigonometrical Sums and Their Applications in the Theory of Numbers. Trans. Camb. Philosophical Soc. 22 (13), 259–276.

Google Scholar

Saatci, E., and Saatci, E. (2020). Period Determination in Cyclo-Stationary Signals by Autocorrelation and Ramanujan Subspaces. IEEE Signal Process. Lett. 27, 266–270. doi:10.1109/lsp.2020.2966877

CrossRef Full Text | Google Scholar

Sharma, A., Patidar, S., Upadhyay, A., and Rajendra Acharya, U. (2019). Accurate Tunable-Q Wavelet Transform Based Method for QRS Complex Detection. Comput. Electr. Eng. 75 (3), 101–111. doi:10.1016/j.compeleceng.2019.01.025

CrossRef Full Text | Google Scholar

Sharma, L. D., and Sunkaria, R. K. (2016). A Robust QRS Detection Using Novel Pre-processing Techniques and Kurtosis Based Enhanced Efficiency. Measurement 87 (11), 194–204. doi:10.1016/j.measurement.2016.03.015

CrossRef Full Text | Google Scholar

Sharma, T., and Sharma, K. K. (2017). QRS Complex Detection in ECG Signals Using Locally Adaptive Weighted Total Variation Denoising. Comput. Biol. Med. 87 (8), 187–199. doi:10.1016/j.compbiomed.2017.05.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, P., Joshi, S. D., Patney, R. K., and Saha, K. (2017). The Fourier Decomposition Method for Nonlinear and Non-stationary Time Series Analysis. Proc. Math. Phys. Eng. Sci. 473 (2199), 20160871. doi:10.1098/rspa.2016.0871

PubMed Abstract | CrossRef Full Text | Google Scholar

Singhal, A., Singh, P., Fatimah, B., and Pachori, R. B. (2020). An Efficient Removal of Power-Line Interference and Baseline Wander from ECG Signals by Employing Fourier Decomposition Technique. Biomed. Signal Process. Control 57 (3), 1–8. doi:10.1016/j.bspc.2019.101741

CrossRef Full Text | Google Scholar

Sugavaneswaran, L., Xie, S., Umapathy, K., and Krishnan, S. (2012). Time-Frequency Analysis via Ramanujan Sums. IEEE Signal Process. Lett. 19 (6), 352–355. doi:10.1109/lsp.2012.2194142

CrossRef Full Text | Google Scholar

Tenneti, S. V. (2018). The Nested Periodic Subspaces: Extensions of Ramanujan Sums for Period Estimation. Ph.D. dissertation (Pasadena, California: Dept. of Electrical Engineering, California Institute of Technology). doi:10.7907/1n4t-5876

CrossRef Full Text

Tenneti, S. V., and Vaidyanathan, P. P. (2015). Nested Periodic Matrices and Dictionaries: New Signal Representations for Period Estimation. IEEE Trans. Signal Process. 63 (14), 3736–3750. doi:10.1109/tsp.2015.2434318

CrossRef Full Text | Google Scholar

Tenneti, S. V., and Vaidyanathan, P. P. (2015). “Ramanujan Filter Banks for Estimation and Tracking of Periodicities,” in IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19-24 April 2015, 3851–3855. doi:10.1109/icassp.2015.7178692

CrossRef Full Text | Google Scholar

Tompkins, W. J. (1993). Biomedical Digital Signal Processing. New Jersey, USA: Prentice-Hall.

Google Scholar

Trevethan, R. (2017). Sensitivity, Specificity, and Predictive Values: Foundations, Pliabilities, and Pitfalls in Research and Practice. Front. Public Health 5, 307–7. doi:10.3389/fpubh.2017.00307

PubMed Abstract | CrossRef Full Text | Google Scholar

Tueche, F., Mohamadou, Y., Djeukam, A., Kouekeu, L. C. N., Seujip, R., and Tonka, M. (2021). Embedded Algorithm for QRS Detection Based on Signal Shape. IEEE Trans. Instrum. Meas. 70, 1–12. doi:10.1109/tim.2021.3051412

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaidyanathan, P. P., and Tenneti, S. V. (2015). “Properties of Ramanujan Filter Banks,” in 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 Aug.- 4 Sept. 2015, 2816–2820. doi:10.1109/eusipco.2015.7362898

CrossRef Full Text | Google Scholar

Yadav, D. K., Kuldeep, G., and Joshi, S. D. (2018). Orthogonal Ramanujan Sums, its Properties, and Applications in Multiresolution Analysis. IEEE Trans. Signal Process. 66 (21), 5789–5798. doi:10.1109/tsp.2018.2871384

CrossRef Full Text | Google Scholar

Yakut, Ö., and Bolat, E. D. (2018). An Improved QRS Complex Detection Method Having Low Computational Load. Biomed. Signal Process. Control 42 (4), 230–241. doi:10.1016/j.bspc.2018.02.004

CrossRef Full Text | Google Scholar

Yazdani, S., Fallet, S., and Vesin, J.-M. (2018). A Novel Short-Term Event Extraction Algorithm for Biomedical Signals. IEEE Trans. Biomed. Eng. 65 (4), 754–762. doi:10.1109/tbme.2017.2718179

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuen, S. K. (1976). Cardalert: A Portable, Battery-Operated, Real-Time Arrhythmia Detector and Alarm System. Ph.D. dissertation (Champaign, IL, USA: Dept. of Computer Science, University of Illinois at Urbana-Champaign).

Zhang, Z., Yu, Q., Zhang, Q., Ning, N., and Li, J. (2020). A Kalman Filtering Based Adaptive Threshold Algorithm for QRS Complex Detection. Biomed. Signal Process. Control 58 (4), 1–8. doi:10.1016/j.bspc.2019.101827

CrossRef Full Text | Google Scholar

Zheng, J., Zhang, J., Danioko, S., Yao, H., Guo, H., and Rakovski, C. (2020). A 12-lead Electrocardiogram Database for Arrhythmia Research Covering More Than 10,000 Patients. Sci. Data 7, 48–8. doi:10.1038/s41597-020-0386-x

PubMed Abstract | CrossRef Full Text | Google Scholar