Depth Map Super-Resolution via Cascaded Transformers Guidance

Depth information captured by affordable depth sensors is characterized by low spatial resolution, which limits potential applications. Several methods have recently been proposed for guided super-resolution of depth maps using convolutional neural networks to overcome this limitation. In a guided super-resolution scheme, high-resolution depth maps are inferred from low-resolution ones with the additional guidance of a corresponding high-resolution intensity image. However, these methods are still prone to texture copying issues due to improper guidance by the intensity image. We propose a multi-scale residual deep network for depth map super-resolution. A cascaded transformer module incorporates high-resolution structural information from the intensity image into the depth upsampling process. The proposed cascaded transformer module achieves linear complexity in image resolution, making it applicable to high-resolution images. Extensive experiments demonstrate that the proposed method outperforms state-of-the-art techniques for guided depth super-resolution.

1 Introduction

Depth information of a scene is crucial in many computer vision applications such as 3D reconstruction (Izadi et al., 2011), driving assistance (Schamm et al., 2009), and augmented reality. Recently, many low-cost consumer depth cameras were introduced, facilitating the use of depth information in various day-to-day scenarios. However, these low-cost sensors often suffer from low spatial resolution, limiting their potential applications. To facilitate such sensors, the depth information usually needs to undergo an upsampling process in which the corresponding high-resolution (HR) depth map is recovered from its low-resolution (LR) counterpart.

The upsampling of depth information is not a trivial task since the fine details in the HR depth map are often missing or severely distorted in the LR depth map, because of the sensor’s limited spatial resolution. Moreover, there often exists an inherent ambiguity in super-resolving the distorted fine details. A naive upsampling of the LR image, e.g., bicubic interpolation, usually produces unsatisfactory results with blurred and unsharp edges. Therefore, numerous advanced methods have been proposed recently for the upsampling, commonly termed super-resolution (SR), of depth information.

Current methods for SR of depth maps can be generally categorized as filter-based methods (Yang et al., 2007; He et al., 2012), energy minimization based methods (Ferstl et al., 2013; Yang et al., 2014; Jiang et al., 2018) and learning-based methods, which rely heavily on the use of convolutional neural networks (CNN) (Riegler et al., 2016b; Hui et al., 2016; Guo et al., 2018; Song et al., 2018; Zuo et al., 2019a). Filter-based methods have a relatively low computational complexity but tend to introduce apparent artifacts in the resulting HR depth map. On the other hand, energy minimization methods often require cumbersome and time-consuming computations. They are heavily reliant on regularization from a statistic or prior that is unavailable for some scenarios. Finally, learning-based methods have blossomed in recent years, and they now provide the best performances in terms of the quality of the upsampled depth map.

In many cases, an LR depth map is accompanied by a corresponding HR intensity image. Many of the more recent methods propose to use this additional image to guide or enhance the SR of the depth map (Park et al., 2011; Kiechle et al., 2013; Kwon et al., 2015; Hui et al., 2016; Guo et al., 2018; Zuo et al., 2019a; Lutio et al., 2019; Li et al., 2020; Ye et al., 2020; Cui et al., 2021; Kim et al., 2021; Zhao et al., 2021). These methods assume that correspondence can be established between an edge in the intensity image and the matching edge in the depth map. Then, given that the intensity image has a higher resolution, its edges can determine depth discontinuities in the super-resolved HR depth map. However, there could be cases in which an edge in the intensity image does not correspond to a depth discontinuity in the depth map or vice versa, e.g., in the case of smooth, highly textured surfaces in the intensity image. These cases lead to texture copying, where color textures are over-transferred to the super-resolved depth map at the boundaries between textured and homogeneous regions. Hence, a more sophisticated guidance scheme needs to be considered.

In this paper, to alleviate the texture copying problem, we propose a Cascaded Transformer Guidance Module (CTGM) for guided depth map SR. Transformers, designed initially for sequence modeling tasks (Vaswani et al., 2017), are notable for their use of attention to model long-range dependencies in the data. Recently, transformers were successfully adapted to computer vision tasks with promising results. Our proposed CTGM is constructed by stacking several transformer blocks, each operating locally within non-overlapping windows that partition the entire input. Window shift is introduced between consecutive transformer blocks to enable inter-window connections to be learned. The CTGM is fed with HR features extracted from the intensity image and is trained to pass only salient and consistent features that are then incorporated into the depth upsampling process. Our proposed CTGM is capable of learning structural and content information from a large receptive field, which was shown to be beneficial for SR tasks (Zhang et al., 2017).

Our overall architecture can be divided into three main parts: a depth branch, an intensity branch, and the CTGM. The proposed depth branch comprises several Residual Dilated Groups (RDG) (Zhang et al., 2018a), and performs the upsampling of the given LR depth map in a multi-scale manner, as in, e.g., Hui et al. (2016). Meanwhile, the intensity image is fed into the intensity branch, which extracts HR features and complements the LR depth structures in the depth branch via the CTGM. This process is repeated according to the desired upsampling factor. This closely guided multi-scale scheme allows the network to learn rich hierarchical features at different levels, and better adapt to the upsampling of both fine-grained and coarse patterns. Moreover, this enables the network to seamlessly utilize the guidance from HR intensity features in multiple scales. In Section 4 we show that our proposed method achieves results with sharper boundaries, more complete details, and better quantitative values in terms of Root Mean Square Error (RMSE) compared to competing guided SR approaches. Our proposed architecture is shown in Figure 1 for the case of an upsampling factor of 2.

FIGURE 1

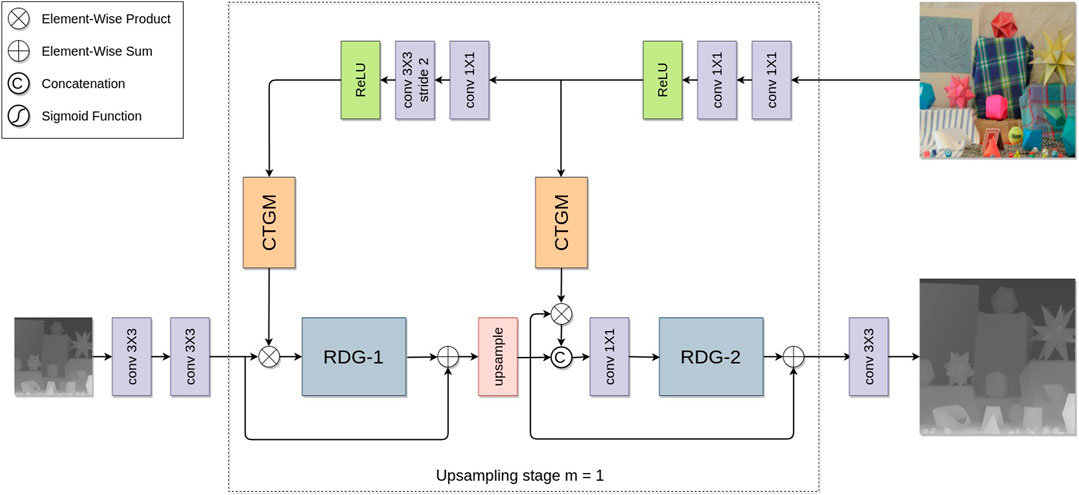
FIGURE 1. Our proposed architecture for guided depth SR for an upsampling factor of 2. The dashed square marks a single upsampling stage i that can be duplicated according to the desired upsampling factor s =2^m.

Our contributions are as follows: (1) We introduce a novel cascaded transformer-based mechanism to produce salient guidance features from the intensity branch. (2) Our proposed CTGM exhibits linear memory constraints, making it applicable even for very large images. (3) Unlike other transformer architectures, our architecture can handle different input resolutions, both during training and inference, making it highly applicable to real-world tasks. (4) We achieve the state of the art performance on several depth upsampling benchmarks.

The remainder of this paper is organized as follows. In Section 2, we present a brief overview of the related work. In Section 3, we present our proposed architecture for depth map SR in detail. In Section 4, we conduct extensive experiments and report our results. Also, an ablation study is performed. Finally, in Section 5, we conclude and discuss future research directions.

2 Related Work

Classic methods for depth map SR were inspired mainly by works from the related field of single color image SR. However, due to the limitation of single depth map SR, such methods usually work well only for small upsampling factors, e.g., 2 or 4. Guided depth map SR, on the other hand, is more robust even for more prominent upsampling factors, e.g., 8 or 16. This improved robustness is achieved by introducing guidance from cross domains, e.g., HR intensity image. A more detailed review of guided depth SR methods is given in the following subsections, emphasizing methods based on deep neural networks.

2.1 Single Depth Map Super Resolution

Earlier works for SR of depth maps, inspired by single image SR methods, mainly focused on filtering-based strategies. Mac Aodha et al. (2012) proposed that the matching HR depth candidate will be searched from a collected database for a given LR depth patch. Selecting the most probable candidate was then formulated as a Markov random field labeling problem. Hornacek et al. (2013) proposed to perform single depth map SR by exploring patch-wise scene self-similarity. Lei et al. (2017) proposed a view synthesis quality-based filtering, which jointly considers depth smoothness, texture similarity, and view synthesis quality.

Other works formulated depth map SR as a global optimization problem. Xie et al. (2015) offered an edge-guided depth map SR method, which applies Markov random field optimization to construct the HR edge map from the LR depth map. Later works considered dictionary learning strategies. Ferstl et al. (2015) used an external database to learn a dictionary of edge priors and then used the learned edge priors to guide the upsampling of an LR depth map in a variational sparse coding framework. Mandal et al. (2016) proposed an edge-preserving constraint to preserve the discontinuity in the depth map and a pyramidal reconstruction framework to better deal with higher scaling factors.

Later, Riegler et al. (2016b) proposed ATGV-Net, which combined a deep CNN with a variational method to recover an accurate HR depth map. Recently, Huang et al. (2019) proposed a pyramid-structured network composed of dense residual blocks that use densely connected layers and residual learning to model the mapping between high-frequency residuals and LR depth maps. A deep supervision scheme in which auxiliary losses were added at various scales within the network was utilized to reduce the difficulty of model training.

2.2 Intensity Guided Depth Map Super Resolution

Unlike an HR depth map, an HR intensity image can usually be easily acquired by color cameras. Thus, in many real-life scenarios, a corresponding intensity image can be used to guide the upsampling process or enhance the low-quality depth maps. Various methods have been proposed to improve the quality of depth maps by the guidance of the HR intensity image. These methods can be categorized as filtering-based methods (He et al., 2010; Liu et al., 2013; Lu and Forsyth, 2015), global optimization-based methods Dong et al. (2016); Ferstl et al. (2013); Ham et al. (2015a,b); Jiang et al. (2018); Liu et al. (2016); Park et al. (2014, 2011); Yang et al. (2012, 2014), sparse representation-based methods (Kiechle et al., 2013; Kwon et al., 2015) and deep learning-based methods (Riegler et al., 2016a; Hui et al., 2016; Zhou et al., 2017; Guo et al., 2018; Zuo et al., 2019a,b; Zhao et al., 2021; Lutio et al., 2019; Kim et al., 2021; Li et al., 2020; Ye et al., 2020; Cui et al., 2021), which are in the focus of this paper.

Liu et al. (2013) utilized geodesic distances to upsample an LR depth map with the guidance of a corresponding HR color image. Lu and Forsyth (2015) used the correlation between edges in a segmentation image and boundaries in depth images to produce detailed HR depth structures. Yang et al. (2012) formulated the depth recovery problem to minimize auto-regressive prediction errors. Ferstl et al. (2013) developed a convex optimization problem for depth image upsampling, which guides the depth upsampling by an anisotropic diffusion tensor calculated from an HR intensity image. Park et al. (2014) extended the non-local structure regularization by combining the additional HR color input when upsampling an LR depth map. Kiechle et al. (2013) introduced a bimodal co-sparse analysis to capture the inter-dependency of registered intensity and depth information. Kwon et al. (2015) proposed a data-driven method for depth map refinement through multi-scale dictionary learning, based on the assumption that a linear combination of basis functions can efficiently represent local patches in both depth and RGB images. Jiang et al. (2018) proposed a depth map SR method in which non-local correlations are exploited by an auto-regressive model in the frequency domain. A multi-directional total variation prior is used in the spatial domain to characterize the geometrical structures.

Inspired by the great success in the SR of color images, deep learning methods for depth map SR have recently attracted more and more attention. Riegler et al. (2016a) used a fully convolutional network to produce an initial estimation for the HR depth. This estimation, in turn, was fed into a non-local variational model to optimize the final result. Hui et al. (2016) proposed an “MSG-Net,” which infers the HR depth map from its LR counterpart in multiple stages, and uses a multi-scale fusion strategy to complement LR depth features with HR intensity features in the high-frequency domain. Zhou et al. (2017) concluded that color images are more helpful for the depth map SR problem when noise is present, and the scaling factor is large. Guo et al. (2018) proposed exploiting multiple level receptive fields by constructing an input pyramid and extracting hierarchical features from the depth map and intensity image. These features are then concatenated, and the residual map between the interpolated depth map and the corresponding HR one is learned via a residual U-Net architecture. Zuo et al. (2019a) proposed a multi-scale upsampling network in which intensity features guide the upsampling process in multiple stages, and both low and high-level features are taken into account in the reconstruction of HR depth maps thanks to local and global connections. Zuo et al. (2019b) proposed another multi-scale network with global and local residual learning. The LR depth map is progressively upsampled, guided by the HR intensity image in multiple scales. Moreover, batch normalization layers were used to improve the performance of depth map denoising. Zhao et al. (2021) proposed to use a discrete cosine transform network in which pairs of color/depth images are fed into the semi-coupled feature extraction module to extract common and unique features from both modalities. The color features are then passed through an edge attention mechanism to highlight the edges useful for upsampling. Finally, a discrete cosine transform was employed to solve the SR optimization problem. Lutio et al. (2019) proposed to find a transformation from the guide image to the target HR depth map, which can be regarded as a pixel-wise translation. Kim et al. (2021) proposed to use deformable convolutions (Dai et al., 2017) for the upsampling of depth maps, where the spatial offsets for convolution are learned from the features of the given HR guidance image. Li et al. (2020) proposed a recumbent Y network for depth map SR. They built the network based on residual channel attention blocks and utilized spatial attention-based feature fusion blocks to suppress the artifacts of texture copying and depth bleeding. Ye et al. (2020) proposed a progressive multi-branch aggregation network by using the multi-branch fusion method to gradually restore the degraded depth map. Cui et al. (2021) proposed an architecture built on two U-Net branches for HR color images and LR depth maps. This architecture uses a dual skip connection structure to leverage the feature interaction of the two branches and a multi-scale fusion to fuse the deeper and multi-scale features of two branch decoders for more effective feature reconstruction.

However, the methods above still use simple schemes such as concatenation to fuse the guidance features extracted from the intensity image with the depth features. At the same time, we propose to use a CTGM, which directs the allocation of available processing resources towards the most informative components of the input, thus achieving superior results, as demonstrated in Section 4.

2.3 Vision Transformers

In recent years, transformer-based architectures (Vaswani et al., 2017) achieved great success in natural language processing tasks, enabling long-range dependencies in the data to be learned via their sophisticated attention mechanism. Their tremendous success in the language domain has led researchers to investigate their adaptation to computer vision, where it has recently demonstrated promising results on certain tasks, specifically image classification (Dosovitskiy et al., 2020; Liu et al., 2021; Wang et al., 2021) and object detection (Carion et al., 2020; Zhu et al., 2020).

A primary transformer encoder, as proposed in Vaswani et al. (2017), usually consists of alternating layers of multiheaded self-attention (MSA) and MLP blocks, with Layer Normalization (LN) before every block and residual connections after every block.

An MSA block takes as input a sequence of length N of d-dimensional embeddings $\mathbf{X}\in {\mathbb{R}}^{N\times d}$ and produces an output sequence $\mathbf{Y}\in {\mathbb{R}}^{N\times d}$ via:

$\begin{array}{cc}\hfill \mathbf{Q}& =\mathbf{X}{\mathbf{W}}_Q,\mathbf{K}=\mathbf{X}{\mathbf{W}}_K,\mathbf{V}=\mathbf{X}{\mathbf{W}}_V\hfill \\ \hfill \mathbf{A}& =\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathbf{Q}{\mathbf{K}}^T/\sqrt{\mathbf{d}}\right)\hfill \\ \hfill \mathbf{Y}& =\mathbf{A}\mathbf{V}\hfill \end{array}(1)$

where W_Q, W_K, and W_V are D × D parameter matrices of 1 × 1 convolutions responsible for projecting the entries of the sequence X into the three standard transformer paradigms; keys, queries, and values, respectively. Each entry of the output sequence Y is a linear combination of values in V weighted by the attention matrix A, which itself is computed from similarities between all pairs of query and key vectors.

The transformer’s expressive power comes from computing the self-attention A and Y. This computation, however, comes with a quadratic cost; it takes O(N²) time and space to compute the pairwise similarities between Q and K and to compute the linear combination of V vectors. This quadratic complexity makes it impractical to apply self-attention to images directly, as even for small images X quickly becomes too long a sequence for self-attention.

In light of this inherent limitation, efforts have been made to restrict these sequence lengths in a modality-aware manner while preserving modeling performance. The pioneering work of Dosovitskiy et al. (2020) proposed to directly apply a transformer architecture on non-overlapping medium-sized image patches for image classification. This local self-attention helps mitigate these memory constraints, as opposed to global self-attention.

3 Proposed Method

3.1 Formulation

A method for guided depth SR aims to find the nonlinear mapping between an LR depth map and the corresponding HR depth map. An HR intensity image guides the process of finding this nonlinear relation. For a given scaling factor s = 2^m we denote the LR depth map as ${\mathbf{D}}_{\text{LR}}\in {\mathbb{R}}^{H/s\times W/s}$ and the respective HR guidance intensity image as ${\mathbf{I}}_{\text{HR}}\in {\mathbb{R}}^{H\times W}$. Then, the corresponding HR depth map ${\mathbf{D}}_{\text{HR}}\in {\mathbb{R}}^{H\times W}$ can be found from:

${\mathbf{D}}_{\text{HR}}=\mathbf{F}\left({\mathbf{D}}_{\text{LR}},{\mathbf{I}}_{\text{HR}};\theta \right)(2)$

where F denotes the nonlinear mapping learned by our proposed architecture, and θ represents the learned network’s parameters. We note that in our proposed architecture, contrary to some other works, D_LR is upsampled in a multi-stage scheme of m stages. In each stage, D_LR is upsampled by a factor of two until it reaches the desired scaling factor s. We note that any upsampling stage m can also perform an upsampling by a factor of three. Thus the overall architecture is flexible enough for real applications and can be configured to achieve upsampling with scaling factors that are not the exponent of 2.

Throughout the section, we use Conv₃ (⋅) to denote a convolution layer with a kernel size of 3 × 3 and Conv₁ (⋅) to denote a convolution layer with a kernel size of 1 × 1.

3.2 Overall Network Architecture

As shown in Figure 1, our architecture mainly consists of three parts: intensity branch, depth branch, and CTGM, which provides guidance from the intensity branch to the depth branch. We now review the general structure of our depth and intensity branches, and more details of the proposed CTGM modules will be given in Section 3.3.

3.2.1 Intensity Branch

Our intensity branch consists of two primary modules; (1) a feature extraction module and (2) a downsampling module. These two basic modules are repeated in each upsampling stage i ∈ {1 … m}. The feature extraction module consists of two consecutive convolution layers with a kernel size of 1 × 1, followed by an element-wise rectified linear unit (ReLU) activation function. This module extracts essential features from the intensity image as guidance for the depth branch. The downsampling module performs a similar operation while also downsampling the feature maps by a factor of two. It consists of a convolution layer with a kernel size of 1 × 1 followed by another convolution layer with a kernel size of 3 × 3 and stride 2, which performs the downsampling. A ReLU activation then follows these two convolution layers. In this manner, the intensity frequency components are progressively downsampled to provide multiple-scale guidance for the depth branch via the CTGM, as elaborated in Section 3.3.

Specifically, a single upsampling stage i ∈ {1 … m} of the intensity branch can be formulated as:

${\mathbf{Y}}_{\text{FE}}^i=\sigma \left({\mathbf{C}\mathbf{o}\mathbf{n}\mathbf{v}}_1\left({\mathbf{C}\mathbf{o}\mathbf{n}\mathbf{v}}_1\left({\mathbf{Y}}_{\text{DS}}^{i-1}\right)\right)\right)(3)$

${\mathbf{Y}}_{\text{DS}}^i=\sigma \left({\mathbf{C}\mathbf{o}\mathbf{n}\mathbf{v}}_{\mathrm{3,2}}\left({\mathbf{C}\mathbf{o}\mathbf{n}\mathbf{v}}_1\left({\mathbf{Y}}_{\text{FE}}^i\right)\right)\right)(4)$

where i ∈ {1 … m} denotes the current upsampling stage, σ is a ReLU activation function, and Conv_3,2 (⋅) is a convolution layer with a kernel size of 3 × 3 and stride 2. The input ${\mathbf{Y}}_{\text{DS}}^{i-1}$ for upsampling stage i is either the output of upsampling stage i−1 or the input HR intensity image I_HR in the case of i = 1, meaning ${\mathbf{Y}}_{\text{DS}}^0={\mathbf{I}}_{\text{HR}}$.

3.2.2 Depth Branch

The depth branch plays the primary role of finding the nonlinear mapping between the LR and the super-resolved HR depth maps. Motivated by Zhang et al. (2018a), we use global and local residual learning, allowing for high-frequency details needed for super-resolving D_HR to be learned in the network and its sub-networks.

In our depth branch, we first extract shallow features from the LR input D_LR by feeding it through two consecutive convolution layers as suggested by, among others, Haris et al. (2018); Zhang et al. (2018b):

${\mathbf{D}}^0={\mathbf{C}\mathbf{o}\mathbf{n}\mathbf{v}}_3\left({\mathbf{C}\mathbf{o}\mathbf{n}\mathbf{v}}_3\left({\mathbf{D}}_{\text{LR}}\right)\right)(5)$

D₀ is then progressively upsampled in m stages by a factor of two in each stage. Each such upsampling stage is composed of an RDG as proposed by Zhang et al. (2018a), followed by an upsampling module, and finally, a second RDG. This upsampling stage is duplicated according to the desired upscaling factor s.

An RDG is composed of stacking G Residual Dilated Blocks (Zhang et al., 2018a), where each such block is composed of stacking L layers of dilated convolution. A long skip connection connects the RDG’s input to its output, stabilizing the training process Haris et al. (2018) and allowing the network to suppress low-frequency information from earlier layers and recover more useful information.

The first RDG in each upsampling stage performs a deep feature extraction. For the RDG to successfully recover high-frequency details from its LR input, we first scale its input via the CTGM, as elaborated in Section 3.3. Features extracted by the first RDG are upsampled by a factor of two via a pixel shuffle module (Shi et al., 2016). Thus the upsampling operators are learned in a data-driven way to improve the representation ability of our model. Finally, the upsampled feature maps are scaled once more by the output of another CTGM and fused with the unscaled feature maps via a convolution layer. The fused feature maps are then passed through a second RDG to explore deeper relations between the depth and intensity features.

A single upsampling stage i can be formulated as:

${\mathbf{F}}_{\text{RDG}1}^i={\mathbf{H}}_{\text{RDG}}^1\left({\mathbf{D}}^{i-1}\otimes {\mathbf{H}}_{\text{CTGM}}^1\right)\oplus {\mathbf{D}}^{i-1}(6)$

${\mathbf{F}}_{\text{UP}}^i={\mathbf{H}}_{\text{PS}}\left({\mathbf{F}}_{\text{RDG}1}^i\right)(7)$

${\mathbf{D}}^i={\mathbf{H}}_{\text{RDG}}^2\left({\mathbf{C}\mathbf{o}\mathbf{n}\mathbf{v}}_1\left({\mathbf{F}}_{\text{UP}}^i\text{©}\left({\mathbf{F}}_{\text{UP}}^i\otimes {\mathbf{H}}_{\text{CTGM}}^2\right)\right)\right)\oplus {\mathbf{F}}_{\text{UP}}^i(8)$

where H_RDG denotes the function learned by our RDG, H_PS is a pixel shuffle upsampling module, ⊗ denotes element-wise product, ⊕ denotes element-wise sum, H_CTGM denotes the scaling features produced from our CTGM, © denotes a concatenation operation and Dⁱ⁻¹ is the output of the previous upsampling stage. More implementation details are given in Section 4.1.

3.3 Cascaded Transformer Guidance Module

Guidance from the intensity image in most previous CNN-based guided SR methods is usually achieved by extracting feature maps from the intensity image and concatenating them to features extracted in the depth branch. This guidance scheme effectively treats all features equally, in both spatial and channel domains, which is not optimal. Moreover, feature maps extracted from the intensity image via CNN usually have a limited receptive field, which affects the guidance quality. In comparison, we propose to exploit long-range dependencies in the guidance image via a novel cascaded transformer guidance module. The motivation is that in image SR, high-frequency features are more informative for HR reconstruction, and a large receptive field is also beneficial (Zhang et al., 2017). Our proposed CTGM is shown in Figure 2.

FIGURE 2

FIGURE 2. Our proposed cascaded transformer guidance module.

Before elaborating on the structure of our proposed CTGM, we observe significant challenges in transferring the transformer’s high performance in the language domain to the visual domain, and specifically to low-level vision tasks. First, unlike word tokens that serve as the essential processing elements in language transformers, images can vary substantially in scale in real-life scenarios. However, in most existing transformer-based models, tokens must all be of a fixed scale. Another difference is the higher number of pixels in images than words text passages. Specifically, the task of SR requires dense prediction at the pixel level while avoiding down-scaling the input as much as possible to prevent loss of HR information. Working with such HR inputs would be intractable for transformers, as the computational complexity of its self-attention is quadratic to image size.

To overcome these issues, we build upon the work of Liu et al. (2021) and propose a cascaded transformer module, which operates on non-overlapping windows that partition the entire input image. The number of pixels in each such window is fixed, and by computing self-attention locally within each window, the complexity becomes linear to image size. Moreover, our proposed CTGM constructs hierarchical representations by applying several such transformer layers consecutively. We shift the partitioning windows with each layer, gradually merging neighboring patches in deeper transformer layers. The shifted windows overlap with the preceding layer windows, providing connections that significantly enhance modeling power. Our transformer model can conveniently extract meaningful information suitable for dense tasks such as SR and encode distant dependencies or heterogeneous interactions with these hierarchical feature maps. Furthermore, the window-based local self-attention is scalable; the linear complexity makes working with large inputs feasible while also enabling working with variable size inputs (given input size is divisible by window size).

Formally, given an intermediate feature map $F_{\text{I}}\in {\mathbb{R}}^{C\times H\times W}$ as input, our CTGM first splits F_I into non-overlapping patches of size (P, P) to form $F_{I,p}\in {\mathbb{R}}^{C\times \widehat{H}\times \widehat{W}}$ where $\widehat{H}=H/P$ and $\widehat{W}=W/P$. A trainable convolution layer with a kernel size of P × P and stride P is applied to construct an initial patch embedding $F_{I,p,emb}\in {\mathbb{R}}^{\widehat{C}\times \widehat{H}\times \widehat{W}}$. Next, we apply window partitioning such that the windows partition F_I,p,emb in a non-overlapping manner, where each window is of size M × M. Every such window is flattened to form the window embeddings $F_{win}\in {\mathbb{R}}^{M^2\times \widehat{C}}$, which forms the input sequence for the cascaded transformer module. During both the patches and windows partitioning, zero padding of the input is applied if necessary.

Similar to Hu et al. (2019), relative position embeddings are added to the window embeddings F_win to retain positional information. We use standard learnable 1D position embeddings since we have not observed significant performance gains from using more advanced 2D-aware or global position embeddings. We refer to this joint embedding Z⁰ which is the input to the following transformer module. Note that for computations efficiency, we batch all $\widehat{H}\times \widehat{W}/(M\times M)$ window embeddings before feeding them to the transformer module.

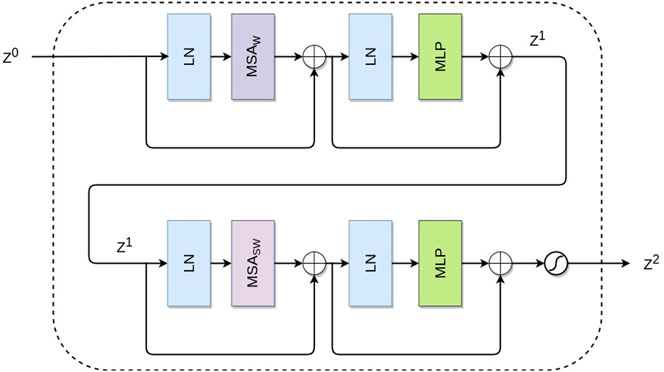
Our proposed transformer module receives Z⁰ as input and computes a hierarchical local self-attention within each window. We construct our transformer module by concatenating two modified transformer blocks, as shown in Figure 2. Each such transformer block is modified from the original transformer block by replacing the standard MSA module with a windows-based MSA (MSA_w) while keeping the other layers unchanged. In an MSA_w module, we apply Eq. 1 locally within each M × M, thus avoiding computing self-attention on the entire input. Specifically, as illustrated in Figure 2, our modified transformer block consists of an MSA_w module, followed by a 2-layer MLP with GELU non-linearity in between. An LN layer is applied before each MLP and MSA_w module, and a residual connection is applied after each module.

We propose a shifted window partitioning approach that alternates between two partitioning configurations in the two consecutive transformer blocks to increase modeling power and introduce cross-window connections. The first block uses a regular window partitioning strategy which starts from the top-left pixel. Then, the next block applies a windowing configuration shifted from the preceding block by displacing the windows by M/2, M/2 pixels from the regularly partitioned windows. We denote the MSA module that operates with the shifted window partitioning approach as MSA_sw. Finally, the two consecutive transformer blocks are computed as -

${\widehat{\mathbf{Z}}}^1={\mathbf{M}\mathbf{S}\mathbf{A}}_{\mathbf{w}}\left(\mathbf{L}\mathbf{N}\left({\mathbf{Z}}^0\right)\right)+{\mathbf{Z}}^0(9)$

${\mathbf{Z}}^1=\mathbf{M}\mathbf{L}\mathbf{P}\left(\mathbf{L}\mathbf{N}\left({\widehat{\mathbf{Z}}}^1\right)\right)+{\widehat{\mathbf{Z}}}^1(10)$

${\widehat{\mathbf{Z}}}^2={\mathbf{M}\mathbf{S}\mathbf{A}}_{\mathbf{sw}}\left(\mathbf{L}\mathbf{N}\left({\mathbf{Z}}^1\right)\right)+{\mathbf{Z}}^1(11)$

${\mathbf{Z}}^2=\mathbf{M}\mathbf{L}\mathbf{P}\left(\mathbf{L}\mathbf{N}\left({\widehat{\mathbf{Z}}}^2\right)\right)+{\widehat{\mathbf{Z}}}^2(12)$

where ${\widehat{\mathbf{Z}}}^1$ and Z¹ denote the output features of the MSA_w and MLP modules of the first block, respectively. Similarly, ${\widehat{\mathbf{Z}}}^2$ and Z² denote the output features of the MSA_sw and MLP modules of the second block, respectively. This shifted window partitioning approach introduces connections between neighboring non-overlapping windows in the previous layer, which improves modeling performance as shown in Section 4.

The overall CTGM module can be summarized as:

${\mathbf{F}}_{\text{CTGM}}=\widehat{\sigma }\left({\mathbf{Z}}^2\right)(13)$

where $\widehat{\sigma }$ denotes the sigmoid function.

Finally, F_CTGM, the features generated by the CTGM are used to scale the corresponding depth features in the depth branch by element-wise multiplication.

4 Experiments

4.1 Training Details

To make a fair comparison to other competing depth map SR methods, we constructed our train and test data similarly to Guo et al. (2018); Huang et al. (2019); Hui et al. (2016), and more. We collected 92 pairs of depth and color images from the MPI Sintel depth dataset (Butler et al., 2012) and from the Middlebury dataset (Scharstein and Szeliski, 2002; Scharstein and Pal, 2007; Scharstein et al., 2014). We followed the same training and validation split as in Hui et al. (2016) and used 82 pairs for training and ten pairs for validation.

Instead of using the full-scale HR depth and intensity images as input in the training process, we randomly extracted patches and used these as input to our network. We opted to use an LR patch size of 96 × 96 pixels, having observed that using a larger patch size did not significantly improve the training accuracy. However, the memory requirements and computation time increase substantially with patch size. Therefore, for upsampling factors of 2 and 4, we extracted HR patches of sizes 192 × 192 and 384 × 384, respectively. For the upsampling factors of 8 and 16, we used smaller LR patch sizes of 48 × 48 and 24 × 24, respectively, due to memory limitations and the fact that some full-scale images had a resolution of $<400$. The LR patches were generated by downsampling each HR patch with bicubic interpolation according to the desired scaling factor. We augmented the extracted patches by randomly performing either a horizontal flip, a vertical flip, or a 90° rotation during training.

4.2 Implementation Details

In our proposed architecture, we set the number of RDBs in each RDG to G = 20 RDBs, and each such RDB has L = 4 dilated convolution layers as described in Section 3.2.2. These values for G and L provided the best performance to network size trade-off in our experiments. All convolution layers throughout our network have a stride of 1, and C = 64 filters, unless otherwise noted. A zero-padding strategy is used to keep size fixed for convolution layers with a kernel size of 3 × 3. The final convolution layer has only one filter, as we output depth values. In our CTGM implementation, we use a patch size of p = 4, an embedding dimension of $\widehat{C}=64$, and set the number of patches in each window to be M = 12 throughout the CTGM. Each MSA_w and MSA_sw module has four attention heads.

We trained a specific network for each upsampling factor s ∈ 2, 4, 8, 16, and used the Pytorch framework Paszke et al. (2019) to train our models. We used a batch size of 4 in all our experiments, with random initialization of the filter weights of each layer. We trained each network for 3 × 10⁵ iterations of back-propagation. Our model was optimized using the ${\mathcal{L}}_1$ loss and the ADAM optimizer Kingma and Ba (2014) with β₁ = 0.9, β₂ = 0.999 and ϵ = 10^–8. The initial learning rate was set to 10^–4 and then divided by 2 every 1 × 10⁵ iterations. All our models were trained on a PC with an i9-9960x CPU, 64GB RAM, and two Titan RTX GPUs.

Our code and trained models will be made public upon publication.

4.3 Results

This section provides both quantitative and qualitative evaluations of our guided depth map SR method. We report the results of bicubic interpolation as a baseline, and compare our results to state-of-the-art global optimization-based methods Ferstl et al. (2013); Liu et al. (2016); Park et al. (2014), a sparse representation-based method (Kiechle et al., 2013) and mainly deep learning-based methods (Guo et al., 2018; Huang et al., 2019; Hui et al., 2016; Zuo et al., 2019a,b; Zhao et al., 2021; Kim et al., 2021; Li et al., 2020; Ye et al., 2020; Cui et al., 2021). We evaluated our proposed method on the noise-free Middlebury dataset and the more challenging noisy Middlebury dataset. Moreover, we demonstrate the generalization capability of our proposed method by evaluating on the NYU Depth v2 dataset.

4.3.1 Results on the Noise-Free Middlebury Dataset

Similar to recent works, we first evaluate the performances of the different methods on the noise-free hole-filled Middlebury RGB-D datasets for various scaling factors s ∈ 2, 4, 8, 16. The Middlebury datasets provide high-quality depth maps and RGB pairs in complex real-world scenes. In Tables 1, 2 we report the RMSE values for different scale factors, where the best RMSE for each evaluation is in boldface, whereas the second best one is underlined. All results in Tables 1, 2 are generated by the authors’ code or calculated directly from the upsampled depth maps provided by the authors.

TABLE 1

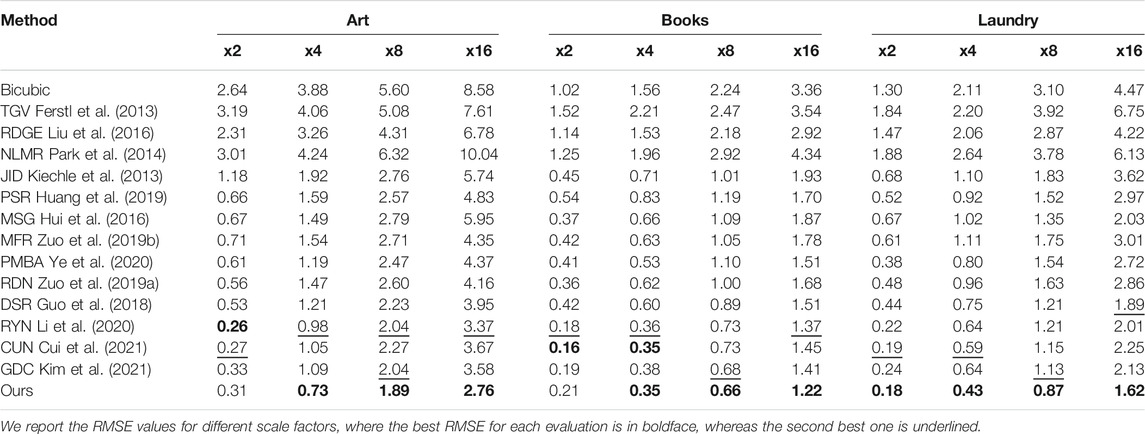
TABLE 1. Quantitative comparisons on “art.” “books” and “laundry” from the noise-free middlebury dataset in terms of RMSE values for different scaling factors.

TABLE 2

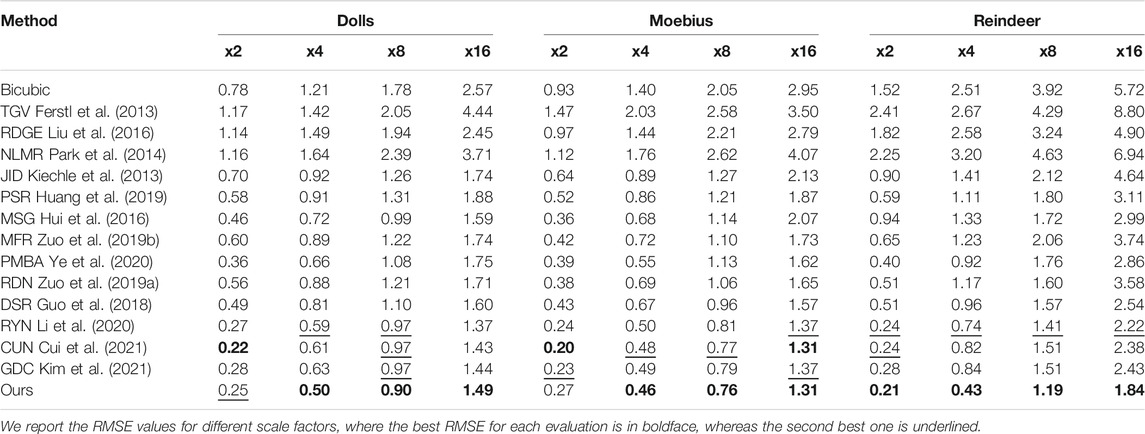
TABLE 2. Quantitative comparisons on “dolls,” “moebius” and “reindeer” from the noise-free middlebury dataset in terms of RMSE values for different scaling factors.

From Tables 1, 2 it can be seen that deep learning based architectures for SR, such as Guo et al. (2018); Huang et al. (2019); Hui et al. (2016); Zuo et al. (2019a,b); Zhao et al. (2021); Kim et al. (2021); Li et al. (2020); Ye et al. (2020); Cui et al. (2021), have obvious advantages compared with other methods. Moreover, our proposed architecture, benefiting from our CTGM, achieves the best performance on almost all scaling factors in terms of RMSE values. This holds especially for large scaling factors, which are difficult for most methods. The average RMSE values obtained by our method on the whole test set are 0.48/1.04/1.70 for scaling factors x4/x8/x16, respectively. Compared to the second-best results, our results outperform them in terms of average RMSE values with a gain of 0.15/0.14/0.25, respectively. For a scale factor of x2, our method achieved similar average RMSE as the second best method.

To further demonstrate the performance of our method, Figure 3 shows upsampled depth maps for different approaches on the “Art” and “Reindeer” datasets and a scale factor of 8. Our results are compared with bicubic interpolation as a baseline and 3 state-of-the-art methods which are RDGR (Liu et al., 2016), MSG (Hui et al., 2016), and DSR (Guo et al., 2018). It is observed that our proposed architecture can alleviate the blurring artifacts better and recover more detailed HR depth boundaries than the competing methods. Moreover, our approach can overcome the texture copying issue apparent with other methods, as marked by a red arrow. The evaluations suggest that our CTGM plays an important role in the success of depth map SR.

FIGURE 3

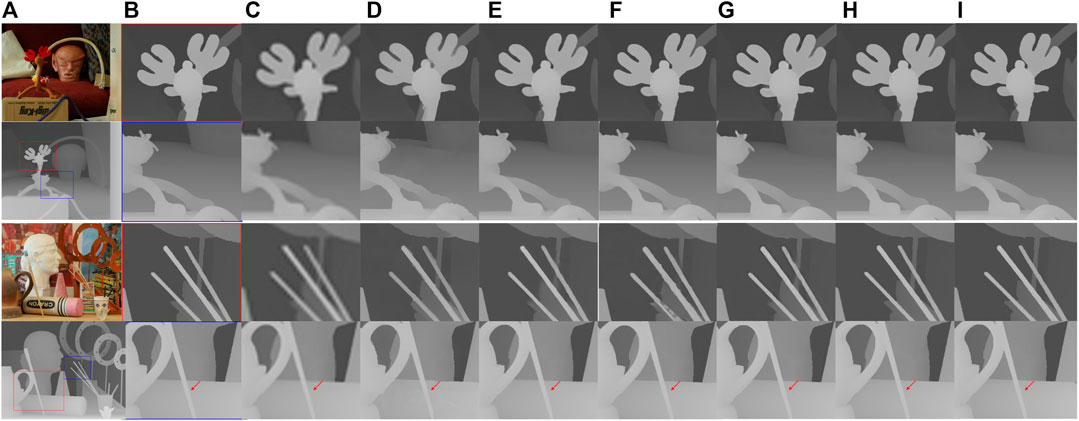
FIGURE 3. A visual quality comparison for depth map SR at a scale factor of 8 on the noise-free “art” and “Reindeer” datasets. (A) HR color and depth images, (B) extracted ground truth patches, and upsampled patches by (C) Bicubic, (D) RDGE (Liu et al., 2016), (E) MSG (Hui et al., 2016), (F) DSR (Guo et al., 2018) (G) RDN (Zuo et al., 2019a) (H) PMBA (Ye et al., 2020) (I) our proposed method (best viewed on the enlarged electronic version).

4.3.2 Results on the Noisy Middlebury Dataset

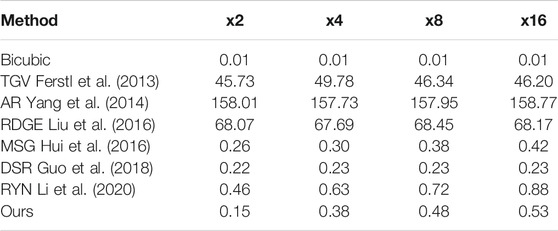
To further test the robustness of our proposed method, we carry additional experiments on the noisy Middlebury dataset. Depth maps are often corrupted by random noise during the acquisition process. Thus we added random Gaussian noise with mean 0 and a SD of 5 to our LR training data, similarly to Guo et al. (2018); Zuo et al. (2019a,b). We retrained all our models and evaluated them on a test set corrupted with the same Gaussian noise. We report the RMSE values for the noisy case in Table 3.

TABLE 3

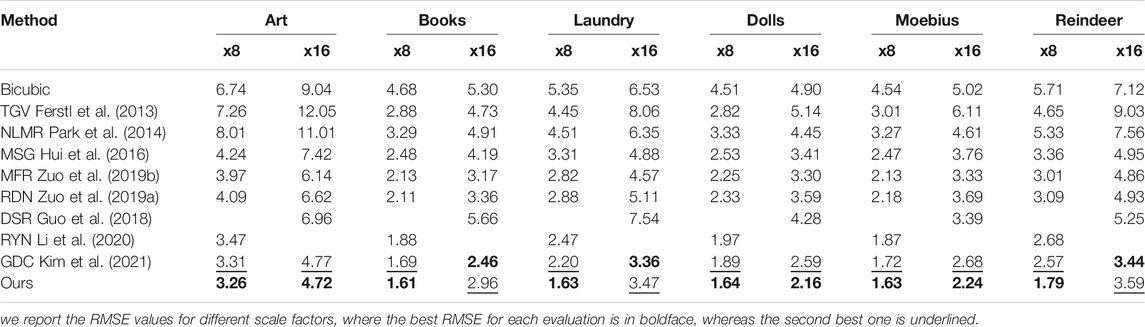
TABLE 3. Quantitative comparisons on the noisy middlebury dataset in terms of RMSE values for scaling factors 4 and 8.

It is observed that noise added to the LR depth maps significantly affects the reconstructed HR depth maps across all methods. However, our proposed architecture still manages to outperform competing methods and generate clean and sharp reconstructions.

To further test our method’s robustness to noise, we added Gaussian noise with a mean 0 and SD of 5 to the guidance HR color images of our training and test data. This simulates a realistic scenario in which data acquired by both the depth and intensity sensors is corrupted with noise. We retrained our models and report the obtained average RMSE values in Table 4.

TABLE 4

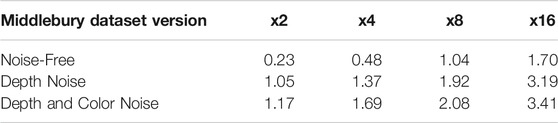
TABLE 4. Average RMSE Values of Our Proposed architecture for Different Scaling Factors on Various Datasets.

Table 4 demonstrate our method’s insensitivity to noise added to the color image. We observe that models evaluated with noise in both LR depth and HR guidance image achieve very similar results to models evaluated with LR depth noise alone, thus demonstrating the effectiveness of our proposed CTGM.

4.3.3 Results on NYU Depth v2 Dataset

In this subsection, to demonstrate the generalization ability of our proposed architecture, we carry out experiments on the challenging NYU Depth v2 public benchmark dataset (Silberman et al., 2012). The NYU Depth v2 dataset comprises 1449 high-quality RGB-D image pairs of natural indoors scenes, taken with a Microsoft Kinect camera. In this dataset, there are unavoidable local structural misalignments between depth maps and color images, which may affect the performance of guided SR methods. We note that no RDB-D pair from the NYU Depth v2 dataset was included in the training data of our models.

In Table 5 we report the RMSE value averaged across all RGB-D pairs in the NYU Depth v2 dataset for a scaling factor of x4, where the best achieved RMSE is boldface. We compare our results with Bicubic interpolation as a baseline and competing guided SR methods; ATGV-Net (Riegler et al., 2016b), MSG (Hui et al., 2016), DSR (Guo et al., 2018), RDN (Zuo et al., 2019a), RYN (Li et al., 2020) and PMBA (Ye et al., 2020). Our proposed architecture achieves the lowest average RMSE, improving over the second-best method by 0.11, demonstrating our proposed method’s generalization ability and robustness.

TABLE 5

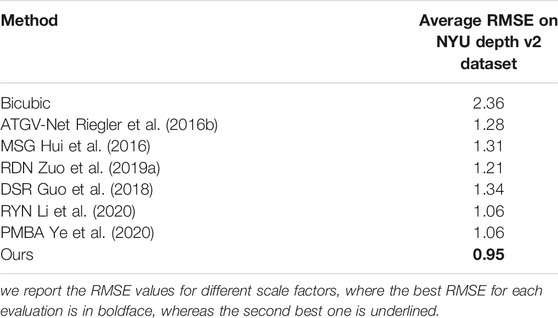
TABLE 5. Quantitative comparisons on the NYU depth v2 dataset in terms of average RMSE values for a scaling factor of 4.

4.3.4 Inference Time

To show the real-world applicability of our proposed method, we compare the inference time of our proposed architecture to competing approaches. Inference times were measured using the same setup described in 4.2 running on a 1320 × 1080 pixels image. We report the average inference times in seconds in Table 6.

TABLE 6

TABLE 6. Average inference time (seconds) for different scaling factors.

From Table 6 we conclude that deep learning based methods, such as our proposed architecture as well as Hui et al. (2016); Li et al. (2020); Guo et al. (2018), achieve significantly faster inference times than traditional methods. Moreover, our proposed method performs similarly to Hui et al. (2016); Guo et al. (2018) and faster then Li et al. (2020) while achieving lower RMSE values. In contrast, the speed of Yang et al. (2014); Liu et al. (2016); Ferstl et al. (2013), which require multiple optimization iterations to achieve good reconstructions, is slower, limiting their practical applications. We also note that methods such as Liu et al. (2016) and Guo et al. (2018) which upsample the LR depth as an initial preprocess step exhibit very similar inference times across different scaling factors.

4.4 Ablation Study

We carry out an ablation study to demonstrate the effectiveness of each component in the proposed architecture. We conduct the following experiments: (1) Our architecture without intensity guidance and the CTGM denoted as “Depth-Only.” (2) Our architecture with fewer RDBs in each RDG, i.e., G = 4, denoted as “proposed (S).” (3) Our architecture without shifted windows in the transformer block denoted as “proposed w/o ws.” (4) Our architecture with absolute position embedding, instead of relative position embedding in the CTGM module denoted as “proposed - ape”. In these experiments, we use the same network parameters with the settings as mentioned earlier. We evaluate the performance using average RMSE on our evaluation dataset at scaling factors 4, 8 and 16. As shown in Table 7, we observe that: (1) As expected, our guided architecture with CTGM performs better than a non-guided version that operates on depth data alone. (2) Our architecture with fewer RDBs still achieves competitive results. However, it is inferior to our full architecture. This implies that the network’s depth also plays a significant role in the success of SR architectures. Our proposed architecture with long and short skip connections and close guidance from the CTGM module enables the effective training of such deep networks. (3) our cascaded transformer with the shifted window partitioning outperforms the counterpart built on a single-window partitioning. The results indicate the effectiveness of using shifted windows to build connections among windows in the preceding layers. (4) Relative position bias improves over absolute position bias, indicating the effectiveness of the relative position bias. Although recent image classification models Dosovitskiy et al. (2020) opted to abandon translation invariance, using an inductive bias that encourages certain translation invariance is still preferable for dense prediction tasks such as SR. Moreover, we observe from Table 7 that the advantages of our complete proposed architecture are more prominent in larger scaling factors, e.g., 8 and 16.

TABLE 7

TABLE 7. Quantitative comparisons of our ablation experiments. Reported results are average RMSE on the noise-free middlebury dataset for scaling factors 4, 8 and 16.

5 Conclusion

We have introduced a new method to address the problem of depth map upsampling by using a cascaded transformer module for guided depth SR. An LR depth map is progressively upsampled using residual dilated blocks and a novel guidance module, based on the cascaded transformer that operates on shifted window partitioning of the image, scales the intermediate feature maps of the network. Our proposed architecture achieves state-of-the-art performance for super-resolving depth maps using such a design.

In future work, we intend to explore even more realistic noise and artifacts in our test sets (e.g., missing depth values, misregistration between RGB image and depth map, etc.). Moreover, we will examine the proposed architecture on upsampling Dynamic Elevation Model (DEM) data using LR DEM and HR raster data, which acts as guidance.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: http://sintel.is.tue.mpg.de/ https://vision.middlebury.edu/stereo/data /https://cs.nyu.edu/∼silberman/datasets/nyu_depth_v2.html.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the PMRI—Peter Munk Research Institute - Technion.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Butler, D. J., Wulff, J., Stanley, G. B., and Black, M. J. (2012). “A Naturalistic Open Source Movie for Optical Flow Evaluation,” in European conference on computer vision (Berlin, Germany: Springer), 611–625. doi:10.1007/978-3-642-33783-3_44

CrossRef Full Text | Google Scholar

Carion, N., Massa, F., Synnaeve, G., Usunier, N., Kirillov, A., and Zagoruyko, S. (2020). “End-to-end Object Detection with Transformers,” in European Conference on Computer Vision (Berlin, Germany: Springer), 213–229. doi:10.1007/978-3-030-58452-8_13

CrossRef Full Text | Google Scholar

Cui, Y., Liao, Q., Yang, W., and Xue, J.-H. (2021). “Rgb Guided Depth Map Super-resolution with Coupled U-Net,” in 2021 IEEE International Conference on Multimedia and Expo (ICME) (Shenzhen, China: IEEE), 1–6. doi:10.1109/icme51207.2021.9428096

CrossRef Full Text | Google Scholar

Dai, J., Qi, H., Xiong, Y., Li, Y., Zhang, G., Hu, H., et al. (2017). “Deformable Convolutional Networks,” in Proceedings of the IEEE international conference on computer vision, 764–773. doi:10.1109/iccv.2017.89

CrossRef Full Text | Google Scholar

Dong, W., Shi, G., Li, X., Peng, K., Wu, J., and Guo, Z. (2016). Color-guided Depth Recovery via Joint Local Structural and Nonlocal Low-Rank Regularization. IEEE Trans. Multimedia 19, 293–301.

Google Scholar

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., et al. (2020). An Image Is worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv preprint arXiv:2010.11929.

Google Scholar

Ferstl, D., Reinbacher, C., Ranftl, R., Rüther, M., and Bischof, H. (2013). “Image Guided Depth Upsampling Using Anisotropic Total Generalized Variation,” in Proceedings of the IEEE International Conference on Computer Vision, 993–1000. doi:10.1109/iccv.2013.127

CrossRef Full Text | Google Scholar

Ferstl, D., Ruther, M., and Bischof, H. (2015). “Variational Depth Superresolution Using Example-Based Edge Representations,” in Proceedings of the IEEE International Conference on Computer Vision, 513–521. doi:10.1109/iccv.2015.66

CrossRef Full Text | Google Scholar

Guo, C., Li, C., Guo, J., Cong, R., Fu, H., and Han, P. (2018). Hierarchical Features Driven Residual Learning for Depth Map Super-resolution. IEEE Trans. Image Process. 28, 2545–2557. doi:10.1109/TIP.2018.2887029

PubMed Abstract | CrossRef Full Text | Google Scholar

Ham, B., Cho, M., and Ponce, J. (2015a). “Robust Image Filtering Using Joint Static and Dynamic Guidance,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 4823–4831. doi:10.1109/cvpr.2015.7299115

CrossRef Full Text | Google Scholar

Ham, B., Dongbo Min, D., and Kwanghoon Sohn, K. (2015b). Depth Superresolution by Transduction. IEEE Trans. Image Process. 24, 1524–1535. doi:10.1109/tip.2015.2405342

PubMed Abstract | CrossRef Full Text | Google Scholar

Haris, M., Shakhnarovich, G., and Ukita, N. (2018). “Deep Back-Projection Networks for Super-resolution,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 1664–1673. doi:10.1109/cvpr.2018.00179

CrossRef Full Text | Google Scholar

He, K., Sun, J., and Tang, X. (2012). Guided Image Filtering. IEEE Trans. Pattern Anal. Mach Intell. 35, 1397–1409. doi:10.1109/TPAMI.2012.213

CrossRef Full Text | Google Scholar

He, K., Sun, J., and Tang, X. (2010). “Guided Image Filtering,” in European conference on computer vision (Berlin, Germany: Springer), 1–14. doi:10.1007/978-3-642-15549-9_1

CrossRef Full Text | Google Scholar

Hornacek, M., Rhemann, C., Gelautz, M., and Rother, C. (2013). “Depth Super Resolution by Rigid Body Self-Similarity in 3d,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 1123–1130. doi:10.1109/cvpr.2013.149

CrossRef Full Text | Google Scholar

Hu, H., Zhang, Z., Xie, Z., and Lin, S. (2019). “Local Relation Networks for Image Recognition,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 3464–3473. doi:10.1109/iccv.2019.00356

CrossRef Full Text | Google Scholar

Huang, L., Zhang, J., Zuo, Y., and Wu, Q. (2019). Pyramid-structured Depth Map Super-resolution Based on Deep Dense-Residual Network. IEEE Signal. Process. Lett. 26, 1723–1727. doi:10.1109/lsp.2019.2944646

CrossRef Full Text | Google Scholar

Hui, T.-W., Loy, C. C., and Tang, X. (2016). “Depth Map Super-resolution by Deep Multi-Scale Guidance,” in European conference on computer vision (Berlin, Germany: Springer), 353–369. doi:10.1007/978-3-319-46487-9_22

CrossRef Full Text | Google Scholar

Izadi, S., Kim, D., Hilliges, O., Molyneaux, D., Newcombe, R., Kohli, P., et al. (2011). “Kinectfusion: Real-Time 3d Reconstruction and Interaction Using a Moving Depth Camera,” in Proceedings of the 24th annual ACM symposium on User interface software and technology, 559–568.

Google Scholar

Jiang, Z., Hou, Y., Yue, H., Yang, J., and Hou, C. (2018). Depth Super-resolution from Rgb-D Pairs with Transform and Spatial Domain Regularization. IEEE Trans. Image Process. 27, 2587–2602. doi:10.1109/tip.2018.2806089

PubMed Abstract | CrossRef Full Text | Google Scholar

Jun Xie, J., Feris, R. S., and Ming-Ting Sun, M.-T. (2015). Edge-guided Single Depth Image Super Resolution. IEEE Trans. Image Process. 25, 428–438. doi:10.1109/TIP.2015.2501749

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiechle, M., Hawe, S., and Kleinsteuber, M. (2013). “A Joint Intensity and Depth Co-sparse Analysis Model for Depth Map Super-resolution,” in Proceedings of the IEEE international conference on computer vision, 15451552. doi:10.1109/iccv.2013.195

CrossRef Full Text | Google Scholar

Kim, J.-Y., Ji, S., Baek, S.-J., Jung, S.-W., and Ko, S.-J. (2021). Depth Map Super-resolution Using Guided Deformable Convolution. IEEE Access 9, 66626–66635. doi:10.1109/access.2021.3076853

CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. (2014). Adam: A Method for Stochastic Optimization. arXiv preprint arXiv:1412.6980.

Google Scholar

Kwon, H., Tai, Y.-W., and Lin, S. (2015). “Data-driven Depth Map Refinement via Multi-Scale Sparse Representation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 159–167. doi:10.1109/cvpr.2015.7298611

CrossRef Full Text | Google Scholar

Lei, J., Li, L., Yue, H., Wu, F., Ling, N., and Hou, C. (2017). Depth Map Super-resolution Considering View Synthesis Quality. IEEE Trans. Image Process. 26, 1732–1745. doi:10.1109/tip.2017.2656463

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, T., Dong, X., and Lin, H. (2020). Guided Depth Map Super-resolution Using Recumbent Y Network. IEEE Access 8, 122695–122708. doi:10.1109/access.2020.3007667

CrossRef Full Text | Google Scholar

Liu, M.-Y., Tuzel, O., and Taguchi, Y. (2013). “Joint Geodesic Upsampling of Depth Images,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 169–176. doi:10.1109/cvpr.2013.29

CrossRef Full Text | Google Scholar

Liu, W., Chen, X., Yang, J., and Wu, Q. (2016). Robust Color Guided Depth Map Restoration. IEEE Trans. Image Process. 26, 315–327. doi:10.1109/TIP.2016.2612826

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., et al. (2021). “Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows,” in International Conference on Computer Vision (ICCV).

CrossRef Full Text | Google Scholar

Lu, J., and Forsyth, D. (2015). “Sparse Depth Super Resolution,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2245–2253. doi:10.1109/cvpr.2015.7298837

CrossRef Full Text | Google Scholar

Lutio, R. d., D’aronco, S., Wegner, J. D., and Schindler, K. (2019). “Guided Super-resolution as Pixel-To-Pixel Transformation,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 8829–8837. doi:10.1109/iccv.2019.00892

CrossRef Full Text | Google Scholar

Mac Aodha, O., Campbell, N. D. F., Nair, A., and Brostow, G. J. (2012). “Patch Based Synthesis for Single Depth Image Super-resolution,” in European conference on computer vision (Berlin, Germany: Springer), 71–84. doi:10.1007/978-3-642-33712-3_6

CrossRef Full Text | Google Scholar

Mandal, S., Bhavsar, A., and Sao, A. K. (2016). Depth Map Restoration from Undersampled Data. IEEE Trans. Image Process. 26, 119–134. doi:10.1109/TIP.2016.2621410

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, J., Kim, H., Tai, Y.-W., Brown, M. S., and Kweon, I. (2011). “High Quality Depth Map Upsampling for 3d-Tof Cameras,” in 2011 International Conference on Computer Vision (Barcelona, Spain: IEEE), 1623–1630. doi:10.1109/iccv.2011.6126423

CrossRef Full Text | Google Scholar

Park, J., Kim, H., Tai, Y.-W., Brown, M. S., and Kweon, I. S. (2014). High-quality Depth Map Upsampling and Completion for Rgb-D Cameras. IEEE Trans. Image Process. 23, 5559–5572. doi:10.1109/tip.2014.2361034

PubMed Abstract | CrossRef Full Text | Google Scholar

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., et al. (2019). “Pytorch: An Imperative Style, High-Performance Deep Learning Library,” in Advances in Neural Information Processing Systems, 8024–8035.

Google Scholar

Riegler, G., Ferstl, D., Rüther, M., and Bischof, H. (2016a). A Deep Primal-Dual Network for Guided Depth Super-resolution. arXiv preprint arXiv:1607.08569. doi:10.5244/c.30.7

CrossRef Full Text | Google Scholar

Riegler, G., Rüther, M., and Bischof, H. (2016b). “Atgv-net: Accurate Depth Super-resolution,” in European conference on computer vision (Berlin, Germany: Springer), 268–284. doi:10.1007/978-3-319-46487-9_17

CrossRef Full Text | Google Scholar

Schamm, T., Strand, M., Gumpp, T., Kohlhaas, R., Zollner, J. M., and Dillmann, R. (2009). “Vision and Tof-Based Driving Assistance for a Personal Transporter,” in 2009 International Conference on Advanced Robotics (Munich, Germany: IEEE), 1–6.

Google Scholar

Scharstein, D., Hirschmüller, H., Kitajima, Y., Krathwohl, G., Nešić, N., Wang, X., et al. (2014). “High-resolution Stereo Datasets with Subpixel-Accurate Ground Truth,” in German conference on pattern recognition (Berlin, Germany: Springer), 31–42. doi:10.1007/978-3-319-11752-2_3

CrossRef Full Text | Google Scholar

Scharstein, D., and Pal, C. (2007). “Learning Conditional Random fields for Stereo,” in 2007 IEEE Conference on Computer Vision and Pattern Recognition (Minneapolis, MN, USA: IEEE), 1–8. doi:10.1109/cvpr.2007.383191

CrossRef Full Text | Google Scholar

Scharstein, D., and Szeliski, R. (2002). A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms. Int. J. Comput. Vis. 47, 7–42. doi:10.1023/a:1014573219977

CrossRef Full Text | Google Scholar

Shi, W., Caballero, J., Huszár, F., Totz, J., Aitken, A. P., Bishop, R., et al. (2016). “Real-time Single Image and Video Super-resolution Using an Efficient Sub-pixel Convolutional Neural Network,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 1874–1883. doi:10.1109/cvpr.2016.207

CrossRef Full Text | Google Scholar

Silberman, N., Hoiem, D., Kohli, P., and Fergus, R. (2012). “Indoor Segmentation and Support Inference from Rgbd Images,” in European conference on computer vision (Berlin, Germany: Springer), 746–760. doi:10.1007/978-3-642-33715-4_54

CrossRef Full Text | Google Scholar

Song, X., Dai, Y., and Qin, X. (2018). Deeply Supervised Depth Map Super-resolution as Novel View Synthesis. IEEE Trans. circuits Syst. video Technol. 29, 2323–2336.

Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). “Attention Is All You Need,” in Advances in neural information processing systems, 5998–6008.

Google Scholar

Wang, W., Xie, E., Li, X., Fan, D.-P., Song, K., Liang, D., et al. (2021). Pyramid Vision Transformer: A Versatile Backbone for Dense Prediction without Convolutions. arXiv preprint arXiv:2102.12122.

CrossRef Full Text | Google Scholar

Yang, J., Ye, X., Li, K., and Hou, C. (2012). “Depth Recovery Using an Adaptive Color-Guided Auto-Regressive Model,” in European conference on computer vision (Berlin, Germany: Springer), 158–171. doi:10.1007/978-3-642-33715-4_12

CrossRef Full Text | Google Scholar

Yang, J., Ye, X., Li, K., Hou, C., and Wang, Y. (2014). Color-guided Depth Recovery from Rgb-D Data Using an Adaptive Autoregressive Model. IEEE Trans. Image Process. 23, 3443–3458. doi:10.1109/tip.2014.2329776

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Q., Yang, R., Davis, J., and Nistér, D. (2007). “Spatial-depth Super Resolution for Range Images,” in 2007 IEEE Conference on Computer Vision and Pattern Recognition (Minneapolis, MN, USA: IEEE), 1–8. doi:10.1109/cvpr.2007.383211

CrossRef Full Text | Google Scholar

Ye, X., Sun, B., Wang, Z., Yang, J., Xu, R., Li, H., et al. (2020). Pmbanet: Progressive Multi-branch Aggregation Network for Scene Depth Super-resolution. IEEE Trans. Image Process. 29, 7427–7442. doi:10.1109/tip.2020.3002664

CrossRef Full Text | Google Scholar

Zhang, K., Zuo, W., Gu, S., and Zhang, L. (2017). “Learning Deep Cnn Denoiser Prior for Image Restoration,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 3929–3938. doi:10.1109/cvpr.2017.300

CrossRef Full Text | Google Scholar

Zhang, Y., Li, K., Li, K., Wang, L., Zhong, B., and Fu, Y. (2018a). “Image Super-resolution Using Very Deep Residual Channel Attention Networks,” in Proceedings of the European Conference on Computer Vision (ECCV), 286–301. doi:10.1007/978-3-030-01234-2_18

CrossRef Full Text | Google Scholar

Zhang, Y., Tian, Y., Kong, Y., Zhong, B., and Fu, Y. (2018b). “Residual Dense Network for Image Super-resolution,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2472–2481. doi:10.1109/cvpr.2018.00262

CrossRef Full Text | Google Scholar

Zhao, Z., Zhang, J., Xu, S., Zhang, C., and Liu, J. (2021). Discrete Cosine Transform Network for Guided Depth Map Super-resolution. arXiv preprint arXiv:2104.06977.

Google Scholar

Zhou, W., Li, X., and Reynolds, D. (2017). “Guided Deep Network for Depth Map Super-resolution: How Much Can Color Help?,” in 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (New Orleans, LA, USA: IEEE), 1457–1461.

Google Scholar

Zhu, X., Su, W., Lu, L., Li, B., Wang, X., and Dai, J. (2020). Deformable Detr: Deformable Transformers for End-To-End Object Detection. arXiv preprint arXiv:2010.04159.

Google Scholar

Zuo, Y., Fang, Y., Yang, Y., Shang, X., and Wang, B. (2019a). Residual Dense Network for Intensity-Guided Depth Map Enhancement. Inf. Sci. 495, 52–64. doi:10.1016/j.ins.2019.05.003

CrossRef Full Text | Google Scholar

Zuo, Y., Wu, Q., Fang, Y., An, P., Huang, L., and Chen, Z. (2019b). “Multi-scale Frequency Reconstruction for Guided Depth Map Super-resolution via Deep Residual Network,” in IEEE Transactions on Circuits and Systems for Video Technology.

Google Scholar