Optimization of Network Throughput of Joint Radar Communication System Using Stochastic Geometry

Recently joint radar communication (JRC) systems have gained considerable interest for several applications such as vehicular communications, indoor localization and activity recognition, covert military communications, and satellite based remote sensing. In these frameworks, bistatic/passive radar deployments with directional beams explore the angular search space and identify mobile users/radar targets. Subsequently, directional communication links are established with these mobile users. Consequently, JRC parameters such as the time trade-off between the radar exploration and communication service tasks have direct implications on the network throughput. Using tools from stochastic geometry (SG), we derive several system design and planning insights for deploying such networks and demonstrate how efficient radar detection can augment the communication throughput in a JRC system. Specifically, we provide a generalized analytical framework to maximize the network throughput by optimizing JRC parameters such as the exploration/exploitation duty cycle, the radar bandwidth, the transmit power and the pulse repetition interval. The analysis is further extended to monostatic radar conditions, which is a special case in our framework. The theoretical results are experimentally validated through Monte Carlo simulations. Our analysis highlights that for a larger bistatic range, a lower operating bandwidth and a higher duty cycle must be employed to maximize the network throughput. Furthermore, we demonstrate how a reduced success in radar detection due to higher clutter density deteriorates the overall network throughput. Finally, we show a peak reliability of 70% of the JRC link metrics for a single bistatic transceiver configuration.

1 Introduction

Over the last decade, joint radar communication (JRC) frameworks are being researched and developed for numerous applications at microwave and millimeter wave (mmWave) frequencies Liu et al. (2020). Through the integration of sensing and communication functionalities on a common platform, JRC based connected systems offer the advantages of increased spectral efficiency through shared spectrum and reduced hardware costs. The most common applications are WiFi/WLAN based indoor detection of humans Falcone et al. (2012); Storrer et al. (2021); Tan et al. (2016); Li et al. (2020); Alloulah and Huang (2019); Yildirim et al. (2021), radar enhanced vehicular communications Ali et al. (2020); Kumari et al. (2017); Dokhanchi et al. (2019); Duggal et al. (2020), covert communications supported by radar based localization Kellett et al. (2019); Hu et al. (2019) and radar remote sensing based on global navigation satellite systems (GNSS) Zavorotny et al. (2014). All of these systems consist of a dual functional (radar-communication) transmitter and either a standalone or integrated radar/communications receiver. When the radar receiver is not co-located with the transmitter, the system constitutes a passive/bistatic radar framework. This is the most common scenario in sub-6 GHz indoor localization systems where the WiFi access point serves as both a radar and communication transmitter and humans activities are sensed for intrusion detection, surveillance, or assisted living. The bistatic scenario is also encountered in GNSS based remote sensing where the ground reflected satellite signals are analyzed, at a passive radar receiver, to estimate land and water surface properties Zavorotny et al. (2014). JRC based systems are also being researched for next generation intelligent transportation services where one of the main objectives is to share environment information for collision avoidance, and pedestrian detection eventually leading to autonomous driving. MmWave communication protocols such as IEEE 802.11 ad/ay characterized by high wide bandwidths and low latency have been identified for vehicular-to-everything (V2X) communications Nitsche et al. (2014); Zhou et al. (2018). However, due to the severe propagation loss at mmWave carrier frequencies, they are meant to operate in short range line-of-sight (LOS) conditions with highly directional beams realized through digital beamforming. In high mobility environments, beam training will result in considerable overhead and significant deterioration of latency. Hence, the integration of the radar functionality within the existing millimeter wave communication frameworks is being explored for rapid beam alignment Kumari et al. (2017); Dokhanchi et al. (2019); Duggal et al. (2019); Grossi et al. (2021). The wide bandwidth supported by the mmWave signals along with the channel estimation capabilities within the packet preamble are uniquely suited for radar remote sensing operations. To summarize, we divide the integrated sensing and communication systems into two broad categories. In the first category, the communication transmitter serves as an opportunistic illuminator whose parameters cannot be modified for maximizing a passive radar receiver’s detection performance. The second category is where a dual functional system is implemented with optimized design parameters - such as antennas, transmit waveform and signal processing algorithms—for enhanced radar detection performance without deterioration in the communication metrics Hassanien et al. (2016); Mishra et al. (2019); Ma et al. (2021). In this work, we consider the second category and focus on the time resource management between the radar and communication functionalities for maximizing communication network throughput. A preliminary work on the detection metrics of a bistatic radar was presented in Ram and Ghatak (2022). Here, we consider a generalized passive/bistatic radar framework that can be used to model the JRC application scenarios described above and analyze the communication network throughput performance as a function of radar detection metrics. The monostatic radar scenario is considered as a limiting case of the bistatic radar and the corresponding results are obtained as a corollary.

Prior works have tackled the time resource management for multi-functional radars Miranda et al. (2007). In Grossi et al. (2017), the radar dwell time was optimized for maximum target detection for a constant false alarm rate. In Ghatak et al. (2021), the time resource management between the localization and communication functionalities was determined as a function of the density of base station deployment. During the radar/localization phase, the transmitter must scan the angular search space and determine the number and location of the mobile users. Then these users must be served during the remaining duration through directional/pencil beams. The exploration and service process must be repeated periodically due to the motion of the mobile user. Now, if the angular beamwidth of the search beams are very narrow, then they will take longer to cover the search space (for a fixed dwell time) and this will result in reduced communication service time. However, the radar link quality will be higher due to the improved gain and result in a larger number of targets being detected. Hence, the overall network throughput is a function of the explore/exploit time management. In this paper, we use stochastic geometry (SG) based formulations to optimize the network throughput as a function of the explore/exploit duty cycle.

SG tools were originally applied to communication problems in cellular networks, mmWave systems, and vehicular networks Chiu et al. (2013); Andrews et al. (2011); Bai and Heath (2014); Thornburg et al. (2016); Ghatak et al. (2018). In all of these scenarios, there is considerable variation in the strength and spatial distribution of the base stations. More recently, they have been used in diverse radar scenarios to study the radar detection performance under interference and clutter conditions Al-Hourani et al. (2017); Munari et al. (2018); Ren et al. (2018); Park and Heath (2018); Fang et al. (2020). These works have considered the significant diversity in the spatial distributions and density of radars. SG offers a mathematical framework to analyze performance metrics of spatial stochastic processes that approximate to Poisson point process distributions without the requirement of computationally expensive system simulation studies or laborious field measurements. Based on the mathematical analysis, insights are obtained of the impact of design parameters on system level performances. In our problem related to JRC, there can be considerable variation in the position of the dual functional base station transmitter, the radar receiver and the communication end users who are the primary radar targets. Additionally, the JRC will encounter reflections from undesired targets/clutter in the environment. We model the discrete clutter scatterers in the bistatic radar environment as a homogeneous Poisson point process (PPP) similar to Chen et al. (2012); Ram et al. (2020, 2021). This generalized framework allows us to regard each specific JRC deployment, not as an individual case, but as a specific instance of an overall spatial stochastic process. Further, the target parameters such as the position and radar cross-section are also modelled as random variables. Using SG we quantify the mean number of mobile users that can be detected by the radar provided the statistics of the target and clutter conditions are known and subsequently determine the network throughput. Then we use the theorem to optimize system parameters such as the explore/exploit duty cycle, transmitted power, radar bandwidth and pulse repetition interval for maximum network throughput. Our results are validated through Monte Carlo simulations carried out in the short range bistatic radar framework.

Our paper is organized as follows. In the following section, we present the system model of the JRC with the bistatic radar framework and describe the explore/exploit time management scheme. In section 4, we provide the theorem for deriving the network throughput as a function of the bistatic radar parameters. In section 5, we offer the key system parameter insights that are drawn from the theorem as well as the Monte Carlo simulation based experimental validation. Finally, we conclude the paper with a discussion on the strengths and limitations of the proposed analytical framework along with directions for future work.

Notation: In this paper, all the random variables are indicated with bold font and constants and realizations of a random variable are indicated with regular font.

2 System Model

We consider a joint radar-communication (JRC) framework with a single base station (BS), multiple mobile users (MU) and a single passive radar receiver (RX) as shown in Figure 1A. The BS serves as a dual functional transmitter that supports both radar and communication functionalities in a time division manner as shown in Figure 1B.During the T_search interval, the BS serves as the radar transmitter or opportunistic illuminator and along with the RX, forms a bistatic radar whose objective is to localize the multiple MU in the presence of clutter/undesirable targets. During this interval, the BS transmits a uniform pulse stream of τ pulse width and T_PRI pulse repetition interval, through a directional and reconfigurable antenna system with gain G_tx and beamwidth Δθ_tx. The radar must scan the entire angular search space within T_search to find the maximum number of MU. If the duration of an antenna beam is fixed at T_beam (based on hardware parameters such as circuit switching speed for electronic scanning or Doppler frequency resolution requirements), then the number of beams that can be searched within T_search is given by

$n_{beam}=\frac{\mathrm{\Omega }}{{\mathrm{\Delta }\theta }_{\text{tx}}}=\frac{T_{search}}{T_{beam}},(1)$

where Ω is the angular search space. In our problem formulation, we set Ω = 2π to correspond to the entire azimuth angle extent. During the remaining duration of T_serve, directional communication links are assumed to be established between the BS and the detected MUs. Thus the beam alignment for communication during T_serve is based on radar enabled localization during T_search. Since the position of the MU does not remain fixed with time, the process of beam alignment is repeated for every T = T_search + T_serve as shown in the figure. An important tuning parameter in the above JRC framework is the duty cycle $ϵ=\frac{T_{search}}{T}$. From (1), it is evident that ${\mathrm{\Delta }\theta }_{\text{tx}}=\frac{\mathrm{\Omega }{T}_{beam}}{ϵT}=\frac{1}{B_0ϵ}$. Here, B₀ is a constant and equal to $\frac{T}{\mathrm{\Omega }{T}_{beam}}$. Note that when the beams become broader, the gain of the radar links become poorer. As a result of the deterioration in the radar link metrics due to larger Δθ_tx, the detection performance becomes poorer and fewer MU (η) are likely to be detected in the search space. Thus η is directly proportional to ϵ. On the other hand, the network throughput (ϒ) of the system is defined as

$\mathrm{\Upsilon }=\eta \left(ϵ\right)\left(1-ϵ\right)D,(2)$

where (1—ϵ) is the duty cycle of the communication service time $(\frac{T_{search}}{T})$. Here, we assume that the communication resources such as spectrum are available to all the η detected MU and all the MU are characterized by identical data rates D. The objective of our work is to present a theorem to optimize the duty cycle ϵ for maximum ϒ under the assumption that the noise, MU and clutter statistics are known and fixed during the radar processing time. These conditions are generally met for microwave or millimeter-wave systems Billingsley (2002); Ruoskanen et al. (2003). The theoretical framework is derived for a generalized bistatic JRC framework where inferences for monostatic conditions are derived from limiting conditions.

FIGURE 1

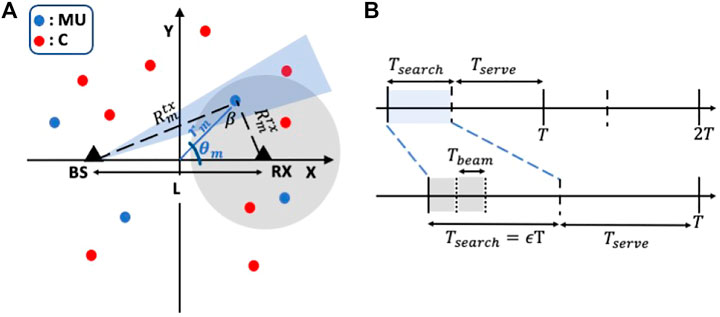
FIGURE 1. (A) Illustration of the joint radar-communication (JRC) scenario. The base station (BS) at $(\frac{L}{2},0)$ and indicated by a triangle is a dual functional transmitter that supports both radar and comm. functionalities with a directional and reconfigurable antenna system of Δθ_tx beamwidth. An omnidirectional receiver (RX) at $(-\frac{L}{2},0)$ forms the passive/bistatic radar receiver. The channel consists of mobile users (MU) at (r_m, θ_m) at distances, $R_m^{tx}$ and $R_m^{rx}$, from BS and MU respectively indicated by blue dots; and undesirable clutter scatterers indicated by red dots. The bistatic radar angle is β. (B) Timing diagram of the JRC framework where each T consists of T_search = ϵT when the BS scans the angular search space for MU using n_beam of T_beam duration. During the remaining T_serve duration, directional beam links are established between BS and MU based on the localization by the radar during T_search.

Next, we discuss the planar bistatic radar geometry that we have considered based on the north-referenced system described in Jackson (1986). We assume that the BS is located in the Cartesian coordinates $(-\frac{L}{2},0)$ while the passive receiver, RX, is assumed to be omnidirectional and located at $(+\frac{L}{2},0)$. High gain transmission links from the BS support high quality communication link metrics. The gain of the passive RX antenna is intentionally kept low so that the common search space of the bistatic radar transmitter and receiver does not become too narrow which would then have to be supported by very time consuming and complicated beam scanning operations. Note that the geometry considered here is specifically suited to model short surveillance based JRC systems (such as indoor/outdoor wireless communication systems). It does not model the bistatic GNSS-R scenario where both the transmitter and receiver are characterized by high gain antennas; and a three-dimensional geometry would have to be considered. The baseline length between the bistatic radar transmitter and receiver is L. The two-dimensional space is assumed to be populated by multiple scatterers - some MU (m) and the remaining discrete clutter (c) scatterers. In real world conditions, there can be significant variation in the number and spatial distribution of the point scatterers (both MU and clutter) in the radar channel. Further, the positions of scatterers are independent of each other. The Poisson point process is a completely random process since it has the property that each point is stochastically independent to all the other points in the process. Consequently, we consider the distribution of scatterers as an independent Poisson point processes (PPP: Φ)—wherein each instance is assumed to be a realization (ϕ) of a spatial stochastic process. We specifically consider a homogeneous PPP wherein the number of the scatterers in each realization follows a Poisson distribution and the positions of these scatterers follow a uniform distribution. Some prior works where discrete scatterers have been modelled as a PPP are Chen et al. (2012); Ram et al. (2020, 2021). We assume that the mean spatial densities of the MU and clutter scatterers are ρ_m and ρ_c respectively where ρ_m ≪ ρ_c. The position of an MU/clutter scatterer is specified in polar coordinates (r_i, θ_i), i ∈ m, c where r_i is the distance from the origin and θ_i is the angle with the positive X axis. The distance from BS and RX are $R_i^{tx}$ and $R_i^{rx}$ respectively and the bistatic range (κ_i) is specified by the geometric mean of both the one-way propagation distances $({\kappa }_i=\sqrt{R_i^{tx}{R}_i^{rx}})$. In bistatic radar geometry, the contours of constant κ_i for a fixed L are called Cassini ovals Willis (2005). Two regions are identified: the first is the cosite region when L ≤ 2κ_i and the contours appear as concentric ovals for different κ_i; and the second is when L > 2κ_i and the oval splits into two circles centered around BS and RX. In our work, we assume that cosite conditions prevail and that the bistatic angle at MU is β. Note that when L is zero, β = 0 and the system becomes a monostatic radar scenario. Here, the Cassini ovals become concentric circles for different values of $R_i^{tx}=R_i^{rx}={\kappa }_i$.

Classically, radar detection metrics and the radar operating curve are obtained from binary hypothesis testing derived from the Neyman-Pearson (NP) theorem Kay (1998). The probability of detection, ${\mathcal{P}}_{\text{d}}$, is the probability that a radar received signal (along with noise and clutter) is above a predefined threshold while the probability of false alarm, ${\mathcal{P}}_{\text{fa}}$, is the probability that the noise and clutter are above the threshold. For a fixed ${\mathcal{P}}_{\text{fa}}$, the ${\mathcal{P}}_{\text{d}}$ is directly proportional to the SCNR. For very simple scenarios (pulse radars in the absence of clutter), the relationship between ${\mathcal{P}}_{\text{d}}$, ${\mathcal{P}}_{\text{fa}}$ and SCNR are given by the Albersheim’s equation Skolnik (1980) while in more complex scenarios, the relationships have to be derived from extensive measurements. In Ram and Ghatak (2022), we presented a metric called the radar detection coverage probability $({\mathcal{P}}_{\text{DC}}^{\text{Bi}})$ to indicate the likelihood of a radar target being detected by a bistatic radar based on the signal-to-clutter-and-noise ratio (SCNR). The metric is analogous to wireless detection coverage probability which is widely studied in communication systems to study the network coverage in wireless links Andrews et al. (2011). We prefer the ${\mathcal{P}}_{\text{DC}}^{\text{Bi}}$ metric is to ${\mathcal{P}}_{\text{d}}$ and ${\mathcal{P}}_{\text{fa}}$ since it offers physics based insights into system performance and because of its tractable problem formulation. Specifically, we use ${\mathcal{P}}_{\text{DC}}^{\text{Bi}}$ to estimate the mean number of detected MU (η) as a function of ϵ and optimize the network throughput (ϒ). An extended discussion on the derivations of ${\mathcal{P}}_{\text{d}}$ and ${\mathcal{P}}_{\text{f}\text{a}}$ metrics are provided in the appendix of previous work on monostatic radar in Ram et al. (2021). If the transmitted power from BS is P_tx and the bistatic radar cross-section (RCS) of the MU, σ_m, is a random variable, then the received signal at RX, S, is given by the Friis radar range equation as

$\mathbf{S}\left({\kappa }_m\right)=P_{tx}{G}_{tx}\left({\theta }_{\mathbf{m}}\right){\sigma }_{\mathbf{m}}\mathcal{H}({\kappa }_{\text{m}}),(3)$

where $\mathcal{H}({\kappa }_{\text{m}})$ is the two-way propagation factor. In line-of-sight (LOS) conditions this is

$\mathcal{H}({\kappa }_{\text{m}})=\frac{{\lambda }^2}{{\left(4\pi \right)}^3{\left(R^{tx}{R}^{rx}\right)}^2}=\frac{H_0}{{\kappa }_m^4},(4)$

where λ is the wavelength of the radar. In the above expression, the gain of RX is assumed to be 1 since it is an omnidirectional antenna. We assume that the gain of the BS is uniform within the main lobe and is inversely proportional to the beam width: $G_{tx}=\frac{G_0}{{\mathrm{\Delta }\theta }_{\text{tx}}}$ where G₀ is the constant of proportionality that accounts for antenna inefficiencies including impedance mismatch, dielectric and conductor efficiencies. If we assume that the MU is within the mainlobe of the radar, then using (1), Equation 3 can be written as

$\mathbf{S}\left({\kappa }_m\right)=\frac{P_{tx}{G}_0{\sigma }_{\mathrm{m}}\mathcal{H}({\kappa }_{\text{m}})}{{\mathrm{\Delta }\theta }_{\text{tx}}}=P_{tx}{G}_0{B}_0ϵ{\sigma }_{\mathrm{m}}\mathcal{H}({\kappa }_{\text{m}}).(5)$

In (3) and (5), we have assumed that only a single MU is within a radar resolution cell, A_c. In the real world, a single radar resolution cell may consist of one or more targets. However, there is no way for the radar operator to distinguish or count the targets that are within a single cell. Hence, it will always be counted/considered as a single target. The amplitude of the target signal will however fluctuate due to interference from the multiple points within the cell and this fluctuation is captured with the Swerling models. Further, in the above discussion, we assume a single tone pulse radar of bandwidth BW. However, the system insights can be equally applied to other wide bandwidth signals as well. The clutter returns, C, at the radar receiver is given by

$\mathbf{C}\left({\kappa }_m\right)=\sum _{\text{c}\in \mathrm{\Phi }\cap {\mathbf{A}}_{\mathbf{c}}({\kappa }_{\text{m}})}{P}_{tx}{G}_{tx}\left({\theta }_{\mathbf{c}}\right){\mathit{\sigma }}_{\mathbf{c}}\mathcal{H}({\kappa }_{\text{c}}).(6)$

In the above expression, we specifically only consider those clutter scatterers that fall within the same resolution cell, A_c, as the MU. We use the generalized Weibull model Sekine et al. (1990) to describe the distribution of the RCS (σ_c) of the clutter points. For a given noise of the radar receiver, N_s = K_BT_sBW where K_B, T_s and BW are the Boltzmann constant, system noise temperature and bandwidth respectively, the signal to clutter and noise ratio is given by $\mathbf{S}\mathbf{C}\mathbf{N}\mathbf{R}({\kappa }_m)=\frac{\mathbf{S}({\kappa }_m)}{\mathbf{C}({\kappa }_m)+N_s}$.

3 Estimation of Network Throughput of Joint Radar-Communication

In this section we present the analytical framework to estimate the network throughput of the communication framework as a function of the explore/exploit duty cycle (ϵ). We use the ${\mathcal{P}}_{\text{DC}}^{\text{Bi}}$ metric defined in Ram and Ghatak (2022) to estimate, η, the number of MU detected by the radar during the search interval T_search = ϵT that will be subsequently served during T_serve.

Theorem 1. The network throughput (ϒ) for an explore/exploit duty cycle (ϵ) for a passive/bistatic radar based JRC system is given by

$\mathrm{\Upsilon }={\mathcal{P}}_{\text{DC}}^{\text{Bi}}\left(2\pi {\kappa }_m-\frac{3\pi L^2}{8{\kappa }_m}\right)\frac{{\rho }_{m}c\tau }{2\sqrt{1-\frac{L^2}{4{\kappa }_m^2}}}\left(1-ϵ\right)D(7)$

where

${\mathcal{P}}_{\text{DC}}^{\text{Bi}}=exp\left(\frac{-\gamma N_s{\kappa }_m^4}{{\sigma }_{m_{avg}}{P}_{\mathrm{tx}}{\text{G}}_0{\text{B}}_0ϵ{\text{H}}_0}+\frac{-\gamma {\rho }_{c}c\tau {\kappa }_m^2{\sigma }_{{\text{c}}_{\text{avg}}}}{B_0ϵ\left({\kappa }_m+\sqrt{{\kappa }_m^2-L^2}\right)\left({\sigma }_{{\text{m}}_{\text{avg}}}+\gamma {\sigma }_{{\text{c}}_{\text{avg}}}\right)}\right)(8)$

Proof.For an MU at bistatic range κ_m, the SCNR is a function of several random variables such as the MU cross-section, the position of MU, the number and spatial distribution of the discrete clutter scatterers and their RCS as shown below

$\mathbf{S}\mathbf{C}\mathbf{N}\mathbf{R}\left({\kappa }_m\right)=\frac{P_{tx}{G}_0{B}_0ϵ{\sigma }_{\mathbf{m}}\mathcal{H}({\kappa }_{\text{m}})}{\sum _{\text{c}\in \mathrm{\Phi }\cap {\mathbf{A}}_{\mathbf{c}}({\kappa }_{\text{m}})}{P}_{tx}{G}_0{B}_0ϵ{\mathbf{\sigma }}_{\mathbf{c}}\mathcal{H}({\kappa }_c)+N_s}=\frac{{\sigma }_{\mathbf{m}}}{\sum _{\text{c}\in \mathrm{\Phi }\cap {\mathbf{A}}_{\mathbf{c}}({\kappa }_{\text{m}})}\frac{{\mathbf{\sigma }}_{\mathbf{c}}\mathcal{H}({\kappa }_{\text{c}})}{\mathcal{H}({\kappa }_{\text{m}})}+\frac{N_s}{P_{\mathrm{tx}}{G}_0{B}_0ϵ\mathcal{H}({\kappa }_{\text{m}})}}.(9)$

We define the bistatic radar detection coverage probability $({\mathcal{P}}_{\text{DC}}^{\text{Bi}})$ as the probability that the SCNR is above a predefined threshold, γ. Therefore,

${\mathcal{P}}_{\text{DC}}^{\text{Bi}}=\mathcal{P}\left(\mathbf{S}\mathbf{C}\mathbf{N}\mathbf{R}\left({\kappa }_m\right)\ge \gamma \right)=\mathcal{P}\left({\sigma }_{\mathbf{m}}\ge \sum _{\text{c}\in \mathrm{\Phi }\cap {\mathbf{A}}_{\mathbf{c}}({\kappa }_{\text{m}})}\frac{\gamma {\sigma }_{\mathbf{c}}{\kappa }_m^4}{{\kappa }_c^4}+\frac{\gamma N_s{\kappa }_m^4}{P_{tx}{G}_0{B}_0ϵH_0}\right).(10)$

The bistatic RCS, σ_m, has been shown to demonstrate similar statistics as monostatic RCS Skolnik (1961). In this work, we consider the MU to have Swerling-1 characteristics, which corresponds to mobile users such as vehicles and humans Raynal et al. (2011a,b), as shown below

$\mathcal{P}\left({\sigma }_m\right)=\frac{1}{{\sigma }_{{\text{m}}_{\text{avg}}}}\mathit{exp}\left(\frac{-{\sigma }_m}{{\sigma }_{{\text{m}}_{\text{avg}}}}\right),(11)$

where, ${\sigma }_{{\text{m}}_{\text{avg}}}$ is the average radar cross-section. Hence, (10) can be expanded to

${\mathcal{P}}_{\text{DC}}^{\text{Bi}}=exp\left(\sum _{\text{c}\in \mathrm{\Phi }\cap {\mathbf{A}}_{\mathbf{c}}({\kappa }_m)}\frac{-\gamma {\sigma }_{\mathbf{c}}}{{\sigma }_{{\text{m}}_{\text{avg}}}}-\frac{\gamma N_s{\kappa }_m^4}{{\sigma }_{{\text{m}}_{\text{avg}}}{\text{P}}_{\text{tx}}{\text{G}}_0{\text{B}}_0ϵ{\text{H}}_0}\right)=exp\left(\frac{-\gamma N_s{\kappa }_m^4}{{\sigma }_{{\text{m}}_{\text{avg}}}{\text{P}}_{\text{tx}}{\text{G}}_0{\text{B}}_0ϵ{\text{H}}_0}\right)I\left({\kappa }_m\right).(12)$

In the above expression, ${\mathcal{P}}_{\text{DC}}^{\text{Bi}}$ consists of two terms. The first term consists entirely of constants and demonstrates the radar detection performance as a function of the signal-to-noise ratio (SNR). The second term, I (κ_m), shows the effect of the signal-to-clutter ratio (SCR). Since, we are specifically considering the clutter points that fall within the same resolution cell, A_c, as the MU we can assume that $\mathcal{H}({\kappa }_c)\approx \mathcal{H}({\kappa }_{\text{m}})$ in (10). We provide further insights into this path loss approximation in our later sections. Finally, the exponent of sum of terms can be written as a product of exponents. Hence, I (κ_m) is

$I\left({\kappa }_m\right)=\underset{{\sigma }_{\text{c}},\text{c}}{\mathbb{E}}\left[\prod _{\text{c}\in \mathrm{\Phi }\cap {\mathbf{A}}_{\mathbf{c}}({\kappa }_{\text{m}})}exp\left(\frac{-\gamma {\sigma }_{\mathbf{c}}}{{\sigma }_{{\mathrm{m}}_{\mathrm{a}\mathrm{v}\mathrm{g}}}}\right)\right],(13)$

where $\underset{{\sigma }_{\text{c}},\text{c}}{\mathbb{E}}$ is the expectation operator with respect to the clutter scatterers and their corresponding cross-section. The probability generating functional (PGFL) of a homogeneous PPP Haenggi (2012) based on stochastic geometry formulations is given as

$I=exp\left(-\underset{{\sigma }_{\text{c}},\text{c}}{\mathbb{E}}\left[{\iint }_{{\mathbf{r}}_{\mathbf{c}},{\varphi }_{\text{c}}}{\rho }_c\left(1-exp\left(\frac{-\gamma {\sigma }_{\mathbf{c}}}{{\sigma }_{{\text{m}}_{\text{avg}}}}\right)\right)d\left({\vec{x}}_c\right)\right]\right),(14)$

where ρ_c is the mean spatial density of the clutter scatterers. The integral specifically considers the clutter scatterers that fall within the same resolution cell as the MU. Bistatic radar literature identifies three types of resolution cells—the range resolution cell, the beamwidth resolution cell and the Doppler resolution cell. In our study, the main objective of the radar is to perform range-azimuth based localization. Hence, we consider the range resolution cell, which based on Willis (2005); Moyer et al. (1989), corresponds to

${\mathbf{A}}_{\mathbf{c}}\left({\kappa }_m\right)=\frac{c\tau R^{tx}\left({\theta }_{\mathbf{m}}\right)\mathrm{\Delta }{\theta }_{tx}}{2{\cos }^2\left(\beta \left({\theta }_{\mathbf{m}}\right)/2\right)}=\frac{c\tau R^{tx}\left({\theta }_{\mathbf{m}}\right)}{B_0ϵ\left(1+\sqrt{1-{\sin }^2\beta \left({\theta }_{\mathbf{m}}\right)}\right)},(15)$

for a pulse width of τ. In the above expression, note that the size of A_c varies as a function of constant κ_m and the random variable θ_m. Prior studies show that sin β takes on the value of sin β_max with a very high probability when $R_m^{tx}\approx {\kappa }_m$ Ram and Ghatak (2022). Based on bistatic geometry $\sin {\beta }_{max}=\sqrt{\frac{L^2}{{\kappa }_m^2}-\frac{L^4}{{\kappa }_m^4}}\approx \frac{L}{{\kappa }_m}$ when κ_m > L. Therefore, (15) reduces to

$A_c\approx \frac{c\tau {\kappa }_m^2}{B_0ϵ\left({\kappa }_m+\sqrt{{\kappa }_m^2-L^2}\right)}(16)$

If we assume that the clutter statistics are uniform within A_c, then the integral in (14) can be further reduced to

$I=exp\left(-\underset{{\sigma }_c}{\mathbb{E}}\left[\left(1-exp\left(\frac{-\gamma {\mathit{\sigma }}_{\mathbf{c}}}{{\sigma }_{{\text{m}}_{\text{avg}}}}\right)\right){\rho }_c{A}_c\right]\right)=exp\left(-\underset{{\sigma }_{\text{c}}}{\mathbb{E}}\left[\left(1-exp\left(\frac{-\gamma {\mathit{\sigma }}_{\mathbf{c}}}{{\sigma }_{{\text{m}}_{\text{avg}}}}\right)\right)\frac{{\rho }_{c}c\tau {\kappa }_m^2}{B_0ϵ\left({\kappa }_m+\sqrt{{\kappa }_m^2-L^2}\right)}\right]\right)(17)$

If we define $J({\kappa }_m)=\frac{{\rho }_{c}c\tau {\kappa }_m^2}{B_0ϵ({\kappa }_m+\sqrt{{\kappa }_m^2-L^2})}$ as a constant independent of σ_c, then it can be pulled out of the integral for computing the expectation as shown below

$I\left({\kappa }_m\right)=exp\left(-J\left({\kappa }_m\right)\underset{0}{\overset{\infty }{\int }}\left(1-exp\left(\frac{-\gamma {\mathit{\sigma }}_{\mathbf{c}}}{{\sigma }_{{\text{m}}_{\text{avg}}}}\right)\right)\mathcal{P}\left({\sigma }_c\right)d{\sigma }_c\right).(18)$

In our work, we specifically consider the contributions from discrete/point clutter responses that arise from direct and multipath reflections from the surrounding environment. We model the radar cross-section of these scatterers using the generalized Weibull model shown in

$\mathcal{P}\left({\sigma }_c\right)=\frac{\alpha }{{\sigma }_{{\text{c}}_{\text{avg}}}}{\left(\frac{{\sigma }_c}{{\sigma }_{{\text{c}}_{\text{avg}}}}\right)}^{\alpha -1}\exp \left(-{\left(\frac{{\sigma }_c}{{\sigma }_{{\text{c}}_{\text{avg}}}}\right)}^{\alpha }\right),(19)$

where ${\sigma }_{{\text{c}}_{\text{avg}}}$ is the average bistatic radar cross-section and α is the corresponding shape parameter. The Weibull distribution has been widely used to model clutter due to its tractable formulation and its adaptability to different environment conditions Sekine et al. (1990). When the scenario is characterized by few dominant scatterers, α is near one and corresponds to the exponential distribution. On the other hand, when there are multiple scatterers of similar strengths, then α tends to two which corresponds to the Rayleigh distribution. The actual value of α in any real world scenario is determined through empirical studies. I (κ_m) in (18) can be numerically evaluated for any value of α. But for α = 1, the expression becomes

$I\left({\kappa }_m\right)=exp\left(-\frac{\gamma J\left({\kappa }_m\right){\sigma }_{{\text{c}}_{\text{avg}}}}{{\sigma }_{m_{avg}}+\gamma {\sigma }_{c_{avg}}}\right).(20)$

Substituting (20) in (12), we obtain

${\mathcal{P}}_{\text{DC}}^{\text{Bi}}=exp\left(\frac{-\gamma N_s{\kappa }_m^4}{{\sigma }_{{\text{m}}_{\text{avg}}}{\text{P}}_{\text{tx}}{\mathrm{G}}_0{\text{B}}_0ϵ{\text{H}}_0}+\frac{-\gamma {\rho }_{c}c\tau {\kappa }_m^2{\sigma }_{{\text{c}}_{\text{avg}}}}{B_0ϵ\left({\kappa }_m+\sqrt{{\kappa }_m^2-L^2}\right)\left({\sigma }_{{\text{m}}_{\text{avg}}}+\gamma {\sigma }_{{\text{c}}_{\text{avg}}}\right)}\right).(21)$

The above expression shows the probability that a MU at κ_m is detected by the bistatic radar based on its SCNR. If we assume a uniform spatial distribution, ρ_m, of the MU in Cartesian space, then the mean number of MU that can be detected within the total radar field-of-view at κ_m bistatic range from the radar will be given by

$\eta ={\mathcal{P}}_{\text{DC}}^{\text{Bi}}\left({\kappa }_m\right){\rho }_m\mathcal{C}\left({\kappa }_m\right)\delta r,(22)$

where $\mathcal{C}({\kappa }_m)$ is the circumference of a Cassini oval and $\delta r=\frac{c\tau }{2\cos (\beta /2)}$ is the range resolution of the radar. The parametric equation for the Cassini oval is given in

${\left(r_m^2+\frac{L^2}{4}\right)}^2-r_m^2{L}^2{\cos }^2{\theta }_m={\kappa }_m^4.(23)$

Hence, the circumference $\mathcal{C}({\kappa }_m)$ can be computed from

$\mathcal{C}\left({\kappa }_m\right)=\underset{0}{\overset{2\pi }{\int }}{r}_m\left({\theta }_m\right)d{\theta }_m=\frac{L}{2}\underset{0}{\overset{2\pi }{\int }}{\left[\cos 2{\theta }_m\pm {\left(\frac{16{\kappa }_m^4}{L^4}-{\sin }^2{\theta }_m\right)}^{1/2}\right]}^{1/2}d{\theta }_m\approx 2\pi {\kappa }_m-\frac{3\pi L^2}{8{\kappa }_m}.(24)$

When κ_m > L, the estimation of (24) can be approximated to the expression shown above. Note that for very large values of κ_m ≫ L, the scenario approaches monostatic conditions. Here, the oval approximates to a circle of circumference 2πκ_m. Also, as mentioned before β can be approximated to β_max. Hence $\cos ({\beta }_{max}/2)\approx \sqrt{1-\frac{L}{4{\kappa }_m^2}}$. Therefore, the mean number of detected MU is

$\eta ={\mathcal{P}}_{\text{DC}}^{\text{Bi}}\left(2\pi {\kappa }_m-\frac{3\pi L^2}{8{\kappa }_m}\right)\frac{{\rho }_{m}c\tau }{2\sqrt{1-\frac{L^2}{4{\kappa }_m^2}}},(25)$

and the resulting network throughput for the communication links that are set up with detected MUs is

$\mathrm{\Upsilon }={\mathcal{P}}_{\text{DC}}^{\text{Bi}}\left(2\pi {\kappa }_m-\frac{3\pi L^2}{8{\kappa }_m}\right)\frac{{\rho }_{m}c\tau }{2\sqrt{1-\frac{L^2}{4{\kappa }_m^2}}}\left(1-ϵ\right)D.(26)$

4 Optimization of Joint Radar-Communication System Parameters for Maximization of Network Throughput

In this section, we discuss the corollaries from the theorem presented in the previous section. Based on these inferences, we present how JRC parameters such as ϵ, τ, Δθ_tx and T_PRI can be optimized for maximum throughput. The results presented in this section are experimentally validated using Monte Carlo simulations. For the simulations, we assume that the bistatic radar transmitter (BS) and receiver (RX) are located at $(\pm \frac{L}{2},0)$ respectively as shown in Figure 2.We consider a [200 m × 200 m] region of interest. Radar, MU and clutter parameters such as $P_{tx},L,{\mathrm{\Delta }\theta }_{\text{tx}},N_s.{\sigma }_{{\text{m}}_{\text{avg}}},\kappa ,{\sigma }_{{\text{c}}_{\text{avg}}}$ and ρ_c are kept fixed and summarized in Table.1. In each realization of the Monte Carlo simulation, the MU’s polar coordinate position, θ_m is drawn from a uniform distribution from (0, 2π) and r_m is computed for a fixed κ_m. The RCS of the MU is drawn from the exponential distribution corresponding to the Swerling-1 model. The mean number of discrete clutter scatterers is equal to ρ_c times the area of the region of interest. The number of clutter scatterers are different for each realization and drawn from a Poisson distribution. The positions of the clutter scatterers are based on a uniform distribution in the two-dimensional Cartesian space while the RCS of each discrete scatterer is drawn from the Weibull model. We compute the SCNR based on the returns from the MU and the clutter scatterers estimated with the Friis bistatic radar range equation. Note that we only consider those point clutter that fall within the BS mainlobe and within δr proximity of the two-way distance of the radar and MU. In other words, they must lie within the radar range limited resolution cell. To do so, we compute the slope of the line joining the scatterer and BS (m₀). Then we compute m₁ = m₀ + tan (Δθ_tx/2) and m₂ = m₀ − tan (Δθ_tx/2) based on the radar BS beamwidth (Δθ_tx). The scatterer is within the radar beamwidth provided the product of the differences (m₁—m₀) and (m₂—m₀) is negative. Then we check if the absolute difference of the two-way path lengths of MU $(R_m^{tx}+R_m^{rx})$ and point clutter $(R_c^{tx}+R_c^{rx})$ is within the range resolution δr. If the resulting SCNR is above the predefined threshold γ, then we assume that the target is detected. The results over a large number of realizations are used to compute the ${\mathcal{P}}_{\text{DC}}^{\text{Bi}}$ for the results presented in Figures 3–8 (a) in this section. Note that the Monte Carlo simulations are useful to test some key assumptions made in SG based analysis such as the path loss approximation of the point clutter within the radar range limited resolution cell to the path loss of the MU.

FIGURE 2

FIGURE 2. Two realizations of Monte Carlo simulations with bistatic radar transmitter (BS) and receiver (RX) indicated by triangles. The BS is characterized by narrow beam indicated by dashed blue lines with slopes m₁ and m₂ while RX is omnidirectional. Target is indicated by black dot while clutter scatterers inside and outside the radar resolution cell are indicated by blue and red dots respectively.

FIGURE 3

FIGURE 3. (A) Detection coverage $({\mathcal{P}}_{DC}^{Bi})$ and (B) network throughput (ϒ) as a function of explore/exploit duty cycle (ϵ) for parametric bistatic range (κ).

FIGURE 4

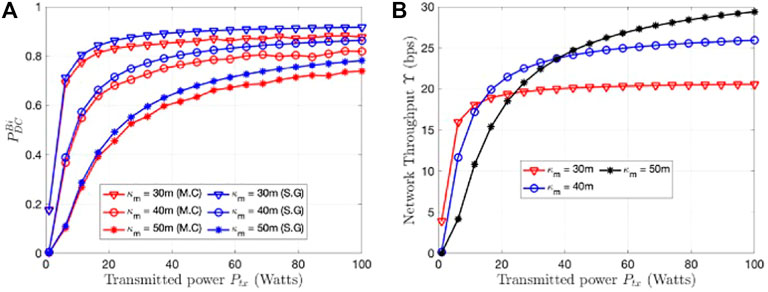
FIGURE 4. (A) Detection coverage $({\mathcal{P}}_{DC}^{Bi})$ and (B) network throughput (ϒ) as a function of transmitted power (P_tx) for parametric bistatic range (κ_m).

FIGURE 5

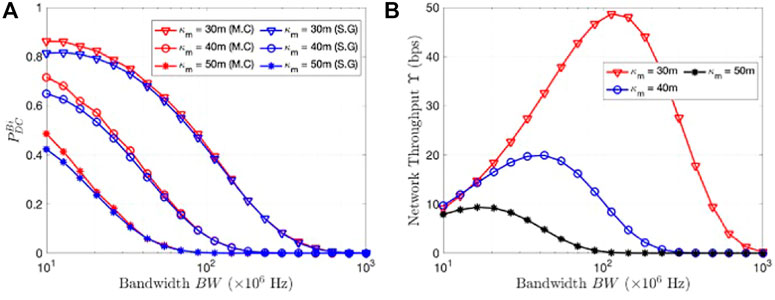
FIGURE 5. (A) Detection coverage $({\mathcal{P}}_{\text{DC}}^{\text{Bi}})$ and (B) network throughput (ϒ) as a function of bandwidth (BW) for parametric bistatic range (κ_m).

FIGURE 6

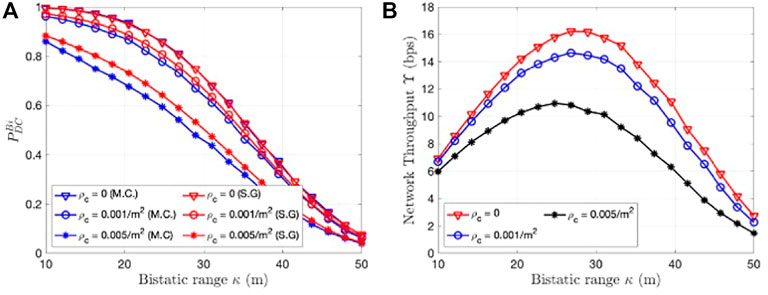
FIGURE 6. (A) Detection coverage $({\mathcal{P}}_{\text{DC}}^{\text{Bi}})$ and (B) network throughput (ϒ) as a function of bistatic range (κ_m) for parametric clutter density (ρ_c).

FIGURE 7

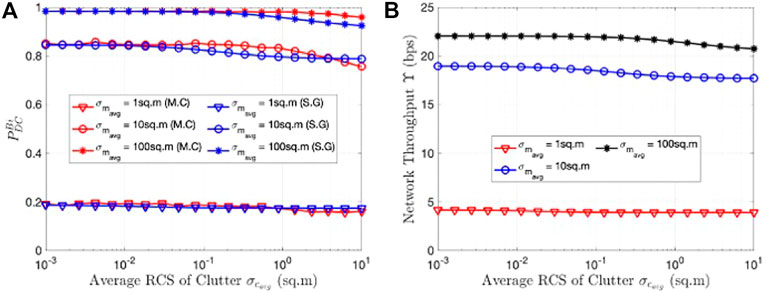
FIGURE 7. (A) Detection coverage $({\mathcal{P}}_{\text{DC}}^{\text{Bi}})$ and (B) network throughput (ϒ) as a function of mean clutter RCS $({\sigma }_{{\text{c}}_{\text{avg}}})$ for parametric mean target RCS $({\sigma }_{{\text{m}}_{\text{avg}}})$.

FIGURE 8

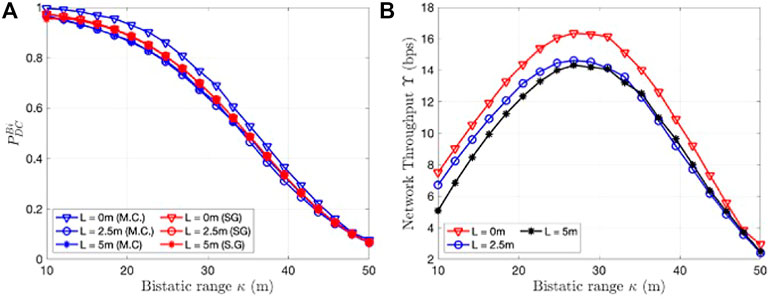
FIGURE 8. (A) Detection coverage $({\mathcal{P}}_{\text{DC}}^{\text{Bi}})$ and (B) network throughput (ϒ) as a function of target bistatic range (κ_m) for parametric bistatic base length (L).

TABLE 1

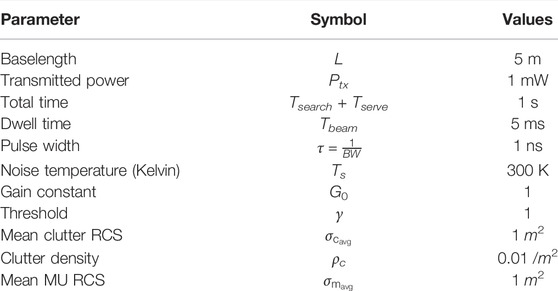
TABLE 1. Radar, target and clutter parameters used in the stochastic geometry formulations and Monte Carlo simulations.

4.1 Explore/Exploit Duty Cycle (ϵ)

In the JRC framework, a key parameter is $ϵ=\frac{T_{search}}{T}$, the duty cycle, of the system. When ϵ is high, there is longer time for radar localization (T_search) but less time for communication service (T_serve) and vice versa. As a result, the radar beams can be narrow while scanning the angular search space. This results in weaker detection performance due to poorer gain. The Theorem (7) shows the dependence of throughput ϒ on ϵ which can be written as

$\mathrm{\Upsilon }\left(ϵ\right)=A_0{e}^{-a/ϵ}\left(1-ϵ\right),(27)$

where

$a=\frac{-\gamma N_s{\kappa }_m^4}{{\sigma }_{{\text{m}}_{\text{avg}}}{P}_{tx}{G}_0{B}_0{H}_0}+\frac{-\gamma {\rho }_{c}c\tau {\kappa }_m^2{\sigma }_{c_{avg}}}{B_0\left({\kappa }_m+\sqrt{{\kappa }_m^2-L^2}\right)\left({\sigma }_{{\text{m}}_{\text{avg}}}+\gamma {\sigma }_{{\text{c}}_{\text{avg}}}\right)}(28)$

and

$A_0=\left(2\pi {\kappa }_m-\frac{3\pi L^2}{8{\kappa }_m}\right)\frac{{\rho }_{m}c\tau D}{2\sqrt{1-\frac{L^2}{4{\kappa }_m^2}}}.(29)$

We find the optimized $\widetilde{ϵ}$ for maximum throughput by equating the first derivative of ϒ to zero.

Corollary 1.1. The optimum explore/exploit duty cycle $(\widetilde{ϵ})$ for maximum throughput is given by

$\widetilde{ϵ}=\frac{\sqrt{a^2+4a}-a}{2}(30)$

The above case shows that the duty cycle is a function of the SCNR of the JRC system (shown in a in (28)). Figure 3 shows the variation of ${\mathcal{P}}_{\text{DC}}^{\text{Bi}}$ and ϒ with respect to ϵ for different values of κ_m.The view graph, Figure 3A, shows that ${\mathcal{P}}_{DC}^{Bi}$ improves with increase in ϵ. In other words, when we have longer search time, we can use finer beams to search for the MU and thus have a greater likelihood of detecting them. However, the same is not true for the throughput (ϒ) shown in Figure 3B. An increase in ϵ initially improves the ϒ but subsequently causes a deterioration due to the reduction in communication service time. The optimum $\widetilde{ϵ}$ in the view graph matches the estimate from corollary (30). Since the above metric is shown to be a function of κ_m, it becomes difficult for a system operator to vary ϵ according to the position of the MU. Instead, we recommend that the above tuning is carried out for the maximum bistatic range of the JRC system which is determined based on the pulse repetition frequency. The selection of the PRF is discussed in subsection 5.4. Note that in the above view graphs, the results obtained from Monte Carlo system simulations closely match the results derived from the SG based analysis.

4.2 Signal-to-Noise Ratio Vs Signal-to-Clutter Ratio

Next, we discuss the effects of noise and clutter on the performance of the JRC. As pointed out earlier, there are two terms within the ${\mathcal{P}}_{DC}^{Bi}$ in (7) and (8).The first term captures the effect of the SNR on the JRC performance while the second term captures the effect of the SCR. Figure 4 shows the effect of increasing the transmitted power P_tx on ${\mathcal{P}}_{DC}^{Bi}$ and ϒ. The results show that ${\mathcal{P}}_{DC}^{Bi}$ and ϒ increase initially with increase in power but subsequently, the performance saturates because the clutter returns also increase proportionately with increase in P_tx. On the other hand, when we consider the radar bandwidth which is the reciprocal of the pulse width $(BW=\frac{1}{\tau })$, we observe that there is an optimum BW for maximum ϒ in Figure 5B. This is because when BW is increased, the range resolution decreases and correspondingly the clutter resolution cell size. As a result, fewer clutter scatterers contribute to the SCNR. But, on the other hand, the radar noise (N_s = K_BT_sBW) also increases which results in poorer quality radar links.

Corollary 1.2. The optimum bandwidth $\widetilde{BW}$ for maximum throughput ϒ is obtained by the derivation of (8) with respect to BW and is given by

$\widetilde{BW}={\left(\frac{{\rho }_{c}c{\sigma }_{{\text{c}}_{\text{avg}}}{\sigma }_{{\text{m}}_{\text{avg}}}{P}_{tx}{G}_0{H}_0}{{\kappa }_m^2{K}_B{T}_s\left({\kappa }_m+\sqrt{{\kappa }_m^2-L^2}\right)\left({\sigma }_{{\text{m}}_{\text{avg}}}+\gamma {\sigma }_{{\text{c}}_{\text{avg}}}\right)}\right)}^{1/2}(31)$

The Monte Carlo results in Figure 5A show good agreement with SG results especially for higher values of wider BW. At low narrow BW, the errors due to the path loss approximation between the point clutter and the MU become more evident. However, in real world scenarios, microwave/millimeter JRC systems are developed specifically for high wide bandwidth waveforms for obtaining fine range resolution of the MU. Next we study the impact of clutter density and clutter RCS in Figure 6 and Figure 7. When the clutter density is low (ρ_c approaches zero), we observe that ${\mathcal{P}}_{DC}^{Bi}$ decays at the fourth power of κ_m as shown in Figure 6 and the throughput is entirely a function of the SNR. For large values of κ_m, the system is dominated by the effects of clutter rather than noise. We observe that the throughput increases initially with increase in κ_m due to the increase in number of MU within the area of interest and then subsequently the throughput falls due to the deterioration in the radar link metrics.The effect of ${\sigma }_{{\text{c}}_{\text{avg}}}$ is less significant on ${\mathcal{P}}_{DC}^{Bi}$ and ϒ as both curves are flat in Figures 7A,B. On the other hand, the performances are far more sensitive to ${\sigma }_{{\text{m}}_{\text{avg}}}$.

4.3 Monostatic Conditions

A monostatic radar is a specific case of bistatic radar where the baseline length, L, and bistatic angle, β, are zero. Here, the one-way propagation distance from the transmitter and receiver to the target are equal. Hence, a monostatic radar can be assumed to be at the origin with the bistatic range κ_m equal to the polar distance r_m. We can, then directly, derive the radar detection coverage metric and throughput for this scenario from the bistatic case by making the corresponding substitutions to (7) and (8) and derive the following corollary.

Corollary 1.3. The radar detection coverage metric $({\mathcal{P}}_{DC}^{Mono})$ and network throughput (ϒ) for a explore/exploit duty cycle (ϵ) for a monostatic radar based JRC system is given by

$\mathrm{\Upsilon }={\mathcal{P}}_{DC}^{Mono}\pi r_m{\rho }_{m}c\tau \left(1-ϵ\right)D(32)$

where

${\mathcal{P}}_{DC}^{Mono}=exp\left(\frac{-\gamma N_s{r}_m^4}{{\sigma }_{m_{avg}}{P}_{tx}{G}_0{B}_0ϵH_0}+\frac{-\gamma {\rho }_{c}c\tau r_m{\sigma }_{c_{avg}}}{2B_0ϵ\left({\sigma }_{{\mathrm{m}}_{\mathrm{avg}}}+\gamma {\sigma }_{{\mathrm{c}}_{\mathrm{avg}}}\right)}\right)(33)$

The corollary again shows that the detection performance in the case of the monostatic radar can be studied through the SNR (the first term within the exponent of (33)) and the SCR (the second term within the exponent). The SNR deteriorates as a function of the fourth power of the target distance while the SCR deteriorates linearly as a function of target radial distance. Hence, at greater distances we are limited by the clutter rather than the noise. We compare the monostatic and bistatic radar performances using the baseline length L as a parameter in Figure 8. Note that for all values of L and κ_m in the above study, the MU remains within the cosite region of the radar. The result show that the ${\mathcal{P}}_{DC}^{Bi}$ does not vary significantly for change from monostatic (L = 0) to bistatic (L > 0) conditions. In other words, the mean number of MU detected does not change significantly in both cases. The throughput, on the other hand, shown in Figures 8B, is higher for the monostatic case and appears to reduce slightly for increase in baseline length. This is because the circumference of the Cassini oval reduces slightly from the monostatic case to the bistatic case as per (24). Hence, fewer MU will be selected for a fixed bistatic range.

4.4 Pulse Repetition Interval

The maximum two-way unambiguous range of a radar, $R_{\text{max}}={(R_m^{tx}+R_m^{rx})}_{\text{max}}$, is equal to cT_PRI. Through the intersection of the ellipse defined for a uniform R_max and the Cassini oval of constant κ_m, the two terms are related through

$R_{\mathit{max}}=c{T}_{PRI}=L^2+2{\kappa }_m^2\left(1+\cos \beta \right).(34)$

Note that in the above expression, the bistatic range changes for the parameter β. The maximum value that cos β can take is 1. Hence, for a given radar’s T_PRI

${\kappa }^{max}=\frac{1}{2}{\left(c^2{T}_{PRI}^2-L^2\right)}^{1/2}.(35)$

If we assume that at this range κ_max ≫ L, then ${\mathcal{P}}_{DC}^{Bi}({\kappa }_{max})$ is given by

${\mathcal{P}}_{\mathrm{DC}}^{Bi}\left({\kappa }_{max}\right)=exp\left(\frac{-\gamma N_s{\left(c^2{T}_{PRI}^2-L^2\right)}^2}{16{\sigma }_{{\text{m}}_{\text{avg}}}{\mathrm{P}}_{\text{tx}}{\text{G}}_0{\text{B}}_0ϵ{\text{H}}_0}+\frac{-\gamma {\rho }_{c}c\tau {\sigma }_{{\text{c}}_{\text{avg}}}{\left(c^2{T}_{PRI}^2-L^2\right)}^{1/2}}{4B_0ϵ\left({\sigma }_{{\text{m}}_{\text{avg}}}+\gamma {\sigma }_{{\text{c}}_{\text{avg}}}\right)}\right),(36)$

and the throughput is given by

$\mathrm{\Upsilon }\left({\kappa }_{max}\right)={\mathcal{P}}_{DC}^{Bi}\left({\kappa }_{max}\right)\frac{\pi }{2}{\left(c^2{T}_{PRI}^2-L^2\right)}^{1/2}{\rho }_{m}c\tau \left(1-ϵ\right)D.(37)$

In the above throughput expression, it is evident that if the T_PRI is larger, the radar detection performance deteriorates. However, a larger number of MU are included in the region-of-interest due to which there are some gains in the throughput. We assume that if the R_max is high enough to ignore the effects of L, the radar operates under clutter limited conditions, and the throughput is a function of T_PRI, as given in

$\mathrm{\Upsilon }\left(T_{PRI}\right)=exp\left(-\frac{\gamma {\rho }_c{\sigma }_{{\text{c}}_{\text{avg}}}{c}^2\tau T_{PRI}}{4B_0ϵ\left({\sigma }_{{\text{m}}_{\text{avg}}}+\gamma {\sigma }_{{\text{c}}_{\text{avg}}}\right)}\right)\frac{\pi }{2}{c}^2\tau T_{PRI}{\rho }_m\left(1-ϵ\right)D.(38)$

Corollary 1.4. Accordingly, the optimum pulse repetition interval, ${\tilde{T}}_{PRI}$, can be estimated for maximum throughput as

${\tilde{T}}_{PRI}=\frac{4B_0ϵ\left({\sigma }_{{\text{m}}_{\text{avg}}}+\gamma {\sigma }_{{\text{c}}_{\text{avg}}}\right)}{\gamma {\rho }_c{\sigma }_{{\text{c}}_{\text{avg}}}{c}^2\tau }.(39)$

The above expression shows that higher ϵ (resulting in narrow beams) and shorter pulse duration (smaller τ) will allow for a longer pulse repetition interval and unambiguous range due to improvement in the link metrics.

4.5 Meta Distribution of Signal-to-Clutter-and-Noise Ratio in a Bistatic Radar

Although the ${\mathcal{P}}_{DC}^{Bi}$ is a useful metric for tuning radar parameters, it only provides an average view of the network across all possible network realizations of the underlying point process. it is simply a spatial average of the detection performance of all radars across all clutter realizations in the region of interest. Hence, it does not reveal the performance of individual radars. This inhibits derivation of link-level reliability of the radar detection performance. In this regard, the meta-distribution, i.e., the distribution of the radar ${\mathcal{P}}_{DC}^{Bi}$ conditioned on a realization of Φ provides a framework to study the same. For that, we introduce the random variable ${\mathcal{P}}_{DC\mathrm{\Phi }}^{Bi}$, which denotes the bistatic detection coverage probability conditioned on the clutter realization, i.e., ${\mathcal{P}}_{DC\mathrm{\Phi }}^{Bi}=\mathbb{P}(\mathbf{S}\mathbf{C}\mathbf{N}\mathbf{R}({\kappa }_m)>\gamma |\mathrm{\Phi })$. The meta-distribution then is simply the distribution of the random variable ${\mathcal{P}}_{DC\mathrm{\Phi }}^{Bi}$. Its complementary CDF, i.e., $F_{{\mathcal{P}}_{DC\mathrm{\Phi }}^{Bi}}(z)=\mathbb{P}\left({\mathcal{P}}_{DC\mathrm{\Phi }}^{Bi}\ge z\right)$, represents the probability with which at least z fraction of the bistatic radar links experience a successful radar detection when the SCNR threshold is set to γ. Mathematically,

${\mathcal{P}}_{\mathrm{DC}\mathrm{\Phi }}^{\mathrm{Bi}}=\mathcal{P}\left(\mathbf{S}\mathbf{C}\mathbf{N}\mathbf{R}\left({\kappa }_m\right)\ge \gamma |\mathrm{\Phi }\right)=\mathcal{P}\left({\mathit{\sigma }}_{\mathit{m}}\ge \sum _{\text{c}\in \mathrm{\Phi }\cap {\mathbf{A}}_{\mathbf{c}}({\kappa }_{\text{m}})}\frac{\gamma {\mathit{\sigma }}_{\mathit{c}}{\kappa }_m^4}{{\kappa }_c^4}+\frac{\gamma N_s{\kappa }_m^4}{P_{tx}{G}_0{B}_0ϵH_0}|\mathrm{\Phi }\right),(40)$

$=\exp \left(-\frac{\gamma N_s{\kappa }_m^4}{{\sigma }_{{\text{m}}_{\text{avg}}}{P}_{tx}{G}_0{B}_0ϵH_0}\right)\left(\prod _{\text{c}\in \mathrm{\Phi }\cap {\mathbf{A}}_{\mathbf{c}}({\kappa }_m)}\left(\frac{\gamma {\sigma }_{{\text{c}}_{\text{avg}}}{\left(R_c^{tx}\right)}^{-2}{\left(R_c^{rx}\right)}^{-2}{\kappa }_m^4}{{\sigma }_{{\text{m}}_{\text{avg}}}+\gamma {\sigma }_{{\text{c}}_{\text{avg}}}{\left(R_c^{tx}\right)}^{-2}{\left(R_c^{rx}\right)}^{-2}{\kappa }_m^4}\right)\right).(41)$

For a point clutter located at a distance, $R_c^{tx}$, from the transmitter at an angle ${\theta }_c^{tx}$, we have ${(R_c^{rx})}^2={(R_c^{tx})}^2+L^2+2R_c^{tx}L\cos ({\theta }_c^{tx})$. The direct evaluation of the exact distribution of ${\mathcal{P}}_{\text{DC}\mathrm{\Phi }}^{\text{Bi}}$ is challenging. Thus, we take an indirect approach to evaluate it through the calculation of its moments. In particular, the bth moment of ${\mathcal{P}}_{\text{DC}\mathrm{\Phi }}^{\text{Bi}}$ is given by:

$\begin{array}{ll}\hfill M_b& =\mathbb{E}\left[\mathcal{T}\left(b,{\kappa }_m\right){\left(\prod _{\text{c}\in \mathrm{\Phi }\cap {\mathbf{A}}_{\mathbf{c}}({\kappa }_{\text{m}})}\left(\frac{\gamma {\sigma }_{{\text{c}}_{\text{avg}}}{\left(R_c^{tx}\right)}^{-2}{\left(R_c^{rx}\right)}^{-2}{\kappa }_m^4}{{\sigma }_{{\text{m}}_{\text{avg}}}+\gamma {\sigma }_{c_{avg}}{\left(R_c^{tx}\right)}^{-2}{\left(R_c^{rx}\right)}^{-2}{\kappa }_m^4}\right)\right)}^b\right]\hfill \\ \hfill & =\mathcal{T}\left(b,m\right)\mathbb{E}\left[{\left(\prod _{c\in \mathrm{\Phi }\cap {\mathbf{A}}_{\mathbf{c}}({\kappa }_m)}\left(\frac{\gamma {\sigma }_{c_{avg}}{\left(R_c^{tx}\right)}^{-2}{\left(R_c^{rx}\right)}^{-2}{\kappa }_m^4}{{\sigma }_{m_{avg}}+\gamma {\sigma }_{c_{avg}}{\left(R_c^{tx}\right)}^{-2}{\left(R_c^{rx}\right)}^{-2}{\kappa }_m^4}\right)\right)}^b\right]\hfill \\ \hfill & =\frac{1}{2\pi }\mathcal{T}\left(b,m\right)\underset{0}{\overset{2\pi }{\int }}\exp \left(-{\rho }_c\underset{{\theta }_m^{tx}-\frac{\mathrm{\Delta }{\theta }_{tx}}{2}}{\overset{{\theta }_m^{tx}+\frac{\mathrm{\Delta }{\theta }_{tx}}{2}}{\int }}\underset{R^{tx}-\frac{\delta r}{2}}{\overset{R^{tx}+\frac{\delta r}{2}}{\int }}1-{\left(\frac{\gamma {\sigma }_{c_{avg}}{y}^{-2}{y}_r^{-2}{\kappa }_m^4}{{\sigma }_{m_{\mathrm{avg}}}+\gamma {\sigma }_{c_{\mathrm{avg}}}{y}^{-2}{y}_r^{-2}{\kappa }_m^4}\right)}^{b}ydyd{\theta }_c^{tx}\right)d{\theta }_m\hfill \\ \hfill & =\frac{1}{2\pi }\mathcal{T}\left(b,m\right)\underset{0}{\overset{2\pi }{\int }}\exp \left(-{\rho }_c\sum _{k=1}^b\left(\genfrac{}{}{0.0pt}{}{b}{k}\right)\underset{{\theta }_m^{tx}-\frac{\mathrm{\Delta }{\theta }_{tx}}{2}}{\overset{{\theta }_m^{tx}+\frac{\mathrm{\Delta }{\theta }_{tx}}{2}}{\int }}\underset{R^{tx}-\frac{\delta r}{2}}{\overset{R^{tx}+\frac{\delta r}{2}}{\int }}{\left(-\frac{\gamma {\sigma }_{c_{avg}}{y}^{-2}{y}_r^{-2}{\kappa }_m^4}{{\sigma }_{m_{\mathrm{avg}}}+\gamma {\sigma }_{c_{\mathrm{avg}}}{y}^{-2}{y}_r^{-2}{\kappa }_m^4}\right)}^{k}ydyd{\theta }_c^{tx}\right)d{\theta }_m,\hfill \end{array}(42)$

where, $\mathcal{T}(b,m)=\exp \left(-\frac{\gamma b{N}_s{\kappa }_m^4}{{\sigma }_{{\text{m}}_{\text{avg}}}{P}_{tx}{G}_0{B}_0ϵH_0}\right)$, $y_r={(y^2+L^2-2yL\cos ({\theta }_c^{tx}))}^{\frac{1}{2}}$. Now, for a large bandwidth, the range-resolution cell is relatively small, and hence, with the path loss approximation $\sqrt{R_c^{tx}{R}_c^{rx}}={\kappa }_m$ for all clutter points within the cell, we have:

$\begin{array}{ll}\hfill M_b& =\exp \left(-\frac{\gamma b{N}_s{\kappa }_m^4}{{\sigma }_{{\text{m}}_{\text{avg}}}{P}_{tx}{G}_0{B}_0ϵH_0}\right){\mathbb{E}}_n\left[{\left(\frac{{\sigma }_{{\text{m}}_{\mathrm{avg}}}}{{\sigma }_{{\text{m}}_{\mathrm{avg}}}+\gamma {\sigma }_{{\text{c}}_{\text{avg}}}}\right)}^{nb}\right]\hfill \\ \hfill & =\exp \left(-\frac{\gamma b{N}_s{\kappa }_m^4}{{\sigma }_{m_{avg}}{P}_{tx}{G}_0{B}_0ϵH_0}\right)\exp \left({\rho }_c{A}_c\left({\kappa }_m\right)\left({\left(\frac{{\sigma }_{m_{\mathrm{avg}}}}{{\sigma }_{m_{\mathrm{avg}}}+\gamma {\sigma }_{c_{\mathrm{avg}}}}\right)}^b-1\right)\right)\hfill \end{array}(43)$

We note here that with the path loss approximation, only the number of clutter points (and not their locations) inside the range resolution cell n impacts the moment. Then, the complementary CDF of the conditional ${\mathcal{P}}_{\text{DC}\mathrm{\Phi }}^{\text{Bi}}$ can be evaluated using the Gil-Pelaez inversion theorem as:

$F_{{\mathcal{P}}_{\text{DC}\mathrm{\Phi }}^{\text{Bi}}}\left(z\right)=\frac{1}{2}-\frac{1}{\pi }{\int }_0^{\infty }\frac{\mathcal{I}\left(\exp \left(-ju\log \left(z\right)\right)\right)M_{ju}}{u}du(44)$

where, $j=\sqrt{-1}$ and M_ju (⋅) is the ju-th moment of ${\mathcal{P}}_{\text{DC}\mathrm{\Phi }}^{\text{Bi}}$.

In Figure 9 we see the impact of the path loss approximation of the clutter points on the meta-distribution of the SCNR.In particular, we see that since with the path loss approximation, the meta-distribution depends only on the number of clutter points within the range resolution cell, the corresponding plot has a stepped behaviour, where each step corresponds to a certain number of clutter points. On the contrary, the plot without the path loss approximation takes into account the relative randomness in the locations of the clutter points within the range resolution cell. For a given κ_m, the path loss approximation may result in either an overestimation or an underestimation of the actual meta-distribution. However, such an analysis is out of scope of the current work and will be investigated in a future work.In Figure 10 we plot the meta-distribution of the SCNR for different SCNR thresholds. This represents, qualitatively, a fine-grained analysis of the radar detection. For a given γ the meta-distribution evaluated at a given z represents the fraction of radar links that experience a successful radar detection at least z% of the time. For example, when the radar detection threshold is set at γ = 0 dB, we observe that about half $(F_{P_{DC\mathrm{\Phi }}}(z)=0.5)$ of the targets are detected with a reliability of at least 70% (i.e., z = 0.7), while virtually no targets $(F_{P_{DC\mathrm{\Phi }}}(z)=0)$ are detected with a reliability of 70% when the detection threshold is set at γ = 3 dB. On the lower reliability regime, interestingly, we observe that with γ = 3 dB, more than 95% of the targets $(F_{P_{DC\mathrm{\Phi }}}(z)=0.95)$ are detected with a reliability of at least 15% (i.e., with z = 0.15) while the same for γ = 0 dB is lower (about 90%). This also indicates that for a lower SCNR threshold, not only the detection probability ${\mathcal{P}}_{DC}^{Bi}$ is higher, but also guaranteeing higher reliability for individual links is more likely. Remarkably, we observe that regardless of the value of ${\mathcal{P}}_{DC}^{Bi}$, none of the targets can be guaranteed to be detected beyond 70% (z = 0.7) reliability, and to achieve that, additional radar transceivers must be deployed.

FIGURE 9

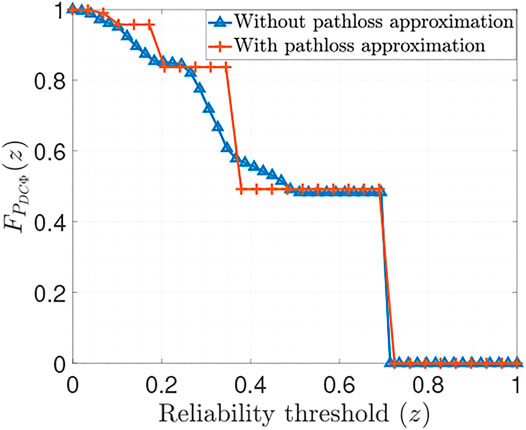
FIGURE 9. Comparison of the meta-distribution of the SCNR with and without the path loss approximation of the clutter points. Here ϵ =0.5.

FIGURE 10

FIGURE 10. Meta distribution of the SCNR for different SCNR thresholds.

5 Conclusion

We have provided an SG based analytical framework to provide system level planning insights into how radar based localization can enhance communication throughput of a JRC system. The key advantage of this framework is that it accounts for the significant variations in the radar, target and clutter conditions that may be encountered in actual deployments without requiring laborious system level simulations or measurement data collection. Specifically, we provide a theorem to optimize JRC system parameters such as the explore/exploit duty cycle, the transmitted power, bandwidth and pulse repetition interval for maximizing the network throughput. The results are presented for generalized bistatic radar scenarios from which the monostatic results are derived through limiting conditions. We also provide a study on the meta-distribution of the radar detection metric which provides the key insight that none of the mobile users can be reliably detected beyond 70% of the time with a single JRC configuration. Our results are validated with Monte Carlo simulations.

The analysis in this work is based on some assumptions: First, we have assumed a planar bistatic radar geometry where all the mobile users/radar targets fall in the cosite region (baseline length is below twice the bistatic range). These assumptions are satisfied in several JRC applications such as indoor localization using WiFi/WLAN devices and in radar enhanced vehicular communications. However, the assumption does not hold for GNSS based bistatic radar remote sensing where the transmitter is the satellite while the receiver is mounted close to the earth and a three-dimensional geometry would have to be considered. Hence, our future work will focus on the modification to the SG based analysis to analyze radar performance metrics under 3D, non-cosite conditions of the bistatic radar.

Second, we have considered short range line-of-sight links in our study which are applicable to mmWave JRC implementations. However, real world deployments encounter blockages that must be accounted for from a JRC system design perspective. Similarly, the radar will receive returns from sidelobes along with the main lobes which has not been considered in our work. Finally, in our throughput analysis, we have assumed that all the mobile users have uniform data rates that can be supported. In real world conditions, the requirements from individual users will differ and there may be system constraints on the maximum resource utilization. Therefore, the study of the performance bounds due to more realistic channel, radar and mobile user models will lead to more accurate estimation of the detection performance and network throughput and would form the basis of future studies.

Third, in this work, we have confined our discussion to a single bistatic radar framework. In the foreseeable future, we may encounter radar networks with a single transmitter and multiple receivers, or even multiple transmitters and receivers. In these conditions, there can be significant diversity in the radar and target geometry which can be effectively analysed through SG. Research into multistatic radar frameworks would form a natural extension to this work.

Data Availability Statement

All the codes used to generate the figures in the document can be accessed at https://essrg.iiitd.edu.in/?page_id=4355.

Author Contributions

The theoretical formulations and derivations and writing of the paper were carried out by SR in collaboration with GG. The Monte Carlo simulations for experimental validation were carried out by SS.

Funding

Project is funded through a grant from Ministry of Electronics and Information Technology, Government of India, No.13 (30/2020-CC&BT).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Hourani, A., Evans, R. J., Kandeepan, S., Moran, B., and Eltom, H. (2017). Stochastic Geometry Methods for Modeling Automotive Radar Interference. IEEE Trans. Intell. Transportation Syst. 19, 333–344. doi:10.1109/tits.2016.2632309

CrossRef Full Text | Google Scholar

Ali, A., González-Prelcic, N., and Ghosh, A. (2020). Passive Radar at the Roadside Unit to Configure Millimeter Wave Vehicle-To-Infrastructure Links. IEEE Trans. Veh. Technol. 69, 14903–14917. doi:10.1109/tvt.2020.3027636

CrossRef Full Text | Google Scholar

Alloulah, M., and Huang, H. (2019). Future Millimeter-Wave Indoor Systems: A Blueprint for Joint Communication and Sensing. Computer 52, 16–24. doi:10.1109/mc.2019.2914018

CrossRef Full Text | Google Scholar

Andrews, J. G., Baccelli, F., and Ganti, R. K. (2011). A Tractable Approach to Coverage and Rate in Cellular Networks. IEEE Trans. Commun. 59, 3122–3134. doi:10.1109/tcomm.2011.100411.100541

CrossRef Full Text | Google Scholar

Bai, T., and Heath, R. W. (2014). Coverage and Rate Analysis for Millimeter-Wave Cellular Networks. IEEE Trans. Wireless Commun. 14, 1100–1114. doi:10.1109/TWC.2014.2364267

CrossRef Full Text | Google Scholar

Billingsley, J. B. (2002). Low-angle Radar Land Clutter: Measurements and Empirical Models. Norwich, NY: IET.

Google Scholar

Chen, X., Tharmarasa, R., Pelletier, M., and Kirubarajan, T. (2012). Integrated Clutter Estimation and Target Tracking Using Poisson point Processes. IEEE Trans. Aerosp. Electron. Syst. 48, 1210–1235. doi:10.1109/taes.2012.6178058

CrossRef Full Text | Google Scholar

Chiu, S. N., Stoyan, D., Kendall, W. S., and Mecke, J. (2013). Stochastic Geometry and its Applications. West Sussex, United Kingdom: John Wiley & Sons.

Google Scholar

Dokhanchi, S. H., Mysore, B. S., Mishra, K. V., and Ottersten, B. (2019). A Mmwave Automotive Joint Radar-Communications System. IEEE Trans. Aerosp. Electron. Syst. 55, 1241–1260. doi:10.1109/taes.2019.2899797

CrossRef Full Text | Google Scholar

Duggal, G., Mishra, K. V., and Ram, S. S. (2019). “Micro-doppler and Micro-range Detection via Doppler-Resilient 802.11ad-Based Vehicle-To-Pedestrian Radar,” in 2019 IEEE Radar Conference (Bostin, MA: IEEE), 1–6. doi:10.1109/radar.2019.8835525

CrossRef Full Text | Google Scholar

Duggal, G., Vishwakarma, S., Mishra, K. V., and Ram, S. S. (2020). Doppler-Resilient 802.11ad-Based Ultrashort Range Automotive Joint Radar-Communications System. IEEE Trans. Aerosp. Electron. Syst. 56, 4035–4048. doi:10.1109/taes.2020.2990393

CrossRef Full Text | Google Scholar

Falcone, P., Colone, F., and Lombardo, P. (2012). Potentialities and Challenges of Wifi-Based Passive Radar. IEEE Aerosp. Electron. Syst. Mag. 27, 15–26. doi:10.1109/maes.2012.6380822

CrossRef Full Text | Google Scholar

Fang, Z., Wei, Z., Chen, X., Wu, H., and Feng, Z. (2020). Stochastic Geometry for Automotive Radar Interference with Rcs Characteristics. IEEE Wireless Commun. Lett. 9, 1817–1820. doi:10.1109/lwc.2020.3003064

CrossRef Full Text | Google Scholar

Ghatak, G., De Domenico, A., and Coupechoux, M. (2018). Coverage Analysis and Load Balancing in Hetnets with Millimeter Wave Multi-Rat Small Cells. IEEE Trans. Wireless Commun. 17, 3154–3169. doi:10.1109/twc.2018.2807426

CrossRef Full Text | Google Scholar

Ghatak, G., Koirala, R., De Domenico, A., Denis, B., Dardari, D., Uguen, B., et al. (2021). Beamwidth Optimization and Resource Partitioning Scheme for Localization Assisted Mm-Wave Communication. IEEE Trans. Commun. 69, 1358–1374. doi:10.1109/TCOMM.2020.3036864

CrossRef Full Text | Google Scholar

Grossi, E., Lops, M., Tulino, A. M., and Venturino, L. (2021). Opportunistic Sensing Using Mmwave Communication Signals: A Subspace Approach. IEEE Trans. Wireless Commun. 20, 4420–4434. doi:10.1109/TWC.2021.3058775

CrossRef Full Text | Google Scholar

Grossi, E., Lops, M., and Venturino, L. (2017). Two-step Sequential Detection in Agile-Beam Radars: Performance and Tradeoffs. IEEE Trans. Aerosp. Electron. Syst. 53, 2199–2213. doi:10.1109/taes.2017.2688878

CrossRef Full Text | Google Scholar

Haenggi, M. (2012). Stochastic Geometry for Wireless Networks. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Hassanien, A., Amin, M. G., Zhang, Y. D., and Ahmad, F. (2016). Signaling Strategies for Dual-Function Radar Communications: An Overview. IEEE Aerosp. Electron. Syst. Mag. 31, 36–45. doi:10.1109/maes.2016.150225

CrossRef Full Text | Google Scholar

Hu, J., Wu, Y., Chen, R., Shu, F., and Wang, J. (2019). Optimal Detection of Uav’s Transmission with Beam Sweeping in covert Wireless Networks. IEEE Trans. Vehicular Techn. 69, 1080–1085.

Google Scholar

Jackson, M. C. (1986). The Geometry of Bistatic Radar Systems. IEE Proc. F Commun. Radar Signal. Process. UK 133, 604–612. doi:10.1049/ip-f-1.1986.0097

CrossRef Full Text | Google Scholar

Kay, S. M. (1998). Fundamentals of Statistical Signal Processing Detection Theory. Upper Saddle River, NJ: Prentice-Hall 146, 222.

Google Scholar

Kellett, D., Garmatyuk, D., Mudaliar, S., Condict, N., and Qualls, I. (2019). Random Sequence Encoded Waveforms for covert Asynchronous Communications and Radar. IET Radar, Sonar & Navigation 13, 1713–1720. doi:10.1049/iet-rsn.2018.5659

CrossRef Full Text | Google Scholar

Kumari, P., Choi, J., González-Prelcic, N., and Heath, R. W. (2017). Ieee 802.11 Ad-Based Radar: An Approach to Joint Vehicular Communication-Radar System. IEEE Trans. Vehicular Techn. 67, 3012–3027. doi:10.1109/TVT.2017.2774762

CrossRef Full Text | Google Scholar

Li, W., Piechocki, R. J., Woodbridge, K., Tang, C., and Chetty, K. (2020). Passive Wifi Radar for Human Sensing Using a Stand-Alone Access point. IEEE Trans. Geosci. Remote Sensing 59, 1986–1998. doi:10.1109/TGRS.2020.3006387

CrossRef Full Text | Google Scholar

Liu, F., Masouros, C., Petropulu, A. P., Griffiths, H., and Hanzo, L. (2020). Joint Radar and Communication Design: Applications, State-Of-The-Art, and the Road Ahead. IEEE Trans. Commun. 68, 3834–3862. doi:10.1109/tcomm.2020.2973976

CrossRef Full Text | Google Scholar

Ma, D., Shlezinger, N., Huang, T., Shavit, Y., Namer, M., Liu, Y., et al. (2021). Spatial Modulation for Joint Radar-Communications Systems: Design, Analysis, and Hardware Prototype. IEEE Trans. Veh. Technol. 70, 2283–2298. doi:10.1109/tvt.2021.3056408

CrossRef Full Text | Google Scholar

Miranda, S. L. C., Baker, C. J., Woodbridge, K., and Griffiths, H. D. (2007). Comparison of Scheduling Algorithms for Multifunction Radar. IET Radar Sonar Navig. 1, 414–424. doi:10.1049/iet-rsn:20070003

CrossRef Full Text | Google Scholar

Mishra, K. V., Bhavani Shankar, M. R., Koivunen, V., Ottersten, B., and Vorobyov, S. A. (2019). Toward Millimeter-Wave Joint Radar Communications: A Signal Processing Perspective. IEEE Signal. Process. Mag. 36, 100–114. doi:10.1109/msp.2019.2913173

CrossRef Full Text | Google Scholar

Moyer, L. R., Morgan, C. J., and Rugger, D. A. (1989). An Exact Expression for Resolution Cell Area in Special Case of Bistatic Radar Systems. IEEE Trans. Aerosp. Electron. Syst. 25, 584–587. doi:10.1109/7.32092

CrossRef Full Text | Google Scholar

Munari, A., Simic, L., and Petrova, M. (2018). Stochastic Geometry Interference Analysis of Radar Network Performance. IEEE Commun. Lett. 22, 2362–2365. doi:10.1109/lcomm.2018.2869742

CrossRef Full Text | Google Scholar

Nitsche, T., Cordeiro, C., Flores, A., Knightly, E., Perahia, E., and Widmer, J. (2014). IEEE 802.11ad: Directional 60 GHz Communication for Multi-Gigabit-Per-Second Wi-Fi [Invited Paper]. IEEE Commun. Mag. 52, 132–141. doi:10.1109/mcom.2014.6979964

CrossRef Full Text | Google Scholar

Park, J., and Heath, R. W. (2018). Analysis of Blockage Sensing by Radars in Random Cellular Networks. IEEE Signal. Process. Lett. 25, 1620–1624. doi:10.1109/lsp.2018.2869279

CrossRef Full Text | Google Scholar

Ram, S. S., and Ghatak, G. (2022). Estimation of Bistatic Radar Detection Performance under Discrete Clutter Conditions Using Stochastic Geometry. arXiv e-prints , arXiv: 2201.03221.

Google Scholar

Ram, S. S., Singh, G., and Ghatak, G. (2020). “Estimating Radar Detection Coverage Probability of Targets in a Cluttered Environment Using Stochastic Geometry,” in 2020 IEEE International Radar Conference (RADAR) (Washington D.C.: IEEE), 665–670. doi:10.1109/radar42522.2020.9114637

CrossRef Full Text | Google Scholar

Ram, S. S., Singh, G., and Ghatak, G. (2021). Optimization of Radar Parameters for Maximum Detection Probability under Generalized Discrete Clutter Conditions Using Stochastic Geometry. IEEE Open J. Signal. Process. 2, 571–585. doi:10.1109/ojsp.2021.3121199

CrossRef Full Text | Google Scholar

Raynal, A. M., Bickel, D. L., Denton, M. M., Bow, W. J., and Doerry, A. W. (2011a). in Radar Cross Section Statistics of Ground Vehicles at Ku-Band (SPIE Proceedings). United States: SPIE 8021.

Google Scholar

Raynal, A. M., Burns, B. L., Verge, T., Bickel, D. L., Dunkel, R., and Doerry, A. W. (2011b). Radar Cross Section Statistics of Dismounts at Ku-Band. Radar Sensor Techn. XV, 8021. doi:10.1117/12.882873

CrossRef Full Text | Google Scholar

Ren, P., Munari, A., and Petrova, M. (2018). Performance Tradeoffs of Joint Radar-Communication Networks. IEEE Wireless Commun. Lett. 8, 165–168. doi:10.1109/LWC.2018.2865360

CrossRef Full Text | Google Scholar

Ruoskanen, J., Eskelinen, P., and Heikkila, H. (2003). Millimeter Wave Radar with Clutter Measurements. IEEE Aerosp. Electron. Syst. Mag. 18, 19–23. doi:10.1109/maes.2003.1244771

CrossRef Full Text | Google Scholar

Sekine, M., Mao, Y., and Mao, Y. (1990). Weibull Radar Clutter. London, United Kingdom: IEE Radar, Sonar, Navigation and Avionics Series 3, by Peter Peregrinus Ltd., 3.

Google Scholar

Skolnik, M. I. (1961). An Analysis of Bistatic Radar. IRE Trans. Aeronaut. Navig. Electron. ANE-8, 19–27. doi:10.1109/tane3.1961.4201772

CrossRef Full Text | Google Scholar

Skolnik, M. I. (1980). Introduction to Radar Systems. New York: McGraw Hill Book Co., 590.

Google Scholar

Storrer, L., Yildirim, H. C., Crauwels, M., Copa, E. I. P., Pollin, S., Louveaux, J., et al. (2021). Indoor Tracking of Multiple Individuals with an 802.11ax Wi-Fi-Based Multi-Antenna Passive Radar. IEEE Sensors J. 21, 20462–20474. doi:10.1109/jsen.2021.3095675

CrossRef Full Text | Google Scholar

Tan, B., Woodbridge, K., and Chetty, K. (2016). Awireless Passive Radar System for Real-Time through-wall Movement Detection. IEEE Trans. Aerosp. Electron. Syst. 52, 2596–2603. doi:10.1109/taes.2016.140207

CrossRef Full Text | Google Scholar

Thornburg, A., Bai, T., and Heath, R. W. (2016). Performance Analysis of Outdoor Mmwave Ad Hoc Networks. IEEE Trans. Signal. Process. 64, 4065–4079. doi:10.1109/tsp.2016.2551690

CrossRef Full Text | Google Scholar

Willis, N. J. (2005). Bistatic Radar, 2. Rayleigh, NC: SciTech Publishing.

Google Scholar

Yildirim, H. C., Determe, J. F., Storrer, L., Rottenberg, F., De Doncker, P., Louveaux, J., et al. (2021). Super Resolution Passive Radars Based on 802.11ax Wi‐Fi Signals for Human Movement Detection. IET Radar, Sonar & Navigation 15, 323–339. doi:10.1049/rsn2.12038

CrossRef Full Text | Google Scholar

Zavorotny, V. U., Gleason, S., Cardellach, E., and Camps, A. (2014). Tutorial on Remote Sensing Using Gnss Bistatic Radar of Opportunity. IEEE Geosci. Remote Sens. Mag. 2, 8–45. doi:10.1109/mgrs.2014.2374220

CrossRef Full Text | Google Scholar

Zhou, P., Cheng, K., Han, X., Fang, X., Fang, Y., He, R., et al. (2018). IEEE 802.11ay-Based mmWave WLANs: Design Challenges and Solutions. IEEE Commun. Surv. Tutorials 20, 1654–1681. doi:10.1109/comst.2018.2816920

CrossRef Full Text | Google Scholar