Contextual Mixing Feature Unet for Multi-Organ Nuclei Segmentation

Nuclei segmentation is fundamental and crucial for analyzing histopathological images. Generally, a pathological image contains tens of thousands of nuclei, and there exists clustered nuclei, so it is difficult to separate each nucleus accurately. Challenges against blur boundaries, inconsistent staining, and overlapping regions have adverse effects on segmentation performance. Besides, nuclei from various organs appear quite different in shape and size, which may lead to the problems of over-segmentation and under-segmentation. In order to capture each nucleus on different organs precisely, characteristics about both nuclei and boundaries are of equal importance. Thus, in this article, we propose a contextual mixing feature Unet (CMF-Unet), which utilizes two parallel branches, nuclei segmentation branch and boundary extraction branch, and mixes complementary feature maps from two branches to obtain rich and integrated contextual features. To ensure good segmentation performance, a multiscale kernel weighted module (MKWM) and a dense mixing feature module (DMFM) are designed. MKWM, used in both nuclei segmentation branch and boundary extraction branch, contains a multiscale kernel block to fully exploit characteristics of images and a weight block to assign more weights on important areas, so that the network can extract discriminative information efficiently. To fuse more beneficial information and get integrated feature maps, the DMFM mixes the feature maps produced by the MKWM from two branches to gather both nuclei information and boundary information and links the feature maps in a densely connected way. Because the feature maps produced by the MKWM and DMFM are both sent into the decoder part, segmentation performance can be enhanced effectively. We test the proposed method on the multi-organ nuclei segmentation (MoNuSeg) dataset. Experiments show that the proposed method not only performs well on nuclei segmentation but also has good generalization ability on different organs.

1 Introduction

Histopathology is one of the most important branches in medical care area, which studies and diagnoses various diseases by examining cells or tissues under a microscope.(Deng et al., 2020). Histopathologists are those who are in charge of analyzing histology images, looking for changes in cells and helping clinicians manage patient care. Nuclei segmentation is a fundamental and vital prerequisite before analyzing and getting medical results. At present, most pathology diagnoses are conducted by histopathologists, so the diagnostic results and opinions are given subjectively. In fact, a histology image is very complicated, which contains tens of thousands of cells and other tissues, and is time-consuming to be analyzed manually. Sometimes, even experienced histopathologists may make wrong judgements and mistakes. In order to help doctors work efficiently, automatic nuclei segmentation by computer technology is indispensable, which can not only display the distribution and structure of nuclei, saving precious time for doctors to focus on key or tough parts, but also provide doctors with consultative opinions, such as the type of disease or disease grading.

However, achieving nuclei segmentation accurately is not an easy task because there are many challenges that hinder obtaining good performance, such as inconsistent staining, blur boundaries, overlapping regions, and various shapes. The examples of challenges are shown in Figure 1. There have been lots of studies that try to solve the mentioned challenges and realize automatic nuclei segmentation. Algorithms such as thresholding (Phansalkar et al., 2011), region growing (Szénási et al., 2011), watershed (Veta et al., 2011), and active contours (Al-Dulaimi et al., 2016) are traditional methods. In addition, in recent years, the development of deep learning shows great potential in the computer vision field. Owing to convolution operation, many classic convolutional neural networks surpass traditional methods and achieve state-of-the-art performance in many image competitions. For segmentation task, the FCN (Long et al., 2015) is the first one using fully convolutional operation in an end-to-end network. In addition, Unet (Ronneberger et al., 2015) is an encoder–decoder network that is designed for medical cell segmentation. Because of the efficiency of Unet, many methods in medical areas are modified and improved based on it, such as Vnet (Milletari et al., 2016), SegNet (Badrinarayanan et al., 2017), and CFPNet-M (Lou et al., 2021).

FIGURE 1

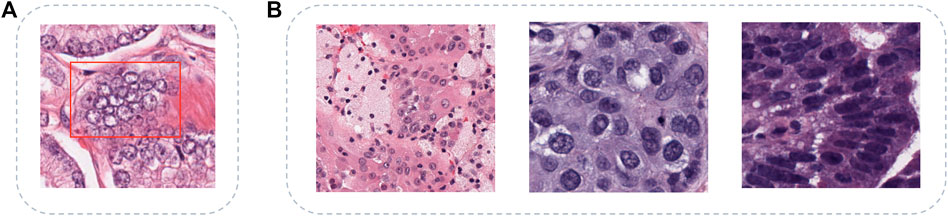
FIGURE 1. Challenges of multi-organ nuclei segmentation task. (A) shows the clustered nuclei (in red box) with the problems of inconsistent staining and blur boundary, (B) shows diverse shapes and sizes of nuclei from different organs, and the organs are kidney, breast, and colon separately.

There are also many Unet-based methods for the multi-organ nuclei segmentation task. Wang et al., (2020) propose a bending loss regularized network and Mahmood et al., (2019) utilize a conditional GAN to train the network in an adversarial pipeline, REMFA-Net. Chen et al., (2020) apply group equivariant convolutions to realize automatic segmentation. In addition, some other methods use multitasks in a whole network. Zhou et al., (2019) both detect boundaries of nuclei and generate binary masks; Xu et al., (2019) detect the center of each nucleus as well as its boundary. But, networks with multitasks often either share the same part of the network, especially for the encoder part, or are trained different tasks independently and use post-processing steps to get the final results. The examples of workflows are shown in Figures 2A, B. These two ways both have their advantages and disadvantages. By sharing parts of the network, the whole network can decrease the parameters. But, the network may fuzzy the goal because the final outputs contain several tasks, and it is hard for the network to learn comprehensively and efficiently. For training independently, each network can focus on one task and is well-directed in forward and backward propagation. However, training independently ignores some features that can be reused and enhances contextual feature maps. To overcome the problems of these two ways, Figure 2C is our proposed method that can not only focus on two sub-tasks dedicatedly and be trained concurrently but also enhance features by mixing the features from two sub-tasks to ensure final performances. For the two sub-tasks, we think that using both nuclei segmentation information and nuclei boundary information can ease the problems of staining inconsistent and blur boundaries. In this study, we propose a contextual mixing feature Unet to solve the multi-organ nuclei segmentation task. The proposed network has two parallel sub-tasks, generating the binary mask and detecting the boundary of each nucleus. In addition, a multiscale kernel weighted module and a dense mixing feature module are designed to ensure that the network obtains rich and integrated features.

FIGURE 2

FIGURE 2. Existing workflows and the proposed method. (A) shares the encoder part between different tasks, (B) trains the network independently for each task, and (C) is our proposed method, training different tasks simultaneously and mixing features from different branches.

The main contributions of our study are summarized as follows:

1) We propose a contextual mixing feature Unet (CMF-Unet) to segment nuclei from various organs. The model mixes the feature maps from both nuclei segmentation branch and boundary extraction branch to get richer and integrated contextual information.

2) We design a multiscale kernel weighted module, which consists of a multiscale kernel block and a weight block to get discriminative features and provide more weights on nuclei and boundaries. In addition, a dense mixing feature module is designed which mixes both information from the two branches to obtain integrated characteristics.

3) We evaluate our proposed method on the MoNuSeg dataset. In addition, experiments demonstrate the effectiveness and generalization ability of our model.

The remaining of this article is organized as followed: Related research on medical image segmentation and multi-organ nuclei segmentation is introduced in Section 2. Details of the proposed method are explained in Section 3. Experiments and results are shown in Section 4. In addition, discussion and conclusion are given in Section 5 and Section 6 separately.

2 Related Work

2.1 Deep Learning–Based Medical Image Segmentation

The medical image segmentation task has been a hot research topic for decades. Since 2012, the rise of deep learning technology brings a brand new future for this field. Image segmentation can be regarded as a pixel-wise classification task. Initially, the same with image classification, segmentation networks use a fully connected way at the end of the network to assign each pixel a class label. In 2014, Long et al., (2015) proposed a fully convolutional network to replace the fully connected layers with convolution operations. Later on, in 2015, Unet (Ronneberger et al., 2015) was proposed, which uses an encoder–decoder structure with skip connection to get the best results on the cell segmentation competition that year. The encoder extracts important features and the decoder expands the obtained feature maps and connects low-level features and high-level features by skip connection. Based on Unet, Unet++ (Zhou et al., 2018) redesigns skip connection and connects layers in a nested way to aggregate feature maps. Due to the powerful ability, the encoder–decoder–based networks become the most popular in segmentation tasks and are widely used in medical segmentation application.

2.2 Nuclei Segmentation

2.2.1 Traditional Methods

Before the popularity of the deep learning technique, many researchers tried to solve the nuclei segmentation task by traditional methods such as thresholding (Phansalkar et al., 2011), region growing algorithm (Szénási et al., 2011), watershed algorithm (Veta et al., 2011), and active contours (Al-Dulaimi et al., 2016). But with pathology images becoming more and more diverse and complicated, the shortcomings of traditional methods are emerging, and segmentation results are not good enough. This is because these methods are often suitable for some specific situations and have limitations on more challenging tasks.

2.2.2 Deep Learning–Based Methods

In recent years, deep learning–based methods are widely used in nuclei segmentation. Many networks are committed to solving the multi-organ segmentation task. Wang et al. (2020) propose a bending loss regularized network to separate overlapping nuclei by giving high penalties for tough contours. Mahmood et al. (2019) utilize a conditional GAN to train the network in an adversarial pipeline and capture more global features. Some methods include several sub-tasks in a network. CIA-Net (Zhou et al., 2019) shares the encoder parts and proposes a multilevel information aggregation module to fully utilize the benefit of complementary information for two task-specific decoders. Unet (Xu et al., 2019) also shares the same encoder and accomplishes the detection task and segmentation task in decoder parts and uses the post-processing step to refine each nucleus. SUNet (Kong et al., 2020) is a two-stage learning framework consisting of two connected, stacked UNets. Pixel-wise segmentation masks on nuclei are the first output, and then the output binary masks are combined with original input images to go through the network together again to obtain final results.

3 Proposed Methods

3.1 Motivation

Since an encoder–decoder structure is effective for the segmentation task, our proposed network is based on this kind of structure. In general, H&E staining is applied to pathological images to see cells and tissues. But, the staining process is made by humans, so some stained images are in poor quality. For example, insufficient staining may cause hollow or unclear boundary for a nucleus. Nuclei segmentation needs to give each pixel a label that belongs to nuclei or the background, so it is necessary to segment objects integrally containing intact nuclei and clear boundaries. In order to segment nuclei from an image in an instance-level, using one encoder–decoder network to generate a binary mask in good quality is a bit difficult. Therefore, besides using a branch to generate nuclei masks, we consider adding a parallel branch to get the boundaries of nuclei so that both nuclei information and boundary information can be obtained, and mixing the features from the two branches can get better representation of an image. In addition, because nuclei on different organs appear quite different, to have good generalization ability, richer feature maps should be obtained as much as possible. Thus, in the encoder parts, kernels with different sizes can be used to fully exploit an image, and more weights can be assigned on nuclei regions and boundary areas. In view of these considerations, we propose a contextual mixing feature Unet with a multiscale kernel weighted module and a dense mixing feature module.

3.2 Image Preprocessing

For pathology images, since tissues and cells at the very beginning are transparent, images need to be dyed with colors. H&E staining procedure, using two dyes hematoxylin and eosin, is the principal stain in histology (Veta et al., 2013). Hematoxylin stains nuclei a purplish blue and eosin stains the extracellular matrix and cytoplasm pink so that a pathologist can easily differentiate between the nuclei and cytoplasm. But, due to different manufacturers, H&E images vary greatly. So, preprocessing steps on H&E images are necessary. Stain separation is the first step to get H channel and E channel by the Beer–Lamber law (Ruifrok and Johnston, 2001), and then SNMF (Vahadane et al., 2016) is applied to factor out a specific color appearance matrix for each image. The normalized H channel images are selected as input images.

3.3 Network Details

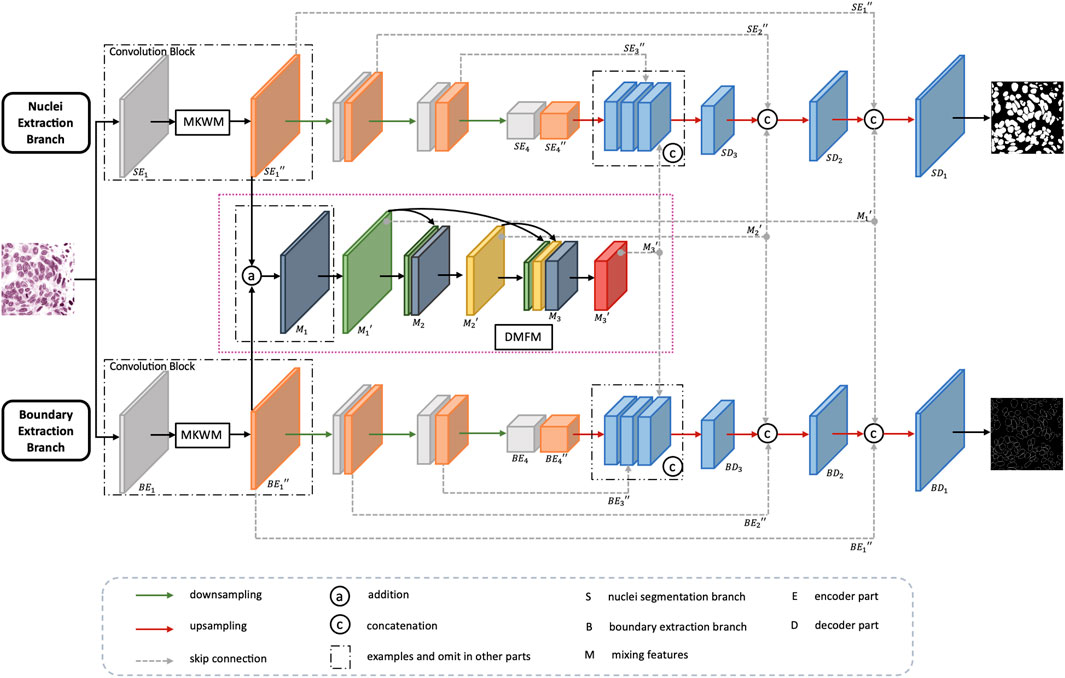
3.3.1 Overall Architecture

Figure 3 shows the overall architecture of CMF-Unet. For an input image, it is sent into two branches to extract features related to nuclei and nuclei boundaries. The two branches are in the same structure, except they use different loss functions to guide them to focus on their own task. The upper branch, nuclei segmentation branch, is chosen as the main example to illustrate the whole process.

FIGURE 3

FIGURE 3. Overall architecture of CMF-Unet.

First, an image is sent into the encoder part which consists of several convolution blocks with downsampling operation to reduce the size of feature maps. Each convolution block contains two convolution layers, and between them, there is a multiscale kernel weighted module (MKWM). This module contains a multiscale kernel block and a weight block, which uses two different kernel sizes to capture more refined features and gives more weight on important areas. Each weighted feature map is combined with the feature maps from the other branch to mix nuclei information and boundary information. The mixed feature maps are densely connected with other feature mixed layers. The whole mixing feature part is called dense mixing feature module (DMFM). Then, back to the upper branch, the last feature maps in the encoder part are enlarged in size through upsampling operation. Then, the enlarged feature maps concatenate with the feature maps in the encoder part and DMFM of the same size, and finally, the segmentation output can be obtained.

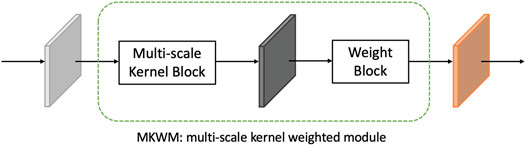
3.3.2 Multiscale Kernel Weighted Module

To fully exploit features of an image, the multiscale kernel weighted module (MKWM) is designed. Details of the MKWM are shown in Figure 4. The aim of this module is to fully excavate features by multiscale kernel block and highlight on the important areas through weight block.

FIGURE 4

FIGURE 4. Constitution of the MKWM.

For multi-organ nuclei segmentation, nuclei on different organs appear in diverse sizes and shapes. In order to capture various nuclei, kernels with different sizes are helpful. This is because kernels with large size can capture more detailed information, and kernels with small size can capture more edge structure information (Tan and Le, 2019). Inspired by the study by Li et al., (2018), besides using 3 × 3 kernel size as a general rule, the multiscale kernel block additionally uses kernel size in 5 × 5 so that the network can adaptively capture characteristics. Moreover, to further utilize the local feature maps extracted from two paths with different kernels, the feature maps from two paths are concatenated with each other mutually to obtain more efficacious information. After that, the two paths are combined together through a 1 × 1 convolution layer to fuse features and reduce computation complexity at the same time. Residual connection is added to link the original feature maps with the strengthened feature maps. The details of the multiscale kernel block are shown in Figure 5A.

FIGURE 5

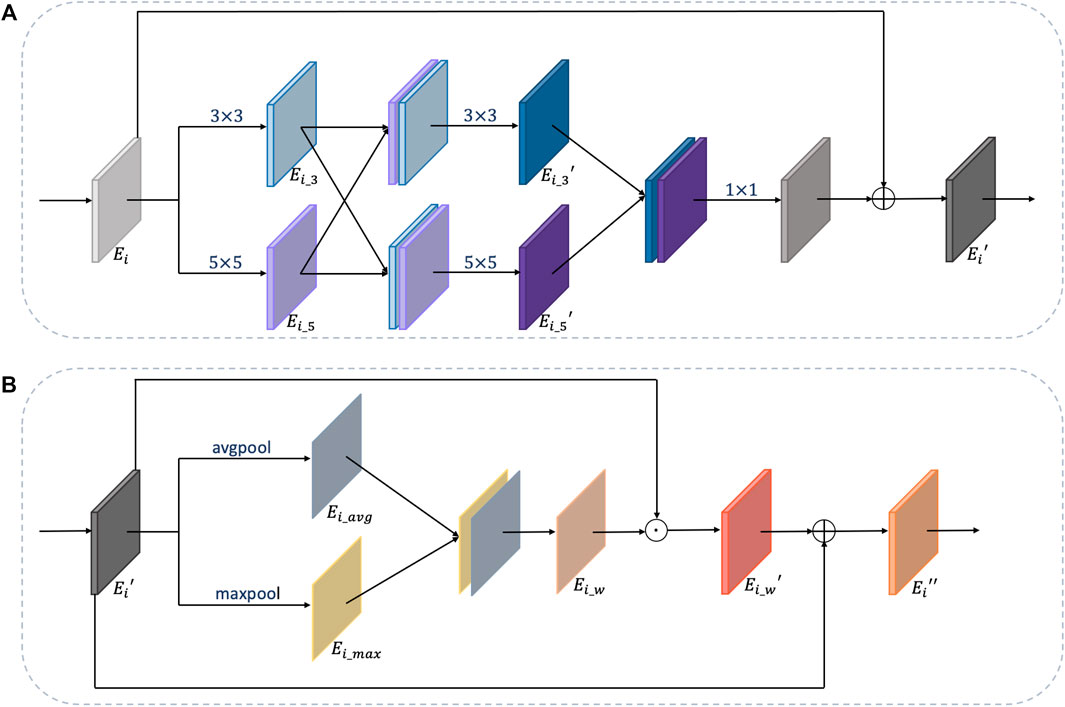
FIGURE 5. Details of multiscale kernel block and weight block. (A) is the multiscale kernel block and (B) is the weight block.

For feature maps $E_i\in {\mathbb{R}}^{H\times W\times C}$, where E means the encoder part, i means the sequence number of the convolution block, and H, W, and C mean height, width, and channel number, respectively, the whole process can be written in the following formulas:

$E_{i\text{\_}3}=\gamma \left(\varphi \left(E_i\right)\right),(1)$

$E_{i\text{\_}5}=\gamma \left(\phi \left(E_i\right)\right),(2)$

$E_{i\text{\_}3}^{\prime }=\gamma \left(\varphi \left(\left[E_{i\text{\_}3},E_{i\text{\_}5}\right]\right)\right),(3)$

$E_{i\text{\_}5}^{\prime }=\gamma \left(\phi \left(\left[E_{i\text{\_}3},E_{i\text{\_}5}\right]\right)\right),(4)$

$E_i^{\prime }=\gamma \left(\omega \left(\left[E_{i\text{\_}3}^{\prime },E_{i\text{\_}5}^{\prime }\right]\right)\right)+E_i,(5)$

where ϕ(⋅), φ(⋅),and ω(⋅) are convolution operations with kernel size of 3 × 3, 5 × 5, and 1 × 1, respectively, γ(⋅) is an activation function, and [⋅] is a concatenation operation. Through these steps, discriminative feature maps $E_i^{\prime }\in {\mathbb{R}}^{H\times W\times C}$ are obtained.

After getting the discriminative feature maps $E_i^{\prime }$, the weight block will calculate the feature importance of each pixel in the space domain, extract key information of an image, and assign more weights. So, the two branches can better focus on nuclei information and boundary information, instead of treating each pixel equally.

The structure of the weight block is shown in Figure 5B. For feature maps $E_i^{\prime }\in {\mathbb{R}}^{H\times W\times C}$, two weight maps, E_{i_avg} and E_{i_ max}, are first obtained by average pooling and max pooling. E_{i_avg} and E_{i_ max} have the same width and height with $E_i^{\prime }$, except that the channel number changes from C to 1. Then, two weight maps are concatenated together and carried on convolution operation and produce $E_{i\text{\_}w}\in {\mathbb{R}}^{H\times W\times 1}$. Following this, E_{i_w} is product-wise with $E_i^{\prime }$ to get $E_{i\text{\_}w}^{\prime }$. Finally, $E_{i\text{\_}w}^{\prime }$ is added with $E_i^{\prime }$ to get the weighted enhanced feature maps $E_i^{\prime \prime }\in {\mathbb{R}}^{H\times W\times C}$. The whole process can be written as follows:

$E_{i\text{\_}w}=\varphi \left(\left[E_{i\text{\_}\mathit{avg}},E_{i\text{\_}\mathit{max}}\right]\right)=\varphi \left(\left[avgpool\left(E_i^{\prime }\right),maxpool\left(E_i^{\prime }\right)\right]\right),(6)$

$E_{i\text{\_}w}^{\prime }=E_i\cdot E_{i\text{\_}w},(7)$

$E_i^{\prime \prime }=E_{i\text{\_}w}^{\prime }+E_i,(8)$

where avgpool (⋅) and maxpool (⋅) are two pooling operations, and ϕ(⋅) is a convolution operation.

Through the MKWM, the network can fully identify distinct and important features from images.

3.3.3 Dense Mixing Feature Module

Although two branches aim to extract features related to nuclei and nuclei boundaries, these two tasks are highly relevant and their feature maps are meaningful for each other. Therefore, mixing the features from the two branches can enhance representation of images. For H&E images with the problems of inconsistent staining and blur boundary, mixing the feature maps containing nuclei information with feature maps related to boundary information is helpful to integrate two kinds of characteristics.

In order to make full use of the extracted features, inspired by the study by Huang et al., (2017), instead of singly concatenating feature maps from two branches, we design a dense mixing feature module (DMFM) to reuse the features from the former layers and further strengthen the information. The details are shown in the pink frame of Figure 3. Taking the first convolution block as an example, through the MKWM, the network gets the enhanced feature maps ${\mathrm{SE}}_1^{\prime \prime }$ and $B{E}_1^{\prime \prime }$, where S and B are short for the segmentation extraction branch and boundary detection branch, E means encoder part, and 1 means the first convolution block. The two feature maps, having already given important areas more weights, are added together so that the feature map M₁ can highlight both the nuclei and boundary areas. Except the last convolution block, other blocks in the encoder part are carried on the same operation. To reuse these feature maps, dense connection is used to improve the representation ability, absorbing the information from multiscale feature maps.

The following formulas describe the workflow of the DFMM:

$M_1^{\prime }=\gamma \left(\varphi \left(M_1\right)\right)=\gamma \left(\varphi \left({\mathrm{SE}}_1^{\prime \prime }+B{E}_1^{\prime \prime }\right)\right),(9)$

$M_2^{\prime }=\gamma \left(\varphi \left(\left[d_2\left(M_1^{\prime }\right),M_2\right]\right)\right)=\gamma \left(\varphi \left[d_2\left(M_1^{\prime }\right),\left({\mathrm{SE}}_2^{\prime \prime }+B{E}_2^{\prime \prime }\right)\right]\right),(10)$

$M_3^{\prime }=\gamma \left(\varphi \left(\left[d_4\left(M_1^{\prime }\right),d_2\left(M_2^{\prime }\right),M_3\right]\right)\right)=\gamma \left(\varphi \left[d_4\left(M_1^{\prime }\right),d_2\left(M_2^{\prime }\right),\left({\mathrm{SE}}_3^{\prime \prime }+B{E}_3^{\prime \prime }\right)\right]\right),(11)$

where ϕ(⋅) is a convolution operation, γ(⋅) is an activation function, [⋅] is a concatenation operation, d_i (⋅) is a downsampling operation, and subscript i is the stride.

Through the DMFM, feature maps can be enhanced by mixing information from two branches and $M_1^{\prime }$, $M_2^{\prime }$, and $M_3^{\prime }$ can be obtained. These three groups of feature maps are used as additional skip connection for the decoder part.

3.4 Loss Function

3.4.1 Loss Function for Nuclei Segmentation Branch

The nuclei segmentation branch aims to judge each pixel that is background or nuclei, so cross-entropy loss (Zhang and Sabuncu, 2018) is used. Binary cross-entropy is a measurement of the difference between two probability distributions. It compares the prediction and the ground truth pixel-wise. The loss function is shown as follows:

$l_1=-\frac{1}{N}{\mathrm{\Sigma }}_{i=1}^N\left(y_{i}log\left(\widehat{y_i}\right)+\left(1-y_i\right)\mathit{log}\left(1-\widehat{y_i}\right)\right),(12)$

where N is the total number of image pixels, i is the i − th pixel, y is a ground truth, and $\widehat{y}$ a prediction result.

In addition, smooth truncated loss (Zhou et al., 2019) is also used in the nuclei segmentation branch to control the contribution of both false positive and false negative, promoting the network learning the beneficial information and relieving over-segmentation. The smooth truncated loss function is shown as follows:

$l_2=\left\{\begin{array}{cccc}\hfill -\mathit{log}\left(\theta \right)+\frac{1}{2}\left(1-\frac{{\widehat{y_i}}^2}{{\theta }^2}\right),& \hfill & \hfill \widehat{y_i}\le \theta & \hfill \\ \hfill -\mathit{log}\left(\widehat{y_i}\right),& \hfill & \hfill \widehat{y_i}\ge \theta \end{array}\right.,(13)$

where $\widehat{y_i}$ is a prediction result on the i − th pixel. If the ground truth y_i = 1, $\widehat{y_i}=\widehat{y}$. Otherwise, $\widehat{y_i}=1-\widehat{y}$. θ is a truncated point, and its value is 0.3.

3.4.2 Loss Function for the Boundary Extraction Branch

Since pixels of nuclei boundaries only take up a small part of the image, pixels are unbalanced between the background and foreground. So, soft dice loss (Sudre et al., 2017) is used for the boundary extraction branch to learn contour information. The formula of soft dice loss is as follows:

$l_3=1-\frac{{\mathrm{\Sigma }}_{i=1}^N\widehat{y_i}{y}_i}{{\mathrm{\Sigma }}_{i=1}^N{\widehat{y_i}}^2+{\mathrm{\Sigma }}_{i=1}^N{y}_i^2},(14)$

where i is the i − th pixel, y is the ground truth, and $\widehat{y}$ is a prediction result.

3.4.3 Loss Function for Whole Network

The total loss function for the whole model is the combination of the two branches. The formula is as follows:

$loss=\alpha l_1+\beta l_2+\mu l_3,(15)$

where α, β, and μ are hyperparameters of three loss functions. We set α = 0.3, β = 1, and μ = 0.5 in our article.

4 Experiments

4.1 Datasets and Implementation Details

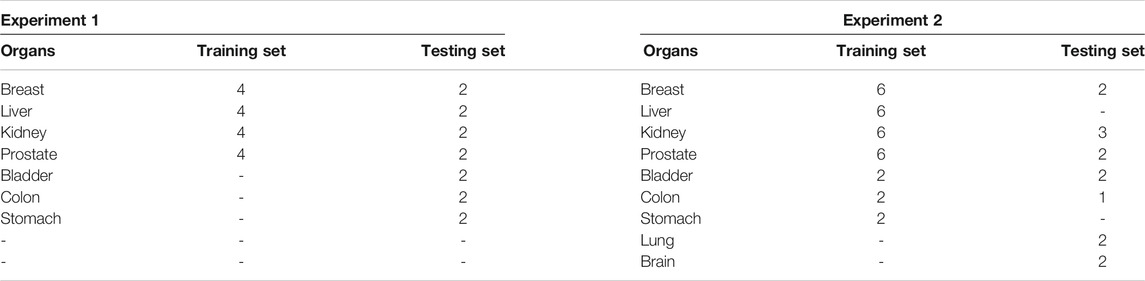
In our experiments, we use the multi-organ nuclei segmentation (MoNuSeg) dataset that comes from the 2018 MICCAI challenge. The dataset contains 30 training images from seven diverse organs (breast, kidney, prostate, liver, colon, bladder, and stomach). In addition, another 14 images are included as testing images from seven organs, where five organs (breast, kidney, prostate, colon, and bladder) are the same categories of the training set, and two additional organs (lung and brain) are not included in the training set. Two experiments are conducted. The first experiment is to split the training image into the training set and testing set. The splitting way is the same as in the study by Kumar et al., (2017). In addition, the second experiment is to use the whole dataset to train and test. Table 1 shows the details of the MoNuSeg dataset on two experiments.

TABLE 1

TABLE 1. Number of images on different organs of the MoNuSeg dataset.

All images are H&E images with the size of 1000 × 1000. In consideration of time overhead, the images are cropped into 512 × 512, and then each patch is further cropped into 256 × 256. So, for one image, 16 patches are obtained. With regard to data augmentation, we use random crop, random flip, random rotation, and elastic transformation. We optimize the loss by using the momentum SGD method with an initial learning rate of 0.001. The learning rate decays by a factor of 10 for every 50 epochs. We implement the proposed network on Pytorch 1.4.0 with NVIDIA GTX1080Ti GPU. In addition, the training loss curves on the two experiments are shown in Figure 6.

FIGURE 6

FIGURE 6. Training loss curves on two experiments.

4.2 Evaluation Metrics

We use four metrics, AJI, F1-score, recall, and precision, to evaluate the effectiveness of our method. AJI, the abbreviation of aggregated Jaccard Index, is proposed by Kumar et al., (2017), and it is an evaluation metric considered in both pixel-level and object-level aspects. The formula of AJI is as follows:

$AJI=\frac{{\mathrm{\Sigma }}_{i=1}^N{G}_i\cap P_j}{{\mathrm{\Sigma }}_{i=1}^N{G}_i\cup P_j+{\mathrm{\Sigma }}_{k\in O}{P}_k},(16)$

where G and P are sets of ground truth and prediction results, respectively, and G = {G₁, G₂, … , G_n}, P = {P₁, P₂, … , P_m}, and $j=argma{x}_k\frac{G_i\cap P_k}{G_i\cup P_k}$. O is the set of indices of prediction results without any intersection to ground truth.

Precision shows that the proportion of positive identifications is actually correct, while recall shows that proportion of actual positives is identified correctly. The formulas of precision and recall are as follows:

$Precision=\frac{TP}{TP+FP},(17)$

$Recall=\frac{TP}{TP+FN},(18)$

where TP is true positive, FP is false positive, and FN is false negative.

F1-score is a measurement based on the metrics of recall and precision, which can judge the ability of a model. The higher the score is, the more robust the model is. The formula of F1 score is as follows:

$F1=\frac{2Precision\cdot Recall}{Precision+Recall}=\frac{2TP}{2TP+FP+FN}.(19)$

4.3 Comparison Results

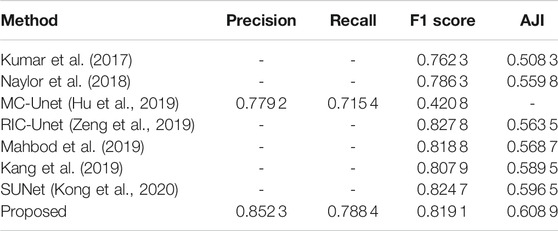
Table 2 shows comparison results of experiment 1. And the proposed method achieves 0.8191 on F1 score and 0.608 9 on AJI score. Although the F1 score of our method is lower than RIC-Unet (Zeng et al., 2019) and SUNet (Kong et al., 2020), our AJI score exceeds other methods.

TABLE 2

TABLE 2. Comparison results of experiment 1 on four evaluation metrics.

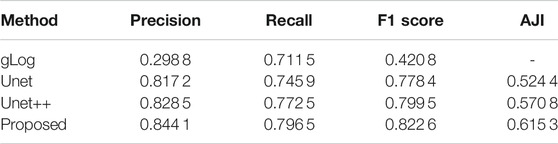
Table 3 is comparison results of experiment 2. gLog (Kong et al., 2013) is a unsupervised method and Unet (Ronneberger et al., 2015) and Unet++(Zhou et al., 2018) are two popular methods used for medical segmentation. This table shows that our proposed method can perform better than Unet and Unet++, which achieves 0.822 6 on F1 score and 0.615 3 on AJI metrics. The visualization results among Unet, Unet++ and the proposed method are displayed in Figure 7. We choose four patches in size of 256 × 256 from four different organs. It is observed that our proposed method can separate tough regions and has less misjudgment than other two methods.

TABLE 3

TABLE 3. Comparison results of experiment 2 on four evaluation metrics.

FIGURE 7

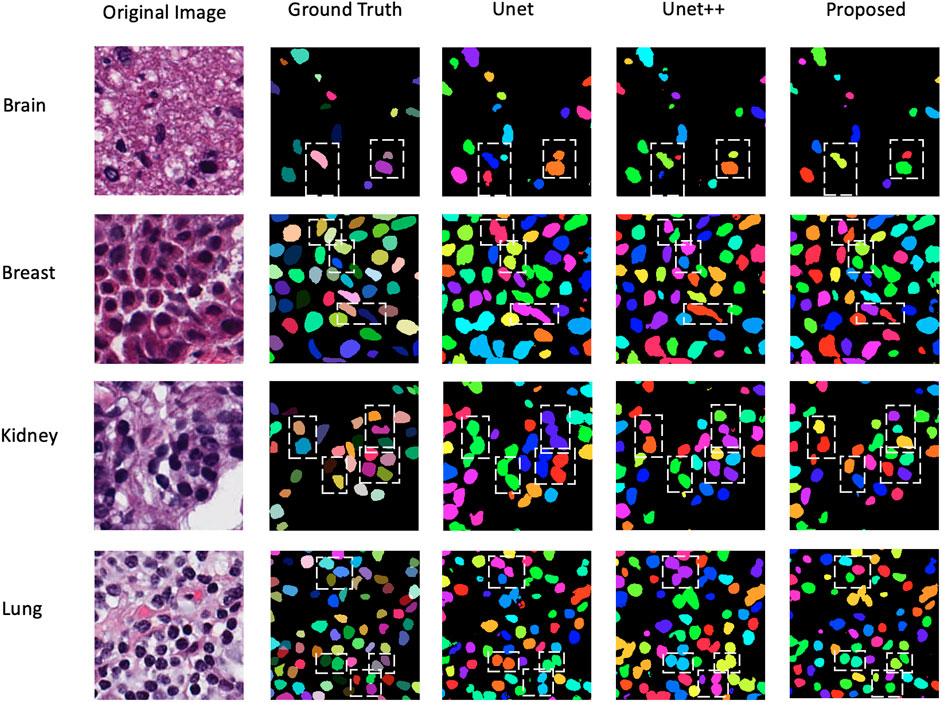
FIGURE 7. Visualization results on four different organs among Unet, Unet++, and the proposed method.

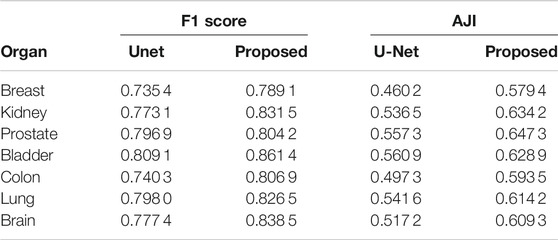
Comparison results between Unet and the proposed method on different organs are shown in Table 4. The performance of the proposed method surpasses the Unet on two evaluation metrics in all 7 organs.

TABLE 4

TABLE 4. Comparison results between Unet and the proposed method on different organs.

5 Discussion

5.1 Ablation Study on the MKWM and DMFM

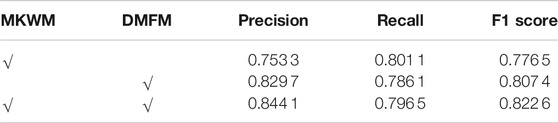
Table 5 shows the ablation study on two modules. In the situation of only using the MKWM, the feature maps from the two branches are simply concatenated, and the network performance is not good. The F1-score is only 0.776 5. This may be because there is a great difference between the nuclei extraction branch and boundary detection branch. In addition, simply concatenating and sending these features directly to the decoder part make the segmentation performance worse. If only using the DMFM, the F1-score is 0.807 4. Despite of not using the MKWM, the DMFM densely connects the feature maps from the two branches and enhances image representations. If both two modules are included in the network, the overall performance is improved. This is because by utilizing the MKWM, the important regions can be highlighted, and it is easier for the DMFM to extract useful features. It can be observed that the performance of mixing the feature maps from the two branches with the MKWM and connecting them in a dense way improves from 0.8074 to 0.8226 on F1-score. This shows that on the one hand, fusing information from the MKWM can make the feature maps highlight both nuclei information and their boundary information, which is helpful to get more integrated features of images; on the other hand, through the DMFM, feature maps in the former layers can be reused to fuse with the latter layers so that the feature maps contain multi-scale characteristics and are helpful for the decoder part.

TABLE 5

TABLE 5. Ablation study on the MKWM and DMFM.

5.2 Comparison Among Unet, Unet++, and CMF-Unet

Unet and Unet++ are two well-known networks and compared to them, our method has the following improvements. First, we add a MKWM to utilize two different sizes of kernels to adaptively extract features and give more weights on important areas, rather than simply using the same kernel size and treating every pixel in equal. Second, we shorten the gap between the encoder part and decoder part through the DMFM. There is a thinking that a huge difference exists between feature maps from an encoder and from a decoder, so concatenating feature maps directly through skip connection has disadvantages. So, Unet++ redesigns a nested way to connect layers in the network. In addition, our method not only densely links different layers but also adds new characteristics for the network to learn and further strengthen feature maps. Thus, CMF-Unet can perform better than Unet and Unet++.

Our proposed method also has limitations. Compared to Unet and Unet++, CMF-Unet has more parameters. Table 6 shows the number of total parameters of the three networks. The number of parameters of Unet++ approaches Unet, but there is a big gap between Unet++ and CMF-Unet. So, the proposed method needs more training time.

TABLE 6

TABLE 6. Number of total parameters of Unet, Unet++, and CMF-Unet.

6 Conclusion

This study proposes a contextual mixing feature Unet (CMF-Unet) to segment nuclei for pathology images. Due to challenges of inconsistent staining, blur boundary, and diverse organs, we consider that using two encoder–decoder structures are beneficial because each branch has a clear goal of extracting nuclei features and nuclei boundaries separately, and these two features are helpful to segment each nucleus. In order to fully exploit image features and improve image representations, two modules, MKWM and DMFM, are designed. The MKWM uses two different kernel sizes to capture both detailed information and margin information and then assigns more weights on important areas so that the nuclei information and the boundary information can be highlighted. The DMFM aims to combine the feature maps through two branches in a densely connected way so as to enhance feature maps. Because the decoder part receives the feature maps with rich information, segmentation performance can be improved. We test our network on the MoNuSeg dataset which contains nuclei from various organs. In addition, experiments show that our method is effective, and the generalization ability also performs well.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author. The datasets MoNuSeg for this study can be found in the Grand Challenge https://monuseg.grand-challenge.org/.

Author Contributions

XX and SK contributed to conception and design of the study. XX wrote the first draft of the manuscript. Both of authors contributed to manuscript revision, read and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Dulaimi, K., Tomeo-Reyes, I., Banks, J., and Chandran, V. (2016). “White Blood Cell Nuclei Segmentation Using Level Set Methods and Geometric Active Contours,” in 2016 International Conference on Digital Image Computing: Techniques and Applications (DICTA) (IEEE), 1–7. doi:10.1109/dicta.2016.7797097

CrossRef Full Text | Google Scholar

Badrinarayanan, V., Kendall, A., and Cipolla, R. (2017). Segnet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 39, 2481–2495. doi:10.1109/tpami.2016.2644615

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Li, X., Hu, K., Chen, Z., and Gao, X. (2020). “Nuclei Segmentation in Histopathology Images Using Rotation Equivariant and Multi-Level Feature Aggregation Neural Network,” in 2020 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) (IEEE), 549–554. doi:10.1109/bibm49941.2020.9313413

CrossRef Full Text | Google Scholar

Deng, S., Zhang, X., Yan, W., Chang, E. I., Fan, Y., Lai, M., et al. (2020). Deep Learning in Digital Pathology Image Analysis: A Survey. Front. Med. 14, 470–487. doi:10.1007/s11684-020-0782-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, H., Zheng, Y., Zhou, Q., Xiao, J., Chen, S., and Guan, Q. (2019). “Mc-unet: Multi-Scale Convolution Unet for Bladder Cancer Cell Segmentation in Phase-Contrast Microscopy Images,” in 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) (IEEE), 1197–1199. doi:10.1109/bibm47256.2019.8983121

CrossRef Full Text | Google Scholar

Huang, G., Liu, Z., Van Der Maaten, L., and Weinberger, K. Q. (2017). “Densely Connected Convolutional Networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 4700–4708. doi:10.1109/cvpr.2017.243

CrossRef Full Text | Google Scholar

Kang, Q., Lao, Q., and Fevens, T. (2019). “Nuclei Segmentation in Histopathological Images Using Two-Stage Learning,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Springer), 703–711. doi:10.1007/978-3-030-32239-7_78

CrossRef Full Text | Google Scholar

Kong, H., Akakin, H. C., and Sarma, S. E. (2013). A Generalized Laplacian of Gaussian Filter for Blob Detection and its Applications. IEEE Trans. Cybern. 43, 1719–1733. doi:10.1109/tsmcb.2012.2228639

PubMed Abstract | CrossRef Full Text | Google Scholar

Kong, Y., Genchev, G. Z., Wang, X., Zhao, H., and Lu, H. (2020). Nuclear Segmentation in Histopathological Images Using Two-Stage Stacked U-Nets with Attention Mechanism. Front. Bioeng. Biotechnol. 8, 573866. doi:10.3389/fbioe.2020.573866

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, N., Verma, R., Sharma, S., Bhargava, S., Vahadane, A., and Sethi, A. (2017). A Dataset and a Technique for Generalized Nuclear Segmentation for Computational Pathology. IEEE Trans. Med. Imaging 36, 1550–1560. doi:10.1109/tmi.2017.2677499

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Fang, F., Mei, K., and Zhang, G. (2018). “Multi-scale Residual Network for Image Super-resolution,” in Proceedings of the European Conference on Computer Vision (ECCV), 517–532.

CrossRef Full Text | Google Scholar

Long, J., Shelhamer, E., and Darrell, T. (2015). “Fully Convolutional Networks for Semantic Segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 3431–3440. doi:10.1109/cvpr.2015.7298965

CrossRef Full Text | Google Scholar

Lou, A., Guan, S., and Loew, M. (2021). Cfpnet-m: A Light-Weight Encoder-Decoder Based Network for Multimodal Biomedical Image Real-Time Segmentation. arXiv preprint arXiv:2105.04075.

Google Scholar

Mahbod, A., Schaefer, G., Ellinger, I., Ecker, R., Smedby, Ö., and Wang, C. (2019). “A Two-Stage U-Net Algorithm for Segmentation of Nuclei in H&E-Stained Tissues,” in European Congress on Digital Pathology (Springer), 75–82. doi:10.1007/978-3-030-23937-4_9

CrossRef Full Text | Google Scholar

Mahmood, F., Borders, D., Chen, R. J., McKay, G. N., Salimian, K. J., Baras, A., et al. (2019). Deep Adversarial Training for Multi-Organ Nuclei Segmentation in Histopathology Images. IEEE Trans. Med. Imaging 39, 3257–3267. doi:10.1109/TMI.2019.2927182

PubMed Abstract | CrossRef Full Text | Google Scholar

Milletari, F., Navab, N., and Ahmadi, S.-A. (2016). “V-net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation,” in 2016 Fourth International Conference on 3D Vision (3DV) (IEEE), 565–571. doi:10.1109/3dv.2016.79

CrossRef Full Text | Google Scholar

Naylor, P., Lae, M., Reyal, F., and Walter, T. (2018). Segmentation of Nuclei in Histopathology Images by Deep Regression of the Distance Map. IEEE Trans. Med. Imaging 38, 448–459. doi:10.1109/TMI.2018.2865709

PubMed Abstract | CrossRef Full Text | Google Scholar

Phansalkar, N., More, S., Sabale, A., and Joshi, M. (2011). “Adaptive Local Thresholding for Detection of Nuclei in Diversity Stained Cytology Images,” in 2011 International Conference on Communications and Signal Processing (IEEE), 218–220. doi:10.1109/iccsp.2011.5739305

CrossRef Full Text | Google Scholar

Ronneberger, O., Fischer, P., and Brox, T. (2015). “U-net: Convolutional Networks for Biomedical Image Segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Springer), 234–241. doi:10.1007/978-3-319-24574-4_28

CrossRef Full Text | Google Scholar

Ruifrok, A. C., and Johnston, D. A. (2001). Quantification of Histochemical Staining by Color Deconvolution. Anal. Quant Cytol. Histol. 23, 291–299.

PubMed Abstract | Google Scholar

Sudre, C. H., Li, W., Vercauteren, T., Ourselin, S., and Jorge Cardoso, M. (2017). “Generalised Dice Overlap as a Deep Learning Loss Function for Highly Unbalanced Segmentations,” in Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support (Springer), 240–248. doi:10.1007/978-3-319-67558-9_28

PubMed Abstract | CrossRef Full Text | Google Scholar

Szénási, S., Vámossy, Z., and Kozlovszky, M. (2011). “Gpgpu-based Data Parallel Region Growing Algorithm for Cell Nuclei Detection,” in 2011 IEEE 12th International Symposium on Computational Intelligence and Informatics (CINTI) (IEEE), 493–499.

Google Scholar

Tan, M., and Le, Q. V. (2019). Mixconv: Mixed Depthwise Convolutional Kernels. arXiv preprint arXiv:1907.09595.

Google Scholar

Vahadane, A., Peng, T., Sethi, A., Albarqouni, S., Wang, L., Baust, M., et al. (2016). Structure-preserving Color Normalization and Sparse Stain Separation for Histological Images. IEEE Trans. Med. Imaging 35, 1962–1971. doi:10.1109/tmi.2016.2529665

PubMed Abstract | CrossRef Full Text | Google Scholar

Veta, M., Huisman, A., Viergever, M. A., van Diest, P. J., and Pluim, J. P. (2011). “Marker-controlled watershed segmentation of nuclei in h&e stained breast cancer biopsy images,” in 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro (IEEE), 618–621.

Google Scholar

Veta, M., Van Diest, P. J., Kornegoor, R., Huisman, A., Viergever, M. A., and Pluim, J. P. W. (2013). Automatic Nuclei Segmentation in H&E Stained Breast Cancer Histopathology Images. PloS one 8, e70221. doi:10.1371/journal.pone.0070221

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Xian, M., and Vakanski, A. (2020). “Bending Loss Regularized Network for Nuclei Segmentation in Histopathology Images,” in 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI) (IEEE), 1–5. doi:10.1109/isbi45749.2020.9098611

CrossRef Full Text | Google Scholar

Xu, Z., Sobhani, F., Moro, C. F., and Zhang, Q. (2019). “Us-net for Robust and Efficient Nuclei Instance Segmentation,” in 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019) (IEEE), 44–47. doi:10.1109/isbi.2019.8759530

CrossRef Full Text | Google Scholar

Zeng, Z., Xie, W., Zhang, Y., and Lu, Y. (2019). Ric-unet: An Improved Neural Network Based on Unet for Nuclei Segmentation in Histology Images. Ieee Access 7, 21420–21428. doi:10.1109/access.2019.2896920

CrossRef Full Text | Google Scholar

Zhang, Z., and Sabuncu, M. R. (2018). “Generalized Cross Entropy Loss for Training Deep Neural Networks with Noisy Labels,” in 32nd Conference on Neural Information Processing Systems (NeurIPS). 1.

Google Scholar

Zhou, Y., Onder, O. F., Dou, Q., Tsougenis, E., Chen, H., and Heng, P.-A. (2019). “Cia-net: Robust Nuclei Instance Segmentation with Contour-Aware Information Aggregation,” in International Conference on Information Processing in Medical Imaging (Springer), 682–693. doi:10.1007/978-3-030-20351-1_53

CrossRef Full Text | Google Scholar

Zhou, Z., Rahman Siddiquee, M. M., Tajbakhsh, N., and Liang, J. (2018). “Unet++: A Nested U-Net Architecture for Medical Image Segmentation,” in Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support (Springer), 3–11. doi:10.1007/978-3-030-00889-5_1

PubMed Abstract | CrossRef Full Text | Google Scholar