Survey of Image Edge Detection

Edge detection technology aims to identify and extract the boundary information of image pixel mutation, which is a research hotspot in the field of computer vision. This technology has been widely used in image segmentation, target detection, and other high-level image processing technologies. In recent years, considering the problems of thick image edge contour, inaccurate positioning, and poor detection accuracy, researchers have proposed a variety of edge detection algorithms based on deep learning, such as multi-scale feature fusion, codec, network reconstruction, and so on. This paper dedicates to making a comprehensive analysis and special research on the edge detection algorithms. Firstly, by classifying the multi-level structure of traditional edge detection algorithms, the theory and method of each algorithm are introduced. Secondly, through focusing on the edge detection algorithm based on deep learning, the technical difficulties, advantages of methods, and backbone network selection of each algorithm are analysed. Then, through the experiments on the BSDS500 and NYUD dataset, the performance of each algorithm is further evaluated. It can be seen that the performance of the current edge detection algorithms is close to or even beyond the human visual level. At present, there are a few comprehensive review articles on image edge detection. This paper dedicates to making a comprehensive analysis of edge detection technology and aims to offer reference and guidance for the relevant personnel to follow up easily the current developments of edge detection and to make further improvements and innovations.

Introduction

Images are always an important source of information for exploring and perceiving the world and representation of the world. In practical applications of image processing, one of the main basic features of an image is its edges, whose information is often used in higher-level image processing techniques. Therefore, edge detection and extraction techniques have become the basis of many image processing-related technologies and have become an important research topic in the current digital image processing discipline.

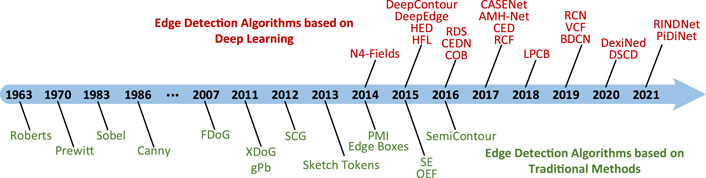
Owing to the importance of image edges, image edge detection has been receiving a lot of attention from researchers since the time it was proposed, and Figure 1 illustrates the development of edge detection algorithms. The earliest edge detection operator was the Robert (Ziou and Tabbone, 1998) operator proposed by Lawrence Roberts in 1963, which is also known as the cross-differential algorithm as the simplest operator, and its underlying principle is to locate the image contour with the help of a local difference operator. It was followed in 1970 by the Prewitt operator (Shrivakshan and Chandrasekar, 2012), which is often applied to high noise, pixel-value fading images. Then came the Sobel operator (Marr and Hildreth, 1980), which introduced the idea of weights, and the Laplacian operator (Xin Wang, 2007), which used second-order differentiation, in the 1980s. Later the optimal Canny operator (Canny, 1986) was proposed in 1986, which continuously optimized the image contour information by filtering, enhancement, and detection steps, and became one of the best operators for detection in the field of edge detection at that time. After that, with the continuous development of deep learning, various methods based on CNN to achieve edge detection have emerged. In 2015 Bertasius et al. changed the traditional bottom-up idea of edge detection and proposed a top-down multi-scale divergent deep network DeepEdge (Bertasius et al., 2015a) for edge detection. In the same year, Xie et al. developed the holistic nested edge detection algorithm HED (Xie and Tu, 2015), which solved the problem of holistic image-based training and prediction and multi-scale multi-level feature learning. In 2017 Liu et al. proposed an accurate edge detector RCF (Liu et al., 2017) using richer convolutional features. In 2019 Deng et al. proposed a novel end-to-end edge detection system DSCD (Deng and Liu, 2020), which effectively utilizes multi-scale and multi-level features to produce high-quality object edge output. In 2021 Su et al. designed PiDiNet (Su et al., 2021), a simple, lightweight, and efficient edge detection architecture.

FIGURE 1

FIGURE 1. Development of edge detection algorithms based on traditional and deep learning methods.

With the development of technology, the recognition performance of edge detection networks has gradually improved, and the accuracy rate has increased. However, at the same time, the depth of the network has been deepened, leading to problems such as oversized parameters, training difficulties, and model complexity. In this paper, we will analyze and classify the classical and latest edge detection models in terms of model structure, technical difficulties, method advantages, and backbone networks from two categories based on traditional methods and deep learning methods. Then we will introduce the backbone networks (AlexNet, VGG16, ResNet), evaluation metrics (ODS, OIS, FPS, PR curve), and datasets (BSDS500, NYUD, PASCAL-VOC, PASCAL-Context, MultiCue, BIPED), which are closely related to edge detection. Finally, the methods mentioned in this paper are briefly summarized, and the problems found and the future directions of edge detection focus are briefly described.

Related Work

Before that, some researchers have already summarized the edge detection algorithms. Starting from the type of edge, Davis, (1975) described in detail the traditional edge detection algorithms based on linear, nonlinear as well as those using planning and prior knowledge from the aspects of formula derivation to algorithm advantages, and described what troubles different noises will cause to the edge detection algorithm. Marr and Hildreth, (1980) divided the theory of edge detection into two parts, namely the change of object scale and the illumination intensity on the object surface, which has a good application and proof of the edge detection method based on Laplace transform. Torre and Poggio, (1986) introduced methods of edge detection through the explanation of filters and derivatives and also summarized the advantages as well as the disadvantages of traditional edge detection algorithms such as DOB, canny and others. Duan et al. (2005) and Maini and Aggarwal, (2009) analyzed and visually compared the most commonly used edge detection techniques based on gradient change and Laplace. Oskoei and Hu, (2010) and Amer and Abushaala, (2015) analyzed and summarized the edge detection algorithms based on traditional methods, classification methods, wavelet transform methods and machine learning methods.

Therefore, previous survey articles on edge detection are mostly based on the research and generalization on traditional algorithms, which rarely involve the knowledge of deep learning and convolutional neural network. At the same time, because these papers appeared earlier, some current edge detection algorithms are seldom summarized. Combined with the contribution of previous work, this paper reorganizes and combs the edge detection algorithms system and makes a unified evaluation of the representative edge detection algorithms in recent years from traditional methods to deep learning methods.

Traditional Methods

Traditional image edge detection methods have been proposed earlier and developed for a longer period of time. Therefore, traditional image edge detection methods are more mature, simple but efficient. However, scholars are still working tirelessly on the road of refining traditional image edge detection methods, trying to make up for the shortcomings of previous algorithms and further improve their performance. In this paper, the traditional edge detection methods are divided into four types: Gradient change-based, Gaussian difference-based, multi-scale feature-based, and structured learning-based.

Edge Detection Method Based on Gradient Change

In conventional based algorithms, image edge refers to the abrupt change between adjacent pixel values of an image, where the difference between two pixel values is manifested significantly (Rong et al., 2014). Thus, image edge detection is to detect and generate image edge gradient by using edge detection operator combined with differential technology through gray mutation between pixels (Arbeláez et al., 2010). The commonly used classical edge detection operators can be divided into first-order and second-order operators: the first-order difference-based operators are mainly Sobel, Prewitt, and Robert; the second-order difference-based operators are mainly Laplace, LOG, and the optimal Canny operator.

The Robert operator proposed by Lawrence Roberts in 1963 (Ziou and Tabbone, 1998) has a small template and is susceptible to noise interference, so it is ineffective in generating image contours with high noise and flat edges, which represent as inaccurate positioning of contours and coarse extracted contour lines. Then in 1970, the Prewitt operator (Shrivakshan and Chandrasekar, 2012) with the size of $3\times 3$ was proposed, which generates the image contour by calculating the difference of pixel gray value and its image contour generation effect in the vertical and horizontal directions is better than that of Robert operator. The Sobel operator (Marr and Hildreth, 1980) proposed in 1983 combined Gaussian smoothing and first-order difference derivation, and sharpened the output image by introducing weight information. The subsequent Laplace operator (Xin Wang, 2007) used second-order differentiation to extract edge contour information, which is more suitable for noise-free images. The Canny operator proposed in 1986 (Canny, 1986) provides further improvement and refinement of the effect of the previous operator, which is less susceptible to noise interference and can detect the weak edges of the image well.

Edge Detection Method Based on Gaussian Difference

Difference of Gaussian (DoG) is an algorithm for blurred image enhancement (Fu et al., 2018), and it is equivalent to a band-pass filter that removes all other frequency information except those frequencies that are retained in the original image.

FDoG (2007): Kang et al. (2007) improved the new edge detection method FDoG based on Gaussian difference and Binary Threshold. The traditional DoG adopts isotropic filter, and the direction information of the edge is not considered in Gaussian convolution (Winnemöller et al., 2006). The FDoG algorithm, on the other hand, integrates the directional information of the local structure of the image when applying the DoG filter. When the boundary tangent stream is constructed from the input image, the image edge information is obtained by calculating the Gaussian difference based on the stream. This algorithm only calculates the Gaussian difference in the normal direction of the edge gradient direction, thus well suppresses the noise and false edges.

XDoG (2011): Since DoG can obtain more aesthetically pleasing edges and lines without post-processing in edge detection (Kyprianidis and Döllner, 2008), the DoG operator has been used in a variety of applications ranging from computer vision to style rendering. Winnemöller, (2011) improved the DoG algorithm and proposed an edge detection algorithm XDoG which can realize the transformation of image advanced style. Algorithm XDoG adjusts the intensity of the cut-off effect of Gaussian difference filtering by introducing a new constant, so as to achieve the effect of image style transformation (Gooch et al., 2004) in edge detection. At the same time, XDoG transforms the threshold bisection function of Gaussian difference into a continuous slope function. Actually, the output of the algorithm is the weighted average of Gaussian blur results and Gaussian difference results, which finally realizes image edge detection with more complex styles and better effects.

Edge Detection Method Based on Multi-Scale Features

The most challenging problem in edge detection is the scale variance of the target. In edge detection, objects always have different shapes and sizes, and there may even be some extremely small, extremely large or shaped objects, which brings great difficulties to the accurate identification and accurate positioning of object edges.

gPb (2011): High quality image segmentation increasingly depends on image edge detection. Arbeláez et al. (2010) simplified the problem of image segmentation into the problem of edge detection, and designed a high-performance edge detection algorithm gPb. The edge detector combines multiple local cues such as multi-scale local brightness, color, and texture into a powerful global structure based on spectral clustering (Arbelaez et al., 2009). By applying directional gradient operator to each position in the image, the local information of the image is calculated, and the incidence matrix of similarity between pixels is established. Then the feature vector of the encoded image edge information can be solved by using the incidence matrix, and combine this feature vector with image local information to obtain the global edge detection result. Compared with other global methods based on similarity information, the algorithm results have been greatly improved.

SGD (2012): Ren et al. (Xiaofeng and Bo, 2012) combined automatic sparse coding with directional gradient and designed an image edge detection algorithm SGD based on Sparse Code Gradients (SCG) unsupervised learning. The algorithm uses K-SVD (Aharon et al., 2006) for dictionary training and orthogonal matching tracking algorithm (Pati et al., 1993) for local neighborhood oriented sparse coding calculation. Before using linear SVM classification, the local information of the image is processed by multi-scale pooling and power transform. Finally, after smoothing and non-maximum suppression, the image edge result graph is generated. Sparse coding can effectively learn the local contrast of the image, and the edge detection performance is obviously better than the coding results of manually designed features.

Edge Detection Method Based on Structured Learning

The early edge detection algorithms consider that the input and output are always in the form of vector, but the actual problems may be more complex, and the input or output may be in the form of sequence and tree. The structured learning methods have better representation ability for high-dimensional data, and can capture the detailed information of the image at the same time.

Sketch Tokens (2013): Lim et al. (2013) applied the idea of Sketch Tokens to the field of image edge detection, and proposed a new edge detection method based on intermediate feature representation of supervised learning and local edge detection (Sketch Tokens). This method extracts the contour from the manually marked sketch edge map to generate a diversified and representative sketch token class (Arbeláez et al., 2010). Then, the sketch token class is grouped by K-means algorithm, which is divided into straight lines to more complex structures. After that, the features of pixels in natural images are extracted, and the classifier is trained by random forest algorithm (Criminisi et al., 2012) using two classes of features, channel index, and self-similarity (Shechtman and Irani, 2007), to determine whether each point of an image pixel belongs to a certain sketch token (i.e., whether it is an edge). Finally, the image edge detection results are output by non-maximal value suppression. This method speeds up the inference of random forest by generating a contour dictionary as the edge features of pixels, which results in good performance in both top-down and bottom-up tasks.

SE (2015): Dollár and Zitnick, (2014) proposed a generalized structured learning algorithm (SE) for edge detection, which transforms the edge detection problem into predicting local segmentation masks given a block of input images. This algorithm uses a random forest structure to capture the structured information inherent to the image edge pixels (Kontschieder et al., 2011), then uses structured labels to determine the splitting function for each branch in the tree. However, since training random forests using structured labels faces the challenge that the structured output space is high-dimensional or complex, and the information gain of structured labels is not clearly defined. Dollár et al. then robustly mapped structured labels to a discrete space where standard information gain measures can be evaluated and each tree predicts an edge pixel label, followed by a random forest to aggregate the final image edge detection results by combining the outputs of multiple trees. The output is also enhanced by introducing sharpening (SH) and multiscale detection (MS) (Ren, 2008) modules.

OEF (2015): Hallman and Fowlkes, (2015) proposed an algorithm for learning boundary detection based on random forest classifier (Oriented Edge Forests, OEF) by studying the success of random decision forest in edge detection (Dollár and Zitnick, 2013). This algorithm trains a random forest classifier to learn the mapping relationship between image pixels and label set, and applies the robustness of random decision forest to detect straight line boundaries in different positions and directions in the image. Although the algorithm ignores some curve boundaries and connection points, it still has great edge detection advantages for most small images that contains large and smooth objects. Compared with the structured forest algorithm, the training time of the algorithm is greatly shortened while the training memory remains is small.

SemiContour (2016): Inspired by Structured Random Forests (SRF) (Kontschieder et al., 2011), Zhang et al. (2016) first tried to apply Semi Supervised Learning (SSL) to image edge detection. Compared with standard Random Forests (RF), SRF has the advantages of fast prediction of high-dimensional data, robustness to label noise (Liu et al., 2013) and good support for arbitrary size output, making SRF a good candidate for SSL. At the same time, it is found that sparse representation technology (Maire et al., 2014) has a strong ability to capture the contour structure of the image. Therefore, by embedding the fast sparse coding algorithm and the construction of low dimensional subspace into the training of the whole SRF, Zhang et al. Designed an image edge detection network (SemiContour) based on semi supervised learning. The network can use very limited training data (three label data) to obtain competitive detection results.

Based on the traditional edge detection algorithm, the implementation is simple and fast, but there are also disadvantages such as thicker generated contour lines, incomplete and discontinuous image contours. Therefore, further refinement of the generated edges is needed to complete the final image edge generation. As shown in Tables 1, 2, through the performance test of the traditional edge detection algorithm in the BSDS500 and NYUD dataset, it is found that traditional edge detection algorithms perform to some extent below the level of human vision. The Optimal Dataset Scale (ODS) and Optimal Image Scale (OIS) in the table are evaluation indicators for the performance of the edge detection algorithms, and the exact meaning will be described in subsection 5.

TABLE 1

TABLE 1. Performance comparison of conventional edge detection based algorithms on the BSDS500 dataset.

TABLE 2

TABLE 2. Performance comparison of conventional edge detection based algorithms on the NYUD dataset.

Deep Learning Methods

With the integration and development of artificial intelligence and machine learning algorithms in recent years, various image edge detection algorithms are emerging in the field of digital image processing. However, because of the influence of many factors such as localization accuracy, edge detection accuracy, noise sensitivity, as well as the different accuracy of detection algorithms, image edge detection methods are continuously being improved to meet the people’s needs. In this paper, edge detection methods for deep learning are classified into three types: Codec-based, network reconstruction-based, and multi-scale feature fusion-based.

Edge Detection Method Based on Codec

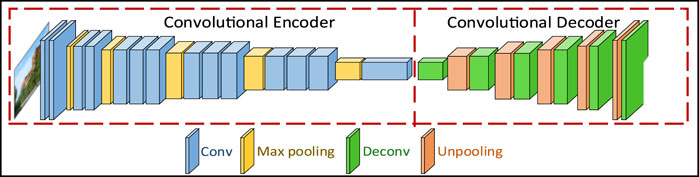
Since convolutional networks reduce the size of an image after multiple convolutions and pooling, the final output does not correspond to every pixel in the original image. Therefore, codec was introduced, as they can accept input images of any size and produce output images of the same size. The function of encoder network is to produce feature images with semantic information, while the function of the decoder network is to map the low-resolution feature image output by the encoder network back to the size of the input image for pixel by pixel classification.

CEDN (2016): Inspired by the success of full convolution network and deconvolution network (Noh et al., 2015) in the field of semantic segmentation, Yang et al. (2016) developed a full convolution codec network CEDN for edge detection, which is shown in Figure 2. Such a CEDN network can operate on any image size. The network uses VGG16 network to initialize the encoder. At the same time, in order to realize the dense prediction of image size, the decoder is constructed by alternating anti-pooling layer and convolution layer, in which the anti-pooling layer uses the maximum pooling to enlarge the feature map. When training, they fixed the encoder parameters and only optimize decoder parameters, which maintains the encoder’s generalization ability, and the decoder network can be easily combined with other tasks through learning.

FIGURE 2

FIGURE 2. Architecture of CEDN.

CASENet (2017): Yu et al. (2017) proposed an end-to-end multi label learning framework CASENet in order to solve the problem of semantic edge detection and classification under the framework of full convolution network. The network includes deep semantic edge learning architecture and jump connection structure improved based on ResNet (He et al., 2016), in which category edge activation is shared in the top convolution layer and fused with the same underlying feature set. At the same time, a multi-label loss function is proposed to supervise fusion activation. The network shows improvement over some popular existing architectures in edge detection and segmentation. Nested architecture and full convolution network are used to retain better low-level edge information, suppress non-edge pixels, and provide detailed edge location and structure information.

RINDNet (2021): Pu et al. (2021) first proposed RINDNet, which is an edge detector that can detect four types of edges simultaneously. Edges can be classified according to different physical properties: Reflectance Edge (RE), Illumination Edge (IE), Normal Edge (NE), and Depth Edge (DE). RINDNet is able to extract efficiently the shared information between different edges, while flexibly modeling the differences between them. RINDNet first extracts general features and spatial cues from the backbone network of all edges, then four independent decoders, namely RE-Decoder, IE-Decoder, NE-Decoder and DE-Decoder, are used to explore the edge effective features with high-level features as input. After that, these features and spatial information are fused for predicting the initial results. Finally, the attention map is obtained by the Attention Module (AM) to aggregate with the initial results to generate the final prediction.

Edge Detection Method Based on Network Reconstruction

With the rapid development of deep learning, various network modules based on deep learning have emerged one after another. Different modules show different advantages for tasks, so the combination of modules with different advantages through network reconstruction has become an important way to improve the results quality of computer vision tasks.

${\mathit{N}}^4$-Fields (2014): Ganin and Lempitsky, (2014) proposed a new architecture $N^4$ -Fields based on a simple combination of convolutional neural networks and nearest neighbor search in order to address the problem that ideal image transformations are too difficult to train for neural networks. In this architecture, convolutional Neural Networks and Nearest Neighbor search are applied sequentially pixel by pixel of an image. Pixels are transformed by CNN to low-dimensional vectors as output, followed by a nearest neighbor search to retrieve annotated pixels with similar CNN activations, and then by averaging overlapping regions to output a transformation of the image. Using nearest neighbor search at the top layer of the neural network can significantly improve the results and address the underfitting effect during neural network training. Thus this architecture yields better generalizability and edge detection quality than single-stage architectures that include CNNs alone or perform nearest neighbor search only on hand-crafted features.

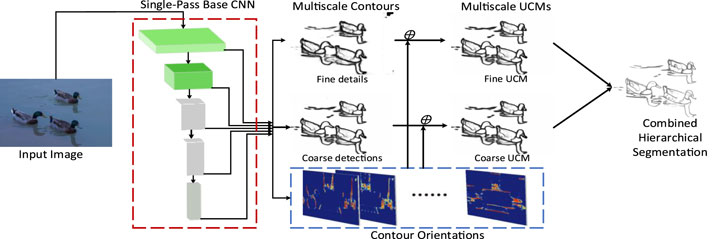
COB (2016): Maninis et al. (2016) proposed an edge detection algorithm COB with convolution-oriented boundary structure, which is shown in Figure 3. The algorithm is a general CNN architecture, which allows end-to-end learning of multi-scale directional contour, and combines such information to build a multi-scale oriented contour detector. Different from previous work, COB uses the duality between contour detection and hierarchical segmentation structure (Pont-Tuset et al., 2016), obtains multi-scale information in a single transmission of the whole image network, and combines pixel by pixel classification with contour direction estimation. At the same time, a novel sparse boundary representation is proposed in hierarchical segmentation. Through the introduction of Ultrametric Contour Map (UCM) (Arbeláez et al., 2010) and Oriented Watershed Transform (OWT), the performance of edge detection algorithm is significantly improved, and it can be extended to unknown categories and datasets.

FIGURE 3

FIGURE 3. Architecture of COB.

AMH-Net (2017): Xu et al. (2018) proposed a new attention guided multi-scale convolutional neural network AMH-Net for edge detection. The network mainly includes two main components: A hierarchical architecture for generating richer and complementary multi-scale feature representations, and a new Attention Gated Conditional Random Fields (AG-CRF) model for robust feature refinement and fusion. Hierarchical networks can learn more multi-scale features than traditional CNN, while AG-CRF seamlessly integrates the attention mechanism (Mnih et al., 2014) into a two-level CNN model in the form of gate (Minka and Gates, 2009) for multi-scale learning. At the same time, AG-CRF model further enhances its ability to represent image edges by using the information obtained from other scales. Finally, the attention mechanism will further improve the quality of multi-scale information representation, so as to improve the overall performance of the model.

Edge Detection Method Based on Multi-Scale Feature Fusion

Convolutional neural networks extract features of the target by layer-by-layer abstraction, in which an important concept is perceptual field. The higher layer network has a larger perceptual field and a strong ability to characterize semantic information while the lower layer network has a smaller perceptual field but a strong ability to characterize geometric detail information. Therefore, fusing features of different scales is an important means to improve the edge detection performance.

DeepEdge (2015): based on the close relationship between object recognition and edge detection tasks, Bertasius et al. (2015a) changed the traditional bottom-up notion of edge detection and proposed DeepEdge, a top-down multiscale bifurcated deep network for edge detection. The network reuses the computational features of the first five convolutional layers of the KNet network (Krizhevsky et al., 2012), which consists of five convolutional layers and a bifurcated fully connected subnetwork to form a multiscale deep network. The image edge information is learned directly from the original pixels through this end-to-end convolutional architecture. Of two branches, one of them learns to predict the edge likelihood (with a classification goal), while the other branch is trained to predict the proportion of human-labeled image edges that are consistent (using regression criteria). DeepEdge can operate on multiple scales simultaneously, resulting in a significant increase in contour detection accuracy by combining local and global information of the image.

HED (2015): To address the problem of holistic image-based training, prediction, multi-scale and multi-level feature learning (Yuille and Poggio, 1986), Xie and Tu, (2015) developed the holistic nested edge detection algorithm HED. by utilizing fully convolutional neural networks and deeply supervised (Lee et al., 2015) network learning models, HED can automatically learn rich hierarchical representations to perform image-to-image prediction. “Holistic” refers to the fact that HED trains and predicts edges in an end-to-end manner despite the absence of an explicitly structured output; “Nested” emphasizes the inherited and progressively refined edge maps generated as side outputs. This algorithm shows good edge detection results in performing image-to-image learning by combining multi-scale and multi-level visual response techniques.

HFL (2015): Inspired by the object-level reasoning used by us humans in determining whether a particular pixel belongs to an image edge (Kourtzi and Kanwisher, 2001), Bertasius et al. (2015b) proposed HFL, a network for predicting image edges by using a pre-trained object classification network and object-level features. The network can be viewed as a high to low approach, where high-level object features provide low-level edge detection process provides information. The final edge probability map is generated sequentially through prediction-related steps of using SE to extract high recall candidate edge points, up-sampling the original image to a larger dimension, deep feature interpolation (Long et al., 2015), and fusing fully connected layers. HFL uses object-level information to predict edges, which is more consistent with human reasoning. This network is accurate and efficient for a variety of datasets, as well as for several advanced vision tasks.

RDS (2016): Liu and Lew, (2016) proposed the use of Relaxed Deep Supervision (RDS) in convolutional neural networks for edge detection. The network was constructed with hierarchical supervised signals and additional relaxed labels to take into account of the diversity of deep neural networks. The relaxed labels are first captured from simple yet effective off-the-shelf detectors such as Canny or SE (Dollár and Zitnick, 2014) and then are merged with general truth maps to generate RDS. Finally, RDS is employed to finely guide and fine-tune the middle layer of the edge network. The RDS contains positive labels (edges), negative labels (non-edges), and additional relaxed labels, where these loose labels can be considered as some false positives (false edges) that are difficult to classify. It is shown that RDS can use a “delay strategy” to handle false edge information and achieve better edge detection performance.

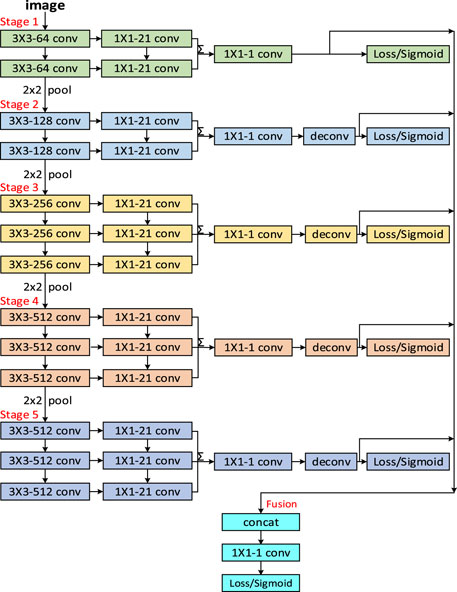
RCF (2017): Many current deep learning-based image contour generation algorithms, that utilize only the last layer of the convolutional network, are missing detailed information at the shallow level of the image, and also lead to the problem of non-convergence of the contour generation model as well as gradient disappearance. Therefore, Liu et al. (2017) proposed an accurate edge detector RCF using richer convolutional features, which is shown in Figure 4. The network is designed as a fully convolutional network with a VGG16 backbone, removing the fully connected layer and the fifth pooling layer. RCF accomplishes image contour generation by fusing the layer-level features of all convolutional layers, and in this structure, all the weight parameters are done by automatic learning. Since the convolutional layers in the original VGG16 network have different perceptual field sizes, the network learns multi-scale information of the image that contributes to contour generation. RCF makes full use of the FPN idea to combine the high-level and underlying feature map for edge detection (Dai et al., 2016).

FIGURE 4

FIGURE 4. Architecture of RCF.

LPCB (2018): In order to solve the problem of thick edge in image prediction, Deng et al. (2018) improved the HED network and obtained a LPCB network. This network takes VGG16 model as the backbone and uses the end-to-end full convolution network of bottom-up/top-down Architecture (Pinheiro et al., 2016) to predict image edges. A new loss function based on image similarity is also introduced, which performs accurate, fast, and convenient image-to-edge prediction, and is also very effective for classifying unbalanced data. The network automatically learns image rich layer features, resolves ambiguities in prediction, and obtains clear prediction results without post-processing. Compared to the original network, LPBC network uses fewer parameters yet demonstrates better edge detection performance benefits.

RCN (2019): Kelm et al. (2019) designed the RefineContourNet (RCN) network based on the RefineNet (Lin et al., 2017) multi-path refinement network. This network prioritizes the efficient use of the high-level abstraction capabilities of the modern classification network ResNet for object edge detection, which starts with a tensor with the highest level of features and combines them with a tensor of lower abstraction levels features layer by layer until it reaches the lowest level. Fusing high-level, mid-level, and low-level features in a specific order is more effective for edge detection than using a simple jump-join architecture. Residual Convolution Unit (RCU), Multi-Resolution Fusion (MRF), and Chained Residual Pooling (CRP) modules are also introduced to enhance the visualization of edge detection.

VCF (2019): Based on the fast feature embedding convolutional architecture (Caffe) and the Visual Geometry Group (VGG16) template, Qu et al. (2019) proposed a new accurate edge detector VCF. Firstly, image features are detected using the Visual Cross Fusion (VCF) network, and then, a custom hierarchical weighted cross-entropy loss function is proposed to maximize the use of the image pixel set and rationalize the organization of contested pixels. Finally, the cross-network fusion layer is used to refine the edge features of the image. the VCF model extracts the features of multi-level hierarchy by two methods, parametric downscaling and cross-fusion of the fully connected layer, respectively, to achieve end-to-end image edge detection. The improvement consists of three main components: the gradual reduction of the feature dimension of the small convolutional kernel, the custom loss function, and the cross-fusion structure.

BDCN (2019): In order to extract edge contours using multi-scale information of images, He et al. (2019) proposed a network structure BDCN using a bidirectional cascade, where the output of each layer is supervised by a contour label of a specific scale that is learned through the network itself. ID Blocks are the basic components of this network, and each ID Block is learned by a bidirectional cascade structure to generate different supervision strategies, while the output of two edge predictions is passed separately to the shallow and high-level structures of the network. To enhance the features output from each layer, a Scale Enhancement Module (SEM) similar to the ASPP structure is again used to generate multi-scale features, which consists of multiple parallel convolutions with different expansion rates, effectively increasing the perceptual field of the network neurons (Chen et al., 2017), and finally outputting the result of multiple multi-scale feature fusion.

DexiNed (2020): Inspired by HED and Xception (Chollet, 2017) networks, Soria et al. (Poma et al., 2020) proposed DexiNed, a deep learning-based edge detector. This network can be used for any edge detection task to generate thin edge maps visible to the human eye without prior training or fine-tuning process. DexiNed can be regarded as two sub-networks: Extremely dense initial network (Dexi) and Up-sampling Block (UB). This network consists of a total of six encoders, and each main block outputs the corresponding feature mapping for generating intermediate edge maps using the up-sampling block. All edge mappings generated by the up-sampling block will be connected at the end of the network to provide filters for learning and to produce fused edge mappings. One of the key components of edge refinement is UB, which consists mainly of convolutional and deconvolutional layers.

DSCD (2020): Deng and Liu, (2020) proposed a novel end-to-end edge detection system, DSCD, which effectively utilizes multi-scale and multi-level features to produce high-quality object edge output (Deng et al., 2018). First, to address localization and sharpness, a novel loss function based on the structural similarity of two images is proposed to effectively minimize the distance between predicted and true values. The system uses a VGG16 (Simonyan and Zisserman, 2014) network as an encoder to extract multi-scale and multi-level features, and a super-convolutional module is constructed on top of the encoder to directly abstract the high-level features and avoid overfitting problems. Finally, the decoder is used to fuse the high-level features and restore them to the original image size. Compared with conventional codec networks, this system is able to classify better background texture and noisy pixels, generate clear and accurate image edges, and also excel in crowd counting.

PiDiNet (2021): It is important to develop lightweight architectures and achieve a better trade-off between accuracy and efficiency of edge detection (Howard et al., 2017). Su et al. (2021) have designed a simple, lightweight and efficient edge detection architecture called Pixel Difference Network (PiDiNet) to address these issues. PiDiNet adopts a novel pixel difference convolution (PDC) to integrate the traditional edge detection operator into the popular convolution operation in modern CNN, which enhances the performance of edge detection task. PDC can easily capture image gradient information conducive to edge detection, while retaining the powerful learning ability of deep CNN to extract information with semantic significance. Also, PDC does not rely on the edge information of the manual detector, but directly integrates the gradient information extraction process into the convolution operation, which has better robustness and edge detection accuracy. Thus, PiDiNet network can still realize edge detection efficiently, robustly, and accurately when it occupies low memory.

The rapid development of deep learning is driving the development process of many tasks including image classification, target detection, and semantic segmentation. Nowadays, image edge detection using CNNs has become a new trend due to their extremely strong learning and characterization capabilities. As shown in Tables 3, 4, experiments on the BSDS500 and NYUD dataset were able to conclude that the performance of deep learning-based edge detection algorithms has surpassed that of human vision.

TABLE 3

TABLE 3. Performance comparison of deep learning-based edge detection algorithms on the BSDS500 dataset.

TABLE 4

TABLE 4. Performance comparison of deep learning-based edge detection algorithms on the NYUD dataset.

Backbone Network

Backbone networks are the basic feature extractors for edge detection tasks, and a powerful backbone network can extract richer image features. Most current deep learning-based edge detection models use AlexNet, VGG16, and ResNet as backbone networks.

AlexNet Network

AlexNet (2012): Alex et al. (Krizhevsky et al., 2012) proposed the AlexNet network at the ImageNet competition in 2012. The network won the ImageNet LSVRC that year. The accuracy rate was much higher than the second place, which was another highlight of deep learning. AlexNet network contains 8 learning layers—5 convolutional layers and 3 fully connected layers, containing 60 million parameters and 650,000 neurons. Relu activation functions, data augmentation, Dropout and cascading pooling operations were also introduced to prevent overfitting and improve the overall generalizability of the model. The authors found that the depth of the model seems to play an important role in the performance of the neural network, a finding that also inspired the later structural design of the VGG and ResNet networks. The edge detection algorithms AMH-Net and $N^4$ -Fields networks based on network reconstruction then use the AlexNet network as the base network.

VGG16 Network

VGG16 (2014): Simonyan and Zisserman, (2014) designed the deep convolutional network VGG16 consisting of 13 convolutional layers and 3 fully connected layers in order to investigate the accuracy of convolutional network depth in large-scale image recognition. Simonyan et al. found that using a very small $3\times 3$ convolutional filter to push the neural network depth to 16–19 weight layers can significantly improve the VGG model. It utilizes a deeper network structure combined with smaller convolutional kernels and pooling kernels, allowing it to obtain more image features while effectively controlling the parameter size of the model, avoiding a large amount of computation and complex structure while achieving advanced performance. In addition, the VGG model has good generalizability and can be well generalized to other image processing fields. So, the model is now the most popular backbone network for deep learning-based image edge detection algorithms.

ResNet Network

ResNet (2016): Although the depth of the network is crucial to the performance of the model, it is empirically believed that deep networks extract more complex feature structures. It has been found experimentally that as the depth of the network increases, the gradient disappears or explodes, leading to saturation or even a decrease in network accuracy. He et al. (2016) designed a deep residual network (Deep Residual Network (ResNet). The authors identified the “Degradation” of the deep model and proposed the solution of “Shortcut Connection”. ResNet, through the introduction of residual learning, has greatly eliminated the problem of difficulty in training neural networks due to excessive depth, making the depth of the network exceed 100 layers for the first time, and can even exceed 1,000 layers. The design of the edge detection models COB and AMH-Net is based on some of the ideas of ResNet.

Evaluation Indicators

Optimal Dataset Scale (ODS) and Optimal Image Scale (OIS) are the most widely used and representative evaluation metrics in assessing image contour generation results, in addition to the Frames Per Second (FPS) and Precision-Recall (PR) curves that are often used. The F in ODS-F and OIS-F represents the F value, which is the summed average of the Precision (P) and Recall (R), and is expressed as

$F-Score=\left(1+{\beta }^2\right)\cdot \frac{Precision\cdot Recall}{{\beta }^2\cdot Precision+Recall}(1)$

So, by adjusting the value of $\beta$, the degree of significance of precision and recall can be controlled. Especially, if $\beta =1$,

$F-Score=\frac{2Precision\cdot Recall}{Precision+Recall}(2)$

then according to Eq. 2, precision rate and recall rate are considered equally important and both have the same weight. If $\beta =0$,

$F-Score=Precision(3)$

else if $\beta =\infty$,

$F-Score=Recall(4)$

According to Eqs 1, 3, 4, if $\beta <1$, then precision rate P is more important; else if $\beta >1$, then recall rate R is more important (unless P = R, Eq. 7). Besides,

$F-Score=Precision\left(1+{\beta }^2\right)(5)$

while $Recall>>{\beta }^{2}Precision$. On the contrary,

$F-Score=Recall\frac{1+{\beta }^2}{{\beta }^2}(6)$

while ${\beta }^{2}Precision>>Recall$. Interestingly enough, when $Precision=Recall$,

$F-Score=Precision=Recall(7)$

which indicates that $F-Score$ is independent of $\beta$. ODS and OIS indicate different ways of setting the threshold $\beta$.

ODS: Fixed contour threshold is also known as global best, dataset fixed scale, and optimal on the detection metric dataset scale, which simply means that the same threshold is set for all images, i.e., a fixed threshold $\beta$ is selected and applied to all images so that the F-score on the whole dataset is maximized.

OIS: Single image optimal threshold is also called optimal on single image, optimal threshold for each image, optimal on the image scale, which simply means that on each image a different threshold $\beta$ is selected that maximizes the F-score of that image.

FPS: Frames per second, i.e., how many images can be detected by the target network per second and how often the images are refreshed. It is used to evaluate the speed of target detection, the shorter is the time the faster is the detection speed.

P-R: PR curve is a curve drawn with two variables, precision and recall, where precision is the vertical coordinate and recall is the horizontal coordinate, and is widely used in the field of information extraction to indicate the proportion of positive samples that are actually positive. It is a descending ranking of the prediction results of the network according to the numerical magnitude of the confidence level, followed by the prediction of the samples in the order of the ranking, and finally the current precision and recall are calculated.

Related Datasets

BSDS500

The Berkeley Segmentation Dataset (BSDS500) was proposed for image segmentation and object contour detection, by the Berkeley computer vision group. The dataset contains a total of 500 images, including 200 training images and 200 test images, and the remaining 100 validation images; the true values of the dataset are saved in. mat files, divided into segmentation and boundaries. Each image is labeled by five people, so there are corresponding five “true” values. BSDS500 is now the most used dataset in the field of edge detection.

NYUD

The NYUD dataset is derived from an ECCV 2012 paper (Indoor Segmentation and Support Inference from RGBD Images) (Silberman et al., 2012), where most existing work ignores physical interactions or applies only to neat rooms and hallways. Instead, this dataset is proposed to parse typical, messy, physically interacting indoor scenes and recover the support relationships. the NYUD dataset consists of 1,449 pairs of densely labeled RGB and depth images, containing 381 training images, 414 validation images and 654 test images, each of $640\times 480$ size.

PASCAL-VOC

PASCAL VOC (Everingham et al., 2015) provides a standardized and excellent dataset for image recognition and classification, and an image recognition challenge was held every year from 2005 to 2012. The main objective of this challenge is to recognize objects in real scenes in a number of categories, and the objects mainly consist of 20 classes. The most widely used datasets are VOC 2017 and VOC 2012. VOC 2007 contains a total of 9,963 labeled images, consisting of training, testing, and validation, with a total of 24,640 labeled objects; the training and validation sets of VOC 2012 contain all the data from the challenge between 2007 and 2011, with a total of 11,540 images and 27,450 labeled objects. The test set contains data from 2008 to 2011. The VOC 2012 training and validation sets for the segmentation task have 2,913 images and 6,929 labeled objects.

PASCAL-Context

The PASCAL-Context (Mottaghi et al., 2014) dataset consists of two parts: the VOC 2010 semantic segmentation dataset and the Context annotation. A total of 10,103 images are included, including 4,998 images in the training set and 5,105 images in the validation set, and a total of 540 categories are annotated, which are divided into three major categories: Objects, materials, and mixtures. Although there are many kinds of objects annotated in PASCAL-Context, there are only 59 commonly used categories, so this sub-category is mostly applied in practical applications for research and experiments.

MultiCue

The MultiCue dataset consists of short binocular videos for edge detection by learning psychophysics. One of the videos consists of 100 frames of images of natural scenes captured by a challenging stereo camera.

BIPED

The BIPED dataset comes from a WACV 2020 article DexiNed, which proposes this dataset with very fine and complete edge information labeling based on the previous datasets that have more or less incomplete edge information, making it difficult to train the model and other problems.

Conclusion

In this paper, we have organised the edge detection algorithms based on traditional learning and deep learning in detail, and have summarized the advantages and structure of each method. We also found that deep learning is more and more widely used in the field of edge detection; while improving the detection accuracy, it sacrifices the complexity of an algorithm, network, and training. Therefore, future developments of edge detection should pay more attention to the lightweight, mobility, and interpretability of the model. In addition, due to the time-consuming and high cost of manually labeling images, the edge detection model should also develop in the direction of weak supervision and no supervision. The future focus can be shown as follows:

1) Multi-scale fusion of information: Both high-level and low-level information are crucial components for an image itself. Therefore, reasonable fusion of multi-scale information of images can significantly improve the visualization and accuracy of edge detection. Parallel multi-branch fusion structure or serial jump connection fusion structure can be used.

2) Lightweight networks: In view of the current problems of complex model structures and training difficulties, we should further reduce the parameters and complexity of the models so that they can run adequately on a variety of devices and resources. Lightweight networks can be mainly divided into two major categories: Lightweight network structure design and model compression, while model compression can be specifically divided into quantization, pruning, distillation, low-rank decomposition, etc.

3) Explainability: Nowadays, most models are designed based on empirical judgment, and the designers cannot explain the specific principles, which also leads to some models having good or bad test results, and the uncertainty inside the network makes the deep learning models not widely and easily applied for better living. The interpretability of the model is to explain the specific reasons why the network is good through our theoretical knowledge and experimental reasoning, rather than just our subjective assumptions.

4) Weakly supervised and unsupervised: Due to the high cost of data labeling and the inability to obtain all truth data labels for many domain tasks, the use of weakly supervised or unsupervised learning becomes a good choice, which can achieve the desired goal by using a small number of data labels. The development of weakly supervised and unsupervised algorithms is important to reduce the cost of labeling and increase the flexibility of the network.

5) Video edge detection: With the development of unmanned vehicles, human pose estimation, etc., video segmentation is getting more and more attention. In all of these, edge contour is one of the most basic features of images, so for video real-time edge detection, more attention should also be paid to developing computationally more efficient algorithms on multiple types of devices.

Author Contributions

TL and RS contributed to conception and design of the study. RS wrote the first draft of the manuscript. QC, ZW, WZ, and AN contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported in part by Natural Science Basic Research Program of Shaanxi (Program No. 2021JC-47), in part by the National Natural Science Foundation of China under Grant 61871259, Grant 61861024, in part by Key Research and Development Program of Shaanxi (ProgramNo.2021ZDLGY08-07), in part by Shaanxi Joint Laboratory of Artificial Intelligence (Program No. 2020SS-03), in part by Serving Local Special Program of Education Department of Shaanxi Province (21JC002), and in part by Xi’an Science and Technology program (21XJZZ0006).

Conflict of Interest

Author WZ is employed by China Electronics Technology Group Corporation Northwest Group Corporation, Xi'an Branch, Xi'an, China.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Lei would like to thank Brunel University London for a visiting position in 2020 to collaborate with Nandi.

References

Aharon, M., Elad, M., and Bruckstein, A. (2006). $rm K$-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Trans. Signal. Process. 54 (11), 4311–4322. doi:10.1109/tsp.2006.881199

CrossRef Full Text | Google Scholar

Amer, G. M. H., and Abushaala, A. M. (2015). “Edge Detection Methods,” in 2015 2nd World Symposium on Web Applications and Networking (WSWAN) (IEEE), 1–7.

CrossRef Full Text | Google Scholar

Arbelaez, P., Maire, M., and Fowlkes, C. (2009). “From Contours to Regions: An Empirical Evaluation,” in 2009 IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2294–2301.

CrossRef Full Text | Google Scholar

Arbeláez, P., Maire, M., Fowlkes, C., and Malik, J. (2010). Contour Detection and Hierarchical Image Segmentation. IEEE Trans. Pattern Anal. Mach Intell. 33 (5), 898–916. doi:10.1109/TPAMI.2010.161

CrossRef Full Text | Google Scholar

Bertasius, G., Shi, J., and Torresani, L. (2015a). “Deepedge: A Multi-Scale Bifurcated Deep Network for Top-Down Contour Detection,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 4380–4389. doi:10.1109/cvpr.2015.7299067

CrossRef Full Text | Google Scholar

Bertasius, G., Shi, J., and Torresani, L. (2015b). “High-for-low and Low-For-High: Efficient Boundary Detection from Deep Object Features and its Applications to High-Level Vision,” in Proceedings of the IEEE International Conference on Computer Vision, 504–512. doi:10.1109/iccv.2015.65

CrossRef Full Text | Google Scholar

Canny, J. (1986). A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-8, 679–698. doi:10.1109/tpami.1986.4767851

CrossRef Full Text | Google Scholar

Chen, L. C., Papandreou, G., Kokkinos, I., Murphy, K., and Yuille, A. L. (2017). Deeplab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected Crfs. IEEE Trans. Pattern Anal. Mach Intell. 40 (4), 834–848. doi:10.1109/TPAMI.2017.2699184

PubMed Abstract | CrossRef Full Text | Google Scholar

Chollet, F. (2017). “Xception: Deep Learning with Depthwise Separable Convolutions,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 1251–1258. doi:10.1109/cvpr.2017.195

CrossRef Full Text | Google Scholar

Criminisi, A., Shotton, J., and Konukoglu, E. (2012). Decision Forests: A Unified Framework for Classification, Regression, Density Estimation, Manifold Learning and Semi-supervised Learning. Foundations Trends. Computer Graphics Vision. 7 (2–3), 81–227. doi:10.1561/0600000035

CrossRef Full Text | Google Scholar

Dai, J., Li, Y., and He, K. (2016). R-fcn: Object Detection via Region-Based Fully Convolutional Networks. Adv. Neural Inf. Process. Syst. 6, 379–387.

Google Scholar

Davis, L. S. (1975). A Survey of Edge Detection Techniques. Computer graphics image Process. 4 (3), 248–270. doi:10.1016/0146-664x(75)90012-x

CrossRef Full Text | Google Scholar

Deng, R., and Liu, S. (2020). “Deep Structural Contour Detection,” in Proceedings of the 28th ACM International Conference on Multimedia, 304–312.

CrossRef Full Text | Google Scholar

Deng, R., Shen, C., and Liu, S. (2018). “Learning to Predict Crisp Boundaries,” in Proceedings of the European Conference on Computer Vision (ECCV), 562–578. doi:10.1007/978-3-030-01231-1_35

CrossRef Full Text | Google Scholar

Dollár, P., and Zitnick, C. L. (2014). Fast Edge Detection Using Structured Forests. IEEE Trans. pattern Anal. machine intelligence. 37 (8), 1558–1570. doi:10.1109/TPAMI.2014.2377715

CrossRef Full Text | Google Scholar

Dollár, P., and Zitnick, C. L. (2013). Structured Forests for Fast Edge Detection. Proc. IEEE Int. Conf. Comput. Vis., 1841–1848. doi:10.1109/iccv.2013.231

CrossRef Full Text | Google Scholar

Duan, R. L., Li, Q. X., and Li, Y. H. (2005). Summary of Image Edge Detection. Opt. Tech. 3 (3), 415–419.

Google Scholar

Everingham, M., Eslami, S. M. A., Van Gool, L., Williams, C. K. I., Winn, J., and Zisserman, A. (2015). The Pascal Visual Object Classes challenge: A Retrospective. Int. J. Comput. Vis. 111 (1), 98–136. doi:10.1007/s11263-014-0733-5

CrossRef Full Text | Google Scholar

Fu, Y., Zeng, H., Ma, L., Ni, Z., Zhu, J., and Ma, K.-K. (2018). Screen Content Image Quality Assessment Using Multi-Scale Difference of Gaussian. IEEE Trans. Circuits Syst. Video Technol. 28 (9), 2428–2432. doi:10.1109/tcsvt.2018.2854176

CrossRef Full Text | Google Scholar

Ganin, Y., and Lempitsky, V. (2014). N^4-Fields: Neural Network Nearest Neighbor Fields for Image Transforms. Asian Conference on Computer Vision, 536–551. doi:10.1007/978-3-319-16808-1_36

CrossRef Full Text | Google Scholar

Gooch, B., Reinhard, E., and Gooch, A. (2004). Human Facial Illustrations. ACM Trans. Graph. 23 (1), 27–44. doi:10.1145/966131.966133

CrossRef Full Text | Google Scholar

Hallman, S., and Fowlkes, C. C. (2015). “Oriented Edge Forests for Boundary Detection,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 1732–1740. doi:10.1109/cvpr.2015.7298782

CrossRef Full Text | Google Scholar

He, J., Zhang, S., and Yang, M. (2019). “Bi-directional cascade Network for Perceptual Edge Detection,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 3828–3837. doi:10.1109/cvpr.2019.00395

CrossRef Full Text | Google Scholar

He, K., Zhang, X., and Ren, S. (2016). “Deep Residual Learning for Image Recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 770–778. doi:10.1109/cvpr.2016.90

CrossRef Full Text | Google Scholar

Howard, A. G., Zhu, M., and Chen, B. (2017). Mobilenets: Efficient Convolutional Neural Networks for mobile Vision Applications. arXiv preprint. arXiv:1704.04861.

Google Scholar

Kang, H., Lee, S., and Chui, C. K. (2007). Coherent Line Drawing. Proceedings of the 5th international symposium on Non-photorealistic animation and rendering, 43–50. doi:10.1145/1274871.1274878

CrossRef Full Text | Google Scholar

Kelm, A. P., Rao, V. S., and Zölzer, U. (2019). “Object Contour and Edge Detection with RefineContourNet,” in International Conference on Computer Analysis of Images and Patterns, 246–258. doi:10.1007/978-3-030-29888-3_20

CrossRef Full Text | Google Scholar

Kontschieder, P., Bulo, S. R., and Bischof, H. (2011). “Structured Class-Labels in Random Forests for Semantic Image Labelling,” in 2011 International Conference on Computer Vision (IEEE), 2190–2197.

CrossRef Full Text | Google Scholar

Kourtzi, Z., and Kanwisher, N. (2001). Representation of Perceived Object Shape by the Human Lateral Occipital Complex. Science 293 (5534), 1506–1509. doi:10.1126/science.1061133

PubMed Abstract | CrossRef Full Text | Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Imagenet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 25, 1097–1105.

Google Scholar

Kyprianidis, J. E., and Döllner, J. (2008). Image Abstraction by Structure Adaptive Filtering. TPCG, 51–58.

Google Scholar

Lee, C. Y., Xie, S., and Gallagher, P. (2015). Deeply-supervised Nets. Artif. intelligence Stat. PMLR 38, 562–570.

Google Scholar

Lim, J. J., Zitnick, C. L., and Dollár, P. (2013). “Sketch Tokens: A Learned Mid-level Representation for Contour and Object Detection,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 3158–3165. doi:10.1109/cvpr.2013.406

CrossRef Full Text | Google Scholar

Lin, G., Milan, A., and Shen, C. (2017). “Refinenet: Multi-Path Refinement Networks for High-Resolution Semantic Segmentation,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 1925–1934. doi:10.1109/cvpr.2017.549

CrossRef Full Text | Google Scholar

Liu, X., Song, M., and Tao, D. (2013). “Semi-supervised Node Splitting for Random forest Construction,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 492–499. doi:10.1109/cvpr.2013.70

CrossRef Full Text | Google Scholar

Liu, Y., Cheng, M. M., and Hu, X. (2017). “Richer Convolutional Features for Edge Detection,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 3000–3009.

CrossRef Full Text | Google Scholar

Liu, Y., and Lew, M. S. (2016). “Learning Relaxed Deep Supervision for Better Edge Detection,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 231–240. doi:10.1109/cvpr.2016.32

CrossRef Full Text | Google Scholar

Long, J., Shelhamer, E., and Darrell, T. (2015). “Fully Convolutional Networks for Semantic Segmentation,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 3431–3440. doi:10.1109/cvpr.2015.7298965

CrossRef Full Text | Google Scholar

Maini, R., and Aggarwal, H. (2009). Study and Comparison of Various Image Edge Detection Techniques. Int. J. image Process. (Ijip). 3 (1), 1–11.

Google Scholar

Maire, M., Stella, X. Y., and Perona, P. (2014). “Reconstructive Sparse Code Transfer for Contour Detection and Semantic Labeling,” in Asian Conference on Computer Vision (Springer, Cham), 273–287.

Google Scholar

Maninis, K.-K., Pont-Tuset, J., Arbeláez, P., and Van Gool, L. (2016). Convolutional Oriented Boundaries. Eur. Conf. Comput. Vis. 9905, 580–596. doi:10.1007/978-3-319-46448-0_35

CrossRef Full Text | Google Scholar

Marr, D., and Hildreth, E. (1980). Theory of Edge Detection. Proc. R. Soc. Lond. B Biol. Sci. 207 (1167), 187–217. doi:10.1098/rspb.1980.0020

PubMed Abstract | CrossRef Full Text | Google Scholar

Minka, T., and Gates, W. J. (2009). NIPS. Vancouver Canada.

Google Scholar

Mnih, V., Heess, N., and Graves, A. (2014). Recurrent Models of Visual Attention. Adv. Neural Inf. Process. Syst., 2204–2212.

Google Scholar

Mottaghi, R., Chen, X., and Liu, X. (2014). “The Role of Context for Object Detection and Semantic Segmentation in the Wild,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 891–898. doi:10.1109/cvpr.2014.119

CrossRef Full Text | Google Scholar

Noh, H., Hong, S., and Han, B. (2015). Learning Deconvolution Network for Semantic Segmentation. Proc. IEEE Int. Conf. Comput. Vis., 1520–1528. doi:10.1109/iccv.2015.178

CrossRef Full Text | Google Scholar

Oskoei, M. A., and Hu, H. (2010). A Survey on Edge Detection Methods. UK: University of Essex.

Google Scholar

Pati, Y. C., Rezaiifar, R., and Krishnaprasad, P. S. (1993). “Orthogonal Matching Pursuit: Recursive Function Approximation with Applications to Wavelet Decomposition,” in Proceedings of 27th Asilomar conference on signals, systems and computers. IEEE, 40–44.

Google Scholar

Pinheiro, P. O., Lin, T.-Y., Collobert, R., and Dollár, P. (2016). Learning to Refine Object Segments. Eur. Conf. Comput. Vis. 9905, 75–91. doi:10.1007/978-3-319-46448-0_5

CrossRef Full Text | Google Scholar

Poma, X. S., Riba, E., and Sappa, A. (2020). “Dense Extreme Inception Network: Towards a Robust Cnn Model for Edge Detection,” in Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, 1923–1932.

Google Scholar

Pont-Tuset, J., Arbelaez, P., T Barron, J., Marques, F., and Malik, J. (2016). Multiscale Combinatorial Grouping for Image Segmentation and Object Proposal Generation. IEEE Trans. Pattern Anal. Mach Intell. 39 (1), 128–140. doi:10.1109/TPAMI.2016.2537320

PubMed Abstract | CrossRef Full Text | Google Scholar

Pu, M., Huang, Y., and Guan, Q. (2021). RINDNet: Edge Detection for Discontinuity in Reflectance. Illumination, Normal Depth. Arxiv Preprint Arxiv. 00616, 2021.

Google Scholar

Qu, Z., Wang, S.-Y., Liu, L., and Zhou, D.-Y. (2019). Visual Cross-Image Fusion Using Deep Neural Networks for Image Edge Detection. IEEE Access 7, 57604–57615. doi:10.1109/access.2019.2914151

CrossRef Full Text | Google Scholar

Ren, X. (2008). Multi-scale Improves Boundary Detection in Natural Images. Eur. Conf. Comput. Vis., 533–545. doi:10.1007/978-3-540-88690-7_40

CrossRef Full Text | Google Scholar

Rong, W., Li, Z., Zhang, W., and Sun, L. (2014). “An Improved CANNY Edge Detection Algorithm,” in 2014 IEEE international conference on mechatronics and automation (IEEE), 577–582.

CrossRef Full Text | Google Scholar

Shechtman, E., and Irani, M. (2007). Matching Local Self-Similarities across Images and Videos. 2007 IEEE Conference on Computer Vision and Pattern Recognition. IEEE., 1–8.

Google Scholar

Shrivakshan, G. T., and Chandrasekar, C. (2012). A Comparison of Various Edge Detection Techniques Used in Image Processing. Int. J. Computer Sci. Issues (Ijcsi). 9 (5), 269.

Google Scholar

Silberman, N., Hoiem, D., Kohli, P., and Fergus, R. (2012). “Indoor Segmentation and Support Inference from RGBD Images,” in European conference on computer vision, 746–760. doi:10.1007/978-3-642-33715-4_54

CrossRef Full Text | Google Scholar

Simonyan, K., and Zisserman, A. (2014). Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv preprint. arXiv:1409.1556.

Google Scholar

Su, Z., Liu, W., and Yu, Z. (2021). Pixel Difference Networks for Efficient Edge Detection. arXiv preprint arXiv. 07009, 2021.

CrossRef Full Text | Google Scholar

Torre, V., and Poggio, T. A. (1986). On Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-8, 147–163. doi:10.1109/tpami.1986.4767769

PubMed Abstract | CrossRef Full Text | Google Scholar

Winnemöller, H. (2011). “Xdog: Advanced Image Stylization with Extended Difference-Of-Gaussians,” in Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Non-Photorealistic Animation and Rendering, 147–156.

Google Scholar

Winnemöller, H., Olsen, S. C., and Gooch, B. (2006). Real-time Video Abstraction. ACM Trans. Graph. 25 (3), 1221–1226. doi:10.1145/1141911.1142018

CrossRef Full Text | Google Scholar

Xiaofeng, R., and Bo, L. (2012). Discriminatively Trained Sparse Code Gradients for Contour Detection. Adv. Neural Inf. Process. Syst., 25.

Google Scholar

Xie, S., and Tu, Z. (2015). Holistically-nested Edge Detection. Proc. IEEE Int. Conf. Comput. Vis., 1395–1403. doi:10.1109/iccv.2015.164

CrossRef Full Text | Google Scholar

Xin Wang, X. (2007). Laplacian Operator-Based Edge Detectors. IEEE Trans. Pattern Anal. Mach. Intell. 29 (5), 886–890. doi:10.1109/tpami.2007.1027

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, D., Ouyang, W., and Alameda-Pineda, X. (2018). Learning Deep Structured Multi-Scale Features Using Attention-Gated Crfs for Contour Prediction. arXiv preprint arXiv. 1801.00524.

Google Scholar

Yang, J., Price, B., and Cohen, S. (2016). “Object Contour Detection with a Fully Convolutional Encoder-Decoder Network,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 193–202. doi:10.1109/cvpr.2016.28

CrossRef Full Text | Google Scholar

Yu, Z., Feng, C., and Liu, M. Y. (2017). “Casenet: Deep Category-Aware Semantic Edge Detection,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 5964–5973. doi:10.1109/cvpr.2017.191

CrossRef Full Text | Google Scholar

Yuille, A. L., and Poggio, T. A. (1986). Scaling Theorems for Zero Crossings. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-8, 15–25. doi:10.1109/tpami.1986.4767748

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Xing, F., Shi, X., and Yang, L. (2016). Semicontour: A Semi-supervised Learning Approach for Contour Detection. Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit 2016, 251–259. doi:10.1109/CVPR.2016.34

PubMed Abstract | CrossRef Full Text | Google Scholar

Ziou, D., and Tabbone, S. (1998). Edge Detection Techniques-An Overview. Pattern Recognition Image Anal. C/C Raspoznavaniye Obrazov Analiz Izobrazhenii. 8, 537–559.

Google Scholar