- Department of Information Engineering, University of Pisa, Pisa, Italy
In this article, we investigate the problem of jointly estimating target location and velocity for widely separated multiple-input multiple-output (MIMO) radar operating in correlated non-Gaussian clutter, modeled by a complex elliptically symmetric (CES) distribution. More specifically, we derive the Cramér–Rao lower bounds (CRLBs) when the target is modeled by the Swerling 0 model and the clutter is complex t-distributed. We thoroughly analyze the impact of the clutter correlation and spikiness to provide accurate performance estimation. Index terms—Cramér–Rao lower bounds (CRLBs), MIMO radar, location and velocity estimation, performance analysis, complex elliptically symmetric (CES) distributed, and complex t-distribution.
1 Introduction
Multiple-input multiple-output (MIMO) radars have attracted increasing attention in recent years, as proved by the many published articles (see, for instance, Fishler et al., 2004; Li and Stoica, 2008; Davis, 2015). MIMO radars can be classified as coherent or noncoherent (He et al., 2010a; Derham et al., 2010), and colocated (Li and Stoica, 2007) or widely distributed (Haimovich et al., 2007).
Estimating target parameters in MIMO radars is one of the far-reaching research topics; hence, various research studies have considered different scenarios, with different antenna deployment (Fishler et al., 2006; Li and Stoica, 2009), target models (in motion or static target) (Hassanien et al., 2012), and various estimation algorithms (Stoica and Nehorai, 1990; Tajer et al., 2010; Min et al., 2011). The Cramér–Rao lower bound (CRLB) is a well-known tool for evaluating target parameter estimation performance in clutter. In Godrich et al., (2008a), Godrich et al., (2010), the CRLBs were derived for target localization in noncoherent and coherent MIMO radars. The CRLB for target velocity was presented in He et al., (2010b), while the CRLB for joint estimation of target location and velocity in case of noncoherent MIMO radars was derived in He et al., (2010a). In Godrich et al., (2008b), He et al., (2008), CRLBs were derived for MIMO radars with widely separated antennas.
In all the cited articles, the clutter is modeled as a Gaussian stochastic process, white or colored. Such assumption is a good approximation in many cases, but not always, particularly when the clutter is very spiky, for e.g., in high resolution radars (Brekke et al., 2010). In MIMO radars, sometime the clutter has been modeled as a non-Gaussian process by the compound-Gaussian (CG) (Farina et al., 1997; Gini, 1998; Gini and Greco, 1999; Sangston et al., 1999; Sangston et al., 2012) or the complex elliptically symmetric (CES) distributions (Ollila et al., 2012; Fortunati et al., 2019) that include a wide variety of distributions such as complex normal (CN) (Goodman, 1963), complex generalized Gaussian (Novey et al., 2009), complex-t
The novel contribution of this article is to derive the CRLBs on the estimation of location and velocity under the assumption that the non-Gaussian correlated clutter is modeled by a
This article is organized as follows: the data model is described in Section 2. In Section 3, the general CES model and the complex t-distribution are summarized. In Section 4, we derive the analytical expression of the CRLBs for the estimation of target location and velocity, and some numerical results are reported in Section 5 to investigate the theoretical findings.
2 Data Model
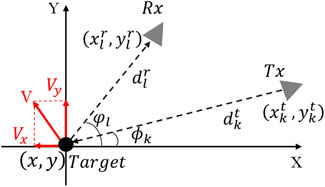
Consider a coherent MIMO radar with M transmit (TX) and N receive (RX) antennas, widely dispersed in a 2-D plane as shown in Figure 1. In order to simplify the CRLB derivation of target location and velocity, we assume an isotropic target whose unknown complex amplitude is ζ = ζR + jζI. The unknown target location is (x, y), and the unknown target velocity is (vx, vy). The known locations of the M transmitters are
The echo at the lth receiver from the transmission of all the M transmitters and reflected from the target, after down-conversion and sampling, is
where ζ is the target complex reflectivity (unknown and deterministic), f0 is the carrier frequency (carrier frequencies of all transmitters are assumed to be identical), Ts is the sampling time (chosen to satisfy the Nyquist criterion), and Ns is the number of samples in the observation period,
τlk represents the time delay of a signal given by
where
flk is the target Doppler frequency shift given by
where λ indicates the wavelength of the carrier frequency.
In our derivation, we assume that the transmitted signals are orthogonal (Peilin Sun et al., 2014). Furthermore, they retain approximately orthogonality, even after a variety of allowed time delays and Doppler frequency shifts, that is,
The orthogonality as given in Eq. 4 is clearly a strong condition if applied to all possible delays and Doppler frequencies. Despite this, for reasonable values of Doppler frequencies and the set of target and radar parameters of this work, we verified that the cross-ambiguity functions are negligible compared to the auto-ambiguity functions; thus, the orthogonal condition can be considered approximately met.
Finally, the Ns-dimensional observation vector at the lth receiver can be expressed as
3 Complex Elliptically Symmetric Distribution
Complex elliptically symmetric (CES) distributions are commonly used to model non-Gaussian heavy-tailed radar clutter (Zhang et al., 2014; Fortunati et al., 2018; Fortunati et al., 2019; Raninen et al., 2021). The m-variate random vector (r.v)
where
Then, the clutter can be represented in short notation by
3.1 t-Distributed Clutter
A particular case of CES-distributions is the
For a complex t-distribution of dimension m, the generating function is given by
and
Here, we investigate two different scenarios for the clutter. Model I: the clutter samples are uncorrelated in space and time. Model II: the clutter samples are temporally uncorrelated but spatially correlated. The mean value is 0, that is, μ = 0.
4 The Joint Cramér–Rao Lower Bound
The CRLB provides a lower bound of the variance of any unbiased estimator of unknown deterministic parameters. Given ψ = [x, y, vx, vy, ζR, ζI] as the vector of all the unknown parameters in the received signal, we derive the CRLBs for the MIMO radar. Since we assume here that the target has already been detected and we want to estimate target range and velocity, we consider the target reflectivity, ζR and ζI, as nuisance parameters (Gini and Reggiannini, 2000; Fortunati et al., 2010), then we derive the CRLBs of the unknown vector βp×1 = [x, y, vx, vy], p = 4.
4.1 CRLB for Target Range and Velocity
In order to derive the CRLB of target location and velocity, the first step is to calculate the Fisher information matrix (FIM) and then to invert it, CRLB(ψ) = [J(ψ)]−1.
The FIM matrix is defined as
where E{.} indicates the expectation operator, ln p(r; ψ) is the log-likelihood (LL) function, and r is the data vector. The FIM is a p × p symmetric positive semi-definite matrix after deleting the rows and columns of the nuisance parameter.
Since (1) is a function of time delay and Doppler frequency shift, we introduce the (2 + NM)-dimensional parameter vector
where
where 0 and I are the zero and identity matrices, respectively, while U is given by
The details on the derivation of the elements of U are in He et al. (2010a). J(Θ) is the Jacobian matrix such that
Matrix J(Θ), computed as in Eq. 12, can be divided into four submatrices as follows:
where
By exploiting the chain rule for Eq. 9, the FIM of ψ is given by
Eventually, since our aim is to calculate the CRLBs of the vector β, we get it as (He et al., 2008)
where the diagonal elements of the CRLB matrix represent the lower bound of the variances of the parameters of interest.
1) CRLB for Clutter Model I: If the clutter is independent in both the time and space domains, then the clutter samples zl[n] (l = 1, … , N n = 1, … , Ns) are IID.
In this case, the log-likelihood function is given by
where C is a generic constant that does not depend on the parameters of interest, and the pdf of each sample rl[n] is given by
where
Each element of the Jacobian matrix is
yielding
Note that, in computing the derivatives of the LL function with respect to the parameters in Eq. 18, we consider the orthogonality conditions in Eq. 4, and then the generic element of Eq. 18 is calculated with the derivative expressions as follows:
where the aforementioned equations represent the first and second derivatives with respect to (w.r.t.) the Doppler frequency. The derivatives w.r.t. time delay and target complex reflectivity are as follows:
The second cross-derivatives w.r.t. Doppler frequency, time delay, and target complex reflectivity are
Note that δ(l − p) = 1 for l = p and 0 elsewhere, and
2) CRLB for Clutter Model II: In this case, the clutter is correlated in the space domain and independent in the time domain, meaning that the Ns clutter vectors
where the
The pdf of the observation vector is given by
where
where ηp,q is the inverse of scatter matrix,
Subsequently, the log-likelihood function is given by
where C is a generic constant, and each element of the Jacobian matrix is
Afterward, the generic element of Eq. 35 is derived using the derivative expressions as follows
The aforementioned equations represent the first and second derivatives w.r.t. Doppler frequency. Next, the derivatives w.r.t. time delay are given as follows:
Furthermore, the derivatives w.r.t. target complex reflectivity are as follows:
Also, these are the cross-derivatives of unknown parameters, for the clutter model II.
The details about derivations are reported in the Supplementary Appendix under Clutter Model II.
5 Numerical Analysis
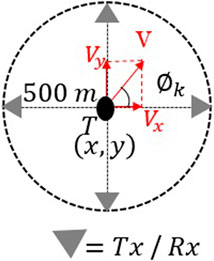
In the following, we investigate the estimation for the circular MIMO radar shown in Figure 2. A M × N = 4 × 4 MIMO radar is considered whose antenna orientations are
Moreover, the carrier frequency is f0 = 10 GHz, the sampling frequency is fS = 9 MHz, the pulse duration is Tp = 0.56 ms, and the observation time is Tobs = 2.2 ms. The received waveforms are
The clutter samples are IID and t-distributed, then
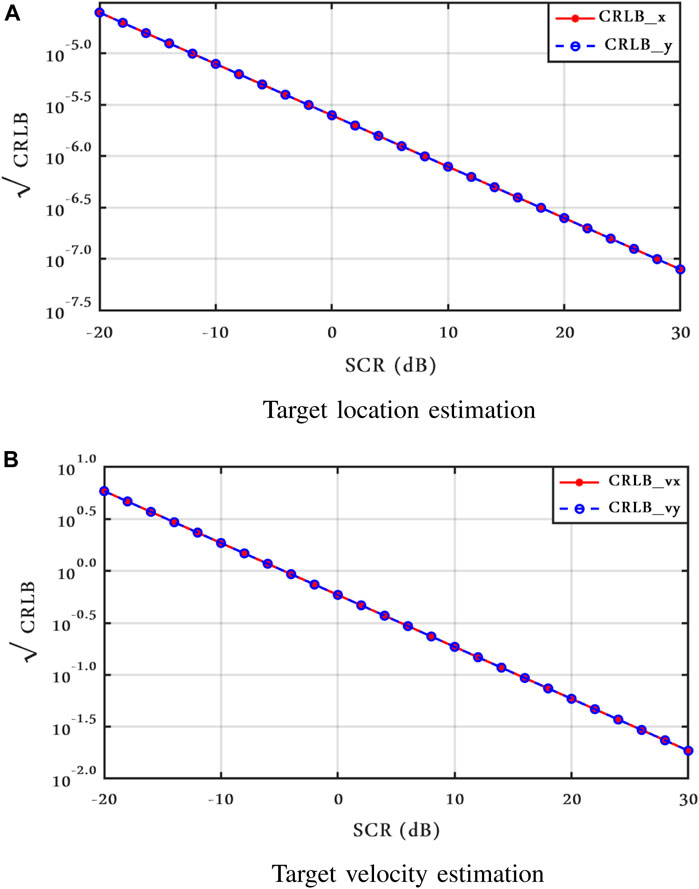
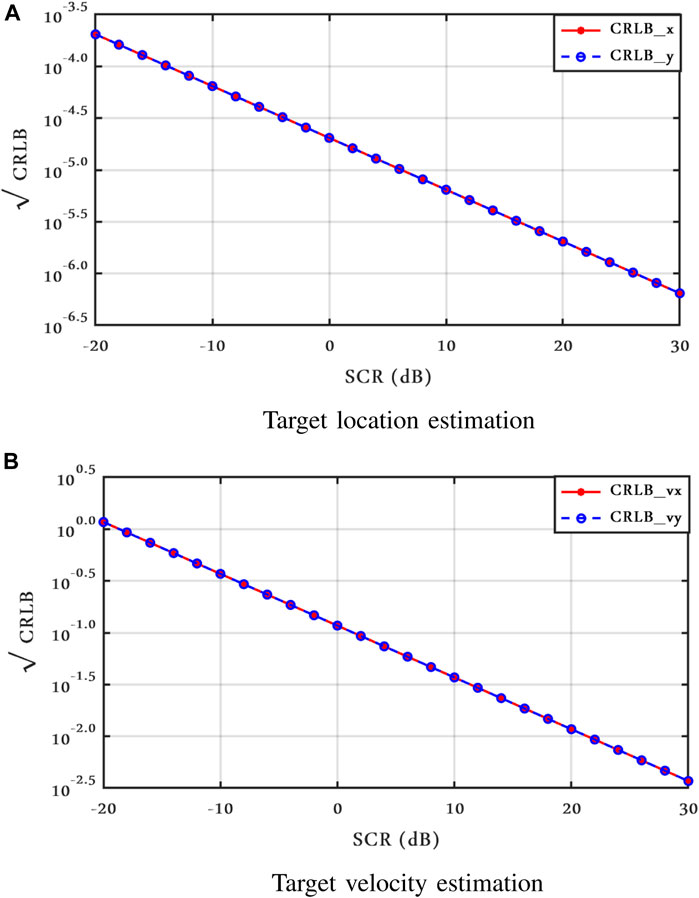
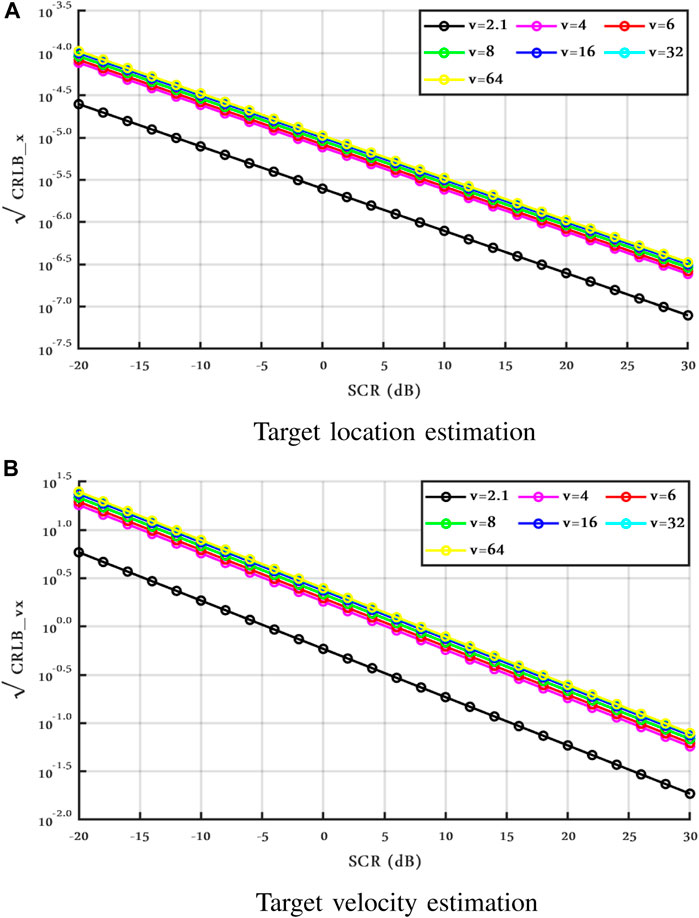
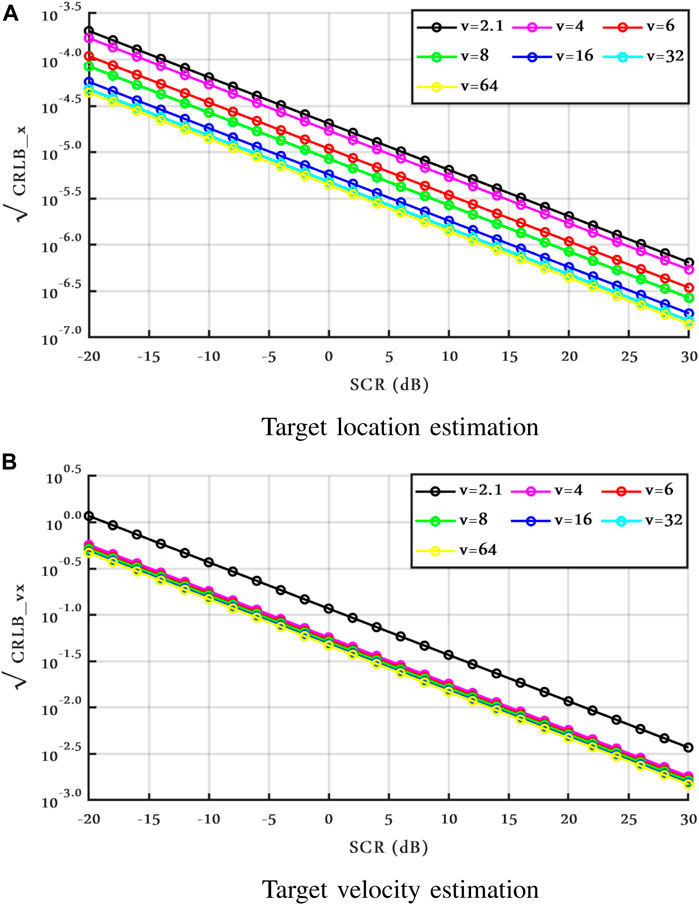
Following this, we chose the spikier clutter case ν = 2.1. Figures 3 and 4 show the range and Doppler frequency CRLBs of the spikier clutter case for both models I and II, respectively. In addition, we set σ2 = 1, and the CRLBs in Figure 4 are shown for spatially correlated clutter.
Considering (Zhang et al., 2014) the spatially correlated clutter is such that
where ρ is a constant value and we chose ρ = 0.9, and Δαp,q is the angular distance from the pth receiver to clutter cell and from clutter to the qth receiver.
In the following figures, the joint CRLBs of target location and velocity for different values ν are presented for both clutter cases. We only show CRLBx and CRLBvx, since we set the same numerical values for x and y as well as for vx and vy; therefore, the CRLBs along the two directions, in this case, are the same.
According to Figure 5, a larger value of ν leads to an increase of the CRLBs in clutter case I. It is worth noting that the clutter power depends on both the scale parameter σ2 and the shape parameter ν. In these figures, σ2 = 1, then to keep constant the SCR for different values of ν, the energy of the transmitted signals is changed accordingly.
In Figure 6, we plot the CRLBs for the correlated clutter (Model II). In this case, the CRLB tends to increase for lower ν. It is apparent, anyway, that the differences in both models I and II are small with varying values of ν, at least in the tested configuration.
To get a better look at the impact of the parameter ν on the target parameter estimation, under both Model I and Model II, Table 1 provides the CRLBs corresponding to x and vx at SCR = 0 dB with different values of ν. CRLBs of y and vy behave quite similarly.
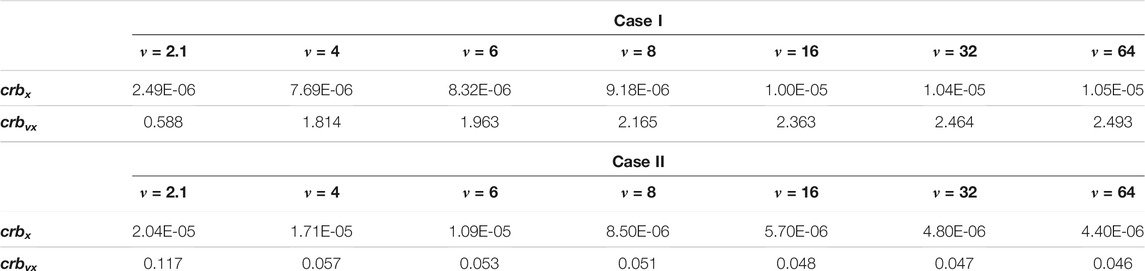
TABLE 1. CRLBs of x and vx in clutter Model I and Model II with different values of ν, SCR = 0 dB, and ρ = 0.9.
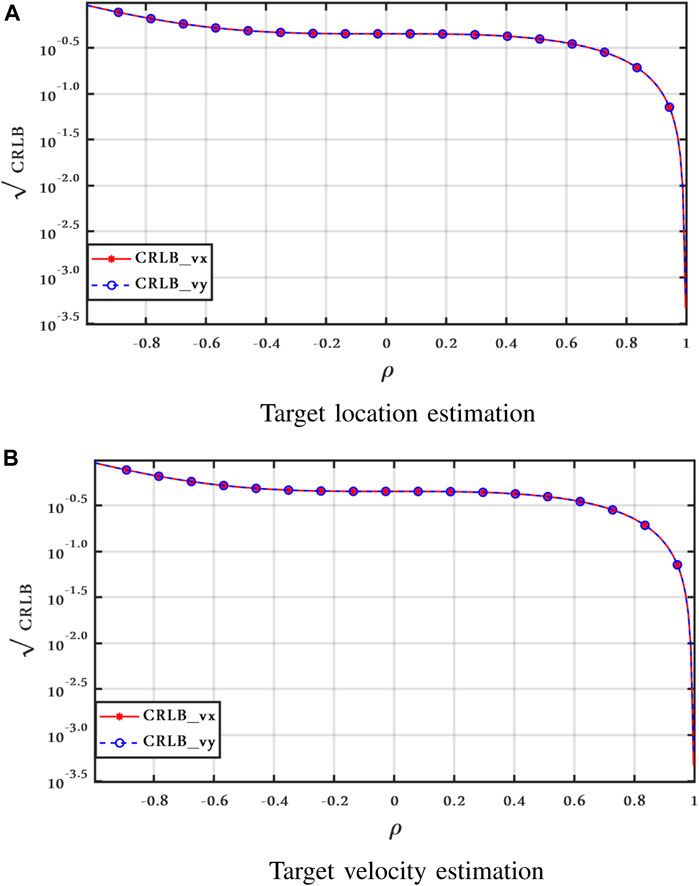
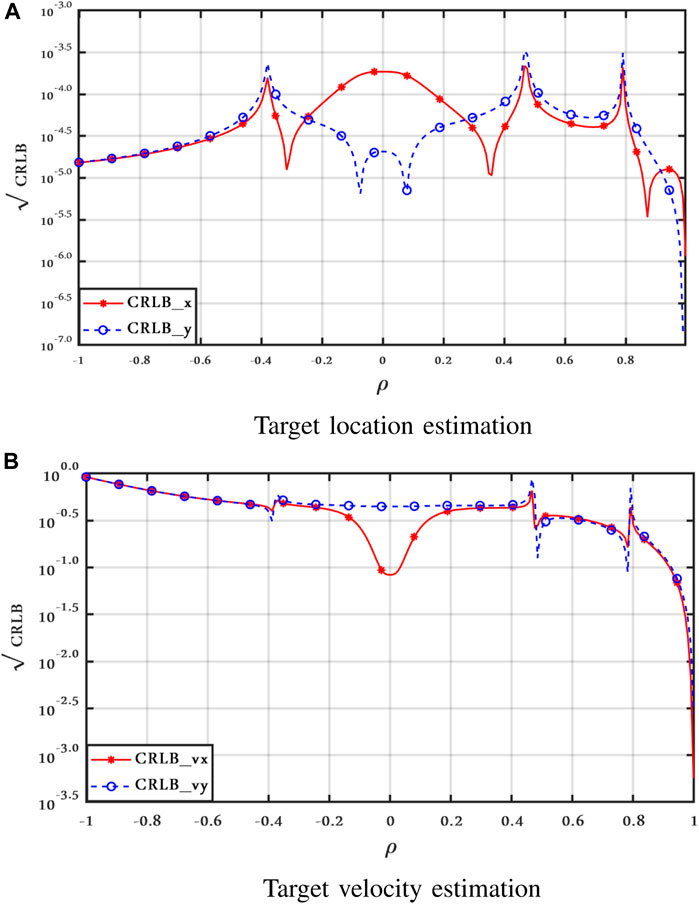
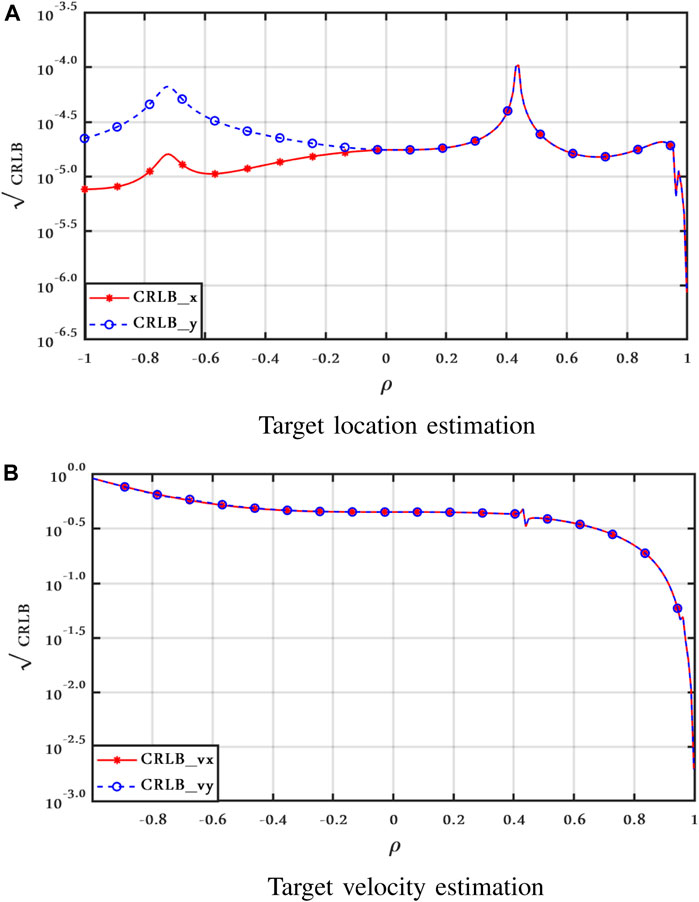
Next, in order to investigate the effect of the correlation coefficient ρ in clutter Model II, Figures 7–9 show the CRLBs as a function of ρ for ν = 2.1 and SCR = 0 dB when the target is still, moving with
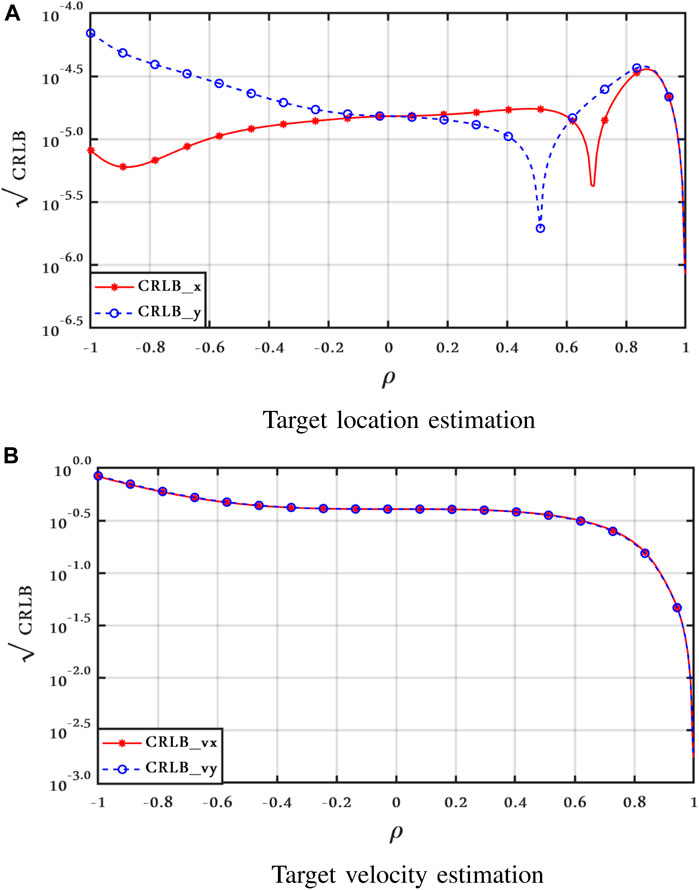
FIGURE 10. CRLBs vs. ρ, Clutter Model II for 45° shifted TX/RX antennas with ν = 2.1, SCR = 0 dB, and vx = vy = 50 m/s.
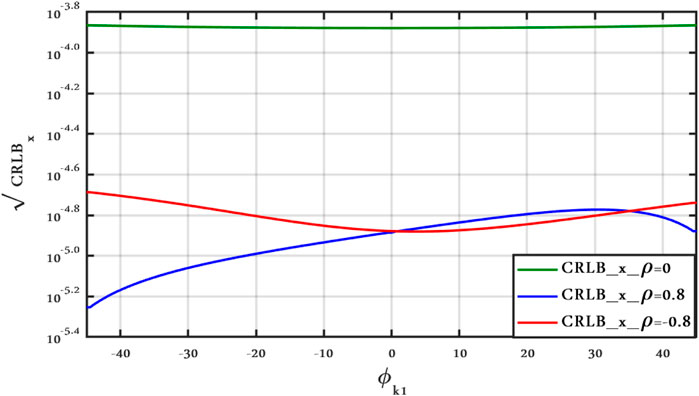
FIGURE 11. CRLBx vs. ϕk1 antenna position, Clutter Model II for different ρ with ν = 2.1, SCR = 0 dB, and vx = vy = 50 m/s.
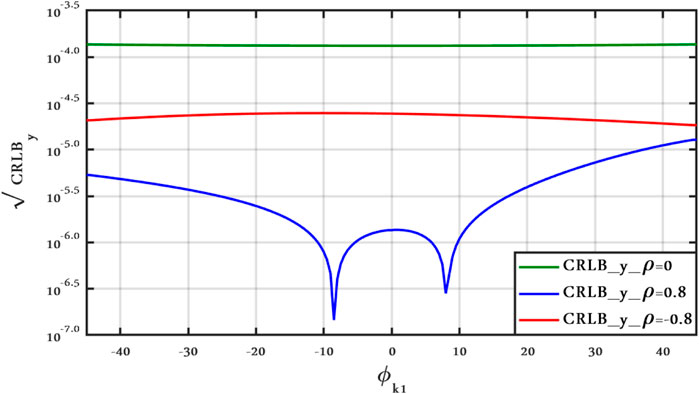
FIGURE 12. CRLBy vs. ϕk1 antenna position, Clutter Model II for different ρ with ν = 2.1, SCR = 0 dB, and vx = vy = 50 m/s.
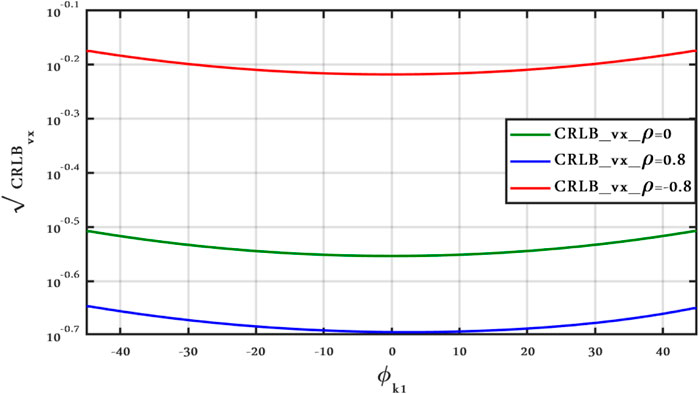
FIGURE 13. CRLBvx vs. ϕk1 antenna position, Clutter Model II for different ρ with ν = 2.1, SCR = 0 dB, and vx = vy = 50 m/s.
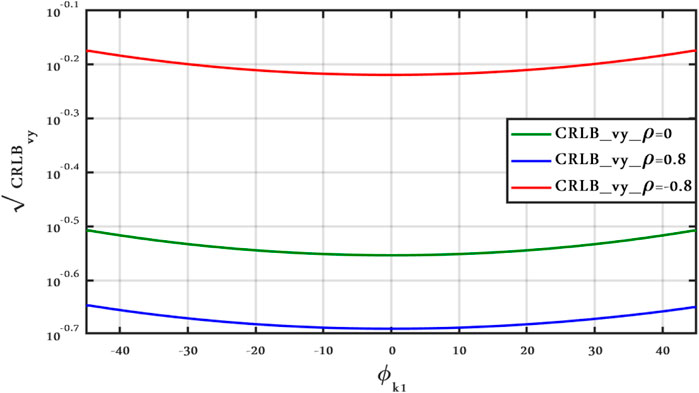
FIGURE 14. CRLBvy vs. ϕk1 antenna position, Clutter Model II for different ρ with ν = 2.1, SCR = 0 dB, and vx = vy = 50 m/s.
In Figures 15 and 16, the relation between the bounds and the number of antennas is shown, when the target is located in (0,0). These figures show the effect of increasing the number of sensors in two different scenarios: 1) the radius of the circle is constant,
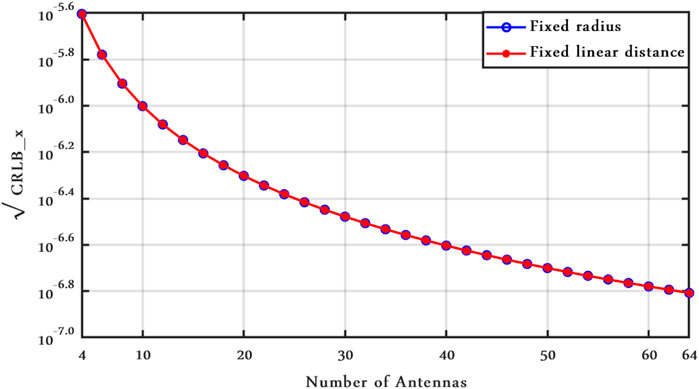
FIGURE 15. CRLBx vs. number of antenna, Clutter Model I with ν = 2.1, SCR = 0 dB, and vx = vy = 50 m/s.
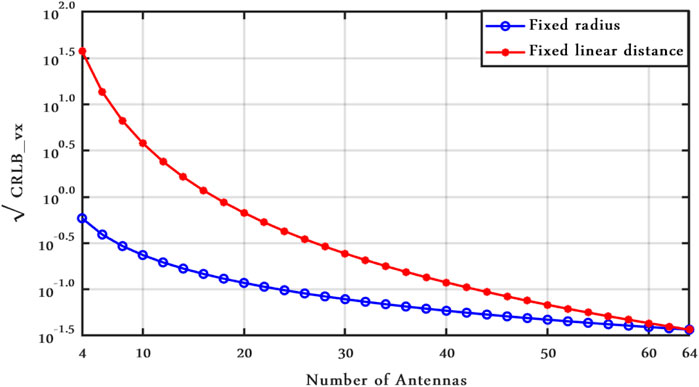
FIGURE 16. CRLBvx vs. number of antenna, Clutter Model I with ν = 2.1, SCR = 0 dB, and vx = vy = 50 m/s.
Additionally, to assess the maximum achievable accuracy of the considered MIMO radar over the area of interest, we define the errors (Maddio et al., 2015; Passafiume et al., 2017; Cidronali et al., 2020) as
Figures 17 and 18 illustrate the maximum achievable accuracy (or the error pattern over the area) attained by Eq. 50, in terms of CRLBs in both the clutter models I and II for varying positions with vx = vy = 50 m/s, while Figures 19 and 20 show the maximum achievable accuracy for a fixed target. These figures are all calculated for SCR = −15 dB and ν = 2.1.
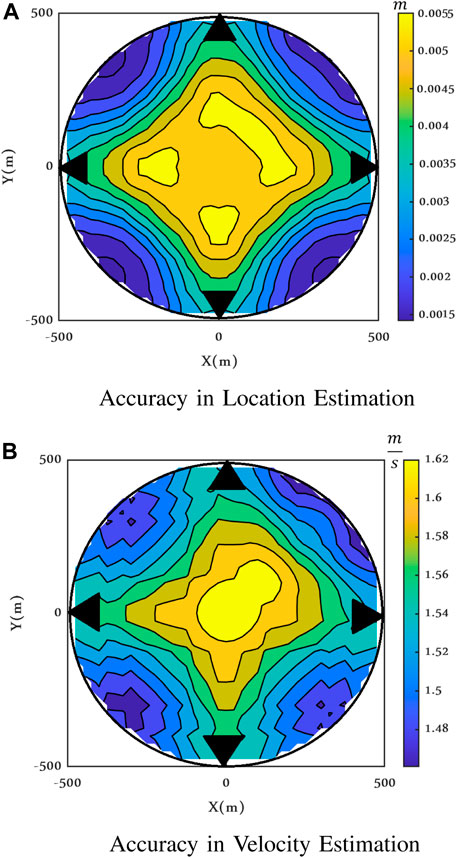
FIGURE 17. Maximum achievable accuracy when the target is moving, Clutter Model I, ν = 2.1 and SCR = −15 dB.
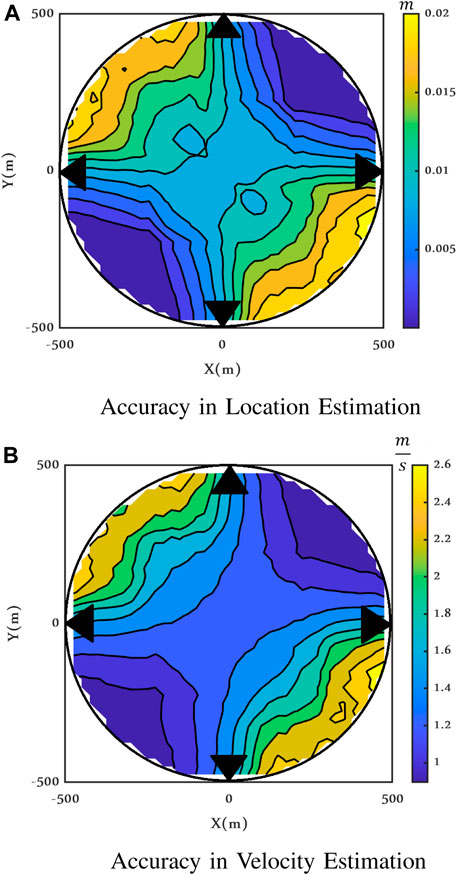
FIGURE 18. Maximum achievable accuracy when the target is moving, Clutter Model II, ρ = 0.9, ν = 2.1, and SCR = −15 dB.
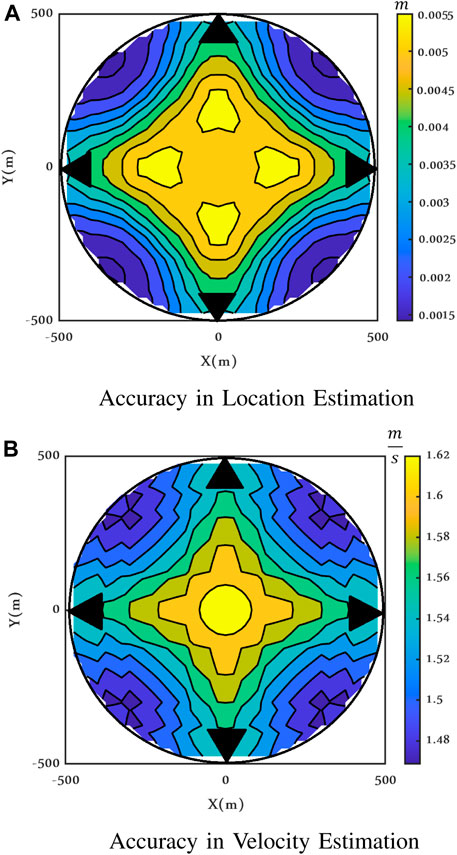
FIGURE 19. Maximum achievable accuracy when the target is still, Clutter Model I, ν = 2.1 and SCR = −15 dB.
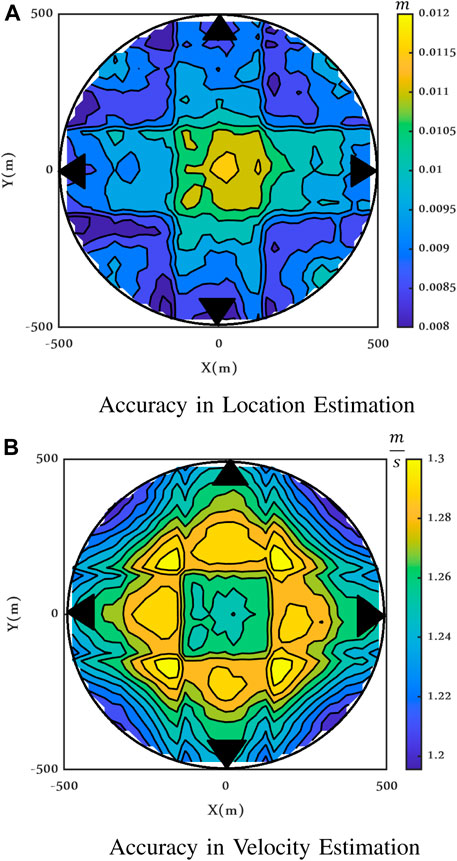
FIGURE 20. Maximum achievable accuracy when the target is still, Clutter Model II, ρ = 0.9, ν = 2.1, and SCR = −15 dB.
Depending on the value of the target velocity along the x and y directions and on the clutter correlation, the shape of the error functioning inside the circle is different, but the range of variations in the considered area is always small, for both range and velocity, for both clutter models I and II.
To check the changes in the CRLBs as a function of the correlation coefficient ρ, in Figure 21, the maximum achievable accuracy is shown for the same scenario described in Figure 18 but for ρ = 0. It is worth observing that ρ = 0 does not mean that the clutter components are independent but only uncorrelated because they are not Gaussian-distributed.
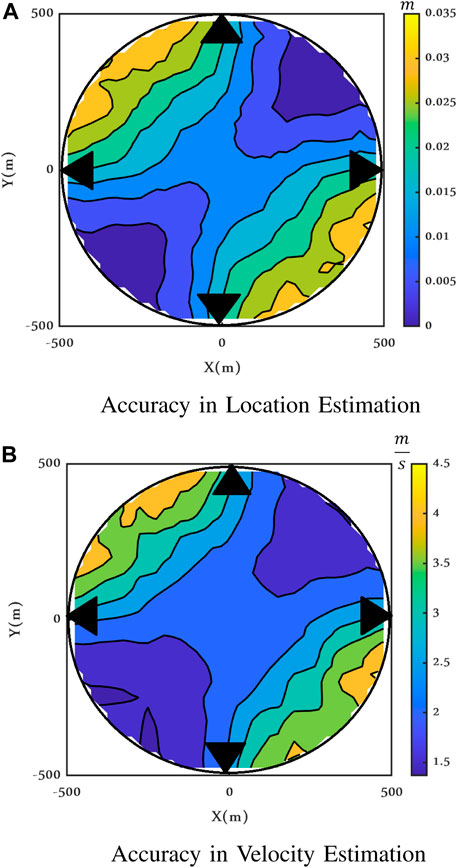
FIGURE 21. Maximum achievable accuracy when the target is moving, Clutter Model II, ρ = 0, ν = 2.1, and SCR = −15 dB.
Finally, to investigate the impact of the position of the transmitters and receivers on the performance of the radar, the error function is shown for a different configuration in Figures 22 and 23, where the receiver antennas are shifted of 45° with respect to the receiver; transmitters and receivers are represented by black and red triangles, respectively. As evident in Figures 22 and 23, configurations with shifted receiver antennas are similar to those of colocated antennas in Figures 17 and 18. The CRLBs are much more affected by the presence of the clutter correlation.
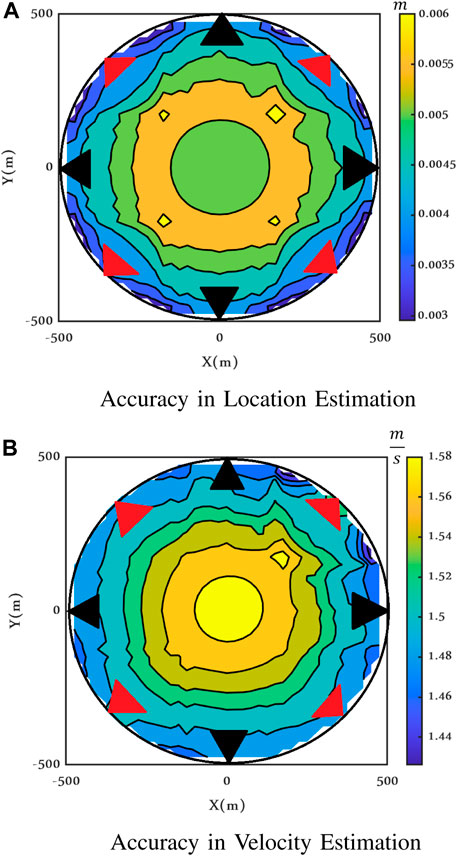
FIGURE 22. Maximum achievable accuracy for shifted receiver antennas when the target is moving, Clutter Model I, ν = 2.1 and SCR = −15 dB.
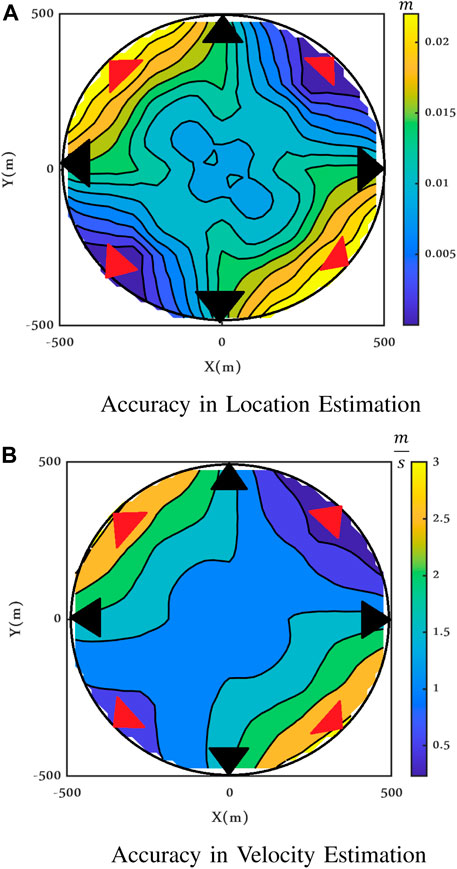
FIGURE 23. Maximum achievable accuracy for shifted receiver antennas when the target is moving, Clutter Model II, ρ = 0, ν = 2.1, and SCR = −15 dB.
6 Conclusion
This article presents the derivation of the CRLBs for the estimation of position and velocity of an isotropic target in a coherent MIMO radar with orthogonally transmitted waveforms in the presence of correlated non-Gaussian clutter, modeled by the complex t-distribution. We derived the CRLBs for two different scenarios: 1) the clutter samples are independent in space and time and 2) the clutter samples are temporally independent but spatially correlated. We then investigated the estimation accuracy as a function of the SCR, the clutter spikiness, and the clutter spatial correlation as well as maximum achievable accuracy in parameter estimation for several radar configurations. The CRLBs show a weak dependency on the spikiness of the clutter but, conversely, a strong dependency on the angular correlation, particularly for the moving target.
Author Disclaimer
The views and conclusions contained are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the Air Force Office of Scientific Research or the United States government.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
The work of MG and FG has been partially supported by the Italian Ministry of Education and Research (MIUR) in the framework of the CrossLab Project (Departments of Excellence) of the University of Pisa, Laboratory of Industrial Internet of Things (IIoT). This work has been partially funded also by EOARD/AFRL grant FA9550-17-1-0344 on “Exploiting Spatial Diversity in MIMO and Massive MIMO Radar Systems.”
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsip.2022.822285/full#supplementary-material
References
Brekke, E., Hallingstad, O., and Glattetre, J. (2010). Tracking Small Targets in Heavy-Tailed Clutter Using Amplitude Information. IEEE J. Oceanic Eng. 35 (2), 314–329. doi:10.1109/joe.2010.2044670
Cidronali, A., Collodi, G., Lucarelli, M., Maddio, S., Passafiume, M., and Pelosi, G. (2020). Assessment of Anchors Constellation Features in Rssi-Based Indoor Positioning Systems for Smart Environments. Electronics 9 (6), 1026. doi:10.3390/electronics9061026
Davis, M. S. (2015). Mimo Radar: Signal Processing, Waveform Design, and Applications to Synthetic Aperture Imaging. Ph.D. dissertation (Atlanta, GA, USA: Georgia Institute of Technology).
Derham, T., Doughty, S., Baker, C., and Woodbridge, K. (2010). Ambiguity Functions for Spatially Coherent and Incoherent Multistatic Radar. IEEE Trans. Aerosp. Electron. Syst. 46 (1), 230–245. doi:10.1109/taes.2010.5417159
Farina, A., Gini, F., Greco, M. V., and Verrazzani, L. (1997). High Resolution Sea Clutter Data: Statistical Analysis of Recorded Live Data. IEE Proc. Radar Sonar Navig. 144 (3), 121–130. doi:10.1049/ip-rsn:19971107
Fishler, E., Haimovich, A., Blum, R., Chizhik, D., Cimini, L., and Valenzuela, R. (2004). “Mimo Radar: An Idea Whose Time Has Come,” in Proceedings of the 2004 IEEE Radar Conference (IEEE Cat. No. 04CH37509) (Philadelphia, PA, USA: IEEE), 71–78.
Fishler, E., Haimovich, A., Blum, R. S., Cimini, L. J., Chizhik, D., and Valenzuela, R. A. (2006). Spatial Diversity in Radars-Models and Detection Performance. IEEE Trans. Signal. Process. 54 (3), 823–838. doi:10.1109/tsp.2005.862813
Fortunati, S., Farina, A., Gini, F., Graziano, A., Greco, M. S., and Giompapa, S. (2010). Least Squares Estimation and Cramér-Rao Type Lower Bounds for Relative Sensor Registration Process. IEEE Trans. Signal Process. 59 (3), 1075–1087.
Fortunati, S., Gini, F., Greco, M. S., Zoubir, A. M., and Rangaswamy, M. (2019). Semiparametric Crb and Slepian-Bangs Formulas for Complex Elliptically Symmetric Distributions. IEEE Trans. Signal. Process. 67 (20), 5352–5364. doi:10.1109/tsp.2019.2939084
Fortunati, S., Gini, F., Greco, M. S., Zoubir, A. M., and Rangaswamy, M. (2018). Semiparametric Inference and Lower Bounds for Real Elliptically Symmetric Distributions. IEEE Trans. Signal Process. 67 (1), 164–177.
Gini, F. (1998). A Radar Application of a Modified Cramer-Rao Bound: Parameter Estimation in Non-gaussian Clutter. IEEE Trans. Signal. Process. 46 (7), 1945–1953. doi:10.1109/78.700966
Gini, F., and Greco, M. V. (1999). Suboptimum Approach to Adaptive Coherent Radar Detection in Compound-Gaussian Clutter. IEEE Trans. Aerosp. Electron. Syst. 35 (3), 1095–1104. doi:10.1109/7.784077
Gini, F., and Reggiannini, R. (2000). On the Use of Cramer-rao-like Bounds in the Presence of Random Nuisance Parameters. IEEE Trans. Commun. 48 (12), 2120–2126. doi:10.1109/26.891222
Godrich, H., Haimovich, A. M., and Blum, R. S. (2008). “Cramer Rao Bound on Target Localization Estimation in Mimo Radar Systems,” in 2008 42nd Annual Conference on Information Sciences and Systems (Princeton, NJ, USA: IEEE), 134–139. doi:10.1109/ciss.2008.4558509
Godrich, H., Haimovich, A. M., and Blum, R. S. (2008). “Target Localization Accuracy and Multiple Target Localization: Tradeoff in Mimo Radars,” in 2008 42nd Asilomar Conference on Signals, Systems and Computers (Pacific Grove, CA, USA: IEEE), 614–618. doi:10.1109/acssc.2008.5074479
Godrich, H., Haimovich, A. M., and Blum, R. S. (2010). Target Localization Accuracy Gain in Mimo Radar-Based Systems. IEEE Trans. Inform. Theor. 56 (6), 2783–2803. doi:10.1109/tit.2010.2046246
Goodman, N. R. (1963). Statistical Analysis Based on a Certain Multivariate Complex Gaussian Distribution (An Introduction). Ann. Math. Statist. 34 (1), 152–177. doi:10.1214/aoms/1177704250
Haimovich, A. M., Blum, R. S., and Cimini, L. J. (2007). Mimo Radar with Widely Separated Antennas. IEEE Signal. Process. Mag. 25 (1), 116–129.
Hassanien, A., Vorobyov, S. A., and Gershman, A. B. (2012). Moving Target Parameters Estimation in Noncoherent Mimo Radar Systems. IEEE Trans. Signal. Process. 60 (5), 2354–2361. doi:10.1109/tsp.2012.2187290
He, Q., Blum, R. S., Godrich, H., and Haimovich, A. M. (2008). “Cramer-rao Bound for Target Velocity Estimation in Mimo Radar with Widely Separated Antennas,” in 2008 42nd Annual Conference on Information Sciences and Systems (Princeton, NJ, USA: IEEE), 123–127. doi:10.1109/ciss.2008.4558507
He, Q., Blum, R. S., Godrich, H., and Haimovich, A. M. (2010). Target Velocity Estimation and Antenna Placement for Mimo Radar with Widely Separated Antennas. IEEE J. Sel. Top. Signal. Process. 4 (1), 79–100. doi:10.1109/jstsp.2009.2038974
He, Q., Blum, R. S., and Haimovich, A. M. (2010). Noncoherent Mimo Radar for Location and Velocity Estimation: More Antennas Means Better Performance. IEEE Trans. Signal. Process. 58 (7), 3661–3680. doi:10.1109/tsp.2010.2044613
Krishnaiah, P. R., and Lin, J. (1986). Complex Elliptically Symmetric Distributions. Commun. Stat. - Theor. Methods 15 (12), 3693–3718. doi:10.1080/03610928608829341
Li, J., and Stoica, P. (2009). Concepts and Applications of a Mimo Radar System with Widely Separated Antennas. Hoboken, NJ, USA: Wiley-IEEE Press.
Li, J., and Stoica, P. (2007). Mimo Radar with Colocated Antennas. IEEE Signal. Process. Mag. 24 (5), 106–114. doi:10.1109/msp.2007.904812
Maddio, S., Passafiume, M., Cidronali, A., and Manes, G. (2015). “A Distributed Positioning System Based on Real-Time Rssi Enabling Decimetric Precision in Unmodified Ieee 802.11 Networks,” in 2015 IEEE MTT-S International Microwave Symposium (Phoenix, AZ, USA: IEEE), 1–4. doi:10.1109/mwsym.2015.7166926
Min, J., Niu, R., and Blum, R. (2011). Bayesian Target Location and Velocity Estimation for Multiple-Input Multiple-Output Radar [j]. IET Radar, Sensor and Navigation 5 (6), 666–670.
Novey, M., Adali, T., and Roy, A. (2009). A Complex Generalized Gaussian Distributionâcharacterization, Generation, and Estimation. IEEE Trans. Signal Process. 58 (3), 1427–1433.
Ollila, E., Tyler, D. E., Koivunen, V., and Poor, H. V. (2012). Complex Elliptically Symmetric Distributions: Survey, New Results and Applications. IEEE Trans. Signal. Process. 60 (11), 5597–5625. doi:10.1109/tsp.2012.2212433
Passafiume, M., Maddio, S., and Cidronali, A. (2017). An Improved Approach for RSSI-Based Only Calibration-free Real-Time Indoor Localization on IEEE 802.11 and 802.15.4 Wireless Networks. Sensors 17 (4), 717. doi:10.3390/s17040717
Peilin Sun, P., Tang, J., and Shuang Wan, S. (2014). Cramer-rao Bound of Joint Estimation of Target Location and Velocity for Coherent Mimo Radar. J. Syst. Eng. Electron. 25 (4), 566–572. doi:10.1109/jsee.2014.00066
Raninen, E., Ollila, E., and Tyler, D. (2021). On the Variability of the Sample Covariance Matrix under Complex Elliptical Distributions. IEEE Signal. Process. Lett. 28, 2092–2096. doi:10.1109/lsp.2021.3117443
Sangston, K. J., Gini, F., and Greco, M. S. (2012). Coherent Radar Target Detection in Heavy-Tailed Compound-Gaussian Clutter. IEEE Trans. Aerosp. Electron. Syst. 48 (1), 64–77. doi:10.1109/taes.2012.6129621
Sangston, K. J., Gini, F., Greco, M. V., and Farina, A. (1999). Structures for Radar Detection in Compound Gaussian Clutter. IEEE Trans. Aerosp. Electron. Syst. 35 (2), 445–458. doi:10.1109/7.766928
Stoica, P., and Nehorai, A. (1990). Music, Maximum Likelihood, and Cramer-Rao Bound: Further Results and Comparisons. IEEE Trans. Acoust. Speech, Signal. Process. 38 (12), 2140–2150. doi:10.1109/29.61541
Tajer, A., Jajamovich, G. H., Wang, X., and Moustakides, G. V. (2010). Optimal Joint Target Detection and Parameter Estimation by Mimo Radar. IEEE J. Sel. Top. Signal. Process. 4 (1), 127–145. doi:10.1109/jstsp.2010.2040104
Zhang, X., El Korso, M. N., and Pesavento, M. (2014). “Mimo Radar Performance Analysis under K-Distributed Clutter,” in 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (Florence, Italy: IEEE), 5287–5291. doi:10.1109/icassp.2014.6854612
Keywords: Cramér–Rao lower bounds (CRLBs), MIMO radar, location and velocity estimation, performance analysis, complex elliptically symmetric (CES) distributed, complex t-distribution
Citation: Rojhani N, Greco MS and Gini F (2022) CRLBs for Location and Velocity Estimation for MIMO Radars in CES-Distributed Clutter. Front. Sig. Proc. 2:822285. doi: 10.3389/frsip.2022.822285
Received: 25 November 2021; Accepted: 28 January 2022;
Published: 25 March 2022.
Edited by:
Vishal Monga, The Pennsylvania State University (PSU), United StatesReviewed by:
Bosung Kang, University of Dayton Research Institute (UDRI), United StatesOmar Aldayel, King Saud University, Saudi Arabia
Copyright © 2022 Rojhani, Greco and Gini. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Neda Rojhani, bmVkYS5yb2poYW5pQGRpaS51bmlwaS5pdA==
 Neda Rojhani
Neda Rojhani Maria Sabrina Greco
Maria Sabrina Greco Fulvio Gini
Fulvio Gini