Abstract
Forward-looking imaging for maneuvering platforms has garnered significant interest in many military and civilian fields. As the maneuvering trajectory in the scanning period can be simplified as the constant acceleration maneuver, monopulse imaging is applied to enhance the azimuthal resolution of the forward-looking image. However, the maneuver causes severe range migration and Doppler shift; this often results in range location error due to the space-varying Doppler shifts and the failure of angle estimation. We propose a decimation keystone algorithm based on the chirp-Z transform (CZT). First, the pulse repetition frequency (PRF) is decimated with an integer; thus, the azimuthal sampling sequence is decimated into many sub-sequences. Then, the linear range walk correction (LRWC) is performed on each sub-sequence using the keystone transform, significantly reducing the influence of the change of Doppler-ambiguity-number on range location. Further, the sub-sequences are regrouped as one sequence, and the range curvature due to the acceleration is compensated in the frequency domain. Finally, the varying Doppler centroid in each coherent processing interval (CPI) is analyzed and compensated for the sum-difference angular measurements. Simulation results demonstrate the effectiveness of the proposed algorithm for forward-looking imaging under constant acceleration maneuvers and the feasibility of range location error correction.
1 Introduction
High-resolution microwave imaging of the front area of an aircraft has raised significant interest among researchers in recent years. Doppler beam sharpening (DBS) and monopulse imaging are two widely-used techniques for enhancing cross-range/angular resolution in airborne scanning radar sensors. Doppler beam sharpening cannot resolve multiple scatterers in the large squint cases because of the severe decline of the Doppler centroid differences, resulting in a “blind area” in the forward-looking direction. Forward-looking monopulse imaging refers to the two-dimensional microwave imaging of the front view of an aircraft based on monopulse techniques. Generally, the radar antenna scans across the front scene, and the monopulse technique is utilized to enhance the azimuthal resolution of the image (Griffiths, 1998; Nickel, 2006; Zhang et al., 2016). The method is characterized by low system complexity, good adaptability for the flight path, and significant resolution enhancement. However, Monopulse technique fails to resolve target multiplicity in the range and azimuth resolution bin of an ordinary monopulse radar. The angle glint caused by target multiplicity may result in imaging blurring in forward-looking images, especially for extended targets comprised of a significant number of scatterers. Combining the amplitude-comparison monopulse technique with the Doppler beam sharpening (DBS) technique, the Doppler difference of the scatterers in the main lobe is used to separate them into different Doppler units (Lu et al., 2011). Then, the sum-difference Doppler estimates are reconstructed and used to estimate the scatterers’ angles. The method can significantly alleviate the image blurring caused by the freedom limit in the angular dimension (Li et al., 2021).
Usually, the uniform motion in the coherent processing interval (CPI) often leads to severe space-varying range migration (Li et al., 2012) and thus affects the focusing performance and positioning accuracy. Therefore, linear range walk correction (LRWC) is implemented based on the keystone transform for forward-looking imaging (Li et al., 2012). However, the change in the Doppler-ambiguity-number due to the varying Doppler shifts of targets in different directions should also be addressed.
The maneuvering trajectory may be simplified as the constant acceleration motion during the CPI for monopulse estimation. And the change of platform velocity in the scanning process causes non-linear range migration and space-varying Doppler shift. So, the range curvature and the Doppler shifts need to be addressed. Especially when the scanning mode is adopted, the change of Doppler-ambiguity-number for scatterers situated at the larger squint angles may cause severe range location error (Li et al., 2022). Moreover, the angle measurement based on the Doppler estimates may suffer from varying Doppler shifts due to accelerations.
Forward-looking radar imaging aims to accumulate the scatterers’ reflective energy coherently. This is like detecting a moving target using a stationary radar system. Both applications must overcome the related motion between the radar’s antenna phase center (APC) and the target. The range migration and the Doppler history of the echoes are similar. Therefore, the methods proposed for detecting targets with uniform acceleration motion may be feasible to compensate for motion error in forward-looking imaging.
To accumulate a target’s energy in the case of constant acceleration motion, the range walk is generally corrected with the keystone transform, and the second-order phase error caused by accelerations is compensated using a dechirping processing (Wu et al., 2009). Li X. et al. (Li et al., 2015) proposed a coherent accumulations algorithm based on the keystone transform and fractional Fourier transform (FrFT). After LRWC, the signals are extracted for FrFT to complete energy accumulation. However, since only the range walk is compensated, the range curvature results in poor accumulation performance when the acceleration cannot be ignored. Sharif R. et al. proposed a method based on the keystone transform and Wigner-Hough (Sharif and Abeysekera, 2007). The second-order keystone transform removes the range curvature (Kirkland, 2011) (Yang et al., 2011). First, the quadratic coupled term of range frequency and the slow time is decoupled through the second-order keystone transform. Second, a matched filter is reconstructed to compensate for the Doppler centroid offset and estimate the accelerations. Finally, the second stage of the second-order keystone transform is used to correct range curvature and accumulate the target energy. However, in all the above research, the change of the Doppler ambiguity number is not considered because only moving targets in the main lobe are concerned in the detection cases. Furthermore, the second-order keystone transforms mean an extensive computation load.
In imaging cases, the motion parameters are usually measured using the GPS/INS mounted on the platform. On the contrary, the range migration and the Doppler shift due to targets or scatterers from the scene differ from the directions. So, space-varying motion compensation plays a vital role in the forward-looking imaging. To resolve the problem, a decimation keystone algorithm is proposed in the paper. First, the range walk is corrected using the decimation keystone transform, which solves the change of the Doppler ambiguity number by reducing the spatial sampling rate. Then, a compensative factor in the frequency domain is constructed to eliminate the range curvature. Finally, the effect of accelerations on the Doppler centroid is considered and removed during angle measurement. Simulation experiments verify the effectiveness of the proposed method.
2 Analysis of the signal model for forward-looking imaging on uniformly accelerated platforms
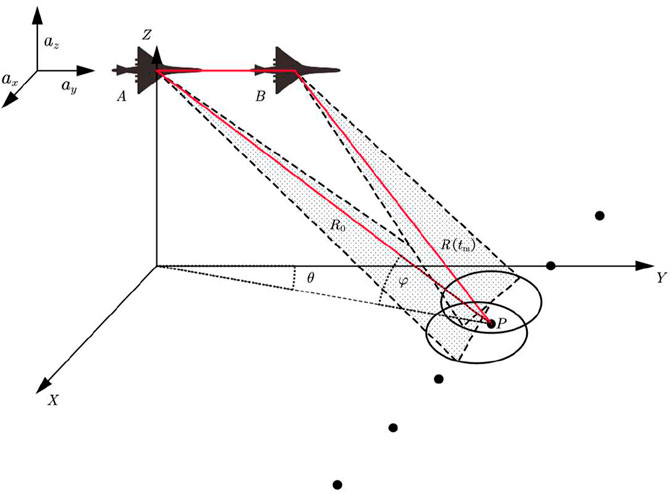
2.1 A geometric model for forward-looking imaging on uniformly accelerated platforms
Forward-looking monopulse imaging based on the scanning mode improves the azimuthal resolution of the real-aperture image of the front scene through the monopulse technique (Wu et al., 2010).
Suppose the radar platform flies from to with an initial forward velocity . is the transverse acceleration, is the forward acceleration, and is the longitudinal acceleration. The radar antenna beam scans the front area uniformly, and the current azimuth angle, with respect to the flight path, is . During the imaging process, the target’s slant range changes due to the platform movement, as illustrated in Figure 1. The coordinates of B and P are and , The instantaneous slant range of the point target , relative to the APC of the radar, iswhere is the instantaneous slant range from to at the initial time, is the slow time, and is the depression angle. For further analysis, 1) is expanded to Taylor’s series.
FIGURE 1
A geometric model for forward-looking imaging of a uniformly accelerated platform.
According to the image geometry, the slant range changes not only over the slow time, but also with the squint angle , and the depression angle , Because the beam scans in the azimuth dimension, the change in can be ignored and considered a constant , The second term in (2) represents the range walk due to the initial velocity, and the third, fourth, and fifth terms mean the range curvature due to the acceleration. Under the condition of far-range imaging and forward-looking imaging, both and are tiny, so the sine of and are also small. Meanwhile, when the platform is flying forward, the lateral accelerations are small, so the influence of lateral acceleration on range migration can be ignored. Since the CPI is small and , the sixth and higher-order terms can be ignored. And 2) can be approximated as
2.2 Range migration and Doppler shift
Assume that the monopulse radar transmits a linear-frequency-modulation (LFM) pulse signal; the time-domain expression of the transmitted signal can be expressed bywhere represents the chirp pulse, represents the pulse sequence number, represents the pulse repetition interval (PRI), represents the center frequency.
The sum-difference channels time-domain echoes of the point target after range pulse compression can be expressed aswhere is the sum channel signal, is the difference channel signal, represents the sum channel’s antenna pattern at the slow time, represents the difference channel’s antenna pattern at the slow time, is the normalized echo envelope, and represents the fast time. Because the range migration and Doppler shift are the same for the sum-difference channels, we only analyze the sum channel signal. By taking a range Fourier transform to and applying the principle of stationary phase (POSP), the signal spectrum can be obtained bywhere is corresponding to the frequency domain of , is the Fourier transform of , By substituting 3) into 6), the signal spectrum becomes
The cross-coupling phase terms are expressed as a range frequency and slow time function. The second exponential term indicates the Doppler shift, and the third shows the linear range walk due to the forward velocity. The fourth term means the extra Doppler shift, and the fifth indicates the range curvature due to the forward acceleration.
3 Range migration correction base on decimation keystone algorithm
According to 7), linear range migration and linear Doppler shift caused by the forward velocity are space-variant for targets in different directions. Traditional methods compensate for the space-variant range walk using the keystone transform (Li et al., 2012).
3.1 Traditional keystone transform and range curve compensation
The keystone transform is performed to correct the range walk in (7) in forward-looking imaging. To decouple the relationship between and in (7), a scaling factor is applied to , such aswhich is the keystone transform (Perry et al., 1999). By substituting 8) into 7), the spectrum signal is recast aswhere the traditional keystone transform eliminates the coupling between and in the second term and compensates for the varying range walk, but, the third exponential term in (9) represents a residual coupling between and introduced by the keystone transform.
For the high-band radar satisfies , as , , 9) can be approximated as
To compensate the range curvature in the fourth exponential term, a frequency-domain factor is proposed to decouple and (Xia, 2011). The compensation factor is expressed by
Considering that the slant angle in the front area is usually less than , the change in is small. Therefore, the difference in the range curvature of targets in different directions can be ignored. The compensation factor is simplified asTherefore, the range curve compensation can be manipulated in the frequency domain. By multiplying by (10), we can obtain
Performing the inverse Fourier transform to (13), yields
The slant range in the envelope indicates that the space-variant range migration has been corrected using the keystone transform and range curve compensation. However, the exponential term means the acceleration introduces an extra Doppler shift.
3.2 The decimation keystone algorithm for Doppler ambiguity compensation
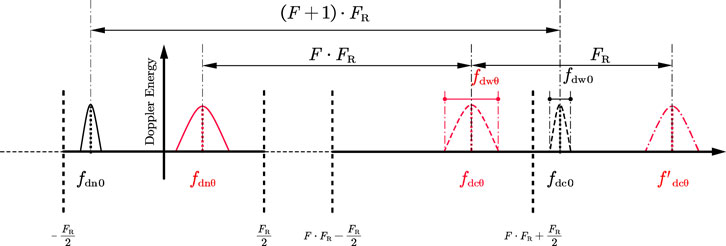
For the high-band radars, as the PRF of the system is much smaller than the Doppler centroid, the Doppler ambiguity occurs. The correction of the Doppler ambiguity must combine with the keystone transform. The dependence on the Doppler ambiguity number is a limitation of the keystone transform (Zhang and Zeng, 2005) (Li, 2006) and is an integer defined aswhere represents the PRF, represents the measured Doppler centroid in the case of Doppler ambiguity, represents the actual Doppler centroid of the main-beam echoes, which is expressed byGenerally, is achieved bywhere is a rounding operator. represents the Doppler bandwidth of the main-beam echoes and is expressed by (Richards, 2005)where is the 3 dB beamwidth. According to (16) and (18), with the increase of , the Doppler centroid decreases, whereas the Doppler width increases, which is illustrated in Figure 2.
FIGURE 2
Schematic diagram of the residual velocity generated by solving Doppler ambiguity.
and represent the actual Doppler centroid and the measured Doppler centroid of the target at , respectively. Similarly, and represent the true Doppler centroid and the measured Doppler centroid of the target at , respectively. In the scanning mode, the Doppler ambiguity number of the front direction is used to compensate for all the echoes from the targets on both sides. Therefore, the residual error of the Doppler centroid for targets at occurs. If is just more significant than , the change of the Doppler ambiguity number is likely to occur for those targets apart from the flight path, producing a residual velocity, as shown in Figure 2.
Since is just larger than , the Doppler ambiguity number is rounded to , Because the actual Doppler ambiguity number for the target at is , it might be shifted to , which means an extra velocity error. Therefore, the wrong Doppler ambiguity number introduces the residual , which can be expressed bywhere is the related velocity from the platform to the target whose Doppler centroid is , The greater the residual rate is, the larger the range location error will be.
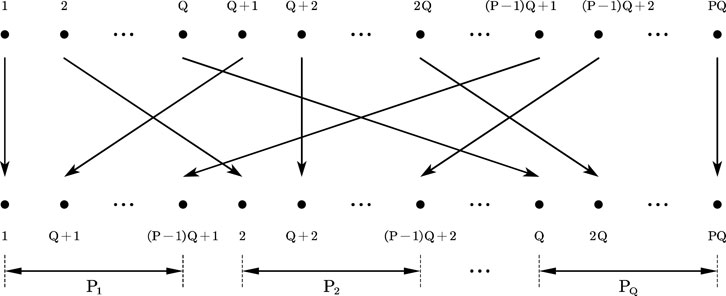
A decimation keystone algorithm is proposed to solve the range location error caused by the Doppler ambiguity compensation. Suppose that the length of the sampling sequence in the slow time dimension is . By down-sampling the original sequence using an integer , the echo sequence is decimated evenly into sub-sequences, as shown in Figure 3. Each sub-sequence consists of sampling points, which index is , The sub-sequences are formed in the order of , as shown in Figure 3.
FIGURE 3
Schematic diagram of sequence decimating and rearranging.
For each sub-sequence , the spatial sampling rate is reduced by times. Then keystone transform is manipulated to the sub-sequence to compensate for the range walk. Although the change in the Doppler ambiguity number cannot be avoided, a low means less residual Doppler ambiguity. For example, when the ambiguity number is changed from to , the residual velocity becomes
The residual velocity is reduced by times compared with the traditional method. By setting an appropriate to make sure more than one sample is achieved in each beam position, the residual range walk can be limited to half a range resolution unit to achieve accurate target positioning. After range walk correction, the sub-sequences are regrouped according to the inverse process, as shown in Figure 3.
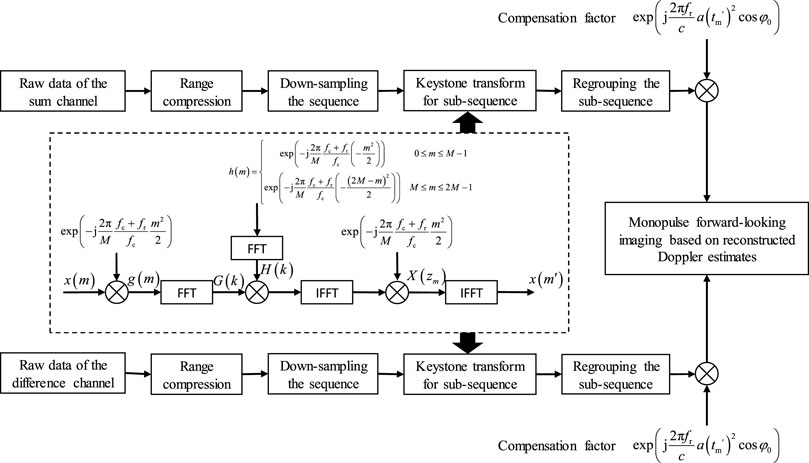
Since the actual signal processing is digitalized, the range frequency and the slow time in the data need to be represented as discrete variables. Three methods to implement the keystone transform have been proposed (Wang and Zhao, 2011): SINC interpolation, DFT-IFFT, and CZT. Because the computational complexity of the CZT is much smaller than the other two methods, it is used to implement the keystone transform. The process can be expressed as follows:where , , , , is the data length of , Performing the inverse FFT to (21), in the case of Doppler ambiguity, the keystone transform can be written aswhere is the Doppler ambiguity number.
The flowchart of the decimation keystone algorithm is shown as Figure 4.
FIGURE 4
Flowchart of decimation keystone algorithm.
After range compression and motion compensation, we utilize the Doppler estimates of the sum-difference measurements to achieve monopulse forward-looking imaging (Li et al., 2021). First, target multiplicity is resolved by exploiting the different Doppler shifts caused by the relative motion between the platform and the targets in different directions. High azimuthal angle measurement accuracy of the Doppler estimates is obtained using the sum-difference amplitude-comparison technique. Subsequently, the intensity of the sum channel estimates is projected onto the image plane according to the range and angle measurements.
3.3 The effect of acceleration on the Doppler centroid and its compensation
In the geometric model for forward-looking imaging illustrated in Figure 1, when the acceleration , the platform is moving uniformly. The Doppler shift of a target situated at the azimuth angle, , is defined by (16). However, if the platform is in a constant acceleration motion, the Doppler shift is affected by the acceleration, as shown in (14). In the CPI, the Doppler centroid of the main beam echoes also varies. To address the problem, 1) is expanded into the Taylor series at , which is the mean time of the CPI.whereand , is the mean velocity in the CPI. Suppose that is the Doppler centroid of the scanning target at , then it can be redefined aswhere the wavelength is, thus, the Doppler bandwidth is also modified as follows:
If the monopulse imaging is performed based on the Doppler estimates of the sum-difference channels, the Doppler parameters must be calculated according to (25) and (26). Otherwise, the scatterers’ energy in the main lobe is missed, and the angle cannot be measured accurately, leading to image blurring.
4 Simulation results
4.1 Point target imaging simulation
The monopulse forward-looking imaging algorithm is used for simulation to verify the proposed method (Li et al., 2021). The simulation parameters are given in Table 1. Suppose that the radar sensor is mounted on an aircraft. The velocity is 240 m/s. The radar transmits coherent linear frequency-modulated signals with pulse width and 50 MHz bandwidth. The center frequency of the transmitted signal is 18 GHz. The beam scans the front scene from -15° to 15°. The pulse number in the scanning illumination is 2500. There are 3 × 21 point targets in the scene in a 30 m × 30 m lattice. Each target has a uniform intensity, and the axis of the scene center is (0, 1700) m in meters on the ground surface. The SNR of the range-compressed data is 20 dB, and the noise follows a complex normal distribution with mean zero and variance . The CPI for the angle measurement is 32. Doppler estimates in the sum-difference channels are reconstructed by CZT and used to measure the azimuth angles of the point targets in monopulse imaging (Li et al., 2021).
TABLE 1
| Parameters | Value |
|---|---|
| Radar center frequency | 18 GHz |
| signal bandwidth | 50 MHz |
| beam scanning area | |
| 3 dB beam width of the sum channel | |
| Signal pulse width | |
| Antenna scanning rate | |
| Center ground range | 1700 m |
| Range × azimuth resolution | 3 m × 3 m |
| Pulse repetition frequency | 2500 Hz |
Simulation parameters for forward-looking scanning radar.
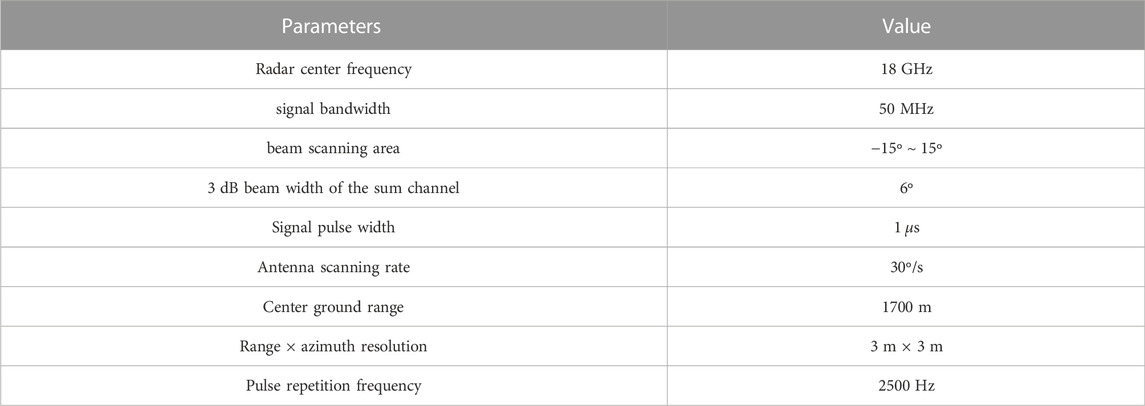
Figure 5 compares the forward-looking imaging results processed using the traditional method and the decimation keystone algorithm. The radar platform obeys a uniform motion. The Doppler ambiguity number of the target at is , The Doppler ambiguity number of the target at is , which means the change in the Doppler ambiguity number occurs in the case. The residual velocity generated by the wrong Doppler ambiguity number is , The point targets at suffer from the residual rate, and their range displacements are approximately proportional to their azimuthal angles. The imaging results in Figure 5A verify the residual velocity’s influence on the range location error. The imaging result of the decimation keystone algorithm is shown in Figure 5B. The decimating factor is . Thus, the residual velocity decreases to , The change in the Doppler ambiguity number is more severe in the sub-sequences, e.g., the Doppler number difference for the point targets at is 4. But the range walk caused by the residual rate is still less than half a range resolution unit owing to the slight residual velocity and the short CPI. Therefore, the targets are located accurately, as shown in Figure 5B.
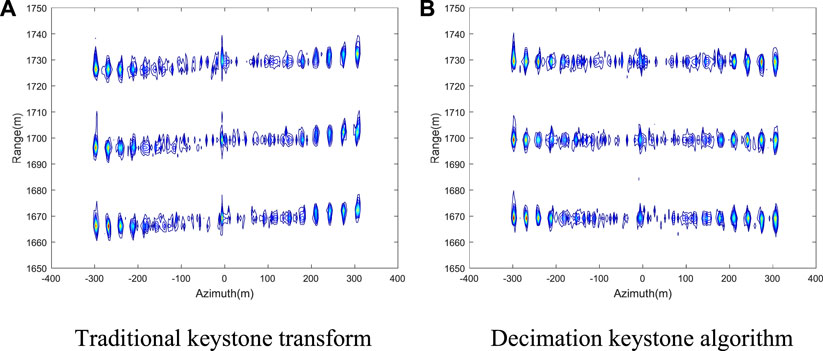
FIGURE 5
Comparison of image results of the uniform motion platform. (A) Traditional keystone transform. (B) Decimation keystone algorithm.
Figure 6 verifies the effectiveness of the range curve compensation on the constant acceleration maneuvers. Figures 6A, B present the imaging results processed by the traditional keystone transform with different accelerations. Because of the change in the Doppler ambiguity number and the range curvature, range positioning error is apparent in the images. Figures 6C, E compare the imaging results processed by the decimation keystone algorithm with the acceleration equals . In Figure 6C, the range curvature due to the acceleration is not compensated. Because of the slight acceleration, the range curvature in Figure 6C is not apparent. Therefore, the decimation keystone transform works well. When the acceleration increases to , the imaging result without range curve compensation in Figure 6D presents apparent range curvatures. And range curve compensation can eliminate the influence of the significant acceleration on the targets’ envelopes, as shown in Figure 6F. Simulation results demonstrated the effectiveness of the decimation keystone transform and range curve compensation in the case of constant acceleration maneuvers.
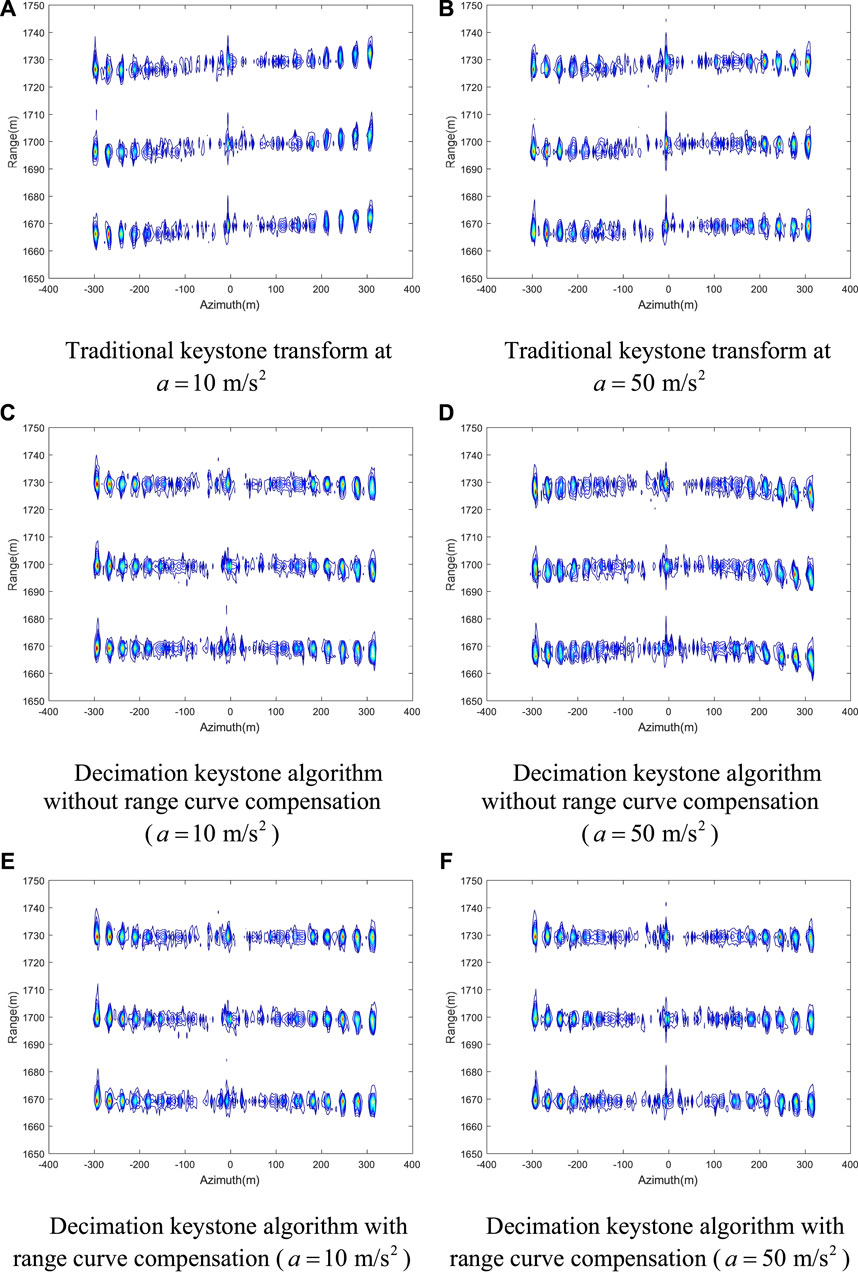
FIGURE 6
Comparison of image results of the uniform acceleration platform. (A) Traditional keystone transform at (B) Traditional keystone transform at . (C) Decimation keystone algorithm without range curve compensation (). (D) Decimation keystone algorithm without range curve compensation (). (E) Decimation keystone algorithm with range curve compensation (). (F) Decimation keystone algorithm with range curve compensation ().
We compare the range profiles of the point target at the azimuth distance of -300 m and the ground range of 1700 m from Figures 6B, D, F, respectively. The normalized range profiles are interpolated by five times. In Figure 7A, the curve in red represents the profile processed using the traditional keystone transform, where the displacement from the actual range is about 3 m. The curve in the blue line represents the profile processed using the decimation keystone transform, where the displacement is invisible. In Figure 7B, the red curve represents the point target’s range profile in Figure 6D. The curve in blue represents the range profile of the point target in Figure 6F. Without compensating for the range curvature, the point targets will be offset by 3 m, resulting in a misalignment of the range positioning. The integrated side lobe ratio (ISLR) is calculated by:
FIGURE 7
Range profiles of targets at the axis (range 1700 m, azimuth −300 m). (A) Comparison of traditional keystone transform and decimation keystone algorithm. (B) Comparison of only decimation and decimation keystone algorithm.
In Figure 7A, the ISLR of the traditional keystone transform is -9.93dB, while the ISLR of the decimation keystone algorithm is −14.65 dB. In Figure 7B, the ISLR of only decimation is −14.34 dB. The energy of the decimation keystone algorithm is more concentrated and has a better focusing effect.
4.2 Scene simulation verification
Point targets simulation verifies the effectiveness of the decimation keystone algorithm. This section demonstrates the proposed method’s feasibility in reconstructing an extended target. In the simulation, a Ku-band SAR image is used as the original scene, and the image was down-sampled by 10 with 3 m × 3 m pixel resolution, as shown in Figure 8A. The red dotted line represents the actual range location of the road’s edges in the image. The image center is at the ground position (01,700) m. The echo data are generated according to the simulation parameters in Table 1 with the acceleration equals . Figures 8B, C show the range-compressed data matrices of the sum-difference channels, respectively. The image results are plotted in the dB scale.
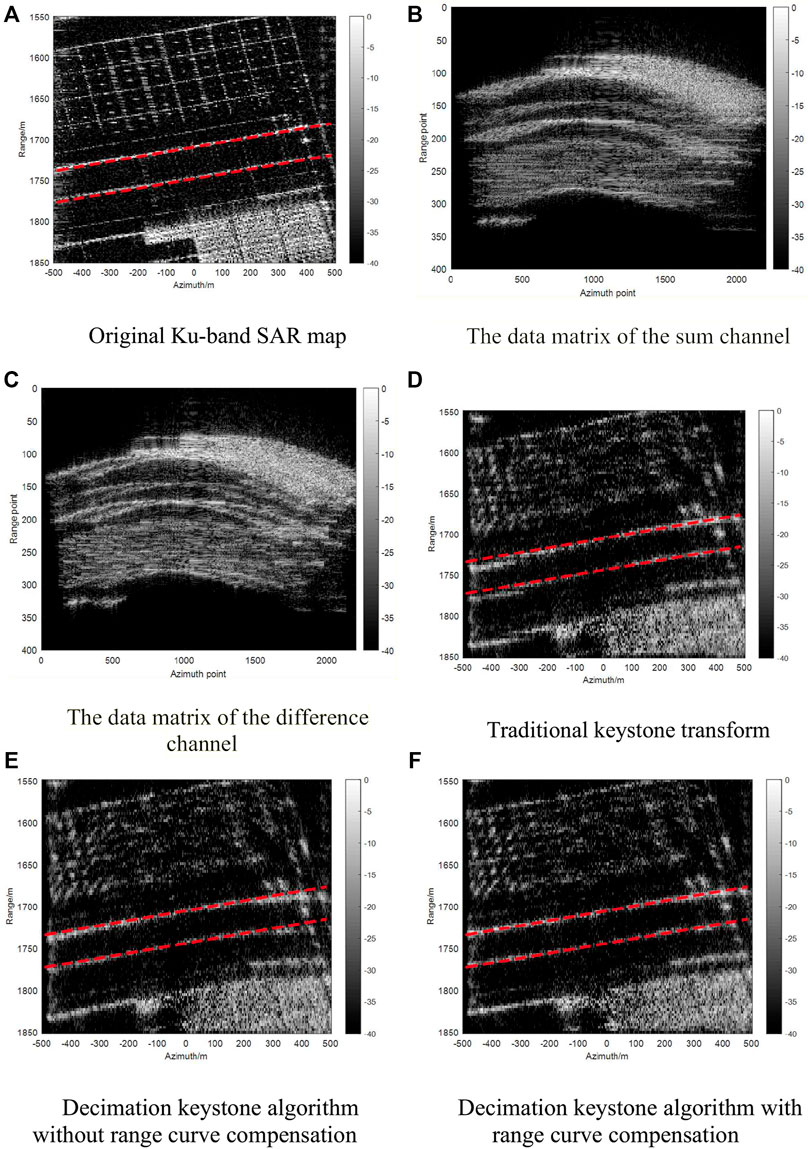
FIGURE 8
Comparison of correction results in simulation scenes. (A) Original Ku-band SAR map. (B) The data matrix of the sum channel. (C) The data matrix of the difference channel. (D) Traditional keystone transform. (E) Decimation keystone algorithm without range curve compensation. (F) Decimation keystone algorithm with range curve compensation.
Figure 8D presents the image result processed with the traditional keystone transform. The road edges are distorted and defocused because of the space-varying Doppler shift and the forward acceleration. The range offset of the targets is severe at the large azimuthal angles. Figure 8E is the imaging result processed with the decimation keystone algorithm without range curve compensation. The distortion of the road edges remains significant owing to the range curvature. Figure 8F demonstrates that the decimation keystone algorithm combined with range curve compensation can reconstruct the scene accurately. The experimental results verify the effectiveness of our proposed method.
5 Conclusion
When the airborne platform adopts the scanning mode in forward-looking imaging, the platform motion leads to range walk and Doppler shift in the target accumulation time. When the keystone transform is used for range walk correction, the point targets on both sides may suffer from the change of Doppler ambiguity number. This paper proposes the decimation keystone algorithm, which can reduce the PRF by decimating, thus reducing the residual velocity and achieving an accurate range position. Furthermore, we analyze the influence of range curvature caused by the acceleration and the Doppler shift on the imaging results for platforms with constant acceleration motion. The decimation keystone algorithm introduces a frequency-domain factor to compensate for the range curvature. Simulation results verify the effectiveness of the proposed method.
Statements
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
Z-SL finished the article under the guidance of Y-LL.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
Griffiths H. (1998). Introduction to airborne radar. (Stimson, G.34, 212.
2
Kirkland D. (2011). Imaging moving targets using the second-order keystone transform. IET Radar Sonar Navig.5 (8), 902–910. 10.1049/iet-rsn.2010.0304
3
Li W. Yang J. Huang Y. (2012). Keystone transform-based space-variant range migration correction for airborne forward-looking scanning radar. Electron. Lett.48 (2), 121–122. 10.1049/el.2011.2774
4
Li X. L. Cui G. L. Yi W. Kong L. J. An efficient coherent integration method for maneuvering target detection[A]. Proceedings of the IET International Radar Conference 2015, October 2015, Hangzhou, 10.1049/cp.2015.1214
5
Li Y. L. Ma M. E. Zhao C. H. Zhou Z. M. Forward-looking imaging via Doppler estimates of sum-difference measurements in scanning monopulse radar[J]. J. Radars, 2021, Vol.10(1): 131–142.
6
Li Y. Range migration compensation and Doppler ambiguity resolution by keystone transform[A]. Proceedings of the 2006 CIE International Conference on Radar[C], October 2006, Shanghai, China.
7
Li Z. S. Li Y. L. Zhang J. F. Frequency domain compensation of the residual range walk after Keystone transform in forward-looking imaging[J]. Chin. J. radio Sci., 2022, 37(4): 568–577.
8
Lu Z. Ding Z. Liu L. Long T. (2011). Adbs Doppler centroid estimation algorithm based on entropy minimization. IEEE Trans. Geosci. Remote Sens.49 (10), 3703–3712. 10.1109/tgrs.2011.2142316
9
Nickel U. (2006). Overview of generalized monopulse estimation. IEEE Aerosp. Electron. Syst. Mag.21 (6), 27–56. 10.1109/maes.2006.1662039
10
Perry R. P. Dipietro R. C. Fante R. L. (1999). SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst.35 (1), 188–200. 10.1109/7.745691
11
Richards M. A. (2005). Fundamentals of radar signal processing. New York: McGraw-Hill.
12
Sharif R. Abeysekera S. (2007). Efficient wideband signal parameter estimation using a radon-ambiguity transform slice. IEEE Trans. Aerosp. Electron. Syst.43 (2), 673–688. 10.1109/taes.2007.4285361
13
Wang J. Zhao Y. B. (2011). Research on implementation of keystone. Transform (1), 45–51.
14
Wu D. Zhu D. Y. Zhu Z. D. Research on monopulse forward-looking imaging algorithm for airborne radar[J]. J. image Graph., 2010, 15(3): 462–469.
15
Wu Z. P. He X. H. Su T. Coherent integration detection of multiple high-speed targets with range migration and Doppler spread[A]. Proceedings of the IET International Radar Conference 2009, April 2009, Guilin.
16
Xia Z. Q. Research on long time accumulation techniques for Pulsed Doppler Radar[D]. Chengdu: University of Electronic Science and Technology of China, 2011.
17
Yang J. G. Huang X. T. Thompson J. Jin T. Zhou Z. M. Low-frequency ultra-wideband synthetic aperture radar ground moving target imaging[J]. IET RADAR SONAR NAVIGATION, 2011, Vol.5(9): 994–1001.
18
Zhang S. S. Zeng T. Weak target detection based on Keystone transform[J]. Acta Electron. Sin., 2005, 33(9): 141–144.
19
Zhang Y. C. Zhang Y. Huang Y. L. Li W. C. Yang J. Y. (2016). Angular superresolution for scanning radar with improved regularized iterative adaptive approach. IEEE Geosci. Remote Sens. Lett.13 (6), 846–850. 10.1109/lgrs.2016.2550491
Summary
Keywords
forward-looking monopulse imaging, decimation keystone algorithm, range migration, Doppler shift, Doppler ambiguity number
Citation
Li Z-S and Li Y-L (2023) Decimation keystone algorithm for forward-looking monopulse imaging on platforms with uniformly accelerated motion. Front. Sig. Proc. 2:1074053. doi: 10.3389/frsip.2022.1074053
Received
19 October 2022
Accepted
06 December 2022
Published
05 January 2023
Volume
2 - 2022
Edited by
Hongmeng Chen, Beijing Institute of Radio Measurement, China
Reviewed by
Shiyang Tang, Xidian University, China
Penghui Huang, Shanghai Jiao Tong University, China
Junjie Wu, University of Electronic Science and Technology of China, China
Updates
Copyright
© 2023 Li and Li.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yue-Li Li, liyueli4uwb@nudt.edu.cn
This article was submitted to Radar Signal Processing, a section of the journal Frontiers in Signal Processing
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.